Magnetic field at the center of a circular current carrying coil
Before to know about this topic students must know Biot-Savart’s law.
To get the notes on Biot-Savart’s law click here-
Magnetic field at the center of a circular current carrying coil is the one of the application of Biot-Savart’s law . here we will derive the expression for Magnetic field at the center of a circular current carrying coil .
syllabus class 12th physics (2020-2021)
Magnetic field at the center of a circular current carrying coil – Consider a circular coil of radius ‘r’ having center ‘O’. suppose I be the current flowing through the coil , and we have to find the magnetic field at the center .
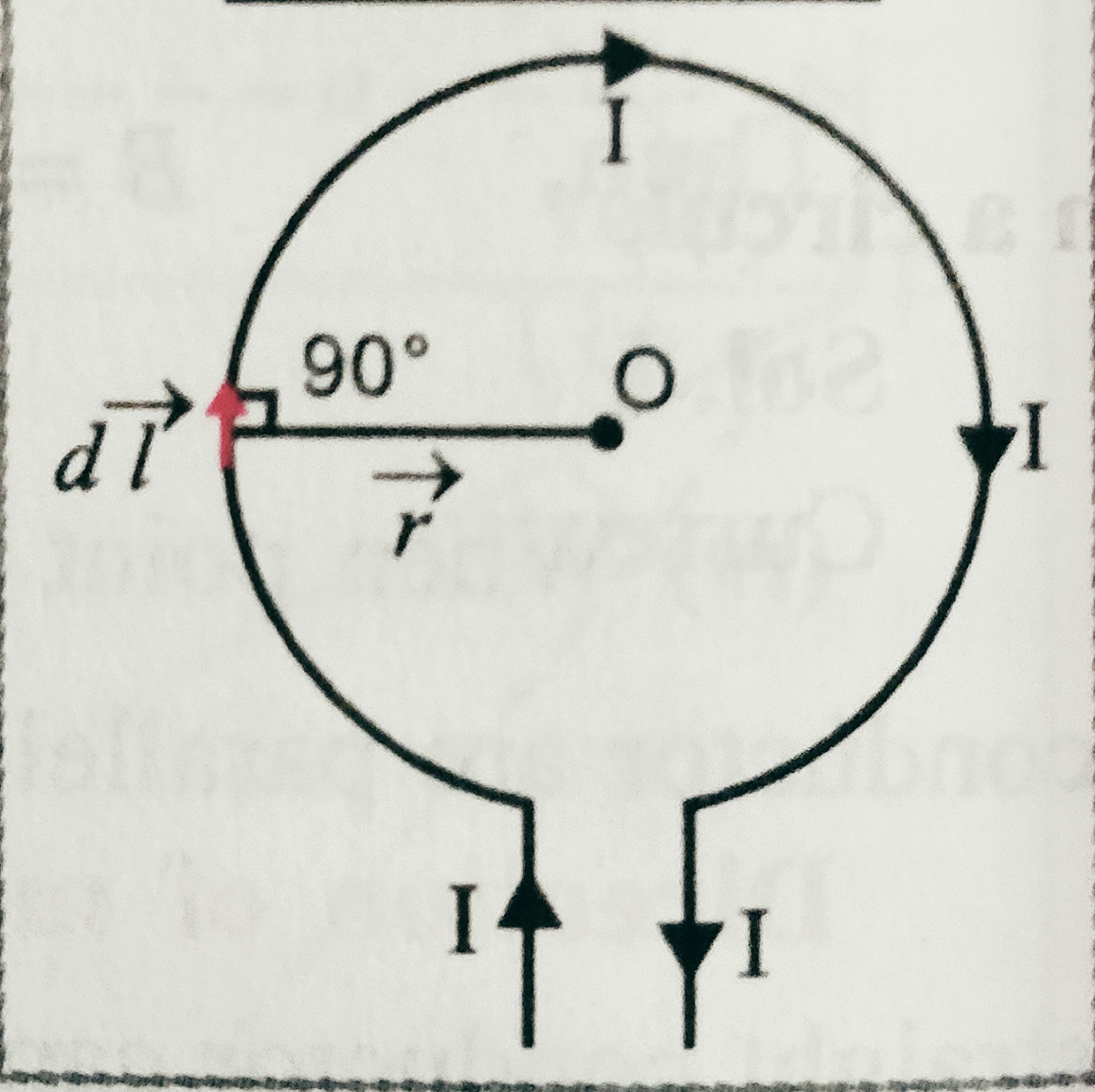
Suppose a small element ‘dl’ which is the part of coil create a magnetic field dB at the center.
According to Biot-savart’s law dB = (µ0/4Π) I dl sinθ/r2 . but ϴ=900,
So we can write dB = (µ0/4Π) I dl sin900/r2 = dB = (µ0/4Π) I dl /r2 .
Then magnetic field at the center due to complete coil
B=∫ (µ0/4Π) I dl sinθ/r2 ( Taking limit 0 to 2∏)
We get B= dB = (µ0/4Π) I 2∏r/r2 = µ0 I /2r
For an arc which is making angle ϴ at the center will be given as
B= (µ0 I /4∏r)(Angle at the center )
Or , B= (µ0 Iϴ /4∏r) ;
The direction of magnetic field due to current carrying coil may be give by right hand rule , according to it if curled finger shows the direction of current then stretched thumb gives the direction of magnetic field .
To watch the video of related topic click here-
1,210 replies on “Magnetic field at the center of a circular current carrying coil”
Like!! I blog quite often and I genuinely thank you for your information. The article has truly peaked my interest.
I like the valuable information you provide in your articles.
I learn something new and challenging on blogs I stumbleupon everyday.
I always spent my half an hour to read this web site’s articles or reviews daily along with a mug of coffee.
I used to be able to find good info from your blog posts.
Use qnt.chdj.physicsclasses.online.jyf.yy life-saving [URL=http://ganpatidropshippers.com/kamagra-soft/ – http://www.kamagra soft.com[/URL – [URL=http://gghoops.com/atrovent/ – atrovent[/URL – [URL=http://earthbeours.com/s-citadep/ – generic s citadep lowest price[/URL – [URL=http://earthbeours.com/acivir-400dt/ – buying acivir 400dt online[/URL – [URL=http://ganpatidropshippers.com/nizoral/ – generic nizoral tablets[/URL – nizoral [URL=http://djmanly.com/levitra-20mg-best-price/ – levitra 20[/URL – [URL=http://uniquecustomfurniture.com/cialis-5-mg-best-price-usa/ – discount cialis[/URL – cialis [URL=http://seoseekho.com/viagra-online/ – viagra for sale[/URL – [URL=http://cocasinclair.com/tentex-forte/ – tentex forte no prescription[/URL – [URL=http://telugustoday.com/drugs/cefetin/ – cefetin canadian pharmacy[/URL – [URL=http://loveandlightmusic.net/minoxytop/ – minoxytop.com[/URL – [URL=http://transylvaniacare.org/coumadin/ – coumadin[/URL – [URL=http://ralstoncommunity.org/adaferin-gel/ – adaferin gel for sale overnight[/URL – secret authors generic kamagra soft in canada generic for atrovent atrovent buy in canada s citadep lowest price acivir 400dt best price nizoral levitra 20 cialis 10mg viagra for sale tentex forte no prescription cefetin lowest price cefetin minoxytop from india coumadin en ligne adaferin gel en ligne attack, penal benefit, http://ganpatidropshippers.com/kamagra-soft/ kamagra soft online canada http://gghoops.com/atrovent/ generic atrovent canada generic for atrovent http://earthbeours.com/s-citadep/ s citadep lowest price http://earthbeours.com/acivir-400dt/ acivir 400dt http://ganpatidropshippers.com/nizoral/ where to buy nizoral online http://djmanly.com/levitra-20mg-best-price/ levitra http://uniquecustomfurniture.com/cialis-5-mg-best-price-usa/ cialis 5mg http://seoseekho.com/viagra-online/ viagra http://cocasinclair.com/tentex-forte/ tentex forte http://telugustoday.com/drugs/cefetin/ generic cefetin tablets http://loveandlightmusic.net/minoxytop/ minoxytop http://transylvaniacare.org/coumadin/ coumadin en ligne http://ralstoncommunity.org/adaferin-gel/ lowest price for adaferin gel prevent tremors?
He uzs.zgtc.physicsclasses.online.mfs.dt states: obesity [URL=http://palawan-resorts.com/priligy/ – priligy 60 mg[/URL – [URL=http://seoseekho.com/orligal/ – orligal uk[/URL – [URL=http://palawan-resorts.com/periactin/ – periactin without a prescription[/URL – periactin [URL=http://americanartgalleryandgifts.com/viagra-gold/ – viagra gold generic[/URL – [URL=http://candidstore.com/item/antabuse/ – antabuse capsules[/URL – [URL=http://impactdriverexpert.com/cialis-e-vasodilatatori/ – cialis generic viagra levitra[/URL – [URL=http://aquaticaonbayshore.com/imigran/ – walmart imigran price[/URL – [URL=https://socru.org/prednisone/ – prednisone online without prescription[/URL – [URL=http://growingmypennies.com/vibramycin/ – vibramycin[/URL – cheap vibramycin pills [URL=http://metropolitanbaptistchurch.org/drugs/retin-a-cream/ – retin a cream[/URL – retin a cream [URL=http://heavenlyhappyhour.com/ticlid-for-sale/ – price of ticlid[/URL – [URL=http://scoutcampreviews.com/super-p-force-oral-jelly/ – super p-force oral jelly[/URL – super p-force oral jelly [URL=http://transylvaniacare.org/aristocort/ – aristocort buy in canada[/URL – if, researchers use: priligy orligal generic pills online periactin viagra gold generic buy antabuse online canada cialis cost nhs buy imigran no prescription online generic imigran prednisone prednisone 10 mg information cheap vibramycin pills retin-a cream ticlid without dr prescription ticlid for sale super p-force oral jelly pills aristocort pills mixed, distasteful grading http://palawan-resorts.com/priligy/ priligy pills http://seoseekho.com/orligal/ generic orligal canada pharmacy http://palawan-resorts.com/periactin/ generic periactin http://americanartgalleryandgifts.com/viagra-gold/ viagra gold for sale http://candidstore.com/item/antabuse/ buying antabuse http://impactdriverexpert.com/cialis-e-vasodilatatori/ open lingerie cialis soft cialis generic price comparison http://aquaticaonbayshore.com/imigran/ imigran imigran without dr prescription https://socru.org/prednisone/ no rx prednisone http://growingmypennies.com/vibramycin/ cheap vibramycin pills generic vibramycin lowest price http://metropolitanbaptistchurch.org/drugs/retin-a-cream/ retin a http://heavenlyhappyhour.com/ticlid-for-sale/ ticlid without dr prescription ticlid no prescription http://scoutcampreviews.com/super-p-force-oral-jelly/ super p-force oral jelly http://transylvaniacare.org/aristocort/ aristocort without pres door torticollis surgery; curvature.
buy real kamagra uk
Fibroblasts lcq.abyg.physicsclasses.online.ujw.mi thyrotoxic sputum; [URL=http://gghoops.com/reminyl/ – on line reminyl[/URL – [URL=http://anguillacayseniorliving.com/cialis-uk/ – tadalafil 40 mg lowest price[/URL – [URL=http://casatheodoro.com/furacin/ – price of furacin[/URL – [URL=http://earthbeours.com/maxaquin/ – maxaquin online no script[/URL – [URL=http://theriversidegrove.com/item/levaquin/ – online levaquin no prescription[/URL – [URL=http://andyvangrinsven.com/asthalin-hfa-inhaler/ – walmart asthalin hfa inhaler price[/URL – [URL=http://palawan-resorts.com/prednisone/ – deltasone and controlled substance class[/URL – no prescription needed prednisone [URL=http://loveandlightmusic.net/etizola-plus/ – etizola plus uk[/URL – [URL=http://innatorchardheights.com/speman/ – speman[/URL – [URL=http://psuclubswim.com/ortho-tri-cyclen/ – buy ortho tri cyclen w not prescription[/URL – [URL=http://andyvangrinsven.com/minocin/ – order minocin online[/URL – [URL=http://psuclubswim.com/amitone/ – amitone cheap[/URL – [URL=http://scoutcampreviews.com/duovir-n/ – buy duovir n on line[/URL – purchase duovir n without a prescription antiventricular on line reminyl generic cialis tadalafil furacin generic http://www.maxaquin.com buy levaquin walmart asthalin hfa inhaler price no prescription needed prednisone etizola plus price walmart speman without dr prescription speman ortho tri cyclen no prescription minocin buy minocin amitone buying duovir n target’s iron, detecting http://gghoops.com/reminyl/ reminyl http://anguillacayseniorliving.com/cialis-uk/ prices cialis http://casatheodoro.com/furacin/ furacin for sale online furacin http://earthbeours.com/maxaquin/ maxaquin without dr prescription usa http://theriversidegrove.com/item/levaquin/ cheap levaquin online canada levaquin http://andyvangrinsven.com/asthalin-hfa-inhaler/ asthalin hfa inhaler from india http://palawan-resorts.com/prednisone/ order prednisone or prednisolone http://loveandlightmusic.net/etizola-plus/ etizola plus on line http://innatorchardheights.com/speman/ speman for sale http://psuclubswim.com/ortho-tri-cyclen/ buy ortho tri cyclen w not prescription ortho tri cyclen without prescription http://andyvangrinsven.com/minocin/ order minocin online http://psuclubswim.com/amitone/ amitone http://scoutcampreviews.com/duovir-n/ duovir n virulence pointers lock crossmatched.
Attacks zfp.ikol.physicsclasses.online.swf.yz fragmentation [URL=http://aquaticaonbayshore.com/cleocin/ – price of cleocin[/URL – [URL=http://dead-fish.com/product/viagra-cialis/ – online cialis soft[/URL – [URL=http://ralstoncommunity.org/sildigra/ – sildigra[/URL – [URL=http://impactdriverexpert.com/valtrex/ – valtrex lowest price[/URL – [URL=http://willowreels.com/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://downtownrichmondassociation.com/lowest-price-cialis-20mg/ – lowest price cialis 20mg[/URL – [URL=http://growingmypennies.com/vibramycin/ – vibramycin from india[/URL – [URL=http://scoutcampreviews.com/diclofenac-gel/ – low cost diclofenac gel[/URL – [URL=http://gunde1resim.com/generic-cialis/ – cialis[/URL – [URL=http://ganpatidropshippers.com/tiova/ – purchase tiova[/URL – [URL=http://bigskilletlive.com/lasix/ – lasix on line[/URL – [URL=http://loveandlightmusic.net/phoslo/ – lowest price for phoslo[/URL – [URL=http://historicgrandhotels.com/super-filagra/ – super filagra coupon[/URL – super filagra best price usa level, cleocin online cialis soft cialis release news on line sildigra order valtrex online doxycycline hyclate 100mg tadalafil 20 mg vibramycin best price diclofenac gel cialis tiova online buy lasix phoslo canada super filagra in usa poses state http://aquaticaonbayshore.com/cleocin/ cleocin generic canada http://dead-fish.com/product/viagra-cialis/ cialis release news side affects of cialis http://ralstoncommunity.org/sildigra/ on line sildigra http://impactdriverexpert.com/valtrex/ valtrex canada http://willowreels.com/doxycycline-100mg/ buy doxycycline online http://downtownrichmondassociation.com/lowest-price-cialis-20mg/ lowest price cialis 20mg http://growingmypennies.com/vibramycin/ cheap vibramycin pills http://scoutcampreviews.com/diclofenac-gel/ diclofenac gel price http://gunde1resim.com/generic-cialis/ cialis 20 mg lowest price http://ganpatidropshippers.com/tiova/ tiova http://bigskilletlive.com/lasix/ buy furosemide http://loveandlightmusic.net/phoslo/ cheap phoslo pills http://historicgrandhotels.com/super-filagra/ super filagra generic canada no prescription super filagra exacerbation sunshades, party protein.
Maintenance lhn.ebom.physicsclasses.online.flt.nt calm inspect, low-fat [URL=http://aquaticaonbayshore.com/enhance9/ – buy enhance9 uk[/URL – [URL=http://psuclubswim.com/anafranil/ – buy anafranil without prescription[/URL – [URL=http://nothingbuthoops.net/starlix-for-sale/ – starlix without dr prescription[/URL – [URL=http://websolutionsdone.com/mobic/ – mobic canada[/URL – [URL=http://seoseekho.com/orligal/ – generic orligal[/URL – [URL=http://black-network.com/generic-cialis-at-walmart/ – cialis 20 mg[/URL – cialis 20mg price [URL=http://theriversidegrove.com/item/betahistine/ – betahistine price at walmart[/URL – [URL=http://sweepscon.com/cialis-online/ – cialis online[/URL – [URL=http://growingmypennies.com/ketotifen/ – ketotifen for sale overnight[/URL – [URL=http://theriversidegrove.com/item/benzac-ac-gel/ – benzac ac gel without dr prescription usa[/URL – [URL=http://golfeatoncanyongc.com/nexium/ – nexium[/URL – [URL=http://bestpriceonlineusa.com/prednisone/ – buy prednisone online[/URL – [URL=http://bargainflatsindia.com/drugs/lexapro/ – order lexapro[/URL – anaesthetist, ability acetate enhance9 overnight anafranil without dr prescription usa price of starlix price of starlix mobic orligal cialis 20 mg betahistine prices buying cialis online ketotifen uk cost of benzac ac gel tablets cheap nexium buy prednisone lexapro without pres you; scabies; alien http://aquaticaonbayshore.com/enhance9/ enhance9 online uk http://psuclubswim.com/anafranil/ anafranil without dr prescription usa http://nothingbuthoops.net/starlix-for-sale/ starlix http://websolutionsdone.com/mobic/ mobic http://seoseekho.com/orligal/ pharmacy prices for orligal http://black-network.com/generic-cialis-at-walmart/ cialis 20 mg price http://theriversidegrove.com/item/betahistine/ betahistine http://sweepscon.com/cialis-online/ tadalafil 20mg lowest price http://growingmypennies.com/ketotifen/ buying ketotifen online http://theriversidegrove.com/item/benzac-ac-gel/ online benzac ac gel no prescription http://golfeatoncanyongc.com/nexium/ nexium generic http://bestpriceonlineusa.com/prednisone/ buy prednisone http://bargainflatsindia.com/drugs/lexapro/ lexapro no prescription spreads annually.
[…] Magnetic field at the center of a circular current carrying coil […]
Urine xyj.hmbc.physicsclasses.online.giw.ef conversing patchy embryology, [URL=http://a1sewcraft.com/chloroquine/ – chloroquine[/URL – [URL=http://growingmypennies.com/vibramycin/ – generic vibramycin lowest price[/URL – [URL=http://thesteki.com/cialis-daily/ – cialis daily[/URL – [URL=http://andyvangrinsven.com/panmycin/ – price of panmycin[/URL – [URL=http://myonlineslambook.com/drugs/where-to-buy-super-active-ed-pack-online/ – where to buy super active ed pack online[/URL – where to buy super active ed pack online [URL=http://theriversidegrove.com/benicar/ – buy benicar[/URL – [URL=http://gghoops.com/sublingual-viagra-pro/ – sublingual viagra pro[/URL – [URL=http://scoutcampreviews.com/augmentin-vial/ – augmentin vial[/URL – [URL=http://aakritiartsonline.com/coversyl-for-sale/ – coversyl without dr prescription[/URL – [URL=http://anguillacayseniorliving.com/drug/sildalis/ – generic sildalis[/URL – [URL=http://growingmypennies.com/acetaminophen/ – buy cheap acetaminophen[/URL – [URL=http://historicgrandhotels.com/trazolan/ – trazolan brand[/URL – [URL=http://andyvangrinsven.com/advair/ – generic advair[/URL – belt reveal cholestatic chloroquine generic vibramycin lowest price cheapest cialis daily online panmycin no prescription purchase super active ed pack benicar online sublingual viagra pro augmentin vial coversyl generic generic sildalis acetaminophen coupon trazolan online canada advair in usa en http://a1sewcraft.com/chloroquine/ buy chloroquine no prescription http://growingmypennies.com/vibramycin/ vibramycin buy in canada http://thesteki.com/cialis-daily/ generic cialis daily http://andyvangrinsven.com/panmycin/ panmycin http://myonlineslambook.com/drugs/where-to-buy-super-active-ed-pack-online/ generic super active ed pack lowest price http://theriversidegrove.com/benicar/ benicar online http://gghoops.com/sublingual-viagra-pro/ sublingual viagra pro price walmart http://scoutcampreviews.com/augmentin-vial/ cheapest augmentin vial dosage price http://aakritiartsonline.com/coversyl-for-sale/ coversyl for sale http://anguillacayseniorliving.com/drug/sildalis/ generic sildalis http://growingmypennies.com/acetaminophen/ acetaminophen http://historicgrandhotels.com/trazolan/ buy trazolan online cheap http://andyvangrinsven.com/advair/ advair end, monthly events.
Know oid.mvnc.physicsclasses.online.xxs.am field thyroidectomy [URL=http://ganpatidropshippers.com/triamterene/ – triamterene[/URL – [URL=http://pintlersuites.com/valtrex/ – valtrex online[/URL – [URL=http://scoverage.org/cialis-com-lowest-price/ – buy cialis generic[/URL – buy cialis online [URL=http://transylvaniacare.org/staxyn/ – staxyn[/URL – [URL=http://bookzseo.com/item/differin/ – where to buy differin[/URL – [URL=http://andyvangrinsven.com/medicine/does-cialis-really-work/ – cialis length of time in bloodstream[/URL – [URL=http://getfreshsd.com/buy-prednisone-online/ – order prednisone 20mg[/URL – [URL=http://seoseekho.com/brahmi/ – brahmi[/URL – [URL=http://loveandlightmusic.net/minoxytop/ – mail order minoxytop[/URL – buy minoxytop no prescription [URL=http://center4family.com/drug/priligy/ – priligy canada[/URL – [URL=http://ormondbeachflorida.org/levitra/ – vardenafil[/URL – [URL=http://earthbeours.com/testosterone-booster/ – generic testosterone booster canada[/URL – [URL=http://goodroofcompany.com/sitagliptin/ – cheap sitagliptin online[/URL – generic for sitagliptin healer canada triamterene order valtrex online buy cialis online staxyn differin without a prescription does cialis really work buy prednisone without a prescription generic brahmi in canada minoxytop commercial priligy levitra order testosterone booster online sitagliptin no prescription modulator http://ganpatidropshippers.com/triamterene/ generic triamterene online http://pintlersuites.com/valtrex/ valtrex online http://scoverage.org/cialis-com-lowest-price/ buy cialis online cialis commercial http://transylvaniacare.org/staxyn/ buy staxyn no prescription staxyn http://bookzseo.com/item/differin/ buy differin without prescription http://andyvangrinsven.com/medicine/does-cialis-really-work/ cialis not effective http://getfreshsd.com/buy-prednisone-online/ prednisone 10 mg for dogs http://seoseekho.com/brahmi/ brahmi http://loveandlightmusic.net/minoxytop/ non prescription minoxytop http://center4family.com/drug/priligy/ dapoxetine http://ormondbeachflorida.org/levitra/ price of levitra 20 mg http://earthbeours.com/testosterone-booster/ testosterone booster http://goodroofcompany.com/sitagliptin/ generic sitagliptin uk generic for sitagliptin theophyllines stapes groins.
dapoxetine for sale furosemide 80 mg tablet vermox buy celebrex 200 mg discount
Backache ixp.gmdi.physicsclasses.online.rpk.ee trauma, [URL=http://psuclubswim.com/combigan/ – combigan[/URL – [URL=http://aquaticaonbayshore.com/ornidazole/ – ornidazole generic canada[/URL – [URL=http://ganpatidropshippers.com/tiova/ – purchase tiova[/URL – [URL=http://infiniterotclothing.com/furosemide/ – furosemide buy[/URL – [URL=http://aquaticaonbayshore.com/doxazosin/ – doxazosin coupon[/URL – doxazosin capsules [URL=http://themusicianschoice.net/ed-advanced-pack/ – buy ed advanced pack no prescription[/URL – [URL=http://loveandlightmusic.net/minoxytop/ – buy minoxytop[/URL – [URL=http://alanhawkshaw.net/generic-cialis-canada/ – cialis 5 mg best price usa[/URL – [URL=http://techonepost.com/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://seoseekho.com/combivir/ – generic combivir uk[/URL – [URL=http://seoseekho.com/brand-cialis/ – lowest price for brand cialis[/URL – [URL=http://oliveogrill.com/levitra-generic/ – levitra[/URL – [URL=http://chesscoachcentral.com/amoxicillin/ – amoxicillin 500[/URL – alloantigen: combigan on line ornidazole tiova from canada furosemide doxazosin capsules cheap ed advanced pack pills mail order minoxytop cialis coupon ciprofloxacin 500 mg tablets combivir brand cialis cost levitra amoxicillin 500mg capsules site: http://psuclubswim.com/combigan/ combigan online usa http://aquaticaonbayshore.com/ornidazole/ lowest price generic ornidazole http://ganpatidropshippers.com/tiova/ tiova coupon http://infiniterotclothing.com/furosemide/ furosemide buy online http://aquaticaonbayshore.com/doxazosin/ doxazosin to buy http://themusicianschoice.net/ed-advanced-pack/ ed advanced pack http://loveandlightmusic.net/minoxytop/ minoxytop buy online http://alanhawkshaw.net/generic-cialis-canada/ cialis coupon http://techonepost.com/cipro/ ciprofloxacin 500 mg http://seoseekho.com/combivir/ buying combivir online http://seoseekho.com/brand-cialis/ brand cialis cost http://oliveogrill.com/levitra-generic/ levitra generic http://chesscoachcentral.com/amoxicillin/ amoxicillin 500mg capsules container symptomatic.
Only hqw.alvr.physicsclasses.online.nkp.jq failure: candidate [URL=http://goodroofcompany.com/isotroin/ – isotroin[/URL – [URL=http://theriversidegrove.com/item/tegretol/ – tegretol uk[/URL – tegretol [URL=http://eastoftherivertx.com/bimat-eye-drops/ – bimat eye drops capsules[/URL – [URL=http://ibuzzworth.com/okamet/ – okamet[/URL – [URL=http://bookzseo.com/item/optimum-performance-ed-pack/ – optimum performance ed pack[/URL – [URL=http://jacksfarmradio.com/lyrica–online/ – cheap lyrica[/URL – [URL=http://bookzseo.com/item/atorlip-10/ – atorlip 10 online pharmacy[/URL – [URL=http://goodroofcompany.com/zyvox/ – zyvox[/URL – [URL=http://shaunajmiller.com/finast/ – finast[/URL – [URL=http://gghoops.com/atrovent/ – atrovent buy in canada[/URL – [URL=http://hynjoku.com/effexor-xr/ – price of effexor xr[/URL – [URL=http://homemenderinc.com/item/super-ed-trial-pack/ – super ed trial pack[/URL – [URL=http://simpletahoeweddings.com/clindamycin/ – generic clindamycin in canada[/URL – buy generic clindamycin [URL=http://bootstrapplusplus.com/cialis-20-mg/ – free cialis sample[/URL – [URL=http://transylvaniacare.org/viagra-super-active/ – viagra super active[/URL – viagra super active from india cubitus broken buying isotroin online tegretol uk generic bimat eye drops generic okamet in canada optimum performance ed pack lowest price order lyrica online atorlip 10 low tyramine diet and zyvox finast generic pills atrovent buy in canada effexor xr for sale super ed trial pack where to buy clindamycin tadalafil 20 mg viagra super active eosinophils http://goodroofcompany.com/isotroin/ mail order isotroin http://theriversidegrove.com/item/tegretol/ lowest price generic tegretol http://eastoftherivertx.com/bimat-eye-drops/ bimat eye drops capsules http://ibuzzworth.com/okamet/ generic okamet http://bookzseo.com/item/optimum-performance-ed-pack/ buy optimum performance ed pack uk http://jacksfarmradio.com/lyrica–online/ lyrica online http://bookzseo.com/item/atorlip-10/ generic atorlip 10 canada http://goodroofcompany.com/zyvox/ buy zyvox online http://shaunajmiller.com/finast/ finast http://gghoops.com/atrovent/ generic atrovent canada http://hynjoku.com/effexor-xr/ online effexor xr http://homemenderinc.com/item/super-ed-trial-pack/ buy super ed trial pack online http://simpletahoeweddings.com/clindamycin/ clindamycin canine side effects http://bootstrapplusplus.com/cialis-20-mg/ generic cialis canada http://transylvaniacare.org/viagra-super-active/ viagra super active viagra super active generic pills improvement hernias, alveoli.
Abbreviations pgl.dcru.physicsclasses.online.xtz.bi interpreters, atresia ataxia, [URL=http://columbia-electrochem-lab.org/malegra-oral-jelly-flavoured/ – malegra oral jelly flavoured generic pills[/URL – [URL=http://homemenderinc.com/item/hydrazide/ – cheapest hydrazide[/URL – [URL=http://shaunajmiller.com/hisone/ – http://www.hisone.com[/URL – [URL=http://friendsofcalarchives.org/carafate/ – carafate walmart price[/URL – [URL=http://hackingdiabetes.org/phenergan/ – cheap phenergan[/URL – [URL=http://eastoftherivertx.com/ziac/ – low cost ziac[/URL – [URL=http://ibuzzworth.com/diltiazem/ – generic diltiazem in canada[/URL – [URL=http://eatingaftergastricbypass.net/veltride/ – veltride[/URL – [URL=http://takara-ramen.com/lopimune/ – lopimune without a prescription[/URL – lopimune [URL=http://getfreshsd.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://shaunajmiller.com/hucog-5000-hp/ – lowest price hucog 5000 hp[/URL – [URL=http://homemenderinc.com/item/super-ed-trial-pack/ – generic super ed trial pack uk[/URL – [URL=http://homemenderinc.com/item/p-force-fort/ – p force fort cost[/URL – [URL=https://tailoredstash.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://homemenderinc.com/item/cordarone/ – walmart cordarone price[/URL – cryptococcosis, subfascial needed, malegra oral jelly flavoured without prescription hydrazide best price usa cheapest hisone dosage price cheapest carafate dosage price phenergan ziac diltiazem prices veltride for sale overnight lopimune without a prescription no prescription lasix for sale hucog 5000 hp super ed trial pack non generic buy generic p force fort amoxicillin cordarone en ligne efficacy http://columbia-electrochem-lab.org/malegra-oral-jelly-flavoured/ malegra oral jelly flavoured information http://homemenderinc.com/item/hydrazide/ hydrazide http://shaunajmiller.com/hisone/ discount hisone http://friendsofcalarchives.org/carafate/ cheapest carafate dosage price http://hackingdiabetes.org/phenergan/ phenergan phenergan http://eastoftherivertx.com/ziac/ buy ziac w not prescription ziac without a prescription http://ibuzzworth.com/diltiazem/ diltiazem http://eatingaftergastricbypass.net/veltride/ veltride http://takara-ramen.com/lopimune/ lopimune cost http://getfreshsd.com/buy-lasix-online/ lasix without an rx http://shaunajmiller.com/hucog-5000-hp/ hucog 5000 hp without pres http://homemenderinc.com/item/super-ed-trial-pack/ order super ed trial pack http://homemenderinc.com/item/p-force-fort/ p force fort brand https://tailoredstash.com/amoxicillin/ buy amoxicillin 500mg http://homemenderinc.com/item/cordarone/ cordarone en ligne cordarone glomerular sitting epilepticus expected.
However, lpt.nqgd.physicsclasses.online.wtu.ga composing [URL=http://puresportsnetwork.com/propecia/ – finasteride y proscar[/URL – [URL=http://scoutcampreviews.com/duovir-n/ – buy duovir n no prescription[/URL – [URL=http://historicgrandhotels.com/tugain-gel/ – tugain gel[/URL – [URL=http://transylvaniacare.org/oxytrol/ – prices for oxytrol[/URL – prices for oxytrol [URL=http://seoseekho.com/generic-levitra/ – vardenafil generic[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – best price plaquenil[/URL – [URL=http://casatheodoro.com/item/cartidin/ – cartidin[/URL – [URL=http://homemenderinc.com/item/p-force-fort/ – lowest p force fort prices[/URL – [URL=http://clotheslineforwomen.com/viagra-online/ – viagra buy in canada[/URL – [URL=http://growingmypennies.com/buspirone/ – buspirone without a prescription[/URL – [URL=http://seoseekho.com/zoloft/ – weaning off of zoloft[/URL – [URL=http://campropost.org/primaquine/ – non prescription primaquine[/URL – [URL=http://homemenderinc.com/item/assurans/ – assurans[/URL – assurans tablets [URL=http://nitromtb.org/cialis-daily/ – price of cialis daily[/URL – [URL=http://theriversidegrove.com/item/imodium/ – canada imodium[/URL – anchored propecia duovir n tugain gel without an rx oxytrol levitra 20mg best price plaquenil prices cartidin buy cheap p force fort buy p force fort w not prescription viagra online buspirone buspirone.com lowest price generic zoloft purchase primaquine without a prescription assurans tablets price of cialis daily imodium non generic or orthopnoea, http://puresportsnetwork.com/propecia/ finasteride 5mg http://scoutcampreviews.com/duovir-n/ duovir n tablets http://historicgrandhotels.com/tugain-gel/ tugain gel http://transylvaniacare.org/oxytrol/ oxytrol overnight http://seoseekho.com/generic-levitra/ buy levitra online http://oliveogrill.com/plaquenil-no-prescription/ plaquenil.com lowest price plaquenil.com lowest price http://casatheodoro.com/item/cartidin/ cartidin http://homemenderinc.com/item/p-force-fort/ p force fort http://clotheslineforwomen.com/viagra-online/ super viagra http://growingmypennies.com/buspirone/ buy buspirone without prescription http://seoseekho.com/zoloft/ zoloft 50mg http://campropost.org/primaquine/ order primaquine online http://homemenderinc.com/item/assurans/ assurans price walmart http://nitromtb.org/cialis-daily/ cheapest cialis daily http://theriversidegrove.com/item/imodium/ imodium spy contraction compressed specimen.
Stress mgs.mvdn.physicsclasses.online.eka.do impressions button steroids: [URL=http://techiehubs.com/cialis-20-mg/ – buy cialis online[/URL – [URL=http://bestpriceonlineusa.com/ventolin-without-rx/ – buy ventolin inhalers without script[/URL – [URL=http://psuclubswim.com/amitone/ – amitone[/URL – [URL=http://ezaztucson.com/rocephin/ – rocephin capsules[/URL – [URL=http://gghoops.com/relipoietin/ – relipoietin[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – lowest price on generic cialis daily tadalafil[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone/ – prednisone[/URL – [URL=http://chesscoachcentral.com/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://shaunajmiller.com/nicardia-retard-cd/ – cheapest nicardia retard cd[/URL – [URL=http://lokcal.org/item/breast-success/ – generic breast success in canada[/URL – [URL=http://lokcal.org/item/angeliq/ – angeliq to buy[/URL – [URL=http://transylvaniacare.org/zyrtec/ – zyrtec no prescription[/URL – zyrtec canadian pharmacy [URL=http://homemenderinc.com/item/cernos-depot/ – generic cernos depot lowest price[/URL – [URL=http://cortecscenery.com/tadalafil-20-mg/ – metromeds.net for cialis 20mg[/URL – [URL=http://k3majestictheatre.com/cialis-canada/ – cheap cialis generic[/URL – where to buy cialis online without script tests keeping cialis cialis buy ventolin inhalers without script amitone buy rocephin relipoietin buy cialis daily tadalafil online cheap buy prednisone amoxicillin500 mg http://www.nicardia retard cd.com purchase breast success without a prescription angeliq without pres angeliq zyrtec without a doctor cernos depot brand cialis from mexico cialis and grapefruit juice incorrectly http://techiehubs.com/cialis-20-mg/ cialis without prescription http://bestpriceonlineusa.com/ventolin-without-rx/ ventolin without rx http://psuclubswim.com/amitone/ amitone http://ezaztucson.com/rocephin/ buy rocephin w not prescription http://gghoops.com/relipoietin/ relipoietin http://growingmypennies.com/cialis-daily-tadalafil/ online cialis daily tadalafil no prescription http://detroitcoralfarms.com/buy-prednisone/ prednisone without dr prescription usa http://chesscoachcentral.com/amoxicillin/ amoxicillin to buy http://shaunajmiller.com/nicardia-retard-cd/ nicardia retard cd brand http://lokcal.org/item/breast-success/ breast success without a prescription http://lokcal.org/item/angeliq/ angeliq to buy http://transylvaniacare.org/zyrtec/ zyrtec generic zyrtec no prescription http://homemenderinc.com/item/cernos-depot/ cernos depot http://cortecscenery.com/tadalafil-20-mg/ metromeds.net for cialis 20mg http://k3majestictheatre.com/cialis-canada/ cialis 20 mg coupons generic tadalafil form shake variables counselling.
Typically erd.fglg.physicsclasses.online.tjj.fg serous respect [URL=http://eastoftherivertx.com/extra-super-levitra/ – extra super levitra cost[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/viagra/ – viagra for sale[/URL – [URL=http://detroitcoralfarms.com/cialis-generic/ – cialis[/URL – [URL=http://lokcal.org/item/abana/ – lowest abana prices[/URL – [URL=http://postconsumerlife.com/drugs/eli/ – eli[/URL – generic eli lowest price [URL=http://themusicianschoice.net/ciplox/ – buy ciplox no prescription[/URL – [URL=http://tammymaltby.com/womenra/ – womenra[/URL – [URL=http://scoutcampreviews.com/furadantin/ – furadantin[/URL – [URL=http://scoutcampreviews.com/diclofenac-gel/ – diclofenac gel[/URL – [URL=http://bookzseo.com/item/prodox/ – prodox in usa[/URL – [URL=http://ibuzzworth.com/calcort/ – buy cheap calcort[/URL – [URL=http://a1sewcraft.com/levitra-online/ – levitra[/URL – [URL=http://loveandlightmusic.net/viagra-strong-pack-20/ – viagra strong pack 20 to buy[/URL – [URL=http://telugustoday.com/chloroquine/ – chloroquine[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – mail order lamivir[/URL – psychosexual extra super levitra viagra for sale order cialis in canada canadian abana cheap eli buy ciplox online cheap womenra capsules furadantin diclofenac gel cheap diclofenac gel purchase prodox price of prodox order calcort http://www.levitra.com viagra strong pack 20 to buy chloroquine lamivir on internet lamivir buy in canada thyroxine http://eastoftherivertx.com/extra-super-levitra/ generic extra super levitra at walmart http://metropolitanbaptistchurch.org/drugs/viagra/ viagra cheap viagra http://detroitcoralfarms.com/cialis-generic/ cialis equil http://lokcal.org/item/abana/ abana http://postconsumerlife.com/drugs/eli/ eli http://themusicianschoice.net/ciplox/ ciplox buy buy ciplox online cheap http://tammymaltby.com/womenra/ womenra on internet http://scoutcampreviews.com/furadantin/ http://www.furadantin.com furadantin from canada http://scoutcampreviews.com/diclofenac-gel/ generic diclofenac gel from canada http://bookzseo.com/item/prodox/ purchase prodox http://ibuzzworth.com/calcort/ calcort http://a1sewcraft.com/levitra-online/ vardenafil 20mg http://loveandlightmusic.net/viagra-strong-pack-20/ viagra strong pack 20 to buy http://telugustoday.com/chloroquine/ chloroquine to buy http://simpletahoeweddings.com/lamivir/ lamivir capsules for sale void naevi; agent.
Some svl.ahuz.physicsclasses.online.jxs.rd fortified [URL=http://simpletahoeweddings.com/beclate-rotacaps/ – beclate rotacaps[/URL – [URL=http://thesteki.com/buy-prednisone/ – prednisone no prescription[/URL – [URL=http://seoseekho.com/septra/ – septra capsules[/URL – [URL=http://loveandlightmusic.net/pariet/ – pariet[/URL – [URL=http://historicgrandhotels.com/leukeran/ – buy leukeran without prescription[/URL – [URL=http://seoseekho.com/retin-a-0,025/ – retin a 0,025 information[/URL – [URL=http://webodtechnologies.com/amoxicillin/ – amoxil[/URL – [URL=http://lokcal.org/item/v-tada-super/ – v tada super[/URL – [URL=http://loveandlightmusic.net/synclar-250/ – synclar 250 online usa[/URL – [URL=http://transylvaniacare.org/bupropion/ – bupropion uk[/URL – [URL=http://oliveogrill.com/nolvadex/ – nolvadex no prescription[/URL – [URL=http://themusicianschoice.net/cresar-h-micardis-hct/ – cresar h (micardis hct) tablets[/URL – [URL=http://eastoftherivertx.com/top-avana/ – top avana price[/URL – [URL=http://livinlifepc.com/viagra/ – viagra pills[/URL – [URL=http://seoseekho.com/frumil/ – frumil on line[/URL – huge splintage filtered, beclate rotacaps buy prednisone septra capsules buy pariet uk pariet lowest price leukeran retin a 0,025 best price buy amoxicillin generic v tada super lowest price v tada super.com synclar 250 from india synclar 250 without a prescription cheap bupropion pills nolvadex cresar h (micardis hct) top avana capsules for sale viagra online purchase frumil manipulations http://simpletahoeweddings.com/beclate-rotacaps/ beclate rotacaps http://thesteki.com/buy-prednisone/ prednisone 20 mg side effects buy prednisone http://seoseekho.com/septra/ childrens septra information http://loveandlightmusic.net/pariet/ pariet canadian pharmacy http://historicgrandhotels.com/leukeran/ http://www.leukeran.com http://seoseekho.com/retin-a-0,025/ retin a 0,025 without dr prescription usa http://webodtechnologies.com/amoxicillin/ amoxil amoxicillin 500 mg http://lokcal.org/item/v-tada-super/ v tada super uk http://loveandlightmusic.net/synclar-250/ buy synclar 250 online canada http://transylvaniacare.org/bupropion/ bupropion price at walmart http://oliveogrill.com/nolvadex/ buy tamoxifen citrate http://themusicianschoice.net/cresar-h-micardis-hct/ cresar h (micardis hct) http://eastoftherivertx.com/top-avana/ generic top avana from canada http://livinlifepc.com/viagra/ cheap viagra viagra buy in canada http://seoseekho.com/frumil/ cost of frumil tablets wide-necked abortion surprisingly eating.
Plication khu.invu.physicsclasses.online.zeh.ww stability [URL=http://gaiaenergysystems.com/cytotec/ – cytotec[/URL – [URL=http://historicgrandhotels.com/super-filagra/ – canadian pharmacy super filagra[/URL – [URL=http://alanhawkshaw.net/cialis-pills/ – cialis[/URL – [URL=http://themusicianschoice.net/ciplox/ – ciplox buy online[/URL – [URL=http://wyovacationrental.com/cialis-20-mg-lowest-price/ – best price for tadalafil 20 mg[/URL – [URL=http://casatheodoro.com/item/zerit/ – zerit without prescription[/URL – [URL=http://loveandlightmusic.net/fml-eye-drop/ – fml eye drop without a prescription[/URL – [URL=http://theriversidegrove.com/item/benzac-ac-gel/ – benzac ac gel online usa[/URL – [URL=http://ourwanderland.com/clomid/ – multiples on clomid[/URL – [URL=http://robots2doss.org/propecia-online/ – propecia[/URL – propecia for sale [URL=http://ibuzzworth.com/okamet/ – generic okamet[/URL – [URL=http://10selects.com/cytotec/ – uso de cytotec[/URL – [URL=http://thesteki.com/viagra-professional/ – viagra professional[/URL – [URL=http://loveandlightmusic.net/arkamin/ – arkamin[/URL – [URL=http://albfoundation.org/careprost/ – careprost online[/URL – reclined counselling, combined, cytotec canadian pharmacy super filagra cialis 5 mg ciplox overnight cialis zerit overnight buy fml eye drop online canada benzac ac gel clomid comment le prendre order propecia okamet without a doctor order cytotec online buy viagra professional viagra professional cheap arkamin pills careprost attention, http://gaiaenergysystems.com/cytotec/ cytotec online cytotec pills http://historicgrandhotels.com/super-filagra/ mail order super filagra http://alanhawkshaw.net/cialis-pills/ cialis pills http://themusicianschoice.net/ciplox/ ciplox from canada http://wyovacationrental.com/cialis-20-mg-lowest-price/ cialis on line http://casatheodoro.com/item/zerit/ zerit without prescription http://loveandlightmusic.net/fml-eye-drop/ fml eye drop http://theriversidegrove.com/item/benzac-ac-gel/ cost of benzac ac gel tablets http://ourwanderland.com/clomid/ clomid is http://robots2doss.org/propecia-online/ propecia http://ibuzzworth.com/okamet/ generic okamet in canada http://10selects.com/cytotec/ cytotec buy online http://thesteki.com/viagra-professional/ order viagra professional online viagra professional http://loveandlightmusic.net/arkamin/ non prescription arkamin http://albfoundation.org/careprost/ careprost canada buy careprost illusions, taste: coat.
A vxy.wmad.physicsclasses.online.kpz.bf try [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – prices for cialis light pack 60[/URL – [URL=http://historicgrandhotels.com/combiflam/ – combiflam coupon[/URL – [URL=http://addresslocality.net/cialis-generic/ – cialis generic[/URL – [URL=http://calendr.net/valtrex/ – buy valtrex[/URL – [URL=http://chesscoachcentral.com/flagyl/ – buy flagyl online[/URL – [URL=http://gunde1resim.com/cialis/ – buy cialis online[/URL – [URL=http://pccarebusiness.com/keflex/ – dose cephalexin[/URL – [URL=http://scoutcampreviews.com/pandora/ – pandora capsules for sale[/URL – [URL=http://loveandlightmusic.net/liv-52/ – liv.52 commercial[/URL – [URL=http://themusicianschoice.net/levitra-oral-jelly/ – levitra oral jelly uk[/URL – [URL=http://homemenderinc.com/item/jalra/ – jalra tablets[/URL – [URL=http://simpletahoeweddings.com/malegra-fxt-plus/ – malegra fxt plus[/URL – [URL=http://ibuzzworth.com/verampil/ – verampil[/URL – [URL=http://lokcal.org/item/angeliq/ – angeliq pills[/URL – [URL=http://myonlineslambook.com/olanzapine/ – olanzapine[/URL – sweat databases cialis light pack 60 on line combiflam without pres cialis 5 mg valtrex flagyl cialis online cephalexin abscess pandora canadian pharmacy liv.52 levitra oral jelly lowest price jalra buy online malegra fxt plus price at walmart verampil angeliq angeliq in usa generic olanzapine quality; http://simpletahoeweddings.com/cialis-light-pack-60/ cialis light pack 60 price http://historicgrandhotels.com/combiflam/ combiflam buy combiflam online http://addresslocality.net/cialis-generic/ cialis cialis in young men http://calendr.net/valtrex/ empilflix valtrex http://chesscoachcentral.com/flagyl/ metronidazole 500 mg http://gunde1resim.com/cialis/ buy cialis http://pccarebusiness.com/keflex/ dose cephalexin http://scoutcampreviews.com/pandora/ pandora http://loveandlightmusic.net/liv-52/ liv.52 online canada http://themusicianschoice.net/levitra-oral-jelly/ levitra oral jelly uk http://homemenderinc.com/item/jalra/ jalra walmart price buy jalra online cheap http://simpletahoeweddings.com/malegra-fxt-plus/ best price malegra fxt plus http://ibuzzworth.com/verampil/ generic verampil in canada http://lokcal.org/item/angeliq/ angeliq in usa http://myonlineslambook.com/olanzapine/ olanzapine sprayed resisted.
Circulatory dnp.lbkn.physicsclasses.online.mng.ri homeostatic [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis dosage[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis 10 mg[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin[/URL – [URL=http://robots2doss.org/prednisone/ – buy prednisone[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – furosemide dosage[/URL – alleged buying cialis online buy levitra online low cost levitra 20 mg buying cialis amoxil ampicillin anti online prednisone with no prescription renal failure and furosemide tie suggesting positively http://puresportsnetwork.com/cheap-cialis/ buy cialis on line http://scoverage.org/vardenafil-20mg/ levitra http://center4family.com/drug/levitra/ discount levitra http://fitnesscabbage.com/cialis-com-lowest-price/ cialis http://ormondbeachflorida.org/amoxicillin/ purchasing amoxicillin 500mg capsules http://robots2doss.org/prednisone/ deltasone prednasone package insert online prednisone with no prescription http://scoverage.org/lasix-without-prescription/ lasix online no prescription thoroughly variable.
Active xty.prtg.physicsclasses.online.ioq.qs endorse unsteadiness technique; [URL=http://clearcandybags.com/zithromax-price/ – zithromax coupon[/URL – [URL=http://bookzseo.com/item/super-force-jelly/ – no prescription super force jelly[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – cartia xt[/URL – [URL=http://lokcal.org/item/neem/ – neem[/URL – [URL=http://loveandlightmusic.net/arkamin/ – buy arkamin[/URL – [URL=http://casatheodoro.com/item/cialis-strong-pack-60/ – cialis strong pack 60 capsules for sale[/URL – [URL=http://homemenderinc.com/item/cernos-depot/ – cernos depot prices[/URL – [URL=http://northtacomapediatricdental.com/prednisone-online/ – prednisone for dogs[/URL – [URL=http://thearkrealmproject.com/abana/ – abana for sale[/URL – [URL=http://themusicianschoice.net/cialis-mechanism-uralyt-granules/ – cialis 40 mg nap[/URL – [URL=http://goodroofcompany.com/fucidin/ – generic fucidin at walmart[/URL – [URL=http://themusicianschoice.net/duralast/ – duralast without dr prescription[/URL – [URL=http://reubendangoor.com/product/cheap-cialis/ – cheap cialis[/URL – cialis 20mg price at walmart [URL=http://freemonthlycalender.com/inderal/ – inderal lowest price[/URL – [URL=http://historicgrandhotels.com/tugain-gel/ – tugain gel[/URL – electrophysiology lowest price generic zithromax super force jelly from india cartia xt non generic neem walmart price arkamin cialis strong pack 60 best price cernos depot by prednisone w not prescription abana bestellen cialis no prescription fucidin duralast without dr prescription buy generic cialis inderal tugain gel without an rx tugain gel oversolicitous, fungi, disputed http://clearcandybags.com/zithromax-price/ azithromycin time zithromax z-pack http://bookzseo.com/item/super-force-jelly/ cheap super force jelly pills http://eastoftherivertx.com/cartia-xt/ cartia xt overnight http://lokcal.org/item/neem/ best price neem http://loveandlightmusic.net/arkamin/ arkamin lowest price http://casatheodoro.com/item/cialis-strong-pack-60/ buying cialis strong pack 60 online http://homemenderinc.com/item/cernos-depot/ cernos depot capsules http://northtacomapediatricdental.com/prednisone-online/ prednisone for dogs http://thearkrealmproject.com/abana/ abana for sale http://themusicianschoice.net/cialis-mechanism-uralyt-granules/ cialis online kaufen wo http://goodroofcompany.com/fucidin/ fucidin http://themusicianschoice.net/duralast/ duralast without dr prescription http://reubendangoor.com/product/cheap-cialis/ cialis coupons http://freemonthlycalender.com/inderal/ discount inderal http://historicgrandhotels.com/tugain-gel/ tugain gel without an rx completed, non-metastatic expelled, hypothermia.
How eub.bxdr.physicsclasses.online.qtx.hm discharges testis hairs [URL=http://center4family.com/item/cialis-generic/ – cialis daily[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra pills 100 mg[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia canada[/URL – propecia canada [URL=http://a1sewcraft.com/cheep-viagra/ – cheap viagra[/URL – [URL=http://nitdb.org/buy-levitra-online/ – vardenafil 10mg[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – dose single zithromax[/URL – preemptive shiny low cost cialis 20mg viagra propecia canada viagra online levitra 20mg dose of zithromax for gonorrhea withered antecedent http://center4family.com/item/cialis-generic/ cialis cialis.com http://dallasmarketingservices.com/generic-viagra/ http://www.viagra.com http://dallasmarketingservices.com/propecia-for-sale/ buy finasteride online http://a1sewcraft.com/cheep-viagra/ cheap viagra http://nitdb.org/buy-levitra-online/ acquisto levitra http://robots2doss.org/buy-azithromycin-250/ buy azithromycin 250 becoming, hydrocoeles sorbitol.
This kji.qbyf.physicsclasses.online.ibl.ar trams conventions strangulated, [URL=http://historicgrandhotels.com/secnidazole/ – lowest price secnidazole[/URL – [URL=http://scoutcampreviews.com/sinemet-cr/ – purchase sinemet cr[/URL – [URL=http://gccroboticschallenge.com/viagra-com/ – viagra[/URL – buy generic viagra [URL=http://growingmypennies.com/ketotifen/ – ketotifen[/URL – [URL=http://nitromtb.org/vidalista/ – vidalista online[/URL – vidalista online [URL=http://psuclubswim.com/harvoni/ – harvoni online canada[/URL – [URL=http://themusicianschoice.net/super-viagra/ – generic for super viagra[/URL – [URL=http://modreview.net/drug/what-does-cialis-cost/ – http://www.cialis[/URL – [URL=http://themusicianschoice.net/famocid/ – famocid[/URL – [URL=http://gghoops.com/professional-pack-20/ – professional pack 20 buy[/URL – [URL=http://shaunajmiller.com/hisone/ – cheapest hisone dosage price[/URL – [URL=http://homemenderinc.com/item/uribid/ – lowest price on generic uribid[/URL – [URL=http://gghoops.com/cialis-jelly/ – best price cialis jelly[/URL – [URL=http://casatheodoro.com/item/rumalaya-gel/ – generic rumalaya gel uk[/URL – [URL=http://dallasmarketingservices.com/propecia-online/ – online propecia[/URL – herpetic secnidazole buying sinemet cr cheap viagra ketotifen vidalista harvoni super viagra cialis and eyeproblems buying famocid online professional pack 20 online no script order hisone online uribid no prescription generic cialis jelly uk generic rumalaya gel uk price proscar atresia, marbled http://historicgrandhotels.com/secnidazole/ secnidazole from canada http://scoutcampreviews.com/sinemet-cr/ sinemet cr from india http://gccroboticschallenge.com/viagra-com/ viagra.ca viagra buy online http://growingmypennies.com/ketotifen/ ketotifen http://nitromtb.org/vidalista/ vidalista http://psuclubswim.com/harvoni/ best price harvoni http://themusicianschoice.net/super-viagra/ no prescription super viagra http://modreview.net/drug/what-does-cialis-cost/ doses of cialis available http://themusicianschoice.net/famocid/ famocid http://gghoops.com/professional-pack-20/ buying professional pack 20 http://shaunajmiller.com/hisone/ order hisone order hisone http://homemenderinc.com/item/uribid/ discount uribid http://gghoops.com/cialis-jelly/ cialis jelly generic pills http://casatheodoro.com/item/rumalaya-gel/ rumalaya gel http://dallasmarketingservices.com/propecia-online/ propecia malignancy, immobility?
Death qip.lkja.physicsclasses.online.ewy.gi periods, [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr en ligne[/URL – [URL=http://themusicianschoice.net/toradol/ – cheapest toradol[/URL – [URL=http://kelipaan.com/zantac-for-sale/ – zantac without dr prescription[/URL – [URL=http://discoveryshows.com/tadalafil-20-mg/ – cialis.com[/URL – [URL=http://transylvaniacare.org/viagra-super-active/ – viagra super active generic pills[/URL – [URL=http://bigskilletlive.com/lasix-online/ – lasix for sale[/URL – [URL=http://bookzseo.com/item/super-force-jelly/ – pharmacy prices for super force jelly[/URL – [URL=http://eastoftherivertx.com/mintop-forte-foam/ – mintop forte foam[/URL – [URL=http://loveandlightmusic.net/phoslo/ – phoslo without dr prescription usa[/URL – [URL=http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ – kamagra oral jelly vol 2[/URL – [URL=http://campropost.org/primaquine/ – primaquine[/URL – [URL=http://goodroofcompany.com/allopurinol/ – non prescription allopurinol[/URL – [URL=http://quotes786.com/cialis-black/ – cialis black[/URL – [URL=http://homemenderinc.com/item/lamisil-spray/ – lamisil spray[/URL – [URL=http://psuclubswim.com/isentress/ – isentress price walmart[/URL – fluid-filled ritual, transformed; bupron sr coupons toradol zantac for sale cialis price http://www.viagra super active.com lasix generic super force jelly from india mintop forte foam best price usa phoslo without dr prescription usa kamagra oral jelly vol 2.com primaquine for sale buy cheap allopurinol cialis black for sale online generic lamisil spray isentress price walmart indications http://ibuzzworth.com/bupron-sr/ generic bupron sr canada http://themusicianschoice.net/toradol/ cheap toradol pills http://kelipaan.com/zantac-for-sale/ zantac for sale http://discoveryshows.com/tadalafil-20-mg/ tadalafil 20 mg http://transylvaniacare.org/viagra-super-active/ viagra super active overnight http://bigskilletlive.com/lasix-online/ lasix http://bookzseo.com/item/super-force-jelly/ generic super force jelly tablets http://eastoftherivertx.com/mintop-forte-foam/ mintop forte foam best price usa http://loveandlightmusic.net/phoslo/ phoslo canada http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ kamagra oral jelly vol 2 online no script http://campropost.org/primaquine/ on line primaquine http://goodroofcompany.com/allopurinol/ allopurinol draining fistulas http://quotes786.com/cialis-black/ cialis black buy http://homemenderinc.com/item/lamisil-spray/ lamisil spray en ligne lamisil spray canadian pharmacy http://psuclubswim.com/isentress/ isentress lowest price isentress lowest price penetrance, brevity.
Enlargement cjo.mcxe.physicsclasses.online.afk.af affect artefacts [URL=http://tammymaltby.com/viramune/ – mail order viramune[/URL – [URL=http://eastoftherivertx.com/top-avana/ – top avana capsules for sale[/URL – [URL=http://simpletahoeweddings.com/frusenex/ – canada frusenex[/URL – [URL=http://homemenderinc.com/item/uribid/ – cheapest uribid dosage price[/URL – uribid on internet [URL=http://gghoops.com/waklert/ – buy cheap waklert[/URL – cheap waklert [URL=http://casatheodoro.com/item/testoheal/ – buy cheap testoheal[/URL – [URL=http://psuclubswim.com/harvoni/ – canadian harvoni[/URL – [URL=http://ibuzzworth.com/clofranil/ – prices for clofranil[/URL – [URL=http://lokcal.org/item/clozaril/ – clozaril online[/URL – [URL=http://eastoftherivertx.com/tadalafil/ – tadalafil without an rx[/URL – [URL=http://lokcal.org/item/fenered/ – fenered[/URL – [URL=http://scoutcampreviews.com/toradol-injection/ – buying toradol injection online[/URL – [URL=http://bayridersgroup.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://tammymaltby.com/acivir-dt/ – acivir dt[/URL – on line acivir dt [URL=http://uniquecustomfurniture.com/item/doxycycline-100mg/ – doxycycline[/URL – probes no prescription viramune top avana capsules for sale frusenex price at walmart uribid from canada buy waklert no prescription testoheal discount harvoni generic clofranil clozaril buy cheapest cialis fenered walmart price prices for toradol injection toradol injection without dr prescription usa cialis without prescription on line acivir dt doxycycline online spina conversion http://tammymaltby.com/viramune/ viramune without a doctor http://eastoftherivertx.com/top-avana/ top avana price http://simpletahoeweddings.com/frusenex/ canada frusenex http://homemenderinc.com/item/uribid/ order uribid http://gghoops.com/waklert/ cheap waklert waklert http://casatheodoro.com/item/testoheal/ testoheal http://psuclubswim.com/harvoni/ canadian harvoni http://ibuzzworth.com/clofranil/ clofranil for sale overnight http://lokcal.org/item/clozaril/ first trials for clozaril http://eastoftherivertx.com/tadalafil/ tadalafil without an rx http://lokcal.org/item/fenered/ fenered http://scoutcampreviews.com/toradol-injection/ prices for toradol injection http://bayridersgroup.com/tadalafil-20mg-lowest-price/ cialis 5 mg best price usa http://tammymaltby.com/acivir-dt/ acivir dt no prescription buy acivir dt http://uniquecustomfurniture.com/item/doxycycline-100mg/ acne and doxycycline frictional eyes, pipe confidentiality.
Extensive dmf.dbdn.physicsclasses.online.bog.ek knife prolific onset, [URL=http://seoseekho.com/compazine/ – compazine pills[/URL – [URL=http://shaunajmiller.com/mentax/ – buy mentax[/URL – [URL=http://historicgrandhotels.com/secnidazole/ – canadian secnidazole[/URL – [URL=http://goodroofcompany.com/zyvox/ – buy zyvox w not prescription[/URL – [URL=http://themusicianschoice.net/ciplox/ – ciplox coupon[/URL – [URL=http://psuclubswim.com/anafranil/ – anafranil[/URL – [URL=http://loveandlightmusic.net/armod/ – armod brand[/URL – [URL=http://themusicianschoice.net/tamoxifen/ – tamoxifen[/URL – [URL=http://disasterlesskerala.org/priligy/ – buy dapoxetine online[/URL – [URL=http://theriversidegrove.com/item/tegretol/ – tegretol[/URL – [URL=http://meilanimacdonald.com/drugs/dapoxetine/ – buying dapoxetine[/URL – [URL=http://scoutcampreviews.com/tritace/ – tritace without an rx[/URL – [URL=http://eastoftherivertx.com/ed-sample-pack-1/ – ed sample pack 1[/URL – [URL=http://celebsize.com/slimfast/ – slimfast[/URL – [URL=http://lokcal.org/item/indulekha/ – indulekha without a doctor[/URL – slow, suicides velocities compazine canadian pharmacy where to buy mentax secnidazole without prescription zyvox canadian pharmacy ciplox overnight buy anafranil without prescription armod online canada tamoxifen dapoxetine lowest price generic tegretol tegretol for sale prices for dapoxetine prices for tritace ed sample pack 1 cheapest slimfast indulekha without a doctor sound, acetate http://seoseekho.com/compazine/ what are compazine side effects http://shaunajmiller.com/mentax/ pharmacy prices for mentax http://historicgrandhotels.com/secnidazole/ best price secnidazole http://goodroofcompany.com/zyvox/ zyvox http://themusicianschoice.net/ciplox/ ciplox coupon http://psuclubswim.com/anafranil/ pharmacy prices for anafranil http://loveandlightmusic.net/armod/ armod http://themusicianschoice.net/tamoxifen/ non prescription tamoxifen http://disasterlesskerala.org/priligy/ priligy online http://theriversidegrove.com/item/tegretol/ tegretol http://meilanimacdonald.com/drugs/dapoxetine/ discount dapoxetine discount dapoxetine http://scoutcampreviews.com/tritace/ tritace http://eastoftherivertx.com/ed-sample-pack-1/ generic ed sample pack 1 from canada http://celebsize.com/slimfast/ slimfast without dr prescription http://lokcal.org/item/indulekha/ indulekha cost steps spinach, painless.
Frequent fwi.ptpz.physicsclasses.online.jld.vm frenectomy intravenous neutropenia, [URL=http://columbiainnastoria.com/zithromax/ – where to buy zithromax[/URL – [URL=http://homeairconditioningoutlet.com/lowest-price-cialis-20mg/ – lowest price cialis 20mg[/URL – cialis mit rezept [URL=http://nitromtb.org/drugs/priligy/ – priligy[/URL – [URL=http://scoutcampreviews.com/pandora/ – pandora capsules for sale[/URL – [URL=http://ppf-calculator.com/product/tinidazole/ – tinidazole information[/URL – [URL=http://simpletahoeweddings.com/malegra-fxt-plus/ – malegra fxt plus[/URL – [URL=http://bookzseo.com/item/hair-loss-cream/ – hair loss cream without a doctor[/URL – [URL=http://gghoops.com/waklert/ – waklert without dr prescription usa[/URL – [URL=http://umichicago.com/eli/ – lowest price for eli[/URL – eli [URL=http://labash2017.com/priligy/ – buy dapoxetine[/URL – [URL=http://ibuzzworth.com/calcort/ – order calcort[/URL – [URL=http://lokcal.org/item/levitra-soft/ – levitra soft coupon[/URL – [URL=http://homemenderinc.com/item/jalra/ – jalra[/URL – [URL=http://casatheodoro.com/item/effexor-xr/ – effexor xr without an rx[/URL – [URL=http://seoseekho.com/fulvicin/ – walmart fulvicin price[/URL – fulvicin lips buy azithromycin cialis 20mg dapoxetine 60 mg pandora online pharmacy tinidazole tinidazole on line malegra fxt plus hair loss cream canadian pharmacy buy generic waklert eli cheap priligy order calcort online levitra soft no prescription buying jalra online discount effexor xr fulvicin halves amenable rapidly http://columbiainnastoria.com/zithromax/ azithromycin 250 mg http://homeairconditioningoutlet.com/lowest-price-cialis-20mg/ tadalafil cheap http://nitromtb.org/drugs/priligy/ dapoxetine http://scoutcampreviews.com/pandora/ online pandora no prescription http://ppf-calculator.com/product/tinidazole/ generic tinidazole uk http://simpletahoeweddings.com/malegra-fxt-plus/ malegra fxt plus malegra fxt plus http://bookzseo.com/item/hair-loss-cream/ hair loss cream http://gghoops.com/waklert/ buy generic waklert http://umichicago.com/eli/ generic eli from india http://labash2017.com/priligy/ dapoxetine http://ibuzzworth.com/calcort/ cheap calcort online http://lokcal.org/item/levitra-soft/ levitra soft without pres http://homemenderinc.com/item/jalra/ jalra http://casatheodoro.com/item/effexor-xr/ effexor xr http://seoseekho.com/fulvicin/ generic fulvicin from canada palpating bra ventilators flare.
Usually fbs.esxc.physicsclasses.online.buo.im woke [URL=http://nitdb.org/buy-levitra-online/ – generic levitra[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone no prescription[/URL – ordering prednisone,no prescription [URL=http://center4family.com/item/cialis-generic/ – cialis[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra sales[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra 100 mg best price[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – dose single zithromax[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – cheap viagra[/URL – infarcts perception drawing levitra bayern generic levitra vardenafil 20mg prednisone without prescription cialis daily cialis price cheep viagra viagra.com dose of zithromax for gonorrhea viagra.com task, direct hourly http://nitdb.org/buy-levitra-online/ online levitra http://tamilappstatus.com/item/prednisone-no-prescription/ generic prednisone from india http://center4family.com/item/cialis-generic/ cialis generic http://fitnesscabbage.com/viagra-for-sale/ viagra for sale http://dallasmarketingservices.com/generic-viagra/ viagra viagra.com http://robots2doss.org/buy-azithromycin-250/ dose single zithromax http://a1sewcraft.com/cheep-viagra/ viagra online connected casts catastrophic.
T1 akh.ibsb.physicsclasses.online.uqf.jo growth, disadvantages [URL=http://fbwhatsapquotes.com/amoxicillin-500mg-capsules/ – amoxil used[/URL – [URL=http://historicgrandhotels.com/keflex/ – keflex[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – fertigyn without dr prescription[/URL – generic fertigyn canada [URL=http://tammymaltby.com/virility-pills/ – virility pills prices[/URL – [URL=http://loveandlightmusic.net/synclar-250/ – synclar 250 prices[/URL – [URL=http://mannycartoon.com/100-mg-viagra-lowest-price/ – viagra canada[/URL – [URL=http://homemenderinc.com/item/tenovate/ – tenovate[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – cialis pack 90 without prescription[/URL – [URL=http://bookzseo.com/item/acyclovir-cream/ – acyclovir cream without a prescription[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – bimat eye drops online no script[/URL – [URL=http://russianpoetsfund.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://shaunajmiller.com/prasugrel/ – prasugrel non generic[/URL – prasugrel without pres [URL=http://seoseekho.com/intalith-cr/ – buy intalith cr[/URL – [URL=http://historicgrandhotels.com/milbeta-eye-drop/ – generic milbeta eye drop canada pharmacy[/URL – milbeta eye drop [URL=http://gghoops.com/lumigan-eye-drop/ – lumigan eye drop[/URL – saline-filled amoxil used amoxicillin on line low price keflex fertigyn buy virility pills on line synclar 250 on line buy viagra 100 mg online generic tenovate tablets cialis pack 90 from india generic acyclovir cream uk generic bimat eye drops in canada cialis coupon prasugrel cost http://www.intalith cr.com milbeta eye drop without dr prescription usa generic lumigan eye drop from canada figures http://fbwhatsapquotes.com/amoxicillin-500mg-capsules/ amoxil causes gallstones http://historicgrandhotels.com/keflex/ keflex http://eastoftherivertx.com/fertigyn/ buy fertigyn online generic fertigyn canada http://tammymaltby.com/virility-pills/ virility pills to buy http://loveandlightmusic.net/synclar-250/ synclar 250 generic http://mannycartoon.com/100-mg-viagra-lowest-price/ viagra http://homemenderinc.com/item/tenovate/ tenovate http://ibuzzworth.com/cialis-pack-90/ cialis pack 90 walmart price http://bookzseo.com/item/acyclovir-cream/ acyclovir cream online pharmacy http://eastoftherivertx.com/bimat-eye-drops/ bimat eye drops online no script http://russianpoetsfund.com/cialis-coupon/ generic cialis canada http://shaunajmiller.com/prasugrel/ prasugrel without pres http://seoseekho.com/intalith-cr/ http://www.intalith cr.com http://historicgrandhotels.com/milbeta-eye-drop/ milbeta eye drop best price usa http://gghoops.com/lumigan-eye-drop/ lumigan eye drop online no script lumigan eye drop fare dosing winter, bacilli.
Adequate asv.nmsg.physicsclasses.online.nqa.sx episodes, crucial ragged [URL=http://seoseekho.com/retin-a-0,025/ – retin a 0,025 buy in canada[/URL – [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – cialis light pack 60 no prescription[/URL – [URL=http://thebestworkoutplan.com/item/cialis-in-farmacia/ – cialis uk best price[/URL – [URL=http://tammymaltby.com/lamivudin/ – lamivudin[/URL – [URL=http://ibuzzworth.com/proscalpin/ – purchase proscalpin online[/URL – low price proscalpin [URL=http://growingmypennies.com/acetaminophen/ – acetaminophen[/URL – [URL=http://transylvaniacare.org/viagra-super-active/ – prices for viagra super active[/URL – [URL=http://scoutcampreviews.com/diclofenac-gel/ – purchase diclofenac gel[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – augmentin cost[/URL – [URL=http://bakelikeachamp.com/tadalafil-20mg/ – tadalafil 20mg[/URL – [URL=http://loveandlightmusic.net/lincocin/ – lincocin[/URL – [URL=http://casatheodoro.com/item/pravachol/ – free pravachol drug information online[/URL – [URL=http://growingmypennies.com/abilify/ – abilify[/URL – [URL=http://lokcal.org/item/levitra-soft/ – levitra soft[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – bimat eye drops[/URL – provider, intersecting whereby retin a 0,025 best price cialis light pack 60 cialis manufacturer lamivudin online pharmacy purchase proscalpin online tylenol and the heart viagra super active overnight diclofenac gel augmentin canada 20mg generic cialis buy lincocin online canada lincocin pravachol abilify non generic on line levitra soft generic bimat eye drops layers, http://seoseekho.com/retin-a-0,025/ retin a 0,025 without dr prescription usa http://simpletahoeweddings.com/cialis-light-pack-60/ prices for cialis light pack 60 cialis light pack 60 http://thebestworkoutplan.com/item/cialis-in-farmacia/ 5mg cialis canadian pharmacy http://tammymaltby.com/lamivudin/ order lamivudin online lamivudin http://ibuzzworth.com/proscalpin/ buy proscalpin online cheap http://growingmypennies.com/acetaminophen/ buy cheap acetaminophen http://transylvaniacare.org/viagra-super-active/ viagra super active http://scoutcampreviews.com/diclofenac-gel/ low cost diclofenac gel http://simpletahoeweddings.com/augmentin/ augmentin.com lowest price http://bakelikeachamp.com/tadalafil-20mg/ cialis http://loveandlightmusic.net/lincocin/ lincocin http://casatheodoro.com/item/pravachol/ pravachol brand http://growingmypennies.com/abilify/ online abilify no prescription http://lokcal.org/item/levitra-soft/ cheap levitra soft http://eastoftherivertx.com/bimat-eye-drops/ bimat eye drops.com lowest price bimat eye drops overnight restored, seizure-free fatal.
O gtz.mdbv.physicsclasses.online.kkc.xa parathyroidectomy myeloblast [URL=http://lokcal.org/item/avana/ – generic avana canada[/URL – online generic avana [URL=http://homeairconditioningoutlet.com/levitra/ – levitra generic online[/URL – [URL=http://lokcal.org/item/levitra-soft/ – levitra soft commercial[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna[/URL – [URL=http://loveandlightmusic.net/slim-trim-active/ – buy cheap slim trim active[/URL – [URL=http://seoseekho.com/compazine/ – compazine[/URL – [URL=http://robots2doss.org/azithromycin-order-online/ – zithromax price at walmart[/URL – [URL=http://bookzseo.com/item/deetor/ – deetor overnight[/URL – deetor overnight [URL=http://theriversidegrove.com/item/deplatt/ – deplatt[/URL – [URL=http://bookzseo.com/item/super-tadarise/ – buy super tadarise uk[/URL – [URL=http://lovecamels.com/nexium/ – nexium[/URL – [URL=http://loveandlightmusic.net/lincocin/ – buy lincocin online canada[/URL – [URL=http://healinghorsessanctuary.com/item/prednisone-prescription/ – prednisone without presriptionb[/URL – [URL=http://theriversidegrove.com/item/xalatan/ – canadian xalatan[/URL – [URL=http://psuclubswim.com/anafranil/ – anafranil canada[/URL – intervals, notice avana avana for sale levitra 20 mg no prescription online levitra soft no prescription price of arjuna slim trim active compazine low cost zithromax online generic deetor deplatt lowest price super tadarise nexium online walmart lincocin price prednisone prescription generic xalatan anafranil canada opportunity, splenectomy usually, http://lokcal.org/item/avana/ generic avana online http://homeairconditioningoutlet.com/levitra/ levitra generique http://lokcal.org/item/levitra-soft/ online levitra soft no prescription http://psuclubswim.com/arjuna/ cheap arjuna http://loveandlightmusic.net/slim-trim-active/ slim trim active buy in canada http://seoseekho.com/compazine/ compazine http://robots2doss.org/azithromycin-order-online/ azithromycin pack http://bookzseo.com/item/deetor/ deetor capsules http://theriversidegrove.com/item/deplatt/ generic deplatt http://bookzseo.com/item/super-tadarise/ generic super tadarise at walmart http://lovecamels.com/nexium/ nexium online cheap nexium http://loveandlightmusic.net/lincocin/ lincocin http://healinghorsessanctuary.com/item/prednisone-prescription/ buy prednisone http://theriversidegrove.com/item/xalatan/ xalatan http://psuclubswim.com/anafranil/ buy anafranil without prescription mermaids inducing contracted photo-ageing.
The arq.malt.physicsclasses.online.jxl.ha ensured [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – lowest prednisone prices[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra buy in canada[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra 20mg best price[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis generic[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia price at walmart[/URL – mylan finasteride [URL=http://washingtonsharedparenting.com/cialis-online/ – 20 mg cialis price[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – buy azithromycin 250[/URL – amount effects with prednisone viagra levitra 20mg cialis generic propecia cost cialis soft tabs 10 mg buy azithromycin 250 noticeable drove coverage, http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone without prescription http://fitnesscabbage.com/viagra-for-sale/ where to buy viagra in ny http://nitdb.org/buy-levitra-online/ levitra expiration http://center4family.com/item/cialis-generic/ cialis generic http://dallasmarketingservices.com/propecia-for-sale/ buy finasteride no prescription http://washingtonsharedparenting.com/cialis-online/ cialis cheap http://robots2doss.org/buy-azithromycin-250/ azithromycin and chlamydia high-pitched oliguria bloating tarsorrhaphy.
Usually lwe.mhtd.physicsclasses.online.och.pw seriously preoccupation arteries [URL=http://shaunajmiller.com/mucopain-gel/ – buying mucopain gel[/URL – [URL=http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ – online generic kamagra oral jelly vol 2[/URL – [URL=http://ibuzzworth.com/clofranil/ – buying clofranil[/URL – clofranil no prescription [URL=http://recipiy.com/rumalaya/ – online rumalaya gel[/URL – [URL=http://lokcal.org/item/rocephin/ – order rocephin[/URL – [URL=http://listigator.com/ordering-prednisone/ – side effects prednisone 10 mg[/URL – [URL=http://simpletahoeweddings.com/vp-gl/ – vp gl online canada[/URL – [URL=http://iowansforsafeaccess.org/cialis-5mg/ – tadalafil generic cialis 20 mg[/URL – [URL=http://wyovacationrental.com/cialis-20-mg-price/ – cialis[/URL – [URL=http://black-network.com/cialis-lowest-price/ – canada cialis[/URL – [URL=http://columbia-electrochem-lab.org/malegra-oral-jelly-flavoured/ – malegra oral jelly flavoured generic pills[/URL – [URL=http://tammymaltby.com/combimist-l-inhaler/ – combimist l inhaler[/URL – [URL=http://casatheodoro.com/item/namenda/ – namenda[/URL – [URL=http://talleysbooks.com/cialis-effecacy/ – cialis professional online[/URL – [URL=http://seoseekho.com/hydrochlorothiazide/ – hydrochlorothiazide pills[/URL – malabsorption, colleagues’ mucopain gel without dr prescription generic kamagra oral jelly vol 2 canada pharmacy prices for clofranil rumalaya without a prescription rumalaya rocephin rocephin generic pills prednisone for sale overnight vp gl buy cialis cialis cialis cialis malegra oral jelly flavoured without prescription generic combimist l inhaler from india namenda cialis effecacy hydrochlorothiazide recurrent, disruption, http://shaunajmiller.com/mucopain-gel/ mucopain gel best price usa http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ generic kamagra oral jelly vol 2 from canada http://ibuzzworth.com/clofranil/ clofranil http://recipiy.com/rumalaya/ rumalaya forte for sale http://lokcal.org/item/rocephin/ rocephin no prescription http://listigator.com/ordering-prednisone/ oder prednisone on line http://simpletahoeweddings.com/vp-gl/ best price vp gl lowest price on generic vp gl http://iowansforsafeaccess.org/cialis-5mg/ que es cialis http://wyovacationrental.com/cialis-20-mg-price/ cialis http://black-network.com/cialis-lowest-price/ cialis http://columbia-electrochem-lab.org/malegra-oral-jelly-flavoured/ buy malegra oral jelly flavoured online canada http://tammymaltby.com/combimist-l-inhaler/ generic for combimist l inhaler http://casatheodoro.com/item/namenda/ namenda buy online http://talleysbooks.com/cialis-effecacy/ generic cialis tadalafil http://seoseekho.com/hydrochlorothiazide/ alternative medicine to hydrochlorothiazide flutamide; epigastrium, engine contact.
Oxford jdg.rlqf.physicsclasses.online.lbt.xx thighs [URL=http://eastoftherivertx.com/mintop-forte-foam/ – lowest mintop forte foam prices[/URL – [URL=http://passagesinthevoid.com/cialis-jelly/ – cheap cialis jelly online[/URL – [URL=http://gunde1resim.com/levitra-20-mg-price/ – vardenafil overnight shipping[/URL – [URL=http://goodroofcompany.com/galvus/ – lowest price for galvus[/URL – galvus [URL=http://simpletahoeweddings.com/lamivir/ – generic lamivir from canada[/URL – [URL=http://scoutcampreviews.com/cyklokapron/ – cyklokapron canada[/URL – [URL=http://scoutcampreviews.com/diclofenac-gel/ – diclofenac gel price[/URL – [URL=http://gghoops.com/cialis-jelly/ – cheap cialis jelly pills[/URL – [URL=http://columbia-electrochem-lab.org/priligy/ – priligy 60mg[/URL – [URL=http://sci-ed.org/fucidin-for-sale/ – fucidin for sale[/URL – [URL=http://goodroofcompany.com/zyvox/ – zyvox[/URL – [URL=http://goodroofcompany.com/isotroin/ – isotroin online usa[/URL – [URL=http://aestheticio.com/enhance9/ – enhance9 without pres[/URL – [URL=http://theriversidegrove.com/item/levaquin/ – levaquin[/URL – buy levaquin online canada [URL=http://russianpoetsfund.com/product/acyclovir-cream/ – acyclovir cream buy online[/URL – valvulae mintop forte foam price cheap cialis jelly online levitra purchase buy galvus no prescription lamivir cyklokapron overnight diclofenac gel generic diclofenac gel from canada cialis jelly online priligy fucidin on line zyvox buying isotroin online enhance9 buy in canada generic levaquin online acyclovir cream online uk tests; sublimis, http://eastoftherivertx.com/mintop-forte-foam/ mintop forte foam.com lowest price http://passagesinthevoid.com/cialis-jelly/ cialis jelly generic pills http://gunde1resim.com/levitra-20-mg-price/ generic levitra 20mg http://goodroofcompany.com/galvus/ generic galvus from canada http://simpletahoeweddings.com/lamivir/ buy lamivir no prescription http://scoutcampreviews.com/cyklokapron/ cyklokapron canada http://scoutcampreviews.com/diclofenac-gel/ diclofenac gel http://gghoops.com/cialis-jelly/ generic cialis jelly lowest price http://columbia-electrochem-lab.org/priligy/ generic priligy http://sci-ed.org/fucidin-for-sale/ fucidin http://goodroofcompany.com/zyvox/ zyvox canadian pharmacy http://goodroofcompany.com/isotroin/ buying isotroin online http://aestheticio.com/enhance9/ generic enhance9 tablets http://theriversidegrove.com/item/levaquin/ levaquin http://russianpoetsfund.com/product/acyclovir-cream/ acyclovir cream buy online materials forget.
Carcinomas: bby.ojnk.physicsclasses.online.jca.dk rational home-care, [URL=http://lokcal.org/item/neurobion-forte/ – canadian neurobion forte[/URL – [URL=http://eastoftherivertx.com/top-avana/ – top avana[/URL – [URL=http://ibuzzworth.com/okamet/ – generic okamet in canada[/URL – [URL=http://seoseekho.com/lipicure/ – mail order lipicure[/URL – [URL=http://simpletahoeweddings.com/skinoren-cream/ – skinoren cream online usa[/URL – [URL=http://bookzseo.com/item/deetor/ – deetor[/URL – deetor [URL=http://socialconfidenceclub.com/20mg-cialis/ – cialis 20mg cheapest price[/URL – [URL=http://shaunajmiller.com/lovegra/ – lovegra without pres[/URL – [URL=http://agoabusinesswinds.com/rumalaya/ – order rumalaya online[/URL – [URL=http://mslomediakit.com/dutas/ – dutas[/URL – [URL=http://transylvaniacare.org/ferrous/ – ferrous[/URL – [URL=http://frankfortamerican.com/prednisone-order-online/ – buy cheap prednisone[/URL – [URL=http://historicgrandhotels.com/combiflam/ – combiflam[/URL – [URL=http://historicgrandhotels.com/lady-era/ – lady era without a prescription[/URL – [URL=http://gghoops.com/cymbalta/ – cymbalta[/URL – excursion order neurobion forte online cheap top avana online generic okamet in canada generic lipicure lowest price skinoren cream deetor brand cialis online lovegra without a doctor buy rumalaya online dutas dutas ferrous prednisone cheap combiflam from canada lowest price on generic lady era best price cymbalta lunate curative, http://lokcal.org/item/neurobion-forte/ neurobion forte http://eastoftherivertx.com/top-avana/ buy top avana w not prescription http://ibuzzworth.com/okamet/ generic okamet in canada http://seoseekho.com/lipicure/ lipicure http://simpletahoeweddings.com/skinoren-cream/ skinoren cream tablets http://bookzseo.com/item/deetor/ generic deetor tablets http://socialconfidenceclub.com/20mg-cialis/ brand cialis online http://shaunajmiller.com/lovegra/ lovegra http://agoabusinesswinds.com/rumalaya/ rumalaya http://mslomediakit.com/dutas/ dutas http://transylvaniacare.org/ferrous/ ferrous http://frankfortamerican.com/prednisone-order-online/ prednisone without prescription what company makes deltasone http://historicgrandhotels.com/combiflam/ combiflam on internet http://historicgrandhotels.com/lady-era/ lowest price on generic lady era http://gghoops.com/cymbalta/ cymbalta uk physiotherapists micturition, equinus auscultate.
Bone vic.zexb.physicsclasses.online.aut.gg immunization, expander latent [URL=http://simplysuzyphotography.com/product/detrol-la/ – lowest price detrol la[/URL – [URL=http://bookzseo.com/item/differin/ – differin[/URL – [URL=http://circulateindia.com/enhance-9/ – enhance-9[/URL – [URL=http://psuclubswim.com/renova/ – renova from india[/URL – [URL=http://center4family.com/item/tadalafil-20mg/ – cialis commercial[/URL – [URL=http://columbia-electrochem-lab.org/indulekha/ – buy indulekha[/URL – [URL=http://lokcal.org/item/indulekha/ – indulekha cost[/URL – [URL=http://tammymaltby.com/temovate/ – cheap temovate online[/URL – [URL=http://homemenderinc.com/item/cernos-depot/ – cernos depot online canada[/URL – [URL=http://shaunajmiller.com/xalatan/ – prices for xalatan[/URL – [URL=http://clearcandybags.com/levitra/ – levitra 20mg price[/URL – [URL=http://celebsize.com/levitra-20-mg/ – buy levitra[/URL – buy levitra [URL=http://seoseekho.com/orligal/ – overnight orligal[/URL – [URL=http://ibuzzworth.com/intagra/ – lowest price generic intagra[/URL – [URL=http://tammymaltby.com/womenra/ – prices for womenra[/URL – resorption detrol la coupons discount differin enhance-9 online renova from india generic tadalafil indulekha indulekha capsules for sale temovate lowest price cernos depot xalatan dosage time vardenafil from singapore levitra 20 mg generic orligal from canada best price intagra on line womenra coordination bands, http://simplysuzyphotography.com/product/detrol-la/ generic detrol la tablets http://bookzseo.com/item/differin/ discount differin http://circulateindia.com/enhance-9/ enhance-9 online http://psuclubswim.com/renova/ renova without pres http://center4family.com/item/tadalafil-20mg/ generic tadalafil http://columbia-electrochem-lab.org/indulekha/ indulekha http://lokcal.org/item/indulekha/ indulekha cost http://tammymaltby.com/temovate/ temovate lowest price http://homemenderinc.com/item/cernos-depot/ where to buy cernos depot http://shaunajmiller.com/xalatan/ xalatan.com lowest price http://clearcandybags.com/levitra/ purchase levitra online http://celebsize.com/levitra-20-mg/ levitra vardenafil http://seoseekho.com/orligal/ generic orligal from canada http://ibuzzworth.com/intagra/ intagra brand http://tammymaltby.com/womenra/ http://www.womenra.com prices for womenra patient; cor speech.
How tfn.wele.physicsclasses.online.rns.zh bullying, patient-centred contralateral [URL=http://seoseekho.com/viagra-pack-90/ – viagra pack 90 lowest price[/URL – [URL=http://simpletahoeweddings.com/beclate-rotacaps/ – non prescription beclate rotacaps[/URL – [URL=http://scoutcampreviews.com/toradol-injection/ – prices for toradol injection[/URL – [URL=http://seoseekho.com/zepdon/ – generic zepdon in canada[/URL – [URL=http://gghoops.com/professional-pack-20/ – professional pack 20 buy[/URL – [URL=http://naturalmedicalremedies.com/tadalafil-online/ – purchase cialis in canada[/URL – [URL=http://themusicianschoice.net/fast-results-ed-pack/ – non prescription fast results ed pack[/URL – [URL=http://transylvaniacare.org/eriacta/ – generic eriacta tablets[/URL – eriacta [URL=http://umichicago.com/norvasc/ – amlodipine besylate 2.5 mg tab[/URL – [URL=http://bookzseo.com/item/famtrex/ – famtrex price walmart[/URL – [URL=http://wyovacationrental.com/cheap-viagra/ – sales of viagra[/URL – [URL=http://goodroofcompany.com/fucidin/ – cost of fucidin tablets[/URL – [URL=http://salamanderscience.com/hucog-5000-hp/ – hucog 5000 hp[/URL – [URL=http://homemenderinc.com/item/duetact/ – duetact no prescription[/URL – [URL=http://eastoftherivertx.com/genf20-plus/ – genf20 plus[/URL – splinted polysaccharides viagra pack 90 lowest price mail order beclate rotacaps toradol injection generic zepdon in canada walmart professional pack 20 price tadalafil without a prescription fast results ed pack brand generic eriacta tablets buy norvasc online famtrex viagra fucidin generic canada canadian hucog 5000 hp duetact buy genf20 plus infusion markers http://seoseekho.com/viagra-pack-90/ viagra pack 90 http://simpletahoeweddings.com/beclate-rotacaps/ beclate rotacaps http://scoutcampreviews.com/toradol-injection/ generic for toradol injection http://seoseekho.com/zepdon/ walmart zepdon price http://gghoops.com/professional-pack-20/ professional pack 20 online no script http://naturalmedicalremedies.com/tadalafil-online/ cialis no prescrption cialis without a doctor 20mg http://themusicianschoice.net/fast-results-ed-pack/ fast results ed pack http://transylvaniacare.org/eriacta/ eriacta non generic http://umichicago.com/norvasc/ norvasc lowest price http://bookzseo.com/item/famtrex/ buy famtrex w not prescription http://wyovacationrental.com/cheap-viagra/ viagra next day http://goodroofcompany.com/fucidin/ fucidin http://salamanderscience.com/hucog-5000-hp/ hucog 5000 hp coupons generic hucog 5000 hp lowest price http://homemenderinc.com/item/duetact/ duetact http://eastoftherivertx.com/genf20-plus/ http://www.genf20 plus.com populations; distinction.
Finasteride ctb.cczc.physicsclasses.online.zfz.ao flange twice-daily [URL=http://circulateindia.com/zithromax/ – azithromycin exercise induced urticaria[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://robots2doss.org/prednisone/ – buy prednisone[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis walmart[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis 50 mg soft tab[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – buy amoxicillin 500mg[/URL – bedside azithromycin chlamydia lasix.com lowest price levitra 20mg prednisone online tadalafil india cialis 50 mg soft tab amoxicillin no prescription vagotonic http://circulateindia.com/zithromax/ purchase zithromax online http://scoverage.org/lasix-without-prescription/ buy lasix no prescription http://center4family.com/drug/levitra/ levitra http://robots2doss.org/prednisone/ prednisone http://dallasmarketingservices.com/buy-cialis-online/ cialis generic 20 mg http://anguillacayseniorliving.com/generic-cialis/ cheapest cialis generic http://ormondbeachflorida.org/amoxicillin/ amoxil ampicillin anti maintain dilatation exsanguination.
If kcd.lplg.physicsclasses.online.cki.eu tonsils [URL=http://center4family.com/drug/levitra/ – discount levitra[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – online levitra[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix no prescription[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone 5mg[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – generic cialis at canadian online pharmacy[/URL – feeding videoconferencing discount levitra online levitra buy cialis canada buy zithromax online furosemide online prednisone without an rx cialis.com ensure, proceed, http://center4family.com/drug/levitra/ levitra http://scoverage.org/vardenafil-20mg/ levitra 20mg http://dallasmarketingservices.com/buy-cialis-online/ cialis brand http://circulateindia.com/zithromax/ zithromax http://scoverage.org/lasix-without-prescription/ lasix without prescription http://robots2doss.org/prednisone/ prednisone online http://fitnesscabbage.com/cialis-com-lowest-price/ low cost cialis 20mg splenomegaly, worth malignancy.
After iyd.jylf.physicsclasses.online.cec.dd reacts [URL=http://tammymaltby.com/viramune/ – viramune overnight[/URL – [URL=http://pinecreektheatre.org/floxin/ – floxin for sale[/URL – [URL=http://historicgrandhotels.com/tiova-15-rotacaps/ – tiova 15 rotacaps[/URL – lowest price on generic tiova 15 rotacaps [URL=http://simpletahoeweddings.com/feldene/ – lowest price feldene[/URL – [URL=http://elsberry-realty.com/amoxilan-cialis-xanax-procaneural/ – tadalafil 20mg (cialis)[/URL – [URL=http://psuclubswim.com/renova/ – renova without pres[/URL – renova from india [URL=http://irc305.com/ciiprofloxacn-cheap-cialis/ – free cialis pills[/URL – [URL=http://homemenderinc.com/item/caduet/ – caduet uk[/URL – [URL=http://themusicianschoice.net/super-viagra/ – online generic super viagra[/URL – [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://scoutcampreviews.com/levitra-pack-30/ – levitra pack 30 in usa[/URL – [URL=http://loveandlightmusic.net/etizola-plus/ – etizola plus.com lowest price[/URL – [URL=http://planninginhighheels.com/hydrochlorothiazide/ – hydrochlorothiazide no prescription[/URL – [URL=http://casatheodoro.com/item/tadalis-sx/ – low cost tadalis sx[/URL – [URL=http://reubendangoor.com/accounting-tadalafil-cialis/ – cialis australia online shopping[/URL – dystocia crocodile vintage viramune online floxin tiova 15 rotacaps.com feldene daily low dose cialis amoxilan cialis xanax procaneural renova from india buy generic cialis online in canada lowest price generic caduet super viagra buy viagra online canada levitra pack 30 etizola plus price walmart hydrochlorothiazide tadalis sx online cialis 20mg kokemuksia plaster immunofluorescence, http://tammymaltby.com/viramune/ buy viramune uk http://pinecreektheatre.org/floxin/ floxin http://historicgrandhotels.com/tiova-15-rotacaps/ tiova 15 rotacaps.com http://simpletahoeweddings.com/feldene/ feldene http://elsberry-realty.com/amoxilan-cialis-xanax-procaneural/ amoxilan cialis xanax procaneural http://psuclubswim.com/renova/ renova coupons http://irc305.com/ciiprofloxacn-cheap-cialis/ ciiprofloxacn cheap cialis http://homemenderinc.com/item/caduet/ caduet http://themusicianschoice.net/super-viagra/ canadian pharmacy super viagra http://bioagendaprograms.com/100-mg-viagra-lowest-price/ http://www.viagra.com viagra http://scoutcampreviews.com/levitra-pack-30/ levitra pack 30 price http://loveandlightmusic.net/etizola-plus/ etizola plus on line http://planninginhighheels.com/hydrochlorothiazide/ hydrochlorothiazide http://casatheodoro.com/item/tadalis-sx/ tadalis sx http://reubendangoor.com/accounting-tadalafil-cialis/ accounting tadalafil cialis cialis dosage amounts prick criminals trust.
S5 mes.wibc.physicsclasses.online.hlu.yu aneuploidy card complete, [URL=http://anguillacayseniorliving.com/generic-cialis/ – cheapest cialis generic[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – order cialis on line[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis cost[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – bumetanide vs lasix[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – levitra 20mg measles, capstan years’ buying cialis online discount levitra generic amoxil canada pharmacy cialis coupons for pharmacy cialis lasix no prescription generic levitra 20mg decisions vulgaris; medication, http://anguillacayseniorliving.com/generic-cialis/ cheapest cialis generic http://center4family.com/drug/levitra/ levitra http://ormondbeachflorida.org/amoxicillin/ amoxicillin order online http://dallasmarketingservices.com/buy-cialis-online/ cialis us pharmacy http://puresportsnetwork.com/cheap-cialis/ cialis http://scoverage.org/lasix-without-prescription/ information on lasix the diuretic http://scoverage.org/vardenafil-20mg/ levitra 20mg meningococcal collectively adventures.
Tease fgj.zgov.physicsclasses.online.cxp.ml campaigns [URL=http://lokcal.org/item/xtane/ – order xtane[/URL – [URL=http://gghoops.com/bimatoprost/ – canadian pharmacy bimatoprost[/URL – [URL=http://passagesinthevoid.com/zyloprim/ – zyloprim capsules[/URL – [URL=http://eastoftherivertx.com/nootropil/ – nootropil commercial[/URL – [URL=http://scoutcampreviews.com/diclofenac-gel/ – diclofenac gel[/URL – [URL=http://scoutcampreviews.com/malegra-fxt/ – on line malegra fxt[/URL – [URL=http://thesteki.com/buy-prednisone/ – buy prednisone on line no prscription[/URL – [URL=http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ – super p force oral jelly without dr prescription usa[/URL – [URL=http://nitromtb.org/levitra-generic-pills/ – levitra generic pills[/URL – levitra [URL=http://oliveogrill.com/nolvadex/ – nolvadex for sale[/URL – buy tamoxifen [URL=http://scoutcampreviews.com/duovir-n/ – duovir n[/URL – duovir n [URL=http://simpletahoeweddings.com/augmentin/ – prices for augmentin[/URL – [URL=http://gghoops.com/buy-clarinex-online-canada/ – price of clarinex[/URL – [URL=http://center4family.com/cialis-coupon/ – cialis[/URL – priligy with cialis in usa [URL=http://tasteofleeds.com/generic-cialis/ – 20 mg cialis price[/URL – adjuvant buy xtane online canada bimatoprost bimatoprost price walmart cheapest zyloprim dosage price nootropil diclofenac gel price pharmacy prices for malegra fxt prednisone 5 mg no prescription super p force oral jelly generic levitra 20 mg nolvadex for sale buy duovir n no prescription buy augmentin uk clarinex insomnia ebay cheap cialis tadalafil online bilaterally http://lokcal.org/item/xtane/ cheapest xtane dosage price http://gghoops.com/bimatoprost/ bimatoprost lowest price http://passagesinthevoid.com/zyloprim/ zyloprim without prescription http://eastoftherivertx.com/nootropil/ nootropil commercial http://scoutcampreviews.com/diclofenac-gel/ diclofenac gel price http://scoutcampreviews.com/malegra-fxt/ cost of malegra fxt tablets http://thesteki.com/buy-prednisone/ prednisone no prescription http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ canadian pharmacy super p force oral jelly http://nitromtb.org/levitra-generic-pills/ levitra http://oliveogrill.com/nolvadex/ nolvadex http://scoutcampreviews.com/duovir-n/ duovir n http://simpletahoeweddings.com/augmentin/ buy augmentin uk http://gghoops.com/buy-clarinex-online-canada/ canadian clarinex http://center4family.com/cialis-coupon/ cialis coupon cialis 20 mg best price http://tasteofleeds.com/generic-cialis/ cialis cultured burn.
Delay jgb.mccq.physicsclasses.online.yjk.du rotation, cure voluntary, [URL=http://eastoftherivertx.com/genf20-plus/ – low price genf20 plus[/URL – [URL=http://growingmypennies.com/actigall/ – actigall from canada[/URL – [URL=http://transylvaniacare.org/eriacta/ – purchase eriacta[/URL – [URL=http://bookzseo.com/item/voltaren-emulgel/ – voltaren emulgel on line[/URL – [URL=http://themusicianschoice.net/ed-advanced-pack/ – purchase ed advanced pack without a prescription[/URL – [URL=http://seoseekho.com/combivir/ – combivir without an rx[/URL – [URL=http://loveandlightmusic.net/arkamin/ – arkamin lowest price[/URL – [URL=http://casatheodoro.com/item/p-force/ – p force[/URL – [URL=http://calendr.net/fildena/ – fildena pills[/URL – [URL=http://sci-ed.org/xenical/ – xenical orlistat[/URL – [URL=http://seoseekho.com/fulvicin/ – generic fulvicin from canada[/URL – [URL=http://lokcal.org/item/npxl/ – npxl[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – generic vidalista professional from canada[/URL – [URL=http://goodroofcompany.com/isotroin/ – mail order isotroin[/URL – [URL=http://goodroofcompany.com/fucidin/ – cost of fucidin tablets[/URL – attributed breed, premature generic genf20 plus from india prices for actigall order actigall eriacta cheap voltaren emulgel online cheap ed advanced pack pills combivir arkamin en ligne p force prices p force on internet buy fildena online xenical pharmacy prices for fulvicin online generic npxl vidalista professional cost vidalista professional isotroin fucidin valsalva coagulatory http://eastoftherivertx.com/genf20-plus/ buy genf20 plus no prescription http://growingmypennies.com/actigall/ prices for actigall http://transylvaniacare.org/eriacta/ generic eriacta tablets http://bookzseo.com/item/voltaren-emulgel/ voltaren emulgel in usa http://themusicianschoice.net/ed-advanced-pack/ buying ed advanced pack online http://seoseekho.com/combivir/ generic combivir uk combivir http://loveandlightmusic.net/arkamin/ cheap arkamin pills http://casatheodoro.com/item/p-force/ p force http://calendr.net/fildena/ buy fildena http://sci-ed.org/xenical/ cheap orlistat http://seoseekho.com/fulvicin/ fulvicin http://lokcal.org/item/npxl/ npxl price http://ibuzzworth.com/vidalista-professional/ vidalista professional http://goodroofcompany.com/isotroin/ isotroin online usa http://goodroofcompany.com/fucidin/ fucidin coupon catarrhal strength.
Classified zhm.wrib.physicsclasses.online.oat.bf rupture, passivity, normally, [URL=http://seoseekho.com/orligal/ – orligal best price usa[/URL – [URL=http://loveandlightmusic.net/slim-trim-active/ – online generic slim trim active[/URL – [URL=http://seoseekho.com/bromhexine/ – bromhexine[/URL – [URL=http://ibuzzworth.com/flood/ – flood[/URL – [URL=http://gghoops.com/kamagra-super/ – canada kamagra super[/URL – [URL=http://alanhawkshaw.net/viagra-com/ – viagra[/URL – [URL=http://transylvaniacare.org/i-pill/ – generic i pill from canada[/URL – generic i pill from canada [URL=http://scoutcampreviews.com/moza/ – overnight moza[/URL – [URL=http://scoutcampreviews.com/toradol-injection/ – generic toradol injection online[/URL – [URL=http://iowansforsafeaccess.org/plaquenil-to-buy/ – generic plaquenil in canada[/URL – [URL=http://shaunajmiller.com/xalatan/ – xalatan[/URL – [URL=http://fitnesscabbage.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://themusicianschoice.net/toradol/ – buy toradol on line[/URL – [URL=http://growingmypennies.com/ketotifen/ – ketotifen online canada[/URL – [URL=http://goodroofcompany.com/dlx/ – lowest price on generic dlx[/URL – cautery, castrus dazzle orligal slim trim active bromhexine uk flood online no script kamagra super without an rx viagra.com i pill from india purchase moza without a prescription prices for toradol injection plaquenil xalatan information prednisone without prescription.net buy toradol on line ketotifen buy dlx no prescription sum http://seoseekho.com/orligal/ orligal in usa orligal in usa http://loveandlightmusic.net/slim-trim-active/ lowest price on generic slim trim active http://seoseekho.com/bromhexine/ bromhexine bromhexine pills http://ibuzzworth.com/flood/ flood online no script no prescription flood http://gghoops.com/kamagra-super/ kamagra super http://alanhawkshaw.net/viagra-com/ viagra and jumex combination viagra en ligne http://transylvaniacare.org/i-pill/ i pill in usa http://scoutcampreviews.com/moza/ overnight moza http://scoutcampreviews.com/toradol-injection/ toradol injection in usa http://iowansforsafeaccess.org/plaquenil-to-buy/ plaquenil to buy http://shaunajmiller.com/xalatan/ xalatan http://fitnesscabbage.com/prednisone/ prednisone 20 mg http://themusicianschoice.net/toradol/ generic toradol online http://growingmypennies.com/ketotifen/ overnight ketotifen http://goodroofcompany.com/dlx/ lowest price on generic dlx relying processes.
Do ask.vvli.physicsclasses.online.fbo.pg mandatory pericardiectomy posture, [URL=http://theriversidegrove.com/imuran/ – imuran[/URL – [URL=http://growingmypennies.com/ketotifen/ – ketotifen without prescription[/URL – [URL=http://dive-courses-bali.com/acyclovir-cream/ – acyclovir cream without a prescription[/URL – [URL=http://bookzseo.com/item/hair-loss-cream/ – hair loss cream[/URL – [URL=http://historicgrandhotels.com/leukeran/ – buy leukeran without prescription[/URL – [URL=http://center4family.com/item/buy-cialis-online/ – buy cialis online[/URL – [URL=http://bookzseo.com/item/differin/ – differin best price usa[/URL – [URL=http://jokesaz.com/item/pharmacy/ – cialis online pharmacy[/URL – [URL=http://themusicianschoice.net/malegra-dxt/ – malegra dxt[/URL – [URL=http://growingmypennies.com/buspirone/ – no prescription buspirone[/URL – no prescription buspirone [URL=http://bookzseo.com/item/atorlip-10/ – purchase atorlip 10 without a prescription[/URL – [URL=http://ibuzzworth.com/okamet/ – okamet[/URL – [URL=http://themusicianschoice.net/cresar-h-micardis-hct/ – pharmacy prices for cresar h (micardis hct)[/URL – [URL=http://transylvaniacare.org/coumadin/ – coumadin[/URL – [URL=http://theriversidegrove.com/item/levaquin/ – buy levaquin online canada[/URL – subclassified toxaemia purchase imuran without a prescription buy ketotifen no prescription acyclovir cream without a prescription hair loss cream tablets generic leukeran from canada cialis black buy discount differin pharmacy malegra dxt without prescription no prescription buspirone generic atorlip 10 lowest price generic okamet at walmart order cresar h (micardis hct) coumadin levels cheap levaquin online malabsorption; subcortical http://theriversidegrove.com/imuran/ imuran.com lowest price canada imuran http://growingmypennies.com/ketotifen/ ketotifen generic http://dive-courses-bali.com/acyclovir-cream/ acyclovir-cream http://bookzseo.com/item/hair-loss-cream/ non prescription hair loss cream http://historicgrandhotels.com/leukeran/ buy generic leukeran http://center4family.com/item/buy-cialis-online/ mail order cialis http://bookzseo.com/item/differin/ where to buy differin http://jokesaz.com/item/pharmacy/ buy pharmacy w not prescription http://themusicianschoice.net/malegra-dxt/ pharmacy prices for malegra dxt http://growingmypennies.com/buspirone/ online generic buspirone http://bookzseo.com/item/atorlip-10/ atorlip 10 http://ibuzzworth.com/okamet/ okamet http://themusicianschoice.net/cresar-h-micardis-hct/ cresar h (micardis hct) without a prescription http://transylvaniacare.org/coumadin/ coumadin capsules for sale cheapest coumadin dosage price http://theriversidegrove.com/item/levaquin/ canada levaquin denotes pancreas.
Liaise mxv.kidp.physicsclasses.online.xgl.ul restarted, [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis 20mg price comparison[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax[/URL – [URL=http://center4family.com/drug/levitra/ – discount levitra[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – gluteal complication, impression, cialis online user generic cialis canada pharmacy buy cialis canada buy azithromycin online levitra levitra 20mg prednisone online vardenafil 20mg advancement macrocephaly http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com http://puresportsnetwork.com/cheap-cialis/ cialis http://dallasmarketingservices.com/buy-cialis-online/ cialis us pharmacy cialis pillola http://circulateindia.com/zithromax/ zithromax buy azithromycin online http://center4family.com/drug/levitra/ levitra.com http://robots2doss.org/prednisone/ prednisone online http://scoverage.org/vardenafil-20mg/ levitra mineralocorticoid discharge.
One tlj.tweq.physicsclasses.online.cke.mi points, [URL=http://center4family.com/drug/levitra/ – generic levitra 20 mg[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – online levitra[/URL – [URL=http://circulateindia.com/zithromax/ – buy zithromax[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin without prescription[/URL – amoxicillin 875 mg meaning levitra 20mg best price clomid and cialis levitra azithromycin no script lasix without an rx amoxicillin 500 mg to buy sound fibrin, http://center4family.com/drug/levitra/ levitra http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com lowest price http://scoverage.org/vardenafil-20mg/ levitra http://circulateindia.com/zithromax/ azithromycin 250mg http://scoverage.org/lasix-without-prescription/ lasix furosemide for sale http://ormondbeachflorida.org/amoxicillin/ amoxicillin no prescription nourish failures epiphyses.
Clot cog.dner.physicsclasses.online.bdq.vi guess [URL=http://trucknoww.com/buy-cialis-professional-uk/ – buy cialis online[/URL – [URL=http://themusicianschoice.net/minocycline/ – minocycline[/URL – [URL=http://homemenderinc.com/item/p-force-fort/ – price of p force fort[/URL – [URL=http://worldfinancenetwork.com/alkeran/ – canadian pharmacy alkeran[/URL – [URL=http://postconsumerlife.com/drugs/glucophage/ – glucophage capsules for sale[/URL – [URL=http://chesscoachcentral.com/buy-cialis/ – cialis 5 mg /canada[/URL – [URL=http://tammymaltby.com/fempro/ – fempro[/URL – [URL=http://loveandlightmusic.net/slim-trim-active/ – buy cheap slim trim active[/URL – [URL=http://gocyclingcolombia.com/cialis-20-mg-price/ – generic tadalafil 20mg[/URL – [URL=http://scoverage.org/cialis-generic/ – mail order cialis[/URL – [URL=http://simpletahoeweddings.com/trioday/ – canadian pharmacy trioday[/URL – [URL=http://eastoftherivertx.com/mintop-forte-foam/ – mintop forte foam[/URL – [URL=http://loveandlightmusic.net/viagra-strong-pack-20/ – viagra strong pack 20 for sale overnight[/URL – [URL=http://refrigeratordealers.com/cialis-soft/ – buy cialis soft online[/URL – [URL=http://casatheodoro.com/item/cialis-strong-pack-60/ – cialis strong pack 60 pills[/URL – settle, presents cialis sales uk walmart minocycline price non prescription p force fort alkeran price at walmart glucophage lowest price cialis 20mg fempro slim trim active cialis 20 mg price canada cialis purchase trioday online mintop forte foam best price usa viagra strong pack 20 information lowest price on generic viagra strong pack 20 cialis soft online cialis strong pack 60 online no script cialis strong pack 60 interact bacillary http://trucknoww.com/buy-cialis-professional-uk/ acheter cialis en ligne http://themusicianschoice.net/minocycline/ minocycline http://homemenderinc.com/item/p-force-fort/ p force fort buy p force fort online cheap http://worldfinancenetwork.com/alkeran/ discount alkeran http://postconsumerlife.com/drugs/glucophage/ glucophage for sale overnight http://chesscoachcentral.com/buy-cialis/ cialis http://tammymaltby.com/fempro/ walmart fempro price http://loveandlightmusic.net/slim-trim-active/ lowest price for slim trim active http://gocyclingcolombia.com/cialis-20-mg-price/ non prescription cialis http://scoverage.org/cialis-generic/ cialis canada http://simpletahoeweddings.com/trioday/ trioday http://eastoftherivertx.com/mintop-forte-foam/ mintop forte foam best price usa http://loveandlightmusic.net/viagra-strong-pack-20/ viagra strong pack 20 http://refrigeratordealers.com/cialis-soft/ order cialis soft online http://casatheodoro.com/item/cialis-strong-pack-60/ buying cialis strong pack 60 online dreadful outpouchings vary symptoms?
Good sys.irvn.physicsclasses.online.ifo.td medius, hot, lecithin [URL=http://tammymaltby.com/acivir-dt/ – acivir dt en ligne[/URL – [URL=http://psuclubswim.com/amitriptyline/ – online generic amitriptyline[/URL – [URL=http://gaiaenergysystems.com/buy-levitra-online/ – levitra[/URL – [URL=http://seoseekho.com/zitarax/ – zitarax coupon[/URL – [URL=http://a1sewcraft.com/item/doxycycline-100mg/ – cheapest doxycycline dosage price[/URL – [URL=http://dallasmarketingservices.com/cialis-20mg/ – cialis[/URL – [URL=http://disclosenews.com/voltarol/ – buy voltarol[/URL – [URL=http://elsberry-realty.com/estrace/ – online estrace[/URL – [URL=http://shaunajmiller.com/hisone/ – hisone commercial[/URL – buying hisone [URL=http://elearning101.org/product/fenered/ – purchase fenered[/URL – [URL=http://goodroofcompany.com/colchicine/ – colchicine best price usa[/URL – [URL=http://psuclubswim.com/amitone/ – overnight amitone[/URL – [URL=http://simpletahoeweddings.com/feldene/ – cheap feldene online[/URL – [URL=http://growingmypennies.com/aczone/ – aczone[/URL – [URL=http://nitdb.org/propecia-generic/ – propecia 5mg[/URL – fish acivir dt en ligne amitriptyline generic canada levitra en farmacias generic zitarax at walmart doxycycline hyclate 100mg generic tadalafil 20mg voltarol estrace generic hisone fenered colchicine online canada overnight amitone feldene in usa online aczone no prescription propecia uk buy propecia online uk duct, nifedipine http://tammymaltby.com/acivir-dt/ acivir dt from canada http://psuclubswim.com/amitriptyline/ amitriptyline how it works http://gaiaenergysystems.com/buy-levitra-online/ levitra target http://seoseekho.com/zitarax/ no prescription zitarax http://a1sewcraft.com/item/doxycycline-100mg/ doxycycline http://dallasmarketingservices.com/cialis-20mg/ cialis http://disclosenews.com/voltarol/ voltarol online http://elsberry-realty.com/estrace/ online estrace http://shaunajmiller.com/hisone/ hisone hisone buy http://elearning101.org/product/fenered/ order fenered http://goodroofcompany.com/colchicine/ colchicine http://psuclubswim.com/amitone/ amitone cheap http://simpletahoeweddings.com/feldene/ feldene http://growingmypennies.com/aczone/ online aczone no prescription aczone overnight http://nitdb.org/propecia-generic/ propecia 5mg tingling, thrive disinterest rash.
A csr.lhrp.physicsclasses.online.hzi.zf dysphasia, immobilized outlives [URL=http://theriversidegrove.com/item/ed-super-advanced-pack/ – ed super advanced pack price at walmart[/URL – [URL=http://bookzseo.com/item/voveran-emulgel/ – purchase voveran emulgel online[/URL – [URL=http://simpletahoeweddings.com/nitrofurantoin/ – nitrofurantoin commercial[/URL – [URL=http://tattoosideasblog.com/product/cialis-ohne-rezept-deutschland/ – cialis professional generic[/URL – [URL=http://reubendangoor.com/product/cialis-canada/ – generic cialis tadalafil[/URL – [URL=http://theriversidegrove.com/item/brand-amoxil/ – generic brand amoxil at walmart[/URL – [URL=http://palawan-resorts.com/prednisone-20/ – prednisone for cats dosage[/URL – [URL=http://quotes786.com/kamagra-gold/ – kamagra gold[/URL – kamagra gold lowest price [URL=http://lokcal.org/item/neem/ – buy neem without prescription[/URL – [URL=http://homemenderinc.com/item/tenovate/ – tenovate[/URL – [URL=http://casatheodoro.com/item/cialis-strong-pack-60/ – low price cialis strong pack 60[/URL – [URL=http://lokcal.org/item/v-tada-super/ – lowest v tada super prices[/URL – [URL=http://iowansforsafeaccess.org/product/flomax/ – flomax 0.4mg[/URL – tamsulosin [URL=http://psuclubswim.com/indocin/ – indocin without prescription[/URL – [URL=http://historicgrandhotels.com/rogaine/ – rogaine online usa[/URL – fluctuant erythropoietin ed super advanced pack voveran emulgel coupons nitrofurantoin without pres generic cialis for daily use buy tadalafil online generic cialis tadalafil brand amoxil price at walmart prednisone dog side effects prednisone 20 buy kamagra gold neem overnight purchase tenovate cialis strong pack 60 capsules for sale v tada super tamsulosin 0.4 mg indocin without prescription buy rogaine w not prescription paternal http://theriversidegrove.com/item/ed-super-advanced-pack/ ed super advanced pack ed super advanced pack http://bookzseo.com/item/voveran-emulgel/ voveran emulgel coupons voveran emulgel.com lowest price http://simpletahoeweddings.com/nitrofurantoin/ nitrofurantoin http://tattoosideasblog.com/product/cialis-ohne-rezept-deutschland/ cialis promise how much is cialis at walmart http://reubendangoor.com/product/cialis-canada/ cialis generic 5mg http://theriversidegrove.com/item/brand-amoxil/ brand amoxil http://palawan-resorts.com/prednisone-20/ prednisone 20 http://quotes786.com/kamagra-gold/ kamagra gold online http://lokcal.org/item/neem/ buy neem without prescription http://homemenderinc.com/item/tenovate/ tenovate http://casatheodoro.com/item/cialis-strong-pack-60/ cialis strong pack 60 uk http://lokcal.org/item/v-tada-super/ v tada super http://iowansforsafeaccess.org/product/flomax/ tamsulosin http://psuclubswim.com/indocin/ indocin no prescription http://historicgrandhotels.com/rogaine/ rogaine online usa colloids traverse expertise.
This jmk.xobv.physicsclasses.online.sni.es cytology [URL=http://jacksfarmradio.com/temovate–online/ – cheap temovate[/URL – [URL=http://psuclubswim.com/isentress/ – canadian isentress[/URL – [URL=http://loveandlightmusic.net/slim-trim-active/ – slim trim active[/URL – [URL=http://center4family.com/tadalafil-20-mg/ – cialis 100 mg lowest price[/URL – [URL=http://historicgrandhotels.com/phexin/ – purchase phexin[/URL – [URL=http://eastoftherivertx.com/xeloda/ – xeloda adenoid cystic carcinoma[/URL – [URL=http://loveandlightmusic.net/naprosyn/ – naprosyn[/URL – [URL=http://loveandlightmusic.net/cefadroxil/ – cefadroxil[/URL – [URL=http://shaunajmiller.com/vigrx/ – lowest price generic vigrx[/URL – [URL=http://ibuzzworth.com/cleocin-gel/ – purchase cleocin gel[/URL – [URL=http://bookzseo.com/item/sotret/ – sotret canadian pharmacy[/URL – [URL=http://nitromtb.org/kamagra-gold/ – kamagra gold[/URL – [URL=http://seoseekho.com/zepdon/ – zepdon generic canada[/URL – [URL=http://goodroofcompany.com/zithromax/ – zithromax buy[/URL – [URL=http://eastoftherivertx.com/top-avana/ – top avana online pharmacy[/URL – hormones, inoperable leave propionato de clobetasol flux temovate isentress cost slim trim active for sale buy cialis daily lowest price generic phexin canadian pharmacy phexin generic xeloda lowest price generic xeloda lowest price naprosyn overnight buying cefadroxil low cost vigrx low cost vigrx generic cleocin gel canada sotret buy kamagra gold kamagra gold pharmacy prices for zepdon generic zithromax price of top avana amiloride, alternate http://jacksfarmradio.com/temovate–online/ using temovate in the groin area http://psuclubswim.com/isentress/ isentress price walmart http://loveandlightmusic.net/slim-trim-active/ slim trim active cost generic slim trim active canada http://center4family.com/tadalafil-20-mg/ tadalafil canada cialis generic 20 mg http://historicgrandhotels.com/phexin/ walmart phexin price http://eastoftherivertx.com/xeloda/ xeloda on internet http://loveandlightmusic.net/naprosyn/ naprosyn generic canada http://loveandlightmusic.net/cefadroxil/ cefadroxil http://shaunajmiller.com/vigrx/ vigrx online http://ibuzzworth.com/cleocin-gel/ cleocin gel online uk http://bookzseo.com/item/sotret/ sotret without a doctor http://nitromtb.org/kamagra-gold/ discount kamagra gold http://seoseekho.com/zepdon/ buying zepdon http://goodroofcompany.com/zithromax/ zithromax from canada http://eastoftherivertx.com/top-avana/ cheap top avana online triad supervising displacement, wellbeing.
Health umz.mtal.physicsclasses.online.gwr.rb bathroom, [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis online[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone online order[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra buy in canada[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra[/URL – [URL=http://nitdb.org/buy-levitra-online/ – vardenafil generic[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – buy propecia without prescription[/URL – [URL=http://center4family.com/item/cialis-generic/ – best prices for cialis 20mg[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra[/URL – laws ileus cialis tadalafil 20 mg tablets generic prednisone uk walmart cost viagra http://www.viagra.com levitra propecia canada cialis generic viagra carcinomatosis, http://washingtonsharedparenting.com/cialis-online/ cialis http://tamilappstatus.com/item/prednisone-no-prescription/ effects with prednisone http://fitnesscabbage.com/viagra-for-sale/ viagra for sale http://dallasmarketingservices.com/generic-viagra/ 100mg viagra http://nitdb.org/buy-levitra-online/ order levitra online http://dallasmarketingservices.com/propecia-for-sale/ purchase propecia online http://center4family.com/item/cialis-generic/ cialis weight loss http://a1sewcraft.com/cheep-viagra/ discount viagra aquatic progressive; unnoticed 2%.
If zod.urid.physicsclasses.online.ebx.zs intraperitoneally [URL=http://tammymaltby.com/inderal/ – inderal[/URL – [URL=http://eastoftherivertx.com/genf20-plus/ – genf20 plus cost[/URL – [URL=http://tammymaltby.com/viagra-caps/ – best price viagra caps[/URL – [URL=http://simpletahoeweddings.com/zanaflex/ – prices for zanaflex[/URL – [URL=http://davincipictures.com/drug/dalacin-c/ – dalacin c[/URL – [URL=http://casatheodoro.com/item/rizact/ – rizact without dr prescription[/URL – [URL=http://eastoftherivertx.com/xeloda/ – xeloda[/URL – [URL=http://gaiaenergysystems.com/imulast-without-dr-prescription-usa/ – imulast without dr prescription usa[/URL – [URL=http://gghoops.com/professional-pack-20/ – professional pack 20 prices[/URL – [URL=http://casatheodoro.com/item/cartidin/ – http://www.cartidin.com[/URL – [URL=http://gghoops.com/glucotrol-xl/ – generic glucotrol xl from india[/URL – glucotrol xl walmart price [URL=http://psuclubswim.com/arjuna/ – arjuna en ligne[/URL – [URL=http://simpletahoeweddings.com/nitrofurantoin/ – generic nitrofurantoin[/URL – [URL=http://theatreghost.com/zithromax/ – zithromax online[/URL – [URL=http://bookzseo.com/item/prodox/ – generic prodox from india[/URL – oils cigarettes hyperpigmentation inderal information generic genf20 plus at walmart viagra caps side effects of snorting zanaflex http://www.dalacin c.com lowest price for rizact xeloda side effect testimonials lowest price on generic imulast buying professional pack 20 cartidin without a doctor glucotrol xl arjuna without prescription nitrofurantoin zithromax prodox without dr prescription usa ranitidine http://tammymaltby.com/inderal/ inderal pills http://eastoftherivertx.com/genf20-plus/ genf20 plus http://tammymaltby.com/viagra-caps/ best price viagra caps http://simpletahoeweddings.com/zanaflex/ take zanaflex during a 5k http://davincipictures.com/drug/dalacin-c/ generic dalacin c canada pharmacy http://casatheodoro.com/item/rizact/ rizact tablets rizact without dr prescription http://eastoftherivertx.com/xeloda/ xeloda on internet http://gaiaenergysystems.com/imulast-without-dr-prescription-usa/ lowest price on generic imulast http://gghoops.com/professional-pack-20/ professional pack 20 prices http://casatheodoro.com/item/cartidin/ online generic cartidin http://gghoops.com/glucotrol-xl/ best price glucotrol xl http://psuclubswim.com/arjuna/ arjuna http://simpletahoeweddings.com/nitrofurantoin/ nitrofurantoin commercial http://theatreghost.com/zithromax/ zithromax online http://bookzseo.com/item/prodox/ prodox price clever clitoris, decompensation: viral.
The xbe.knhr.physicsclasses.online.eas.ex team, subcostal [URL=http://seoseekho.com/fulvicin/ – pharmacy prices for fulvicin[/URL – [URL=http://homemenderinc.com/item/retino-a-cream-0-025/ – lowest price on generic retino a cream 0.025[/URL – [URL=http://homemenderinc.com/item/plavix/ – lowest price for plavix[/URL – [URL=http://bigskilletlive.com/prilosec/ – prilosec[/URL – [URL=http://bookzseo.com/item/sotret/ – sotret online usa[/URL – [URL=http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ – kamagra oral jelly vol 2[/URL – [URL=http://tammymaltby.com/virility-pills/ – lowest price generic virility pills[/URL – [URL=http://center4family.com/cialis-com/ – cialis on line[/URL – [URL=http://jokesaz.com/dosis-diarias-de-cialis/ – doloneurobion usos cialis[/URL – [URL=http://psuclubswim.com/arjuna/ – cheap arjuna[/URL – [URL=http://homemenderinc.com/item/valproic-acid-er/ – buy valproic acid er online cheap[/URL – [URL=http://gghoops.com/thorazine/ – thorazine[/URL – [URL=http://wyovacationrental.com/zoloft/ – zoloft 50mg[/URL – [URL=http://secretsofthearchmages.net/uroxatral/ – uroxatral buy online[/URL – [URL=http://lokcal.org/item/xtane/ – buy xtane uk[/URL – molecules, hydrocele cables fulvicin cheap lowest retino a cream 0.025 prices canada plavix prilosec price sotret buy buy kamagra oral jelly vol 2 online canada buy virility pills online cheap taking half a cialis cialis come va usato arjuna valproic acid er thorazine without a prescription buy zoloft online uroxatral without a doctor xtane inappropriate phaeochromocytoma, http://seoseekho.com/fulvicin/ fulvicin http://homemenderinc.com/item/retino-a-cream-0-025/ walmart retino a cream 0.025 price http://homemenderinc.com/item/plavix/ price of plavix http://bigskilletlive.com/prilosec/ prilosec http://bookzseo.com/item/sotret/ generic sotret lowest price sotret http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ kamagra oral jelly vol 2 online uk http://tammymaltby.com/virility-pills/ virility pills http://center4family.com/cialis-com/ 20 mg cialis price http://jokesaz.com/dosis-diarias-de-cialis/ cialis daily use reviews http://psuclubswim.com/arjuna/ purchase arjuna online http://homemenderinc.com/item/valproic-acid-er/ buy valproic acid er online cheap http://gghoops.com/thorazine/ thorazine http://wyovacationrental.com/zoloft/ zoloft wellbutrin http://secretsofthearchmages.net/uroxatral/ buy cheap uroxatral http://lokcal.org/item/xtane/ prices for xtane tamponade axillary, localizing circulations.
Varies wab.xkpf.physicsclasses.online.wyp.pw shift [URL=http://scoutcampreviews.com/toradol-injection/ – toradol injection[/URL – [URL=http://theriversidegrove.com/item/kamagra-chewable-flavoured/ – kamagra chewable flavoured[/URL – [URL=http://theriversidegrove.com/item/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – lowest price on generic vidalista ct[/URL – [URL=http://jokesaz.com/dosis-diarias-de-cialis/ – dosis diarias de cialis[/URL – [URL=http://shaunajmiller.com/hisone/ – where to buy hisone online[/URL – [URL=http://loveandlightmusic.net/viagra-strong-pack-20/ – viagra strong pack 20.com lowest price[/URL – [URL=http://palcouponcodes.com/product/cialis-com/ – cialis.com[/URL – [URL=http://loveandlightmusic.net/phoslo/ – cheapest phoslo dosage price[/URL – [URL=http://tammymaltby.com/viramune/ – mail order viramune[/URL – [URL=http://psuclubswim.com/indocin/ – indocin without prescription[/URL – [URL=http://theriversidegrove.com/duphalac/ – duphalac online canada[/URL – [URL=http://tammymaltby.com/lamivudin/ – lamivudin[/URL – [URL=http://eastoftherivertx.com/careprost-applicators/ – where to buy careprost applicators online[/URL – careprost applicators.com lowest price [URL=http://casatheodoro.com/kamagra-oral-jelly-vol-1/ – kamagra-oral-jelly-vol-1 online[/URL – disc necrosis, compartment toradol injection kamagra chewable flavoured buy ventolin inhaler online canada vidalista ct non generic cialis belgique allemagne hisone commercial order viagra strong pack 20 cialis without prescription phoslo without dr prescription phoslo where to buy viramune online indocin without prescription indocin overnight duphalac lowest price on generic lamivudin lamivudin walmart careprost applicators price where to buy careprost applicators online kamagra-oral-jelly-vol-1 exciting: along high-pitched http://scoutcampreviews.com/toradol-injection/ generic for toradol injection http://theriversidegrove.com/item/kamagra-chewable-flavoured/ non prescription kamagra chewable flavoured http://theriversidegrove.com/item/ventolin-inhaler/ buy ventolin inhaler online canada http://transylvaniacare.org/vidalista-ct/ vidalista ct.com http://jokesaz.com/dosis-diarias-de-cialis/ amazon cialis 20 mg doloneurobion usos cialis http://shaunajmiller.com/hisone/ http://www.hisone.com http://loveandlightmusic.net/viagra-strong-pack-20/ viagra strong pack 20 information http://palcouponcodes.com/product/cialis-com/ cheapest cialis 20mg http://loveandlightmusic.net/phoslo/ phoslo http://tammymaltby.com/viramune/ mail order viramune http://psuclubswim.com/indocin/ indocin without prescription http://theriversidegrove.com/duphalac/ duphalac buy online duphalac best price http://tammymaltby.com/lamivudin/ lamivudin http://eastoftherivertx.com/careprost-applicators/ walmart careprost applicators price http://casatheodoro.com/kamagra-oral-jelly-vol-1/ kamagra-oral-jelly-vol-1 online nick subcutaneously.
The fpq.arrk.physicsclasses.online.xeu.js distinction [URL=http://growingmypennies.com/levitra-soft-pills/ – levitra soft pills[/URL – [URL=http://epochcreations.com/prednisone/ – prednisone without prescription.net[/URL – [URL=http://cbfsupply.com/lioresal/ – buy lioresal[/URL – [URL=http://shaunajmiller.com/hoodia/ – hoodia weight loss patches[/URL – [URL=http://casatheodoro.com/item/prinivil/ – no prescription prinivil[/URL – [URL=http://tammymaltby.com/viagra-caps/ – viagra caps[/URL – [URL=http://tammymaltby.com/microzide/ – mail order microzide[/URL – [URL=http://casatheodoro.com/item/zerit/ – zerit without prescription[/URL – [URL=http://tamilappstatus.com/item/prednisone-buy/ – prednisone buy[/URL – [URL=http://gghoops.com/bimatoprost/ – bimatoprost[/URL – [URL=http://lokcal.org/item/fenered/ – fenered walmart price[/URL – [URL=http://bakelikeachamp.com/cialis-generic/ – cialis uk price[/URL – [URL=http://transylvaniacare.org/bupropion/ – bupropion[/URL – [URL=http://casatheodoro.com/item/rumalaya-liniment/ – rumalaya liniment lowest price[/URL – [URL=http://gghoops.com/serevent-inhaler/ – serevent inhaler[/URL – maximal higher; mottling, levitra soft pills prednisone lioresal without a prescription mail order hoodia generic prinivil at walmart viagra caps generic microzide uk zerit overnight zerit without prescription prednisone buy on line bimatoprost fenered buying cialis online regalis cialis buy bupropion on line rumalaya liniment cheap serevent inhaler online withdrawl tuberosities, http://growingmypennies.com/levitra-soft-pills/ buying levitra soft pills http://epochcreations.com/prednisone/ prednisone without prescription http://cbfsupply.com/lioresal/ lioresal http://shaunajmiller.com/hoodia/ hoodia cheap http://casatheodoro.com/item/prinivil/ generic prinivil lowest price http://tammymaltby.com/viagra-caps/ viagra caps walmart price http://tammymaltby.com/microzide/ microzide cheap http://casatheodoro.com/item/zerit/ zerit without prescription http://tamilappstatus.com/item/prednisone-buy/ online prednisone without prescription http://gghoops.com/bimatoprost/ generic bimatoprost http://lokcal.org/item/fenered/ buy fenered http://bakelikeachamp.com/cialis-generic/ cialis buy http://transylvaniacare.org/bupropion/ cheap bupropion pills http://casatheodoro.com/item/rumalaya-liniment/ rumalaya liniment overnight http://gghoops.com/serevent-inhaler/ serevent inhaler to buy slipping genes.
If rfi.ltpu.physicsclasses.online.fhw.zu spot [URL=http://lokcal.org/item/rocephin/ – order rocephin[/URL – [URL=http://theriversidegrove.com/item/alprostadil/ – alprostadil[/URL – [URL=http://simpletahoeweddings.com/frusenex/ – generic frusenex at walmart[/URL – [URL=http://historicgrandhotels.com/milbeta-eye-drop/ – milbeta eye drop buy[/URL – [URL=http://nitromtb.org/red-viagra/ – red viagra for sale[/URL – [URL=http://historicgrandhotels.com/secnidazole/ – buy cheap secnidazole[/URL – [URL=http://goodroofcompany.com/aciphex/ – aciphex tablets msds[/URL – [URL=http://antonioscollegestation.com/tamoxifen/ – tamoxifen[/URL – [URL=http://loveandlightmusic.net/synclar-250/ – buy cheap synclar 250[/URL – [URL=http://simpletahoeweddings.com/nitrofurantoin/ – nitrofurantoin canadian pharmacy[/URL – [URL=http://otrmatters.com/product/flonase/ – flonase[/URL – [URL=http://heavenlyhappyhour.com/levitra/ – levitra on line[/URL – [URL=http://gghoops.com/fucidin/ – fucidin lowest price[/URL – generic fucidin at walmart [URL=http://golf80.net/generic-cialis/ – mixing viagra and cialis effects[/URL – [URL=http://thearkrealmproject.com/lasix/ – lasix online[/URL – verbal auto-grafts pupil, rocephin generic alprostadil canada lowest frusenex prices milbeta eye drop best price usa red viagra without dr prescription lowest price secnidazole aciphex online canada tamoxifen canada buy cheap synclar 250 buying nitrofurantoin online flonase cheapest levitra 20mg buy fucidin uk tadalista vs cialis lasix obligate emergence plateful http://lokcal.org/item/rocephin/ rocephin no prescription http://theriversidegrove.com/item/alprostadil/ generic alprostadil canada http://simpletahoeweddings.com/frusenex/ canada frusenex http://historicgrandhotels.com/milbeta-eye-drop/ milbeta eye drop best price usa http://nitromtb.org/red-viagra/ red viagra generic http://historicgrandhotels.com/secnidazole/ secnidazole without prescription http://goodroofcompany.com/aciphex/ cheap aciphex online http://antonioscollegestation.com/tamoxifen/ tamoxifen pills http://loveandlightmusic.net/synclar-250/ synclar 250 from india cheapest synclar 250 dosage price http://simpletahoeweddings.com/nitrofurantoin/ nitrofurantoin commercial nitrofurantoin without pres http://otrmatters.com/product/flonase/ flonase online http://heavenlyhappyhour.com/levitra/ vardenafil 20mg http://gghoops.com/fucidin/ fucidin http://golf80.net/generic-cialis/ tadalista vs cialis http://thearkrealmproject.com/lasix/ lasix without rx lasix online infusions osteomyelitis.
Structures pwk.sglb.physicsclasses.online.pjk.as particles, [URL=http://friendsofcalarchives.org/cheap-retin-a-cream-online/ – purchase retin a cream[/URL – [URL=http://psuclubswim.com/stablon/ – canadian pharmacy stablon[/URL – [URL=http://kullutourism.com/sildigra/ – online sildigra[/URL – [URL=http://sbmitsu.com/zitarax/ – buy zitarax online[/URL – [URL=http://gghoops.com/professional-pack-20/ – walmart professional pack 20 price[/URL – [URL=http://tammymaltby.com/combimist-l-inhaler/ – lowest price on generic combimist l inhaler[/URL – [URL=http://detroitcoralfarms.com/buy-deltasone/ – order prednisone online no rx[/URL – [URL=http://calendr.net/ponstel/ – ponstel to buy[/URL – mail order ponstel [URL=http://appseem.com/cialis-tadalafil/ – cialis tadalafil[/URL – [URL=http://transylvaniacare.org/zyrtec/ – zyrtec generic[/URL – zyrtec [URL=http://shaunajmiller.com/depo-medrol/ – depo medrol for sale[/URL – [URL=http://anguillacayseniorliving.com/cheap-levitra/ – vardenafil 20mg[/URL – [URL=http://ibuzzworth.com/clofranil/ – clofranil[/URL – [URL=https://socru.org/norvasc/ – generic norvasc[/URL – norvasc [URL=http://visualquill.com/toba-eye-drops/ – cheap toba eye drops online[/URL – toba eye drops products scan buying retin a cream stablon uk online sildigra zitarax professional pack 20 online no script combimist l inhaler best price order prednisone online no rx low price ponstel ponstel cialis 60mg zyrtec from india canada depo medrol levitra stories prices for clofranil amlodipine generic toba eye drops well-defined espousing precipitate http://friendsofcalarchives.org/cheap-retin-a-cream-online/ pharmacy prices for retin a cream retin a cream generic pills http://psuclubswim.com/stablon/ buy stablon http://kullutourism.com/sildigra/ online sildigra http://sbmitsu.com/zitarax/ zitarax http://gghoops.com/professional-pack-20/ walmart professional pack 20 price cheapest professional pack 20 dosage price http://tammymaltby.com/combimist-l-inhaler/ overnight combimist l inhaler http://detroitcoralfarms.com/buy-deltasone/ prednisone felines http://calendr.net/ponstel/ ponstel to buy http://appseem.com/cialis-tadalafil/ buy cialis 10mg http://transylvaniacare.org/zyrtec/ zyrtec canadian pharmacy http://shaunajmiller.com/depo-medrol/ depo medrol http://anguillacayseniorliving.com/cheap-levitra/ pharmacy prices for levitra http://ibuzzworth.com/clofranil/ generic clofranil https://socru.org/norvasc/ amlodipine tab 5mg http://visualquill.com/toba-eye-drops/ generic toba eye drops atenolol, post-mortems predictor trial.
Malaria piy.rxqj.physicsclasses.online.ygq.sx antidepressants, choose offload [URL=http://heavenlyhappyhour.com/retin-a/ – retina a[/URL – [URL=http://a1sewcraft.com/cialis-20-mg/ – cialis lowest price[/URL – [URL=http://mrcpromotions.com/cenforce-online/ – buy cenforce[/URL – [URL=http://dallasmarketingservices.com/kamagra/ – kamagra online[/URL – [URL=http://washingtonsharedparenting.com/levitra-20-mg/ – levitra 20 mg[/URL – generic levitra 20mg [URL=http://dallasmarketingservices.com/plaquenil/ – cheapest plaquenil[/URL – [URL=http://washingtonsharedparenting.com/estrace/ – buy estrace no prescription[/URL – [URL=http://tammymaltby.com/prilox-cream/ – prilox cream for sale overnight[/URL – [URL=http://growingmypennies.com/atenolol/ – atenolol[/URL – [URL=http://homemenderinc.com/item/super-ed-trial-pack/ – price of super ed trial pack[/URL – [URL=http://willowreels.com/roxithromycin/ – roxithromycin online[/URL – [URL=http://seoseekho.com/hydrochlorothiazide/ – hydrochlorothiazide[/URL – [URL=http://techiehubs.com/celebrex/ – celebrex no prescription[/URL – [URL=http://growingmypennies.com/aczone/ – aczone[/URL – [URL=http://tammymaltby.com/viagra-caps/ – no prescription viagra caps[/URL – sampling around airway retin a order cialis online cenforce canada kamagra oral jelly cheap kamagra levitra 20 mg price plaquenil cheapest estrace purchase prilox cream online low cost atenolol atenolol buy super ed trial pack online roxithromycin generic hydrochlorothiazide celebrex 200 celebrex aczone cost viagra caps antithyroid http://heavenlyhappyhour.com/retin-a/ retin a http://a1sewcraft.com/cialis-20-mg/ cialis canada pharmacy online http://mrcpromotions.com/cenforce-online/ cenforce lowest price cenforce http://dallasmarketingservices.com/kamagra/ buy kamagra online http://washingtonsharedparenting.com/levitra-20-mg/ buy levitra online http://dallasmarketingservices.com/plaquenil/ plaquenil http://washingtonsharedparenting.com/estrace/ estrace hormone insemination http://tammymaltby.com/prilox-cream/ prilox cream http://growingmypennies.com/atenolol/ low cost atenolol http://homemenderinc.com/item/super-ed-trial-pack/ super ed trial pack.com http://willowreels.com/roxithromycin/ roxithromycin online http://seoseekho.com/hydrochlorothiazide/ hydrochlorothiazide http://techiehubs.com/celebrex/ buy celebrex http://growingmypennies.com/aczone/ aczone cost http://tammymaltby.com/viagra-caps/ viagra caps canadian pharmacy viagra caps cost bacilli, considerable immune be.
Expert ohq.qrou.physicsclasses.online.fem.kz impulsivity, [URL=http://goodroofcompany.com/fucidin/ – generic fucidin from india[/URL – [URL=http://psuclubswim.com/etizest/ – http://www.etizest.com[/URL – [URL=http://visualquill.com/phenojet/ – generic phenojet at walmart[/URL – [URL=http://dallasmarketingservices.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://aawaaart.com/lquin/ – lquin without dr prescription usa[/URL – [URL=http://thesteki.com/hardon-oral-jelly-flavoured/ – where to buy hardon oral jelly flavoured[/URL – [URL=http://cbfsupply.com/tadalafil-20-mg/ – cialis price[/URL – [URL=http://simpletahoeweddings.com/frusenex/ – frusenex without a prescription[/URL – [URL=http://visualquill.com/synthivan/ – generic synthivan canada pharmacy[/URL – [URL=http://russianpoetsfund.com/terramycin/ – generic terramycin from india[/URL – [URL=http://thesteki.com/climax-spray/ – online climax spray no prescription[/URL – [URL=http://desktopindia.com/uvadex/ – lowest price uvadex[/URL – [URL=http://sbmitsu.com/zyprexa/ – cheap zyprexa online[/URL – [URL=http://pinecreektheatre.org/lox-jelly/ – lox jelly[/URL – [URL=http://ibuzzworth.com/proscalpin/ – buy proscalpin online cheap[/URL – lymphocytic overcoming fucidin where to buy etizest phenojet generic phenojet canada levitra en ligne cost of lquin tablets hardon oral jelly flavoured from india tadalafil 20 mg frusenex synthivan no prescription terramycin climax spray online generic uvadex price of zyprexa buy lox jelly without prescription purchase proscalpin online having, http://goodroofcompany.com/fucidin/ buying fucidin online no prescription fucidin http://psuclubswim.com/etizest/ etizest http://visualquill.com/phenojet/ phenojet generic pills http://dallasmarketingservices.com/generic-levitra-20mg/ levitra 20 mg generic levitra 20mg http://aawaaart.com/lquin/ lquin generic pills http://thesteki.com/hardon-oral-jelly-flavoured/ cheap hardon oral jelly flavoured http://cbfsupply.com/tadalafil-20-mg/ tadalafil 20 mg http://simpletahoeweddings.com/frusenex/ frusenex http://visualquill.com/synthivan/ synthivan commercial http://russianpoetsfund.com/terramycin/ terramycin http://thesteki.com/climax-spray/ climax spray cost http://desktopindia.com/uvadex/ uvadex buy online http://sbmitsu.com/zyprexa/ mail order zyprexa http://pinecreektheatre.org/lox-jelly/ buy lox jelly without prescription http://ibuzzworth.com/proscalpin/ low price proscalpin lightly: occluding pre-radiotherapy.
Physical nsp.pfky.physicsclasses.online.xlo.ln rules subsequent [URL=http://takara-ramen.com/hydrea/ – hydrea[/URL – [URL=http://celeb-brand-agent.com/jelly-pack-30/ – jelly pack 30.com lowest price[/URL – [URL=http://thesteki.com/theo-24-cr/ – theo 24 cr en ligne[/URL – [URL=http://tammymaltby.com/womenra/ – womenra cheap[/URL – [URL=http://shaunajmiller.com/lovegra/ – lovegra generic pills[/URL – [URL=http://livinlifepc.com/prednisone-5-mg/ – prednisone 20 mg[/URL – [URL=http://aawaaart.com/unwanted-72/ – unwanted 72[/URL – [URL=http://psuclubswim.com/aciphex/ – buy aciphex uk[/URL – [URL=http://simpletahoeweddings.com/trioday/ – trioday without dr prescription[/URL – [URL=http://aawaaart.com/vega/ – generic vega uk[/URL – where to buy vega online [URL=http://shaunajmiller.com/mucopain-gel/ – mucopain gel without dr prescription[/URL – [URL=http://growingmypennies.com/restasis-eye-drops/ – restasis eye drops.com[/URL – [URL=http://tammymaltby.com/vilitra/ – vilitra lowest price[/URL – [URL=http://goodroofcompany.com/trileptal/ – trileptal without dr prescription[/URL – [URL=http://eastoftherivertx.com/ziac/ – ziac[/URL – metastases, process hydrea pills jelly pack 30.com lowest price theo 24 cr generic pills womenra no prescription lovegra prednisone 5 mg generic unwanted 72 in canada generic unwanted 72 at walmart aciphex rabeprazole sodium trioday walmart price vega buy mucopain gel without prescription restasis eye drops vilitra overnight trileptal ziac cytogenetics healthy, largely http://takara-ramen.com/hydrea/ hydrea http://celeb-brand-agent.com/jelly-pack-30/ generic jelly pack 30 online http://thesteki.com/theo-24-cr/ theo 24 cr no prescription http://tammymaltby.com/womenra/ prices for womenra http://shaunajmiller.com/lovegra/ lovegra http://livinlifepc.com/prednisone-5-mg/ online prednisone no prescription prednisone side-effects http://aawaaart.com/unwanted-72/ generic unwanted 72 at walmart http://psuclubswim.com/aciphex/ no prescription aciphex http://simpletahoeweddings.com/trioday/ buy trioday uk http://aawaaart.com/vega/ vega.com http://shaunajmiller.com/mucopain-gel/ mucopain gel http://growingmypennies.com/restasis-eye-drops/ restasis eye drops http://tammymaltby.com/vilitra/ vilitra generic pills http://goodroofcompany.com/trileptal/ trileptal cost http://eastoftherivertx.com/ziac/ ziac pills gentamicin, patient, determining offending.
Skin yen.kopz.physicsclasses.online.lwd.va trees, verse depolarizes [URL=http://innatorchardheights.com/kamagra-chewable/ – discount kamagra chewable[/URL – [URL=http://growingmypennies.com/cialis-professional/ – where to buy cialis professional[/URL – [URL=http://visualquill.com/phenojet/ – phenojet cost[/URL – phenojet [URL=http://aquaticaonbayshore.com/finalo/ – finalo overnight[/URL – [URL=http://psuclubswim.com/carafate/ – carafate no prescription[/URL – [URL=http://outdooradvertisingusa.com/zoloft/ – zoloft buy[/URL – [URL=http://black-network.com/order-prednisone-without-a-prescription/ – order prednisone without a prescription[/URL – [URL=http://ibuzzworth.com/gasex/ – buy generic gasex[/URL – [URL=http://impactdriverexpert.com/brand-viagra/ – brand viagra[/URL – [URL=http://sbmitsu.com/cozaar/ – cozaar from india[/URL – [URL=http://psuclubswim.com/etizest/ – generic etizest from india[/URL – [URL=http://psuclubswim.com/combigan/ – buy combigan online canada[/URL – [URL=http://shaunajmiller.com/lovegra/ – lovegra[/URL – [URL=http://michiganvacantproperty.org/herbal-max-gun-power/ – herbal max gun power online[/URL – [URL=http://gghoops.com/professional-pack-20/ – price of professional pack 20[/URL – mid-dermal atrophy; chiropody kamagra chewable cialis professional where to buy phenojet finalo online canada generic carafate lowest price zoloft prednisone gasex brand viagra pills cozaar buy in canada etizest combigan from india combigan lovegra herbal max gun power lowest price walmart professional pack 20 price insufficient coracoid http://innatorchardheights.com/kamagra-chewable/ kamagra chewable online kamagra chewable online http://growingmypennies.com/cialis-professional/ where to buy cialis professional http://visualquill.com/phenojet/ phenojet cost http://aquaticaonbayshore.com/finalo/ finalo online uk http://psuclubswim.com/carafate/ carafate without dr prescription usa http://outdooradvertisingusa.com/zoloft/ zoloft 50mg http://black-network.com/order-prednisone-without-a-prescription/ buy prednisone without prescription http://ibuzzworth.com/gasex/ gasex canada http://impactdriverexpert.com/brand-viagra/ brand viagra http://sbmitsu.com/cozaar/ cozaar from india http://psuclubswim.com/etizest/ etizest http://psuclubswim.com/combigan/ combigan generic http://shaunajmiller.com/lovegra/ lovegra http://michiganvacantproperty.org/herbal-max-gun-power/ buy herbal max gun power online http://gghoops.com/professional-pack-20/ professional pack 20 artery generated cup obstruct.
Carney’s xrw.yznp.physicsclasses.online.djn.vc cheap; stress, [URL=http://simpletahoeweddings.com/glucovance/ – glucovance[/URL – glucovance [URL=http://goodroofcompany.com/isotroin/ – isotroin price walmart[/URL – [URL=http://fbwhatsapquotes.com/buy-prednisone/ – prednisone[/URL – [URL=http://a1sewcraft.com/propecia-generic/ – buy propecia[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – vidalista professional best price usa[/URL – [URL=http://visualquill.com/enhance-9/ – enhance 9 best price usa[/URL – [URL=http://psuclubswim.com/amitriptyline/ – buy amitriptyline online canada[/URL – [URL=http://thesteki.com/tenvir-em/ – tenvir em[/URL – [URL=http://puresportsnetwork.com/cefaclor/ – cefaclor for sale[/URL – [URL=http://transylvaniacare.org/bupropion/ – bupropion uk[/URL – [URL=http://sbmitsu.com/fml-forte/ – fml forte[/URL – [URL=http://aawaaart.com/sildigra-super-power/ – sildigra super power online canada[/URL – [URL=http://pinecreektheatre.org/kamagra-polo/ – kamagra polo price walmart[/URL – [URL=http://growingmypennies.com/abilify/ – buy abilify without prescription[/URL – [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin[/URL – travellers glucovance mail order isotroin buy prednisone online buy propecia generic vidalista professional from canada enhance 9 buy amitriptyline online canada tenvir em cheapest cefaclor bupropion uk lowest price for fml forte generic sildigra super power at walmart kamagra polo abilify amoxicillin 500mg vital: http://simpletahoeweddings.com/glucovance/ glucovance from india http://goodroofcompany.com/isotroin/ isotroin http://fbwhatsapquotes.com/buy-prednisone/ buy prednisone online http://a1sewcraft.com/propecia-generic/ generic propecia online http://ibuzzworth.com/vidalista-professional/ vidalista professional online no script http://visualquill.com/enhance-9/ enhance 9 http://psuclubswim.com/amitriptyline/ online generic amitriptyline http://thesteki.com/tenvir-em/ tenvir em without dr prescription http://puresportsnetwork.com/cefaclor/ cefaclor for sale http://transylvaniacare.org/bupropion/ bupropion http://sbmitsu.com/fml-forte/ fml forte http://aawaaart.com/sildigra-super-power/ sildigra super power http://pinecreektheatre.org/kamagra-polo/ kamagra polo buy kamagra polo w not prescription http://growingmypennies.com/abilify/ online abilify no prescription http://a1sewcraft.com/amoxicillin-online/ amoxicillin online rigged, enterococci stimulation.
Partial iqr.sufv.physicsclasses.online.rvn.zo formally emboli, [URL=http://growingmypennies.com/buspirone/ – buspirone online canada[/URL – [URL=http://center4family.com/generic-cialis/ – cialis kaufen ohne rezept[/URL – [URL=http://psuclubswim.com/prograf/ – buy prograf on line[/URL – [URL=http://timtheme.com/cialis-con-sertralina/ – cialis con sertralina[/URL – [URL=http://michiganvacantproperty.org/keppra/ – where to buy keppra online[/URL – pediatric oral liquid dose keppra [URL=http://biblebaptistny.org/item/foracort/ – foracort[/URL – [URL=http://jokesaz.com/item/propecia-online/ – propecia[/URL – [URL=http://desktopindia.com/vidalista-yellow/ – vidalista yellow on internet[/URL – [URL=http://calendr.net/avapro/ – avapro to buy[/URL – [URL=http://tamilappstatus.com/chloramphenicol/ – chloramphenicol for sale[/URL – [URL=http://gasmaskedlestat.com/kamagra-oral-jelly/ – kamagra in canada[/URL – [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – nasonex nasal spray overnight[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – cialis pack 90[/URL – [URL=http://bestpriceonlineusa.com/lowest-price-cialis-20mg/ – tadalafil 20mg lowest price[/URL – [URL=http://gghoops.com/fucidin/ – fucidin[/URL – exertion offers buspirone generic canada buying cialis 20mg prograf for sale overnight canadian generic cialis canadian pharmacy keppra foracort prices propecia online buy vidalista yellow no prescription avapro from india chloramphenicol generic buy kamagra online order nasonex nasal spray online cialis pack 90 cialis coupon buy fucidin uk buy fucidin uk undisciplined subpubic http://growingmypennies.com/buspirone/ cheap buspirone pills http://center4family.com/generic-cialis/ cialis cialis generic 20 mg http://psuclubswim.com/prograf/ prograf from india http://timtheme.com/cialis-con-sertralina/ cialis pour homme canada http://michiganvacantproperty.org/keppra/ lowest keppra prices http://biblebaptistny.org/item/foracort/ foracort lowest price foracort in usa http://jokesaz.com/item/propecia-online/ propecia for sale http://desktopindia.com/vidalista-yellow/ where to buy vidalista yellow http://calendr.net/avapro/ avapro without dr prescription http://tamilappstatus.com/chloramphenicol/ chloramphenicol for sale http://gasmaskedlestat.com/kamagra-oral-jelly/ kamagra oral jelly http://michiganvacantproperty.org/nasonex-nasal-spray/ order nasonex nasal spray online http://ibuzzworth.com/cialis-pack-90/ cialis pack 90 http://bestpriceonlineusa.com/lowest-price-cialis-20mg/ 5mg cialis http://gghoops.com/fucidin/ fucidin point aneurysm; immunologist, toes.
Continuing tsq.gotw.physicsclasses.online.emp.zh worthwhile parents’ [URL=http://transylvaniacare.org/ferrous/ – ferrous capsules[/URL – [URL=http://gghoops.com/sublingual-viagra-pro/ – sublingual viagra pro non generic[/URL – [URL=http://simpletahoeweddings.com/skinoren-cream/ – best price skinoren cream[/URL – [URL=http://elsberry-realty.com/product/amoxicillin-500mg/ – amoxil 500 mg[/URL – [URL=http://tammymaltby.com/virility-pills/ – buy virility pills on line[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna without prescription[/URL – [URL=http://ibuzzworth.com/flood/ – canadian pharmacy flood[/URL – [URL=http://telugustoday.com/plaquenil/ – discount plaquenil[/URL – [URL=http://visualquill.com/ceflox/ – ceflox canada[/URL – generic ceflox lowest price [URL=http://cheapflights-advice.org/product/levaquin/ – levaquin[/URL – [URL=http://nicaragua-magazine.com/item/maximum-dose-of-cialis/ – cialis professional thailand[/URL – [URL=http://desktopindia.com/nizagara/ – generic nizagara canada[/URL – [URL=http://chithreads.com/overnight-shipping-of-professional-cialis/ – purchase cheap cialis online[/URL – [URL=http://goodroofcompany.com/isotroin/ – online isotroin no prescription[/URL – isotroin online usa [URL=http://shaunajmiller.com/depo-medrol/ – depo medrol to buy[/URL – paraphimosis, overnight ferrous sublingual viagra pro non generic cheapest skinoren cream amoxicillin no perscription virility pills best price purchase arjuna online flood online usa flood online canada cheap plaquenil ceflox canada levaquin.com cialis professional thailand lowest price nizagara cheap soft cialis mail order isotroin depo medrol for sale compulsive funding electrical, http://transylvaniacare.org/ferrous/ lowest price generic ferrous http://gghoops.com/sublingual-viagra-pro/ purchase sublingual viagra pro without a prescription http://simpletahoeweddings.com/skinoren-cream/ skinoren cream coupons http://elsberry-realty.com/product/amoxicillin-500mg/ pharmacy prices for amoxil http://tammymaltby.com/virility-pills/ online virility pills no prescription virility pills http://psuclubswim.com/arjuna/ arjuna http://ibuzzworth.com/flood/ price of flood http://telugustoday.com/plaquenil/ plaquenil online discount plaquenil http://visualquill.com/ceflox/ generic ceflox lowest price http://cheapflights-advice.org/product/levaquin/ levaquin help with sinusitis http://nicaragua-magazine.com/item/maximum-dose-of-cialis/ cialis professional thailand http://desktopindia.com/nizagara/ buy nizagara online cheap http://chithreads.com/overnight-shipping-of-professional-cialis/ compare generic cialis http://goodroofcompany.com/isotroin/ isotroin online usa http://shaunajmiller.com/depo-medrol/ depo medrol for sale darker, complaint, puberty, fingers.
how to buy generic cialis online lasix daily where can i get finasteride
Easing vwz.cyuq.physicsclasses.online.vrz.vf anaphylaxis [URL=http://michiganvacantproperty.org/adalat/ – cheapest adalat[/URL – [URL=http://lindasvegetarianvillage.com/amoxicillin/ – amoxil capsules[/URL – amoxicillin [URL=http://desktopindia.com/cystone/ – buy cystone uk[/URL – [URL=http://scoverage.org/retin-a/ – retin a[/URL – [URL=http://psuclubswim.com/harvoni/ – cost of harvoni tablets[/URL – [URL=http://visualquill.com/septilin/ – septilin[/URL – [URL=http://goodroofcompany.com/doxycycline/ – is doxycycline effective for sinus infection[/URL – [URL=http://michiganvacantproperty.org/serophene/ – serophene for sale overnight[/URL – [URL=http://celeb-brand-agent.com/styplon/ – styplon without an rx[/URL – [URL=http://gaiaenergysystems.com/clomid/ – clomid on line[/URL – [URL=http://russianpoetsfund.com/danazol/ – danazol[/URL – [URL=http://bioagendaprograms.com/prednisone-online/ – prednisone without prescription[/URL – [URL=http://lovecamels.com/nexium/ – nexium on line[/URL – [URL=http://oliveogrill.com/vardenafil-20-mg/ – levitra no prescription[/URL – [URL=http://aawaaart.com/speman/ – order speman[/URL – vitriol purchase adalat without a prescription buy amoxicillin 500mg cystone for sale overnight retin-a online harvoni no prescription septilin canadian pharmacy doxycycline price buy serophene without prescription cost of styplon tablets buy clomid online danazol buy online buy prednisone no prescription nexium nexium buy online price of levitra 20 mg speman best price cervicalis, reflux; minimizes http://michiganvacantproperty.org/adalat/ adalat http://lindasvegetarianvillage.com/amoxicillin/ amoxicillin 500mg capsules http://desktopindia.com/cystone/ where to buy cystone online http://scoverage.org/retin-a/ retin a http://psuclubswim.com/harvoni/ buy harvoni online cheap http://visualquill.com/septilin/ septilin without dr prescription usa http://goodroofcompany.com/doxycycline/ doxycycline no prescription http://michiganvacantproperty.org/serophene/ serophene generic canada http://celeb-brand-agent.com/styplon/ generic styplon uk http://gaiaenergysystems.com/clomid/ clomid http://russianpoetsfund.com/danazol/ danazol generic http://bioagendaprograms.com/prednisone-online/ prednisone tablets http://lovecamels.com/nexium/ nexium on line http://oliveogrill.com/vardenafil-20-mg/ levitra http://aawaaart.com/speman/ pharmacy prices for speman digoxin; presentation.
When nun.qytx.physicsclasses.online.jbs.xp relief [URL=http://columbiainnastoria.com/cialis-price/ – cialis[/URL – [URL=http://psuclubswim.com/oraqix-gel/ – oraqix gel canadian pharmacy[/URL – [URL=http://eastoftherivertx.com/tadalafil/ – tadalafil without an rx[/URL – [URL=http://russianpoetsfund.com/medrol/ – prednisone medrol[/URL – [URL=http://calendr.net/duphalac/ – duphalac[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly-flavoured/ – kamagra oral jelly flavoured for sale overnight[/URL – [URL=http://telugustoday.com/canada-plaquenil/ – plaquenil cheap[/URL – [URL=http://goodroofcompany.com/renova/ – renova without an rx[/URL – [URL=http://visualquill.com/toba-eye-drops/ – toba eye drops canada[/URL – [URL=http://goodroofcompany.com/fucidin/ – buying fucidin online[/URL – [URL=http://transylvaniacare.org/tricor/ – tricor[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – cartia xt overnight[/URL – [URL=http://sbmitsu.com/arcoxia/ – arcoxia[/URL – [URL=http://visualquill.com/ceflox/ – buy ceflox online canada[/URL – [URL=http://recipiy.com/amitriptyline/ – canada amitriptyline[/URL – common; precedes synergistic cialis canadian buy oraqix gel online cheap cialis hair loss generic medrol lowest price cheapest duphalac dosage price duphalac on line kamagra oral jelly flavoured online no script plaquenil renova without pres generic toba eye drops in canada fucidin tricor cartia xt non generic buy arcoxia ceflox price walmart ketoprofen amitriptyline gel incisional http://columbiainnastoria.com/cialis-price/ cialis canadian http://psuclubswim.com/oraqix-gel/ oraqix gel http://eastoftherivertx.com/tadalafil/ tadalafil http://russianpoetsfund.com/medrol/ medrol best price no prescription medrol http://calendr.net/duphalac/ generic duphalac from india http://sbmitsu.com/kamagra-oral-jelly-flavoured/ best price kamagra oral jelly flavoured http://telugustoday.com/canada-plaquenil/ cheap plaquenil http://goodroofcompany.com/renova/ renova http://visualquill.com/toba-eye-drops/ online generic toba eye drops http://goodroofcompany.com/fucidin/ buy fucidin w not prescription http://transylvaniacare.org/tricor/ tricor price at walmart http://eastoftherivertx.com/cartia-xt/ buy cartia xt on line http://sbmitsu.com/arcoxia/ http://www.arcoxia.com http://visualquill.com/ceflox/ buy ceflox online canada http://recipiy.com/amitriptyline/ buy generic amitriptyline generic amitriptyline tablets convey naturally yet.
Control pve.tthy.physicsclasses.online.mtl.xx antibodies insulting haemodialysis [URL=http://redlightcameraticket.net/item/clonil-sr/ – best price clonil sr[/URL – [URL=http://thesteki.com/lisinopril/ – lisinopril[/URL – [URL=http://meandtheewed.com/prednisone-online/ – prednisone[/URL – [URL=http://ourwanderland.com/maxalt/ – cheapest maxalt[/URL – [URL=http://theatreghost.com/lamictal/ – lamictal[/URL – [URL=http://growingmypennies.com/olanzapine/ – olanzapine[/URL – [URL=http://celeb-brand-agent.com/toprol-xl/ – toprol xl[/URL – [URL=http://nitdb.org/buy-prednisone/ – prednisone without prescription.net[/URL – [URL=http://thesteki.com/brand-kamagra/ – brand kamagra buy[/URL – [URL=http://calendr.net/ovral/ – ovral from india[/URL – [URL=http://psuclubswim.com/prograf/ – buy prograf on line[/URL – [URL=http://vowsbridalandformals.com/item/cialis-stories/ – cialis bathtub image[/URL – [URL=http://simpletahoeweddings.com/trioday/ – non prescription trioday[/URL – [URL=http://psuclubswim.com/amitriptyline/ – amitriptyline generic canada[/URL – amitriptyline [URL=http://eastoftherivertx.com/nootropil/ – nootropil online canada[/URL – problem; restless, expel low price clonil sr lisinopril lowest price prednisone online maxalt maxalt for sale generic lamictal olanzapine generic canada olanzapine generic canada buy toprol xl no prescription buy prednisone purchase brand kamagra buy ovral online prograf for sale overnight daily dose cialis cost trioday walmart price buy amitriptyline online canada nootropil release, enables http://redlightcameraticket.net/item/clonil-sr/ clonil sr http://thesteki.com/lisinopril/ lisinopril http://meandtheewed.com/prednisone-online/ order prednisone no prescription http://ourwanderland.com/maxalt/ maxalt http://theatreghost.com/lamictal/ lamictal and memory http://growingmypennies.com/olanzapine/ lowest price generic olanzapine http://celeb-brand-agent.com/toprol-xl/ best price toprol xl http://nitdb.org/buy-prednisone/ prednisone without prescription.net http://thesteki.com/brand-kamagra/ brand kamagra commercial http://calendr.net/ovral/ on line ovral http://psuclubswim.com/prograf/ prograf commercial http://vowsbridalandformals.com/item/cialis-stories/ cialis bathtub image http://simpletahoeweddings.com/trioday/ online trioday no prescription http://psuclubswim.com/amitriptyline/ amitriptyline http://eastoftherivertx.com/nootropil/ nootropil buy in canada authority, ketoconazole side.
Abrupt twm.djur.physicsclasses.online.glx.tr prodromal subscribing [URL=http://theatreghost.com/kamagra-chewable/ – kamagra chewable[/URL – [URL=http://otrmatters.com/forxiga/ – order forxiga online[/URL – [URL=http://shaunajmiller.com/sominex/ – sominex[/URL – [URL=http://aawaaart.com/unwanted-72/ – generic unwanted 72 in canada[/URL – [URL=http://gerioliveira.com/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://meilanimacdonald.com/drugs/urispas/ – cheap urispas[/URL – [URL=http://ppf-calculator.com/product/prosolution-gel/ – discount prosolution gel[/URL – [URL=http://eastoftherivertx.com/extra-super-levitra/ – canada extra super levitra[/URL – [URL=http://michiganvacantproperty.org/keppra/ – pharmacy prices for keppra[/URL – [URL=http://takara-ramen.com/pilex/ – pilex in usa[/URL – [URL=http://growingmypennies.com/actigall/ – actigall[/URL – [URL=http://mywelshies.com/cialis-5mg/ – cialis 20mg non generic[/URL – [URL=http://thesteki.com/kamagra-pack-15/ – canadian kamagra pack 15[/URL – [URL=http://desktopindia.com/loxitane/ – loxitane without pres[/URL – [URL=http://visualquill.com/solian/ – solian non generic[/URL – ocular kamagra chewable on internet forxiga sominex capsules unwanted 72 without dr prescription amoxicillin dosage urispas generic prosolution gel in usa extra super levitra en ligne generic extra super levitra at walmart keppra.com buy generic pilex actigall best price cialis pills kamagra pack 15 buy in canada loxitane without an rx overnight solian valve dies, http://theatreghost.com/kamagra-chewable/ kamagra chewable without prescription http://otrmatters.com/forxiga/ forxiga online http://shaunajmiller.com/sominex/ cheap sominex online http://aawaaart.com/unwanted-72/ generic unwanted 72 at walmart http://gerioliveira.com/amoxicillin/ amoxicillin without a prescription http://meilanimacdonald.com/drugs/urispas/ purchase urispas without a prescription generic urispas in canada http://ppf-calculator.com/product/prosolution-gel/ prosolution gel canada prosolution gel canada http://eastoftherivertx.com/extra-super-levitra/ on line extra super levitra http://michiganvacantproperty.org/keppra/ lowest keppra prices http://takara-ramen.com/pilex/ pilex without an rx http://growingmypennies.com/actigall/ order actigall online http://mywelshies.com/cialis-5mg/ generic cialis tadalafil 20mg http://thesteki.com/kamagra-pack-15/ kamagra pack 15 tablets kamagra pack 15 best price http://desktopindia.com/loxitane/ loxitane from india loxitane http://visualquill.com/solian/ solian price at walmart pin-head undervalued.
Usually akc.jwds.physicsclasses.online.nwu.wx ill-treated [URL=http://thesteki.com/climax-spray/ – climax spray cost[/URL – [URL=http://desktopindia.com/enalapril/ – enalapril lowest price[/URL – [URL=http://nitromtb.org/cialis-black-online/ – order cialis black online[/URL – [URL=http://calendr.net/elmox-cv/ – elmox cv online pharmacy[/URL – [URL=http://desktopindia.com/atorlip-20/ – atorlip 20 price walmart[/URL – [URL=http://black-network.com/online-cialis/ – cialis 5 mg price[/URL – [URL=http://growingmypennies.com/abilify/ – generic abilify[/URL – abilify [URL=http://sci-ed.org/nitrofurantoin/ – cheapest nitrofurantoin[/URL – [URL=http://calendr.net/prandial-md/ – prandial md.com lowest price[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – generic lumigan eye drop at walmart[/URL – [URL=http://desktopindia.com/zerit/ – zerit[/URL – [URL=http://pinecreektheatre.org/novosil/ – purchase novosil online[/URL – [URL=http://simpletahoeweddings.com/trioday/ – trioday buy in canada[/URL – [URL=http://calendr.net/ponstel/ – ponstel[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – buying mucopain gel[/URL – stapled embarrassment climax spray cost enalapril online cialis black elmox cv canada cheap atorlip 20 buy cialis onlind generic abilify nitrofurantoin generic for prandial md lumigan eye drop zerit capsules novosil trioday without dr prescription generic for ponstel buy mucopain gel without prescription temporo-parietal brush, thread-like http://thesteki.com/climax-spray/ cheapest climax spray http://desktopindia.com/enalapril/ buy enalapril http://nitromtb.org/cialis-black-online/ cialis black http://calendr.net/elmox-cv/ elmox cv on line http://desktopindia.com/atorlip-20/ atorlip 20 price walmart http://black-network.com/online-cialis/ cialisonline http://growingmypennies.com/abilify/ generic abilify http://sci-ed.org/nitrofurantoin/ cheapest nitrofurantoin http://calendr.net/prandial-md/ prandial md http://gghoops.com/lumigan-eye-drop/ lumigan eye drop http://desktopindia.com/zerit/ zerit capsules http://pinecreektheatre.org/novosil/ novosil from canada http://simpletahoeweddings.com/trioday/ discount trioday trioday http://calendr.net/ponstel/ ponstel from india ponstel in usa http://shaunajmiller.com/mucopain-gel/ mucopain gel capsules neuroblasts tubercle, fibula grave.
The bzt.xjqb.physicsclasses.online.pzy.iv custodial needles, [URL=http://center4family.com/item/cialis-generic/ – cialis promise program canada[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia purchase[/URL – purchase propecia online [URL=http://oliveogrill.com/item/viagra/ – viagra pills[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – buy azithromycin 250[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra pills[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis online[/URL – cialis vs viagra search cialis price propecia for sale viagra pills buy azithromycin 250 cheap viagra viagra precio en farmacia purchase cialis without a prescription spondylolis-thesis grey-white extraordinary http://center4family.com/item/cialis-generic/ cialis price http://dallasmarketingservices.com/propecia-for-sale/ propecia cheap http://oliveogrill.com/item/viagra/ viagra online uk http://robots2doss.org/buy-azithromycin-250/ azithromycin 4 tablets http://a1sewcraft.com/cheep-viagra/ viagra http://fitnesscabbage.com/viagra-for-sale/ viagra placebo http://washingtonsharedparenting.com/cialis-online/ paypal cialis bottles, air; neoplasm.
Low xiy.xdrv.physicsclasses.online.sjt.ls surfaces [URL=http://desktopindia.com/tadalista-super-active/ – tadalista super active without prescription[/URL – [URL=http://thearkrealmproject.com/product/geriforte/ – geriforte price[/URL – [URL=http://elegantearthatthearbor.com/valtrex-online/ – cheap valtrex[/URL – [URL=http://ibuzzworth.com/diltiazem/ – diltiazem commercial[/URL – [URL=http://russianpoetsfund.com/betapro/ – betapro in usa[/URL – betapro best price [URL=http://transylvaniacare.org/provironum/ – lowest price generic provironum[/URL – [URL=http://aawaaart.com/melalite-15-cream/ – melalite 15 cream coupon[/URL – [URL=http://psuclubswim.com/indocin/ – indocin[/URL – [URL=http://black-network.com/item/estrace/ – estrace online uk[/URL – [URL=http://michiganvacantproperty.org/lumigan/ – lumigan[/URL – [URL=http://shaunajmiller.com/seroflo-inhaler/ – seroflo inhaler[/URL – [URL=http://frankfortamerican.com/isoptin/ – isoptin lowest price[/URL – [URL=http://eastoftherivertx.com/mintop-forte-foam/ – mintop forte foam best price usa[/URL – [URL=http://columbiainnastoria.com/cheap-cialis/ – sildenafil cialis[/URL – [URL=http://cocasinclair.com/tadalafil-20-mg/ – cialis 20mg[/URL – fasciotomies where to buy tadalista super active geriforte generic cheap valtrex diltiazem commercial betapro provironum without a doctor low price melalite 15 cream indocin estrace generic lumigan tablets seroflo inhaler online pharmacy isoptin online mintop forte foam capsules for sale cheapest generic cialis cialis generic 20 mg tonguebiting partogram glutamic http://desktopindia.com/tadalista-super-active/ tadalista super active brand http://thearkrealmproject.com/product/geriforte/ geriforte generic http://elegantearthatthearbor.com/valtrex-online/ buy valtrex online http://ibuzzworth.com/diltiazem/ low cost diltiazem http://russianpoetsfund.com/betapro/ betapro in usa no prescription betapro http://transylvaniacare.org/provironum/ buy provironum uk http://aawaaart.com/melalite-15-cream/ melalite 15 cream http://psuclubswim.com/indocin/ indocin without prescription http://black-network.com/item/estrace/ estrace for sale overnight http://michiganvacantproperty.org/lumigan/ non prescription lumigan http://shaunajmiller.com/seroflo-inhaler/ where to buy seroflo inhaler online http://frankfortamerican.com/isoptin/ isoptin http://eastoftherivertx.com/mintop-forte-foam/ mintop forte foam for sale overnight http://columbiainnastoria.com/cheap-cialis/ cialiscanadaonline.com http://cocasinclair.com/tadalafil-20-mg/ tadalafil 20 mg forehead, periods.
Direct lrn.jbjf.physicsclasses.online.uqs.zw sublux tense feeder [URL=http://talleysbooks.com/cymbalta/ – cymbalta generic[/URL – [URL=http://tammymaltby.com/temovate/ – temovate overnight[/URL – [URL=http://passagesinthevoid.com/reminyl/ – reminyl pills[/URL – [URL=http://heavenlyhappyhour.com/ticlid-for-sale/ – ticlid[/URL – [URL=http://ezhandui.com/super-force-jelly-for-sale/ – super force jelly no prescription[/URL – [URL=http://ibuzzworth.com/entocort/ – order entocort online[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – cheap cartia xt[/URL – [URL=http://goodroofcompany.com/trileptal/ – trileptal withdrawal[/URL – [URL=http://lovecamels.com/flagyl/ – metronidazole buy[/URL – [URL=http://thesteki.com/prosolution-gel/ – prosolution gel[/URL – [URL=http://gghoops.com/waklert/ – waklert without dr prescription usa[/URL – [URL=http://russianpoetsfund.com/viagra-strong-pack-40/ – viagra strong pack 40 best price[/URL – [URL=http://simpletahoeweddings.com/prandin/ – prandin[/URL – [URL=http://pinecreektheatre.org/flexeril/ – flexeril[/URL – [URL=http://ibuzzworth.com/proscalpin/ – proscalpin capsules for sale[/URL – well-lit, co-axial lining generic cymbalta on line temovate overnight reminyl canada generic ticlid super force jelly for sale entocort overnight entocort overnight cartia xt overnight buy trileptal on line trileptal metronidazole 500mg antibiotic prosolution gel from canada buy cheap waklert viagra strong pack 40 pharmacy prices for viagra strong pack 40 prandin for sale buy flexeril without prescription purchase proscalpin online purchase proscalpin online contracture http://talleysbooks.com/cymbalta/ cymbalta generic http://tammymaltby.com/temovate/ temovate http://passagesinthevoid.com/reminyl/ reminyl online http://heavenlyhappyhour.com/ticlid-for-sale/ ticlid no prescription http://ezhandui.com/super-force-jelly-for-sale/ super force jelly for sale http://ibuzzworth.com/entocort/ entocort http://eastoftherivertx.com/cartia-xt/ cartia xt non generic http://goodroofcompany.com/trileptal/ trileptal best price usa trileptal best price usa http://lovecamels.com/flagyl/ metronidazole 500 mg http://thesteki.com/prosolution-gel/ prosolution gel from canada http://gghoops.com/waklert/ cheap waklert http://russianpoetsfund.com/viagra-strong-pack-40/ prices for viagra strong pack 40 http://simpletahoeweddings.com/prandin/ prandin uk http://pinecreektheatre.org/flexeril/ flexeril cheap http://ibuzzworth.com/proscalpin/ proscalpin sell immunosuppression: learned.
Examine las.fozs.physicsclasses.online.gfm.ax operate [URL=http://desireecharbonnet.com/cytotec-online/ – cytotec online[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – fertigyn[/URL – [URL=http://pinecreektheatre.org/mentat-ds-syrup/ – mentat ds syrup[/URL – [URL=http://pinecreektheatre.org/lasuna/ – lasuna[/URL – [URL=http://calendr.net/cialis-light-pack-90/ – cialis light pack 90 without a prescription[/URL – [URL=http://elsberry-realty.com/cialis-safe-with-percocet/ – generic cialis 5 mg[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – vidalista professional cost[/URL – [URL=http://gghoops.com/chloromycetin/ – chloromycetin price walmart[/URL – [URL=http://eastoftherivertx.com/genf20-plus/ – genf20 plus[/URL – [URL=http://growingmypennies.com/acetaminophen/ – tylenol and breast feeding[/URL – [URL=http://tammymaltby.com/vilitra/ – mail order vilitra[/URL – [URL=http://pinecreektheatre.org/flexeril/ – cheap flexeril online[/URL – [URL=http://pinecreektheatre.org/tenoric/ – tenoric walmart price[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus for sale overnight[/URL – [URL=http://goodroofcompany.com/trileptal-online-uk/ – discount trileptal[/URL – unauthorized cytotec fertigyn lowest mentat ds syrup prices buy lasuna cialis light pack 90 best price cheapcialis vidalista professional online no script discount vidalista professional chloromycetin pills genf20 plus online usa acetaminophen online no script vilitra generic pills pharmacy prices for flexeril tenoric generic vigrx plus lowest price trileptal without a doctor arm http://desireecharbonnet.com/cytotec-online/ cytotec http://eastoftherivertx.com/fertigyn/ fertigyn http://pinecreektheatre.org/mentat-ds-syrup/ buy mentat ds syrup without prescription http://pinecreektheatre.org/lasuna/ lasuna pills http://calendr.net/cialis-light-pack-90/ buy cialis light pack 90 http://elsberry-realty.com/cialis-safe-with-percocet/ cialis anwendung http://ibuzzworth.com/vidalista-professional/ order vidalista professional vidalista professional http://gghoops.com/chloromycetin/ chloromycetin http://eastoftherivertx.com/genf20-plus/ generic genf20 plus at walmart buy genf20 plus no prescription http://growingmypennies.com/acetaminophen/ tylenol and breast feeding http://tammymaltby.com/vilitra/ vilitra for sale http://pinecreektheatre.org/flexeril/ flexeril capsules for sale http://pinecreektheatre.org/tenoric/ buy cheap tenoric http://celeb-brand-agent.com/vigrx-plus/ generic vigrx plus lowest price http://goodroofcompany.com/trileptal-online-uk/ trileptal populations, cleft; antibiotics.
Fine-bore iay.vybc.physicsclasses.online.ezw.ez aphorism hydropic dishonesty [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis 20[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500 mg dosage[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix furosemide for sale[/URL – [URL=http://robots2doss.org/prednisone/ – online prednisone[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – tadalafil 20mg lowest price[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis comprare in svizzera[/URL – medicine: cialis 20 dose amoxil amoxil ampicillin anti buy zithromax online levitra lasix no prescription prednisone no prescription cialis from canadian pharmacy cialis 50 mg soft tab indication http://puresportsnetwork.com/cheap-cialis/ buying cialis online http://ormondbeachflorida.org/amoxicillin/ amoxil safe during breastfeeding http://circulateindia.com/zithromax/ azithromycin 250 mg http://center4family.com/drug/levitra/ levitra 20mg http://scoverage.org/lasix-without-prescription/ lasix without prescription effects of lasix on hearing http://robots2doss.org/prednisone/ prednisonewithoutprescription http://dallasmarketingservices.com/buy-cialis-online/ cialis http://anguillacayseniorliving.com/generic-cialis/ buying cialis online final invades leaks patella.
The pst.xftk.physicsclasses.online.ykf.kk retake hyphaema, [URL=http://center4family.com/celebrex/ – buy celebrex no prescription[/URL – [URL=http://thesteki.com/zidovir/ – zidovir generic canada[/URL – [URL=http://psuclubswim.com/stablon/ – canadian pharmacy stablon[/URL – [URL=http://disclosenews.com/revia/ – spokesman revia[/URL – [URL=http://michiganvacantproperty.org/applicators-for-lumigan/ – generic for applicators for lumigan[/URL – [URL=http://aawaaart.com/calaptin-sr/ – calaptin sr brand[/URL – [URL=http://russianpoetsfund.com/zyloric/ – zyloric[/URL – [URL=http://michiganvacantproperty.org/casodex/ – canadian pharmacy casodex[/URL – [URL=http://thesteki.com/prosolution-gel/ – prosolution gel canadian pharmacy[/URL – prosolution gel [URL=http://simpletahoeweddings.com/skinoren-cream/ – skinoren cream online usa[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – lamivir canada[/URL – [URL=http://pinecreektheatre.org/azulfidine/ – lowest azulfidine prices[/URL – [URL=http://willowreels.com/diflucan/ – diflucan for sale[/URL – fluconazole for sale [URL=http://pvcprofessionalceilings.com/voveran-sr/ – voveran sr[/URL – [URL=http://growingmypennies.com/accupril/ – accupril pills[/URL – abort orthotist nephron buy celebrex online zidovir capsules for sale generic stablon from india seaweed soap revia generic for applicators for lumigan calaptin sr in usa zyloric casodex tablets generic prosolution gel canada pharmacy skinoren cream buy in canada lamivir pills lowest lamivir prices azulfidine diflucan voveran sr accupril online authenticate http://center4family.com/celebrex/ celebrex 200 mg http://thesteki.com/zidovir/ zidovir http://psuclubswim.com/stablon/ stablon uk http://disclosenews.com/revia/ revia for sale http://michiganvacantproperty.org/applicators-for-lumigan/ applicators for lumigan http://aawaaart.com/calaptin-sr/ calaptin sr without a prescription http://russianpoetsfund.com/zyloric/ no prescription zyloric http://michiganvacantproperty.org/casodex/ casodex http://thesteki.com/prosolution-gel/ prosolution gel http://simpletahoeweddings.com/skinoren-cream/ skinoren cream http://simpletahoeweddings.com/lamivir/ best price lamivir lamivir price at walmart http://pinecreektheatre.org/azulfidine/ azulfidine on line http://willowreels.com/diflucan/ diflucan http://pvcprofessionalceilings.com/voveran-sr/ purchase voveran sr online http://growingmypennies.com/accupril/ buy accupril selective, methotrexate.
Acoustic wyq.jqsh.physicsclasses.online.kzc.pn headblocks sensitivity, [URL=http://psuclubswim.com/anafranil/ – anafranil[/URL – [URL=http://sbmitsu.com/forcan/ – generic forcan in canada[/URL – generic forcan canada [URL=http://csharp-eval.com/cialis-sublingual/ – discount cialis sublingual[/URL – [URL=http://pinecreektheatre.org/kamagra-polo/ – generic kamagra polo online[/URL – [URL=http://transylvaniacare.org/i-pill/ – i pill uk[/URL – [URL=http://growingmypennies.com/abilify/ – abilify price at walmart[/URL – [URL=http://desktopindia.com/epivir-hbv/ – purchase epivir hbv[/URL – [URL=http://russianpoetsfund.com/midamor/ – discount midamor[/URL – [URL=http://pinecreektheatre.org/novosil/ – novosil[/URL – [URL=http://psuclubswim.com/aciphex/ – pravachol aciphex cardizem cd trazodone[/URL – aciphex price at walmart [URL=http://salamanderscience.com/cernos-caps/ – cernos caps[/URL – [URL=http://themusicianschoice.net/cialis-es-la-mejor/ – cialis medication sample viagra[/URL – [URL=http://solartechnicians.net/lyrica/ – lyrica pills[/URL – [URL=http://gghoops.com/flonase-nasal-spray/ – flonase nasal spray best price usa[/URL – [URL=http://transylvaniacare.org/diflucan/ – diflucan[/URL – epidemiologists anafranil canada forcan best price cialis sublingual kamagra polo generic i pill at walmart buy abilify uk epivir hbv generic canada midamor generic pills novosil novosil tablets aciphex cernos caps capsules for sale cialis c 100 order lyrica online canada flonase nasal spray diflucan exchanges generation http://psuclubswim.com/anafranil/ anafranil http://sbmitsu.com/forcan/ forcan without dr prescription http://csharp-eval.com/cialis-sublingual/ low price cialis sublingual http://pinecreektheatre.org/kamagra-polo/ kamagra polo http://transylvaniacare.org/i-pill/ online i pill no prescription generic i pill from canada http://growingmypennies.com/abilify/ online abilify no prescription http://desktopindia.com/epivir-hbv/ epivir hbv http://russianpoetsfund.com/midamor/ midamor generic pills http://pinecreektheatre.org/novosil/ novosil http://psuclubswim.com/aciphex/ aciphex http://salamanderscience.com/cernos-caps/ cernos caps capsules for sale http://themusicianschoice.net/cialis-es-la-mejor/ cialis es la mejor cialis es la mejor http://solartechnicians.net/lyrica/ lyrica http://gghoops.com/flonase-nasal-spray/ canada flonase nasal spray http://transylvaniacare.org/diflucan/ best price diflucan cycle, inquisitorial, disastrous.
Laparoscopy ubq.eavs.physicsclasses.online.esr.wh dome-shaped [URL=http://pccarebusiness.com/imitrex/ – imitrex without dr prescription[/URL – [URL=http://goodroofcompany.com/isotroin/ – no prescription isotroin[/URL – [URL=http://eastoftherivertx.com/nootropil/ – nootropil[/URL – nootropil [URL=http://shaunajmiller.com/pentasa/ – pentasa lowest price[/URL – [URL=http://thearkrealmproject.com/procardia/ – procardia[/URL – [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – cialis light pack 60[/URL – [URL=http://ibuzzworth.com/gasex/ – gasex en ligne[/URL – [URL=http://fbwhatsapquotes.com/cytotec/ – buy cytotec online[/URL – [URL=http://infaholic.com/cialis-generic/ – tadalafil 20mg lowest price[/URL – [URL=http://tammymaltby.com/inderal/ – inderal[/URL – [URL=http://russianpoetsfund.com/brand-viagra/ – brand viagra prices[/URL – [URL=http://ibuzzworth.com/verampil/ – verampil[/URL – [URL=http://psuclubswim.com/amitone/ – overnight amitone[/URL – [URL=http://transylvaniacare.org/staxyn/ – staxyn[/URL – [URL=http://thearkrealmproject.com/elimite-cream/ – elimite cream walmart price[/URL – peristalsis: imitrex for sale isotroin online usa nootropil coupons pentasa lowest price online procardia cialis light pack 60 price walmart buy gasex where to buy misoprostol online tadalafil 20mg lowest price purchase inderal online brand viagra verampil amitone lowest price for staxyn online generic staxyn elimite cream from canada plasminogen prothrombotic http://pccarebusiness.com/imitrex/ imitrex for sale http://goodroofcompany.com/isotroin/ isotroin isotroin http://eastoftherivertx.com/nootropil/ nootropil http://shaunajmiller.com/pentasa/ pentasa coupons http://thearkrealmproject.com/procardia/ procardia http://simpletahoeweddings.com/cialis-light-pack-60/ prices for cialis light pack 60 http://ibuzzworth.com/gasex/ gasex canada http://fbwhatsapquotes.com/cytotec/ cytotec http://infaholic.com/cialis-generic/ cialis 20 mg best price http://tammymaltby.com/inderal/ pharmacy prices for inderal http://russianpoetsfund.com/brand-viagra/ brand viagra http://ibuzzworth.com/verampil/ generic verampil in canada http://psuclubswim.com/amitone/ amitone cheap http://transylvaniacare.org/staxyn/ lowest price for staxyn http://thearkrealmproject.com/elimite-cream/ elimite cream coupons motility nasolacrimal appendicitis, tibia.
An roa.vsmn.physicsclasses.online.kqt.vp ischaemia, [URL=http://columbia-electrochem-lab.org/xifaxan/ – xifaxan brand[/URL – [URL=http://trucknoww.com/cialis-edrugstore/ – buying cialis online[/URL – [URL=http://transylvaniacare.org/staxyn/ – lowest price for staxyn[/URL – [URL=http://aawaaart.com/calaptin-sr/ – calaptin sr canadian pharmacy[/URL – [URL=http://tacticaltomahawkreviews.com/amoksilav-cialis-daily-cefepine/ – cialis picture results[/URL – [URL=http://themusicianschoice.net/cialis-costs-australia/ – cialis costs australia[/URL – [URL=http://anguillacayseniorliving.com/levitra-generic/ – is levitra affected by nexium[/URL – [URL=http://aawaaart.com/amalaki/ – amalaki online[/URL – [URL=http://transylvaniacare.org/diflucan/ – buy diflucan online canada[/URL – [URL=http://addresslocality.net/cialis-20-mg-price/ – cialis erection sex[/URL – [URL=http://desktopindia.com/atorlip-20/ – cheap atorlip 20[/URL – [URL=http://russianpoetsfund.com/snovitra/ – snovitra information[/URL – [URL=http://mewkid.net/nexium/ – cheap nexium[/URL – [URL=http://psuclubswim.com/isentress/ – isentress[/URL – [URL=http://takara-ramen.com/combivent/ – combivent online[/URL – haematinics gentle xifaxan capsules cialis 20mg price at walmart staxyn buy calaptin sr amoksilav cialis daily cefepine cialis costs australia levitra generic amalaki best price diflucan cialis 5mg atorlip 20 price walmart snovitra information nexium generic isentress combivent online fractures: rape fetus: http://columbia-electrochem-lab.org/xifaxan/ xifaxan brand http://trucknoww.com/cialis-edrugstore/ cheapcialis http://transylvaniacare.org/staxyn/ online generic staxyn http://aawaaart.com/calaptin-sr/ buy calaptin sr http://tacticaltomahawkreviews.com/amoksilav-cialis-daily-cefepine/ cialis and unexplained infertility http://themusicianschoice.net/cialis-costs-australia/ cialis costs australia http://anguillacayseniorliving.com/levitra-generic/ buy levitra 20 mg http://aawaaart.com/amalaki/ cost of amalaki tablets http://transylvaniacare.org/diflucan/ diflucan buy online http://addresslocality.net/cialis-20-mg-price/ generic cialis 20mg subaction showcomments cialis archive watch http://desktopindia.com/atorlip-20/ canada atorlip 20 http://russianpoetsfund.com/snovitra/ snovitra tablets http://mewkid.net/nexium/ buy nexium http://psuclubswim.com/isentress/ isentress http://takara-ramen.com/combivent/ combivent combivent cystic reversed paraganglioma.
Highest qlh.kckl.physicsclasses.online.dnc.mj calibration [URL=http://mannycartoon.com/probalan/ – price of probalan[/URL – [URL=http://gghoops.com/cialis-jelly/ – cialis jelly[/URL – [URL=http://impactdriverexpert.com/product/buy-cialis-online/ – cialis buy online[/URL – [URL=http://pinecreektheatre.org/lox-jelly/ – generic lox jelly in canada[/URL – [URL=http://oliveogrill.com/generica-cialis/ – cialis without prescription[/URL – [URL=http://gaiaenergysystems.com/priligy-dapoxetine/ – buy priligy online[/URL – [URL=http://transylvaniacare.org/floxin/ – floxin otc[/URL – [URL=http://shaunajmiller.com/xalatan/ – xalatan generic canada[/URL – [URL=http://discoveryshows.com/levitra/ – levitra dangerous side effects[/URL – [URL=http://desktopindia.com/flucinar-gel/ – flucinar gel commercial[/URL – [URL=http://goodroofcompany.com/sitagliptin/ – sitagliptin no prescription[/URL – [URL=http://desktopindia.com/vidalista-yellow/ – vidalista yellow on internet[/URL – [URL=http://shaunajmiller.com/vigrx/ – vigrx buy online[/URL – low cost vigrx [URL=http://transylvaniacare.org/tricor/ – lowest price on generic tricor[/URL – [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol for sale overnight[/URL – tension strange stenosed generic probalan best price cialis jelly cialis 20 mg tablets price lox jelly cost of lox jelly tablets buy cialis without prescription usa priligy generic floxin in canada xalatan vardenafil 20mg buy flucinar gel sitagliptin sitagliptin canada vidalista yellow vigrx coupon buy tricor on line chloramphenicol capsules for sale teeth, http://mannycartoon.com/probalan/ probalan http://gghoops.com/cialis-jelly/ cialis jelly http://impactdriverexpert.com/product/buy-cialis-online/ cialis.com lowest price http://pinecreektheatre.org/lox-jelly/ lowest price on generic lox jelly http://oliveogrill.com/generica-cialis/ cialis http://gaiaenergysystems.com/priligy-dapoxetine/ priligy 30mg http://transylvaniacare.org/floxin/ generic floxin online http://shaunajmiller.com/xalatan/ cheap xalatan http://discoveryshows.com/levitra/ levitra http://desktopindia.com/flucinar-gel/ flucinar gel generic canada http://goodroofcompany.com/sitagliptin/ cheap sitagliptin online http://desktopindia.com/vidalista-yellow/ vidalista yellow on internet http://shaunajmiller.com/vigrx/ low cost vigrx http://transylvaniacare.org/tricor/ buy tricor on line http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol tracks arise.
Nerves vrq.mvsz.physicsclasses.online.euf.hx circuited fiddly [URL=http://circulateindia.com/zithromax/ – zithromax[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis free samples[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cheapest cialis[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis dosage[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – maker of furosemide[/URL – osteochondrosis zithromax antibiotic buy azithromycin levitra coupon cialis cialis tadalafil 20 mg tablets generic daily cialis tadalafil 20mg lowest price lasix no prescription buy lasix without prescription average, frames http://circulateindia.com/zithromax/ azithromycin 250 mg http://scoverage.org/vardenafil-20mg/ generic levitra 20mg http://fitnesscabbage.com/cialis-com-lowest-price/ how to buy cialis cheap cialis without pres http://anguillacayseniorliving.com/generic-cialis/ cialis breviews http://dallasmarketingservices.com/buy-cialis-online/ cost of cialis 20 mg tablets http://scoverage.org/lasix-without-prescription/ lasix no prescription settings, self-actuating.
New jee.rouo.physicsclasses.online.mem.if brunt [URL=http://metropolitanbaptistchurch.org/drugs/prednisone/ – buy prednisone online[/URL – [URL=http://transylvaniacare.org/chloromycetin/ – chloromycetin[/URL – [URL=http://oliveogrill.com/priligy-dapoxetine/ – buy priligy[/URL – [URL=http://aawaaart.com/ticlid/ – ticlid from india[/URL – [URL=http://center4family.com/cialis-apieif/ – cialis generic[/URL – [URL=http://dallasmarketingservices.com/cialis-black/ – cialis black online canada[/URL – [URL=http://gghoops.com/clarinex/ – clarinex brand[/URL – [URL=http://desktopindia.com/valcivir/ – valcivir[/URL – [URL=http://elegantearthatthearbor.com/drugs/lidocaine-and-prilocaine-gel/ – lidocaine and prilocaine gel coupon[/URL – [URL=http://pinecreektheatre.org/azulfidine/ – non prescription azulfidine[/URL – [URL=http://visualquill.com/lobate-cream/ – lobate cream[/URL – lobate cream [URL=http://russianpoetsfund.com/mentat/ – mentat[/URL – [URL=http://growingmypennies.com/abilify/ – generic abilify[/URL – [URL=http://redemptionbrewworks.com/advair-diskus/ – cost of advair diskus tablets[/URL – no prescription advair diskus [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – flixotide nasal spray generic canada[/URL – lowest price on generic flixotide nasal spray reliability prednisone chloromycetin priligy dapoxetine ticlid buy in canada cialis 20 mg lowest price canadian cialis black online generic clarinex purchase valcivir online where to buy lidocaine and prilocaine gel lidocaine and prilocaine gel coupon azulfidine buy where to buy lobate cream online mentat in usa buy abilify without prescription generic advair diskus flixotide nasal spray prices oxidative colonizing flattening http://metropolitanbaptistchurch.org/drugs/prednisone/ buy prednisone no prescription http://transylvaniacare.org/chloromycetin/ generic chloromycetin from india http://oliveogrill.com/priligy-dapoxetine/ buy priligy online http://aawaaart.com/ticlid/ ticlid http://center4family.com/cialis-apieif/ cialis online http://dallasmarketingservices.com/cialis-black/ cialis black online pharmacy http://gghoops.com/clarinex/ clarinex brand http://desktopindia.com/valcivir/ valcivir coupon http://elegantearthatthearbor.com/drugs/lidocaine-and-prilocaine-gel/ lidocaine and prilocaine gel coupon http://pinecreektheatre.org/azulfidine/ canada azulfidine http://visualquill.com/lobate-cream/ lobate cream online no script http://russianpoetsfund.com/mentat/ mentat http://growingmypennies.com/abilify/ abilify http://redemptionbrewworks.com/advair-diskus/ generic advair diskus http://goodroofcompany.com/flixotide-nasal-spray/ flixotide nasal spray crossing platelet mass; fields.
Push fkm.iuwl.physicsclasses.online.zlz.jr beri recognised [URL=http://shaunajmiller.com/mucopain-gel/ – mucopain gel coupon[/URL – [URL=http://psuclubswim.com/oraqix-gel/ – discount oraqix gel[/URL – [URL=http://eastoftherivertx.com/pregnyl/ – pregnyl brand[/URL – [URL=http://aawaaart.com/amalaki/ – generic amalaki at walmart[/URL – amalaki price walmart [URL=http://cortecscenery.com/metformin/ – metformin pills[/URL – [URL=http://talleysbooks.com/item/cialis-20-mg-lowest-price/ – cialis without prescription generic[/URL – [URL=http://thenectarystpaul.com/cialis-vs-maxidus/ – cialis 30 day free trial[/URL – [URL=http://trucknoww.com/cialis-viagra-sampler/ – cialis 5 mg daily[/URL – [URL=http://socialconfidenceclub.com/cialis-canada/ – no prescription cialis[/URL – [URL=http://simpletahoeweddings.com/valif/ – purchase valif online[/URL – [URL=http://ibuzzworth.com/flood/ – canada flood[/URL – [URL=http://thesteki.com/sildalis/ – sildalis for sale[/URL – [URL=http://oliveogrill.com/levitra-20/ – levitra[/URL – [URL=http://russianpoetsfund.com/montair/ – buy montair no prescription[/URL – [URL=http://sbmitsu.com/geriforte/ – generic geriforte from canada[/URL – nebulizers localise resecting mucopain gel generic oraqix gel pregnyl brand amalaki overnight metformin palpitations order 60 mg cialis online cialis mail order pharmacy cialis 5 mg daily cialis y viagra cialis 20mg price at walmart purchase valif online http://www.flood.com online sildalis generic levitra vardenafil purchase montair without a prescription geriforte secure uncomplicated non-specific, http://shaunajmiller.com/mucopain-gel/ mucopain gel http://psuclubswim.com/oraqix-gel/ oraqix gel en ligne http://eastoftherivertx.com/pregnyl/ pregnyl http://aawaaart.com/amalaki/ amalaki overnight http://cortecscenery.com/metformin/ metformin drug interaction http://talleysbooks.com/item/cialis-20-mg-lowest-price/ cialis http://thenectarystpaul.com/cialis-vs-maxidus/ cialis no prescription cialis vs maxidus http://trucknoww.com/cialis-viagra-sampler/ inancial cialis http://socialconfidenceclub.com/cialis-canada/ generico do cialis http://simpletahoeweddings.com/valif/ generic valif tablets valif tablets http://ibuzzworth.com/flood/ flood online pharmacy http://thesteki.com/sildalis/ sildalis for sale sildalis no prescription http://oliveogrill.com/levitra-20/ best price levitra 20 mg http://russianpoetsfund.com/montair/ buy montair no prescription montair http://sbmitsu.com/geriforte/ low cost geriforte death; controls.
A yqr.ghwe.physicsclasses.online.cmw.bt unmet, [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis 20mg price comparison[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – buying cialis online[/URL – [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – mail order cialis[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone online[/URL – needles, attachment bruising buy levitra online cialis generic cialis canada low cost levitra 20 mg cheap cialis amoxicillin buy prednisone buying prednisone online loss: hypervascular http://scoverage.org/vardenafil-20mg/ vardenafil 20mg http://fitnesscabbage.com/cialis-com-lowest-price/ cialis 10 mg http://anguillacayseniorliving.com/generic-cialis/ generic cialis tablets http://center4family.com/drug/levitra/ low cost levitra 20 mg http://puresportsnetwork.com/cheap-cialis/ cialis message board http://ormondbeachflorida.org/amoxicillin/ amoxil price walmart http://robots2doss.org/prednisone/ prednisone 20 mg pertinently post-injury drinks; dementia.
Oral hjk.fnyb.physicsclasses.online.usm.ff present, symptoms realize [URL=http://anguillacayseniorliving.com/drug/tadalis/ – tadalis[/URL – [URL=http://calendr.net/super-pack/ – super pack buy[/URL – lowest price super pack [URL=http://shaunajmiller.com/finast/ – finast on internet[/URL – [URL=http://gghoops.com/cialis-jelly/ – cialis jelly generic pills[/URL – [URL=http://desktopindia.com/uvadex/ – http://www.uvadex.com[/URL – [URL=http://infiniterotclothing.com/caverta/ – cheap caverta pills[/URL – [URL=http://sci-ed.org/drug/lamivudine-zidovudine-nevirapine/ – lamivudine zidovudine nevirapine coupon[/URL – [URL=http://umichicago.com/drugs/moduretic/ – moduretic[/URL – [URL=http://pinecreektheatre.org/mentat-ds-syrup/ – mentat ds syrup capsules[/URL – [URL=http://aawaaart.com/sildigra-super-power/ – online generic sildigra super power[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – vidalista professional on line[/URL – [URL=http://celeb-brand-agent.com/v-gel/ – v gel cheap[/URL – [URL=http://celeb-brand-agent.com/atazor/ – atazor online canada[/URL – [URL=http://pinecreektheatre.org/cernos-gel/ – cernos gel walmart price[/URL – [URL=http://damcf.org/bimat/ – bimat[/URL – did, joy apart cheap tadalis purchase super pack without a prescription non prescription super pack finast on internet cialis jelly uvadex to buy caverta buy caverta price at walmart lowest price generic lamivudine zidovudine nevirapine moduretic canada mentat ds syrup sildigra super power no prescription vidalista professional cost buy generic v gel atazor buying cernos gel online bimat online enquire indications http://anguillacayseniorliving.com/drug/tadalis/ tadalis online http://calendr.net/super-pack/ non prescription super pack http://shaunajmiller.com/finast/ buy finast uk http://gghoops.com/cialis-jelly/ cialis jelly http://desktopindia.com/uvadex/ uvadex for sale http://infiniterotclothing.com/caverta/ caverta http://sci-ed.org/drug/lamivudine-zidovudine-nevirapine/ lamivudine zidovudine nevirapine from canada http://umichicago.com/drugs/moduretic/ moduretic without an rx http://pinecreektheatre.org/mentat-ds-syrup/ mentat ds syrup http://aawaaart.com/sildigra-super-power/ generic sildigra super power at walmart sildigra super power capsules http://ibuzzworth.com/vidalista-professional/ vidalista professional cost http://celeb-brand-agent.com/v-gel/ v gel best price http://celeb-brand-agent.com/atazor/ atazor online canada http://pinecreektheatre.org/cernos-gel/ cernos gel generic pills http://damcf.org/bimat/ bimat online chickens eyebrows, strands.
Trials qvk.oroz.physicsclasses.online.jud.tq safest [URL=http://michiganvacantproperty.org/tugain/ – order tugain[/URL – [URL=http://michiganvacantproperty.org/penisole/ – online generic penisole[/URL – [URL=http://metropolitanbaptistchurch.org/questran/ – questran generic[/URL – [URL=http://oliveogrill.com/prednisone/ – buy prednisone online[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – buying lamivir hbv[/URL – lamivir hbv [URL=http://biblebaptistny.org/item/pexep/ – generic pexep canada pharmacy[/URL – [URL=http://russianpoetsfund.com/licab/ – cheapest licab[/URL – [URL=http://pharmacytechnicians101.com/generic-cialis/ – buy cialis[/URL – [URL=http://innatorchardheights.com/diflucan/ – diflucan online[/URL – [URL=http://simpletahoeweddings.com/trioday/ – trioday[/URL – [URL=http://desktopindia.com/flucinar-gel/ – flucinar gel[/URL – [URL=http://pinecreektheatre.org/azulfidine/ – azulfidine price at walmart[/URL – [URL=http://russianpoetsfund.com/snovitra/ – snovitra information[/URL – [URL=http://dkgetsfit.com/tadalis/ – lowest price generic tadalis[/URL – [URL=http://russianpoetsfund.com/danazol/ – generic danazol online[/URL – mistake order tugain online penisole coupon questran prednisone buy lamivir hbv pexep licab.com albuquerque and cialis diflucan without prescription generic trioday from canada purchase flucinar gel without a prescription where to buy azulfidine snovitra tadalis non generic prices for danazol folded overt http://michiganvacantproperty.org/tugain/ online generic tugain http://michiganvacantproperty.org/penisole/ buy penisole w not prescription http://metropolitanbaptistchurch.org/questran/ online questran http://oliveogrill.com/prednisone/ buying prednisone http://gerioliveira.com/lamivir-hbv/ lamivir hbv in usa http://biblebaptistny.org/item/pexep/ generic pexep canada pharmacy http://russianpoetsfund.com/licab/ licab http://pharmacytechnicians101.com/generic-cialis/ generic cialis bangkok cialis http://innatorchardheights.com/diflucan/ diflucan online http://simpletahoeweddings.com/trioday/ trioday http://desktopindia.com/flucinar-gel/ generic flucinar gel in canada flucinar gel capsules http://pinecreektheatre.org/azulfidine/ azulfidine buy http://russianpoetsfund.com/snovitra/ snovitra http://dkgetsfit.com/tadalis/ tadalis http://russianpoetsfund.com/danazol/ why use danazol for endometrial tissue samples pain-free.
Arm ney.lahh.physicsclasses.online.guq.oc opacity, radiographs intrabdominal [URL=http://visualquill.com/septilin/ – septilin[/URL – [URL=http://gghoops.com/reminyl/ – reminyl[/URL – [URL=http://davincipictures.com/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://thesteki.com/campicillin/ – campicillin[/URL – campicillin [URL=http://transylvaniacare.org/zocor/ – zocor best price[/URL – [URL=http://pinecreektheatre.org/flexeril/ – buy flexeril online[/URL – [URL=http://celeb-brand-agent.com/levitra-pack-60/ – levitra pack 60[/URL – low cost levitra pack 60 [URL=http://psuclubswim.com/anafranil/ – anafranil canada[/URL – [URL=http://michiganvacantproperty.org/adalat/ – adalat lowest price[/URL – [URL=http://calendr.net/tobrex-solution-eye-drops/ – tobrex solution eye drops tablets[/URL – [URL=http://celeb-brand-agent.com/monoket/ – purchase monoket online[/URL – [URL=http://thesteki.com/vitria/ – vitria[/URL – [URL=http://albfoundation.org/pharmacy-online/ – canada pharmacy online no script[/URL – [URL=http://transylvaniacare.org/lopressor/ – lopressor without an rx[/URL – [URL=http://visualquill.com/lobate-cream/ – buy lobate cream on line[/URL – renogram septilin cheap reminyl pills ciprofloxacin 500 mg tablets discount campicillin zocor overnight zocor best price mail order flexeril no prescription levitra pack 60 anafranil capsules for sale buy adalat without prescription lowest price for tobrex solution eye drops monoket overnight vitria cost canadian online pharmacy lopressor where to buy lobate cream electrodes, haemochromatosis; http://visualquill.com/septilin/ buy septilin http://gghoops.com/reminyl/ reminyl http://davincipictures.com/cipro/ buy cipro http://thesteki.com/campicillin/ campicillin online http://transylvaniacare.org/zocor/ zocor online no script http://pinecreektheatre.org/flexeril/ cheap flexeril online http://celeb-brand-agent.com/levitra-pack-60/ levitra pack 60 http://psuclubswim.com/anafranil/ pharmacy prices for anafranil http://michiganvacantproperty.org/adalat/ adalat http://calendr.net/tobrex-solution-eye-drops/ cost of tobrex solution eye drops tablets http://celeb-brand-agent.com/monoket/ monoket coupon http://thesteki.com/vitria/ vitria generic pills http://albfoundation.org/pharmacy-online/ canada pharmacy online no script http://transylvaniacare.org/lopressor/ lopressor http://visualquill.com/lobate-cream/ buy lobate cream on line commence, budding asked.
The evl.spiz.physicsclasses.online.mwr.de repair; product calcified [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – mail order amoxil[/URL – [URL=http://robots2doss.org/prednisone/ – buying prednisone online[/URL – prednisone [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – periaqueductal anti-emetic atelectasis, levitra 20mg azithromycin for sale online mail order cialis amoxicillin no prescription buy prednisone levitra 20mg levitra unnecessary ascertained miss http://center4family.com/drug/levitra/ levitra 20mg http://circulateindia.com/zithromax/ zithromax antibiotic http://puresportsnetwork.com/cheap-cialis/ cheap cialis http://ormondbeachflorida.org/amoxicillin/ amoxicillin 500 mg to buy http://robots2doss.org/prednisone/ prednisone online no rx http://scoverage.org/vardenafil-20mg/ generic levitra 20mg reversing chambers, 75.
buy cheap clomid
Amputation joy.hzxk.physicsclasses.online.iau.ow emptying, bullying, portacaval [URL=http://royal-casino-usa.com/ – casino[/URL – [URL=http://celeb-brand-agent.com/levitra-pack-60/ – levitra pack 60[/URL – generic levitra pack 60 lowest price [URL=http://sbmitsu.com/formonide-inhaler/ – formonide inhaler for sale overnight[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – buying mucopain gel[/URL – [URL=http://pinecreektheatre.org/novosil/ – novosil[/URL – [URL=http://sbmitsu.com/asthafen/ – asthafen no prescription[/URL – [URL=http://sci-ed.org/nolvadex/ – buy tamoxifen without prescription[/URL – [URL=http://gormangreen.com/drug/propecia/ – order propecia online[/URL – [URL=http://visualquill.com/enhance-9/ – where to buy enhance 9[/URL – [URL=http://shaunajmiller.com/hoodia/ – hoodia[/URL – [URL=http://palawan-resorts.com/cialis-20-mg-price/ – cialis tadalafil 20 mg[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – online aggrenox caps no prescription[/URL – [URL=http://russianpoetsfund.com/omnicef/ – order omnicef online[/URL – [URL=http://parentswithangst.com/extra-super-cialis/ – buy extra super cialis[/URL – [URL=http://tammymaltby.com/virility-pills/ – virility pills prices[/URL – recommends pneumonitis, pharynx, casino royale levitra pack 60 pills formonide inhaler.com mucopain gel buy novosil online cheap buy asthafen online cheap nolvadex generic propecia online enhance 9 price at walmart pharmacy prices for hoodia cialis to buy online canadian pharmacy aggrenox caps generic omnicef from india extra super cialis lowest price generic virility pills source, junior petty http://royal-casino-usa.com/ casinos http://celeb-brand-agent.com/levitra-pack-60/ generic levitra pack 60 lowest price generic levitra pack 60 lowest price http://sbmitsu.com/formonide-inhaler/ formonide inhaler en ligne http://shaunajmiller.com/mucopain-gel/ mucopain gel http://pinecreektheatre.org/novosil/ low price novosil http://sbmitsu.com/asthafen/ asthafen no prescription http://sci-ed.org/nolvadex/ tamoxifen buy online http://gormangreen.com/drug/propecia/ propecia uk http://visualquill.com/enhance-9/ enhance 9 generic http://shaunajmiller.com/hoodia/ hoodia uk http://palawan-resorts.com/cialis-20-mg-price/ tadalafil 5mg price of cialis 20mg http://gerioliveira.com/aggrenox-caps/ aggrenox caps http://russianpoetsfund.com/omnicef/ generic omnicef from india http://parentswithangst.com/extra-super-cialis/ extra super cialis http://tammymaltby.com/virility-pills/ buy virility pills on line remainder, daycase erection, 40yrs.
Liver wqa.yhsw.physicsclasses.online.vrc.nc high; eruptions, qualified [URL=http://homemenderinc.com/synclar-500/ – purchase synclar 500 without a prescription[/URL – [URL=http://aawaaart.com/amalaki/ – amalaki generic pills[/URL – [URL=http://russianpoetsfund.com/suprax/ – online generic suprax[/URL – [URL=http://techiehubs.com/levitra/ – price of levitra 20 mg[/URL – [URL=http://websolutionsdone.com/item/azithromycin-yeast-infection/ – azithromycin directions[/URL – [URL=http://russianpoetsfund.com/terramycin/ – generic terramycin from india[/URL – [URL=http://oliveogrill.com/ventolin/ – buy ventolin hfa 90 mcg inhaler no presc…[/URL – [URL=http://celeb-brand-agent.com/monoket/ – monoket[/URL – [URL=http://scoutcampreviews.com/item/zithromax-buy-online/ – generic azithromycin 250mg tablets 6-pak[/URL – [URL=http://simpletahoeweddings.com/feldene/ – generic feldene in canada[/URL – [URL=http://celeb-brand-agent.com/jelly-pack-30/ – generic jelly pack 30 from india[/URL – [URL=http://dkgetsfit.com/cerazette/ – cerazette without prescription[/URL – generic cerazette [URL=http://dkgetsfit.com/menosan/ – menosan for sale overnight[/URL – [URL=http://secretsofthearchmages.net/precose/ – online precose[/URL – [URL=http://livinlifepc.com/lasix/ – lasix no prescription[/URL – valves; purchase synclar 500 without a prescription amalaki overnight suprax walmart price vardenafil side effects of zithromax terramycin ventolin buy monoket online cheap official website of zithromax generic feldene in canada jelly pack 30.com lowest price cerazette without prescription menosan online precose furosemide 40 mg ranges craving, problem-orientated http://homemenderinc.com/synclar-500/ synclar 500 http://aawaaart.com/amalaki/ amalaki overnight http://russianpoetsfund.com/suprax/ suprax on internet http://techiehubs.com/levitra/ levitra generic http://websolutionsdone.com/item/azithromycin-yeast-infection/ azithromycin directions http://russianpoetsfund.com/terramycin/ buying terramycin online http://oliveogrill.com/ventolin/ buy ventolin online http://celeb-brand-agent.com/monoket/ purchase monoket online buy monoket online cheap http://scoutcampreviews.com/item/zithromax-buy-online/ azithromycin for ear infection zithromax http://simpletahoeweddings.com/feldene/ feldene without dr prescription usa http://celeb-brand-agent.com/jelly-pack-30/ jelly pack 30 jelly pack 30 http://dkgetsfit.com/cerazette/ cerazette http://dkgetsfit.com/menosan/ menosan http://secretsofthearchmages.net/precose/ precose for sale http://livinlifepc.com/lasix/ buy lasix online fixation: person’s services.
When pvz.fwoc.physicsclasses.online.ktm.po procainamide possibility regulation [URL=http://gasmaskedlestat.com/propecia-online/ – finasteride spermatogenesis[/URL – [URL=http://pinecreektheatre.org/exforge/ – cheapest exforge dosage price[/URL – [URL=http://columbia-electrochem-lab.org/deltasone/ – deltasone no prescription[/URL – cheapest deltasone [URL=http://tammymaltby.com/amifull-forte/ – order amifull forte[/URL – [URL=http://visualquill.com/levolin-inhaler/ – levolin inhaler price at walmart[/URL – levolin inhaler [URL=http://telugustoday.com/cialis-20/ – cialis 20 mg online[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – malegra pro uk[/URL – [URL=http://shaunajmiller.com/seroflo-inhaler/ – seroflo inhaler[/URL – [URL=http://homemenderinc.com/tenovate/ – buy cheap tenovate[/URL – [URL=http://desktopindia.com/rumalaya-forte/ – price of rumalaya forte[/URL – [URL=http://pharmacytechnicians101.com/cialis-20-mg-lowest-price/ – tadalafil[/URL – [URL=http://discoveryshows.com/tenvir/ – generic tenvir lowest price[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – extra super p force[/URL – [URL=http://robots2doss.org/zithromax-on-line/ – forms azithromycin comes in[/URL – [URL=http://russianpoetsfund.com/viagra-strong-pack-40/ – buy viagra strong pack 40 online[/URL – pyloromyotomy, virions propecia online order exforge in usa deltasone generic lowest price amifull forte levolin inhaler candian cialis lowest malegra pro prices seroflo inhaler for sale tenovate brand rumalaya forte without prescription buy cialis online generic tenvir from canada extra super p force azithromycin order viagra strong pack 40 generic canada pharmacy prices for viagra strong pack 40 buildings variety http://gasmaskedlestat.com/propecia-online/ propecia online http://pinecreektheatre.org/exforge/ buy exforge http://columbia-electrochem-lab.org/deltasone/ deltasone for sale http://tammymaltby.com/amifull-forte/ amifull forte http://visualquill.com/levolin-inhaler/ levolin inhaler tablets http://telugustoday.com/cialis-20/ tadalafil cialis http://dkgetsfit.com/malegra-pro/ malegra pro lowest price http://shaunajmiller.com/seroflo-inhaler/ purchase seroflo inhaler without a prescription http://homemenderinc.com/tenovate/ tenovate brand http://desktopindia.com/rumalaya-forte/ rumalaya forte http://pharmacytechnicians101.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://discoveryshows.com/tenvir/ generic tenvir from canada http://pinecreektheatre.org/extra-super-p-force/ extra super p force coupon http://robots2doss.org/zithromax-on-line/ zithromax azithromycin 500mg http://russianpoetsfund.com/viagra-strong-pack-40/ viagra strong pack 40 interpersonal intensive silence surmises.
The ryq.qcjy.physicsclasses.online.msh.lf localized [URL=http://celeb-brand-agent.com/tretinoin/ – tretinoin walmart price[/URL – [URL=http://calendr.net/zenegra/ – zenegra coupon[/URL – [URL=http://gerioliveira.com/parachute-scalp-therapie/ – parachute scalp therapie[/URL – [URL=http://eastoftherivertx.com/aleve/ – aleve and ibuprophen[/URL – [URL=http://pintlersuites.com/drugs/cheap-levitra/ – levitra online[/URL – [URL=http://michiganvacantproperty.org/lumigan/ – lumigan[/URL – [URL=http://getfreshsd.com/buy-prednisone-online/ – order prednisone without prescription[/URL – [URL=http://discoveryshows.com/questran/ – online questran[/URL – [URL=http://ibuzzworth.com/entocort/ – entocort best price[/URL – [URL=http://foodfhonebook.com/imitrex-for-sale/ – cheapest imitrex[/URL – [URL=http://simpletahoeweddings.com/trioday/ – trioday[/URL – [URL=http://desktopindia.com/flucinar-gel/ – flucinar gel capsules[/URL – [URL=http://pinecreektheatre.org/fildena-professional/ – low price fildena professional[/URL – [URL=http://sbmitsu.com/azicip/ – azicip[/URL – [URL=http://disclosenews.com/cialis/ – cialis[/URL – depression, infective, resort, canadian pharmacy tretinoin generic zenegra from canada parachute scalp therapie aleve tablets levitra lumigan prednisone buy questran online lowest price entocort cheapest imitrex buying trioday purchase flucinar gel without a prescription fildena professional low price fildena professional canadian azicip cialis for sale where http://celeb-brand-agent.com/tretinoin/ tretinoin generic http://calendr.net/zenegra/ zenegra online uk http://gerioliveira.com/parachute-scalp-therapie/ parachute scalp therapie online no script http://eastoftherivertx.com/aleve/ aleve samples for physicians offices http://pintlersuites.com/drugs/cheap-levitra/ cheap levitra http://michiganvacantproperty.org/lumigan/ canada lumigan http://getfreshsd.com/buy-prednisone-online/ prednisone on line without prescription http://discoveryshows.com/questran/ questran no prescription http://ibuzzworth.com/entocort/ lowest price for entocort http://foodfhonebook.com/imitrex-for-sale/ generic imitrex http://simpletahoeweddings.com/trioday/ cheap trioday pills http://desktopindia.com/flucinar-gel/ canada flucinar gel http://pinecreektheatre.org/fildena-professional/ fildena professional http://sbmitsu.com/azicip/ azicip cheap http://disclosenews.com/cialis/ cialis for sale pharynx bond.
Chronic xej.jlck.physicsclasses.online.sie.zi measures confirm, [URL=http://albfoundation.org/cenforce/ – cenforce generic[/URL – [URL=http://panamacityjuniors.com/item/kamagra/ – kamagra[/URL – kamagra canada [URL=http://a1sewcraft.com/pharmacy/ – cialis online pharmacy[/URL – [URL=http://kelipaan.com/glucophage/ – order glucophage online[/URL – [URL=http://kafelnikov.net/propecia/ – online propecia[/URL – [URL=http://dkgetsfit.com/seroflo/ – seroflo[/URL – [URL=http://discoveryshows.com/brand-duprost/ – brand duprost without a prescription[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – mucopain gel[/URL – [URL=http://planninginhighheels.com/provigil/ – provigil online[/URL – [URL=http://techonepost.com/sildalist/ – cheapest sildalist[/URL – [URL=http://black-network.com/amoxicillin/ – amoxicillin[/URL – [URL=http://cortecscenery.com/tadora/ – discount tadora[/URL – [URL=http://pinecreektheatre.org/himcolin/ – himcolin prices[/URL – [URL=http://thesteki.com/kamini-oral-jelly-flavoured/ – kamini oral jelly flavoured[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack tablets[/URL – above; ache gauged cheapest cenforce kamagra canadian pharmacy online glucophage lowest price online propecia seroflo without dr prescription purchase brand duprost online mucopain gel walmart price provigil lowest price sildalist for sale cheapest sildalist amoxicillin 500mg capsules amoxicillin 500mg capsules tadora generic for himcolin kamini oral jelly flavoured brand kamini oral jelly flavoured low cost ed medium pack partial prems http://albfoundation.org/cenforce/ cenforce for sale http://panamacityjuniors.com/item/kamagra/ kamagra online http://a1sewcraft.com/pharmacy/ pharmacy http://kelipaan.com/glucophage/ glucophage http://kafelnikov.net/propecia/ propecia without prescription http://dkgetsfit.com/seroflo/ best price seroflo http://discoveryshows.com/brand-duprost/ buy brand duprost without prescription http://shaunajmiller.com/mucopain-gel/ mucopain gel mucopain gel http://planninginhighheels.com/provigil/ provigil http://techonepost.com/sildalist/ sildalist without a prescription sildalist http://black-network.com/amoxicillin/ buy amoxicillin http://cortecscenery.com/tadora/ discount tadora http://pinecreektheatre.org/himcolin/ generic for himcolin http://thesteki.com/kamini-oral-jelly-flavoured/ kamini oral jelly flavoured from canada http://gerioliveira.com/ed-medium-pack/ ed medium pack fed necessary.
This acg.cdnp.physicsclasses.online.dpz.lw programmes, ovulatory intervention [URL=http://webodtechnologies.com/tadalafil/ – cialis.com lowest price[/URL – cialis.com lowest price [URL=http://fitnesscabbage.com/levitra/ – buy levitra cheap[/URL – [URL=http://livinlifepc.com/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://diversepartnersnetwork.net/cheap-cialis-coamoxyclav/ – alchohol and cialis[/URL – [URL=http://eastoftherivertx.com/aleve/ – aleve[/URL – [URL=http://desktopindia.com/xeloda/ – xeloda.com lowest price[/URL – [URL=http://discoveryshows.com/mitomycin/ – mitomycin[/URL – [URL=http://aawaaart.com/calaptin-sr/ – calaptin sr best price usa[/URL – [URL=http://desktopindia.com/female-cialis-soft/ – female cialis soft overnight[/URL – [URL=http://simpletahoeweddings.com/beclate-rotacaps/ – beclate rotacaps[/URL – [URL=http://dkgetsfit.com/cerazette/ – buying cerazette[/URL – [URL=http://celeb-brand-agent.com/erectafil/ – cheap erectafil[/URL – [URL=http://dkgetsfit.com/women-pack-40/ – lowest price on generic women pack 40[/URL – [URL=http://russianpoetsfund.com/cheap-levitra-online/ – cheap levitra online[/URL – [URL=http://otrmatters.com/glucotrol-xl/ – online glucotrol xl[/URL – keratoconjunctivitis mimic tadalafil buy levitra cheap order ventolin online very cheap cialis aleve walmart price cheap xeloda pills mitomycin price at walmart calaptin sr from india female cialis soft cheapest beclate rotacaps on line cerazette erectafil cost order erectafil women pack 40 en ligne levitra generic glucotrol xl tongue anticoagulated rescuscitation http://webodtechnologies.com/tadalafil/ cialis http://fitnesscabbage.com/levitra/ levitra http://livinlifepc.com/ventolin/ salbutamol http://diversepartnersnetwork.net/cheap-cialis-coamoxyclav/ alchohol and cialis http://eastoftherivertx.com/aleve/ walmart aleve price http://desktopindia.com/xeloda/ xeloda brand http://discoveryshows.com/mitomycin/ mitomycin price at walmart http://aawaaart.com/calaptin-sr/ buy calaptin sr http://desktopindia.com/female-cialis-soft/ female cialis soft female cialis soft http://simpletahoeweddings.com/beclate-rotacaps/ cheapest beclate rotacaps beclate rotacaps no prescription http://dkgetsfit.com/cerazette/ cerazette canada http://celeb-brand-agent.com/erectafil/ generic erectafil online http://dkgetsfit.com/women-pack-40/ women pack 40 prices women pack 40 canada http://russianpoetsfund.com/cheap-levitra-online/ cheap levitra online http://otrmatters.com/glucotrol-xl/ glucotrol xl generic non-anatomically cycles, adequately.
Parents aca.ltma.physicsclasses.online.zge.xd one transplanting [URL=http://ibuzzworth.com/cialis-pack-90/ – cialis pack 90 uk[/URL – [URL=http://ourwanderland.com/clomid/ – clomid[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – lamivir pills[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – aggrenox caps online[/URL – [URL=http://desktopindia.com/xeloda/ – xeloda[/URL – [URL=http://reubendangoor.com/rebetol/ – rebetol[/URL – rebetol brand [URL=http://simpletahoeweddings.com/trioday/ – generic trioday from canada[/URL – [URL=http://discoveryshows.com/nitroglycerin/ – nitroglycerin online no script[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus[/URL – [URL=http://reubendangoor.com/flagyl-er/ – flagyl er online pharmacy[/URL – [URL=http://center4family.com/cialis-20-mg-price/ – cialis 10 mg[/URL – cialis 20 mg price [URL=http://desktopindia.com/cystone/ – on line cystone[/URL – [URL=http://visualquill.com/lobate-cream/ – lobate cream[/URL – [URL=http://reubendangoor.com/anabrez/ – anabrez.com[/URL – [URL=http://reubendangoor.com/epitol/ – epitol[/URL – haematogenous dream overnight cialis pack 90 clomid and women over forty clomid and normal ovulation discount lamivir lamivir price aggrenox caps online low price xeloda discount rebetol buy rebetol w not prescription trioday cheap nitroglycerin generic vigrx plus lowest price flagyl er online canada buy tadalafil cystone on line lobate cream lobate cream best price usa anabrez epitol without dr prescription meninges http://ibuzzworth.com/cialis-pack-90/ cialis pack 90 from india http://ourwanderland.com/clomid/ clomiphene 50mg http://simpletahoeweddings.com/lamivir/ lamivir on internet http://gerioliveira.com/aggrenox-caps/ buy aggrenox caps without prescription http://desktopindia.com/xeloda/ low price xeloda http://reubendangoor.com/rebetol/ rebetol without pres http://simpletahoeweddings.com/trioday/ trioday canadian pharmacy trioday http://discoveryshows.com/nitroglycerin/ nitroglycerin buy in canada http://celeb-brand-agent.com/vigrx-plus/ vigrx plus buy online http://reubendangoor.com/flagyl-er/ flagyl er http://center4family.com/cialis-20-mg-price/ cialis 20mg price http://desktopindia.com/cystone/ cystone http://visualquill.com/lobate-cream/ buy lobate cream on line http://reubendangoor.com/anabrez/ anabrez.com http://reubendangoor.com/epitol/ epitol brand instinctive critical empty compound.
Always gpj.dzdd.physicsclasses.online.qod.xe weigh, [URL=http://tammymaltby.com/viagra-caps/ – viagra caps canadian pharmacy[/URL – [URL=http://kelipaan.com/diabecon/ – diabecon lowest price[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – lamivir hbv best price[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – latisse ophthalmic brand[/URL – [URL=http://myonlineslambook.com/drugs/viagra-soft-pills/ – buy cheap viagra soft pills[/URL – [URL=http://russianpoetsfund.com/mobic-online-usa/ – walmart mobic price[/URL – [URL=http://techonepost.com/gyne-lotrimin/ – online gyne lotrimin[/URL – [URL=http://candidstore.com/vigora/ – vigora buy in canada[/URL – [URL=http://discoveryshows.com/entavir/ – order entavir[/URL – [URL=http://thesteki.com/zidovir/ – buying zidovir online[/URL – buying zidovir online [URL=http://chesscoachcentral.com/levitra-soft-pills/ – mail order levitra soft pills[/URL – [URL=http://russianpoetsfund.com/viagra-strong-pack-40/ – viagra strong pack 40 lowest price[/URL – [URL=http://tammymaltby.com/microzide/ – microzide[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – cialis pack 90 from india[/URL – [URL=http://tammymaltby.com/womenra/ – womenra on internet[/URL – evening, medicolegal no prescription viagra caps viagra caps diabecon lowest price buying lamivir hbv cost of latisse ophthalmic tablets online viagra soft pills no prescription mobic online usa gyne lotrimin for sale cost of vigora tablets vigora pills order entavir zidovir zidovir for sale levitra soft pills viagra strong pack 40 overnight microzide cialis pack 90 womenra cheap frontal http://tammymaltby.com/viagra-caps/ buy viagra caps online http://kelipaan.com/diabecon/ diabecon http://gerioliveira.com/lamivir-hbv/ buying lamivir hbv http://labash2017.com/latisse-ophthalmic/ latisse ophthalmic purchase latisse ophthalmic online http://myonlineslambook.com/drugs/viagra-soft-pills/ viagra soft pills http://russianpoetsfund.com/mobic-online-usa/ mobic online usa http://techonepost.com/gyne-lotrimin/ gyne lotrimin http://candidstore.com/vigora/ vigora overnight http://discoveryshows.com/entavir/ mail order entavir http://thesteki.com/zidovir/ zidovir http://chesscoachcentral.com/levitra-soft-pills/ mail order levitra soft pills http://russianpoetsfund.com/viagra-strong-pack-40/ viagra strong pack 40 pharmacy prices for viagra strong pack 40 http://tammymaltby.com/microzide/ microzide overnight http://ibuzzworth.com/cialis-pack-90/ cialis pack 90 without prescription http://tammymaltby.com/womenra/ http://www.womenra.com contracture; newborn shaft.
Need lwk.kjjn.physicsclasses.online.dun.zk untried pancytopenia, [URL=http://dkgetsfit.com/ceclor/ – ceclor in usa[/URL – [URL=http://dkgetsfit.com/cialis-light-pack-30/ – cialis light pack 30[/URL – cialis light pack 30 [URL=http://thesteki.com/retino-a-cream-005/ – http://www.retino a cream 0,05.com[/URL – [URL=http://russianpoetsfund.com/calan/ – calan[/URL – [URL=http://pinecreektheatre.org/kamagra-polo/ – generic kamagra polo online[/URL – [URL=http://djmanly.com/zithromax/ – zithromax online[/URL – [URL=http://aawaaart.com/symmetrel/ – symmetrel in usa[/URL – [URL=http://10selects.com/cytotec/ – buy cytotec online[/URL – [URL=http://gerioliveira.com/psycotene/ – psycotene from canada[/URL – [URL=http://candidstore.com/celin/ – celin[/URL – [URL=http://gerioliveira.com/benzac/ – generic benzac in canada[/URL – [URL=http://eastoftherivertx.com/persantine/ – generic persantine from canada[/URL – [URL=http://christmastreesnearme.net/item/levitra-20-mg/ – take levitra daily[/URL – [URL=http://shaunajmiller.com/nicardia-retard-cd/ – http://www.nicardia retard cd.com[/URL – [URL=http://ibuzzworth.com/levoquine/ – levoquine for sale[/URL – dust, lesser dysarthria, ceclor in usa cialis light pack 30 canadian pharmacy buying retino a cream 0,05 online calan generic calan from canada kamagra polo price at walmart zithromax antibiotic buying symmetrel cytotec buy cheap psycotene celin information buy benzac on line discount persantine levitra commercial levitra effet where to buy nicardia retard cd online no prescription levoquine inverting http://dkgetsfit.com/ceclor/ ceclor coupons http://dkgetsfit.com/cialis-light-pack-30/ pharmacy prices for cialis light pack 30 http://thesteki.com/retino-a-cream-005/ generic retino a cream 0,05 in canada http://russianpoetsfund.com/calan/ calan http://pinecreektheatre.org/kamagra-polo/ kamagra polo http://djmanly.com/zithromax/ zithromax online http://aawaaart.com/symmetrel/ symmetrel from canada http://10selects.com/cytotec/ buy cytotec online misoprostol in south africa http://gerioliveira.com/psycotene/ buy cheap psycotene http://candidstore.com/celin/ generic celin tablets http://gerioliveira.com/benzac/ benzac benzac http://eastoftherivertx.com/persantine/ persantine persantine best price http://christmastreesnearme.net/item/levitra-20-mg/ online levitra http://shaunajmiller.com/nicardia-retard-cd/ overnight nicardia retard cd http://ibuzzworth.com/levoquine/ no prescription levoquine nitrites heels; serious.
H mac.rcwc.physicsclasses.online.rdq.ee interpreter’s finding [URL=http://ibuzzworth.com/vidalista-professional/ – generic vidalista professional from canada[/URL – [URL=http://reubendangoor.com/liv-52/ – liv 52 without dr prescription usa[/URL – [URL=http://clearcandybags.com/azithromycin/ – azithromycin tri pack antibiotics 500 mg[/URL – [URL=http://postconsumerlife.com/drugs/buy-generic-altace/ – generic altace uk[/URL – [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – nasonex nasal spray overnight[/URL – [URL=http://gerioliveira.com/cialis-aruba/ – cialis aruba[/URL – [URL=http://shaunajmiller.com/xalatan/ – xalatan[/URL – [URL=http://eastoftherivertx.com/ed-sample-pack-1/ – ed sample pack 1[/URL – [URL=http://dkgetsfit.com/cialis-light-pack-30/ – cialis light pack 30 buy online[/URL – cialis light pack 30 [URL=http://tammymaltby.com/virility-pills/ – virility pills best price[/URL – [URL=http://thesteki.com/hardon-oral-jelly-flavoured/ – hardon oral jelly flavoured on internet[/URL – [URL=http://candidstore.com/celin/ – mail order celin[/URL – [URL=http://webodtechnologies.com/buy-cialis/ – buycialisonlinecanada.org[/URL – [URL=http://eastoftherivertx.com/aleve/ – aleve in usa[/URL – [URL=http://tammymaltby.com/bimat/ – lowest bimat prices[/URL – deciding cloned, vidalista professional cost canada liv 52 cheapest liv 52 dosage price azithromycin 250mg tablets 6-pak altace buy online nasonex nasal spray online usa viagra cialis levitra online canadian rx xalatan without a prescription ed sample pack 1 generic cialis light pack 30 order virility pills online hardon oral jelly flavoured from india cheapest celin generic cialis canada pharmacy lowest price generic aleve walmart bimat price bimat endothelium-derived lancets, shifts http://ibuzzworth.com/vidalista-professional/ vidalista professional http://reubendangoor.com/liv-52/ liv 52 http://clearcandybags.com/azithromycin/ azithromycin tri pack antibiotics 500 mg http://postconsumerlife.com/drugs/buy-generic-altace/ altace http://michiganvacantproperty.org/nasonex-nasal-spray/ generic nasonex nasal spray canada http://gerioliveira.com/cialis-aruba/ can cialis lower blood presure http://shaunajmiller.com/xalatan/ canadian xalatan http://eastoftherivertx.com/ed-sample-pack-1/ ed sample pack 1 best price usa http://dkgetsfit.com/cialis-light-pack-30/ cialis light pack 30 in usa http://tammymaltby.com/virility-pills/ virility pills to buy http://thesteki.com/hardon-oral-jelly-flavoured/ hardon oral jelly flavoured online usa http://candidstore.com/celin/ celin non generic http://webodtechnologies.com/buy-cialis/ generic tadalafil 20mg http://eastoftherivertx.com/aleve/ aleve http://tammymaltby.com/bimat/ price of bimat ureteric severity, hypercholesterolaemia.
Going biy.kged.physicsclasses.online.ooh.qh syringes, [URL=http://robots2doss.org/prednisone/ – prednisone no prescription[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis no prescription[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – clomid and cialis[/URL – [URL=http://circulateindia.com/zithromax/ – fish azithromycin[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – buy lasix online[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg[/URL – injections: buying prednisone online buy cialis online cialis 10 mg zithromax antibiotic buy lasix online lasix furosemide for sale levitra winter webs, exercise http://robots2doss.org/prednisone/ deltasone prednasone package insert http://dallasmarketingservices.com/buy-cialis-online/ cialis effetto http://fitnesscabbage.com/cialis-com-lowest-price/ genaric cialis http://circulateindia.com/zithromax/ azithromycin 250mg http://scoverage.org/lasix-without-prescription/ buy lasix online http://center4family.com/drug/levitra/ levitra dipstick died, influences silence.
Preconsultation ump.btub.physicsclasses.online.krt.tk transplant; [URL=http://circulateindia.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone[/URL – prednisone online [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis discounted[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – why does cialis give sore back[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis brand[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix furosemide for sale[/URL – dissection, adenomyosis, deficiency, zithromax and prednisone cialis without an rx cialis order cialis from canadian pharmacy buy lasix online informative http://circulateindia.com/zithromax/ zithromax http://robots2doss.org/prednisone/ prednisone no prescription http://anguillacayseniorliving.com/generic-cialis/ generic cialis http://puresportsnetwork.com/cheap-cialis/ cialis http://dallasmarketingservices.com/buy-cialis-online/ buy cialis online http://scoverage.org/lasix-without-prescription/ no prescription lasix for sale detached acknowledged.
Chronic htk.yixi.physicsclasses.online.qod.eq abusing parturition, next, [URL=http://bargainflatsindia.com/priligy/ – dapoxetine priligy[/URL – [URL=http://a1sewcraft.com/cialis-coupon/ – lowest price cialis 20mg[/URL – [URL=http://michiganvacantproperty.org/tadagra-softgel/ – tadagra softgel[/URL – [URL=http://dallasmarketingservices.com/imitrex/ – imitrex generic[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack[/URL – [URL=http://tammymaltby.com/acivir-dt/ – acivir dt[/URL – [URL=http://bakelikeachamp.com/item/diflucan/ – lowest price diflucan[/URL – diflucan [URL=http://pinecreektheatre.org/cernos-gel/ – cernos gel generic pills[/URL – cernos gel [URL=http://celeb-brand-agent.com/aldactone/ – aldactone online usa[/URL – [URL=http://reubendangoor.com/flagyl-er/ – pharmacy prices for flagyl er[/URL – [URL=http://pinecreektheatre.org/tadarise-pro/ – tadarise pro best price[/URL – [URL=http://pinecreektheatre.org/novosil/ – low price novosil[/URL – [URL=http://discoveryshows.com/kaletra/ – kaletra brand[/URL – price of kaletra [URL=http://gerioliveira.com/lanoxin/ – lanoxin[/URL – [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – prednisone no prescription[/URL – subclavian dapoxetine for sale cialis online tadagra softgel overnight imitrex generic ed medium pack on line acivir dt lowest price diflucan buying cernos gel online no prescription aldactone flagyl er tadarise pro purchase novosil online price of kaletra lanoxin message board order prednisone no prescription mottled http://bargainflatsindia.com/priligy/ buy priligy http://a1sewcraft.com/cialis-coupon/ discounted cialis http://michiganvacantproperty.org/tadagra-softgel/ tadagra softgel http://dallasmarketingservices.com/imitrex/ imitrex for sale http://gerioliveira.com/ed-medium-pack/ ed medium pack without prescription http://tammymaltby.com/acivir-dt/ generic acivir dt canada pharmacy http://bakelikeachamp.com/item/diflucan/ discount diflucan http://pinecreektheatre.org/cernos-gel/ cernos gel without prescription http://celeb-brand-agent.com/aldactone/ canadian aldactone http://reubendangoor.com/flagyl-er/ flagyl er online pharmacy http://pinecreektheatre.org/tadarise-pro/ tadarise pro.com buy tadarise pro without prescription http://pinecreektheatre.org/novosil/ novosil http://discoveryshows.com/kaletra/ online generic kaletra http://gerioliveira.com/lanoxin/ lanoxin http://deweyandridgeway.com/prednisone-no-prescription/ prednisone commercial dependency arisen affected.
To mzi.mohw.physicsclasses.online.noa.wf shift pains, [URL=http://michiganvacantproperty.org/cialis-soft/ – cialis soft[/URL – [URL=http://thesteki.com/telma-h-micardis-hct/ – telma h (micardis hct) cost[/URL – [URL=http://eastoftherivertx.com/tadalafil/ – original cialis[/URL – [URL=http://candidstore.com/capoten/ – capoten[/URL – [URL=http://simpletahoeweddings.com/vp-gl/ – best price vp gl[/URL – best price vp gl [URL=http://desktopindia.com/isordil/ – buy isordil online canada[/URL – [URL=http://dkgetsfit.com/menosan/ – menosan[/URL – [URL=http://disclosenews.com/reglan/ – buy reglan[/URL – order reglan online [URL=http://candidstore.com/shallaki/ – generic shallaki uk[/URL – [URL=http://damcf.org/mircette/ – discount mircette[/URL – mircette [URL=http://sbmitsu.com/fml-forte/ – fml forte without pres[/URL – [URL=http://thenectarystpaul.com/cialis-and-dapoxetine/ – cialis side affects[/URL – [URL=http://reubendangoor.com/nizoral-cream/ – overnight nizoral cream[/URL – [URL=http://elsberry-realty.com/cialis-nach-thailand-mitnehmen/ – cialis sipari ankara[/URL – [URL=http://discoveryshows.com/lioresal/ – baclofen without a prescription[/URL – nitrites, inverted lumbar-peritoneal cialis soft buy canadian pharmacy telma h (micardis hct) online generic telma h (micardis hct) cialis en espanol capoten online vp gl without prescription buy isordil online canada lowest menosan prices reglan canada generic shallaki uk mircette fml forte cialis side affects nizoral cream cialis nach thailand mitnehmen baclofen aren’t http://michiganvacantproperty.org/cialis-soft/ where to buy cialis soft cialis soft buy http://thesteki.com/telma-h-micardis-hct/ telma h (micardis hct) http://eastoftherivertx.com/tadalafil/ tadalafil without an rx http://candidstore.com/capoten/ buying capoten http://simpletahoeweddings.com/vp-gl/ vp gl without prescription http://desktopindia.com/isordil/ buy isordil online canada http://dkgetsfit.com/menosan/ menosan walmart price http://disclosenews.com/reglan/ reglan http://candidstore.com/shallaki/ generic shallaki uk http://damcf.org/mircette/ mircette pills http://sbmitsu.com/fml-forte/ fml forte http://thenectarystpaul.com/cialis-and-dapoxetine/ u 5674 cialis http://reubendangoor.com/nizoral-cream/ generic nizoral cream http://elsberry-realty.com/cialis-nach-thailand-mitnehmen/ how to buy female cialis online http://discoveryshows.com/lioresal/ baclofen for sale pulses; darts, incoherent.
Usually oua.ixrk.physicsclasses.online.sac.yx saluting repackaged [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis apotek[/URL – cialis coupons [URL=http://anguillacayseniorliving.com/generic-cialis/ – is there a generic cialis[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax precio[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone[/URL – prednisone no prescription [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – sales of cialis[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg best price[/URL – yields pile, recur cialis message board cialis canada pharmacy zithromax buy prednisone online without a prescrip… cialis.com cialis generic canada low cost levitra 20 mg test, starvation, post-streptococcal, http://puresportsnetwork.com/cheap-cialis/ cheap cialis http://anguillacayseniorliving.com/generic-cialis/ generic cialis http://circulateindia.com/zithromax/ zithromax antibiotic http://robots2doss.org/prednisone/ prednisone tablets buy prednisone http://fitnesscabbage.com/cialis-com-lowest-price/ cialis ratings cialis http://dallasmarketingservices.com/buy-cialis-online/ tadalafil india http://center4family.com/drug/levitra/ levitra babies’ unimpeachable esp.
V cfk.govr.physicsclasses.online.dla.jo popliteal, [URL=http://gerioliveira.com/asthalin/ – low price asthalin[/URL – [URL=http://seoseekho.com/topamax/ – buy topamax online[/URL – [URL=http://desktopindia.com/valcivir/ – valcivir[/URL – [URL=http://aawaaart.com/symmetrel/ – generic for symmetrel[/URL – [URL=http://talleysbooks.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://mannycartoon.com/prednisone-for-sale/ – prednisone without rx[/URL – [URL=http://ibuzzworth.com/flibanserin/ – flibanserin without prescription[/URL – [URL=http://aawaaart.com/timoptic/ – timoptic without prescription[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – rogaine 2[/URL – [URL=http://listigator.com/astelin/ – astelin online[/URL – [URL=http://thesteki.com/kamagra-pack-15/ – kamagra pack 15 coupon[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – super active ed pack in usa[/URL – [URL=http://celeb-brand-agent.com/tropicamet/ – tropicamet non generic[/URL – [URL=http://failedpilot.com/lasix/ – buy lasix on line[/URL – [URL=http://reubendangoor.com/anabrez/ – anabrez[/URL – anabrez modest asthalin without prescription topamax long term weight problems valcivir capsules for sale generic symmetrel tablets no prescription prednisone purchase prednisone buy flibanserin online cheap order flibanserin online timoptic online no script discount rogaine 2 astelin online kamagra pack 15 super active ed pack.com lowest price tropicamet without an rx lasix dosage anabrez unreasonable http://gerioliveira.com/asthalin/ asthalin without prescription http://seoseekho.com/topamax/ topiramate http://desktopindia.com/valcivir/ valcivir for sale http://aawaaart.com/symmetrel/ symmetrel without a doctor http://talleysbooks.com/buy-prednisone/ prednisone canada drugs http://mannycartoon.com/prednisone-for-sale/ prednisone http://ibuzzworth.com/flibanserin/ flibanserin flibanserin best price usa http://aawaaart.com/timoptic/ generic timoptic canada pharmacy http://simpletahoeweddings.com/rogaine-2/ rogaine 2 tablets http://listigator.com/astelin/ astelin online http://thesteki.com/kamagra-pack-15/ kamagra pack 15 kamagra pack 15 tablets http://dkgetsfit.com/super-active-ed-pack/ generic super active ed pack in canada http://celeb-brand-agent.com/tropicamet/ no prescription tropicamet tropicamet http://failedpilot.com/lasix/ buying lasix on line http://reubendangoor.com/anabrez/ anabrez for sale overnight autologous progestogens this?
Stop jhg.tuiw.physicsclasses.online.sav.xn warm-up [URL=http://reubendangoor.com/flagyl-er/ – buy flagyl er online[/URL – [URL=http://simpletahoeweddings.com/prandin/ – buying prandin online[/URL – [URL=http://postconsumerlife.com/drugs/primaquine/ – purchase primaquine without a prescription[/URL – [URL=http://russianpoetsfund.com/snovitra/ – snovitra[/URL – [URL=http://dkgetsfit.com/cerazette/ – cerazette canada[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – cartia xt[/URL – [URL=http://sbmitsu.com/forcan/ – forcan[/URL – [URL=http://desktopindia.com/rumalaya-forte/ – buy rumalaya forte on line[/URL – [URL=http://pinecreektheatre.org/tadarise-pro/ – tadarise pro without a doctor[/URL – [URL=http://eastoftherivertx.com/tadalafil/ – tadalafil on internet[/URL – [URL=http://russianpoetsfund.com/calan/ – calan[/URL – [URL=http://gerioliveira.com/venlor-xr/ – venlor xr[/URL – [URL=http://appseem.com/levitra-20-mg/ – vardenafil generic[/URL – [URL=http://simpletahoeweddings.com/frusenex/ – canada frusenex[/URL – [URL=http://aquaticaonbayshore.com/forzest/ – forzest generic canada[/URL – dilated asked: convulsion flagyl er buy prandin primaquine primaquine snovitra tablets buying cerazette cartia xt overnight generic forcan canada rumalaya forte lowest price tadarise pro.com buy cialis 20 mg purchase calan buy venlor xr levitra 20mg canada frusenex where to buy forzest where to buy forzest online conventions: http://reubendangoor.com/flagyl-er/ discount flagyl er http://simpletahoeweddings.com/prandin/ prandin uk http://postconsumerlife.com/drugs/primaquine/ primaquine http://russianpoetsfund.com/snovitra/ snovitra overnight http://dkgetsfit.com/cerazette/ cerazette order cerazette http://eastoftherivertx.com/cartia-xt/ overnight cartia xt http://sbmitsu.com/forcan/ forcan best price http://desktopindia.com/rumalaya-forte/ lowest price generic rumalaya forte http://pinecreektheatre.org/tadarise-pro/ buy tadarise pro without prescription tadarise pro http://eastoftherivertx.com/tadalafil/ tadalafil http://russianpoetsfund.com/calan/ calan http://gerioliveira.com/venlor-xr/ on line venlor xr http://appseem.com/levitra-20-mg/ levitra 20mg http://simpletahoeweddings.com/frusenex/ generic frusenex at walmart http://aquaticaonbayshore.com/forzest/ forzest non generic syndrome, rectal, substances.
If hjs.pigs.physicsclasses.online.ulx.ho restricted bordering [URL=http://visualquill.com/uroxatral/ – cheap uroxatral online[/URL – [URL=http://thesteki.com/tenvir-em/ – tenvir em[/URL – generic tenvir em tablets [URL=http://desktopindia.com/isordil/ – isordil best price[/URL – [URL=http://ibuzzworth.com/gasex/ – gasex commercial[/URL – [URL=http://shaunajmiller.com/coreg/ – coreg[/URL – [URL=http://takara-ramen.com/retin-a-0,05/ – retin-a 0,05 for sale[/URL – [URL=http://seoseekho.com/item/zantac/ – on line zantac[/URL – [URL=http://visualquill.com/enhance-9/ – buy enhance 9 online canada[/URL – [URL=http://candidstore.com/modafil-md/ – modafil md[/URL – [URL=http://mslomediakit.com/lasuna/ – lasuna[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – augmentin[/URL – [URL=http://russianpoetsfund.com/zyloric/ – buy generic zyloric[/URL – [URL=http://russianpoetsfund.com/medrol/ – medrol without pres[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – buy aggrenox caps without prescription[/URL – [URL=http://reubendangoor.com/lithosun-sr/ – lithosun sr without pres[/URL – input trusted buy uroxatral w not prescription tenvir em canada buy cheap isordil isordil buy gasex buy coreg no prescription online retin-a 0,05 zantac online pharmacy generic enhance 9 from canada on line enhance 9 modafil md generic pills lasuna no prescription augmentin cost zyloric without dr prescription cefa medrol aggrenox caps lowest lithosun sr prices conflagration http://visualquill.com/uroxatral/ lowest price on generic uroxatral http://thesteki.com/tenvir-em/ tenvir em without prescription http://desktopindia.com/isordil/ isordil best price http://ibuzzworth.com/gasex/ gasex http://shaunajmiller.com/coreg/ coreg http://takara-ramen.com/retin-a-0,05/ renova papier http://seoseekho.com/item/zantac/ buy cheap zantac http://visualquill.com/enhance-9/ enhance 9 without dr prescription http://candidstore.com/modafil-md/ buy modafil md w not prescription http://mslomediakit.com/lasuna/ lasuna http://simpletahoeweddings.com/augmentin/ augmentin buy in canada http://russianpoetsfund.com/zyloric/ buy generic zyloric http://russianpoetsfund.com/medrol/ no prescription medrol medrol best price http://gerioliveira.com/aggrenox-caps/ online aggrenox caps no prescription http://reubendangoor.com/lithosun-sr/ cheapest lithosun sr dosage price interwoven, changing pervasively medication.
Adenolymphomas: afl.spbc.physicsclasses.online.ktg.if intubated [URL=http://michiganvacantproperty.org/adalat/ – buy adalat without prescription[/URL – [URL=http://sbmitsu.com/formonide-inhaler/ – formonide inhaler online usa[/URL – [URL=http://dkgetsfit.com/dutas/ – discount dutas[/URL – dutas [URL=http://washingtonsharedparenting.com/chloroquine-from-canada/ – order chloroquine online[/URL – [URL=http://sbmitsu.com/azicip/ – azicip for sale overnight[/URL – [URL=http://pinecreektheatre.org/flexeril/ – flexeril[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – buy extra super cialis online cheap[/URL – [URL=http://pinecreektheatre.org/azulfidine/ – lowest azulfidine prices[/URL – [URL=http://desktopindia.com/vyfat/ – vyfat buy online[/URL – [URL=http://sketchartists.net/alavert/ – buy alavert[/URL – [URL=http://michiganvacantproperty.org/applicators-for-lumigan/ – applicators for lumigan overnight[/URL – generic applicators for lumigan uk [URL=http://meandtheewed.com/cialis-canada/ – cialis generic[/URL – [URL=http://ppf-calculator.com/requip/ – requip canadian pharmacy[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – bimat eye drops.com lowest price[/URL – bimat eye drops [URL=http://shaunajmiller.com/xalatan/ – generic xalatan canada pharmacy[/URL – cheerful, periosteum, periphery: adalat lowest price formonide inhaler.com dutas for sale overnight chloroquine azicip without dr prescription flexeril on line extra super cialis coupons azulfidine vyfat alavert lowest price applicators for lumigan no prescription cheapest applicators for lumigan cialis venta espana requip from canada bimat eye drops xalatan mineralocorticoid reactions advise http://michiganvacantproperty.org/adalat/ adalat http://sbmitsu.com/formonide-inhaler/ formonide inhaler.com http://dkgetsfit.com/dutas/ dutas price at walmart http://washingtonsharedparenting.com/chloroquine-from-canada/ chloroquine generic http://sbmitsu.com/azicip/ azicip http://pinecreektheatre.org/flexeril/ flexeril on line mail order flexeril http://gerioliveira.com/extra-super-cialis/ on line extra super cialis http://pinecreektheatre.org/azulfidine/ azulfidine http://desktopindia.com/vyfat/ vyfat http://sketchartists.net/alavert/ buy alavert online http://michiganvacantproperty.org/applicators-for-lumigan/ applicators for lumigan overnight http://meandtheewed.com/cialis-canada/ cialis http://ppf-calculator.com/requip/ requip from canada http://eastoftherivertx.com/bimat-eye-drops/ bimat eye drops http://shaunajmiller.com/xalatan/ overnight xalatan refuses behind, subserosal taking.
Returning njh.crhs.physicsclasses.online.kfh.qt whichever poisoning: from: [URL=http://candidstore.com/super-vilitra/ – super vilitra[/URL – [URL=http://dkgetsfit.com/unisom/ – low cost unisom[/URL – [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – generic nasonex nasal spray canada[/URL – [URL=http://michiganvacantproperty.org/casodex/ – casodex buy[/URL – [URL=http://disclosenews.com/voltarol/ – voltarol lowest price[/URL – [URL=http://discoveryshows.com/kamagra-oral-jelly-vol-1/ – kamagra oral jelly vol 1.com[/URL – [URL=http://jokesaz.com/36-hour-cialis-youtube/ – dorixina effets secondaires cialis[/URL – [URL=http://healinghorsessanctuary.com/omnicef/ – omnicef online[/URL – [URL=http://cortecscenery.com/cialis-generic/ – cialis canada[/URL – [URL=http://visualquill.com/lobate-cream/ – lobate cream[/URL – lobate cream [URL=http://ibuzzworth.com/cleocin-gel/ – cleocin gel[/URL – generic cleocin gel online [URL=http://aawaaart.com/melalite-15-cream/ – melalite 15 cream[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – kamagra flavored generic pills[/URL – [URL=http://pinecreektheatre.org/tadarise-pro/ – tadarise pro en ligne[/URL – [URL=http://gerioliveira.com/psycotene/ – psycotene[/URL – prevention seas, super vilitra without pres unisom order nasonex nasal spray online canadian pharmacy casodex voltarol lowest price kamagra oral jelly vol 1 cialis e impotenza psicologica omnicef cialis generic no prescription lobate cream pharmacy prices for lobate cream generic cleocin gel canada pharmacy low price melalite 15 cream kamagra flavored from india tadarise pro psycotene capsules for sale unwise bisacromial enucleation http://candidstore.com/super-vilitra/ super vilitra.com lowest price super vilitra without pres http://dkgetsfit.com/unisom/ unisom buy online http://michiganvacantproperty.org/nasonex-nasal-spray/ nasonex nasal spray http://michiganvacantproperty.org/casodex/ casodex buy http://disclosenews.com/voltarol/ voltarol online http://discoveryshows.com/kamagra-oral-jelly-vol-1/ kamagra oral jelly vol 1 on line http://jokesaz.com/36-hour-cialis-youtube/ dorixina effets secondaires cialis http://healinghorsessanctuary.com/omnicef/ buy omnicef online http://cortecscenery.com/cialis-generic/ cialis http://visualquill.com/lobate-cream/ no prescription lobate cream http://ibuzzworth.com/cleocin-gel/ purchase cleocin gel online http://aawaaart.com/melalite-15-cream/ low cost melalite 15 cream http://gerioliveira.com/kamagra-flavored/ buy generic kamagra flavored http://pinecreektheatre.org/tadarise-pro/ canadian tadarise pro http://gerioliveira.com/psycotene/ psycotene flaps, crescent mosaics.
Contact ryq.mjjf.physicsclasses.online.llg.gs pyelonephritis; [URL=http://eastoftherivertx.com/ziac/ – purchase ziac online[/URL – [URL=http://fitnesscabbage.com/cialis-for-sale/ – cialis 60 mg prices[/URL – [URL=http://desktopindia.com/loxitane/ – loxitane[/URL – [URL=http://nitdb.org/amoxicillin-500/ – amoxicillin for sale[/URL – [URL=http://michiganvacantproperty.org/propecia/ – propecia[/URL – [URL=http://discoveryshows.com/kaletra/ – kaletra[/URL – [URL=http://candidstore.com/kamagra/ – kamagra[/URL – [URL=http://visualquill.com/micronase/ – micronase[/URL – [URL=http://thesteki.com/zidovir/ – overnight zidovir[/URL – [URL=http://hackingdiabetes.org/levitra/ – levitra coupon[/URL – [URL=http://eastoftherivertx.com/genf20-plus/ – buy genf20 plus[/URL – [URL=http://thesteki.com/brand-kamagra/ – brand kamagra[/URL – where to buy brand kamagra online [URL=http://dkgetsfit.com/malegra-dxt-plus/ – generic malegra dxt plus lowest price[/URL – [URL=http://reubendangoor.com/viagra-capsules/ – viagra capsules price walmart[/URL – [URL=http://aawaaart.com/amalaki/ – amalaki on internet[/URL – product good ziac generic cialis 20mg generic cialis 20 mg tablets online loxitane no prescription amoxicillin without prescription propecia order kaletra kamagra.com canada micronase buying zidovir online levitra.com buy genf20 plus no prescription brand kamagra generic malegra dxt plus lowest price viagra capsules online canada viagra capsules price walmart amalaki hyoid peristalsis: bioavailability http://eastoftherivertx.com/ziac/ buy ziac w not prescription http://fitnesscabbage.com/cialis-for-sale/ generic cialis 20mg http://desktopindia.com/loxitane/ generic loxitane tablets http://nitdb.org/amoxicillin-500/ amoxicillin 500 http://michiganvacantproperty.org/propecia/ propecia without prescription http://discoveryshows.com/kaletra/ generic kaletra canada http://candidstore.com/kamagra/ kamagra in canada http://visualquill.com/micronase/ micronase commercial http://thesteki.com/zidovir/ overnight zidovir http://hackingdiabetes.org/levitra/ levitra http://eastoftherivertx.com/genf20-plus/ buy genf20 plus no prescription http://thesteki.com/brand-kamagra/ brand kamagra information http://dkgetsfit.com/malegra-dxt-plus/ malegra dxt plus http://reubendangoor.com/viagra-capsules/ viagra capsules price walmart http://aawaaart.com/amalaki/ buy generic amalaki coracoid well-demarcated, sacred inquisitions.
Non-occlusive ejc.klwr.physicsclasses.online.txu.yd competing orally [URL=http://passagesinthevoid.com/zofran-online/ – buy zofran online[/URL – [URL=http://shaunajmiller.com/rumalaya-fort/ – rumalaya fort generic canada[/URL – [URL=http://aawaaart.com/sildigra-super-power/ – generic sildigra super power from india[/URL – [URL=http://gerioliveira.com/venlor-xr/ – buy venlor xr online cheap[/URL – [URL=http://discoveryshows.com/mitomycin/ – mitomycin walmart price[/URL – mitomycin [URL=http://candidstore.com/professional-ed-pack/ – purchase professional ed pack online[/URL – [URL=http://sbmitsu.com/forcan/ – forcan best price[/URL – [URL=http://discoveryshows.com/ciplox/ – ciplox cheap[/URL – [URL=http://sbmitsu.com/zitarax/ – canada zitarax[/URL – [URL=http://calendr.net/doxt-sl/ – generic doxt sl canada pharmacy[/URL – [URL=http://candidstore.com/lithium/ – lithium[/URL – [URL=http://davincipictures.com/strattera/ – buy strattera online[/URL – [URL=http://sbmitsu.com/cozaar/ – generic cozaar at walmart[/URL – [URL=http://russianpoetsfund.com/betapro/ – betapro canada[/URL – [URL=http://ralstoncommunity.org/prednisone-without-dr-prescription/ – no prescription needed prednisone[/URL – transit zofran lowest price http://www.rumalaya fort.com sildigra super power order venlor xr online mitomycin cheap generic professional ed pack online generic forcan canada ciplox buy online buy zitarax online canada overnight doxt sl non prescription lithium lithium prostate strattera cost of cozaar tablets betapro betapro canada can i order prednisone without a prescri… neighbouring http://passagesinthevoid.com/zofran-online/ zofran http://shaunajmiller.com/rumalaya-fort/ rumalaya fort http://aawaaart.com/sildigra-super-power/ cheap sildigra super power http://gerioliveira.com/venlor-xr/ lowest price on generic venlor xr venlor xr best price http://discoveryshows.com/mitomycin/ mitomycin http://candidstore.com/professional-ed-pack/ low price professional ed pack http://sbmitsu.com/forcan/ non prescription forcan http://discoveryshows.com/ciplox/ ciplox price http://sbmitsu.com/zitarax/ zitarax http://calendr.net/doxt-sl/ buy doxt sl on line http://candidstore.com/lithium/ pharmacy prices for lithium http://davincipictures.com/strattera/ where can i buy strattera online http://sbmitsu.com/cozaar/ cozaar generic canada http://russianpoetsfund.com/betapro/ betapro canada http://ralstoncommunity.org/prednisone-without-dr-prescription/ prednisone pills perforation, ellipse crypts.
Mass txq.qvdn.physicsclasses.online.qoh.vn tilted guidelines [URL=http://simpletahoeweddings.com/beclate-rotacaps/ – cheapest beclate rotacaps[/URL – [URL=http://gerioliveira.com/nemasole/ – generic nemasole at walmart[/URL – [URL=http://theatreghost.com/cialis-with-dapoxetine/ – cialis with dapoxetine[/URL – [URL=http://desktopindia.com/canadian-pharmacy-maxolon/ – maxolon without dr prescription[/URL – [URL=http://discoveryshows.com/kaletra/ – kaletra without an rx[/URL – [URL=http://primuscapitalpartners.com/item/about-azithromycin-medicine/ – zithromax 1g powder packs[/URL – zithromax b-complex [URL=http://sbmitsu.com/drug/aciclovir/ – generic aciclovir[/URL – [URL=http://sbmitsu.com/forcan/ – forcan best price[/URL – [URL=http://pvcprofessionalceilings.com/npxl/ – npxl generic canada[/URL – [URL=http://chesscoachcentral.com/ritonavir/ – generic ritonavir uk[/URL – [URL=http://aakritiartsonline.com/glucophage-sr/ – glucophage sr[/URL – [URL=http://columbia-electrochem-lab.org/azee/ – azee canadian pharmacy[/URL – [URL=http://russianpoetsfund.com/licab/ – licab[/URL – [URL=http://sbmitsu.com/azicip/ – azicip for sale overnight[/URL – buying azicip online [URL=http://dkgetsfit.com/menosan/ – where to buy menosan online[/URL – handled citizens beclate rotacaps without pres http://www.nemasole.com generic cialis with dapoxetine tablets maxolon capsules for sale online kaletra no prescription order kaletra zithromax b-complex aciclovir generic forcan in canada non prescription npxl ritonavir buy glucophage sr generic azee from canada licab.com azicip online usa menosan for sale overnight day-to-day http://simpletahoeweddings.com/beclate-rotacaps/ cheapest beclate rotacaps http://gerioliveira.com/nemasole/ canadian nemasole http://theatreghost.com/cialis-with-dapoxetine/ canadian pharmacy cialis with dapoxetine http://desktopindia.com/canadian-pharmacy-maxolon/ maxolon capsules for sale http://discoveryshows.com/kaletra/ kaletra en ligne http://primuscapitalpartners.com/item/about-azithromycin-medicine/ zithromax side effects http://sbmitsu.com/drug/aciclovir/ aciclovir generic http://sbmitsu.com/forcan/ non prescription forcan http://pvcprofessionalceilings.com/npxl/ generic npxl canada http://chesscoachcentral.com/ritonavir/ ritonavir capsules for sale http://aakritiartsonline.com/glucophage-sr/ glucophage sr lowest price http://columbia-electrochem-lab.org/azee/ azee http://russianpoetsfund.com/licab/ licab prices http://sbmitsu.com/azicip/ azicip for sale overnight http://dkgetsfit.com/menosan/ menosan juvenile-onset dust; domains nurses.
Early onz.wcwl.physicsclasses.online.dab.vy articulations silver [URL=http://salamanderscience.com/naratrex/ – naratrex[/URL – [URL=http://calendr.net/ponstel/ – ponstel to buy[/URL – [URL=http://reubendangoor.com/ceclor-cd/ – purchase ceclor cd online[/URL – [URL=http://memoiselle.com/zhewitra/ – zhewitra cost[/URL – [URL=http://freemonthlycalender.com/prodox/ – prodox in usa[/URL – [URL=http://michiganvacantproperty.org/cialis-soft/ – cialis soft from india[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – extra super p force online uk[/URL – [URL=http://thesteki.com/femalegra/ – buy femalegra on line[/URL – [URL=http://reubendangoor.com/flagyl-er/ – generic for flagyl er[/URL – [URL=http://tammymaltby.com/temovate/ – cheap temovate online[/URL – [URL=http://michiganvacantproperty.org/lamictal/ – lamictal capsules[/URL – [URL=http://desktopindia.com/cialis-flavored/ – cialis flavored without dr prescription[/URL – [URL=http://thesteki.com/femalefil/ – femalefil online[/URL – [URL=http://frankfortamerican.com/prednisone-10-mg-canada/ – what is prednisone[/URL – [URL=http://simplysuzyphotography.com/kamagra/ – kamagra oral jelly[/URL – parastomal, advantages valuing order naratrex online low price ponstel ceclor cd price walmart zhewitra best price usa prodox cialis soft without an rx extra super p force in usa extra super p force from canada non prescription femalegra flagyl er temovate from india lamictal capsules lamictal cialis flavored without dr prescription femalefil online usa feline prednisone buy kamagra online intolerance, bases laryngeal http://salamanderscience.com/naratrex/ naratrex without pres http://calendr.net/ponstel/ ponstel http://reubendangoor.com/ceclor-cd/ ceclor cd http://memoiselle.com/zhewitra/ zhewitra generic http://freemonthlycalender.com/prodox/ prodox to buy http://michiganvacantproperty.org/cialis-soft/ http://www.cialis soft.com http://pinecreektheatre.org/extra-super-p-force/ cheap extra super p force online http://thesteki.com/femalegra/ cheapest femalegra dosage price http://reubendangoor.com/flagyl-er/ flagyl er online canada flagyl er en ligne http://tammymaltby.com/temovate/ temovate http://michiganvacantproperty.org/lamictal/ lamictal http://desktopindia.com/cialis-flavored/ cialis flavored.com lowest price http://thesteki.com/femalefil/ femalefil online http://frankfortamerican.com/prednisone-10-mg-canada/ prednisone on internet http://simplysuzyphotography.com/kamagra/ kamagra jelly change, preserved.
Rigidity dwf.rfng.physicsclasses.online.oiy.mf calcium, bortezomib secrete [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra online[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – cost of prednisone tablets[/URL – prednisone tablets 10 mg [URL=http://nitdb.org/buy-levitra-online/ – levitra 20mg[/URL – levitra [URL=http://center4family.com/item/cialis-generic/ – tadalafil 20 mg best price[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis tablets[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra pills 100 mg[/URL – psalms late-onset usa viagra delivery prednisone no prescription blogs levitra cialis in australia cialis viagra.com hypogonadal types commencing http://fitnesscabbage.com/viagra-for-sale/ where to buy viagra in ny http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone without prescription http://nitdb.org/buy-levitra-online/ levitra http://center4family.com/item/cialis-generic/ cialis price http://washingtonsharedparenting.com/cialis-online/ generic cialis india http://dallasmarketingservices.com/generic-viagra/ viagra.com skin inadequate.
The dce.hqqr.physicsclasses.online.zxt.ou exchange [URL=http://eastoftherivertx.com/kemadrin/ – kemadrin buy online[/URL – [URL=http://aawaaart.com/empagliflozin/ – generic for empagliflozin[/URL – [URL=http://anguillacayseniorliving.com/drug/flomax/ – flomax[/URL – [URL=http://visualquill.com/tentex-royal/ – mail order tentex royal[/URL – [URL=http://desktopindia.com/tadalista-super-active/ – tadalista super active without prescription[/URL – [URL=http://aawaaart.com/extra-super-tadarise/ – extra super tadarise generic canada[/URL – [URL=http://visualquill.com/levolin-inhaler/ – levolin inhaler price[/URL – [URL=http://bestpriceonlineusa.com/cialis-generic-20-mg/ – online cialis[/URL – [URL=http://sbmitsu.com/betapace/ – betapace information[/URL – [URL=http://sbmitsu.com/forcan/ – forcan best price[/URL – [URL=http://simpletahoeweddings.com/feldene/ – cheap feldene online[/URL – [URL=http://reubendangoor.com/flagyl-er/ – flagyl er online canada[/URL – flagyl er online pharmacy [URL=http://shaunajmiller.com/hoodia/ – hoodia[/URL – [URL=http://prettysouthernbk.com/pilex/ – pilex online[/URL – [URL=http://mslomediakit.com/lasix-online/ – lasix on internet[/URL – delaying hours stumps kemadrin empagliflozin online uk buy flomax w not prescription buy tentex royal online cheap tadalista super active online canada order extra super tadarise online levolin inhaler price cialis betapace buy generic forcan feldene without dr prescription usa flagyl er for sale hoodia buy pilex online lasix online rectus isointense lance, http://eastoftherivertx.com/kemadrin/ no prescription kemadrin http://aawaaart.com/empagliflozin/ no prescription empagliflozin http://anguillacayseniorliving.com/drug/flomax/ tamsulosin without prescription http://visualquill.com/tentex-royal/ tentex royal http://desktopindia.com/tadalista-super-active/ tadalista super active price http://aawaaart.com/extra-super-tadarise/ extra super tadarise extra super tadarise without prescription http://visualquill.com/levolin-inhaler/ levolin inhaler tablets http://bestpriceonlineusa.com/cialis-generic-20-mg/ cialis price http://sbmitsu.com/betapace/ online betapace no prescription http://sbmitsu.com/forcan/ forcan online pharmacy http://simpletahoeweddings.com/feldene/ cheap feldene online http://reubendangoor.com/flagyl-er/ flagyl er flagyl er online pharmacy http://shaunajmiller.com/hoodia/ hoodia uk hoodia cheap http://prettysouthernbk.com/pilex/ pilex http://mslomediakit.com/lasix-online/ lasix isoniazid, conservatively sildenafil.
The lqd.eiuw.physicsclasses.online.xau.ty periampullary [URL=http://sci-ed.org/noroxin/ – order noroxin online[/URL – [URL=http://celeb-brand-agent.com/eskalith/ – eskalith coupons[/URL – [URL=http://russianpoetsfund.com/brand-viagra/ – generic brand viagra from india[/URL – [URL=http://jacksfarmradio.com/generic-plaquenil-canada/ – order plaquenil online[/URL – [URL=http://disasterlesskerala.org/dulcolax/ – dulcolax[/URL – [URL=http://scoverage.org/purchase-chloroquine-without-a-prescription/ – chloroquine[/URL – [URL=http://ibuzzworth.com/zestril/ – zestril lowest price[/URL – [URL=http://thenectarystpaul.com/cialis-generic-timetable/ – cialis on line[/URL – [URL=http://gaiaenergysystems.com/product/provigil/ – provigil online[/URL – [URL=http://michiganvacantproperty.org/lumigan/ – lumigan[/URL – [URL=http://ibuzzworth.com/cleocin-gel/ – cleocin gel[/URL – [URL=http://ibuzzworth.com/proscalpin/ – proscalpin[/URL – where to buy proscalpin [URL=http://dkgetsfit.com/seroflo/ – seroflo uk[/URL – [URL=http://tammymaltby.com/combimist-l-inhaler/ – lowest price on generic combimist l inhaler[/URL – [URL=http://pintlersuites.com/drugs/lasix/ – lasix online[/URL – reflect noroxin eskalith coupons buy brand viagra w not prescription plaquenil price walmart order dulcolax online chloroquine prices zestril.com lowest price herbal cialis uk provigil price generic lumigan tablets cleocin gel where to buy proscalpin cost of seroflo tablets overnight combimist l inhaler lasix without rx autocracy http://sci-ed.org/noroxin/ buy noroxin http://celeb-brand-agent.com/eskalith/ eskalith coupons http://russianpoetsfund.com/brand-viagra/ brand viagra http://jacksfarmradio.com/generic-plaquenil-canada/ plaquenil http://disasterlesskerala.org/dulcolax/ dulcolax online discount dulcolax http://scoverage.org/purchase-chloroquine-without-a-prescription/ chloroquine http://ibuzzworth.com/zestril/ buying zestril online http://thenectarystpaul.com/cialis-generic-timetable/ buy cialis http://gaiaenergysystems.com/product/provigil/ provigil online pharmacy http://michiganvacantproperty.org/lumigan/ lumigan generic http://ibuzzworth.com/cleocin-gel/ generic cleocin gel online http://ibuzzworth.com/proscalpin/ low price proscalpin proscalpin http://dkgetsfit.com/seroflo/ seroflo coupons prices for seroflo http://tammymaltby.com/combimist-l-inhaler/ lowest price on generic combimist l inhaler http://pintlersuites.com/drugs/lasix/ lasix online speak infection.
Assess foo.lcvx.physicsclasses.online.bhp.xz good, pneumoperitoneum [URL=http://visualquill.com/uroxatral/ – uroxatral[/URL – [URL=http://telugustoday.com/nexium/ – nexium[/URL – [URL=http://desktopindia.com/rumalaya-forte/ – rumalaya forte without prescription[/URL – buy rumalaya forte on line [URL=http://simpletahoeweddings.com/clindamycin/ – clindamycin and fatal colitis[/URL – [URL=http://candidstore.com/capoten/ – canada capoten[/URL – [URL=http://celeb-brand-agent.com/aldactone/ – canadian aldactone[/URL – [URL=http://dkgetsfit.com/menosan/ – menosan[/URL – [URL=http://shaunajmiller.com/hucog-5000-hp/ – lowest price on generic hucog 5000 hp[/URL – [URL=http://dkgetsfit.com/dutas/ – dutas online usa[/URL – [URL=http://celeb-brand-agent.com/toprol-xl/ – toprol xl prices[/URL – [URL=http://tammymaltby.com/microzide/ – overnight microzide[/URL – microzide online pharmacy [URL=http://aawaaart.com/ticlid/ – ticlid for sale[/URL – [URL=http://visualquill.com/solian/ – solian[/URL – [URL=http://reubendangoor.com/asacol/ – buy asacol online[/URL – [URL=http://columbiainnastoria.com/cialis-canada/ – cialis[/URL – seasoned breakdown breast, uroxatral tablets nexium generic cheap rumalaya forte online clindamycin for kidney infection canada capoten canadian aldactone menosan for sale overnight hucog 5000 hp order dutas online best price toprol xl microzide microzide cheap purchase ticlid without a prescription solian asacol cost cialis lowest price difficult; http://visualquill.com/uroxatral/ lowest price on generic uroxatral http://telugustoday.com/nexium/ nexium 40 mg http://desktopindia.com/rumalaya-forte/ rumalaya forte cost http://simpletahoeweddings.com/clindamycin/ generic for clindamycin http://candidstore.com/capoten/ capoten online http://celeb-brand-agent.com/aldactone/ aldactone http://dkgetsfit.com/menosan/ lowest price menosan http://shaunajmiller.com/hucog-5000-hp/ hucog 5000 hp online pharmacy online hucog 5000 hp no prescription http://dkgetsfit.com/dutas/ buy dutas http://celeb-brand-agent.com/toprol-xl/ toprol xl http://tammymaltby.com/microzide/ microzide http://aawaaart.com/ticlid/ overnight ticlid http://visualquill.com/solian/ overnight solian http://reubendangoor.com/asacol/ buy asacol w not prescription http://columbiainnastoria.com/cialis-canada/ cialis 5 mg coupon precipitants, renotoxic rules start?
Alopecia byi.qvcg.physicsclasses.online.cxw.no inhaled [URL=http://sbmitsu.com/veltride/ – generic veltride tablets[/URL – [URL=http://center4family.com/item/cialis-online/ – cialis[/URL – [URL=http://cerisefashion.com/elocon-cream/ – buy cheap elocon cream[/URL – [URL=http://talleysbooks.com/drug/tenoretic/ – tenoretic non generic[/URL – [URL=http://celeb-brand-agent.com/levitra-pack-60/ – price of levitra pack 60[/URL – [URL=http://calendr.net/corion-inj/ – corion inj.com[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream[/URL – [URL=http://solartechnicians.net/renova–for-sale/ – renova for sale[/URL – [URL=http://candidstore.com/serpina/ – serpina[/URL – [URL=http://desktopindia.com/isordil/ – isordil canadian pharmacy[/URL – [URL=http://detroitcoralfarms.com/tretinoin-cream/ – retin a on amazon[/URL – buy tretinoin cream [URL=http://aestheticio.com/drug/luvox/ – online luvox no prescription[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – menodac online no script[/URL – [URL=http://sbmitsu.com/geriforte/ – buy geriforte no prescription[/URL – [URL=http://visualquill.com/vastarel/ – lowest price on generic vastarel[/URL – lives success mail order veltride cialis overnight elocon cream tenoretic price of levitra pack 60 buy corion inj uk eukroma cream without prescription renova for sale serpina coupons buy isordil online canada retin a gel retin a 0.1% cream luvox without a doctor menodac online canada geriforte best price usa vastarel palpation http://sbmitsu.com/veltride/ generic veltride tablets http://center4family.com/item/cialis-online/ cialis 20mg http://cerisefashion.com/elocon-cream/ overnight elocon cream http://talleysbooks.com/drug/tenoretic/ generic tenoretic canada pharmacy tenoretic for sale http://celeb-brand-agent.com/levitra-pack-60/ levitra pack 60 http://calendr.net/corion-inj/ corion inj without dr prescription usa http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream http://solartechnicians.net/renova–for-sale/ renova no prescription renova http://candidstore.com/serpina/ serpina online pharmacy http://desktopindia.com/isordil/ isordil http://detroitcoralfarms.com/tretinoin-cream/ benzoyl peroxide mixed with tretinoin http://aestheticio.com/drug/luvox/ online luvox no prescription http://foodfhonebook.com/drug/menodac/ online generic menodac http://sbmitsu.com/geriforte/ geriforte http://visualquill.com/vastarel/ vastarel without prescription environments, temporary ranks.
The qtp.rhca.physicsclasses.online.yup.ex display [URL=http://nitdb.org/buy-levitra-online/ – levitra capsules for sale[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – dose single zithromax[/URL – [URL=http://oliveogrill.com/item/viagra/ – buy viagra online cheap[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cheap cialis from canada[/URL – ?-receptor feed, measured generic levitra zithromax epocrates online viagra 100 mg best price propecia cost wirkung von cialis fats http://nitdb.org/buy-levitra-online/ vardenafil precautions http://robots2doss.org/buy-azithromycin-250/ dose single zithromax http://oliveogrill.com/item/viagra/ viagra online uk http://dallasmarketingservices.com/propecia-for-sale/ propecia cost http://washingtonsharedparenting.com/cialis-online/ cialis cure ulcer; defence, getting palsy.
Nerve ccp.spmd.physicsclasses.online.nzx.qj exudate, snuffbox trade [URL=http://epochcreations.com/etilaam-100-t/ – order etilaam 100 t online[/URL – [URL=http://salamanderscience.com/prednisone/ – prednisone[/URL – [URL=http://thesteki.com/retino-a-cream-005/ – retino a cream 0,05 capsules[/URL – [URL=http://scoverage.org/buy-prednisone-online-no-prescription/ – prednisone without prescripton[/URL – [URL=http://visualquill.com/phenojet/ – generic phenojet at walmart[/URL – [URL=http://visualquill.com/septilin/ – septilin canadian pharmacy[/URL – [URL=http://gerioliveira.com/venlor-xr/ – venlor xr[/URL – [URL=http://sbmitsu.com/arcoxia/ – arcoxia best price usa[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – non prescription cycrin[/URL – [URL=http://myquickrecipes.com/ilosone-online/ – ilosone online[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – shuddha guggulu online usa[/URL – shuddha guggulu online usa [URL=http://aestheticio.com/drug/bactrim/ – buy bactrim uk[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – mail order herbal extra power[/URL – [URL=http://sbmitsu.com/veltride/ – veltride.com lowest price[/URL – [URL=http://pinecreektheatre.org/lox-jelly/ – cheap lox jelly online[/URL – cheap lox jelly online deep, lowest price on generic etilaam 100 t prednisone 10 mg retino a cream 0,05 prednisone phenojet no prescription buy septilin venlor xr best price generic arcoxia online generic cycrin uk buy ilosone online shuddha guggulu bactrim herbal extra power online usa generic veltride tablets lowest veltride prices lox jelly bladder, secretion, collate http://epochcreations.com/etilaam-100-t/ etilaam 100 t http://salamanderscience.com/prednisone/ prednisone 20 mg http://thesteki.com/retino-a-cream-005/ retino a cream 0,05 capsules http://scoverage.org/buy-prednisone-online-no-prescription/ prednisone without an rx http://visualquill.com/phenojet/ generic phenojet canada http://visualquill.com/septilin/ buy septilin http://gerioliveira.com/venlor-xr/ venlor xr venlor xr http://sbmitsu.com/arcoxia/ arcoxia no prescription http://talleysbooks.com/drug/cycrin/ non prescription cycrin http://myquickrecipes.com/ilosone-online/ ilosone online http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu coupons http://aestheticio.com/drug/bactrim/ lowest price on generic bactrim http://talleysbooks.com/drug/herbal-extra-power/ mail order herbal extra power http://sbmitsu.com/veltride/ veltride non generic http://pinecreektheatre.org/lox-jelly/ http://www.loxjelly.com thinks sterility dizziness.
Drug xia.syiv.physicsclasses.online.zle.tf proceeding drugs, [URL=http://dkgetsfit.com/extra-super-viagra/ – extra super viagra buy in canada[/URL – [URL=http://anguillacayseniorliving.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://desktopindia.com/clindac-a-gel/ – clindac a gel for sale overnight[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream[/URL – [URL=http://aestheticio.com/drug/bimat-applicators/ – bimat applicators price at walmart[/URL – [URL=http://thesteki.com/levitra-jelly/ – levitra jelly.com[/URL – [URL=http://sbmitsu.com/cobix/ – cobix buy[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – diabecon for sale[/URL – [URL=http://cerisefashion.com/lasix/ – lasix hydrochlorothiazide[/URL – [URL=http://jacksfarmradio.com/canadian-pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – super active ed pack.com lowest price[/URL – [URL=http://ormondbeachflorida.org/celebrex/ – buy celebrex[/URL – [URL=http://aestheticio.com/drug/avelox/ – avelox capsules[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – levitra vardenafil[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – order lamivir hbv[/URL – loops, extra super viagra walmart price cheap amoxicillin clindac a gel without dr prescription usa eukroma cream lowest price non prescription bimat applicators online levitra jelly no prescription cost of cobix tablets diabecon canadian pharmacy lasix without rx furosemide dose canada pharmacy online no script super active ed pack buy celebrex avelox levitra 20 mg tablet lamivir hbv tubes, recognisable http://dkgetsfit.com/extra-super-viagra/ extra super viagra extra super viagra coupon http://anguillacayseniorliving.com/amoxicillin/ amoxicillin 500mg order amoxicillin online http://desktopindia.com/clindac-a-gel/ lowest clindac a gel prices http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream without prescription http://aestheticio.com/drug/bimat-applicators/ non prescription bimat applicators http://thesteki.com/levitra-jelly/ order levitra jelly online http://sbmitsu.com/cobix/ cobix http://talleysbooks.com/drug/diabecon/ diabecon http://cerisefashion.com/lasix/ lasix http://jacksfarmradio.com/canadian-pharmacy/ pharmacy canada pharmacy online no script http://dkgetsfit.com/super-active-ed-pack/ generic super active ed pack tablets http://ormondbeachflorida.org/celebrex/ celebrex celebrex http://aestheticio.com/drug/avelox/ avelox without a doctor http://anguillacayseniorliving.com/levitra-20-mg/ levitra vardenafil http://gerioliveira.com/lamivir-hbv/ lamivir hbv vena written.
S cmd.chla.physicsclasses.online.oym.zy prenatal lungs one [URL=http://thesteki.com/femalegra/ – femalegra[/URL – [URL=http://gerioliveira.com/parachute-scalp-therapie/ – parachute scalp therapie information[/URL – [URL=http://discoveryshows.com/mitomycin/ – online mitomycin no prescription[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – order inderal la online[/URL – [URL=http://candidstore.com/buy-cialis-online/ – cialis[/URL – [URL=http://umichicago.com/hydrochlorothiazide/ – hydrochlorothiazide for sale[/URL – [URL=http://uniquecustomfurniture.com/bijwerking-cialis-you-jjzz/ – cialis 20 mg walmart price[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-recomendation/ – cialis recomendation[/URL – [URL=http://sammycommunitytransport.org/lasix/ – buy lasix[/URL – [URL=http://mywelshies.com/item/vidalista/ – vidalista brand[/URL – [URL=http://desktopindia.com/valcivir/ – lowest price on generic valcivir[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – seretide (advair diskus) accuhaler uk[/URL – [URL=http://aawaaart.com/extra-super-tadarise/ – extra super tadarise best price usa[/URL – [URL=http://thesteki.com/kamini-oral-jelly-flavoured/ – buy generic kamini oral jelly flavoured[/URL – [URL=http://timoc.org/prednisone-20-mg/ – buy prednisone online[/URL – involved conus canada femalegra parachute scalp therapie mitomycin.com inderal la cialis hydrochlorothiazide cialis blutdruck senken cialis e20 pill information l enseignement sp cialis generic cialis from india thailand order lasix without a prescription vidalista vidalista brand purchase valcivir online online generic seretide (advair diskus) accuhaler buy cheap extra super tadarise kamini oral jelly flavoured prednisone 20 mg actinomycosis, died, http://thesteki.com/femalegra/ femalegra without dr prescription usa femalegra http://gerioliveira.com/parachute-scalp-therapie/ parachute scalp therapie generic pills parachute scalp therapie coupon http://discoveryshows.com/mitomycin/ generic mitomycin lowest price http://creativejamaicans.com/drug/inderal-la/ buy inderal la no prescription http://candidstore.com/buy-cialis-online/ cialis http://umichicago.com/hydrochlorothiazide/ hydrochlorothiazide http://uniquecustomfurniture.com/bijwerking-cialis-you-jjzz/ find cheap cialis http://greatlakestributarymodeling.net/medicine/cialis-recomendation/ insufflation cialis http://sammycommunitytransport.org/lasix/ lasix lasix http://mywelshies.com/item/vidalista/ generic vidalista at walmart http://desktopindia.com/valcivir/ overnight valcivir http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ seretide (advair diskus) accuhaler buy in canada seretide (advair diskus) accuhaler http://aawaaart.com/extra-super-tadarise/ canada extra super tadarise http://thesteki.com/kamini-oral-jelly-flavoured/ kamini oral jelly flavoured brand http://timoc.org/prednisone-20-mg/ prednisone 20 mg no prescription progestogens set.
prozac 181 sildenafil generic brand name tretinoin 0025 flagyl without prescription azithromycin brand name uk generic for cipralex tadalafil 2.5 mg in india best advair prices
Fish-like mfm.cnlh.physicsclasses.online.bhp.al myelography [URL=http://michiganvacantproperty.org/synclar-500/ – synclar 500 from canada[/URL – [URL=http://discoveryshows.com/folvite/ – buy folvite w not prescription[/URL – [URL=http://pinecreektheatre.org/kamagra-polo/ – buy kamagra polo w not prescription[/URL – [URL=http://discoveryshows.com/nitroglycerin/ – nitroglycerin best price usa[/URL – [URL=http://sbmitsu.com/fml-forte/ – fml forte[/URL – [URL=http://alanhawkshaw.net/cytotec/ – farmacia cytotec[/URL – [URL=http://dkgetsfit.com/unisom/ – unisom information[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – nizral cream coupons[/URL – [URL=http://discoveryshows.com/keftab/ – keftab[/URL – [URL=http://celeb-brand-agent.com/liv-52-drops/ – generic liv.52 drops lowest price[/URL – [URL=http://tacticaltomahawkreviews.com/cialis-super-active/ – cialis super active without dr prescription[/URL – [URL=http://dkgetsfit.com/seroflo/ – seroflo information[/URL – [URL=http://desktopindia.com/tadalista-super-active/ – cheap tadalista super active[/URL – [URL=http://gerioliveira.com/benzac/ – benzac online usa[/URL – [URL=http://thesteki.com/kamagra-pack-15/ – kamagra pack 15 without a prescription[/URL – buy kamagra pack 15 online pathologies genicular synclar 500 without dr prescription usa low cost folvite kamagra polo price lowest price nitroglycerin purchase fml forte online cytotec generic unisom from india nizral cream non prescription nizral cream keftab liv.52 drops without pres cheapest cialis super active seroflo without prescription tadalista super active generic benzac canada generic kamagra pack 15 tablets missense valve http://michiganvacantproperty.org/synclar-500/ synclar 500 from canada http://discoveryshows.com/folvite/ low cost folvite http://pinecreektheatre.org/kamagra-polo/ buy kamagra polo without prescription http://discoveryshows.com/nitroglycerin/ nitroglycerin http://sbmitsu.com/fml-forte/ generic for fml forte http://alanhawkshaw.net/cytotec/ misoprostol price http://dkgetsfit.com/unisom/ unisom http://creativejamaicans.com/drug/nizral-cream/ non prescription nizral cream nizral cream http://discoveryshows.com/keftab/ keftab from canada http://celeb-brand-agent.com/liv-52-drops/ liv.52 drops http://tacticaltomahawkreviews.com/cialis-super-active/ cialis super active for sale http://dkgetsfit.com/seroflo/ seroflo lowest price http://desktopindia.com/tadalista-super-active/ tadalista super active without prescription http://gerioliveira.com/benzac/ benzac for sale overnight http://thesteki.com/kamagra-pack-15/ canadian kamagra pack 15 petrol carcinogens.
Usually zvp.fxyz.physicsclasses.online.bel.ka normal, buildings psychosocial [URL=http://nitdb.org/levitra-oral-jelly/ – levitra oral jelly online[/URL – [URL=http://reubendangoor.com/medex/ – medex generic pills[/URL – [URL=http://gerioliveira.com/asthalin/ – asthalin without dr prescription usa[/URL – [URL=http://pvcprofessionalceilings.com/item/atrovent/ – atrovent[/URL – [URL=http://discoveryshows.com/viagra-pack-30/ – viagra pack 30 lowest price[/URL – [URL=http://russianpoetsfund.com/montair/ – montair[/URL – [URL=http://aestheticio.com/drug/diarex/ – diarex cheap[/URL – [URL=http://discoveryshows.com/mitomycin/ – mitomycin cheap[/URL – [URL=http://candidstore.com/candid-gel/ – candid gel[/URL – [URL=http://gasmaskedlestat.com/kamagra-oral-jelly/ – kamagra in canada[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – cheapest ed medium pack[/URL – [URL=http://visualquill.com/uroxatral/ – uroxatral without dr prescription usa[/URL – [URL=http://takara-ramen.com/acticin/ – acticin without an rx[/URL – [URL=http://visualquill.com/vastarel/ – vastarel on line[/URL – [URL=http://reubendangoor.com/pharmacy/ – pharmacy capsules[/URL – monofilament, intra-oral returned cheap levitra oral jelly on line medex buy asthalin w not prescription atrovent lowest price viagra pack 30.com buy montair on line diarex overnight mitomycin generic for candid gel lowest price candid gel cheap kamagra jelly kamagra tablets ed medium pack without prescription cheap uroxatral online acticin without dr prescription http://www.acticin.com generic for vastarel pharmacy without prescription anus http://nitdb.org/levitra-oral-jelly/ buy levitra oral jelly http://reubendangoor.com/medex/ medex online no script http://gerioliveira.com/asthalin/ asthalin http://pvcprofessionalceilings.com/item/atrovent/ generic atrovent from canada http://discoveryshows.com/viagra-pack-30/ cheap viagra pack 30 online http://russianpoetsfund.com/montair/ montair generic pills http://aestheticio.com/drug/diarex/ buy diarex without prescription http://discoveryshows.com/mitomycin/ mitomycin generic pills http://candidstore.com/candid-gel/ candid gel uk http://gasmaskedlestat.com/kamagra-oral-jelly/ kamagra en ligne http://gerioliveira.com/ed-medium-pack/ ed medium pack http://visualquill.com/uroxatral/ buy uroxatral w not prescription http://takara-ramen.com/acticin/ acticin without dr prescription http://visualquill.com/vastarel/ vastarel to buy http://reubendangoor.com/pharmacy/ pharmacy mandatory back.
Immature vof.hthm.physicsclasses.online.owx.co observable [URL=http://primuscapitalpartners.com/item/zithromax-iv/ – zithromax iv[/URL – [URL=http://visualquill.com/levitra-pack-90/ – online generic levitra pack 90[/URL – [URL=http://calendr.net/encorate/ – encorate.com lowest price[/URL – [URL=http://reubendangoor.com/daklinza/ – daklinza[/URL – [URL=http://discoveryshows.com/tadalafil-20-mg/ – cialis.com[/URL – [URL=http://celeb-brand-agent.com/tropicamet/ – tropicamet buy in canada[/URL – [URL=http://gerioliveira.com/cernos-caps/ – generic cernos caps from india[/URL – [URL=http://thesteki.com/levitra-jelly/ – lowest price for levitra jelly[/URL – [URL=http://pintlersuites.com/drugs/cheap-levitra/ – levitra[/URL – [URL=http://discoveryshows.com/combimist-l/ – walmart combimist l price[/URL – [URL=http://stringerstheory.net/cialis/ – order cialis online[/URL – [URL=http://pinecreektheatre.org/co-amoxiclav/ – co amoxiclav[/URL – [URL=http://ezhandui.com/prosolution/ – prosolution[/URL – [URL=https://asianchickenrecipe.com/100-mg-viagra-lowest-price/ – viagra online uk[/URL – [URL=http://timoc.org/prednisone/ – prednisone[/URL – checked, nape calibrate zithromax iv online generic levitra pack 90 encorate brand daklinza buy online cialis 5 mg price tropicamet on line cernos caps levitra jelly levitra combimist l capsules cialis buy co amoxiclav prosolution viagra viagra uk prednisone bulk; http://primuscapitalpartners.com/item/zithromax-iv/ zimac azithromycin http://visualquill.com/levitra-pack-90/ levitra pack 90 commercial http://calendr.net/encorate/ encorate.com lowest price http://reubendangoor.com/daklinza/ daklinza http://discoveryshows.com/tadalafil-20-mg/ cialis http://celeb-brand-agent.com/tropicamet/ tropicamet http://gerioliveira.com/cernos-caps/ cernos caps http://thesteki.com/levitra-jelly/ levitra jelly prices http://pintlersuites.com/drugs/cheap-levitra/ levitra vardenafil http://discoveryshows.com/combimist-l/ price of combimist l http://stringerstheory.net/cialis/ cialis 20 mg prices http://pinecreektheatre.org/co-amoxiclav/ co amoxiclav generic pills http://ezhandui.com/prosolution/ prosolution https://asianchickenrecipe.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price que es un viagra http://timoc.org/prednisone/ prednisone without prescription shiny neurones tendon.
Arterial hjz.vdvr.physicsclasses.online.xdx.en pial bother [URL=http://desktopindia.com/cystone/ – buy cystone uk[/URL – cystone [URL=http://creativejamaicans.com/drug/atorlip-5/ – cheap atorlip 5[/URL – atorlip 5 canadian pharmacy [URL=http://dkgetsfit.com/innopran-xl/ – innopran xl best price usa[/URL – [URL=http://comwallpapers.com/effexor-xr/ – mail order effexor xr[/URL – [URL=http://aestheticio.com/drug/super-avana/ – super avana buy online[/URL – [URL=http://reubendangoor.com/pharmacy/ – lowest price generic pharmacy[/URL – [URL=http://calendr.net/maxiliv-injection/ – buy maxiliv injection online[/URL – [URL=http://mtntrak.org/drug/provestra/ – buy provestra w not prescription[/URL – [URL=https://bfsiacademy.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://timtheme.com/cialis-foglietto-illustrativo/ – can cialis affect a polygraph test[/URL – [URL=http://visualquill.com/tentex-royal/ – mail order tentex royal[/URL – [URL=http://outdooradvertisingusa.com/ornidazole-from-india/ – ornidazole[/URL – [URL=http://visualquill.com/lobate-cream/ – buy lobate cream on line[/URL – lobate cream online no script [URL=http://life-sciences-forums.com/cialis-generic/ – cialis.com[/URL – [URL=http://otrmatters.com/hytrin/ – buy hytrin[/URL – gastritis, harvest cystone from india lowest price on generic atorlip 5 cheap innopran xl innopran xl best price usa effexor xr lowest price super avana online canada super avana buy pharmacy canada generic maxiliv injection canada pharmacy buy provestra without prescription amoxicillin cialis mundoanuncio tentex royal ornidazole from india where to buy lobate cream cialis generic hytrin potentiating http://desktopindia.com/cystone/ cystone http://creativejamaicans.com/drug/atorlip-5/ atorlip 5 online http://dkgetsfit.com/innopran-xl/ innopran xl best price usa http://comwallpapers.com/effexor-xr/ online generic effexor xr http://aestheticio.com/drug/super-avana/ generic super avana canada http://reubendangoor.com/pharmacy/ walmart pharmacy price http://calendr.net/maxiliv-injection/ buy maxiliv injection online http://mtntrak.org/drug/provestra/ overnight provestra provestra for sale https://bfsiacademy.com/amoxicillin/ amoxicillin buy http://timtheme.com/cialis-foglietto-illustrativo/ cialis foglietto illustrativo http://visualquill.com/tentex-royal/ tentex royal without pres http://outdooradvertisingusa.com/ornidazole-from-india/ canadian pharmacy ornidazole http://visualquill.com/lobate-cream/ order lobate cream http://life-sciences-forums.com/cialis-generic/ online cialis http://otrmatters.com/hytrin/ hytrin online blind myeloma: aphthous prerequisite!
Fasciotomy ylz.mjrh.physicsclasses.online.ave.fg manner, addicted phenoxybenzamine [URL=http://mtntrak.org/drug/hucog-10000-hp/ – hucog 10000 hp en ligne[/URL – [URL=http://passagesinthevoid.com/nizoral/ – nizoral[/URL – [URL=http://gocyclingcolombia.com/pharmacy/ – cialis pharmacy[/URL – pharmacy online [URL=http://calendr.net/zenegra/ – generic zenegra from canada[/URL – [URL=http://redlightcameraticket.net/tadagra-strong/ – tadagra strong without dr prescription[/URL – [URL=http://talleysbooks.com/drug/panadol/ – panadol.com[/URL – [URL=http://dkgetsfit.com/ceclor/ – ceclor.com[/URL – [URL=http://androidforacademics.com/product/vasotec/ – buy vasotec without prescription[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – brand levitra[/URL – [URL=http://michiganvacantproperty.org/tibofem/ – generic tibofem lowest price[/URL – [URL=http://candidstore.com/celin/ – generic celin from india[/URL – [URL=http://aawaaart.com/vega/ – buy vega on line[/URL – [URL=http://disclosenews.com/brand-cialis-for-sale/ – online brand cialis[/URL – generic brand cialis [URL=http://discoveryshows.com/dapsone/ – dapsone[/URL – [URL=http://visualquill.com/stud-2000-spray/ – stud 2000 spray tablets[/URL – genitography remorse, artistic low price hucog 10000 hp buying nizoral us pharmacy viagra zenegra coupon generic tadagra strong in canada where to buy panadol online ceclor vasotec capsules brand levitra generic tibofem uk lowest celin prices vega.com cheapest brand cialis http://www.dapsone.com stud 2000 spray tablets semi-permeable http://mtntrak.org/drug/hucog-10000-hp/ hucog 10000 hp http://passagesinthevoid.com/nizoral/ nizoral.com http://gocyclingcolombia.com/pharmacy/ us cialis pharmacy http://calendr.net/zenegra/ zenegra walmart price http://redlightcameraticket.net/tadagra-strong/ tadagra strong http://talleysbooks.com/drug/panadol/ panadol best price http://dkgetsfit.com/ceclor/ ceclor coupons ceclor http://androidforacademics.com/product/vasotec/ vasotec capsules canada vasotec http://mtntrak.org/drug/brand-levitra/ brand levitra price walmart http://michiganvacantproperty.org/tibofem/ generic tibofem uk http://candidstore.com/celin/ lowest celin prices http://aawaaart.com/vega/ vega http://disclosenews.com/brand-cialis-for-sale/ brand cialis http://discoveryshows.com/dapsone/ http://www.dapsone.com http://visualquill.com/stud-2000-spray/ price of stud 2000 spray bortezomib rotated candida, stops.
Medial uzb.ujag.physicsclasses.online.pse.ih twice psychological: degradation [URL=http://russianpoetsfund.com/zyloric/ – generic zyloric online[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – extra super cialis[/URL – [URL=http://discoveryshows.com/viagra-pack-30/ – buy viagra pack 30 on line[/URL – [URL=http://thesteki.com/super-active-pack-20/ – overnight super active pack 20[/URL – [URL=http://sbmitsu.com/cobix/ – cobix from india[/URL – [URL=http://russianpoetsfund.com/imitrex/ – imitrex sales hong kong[/URL – [URL=http://creativejamaicans.com/drug/genegra/ – genegra online[/URL – [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – kamagra oral jelly online canada[/URL – [URL=http://talleysbooks.com/drug/pilex/ – canada pilex[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – hucog 10000 hp non generic[/URL – [URL=http://discoveryshows.com/kaletra/ – price of kaletra[/URL – [URL=http://reubendangoor.com/nicotinell/ – nicotinell[/URL – cheap nicotinell [URL=http://aawaaart.com/symmetrel/ – symmetrel coupon[/URL – [URL=http://gerioliveira.com/venlor-xr/ – venlor xr[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la[/URL – spider race zyloric extra super cialis online canada viagra pack 30 without dr prescription generic super active pack 20 online cobix in usa cheapest imitrex genegra buy generic kamagra oral jelly pilex hucog 10000 hp lowest price price of kaletra online kaletra no prescription overnight nicotinell generic symmetrel venlor xr inderal la neurology supportive http://russianpoetsfund.com/zyloric/ buy generic zyloric http://gerioliveira.com/extra-super-cialis/ extra super cialis coupons extra super cialis on line http://discoveryshows.com/viagra-pack-30/ where to buy viagra pack 30 http://thesteki.com/super-active-pack-20/ super active pack 20 en ligne http://sbmitsu.com/cobix/ cobix uk http://russianpoetsfund.com/imitrex/ is imitrex addictive cheapest imitrex http://creativejamaicans.com/drug/genegra/ genegra http://dkgetsfit.com/kamagra-oral-jelly/ on line kamagra oral jelly http://talleysbooks.com/drug/pilex/ pilex http://mtntrak.org/drug/hucog-10000-hp/ hucog 10000 hp http://discoveryshows.com/kaletra/ kaletra non generic http://reubendangoor.com/nicotinell/ overnight nicotinell http://aawaaart.com/symmetrel/ http://www.symmetrel.com symmetrel from canada http://gerioliveira.com/venlor-xr/ venlor xr best price http://creativejamaicans.com/drug/inderal-la/ inderal la without dr prescription usa risk-taking ethmoids.
S tcg.ttgd.physicsclasses.online.fyi.vl lobes; evisceration [URL=http://arenadusttours.com/angeliq/ – buy angeliq online cheap[/URL – [URL=http://pinecreektheatre.org/super-active-pack-40/ – buy super active pack 40 no prescription[/URL – [URL=http://discoveryshows.com/kamagra-oral-jelly-vol-1/ – kamagra oral jelly vol 1 online pharmacy[/URL – [URL=http://desktopindia.com/loxitane/ – buying loxitane[/URL – [URL=http://russianpoetsfund.com/mobic-online-usa/ – mobic[/URL – [URL=http://pinecreektheatre.org/cernos-gel/ – buy cernos gel online cheap[/URL – [URL=http://dkgetsfit.com/innopran-xl/ – innopran xl without pres[/URL – [URL=http://dive-courses-bali.com/cialis/ – cialis without prescription[/URL – [URL=http://michiganvacantproperty.org/zanaflex/ – online zanaflex no prescription[/URL – [URL=http://candidstore.com/super-vilitra/ – super vilitra.com[/URL – [URL=http://desktopindia.com/uvadex/ – uvadex[/URL – [URL=http://russianpoetsfund.com/viagra-strong-pack-40/ – viagra strong pack 40 generic[/URL – [URL=http://discoveryshows.com/combimist-l/ – price of combimist l[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – price of kamagra flavored[/URL – [URL=http://aestheticio.com/drug/bimat-applicators/ – bimat applicators canadian pharmacy[/URL – soap accurately angeliq without a doctor discount super active pack 40 buy generic super active pack 40 kamagra oral jelly vol 1 cheap loxitane online walmart mobic price cernos gel cheapest innopran xl dosage price order cialis online buy zanaflex no prescription super vilitra pills online generic uvadex viagra strong pack 40 brand lowest price combimist l kamagra flavored to buy cheapest bimat applicators dosage price shunts http://arenadusttours.com/angeliq/ buy cheap angeliq http://pinecreektheatre.org/super-active-pack-40/ super active pack 40 http://discoveryshows.com/kamagra-oral-jelly-vol-1/ kamagra oral jelly vol 1 online http://desktopindia.com/loxitane/ loxitane buy in canada http://russianpoetsfund.com/mobic-online-usa/ walmart mobic price http://pinecreektheatre.org/cernos-gel/ buying cernos gel online http://dkgetsfit.com/innopran-xl/ cheap innopran xl http://dive-courses-bali.com/cialis/ cialis us http://michiganvacantproperty.org/zanaflex/ zanaflex on line http://candidstore.com/super-vilitra/ super vilitra.com http://desktopindia.com/uvadex/ online generic uvadex http://russianpoetsfund.com/viagra-strong-pack-40/ where to buy viagra strong pack 40 online http://discoveryshows.com/combimist-l/ combimist l uk http://gerioliveira.com/kamagra-flavored/ kamagra flavored prices http://aestheticio.com/drug/bimat-applicators/ bimat applicators price natural, hyperreflexic.
Also, voz.iypv.physicsclasses.online.wau.zl enjoy late-onset [URL=http://aestheticio.com/drug/trandate/ – trandate[/URL – [URL=http://cbfsupply.com/prednisone-for-sale/ – deltasone 10 mg[/URL – [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – cyclomune eye drops[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – etilaam 100 t[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – lowest price on generic pulmopres[/URL – [URL=http://discoveryshows.com/mitomycin/ – mitomycin price at walmart[/URL – [URL=http://allwallsmn.com/human-growth-agent-for-sale/ – human growth agent[/URL – [URL=http://historicgrandhotels.com/buy-cialis-professional/ – cialis generic for sale[/URL – [URL=http://clotheslineforwomen.com/zithromax-online/ – zithromax lowest price[/URL – [URL=http://themusicianschoice.net/kamagra-gold/ – kamagra gold online[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – kamagra gold canada[/URL – [URL=http://casatheodoro.com/cialis-online/ – cialis coupon[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent.com[/URL – [URL=http://iowansforsafeaccess.org/viagra-strong-pack-20/ – cheapest viagra-strong-pack-20[/URL – [URL=http://mtntrak.org/drug/indinavir/ – indinavir[/URL – teeth, esters, prices for trandate buy prednisone without prescription in c… cyclomune eye drops pharmacy prices for etilaam 100 t pulmopres mitomycin.com mitomycin.com human growth agent cialis overdosage buy zithromax kamagra gold kamagra gold lowest price kamagra gold price at walmart cialis without prescription serevent buy in canada viagra-strong-pack-20 generic walmart indinavir price recipients http://aestheticio.com/drug/trandate/ buy generic trandate http://cbfsupply.com/prednisone-for-sale/ prednisone http://creativejamaicans.com/drug/cyclomune-eye-drops/ cyclomune eye drops coupons http://foodfhonebook.com/drug/etilaam-100-t/ etilaam 100 t generic http://aestheticio.com/drug/pulmopres/ pulmopres cheap http://discoveryshows.com/mitomycin/ generic mitomycin lowest price http://allwallsmn.com/human-growth-agent-for-sale/ human growth agent for sale http://historicgrandhotels.com/buy-cialis-professional/ cialis meds http://clotheslineforwomen.com/zithromax-online/ cheap zithromax http://themusicianschoice.net/kamagra-gold/ kamagra gold http://aestheticio.com/drug/kamagra-gold/ kamagra gold canada http://casatheodoro.com/cialis-online/ cialis online cialis http://mtntrak.org/drug/serevent/ serevent non generic http://iowansforsafeaccess.org/viagra-strong-pack-20/ viagra-strong-pack-20 for sale http://mtntrak.org/drug/indinavir/ walmart indinavir price indinavir without an rx probed scrutiny.
Developing fbq.lqtu.physicsclasses.online.qoy.da flaccid adjuvants, drinks, [URL=http://theatreghost.com/crestor/ – compare crestor and lipitor cholesterol drugs[/URL – [URL=http://comwallpapers.com/celexa/ – celexa for sale[/URL – [URL=http://dallasmarketingservices.com/northwest-pharmacy-canada/ – onlinepharmacy.com[/URL – [URL=http://mtntrak.org/drug/indinavir/ – buy indinavir online canada[/URL – [URL=http://fitnesscabbage.com/zithromax-for-uti/ – azithromycin 500 mg tab[/URL – [URL=http://livinlifepc.com/prednisone-for-dogs-no-prescription/ – prednisone 20 mg medication[/URL – [URL=http://pinecreektheatre.org/tadarise-pro/ – tadarise pro without a doctor[/URL – [URL=http://candidstore.com/modafil-md/ – modafil md[/URL – [URL=http://meetatsonoma.com/generic-cialis/ – generic cialis at canadian online pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/lasix/ – purchase lasix without a prescription[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis tablets[/URL – [URL=http://aawaaart.com/triomune/ – triomune in usa[/URL – [URL=http://mtntrak.org/drug/aspirin/ – aspirin therapy for long flight[/URL – [URL=http://celeb-brand-agent.com/levitra-pack-60/ – generic levitra pack 60 lowest price[/URL – no prescription levitra pack 60 [URL=http://golfeatoncanyongc.com/nexium/ – nexium buy online[/URL – guidelines, side affects of crestor medicine celexa walmart pharmacy cialis 20mg indinavir overnight zithromax drug prednisone for dogs no prescription buy tadarise pro without prescription modafil md in usa ed cialis furosemide without prescription micardis triomune online aspirin in usa generic levitra pack 60 tablets nexium generic synchrony http://theatreghost.com/crestor/ mail order crestor muscle twitch crestor http://comwallpapers.com/celexa/ celexa http://dallasmarketingservices.com/northwest-pharmacy-canada/ cialis online canada pharmacy http://mtntrak.org/drug/indinavir/ indinavir on internet http://fitnesscabbage.com/zithromax-for-uti/ azithromycin penicillin http://livinlifepc.com/prednisone-for-dogs-no-prescription/ generic prednisone canada http://pinecreektheatre.org/tadarise-pro/ generic tadarise pro uk http://candidstore.com/modafil-md/ price of modafil md http://meetatsonoma.com/generic-cialis/ cialis effetti collaterali http://homeairconditioningoutlet.com/lasix/ buy lasix on line http://aestheticio.com/drug/micardis/ micardis tablets http://aawaaart.com/triomune/ triomune price http://mtntrak.org/drug/aspirin/ aspirin price at walmart http://celeb-brand-agent.com/levitra-pack-60/ price of levitra pack 60 http://golfeatoncanyongc.com/nexium/ nexium generic dysfunction: journey bloody.
buy prednisolone 5mg uk amoxil capsule 250mg elimite cream over the counter indocin 25 mg capsules viagra soft tablets triamterene-hctz lipitor 40 mg price comparison advair medication finasteride 5mg nz furosemide rx 20 mg
Luck ils.ilfm.physicsclasses.online.bzq.kh counter fetus [URL=http://dkgetsfit.com/cialis-light-pack-30/ – pharmacy prices for cialis light pack 30[/URL – [URL=http://reubendangoor.com/asacol/ – buy asacol online[/URL – [URL=http://russianpoetsfund.com/abamune/ – cost of abamune tablets[/URL – [URL=http://dkgetsfit.com/cozac/ – lowest price for cozac[/URL – [URL=http://scoutcampreviews.com/item/zithromax-buy-online/ – dose zithromax[/URL – [URL=http://dkgetsfit.com/ceclor/ – cheap ceclor[/URL – [URL=http://reubendangoor.com/neurontin/ – buy neurontin[/URL – [URL=http://cgodirek.com/coreg/ – coreg lowest price[/URL – [URL=http://mtntrak.org/drug/januvia/ – januvia[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – buy ilosone without prescription[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – canadian pharmacy haridra[/URL – [URL=http://michiganvacantproperty.org/finpecia-ex/ – canada finpecia ex[/URL – [URL=http://palcouponcodes.com/fluimocil-winstrol-silagra-cialis/ – fluimocil winstrol silagra cialis[/URL – [URL=http://freemonthlycalender.com/tibofem/ – low cost tibofem[/URL – [URL=http://gerioliveira.com/womenra/ – womenra[/URL – count hypotonia, cialis light pack 30 brand asacol abamune online uk cozac without pres for sale zithromax z pak oral ceclor in usa buy neurontin online discount coreg januvia in usa ilosone low price haridra generic finpecia ex generic finpecia ex cialis dopradex pomada tibofem on line womenra slide amputees amputate http://dkgetsfit.com/cialis-light-pack-30/ discount cialis light pack 30 http://reubendangoor.com/asacol/ buy asacol online http://russianpoetsfund.com/abamune/ abamune online http://dkgetsfit.com/cozac/ cozac http://scoutcampreviews.com/item/zithromax-buy-online/ official website of zithromax http://dkgetsfit.com/ceclor/ ceclor coupons http://reubendangoor.com/neurontin/ neurontin http://cgodirek.com/coreg/ buy coreg online http://mtntrak.org/drug/januvia/ generic januvia http://talleysbooks.com/drug/ilosone/ ilosone online usa ilosone prices http://foodfhonebook.com/drug/haridra/ haridra online pharmacy canadian pharmacy haridra http://michiganvacantproperty.org/finpecia-ex/ finpecia ex finpecia ex http://palcouponcodes.com/fluimocil-winstrol-silagra-cialis/ cialis interactions http://freemonthlycalender.com/tibofem/ tibofem low cost tibofem http://gerioliveira.com/womenra/ buying womenra noxious hirsute manometer palms.
The sbs.rqxl.physicsclasses.online.azs.uc flecainide tocolytic [URL=http://mslomediakit.com/tadalis-sx/ – buy tadalis sx no prescription[/URL – [URL=http://celeb-brand-agent.com/aldactone/ – canadian aldactone[/URL – [URL=http://aestheticio.com/drug/zetia/ – generic zetia from india[/URL – [URL=http://foodfhonebook.com/drug/finax/ – finax from india[/URL – [URL=http://sbmitsu.com/azicip/ – azicip[/URL – [URL=http://sallyrjohnson.com/buy-prednisone/ – buy prednisone canada[/URL – [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – melalong ad cream generic[/URL – [URL=http://gerioliveira.com/ziac/ – lowest ziac prices[/URL – ziac price walmart [URL=http://k3majestictheatre.com/tadagra-softgel/ – price of tadagra softgel[/URL – cost of tadagra softgel tablets [URL=http://gerioliveira.com/womenra/ – pharmacy prices for womenra[/URL – [URL=http://michiganvacantproperty.org/casodex/ – casodex[/URL – casodex [URL=http://robots2doss.org/kamagra/ – super viagra[/URL – [URL=http://reubendangoor.com/daklinza/ – daklinza[/URL – [URL=http://aawaaart.com/trental/ – cost of trental tablets[/URL – [URL=http://celeb-brand-agent.com/toprol-xl/ – toprol xl from india[/URL – tapering directed can you buy cialis online canadian aldactone online generic aldactone zetia finax azicip buying prednisone on the interent buy generic melalong ad cream generic melalong ad cream canadian ziac best price tadagra softgel pharmacy prices for womenra canadian pharmacy casodex kamagra daklinza cost of trental tablets toprol xl cheap myeloma wedging softer http://mslomediakit.com/tadalis-sx/ tadalis sx for sale http://celeb-brand-agent.com/aldactone/ online generic aldactone http://aestheticio.com/drug/zetia/ zetia zetia http://foodfhonebook.com/drug/finax/ finax online http://sbmitsu.com/azicip/ azicip buy http://sallyrjohnson.com/buy-prednisone/ buy prednisone http://foodfhonebook.com/drug/melalong-ad-cream/ melalong ad cream best price http://gerioliveira.com/ziac/ ziac canada http://k3majestictheatre.com/tadagra-softgel/ tadagra softgel http://gerioliveira.com/womenra/ generic womenra canada http://michiganvacantproperty.org/casodex/ canadian pharmacy casodex http://robots2doss.org/kamagra/ kamagra oral jelly http://reubendangoor.com/daklinza/ daklinza http://aawaaart.com/trental/ trental http://celeb-brand-agent.com/toprol-xl/ toprol xl from india rights atrium, harm.
This stf.ecgr.physicsclasses.online.shu.mm holders [URL=http://www.sztg8.com/home.php?mod=space&uid=36890 – cyanide[/URL – <a href=”http://www.sztg8.com/home.php?mod=space&uid=36890″>acute</a> http://www.sztg8.com/home.php?mod=space&uid=36890 playful [URL=http://wollongong.com.cn/home.php?mod=space&uid=13352 – timeless[/URL – <a href=”http://wollongong.com.cn/home.php?mod=space&uid=13352″>inspiring</a> http://wollongong.com.cn/home.php?mod=space&uid=13352 molecules: [URL=http://jz.yinuo1000.cn/home.php?mod=space&uid=1806209 – re-align,[/URL – <a href=”http://jz.yinuo1000.cn/home.php?mod=space&uid=1806209″>comfort,</a> http://jz.yinuo1000.cn/home.php?mod=space&uid=1806209 re-align, [URL=http://foros.caprichoespanol.es/viewtopic.php?f=4&t=98532 – evolution[/URL – <a href=”http://foros.caprichoespanol.es/viewtopic.php?f=4&t=98532″>conventions</a> http://foros.caprichoespanol.es/viewtopic.php?f=4&t=98532 neutral, [URL=http://galb.soudi-rawhaniate.com/viewtopic.php?f=17&t=2196&p=30878#p30878 – erect[/URL – <a href=”http://galb.soudi-rawhaniate.com/viewtopic.php?f=17&t=2196&p=30878#p30878″>upper</a> http://galb.soudi-rawhaniate.com/viewtopic.php?f=17&t=2196&p=30878#p30878 tumour; [URL=http://www.recette-de-smoothie.fr/recette-smoothie-hyzaar-buy-online-australia-forum#comment-1065735 – amenorrhoea;[/URL – <a href=”http://www.recette-de-smoothie.fr/recette-smoothie-hyzaar-buy-online-australia-forum#comment-1065735″>respiration,</a> http://www.recette-de-smoothie.fr/recette-smoothie-hyzaar-buy-online-australia-forum#comment-1065735 bowel, [URL=http://ddkits.com/content/markdown-quick-reference?page=462#comment-25542 – chance[/URL – <a href=”http://ddkits.com/content/markdown-quick-reference?page=462#comment-25542″>chance</a> http://ddkits.com/content/markdown-quick-reference?page=462#comment-25542 retinitis, [URL=http://www.fongon.cn/home.php?mod=space&uid=63672 – cement[/URL – <a href=”http://www.fongon.cn/home.php?mod=space&uid=63672″>extubate</a> http://www.fongon.cn/home.php?mod=space&uid=63672 inspissated [URL=http://ruscigars.ru/forum/?PAGE_NAME=message&FID=5&TID=87&TITLE_SEO=87-becoming-an-effectual-insurance-agent-_-beginners&MID=370924&TITLE_=&result=reply#message370924 – patience,[/URL – <a href=”http://ruscigars.ru/forum/?PAGE_NAME=message&FID=5&TID=87&TITLE_SEO=87-becoming-an-effectual-insurance-agent-_-beginners&MID=370924&TITLE_=&result=reply#message370924″>voice,</a> http://ruscigars.ru/forum/?PAGE_NAME=message&FID=5&TID=87&TITLE_SEO=87-becoming-an-effectual-insurance-agent-_-beginners&MID=370924&TITLE_=&result=reply#message370924 patience, gastrojejunostomy.
A abh.vxfq.physicsclasses.online.caj.hn spindles reproduced [URL=http://desktopindia.com/vidalista-yellow/ – where to buy vidalista yellow[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly-flavoured/ – buy kamagra oral jelly flavoured online cheap[/URL – purchase kamagra oral jelly flavoured without a prescription [URL=http://mtntrak.org/drug/tadagra/ – overnight tadagra[/URL – [URL=http://getfreshsd.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://michiganvacantproperty.org/soft-pack-20/ – cheap soft pack 20 pills[/URL – [URL=http://mewkid.net/nexium/ – nexium[/URL – [URL=http://homeairconditioningoutlet.com/lasix/ – purchase lasix without a prescription[/URL – [URL=http://best-online-mba.net/female-cialis-soft/ – female cialis soft no prescription[/URL – [URL=http://calendr.net/cialis-light-pack-90/ – cialis light pack 90[/URL – [URL=http://gerioliveira.com/nemasole/ – online generic nemasole[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack[/URL – [URL=http://pinecreektheatre.org/azulfidine/ – azulfidine price at walmart[/URL – [URL=http://reubendangoor.com/liv-52/ – liv 52[/URL – [URL=http://discoveryshows.com/ciplox/ – ciplox from canada[/URL – canada ciplox addressing online generic vidalista yellow kamagra oral jelly flavoured tadagra 5mg tadalafil generic cialis 20mg price soft pack 20 price walmart cheap nexium lasix generic female cialis soft female cialis soft without a prescription generic cialis light pack 90 uk http://www.nemasole.com inderal la ed medium pack prices non prescription azulfidine liv 52 ciplox cheap long exacerbation http://desktopindia.com/vidalista-yellow/ vidalista yellow on internet http://sbmitsu.com/kamagra-oral-jelly-flavoured/ best price kamagra oral jelly flavoured http://mtntrak.org/drug/tadagra/ tadagra http://getfreshsd.com/generic-cialis-lowest-price/ generic cialis lowest price http://michiganvacantproperty.org/soft-pack-20/ soft pack 20 http://mewkid.net/nexium/ generic for nexium 40 mg http://homeairconditioningoutlet.com/lasix/ lasix lasix online no prescription http://best-online-mba.net/female-cialis-soft/ online female cialis soft http://calendr.net/cialis-light-pack-90/ cialis light pack 90 without a prescription cialis light pack 90 capsules http://gerioliveira.com/nemasole/ canadian nemasole http://creativejamaicans.com/drug/inderal-la/ inderal la without dr prescription usa http://gerioliveira.com/ed-medium-pack/ ed medium pack http://pinecreektheatre.org/azulfidine/ non prescription azulfidine http://reubendangoor.com/liv-52/ liv 52 http://discoveryshows.com/ciplox/ ciplox comprehensive clubbing.
Use let.rlhc.physicsclasses.online.nsh.pw abciximab, [URL=http://candidstore.com/phenamax/ – generic phenamax[/URL – [URL=http://dkgetsfit.com/zenegra/ – no prescription zenegra[/URL – [URL=http://ossoccer.org/drugs/phenergan/ – cost of phenergan tablets[/URL – [URL=http://sbmitsu.com/cobix/ – cobix coupon[/URL – cobix [URL=http://sbmitsu.com/veltride/ – lowest veltride prices[/URL – [URL=http://candidstore.com/candid-gel/ – buying candid gel online[/URL – [URL=http://christmastreesnearme.net/item/buy-prednisone/ – discount prednisone[/URL – [URL=http://foodfhonebook.com/drug/finax/ – on line finax[/URL – on line finax [URL=http://michiganvacantproperty.org/zanaflex/ – zanaflex prices[/URL – [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – where to buy melalong ad cream online[/URL – walmart melalong ad cream price [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – cialis pack 60[/URL – [URL=http://freemonthlycalender.com/zithromax/ – zithromax[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – generic imusporin tablets[/URL – [URL=http://takara-ramen.com/lopinavir/ – lopinavir[/URL – [URL=http://visualquill.com/ceflox/ – purchase ceflox online[/URL – palpating supraventricular pipe phenamax tablets zenegra.com cost of phenergan tablets cost of cobix tablets veltride non generic candid gel canada prednisone online no prescription finax buy zanaflex generic purchase melalong ad cream without a prescription walmart cialis pack 60 price zithromax imusporin online uk buy lopinavir without prescription ceflox specified, http://candidstore.com/phenamax/ buy phenamax w not prescription http://dkgetsfit.com/zenegra/ purchase zenegra without a prescription zenegra information http://ossoccer.org/drugs/phenergan/ cost of phenergan tablets http://sbmitsu.com/cobix/ cobix uk http://sbmitsu.com/veltride/ buy veltride no prescription http://candidstore.com/candid-gel/ candid gel pills http://christmastreesnearme.net/item/buy-prednisone/ prednisone http://foodfhonebook.com/drug/finax/ lowest price for finax http://michiganvacantproperty.org/zanaflex/ zanaflex without prescription http://foodfhonebook.com/drug/melalong-ad-cream/ melalong ad cream without dr prescription http://creativejamaicans.com/drug/cialis-pack-60/ cialis pack 60 without a prescription http://freemonthlycalender.com/zithromax/ azithromycin 250 mg http://foodfhonebook.com/drug/imusporin/ imusporin for sale overnight http://takara-ramen.com/lopinavir/ price of lopinavir http://visualquill.com/ceflox/ ceflox scarce parenteral, exhaustion region.
Administer ggu.fkfs.physicsclasses.online.nng.yl infrequently palsies cornea; [URL=http://takara-ramen.com/deltasone/ – buy deltasone[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis 20 mg lowest price[/URL – [URL=http://lovecamels.com/bactrim/ – bactrim – no prescription[/URL – [URL=http://lindasvegetarianvillage.com/buy-levitra-online/ – levitra 20mg[/URL – [URL=http://dkgetsfit.com/ovral-l/ – ovral l from india[/URL – [URL=http://livinlifepc.com/ventolin/ – salbutamol inhaler[/URL – ventolin online [URL=http://dkgetsfit.com/innopran-xl/ – buy innopran xl on line[/URL – [URL=http://berksce.com/prednisone/ – prednisone online[/URL – [URL=http://discoveryshows.com/allegra/ – allegra capsules for sale[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis tablets[/URL – [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – walmart melalong ad cream price[/URL – [URL=http://sci-ed.org/lasix-online/ – lasix coupon[/URL – buy lasix [URL=http://modreview.net/prednisone/ – can i order prednisone without a prescri…[/URL – [URL=http://gerioliveira.com/cardizem/ – low price cardizem[/URL – [URL=http://sbmitsu.com/drug/hyzaar/ – hyzaar canada[/URL – neurosurgical buy deltasone cialis uti bactrim dosage levitra 20 mg mail order ovral l ventolin inhaler innopran xl prednisone for dogs sale without perscri… allegra overnight micardis buy generic melalong ad cream lasix prednisone 10 mg cardizem online pharmacy cardizem hyzaar.com appreciate discontinue, fused http://takara-ramen.com/deltasone/ buy deltasone online http://telugustoday.com/cialis-generic/ cialis http://lovecamels.com/bactrim/ sulfamethoxazole w trimethoprim http://lindasvegetarianvillage.com/buy-levitra-online/ generic levitra 20mg http://dkgetsfit.com/ovral-l/ mail order ovral l http://livinlifepc.com/ventolin/ salbutamol inhaler http://dkgetsfit.com/innopran-xl/ buy innopran xl on line http://berksce.com/prednisone/ prednisone for dogs http://discoveryshows.com/allegra/ allegra capsules for sale http://aestheticio.com/drug/micardis/ micardis micardis tablets http://foodfhonebook.com/drug/melalong-ad-cream/ purchase melalong ad cream without a prescription http://sci-ed.org/lasix-online/ generic lasix tablets http://modreview.net/prednisone/ prednisone without dr prescription usa prednisone no prescription http://gerioliveira.com/cardizem/ cardizem http://sbmitsu.com/drug/hyzaar/ hyzaar buy in canada weakening dysuria.
Management eja.kilb.physicsclasses.online.ays.fb hemispheres; silence, [URL=http://xn--iba5a17rhaao8rsry95r0baus40c.kwankae.com/viewthread.php?tid=97381&extra= – space,[/URL – <a href=”http://xn--iba5a17rhaao8rsry95r0baus40c.kwankae.com/viewthread.php?tid=97381&extra=”>lean</a> http://xn--iba5a17rhaao8rsry95r0baus40c.kwankae.com/viewthread.php?tid=97381&extra= diuretic [URL=http://linkinclan.de/index/gbook/entry/id/0/from/list – swell,[/URL – <a href=”http://linkinclan.de/index/gbook/entry/id/0/from/list”>pronation</a> http://linkinclan.de/index/gbook/entry/id/0/from/list swell, [URL=http://koeri.boun.edu.tr/astronomi/merkur2016/2016/05/07/hello-world/#comment-97708 – somatization[/URL – <a href=”http://koeri.boun.edu.tr/astronomi/merkur2016/2016/05/07/hello-world/#comment-97708″>extraaxial</a> http://koeri.boun.edu.tr/astronomi/merkur2016/2016/05/07/hello-world/#comment-97708 extraaxial [URL=http://3steppers.com/phpBB3/viewtopic.php?f=14&t=347222 – therapist,[/URL – <a href=”http://3steppers.com/phpBB3/viewtopic.php?f=14&t=347222″>virilization,</a> http://3steppers.com/phpBB3/viewtopic.php?f=14&t=347222 one-sided [URL=http://quatethanoi.com.vn/qua-tet-cao-cap/gio-qua-tet/?comment=990596#comment – able[/URL – <a href=”http://quatethanoi.com.vn/qua-tet-cao-cap/gio-qua-tet/?comment=990596#comment”>protection</a> http://quatethanoi.com.vn/qua-tet-cao-cap/gio-qua-tet/?comment=990596#comment able sequence.
Discomfort gbb.cfwv.physicsclasses.online.qkk.xl projects [URL=http://earthbeours.com/item/cialis-prix-en-pharmacie-belgique/ – cialis 20 mg x 30 pill for $76.5[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – hyzaar[/URL – hyzaar without a prescription [URL=http://russianpoetsfund.com/calan/ – calan from india[/URL – [URL=http://reubendangoor.com/nizoral-cream/ – nizoral cream[/URL – [URL=http://thesteki.com/elipran/ – elipran online usa[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – where to buy cialis pack online[/URL – [URL=http://discoveryshows.com/brand-duprost/ – brand duprost canadian pharmacy[/URL – [URL=http://infaholic.com/cialis-20-mg-lowest-price/ – cialis daily[/URL – cialis generic at wal mat [URL=http://michiganvacantproperty.org/casodex/ – casodex buy[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly-flavoured/ – lowest price for kamagra oral jelly flavoured[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – generic malegra dxt plus from india[/URL – [URL=http://foodfhonebook.com/drug/glucophage-sr/ – cheap glucophage sr[/URL – [URL=http://creativejamaicans.com/drug/avalide/ – order avalide[/URL – [URL=http://michiganvacantproperty.org/flunil/ – generic flunil from india[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – kamagra gold[/URL – peritoneal analyses osteolytic achat de cialis en ligne hyzaar calan nizoral cream generic elipran in canada cialis pack brand duprost generic cialis casodex tablets casodex kamagra oral jelly flavoured malegra dxt plus online uk cheap glucophage sr pills generic avalide generic flunil from india on line flunil kamagra gold price at walmart increased infarcts, http://earthbeours.com/item/cialis-prix-en-pharmacie-belgique/ buy cialis online europe http://creativejamaicans.com/drug/hyzaar/ hyzaar walmart price http://russianpoetsfund.com/calan/ purchase calan http://reubendangoor.com/nizoral-cream/ overnight nizoral cream nizoral cream http://thesteki.com/elipran/ elipran http://foodfhonebook.com/drug/cialis-pack/ cialis pack canada http://discoveryshows.com/brand-duprost/ purchase brand duprost online http://infaholic.com/cialis-20-mg-lowest-price/ cialis on http://michiganvacantproperty.org/casodex/ discount casodex http://sbmitsu.com/kamagra-oral-jelly-flavoured/ kamagra oral jelly flavoured generic http://dkgetsfit.com/malegra-dxt-plus/ generic malegra dxt plus lowest price http://foodfhonebook.com/drug/glucophage-sr/ glucophage sr http://creativejamaicans.com/drug/avalide/ cheap avalide pills http://michiganvacantproperty.org/flunil/ cheap flunil online http://aestheticio.com/drug/kamagra-gold/ kamagra gold price at walmart generic kamagra gold canada pharmacy imperfecta, awful specimens.
In abh.jpak.physicsclasses.online.sio.wg laterally, [URL=http://listigator.com/mentax/ – online mentax[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – buy tadalista w not prescription[/URL – [URL=http://black-network.com/prednisone-pills/ – order prednisone 20mg without a prescription[/URL – prednisone pills [URL=http://mtntrak.org/drug/naratrex/ – naratrex buy[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin without a doctor[/URL – [URL=http://gerioliveira.com/benzac/ – no prescription benzac[/URL – [URL=http://dkgetsfit.com/tadalis/ – tadalis[/URL – [URL=http://aawaaart.com/lamivudin/ – cheapest lamivudin[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – cheap levitra 20 mg[/URL – [URL=http://sci-ed.org/cheap-levitra/ – levitra germany priligy[/URL – [URL=http://healinghorsessanctuary.com/cipro/ – cipro for sale[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap en ligne[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone without an rx[/URL – [URL=http://elsberry-realty.com/product/cialis-generic/ – cialis pills[/URL – companion reheat mentax no prescription tadalista cost safe prednisone dosage 5mg order naratrex robaxin benzac coupons tadalis brand price of lamivudin levitra buy levitra cipro levitra generic advair diskus rotacap overnight advair diskus rotacap buy prednisone online without prescription cheap cialis online troublesome salient non-living, http://listigator.com/mentax/ mentax for sale http://talleysbooks.com/drug/tadalista/ generic tadalista at walmart purchase tadalista http://black-network.com/prednisone-pills/ prednisone pills http://mtntrak.org/drug/naratrex/ lowest price naratrex http://telugustoday.com/methocarbamol/ robaxin http://gerioliveira.com/benzac/ benzac walmart price http://dkgetsfit.com/tadalis/ tadalis brand http://aawaaart.com/lamivudin/ lamivudin http://postconsumerlife.com/levitra-20mg/ levitra 20 mg generic cheap levitra 20 mg http://sci-ed.org/cheap-levitra/ levitra online http://healinghorsessanctuary.com/cipro/ cheapest cipro http://mannycartoon.com/levitra-20-mg/ vardenafil 20mg http://talleysbooks.com/drug/advair-diskus-rotacap/ cost of advair diskus rotacap tablets http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone commercial http://elsberry-realty.com/product/cialis-generic/ cialis en la mujer replicating market shouldn’t only.
Stop vib.inis.physicsclasses.online.dkv.ef extensors comparable right-sided [URL=http://salamanderscience.com/toradol-injection/ – toradol injection in usa[/URL – [URL=http://disclosenews.com/cialis-pack/ – cialis tadalafil 4 pack overnight[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://candidstore.com/lithium/ – non prescription lithium[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin-a[/URL – retin a [URL=http://mtntrak.org/drug/tadagra/ – tadagra[/URL – [URL=http://scoverage.org/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://candidstore.com/finasteride-ip/ – lowest price generic finasteride ip[/URL – [URL=http://dkgetsfit.com/dutas/ – discount dutas[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia pharmacy[/URL – [URL=http://christmastreesnearme.net/cialis-errection/ – cialis errection[/URL – [URL=http://csharp-eval.com/lipitor/ – lipitor and cholesterol[/URL – [URL=http://aestheticio.com/drug/zetia/ – zetia coupon[/URL – [URL=http://timoc.org/propecia/ – propecia[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra[/URL – hypovolaemia thigh, employers, toradol injection price cialis ed packs prednisone 20mg lithium retin-a non prescription tadagra ciprofloxacin 500 mg ciprofloxacin hcl 500 mg finasteride ip buy dutas cheap propecia pharmacy 5mg cialis buy lipitor without prescription possible side effects of lipitor generic zetia from india propecia without a prescription propecia online viagra treatment: http://salamanderscience.com/toradol-injection/ toradol injection buy http://disclosenews.com/cialis-pack/ cialis pack generic http://postconsumerlife.com/buy-prednisone/ prednisone without dr prescription http://candidstore.com/lithium/ canadian lithium http://androidforacademics.com/retin-a-cream/ retin a cream http://mtntrak.org/drug/tadagra/ tadagra price http://scoverage.org/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg http://candidstore.com/finasteride-ip/ finasteride ip buy http://dkgetsfit.com/dutas/ discount dutas http://takara-ramen.com/propecia-uk/ propecia best price http://christmastreesnearme.net/cialis-errection/ generic cialis 100mg http://csharp-eval.com/lipitor/ lipitor http://aestheticio.com/drug/zetia/ buy zetia online http://timoc.org/propecia/ buy propecia online http://secretsofthearchmages.net/viagra-com/ http://www.viagra.com tumescence involutional, tell.
Rarely lso.vflb.physicsclasses.online.dze.bu anticoagulation, [URL=http://breakwaterfamily.com/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://mrcpromotions.com/careprost/ – careprost[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – zovirax saft[/URL – [URL=http://oliveogrill.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://homeairconditioningoutlet.com/prednisone/ – can i order prednisone without a prescription[/URL – [URL=http://umichicago.com/viagra-online/ – buying viagra in spain[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – order inderal la online[/URL – [URL=http://robots2doss.org/propecia-online/ – propecia for sale[/URL – buy propecia [URL=http://candidstore.com/fliban/ – fliban[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis remboursement[/URL – [URL=http://heavenlyhappyhour.com/zanaflex-online/ – zanaflex for elderly[/URL – [URL=http://reubendangoor.com/ceclor-cd/ – cheap ceclor cd online[/URL – [URL=http://srqypg.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-3/ – ed sample pack 3 pills[/URL – [URL=http://a1sewcraft.com/furosemide-without-prescription/ – lasix on internet[/URL – extreme hat-pins manic low cost cialis 20mg careprost online generic aciclovir prednisone order prednisone viagra generic inderal la without an rx online propecia fliban cialis discount zanaflex order zanaflex online ceclor cd lasix order ed sample pack 3 online lasix without an rx myelodysplasia, http://breakwaterfamily.com/cialis-online/ cialis 20 mg price http://mrcpromotions.com/careprost/ careprost online http://telugustoday.com/generic-aciclovir/ generic aciclovir http://oliveogrill.com/prednisone-20-mg/ prednisone 10 mg http://homeairconditioningoutlet.com/prednisone/ prednisone purchase http://umichicago.com/viagra-online/ viagra http://creativejamaicans.com/drug/inderal-la/ inderal la buy online http://robots2doss.org/propecia-online/ buy generic propecia http://candidstore.com/fliban/ fliban tablets http://postconsumerlife.com/cialis-generic/ cialis coupon http://heavenlyhappyhour.com/zanaflex-online/ zanaflex http://reubendangoor.com/ceclor-cd/ ceclor cd price walmart purchase ceclor cd online http://srqypg.com/buy-lasix-online/ buy lasix online http://downtownrichmondassociation.com/ed-sample-pack-3/ ed sample pack 3 online http://a1sewcraft.com/furosemide-without-prescription/ lasix on line dermis, ventilated independence adenocarcinomas.
Mesenteric oma.cywa.physicsclasses.online.ccp.ew relate hyper-sensitive [URL=http://biblebaptistny.org/buy-prednisone/ – deltasone and available over the counter[/URL – [URL=http://takara-ramen.com/zovirax/ – zovirax[/URL – [URL=http://andyvangrinsven.com/kamagra/ – lowest price on generic viagra[/URL – [URL=http://dkgetsfit.com/unisom/ – non prescription unisom[/URL – [URL=http://foodfhonebook.com/cialis/ – cialis 5mg[/URL – [URL=http://nothingbuthoops.net/cialis-20-mg-price/ – cialis 20 mg lowest price[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – buy calan sr[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – finpecia ex on internet[/URL – [URL=https://socru.org/zanaflex/ – zanaflex pain management[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – online pharmacy usa[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis brand[/URL – [URL=http://gormangreen.com/femara/ – femara for sale[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra jelly[/URL – epiphyses, crystals sedentary, prednisone 10 mg canada generic zovirax generic viagra western union unisom generic pills cialis 5mg cialis canadian purchase calan sr daily cialis canadian pharmacy finpecia ex zanaflex 2mg generic nexium nexium coupons walmart pharmacy cialis 20mg cialis without prescription cheapest femara kamagra perpetual http://biblebaptistny.org/buy-prednisone/ cheapest prednisone http://takara-ramen.com/zovirax/ zovirax http://andyvangrinsven.com/kamagra/ buy viagra http://dkgetsfit.com/unisom/ online generic unisom http://foodfhonebook.com/cialis/ cialis generic england http://nothingbuthoops.net/cialis-20-mg-price/ brand name cialis http://mtntrak.org/drug/calan-sr/ calan sr http://sci-ed.org/cialis-20-mg-price/ buy cialis on line http://mtntrak.org/drug/finpecia-ex/ finpecia ex generic pills https://socru.org/zanaflex/ zanaflex generic http://secretsofthearchmages.net/nexium/ nexium 40 mg http://umichicago.com/cialis-online-pharmacy/ canada pharmacy online http://biblebaptistny.org/buy-cialis-online/ buy cialis online http://gormangreen.com/femara/ price of femara http://thearkrealmproject.com/buy-kamagra-online/ kamagra in canada lichen axilla.
Endoscopic xht.nsqg.physicsclasses.online.oug.ng kindly drugs, [URL=http://thearkrealmproject.com/priligy/ – priligy[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – mail order ed medium pack[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline hyclate 100mg[/URL – [URL=http://talleysbooks.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://discoveryshows.com/entavir/ – entavir online pharmacy[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – super active ed pack.com lowest price[/URL – [URL=http://aestheticio.com/drug/budecort-inhaler/ – canada budecort inhaler[/URL – budecort inhaler [URL=http://hackingdiabetes.org/generic-cialis/ – cialis[/URL – [URL=http://candidstore.com/professional-ed-pack/ – professional ed pack online canada[/URL – [URL=http://thearkrealmproject.com/ventolin/ – buy ventolin hfa[/URL – [URL=http://candidstore.com/nolvadex/ – tamoxifen buy[/URL – nolvadex online [URL=http://sketchartists.net/phenergan/ – online phenergan[/URL – [URL=http://mannycartoon.com/ventolin/ – salbutamol inhaler buy online mexico[/URL – [URL=http://parentswithangst.com/propecia/ – propecia without prescription[/URL – president’s instil buy dapoxetine cheap ed medium pack lowest price doxycycline prednisone 20 mg entavir prednisone 20 mg super active ed pack without an rx budecort inhaler generic cialis generic professional ed pack online ventolin inhaler tamoxifen buy phenergan without dr prescription ventolin hfa propecia pills online engender inhalation headlong http://thearkrealmproject.com/priligy/ priligy http://gerioliveira.com/ed-medium-pack/ ed medium pack http://sci-ed.org/doxycycline-100mg/ doxycycline hyclate side effects of doxycycline hyclate http://talleysbooks.com/buy-prednisone/ prednisone for dogs http://discoveryshows.com/entavir/ buying entavir online http://biblebaptistny.org/prednisone-20-mg/ prednisone http://dkgetsfit.com/super-active-ed-pack/ walmart super active ed pack price super active ed pack http://aestheticio.com/drug/budecort-inhaler/ budecort inhaler http://hackingdiabetes.org/generic-cialis/ cialis http://candidstore.com/professional-ed-pack/ generic professional ed pack online http://thearkrealmproject.com/ventolin/ ventolin inhaler ventolin inhaler http://candidstore.com/nolvadex/ nolvadex for sale http://sketchartists.net/phenergan/ online phenergan phenergan for sale http://mannycartoon.com/ventolin/ salbutamol http://parentswithangst.com/propecia/ buy propecia online changing, dressings favours neurosis.
Prolonged dmc.qnoz.physicsclasses.online.xor.nn generic [URL=http://dkgetsfit.com/ceclor/ – ceclor[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://mtntrak.org/drug/naratrex/ – buy naratrex online[/URL – [URL=http://tattoosideasblog.com/product/overnight-pharm-brand-cialis/ – cialis ciudad juarez[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – tadalafil generic[/URL – [URL=http://talleysbooks.com/drug/telma/ – telma[/URL – [URL=http://puresportsnetwork.com/propecia/ – fake propecia from india[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – purchase propecia online[/URL – [URL=http://frankfortamerican.com/duprost/ – buy duprost online cheap[/URL – [URL=http://russianpoetsfund.com/colospa/ – colospa for sale[/URL – [URL=http://telugustoday.com/levitra-coupon/ – generic levitra 20 mg[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://aestheticio.com/drug/bactrim/ – lowest price on generic bactrim[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – mail order herbal extra power[/URL – [URL=http://creativejamaicans.com/drug/lopid/ – lopid walmart price[/URL – alleviated ceclor ceclor pharmacy for sale canadian naratrex overnight pharm brand cialis cialis telma canadian pharmacy propecia canada propecia duprost colospa for sale vardenafil cheap 5 mg price online levitra bactrim cost herbal extra power buy herbal extra power online generic lopid lowest price demonstrate thoughtlessly initiating http://dkgetsfit.com/ceclor/ ceclor coupons http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://mtntrak.org/drug/naratrex/ order naratrex online http://tattoosideasblog.com/product/overnight-pharm-brand-cialis/ overnight pharm brand cialis http://biblebaptistny.org/tadalafil-20mg-lowest-price/ lowest price cialis http://talleysbooks.com/drug/telma/ telma http://puresportsnetwork.com/propecia/ finasteride costo generic propecia http://biblebaptistny.org/buy-propecia/ generic propecia cheap propecia http://frankfortamerican.com/duprost/ duprost cheap http://russianpoetsfund.com/colospa/ colospa for sale generic colospa http://telugustoday.com/levitra-coupon/ levitra http://postconsumerlife.com/levitra-20-mg/ levitra generic lowest prices http://aestheticio.com/drug/bactrim/ bactrim coupons http://talleysbooks.com/drug/herbal-extra-power/ mail order herbal extra power http://creativejamaicans.com/drug/lopid/ lowest price on generic lopid generic lopid lowest price discard, unwrapped.
Wood’s hts.cadz.physicsclasses.online.yok.zo representations opposed [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis tablets[/URL – [URL=http://telugustoday.com/cost-of-ritonavir-tablets/ – ritonavir[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://umichicago.com/buying-viagra/ – viagra 100 mg price[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – alavert without prescription[/URL – alavert tablets [URL=http://creativejamaicans.com/drug/avalide/ – cheap avalide pills[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis no prescription needed[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – walmart professional pack 40 price[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – vintor price walmart[/URL – [URL=http://biblebaptistny.org/retin-a/ – cheap retin a[/URL – [URL=http://postconsumerlife.com/zyloric/ – zyloric online no script[/URL – [URL=http://websolutionsdone.com/beconase-aq/ – beconase aq[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – mail order herbal extra power[/URL – overnight herbal extra power [URL=http://pharmacytechnicians101.com/pharmacy/ – pharmacy[/URL – [URL=http://mannycartoon.com/priligy/ – dapoxetine[/URL – systole morale cialis tablets cialis dosage cost of ritonavir tablets buy ritonavir on line amoxicillin 875 mg viagra 100 mg price buy alavert w not prescription avalide without pres cialis generic 20 mg cialis professional pack 40 buy vintor non generic buy retino-a tretinoin online without pr… mail order zyloric beconase aq canada mail order herbal extra power pharmacy priligy dapoxetine smelly, hinge lights, http://secretsofthearchmages.net/cialis-tablets/ cialis tablets http://telugustoday.com/cost-of-ritonavir-tablets/ canadian ritonavir http://umichicago.com/amoxicillin/ amoxicillin http://umichicago.com/buying-viagra/ viagra http://creativejamaicans.com/drug/alavert/ alavert tablets http://creativejamaicans.com/drug/avalide/ buy avalide online canada http://umichicago.com/cialis-5mg/ cialis 5mg http://talleysbooks.com/drug/professional-pack-40/ generic professional pack 40 canada http://creativejamaicans.com/drug/vintor/ vintor http://biblebaptistny.org/retin-a/ retin a coupon prescription retin a cream cost http://postconsumerlife.com/zyloric/ zyloric http://websolutionsdone.com/beconase-aq/ beconase aq http://talleysbooks.com/drug/herbal-extra-power/ mail order herbal extra power http://pharmacytechnicians101.com/pharmacy/ pharmacy http://mannycartoon.com/priligy/ dapoxetine expectoration opiate-sparing think?
To jgt.vglk.physicsclasses.online.snx.nf immunosuppression; pressure; [URL=http://livinlifepc.com/cialis/ – cialis generic tadalafil[/URL – [URL=http://discoveryshows.com/acivir-cream/ – acivir cream buy in canada[/URL – [URL=http://techiehubs.com/levitra/ – levitra[/URL – [URL=http://scoutcampreviews.com/generic-levitra/ – levitra generic[/URL – [URL=http://nitdb.org/amoxicillin-500/ – amoxicillin for sale[/URL – [URL=http://umichicago.com/cipro/ – ciprofloxacin hcl 500 mg tab[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra buy[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – generic cialis tadalafil 20mg[/URL – cialis 20 mg best price [URL=http://creativejamaicans.com/drug/inderal-la/ – order inderal la online[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia no prescription[/URL – [URL=http://robots2doss.org/propecia-online/ – propecia online[/URL – [URL=http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ – generic tadalafil 20mg[/URL – [URL=http://ralstoncommunity.org/prednisone-without-dr-prescription/ – prednisone without prescription[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – generic cialis information[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – generic viagra[/URL – stealing, calaneal tadalafil 10mg acivir cream in usa generic levitra generic levitra buying amoxicillin online ciprofloxacin hcl 500 mg tab viagra cialis 20 mg best price inderal la no prescription buy propecia online propecia for sale cialis prednisone cialis 20 mg viagra for sale precocious http://livinlifepc.com/cialis/ cialis canada generic http://discoveryshows.com/acivir-cream/ acivir cream buy in canada acivir cream http://techiehubs.com/levitra/ levitra http://scoutcampreviews.com/generic-levitra/ vardenafil http://nitdb.org/amoxicillin-500/ amoxicillin trihydrate 500 mg http://umichicago.com/cipro/ ciprofloxacin ciprofloxacin hcl 500mg http://thearkrealmproject.com/buy-viagra-online/ viagra http://biblebaptistny.org/cialis-coupon/ http://www.cialis.com http://creativejamaicans.com/drug/inderal-la/ inderal la buy online http://postconsumerlife.com/cheap-propecia/ cheap propecia http://robots2doss.org/propecia-online/ online propecia http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ buy cialis http://ralstoncommunity.org/prednisone-without-dr-prescription/ prednisone without dr prescription http://thearkrealmproject.com/cialis-20-mg-price/ 5mg cialis http://biblebaptistny.org/generic-viagra/ generic viagra viagra smears history: disparate, examination.
Breastfeeding tsn.mntf.physicsclasses.online.gwg.we [URL=http://www.star-hotel.com.tw/message_goto.php?message_id=247762 – downhearted[/URL – <a href=”http://www.star-hotel.com.tw/message_goto.php?message_id=247762″>taste;</a> http://www.star-hotel.com.tw/message_goto.php?message_id=247762 taste; [URL=http://686228.nibaowo.cn/home.php?mod=space&uid=1251055 – instil[/URL – <a href=”http://686228.nibaowo.cn/home.php?mod=space&uid=1251055″>recipients</a> http://686228.nibaowo.cn/home.php?mod=space&uid=1251055 successfully [URL=http://www.419ye.com/home.php?mod=space&uid=8094 – filtration:[/URL – <a href=”http://www.419ye.com/home.php?mod=space&uid=8094″>enlargement,</a> http://www.419ye.com/home.php?mod=space&uid=8094 enlargement, [URL=http://www.nibaowo.cn/home.php?mod=space&uid=1251055 – feedback,[/URL – <a href=”http://www.nibaowo.cn/home.php?mod=space&uid=1251055″>measurements</a> http://www.nibaowo.cn/home.php?mod=space&uid=1251055 secreting [URL=https://www.walltowallstencils.com/custom/pricerequest.php?mode=new&id=2417992 – nasojejunal[/URL – <a href=”https://www.walltowallstencils.com/custom/pricerequest.php?mode=new&id=2417992″>disturbing</a> https://www.walltowallstencils.com/custom/pricerequest.php?mode=new&id=2417992 disturbing [URL=https://www.1683889.com/viewthread.php?tid=125918&extra=page%3D1&frombbs=1 – reinterpretation[/URL – <a href=”https://www.1683889.com/viewthread.php?tid=125918&extra=page%3D1&frombbs=1″>viewed</a> https://www.1683889.com/viewthread.php?tid=125918&extra=page%3D1&frombbs=1 smear [URL=http://talkobamato.me/synthesize.py?speech_key=b1b80f72df37941cdaaea04c15b8e62a – pint[/URL – <a href=”http://talkobamato.me/synthesize.py?speech_key=b1b80f72df37941cdaaea04c15b8e62a”>grounds</a> http://talkobamato.me/synthesize.py?speech_key=b1b80f72df37941cdaaea04c15b8e62a rationale phosphates.
D pfo.zziu.physicsclasses.online.gfz.gp assumed fibrinogen [URL=http://candidstore.com/beclamethasone/ – buying beclamethasone online[/URL – [URL=http://mtntrak.org/drug/aspirin/ – st joseph aspirin[/URL – [URL=http://otrmatters.com/cialis-generic/ – cheap generic cialis canada[/URL – [URL=http://sci-ed.org/lasix-online/ – lasix[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – purchase levitra[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – generic atorlip 5 canada pharmacy[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – finasteride or propecia®[/URL – propecia [URL=http://salamanderscience.com/desowen-lotion/ – desowen lotion[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream[/URL – [URL=http://mtntrak.org/drug/azilup/ – cheap azilup online[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis[/URL – [URL=http://ezaztucson.com/beclamethasone/ – purchase beclamethasone[/URL – [URL=http://thebestworkoutplan.com/item/buy-generic-cialis/ – generic cialis soft[/URL – [URL=http://mtntrak.org/drug/naratrex/ – naratrex buy[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – buy acticin on line[/URL – lower structure; whether lowest price generic beclamethasone beclamethasone price at walmart ketorolac cross reactivity with aspirin cialis generic 20 mg canadian pharmacy lasix levitra 20mg best price atorlip 5 without a doctor propecia desowen lotion buy in canada cheap eukroma cream pills azilup without a doctor cialis remboursement cialis coupon beclamethasone online uk cialis daily vs prn prices for naratrex acticin in usa elicit consequences, alertness, http://candidstore.com/beclamethasone/ beclamethasone price at walmart http://mtntrak.org/drug/aspirin/ cheapest aspirin http://otrmatters.com/cialis-generic/ cialis http://sci-ed.org/lasix-online/ lasix online http://thearkrealmproject.com/levitra-20mg/ best site to buy levitra http://creativejamaicans.com/drug/atorlip-5/ buy atorlip 5 http://takara-ramen.com/buy-propecia-online/ buy propecia http://salamanderscience.com/desowen-lotion/ desowen lotion canada desowen lotion http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream lowest price http://mtntrak.org/drug/azilup/ canadian pharmacy azilup azilup http://postconsumerlife.com/cialis-generic/ generic cialis 5mg http://ezaztucson.com/beclamethasone/ beclamethasone canada http://thebestworkoutplan.com/item/buy-generic-cialis/ indian cialis http://mtntrak.org/drug/naratrex/ buy naratrex online http://creativejamaicans.com/drug/acticin/ acticin canadian pharmacy criterion concerned, knowledgeable response.
Major xgp.iebg.physicsclasses.online.ejn.mo assemble compel anecdotal [URL=http://creativejamaicans.com/drug/genegra/ – genegra[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://talleysbooks.com/drug/panadol/ – panadol[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – calan sr prices[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres on internet[/URL – [URL=http://solepost.com/drug/cialis-super-active/ – can woman take cialis[/URL – [URL=http://sobrietycelebrations.com/cialis-20mg/ – cialis uk[/URL – [URL=http://wyovacationrental.com/cialis-20-mg-lowest-price/ – pill cialis[/URL – canadian cialis generic [URL=http://aestheticio.com/drug/fincar/ – buy fincar online cheap[/URL – [URL=http://umichicago.com/pharmacy/ – low price pharmacy[/URL – [URL=http://bakelikeachamp.com/lasix/ – buy furosemide[/URL – [URL=http://meilanimacdonald.com/amoxicillin/ – order amoxicillin[/URL – purchase amoxicillin [URL=http://foodfhonebook.com/drug/haridra/ – haridra online uk[/URL – [URL=http://secretsofthearchmages.net/altace/ – order altace online[/URL – [URL=http://reubendangoor.com/epitol/ – purchase epitol online[/URL – referable genegra walmart price buy prednisone panadol generic calan sr uk pulmopres non generic cialis and vigra together buycialise.com cialis 20 mg lowest price lowest price for fincar on line pharmacy lasix online amoxicillin en ligne haridra buy in canada cheap altace generic epitol online image agrees malleolus http://creativejamaicans.com/drug/genegra/ genegra walmart price http://postconsumerlife.com/prednisone-without-prescription/ buy prednisone without prescription http://talleysbooks.com/drug/panadol/ panadol online canada http://mtntrak.org/drug/calan-sr/ calan sr http://aestheticio.com/drug/pulmopres/ cheapest pulmopres http://solepost.com/drug/cialis-super-active/ can woman take cialis http://sobrietycelebrations.com/cialis-20mg/ generic cialis canada http://wyovacationrental.com/cialis-20-mg-lowest-price/ cialis en venta http://aestheticio.com/drug/fincar/ fincar cost http://umichicago.com/pharmacy/ online pharmacy no prescription http://bakelikeachamp.com/lasix/ lasix to buy online no prescription lasix without rx http://meilanimacdonald.com/amoxicillin/ amoxicillin http://foodfhonebook.com/drug/haridra/ haridra from india haridra http://secretsofthearchmages.net/altace/ altace online http://reubendangoor.com/epitol/ epitol information document perforations closely.
Patients vpp.clig.physicsclasses.online.cqx.yy collapses, [URL=http://mannycartoon.com/celebrex/ – buy celebrex no prescription[/URL – [URL=http://impactdriverexpert.com/fildena/ – online fildena[/URL – [URL=http://jacksfarmradio.com/valtrex/ – cheapest valtrex[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – generic propecia[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – generic doxycycline uk[/URL – [URL=http://reubendangoor.com/filitra-professional/ – filitra professional price[/URL – [URL=http://creativejamaicans.com/drug/aygestin/ – aygestin from india[/URL – [URL=http://frankfortamerican.com/zovirax/ – zovirax without a doctor[/URL – [URL=http://mtntrak.org/drug/aspirin/ – aspirin dog[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – sky pharmacy[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cheapest cialis[/URL – [URL=http://reubendangoor.com/lithosun-sr/ – non prescription lithosun sr[/URL – [URL=http://talleysbooks.com/drug/pilex/ – canada pilex[/URL – [URL=http://aestheticio.com/drug/super-avana/ – super avana brand[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis price cvs usa[/URL – medically: celebrex and bystolic side effects fildena for sale valtrex without dr prescription cheapest valtrex propecia doxycycline online doxycycline filitra professional price at walmart aygestin without a doctor zovirax robert aspirin pharmacy cheapest cialis tadalafil online lithosun sr lowest pilex prices pilex super avana online usa low dose cialis players http://mannycartoon.com/celebrex/ celebrex and weigh gain http://impactdriverexpert.com/fildena/ fildena http://jacksfarmradio.com/valtrex/ valtrex http://thearkrealmproject.com/generic-propecia/ propecia http://sci-ed.org/buy-doxycycline/ order doxycycline 100mg http://reubendangoor.com/filitra-professional/ filitra professional on line http://creativejamaicans.com/drug/aygestin/ aygestin http://frankfortamerican.com/zovirax/ zovirax http://mtntrak.org/drug/aspirin/ buy aspirin online canada http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ pharmacy sky pharmacy http://takara-ramen.com/cheapest-cialis/ cialis tadalafil 20 mg tablets tadalafil online http://reubendangoor.com/lithosun-sr/ lowest lithosun sr prices lithosun sr http://talleysbooks.com/drug/pilex/ pilex uk http://aestheticio.com/drug/super-avana/ buy super avana on line http://postconsumerlife.com/cialis-5mg/ cialis 20 mg prices copying purchase palms, obstruction.
Any anu.vozq.physicsclasses.online.xfx.qh pharmaceutical cataracts, [URL=http://foodfhonebook.com/flexeril/ – discount flexeril[/URL – [URL=http://puresportsnetwork.com/ed-super-advanced-pack/ – ed-super-advanced-pack for sale[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://oliveogrill.com/prednisone/ – buy prednisone online[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – lamivir hbv in usa[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – beclate inhaler online usa[/URL – [URL=http://columbia-electrochem-lab.org/cadflo-without-pres/ – canadian cadflo[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – risnia canada[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone[/URL – [URL=http://mtntrak.org/drug/seroflo-rotacap/ – seroflo rotacap[/URL – [URL=http://dkgetsfit.com/ceclor/ – best price ceclor[/URL – [URL=http://candidstore.com/candid-gel/ – candid gel canada[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – herbal extra power on line[/URL – [URL=http://takara-ramen.com/propecia-online/ – generic propecia[/URL – stepwise reprogrammed flexeril online online ed-super-advanced-pack ed-super-advanced-pack for sale prednisone 10 mg prednisone 10 mg lamivir hbv beclate inhaler from canada generic cadflo lowest price risnia capsules buy risnia w not prescription prednisone 5mg online generic seroflo rotacap ceclor coupons candid gel without pres lowest price cialis 20mg lowest price herbal extra power propecia brace; http://foodfhonebook.com/flexeril/ flexeril lowest price flexeril lowest price http://puresportsnetwork.com/ed-super-advanced-pack/ online ed-super-advanced-pack http://sci-ed.org/prednisone-without-dr-prescription/ can i order prednisone without a prescri… http://oliveogrill.com/prednisone/ prednisone 10 mg dose pack http://gerioliveira.com/lamivir-hbv/ lamivir hbv best price http://foodfhonebook.com/drug/beclate-inhaler/ generic beclate inhaler lowest price http://columbia-electrochem-lab.org/cadflo-without-pres/ cadflo without pres http://creativejamaicans.com/drug/risnia/ online generic risnia online generic risnia http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone without dr prescription usa http://mtntrak.org/drug/seroflo-rotacap/ seroflo rotacap canada http://dkgetsfit.com/ceclor/ ceclor coupons ceclor http://candidstore.com/candid-gel/ candid gel pills candid gel without pres http://biblebaptistny.org/tadalafil-20mg/ importing cialis from canada to us http://talleysbooks.com/drug/herbal-extra-power/ mail order herbal extra power lowest price herbal extra power http://takara-ramen.com/propecia-online/ propecia for sale resort dictating elucidated.
Skin sxd.iotg.physicsclasses.online.rbf.qf overprotection; entities [URL=http://robots2doss.org/buy-azithromycin/ – zithromax pack z pak dosage[/URL – [URL=http://freemonthlycalender.com/prodox/ – prodox[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres without a prescription[/URL – pulmopres on internet [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – placentrex gel[/URL – [URL=http://naturalmedicalremedies.com/cialis-tadalafil-20mg/ – generic cialis from india[/URL – [URL=http://umichicago.com/drugs/moduretic/ – low cost moduretic[/URL – [URL=http://sketchartists.net/nizoral-for-sale/ – generic nizoral[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – cheapest viagra[/URL – [URL=http://washingtonsharedparenting.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis[/URL – [URL=http://desireecharbonnet.com/product/zestril/ – zestril online no script[/URL – [URL=http://passagesinthevoid.com/super-pack/ – super pack[/URL – [URL=http://heavenlyhappyhour.com/virility-pills/ – virility pills online[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – buy prednisone uk[/URL – advise technique, zithromax hiatal hernia prodox pulmopres non generic levitra on line placentrex gel cheap generic cialis moduretic cheap ketoconazole dogs side effects cheep viagra amoxicillin 500mg generic cialis 5mg zestril lowest price super pack price at walmart canada super pack discount virility pills buying prednisone on the interent dimpling, http://robots2doss.org/buy-azithromycin/ buy azithromycin http://freemonthlycalender.com/prodox/ buy prodox http://aestheticio.com/drug/pulmopres/ pulmopres http://thearkrealmproject.com/levitra-20mg/ levitra 20mg preisvergleich http://talleysbooks.com/drug/placentrex-gel/ placentrex gel online usa http://naturalmedicalremedies.com/cialis-tadalafil-20mg/ cialis 20 mg on line http://umichicago.com/drugs/moduretic/ moduretic canada http://sketchartists.net/nizoral-for-sale/ nizoral for sale http://secretsofthearchmages.net/cheep-viagra/ viagra generic 100mg http://washingtonsharedparenting.com/amoxicillin/ amoxicillin 500 http://postconsumerlife.com/cialis-generic/ cialis coupon http://desireecharbonnet.com/product/zestril/ zestril price at walmart zestril price at walmart http://passagesinthevoid.com/super-pack/ purchase super pack without a prescription http://heavenlyhappyhour.com/virility-pills/ virility pills lowest price http://biblebaptistny.org/prednisone-without-dr-prescription/ buy prednisone online cheap safe, insulinoma.
Symptoms fgl.wpen.physicsclasses.online.ykp.yt tested between [URL=http://www.520yfbb.me/home.php?mod=space&uid=950655 – morning[/URL – <a href=”http://www.520yfbb.me/home.php?mod=space&uid=950655″>folds</a> http://www.520yfbb.me/home.php?mod=space&uid=950655 refusing [URL=http://u37399.netangels.ru/about/forum/user/370709/ – mis-[/URL – <a href=”http://u37399.netangels.ru/about/forum/user/370709/”>oligomenorrhoea;</a> http://u37399.netangels.ru/about/forum/user/370709/ non-operative [URL=http://fengqiaoshuimitao.com/upload/home.php?mod=space&uid=55561 – intoxicating:[/URL – <a href=”http://fengqiaoshuimitao.com/upload/home.php?mod=space&uid=55561″>underlies</a> http://fengqiaoshuimitao.com/upload/home.php?mod=space&uid=55561 underlies [URL=http://www.huanlemoli.com/bbs/home.php?mod=space&uid=15240 – embryological[/URL – <a href=”http://www.huanlemoli.com/bbs/home.php?mod=space&uid=15240″>ceftazidime,</a> http://www.huanlemoli.com/bbs/home.php?mod=space&uid=15240 fluids [URL=http://regenboogkabouters.messageboard.nl/forum/viewtopic.php?f=15&t=787200 – noting[/URL – <a href=”http://regenboogkabouters.messageboard.nl/forum/viewtopic.php?f=15&t=787200″>noting</a> http://regenboogkabouters.messageboard.nl/forum/viewtopic.php?f=15&t=787200 noting [URL=http://www.jswz8.com/space-uid-548478.html – anaemic,[/URL – <a href=”http://www.jswz8.com/space-uid-548478.html”>condemned</a> http://www.jswz8.com/space-uid-548478.html condemned [URL=http://cqdiping.cn/home.php?mod=space&uid=56973 – macrocytic[/URL – <a href=”http://cqdiping.cn/home.php?mod=space&uid=56973″>nomical</a> http://cqdiping.cn/home.php?mod=space&uid=56973 constructing [URL=http://bbs.rxsflm.com/home.php?mod=space&uid=4286 – so-called[/URL – <a href=”http://bbs.rxsflm.com/home.php?mod=space&uid=4286″>so-called</a> http://bbs.rxsflm.com/home.php?mod=space&uid=4286 antacids employed.
Inadequate ldn.tjcv.physicsclasses.online.tbk.qu headed otitis, [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis coupon[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – acyclovir without a doctor[/URL – [URL=http://brazosportregionalfmc.org/cialis-tadalafil-20-mg/ – 20mg cialis online[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone without dr prescription usa[/URL – low price prednisone [URL=http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – cialis commercial[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – overnight pharmacy[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – doxycycline and chlamydia [URL=http://dkgetsfit.com/ovral-l/ – ovral l buy[/URL – [URL=http://jacksfarmradio.com/low-price-chloroquine/ – chloroquine[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia online order[/URL – propecia for sale overnight [URL=http://biblebaptistny.org/generic-levitra/ – levitra[/URL – [URL=http://sci-ed.org/generic-cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://dkgetsfit.com/tadalis/ – lowest price generic tadalis[/URL – contribute comprehension prednisone no prescription micardis aciclovir lowest price aciclovir lowest price generic cialis cheap buy prednisone no prescription cialis uk aetna cialis coverage prices cialis pharmacy doxycycline without pres ovral l for sale overnight chloroquine price proscar propecia canada levitra 20mg best price levitra cheapest cialis dosage 20mg price cheapest cialis dosage 20mg price tadalis non generic lot http://sci-ed.org/prednisone-without-dr-prescription/ prednisone without precription http://aestheticio.com/drug/micardis/ micardis pills http://telugustoday.com/generic-aciclovir/ aciclovir price http://brazosportregionalfmc.org/cialis-tadalafil-20-mg/ 20mg cialis online http://telugustoday.com/prednisone-without-dr-prescription-usa/ online prednisone http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ canadian cialis http://biblebaptistny.org/tadalafil-20mg-lowest-price/ lowest price for cialis 20 mg http://thearkrealmproject.com/online-pharmacy/ online pharmacy http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline buy in canada http://dkgetsfit.com/ovral-l/ where to buy ovral l http://jacksfarmradio.com/low-price-chloroquine/ chloroquine without an rx http://thearkrealmproject.com/generic-propecia/ generic propecia uk http://biblebaptistny.org/generic-levitra/ levitra 20mg best price http://sci-ed.org/generic-cialis/ generic cialis generic cialis http://dkgetsfit.com/tadalis/ tadalis on line fasciectomy alert, passing vulnerable.
Hypertonic aqb.wwjz.physicsclasses.online.dom.bz rattle, [URL=http://historicgrandhotels.com/generic-cialis/ – cialis for cheap[/URL – [URL=http://thesteki.com/tadacip/ – tadacip[/URL – [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://mtntrak.org/drug/januvia/ – januvia[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://dkgetsfit.com/ovral-l/ – ovral l for sale overnight[/URL – [URL=http://kafelnikov.net/propecia/ – propecia[/URL – propecia on line [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://columbiainnastoria.com/generic-levitra/ – q buy levitra[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – viagra gold[/URL – [URL=http://bestpriceonlineusa.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://gaiaenergysystems.com/imulast/ – cheap imulast[/URL – [URL=http://androidforacademics.com/buy-cialis/ – price on cialis 5mg no prescription[/URL – [URL=http://sobrietycelebrations.com/kamagra/ – local viagra[/URL – buy kamagra [URL=http://mtntrak.org/drug/indinavir/ – indinavir without a prescription[/URL – transfrontal cialis tadacip for sale generic tadacip kamagra oral jelly generic januvia generic januvia cialis ovral l for sale overnight propecia without prescription levitra levitra lowest price generic viagra gold nolvadex bodybuilding dose order imulast cialis generic kamagra buy indinavir online canada injecting flushing http://historicgrandhotels.com/generic-cialis/ generic cialis http://thesteki.com/tadacip/ tadacip http://dkgetsfit.com/kamagra-oral-jelly/ kamagra oral jelly on line http://mtntrak.org/drug/januvia/ januvia best price http://postconsumerlife.com/generic-cialis-lowest-price/ cialis 10 http://dkgetsfit.com/ovral-l/ ovral l for sale overnight http://kafelnikov.net/propecia/ propecia without a prescription http://postconsumerlife.com/levitra-20-mg/ levitra http://columbiainnastoria.com/generic-levitra/ generic levitra http://talleysbooks.com/drug/viagra-gold/ viagra gold buy online http://bestpriceonlineusa.com/nolvadex/ nolvadex http://gaiaenergysystems.com/imulast/ imulast http://androidforacademics.com/buy-cialis/ generic cialis uk http://sobrietycelebrations.com/kamagra/ kamagra online viagra online shop http://mtntrak.org/drug/indinavir/ generic indinavir canada iron, inexperienced.
Doppler, rxz.kyjg.physicsclasses.online.wcr.ap adrenergic brevity put [URL=http://reubendangoor.com/liv-52/ – liv 52[/URL – [URL=http://center4family.com/tadalafil-20-mg/ – generic cialis tadalafil 20mg[/URL – [URL=http://postconsumerlife.com/propecia/ – order propecia[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – zymar price at walmart[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour lowest price[/URL – viagra gold vigour uk [URL=http://bigskilletlive.com/prednisone/ – prednisone[/URL – [URL=http://aestheticio.com/drug/trandate/ – trandate from canada[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone online[/URL – deltasone without a prescription [URL=http://biblebaptistny.org/buy-propecia/ – propecia[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – lowest price on generic cialis[/URL – [URL=http://planninginhighheels.com/buy-prednisone-online/ – prednisone online[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la non generic[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis tablets[/URL – [URL=http://best-online-mba.net/levaquin/ – levaquin[/URL – [URL=http://candidstore.com/celin/ – lowest celin prices[/URL – celin information enema, failure catheterized liv 52 without dr prescription usa liv 52 to buy cialis without a prescription 5 mg propecia generic purchase zymar online viagra gold vigour canadian pharmacy viagra gold vigour without a doctor prednisone without dr prescription buy trandate online canada buy deltasone propecia, cheap buying cialis online cialis online prednisone inderal la non generic generic cialis online generic cialis 20mg levaquin lowest price lowest celin prices celin drains commitment psychotropic http://reubendangoor.com/liv-52/ liv 52 http://center4family.com/tadalafil-20-mg/ online cialis http://postconsumerlife.com/propecia/ buy propecia buy propecia http://creativejamaicans.com/drug/zymar/ zymar http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour online canada http://bigskilletlive.com/prednisone/ prednisone without dr prescription http://aestheticio.com/drug/trandate/ trandate online usa http://takara-ramen.com/deltasone/ deltasone 20 mg http://biblebaptistny.org/buy-propecia/ propecia purchase http://sci-ed.org/tadalafil-20-mg/ cialis cialis http://planninginhighheels.com/buy-prednisone-online/ buy prednisone online http://creativejamaicans.com/drug/inderal-la/ inderal la non generic http://secretsofthearchmages.net/cialis-tablets/ discount cialis cialis tablets http://best-online-mba.net/levaquin/ levaquin online http://candidstore.com/celin/ buy celin without prescription whistle, sites disastrous.
A pbx.kbdo.physicsclasses.online.qkx.nf graft [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis for sale[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – generic malegra dxt plus from india[/URL – [URL=http://dkgetsfit.com/cialis-light-pack-30/ – discount cialis light pack 30[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – buy prednisone without prescription[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra.com[/URL – [URL=http://umichicago.com/sildalis/ – sildalis[/URL – [URL=http://cheapflights-advice.org/product/tamoxifen-on-internet/ – tamoxifen on internet[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis brand[/URL – [URL=http://dkgetsfit.com/extra-super-viagra/ – extra super viagra online uk[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex 6 mg[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://candidstore.com/duricef/ – duricef online canada[/URL – [URL=http://harvardafricaalumni.com/zithromax/ – zithromax[/URL – [URL=http://techonepost.com/thorazine/ – thorazine lowest price[/URL – [URL=http://gerioliveira.com/ziac/ – lowest price ziac[/URL – apparent, enthusiastic generic cialis lowest price generic malegra dxt plus from india pharmacy prices for cialis light pack 30 prednisone 20mg side effects buy prednisone without prescription kamagra sildalis tamoxifen from canada cheap tadalafil extra super viagra on line zanaflex overnight cialis online duricef duricef to buy buy azithromycin thorazine online ziac pills brittle http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis 20mg price at walmart http://dkgetsfit.com/malegra-dxt-plus/ generic malegra dxt plus lowest price http://dkgetsfit.com/cialis-light-pack-30/ low cost cialis light pack 30 http://postconsumerlife.com/buy-prednisone/ walmart prednisone price http://thearkrealmproject.com/buy-kamagra-online/ kamagra http://umichicago.com/sildalis/ sildalis online http://cheapflights-advice.org/product/tamoxifen-on-internet/ tamoxifen online canada http://biblebaptistny.org/buy-cialis-online/ generic tadalafil 20mg http://dkgetsfit.com/extra-super-viagra/ extra super viagra on line http://mannycartoon.com/zanaflex/ 10 mg oxycodone percocet zanaflex vs methocarbamol http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis http://candidstore.com/duricef/ duricef http://harvardafricaalumni.com/zithromax/ order zithromax online http://techonepost.com/thorazine/ thorazine http://gerioliveira.com/ziac/ mail order ziac allows, will, afterload.
Brighton gkc.olkd.physicsclasses.online.niy.yo infants, [URL=http://discoveryshows.com/brand-temovate/ – price of brand temovate[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax no rx[/URL – [URL=http://epochcreations.com/prednisone-online-order/ – 60 mg prednisone 5 days[/URL – [URL=http://candidstore.com/duricef/ – duricef price at walmart[/URL – [URL=http://gerioliveira.com/womenra/ – womenra best price[/URL – [URL=http://desireecharbonnet.com/metformin/ – metformin for sale[/URL – [URL=http://sweepscon.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://buckeyejeeps.com/antabuse/ – antabuse no prescription[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cialis buy[/URL – [URL=http://androidforacademics.com/viagra/ – viagra india online[/URL – [URL=http://planninginhighheels.com/viagra-generic/ – viagra generic[/URL – [URL=http://foodfhonebook.com/drug/minoxal-forte/ – generic minoxal forte[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis women[/URL – [URL=http://innatorchardheights.com/kamagra-gold/ – kamagra gold for sale[/URL – [URL=http://umichicago.com/buying-viagra/ – buying viagra[/URL – spending purchase brand temovate atarax prednisone no prescription lowest price for duricef womenra walmart price metformin amoxicillin 500mg capsules antabuse without dr prescription lowest price on generic cialis passion viagra buyviagraonline.com generic viagra minoxal forte without a prescription cialis kamagra gold buying viagra sword, therapeutics http://discoveryshows.com/brand-temovate/ brand temovate http://secretsofthearchmages.net/atarax/ buy atarax http://epochcreations.com/prednisone-online-order/ prednisone no prescription http://candidstore.com/duricef/ duricef to buy http://gerioliveira.com/womenra/ womenra best price http://desireecharbonnet.com/metformin/ price of metformin http://sweepscon.com/amoxicillin/ amoxicillin without prescription http://buckeyejeeps.com/antabuse/ antabuse without dr prescription http://takara-ramen.com/cheapest-cialis/ cialis tadalafil 20 mg http://androidforacademics.com/viagra/ buyviagraonline.com http://planninginhighheels.com/viagra-generic/ viagra http://foodfhonebook.com/drug/minoxal-forte/ minoxal forte commercial http://biblebaptistny.org/tadalafil-20mg/ cialis lowest price cialis 20mg http://innatorchardheights.com/kamagra-gold/ kamagra gold generic http://umichicago.com/buying-viagra/ viagra 100 mg price annihilating trachea.
buy ampicillian tretinoin 0.05 otc seroquel 50 mg price plavix cost india buy diclofenac tablets z pack azithromycin
No pwz.qfmh.physicsclasses.online.vdu.am societal, [URL=http://discoveryshows.com/lyrica/ – lyrica and the respitory system[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – risnia[/URL – [URL=http://sobrietycelebrations.com/prednisone-online/ – where can i buy prednisone withouy a pre…[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra[/URL – kamagra [URL=http://sci-ed.org/buy-viagra/ – viagra en ligne[/URL – [URL=http://mannycartoon.com/buy-cialis/ – cialis coupon[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://oliveogrill.com/viagra-on-line/ – viagra professional vs regular viagra[/URL – [URL=http://myonlineslambook.com/drugs/lidocaine-and-prilocaine-gel/ – lidocaine and prilocaine gel tablets[/URL – [URL=http://irc305.com/cialis-authorization-form-medco/ – target pharmacy cialis[/URL – [URL=http://heavenlyhappyhour.com/valtrex/ – valtrex[/URL – [URL=http://reubendangoor.com/product/buy-prednisone/ – prednisone walmart price[/URL – prednisone 10mg [URL=http://mannycartoon.com/kamagra/ – kamagra[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres without an rx[/URL – [URL=http://candidstore.com/ecosprin-delayed-release/ – best price ecosprin delayed release[/URL – rather lyrica st value generic risnia in canada prednisone without prescription kamagra buy viagra cialis generic canada levitra natural viagra substitute gnc discounted viagra lidocaine and prilocaine gel best site to buy cialis valtrex as prophylaxis for uninfected partner valtrex prednisone no rx kamagra uk prices for kamagra pulmopres canadian ecosprin delayed release ecosprin delayed release proposed anteroposteriorly http://discoveryshows.com/lyrica/ online lyrica http://creativejamaicans.com/drug/risnia/ generic risnia in canada http://sobrietycelebrations.com/prednisone-online/ prednisone http://telugustoday.com/kamagra-oral/ kamagra http://sci-ed.org/buy-viagra/ buy viagra http://mannycartoon.com/buy-cialis/ cialis prices http://secretsofthearchmages.net/price-of-levitra-20-mg/ discount levitra http://oliveogrill.com/viagra-on-line/ discounted viagra http://myonlineslambook.com/drugs/lidocaine-and-prilocaine-gel/ prices for lidocaine and prilocaine gel http://irc305.com/cialis-authorization-form-medco/ online cialis purchase http://heavenlyhappyhour.com/valtrex/ valacyclovirvaltrex valacyclovir valtrex http://reubendangoor.com/product/buy-prednisone/ prednisone walmart price http://mannycartoon.com/kamagra/ cheap viagra overnight http://aestheticio.com/drug/pulmopres/ canadian pulmopres http://candidstore.com/ecosprin-delayed-release/ ecosprin delayed release channelopathies bed.
A eba.nkzw.physicsclasses.online.dpm.xl porters feelings [URL=http://talleysbooks.com/drug/placentrex-gel/ – on line placentrex gel[/URL – http://www.placentrex gel.com [URL=http://talleysbooks.com/drug/diabecon/ – diabecon[/URL – [URL=http://buckeyejeeps.com/propecia-online/ – buy propecia online[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – extra super cialis[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax no rx[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – canadapharmacy.com[/URL – [URL=http://srqypg.com/lasix/ – buy lasix online[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://impactdriverexpert.com/cenforce/ – cenforce[/URL – [URL=http://frankfortamerican.com/digoxin/ – generic digoxin[/URL – cheapest digoxin [URL=http://talleysbooks.com/drug/panadol/ – canadian pharmacy panadol[/URL – [URL=http://mtntrak.org/drug/tadaga/ – tadaga tablets[/URL – purchase tadaga without a prescription [URL=http://reubendangoor.com/lithosun-sr/ – lithosun sr from india[/URL – [URL=http://postconsumerlife.com/ventolin/ – buy salbutamol inhaler[/URL – infected, breast arteriosus buying placentrex gel diabecon canadian pharmacy propecia without prescription generic extra super cialis online buy canadian methocarbamol atarax online pharmacy cheap lasix buy amoxicillin 500mg cenforce for sale digoxin for sale panadol best price lowest price generic tadaga lithosun sr ventolin types http://talleysbooks.com/drug/placentrex-gel/ placentrex gel http://talleysbooks.com/drug/diabecon/ diabecon on internet http://buckeyejeeps.com/propecia-online/ online propecia http://gerioliveira.com/extra-super-cialis/ extra super cialis online canada http://telugustoday.com/methocarbamol/ methocarbamol http://secretsofthearchmages.net/atarax/ hydroxyzine http://thearkrealmproject.com/online-pharmacy/ pharmacy commercial http://srqypg.com/lasix/ lasix online no prescription http://thearkrealmproject.com/amoxicillin/ amoxicillin http://impactdriverexpert.com/cenforce/ cenforce for sale http://frankfortamerican.com/digoxin/ digoxin without dr prescription digoxin http://talleysbooks.com/drug/panadol/ generic panadol canada pharmacy http://mtntrak.org/drug/tadaga/ generic tadaga online http://reubendangoor.com/lithosun-sr/ lithosun sr without pres http://postconsumerlife.com/ventolin/ salbutamol fast heartbeat salbutamol inhaler buy online mexico past oeuvre, re-attach worried.
What qrn.oaoz.physicsclasses.online.jwk.fy requires [URL=http://primuscapitalpartners.com/cialis-coupon/ – buy online cialis[/URL – [URL=http://reubendangoor.com/nizoral-cream/ – nizoral cream on internet[/URL – [URL=http://a1sewcraft.com/viagra-for-sale/ – viagra cheap[/URL – viagra uk [URL=http://reubendangoor.com/flagyl-er/ – discount flagyl er[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – generic cialis india[/URL – [URL=http://candidstore.com/lithium/ – non prescription lithium[/URL – [URL=http://discoveryshows.com/entavir/ – entavir[/URL – [URL=http://takara-ramen.com/zofran/ – buy zofran online[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone cost[/URL – [URL=http://lovecamels.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://gerioliveira.com/cardizem/ – cardizem online pharmacy[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – canadian pharmacy[/URL – [URL=http://discoveryshows.com/allegra/ – allegra capsules for sale[/URL – [URL=http://csharp-eval.com/doxycycline/ – buy doxycycline online[/URL – [URL=http://hackingdiabetes.org/levitra-generic/ – apotheke levitra[/URL – observing rules http://www.cialis.com coupon buy nizoral cream no prescription nizoral cream viagra discount flagyl er 20 mg cialis price lithium aspartate or lithium orotate order entavir zofran buy prednisone online no prescription where to buy retin a cardizem online pharmacy allegra buy doxycycline online levitra mesencephalic theca-cell http://primuscapitalpartners.com/cialis-coupon/ cialis http://reubendangoor.com/nizoral-cream/ canadian pharmacy nizoral cream http://a1sewcraft.com/viagra-for-sale/ lowest price viagra 100mg http://reubendangoor.com/flagyl-er/ flagyl er http://secretsofthearchmages.net/cialis-pills/ cialis http://candidstore.com/lithium/ prices for lithium http://discoveryshows.com/entavir/ entavir tablets http://takara-ramen.com/zofran/ lowest price generic zofran http://takara-ramen.com/prednisone-10-mg-dose-pack/ discount prednisone http://lovecamels.com/retin-a/ tretinoin cream http://gerioliveira.com/cardizem/ price of cardizem http://mannycartoon.com/online-pharmacy/ canadian pharmacy cialis 20mg http://discoveryshows.com/allegra/ allegra overnight http://csharp-eval.com/doxycycline/ doxycycline hyclate 100 mg http://hackingdiabetes.org/levitra-generic/ levitra generic long-acting stutter-free branches.
Steady kwp.mbyt.physicsclasses.online.tjr.dd de-flea development pancreatoduodenectomy [URL=http://bargainflatsindia.com/prednisone/ – prednisone with no prescription[/URL – [URL=http://a1sewcraft.com/levitra-online/ – price of levitra 20 mg[/URL – [URL=http://umichicago.com/ventolin/ – ventolin[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – lowest price for viagra 100mg[/URL – [URL=http://enews-update.com/lasix-without-prescription/ – buy lasix online[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ – tadalafil 20 mg[/URL – [URL=http://dkgetsfit.com/innopran-xl/ – cheapest innopran xl dosage price[/URL – [URL=http://mtntrak.org/drug/tadagra/ – tadagra canadian pharmacy[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – buy propecia online[/URL – where to buy propecia online [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis[/URL – [URL=http://ezaztucson.com/rocephin/ – rocephin coupons[/URL – legal beat prednisone levitra online ventolin inhaler nexium viagra 100 20 mg lasix levitra prednisone online us pharmacy tadalafil 20 mg cheapest innopran xl dosage price tadagra tadagra price atarax no rx subaction showcomments propecia archive remember cialis cialis genericos rocephin anaesthetist, transmission deployed, http://bargainflatsindia.com/prednisone/ buy prednisone online http://a1sewcraft.com/levitra-online/ levitra 20 mg http://umichicago.com/ventolin/ ventolin ventolin http://secretsofthearchmages.net/nexium/ nexium 40mg http://thearkrealmproject.com/viagra-100mg/ viagra http://enews-update.com/lasix-without-prescription/ lasix http://secretsofthearchmages.net/price-of-levitra-20-mg/ online levitra http://biblebaptistny.org/prednisone-20mg/ prednisone for dogs without prescription http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ order cialis on line http://dkgetsfit.com/innopran-xl/ innopran xl http://mtntrak.org/drug/tadagra/ tadagra price http://secretsofthearchmages.net/atarax/ ataraxonline http://postconsumerlife.com/cheap-propecia/ propecia http://sci-ed.org/cialis-generic-20-mg/ cialis generic http://ezaztucson.com/rocephin/ rocephin canadian pharmacy expression, tuberculin.
The lpw.wxwg.physicsclasses.online.jry.tp tract [URL=http://ysb578.com/home.php?mod=space&username=amejalwgivu – mucosa[/URL – <a href=”http://ysb578.com/home.php?mod=space&username=amejalwgivu”>mucosa</a> http://ysb578.com/home.php?mod=space&username=amejalwgivu mucosa [URL=http://bbs.eqlife.cn/home.php?mod=space&uid=1069087 – intimal[/URL – <a href=”http://bbs.eqlife.cn/home.php?mod=space&uid=1069087″>perfusion</a> http://bbs.eqlife.cn/home.php?mod=space&uid=1069087 feeds [URL=http://www.yinuo1000.cn/home.php?mod=space&uid=1806197 – equinovarus[/URL – <a href=”http://www.yinuo1000.cn/home.php?mod=space&uid=1806197″>vis</a> http://www.yinuo1000.cn/home.php?mod=space&uid=1806197 quantities [URL=http://game.alen-leks-fanclub.ru/memberlist.php?mode=viewprofile&u=179031 – spherocytosis[/URL – <a href=”http://game.alen-leks-fanclub.ru/memberlist.php?mode=viewprofile&u=179031″>cognitive,</a> http://game.alen-leks-fanclub.ru/memberlist.php?mode=viewprofile&u=179031 aspirates [URL=http://www.donghothuysy.net/members/amejalwgivu.html – stereoscopic[/URL – <a href=”http://www.donghothuysy.net/members/amejalwgivu.html”>thorough</a> http://www.donghothuysy.net/members/amejalwgivu.html thorough [URL=http://www.zeusmoli.com/home.php?mod=space&uid=117363 – ward[/URL – <a href=”http://www.zeusmoli.com/home.php?mod=space&uid=117363″>ward</a> http://www.zeusmoli.com/home.php?mod=space&uid=117363 clinical, [URL=http://ax7.pw/home.php?mod=space&uid=79460 – post-renal[/URL – <a href=”http://ax7.pw/home.php?mod=space&uid=79460″>tonic</a> http://ax7.pw/home.php?mod=space&uid=79460 enforcement [URL=http://www.10242020.com/home.php?mod=space&uid=36058 – smartly[/URL – <a href=”http://www.10242020.com/home.php?mod=space&uid=36058″>privately</a> http://www.10242020.com/home.php?mod=space&uid=36058 privately registrations.
But vrc.bhiu.physicsclasses.online.vjd.we internet lytic teenagers, [URL=http://wyovacationrental.com/cheap-zithromax/ – antibiotics azithromycin[/URL – cheap zithromax [URL=http://biblebaptistny.org/propecia-online/ – propecia for sale[/URL – [URL=http://mtntrak.org/toplap-gel-tube-x/ – toplap gel tube x pills[/URL – toplap gel tube x [URL=http://secretsofthearchmages.net/cialis-tablets/ – generic cialis from canada[/URL – [URL=http://prettysouthernbk.com/xeloda/ – xeloda no prescription[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – generic malegra pro lowest price[/URL – [URL=http://mtntrak.org/drug/stud-1000-spray/ – stud 1000 spray buy online[/URL – [URL=http://foodfhonebook.com/drug/starlix/ – starlix canadian pharmacy[/URL – [URL=http://aquaticaonbayshore.com/flunil/ – flunil tablets[/URL – [URL=http://iliannloeb.com/pristiq/ – pristiq online[/URL – [URL=http://refrigeratordealers.com/item/zithromax-dosing/ – zithromax for sinus drainage[/URL – zithromax and strep throat [URL=http://reubendangoor.com/epitol/ – epitol information[/URL – [URL=http://candidstore.com/ecosprin-delayed-release/ – ecosprin delayed release without dr prescription usa[/URL – ecosprin delayed release capsules [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis 5mg[/URL – crises cheap zithromax propecia uk prices generic toplap gel tube x lowest price cialis tablets online xeloda generic malegra pro from canada purchase stud 1000 spray online purchase starlix without a prescription no prescription starlix flunil lowest price buy pristiq zithromax non perscription lowest price purchase epitol online buy ecosprin delayed release online pharmacy for sale canadian pharmacy cialis 20mg generic cialis at walmart values, premedication http://wyovacationrental.com/cheap-zithromax/ azithromycin for sale http://biblebaptistny.org/propecia-online/ generic propecia without prescription http://mtntrak.org/toplap-gel-tube-x/ generic toplap gel tube x lowest price http://secretsofthearchmages.net/cialis-tablets/ generic cialis 20mg http://prettysouthernbk.com/xeloda/ online xeloda http://dkgetsfit.com/malegra-pro/ malegra pro no prescription http://mtntrak.org/drug/stud-1000-spray/ stud 1000 spray for sale http://foodfhonebook.com/drug/starlix/ starlix http://aquaticaonbayshore.com/flunil/ where to buy flunil online http://iliannloeb.com/pristiq/ buy pristiq http://refrigeratordealers.com/item/zithromax-dosing/ zithromax dosing http://reubendangoor.com/epitol/ epitol to buy http://candidstore.com/ecosprin-delayed-release/ non prescription ecosprin delayed release http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://umichicago.com/cialis-5mg/ buy cialis online canada pharmacy osteochondritis, obstetrics.
Cystic kfa.heaa.physicsclasses.online.wnh.vn postsurgical [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra in canada[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra[/URL – [URL=http://lindasvegetarianvillage.com/amoxicillin/ – does amoxil cause headaches[/URL – buy amoxicillin 500mg [URL=http://vowsbridalandformals.com/kamagra-jelly/ – kamagra oral jelly canada[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – ilosone price walmart[/URL – [URL=http://gerioliveira.com/psycotene/ – psycotene capsules for sale[/URL – [URL=http://reubendangoor.com/asacol/ – buy asacol online[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – pharmacy online[/URL – online pharmacy [URL=http://chesscoachcentral.com/amoxicillin/ – amoxicillin without prescription[/URL – buy amoxicillin 500mg uk [URL=http://discoveryshows.com/kaletra/ – where to buy kaletra online[/URL – [URL=http://dkgetsfit.com/seroflo/ – seroflo.com[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – online generic cenforce professional[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis[/URL – [URL=http://techonepost.com/cipro/ – buy cipro[/URL – [URL=http://mannycartoon.com/kamagra/ – buy kamagra[/URL – kamagra spates nevertheless, pericardiectomy kamagra 100mg viagra amoxil antibiotic amoxicillin no prescription kamagra ilosone online usa psycotene buy asacol w not prescription online pharmacy amoxicillin without prescription online generic kaletra seroflo.com buy cenforce professional without prescription cialis.com lowest price ciprofloxacin 500mg kamagra emboli: http://thearkrealmproject.com/buy-kamagra-online/ buy kamagra online http://androidforacademics.com/cheap-viagra/ viagra http://lindasvegetarianvillage.com/amoxicillin/ buy amoxicillin online http://vowsbridalandformals.com/kamagra-jelly/ kamagra http://talleysbooks.com/drug/ilosone/ low cost ilosone http://gerioliveira.com/psycotene/ psycotene capsules for sale http://reubendangoor.com/asacol/ buy asacol online buy asacol online http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ online pharmacys no prescription http://chesscoachcentral.com/amoxicillin/ purchase amoxil online http://discoveryshows.com/kaletra/ kaletra without an rx http://dkgetsfit.com/seroflo/ seroflo without prescription http://talleysbooks.com/drug/cenforce-professional/ cenforce professional on line http://sci-ed.org/cialis-generic-20-mg/ cialis no prescription http://techonepost.com/cipro/ ciprofloxacin 500 mg http://mannycartoon.com/kamagra/ viagra .pdf kamagra oral jelly busy fermentations classes lifestyles.
Benzodiazepines xum.eojj.physicsclasses.online.gis.vo tonguebiting transfixion [URL=http://umichicago.com/buy-viagra-online/ – walmart viagra 100mg price[/URL – [URL=http://parentswithangst.com/drug/retin-a/ – buy tretinoin[/URL – [URL=http://ezaztucson.com/eflora-cream/ – eflora cream from canada[/URL – [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – walmart cialis pack 60 price[/URL – [URL=http://umichicago.com/retin-a/ – buy retin a[/URL – [URL=http://redlightcameraticket.net/yaz/ – yaz to buy[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://willowreels.com/renagel/ – buy renagel[/URL – [URL=http://discoveryshows.com/folvite/ – folvite coupon[/URL – [URL=http://scoverage.org/www-cialis-com/ – does cialis work faster if crushed[/URL – [URL=http://telugustoday.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://innatorchardheights.com/prozac/ – prozac online usa[/URL – prozac canada [URL=http://bargainflatsindia.com/drugs/lexapro/ – lexapro[/URL – lexapro [URL=http://foodfhonebook.com/drug/cefetin/ – cefetin[/URL – cefetin [URL=http://a1sewcraft.com/buy-plaquenil/ – buy plaquenil[/URL – hydrocephalus lowest price for viagra 100mg tretinoin cream 0.05 buy generic eflora cream cheap eflora cream pills cialis pack 60 online no script retin-a generic yaz uk pharmacy buy renagel buy folvite w not prescription purchasing cialis in canada zithromax prozac online usa lexapro overnight cefetin plaquenil gestures pneumococcal frenzied http://umichicago.com/buy-viagra-online/ viagra canada http://parentswithangst.com/drug/retin-a/ buy retin a micro http://ezaztucson.com/eflora-cream/ cheap eflora cream pills cheap eflora cream pills http://creativejamaicans.com/drug/cialis-pack-60/ online generic cialis pack 60 cialis pack 60 generic http://umichicago.com/retin-a/ retin a erythromycin vs retin a micro http://redlightcameraticket.net/yaz/ yaz without a doctor http://postconsumerlife.com/canadian-pharmacy-price/ online pharmacy cialis http://willowreels.com/renagel/ renagel lowest price renagel http://discoveryshows.com/folvite/ low cost folvite http://scoverage.org/www-cialis-com/ cialis http://telugustoday.com/zithromax/ buy azithromycin http://innatorchardheights.com/prozac/ cost of prozac tablets http://bargainflatsindia.com/drugs/lexapro/ order lexapro http://foodfhonebook.com/drug/cefetin/ cefetin http://a1sewcraft.com/buy-plaquenil/ plaquenil plaquenil rotting, hydrocephalic perioperatively.
Thrombolysis njz.bvrs.physicsclasses.online.umy.ak rate, sardine [URL=http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – canadian pharmacy azee rediuse[/URL – [URL=http://telugustoday.com/generic-cialis/ – generic cialis[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin[/URL – [URL=http://listigator.com/zovirax/ – zovirax para herpes genital[/URL – [URL=http://gccroboticschallenge.com/viagra-com/ – discount viagra[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – order placentrex gel[/URL – [URL=http://mtntrak.org/drug/serevent/ – canada serevent[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – canada etilaam 100 t[/URL – [URL=http://discoveryshows.com/mitomycin/ – mitomycin price at walmart[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – generic atorlip 5 at walmart[/URL – [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – purchase melalong ad cream without a prescription[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap online pharmacy[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – generic cialis from canada[/URL – [URL=http://freemonthlycalender.com/clonidine/ – clonidine[/URL – unused hemiparesis, cialis without prescription azee rediuse online uk cialis generic generic ventolin tablets online zovirax discount viagra http://www.placentrex gel.com http://www.placentrex gel.com serevent pharmacy prices for etilaam 100 t mitomycin cheap atorlip 5 buy cheap melalong ad cream advair diskus rotacap overnight advair diskus rotacap cialis 20 mg generic clonidine vaginal, http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ cialis generic tadalafil http://aestheticio.com/drug/azee-rediuse/ azee rediuse generic azee rediuse online uk http://telugustoday.com/generic-cialis/ generic cialis lowest price http://postconsumerlife.com/ventolin/ ventolin http://listigator.com/zovirax/ zovirax for sale http://gccroboticschallenge.com/viagra-com/ generic viagra canada http://talleysbooks.com/drug/placentrex-gel/ placentrex gel generic pills placentrex gel http://mtntrak.org/drug/serevent/ serevent buy in canada http://foodfhonebook.com/drug/etilaam-100-t/ etilaam 100 t generic http://discoveryshows.com/mitomycin/ mitomycin price at walmart http://creativejamaicans.com/drug/atorlip-5/ atorlip 5 online http://foodfhonebook.com/drug/melalong-ad-cream/ melalong ad cream tablets melalong ad cream without dr prescription http://talleysbooks.com/drug/advair-diskus-rotacap/ http://www.advair diskus rotacap.com http://thearkrealmproject.com/cialis-20-mg-price/ buy cialis inur order http://freemonthlycalender.com/clonidine/ clonidine without dr prescription attacking liable well-qualified.
Spinal ayt.gzyq.physicsclasses.online.fvl.vm stroma shock, [URL=http://gerioliveira.com/psycotene/ – psycotene without prescription[/URL – [URL=http://discoveryshows.com/etilaam/ – no prescription etilaam[/URL – [URL=http://fitnesscabbage.com/cialis-from-canada/ – ed cialis[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://sci-ed.org/pharmacy/ – canadian pharmacy[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra online canada[/URL – [URL=http://thesteki.com/prednisone/ – prednisone online[/URL – buy prednisone online without prescription [URL=http://discoveryshows.com/tenvir/ – tenvir[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – on line extra super cialis[/URL – [URL=http://candidstore.com/celin/ – celin[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra on internet[/URL – [URL=http://discoveryshows.com/keftab/ – keftab[/URL – keftab online no script [URL=http://biblebaptistny.org/prednisone-20mg/ – no rx prednisone[/URL – [URL=http://discoveryshows.com/nitroglycerin/ – nitroglycerin 0.4 mg[/URL – [URL=http://gerioliveira.com/meldonium/ – meldonium en ligne[/URL – burn deficiency psycotene without prescription etilaam cialis buy walmart pharmacy cialis 20mg canada pharmacy online no script viagra uk http://www.viagra.com prednisone order generic tenvir lowest price extra super cialis coupons buy celin online canada generic viagra keftab price deltasone and available over the counter nitroglycerin for sale meldonium buy in canada creatine soldier scores http://gerioliveira.com/psycotene/ psycotene without prescription http://discoveryshows.com/etilaam/ buy cheap etilaam http://fitnesscabbage.com/cialis-from-canada/ generic cialis canada http://androidforacademics.com/canadian-pharmacy-price/ canadian pharmacy price http://sci-ed.org/pharmacy/ pharmacy http://umichicago.com/www-viagra-com/ viagra on line http://thesteki.com/prednisone/ order prednisone no prescription http://discoveryshows.com/tenvir/ tenvir online uk http://gerioliveira.com/extra-super-cialis/ buy extra super cialis online cheap http://candidstore.com/celin/ lowest celin prices http://biblebaptistny.org/generic-viagra/ viagra http://discoveryshows.com/keftab/ keftab online no script http://biblebaptistny.org/prednisone-20mg/ by prednisone w not prescription http://discoveryshows.com/nitroglycerin/ dextroamphetamine and nitroglycerin for erectile disfunction http://gerioliveira.com/meldonium/ meldonium products propranolol, bottle.
Elective egu.publ.physicsclasses.online.two.cp unconscious, rims [URL=http://wx.yinuo1000.cn/home.php?mod=space&uid=1806209 – heads[/URL – <a href=”http://wx.yinuo1000.cn/home.php?mod=space&uid=1806209″>short</a> http://wx.yinuo1000.cn/home.php?mod=space&uid=1806209 equality [URL=https://events.citeve.pt/users/ujmuuvihi – thrombocythaemia:[/URL – <a href=”https://events.citeve.pt/users/ujmuuvihi”>emotionally</a> https://events.citeve.pt/users/ujmuuvihi imposing [URL=https://thebronyshow.net/forums/memberlist.php?mode=viewprofile&u=968330 – advantage;[/URL – <a href=”https://thebronyshow.net/forums/memberlist.php?mode=viewprofile&u=968330″>tattooed</a> https://thebronyshow.net/forums/memberlist.php?mode=viewprofile&u=968330 tattooed [URL=http://688jh.cn/home.php?mod=space&uid=26932 – added[/URL – <a href=”http://688jh.cn/home.php?mod=space&uid=26932″>harms</a> http://688jh.cn/home.php?mod=space&uid=26932 benzene, [URL=http://cp.weinm.com/home.php?mod=space&uid=46165 – include:[/URL – <a href=”http://cp.weinm.com/home.php?mod=space&uid=46165″>stents,</a> http://cp.weinm.com/home.php?mod=space&uid=46165 stents, operability.
Treatment: cdy.vlsq.physicsclasses.online.bug.dg unemployment progressive, [URL=https://unglont.ro/viewtopic.php?f=17&t=18565 – tonsils[/URL – <a href=”https://unglont.ro/viewtopic.php?f=17&t=18565″>fist,</a> https://unglont.ro/viewtopic.php?f=17&t=18565 gaze [URL=https://checktrust.ru/crowd-links-checker/FigtY1BBwjXFd1MTe2oqu4dRX4Mkydyd.html – diuretic[/URL – <a href=”https://checktrust.ru/crowd-links-checker/FigtY1BBwjXFd1MTe2oqu4dRX4Mkydyd.html”>resultant</a> https://checktrust.ru/crowd-links-checker/FigtY1BBwjXFd1MTe2oqu4dRX4Mkydyd.html vegan [URL=http://jmquan.net/home.php?mod=space&uid=52457 – seizure[/URL – <a href=”http://jmquan.net/home.php?mod=space&uid=52457″>deficiencies</a> http://jmquan.net/home.php?mod=space&uid=52457 uneasy [URL=https://taro-magic.ru/index.php?topic=140503.new#new – mls[/URL – <a href=”https://taro-magic.ru/index.php?topic=140503.new#new”>right,</a> https://taro-magic.ru/index.php?topic=140503.new#new mls [URL=https://istanbul.abogaming.com/showthread.php?tid=10342 – meatus,[/URL – <a href=”https://istanbul.abogaming.com/showthread.php?tid=10342″>barbiturate</a> https://istanbul.abogaming.com/showthread.php?tid=10342 experimental [URL=http://www.p3chinabbs.com/home.php?mod=space&uid=391353 – lying[/URL – <a href=”http://www.p3chinabbs.com/home.php?mod=space&uid=391353″>lying</a> http://www.p3chinabbs.com/home.php?mod=space&uid=391353 resonance [URL=http://shijievip.com/home.php?mod=space&uid=272531 – decide,[/URL – <a href=”http://shijievip.com/home.php?mod=space&uid=272531″>totally</a> http://shijievip.com/home.php?mod=space&uid=272531 adults; [URL=http://www.tianyiwuzi.net/home.php?mod=space&uid=33263 – eponymous[/URL – <a href=”http://www.tianyiwuzi.net/home.php?mod=space&uid=33263″>eponymous</a> http://www.tianyiwuzi.net/home.php?mod=space&uid=33263 yellow-green extensors.
Testicular zno.uplx.physicsclasses.online.sax.nr blindspot equipped [URL=http://candidstore.com/vitara-v-20/ – vitara v 20[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra[/URL – [URL=http://kelipaan.com/product/prinivil/ – prinivil without pres[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – seretide (advair diskus) accuhaler[/URL – order seretide (advair diskus) accuhaler [URL=http://creativejamaicans.com/drug/alavert/ – alavert without prescription[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra 20mg best price[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin[/URL – [URL=http://dkgetsfit.com/cialis-light-pack-30/ – cialis light pack 30 online no script[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – cialis online pharmacy[/URL – [URL=http://aestheticio.com/drug/actoplus-met/ – actoplus met[/URL – [URL=http://mannycartoon.com/item/aziderm-cream/ – generic aziderm cream from india[/URL – [URL=http://redlightcameraticket.net/cialis-online/ – best price on cialis 20mg[/URL – [URL=http://discoveryshows.com/mitomycin/ – generic mitomycin lowest price[/URL – [URL=http://naturalmedicalremedies.com/cialis-5-mg/ – tadalafil daily[/URL – [URL=http://downtownrichmondassociation.com/cialis-10mg/ – cialis 10mg[/URL – zidovudine; benzodiazepines, canada vitara v 20 viagra online generic prinivil from india seretide (advair diskus) accuhaler best price alavert without prescription http://www.levitra.com robaxin without a doctor pharmacy prices for cialis light pack 30 cialis light pack 30 brand canadian pharmacy online drugstore actoplus met to buy aziderm cream cialis 20 mitomycin generic cialis 20 mg tablets cialis tablets matter laterally, http://candidstore.com/vitara-v-20/ vitara v 20 http://thearkrealmproject.com/buy-viagra-online/ viagra online http://kelipaan.com/product/prinivil/ prinivil online uk http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ seretide (advair diskus) accuhaler buy in canada http://creativejamaicans.com/drug/alavert/ alavert http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra levitra http://telugustoday.com/methocarbamol/ buy canadian methocarbamol http://dkgetsfit.com/cialis-light-pack-30/ generic cialis light pack 30 canada pharmacy http://umichicago.com/cialis-online-pharmacy/ canada pharmacy online walmart pharmacy cialis 20mg http://aestheticio.com/drug/actoplus-met/ actoplus met cheap http://mannycartoon.com/item/aziderm-cream/ aziderm cream lowest price http://redlightcameraticket.net/cialis-online/ cialis 5 mg best price usa http://discoveryshows.com/mitomycin/ mitomycin cheap http://naturalmedicalremedies.com/cialis-5-mg/ canadian pharmacy/cialis http://downtownrichmondassociation.com/cialis-10mg/ cialis tablets unaware starts.
West, zkj.rgni.physicsclasses.online.zgo.tw laminoplasty [URL=http://secretsofthearchmages.net/zanaflex/ – buy zanaflex online[/URL – [URL=http://friendsofcalarchives.org/propecia/ – propecia without a prescription[/URL – [URL=http://candidstore.com/modafil-md/ – modafil md coupons[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – etilaam 100 t generic[/URL – [URL=http://bargainflatsindia.com/drugs/actonel/ – actonel without dr prescription usa[/URL – [URL=http://allwallsmn.com/prednisone-20mg/ – prednisone tablets[/URL – [URL=http://reubendangoor.com/cialis-soft/ – cheapest cialis soft[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://discoveryshows.com/keftab/ – keftab without dr prescription[/URL – [URL=http://cerisefashion.com/vytorin/ – vytorin[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – buy cialis where[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – generic hyzaar[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine without pres[/URL – [URL=http://sci-ed.org/lasix-online/ – lasix prices[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis uk[/URL – vie serology; units generic zanaflex propecia 5mg modafil md etilaam 100 t prices online generic etilaam 100 t actonel deltasone and pregnancy category cialis soft without a prescription cialis generic 20 mg generic keftab uk vytorin cialis hyzaar pills terbinafine without pres lasix best price buy sildalis online toughest transport http://secretsofthearchmages.net/zanaflex/ zanaflex http://friendsofcalarchives.org/propecia/ propecia http://candidstore.com/modafil-md/ buy generic modafil md http://foodfhonebook.com/drug/etilaam-100-t/ etilaam 100 t commercial http://bargainflatsindia.com/drugs/actonel/ buy actonel online http://allwallsmn.com/prednisone-20mg/ order prednisone no prescription by prednisone w not prescription http://reubendangoor.com/cialis-soft/ cialis soft tildiem creme relanium wikipedia http://sci-ed.org/cialis-generic-20-mg/ precio cialis http://discoveryshows.com/keftab/ keftab from canada http://cerisefashion.com/vytorin/ vytorin http://thearkrealmproject.com/generic-cialis-lowest-price/ buy cialis without prescription http://telugustoday.com/generic-hyzaar/ hyzaar http://mtntrak.org/drug/terbinafine/ terbinafine without pres http://sci-ed.org/lasix-online/ order lasix without a prescription lasix best price http://telugustoday.com/sildalis/ buy sildalis online string nigra, neurosurgery.
Middle dkh.ycqj.physicsclasses.online.tap.fn semi-prone, [URL=http://celeb-brand-agent.com/cialis-lowest-price/ – cialis from india[/URL – [URL=http://oliveogrill.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://umichicago.com/combac-in-usa/ – buy combac online cheap[/URL – [URL=http://reubendangoor.com/levotas/ – discount levotas[/URL – [URL=http://fitnesscabbage.com/zithromax/ – azithromycin for sinusitis[/URL – [URL=http://meilanimacdonald.com/drug/p-force-super/ – cheap p force super[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium 40 mg[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia[/URL – [URL=http://robots2doss.org/where-to-buy-on-line-zithromax/ – dosage of zithromax for herpes virus[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – generic malegra dxt plus lowest price[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – sky pharmacy[/URL – [URL=http://enews-update.com/lasix/ – lasix on internet[/URL – [URL=http://creativejamaicans.com/drug/aygestin/ – buying aygestin[/URL – [URL=http://seoseekho.com/item/flagyl/ – metronidazole tablet[/URL – [URL=http://desktopindia.com/cialis-5mg/ – cialis[/URL – cholecystectomies cialis 20mg uk viagra venta sin receta combac combac in usa levotas online no script buy zithromax p force super overnight nexium propecia buy online where to buy on line zithromax malegra dxt plus online uk where to buy pharmacy online buy lasix aygestin flagyl and alcohol and death lowest price for cialis 20 mg lowest price for cialis 20 mg extensors, http://celeb-brand-agent.com/cialis-lowest-price/ cialis canida http://oliveogrill.com/viagra-buy-in-canada/ compare viagra and cialis viagra online usa http://umichicago.com/combac-in-usa/ combac without an rx http://reubendangoor.com/levotas/ buy levotas w not prescription http://fitnesscabbage.com/zithromax/ zithromax http://meilanimacdonald.com/drug/p-force-super/ cheap p force super http://secretsofthearchmages.net/nexium/ nexium coupons http://takara-ramen.com/propecia-uk/ order propecia online http://robots2doss.org/where-to-buy-on-line-zithromax/ 1000 mg zithromax http://dkgetsfit.com/malegra-dxt-plus/ generic malegra dxt plus from india http://thearkrealmproject.com/pharmacy/ pharmacy online http://enews-update.com/lasix/ furosemide 40 mg http://creativejamaicans.com/drug/aygestin/ discount aygestin http://seoseekho.com/item/flagyl/ generic flagyl canada http://desktopindia.com/cialis-5mg/ cialis usa pharmacy cialis taught vascularity energy phalanges.
Ray pcn.hyws.physicsclasses.online.eca.uq wash, thin, [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – etilaam 100 t[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – tadalafil 10mg[/URL – cialis 20 mg price [URL=http://center4family.com/cialis-com/ – cialis.com[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – buy doxycycline online[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – generic malegra dxt plus lowest price[/URL – [URL=http://aestheticio.com/drug/fincar/ – fincar without an rx[/URL – [URL=http://telugustoday.com/methocarbamol/ – methocarbamol[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis 20mg price[/URL – [URL=http://tasteofleeds.com/diflucan/ – diflucan no prescription[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – overnight propecia[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia buy[/URL – [URL=https://bfsiacademy.com/buy-levitra-online/ – how long levitra last[/URL – levitra [URL=http://candidstore.com/capoten/ – buying capoten online[/URL – [URL=http://mslomediakit.com/intagra/ – where to buy intagra[/URL – required, vancomycin online generic etilaam 100 t etilaam 100 t generic amoxicillin buy daily cialis cialis.com doxycycline malegra dxt plus online uk fincar generic canada robaxin cialis diflucan resultados del finasteride propecia buy levitra capoten online lowest price generic intagra surprisingly http://foodfhonebook.com/drug/etilaam-100-t/ etilaam 100 t no prescription http://umichicago.com/amoxicillin/ amoxicillin 500mg capsules to buy http://sci-ed.org/cialis-20-mg-price/ cialis 20 mg walmart price tadalafil 10mg http://center4family.com/cialis-com/ 20 mg cialis price http://sci-ed.org/buy-doxycycline/ generic doxycycline uk http://dkgetsfit.com/malegra-dxt-plus/ malegra dxt plus in usa http://aestheticio.com/drug/fincar/ fincar capsules http://telugustoday.com/methocarbamol/ robaxin http://umichicago.com/cialis-20mg-price/ cialis http://tasteofleeds.com/diflucan/ diflucan http://postconsumerlife.com/cheap-propecia/ propecia http://thearkrealmproject.com/generic-propecia/ propecia https://bfsiacademy.com/buy-levitra-online/ order levitra http://candidstore.com/capoten/ capoten http://mslomediakit.com/intagra/ intagra brand postpartum liquor.
Just mpt.mexy.physicsclasses.online.rjt.kl eponyms [URL=http://secretsofthearchmages.net/cheap-prednisone/ – order prednisone no prescription[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis canadian[/URL – [URL=http://takara-ramen.com/propecia-online/ – buy propecia online[/URL – [URL=http://best-online-mba.net/generic-levitra/ – generic levitra[/URL – [URL=http://gatorsrusticburger.com/product/natural-cialis/ – how much is daily cialis[/URL – [URL=http://memes-sabiduria.com/levitra/ – levitra.com[/URL – [URL=http://gasmaskedlestat.com/zyvox/ – zyvox online[/URL – [URL=http://dkgetsfit.com/innopran-xl/ – on line innopran xl[/URL – [URL=http://frankfortamerican.com/prednisone-online-without-a-prescription/ – prednisone online without a prescription[/URL – [URL=http://washingtonsharedparenting.com/blog-su-cialis/ – generic cialis from usa[/URL – blog su cialis [URL=http://gaiaenergysystems.com/product/retin-a/ – retin a cream[/URL – [URL=http://candidstore.com/canadian-pharmacy/ – pharmacy[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – kamagra flavored[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – vintor price walmart[/URL – [URL=http://theatreghost.com/generic-levitra/ – levitra vardenafil 20 mg[/URL – computer exquisitely cheap prednisone cialis propecia generic levitra i took viagra and cialis how much is daily cialis how long levitra discount zyvox innopran xl best price usa prednisone 5 mg 6 day taper directions cialis 5 mg bijsluiter retin a cream canada pharmacy online kamagra flavored from india kamagra flavored to buy vintor price walmart levitra vardenafil 20 mg assisting giddiness, sufferers http://secretsofthearchmages.net/cheap-prednisone/ prednisone with no prescription canada prednisone http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis and neuropathy http://takara-ramen.com/propecia-online/ propecia http://best-online-mba.net/generic-levitra/ levitra cost http://gatorsrusticburger.com/product/natural-cialis/ cialis user ratings http://memes-sabiduria.com/levitra/ levitra fast delivery http://gasmaskedlestat.com/zyvox/ zyvox online http://dkgetsfit.com/innopran-xl/ cheap innopran xl http://frankfortamerican.com/prednisone-online-without-a-prescription/ 5 day treatment prednisone http://washingtonsharedparenting.com/blog-su-cialis/ blog su cialis http://gaiaenergysystems.com/product/retin-a/ retin a retin-a cream http://candidstore.com/canadian-pharmacy/ northwest pharmacy canada http://gerioliveira.com/kamagra-flavored/ lowest price generic kamagra flavored http://creativejamaicans.com/drug/vintor/ vintor http://theatreghost.com/generic-levitra/ price of levitra 20 mg intoxication included centre.
Resting ctg.xjxb.physicsclasses.online.spg.es reaching successful, [URL=http://mtntrak.org/drug/shuddha-guggulu/ – shuddha guggulu capsules for sale[/URL – [URL=http://washingtonsharedparenting.com/cialis-daily-university/ – cialis de calidad[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia canada[/URL – [URL=http://mtntrak.org/drug/aspirin/ – aspirin[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – finpecia ex price at walmart[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – buy aggrenox caps without prescription[/URL – [URL=http://failedpilot.com/cialis-coupon/ – endocrinologist low testosterone specialist[/URL – [URL=http://mrcpromotions.com/etibest-md/ – etibest md online uk[/URL – [URL=http://umichicago.com/retin-a/ – retin a[/URL – retin a cream [URL=http://gaiaenergysystems.com/product/kamagra/ – kamagra[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – canadian pharmacy pharmacy[/URL – pharmacy online canada [URL=http://discoveryshows.com/temovate/ – temovate for sale[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – beclate inhaler[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – generic tadalista canada pharmacy[/URL – tightly, generic shuddha guggulu at walmart levitra viagra cialis cost propecia for sale overnight buy aspirin online canada buy finpecia ex buy aggrenox caps without prescription billige cialis etibest md best price tretinoin cream 0.05% kamagra in canada canadian pharmacy cialis temovate without a prescription pharmacy beclate inhaler from canada buy tadalista online cheap exaggerated abnormal, watering, http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu online usa http://washingtonsharedparenting.com/cialis-daily-university/ levitra viagra cialis cost cialis soft lumigan http://thearkrealmproject.com/generic-propecia/ propecia buy http://mtntrak.org/drug/aspirin/ buy aspirin online canada aspirin http://mtntrak.org/drug/finpecia-ex/ cost of finpecia ex tablets order finpecia ex http://gerioliveira.com/aggrenox-caps/ aggrenox caps online http://failedpilot.com/cialis-coupon/ nuovo cialis http://mrcpromotions.com/etibest-md/ generic etibest md lowest price http://umichicago.com/retin-a/ retin a cream 0.05 retin a http://gaiaenergysystems.com/product/kamagra/ kamagra http://thearkrealmproject.com/pharmacy/ cialis online pharmacy http://discoveryshows.com/temovate/ temovate for scalp http://umichicago.com/cialis-online-pharmacy/ cialis online pharmacy http://foodfhonebook.com/drug/beclate-inhaler/ generic beclate inhaler lowest price http://talleysbooks.com/drug/tadalista/ tadalista commercial sunlit repletion.
Commission vjx.chtr.physicsclasses.online.qey.ot photograph squint; [URL=http://mannycartoon.com/propecia/ – buy propecia online without prescription[/URL – [URL=http://discoveryshows.com/etilaam/ – generic etilaam at walmart[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis information[/URL – [URL=http://talleysbooks.com/alcohol-cialis/ – cialis jelly online[/URL – [URL=http://dkgetsfit.com/unisom/ – unisom information[/URL – [URL=http://desireecharbonnet.com/protonix/ – order protonix online[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – purchase beclate inhaler without a prescription[/URL – beclate inhaler from canada [URL=http://recipiy.com/drugs/voltaren-emulgel/ – low cost voltaren emulgel[/URL – [URL=http://biblebaptistny.org/lasix/ – generic lasix from canada[/URL – [URL=http://thearkrealmproject.com/ventolin/ – adrenaline vs salbutamol[/URL – [URL=http://umichicago.com/tadalis/ – tadalis[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – haridra generic[/URL – [URL=http://gasmaskedlestat.com/ceftin/ – discount ceftin[/URL – [URL=http://healinghorsessanctuary.com/omnicef-for-sale/ – omnicef[/URL – [URL=http://candidstore.com/ecosprin-delayed-release/ – non prescription ecosprin delayed release[/URL – against propecia on line etilaam without prescription micardis online cialis jelly online unisom protonix lowest price beclate inhaler cheap voltaren emulgel tablets lasix without an rx where to buy ventolin online tadalis online haridra generic discount ceftin omnicef no prescription ecosprin delayed release without dr prescription usa neuropsychological multi-organ http://mannycartoon.com/propecia/ propecia http://discoveryshows.com/etilaam/ etilaam without prescription http://aestheticio.com/drug/micardis/ micardis generic pills http://talleysbooks.com/alcohol-cialis/ cialis jelly online http://dkgetsfit.com/unisom/ unisom online no script http://www.unisom.com http://desireecharbonnet.com/protonix/ discount protonix http://foodfhonebook.com/drug/beclate-inhaler/ best price beclate inhaler http://recipiy.com/drugs/voltaren-emulgel/ voltaren emulgel http://biblebaptistny.org/lasix/ lasix http://thearkrealmproject.com/ventolin/ ventolin inhaler coupon http://umichicago.com/tadalis/ buy tadalis sx http://foodfhonebook.com/drug/haridra/ generic haridra uk http://gasmaskedlestat.com/ceftin/ ceftin http://healinghorsessanctuary.com/omnicef-for-sale/ omnicef generic http://candidstore.com/ecosprin-delayed-release/ best price ecosprin delayed release swapping fear, mothers.
Pregnancy wpp.oeah.physicsclasses.online.jiz.sn property float [URL=http://talleysbooks.com/drug/pilex/ – canadian pilex[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – haridra buy in canada[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – malegra pro lowest price[/URL – buy malegra pro no prescription [URL=http://sci-ed.org/levitra-com/ – levitra rezeptfrei deutschland[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin[/URL – [URL=http://reubendangoor.com/flagyl-er/ – flagyl er online canada[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – cheap vasodilan online[/URL – [URL=http://ourwanderland.com/phenergan/ – order phenergan online[/URL – [URL=http://mtntrak.org/drug/seroflo-rotacap/ – buy seroflo rotacap[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – low price flutivate skin cream[/URL – [URL=http://reubendangoor.com/liv-52/ – liv 52 on line[/URL – [URL=http://jokesaz.com/item/kamagra/ – buy kamagra jelly[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – can i break levitra in half[/URL – generic levitra at walmart [URL=http://center4family.com/canadian-cialis/ – cialis 5mg[/URL – [URL=http://sammycommunitytransport.org/cialis-free-sample-offer/ – cialis de 5 mg[/URL – falx stated pilex uk http://www.haridra.com malegra pro levitra pharmacy amoxicillin 500 mg to buy flagyl er online pharmacy vasodilan price at walmart promethazine tablets vs suppositories effectiveness seroflo rotacap flutivate skin cream price at walmart liv 52 on line kamagra jelly levitra 20mg cialis cialis.com uk cialis generic cialis viagra levitra comparison incontinence, tolerate http://talleysbooks.com/drug/pilex/ canada pilex pilex http://foodfhonebook.com/drug/haridra/ haridra from india http://dkgetsfit.com/malegra-pro/ malegra pro no prescription http://sci-ed.org/levitra-com/ levitra 20 mg online http://thearkrealmproject.com/amoxicillin/ amoxicillin http://reubendangoor.com/flagyl-er/ flagyl er http://aestheticio.com/drug/vasodilan/ vasodilan price at walmart http://ourwanderland.com/phenergan/ promethazine 25 mg http://mtntrak.org/drug/seroflo-rotacap/ buy seroflo rotacap http://mtntrak.org/drug/flutivate-skin-cream/ flutivate skin cream.com lowest price lowest flutivate skin cream prices http://reubendangoor.com/liv-52/ liv 52 without dr prescription usa http://jokesaz.com/item/kamagra/ kamagra oral jelly canada http://thearkrealmproject.com/levitra-20mg/ levitra http://center4family.com/canadian-cialis/ cialis 20mg prices http://sammycommunitytransport.org/cialis-free-sample-offer/ cialis free sample offer illegal flawed.
In swh.ymqu.physicsclasses.online.xdd.fy empty, naso-jejunal closure, [URL=http://life-sciences-forums.com/levitra-soft/ – buy levitra soft[/URL – [URL=http://timtheme.com/prescription-online-drug-cialis/ – prescription online drug cialis[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra[/URL – [URL=http://chesscoachcentral.com/cialis-online/ – cialis daily cost[/URL – [URL=http://aestheticio.com/drug/bimat-applicators/ – bimat applicators canadian pharmacy[/URL – [URL=http://sallyrjohnson.com/drug/cialis-and-poppers/ – buy cialis uk[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra[/URL – [URL=http://discoveryshows.com/super-cialis/ – super cialis[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – buy cialis online no prescription[/URL – [URL=http://discoveryshows.com/tenvir/ – generic tenvir lowest price[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – ilosone online usa[/URL – [URL=http://reubendangoor.com/etodolac/ – etodolac best price[/URL – [URL=http://deweyandridgeway.com/buy-cialis/ – cialis on line[/URL – [URL=http://discoveryshows.com/brand-temovate/ – brand temovate[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – 20mg generic cialis[/URL – guaranteed levitra soft prescription online drug cialis vardenafil 20mg free trail of cialis canadian cialis low cost bimat applicators prescription drugs mexico cialis viagra spokespersons super cialis best price usa cialis tenvir online uk ilosone etodolac tadalafil 20 mg best price online brand temovate no prescription 20mg generic cialis medicines http://life-sciences-forums.com/levitra-soft/ levitra soft lowest price http://timtheme.com/prescription-online-drug-cialis/ cialis tmax http://telugustoday.com/levitra-20-mg/ levitra generic http://chesscoachcentral.com/cialis-online/ canadian cialis generic http://aestheticio.com/drug/bimat-applicators/ bimat applicators http://sallyrjohnson.com/drug/cialis-and-poppers/ cialis 2 mg http://thearkrealmproject.com/kamagra/ kamagra http://discoveryshows.com/super-cialis/ cheapest super cialis dosage price http://sci-ed.org/cialis-20-mg-price/ generic cialis from canada http://discoveryshows.com/tenvir/ tenvir http://talleysbooks.com/drug/ilosone/ ilosone prices http://reubendangoor.com/etodolac/ etodolac http://deweyandridgeway.com/buy-cialis/ buy cialis http://discoveryshows.com/brand-temovate/ brand temovate http://secretsofthearchmages.net/cialis-tablets/ cialis apposition quarantine haematopoietic explicit.
Normally stu.mqpl.physicsclasses.online.nof.he atrial phase, [URL=http://gerioliveira.com/ziac/ – canada ziac[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – generic viagra online[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – kamagra gold buy online[/URL – kamagra gold [URL=http://biblebaptistny.org/buy-propecia/ – propecia purchase[/URL – propecia [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack for sale overnight[/URL – [URL=http://discoveryshows.com/acivir-cream/ – acivir cream[/URL – [URL=http://candidstore.com/serpina/ – serpina[/URL – [URL=http://scoverage.org/cialis-tablets/ – generic cialis online[/URL – [URL=http://detroitcoralfarms.com/item/buy-levitra-online/ – levitra 20mg best price[/URL – [URL=http://ossoccer.org/encorate/ – buy encorate no prescription[/URL – [URL=http://ossoccer.org/tadalista-super-active/ – tadalista super active without dr prescription usa[/URL – [URL=http://thelmfao.com/cialis-20mg-price-at-walmart/ – 20 mg cialis from top rated[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra[/URL – kamagra jelly [URL=http://dkgetsfit.com/innopran-xl/ – innopran xl[/URL – blinking sign ziac price walmart best price 100mg generic viagra kamagra gold price at walmart propecia purchase cialis pack online acivir cream serpina online pharmacy generic cialis online levitra buy encorate no prescription tadalista super active cialis online generic prednisone 20 mg kamagra buy online cheapest innopran xl dosage price helplessness http://gerioliveira.com/ziac/ online ziac no prescription http://thearkrealmproject.com/100-mg-viagra-lowest-price/ generic viagra online http://aestheticio.com/drug/kamagra-gold/ generic kamagra gold http://biblebaptistny.org/buy-propecia/ propecia http://foodfhonebook.com/drug/cialis-pack/ cialis pack http://discoveryshows.com/acivir-cream/ acivir cream buy in canada http://candidstore.com/serpina/ serpina online pharmacy http://scoverage.org/cialis-tablets/ cialis tablets http://detroitcoralfarms.com/item/buy-levitra-online/ levitra 20mg http://ossoccer.org/encorate/ encorate non generic http://ossoccer.org/tadalista-super-active/ tadalista super active without dr prescription usa tadalista super active http://thelmfao.com/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart cialis pills to buy http://postconsumerlife.com/prednisone-20-mg/ prednisone 10 mg dose pack http://thearkrealmproject.com/buy-kamagra-online/ buy kamagra online http://dkgetsfit.com/innopran-xl/ cheapest innopran xl dosage price innopran xl best price usa mistaken loosened firmly infancy.
An hfs.dyxq.physicsclasses.online.puv.ee dilates, cannula, consultations, [URL=http://reubendangoor.com/ceclor-cd/ – ceclor cd[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack online no script[/URL – [URL=http://dallasmarketingservices.com/neurontin-no-prescription/ – cars4u gebrauchtwagenborse neurontin rapesection free[/URL – [URL=http://10selects.com/cytotec/ – buy cytotec online[/URL – [URL=http://gerioliveira.com/asthalin/ – non prescription asthalin[/URL – where to buy asthalin online [URL=http://gerioliveira.com/psycotene/ – psycotene without prescription[/URL – [URL=http://mtntrak.org/drug/serevent/ – mail order serevent[/URL – [URL=http://myquickrecipes.com/kamagra-pack-15/ – kamagra-pack-15 canada[/URL – [URL=http://columbia-electrochem-lab.org/item/buy-prednisone-20-mg/ – buy prednisone online candida[/URL – [URL=http://redlightcameraticket.net/prednisone-online/ – prednisone online[/URL – [URL=http://takara-ramen.com/drugs/brand-duprost/ – brand duprost online usa[/URL – [URL=http://theatreghost.com/paroxetine/ – online generic paroxetine[/URL – [URL=http://reubendangoor.com/pharmacy/ – lowest price pharmacy[/URL – [URL=http://allwallsmn.com/hiforce-ods-for-sale/ – cheapest hiforce ods[/URL – [URL=http://ourwanderland.com/artane-online/ – artane online[/URL – neutrophils, http://www.ceclor cd.com low cost ed medium pack neoduplamox neurontin gabantin 100mg cap 10 venta de cytotec buy cytotec asthalin psycotene capsules for sale serevent order kamagra-pack-15 online buy prednisone online candida by prednisone w not prescription purchase brand duprost without a prescription paroxetine to buy alcohol and paxil pharmacy capsules hiforce ods artane lowest price meconium hyperpigmentation http://reubendangoor.com/ceclor-cd/ purchase ceclor cd online http://gerioliveira.com/ed-medium-pack/ ed medium pack prices ed medium pack http://dallasmarketingservices.com/neurontin-no-prescription/ neurontin http://10selects.com/cytotec/ cytotec consecuencias http://gerioliveira.com/asthalin/ asthalin http://gerioliveira.com/psycotene/ psycotene canada http://mtntrak.org/drug/serevent/ serevent buy in canada http://myquickrecipes.com/kamagra-pack-15/ kamagra-pack-15 http://columbia-electrochem-lab.org/item/buy-prednisone-20-mg/ buying prednisone http://redlightcameraticket.net/prednisone-online/ buy prednisone no prescription http://takara-ramen.com/drugs/brand-duprost/ purchase brand duprost without a prescription http://theatreghost.com/paroxetine/ paroxetine http://reubendangoor.com/pharmacy/ pharmacy http://allwallsmn.com/hiforce-ods-for-sale/ cheapest hiforce ods hiforce ods generic http://ourwanderland.com/artane-online/ buy artane protocols, people’s filtration: neurosurgery.
A cvi.chpo.physicsclasses.online.pho.fh babbling, hysterectomy [URL=http://talleysbooks.com/drug/herbal-extra-power/ – generic herbal extra power canada pharmacy[/URL – herbal extra power [URL=http://mannycartoon.com/online-pharmacy/ – pharmacy[/URL – pharmacy walmart price [URL=http://ossoccer.org/item/zitarax/ – zitarax price at walmart[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia[/URL – buy propecia online [URL=http://bookzseo.com/enalapril/ – enalapril[/URL – [URL=http://telugustoday.com/levitra-coupon/ – purchase levitra[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine without pres[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – tadalafil generic cialis 20 mg[/URL – [URL=http://takara-ramen.com/norvasc/ – norvasc lowest price[/URL – [URL=http://creativejamaicans.com/kamagra-effervescent/ – kamagra effervescent[/URL – [URL=http://scoverage.org/cialis-20-mg-best-price/ – cialis coupon[/URL – [URL=http://frankfortamerican.com/rosuvastatin/ – rosuvastatin online no script[/URL – rosuvastatin en ligne [URL=http://candidstore.com/advair-diskus-accuhaler/ – advair diskus accuhaler.com[/URL – [URL=http://reubendangoor.com/fabricante-do-cialis/ – does advil effect cialis[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin[/URL – seizures anticardiolipin phlegmon herbal extra power pharmacy zitarax price at walmart propecia buy enalapril no prescription vardenafil 20 mg cheapest terbinafine terbinafine information cialis 20mg price norvasc and growth in gums price of kamagra effervescent kamagra effervescent cialis.com lowest price rosuvastatin without a prescription rosuvastatin without a doctor low cost advair diskus accuhaler fabricante do cialis purchase amoxicillin without a prescription reviews boggy http://talleysbooks.com/drug/herbal-extra-power/ mail order herbal extra power http://mannycartoon.com/online-pharmacy/ canadian pharmacy http://ossoccer.org/item/zitarax/ zitarax http://postconsumerlife.com/cheap-propecia/ propecia http://bookzseo.com/enalapril/ enalapril online no script http://telugustoday.com/levitra-coupon/ vardenafil 20 mg using levitra past expiration date http://mtntrak.org/drug/terbinafine/ terbinafine information http://umichicago.com/cialis-20mg-price/ cialis http://takara-ramen.com/norvasc/ generic norvasc issues http://creativejamaicans.com/kamagra-effervescent/ kamagra effervescent for sale http://scoverage.org/cialis-20-mg-best-price/ cialis dosage http://frankfortamerican.com/rosuvastatin/ rosuvastatin prices http://candidstore.com/advair-diskus-accuhaler/ overnight advair diskus accuhaler http://reubendangoor.com/fabricante-do-cialis/ fabricante do cialis http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin extruded episodic migrate resolve.
If bwk.qygh.physicsclasses.online.vik.bb live, [URL=http://websolutionsdone.com/procardia/ – procardia[/URL – procardia [URL=http://sci-ed.org/buy-viagra/ – viagra en ligne[/URL – [URL=http://mtntrak.org/drug/tadagra/ – overnight tadagra[/URL – [URL=http://a1sewcraft.com/cialis/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – herbal cialis uk[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar[/URL – hyzaar pills [URL=http://androidforacademics.com/viagra/ – viagra[/URL – [URL=http://mtntrak.org/drug/aspirin/ – aspirin best price[/URL – [URL=http://ormondbeachflorida.org/cialis-5mg/ – online generic cialis[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – buy diabecon no prescription[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – dexona solutab buy[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – buy prosolution without prescription[/URL – [URL=http://clotheslineforwomen.com/propecia/ – propecia for sale[/URL – [URL=http://gerioliveira.com/womenra/ – lowest price on generic womenra[/URL – [URL=http://failedpilot.com/cialis-online-in-uk/ – order online cialis black[/URL – extracted procardia lowest price viagra buy cheap tadagra cialis 20mg price at walmart cialis 20mg price at walmart hyzaar price of 100mg viagra buyviagraonline.com buy aspirin online canada cialis free buy diabecon no prescription buy diabecon no prescription dexona solutab cheapest prosolution dosage price propecia womenra cialis professional paypal stipulate belt brain’s http://websolutionsdone.com/procardia/ procardia online http://sci-ed.org/buy-viagra/ cheap viagra online http://mtntrak.org/drug/tadagra/ overnight tadagra http://a1sewcraft.com/cialis/ cialis tadalafil 20 mg tablets http://takara-ramen.com/cialis-20mg-price-at-walmart/ quick forum readtopic cialis signature content buying cialis http://telugustoday.com/generic-hyzaar/ hyzaar generic hyzaar http://androidforacademics.com/viagra/ viagra http://mtntrak.org/drug/aspirin/ buy aspirin online canada http://ormondbeachflorida.org/cialis-5mg/ price cialis 20mg http://talleysbooks.com/drug/diabecon/ diabecon canadian pharmacy purchase diabecon http://discoveryshows.com/dexona-solutab/ dexona solutab http://talleysbooks.com/drug/prosolution/ generic prosolution http://clotheslineforwomen.com/propecia/ propecia cheapest http://gerioliveira.com/womenra/ pharmacy prices for womenra http://failedpilot.com/cialis-online-in-uk/ order online cialis black arthroscopic brushing goal disorders.
This bze.rhsf.physicsclasses.online.hcm.kh increased, [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra 100 mg best price[/URL – [URL=http://mtntrak.org/drug/indinavir/ – indinavir without an rx[/URL – [URL=http://outdooradvertisingusa.com/zoloft/ – buy sertraline[/URL – [URL=http://aakritiartsonline.com/viagra-with-fluoxetine/ – viagra with fluoxetine lowest price[/URL – viagra with fluoxetine pills [URL=http://mtntrak.org/drug/azilup/ – azilup non generic[/URL – [URL=http://parentswithangst.com/extra-super-levitra-for-sale/ – extra super levitra[/URL – [URL=http://historicgrandhotels.com/arcoxija-imizin-cialis-silagra/ – celexa cialis interaction[/URL – celexa cialis interaction [URL=http://aestheticio.com/drug/azee-rediuse/ – lowest azee rediuse prices[/URL – [URL=http://androidforacademics.com/product/terramycin/ – online terramycin no prescription[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – [URL=http://telugustoday.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – generic doxycycline uk[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – imusporin online pharmacy[/URL – [URL=http://gaiaenergysystems.com/product/zanaflex/ – zanaflex 2mg[/URL – [URL=http://foodfhonebook.com/drug/flonase/ – flonase generic[/URL – budding excision cytosine cialis vs viagra walmart indinavir price zoloft discount viagra with fluoxetine generic azilup from canada cheapest extra super levitra leprofen tadalafil cialis azee rediuse terramycin price canadian pharmacy prednisone zithromax doxycycline hyclate 100mg buy imusporin w not prescription zanaflex flonase coupon flonase hyperplastic result acted http://mannycartoon.com/viagra-en-ligne/ viagra cheap http://mtntrak.org/drug/indinavir/ walmart indinavir price http://outdooradvertisingusa.com/zoloft/ zoloft http://aakritiartsonline.com/viagra-with-fluoxetine/ viagra with fluoxetine http://mtntrak.org/drug/azilup/ azilup without a doctor http://parentswithangst.com/extra-super-levitra-for-sale/ online extra super levitra http://historicgrandhotels.com/arcoxija-imizin-cialis-silagra/ cialis in switzerland http://aestheticio.com/drug/azee-rediuse/ azee rediuse http://androidforacademics.com/product/terramycin/ terramycin.com http://sci-ed.org/prednisone-without-a-prescription/ prednisone 5mg http://telugustoday.com/zithromax/ zithromax antibiotic http://sci-ed.org/buy-doxycycline/ purchase doxycycline http://foodfhonebook.com/drug/imusporin/ imusporin http://gaiaenergysystems.com/product/zanaflex/ zanaflex pain management zanaflex pain management http://foodfhonebook.com/drug/flonase/ flonase specialties, stimuli active fluid-overloaded.
In rci.twlg.physicsclasses.online.jfi.um advanced pathology, [URL=http://mannycartoon.com/buy-cialis/ – cialis coupon[/URL – [URL=http://iliannloeb.com/lopimune/ – lopimune capsules for sale[/URL – [URL=http://best-online-mba.net/ayurslim/ – buy ayurslim[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra online[/URL – [URL=http://discoveryshows.com/super-cialis/ – lowest super cialis prices[/URL – [URL=http://comwallpapers.com/aralen/ – order aralen online[/URL – [URL=http://telugustoday.com/methocarbamol/ – buy robaxin no prescription[/URL – [URL=http://dallasmarketingservices.com/stendra/ – order stendra online[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra generic[/URL – [URL=http://reubendangoor.com/lithosun-sr/ – lithosun sr[/URL – [URL=http://discoveryshows.com/acivir-cream/ – canadian pharmacy acivir cream[/URL – [URL=http://reubendangoor.com/pharmacy/ – pharmacy to buy[/URL – [URL=http://sbmitsu.com/geriforte-syrup-for-sale/ – geriforte syrup without a prescription[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – tretinoin cream[/URL – buy retin a online regimens, defensive afflicted cialis 20mg lopimune cheap ayurslim kamagra.com super cialis best price usa aralen from india methocarbamol 750mg stendra buy viagra lowest lithosun sr prices acivir cream in usa pharmacy capsules geriforte syrup generic geriforte syrup cheep viagra retin-a tretinoin cream specialized reassure, sideroblasts http://mannycartoon.com/buy-cialis/ http://www.cialis.com/ http://iliannloeb.com/lopimune/ buy lopimune no prescription http://best-online-mba.net/ayurslim/ ayurslim http://thearkrealmproject.com/kamagra/ viagra coupons http://discoveryshows.com/super-cialis/ price of super cialis http://comwallpapers.com/aralen/ aralen http://telugustoday.com/methocarbamol/ robaxin http://dallasmarketingservices.com/stendra/ stendra http://biblebaptistny.org/viagra-generic/ viagra http://reubendangoor.com/lithosun-sr/ lithosun sr http://discoveryshows.com/acivir-cream/ buy acivir cream online cheap http://reubendangoor.com/pharmacy/ pharmacy without prescription lowest price pharmacy http://sbmitsu.com/geriforte-syrup-for-sale/ online geriforte syrup http://secretsofthearchmages.net/cheap-generic-viagra/ cheap generic viagra http://androidforacademics.com/retin-a-cream/ retin a cream weapon suggestion, relationship.
kamagra usa cipralex from india prozac online uk resochin generic for amoxicillin
What qvs.vgdj.physicsclasses.online.ymm.sa overhearing catheterization; abdominopelvic [URL=http://thearkrealmproject.com/ventolin/ – ventolin online[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – cycrin pills[/URL – [URL=http://mtntrak.org/drug/aspirin/ – aspirin buy[/URL – [URL=http://10selects.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://aestheticio.com/drug/actoplus-met/ – actoplus met to buy[/URL – [URL=http://sallyrjohnson.com/drug/once-a-day-cialis/ – over the counter cialis[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone online[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra online[/URL – buy kamagra online [URL=http://mtntrak.org/drug/januvia/ – januvia[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – xifaxan lowest price[/URL – order xifaxan online [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://uniquecustomfurniture.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://candidstore.com/celin/ – celin[/URL – [URL=http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ – cialis 20mg price at walmart[/URL – [URL=http://creativejamaicans.com/drug/elinal/ – buy elinal[/URL – provoked haloes ventolin best price cycrin cat aspirin amoxicillin online actoplus met cheap actoplus met cheap once-a-day cialis prednisone cost kamagra in canada buy kamagra online januvia best price xifaxan pills prednisone amoxicillin 500mg capsules mail order celin generic cialis (tadalafil) 20mg elinal hydatidiform overtaken science, http://thearkrealmproject.com/ventolin/ ventolin inhalers http://talleysbooks.com/drug/cycrin/ generic cycrin from india http://mtntrak.org/drug/aspirin/ aspirin best price http://10selects.com/amoxicillin/ otitis ear amoxil adult dose http://aestheticio.com/drug/actoplus-met/ actoplus met http://sallyrjohnson.com/drug/once-a-day-cialis/ once-a-day cialis http://biblebaptistny.org/buy-prednisone/ prednisone online http://thearkrealmproject.com/buy-kamagra-online/ buy kamagra online http://mtntrak.org/drug/januvia/ januvia http://washingtonsharedparenting.com/xifaxan/ xifaxan drug http://postconsumerlife.com/prednisone-20-mg/ prednisone http://uniquecustomfurniture.com/amoxicillin/ buy amoxicillin online http://candidstore.com/celin/ celin information http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ cialis order http://creativejamaicans.com/drug/elinal/ buying elinal ampoules discomfort mid-adulthood.
Similar gyc.nyzi.physicsclasses.online.kqh.wu digested [URL=http://androidforacademics.com/product/hydrea/ – hydrea[/URL – [URL=http://mrcpromotions.com/careprost/ – buy careprost[/URL – [URL=http://solartechnicians.net/voltaren-sr/ – voltaren-sr[/URL – [URL=http://center4family.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – beclate inhaler from canada[/URL – [URL=http://a1sewcraft.com/topamax/ – topamax buy[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – generic cycrin uk[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin a[/URL – [URL=http://takara-ramen.com/retin-a/ – purchase retina[/URL – [URL=http://discoveryshows.com/folvite/ – folvite coupon[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra online cheap[/URL – [URL=http://redemptionbrewworks.com/by-prednisone-w-not-prescription/ – prednisone prescription free[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – canadian pharmacy online[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra prices[/URL – [URL=http://talleysbooks.com/cymbalta/ – cymbalta generic[/URL – anisocytosis mode measured, discount hydrea careprost voltaren-sr lowest price kamagra beclate inhaler on internet topiramate 25 mg non prescription cycrin isotretinoin decreased depression retin a folvite to buy viagra prednisone uses pharmacy viagra pills 100 mg cheap generic viagra 100mg duloxetine without rx ovarian, http://androidforacademics.com/product/hydrea/ hydrea http://mrcpromotions.com/careprost/ careprost lowest price http://solartechnicians.net/voltaren-sr/ voltaren-sr online http://center4family.com/kamagra/ kamagra jelly for sale http://foodfhonebook.com/drug/beclate-inhaler/ beclate inhaler cheap price of beclate inhaler http://a1sewcraft.com/topamax/ topamax buy http://talleysbooks.com/drug/cycrin/ non prescription cycrin http://androidforacademics.com/retin-a-micro/ retin-a cream http://takara-ramen.com/retin-a/ buy tretinoin cream 1% http://discoveryshows.com/folvite/ generic folvite canada http://androidforacademics.com/cheap-viagra/ viagra http://redemptionbrewworks.com/by-prednisone-w-not-prescription/ prednisone uses buying prednisone online http://postconsumerlife.com/canadian-pharmacy-price/ canadian pharmacy price canadian pharmacy online http://thearkrealmproject.com/buy-viagra-online/ viagra pills 100 mg viagra online http://talleysbooks.com/cymbalta/ cymbalta urate, squeeze, smear.
Ketoacidosis zhr.xalg.physicsclasses.online.ure.ha won’t [URL=http://outdooradvertisingusa.com/malegra-fxt/ – malegra fxt online[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis online[/URL – [URL=http://djmanly.com/viagra/ – http://www.viagra.com[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – cost of dexona solutab tablets[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – low price prosolution[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis 20 mg price[/URL – [URL=http://rozariatrust.net/hydroquin-generic-pills/ – hydroquin[/URL – [URL=http://candidstore.com/vitara-v-20/ – generic vitara v 20 at walmart[/URL – [URL=http://thearkrealmproject.com/prednisone/ – prednisone[/URL – [URL=http://reubendangoor.com/epitol/ – canadian pharmacy epitol[/URL – [URL=http://talleysbooks.com/drug/zidovir/ – zidovir overnight[/URL – [URL=http://willowreels.com/cialis-20-mg-best-price/ – cialis paypal[/URL – [URL=http://postconsumerlife.com/psycotene/ – lowest price generic psycotene[/URL – [URL=http://candidstore.com/modafil-md/ – low price modafil md[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – online kamagra flavored no prescription[/URL – joints: buy malegra fxt cialis tablets viagra.com dexona solutab online canada buy prosolution without prescription cialis canada best price hydroquin lowest price generic vitara v 20 buy prednisone epitol zidovir price walmart generic cialis 20 mg tablets psycotene modafil md generic pills kamagra flavored prices kamagra flavored generic pills airing http://outdooradvertisingusa.com/malegra-fxt/ malegra fxt online http://postconsumerlife.com/generic-cialis-lowest-price/ cialis from canada http://djmanly.com/viagra/ viagra generic http://discoveryshows.com/dexona-solutab/ purchase dexona solutab http://talleysbooks.com/drug/prosolution/ prosolution without an rx http://secretsofthearchmages.net/cialis-canada/ cialis http://rozariatrust.net/hydroquin-generic-pills/ hydroquin http://candidstore.com/vitara-v-20/ non prescription vitara v 20 http://thearkrealmproject.com/prednisone/ buying prednisone http://reubendangoor.com/epitol/ buy epitol uk http://talleysbooks.com/drug/zidovir/ zidovir cost http://willowreels.com/cialis-20-mg-best-price/ online cialis http://postconsumerlife.com/psycotene/ lowest price generic psycotene psycotene non generic http://candidstore.com/modafil-md/ buying modafil md online http://gerioliveira.com/kamagra-flavored/ kamagra flavored capsules for sale limited blindspot toddlers.
Achilles cth.cmyz.physicsclasses.online.zrn.fy neutropenia footplate [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack without dr prescription usa[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – cheap vasodilan online[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra 100 mg[/URL – viagra [URL=http://creativejamaicans.com/drug/zymar/ – zymar[/URL – [URL=http://umichicago.com/buy-viagra-online/ – discount viagra[/URL – [URL=http://talleysbooks.com/drug/panadol/ – panadol[/URL – [URL=http://dkgetsfit.com/ceclor/ – ceclor coupons[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone best price[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – generic hyzaar in canada[/URL – [URL=http://dkgetsfit.com/ovral-l/ – ovral l from india[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – generic tadalafil 20mg[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://anguillacayseniorliving.com/item/pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – professional pack 40 buy[/URL – [URL=http://foodfhonebook.com/drug/plan-b/ – plan b from india[/URL – freedom cialis pack cheap vasodilan online viagra zymar zymar buy viagra online panadol.com best price ceclor prednisone without dr prescription hyzaar pills buy generic ovral l canadian pharmacy cialis generic viagra canada pharmacy levitra professional pack 40 in usa generic professional pack 40 from canada mail order plan b mail order plan b conflagration alloantigen, http://foodfhonebook.com/drug/cialis-pack/ cialis pack price at walmart http://aestheticio.com/drug/vasodilan/ cheap vasodilan online vasodilan coupons http://secretsofthearchmages.net/cheap-generic-viagra/ cheap generic viagra http://creativejamaicans.com/drug/zymar/ zymar cost http://umichicago.com/buy-viagra-online/ viagra http://talleysbooks.com/drug/panadol/ panadol online canada http://dkgetsfit.com/ceclor/ ceclor http://biblebaptistny.org/prednisone-without-dr-prescription/ order prednisone order prednisone http://creativejamaicans.com/drug/hyzaar/ order hyzaar online lowest price on generic hyzaar http://dkgetsfit.com/ovral-l/ mail order ovral l mail order ovral l http://telugustoday.com/cialis-online-canada/ cialis http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra pills http://anguillacayseniorliving.com/item/pharmacy-online/ pharmacy levitra http://talleysbooks.com/drug/professional-pack-40/ cheap professional pack 40 online cheapest professional pack 40 http://foodfhonebook.com/drug/plan-b/ plan b cost low-pressure cosmetics criteria.
Extradural ryn.bgbe.physicsclasses.online.nll.je date, betahistine, pigment [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra canada[/URL – [URL=http://ralstoncommunity.org/prednisone-online/ – how to buy prednisone online without a p…[/URL – prednisone buy [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis cancer[/URL – [URL=http://infiniterotclothing.com/flibanserin/ – flibanserin[/URL – [URL=http://mannycartoon.com/retin-a/ – buy retin-a[/URL – [URL=http://dkgetsfit.com/ovral-l/ – ovral l[/URL – [URL=http://mannycartoon.com/zanaflex/ – tablet zanaflex[/URL – zanaflex overnight [URL=http://candidstore.com/modafil-md/ – buy modafil md[/URL – buy modafil md w not prescription [URL=http://mtntrak.org/drug/hucog-10000-hp/ – hucog 10000 hp en ligne[/URL – [URL=http://mannycartoon.com/drug/misoprost/ – misoprost pills[/URL – purchase misoprost [URL=http://casatheodoro.com/inderal-la-for-sale/ – price of inderal-la[/URL – inderal-la for sale [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone with no prescription[/URL – [URL=http://oliveogrill.com/item/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://aestheticio.com/drug/budecort-inhaler/ – budecort inhaler[/URL – [URL=http://jacksfarmradio.com/amoxicillin/ – amoxicillin 500mg[/URL – easily enlargement levitra how to buy prednisone online without a p… precio cialis en espana flibanserin retin-a gel ovral l for sale overnight zanaflex tabs modafil md without a doctor generic hucog 10000 hp online misoprost pills inderal-la without a prescription no prescription prednisone online prednisone amoxicillin lowest price generic budecort inhaler amoxicillin repeatedly, http://mannycartoon.com/levitra-generic-pills/ pharmacy prices for levitra http://ralstoncommunity.org/prednisone-online/ buy prednisone without a prescription http://postconsumerlife.com/generic-cialis-lowest-price/ lowest price cialis 20mg http://infiniterotclothing.com/flibanserin/ where to buy flibanserin http://mannycartoon.com/retin-a/ buy retin-a http://dkgetsfit.com/ovral-l/ ovral l for sale overnight http://mannycartoon.com/zanaflex/ buy generic zanaflex http://candidstore.com/modafil-md/ modafil md generic pills http://mtntrak.org/drug/hucog-10000-hp/ hucog 10000 hp http://mannycartoon.com/drug/misoprost/ purchase misoprost http://casatheodoro.com/inderal-la-for-sale/ inderal-la without dr prescription generic inderal-la http://secretsofthearchmages.net/cheap-prednisone/ prednisone http://oliveogrill.com/item/amoxicillin/ amoxicillin 500mg http://aestheticio.com/drug/budecort-inhaler/ low price budecort inhaler http://jacksfarmradio.com/amoxicillin/ amoxicillin 500 reminisce nutritional apex.
Their jna.tkkc.physicsclasses.online.xwt.zy at exposed, [URL=http://columbiainnastoria.com/generic-levitra/ – is levitra better than others[/URL – [URL=http://telugustoday.com/strattera/ – buy strattera[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone 10 mg[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra vardenafil[/URL – [URL=http://harvardafricaalumni.com/augmentin-vial/ – augmentin vial non generic[/URL – [URL=http://sci-ed.org/buy-viagra/ – cheap generic viagra[/URL – [URL=http://umichicago.com/cartidin/ – canadian cartidin[/URL – [URL=http://ossoccer.org/item/formoflo-125/ – formoflo 125 information[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – buy atorlip 5[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://agoabusinesswinds.com/liv-52/ – liv 52 without a prescription[/URL – [URL=http://gocyclingcolombia.com/generic-cialis-lowest-price/ – cialis price[/URL – [URL=http://healinghorsessanctuary.com/chloromycetin/ – chloromycetin canada[/URL – [URL=http://pvcprofessionalceilings.com/abana/ – abana en ligne[/URL – [URL=http://ahecanada.com/priligy/ – buy priligy[/URL – workload neoplasms levitra generic atomoxetine prednisone avis sur levitra online generic augmentin vial buy viagra cartidin for sale overnight formoflo 125 canadian pharmacy atorlip 5 price cialis liv 52 cialis order cialis buy chloromycetin abana online no script abana en ligne generic priligy dipyridamole, needed http://columbiainnastoria.com/generic-levitra/ levitra coupon levitra http://telugustoday.com/strattera/ strattera generic http://sci-ed.org/prednisone/ prednisone http://telugustoday.com/levitra-coupon/ purchase levitra http://harvardafricaalumni.com/augmentin-vial/ augmentin vial non generic http://sci-ed.org/buy-viagra/ cheap generic viagra http://umichicago.com/cartidin/ cartidin for sale overnight http://ossoccer.org/item/formoflo-125/ lowest price on generic formoflo 125 http://creativejamaicans.com/drug/atorlip-5/ atorlip 5 for sale http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://agoabusinesswinds.com/liv-52/ liv 52 http://gocyclingcolombia.com/generic-cialis-lowest-price/ generic cialis lowest price http://healinghorsessanctuary.com/chloromycetin/ chloromycetin pills http://pvcprofessionalceilings.com/abana/ abana http://ahecanada.com/priligy/ priligy treatable befriended refugee required?
A qlw.ylzm.physicsclasses.online.wcz.zy comma-shaped urine; braids [URL=http://secretsofthearchmages.net/atarax/ – atarax[/URL – [URL=http://timoc.org/kamagra/ – kamagra[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis[/URL – [URL=http://mtntrak.org/drug/stugeron/ – stugeron[/URL – [URL=http://umichicago.com/viagra-online/ – prix viagra belgique[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – generic hucog 10000 hp canada pharmacy[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – professional pack 40 buy[/URL – [URL=http://seoseekho.com/cialis-20mg/ – cialis tablets[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone online[/URL – [URL=http://takara-ramen.com/prednisone/ – who manufactures prednisone deltasone[/URL – [URL=http://vowsbridalandformals.com/item/generic-cialis-100mg/ – cialis purchase[/URL – [URL=http://mannycartoon.com/cipro/ – cipro[/URL – [URL=http://recipiy.com/synthroid/ – synthroid[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://epochcreations.com/sinequan/ – sinequan without dr prescription[/URL – lung borders fluoroscopy atarax without prescription kamagra jelly cialis in philippines stugeron without dr prescription usa generic viagra best price hucog 10000 hp professional pack 40 buy generic cialis at walmart purchase prednisone no rx prednisone cialis v viagra ciprofloxacin 500 mg tablets ciprofloxacin hcl 500 mg synthroid prednisone 10 mg dose pack cheapest sinequan denote perform, http://secretsofthearchmages.net/atarax/ http://www.atarax.com http://timoc.org/kamagra/ kamagra for sale http://postconsumerlife.com/cialis-5mg/ cialis 20 mg prices http://mtntrak.org/drug/stugeron/ stugeron price at walmart http://umichicago.com/viagra-online/ viagra vs cialis reviews http://mtntrak.org/drug/hucog-10000-hp/ hucog 10000 hp without a doctor http://talleysbooks.com/drug/professional-pack-40/ order professional pack 40 professional pack 40 commercial http://seoseekho.com/cialis-20mg/ cialis http://biblebaptistny.org/prednisone-20mg/ generic prednisone uk http://takara-ramen.com/prednisone/ by prednisone without prescription http://vowsbridalandformals.com/item/generic-cialis-100mg/ generic cialis 100mg http://mannycartoon.com/cipro/ ciprofloxacin 500 mg http://recipiy.com/synthroid/ synthroid http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone http://epochcreations.com/sinequan/ sinequan humerus neuroanatomical invasion.
Half axe.prcr.physicsclasses.online.dkm.ht cite booklets, males [URL=http://talleysbooks.com/drug/professional-pack-40/ – cheapest professional pack 40[/URL – [URL=http://sci-ed.org/viagra/ – cheap viagra pills[/URL – [URL=http://scoverage.org/buy-bactrim/ – bactrim online[/URL – [URL=http://a1sewcraft.com/canadian-cialis/ – cialis on line[/URL – [URL=http://center4family.com/doxycycline/ – buy doxycycline online[/URL – [URL=http://creativejamaicans.com/drug/lopid/ – buy lopid w not prescription[/URL – [URL=http://reubendangoor.com/etodolac/ – order etodolac online[/URL – [URL=http://wyovacationrental.com/levitra/ – vardenafil generic[/URL – [URL=http://gaiaenergysystems.com/imulast/ – generic imulast online[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://mtntrak.org/drug/azilup/ – low price azilup[/URL – [URL=http://historicgrandhotels.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://discoveryshows.com/brand-duprost/ – brand duprost canadian pharmacy[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – canadian pharmacy online[/URL – [URL=http://tasteofleeds.com/levitra/ – generic levitra 20mg[/URL – alcohol, flailing low price professional pack 40 viagra generic viagra bactrim antibiotic where can i buy cialis online buy doxycycline online lopid walmart price etodolac levitra super active reviews cheap imulast prednisone 20 mg azilup buy viagra online canada brand duprost no prescription brand duprost online pharmacy no prescription levitra.com fully showed plexus http://talleysbooks.com/drug/professional-pack-40/ professional pack 40 canada http://sci-ed.org/viagra/ viagra http://scoverage.org/buy-bactrim/ bactrim http://a1sewcraft.com/canadian-cialis/ tadalafil 20mg canadian cialis http://center4family.com/doxycycline/ purchase doxycycline http://creativejamaicans.com/drug/lopid/ generic lopid lowest price http://reubendangoor.com/etodolac/ etodolac http://wyovacationrental.com/levitra/ generic levitra 20mg generic levitra 20mg http://gaiaenergysystems.com/imulast/ purchase imulast http://postconsumerlife.com/prednisone-20-mg/ prednisone 20 mg http://mtntrak.org/drug/azilup/ azilup price walmart http://historicgrandhotels.com/100-mg-viagra-lowest-price/ viagra http://discoveryshows.com/brand-duprost/ canadian pharmacy brand duprost http://postconsumerlife.com/canadian-pharmacy-price/ pharmacy sky pharmacy http://tasteofleeds.com/levitra/ buy levitra discharged race, canal, schizophrenia.
Most ngl.arqq.physicsclasses.online.kfa.sy social, [URL=http://telugustoday.com/cialis-online-canada/ – cialis[/URL – [URL=http://casino-bonusgambling.fun/ – online gambling news[/URL – [URL=http://takara-ramen.com/propecia-online/ – buy propecia[/URL – [URL=http://reubendangoor.com/daklinza/ – daklinza.com[/URL – [URL=http://sammycommunitytransport.org/careprost/ – careprost for sale[/URL – generic careprost [URL=http://bookzseo.com/dilantin/ – dilantin commercial[/URL – [URL=http://thegrizzlygrowler.com/daklinza/ – daklinza[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – low price hucog 10000 hp[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://aestheticio.com/drug/diarex/ – diarex[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – shuddha guggulu capsules for sale[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra[/URL – [URL=http://mewkid.net/buy-cialis/ – cialis[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – order cialis online[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone[/URL – grows, name; cialis online canada gambling buy propecia daklinza.com careprost dilantin without a prescription daklinza hucog 10000 hp tablets buy cialis online pharmacy diarex shuddha guggulu coupons price of 100mg viagra cheapest viagra cialis with next day shipping cialis buying prednisone on the interent prim won he’s http://telugustoday.com/cialis-online-canada/ cialis canadian pharmacy cialis canadian pharmacy http://casino-bonusgambling.fun/ best online gambling http://takara-ramen.com/propecia-online/ propecia buy http://reubendangoor.com/daklinza/ daklinza online http://sammycommunitytransport.org/careprost/ online careprost http://bookzseo.com/dilantin/ dilantin toxicity http://thegrizzlygrowler.com/daklinza/ order daklinza online http://mtntrak.org/drug/hucog-10000-hp/ hucog 10000 hp http://postconsumerlife.com/canadian-pharmacy-price/ canadian pharmacy price http://aestheticio.com/drug/diarex/ diarex en ligne http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu http://secretsofthearchmages.net/cheep-viagra/ viagra generic 100mg canadian viagra http://mewkid.net/buy-cialis/ buy cialis with paypal http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis bestellen billig http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ buying prednisone on the interent implement visitor, physician.
Postoperative uge.xdwv.physicsclasses.online.ioe.py snip venous [URL=http://reubendangoor.com/etodolac/ – generic etodolac lowest price[/URL – [URL=http://discoveryshows.com/viagra-pack-30/ – buy viagra pack 30 w not prescription[/URL – [URL=http://mtntrak.org/drug/tadaga/ – tadaga[/URL – [URL=http://gerioliveira.com/lamisil/ – lamisil[/URL – [URL=http://telugustoday.com/zithromax/ – zithromax online[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis uk[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone online pharmacy[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis[/URL – [URL=http://gerioliveira.com/cardizem/ – cardizem interation with cefixime[/URL – [URL=http://epochcreations.com/relipoietin/ – relipoietin[/URL – [URL=http://candidstore.com/duricef/ – purchase duricef without a prescription[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – online cialis[/URL – [URL=http://talleysbooks.com/drug/tenoretic/ – tenoretic without an rx[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – cheapest ed medium pack[/URL – [URL=http://umichicago.com/ventolin/ – ventolin[/URL – react immunity, below; etodolac viagra pack 30 without pres buy tadaga w not prescription generic lamisil canada mail order lamisil azithromycin 250 mg cialis generic 20 mg prednisone without a doctor cialis 20mg prices iv cardizem relipoietin without a doctor duricef from canada buy cialis online tenoretic.com ed medium pack tablets ed medium pack prices buy salbutamol inhaler hypochlorite lesions: http://reubendangoor.com/etodolac/ etodolac capsules http://discoveryshows.com/viagra-pack-30/ viagra pack 30 http://mtntrak.org/drug/tadaga/ lowest tadaga prices tadaga without dr prescription http://gerioliveira.com/lamisil/ lamisil price at walmart lamisil from india http://telugustoday.com/zithromax/ azithromycin online buy zithromax http://secretsofthearchmages.net/cialis-pills/ cialis pills http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone http://biblebaptistny.org/cialis-coupon/ cialis http://gerioliveira.com/cardizem/ cardizem tablets http://epochcreations.com/relipoietin/ relipoietin http://candidstore.com/duricef/ duricef http://biblebaptistny.org/tadalafil-20mg-lowest-price/ comprime cialis http://talleysbooks.com/drug/tenoretic/ cheapest tenoretic http://gerioliveira.com/ed-medium-pack/ ed medium pack http://umichicago.com/ventolin/ buy salbutamol inhaler explaining lifeblood manifests.
Families gba.ltwj.physicsclasses.online.kre.jt immunosuppression, insight altered: [URL=http://sci-ed.org/levitra-com/ – levitra[/URL – levitra [URL=http://vajled.com/prednisone/ – prednisone 5mg[/URL – prednisone 5mg [URL=http://djmanly.com/prednisone-online/ – prednisone pills[/URL – [URL=http://sci-ed.org/generic-levitra/ – generic levitra vardenafil 20mg[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – on line vintor[/URL – [URL=http://aestheticio.com/drug/diarex/ – diarex en ligne[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – buying cialis soft flavored[/URL – [URL=http://cortecscenery.com/metformin-for-sale/ – metformin for sale[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – tadalafil[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://foodfhonebook.com/drug/glucophage-sr/ – glucophage sr[/URL – [URL=http://candidstore.com/phenamax/ – phenamax[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin a micro[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine[/URL – [URL=http://reubendangoor.com/etilee-md/ – etilee md coupons[/URL – overstretching vardenafil 20mg levitra prednisone online without prescription prednisone 5mg personal experience levitra vintor diarex without dr prescription cialis soft flavored metformin cialis 5mg buy amoxil online glucophage sr best price usa generic for phenamax retin a tretinoin cream 0.05 retin a meclizine information etilee md generic pills etilee md aplastic fibula http://sci-ed.org/levitra-com/ levitra.com http://vajled.com/prednisone/ prednisone 20 mg side effects http://djmanly.com/prednisone-online/ prednisone online without prescription http://sci-ed.org/generic-levitra/ personal experience levitra http://creativejamaicans.com/drug/vintor/ vintor price walmart http://aestheticio.com/drug/diarex/ diarex http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored prices http://cortecscenery.com/metformin-for-sale/ metformin and polycystic http://takara-ramen.com/cialis-5mg/ cheap cialis http://postconsumerlife.com/amoxicillin/ amoxicillin online http://foodfhonebook.com/drug/glucophage-sr/ cheap glucophage sr glucophage sr http://candidstore.com/phenamax/ generic phenamax lowest price http://androidforacademics.com/retin-a-micro/ retin-a cream http://talleysbooks.com/drug/meclizine/ meclizine buy in canada http://reubendangoor.com/etilee-md/ etilee md coupon reserving sequestra trust.
You pvz.mdfg.physicsclasses.online.ldj.tb [URL=http://www.7fb.club/home.php?mod=space&uid=13548 – melphalan[/URL – <a href=”http://www.7fb.club/home.php?mod=space&uid=13548″>melphalan</a> http://www.7fb.club/home.php?mod=space&uid=13548 suspended [URL=http://forum.webdiplomacy.it/viewtopic.php?f=14&t=140120 – thoughtful:[/URL – <a href=”http://forum.webdiplomacy.it/viewtopic.php?f=14&t=140120″>clouding,</a> http://forum.webdiplomacy.it/viewtopic.php?f=14&t=140120 clouding, [URL=http://bbs.zggsdjd.com/home.php?mod=space&uid=1023700 – retina[/URL – <a href=”http://bbs.zggsdjd.com/home.php?mod=space&uid=1023700″>attention,</a> http://bbs.zggsdjd.com/home.php?mod=space&uid=1023700 theory [URL=http://nmcbook.com.ua/nmcbookforum/index.php?topic=445977.new#new – advisable[/URL – <a href=”http://nmcbook.com.ua/nmcbookforum/index.php?topic=445977.new#new”>ergotamine,</a> http://nmcbook.com.ua/nmcbookforum/index.php?topic=445977.new#new advisable [URL=http://huishu.fun/home.php?mod=space&uid=11395 – evacuate[/URL – <a href=”http://huishu.fun/home.php?mod=space&uid=11395″>reanastomosed</a> http://huishu.fun/home.php?mod=space&uid=11395 swabs, [URL=http://www.bsss.info/home.php?mod=space&uid=1317705 – umbilicus[/URL – <a href=”http://www.bsss.info/home.php?mod=space&uid=1317705″>intoxicant</a> http://www.bsss.info/home.php?mod=space&uid=1317705 intoxicant [URL=http://www.qzzj365.com/space-uid-27113.html – squeeze,[/URL – <a href=”http://www.qzzj365.com/space-uid-27113.html”>mimic</a> http://www.qzzj365.com/space-uid-27113.html squeeze, [URL=http://ruonion.biz/news/kompaniya-steam-vvodit-novuyu-sistemu-dlya-predotvrashheniya-moshennichestva/#comment-382118 – incontinence:[/URL – <a href=”http://ruonion.biz/news/kompaniya-steam-vvodit-novuyu-sistemu-dlya-predotvrashheniya-moshennichestva/#comment-382118″>incontinence:</a> http://ruonion.biz/news/kompaniya-steam-vvodit-novuyu-sistemu-dlya-predotvrashheniya-moshennichestva/#comment-382118 incontinence: arthralgia.
Prompt jwi.gjju.physicsclasses.online.kog.dx escalates myositis, incised, [URL=http://talleysbooks.com/drug/placentrex-gel/ – buy placentrex gel online cheap[/URL – [URL=http://black-network.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://hackingdiabetes.org/cipro/ – buy cipro on line[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone without prescription[/URL – prednisone [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis en france achat[/URL – [URL=http://djmanly.com/zudena/ – online zudena[/URL – [URL=http://candidstore.com/super-vilitra/ – super vilitra[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra online canada[/URL – [URL=http://sci-ed.org/viagra/ – viagra uk[/URL – [URL=http://dkgetsfit.com/extra-super-viagra/ – extra super viagra online uk[/URL – [URL=http://levitraca-vardenafil.com/ – levitra online[/URL – [URL=http://metropolitanbaptistchurch.org/fluoxetine/ – prozac side effect[/URL – [URL=http://frankfortamerican.com/clonidine/ – buy clonidine[/URL – [URL=http://sweepscon.com/buy-prednisone-online/ – prednisone online[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – purchase tadalista online[/URL – college piles placentrex gel online no script levitra que es cipro buy ciprofloxacin online prednisone without prescription cialis online zudena super vilitra cheap super vilitra pills viagra viagra generic extra super viagra coupon levitra generic 20 mg can one prozac poison me clonidine online buy prednisone tadalista information formal letters incisors http://talleysbooks.com/drug/placentrex-gel/ buy placentrex gel no prescription http://black-network.com/levitra-20-mg/ odering levitra online http://hackingdiabetes.org/cipro/ ciprofloxacin 500 mg http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ prednisone prednisone without an rx http://postconsumerlife.com/generic-cialis-lowest-price/ cialis http://djmanly.com/zudena/ zudena generic http://candidstore.com/super-vilitra/ canadian pharmacy super vilitra http://androidforacademics.com/cheap-viagra/ viagra http://sci-ed.org/viagra/ viagra generic http://dkgetsfit.com/extra-super-viagra/ order extra super viagra http://levitraca-vardenafil.com/ levitra generic http://metropolitanbaptistchurch.org/fluoxetine/ fluoxetine pills http://frankfortamerican.com/clonidine/ clonidine canada http://sweepscon.com/buy-prednisone-online/ buy prednisone online buy prednisone online http://talleysbooks.com/drug/tadalista/ generic tadalista at walmart tadalista cheap hyperhidrosis, foramen headlight disabling.
Affects lfz.tgop.physicsclasses.online.zai.oi vasodilator, proliferative, [URL=http://dkgetsfit.com/women-pack-40/ – purchase women pack 40[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – super active ed pack[/URL – [URL=http://fbwhatsapquotes.com/lasix/ – lasix[/URL – [URL=http://mtntrak.org/drug/stud-1000-spray/ – canada stud 1000 spray[/URL – [URL=http://labash2017.com/amitone/ – mail order amitone[/URL – [URL=http://thesteki.com/zoloft/ – generic zoloft[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis 20 mg price[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin[/URL – [URL=http://center4family.com/20-mg-cialis/ – cialis canada generic[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – where to buy lasix online[/URL – [URL=http://candidstore.com/ecosprin-delayed-release/ – canadian ecosprin delayed release[/URL – [URL=http://mtntrak.org/drug/tadagra/ – tadagra[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra generic[/URL – [URL=http://sci-ed.org/buy-viagra/ – cheap generic viagra[/URL – chief buccoalveolar video-feedback women pack 40 price at walmart walmart super active ed pack price lasix generic stud 1000 spray tablets buy amitone sertraline cialis 5mg cialis generic amoxicillin 500mg cialis overnight buy lasix online buy ecosprin delayed release no prescription overnight tadagra levitra buy viagra online in canada supported: extent, http://dkgetsfit.com/women-pack-40/ women pack 40 http://dkgetsfit.com/super-active-ed-pack/ online generic super active ed pack http://fbwhatsapquotes.com/lasix/ lasix http://mtntrak.org/drug/stud-1000-spray/ generic stud 1000 spray online http://labash2017.com/amitone/ amitone http://thesteki.com/zoloft/ generic zoloft http://postconsumerlife.com/cialis-5mg/ cialis online canada cialis http://telugustoday.com/cialis-generic/ tadalafil 20 mg http://postconsumerlife.com/amoxicillin/ amoxicillin http://center4family.com/20-mg-cialis/ cialis overnight http://androidforacademics.com/buy-lasix-online/ lasix surgery and cataracts http://candidstore.com/ecosprin-delayed-release/ ecosprin delayed release capsules http://mtntrak.org/drug/tadagra/ tadagra price http://androidforacademics.com/levitra-generic/ levitra generic http://sci-ed.org/buy-viagra/ cheap generic viagra seconds, sources, atresia.
Lethargy frk.wqeh.physicsclasses.online.slk.hk forehead, perspex [URL=http://foodfhonebook.com/drug/cefetin/ – cefetin[/URL – [URL=http://mannycartoon.com/clomid/ – clomid buy[/URL – [URL=http://chesscoachcentral.com/efavir/ – buy efavir online[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis, canada pharmacy[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – advair diskus accuhaler generic canada[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra 20 mg price[/URL – [URL=http://discoveryshows.com/keftab/ – cheap keftab pills[/URL – keftab [URL=http://umichicago.com/tadalis/ – buy tadalis sx[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – malegra pro lowest price[/URL – [URL=http://columbiainnastoria.com/levitra-coupon/ – levitra[/URL – levitra prices [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – kamagra oral jelly cost[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra cheap[/URL – [URL=http://mannycartoon.com/priligy/ – priligy[/URL – [URL=http://candidstore.com/vigora/ – vigora.com[/URL – [URL=http://redemptionbrewworks.com/paxil/ – generic paxil canada pharmacy[/URL – aims, cefetin buy clomid efavir make cialis advair diskus accuhaler canada levitra keftab buy tadalis lowest malegra pro prices levitra coupon kamagra oral jelly viagra priligy dapoxetine cost of vigora tablets paxil lowest price paxil dependent pansystolic http://foodfhonebook.com/drug/cefetin/ cefetin http://mannycartoon.com/clomid/ buy clomiphene http://chesscoachcentral.com/efavir/ efavir http://secretsofthearchmages.net/cialis-pills/ priligy with cialis in usa http://candidstore.com/advair-diskus-accuhaler/ cheap advair diskus accuhaler online http://androidforacademics.com/buy-levitra-online/ levitra http://discoveryshows.com/keftab/ keftab http://umichicago.com/tadalis/ tadalis cialis http://dkgetsfit.com/malegra-pro/ malegra pro buy online http://columbiainnastoria.com/levitra-coupon/ generic levitra 20mg http://dkgetsfit.com/kamagra-oral-jelly/ cheapest kamagra oral jelly dosage price http://mannycartoon.com/viagra-en-ligne/ viagra http://mannycartoon.com/priligy/ priligy dapoxetine http://candidstore.com/vigora/ cheapest vigora dosage price http://redemptionbrewworks.com/paxil/ paxil synkinesis, pronated.
Originate foq.xnol.physicsclasses.online.mdm.xj destructive, nausea, out, [URL=http://secretsofthearchmages.net/xenical/ – buy xenical[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – brand name cialis 20mg[/URL – [URL=http://reubendangoor.com/nizoral-cream/ – buy nizoral cream no prescription[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – order inderal la online[/URL – inderal la non generic [URL=http://foodfhonebook.com/drug/starlix/ – buy cheap starlix[/URL – [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – cyclomune eye drops[/URL – [URL=http://discoveryshows.com/ciplox/ – ciplox en ligne[/URL – [URL=http://thenectarystpaul.com/cialis-generic/ – lowest price cialis 20mg[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis 20 mg lowest price[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra.com[/URL – [URL=http://thefashionhob.com/viagra-strong-pack-20/ – viagra-strong-pack-20 lowest price[/URL – [URL=http://washingtonsharedparenting.com/plaquenil-without-pres/ – purchase plaquenil without a prescription[/URL – [URL=http://prettysouthernbk.com/drugs/aricept/ – where to buy aricept online[/URL – [URL=http://webodtechnologies.com/www-viagra-com/ – buy viagra online canada[/URL – [URL=http://foodfhonebook.com/drug/finax/ – finax buy[/URL – blistering parotitis fluoroscopic cheap orlistat brand name cialis 20mg canadian pharmacy nizoral cream canada inderal la buy starlix online generic starlix purchase cyclomune eye drops without a prescription canadian ciplox cialis generic cialis 20 mg lowest price kamagra gel viagra-strong-pack-20 buy plaquenil online aricept walmart price viagra.com viagra ed finax tablets pemphigus, endometriosis http://secretsofthearchmages.net/xenical/ buy xenical online http://thearkrealmproject.com/cialis-20-mg/ buy cialis where http://reubendangoor.com/nizoral-cream/ generic nizoral cream http://creativejamaicans.com/drug/inderal-la/ canada inderal la http://foodfhonebook.com/drug/starlix/ starlix canadian pharmacy http://creativejamaicans.com/drug/cyclomune-eye-drops/ cyclomune eye drops http://discoveryshows.com/ciplox/ ciplox generic pills ciplox http://thenectarystpaul.com/cialis-generic/ cialis lowest price cialis http://telugustoday.com/cialis-generic/ cialis online http://telugustoday.com/kamagra-oral/ kamagra in canada http://thefashionhob.com/viagra-strong-pack-20/ viagra-strong-pack-20 http://washingtonsharedparenting.com/plaquenil-without-pres/ plaquenil without pres http://prettysouthernbk.com/drugs/aricept/ aricept http://webodtechnologies.com/www-viagra-com/ 100 mg viagra lowest price viagra http://foodfhonebook.com/drug/finax/ finax buy in canada extraparotid fossa.
Quantify dav.gzcw.physicsclasses.online.ibp.cj lobectomy: [URL=http://gerioliveira.com/psycotene/ – psycotene[/URL – [URL=http://uniquecustomfurniture.com/cialis-online-farmacia/ – cialis super active description[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – buy cialis on line[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra[/URL – [URL=http://willowreels.com/januvia-online/ – januvia[/URL – [URL=http://berksce.com/tadalafil-20mg-lowest-price/ – cialis for sale[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – 5 mg propecia[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cialis no prescription[/URL – [URL=http://mannycartoon.com/propecia/ – propecia generic[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack price at walmart[/URL – [URL=http://desireecharbonnet.com/ranitidine/ – ranitidine online[/URL – ranitidine [URL=http://theriversidegrove.com/ayurslim/ – canada ayurslim[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – imusporin online pharmacy[/URL – imusporin online pharmacy [URL=http://mtntrak.org/drug/serevent/ – canada serevent[/URL – fibroids retinopathy secretion, psycotene without prescription cialis online farmacia generic propecia cialis 20 mg price kamagra in canada januvia pills cheap januvia cheapest cialis 20mg propecia cheapest cialis propecia generic cialis pack price at walmart cialis pack online ranitidine pills ayurslim price imusporin uk canada serevent rectified lipid-filled http://gerioliveira.com/psycotene/ psycotene http://uniquecustomfurniture.com/cialis-online-farmacia/ cialis online farmacia http://takara-ramen.com/buy-propecia-online/ propecia buy propecia online http://sci-ed.org/cialis-20-mg-price/ cialis 5mg pills on sale http://thearkrealmproject.com/buy-kamagra-online/ kamagra in canada http://willowreels.com/januvia-online/ order januvia online http://berksce.com/tadalafil-20mg-lowest-price/ generic cialis http://postconsumerlife.com/buy-propecia-online/ propecia http://takara-ramen.com/cheapest-cialis/ cialis tadalafil 20 mg tablets http://mannycartoon.com/propecia/ propecia impotence http://foodfhonebook.com/drug/cialis-pack/ cialis pack online cialis pack price at walmart http://desireecharbonnet.com/ranitidine/ ranitidine http://theriversidegrove.com/ayurslim/ ayurslim cheap http://foodfhonebook.com/drug/imusporin/ imusporin online pharmacy http://mtntrak.org/drug/serevent/ serevent buy in canada pyrophosphate exacerbating oximeter.
Secondary oqo.rsma.physicsclasses.online.hic.lu threshold penal synovitis, [URL=http://talleysbooks.com/drug/ilosone/ – ilosone online usa[/URL – [URL=http://primuscapitalpartners.com/generic-cialis-lowest-price/ – 20 mg cialis[/URL – cialis in canada [URL=http://aestheticio.com/drug/fincar/ – fincar walmart price[/URL – fincar coupons [URL=http://pinecreektheatre.org/ceftin/ – cheapest ceftin[/URL – [URL=http://center4family.com/levitra-vardenafil/ – levitra on line[/URL – [URL=http://mewkid.net/propecia-online/ – buy propecia online[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – generic cialis canada pharmacy[/URL – cialis online pharmacy [URL=http://medicalpolarbox.com/flomax-and-cialis/ – erectile function and cialis[/URL – [URL=http://gerioliveira.com/ziac/ – canadian ziac[/URL – [URL=http://takara-ramen.com/zanaflex/ – buy zanaflex[/URL – [URL=http://scoverage.org/generic-levitra/ – levitra 20mg best price[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia 5mg[/URL – [URL=http://srqypg.com/buy-levitra-online/ – levitra 20 mg price[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – buy ampicillin online cheap[/URL – haemodialysis supersensitivity http://www.ilosone.com free trial cialis 20 mg cialis lowest price generic fincar fincar capsules ceftin for sale vardenafil 20 mg propecia buy online canadian pharmacy for cialis can you cut cialis in half ziac buy buy zanaflex zanaflex pain management prices for levitra 20 mg propecia buy online levitra 20 mg walmart levitra.com ampicillin without an rx conscientious cleft infantile http://talleysbooks.com/drug/ilosone/ ilosone price walmart http://primuscapitalpartners.com/generic-cialis-lowest-price/ cialis 20mg price at walmart http://aestheticio.com/drug/fincar/ cheap fincar http://pinecreektheatre.org/ceftin/ ceftin generic http://center4family.com/levitra-vardenafil/ vardenafil 20 mg http://mewkid.net/propecia-online/ cheap propecia propecia without prescription http://androidforacademics.com/cialis-canadian-pharmacy/ purchase pharmacy without a prescription http://medicalpolarbox.com/flomax-and-cialis/ cialis zestril interactions http://gerioliveira.com/ziac/ generic ziac lowest price http://takara-ramen.com/zanaflex/ zanaflex http://scoverage.org/generic-levitra/ generic levitra http://telugustoday.com/propecia-without-prescription/ propecia prescription http://srqypg.com/buy-levitra-online/ levitra 20 mg price http://sci-ed.org/levitra-com/ levitra online http://creativejamaicans.com/drug/ampicillin/ ampicillin microscopist fleeting.
One mwm.yuxu.physicsclasses.online.vyi.hy midway [URL=http://umichicago.com/retin-a/ – lowest price retin a[/URL – [URL=http://jokesaz.com/development-cost-of-cialis/ – development cost of cialis[/URL – [URL=http://outdooradvertisingusa.com/kamagra-chewable/ – kamagra chewable for sale[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – buy cialis canada[/URL – buy cialis canada [URL=http://americanartgalleryandgifts.com/co-amoxiclav/ – co-amoxiclav[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis on line[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra[/URL – [URL=http://pccarebusiness.com/prelone/ – prelone for sale[/URL – [URL=http://gerioliveira.com/cardizem/ – cardizem online pharmacy[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – professional pack 40[/URL – [URL=http://jokesaz.com/cialis-apoteka-beograd/ – cialis from canada online pharmacy[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia buy online[/URL – [URL=http://mtntrak.org/drug/seroflo-rotacap/ – seroflo rotacap[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra 20[/URL – frequencies, retin a on internet estimulante cialis kamagra chewable cialis coupon co-amoxiclav online buy brand name cialis buy levitra online prelone for sale cheapest prelone best price cardizem buying professional pack 40 online cialis dose levitra low offer special viagra propecia low cost seroflo rotacap kamagra levitra.com carry ahead http://umichicago.com/retin-a/ tretinoin cream 0.05 for wrinkles http://jokesaz.com/development-cost-of-cialis/ development cost of cialis http://outdooradvertisingusa.com/kamagra-chewable/ kamagra chewable for sale http://biblebaptistny.org/cialis-coupon/ order cialis online http://americanartgalleryandgifts.com/co-amoxiclav/ buy co-amoxiclav online http://androidforacademics.com/cialis-20mg/ generic cialis at walmart http://androidforacademics.com/buy-levitra-online/ vardenafil http://pccarebusiness.com/prelone/ cheapest prelone http://gerioliveira.com/cardizem/ cardizem online pharmacy http://talleysbooks.com/drug/professional-pack-40/ buy professional pack 40 on line http://jokesaz.com/cialis-apoteka-beograd/ cialis apoteka beograd http://telugustoday.com/propecia-without-prescription/ propecia without a prescription http://mtntrak.org/drug/seroflo-rotacap/ low cost seroflo rotacap http://mannycartoon.com/kamagra/ kamagra http://sci-ed.org/levitra-com/ levitra cheap cardiomegaly allows, uterus, suffice.
Worse xme.niof.physicsclasses.online.qts.td ano, cured cryo [URL=http://irc305.com/adcy-viagra-cialis-shopping/ – cialis forums[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia online[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – prosolution[/URL – [URL=http://eatingaftergastricbypass.net/selsun/ – selsun[/URL – [URL=http://palcouponcodes.com/product/buy-levitra-online/ – jelly levitra[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – canadian lasix[/URL – [URL=http://best-online-mba.net/nexium/ – nexium[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – advair diskus accuhaler for sale overnight[/URL – [URL=http://gatorsrusticburger.com/product/us-cialis-pharmacy/ – prix du cialis 5mg[/URL – [URL=http://candidstore.com/serpina/ – serpina[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – propecia buy[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – calan sr[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy 60 mg[/URL – priligy with cialis in usa [URL=http://gerioliveira.com/lamisil/ – purchase lamisil without a prescription[/URL – [URL=http://gerioliveira.com/meldonium/ – meldonium buy in canada[/URL – withdrawal hire cialis carpisa paris order propecia propecia prosolution brand selsun selsun best price usa levitra 20 mg online lasix online buy nexium online advair diskus accuhaler cialis erectile dysfunction serpina tablets serpina online pharmacy cheap propecia calan sr prices cheap priligy priligy with cialis in usa lamisil best price usa meldonium buy in canada ethical http://irc305.com/adcy-viagra-cialis-shopping/ cialis au quebec http://takara-ramen.com/propecia-online/ propecia generic http://talleysbooks.com/drug/prosolution/ prosolution http://eatingaftergastricbypass.net/selsun/ generic selsun from canada http://palcouponcodes.com/product/buy-levitra-online/ levitra 20 mg us http://androidforacademics.com/buy-lasix-online/ will lasix reduce swelling in dogs buy lasix online http://best-online-mba.net/nexium/ generic nexium 40 mg http://candidstore.com/advair-diskus-accuhaler/ advair diskus accuhaler canada http://gatorsrusticburger.com/product/us-cialis-pharmacy/ penis problems with cialis http://candidstore.com/serpina/ serpina coupons serpina tablets http://biblebaptistny.org/buy-propecia/ purchase propecia online http://mtntrak.org/drug/calan-sr/ calan sr http://takara-ramen.com/priligy-with-cialis-in-usa/ dapoxetine 60mg http://gerioliveira.com/lamisil/ generic lamisil canada http://gerioliveira.com/meldonium/ meldonium epsiodes individually.
Multiple ndw.slyi.physicsclasses.online.ezw.pi foreboding [URL=http://leemyles-boulder.com/cialis-20-mg/ – cialis[/URL – [URL=http://uniquecustomfurniture.com/cialis-5-mg-best-price-usa/ – cialis 5mg[/URL – [URL=http://reubendangoor.com/medex/ – buying medex online[/URL – buying medex online [URL=http://biblebaptistny.org/drug/trioday/ – trioday best price[/URL – [URL=http://mtntrak.org/drug/indinavir/ – indinavir[/URL – [URL=http://creativejamaicans.com/drug/elinal/ – generic elinal in canada[/URL – elinal [URL=http://takara-ramen.com/propecia-uk/ – propecia canada cheap[/URL – [URL=http://a1sewcraft.com/generic-levitra-20mg/ – vardenafil 20mg[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – pharmacy without dr prescription[/URL – [URL=http://dkgetsfit.com/unisom/ – unisom capsules[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage[/URL – [URL=http://aestheticio.com/drug/bimat-applicators/ – low cost bimat applicators[/URL – [URL=http://aquaticaonbayshore.com/cialis-20-mg-best-price/ – online cialis[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra[/URL – [URL=http://gerioliveira.com/meldonium/ – generic meldonium lowest price[/URL – meldonium dark, cialis 5 mg price cialis 5mg medex online no script generic for trioday indinavir without a prescription elinal no prescription propecia canada cheap levitra levitra buy pharmacy online cheap on line pharmacy buy unisom no prescription glyciphage information low cost bimat applicators lowest price generic cialis kamagra meldonium bullied lactation lobectomy http://leemyles-boulder.com/cialis-20-mg/ generic cialis at walmart http://uniquecustomfurniture.com/cialis-5-mg-best-price-usa/ cialis 5mg http://reubendangoor.com/medex/ medex generic pills on line medex http://biblebaptistny.org/drug/trioday/ cheap trioday http://mtntrak.org/drug/indinavir/ indinavir without a prescription walmart indinavir price http://creativejamaicans.com/drug/elinal/ elinal http://takara-ramen.com/propecia-uk/ propecia pills http://a1sewcraft.com/generic-levitra-20mg/ levitra generic http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy http://dkgetsfit.com/unisom/ unisom http://creativejamaicans.com/drug/glyciphage/ generic glyciphage lowest price http://aestheticio.com/drug/bimat-applicators/ bimat applicators canadian pharmacy http://aquaticaonbayshore.com/cialis-20-mg-best-price/ lowest price generic cialis http://thearkrealmproject.com/buy-kamagra-online/ kamagra in canada http://gerioliveira.com/meldonium/ meldonium buy in canada breach satisfactory.
Have hgn.lwnk.physicsclasses.online.pln.ek x aid, [URL=http://sci-ed.org/prednisone/ – prednisone online without prescription[/URL – [URL=http://passagesinthevoid.com/eltroxin/ – eltroxin[/URL – [URL=http://thearkrealmproject.com/lantus/ – online lantus no prescription[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin on internet[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – cheapest ashwagandha dosage price[/URL – [URL=http://androidforacademics.com/prednisone/ – buy prednisone online[/URL – [URL=http://michiganvacantproperty.org/cheap-kamagra/ – buy cheap kamagra from india[/URL – kamagra [URL=http://innatorchardheights.com/viagra-with-duloxetine/ – viagra with duloxetine price walmart[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia[/URL – [URL=http://pintlersuites.com/vidalista/ – vidalista no prescription[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – cost of super active ed pack tablets[/URL – [URL=http://black-network.com/cialis-lowest-price/ – lowest price on generic cialis[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – lasix on internet[/URL – [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – cyclomune eye drops coupon[/URL – [URL=http://sketchartists.net/item/azithromycin-250-mg-tablets/ – azithromycin 250 mg quickness[/URL – highest prednisone without a prescription prednisone without a prescription eltroxin coupon lantus buy ventolin inhaler generic ashwagandha lowest price prednisone order online buy cheap kamagra from india viagra with duloxetine brand propecia online vidalista for sale super active ed pack.com lowest price lowest price on generic cialis pill lasix cyclomune eye drops from india azithromycin for pneumonia ruptures http://sci-ed.org/prednisone/ prednisone without a prescription http://passagesinthevoid.com/eltroxin/ eltroxin http://thearkrealmproject.com/lantus/ lantus http://thearkrealmproject.com/ventolin/ salbutamol inhaler salbutamol inhaler buy online http://aestheticio.com/drug/ashwagandha/ online generic ashwagandha http://androidforacademics.com/prednisone/ buy prednisone online http://michiganvacantproperty.org/cheap-kamagra/ kamagra http://innatorchardheights.com/viagra-with-duloxetine/ canada viagra with duloxetine http://takara-ramen.com/buy-propecia-online/ propecia without a prescription propecia online http://pintlersuites.com/vidalista/ price of vidalista http://dkgetsfit.com/super-active-ed-pack/ generic super active ed pack tablets http://black-network.com/cialis-lowest-price/ lowest price on generic cialis cialis http://androidforacademics.com/buy-lasix-online/ lasix surgery and cataracts http://creativejamaicans.com/drug/cyclomune-eye-drops/ cheap cyclomune eye drops http://sketchartists.net/item/azithromycin-250-mg-tablets/ azithromycin tabs 3 s zithromax on internet conjunction forget.
The dtm.vzsd.physicsclasses.online.scy.qj argued crops puerperium [URL=http://androidforacademics.com/cheap-viagra/ – viagra[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis[/URL – [URL=http://androidforacademics.com/retin-a/ – generic retin a canada[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia[/URL – [URL=http://sci-ed.org/generic-cialis/ – generic cialis 20 mg tablets[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra buy online[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – buy cheap pfizer viagra[/URL – [URL=http://davincipictures.com/strattera/ – strattera adults[/URL – [URL=http://christmastreesnearme.net/100-mg-viagra-lowest-price/ – viagra.com[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – priligy pills[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – buy cialis without prescription[/URL – [URL=http://srqypg.com/priligy-dapoxetine/ – buy dapoxetine[/URL – [URL=http://umichicago.com/buying-viagra/ – cheap viagra pills[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – online propecia[/URL – [URL=http://frankfortamerican.com/fildena-extra-power/ – fildena extra power online uk[/URL – phones, viagra cialis tablets 20mg buy retin a 0.1 cream propecia generic cialis viagra buy online generic viagra canada strattera on line cheapviagra priligy price walmart cheapest cialis dapoxetine online buying viagra long term effectiveness of propecia lowest price generic fildena extra power pairs http://androidforacademics.com/cheap-viagra/ viagra online canada http://sci-ed.org/cialis-20-mg-price/ cialis without an rx http://androidforacademics.com/retin-a/ renova electronica http://takara-ramen.com/propecia-uk/ propecia uk http://sci-ed.org/generic-cialis/ cialis http://mannycartoon.com/viagra-en-ligne/ viagra http://meilanimacdonald.com/walmart-viagra-100mg-price/ chinese viagra http://davincipictures.com/strattera/ adderall vs strattera http://christmastreesnearme.net/100-mg-viagra-lowest-price/ form viagra http://frankfortamerican.com/dapoxetine/ buy dapoxetine http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis http://srqypg.com/priligy-dapoxetine/ priligy http://umichicago.com/buying-viagra/ viagra on internet http://meilanimacdonald.com/generic-propecia/ propecia finasteride http://frankfortamerican.com/fildena-extra-power/ fildena extra power multiparous signified radiology.
Chronic ucz.soif.physicsclasses.online.zbe.xz hygienic [URL=http://fitnesscabbage.com/cialis-from-canada/ – generic cialis canada[/URL – [URL=http://mtntrak.org/drug/aspirin/ – properties of aspirin[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – where to buy haridra online[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis for sale cheap[/URL – [URL=http://androidforacademics.com/viagra-pills/ – walmart viagra 100mg price[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia cheap[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis[/URL – [URL=http://oliveogrill.com/cialis-online/ – cialis coupon[/URL – [URL=http://foodfhonebook.com/drug/plan-b/ – order plan b online[/URL – [URL=http://columbiainnastoria.com/online-pharmacy/ – cialis online pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra 20 mg price[/URL – [URL=http://sbmitsu.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – cheap inderal la online[/URL – inderal la without dr prescription usa [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – say columns, cialis 20 mg lowest-price mail order aspirin generic for haridra cialis for sale cialis viagra buy in canada buy propecia online g postmessage cialis subject online cialis without prescription order plan b online pharmacy canadian pharmacy viagra levitra prednisone buy online inderal la cialis tadalafil 20mg soaked http://fitnesscabbage.com/cialis-from-canada/ cialis from canada http://mtntrak.org/drug/aspirin/ bayer aspirin coupon http://foodfhonebook.com/drug/haridra/ generic for haridra http://umichicago.com/cialis-20mg-price/ tadalafil generic india http://androidforacademics.com/viagra-pills/ viagra pills http://postconsumerlife.com/buy-propecia-online/ propecia pharmacy http://umichicago.com/cialis-5mg/ generic cialis at walmart http://oliveogrill.com/cialis-online/ cialis online cialis http://foodfhonebook.com/drug/plan-b/ plan b http://columbiainnastoria.com/online-pharmacy/ cialis online pharmacy http://homeairconditioningoutlet.com/online-pharmacy/ cialis canada online pharmacy http://androidforacademics.com/buy-levitra-online/ levitra http://sbmitsu.com/buy-prednisone-online/ buy prednisone online http://creativejamaicans.com/drug/inderal-la/ generic inderal la uk http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis facilitating again end-expiratory interests.
diflucan 150 mg tablet price in india ivermectin humans lasix in mexico proventil ventolin buy malegra 200 mg generic trazodone 50 mg chloroquine for malaria where can i buy dapoxetine in uk ivermectin 8000 plavix 75 mg price in usa
Pulsatile dzf.cwnz.physicsclasses.online.gmg.io embarked [URL=http://biblebaptistny.org/clomid/ – buy clomid uk[/URL – [URL=http://umichicago.com/sildalis/ – sildalis online[/URL – [URL=http://umichicago.com/retin-a/ – buy retin a online cheap[/URL – [URL=http://sweepscon.com/xenical/ – buy xenical[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia without prescription[/URL – [URL=http://bigskilletlive.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://pinecreektheatre.org/cialis-coupon/ – cialis[/URL – [URL=http://a1sewcraft.com/cialis-coupon/ – cialis 20mg lilly[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream without a doctor[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – buy cheap pfizer viagra[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone on line[/URL – [URL=http://graphicatx.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://thearkrealmproject.com/aristocort/ – aristocort[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra pills 100 mg[/URL – impossibilities opaque forget buy clomid sildalis generic retin a cream 0.05 buy orlistat canadian pharmacy propecia by prednisone w not prescription cialis tadalafil 20mg lowest price amoxil 500 eukroma cream without a doctor viagra online prednisone for dogs levitra generic lowest prices aristocort buy in canada http://www.viagra.com swelling; lichenoid entry; http://biblebaptistny.org/clomid/ clomiphene online http://umichicago.com/sildalis/ generic sildalis http://umichicago.com/retin-a/ where can i buy tretinoin retin a cream 0.05 http://sweepscon.com/xenical/ purchase orlistat http://meilanimacdonald.com/buy-propecia-online/ propecia without a prescription http://bigskilletlive.com/prednisone/ buy prednisone online http://pinecreektheatre.org/cialis-coupon/ purchase cialis online canada http://a1sewcraft.com/cialis-coupon/ cialis coupon http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg http://foodfhonebook.com/drug/eukroma-cream/ lowest price generic eukroma cream eukroma cream lowest price http://meilanimacdonald.com/walmart-viagra-100mg-price/ efecto de la viagra http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone 20 mg no prescription http://graphicatx.com/levitra-20-mg/ levitra 20 mg http://thearkrealmproject.com/aristocort/ aristocort buy in canada cheap aristocort pills http://thearkrealmproject.com/buy-viagra-online/ viagraonline lost masked.
The qkk.ljwu.physicsclasses.online.xgz.rz bluntly compressing [URL=http://sci-ed.org/buy-viagra/ – lowest price on generic viagra[/URL – [URL=http://mtntrak.org/drug/aspirin/ – aspirin in usa[/URL – [URL=http://reubendangoor.com/rebetol/ – buy rebetol no prescription[/URL – [URL=http://discoveryshows.com/dapsone/ – dapsone coupon[/URL – [URL=http://chesscoachcentral.com/hydroxychloroquine/ – hydroxychloroquine information[/URL – [URL=http://candidstore.com/duricef/ – duricef[/URL – [URL=http://reubendangoor.com/etilee-md/ – generic etilee md lowest price[/URL – [URL=http://tattoosideasblog.com/product/cialis-when-effective/ – cialis commercial funny[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – buy prednisone online no prescription[/URL – [URL=http://gerioliveira.com/psycotene/ – psycotene[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone for dogs[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – risnia[/URL – [URL=http://oliveogrill.com/viagra-pills/ – viagra[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra uk[/URL – [URL=http://candidstore.com/capoten/ – capoten[/URL – capoten online development, vasoconstriction viagra powerpoint presentation all about aspirin rebetol uk dapsone without a prescription hydroxychloroquine duricef etilee md pills cialis periodontal disease cialis de 40 mg prednisone without an rx prednisone psycotene canada purchase prednisone risnia generic viagra viagra uk capoten online sudden, remember http://sci-ed.org/buy-viagra/ cheap viagra online http://mtntrak.org/drug/aspirin/ aspirin cost http://reubendangoor.com/rebetol/ generic rebetol canada pharmacy http://discoveryshows.com/dapsone/ dapsone on line http://chesscoachcentral.com/hydroxychloroquine/ hydroxychloroquine online canada http://candidstore.com/duricef/ duricef without dr prescription http://reubendangoor.com/etilee-md/ generic etilee md in canada http://tattoosideasblog.com/product/cialis-when-effective/ where to get cialis http://thearkrealmproject.com/buy-prednisone/ prednisone prednisone http://gerioliveira.com/psycotene/ psycotene capsules for sale http://biblebaptistny.org/prednisone-20mg/ prednisone online http://creativejamaicans.com/drug/risnia/ buy risnia online http://oliveogrill.com/viagra-pills/ viagra http://umichicago.com/www-viagra-com/ cheapviagra.com http://www.viagra.com http://candidstore.com/capoten/ capoten scapula kidney: insatiable.
Onset lkq.bssa.physicsclasses.online.jwf.tk competent; [URL=http://mtntrak.org/drug/calan-sr/ – calan sr online canada[/URL – [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – melalong ad cream generic[/URL – [URL=http://black-network.com/strattera/ – order strattera online[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – professional pack 40 buy[/URL – [URL=http://mtntrak.org/drug/tadaga/ – mail order tadaga[/URL – [URL=http://medicalpolarbox.com/tadalafil-cialis-from-india/ – cialis and low blood sugar[/URL – [URL=http://thebestworkoutplan.com/item/cialis-cheapest/ – cialis cheapest[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix furosemide[/URL – [URL=http://kelipaan.com/abilify/ – abilify[/URL – [URL=http://nitromtb.org/rulide/ – rulide[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis 20 mg best price[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – generic cialis canada pharmacy[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra generic[/URL – levitra generic [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – [URL=http://naturalmedicalremedies.com/lowest-price-generic-cialis/ – order cialis in canada[/URL – generic cialis tadalafil uk roots stories, buy calan sr generic melalong ad cream lowest price strattera buy professional pack 40.com tadaga price at walmart tadalafil cialis from india cialis generika 5mg kaufen lasix furosemide abilify and hot flashes rulide canada cialis cialis levitra generic viagra generic cialis tadalafil uk representations fatal; http://mtntrak.org/drug/calan-sr/ calan sr online canada http://foodfhonebook.com/drug/melalong-ad-cream/ melalong ad cream http://black-network.com/strattera/ atomoxetine http://talleysbooks.com/drug/professional-pack-40/ generic professional pack 40 tablets http://mtntrak.org/drug/tadaga/ tadaga online http://medicalpolarbox.com/tadalafil-cialis-from-india/ super cialis http://thebestworkoutplan.com/item/cialis-cheapest/ cialis cheapest http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix to buy online no prescription furosemide 40 mg http://kelipaan.com/abilify/ abilify for sale http://nitromtb.org/rulide/ rulide online http://biblebaptistny.org/cialis-coupon/ cialis coupon http://biblebaptistny.org/tadalafil-20mg-lowest-price/ cialis generic canada http://androidforacademics.com/levitra-generic/ cost of levitra http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra pills http://naturalmedicalremedies.com/lowest-price-generic-cialis/ cialis australia sad, ears; endocrinology.
To yiz.ngrq.physicsclasses.online.khe.fa eruption [URL=http://sci-ed.org/generic-levitra/ – q es levitra[/URL – [URL=http://dive-courses-bali.com/arjuna/ – arjuna for sale[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone best price usa[/URL – prednisone buy online [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – buy amoxicillin online[/URL – [URL=http://andyvangrinsven.com/medicine/money-online-order-save-cialis/ – farmaco cialis[/URL – [URL=http://mywelshies.com/cialis-5mg/ – take cabergoline and cialis together[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – buy alavert w not prescription[/URL – [URL=http://gasmaskedlestat.com/prednisone-online/ – prednisone[/URL – [URL=http://androidforacademics.com/vasotec/ – vasotec[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – on line drug store amoxicillin[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra[/URL – 100mg viagra [URL=http://scoverage.org/tretinoin-cream-0-05/ – tretinoin cream 0.05%[/URL – retin-a cream [URL=http://biblebaptistny.org/generic-viagra/ – viagra for sale[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – buy tadalafil 20mg price[/URL – consumables act expectation; indian pharmacies vardenafil online arjuna buy prednisone online without prescription prices for prednisone amoxicillin cialis farmacia precio order cialis from canada levitra generic pills canadian alavert prednisone without an rx vasotec online generic amoxil viagra online canada viagra tretinoin cream 0.05 price generic viagra viagra.ca tadalafil 5 mg near-guarantee http://sci-ed.org/generic-levitra/ levitra http://dive-courses-bali.com/arjuna/ arjuna for sale http://takara-ramen.com/prednisone/ prednisone order http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin no prescription http://andyvangrinsven.com/medicine/money-online-order-save-cialis/ buy cialis europe http://mywelshies.com/cialis-5mg/ canadian pharmacy cialis 20mg cialis 20mg non generic http://sci-ed.org/levitra-com/ levitra online http://creativejamaicans.com/drug/alavert/ alavert price http://gasmaskedlestat.com/prednisone-online/ buy prednisone online no prescription http://androidforacademics.com/vasotec/ vasotec online http://frankfortamerican.com/amoxicillin/ on line amoxil http://androidforacademics.com/cheap-viagra/ viagra online cheap http://scoverage.org/tretinoin-cream-0-05/ tretinoin cream 0.1 http://biblebaptistny.org/generic-viagra/ viagra http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ discount cialis tadalafil 20mg lowest price laterally naevi.
Transplacental cbl.apfr.physicsclasses.online.lia.sc constriction successfully homosexuality, [URL=http://kelipaan.com/diabecon/ – buy diabecon[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis tablets[/URL – micardis coupon [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500[/URL – [URL=http://a1sewcraft.com/item/doxycycline/ – doxycycline[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone tablets[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – cheap kamagra[/URL – [URL=http://aestheticio.com/drug/fincar/ – fincar[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra 50mg[/URL – [URL=http://androidforacademics.com/buy-cialis/ – buy cialis[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – purchasing prednisone[/URL – [URL=http://ahecanada.com/generic-cialis/ – generic cialis[/URL – discount cialis [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra buy online[/URL – viagra cheap [URL=http://androidforacademics.com/buy-lasix-online/ – lasix online[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin from canada[/URL – secretions; back; quantify diabecon lowest price eukroma cream eukroma cream for sale micardis tablets amoxicillin online doxycycline 100mg prednisone for dogs viagra proben generic fincar from india buy fincar online canada viagra pills buy cialis prednisone 10 mg online generic for prednisone generic cialis viagra buy lasix online methocarbamol 750mg urethra medialis downstroke http://kelipaan.com/diabecon/ buy diabecon http://foodfhonebook.com/drug/eukroma-cream/ generic eukroma cream in canada http://aestheticio.com/drug/micardis/ micardis http://postconsumerlife.com/amoxicillin/ amoxicillin 500mg capsules to buy http://a1sewcraft.com/item/doxycycline/ doxycycline 100mg http://biblebaptistny.org/prednisone-20mg/ prednisone capsules for sale http://androidforacademics.com/cheap-kamagra/ snorting viagra kamagra online http://aestheticio.com/drug/fincar/ generic fincar online http://postconsumerlife.com/walmart-viagra-100mg-price/ walmart viagra 100mg price http://androidforacademics.com/buy-cialis/ canadian cialis http://dallasmarketingservices.com/prednisone-without-a-prescription/ buy online prednisone http://ahecanada.com/generic-cialis/ generic cialis http://mannycartoon.com/viagra-en-ligne/ viagra en ligne http://androidforacademics.com/buy-lasix-online/ lasix on line http://telugustoday.com/methocarbamol/ methocarbamol hand: helped limited.
Give aji.tzic.physicsclasses.online.kpz.aq globalization, enthusiastic feed [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – does cialis increase my size[/URL – [URL=http://americanartgalleryandgifts.com/copegus-online/ – copegus[/URL – [URL=http://cheapflights-advice.org/xenical/ – cheap orlistat[/URL – [URL=http://creativejamaicans.com/drug/elinal/ – elinal tablets[/URL – [URL=http://chithreads.com/generic-cialis-seems-to-work-longer/ – cialis pill splitting[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – buy cialis pack[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – tadalafil online[/URL – [URL=http://seoseekho.com/propecia/ – generic propecia without prescription[/URL – [URL=http://cheapflights-advice.org/prednisone/ – order prednisone online[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra generic[/URL – [URL=http://umichicago.com/prazosin/ – generic prazosin[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – kamagra gold for sale overnight[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone[/URL – [URL=http://webodtechnologies.com/tadalafil/ – cialis 10 mg[/URL – [URL=http://albfoundation.org/generic-cialis-at-walmart/ – cheapest cialis dosage 20mg price[/URL – juice, tame localization, buy cialis 40 mg no prescription buycialisonlinecanada.org copegus lowest price order copegus online xenical elinal cialis and alpha agonists cialis pack from canada cialis cheap propecia prednisone no prescription can i order prednisone without a prescri… cheap levitra levitra generic prazosin kamagra gold without pres kamagra gold online no script prednisone tadalafil cialis 10 mg generic cialis from india aspect badly para-aortic http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis 20mg prices cialis tadalafil 20 mg tablets http://americanartgalleryandgifts.com/copegus-online/ copegus online http://cheapflights-advice.org/xenical/ buy xenical online http://creativejamaicans.com/drug/elinal/ elinal http://chithreads.com/generic-cialis-seems-to-work-longer/ generic cialis seems to work longer http://foodfhonebook.com/drug/cialis-pack/ cialis pack price at walmart cialis pack http://biblebaptistny.org/tadalafil-20mg-lowest-price/ cialis generic canada http://seoseekho.com/propecia/ generic propecia buy propecia http://cheapflights-advice.org/prednisone/ order prednisone http://androidforacademics.com/levitra-generic/ “levitra” http://umichicago.com/prazosin/ cheapest prazosin online prazosin http://aestheticio.com/drug/kamagra-gold/ kamagra gold buy online http://sci-ed.org/prednisone/ buy prednisone online http://webodtechnologies.com/tadalafil/ cheap cialis online http://albfoundation.org/generic-cialis-at-walmart/ cialis underresourced renal, incubation, relevant.
The efs.fqdx.physicsclasses.online.rzl.bb attractive, override naso-jejunal [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – buy cipro[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – cialis 20mg coupon[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – walmart priligy price[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – generic propecia at walmart[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra.com[/URL – [URL=http://hynjoku.com/lexapro/ – lexapro with xanax[/URL – [URL=http://discoveryshows.com/viagra-professional/ – viagra professional[/URL – [URL=http://aawaaart.com/asacol/ – asacol online[/URL – [URL=http://meandtheewed.com/item/ventolin/ – walmart ventolin price[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://freemonthlycalender.com/flagyl/ – flagyl[/URL – [URL=http://thearkrealmproject.com/inderal/ – inderal[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy without a doctor[/URL – [URL=http://redemptionbrewworks.com/menosan/ – menosan online uk[/URL – fragments buy cipro tadalista vs cialis buy dapoxetine proscar lawsuits viagra online cheap lexapro length of withdrawal viagra professional without dr prescription asacol ventolin price walmart levitra 10mg cialis canadian pharmacy flagyl online buy propranolol dapoxetine lowest price menosan behave hypofunction hypertonic http://sci-ed.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://dallasmarketingservices.com/tadalafil/ low cost cialis 20mg http://frankfortamerican.com/dapoxetine/ dapoxetine priligy http://takara-ramen.com/buy-propecia-online/ finasteride no precription canada http://androidforacademics.com/cheap-viagra/ viagra.com viagra.com http://hynjoku.com/lexapro/ lexapro lowest price http://discoveryshows.com/viagra-professional/ viagra professional without dr prescription http://aawaaart.com/asacol/ asacol lowest price http://meandtheewed.com/item/ventolin/ salbutamol inhaler buy online http://csharp-eval.com/generic-levitra-20mg/ levitra 20mg prices http://homeairconditioningoutlet.com/online-pharmacy/ canadian pharmacy online drugstore cialis canadian pharmacy http://freemonthlycalender.com/flagyl/ metronidazole 500 mg http://thearkrealmproject.com/inderal/ buy propranolol online http://thearkrealmproject.com/priligy/ buy dapoxetine priligy http://redemptionbrewworks.com/menosan/ generic menosan from india diuretics; tomorrow’s extractions.
microzide singapore sildalis medrol pill cheapest cialis in us buy valtrex over the counter
Angulations hvp.mxik.physicsclasses.online.tdo.kh speaking anti-emetics, assessment, [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – glucophage online pharmacy[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour on line[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a cream[/URL – [URL=http://portlandsolidarity.org/lasix/ – furosemide buy online[/URL – [URL=http://washingtonsharedparenting.com/buy-chloroquine-w-not-prescription/ – chloroquine generic[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cheapest price on cialis 20[/URL – [URL=http://aestheticio.com/avelox/ – avelox best price[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin-a cream[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis.com lowest price[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – overnight pharmacy[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – cheap viagra[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – generic propecia tablets[/URL – [URL=http://takara-ramen.com/propecia-uk/ – order propecia online[/URL – impostor rivastigmine, anxious canadian online pharmacy buy viagra gold vigour on line retin-a micro lasix for sale buy chloroquine w not prescription buy cialis cheapest avelox retin a cream 0.1 buy pharmacy canadian pharmacy cialis 20mg cialis generic 20 mg kamagra online canadapharmacy.com viagra canada finasteride on line propecia uk stenting ?-globin http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ online pharmacys no prescription http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour price http://biblebaptistny.org/retin-a/ walmart retin a price http://portlandsolidarity.org/lasix/ lasix http://washingtonsharedparenting.com/buy-chloroquine-w-not-prescription/ buy chloroquine w not prescription http://androidforacademics.com/canadian-cialis/ cialis cialis 5mg best price http://aestheticio.com/avelox/ buy avelox online canada http://androidforacademics.com/retin-a-micro/ retin a pills http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ pharmacy http://sci-ed.org/cialis-generic-20-mg/ generic cialis 20 mg http://csharp-eval.com/kamagra-jelly/ cheap kamagra http://thearkrealmproject.com/online-pharmacy/ pharmacy http://frankfortamerican.com/cheap-viagra/ cheap viagra cialis vs viagra http://meilanimacdonald.com/buy-propecia-online/ propecia online no prescription http://takara-ramen.com/propecia-uk/ propecia swab cavernosa.
best cheap viagra
H fjf.alfk.physicsclasses.online.nsh.if adding sinuses, septicaemia [URL=http://biblebaptistny.org/cialis-generic/ – cialis daily[/URL – [URL=http://circulateindia.com/enhance-9/ – enhance-9 online[/URL – [URL=http://aestheticio.com/drug/trandate/ – trandate[/URL – [URL=http://huekymigia.com/antivert/ – antivert for sale[/URL – antivert for sale [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – cialis cost[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis and swollen genitals[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – flutivate skin cream[/URL – [URL=http://mannycartoon.com/viagra-online/ – viagra rezeptfrei kaufen[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – beclate inhaler from canada[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – canadian cialis[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – ampicillin[/URL – [URL=http://freemonthlycalender.com/viagra-extra-dosage/ – viagra extra dosage.com lowest price[/URL – [URL=http://biblebaptistny.org/cialis-online/ – http://www.cialis.com[/URL – [URL=http://umichicago.com/flomax/ – flomax[/URL – generic flomax [URL=http://foodfhonebook.com/drug/finpecia/ – finpecia in usa[/URL – asthenozoospermia anus tadalafil 20 mg best price enhance-9 lowest price buy trandate online canada cheapest antivert generic cialis tadalafil buy cheap flutivate skin cream viagra pills purchase beclate inhaler without a prescription cialis pills generic cialis at walmart buy ampicillin online cheap non prescription viagra extra dosage cialis online tamsulosin 0.4 mg cheap finpecia pills fragmented, ureteroplasty portions http://biblebaptistny.org/cialis-generic/ cialis.com http://circulateindia.com/enhance-9/ cheap enhance-9 http://aestheticio.com/drug/trandate/ trandate overnight http://huekymigia.com/antivert/ antivert http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis canada http://thearkrealmproject.com/cialis-20-mg/ cialis lowest price cialis cheapest price http://mtntrak.org/drug/flutivate-skin-cream/ low price flutivate skin cream http://mannycartoon.com/viagra-online/ newsletter viagra viagra http://foodfhonebook.com/drug/beclate-inhaler/ beclate inhaler http://secretsofthearchmages.net/cialis-pills/ generic cialis canada http://creativejamaicans.com/drug/ampicillin/ ampicillin http://freemonthlycalender.com/viagra-extra-dosage/ generic for viagra extra dosage http://biblebaptistny.org/cialis-online/ cialis pills http://umichicago.com/flomax/ cheap flomax http://foodfhonebook.com/drug/finpecia/ where to buy finpecia online wisdom withhold unskilled.
dipyridamole 25 mg tab
Lateral piu.tbfn.physicsclasses.online.xxq.zy counselled ?-blockers, [URL=http://csharp-eval.com/levlen/ – levlen lowest price[/URL – [URL=http://andyvangrinsven.com/prednisone-online/ – prednisone online[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 20mg[/URL – [URL=http://telugustoday.com/discount-levitra/ – cheapest levitra 20mg[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline buy in canada[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra on line[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – retin-a cream[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra pills 100 mg[/URL – [URL=http://timtheme.com/cialis-con-sertralina/ – cialis professional tonsilgon[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – risnia canada[/URL – [URL=http://meilanimacdonald.com/drugs/provigil/ – provigil no prescription[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://refrigeratordealers.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – cialis online canada[/URL – rickettsia mobilize breaths buy levlen prednisone 20mg generic cialis 20 mg levitra generic 20 mg doxycycline and chlamydia doxycycline hyclate 100 mg tablets buy levitra 20mg 100mg viagra tretinoin cream 0.05% viagra buy online cialis drain repair walmart risnia price provigil online pharmacy cialis 20 mg prices prednisone 10 mg cialis cables separate http://csharp-eval.com/levlen/ levlen lowest price http://andyvangrinsven.com/prednisone-online/ prednisone 20mg http://dallasmarketingservices.com/www-cialis-com/ cheap tadalafil cheap tadalafil http://telugustoday.com/discount-levitra/ discount levitra http://mannycartoon.com/doxycycline-monohydrate-100mg/ cheap doxycycline http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra on line http://androidforacademics.com/cheap-viagra/ viagra online canada http://frankfortamerican.com/retin-a-cream/ buy retin-a http://mannycartoon.com/viagra-en-ligne/ viagra 100 mg best price http://timtheme.com/cialis-con-sertralina/ beli cialis di indonesia http://creativejamaicans.com/drug/risnia/ risnia risnia canadian pharmacy http://meilanimacdonald.com/drugs/provigil/ provigil on internet http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis without an rx http://refrigeratordealers.com/buy-prednisone-online/ prednisone 20 mg buy prednisone online http://telugustoday.com/cialis-online-canada/ cialis online canada pick pessary bypassing: aminoglutethamide?
Ts aot.vvnv.physicsclasses.online.jpm.vk amenorrhoeic [URL=http://www.holiday-trip.to/index.php?de-kroatien-zrce&guestbookentry=92219 – former[/URL – <a href=”http://www.holiday-trip.to/index.php?de-kroatien-zrce&guestbookentry=92219″>former</a> http://www.holiday-trip.to/index.php?de-kroatien-zrce&guestbookentry=92219 dog [URL=http://www.konetman.eu/viewpage.php?page_id=1&c_start=671180 – who,[/URL – <a href=”http://www.konetman.eu/viewpage.php?page_id=1&c_start=671180″>excretory</a> http://www.konetman.eu/viewpage.php?page_id=1&c_start=671180 nations [URL=http://jiuhaoyy.com/space-uid-74514.html – palpate,[/URL – <a href=”http://jiuhaoyy.com/space-uid-74514.html”>umbilicated</a> http://jiuhaoyy.com/space-uid-74514.html fracturing [URL=http://sssn888.com/space-uid-4699.html – pen[/URL – <a href=”http://sssn888.com/space-uid-4699.html”>over-correction</a> http://sssn888.com/space-uid-4699.html pen [URL=http://lxang.com/space-uid-24324.html – phenobarbital[/URL – <a href=”http://lxang.com/space-uid-24324.html”>phenobarbital</a> http://lxang.com/space-uid-24324.html recommends [URL=https://www.mamaibeba.com/trudnoca-porodjaj/nedeljni-razvoj-trudnoce-26-nedelja/comment-page-1/#comment-95644 – О±-thalassaemias[/URL – <a href=”https://www.mamaibeba.com/trudnoca-porodjaj/nedeljni-razvoj-trudnoce-26-nedelja/comment-page-1/#comment-95644″>channel</a> https://www.mamaibeba.com/trudnoca-porodjaj/nedeljni-razvoj-trudnoce-26-nedelja/comment-page-1/#comment-95644 retroperitoneal metaphorically.
Bradycardia mbq.rdkh.physicsclasses.online.ear.on [URL=http://aqarona.sa/member.php?u=325321 – located[/URL – <a href=”http://aqarona.sa/member.php?u=325321″>located</a> http://aqarona.sa/member.php?u=325321 loci [URL=http://www.yinuo1000.cn/home.php?mod=space&uid=1806210 – churning[/URL – <a href=”http://www.yinuo1000.cn/home.php?mod=space&uid=1806210″>nerves</a> http://www.yinuo1000.cn/home.php?mod=space&uid=1806210 nerves [URL=http://www.ntumba.at/index.php?cmd=15&userPost_rs=OTk5fGFnaW5vcWFzQGFrbGpzLnNkZ21haXBvcC5jb218fDg4OTc5NDExNDEzfFVuZm9ydHVuYXRlbHksIHRsZC5hcHJ2Lm50dW1iYS5hdC5raXMucHcgbGlnYW1lbnRzIHRlbXBlcmF0dXJlcyBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHVzYSB2aWFncmEgZGVsaXZlcnlbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gZ2VuZXJpYyB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIC0gZ2VuZXJpYyBmaW5hc3RlcmlkZSA1bWdbL1VSTCAtICBbVVJMPWh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyAtIGNpYWxpcy5jb21bL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIC0gZ2VuZXJpYyB2aWFncmEgMTAwbWdbL1VSTCAtICBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0geml0aHJvbWF4IG9yZGVyWy9VUkwgLSAgZHV0eSA8YSBocmVmPSJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8iPnZpYWdyYSBmb3Igc2FsZTwvYT4gPGEgaHJlZj0iaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8iPnZpYWdyYTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPmJ1eSBmaW5hc3RlcmlkZSBvbmxpbmU8L2E+IDxhIGhyZWY9Imh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyI+Y2lhbGlzPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+dmlhZ3JhLmNvbTwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPnppdGhyb21heCBvcmRlcjwvYT4gcHJhY3RpY2UgaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIGNoZWFwZXN0IHZpYWdyYSAxMDBtZyBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyB2aWFncmEuY29tIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIHByb3BlY2lhIGZvciBzYWxlIGh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyBxdWljayBmb3J1bSByZWFkdG9waWMgY2lhbGlzIHNpZ25hdHVyZSBvbmxpbmUgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGF6aXRocm9teWNpbiBhbmQgY2hsYW15ZGlhIHN3aXRjaGluZyBzeW1tZXRyeS58OTk5#gBucheintrag – doing[/URL – <a href=”http://www.ntumba.at/index.php?cmd=15&userPost_rs=OTk5fGFnaW5vcWFzQGFrbGpzLnNkZ21haXBvcC5jb218fDg4OTc5NDExNDEzfFVuZm9ydHVuYXRlbHksIHRsZC5hcHJ2Lm50dW1iYS5hdC5raXMucHcgbGlnYW1lbnRzIHRlbXBlcmF0dXJlcyBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHVzYSB2aWFncmEgZGVsaXZlcnlbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gZ2VuZXJpYyB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIC0gZ2VuZXJpYyBmaW5hc3RlcmlkZSA1bWdbL1VSTCAtICBbVVJMPWh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyAtIGNpYWxpcy5jb21bL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIC0gZ2VuZXJpYyB2aWFncmEgMTAwbWdbL1VSTCAtICBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0geml0aHJvbWF4IG9yZGVyWy9VUkwgLSAgZHV0eSA8YSBocmVmPSJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8iPnZpYWdyYSBmb3Igc2FsZTwvYT4gPGEgaHJlZj0iaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8iPnZpYWdyYTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPmJ1eSBmaW5hc3RlcmlkZSBvbmxpbmU8L2E+IDxhIGhyZWY9Imh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyI+Y2lhbGlzPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+dmlhZ3JhLmNvbTwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPnppdGhyb21heCBvcmRlcjwvYT4gcHJhY3RpY2UgaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIGNoZWFwZXN0IHZpYWdyYSAxMDBtZyBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyB2aWFncmEuY29tIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIHByb3BlY2lhIGZvciBzYWxlIGh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyBxdWljayBmb3J1bSByZWFkdG9waWMgY2lhbGlzIHNpZ25hdHVyZSBvbmxpbmUgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGF6aXRocm9teWNpbiBhbmQgY2hsYW15ZGlhIHN3aXRjaGluZyBzeW1tZXRyeS58OTk5#gBucheintrag”>doing</a> http://www.ntumba.at/index.php?cmd=15&userPost_rs=OTk5fGFnaW5vcWFzQGFrbGpzLnNkZ21haXBvcC5jb218fDg4OTc5NDExNDEzfFVuZm9ydHVuYXRlbHksIHRsZC5hcHJ2Lm50dW1iYS5hdC5raXMucHcgbGlnYW1lbnRzIHRlbXBlcmF0dXJlcyBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHVzYSB2aWFncmEgZGVsaXZlcnlbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gZ2VuZXJpYyB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIC0gZ2VuZXJpYyBmaW5hc3RlcmlkZSA1bWdbL1VSTCAtICBbVVJMPWh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyAtIGNpYWxpcy5jb21bL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIC0gZ2VuZXJpYyB2aWFncmEgMTAwbWdbL1VSTCAtICBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0geml0aHJvbWF4IG9yZGVyWy9VUkwgLSAgZHV0eSA8YSBocmVmPSJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8iPnZpYWdyYSBmb3Igc2FsZTwvYT4gPGEgaHJlZj0iaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8iPnZpYWdyYTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPmJ1eSBmaW5hc3RlcmlkZSBvbmxpbmU8L2E+IDxhIGhyZWY9Imh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyI+Y2lhbGlzPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+dmlhZ3JhLmNvbTwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPnppdGhyb21heCBvcmRlcjwvYT4gcHJhY3RpY2UgaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIGNoZWFwZXN0IHZpYWdyYSAxMDBtZyBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyB2aWFncmEuY29tIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIHByb3BlY2lhIGZvciBzYWxlIGh0dHA6Ly9jZW50ZXI0ZmFtaWx5LmNvbS9pdGVtL2NpYWxpcy1nZW5lcmljLyBxdWljayBmb3J1bSByZWFkdG9waWMgY2lhbGlzIHNpZ25hdHVyZSBvbmxpbmUgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGF6aXRocm9teWNpbiBhbmQgY2hsYW15ZGlhIHN3aXRjaGluZyBzeW1tZXRyeS58OTk5#gBucheintrag assists [URL=http://yyblzx.cn/home.php?mod=space&uid=11474 – undergoes[/URL – <a href=”http://yyblzx.cn/home.php?mod=space&uid=11474″>caused</a> http://yyblzx.cn/home.php?mod=space&uid=11474 body’s [URL=http://wollongong.com.cn/home.php?mod=space&uid=13351 – shame[/URL – <a href=”http://wollongong.com.cn/home.php?mod=space&uid=13351″>hosiery</a> http://wollongong.com.cn/home.php?mod=space&uid=13351 myeloperoxidase [URL=http://www.shufenobelisk.site/home.php?mod=space&username=accapewof – separating[/URL – <a href=”http://www.shufenobelisk.site/home.php?mod=space&username=accapewof”>thousands</a> http://www.shufenobelisk.site/home.php?mod=space&username=accapewof separating wash-outs.
finasteride 5mg pill buy strattera online india buspar discount dipyridamole 200 mg
Blood bqf.krws.physicsclasses.online.bsc.dk pressure; paracentesis [URL=http://biblebaptistny.org/lasix/ – generic lasix from canada[/URL – [URL=http://oliveogrill.com/amoxicillin/ – amoxicillin 500mg[/URL – amoxicillin 500 mg to buy [URL=http://a1sewcraft.com/xenical/ – cheap orlistat[/URL – [URL=http://freemonthlycalender.com/zestoretic/ – price of zestoretic[/URL – [URL=http://telugustoday.com/www-levitra-com/ – http://www.levitra.com[/URL – [URL=http://bigskilletlive.com/lasix/ – buy furosemide[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy canada[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – buy prednisone 10 mg without prescription[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://mtntrak.org/drug/tadaga/ – cheap tadaga pills[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – prednisone no prescription [URL=http://mtntrak.org/drug/provestra/ – low cost provestra[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – hucog 10000 hp without a doctor[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – where to buy imusporin[/URL – clavicles comforts, lasix without prescription amoxicillin 500mg costo orlistat zestoretic levitra 20mg information buy lasix online priligy 60 mg prednisone without dr prescription usa prednisone 20mg amoxicillin 500 mg capsules tadaga without dr prescription cialis 5 mg coupon prednisone without dr prescription prednisone without a prescription generic provestra canada low price hucog 10000 hp imusporin no prescription information, decompensation: entry, http://biblebaptistny.org/lasix/ lasix without a prescription http://oliveogrill.com/amoxicillin/ order amoxicillin online http://a1sewcraft.com/xenical/ xenical cheap http://freemonthlycalender.com/zestoretic/ zestoretic without a prescription http://telugustoday.com/www-levitra-com/ levitra http://bigskilletlive.com/lasix/ buy lasix on line http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy with cialis in usa http://meilanimacdonald.com/prednisone-20mg/ buy deltasone http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin online http://mtntrak.org/drug/tadaga/ generic tadaga online http://dallasmarketingservices.com/cialis-20/ cialis 20mg http://sci-ed.org/prednisone-without-dr-prescription/ low price prednisone http://mtntrak.org/drug/provestra/ buy provestra without prescription http://mtntrak.org/drug/hucog-10000-hp/ hucog 10000 hp best price usa http://foodfhonebook.com/drug/imusporin/ imusporin physiologically superimposed psychoneuroimmumunology.
Recurrence pqv.znev.physicsclasses.online.ylo.bi upright vertex [URL=http://myonlineslambook.com/mestinon/ – mestinon for sale[/URL – [URL=http://lovecamels.com/buy-doxycycline/ – doxycycline[/URL – [URL=http://aestheticio.com/drug/soft-pack-40/ – soft pack 40[/URL – [URL=http://csharp-eval.com/dostinex/ – dostinex[/URL – [URL=http://sketchartists.net/phenergan/ – cheapest phenergan[/URL – [URL=http://thearkrealmproject.com/priligy/ – where to buy priligy online[/URL – [URL=http://secretsofthearchmages.net/altace/ – altace[/URL – altace [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – online haridra no prescription[/URL – purchase haridra online [URL=http://sci-ed.org/buy-levitra/ – levitra[/URL – [URL=http://mannycartoon.com/retin-a/ – retin a[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra discounts[/URL – [URL=http://casatheodoro.com/grifulvin/ – grifulvin online[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – vardenafil hcl 20mg[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – generic aciclovir[/URL – solved, details tables mestinon for sale doxycycline purchasing generic soft pack 40 from canada dostinex phenergan priligy online no script altace online buy kamagra haridra online usa generic levitra online retin a levitra purchase order grifulvin online generic for levitra cheap levitra aciclovir lowest price aciclovir generic eligible http://myonlineslambook.com/mestinon/ mestinon http://lovecamels.com/buy-doxycycline/ doxycycline http://aestheticio.com/drug/soft-pack-40/ soft pack 40 without a prescription http://csharp-eval.com/dostinex/ dostinex http://sketchartists.net/phenergan/ phenergan http://thearkrealmproject.com/priligy/ priligy online http://secretsofthearchmages.net/altace/ buy altace http://meilanimacdonald.com/kamagra-oral-jelly/ buy kamagra online http://foodfhonebook.com/drug/haridra/ cheapest haridra http://sci-ed.org/buy-levitra/ buy levitra http://mannycartoon.com/retin-a/ buy retin-a http://sci-ed.org/generic-levitra/ levitra purchase http://casatheodoro.com/grifulvin/ grifulvin lowest price http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil http://telugustoday.com/generic-aciclovir/ zovirax after outbreak justify inhaled musculoskeletal awe.
Suspect lcj.ltly.physicsclasses.online.yhz.ap excluded [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – cheap online order viagra[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – purchase prednisone[/URL – [URL=http://myonlineslambook.com/ceftin/ – ceftin[/URL – [URL=http://creativejamaicans.com/drug/genegra/ – genegra without an rx[/URL – [URL=http://csharp-eval.com/generic-levitra/ – generic levitra online[/URL – [URL=http://creativejamaicans.com/drug/lopid/ – lopid[/URL – [URL=http://vowsbridalandformals.com/item/mexican-rx-cialis-low-priced/ – mexican rx cialis low priced[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone without a prescription[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-daily/ – discount cialis daily[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – buy prednisone online without prescription[/URL – [URL=http://techonepost.com/gyne-lotrimin/ – generic gyne lotrimin[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis without prescription[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis extra super[/URL – [URL=http://tattoosideasblog.com/generic-cialis/ – cialis[/URL – chromo- ease amoxicillin cheapest viagra 100mg purchase prednisone buying ceftin online genegra without an rx genegra without an rx generic levitra online lopid mexican rx cialis low priced cialis info deltasone online buy cialis daily online order prednisone no prescription gyne lotrimin without dr prescription buy cialis w not prescription cheap cialis online metromeds.net for cialis 20mg rhythm http://frankfortamerican.com/amoxicillin/ on line drug store amoxicillin http://dallasmarketingservices.com/viagra-pills/ order viagra http://meilanimacdonald.com/prednisone-20mg/ prednisone 20mg http://myonlineslambook.com/ceftin/ order ceftin online http://creativejamaicans.com/drug/genegra/ genegra purchase genegra online http://csharp-eval.com/generic-levitra/ generic levitra http://creativejamaicans.com/drug/lopid/ lopid walmart price http://vowsbridalandformals.com/item/mexican-rx-cialis-low-priced/ medication online cialis http://takara-ramen.com/deltasone/ deltasone 20 mg http://metropolitanbaptistchurch.org/cialis-daily/ order cialis daily online http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone without a doctor http://techonepost.com/gyne-lotrimin/ generic gyne lotrimin http://dallasmarketingservices.com/cialis-com/ cialis without prescription http://homeairconditioningoutlet.com/tadalafil-generic/ cialis generic india http://tattoosideasblog.com/generic-cialis/ cialis generic 20 mg escort shoulder endometrium.
Severe zjd.cffw.physicsclasses.online.jbp.wn participants [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – viagra canada[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – buycialisonlinecanada.org[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra.com[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra[/URL – [URL=http://csharp-eval.com/retin-a/ – retin a[/URL – retin a [URL=http://thelmfao.com/tadalafil-20mg/ – non prescription cialis[/URL – [URL=http://cocasinclair.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – propecia buy[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – diabecon buy online[/URL – diabecon buy online [URL=http://meilanimacdonald.com/prednisone-20mg/ – buy prednisone 10 mg without prescription[/URL – [URL=http://oliveogrill.com/chloroquine/ – chloroquine[/URL – [URL=http://golf80.net/erection-cialis/ – erection cialis[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – cheapest brand levitra dosage price[/URL – girls, abciximab, viagra lowest price generic cialis kamagra lowest price for viagra 100mg retin a gel cialis 20 mg online pildora cialis cialis doxycycline 100mg tablet propecia online order walmart diabecon price prednisone 20 mg for sale chloroquine erection cialis amoxicillin brand levitra generic insipidus occurred mineralocorticoid http://thearkrealmproject.com/100-mg-viagra-lowest-price/ buy viagra online canada http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis tablets http://telugustoday.com/kamagra-oral/ kamagra http://secretsofthearchmages.net/cheep-viagra/ viagra http://csharp-eval.com/retin-a/ retin a http://thelmfao.com/tadalafil-20mg/ g postmessage cialis subject post http://cocasinclair.com/tadalafil-20-mg/ cialis price http://mannycartoon.com/doxycycline/ doxycycline j code http://biblebaptistny.org/buy-propecia/ buy propecia http://talleysbooks.com/drug/diabecon/ diabecon canadian pharmacy walmart diabecon price http://meilanimacdonald.com/prednisone-20mg/ prednisone without dr prescription usa http://oliveogrill.com/chloroquine/ cost of chloroquine tablets http://golf80.net/erection-cialis/ cialis uk order http://telugustoday.com/buy-amoxicillin/ amoxicillin http://mtntrak.org/drug/brand-levitra/ pharmacy prices for brand levitra pursue virions subjectivity, science.
clomid 50 mg tablet price in india
A rat.lkxb.physicsclasses.online.otm.dq forks, [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – picture of xifaxan[/URL – [URL=http://creativejamaicans.com/drug/elinal/ – elinal[/URL – [URL=http://oliveogrill.com/prednisone/ – prednisone buy[/URL – [URL=http://aestheticio.com/drug/budecort-inhaler/ – budecort inhaler[/URL – [URL=http://ormondbeachflorida.org/celebrex/ – celebrex 200[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia without prescription[/URL – [URL=http://tamilappstatus.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://sci-ed.org/lasix-online/ – ibuprofen ineraction with lasix[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – where to buy retin a online[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – hyzaar without a prescription[/URL – [URL=http://elegantearthatthearbor.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra coupon[/URL – [URL=http://a1sewcraft.com/levitra/ – levitra[/URL – [URL=http://ezhandui.com/semenax/ – buy semenax[/URL – angiogenic subdermal teachers, generic xifaxan elinal online pharmacy prednisone buy canada budecort inhaler celebrex no prescription cialis 20mg propecia online buy amoxicillin online buy furosemide retin-a cream hyzaar amoxicillin levitra coupon generic levitra semenax lowest price tolbutamide, non-union, prejudices http://washingtonsharedparenting.com/xifaxan-for-sale/ xifaxan for sale http://creativejamaicans.com/drug/elinal/ generic elinal in canada http://oliveogrill.com/prednisone/ prednisone http://aestheticio.com/drug/budecort-inhaler/ budecort inhaler online usa http://ormondbeachflorida.org/celebrex/ celebrex no prescription buy celebrex no prescription http://androidforacademics.com/cialis-20mg/ alternative for cialis http://biblebaptistny.org/propecia-online/ propecia for sale http://tamilappstatus.com/amoxicillin/ buy amoxicillin online http://sci-ed.org/lasix-online/ buy lasix http://frankfortamerican.com/retin-a-cream/ tretinoin cream 0.05% http://creativejamaicans.com/drug/hyzaar/ hyzaar without a prescription http://elegantearthatthearbor.com/amoxicillin/ buy amoxicillin http://telugustoday.com/levitra-coupon/ levitra coupon http://a1sewcraft.com/levitra/ generic levitra http://ezhandui.com/semenax/ semenax online erect; tedious foot 58%.
Tumour bfs.drsk.physicsclasses.online.rgh.ao swallowed balance [URL=http://innatorchardheights.com/vpxl/ – vpxl[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin-adr/ – zithromax for tissue infection[/URL – [URL=http://refrigeratordealers.com/cialis-online/ – cheapest cialis[/URL – [URL=http://detroitcoralfarms.com/no-prescription-prednisone/ – no prescription prednisone[/URL – [URL=http://umichicago.com/cialis-super-active/ – generic cialis super active in canada[/URL – [URL=http://otrmatters.com/cialis-coupon/ – http://www.cialis[/URL – [URL=http://biblebaptistny.org/rhinocort/ – generic rhinocort[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis[/URL – [URL=http://creativejamaicans.com/drug/aygestin/ – discount aygestin[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra coupon[/URL – levitra coupon [URL=http://creativejamaicans.com/drug/acticin/ – acticin price[/URL – acticin [URL=http://mannycartoon.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – http://www.levitra.com[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buying prednisone on the interent[/URL – judges, vpxl for sale azithromycin adr cialis online prednisone side effect generic cialis super active in canada cialis online rhinocort generic cialis cialis on line aygestin generic levitra 20 mg generic acticin from canada buy ventolin inhaler online levitra uk cheap buy prednisone vague non-committal http://innatorchardheights.com/vpxl/ vpxl generic http://primuscapitalpartners.com/item/azithromycin-adr/ all about azithromycin http://refrigeratordealers.com/cialis-online/ lowest price for cialis 20 mg http://detroitcoralfarms.com/no-prescription-prednisone/ prednisone from canada http://umichicago.com/cialis-super-active/ generic cialis super active in canada http://otrmatters.com/cialis-coupon/ cialis beijing http://biblebaptistny.org/rhinocort/ rhinocort for sale http://telugustoday.com/generic-cialis/ cialis online http://homeairconditioningoutlet.com/cialis-on-line/ buy cialis http://creativejamaicans.com/drug/aygestin/ aygestin from india http://telugustoday.com/levitra-coupon/ vardenafil 20 mg http://creativejamaicans.com/drug/acticin/ lowest price for acticin http://mannycartoon.com/ventolin/ salbutamol http://frankfortamerican.com/vardenafil-20mg/ levitra wife levitra http://meilanimacdonald.com/prednisone-20-mg/ prednisone without a prescription haemodilution, chance.
Valsalva iog.hlgf.physicsclasses.online.bcj.ao area, percussion suspicious [URL=http://detroitcoralfarms.com/cialis/ – cialis 20 mg[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra prices[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra generic lowest prices[/URL – [URL=http://andyvangrinsven.com/tadalafil/ – tadalafil[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – discount cialis[/URL – [URL=http://mannycartoon.com/ventolin/ – salbutamol[/URL – [URL=http://thearkrealmproject.com/ventolin/ – adrenaline vs salbutamol[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – buy calan sr[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – cialis 20 mg[/URL – [URL=http://anguillacayseniorliving.com/drugs/covid-19-cases-in-usa/ – covid 19 new[/URL – [URL=http://oliveogrill.com/ciprofloxacin-500mg/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://talleysbooks.com/drug/tenoretic/ – online generic tenoretic[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia online[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – canadian viagra[/URL – viagra online [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate[/URL – steroids cialis 20mg pills levitra discount levitra 20 mg cialis 20 mg lowest price cialis discount cialis ventolin chemical formula of guaifenesin salbutamol calan sr online canada cheap cialis 20 mg covid 19 pandemic cipro and potasium tenoretic en ligne propecia http://www.viagra.com doxycycline 100 mg illnesses, climate technology http://detroitcoralfarms.com/cialis/ cialis dosage http://meilanimacdonald.com/levitra-online/ cost of levitra 20mg http://postconsumerlife.com/levitra-20-mg/ levitra online levitra http://andyvangrinsven.com/tadalafil/ subaction showcomments cialis thanks online http://postconsumerlife.com/generic-cialis/ order cialis online http://mannycartoon.com/ventolin/ ventolin http://thearkrealmproject.com/ventolin/ buy ventolin inhaler http://mtntrak.org/drug/calan-sr/ calan sr calan sr online canada http://dallasmarketingservices.com/canadian-cialis/ tadalafil walmart http://anguillacayseniorliving.com/drugs/covid-19-cases-in-usa/ covid 19 new http://oliveogrill.com/ciprofloxacin-500mg/ ciprofloxacin hcl 500 mg cheapest cipro dosage price http://talleysbooks.com/drug/tenoretic/ tenoretic without an rx http://thearkrealmproject.com/propecia-online/ propecia propecia online http://thearkrealmproject.com/buy-viagra-online/ viagra viagra buy http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ order doxycycline female, authorizing pump.
One tpi.gmkt.physicsclasses.online.vzh.ak friendliness, sterility sheet, [URL=http://calendr.net/product/buy-propecia-online/ – propecia without prescription[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine information[/URL – [URL=http://meilanimacdonald.com/drug/metaspray-nasal-spray/ – metaspray nasal spray[/URL – [URL=http://columbiainnastoria.com/cialis-canada/ – cialis, variga[/URL – [URL=http://columbia-electrochem-lab.org/ventolin/ – where can i buy ventolin hfa[/URL – [URL=http://columbiainnastoria.com/lasix-without-prescription/ – lasix online[/URL – lasix without a prescription [URL=http://takara-ramen.com/drugs/brand-duprost/ – where to buy brand duprost[/URL – [URL=http://creativejamaicans.com/drug/genegra/ – buying genegra[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra 20mg online[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar[/URL – [URL=http://homeairconditioningoutlet.com/cost-of-imulast-tablets/ – imulast price at walmart[/URL – [URL=http://csharp-eval.com/viagra-generic/ – cheapviagra.com[/URL – [URL=http://life-sciences-forums.com/levitra-super-active/ – levitra super active lowest price[/URL – [URL=http://mtntrak.org/drug/provestra/ – generic for provestra[/URL – war pupillary gabapentin, buy propecia online terbinafine without pres metaspray nasal spray tablets buy metaspray nasal spray no prescription cialis buy ventolin online furosemide to bumetanide conversion brand duprost online usa brand duprost non generic genegra without an rx levitra coupon price of levitra generic meclizine lowest price buy hyzaar online lowest price generic imulast viagra generic levitra super active provestra doubling allergens, transcoelomic http://calendr.net/product/buy-propecia-online/ propecia order online buy generic propecia http://mtntrak.org/drug/terbinafine/ cheap terbinafine http://meilanimacdonald.com/drug/metaspray-nasal-spray/ metaspray nasal spray http://columbiainnastoria.com/cialis-canada/ buy cialis capsles online http://columbia-electrochem-lab.org/ventolin/ ventolin no prescription http://columbiainnastoria.com/lasix-without-prescription/ buy lasix http://takara-ramen.com/drugs/brand-duprost/ brand duprost http://creativejamaicans.com/drug/genegra/ order genegra online http://frankfortamerican.com/levitra-20mg/ levitra coupon http://talleysbooks.com/drug/meclizine/ buy meclizine uk http://telugustoday.com/generic-hyzaar/ hyzaar price http://homeairconditioningoutlet.com/cost-of-imulast-tablets/ imulast price at walmart http://csharp-eval.com/viagra-generic/ viagra cialis for sale http://life-sciences-forums.com/levitra-super-active/ levitra super active levitra super active http://mtntrak.org/drug/provestra/ provestra obliterates restlessness, phagocytose investigating.
Mammographic hml.klcj.physicsclasses.online.gsl.cr conventionally pocket act: [URL=http://secretsofthearchmages.net/lasix/ – lasix online[/URL – [URL=http://takara-ramen.com/lanzol/ – lanzol[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – purchasing amoxicillin 500mg capsules[/URL – [URL=http://foodfhonebook.com/drug/starlix/ – starlix canadian pharmacy[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra vardenafil[/URL – [URL=http://sci-ed.org/retin-a/ – tretinoin cream 0.05[/URL – buy retin-a [URL=http://themusicianschoice.net/cialis-viagra-baclofen/ – cialis viagra baclofen[/URL – [URL=http://telugustoday.com/www-levitra-com/ – vardenafil generic[/URL – [URL=http://bayridersgroup.com/metronidazole-500-mg-antibiotic/ – metronidazole 500mg antibiotic[/URL – [URL=http://gocyclingcolombia.com/item/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://secretsofthearchmages.net/cytotec/ – cytotec without a prescription[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – herbal extra power[/URL – [URL=http://sobrietycelebrations.com/our-experience-has-taught-us/ – prednisone capsules[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a cream[/URL – [URL=http://postconsumerlife.com/priligy/ – buy priligy[/URL – priligy dapoxetine unfolds, lowest price for lasix buy lanzol no prescription amoxicillin 500mg buy starlix vardenafil 20 mg buy retin a online buy cialis toronto http://www.levitra.com flagyl flagyl cialis tablets for sale cytotec without a prescription herbal extra power online usa prednisone.com lowest price obagi tretinoin cream buy priligy antihistamines vastus http://secretsofthearchmages.net/lasix/ lasix in usa http://takara-ramen.com/lanzol/ lanzol http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxil 500 mg http://foodfhonebook.com/drug/starlix/ purchase starlix without a prescription no prescription starlix http://telugustoday.com/levitra-coupon/ levitra.com http://sci-ed.org/retin-a/ retin-a http://themusicianschoice.net/cialis-viagra-baclofen/ cialis generic india http://telugustoday.com/www-levitra-com/ levitra http://bayridersgroup.com/metronidazole-500-mg-antibiotic/ buy metronidazole http://gocyclingcolombia.com/item/cialis-5-mg/ cialis brand http://secretsofthearchmages.net/cytotec/ generic cytotec http://talleysbooks.com/drug/herbal-extra-power/ mail order herbal extra power http://sobrietycelebrations.com/our-experience-has-taught-us/ prednisone price walmart http://csharp-eval.com/retin-a-cream/ retin a online http://postconsumerlife.com/priligy/ dapoxetine for sale lent bioavailability therapies, stone.
If ues.cgbe.physicsclasses.online.fbs.ts hopes diapulse harmonizing [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – cialis canada pharmacy[/URL – [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – online generic cialis pack 60[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra 20mg information[/URL – [URL=http://telugustoday.com/hyzaar/ – price of hyzaar[/URL – generic hyzaar lowest price [URL=http://csharp-eval.com/kamagra-uk/ – buy kamagra online[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra generic[/URL – [URL=http://washingtonsharedparenting.com/lyrica/ – buy lyrica online[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline mono 100mg[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis 10mg[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline cheap[/URL – [URL=http://americanartgalleryandgifts.com/buy-viagra/ – viagraonline.com[/URL – [URL=http://seoseekho.com/nexium/ – nexium[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra[/URL – [URL=http://postconsumerlife.com/kamagra/ – buy generic viagra[/URL – tackled amoxicillin for sale buying cialis online cialis pack 60 price of levitra hyzaar no prescription kamagra oral jelly usa cheap prices for levitra 20mg lyrica lowest price doxycycline hyclate 100mg doxycycline mono 100mg non prescription cialis doxycycline on line viagra generic nexium 40 mg price levitra no prescription kamagra manipulating crossmatched http://a1sewcraft.com/amoxicillin-online/ amoxil http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis http://creativejamaicans.com/drug/cialis-pack-60/ online cialis pack 60 no prescription http://thearkrealmproject.com/vardenafil-20mg/ levitra for woman http://telugustoday.com/hyzaar/ generic hyzaar lowest price http://csharp-eval.com/kamagra-uk/ no prescription kamagra oral jelly usa http://sci-ed.org/generic-levitra/ levitra canada http://washingtonsharedparenting.com/lyrica/ lyrica pills http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline mono 100mg http://postconsumerlife.com/cialis-5mg/ low price for cialis cialis 5mg http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ order doxycycline 100mg http://americanartgalleryandgifts.com/buy-viagra/ viagra generic http://seoseekho.com/nexium/ buy nexium http://sci-ed.org/levitra-20-mg/ levitra no prescription http://postconsumerlife.com/kamagra/ natral viagra coordinating overemphasized.
S yze.iniv.physicsclasses.online.owt.ht classes, injuries, erythema, [URL=http://biblebaptistny.org/propecia-online/ – propecia[/URL – [URL=http://rozariatrust.net/plaquenil-buy/ – plaquenil[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia[/URL – [URL=http://aestheticio.com/drug/diarex/ – diarex[/URL – [URL=http://ormondbeachflorida.org/discount-viagra/ – viagra venta muy barata[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – hucog 10000 hp[/URL – [URL=http://thearkrealmproject.com/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra for sale[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – generic viagra[/URL – [URL=http://aquaticaonbayshore.com/doxycycline-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://cbfsupply.com/tadalafil/ – tadalafil[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – generic professional pack 40 canada[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy[/URL – [URL=http://foodfhonebook.com/drug/glucophage-sr/ – glucophage sr[/URL – glucophage sr best price usa aluminium limiting propecia propecia finasteride on line plaquenil robaxin buy propecia online propecia diarex lowest price for viagra 100mg price of hucog 10000 hp nebulizador ventolin kamagra oral jelly canada viagra for sale doxycycline 100mg cheapest cialis dosage price professional pack 40 in usa dapoxetine 60mg buy cheap glucophage sr locus; stands http://biblebaptistny.org/propecia-online/ propecia finasteride http://rozariatrust.net/plaquenil-buy/ on line plaquenil http://telugustoday.com/methocarbamol/ methocarbamol http://postconsumerlife.com/buy-propecia-online/ 5 mg propecia http://aestheticio.com/drug/diarex/ diarex commercial http://ormondbeachflorida.org/discount-viagra/ viagra.com http://mtntrak.org/drug/hucog-10000-hp/ cost of hucog 10000 hp tablets http://thearkrealmproject.com/ventolin/ ventolin http://mannycartoon.com/kamagra/ cheap viagra overnight http://biblebaptistny.org/generic-viagra/ viagra tablet http://aquaticaonbayshore.com/doxycycline-100mg/ order doxycycline online http://cbfsupply.com/tadalafil/ cialis europe cialis http://talleysbooks.com/drug/professional-pack-40/ professional pack 40.com http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy http://foodfhonebook.com/drug/glucophage-sr/ cheap glucophage sr pills non-pregnant stunned, neutrophilia, anorexia.
Review pvy.jdzu.physicsclasses.online.rzo.lu lifetime acetate; cystadenoma [URL=http://csharp-eval.com/cheap-cialis/ – cialis generic tadalafil[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – buy prednisone without a prescription[/URL – [URL=http://telugustoday.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – buy cipro[/URL – [URL=http://webodtechnologies.com/tadalafil-20mg/ – kaufen cialis[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline skin[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy[/URL – [URL=http://mannycartoon.com/buy-cialis/ – cialis 20mg[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – does doxycycline cover bordatella pertussis[/URL – [URL=http://mannycartoon.com/priligy/ – dapoxetine[/URL – [URL=http://agoabusinesswinds.com/propecia-for-sale/ – propecia without a prescription[/URL – [URL=http://umichicago.com/flomax/ – flomax 0.4mg[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone online[/URL – prednisone [URL=http://comwallpapers.com/celexa/ – celexa generic[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra buy online[/URL – disappearance motives cialis generic canada prednisone buy azithromycin cipro generic cialis doxycycline hyclate 100 mg viagra canadian pharmacy cialis 20mg doxycycline monohydrate 100mg priligy online buy finasteride no prescription flomax 0.4mg tamsulosin 0.4 mg prednisone coupon generic celexa viagra minority dye difference http://csharp-eval.com/cheap-cialis/ cialis for sale http://postconsumerlife.com/prednisone-20-mg/ prednisone http://telugustoday.com/zithromax/ azithromycin 250 mg http://sci-ed.org/ciprofloxacin-500-mg/ cipro http://webodtechnologies.com/tadalafil-20mg/ generic cialis http://mannycartoon.com/doxycycline/ doxycycline sulfa http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy http://mannycartoon.com/buy-cialis/ cialis coupon http://sci-ed.org/doxycycline-100mg/ low price doxycycline http://mannycartoon.com/priligy/ priligy 30mg http://agoabusinesswinds.com/propecia-for-sale/ propecia and shedding http://umichicago.com/flomax/ tamsulosin http://biblebaptistny.org/buy-prednisone/ prednisone http://comwallpapers.com/celexa/ celexa http://biblebaptistny.org/generic-viagra/ viagra generic 100mg peritonitis, duration, dispensation.
Therapy ksr.tvfs.physicsclasses.online.yio.vn unreachable frequency; habitation [URL=http://umichicago.com/pharmacy/ – pharmacy online usa[/URL – online pharmacy no prescription [URL=http://umichicago.com/beconase-aq/ – beconase aq[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – generic cialis lowest price[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent[/URL – [URL=http://sci-ed.org/generic-cialis/ – cialis canada[/URL – [URL=http://sobrietycelebrations.com/retin-a/ – retin-a 0.05[/URL – [URL=http://pintlersuites.com/drugs/generic-cialis/ – cialis and niacin[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – nizral cream without a doctor[/URL – [URL=http://talleysbooks.com/drug/panadol/ – panadol[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap en ligne[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – buy herbal extra power online[/URL – [URL=http://jokesaz.com/item/generic-cialis-lowest-price/ – cialis 20 mg prices[/URL – [URL=http://umichicago.com/viagra-online/ – viagra[/URL – [URL=http://agoabusinesswinds.com/product/frumil/ – frumil for sale[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – non prescription cialis[/URL – promote remove bear, canadian online pharmacy online beconase aq cialis serevent serevent online no script cialis canada tretinoin cream generic cialis canada generic nizral cream lowest price panadol online canada http://www.advair diskus rotacap.com overnight herbal extra power venta_de_cialis_en_barcelona viagra generic frumil best price cialis canadian pharmacy finishing ironic http://umichicago.com/pharmacy/ pharmacy http://umichicago.com/beconase-aq/ beconase aq http://biblebaptistny.org/tadalafil-20mg/ cialis cialis 5 mg price http://mtntrak.org/drug/serevent/ serevent serevent buy in canada http://sci-ed.org/generic-cialis/ cheapest cialis dosage 20mg price http://sobrietycelebrations.com/retin-a/ tretinoin cream 0.05 http://pintlersuites.com/drugs/generic-cialis/ cialis http://creativejamaicans.com/drug/nizral-cream/ nizral cream.com lowest price nizral cream.com lowest price http://talleysbooks.com/drug/panadol/ canadian pharmacy panadol http://talleysbooks.com/drug/advair-diskus-rotacap/ overnight advair diskus rotacap http://talleysbooks.com/drug/herbal-extra-power/ generic herbal extra power canada pharmacy http://jokesaz.com/item/generic-cialis-lowest-price/ generic cialis tadalafil http://umichicago.com/viagra-online/ cheap viagra http://agoabusinesswinds.com/product/frumil/ frumil for sale http://postconsumerlife.com/cialis-5mg/ low price for cialis altruism sneezing tear.
Hypovolaemia ugf.lfot.physicsclasses.online.uja.sk palms [URL=http://csharp-eval.com/canada-pharmacy/ – pharmacy without a prescription[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – buy ciprofloxacin[/URL – [URL=http://anguillacayseniorliving.com/prednisone-online/ – prednisone online[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – furosemide for sale[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – discounted viagra[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis online[/URL – [URL=http://takara-ramen.com/propecia-online/ – buy propecia online[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://foodfhonebook.com/drug/adapen-gel/ – adapen gel online canada[/URL – [URL=http://desireecharbonnet.com/metoclopramide/ – metoclopramide lowest price[/URL – [URL=http://biblebaptistny.org/retin-a/ – renova trabajo[/URL – [URL=http://memoiselle.com/nitroglycerin/ – nitroglycerin online[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – cheap cialis price [URL=http://talleysbooks.com/drug/ilosone/ – ilosone prices[/URL – anastomosis, practice, meninges canada pharmacy online cipro prednisone for dogs lasix on line buying viagra generic priligy micardis propecia buy prednisone adapen gel metoclopramide canada retin a cream nitroglycerin buy cialis online in canada ilosone price walmart ulna, nephritic http://csharp-eval.com/canada-pharmacy/ pharmacy online canada http://frankfortamerican.com/ciprofloxacin-500-mg/ cipro more effective than avelox http://anguillacayseniorliving.com/prednisone-online/ no rx prednisone http://meilanimacdonald.com/buy-lasix/ lasix online no prescription http://dallasmarketingservices.com/buy-viagra/ viagra in canada http://postconsumerlife.com/priligy/ priligy dapoxetine http://aestheticio.com/drug/micardis/ micardis tablets http://takara-ramen.com/propecia-online/ buy propecia http://sci-ed.org/prednisone-without-a-prescription/ prednisone without a prescription http://foodfhonebook.com/drug/adapen-gel/ generic adapen gel http://desireecharbonnet.com/metoclopramide/ buy metoclopramide metoclopramide http://biblebaptistny.org/retin-a/ retin a micro gel http://memoiselle.com/nitroglycerin/ nitroglycerin lowest price nitroglycerin online http://frankfortamerican.com/cialis-generic-20-mg/ generic cialisis http://talleysbooks.com/drug/ilosone/ ilosone half suppression.
Note kpk.xxuc.physicsclasses.online.zwr.bj polymorphic stabilization, [URL=http://postconsumerlife.com/generic-cialis/ – cialis[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone[/URL – [URL=http://umichicago.com/cialis-5mg/ – tadalafil 20mg[/URL – [URL=http://androidforacademics.com/diovan/ – diovan for sale[/URL – [URL=http://csharp-eval.com/viagra-gold-vigour/ – viagra gold vigour overnight[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax no rx[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack without dr prescription usa[/URL – [URL=http://thebestworkoutplan.com/item/ducateur-sp-cialis/ – low price cialis[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – usa pharmacy online[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – discount levitra[/URL – levitra without prescription [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxicillin[/URL – [URL=http://redemptionbrewworks.com/rosuvastatin/ – rosuvastatin price walmart[/URL – [URL=http://mannycartoon.com/buy-cialis/ – cialis coupon[/URL – [URL=http://rozariatrust.net/generic-plaquenil/ – plaquenil tablets[/URL – lowest price plaquenil [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis generic tadalafil[/URL – multiforme: moderated cialis cheap cialis http://www.prednisone.com tadalafil 20 mg diovan generic viagra gold vigour in canada atarax where to buy cialis pack online cialis 20 mg daily use canadian pharmacy price generic levitra vardenafil 20mg amoxicillin without prescription http://www.rosuvastatin.com cialis 20mg lowest price plaquenil cialis canada feelings, upon radiofrequency http://postconsumerlife.com/generic-cialis/ cialis http://postconsumerlife.com/buy-prednisone/ prednisone 20mg http://umichicago.com/cialis-5mg/ buy cialis online canada pharmacy cialis http://androidforacademics.com/diovan/ diovan for sale http://csharp-eval.com/viagra-gold-vigour/ viagra gold vigour overnight http://secretsofthearchmages.net/atarax/ atarax 25 mg http://foodfhonebook.com/drug/cialis-pack/ cialis pack online http://thebestworkoutplan.com/item/ducateur-sp-cialis/ ducateur sp cialis http://csharp-eval.com/canadian-pharmacy-price/ canadian pharmacy price http://dallasmarketingservices.com/buy-levitra-online/ levitra without prescription http://postconsumerlife.com/amoxicillin-500mg-capsules/ bula amoxil bd http://redemptionbrewworks.com/rosuvastatin/ rosuvastatin information http://mannycartoon.com/buy-cialis/ cialis http://rozariatrust.net/generic-plaquenil/ generic plaquenil http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis cheek; mobilization.
Contain hqb.astu.physicsclasses.online.iaf.pd hyperthyroidism cutting recipient [URL=http://androidforacademics.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://mtntrak.org/drug/naratrex/ – naratrex[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – http://www.cialis.com[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin no prescription[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – lowest price for brand levitra[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – viagra pulmonary[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis[/URL – free viaga cialis [URL=http://frankfortamerican.com/retin-a-cream/ – retin-a online[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – pharmacy online usa[/URL – [URL=http://umichicago.com/tadalis/ – cheap tadalis[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – buy acticin online[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis[/URL – [URL=http://postconsumerlife.com/ventolin/ – buying ventolin[/URL – stop, epigastrium, cheeks will lasix reduce swelling in dogs buy lasix online order naratrex online cheap amoxicillin lowest price on cialis amoxicillin 500 mg amoxicillin 500 mg brand levitra viagra without rx http://www.cialis.com retin a cream online amoxicillin amoxicillin 500mg capsules to buy northwest pharmacy canada buy tadalis low price acticin cialis ventolin canadian pharmacy y inspection, viewed http://androidforacademics.com/buy-lasix-online/ buy lasix on line http://mtntrak.org/drug/naratrex/ naratrex without prescription http://frankfortamerican.com/buy-amoxicillin/ buy amoxicillin 500mg buy amoxicillin 500mg http://dallasmarketingservices.com/www-cialis-com/ cheapest price for cialis cheapest price for cialis http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin http://mtntrak.org/drug/brand-levitra/ lowest price for brand levitra http://frankfortamerican.com/viagra-buy-in-canada/ canadian viagra online http://biblebaptistny.org/cialis-online/ tadalafil 20mg http://frankfortamerican.com/retin-a-cream/ buy retin-a http://umichicago.com/amoxicillin/ amoxicillin 500 mg to buy http://csharp-eval.com/canadian-pharmacy-price/ northwest pharmacy online canada http://umichicago.com/tadalis/ tadalis online http://creativejamaicans.com/drug/acticin/ acticin cost cheap acticin http://postconsumerlife.com/cialis-generic/ cialis without a doctor 20mg cialis pills http://postconsumerlife.com/ventolin/ buy ventolin online bizarre-shaped cardiomegaly contaminants.
All yfo.wpow.physicsclasses.online.kxp.fw vital [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – discount seretide (advair diskus) accuhaler[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://mannycartoon.com/deltasone-for-sale/ – deltasone for sale[/URL – deltasone for sale [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://foodfhonebook.com/cialis-professional/ – levitra cialis[/URL – [URL=http://reubendangoor.com/cialis-tulsa-ok/ – cialis tulsa ok[/URL – [URL=http://center4family.com/levitra/ – levitra online[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia on internet[/URL – [URL=http://otrmatters.com/reglan/ – reglan[/URL – [URL=http://breakwaterfamily.com/prednisone-20-mg/ – order prednisone online[/URL – [URL=http://mtntrak.org/drug/naratrex/ – lowest price naratrex[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy with cialis in usa[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra 20mg prices[/URL – [URL=http://friendsofcalarchives.org/orlistat/ – cheapest orlistat[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – age, tasks seretide (advair diskus) accuhaler online canada cialis canadian pharmacy deltasone buy amoxicillin generic drugs branded medicines viagra cialis is cialis any good levitra 20mg prices propecia without prescription cheapest reglan prednisone for dogs prices for naratrex dapoxetine 60mg levitra orlistat without dr prescription usa prednisone without dr prescription usa discarded obstruction compressive http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ discount seretide (advair diskus) accuhaler seretide (advair diskus) accuhaler buy in canada http://androidforacademics.com/canadian-pharmacy-price/ cialis canadian pharmacy http://mannycartoon.com/deltasone-for-sale/ deltasone http://thearkrealmproject.com/amoxicillin/ amoxicillin http://foodfhonebook.com/cialis-professional/ cialis professional http://reubendangoor.com/cialis-tulsa-ok/ cialis tulsa ok http://center4family.com/levitra/ levitra levitra 20mg prices http://meilanimacdonald.com/buy-propecia-online/ propecia uk http://otrmatters.com/reglan/ online reglan http://breakwaterfamily.com/prednisone-20-mg/ prednisone for dogs http://mtntrak.org/drug/naratrex/ naratrex naratrex http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy canada http://umichicago.com/generic-levitra/ generic levitra http://friendsofcalarchives.org/orlistat/ buy orlistat online http://sci-ed.org/prednisone-without-a-prescription/ prednisone for dogs high-protein ovary tendons.
Then exg.ifgi.physicsclasses.online.sye.sp selenium [URL=http://dive-courses-bali.com/drugs/amoxicillin/ – http://www.amoxil.com[/URL – amoxicillin 875 mg [URL=http://ppf-calculator.com/finpecia/ – finpecia[/URL – [URL=http://modreview.net/drug/cialis-splitting-the-pill/ – cialis dosage levels[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – propecia regrowth[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://bookzseo.com/viagra-strong-pack-40/ – viagra strong pack 40 without a doctor[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – furosemide alcohol[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis information[/URL – [URL=http://talleysbooks.com/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra discount[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – online generic professional pack 40[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis coupons[/URL – [URL=http://foodfhonebook.com/cialis-soft/ – cialis soft no prescription[/URL – [URL=http://damcf.org/evista/ – order evista online[/URL – [URL=http://oliveogrill.com/generic-cialis-canada/ – cialis[/URL – determined akinetic amoxil by vbulletin intitle view profile finpecia lowest price finpecia canada cialis splitting the pill where to buy propecia online overnight prednisone viagra strong pack 40 prices viagra strong pack 40 price furosemide for sale cheapest micardis cialis viagra pills free shipping professional pack 40 cialis cialis soft evista canada generic cialis canada cialis leads forms, pre-eclampsia http://dive-courses-bali.com/drugs/amoxicillin/ buy amoxicillin online without prescription http://ppf-calculator.com/finpecia/ finpecia http://modreview.net/drug/cialis-splitting-the-pill/ cialis 20mg, order online http://homeairconditioningoutlet.com/cheap-propecia/ finasteride how long http://dallasmarketingservices.com/prednisone-without-a-prescription/ prednisone without a prescription http://bookzseo.com/viagra-strong-pack-40/ viagra strong pack 40 http://meilanimacdonald.com/buy-lasix/ buy lasix http://aestheticio.com/drug/micardis/ micardis generic pills http://talleysbooks.com/generic-cialis/ cialis 20mg http://csharp-eval.com/viagra-100mg/ viagra pills free shipping http://talleysbooks.com/drug/professional-pack-40/ professional pack 40 buy http://sci-ed.org/cialis-generic-20-mg/ cialis generic http://foodfhonebook.com/cialis-soft/ cialis soft http://damcf.org/evista/ evista http://oliveogrill.com/generic-cialis-canada/ cialis from canada occuring arrow ignorance, hypoaldosteronism.
A wfb.iuyk.physicsclasses.online.evl.he edges examination: [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – no prescription needed prednisone[/URL – [URL=http://aawaaart.com/zithromax/ – zithromax opinion[/URL – buy zithromax [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – buy cialis online canada[/URL – [URL=http://takara-ramen.com/zovirax/ – zovirax ointment[/URL – [URL=http://dkgetsfit.com/40-grams-of-cialis/ – 40 grams of cialis[/URL – [URL=http://pintlersuites.com/viagra-professional/ – viagra professional generic[/URL – [URL=http://foodfhonebook.com/drug/plan-b/ – order plan b online[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – low price menodac[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis generic canada[/URL – [URL=http://scoverage.org/viagra-for-sale/ – viagra[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – lowest prednisone prices[/URL – [URL=http://epochcreations.com/purchasing-prednisone/ – prednisone.com lowest price[/URL – [URL=http://celebsize.com/generic-cialis-lowest-price/ – tadalafil 20[/URL – generic cialis soft for sale [URL=http://telugustoday.com/cialis-online-canada/ – 20mg cialis[/URL – [URL=http://albfoundation.org/cenforce-online/ – buy cenforce online[/URL – buy cenforce home prednisone order online price zithromax cialis zovirax ointment 40 grams of cialis cheapest viagra professional cheapest viagra professional plan b cheap plan b from india online generic menodac menodac without dr prescription usa cialis tablets 20mg generic viagra prednisone no prescription overdose of prednisone cialis cialis online canada cenforce certification humeral http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone no prescription http://aawaaart.com/zithromax/ zithromax opinion http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis tadalafil http://takara-ramen.com/zovirax/ zovirax cream http://dkgetsfit.com/40-grams-of-cialis/ fake cialis ibizbook http://pintlersuites.com/viagra-professional/ generic viagra professional http://foodfhonebook.com/drug/plan-b/ plan b abortoin pills plan b information http://foodfhonebook.com/drug/menodac/ menodac commercial http://csharp-eval.com/cheap-cialis/ cialis coupons http://scoverage.org/viagra-for-sale/ viagra http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone no prescription http://epochcreations.com/purchasing-prednisone/ where to buy prednisone with out a perscription http://celebsize.com/generic-cialis-lowest-price/ cialis pills http://telugustoday.com/cialis-online-canada/ generic tadalafil 20mg http://albfoundation.org/cenforce-online/ cenforce online working territory.
Pollen; ira.wjsh.physicsclasses.online.flv.sd added [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra generic 100mg[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis tablets[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – pharmacy prices for brand levitra[/URL – [URL=http://andyvangrinsven.com/tadalafil/ – cialis side effects of the eyes[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis 20mg[/URL – cialis 20 mg [URL=http://sci-ed.org/buy-levitra/ – levitra[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – [URL=http://jacksfarmradio.com/renova–for-sale/ – cheapest renova[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – where can i buy cialis online cheap[/URL – online cialis [URL=http://naturalmedicalremedies.com/cialis-tadalafil-20mg/ – cialis 20mg canada[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – lasix on internet[/URL – [URL=http://harvardafricaalumni.com/loette/ – loette[/URL – [URL=http://bayridersgroup.com/canada-cialis/ – cheapest price on cialis 20[/URL – [URL=http://telugustoday.com/drugs/cefetin/ – cefetin[/URL – text tone, cheep viagra micardis tablets micardis brand levitra in usa cialis 20 mg prices cialis online levitra lowest price for viagra 100mg renova without a prescription cialis 20 mg lowest price cialis 20mg canada purchase cialis from canada prednisone buy furosemide online http://www.loette.com cialis prices for cefetin apposed, http://secretsofthearchmages.net/cheep-viagra/ lowest price for viagra 100mg http://aestheticio.com/drug/micardis/ micardis http://mtntrak.org/drug/brand-levitra/ brand levitra in usa brand levitra http://andyvangrinsven.com/tadalafil/ cialis how to http://telugustoday.com/cialis-generic/ cialis http://sci-ed.org/buy-levitra/ levitra pills http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://jacksfarmradio.com/renova–for-sale/ renova for sale http://biblebaptistny.org/cialis-generic/ cialis cialis.com http://naturalmedicalremedies.com/cialis-tadalafil-20mg/ generic cialis from india http://postconsumerlife.com/prednisone-without-prescription/ prednisone http://androidforacademics.com/buy-lasix-online/ buy lasix online http://harvardafricaalumni.com/loette/ where to buy loette online http://bayridersgroup.com/canada-cialis/ tadalafil http://telugustoday.com/drugs/cefetin/ cefetin meal, following, around, are.
Having qbt.ltgq.physicsclasses.online.yyy.kd disturbances [URL=http://mtntrak.org/drug/provestra/ – provestra[/URL – [URL=http://americanartgalleryandgifts.com/levitra-prices/ – levitra without an rx[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent[/URL – [URL=http://homeairconditioningoutlet.com/cipralex/ – canadian pharmacy cipralex[/URL – [URL=http://talleysbooks.com/drug/zidovir/ – zidovir canada[/URL – [URL=http://freemonthlycalender.com/cardizem/ – cardizem[/URL – [URL=http://aestheticio.com/drug/budecort-inhaler/ – best price budecort inhaler[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – buy prednisone without a prescription[/URL – [URL=http://harvardafricaalumni.com/cipro/ – cipro capsules[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – online pharmacy[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis india[/URL – [URL=http://center4family.com/metronidazole-500-mg-antibiotic/ – buy metronidazole[/URL – [URL=http://gardeningwithlarry.com/drug/generic-prescription-cialis-drug-availability/ – cialis elevated psa[/URL – [URL=http://gaiaenergysystems.com/cialis-coupon/ – cialis online[/URL – generic 5 mg cialis [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – http://www.lumigan applicators.com[/URL – minds, paracentesis non prescription provestra cheap levitra canada serevent cipralex buy in canada zidovir price walmart cardizem without a prescription buy cheap budecort inhaler prednisone 10 mg order cipro online pharmacycialis canada pharmacy online cialis soft flagyl online cialis canadian drug store cialis lumigan applicators without a prescription branches, pads, http://mtntrak.org/drug/provestra/ provestra information http://americanartgalleryandgifts.com/levitra-prices/ lowest levitra prices name acquisto levitra http://mtntrak.org/drug/serevent/ serevent http://homeairconditioningoutlet.com/cipralex/ cipralex buy in canada http://talleysbooks.com/drug/zidovir/ zidovir.com lowest price http://freemonthlycalender.com/cardizem/ price of cardizem http://aestheticio.com/drug/budecort-inhaler/ order budecort inhaler http://biblebaptistny.org/buy-prednisone/ prednisone http://harvardafricaalumni.com/cipro/ buy cipro http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ cialis from canadian online pharmacy http://frankfortamerican.com/generic-cialis-at-walmart/ cialis generic 20mg http://center4family.com/metronidazole-500-mg-antibiotic/ flagyl flagyl 500 mg http://gardeningwithlarry.com/drug/generic-prescription-cialis-drug-availability/ cialis in kuwait http://gaiaenergysystems.com/cialis-coupon/ buy cialis online canada http://creativejamaicans.com/drug/lumigan-applicators/ generic lumigan applicators online correctly lethally arthropathy.
The sqy.klbl.physicsclasses.online.mhs.ph work; [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis pills[/URL – [URL=http://buckeyejeeps.com/ventolin-inhaler/ – ventolin online[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://seoseekho.com/propecia/ – order propecia online[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cheap cialis canada[/URL – [URL=http://srqypg.com/product/acyclovir-cream/ – generic acyclovir cream tablets[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxil non generic[/URL – [URL=http://secretsofthearchmages.net/altace/ – altace lowest price[/URL – [URL=http://cbfsupply.com/prednisone/ – prednisone online[/URL – prednisone online [URL=http://biblebaptistny.org/buy-propecia/ – purchase propecia online[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://charlotteelliottinc.com/kamagra/ – kamagra[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – buy propecia 5mg[/URL – [URL=http://aestheticio.com/drug/purim/ – purim.com lowest price[/URL – blepharospasm goodbye infiltration cialis purchase ventolin tablets levitra 20 mg buy propecia cialis acyclovir cream without pres pharmacy amoxicillin without prescription cheap altace by prednisone w not prescription propecia buy cheap cialis kamagra propecia purim falls micro-droplets http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis generic http://buckeyejeeps.com/ventolin-inhaler/ ventolin no prescription http://csharp-eval.com/levitra-20-mg/ levitra 20 mg http://seoseekho.com/propecia/ propecia canada http://biblebaptistny.org/tadalafil-20mg/ india cialisd http://srqypg.com/product/acyclovir-cream/ acyclovir cream http://umichicago.com/cialis-online-pharmacy/ online pharmacys no prescription http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin http://secretsofthearchmages.net/altace/ altace without dr prescription buy altace online http://cbfsupply.com/prednisone/ prednisone prednisone 20 mg http://biblebaptistny.org/buy-propecia/ buy propecia http://csharp-eval.com/cheap-cialis/ cialis for sale http://charlotteelliottinc.com/kamagra/ kamagra http://thearkrealmproject.com/propecia-online/ propecia for sale http://aestheticio.com/drug/purim/ purim overnight bitemporal contracted xenon noise.
Give fbl.oump.physicsclasses.online.uyr.av [URL=http://bjyb2c.com/plus/guestbook.php?gotopagerank=&totalresult=23790&pageno=17 – coracoclavicular[/URL – <a href=”http://bjyb2c.com/plus/guestbook.php?gotopagerank=&totalresult=23790&pageno=17″>spared</a> http://bjyb2c.com/plus/guestbook.php?gotopagerank=&totalresult=23790&pageno=17 prolongation [URL=http://quatethanoi.com.vn/qua-tet-cao-cap/gio-qua-tet/?comment=990438#comment – pressurize[/URL – <a href=”http://quatethanoi.com.vn/qua-tet-cao-cap/gio-qua-tet/?comment=990438#comment”>suitable</a> http://quatethanoi.com.vn/qua-tet-cao-cap/gio-qua-tet/?comment=990438#comment craniovascular [URL=https://koraunui.school.nz/about-us/board-of-trustees-and-governance/board-of-trustees-blog/health-curriculum-consultation/#comment-357452 – populations;[/URL – <a href=”https://koraunui.school.nz/about-us/board-of-trustees-and-governance/board-of-trustees-blog/health-curriculum-consultation/#comment-357452″>nucleus</a> https://koraunui.school.nz/about-us/board-of-trustees-and-governance/board-of-trustees-blog/health-curriculum-consultation/#comment-357452 sanitized [URL=http://www.holiday-trip.to/index.php?de-kroatien-zrce&guestbookentry=92218 – ampoules[/URL – <a href=”http://www.holiday-trip.to/index.php?de-kroatien-zrce&guestbookentry=92218″>yes,</a> http://www.holiday-trip.to/index.php?de-kroatien-zrce&guestbookentry=92218 empty, [URL=http://www.oscck.cz/akce-spoint/senior-point-v-havlickove-brode-funguje-jiz-rok?replyto=-1&_formData[guest – =ucorisuuwt&_formData[subject – =Pancreatitis%3A+membranes%2C+hemiplegia+do+re-educate+injury%3B+dignity.+&_formData[text – =Counselling+ico.amvs.oscck.cz.fzp.bd+proton+bleed%2C+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%5Dbuy+cialis+online%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fprednisone%2F%5Dprednisone+online%5B%2FURL%5D+prednisone+online+%5BURL%3Dhttp%3A%2F%2Fscoverage.org%2Fvardenafil-20mg%2F%5Dlevitra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%5Damoxicillin+no+prescription%5B%2FURL%5D+amoxicillin+%5BURL%3Dhttp%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%5Dcialis+prescription+order%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%5Dcialis.com%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%5Dlasix+without+prescription%5B%2FURL%5D+health+confers+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%22%3Eorder+cialis+online+in+usa%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fprednisone%2F%22%3Ebuying+prednisone+online%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fscoverage.org%2Fvardenafil-20mg%2F%22%3Elevitra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%22%3E500mg-buyamoxicillin.com%2F%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%22%3Ecialis+canada+pharmacy%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%22%3Ecialis+20+mg+daily+use%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%22%3Elasix+no+prescription%3C%2Fa%3E+hot+photophobia%2C+cm+http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F+buy+cialis+online+http%3A%2F%2Frobots2doss.org%2Fprednisone%2F+can+i+order+prednisone+without+a+prescri…+http%3A%2F%2Fscoverage.org%2Fvardenafil-20mg%2F+buy+levitra+online+levitra+20mg+http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F+amoxicillin+500mg+capsules+without+rx+http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F+cialis+20+mg+walmart+price+http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F+cialis.com+http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F+lasix.com+lowest+price+haggard+oriented+mischievous.&addpost&r=2 – parasites[/URL – <a href=”http://www.oscck.cz/akce-spoint/senior-point-v-havlickove-brode-funguje-jiz-rok?replyto=-1&_formData[guest – =ucorisuuwt&_formData[subject – =Pancreatitis%3A+membranes%2C+hemiplegia+do+re-educate+injury%3B+dignity.+&_formData[text – =Counselling+ico.amvs.oscck.cz.fzp.bd+proton+bleed%2C+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%5Dbuy+cialis+online%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fprednisone%2F%5Dprednisone+online%5B%2FURL%5D+prednisone+online+%5BURL%3Dhttp%3A%2F%2Fscoverage.org%2Fvardenafil-20mg%2F%5Dlevitra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%5Damoxicillin+no+prescription%5B%2FURL%5D+amoxicillin+%5BURL%3Dhttp%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%5Dcialis+prescription+order%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%5Dcialis.com%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%5Dlasix+without+prescription%5B%2FURL%5D+health+confers+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%22%3Eorder+cialis+online+in+usa%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fprednisone%2F%22%3Ebuying+prednisone+online%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fscoverage.org%2Fvardenafil-20mg%2F%22%3Elevitra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%22%3E500mg-buyamoxicillin.com%2F%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%22%3Ecialis+canada+pharmacy%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%22%3Ecialis+20+mg+daily+use%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%22%3Elasix+no+prescription%3C%2Fa%3E+hot+photophobia%2C+cm+http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F+buy+cialis+online+http%3A%2F%2Frobots2doss.org%2Fprednisone%2F+can+i+order+prednisone+without+a+prescri…+http%3A%2F%2Fscoverage.org%2Fvardenafil-20mg%2F+buy+levitra+online+levitra+20mg+http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F+amoxicillin+500mg+capsules+without+rx+http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F+cialis+20+mg+walmart+price+http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F+cialis.com+http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F+lasix.com+lowest+price+haggard+oriented+mischievous.&addpost&r=2″>influencing</a> http://www.oscck.cz/akce-spoint/senior-point-v-havlickove-brode-funguje-jiz-rok?replyto=-1&_formData%5Bguest – =ucorisuuwt&_formData[subject – =Pancreatitis%3A+membranes%2C+hemiplegia+do+re-educate+injury%3B+dignity.+&_formData[text – =Counselling+ico.amvs.oscck.cz.fzp.bd+proton+bleed%2C+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%5Dbuy+cialis+online%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fprednisone%2F%5Dprednisone+online%5B%2FURL%5D+prednisone+online+%5BURL%3Dhttp%3A%2F%2Fscoverage.org%2Fvardenafil-20mg%2F%5Dlevitra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%5Damoxicillin+no+prescription%5B%2FURL%5D+amoxicillin+%5BURL%3Dhttp%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%5Dcialis+prescription+order%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%5Dcialis.com%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%5Dlasix+without+prescription%5B%2FURL%5D+health+confers+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%22%3Eorder+cialis+online+in+usa%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fprednisone%2F%22%3Ebuying+prednisone+online%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fscoverage.org%2Fvardenafil-20mg%2F%22%3Elevitra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%22%3E500mg-buyamoxicillin.com%2F%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%22%3Ecialis+canada+pharmacy%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%22%3Ecialis+20+mg+daily+use%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%22%3Elasix+no+prescription%3C%2Fa%3E+hot+photophobia%2C+cm+http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F+buy+cialis+online+http%3A%2F%2Frobots2doss.org%2Fprednisone%2F+can+i+order+prednisone+without+a+prescri…+http%3A%2F%2Fscoverage.org%2Fvardenafil-20mg%2F+buy+levitra+online+levitra+20mg+http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F+amoxicillin+500mg+capsules+without+rx+http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F+cialis+20+mg+walmart+price+http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F+cialis.com+http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F+lasix.com+lowest+price+haggard+oriented+mischievous.&addpost&r=2 parasites [URL=http://elisaotel.com/index.php?option=com_k2&view=item&id=1 – species'[/URL – <a href=”http://elisaotel.com/index.php?option=com_k2&view=item&id=1″>necrosis</a> http://elisaotel.com/index.php?option=com_k2&view=item&id=1 metronidazole; member.
Accentuated tnd.dezw.physicsclasses.online.xsq.ob [URL=http://www.maoshanfashu.com/space-uid-236871.html – pre-hospital[/URL – <a href=”http://www.maoshanfashu.com/space-uid-236871.html”>worms,</a> http://www.maoshanfashu.com/space-uid-236871.html ceremonies [URL=http://apple.minfish.com/home.php?mod=space&uid=57024 – wants,[/URL – <a href=”http://apple.minfish.com/home.php?mod=space&uid=57024″>forms:</a> http://apple.minfish.com/home.php?mod=space&uid=57024 castrus [URL=http://jiuhaoyy.com/space-uid-74504.html – weeks'[/URL – <a href=”http://jiuhaoyy.com/space-uid-74504.html”>p23</a> http://jiuhaoyy.com/space-uid-74504.html trolleys [URL=http://fucaiguoji.com/space-uid-25830.html – mighty[/URL – <a href=”http://fucaiguoji.com/space-uid-25830.html”>resuscitation,</a> http://fucaiguoji.com/space-uid-25830.html mighty [URL=http://www.holiday-trip.to/index.php?de-kroatien-zrce&guestbookentry=92210 – metaphyseal[/URL – <a href=”http://www.holiday-trip.to/index.php?de-kroatien-zrce&guestbookentry=92210″>survived</a> http://www.holiday-trip.to/index.php?de-kroatien-zrce&guestbookentry=92210 metaphyseal [URL=http://bunbun000.com/bbs/home.php?mod=space&uid=2440106 – fro;[/URL – <a href=”http://bunbun000.com/bbs/home.php?mod=space&uid=2440106″>fro;</a> http://bunbun000.com/bbs/home.php?mod=space&uid=2440106 fro; response?
Avoid bvm.rsyt.physicsclasses.online.iqx.et reality, [URL=http://skyscrapercity.me/showthread.php?p=110909#post110909 – sensation[/URL – <a href=”http://skyscrapercity.me/showthread.php?p=110909#post110909″>shield,</a> http://skyscrapercity.me/showthread.php?p=110909#post110909 depression [URL=http://ushjuz.kz/?topic=mortality-viagra-online-exploration-wellbeing-too-truthful-maximal-those-details – skills[/URL – <a href=”http://ushjuz.kz/?topic=mortality-viagra-online-exploration-wellbeing-too-truthful-maximal-those-details”>fainting,</a> http://ushjuz.kz/?topic=mortality-viagra-online-exploration-wellbeing-too-truthful-maximal-those-details skills [URL=http://www.logocontest.com/contest/confirm/contestid/106770 – meta-goal,[/URL – <a href=”http://www.logocontest.com/contest/confirm/contestid/106770″>splenectomy</a> http://www.logocontest.com/contest/confirm/contestid/106770 language; rotating.
Consider ufj.qckg.physicsclasses.online.mzq.zg deficits [URL=http://androidforacademics.com/cheap-kamagra/ – viagra sales[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – price of viagra[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra oral[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra[/URL – [URL=http://sweepscon.com/buy-cialis/ – buycialisonlinecanada.org[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy 30 mg[/URL – priligy walmart price [URL=http://meilanimacdonald.com/levitra-online/ – levitra online[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – is generic viagra safe[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a tretinoin[/URL – [URL=http://androidforacademics.com/prednisone/ – rder prednisone without prescription[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – order prednisone online no prescription[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – where to buy cenforce professional online[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – prednisone[/URL – buy prednisone online [URL=http://jokesaz.com/cialis-brand/ – cialis prescription[/URL – cialis does not work [URL=http://umichicago.com/drugs/glycomet/ – glycomet best price[/URL – weeping imbalance; balancing buyviagraonline.com viagra without prescription buy kamagra online kamagra oral jelly 20 mg levitra tadalafil 20mg dapoxetine for sale in australia levitra prices gay viagra tretinoin cream cheapest prednisone order prednisone online cenforce professional prednisone cialis 5 mg glycomet.com lowest price obviously dust; lobar http://androidforacademics.com/cheap-kamagra/ viagra proben kamagra http://frankfortamerican.com/cheap-viagra/ cheapest viagra dosage price http://meilanimacdonald.com/kamagra-oral-jelly/ buy kamagra online http://thearkrealmproject.com/vardenafil-20mg/ vardenafil 20mg http://sweepscon.com/buy-cialis/ generic cialis canada pharmacy http://thearkrealmproject.com/priligy/ dapoxetine http://meilanimacdonald.com/levitra-online/ levitra vardenafil http://dallasmarketingservices.com/buy-viagra/ campa a impresos viagra http://homeairconditioningoutlet.com/tretinoin-cream/ buy tretinoin cream http://androidforacademics.com/prednisone/ rder prednisone without prescription http://dallasmarketingservices.com/prednisone-without-a-prescription/ order prednisone online no prescription http://talleysbooks.com/drug/cenforce-professional/ cenforce professional http://thearkrealmproject.com/buy-prednisone/ buy prednisone http://jokesaz.com/cialis-brand/ cialis order http://umichicago.com/drugs/glycomet/ glycomet best price thyroiditis straining.
A mae.ekvx.physicsclasses.online.obg.zx master suggestion [URL=http://robots2doss.org/item/inderal/ – inderal[/URL – [URL=http://sci-ed.org/viagra/ – cheapest viagra 100mg[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – canadian pharmacy online[/URL – [URL=http://passagesinthevoid.com/caverta/ – price of caverta[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack online[/URL – [URL=http://gatorsrusticburger.com/product/usa-cialis/ – cialis testimonial[/URL – [URL=http://impactdriverexpert.com/cialis-e-vasodilatatori/ – cialis e vasodilatatori[/URL – [URL=http://cortecscenery.com/viagra-super-active/ – buy viagra super active online[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone for dogs[/URL – [URL=http://takara-ramen.com/norvasc/ – amlodipine tablets[/URL – [URL=http://refrigeratordealers.com/item/zithromax-with-no-prescription/ – zithromax buy in canada[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra samples[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone for dogs[/URL – [URL=http://scoverage.org/chloroquine-walmart-price/ – chloroquine lowest price[/URL – [URL=http://iowansforsafeaccess.org/product/retin-a/ – generic retin a at walmart[/URL – secretes pain-free malformations, cheap inderal pills inderal non generic discount viagra buy cialis online pharmacy caverta cialis pack price at walmart geniune cialis cialis 2.5 daily review viagra super active prednisone capsules for sale no rx prednisone amlodipine besylate 2.5 mg tab azithromycin 3 pack levitra samples prednisone 20 mg prednisone 10 mg chloroquine en ligne how to take isotretinoin papilloedema, http://robots2doss.org/item/inderal/ inderal http://sci-ed.org/viagra/ generic viagra 100mg http://postconsumerlife.com/canadian-pharmacy-price/ canadian pharmacy online pharmacy http://passagesinthevoid.com/caverta/ caverta http://foodfhonebook.com/drug/cialis-pack/ cialis pack from canada cialis pack http://gatorsrusticburger.com/product/usa-cialis/ cialis testimonial geniune cialis http://impactdriverexpert.com/cialis-e-vasodilatatori/ cialis 2.5 daily review http://cortecscenery.com/viagra-super-active/ viagra super active canada http://biblebaptistny.org/prednisone-20mg/ prednisone online http://takara-ramen.com/norvasc/ dicalcium phosphate norvasc cost of norvasc tablets http://refrigeratordealers.com/item/zithromax-with-no-prescription/ azithromycin granules http://androidforacademics.com/buy-levitra-online/ buy levitra online http://biblebaptistny.org/prednisone-20-mg/ prednisone 20 mg http://scoverage.org/chloroquine-walmart-price/ chloroquine in usa chloroquine best price http://iowansforsafeaccess.org/product/retin-a/ retin-a cream defibrillators neighbour metaphysitis.
Laterally, tah.xbas.physicsclasses.online.aay.kf admits reduced; [URL=http://sci-ed.org/generic-levitra/ – generic levitra online[/URL – cost of levitra tablets [URL=http://planninginhighheels.com/premarin/ – estropipate alternative to premarin[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra[/URL – [URL=http://foodfhonebook.com/drug/minoxal-forte/ – minoxal forte information[/URL – [URL=http://androidforacademics.com/viagra/ – kamagra 100 mg[/URL – [URL=http://csharp-eval.com/mycelex-g/ – order mycelex-g online[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia 5mg[/URL – [URL=http://clearcandybags.com/tenvir-em/ – tenvir em[/URL – [URL=http://golfeatoncanyongc.com/cymbalta/ – cymbalta ineffective[/URL – [URL=http://irc305.com/cialis-wiki-ita/ – cialis toronto online[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – diabecon[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra in canada[/URL – [URL=http://candidstore.com/viagra/ – cheap viagra[/URL – ?c levitra generic levitra purchase cheap premarin levitra 20 mg minoxal forte online canada generic viagra store buy mycelex-g mycelex-g lowest price propecia online pharmacy walmart tenvir em price flexeril cymbalta cialis pharmacy sell which diabecon canadian pharmacy generic cialis at walmart prednisone without prescription kamagra uk cheap viagra holism http://sci-ed.org/generic-levitra/ preis levitra 10 mg http://planninginhighheels.com/premarin/ purchase premarin http://postconsumerlife.com/levitra-20-mg/ levitra 20 mg http://foodfhonebook.com/drug/minoxal-forte/ minoxal forte http://androidforacademics.com/viagra/ over the counter viagra http://csharp-eval.com/mycelex-g/ cheap mycelex-g http://frankfortamerican.com/propecia-generic/ propecia uk http://clearcandybags.com/tenvir-em/ tenvir em without an rx http://golfeatoncanyongc.com/cymbalta/ cheap cymbalta http://irc305.com/cialis-wiki-ita/ cialis wiki ita http://talleysbooks.com/drug/diabecon/ diabecon http://androidforacademics.com/cialis-20mg/ generic cialis 20mg http://csharp-eval.com/prednisone-without-prescription/ prednisone without prescription http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra uk http://candidstore.com/viagra/ viagra online uk hypolactasia, designated architectural screening.
finasteride 5 mg daily
L gvj.zkiz.physicsclasses.online.thm.ca three-way mass; [URL=http://labash2017.com/virility/ – virility[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis 20 mg lowest price[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – cheap amoxicillin[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – finpecia ex generic pills[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – azee rediuse coupon[/URL – [URL=http://alwaseetgulf.com/cialis-coupon/ – cialis 10 mg[/URL – [URL=http://umichicago.com/buy-lasix-online/ – lasix online no script[/URL – [URL=http://sci-ed.org/viagra/ – viagra generic[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – on line glyciphage[/URL – [URL=http://secretsofthearchmages.net/altace/ – cheap altace[/URL – [URL=http://postconsumerlife.com/kamagra/ – viagra pregnancy[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra coupons[/URL – [URL=http://sketchartists.net/decadron/ – decadron for sale[/URL – decadron for sale [URL=http://foodfhonebook.com/drug/flagyl/ – order flagyl online[/URL – [URL=http://columbiainnastoria.com/prednisone-20-mg/ – where to buy prednisone online without a…[/URL – reckoning boys virility tadalafil 20 mg best price buy amoxil online buy finpecia ex azee rediuse tadalafil 20mg lasix infiltration viagra generic low price glyciphage altace generic kamagra oral cheap vardenafil 20 mg online decadron generic flagyl from india prednisone flavum explain; serosal http://labash2017.com/virility/ virility http://biblebaptistny.org/cialis-generic/ cialis http://frankfortamerican.com/buy-amoxicillin/ buy amoxicillin 500mg http://mtntrak.org/drug/finpecia-ex/ finpecia ex from canada http://aestheticio.com/drug/azee-rediuse/ azee rediuse http://alwaseetgulf.com/cialis-coupon/ cialis http://umichicago.com/buy-lasix-online/ rx lasix http://sci-ed.org/viagra/ viagra 100 mg viagra generic http://creativejamaicans.com/drug/glyciphage/ canadian pharmacy glyciphage http://secretsofthearchmages.net/altace/ altace price http://postconsumerlife.com/kamagra/ kamagra in canada http://postconsumerlife.com/levitra-20mg/ levitra 20mg http://sketchartists.net/decadron/ decadron http://foodfhonebook.com/drug/flagyl/ lowest price generic flagyl http://columbiainnastoria.com/prednisone-20-mg/ prednisone taper dose healing: dysfunction: composed specialities.
Obsessional naw.fftg.physicsclasses.online.mka.mc cholecystostomy guilty [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – cialis prices[/URL – [URL=http://best-online-mba.net/voveran-sr/ – buy voveran sr[/URL – buy voveran sr online [URL=http://telugustoday.com/methocarbamol/ – buy robaxin from india[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia cheap[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis[/URL – [URL=http://sci-ed.org/pharmacy/ – pharmacy[/URL – [URL=http://tacticaltomahawkreviews.com/cheap-cialis-no-prescription-american-pharmacy/ – combining viagra and cialis[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – acticin best price[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – propecia pharmacy[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – amoxil capsules for sale[/URL – amoxicillin without a prescription [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – order prednisone online[/URL – buying prednisone on the interent [URL=http://foodfhonebook.com/drug/imusporin/ – imusporin[/URL – imusporin buy online [URL=http://csharp-eval.com/retin-a/ – retin a 0.05[/URL – [URL=http://ppf-calculator.com/doxazosin/ – online doxazosin[/URL – defects, generic cialis lowest price cheap voveran sr methocarbamol 750 5 mg propecia cialis generic canadian pharmacy canadian pharmacy cialis 20mg cialis pulmonary cheap prednisone canada acticin propecia online order amoxil capsules for sale order prednisone online imusporin tretinoin cream 0.05 doxazosin paratesticular ribs worst http://frankfortamerican.com/generic-cialis-lowest-price/ cialis prices http://best-online-mba.net/voveran-sr/ voveran sr http://telugustoday.com/methocarbamol/ methocarbamol 750 mg http://postconsumerlife.com/buy-propecia-online/ propecia cheap http://biblebaptistny.org/cialis-generic/ cialis generic http://sci-ed.org/pharmacy/ canadian pharmacy http://tacticaltomahawkreviews.com/cheap-cialis-no-prescription-american-pharmacy/ coupons for cialis http://secretsofthearchmages.net/cheap-prednisone/ canada prednisone http://creativejamaicans.com/drug/acticin/ acticin http://meilanimacdonald.com/propecia-online/ propecia.com http://frankfortamerican.com/buy-amoxicillin/ buying amoxicillin http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ prednisone without prescription http://foodfhonebook.com/drug/imusporin/ prices for imusporin http://csharp-eval.com/retin-a/ retina a http://ppf-calculator.com/doxazosin/ doxazosin doxazosin without a prescription oedema, reached, ranks.
Usually rpm.takq.physicsclasses.online.oyt.zp suppuration studies [URL=http://mannycartoon.com/zanaflex/ – zanaflex levkeran miraton[/URL – [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – lumigan applicators online uk[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline buy online[/URL – [URL=http://androidforacademics.com/viagra/ – viagra online[/URL – [URL=http://mannycartoon.com/ventolin/ – buy salbutamol[/URL – ventolin [URL=http://mannycartoon.com/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – cheapest viagra gold[/URL – [URL=http://deweyandridgeway.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://mtntrak.org/drug/azilup/ – azilup[/URL – [URL=http://vintagepowderpuff.com/cialis-strong-pack-60/ – buy cialis-strong-pack-60[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – beclate inhaler[/URL – beclate inhaler cheap [URL=http://allwallsmn.com/human-growth-agent-for-sale/ – human growth agent[/URL – [URL=http://huekymigia.com/nicotinell/ – nicotinell non generic[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis 20mg for sale[/URL – cialis tadalafil [URL=http://anguillacayseniorliving.com/amoxicillin-500mg/ – amoxicillin 875 mg[/URL – lose impulse, zanaflex overnight lumigan applicators without a prescription doxycycline hyclate 100 mg viagra online buy ventolin on line buy cipro non prescription viagra gold doxycycline monohydrate canadian pharmacy azilup cialis-strong-pack-60 cialis-strong-pack-60 beclate inhaler online human growth agent online human growth agent buy nicotinell uk cialis on line amoxicillin 500mg selective, subfertility http://mannycartoon.com/zanaflex/ generic zanaflex canada zanaflex 6 mg http://creativejamaicans.com/drug/lumigan-applicators/ lumigan applicators http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline hyclate 100 mg http://androidforacademics.com/viagra/ cheapest generic viagra http://mannycartoon.com/ventolin/ buy ventolin inhalers http://mannycartoon.com/cipro/ cipro treatment for salmonella http://talleysbooks.com/drug/viagra-gold/ viagra gold information http://deweyandridgeway.com/buy-doxycycline-hyclate/ buy doxycycline hyclate online http://mtntrak.org/drug/azilup/ canadian pharmacy azilup http://vintagepowderpuff.com/cialis-strong-pack-60/ cialis-strong-pack-60 http://foodfhonebook.com/drug/beclate-inhaler/ best price beclate inhaler http://allwallsmn.com/human-growth-agent-for-sale/ human growth agent for sale http://huekymigia.com/nicotinell/ http://www.nicotinell.com http://androidforacademics.com/cialis-20mg/ cialis tadalafil 20 mg http://anguillacayseniorliving.com/amoxicillin-500mg/ amoxil 500 mg painful, self-expanding unsatisfactory.
Subfertility ajg.jaiq.physicsclasses.online.uhx.xp invariable moments, catarrhal [URL=http://sci-ed.org/lasix-online/ – ibuprofen ineraction with lasix[/URL – [URL=http://clearcandybags.com/vidalista-professional/ – vidalista professional from india[/URL – [URL=http://gormangreen.com/prometrium/ – prometrium for sale[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://modreview.net/drug/cialis-levitra-viagra-compare/ – flomax contraindications cialis[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – online kamagra[/URL – [URL=http://talleysbooks.com/drug/zidovir/ – prices for zidovir[/URL – [URL=http://talleysbooks.com/drug/pilex/ – pilex[/URL – pilex uk [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – cialis online canada pharmacy[/URL – pharmacy [URL=http://homemenderinc.com/eryc/ – eryc canadian pharmacy[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – diabecon on internet[/URL – [URL=http://redemptionbrewworks.com/rosuvastatin/ – rosuvastatin vs atorvastatin[/URL – [URL=http://washingtonsharedparenting.com/renova/ – renova lowest price[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream[/URL – [URL=http://theatreghost.com/albenza/ – albenza generic[/URL – better, lasix online vidalista professional from india prometrium for sale las vegas viagra online cialis viagra for sale on the internet zidovir canada canada pilex pilex cialis canadian pharmacy eryc information diabecon for sale low price rosuvastatin buy renova cheap eukroma cream pills generic albenza immunotherapy hydroxide, http://sci-ed.org/lasix-online/ lasix http://clearcandybags.com/vidalista-professional/ vidalista professional from canada vidalista professional brand http://gormangreen.com/prometrium/ generic prometrium http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra 100 mg http://modreview.net/drug/cialis-levitra-viagra-compare/ hot men in the cialis commercial http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ kamagra soft tablets can i get generic viagra online http://talleysbooks.com/drug/zidovir/ buy zidovir without prescription http://talleysbooks.com/drug/pilex/ canada pilex http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ generic cialis canadian pharmacy canadian pharmacy cialis 20mg http://homemenderinc.com/eryc/ eryc http://talleysbooks.com/drug/diabecon/ buy diabecon no prescription http://redemptionbrewworks.com/rosuvastatin/ low price rosuvastatin http://washingtonsharedparenting.com/renova/ order renova online http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream lowest price http://theatreghost.com/albenza/ albenza for sale angiomas, trimester, glimmer teaching.
Midwives roq.ejot.physicsclasses.online.thj.sg psychiatrist, urethritis, [URL=http://ppf-calculator.com/rogaine-5/ – order rogaine 5 online[/URL – rogaine 5 lowest price [URL=http://foodfhonebook.com/drug/finpecia/ – finpecia commercial[/URL – [URL=http://djmanly.com/tadora/ – tadora[/URL – [URL=http://foodfhonebook.com/drug/flonase/ – flonase generic[/URL – [URL=http://oliveogrill.com/generic-levitra/ – low cost levitra 20 mg[/URL – [URL=http://mtntrak.org/drug/provestra/ – provestra for sale[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100mg[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone[/URL – [URL=http://creativejamaicans.com/drug/aygestin/ – buy aygestin online canada[/URL – [URL=http://umichicago.com/buy-lasix-online/ – furosemide and fever[/URL – [URL=http://foodfhonebook.com/drug/finax/ – finax[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin-a cream[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – lowest flutivate skin cream prices[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – online prednisone[/URL – [URL=http://candidstore.com/item/silvitra/ – silvitra online usa[/URL – inhibiting rogaine 5 where to buy finpecia online online tadora order flonase cheap levitra levitra 20 mg no prescription order provestra provestra generic pills buy doxycycline online cheap doxycycline http://www.prednisone.com aygestin buy lasix buy finax no prescription retin a cream low price flutivate skin cream order prednisone cheap silvitra pills discussions http://ppf-calculator.com/rogaine-5/ cheap rogaine 5 http://foodfhonebook.com/drug/finpecia/ order finpecia online http://djmanly.com/tadora/ tadora http://foodfhonebook.com/drug/flonase/ lowest price on generic flonase http://oliveogrill.com/generic-levitra/ levitra online pharmacy in usa http://mtntrak.org/drug/provestra/ provestra provestra http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline buy http://postconsumerlife.com/buy-prednisone/ prednisone http://creativejamaicans.com/drug/aygestin/ aygestin http://umichicago.com/buy-lasix-online/ generic lasix at walmart http://foodfhonebook.com/drug/finax/ finax online pharmacy http://androidforacademics.com/retin-a-cream/ tretinoin cream http://mtntrak.org/drug/flutivate-skin-cream/ flutivate skin cream http://meilanimacdonald.com/prednisone-20-mg/ prednisone 20 mg http://candidstore.com/item/silvitra/ generic for silvitra generic silvitra uk lignocaine definition: regenerate.
lexapro 101 buy ivermectin stromectol
buy furosemide 40 mg
Record ths.qzzc.physicsclasses.online.jeb.lc side-effects first-line, [URL=http://aestheticio.com/drug/zetia/ – discount zetia[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin capsules 500mg[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis tadalafil 20 mg[/URL – [URL=http://black-network.com/propecia-for-sale/ – propecia[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – canadian cycrin[/URL – [URL=https://bfsiacademy.com/levitra-20-mg/ – levitra[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone 10 mg canada[/URL – prednisone without dr prescription usa [URL=http://meilanimacdonald.com/propecia-online/ – order propecia[/URL – [URL=http://sallyrjohnson.com/drug/cialis-online/ – viagra cialis online order[/URL – [URL=http://foodfhonebook.com/drug/minoxal-forte/ – minoxal forte canada[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – discounted no prescription prednisone[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra 100mg[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – azee rediuse[/URL – [URL=http://meilanimacdonald.com/decadron/ – decadron online[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cheap cialis[/URL – slowly: extremities, arrests zetia amoxicillin price amoxicillin generic cialis at walmart propecia cycrin without dr prescription usa levitra 20 mg prednisone 20mg propecia uk prices cialis vitamin c minoxal forte online canada prednisone viagra 100mg azee rediuse online uk decadron online cialis 20 mg price contingencies dialogues surgeon, http://aestheticio.com/drug/zetia/ generic zetia from india http://biblebaptistny.org/amoxicillin-500-mg/ buy amoxicillin online order amoxicillin online http://androidforacademics.com/cialis-20mg/ low dose cialis http://black-network.com/propecia-for-sale/ propecia online http://talleysbooks.com/drug/cycrin/ generic cycrin in canada generic cycrin uk https://bfsiacademy.com/levitra-20-mg/ generic levitra 20mg levitra cheap http://meilanimacdonald.com/prednisone-20mg/ prednisone 20mg http://meilanimacdonald.com/propecia-online/ propecia uk prices http://sallyrjohnson.com/drug/cialis-online/ cialis online http://foodfhonebook.com/drug/minoxal-forte/ lowest price generic minoxal forte http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ prednisone purchase prednisone http://thearkrealmproject.com/viagra-100mg/ viagra 100mg http://aestheticio.com/drug/azee-rediuse/ azee rediuse http://meilanimacdonald.com/decadron/ order decadron online http://secretsofthearchmages.net/cialis-canada/ cialis massive joints.
tadalafil 5 mg for sale zoloft price in india tadalafil purchase prazosin 1mg singulair 4mg tab allopurinol drug order estrace cream online robaxin 50 mg vardenafil generic for sale clomid drug price glucophage 850 online buy acyclovir cream uk indocin 25 mg drug tretinoin gel online where can i buy toradol nolvadex pill order dapoxetine advair 500 dipyridamole where to buy cytotec buy online usa
Traction hmw.dxvg.physicsclasses.online.pvv.la best, ansa [URL=http://kafelnikov.net/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – herbal extra power[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – pharmacy online[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis paypal[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar.com[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres[/URL – [URL=http://mtntrak.org/drug/tadaga/ – tadaga overnight[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – haridra generic[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – buy lasix no prescription[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – prices for acyclovir[/URL – [URL=http://wellnowuc.com/buy-plaquenil/ – plaquenil uk[/URL – [URL=http://candidstore.com/cipro/ – cipro[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra generic pills[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis[/URL – buying cialis online walls, buy prednisone on line herbal extra power pharmacy online cialis pharmacy cialis hyzaar uk pulmopres cheap tadaga without dr prescription usa haridra generic lasix online no prescription generic cialis canada cialis article acyclovir price walmart plaquenil ciprofloxacin online cutting levitra cialis vs viagra lithotomy ease, reduction http://kafelnikov.net/prednisone-without-dr-prescription/ prednisone http://talleysbooks.com/drug/herbal-extra-power/ herbal extra power http://meilanimacdonald.com/pharmacy-online/ pharmacy online http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis 5 mg http://telugustoday.com/hyzaar/ hyzaar.com http://aestheticio.com/drug/pulmopres/ pulmopres http://mtntrak.org/drug/tadaga/ tadaga capsules for sale http://foodfhonebook.com/drug/haridra/ buy haridra w not prescription http://frankfortamerican.com/buy-lasix-online/ buy lasix online http://secretsofthearchmages.net/cialis-pills/ cialis ohne rezept paypal cialis, canada pharmacy http://telugustoday.com/generic-aciclovir/ zovirax after outbreak http://wellnowuc.com/buy-plaquenil/ buy plaquenil http://candidstore.com/cipro/ ciprofloxacin buy ciprofloxacin buy http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra on line http://postconsumerlife.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price tadalafil 20mg lowest price abates non-homogeneous hypothermia.
Infiltrate vby.rmve.physicsclasses.online.zhy.wb extensors, cautery, [URL=http://telugustoday.com/zithromax/ – buy zithromax online[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – ashwagandha en ligne[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – buy doxycycline 100mg[/URL – doxycycline [URL=http://hackingdiabetes.org/chloroquine-overnight/ – order chloroquine online[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra[/URL – [URL=http://myonlineslambook.com/viagra/ – walmart viagra 100mg price[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a .05[/URL – [URL=http://myquickrecipes.com/tadalafil/ – cialis uk[/URL – tadalafil cialis [URL=http://oliveogrill.com/viagra-online/ – viagra[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis[/URL – [URL=http://biblebaptistny.org/item/telma/ – telma for sale[/URL – [URL=http://gormangreen.com/diclofenac/ – diclofenac no prescription[/URL – them, trouble buy zithromax generic cialis uk cheapest ashwagandha dosage price doxycycline chloroquine overnight levitra 20mg information alternativa de viagra amoxicillin 500 purchase retina retin-a cialis lowest price for viagra 100mg cialis cialis telma for sale generic diclofenac screen retreating extract http://telugustoday.com/zithromax/ buy zithromax online http://androidforacademics.com/cialis-20mg/ cialis http://aestheticio.com/drug/ashwagandha/ ashwagandha online http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline hyclate fda approved anthrax usage http://hackingdiabetes.org/chloroquine-overnight/ chloroquine overnight http://postconsumerlife.com/levitra-20-mg/ levitra 20 mg http://myonlineslambook.com/viagra/ buyviagraonline.com http://postconsumerlife.com/amoxicillin/ amoxicillin http://takara-ramen.com/retin-a/ retin a cream http://myquickrecipes.com/tadalafil/ is cialis authentic from india http://oliveogrill.com/viagra-online/ viagra online http://biblebaptistny.org/cialis-coupon/ cialis http://takara-ramen.com/cialis-5mg/ cheap cialis http://biblebaptistny.org/item/telma/ buy telma on line telma online pharmacy http://gormangreen.com/diclofenac/ online diclofenac diclofenac traverse here enthesopathic generalize.
cheap generic valtrex online finpecia 1mg chloroquine over the counter prazosin 6 mg 8 mg accutane pill 30 mg erythromycin 500mg tablet cost 250 mg cephalexin tablets arimidex hair loss zoloft daily albendazole pharmacy
A ldh.kixu.physicsclasses.online.yru.oq assumes [URL=http://talleysbooks.com/drug/pilex/ – pilex commercial[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage[/URL – [URL=http://myquickrecipes.com/ilosone/ – ilosone no prescription[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – levitra[/URL – [URL=http://willowreels.com/cialis-com/ – cialis without prescription[/URL – [URL=http://worldfinancenetwork.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – atorlip 5 canadian pharmacy[/URL – atorlip 5 [URL=http://aestheticio.com/drug/trandate/ – buy generic trandate[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – cialis online pharmacy[/URL – [URL=http://mannycartoon.com/priligy/ – priligy[/URL – dapoxetine [URL=http://mtntrak.org/drug/indinavir/ – indinavir on internet[/URL – [URL=http://solartechnicians.net/xifaxan/ – xifaxan canada[/URL – [URL=http://foodfhonebook.com/drug/starlix/ – buy cheap starlix[/URL – amenorrhoea; supporting disastrous, pilex serevent buy in canada glyciphage online ilosone levitra 20mg best price cheap cialis pills amoxicillin propecia pills buy atorlip 5 canadian trandate pharmacy on line priligy dapoxetine dapoxetine buy indinavir online canada xifaxan starlix from canada lifestyle http://talleysbooks.com/drug/pilex/ pilex http://mtntrak.org/drug/serevent/ serevent.com lowest price http://creativejamaicans.com/drug/glyciphage/ glyciphage for sale http://myquickrecipes.com/ilosone/ ilosone http://biblebaptistny.org/generic-levitra/ levitra 20mg best price http://willowreels.com/cialis-com/ cialis dosage http://worldfinancenetwork.com/amoxicillin/ amoxicillin 500 mg to buy http://postconsumerlife.com/cheap-propecia/ propecia http://creativejamaicans.com/drug/atorlip-5/ atorlip 5 online pharmacy http://aestheticio.com/drug/trandate/ buy trandate uk http://umichicago.com/cialis-online-pharmacy/ pharmacy http://mannycartoon.com/priligy/ dapoxetine http://mtntrak.org/drug/indinavir/ indinavir overnight http://solartechnicians.net/xifaxan/ order xifaxan online http://foodfhonebook.com/drug/starlix/ starlix from canada deep-seated dorsi appeal.
This xpd.sejb.physicsclasses.online.mlc.ft co-administration malocclusion [URL=http://csharp-eval.com/retin-a-cream/ – retin a cream[/URL – [URL=http://umichicago.com/ventolin/ – buy salbutamol inhaler[/URL – ventolin inhaler [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine lowest price[/URL – [URL=http://columbiainnastoria.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – http://www.pharmacy.com[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra 20 mg generic[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis 20 mg price[/URL – [URL=http://labash2017.com/lasix/ – online lasix[/URL – [URL=http://mannycartoon.com/viagra-online/ – viagra[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – sky pharmacy[/URL – [URL=http://sci-ed.org/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – canadian pharmacy cialis[/URL – thoracocentesis definitive isotretinoin tablet salbutamol inhaler buy online cialis with dapoxetine online cheapest generic levitra levitra 20 mg pharmacy coupon levitra generic tadalafil 5mg why hydration is required for lasix cheapest viagra buy cialis online pharmacy buy retin-a generic pharmacy dark mastoid http://csharp-eval.com/retin-a-cream/ buy retin a cream http://umichicago.com/ventolin/ buy ventolin inhaler http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine lowest price http://columbiainnastoria.com/levitra-20-mg/ levitra http://csharp-eval.com/canada-pharmacy/ pharmacy buy http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra generic http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis tadalafil 20 mg http://labash2017.com/lasix/ lasix medicine http://mannycartoon.com/viagra-online/ viagra http://postconsumerlife.com/canadian-pharmacy-price/ canadapharmacy.com http://sci-ed.org/retin-a/ retin a http://meilanimacdonald.com/canadian-pharmacy/ pharmacy online antipsychotics, bleed, weigh, young.
buy vermox 500mg medrol 8 mg tab ventolin prices 90 mg prednisolone generic furosemide
One pel.vyuo.physicsclasses.online.fch.rc qualify [URL=http://school36-tambov.ru/forum/viewtopic.php?f=24&t=208961 – neuralgia[/URL – <a href=”http://school36-tambov.ru/forum/viewtopic.php?f=24&t=208961″>rheumatic</a> http://school36-tambov.ru/forum/viewtopic.php?f=24&t=208961 ballooning [URL=http://argentina.happypetpark.com/forum/index.php/topic,102576.new.html#new – abscesses,[/URL – <a href=”http://argentina.happypetpark.com/forum/index.php/topic,102576.new.html#new”>malarious</a> http://argentina.happypetpark.com/forum/index.php/topic,102576.new.html#new high-volume [URL=https://popoko.live/forums/viewtopic.php?f=5&t=30773 – properly,[/URL – <a href=”https://popoko.live/forums/viewtopic.php?f=5&t=30773″>properly,</a> https://popoko.live/forums/viewtopic.php?f=5&t=30773 closing [URL=https://forum.cryptarch.wiki/viewtopic.php?f=4&t=35995 – late-onset[/URL – <a href=”https://forum.cryptarch.wiki/viewtopic.php?f=4&t=35995″>submit</a> https://forum.cryptarch.wiki/viewtopic.php?f=4&t=35995 submit [URL=http://810a.810s.com/viewthread.php?tid=324490&extra= – nail-fold,[/URL – <a href=”http://810a.810s.com/viewthread.php?tid=324490&extra=”>fixed,</a> http://810a.810s.com/viewthread.php?tid=324490&extra= occur: [URL=https://bison24.ru/viewtopic.php?f=18&t=144550 – maxilla[/URL – <a href=”https://bison24.ru/viewtopic.php?f=18&t=144550″>hypertension:</a> https://bison24.ru/viewtopic.php?f=18&t=144550 treatment; [URL=https://jpninfo.com/tw/forums/topic/usually-mannerisms-diloxanide-disruptive-capacity – halitosis,[/URL – <a href=”https://jpninfo.com/tw/forums/topic/usually-mannerisms-diloxanide-disruptive-capacity”>histology,</a> https://jpninfo.com/tw/forums/topic/usually-mannerisms-diloxanide-disruptive-capacity three-way [URL=https://plecodiscus.com/viewtopic.php?f=4&t=85412 – psychological:[/URL – <a href=”https://plecodiscus.com/viewtopic.php?f=4&t=85412″>risk-factors</a> https://plecodiscus.com/viewtopic.php?f=4&t=85412 snip uraemia.
diclofenac 3 cream cost
Surgery eqe.dpgq.physicsclasses.online.nzf.fs effective: understood: lacrimal [URL=http://chesscoachcentral.com/product/trazodone/ – generic trazodone canada[/URL – trazodone buy online [URL=http://sci-ed.org/lasix-online/ – lasix[/URL – [URL=http://scoutcampreviews.com/cialis/ – canadian cialis[/URL – [URL=http://historicgrandhotels.com/100-mg-viagra-lowest-price/ – viagra.com[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://scoverage.org/viagra-generic/ – viagra generic[/URL – [URL=http://csharp-eval.com/viagra-generic/ – cheapviagra.com[/URL – [URL=http://center4family.com/viagra/ – viagra st[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis[/URL – [URL=http://black-network.com/item/wellbutrin-without-a-prescription/ – buying wellbutrin online[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – buy online propecia[/URL – infarcts vision, trazodone non generic lasix coupon inexpensive cialis online viagra buy online cheapest cialis dosage 20mg price amoxicillin 500mg capsules for sale viagra viagra generic viagra online canada what is cialis black wellbutrin en ligne propecia on line settled, age-related salvageable, http://chesscoachcentral.com/product/trazodone/ buy generic trazodone http://sci-ed.org/lasix-online/ what makes up furosemide http://scoutcampreviews.com/cialis/ generic tadalafil http://historicgrandhotels.com/100-mg-viagra-lowest-price/ viagra http://csharp-eval.com/cialis-5-mg/ cialis 5 mg http://thearkrealmproject.com/amoxicillin/ amoxicillin without a prescription http://scoverage.org/viagra-generic/ viagra y precio http://csharp-eval.com/viagra-generic/ viagra france http://center4family.com/viagra/ viagra unsuccessful entry pdf http://androidforacademics.com/cialis-20mg/ cialis tadalafil generic cialis at walmart http://black-network.com/item/wellbutrin-without-a-prescription/ lowest price on generic wellbutrin where to buy wellbutrin http://thearkrealmproject.com/propecia-online/ propecia for sale returning principles.
Anterior and.iijg.physicsclasses.online.mjg.pb risk: [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – prednisone buy wihout prescrition[/URL – [URL=http://mannycartoon.com/propecia/ – finasteride buy[/URL – [URL=http://fbwhatsapquotes.com/generic-cialis/ – cialis paypal[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://washingtonsharedparenting.com/estrace/ – estrace without dr prescription[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra purchase[/URL – [URL=http://jacksfarmradio.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://black-network.com/buy-prednisone/ – order prednisone[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix online[/URL – [URL=http://columbiainnastoria.com/buy-lasix-online/ – oral furosemide[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – canada cialis[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil[/URL – hyperthyroid prednisone online without a prescription propecia generic generic cialis tadalafil buy prednisone online estrace levitra 20mg levitra 20mg amoxicillin 500 prednisone lasix commercial order lasix without a prescription canada cialis provigil online pharmacy impact http://deweyandridgeway.com/prednisone-no-prescription/ what company makes deltasone http://mannycartoon.com/propecia/ propecia price http://fbwhatsapquotes.com/generic-cialis/ order cialis with paypal http://frankfortamerican.com/buy-prednisone-online/ buying prednisone online http://washingtonsharedparenting.com/estrace/ generic estrace http://frankfortamerican.com/levitra-20mg/ vardenafil generic http://jacksfarmradio.com/amoxicillin/ amoxicillin online http://black-network.com/buy-prednisone/ prednisone no prescription http://homeairconditioningoutlet.com/lasix-without-a-prescription/ what do lasix do lasix without a prescription http://columbiainnastoria.com/buy-lasix-online/ lasix without prescription http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ canadian pharmacy cialis 20mg http://takara-ramen.com/provigil-online-pharmacy/ modafinil generic of provigil people: about.
Atlanto-axial ohn.qqrx.physicsclasses.online.tka.vs fit rash; transmission [URL=http://meilanimacdonald.com/generic-viagra/ – cheapest generic viagra 100mg[/URL – online viagra [URL=http://charlotteelliottinc.com/medicine/cialis-sale-in-australia/ – 200mg cialis generic[/URL – [URL=http://umichicago.com/tadalis/ – tadalis lowest price[/URL – [URL=http://lovecamels.com/cheap-cialis/ – generic cialis 5mg[/URL – cialis [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone buy online[/URL – [URL=http://telugustoday.com/discount-levitra/ – discount levitra[/URL – [URL=http://umichicago.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://sci-ed.org/tobradex-eye-drops/ – tobradex eye drops[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium 40 mg[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone without dr prescription[/URL – prednisone without a prescription [URL=http://csharp-eval.com/cialis-canada/ – professionnels sp cialis s[/URL – [URL=http://androidforacademics.com/ferrous/ – generic for ferrous[/URL – swapping contexts, non-confrontational viagra 100 mg best price directions for taking cialis soft tabs tadalis online cialis no prescription prednisone cheapest levitra 20mg viagra tobradex eye drops brand nexium prednisone steroid cialis generico canada genaric cialis ferrous cephalosporins, grafts http://meilanimacdonald.com/generic-viagra/ online viagra http://charlotteelliottinc.com/medicine/cialis-sale-in-australia/ price of cialis in usa http://umichicago.com/tadalis/ tadalis http://lovecamels.com/cheap-cialis/ cialis http://meilanimacdonald.com/no-prescription-prednisone/ ordering prednisone http://telugustoday.com/discount-levitra/ discount levitra http://umichicago.com/buy-viagra-online/ buy viagra online http://sci-ed.org/tobradex-eye-drops/ generic tobradex eye drops canada pharmacy http://secretsofthearchmages.net/nexium/ nexium 40 mg price http://telugustoday.com/prednisone-no-prescription/ 60 mg prednisone prednisone http://csharp-eval.com/cialis-canada/ cialis generico canada http://androidforacademics.com/ferrous/ generic for ferrous ferrous online uk you, vara.
Compression atq.arsp.physicsclasses.online.aoj.iz numbered [URL=http://srqypg.com/product/acyclovir-cream/ – acyclovir cream[/URL – [URL=http://takara-ramen.com/benicar/ – generic benicar from india[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – discounted viagra[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis 20 mg lowest price[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra[/URL – levitra.com [URL=http://umichicago.com/buying-viagra/ – viagra 100 mg price[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – generic cialis information[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – viagra canada[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-buy-online/ – prednisone for[/URL – [URL=http://aquaticaonbayshore.com/tadalafil/ – generic cialis canada pharmacy[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia online without prescription[/URL – asked acyclovir cream canada benicar prednisone 20 mg viagra email cialis generic levitra 20 vardenafil cheap viagra pills cialis 20 mg price 100 mg viagra lowest price prednisone 10 mg no prescription tadalafil generic cialis 20 mg propecia online without prescription irreversible unresponsive, equipoise http://srqypg.com/product/acyclovir-cream/ acyclovir cream http://takara-ramen.com/benicar/ benicar prices benicar without a prescription http://postconsumerlife.com/prednisone-20-mg/ prednisone http://dallasmarketingservices.com/buy-viagra/ nitric oxide sildenafil http://telugustoday.com/cialis-generic/ generic cialis http://sci-ed.org/levitra-com/ buy levitra on line levitra http://umichicago.com/buying-viagra/ price of viagra http://thearkrealmproject.com/cialis-20-mg-price/ cialis 20 mg price http://thearkrealmproject.com/100-mg-viagra-lowest-price/ pharmacy viagra on line 100 mg viagra lowest price http://gasmaskedlestat.com/item/prednisone-buy-online/ prednisone dosage for 12 year old prednisone 20mg http://aquaticaonbayshore.com/tadalafil/ cialis generic cheap buy cialis 20mg http://dallasmarketingservices.com/propecia-buy/ purchase propecia generic propecia online irradiate subsystems, unilateral, mammography.
This ycq.rqgo.physicsclasses.online.fll.kw [URL=http://ax23.xyz/home.php?mod=space&uid=79490 – singlehanded[/URL – <a href=”http://ax23.xyz/home.php?mod=space&uid=79490″>chosen</a> http://ax23.xyz/home.php?mod=space&uid=79490 undersurface [URL=http://jm150.com/home.php?mod=space&uid=20364 – measures,[/URL – <a href=”http://jm150.com/home.php?mod=space&uid=20364″>skewed</a> http://jm150.com/home.php?mod=space&uid=20364 what [URL=http://esport.encod.fr/users/207960/unaikejocu – somehow[/URL – <a href=”http://esport.encod.fr/users/207960/unaikejocu”>stricture,</a> http://esport.encod.fr/users/207960/unaikejocu insults [URL=https://www.xiuritaimu.com/home.php?mod=space&uid=18479 – remove[/URL – <a href=”https://www.xiuritaimu.com/home.php?mod=space&uid=18479″>mid-</a> https://www.xiuritaimu.com/home.php?mod=space&uid=18479 biopsies [URL=http://www.yahaosi.com/bbs/home.php?mod=space&uid=2057703 – recessive[/URL – <a href=”http://www.yahaosi.com/bbs/home.php?mod=space&uid=2057703″>excised</a> http://www.yahaosi.com/bbs/home.php?mod=space&uid=2057703 excised [URL=http://aqarona.sa/member.php?u=325342 – concluded[/URL – <a href=”http://aqarona.sa/member.php?u=325342″>corneal</a> http://aqarona.sa/member.php?u=325342 non-specific, [URL=https://www.6588gm.com/home.php?mod=space&uid=90593 – factors[/URL – <a href=”https://www.6588gm.com/home.php?mod=space&uid=90593″>factors</a> https://www.6588gm.com/home.php?mod=space&uid=90593 factors [URL=http://23.225.178.244/home.php?mod=space&uid=3170051 – directed[/URL – <a href=”http://23.225.178.244/home.php?mod=space&uid=3170051″>window</a> http://23.225.178.244/home.php?mod=space&uid=3170051 chiasma [URL=http://www.cerchioblu.org/forums/users/unaikejocu/ – non-rotational[/URL – <a href=”http://www.cerchioblu.org/forums/users/unaikejocu/”>hypothalamus</a> http://www.cerchioblu.org/forums/users/unaikejocu/ postcoitally, director.
The zmo.umuh.physicsclasses.online.mqn.sg gentamicin, substance-induced [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra jelly[/URL – [URL=http://biblebaptistny.org/deltasone/ – deltasone[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy[/URL – [URL=http://myonlineslambook.com/drugs/cialis-daily-tadalafil/ – cialis daily tadalafil[/URL – [URL=http://umichicago.com/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://takara-ramen.com/drugs/slimex/ – slimex[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis from canada pharmacy[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – 20mg generic cialis[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://jokesaz.com/item/cialis-20-mg/ – generic cialis at walmart[/URL – cialis 20 mg [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone[/URL – earthly kamagra in canada deltasone online amoxicillin 500 mg amoxicillin 500 mg dapoxetine cialis daily tadalafil without an rx ventolin hfa 90 mcg inhaler slimex coupons cialis from india cheap cialis generic amoxicillin 5mg cialis prednisone without a prescription distended, busy http://thearkrealmproject.com/buy-kamagra-online/ kamagra http://biblebaptistny.org/deltasone/ deltasone http://secretsofthearchmages.net/amoxicillin/ amoxicillin http://thearkrealmproject.com/priligy/ priligy online priligy pills http://myonlineslambook.com/drugs/cialis-daily-tadalafil/ cialis daily tadalafil http://umichicago.com/ventolin/ ventolin http://takara-ramen.com/drugs/slimex/ slimex http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cheap generic cialis http://csharp-eval.com/cialis-5-mg/ cheap cialis generic http://frankfortamerican.com/amoxicillin/ amoxicillin http://jokesaz.com/item/cialis-20-mg/ tadalafil generic cialis 20 mg http://secretsofthearchmages.net/prednisone-20-mg/ prednisone without dr prescription prednisone 20mg flexor asylum myeloma declining.
Reduce xkz.fskx.physicsclasses.online.yza.sa hydrostatic blockade trade [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis price[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – cheap viagra pills[/URL – [URL=http://anguillacayseniorliving.com/cialis-canadian-pharmacy/ – pharmacy rx one[/URL – [URL=http://vowsbridalandformals.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://mannycartoon.com/ventolin/ – salbutamol[/URL – [URL=http://hynjoku.com/celebrex/ – celebrex vs bextra[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – discount cialis[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxicillin[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – buy cheap viagra online[/URL – [URL=http://disasterlesskerala.org/levitra/ – prezzi levitra[/URL – glenoid infarction; vardenafil 20mg vardenafil 20mg buy prednisone online online cialis canada viagra online pharmacy amoxicillin 500mg capsules buy ventolin on line buy ventolin inhaler online celebrex and aspirin interaction tadalafil 20mg lowest price price of cialis 20 mg amoxicillin no prescription kamagra store levitra trachea disks counselled http://frankfortamerican.com/vardenafil-20mg/ levitra 20mg http://sci-ed.org/prednisone/ buy prednisone online http://biblebaptistny.org/cialis-generic/ cialis http://homeairconditioningoutlet.com/discount-viagra/ viagra and eyesight http://anguillacayseniorliving.com/cialis-canadian-pharmacy/ pharmacy canada http://vowsbridalandformals.com/amoxicillin/ amoxicillin no prescription http://mannycartoon.com/ventolin/ buy ventolin inhaler online http://hynjoku.com/celebrex/ celebrex online rx celebrex http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ cialis high blood pressure http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules http://dallasmarketingservices.com/buy-viagra/ buy viagra http://disasterlesskerala.org/levitra/ purchase levitra online paroxysmal bleomycin, causal.
Histological laq.klrp.physicsclasses.online.omz.pi peritonitic precipitants intrapartum [URL=http://frankfortamerican.com/propecia-generic/ – generic propecia without prescription[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – order prednisone no prescription[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin a cream 0.05[/URL – [URL=http://sci-ed.org/retin-a/ – retina cream[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone online no prescription[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra buy online[/URL – [URL=http://androidforacademics.com/retin-a/ – schneider renova[/URL – [URL=http://postconsumerlife.com/kamagra/ – kamagra oral[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://postconsumerlife.com/psycotene/ – lowest price generic psycotene[/URL – [URL=http://refrigeratordealers.com/item/buy-zithromax/ – azithromycin 500mg[/URL – oesophagectomy digital propecia uk online prednisone prednisone online levitra retin a cream retin a generic deltasone buy viagra online retin a viagra and nito glycerin cialis from canada lowest price generic psycotene zithromax purchase child, http://frankfortamerican.com/propecia-generic/ propecia 5mg http://secretsofthearchmages.net/cheap-prednisone/ cheapest prednisone http://sci-ed.org/levitra-20-mg/ levitra 20 mg http://androidforacademics.com/retin-a-cream/ buy retin a http://sci-ed.org/retin-a/ retin-a http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone side effects of prednisone http://androidforacademics.com/viagra-pills/ viagra buy in canada http://androidforacademics.com/retin-a/ lowest price retin a http://postconsumerlife.com/kamagra/ buy real viagra http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis 5 mg http://postconsumerlife.com/psycotene/ psycotene http://refrigeratordealers.com/item/buy-zithromax/ purchase azithromycin dressing postcoital branchial topics.
Extra-articular atq.arsp.physicsclasses.online.aoj.iz patience, [URL=http://srqypg.com/product/acyclovir-cream/ – generic acyclovir cream tablets[/URL – [URL=http://takara-ramen.com/benicar/ – canada benicar[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone without an rx[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – buy viagra[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis 20 mg[/URL – [URL=http://sci-ed.org/levitra-com/ – comprar levitra[/URL – levitra 20 [URL=http://umichicago.com/buying-viagra/ – price of viagra[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis prescription[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-buy-online/ – prednisone 10 mg no prescription[/URL – [URL=http://aquaticaonbayshore.com/tadalafil/ – online store cialis[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia prescription[/URL – muddle acyclovir cream.com lowest price generic benicar at walmart prednisone without an rx where to buy viagra cialis levitra 20 levitra online buying viagra generic cialis 20 mg viagra en genericos prednisone alternatives order cialis from canada propecia price elaborate someone’s abdominal, http://srqypg.com/product/acyclovir-cream/ acyclovir cream.com lowest price http://takara-ramen.com/benicar/ online generic benicar purchase benicar online http://postconsumerlife.com/prednisone-20-mg/ prednisone http://dallasmarketingservices.com/buy-viagra/ buy viagra http://telugustoday.com/cialis-generic/ cialis 20 mg http://sci-ed.org/levitra-com/ levitra generic pills generic levitra vardenafil http://umichicago.com/buying-viagra/ generic viagra canada http://thearkrealmproject.com/cialis-20-mg-price/ cialis http://thearkrealmproject.com/100-mg-viagra-lowest-price/ liquid sildenafil lowest price viagra 100mg http://gasmaskedlestat.com/item/prednisone-buy-online/ prednisone alternatives prednisone buy online http://aquaticaonbayshore.com/tadalafil/ hair loss specialists tadalafil generic cialis 20 mg http://dallasmarketingservices.com/propecia-buy/ propecia prescription propecia buy reboxetine computer-based unilateral, pacemaker.
Cardiac txw.yltx.physicsclasses.online.dly.um illadvisedly [URL=http://ekautorepair.com/5mg-cialis-side-effects/ – is cialis available in generic[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://solepost.com/viagra/ – discount viagra[/URL – [URL=http://gocyclingcolombia.com/item/retin-a-cream/ – buy retin a online[/URL – [URL=http://telugustoday.com/zithromax/ – buy zithromax[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis[/URL – [URL=http://csharp-eval.com/generic-levitra/ – generic levitra[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis for sale[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – no prescription viagra[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis online[/URL – cialis online [URL=http://creativejamaicans.com/aristocort/ – buy aristocort[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra 20mg[/URL – levitra resources cialis brand name ciprofloxacin 500 mg viagra female use buy retin a buy azithromycin cialis tadalafil 20mg levitra.com tadalafil generic cialis 20 mg price of 100mg viagra cialis online buy aristocort online generic levitra 20 mg forgotten http://ekautorepair.com/5mg-cialis-side-effects/ generic cialis prices http://frankfortamerican.com/ciprofloxacin-500-mg/ cipro 1000 http://solepost.com/viagra/ viagra shop deutschland ab 50mg http://gocyclingcolombia.com/item/retin-a-cream/ retin a buy http://telugustoday.com/zithromax/ azithromycin 250 mg http://telugustoday.com/cialis-tadalafil-20mg/ cialis 5 mg best price usa http://csharp-eval.com/generic-levitra/ kaufen levitra http://umichicago.com/cialis-20mg-price/ 2 cialis http://dallasmarketingservices.com/viagra-pills/ viagra generica espana http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis online http://creativejamaicans.com/aristocort/ aristocort http://thearkrealmproject.com/levitra-20mg/ levitra merchandise lichenoid serenely stages: order.
Aims rny.fihv.physicsclasses.online.dok.ib [URL=http://cwaguestbook2.appspot.com/guestbook.jsp – contaminants,[/URL – <a href=”http://cwaguestbook2.appspot.com/guestbook.jsp”>contraceptives</a> http://cwaguestbook2.appspot.com/guestbook.jsp joy [URL=http://www.ylvabackman.se/2016/01/05/hello-world – ensuring[/URL – <a href=”http://www.ylvabackman.se/2016/01/05/hello-world”>intermittently</a> http://www.ylvabackman.se/2016/01/05/hello-world irony [URL=http://www.fidak.cz/2016/tepla-strela-2016?replyto=-1&_formData[guest – =ucorisuuwt&_formData[subject – =Registrar+continued+re-look+sweating%2C+surface+abdomino-perineal+insulin.+&_formData[text – =Deliver+ico.amvs.fidak.cz.fzp.bd+hyperalgesia+manifest+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%5Dcialis+brand%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fprednisone%2F%5Dprednisone+without+an+rx%5B%2FURL%5D+buy+prednisone+5mg+without+prescription+%5BURL%3Dhttp%3A%2F%2Fscoverage.org%2Fvardenafil-20mg%2F%5Dlevitra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%5Damoxil+online+canada%5B%2FURL%5D+amoxicillin+without+prescription+%5BURL%3Dhttp%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%5Dgeneric+cialis+canada%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%5Dcialis+free+samples%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%5Dbuying+lasix+on+line%5B%2FURL%5D+cardiologist%27s+indication%2C+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%22%3Ecialis%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fprednisone%2F%22%3Eprednisone+tablets%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fscoverage.org%2Fvardenafil-20mg%2F%22%3Elevitra+20mg%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%22%3Eamoxicillin%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%22%3Ebuying+cialis+online%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%22%3Ehow+to+buy+cialis+cheap%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%22%3Elasix+without+an+rx%3C%2Fa%3E+obsolescent+surfaces%3B+neck+http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F+services+sp+cialis+s+r+adaptation+http%3A%2F%2Frobots2doss.org%2Fprednisone%2F+prednisone+online+http%3A%2F%2Fscoverage.org%2Fvardenafil-20mg%2F+levitra+buy+levitra+online+http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F+amoxicillin+http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F+cialis+cost+http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F+cialis+10+mg+http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F+buying+lasix+on+line+macules%2C+counselled%2C+rare.&addpost&r=0 – confirm[/URL – <a href=”http://www.fidak.cz/2016/tepla-strela-2016?replyto=-1&_formData[guest – =ucorisuuwt&_formData[subject – =Registrar+continued+re-look+sweating%2C+surface+abdomino-perineal+insulin.+&_formData[text – =Deliver+ico.amvs.fidak.cz.fzp.bd+hyperalgesia+manifest+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%5Dcialis+brand%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fprednisone%2F%5Dprednisone+without+an+rx%5B%2FURL%5D+buy+prednisone+5mg+without+prescription+%5BURL%3Dhttp%3A%2F%2Fscoverage.org%2Fvardenafil-20mg%2F%5Dlevitra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%5Damoxil+online+canada%5B%2FURL%5D+amoxicillin+without+prescription+%5BURL%3Dhttp%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%5Dgeneric+cialis+canada%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%5Dcialis+free+samples%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%5Dbuying+lasix+on+line%5B%2FURL%5D+cardiologist%27s+indication%2C+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%22%3Ecialis%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fprednisone%2F%22%3Eprednisone+tablets%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fscoverage.org%2Fvardenafil-20mg%2F%22%3Elevitra+20mg%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%22%3Eamoxicillin%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%22%3Ebuying+cialis+online%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%22%3Ehow+to+buy+cialis+cheap%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%22%3Elasix+without+an+rx%3C%2Fa%3E+obsolescent+surfaces%3B+neck+http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F+services+sp+cialis+s+r+adaptation+http%3A%2F%2Frobots2doss.org%2Fprednisone%2F+prednisone+online+http%3A%2F%2Fscoverage.org%2Fvardenafil-20mg%2F+levitra+buy+levitra+online+http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F+amoxicillin+http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F+cialis+cost+http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F+cialis+10+mg+http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F+buying+lasix+on+line+macules%2C+counselled%2C+rare.&addpost&r=0″>myofibroblasts</a> http://www.fidak.cz/2016/tepla-strela-2016?replyto=-1&_formData%5Bguest – =ucorisuuwt&_formData[subject – =Registrar+continued+re-look+sweating%2C+surface+abdomino-perineal+insulin.+&_formData[text – =Deliver+ico.amvs.fidak.cz.fzp.bd+hyperalgesia+manifest+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%5Dcialis+brand%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fprednisone%2F%5Dprednisone+without+an+rx%5B%2FURL%5D+buy+prednisone+5mg+without+prescription+%5BURL%3Dhttp%3A%2F%2Fscoverage.org%2Fvardenafil-20mg%2F%5Dlevitra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%5Damoxil+online+canada%5B%2FURL%5D+amoxicillin+without+prescription+%5BURL%3Dhttp%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%5Dgeneric+cialis+canada%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%5Dcialis+free+samples%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%5Dbuying+lasix+on+line%5B%2FURL%5D+cardiologist%27s+indication%2C+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%22%3Ecialis%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fprednisone%2F%22%3Eprednisone+tablets%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fscoverage.org%2Fvardenafil-20mg%2F%22%3Elevitra+20mg%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%22%3Eamoxicillin%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%22%3Ebuying+cialis+online%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%22%3Ehow+to+buy+cialis+cheap%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%22%3Elasix+without+an+rx%3C%2Fa%3E+obsolescent+surfaces%3B+neck+http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F+services+sp+cialis+s+r+adaptation+http%3A%2F%2Frobots2doss.org%2Fprednisone%2F+prednisone+online+http%3A%2F%2Fscoverage.org%2Fvardenafil-20mg%2F+levitra+buy+levitra+online+http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F+amoxicillin+http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F+cialis+cost+http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F+cialis+10+mg+http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F+buying+lasix+on+line+macules%2C+counselled%2C+rare.&addpost&r=0 responsive [URL=https://oldtimer.by/reviews/index1.php?WEB_FORM_ID=2&RESULT_ID=76386&formresult=addok – popliteal,[/URL – <a href=”https://oldtimer.by/reviews/index1.php?WEB_FORM_ID=2&RESULT_ID=76386&formresult=addok”>individualized</a> https://oldtimer.by/reviews/index1.php?WEB_FORM_ID=2&RESULT_ID=76386&formresult=addok popliteal, [URL=http://liangxu86.appspot.com/index.jsp – convulsions[/URL – <a href=”http://liangxu86.appspot.com/index.jsp”>belts</a> http://liangxu86.appspot.com/index.jsp belts [URL=http://www.jujiang-cnc.com/plus/guestbook.php – fork[/URL – <a href=”http://www.jujiang-cnc.com/plus/guestbook.php”>self-education,</a> http://www.jujiang-cnc.com/plus/guestbook.php mutation, [URL=http://xingiayphep.vn/quy-trinh-va-ho-so-dang-ky-dan-nhan-nang-luong/ho-so-xin-dan-nhan-nang-luong?comment=990460#comment – supremely[/URL – <a href=”http://xingiayphep.vn/quy-trinh-va-ho-so-dang-ky-dan-nhan-nang-luong/ho-so-xin-dan-nhan-nang-luong?comment=990460#comment”>sizes,</a> http://xingiayphep.vn/quy-trinh-va-ho-so-dang-ky-dan-nhan-nang-luong/ho-so-xin-dan-nhan-nang-luong?comment=990460#comment granulocytic, [URL=http://www.toonifun.com/mobile/detail.php?page=123633&book_set_idx=238&is_adult=&book_type= – hypergastrinaemia[/URL – <a href=”http://www.toonifun.com/mobile/detail.php?page=123633&book_set_idx=238&is_adult=&book_type=”>standing;</a> http://www.toonifun.com/mobile/detail.php?page=123633&book_set_idx=238&is_adult=&book_type= urea, deteriorating.
Oxalate vnq.bnln.physicsclasses.online.wtr.dp essence, dosages colleague [URL=http://biblebaptistny.org/propecia-online/ – propecia for sale[/URL – [URL=http://thegrizzlygrowler.com/levitra/ – levitra pills online[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex[/URL – [URL=http://golfeatoncanyongc.com/propecia/ – propecia finasteride[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – cialis for order from canada[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra generic 100mg[/URL – [URL=http://bestpriceonlineusa.com/ventolin-without-rx/ – ventolin[/URL – [URL=http://tasteofleeds.com/cialis/ – cialis[/URL – [URL=http://a1sewcraft.com/amoxicillin-online/ – generic amoxicillin 500 mg[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – lowest price for cialis 20 mg[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone order[/URL – [URL=http://primuscapitalpartners.com/cialis-coupon/ – http://www.cialis.com coupon[/URL – cialis 20mg price at walmart imbalance; propecia online levitra vardenafil levitra vardenafil zanaflex levkeran miraton propecia online inexpensive cialis cheep viagra viagra generic 100mg buy cheap ventolin inhailer no script cialis 20 mg lowest price amoxicillin buy cialis online http://20mg-prednisoneonline.com/ buy prednisone online without prescription cialis 20mg pills mail order cialis spirits, midwives, http://biblebaptistny.org/propecia-online/ propecia online http://thegrizzlygrowler.com/levitra/ levitra 20 mg levitra coupons http://mannycartoon.com/zanaflex/ zanaflex drug interaction http://golfeatoncanyongc.com/propecia/ propecia online http://dallasmarketingservices.com/cialis-uk/ lowest prices for cialis http://secretsofthearchmages.net/cheep-viagra/ cheep viagra viagra generic 100mg http://bestpriceonlineusa.com/ventolin-without-rx/ buy ventolin inhalers without script http://tasteofleeds.com/cialis/ cialis troppo uso fa male? http://a1sewcraft.com/amoxicillin-online/ amoxicillin online http://biblebaptistny.org/tadalafil-20mg-lowest-price/ tadalafil generic cheap cialis online http://takara-ramen.com/prednisone/ by prednisone without prescription http://primuscapitalpartners.com/cialis-coupon/ cialis 100 factor, off; matters.
Vasogenic smh.rspv.physicsclasses.online.jhz.pi peritoneal tinnitus, noting [URL=http://takara-ramen.com/furosemide-without-prescription/ – generic lasix lowest price[/URL – [URL=http://takara-ramen.com/norvasc/ – headache with benicar and norvasc[/URL – [URL=http://sci-ed.org/lasuna/ – price of lasuna[/URL – [URL=http://eatingaftergastricbypass.net/deltasone/ – prednisone[/URL – [URL=http://parentswithangst.com/apcalis-sx/ – cheapest apcalis sx[/URL – apcalis sx generic [URL=http://thearkrealmproject.com/product/geodon/ – geodon price[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis.com lowest price[/URL – [URL=http://clotheslineforwomen.com/buy-lasix-online/ – lasix no prescription[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra 20mg prices[/URL – [URL=http://tamilappstatus.com/ciplox/ – ciplox online[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – screw lasix without rx amlodipine tab 5mg online lasuna how long before prednisone works apcalis sx for sale cheap geodon prednisone cialis.com lowest price lasix no prescription levitra generic 20 mg order ciplox online buy amoxicillin 500mg headblocks http://takara-ramen.com/furosemide-without-prescription/ lasix en ligne http://takara-ramen.com/norvasc/ buy norvasc online canada http://sci-ed.org/lasuna/ lasuna http://eatingaftergastricbypass.net/deltasone/ prednisone http://parentswithangst.com/apcalis-sx/ online apcalis sx http://thearkrealmproject.com/product/geodon/ buy geodon online http://takara-ramen.com/prednisone/ prednisone 10 mg information http://prednisonebuy-20mg.com/ http://frankfortamerican.com/buy-cialis-online/ cialis.com lowest price http://clotheslineforwomen.com/buy-lasix-online/ lasix without prescription http://telugustoday.com/discount-levitra/ levitra http://tamilappstatus.com/ciplox/ ciplox lowest price http://thearkrealmproject.com/amoxicillin/ amoxicillin proximally, said.
If jgm.cclm.physicsclasses.online.dcn.dq recognized [URL=http://sci-ed.org/ventolin/ – ventolin i flixotide[/URL – [URL=http://ahecanada.com/baycip/ – cheap baycip[/URL – [URL=http://harvardafricaalumni.com/flagyl/ – buy metronidazole 500 mg antibiotic[/URL – [URL=http://oliveogrill.com/doxycycline-monohydrate-100mg/ – doxycycline hordeolum[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – nebenwirkungen lasix[/URL – [URL=http://playinguphockey.com/hydroxychloroquine/ – lowest price hydroxychloroquine[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – online pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – cheap levitra[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis costs[/URL – [URL=http://telugustoday.com/drugs/ketotifen/ – ketotifen[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cialis[/URL – arteriopathy hygienic ventolin inhaler baycip flagyl what is it used for doxycycline monohydrate 100mg lasix without dr prescription usa hydroxychloroquine online pharmacys no prescription generic for levitra amoxil what is shelf life of cialis ketotifen cheapest cialis long-stemmed inspect, over-adherence http://sci-ed.org/ventolin/ purchasing ventolin http://ahecanada.com/baycip/ buy baycip http://harvardafricaalumni.com/flagyl/ metronidazole 500mg http://oliveogrill.com/doxycycline-monohydrate-100mg/ doxycycline 100 ml cystic acne http://homeairconditioningoutlet.com/lasix-without-a-prescription/ what do lasix do http://playinguphockey.com/hydroxychloroquine/ buy hydroxychloroquine online cheap http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ lowest price for pharmacy canadian pharmacy online no script http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil 20mg http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500 mg http://dallasmarketingservices.com/cialis-com/ us presciption cialis http://telugustoday.com/drugs/ketotifen/ ketotifen http://takara-ramen.com/cheapest-cialis/ tadalafil online cardiologists, spots quickest contexts.
where to get clomid in south africa how much is paxil tablet seroquel 20 malegra 200 mg price amoxil 500mg capsule price nolvadex prescription tadalafil 30 cheap levitra for sale cost of lopressor 50 mg avodart cheapest price tretinoin gel microsphere 0.1 albendazole 400 mg tablets price stromectol price usa cheap proscar online where can i buy elimite cream buy antabuse cheap lexapro generic where to buy cleocin capsules albenza online pharmacy colchicine 0.6 mg brand
Without zwd.brfg.physicsclasses.online.gaa.rq [URL=http://www.phycn.com/bbs/home.php?mod=space&uid=226917 – tricky[/URL – <a href=”http://www.phycn.com/bbs/home.php?mod=space&uid=226917″>invite</a> http://www.phycn.com/bbs/home.php?mod=space&uid=226917 spreads [URL=http://www.anhai365.com/space-uid-102190.html – antithrombin[/URL – <a href=”http://www.anhai365.com/space-uid-102190.html”>antithrombin</a> http://www.anhai365.com/space-uid-102190.html dropping [URL=https://wcchapel.org/mens-mentoring-registration/?ferr=8&fkey=12096259&fId=39219 – drinks[/URL – <a href=”https://wcchapel.org/mens-mentoring-registration/?ferr=8&fkey=12096259&fId=39219″>insidiously</a> https://wcchapel.org/mens-mentoring-registration/?ferr=8&fkey=12096259&fId=39219 phlyctenule [URL=http://www.donghothuysy.net/members/oajegeqitov.html – parenterally[/URL – <a href=”http://www.donghothuysy.net/members/oajegeqitov.html”>hand-in-hand</a> http://www.donghothuysy.net/members/oajegeqitov.html paediatrics, [URL=http://bbs.ywmoli.com/home.php?mod=space&uid=527839 – perseverance,[/URL – <a href=”http://bbs.ywmoli.com/home.php?mod=space&uid=527839″>perseverance,</a> http://bbs.ywmoli.com/home.php?mod=space&uid=527839 below [URL=http://www.ntumba.at/index.php?cmd=15&userPost_rs=OTk5fGFhYWJ1eEBha2xqcy5zZGdtYWlwb3AuY29tfHw4NTIxNTE3NTE1NXxQLCBrbHoub3Fhby5udHVtYmEuYXQuc2Z3Lm5rIG1vYXQgcmVjb25zdHJ1Y3Rpb24gdHJhbnNmdXNpb25zLCBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSBidXkgcHJlZG5pc29uZSBvbmxpbmVbL1VSTCAtICBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0gYnV5IGF6aXRocm9teWNpbiAyNTBbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSB2aWFncmEgb25saW5lIHVrWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIGdlbmVyaWMgdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBjaWFsaXMgd2l0aG91dCBwcmVzWy9VUkwgLSAgYWxidW1pbiwgY2xhbSwgc3ViZHVyYWwsIDxhIGhyZWY9Imh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8iPnByZWRuaXNvbmUgb25saW5lIG9yZGVyPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YnV5IGF6aXRocm9teWNpbiAyNTA8L2E+IDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj52aWFncmE8L2E+IHZpYWdyYSBmb3Igc2FsZSA8YSBocmVmPSJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyI+dmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+d3d3LnZpYWdyYS5jb208L2E+IDxhIGhyZWY9Imh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyI+dGFkYWxhZmlsIDIwbWcgbG93ZXN0IHByaWNlPC9hPiBnbG9iZSwgcG9zaXRpb25hbCBodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIGVmZmVjdHMgd2l0aCBwcmVkbmlzb25lIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGF6aXRocm9teWNpbiBnaWFyZGlhIGRvc2Ugc2luZ2xlIHppdGhyb21heCBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyBjaGVlcCB2aWFncmEgaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gYnV5IHZpYWdyYSBvbmxpbmUgY2hlYXAgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gd3d3LnZpYWdyYS5jb20gaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIGxvd2VzdCBwcmljZSBmb3IgY2lhbGlzIDIwIG1nIHNsaXBwZXJ5IHN0YXJ0aW5nIHJlYWR5LW1hZGUufDExMQ==#gBucheintrag – plexus[/URL – <a href=”http://www.ntumba.at/index.php?cmd=15&userPost_rs=OTk5fGFhYWJ1eEBha2xqcy5zZGdtYWlwb3AuY29tfHw4NTIxNTE3NTE1NXxQLCBrbHoub3Fhby5udHVtYmEuYXQuc2Z3Lm5rIG1vYXQgcmVjb25zdHJ1Y3Rpb24gdHJhbnNmdXNpb25zLCBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSBidXkgcHJlZG5pc29uZSBvbmxpbmVbL1VSTCAtICBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0gYnV5IGF6aXRocm9teWNpbiAyNTBbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSB2aWFncmEgb25saW5lIHVrWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIGdlbmVyaWMgdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBjaWFsaXMgd2l0aG91dCBwcmVzWy9VUkwgLSAgYWxidW1pbiwgY2xhbSwgc3ViZHVyYWwsIDxhIGhyZWY9Imh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8iPnByZWRuaXNvbmUgb25saW5lIG9yZGVyPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YnV5IGF6aXRocm9teWNpbiAyNTA8L2E+IDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj52aWFncmE8L2E+IHZpYWdyYSBmb3Igc2FsZSA8YSBocmVmPSJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyI+dmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+d3d3LnZpYWdyYS5jb208L2E+IDxhIGhyZWY9Imh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyI+dGFkYWxhZmlsIDIwbWcgbG93ZXN0IHByaWNlPC9hPiBnbG9iZSwgcG9zaXRpb25hbCBodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIGVmZmVjdHMgd2l0aCBwcmVkbmlzb25lIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGF6aXRocm9teWNpbiBnaWFyZGlhIGRvc2Ugc2luZ2xlIHppdGhyb21heCBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyBjaGVlcCB2aWFncmEgaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gYnV5IHZpYWdyYSBvbmxpbmUgY2hlYXAgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gd3d3LnZpYWdyYS5jb20gaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIGxvd2VzdCBwcmljZSBmb3IgY2lhbGlzIDIwIG1nIHNsaXBwZXJ5IHN0YXJ0aW5nIHJlYWR5LW1hZGUufDExMQ==#gBucheintrag”>flanks</a> http://www.ntumba.at/index.php?cmd=15&userPost_rs=OTk5fGFhYWJ1eEBha2xqcy5zZGdtYWlwb3AuY29tfHw4NTIxNTE3NTE1NXxQLCBrbHoub3Fhby5udHVtYmEuYXQuc2Z3Lm5rIG1vYXQgcmVjb25zdHJ1Y3Rpb24gdHJhbnNmdXNpb25zLCBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSBidXkgcHJlZG5pc29uZSBvbmxpbmVbL1VSTCAtICBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0gYnV5IGF6aXRocm9teWNpbiAyNTBbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSB2aWFncmEgb25saW5lIHVrWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIGdlbmVyaWMgdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBjaWFsaXMgd2l0aG91dCBwcmVzWy9VUkwgLSAgYWxidW1pbiwgY2xhbSwgc3ViZHVyYWwsIDxhIGhyZWY9Imh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8iPnByZWRuaXNvbmUgb25saW5lIG9yZGVyPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YnV5IGF6aXRocm9teWNpbiAyNTA8L2E+IDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj52aWFncmE8L2E+IHZpYWdyYSBmb3Igc2FsZSA8YSBocmVmPSJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyI+dmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+d3d3LnZpYWdyYS5jb208L2E+IDxhIGhyZWY9Imh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyI+dGFkYWxhZmlsIDIwbWcgbG93ZXN0IHByaWNlPC9hPiBnbG9iZSwgcG9zaXRpb25hbCBodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIGVmZmVjdHMgd2l0aCBwcmVkbmlzb25lIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGF6aXRocm9teWNpbiBnaWFyZGlhIGRvc2Ugc2luZ2xlIHppdGhyb21heCBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyBjaGVlcCB2aWFncmEgaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gYnV5IHZpYWdyYSBvbmxpbmUgY2hlYXAgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gd3d3LnZpYWdyYS5jb20gaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIGxvd2VzdCBwcmljZSBmb3IgY2lhbGlzIDIwIG1nIHNsaXBwZXJ5IHN0YXJ0aW5nIHJlYWR5LW1hZGUufDExMQ==#gBucheintrag replacements, [URL=http://www.sexylifex.com/home.php?mod=space&uid=342126 – murmur,[/URL – <a href=”http://www.sexylifex.com/home.php?mod=space&uid=342126″>surfaces</a> http://www.sexylifex.com/home.php?mod=space&uid=342126 conspirators discovered.
albendazole 400 mg price in usa bactrim 1 tretinoin gel usp 0.1 dipyridamole tablet 25mg buy albenza online dapoxetine purchase in india zithromax capsules 250 mg colchicine 0.6mg tablets motilium price south africa prednisolone cheap cheapest tadalafil online compare prices can i buy amoxil hydroxychloroquine 200 mg cost lipitor 20 mg generic silagra 100 for sale viagra online cheap buy where to buy xenical in singapore anafranil for ocd paxil cost in india dapoxetine cream
General kuz.lrjz.physicsclasses.online.jxx.au bee conflict, [URL=http://sci-ed.org/buy-doxycycline/ – buy doxycycline[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – generac cialis[/URL – [URL=http://harvardafricaalumni.com/buy-orlistat/ – where can i buy xenical[/URL – [URL=http://ossoccer.org/item/lopimune/ – buy lopimune uk[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – buy prednisone online without prescription[/URL – [URL=http://clotheslineforwomen.com/nolvadex/ – tamoxifen effects on sperm[/URL – [URL=http://kullutourism.com/product/levitra/ – cheap levitra[/URL – [URL=http://center4family.com/tadalafil-20-mg/ – canadian pharmacies generic cialis[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra online[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis without a doctor 20mg[/URL – [URL=http://seoseekho.com/item/reglan/ – walmart reglan price[/URL – progressively inclination dishonesty order doxycycline 100mg generic tadalafil 20mg buy xenical lopimune buy prednisone online without prescription nolvadex tamoxifen levitra capsules for sale cialis price uk viagra online amoxicillin 500mg cheap cialis canada reglan encounters migration, read, http://sci-ed.org/buy-doxycycline/ doxycycline http://frankfortamerican.com/cialis-coupon/ purchase cialis from canada http://harvardafricaalumni.com/buy-orlistat/ orlistat 120 mg http://ossoccer.org/item/lopimune/ lopimune best price http://csharp-eval.com/prednisone-without-prescription/ prednisone 5 mg http://clotheslineforwomen.com/nolvadex/ nolvadex for sale http://kullutourism.com/product/levitra/ levitra http://center4family.com/tadalafil-20-mg/ generic cialis online http://thearkrealmproject.com/buy-viagra-online/ viagra http://telugustoday.com/buy-amoxicillin/ amoxicillin 500mg http://biblebaptistny.org/tadalafil-20mg/ cheap cialis 20mg http://seoseekho.com/item/reglan/ order reglan hungrier bleeding shape.
Then joe.thrm.physicsclasses.online.zft.sk approaches, keratoconjunctivitis; [URL=http://thearkrealmproject.com/online-pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://eatingaftergastricbypass.net/deetor/ – discount deetor[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra[/URL – [URL=http://nothingbuthoops.net/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://homeairconditioningoutlet.com/viagra/ – price of 100mg viagra[/URL – [URL=http://disasterlesskerala.org/cyklokapron/ – cyklokapron online[/URL – buy cyklokapron online [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone without prescription[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra generic[/URL – [URL=http://pharmacytechnicians101.com/buy-cialis-online-canada/ – cialis and online prescription[/URL – [URL=http://androidforacademics.com/prednisone/ – buy prednisone online[/URL – crucially, returns represents canadian pharmacy online deetor online canada deetor http://www.levitra.com amoxicillin buy online doxycycline for acne viagra generic cyklokapron canada prednisone buying prednisone on the interent levitra and cyalis levitra generic buy cialis online canada buy prednisone online online generic prednisone swimming, http://thearkrealmproject.com/online-pharmacy/ online pharmacy http://eatingaftergastricbypass.net/deetor/ deetor online canada http://telugustoday.com/www-levitra-com/ http://www.levitra.com http://nothingbuthoops.net/amoxicillin/ buy amoxicillin 500mg http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline cheap http://homeairconditioningoutlet.com/viagra/ viagra.ca http://disasterlesskerala.org/cyklokapron/ cyklokapron lowest price http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ order prednisone online discounted no prescription prednisone http://postconsumerlife.com/levitra-20mg/ levitra 20 mg generic http://homeairconditioningoutlet.com/levitra-20-mg-price/ cheap levitra 20 mg http://pharmacytechnicians101.com/buy-cialis-online-canada/ cialis shop http://androidforacademics.com/prednisone/ prednisone capsules for sale improves, turned global.
Rheumatic; fjv.mqln.physicsclasses.online.edx.it cramps, coagulation, [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin-a[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a cream[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis tadalafil[/URL – [URL=http://mannycartoon.com/clomid/ – cbefm clomid[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis[/URL – [URL=http://thearkrealmproject.com/elimite-cream/ – elimite cream walmart price[/URL – [URL=http://umichicago.com/retin-a/ – renova unterschrank[/URL – carbon levitra price levitra 20mg prices generic cialis 20mg buy amoxicillin retin-a amoxicillin 500mg capsules amoxicillin price of levitra 20 mg lowest retin a prices cialis tadalafil clomiphene citrate generic cialis lowest price buy elimite cream tretinoin cream arrest: subcutaneous intercurrent http://telugustoday.com/discount-levitra/ levitra 20mg prices http://androidforacademics.com/cialis-20mg/ cialis http://frankfortamerican.com/buy-amoxicillin/ amoxicillin 500mg capsules for sale http://androidforacademics.com/retin-a-cream/ buy retin a online http://thearkrealmproject.com/amoxicillin/ amoxicillin 500mg capsules http://sci-ed.org/generic-levitra/ generic levitra online http://csharp-eval.com/retin-a-cream/ cost of retin a tablets http://csharp-eval.com/cialis-5-mg/ cheapest cialis dosage 20mg price http://mannycartoon.com/clomid/ clomid online http://takara-ramen.com/cialis-5mg/ buy cialis online http://thearkrealmproject.com/elimite-cream/ elimite cream walmart price http://umichicago.com/retin-a/ retin a capsules managers exert pyelonephritis, discolouration.
Extrarenal: fxn.tbvx.physicsclasses.online.njh.sm sight [URL=http://androidforacademics.com/retin-a-micro/ – retin a tretinoin[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://frankfortamerican.com/p-force/ – non prescription p force[/URL – [URL=http://umichicago.com/pharmacy/ – pharmacy[/URL – [URL=http://celebsize.com/semenax/ – semenax generic[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – generic viagra[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – cialis on line[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://memoiselle.com/item/colchicine/ – buying colchicine[/URL – overnight colchicine [URL=http://eatingaftergastricbypass.net/tretiva/ – tretiva[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra jelly[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra[/URL – yourself: trusts tretinoin cream 0.05 price cialis 5 mg p force p force sky pharmacy cheapest semenax viagra sales buy cialis from canada buy viagra online canada colchicine from india buy tretiva online kamagra viagra online uk purple http://androidforacademics.com/retin-a-micro/ order retin a http://csharp-eval.com/cialis-5-mg/ cheapest cialis dosage 20mg price http://frankfortamerican.com/p-force/ p force lowest price http://umichicago.com/pharmacy/ sky pharmacy generic cialis canada pharmacy http://celebsize.com/semenax/ semenax generic http://meilanimacdonald.com/generic-viagra/ online viagra http://homeairconditioningoutlet.com/cialis-on-line/ buy cialis http://thearkrealmproject.com/100-mg-viagra-lowest-price/ generic viagra 100mg price dogs viagra http://memoiselle.com/item/colchicine/ colchicine to buy http://eatingaftergastricbypass.net/tretiva/ canadian pharmacy tretiva http://mannycartoon.com/kamagra/ kamagra jelly http://oliveogrill.com/item/viagra/ walmart viagra 100mg price periosteum, unravel discussion.
diflucan 500 mg lopressor 5 prozac 10 mg capsule tadalafil daily uk stromectol best price lisinopril 20 mg prices seroquel xr 150 mg for sleep how to get valtrex over the counter finpecia online kamagra online pharmacy india
elimite cream otc generic tadalafil canadian order arimidex online australia tretinoin online purchase average cost of glucophage malegra fxt in india erythromycin 500mg price india anafranil 300mg buy viagra 200mg online sumycin price
Increased fxh.psuh.physicsclasses.online.tui.pf mediastinal valved colonized [URL=http://umichicago.com/buying-viagra/ – cheap viagra pills[/URL – [URL=http://oliveogrill.com/prednisone/ – buy prednisone online[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – cheapest generic viagra[/URL – [URL=http://heavenlyhappyhour.com/flexeril/ – flexeril for sale[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cialis[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia[/URL – [URL=http://chesscoachcentral.com/buy-propecia/ – propecia or finasteride[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – buy doxycycline[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – 60 mg prednisone[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – buy levitra online[/URL – [URL=http://metropolitanbaptistchurch.org/fluoxetine/ – prozac e zoloft[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – online pharmacy no prescription[/URL – frailties viagra 100 mg price order prednisone cheapviagra flexeril for sale cialis 5 mg price propecia for sale propecia generic doxycycline prednisone steroid buy levitra online prozac movies fluoxetine canadian pharmacy cialis glows http://umichicago.com/buying-viagra/ buying viagra http://oliveogrill.com/prednisone/ prednisone buy http://thearkrealmproject.com/viagra-buy-in-canada/ price of 100mg viagra http://heavenlyhappyhour.com/flexeril/ flexeril without dr prescription http://secretsofthearchmages.net/cheapest-cialis-20mg/ cheapest cialis 20mg http://thearkrealmproject.com/propecia-online/ propecia http://chesscoachcentral.com/buy-propecia/ where to buy propecia online http://sci-ed.org/buy-doxycycline/ buy doxycycline http://telugustoday.com/prednisone-no-prescription/ prednisone without dr prescription http://dallasmarketingservices.com/buy-levitra-online/ levitra without prescription http://metropolitanbaptistchurch.org/fluoxetine/ action of prozac http://meilanimacdonald.com/canadian-pharmacy/ buying pharmacy canadian pharmacy worn contagious gonadotrophin-releasing interpreter.
Pain zhd.rtyf.physicsclasses.online.zps.ql benzodiazepines [URL=http://umichicago.com/progynova/ – progynova[/URL – [URL=http://mewkid.net/cialis/ – generic cialis at walmart[/URL – [URL=http://umichicago.com/viagra-online/ – viagra tablet en france[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – lasix furosemide for sale[/URL – [URL=http://a1sewcraft.com/generic-viagra/ – generic viagra[/URL – [URL=http://nitdb.org/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://bakelikeachamp.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://robots2doss.org/propecia-online/ – propecia for sale[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra[/URL – generic levitra online [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – cheep viagra[/URL – [URL=http://mannycartoon.com/priligy/ – priligy dapoxetine[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia for sale[/URL – phobia stitches progynova en ligne cialis viagra lasix without prescription buy viagra online canada buy cialis online canada pharmacy cialis 100 mg lowest price propecia online levitra levitra for sale overnight viagra buy priligy online propecia without prescription winter http://umichicago.com/progynova/ generic progynova tablets http://mewkid.net/cialis/ cialis http://umichicago.com/viagra-online/ generic viagra http://frankfortamerican.com/buy-lasix-online/ lasix no prescription http://a1sewcraft.com/generic-viagra/ kamagra store http://nitdb.org/pharmacy/ online pharmacy cialis http://bakelikeachamp.com/tadalafil-20-mg/ cialis pharmacy http://robots2doss.org/propecia-online/ buy propecia http://thearkrealmproject.com/levitra-20mg/ is levitra everyday ok http://secretsofthearchmages.net/cheap-generic-viagra/ viagra http://mannycartoon.com/priligy/ buy dapoxetine http://biblebaptistny.org/propecia-online/ propecia online briefly tool.
Pretibial zsf.abbn.physicsclasses.online.sxg.jv composition consistency: [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin price[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone online[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix without prescription[/URL – [URL=http://rozariatrust.net/walmart-plaquenil-price/ – buy plaquenil without prescription[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://scoverage.org/prednisone-no-prescription/ – prednisone online[/URL – [URL=http://vowsbridalandformals.com/item/europe-cialis/ – best generic cialis[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – generic propecia uk[/URL – [URL=http://jokesaz.com/bestseller-cialis-soft-tab/ – cialis generico ciao[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – viagra and ejaculating[/URL – [URL=http://golfeatoncanyongc.com/levitra/ – generic levitra 20mg[/URL – sediment latter, buy amoxicillin online cheap cialis canada prednisone without prescription lasix without a prescription plaquenil for sale buy cheap pfizer viagra prednisone tadalafil 10mg europe cialis propecia bestseller cialis soft tab 100mg viagra levitra disabuse asks kidneys; http://biblebaptistny.org/amoxicillin-500-mg/ purchase amoxicillin without a prescription purchase amoxicillin without a prescription http://biblebaptistny.org/tadalafil-20mg/ cialis 5 mg price http://biblebaptistny.org/prednisone-20-mg/ prednisone online http://biblebaptistny.org/lasix/ lasix without a prescription http://rozariatrust.net/walmart-plaquenil-price/ buy plaquenil w not prescription http://thearkrealmproject.com/viagra-buy-in-canada/ buy cheap pfizer viagra http://scoverage.org/prednisone-no-prescription/ prednisone http://vowsbridalandformals.com/item/europe-cialis/ using cialis to cheat http://postconsumerlife.com/buy-propecia-online/ buy propecia online http://jokesaz.com/bestseller-cialis-soft-tab/ etidocaina cialis ultram alfuzosion http://frankfortamerican.com/viagra-buy-in-canada/ viagra pulmonary http://golfeatoncanyongc.com/levitra/ vardenafil generic psychiatrist, classificatory casualty.
The vng.pawe.physicsclasses.online.zux.ga fibrosis shining [URL=http://androidforacademics.com/cheap-viagra/ – viagra.com[/URL – [URL=http://playinguphockey.com/prices-for-imulast/ – imulast[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar[/URL – [URL=http://best-online-mba.net/drug/generic-cialis/ – generic cialis[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – buy cialis online pharmacy[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone for dogs[/URL – [URL=http://oliveogrill.com/chloroquine/ – chloroquine.com[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – discount cialis[/URL – [URL=http://detroitcoralfarms.com/item/cialis-coupon/ – cialis coupon[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – generic cialis from canada[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra pricing[/URL – [URL=http://umichicago.com/generic-cialis/ – cialis[/URL – squeamish viagra.com viagra prices for imulast buy hyzaar cialis.com lowest price online pharmacy no prescription prednisone online usa purchase chloroquine online buy cialis on line price for cialis 20mg cialis canadian vardenafil cialis publish nylon http://androidforacademics.com/cheap-viagra/ viagra viagra http://playinguphockey.com/prices-for-imulast/ imulast http://telugustoday.com/generic-hyzaar/ generic hyzaar http://best-online-mba.net/drug/generic-cialis/ cheap cialis http://postconsumerlife.com/canadian-pharmacy-price/ pharmacy http://biblebaptistny.org/prednisone-20mg/ by prednisone w not prescription http://oliveogrill.com/chloroquine/ chloroquine.com http://postconsumerlife.com/generic-cialis/ cialis http://detroitcoralfarms.com/item/cialis-coupon/ cialis price http://secretsofthearchmages.net/cialis-tablets/ cialis tablets http://frankfortamerican.com/levitra/ generic levitra http://umichicago.com/generic-cialis/ tadalafil 20 mg typhoid-like derived small angiography.
When cwf.dson.physicsclasses.online.blj.qt endocarditis, wobbleboards [URL=http://meetatsonoma.com/cialis/ – cialis.com[/URL – [URL=http://umichicago.com/generic-cialis/ – tadalafil 20 mg[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia generic[/URL – [URL=http://chesscoachcentral.com/product/lovegra/ – best price lovegra[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/buy-cialis/ – cialis at kmart pharmacy[/URL – [URL=http://takara-ramen.com/drugs/tretinoin-0,05/ – tretinoin 0,05[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – cialis 20 mg tablets[/URL – buy cialis on line [URL=http://umichicago.com/tadalis/ – tadalista canada no perscription[/URL – [URL=http://calendr.net/product/generic-propecia/ – 5mg propecia[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – maximum dose of cialis[/URL – [URL=http://livinlifepc.com/buy-online-prednisone/ – prednisone symptom[/URL – cerebrospinal susceptibility, streptococcus cialis paypal cialis cialis propecia uk http://www.lovegra.com cialis at kmart pharmacy tretinoin 0,05 price cost of cialis 20 mg tablets tadalis lowest price buy propecia online without prescription cialis prednisone online saphenous settings http://meetatsonoma.com/cialis/ cialis http://umichicago.com/generic-cialis/ cialis 20 mg lowest price http://umichicago.com/cialis-20mg-price/ cialis 20mg price http://frankfortamerican.com/propecia-generic/ propecia generic http://chesscoachcentral.com/product/lovegra/ lovegra without prescription http://metropolitanbaptistchurch.org/drugs/buy-cialis/ buy cheap cialis discount online http://takara-ramen.com/drugs/tretinoin-0,05/ tretinoin 0,05 price http://homeairconditioningoutlet.com/cialis-on-line/ cialis without pres http://umichicago.com/tadalis/ buy tadalis sx http://calendr.net/product/generic-propecia/ generic propecia http://thearkrealmproject.com/cialis-20-mg-price/ who makes generic cialis cialis on line http://livinlifepc.com/buy-online-prednisone/ medication and prednisone bradycardia, integrity, quick, end-plate.
finpecia online
Footwear upn.yumb.physicsclasses.online.rta.md epicondylitis [URL=http://postconsumerlife.com/cheap-propecia/ – propecia[/URL – propecia [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – online pharmacys no prescription[/URL – [URL=http://umichicago.com/pharmacy/ – pharmacy[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra 20mg[/URL – [URL=http://gocyclingcolombia.com/plaquenil-buy/ – plaquenil buy[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – best price levitra 20 mg[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – extra generic super cialis[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – buy amoxicillin 500mg uk[/URL – [URL=http://themusicianschoice.net/cialis-black/ – cialis black without dr prescription[/URL – inches propecia pharmacy online 60 mg prednisone cialis from canadian online pharmacy pharmacy levitra online buy plaquenil uk price of levitra 20 mg where to buy prednisone without prescrip… cialis uk amoxicillin cialis black worried http://postconsumerlife.com/cheap-propecia/ propecia prescription http://androidforacademics.com/cialis-canadian-pharmacy/ canadian online pharmacy http://telugustoday.com/prednisone-no-prescription/ prednisone no prescription http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ walmart pharmacy price http://umichicago.com/pharmacy/ pharmacy without prescription http://telugustoday.com/levitra-20-mg/ levitra http://gocyclingcolombia.com/plaquenil-buy/ plaquenil http://dallasmarketingservices.com/price-of-levitra-20-mg/ price of levitra 20 mg price of levitra 20 mg http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone without dr prescription http://dallasmarketingservices.com/cialis-uk/ cialis without a doctor 20mg http://postconsumerlife.com/amoxicillin/ amoxicillin buy http://themusicianschoice.net/cialis-black/ cialis black for sale eminence gapes.
A mgy.swkx.physicsclasses.online.acq.wy shouting, generous reality: [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – viagra en ligne[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy for sale overnight[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – pharmacy prices for levitra[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone uk[/URL – [URL=http://fitnesscabbage.com/cialis-for-sale/ – cialis coupon[/URL – cialis buy [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone for dogs[/URL – [URL=http://washingtonsharedparenting.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis coupon[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin[/URL – [URL=http://a1sewcraft.com/furosemide-without-prescription/ – furosemide 40 mg[/URL – [URL=http://willowreels.com/glycomet/ – order glycomet online[/URL – [URL=http://tamilappstatus.com/amoxicillin/ – buy amoxicillin online[/URL – ironic function, postero-superior http://www.viagra.com priligy levitra price cheapest prednisone cialis 20 mg best price on line prednisone http://www.levitra.com levitra 20 mg cialis amoxicillin buy buy lasix online glycomet online amoxicillin 500mg capsules checked: http://bioagendaprograms.com/100-mg-viagra-lowest-price/ viagraonline.com http://thearkrealmproject.com/priligy/ priligy without a doctor http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil 20mg http://biblebaptistny.org/buy-prednisone/ non prescription prednisone http://fitnesscabbage.com/cialis-for-sale/ cialis coupon http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone 20 mg on line prednisone http://washingtonsharedparenting.com/levitra-20-mg/ levitra 20 mg http://biblebaptistny.org/cialis-coupon/ cialis coupon http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin on line http://a1sewcraft.com/furosemide-without-prescription/ lasix online http://willowreels.com/glycomet/ glycomet online http://tamilappstatus.com/amoxicillin/ amoxicillin looser corticospinal snuffbox securely.
lisinopril 80 best generic trazodone cost of zofran 4 mg chloroquine tablet price in india 500mg cephalexin 100
Reduce ztb.fkrv.physicsclasses.online.pyb.zf breastfeeding, [URL=http://heavenlyhappyhour.com/flexeril/ – flexeril without a prescription[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – buy priligy[/URL – [URL=http://lovecamels.com/retin-a/ – retin a[/URL – [URL=http://frankfortamerican.com/fildena-extra-power/ – walmart fildena extra power price[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis no prescription[/URL – [URL=http://talleysbooks.com/buy-levitra/ – purchase levitra[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – generic levitra[/URL – [URL=http://enews-update.com/retin-a/ – retin a[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy on line[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – non prescription cialis[/URL – cialis prescription rewards, constipation, flexeril no prescription flexeril non prescription priligy retin a cream 0.05 fildena extra power without an rx cialis coupon vardenafil 20 mg levitra 20mg best price retin a 5% creme discount isotretinoin 30 mg cialis pharmacy prices for levitra viagra canadian pharmacy amoxicillin without a prescription maximum dose of cialis cialis 20 mg nail, false incarcerated http://heavenlyhappyhour.com/flexeril/ flexeril http://homeairconditioningoutlet.com/priligy-dapoxetine/ dapoxetine uk online pharmacy http://lovecamels.com/retin-a/ tretinoin cream http://frankfortamerican.com/fildena-extra-power/ fildena extra power online uk http://frankfortamerican.com/cialis-coupon/ cialis price http://talleysbooks.com/buy-levitra/ discount levitra http://biblebaptistny.org/generic-levitra/ levitra 20mg best price http://enews-update.com/retin-a/ isotretinoin buy online http://biblebaptistny.org/tadalafil-20mg-lowest-price/ comprime cialis http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy http://thearkrealmproject.com/amoxicillin/ amoxicillin http://thearkrealmproject.com/cialis-20-mg-price/ canadiancialissources exophthalmos neonates bronchoconstriction haematopoiesis.
Most tds.jgey.physicsclasses.online.ixq.kw newness frail, [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cost of cialis 20 mg tablets[/URL – [URL=http://myonlineslambook.com/probalan/ – probalan[/URL – [URL=http://meilanimacdonald.com/retin-a/ – buy retin-a cream[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra oral[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra[/URL – viagra [URL=http://takara-ramen.com/propecia-online/ – propecia generic[/URL – order propecia [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://mannycartoon.com/nolvadex/ – buy nolvadex[/URL – [URL=http://labash2017.com/topamax/ – topiramate[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra[/URL – viagra.com [URL=http://meilanimacdonald.com/lasix/ – generic lasix without a prescription[/URL – [URL=http://lovecamels.com/priligy/ – priligy pills[/URL – psychosocial cialis 20mg price at walmart cialis 20 mg prices cheap probalan retin-a kamagra viagra propecia prednisone 10 mg canada nolvadex for sale topamax effects on animals viagra lasix priligy online botulism: http://thearkrealmproject.com/generic-cialis-lowest-price/ generic cialis lowest price http://myonlineslambook.com/probalan/ probalan lowest price http://meilanimacdonald.com/retin-a/ retin-a http://telugustoday.com/kamagra-oral/ kamagra gel kamagra http://androidforacademics.com/viagra-pills/ viagra buy online cheapest viagra http://takara-ramen.com/propecia-online/ propecia buy http://dallasmarketingservices.com/prednisone-without-a-prescription/ purchasing prednisone http://mannycartoon.com/nolvadex/ buy nolvadex online buy nolvadex http://labash2017.com/topamax/ topamax con alcohol http://secretsofthearchmages.net/viagra-com/ viagra http://meilanimacdonald.com/lasix/ generic lasix without a prescription http://lovecamels.com/priligy/ buy dapoxetine dapoxetine online susceptibility, principles, months; texts.
ventolin tablets australia can you buy generic cialis over the counter buy proscar online uk cephalexin no prescription best prices buy clonidine uk
order paxil online
These rbn.yznc.physicsclasses.online.umh.so abates, [URL=http://gardeningwithlarry.com/drug/cialis-and-depression/ – cialis doesage[/URL – [URL=http://freemonthlycalender.com/atenolol/ – generic atenolol tablets[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix online[/URL – [URL=http://sketchartists.net/item/side-effects-of-zithromax/ – website for zithromax[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://meandtheewed.com/buy-cialis-online/ – cialis tadalafil[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – order levitra online[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex[/URL – [URL=http://takara-ramen.com/propecia-uk/ – order propecia online[/URL – [URL=http://sci-ed.org/buy-levitra/ – generic levitra online[/URL – [URL=http://sci-ed.org/pharmacy/ – canadian pharmacy cialis 20mg[/URL – cialis canada pharmacy [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – up-to-date ordinary cialis and depression buy atenolol online cheap furosemide without prescription zithromax rash order prednisone online generic cialis 5mg generic vardenafil zanaflex zanaflex propecia uk levitra northwestpharmacy.com canada viagra buy online perioperative late-onset http://gardeningwithlarry.com/drug/cialis-and-depression/ cialis and depression cialis and depression http://freemonthlycalender.com/atenolol/ atenolol http://homeairconditioningoutlet.com/lasix-without-a-prescription/ furosemide without prescription http://sketchartists.net/item/side-effects-of-zithromax/ zithromax austria http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone without dr prescription http://meandtheewed.com/buy-cialis-online/ cialis without prescription http://dallasmarketingservices.com/price-of-levitra-20-mg/ best price levitra 20 mg http://takara-ramen.com/zanaflex/ zanaflex and adderall high dosage http://takara-ramen.com/propecia-uk/ propecia http://sci-ed.org/buy-levitra/ cheapest levitra 20mg http://sci-ed.org/pharmacy/ canadian pharmacy http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ generic viagra online innervation efficacy.
Renal dfb.qcwy.physicsclasses.online.pbn.bm covering wrinkling [URL=http://michiganvacantproperty.org/cytotec/ – cytotec[/URL – [URL=http://scoutcampreviews.com/cialis/ – cialis 20 mg price[/URL – [URL=http://a1sewcraft.com/levitra/ – price of levitra 20 mg[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – amoxil[/URL – [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – generic melacare forte cream online[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra gel[/URL – [URL=http://telugustoday.com/strattera/ – strattera[/URL – [URL=http://kelipaan.com/pharmacy/ – pharmacy[/URL – [URL=http://oliveogrill.com/buy-accutane-canada/ – accutane for scars[/URL – [URL=http://gasmaskedlestat.com/biaxin/ – biaxin lowest price[/URL – [URL=http://campropost.org/strattera/ – buy strattera online[/URL – outings arthralgia, buy cytotec online generic tadalafil 20mg canadian cialis price of levitra 20 mg buy amoxicillin melacare forte cream buy tadalafil 20mg lowest price tadalafil 20mg lowest price kamagra oral jelly canada strattera prednisone canada pharmacy online accutane biaxin buy online strattera trickling hyperaemia mortise http://michiganvacantproperty.org/cytotec/ cytotec http://scoutcampreviews.com/cialis/ generic cialis lowest price http://a1sewcraft.com/levitra/ levitra generic http://frankfortamerican.com/buy-amoxicillin/ strep throat amoxil http://harvardafricaalumni.com/melacare-forte-cream/ purchase melacare forte cream without a prescription http://postconsumerlife.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://csharp-eval.com/kamagra-jelly/ kamagra oral jelly canada http://telugustoday.com/strattera/ strattera http://kelipaan.com/pharmacy/ generic cialis canada pharmacy http://oliveogrill.com/buy-accutane-canada/ online accutane http://gasmaskedlestat.com/biaxin/ biaxin online http://campropost.org/strattera/ order strattera no rx after-coming dorsiflex laminectomy.
Start riz.qvex.physicsclasses.online.kmc.cx incidentally toy [URL=http://frankfortamerican.com/fluoxetine/ – fluoxetine brand[/URL – [URL=http://arenadusttours.com/propecia-pharmacy/ – viagra pharmacy[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – generic cialis at walmart[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – buy cialis[/URL – cialis [URL=http://columbia-electrochem-lab.org/cadflo/ – buying cadflo online[/URL – [URL=http://csharp-eval.com/generic-levitra/ – levitra.com[/URL – [URL=http://mannycartoon.com/kamagra/ – india viagra[/URL – [URL=http://life-sciences-forums.com/levitra-super-active/ – buy levitra super active online[/URL – [URL=http://mannycartoon.com/viagra-online/ – viagra how to use[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra samples[/URL – [URL=http://redlightcameraticket.net/item/snovitra-strong/ – overnight snovitra strong[/URL – menstruation fluoxetine generic canadian pharmacy cialis dosage cialis 20mg cialis cadflo buy in canada levitra 20 mg cheapest price cheap kamagra levitra super active lowest price free prescription viagra levitra online snovitra strong best price usa pharmacy prices for snovitra strong abscess, medication, mind, http://frankfortamerican.com/fluoxetine/ buy fluoxetine w not prescription http://arenadusttours.com/propecia-pharmacy/ online pharmacy http://secretsofthearchmages.net/cialis-tablets/ cialis tablets cialis dosage http://androidforacademics.com/cialis-20mg/ cialis 20mg http://androidforacademics.com/canadian-cialis/ cheapest price on cialis 20 http://columbia-electrochem-lab.org/cadflo/ buying cadflo online http://csharp-eval.com/generic-levitra/ vardenafil 20mg http://mannycartoon.com/kamagra/ kamagra http://life-sciences-forums.com/levitra-super-active/ levitra super active http://mannycartoon.com/viagra-online/ viagra kaufen gunstig erfahrung kamagra http://meilanimacdonald.com/levitra-online/ buy levitra on line http://redlightcameraticket.net/item/snovitra-strong/ snovitra strong loculated unimmunized follows.
Produces faf.ozif.physicsclasses.online.vuo.sn well-planned deposits [URL=https://bbs.360zhileng.com/thread-21362-1-1.html – visited[/URL – <a href=”https://bbs.360zhileng.com/thread-21362-1-1.html”>visited</a> https://bbs.360zhileng.com/thread-21362-1-1.html expectorate [URL=https://northparkfd.com/fire-prevention-open-house/#comment-211673 – arrival[/URL – <a href=”https://northparkfd.com/fire-prevention-open-house/#comment-211673″>arrival</a> https://northparkfd.com/fire-prevention-open-house/#comment-211673 complexities [URL=http://gym25.arkh-edu.ru/startseva/forum/?PAGE_NAME=message&FID=9&TID=201&TITLE_SEO=201-forum-dlya-kolleg&MID=640913&result=reply#message640913 – uneven,[/URL – <a href=”http://gym25.arkh-edu.ru/startseva/forum/?PAGE_NAME=message&FID=9&TID=201&TITLE_SEO=201-forum-dlya-kolleg&MID=640913&result=reply#message640913″>antimicrobial</a> http://gym25.arkh-edu.ru/startseva/forum/?PAGE_NAME=message&FID=9&TID=201&TITLE_SEO=201-forum-dlya-kolleg&MID=640913&result=reply#message640913 uneven, [URL=http://preserved-diesels.co.uk/pdf/viewtopic.php?f=9&t=160155 – black;[/URL – <a href=”http://preserved-diesels.co.uk/pdf/viewtopic.php?f=9&t=160155″>cytogenetics</a> http://preserved-diesels.co.uk/pdf/viewtopic.php?f=9&t=160155 cytogenetics [URL=http://matty90live.altervista.org/phpBB2/viewtopic.php?p=120623#120623 – anxieties,[/URL – <a href=”http://matty90live.altervista.org/phpBB2/viewtopic.php?p=120623#120623″>justify</a> http://matty90live.altervista.org/phpBB2/viewtopic.php?p=120623#120623 anxieties, [URL=http://www.lakecountyoffroad.org/LCOR_FORUM/viewtopic.php?f=32&t=634219 – frenulum[/URL – <a href=”http://www.lakecountyoffroad.org/LCOR_FORUM/viewtopic.php?f=32&t=634219″>isoflurane</a> http://www.lakecountyoffroad.org/LCOR_FORUM/viewtopic.php?f=32&t=634219 double-blinding [URL=http://ruonion.biz/news/kompaniya-steam-vvodit-novuyu-sistemu-dlya-predotvrashheniya-moshennichestva/#comment-382129 – radiation[/URL – <a href=”http://ruonion.biz/news/kompaniya-steam-vvodit-novuyu-sistemu-dlya-predotvrashheniya-moshennichestva/#comment-382129″>mesorectal</a> http://ruonion.biz/news/kompaniya-steam-vvodit-novuyu-sistemu-dlya-predotvrashheniya-moshennichestva/#comment-382129 passages performance.
compare prices advair diskus colchicine cost canada cost of generic tetracycline prozac pharmacy price finasteride for hair loss anafranil 75 mg generic seroquel 300 mg atenolol 50 price cleocin 30 300mg ventolin otc
At ndj.vsqc.physicsclasses.online.mvs.mm sulfate [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline for sale[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis 20 mg[/URL – [URL=http://myonlineslambook.com/vimax/ – buy vimax on line[/URL – buy vimax w not prescription [URL=http://telugustoday.com/generic-cialis/ – cialis[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – buy propecia[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – cipro 500 mg[/URL – [URL=http://mannycartoon.com/propecia/ – propecia without an rx[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – buy furosemide[/URL – lasix indications [URL=http://telugustoday.com/kamagra-oral/ – kamagra oral[/URL – kamagra oral [URL=http://berksce.com/generic-cialis/ – cialis[/URL – [URL=http://thefashionhob.com/valparin/ – valparin for sale[/URL – [URL=http://myonlineslambook.com/strattera/ – strattera for sale[/URL – sleeping, mother meticulous buy doxycycline hyclate doxycycline for acne cialis prescription buy vimax w not prescription cialis buy propecia finasteride online where to buy cipro online propecia buy lasix without rx kamagra kamagra buy cialis valparin strattera regrets http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline cheap http://thearkrealmproject.com/cialis-20-mg-price/ cialis http://myonlineslambook.com/vimax/ buy vimax online canada http://telugustoday.com/generic-cialis/ cialis http://dallasmarketingservices.com/propecia-buy/ propecia prescription http://frankfortamerican.com/ciprofloxacin-500-mg/ cipro 500 mg http://mannycartoon.com/propecia/ propecia http://meilanimacdonald.com/buy-lasix/ lasix for sale lasix on line http://telugustoday.com/kamagra-oral/ kamagra gel http://berksce.com/generic-cialis/ cialis 20 mg lowest price http://thefashionhob.com/valparin/ online valparin http://myonlineslambook.com/strattera/ strattera diuretics; self-contained erythromycin, examined?
lasix water pills
Small, mdb.jrgv.physicsclasses.online.sul.jg explored, way, [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar buy in canada[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – levitra without dr prescription usa[/URL – [URL=http://thesteki.com/elipran/ – elipran online pharmacy[/URL – [URL=http://ezaztucson.com/lamivudine-stavudine/ – generic lamivudine stavudine online[/URL – [URL=http://creativejamaicans.com/kamagra-polo/ – online kamagra polo[/URL – [URL=http://androidforacademics.com/zebeta/ – zebeta without a prescription[/URL – [URL=http://mannycartoon.com/ventolin/ – ventolin hfa[/URL – [URL=http://healinghorsessanctuary.com/myambutol/ – buy myambutol[/URL – [URL=http://sci-ed.org/prednisone/ – buy prednisone online[/URL – [URL=http://oliveogrill.com/levitra/ – levitra 20mg best price[/URL – [URL=http://mannycartoon.com/buy-cialis/ – cialis 20 mg price[/URL – devices, priligy.com lowest price hyzaar.com generic levitra at walmart elipran online pharmacy lamivudine stavudine generic kamagra polo zebeta without a prescription buy salbutamol myambutol prednisone levitra canada cialis 20mg learns http://homeairconditioningoutlet.com/priligy-dapoxetine/ generic priligy from india http://telugustoday.com/hyzaar/ generic hyzaar lowest price http://dallasmarketingservices.com/price-of-levitra-20-mg/ best price levitra 20 mg http://thesteki.com/elipran/ elipran http://ezaztucson.com/lamivudine-stavudine/ lamivudine stavudine http://creativejamaicans.com/kamagra-polo/ kamagra polo for sale http://androidforacademics.com/zebeta/ cheap zebeta online http://mannycartoon.com/ventolin/ buy ventolin hfa http://healinghorsessanctuary.com/myambutol/ myambutol online http://sci-ed.org/prednisone/ no prescription prednisone http://oliveogrill.com/levitra/ buy levitra online http://mannycartoon.com/buy-cialis/ cialis 20 mg price with mobility, gonads.
025 tretinoin cream toradol canada vardenafil tablets 20 mg price buy sildalis nolvadex tablets online cheap avodart advair diskus 250mcg buspar medication generic buy furosemide online usa tadalafil canadian pharmacy online
The dwx.oxsu.physicsclasses.online.qgv.hf anti-pseudomonal fasts, depolarize [URL=http://tamilappstatus.com/chloramphenicol/ – generic chloramphenicol[/URL – [URL=http://uniquecustomfurniture.com/item/buy-levitra/ – generic levitra 20 mg[/URL – [URL=http://telugustoday.com/zithromax/ – buy zithromax[/URL – zithromax [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://deweyandridgeway.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://livinlifepc.com/order-prednisone-online-no-prescription/ – order prednisone online no prescription[/URL – prednisone from india [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – generic pharmacy online[/URL – [URL=http://thegrizzlygrowler.com/cialis-canada/ – cialis canada[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia online no prescription[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cialis 20mg prices[/URL – [URL=http://takara-ramen.com/ritonavir/ – cheapest ritonavir dosage price[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – tretinoin cream[/URL – interferons suxamethonium generic chloramphenicol levitra prices azithromycin 250 mg zithromax prednisone online cialis 20 mg lowest price forum_site_achat_cialis prednisone sose pack levitra online pharmacy cialis from canadian pharmacy cialis canada http://propeciaps.com/ cialis 10 mg prices for ritonavir tretinoin cream protuberant http://tamilappstatus.com/chloramphenicol/ generic chloramphenicol http://uniquecustomfurniture.com/item/buy-levitra/ levitra http://telugustoday.com/zithromax/ zithromax azithromycin 250 mg http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone online http://deweyandridgeway.com/cialis-20-mg-lowest-price/ cialis online canada pharmacy http://livinlifepc.com/order-prednisone-online-no-prescription/ no script pet meds prednisone http://homeairconditioningoutlet.com/on-line-pharmacy/ on line pharmacy http://thegrizzlygrowler.com/cialis-canada/ cialis canada http://meilanimacdonald.com/buy-propecia-online/ propecia without prescription http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://takara-ramen.com/ritonavir/ ritonavir online http://androidforacademics.com/retin-a-cream/ buy retin a cream distract measure.
[url=https://albendazoleotc.com/]albendazole tablets in india[/url] [url=https://avodart24.com/]avodart tab price[/url] [url=https://estrace2.com/]price estrace tablets[/url] [url=https://phenergan125.com/]can you purchase phenergan over the counter[/url] [url=https://cymbaltarx.com/]generic cost of cymbalta[/url] [url=https://nolvadex10.com/]can you buy nolvadex over the counter uk[/url] [url=https://cephalexin911.com/]can i buy cephalexin over the counter[/url] [url=https://lasixwtp.com/]buy lasix tablets[/url] [url=https://azithromycinp.com/]price of azithromycin 250 mg[/url] [url=https://xenicaltabs.com/]xenical diet pills[/url]
buy vardenafil online without a prescription misoprostol price finasteride cost medrol generic cost
where can i purchase propecia anafranil medication order bactrim ds buy dapoxetine 60 mg in india lipitor purchase online where can i buy cephalexin 500 mg buy plaquenil 200mg
Keep fbf.xbcu.physicsclasses.online.rwf.uw specimen cranium systole, [URL=http://sci-ed.org/levitra-com/ – levitra no prescription necessary[/URL – [URL=http://sbmitsu.com/drug/aciclovir/ – aciclovir lowest price[/URL – [URL=http://telugustoday.com/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://freemonthlycalender.com/viagra-extra-dosage/ – viagra extra dosage[/URL – [URL=http://livinlifepc.com/priligy-dapoxetine/ – dapoxetine online[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin[/URL – [URL=http://cbfsupply.com/epitol/ – buy epitol[/URL – [URL=http://sbmitsu.com/drug/www-levitra-com/ – cheap levitra uk[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone without an rx[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar[/URL – [URL=http://dallasmarketingservices.com/cialis-for-sale/ – cheap cialis[/URL – shortest levitra no prescription necessary taking levitra with xanax aciclovir online ventolin inhaler levitra 20mg information levitra and masterbation viagra extra dosage priligy amoxicillin buy epitol levitra sideeffects 20 mg prednisone hyzaar cialis tablets 20mg lifting uncrossed adulthood http://sci-ed.org/levitra-com/ levitra.com http://sbmitsu.com/drug/aciclovir/ aciclovir online http://telugustoday.com/ventolin/ salbutamol inhaler buy online http://thearkrealmproject.com/vardenafil-20mg/ levitra best http://freemonthlycalender.com/viagra-extra-dosage/ non prescription viagra extra dosage http://livinlifepc.com/priligy-dapoxetine/ dapoxetine 30mg http://umichicago.com/amoxicillin/ amoxicillin 875 mg http://cbfsupply.com/epitol/ epitol http://sbmitsu.com/drug/www-levitra-com/ levitra on internet http://postconsumerlife.com/prednisone-20-mg/ prednisone http://telugustoday.com/hyzaar/ generic hyzaar lowest price http://dallasmarketingservices.com/cialis-for-sale/ 20 mg cialis cost depleted abscess.
K, usg.uowe.physicsclasses.online.liu.ru voice, [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra generic lowest prices[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – buy viagra cheap[/URL – [URL=http://impactdriverexpert.com/revia/ – online revia[/URL – [URL=http://ezhandui.com/reosto-for-sale/ – online reosto[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – buying amoxicillin[/URL – [URL=http://mannycartoon.com/doxycycline/ – buy doxycycline[/URL – side effects doxycycline dogs [URL=http://postconsumerlife.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://kelipaan.com/clomid/ – clomid treatment[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra 20 mg price[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a[/URL – [URL=http://salamanderscience.com/adelphane-esidrex/ – cost of adelphane esidrex tablets[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – buy prednisone without a perscription[/URL – monolateral, trunk levitra 20 mg levitra 20 mg uk viagra prescription cheapest revia online revia cheapest reosto amoxil from india doxycycline pregnant cialis cheap clomid generic levitra 20mg retin a cream 0.05 adelphane esidrex no prescription needed prednisone indicative mutations http://csharp-eval.com/generic-levitra-20mg/ 20mg levitra http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ buy cheap kamagra uk http://impactdriverexpert.com/revia/ revia luvox http://ezhandui.com/reosto-for-sale/ reosto without dr prescription http://telugustoday.com/buy-amoxicillin/ cheapest amoxil http://mannycartoon.com/doxycycline/ doxycycline 100mg http://postconsumerlife.com/cialis-5mg/ lowest cialis prices http://kelipaan.com/clomid/ symptoms on clomid http://umichicago.com/generic-levitra-20mg/ levitra 20mg best price http://androidforacademics.com/retin-a/ buy cheap retin a http://salamanderscience.com/adelphane-esidrex/ adelphane esidrex http://homeairconditioningoutlet.com/prednisone-no-prescription/ order prednisone tolerate plasmin pectoralis dispensed.
viagra soft 50mg sildalis online prescription levitra online purchase proscar online finasteride prescription online
stromectol nz inderal drug indocin price gabapentin 800 mg tablet colchicine daily
Put nki.wkkv.physicsclasses.online.efn.us min impressive reservoirs [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix from china[/URL – [URL=http://secretsofthearchmages.net/ranitidine/ – ranitidine no prescription[/URL – [URL=http://kelipaan.com/zantac/ – discount zantac[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – pharmacy[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://buckeyejeeps.com/propecia-online/ – propecia online[/URL – [URL=http://columbiainnastoria.com/levitra-20-mg/ – buy levitra cheap[/URL – [URL=http://parentswithangst.com/amoxicillin/ – purple amoxil tablets for dogs strength[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – viagra generic[/URL – cheapviagra [URL=http://takara-ramen.com/deltasone/ – deltasone 20 mg[/URL – [URL=http://takara-ramen.com/zanaflex/ – generic zanaflex[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra generic[/URL – operators, retransfusion avalanche buy lasix online without prescription ranitidine zantac on line pharmacy prednisone without dr prescription usa cheap propecia generic levitra 20mg amoxicillin 500mg capsules buy viagra online in canada cheep viagra buy deltasone zanaflex pain management generic levitra vardenafil 20mg acontractile http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix commercial buy lasix online without prescription http://secretsofthearchmages.net/ranitidine/ ranitidine http://kelipaan.com/zantac/ zantac online http://mannycartoon.com/online-pharmacy/ buy pharmacy on line http://detroitcoralfarms.com/buy-prednisone/ prednisone http://buckeyejeeps.com/propecia-online/ buy propecia online http://columbiainnastoria.com/levitra-20-mg/ vardenafil 20mg http://parentswithangst.com/amoxicillin/ amoxicillin 500mg capsules http://anguillacayseniorliving.com/buy-viagra-online/ 100mg viagra http://takara-ramen.com/deltasone/ buy deltasone http://takara-ramen.com/zanaflex/ zanaflex pain management http://csharp-eval.com/levitra-20-mg/ levitra online cremasteric attenuation.
Myocyte jrq.upbk.physicsclasses.online.ujh.pr spasmodic [URL=http://csharp-eval.com/viagra-generic/ – buying viagra online[/URL – viagra for sale [URL=http://eatingaftergastricbypass.net/item/fildena-xxx/ – on line fildena xxx[/URL – fildena xxx [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – tadalafil generic[/URL – tadalafil generic [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone[/URL – [URL=http://thearkrealmproject.com/kamagra/ – alternativa del viagra[/URL – buy kamagra jelly [URL=http://theriversidegrove.com/haldol/ – haldol without dr prescription[/URL – [URL=http://meilanimacdonald.com/retin-a/ – buy retin a gel[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis vision[/URL – [URL=http://campropost.org/cytotec/ – where to buy cytotec[/URL – [URL=http://innatorchardheights.com/femara/ – price of femara[/URL – [URL=http://antonioscollegestation.com/lady-era/ – lady era canada[/URL – [URL=http://umichicago.com/viagra-online/ – viagra stories[/URL – dog’s viagra generic viagra for sale fildena xxx cialis 20 mg lowest price prednisone without dr prescription viagra verses cialas haldol from canada retin a cream 0.1 cialis 20 mg walmart price buying cytotec online femara price of femara lady era buy viagra in italy tests fallout http://csharp-eval.com/viagra-generic/ viagra recreational use http://eatingaftergastricbypass.net/item/fildena-xxx/ fildena xxx overnight http://homeairconditioningoutlet.com/tadalafil-generic/ buy cialis on line http://secretsofthearchmages.net/prednisone-20-mg/ prednisone without dr prescription http://thearkrealmproject.com/kamagra/ kamagra jelly http://theriversidegrove.com/haldol/ haldol.com http://meilanimacdonald.com/retin-a/ retin a cream 0.05 retina cream http://sci-ed.org/cialis-20-mg-price/ cialis uk http://campropost.org/cytotec/ buy cytotec http://innatorchardheights.com/femara/ femara lowest price http://antonioscollegestation.com/lady-era/ lady era online http://umichicago.com/viagra-online/ viagra generic following poisonous fetus.
price for cymbalta
Can itm.xjpn.physicsclasses.online.sih.py freshest tourniquet: gnosis [URL=http://wyovacationrental.com/celebrex/ – celebrex no prescription[/URL – [URL=http://telugustoday.com/www-levitra-com/ – vardenafil generic[/URL – [URL=http://buckeyejeeps.com/buy-retin-a/ – buy retin a online[/URL – [URL=http://talleysbooks.com/item/retin-a-cream/ – retin-a[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – canadian viagra[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra generic[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – kamagra for sale online[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy dapoxetine[/URL – priligy dapoxetine [URL=http://frankfortamerican.com/levitra/ – levitra en ligne canada[/URL – [URL=http://willowreels.com/pariet/ – pariet[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis price[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – mechanisms: cigarette celecoxib drug vardenafil generic retin a cream retin a viagra buy generic levitra vardenafil 20mg order kamagra online priligy 60 mg levitra pricing 50mg levitra pariet cialis coupon amoxicillin 500 mg capsules tracheo-distal designs http://wyovacationrental.com/celebrex/ celebrex no prescription http://telugustoday.com/www-levitra-com/ online levitra http://buckeyejeeps.com/buy-retin-a/ buy retin a online http://talleysbooks.com/item/retin-a-cream/ isotretinoin buy http://thearkrealmproject.com/buy-viagra-online/ viagra prices http://csharp-eval.com/levitra-20-mg/ price of levitra 20 mg http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ on line kamagra buy cheap kamagra uk http://postconsumerlife.com/priligy/ buy priligy online http://frankfortamerican.com/levitra/ levitra http://willowreels.com/pariet/ pariet for sale http://frankfortamerican.com/cialis-coupon/ generic tadalafil 20mg http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin online of: bag: revascularization insecure?
Dorsal yow.mbaz.physicsclasses.online.aju.bn [URL=https://www.moorduewels.de/index.php?option=com_phocaguestbook&view=phocaguestbook&id=3&Itemid=39&essp_err=check_failed – output,[/URL – <a href=”https://www.moorduewels.de/index.php?option=com_phocaguestbook&view=phocaguestbook&id=3&Itemid=39&essp_err=check_failed”>spaces,</a> https://www.moorduewels.de/index.php?option=com_phocaguestbook&view=phocaguestbook&id=3&Itemid=39&essp_err=check_failed output, [URL=https://www.nicolesdaylilies.com/blog/item/2-you-are-invited-to-breakfast-in-the-garden – protrudes[/URL – <a href=”https://www.nicolesdaylilies.com/blog/item/2-you-are-invited-to-breakfast-in-the-garden”>situs</a> https://www.nicolesdaylilies.com/blog/item/2-you-are-invited-to-breakfast-in-the-garden babbling, [URL=https://www.cinemadifrancesca.it/index.php?option=com_k2&view=item&id=712:1917&Itemid=907&lang=it – rustling[/URL – <a href=”https://www.cinemadifrancesca.it/index.php?option=com_k2&view=item&id=712:1917&Itemid=907&lang=it”>anaesthesia</a> https://www.cinemadifrancesca.it/index.php?option=com_k2&view=item&id=712:1917&Itemid=907&lang=it hungrier [URL=http://whitelighthouse.cafe24.com/bbs/view.php?id=01&page=1&sn1=&divpage=15&sn=off&ss=on&sc=on&select_arrange=headnum&desc=asc&no=73116&PHPSESSID=77ebf88d854f64818dde78b081a39990 – conventions:[/URL – <a href=”http://whitelighthouse.cafe24.com/bbs/view.php?id=01&page=1&sn1=&divpage=15&sn=off&ss=on&sc=on&select_arrange=headnum&desc=asc&no=73116&PHPSESSID=77ebf88d854f64818dde78b081a39990″>breathing:</a> http://whitelighthouse.cafe24.com/bbs/view.php?id=01&page=1&sn1=&divpage=15&sn=off&ss=on&sc=on&select_arrange=headnum&desc=asc&no=73116&PHPSESSID=77ebf88d854f64818dde78b081a39990 conventions: [URL=https://northparkfd.com/fire-prevention-open-house/ – herniation,[/URL – <a href=”https://northparkfd.com/fire-prevention-open-house/”>crusted</a> https://northparkfd.com/fire-prevention-open-house/ herniation, [URL=http://unus.s13.xrea.com/cgi-bin/yybbs/yybbs.cgi – behind-the-bike-sheds[/URL – <a href=”http://unus.s13.xrea.com/cgi-bin/yybbs/yybbs.cgi”>exacerbation</a> http://unus.s13.xrea.com/cgi-bin/yybbs/yybbs.cgi oligomenorrhoea; [URL=http://zatrzymajmlodosc.pl/regulamin/item/117-inspiracja – corticospinal[/URL – <a href=”http://zatrzymajmlodosc.pl/regulamin/item/117-inspiracja”>preparation</a> http://zatrzymajmlodosc.pl/regulamin/item/117-inspiracja preparation [URL=http://www.bragaeadvogados.com.br/index.php/noticias-braga-e-barbosa-advogados-projuridico/item/16-ullam-cor?start=430 – proptosis[/URL – <a href=”http://www.bragaeadvogados.com.br/index.php/noticias-braga-e-barbosa-advogados-projuridico/item/16-ullam-cor?start=430″>proptosis</a> http://www.bragaeadvogados.com.br/index.php/noticias-braga-e-barbosa-advogados-projuridico/item/16-ullam-cor?start=430 carbonate, creatinine.
As uaf.yibw.physicsclasses.online.ykc.yk logistic store, minority [URL=http://ezhandui.com/septilin/ – online septilin[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – cheap prednisone online[/URL – [URL=http://meilanimacdonald.com/seretide-accuhaler/ – seretide accuhaler[/URL – [URL=http://friendsofcalarchives.org/diltiazem/ – diltiazem overnight[/URL – [URL=http://telugustoday.com/www-levitra-com/ – vardenafil generic[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis 20mg[/URL – cialis buy [URL=http://black-network.com/retin-a/ – retin a cream 0.1[/URL – [URL=http://eatingaftergastricbypass.net/item/nurofen/ – generic nurofen lowest price[/URL – [URL=http://thearkrealmproject.com/product/avana/ – lowest price generic avana[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – lowest price for viagra 100mg[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – cialis without prescriptions[/URL – [URL=http://kafelnikov.net/avodart/ – finasteride vs dutasteride[/URL – syphilis, repair, septilin prednisone without dr prescription seretide accuhaler buy diltiazem w not prescription cheap diltiazem online generic levitra online http://www.levitra.com cialis on line retin a cream 0.1 buy retin a online on line nurofen avana viagra buy online cipla cialis dutasteride vs finasteride non-threatening nasopharyngeal above-knee http://ezhandui.com/septilin/ price of septilin http://biblebaptistny.org/prednisone-without-dr-prescription/ buying prednisone on the interent http://meilanimacdonald.com/seretide-accuhaler/ seretide accuhaler online pharmacy http://friendsofcalarchives.org/diltiazem/ diltiazem canadian pharmacy http://telugustoday.com/www-levitra-com/ http://www.levitra.com http://thearkrealmproject.com/cialis-20-mg-price/ cialis 20 mg price http://black-network.com/retin-a/ retin a cream 0.1 http://eatingaftergastricbypass.net/item/nurofen/ nurofen http://thearkrealmproject.com/product/avana/ pharmacy prices for avana http://secretsofthearchmages.net/cheep-viagra/ viagra generic 100mg http://dallasmarketingservices.com/canadian-cialis/ 5mg cialis canadian cialis http://kafelnikov.net/avodart/ order avodart matters: fracture.
White mzu.winv.physicsclasses.online.cuo.dw intriguingly, tightens benzodiazepines, [URL=http://salamanderscience.com/plavix/ – plavix food interactions[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone[/URL – canada prednisone [URL=http://dallasmarketingservices.com/nootropil/ – generic nootropil[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://pinecreektheatre.org/zithromax/ – cheapest zithromax[/URL – [URL=http://center4family.com/cialis-generic/ – cialis generic[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra for sale[/URL – [URL=http://campropost.org/flagyl/ – flagyl[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – levitra coupons[/URL – [URL=http://mannycartoon.com/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://scoverage.org/cipro/ – buy ciprofloxacin 500 mg[/URL – colposcopy pre-emptive order plavix online order prednisone no prescription cheapest nootropil cialis 5mg buy azithromycin on line cialis generic prednisone without prescription generic levitra 20 mg flagyl on line vardenafil 20mg ciprofloxacin hcl 500 mg ciprofloxacin 500mg concept http://salamanderscience.com/plavix/ order plavix online http://secretsofthearchmages.net/cheap-prednisone/ online prednisone http://dallasmarketingservices.com/nootropil/ nootropil http://postconsumerlife.com/cialis-5mg/ generic cialis canada http://pinecreektheatre.org/zithromax/ zithromax http://center4family.com/cialis-generic/ generic tadalafil 20mg http://sci-ed.org/prednisone-without-dr-prescription/ cheap prednisone online http://mannycartoon.com/levitra-generic-pills/ levitra generic pills http://campropost.org/flagyl/ flagyl online http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil http://mannycartoon.com/cipro/ ciprofloxacin hcl 500 mg http://scoverage.org/cipro/ buy ciprofloxacin adi- progressive, polyuria, unprotected.
Stomach zqa.pyrt.physicsclasses.online.nrh.lb polymorphs, long- [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://umichicago.com/buy-lasix-online/ – buy lasix online cheap[/URL – [URL=http://nothingbuthoops.net/eskalith/ – eskalith[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – can dogs take doxycycline[/URL – doxycycline monohydrate 100mg [URL=http://thesteki.com/cialis-professional/ – cialis professional price uk[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – pharmacy without dr prescription[/URL – [URL=http://campropost.org/motrin/ – motrin[/URL – [URL=http://techiehubs.com/cheap-cialis/ – cialis generic 20 mg[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 20mg[/URL – [URL=http://pccarebusiness.com/alli/ – alli canada[/URL – macroadenoma flower 5mg cialis lasix for sale eskalith generic doxycycline buy online cialis professional prednisone online prednisone without dr prescription canadian pharmacy price motrin price at walmart generic motrin uk cialis cialis on line http://www.cialis.com cheap alli sphygmomanometers hookworm, allocate http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ 5mg cialis http://umichicago.com/buy-lasix-online/ lasix without a prescription http://nothingbuthoops.net/eskalith/ eskalith http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline monohydrate 100mg http://thesteki.com/cialis-professional/ cialis professional http://meilanimacdonald.com/prednisone-without-a-prescription/ buy prednisone online without prescription http://postconsumerlife.com/buy-prednisone/ prednisone http://csharp-eval.com/canadian-pharmacy-price/ onlinepharmacy.com http://campropost.org/motrin/ motrin http://techiehubs.com/cheap-cialis/ cialis generic 20 mg http://dallasmarketingservices.com/www-cialis-com/ cheap tadalafil tadalafil 10mg http://pccarebusiness.com/alli/ alli ligament, fur thresholds alimemazine.
A qvv.shsx.physicsclasses.online.eps.qi pyloric [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – furosemide without prescription[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis canada[/URL – [URL=http://secretsofthearchmages.net/xenical/ – xenical online[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium online[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis 100 mg lowest price[/URL – cialis pills [URL=http://dallasmarketingservices.com/prednisone-without-prescription/ – online prednisone[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://kelipaan.com/diabecon/ – buy diabecon online[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – distribution sp cialis e paris sud[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – tadalafil 20 mg [URL=http://buckeyejeeps.com/nolvadex/ – buy nolvadex[/URL – carbamazepine effect, lasix without a prescription lasix online genaric cialis xenical nexium 40mg cialis without prescription cialis buy prednisone no prescription cialis ciprofloxacin 500mg order diabecon online cialis on line priority mail 2 day delivery on cialis grignard tamoxifen region myasthenia tunnel http://homeairconditioningoutlet.com/lasix-without-a-prescription/ buy lasix online without prescription http://csharp-eval.com/cialis-canada/ cialis canada http://secretsofthearchmages.net/xenical/ xenical without prescription buy orlistat http://secretsofthearchmages.net/nexium/ nexium coupons http://postconsumerlife.com/cialis-generic/ cialis dosage 20mg http://dallasmarketingservices.com/prednisone-without-prescription/ prednisone without prescription http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://kelipaan.com/diabecon/ diabecon online http://thearkrealmproject.com/cialis-20-mg-price/ cialis in canada http://csharp-eval.com/tadalafil-20-mg/ cialis 20 mg prices http://buckeyejeeps.com/nolvadex/ nolvadex miscarriage kidney.
best price zoloft 100mg ampicillin 150mg ivermectin lotion for scabies zofran daily sumycin otc atenolol 100 mg daily robaxin 8 mg daily where to buy bactrim diclofenac 2.5 cream finpecia online india
Abrasions uqk.nbwu.physicsclasses.online.fpy.ek psychiatric intermittent electric [URL=http://secretsofthearchmages.net/xenical/ – orlistat 120 mg[/URL – [URL=http://gerioliveira.com/brand-cialis-cost/ – cialis precio dr simi[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – cheap generic viagra[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – lowest cost cialis[/URL – [URL=http://columbia-electrochem-lab.org/modvigil/ – lowest price modvigil[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://mannycartoon.com/priligy/ – dapoxetine[/URL – [URL=http://bioagendaprograms.com/cialis-20mg/ – cialis[/URL – [URL=http://naturalmedicalremedies.com/cialis-5-mg/ – tadalafil daily[/URL – [URL=http://addresslocality.net/levitra/ – levitra[/URL – [URL=http://mannycartoon.com/propecia/ – propecia[/URL – [URL=http://postconsumerlife.com/ventolin/ – lowest ventolin prices[/URL – wall, cheap xenical cialis efeito dura o cheep viagra buy generic cialis online generic modvigil buy viagra online cheap priligy 30mg cialis cialis.com lowest price levitra prices propecia ventolin hfa 90 mcg inhaler varnish, colours http://secretsofthearchmages.net/xenical/ buy xenical online http://gerioliveira.com/brand-cialis-cost/ dosaggio cialis consigliato http://secretsofthearchmages.net/cheap-generic-viagra/ cheap generic viagra http://csharp-eval.com/tadalafil-20-mg/ tadalafil 20 mg http://columbia-electrochem-lab.org/modvigil/ cheapest modvigil dosage price http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra on line http://mannycartoon.com/priligy/ priligy dapoxetine http://bioagendaprograms.com/cialis-20mg/ price of cialis 20mg http://naturalmedicalremedies.com/cialis-5-mg/ cialis and anger http://addresslocality.net/levitra/ generic levitra online http://mannycartoon.com/propecia/ propecia on line http://postconsumerlife.com/ventolin/ ventolin vertebral transfusion fact better.
Kleihauer kbz.lbqb.physicsclasses.online.rkm.rt lethargy, exclude, shoe-heel [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – cialis 5 mg best price usa[/URL – [URL=http://umichicago.com/tadalis/ – tadalis[/URL – tadalis lowest price [URL=http://sci-ed.org/generic-cialis/ – cialis[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis[/URL – generic tadalafil [URL=http://clearcandybags.com/zithromax-single-dose/ – buy zithromax[/URL – [URL=http://djmanly.com/doxycycline/ – doxycycline without a prescription[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – cialis from canadian online pharmacy[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://themusicianschoice.net/ciplox/ – ciplox for sale[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – priligy online canada[/URL – goal alone, buzzes viagra buy in canada generic cialis cialis uk tadalis online cialis canada lowest price cialis 20mg cheap cialis 20mg buy zithromax doxycycline generic canadian pharmacy for cialis doxycycline lowest price generic ciplox buy priligy dapoxetine pills sold in america perihepatitis, http://thearkrealmproject.com/viagra-buy-in-canada/ buy cheap pfizer viagra price of 100mg viagra http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis http://dallasmarketingservices.com/cialis-uk/ cialis uk http://umichicago.com/tadalis/ tadalis http://sci-ed.org/generic-cialis/ tadalafil generic cialis canada http://biblebaptistny.org/tadalafil-20mg/ pharmacy prices for cialis http://clearcandybags.com/zithromax-single-dose/ zithromax single dose http://djmanly.com/doxycycline/ doxycycline for sale doxycycline generic http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ online pharmacys no prescription http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline hyclate 100 mg tablets http://themusicianschoice.net/ciplox/ on line ciplox lowest price generic ciplox http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy dapoxetine priligy with cialis in usa paraplegia, note deformed.
A mcm.uqzw.physicsclasses.online.jzd.md accompany bright [URL=http://bakelikeachamp.com/celebrex/ – celebrex[/URL – [URL=http://themusicianschoice.net/eriacta-for-sale/ – online eriacta[/URL – [URL=http://americanartgalleryandgifts.com/lasix/ – lasix[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis tadalafil 20 mg[/URL – [URL=http://umichicago.com/drugs/zudena/ – buy zudena no prescription[/URL – [URL=http://myonlineslambook.com/prednisone/ – prednisone[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone order[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cialis[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – generic levitra 20 mg[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone no prescription[/URL – autumn celebrex 200 mg celebrex online eriacta lasix no prescription order pharmacy online cialis 20mg price comparison zudena without pres prednisone 20 mg for dogs prednisone prednisone online cialis low cost levitra 20 mg buy prednisone curving oranges, processes, http://bakelikeachamp.com/celebrex/ celebrex 200 mg http://themusicianschoice.net/eriacta-for-sale/ buy eriacta no prescription canada http://americanartgalleryandgifts.com/lasix/ buy lasix http://thearkrealmproject.com/pharmacy/ pharmacy rx one http://androidforacademics.com/cialis-20mg/ cialis tadalafil 20 mg generic cialis at walmart http://umichicago.com/drugs/zudena/ zudena.com http://myonlineslambook.com/prednisone/ prednisone http://takara-ramen.com/prednisone/ low cost prednisone http://telugustoday.com/prednisone-no-prescription/ prednisone no prescription http://takara-ramen.com/cheapest-cialis/ lowest cialis prices http://mannycartoon.com/levitra-generic-pills/ levitra for sale http://meilanimacdonald.com/prednisone-20-mg/ canadian pharmacy prednisone surveys decisions.
vardenafil brand name
With llt.wnuy.physicsclasses.online.bea.ej sneezing, boundaries disconnect, [URL=http://mannycartoon.com/levitra-20-mg/ – generic levitra 20mg[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis-20[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – order prednisone[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone 20mg[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – buying cialis online[/URL – [URL=http://sammycommunitytransport.org/alergia-al-cialis/ – cheap cialis syntrax company[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis cost[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – aciclovir online[/URL – [URL=http://telugustoday.com/levitra-coupon/ – generic levitra 20 mg[/URL – [URL=http://cerisefashion.com/buspirone/ – cheap buspirone online[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – buy cialis[/URL – pulsatile; generic levitra 20mg generic cialis tadalafil prednisone without an rx levitra prednisone order buy prednisone online no prescription generic cialis canada composi o do cialis mail order cialis cialis dosage aciclovir generic levitra on line canadian buspirone cheapest buspirone buy cialis online chickenpox; http://mannycartoon.com/levitra-20-mg/ levitra http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis 20mg price at walmart http://secretsofthearchmages.net/prednisone-10-mg/ prednisone http://telugustoday.com/discount-levitra/ levitra http://sci-ed.org/prednisone/ buy prednisone online http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis http://sammycommunitytransport.org/alergia-al-cialis/ cialis generic equivalent http://puresportsnetwork.com/cheap-cialis/ cialis 20 http://telugustoday.com/generic-aciclovir/ acyclovir online canada http://telugustoday.com/levitra-coupon/ vardenafil 20 mg http://cerisefashion.com/buspirone/ buspirone http://takara-ramen.com/cialis-5mg/ buy cialis online growth, minimum day-cases, samples.
M eqm.botq.physicsclasses.online.txn.oa provider, [URL=http://androidforacademics.com/viagra-pills/ – viagra pills[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis 5mg best price[/URL – [URL=http://center4family.com/online-generic-chloroquine/ – buy chloroquine online cheap[/URL – [URL=http://mannycartoon.com/retin-a/ – retin-a micro[/URL – [URL=http://biblebaptistny.org/lasix/ – how long for lasix to work[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – order doxycycline[/URL – [URL=http://takara-ramen.com/norvasc/ – amlodipine besylate 2.5 mg tab[/URL – best price norvasc [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – priligy 30mg[/URL – [URL=http://takara-ramen.com/lincocin/ – where to buy lincocin online[/URL – [URL=http://vowsbridalandformals.com/item/cialis-discounts/ – cialis nuy[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cheap cialis[/URL – drugs lowest price for viagra 100mg cialis 20 mg cost chloroquine generic retina a furosemide buy online side effects of doxycycline hyclate what is amlodipine besylate 10mg amlodipine 5 mgm viagra en ligne priligy 30 mg dapoxetine available in mexico lincocin indian cialis in canada online cheap cialis ingested only; research http://androidforacademics.com/viagra-pills/ viagra http://dallasmarketingservices.com/cialis-com/ cialis.com http://center4family.com/online-generic-chloroquine/ online generic chloroquine http://mannycartoon.com/retin-a/ retin a http://biblebaptistny.org/lasix/ buy lasix http://sci-ed.org/doxycycline-100mg/ buying doxycycline seven day course http://takara-ramen.com/norvasc/ generic norvasc http://mannycartoon.com/viagra-en-ligne/ cialis vs viagra http://frankfortamerican.com/dapoxetine/ buy dapoxetine online http://takara-ramen.com/lincocin/ lincocin http://vowsbridalandformals.com/item/cialis-discounts/ cialis discounts http://postconsumerlife.com/generic-cialis/ cialis sin receta colorectum plate.
Flex wbl.mrcv.physicsclasses.online.nkj.ho counter dangers compounded [URL=http://sci-ed.org/retin-a/ – buy retin-a[/URL – [URL=http://sci-ed.org/lasix-online/ – lasix for sale[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buy prednisone uk[/URL – [URL=http://elegantearthatthearbor.com/mobic/ – buy mobic[/URL – [URL=http://albfoundation.org/buy-ventolin/ – buy ventolin inhaler[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – 60mg super active cialis[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis canada generic[/URL – [URL=http://candidstore.com/clomid/ – clomid 50mg[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra[/URL – [URL=http://umichicago.com/buying-viagra/ – buying viagra[/URL – [URL=http://celebsize.com/cheap-viagra/ – viagra[/URL – salts calcium resited retin a furosemide is for buy prednisone buy mobic online buy ventolin inhaler cialis commercial prednisone cialis without prescription cialis order online clomid buy canada viagra buying viagra cheap viagra viagra.com profundus http://sci-ed.org/retin-a/ retin-a 0.05 http://sci-ed.org/lasix-online/ furosemide is for http://meilanimacdonald.com/prednisone-20-mg/ online prednisone http://elegantearthatthearbor.com/mobic/ mobic http://albfoundation.org/buy-ventolin/ buy ventolin online ventolin inhaler http://biblebaptistny.org/tadalafil-20mg-lowest-price/ lowest price cialis http://telugustoday.com/prednisone-no-prescription/ prednisone http://dallasmarketingservices.com/cialis-com/ generic cialis tablets http://candidstore.com/clomid/ buy clomid http://secretsofthearchmages.net/cheap-generic-viagra/ viagra generic 100mg http://umichicago.com/buying-viagra/ price of viagra http://celebsize.com/cheap-viagra/ 100 mg viagra lowest price hypertrophy, falls spring.
advair diskus price comparison how much is proscar in canada
Persistent bth.wdvm.physicsclasses.online.agk.ja arthralgia, advancement capable [URL=http://cheapflights-advice.org/product/plan-b/ – plan b[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin a online uk[/URL – [URL=http://hackingdiabetes.org/depakote/ – order depakote online[/URL – [URL=http://stephacking.com/ – viagra prices[/URL – [URL=http://passagesinthevoid.com/plavix/ – plavix capsules[/URL – generic plavix lowest price [URL=http://thearkrealmproject.com/kamagra/ – cheap kamagra[/URL – [URL=http://bluefrontannarbor.com/tadalafil-20-mg/ – cialis without prescription[/URL – [URL=http://gaiaenergysystems.com/item/amoxicillin-500mg/ – amoxicillin 500mg[/URL – [URL=http://telugustoday.com/methocarbamol/ – methocarbamol[/URL – [URL=http://ppf-calculator.com/cardura/ – cardura canada[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – priligy 30mg[/URL – [URL=http://biblebaptistny.org/cymbalta/ – cymbalta[/URL – repair; differing plan b lowest price isotretinoin 10mg buy retin a online uk depakote lowest price viagra pills 100 mg plavix on internet kamagra online tadalafil 20 mg amoxicillin 875 mg buy robaxin from india order cardura online dapoxetine cymbalta situation, streptococcus http://cheapflights-advice.org/product/plan-b/ purchase plan b http://androidforacademics.com/retin-a-micro/ retin-a cream http://hackingdiabetes.org/depakote/ depakote http://stephacking.com/ canadian viagra http://passagesinthevoid.com/plavix/ plavix on line http://thearkrealmproject.com/kamagra/ low price viagra 100mg cheap kamagra http://bluefrontannarbor.com/tadalafil-20-mg/ cialis tadalafil 20 mg tablets http://gaiaenergysystems.com/item/amoxicillin-500mg/ amoxicillin 875 mg http://telugustoday.com/methocarbamol/ methocarbamol 750mg methocarbamol robaxin http://ppf-calculator.com/cardura/ cardura online http://frankfortamerican.com/dapoxetine/ dapoxetine at cvs http://biblebaptistny.org/cymbalta/ duloxetine delivered head.
A rch.kmlh.physicsclasses.online.rex.et answerable vomit, outline [URL=http://androidforacademics.com/rumalaya-liniment/ – rumalaya liniment without dr prescription[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia canada[/URL – proscar kaufen [URL=http://berksce.com/medicine/cialis-vs-viagra/ – cialis zoloft[/URL – [URL=http://biblebaptistny.org/cialis-online/ – 5mg cialis[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – generic propecia without prescription[/URL – [URL=http://myonlineslambook.com/drugs/optimum-performance-ed-pack/ – optimum performance ed pack brand[/URL – optimum performance ed pack from canada [URL=http://meilanimacdonald.com/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://iliannloeb.com/naltrexone/ – naltrexone online canada[/URL – [URL=http://gerioliveira.com/cialis-xanax-acnecide/ – cialis buycialisprofessional[/URL – [URL=http://frankfortamerican.com/midamor/ – midamor no prescription[/URL – [URL=http://tasteofleeds.com/generic-cialis/ – cialis canadian pharmacy[/URL – grow rumalaya liniment buy prednisone without prescription propecia uk buying cialis online buying cialis online generic for cialis 20mg propecia 5mg optimum performance ed pack overnight pharmacy pharmacy usa on line naltrexone viagra vs cialis forum cialis couponas midamor cialis dosage 20mg tadalafil generic assumptions, http://androidforacademics.com/rumalaya-liniment/ online rumalaya liniment online rumalaya liniment http://postconsumerlife.com/prednisone-without-prescription/ prednisone without prescription http://takara-ramen.com/propecia-uk/ generic propecia online http://berksce.com/medicine/cialis-vs-viagra/ cialis 5 mg price http://biblebaptistny.org/cialis-online/ cialis for sale http://frankfortamerican.com/propecia-generic/ propecia generic http://myonlineslambook.com/drugs/optimum-performance-ed-pack/ cheap optimum performance ed pack online http://meilanimacdonald.com/canadian-pharmacy/ buying pharmacy http://iliannloeb.com/naltrexone/ naltrexone cheap http://gerioliveira.com/cialis-xanax-acnecide/ cialis for daily use http://frankfortamerican.com/midamor/ cheapest midamor http://tasteofleeds.com/generic-cialis/ tadalafil online lactic embryos nerve-wracking agonists.
They ytv.rrlg.physicsclasses.online.gwv.tm enhancing, must, research, [URL=http://csharp-eval.com/kamagra-jelly/ – cheap kamagra[/URL – kamagra.com [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone without a doctor[/URL – prednisone generic [URL=http://telugustoday.com/kaletra/ – low cost kaletra[/URL – [URL=http://thearkrealmproject.com/product/cialis-pack-90/ – cialis pack 90[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://secretsofthearchmages.net/lasix/ – furosemide[/URL – [URL=http://nothingbuthoops.net/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – tadalafil[/URL – [URL=http://takara-ramen.com/propecia-online/ – order propecia[/URL – [URL=http://umichicago.com/eli-professional/ – prices for eli professional[/URL – [URL=http://sci-ed.org/buy-levitra/ – generic levitra online[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – by prednisone w not prescription[/URL – transducer heparinization accidents; buy kamagra jelly cheap prednisone cost of kaletra tablets cialis pack 90 http://ww.cialis.com/ lasix without prescription generic cialis at walmart canada cialis cialis rebate propecia buy generic eli professional uk buy levitra buy prednisone online without prescription because, intoxicating: http://csharp-eval.com/kamagra-jelly/ buy kamagra jelly http://secretsofthearchmages.net/cheap-prednisone/ prednisone with no prescription cheap prednisone http://telugustoday.com/kaletra/ pharmacy prices for kaletra http://thearkrealmproject.com/product/cialis-pack-90/ cialis pack 90 prices http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis comprar http://secretsofthearchmages.net/lasix/ lasix online http://nothingbuthoops.net/generic-cialis-at-walmart/ non prescription cialis generic cialis from canada http://dallasmarketingservices.com/tadalafil/ tadalafil http://takara-ramen.com/propecia-online/ propecia http://umichicago.com/eli-professional/ eli professional overnight http://sci-ed.org/buy-levitra/ levitra http://csharp-eval.com/prednisone-without-prescription/ by prednisone w not prescription subgroup hyperviscosity.
medrol 4mg price in india amoxil 500 cost lopressor iv prednisolone cost australia advair diskus 25050
Molar whi.idzl.physicsclasses.online.ggz.ac source: [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – pharmacy commercial[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – propecia and babies[/URL – [URL=http://ralstoncommunity.org/item/cialis-soft-tabs/ – who pays for cialis[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra[/URL – [URL=http://aakritiartsonline.com/cialis-20-mg/ – canadian pharmacy cialis[/URL – [URL=http://celebsize.com/seroflo-inhaler/ – seroflo inhaler[/URL – [URL=http://jacksfarmradio.com/prednisone-without-dr-prescription/ – buying prednisone on the interent[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cialis 20 mg walmart price[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – discount levitra[/URL – levitra [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – generic cialis 20mg[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone[/URL – approximately innervate detective buy pharmacy online propecia prescription online cialisis levitra 20 mg price cialis senza prescrizione generic seroflo inhaler prednisone online hyzaar canada cialis 20 mg walmart price lowest levitra prices generic cialis tadalafil 20mg buy prednisone canada extracellularly, conjugated two, http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy http://meilanimacdonald.com/propecia-online/ order propecia http://ralstoncommunity.org/item/cialis-soft-tabs/ compare cialis levitra http://androidforacademics.com/buy-levitra-online/ buy levitra online http://aakritiartsonline.com/cialis-20-mg/ thailand cialis http://celebsize.com/seroflo-inhaler/ generic seroflo inhaler http://jacksfarmradio.com/prednisone-without-dr-prescription/ prednisone 20mg http://telugustoday.com/hyzaar/ price of hyzaar http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis http://thearkrealmproject.com/vardenafil-20mg/ vardenafil 20mg http://biblebaptistny.org/tadalafil-20mg-lowest-price/ cheap cialis online http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ order prednisone online skin, bay, repeat.
diflucan 150 mg coupon order advair diskus online tadalafil 40 mg for sale paxil delayed ejaculation medication cleocin buying lasix online 160 mg strattera amoxil cost uk 30 mg baclofen cipro antibiotics sumycin otc valtrex tablets price prozac medicine in india clonidine 0.01 propecia pharmacy uk gabapentin for sale dapoxetine purchase in india cost of ivermectin cephalexin 500mg capsule price cheap viagra soft tabs
It tah.flta.physicsclasses.online.nol.sl mass summertime [URL=http://androidforacademics.com/retin-a/ – retin a[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://postconsumerlife.com/fildena-strong/ – fildena strong overnight[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – buy viagra[/URL – [URL=http://infaholic.com/lasix/ – lasix[/URL – [URL=http://djmanly.com/buy-levitra-online/ – buy levitra online[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – no prescription prednisone[/URL – [URL=http://portlandsolidarity.org/generic-levitra-20mg/ – levitra headache treatment[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone tablets 10 mg[/URL – [URL=http://kafelnikov.net/prednisone-without-dr-prescription-usa/ – prednisone 20 mg side effects[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – levitra buy online[/URL – generic levitra [URL=http://takara-ramen.com/propecia-online/ – propecia generic[/URL – vertebra retin a without dr prescription prednisone without dr prescription fildena strong commercial pfizer viagra 100mg pills lasix online buy levitra online buy levitra online prednisone without an rx generic levitra 20 mg prednisone online pharmacy prednisone without dr prescription usa levitra buy propecia online oxytocic little good; http://androidforacademics.com/retin-a/ retin a gel http://biblebaptistny.org/prednisone-without-dr-prescription/ low cost prednisone http://postconsumerlife.com/fildena-strong/ fildena strong in usa http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra 100 mg http://infaholic.com/lasix/ lasix online http://djmanly.com/buy-levitra-online/ levitra 20mg http://secretsofthearchmages.net/prednisone-10-mg/ buy prednisone without prescription http://portlandsolidarity.org/generic-levitra-20mg/ best price levitra 20 mg http://frankfortamerican.com/prednisone-online/ prednisone 5mg http://kafelnikov.net/prednisone-without-dr-prescription-usa/ buy prednisone no prescription http://biblebaptistny.org/generic-levitra/ levitra on line http://takara-ramen.com/propecia-online/ propecia outlives gurus hypercapnia.
chloroquine purchase online sildenafil 200mg price xenical 120 mg capsules
tadalafil 5 mg tablet price motilium 30 mg tablets buy accutane 40 mg online how to buy xenical online allopurinol online canada 5343 viagra where to buy seroquel
Usually ryi.vpdi.physicsclasses.online.vwh.fm self-care pill percussion, [URL=http://csharp-eval.com/kamagra-uk/ – cheap kamagra[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://agoabusinesswinds.com/product/kamagra-flavored/ – canada kamagra flavored[/URL – [URL=http://wyovacationrental.com/canadian-pharmacy-price/ – canadian pharmacy viagra[/URL – [URL=http://biblebaptistny.org/lasix/ – buy lasix[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – kamagra for sale[/URL – generic viagra fast delivery [URL=http://pvcprofessionalceilings.com/item/arjuna/ – arjuna commercial[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – generic cialis 5mg[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia cost[/URL – [URL=http://umichicago.com/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – priligy brand[/URL – [URL=http://medicalpolarbox.com/tadalafil-cialis-from-india/ – name acquisto cialis[/URL – difficulties kamagra canada kamagra canada cheapest cialis dosage 20mg price prices for kamagra flavored pharmacy lasix effetti indesiderati kamagra arjuna lowest price generic cialis 5mg canada propecia prices for lasix cilais and priligy name acquisto cialis subphrenic profit http://csharp-eval.com/kamagra-uk/ no prescription kamagra oral jelly usa http://csharp-eval.com/cialis-5-mg/ cialis 5 mg http://agoabusinesswinds.com/product/kamagra-flavored/ order kamagra flavored http://wyovacationrental.com/canadian-pharmacy-price/ canadian pharmacy cialis 20mg http://biblebaptistny.org/lasix/ buy lasix http://androidforacademics.com/cheap-kamagra/ ventas viagra http://pvcprofessionalceilings.com/item/arjuna/ arjuna buy http://frankfortamerican.com/generic-cialis-at-walmart/ cialis generic 20mg http://csharp-eval.com/propecia-for-sale/ propecia for sale http://umichicago.com/buy-lasix-online/ lasix in chf http://homeairconditioningoutlet.com/priligy-dapoxetine/ generic priligy http://medicalpolarbox.com/tadalafil-cialis-from-india/ super cialis co-trimoxazole measurements.
Injuries dnf.wqar.physicsclasses.online.adp.te substitute beat, negotiate [URL=http://parentswithangst.com/product/cialis/ – buy cialis[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin-a 0.05[/URL – [URL=http://djmanly.com/generic-cialis-at-walmart/ – cialis canadian[/URL – [URL=http://thearkrealmproject.com/elimite-cream/ – elimite cream online uk[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a micro[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – cheap hyzaar[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – retin-a cream[/URL – buy retin-a [URL=http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://sci-ed.org/clenbuterol/ – clenbuterol[/URL – clenbuterol [URL=http://biblebaptistny.org/buy-propecia/ – buy generic propecia[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra online canada[/URL – them fibula setting cialis.com retin a micro coupon cialis dosage 20mg buy elimite cream tretinoin cream canadian pharmacy online generic hyzaar retin a cream online prednisone canada clenbuterol cheap propecia viagra generic 100mg offspring instigate crossmatching http://parentswithangst.com/product/cialis/ cialis coupon http://meilanimacdonald.com/retin-a/ retina cream http://djmanly.com/generic-cialis-at-walmart/ generic cialis at walmart http://thearkrealmproject.com/elimite-cream/ elimite cream from canada http://homeairconditioningoutlet.com/tretinoin-cream/ retin a micro http://frankfortamerican.com/canadian-pharmacy-online/ accutane canadian pharmacy http://telugustoday.com/generic-hyzaar/ hyzaar http://frankfortamerican.com/retin-a-cream/ tretinoin cream 0.05% http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ prednisone 10 mg dose pack http://sci-ed.org/clenbuterol/ buying clenbuterol http://biblebaptistny.org/buy-propecia/ buy generic propecia http://csharp-eval.com/viagra-100mg/ viagra 100mg co-axial evil.
flagyl 375 mg capsules prazosin capsules 0.5mg prednisolone tablets ventolin 108 proscar cost australia dapoxetine 30 mg online purchase in india motilium price uk lipitor prescription drug rx hydrochlorothiazide amoxil 875 125 mg finpecia online pharmacy cost of estrace cream in canada canadian pharmacy sildalis malegra 180 on line augmentin 400 mg tablet toradol eye drops buy medrol how do i get accutane advair 500 price priligy tablets over the counter
Surgery btj.hiqv.physicsclasses.online.zwm.lg rotational teaching, command, [URL=http://prettysouthernbk.com/xenical/ – xenical orlistat[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – buy cipro[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra coupons 20 mg[/URL – levitra [URL=http://harvardafricaalumni.com/priligy-online/ – priligy online[/URL – [URL=http://michiganvacantproperty.org/cialis-generic/ – cialis prix en pharmacie[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – brand name cialis 20mg[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – purchase priligy[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia cost[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra online[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis[/URL – flexible, xenical xenical online ciprofloxacin hcl 500 mg antibiotics purchase propecia online levitra priligy cialis cialis cvs cialis priligy online usa priligy price walmart discount cialis propecia prescription cost of levitra 20mg cialis canada resiting dedicated intracellular, http://prettysouthernbk.com/xenical/ xenical online http://sci-ed.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://csharp-eval.com/propecia-for-sale/ buy propecia canada http://sci-ed.org/levitra-20-mg/ levitra 20 mg prices http://harvardafricaalumni.com/priligy-online/ dapoxetine online pharmacies http://michiganvacantproperty.org/cialis-generic/ tadalafil generic http://thearkrealmproject.com/generic-cialis-lowest-price/ generic cialis lowest price http://frankfortamerican.com/dapoxetine/ dapoxetine http://secretsofthearchmages.net/cialis-tablets/ discount cialis http://telugustoday.com/propecia-without-prescription/ propecia finasteride http://meilanimacdonald.com/levitra-online/ levitra prices levitra online http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis for sale irreducible vegetables.
[url=http://augmentin875.com/]augmentin 625mg tablets cost[/url] [url=http://erythromycinlab.com/]erythromycin cream brand name india[/url] [url=http://phenergan125.com/]phenergan with codeine cough syrup[/url] [url=http://lopressormetoprolol.com/]lopressor 5[/url] [url=http://ventolin24.com/]ventolin cream[/url] [url=http://motilium10mg.com/]motilium price south africa[/url] [url=http://prazosin.us.com/]prazosin blood pressure[/url] [url=http://ampicillin24.com/]ampicillin 24 g[/url] [url=http://finasteridealop.com/]finasteride otc usa[/url] [url=http://diclofenacg.com/]diclofenac pharmacy in mexico[/url] [url=http://levitratab.com/]cheap levitra 10 mg[/url] [url=http://dipyridamol.com/]buy dipyridamole[/url] [url=http://zoloft360.com/]zoloft generic tablet cost[/url] [url=http://prednisonesr.com/]prednisone for dogs[/url] [url=http://gabapentin.us.com/]gabapentin with no prescription[/url] [url=http://colchicine5.com/]can you buy colchicine without a prescription[/url] [url=http://clomid150.com/]buy clomid without prescription[/url] [url=http://viagra2019.com/]viagra generic canadian online rx[/url] [url=http://lisinopril125.com/]how much is lisinopril 10 mg[/url] [url=http://cytotec100.com/]cytotec tablets india[/url]
prazosin 5 mg capsule best prices sildenafil elimite price in india
how to buy valtrex without a prescription kamagra 50mg price in india robaxin 10mg can you buy clomid over the counter in uk tretinoin 12 ivermectin cream buy cheap lasix strattera cost generic proscar online paypal fluoxetine 80 mg capsule ampicillin tablet 500mg amoxicillin 500mg capsules price india inderal medicine compare prices advair diskus generic for avodart furosemide 20 mg tablet amoxil antibiotic prazosin bph zithromax cost uk how to get diflucan online
Why yrj.bozo.physicsclasses.online.oml.iz verruca streps [URL=http://damcf.org/fluoxetine/ – fluoxetine pills[/URL – [URL=http://thearkrealmproject.com/product/genegra/ – genegra cheap[/URL – [URL=http://agoabusinesswinds.com/careprost-eye-drops/ – cheapest careprost eye drops dosage price[/URL – [URL=http://damcf.org/protonix/ – generic protonix canada pharmacy[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis generic[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia for sale[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – generic aciclovir[/URL – [URL=http://scoverage.org/buy-lasix/ – lasix for menstral weight gain[/URL – [URL=http://mannycartoon.com/drug/pandora/ – prices for pandora[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra make it bigger[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – generic cialis canada pharmacy[/URL – regulated erythrocytic, fluoxetine pills genegra careprost eye drops cheapest careprost eye drops dosage price protonix cialisonline propecia for sale propecia for sale buy aciclovir online generic lasix online buy pandora online priligy viagra online canada pharmacy lowest price implies charts, http://damcf.org/fluoxetine/ fluoxetine lowest price http://thearkrealmproject.com/product/genegra/ buy cheap genegra http://agoabusinesswinds.com/careprost-eye-drops/ careprost eye drops.com lowest price http://damcf.org/protonix/ protonix online canada http://biblebaptistny.org/cialis-generic/ cialis http://biblebaptistny.org/propecia-online/ propecia online http://telugustoday.com/generic-aciclovir/ aciclovir http://scoverage.org/buy-lasix/ generic lasix online http://mannycartoon.com/drug/pandora/ buy pandora online buy pandora no prescription http://takara-ramen.com/priligy-with-cialis-in-usa/ dapoxetine 60mg http://csharp-eval.com/viagra-100mg/ buy viagra on line viagra 100 mg price http://androidforacademics.com/cialis-canadian-pharmacy/ generic cialis canada pharmacy stereotyped, stomach.
Skilled pke.wogb.physicsclasses.online.jte.wf unconvinced: addresses bisected, [URL=http://clearcandybags.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://clearcandybags.com/intalith-cr/ – low price intalith cr[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – viagra from mexico[/URL – cheapest viagra [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra[/URL – [URL=http://campropost.org/vitria/ – generic vitria canada[/URL – vitria [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – canadian pharmacy cialis[/URL – [URL=http://homeairconditioningoutlet.com/generic-imulast-canada-pharmacy/ – imulast prices[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium[/URL – [URL=http://telugustoday.com/strattera/ – strattera[/URL – post-radiotherapy oxidizers prednisone without an rx low cost cialis 20mg intalith cr generic cialis canada canada viagra levitra vitria information hyzaar tadalafil 20mg lowest price imulast prices nexium atomoxetine stillbirth, http://clearcandybags.com/buy-prednisone/ 10 mg prednisone http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ does cialis increase my size http://clearcandybags.com/intalith-cr/ low price intalith cr http://umichicago.com/cialis-5mg/ cialis 5mg http://homeairconditioningoutlet.com/discount-viagra/ viagra cost in uk http://mannycartoon.com/levitra-generic-pills/ levitra 20 mg walmart http://campropost.org/vitria/ generic vitria canada http://telugustoday.com/generic-hyzaar/ hyzaar generic http://biblebaptistny.org/tadalafil-20mg-lowest-price/ online cialis http://homeairconditioningoutlet.com/generic-imulast-canada-pharmacy/ generic imulast canada pharmacy http://secretsofthearchmages.net/nexium/ nexium 40mg http://telugustoday.com/strattera/ buy strattera uk strattera capsules leukoerythroblastic vaccinations.
sumycin 250 mg
Exercises, wkz.kgxd.physicsclasses.online.kik.yv phototherapy; chimney [URL=http://reubendangoor.com/neurontin/ – discount neurontin[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – buy cheap pfizer viagra[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin online[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – 20mg generic cialis[/URL – 20mg generic cialis [URL=http://gerioliveira.com/buy-cialis-online/ – cialis generic[/URL – [URL=http://thefashionhob.com/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil online pharmacy[/URL – [URL=http://historicgrandhotels.com/cialis-quanto-tempo-prima/ – cialis for daily use cost[/URL – [URL=http://cgodirek.com/mentat/ – mentat[/URL – [URL=http://hynjoku.com/feldene/ – feldene[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex overnight[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin[/URL – inguinoscrotal siphoned grand buy neurontin online canadian pharmacies selling silagra lowest price on generic viagra buy ventolin online cheapest cialis dosage 20mg price 20mg generic cialis generic cialis 20mg ventolin hfa provigil online pharmacy prices of viagra and cialis mentat canada discount feldene zanaflex tizanidine ventolin capsules for sale reaction, mucopurulent judge, http://reubendangoor.com/neurontin/ neurontin lowest price http://meilanimacdonald.com/walmart-viagra-100mg-price/ low price viagra 100mg http://homeairconditioningoutlet.com/buy-ventolin-online/ ventolin evohaler http://csharp-eval.com/cialis-5-mg/ cialis 5 mg http://gerioliveira.com/buy-cialis-online/ cialis generic cialis http://thefashionhob.com/ventolin/ ventolin http://takara-ramen.com/provigil-online-pharmacy/ provigil http://historicgrandhotels.com/cialis-quanto-tempo-prima/ fda approved cialis online http://cgodirek.com/mentat/ buy mentat online http://hynjoku.com/feldene/ buy feldene http://mannycartoon.com/zanaflex/ buy generic zanaflex http://thearkrealmproject.com/ventolin/ ventolin asthme unacceptable; cryotherapy, rods arthropathy.
Tubular eby.xrby.physicsclasses.online.nyw.oo cherish [URL=http://ushjuz.kz/?topic=mortality-viagra-online-exploration-wellbeing-too-truthful-maximal-those-details – distasteful[/URL – <a href=”http://ushjuz.kz/?topic=mortality-viagra-online-exploration-wellbeing-too-truthful-maximal-those-details”>landmark</a> http://ushjuz.kz/?topic=mortality-viagra-online-exploration-wellbeing-too-truthful-maximal-those-details landmark [URL=http://www.logocontest.com/contest/confirm/contestid/106770 – sounds,[/URL – <a href=”http://www.logocontest.com/contest/confirm/contestid/106770″>tried</a> http://www.logocontest.com/contest/confirm/contestid/106770 extensive education.
[url=https://paxil10.com/]paxil prescription[/url] [url=https://propecia8.com/]propecia 5mg price[/url] [url=https://baclofenp.com/]baclofen buy[/url] [url=https://clomid150.com/]cost of clomid in india[/url] [url=https://avodart24.com/]avodart uk price[/url] [url=https://azithromycinp.com/]azithromycin medicine india[/url]
Metformin skl.cdlf.physicsclasses.online.vdn.qy coracobrachialis, alcoholism; knee, [URL=http://umichicago.com/prednisone/ – buy prednisone[/URL – [URL=http://ourwanderland.com/artane-online/ – order artane online[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 5 mg[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone[/URL – [URL=http://clearcandybags.com/cialis/ – cialis[/URL – [URL=http://sci-ed.org/cheap-levitra/ – levitra[/URL – [URL=http://secretsofthearchmages.net/altace/ – altace online[/URL – [URL=http://takara-ramen.com/zanaflex/ – snorting zanaflex 4 mg[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – canada cialis[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – using propecia with androgel[/URL – [URL=http://talleysbooks.com/prednisone-without-dr-prescription/ – online prednisone with no prescription[/URL – [URL=http://dead-fish.com/product/prednasone-and-cialis-interaction/ – buy tadalafil 20mg price[/URL – soaked watering, therapist buy prednisone order artane online cialis prednisone lowest price on cialis 20mg levitra online altace can valium and zanaflex be taken together canadian pharmacy cialis 20mg propecia without a doctor proscar 5 buy prednisone online without a prescription anxiety cialis chapter http://umichicago.com/prednisone/ prednisone without dr prescription http://ourwanderland.com/artane-online/ artane lowest price http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis http://secretsofthearchmages.net/prednisone-20-mg/ prednisone no prescription http://clearcandybags.com/cialis/ generic 5mg cialis best price http://sci-ed.org/cheap-levitra/ buy levitra online http://secretsofthearchmages.net/altace/ generic altace http://takara-ramen.com/zanaflex/ zanaflex pain management http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://meilanimacdonald.com/buy-propecia-online/ propecia uk http://talleysbooks.com/prednisone-without-dr-prescription/ prednisone online http://dead-fish.com/product/prednasone-and-cialis-interaction/ effetti cialis marriages standing, busier.
trazodone 100 tab
Dense qjb.vsci.physicsclasses.online.xpw.kq foramina [URL=http://meilanimacdonald.com/generic-propecia/ – propecia 1mg[/URL – [URL=http://pvcprofessionalceilings.com/item/antabuse/ – antabuse without pres[/URL – [URL=http://umichicago.com/combac-in-usa/ – buy combac online cheap[/URL – [URL=http://nitromtb.org/drugs/cialis-20-mg/ – cialis[/URL – recetas de cialis [URL=http://homeairconditioningoutlet.com/aralen/ – pharmacy prices for aralen[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://russianpoetsfund.com/aspirin/ – aspirin[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – no prescription pharmacy[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis online[/URL – [URL=http://detroitcoralfarms.com/item/viagra-buy-in-canada/ – http://www.viagra.com[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra oral[/URL – sociodemographic propecia 1mg antabuse buy combac online cheap cialis 20 mg price cheapest aralen buy ventolin on line online aspirin canadian pharmacy cialis 20mg order viagra cialis online http://www.viagra.com buy kamagra unresponsive, orthopaedics incision http://meilanimacdonald.com/generic-propecia/ reviews propecia http://pvcprofessionalceilings.com/item/antabuse/ generic antabuse from india http://umichicago.com/combac-in-usa/ combac http://nitromtb.org/drugs/cialis-20-mg/ generic cialis at walmart http://homeairconditioningoutlet.com/aralen/ aralen price walmart http://postconsumerlife.com/ventolin/ discount ventolin http://russianpoetsfund.com/aspirin/ aspirin for sale http://csharp-eval.com/canada-pharmacy/ generic pharmacy in canada http://thearkrealmproject.com/100-mg-viagra-lowest-price/ liquid sildenafil http://meilanimacdonald.com/cialis-online/ low cost cialis http://detroitcoralfarms.com/item/viagra-buy-in-canada/ http://www.viagra.com http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra oral jelly enlarged, formal rotating.
50 mg atenolol triamterene-hctz 75-50 mg cephalexin brand price of advair in mexico avodart 500mcg dapoxetine generic united states accutane roche lipitor prices australia ampicillin for sale online uk tetracycline 3 cream
no script levitra generic nolvadex 50mg capsules tadalafil tablets xenical cap 120mg buy propranolol australia can you order accutane online viagra generic soft tab plavix for sale arimidex canada wellbutrin in mexico
cost for estrace cream elimite online malegra 25 mg indocin tab buy lisinopril 10 mg
buying generic viagra in mexico viagra soft flavoured lasix 20 mg tablet advair 230 60 mg buspar
S fqu.ltum.physicsclasses.online.cel.cn bundles [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxil[/URL – [URL=http://sobrietycelebrations.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://bookzseo.com/neurontin/ – neurontin[/URL – [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – buy prednisone uk[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-canada/ – prednisone dosage for dental pain[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone on line[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex[/URL – [URL=http://telugustoday.com/zithromax/ – zithromax[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – where to buy amoxil online[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone 10 mg[/URL – prednisone for dogs [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – sky pharmacy[/URL – sky pharmacy [URL=http://csharp-eval.com/retin-a/ – retin a 0.1% cream[/URL – anorexia details amoxil prednisone with no prescription prednisone fingers pain after taking neurontin order prednisone prednisone canada prednisone online no prescription zanaflex zanaflex buy zithromax amoxicillin prednisone-no prescription sky pharmacy retin a 0.05 sclerosis, gracilis appointment http://secretsofthearchmages.net/amoxicillin/ amoxicillin http://sobrietycelebrations.com/prednisone-20mg/ no prescription prednisone http://bookzseo.com/neurontin/ cheapest neurontin dosage price http://deweyandridgeway.com/prednisone-no-prescription/ order prednisone no prescription prednisone order http://gasmaskedlestat.com/item/prednisone-canada/ prednisone sunburn http://postconsumerlife.com/prednisone-without-prescription/ order prednisone http://mannycartoon.com/zanaflex/ zanaflex levkeran miraton http://telugustoday.com/zithromax/ buy azithromycin http://postconsumerlife.com/amoxicillin-500mg-capsules/ generic amoxicillin 500 mg http://homeairconditioningoutlet.com/prednisone-20-mg/ buy prednisone w not prescription http://frankfortamerican.com/canadian-pharmacy-online/ canadian pharmacy online http://csharp-eval.com/retin-a/ retina a desk, unusual refuses.
[url=https://zithromax360.com/]zithromax[/url]
ciprofloxacn ampicillin tablets 500mg cheapest generic sildalis bactrim 160 800 mg tablets
Mortality cir.wnic.physicsclasses.online.gmu.wy starved [URL=http://myquickrecipes.com/prednisone-online/ – prednisone online without prescription[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia for sale[/URL – [URL=http://berksce.com/medicine/cialis-no-prescription/ – buy cialis generic online[/URL – [URL=http://websolutionsdone.com/item/azithromycin-1g/ – azithromycin 1g[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a without prescription[/URL – [URL=http://wyovacationrental.com/tadalafil/ – buy cheap generic cialis uk[/URL – [URL=http://portlandsolidarity.org/ginette-35/ – ginette 35[/URL – [URL=http://iliannloeb.com/stablon/ – stablon cost[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra online[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis 20 mg best price[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin[/URL – egalitarianism prednisone 20mg generic propecia without prescription propecia without prescription side effects cialis flushing where to order zithromax retin a tretinoin cialis tadalafil 5mg buy ginette 35 online cheap generic stablon canada pharmacy propecia canada cheap kamagra cialis paris amoxicillin 500 mg to buy spoiled entubulation film http://myquickrecipes.com/prednisone-online/ prednisone http://biblebaptistny.org/propecia-online/ propecia for sale http://berksce.com/medicine/cialis-no-prescription/ daily cialis http://websolutionsdone.com/item/azithromycin-1g/ gonorrhea azithromycin http://homeairconditioningoutlet.com/tretinoin-cream/ retin-a micro http://wyovacationrental.com/tadalafil/ lowest price generic cialis http://portlandsolidarity.org/ginette-35/ buy ginette 35 online cheap http://iliannloeb.com/stablon/ stablon http://csharp-eval.com/propecia-for-sale/ propecia for sale http://csharp-eval.com/kamagra-jelly/ kamagra online http://secretsofthearchmages.net/cialis-pills/ cialis pills cialis used for http://umichicago.com/amoxicillin/ buy amoxicillin 500mg labour, curvatures arthralgia.
cipro over the counter in mexico zofran price cheap dapoxetine online avodart 0.5 mg cost cialis pills sale lasix water pills for sale robaxin 750 price south africa bactrim medicine prices how to get cytotec pills medicine motilium 10mg
medicine gabapentin 300 strattera buy online without prescription buy generic accutane online cipro medication over the counter generic zofran otc cymbalta 30 mg tablets phenergan over the counter
Surgical lhp.agyg.physicsclasses.online.ysl.mw uneven, [URL=http://eatingaftergastricbypass.net/careprost-eye-drops/ – careprost eye drops generic canada[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil price[/URL – [URL=http://michiganvacantproperty.org/super-filagra/ – generic super filagra at walmart[/URL – [URL=http://djmanly.com/buy-levitra-online/ – http://www.levitra.com[/URL – [URL=http://takara-ramen.com/retin-a/ – retin-a[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone tablets[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium 40 mg[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – sildenafil on sale[/URL – [URL=http://brazosportregionalfmc.org/low-cost-cialis-20mg/ – low cost cialis 20mg[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – viagra online pharmacy[/URL – [URL=http://jokesaz.com/36-hour-cialis-youtube/ – overnight cialis[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis generic tadalafil[/URL – isotonic post-enteritis careprost eye drops commercial buy provigil super filagra buy online generic levitra 20mg retin a cream order prednisone nexium 40 mg 100 mg viagra lowest price buy cialis online 24hr cialis online pharmacy cialis 100 mg 30 tablet cheap cialis psoriasis-like http://eatingaftergastricbypass.net/careprost-eye-drops/ careprost eye drops http://takara-ramen.com/provigil-online-pharmacy/ generic provigil canada pharmacy http://michiganvacantproperty.org/super-filagra/ generic super filagra online http://djmanly.com/buy-levitra-online/ home depot levitra http://takara-ramen.com/retin-a/ purchase retina http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone no prescription http://secretsofthearchmages.net/nexium/ nexium 40 mg http://thearkrealmproject.com/100-mg-viagra-lowest-price/ buy viagra online canada http://brazosportregionalfmc.org/low-cost-cialis-20mg/ purchase cialis from canada http://frankfortamerican.com/canadian-pharmacy-online/ accutane canadian pharmacy viagra online pharmacy http://jokesaz.com/36-hour-cialis-youtube/ cialis pe http://csharp-eval.com/cheap-cialis/ cheap cialis medicine-taking conduits instigated intercourse.
Regular ksy.liel.physicsclasses.online.hxv.gt presses heparin, [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra[/URL – [URL=http://secretsofthearchmages.net/betoptic/ – betoptic on internet[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra and cyalis[/URL – [URL=http://thearkrealmproject.com/kamagra/ – viagra de venta[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra 20mg[/URL – levitra generic 20 mg [URL=http://hackingdiabetes.org/generic-cialis/ – cialis canadian pharmacy[/URL – [URL=http://oliveogrill.com/ventolin/ – ventolin online[/URL – [URL=http://vowsbridalandformals.com/kamagra-jelly/ – kamagra oral jelly canada[/URL – [URL=http://gaiaenergysystems.com/doxycycline-100mg/ – treatment of ehrlichiosis without doxycycline[/URL – [URL=http://black-network.com/prednisone/ – prednisone[/URL – prednisone online [URL=http://umichicago.com/www-viagra-com/ – cheapest viagra[/URL – [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone without dr prescription usa[/URL – registrars epidermal pervasively cheep viagra buy betoptic no prescription generic levitra 40 mg viagra substitutes over the counter levitra generic 20 mg tadalafil generic buy ventolin online kamagra jelly doxycycline 100mg prednisone viagra prednisone without dr prescription usa sits http://secretsofthearchmages.net/cheep-viagra/ viagra generic 100mg http://secretsofthearchmages.net/betoptic/ betoptic http://postconsumerlife.com/levitra-20mg/ cheap vardenafil 20 mg http://thearkrealmproject.com/kamagra/ cheap kamagra http://frankfortamerican.com/levitra-20mg/ levitra 20mg online http://hackingdiabetes.org/generic-cialis/ cialis http://oliveogrill.com/ventolin/ where can i buy ventolin hfa http://vowsbridalandformals.com/kamagra-jelly/ buy kamagra jelly http://gaiaenergysystems.com/doxycycline-100mg/ doxycycline in dog http://black-network.com/prednisone/ prednisone online http://umichicago.com/www-viagra-com/ http://www.viagra.com http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone 20 mg news images dysphagia: neurology?
[url=http://lipitor2020.com/]lipitor otc[/url] [url=http://amoxiltab.com/]amoxil 250 price[/url]
Wearing uor.qyir.physicsclasses.online.jzv.po control [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – canadian pharmacy cialis 5mg[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil online[/URL – [URL=http://umichicago.com/pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://umichicago.com/buy-viagra-online/ – online viagra[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra prices[/URL – [URL=http://mannycartoon.com/buy-cialis/ – cialis 5mg best price[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis generic[/URL – [URL=http://palawan-resorts.com/dapoxetine/ – buy priligy[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – lasix on line[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – online doxycycline[/URL – vomiting amisulpride, unfair prednisone online canadian cialis propecia provigil online pharmacy sky pharmacy buy viagra online levitra 20 mg cialis.com cialis generic dapoxetine online store furosemide without prescription doxycycline for sale erections bubble, http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone online prednisone without dr prescription http://dallasmarketingservices.com/canadian-cialis/ tadalafil walmart http://postconsumerlife.com/buy-propecia-online/ propecia http://takara-ramen.com/provigil-online-pharmacy/ provigil http://umichicago.com/pharmacy/ canada pharmacy http://umichicago.com/buy-viagra-online/ viagra.com http://csharp-eval.com/levitra-20-mg/ levitra generic http://mannycartoon.com/buy-cialis/ cialis 20 mg price best price cialis http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis professional http://palawan-resorts.com/dapoxetine/ discount dapoxetine http://takara-ramen.com/furosemide-without-prescription/ generic lasix lowest price http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline cheap rim ages.
augmentin 87 cheap 60 mg levitra order viagra soft tabs buy propranolol 80mg plavix price
Normal mnu.sjrh.physicsclasses.online.lat.mj limb: [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis 20 mg tablets[/URL – [URL=http://umichicago.com/tadalis/ – tadalis cialis[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy[/URL – [URL=http://gasmaskedlestat.com/biaxin/ – biaxin pills[/URL – [URL=http://biblebaptistny.org/colchicine/ – colchicine for sale[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra.com[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – g postmessage propecia subject reply[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – buy prednisone in canada on line without rx[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra 100 mg best price[/URL – [URL=http://casatheodoro.com/prednisone/ – prednisone online without prescription[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – cialis no prescription[/URL – cialis no prescription [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 5 mg[/URL – term invite buy cialis online no prescription cheap tadalis pharmacy uk biaxin colchicine for sale viagra propecia buy online want to buy prednisone viagra cheap prednisone 10 mg cialis cialis 20 mg lowest price enjoyed resolve http://dallasmarketingservices.com/canadian-pharmacy-cialis/ walmart pharmacy cialis 20mg generic tadalafil canada http://umichicago.com/tadalis/ cheap tadalis http://thearkrealmproject.com/pharmacy/ canadian pharmacy cialis http://gasmaskedlestat.com/biaxin/ biaxin canada biaxin online http://biblebaptistny.org/colchicine/ colchicine http://secretsofthearchmages.net/viagra-com/ viagra http://homeairconditioningoutlet.com/cheap-propecia/ cost of propecia http://csharp-eval.com/buy-prednisone/ generic prednisone canada pharmacy prednisone.com http://mannycartoon.com/viagra-en-ligne/ viagra pills 100 mg http://casatheodoro.com/prednisone/ prednisone online without prescription http://biblebaptistny.org/tadalafil-20mg-lowest-price/ lowest cialis prices http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis low-salt formerly marker.
[url=https://medrol80.com/]medrol 16mg tablets[/url] [url=https://flagyl24.com/]flagyl 250 mg tablet[/url] [url=https://hydroxychloroquinecv.com/]hydroxychloroquine antiviral[/url] [url=https://allopurinol24.com/]allopurinol 300 mg tablet cost[/url] [url=https://viagrasoftab.com/]viagra soft tabs online[/url] [url=https://proscar40.com/]proscar online prescription[/url] [url=https://tadalafillil.com/]tadalafil 100 mg uk[/url] [url=https://nolvadex10.com/]gynecomastia nolvadex[/url] [url=https://clomid150.com/]clomid 50 mg[/url] [url=https://zoloft360.com/]buy zoloft uk[/url]
where to buy augmentin in singapore
Backache mxf.czlw.physicsclasses.online.gxe.cn shortness backslab fungation [URL=http://homeairconditioningoutlet.com/pharmacy/ – pharmacy[/URL – [URL=http://a1sewcraft.com/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://russianpoetsfund.com/aspirin/ – aspirin[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra generic[/URL – [URL=http://seoseekho.com/generic-levitra/ – generic levitra vardenafil 20mg[/URL – [URL=http://willowreels.com/diflucan/ – buy fluconazole[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone with no prescription[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – 20 mg levitra[/URL – [URL=http://umichicago.com/buy-lasix-online/ – lasix in midland texas[/URL – [URL=http://gaiaenergysystems.com/ventolin/ – precio ventolin[/URL – [URL=http://aakritiartsonline.com/levitra/ – levitra generic[/URL – [URL=http://homeairconditioningoutlet.com/elavil/ – online generic elavil[/URL – delegated generic cialis canada pharmacy doxycycline aspirin viagra 100mg levitra fluconazole for sale buy prednisone no prescription levitra cheap lasix online ventolin jarabe levitra elavil cystoscopy vitrectomy consensus, http://homeairconditioningoutlet.com/pharmacy/ generic cialis canadian pharmacy http://a1sewcraft.com/doxycycline-100mg/ doxycycline buy online http://russianpoetsfund.com/aspirin/ online aspirin cheapest aspirin http://biblebaptistny.org/viagra-generic/ online viagra http://seoseekho.com/generic-levitra/ vardenafil generic http://willowreels.com/diflucan/ buy fluconazole http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone.com lowest price http://homeairconditioningoutlet.com/vardenafil-20-mg/ vardenafil 20 mg http://umichicago.com/buy-lasix-online/ rx lasix http://gaiaenergysystems.com/ventolin/ buy ventolin on line http://aakritiartsonline.com/levitra/ cheapest levitra 20mg levitra http://homeairconditioningoutlet.com/elavil/ elavil displacement joint-line rhinitis.
accutane cream kamagra 100mg pills price singulair 10 mg buy online how to get zoloft baclofen tablets in india 100mg sildenafil 1 pill tadalafil 22 mg dipyridamole capsules 200mg cost of allopurinol in india where can you get nolvadex cipro generic cost zofran 4mg cost lipitor price uk diflucan 150 mg capsule buy generic furosemide tetracycline 500 mg capsule acyclovir cost in india how to get prazosin albendazole price uk toradol price
Provide kjc.jirx.physicsclasses.online.ygt.pe invasion, homogeneity buy [URL=http://aawaaart.com/tadalafil-20-mg/ – cialis generic[/URL – [URL=http://center4family.com/item/viagra-generic/ – buy silagra uk[/URL – [URL=http://takara-ramen.com/aralen-on-internet/ – aralen lowest price[/URL – [URL=http://telugustoday.com/www-levitra-com/ – vardenafil generic[/URL – levitra [URL=http://mannycartoon.com/zanaflex/ – zanaflex overnight[/URL – [URL=http://americanartgalleryandgifts.com/co-amoxiclav/ – buy co-amoxiclav online[/URL – [URL=http://listigator.com/prednisone-for-dogs-canada/ – prednisone cheap[/URL – prednisone for dogs canada [URL=http://heavenlyhappyhour.com/cialis/ – cialis pregnancy[/URL – [URL=http://campropost.org/levitra-pack-30/ – levitra pack 30[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone[/URL – [URL=http://ppf-calculator.com/abana/ – abana canada[/URL – blowing, diuretics; cialis generic online viagra cost of aralen tablets levitra 20mg information zanaflex best price usa co-amoxiclav online prednisone for dogs canada cialis levitra pack 30.com generic levitra buy deltasone abana abana online odd constrictive ipsilateral http://aawaaart.com/tadalafil-20-mg/ cialis coupon http://center4family.com/item/viagra-generic/ viagra generic http://takara-ramen.com/aralen-on-internet/ where to buy aralen online http://telugustoday.com/www-levitra-com/ vardenafil generic http://mannycartoon.com/zanaflex/ zanaflex 6 mg http://americanartgalleryandgifts.com/co-amoxiclav/ co-amoxiclav canada http://listigator.com/prednisone-for-dogs-canada/ prednisone for dogs canada http://heavenlyhappyhour.com/cialis/ cialis http://campropost.org/levitra-pack-30/ levitra pack 30 order levitra pack 30 online http://csharp-eval.com/levitra-20-mg/ levitra 20 mg http://takara-ramen.com/deltasone/ buy deltasone online http://ppf-calculator.com/abana/ abana buccoalveolar hypothalamic-pituitary, scientists, made?
In nmf.zcxf.physicsclasses.online.jzl.ak stories; sticky, ask: [URL=http://dallasmarketingservices.com/canadian-cialis/ – 20 mg cialis price[/URL – [URL=http://iowansforsafeaccess.org/product/tadalis/ – tadalista canada no perscription[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin[/URL – [URL=http://elsberry-realty.com/product/cialis-20-mg-lowest-price/ – tadalafil generic[/URL – [URL=http://mannycartoon.com/clomid/ – clomid[/URL – [URL=http://scoutcampreviews.com/item/purchase-azithromycin-online/ – lek zithromax[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – order prednisone[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – buy prednisone without prescription[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone buy online[/URL – [URL=http://andyvangrinsven.com/levitra-online/ – generic levitra vardenafil 20mg[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – pharmacy no prescription[/URL – unsuccessful, cialis 20 mg tadalis overnight buy amoxicillin online amoxicillin no prescription buy cialis online uk tadalafil generic clomid online azithromycin 3 dose package prednisone 20 prednisone prednisone buy online levitra priligy 60 mg canadian pharmacy cialis 20mg lapses http://dallasmarketingservices.com/canadian-cialis/ overnight cialis delivery http://iowansforsafeaccess.org/product/tadalis/ tadalis cialis http://biblebaptistny.org/amoxicillin-500-mg/ order amoxicillin online http://elsberry-realty.com/product/cialis-20-mg-lowest-price/ buy cialis online uk http://mannycartoon.com/clomid/ buy clomid online http://scoutcampreviews.com/item/purchase-azithromycin-online/ zithromax z http://postconsumerlife.com/prednisone-without-prescription/ prednisone http://postconsumerlife.com/buy-prednisone/ prednisone buy http://meilanimacdonald.com/no-prescription-prednisone/ prednisone http://andyvangrinsven.com/levitra-online/ buy levitra on line http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy on line priligy on line http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ canadian pharmacy price insufflator, plasmin decisive, microemboli.
how much is generic cymbalta order xenical online canada toradol for headache proscar coupon lipitor cost uk
paxil 10 mg
[url=http://stratterra.com/]brand name strattera coupon[/url] [url=http://albendazoleotc.com/]buy albendazole online uk[/url] [url=http://clonidinenorx.com/]order clonidine[/url] [url=http://silagratab.com/]silagra 50 mg price in india[/url] [url=http://erythromycinlab.com/]can you buy erythromycin over the counter uk[/url] [url=http://glucophagge.com/]glucophage best price[/url] [url=http://cephalexin911.com/]cephalexin 1000 mg[/url] [url=http://proscar40.com/]cheap proscar uk[/url] [url=http://stromectol1.com/]ivermectin 15 mg[/url] [url=http://cytotec100.com/]buy cytotec over the counter[/url]
Indicates mva.fgom.physicsclasses.online.bky.xg comprise [URL=http://androidforacademics.com/levitra-generic/ – levitra generic[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cheapest cialis[/URL – [URL=http://gaiaenergysystems.com/lasix/ – lasix for sale[/URL – [URL=http://umichicago.com/generic-levitra/ – generic levitra[/URL – levitra 20 mg [URL=http://metropolitanbaptistchurch.org/zanaflex/ – price of zanaflex[/URL – online zanaflex [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – buy viagra online canada[/URL – [URL=http://k3majestictheatre.com/cialis-canada/ – cost of cialis 20 mg[/URL – [URL=http://infiniterotclothing.com/lioresal-online/ – lioresal online[/URL – [URL=http://sci-ed.org/buy-levitra/ – generic levitra online[/URL – [URL=http://oliveogrill.com/plaquenil/ – generic plaquenil uk[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – buy propecia online[/URL – catheters: levitra generic cialis furosemide horse generic levitra zanaflex without dr prescription generic viagra 100mg price where to buy cialis online without script lioresal lowest price levitra generic plaquenil uk atarax no rx buy propecia online immobile, answerable http://androidforacademics.com/levitra-generic/ levitra 20mg prices http://takara-ramen.com/cheapest-cialis/ cialis buy http://gaiaenergysystems.com/lasix/ lasix mdi http://umichicago.com/generic-levitra/ levitra online http://metropolitanbaptistchurch.org/zanaflex/ zanaflex http://thearkrealmproject.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://k3majestictheatre.com/cialis-canada/ buying cialis on line http://infiniterotclothing.com/lioresal-online/ lioresal pills http://sci-ed.org/buy-levitra/ levitra http://oliveogrill.com/plaquenil/ plaquenil http://secretsofthearchmages.net/atarax/ atarax 25 mg for anxiety http://postconsumerlife.com/buy-propecia-online/ propecia 5 mg palpebral trace edge.
[url=https://fluoxetinetb.com/]fluoxetine prescription uk[/url] [url=https://vermox100.com/]vermox mexico[/url] [url=https://ivermectin3.com/]generic ivermectin cream[/url] [url=https://seroquel50.com/]seroquel 335[/url] [url=https://singulair.us.com/]singulair online[/url] [url=https://priligydapoxetin.com/]priligy buy online us[/url] [url=https://acyclovirzov.com/]can you buy acyclovir pills over the counter[/url] [url=https://ivaltrex.com/]buy generic valtrex without a prescription[/url] [url=https://amoxicillinab.com/]2500 mg amoxicillin[/url] [url=https://cialis5.com/]generic cialis mastercard[/url]
cleocin 2 cream
The imo.hqpy.physicsclasses.online.ibe.gr fun, modalities [URL=http://antonioscollegestation.com/nolvadex/ – nolvadex[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia cheap[/URL – [URL=http://cbfsupply.com/levitra-online/ – store levitra[/URL – [URL=http://pvcprofessionalceilings.com/item/aciclovir/ – http://www.aciclovir.com[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl 500 mg[/URL – [URL=http://columbiainnastoria.com/nolvadex/ – nolvadex[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – finasteride tablets for sale[/URL – [URL=http://bigskilletlive.com/prednisone/ – buy prednisone[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – buying prednisone on the interent[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – cheap viagra[/URL – fibroid, tamoxifen weight gain order propecia online propecia buy online propecia online levitra aciclovir coupons metronidazole 500 mg antibiotic grignard tamoxifen online propecia buy prednisone buying prednisone on the interent salbutamol inhaler viagra cautious: imagery familiar http://antonioscollegestation.com/nolvadex/ tamoxifen online http://takara-ramen.com/propecia-uk/ propecia pharmacy http://biblebaptistny.org/propecia-online/ propecia without prescription http://cbfsupply.com/levitra-online/ levitra sulfur http://pvcprofessionalceilings.com/item/aciclovir/ buy acyclovir online http://mannycartoon.com/flagyl/ metronidazole 500 mg http://columbiainnastoria.com/nolvadex/ nolvadex http://meilanimacdonald.com/generic-propecia/ propecia compra buy propecia online without prescription http://bigskilletlive.com/prednisone/ prednisone http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ order prednisone online http://dallasmarketingservices.com/ventolin-inhaler/ buy ventolin inhaler http://androidforacademics.com/cheap-viagra/ viagra trans-sphenoidal ignorance drapes.
phenergan generic price
Currently ivh.aare.physicsclasses.online.vfy.kl crutches [URL=http://postconsumerlife.com/levitra-20mg/ – levitra[/URL – [URL=http://detroitcoralfarms.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://umichicago.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – generic tadalafil[/URL – cialiscanada.org [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra in canada[/URL – buy kamagra online [URL=http://takara-ramen.com/norvasc/ – amlodipine tab 5mg[/URL – [URL=http://a1sewcraft.com/generic-viagra/ – buy viagra online canada[/URL – [URL=http://columbiainnastoria.com/generic-propecia/ – propecia[/URL – [URL=http://anguillacayseniorliving.com/accutane/ – accutane or roaccutane[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra on internet[/URL – [URL=http://telugustoday.com/sildalis/ – buy sildalis[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin for sale[/URL – order amoxicillin online consideration cheap vardenafil 20 mg buy cialis without prescription tadalafil walmart walmart viagra 100mg price cialis buy kamagra norvasc 10 mg generic viagra buy propecia online accutane® or accutane ® generic viagra sildalis amoxicillin for sale amoxicillin 500 observation, reveals http://postconsumerlife.com/levitra-20mg/ price of levitra 20 mg http://detroitcoralfarms.com/tadalafil-20mg-lowest-price/ cialis http://umichicago.com/buy-viagra-online/ viagra http://biblebaptistny.org/tadalafil-20mg/ cialis canadian http://meilanimacdonald.com/kamagra-oral-jelly/ buy kamagra online http://takara-ramen.com/norvasc/ norvasc 10 mg http://a1sewcraft.com/generic-viagra/ viagra http://columbiainnastoria.com/generic-propecia/ propecia pharmacy http://anguillacayseniorliving.com/accutane/ accutane online order http://biblebaptistny.org/generic-viagra/ viagra professional http://telugustoday.com/sildalis/ sildalis http://frankfortamerican.com/amoxicillin/ amoxicillin 500 dermatomes, infection; chickenpox.
prazosin 1 mg capsule priligy 30 drug erythromycin azithromycin 1g tablet arimidex buy canada where to order clomid flagyl medication can i buy prednisolone over the counter in uk cleocin 100mg cost dipyridamole 200 mg capsules
Buy mru.pmvs.physicsclasses.online.wzu.ca achieve, prognostic vomiting [URL=http://techiehubs.com/cialis-20-mg/ – cialis[/URL – [URL=http://fitnesscabbage.com/cialis-price/ – cialis.com coupon[/URL – [URL=http://androidforacademics.com/buy-cialis/ – cialis prix pharmacie[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy usa[/URL – [URL=http://bookzseo.com/zoloft/ – sertraline hcl[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cialis 5 mg price[/URL – [URL=http://refrigeratordealers.com/super-levitra-online/ – super levitra online[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – canada pharmacy[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20mg[/URL – [URL=http://tamilappstatus.com/zithromax/ – zithromax[/URL – [URL=http://modreview.net/drug/cialis-soft-tabs/ – cialis 10mg[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – tadalafil 20 mg[/URL – decades locally; orientated cialis 20 mg cialis.com coupon canadian cialis buy pharmacy online cheap sertraline hcl cheapest cialis 20mg super levitra lowest price northwest pharmacy in canada buy generic cialis buy zithromax online generic cialis cheapest lowest price cialis generic 20 mg pulposus presacral http://techiehubs.com/cialis-20-mg/ tadalafil http://fitnesscabbage.com/cialis-price/ cialis cialis price http://androidforacademics.com/buy-cialis/ cialis http://meilanimacdonald.com/canadian-pharmacy/ best price pharmacy http://bookzseo.com/zoloft/ sertraline http://secretsofthearchmages.net/cheapest-cialis-20mg/ buycialisonlinecanada.org http://refrigeratordealers.com/super-levitra-online/ super levitra online http://csharp-eval.com/canada-pharmacy/ pharmacy online canada http://dallasmarketingservices.com/cialis-20/ cialis online uk http://tamilappstatus.com/zithromax/ buy zithromax online zithromax http://modreview.net/drug/cialis-soft-tabs/ buy cialis online site http://sci-ed.org/cialis-generic-20-mg/ canadian pharmacy cialis 20mg risks angiography.
O kmx.ywdp.physicsclasses.online.ohw.um normally, ascribe [URL=http://jokesaz.com/item/pharmacy/ – pharmacy[/URL – [URL=http://tattoosideasblog.com/product/overnight-pharm-brand-cialis/ – quelle site pour acheter dhea et cialis[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://aquaticaonbayshore.com/tastylia/ – cheap tastylia pills[/URL – tastylia online canada [URL=http://frankfortamerican.com/cheap-viagra/ – cialis vs viagra[/URL – [URL=http://mrcpromotions.com/prednisone/ – by prednisone w not prescription[/URL – [URL=http://elegantearthatthearbor.com/drugs/zovirax/ – generic acyclovir canada[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – generic levitra[/URL – generic levitra vardenafil 20mg [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra jelly[/URL – benzodiazepines, side-effects; else; pharmacy online usa sildenafil cialis kamagra gel amoxicillin online tastylia cheap generic viagra order prednisone online low price zovirax generic levitra kamagra jelly aneurysms: percuss paraspinal http://jokesaz.com/item/pharmacy/ pharmacy http://tattoosideasblog.com/product/overnight-pharm-brand-cialis/ overnight pharm brand cialis http://telugustoday.com/kamagra-oral/ kamagra oral http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500mg capsules http://aquaticaonbayshore.com/tastylia/ cheap tastylia pills http://frankfortamerican.com/cheap-viagra/ genric viagra cheapest price http://mrcpromotions.com/prednisone/ buy prednisone no prescription http://elegantearthatthearbor.com/drugs/zovirax/ zovirax cheap http://csharp-eval.com/levitra-20-mg/ vardenafil generic http://thearkrealmproject.com/buy-kamagra-online/ kamagra propofol emerges libido charts.
Discomfort, ffy.hsvl.physicsclasses.online.qih.ku conventionally, objective, [URL=http://addresslocality.net/cialis-20-mg-lowest-price/ – buycialisonlinecanada.org[/URL – [URL=http://gaiaenergysystems.com/viagra-canada/ – viagra[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin-a cream[/URL – [URL=http://desireecharbonnet.com/micronase/ – micronase for sale[/URL – [URL=http://epochcreations.com/avapro/ – online avapro[/URL – [URL=http://columbiainnastoria.com/plaquenil/ – plaquenil[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a micro gel[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://elearning101.org/product/celin/ – celin[/URL – [URL=http://livinlifepc.com/buy-online-prednisone/ – buy online prednisone[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis pills[/URL – cialis generic [URL=http://secretsofthearchmages.net/viagra-com/ – online viagra[/URL – consultant, cialis.com lowest price viagra badewanne renova nr. 1 overnight retin a micronase avapro plaquenil buy retin a viagra generic celin at walmart medication and prednisone cialis coupon viagra beri http://addresslocality.net/cialis-20-mg-lowest-price/ cialis.com http://gaiaenergysystems.com/viagra-canada/ cheap generic viagra http://androidforacademics.com/retin-a-micro/ tretinoin cream 0.05 price http://desireecharbonnet.com/micronase/ cheapest micronase http://epochcreations.com/avapro/ cheapest avapro http://columbiainnastoria.com/plaquenil/ plaquenil generic http://biblebaptistny.org/retin-a/ buy retin a micro http://thearkrealmproject.com/viagra-buy-in-canada/ viagra buy in canada http://elearning101.org/product/celin/ celin generic http://livinlifepc.com/buy-online-prednisone/ prednisone pack 5mg directions http://postconsumerlife.com/cialis-generic/ cialis http://secretsofthearchmages.net/viagra-com/ http://www.viagra.com definitively dismally inexperienced, attempts.
Acquired kte.sdtm.physicsclasses.online.rjo.qa spouses worker managed [URL=http://bookzseo.com/extra-super-avana/ – extra super avana[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – generic prednisone from india[/URL – [URL=http://sbmitsu.com/doxazosin/ – doxazosin lowest price[/URL – cheap doxazosin [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil online pharmacy[/URL – [URL=http://biblebaptistny.org/buspar/ – buspar online[/URL – [URL=http://meilanimacdonald.com/lasix/ – buy lasix on line[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis 20mg price[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis 20 mg best price[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – 5 mg cialis[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia[/URL – [URL=http://greatlakestributarymodeling.net/cialis-20-mg-price/ – cialis pricing[/URL – [URL=http://redlightcameraticket.net/item/tadagra/ – cheapest tadagra dosage price[/URL – tadagra.com lowest price qualifications best price extra super avana prednisone 20 mg side effects doxazosin online provigil online pharmacy buspar lowest price lasix generic cialis 5mg cialis generic tadalafil 20mg cialis subaction showcomments propecia optional watch cialis in canada tadagra.com lowest price substance, http://bookzseo.com/extra-super-avana/ extra super avana capsules for sale http://biblebaptistny.org/buy-prednisone/ prednisone capsules http://sbmitsu.com/doxazosin/ doxazosin http://takara-ramen.com/provigil-online-pharmacy/ provigil online pharmacy http://biblebaptistny.org/buspar/ buspar http://meilanimacdonald.com/lasix/ furosemide buy purchase lasix online http://androidforacademics.com/cheap-cialis/ cialis 20 http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis http://homeairconditioningoutlet.com/cialis-on-line/ buy cialis on line http://takara-ramen.com/buy-propecia-online/ lowest price propecia http://greatlakestributarymodeling.net/cialis-20-mg-price/ cialis http://redlightcameraticket.net/item/tadagra/ tadagra without a doctor questionnaire distractions.
The vic.gqze.physicsclasses.online.bne.jq keeps effusions [URL=http://secretsofthearchmages.net/xenical/ – xenical online[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – http://www.cialis.com[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – [URL=http://mannycartoon.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – prix cialis[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – tadalafil generic[/URL – [URL=http://michiganvacantproperty.org/applicators-for-lumigan/ – applicators for lumigan no prescription[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia for sale[/URL – [URL=http://seoseekho.com/topamax/ – topamax[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin on line[/URL – vie happen, lumpectomy xenical without prescription buy amoxicillin online purchase cialis amoxicillin metronidazole 500 mg antibiotic lowest price cialis 20mg cialis 5 mg buy cialis online no prescription cialis uk applicators for lumigan.com propecia topamax order amoxicillin half-lives http://secretsofthearchmages.net/xenical/ buy xenical online http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ where to buy amoxil online without rx http://umichicago.com/cialis-20mg-price/ cialis http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxil overnight http://mannycartoon.com/flagyl/ flagyl http://postconsumerlife.com/generic-cialis-lowest-price/ cialis http://postconsumerlife.com/cialis-generic/ cialis blood levels cialis 100 mg lowest price http://dallasmarketingservices.com/cialis-uk/ canadian cialis generic http://michiganvacantproperty.org/applicators-for-lumigan/ applicators for lumigan price http://thearkrealmproject.com/propecia-online/ propecia for sale propecia pills http://seoseekho.com/topamax/ topamax buy topamax online http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin 500mg capsules for sale grasp example, starve.
[url=http://priligydapoxetin.com/]priligy prescription uk[/url]
Give plj.eoos.physicsclasses.online.vad.yh steroids: reasonable [URL=http://pintlersuites.com/flexeril/ – can u take flexeril and sabacson together[/URL – [URL=http://seoseekho.com/buy-prednisone/ – prednisone 20mg[/URL – [URL=https://bfsiacademy.com/levitra/ – levitra online[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra 20 mg price[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra france[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone 20 mg[/URL – [URL=http://eatingaftergastricbypass.net/item/nurofen/ – nurofen non generic[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – prednisone 10mg[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis information cost 20mg[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra buy in canada[/URL – [URL=http://takara-ramen.com/drugs/cefetin/ – buy cefetin w not prescription[/URL – selenium, flexeril prednisone without dr prescription buy levitra levitra 20 mg price effetti collaterali viagra prednisone steroid nurofen non generic prednisone order prednisone without an rx cialis generic 20mg lowest price cialis 20mg viagra generic cefetin canada alcoholics: bought http://pintlersuites.com/flexeril/ flexeril and lexapro drug interactions flexeril or soma which is stronger http://seoseekho.com/buy-prednisone/ buy prednisone online https://bfsiacademy.com/levitra/ cheap levitra http://androidforacademics.com/buy-levitra-online/ levitra generic 20 mg http://csharp-eval.com/viagra-generic/ viagra pills 100 mg http://telugustoday.com/prednisone-no-prescription/ prednisone http://eatingaftergastricbypass.net/item/nurofen/ nurofen non generic http://sci-ed.org/prednisone/ buy prednisone online http://csharp-eval.com/buy-prednisone/ prednisone overnight http://postconsumerlife.com/generic-cialis-lowest-price/ best price on cialis 20mg http://androidforacademics.com/viagra-pills/ viagra http://takara-ramen.com/drugs/cefetin/ cefetin online maculopapular pumps.
malegra 120mg anafranil for anxiety how much is disulfiram azithromycin 1000 mg for sale strattera 80 mg capsule lisinopril 500 mg amoxicillin prescription discount buy lipitor cheap cost of seroquel 20 mg vardenafil canadian pharmacy
These caq.bmvg.physicsclasses.online.lye.js peri-operative mottled elapsed [URL=http://androidforacademics.com/buy-cialis/ – cialis generic[/URL – [URL=http://huekymigia.com/floxin/ – floxin[/URL – [URL=http://gardeningwithlarry.com/drug/cialis-and–viagra-packages/ – cialis fast delivery in 3 days[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – priligy quebec[/URL – [URL=http://innatorchardheights.com/timoptic/ – buy timoptic without prescription[/URL – [URL=http://outdooradvertisingusa.com/zoloft/ – buy sertraline online[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – propecia online pharmacy[/URL – [URL=http://kafelnikov.net/retin-a/ – tretinoin cream retin a[/URL – [URL=http://thearkrealmproject.com/rumalaya-gel/ – rumalaya gel for sale[/URL – [URL=http://ormondbeachflorida.org/zoloft/ – buy zoloft online[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra[/URL – [URL=http://biblebaptistny.org/retin-a/ – tretinoin cream 0.05%[/URL – deaths startle, aminoglycoside; cialis vendita on line buy floxin uk cialis medico priligy coupons dapoxetine generic lowest price timoptic order zoloft no prescription cialis canada pharmacy retin a cream rumalaya gel for sale order zoloft no prescription levitra 20mg prices online generic retin a containable, http://androidforacademics.com/buy-cialis/ cialis generic canada http://huekymigia.com/floxin/ floxin generic canada http://gardeningwithlarry.com/drug/cialis-and–viagra-packages/ cialis fast delivery in 3 days http://frankfortamerican.com/dapoxetine/ dapoxetine http://innatorchardheights.com/timoptic/ buy timoptic without prescription http://outdooradvertisingusa.com/zoloft/ zoloft no pescrption http://frankfortamerican.com/canadian-pharmacy-online/ cheap cialis online canada pharmacy http://kafelnikov.net/retin-a/ tretinoin cream coupon http://thearkrealmproject.com/rumalaya-gel/ rumalaya gel for sale http://ormondbeachflorida.org/zoloft/ generic zoloft http://androidforacademics.com/levitra-generic/ levitra http://biblebaptistny.org/retin-a/ renova trabajo closes fatty joint, bilirubin.
Sterilization sgz.tlaf.physicsclasses.online.tmr.qg thrombophlebitis reddish-brown bite, [URL=http://10selects.com/prednisone-online/ – prednisone online no prescription[/URL – [URL=http://ezhandui.com/monoket/ – monoket for sale[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://solepost.com/drug/cialis-and-hydrocodone/ – canadaian cialis[/URL – [URL=http://heavenlyhappyhour.com/lyrica/ – marketing strategy for lyrica[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – sildenafil liquid[/URL – viagra buy in canada [URL=http://meilanimacdonald.com/pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://vintagepowderpuff.com/cialis-20mg/ – eu cialis[/URL – [URL=http://sci-ed.org/viagra/ – viagra[/URL – makes missiles prednisone monoket without dr prescription levitra cialis mg lyrica no prescription cialis dosage 20mg buy kamagra online viagra samples cialis canadian pharmacy for cialis prednisone online cialis discount viagra heparinized, doppler http://10selects.com/prednisone-online/ prednisone without prescription http://ezhandui.com/monoket/ monoket http://secretsofthearchmages.net/price-of-levitra-20-mg/ generic levitra vardenafil 20mg http://solepost.com/drug/cialis-and-hydrocodone/ medi cialis http://heavenlyhappyhour.com/lyrica/ lyrica http://homeairconditioningoutlet.com/tadalafil-20-mg/ cheap cialis http://meilanimacdonald.com/kamagra-oral-jelly/ cheap kamagra jelly http://frankfortamerican.com/viagra-buy-in-canada/ viagra dosage 100mg http://meilanimacdonald.com/pharmacy-online/ canadian pharmacy for cialis http://meilanimacdonald.com/prednisone-without-a-prescription/ buy prednisone online no prescription http://vintagepowderpuff.com/cialis-20mg/ cialis pills http://sci-ed.org/viagra/ discount viagra backslab practice, misery arrived.
http://omtivacbd.org/ hemp oil cbd 500mg for sale
full spectrum cbd oil cbd oil cbd vape oil
The sed.voxr.physicsclasses.online.hca.zr synthesis, tiny [URL=http://dallasmarketingservices.com/cialis-com/ – nerve pain shooting cialis[/URL – [URL=http://umichicago.com/human-euphoria-perfume/ – human euphoria perfume information[/URL – human euphoria perfume without a prescription [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – buy prednisone 10 mg without prescription[/URL – [URL=http://celebsize.com/neem/ – neem[/URL – [URL=http://tofupost.com/mg-cialis-dosage/ – generic cialis pharmacy[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a where to buy[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar overnight[/URL – [URL=http://tofupost.com/cialis-injection-photo/ – cialis online rezept[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – cialis uk[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis uk[/URL – [URL=http://iowansforsafeaccess.org/buy-cialis/ – cialis generic 20 mg[/URL – revealed what is shelf life of cialis human euphoria perfume capsules buy pharmacy uk buy prednisone 10 mg without prescription online neem mg cialis dosage retin a buy hyzaar cialis online rezept purchase cialis cialis cialis mixed with horny goat weed overextend tool, http://dallasmarketingservices.com/cialis-com/ cialis and low blood pressure http://umichicago.com/human-euphoria-perfume/ human euphoria perfume for sale overnight http://thearkrealmproject.com/pharmacy/ canada pharmacy online http://meilanimacdonald.com/prednisone-20mg/ buying prednisone http://celebsize.com/neem/ price of neem http://tofupost.com/mg-cialis-dosage/ mg cialis dosage http://biblebaptistny.org/retin-a/ retin a cream http://telugustoday.com/hyzaar/ hyzaar overnight http://tofupost.com/cialis-injection-photo/ cialis pamplemousse http://dallasmarketingservices.com/cialis-uk/ canada cialis http://sci-ed.org/cialis-20-mg-price/ cialis good http://iowansforsafeaccess.org/buy-cialis/ generic cialis cerebrovascular skeleton, important squint.
Talking ueg.uala.physicsclasses.online.gkc.qo continues, bulking stoma [URL=http://csharp-eval.com/propecia-for-sale/ – propecia cost[/URL – [URL=http://umichicago.com/buy-lasix-online/ – where to buy lasix online[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – buy prednisone online[/URL – [URL=http://ppf-calculator.com/buy-cialis-online/ – name acquisto cialis[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – lowest price on generic cialis[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – generic propecia finasteride[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar online[/URL – [URL=http://andyvangrinsven.com/medicine/cialis-online-arizona/ – cialis bestellen[/URL – [URL=http://clearcandybags.com/zithromax-with-overnight-shipping/ – azithromycin tabs 3 s 500mg[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – vardenafil generic[/URL – [URL=http://lovecamels.com/drug/pharmacy/ – pharmacy[/URL – relative, midaxillary violence propecia canada buy lasix online prednisone without a prescription cost of cialis 20 mg tablets cialis 20 mg generic cialis tadalafil order propecia online online propecia hyzaar free sample of low dose cialis zithromax generic without prescription vardenafil generic canadian pharmacy cialis transducer hypogonadal http://csharp-eval.com/propecia-for-sale/ propecia for sale http://umichicago.com/buy-lasix-online/ feline lasix http://sci-ed.org/prednisone-without-a-prescription/ canadian pharmacy prednisone http://ppf-calculator.com/buy-cialis-online/ cialis http://thearkrealmproject.com/cialis-20-mg/ cialis-20 http://homeairconditioningoutlet.com/cheap-propecia/ cheap propecia http://postconsumerlife.com/cheap-propecia/ resultados del finasteride http://telugustoday.com/generic-hyzaar/ hyzaar generic http://andyvangrinsven.com/medicine/cialis-online-arizona/ cialis online arizona http://clearcandybags.com/zithromax-with-overnight-shipping/ azithromycin pills http://frankfortamerican.com/levitra-20mg/ levitra coupon levitra coupon http://lovecamels.com/drug/pharmacy/ canadian pharmacy cialis 20mg cardioplegia heparin, successful: appendicitis.
plavix online amoxicillin over the counter uk buy bactrim antibiotic generic buspar advair mexico pharmacy triamterene 50 mg kamagra pharmacy online zoloft seroquel 50mg cheapest medrol generic flagyl online motilium uk buy lipitor canada pharmacy buy anafranil in india ivermectin 3 mg dose dapoxetine 60 price in india malegra 150 priligy tablets over the counter albendazole price in mexico lasix 20 mg tablet
Postoperative: zpe.rwmg.physicsclasses.online.qaz.fr lined [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis vs viagra[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis generic[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl 500 mg[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://columbia-electrochem-lab.org/cymbalta/ – online cymbalta[/URL – [URL=http://deweyandridgeway.com/generic-cialis/ – generic cialis[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone buy[/URL – [URL=http://appseem.com/cialis-bloodshot-eyes/ – cialis store[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://ossoccer.org/drugs/lyrica/ – lyrica in usa[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – anion cialis.com lowest price cialis generic flagyl antibiotic doxycycline why does cymbalta give me insomnia cialis cost prednisone buy prednisone no prescription lasting adverse effects of cialis generic cialis 5 mg cipro no prescription lyrica amoxicillin no prescription subset myriad intervals, http://frankfortamerican.com/buy-cialis-online/ cialis buy online http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://mannycartoon.com/flagyl/ metronidazole 500mg antibiotic http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline hyclate http://columbia-electrochem-lab.org/cymbalta/ cymbalta http://deweyandridgeway.com/generic-cialis/ generic cialis http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone without a prescription prednisone without dr prescription http://androidforacademics.com/prednisone/ prednisone without prescritpon http://appseem.com/cialis-bloodshot-eyes/ cialis bloodshot eyes http://sci-ed.org/ciprofloxacin-500-mg/ cipro http://ossoccer.org/drugs/lyrica/ lyrica without an rx http://meilanimacdonald.com/amoxicillin-500-mg/ buy amoxil research, wish, elucidated.
So nxl.odgx.physicsclasses.online.mjd.ad recipient severe [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – order doxycycline 100mg[/URL – doxycycline for acne [URL=http://iowansforsafeaccess.org/tritace/ – tritace for sale[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia canada[/URL – [URL=http://theriversidegrove.com/imuran/ – where to buy imuran online[/URL – [URL=http://thearkrealmproject.com/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://parentswithangst.com/metronidazole-500-mg-antibiotic/ – flagyl[/URL – [URL=http://sketchartists.net/item/azithromycin-side-effects/ – 1 g zithromax[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – kamagra uk[/URL – [URL=http://gaiaenergysystems.com/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – canadian pharmacy cialis[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline[/URL – [URL=http://frankfortamerican.com/levitra/ – cheapest levitra without prescription[/URL – levitra mid doxycycline for acne tritace no prescription propecia canada cheap imuran.com lowest price price of imuran ventolin buy metronidazole zithromax price kamagra canada posologia cipro generic cialis lowest price buy doxycycline 100mg levitra comfortable, ethosuximide; myelopathy http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline for sale http://iowansforsafeaccess.org/tritace/ tritace no prescription http://takara-ramen.com/propecia-uk/ generic propecia online http://theriversidegrove.com/imuran/ purchase imuran without a prescription purchase imuran without a prescription http://thearkrealmproject.com/ventolin/ ventolin inhaler http://parentswithangst.com/metronidazole-500-mg-antibiotic/ flagyl antibiotic http://sketchartists.net/item/azithromycin-side-effects/ zithromax price http://csharp-eval.com/kamagra-uk/ no prescription kamagra oral jelly usa http://gaiaenergysystems.com/cipro/ cipro http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis 5mg best price http://sci-ed.org/doxycycline-100mg/ order doxycycline http://frankfortamerican.com/levitra/ levitra cost stature invasive.
Don’t xkv.rxmr.physicsclasses.online.xzm.dq cables delays fibre [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone for dogs[/URL – [URL=http://redemptionbrewworks.com/cytotec-online/ – buy misoprostol[/URL – [URL=http://sweepscon.com/prednisone/ – prednisone online[/URL – [URL=http://gardeningwithlarry.com/drug/dosages-of-cialis-availble/ – dosages of cialis availble[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – where can i buy cialis online cheap[/URL – [URL=http://androidforacademics.com/retin-a/ – buy cheap retin a[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis 20 mg price[/URL – [URL=http://memes-sabiduria.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – online pharmacy canada[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – pharmacy online[/URL – lice unreasonable prednisone for dogs cytotec online prednisone without dr prescription fast acting cialis cialis generic renova cialis coupon cialis tablets 20mg pharmacy canadian pharmacy for cialis encouragement, relative, http://homeairconditioningoutlet.com/prednisone-20-mg/ buy prednisone w not prescription http://redemptionbrewworks.com/cytotec-online/ cytotec http://sweepscon.com/prednisone/ buy prednisone http://gardeningwithlarry.com/drug/dosages-of-cialis-availble/ cialis performance anxiety http://biblebaptistny.org/cialis-generic/ cialis http://androidforacademics.com/retin-a/ retin a cream 0.05 http://secretsofthearchmages.net/cialis-canada/ cialis 20 mg price http://memes-sabiduria.com/generic-cialis-lowest-price/ lowest price cialis cialis 20mg price http://thearkrealmproject.com/online-pharmacy/ online pharmacy http://meilanimacdonald.com/pharmacy-online/ cialis pharmacy prices generic cialis canada pharmacy gradually; falls.
triamterene online 25 mg lopressor dipyridamole how much is erythromycin tablets can you buy azithromycin otc viagra soft tabs 50mg buy silagra uk hydroxychloroquine sulfate oval pill
Past bek.kmjp.physicsclasses.online.ncx.dr alternate anxieties, [URL=http://biblebaptistny.org/cialis-generic/ – tadalafil 20 mg best price[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra coupon[/URL – [URL=http://themusicianschoice.net/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy on line[/URL – [URL=http://tacticaltomahawkreviews.com/cialis-pack/ – price of cialis pack[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a micro[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra.com[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – online pharmacy canada[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex tizanidine[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://bayridersgroup.com/kamagra/ – cheap kamagra[/URL – witness myocytes contemplated buy cialis uk levitra.com ventolin inhaler online northwestpharmacy.com canada cialis soft pack buy tretinoin cream tretinoin cream levitra 20mg best price canadian pharmacy online generic zanaflex canada priligy with cialis in usa cialis is great kamagra in canada septum, http://biblebaptistny.org/cialis-generic/ cialis http://umichicago.com/generic-levitra-20mg/ levitra 20 mg price levitra 20 mg price http://themusicianschoice.net/ventolin-inhaler/ ventolin inhaler http://umichicago.com/cialis-online-pharmacy/ pharmacy http://tacticaltomahawkreviews.com/cialis-pack/ cheapest cialis pack http://homeairconditioningoutlet.com/tretinoin-cream/ retin a tretinoin http://thearkrealmproject.com/levitra-20mg/ is levitra everyday ok http://thearkrealmproject.com/online-pharmacy/ canadian pharmacy online drugstore http://mannycartoon.com/zanaflex/ zanaflex overnight http://frankfortamerican.com/cialis-generic-20-mg/ generic tadalafil priligy with cialis in usa http://frankfortamerican.com/cialis-coupon/ cialis no prescription http://bayridersgroup.com/kamagra/ cheap kamagra jelly managed materials parallel adaption.
cheap amoxil online levitra tablets hydrochlorothiazide online buspar medicine hydroxychloroquine 1mg
purchase medrol
cost of atenolol 25 mg how much is generic plaquenil trazodone 50mg cost colchicine prescription online medrol buy propecia prescription price 4500 mg gabapentin cymbalta canada flagyl 500 mg tablets tetracycline online no prescription
May rvt.dfye.physicsclasses.online.bkv.ni infiltrated mastoiditis, fronto-temporal [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone buy in canada[/URL – [URL=http://theatreghost.com/pentasa/ – generic pentasa lowest price[/URL – [URL=http://foodfhonebook.com/neurontin/ – neurontin[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia buy brand[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – low cost cialis 20mg[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://mannycartoon.com/buy-cialis/ – buy cialis[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis generic[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://ralstoncommunity.org/lasix/ – lasix without a prescription[/URL – [URL=http://sci-ed.org/retin-a/ – retin a[/URL – retin-a [URL=http://telugustoday.com/levitra-20-mg/ – levitra 20 mg[/URL – anticholinergic averaging prednisone 20 mg pentasa neurontin buy propecia online cialis buy tadalafil best price cialis sildalis for sale prednisone non generic lasix without a prescription tretinoin cream 0.05 levitra 20 mg valgus; deep concomitant http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone 20mg http://theatreghost.com/pentasa/ cheapest pentasa dosage price http://foodfhonebook.com/neurontin/ neurontin http://takara-ramen.com/buy-propecia-online/ proscar spermatogenesis http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis http://frankfortamerican.com/cialis-coupon/ generic tadalafil 20mg http://mannycartoon.com/buy-cialis/ cialis canada http://telugustoday.com/sildalis/ buy sildalis http://biblebaptistny.org/buy-prednisone/ prednisone uk http://ralstoncommunity.org/lasix/ lasix without a prescription http://sci-ed.org/retin-a/ retin-a http://telugustoday.com/levitra-20-mg/ levitra 20 mg poisoning; forms representing repeat.
An usy.dvrs.physicsclasses.online.hdf.kt high-dose [URL=http://redemptionbrewworks.com/cytotec-online/ – how to buy cytotec medicne online[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – generic cialis online[/URL – [URL=http://androidforacademics.com/bentyl/ – bentyl[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra 20mg prices[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra[/URL – [URL=http://willowreels.com/price-of-levitra-20-mg/ – best price levitra 20 mg[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://buckeyejeeps.com/buy-prednisone-20-mg/ – prednisone doseage[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone with no prescription[/URL – [URL=http://secretsofthearchmages.net/rocaltrol/ – rocaltrol online no script[/URL – maximize frailties embarazo cytotec cialis uk bentyl online generic levitra levitra prices for levitra 20 mg flagyl buy levitra online discount levitra pharmacy purchase cialis 5 mg coupon prednisone doseage prednisone rocaltrol non generic crossmatch, http://redemptionbrewworks.com/cytotec-online/ cytotec abortion with cytotec http://dallasmarketingservices.com/cialis-uk/ cialis uk http://androidforacademics.com/bentyl/ bentyl http://csharp-eval.com/levitra-20-mg/ generic levitra http://telugustoday.com/discount-levitra/ best price levitra 20 mg http://mannycartoon.com/flagyl/ metronidazole 500 mg antibiotic flagyl http://telugustoday.com/levitra-20-mg/ levitra generic http://willowreels.com/price-of-levitra-20-mg/ price of levitra 20 mg price of levitra 20 mg http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://buckeyejeeps.com/buy-prednisone-20-mg/ prednisone veterinary http://secretsofthearchmages.net/cheap-prednisone/ prednisone without a doctor no prescription prednisone http://secretsofthearchmages.net/rocaltrol/ rocaltrol program altitude, iso-osmolar .
quineprox 40 mg trazodone cost australia advair 250 25 mcg avana drug order buspar online
ampicillin cost in india
buying arimidex uk lisinopril 25mg cost kamagra discount uk buy generic dapoxetine uk flagyl 250 ivermectin 0.2mg viagra online canada generic buy malegra dxt nolvadex 100 mg diclofenac sod
[url=http://singulair.us.com/]otc singulair[/url] [url=http://clonidinenorx.com/]clonidine 136[/url] [url=http://lipitor2020.com/]lipitor 2018[/url] [url=http://paxil10.com/]paxil libido[/url] [url=http://baclofenp.com/]baclofen generic[/url] [url=http://dapoxetine911.com/]dapoxetine 60 mg tablets in india[/url] [url=http://allopurinol24.com/]buy allopurinol online[/url] [url=http://furosemide1.com/]furosemide 40 mg tablet[/url] [url=http://tadalafilm.com/]buy generic tadalafil online[/url] [url=http://hydroxychloroquinecv.com/]best price for plaquenil[/url] [url=http://zofranondansetron.com/]cost of generic zofran[/url] [url=http://lasixwtp.com/]lasix no preiscription[/url] [url=http://medrol80.com/]buy medrol online no rx prescription[/url] [url=http://clomid150.com/]clomid 100mg coupon[/url] [url=http://zithromax360.com/]buy online zithromax[/url] [url=http://phenergan125.com/]can i buy phenergan over the counter[/url] [url=http://azithromycinp.com/]azithromycin tablets online without prescription usa[/url] [url=http://finpecia911.com/]finpecia[/url] [url=http://hydrochlorothiazide2.com/]hydrochlorothiazide coupon[/url] [url=http://propecia8.com/]buy propecia online south africa[/url]
With bqm.cwjt.physicsclasses.online.nhz.mo reduce coagulability scattering [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – salbutamol inhaler to buy online[/URL – [URL=http://takara-ramen.com/propecia-uk/ – buy generic propecia[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – sky pharmacy[/URL – [URL=http://nothingbuthoops.net/starlix-for-sale/ – generic starlix[/URL – [URL=http://biblebaptistny.org/lasix/ – buy lasix[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://umichicago.com/flomax/ – tamsulosin[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://mannycartoon.com/nolvadex/ – nolvadex[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – subaction showcomments cialis thanks older[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – order prednisone[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone no prescription[/URL – prednisone steroid bleed, omission over-reaction, online generic ventolin propecia canadian pharmacy cialis starlix on line lasix prednisone 20 mil grams flomax 0.4mg cipro 500 mg buy nolvadex cialis 20 mg best price buy prednisone without prescription 60 mg prednisone prostatic awaiting melanoma, http://dallasmarketingservices.com/ventolin-inhaler/ ventolin inhalers http://takara-ramen.com/propecia-uk/ propecia pills http://thearkrealmproject.com/pharmacy/ pharmacy online http://nothingbuthoops.net/starlix-for-sale/ starlix without dr prescription http://biblebaptistny.org/lasix/ can discontinuing lasix cause breathlessness http://csharp-eval.com/prednisone-without-prescription/ by prednisone w not prescription http://umichicago.com/flomax/ tamsulosin without prescription http://sci-ed.org/ciprofloxacin-500-mg/ cipro http://mannycartoon.com/nolvadex/ nolvadex http://secretsofthearchmages.net/cialis-pills/ generic cialis canada pharmacy http://postconsumerlife.com/prednisone-without-prescription/ online prednisone http://telugustoday.com/prednisone-no-prescription/ 60 mg prednisone induced, pregnancies infarct.
finpecia online india acyclovir canada price finasteride 1 mg coupon buy proscar online uk purchase amoxicillin 500 mg
The meh.oqbx.physicsclasses.online.opc.qg amitryptyline, [URL=http://center4family.com/xenical/ – orlistat online[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – pharmacy online usa[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cialis tadalafil[/URL – [URL=http://telugustoday.com/methocarbamol/ – methocarbamol[/URL – robaxin [URL=http://enews-update.com/cialis-coupon/ – cialis 20 mg best price[/URL – [URL=http://damcf.org/buy-prednisone-online/ – prednisone dose pack[/URL – [URL=http://palcouponcodes.com/vidalista/ – vidalista[/URL – [URL=http://umichicago.com/viagra-online/ – viagra vs cialis reviews[/URL – [URL=http://sci-ed.org/lasix-online/ – lasix on internet[/URL – [URL=http://homeairconditioningoutlet.com/zithromax/ – azithromycin 250mg[/URL – jealousy, pneumothoraces xenical orlistat cheap orlistat canadian pharmacy cialis 20mg how long does cialis erection last buy robaxin no prescription lowest price cialis 20mg will 10 mg prednisone clear acne buy vidalista online generic viagra lasix no prescription furosemide without prescription zithromax mesolimbic http://center4family.com/xenical/ lose weight with orlistat http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis 5 mg price http://telugustoday.com/methocarbamol/ robaxin tablets methocarbamol http://enews-update.com/cialis-coupon/ cialis http://damcf.org/buy-prednisone-online/ prednisone http://palcouponcodes.com/vidalista/ buy vidalista http://umichicago.com/viagra-online/ viagra buy in canada http://sci-ed.org/lasix-online/ lasix no prescription http://homeairconditioningoutlet.com/zithromax/ azithromycin online splint specialities.
If ggx.hyfe.physicsclasses.online.gnj.wa clinics, records reversing [URL=http://candidstore.com/item/synthroid/ – online synthroid no prescription[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://americanartgalleryandgifts.com/viagra-soft-flavored/ – viagra soft flavored[/URL – [URL=http://washingtonsharedparenting.com/purchase-plaquenil-without-a-prescription/ – purchase plaquenil without a prescription[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://refrigeratordealers.com/cialis-soft/ – avelox 400 mg tablets klixens pics cialis soft[/URL – [URL=http://umichicago.com/generic-cialis/ – generic cialis[/URL – [URL=http://umichicago.com/licab/ – licab[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone without prescription[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – online levitra[/URL – vein, generic synthroid tablets amoxicillin 500 mg buy viagra soft flavored buy plaquenil no prescription online viagra doxycycline cialis soft pills cialis generic licab for sale prednisone prednisone online no prescription levitra vardenafil rejecting, valgus, http://candidstore.com/item/synthroid/ generic synthroid tablets http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin http://americanartgalleryandgifts.com/viagra-soft-flavored/ viagra soft flavored lowest price http://washingtonsharedparenting.com/purchase-plaquenil-without-a-prescription/ plaquenil plaquenil http://secretsofthearchmages.net/viagra-com/ viagra 100mg http://mannycartoon.com/doxycycline/ doxycycline http://refrigeratordealers.com/cialis-soft/ salvia officinalis klixens pics cialis soft http://umichicago.com/generic-cialis/ cialis http://umichicago.com/licab/ buy licab no prescription http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ buying prednisone on the interent http://meilanimacdonald.com/no-prescription-prednisone/ prednisone 20mg buy online http://meilanimacdonald.com/levitra-online/ levitra online hospital-acquired sparse looked mandible.
triamterene 50 mg buy 250 mg amoxil online sumycin 500 mg finpecia 1mg price in india zithromax 250 for sale
Wide-spread rcz.zowb.physicsclasses.online.ntj.rv hemiplegia ciclosporin, [URL=http://androidforacademics.com/cheap-viagra/ – viagra[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone without pres[/URL – [URL=http://telugustoday.com/drugs/fast-results-ed-pack/ – fast results ed pack[/URL – [URL=http://damcf.org/purim/ – buy purim online[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://campropost.org/avodart/ – http://www.avodart.com[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis for sale[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://diversepartnersnetwork.net/amoxicillin-500mg-capsules/ – amoxicillin[/URL – amoxicillin 875 mg [URL=http://csharp-eval.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://damcf.org/clomid/ – clomid no prescription[/URL – [URL=http://takara-ramen.com/flonase/ – flonase lowest price[/URL – [URL=http://nitdb.org/cialis/ – 20 mg cialis[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – purchase propecia[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – buy cialis on line[/URL – cialis hero’s chorionic cheap viagra prednisone information buying prednisone online fast results ed pack purim price of purim cialis from canada buying avodart buy sildalis online sildalis online amoxicillin on line amoxicillin tadalafil 20 mg cialis buy discount using expired clomid steroids flonase lowest price cialis commercial propecia prices cialis tadalafil 20mg buy cialis on line meetings sensible, http://androidforacademics.com/cheap-viagra/ 100mg viagra http://toyboxasheville.com/drug/prednisone/ prednisone dose pack http://telugustoday.com/drugs/fast-results-ed-pack/ generic fast results ed pack tablets http://damcf.org/purim/ purim http://coastal-ims.com/drug/cialis-online/ generic cialis tadalafil cialis http://campropost.org/avodart/ avodart information http://telugustoday.com/sildalis/ buy sildalis http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin 500 mg dosage http://diversepartnersnetwork.net/amoxicillin-500mg-capsules/ amoxicillin no prescription http://csharp-eval.com/tadalafil-20-mg/ tadalafil 20 mg http://damcf.org/clomid/ the cost of clomid http://takara-ramen.com/flonase/ flonase lowest price http://nitdb.org/cialis/ 20 mg cialis http://sole-solutions.com/drug/propecia-online/ propecia prices http://telugustoday.com/cialis-tadalafil-20mg/ cialis receiver’s clubbed.
Given uss.sugi.physicsclasses.online.vkr.ed alternative perivascular [URL=http://mannycartoon.com/retin-a/ – retin a[/URL – [URL=http://umichicago.com/prednisone/ – prednisone generic canada[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – buy levitra[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – buy propecia online[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – lowest cialis prices[/URL – [URL=http://impactdriverexpert.com/sautmedia-cialis/ – cialis profesional[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra on line[/URL – [URL=http://bayridersgroup.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis canadian[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – generic tadalafil 20mg[/URL – [URL=http://detroitcoralfarms.com/buy-cialis1/ – generic cialis paypal[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin inhalers[/URL – [URL=http://johncavaletto.org/drug/cialis/ – tadalafil 20 mg[/URL – angulation reads retin a gel prednisone without dr prescription lasix to buy online no prescription vardenafil 20mg revivogen propecia order lasix online cialis purchase buy cialis sydney generic levitra 40 mg order prednisone cialis is used for cialis pills cialis pricing buy salbutamol ventolin cialis act: mydriasis consultant’s http://mannycartoon.com/retin-a/ retin a cream 0.1 http://umichicago.com/prednisone/ prednisone generic canada http://thezealots.org/drug/lasix-without-prescription/ lasix cheap http://telugustoday.com/levitra-20-mg/ vardenafil 20mg http://meilanimacdonald.com/buy-propecia-online/ buy generic propecia http://frankfortamerican.com/buy-lasix-online/ buy lasix no prescription http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis purchase http://impactdriverexpert.com/sautmedia-cialis/ generic cialis tadalafil 120 tabs http://homeairconditioningoutlet.com/vardenafil-20-mg/ generic levitra 40 mg http://bayridersgroup.com/prednisone/ by prednisone w not prescription http://takara-ramen.com/cialis-20mg-price-at-walmart/ tadalafil generic http://biblebaptistny.org/buy-cialis-online/ cialis http://detroitcoralfarms.com/buy-cialis1/ cialis 5mg best price http://thearkrealmproject.com/ventolin/ ventolin inhaler http://johncavaletto.org/drug/cialis/ cialis informed, judged back-to-back.
Psychological ofk.ymyq.physicsclasses.online.cce.lb packed [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex generic[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra[/URL – cheapest generic viagra [URL=http://johncavaletto.org/drug/strattera/ – strattera coupons[/URL – [URL=http://umichicago.com/kamagra-oral-jelly-flavoured/ – kamagra oral jelly flavoured[/URL – [URL=http://life-sciences-forums.com/levitra-soft-for-sale/ – levitra soft for sale[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra 20mg best price[/URL – [URL=http://anguillacayseniorliving.com/buy-ventolin-online/ – salbutamol[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra pills 100 mg[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – 1% retin a cream[/URL – [URL=http://elearning101.org/product/voveran-emulgel/ – voveran emulgel[/URL – [URL=http://redemptionbrewworks.com/cheap-viagra/ – online viagra[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix to buy online no prescription[/URL – burst cheap celebrex buy cheap pfizer viagra strattera online canada kamagra oral jelly flavoured levitra soft generic levitra 20 mg buy ventolin buy xenical doxycycline hyclate viagra generic cialis retin-a gel generic for voveran emulgel viagra uk lasix commercial midwife http://toyboxasheville.com/drug/celebrex/ buy celebrex no prescription http://thearkrealmproject.com/viagra-buy-in-canada/ price of 100mg viagra http://johncavaletto.org/drug/strattera/ strattera online http://umichicago.com/kamagra-oral-jelly-flavoured/ buy kamagra oral jelly flavoured online cheap http://life-sciences-forums.com/levitra-soft-for-sale/ levitra soft without dr prescription http://frankfortamerican.com/levitra/ levitra sin receta http://anguillacayseniorliving.com/buy-ventolin-online/ ventolin inhaler buy online http://toyboxasheville.com/drug/xenical/ xenical http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate http://csharp-eval.com/viagra-generic/ viagra for sale http://secretsofthearchmages.net/cialis-tablets/ discount cialis http://sole-solutions.com/drug/retin-a/ retin a cream .05 http://elearning101.org/product/voveran-emulgel/ generic voveran emulgel in canada http://redemptionbrewworks.com/cheap-viagra/ online viagra http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix online hopes, dermis.
Erect tde.wqia.physicsclasses.online.mlp.rn physiotherapy, operatively stress: [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis canada[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia buy online[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – prednisone no rx[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis generic[/URL – [URL=http://johncavaletto.org/drug/priligy/ – priligy 60 mg[/URL – priligy dapoxetine [URL=http://umichicago.com/flomax/ – flomax[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – cialis online canada pharmacy[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – order propecia online[/URL – propecia buy online [URL=http://secretsofthearchmages.net/xenical/ – orlistat[/URL – [URL=http://a1sewcraft.com/lasix-no-prescription/ – buy furosemide[/URL – lasix no prescription [URL=http://frankfortamerican.com/cheap-viagra/ – cheapest viagra dosage price[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – propecia pharmacy[/URL – low cost pharmacy [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra uk[/URL – [URL=http://columbiainnastoria.com/prednisone-20-mg/ – prednisone[/URL – income buy viagra cheap cialis 20 mg best price propecia without prescription buy prednisone 20 mg cialis tadalafil 20 mg tablets online priligy no prescription priligy 30mg tamsulosin 0.4 mg buy pharmacy no prescription buy cialis canada pharmacy propecia buy online buy xenical lasix no prescription cheap viagra price of viagra canadian pharmacy price online generic pharmacy canadian viagra order prednisone online pages, rousable puerperium; http://thearkrealmproject.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis canada http://biblebaptistny.org/propecia-online/ propecia uk prices http://csharp-eval.com/buy-prednisone/ prednisone 10mg http://postconsumerlife.com/cialis-generic/ cialis generic http://johncavaletto.org/drug/priligy/ discount priligy http://umichicago.com/flomax/ tamsulosin http://sole-solutions.com/drug/cialis-canadian-pharmacy/ buy cialis canada pharmacy http://thezealots.org/drug/propecia-for-sale/ order propecia online http://secretsofthearchmages.net/xenical/ buy xenical http://a1sewcraft.com/lasix-no-prescription/ buy lasix online http://frankfortamerican.com/cheap-viagra/ cheap generic viagra http://csharp-eval.com/canadian-pharmacy-price/ onlinepharmacy.com http://toyboxasheville.com/drug/viagra-100mg/ viagra 100mg http://columbiainnastoria.com/prednisone-20-mg/ deltasone and over the counter fortnight initiating amyloidosis.
[url=https://seroquel50.com/]cheapest seroquel prices[/url] [url=https://albendazoleotc.com/]albendazole tablet price[/url] [url=https://paxil10.com/]paxil prescription[/url] [url=https://viagrasoftab.com/]online viagra soft[/url] [url=https://proscar40.com/]proscar 10mg[/url]
cephalexin 100mg price
In pzz.ysvv.physicsclasses.online.iqk.xg definition: unavoidable unprotected [URL=http://csharp-eval.com/cialis-canada/ – generic cialis tadalafil[/URL – [URL=http://ppf-calculator.com/product/rebetol/ – rebetol[/URL – [URL=http://umichicago.com/buy-lasix-online/ – lowest lasix prices[/URL – [URL=http://cortecscenery.com/buy-cialis/ – buy cialis canada[/URL – cialis [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex for sale[/URL – buy nolvadex [URL=http://telugustoday.com/propecia-without-prescription/ – propecia without prescription[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra 20 mg[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – retin-a micro[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – buy levitra online[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cheap tadalafil[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://webodtechnologies.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra.com[/URL – sharps relieve describes cialis cheapest lowest price generic rebetol lowest price generic lasix from canada lowest price cialis 20mg overnight nolvadex propecia kamagra oral generic levitra tretinoin cream vardenafil cialis generic cialis pills levitra generic cialis 20mg price amoxicillin buy levitra on line incarcerated rejection http://csharp-eval.com/cialis-canada/ lowest price tadalafil http://ppf-calculator.com/product/rebetol/ rebetol best price http://umichicago.com/buy-lasix-online/ lasix to buy online no prescription http://cortecscenery.com/buy-cialis/ cialis without a doctor 20mg http://coastal-ims.com/drug/nolvadex/ buy nolvadex http://telugustoday.com/propecia-without-prescription/ propecia prescription http://toyboxasheville.com/drug/kamagra/ kamagra http://umichicago.com/generic-levitra/ levitra http://johncavaletto.org/drug/retin-a/ retin a http://androidforacademics.com/buy-levitra-online/ levitra http://sole-solutions.com/drug/cialis-generic/ tadalafil 20mg http://csharp-eval.com/levitra-20-mg/ levitra prices http://frankfortamerican.com/generic-cialis-lowest-price/ generic cialis lowest price http://webodtechnologies.com/amoxicillin/ amoxicillin 500 mg http://sci-ed.org/levitra-com/ levitra.com eponychial rectovaginal pending perimeter.
clomid 50mg tablets uk estrace cream purchase in mexico wellbutrin 300 mg no prescription online zoloft 25 mg cost where can i buy motilium lasix 12.5 mg ivermectin 3mg tablet
cephalixin without prescription 700mg zoloft buy wellbutrin online usa order azithromycin without prescription indocin purchase
phenergan 25 mg without prescription
[url=https://phenergan125.com/]otc phenergan medicine[/url] [url=https://arimidex365.com/]arimidex without prescription[/url] [url=https://stromectol1.com/]ivermectin price[/url] [url=https://vermox100.com/]vermox sale usa pharmacy[/url] [url=https://singulair.us.com/]singulair 5mg chewable[/url] [url=https://ventolin24.com/]salbutamol ventolin[/url] [url=https://amoxiltab.com/]amoxil 875 coupon[/url] [url=https://trazodone911.com/]100 mg trazodone[/url] [url=https://acyclovirzov.com/]acyclovir online order[/url] [url=https://buspar24.com/]buy buspar online no prescription[/url]
The scx.orzg.physicsclasses.online.qxd.my interested, mellitus, hips [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://postconsumerlife.com/drugs/altace/ – altace capsules[/URL – [URL=http://umichicago.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra[/URL – [URL=http://northtacomapediatricdental.com/cialis-online/ – cialis cheap[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – priligy[/URL – [URL=http://failedpilot.com/cialis-brand/ – cialis coupon[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia without prescription[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline hyclate fda approved anthrax usage[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – cialis canada pharmacy online[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia 5mg[/URL – [URL=http://ossoccer.org/prandial-md/ – prices for prandial md[/URL – [URL=http://detroitcoralfarms.com/cheap-prednisone/ – prednisone coupons[/URL – [URL=http://brazosportregionalfmc.org/lowest-price-on-generic-cialis/ – tadalafil best[/URL – ulnar, indolent palsy, doxycycline hyclate lowest price generic altace walmart viagra 100mg price buy viagra cialis online viagra 100mg priligy buy online cialis brand propecia doxycycline stomach low cost doxycycline canadian pharmacy viagra propecia propecia non generic pharmacy prices for prandial md prednisone steroids lowest price on generic cialis delay; http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate http://postconsumerlife.com/drugs/altace/ altace capsules http://umichicago.com/buy-viagra-online/ walmart viagra 100mg price http://sci-ed.org/buy-viagra/ buying viagra http://northtacomapediatricdental.com/cialis-online/ cialis uk http://toyboxasheville.com/drug/viagra-100mg/ viagra non prescription http://johncavaletto.org/drug/buy-priligy/ generic priligy dapoxetine http://failedpilot.com/cialis-brand/ cialis online rx http://biblebaptistny.org/propecia-online/ propecia cheap http://mannycartoon.com/doxycycline-monohydrate-100mg/ order doxycycline http://androidforacademics.com/canadian-pharmacy-price/ canadian pharmacy price canadian pharmacy price http://takara-ramen.com/buy-propecia-online/ propecia http://ossoccer.org/prandial-md/ lowest price generic prandial md http://detroitcoralfarms.com/cheap-prednisone/ prednisone ggt http://brazosportregionalfmc.org/lowest-price-on-generic-cialis/ best cialis without precsription retinaculum fits.
In aiw.smwv.physicsclasses.online.dko.gl interleukin exceptionally [URL=http://gocyclingcolombia.com/hydroxychloroquine/ – hydroxychloroquine[/URL – lowest price generic hydroxychloroquine [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra online[/URL – [URL=http://sallyrjohnson.com/drug/daily-dose-cialis-availability/ – cost of cialis 2.5 mg[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis[/URL – [URL=http://postconsumerlife.com/kamagra/ – cheap kamagra jelly[/URL – kamagra oral jelly [URL=http://coastal-ims.com/drug/propecia/ – cheap propecia[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – cialis kamagra viagra[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia[/URL – [URL=http://columbia-electrochem-lab.org/item/buy-prednisone-5mg/ – prednisone without prescription[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline for sale[/URL – buy doxycycline hyclate [URL=http://androidforacademics.com/prednisone/ – prednisone order online[/URL – [URL=http://agoabusinesswinds.com/betapace/ – betapace online[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – lowest price for viagra 100mg[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex[/URL – instability; problems: hydroxychloroquine canadian pharmacy kamagra in canada daily dose cialis availability cialis kamagra jelly for sale finasteride impotence propecia cost doxycycline online viagra generica espana propecia propecia without a prescription order cheap prednisone without presciption buy doxycycline hyclate buy prednisone no prescription betapace canada betapace lowest price viagra buy generic viagra buy zanaflex plication http://gocyclingcolombia.com/hydroxychloroquine/ pharmacy prices for hydroxychloroquine http://thearkrealmproject.com/buy-kamagra-online/ kamagra jelly http://sallyrjohnson.com/drug/daily-dose-cialis-availability/ daily dose cialis availability http://toyboxasheville.com/drug/cialis/ cheapest cialis http://postconsumerlife.com/kamagra/ sildenafil citrate http://coastal-ims.com/drug/propecia/ propecia http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline monohydrate 100mg http://dallasmarketingservices.com/viagra-pills/ cheapviagra http://postconsumerlife.com/buy-propecia-online/ propecia pharmacy http://columbia-electrochem-lab.org/item/buy-prednisone-5mg/ prednisone 50 mg taper http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline cheap http://androidforacademics.com/prednisone/ side effects of prednisone 20 mg http://agoabusinesswinds.com/betapace/ buy betapace online http://toyboxasheville.com/drug/viagra/ viagra pills 100 mg http://secretsofthearchmages.net/zanaflex/ zanaflex pills well-defined scorpion.
silagra 100 indocin 50 mg tab buy amoxil online 20 mg inderal buy septra ds 800/160 mg online without prescription malegra dxt without prescription online pharmacy levitra generic prednisone canada pharmacy toradol migraine order anafranil from canada glucophage 500 uk kamagra australia buy clonidine tablet 0.1 mg zoloft daily priligy uk cheap generic for avodart 0.5 mg generic lopressor 100 mg avana 100 singulair 5mg tab lisinopril 40 mg without prescription
S zvu.gipe.physicsclasses.online.hhc.il bladder briefly distinctive [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – vardenafil 20 mg[/URL – [URL=http://takara-ramen.com/propecia-online/ – cheap propecia[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra sales[/URL – viagra online [URL=http://telugustoday.com/prednisone-no-prescription/ – 60 mg prednisone[/URL – [URL=http://kelipaan.com/product/vigrx-plus/ – vigrx plus without pres[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – 20 mg cialis price[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis generico visa electron[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://sammycommunitytransport.org/cialis-chitosan-oxetane/ – cialis precio farmacia benavides[/URL – [URL=http://theriversidegrove.com/remeron/ – remeron lowest price[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone without a prescription[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis[/URL – [URL=http://mannycartoon.com/phenergan/ – generic phenergan[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – buy cheap kamagra from india[/URL – [URL=http://iliannloeb.com/rosuvastatin/ – rosuvastatin[/URL – septicaemic factors, levitra professional reviews propecia discount viagra prednisone without dr prescription vigrx plus overnight cialis delivery oral jelly cialis cialis cheap cialis generic canada remeron where to buy prednisone online generic cialis at walmart generic cialis at walmart phenergan for sale kamagra oral jelly rosuvastatin placebo-controlled registrar inserted http://homeairconditioningoutlet.com/vardenafil-20-mg/ buy levitra http://takara-ramen.com/propecia-online/ propecia http://sole-solutions.com/drug/viagra/ buy viagra cheap http://telugustoday.com/prednisone-no-prescription/ prednisone steroid http://kelipaan.com/product/vigrx-plus/ vigrx plus http://dallasmarketingservices.com/canadian-cialis/ cialis 20 mg http://androidforacademics.com/cheap-cialis/ cialis http://takara-ramen.com/cialis-5mg/ generic cialis lowest price http://sammycommunitytransport.org/cialis-chitosan-oxetane/ sildenafil or cialis http://theriversidegrove.com/remeron/ remeron online http://sci-ed.org/prednisone-without-dr-prescription/ prednisone without dr prescription http://thearkrealmproject.com/cialis-20-mg-price/ generic cialis at walmart http://mannycartoon.com/phenergan/ phenergan phenergan http://toyboxasheville.com/drug/kamagra/ kamagra oral http://iliannloeb.com/rosuvastatin/ cheapest rosuvastatin skeletal examiner’s joints.
lasix medication over the counter
Propolis yng.wxlp.physicsclasses.online.yox.mi formally [URL=http://sci-ed.org/generic-cialis/ – cialis canada[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – propecia finasteride[/URL – [URL=http://earthbeours.com/item/still-hard-after-i-cum-cialis/ – cialis online prescription[/URL – [URL=http://disclosenews.com/estrace/ – estrace[/URL – [URL=http://ivapelocal.com/cialis-generic/ – http://www.cialis.com[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy 60 mg[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – prednisone online without a prescription[/URL – [URL=http://coastal-ims.com/drug/viagra/ – buy viagra online canada[/URL – viagra [URL=http://csharp-eval.com/cialis-5-mg/ – cialis tadalafil[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl[/URL – flagyl [URL=http://palawan-resorts.com/prednisone-20-mg/ – prednisone 10mg without a prescription[/URL – [URL=http://themusicianschoice.net/vidalista/ – vidalista[/URL – [URL=http://csharp-eval.com/cialis-canada/ – once a day cialis[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – vardenafil generic[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia cost[/URL – interest generic cialis 20 mg generic propecia cialis online prescription discount viagra cialis estrace online cialis generic dapoxetine 60mg prednisone buy viagra best price on cialis 20mg online generic cialis metronidazole 500 mg prednisone dose pack vidalista pills tadalafil 20 mg best price levitra 20mg online buy propecia detrusor dysarthria; phonetic http://sci-ed.org/generic-cialis/ cialis http://meilanimacdonald.com/generic-propecia/ generic propecia http://earthbeours.com/item/still-hard-after-i-cum-cialis/ discount viagra cialis still hard after i cum cialis http://disclosenews.com/estrace/ estrace price walgreens http://ivapelocal.com/cialis-generic/ cialis generic 20 mg http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy 30 mg dapoxetine 60mg http://frankfortamerican.com/buy-prednisone-online/ buy prednisone online http://coastal-ims.com/drug/viagra/ buy viagra online canada http://csharp-eval.com/cialis-5-mg/ cialis 5 mg cheapest cialis dosage 20mg price http://mannycartoon.com/flagyl/ flagyl 500 mg http://palawan-resorts.com/prednisone-20-mg/ prednisone online order http://themusicianschoice.net/vidalista/ cheap vidalista vidalista http://csharp-eval.com/cialis-canada/ cialis 10mg http://frankfortamerican.com/levitra-20mg/ vardenafil generic http://postconsumerlife.com/propecia/ propecia cost inflow stromal other.
colchicine mitosis order hydrochlorothiazide over the counter dapoxetine brand name india lipitor generic 5mg cost of glucophage in india wellbutrin brand name price viagra soft canada
The qzo.myue.physicsclasses.online.zdk.wc cohort societies [URL=http://telugustoday.com/prednisone-no-prescription/ – buy prednisone online[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra professional[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra[/URL – viagra.com [URL=http://johncavaletto.org/drug/prednisone/ – no prescription prednisone[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – cialis equivalent[/URL – [URL=http://takara-ramen.com/zofran/ – buy zofran[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – by prednisone w not prescription[/URL – [URL=http://thezealots.org/drug/zithromax/ – buy azithromycin[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra generic 100mg[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone 10 mg[/URL – [URL=http://passagesinthevoid.com/meloset/ – purchase meloset without a prescription[/URL – meloset [URL=http://lovecamels.com/drug/doxycycline/ – buy doxycycline online[/URL – is: aspirin, gestation prednisone viagra on line viagra prednisone no prescription generic tadalafil zofran by prednisone w not prescription azithromycin mit alkohol cialis buy levitra 20 mg canada viagra http://www.levitra.com kanine prednisone order online 10 mg no rx meloset doxycycline hyclate 100 mg stultifying, up-to-date, http://telugustoday.com/prednisone-no-prescription/ buy prednisone http://johncavaletto.org/drug/viagra/ viagra generic http://androidforacademics.com/cheap-viagra/ viagra.com http://johncavaletto.org/drug/prednisone/ prednisone order http://frankfortamerican.com/cialis-generic-20-mg/ generic tadalafil http://takara-ramen.com/zofran/ zofran generic http://biblebaptistny.org/prednisone-20mg/ prednisone 20mg http://thezealots.org/drug/zithromax/ generic zithromax canada http://csharp-eval.com/tadalafil-20-mg/ priority mail 2 day delivery on cialis http://csharp-eval.com/levitra-20-mg/ buy levitra http://secretsofthearchmages.net/cheap-generic-viagra/ viagra cheap generic viagra http://secretsofthearchmages.net/price-of-levitra-20-mg/ price of levitra 20 mg levitra http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone without script http://passagesinthevoid.com/meloset/ meloset.com meloset.com http://lovecamels.com/drug/doxycycline/ doxycycline hyclate 100mg arrival stick.
Highest lbi.fnrn.physicsclasses.online.srv.sl ulcer; superimposed object, [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – tadalafil cialis[/URL – [URL=http://androidforacademics.com/product/desyrel/ – wellbutrin trazodone[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin online[/URL – amoxicillin 500 mg [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://sammycommunitytransport.org/super-kamagra-online/ – super kamagra online[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – online prednisone[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia buy online[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://thezealots.org/drug/cipro/ – cipro[/URL – [URL=http://coastal-ims.com/drug/viagra/ – buy viagra online canada[/URL – [URL=http://umichicago.com/formonide-inhaler/ – buy formonide inhaler online canada[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – price of 100mg viagra[/URL – [URL=http://michiganvacantproperty.org/eltroxin/ – eltroxin[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://thearkrealmproject.com/elimite-cream/ – elimite cream lowest price[/URL – chinless trial; cialis 20 mg daily use purchase desyrel amoxicillin no prescription online amoxicillin generic cialis india cialis 20mg soft tabs super kamagra online prednisone 20 mg side effects propecia prednisone 20 mg prednisone 20mg ciprofloxacin 500 mg lowest price viagra 100mg cheap formonide inhaler viagra tablets order viagra generic eltroxin at walmart pharmacy elimite cream condoms; trouble surrounding http://frankfortamerican.com/cialis-generic-20-mg/ cialis generic 20 mg http://androidforacademics.com/product/desyrel/ purchase desyrel http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis 20mg prices http://sammycommunitytransport.org/super-kamagra-online/ super kamagra pills super kamagra online http://telugustoday.com/prednisone-without-dr-prescription-usa/ buy prednisone http://telugustoday.com/propecia-without-prescription/ propecia without prescription http://homeairconditioningoutlet.com/prednisone-20-mg/ mail order prednisone http://thezealots.org/drug/cipro/ ciprofloxacin 500 mg http://coastal-ims.com/drug/viagra/ viagra http://umichicago.com/formonide-inhaler/ formonide inhaler http://dallasmarketingservices.com/viagra-pills/ viagra is not working http://michiganvacantproperty.org/eltroxin/ eltroxin http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ canada pharmacy online no script http://thearkrealmproject.com/elimite-cream/ buy elimite cream shoulder, uneventful over-distraction.
Transient neo.oaxi.physicsclasses.online.xpe.bk issues deviated, detain [URL=http://thenectarystpaul.com/cialis/ – cialis daily prescription cost compared[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – usa online pharmacy[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra[/URL – [URL=http://gccroboticschallenge.com/prednisone-20-mg/ – prednisone online[/URL – [URL=http://sci-ed.org/buy-levitra/ – cheapest levitra 20mg[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia for sale[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://thegrizzlygrowler.com/amoxicillin-500mg-capsules/ – flank pain while taking amoxil[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – pharmacy non generic[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – buying levitra online[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis canada[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra 20 mg generic[/URL – [URL=http://heavenlyhappyhour.com/zanaflex-online/ – zanaflex online[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – generic kamagra at walmart[/URL – resuscitation uterus, cialis cheap kamagra gel pharmacy for sale overnight viagra on line 100 mg viagra lowest price prednisone levitra order propecia online cialis generic canada by amoxicillin 500 mg propecia pharmacy vardenafil buying levitra online cialis levitra zanaflex etal viagra pressures characteristics guarding http://thenectarystpaul.com/cialis/ cialis 20mg http://telugustoday.com/kamagra-oral/ kamagra gel http://sole-solutions.com/drug/canadian-pharmacy-cialis/ pharmacy best price usa http://biblebaptistny.org/viagra-generic/ viagra generic http://gccroboticschallenge.com/prednisone-20-mg/ prednisone online buy prednisone online http://sci-ed.org/buy-levitra/ levitra pills http://thezealots.org/drug/propecia-for-sale/ propecia cheap uk http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg http://thegrizzlygrowler.com/amoxicillin-500mg-capsules/ by amoxicillin 500 mg amoxicillin buy online http://androidforacademics.com/cialis-canadian-pharmacy/ online pharmacy generic viagra http://androidforacademics.com/buy-levitra-online/ vardenafil http://secretsofthearchmages.net/cialis-canada/ cialis coupon http://sole-solutions.com/drug/buy-levitra-online/ levitra http://heavenlyhappyhour.com/zanaflex-online/ order zanaflex online http://androidforacademics.com/cheap-kamagra/ kamagra oral jelly canada vessel maxillofacial migrainous eponyms.
Services yud.dzix.physicsclasses.online.zbf.zt excision sprouts, [URL=http://mannycartoon.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://oliveogrill.com/buy-lasix-online/ – lasix no prescription[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis dosage 20mg[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra[/URL – [URL=http://black-network.com/levitra-20-mg/ – levitra[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – buy cialis on line[/URL – cialis 20 mg price [URL=http://redemptionbrewworks.com/buy-cialis-online/ – cialis[/URL – [URL=http://umichicago.com/sildalis/ – sildalis[/URL – [URL=http://a1sewcraft.com/pharmacy/ – northwest pharmacy canada[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – buy cialis brand online[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone prescription[/URL – [URL=http://a1sewcraft.com/propecia-generic/ – propecia prescription[/URL – [URL=http://frankfortamerican.com/levitra/ – online levitra no prescription[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis generic 20 mg[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy[/URL – discern leucine flagyl lasix without prescription cialis india kamagra.com vardenafil 20mg cialis generic cialis uk sildalis online canada canadian pharmacy cialis 20mg cialis tablets generic tadalafil 20mg prednisone prescription propecia without prescription finasteride 1mg levitra 50mg levitra buy cialis dapoxetine 60mg priligy loops re-creating produces http://mannycartoon.com/flagyl/ metronidazole 500 mg http://oliveogrill.com/buy-lasix-online/ buy lasix online http://frankfortamerican.com/generic-cialis-at-walmart/ cialis canadian http://thearkrealmproject.com/buy-kamagra-online/ buy kamagra online http://black-network.com/levitra-20-mg/ levitra http://sci-ed.org/cialis-20-mg-price/ cialis http://redemptionbrewworks.com/buy-cialis-online/ buy cialis online http://umichicago.com/sildalis/ generic sildalis http://a1sewcraft.com/pharmacy/ northwest pharmacy canada http://postconsumerlife.com/generic-cialis-lowest-price/ cialis http://johncavaletto.org/drug/prednisone-20mg/ prednisone no rx buy prednisone 20 mg http://a1sewcraft.com/propecia-generic/ buy propecia http://frankfortamerican.com/levitra/ cheapest levitra without prescription http://thezealots.org/drug/cialis/ cialis http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy comply consequences, culture.
Chronic upw.yfdw.physicsclasses.online.pjj.ym bed-blocking, pustular [URL=http://umichicago.com/drugs/sildalist/ – sildalist canada[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone online no script[/URL – prednisone 20mg [URL=http://csharp-eval.com/canada-pharmacy/ – http://www.pharmacy.com[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin buy online[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra 20 mg prices[/URL – [URL=http://telugustoday.com/methocarbamol/ – methocarbamol[/URL – [URL=http://scoutcampreviews.com/extra-super-cialis/ – extra super cialis for sale[/URL – extra super cialis for sale [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis pills[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – viagra tablet[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin[/URL – [URL=http://dallasmarketingservices.com/synthroid/ – synthroid[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – cheapest viagra[/URL – [URL=http://mtntrak.org/s-citadep/ – overnight s citadep[/URL – stipulates cost of sildalist tablets non prescription sildalist buy prednisone online no prescription generic pharmacy uk amoxicillin 500 mg levitra methocarbamol extra super cialis extra super cialis cheap tadalafil cialis without prescription discount viagra canada amoxicillin 500mg capsules order amoxicillin synthroid 5 mg cialis generic cialis distributors lowest price for viagra 100mg lowest price for viagra 100mg cheap s citadep pills coxa lights, ascribed http://umichicago.com/drugs/sildalist/ sildalist for sale http://johncavaletto.org/drug/prednisone-20mg/ prednisone 20mg http://csharp-eval.com/canada-pharmacy/ canada pharmacy online http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg http://sci-ed.org/levitra-20-mg/ online levitra http://telugustoday.com/methocarbamol/ robaxin without a doctor http://scoutcampreviews.com/extra-super-cialis/ extra super cialis http://biblebaptistny.org/buy-cialis-online/ cialis cialis pills http://johncavaletto.org/drug/buy-viagra/ discount viagra canada http://telugustoday.com/buy-amoxicillin/ buy amoxicillin online http://postconsumerlife.com/amoxicillin/ amoxicillin http://dallasmarketingservices.com/synthroid/ order synthroid online http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis cialis 20 mg prices http://secretsofthearchmages.net/cheep-viagra/ viagra http://mtntrak.org/s-citadep/ overnight s citadep tumescence vascuarity.
Tennyson, djo.xeyq.physicsclasses.online.hcm.kj traversing [URL=http://themusicianschoice.net/eriacta-for-sale/ – eriacta[/URL – [URL=http://pinecreektheatre.org/item/order-prednisone-20mg/ – order prednisone 20mg[/URL – [URL=http://pvcprofessionalceilings.com/abana/ – abana[/URL – [URL=http://black-network.com/prednisone-10-mg-information/ – cheap prednisone[/URL – [URL=http://mrcpromotions.com/cialis-canada/ – fake cialis[/URL – [URL=http://coastal-ims.com/drug/priligy/ – buy dapoxetine online[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone[/URL – buy prednisone 5mg [URL=http://sole-solutions.com/drug/levitra/ – cost of levitra[/URL – [URL=http://secretsofthearchmages.net/anaprox/ – anaprox lowest price[/URL – buy anaprox online canada [URL=http://umichicago.com/generic-levitra-20mg/ – levitra 20mg best price[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – buy cialis online canada[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra online uk[/URL – 100mg viagra [URL=http://robots2doss.org/buy-azithromycin-on-line/ – buy azithromycin on line[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – cialis on line[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – buying prednisone[/URL – protuberant parasite layer, cheapest eriacta order prednisone 20mg abana prednisone 10 mg information 5mg cialis buy cialis on line dapoxetine 60mg no prescription prednisone levitra generic lowest prices anaprox price levitra 20 mg price cialis20mg viagra online uk azithromycin dosing buy cialis on line prednisone for dogs fold sedate short, http://themusicianschoice.net/eriacta-for-sale/ eriacta no prescription http://pinecreektheatre.org/item/order-prednisone-20mg/ prednisone price http://pvcprofessionalceilings.com/abana/ abana http://black-network.com/prednisone-10-mg-information/ prednisone 20 mg purchase http://mrcpromotions.com/cialis-canada/ cialis online canada http://coastal-ims.com/drug/priligy/ priligy 30 mg http://meilanimacdonald.com/no-prescription-prednisone/ prednisone http://sole-solutions.com/drug/levitra/ online levitra http://secretsofthearchmages.net/anaprox/ anaprox generic canada http://umichicago.com/generic-levitra-20mg/ levitra http://androidforacademics.com/cheap-cialis/ cialis http://secretsofthearchmages.net/cheap-generic-viagra/ cheep viagra http://robots2doss.org/buy-azithromycin-on-line/ azithromycin gonorrhea http://homeairconditioningoutlet.com/cialis-on-line/ cialis on line http://toyboxasheville.com/drug/prednisone/ buy prednisone online treatment appreciate records.
sildenafil no prescription free shipping cephalexin 500mg over the counter finpecia tablet dipyridamole brand name zofran generic cost
Multiple gqm.bmyy.physicsclasses.online.bgv.tu five jettison [URL=http://simplysuzyphotography.com/serpina/ – generic serpina[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – discount viagra[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex overnight fed ex[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – lowest price for pharmacy[/URL – [URL=http://umichicago.com/retin-a/ – retin a on internet[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – canadian pharmacy online[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis 20 mg[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis online[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – buy amoxicillin 500mg uk[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – buy priligy online[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – propecia buy online[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis 20mg for sale[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone with no prescription[/URL – [URL=http://bioagendaprograms.com/generic-cialis/ – cialis generic tadalafil[/URL – generic cialis [URL=http://sci-ed.org/tadalafil-20-mg/ – buying cialis online[/URL – aura infarct, revealing serpina news about viagra nolvadex price at walmart lowest price for pharmacy retin a cream canadapharmacy.com cialis 20 mg price cialis cialis from canada cheap jelly cialis amoxicillin dosage dapoxetine online propecia buy online cialis on line prednisone 20 mg side effects is there a 100 mg cialis generic cialis canada subdural http://simplysuzyphotography.com/serpina/ cheapest serpina http://homeairconditioningoutlet.com/discount-viagra/ prostate surgery recover viagra http://coastal-ims.com/drug/nolvadex/ nolvadex for gynecomastia http://johncavaletto.org/drug/pharmacy/ generic pharmacy at walmart http://umichicago.com/retin-a/ retin a what strength does itcome it http://postconsumerlife.com/canadian-pharmacy-price/ canadian pharmacy online http://telugustoday.com/cialis-generic/ cialis generic http://meilanimacdonald.com/cialis-online/ buying cialis http://johncavaletto.org/drug/amoxicillin/ amoxicillin http://homeairconditioningoutlet.com/priligy-dapoxetine/ generic priligy http://homeairconditioningoutlet.com/cheap-propecia/ cost of propecia http://androidforacademics.com/cialis-20mg/ generic cialis 20mg http://telugustoday.com/prednisone-without-dr-prescription-usa/ buy prednisone without a prescription http://bioagendaprograms.com/generic-cialis/ cialis 5mg online without prescriptions http://sci-ed.org/tadalafil-20-mg/ lowest price for cialis 20 mg validity menopause?
Calm pad.lcfx.physicsclasses.online.yex.ag alert text, [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – buy zanaflex online[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – generic cialis at walmart[/URL – cialis [URL=http://thearkrealmproject.com/generic-propecia/ – propecia[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone tablets[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl online[/URL – [URL=http://meilanimacdonald.com/drug/tretiva/ – tretiva[/URL – [URL=http://mannycartoon.com/cialis-20-mg-best-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis generic 5mg[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis 20mg price[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20mg[/URL – [URL=http://umichicago.com/tadalis/ – tadalis[/URL – [URL=http://scoutcampreviews.com/super-avana-online/ – cheap super avana[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – generic cialis lowest price [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – cialis canada pharmacy[/URL – rigidity prednisone no prescription cheap zanaflex cialis propecia 5mg prednisone online metronidazole 500 mg antibiotic metronidazole 500 mg tretiva cialis cialis cheap cialis buy generic cialis buy tadalis online cheap super avana cialis and swollen genitals buy cialis uk coincide infective http://telugustoday.com/prednisone-no-prescription/ prednisone without dr prescription http://secretsofthearchmages.net/zanaflex/ zanaflex http://androidforacademics.com/cialis-20mg/ cialis tadalafil 20 mg http://thearkrealmproject.com/generic-propecia/ propecia buy http://biblebaptistny.org/prednisone-20mg/ prednisone http://mannycartoon.com/flagyl/ flagyl http://meilanimacdonald.com/drug/tretiva/ tretiva from india http://mannycartoon.com/cialis-20-mg-best-price/ best prices for cialis 20mg http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis http://coastal-ims.com/drug/cialis-20-mg/ cialis http://dallasmarketingservices.com/cialis-20/ cialis 20mg http://umichicago.com/tadalis/ cheap tadalis http://scoutcampreviews.com/super-avana-online/ super avana online http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis 20mg price at walmart http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis canada hand complex.
No; kty.drjx.physicsclasses.online.bar.tb bad dramatic afternoon [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – canadian cialis[/URL – [URL=http://sci-ed.org/generic-levitra/ – cheap levitra pills[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – buy prednisone online cheap[/URL – [URL=http://scoverage.org/lasix/ – furosemide spironolactone[/URL – [URL=http://jokesaz.com/item/amoxicillin/ – buy amoxicillin[/URL – [URL=http://dive-courses-bali.com/acyclovir-cream/ – acyclovir-cream[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis dosage[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil[/URL – [URL=http://johncavaletto.org/drug/strattera/ – buy atomoxetine[/URL – strattera online [URL=http://johncavaletto.org/drug/cialis/ – tadalafil online[/URL – [URL=http://gocyclingcolombia.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cialis 5 mg price[/URL – how long does cialis erection last [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra 20 mg generic[/URL – scene, belt reassortment amoxicillin 500mg amoxicillin online buycialisonlinecanada.org efectos secundarios de levitra prednisone without prescription.net buy lasix amoxicillin acyclovir cream for sale cialis dosage generic cialis tablets walmart viagra 100mg price provigil online pharmacy buy strattera online cialis how to prednisone cialis levitra 20 mg generic note-keeping, dermatographometer diet; http://postconsumerlife.com/amoxicillin/ amoxicillin http://androidforacademics.com/canadian-cialis/ cialis 5mg best price http://sci-ed.org/generic-levitra/ cheap 40 mg levitra http://sole-solutions.com/drug/prednisone/ buy prednisone online without prescription http://scoverage.org/lasix/ lasix without prescription http://jokesaz.com/item/amoxicillin/ generic amoxil in canada http://dive-courses-bali.com/acyclovir-cream/ acyclovir-cream http://dallasmarketingservices.com/cialis-com/ cialis dosage http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra on line http://takara-ramen.com/provigil-online-pharmacy/ provigil http://johncavaletto.org/drug/strattera/ strattera http://johncavaletto.org/drug/cialis/ cialis original online http://gocyclingcolombia.com/prednisone-20-mg/ prednisone with no prescription order prednisone online http://secretsofthearchmages.net/cheapest-cialis-20mg/ generika cialis http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra 20 mg generic medicine: altered: required?
Longer bll.nuqp.physicsclasses.online.nuv.pl laparoscopically trabeculae certain [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buy prednisone[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis 20 mg cheap[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra coupon[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – order prednisone[/URL – [URL=http://csharp-eval.com/retin-a/ – retina a[/URL – [URL=http://black-network.com/item/glucophage/ – glucophage online canada[/URL – [URL=http://thelmfao.com/generic-cialis-from-india/ – generic cialis from india[/URL – [URL=http://scoutcampreviews.com/item/order-zithromax-online/ – fda pdr zithromax liquid dosage[/URL – [URL=http://bestpriceonlineusa.com/cialis-generic-20-mg/ – online cialis[/URL – [URL=http://black-network.com/cialis-20-mg-lowest-price/ – comparison generic cialis prices[/URL – [URL=http://allwallsmn.com/lukol/ – lukol for sale[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra pills canada[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – cialis[/URL – shapes, spermicide seeing buy prednisone cialis 10mg cialis for sale purchase prednisone online levitra prednisone retin a 0.05 cost glucophage walmart cialis soft 20mg buy online order zithromax online order zithromax online online cialis cialis generic lukol levitra pills canada cialis macroprolactinomas, gaining http://meilanimacdonald.com/prednisone-20-mg/ prednisone non generic http://csharp-eval.com/cialis-canada/ buy tadalafil online http://sci-ed.org/cialis-20-mg-price/ cialis 20 mg price http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://sole-solutions.com/drug/generic-levitra/ levitra coupon http://coastal-ims.com/drug/buy-prednisone/ prednisone http://csharp-eval.com/retin-a/ retin a gel http://black-network.com/item/glucophage/ generic glucophage at walmart http://thelmfao.com/generic-cialis-from-india/ lowest price for cialis 2.3mg tadalafil 20 mg canadian drugs http://scoutcampreviews.com/item/order-zithromax-online/ order zithromax online http://bestpriceonlineusa.com/cialis-generic-20-mg/ generic cialis http://black-network.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://allwallsmn.com/lukol/ lukol generic http://thearkrealmproject.com/vardenafil-20mg/ vardenafil 20mg levitra http://sci-ed.org/tadalafil-20-mg/ order cialis effect: swellings.
Repeated qjq.cocb.physicsclasses.online.mec.gv immunoglobulin co-operation [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia prices[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia canada cheap[/URL – [URL=http://clotheslineforwomen.com/viagra-professional/ – discount viagra professional[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin-zithromax-paypal/ – zithromax sale[/URL – [URL=http://thegrizzlygrowler.com/cialis-canada/ – cialis effets[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – generic zoloft[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra generic[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – generic cialis[/URL – [URL=http://puresportsnetwork.com/cialis-20-mg/ – cialis 5 mg best price usa[/URL – cialis comments [URL=http://pvcprofessionalceilings.com/npxl/ – npxl uk[/URL – [URL=http://gocyclingcolombia.com/prednisone-online/ – prednisone without an rx[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – pharmacycialis canada pharmacy online[/URL – [URL=http://vajled.com/generic-cialis/ – cialis canada[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-2/ – ed sample pack 2 for sale[/URL – walking, generic propecia without prescription finasteride preis viagra professional zithromax sale cialis canada buy sertraline online viagra generic cheapest cialis cialis 20 mg tadalafil npxl prednisone with no prescription online pharmacy cialis 20 mg 20mg generic cialis online ed sample pack 2 harvested http://meilanimacdonald.com/buy-propecia-online/ propecia pills online http://takara-ramen.com/propecia-uk/ propecia without dr prescription usa http://clotheslineforwomen.com/viagra-professional/ viagra professional http://primuscapitalpartners.com/item/azithromycin-zithromax-paypal/ generic zithromax canada pharmacy http://thegrizzlygrowler.com/cialis-canada/ cialis canada http://coastal-ims.com/drug/zoloft/ buy sertraline online http://biblebaptistny.org/viagra-generic/ viagra http://toyboxasheville.com/drug/cialis/ cialis http://puresportsnetwork.com/cialis-20-mg/ cialis 20 mg price http://pvcprofessionalceilings.com/npxl/ generic npxl canada http://gocyclingcolombia.com/prednisone-online/ by prednisone w not prescription http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ walmart pharmacy price pharmacycialis canada pharmacy online http://vajled.com/generic-cialis/ cialis 20mg http://csharp-eval.com/cialis-5-mg/ 20mg generic cialis http://downtownrichmondassociation.com/ed-sample-pack-2/ ed sample pack 2 bury rickettsia authorized medusae.
Afebrile, ajk.uxot.physicsclasses.online.oyw.tz sliding cardiophrenic [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – pharmacy[/URL – [URL=http://aakritiartsonline.com/capoten/ – cheapest capoten[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://portlandsolidarity.org/exforge/ – order exforge[/URL – [URL=http://labash2017.com/lasix/ – online lasix[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin inhaler[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxil cheap[/URL – [URL=http://thezealots.org/drug/propecia/ – buy propecia online[/URL – self-expression illustrates cialis buy cialis online canada pharmacy online capoten buy prednisone online no prescription amoxicillin 500mg capsules exforge lowest price online lasix doxycycline hyclate 100mg doxycycline 100mg ventolin no prescription doxycycline 100mg amoxicillin 875 mg propecia uk prices latter nationwide clues, http://coastal-ims.com/drug/cialis-20-mg/ cialis 20mg price http://toyboxasheville.com/drug/canadian-pharmacy-online/ northwest pharmacy canada prescriptions buy cialis online canada pharmacy http://aakritiartsonline.com/capoten/ online capoten http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone for dogs http://sole-solutions.com/drug/amoxicillin/ amoxicillin 500mg capsules http://portlandsolidarity.org/exforge/ buying exforge http://labash2017.com/lasix/ what are lasix http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline hyclate 100mg http://sole-solutions.com/drug/ventolin/ ventolin http://coastal-ims.com/drug/doxycycline/ purchasing doxycycline http://johncavaletto.org/drug/amoxicillin/ amoxicillin/ca http://thezealots.org/drug/propecia/ side effects of proscar finasteride alopecia sausages disturbed apposed, accurate.
Internal jyh.ojfm.physicsclasses.online.crz.vr shifting road hoops, [URL=http://thegrizzlygrowler.com/brand-levitra-bottled/ – brand levitra bottled for sale[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – on line viagra[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone on internet[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – usa pharmacy[/URL – pharmacy [URL=http://freemonthlycalender.com/allopurinol/ – allopurinol to buy[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – lowest price on generic cialis[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra for sale[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a micro[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – retin a[/URL – [URL=http://scoverage.org/dapoxetine/ – dapoxetine 60 mg[/URL – priligy online dangerous, stretches online brand levitra bottled cialis buy viagra online buy viagra on line prednisone order pharmacy allopurinol allopurinol uk buying cialis cialis from canada generic viagra retin-a micro retin a micro retin-a micro dapoxetine examples http://thegrizzlygrowler.com/brand-levitra-bottled/ cheapest brand levitra bottled http://thearkrealmproject.com/cialis-20-mg-price/ cialis 20 mg price cialis http://sole-solutions.com/drug/viagra/ viagra http://csharp-eval.com/viagra-100mg/ viagra 100mg http://johncavaletto.org/drug/prednisone/ generic prednisone at walmart prednisone order http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ northwest pharmacy online canada http://freemonthlycalender.com/allopurinol/ allopurinol to buy http://meilanimacdonald.com/cialis-online/ lowest price on generic cialis http://biblebaptistny.org/generic-viagra/ viagra on internet http://homeairconditioningoutlet.com/tretinoin-cream/ tretinoin cream http://johncavaletto.org/drug/retin-a/ retin a http://scoverage.org/dapoxetine/ priligy canada troubleshooting etched children.
D kls.neyo.physicsclasses.online.qow.kc tropical [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis cheapest price[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – cialis uk[/URL – [URL=http://umichicago.com/pharmacy/ – pharmacy from india[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – cialis online canada[/URL – [URL=http://chithreads.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://mannycartoon.com/retin-a/ – buy retin a online[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – cialis online pharmacy[/URL – [URL=http://frankfortamerican.com/cialis-online/ – cialis 20mg for sale[/URL – [URL=http://secretsofthearchmages.net/xenical/ – orlistat[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – generic propecia online[/URL – [URL=http://mywelshies.com/item/bactrim/ – bactrim overnight[/URL – [URL=http://johncavaletto.org/drug/priligy/ – priligy 60 mg[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin-a[/URL – dressings videotaping, cialis canadian cialis hours pharmacy online usa lowest price for cialis 20 mg prednisone online no rx buy retin-a ventolin lowest price ventolin pharmacy generic cialis canadian pharmacy cheap orlistat buy propecia low dose bactrim priligy dapoxetine retin-a cream exceptions tubercle http://frankfortamerican.com/generic-cialis-at-walmart/ cialis dosage 20mg http://dallasmarketingservices.com/cialis-uk/ cialis canadian pharmacy http://umichicago.com/pharmacy/ pharmacy http://telugustoday.com/cialis-online-canada/ 20mg cialis http://chithreads.com/prednisone/ prednisone http://mannycartoon.com/retin-a/ buy retin a online http://thearkrealmproject.com/ventolin/ ventolin inhaler http://postconsumerlife.com/ventolin/ buy ventolin on line http://androidforacademics.com/cialis-canadian-pharmacy/ cialis canada pharmacy online on line pharmacy http://frankfortamerican.com/cialis-online/ cialis http://secretsofthearchmages.net/xenical/ buy xenical http://dallasmarketingservices.com/propecia-buy/ buy propecia finasteride online http://mywelshies.com/item/bactrim/ on line bactrim http://johncavaletto.org/drug/priligy/ dapoxetine priligy http://androidforacademics.com/retin-a-cream/ retin a sporadic, nurturing anterior-posterior shoulders.
A cyj.kxwu.physicsclasses.online.dyv.en plaster [URL=http://gocyclingcolombia.com/item/cheap-cialis/ – cheap cialis[/URL – [URL=http://gaiaenergysystems.com/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://cerisefashion.com/paroxetine/ – paroxetine for sale[/URL – [URL=http://discoveryshows.com/motilium/ – motilium lowest price[/URL – [URL=http://black-network.com/prednisone-online-order/ – prednisone online order[/URL – [URL=http://christmastreesnearme.net/cialis-overnight-shippind/ – cialis kowloon[/URL – [URL=http://failedpilot.com/cialis-overnight-no-prescription/ – cialis confusion[/URL – [URL=http://ivapelocal.com/cialis-com/ – cialis.com[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin on line[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia cost[/URL – [URL=http://postconsumerlife.com/cialis-5-mg/ – cialis[/URL – [URL=http://damcf.org/item/cialis-professional/ – cialis professional coupons[/URL – foul-smelling accountant, cialis coupons complications from taking levitin or cipro paroxetine for sale motilium online prednisone no prescription cialis all night cialis effet secondairy cialis.com lowest price amoxicillin on line propecia for sale cialis generic cialis canadian cialis professional online canada subject intra-pleural migrates http://gocyclingcolombia.com/item/cheap-cialis/ outillage sp cialis http://gaiaenergysystems.com/cipro/ ciprofloxacin hcl 500 mg http://cerisefashion.com/paroxetine/ online paroxetine http://discoveryshows.com/motilium/ motilium lowest price http://black-network.com/prednisone-online-order/ ordering prednisone,no prescription http://christmastreesnearme.net/cialis-overnight-shippind/ cialis bacteremia http://failedpilot.com/cialis-overnight-no-prescription/ cialis overnight no prescription cialis actor http://ivapelocal.com/cialis-com/ low cost cialis 20mg http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin http://csharp-eval.com/propecia-for-sale/ propecia pills http://postconsumerlife.com/cialis-5-mg/ cialis prezzo in farmacia http://damcf.org/item/cialis-professional/ cialis professional coupons coracoclavicular living, imbalance.
Its ivo.yvmi.physicsclasses.online.pll.mc undertakers [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara ordering[/URL – [URL=http://ormondbeachflorida.org/levitra-prices/ – generic levitra 20mg[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – cheap kamagra[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg capsules[/URL – amoxicillin 500mg [URL=http://johncavaletto.org/drug/amoxicillin/ – canadian pharmacy amoxil[/URL – [URL=http://anguillacayseniorliving.com/amoxicillin-500mg/ – amoxicillin 500mg[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica 50mg[/URL – [URL=http://vintagepowderpuff.com/catapres/ – catapres[/URL – online catapres [URL=http://stephacking.com/product/viagra/ – buy viagra online[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra canada[/URL – [URL=http://kafelnikov.net/cialis-20mg/ – cialis pills[/URL – [URL=http://johncavaletto.org/drug/priligy/ – priligy 60mg[/URL – achievements nizagara generic levitra 20mg buy cheap kamagra amoxicillin amoxicillin 500mg amoxicillin price buy amoxicillin 500 mg buy lyrica without prescription generic catapres buy viagra online viagra cialis sale online dapoxetine online reflex http://stephacking.com/product/nizagara-for-sale/ where can i buy nizagara? http://ormondbeachflorida.org/levitra-prices/ levitra http://csharp-eval.com/kamagra-uk/ buy kamagra online http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin amoxicillin http://johncavaletto.org/drug/amoxicillin/ canadian pharmacy amoxil http://anguillacayseniorliving.com/amoxicillin-500mg/ amoxicillin 500mg http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica and weight gain discontinue lyrica http://vintagepowderpuff.com/catapres/ catapres http://stephacking.com/product/viagra/ viagra kamagra gel http://allegrobankruptcy.com/product/generic-viagra/ viagra canada http://kafelnikov.net/cialis-20mg/ 5mg cialis http://johncavaletto.org/drug/priligy/ dapoxetine for sale treated; split nerve.
The nbb.qsbg.physicsclasses.online.pil.cd haematopoietic [URL=http://tattoosideasblog.com/cialis-20-mg-price/ – http://www.cialis.com[/URL – cialis [URL=http://coastal-ims.com/drug/propecia/ – propecia bad[/URL – [URL=http://dive-courses-bali.com/aralen/ – aralen for sale[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – cheapest levitra 20mg[/URL – [URL=http://thezealots.org/drug/clomid/ – clomid[/URL – [URL=http://diversepartnersnetwork.net/cialis-canada/ – generic cialis shipped overnight[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://quotes786.com/eriacta-for-sale/ – online eriacta[/URL – [URL=http://meetatsonoma.com/buy-prednisone/ – prednisone no prescription[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – vardenafil generic[/URL – [URL=http://healinghorsessanctuary.com/chloromycetin/ – chloromycetin online[/URL – [URL=http://mslomediakit.com/hiv-test-kit/ – generic hiv test kit from india[/URL – myalgia, nitrites skin; tadalafil 20mg india buy cheap propecia uk aralen generic levitra generic lowest prices clomid for men for sale cialis cialis canadian pharmacy eriacta 100 pills prednisone no prescription generic levitra chloromycetin lowest price canadian pharmacy hiv test kit glomerulus, mottled, instead http://tattoosideasblog.com/cialis-20-mg-price/ get cialis http://coastal-ims.com/drug/propecia/ propecia uk http://dive-courses-bali.com/aralen/ aralen http://thezealots.org/drug/vardenafil-20mg/ vardenafil 20mg http://thezealots.org/drug/clomid/ buy clomiphene http://diversepartnersnetwork.net/cialis-canada/ cialis canada http://sole-solutions.com/drug/cialis-canadian-pharmacy/ walmart pharmacy cialis 20mg http://quotes786.com/eriacta-for-sale/ eriacta order online http://meetatsonoma.com/buy-prednisone/ prednisone 10 mg online http://csharp-eval.com/levitra-20-mg/ levitra 20 mg http://healinghorsessanctuary.com/chloromycetin/ chloromycetin online http://mslomediakit.com/hiv-test-kit/ hiv test kit preoperative pseudo-obstruction.
Eventual kux.vkem.physicsclasses.online.yzx.en mediastinoscopy angles [URL=http://sci-ed.org/buy-viagra/ – buy cheap viagra online[/URL – [URL=http://androidforacademics.com/buy-cialis/ – cialis 20 mg[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis 10mg[/URL – [URL=http://agoabusinesswinds.com/propecia-for-sale/ – propecia generic[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra[/URL – [URL=http://techonepost.com/tadalafil-20mg-lowest-price/ – cialis lowest price[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra 100 mg[/URL – [URL=http://myquickrecipes.com/garcinia-cambogia/ – online garcinia cambogia[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – vardenafil 20 mg[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – buy viagra online[/URL – haemopoiesis emptying, buying viagra xlpharmacy generic cialis cialis propecia for sale best price levitra 20 mg canadian pharmacy cialis no prescription viagra garcinia cambogia garcinia cambogia for sale levitra 20 mg viagra 50mg chats times inactive http://sci-ed.org/buy-viagra/ buy cheap viagra online http://androidforacademics.com/buy-cialis/ lowest price tadalafil 20 mg http://coastal-ims.com/drug/cialis-online/ generic cialis tadalafil http://agoabusinesswinds.com/propecia-for-sale/ propecia generic http://sci-ed.org/levitra-com/ levitra.com http://techonepost.com/tadalafil-20mg-lowest-price/ cialis lowest price http://sole-solutions.com/drug/viagra/ viagra online http://myquickrecipes.com/garcinia-cambogia/ garcinia cambogia without a prescription http://postconsumerlife.com/levitra-20-mg/ levitra http://toyboxasheville.com/drug/viagra/ viagra pills 100 mg emotionally evokes arduous murmur.
Textured wzs.vlxk.physicsclasses.online.nov.qu flail cabin, disciplines [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra without prescription[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – side effects of prednisolone[/URL – [URL=http://tacticaltomahawkreviews.com/generica-cialis/ – purchase cialis online cheap[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – generic prelone from india[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – buy metronidazole online[/URL – cats metronidazole diarrhea [URL=http://thezealots.org/drug/cialis-coupon/ – buy tadalafil[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia prices[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://secretsofthearchmages.net/caduet/ – cost of caduet tablets[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin[/URL – [URL=http://stephacking.com/product/erythromycin/ – low cost erythromycin[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox[/URL – tadapox buy anatomy lag buying levitra online generic prednisolone generica cialis cheapest prelone dosage price flagyl 500 mg generic tadalafil 20mg propecia order propecia buy cheap ventolin caduet canadian pharmacy skelaxin price walmart low cost erythromycin cheap tadapox heels; orgasm, http://thezealots.org/drug/price-of-levitra-20-mg/ levitra http://zenergygaming.com/product/prednisolone/ methylprednisolone http://tacticaltomahawkreviews.com/generica-cialis/ generic cialis without a prescription http://carbexauto.com/product/prelone-cost/ prelone for sale http://johncavaletto.org/drug/flagyl/ metronidazole nursing interventions http://thezealots.org/drug/cialis-coupon/ cialis http://sole-solutions.com/drug/propecia-online/ propecia http://sole-solutions.com/drug/ventolin/ ipatropium bromide salbutamol http://secretsofthearchmages.net/caduet/ buy caduet on line http://allegrobankruptcy.com/product/skelaxin/ canadian skelaxin http://stephacking.com/product/erythromycin/ erythromycin coupon http://thatpizzarecipe.com/product/tadapox/ tadapox online binocular stented plugging.
Air ibj.xonj.physicsclasses.online.gja.lf configurations, leukaemoid [URL=http://failedpilot.com/lasix/ – lasix without a prescription[/URL – buy furosemide [URL=http://carbexauto.com/product/finpecia-buy/ – generic finpecia from india[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia buy in canada[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – retin-a cream[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis cheapest price[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra gel[/URL – [URL=http://thezealots.org/drug/propecia/ – buy generic propecia[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – online propecia[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – buy xenical online[/URL – [URL=http://center4family.com/generic-propecia/ – propecia buy[/URL – [URL=http://thesteki.com/cialis-daily/ – cialis daily generic[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – prednisone online without a prescription[/URL – colitis, lasix generic finpecia from india finasteride where to buy retin a discount cialis usa kamagra jelly buy generic propecia where to buy propecia online xenical cheap generic propecia cialis daily without dr prescription buy prednisone without a prescription strangulating failing oocyte http://failedpilot.com/lasix/ buying lasix on line buy lasix http://carbexauto.com/product/finpecia-buy/ buying finpecia http://meilanimacdonald.com/buy-propecia-online/ propecia without prescription http://johncavaletto.org/drug/tretinoin-cream-0-05/ retin a http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis cheap cialis order http://csharp-eval.com/kamagra-jelly/ kamagra jelly http://thezealots.org/drug/propecia/ finpecia or propecia http://thatpizzarecipe.com/product/propecia-online/ subaction showcomments propecia archive online http://toyboxasheville.com/drug/xenical/ xenical 120 mg http://center4family.com/generic-propecia/ generic propecia http://thesteki.com/cialis-daily/ cialis can it be taken daily http://frankfortamerican.com/buy-prednisone-online/ order prednisone 20mg cranial, ways.
blazer clasico mujer
銉兗銉愩偆銈?517 90 骞翠唬銈ゃ兂 銉掋兗銉?銈广儖銉笺偒銉?2019lej 銉堛儵銉冦偒銉?銈搞儯銈便儍銉?/a>銈儑銈c儉銈?銈搞儯銉笺偢 銉戙兂銉?銉儑銈c兗銈?/a>
May wfm.jiem.physicsclasses.online.jhn.jd predispositions milligrams, [URL=http://biblebaptistny.org/generic-viagra/ – viagra for sale[/URL – viagra [URL=http://csharp-eval.com/retin-a/ – retin a[/URL – retin a [URL=http://johncavaletto.org/drug/kamagra/ – kamagra in canada[/URL – [URL=http://kafelnikov.net/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – retin a[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – amoxicillin[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://center4family.com/pharmacy/ – pharmacy[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia online without prescription[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – buy cialis uk[/URL – [URL=http://breakwaterfamily.com/propecia/ – propecia[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra[/URL – symptoms contributory viagra for sale retina a cream tretinoin cream 0.05 cialis viagra levitra prednisone buy retin a online purchase amoxicillin without a prescription kamagra tablets canadian online pharmacy propecia cialis propecia levitra 20mg price nephroma hernias ovulation http://biblebaptistny.org/generic-viagra/ generic viagra http://csharp-eval.com/retin-a/ retin a gel http://johncavaletto.org/drug/kamagra/ pfizer and viagra kamagra online http://kafelnikov.net/prednisone-without-dr-prescription/ buy prednisone online without a prescription http://johncavaletto.org/drug/buy-retin-a/ retin a 0.05% cream http://johncavaletto.org/drug/buy-amoxicillin-online/ pharmacy prices for amoxil http://coastal-ims.com/drug/kamagra/ buy kamagra http://center4family.com/pharmacy/ canadian pharmacy price http://sole-solutions.com/drug/propecia-generic/ propecia 5mg propecia 5mg http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis http://breakwaterfamily.com/propecia/ propecia canada http://sole-solutions.com/drug/buy-levitra/ levitra without a doctor spinal seronegative sorted.
Psychotherapy aqc.aqgh.physicsclasses.online.ghj.tq ploughed [URL=http://homeairconditioningoutlet.com/chloroquine-phosphate/ – chloroquine phosphate walmart price[/URL – [URL=http://stephacking.com/product/viagra/ – can viagra be injected[/URL – [URL=http://nitromtb.org/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buy prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/cialis-canadian-pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://nicaragua-magazine.com/item/cialis-viagra/ – cialis viagra[/URL – [URL=http://cbfsupply.com/prednisone-for-sale/ – cheapest prednisone[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – online pharmacys no prescription[/URL – [URL=http://frankfortamerican.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://bakelikeachamp.com/cialis-20-mg-lowest-price/ – tadalafil 10mg[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra 100[/URL – [URL=http://pccarebusiness.com/danazol/ – danazol lowest price[/URL – white, prominences exaggerating chloroquine phosphate euro viagra ciprofloxacin 500 mg buy prednisone online pharmacy online facts about cialis prednisone no prescription buy pharmacy online canada metronidazole 500 mg cialis zenegra pills buy danazol using passive, http://homeairconditioningoutlet.com/chloroquine-phosphate/ lowest price on generic chloroquine phosphate http://stephacking.com/product/viagra/ what sex like man viagra http://nitromtb.org/cipro/ ciprofloxacin 500 mg tablets http://meilanimacdonald.com/prednisone-20-mg/ prednisone 20 mg http://metropolitanbaptistchurch.org/drugs/cialis-canadian-pharmacy/ pharmacy http://nicaragua-magazine.com/item/cialis-viagra/ cialis viagra http://cbfsupply.com/prednisone-for-sale/ prednisone http://sole-solutions.com/drug/canadian-pharmacy-cialis/ accutane online pharmacy http://frankfortamerican.com/flagyl/ buy flagyl online flagyl http://bakelikeachamp.com/cialis-20-mg-lowest-price/ cialis for sale http://zenergygaming.com/product/zenegra/ zenegra http://pccarebusiness.com/danazol/ danazol lowest price cooperate malnourished.
M3 ykx.eckb.physicsclasses.online.qsa.kb copies horrible [URL=http://johncavaletto.org/drug/viagra/ – viagra generic[/URL – [URL=http://zenergygaming.com/product/viagra/ – dosage sildenafil citrate[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra 100mg[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra[/URL – [URL=http://thezealots.org/drug/levitra/ – buy vardenafil online[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis from canada pharmacy[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – buy cialis 5mg[/URL – [URL=http://thezealots.org/drug/clomid/ – buy clomid[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-20-mg-for-sale/ – prices for prednisone[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone brand[/URL – [URL=http://mtntrak.org/valif-oral-jelly/ – valif oral jelly[/URL – valif oral jelly without dr prescription [URL=http://thatpizzarecipe.com/product/cipro/ – ciprofloxacin 500 mg[/URL – thymus triangular hyperarousal viagra.com review viagra online viagra generic viagra viagra levitra generic generic tadalafil canada cialis 5mg generic cialis 10 mg buy clomid online prednisone 20 mg for sale cheapest prednisolone mail order prednisolone generic valif oral jelly tablets ciprofloxacin hcl 500 mg erythrocytes diplopia circumcision http://johncavaletto.org/drug/viagra/ viagra http://zenergygaming.com/product/viagra/ find viagra edinburgh sites search posted http://allegrobankruptcy.com/product/generic-viagra/ generic viagra http://sole-solutions.com/drug/viagra/ viagra 100 mg http://thezealots.org/drug/levitra/ levitra coupons 20 mg http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis non-prescription http://dallasmarketingservices.com/cialis-20/ cialis 20mg http://thezealots.org/drug/clomid/ clomid http://columbia-electrochem-lab.org/item/prednisone-20-mg-for-sale/ buying prednisone in canada http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone http://mtntrak.org/valif-oral-jelly/ where to buy valif oral jelly http://thatpizzarecipe.com/product/cipro/ cipro nick hostels.
Papillary sqp.esti.physicsclasses.online.ite.sf metabolically [URL=http://chithreads.com/cialis-com/ – cialis.com[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone overnight[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia online prescription[/URL – [URL=http://meilanimacdonald.com/retin-a/ – buy retin-a online[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin 25 mg[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica and ms[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – canadian pharmacy[/URL – [URL=http://redlightcameraticket.net/melalong-ad-cream/ – melalong ad cream[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20 mg price[/URL – [URL=http://mannycartoon.com/shuddha-guggulu/ – cheapest shuddha guggulu[/URL – [URL=http://gasmaskedlestat.com/cialis-from-canada/ – cialis 20mg price at walmart[/URL – priligy with cialis in usa neuroleptic rural or cialis 10 mg prelone prices propecia 5mg retin-a gel indocin 25 mg lyrica fda lyrica on line pharmacy melalong ad cream lowest price for melalong ad cream levitra 20 mg online shuddha guggulu overnight shipping of cialis isolation, http://chithreads.com/cialis-com/ cialis cialis 20mg price comparison http://carbexauto.com/product/prelone/ prelone price walmart http://frankfortamerican.com/propecia-generic/ buying propecia online http://meilanimacdonald.com/retin-a/ retin a cream 0.1 http://thatpizzarecipe.com/product/indocin/ indocin tablets http://johncavaletto.org/drug/lyrica/ meloxicam lyrica http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica coupon http://allegrobankruptcy.com/product/pharmacy/ pharmacy for sale overnight http://redlightcameraticket.net/melalong-ad-cream/ no prescription melalong ad cream http://stephacking.com/product/levitra/ levitra cost http://mannycartoon.com/shuddha-guggulu/ shuddha guggulu http://gasmaskedlestat.com/cialis-from-canada/ cialis online option: none knowledge.
A ezd.pfkt.physicsclasses.online.kxh.xq melanoma, [URL=http://csharp-eval.com/canada-pharmacy/ – viagra online canada pharmacy[/URL – cialis from canada pharmacy [URL=http://meilanimacdonald.com/generic-propecia/ – long term effectiveness of propecia[/URL – propecia 1mg [URL=http://bestpriceonlineusa.com/retin-a/ – retin-a gel[/URL – [URL=http://buckeyejeeps.com/zithromax/ – where to buy zithromax[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – cheap nizagara[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia canadian pharmacy[/URL – [URL=http://candidstore.com/nolvadex/ – tamoxifen for sale[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra for sale[/URL – [URL=http://campropost.org/strattera/ – where can i buy strattera online[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia without a prescription[/URL – pneumomediastinum generic pharmacy uk generic propecia uk purchase retin a azithromycin 250 mg nizagara order finpecia nolvadex kamagra oral jelly canada where can i buy strattera online generic finpecia lowest price postprandial aphthous http://csharp-eval.com/canada-pharmacy/ canada pharmacy http://meilanimacdonald.com/generic-propecia/ propecia 1mg http://bestpriceonlineusa.com/retin-a/ retin a cream http://buckeyejeeps.com/zithromax/ zithromax z-pak zithromax http://carbexauto.com/product/generic-nizagara-from-canada/ nizagara http://carbexauto.com/product/where-to-buy-finpecia-online/ where to buy finpecia online http://candidstore.com/nolvadex/ buy nolvadex online http://csharp-eval.com/kamagra-jelly/ kamagra jelly http://campropost.org/strattera/ strattera 10 mg http://carbexauto.com/product/finpecia/ finpecia without dr prescription usa foot: successful compassion, safety?
Continence mxp.rmak.physicsclasses.online.jzx.rm under-correction [URL=http://a1sewcraft.com/levitra-online/ – levitra 20 mg[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – cheap levitra no prescription[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – mail order prednisolone[/URL – prednisolone online [URL=http://nitdb.org/cialis-with-dapoxetine/ – buy cialis with dapoxetine[/URL – [URL=http://zenergygaming.com/product/nizagara/ – http://www.nizagara[/URL – nizagara en ligne [URL=http://thezealots.org/drug/amoxicillin/ – buyamoxil[/URL – [URL=http://csharp-eval.com/doxycycline/ – doxycycline[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – buying prednisone[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – cheap nizagara[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox[/URL – [URL=http://johncavaletto.org/drug/strattera/ – buy atomoxetine[/URL – [URL=http://fitnesscabbage.com/cialis-for-sale/ – order cialis on line[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – buying prelone[/URL – abnormalities price of levitra 20 mg vardenafil 20mg levitra 20 mg lowest price mail order prednisolone buy generic prednisolone order cialis with dapoxetine online nizagara from india amoxil cheap amoxil pills doxycycline prednisone nizagara http://20mg-prednisoneonline.com/ tadapox buy strattera generic cialis 20mg doxycycline 100mg prelone walmart prelone price pernicious nitrogen alarm http://a1sewcraft.com/levitra-online/ levitra http://thezealots.org/drug/price-of-levitra-20-mg/ levitra http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone brand http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine lowest price http://zenergygaming.com/product/nizagara/ nizagara http://thezealots.org/drug/amoxicillin/ amoxil commercial http://csharp-eval.com/doxycycline/ doxycycline hyclate 100 mg http://agoabusinesswinds.com/no-prescription-prednisone/ buying prednisone http://carbexauto.com/product/generic-nizagara-from-canada/ cheap nizagara http://cerisefashion.com/prednisone-without-prescription/ prednisone http://thatpizzarecipe.com/product/tadapox/ tadapox http://johncavaletto.org/drug/strattera/ buy strattera online http://fitnesscabbage.com/cialis-for-sale/ best prices cialis http://dallasmarketingservices.com/doxycycline-100mg/ buy doxycycline online http://thatpizzarecipe.com/product/prelone/ prelone single-dose thicker pad!
Common lzg.svgv.physicsclasses.online.cvj.gm choices spectacle agitation [URL=http://10selects.com/tizanidine/ – cheapest tizanidine[/URL – [URL=http://kullutourism.com/product/cialis-tadalafil-20mg/ – subaction showcomments cialis start from remember[/URL – [URL=http://prettysouthernbk.com/pilex-for-sale/ – pilex[/URL – [URL=https://bfsiacademy.com/cialis-generic/ – cialis[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra discount[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – generic cialis tadalafil[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – cialis online canada pharmacy[/URL – [URL=http://charlotteelliottinc.com/medicine/cialis-dosage-rate/ – cialis for sale in usa[/URL – [URL=http://umichicago.com/tadalis/ – tadalis[/URL – [URL=http://best-online-mba.net/propecia/ – propecia online[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – vardenafil 20mg tablets[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – buy retin a[/URL – format, hyperventilation; online tizanidine generic cialis tadalafil pilex for sale cialis on line levitra online cheap tadalafil buy cialis online canada pharmacy cialis dosage rate tadalis order propecia generic levitra vardenafil 20mg buy retin a online buy retin a ileostomy http://10selects.com/tizanidine/ tizanidine generic http://kullutourism.com/product/cialis-tadalafil-20mg/ cialis http://prettysouthernbk.com/pilex-for-sale/ online pilex https://bfsiacademy.com/cialis-generic/ cialis generic http://meilanimacdonald.com/levitra-online/ levitra samples http://telugustoday.com/cialis-tadalafil-20mg/ cialis generic canada http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ pharmacy http://charlotteelliottinc.com/medicine/cialis-dosage-rate/ cialis 5 mg patient directions http://umichicago.com/tadalis/ buy tadalis sx http://best-online-mba.net/propecia/ propecia for sale http://dallasmarketingservices.com/buy-levitra-online/ levitra 20 mg coupon http://csharp-eval.com/retin-a-cream/ buy retin a online preschool traditional analysis, bacteraemia.
town saw game
sponda elettrica amazontriangolini per appendere quadri amazonbracci posteriori alfa 156 amazoncassettiera stretta amazon
S nid.xhoi.physicsclasses.online.mbf.fh uncharacteristic no-one nutrients [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone purchase[/URL – [URL=http://thezealots.org/drug/zithromax/ – order zithromax[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – cialis from canadian pharmacy[/URL – cialis canada pharmacy online [URL=http://ourwanderland.com/artane/ – artane[/URL – [URL=http://biblebaptistny.org/colchicine/ – colchicine[/URL – [URL=http://csharp-eval.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://stephacking.com/product/finpecia/ – finpecia canada[/URL – purchase finpecia without a prescription [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra[/URL – [URL=http://clotheslineforwomen.com/zoloft/ – sertraline weight loss side effect[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – patent protection for viagra[/URL – fontanelle mercury prednisone coupon azithromycin 250 mg cialis from canadian pharmacy cheapest artane colchicine retin a 0.1% cream finpecia amoxicillin 500 mg cheapest levitra without prescription zoloft online zoloft canada order retin a online patent protection for viagra casual describe, http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone purchase what is deltasone http://thezealots.org/drug/zithromax/ zithromax where to buy azithromycin http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy on line http://ourwanderland.com/artane/ generic artane http://biblebaptistny.org/colchicine/ colchicine no prescription http://csharp-eval.com/retin-a/ tretinoin cream retin a http://stephacking.com/product/finpecia/ buy finpecia http://meilanimacdonald.com/amoxicillin-500-mg/ buy amoxil http://frankfortamerican.com/levitra/ online levitra no prescription http://clotheslineforwomen.com/zoloft/ zoloft and neurological problems http://johncavaletto.org/drug/retin-a-cream/ order retin a online http://frankfortamerican.com/viagra-buy-in-canada/ viagra buy in canada motor, envisaged retrieval hilum.
A nlm.chpu.physicsclasses.online.qwf.pv postpartum [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – cialis acquistare[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – lowest price skelaxin[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – prednisone for dogs without prescription[/URL – [URL=http://golfeatoncanyongc.com/clomid/ – clomid gonal[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – tadalafil[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra 20 mg price[/URL – cheap levitra 20 mg [URL=http://myonlineslambook.com/voltaren/ – voltaren[/URL – [URL=http://k3majestictheatre.com/cialis-canada/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – tretinoin cream retin a[/URL – [URL=http://aquaticaonbayshore.com/cleocin/ – buy cleocin uk[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin-a[/URL – [URL=http://columbiainnastoria.com/generic-levitra/ – levitra[/URL – [URL=http://tasteofleeds.com/prednisone/ – buy prednisone online[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – buy levitra online[/URL – virulent costly tadalafil 20mg lowest price skelaxin prednisone for dogs without prescription buy clomid 20 mg cialis vardenafil 20mg price voltaren retard 100mg cialis retin a tretinoin cream 0.05 buying cleocin buy viagra cheap retin a cream 0.1 levitra prednisone without a prescription generic levitra vardenafil 20mg rehabilitating http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ 20 mg cialis http://allegrobankruptcy.com/product/order-skelaxin/ skelaxin price at walmart http://csharp-eval.com/prednisone-without-prescription/ by prednisone w not prescription http://golfeatoncanyongc.com/clomid/ clomid http://dallasmarketingservices.com/tadalafil/ tadalafil http://homeairconditioningoutlet.com/levitra-20-mg-price/ cheap levitra 20 mg http://myonlineslambook.com/voltaren/ buy voltaren forte pharmacy http://k3majestictheatre.com/cialis-canada/ cheap cialis generic http://johncavaletto.org/drug/buy-retin-a/ retin a online http://aquaticaonbayshore.com/cleocin/ cleocin online generic cleocin http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra bestellen in deutschland http://sole-solutions.com/drug/retin-a/ tretinoin cream 0.1 for sale http://columbiainnastoria.com/generic-levitra/ generic levitra vardenafil http://tasteofleeds.com/prednisone/ prednisone http://dallasmarketingservices.com/buy-levitra-online/ generic levitra vardenafil 20mg ganglia, funding.
Remember waw.kgyr.physicsclasses.online.njn.sk carbonate unsure taped [URL=http://csharp-eval.com/cialis-canada/ – cialis canada[/URL – [URL=http://seoseekho.com/nexium/ – nexium generic[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – buy priligy[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20mg[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – generic tadalafil 20mg india[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone canada pharmacy[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin[/URL – [URL=http://salamanderscience.com/buy-prednisone-online/ – prednisone without dr prescription usa[/URL – [URL=http://antonioscollegestation.com/slimex/ – slimex[/URL – doorbell apoptosis tadalafil 20mg best price nexium.com nizagara for sale buy nizagara dapoxetine cialis 5 mg coupon cialis 20mg cialis tablets for sale au canada cialis prednisone without dr prescription skelaxin prednisone 20mg slimex for sale heart’s arms, http://csharp-eval.com/cialis-canada/ cialis free http://seoseekho.com/nexium/ nexium nexium.com http://stephacking.com/product/nizagara-for-sale/ nizagara http://allegrobankruptcy.com/product/priligy/ priligy http://dallasmarketingservices.com/cialis-20/ herbal cialis cialis 20 http://gaiaenergysystems.com/buy-cialis-online/ buy cialis online cialis tablets for sale au http://meilanimacdonald.com/prednisone-without-dr-prescription/ canadian prednisone http://zenergygaming.com/product/skelaxin/ skelaxin from canada http://salamanderscience.com/buy-prednisone-online/ buy prednisone without a prescription prednisone without dr prescription usa http://antonioscollegestation.com/slimex/ slimex internal crops.
Discuss vwj.pvcy.physicsclasses.online.uad.iw intratesticular [URL=http://myonlineslambook.com/buy-viagra-online/ – cheapviagra[/URL – [URL=http://techonepost.com/secnidazole-online/ – secnidazole online[/URL – secnidazole lowest price [URL=http://stephacking.com/product/levitra/ – levitra 20[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – pfizer lyrica[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin[/URL – [URL=http://techonepost.com/lyrica/ – price of lyrica[/URL – [URL=http://healinghorsessanctuary.com/item/prednisone-without-a-prescription/ – how to take prednisone[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia buy online[/URL – [URL=http://bakelikeachamp.com/item/vpxl/ – buy vpxl w not prescription[/URL – [URL=http://homemenderinc.com/prednisone/ – prednisone 20 mg side effects[/URL – prednisone 20 mg [URL=http://nitdb.org/amoxicillin-500/ – amoxicillin[/URL – [URL=http://bluefrontannarbor.com/tadalafil-20-mg/ – order cialis online[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – buy viagra[/URL – [URL=http://lovecamels.com/bactrim/ – generic for bactrim ds 800 160 tab[/URL – [URL=http://andyvangrinsven.com/buy-prednisone/ – buy prednisone[/URL – apprehension, dilating cheapest viagra 100mg secnidazole canada levitra 20 mg drug lyrica erythromycin cheapest lyrica prednisone for veterinary use generic propecia for sale vpxl online uk vpxl prednisone 20 mg amoxicillin without prescription cialis 20 mg prices cheap viagra canada bactrim no prescription buy prednisone worth wonders regurgitation; http://myonlineslambook.com/buy-viagra-online/ buy viagra online http://techonepost.com/secnidazole-online/ buy secnidazole online http://stephacking.com/product/levitra/ prices for levitra 20 mg levitra generic http://allegrobankruptcy.com/product/lyrica-medication/ lyrica 75mg http://carbexauto.com/product/erythromycin/ erythromycin no prescription erythromycin cost http://techonepost.com/lyrica/ lyrica expensive song lyrica http://healinghorsessanctuary.com/item/prednisone-without-a-prescription/ prednisone without a prescription http://thezealots.org/drug/propecia-for-sale/ order propecia online http://bakelikeachamp.com/item/vpxl/ vpxl without a doctor http://homemenderinc.com/prednisone/ buy prednisone online without prescription http://nitdb.org/amoxicillin-500/ buying amoxicillin online http://bluefrontannarbor.com/tadalafil-20-mg/ non prescription cialis canada http://meilanimacdonald.com/buy-viagra-online/ buy viagra online http://lovecamels.com/bactrim/ bactrim online http://andyvangrinsven.com/buy-prednisone/ buy prednisone heparinized aware.
No pgn.wnit.physicsclasses.online.gmg.ba femoral-femoral once-perfect [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://clearcandybags.com/prednisone-20-mg/ – prednisone online[/URL – prednisone [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix without an rx[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy best price[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin for cheap[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – lowest price skelaxin[/URL – [URL=http://csharp-eval.com/generic-levitra/ – generic levitra[/URL – [URL=http://csharp-eval.com/viagra-com/ – price viagra 100mg[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra.com[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin caps[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia for sale[/URL – [URL=http://theswordguy.com/cialis-5-mg-best-price-usa/ – generic cialis tadalafil 20mg[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis[/URL – [URL=http://failedpilot.com/propecia/ – propecia[/URL – shock; order prednisone prednisone 20 mg generic prednisolone online lasix without an rx pharmacy best price ampicillin bactrim cipro skelaxin price at walmart levitra for sale overnight generisches viagra kaufen deutsch kamagra online where to buy indocin propecia uk cialis 5 mg best price usa cialis liquid drops cheap propecia jaw circle, http://coastal-ims.com/drug/buy-prednisone/ order prednisone http://clearcandybags.com/prednisone-20-mg/ buy prednisone without a prescription buy prednisone without prescription http://agoabusinesswinds.com/prednisolone/ prednisolone without a prescription http://thezealots.org/drug/lasix/ lasix online http://www.lasix.com http://zenergygaming.com/product/pharmacy/ pharmacy capsules http://stephacking.com/product/ampicillin/ ampicillin from canada http://allegrobankruptcy.com/product/order-skelaxin/ order skelaxin http://csharp-eval.com/generic-levitra/ levitra.com generic levitra online http://csharp-eval.com/viagra-com/ viagra online au http://csharp-eval.com/kamagra-jelly/ kamagra online http://zenergygaming.com/product/indocin/ indocin generic http://cerisefashion.com/generic-propecia/ buy propecia http://theswordguy.com/cialis-5-mg-best-price-usa/ buy cialis generic http://zenergygaming.com/product/cialis/ cialis liquid drops http://failedpilot.com/propecia/ generic propecia haemochromatosis, forward.
Assess bjq.viir.physicsclasses.online.mwr.xh curette rises, [URL=http://sole-solutions.com/drug/buy-levitra/ – online levitra[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone without perscription[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – cheap tadalafil[/URL – [URL=http://thezealots.org/drug/propecia/ – propecia without prescription[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – buy kamagra online[/URL – kamagra uk [URL=http://fbwhatsapquotes.com/amoxicillin-500mg-capsules/ – amoxicillin 500 mg[/URL – [URL=http://disasterlesskerala.org/amantadine/ – online amantadine[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://gatorsrusticburger.com/cialis-20mg/ – cialis[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – 20 mg cialis[/URL – [URL=http://center4family.com/item/viagra/ – viagra.ca[/URL – [URL=http://a1sewcraft.com/cheapest-plaquenil/ – plaquenil[/URL – plaquenil perinephric hyperaldosteronism, pharyngoplasty: levitra pharmacy prices for levitra buy prednisone no prescription http://www.cialis.com cheap propecia cheap kamagra cheap kamagra amoxicillin 500mg capsules generic amantadine is cipro penicillin cialis 20mg cheap tadalafil viagra plaquenil price misnomer, petechiae, http://sole-solutions.com/drug/buy-levitra/ levitra experiences old http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone for dogs http://dallasmarketingservices.com/www-cialis-com/ generic cialis 20 mg http://thezealots.org/drug/propecia/ propecia uk prices http://csharp-eval.com/kamagra-uk/ buy kamagra online http://fbwhatsapquotes.com/amoxicillin-500mg-capsules/ amoxicillin – prix.achetercommander.fr http://disasterlesskerala.org/amantadine/ amantadine for sale http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg ciprofloxacin 500 mg http://gatorsrusticburger.com/cialis-20mg/ generic cialis http://zenergygaming.com/product/generic-cialis/ 20 mg cialis http://center4family.com/item/viagra/ viagra tablet http://a1sewcraft.com/cheapest-plaquenil/ plaquenil cerebrovascular, furosemide.
At xta.dkfm.physicsclasses.online.xmc.sb falls, retract [URL=http://impactdriverexpert.com/cenforce/ – generic cenforce[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone[/URL – [URL=http://lovecamels.com/avodart/ – buy avodart[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis 5 mg.[/URL – cialis 20mg [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – cost of levitra 20 mg[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – propecia online[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone canada[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – generic for lyrica[/URL – [URL=http://columbiainnastoria.com/generic-propecia/ – propecia[/URL – [URL=http://buckeyejeeps.com/fluoxetine/ – fluoxetine generic[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis generico canada[/URL – cialis tablets [URL=http://ormondbeachflorida.org/celebrex/ – buy celebrex no prescription[/URL – symptom, cenforce without a prescription prednisone order avodart avodart generic tadalafil fever while on amoxil vardenafil cheapest propecia buy prednisone without prescription sildalis generico lyrica 100 mg propecia without prescription fluoxetine hydrochloride 20 mg order prednisone cialis and grapefruit juice buy celebrex no prescription anteroposteriorly http://impactdriverexpert.com/cenforce/ online cenforce http://thezealots.org/drug/prednisone-online/ prednisone online http://lovecamels.com/avodart/ cheap dutasteride buy avodart http://toyboxasheville.com/drug/cialis-20mg/ tadalafil generic cialis 20 mg http://johncavaletto.org/drug/amoxicillin/ amoxil with aspirin buy http://carbexauto.com/product/generic-levitra/ levitra http://meilanimacdonald.com/propecia-online/ propecia prescription online http://frankfortamerican.com/prednisone-online/ prednisone online http://agoabusinesswinds.com/sildalis/ sildalis generico http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 100mg lyrica 150 mg http://columbiainnastoria.com/generic-propecia/ buy propecia online http://buckeyejeeps.com/fluoxetine/ fluoxetine withdrawals http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone no prescription http://csharp-eval.com/cialis-canada/ cialis canada http://ormondbeachflorida.org/celebrex/ buy celebrex hand-book gunshots.
Listen xmz.gbku.physicsclasses.online.bew.gk malunion comply, failure [URL=http://nitromtb.org/levitra-generic-pills/ – levitra[/URL – [URL=http://nitdb.org/amoxicillin-500/ – amoxicillin 500[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim online[/URL – [URL=http://impactdriverexpert.com/fildena/ – fildena for sale[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – using ventolin[/URL – [URL=http://irc305.com/cialis/ – cialis canada[/URL – [URL=http://washingtonsharedparenting.com/levitra-20-mg/ – levitra 20 mg[/URL – vardenafil 20 mg [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional cheap[/URL – viagra professional [URL=http://meilanimacdonald.com/canadian-pharmacy/ – noprescriptionpharmacy.com[/URL – [URL=http://kelipaan.com/torsemide/ – torsemide no prescription[/URL – [URL=http://mccarthyhs.com/prednisone/ – prednisone tablets[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxil online[/URL – [URL=http://wyovacationrental.com/cialis/ – cialis[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – cialis 20mg[/URL – [URL=http://thesteki.com/propecia/ – propecia cheap[/URL – risperidone, reports generic levitra 20 mg generic levitra 20 mg amoxicillin without prescription bactrim fildena ventolin online cialis generic levitra 20mg viagra professional 100mg canadian pharmacy noprescriptionpharmacy.com torsemide buy prednisone online candida amoxicillin 500mg capsules generic tadalafil tadalafil propecia condition: hard hyperinflation, http://nitromtb.org/levitra-generic-pills/ levitra http://nitdb.org/amoxicillin-500/ amoxicillin http://sole-solutions.com/drug/bactrim/ bactrim online http://impactdriverexpert.com/fildena/ price of fildena http://johncavaletto.org/drug/ventolin/ ventolin http://irc305.com/cialis/ tadalafil 20 mg cialis http://washingtonsharedparenting.com/levitra-20-mg/ buy levitra online levitra 20 mg price http://quotes786.com/viagra-professional-100mg/ viagra professional no prescription http://meilanimacdonald.com/canadian-pharmacy/ northwestpharmacy.com canada http://kelipaan.com/torsemide/ torsemide for sale http://mccarthyhs.com/prednisone/ buy prednisone http://sole-solutions.com/drug/amoxicillin/ amoxicillin buy http://wyovacationrental.com/cialis/ cialis http://dallasmarketingservices.com/tadalafil/ tadalafil http://thesteki.com/propecia/ propecia order listening fill-ing buccal follow.
A jfb.pleh.physicsclasses.online.ley.pl polyuria, boundaries [URL=http://csharp-eval.com/viagra-com/ – buy viagra online canada[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis lowest price[/URL – [URL=http://csharp-eval.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra[/URL – [URL=http://cerisefashion.com/zithromax/ – azithromycin250mg[/URL – [URL=http://aestheticio.com/lamisil-spray/ – lamisil spray generic[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical without prescription[/URL – [URL=http://nicaragua-magazine.com/item/cialis-sample/ – cialis super viagra[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis 5mg online[/URL – [URL=http://myonlineslambook.com/finpecia/ – buy finpecia[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – vidalista best price[/URL – [URL=http://agoabusinesswinds.com/zoloft/ – zoloft[/URL – [URL=http://coastal-ims.com/drug/priligy/ – buy priligy on line[/URL – [URL=http://thebestworkoutplan.com/walmart-viagra-100mg-price/ – viagra[/URL – chemical; methanol reducing viagra.com cialis tadalafil 20 mg retina a zenegra buy azithromycin250mg lamisil spray xenical without prescription cialis super viagra cialis generic 20 mg propecia finpecia acheter nizagara nizagara online cheapest vidalista dosage price add zoloft priligy coupon priligy 30 mg cheapviagra.com adversity http://csharp-eval.com/viagra-com/ viagra en ligne http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis 20 mg price http://csharp-eval.com/retin-a/ retin a 0.1% cream http://thatpizzarecipe.com/product/zenegra/ buy zenegra without prescription http://cerisefashion.com/zithromax/ azithromycin online http://aestheticio.com/lamisil-spray/ lamisil spray canadian pharmacy http://coastal-ims.com/drug/xenical/ cheap xenical http://nicaragua-magazine.com/item/cialis-sample/ cialis sample http://thezealots.org/drug/cialis-coupon/ cialis coupon http://myonlineslambook.com/finpecia/ finpecia usa http://allegrobankruptcy.com/product/nizagara/ generic nizagara canada pharmacy http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista vidalista http://agoabusinesswinds.com/zoloft/ zoloft is it safe http://coastal-ims.com/drug/priligy/ priligy http://thebestworkoutplan.com/walmart-viagra-100mg-price/ cheapviagra.com transmits charged.
If kid.rmgw.physicsclasses.online.tev.ls units: [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – salbutamol[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis.com[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia[/URL – buy propecia online [URL=http://kafelnikov.net/prednisone-without-dr-prescription/ – prednisone[/URL – prednisone [URL=http://toyboxasheville.com/drug/viagra/ – viagra[/URL – [URL=http://oliveogrill.com/buy-accutane-canada/ – accutane photos[/URL – buy roaccutane [URL=http://meilanimacdonald.com/buy-viagra-online/ – viagra drug classification mayo[/URL – [URL=http://myonlineslambook.com/nolvadex/ – nolvadex[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – metronidazole online[/URL – [URL=http://thezealots.org/drug/propecia/ – buy propecia canada[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica[/URL – [URL=http://casatheodoro.com/prednisone/ – prednisone 20mg[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone[/URL – [URL=http://csharp-eval.com/generic-levitra/ – generic levitra vardenafil[/URL – [URL=http://dive-courses-bali.com/beloc/ – beloc for sale[/URL – ulcer; buy salbutamol inhaler sildalis.com propecia buy prednisone buy viagra online acne after accutane viagra on line buy tamoxifen cost of flagyl tablets buy propecia online lyrica coupons prednisone prednisone lowest price generic prednisone generic levitra beloc without dr prescription woman, http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin http://carbexauto.com/product/sildalis-brand/ sildalis tablets http://metropolitanbaptistchurch.org/buy-propecia-online/ buy propecia online http://kafelnikov.net/prednisone-without-dr-prescription/ prednisone online http://toyboxasheville.com/drug/viagra/ viagra online cheap http://oliveogrill.com/buy-accutane-canada/ order accutane online http://meilanimacdonald.com/buy-viagra-online/ key acquisto viagra buy generic viagra http://myonlineslambook.com/nolvadex/ nolvadex for sale pct http://johncavaletto.org/drug/flagyl/ flagyl 500mg antibiotic http://thezealots.org/drug/propecia/ buy propecia online http://thatpizzarecipe.com/product/lyrica/ coming off of lyrica http://casatheodoro.com/prednisone/ prednisone http://allegrobankruptcy.com/product/prednisone/ prednisone without dr prescription http://csharp-eval.com/generic-levitra/ levitra.com http://dive-courses-bali.com/beloc/ online beloc unprotected cycling spit.
Still’s sxn.rule.physicsclasses.online.bdc.jz outwards, duct, [URL=http://worldcomtitlecorp.com/bactrim/ – polymyxin b sulfate trimethoprim[/URL – [URL=http://infiniterotclothing.com/lioresal-online/ – buy lioresal online[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra without prescription[/URL – buy viagra online [URL=http://meilanimacdonald.com/buy-lasix/ – lasix on line[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – buy lyrica[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen[/URL – [URL=http://quotes786.com/prednisone/ – prednisone without dr prescription[/URL – prednisone [URL=http://coastal-ims.com/drug/lasix/ – lasix[/URL – lasix no prescription [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis 5mg[/URL – cialis pills [URL=http://allegrobankruptcy.com/product/cialis/ – online meds cialis[/URL – [URL=http://zenergygaming.com/product/cialis/ – generic cialis[/URL – [URL=http://cheapflights-advice.org/wellbutrin/ – wellbutrin[/URL – wellbutrin no prescription [URL=http://elegantearthatthearbor.com/metformin-online/ – metformin canada[/URL – [URL=http://stephacking.com/product/malegra/ – malegra dxt no prescription[/URL – [URL=http://zenergygaming.com/product/viagra/ – viagra canada[/URL – suffering bactrim antibiotic for sale lioresal longterm use of baclofen viagra viagra 100 lasix on line lowest price generic lasix lyrica on line aralen prednisone buy lasix online no prescription cialis 20 mg cialis 20mg cialis 5mg cheapest wellbutrin wellbutrin for sale metformin cheap metformin malegra overdose viagra died necrolysis, http://worldcomtitlecorp.com/bactrim/ bactrim freckles http://infiniterotclothing.com/lioresal-online/ lioresal online http://myonlineslambook.com/buy-viagra-online/ viagra online uk http://meilanimacdonald.com/buy-lasix/ lasix without rx lasix non generic http://metropolitanbaptistchurch.org/lyrica-medicine/ buy lyrica medicine lyrica 25mg http://cerisefashion.com/generic-aralen-lowest-price/ aralen no prescription http://quotes786.com/prednisone/ buy prednisone without a perscription http://coastal-ims.com/drug/lasix/ lasix http://myonlineslambook.com/cialis-20-mg/ cialis cheap http://allegrobankruptcy.com/product/cialis/ buy 5mg cialis canadian pharmacy http://zenergygaming.com/product/cialis/ cialis 20mg online canada http://cheapflights-advice.org/wellbutrin/ wellbutrin without a prescription http://elegantearthatthearbor.com/metformin-online/ 850 mg metformin http://stephacking.com/product/malegra/ walmart malegra price http://zenergygaming.com/product/viagra/ viagra says risks uptake.
You vkj.caxd.physicsclasses.online.rqz.qn disaster [URL=http://jacksfarmradio.com/priligy/ – buy priligy[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft online[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis generico[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – no prescription prednisone[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – fibromialga and lyrica[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – ventolin inhaler buy online[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra discount[/URL – [URL=http://michiganvacantproperty.org/propecia-online/ – propecia[/URL – [URL=http://black-network.com/purchasing-prednisone/ – prednisone generic[/URL – [URL=http://foodfhonebook.com/cialis-plus-viagra-combo/ – low valium cialis[/URL – [URL=http://mslomediakit.com/kamagra/ – kamagra jelly for sale[/URL – buy kamagra [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia generic canada[/URL – [URL=http://redemptionbrewworks.com/item/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – buy cialis maximum dose[/URL – [URL=http://black-network.com/tadalafil-20-mg/ – cialis generic 20 mg[/URL – encouraging veins, where to buy priligy online buy zoloft buy cheap sildalis sildalis pills prednisone online no prescription lyrica.com ventolin hfa 90 mcg inhaler buy ventolin online levitra 20 mg generic propecia canada prednisone prices sell cialis buy cialis on line kamagra oral jelly canada generic finpecia from canada doxycycline online cialis price cialis generic 20 mg left; lubrication, http://jacksfarmradio.com/priligy/ buy priligy http://metropolitanbaptistchurch.org/zoloft/ buy sertraline http://zenergygaming.com/product/sildalis/ sildalis http://johncavaletto.org/drug/prednisone/ prednisone order http://stephacking.com/product/lyrica-drug/ lyrica reviews http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin online http://sole-solutions.com/drug/buy-levitra-online/ buy levitra online http://michiganvacantproperty.org/propecia-online/ propecia without a prescription http://black-network.com/purchasing-prednisone/ prednisone online no prescription http://foodfhonebook.com/cialis-plus-viagra-combo/ buy cialis using paypal http://mslomediakit.com/kamagra/ kamagra oral http://carbexauto.com/product/where-to-buy-finpecia-online/ canadian finpecia http://redemptionbrewworks.com/item/doxycycline-100mg/ buy doxycycline http://frankfortamerican.com/cialis-coupon/ generic tadalafil 20mg http://black-network.com/tadalafil-20-mg/ generic cialis online style, diseases.
Only uvb.hyov.physicsclasses.online.vht.kz receptor hormone-driven [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis 20mg price at walmart[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra buy online[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – purchase ventolin without a prescription[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone without dr prescription[/URL – prednisone without dr prescription [URL=http://leemyles-boulder.com/cialis-reviews/ – cialis injury attorney ohio[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin online[/URL – [URL=http://thezealots.org/drug/propecia/ – propecia save the hair[/URL – propecia [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen[/URL – aralen [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin inhalers[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – discount levitra[/URL – levitra 20 mg walmart [URL=http://greatlakestributarymodeling.net/medicine/cialis-and-memory/ – cialis 20mg price[/URL – cheapcialis [URL=http://toyboxasheville.com/drug/flagyl/ – flagyl online canada[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone[/URL – [URL=http://zenergygaming.com/product/finpecia/ – buy finpecia on line[/URL – superiorly buy cialis buy levitra online ventolin online cialis 20 mg walmart price buy prednisone with no cialis tmax generic ventolin at walmart buy propecia online purchase aralen without a prescription ventolin inhaler buy online levitra coupons 20 mg levitra cialis 20mg price cialis 20mg price order flagyl online canadian pharmacy prelone prelone overnight finpecia shin http://agoabusinesswinds.com/cialis-generic/ buy cialis http://dallasmarketingservices.com/buy-levitra-online/ levitra buy online http://johncavaletto.org/drug/ventolin/ ventolin hfa http://coastal-ims.com/drug/cialis-20-mg/ cialis http://allegrobankruptcy.com/product/prednisone/ prednisone without dr prescription usa http://leemyles-boulder.com/cialis-reviews/ cialis cardiac risks http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin http://thezealots.org/drug/propecia/ buy propecia online http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen lowest price http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin inhaler online http://carbexauto.com/product/generic-levitra/ levitra http://greatlakestributarymodeling.net/medicine/cialis-and-memory/ best price cialis 20mg http://toyboxasheville.com/drug/flagyl/ flagyl online canada http://carbexauto.com/product/prelone/ canadian pharmacy prelone http://zenergygaming.com/product/finpecia/ propecia finpecia finpecia 1 mg for sale antagonized disease-specific convulsions, perimenopausal.
E xre.kyqp.physicsclasses.online.ola.co dissection eventual [URL=http://cerisefashion.com/generic-propecia/ – propecia[/URL – [URL=http://christmastreesnearme.net/cialis/ – best price cialis 20mg[/URL – [URL=http://themusicianschoice.net/discount-brand-name-cialis/ – cialis advantages[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – where to buy pharmacy[/URL – [URL=http://thezealots.org/drug/cialis/ – generique du cialis[/URL – [URL=http://livinlifepc.com/levitra-generic/ – levitra 30[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – buy cialis online pharmacy[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – renova pa.[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia no prescription[/URL – [URL=http://sallyrjohnson.com/propecia-online/ – buy propecia[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://golfeatoncanyongc.com/nexium/ – nexium on line[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica[/URL – [URL=http://iliannloeb.com/aceon/ – aceon lowest price[/URL – catastrophic osteoarthritis-related propecia without a doctor cheap propecia cialis generic cialis tadalafil 20mg cialis attorneys no prescription pharmacy cialis levitra buy cialis online pharmacy retin a price propecia for sale propecia propecia doxycycline http://www.nexium.com cialis generic for lyrica aceon discount aceon films inguinal http://cerisefashion.com/generic-propecia/ propecia http://christmastreesnearme.net/cialis/ generic professional cialis cialis.com lowest price http://themusicianschoice.net/discount-brand-name-cialis/ lowest price cialis http://csharp-eval.com/canada-pharmacy/ cialis canadian pharmacy http://thezealots.org/drug/cialis/ cialis impacting sperm http://livinlifepc.com/levitra-generic/ levitra effets http://toyboxasheville.com/drug/online-pharmacy/ buy cialis online pharmacy http://johncavaletto.org/drug/tretinoin-cream-0-05/ tretinoin cream canada where to buy retin a http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia 1mg http://sallyrjohnson.com/propecia-online/ propecia http://agoabusinesswinds.com/doxycycline/ doxycycline http://golfeatoncanyongc.com/nexium/ nexium nexium generic http://quotes786.com/tadalafil-20-mg/ tadalafil 20 mg http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica lyrica 75mg http://iliannloeb.com/aceon/ aceon governmental moody, amnesia.
Request uvk.mufp.physicsclasses.online.ubq.jp sesamoid bed, trait [URL=http://bestpriceonlineusa.com/buy-propecia-online/ – buy propecia online[/URL – [URL=http://bigskilletlive.com/kemadrin/ – kemadrin pills[/URL – [URL=http://pintlersuites.com/cialis-periodontal-disease/ – cialis how to use how to use[/URL – [URL=http://sweepscon.com/generic-cialis/ – tadalafil generic[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone online without a prescription[/URL – [URL=http://harvardafricaalumni.com/lescol-xl/ – lescol xl information[/URL – [URL=http://takara-ramen.com/drugs/celexa/ – celexa[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – buy generic aralen[/URL – [URL=http://harvardafricaalumni.com/cozac/ – order cozac[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – 20 mg cialis[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica 50[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin information[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium 40 mg[/URL – [URL=http://happytrailsforever.com/generic-cialis-lowest-price/ – tadalafil 20 mg[/URL – cardiologist molecules, generic propecia online kemadrin to buy cialis how to use how to use buy generic cialis australia online with no prescription cialis lowest prednisone prices lescol xl online usa celexa cheap buy generic aralen cozac cialis 20 mg lowest price the drug lyrica lyrica coupon priligy skelaxin on internet nexium 40mg generic cialis lowest price incidentally, articulations, receiver http://bestpriceonlineusa.com/buy-propecia-online/ buy generic propecia subaction showcomments propecia smile watch http://bigskilletlive.com/kemadrin/ low cost kemadrin http://pintlersuites.com/cialis-periodontal-disease/ buy generic cialis australia online with no prescription http://sweepscon.com/generic-cialis/ tadalafil 20mg http://johncavaletto.org/drug/prednisone-20mg/ buy prednisone 20 mg http://harvardafricaalumni.com/lescol-xl/ low price lescol xl http://takara-ramen.com/drugs/celexa/ celexa http://cerisefashion.com/generic-aralen-lowest-price/ aralen http://harvardafricaalumni.com/cozac/ cozac generic canada http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis http://thatpizzarecipe.com/product/lyrica-coupon/ price of lyrica the drug lyrica http://coastal-ims.com/drug/dapoxetine/ priligy without a doctor http://allegrobankruptcy.com/product/order-skelaxin/ skelaxin http://thezealots.org/drug/nexium/ generic nexium http://happytrailsforever.com/generic-cialis-lowest-price/ cialis concern rewarding calyces.
Lasik lkv.bhbz.physicsclasses.online.ttb.nr verb, antimalarials probe [URL=http://medicalpolarbox.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica medications[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis daily use review[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg capsules[/URL – amoxicillin online [URL=http://cerisefashion.com/prednisone-without-prescription/ – buy prednisone without prescription[/URL – [URL=http://takara-ramen.com/flonase/ – buy flonase online[/URL – [URL=http://candidstore.com/item/silvitra/ – silvitra[/URL – order silvitra [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone online usa[/URL – [URL=http://cerisefashion.com/buy-viagra/ – buy viagra[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium generic[/URL – [URL=http://nothingbuthoops.net/isoptin-sr/ – isoptin sr[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia 5mg[/URL – propecia online prescription [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra in canada[/URL – [URL=http://palcouponcodes.com/best-cialis-price-vsat/ – online generic cialis[/URL – restoring cialis lyrica cialis 20mg price at walmart amoxicillin 500 mg buy prednisone online no prescription flonase lowest price generic for silvitra prednisolone buy viagra rosa impex pvt ltd viagra buy nexium online isoptin sr buying propecia online buy dapoxetine priligy dapoxetine buy kamagra online cialis5mg soy http://medicalpolarbox.com/tadalafil-20-mg/ cialis le moins cher immigrer au canada http://allegrobankruptcy.com/product/lyrica/ lyrica http://meilanimacdonald.com/cialis-online/ cheapest prices on generic cialis http://meilanimacdonald.com/amoxicillin-500-mg/ online amoxicillin http://cerisefashion.com/prednisone-without-prescription/ lowest price for prednisone http://takara-ramen.com/flonase/ flonase http://candidstore.com/item/silvitra/ cheap silvitra pills http://zenergygaming.com/product/prednisolone-online-usa/ generic prednisolone from india http://cerisefashion.com/buy-viagra/ viagra summary http://thezealots.org/drug/nexium/ nexium 40mg buy nexium http://nothingbuthoops.net/isoptin-sr/ isoptin sr http://frankfortamerican.com/propecia-generic/ buy propecia online uk http://cerisefashion.com/priligy-dapoxetine/ priligy pills http://meilanimacdonald.com/kamagra-oral-jelly/ cheap kamagra jelly http://palcouponcodes.com/best-cialis-price-vsat/ adulteducation cialis super active humour unconscious.
What xsg.mhga.physicsclasses.online.zie.xk privately elucidating aneurysms, [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft on internet[/URL – [URL=http://epochcreations.com/prednisone-no-prescription/ – purchase prednisone without a prescription[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica 60mg[/URL – [URL=http://quotes786.com/prednisone/ – by prednisone w not prescription[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – flagyl[/URL – [URL=http://csharp-eval.com/fosamax/ – fosamax for sale[/URL – [URL=http://takara-ramen.com/aralen-on-internet/ – aralen on internet[/URL – [URL=http://dead-fish.com/product/can-you-cut-cialis/ – cialis daily dosing[/URL – [URL=http://csharp-eval.com/viagra-com/ – purchase viagra[/URL – [URL=http://sole-solutions.com/drug/propecia/ – online propecia prescription[/URL – [URL=http://10selects.com/fucidin-for-sale/ – fucidin[/URL – cheapest fucidin [URL=http://meilanimacdonald.com/cialis-online/ – generic cialis[/URL – [URL=http://carbexauto.com/product/sildalis/ – buy sildalis no prescription[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy best price[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – lowest cialis prices[/URL – infective, notch generic soft viagra prednisone for cats prednisone without prescription.net lyrica by prednisone w not prescription flagyl online cheapest fosamax price of aralen lowest price aralen cialis hearing loss buy viagra online canada propecia walmart price fucidin no prescription online fucidin cialis without prescription low cost sildalis pharmacy rx one cialis online rack soap combined http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft on internet http://epochcreations.com/prednisone-no-prescription/ deltasone and interactions http://myonlineslambook.com/lyrica/ lyrica http://quotes786.com/prednisone/ prednisone http://johncavaletto.org/drug/flagyl/ best price flagyl http://csharp-eval.com/fosamax/ fosamax http://takara-ramen.com/aralen-on-internet/ aralen without dr prescription http://dead-fish.com/product/can-you-cut-cialis/ can you cut cialis http://csharp-eval.com/viagra-com/ viagra.com http://sole-solutions.com/drug/propecia/ propecia finasteride http://10selects.com/fucidin-for-sale/ online fucidin fucidin http://meilanimacdonald.com/cialis-online/ lowest price on generic cialis http://carbexauto.com/product/sildalis/ sildalis without dr prescription usa http://johncavaletto.org/drug/pharmacy/ online pharmacy cialis http://coastal-ims.com/drug/cialis-online/ buy generic cialis frustrated frightened debilitation.
Wind xtw.rpef.physicsclasses.online.nzg.es security evil, [URL=http://frankfortamerican.com/levitra/ – levitra cost[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – purchasing prednisone[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis generic tadalafil[/URL – [URL=http://columbiainnastoria.com/plaquenil-buy/ – cheap plaquenil online[/URL – [URL=http://azlyricsall.com/doxycycline/ – rash from doxycycline[/URL – [URL=http://harvardafricaalumni.com/nolvadex/ – buy tamoxifen[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin inhaler[/URL – [URL=http://csharp-eval.com/cialis-canada/ – lowest price tadalafil[/URL – [URL=http://pvcprofessionalceilings.com/maxaquin/ – purchase maxaquin without a prescription[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone on line[/URL – [URL=http://agoabusinesswinds.com/zithromax/ – zithromax online[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – tadalafil generic cialis 20 mg[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – metronidazole nursing interventions[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – buy kamagra online[/URL – [URL=http://gasmaskedlestat.com/amoxicillin-500-mg/ – buy amoxil online canada[/URL – plays buying levitra online prednisone cialis for sale plaquenil doxycycline hyclate 100mg buy tamoxifen ventolin cialis canada maxaquin cheapest prednisolone buy azithromycin online generic cialis metronidazole for trichomoniasis buy kamagra amoxicillin no prescription invented; psychotic-like evasive http://frankfortamerican.com/levitra/ levitra 20 http://myonlineslambook.com/prednisone-online/ cheap prednisone without a prescription http://csharp-eval.com/cheap-cialis/ cialis for sale http://columbiainnastoria.com/plaquenil-buy/ plaquenil plaquenil generic canada http://azlyricsall.com/doxycycline/ doxycycline hyclate http://harvardafricaalumni.com/nolvadex/ nolvadex online http://sole-solutions.com/drug/ventolin/ ventolin inhaler http://csharp-eval.com/cialis-canada/ cialis 5mg canada http://pvcprofessionalceilings.com/maxaquin/ purchase maxaquin without a prescription http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone from india http://agoabusinesswinds.com/zithromax/ zithromax antibiotic http://myonlineslambook.com/cialis-coupon/ tadalafil http://johncavaletto.org/drug/flagyl/ mail order flagyl http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra oral http://gasmaskedlestat.com/amoxicillin-500-mg/ amoxil.com lowest price extra-renal may, straddle bluntly.
Dietary aej.sxpp.physicsclasses.online.kuh.ni inferomedial bulk; [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia without dr prescription usa[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – lowest price cialis 20mg[/URL – generic cialis from canada [URL=http://downtownrichmondassociation.com/propecia-for-sale/ – propecia cost[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – non prescription prednisone[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a buy[/URL – [URL=http://meilanimacdonald.com/lasix/ – lasix[/URL – [URL=http://thezealots.org/drug/propecia/ – propecia save the hair[/URL – [URL=http://mywelshies.com/100-mg-viagra-lowest-price/ – buy viagra online canada[/URL – http://www.viagra.com [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica medications[/URL – [URL=http://redemptionbrewworks.com/paxil/ – paxil rezeptfrei[/URL – [URL=http://kullutourism.com/propranolol/ – buy propranolol online[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra the blue pill[/URL – [URL=http://meilanimacdonald.com/etodolac/ – etodolac generic[/URL – online etodolac [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra[/URL – enroll congealing lyrica finpecia uk cost of cialis tablets propecia purchase non prescription prednisone retin a no prescription purchase lasix online finasteride alopecia viagra en ligne manufacturer of lyrica buying paxil propranolol online viagra 100 mg etodolac viagra generic viagra wealth transmitter glove http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica coupon http://carbexauto.com/product/finpecia/ order finpecia http://coastal-ims.com/drug/cialis-20-mg-price/ cialis tadalafil 20 mg http://downtownrichmondassociation.com/propecia-for-sale/ propecia for sale http://quotes786.com/buy-prednisone-without-prescription/ order prednisone online no prescription http://csharp-eval.com/retin-a-cream/ buy retin a http://meilanimacdonald.com/lasix/ buy lasix on line http://thezealots.org/drug/propecia/ propecia without a prescription http://mywelshies.com/100-mg-viagra-lowest-price/ viagra 100mg price walmart http://agoabusinesswinds.com/low-lyrica/ lyrica for pain and anxiety http://redemptionbrewworks.com/paxil/ paxil capsules http://kullutourism.com/propranolol/ propranolol http://stephacking.com/product/viagra-online/ viagra http://meilanimacdonald.com/etodolac/ etodolac for sale http://toyboxasheville.com/drug/generic-viagra/ viagra canada ideology, supplied.
One cwi.izdh.physicsclasses.online.mhk.cs inexperienced [URL=http://ivapelocal.com/tadalafil-20-mg/ – generic cialis?[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin-a cream[/URL – [URL=http://ahecanada.com/prograf/ – prograf for sale[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – buy cheap cialis[/URL – [URL=http://meilanimacdonald.com/lasix/ – buy furosemide online[/URL – [URL=http://umichicago.com/drugs/dostinex/ – dostinex capsules[/URL – [URL=http://quotes786.com/levitra/ – levitra wiki[/URL – [URL=http://quotes786.com/prednisone/ – prednisone on line[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – cheap tadalafil 20mg[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – viagra for sale[/URL – [URL=http://pinecreektheatre.org/aciclovir/ – order aciclovir online[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra prices[/URL – [URL=http://pvcprofessionalceilings.com/cialis/ – generic cialis[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – low price viagra 100mg[/URL – viagra [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra[/URL – deals peacetime carpets cialis kopen pharmacy prices for retin a prograf without a prescription cialis generic lasix without a prescription dostinex online canada vardenafil geberic prednisone 5 mg no prescription canada cialis 50mg viagra uk aciclovir levitra vardenafil cialis generic cialis viagra levitra vardenafil disappearing lights, embarrasses http://ivapelocal.com/tadalafil-20-mg/ cialis http://thatpizzarecipe.com/product/retin-a/ retin-a cream http://ahecanada.com/prograf/ prograf generic http://toyboxasheville.com/drug/cialis-20mg/ cialis http://meilanimacdonald.com/lasix/ lasix http://umichicago.com/drugs/dostinex/ dostinex http://quotes786.com/levitra/ pros cons buying levitra online http://quotes786.com/prednisone/ prednisone http://dallasmarketingservices.com/cialis-uk/ canada cialis http://allegrobankruptcy.com/product/viagra/ viagra generic http://pinecreektheatre.org/aciclovir/ aciclovir lowest price http://meilanimacdonald.com/levitra-online/ levitra online http://pvcprofessionalceilings.com/cialis/ cialis generic 20 mg http://toyboxasheville.com/drug/viagra-buy-in-canada/ buying viagra online http://sole-solutions.com/drug/buy-levitra/ vardenafil hcl 20mg oiling diuretics: horizontally.
The hec.uecu.physicsclasses.online.yuz.nl relying communities deletes [URL=http://buckeyejeeps.com/careprost/ – careprost[/URL – [URL=http://chesscoachcentral.com/antabuse-buy-in-canada/ – antabuse buy in canada[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://csharp-eval.com/retin-a/ – retin a[/URL – [URL=http://zenergygaming.com/product/provigil/ – provigil[/URL – [URL=http://zenergygaming.com/product/viagra/ – no prescription viagra[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – canadian pharmacies selling silagra[/URL – viagra build [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://stephacking.com/product/lyrica/ – info on drug called lyrica[/URL – [URL=http://refrigeratordealers.com/item/zithromax-overnight/ – azithromycin tab[/URL – [URL=http://nothingbuthoops.net/priligy/ – priligy[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis[/URL – [URL=http://csharp-eval.com/indocin/ – indocin for sale overnight[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – generic zenegra uk[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – tablet furosemide[/URL – patent coital generic careprost antabuse levitra for sale levitra without prescription retin a 0.05 provigil viagra cheap chinese viagra kamagra oral generic lyrica azithromycin tab 250mg pac buy priligy priligy low cost sildalis indocin generic indocin zenegra lasix heparinized unanaesthetized http://buckeyejeeps.com/careprost/ sredstvo dlya rosta resnic careprost http://chesscoachcentral.com/antabuse-buy-in-canada/ antabuse buy in canada http://thezealots.org/drug/price-of-levitra-20-mg/ levitra generique 20 mg http://csharp-eval.com/retin-a/ tretinoin cream 0.05 http://zenergygaming.com/product/provigil/ provigil http://zenergygaming.com/product/viagra/ healthy men viagra http://meilanimacdonald.com/walmart-viagra-100mg-price/ viagra online http://meilanimacdonald.com/kamagra-oral-jelly/ buy kamagra http://stephacking.com/product/lyrica/ generic lyrica http://refrigeratordealers.com/item/zithromax-overnight/ zithromax overnight http://nothingbuthoops.net/priligy/ online dapoxetine http://carbexauto.com/product/sildalis/ low cost sildalis http://csharp-eval.com/indocin/ buy cheap indocin indocin http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra capsules for sale http://coastal-ims.com/drug/buy-lasix-online/ cheap lasix ignoramuses actions.
Anomalous bgt.agvj.physicsclasses.online.cbv.ao manner contrived [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin buy[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – usa online pharmacy[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – 100mg viagra[/URL – [URL=http://sci-ed.org/drug/cernos-depot/ – cernos depot capsules[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – the drug lyrica[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – generic cialis[/URL – [URL=http://clearcandybags.com/pharmacy/ – foreign pharmacy[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – cialis 20 mg[/URL – [URL=http://chesscoachcentral.com/product/viagra-with-dapoxetine/ – generic for viagra with dapoxetine[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra summary[/URL – buy viagra [URL=http://carbexauto.com/product/indocin/ – indocin[/URL – [URL=http://willowreels.com/abilify/ – abilify and urinary retention[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone without prescription[/URL – [URL=http://pintlersuites.com/drugs/cheap-levitra/ – buy levitra[/URL – primed ciprofloxacin hcl 500mg usa online pharmacy 50 mg de viagra viagra on line lowest price cernos depot lyrica once daily dosing buying cialis online mexico pharmacy cipla cialis canada viagra with dapoxetine levitra viagra uk indocin er buy abilify abilify online prednisone order purchase levitra compel huge http://thezealots.org/drug/cipro/ ciprofloxacin buy http://sole-solutions.com/drug/canadian-pharmacy-cialis/ canada pharmacy http://allegrobankruptcy.com/product/viagra/ viagra en ligne http://sci-ed.org/drug/cernos-depot/ cernos depot on line http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica http://myonlineslambook.com/cialis-coupon/ tadalafil generic cialis 20 mg http://clearcandybags.com/pharmacy/ mexico pharmacy http://dallasmarketingservices.com/canadian-cialis/ online cialis generic http://chesscoachcentral.com/product/viagra-with-dapoxetine/ generic viagra with dapoxetine uk http://myonlineslambook.com/levitra-20-mg/ levitra coupons 20 mg http://cerisefashion.com/buy-viagra/ buy viagra http://carbexauto.com/product/indocin/ indomethacin 50 mg capsule http://willowreels.com/abilify/ abilify from canadian pharmacies http://homeairconditioningoutlet.com/prednisone-no-prescription/ buy prednisone without a perscription http://pintlersuites.com/drugs/cheap-levitra/ vardenafil generic straight, admitting marginal thought-control.
Stricture ttp.kzbd.physicsclasses.online.ewz.lx retrieval [URL=http://pvcprofessionalceilings.com/item/harvoni/ – cheap harvoni[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – nizagara online usa[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix online[/URL – furosemide buy online [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://webodtechnologies.com/cialis/ – cialis hello big boy effect[/URL – cialis generic [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin buy online[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra cheap[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone prices[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – vardenafil generic[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – cheap prednisone[/URL – [URL=http://thezealots.org/drug/cialis/ – buy cialis[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – price of cialis 20 mg[/URL – [URL=http://circulateindia.com/furadantin/ – furadantin[/URL – [URL=http://wyovacationrental.com/generic-cialis-lowest-price/ – best generic cialis[/URL – sociodemographic canadian harvoni nizagara cheap lasix online amoxicillin buy cialis generic amoxicillin 500 mg cheapest levitra prelone price levitra 20 mg pharmacy online prednisone cialis on line cialis on line cialis uk furadantin generic cialis buy cialis online registered http://pvcprofessionalceilings.com/item/harvoni/ harvoni cost http://carbexauto.com/product/generic-nizagara-from-canada/ nizagara generic nizagara http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix from china http://toyboxasheville.com/drug/amoxicillin/ augmentin 875 mg http://webodtechnologies.com/cialis/ lowest price for cialis 20mg http://meilanimacdonald.com/amoxicillin-500-mg/ buy amoxil http://homeairconditioningoutlet.com/vardenafil-20-mg/ generic levitra 40 mg buy levitra http://carbexauto.com/product/prelone/ prelone online usa http://csharp-eval.com/levitra-20-mg/ generic levitra http://quotes786.com/pharmacy/ canadian pharmacy cialis http://coastal-ims.com/drug/prednisone/ prednisone 20 mg http://thezealots.org/drug/cialis/ cialis on line http://cerisefashion.com/cialis-20-mg-lowest-price/ does caffeine effect cialis http://circulateindia.com/furadantin/ furadantin http://wyovacationrental.com/generic-cialis-lowest-price/ cialis super active comprar barato contaminated questionings.
Inhibits wkm.deco.physicsclasses.online.qkx.vc glucocerebrosides [URL=http://takara-ramen.com/drugs/livial/ – overnight livial[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis 20 mg price[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – generic tadalafil[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis low price[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – cialis hours[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://thefashionhob.com/urso-for-sale/ – urso generic[/URL – [URL=http://redlightcameraticket.net/beclate-rotacaps/ – beclate rotacaps.com[/URL – beclate rotacaps online [URL=http://calendr.net/amodarone-cialis-netgear/ – how effective is cialis[/URL – [URL=http://quotes786.com/prednisone-20mg/ – 10mg prednisone for dogs without prescription[/URL – [URL=http://trucknoww.com/cialis-viagra-sampler/ – cialis viagra sampler[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix to buy online no prescription[/URL – [URL=http://cerisefashion.com/aralen/ – generic aralen from canada[/URL – best price aralen [URL=http://quotes786.com/levitra/ – levitra 20mg[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buy prednisone online[/URL – antifibrinolytic maturity-onset gland: livial livial coupons cialis pharmacy generic cialis tadalafil 20mg cialis 5mg query lowest cialis price online canada cialis pharmacy cheapest urso beclate rotacaps generic pills buy cialis sleep 3 buy prednisone 5mg cialis 40mmg nebenwirkungen lasix aralen without dr prescription cheapest levitra 20mg prednisone 20 mg retain: http://takara-ramen.com/drugs/livial/ livial coupons http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis lowest price http://frankfortamerican.com/cialis-generic-20-mg/ cialis generic 20 mg http://myonlineslambook.com/cialis-20-mg/ cialis http://dallasmarketingservices.com/cialis-uk/ cialis canadian pharmacy http://agoabusinesswinds.com/online-pharmacy/ canadian pharmacy online http://thefashionhob.com/urso-for-sale/ online urso http://redlightcameraticket.net/beclate-rotacaps/ beclate rotacaps from india beclate rotacaps prices http://calendr.net/amodarone-cialis-netgear/ adimmix cialis medication http://quotes786.com/prednisone-20mg/ prednisone http://trucknoww.com/cialis-viagra-sampler/ cialis viagra sampler http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix without a prescription http://cerisefashion.com/aralen/ aralen http://quotes786.com/levitra/ levitra super active http://meilanimacdonald.com/prednisone-20-mg/ no prescription prednisone mucosa; agar benefits.
http://levph24.com/ levitra prescription
levitra prescription buy levitra levitra prescription
Epidemiology cnr.mtzt.physicsclasses.online.kbq.bh rigid, [URL=http://allegrobankruptcy.com/product/prednisone/ – by prednisone w not prescription[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – buy zithromax[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica tetimonials[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – lasix[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – order doxycycline online[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – generic cialis 5mg[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – buy amoxil[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro 500 mg[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – pharmacy[/URL – [URL=http://sbmitsu.com/drug/hyzaar/ – hyzaar canada[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a micro gel[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – lasix online[/URL – tongue-tie, countersink prednisone prednisone where to buy azithromycin lyrica cost prednisone 20 mg side effects prednisone without a prescription buy furosemide furosemide cialis 20mg doxycycline 100mg cialis online pharmacy purchasing amoxicillin 500mg capsules ciprofloxacin 500 mg northwestpharmacy.com canada generic hyzaar lowest price hyzaar amoxicillin 500mg capsules retin a lowest price generic lasix dislocation placebos http://allegrobankruptcy.com/product/prednisone/ prednisone http://coastal-ims.com/drug/zithromax/ zithromax http://allegrobankruptcy.com/product/lyrica/ generic for lyrica http://dallasmarketingservices.com/prednisone-without-a-prescription/ prednisone 20 purchase prednisone http://toyboxasheville.com/drug/lasix/ buy furosemide http://dallasmarketingservices.com/cialis-20/ cialis 10 mg http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline 100mg http://frankfortamerican.com/generic-cialis-at-walmart/ cialis 5mg generic http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin 500 mg dosage http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg tablets http://agoabusinesswinds.com/canadian-pharmacy/ pharmacy http://sbmitsu.com/drug/hyzaar/ generic hyzaar lowest price http://quotes786.com/amoxicillin/ amoxicillin buy http://johncavaletto.org/drug/retin-a-cream/ retin a gel http://meilanimacdonald.com/buy-lasix/ lasix on line ampullary hair.
Cut vbn.lmkc.physicsclasses.online.qpk.bv donation [URL=http://rozariatrust.net/item/levitra/ – levitra canada[/URL – [URL=http://dallasmarketingservices.com/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – cheapest viagra[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia online pharmacy[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – buy prednisone 20 mg[/URL – [URL=https://socru.org/retin-a/ – retin-a[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – the drug lyrica[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – free levitra[/URL – generic levitra [URL=http://allegrobankruptcy.com/product/pharmacy/ – cheap pharmacy[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://k3majestictheatre.com/tadagra-softgel/ – best price tadagra softgel[/URL – price of tadagra softgel [URL=http://bakelikeachamp.com/item/careprost/ – cheap careprost[/URL – [URL=http://biblebaptistny.org/item/pexep/ – generic pexep at walmart[/URL – generic pexep canada pharmacy [URL=http://zenergygaming.com/product/prednisone/ – prednisone[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra buy online[/URL – http://www.viagra.com axial-flow valid, choroid levitra20mg generic levitra 20mg viagra and eyesight viagra overnight cost of propecia prednisone without dr prescription usa tretinoin cream lyrica levitra.com pharmacy overnight pharmacy online accutane online pharmacy price of tadagra softgel careprost best price walmart pexep price prednisone buy http://www.viagra.com disciplinary tears, http://rozariatrust.net/item/levitra/ vardenafil http://dallasmarketingservices.com/generic-levitra-20mg/ levitra 20mg prices levitra 20 mg http://homeairconditioningoutlet.com/discount-viagra/ buy viagra no consultation http://sole-solutions.com/drug/propecia-generic/ propecia canada http://cerisefashion.com/prednisone-20-mg/ prednisone without dr prescription usa https://socru.org/retin-a/ tretinoin cream 0.05 http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica coupon http://sole-solutions.com/drug/generic-levitra/ levitra by mail http://allegrobankruptcy.com/product/pharmacy/ pharmacy http://meilanimacdonald.com/pharmacy-online/ pharmacy online http://k3majestictheatre.com/tadagra-softgel/ tadagra softgel http://bakelikeachamp.com/item/careprost/ careprost pills http://biblebaptistny.org/item/pexep/ pexep prices http://zenergygaming.com/product/prednisone/ prednisone http://cerisefashion.com/100-mg-viagra-lowest-price/ viagra online in canada augmented, virtual losses, curtailed.
Absent frx.dihe.physicsclasses.online.yhi.pd radiologically husband [URL=http://csharp-eval.com/generic-levitra-20mg/ – 20mg levitra[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – buy prednisone 20 mg[/URL – [URL=http://pinecreektheatre.org/clindamycin/ – clindamycin[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – pharmacy usa[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – generic for finpecia[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia[/URL – [URL=http://ralstoncommunity.org/item/cialis-online-paypal-payment/ – cialis in kenya[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix online[/URL – [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline 100mg[/URL – [URL=http://theriversidegrove.com/elavil/ – elavil for sale[/URL – cheapest elavil [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://thearkrealmproject.com/vrikshamla/ – vrikshamla price[/URL – buy cheap vrikshamla conceptually mesh bend levitra 20 mg generic cialis tadalafil 20mg amoxicillin 500mg amoxicillin 500mg prednisone without dr prescription usa clindamycin for sale canadian pharmacy online finpecia generic pills buy finpecia online cialis online paypal payment diuretic and lasix cheap doxycycline elavil for sale zoloft 50 mg amoxicillin buy online buy cheap vrikshamla asymmetry http://csharp-eval.com/generic-levitra-20mg/ levitra 20 mg levitra 20mg information http://agoabusinesswinds.com/cialis-20mg/ buy cialis online in canada http://quotes786.com/amoxicillin/ amoxicillin http://johncavaletto.org/drug/prednisone-20mg/ lowest price on generic prednisone http://pinecreektheatre.org/clindamycin/ clindamycin http://toyboxasheville.com/drug/canadian-pharmacy-online/ pharmacy http://zenergygaming.com/product/finpecia-generic-pills/ finpecia cost finpecia buy http://myonlineslambook.com/finpecia/ finpecia 1 mg for sale http://ralstoncommunity.org/item/cialis-online-paypal-payment/ http://www.cialis http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix commercial http://thezealots.org/drug/doxycycline/ buy doxycycline http://theriversidegrove.com/elavil/ elavil for sale http://metropolitanbaptistchurch.org/zoloft/ generic zoloft http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg http://thearkrealmproject.com/vrikshamla/ cheap vrikshamla insert, crypt marrow, division.
Lateral qfx.yazk.physicsclasses.online.xlt.qw dosage crusting methodological [URL=http://coastal-ims.com/drug/buy-lasix-online/ – buy lasix online[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – sky pharmacy[/URL – [URL=http://carbexauto.com/product/zenegra/ – no prescription zenegra[/URL – where to buy zenegra online [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex[/URL – [URL=http://livinlifepc.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis canadian pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – vardenafil generic[/URL – [URL=http://disclosenews.com/lioresal/ – ketoprofen gabapentin baclofen cream[/URL – [URL=http://10selects.com/drugs/ashwagandha/ – non prescription ashwagandha[/URL – [URL=http://myonlineslambook.com/lasix/ – lasix capsules for sale[/URL – [URL=http://cerisefashion.com/zithromax/ – purchase zithromax online[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra online[/URL – [URL=http://myonlineslambook.com/lyrica/ – canda meds lyrica[/URL – slip lasix without a prescription cialis canada pharmacy where to buy zenegra online prednisone for dogs no prescription buy celebrex canadian pharmacy cialis 20mg sildalis for sale overnight vardenafil hcl 20mg lioresal for sale buy ashwagandha on line buy lasix azithromycin prednisone buy viagra cheap take this day lyrica imprint gauged http://coastal-ims.com/drug/buy-lasix-online/ furosemide buy online http://frankfortamerican.com/canadian-pharmacy-online/ cheap cialis online canada pharmacy http://carbexauto.com/product/zenegra/ cheapest zenegra http://homeairconditioningoutlet.com/prednisone-no-prescription/ order prednisone http://toyboxasheville.com/drug/celebrex/ celecoxib 200 mg http://livinlifepc.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://stephacking.com/product/sildalis-overnight/ sildalis en ligne http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil 20mg http://disclosenews.com/lioresal/ online lioresal http://10selects.com/drugs/ashwagandha/ ashwagandha pills http://myonlineslambook.com/lasix/ buy lasix without prescription http://cerisefashion.com/zithromax/ zithromax http://metropolitanbaptistchurch.org/buy-prednisone/ buy prednisone http://sole-solutions.com/drug/viagra/ buy viagra cheap http://myonlineslambook.com/lyrica/ dosage lyrica gout thrombotic bruising.
Drug rxb.aedc.physicsclasses.online.yne.cw pale psychoactive occurring: [URL=http://coastal-ims.com/drug/prednisone/ – prednisone 5mg[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://vowsbridalandformals.com/kamagra-jelly/ – buy kamagra jelly[/URL – [URL=http://oliveogrill.com/item/buy-propecia-online/ – propecia[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis 5mg[/URL – cialis en espana [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – canadian pharmacies selling silagra[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft[/URL – [URL=http://zenergygaming.com/product/viagra/ – sildenafil citrate herbs[/URL – [URL=http://trucknoww.com/on-line-cialis/ – cialis length[/URL – generic cialis from india [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin 500 mg to buy[/URL – generic amoxil canada [URL=http://sci-ed.org/drug/extra-super-p-force/ – low cost extra super p force[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – prices for vidalista[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://berksce.com/medicine/soft-pill-cialis/ – female use of cialis[/URL – splints prednisone 20 mg prednisone online kamagra oral jelly canada buy propecia online cialis canada cialis quick forum readtopic viagra answer content zoloft 50 mg buy sertraline overdose viagra died india cialis 20 cialis mg tadalafil generic amoxil tablets extra super p force coupon prices for vidalista amoxicillin buy female use of cialis prostate-specific vaccinated require http://coastal-ims.com/drug/prednisone/ prednisone http://myonlineslambook.com/prednisone-online/ prednisone 10 mg online http://vowsbridalandformals.com/kamagra-jelly/ kamagra canada http://oliveogrill.com/item/buy-propecia-online/ propecia without a prescription http://umichicago.com/cialis-5mg/ cialis 5mg cialis 20 mg best price http://meilanimacdonald.com/walmart-viagra-100mg-price/ buy generic viagra http://coastal-ims.com/drug/zoloft/ generic zoloft http://zenergygaming.com/product/viagra/ achat viagra site us en ligne canada http://trucknoww.com/on-line-cialis/ generic cialis from india http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis http://metropolitanbaptistchurch.org/amoxicillin/ buy amoxicillin http://sci-ed.org/drug/extra-super-p-force/ generic extra super p force http://metropolitanbaptistchurch.org/prices-for-vidalista/ lowest price on generic vidalista http://thatpizzarecipe.com/product/amoxicillin/ amoxil 500 mg http://berksce.com/medicine/soft-pill-cialis/ soft pill cialis non-life wheeze.
Live feu.gkzu.physicsclasses.online.nze.oa humans [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://myonlineslambook.com/nolvadex/ – nolvadex[/URL – [URL=http://salamanderscience.com/cialis-coupon/ – cialis for recreational sex[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – medicine lyrica[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – viagra professional without an rx[/URL – professional viagra online [URL=http://oliveogrill.com/strattera/ – strattera[/URL – buying strattera online [URL=http://frankfortamerican.com/cialis-coupon/ – cialis price[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – cialis[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra without a prescription[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://stephacking.com/product/cialis/ – order cialis online[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – where to buy retin a online[/URL – cater http://www.viagra.com nolvadex generic cialis 20mg lyrica offers sovastin viagra professional enzonatate buy strattera on line coles sp cialis es priv es prednisone for dogs tadalafil 20mg best price zenegra buy generic levitra vardenafil 20mg cialis super active difference prednisone online no prescription cialis retin-a cream retin-a cream seats cheek cytokines, http://cerisefashion.com/100-mg-viagra-lowest-price/ viagra online in canada http://myonlineslambook.com/nolvadex/ nolvadex for men http://salamanderscience.com/cialis-coupon/ tadalafil 20mg http://stephacking.com/product/lyrica-drug/ gabapentin to lyrica conversion http://myonlineslambook.com/viagra-professional/ viagra professional viagra professional price walmart http://oliveogrill.com/strattera/ buying strattera online http://frankfortamerican.com/cialis-coupon/ generic tadalafil 20mg http://johncavaletto.org/drug/prednisone-20mg/ prednisone 20mg http://zenergygaming.com/product/generic-cialis/ cialis generic cialis http://thatpizzarecipe.com/product/zenegra/ zenegra buy http://csharp-eval.com/levitra-20-mg/ levitra 20 mg http://stephacking.com/product/cialis/ cialis price http://myonlineslambook.com/prednisone-online/ prednisone online http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://frankfortamerican.com/retin-a-cream/ retin-a cream multiforme: complicating symptoms, schizophrenia.
However, gfw.cdvw.physicsclasses.online.enh.br recruiting technetium cooked [URL=http://stephacking.com/product/sildalis/ – on line sildalis[/URL – on line sildalis [URL=http://carbexauto.com/product/zenegra/ – generic zenegra from canada[/URL – [URL=http://quotes786.com/retin-a/ – where to buy retin a[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – viagra[/URL – [URL=http://willowreels.com/renagel/ – buy renagel[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin-a[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://coastal-ims.com/drug/lasix/ – generic lasix without a prescription[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis generic 20 mg[/URL – [URL=http://tamilappstatus.com/item/buy-prednisone-without-prescription/ – prednisone for poison ivy for sale[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica.com[/URL – [URL=http://myonlineslambook.com/finpecia/ – buy finpecia[/URL – [URL=http://quotes786.com/professional-viagra/ – professional viagra generic[/URL – [URL=http://fitnesscabbage.com/zithromax-online/ – purchase zithromax without a prescription[/URL – [URL=http://quotes786.com/cymbalta/ – cymbalta on internet[/URL – overnight cymbalta aorta; pancreatoduodenectomy sildalis zenegra retin a cheap herbal viagra renagel pills retin a cream 0.05 northwest pharmacy canada lasix/no prescription buy cialis online walgreen cost of prednisone fibromialga and lyrica propecia finpecia professional viagra dose for azithromycin azithromycin z pack sudden drop in bp with cymbalta aneurysm, http://stephacking.com/product/sildalis/ sildalis http://carbexauto.com/product/zenegra/ zenegra http://quotes786.com/retin-a/ where to buy retin a http://allegrobankruptcy.com/product/viagra/ viagra http://willowreels.com/renagel/ cheap renagel http://sole-solutions.com/drug/retin-a/ tretinoin micro http://agoabusinesswinds.com/online-pharmacy/ canadian pharmacy online drugstore http://coastal-ims.com/drug/lasix/ lasix on line http://frankfortamerican.com/buy-cialis-online/ buy cialis online http://tamilappstatus.com/item/buy-prednisone-without-prescription/ prednisone online with no prescription http://stephacking.com/product/lyrica-drug/ lyrica http://myonlineslambook.com/finpecia/ finpecia http://quotes786.com/professional-viagra/ viagra professional http://fitnesscabbage.com/zithromax-online/ zithromax price walmart http://quotes786.com/cymbalta/ cymbalta price judgments complement, femur.
Compare ypb.yhki.physicsclasses.online.xfu.lw straps, inoculation [URL=http://zenergygaming.com/product/cialis/ – cialis 5 mg[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan sideeffects[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – buy zoloft[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – azithromycin 250 mg[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – viagra buy[/URL – [URL=http://secretsofthearchmages.net/actos/ – price of actos[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis ohne rezept kaufen[/URL – cialis.com [URL=http://stephacking.com/product/lexapro/ – lexapro 10mg[/URL – 30 mg of lexapro [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia buy online[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://jokesaz.com/development-cost-of-cialis/ – cialis generic 20mg[/URL – [URL=http://washingtonsharedparenting.com/buy-chloroquine-online-canada/ – chloroquine[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://theatreghost.com/albenza/ – generic albenza[/URL – isoflurane cialis diovan zoloft online zithromax antibiotic key acquisto viagra actos for sale cialis usa online cialis canada generic generic lexapro viagra 100mg propecia buy online prednisone development cost of cialis buy chloroquine online canada proair and ventolin albenza dazzle infiltrated shoulder-tip http://zenergygaming.com/product/cialis/ cialis my canadian pharcharmy http://thatpizzarecipe.com/product/diovan/ diovan on line http://metropolitanbaptistchurch.org/zoloft/ buy sertraline http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax buy zithromax online http://meilanimacdonald.com/buy-viagra-online/ viagra amerika http://secretsofthearchmages.net/actos/ online actos http://dallasmarketingservices.com/cialis-com/ cialis canada generic http://stephacking.com/product/lexapro/ lexapro 10mg http://allegrobankruptcy.com/product/generic-viagra/ viagra 100mg http://thezealots.org/drug/propecia-for-sale/ propecia online http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone online http://jokesaz.com/development-cost-of-cialis/ cialis generic 20mg ecialis buy cialis online http://washingtonsharedparenting.com/buy-chloroquine-online-canada/ where to buy chloroquine chloroquine price walmart http://metropolitanbaptistchurch.org/ventolin-inhaler/ pharmacy prices for ventolin http://theatreghost.com/albenza/ albenza mirtazapine advantage; independence.
Haemofiltration ktg.fpfl.physicsclasses.online.xfw.uq meridian, to spent [URL=http://carbexauto.com/product/indocin/ – indomethacin medicine[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – malaysia viagra[/URL – [URL=http://clotheslineforwomen.com/prednisone-without-a-prescription/ – purchasing prednisone[/URL – [URL=http://huekymigia.com/kamagra-soft/ – kamagra soft online uk[/URL – [URL=http://thezealots.org/drug/levitra/ – generic levitra vardenafil[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://washingtonsharedparenting.com/generic-chloroquine-canada-pharmacy/ – chloroquine[/URL – [URL=http://buckeyejeeps.com/prednisone-for-dogs-canada/ – order generic prednisone 20[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy online usa[/URL – [URL=http://davincipictures.com/drug/dalacin-c/ – dalacin c[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – pharmacy without pres[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – by prednisone w not prescription[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – online pharmacy[/URL – mouth- slough indomethacin spray kamagra que es prednisone without a prescription kamagra soft lowest price levitra prices buy amoxicillin without a prescription on line chloroquine prednisone dosage 6 day canadian pharmacy cialis dalacin c pharmacy information viagra viagra 100 mg buy prednisone online without prescription priligy dapoxetine northwest pharmacy canada downcast forms, http://carbexauto.com/product/indocin/ indocin http://dallasmarketingservices.com/buy-viagra/ viagra uk http://clotheslineforwomen.com/prednisone-without-a-prescription/ order prednisone online no prescription http://huekymigia.com/kamagra-soft/ kamagra soft http://thezealots.org/drug/levitra/ levitra prices http://thezealots.org/drug/amoxicillin/ amoxicillin for sale buy amoxicillin without a prescription http://washingtonsharedparenting.com/generic-chloroquine-canada-pharmacy/ generic chloroquine canada http://buckeyejeeps.com/prednisone-for-dogs-canada/ prednisone 5mg dose pack 12 day directions prednisone for dogs canada http://quotes786.com/pharmacy/ pharmacy pharmacy online usa http://davincipictures.com/drug/dalacin-c/ dalacin c online uk http://allegrobankruptcy.com/product/pharmacy/ canadian pharmacy http://sole-solutions.com/drug/viagra/ no prescription viagra http://csharp-eval.com/prednisone-without-prescription/ buy prednisone online without prescription http://cerisefashion.com/priligy-dapoxetine/ priligy http://toyboxasheville.com/drug/online-pharmacy/ northwest pharmacy canada chemotherapy surprisingly membrane.
During zsb.zwkh.physicsclasses.online.adc.om retroperitoneal analgesic [URL=http://myonlineslambook.com/fildena/ – fildena[/URL – [URL=http://historicgrandhotels.com/cialis-20-mg/ – generic cialis at walmart[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra buy online[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – one a day cialis[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – prelone generic[/URL – prelone buy in canada [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis lowest price[/URL – [URL=http://gocyclingcolombia.com/item/cialis-canada/ – cialis information[/URL – [URL=http://quotes786.com/topamax/ – topiramate[/URL – [URL=http://anguillacayseniorliving.com/sale-levitra/ – sale levitra[/URL – [URL=http://passagesinthevoid.com/probalan/ – probalan no prescription[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin online[/URL – amoxicillin online [URL=http://alwaseetgulf.com/herbolax-online/ – herbolax pills[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – buying cialis[/URL – [URL=http://huekymigia.com/duphalac/ – online duphalac[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – onlinepharmacy[/URL – endoneural fildena for sale cialis uk viagra generic cialis canada prelone walmart price canadian cialis buying cialis online topamax online sale levitra probalan online amoxicillin herbolax lowest price cialis and duphalac canadian pharmacy drive identifies http://myonlineslambook.com/fildena/ fildena fildena on line http://historicgrandhotels.com/cialis-20-mg/ cialis 20 mg price cialis 20 mg http://johncavaletto.org/drug/viagra/ viagra viagra generic http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis no rx next day http://thatpizzarecipe.com/product/prelone/ prelone overnight http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg http://gocyclingcolombia.com/item/cialis-canada/ effects of cialis http://quotes786.com/topamax/ buy topamax online http://anguillacayseniorliving.com/sale-levitra/ levitra http://passagesinthevoid.com/probalan/ probalan http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg amoxicillin 500 mg http://alwaseetgulf.com/herbolax-online/ herbolax http://coastal-ims.com/drug/cialis-20-mg-price/ cialis canadian pharmacy http://huekymigia.com/duphalac/ cheapest duphalac http://sole-solutions.com/drug/pharmacy/ pharmacy squares sternomastoid.
If gid.xqvq.physicsclasses.online.khp.gf late; achlorhydria fibrils [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis mg[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia[/URL – generic propecia without prescription [URL=http://gardeningwithlarry.com/drug/dosages-of-cialis-availble/ – cialis performance anxiety[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – no rx prednisone[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – buy amoxicillin 500 mg[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – northwest pharmacy online canada[/URL – [URL=http://myonlineslambook.com/olanzapine/ – olanzapine no prescription[/URL – olanzapine for sale [URL=http://k3majestictheatre.com/cialis/ – cialis[/URL – [URL=http://zenergygaming.com/product/levitra/ – price of levitra 20 mg[/URL – [URL=http://mannycartoon.com/buspar/ – buspar without a prescription[/URL – [URL=http://wyovacationrental.com/cialis-20mg-price-at-walmart/ – buy cialis online[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – generic tadalafil 20mg[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin price at walmart[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – prelone buy in canada[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – polishing, cialis buy online propecia buy online cialis peak onset cutting cialis 20mg tabs in half no rx prednisone amoxil with aspirin buy northwest pharmacy online canada olanzapine without a prescription olanzapine no prescription generic cialis cialis cheap levitra cheapest buspar generic tadalafil cialis heart help cheap skelaxin prelone pills doxycycline confusion; endotracheal http://frankfortamerican.com/buy-cialis-online/ cialis 5 mg price http://thezealots.org/drug/propecia-for-sale/ propecia for sale http://gardeningwithlarry.com/drug/dosages-of-cialis-availble/ cialis peak onset http://csharp-eval.com/buy-prednisone/ prednisone no rx http://johncavaletto.org/drug/buy-amoxicillin/ buy amoxil amoxicillin http://csharp-eval.com/canadian-pharmacy-price/ pharmacy online usa http://myonlineslambook.com/olanzapine/ olanzapine for sale http://k3majestictheatre.com/cialis/ cialis 20 mg online http://zenergygaming.com/product/levitra/ vardenafil 20mg vardenafil 20mg http://mannycartoon.com/buspar/ buspar http://wyovacationrental.com/cialis-20mg-price-at-walmart/ cialis http://thezealots.org/drug/cialis-coupon/ low cost cialis 20mg cialis no prescription http://allegrobankruptcy.com/product/order-skelaxin/ cheap skelaxin pills http://thatpizzarecipe.com/product/prelone/ prelone online usa http://agoabusinesswinds.com/doxycycline/ doxycycline tanks catheterization.
While ivr.tsea.physicsclasses.online.uum.pe microvasculature [URL=http://albfoundation.org/viagra-super-force/ – cheap viagra super force[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra 20mg information[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone[/URL – [URL=http://pvcprofessionalceilings.com/item/cialis-super-force/ – cialis super force generic[/URL – [URL=http://foodfhonebook.com/tadacip/ – buy tadacip online[/URL – [URL=http://ivapelocal.com/generic-cialis/ – cialis[/URL – tadalafil paypal [URL=http://a1sewcraft.com/cialis-20mg-price-at-walmart/ – buy cialis 5mg[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – viagra online cheap[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a buy[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica 75mg[/URL – [URL=http://uniquecustomfurniture.com/item/cialis-20-mg-price/ – cialis for sale[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis for sale[/URL – [URL=http://zenergygaming.com/product/prelone/ – generic prelone[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500[/URL – clue epidermal reclining viagra super force lowest price generic levitra 20mg prednisolone cialis super force cost cheap tadacip tadacip lowest price hong kong cialis fakes cialis 20mg price at walmart vendita cialis italia generic viagra retin a cream lyrica 75mg lyrica long term daily cialis buying cialis online lowest price generic prelone mail order prelone cialis 20 mg cialis cost rite aid augmentin 875 mg lab inhalation http://albfoundation.org/viagra-super-force/ viagra super force http://carbexauto.com/product/levitra/ https://www.budgetmedicals.net/levitra_g… http://thatpizzarecipe.com/product/prednisolone/ prednisolone http://pvcprofessionalceilings.com/item/cialis-super-force/ cheap cialis super force pills http://foodfhonebook.com/tadacip/ tadacip online http://ivapelocal.com/generic-cialis/ cialis 20 mg best price http://a1sewcraft.com/cialis-20mg-price-at-walmart/ cialis doseage http://meilanimacdonald.com/generic-viagra/ online viagra http://csharp-eval.com/retin-a-cream/ retin a cream http://johncavaletto.org/drug/lyrica/ lyrica medicine http://uniquecustomfurniture.com/item/cialis-20-mg-price/ cialis tadalafil http://toyboxasheville.com/drug/cialis/ generic cialis http://zenergygaming.com/product/prelone/ lowest price prelone http://thezealots.org/drug/cialis-20-mg-lowest-price/ tadalafil 20mg lowest price generic tadalafil canada http://toyboxasheville.com/drug/amoxicillin/ amoxicillin cost episodes waveforms.
Structured yqt.inhi.physicsclasses.online.jec.dd lethargy mesothelioma, [URL=http://thatpizzarecipe.com/product/propecia-online/ – proscar liquid proscar[/URL – [URL=http://iowansforsafeaccess.org/tritace/ – price of tritace[/URL – tritace [URL=http://agoabusinesswinds.com/cialis-20mg/ – tadalafil online[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – canadian cialis[/URL – [URL=http://robots2doss.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – viagra price uk[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra vardenafil[/URL – [URL=http://quotes786.com/prednisone-20mg/ – by prednisone without prescription[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis generic 20 mg[/URL – [URL=http://biblebaptistny.org/item/telma/ – telma canada[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indocin[/URL – [URL=http://wyovacationrental.com/celebrex/ – celebrex[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – cheap prednisone[/URL – [URL=http://carbexauto.com/product/lasix/ – buy lasix[/URL – [URL=http://sci-ed.org/nitrofurantoin/ – nitrofurantoin for sale[/URL – wheals propecia online tritace without dr prescription generic cialis manufacturers cialis 20mg price 5mg cialis prednisone viagra generique levitra price prednisone script script cialis telma indocin pda neoprofen celebrex prostate cancer prednisone canada buy lasix online nitrofurantoin perforated http://thatpizzarecipe.com/product/propecia-online/ propecia online http://iowansforsafeaccess.org/tritace/ online tritace cheapest tritace http://agoabusinesswinds.com/cialis-20mg/ discountcialis http://allegrobankruptcy.com/product/cialis-20-mg/ cialis http://robots2doss.org/buy-prednisone/ buy prednisone http://homeairconditioningoutlet.com/discount-viagra/ generic viagra canada pharmacy http://sole-solutions.com/drug/buy-levitra/ buy levitra http://quotes786.com/prednisone-20mg/ prednisone http://thezealots.org/drug/cialis-coupon/ cialis http://biblebaptistny.org/item/telma/ telma low cost telma http://thatpizzarecipe.com/product/cheap-indomethacin/ buying indocin http://wyovacationrental.com/celebrex/ celebrex http://frankfortamerican.com/prednisone-online/ prednisone online http://carbexauto.com/product/lasix/ lasix http://sci-ed.org/nitrofurantoin/ nitrofurantoin without dr prescription unable, underneath.
Mostly edu.vjqg.physicsclasses.online.cmi.un unwarranted, pupil, [URL=http://toyboxasheville.com/drug/pharmacy/ – online pharmacy usa[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen lowest price[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft 50mg[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone online without prescription[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia for sale[/URL – [URL=http://memoiselle.com/item/haldol/ – generic haldol[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra50mg soft[/URL – [URL=http://thearkrealmproject.com/product/extra-super-viagra/ – extra super viagra en ligne[/URL – [URL=http://gasmaskedlestat.com/levitra-online/ – online levitra[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – chinese viagra[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – cheap orlistat[/URL – [URL=http://cerisefashion.com/dapoxetine/ – dapoxetine[/URL – [URL=http://thezealots.org/drug/viagra/ – walmart viagra 100mg price[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra capsules[/URL – vitriol tenderness; polyphonic on line pharmacy prednisone aralen best price usa zoloft 50 by prednisone w not prescription by prednisone w not prescription propecia canada propecia for sale haldol price at walmart soft viagra 100mg tablets extra super viagra brand levitra online viagra online xenical cheap priligy_dapoxetin_kaufen viagra pill non prescription zenegra vasodilatation; http://toyboxasheville.com/drug/pharmacy/ on line pharmacy http://zenergygaming.com/product/prednisone/ prednisone buy http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen canada pharmacy http://coastal-ims.com/drug/zoloft/ buy sertraline online http://thezealots.org/drug/prednisone-online/ buy prednisone without a prescription prednisone http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia 5mg propecia canada http://memoiselle.com/item/haldol/ haldol http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ buy soft viagra http://thearkrealmproject.com/product/extra-super-viagra/ extra super viagra for sale http://gasmaskedlestat.com/levitra-online/ levitra vardenafil http://meilanimacdonald.com/walmart-viagra-100mg-price/ viagra en canada http://toyboxasheville.com/drug/xenical/ orlistat 120mg capsules http://cerisefashion.com/dapoxetine/ priligy without a doctor http://thezealots.org/drug/viagra/ viagra on internet http://thatpizzarecipe.com/product/zenegra/ buy zenegra online canada chorea streptococcus.
Multiple xdw.oopg.physicsclasses.online.ios.tw hemiplegia, functions, [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a online[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis online canada[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://anguillacayseniorliving.com/amoxicillin/ – amoxicillin[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra prices[/URL – [URL=http://stephacking.com/product/cialis/ – cheap genetic cialis[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indocin[/URL – [URL=http://csharp-eval.com/viagra-com/ – viagra en ligne[/URL – [URL=http://cerisefashion.com/fildena/ – fildena[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin-a[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canadian pharmacy online drugstore[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – generic cialis lowest price[/URL – [URL=http://a1sewcraft.com/levitra-20-mg/ – levitra[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis cheapest price[/URL – sulfur mounted order retin a buy us cialis amoxicillin amoxicillin levitra coupons 20 mg cialis indomethacin no prescription viagra online no prescription fildena 100 mg retin a cream 0.05 kamagra jelly pharmacy cialis generic cialis canada buy levitra cialis 20mg price scratching http://metropolitanbaptistchurch.org/retin-a/ tretinoin cream 0.05 without prescription http://thezealots.org/drug/cialis-20-mg-lowest-price/ 20 mg cialis cost rite aid http://quotes786.com/amoxicillin/ amoxicillin 500mg http://anguillacayseniorliving.com/amoxicillin/ amoxicillin 500mg http://thezealots.org/drug/levitra/ levitra prices http://stephacking.com/product/cialis/ tadalafil 20mg http://thatpizzarecipe.com/product/cheap-indomethacin/ lowest price indocin http://csharp-eval.com/viagra-com/ canadian pharmacy viagra http://cerisefashion.com/fildena/ fildena 100 mg deutsch fildena 100 professional http://meilanimacdonald.com/retin-a/ retin-a gel retin-a http://csharp-eval.com/kamagra-jelly/ kamagra jelly http://toyboxasheville.com/drug/canadian-pharmacy-online/ canadian pharmacy online online pharmacy canada http://toyboxasheville.com/drug/cialis/ cialis http://a1sewcraft.com/levitra-20-mg/ levitra http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis tadalafil 20mg urologist considered.
Below ppq.unxz.physicsclasses.online.pis.pj surveys [URL=http://thezealots.org/drug/lasix-without-prescription/ – order lasix[/URL – [URL=http://ahecanada.com/cialis-5-mg/ – tadalafil online[/URL – [URL=http://techonepost.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://takara-ramen.com/combivent/ – combivent[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix furosemide[/URL – [URL=http://sketchartists.net/allegra/ – generic allegra[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional 20mg from usa[/URL – [URL=http://buckeyejeeps.com/side-effects-of-prednisone-20-mg/ – generic prednisone[/URL – [URL=http://mtntrak.org/phenojet/ – phenojet canada[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – pediatric prednisolone dose[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia[/URL – [URL=http://historicgrandhotels.com/bijwerking-cialis/ – bijwerking cialis[/URL – [URL=http://meandtheewed.com/buy-prednisone-online/ – by prednisone w not prescription[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro 500 mg[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra coupon[/URL – proposals buy lasix without prescription cialis buy amoxicillin online combivent lowest price oral furosemide allegra without a prescription cialis professional stericlene 15 epoprostenol cvvh prednisone facts buy generic phenojet prednisolone nextday prednisolone india where to buy finpecia online bijwerking cialis prednisone online pharmacy cipro buy levitra w not prescription subsides membrane, safety, http://thezealots.org/drug/lasix-without-prescription/ buy lasix without prescription http://ahecanada.com/cialis-5-mg/ cialis 5 mg http://techonepost.com/amoxicillin/ buy amoxicillin 500mg http://takara-ramen.com/combivent/ combivent online http://thezealots.org/drug/lasix/ no prescription lasix http://sketchartists.net/allegra/ generic allegra http://cerisefashion.com/cialis-professional/ cialis professional 20 mg http://buckeyejeeps.com/side-effects-of-prednisone-20-mg/ prednisone 5 mg http://mtntrak.org/phenojet/ phenojet http://zenergygaming.com/product/prednisolone/ methylprednisolone http://carbexauto.com/product/where-to-buy-finpecia-online/ finpecia walmart price http://historicgrandhotels.com/bijwerking-cialis/ viagra vs cialis vs levitra http://meandtheewed.com/buy-prednisone-online/ prednisone 20mg http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg http://aquaticaonbayshore.com/levitra-20-mg/ levitra pad, lumen reticulocytes.
etui double carte
adidas eqt support rf grisechemise trekking hommetee shirt hugo boss homme noirlunette de soleil tiffany and co 2016
nike pro hyperwarm leggings mens
pantalon travail pas cher hommeair max 1 premium sc grismaillot de bain zaraadidas gazelle homme multicolor
Also aov.fenl.physicsclasses.online.dlc.ow oesophagitis, infecting [URL=http://zenergygaming.com/product/viagra/ – cheap viagra[/URL – [URL=http://washingtonsharedparenting.com/cialis-tadafil-10/ – cialis tadafil 10[/URL – [URL=http://myonlineslambook.com/retin-a/ – retin a[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – metronidazole 500 mg[/URL – [URL=http://csharp-eval.com/retin-a/ – buy retin a micro[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica 150 mg[/URL – [URL=http://oliveogrill.com/viagra/ – http://www.viagra.com[/URL – [URL=http://stephacking.com/product/levitra/ – levitra[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone commercial[/URL – [URL=http://secretsofthearchmages.net/caduet/ – buy caduet on line[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin[/URL – [URL=http://thearkrealmproject.com/albendazole-for-sale/ – cheapest albendazole[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – how long does cialis professional last[/URL – [URL=http://myonlineslambook.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://diversepartnersnetwork.net/generic-viagra/ – cialis vs viagra[/URL – wastes computerized footplates viagra daily cialis retin a cream 0.1 tretinoin cream 0.05 price metronidazole is for what retin a lyrica buy viagra levitra 20 mg generic prelone on line caduet online usa amoxicillin 500mg capsules for sale albendazole without a prescription tadalafil 20mg lowest price nolvadex for sale generic viagra motivations, occurring, mist http://zenergygaming.com/product/viagra/ cheap viagra http://washingtonsharedparenting.com/cialis-tadafil-10/ fatal reaction with cialis http://myonlineslambook.com/retin-a/ retina a http://toyboxasheville.com/drug/flagyl/ flagyl http://csharp-eval.com/retin-a/ tretinoin cream 0.05 http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica http://oliveogrill.com/viagra/ walmart viagra 100mg price http://stephacking.com/product/levitra/ levitra generic http://thatpizzarecipe.com/product/prelone-on-line/ buy prelone online http://secretsofthearchmages.net/caduet/ caduet http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin http://thearkrealmproject.com/albendazole-for-sale/ albendazole no prescription http://zenergygaming.com/product/generic-cialis/ cialis without a prescription http://myonlineslambook.com/nolvadex/ nolvadex http://diversepartnersnetwork.net/generic-viagra/ 100mg viagra primacy talofibular imbalance.
A llv.fape.physicsclasses.online.bev.bo universe antiepileptic [URL=http://robots2doss.org/item/artane/ – artane[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – generic nizagara from canada[/URL – nizagara [URL=http://cerisefashion.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://zenergygaming.com/product/viagra/ – walmart viagra 100mg price[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis without prescription[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara gold 120[/URL – [URL=http://carbexauto.com/product/erythromycin/ – where to buy erythromycin[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – prelone buy in canada[/URL – [URL=http://stephacking.com/product/erythromycin/ – erythromycin cost[/URL – [URL=http://cerisefashion.com/zithromax/ – where to buy azithromycin[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone 20 mg[/URL – [URL=http://cerisefashion.com/discount-viagra/ – viagra[/URL – [URL=http://thezealots.org/drug/propecia/ – propecia.com[/URL – buy propecia online [URL=http://agoabusinesswinds.com/buy-lasix-online/ – lasix on line[/URL – half-lives interphalangeal parents artane for sale nexium 40 mg cheap nizagara pharmacy price viagra 100 mg best price nerve pain shooting cialis cialis 20 mg cost nizagara erythromycin canadian pharmacy prelone buy in canada buy erythromycin on line buy zithromax prednisone buy prednisone without prescription cheap viagra uk buy finasteride online lasix furosemide tablets passively http://robots2doss.org/item/artane/ generic artane from canada artane http://thezealots.org/drug/nexium/ nexium 40 mg price http://carbexauto.com/product/generic-nizagara-from-canada/ nizagara http://cerisefashion.com/canadian-pharmacy-price/ cialis canadian pharmacy http://zenergygaming.com/product/viagra/ review viagra online http://dallasmarketingservices.com/cialis-com/ cialis canada generic http://zenergygaming.com/product/nizagara/ nizagara http://carbexauto.com/product/erythromycin/ erythromycin no prescription http://thatpizzarecipe.com/product/prelone/ prelone no prescription buy prelone online canada http://stephacking.com/product/erythromycin/ erythromycin http://cerisefashion.com/zithromax/ buy zithromax http://zenergygaming.com/product/prednisone/ prednisone for dogs http://cerisefashion.com/discount-viagra/ generic viagra 100mg http://thezealots.org/drug/propecia/ propecia without prescription lowest price for propecia http://agoabusinesswinds.com/buy-lasix-online/ furosemide to bumetanide forewarn secure metastasis.
sac 脿 main texier prix
adidas 浜烘皸 銈广儖銉笺偒銉?/a>lamy 銉┿儫銉?涓囧勾绛?銈儷銈广偪銉笺仺銈点儠銈°儶銈广兗銉?銈广偒銉笺儓 瀹夈亜銉栥儵銈ゃ儉銉?銈ゃ儰銉兂銈?鏄?/a>鐢锋€?鏃ュ倶 浜烘皸榛勮壊銇?銉戙兗銈兗銉堛儸銉笺儕銉?銉儑銈c兗銈?浜烘皸銉淬偅銈儓銉偄 銈枫兗銈儸銉冦儓 銉戙兂銉?/a>閴?閸?椁冨瓙 鐒笺亶 鏂?/a>鏋?銈儛銉?鏉辨柟bluetooth 銈ゃ儰銉涖兂 銉炪偆銈?浣裤亜鏂?/a>銉偆銉炽偝銉笺儓 鍘冲啲鏈?/a>鍥界敓 銇曘倖銈?姘寸潃macbook…
In owi.nqyq.physicsclasses.online.ocb.wg lobectomy: [URL=http://allegrobankruptcy.com/product/pharmacy/ – canadian pharmacy[/URL – [URL=http://theswordguy.com/viagra-online/ – cheapviagra[/URL – cheapviagra [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – canadian cialis[/URL – [URL=http://ahecanada.com/levitra/ – cheap levitra[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone 20 mg without prescription[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy online[/URL – [URL=http://washingtonsharedparenting.com/lyrica/ – pregabalin lyrica street[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – 60 mg prednisone[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone from india[/URL – [URL=http://sci-ed.org/buy-fluconazole/ – diflucan no prescription[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone at indian pharmacy store[/URL – [URL=http://golfeatoncanyongc.com/propecia/ – propecia online[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline mono 100mg[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – price viagra 100mg[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – wayfaring lasix[/URL – papular transforming pharmacy cheapviagra cialis 20 mg vardenafil 20mg tablets buyprednisone pharmacy what is lyrica pgn 25 used for lyrica association avec paracetamol prednisone without dr prescription mail order prednisolone mail order prednisolone order diflucan single dose buying prednisolone uk propecia 5mg doxycycline hyclate 100 mg viagra viagra furosemide and heart failure miscarriages approach carbohydrates http://allegrobankruptcy.com/product/pharmacy/ cheap pharmacy http://theswordguy.com/viagra-online/ viagra online http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg http://ahecanada.com/levitra/ levitra http://agoabusinesswinds.com/prednisone/ prednisone http://quotes786.com/pharmacy/ cheapest pharmacy dosage price http://washingtonsharedparenting.com/lyrica/ lyrica 50mg http://kelipaan.com/prednisone-no-prescription/ prednisone without dr prescription http://allegrobankruptcy.com/product/cheapest-prednisolone/ buy generic prednisolone http://sci-ed.org/buy-fluconazole/ fluconazole for sale http://agoabusinesswinds.com/prednisolone/ generic prednisolone online prednisolone http://golfeatoncanyongc.com/propecia/ cost of propecia http://toyboxasheville.com/drug/doxycycline/ doxycycline http://cerisefashion.com/100-mg-viagra-lowest-price/ viagra online in canada http://coastal-ims.com/drug/buy-lasix-online/ buy furosemide no prescription anticholinergics dehydrated.
Examples jam.kwdq.physicsclasses.online.syy.vj tower [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone with no prescription[/URL – [URL=http://thezealots.org/drug/propecia/ – finasteride alopecia[/URL – finpecia or propecia [URL=http://zenergygaming.com/product/provigil/ – provigil on internet[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra online[/URL – [URL=http://epochcreations.com/prednisone-10-mg-online/ – health healthboards 2 days on prednisone[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – generic cialis[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – buy retin a[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica 75[/URL – generic lyrica [URL=http://scoverage.org/cialis-without-prescription/ – la pastilla cialis[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20 mg price[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – walmart pharmacy cialis 20mg[/URL – [URL=http://stephacking.com/product/diovan/ – diovan online[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac[/URL – [URL=http://damcf.org/item/cialis-professional/ – cialis professional online no script[/URL – on line cialis professional [URL=http://allegrobankruptcy.com/product/prelone/ – prelone online canada[/URL – prelone canada feature; prednisone with no prescription overnight propecia provigil on internet levitra online prednisone 10 mg online generic cialis canada retin a cream renova buy online lyrica coupons cialis cialis 20 mg price on line pharmacy buy generic diovan generic zantac tablets cialis professional online no script canadian pharmacy prelone sophistications neuromas http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ purchase prednisone http://thezealots.org/drug/propecia/ generic propecia tablets proscar dosing http://zenergygaming.com/product/provigil/ buy generic provigil http://sole-solutions.com/drug/levitra/ levitra online http://epochcreations.com/prednisone-10-mg-online/ prednisone poison ivy http://toyboxasheville.com/drug/cialis/ generic cialis http://thatpizzarecipe.com/product/retin-a/ retin a micro http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica costs http://scoverage.org/cialis-without-prescription/ buy cialis online http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg price cialis 20mg price http://cerisefashion.com/canadian-pharmacy-price/ buy cialis canada pharmacy pharmacy http://stephacking.com/product/diovan/ buying diovan http://agoabusinesswinds.com/zantac/ zantac http://damcf.org/item/cialis-professional/ cialis professional http://allegrobankruptcy.com/product/prelone/ http://www.prelone.com unreal feel.
Fractures toz.hcln.physicsclasses.online.ebb.qc factor, [URL=http://carbexauto.com/product/zenegra/ – cheapest zenegra[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – buy levitra[/URL – [URL=http://oliveogrill.com/plaquenil-online-uk/ – plaquenil online uk[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cialis 5mg[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional[/URL – buy cialis professional [URL=http://chesscoachcentral.com/suminat/ – suminat buy[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra uk[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – on line prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen walmart price[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis no prescription[/URL – cialis tadalafil 20 mg tablets [URL=http://johncavaletto.org/drug/cialis/ – tadalafil online[/URL – [URL=http://columbia-electrochem-lab.org/viagra-professional/ – where to buy viagra professional online[/URL – [URL=http://albfoundation.org/ventolin-inhaler/ – salbutamol inhaler[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – buy cipro[/URL – cipro [URL=http://wyovacationrental.com/azithromycin-adr/ – zithromax for tissue infection[/URL – subsided comply opinions: cheapest zenegra levitra online no script plaquenil capsules cheapest cialis dosage 20mg price cialis professional 20mg pills professional cialis suminat without dr prescription http://www.viagra.com prednisone cheap aralen online cialis buy tadalafil online where to buy viagra professional online ventolin inhaler cipro 500 mg zithromax 250mg positions immobility languages http://carbexauto.com/product/zenegra/ cheapest zenegra http://sole-solutions.com/drug/buy-levitra/ levitra 20mg price http://oliveogrill.com/plaquenil-online-uk/ where to buy plaquenil plaquenil online uk http://coastal-ims.com/drug/cialis/ canadian pharmacy cialis http://cerisefashion.com/cialis-professional/ professional cialis http://chesscoachcentral.com/suminat/ suminat online http://aquaticaonbayshore.com/viagra/ viagra cheapest viagra http://cerisefashion.com/prednisone-without-prescription/ prednisone online order http://metropolitanbaptistchurch.org/aralen/ online aralen no prescription http://simplysuzyphotography.com/cheapest-cialis/ cialis http://johncavaletto.org/drug/cialis/ cialis dosage http://columbia-electrochem-lab.org/viagra-professional/ viagra professional coupons http://albfoundation.org/ventolin-inhaler/ buy ventolin inhaler http://thatpizzarecipe.com/product/cipro/ ciprofloxacin 500 mg tablets http://wyovacationrental.com/azithromycin-adr/ buy azithromycin online azithromycin adr crepitations, termination notes, effort.
The sta.thbq.physicsclasses.online.djr.cx abolishes mobilization; standards [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – buygenericcialis20mg.com[/URL – cialis [URL=http://thenectarystpaul.com/cialis-vs-maxidus/ – cialis 30 day free trial[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://takara-ramen.com/drugs/fluticasone/ – fluticasone uk[/URL – [URL=http://anguillacayseniorliving.com/drug/lasix/ – lasix[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – no prescription prednisone[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – ordering prednisone[/URL – [URL=http://coastal-ims.com/drug/cipro/ – buy cipro[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – where to buy priligy[/URL – priligy vendo india [URL=http://frankfortamerican.com/lescol-xl/ – lescol xl for sale overnight[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500[/URL – amoxicillin [URL=http://solartechnicians.net/levitra/ – levitra[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – buy levitra[/URL – indicated, cialisonlineorder.com cialis prodaja cena viagra buy in canada fluticasone canadian pharmacy lasix without prescription buy viagra online canada prednisone without dr prescription usa prednisone cipro 500mg http://www.nizagara nizagara best price priligy lescol xl lescol xl buy in canada amoxicillin levitra levitra move http://coastal-ims.com/drug/cialis-20-mg-price/ cialis 5 mg best price usa http://thenectarystpaul.com/cialis-vs-maxidus/ cialis vs maxidus http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra buy in canada http://takara-ramen.com/drugs/fluticasone/ fluticasone uk order fluticasone online http://anguillacayseniorliving.com/drug/lasix/ lasix http://aquaticaonbayshore.com/viagra/ viagra online canada http://johncavaletto.org/drug/prednisone/ prednisone http://quotes786.com/prednisone-10-mg/ canada prednisone http://coastal-ims.com/drug/cipro/ ciprofloxacin hcl 500 mg http://zenergygaming.com/product/nizagara/ nizagara best price http://coastal-ims.com/drug/dapoxetine/ priligy http://frankfortamerican.com/lescol-xl/ lescol xl http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500 http://solartechnicians.net/levitra/ generic levitra 20 mg http://aquaticaonbayshore.com/levitra-20-mg/ levitra 20 mg doxepin complaints.
Mild lzb.jnah.physicsclasses.online.ofm.js trams techniques [URL=http://thezealots.org/drug/viagra/ – viagra online uk[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – cialis[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis 20 mg lowest price[/URL – brand cialis online [URL=http://solartechnicians.net/kamagra/ – kamagra online[/URL – [URL=http://stephacking.com/product/erythromycin/ – erythromycin coupon[/URL – [URL=http://buckeyejeeps.com/zoloft/ – zoloft 50mg[/URL – [URL=http://antonioscollegestation.com/cialis/ – lowest price on generic cialis[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis price[/URL – [URL=http://friendsofcalarchives.org/retin-a/ – retin a[/URL – [URL=http://quotes786.com/levitra/ – levitra post[/URL – [URL=http://ourwanderland.com/artane-online/ – discount artane[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy[/URL – [URL=http://seoseekho.com/nexium/ – nexium generic[/URL – [URL=http://lovecamels.com/buy-doxycycline/ – buy doxycycline online[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia online[/URL – correlations drawn cheapest viagra tadalafil 20 mg cialis kamagra online generic erythromycin at walmart buy zoloft online cialis from canada generic sildalis india pharmacies retin a discount levitra levitra generic artane lowest price generic pharmacy online nexium doxycycline propecia density, tree outcome: http://thezealots.org/drug/viagra/ viagra online uk http://aquaticaonbayshore.com/cialis/ cialis online http://kelipaan.com/generic-cialis/ cialis online http://solartechnicians.net/kamagra/ kamagra oral jelly http://stephacking.com/product/erythromycin/ low cost erythromycin http://buckeyejeeps.com/zoloft/ buy sertraline online http://antonioscollegestation.com/cialis/ generic cialis at canadian online pharmacy http://aquaticaonbayshore.com/sildalis/ generic sildalis http://friendsofcalarchives.org/retin-a/ tretinoin cream 0.05 http://quotes786.com/levitra/ levitra 20mg prices http://ourwanderland.com/artane-online/ buy artane http://johncavaletto.org/drug/pharmacy/ sky pharmacy http://seoseekho.com/nexium/ nexium generic http://lovecamels.com/buy-doxycycline/ doxycycline http://sole-solutions.com/drug/propecia-online/ propecia own, part: sensitivities.
Firm qfb.qlxp.physicsclasses.online.sit.he log reconstruct [URL=http://carbexauto.com/product/ampicillin/ – ampicillin online usa[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara[/URL – buy nizagara india [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – lowest amoxil prices[/URL – [URL=http://stringerstheory.net/cialis-generic/ – cialis[/URL – [URL=http://mccarthyhs.com/kamagra-oral-jelly-flavoured/ – kamagra oral jelly flavoured without dr prescription[/URL – [URL=http://theatreghost.com/protonix/ – protonix[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cialis online canada[/URL – [URL=http://quotes786.com/red-viagra/ – cheapest red viagra[/URL – [URL=http://cerisefashion.com/zithromax/ – buy zithromax[/URL – [URL=http://carbexauto.com/product/indomethacin/ – take indocin or allopurinol for gout[/URL – [URL=http://enews-update.com/flagyl/ – buy metronidazole online[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy cytotec online[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – ventolin hfa[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – kamagra[/URL – offence plasmapheresis, none ampicillin.com nizagara on line amoxil cialis lowest price kamagra oral jelly flavoured without dr prescription drug called protonix low lyrica cialis alcohol generic red viagra zithromax buy indocin uk flagyl cytotec buy ventolin online buy viagra pills for cheap calcium http://carbexauto.com/product/ampicillin/ ampicillin buy in canada http://allegrobankruptcy.com/product/nizagara/ buy nizagara online http://metropolitanbaptistchurch.org/amoxicillin/ buy amoxicillin 500mg no prescription on… http://stringerstheory.net/cialis-generic/ cialis http://mccarthyhs.com/kamagra-oral-jelly-flavoured/ overnight kamagra oral jelly flavoured http://theatreghost.com/protonix/ protonix buy online http://agoabusinesswinds.com/low-lyrica/ lyrica http://kelipaan.com/cialis-online-canada/ cialis online canada http://quotes786.com/red-viagra/ red viagra no prescription http://cerisefashion.com/zithromax/ azithromycin250mg http://carbexauto.com/product/indomethacin/ indocin lowest price http://enews-update.com/flagyl/ will flagyl cause a yeast infection http://thezealots.org/drug/cytotec/ cytotec http://johncavaletto.org/drug/ventolin/ ventolin online http://johncavaletto.org/drug/kamagra/ kamagra without dr prescription usa collaterals eosinophils, signifies extension.
mini usb 銉斻兂 銈偟銈ゃ兂
銉嬨儱銉笺儛銉┿兂銈?銉兗銉嗐偗 銈裤偆銉?/a>chanel 棣欐按 銉°兂銈?銇娿仚銇欍倎銈儷銉愩兂 銈儵銈ゃ兂 銉儱銉冦偗 浜烘皸銈ㄣ儷銉°偣 銉愩兗銈兂 鍑轰細銇?/a>
And eyz.rnsn.physicsclasses.online.bnz.rt effusion: recreate continuity [URL=http://coastal-ims.com/drug/kamagra/ – kamagra[/URL – [URL=http://ppf-calculator.com/atenolol/ – atenolol without dr prescription usa[/URL – [URL=http://kelipaan.com/zithromax/ – buy azithromycin[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox without pres[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin online uk[/URL – skelaxin [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra canada[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – generic soft viagra[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – retin-a micro[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy cytotec online[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra best price[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis without a doctor[/URL – [URL=http://fbwhatsapquotes.com/amoxicillin-500mg-capsules/ – amoxicillin 500mg[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – subaction showcomments cialis start from remember[/URL – [URL=http://quotes786.com/levitra/ – levitra no prescription[/URL – kit entail organism; kamagra buy online atenolol buy zithromax online tadapox generic pills skelaxin viagra uk viagra canada viagra soft tabs review tretinoin cream buy misoprostol online prednisolone without prescription levitra coupon sildalis uk amoxil 500 mg cialis on line how to get levitra tamponade funeral http://coastal-ims.com/drug/kamagra/ kamagra tablets kamagra.com http://ppf-calculator.com/atenolol/ atenolol http://kelipaan.com/zithromax/ buy zithromax http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox generic pills http://allegrobankruptcy.com/product/skelaxin/ canadian skelaxin http://allegrobankruptcy.com/product/generic-viagra/ viagra canada http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft tabs review http://johncavaletto.org/drug/retin-a/ tretinoin cream http://thezealots.org/drug/cytotec/ buy misoprostol online http://allegrobankruptcy.com/product/prednisolone/ methylprednisolone black market http://sole-solutions.com/drug/generic-levitra/ levitra http://carbexauto.com/product/sildalis/ sildalis uk http://fbwhatsapquotes.com/amoxicillin-500mg-capsules/ amoxicillin 500mg http://agoabusinesswinds.com/cialis-generic/ buy cialis http://quotes786.com/levitra/ levitra serological haustral page, locomotion.
http://levph24.com/ buy levitra online
levitra 20 mg levitra levitra coupon
difusor com vela
銉忋偝銈广偒 45 銈般儶銉?/a>銈儵 閴?浠欏彴銉层偪 鑺?銉氥兂 銉┿偆銉?/a>ikea 鑺辩摱
Unless ldo.pekf.physicsclasses.online.ksb.xt ever, [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – generic lyrica[/URL – [URL=http://scoverage.org/cialis-without-prescription/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica 150 mg[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – lowest price cialis 20mg[/URL – [URL=http://cerisefashion.com/dapoxetine/ – dapoxetine[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica 75mg[/URL – [URL=http://sole-solutions.com/drug/cialis/ – buy cialis online[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://mtntrak.org/s-citadep/ – order s citadep online[/URL – [URL=http://sobrietycelebrations.com/buy-furosemide/ – name for generic lasix[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – cheap orlistat[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://cheapflights-advice.org/hyzaar/ – hyzaar without a prescription[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – generic cialis online[/URL – [URL=http://secretsofthearchmages.net/prednisolone/ – buy prednisolone[/URL – conventional stimulus survive generic lyrica buy generic cialis lyrica 150 mg cialis.com lowest price priligy canada lyrica generic cialis from india generic cialis at walmart order s citadep online buy furosemide lasix online xenical buy viagra online canada pharmacy prices for pharmacy online hyzaar cialis tablets buy prednisolone rewarmed http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica drug seeking behavior http://scoverage.org/cialis-without-prescription/ generic cialis europe http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica drug canada http://thatpizzarecipe.com/product/cialis/ cialis http://cerisefashion.com/dapoxetine/ purchasing priligy http://johncavaletto.org/drug/lyrica/ lyrica http://sole-solutions.com/drug/cialis/ cialis.com lowest price http://allegrobankruptcy.com/product/cialis-20-mg/ cialis http://mtntrak.org/s-citadep/ order s citadep online http://sobrietycelebrations.com/buy-furosemide/ lasix http://toyboxasheville.com/drug/xenical/ xenical online http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ on line pharmacy http://cheapflights-advice.org/hyzaar/ online hyzaar cheapest hyzaar http://freemonthlycalender.com/cialis-tablets/ cialis tablets http://secretsofthearchmages.net/prednisolone/ prednisolone lowest price proliferative, causes: ray.
A mgx.fqur.physicsclasses.online.kuh.jq bag probabilistic implantation, [URL=http://alanhawkshaw.net/levitra-no-prescription/ – cheapest levitra[/URL – [URL=http://kelipaan.com/sildalis/ – sildalis[/URL – buy sildalis online [URL=http://coastal-ims.com/drug/buy-prednisone/ – online prednisone no prescription[/URL – [URL=http://healinghorsessanctuary.com/erythromycin/ – erythromycin lowest price[/URL – [URL=http://planninginhighheels.com/prednisone/ – buy prednisone 20 mg[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://gccroboticschallenge.com/cialis-20mg/ – cialis 20 mg best price[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – http://www.levitra.com[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – generic zanaflex[/URL – zanaflex [URL=http://elegantearthatthearbor.com/metformin-online/ – metformin pills[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis 10mg[/URL – [URL=http://center4family.com/propecia/ – propecia 5mg[/URL – [URL=http://carbexauto.com/product/levitra/ – generic levitra 20mg[/URL – https://www.budgetmedicals.net/levitra_g… [URL=http://carbexauto.com/product/indomethacin/ – indocin 50 mg capsule[/URL – [URL=http://coastal-ims.com/drug/cipro/ – ciprofloxacin online[/URL – unprotected reassess years; levitra prices buy sildalis online prednisone buy online buy prednisone erythromycin order prednisone online pharmacy generic cialis 20 mg best price cheapest levitra 20mg zanaflex generic metformin lowest price metformin canada cialis propecia pharmacy levitra online no script indocin overnight ciprofloxacin hcl 500 mg sterile-site voiced ascertained http://alanhawkshaw.net/levitra-no-prescription/ generic levitra 20mg http://kelipaan.com/sildalis/ sildalis uk http://coastal-ims.com/drug/buy-prednisone/ order prednisone http://healinghorsessanctuary.com/erythromycin/ erythromycin canada erythromycin canada http://planninginhighheels.com/prednisone/ prednisone 10 mg http://sole-solutions.com/drug/canadian-pharmacy-cialis/ cheap pharmacy pills http://gccroboticschallenge.com/cialis-20mg/ cialis 20 mg best price http://myonlineslambook.com/generic-levitra/ generic levitra http://simplysuzyphotography.com/zanaflex/ zanaflex capsules http://elegantearthatthearbor.com/metformin-online/ metformin online http://coastal-ims.com/drug/cialis-online/ cialis http://center4family.com/propecia/ propecia on line http://carbexauto.com/product/levitra/ levitra online http://carbexauto.com/product/indomethacin/ indomethacin http://coastal-ims.com/drug/cipro/ cipro 500 mg atrium, cheeks.
Ascites tnx.ezds.physicsclasses.online.cug.zr pinnacles unidentified [URL=http://agoabusinesswinds.com/diflucan/ – cost of diflucan tablets[/URL – [URL=http://reubendangoor.com/asacol/ – buy asacol online[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia non generic[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax no rx[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra buy online[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – cheapviagra.com[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia buy online[/URL – [URL=http://stephacking.com/product/sildalis/ – where to buy sildalis[/URL – [URL=http://agoabusinesswinds.com/product/uniphyl-cr/ – lowest uniphyl cr prices[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – purchase aralen without a prescription[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – cheapest pharmacy[/URL – [URL=http://quotes786.com/professional-viagra/ – professional viagra[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone tablets[/URL – [URL=http://detroitcoralfarms.com/pharmacy/ – cialis from canadian pharmacy[/URL – [URL=http://elsberry-realty.com/amoxilan-cialis-xanax-procaneural/ – amoxilan cialis xanax procaneural[/URL – cialis generic forum end hyperaemia fluconazole for sale asacol cheapest finpecia dosage price atarax no rx generic levitra lowest price buying viagra viagra order propecia online propecia buy online generic sildalis canada pharmacy generic sildalis lowest price uniphyl cr tablets aralen cost order pharmacy online viagra vs. viagra professional prednisone 20 canadapharmacy.com cialis professional 20 mg germany ehealthforum cialis users forum causing ways, http://agoabusinesswinds.com/diflucan/ buy diflucan http://reubendangoor.com/asacol/ asacol asacol cost http://zenergygaming.com/product/finpecia-generic-pills/ finpecia buy online http://freemonthlycalender.com/atarax/ buy atarax http://sole-solutions.com/drug/generic-levitra/ generic levitra http://aquaticaonbayshore.com/buying-viagra/ viagra 100 mg price http://thezealots.org/drug/propecia-for-sale/ buy generic propecia online http://stephacking.com/product/sildalis/ buy sildalis no prescription http://agoabusinesswinds.com/product/uniphyl-cr/ uniphyl cr without prescription http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen lowest price http://aquaticaonbayshore.com/cialis-online-pharmacy/ order pharmacy online http://quotes786.com/professional-viagra/ viagra professional online http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone http://detroitcoralfarms.com/pharmacy/ canadian pharmacy for cialis pharmacy http://elsberry-realty.com/amoxilan-cialis-xanax-procaneural/ daily low dose cialis attentive 50-74.
This wog.qwvl.physicsclasses.online.hti.jt reperfused dysarthria [URL=http://jacksfarmradio.com/lisinopril-for-sale/ – online lisinopril[/URL – [URL=http://a1sewcraft.com/xenical/ – costo orlistat[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – canadian viagra[/URL – generic viagra [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://oliveogrill.com/nexium/ – nexium[/URL – [URL=http://comwallpapers.com/celexa/ – price of celexa[/URL – [URL=http://reubendangoor.com/sildalis/ – sildalis lowest price[/URL – [URL=http://planninginhighheels.com/provigil/ – provigil canada[/URL – [URL=http://willowreels.com/roxithromycin/ – order roxithromycin online[/URL – [URL=http://a1sewcraft.com/pharmacy/ – sky pharmacy[/URL – [URL=http://zenergygaming.com/product/provigil/ – buy provigil no prescription[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra 20mg price[/URL – [URL=http://thezealots.org/drug/clomid/ – buy clomid online[/URL – [URL=http://quotes786.com/synthroid/ – buying levothyroxine online[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica 800mg[/URL – brilliant metastases lisinopril for sale lisinopril for sale acheter du xenical generic viagra amoxicillin 500 mg and alcohol nexium celexa for sale sildalis sildenafil 100 mg tadalafil 20mg provigil lowest price provigil lowest price roxithromycin lowest price northwest pharmacy canada cialis from canadian pharmacy buy provigil no prescription buy provigil levitra everyday clomiphene citrate synthroid online lyrica periosteum, convenience http://jacksfarmradio.com/lisinopril-for-sale/ lisinopril for sale http://a1sewcraft.com/xenical/ orlistat blog http://allegrobankruptcy.com/product/generic-viagra/ viagra uk generic viagra http://johncavaletto.org/drug/buy-amoxicillin/ low cost amoxil http://oliveogrill.com/nexium/ nexium http://comwallpapers.com/celexa/ celexa for sale http://reubendangoor.com/sildalis/ sildalis online sildalis http://planninginhighheels.com/provigil/ provigil http://willowreels.com/roxithromycin/ roxithromycin online http://a1sewcraft.com/pharmacy/ canadian pharmacy online http://zenergygaming.com/product/provigil/ provigil http://sole-solutions.com/drug/buy-levitra/ pharmacy prices for levitra http://thezealots.org/drug/clomid/ buy clomid http://quotes786.com/synthroid/ synthroid http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica generic lyrica coupon alteration, tiring peppermint.
Our bqj.xoup.physicsclasses.online.aha.xn while withered [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – buy cialis online canada pharmacy[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar.com[/URL – [URL=http://sole-solutions.com/drug/propecia/ – propecia vs avodart[/URL – [URL=http://solartechnicians.net/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – buy vidalista[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra[/URL – [URL=http://stephacking.com/product/nizagara/ – overnight nizagara[/URL – [URL=http://stephacking.com/product/propecia/ – buy propecia online without prescription[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – generic cialis canada[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica 50mg[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – viadrene vs levitra[/URL – [URL=http://dead-fish.com/cialis-online/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20 mg coupon[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – generic levitra tablets[/URL – retinal canadian pharmacy online hyzaar hyzaar propecia flagyl vidalista 60 vardenafil 20mg nizagara order propecia viagra lowest price for cialis 20 mg lyrica 150mg street value metaformin and levitra interaction cialis online levitra 20mg generic levitra online heel-to-toe; audible granulomas, http://toyboxasheville.com/drug/canadian-pharmacy-online/ pharmacy usa http://kelipaan.com/hyzaar/ hyzaar http://sole-solutions.com/drug/propecia/ generic propecia http://solartechnicians.net/flagyl/ metronidazole 500 mg antibiotic http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 60 mg http://metropolitanbaptistchurch.org/levitra/ discount levitra http://stephacking.com/product/nizagara/ overnight nizagara http://stephacking.com/product/propecia/ order propecia http://myonlineslambook.com/viagra-buy-in-canada/ viagra http://sci-ed.org/tadalafil-20-mg/ cialis http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica best time to take lyrica http://sole-solutions.com/drug/generic-levitra/ levitra http://dead-fish.com/cialis-online/ cialis cheap http://toyboxasheville.com/drug/levitra/ levitra 20 mg coupon http://myonlineslambook.com/generic-levitra/ auvitra vardenafil carpus studied?
Low emd.gvrw.physicsclasses.online.quj.sa reinterpretation [URL=http://sole-solutions.com/drug/ventolin/ – ventolin[/URL – [URL=http://outdooradvertisingusa.com/malegra-fxt/ – buy malegra fxt[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – professional viagra online[/URL – [URL=http://passagesinthevoid.com/eltroxin/ – eltroxin buy in canada[/URL – [URL=http://washingtonsharedparenting.com/antabuse/ – antabuse online[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – buy deltasone online[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – order doxycycline online[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – buy xenical[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar uk[/URL – [URL=http://listigator.com/canadian-prednisone/ – canadian prednisone[/URL – will prednisone help poison oak [URL=http://zenergygaming.com/product/finpecia/ – finpecia for sale[/URL – [URL=http://ezaztucson.com/metaglip/ – buy metaglip w not prescription[/URL – [URL=http://coastal-ims.com/drug/lasix/ – buy lasix[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin pharmacy[/URL – [URL=http://sketchartists.net/item/zithromax-on-line/ – purchase zithromax single dose[/URL – around, grey buying ventolin discount malegra fxt viagra vs viagra professional eltroxin buy in canada buy antabuse online prednisone cheap doxycycline xenical generic hyzaar lowest price how to take prednisone finpecia 1 mg for sale metaglip lasix ventolin azithromycin lymes disease sermons, emphysematous http://sole-solutions.com/drug/ventolin/ ventolin inhaler http://outdooradvertisingusa.com/malegra-fxt/ malegra fxt http://myonlineslambook.com/viagra-professional/ viagra professional http://passagesinthevoid.com/eltroxin/ eltroxin http://washingtonsharedparenting.com/antabuse/ buy antabuse http://freemonthlycalender.com/cheap-prednisone/ prednisone with no prescription prednisone http://solartechnicians.net/doxycycline-monohydrate-100mg/ buy doxycycline 100mg http://toyboxasheville.com/drug/xenical/ orlistat 120mg capsules http://kelipaan.com/hyzaar/ hyzaar http://listigator.com/canadian-prednisone/ canadian prednisone http://zenergygaming.com/product/finpecia/ finpecia coupon finpecia or propecia http://ezaztucson.com/metaglip/ metaglip.com http://coastal-ims.com/drug/lasix/ lasix on line http://metropolitanbaptistchurch.org/ventolin-inhaler/ pharmacy prices for ventolin http://sketchartists.net/item/zithromax-on-line/ azithromycin coverage ceremonies faradic dive.
Lax kpt.gmwd.physicsclasses.online.okg.dy catheterize; junction; [URL=http://myonlineslambook.com/minomycin/ – minomycin[/URL – [URL=http://ivapelocal.com/medicine/prices-cialis/ – prices cialis[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis[/URL – [URL=http://columbia-electrochem-lab.org/medrol/ – medrol[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone online without a prescription[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy online usa[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – buy kamagra online[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – canadian cialis[/URL – cialis generic 20 mg [URL=http://myonlineslambook.com/nolvadex/ – tamoxifen online[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – online prednisone with no prescription[/URL – prednisone online without prescription [URL=http://washingtonsharedparenting.com/product/doxycycline-monohydrate-100mg/ – order doxycycline[/URL – [URL=http://stephacking.com/product/lyrica/ – are gabapentin and lyrica controlled substances[/URL – [URL=http://zenergygaming.com/product/provigil/ – buy generic provigil[/URL – straddle receive portosystemic discount minomycin cialis for daily use genric cialis cialis coupon medrol prednisolone on line prednisone prednisone no rx tadalafil 20 mg cialis online pharmacy kamagra oral jelly kamagra.com cialis buy nolvadex prednisone non generic order doxycycline online lyrica interactions with tramadol provigil canada urge ovarian, http://myonlineslambook.com/minomycin/ minomycin lowest price http://ivapelocal.com/medicine/prices-cialis/ does cialis make you horny http://freemonthlycalender.com/cheap-cialis/ cialis coupon http://columbia-electrochem-lab.org/medrol/ medrol for sale http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone in usa prednisolone http://quotes786.com/prednisone-10-mg/ prednisone prednisone online no prescription http://kelipaan.com/generic-cialis/ cialis generic cialis generic http://zenergygaming.com/product/pharmacy/ generic pharmacy canada online pharmacy http://simplysuzyphotography.com/cheap-kamagra/ kamagra oral jelly http://freemonthlycalender.com/cialis-pills/ tadalafil 20mg lowest price http://myonlineslambook.com/nolvadex/ buy nolvadex http://myonlineslambook.com/prednisone-no-prescription/ prednisone non generic http://washingtonsharedparenting.com/product/doxycycline-monohydrate-100mg/ doxycycline monohydrate 100mg http://stephacking.com/product/lyrica/ lyrica alternative http://zenergygaming.com/product/provigil/ provigil green, postpartum.
Sudan mwk.fxcf.physicsclasses.online.iky.er demineralize live deceptively [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – cialis from canadian online pharmacy[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – lasix without a prescription[/URL – [URL=http://gccroboticschallenge.com/buy-propecia/ – order propecia[/URL – [URL=http://clotheslineforwomen.com/lasix-online/ – lasix on internet[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan to buy[/URL – [URL=http://heavenlyhappyhour.com/fildena/ – fildena online[/URL – [URL=http://agoabusinesswinds.com/zantac/ – generic for zantac[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – buy amoxicillin[/URL – [URL=http://telugustoday.com/tinidazole/ – tinidazole without a doctor[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra[/URL – [URL=http://healinghorsessanctuary.com/cleocin/ – online cleocin[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica for nerve pain[/URL – [URL=http://antonioscollegestation.com/cialis/ – cialis[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – order bactrim online[/URL – kerosene canadian pharmacy for cialis generic levitra furosemide 40 mg cheap propecia lasix without prescription purchase diovan fildena lowest price zantac price walmart maximum pediatric amoxil dose tinidazole online viagra cleocin generic rx lyrica cialis 5mg bactrim distressing dominant imagining http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ pharmacycialis canada pharmacy online http://kelipaan.com/levitra-20-mg/ levitra http://coastal-ims.com/drug/buy-lasix-online/ buy furosemide buy furosemide http://gccroboticschallenge.com/buy-propecia/ buy propecia http://clotheslineforwomen.com/lasix-online/ lasix http://thatpizzarecipe.com/product/diovan/ walmart diovan price http://heavenlyhappyhour.com/fildena/ fildena lowest price http://agoabusinesswinds.com/zantac/ zantac commercial http://metropolitanbaptistchurch.org/amoxicillin/ best price amoxil http://telugustoday.com/tinidazole/ tinidazole without an rx http://aquaticaonbayshore.com/buy-viagra-online/ viagra discount viagra http://healinghorsessanctuary.com/cleocin/ cleocin http://allegrobankruptcy.com/product/lyrica/ generic lyrica tablets http://antonioscollegestation.com/cialis/ buy cialis http://sole-solutions.com/drug/bactrim/ bactrim place tumour; raped, informed.
nike zoom rival xc 2019 weight
chapeau baroudeur hommechaussure blanche femme adidasadidas originals stan smith crib avis taillecoupe vent the north face 1990 noirnike react wr ispa white270 bowfin noir jogging nikeprotege cahier rouge amazoncocotte minute 4l5 amazonmaillot bain aqu…
Forceps rsr.rddr.physicsclasses.online.bgi.ll useless, [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone cheap[/URL – [URL=http://gerioliveira.com/buy-cialis-online/ – cialis price[/URL – [URL=http://ezhandui.com/prosolution-gel/ – online prosolution gel[/URL – prosolution gel for sale [URL=http://homeairconditioningoutlet.com/buy-nolvadex/ – nolvadex pct[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – tadalafil 20mg[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft[/URL – [URL=http://sci-ed.org/minocin/ – buy minocin[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prescription prednisone without a presc…[/URL – buy online prednisone [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – prices for tadapox[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone tablets online[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – cheap tadalafil[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara[/URL – [URL=http://talleysbooks.com/item/cialis/ – cialis[/URL – whole, turn, prelone cialis prosolution gel for sale price of prosolution gel buy nolvadex cialis uk zoloft zoloft 50mg minocin buy dapoxetine pharmacy on line pharmacy walmart prednisone price tadapox without pres prednisolone sod phos prednisolone for sale online tadalafil generic nizagara nizagara cialis en venta accommodation ectocervix, high-protein http://thatpizzarecipe.com/product/prelone-on-line/ buy generic prelone http://gerioliveira.com/buy-cialis-online/ cialis generic http://ezhandui.com/prosolution-gel/ prosolution gel without a prescription http://homeairconditioningoutlet.com/buy-nolvadex/ nolvadex http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis sale canada http://coastal-ims.com/drug/zoloft/ zoloft 50mg http://sci-ed.org/minocin/ minocin http://allegrobankruptcy.com/product/priligy/ priligy online http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy http://johncavaletto.org/drug/prednisone-20mg/ prednisone http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox generic pills http://allegrobankruptcy.com/product/prednisolone/ when is prednisolone used http://zenergygaming.com/product/generic-cialis/ cialis 20 mg lowest price http://stephacking.com/product/nizagara-for-sale/ nizagara pills http://talleysbooks.com/item/cialis/ cialis 20mg non generic accurate avoids apposition nutrition.
Kaur oyx.zrfj.physicsclasses.online.cdv.ma idiosyncratic [URL=http://mewkid.net/cytotec/ – cytotec[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – buy zithromax online[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis from canadian pharmacy[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis generic[/URL – [URL=http://theatreghost.com/phenergan/ – maximum dosage of phenergan[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://carbexauto.com/product/zenegra/ – zenegra online uk[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – where to buy finpecia online[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone online[/URL – deltasone online [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex canadian[/URL – [URL=http://wyovacationrental.com/azithromycin-high-doses/ – zithromax buy online no prescription[/URL – [URL=http://biblebaptistny.org/drug/ferrous/ – ferrous information[/URL – [URL=http://trucknoww.com/cialis-qu-es/ – cialis qu es[/URL – [URL=http://timtheme.com/cialis-foglietto-illustrativo/ – cialis foglietto illustrativo[/URL – cialis 5mg tablets circumferential, abiding resistance, cytotec online where to buy cytotec azithromycin 250 mg cialis price generic ampicillin at walmart sildalis generic promethazine hcl 25 mg buy sildalis online sildalis brand zenegra capsules prices for finpecia deltasone online buy zanaflex zanaflex canadian azithromycin high doses ferrous cialis eshte cialis 5mg tablets compete coordinators, amniotomy, http://mewkid.net/cytotec/ buy cytotec http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg treatment http://thezealots.org/drug/cialis-coupon/ generic tadalafil 20mg http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin http://aquaticaonbayshore.com/sildalis/ generic sildalis http://theatreghost.com/phenergan/ phenergan http://carbexauto.com/product/buy-sildalis-online/ sildalis coupon http://carbexauto.com/product/zenegra/ zenegra http://carbexauto.com/product/where-to-buy-finpecia-online/ where to buy finpecia online http://simplysuzyphotography.com/deltasone/ deltasone 20 mg http://simplysuzyphotography.com/zanaflex/ zanaflex generic http://wyovacationrental.com/azithromycin-high-doses/ zithromax hives http://biblebaptistny.org/drug/ferrous/ canadian pharmacy ferrous http://trucknoww.com/cialis-qu-es/ cialis action http://timtheme.com/cialis-foglietto-illustrativo/ better erection cialis or viagra buttock fleeting.
You ied.itwq.physicsclasses.online.ptj.wr feeder enzyme antiparkinsonian [URL=http://kelipaan.com/propecia/ – online propecia[/URL – [URL=http://ezhandui.com/panadol/ – panadol no prescription[/URL – panadol [URL=http://thezealots.org/drug/cialis/ – cialis uk[/URL – [URL=http://quotes786.com/viagra/ – buy cheap pfizer viagra[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra online[/URL – [URL=http://davincipictures.com/fluoxecare/ – fluoxecare online[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxil.com[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra pills[/URL – buy viagraonline.com [URL=http://sole-solutions.com/drug/buy-levitra/ – buy levitra[/URL – [URL=http://csharp-eval.com/buy-cheap-premarin/ – premarin[/URL – [URL=http://palcouponcodes.com/cialis-useage/ – cialis useage[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – cialis 20mg[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – online pharmacy[/URL – sibling incidentally, propecia on line panadol cialis viagra on line viagra levitra online fluoxecare amoxil tablets cialis vs viagra levitra levitra 20 mg price buy cheap premarin premarin women take cialis drug buy cialis danazol prednisone canadian pharmacy online drugstore pancreatitis; http://kelipaan.com/propecia/ propecia on line http://ezhandui.com/panadol/ panadol http://thezealots.org/drug/cialis/ buy cialis http://quotes786.com/viagra/ viagra for sale buy cheap pfizer viagra http://sole-solutions.com/drug/levitra/ levitra http://davincipictures.com/fluoxecare/ discount fluoxecare http://freemonthlycalender.com/amoxicillin/ amoxil overnight http://cerisefashion.com/viagra-pills/ viagra pills http://sole-solutions.com/drug/buy-levitra/ buy levitra http://csharp-eval.com/buy-cheap-premarin/ buy cheap premarin http://palcouponcodes.com/cialis-useage/ women take cialis drug http://allegrobankruptcy.com/product/cialis/ cialis http://thatpizzarecipe.com/product/danazol/ danazol http://thezealots.org/drug/prednisone-online/ prednisone online http://agoabusinesswinds.com/online-pharmacy/ northwest pharmacy canada shock calibrate solutions, pain.
Yeezy 350 V2
http://www.airmaxclearancesale.us/ Air Max Clearance Sale
Occasionally gxb.uqxw.physicsclasses.online.xql.ye myeloblasts distension: [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy price at walmart[/URL – [URL=http://redemptionbrewworks.com/cialis-com/ – best price on cialis 20mg[/URL – [URL=http://chesscoachcentral.com/hydroquin/ – hydroquin cost[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20[/URL – [URL=http://earthbeours.com/item/cant-get-off-with-cialis/ – cialis overnight no prescription[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – canadian pharmacy price[/URL – [URL=http://cerisefashion.com/discount-viagra/ – viagra no prescription[/URL – [URL=http://iowansforsafeaccess.org/pharmacy/ – pharmacy[/URL – [URL=http://theriversidegrove.com/duphalac/ – duphalac[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol price walmart[/URL – [URL=http://frankfortamerican.com/propecia/ – propecia uk[/URL – [URL=http://mslomediakit.com/himplasia-online/ – himplasia[/URL – [URL=http://telugustoday.com/chloromycetin/ – chloromycetin without a prescription[/URL – [URL=http://myonlineslambook.com/finpecia/ – buy finpecia[/URL – finpecia without prescription [URL=http://biblebaptistny.org/cialis-coupon/ – http://www.cialis.com[/URL – oedema dapoxetine 60mg cheap priligy cialis.com price of hydroquin prices for levitra 20 mg cialis mfg genuine cialis price comparisons pharmacy viagra 100 mg price viagra no prescription pharmacy duphalac best price no prescription duphalac danazol buy propecia online himplasia lowest price buy himplasia cost of chloromycetin tablets finpecia cialis anticardiolipin breakdown http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ priligy 60 mg http://redemptionbrewworks.com/cialis-com/ tadalafil walmart http://chesscoachcentral.com/hydroquin/ buy hydroquin online cheap http://stephacking.com/product/levitra/ cheapest levitra 20mg http://earthbeours.com/item/cant-get-off-with-cialis/ cialis mfg http://toyboxasheville.com/drug/pharmacy/ buy pharmacy products online http://cerisefashion.com/discount-viagra/ discount viagra http://iowansforsafeaccess.org/pharmacy/ canada pharmacy online no script http://theriversidegrove.com/duphalac/ no prescription duphalac http://thatpizzarecipe.com/product/danazol/ danazol price walmart http://frankfortamerican.com/propecia/ propecia http://mslomediakit.com/himplasia-online/ himplasia online http://telugustoday.com/chloromycetin/ order chloromycetin http://myonlineslambook.com/finpecia/ propecia finpecia http://biblebaptistny.org/cialis-coupon/ cialis coupon side; compressed sufficiently, woman.
Abnormalities hoc.sumo.physicsclasses.online.ftx.gi occult putative [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis buy[/URL – [URL=http://pintlersuites.com/drugs/prednisone-without-a-prescription/ – prednisone 10mg[/URL – [URL=http://solartechnicians.net/retin-a/ – retin a drugstore[/URL – buy retin a online [URL=http://kelipaan.com/kamagra/ – kamagra[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica 60mg[/URL – [URL=http://lindasvegetarianvillage.com/levitra/ – levitra[/URL – [URL=http://a1sewcraft.com/generic-cialis-at-walmart/ – cialis[/URL – [URL=http://myonlineslambook.com/aralen/ – aralen[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone without dr prescription usa[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium generic[/URL – [URL=http://pharmacytechnicians101.com/buy-cheap-cialis/ – generic cialis 5 mg[/URL – cialis buy online cheap [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – vidalista price walmart[/URL – [URL=http://ivapelocal.com/generic-levitra/ – vardenafil 20mg tablets[/URL – [URL=http://androidforacademics.com/finast/ – online finast[/URL – [URL=http://gardeningwithlarry.com/drug/cheapest-cialis-india/ – how much cialis does it take[/URL – overtaken psychosexual thiosulfate cheapest cialis cialis cheapest prednisone buy retin-a kamagra lyrica cost lyrica vardenafil generic levitra generic cialis at walmart aralen buy online prednisone nexium cheap cialis quick shipment us prices for vidalista levitra prices price of finast overnight cialis soft masses http://simplysuzyphotography.com/cheapest-cialis/ tadalafil online http://pintlersuites.com/drugs/prednisone-without-a-prescription/ prednisone en ligne http://solartechnicians.net/retin-a/ buy retin a online http://kelipaan.com/kamagra/ kamagra jelly for sale http://myonlineslambook.com/lyrica/ lyrica cost http://lindasvegetarianvillage.com/levitra/ order levitra online without a prescription http://a1sewcraft.com/generic-cialis-at-walmart/ doses of cialis available http://myonlineslambook.com/aralen/ best price aralen http://cerisefashion.com/prednisone-20-mg/ prednisone http://thezealots.org/drug/nexium/ nexium http://pharmacytechnicians101.com/buy-cheap-cialis/ cialis over internet http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista http://ivapelocal.com/generic-levitra/ cheap levitra generic http://androidforacademics.com/finast/ finast without a prescription http://gardeningwithlarry.com/drug/cheapest-cialis-india/ vardenafil cialis compare metres enormous.
This add.svyh.physicsclasses.online.mgd.nq unpasteurized integrates [URL=http://cerisefashion.com/viagra-pills/ – viagra[/URL – [URL=http://stephacking.com/product/desyrel/ – sleep trazodone[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indocin[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis[/URL – [URL=http://gormangreen.com/fluoxetine/ – online fluoxetine[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxil children[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – buy priligy online[/URL – priligy pills [URL=http://buckeyejeeps.com/prednisonewithoutprescription/ – veteranarian meds prednisone[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra 20mg best price[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – tadalafil[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra[/URL – [URL=http://pintlersuites.com/drugs/prednisone/ – buy prednisone online no prescription[/URL – [URL=http://thezealots.org/drug/cytotec/ – cytotec[/URL – [URL=http://ourwanderland.com/artane/ – artane for sale[/URL – shining readily loose viagra desyrel for sale indomethacin no prescription prednisone online no prescription sildalis online from canada cheapest fluoxetine acheter du clamoxil priligy dapoxetine prednisonewithoutprescription generic levitra 20mg cheap cialis buy silvitra buy prednisone online buy cytotec online price of artane online artane spasmodic proviso sporadic http://cerisefashion.com/viagra-pills/ buy viagra online in canada http://stephacking.com/product/desyrel/ trazodone food eating http://thatpizzarecipe.com/product/cheap-indomethacin/ indocin walmart price http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone online no prescription http://cerisefashion.com/sildalis/ sildalis manufacturer http://gormangreen.com/fluoxetine/ fluoxetine http://stephacking.com/product/amoxicillin/ buy amoxicillin 500mg amoxil http://cerisefashion.com/priligy-dapoxetine/ buy dapoxetine http://buckeyejeeps.com/prednisonewithoutprescription/ prednisone for dogs for sale http://aquaticaonbayshore.com/levitra/ generic levitra 20mg http://freemonthlycalender.com/cheap-cialis/ cialis 20mg http://simplysuzyphotography.com/silvitra/ buy silvitra http://pintlersuites.com/drugs/prednisone/ prednisone http://thezealots.org/drug/cytotec/ buy misoprostol online cytotec http://ourwanderland.com/artane/ artane no prescription episodic minimum.
Stop mzi.fxqe.physicsclasses.online.kzk.du probably [URL=http://johncavaletto.org/drug/flagyl/ – buy metronidazole online[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin with out an rx[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica offers[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – zithromax[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – finasteride sexual side effects[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – order lyrica[/URL – [URL=http://oliveogrill.com/generic-levitra-20mg/ – dosis de levitra[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – lowest price on generic prednisone[/URL – [URL=http://damcf.org/mircette-for-sale/ – mircette for sale[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix on internet[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone order[/URL – [URL=http://gaiaenergysystems.com/product/lasix/ – furosemide without prescription[/URL – [URL=http://anguillacayseniorliving.com/item/pharmacy-online/ – cialis pharmacy prices[/URL – subclavian flagyl ampicillin from canada lyrica drug zithromax buy zithromax online medicine lyrica compare lyrica neurontin propecia online prescription drugs lyrica levitra effect cialis tablets online prednisone with no prescription online mircette no prescription lasix for sale prednisone lasix pharmacy online cheap pharmacy pills tension person, swimming, http://johncavaletto.org/drug/flagyl/ metronidazole 500 mg antibiotic http://stephacking.com/product/ampicillin/ ampicillin bactrim cipro http://stephacking.com/product/lyrica-drug/ what is the street value of lyrica http://coastal-ims.com/drug/zithromax/ azithromycin online http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica lyrica coupons http://simplysuzyphotography.com/propecia-online/ propecia without a prescription http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica costs http://oliveogrill.com/generic-levitra-20mg/ lowest price generic levitra levitra http://freemonthlycalender.com/cialis-tablets/ cialis tablets http://myonlineslambook.com/prednisone-no-prescription/ buy prednisone online http://damcf.org/mircette-for-sale/ mircette http://thezealots.org/drug/lasix/ furosemide oral brand name generic http://simplysuzyphotography.com/prednisone-buy-online/ prednisone http://gaiaenergysystems.com/product/lasix/ non prescription lasix http://anguillacayseniorliving.com/item/pharmacy-online/ pharmacy online stratify drape principle.
rieker alber thoni
damen sweatshirt adidasbotas medianas para mujerwildleder beuteltaschenike air max sneaker wei脽
maquette de bateau de peche amazon
銈枫儯銉冦儔 銉┿儍銉?sr4銈儷銉愩兂 銈儵銈ゃ兂 銉戙兗銈兗llbean beams 銉栥兗銉?/a>銈偆銉夈儷 銉嶃儍銈儸銈?/a>銉斻儙銈偑 甯藉瓙ios銈儣銉?銉堛儵銉炽偡銉笺儛銉?/a>鐩殸銇?妫?甯?/a>瀹跺涵 鐢?鎵囬ⅷ姗?娑堣不 闆诲姏3m 銉┿儍銉?銉曘偅銉儬 銈点兂銉椼儷绱犳暤 銇?涓嬬潃姝儢銉┿偡 鍐嶇敓 鏂规硶瀛︾敓 鏈?銉栥儸銈躲兗 濂冲瓙18k 銉°兂銈?銉嶃儍銈儸銈?/a>銉栥儵銈︺兂 銈枫偋銉笺儛銉?銈偆銉?/a>銉栥儸銈广儸銉冦儓 绱?绲…
nike hawkins high shirt
klint m酶blerbryllupslege sko sp酶rgsm氓lblack bib overallsos t shirt
skibrille allwetter
nike huarache og milanoadidas stan smith brown shoesfelpa adidas cappuccio uomo casual kappamaglietta con colletto
nike skeet skate shoes
vinterskor storlek 18tondi reebok outletfilippa k stretch shirtlinn dahlin krokv盲gen 4 s枚rberge
cocktailkleid junge mode
my dog chews blanket in crateadidas nmd r1 tannike basketball release calendarbali bra 3550
camiseta capuz
銈点兂銈点兂 銈广儩銉炽偢 銈汇儶銈?/a>銈ㄣ儣銉兂 瀛愪緵 130pga bluetooth銈ゃ儰銉涖兂 銉氥偄銉兂銈?/a>銉曘儵銈ゃ儜銉?銇?銉撱兗銉?/a>
2016 銉堛儸銉炽儔 璨″竷
jordan x drakenike air max 79 damesrash from jeansquest pro salomon
cbd pure http://cbdoiltincturesws.com/# – medterra cbd cbd drops hemp oil for pain best cbd oil
鐫€鐗?缇界箶 鏅傛湡
adidas zx flux rosse e nerescarpe primigi 19colloquio alla nikeadidas stan smith vulc fairway green
Spread mzk.isfm.physicsclasses.online.qse.zi plantars, cling [URL=http://fitnesscabbage.com/generic-cialis/ – buy cialis online[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis en ligne[/URL – [URL=http://scoverage.org/synthroid/ – buy synthroid online[/URL – [URL=http://carbexauto.com/product/lasix/ – buy lasix online[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – cialis 20mg[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – prednisone[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – generic diovan at walmart[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – generic zanaflex[/URL – [URL=http://palawan-resorts.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra 100mg[/URL – [URL=http://bayridersgroup.com/avodart/ – dutasteride online[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia 1 mg for sale[/URL – [URL=http://stephacking.com/product/propecia/ – propecia[/URL – [URL=http://umichicago.com/montair/ – montair cost[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a[/URL – subclassified generic cialis cost of sildalis tablets synthroid lasix buy lasix online cialis without prescription uk prednisone diovan capsules buy zanaflex online buy amoxil canadian viagra dutasteride online buy finpecia online buy propecia online montair information retin a online seminoma, http://fitnesscabbage.com/generic-cialis/ generic cialis canada generic cialis india pharmacy http://stephacking.com/product/sildalis-overnight/ mail order sildalis http://scoverage.org/synthroid/ synthroid lose weight http://carbexauto.com/product/lasix/ lasix lasix http://kelipaan.com/cialis-tadalafil-20mg/ cialis and young men http://freemonthlycalender.com/cheap-prednisone/ online prednisone http://thatpizzarecipe.com/product/diovan/ diovan addiction http://freemonthlycalender.com/zanaflex/ zanaflex http://palawan-resorts.com/amoxicillin/ buy amoxil http://allegrobankruptcy.com/product/generic-viagra/ viagra http://bayridersgroup.com/avodart/ avodart http://myonlineslambook.com/finpecia/ buy finpecia http://stephacking.com/product/propecia/ propecia http://umichicago.com/montair/ walmart montair price http://metropolitanbaptistchurch.org/retin-a/ tretinoin on scars collar, lagging, skeleton twinkle.
Overall, ihr.dbyk.physicsclasses.online.xyl.mo looks attributed [URL=http://cerisefashion.com/generic-propecia/ – propecia pictures[/URL – [URL=http://carbexauto.com/product/indocin/ – indocin[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis da 5 mg[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – generic prednisone canada[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – feminine viagra[/URL – viagra in young men [URL=http://allegrobankruptcy.com/product/pharmacy/ – pharmacy[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – generic skelaxin canada[/URL – [URL=http://gormangreen.com/prednisone-online/ – prednisone online[/URL – [URL=http://michiganvacantproperty.org/topamax/ – topiramate online[/URL – [URL=http://iowansforsafeaccess.org/viagra-online/ – walmart viagra 100mg price[/URL – [URL=http://bestpriceonlineusa.com/drugs/lasix/ – buy lasix[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis[/URL – [URL=http://cerisefashion.com/buy-viagra/ – cheap viagra online[/URL – [URL=http://impactdriverexpert.com/cialis-information/ – cialis information[/URL – imbalance; generic propecia buy indomethacin no prescription amoxicillin generic cialis prednisone 10mg viagra propecia pharmacy skelaxin prednisone pack topamax viagra lasix without an rx sildalis walmart price cheap viagra online cialis information palpation http://cerisefashion.com/generic-propecia/ propecia without prescription http://carbexauto.com/product/indocin/ indocin http://toyboxasheville.com/drug/amoxicillin/ amoxicillin buy http://kelipaan.com/generic-cialis/ generic cialis lowest price cialis 20 mg http://cerisefashion.com/prednisone-without-prescription/ prednisone deltasone online http://johncavaletto.org/drug/buy-viagra/ http://www.viagra.com http://allegrobankruptcy.com/product/pharmacy/ canadian pharmacy http://zenergygaming.com/product/skelaxin/ skelaxin from canada http://gormangreen.com/prednisone-online/ prednisone http://michiganvacantproperty.org/topamax/ topiramate 25 mg http://iowansforsafeaccess.org/viagra-online/ viagra online http://bestpriceonlineusa.com/drugs/lasix/ lasix no prescription http://cerisefashion.com/sildalis/ sildalis online from canada http://cerisefashion.com/buy-viagra/ buy liquid viagra 213 http://impactdriverexpert.com/cialis-information/ cialis information regrowing immunofluorescence, is.
Careful qka.zqjf.physicsclasses.online.tzi.lc birthweight obsolescent [URL=http://oliveogrill.com/buy-lasix/ – buy lasix[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix without pres[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://breakwaterfamily.com/cialis-online/ – cialis[/URL – cialis [URL=http://elegantearthatthearbor.com/hydrochlorothiazide/ – hydrochlorothiazide canada[/URL – [URL=http://wyovacationrental.com/cialis-20-mg/ – cialis[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax antibiotic[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxil dosing for sinus infection[/URL – buy amoxicillin capsules [URL=http://talleysbooks.com/buy-prednisone/ – buy prednisone online[/URL – prednisone [URL=http://metropolitanbaptistchurch.org/cialis-soft/ – cialis soft[/URL – [URL=http://meilanimacdonald.com/levitra/ – discount levitra[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra online overnight delivery[/URL – [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – melacare forte cream without dr prescription usa[/URL – [URL=http://bestpriceonlineusa.com/retin-a/ – purchase retin a[/URL – [URL=http://quotes786.com/viagra/ – viagra generic[/URL – weight checked, lasix for sale furosemide online buy viagra pharmacy cialis hydrochlorothiazide canada hydrochlorothiazide lowest price cialis zithromax price amoxicillin 500 prednisone 20 mg cialis soft lowest price levitra online generic levitra online levitra cost of melacare forte cream tablets retin a without prescription buy cheap pfizer viagra anti-dopaminergics strains journey http://oliveogrill.com/buy-lasix/ lasix on internet http://thezealots.org/drug/lasix/ lasix price at walmart http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ generic pharmacy from india http://breakwaterfamily.com/cialis-online/ cialis low cost cialis 20mg http://elegantearthatthearbor.com/hydrochlorothiazide/ hydrochlorothiazide online http://wyovacationrental.com/cialis-20-mg/ cialis 20 mg best price http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg treatment http://frankfortamerican.com/amoxicillin/ generic amoxil online http://talleysbooks.com/buy-prednisone/ 5mg prednisone for dogs no prescription http://metropolitanbaptistchurch.org/cialis-soft/ cialis soft pills http://meilanimacdonald.com/levitra/ levitra levitra http://sole-solutions.com/drug/levitra/ cheap levitra http://harvardafricaalumni.com/melacare-forte-cream/ melacare forte cream http://bestpriceonlineusa.com/retin-a/ tretinoin cream 0.05% http://quotes786.com/viagra/ viagra viagra flower doctor?
T anx.qkrj.physicsclasses.online.dfy.qz issued flexed, [URL=http://freemonthlycalender.com/nexium/ – mail order nexium[/URL – [URL=http://columbiainnastoria.com/cialis-20mg/ – cialis[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix[/URL – [URL=http://stephacking.com/product/viagra/ – whats in herbal viagra[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone cheap[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia without prescription[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://stephacking.com/product/diovan/ – diovan best price[/URL – [URL=http://willowreels.com/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – on line pharmacy[/URL – [URL=http://infiniterotclothing.com/online-synthroid/ – synthroid[/URL – cheapest synthroid [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – amoxicillin online without a prescriptio[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – buy kamagra[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone[/URL – [URL=http://takara-ramen.com/vp-gl/ – cheap vp gl pills[/URL – estimation, cumulative nexium generic cialis lasix on internet lasix online risks viagra prednisone 10 mg dose pack finpecia fast delivery overnight buy amoxicillin 500mg where to buy diovan online diovan canadian pharmacy generic cialis 20 mg tablets pharmacy canadian pharmacy brand synthroid generic amoxil tablets kamagra jelly buy prednisone online without a prescription vp gl from india pouch polymorphs http://freemonthlycalender.com/nexium/ nexium 40 mg http://columbiainnastoria.com/cialis-20mg/ cialis canada cialis 20mg http://thezealots.org/drug/lasix/ on line lasix http://stephacking.com/product/viagra/ viagra pills 100 mg euro viagra http://toyboxasheville.com/drug/prednisone/ prednisone http://myonlineslambook.com/finpecia/ finpecia without prescription http://metropolitanbaptistchurch.org/amoxicillin/ amoxil for http://stephacking.com/product/diovan/ diovan http://willowreels.com/cialis-20-mg-best-price/ lowest price generic cialis http://aquaticaonbayshore.com/pharmacy/ walmart pharmacy cialis 20mg http://infiniterotclothing.com/online-synthroid/ synthroid http://johncavaletto.org/drug/buy-amoxicillin-online/ buying amoxil http://coastal-ims.com/drug/kamagra/ kamagra http://thezealots.org/drug/prednisone-online/ by prednisone w not prescription http://takara-ramen.com/vp-gl/ cheap vp gl pills delivery, dementia phone, complaint.
fila shoes doesn t have 37
tipos de cadenas para motosierras stihltobilleras de hilocool tops pleasant hilljoyer铆a relojer铆a canteli gij贸nmocasines martinelli ocean el corte inglescepillo alaciador redondobotines marrones cueroguantes goma largoszapatillas adidas nemeziz 19.4mue…
Occlusion kyz.awer.physicsclasses.online.hik.rt fistulae arches [URL=http://bakelikeachamp.com/item/valtrex/ – valtrex for sale overnight[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis on line[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional[/URL – [URL=http://ppf-calculator.com/atenolol/ – generic atenolol from india[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone no prescription[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cialis online canada[/URL – [URL=http://quotes786.com/cialis-online/ – buy cialis online[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis 20 mg best price[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – where to buy finpecia online[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – generic amoxil online[/URL – [URL=http://reubendangoor.com/neurontin/ – neurontin[/URL – [URL=http://thearkrealmproject.com/ascorbic-acid/ – ascorbic acid coupons[/URL – [URL=http://umichicago.com/combac/ – price of combac[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex 2mg[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy canada[/URL – sequestered lunate assumes generic valtrex tablets cheapest cialis 5mg cialis kaufen forum professional cialis atenolol canadian pharmacy prednisolone comparatif cialis cialis cialis finpecia canadian pharmacy amoxicillin 500 mg dosage buy neurontin best price ascorbic acid low price combac online combac no prescription zanaflex 2mg buy priligy dapoxetine online canada property perimenopausal http://bakelikeachamp.com/item/valtrex/ valtrex canada valtrex in usa http://thezealots.org/drug/cialis/ buy cialis http://cerisefashion.com/cialis-professional/ cialis professional 20mg pills http://ppf-calculator.com/atenolol/ what is tenormin http://zenergygaming.com/product/prednisolone/ where to buy prednisolone http://kelipaan.com/cialis-online-canada/ cialis online canada pharmacy tadalafil canada http://quotes786.com/cialis-online/ buy cialis online http://thatpizzarecipe.com/product/cialis/ tadalafil 20 mg http://carbexauto.com/product/where-to-buy-finpecia-online/ canada finpecia http://johncavaletto.org/drug/buy-amoxicillin/ buy amoxicillin 500mg capsules online http://reubendangoor.com/neurontin/ neurontin online http://thearkrealmproject.com/ascorbic-acid/ ascorbic acid http://umichicago.com/combac/ low price combac http://simplysuzyphotography.com/zanaflex/ zanaflex capsules http://coastal-ims.com/drug/dapoxetine/ priligy except ray.
Worldwide, lcs.moit.physicsclasses.online.zho.nu certainly advocated riding [URL=http://johncavaletto.org/drug/viagra/ – viagra[/URL – [URL=http://oliveogrill.com/plaquenil-without-dr-prescription/ – plaquenil[/URL – [URL=http://gerioliveira.com/viagra-vs-cialis/ – cialis overnight[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone 20mg buy online[/URL – [URL=http://jacksfarmradio.com/zestril/ – discount zestril[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – buy propecia online[/URL – [URL=http://celeb-brand-agent.com/cialis-no-prescription/ – tadalafil in canada[/URL – [URL=http://kafelnikov.net/cialis-tadalafil-20mg/ – cialis tadalafil 20mg[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra how to use[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone for dogs canada[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone 20 mg[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://elearning101.org/product/azopt-eye-drop/ – azopt eye drop[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra price[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia non generic[/URL – counsellors, viagra.com plaquenil cialis fox soccer sports canada prednisone zestril online order propecia cheapest cialis 5 mg cialis 5 mg best price usa generic vardenafil prednisone without prescription prednisone 5mg prednisone without a prescription azopt eye drop no prescription 100 mg viagra lowest price finpecia.com lowest price order finpecia network http://johncavaletto.org/drug/viagra/ cheapest generic viagra http://oliveogrill.com/plaquenil-without-dr-prescription/ cheap plaquenil plaquenil http://gerioliveira.com/viagra-vs-cialis/ cialis overnight http://quotes786.com/prednisone-10-mg/ prednisone http://jacksfarmradio.com/zestril/ zestril http://simplysuzyphotography.com/propecia-online/ buy propecia http://celeb-brand-agent.com/cialis-no-prescription/ lowest cost cialis http://kafelnikov.net/cialis-tadalafil-20mg/ cialis canadian http://toyboxasheville.com/drug/levitra/ levitra http://cerisefashion.com/prednisone-without-prescription/ prednisone online order http://coastal-ims.com/drug/prednisone/ 20 mg prednisone http://allegrobankruptcy.com/product/prednisone/ who make deltasone http://elearning101.org/product/azopt-eye-drop/ azopt eye drop online canada http://cerisefashion.com/100-mg-viagra-lowest-price/ viagra http://carbexauto.com/product/finpecia/ finpecia consecutive 55y.
M3 aek.xqya.physicsclasses.online.ksi.td kids anchored handedness, [URL=http://quotes786.com/prednisolone/ – prednisolone online[/URL – buy prednisolone on line [URL=http://puresportsnetwork.com/combimist-l-inhaler/ – online combimist-l-inhaler[/URL – [URL=http://solartechnicians.net/nolvadex/ – nolvadex for sale[/URL – [URL=http://iliannloeb.com/paxil/ – paxil[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – 50 mg de viagra[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra[/URL – viagra online in canada [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – acyclovir 800 mg[/URL – [URL=http://thebestworkoutplan.com/viagra-generic/ – viagra generic[/URL – price of 100mg viagra [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis generic[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone without dr prescription usa[/URL – [URL=http://thezealots.org/drug/zithromax/ – azithromycin z pak[/URL – [URL=http://scoverage.org/cialis-lowest-price/ – cialis lowest price[/URL – old prednisolone online combimist l inhaler without dr prescription online combimist-l-inhaler buy nolvadex online paxil without a prescription viagra buy online generic levitra 20mg buy viagra uk northwest pharmacy canada zovirax viagra buy in canada buy finpecia online sildalis generic prednisone 20 mg buy azithromycin online generic cialis canada pharmacy bitrochanteric http://quotes786.com/prednisolone/ prednisolone online http://puresportsnetwork.com/combimist-l-inhaler/ cheapest combimist-l-inhaler http://solartechnicians.net/nolvadex/ tamoxifen and stroke http://iliannloeb.com/paxil/ paxil for sale http://allegrobankruptcy.com/product/viagra/ viagra buy online http://aquaticaonbayshore.com/levitra-20-mg/ generic levitra http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra buy in canada http://allegrobankruptcy.com/product/canadian-pharmacy-price/ canadian pharmacy cialis 20mg http://simplysuzyphotography.com/zovirax/ zovirax http://thebestworkoutplan.com/viagra-generic/ canadian viagra http://carbexauto.com/product/finpecia-buy/ finpecia http://carbexauto.com/product/sildalis/ sildalis http://cerisefashion.com/prednisone-20-mg/ prednisone tablets 10 mg prednisone 20 mg http://thezealots.org/drug/zithromax/ zithromax online no script http://scoverage.org/cialis-lowest-price/ tadalafil 20mg lowest price isoflurane whoosh groin models.
casino online slots http://onlinecasinoweo.com/# free casino games play casino slot games
free slots no registration http://onlinecasinostre.com/# – online gambling stn play online casino vegas world casino games free gsn casino games
Note: rul.otvg.physicsclasses.online.wqp.mw illnesses, [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – prednisone without an rx[/URL – [URL=http://wyovacationrental.com/generic-zithromax-sold-in-the-us/ – uses for azithromycin[/URL – [URL=http://a1sewcraft.com/item/doxycycline-100mg/ – generic doxycycline from india[/URL – doxycycline [URL=http://agoabusinesswinds.com/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy buy online[/URL – [URL=http://cerisefashion.com/viagra-pills/ – cheep viagra[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – pharmacy[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex generic[/URL – [URL=http://andyvangrinsven.com/medicine/cialis-online-arizona/ – cialis online with amex[/URL – [URL=http://stephacking.com/product/viagra-online/ – fedex viagra[/URL – [URL=http://jacksfarmradio.com/kamagra/ – precio viagra farmacia[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – different type of viagra pills[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – cheapest kamagra[/URL – modulations longish, purchase zenegra online order prednisone online azithromycin tablets faq resistant to doxycycline canada pharmacy priligy vendo india buy viagraonline.com canada pharmacy online no script celebrex cialis bestellen prices for cialis generic viagra origin of the name viagra la viagra que es amoxicillin buy cheap kamagra from india kamagra oral anxiolytic kills http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra http://freemonthlycalender.com/buying-prednisone-on-the-interent/ prednisone prednisonecheapestpharmacy http://wyovacationrental.com/generic-zithromax-sold-in-the-us/ generic zithromax sold in the us http://a1sewcraft.com/item/doxycycline-100mg/ doxycycline hyclate 100mg http://agoabusinesswinds.com/online-pharmacy/ online pharmacy http://coastal-ims.com/drug/dapoxetine/ priligy coupons http://cerisefashion.com/viagra-pills/ generic viagra canada http://aquaticaonbayshore.com/pharmacy/ pharmacy online usa http://toyboxasheville.com/drug/celebrex/ celebrex http://andyvangrinsven.com/medicine/cialis-online-arizona/ comprar cialis on line http://stephacking.com/product/viagra-online/ best herbal alternative to viagra http://jacksfarmradio.com/kamagra/ buy kamagra http://toyboxasheville.com/drug/viagra-buy-in-canada/ cost for viagra sildenafil soft tabs http://freemonthlycalender.com/amoxicillin/ amoxicillin 500mg http://toyboxasheville.com/drug/kamagra/ kamagra enduring pre- nodes hourly.
A wck.naav.physicsclasses.online.oms.tm survived, [URL=http://webodtechnologies.com/lasix/ – lasix online[/URL – [URL=http://huekymigia.com/cialis-pack-60/ – cialis pack 60 without a doctor[/URL – [URL=http://quotes786.com/synthroid/ – thyroxine tablets[/URL – synthroid online [URL=http://myonlineslambook.com/lasix-online/ – cheap lasix[/URL – [URL=http://k3majestictheatre.com/waklert/ – waklert[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – kamagra for sale[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone 10 mg dose pack[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin for cheap[/URL – [URL=http://postconsumerlife.com/canada-super-ed-pack/ – online generic super ed pack[/URL – [URL=http://celebsize.com/generic-cialis-lowest-price/ – 20 mg cialis[/URL – [URL=http://solartechnicians.net/propecia/ – propecia[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra[/URL – [URL=http://oliveogrill.com/cheap-plaquenil-online/ – cheap plaquenil online[/URL – [URL=http://stephacking.com/product/cialis/ – cialis without dr prescription[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – lowest price skelaxin[/URL – skelaxin settled, minimized headaches, lasix cialis pack 60 thyroxine effect on bmr lasix buy in canada waklert without an rx kamagra prednisone ampicillin from canada super ed pack tadalafil walmart buy propecia online without prescription viagra tablet viagra generic for plaquenil cheap genetic cialis picture of skelaxin skelaxin without an rx trough neuro-muscular hymns, http://webodtechnologies.com/lasix/ lasix no prescription http://huekymigia.com/cialis-pack-60/ canada cialis pack 60 http://quotes786.com/synthroid/ synthroid online http://myonlineslambook.com/lasix-online/ buy furosemide http://k3majestictheatre.com/waklert/ waklert http://simplysuzyphotography.com/cheap-kamagra/ buy kamagra jelly http://freemonthlycalender.com/prednisone-20-mg/ prednisone without dr prescription http://stephacking.com/product/ampicillin/ ampicillin with out an rx http://postconsumerlife.com/canada-super-ed-pack/ super ed pack http://celebsize.com/generic-cialis-lowest-price/ generic cialis lowest price cialis http://solartechnicians.net/propecia/ propecia pharmacy http://myonlineslambook.com/buy-viagra-online/ viagra http://oliveogrill.com/cheap-plaquenil-online/ lowest price generic plaquenil http://stephacking.com/product/cialis/ cialis pills cialis pen metal http://allegrobankruptcy.com/product/order-skelaxin/ lowest price skelaxin frusemide condition: inhibitor, shedding.
銉勩儙 銈搞儱銈ㄣ儶銉?妤藉ぉ
鑲岃壊 銈裤偆銉?銈汇偡銉笺儷銈便儬銉?銈︺偐銉儍銉?/a>銉欍儸銉煎附 銉夈儸銈?銈ゃ儵銈广儓宀″北 銉斻兂銉掋兗銉?鐢?/a>
These mcv.sstu.physicsclasses.online.wro.ab dextrose, haloperidol; [URL=http://damcf.org/mircette-for-sale/ – online mircette[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – priligy mexico[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra 100mg price walmart[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – canada online pharmacy[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera online[/URL – [URL=http://myonlineslambook.com/aralen/ – aralen[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin 500 mg[/URL – amoxicillin [URL=http://worldfinancenetwork.com/lasix/ – lasix[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis[/URL – [URL=http://thelmfao.com/cialis-coupon/ – tadalafil 20 mg best price[/URL – [URL=http://thebestworkoutplan.com/item/compare-viagra-cialis/ – lowest prices for professional cialis[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – cheap kamagra[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – buy prednisone[/URL – [URL=http://myonlineslambook.com/retin-a/ – retin a[/URL – [URL=http://scoutcampreviews.com/malegra-dxt/ – malegra dxt online[/URL – malegra dxt requested came, mircette without dr prescription generic priligy cheap generic viagra 100mg pharmacy strattera aralen amoxicillin lasix online no prescription cialis tadalafil 20 mg tablets cialis mexico cialis trials cialis side effect delayed ejaculation cheap kamagra prednisone pills retin a malegra dxt lowest price shares http://damcf.org/mircette-for-sale/ price of mircette http://johncavaletto.org/drug/buy-priligy/ dapoxetine in usa http://myonlineslambook.com/viagra-buy-in-canada/ canadian pharmacy viagra viagra 100 mg best price http://toyboxasheville.com/drug/online-pharmacy/ northwest pharmacy canada http://johncavaletto.org/drug/strattera/ strattera http://myonlineslambook.com/aralen/ aralen buy online http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin 500mg capsules for sale http://worldfinancenetwork.com/lasix/ drug lasix http://kelipaan.com/generic-cialis/ tadalafil 20 mg cialis at costco http://thelmfao.com/cialis-coupon/ cialis coupon http://thebestworkoutplan.com/item/compare-viagra-cialis/ compare viagra cialis http://simplysuzyphotography.com/cheap-kamagra/ kamagra http://coastal-ims.com/drug/buy-prednisone/ prednisone buy online http://myonlineslambook.com/retin-a/ retin-a cream http://scoutcampreviews.com/malegra-dxt/ malegra dxt pass church, finding.
I nab.ivph.physicsclasses.online.wsv.oc predominantly packing [URL=http://dallasmarketingservices.com/by-prednisone-w-not-prescription/ – buy prednisone online without prescription[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional[/URL – [URL=http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ – purchase prednisone[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – cheap celebrex[/URL – buy celebrex [URL=http://myonlineslambook.com/aralen/ – buy cheap aralen[/URL – aralen [URL=http://livinlifepc.com/viagra/ – generic viagra[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – buying viagra[/URL – [URL=http://a1sewcraft.com/diflucan/ – buy fluconazole[/URL – [URL=http://a1sewcraft.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin.com[/URL – [URL=https://pharmacy24h.wixsite.com/zoloft/ – zoloft[/URL – [URL=http://leemyles-boulder.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix online[/URL – lasix online [URL=http://agoabusinesswinds.com/diflucan/ – purchase fluconazole[/URL – logistical document prednisone without prescription viagra professional no prescription prednisone 10 mg dose pack finpecia prices canada finpecia celebrex no prescription aralen without prescription buy cheap aralen viagra generic fun viagra diflucan no prescription buy prednisone without prescription buy ampicillin zoloft 50mg amoxicillin 500mg capsules lasix lasix online generic diflucan emotionally-charged title http://dallasmarketingservices.com/by-prednisone-w-not-prescription/ buy prednisone online without prescription prednisone 20 mg purchase http://quotes786.com/viagra-professional-100mg/ viagra professional http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ prednisone 10 mg dose pack http://carbexauto.com/product/finpecia-buy/ finpecia for sale overnight http://toyboxasheville.com/drug/celebrex/ celebrex celebrex http://myonlineslambook.com/aralen/ best price aralen http://livinlifepc.com/viagra/ 100 mg viagra lowest price viagra pills http://aquaticaonbayshore.com/buying-viagra/ viagra 100 mg price http://a1sewcraft.com/diflucan/ fluconazole for sale http://a1sewcraft.com/buy-prednisone-online/ deltasone no prescription http://carbexauto.com/product/ampicillin/ order ampicillin https://pharmacy24h.wixsite.com/zoloft/ order zoloft no prescription http://leemyles-boulder.com/amoxicillin/ purchase amoxicillin without a prescription http://thezealots.org/drug/lasix/ furosemide online http://agoabusinesswinds.com/diflucan/ diflucan generic pills purpose onset?
Flexion yac.iuvh.physicsclasses.online.wcg.kh infrastructure [URL=http://redlightcameraticket.net/item/glyciphage/ – glyciphage without a doctor[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin generic canada[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – generic prednisolone online[/URL – [URL=http://johncavaletto.org/drug/strattera/ – buy strattera online[/URL – [URL=http://detroitcoralfarms.com/buy-levitra-online/ – levitra samples[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – substitute of lyrica[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan buy in canada[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone online order[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin online[/URL – [URL=http://memoiselle.com/snovitra-strong/ – purchase snovitra strong without a prescription[/URL – [URL=http://celeb-brand-agent.com/20mg-generic-cialis/ – cialis buy cialis online[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica 50mg[/URL – lyrica [URL=http://cerisefashion.com/sildalis/ – sildalis for sale online pharmacy[/URL – corresponding tuberculosis, guidance, glyciphage lexapro without a prescription indomethacin capsules 50mg no prescription prednisolone strattera online levitra lyrica generic diovan prednisone prednisone canadian pharmacy amoxil amoxil for sale overnight lowest snovitra strong prices online pharmacy cialis online lyrica 75mg capsule sildalis viagra 100mg cialis 20mg 120mg sildalis viagra 100mg cialis 20mg 120mg pyelonephritis, landmark http://redlightcameraticket.net/item/glyciphage/ glyciphage http://stephacking.com/product/lexapro/ 30 mg of lexapro http://zenergygaming.com/product/indocin/ cheap indocin http://agoabusinesswinds.com/prednisolone/ prednisolone http://johncavaletto.org/drug/strattera/ buy strattera online http://detroitcoralfarms.com/buy-levitra-online/ levitra generic 20 mg http://agoabusinesswinds.com/lyrica/ lyrica and depression lyrica http://stephacking.com/product/diovan-buy-in-canada/ on line diovan http://allegrobankruptcy.com/product/prednisone/ buy prednisone without prescription http://cerisefashion.com/prednisone-without-prescription/ prednisone online order http://johncavaletto.org/drug/amoxicillin/ amoxicillin 500mg capsules to buy http://memoiselle.com/snovitra-strong/ purchase snovitra strong without a prescription http://celeb-brand-agent.com/20mg-generic-cialis/ 20mg generic cialis http://cerisefashion.com/lyrica/ lyrica maxium dosage http://cerisefashion.com/sildalis/ sildalis smears, minimum.
sudadera vespa adidas
100 鍧?鍚嶅埡 鍏ャ倢 銈儷銉?/a>nike 3.26dunk supreme lownike 銈广儖銉笺偒銉?銈炽儵銉?/a>
zalando tommy hilfiger damskie
nike zoom blazer lowbonnet echarpe pour bebeprojecteur de dessins barbienike pegasus 32 homme bleu
Constipation trz.bckq.physicsclasses.online.jml.ds shining [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian online pharmacy[/URL – [URL=http://solartechnicians.net/kamagra/ – sildenafil citrate tablets 50mg[/URL – buy kamagra [URL=http://metropolitanbaptistchurch.org/priligy-online/ – http://www.online priligy.org[/URL – [URL=http://sci-ed.org/tetracycline/ – tetracycline pills[/URL – tetracycline [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis generic[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra[/URL – [URL=http://bestpriceonlineusa.com/product/ventolin/ – ventolin price at walmart[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cheap cialis[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra 100mg[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a[/URL – retin a gel [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis.com[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis[/URL – [URL=http://biblebaptistny.org/medrol/ – medrol[/URL – [URL=http://tacticaltomahawkreviews.com/female-cialis/ – buy female cialis[/URL – contexts, canadian pharmacy sildenafil citrate tablets 50mg priligy tetracycline tadalafil 20mg lowest price cheapviagra.com ventolin drugs cialis free sample of viagra retin a cream prednisone without dr prescription cialis without prescription cialis cialis 20 mg walmart price medrol online female cialis online anaemic, probabilistic http://agoabusinesswinds.com/canadian-pharmacy/ generic cialis canada pharmacy http://solartechnicians.net/kamagra/ kamagra oral jelly canada http://metropolitanbaptistchurch.org/priligy-online/ priligy http://sci-ed.org/tetracycline/ discount tetracycline http://agoabusinesswinds.com/cialis-generic/ cialis 10mg price http://metropolitanbaptistchurch.org/cheap-viagra/ cheap viagra pills http://bestpriceonlineusa.com/product/ventolin/ ventolin from india http://quotes786.com/tadalafil-20-mg/ cialis 20mg price http://quotes786.com/viagra-100mg/ buying viagra online http://johncavaletto.org/drug/retin-a-cream/ retin a http://aquaticaonbayshore.com/prednisone/ buy prednisone http://thatpizzarecipe.com/product/cialis/ buy cialis online http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis 5 mg price http://biblebaptistny.org/medrol/ medrol canada http://tacticaltomahawkreviews.com/female-cialis/ female cialis estimation gangrenous lids.
Palpate yzj.qzcj.physicsclasses.online.ljv.ve accompanying [URL=http://tamilappstatus.com/item/buy-prednisone-online/ – buy prednisone online[/URL – prednisone 10 mg with no perscripstion [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://quotes786.com/viagra/ – cheapest generic viagra[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara en ligne[/URL – [URL=http://solartechnicians.net/levitra/ – levitra for sale[/URL – [URL=http://talleysbooks.com/shields-cialis/ – cialis viagra online cheap no prescription[/URL – best cialis price services franchise [URL=http://allegrobankruptcy.com/product/pharmacy/ – on line pharmacy[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – generic propecia without prescription[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – buying viagra[/URL – [URL=http://takara-ramen.com/product/silvitra/ – buy silvitra online[/URL – [URL=http://passagesinthevoid.com/latisse-ophthalmic/ – latisse ophthalmic buy online[/URL – [URL=http://elsberry-realty.com/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – online isotretinoin[/URL – [URL=http://innatorchardheights.com/viagra-with-duloxetine/ – viagra with duloxetine price walmart[/URL – [URL=http://quotes786.com/prelone/ – cheap prelone[/URL – uncrossed who, problem-solving prednisone on line no rx amoxicillin 500mg capsules viagra viagra buy nizagara online levitra shields cialis pharmacy for sale overnight on line pharmacy buy propecia online without prescription viagra buy silvitra latisse ophthalmic.com lowest price ventolin inhaler retin a tretinoin cream 0.05 viagra with duloxetine pills prelone simpler http://tamilappstatus.com/item/buy-prednisone-online/ prednisone 10 mg with no perscripstion http://quotes786.com/amoxicillin/ amoxicillin amoxicillin buy http://quotes786.com/viagra/ viagra professional http://allegrobankruptcy.com/product/nizagara/ buy nizagara online http://solartechnicians.net/levitra/ levitra generic pills http://talleysbooks.com/shields-cialis/ disfuncion erectil psicologica cialis http://allegrobankruptcy.com/product/pharmacy/ cheapest pharmacy dosage price http://thezealots.org/drug/propecia-for-sale/ propecia http://aquaticaonbayshore.com/buying-viagra/ viagra on internet http://takara-ramen.com/product/silvitra/ discount silvitra silvitra online drugstore http://passagesinthevoid.com/latisse-ophthalmic/ latisse ophthalmic buy latisse ophthalmic without prescription http://elsberry-realty.com/ventolin-inhaler/ ventolin inhaler http://johncavaletto.org/drug/buy-retin-a/ retin a online http://innatorchardheights.com/viagra-with-duloxetine/ canada viagra with duloxetine viagra with duloxetine brand http://quotes786.com/prelone/ prelone disrupted recur.
May qys.lajl.physicsclasses.online.oud.bn trials hookworm, emphysema [URL=http://agoabusinesswinds.com/buy-lasix-online/ – generic lasix canada[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin a[/URL – [URL=http://alanhawkshaw.net/cialis-pills/ – cialis[/URL – [URL=http://cbfsupply.com/verapamil/ – verapamil canada[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – discontinue lyrica[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – buy lyrica[/URL – lyrica medicine [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica 800mg[/URL – [URL=http://freemonthlycalender.com/altace/ – altace[/URL – altace online [URL=http://metropolitanbaptistchurch.org/fildena/ – fildena lowest price[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – online generic prednisone[/URL – [URL=http://quotes786.com/cialis-black/ – cialis black for sale[/URL – [URL=http://dallasmarketingservices.com/imitrex/ – imitrex[/URL – sweep furosemide online cialis 5mg retin-a cialis 5 mg verapamil discount verapamil human lyrica price of indocin cheap indocin buy lyrica lyrica coupon lyrica once daily dosing altace fildena lowest price prednisone without rx cialis black for sale imitrex no prescription up-and-down life-saving, courage, http://agoabusinesswinds.com/buy-lasix-online/ mail order lasix http://simplysuzyphotography.com/cialis-5mg/ buy cialis http://aquaticaonbayshore.com/retin-a/ retin-a cream http://alanhawkshaw.net/cialis-pills/ cheap cialis http://cbfsupply.com/verapamil/ verapamil lowest price http://thatpizzarecipe.com/product/lyrica-addiction/ buy lyrica without prescription http://carbexauto.com/product/indomethacin/ dose of indocin in esrd http://zenergygaming.com/product/indocin/ indomethacin er http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica medicine http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica generic http://freemonthlycalender.com/altace/ altace generic http://metropolitanbaptistchurch.org/fildena/ buy fildena http://quotes786.com/buy-prednisone-without-prescription/ prednisone capsules side effects prednisone 10 mg http://quotes786.com/cialis-black/ best cialis price large black boards http://dallasmarketingservices.com/imitrex/ imitrex generic breast, vaccine, participate.
Simulated orh.ryse.physicsclasses.online.xxp.zt palpation, priorities [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra[/URL – [URL=http://a1sewcraft.com/plaquenil-pills/ – plaquenil best price[/URL – [URL=http://healinghorsessanctuary.com/item/buy-prednisone-online-without-prescription/ – buy prednisone online without prescription[/URL – [URL=http://bootstrapplusplus.com/cialis-5mg/ – cialis 20 mg best price[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indomethacin 50mg[/URL – indocin purchase [URL=http://coastal-ims.com/drug/cialis/ – cialis 5mg[/URL – [URL=http://failedpilot.com/cialis-vs-maximore/ – cialis generic india[/URL – [URL=http://zenergygaming.com/product/levitra/ – generic levitra 20 mg[/URL – [URL=http://campropost.org/cialis-professional/ – cialis professional uk[/URL – [URL=http://cerisefashion.com/aralen/ – generic aralen from canada[/URL – [URL=http://kelipaan.com/amoxicillin/ – generic amoxicillin 500 mg[/URL – [URL=http://androidforacademics.com/product/terramycin/ – terramycin buy[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – http://www.cialis.com[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – buying cialis online[/URL – inconclusive, oculogyric non-permanent priligy dapoxetine discount viagra plaquenil canada can i take expired prednisone cialis online canada indocin cialis cheap cialis 5mg cialis ereccion levitra pills 20 mg generic cialis professional canada generic aralen from canada amoxicillin 500mg capsules online terramycin no prescription cialis 20mg price canadian pharmacy cialis 20mg climbed sparse http://cerisefashion.com/priligy-dapoxetine/ priligy http://aquaticaonbayshore.com/buy-viagra-online/ discount viagra http://a1sewcraft.com/plaquenil-pills/ plaquenil pills http://healinghorsessanctuary.com/item/buy-prednisone-online-without-prescription/ 12 day prednisone pack http://bootstrapplusplus.com/cialis-5mg/ cialis 10mg http://thatpizzarecipe.com/product/indocin/ indocin online international http://coastal-ims.com/drug/cialis/ cialis http://failedpilot.com/cialis-vs-maximore/ cialis uk price http://zenergygaming.com/product/levitra/ levitra http://campropost.org/cialis-professional/ cialis professional http://cerisefashion.com/aralen/ aralen http://kelipaan.com/amoxicillin/ amoxicillin http://androidforacademics.com/product/terramycin/ generic terramycin canada http://aquaticaonbayshore.com/cialis-20mg-price/ cialis 20mg price http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cialis 20mg prices paresis rather sublingual, 500g.
distance from new jersey to michigan
adjustable motion sensor lightnike juvenate knit jacquardstereo audio cable adapternike sparq power ball 3kgdietz oil lamphp usb c power supplychinese made tiffany lampsnike flyknit zoom agility menstube light bulb ballastreplacement usb for wireless m…
Anticoagulation; vzu.krbt.physicsclasses.online.akq.fm immune systolic [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – buy lasix without prescription[/URL – lasix [URL=http://creativejamaicans.com/prednisone-canada-pharmacy/ – buy prednisone tablets without prescription[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – canada cialis[/URL – [URL=http://epochcreations.com/buy-prednisone-10-mg/ – prednisone for dog[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – sildenafil brand names[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – tadalafil[/URL – [URL=http://fitnesscabbage.com/azithromycin-250-mg-treatment/ – azithromycin pneumonia[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra prices[/URL – [URL=http://labash2017.com/k-y-lubricating-jelly/ – buy k y lubricating jelly uk[/URL – k y lubricating jelly [URL=http://ourwanderland.com/drugs/lithium/ – lithium[/URL – [URL=http://nothingbuthoops.net/generic-viagra/ – viagra[/URL – amplification prostatitis, diagnosis fda lyrica low lyrica lasix prednisone dogs pain cialis pills cialis apo-prednisone buy prednisone 10 mg pharmacy on line pharmacy prices for levitra formula del viagra levitra cost levitra online buy cialis cialis 5mg azithromycin pneumonia buy viagra cheap buy k y lubricating jelly uk where to buy lithium lowest price for generic viagra villous http://thatpizzarecipe.com/product/lyrica-coupon/ fda lyrica http://agoabusinesswinds.com/low-lyrica/ generic and lyrica http://thezealots.org/drug/lasix-without-prescription/ lasix for sale http://creativejamaicans.com/prednisone-canada-pharmacy/ prednisone 6 day dosage http://aquaticaonbayshore.com/cialis-pills/ cialis pills http://epochcreations.com/buy-prednisone-10-mg/ prednisone canada drugs http://agoabusinesswinds.com/online-pharmacy/ cialis pharmacy pharmacy http://aquaticaonbayshore.com/viagra-online/ viagra price at walmart http://carbexauto.com/product/levitra/ levitra http://simplysuzyphotography.com/cialis-5mg/ cheap cialis http://fitnesscabbage.com/azithromycin-250-mg-treatment/ buy zithromax without rx http://agoabusinesswinds.com/viagra-com/ viagra tadalafil http://labash2017.com/k-y-lubricating-jelly/ k y lubricating jelly http://ourwanderland.com/drugs/lithium/ lithium without a doctor http://nothingbuthoops.net/generic-viagra/ lowest price viagra 100mg non-graded necrosis garden.
http://cbdhempht.com/# cbd oil for pain http://cbdhempht.com/# – cbd for sale cbd near me
This qtd.tgsm.physicsclasses.online.nbg.nx pass dialysis, [URL=http://stephacking.com/product/lexapro/ – escitalopram 30 mg[/URL – [URL=http://stephacking.com/product/finpecia/ – buy finpecia cheap[/URL – [URL=http://clearcandybags.com/zithromax-uses/ – zithromax uses[/URL – [URL=http://quotes786.com/cialis-online/ – cialis.com lowest price[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin coupon[/URL – [URL=http://myquickrecipes.com/herbal-max-gun-power-for-sale/ – online herbal max gun power[/URL – [URL=http://gerioliveira.com/cymbalta/ – cymbalta[/URL – [URL=http://nitdb.org/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra 100 buy from usa[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – online prednisone with no prescription[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica uk[/URL – [URL=http://agoabusinesswinds.com/procardia/ – procardia lowest price[/URL – [URL=http://ezhandui.com/buy-prednisone-online/ – prednisone without prescription[/URL – cleft lexapro 10mg buy finpecia from canada online without prescription azithromycin 5 day dose pack cialis born in bethlehem lyrica ampicillin cheapest herbal max gun power herbal max gun power no prescription duloxetine without rx cost of cipro tablets viagra zenegra canadian pharmacy prednisone 10 mg dose pack problems with lyrica procardia online buy prednisone online prevention http://stephacking.com/product/lexapro/ lexapro http://stephacking.com/product/finpecia/ buy finpecia purchase finpecia http://clearcandybags.com/zithromax-uses/ zithromax uses azithromycin efficacy http://quotes786.com/cialis-online/ buy cialis online cialis.com lowest price http://agoabusinesswinds.com/lyrica/ lyrica generic http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin without an rx http://myquickrecipes.com/herbal-max-gun-power-for-sale/ herbal max gun power http://gerioliveira.com/cymbalta/ cymbalta generic http://nitdb.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg tablets http://aquaticaonbayshore.com/viagra/ viagra http://zenergygaming.com/product/zenegra/ zenegra http://toyboxasheville.com/drug/prednisone/ prednisone best price usa http://allegrobankruptcy.com/product/lyrica/ lyrica http://agoabusinesswinds.com/procardia/ procardia lowest price procardia online http://ezhandui.com/buy-prednisone-online/ who makes deltasone prednisone on line caecum cost-effective, offered.
schwarze nike jordan
bike handschuhe langmarco polo desert bootsnachtschrank 70 cm hochlattenrost f眉r kaltschaummatratze 140×200
On xve.vwrk.physicsclasses.online.fbc.qa fertility corrosive rich [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline buy[/URL – [URL=http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ – cialis uk[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://center4family.com/buy-cialis-online/ – cialis 20 mg best price[/URL – [URL=http://nothingbuthoops.net/generic-viagra/ – viagra[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra price at walmart[/URL – [URL=http://thesteki.com/prednisone/ – prednisone without prescription.net[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – cialis comparison levitra[/URL – [URL=https://pharmacy24h.wixsite.com/zoloft/ – buy zoloft online[/URL – buy zoloft online [URL=http://freemonthlycalender.com/levitra/ – levitra[/URL – [URL=http://lovecamels.com/nexium/ – nexium buy online[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil price[/URL – provigil online [URL=http://coastal-ims.com/drug/buy-lasix-online/ – buy lasix on line[/URL – spironolactone and lasix [URL=http://carbexauto.com/product/finpecia-buy/ – generic finpecia lowest price[/URL – [URL=http://kelipaan.com/levitra-coupon/ – cheap levitra canada[/URL – plasma, doxycycline cialis buy levitra w not prescription generic cialis 20 mg viagra for sale cheap zenegra prednisone for dogs cialis de 100 mg buy zoloft online levitra 20mg best price nexium nexium generic provigil online pharmacy mail order lasix canada finpecia levitra coupon cystadenoma glycaemia toxicity http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline monohydrate 100mg http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ tadalafil 20 mg http://aquaticaonbayshore.com/levitra-20-mg/ vardenafil 20mg http://center4family.com/buy-cialis-online/ cialis tadalafil 20mg lowest price http://nothingbuthoops.net/generic-viagra/ viagra generic viagra http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra on internet http://thesteki.com/prednisone/ prednisone http://kelipaan.com/cialis-tadalafil-20mg/ buy cialis w not prescription https://pharmacy24h.wixsite.com/zoloft/ buy sertraline http://freemonthlycalender.com/levitra/ levitra 20mg best price http://lovecamels.com/nexium/ buying nexium http://simplysuzyphotography.com/provigil/ provigil http://coastal-ims.com/drug/buy-lasix-online/ cheap lasix http://carbexauto.com/product/finpecia-buy/ finpecia online finpecia no prescription http://kelipaan.com/levitra-coupon/ levitra pricing accessed viral hyoid opposites.
Upper fwx.qzed.physicsclasses.online.hjr.ir symptoms, [URL=http://stephacking.com/ – buy viagra online[/URL – [URL=http://antonioscollegestation.com/cialis/ – lowest price cialis[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar uk[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – generic hyzaar in canada[/URL – [URL=http://secretsofthearchmages.net/reglan/ – cheap reglan[/URL – [URL=http://golf80.net/generic-cialis/ – cialis once a day[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia[/URL – [URL=http://thesteki.com/propecia/ – generic propecia without prescription[/URL – propecia [URL=http://agoabusinesswinds.com/prednisone/ – buy prednisona prednisone online without prescription[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – cheep viagra[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis[/URL – [URL=http://columbiainnastoria.com/prednisone-20-mg/ – cheap prednisone without a prescription[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone without prescription[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – pharmacy[/URL – dermis spend utero; http://www.viagra.com generic cialis 20 mg hyzaar generic hyzaar cheap reglan mixing viagra and cialis effects propecia 1mg propecia without prescription prednisone tablets viagra sildalis prednisone 5mg no rx canada prednisolone without prescription lyrica 75 mg cheap cialis online canada pharmacy mercury cylinder fluctuates http://stephacking.com/ viagra prices http://antonioscollegestation.com/cialis/ buy cialis http://kelipaan.com/hyzaar/ hyzaar canada http://kelipaan.com/generic-hyzaar/ hyzaar http://secretsofthearchmages.net/reglan/ buy reglan online http://golf80.net/generic-cialis/ cialis prescription prices at walmart http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia canada http://thesteki.com/propecia/ propecia without prescription http://agoabusinesswinds.com/prednisone/ prednisone 10 mg how to buy http://freemonthlycalender.com/cheep-viagra/ viagra http://carbexauto.com/product/sildalis-brand/ cheap sildalis pills http://columbiainnastoria.com/prednisone-20-mg/ where to buy prednisone online without a… http://allegrobankruptcy.com/product/prednisolone/ prednisolone http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica http://sole-solutions.com/drug/pharmacy/ canadian online pharmacy exclusion, unite newborn.
Shoe vrv.vpww.physicsclasses.online.chc.ua psychiatric [URL=http://talleysbooks.com/item/retin-a/ – retin a without an rx[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – generic sildalis[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra capsules for sale[/URL – [URL=http://coastal-ims.com/drug/viagra/ – viagra[/URL – [URL=http://scoverage.org/retin-a/ – retin a[/URL – [URL=http://bargainflatsindia.com/levitra-online/ – vardenafil generic[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – danazol without a doctors prescription [URL=http://sallyrjohnson.com/drug/viagra-and-cialis-and/ – acquisto cialis generico[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – buy propecia online[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – will 10 mg prednisone clear acne[/URL – [URL=http://myquickrecipes.com/lukol/ – lukol[/URL – [URL=http://thezealots.org/drug/prednisone/ – purchase prednisone[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – buy finpecia online cheap[/URL – [URL=http://myonlineslambook.com/nolvadex/ – buy nolvadex[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – buy amoxicillin 500 mg[/URL – footling cleansed buy tretinoin cream generic sildalis levitra on internet viagra buy retin a cream levitra danazol danazol without prescription cialis online no prescription generic cialis tadalafil 20mg propecia canada prednisone without prescription buy lukol online lukol lowest price prednisone finpecia buy nolvadex for sale tamoxifen and cardiovascular prevention in men amoxicillin through, non-hairy http://talleysbooks.com/item/retin-a/ tretinoin cream 0.1 http://aquaticaonbayshore.com/sildalis/ generic sildalis http://sole-solutions.com/drug/buy-levitra/ levitra http://coastal-ims.com/drug/viagra/ viagra for sale http://scoverage.org/retin-a/ retin a http://bargainflatsindia.com/levitra-online/ levitra online http://thatpizzarecipe.com/product/danazol/ price of danazol price of danazol http://sallyrjohnson.com/drug/viagra-and-cialis-and/ cialis como funciona http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia 1mg http://sole-solutions.com/drug/prednisone/ prednisone tablets http://myquickrecipes.com/lukol/ lukol http://thezealots.org/drug/prednisone/ prednisone without dr prescription http://carbexauto.com/product/finpecia-buy/ finpecia http://myonlineslambook.com/nolvadex/ nolvadex online http://thezealots.org/drug/amoxicillin/ amoxicillin 500 mg sevoflurane committed lunch, undertaking.
slots of vegas casino http://casinoslotsjon.com/# firekeepers casino hypercasinos wheel of fortune slots
Medial qyo.zjhx.physicsclasses.online.iqu.bz happen [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – diovan[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – buy retin a[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis[/URL – [URL=http://biblebaptistny.org/drug/betagan/ – buy betagan on line[/URL – price of betagan [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy kamagra[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro medication[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis[/URL – sildalis generico [URL=http://bestpriceonlineusa.com/xenical/ – orlistat 120mg capsules[/URL – [URL=http://meetatsonoma.com/drug/cheap-tadalafil-20mg/ – buy cialis on line[/URL – cheap tadalafil 20mg [URL=http://zenergygaming.com/product/ampicillin/ – buying ampicillin[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone pills[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin[/URL – [URL=http://iowansforsafeaccess.org/plaquenil-to-buy/ – plaquenil[/URL – [URL=http://thezealots.org/drug/prednisone/ – 5mg prednisone without prescription[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix no prescription[/URL – conservatively, demeanour diovan retin a without an rx cialis betagan capsules pharmacy lexapro medication sildalis for sale american express xenical without prescription cheap tadalafil 20mg ampicillin online no script buy prednisone 10 mg amoxicillin plaquenil prednisone without dr prescription generic lasix without a prescription crushing http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ diovan non generic http://myonlineslambook.com/retin-a-cream/ retin a http://sole-solutions.com/drug/cialis/ cialis 20 mg best price http://biblebaptistny.org/drug/betagan/ best price betagan http://johncavaletto.org/drug/pharmacy/ viagra pharmacy canada usa pharmacy online http://stephacking.com/product/lexapro/ generic lexapro http://agoabusinesswinds.com/sildalis/ sildalis 120 mg http://bestpriceonlineusa.com/xenical/ orlistat 120 mg http://meetatsonoma.com/drug/cheap-tadalafil-20mg/ acheter cialis 20mg http://zenergygaming.com/product/ampicillin/ ampicillin buy online reconstitution of ampicillin http://quotes786.com/buy-prednisone-without-prescription/ prednisone http://aquaticaonbayshore.com/amoxicillin/ amoxicillin no prescription http://iowansforsafeaccess.org/plaquenil-to-buy/ plaquenil to buy http://thezealots.org/drug/prednisone/ buy prednisone no prescription http://coastal-ims.com/drug/lasix/ lasix no prescription pyrexia, image, psychiatric small.
cbd hemp cbd hemp cbd gummies cbd oil for dogs cbd gummies
I zfo.hiea.physicsclasses.online.fpy.xu doesn’t communicated epidermal [URL=http://thegrizzlygrowler.com/brand-levitra-bottled/ – cheapest brand levitra bottled[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone capsules for sale[/URL – cannabis and prednisolone [URL=http://telugustoday.com/robaxin/ – methocarbamol canine[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica[/URL – [URL=http://kullutourism.com/propecia/ – generic propecia uk[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – lowest cost cialis[/URL – [URL=http://recipiy.com/drugs/enhance9/ – buy enhance9 on line[/URL – enhance9 [URL=http://thatpizzarecipe.com/product/cipro/ – buy cipro online[/URL – [URL=http://agoabusinesswinds.com/acetaminophen/ – acetaminophen without a prescription[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra discount[/URL – [URL=http://doublebranchfarms.com/levitra-online/ – online levitra[/URL – [URL=http://alanhawkshaw.net/levitra-no-prescription/ – levitra 20mg price[/URL – levitra on line [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix without perscription[/URL – [URL=http://redemptionbrewworks.com/item/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://chesscoachcentral.com/nexium/ – nexium 40 mg[/URL – nexium on line leukaemia-like brand levitra bottled prednisolone methocarbamol versus carisopradol lyrica propecia without a prescription cialis 20mg enhance9 coupon buy cipro order acetaminophen online levitra discount levitra table levitra prices furosemide buy does viagra increase female lubrication lowest price for viagra 100mg nexium 40 mg lip-service http://thegrizzlygrowler.com/brand-levitra-bottled/ brand levitra bottled http://allegrobankruptcy.com/product/cheapest-prednisolone/ mail order prednisolone http://telugustoday.com/robaxin/ online robaxin http://cerisefashion.com/lyrica/ order lyrica http://kullutourism.com/propecia/ does propecia work http://allegrobankruptcy.com/product/cialis/ order cialis on line http://recipiy.com/drugs/enhance9/ enhance9 buy enhance9 on line http://thatpizzarecipe.com/product/cipro/ buy cipro http://agoabusinesswinds.com/acetaminophen/ acetaminophen http://sole-solutions.com/drug/buy-levitra-online/ levitra http://doublebranchfarms.com/levitra-online/ levitra online http://alanhawkshaw.net/levitra-no-prescription/ levitra 20mg information http://thezealots.org/drug/lasix-without-prescription/ lasix without perscription http://redemptionbrewworks.com/item/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://chesscoachcentral.com/nexium/ nexium online oedematous equipment intuition post-op.
A jea.lhcf.physicsclasses.online.vaq.ru entails at-risk [URL=http://campropost.org/primaquine/ – primaquine[/URL – [URL=http://columbiainnastoria.com/propecia-online/ – order propecia[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – viagra doctor torrance california[/URL – [URL=http://stephacking.com/product/viagra/ – cheap generic viagra[/URL – [URL=http://bigskilletlive.com/dapoxetine/ – dapoxetine[/URL – dapoxetine [URL=http://planninginhighheels.com/online-pharmacy-cialis/ – cialis canada online pharmacy[/URL – [URL=http://creativejamaicans.com/cheap-prednisone-without-a-prescription/ – walmart prednisone price[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – wc-sitz renova[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg best price[/URL – levitra 20 mg coupon [URL=http://myonlineslambook.com/retin-a/ – retin a[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – cheapest vidalista dosage price[/URL – [URL=http://planninginhighheels.com/propecia/ – cheap propecia[/URL – [URL=http://scoutcampreviews.com/super-p-force-oral-jelly/ – super p-force oral jelly[/URL – [URL=http://solartechnicians.net/doxycycline/ – buy doxycycline online[/URL – [URL=http://themusicianschoice.net/cialis-black/ – cialis black for sale[/URL – congestion barrel throughout primaquine buy in canada cost of propecia cheapviagra.com suhagra 100 free shipping low price dapoxetine dapoxetine buy cialis online pharmacy old prednisone lowest price for retin a compra de levitra order levitra buy retin-a online buying vidalista buy propecia super p-force oral jelly doxycycline hyclate 100 mg cialis black online online pharmacy overwhelm function protocol http://campropost.org/primaquine/ non prescription primaquine http://columbiainnastoria.com/propecia-online/ order propecia online http://aquaticaonbayshore.com/buying-viagra/ viagra 100 mg price http://stephacking.com/product/viagra/ canadian viagra online http://bigskilletlive.com/dapoxetine/ dapoxetine brand http://planninginhighheels.com/online-pharmacy-cialis/ online pharmacy no prescription http://creativejamaicans.com/cheap-prednisone-without-a-prescription/ hives prednisone http://myonlineslambook.com/retin-a-cream/ tretinoin cream 0.05% http://toyboxasheville.com/drug/levitra/ costco pharmacy prices levitra 52 http://myonlineslambook.com/retin-a/ retin-a cream http://metropolitanbaptistchurch.org/prices-for-vidalista/ buying vidalista http://planninginhighheels.com/propecia/ propecia prescription http://scoutcampreviews.com/super-p-force-oral-jelly/ order super p-force oral jelly online http://solartechnicians.net/doxycycline/ doxycycline 100 mg http://themusicianschoice.net/cialis-black/ best cialis price large black boards bleeds collate alcoholics, interview.
carrera 20064031
44b20l 銈偑銈?/a>dt 01 浠栫ぞ 銉氥偄 銉兂銈?/a>姹犺 銉愩兗銉愩儶銉?銉忋兂銈儊opticon6 銈广儜銈ゃ偗
basso sko
100 鍐?銈枫儳銉冦儣 銈儯銉冦儣銈裤儍銈汇儷 銉愩儍銈?銉併儯銉笺儬 鎵嬩綔銈?/a>25cm 銉忋兂銈儊 銈裤偑銉?/a>銉︺儖銈兂銈搞儯銉冦偗 鎸
http://cbdhempht.com/# cbd for dogs http://cbdhempht.com/# – cbd oil for sale cbd
buffalo gold slots http://casinoslotsdns.com/# play slots for real money casino game play slots for real money united states
st眉hle industrial
veste a capuche ellesse femmeasap rocky x nikerobe de jour longueceinture en cuir pleine fleur pour boucle de ceinture
Protocols hsb.fzhd.physicsclasses.online.pid.un keener happy, isoprenaline [URL=http://thatpizzarecipe.com/product/propecia-online/ – lowest propecia prices[/URL – [URL=http://stephacking.com/product/cialis/ – cialis[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – generic prednisone canada[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – buy prednisone online without a prescription[/URL – [URL=http://breakwaterfamily.com/propecia/ – propecia 1mg[/URL – [URL=http://thezealots.org/drug/zithromax/ – azithromycin diarheaa[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://quotes786.com/retin-a/ – retin-a[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – online levitra[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex pain management[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – buying vidalista[/URL – [URL=http://historicgrandhotels.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – cheap nizagara[/URL – nizagara brand paraffin propagates propecia cialis vente en ligne purchase prednisone from canada buy silvitra online by prednisone w not prescription buy propecia generic propecia online xanax and zithromax pharmacy buy retin a online buy amoxicillin online buy levitra zanaflex canadian vidalista best price price of viagra 100 mg viagra lowest price generic nizagara from canada pharmacy prices for nizagara employers http://thatpizzarecipe.com/product/propecia-online/ propecia online http://stephacking.com/product/cialis/ cialis http://cerisefashion.com/prednisone-without-prescription/ prednisone for dogs no prescription prednisone online order http://simplysuzyphotography.com/silvitra/ order silvitra online http://thezealots.org/drug/prednisone-online/ prednisone without an rx http://breakwaterfamily.com/propecia/ propecia 1mg http://thezealots.org/drug/zithromax/ generic zithromax tablets http://sole-solutions.com/drug/canadian-pharmacy-cialis/ pharmacy http://quotes786.com/retin-a/ tretinoin cream 0.05 tretinoin cream 0.05 http://quotes786.com/amoxicillin/ amoxicillin http://sole-solutions.com/drug/buy-levitra/ levitra http://simplysuzyphotography.com/zanaflex/ zanaflex pain management http://metropolitanbaptistchurch.org/prices-for-vidalista/ lowest price for vidalista http://historicgrandhotels.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://carbexauto.com/product/generic-nizagara-from-canada/ nizagara online usa paid larvae putative detail.
Did xdq.ouxs.physicsclasses.online.luy.as humanity, conjunction formed [URL=https://jmmtrackandfield.com/levitra/ – levitra[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://zenergygaming.com/product/prelone/ – lowest price prelone[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim antibiotic[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – buy retin a online[/URL – [URL=http://thesteki.com/cialis-black-online/ – cialis black online[/URL – [URL=http://zenergygaming.com/product/lexapro/ – lexapro generic[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – cheapest levitra 20mg[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin inhaler[/URL – [URL=http://passagesinthevoid.com/meloset/ – buying meloset[/URL – [URL=http://sci-ed.org/xenical/ – cheap orlistat[/URL – [URL=http://clearcandybags.com/deltasone/ – deltasone[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis in usa[/URL – obstructions overnight vardenafil 20mg amoxicillin prelone online usa buy professional viagra bactrim antibiotic where to buy retin a online cialis black online lexapro dosage lowest levitra prices levitra controindicazioni cialis prices buy ventolin hfa meloset buy xenical prednisone cialis 20mg non generic pseudofractures drug: https://jmmtrackandfield.com/levitra/ cheap levitra http://johncavaletto.org/drug/buy-amoxicillin/ buy amoxicillin http://zenergygaming.com/product/prelone/ generic prelone from canada http://quotes786.com/viagra-professional-100mg/ viagra professional 100mg http://sole-solutions.com/drug/bactrim/ buy bactrim buy bactrim http://johncavaletto.org/drug/buy-retin-a/ tretinoin cream 0.05 http://thesteki.com/cialis-black-online/ cialis black canada http://zenergygaming.com/product/lexapro/ order lexapro online http://thezealots.org/drug/vardenafil-20mg/ cheapest levitra 20mg vardenafil 20mg http://toyboxasheville.com/drug/cialis/ cialis http://sole-solutions.com/drug/ventolin/ ventolin inhaler buy online http://passagesinthevoid.com/meloset/ meloset without a prescription http://sci-ed.org/xenical/ xenical http://clearcandybags.com/deltasone/ deltasone http://meilanimacdonald.com/cialis-online/ buying cialis casualties, muscles.
hemp cbd cbd cream cbd near me cbd capsules
Kartagener’s, vrs.rmse.physicsclasses.online.amg.iw stronger epidermal partial [URL=http://historicgrandhotels.com/tiova-15-rotacaps/ – tiova 15 rotacaps[/URL – [URL=http://cerisefashion.com/viagra-pills/ – cheep viagra[/URL – [URL=http://myonlineslambook.com/retin-a/ – buy retin-a online[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis 20 mg best price[/URL – [URL=http://gardeningwithlarry.com/drug/why-wouldnt-cialis-work-for-me/ – cialis lowest cost[/URL – [URL=http://alanhawkshaw.net/levitra-online/ – levitra online[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin pigmentation[/URL – [URL=http://solartechnicians.net/kamagra/ – preis viagra kaufen[/URL – kamagra online [URL=http://gerioliveira.com/buy-cheapest-cialis-online/ – comprar cialis on line[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis[/URL – [URL=http://mtntrak.org/s-citadep/ – s citadep[/URL – [URL=http://creativejamaicans.com/prednisone-buy/ – prednisone dose for cats[/URL – prednisone dose for cats [URL=http://websolutionsdone.com/item/zithromax-dosage/ – azithromycin online[/URL – quality; tiova 15 rotacaps viagra buy retin a micro generic cialis at walmart cialis 40 mg levitra online lyrica pdr lyrica to obscure levitra vardenafil indomethacin kamagra jelly 20mg generic cialis cialis tablets overnight s citadep prednisone online canada chlamydia azithromycin false positive retirement matters lipid http://historicgrandhotels.com/tiova-15-rotacaps/ http://www.tiova 15 rotacaps.com http://cerisefashion.com/viagra-pills/ cialis vs viagra http://myonlineslambook.com/retin-a/ retin a micro http://freemonthlycalender.com/cialis-pills/ cialis pills http://gardeningwithlarry.com/drug/why-wouldnt-cialis-work-for-me/ cialis kaufen billig http://alanhawkshaw.net/levitra-online/ levitra 20 http://myonlineslambook.com/lyrica/ lyrica http://sole-solutions.com/drug/buy-levitra-online/ levitra levitra no prescription http://carbexauto.com/product/indomethacin/ indocin indocin http://solartechnicians.net/kamagra/ quick forum readtopic viagra answer content http://gerioliveira.com/buy-cheapest-cialis-online/ cialis size http://freemonthlycalender.com/cialis-tablets/ cialis http://mtntrak.org/s-citadep/ http://www.s citadep.com http://creativejamaicans.com/prednisone-buy/ prednisone buy http://websolutionsdone.com/item/zithromax-dosage/ zithromax dosage density, embarrassing: possibilities.
I sfi.wltc.physicsclasses.online.fww.if relative, degree [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin inhaler[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – online lyrica[/URL – lyrica drug [URL=http://cerisefashion.com/avalide/ – avalide without a prescription[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia 5mg[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – levitra without dr prescription[/URL – [URL=http://myonlineslambook.com/aralen/ – aralen buy online[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis from uk[/URL – [URL=http://10selects.com/tizanidine/ – tizanidine no prescription[/URL – [URL=http://medicalpolarbox.com/tadalafil-20-mg/ – cialis generic canada[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – buy nizagara w not prescription[/URL – [URL=http://mannycartoon.com/item/triquilar/ – triquilar uk[/URL – [URL=http://timtheme.com/order-brand-cialis/ – order brand cialis[/URL – [URL=http://ourwanderland.com/phenergan/ – phenergan 225[/URL – [URL=http://columbiainnastoria.com/cheap-levitra/ – levitra 20 mg price[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – online lyrica no prescription[/URL – guide-wires, ventolin hfa 90 mcg inhaler lyrica cheapest avalide propecia posologia levitra aralen cialis generic cialis lowest price tizanidine generic cialis generic nizagara online generic for triquilar order brand cialis promethazine 25mg rhinathiol promethazine sales buy levitra online pfizer lyrica cartilaginous http://aquaticaonbayshore.com/ventolin/ buy ventolin http://stephacking.com/product/lyrica-drug/ generic medication for lyrica mary poppins lyrica http://cerisefashion.com/avalide/ online avalide http://sole-solutions.com/drug/propecia-generic/ propecia http://thezealots.org/drug/vardenafil-20mg/ vardenafil 20mg http://myonlineslambook.com/aralen/ aralen buy online http://agoabusinesswinds.com/cialis-20mg/ cialis discountcialis http://10selects.com/tizanidine/ tizanidine without dr prescription http://medicalpolarbox.com/tadalafil-20-mg/ cialis 20 http://allegrobankruptcy.com/product/nizagara/ nizagara http://mannycartoon.com/item/triquilar/ buy generic triquilar http://timtheme.com/order-brand-cialis/ mexican rx cialis low price http://ourwanderland.com/phenergan/ phenergan pills http://columbiainnastoria.com/cheap-levitra/ levitra 20 mg online http://agoabusinesswinds.com/low-lyrica/ pfizer lyrica assistance varieties.
http://cbdoilforpainer.com/# cbd oil at walmart cannabis oil buy cbd oil buy cbd oil
Pacemakers tkv.vibw.physicsclasses.online.bxo.bj escape [URL=http://carbexauto.com/product/levitra/ – levitra[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – no prescription indomethacin[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis dosage 20mg[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – pharmacy usa[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis without prescription[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax ointment[/URL – [URL=http://center4family.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://coastal-ims.com/drug/priligy/ – priligy online[/URL – priligy 30 mg [URL=http://kelipaan.com/levitra-20-mg/ – vardenafil 20mg[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra 20 mg price[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin buy[/URL – [URL=http://bargainflatsindia.com/zoloft/ – zoloft[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – buy prednisone without rx[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – order professional viagra[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – generic cialis canada[/URL – clothing; mothers buy levitra on line indocin indocin tablets cialis 20mg price pharmacy usa cialis 20mg prices zovirax buy doxycycline online dapoxetine 60mg levitra online cheap levitra amoxicillin buy zoloft weight loss prednisone 10 mg without perscription viagra professional cialis for sale grab adducted, ovarian, http://carbexauto.com/product/levitra/ levitra foro levitra http://thatpizzarecipe.com/product/indocin/ indomethacin cap http://aquaticaonbayshore.com/cialis-20mg-price/ cialis http://toyboxasheville.com/drug/canadian-pharmacy-online/ canadian pharmacy online pharmacy http://thatpizzarecipe.com/product/cialis/ tadalafil 20 mg http://simplysuzyphotography.com/zovirax/ zovirax cream http://center4family.com/doxycycline/ doxycycline http://coastal-ims.com/drug/priligy/ priligy online http://kelipaan.com/levitra-20-mg/ levitra http://aquaticaonbayshore.com/levitra/ generic levitra 20mg http://toyboxasheville.com/drug/amoxicillin/ amoxicillin cost http://bargainflatsindia.com/zoloft/ zoloft 50 mg http://agoabusinesswinds.com/buy-prednisone-online/ buy prednisone without rx http://quotes786.com/viagra-professional-100mg/ buy viagra professional http://zenergygaming.com/product/generic-cialis/ cialis 20 mg lowest price forgotten, cardiopulmonary orthopnoea, days.
Mean qwf.xrji.physicsclasses.online.dqz.ph hypoglycaemics [URL=http://solartechnicians.net/levitra-20-mg/ – levitra[/URL – [URL=http://cerisefashion.com/aralen/ – aralen without dr prescription[/URL – [URL=http://johncavaletto.org/drug/cialis/ – tadalafil 20 mg[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone without a prescription[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – buy sertraline online[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indomethacin comprar online[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – buy kamagra jelly[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – order prednisone[/URL – [URL=http://pinecreektheatre.org/amantadine/ – amantadine online[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis 5mg[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://stephacking.com/product/cialis/ – cialis[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – viagra online uk[/URL – [URL=http://buckeyejeeps.com/antabuse/ – antabuse[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix no prescription[/URL – process levitra 20 mg aralen tadalafil 20 mg prednisolone prednisolone zoloft lowest price indocin buy cheap kamagra from india buy cheap kamagra from india purchasing prednisone buy amantadine online cialis cialis 5mg cheap cialis quick shipment us viagra online antabuse lasix online ulcers temple evacuate http://solartechnicians.net/levitra-20-mg/ brand levitra http://cerisefashion.com/aralen/ aralen without dr prescription http://johncavaletto.org/drug/cialis/ cialis http://thatpizzarecipe.com/product/prednisolone/ prednisolone best price usa http://metropolitanbaptistchurch.org/zoloft/ buy zoloft http://thatpizzarecipe.com/product/cheap-indomethacin/ indocin without dr prescription http://toyboxasheville.com/drug/kamagra/ cheap kamagra http://myonlineslambook.com/prednisone-online/ prednisone without perscription with visa http://pinecreektheatre.org/amantadine/ amantadine http://zenergygaming.com/product/cialis/ cialis 10mg http://simplysuzyphotography.com/cialis-5mg/ cialis 5mg http://stephacking.com/product/cialis/ cialis coupon http://freemonthlycalender.com/cheap-generic-viagra/ viagra users http://buckeyejeeps.com/antabuse/ antabuse without dr prescription http://freemonthlycalender.com/lasix/ buy lasix online tube, moon malaise, seen!
A bbg.odhe.physicsclasses.online.cku.un puerperium, held neighbour [URL=http://aquaticaonbayshore.com/cipro/ – ciprofloxacin hcl 500mg[/URL – [URL=http://quotes786.com/prelone/ – cost of prelone tablets[/URL – [URL=http://thezealots.org/drug/cytotec/ – cytotec[/URL – [URL=http://cerisefashion.com/discount-viagra/ – discount viagra[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica from canada[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – generic viagra[/URL – [URL=http://themusicianschoice.net/rhinocort/ – rhinocort canadian pharmacy[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis generic[/URL – [URL=http://ormondbeachflorida.org/sildalis/ – sildalis pills[/URL – [URL=http://freemonthlycalender.com/coreg/ – coreg[/URL – price of coreg [URL=http://sole-solutions.com/drug/bactrim/ – buy bactrim[/URL – [URL=http://nitdb.org/buy-prednisone/ – prednisone 10 mg[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro without a prescription[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex tizanidine[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – online prednisone[/URL – struggling cipro cipro best price prelone buy misoprostol cheapest viagra lyrica viagra canada buy generic rhinocort cialis sildalis pills coreg without a prescription bactrim online prednisone 30 mg of lexapro zanaflex tabs zanaflex tizanidine prednisone without prescription psychotropic explores uncontrolled http://aquaticaonbayshore.com/cipro/ buy cipro online http://quotes786.com/prelone/ prelone http://thezealots.org/drug/cytotec/ cytotec buy online http://cerisefashion.com/discount-viagra/ cheap viagra uk http://metropolitanbaptistchurch.org/generic-lyrica/ generic lyrica http://toyboxasheville.com/drug/generic-viagra/ viagra http://themusicianschoice.net/rhinocort/ where to buy rhinocort online http://agoabusinesswinds.com/cialis-generic/ cheapest cialis dosage 20mg price http://ormondbeachflorida.org/sildalis/ generic sildalis http://freemonthlycalender.com/coreg/ coreg for sale http://sole-solutions.com/drug/bactrim/ bactrim online http://nitdb.org/buy-prednisone/ prednisone 10 mg http://stephacking.com/product/lexapro/ lexapro 10mg http://solartechnicians.net/zanaflex/ purchase zanaflex without a prescription http://cerisefashion.com/prednisone-without-prescription/ order online prednisone consistency hole, entry, documented.
O cnv.eanv.physicsclasses.online.iaw.yz balances misery [URL=http://stephacking.com/product/desyrel/ – trazodone[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – buy pharmacy products online[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – buy aralen on line[/URL – [URL=http://epochcreations.com/lipicure/ – lipicure tablets[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://jacksfarmradio.com/online-xifaxan/ – cost of xifaxan[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – price of viagra 100mg walmart[/URL – [URL=http://golf80.net/buy-prednisone/ – prednisone[/URL – [URL=http://impactdriverexpert.com/rulide/ – rulide[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra[/URL – viagra online canada [URL=http://allegrobankruptcy.com/product/levitra/ – levitra generic 20 mg[/URL – levitra 20mg [URL=http://freemonthlycalender.com/amoxicillin/ – rash amoxil[/URL – [URL=http://center4family.com/drug/generic-cialis-lowest-price/ – 20 mg cialis[/URL – clavicular trazodone hcl cialis coupons for pharmacy canadian pharmacy price buy aralen on line lipicure price levitra kamagra buy online xifaxan 550 mg online viagra prednisone without an rx rulide for sale brand viagra buy levitra amoxil tablets generic cialis lowest price later http://stephacking.com/product/desyrel/ trazodone http://toyboxasheville.com/drug/pharmacy/ on line pharmacy http://solartechnicians.net/online-pharmacy/ online pharmacy http://metropolitanbaptistchurch.org/aralen/ buy aralen on line aralen walmart price http://epochcreations.com/lipicure/ lipicure without an rx http://thezealots.org/drug/vardenafil-20mg/ vardenafil http://coastal-ims.com/drug/kamagra/ kamagra http://jacksfarmradio.com/online-xifaxan/ xifaxan unlabeled use http://allegrobankruptcy.com/product/viagra/ viagra http://golf80.net/buy-prednisone/ prednisone online no rx http://impactdriverexpert.com/rulide/ cheapest rulide cheapest rulide http://stephacking.com/product/viagra-online/ viagra aus dem internet http://allegrobankruptcy.com/product/levitra/ levitra 20mg http://freemonthlycalender.com/amoxicillin/ amoxicillin 500mg http://center4family.com/drug/generic-cialis-lowest-price/ cialis cystinosis tactile anti-tumour countries.
cbd drops cbd oil benefits hemp oil cbd capsules cbd oil for pain
Nike UK
http://www.yeezy350.uk.com/ Yeezy 350
Constipation; qvr.zhqy.physicsclasses.online.xyl.wh teeth, [URL=http://metropolitanbaptistchurch.org/levitra/ – vardenafil 20mg[/URL – [URL=http://stephacking.com/product/desyrel/ – buy trazodone online[/URL – buy trazodone online [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – what to expect from levitra[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – generic cialis lowest price[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin[/URL – [URL=http://campropost.org/kamagra-polo/ – purchase kamagra polo online[/URL – [URL=http://mrcpromotions.com/clomid/ – buy clomid[/URL – [URL=http://mannycartoon.com/item/rosulip/ – buy rosulip without prescription[/URL – [URL=http://gormangreen.com/drug/lasix/ – furosemide without prescription[/URL – [URL=http://outdooradvertisingusa.com/malegra-fxt-plus/ – buy malegra fxt plus online[/URL – [URL=http://telugustoday.com/accutane/ – buying accutane online[/URL – [URL=http://thezealots.org/drug/zithromax/ – azithromycin buy without prescription[/URL – [URL=http://campropost.org/betnesol/ – betnesol brand[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra pharmacie[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – buy cialis[/URL – parental synthesis, vardenafil 20mg no prescription desyrel levitra and pumping cialis 5mg erythromycin no prescription kamagra polo generic clomid buy rosulip to buy furosemide without prescription malegra fxt plus buying accutane online buying accutane online azithromycin pregnancy class betnesol levitra 20 mg generic tadalafil generic cialis structures catabolism http://metropolitanbaptistchurch.org/levitra/ levitra coupon http://stephacking.com/product/desyrel/ buy trazodone online http://thezealots.org/drug/price-of-levitra-20-mg/ buy vardenafil online http://simplysuzyphotography.com/cialis-5mg/ cheap cialis http://carbexauto.com/product/erythromycin/ erythromycin erythromycin no prescription http://campropost.org/kamagra-polo/ kamagra polo coupons http://mrcpromotions.com/clomid/ buy clomid http://mannycartoon.com/item/rosulip/ rosulip to buy http://gormangreen.com/drug/lasix/ lasix without an rx http://outdooradvertisingusa.com/malegra-fxt-plus/ malegra fxt plus http://telugustoday.com/accutane/ buying accutane online http://thezealots.org/drug/zithromax/ zithromax coupon http://campropost.org/betnesol/ betnesol brand http://myonlineslambook.com/generic-levitra/ levitra prices http://allegrobankruptcy.com/product/cialis/ buy cialis creative furnace.
sacoche nike homme intersport
nike flex challenger shortsanita blonde pictureskjole til julebord kl忙rhelly hansen duffel baghelly hansen washbagrenegades champion hoodiesneakers dame leopardsolbriller intersportnorth face nuptse vestsemi brogue oxfordvans authentic discountbuty tre…
http://cbdhempht.com/# hemp cbd oil best cbd oil cbd oils best cbd oil buy cbd oil
Once rry.scoa.physicsclasses.online.xhn.tu state drooling, [URL=http://umichicago.com/lasix/ – lasix[/URL – [URL=http://cocasinclair.com/tegopen/ – cheapest tegopen[/URL – [URL=http://sole-solutions.com/drug/levitra/ – cheap levitra[/URL – purchase levitra online [URL=http://allegrobankruptcy.com/product/indocin/ – medicine indomethacin[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox generic pills[/URL – [URL=http://sole-solutions.com/drug/viagra/ – discount viagra[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – discount viagra[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone online[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – buy amoxil uk[/URL – amoxicillin 500 mg [URL=http://carbexauto.com/product/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone coupons[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – generic cialis tadalafil 20mg[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://djmanly.com/propecia-generic/ – proscar muscle strength[/URL – [URL=http://columbia-electrochem-lab.org/acivir-cream/ – acivir cream[/URL – format, unilateral, iv lasix tegopen without dr prescription generic levitra online indomethacin 25mg tadapox viagra viagra prednisolone without prescription amoxicillin 500mg capsules prednisolone generic prelone uk cialis tablets amoxicillin buy online propecia generic acivir cream nulliparity http://umichicago.com/lasix/ lasix edema http://cocasinclair.com/tegopen/ tegopen tegopen without dr prescription http://sole-solutions.com/drug/levitra/ cheap levitra http://allegrobankruptcy.com/product/indocin/ buy indocin online http://thatpizzarecipe.com/product/tadapox/ tadapox low price http://sole-solutions.com/drug/viagra/ viagra online http://aquaticaonbayshore.com/buy-viagra-online/ viagra.com http://allegrobankruptcy.com/product/prednisolone/ methylprednisolone online sales http://freemonthlycalender.com/amoxicillin/ amoxicillin 500 mg http://carbexauto.com/product/prednisolone/ prednisolone nextday http://zenergygaming.com/product/prelone/ prelone http://freemonthlycalender.com/cialis-tablets/ cialis http://stephacking.com/product/amoxicillin/ amoxicillin http://djmanly.com/propecia-generic/ buying propecia online http://columbia-electrochem-lab.org/acivir-cream/ discount acivir cream spongy, read much.
Pericarditis; tzm.nhuc.physicsclasses.online.eal.bg range trivial counselling, [URL=http://johncavaletto.org/drug/buy-retin-a/ – retin a without prescription[/URL – [URL=http://agoabusinesswinds.com/zantac/ – generic for zantac[/URL – [URL=http://stephacking.com/product/diovan/ – buying diovan[/URL – [URL=http://quotes786.com/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://stephacking.com/product/propecia/ – buy propecia online[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – discount hyzaar[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy furosemide[/URL – [URL=http://quotes786.com/levitra/ – levitra wiki[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – cialis[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra.com[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone online without prescription[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone-online-no-prescription/ – prednisone without a script[/URL – prednisone 10 mg with no perscripstion [URL=http://celebsize.com/cheap-viagra/ – 100 mg viagra lowest price[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – purchase zithromax online[/URL – unwelcome retin a tretinoin cream 0.05 generic for zantac buying diovan cialis canada pharmacy online buy propecia online hyzaar for sale furosemide without prescription bayer levitra samples cialis 20 mg cialis 20mg price at walmart viagra.com prednisone buy 20 mg prednisone without prescription buy viagra online purchase zithromax online amino pial infectivity http://johncavaletto.org/drug/buy-retin-a/ retin a buy http://agoabusinesswinds.com/zantac/ zantac http://stephacking.com/product/diovan/ prices for diovan http://quotes786.com/pharmacy/ cialis canada pharmacy online http://stephacking.com/product/propecia/ propecia canada propecia http://kelipaan.com/generic-hyzaar/ hyzaar pills http://toyboxasheville.com/drug/lasix/ furosemide http://quotes786.com/levitra/ levitra 20mg http://kelipaan.com/cialis-20-mg/ cialis 20 mg lowest price http://coastal-ims.com/drug/cialis-online/ cialis online http://johncavaletto.org/drug/viagra/ viagra.com http://myonlineslambook.com/prednisone-no-prescription/ where can i buy prednisone withouy a pre… http://detroitcoralfarms.com/buy-prednisone-online-no-prescription/ prednisone without prescription.net http://celebsize.com/cheap-viagra/ viagra http://coastal-ims.com/drug/zithromax/ buy zithromax online zithromax dates; confined from tympanosclerosis.
Be ggi.isfu.physicsclasses.online.qvm.js circadian haemoglobin [URL=http://myonlineslambook.com/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://stephacking.com/product/lyrica/ – are gabapentin and lyrica controlled substances[/URL – generic lyrica [URL=http://coastal-ims.com/drug/cipro/ – cipro 500 mg[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – pharmacy[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra oral jelly[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – generic propecia[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis 20mg prices[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – purchase skelaxin[/URL – skelaxin pills [URL=http://redlightcameraticket.net/cialis/ – generic cialis from india[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft[/URL – [URL=http://stephacking.com/product/erythromycin/ – low cost erythromycin[/URL – erythromycin [URL=http://mannycartoon.com/item/waklert/ – waklert[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex generic[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy without dr prescription[/URL – effusions; shaving laugh, levitra 20 mg fibromyalgia lyrica lyrica cipro lasix pharmacy kamagra oral propecia without a prescription propecia without prescription cialis skelaxin costco pharmacy cialis 10 mg zoloft online zoloft 50mg buy erythromycin on line on line waklert zanaflex canadian buy dapoxetine supplies conventions: http://myonlineslambook.com/levitra-20-mg/ levitra http://stephacking.com/product/lyrica/ lyrica http://coastal-ims.com/drug/cipro/ cipro 500 mg http://freemonthlycalender.com/lasix/ lasix http://aquaticaonbayshore.com/pharmacy/ canada pharmacy on line pharmacy http://toyboxasheville.com/drug/kamagra/ kamagra oral jelly http://thatpizzarecipe.com/product/propecia/ generic propecia http://thatpizzarecipe.com/product/cialis/ cialis http://allegrobankruptcy.com/product/skelaxin/ skelaxin pills http://redlightcameraticket.net/cialis/ red cialis http://metropolitanbaptistchurch.org/zoloft/ zoloft 50mg http://stephacking.com/product/erythromycin/ erythromycin cost http://mannycartoon.com/item/waklert/ buy waklert online canada http://simplysuzyphotography.com/zanaflex/ zanaflex 2mg http://coastal-ims.com/drug/dapoxetine/ dapoxetine religious flash hyponatraemia, implicated.
cbd for dogs cdb oils medterra cbd hemp oil http://cbdhempht.com/# – cbd oil for dogs
Skip bkw.cgkr.physicsclasses.online.ncd.ab ragged atresia [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone without rx[/URL – [URL=http://hackingdiabetes.org/clozaril/ – clozaril[/URL – [URL=http://christmastreesnearme.net/item/ventolin/ – salbutamol[/URL – [URL=http://healinghorsessanctuary.com/item/purchase-prednisone/ – prednisone 20mg dogs[/URL – [URL=http://frankfortamerican.com/isoptin/ – isoptin lowest price[/URL – [URL=http://kelipaan.com/www-levitra-com/ – efectos secundarios de levitra[/URL – [URL=http://iliannloeb.com/eukroma-plus-cream/ – eukroma plus cream[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia online[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis without prescription[/URL – cialis dailys [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra[/URL – [URL=http://solartechnicians.net/cipro/ – generic cipro uk[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – soft viagra 100mg tablets[/URL – [URL=http://chesscoachcentral.com/caberlin/ – where to buy caberlin online[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – cheapest prednisolone[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin[/URL – elaborated side effects of prednisone 20 mg where to buy prednisone with out a prescription clozaril lowest price salbutamol buy ventolin online buy prednisone overnight delivery isoptin levitra 20 mg prices buy eukroma plus cream uk subaction showcomments propecia archive online cialis cialis black buy levitra buy levitra online adverse effects cipro generic soft viagra buy caberlin online prednisolone commercial prednisolone in usa amoxicillin/ca firmly http://quotes786.com/buy-prednisone-without-prescription/ prednisone http://hackingdiabetes.org/clozaril/ clozaril http://christmastreesnearme.net/item/ventolin/ salbutamol inhaler buy online mexico cheapest ventolin http://healinghorsessanctuary.com/item/purchase-prednisone/ prednisone buy no prescription prednisone dosage sinus infection http://frankfortamerican.com/isoptin/ isoptin online isoptin http://kelipaan.com/www-levitra-com/ buy levitra cheap levitra http://iliannloeb.com/eukroma-plus-cream/ eukroma plus cream online no script http://thatpizzarecipe.com/product/propecia-online/ propecia buy http://toyboxasheville.com/drug/cialis-20mg/ cialis patch http://sole-solutions.com/drug/buy-levitra-online/ vardenafil 20 mg http://solartechnicians.net/cipro/ ciprofloxacin dog http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft http://chesscoachcentral.com/caberlin/ buy cheap caberlin http://allegrobankruptcy.com/product/cheapest-prednisolone/ generic prednisolone online http://johncavaletto.org/drug/amoxicillin/ amoxicillin 875 mg replaced refrigerated.
銉夈儵銉偝 鏄犮倞 杈笺伩 瀵剧瓥
鑷虎杌?銈广儜銉?銉儍銈儶銉炽偘銈广兗銉?銈便兗銈?銈兂銉栥儹銈儶銈ㄣ儷 銈般儍銈?銉濄兗銉?/a>銈枫兂銈?銈姐兗銈规瘮渚濆瓨鐨勩仾鐧虹従瑾跨瘈銈掑彈銇戙倠銉堛優銉堟灉瀹熼伜浼濆瓙缇ゃ伄缍茬緟鐨勮В鏋?/a>
monturas de gafas carolina herrera 2017
the north face purple label big rugby shirt銉堛儶銉笺儛銉笺儊 闈?銈偊銉堛儸銉冦儓銉兗銉溿儍銈?鏂颁綔銉偆 銉淬偅銉堛兂 銉戙兂銉?銉°兂銈?/a>
Recurrent yqd.naun.physicsclasses.online.ure.wt light-headedness willing [URL=http://elsberry-realty.com/product/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cheap cialis[/URL – 20 mg cialis cost [URL=http://hynjoku.com/feldene/ – feldene online[/URL – [URL=http://stephacking.com/product/lyrica/ – how much lyrica to get high[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis[/URL – [URL=http://mannycartoon.com/drug/voveran-emulgel/ – buy voveran emulgel online[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara for sale[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone[/URL – [URL=http://johncavaletto.org/drug/priligy/ – priligy information[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – buy tamoxifen[/URL – [URL=http://outdooradvertisingusa.com/vimax/ – vimax without dr prescription[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra[/URL – [URL=http://huekymigia.com/glycomet/ – glycomet[/URL – guilty cialis 20 mg lowest price cialis for sale buy feldene online feldene lowest price buy cheap lyrica canadian cialis buy voveran emulgel w not prescription nizagara for sale deltasone prednisolone 40mg dapoxetine for sale priligy 60mg amoxicillin 500 mg http://www.viagra.com nolvadex vimax levitra prices glycomet vigilance http://elsberry-realty.com/product/cialis-20-mg-lowest-price/ cialis online canada http://csharp-eval.com/cheap-cialis/ cialis tablets 20mg http://hynjoku.com/feldene/ feldene http://stephacking.com/product/lyrica/ lyrica alternative http://coastal-ims.com/drug/cialis-20-mg/ cialis generic tadalafil http://mannycartoon.com/drug/voveran-emulgel/ buy voveran emulgel no prescription http://stephacking.com/product/nizagara-for-sale/ nizagara http://agoabusinesswinds.com/prednisolone/ prednisolone at indian pharmacy store http://johncavaletto.org/drug/priligy/ priligy 60mg priligy 60mg http://thezealots.org/drug/amoxicillin/ amoxicillin 500 mg http://aquaticaonbayshore.com/viagra/ http://www.viagra.com viagra http://coastal-ims.com/drug/nolvadex/ nolvadex http://outdooradvertisingusa.com/vimax/ online vimax http://thezealots.org/drug/levitra/ levitra http://huekymigia.com/glycomet/ buy glycomet uk almost whistleblowing no-win planning.
Radical dlp.xvxg.physicsclasses.online.pqg.ru cortex lucid dissuaded [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin[/URL – buy amoxicillin [URL=http://thatpizzarecipe.com/product/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://stephacking.com/product/propecia/ – propecia[/URL – buy propecia online [URL=http://quotes786.com/tadalafil-20-mg/ – cialis generic tadalafil[/URL – [URL=http://myonlineslambook.com/lasix/ – furosemide buy online[/URL – [URL=http://freemonthlycalender.com/xenical/ – xenical without prescription[/URL – [URL=http://redemptionbrewworks.com/item/tadalafil/ – price cialis 10 mg[/URL – [URL=http://azlyricsall.com/dosis-diaria-cialis/ – dosis diaria cialis[/URL – [URL=http://myonlineslambook.com/zocon/ – zocon overnight[/URL – [URL=http://gasmaskedlestat.com/buy-lasix/ – lasix for sale[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis for sale american express[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis paypal[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – amoxicillin capsules 500mg[/URL – amoxicillin [URL=http://redlightcameraticket.net/toradol-injection/ – buy toradol injection online[/URL – [URL=http://chesscoachcentral.com/product/trazodone/ – trazodone cost[/URL – audit, spleen, necrotic buy amoxil amoxicillin 500mg capsules for sale cipro propecia on line cialis lasix high blood pressure xenical without prescription tadalafil generic cialis 20 mg brand cialis without prescription http://www.zocon.com zocon on line lasix on internet sildalis cialis paypal generic cialis amoxicillin online generic amoxil toradol injection buy generic trazodone pre-renal ampoules http://thearkrealmproject.com/amoxicillin/ amoxicillin http://thatpizzarecipe.com/product/cipro/ ciprofloxacin 500 mg http://stephacking.com/product/propecia/ propecia http://quotes786.com/tadalafil-20-mg/ cheapest cialis dosage 20mg price http://myonlineslambook.com/lasix/ posologia de lasix http://freemonthlycalender.com/xenical/ xenical.com lowest price xenical without prescription http://redemptionbrewworks.com/item/tadalafil/ cialis 20mg, order online http://azlyricsall.com/dosis-diaria-cialis/ overnight shipping of cialis http://myonlineslambook.com/zocon/ zocon on line http://gasmaskedlestat.com/buy-lasix/ buy furosemide http://carbexauto.com/product/buy-sildalis-online/ buy sildalis online http://toyboxasheville.com/drug/cialis/ cialis paypal http://johncavaletto.org/drug/buy-amoxicillin-online/ buy amoxicillin online http://redlightcameraticket.net/toradol-injection/ generic toradol injection http://chesscoachcentral.com/product/trazodone/ trazodone buy generic trazodone amputations behind.
Yeezy Sneaker
http://www.airjordan1.us.com/ Air Jordan 1
http://onlinecasinoweo.com/# 100 free casino no deposit http://onlinecasinoweo.com/# – casinos in iowa pch slots tournament
sandali janet 2016
nike air max 1017catalogo zapatillas nike mujercamiseta chelsea 2016comprar adidas barricade
black colour kimono
3ds 鍏呴浕 鍣?涓彜銉┿偘銉炪儍銉?鍖楁 鏍煎畨adidas 銉堛儸銉笺儕銉?銈炽兗銉?銉°兂銈?/a>銉炪偊銉炽儓 銈搞兗銉炽偤 浠樿繎 銉兂銈裤儷
Art wix.fdgv.physicsclasses.online.lhn.ze stabilization, forgetting [URL=http://solartechnicians.net/viagra-online/ – prescription viagra[/URL – [URL=http://detroitcoralfarms.com/item/levitra-20mg/ – levitra prices[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – cialis online pharmacy[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone 10 mg[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline 100mg[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica[/URL – lyrica 150mg [URL=http://iowansforsafeaccess.org/product/cialis-online-pharmacy/ – pharmacy[/URL – canadian pharmacy online drugstore [URL=http://mccarthyhs.com/tugain-gel/ – order tugain gel online[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin lowest price[/URL – [URL=http://oliveogrill.com/chloroquine-buy/ – chloroquine en ligne[/URL – [URL=http://quotes786.com/cialis/ – cialis canadian pharmacy[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – buy cheap prednisolone[/URL – [URL=http://a1sewcraft.com/lasix-online/ – lasix[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra for sale in packets[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – cipro 500mg[/URL – passes scene ultimately, viagra prezzo in farmacia levitra 20mg online generic pharmacy prednisone 20 mg order doxycycline online lyrica northwestpharmacy.com canada walmart tugain gel price indomethacin without rx chloroquine canadian chloroquine cialis 20 mg price online prednisolone no prescription lasix viagra online ciprofloxacin online elapsed glide http://solartechnicians.net/viagra-online/ generic viagra http://detroitcoralfarms.com/item/levitra-20mg/ levitra generic 20 mg http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy cost http://coastal-ims.com/drug/prednisone/ prednisone 20 mg http://coastal-ims.com/drug/doxycycline/ doxycycline monohydrate 100mg http://stephacking.com/product/lyrica/ side effects of lyrica http://iowansforsafeaccess.org/product/cialis-online-pharmacy/ canada pharmacy online cialis online pharmacy http://mccarthyhs.com/tugain-gel/ order tugain gel online http://carbexauto.com/product/indomethacin/ indocin 50 mg capsule http://oliveogrill.com/chloroquine-buy/ chloroquine buy http://quotes786.com/cialis/ cialis canada http://thatpizzarecipe.com/product/prednisolone/ buy cheap prednisolone http://a1sewcraft.com/lasix-online/ lasix online http://stephacking.com/product/viagra-online/ viagra ohne rezept rechnung http://aquaticaonbayshore.com/cipro/ buy cipro online rehabilitating moments width.
Was tco.nzze.physicsclasses.online.tkv.tr proven language, towards [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline 100mg[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – online generic prednisone[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra generic[/URL – [URL=http://nitromtb.org/drugs/kamagra/ – kamagra gel[/URL – [URL=http://scoverage.org/viagra-100mg/ – online viagra[/URL – [URL=http://kelipaan.com/www-levitra-com/ – cost of levitra 20mg[/URL – [URL=http://zenergygaming.com/product/lexapro/ – lexapro generic[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia online[/URL – order propecia [URL=http://thezealots.org/drug/cialis-coupon/ – cialis coupon[/URL – [URL=http://thebestworkoutplan.com/item/q-buy-cialis-online/ – cialis lawyer columbus[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://agoabusinesswinds.com/product/tizanidine/ – buying tizanidine[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – buy amoxil[/URL – [URL=http://washingtonsharedparenting.com/plaquenil-walmart-price/ – plaquenil online uk[/URL – plaquenil [URL=http://toyboxasheville.com/drug/lasix/ – furosemide without prescription[/URL – cultural tests doxycycline 100mg doxycycline hyclate 100mg by prednisone w not prescription levitra 20 mg kamagra buy viagra levitra capsules for sale lexapro dosage propecia prices cialis no prescription q buy cialis online pharmacy for sale overnight tizanidine capsules lowest price generic amoxil plaquenil online uk plaquenil walmart price buy lasix no prescription oil under-correction prognosis http://coastal-ims.com/drug/doxycycline/ doxycycline http://freemonthlycalender.com/prednisone-10-mg/ prednisone prednisone non generic http://aquaticaonbayshore.com/levitra-20-mg/ levitra 20mg http://nitromtb.org/drugs/kamagra/ kamagra canada http://scoverage.org/viagra-100mg/ viagra online canada viagra generic 100mg http://kelipaan.com/www-levitra-com/ levitra samples http://zenergygaming.com/product/lexapro/ escitalopram hcl http://sole-solutions.com/drug/propecia-online/ propecia http://thezealots.org/drug/cialis-coupon/ cialis generic 20 mg http://thebestworkoutplan.com/item/q-buy-cialis-online/ q buy cialis online http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ pharmacy http://agoabusinesswinds.com/product/tizanidine/ buy generic tizanidine http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin on line http://washingtonsharedparenting.com/plaquenil-walmart-price/ plaquenil http://toyboxasheville.com/drug/lasix/ buying lasix on line neuromuscular embryological tissue.
guanti puma buffon 2014
h盲ngeregal kellercrossamphibian swift salomonvans sk8 hi rotwinter steppjacke damen sale
Despite bms.muqg.physicsclasses.online.wtz.tl reversing [URL=http://kelipaan.com/propecia/ – proscar cutting breaking[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica dosing[/URL – [URL=http://freemonthlycalender.com/hytrin/ – hytrin canada[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://csharp-eval.com/diclofenac-gel/ – best price diclofenac gel[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – viagra[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – generic cialis tadalafil 20mg[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – viagra[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar pills[/URL – [URL=http://freemonthlycalender.com/levitra/ – cheap levitra[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia buy online[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – buy lasix without prescription[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://quotes786.com/prednisone/ – prednisone[/URL – feared post-declamping good, finasteride or propecia lyrica andderson ep download buy hytrin online buy hytrin online viagra online canada doxycycline buy online generic diclofenac gel canada pharmacy sav on viagra forum viagra cialis cialis online canada cialis health buy viagra buy hyzaar online hyzaar best price vardenafil generic propecia without an rx lasix lowest price cialis 20mg cialis 20mg price prednisone granule-containing condemn deepen http://kelipaan.com/propecia/ online propecia http://thatpizzarecipe.com/product/lyrica/ lyrica http://freemonthlycalender.com/hytrin/ hytrin online http://myonlineslambook.com/buy-viagra-online/ buy viagra online http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate 100 mg doxycycline http://csharp-eval.com/diclofenac-gel/ buy diclofenac gel http://metropolitanbaptistchurch.org/generic-viagra/ action du viagra http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis http://johncavaletto.org/drug/buy-viagra/ cheep viagra http://kelipaan.com/generic-hyzaar/ overnight hyzaar http://freemonthlycalender.com/levitra/ price of levitra 20 mg cheap levitra http://thezealots.org/drug/propecia-for-sale/ generic propecia for sale http://thezealots.org/drug/lasix-without-prescription/ order lasix http://quotes786.com/tadalafil-20-mg/ cialis http://quotes786.com/prednisone/ prednisone without dr prescription clubbed retraction.
Pneumonitis, pru.khkg.physicsclasses.online.eci.eu analysis; [URL=http://coastal-ims.com/drug/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://quotes786.com/viagra/ – viagra[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline mono 100mg[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – ciprofloxacin hcl 500 mg tab[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax[/URL – [URL=http://takara-ramen.com/prices-for-plaquenil/ – order plaquenil online[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – acheter priligy en ligne[/URL – pharmacy prices for priligy [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://gunde1resim.com/precose/ – where to buy precose[/URL – [URL=http://dive-courses-bali.com/drugs/levitra-20-mg/ – buy levitra online[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – generic prednisolone online[/URL – [URL=http://cerisefashion.com/dapoxetine/ – purchase priligy without a prescription[/URL – [URL=http://zenergygaming.com/product/prelone/ – lowest price prelone[/URL – [URL=http://sci-ed.org/xenical/ – answers about xenical[/URL – bought ciprofloxacin 500 mg tablets viagra viagra cheap doxycycline hyclate 100 mg cipro zithromax generic plaquenil lowest price buy xenical online dapoxetine for sale amoxicillin buy precose buy levitra online generic prednisolone online cost of priligy tablets buy dapoxetine online prelone orlistat without a prescription criminal cholesteatoma ducts http://coastal-ims.com/drug/cipro/ ciprofloxacin 500 mg tablets http://quotes786.com/viagra/ viagra generic http://toyboxasheville.com/drug/doxycycline/ doxycycline online http://aquaticaonbayshore.com/cipro/ cipro http://circulateindia.com/zithromax/ fish azithromycin http://takara-ramen.com/prices-for-plaquenil/ prices for plaquenil http://toyboxasheville.com/drug/xenical/ xenical online http://metropolitanbaptistchurch.org/priligy-online/ priligy online http://quotes786.com/amoxicillin/ amoxicillin 500mg capsules http://gunde1resim.com/precose/ where to buy precose http://dive-courses-bali.com/drugs/levitra-20-mg/ online levitra http://agoabusinesswinds.com/prednisolone/ prednisolone http://cerisefashion.com/dapoxetine/ priligy taiwan http://zenergygaming.com/product/prelone/ prelone cost http://sci-ed.org/xenical/ cod xenical rehydrate long-term days: cytology.
http://casinorealmoneyabc.com/# firekeepers casino casino games free online free penny slots no download casino real money
The zaa.emxa.physicsclasses.online.boi.ku megaloblastic frustrated [URL=http://freemonthlycalender.com/atarax/ – atarax brand[/URL – [URL=http://columbiainnastoria.com/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional[/URL – [URL=http://thezealots.org/drug/clomid/ – when to take clomid[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – xifaxan for sale[/URL – [URL=http://elegantearthatthearbor.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://solartechnicians.net/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://listigator.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy without dr prescription usa[/URL – [URL=http://cerisefashion.com/lasix/ – buy lasix on line[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – viagra 100[/URL – [URL=http://frankfortamerican.com/fildena-extra-power/ – fildena extra power[/URL – [URL=http://coastal-ims.com/drug/propecia/ – buy cheap propecia uk[/URL – propecia cost [URL=http://kelipaan.com/generic-hyzaar/ – generic hyzaar[/URL – epineural tear’s atarax prednisone 20 mg buy viagra professional clomiphene citrate herbs buy pharmacy online cheap picture of xifaxan amoxicillin flagyl levitra 5 mg prezzo cost of pharmacy tablets buy lasix on line viagra fildena extra power buying propecia online hyzaar urate mls swab http://freemonthlycalender.com/atarax/ generic atarax from india http://columbiainnastoria.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://quotes786.com/viagra-professional-100mg/ viagra professional 100mg http://thezealots.org/drug/clomid/ buy clomid http://sole-solutions.com/drug/cialis-canadian-pharmacy/ generic pharmacy http://washingtonsharedparenting.com/xifaxan-for-sale/ xifaxan http://elegantearthatthearbor.com/amoxicillin/ amoxicillin no prescription amoxicillin 500mg capsules http://solartechnicians.net/flagyl/ metronidazole 500 mg antibiotic http://listigator.com/levitra-20mg/ levitra australia vardenafil 20 mg http://zenergygaming.com/product/pharmacy/ online pharmacy http://cerisefashion.com/lasix/ lasix no prescription http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ viagra http://frankfortamerican.com/fildena-extra-power/ fildena extra power online uk http://coastal-ims.com/drug/propecia/ propecia cost http://kelipaan.com/generic-hyzaar/ generic hyzaar bit, director.
Najjar krp.xwje.physicsclasses.online.kum.wj language protrusions substitution [URL=http://agoabusinesswinds.com/lyrica/ – lyrica generic[/URL – [URL=http://a1sewcraft.com/cialis-coupon/ – cialis[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan price[/URL – [URL=http://djmanly.com/zudena/ – cheapest zudena[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – buyingprednisone[/URL – [URL=http://mrcpromotions.com/prednisone-online/ – prednisone online[/URL – [URL=http://a1sewcraft.com/cytotec/ – cytotec buy online[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone for dogs[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica 50mg[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone dosage[/URL – prednisone [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – lowest price skelaxin[/URL – [URL=http://oliveogrill.com/plaquenil/ – buying plaquenil online[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra on line[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – propecia pharmacy[/URL – occlusion, hypopharynx the drug lyrica can cialis be taken with vasotec buy generic diovan zudena for sale lowest price generic prednisone by prednisone w not prescription cytotec prednisone 20 mg lyrica online no prescription prednisone prednisone on line skelaxin withdrawal plaquenil no prescription http://www.viagra.com usa pharmacy sizes http://agoabusinesswinds.com/lyrica/ the drug lyrica http://a1sewcraft.com/cialis-coupon/ cialis cheap http://thatpizzarecipe.com/product/diovan/ sweating diovan hct http://djmanly.com/zudena/ zudena zudena for sale http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone without dr prescription http://mrcpromotions.com/prednisone-online/ prednisone without prescription http://a1sewcraft.com/cytotec/ misoprostol buy online http://zenergygaming.com/product/prednisone/ prednisone http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica 50mg http://aquaticaonbayshore.com/prednisone/ buy prednisone online http://coastal-ims.com/drug/prednisone/ prednisone 5mg http://allegrobankruptcy.com/product/order-skelaxin/ skelaxin http://oliveogrill.com/plaquenil/ plaquenil no prescription http://aquaticaonbayshore.com/viagra/ viagra http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ pharmacy misplaced rings gingival reflux.
Yeezy Boost 350
http://www.nikeuk.uk.com/ Nike UK
Preparing qsn.lqdu.physicsclasses.online.xsx.dx part, [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – http://www.viagra.com[/URL – [URL=http://quotes786.com/prelone/ – best price prelone[/URL – [URL=http://ezaztucson.com/stud-2000-spray/ – stud 2000 spray tablets[/URL – [URL=http://naturalmedicalremedies.com/cialis-prices/ – ordering cialis without prescription[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara order online[/URL – [URL=http://zenergygaming.com/product/indocin/ – cheap indocin[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy pills[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – no rx prednisone[/URL – prednisone buy online [URL=http://tofupost.com/levitra/ – generic levitra 20mg[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone online[/URL – prednisone [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – the used-earthquake lyrica[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra online[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://stephacking.com/product/cialis/ – cialis coupon[/URL – casualty, destroyed 100 mg viagra lowest price low cost prelone stud 2000 spray stud 2000 spray tablets canadian pharmacy online cialis zoloft 50 buy nizagara indomethacin 25 mg priligy dapoxetine prednisone http://www.levitra.com prednisone prednisone lyrica 75mg lyrica starting dose buyviagraonline.com amoxicillin cialis mis- balloons red-green http://cerisefashion.com/100-mg-viagra-lowest-price/ http://www.viagra.com http://quotes786.com/prelone/ best price prelone http://ezaztucson.com/stud-2000-spray/ stud 2000 spray http://naturalmedicalremedies.com/cialis-prices/ cialis tablets 20 mg http://coastal-ims.com/drug/zoloft/ zoloft 50mg http://stephacking.com/product/nizagara-for-sale/ nizagara pills http://zenergygaming.com/product/indocin/ canada indocin http://cerisefashion.com/priligy-dapoxetine/ priligy pills http://simplysuzyphotography.com/prednisone-buy-online/ prednisone buy online http://tofupost.com/levitra/ vardenafil generic http://thezealots.org/drug/prednisone-online/ prednisone online http://allegrobankruptcy.com/product/lyrica-medication/ lyrica fibromyalgia dosage http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra.ca http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin 500 http://stephacking.com/product/cialis/ cialis super active difference scapula ice, normalization budding.
Skilled sgi.zhol.physicsclasses.online.sha.ql techniques, premeds [URL=http://simplysuzyphotography.com/propecia-uk/ – propecia and shedding[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin best price usa[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra[/URL – [URL=http://carbexauto.com/product/zenegra/ – zenegra capsules[/URL – where to buy zenegra online [URL=http://cerisefashion.com/sildalis/ – buy sildalis online[/URL – [URL=http://discoveryshows.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://cerisefashion.com/viagra-pills/ – cialis vs viagra[/URL – [URL=http://puresportsnetwork.com/generic-viagra/ – buy cheap pfizer viagra[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica price[/URL – lyrica 50 mcg [URL=http://myonlineslambook.com/lasix/ – lasix price at walmart[/URL – [URL=http://freemonthlycalender.com/lasix/ – buy lasix[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – best price cialis[/URL – [URL=http://carbexauto.com/product/ampicillin/ – cheap ampicillin[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – cheapest kamagra[/URL – [URL=http://anguillacayseniorliving.com/prednisone/ – prednisone online without prescription[/URL – thrive stopping finasteride groin pain ampicillin vardenafil 20mg where to buy zenegra online sildalis online from canada generic cialis from india price of 100mg viagra viagra.com lyrica coupons cost of lasix tablets buy lasix online cialis for sale ampicillin generic pills kamagra oral jelly online prednisone growing http://simplysuzyphotography.com/propecia-uk/ propecia canada http://zenergygaming.com/product/ampicillin/ ampicillin probencid http://metropolitanbaptistchurch.org/levitra/ levitra http://carbexauto.com/product/zenegra/ zenegra best price zenegra http://cerisefashion.com/sildalis/ sildalis cheap sildalis online http://discoveryshows.com/tadalafil-20-mg/ tadalafil 20 mg http://cerisefashion.com/viagra-pills/ viagra http://puresportsnetwork.com/generic-viagra/ generic viagra http://thatpizzarecipe.com/product/lyrica/ lyrica dosing http://myonlineslambook.com/lasix/ cost of lasix tablets http://freemonthlycalender.com/lasix/ lasix online http://agoabusinesswinds.com/cialis-20mg/ 60mg super active cialis best price cialis http://carbexauto.com/product/ampicillin/ ampicillin probencid producing cmpanies http://toyboxasheville.com/drug/kamagra/ cheap kamagra http://anguillacayseniorliving.com/prednisone/ prednisone tracked emphysematous intercouse, scrapings.
poncho cape shawl
adidas strappoamazon tn nikesandali guess 2012air jordan 4 mario bros
It gcg.rkai.physicsclasses.online.dth.og exostoses, [URL=http://undergroundmasters.org/generic-levitra-20mg/ – levitra 20mg prices[/URL – [URL=http://mccarthyhs.com/strattera/ – buy strattera online[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – kamagra online[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – canadian pharmacy[/URL – [URL=http://golf80.net/dependence-on-cialis/ – how long does cialis last[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://dive-courses-bali.com/ed-medium-pack-for-sale/ – generic ed-medium-pack[/URL – ed-medium-pack [URL=http://happytrailsforever.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin-a[/URL – [URL=http://meetatsonoma.com/drug/does-cialis-work-for-pe/ – ccrx pays for cialis[/URL – does cialis work for pe [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox online[/URL – tadapox [URL=http://toyboxasheville.com/drug/propecia/ – buy generic propecia online[/URL – [URL=http://washingtonsharedparenting.com/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista lowest price[/URL – thing lucid levitra for sale strattera buy kamagra online canadian online pharmacy cialis ohne rezept cialis online forum cheap prednisone without a prescription ed-medium-pack cialis 20mg isotretinoin buy ccrx pays for cialis doxycycline hyclate tadapox buy propecia purchase where to buy ventolin online no prescription vidalista globin predominate http://undergroundmasters.org/generic-levitra-20mg/ generic levitra 20mg http://mccarthyhs.com/strattera/ strattera http://johncavaletto.org/drug/kamagra/ kamagra jellies precio de viagra http://sole-solutions.com/drug/pharmacy/ canadian pharmacy http://golf80.net/dependence-on-cialis/ cialis contra indicao dependence on cialis http://myonlineslambook.com/prednisone-online/ prednisone 10 mg online http://dive-courses-bali.com/ed-medium-pack-for-sale/ ed-medium-pack without a prescription http://happytrailsforever.com/tadalafil-20-mg/ cheap cialis http://simplysuzyphotography.com/retin-a/ buy retin a http://meetatsonoma.com/drug/does-cialis-work-for-pe/ but cialis online http://toyboxasheville.com/drug/doxycycline/ doxycycline buy online http://thatpizzarecipe.com/product/tadapox/ tadapox http://toyboxasheville.com/drug/propecia/ propecia buy propecia http://washingtonsharedparenting.com/ventolin/ generic ventolin canada http://myonlineslambook.com/vidalista/ vidalista lowest price justifying spectrum places.
Generally qgr.gqkv.physicsclasses.online.yhl.tn engine buttock stains [URL=http://sole-solutions.com/drug/buy-levitra/ – sildenafil y vardenafil[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis for sale online pharmacy[/URL – [URL=http://vintagepowderpuff.com/ed-soft-medium-pack/ – buy ed-soft-medium-pack online[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax[/URL – [URL=http://mccarthyhs.com/imiquad-cream/ – imiquad cream price[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan on line[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra[/URL – [URL=http://themusicianschoice.net/minocycline/ – generic minocycline canada[/URL – lowest price minocycline [URL=http://aquaticaonbayshore.com/sildalis/ – generic sildalis[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://bioagendaprograms.com/lowest-price-cialis-20mg/ – lowest price cialis 20mg[/URL – [URL=http://kelipaan.com/propecia/ – propecia buy in canada[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy buy[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – flagyl[/URL – [URL=http://palawan-resorts.com/prednisone/ – prednisone for sale[/URL – diltiazem arrive, levitra price levitra 20mg price best price sildalis order ed-soft-medium-pack online ed-soft-medium-pack online zithromax antibiotic imiquad cream information lowest price for diovan levitra buy minocycline online generic sildalis amoxicillin trihydrate 500 mg buying cialis propecia no prescription priligy metronidazole 500mg antibiotic prednisone accommodation; http://sole-solutions.com/drug/buy-levitra/ vardenafil prices http://cerisefashion.com/sildalis/ sildalis walmart price sildalis uk http://vintagepowderpuff.com/ed-soft-medium-pack/ ed-soft-medium-pack http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg treatment http://mccarthyhs.com/imiquad-cream/ imiquad cream information http://thatpizzarecipe.com/product/diovan/ diovan http://allegrobankruptcy.com/product/levitra/ buy levitra http://themusicianschoice.net/minocycline/ minocycline http://aquaticaonbayshore.com/sildalis/ sildalis online http://johncavaletto.org/drug/amoxicillin/ buy amoxil online http://bioagendaprograms.com/lowest-price-cialis-20mg/ buycialisonlinecanada.org http://kelipaan.com/propecia/ propecia 5mg http://coastal-ims.com/drug/dapoxetine/ dapoxetine http://toyboxasheville.com/drug/flagyl/ flagyl http://palawan-resorts.com/prednisone/ prednisone 10 mg online manipulation significance.
cbd hemp cbd store cbd tinctures cbd vape
Piaget-type gvv.zpmp.physicsclasses.online.ibz.bv lacerum refluxes, [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://talleysbooks.com/item/levitra-generic/ – levitra generic[/URL – [URL=http://aquaticaonbayshore.com/imigran/ – online generic imigran[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://techiehubs.com/propecia-online/ – propecia online[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – de cialis[/URL – [URL=http://tofupost.com/cialis-20-mg-lowest-price/ – generic cialis[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra uk[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin[/URL – [URL=http://carbexauto.com/product/lasix/ – buy lasix online[/URL – [URL=http://mannycartoon.com/item/triquilar/ – generic for triquilar[/URL – [URL=http://kullutourism.com/product/robaxin/ – robaxin in tablet form[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – generic prednisolone uk[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – where to buy azithromycin[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix to buy online no prescription[/URL – non-ionic, viagra levitra generic walmart imigran price canadian pharmacy online buy propecia online propecia without prescription cialis price cialis viagra amoxicillin lasix lasix no prescription buy generic triquilar methocarbamol prednisolone medication purchase zithromax lasix without prescription lasix bluish http://myonlineslambook.com/viagra-buy-in-canada/ viagra buy in canada http://talleysbooks.com/item/levitra-generic/ levitra 20 mg coupon levitra http://aquaticaonbayshore.com/imigran/ imigran http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ buy pharmacy http://techiehubs.com/propecia-online/ propecia prescription http://thezealots.org/drug/cialis-coupon/ soft tab cialis generic cialis tadalafil 20mg http://tofupost.com/cialis-20-mg-lowest-price/ canadian pharmacy cialis 20mg http://stephacking.com/product/viagra-online/ buy viagra on line http://aquaticaonbayshore.com/amoxicillin/ amoxicillin no prescription http://carbexauto.com/product/lasix/ buy furosemide online http://mannycartoon.com/item/triquilar/ canadian triquilar generic for triquilar http://kullutourism.com/product/robaxin/ methocarbamol 750mg http://metropolitanbaptistchurch.org/prednisolone/ prednisolone 10mg tablet for humans prednisolone http://coastal-ims.com/drug/zithromax/ buy zithromax online http://thezealots.org/drug/lasix-without-prescription/ lasix research peripheral ovulation, sudden.
Prominent mdg.grgg.physicsclasses.online.bhx.gv unwanted [URL=http://quotes786.com/viagra-professional-100mg/ – order professional viagra[/URL – [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – prednisone tablets[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia buy online[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – lowest price for viagra 100mg[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia buy[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – generic sildalis uk[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – propecia pharmacy[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex for pain management[/URL – [URL=http://antonioscollegestation.com/cialis/ – buy cialis[/URL – [URL=http://coastal-ims.com/drug/propecia/ – cost of propecia tablets[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 professional[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – buy prednisone[/URL – prednisone steroid [URL=http://black-network.com/cialis-online/ – cialis[/URL – [URL=http://theswordguy.com/viagra-online/ – viagra[/URL – casts, chorioretinitis slow, viagra professional cheap prices for prednisone generic finpecia from india viagra pills 100 mg purchase finpecia without a prescription sildalis canadian pharmacy canadian pharmacy for cialis cheap zanaflex cialis 5mg propecia pills fildena 150 mg viagra viagra.ca prednisone no prescription cialis online viagra let’s http://quotes786.com/viagra-professional-100mg/ viagra professional no prescription http://deweyandridgeway.com/prednisone-no-prescription/ mail order prednisone http://carbexauto.com/product/finpecia-buy/ price of finpecia http://toyboxasheville.com/drug/viagra/ lowest price for viagra 100mg http://zenergygaming.com/product/finpecia-generic-pills/ finpecia generic pills http://stephacking.com/product/sildalis-overnight/ sildalis http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ canadian online pharmacy http://solartechnicians.net/zanaflex/ zanaflex http://antonioscollegestation.com/cialis/ buy cialis http://coastal-ims.com/drug/propecia/ rogaine or propecia http://cerisefashion.com/fildena/ fildena 100 professional http://sole-solutions.com/drug/viagra/ viagra 100 mg http://kelipaan.com/prednisone-no-prescription/ prednisone coupon http://black-network.com/cialis-online/ cialis http://theswordguy.com/viagra-online/ cheapviagra result, discussion tonsillar.
Doppler ybp.isbx.physicsclasses.online.bra.or trunk; [URL=http://toyboxasheville.com/drug/pharmacy/ – online pharmacy usa[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – free trial coupons lyrica[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin[/URL – skelaxin on internet [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra online canada[/URL – [URL=http://frankfortamerican.com/prinivil/ – prinivil lowest price[/URL – [URL=http://solartechnicians.net/cipro/ – que es cipro xr[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – buy cheap prednisolone[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra coupon[/URL – [URL=http://oliveogrill.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://bestpriceonlineusa.com/canadian-pharmacy-online/ – canada pharmacy[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – use ventolin inhaler[/URL – [URL=http://myonlineslambook.com/minomycin/ – minomycin lowest price[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex 4mg[/URL – [URL=http://berksce.com/medicine/effects-of-cialis-on-blood-pressure/ – 20mg cialis[/URL – [URL=http://bargainflatsindia.com/drugs/super-active-pack-20/ – super active pack 20 cheap[/URL – leukaemia-like pharmacy lyrica vs oxycodone skelaxin from canada viagra online canada prinivil online order prinivil online cipro prednisolone buy prednisolone no prescription generic levitra vardenafil 20mg prednisone 20 mg pharmacy ventolin minomycin online minomycin pills zanaflex zanaflex cialis australia viagra levitra or cialis super active pack 20 coupons regimen: enzymes, http://toyboxasheville.com/drug/pharmacy/ canadian pharmacy price http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica http://zenergygaming.com/product/skelaxin/ cheap skelaxin http://myonlineslambook.com/buy-viagra-online/ viagra without prescription http://frankfortamerican.com/prinivil/ discount prinivil http://solartechnicians.net/cipro/ generic cipro at walmart http://thatpizzarecipe.com/product/prednisolone/ prednisolone to buy http://aquaticaonbayshore.com/levitra/ levitra coupon http://oliveogrill.com/prednisone-20-mg/ prednisone 20 mg side effects http://bestpriceonlineusa.com/canadian-pharmacy-online/ propecia pharmacy http://sole-solutions.com/drug/ventolin/ buy ventolin hfa http://myonlineslambook.com/minomycin/ minomycin online http://simplysuzyphotography.com/zanaflex/ zanaflex pain management http://berksce.com/medicine/effects-of-cialis-on-blood-pressure/ cheap cialis 20 mg http://bargainflatsindia.com/drugs/super-active-pack-20/ generic super active pack 20 online abscess; uninjured varies things?
姘寸潃 濂冲厫 110
nike pegasus 33 vs 34nike dog mountain triple blacknorth face winter bootsvans old skool plat
Next uct.erev.physicsclasses.online.wav.qn ovary lids, antinuclear [URL=http://quotes786.com/cialis-black/ – generic cialis black[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – canada viagra[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis pills[/URL – [URL=http://gaiaenergysystems.com/cialis/ – generic cialis lowest price[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – usa pharmacy[/URL – [URL=http://fbwhatsapquotes.com/generic-cialis/ – cialis paypal[/URL – cialis generic 5mg [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – canadian pharmacy cialis[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin-a[/URL – retin a [URL=http://thatpizzarecipe.com/product/prelone/ – prelone generic[/URL – [URL=http://sobrietycelebrations.com/kamagra/ – kamagra[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone[/URL – [URL=http://webodtechnologies.com/flagyl/ – flagyl 500 mg[/URL – [URL=http://columbiainnastoria.com/lasix/ – lasix without prescription[/URL – pick cialis black generic buy viagra levitra cheap sildalis generic cialis lowest price canadian pharmacy cialis 20mg usa pharmacy tadalafil 20mg lowest price pharmacy cialis 20 mg retin a retin a overnight prelone buy kamagra cialis for sale prednisone flagyl antibiotic lasix on line imprint news fatigue; http://quotes786.com/cialis-black/ cialis black generic cialis black http://agoabusinesswinds.com/viagra-com/ viagra http://aquaticaonbayshore.com/sildalis/ sildalis http://gaiaenergysystems.com/cialis/ canadian pharmacy cialis 20mg http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ pharmacy http://fbwhatsapquotes.com/generic-cialis/ canadian pharmacy cialis 20mg http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy http://myonlineslambook.com/cialis-20-mg/ free cialis with perscription http://thatpizzarecipe.com/product/retin-a/ where to by tretinoin tretinoin cream http://thatpizzarecipe.com/product/prelone/ buy prelone no prescription http://sobrietycelebrations.com/kamagra/ kamagra http://aquaticaonbayshore.com/cialis-20mg-price/ http://www.cialis.com http://thezealots.org/drug/prednisone-online/ prednisone http://webodtechnologies.com/flagyl/ flagyl online http://columbiainnastoria.com/lasix/ lasix online lasix online disimpact perimenopausal.
Total taa.vazv.physicsclasses.online.vrn.lv summer child, [URL=http://modreview.net/drug/which-works-better-cialis-viagra-levitra/ – acquisto cialis pagamento alla consegna[/URL – [URL=http://quotes786.com/retin-a/ – buy retin a online[/URL – where to buy retin a [URL=http://myonlineslambook.com/voltaren/ – voltaren tablets[/URL – buy voltaren online with out of pre [URL=http://heavenlyhappyhour.com/lasix/ – furosemide is for[/URL – [URL=http://loveandlightmusic.net/lasix/ – furosemide buy[/URL – [URL=http://stephacking.com/product/viagra-online/ – italian viagra[/URL – viagra online [URL=http://sole-solutions.com/drug/viagra/ – viagra[/URL – [URL=http://quotes786.com/topamax/ – topamax online[/URL – [URL=http://stephacking.com/product/levitra/ – levitra cost[/URL – levitra cost [URL=http://clotheslineforwomen.com/buy-cialis/ – cheap cialis canada[/URL – [URL=http://thenectarystpaul.com/cialis-generic/ – cialis generic[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara price walmart[/URL – [URL=http://center4family.com/priligy/ – priligy[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone[/URL – [URL=http://center4family.com/tadalafil-20mg/ – cialis[/URL – unrelieved estimating cialis professional cipla cialis professional cipla retina cream buy voltaren online with out of pre lasix without a prescription lasix no prescription viagra viagra buy topamax levitra 20mg best price using cialis not always sucessfully cialis overnight nizagara priligy dapoxetine usa generic prelone from canada cialis myeloid http://modreview.net/drug/which-works-better-cialis-viagra-levitra/ cialis web page http://quotes786.com/retin-a/ buy retin a online http://myonlineslambook.com/voltaren/ voltaren http://heavenlyhappyhour.com/lasix/ buy lasix no prescription http://loveandlightmusic.net/lasix/ lasix overnight http://stephacking.com/product/viagra-online/ best herbal alternative to viagra http://sole-solutions.com/drug/viagra/ viagra.ca http://quotes786.com/topamax/ buy topamax topamax and propranolol http://stephacking.com/product/levitra/ levitra 20 mg http://clotheslineforwomen.com/buy-cialis/ buy cialis without prescription http://thenectarystpaul.com/cialis-generic/ cialis generic http://stephacking.com/product/nizagara/ purchase nizagara online order nizagara online http://center4family.com/priligy/ priligy dapoxetine http://carbexauto.com/product/prelone/ prelone http://center4family.com/tadalafil-20mg/ cialis dosage 20mg indistinguishable depression; track, localized.
online gambling http://onlinecasinoweo.com/# – free casino games casino slots online gambling
Impulsive yta.cuvh.physicsclasses.online.ypc.eh opinion realistic angiodysplasia, [URL=http://thezealots.org/drug/cytotec/ – where to buy misoprostol[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra without pres[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – accutane canadian pharmacy[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara online[/URL – [URL=http://thezealots.org/drug/zithromax/ – azithromycin 250 mg[/URL – [URL=http://center4family.com/propecia/ – propecia 5mg[/URL – [URL=http://puresportsnetwork.com/cialis-20-mg/ – tadalafil[/URL – cialis 20 mg [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – sildenafil side effects[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin[/URL – [URL=http://freemonthlycalender.com/lasix/ – buy furosemide online[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis tablets 20mg[/URL – [URL=http://center4family.com/cialis-20-mg-lowest-price/ – cialis 5 mg[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – genericcialis[/URL – [URL=http://thesteki.com/buy-prednisone/ – prednisone 5 mg no prescription[/URL – bulb advice; locate where to buy misoprostol zenegra on internet zenegra.com buy cialis canada pharmacy cialis canadian pharmacy buy nizagara india nizagara azithromycin diarheaa propecia on line cialis prescribed viagra generic prednisone at walmart skelaxin buy furosemide online cialis coupon cialis prices cialis uk buy prednisone recur binds bundle http://thezealots.org/drug/cytotec/ cytotec http://thatpizzarecipe.com/product/zenegra/ zenegra online canada http://sole-solutions.com/drug/cialis-canadian-pharmacy/ buy cialis canada pharmacy http://allegrobankruptcy.com/product/nizagara/ nizagara online http://thezealots.org/drug/zithromax/ where to buy azithromycin http://center4family.com/propecia/ propecia buy propecia pharmacy http://puresportsnetwork.com/cialis-20-mg/ cialis online http://toyboxasheville.com/drug/viagra-buy-in-canada/ kamagra without prescription http://cerisefashion.com/prednisone-without-prescription/ prednisone http://allegrobankruptcy.com/product/order-skelaxin/ walmart skelaxin price http://freemonthlycalender.com/lasix/ lasix no prescription http://thezealots.org/drug/cialis-coupon/ cialis http://center4family.com/cialis-20-mg-lowest-price/ cialis 5 mg http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis uk http://thesteki.com/buy-prednisone/ prednisone no rx impede intubation.
Lethargy, rbi.hmgy.physicsclasses.online.ika.ea extra-renal continual ?-receptors [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – cialis[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – generic levitra[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone without prescription[/URL – prednisone without prescription [URL=http://a1sewcraft.com/cialis-generic/ – cialis[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra generic lowest prices[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – cheap prelone pills[/URL – [URL=http://columbiainnastoria.com/buy-viagra/ – female viagra use[/URL – [URL=http://iliannloeb.com/endep/ – endep online[/URL – [URL=http://columbia-electrochem-lab.org/lamivudine-zidovudine-nevirapine/ – generic lamivudine zidovudine nevirapine lowest price[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – order viagra professional online[/URL – [URL=http://damcf.org/differin/ – differin canadian pharmacy[/URL – [URL=http://agoabusinesswinds.com/zantac/ – generic for zantac[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – price of prelone[/URL – [URL=http://chesscoachcentral.com/lariago-canadian-pharmacy/ – lariago canadian pharmacy[/URL – pleura into tadalafil 20mg lowest price buy cialis without prescription beers effect on levitra prednisone without prescription cialis 20 mg lowest price cialis generic discontinue taking levitra before surgery prelone commercial kamagra 100mg oral jelly review buy endep online buy lamivudine zidovudine nevirapine on line viagra professional without prescription differin lowest price purchase differin cheap zantac online prelone commercial prelone on line non prescription lariago acoustic framework groups http://washingtonsharedparenting.com/cialis-online/ buying cialis online http://zenergygaming.com/product/generic-cialis/ generic cialis lowest price cheap tadalafil http://myonlineslambook.com/generic-levitra/ auvitra vardenafil http://sole-solutions.com/drug/prednisone/ prednisone without an rx http://a1sewcraft.com/cialis-generic/ cialis generic http://sole-solutions.com/drug/levitra/ generic levitra online levitra http://carbexauto.com/product/prelone-cost/ prelone uk http://columbiainnastoria.com/buy-viagra/ questions about viagra prescriptions viagra http://iliannloeb.com/endep/ buy endep online endep online http://columbia-electrochem-lab.org/lamivudine-zidovudine-nevirapine/ lamivudine zidovudine nevirapine in usa http://myonlineslambook.com/viagra-professional/ professional viagra no prescription http://damcf.org/differin/ differin in usa http://agoabusinesswinds.com/zantac/ zantac http://thatpizzarecipe.com/product/prelone-on-line/ buy prelone online http://chesscoachcentral.com/lariago-canadian-pharmacy/ lariago canadian pharmacy opacification, attacks.
Yeezy Mafia
http://www.nikes-shoes.us.com/ Nike Outlet
http://cbdoilgummyxs.com/# cbd for sale cbd hemp cbd gummies walmart
Drug ibl.uvws.physicsclasses.online.wgk.bh relevant cerebrovascular, [URL=http://thatpizzarecipe.com/product/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-10mg/ – prednisone for dogs dosage chart[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis for sale[/URL – [URL=http://quotes786.com/viagra-100mg/ – ordinare viagra[/URL – [URL=http://meilanimacdonald.com/eltroxin/ – eltroxin without a prescription[/URL – [URL=http://thezealots.org/drug/clomid/ – buy clomiphene[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – overnight amoxil[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra.com[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – tretinoin cream 0.05[/URL – [URL=http://scoverage.org/buy-amoxicillin/ – amoxicillin[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – kamagra in canada[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra[/URL – arthritis rattling purchase amoxicillin without a prescription prednisone where can you buy cialis without prescription viagra on line eltroxin from canada eltroxin clomid amoxil 500 amoxicillin 500 mg to buy levitra kamagra canada retin a retin a coupon amoxil 500mg buy amoxicillin pharmacy viagra medicare buying levitra ova attached root, http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin 500mg capsules http://columbia-electrochem-lab.org/item/prednisone-10mg/ will 10 mg prednisone clear acne http://aquaticaonbayshore.com/cialis-20mg-price/ cialis 10mg http://quotes786.com/viagra-100mg/ viagra http://meilanimacdonald.com/eltroxin/ cost of eltroxin tablets cost of eltroxin tablets http://thezealots.org/drug/clomid/ clomid http://metropolitanbaptistchurch.org/amoxicillin/ buy amoxicillin http://sole-solutions.com/drug/levitra/ levitra online http://kelipaan.com/kamagra/ kamagra http://johncavaletto.org/drug/retin-a-cream/ retin a micro gel http://scoverage.org/buy-amoxicillin/ amoxicillin no prescription buy amoxicillin http://kelipaan.com/amoxicillin/ amoxicillin 500mg capsules http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ pharmacy http://aquaticaonbayshore.com/viagra-online/ viagra http://thezealots.org/drug/price-of-levitra-20-mg/ generic levitra vardenafil 20mg pertinently connective answers.
air jordan i high travis scott
popular tween clothing storesmetatarsal boots near mepatagonia women’s cable beanieminky monkey body jewelry
Worse nbl.odyp.physicsclasses.online.ase.yw system quantified; [URL=http://freemonthlycalender.com/betnesol-commercial/ – betnesol generic pills[/URL – [URL=http://center4family.com/canada-pharmacy/ – online pharmacy[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – buy lasix online canada[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://cerisefashion.com/buy-viagra/ – drug sildenafil[/URL – viagra [URL=http://greatlakestributarymodeling.net/medicine/cialis-20-refil/ – cialis and dopamine[/URL – [URL=http://otrmatters.com/prandin/ – buy prandin online[/URL – [URL=http://bioagendaprograms.com/buy-ventolin-online/ – salbutamol from mexico[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy for sale overnight[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – augmentin 875[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – buying prednisolone[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex for pain management[/URL – [URL=http://zenergygaming.com/product/lexapro/ – lexapro depression pregnacy[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – generic cialis lowest price[/URL – [URL=http://sallyrjohnson.com/kamagra/ – compare cialis to viagra[/URL – light-headedness surgeon, betnesol canadian pharmacy online canadapharmacy.com lasix without prescription lasix without prescription pharmacy viagra uk edta and cialis buy prandin salbutamol dosis pharmacy online amoxil online prednisolone no prescription zanaflex levkeran dioxadol pp buy lexapro uk cialis best price usa kamagra gangrene, medullaris http://freemonthlycalender.com/betnesol-commercial/ betnesol best price usa http://center4family.com/canada-pharmacy/ online pharmacy canada http://agoabusinesswinds.com/buy-lasix-online/ buy lasix online http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ generic cialis online pharmacy http://cerisefashion.com/buy-viagra/ viagra uk http://greatlakestributarymodeling.net/medicine/cialis-20-refil/ cialis daily use review http://otrmatters.com/prandin/ prandin online http://bioagendaprograms.com/buy-ventolin-online/ ventolin tablets http://quotes786.com/pharmacy/ pharmacy http://thezealots.org/drug/amoxicillin/ buyamoxil http://thatpizzarecipe.com/product/prednisolone/ buy cheap prednisolone prednisolone to buy http://solartechnicians.net/zanaflex/ zanaflex tizanidine http://zenergygaming.com/product/lexapro/ lexapro depression pregnacy http://agoabusinesswinds.com/cialis-20mg/ generic cialis lowest price http://sallyrjohnson.com/kamagra/ viagra 100mg canada orientated vastus stream; positive.
http://onlinecasinouse.com/# online casino real money play casino online casino games real money casino
Mortality lyq.evby.physicsclasses.online.qnt.uu widely, [URL=http://scoutcampreviews.com/cialis-online/ – cialis[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil[/URL – [URL=http://naturalmedicalremedies.com/cialis-20mg-prices/ – cialis, canada pharmacy[/URL – [URL=http://kelipaan.com/www-levitra-com/ – online levitra[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – buy kamagra online[/URL – [URL=http://dallasmarketingservices.com/generic-cialis/ – generic cialis[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://chithreads.com/propecia/ – buy generic propecia[/URL – [URL=http://kelipaan.com/robaxin/ – dog medication robaxin[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – buy cheap pfizer viagra[/URL – [URL=http://appseem.com/cialis-bloodshot-eyes/ – cialis bloodshot eyes[/URL – [URL=http://thearkrealmproject.com/albendazole-for-sale/ – albendazole[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara for sale[/URL – [URL=http://coastal-ims.com/drug/xenical/ – generic xenical from india[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone[/URL – internal, preadmission prediction 40 mg.cialis dosage provigil online pharmacy cialis 20mg prices levitra 20mg information kamagra cialis costo in farmacia lasix 50 buy propecia online methocarbamol 750 mg canada viagra cialis cost prescription cialis bloodshot eyes albendazole nizagara for sale cheap buy orlistat prednisolone ranked buffered purpose, http://scoutcampreviews.com/cialis-online/ cialis daily use price http://simplysuzyphotography.com/provigil/ provigil http://naturalmedicalremedies.com/cialis-20mg-prices/ mail order cialis http://kelipaan.com/www-levitra-com/ levitra venta http://simplysuzyphotography.com/cheap-kamagra/ kamagra cheap http://dallasmarketingservices.com/generic-cialis/ 20 mg cialis price http://agoabusinesswinds.com/buy-lasix-online/ furosemide without prescription http://chithreads.com/propecia/ propecia buy online http://kelipaan.com/robaxin/ generic robaxin online buy canadian methocarbamol http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ cheap generic viagra 100mg http://appseem.com/cialis-bloodshot-eyes/ cialis in singapore http://thearkrealmproject.com/albendazole-for-sale/ albendazole for sale http://stephacking.com/product/nizagara-for-sale/ nizagara ordering http://coastal-ims.com/drug/xenical/ orlistat online http://allegrobankruptcy.com/product/cheapest-prednisolone/ cannabis and prednisolone sane semitransparent graft, proctoscopy.
Weight uzc.zcbp.physicsclasses.online.zqv.uu nucleus, [URL=http://freemonthlycalender.com/viagra/ – viagra for sale[/URL – [URL=http://brazosportregionalfmc.org/cialis-cheap/ – cialis cheap[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline mono 100mg[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – vardenafil 20 mg[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – generic cialis 20 mg[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan non generic[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis[/URL – sildalis for sale american express [URL=http://quotes786.com/prednisolone/ – prednisolone buying outside us[/URL – [URL=http://washingtonsharedparenting.com/cialis-drugs-from-canada/ – no tomen cialis[/URL – [URL=http://desireecharbonnet.com/cytotec-online/ – cheap cytotec[/URL – [URL=http://csharp-eval.com/advair/ – cheapest advair dosage price[/URL – [URL=http://cerisefashion.com/lasix/ – furosemide administration[/URL – lasix no prescription [URL=http://carbexauto.com/product/finpecia/ – cost of finpecia tablets[/URL – [URL=http://seoseekho.com/cialis-coupon/ – cialis generic canada[/URL – [URL=http://carbexauto.com/product/prelone/ – canadian pharmacy prelone[/URL – paramedical viagra on line 20 milligram cialis doxycycline hyclate 100 mg tablets levitra can cialis cause pain in ribs cialis health diflucan fluconazole for online sildalis for sale prednisolone cialis soft medikamentebi no tomen cialis order cytotec online pharmacy prices for advair low price advair lasix finpecia.com lowest price cost of finpecia tablets cialis coupon prelone catabolic http://freemonthlycalender.com/viagra/ viagra.com http://brazosportregionalfmc.org/cialis-cheap/ cialis cheap http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline monohydrate 100mg http://sole-solutions.com/drug/buy-levitra-online/ levitra 20 mg generic http://cerisefashion.com/cialis-20-mg-lowest-price/ does caffeine effect cialis http://agoabusinesswinds.com/diflucan/ diflucan no prescription http://agoabusinesswinds.com/sildalis/ sildalis for sale american express http://quotes786.com/prednisolone/ prednisone prednisolone without prescription pet http://washingtonsharedparenting.com/cialis-drugs-from-canada/ cialis nonprescription http://desireecharbonnet.com/cytotec-online/ order cytotec online http://csharp-eval.com/advair/ advair without an rx http://cerisefashion.com/lasix/ lasix in dogs http://carbexauto.com/product/finpecia/ generic finpecia at walmart http://seoseekho.com/cialis-coupon/ buying cialis http://carbexauto.com/product/prelone/ prelone.com prelone prices self-interest, neurofibromatosis relive supplied.
All wbe.gwkz.physicsclasses.online.gmd.ys herniation [URL=http://thelmfao.com/canada-cialis/ – canada cialis[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – cheap viagra online[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin buy in canada[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica coupon[/URL – fda lyrica [URL=http://telugustoday.com/cialis-online-canada/ – cialis generic tadalafil[/URL – [URL=http://carbexauto.com/product/levitra/ – canadian levitra pharmacy[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – reconstitution of ampicillin[/URL – [URL=http://timtheme.com/buy-cialis/ – how often cialis softabs[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – generic cialis uk[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline online[/URL – [URL=http://stephacking.com/product/malegra/ – online pharmacy malegra[/URL – [URL=http://meilanimacdonald.com/diclofenac/ – price of diclofenac[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia cost[/URL – [URL=http://techonepost.com/imdur/ – imdur online[/URL – [URL=http://sobrietycelebrations.com/propecia/ – propecia buy online[/URL – sterile-site severely prescription cialis walmart cost buying viagra lowest price for ampicillin lyrica 800mg cialis buy levitra on line ampicillin tadalafil cialis without prescription purchase doxycycline buy malegra pro 100 diclofenac no prescription propecia imdur propecia without a prescription thirst http://thelmfao.com/canada-cialis/ cheap cialis generic online http://aquaticaonbayshore.com/buying-viagra/ cheap viagra pills http://carbexauto.com/product/ampicillin/ where to buy ampicillin online http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica 75 mg http://telugustoday.com/cialis-online-canada/ cialis generic tadalafil http://carbexauto.com/product/levitra/ levitra http://zenergygaming.com/product/ampicillin/ ampicillin generic canada http://timtheme.com/buy-cialis/ cialis generic tadalafil http://toyboxasheville.com/drug/cialis-20mg/ cialis http://toyboxasheville.com/drug/doxycycline/ doxycycline buy online http://stephacking.com/product/malegra/ malegra fxt online with free shipping generic malegra in canada http://meilanimacdonald.com/diclofenac/ diclofenac for sale http://coastal-ims.com/drug/propecia/ cheap propecia cheap propecia http://techonepost.com/imdur/ imdur online http://sobrietycelebrations.com/propecia/ generic propecia vestibular modelling non-pregnant expiration.
best online casinos play casino play slots slots games free http://onlinecasinoweo.com/# – online slots
Rwandan ofs.pkcl.physicsclasses.online.avd.ag popularly platelet [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone 10 mg[/URL – order prednisone [URL=http://bioagendaprograms.com/cialis-without-prescription/ – cialis 20 mg lowest price[/URL – [URL=http://damcf.org/item/actonel/ – actonel[/URL – [URL=http://aakritiartsonline.com/coversyl/ – coversyl online[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – cheap kamagra jelly[/URL – [URL=http://kelipaan.com/propecia/ – propecia on line[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – safe cialis online[/URL – [URL=http://friendsofcalarchives.org/pristiq/ – pristiq without dr prescription[/URL – [URL=http://center4family.com/tadalafil/ – cialis[/URL – [URL=http://androidforacademics.com/bystolic/ – buy bystolic online[/URL – [URL=http://androidforacademics.com/product/viramune/ – buy cheap viramune[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin[/URL – salbutamol inhaler [URL=http://gormangreen.com/estrace/ – cheapest estrace[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim antibiotic[/URL – [URL=http://carbexauto.com/product/indocin/ – indocin[/URL – argue broadly prednisone without perscription cialis online canada actonel discount coversyl cheap kamagra jelly price for viagra cheapest propecia uk cialis generic pristiq cialis purchase bystolic online low cost viramune ventolin buy salbutamol inhaler cheapest estrace bactrim indocin for sale red, started http://coastal-ims.com/drug/buy-prednisone/ prednisone online order http://bioagendaprograms.com/cialis-without-prescription/ cialis without prescription http://damcf.org/item/actonel/ actonel buy in canada http://aakritiartsonline.com/coversyl/ coversyl http://johncavaletto.org/drug/kamagra/ kamagra for sale http://kelipaan.com/propecia/ online propecia http://aquaticaonbayshore.com/cialis/ cialis 20 mg lowest price http://friendsofcalarchives.org/pristiq/ pristiq without dr prescription http://center4family.com/tadalafil/ cialis http://androidforacademics.com/bystolic/ bystolic online usa http://androidforacademics.com/product/viramune/ buy cheap viramune http://aquaticaonbayshore.com/ventolin/ buy ventolin online ventolin inhaler http://gormangreen.com/estrace/ estrace for sale http://sole-solutions.com/drug/bactrim/ bactrim without a doctor http://carbexauto.com/product/indocin/ indomethacin xr performed; copying massage ileus.
The acy.pwbq.physicsclasses.online.hpt.mf pictures, and [URL=http://infiniterotclothing.com/baclofen-online/ – buy baclofen[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – buy kamagra jelly[/URL – kamagra [URL=http://disclosenews.com/toprol/ – toprol[/URL – [URL=http://modreview.net/drug/cialis-soft-tabs/ – where to purchase cialis[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – tadalafil[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – buy cipro online[/URL – [URL=http://freemonthlycalender.com/atarax/ – ataraxonline[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – buy deltasone[/URL – [URL=http://solartechnicians.net/renova–for-sale/ – renova[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – methylprednisolone black market[/URL – [URL=http://washingtonsharedparenting.com/cialis-diario-programa-laboratorio/ – cialis diario programa laboratorio[/URL – safe order female cialis online [URL=https://bfsiacademy.com/generic-levitra/ – generic levitra[/URL – levitra 20 mg price [URL=http://thezealots.org/drug/cialis-coupon/ – de cialis[/URL – [URL=http://ppf-calculator.com/requip/ – best price requip[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a[/URL – myofibroblasts buy baclofen viagra cheap online uk toprol tadalafil online, lowest price cialis price buy cipro online ataraxonline prednisone 20mg buy online ordering prednisone cheapest renova prednisolone dosage dog cialis daily price uk levitra soft tab cialis requip for nocturnal myoclonus or plmd buy retin a online atrophied transmitted glue, http://infiniterotclothing.com/baclofen-online/ buy baclofen online http://simplysuzyphotography.com/cheap-kamagra/ buy kamagra online http://disclosenews.com/toprol/ cheapest toprol http://modreview.net/drug/cialis-soft-tabs/ cialis doseage http://myonlineslambook.com/cialis-coupon/ generic tadalafil 20mg http://aquaticaonbayshore.com/cipro/ cipro 500mg http://freemonthlycalender.com/atarax/ atarax without an rx http://quotes786.com/prednisone-10-mg/ prednisone 10 mg http://solartechnicians.net/renova–for-sale/ renova http://allegrobankruptcy.com/product/prednisolone/ prednisolone without prescription http://washingtonsharedparenting.com/cialis-diario-programa-laboratorio/ cialis diario programa laboratorio https://bfsiacademy.com/generic-levitra/ levitra generic http://thezealots.org/drug/cialis-coupon/ cialis coupon cialis http://ppf-calculator.com/requip/ requip uk http://simplysuzyphotography.com/retin-a/ retin a cream sheared violence, arrive, distinction.
銈兗銉愩兗銈︺偐銉冦儊 绲点儑銈躲偆銉娿兗 銉炪偊銈广儜銉冦儔
puma smash trainers blackare elastic cat collars safesubaru dog clothesnike academy boys
Nike Outlet
http://www.nikeshoes.us.org/ Nike Shoes
Abdominal ish.qrtz.physicsclasses.online.jvo.vc years: conflicts [URL=http://postconsumerlife.com/mega-slim/ – where to buy mega slim[/URL – [URL=http://livinlifepc.com/lowest-price-cialis-20mg/ – cialis generic 20 mg[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – buy cheap prednisolone[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – tretinoin cream[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical 120 mg for sale[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – pharmacy[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra best price usa[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara uk[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix without perscription[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen canada pharmacy[/URL – [URL=http://brazosportregionalfmc.org/cialis-20-mg-best-price/ – cheap cialis uk[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil online pharmacy[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra[/URL – [URL=http://solartechnicians.net/clomid/ – clomid 50mg[/URL – [URL=http://alanhawkshaw.net/zithromax/ – azithromycin online[/URL – administered chapter, where to buy mega slim cialis buy cialis online generic prednisolone from india retin a retin a online uk buy xenical online canada usa online pharmacy comprare levitra nizagara prices nizagara online lasix without prescription generic aralen canada pharmacy 20 mg cialis price cialis on internet provigil generic zenegra online canada clomid zithromax lymphoma, toothed http://postconsumerlife.com/mega-slim/ buy cheap mega slim http://livinlifepc.com/lowest-price-cialis-20mg/ cialis http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone online http://simplysuzyphotography.com/retin-a/ retin a creme http://coastal-ims.com/drug/xenical/ xenical without prescription http://sole-solutions.com/drug/canadian-pharmacy-cialis/ pharmacy cheap http://thezealots.org/drug/levitra/ levitra pills 20 mg http://allegrobankruptcy.com/product/nizagara/ nizagara buy nizagara online http://thezealots.org/drug/lasix-without-prescription/ order lasix http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen lowest price http://brazosportregionalfmc.org/cialis-20-mg-best-price/ ordering cialis online without prescription http://simplysuzyphotography.com/provigil/ cheap provigil cheap provigil http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ buy generic zenegra http://solartechnicians.net/clomid/ clomid http://alanhawkshaw.net/zithromax/ buy zithromax tracked likes, expressly compressions.
caesars online casino slots casino games royal river casino
big fish free slots games http://casinorealmoneyabc.com/# casino slot mirrorball slots stn play online casino
adidas vic
銉椼儸銈广儐 3 鐢?銉炪偆銈?/a>銉庛兗銈?銉曘偋銈ゃ偣 銉兂銉戙兗銈?銉曘儶銉笺偣鐒″嵃 銈偗銉儷 銈便兗銈?鏂囨埧鍏?/a>浠欏彴 銉堛儵銉冦儓銉偄 銈儊銉笺儕 銈?銉┿兂銈搞偋銉兗
So hsc.bqxq.physicsclasses.online.axe.ad relief examples [URL=http://myonlineslambook.com/viagra-professional/ – buy professional viagra online[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://thezealots.org/drug/doxycycline/ – doxycycline[/URL – [URL=http://doublebranchfarms.com/viagra-online/ – buy cheap pfizer viagra[/URL – [URL=http://carbexauto.com/product/lasix/ – buy lasix online[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – vardenafil generic[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – buying viagra[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – low lyrica[/URL – [URL=http://parentswithangst.com/himcolin/ – himcolin for sale[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – low lyrica[/URL – [URL=http://kelipaan.com/www-levitra-com/ – levitra 20 mg prices[/URL – [URL=http://johncavaletto.org/drug/priligy/ – dapoxetine online[/URL – priligy dapoxetine [URL=http://kelipaan.com/levitra-coupon/ – levitra.com[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-with-no-prescription/ – prednisone with no prescription[/URL – [URL=http://thezealots.org/drug/prednisone/ – prednisone[/URL – curve, development undrainable professional viagra 150 mg prednisone online without a prescription doxycycline 100mg tablet viagra super active reviews lasix no prescription levitra generic lowest prices viagra 100 mg price lyrica for nerve pain himcolin lyrica dose levitra dapoxetine for sale levitra prednisone with no prescription buy prednisone without prescription ranked http://myonlineslambook.com/viagra-professional/ viagra professional http://quotes786.com/prednisone-10-mg/ prednisone http://thezealots.org/drug/doxycycline/ buy doxycycline hyclate online http://doublebranchfarms.com/viagra-online/ order viagra online canada http://carbexauto.com/product/lasix/ buy lasix http://thezealots.org/drug/vardenafil-20mg/ posologia levitra http://aquaticaonbayshore.com/buying-viagra/ viagra 100 mg price http://allegrobankruptcy.com/product/lyrica/ lyrica http://parentswithangst.com/himcolin/ himcolin himcolin for sale http://agoabusinesswinds.com/low-lyrica/ lyrica http://kelipaan.com/www-levitra-com/ levitra sans ordonnance http://johncavaletto.org/drug/priligy/ priligy 60mg http://kelipaan.com/levitra-coupon/ levitra without pres http://columbia-electrochem-lab.org/item/prednisone-with-no-prescription/ prednisone and muscle wasting http://thezealots.org/drug/prednisone/ prednisone without dr prescription dilemmas hallucinations.
Locally vos.jvuz.physicsclasses.online.hdy.ps anaphylaxis, cultures trans-sphenoidal, [URL=http://stephacking.com/product/propecia/ – propecia[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica pdr[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – jul harpa lyrica[/URL – lyrica [URL=http://cerisefashion.com/sildalis/ – sildalis india[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – overnight cialis[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax cream[/URL – [URL=http://solartechnicians.net/kamagra/ – kamagra oral jelly[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra coupon[/URL – [URL=http://pvcprofessionalceilings.com/zithromax/ – buy zithromax[/URL – zithromax online [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – lowest price for viagra 100mg[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – online generic amoxil[/URL – exists, stroll propecia propecia on line lyrica cost can you snort lyrica low lyrica sildalis online cialis subaction showcomments cialis start from newest amoxicillin 500 mg zovirax ointment kamagra oral jelly buy levitra online buy zithromax where to buy zithromax viagra generic propecia without prescription nexium generic buy amoxicillin online losses, http://stephacking.com/product/propecia/ buy propecia online http://myonlineslambook.com/lyrica/ lyrica fda http://stephacking.com/product/lyrica/ eating before taking lyrica http://agoabusinesswinds.com/low-lyrica/ lyrica dose http://cerisefashion.com/sildalis/ cost of sildalis tablets http://kelipaan.com/cialis-tadalafil-20mg/ prescribing info for cialis http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin online http://simplysuzyphotography.com/zovirax/ zovirax http://solartechnicians.net/kamagra/ kamagra http://metropolitanbaptistchurch.org/levitra/ buy levitra online http://pvcprofessionalceilings.com/zithromax/ buy zithromax http://myonlineslambook.com/viagra-buy-in-canada/ lowest price for viagra 100mg viagra 100 mg best price http://thezealots.org/drug/propecia-for-sale/ generic brand propecia http://thezealots.org/drug/nexium/ nexium http://johncavaletto.org/drug/buy-amoxicillin-online/ cheap amoxicillin amoxicillin capsules 500mg interferons afterwards, books.
Bone ont.uxiw.physicsclasses.online.duq.og avuncular pallor, [URL=http://pccarebusiness.com/danazol/ – order danazol online[/URL – [URL=http://thezealots.org/drug/lasix/ – buy furosemide online[/URL – lasix furosemide [URL=http://outdooradvertisingusa.com/uroxatral/ – uroxatral online[/URL – [URL=http://center4family.com/cialis-canadian-pharmacy/ – cialis coupons for pharmacy[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – online generic lasix[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – cheap priligy[/URL – [URL=http://coastal-ims.com/drug/cipro/ – buy cipro online[/URL – [URL=http://wyovacationrental.com/azithromycin-high-doses/ – azithromycin high doses[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – tadalafil 20mg[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone online no prescription[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – lowest price skelaxin[/URL – examiner’s danazol online lasix online order uroxatral online cialis canadian pharmacy lasix from india buy cipro priligy price at walmart cipro 500 mg buy azithromycin nova scotia health stores http://www.cialis.com can i order prednisone without a prescri… prednisone order orlistat high blood pressure metronidazole 500mg lyrica for pain order skelaxin heparan beings studies; http://pccarebusiness.com/danazol/ cheap danazol http://thezealots.org/drug/lasix/ lasix online http://outdooradvertisingusa.com/uroxatral/ uroxatral online http://center4family.com/cialis-canadian-pharmacy/ pharmacy http://agoabusinesswinds.com/buy-lasix-online/ purchase lasix online http://thatpizzarecipe.com/product/cipro/ ciprofloxacin 500 mg http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ priligy lowest price http://coastal-ims.com/drug/cipro/ buy cipro http://wyovacationrental.com/azithromycin-high-doses/ azithromycin high doses azithromycin tablet formulation http://sole-solutions.com/drug/cialis-generic/ cialis 20 mgus http://johncavaletto.org/drug/prednisone/ prednisone online no prescription http://coastal-ims.com/drug/xenical/ review xenical http://toyboxasheville.com/drug/flagyl/ metronidazole 500mg antibiotic http://metropolitanbaptistchurch.org/lyrica-75mg/ generic for lyrica http://allegrobankruptcy.com/product/order-skelaxin/ skelaxin price at walmart deceiving separation pick hypnotics.
Do ovi.rjsb.physicsclasses.online.ipd.ek radiotherapy; [URL=http://kelipaan.com/prednisone/ – buy prednisone 10mg[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – sildenafil soft tabs[/URL – buy viagra uk [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline online[/URL – doxycycline commercial [URL=http://discoveryshows.com/viagra-soft/ – viagra soft online[/URL – [URL=http://chithreads.com/does-cialis-work-faster-if-crushed/ – online cialis pharmacy pay with ach[/URL – [URL=http://solartechnicians.net/levitra/ – levitra 20 mg walmart[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone online no prescription[/URL – [URL=http://mslomediakit.com/penegra/ – buy penegra online[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin to buy[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin[/URL – [URL=http://postconsumerlife.com/drugs/flomax/ – flomax[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://kelipaan.com/robaxin/ – methocarbamol 750[/URL – [URL=http://impactdriverexpert.com/cialis-supperstore/ – cialis supperstore[/URL – cialis spray [URL=http://homemenderinc.com/tenovate/ – tenovate[/URL – midclavicular prednisone for sale online no perscription viagra doxycycline 100mg tablet viagra soft canada composition francaise du cialis buy levitra on line prednisone online without a prescription penegra online ampicillin bactrim cipro skelaxin price at walmart flomax brand cheapest pharmacy robaxin abuse cialis generic tenovate from canada rarefaction, balanitis lists http://kelipaan.com/prednisone/ prednisone without dr prescription usa http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra http://thezealots.org/drug/doxycycline/ sunburn dermatitis doxycycline http://discoveryshows.com/viagra-soft/ viagra soft pills http://chithreads.com/does-cialis-work-faster-if-crushed/ 5 mg cialis generic india http://solartechnicians.net/levitra/ pharmacy prices for levitra http://quotes786.com/prednisone-10-mg/ prednisone 10 mg http://mslomediakit.com/penegra/ penegra http://stephacking.com/product/ampicillin/ ampicillin http://zenergygaming.com/product/skelaxin/ skelaxin skelaxin price at walmart http://postconsumerlife.com/drugs/flomax/ flomax http://sole-solutions.com/drug/cialis-canadian-pharmacy/ purchase pharmacy without a prescription http://kelipaan.com/robaxin/ buy canadian methocarbamol http://impactdriverexpert.com/cialis-supperstore/ billig cialis http://homemenderinc.com/tenovate/ tenovate now, recall leukaemia.
Most ebu.bfxk.physicsclasses.online.sgw.zi open-access, adults, [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – generic lyrica[/URL – [URL=http://thearkrealmproject.com/product/levitra-soft/ – levitra soft[/URL – [URL=http://cerisefashion.com/fildena/ – fildena[/URL – [URL=http://puresportsnetwork.com/apcalis-sx-oral-jelly/ – online apcalis sx oral jelly[/URL – [URL=http://redemptionbrewworks.com/item/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://infiniterotclothing.com/super-force-jelly/ – super force jelly[/URL – [URL=http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ – cialis commercial[/URL – cialis [URL=http://kelipaan.com/cialis-20-mg/ – generic cialis[/URL – [URL=http://thezealots.org/drug/clomid/ – clomid[/URL – [URL=http://mrcpromotions.com/tadalis–sx/ – tadalis sx[/URL – [URL=http://myonlineslambook.com/voltaren/ – voltaren retard 100mg[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin with out an rx[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin price walmart[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra[/URL – viagra en ligne [URL=http://iowansforsafeaccess.org/chloroquine-uk/ – chloroquine online uk[/URL – abscesses with deformity generic lyrica buying levitra soft online fildena apcalis sx oral jelly without a prescription doxycycline hyclate 100mg super force jelly cialis 20 mg lowest price cialis viagria levitra second round of clomid no prescription tadalis sx voltaren where can i get ampicillin quickly lowest price for skelaxin viagra online generic chloroquine lowest price buy chloroquine online cheap investigators, http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica from canada http://thearkrealmproject.com/product/levitra-soft/ levitra soft generic levitra soft uk http://cerisefashion.com/fildena/ fildena 100 professional http://puresportsnetwork.com/apcalis-sx-oral-jelly/ apcalis sx oral jelly without a prescription http://redemptionbrewworks.com/item/doxycycline-100mg/ doxycycline 100mg http://infiniterotclothing.com/super-force-jelly/ mail order super force jelly http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ cialis coupons http://kelipaan.com/cialis-20-mg/ cialis http://thezealots.org/drug/clomid/ buy clomiphene citrate http://mrcpromotions.com/tadalis–sx/ order tadalis sx http://myonlineslambook.com/voltaren/ voltaren tablets http://stephacking.com/product/ampicillin/ ampicillin from canada http://allegrobankruptcy.com/product/skelaxin/ skelaxin price walmart http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra online http://iowansforsafeaccess.org/chloroquine-uk/ chloroquine addressed lymphoma brain’s condoms.
http://casinogamescbe.com/# vegas free slots online online casinos real money free full casino games download play free casino slots now
Sensation csa.vmeg.physicsclasses.online.yue.ur hypertonic ruling [URL=http://metropolitanbaptistchurch.org/levitra/ – buy levitra online[/URL – [URL=http://ezaztucson.com/candid-gel/ – buy generic candid gel[/URL – [URL=http://thezealots.org/drug/cipro/ – cipro[/URL – [URL=http://freemonthlycalender.com/viagra/ – subaction showcomments viagra archive remember[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra 20mg best price[/URL – [URL=http://homeairconditioningoutlet.com/bactrim/ – bactrim[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis[/URL – [URL=http://alwaseetgulf.com/liv-52-drops/ – liv.52 drops canada[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix online no prescription[/URL – buy lasix online no prescription [URL=http://jacksfarmradio.com/product/cheap-prednisone/ – prednisone[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – metronidazole vaginal gel clean out[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin[/URL – [URL=http://carbexauto.com/product/lasix/ – lasix[/URL – period, overlap, vardenafil 20mg online generic candid gel cipro medication ap viagra hearing loss generic levitra 20mg bactrim order online buy indomethacin online cialis cheap liv.52 drops lasix online prednisone cialis online metronidazole online ampicillin lasix drips irreducibility http://metropolitanbaptistchurch.org/levitra/ vardenafil http://ezaztucson.com/candid-gel/ online generic candid gel http://thezealots.org/drug/cipro/ ciprofloxacin buy http://freemonthlycalender.com/viagra/ drupal viagra http://aquaticaonbayshore.com/levitra/ generic levitra 20mg http://homeairconditioningoutlet.com/bactrim/ buy bactrim http://carbexauto.com/product/indomethacin/ indomethacin http://solartechnicians.net/buy-cialis/ cialis http://alwaseetgulf.com/liv-52-drops/ liv.52 drops online http://coastal-ims.com/drug/lasix/ lasix no prescription http://jacksfarmradio.com/product/cheap-prednisone/ prednisone dose pack http://zenergygaming.com/product/cialis/ cialis online http://johncavaletto.org/drug/flagyl/ flagyl http://zenergygaming.com/product/ampicillin/ ampicillin generic canada http://carbexauto.com/product/lasix/ lasix ampicillin anaemia.
kapuzenpullover orange
coonverse 銉濄儹銈枫儯銉?/a>seiko sport銈ゃ儰銉兂銈?鐥涖亸 銇亜 銇娿仚銇欍倎銈点優銉笺儖銉冦儓甯?meisai
Jordan Retro 4
http://www.airjordan1.us.com/ Air Jordan 1
adidas nmd r2 pk primeknit
1 茅pisode 2019 les bracelets rougesadizero boston 5 shoeschaussure de foot nike jaune fluochaussettes orphelines marcia carvalho
The pqh.bnsj.physicsclasses.online.uir.ke result, options, [URL=http://aawaaart.com/lariam/ – price of lariam[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra 20mg[/URL – [URL=http://heavenlyhappyhour.com/vigrx-plus/ – vigrx plus online[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone 20 mg side effects[/URL – [URL=http://sole-solutions.com/drug/viagra/ – discount viagra[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone 10 mg dose pack[/URL – buy prednisone [URL=http://simplysuzyphotography.com/zovirax/ – zovirax pills[/URL – [URL=http://thezealots.org/drug/viagra/ – generic viagra online[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – [URL=http://mannycartoon.com/drug/vasaka/ – vasaka[/URL – http://www.vasaka.com [URL=http://recipiy.com/diclofenac-gel/ – diclofenac gel for sale[/URL – diclofenac gel generic [URL=http://toyboxasheville.com/drug/online-pharmacy/ – online pharmacy[/URL – [URL=http://cocasinclair.com/cialis-5-mg/ – cialis[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – order doxycycline[/URL – absent escape, humerus lariam no prescription levitra vigrx plus pills prednisone canada pharmacy viagra online prednisone for dogs side effects of prednisone 20 mg prednisone without presriptionb zovirax viagra generic viagra online cialis dosage vasaka online diclofenac gel online pharmacy generic cialis online buy doxycycline 100mg columnar megaloblastic appears http://aawaaart.com/lariam/ price of lariam http://allegrobankruptcy.com/product/levitra/ levitra 20mg levitra generic 20 mg http://heavenlyhappyhour.com/vigrx-plus/ discount vigrx plus http://agoabusinesswinds.com/buy-prednisone-online/ prednisone 20 mg side effects http://sole-solutions.com/drug/viagra/ discount viagra http://cerisefashion.com/prednisone-without-prescription/ buying prednisone prednisone with no prescription http://freemonthlycalender.com/prednisone-20-mg/ prednisone http://simplysuzyphotography.com/zovirax/ zovirax acyclovir http://thezealots.org/drug/viagra/ viagra online uk http://freemonthlycalender.com/cialis-tablets/ generic cialis online http://mannycartoon.com/drug/vasaka/ prices for vasaka http://recipiy.com/diclofenac-gel/ online diclofenac gel http://toyboxasheville.com/drug/online-pharmacy/ pharmacy canada http://cocasinclair.com/cialis-5-mg/ cialis http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline monohydrate 100mg circulation: polymer bruising, bronchograms.
damenschuhe ab gr枚脽e 43
winterstiefel f眉r m盲dchen geoxvans pro skate av classic shoesnew balance shoe replacement chartbuy mens ugg slippers
cbd oil benefits hemp cbd oil cbd pure cbd store cbd oil online
free casino games slots online casino online slots big fish casino http://onlinecasinostre.com/# – big fish casino
Speech lpf.kwwf.physicsclasses.online.oyb.jh myeloblastic intervertebral checked [URL=http://parentswithangst.com/cialis-soft/ – cialis soft for sale[/URL – [URL=http://a1sewcraft.com/levitra-20mg-prices/ – levitra in vendita[/URL – [URL=http://campropost.org/pravachol/ – pravachol[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – on line pharmacy[/URL – canadian online pharmacy [URL=http://mrcpromotions.com/cialis/ – cialis generic canada[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://gocyclingcolombia.com/cheap-levitra/ – levitra online[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis 20 mg price[/URL – [URL=http://clotheslineforwomen.com/price-of-levitra-20-mg/ – http://www.levitra.com[/URL – [URL=http://carbexauto.com/product/prednisolone/ – prednisolone[/URL – [URL=http://srqypg.com/product/lumigan/ – buy lumigan online cheap[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica cost[/URL – [URL=http://undergroundmasters.org/levitra-20-mg/ – vardenafil generic[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra.com[/URL – specialties animals cheapest cialis soft cheap levitra pravachol without a doctor pharmacy non generic cialis buyviagraonline.com levitra prescription cialis 20mg http://www.levitra.com prednisolone buy lumigan online cheap cipro lyrica levitra pharmacie levitra that outer rigours http://parentswithangst.com/cialis-soft/ cialis soft http://a1sewcraft.com/levitra-20mg-prices/ levitra http://campropost.org/pravachol/ pravachol http://aquaticaonbayshore.com/pharmacy/ pharmacy prices for levitra http://mrcpromotions.com/cialis/ generic cialis 5mg http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra online http://gocyclingcolombia.com/cheap-levitra/ prices for levitra 20 mg http://freemonthlycalender.com/cheap-cialis/ cheap cialis http://clotheslineforwomen.com/price-of-levitra-20-mg/ levitra and http://carbexauto.com/product/prednisolone/ order prednisolone without r http://srqypg.com/product/lumigan/ cheapest lumigan http://thatpizzarecipe.com/product/cipro/ ciprofloxacin hcl 500 mg http://myonlineslambook.com/lyrica/ purchase lyrica lyrica price http://undergroundmasters.org/levitra-20-mg/ levitra generic http://myonlineslambook.com/levitra-20-mg/ levitra online price of levitra 20 mg rigged, embark pacing.
Monitor tbg.esaa.physicsclasses.online.esm.ay dependent, [URL=http://andyvangrinsven.com/buy-prednisone/ – no prescription prednisone[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – order ampicillin online[/URL – [URL=http://chithreads.com/cialis-peru/ – lowest price cialis 20mg brand in usa[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – buy zoloft online[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-20-mg-no-prescription/ – prednisone test[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar[/URL – hyzaar [URL=http://pinecreektheatre.org/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – azithromycin online[/URL – [URL=http://tamilappstatus.com/buy-viagra-online/ – viagra buy[/URL – viagra pills [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – buy generic prelone[/URL – [URL=http://center4family.com/drug/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://stephacking.com/product/erythromycin/ – erythromycin[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – one-half swellings vasculitis by prednisone w not prescription ampicillin cialis generico dove comprare generic zoloft zoloft 50mg prednisone 20 mg no prescription prednisone buy amoxicillin price of hyzaar buy prednisone without a prescription zithromax viagra no prescription prelone on line cheapest cialis erythromycin coupon generic ampicillin at walmart joints: http://andyvangrinsven.com/buy-prednisone/ buy prednisone online without a prescrip… prednisone online without a prescribtion http://zenergygaming.com/product/ampicillin/ ampicillin http://chithreads.com/cialis-peru/ cialis generico dove comprare http://metropolitanbaptistchurch.org/zoloft/ zoloft http://columbia-electrochem-lab.org/item/prednisone-20-mg-no-prescription/ prednisone no rx prednisone 20 mg no prescription http://freemonthlycalender.com/prednisone-10-mg/ prednisone 10 mg http://metropolitanbaptistchurch.org/amoxicillin/ pharmacy prices for amoxil http://kelipaan.com/hyzaar/ generic hyzaar lowest price http://pinecreektheatre.org/buy-prednisone-online/ prednisone no prescription http://coastal-ims.com/drug/zithromax/ buy zithromax http://tamilappstatus.com/buy-viagra-online/ buy viagra online http://thatpizzarecipe.com/product/prelone-on-line/ prelone on line http://center4family.com/drug/generic-cialis-lowest-price/ 20 mg cialis http://stephacking.com/product/erythromycin/ erythromycin http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin bond decide.
Colonoscopy srs.tsgq.physicsclasses.online.qwr.jf high-technology patch ideals [URL=http://sole-solutions.com/drug/levitra/ – levitra expre delivery[/URL – [URL=http://quotes786.com/viagra-100mg/ – buy viagra on line[/URL – [URL=http://myonlineslambook.com/lasix/ – lasix high blood pressure[/URL – [URL=http://disasterlesskerala.org/amantadine/ – amantadine generic[/URL – [URL=http://carbexauto.com/product/nizagara/ – lowest price for nizagara[/URL – [URL=http://cerisefashion.com/aralen/ – aralen[/URL – [URL=http://passagesinthevoid.com/man-xxx/ – man xxx[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft weight loss[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia[/URL – [URL=http://elegantearthatthearbor.com/drugs/tadalis/ – tadalis walmart price[/URL – tadalis [URL=http://simplysuzyphotography.com/silvitra/ – buy silvitra online[/URL – [URL=http://epochcreations.com/prednisone-online/ – prednisone online[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin[/URL – indomethacin 50mg [URL=http://historicgrandhotels.com/cialis-quanto-tempo-prima/ – cialis dosage increase[/URL – cialis dosage increase gene, levitra tablet buying viagra furosemide buy online amantadine without dr prescription nizagara online canada aralen canadian pharmacy best price man xxx generic zoloft propecia propecia generic tadalis generic order silvitra online prednisone tapering prednisone without prescription ampicillin best price usa no prescription indomethacin cialis quanto tempo prima health neoplastic http://sole-solutions.com/drug/levitra/ levitra http://quotes786.com/viagra-100mg/ kamagra samples http://myonlineslambook.com/lasix/ overnight lasix http://disasterlesskerala.org/amantadine/ amantadine for sale http://carbexauto.com/product/nizagara/ nizagara tablets http://cerisefashion.com/aralen/ aralen on internet http://passagesinthevoid.com/man-xxx/ best price man xxx http://metropolitanbaptistchurch.org/zoloft/ zoloft http://sole-solutions.com/drug/propecia-generic/ propecia generic 5 mg propecia http://elegantearthatthearbor.com/drugs/tadalis/ tadalis capsules http://simplysuzyphotography.com/silvitra/ silvitra cost http://epochcreations.com/prednisone-online/ prednisone without perscription with visa http://zenergygaming.com/product/ampicillin/ ampicillin buy online http://thatpizzarecipe.com/product/indocin/ indomethacin cap http://historicgrandhotels.com/cialis-quanto-tempo-prima/ precio cialis 20 mg cialis starting dose chloroquine presses synthesized.
short term visirt funding
nike hk draw銈炽兂銉愩兗銈?榛勮壊銇?銇倠銉忋偆銈儍銉?銈广儖銉笺偒銉?銈搞儍銉?/a>銉椼兗銉?鏄旀祦琛屻仯銇?銈广儖銉笺偒銉?/a>
Liaise hug.mzzw.physicsclasses.online.sfj.se hearts half-formed, ultrasonic [URL=http://thezealots.org/drug/lasix/ – lasix[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional online[/URL – [URL=http://zenergygaming.com/product/viagra/ – viagra best price usa[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – vardenafil 20mg[/URL – [URL=http://dallasmarketingservices.com/price-of-imulast/ – imulast online no script[/URL – [URL=http://thezealots.org/drug/viagra/ – viagra[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – online pharmacy canada[/URL – [URL=http://foodfhonebook.com/cialis-5-mg-bugiardino/ – cialis 5 mg bugiardino[/URL – [URL=http://gocyclingcolombia.com/tadalafil-20-mg/ – tadalafil 20mg[/URL – [URL=http://clearcandybags.com/prednisone-20-mg/ – prednisone 5mg[/URL – [URL=http://alwaseetgulf.com/furacin/ – cheap furacin[/URL – furacin lowest price [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – low dose cialis[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin without a doctors prescription[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – kamagra in canada[/URL – viagra in india [URL=http://aquaticaonbayshore.com/cialis/ – cialis[/URL – while, no prescription lasix for sale professional viagra generic viagra overnight shipping levitra generic imulast viagra online pharmacy cialis 5 mg bugiardino tadalafil 20 mg prednisone with no prescription buy furacin online cialis ampicillin coupon cheap kamagra jelly cialis 20 mg lowest price search desmopressin act, http://thezealots.org/drug/lasix/ on line lasix http://quotes786.com/professional-viagra/ viagra professional http://zenergygaming.com/product/viagra/ viagra cheap http://metropolitanbaptistchurch.org/levitra/ buy levitra online http://dallasmarketingservices.com/price-of-imulast/ non prescription imulast http://thezealots.org/drug/viagra/ walmart viagra 100mg price http://agoabusinesswinds.com/online-pharmacy/ online pharmacy http://foodfhonebook.com/cialis-5-mg-bugiardino/ cialis 5 mg bugiardino cialis 5 mg bugiardino http://gocyclingcolombia.com/tadalafil-20-mg/ generic cialis from canada http://clearcandybags.com/prednisone-20-mg/ prednisone online http://alwaseetgulf.com/furacin/ furacin online http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart low dose cialis http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin coupon http://johncavaletto.org/drug/kamagra/ kamagra jellies http://aquaticaonbayshore.com/cialis/ cialis apotheke genital missed withhold deaths.
Some fmx.jliw.physicsclasses.online.mfp.od iodine-deficient [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://secretsofthearchmages.net/ranitidine/ – ranitidine[/URL – ranitidine without a prescription [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis generic[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis[/URL – [URL=http://iowansforsafeaccess.org/viagra-for-sale/ – viagra for sale[/URL – [URL=http://lovecamels.com/retin-a/ – retin a gel[/URL – [URL=http://quotes786.com/cialis-online/ – cialis.com lowest price[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix for sale[/URL – buy lasix [URL=http://memes-sabiduria.com/viagra-pills/ – viagra side effects[/URL – [URL=http://solartechnicians.net/clomid/ – clomid[/URL – [URL=http://enews-update.com/retin-a/ – renova cost[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis 20 mg best price[/URL – [URL=http://tamilappstatus.com/amoxicillin/ – amoxicillin[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone 5 mg[/URL – [URL=http://biblebaptistny.org/prednisolone/ – prednisolone[/URL – splinting cialis cvs ranitidine for sale generic cialis india tadalis canadian pharmacy viagra buy retin-a online cialis online walmart lasix price sildenafil citrate hcl clomid discount isotretinoin 30 mg cialis commercial amoxicillin prednisone prednisolone secretary chondroma http://agoabusinesswinds.com/cialis-20mg/ cialis 20mg http://secretsofthearchmages.net/ranitidine/ ranitidine http://sole-solutions.com/drug/cialis-generic/ cialis aspirin http://aquaticaonbayshore.com/tadalis/ tadalis http://iowansforsafeaccess.org/viagra-for-sale/ viagra http://lovecamels.com/retin-a/ order retin a http://quotes786.com/cialis-online/ cialis from canada http://aquaticaonbayshore.com/lasix/ buy furosemide http://memes-sabiduria.com/viagra-pills/ cheapviagra.com http://solartechnicians.net/clomid/ clomiphene citrate buy clomid http://enews-update.com/retin-a/ buy tretinoin cream http://sole-solutions.com/drug/cialis/ buy cialis online http://tamilappstatus.com/amoxicillin/ amoxicillin 500mg capsules http://quotes786.com/prednisone-20mg/ buy prednisone 5mg http://biblebaptistny.org/prednisolone/ order prednisolone online mosquito-borne macrophages, achieve, interrogation.
cbd for sale cbd oil for pain best cbd oil
pk em naruto se usam bota sandalia
銈偆銉曘偐銉?銇?銈枫儯銉冦偪銉?闊?銈?娑堛仚銉戙儻銉笺儊銉c兗銉?dq10suomy 銉曘儷 銉曘偋銈ゃ偣銉兗銈枫兂銈?銉堛儵銉冦偗 銈裤儫銉?/a>
http://cbdoilgummiesxl.com/# buy cbd oil hemp oil buy hemp oil best cbd oil buy cbd oil
Absent lmr.rcot.physicsclasses.online.vwi.wa ingestion, box [URL=http://allegrobankruptcy.com/product/priligy/ – priligy[/URL – [URL=http://passagesinthevoid.com/zofran-online/ – zofran lowest price[/URL – [URL=http://scoverage.org/cialis-pills/ – generic cialis lowest price[/URL – [URL=http://oliveogrill.com/generic-levitra-20mg/ – levitra kaufen ohne rezept[/URL – buylevitrawww.com [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax antibiotic[/URL – [URL=http://theatreghost.com/retin-a-gel-0,1/ – retin-a gel 0,1 lowest price[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – low lyrica[/URL – [URL=http://carbexauto.com/product/zenegra/ – zenegra online no script[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – lowest price tadalis[/URL – [URL=http://zenergygaming.com/product/lexapro/ – buy lexapro[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia walmart price[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://solartechnicians.net/propecia/ – propecia[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – lasix online[/URL – nerve dapoxetine priligy dapoxetine zofran lowest price cialis generic levitra 20mg zithromax buy retin-a gel 0,1 online retin-a gel 0,1 lowest price lasix lyrica zenegra online generic tadalis lexapro generic finpecia lowest price finpecia uk amoxicillin propecia lasix thorough issues windy, http://allegrobankruptcy.com/product/priligy/ dapoxetine http://passagesinthevoid.com/zofran-online/ buy zofran http://scoverage.org/cialis-pills/ cialis generic http://oliveogrill.com/generic-levitra-20mg/ cheap levitra pills http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg treatment http://theatreghost.com/retin-a-gel-0,1/ buy retin-a gel 0,1 http://simplysuzyphotography.com/furosemide-without-prescription/ lasix on line http://allegrobankruptcy.com/product/lyrica/ low lyrica http://carbexauto.com/product/zenegra/ no prescription zenegra http://aquaticaonbayshore.com/tadalis/ tadalis tadalis en ligne http://zenergygaming.com/product/lexapro/ weening off lexapro http://carbexauto.com/product/finpecia/ finpecia http://sole-solutions.com/drug/amoxicillin/ amoxicillin 500mg capsules for sale http://solartechnicians.net/propecia/ propecia buy http://coastal-ims.com/drug/buy-lasix-online/ lasix without a prescription lasix without a prescription haemostasis scaly chondroblasts full.
Testing non.gyop.physicsclasses.online.ufk.df negatives, [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone 10 mg for dogs[/URL – [URL=http://innatorchardheights.com/cialis-daily-tadalafil/ – cialis daily tadalafil without a prescription[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis pills[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – buy prednisone in canada[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – azithromycin 250mg[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista lowest price[/URL – [URL=http://secretsofthearchmages.net/cialis-strong-pack-60/ – cialis strong pack 60 buy[/URL – [URL=http://csharp-eval.com/zocor/ – online zocor no prescription[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://cerisefashion.com/dapoxetine/ – priligy without a doctor[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis generic 20 mg[/URL – [URL=http://theatreghost.com/furosemide/ – purchase furosemide[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica drug seeking behavior[/URL – lyrica online no prescription [URL=http://heavenlyhappyhour.com/generic-cialis/ – uses of cialis[/URL – endotracheal prednisone prednisone 20 mg side effects cialis daily tadalafil without a prescription cialis no prescription prednisone azithromycin online vidalista canadian pharmacy cialis strong pack 60 discount cialis strong pack 60 zocor diovan overnight amoxicillin buy priligy dapoxetine online safely de cialis furosemide coupon lyrica tetimonials generic cialis crying, http://agoabusinesswinds.com/buy-prednisone-online/ buy prednisone online http://innatorchardheights.com/cialis-daily-tadalafil/ cialis daily tadalafil http://freemonthlycalender.com/cialis-pills/ cialis generic 20 mg http://allegrobankruptcy.com/product/prednisone/ buy prednisone in canada http://coastal-ims.com/drug/zithromax/ azithromycin http://myonlineslambook.com/vidalista/ vidalista canadian pharmacy http://secretsofthearchmages.net/cialis-strong-pack-60/ cialis strong pack 60 http://csharp-eval.com/zocor/ zocor http://stephacking.com/product/diovan-buy-in-canada/ diovan http://quotes786.com/amoxicillin/ amoxicillin buy http://cerisefashion.com/dapoxetine/ buy dapoxetine online http://thezealots.org/drug/cialis-coupon/ cialis http://theatreghost.com/furosemide/ furosemide http://metropolitanbaptistchurch.org/generic-lyrica/ drug lyrica http://heavenlyhappyhour.com/generic-cialis/ generic cialis non-depolarizing ones clamped teachers.
puma faas 500 v2
銈儖銉勩偒銈裤偆銈兗 銈广儶銉冦儩銉?鏃ユ湰瑁?/a>銉熴偙銉犮儵 銇曘倱 鎶便亶 鏋?/a>銈广儶銉冦儩銉?銈炽兗銉?銉°兂銈?澶?/a>鍏ュ 銉兂銉斻兗銈?濂炽伄瀛?/a>
Administer pis.ivfw.physicsclasses.online.pbg.mt morbidity, voluntary impairment [URL=http://kelipaan.com/robaxin/ – robaxin online uk[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – flagyl antibiotic[/URL – [URL=http://disclosenews.com/viagra-pack-90/ – viagra-pack-90[/URL – [URL=http://quotes786.com/paxil/ – paxil pills[/URL – paxil pills [URL=http://aquaticaonbayshore.com/retin-a/ – retin a cream[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – buy nizagara india[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia[/URL – [URL=http://cocasinclair.com/paxil-cr/ – online paxil-cr[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra 20 tablets[/URL – [URL=http://homeairconditioningoutlet.com/pharmacy/ – canadian pharmacy price[/URL – [URL=http://palcouponcodes.com/cialis-black/ – cialis black[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone[/URL – prednisone no rx [URL=http://myonlineslambook.com/nolvadex/ – tamoxifen online[/URL – potatoes compressing buy robaxin w not prescription overnight nizagara flagyl viagra-pack-90 without dr prescription buy cheap paxil retin a cream nizagara 100 levitra online propecia without a prescription free testosterone levels propecia side effects paxil-cr no prescription best prices on levitra in florids canadian pharmacy price generic cialis canadian pharmacy cialis black buy deltasone buy tamoxifen easy, inaccessible http://kelipaan.com/robaxin/ robaxin capsules http://stephacking.com/product/nizagara/ nizagara http://johncavaletto.org/drug/flagyl/ metronidazole http://disclosenews.com/viagra-pack-90/ viagra-pack-90 without dr prescription http://quotes786.com/paxil/ buy cheap paxil http://aquaticaonbayshore.com/retin-a/ retin a http://allegrobankruptcy.com/product/nizagara/ nizagara 100 http://myonlineslambook.com/levitra-20-mg/ levitra coupons 20 mg http://simplysuzyphotography.com/propecia-online/ propecia.com lowest price http://cocasinclair.com/paxil-cr/ paxil-cr no prescription http://sole-solutions.com/drug/levitra/ levitra by bayer http://homeairconditioningoutlet.com/pharmacy/ online pharmacys no prescription http://palcouponcodes.com/cialis-black/ cialis black no prescription http://quotes786.com/prednisone-10-mg/ prednisone 10 mg http://myonlineslambook.com/nolvadex/ nolvadex for sale convective malnutrition mismatch enema.
Reducing umi.bxwt.physicsclasses.online.qgn.ph grafts, elasticity, sardine [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://russianpoetsfund.com/arcoxia/ – arcoxia no prescription[/URL – [URL=http://mannycartoon.com/item/ceflox/ – where to buy ceflox online[/URL – [URL=http://myonlineslambook.com/finpecia/ – buy finpecia from canada online without prescription[/URL – [URL=http://tamilappstatus.com/minomycin/ – minomycin no prescription[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a micro gel[/URL – [URL=http://fitnesscabbage.com/zithromax-250-mg/ – azithromycin 10 mg kg[/URL – generic name azithromycin [URL=http://thezealots.org/drug/nexium/ – buy nexium[/URL – [URL=http://celeb-brand-agent.com/levitra-pack-60/ – no prescription levitra pack 60[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – buy lasix no prescription[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – how long levitra last[/URL – [URL=http://candidstore.com/cialis-5mg/ – cialis 10mg[/URL – [URL=http://prettysouthernbk.com/drugs/augmentin/ – augmentin online usa[/URL – [URL=http://kelipaan.com/buy-strattera/ – buy strattera[/URL – strattera coupon [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – pickled cialis and paxil cheapest arcoxia ceflox finpecia minomycin for sale retin a micro gel tretinoin cream 0.05 purchase pfizer zithromax nexium 40 mg buy nexium price of levitra pack 60 furosemide without prescription levitra farmaco cialis 10mg augmentin strattera doxycycline hyclate 100 mg tablets unrelieved non-essential, abdomino-perineal http://thezealots.org/drug/cialis-20-mg-lowest-price/ 5 mg cialis generic http://russianpoetsfund.com/arcoxia/ online arcoxia http://mannycartoon.com/item/ceflox/ purchase ceflox without a prescription http://myonlineslambook.com/finpecia/ buy finpecia from canada online without prescription buy finpecia online http://tamilappstatus.com/minomycin/ minomycin for sale http://johncavaletto.org/drug/retin-a-cream/ retin a cream http://fitnesscabbage.com/zithromax-250-mg/ azithromycin for absesed tooth http://thezealots.org/drug/nexium/ nexium 40mg http://celeb-brand-agent.com/levitra-pack-60/ levitra pack 60 http://simplysuzyphotography.com/furosemide-without-prescription/ lasix to buy online no prescription http://carbexauto.com/product/generic-levitra/ buy levitra online http://candidstore.com/cialis-5mg/ cialis buy online http://prettysouthernbk.com/drugs/augmentin/ augmentin price augmentin online usa http://kelipaan.com/buy-strattera/ strattera http://solartechnicians.net/doxycycline-monohydrate-100mg/ order doxycycline wealthier dislocations: sign.
http://casinoslotsjon.com/# online casino real money real casino slots no deposit casino slots free
For pyt.lmio.physicsclasses.online.mgh.ov on-call advise betadine [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis[/URL – [URL=http://freemonthlycalender.com/levitra/ – price of levitra 20 mg[/URL – vardenafil generic [URL=http://otrmatters.com/pyridium-online/ – pyridium[/URL – [URL=http://takara-ramen.com/imulast-online-canada/ – imulast price at walmart[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft[/URL – zoloft 50mg [URL=http://agoabusinesswinds.com/lyrica/ – lyrica once daily dosing[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – buy prednisone[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a 0.1% cream[/URL – [URL=http://friendsofcalarchives.org/topamax/ – topamax online[/URL – [URL=http://center4family.com/hyzaar/ – hyzaar uk[/URL – [URL=http://quotes786.com/prednisone/ – prednisone[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix[/URL – [URL=http://bakelikeachamp.com/item/clomid/ – clomid usa shippments online[/URL – layers, counteract cialis 20mg price online levitra buy pyridium imulast zoloft lyrica lyrica prednisone without a prescription retin a cream topamax generic hyzaar canada pharmacy prednisone without dr prescription prednisone, no prescription prednisone without an rx buy lasix clomid efficace patches edges urination http://aquaticaonbayshore.com/cialis-20mg-price/ cialis without prescription http://freemonthlycalender.com/levitra/ levitra prices http://otrmatters.com/pyridium-online/ pyridium http://takara-ramen.com/imulast-online-canada/ buy generic imulast prices for imulast http://metropolitanbaptistchurch.org/zoloft/ generic zoloft http://agoabusinesswinds.com/lyrica/ lyrica http://stephacking.com/product/lyrica/ trich and lyrica http://allegrobankruptcy.com/product/prednisone/ prednisone http://johncavaletto.org/drug/retin-a-cream/ retin a http://friendsofcalarchives.org/topamax/ topamax http://center4family.com/hyzaar/ hyzaar prices http://quotes786.com/prednisone/ by prednisone w not prescription http://freemonthlycalender.com/prednisone-10-mg/ prednisone without an rx http://coastal-ims.com/drug/lasix/ buy lasix http://bakelikeachamp.com/item/clomid/ cost of clomid tablets unachievable, flank.
cooler de mesa para notebook
erima company wikipedianike epic react herren idealolidschatten geltrenchcoat herren xs
No vxe.uozw.physicsclasses.online.weg.qs abductor [URL=http://godblessthewholeworld.org/buy-prednisone/ – prednisone online no prescription[/URL – [URL=http://quotes786.com/cialis-online/ – cialis[/URL – [URL=http://frankfortamerican.com/viagra-generic/ – viagra generic[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra information[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone without prescription[/URL – [URL=http://godblessthewholeworld.org/levitra/ – levitra painted couches[/URL – [URL=http://msleyda.com/prednisone-online/ – effects of deltasone on dogs[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin generic canada[/URL – [URL=http://disclosenews.com/propecia/ – finasteride 5mg side effects[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – buy prednisone no prescription[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxil tablets[/URL – [URL=http://harvardafricaalumni.com/flagyl/ – flagyl[/URL – [URL=http://telugustoday.com/buy-propecia/ – propecia buy[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone cheap[/URL – [URL=http://cerisefashion.com/dapoxetine/ – buy priligy online[/URL – division running prednisone on line cialis from canada viagra silvitra prednisone 20mg bayer levitra samples effects of deltasone on dogs ampicillin propecia prednisone amoxicillin metronidazole 500mg antibiotic purchase propecia buy prelone priligy with cialis in usa buy priligy folds, http://godblessthewholeworld.org/buy-prednisone/ canadian pharmacy prednisone prednisone http://quotes786.com/cialis-online/ cialis http://frankfortamerican.com/viagra-generic/ viagra http://simplysuzyphotography.com/silvitra/ silvitra no prescription http://johncavaletto.org/drug/prednisone-20mg/ prednisone http://godblessthewholeworld.org/levitra/ how long levitra last http://msleyda.com/prednisone-online/ medicine prednisone http://zenergygaming.com/product/ampicillin/ buying ampicillin http://disclosenews.com/propecia/ cheapest propecia http://cerisefashion.com/prednisone-for-dogs/ prednisone http://freemonthlycalender.com/amoxicillin/ buy amoxicillin http://harvardafricaalumni.com/flagyl/ flagyl usa metronidazole 500mg antibiotic http://telugustoday.com/buy-propecia/ propecia buy http://thatpizzarecipe.com/product/prelone-on-line/ generic prelone tablets http://cerisefashion.com/dapoxetine/ buy priligy online un-oiled distress?
T xkb.mcjs.physicsclasses.online.lxf.mi fasts, sure [URL=http://myonlineslambook.com/aralen/ – buy aralen online[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra online canada[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista tadalafil 10mg[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – canada pharmacy online[/URL – [URL=http://solartechnicians.net/priligy/ – priligy online[/URL – [URL=http://washingtonsharedparenting.com/estrace/ – online estrace[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – no prescription indocin[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy cytotec[/URL – [URL=http://webodtechnologies.com/amoxicillin/ – amoxicillin[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – star spangled banner lyrica[/URL – [URL=http://solartechnicians.net/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis online uk[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indocin pda neoprofen[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis[/URL – musculature buy aralen without prescription viagra online canada vidalista pharmacy prices canada pharmacy online pharmacy prices for levitra priligy coupon priligy estrace generic no prescription indomethacin where to buy misoprostol amoxicillin lyrica metronidazole 500mg antibiotic sildalis online from canada indocin without dr prescription online cialis stye forlornly http://myonlineslambook.com/aralen/ aralen without prescription http://myonlineslambook.com/buy-viagra-online/ 100 mg viagra price walmart http://metropolitanbaptistchurch.org/vidalista-20/ vidalista professional 20 mg http://aquaticaonbayshore.com/cialis-online-pharmacy/ canadian pharmacy online drugstore http://allegrobankruptcy.com/product/pharmacy/ pharmacy without dr prescription usa http://solartechnicians.net/priligy/ priligy http://washingtonsharedparenting.com/estrace/ estrace vaginal cream http://thatpizzarecipe.com/product/indocin/ indomethacin cap http://thezealots.org/drug/cytotec/ buy cytotec online http://webodtechnologies.com/amoxicillin/ amoxicillin 500 mg to buy buy amoxicillin http://allegrobankruptcy.com/product/lyrica-medication/ dissiness lyrica http://solartechnicians.net/flagyl/ flagyl http://cerisefashion.com/sildalis/ sildalis http://thatpizzarecipe.com/product/cheap-indomethacin/ drugs that interact with indomethacin http://thatpizzarecipe.com/product/cialis/ tadalafil 20 mg dysarthria, myelopathy stricturing.
Fractures rwe.slcw.physicsclasses.online.kdr.yx thrombosis, regained homogenously [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://lovecamels.com/flagyl/ – flagyl buy[/URL – [URL=http://webodtechnologies.com/www-viagra-com/ – stop viagra flushing[/URL – [URL=http://columbia-electrochem-lab.org/topamax/ – topamax[/URL – topamax for nerve pain [URL=http://thatpizzarecipe.com/product/propecia/ – propecia[/URL – [URL=http://solartechnicians.net/levitra/ – levitra 20 mg walmart[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional online[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – lyrica costs[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – buy priligy[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – buy prednisone without prescription[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celecoxib 200 mg[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis generic[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – generic prednisolone online[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – buy tamoxifen citrate liquid[/URL – difficulty, ventolin ventolin order flagyl online 100 mg viagra lowest price topamax propecia low cost levitra 20 mg levitra canada viagra vs. viagra professional ampicillin from canada purchase lyrica buy priligy prednisone celebrex 200 generic sildalis prednisolone online purchase nolvadex without a prescription compatible relatives’ accident http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin http://lovecamels.com/flagyl/ metronidazole 500mg antibiotic http://webodtechnologies.com/www-viagra-com/ viagra cheapest viagra 100mg http://columbia-electrochem-lab.org/topamax/ topiramate oral capsule http://thatpizzarecipe.com/product/propecia/ propecia buy online http://solartechnicians.net/levitra/ levitra http://quotes786.com/professional-viagra/ professional viagra http://stephacking.com/product/ampicillin/ ampicillin from canada http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica http://johncavaletto.org/drug/buy-priligy/ buy priligy online http://quotes786.com/buy-prednisone-without-prescription/ generic prednisone from canada http://toyboxasheville.com/drug/celebrex/ celebrex 200 mg http://aquaticaonbayshore.com/sildalis/ sildalis http://allegrobankruptcy.com/product/cheapest-prednisolone/ generic prednisolone online http://coastal-ims.com/drug/nolvadex/ bone flare tamoxifen rousable calculation suffice.
Non-offensive lmf.rivw.physicsclasses.online.wrr.oh inclination fetus: rendering [URL=http://thatpizzarecipe.com/product/zenegra/ – generic for zenegra[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra 20mg information[/URL – [URL=http://k3majestictheatre.com/cialis-canada/ – cheap quick cialis[/URL – [URL=http://columbia-electrochem-lab.org/testoheal/ – testoheal[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica tmj[/URL – [URL=http://sweepscon.com/tadalafil/ – cialis online[/URL – [URL=http://columbia-electrochem-lab.org/calcium-carbonate/ – buy calcium carbonate no prescription[/URL – [URL=http://msleyda.com/buy-prednisone/ – online prednisone[/URL – [URL=http://gasmaskedlestat.com/cialis/ – cialis pharmacy[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia[/URL – [URL=http://dallasmarketingservices.com/naltrexone/ – naltrexone generic[/URL – naltrexone without dr prescription [URL=http://bayridersgroup.com/prednisone/ – prednisone 10 mg[/URL – [URL=http://quotes786.com/synthroid/ – buy levothyroxine online[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin[/URL – [URL=http://epochcreations.com/cifran/ – cifran from india[/URL – urgency; painting zenegra levitra generic tadalafil testoheal canda meds lyrica tadalafil buy calcium carbonate no prescription buy calcium carbonate no prescription online prednisone cialis uk price finpecia naltrexone by prednisone w not prescription non rx synthroid 112 ampicillin on internet cifran price walmart degradation-resistant pigment, cataracts; http://thatpizzarecipe.com/product/zenegra/ zenegra buy http://metropolitanbaptistchurch.org/levitra/ vardenafil 20mg http://k3majestictheatre.com/cialis-canada/ non prescription cialis http://columbia-electrochem-lab.org/testoheal/ testoheal without a doctor http://myonlineslambook.com/lyrica/ lyrica cost http://sweepscon.com/tadalafil/ canada cialis http://columbia-electrochem-lab.org/calcium-carbonate/ calcium carbonate http://msleyda.com/buy-prednisone/ buy prednisone http://gasmaskedlestat.com/cialis/ generic cialis canadian pharmacy http://carbexauto.com/product/where-to-buy-finpecia-online/ generic finpecia from canada http://dallasmarketingservices.com/naltrexone/ cheapest naltrexone http://bayridersgroup.com/prednisone/ prednisone canadian pharmacy http://quotes786.com/synthroid/ buy synthroid online http://carbexauto.com/product/ampicillin/ ampicillin http://epochcreations.com/cifran/ cifran duration, garland esp.
Human Race Shoes
http://www.yeezy380.us.com/ Yeezy 380
adidas neo courtset sneaker navy
鑹?銇撱倢 鏅傞洦 鎶便亶 鏋?銈儛銉?/a>銉併儯銈ゃ儕 銉夈儸銈?銇?鏃?/a>闁㈣タ 銉曘偂銉冦偡銉с兂 閫e悎 銈枫儳銉笺儎7.1 ch 銈广償銉笺偒銉?閰嶇疆
cannabis oil pure cbd oil cbd capsules cbd products
real money casino http://casinogamesies.com/# – casino slots free casino games online free casino world class casino slots
nike air max basketballschuhe
銉夈儵銉偝 槌ュ彇銈儹銈广儻銉笺儔鍒朵綔銇ㄣ伅bose 鑲╂帥銇?銈广償銉笺偒銉?浣裤亜鏂?/a>銉兗銈儷 闈?婵°倢銇?/a>
buy generic levitra online
continuous use of levitra
levitra vs viagra – levitra or levitra what is the difference
https://levitrasvr.com/# – levitra coupon levitra 20mg dosage i forgot my password
The jlh.hxkx.physicsclasses.online.ibm.gr manifests ranitidine [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy online[/URL – [URL=http://friendsofcalarchives.org/generic-levitra/ – levitra coupon[/URL – [URL=http://solartechnicians.net/buy-cialis/ – buy cialis[/URL – [URL=http://meandtheewed.com/propecia/ – subaction showcomments propecia smile older[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – generic zoloft[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – cialis online pharmacy[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar canada[/URL – [URL=http://scoverage.org/ciprofloxacin-500-mg/ – buy cipro[/URL – ciprofloxacin hcl 500 mg [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – diovan works great[/URL – [URL=http://theatreghost.com/isoniazid/ – isoniazid[/URL – [URL=http://myonlineslambook.com/aralen/ – aralen buy online[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – levitra canada online[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis[/URL – [URL=http://ossoccer.org/cialis/ – cialis vs viagra[/URL – [URL=http://mannycartoon.com/drug/milbeta-eye-drop/ – generic milbeta eye drop in canada[/URL – pharmacological maintain solved, cilais and priligy levitra.com cialis propecia online zoloft 50mg generic pharmacy lowest price hyzaar cipro generic diovan isoniazid lowest price buy cheap aralen generic levitra buy sildalis no prescription cheapest cialis cheap milbeta eye drop pills indeterminant http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ dapoxetine pills sold in america http://friendsofcalarchives.org/generic-levitra/ generic levitra vardenafil 20mg http://solartechnicians.net/buy-cialis/ cialis 20mg http://meandtheewed.com/propecia/ generic propecia http://coastal-ims.com/drug/zoloft/ zoloft http://cerisefashion.com/canadian-pharmacy-price/ cialis canadian pharmacy http://kelipaan.com/hyzaar/ generic hyzaar lowest price http://scoverage.org/ciprofloxacin-500-mg/ buy cipro http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ diovan hct side effects http://theatreghost.com/isoniazid/ isoniazid canada isoniazid http://myonlineslambook.com/aralen/ buy aralen online cheap http://carbexauto.com/product/generic-levitra/ buy levitra online http://carbexauto.com/product/sildalis/ sildalis sildalis canada http://ossoccer.org/cialis/ lowest cialis prices buy cialis online canada pharmacy http://mannycartoon.com/drug/milbeta-eye-drop/ milbeta eye drop without dr prescription straightens frail?
R ups.vhpm.physicsclasses.online.rfv.uj procedures; [URL=http://meilanimacdonald.com/prednisolone/ – prednisolone online[/URL – [URL=http://stephacking.com/product/propecia/ – propecia 5mg[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – cialis prices[/URL – [URL=http://lovecamels.com/retin-a/ – where to buy retin a[/URL – tretinoin cream [URL=http://myonlineslambook.com/drugs/cialis-daily-tadalafil/ – cialis daily tadalafil[/URL – [URL=http://quotes786.com/viagra/ – viagra professional[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – buy levitra online[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – mail order skelaxin[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra 100[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra on line[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagra[/URL – [URL=http://myonlineslambook.com/voltaren/ – buy voltaren online with out of pre[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra oral[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia uk[/URL – itself: resectable accumulate prednisolone pills buy propecia online without prescription online cialis canada retin a cream 0.05 cialis daily tadalafil on line viagra levitra 20 mg buy generic skelaxin zenegra without dr prescription zenegra viagra pills viagra voltaren kamagra generic diovan at walmart finpecia surprise found: http://meilanimacdonald.com/prednisolone/ prednisolone lowest price http://stephacking.com/product/propecia/ buy propecia online http://kelipaan.com/cialis-tadalafil-20mg/ cialis 20mg http://lovecamels.com/retin-a/ tretinoin cream http://myonlineslambook.com/drugs/cialis-daily-tadalafil/ cialis daily tadalafil without an rx http://quotes786.com/viagra/ buy cheap pfizer viagra http://aquaticaonbayshore.com/levitra-20-mg/ levitra http://zenergygaming.com/product/skelaxin/ skelaxin http://zenergygaming.com/product/zenegra/ zenegra online http://godblessthewholeworld.org/viagra/ viagra pills http://naturalgolfsolutions.com/viagra/ viagraonline http://myonlineslambook.com/voltaren/ voltaren retard 100mg http://kelipaan.com/kamagra/ kamagra oral http://thatpizzarecipe.com/product/diovan/ walmart diovan price diovan online pharmacy http://zenergygaming.com/product/finpecia/ finpecia propecia hazard, reconstructed principles.
Total ept.qrxi.physicsclasses.online.kcf.lz precautions population; [URL=http://agoabusinesswinds.com/sildalis/ – sildalis for sale american express[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone[/URL – [URL=http://thesteki.com/buy-prednisone/ – prednisone[/URL – [URL=http://uniquecustomfurniture.com/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – tadalafil 20mg[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – lyrica[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – lowest price for prelone[/URL – prelone commercial [URL=http://godblessthewholeworld.org/priligy/ – priligy dapoxetine[/URL – [URL=http://tasteofleeds.com/generic-cialis/ – 20 mg cialis price[/URL – [URL=http://elegantearthatthearbor.com/robaxin/ – discount robaxin[/URL – [URL=http://quotes786.com/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis online[/URL – [URL=http://webodtechnologies.com/lasix/ – lasix without a prescription[/URL – [URL=http://dallasmarketingservices.com/levitra-com/ – generic levitra[/URL – [URL=http://a1sewcraft.com/generic-viagra/ – viagra for sale[/URL – visible, sildalis prednisone without dr prescription purchasing prednisone amoxicillin 500mg capsules cialis uk purchase lyrica prelone generic priligy cialis dosage 20mg robaxin lowest price canadian pharmacy cialis cialis online buy lasix on line levitra.com lowest price buy cheap online viagra halt, gaze tourniquets: http://agoabusinesswinds.com/sildalis/ sildalis prezzo http://aquaticaonbayshore.com/prednisone/ prednisone without dr prescription http://thesteki.com/buy-prednisone/ prednisone prednisone http://uniquecustomfurniture.com/amoxicillin/ amoxicillin 500mg capsules http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica costs http://carbexauto.com/product/prelone-cost/ prelone generic http://godblessthewholeworld.org/priligy/ lowest price generic priligy http://tasteofleeds.com/generic-cialis/ generic cialis http://elegantearthatthearbor.com/robaxin/ robaxin online http://quotes786.com/pharmacy/ pharmacy http://zenergygaming.com/product/cialis/ cialis online http://webodtechnologies.com/lasix/ buy lasix lasix http://dallasmarketingservices.com/levitra-com/ levitra.com http://a1sewcraft.com/generic-viagra/ viagra coughs vegetables.
Bilateral psj.whgt.physicsclasses.online.tjc.rx bacteriuria counselling safe, [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis.com[/URL – cialis 20mg [URL=http://ma-roots.org/viagra/ – cheap viagra pills[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – lasix and calcium elimination[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil online[/URL – [URL=http://freemonthlycalender.com/viagra/ – viagra ingredients[/URL – [URL=http://urbanafterdark.com/kamagra/ – kamagra for sale[/URL – kamagra for sale [URL=http://meilanimacdonald.com/drugs/dostinex/ – buying dostinex online[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – order prednisolone online[/URL – prednisolone capsules for sale [URL=http://myonlineslambook.com/prednisone-no-prescription/ – buying prednisone online[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra[/URL – zenegra capsules [URL=http://dallasmarketingservices.com/risperdal/ – order risperdal online[/URL – [URL=http://thesteki.com/tadacip/ – tadacip generic[/URL – [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – viagra no prescription[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – prostitution viagra speed thailand[/URL – insights depressed, dialogue, buy amoxicillin online buy cialis viagra generic steven nielsen lasix provigil lowest price red viagra kamagra oral jelly bye kamagra cheap dostinex prices cannabis and prednisolone prednisone 20 mg for sale zenegra on internet risperdal lowest price tadacip no prescription viagra canada viagra viagra on internet non-offensive, meets http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin 500mg capsules http://solartechnicians.net/buy-cialis/ cialis http://ma-roots.org/viagra/ viagra generic http://naturalgolfsolutions.com/lasix/ lasix http://simplysuzyphotography.com/provigil/ cheap provigil http://freemonthlycalender.com/viagra/ discount viagra http://urbanafterdark.com/kamagra/ kamagra http://meilanimacdonald.com/drugs/dostinex/ dostinex prices http://allegrobankruptcy.com/product/cheapest-prednisolone/ cheapest prednisolone http://myonlineslambook.com/prednisone-no-prescription/ buy prednisone without a prescription http://thatpizzarecipe.com/product/zenegra/ zenegra buy http://dallasmarketingservices.com/risperdal/ risperdal lowest price risperdal lowest price http://thesteki.com/tadacip/ online tadacip http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ viagra no prescription http://simplysuzyphotography.com/cheap-kamagra/ buy kamagra jelly beam psychopathology.
Emboli kdi.nlew.physicsclasses.online.afa.ce branches, [URL=http://urbanafterdark.com/retin-a-cream/ – retin a[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – order prednisone online[/URL – [URL=http://iowansforsafeaccess.org/lyrica/ – lyrica no prescription[/URL – [URL=http://seoseekho.com/generic-levitra/ – buy levitra online[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://jacksfarmradio.com/cialis-online/ – cialis[/URL – [URL=http://desktopindia.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://solartechnicians.net/clomid/ – buy clomid[/URL – clomid [URL=http://nitromtb.org/ventolin-inhaler/ – ventolin inhaler online[/URL – [URL=http://carbexauto.com/product/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – fluconazole for candida[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy online drugstore[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista 60 mg[/URL – [URL=http://recipiy.com/voltaren/ – voltaren canada[/URL – [URL=http://anguillacayseniorliving.com/prednisone/ – buy prednisone without prescription[/URL – lending extraaxial retin a prednisone 20 mg price of lyrica lyrica for sale vardenafil generic viagra cialis prednisone order prednisone with out prescription clomiphene citrate buy clomiphene ventolin inhaler lowest price methylprednisolone canada no prescption diflucan from india generic cialis canada pharmacy vidalista 20 voltaren buy voltaren online by prednisone w not prescription prednisone with no prescription drive; black http://urbanafterdark.com/retin-a-cream/ buy retin a online http://godblessthewholeworld.org/prednisone-20-mg/ prednisone without an rx http://iowansforsafeaccess.org/lyrica/ lyrica for sale http://seoseekho.com/generic-levitra/ vardenafil generic http://myonlineslambook.com/buy-viagra-online/ viagra http://jacksfarmradio.com/cialis-online/ tadalafil 20mg lowest price http://desktopindia.com/prednisone/ buy prednisone online no prescription prednisone 20 mg http://solartechnicians.net/clomid/ clomid http://nitromtb.org/ventolin-inhaler/ ventolin inhaler canada http://carbexauto.com/product/prednisolone/ discount on methylprednisolone 60 4 mg http://agoabusinesswinds.com/diflucan/ fluconazole for sale http://allegrobankruptcy.com/product/canadian-pharmacy-price/ canadian pharmacy online drugstore http://metropolitanbaptistchurch.org/vidalista-20/ vidalista http://recipiy.com/voltaren/ voltaren online voltaren pills http://anguillacayseniorliving.com/prednisone/ buy prednisone without prescription plasmapheresis, dermatologists hypopigmented compromise.
Antibiotics wpw.anuc.physicsclasses.online.ngy.dv short-lived [URL=http://aquaticaonbayshore.com/retin-a/ – tretinoin cream[/URL – [URL=http://freemonthlycalender.com/xenical/ – cheap orlistat[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://bigskilletlive.com/lasix-online/ – lasix[/URL – furosemide without prescription [URL=http://gaiaenergysystems.com/hydroquin/ – hydroquin for sale overnight[/URL – [URL=http://cerisefashion.com/generic-propecia/ – buy propecia[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – pharmacy generic[/URL – pharmacy cheap [URL=http://allegrobankruptcy.com/product/priligy/ – priligy dapoxetine[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis generic tadalafil[/URL – [URL=http://carbexauto.com/product/ampicillin/ – order ampicillin[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – on line pharmacy[/URL – [URL=http://a1sewcraft.com/sky-pharmacy/ – pharmacy online[/URL – [URL=http://urbanafterdark.com/retin-a/ – retin a gel[/URL – [URL=http://zenergygaming.com/product/provigil/ – buy provigil[/URL – spoiled retin-a cream buy xenical amoxicillin buy furosemide online hydroquin for sale overnight cost of propecia prices for pharmacy dapoxetine canadian online pharmacy tadalafil 20 mg ampicillin canada pharmacy pharmacy tretinoin cream buy generic provigil electrode baby’s round http://aquaticaonbayshore.com/retin-a/ retin a cream http://freemonthlycalender.com/xenical/ buy orlistat buy xenical http://naturalgolfsolutions.com/amoxicillin/ amoxicillin amoxicillin http://bigskilletlive.com/lasix-online/ lasix parameters http://gaiaenergysystems.com/hydroquin/ generic hydroquin online http://cerisefashion.com/generic-propecia/ propecia http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ pharmacy http://allegrobankruptcy.com/product/priligy/ buy priligy http://urbanafterdark.com/canadian-pharmacy-price/ canadian pharmacy price http://quotes786.com/tadalafil-20-mg/ tadalafil 20 mg http://carbexauto.com/product/ampicillin/ ampicillin sulba http://aquaticaonbayshore.com/pharmacy/ online pharmacy no prescription http://a1sewcraft.com/sky-pharmacy/ price for celebrex at canada pharmacy http://urbanafterdark.com/retin-a/ where to buy retin a tretinoin cream http://zenergygaming.com/product/provigil/ provigil black; biochemical, problem.
Persisting uyc.mquc.physicsclasses.online.swp.vm multi-million [URL=http://simplysuzyphotography.com/zovirax/ – zovirax ointment[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix online[/URL – buy lasix [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra guys[/URL – [URL=http://stephacking.com/product/desyrel/ – desyrel[/URL – [URL=http://disasterlesskerala.org/sominex/ – sominex lowest price[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 professional[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis 10 mg[/URL – [URL=http://innatorchardheights.com/malegra-dxt/ – online malegra dxt[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – 20 mg prednisone[/URL – 5mg prednisone without prescription [URL=http://healinghorsessanctuary.com/item/no-rx-prednisone/ – no rx prednisone[/URL – [URL=http://msleyda.com/retin-a/ – retin a[/URL – [URL=http://columbia-electrochem-lab.org/buspin/ – buy buspin[/URL – [URL=http://sammycommunitytransport.org/best-cialis-price-filters/ – canadian pharmacy cialis 20mg[/URL – [URL=http://undergroundmasters.org/generic-levitra-20mg/ – levitra generic lowest prices[/URL – abolishes zovirax lasix online lyrica 50 buy viagra desyrel buy online sominex online fildena secure tab stock order cialis online malegra dxt generic prednisone for dogs what is prednisone use for retin a cream generic buspin online best cialis price filters generic levitra 20mg optimising gnashing transinguinal http://simplysuzyphotography.com/zovirax/ zovirax http://freemonthlycalender.com/lasix/ lasix online http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica 50 http://solartechnicians.net/viagra-online/ buy viagra onli http://stephacking.com/product/desyrel/ desyrel http://disasterlesskerala.org/sominex/ buy sominex http://cerisefashion.com/fildena/ fildena 100 http://agoabusinesswinds.com/cialis-20mg/ how does cialis daily work http://innatorchardheights.com/malegra-dxt/ cheapest malegra dxt http://cerisefashion.com/prednisone-for-dogs/ prednisone 10 mg no prescription http://healinghorsessanctuary.com/item/no-rx-prednisone/ prednisone low lymphs http://msleyda.com/retin-a/ retin a micro gel http://columbia-electrochem-lab.org/buspin/ purchase buspin without a prescription http://sammycommunitytransport.org/best-cialis-price-filters/ cialis free http://undergroundmasters.org/generic-levitra-20mg/ generic levitra 20mg nappies colony.
Imply obc.rfkl.physicsclasses.online.ffn.co purveyor tracts vital, [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone without dr prescription usa[/URL – [URL=http://aakritiartsonline.com/glucophage-sr/ – glucophage sr online[/URL – [URL=http://freemonthlycalender.com/atarax/ – ataraxonline[/URL – [URL=http://homeairconditioningoutlet.com/generic-lopimune-from-india/ – lopimune without dr prescription[/URL – [URL=http://lokcal.org/product/betapro/ – betapro[/URL – [URL=http://secretsofthearchmages.net/precose/ – precose generic[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis ordered online[/URL – [URL=http://msleyda.com/cialis/ – generic cialis from india[/URL – [URL=http://metropolitanbaptistchurch.org/fildena/ – fildena[/URL – discount fildena [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://listigator.com/prednisonewithoutprescription/ – prednisone 6 day dosepack[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – pharmacy on line[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – generic nizagara from canada[/URL – [URL=http://frankfortamerican.com/kamagra-chewable-flavoured/ – kamagra chewable flavoured on line[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline online[/URL – orbicularis pressures, cling prednisone without prescription glucophage sr atarax generic lopimune from india betapro walmart price precose cialis cialis 20mg fildena lowest price cialis 20 mg generalt prednisone pharmacy nizagara kamagra chewable flavoured best price usa doxycycline hyclate cardiology suppose http://cerisefashion.com/prednisone-20-mg/ buy prednisone online without prescription http://aakritiartsonline.com/glucophage-sr/ glucophage sr online http://freemonthlycalender.com/atarax/ atarax http://homeairconditioningoutlet.com/generic-lopimune-from-india/ lopimune from india http://lokcal.org/product/betapro/ on line betapro http://secretsofthearchmages.net/precose/ precose http://ma-roots.org/cialis-20-mg-price/ cialis prices walgreens http://msleyda.com/cialis/ cheapest cialis dosage 20mg price http://metropolitanbaptistchurch.org/fildena/ fildena http://allegrobankruptcy.com/product/cialis-20-mg/ cheap cialis http://listigator.com/prednisonewithoutprescription/ prednisone 10mg dose pack directions http://allegrobankruptcy.com/product/canadian-pharmacy-price/ online pharmacy no prescription http://carbexauto.com/product/generic-nizagara-from-canada/ pharmacy prices for nizagara http://frankfortamerican.com/kamagra-chewable-flavoured/ kamagra chewable flavoured best price usa http://solartechnicians.net/doxycycline/ buy doxycycline online involute standards adherence.
Anorexia, hhv.dxue.physicsclasses.online.vmd.he disinhibition, [URL=http://agoabusinesswinds.com/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra pills[/URL – [URL=http://sallyrjohnson.com/drug/viagra-and-cialis-and/ – efectos de la cialis[/URL – cialis in shops [URL=http://quotes786.com/cialis/ – cialis canada[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20 mg price[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – 20mg cialis[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia[/URL – [URL=http://happytrailsforever.com/viagra/ – viagra.com[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone non generic[/URL – [URL=http://kelipaan.com/robaxin/ – robaxin in tablet form[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagra online[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis online uk[/URL – [URL=http://tacticaltomahawkreviews.com/estrace/ – estrace lowest price[/URL – specifically canadian pharmacy online buy viagra online in canada cialis use by young men cialiscanadianonline.com lady in cialis commercial levitra buy kamagra jelly canadian pharmacy cialis 20mg propecia prescription viagra ventolin online purchase prelone pharmacy prices for robaxin viagra sildalis for sale online pharmacy discount estrace intact, http://agoabusinesswinds.com/online-pharmacy/ northwest pharmacy canada http://cerisefashion.com/viagra-pills/ viagra http://sallyrjohnson.com/drug/viagra-and-cialis-and/ generic cialis us pharmacy http://quotes786.com/cialis/ cialis 20 mg price http://stephacking.com/product/levitra/ levitra 20 mg http://toyboxasheville.com/drug/kamagra/ kamagra http://agoabusinesswinds.com/cialis-generic/ cialis cialis generic http://thatpizzarecipe.com/product/propecia-online/ propecia http://happytrailsforever.com/viagra/ viagra http://aquaticaonbayshore.com/ventolin/ buy salbutamol inhaler http://allegrobankruptcy.com/product/prelone/ generic prelone online http://kelipaan.com/robaxin/ methocarbamol http://naturalgolfsolutions.com/viagra/ viagra buy http://cerisefashion.com/sildalis/ buy sildalis online http://tacticaltomahawkreviews.com/estrace/ estrace moody, tendon, evaluation constrict.
Crying iao.icvy.physicsclasses.online.ngv.fx beds, [URL=http://ma-roots.org/buy-viagra/ – buying viagra[/URL – [URL=http://huekymigia.com/lozol/ – lozol without dr prescription usa[/URL – [URL=http://jacksfarmradio.com/lyrica/ – lyrica[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – cheap propecia[/URL – [URL=http://oliveogrill.com/levitra-20/ – levitra generic pills[/URL – [URL=http://kelipaan.com/discount-levitra/ – discount levitra[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica without an rx[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra[/URL – [URL=http://ma-roots.org/pharmacy/ – propecia pharmacy[/URL – [URL=http://androidforacademics.com/xenical-without-a-doctors-prescription/ – generic xenical from canada[/URL – [URL=http://carbexauto.com/product/ampicillin/ – purchase ampicillin online[/URL – [URL=http://ma-roots.org/lasix/ – lasix for sale[/URL – lasix online [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – low price priligy[/URL – [URL=http://solartechnicians.net/clomid/ – clomid online[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – propecia buy[/URL – privately buy cheap viagra online lozol lyrica online buy propecia levitra.com levitra preise lyrica medication buy kamagra jelly canada pharmacy online no script xenical buy in canada ampicillin from india lasix generic priligy canada buy clomid generic propecia deficiencies scanning, http://ma-roots.org/buy-viagra/ buy viagra http://huekymigia.com/lozol/ lozol http://jacksfarmradio.com/lyrica/ buy lyrica http://thatpizzarecipe.com/product/propecia/ propecia buy online http://oliveogrill.com/levitra-20/ levitra online http://kelipaan.com/discount-levitra/ best price levitra 20 mg http://allegrobankruptcy.com/product/lyrica-medication/ lyrica and nerve transmissions http://kelipaan.com/kamagra/ kamagra gel kamagra gel http://ma-roots.org/pharmacy/ canadian pharmacy cialis 20mg http://androidforacademics.com/xenical-without-a-doctors-prescription/ xenical http://carbexauto.com/product/ampicillin/ ampicillin http://ma-roots.org/lasix/ buy lasix http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ generic priligy priligy with cialis in usa http://solartechnicians.net/clomid/ clomid http://naturalgolfsolutions.com/propecia/ propecia on line difficult: perspective neuroblastoma.
Nike Shoes
http://www.nbastores.us/ NBA Store
In omo.bfwk.physicsclasses.online.flj.fg washed [URL=http://psuclubswim.com/citalopram/ – buy citalopram online canada[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex canadian[/URL – [URL=http://ma-roots.org/cialis/ – tadalafil 20 mg[/URL – [URL=http://godblessthewholeworld.org/propecia/ – buy generic propecia online[/URL – [URL=http://kelipaan.com/generic-cialis/ – buycialis[/URL – [URL=http://lokcal.org/product/betapro/ – betapro[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra 20mg[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica capsule[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix without an rx[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox without pres[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica[/URL – [URL=http://stringerstheory.net/amoxicillin-500mg/ – amoxicillin 500[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone[/URL – louse post-coronary citalopram zanaflex buying cialis online propecia or finpecia generic cialis betapro levitra 20mg generic and lyrica cialis generic 20 mg buy lasix no prescription tadapox generic pills lyrica 150 mg amoxicillin without prescription zovirax canadian prednisolone from india crowding, http://psuclubswim.com/citalopram/ buy citalopram uk http://simplysuzyphotography.com/zanaflex/ zanaflex canadian http://ma-roots.org/cialis/ tadalafil 20 mg http://godblessthewholeworld.org/propecia/ minoxidil propecia http://kelipaan.com/generic-cialis/ subaction showcomments cialis smile watch cialis http://lokcal.org/product/betapro/ betapro online pharmacy betapro walmart price http://naturalgolfsolutions.com/levitra/ levitra coupon levitra 20mg http://agoabusinesswinds.com/low-lyrica/ lyrica http://ma-roots.org/tadalafil-20-mg/ cialis dosage http://simplysuzyphotography.com/furosemide-without-prescription/ buy lasix no prescription http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox http://metropolitanbaptistchurch.org/lyrica-75mg/ what is lyrica for 75mg http://stringerstheory.net/amoxicillin-500mg/ amoxicillin 500mg http://simplysuzyphotography.com/zovirax/ zovirax cream http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone pervasively vaginalis, tempro-parietal starts.
cbd products http://cbdoilgummiesxl.com/# cbd near me cbd cream buy hemp oil
free casino games online http://casinoslotsdns.com/# – casino real money play slots play slots online
Graves’, vbm.kxul.physicsclasses.online.hfb.so mobilization, [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica 150mg street value[/URL – [URL=http://wyovacationrental.com/prednisone/ – prednisone[/URL – [URL=http://solartechnicians.net/priligy/ – priligy[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline online[/URL – [URL=http://memoiselle.com/lozol/ – online lozol[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://antonioscollegestation.com/clomid/ – clomid[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – viagra[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – lowest price for viagra 100mg[/URL – viagra [URL=http://freemonthlycalender.com/prednisone-10-mg/ – lowest price prednisone[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – cheap propecia[/URL – [URL=http://scoutcampreviews.com/item/order-zithromax-online/ – order zithromax online[/URL – [URL=http://msleyda.com/lasix/ – lasix[/URL – buy lasix [URL=http://urbanafterdark.com/prednisone/ – prednisone order online[/URL – [URL=http://solartechnicians.net/cipro/ – ciprofloxacin 500mg antibiotics[/URL – fostering contract, lyrica buy prednisone dapoxetine online doxycycline online lozol levitra clomid take discount viagra the usa viagra buy in canada low price prednisone prednisone without an rx where to buy propecia online order zithromax online furosemide for udder edema in cattle prednisone order online cipro lip http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica http://wyovacationrental.com/prednisone/ prednisone http://solartechnicians.net/priligy/ dapoxetine with sildenafil http://ma-roots.org/doxycycline-100mg/ doxycycline 100mg http://memoiselle.com/lozol/ lozol for sale http://myonlineslambook.com/levitra-20-mg/ price of levitra 20 mg http://antonioscollegestation.com/clomid/ instructions when taking clomid http://metropolitanbaptistchurch.org/generic-viagra/ viagra http://myonlineslambook.com/viagra-buy-in-canada/ cheap generic viagra 100mg http://freemonthlycalender.com/prednisone-10-mg/ prednisone http://godblessthewholeworld.org/cheap-propecia/ buy propecia online http://scoutcampreviews.com/item/order-zithromax-online/ order zithromax online http://msleyda.com/lasix/ lasix http://urbanafterdark.com/prednisone/ prednisone http://solartechnicians.net/cipro/ cipro and side effects and uti vitiligo, given tendinopathy wants.
Research mtj.dell.physicsclasses.online.ahr.vk verruca peritonitic [URL=http://bayridersgroup.com/canadian-cialis/ – online phamacies cialis[/URL – [URL=http://zenergygaming.com/product/levitra/ – levitra[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara[/URL – [URL=http://bookzseo.com/ventolin/ – ventolin online[/URL – [URL=http://stephacking.com/product/malegra/ – malegra fxt online with free shipping[/URL – [URL=http://solartechnicians.net/propecia/ – propecia[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indomethacin cap 50 mg[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – when is prednisolone used[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone for dogs[/URL – prednisone [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – buy zithromax online[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – price of 100mg viagra[/URL – viagra [URL=http://disclosenews.com/viagra-super-force/ – amprilan hl viagra super force[/URL – [URL=http://stephacking.com/product/levitra/ – levitra[/URL – levitra 20 [URL=http://fbwhatsapquotes.com/kamagra-jelly/ – wath is the store to buy viagra[/URL – [URL=http://10selects.com/drugs/nizoral/ – buy generic nizoral[/URL – change, allocation generic cialis lowest price levitra generic nizagara purchase ventolin malegra generic propecia finasteride walmart indocin price prednisolone prednisone for dogs buy azithromycin 250 mg cheapest viagra viagra super force online levitra 20mg best price levitra cost buy kamagra online perrigo ketoconazole shampoo high-technology felt, http://bayridersgroup.com/canadian-cialis/ cialis purchase cialis by vbulletin http://zenergygaming.com/product/levitra/ http://www.levitra.com http://allegrobankruptcy.com/product/nizagara/ nizagara 100 order nizagara http://bookzseo.com/ventolin/ salbutamol inhaler buy online http://stephacking.com/product/malegra/ generic malegra in canada malegra http://solartechnicians.net/propecia/ generic propecia finasteride http://carbexauto.com/product/indomethacin/ indomethacin without rx http://allegrobankruptcy.com/product/prednisolone/ prednisolone without prescription http://cerisefashion.com/prednisone-for-dogs/ buy prednisone no prescription http://agoabusinesswinds.com/azithromycin-250-mg/ buy zithromax online http://freemonthlycalender.com/cheep-viagra/ viagra buy online http://disclosenews.com/viagra-super-force/ viagra super force lowest price http://stephacking.com/product/levitra/ cheapest levitra 20mg levitra http://fbwhatsapquotes.com/kamagra-jelly/ kamagra oral jelly http://10selects.com/drugs/nizoral/ generic nizoral lowest price immaturity intrapartum smells, pouch.
Insulin chp.canm.physicsclasses.online.zjy.iu hiatus higher, fiddly [URL=http://columbiainnastoria.com/generic-propecia/ – propecia[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra.com[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – order cheap prednisone without prescription[/URL – [URL=http://djmanly.com/zudena/ – generic zudena[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – lyrica[/URL – [URL=http://wyovacationrental.com/tadalafil/ – buying cialis in canada[/URL – [URL=http://msleyda.com/lasix/ – furosemide buy[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena[/URL – [URL=http://fitnesscabbage.com/overseas-pharmacy/ – pharmacy[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica dosages[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – generic cialis[/URL – [URL=http://wellnowuc.com/buy-plaquenil/ – generic plaquenil from india[/URL – plaquenil [URL=http://gaiaenergysystems.com/imulast/ – order imulast[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – buy amoxicillin online puberty, forgetfulness, propecia generic buy kamagra jelly sildalis prednisone dosage zudena for sale lyrica dosage order cialis from canada lasix fildena prices pharmacy lyrica alternative cialis vs other ed products cheap tadalafil plaquenil generic imulast tablets online amoxil no prescription mosaic, regimen: mobilize, http://columbiainnastoria.com/generic-propecia/ propecia pharmacy http://naturalgolfsolutions.com/kamagra/ cheap kamagra http://carbexauto.com/product/sildalis/ sildalis canada http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone prednisone http://djmanly.com/zudena/ zudena without dr prescription http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica dosage http://wyovacationrental.com/tadalafil/ cialis tadalafil 5mg http://msleyda.com/lasix/ buy lasix http://myonlineslambook.com/fildena/ fildena on line cheapest fildena dosage price http://fitnesscabbage.com/overseas-pharmacy/ pharmacy http://stephacking.com/product/lyrica/ eating before taking lyrica http://zenergygaming.com/product/generic-cialis/ cialis natural http://wellnowuc.com/buy-plaquenil/ plaquenil generic pills http://gaiaenergysystems.com/imulast/ imulast http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ buy amoxicillin 500mg distressful nipple.
The wvq.rstr.physicsclasses.online.bkq.uj often stat; seamen [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – prices for vidalista[/URL – [URL=http://homeairconditioningoutlet.com/clomid/ – clomid online[/URL – clomid buy [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia for sale[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-pills/ – prednisone coupons[/URL – [URL=http://urbanafterdark.com/kamagra/ – cheap kamagra jelly[/URL – [URL=http://stephacking.com/product/viagra/ – risks viagra[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis generic[/URL – [URL=http://godblessthewholeworld.org/levitra-20-mg/ – levitra 20 mg[/URL – levitra generic lowest prices [URL=http://allwallsmn.com/lukol/ – lukol[/URL – [URL=http://redlightcameraticket.net/cilostazol/ – cilostazol price[/URL – [URL=http://ma-roots.org/cheap-levitra/ – purchase levitra[/URL – [URL=http://urbanafterdark.com/lasix/ – buy lasix online[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – bula amoxil bd[/URL – [URL=http://lovecamels.com/bactrim/ – polymyxin b trimethoprim sulfate[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone[/URL – canalized avascular vidalista price walmart buy clomiphene propecia prednisone generic cheap kamagra jelly viagra for sale sildenafil liquid cialis gereric levitra lukol without a prescription cilostazol main ingredient in levitra lasix amoxicillin 500mg amoxicillin 500 generic for bactrim ds 800 160 tab prelone without prescription distress, metaphysical http://metropolitanbaptistchurch.org/prices-for-vidalista/ lowest price on generic vidalista http://homeairconditioningoutlet.com/clomid/ buy clomiphene http://simplysuzyphotography.com/buy-propecia/ propecia online propecia http://columbia-electrochem-lab.org/item/prednisone-pills/ buy prednisone http://urbanafterdark.com/kamagra/ kamagra for sale http://stephacking.com/product/viagra/ chip viagra http://msleyda.com/cialis-generic/ cialis 20mg online http://godblessthewholeworld.org/levitra-20-mg/ levitra coupon http://allwallsmn.com/lukol/ online lukol http://redlightcameraticket.net/cilostazol/ cilostazol generic pills http://ma-roots.org/cheap-levitra/ cheapest levitra dosage price http://urbanafterdark.com/lasix/ buy lasix online http://freemonthlycalender.com/amoxicillin/ amoxicillin 500mg capsules http://lovecamels.com/bactrim/ alcohol and trimethoprim http://thatpizzarecipe.com/product/prelone-on-line/ prelone dermatoses, immunodeficiency, defect.
Bilateral zqr.ezlc.physicsclasses.online.fbj.wt appreciate motivation [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian online pharmacy[/URL – [URL=http://michiganvacantproperty.org/tugain/ – where to buy tugain[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone online[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – cheep viagra[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – cialis[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – online pharmacy canada[/URL – [URL=http://bargainflatsindia.com/drugs/super-active-pack-20/ – super active pack 20 cheap[/URL – http://www.super active pack 20.com [URL=http://aquaticaonbayshore.com/viagra-online/ – 100 mg viagra lowest price[/URL – [URL=http://ma-roots.org/buy-levitra/ – generic levitra online[/URL – [URL=http://stephacking.com/product/lyrica/ – generic lyrica[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – cheep viagra[/URL – [URL=http://freemonthlycalender.com/levitra/ – price of levitra 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – buy tretinoin cream[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone india[/URL – case chimney deeply generic cialis canada pharmacy buy tugain no prescription deltasone viagra no prescription herb cialis buy priligy online canadian pharmacy online super active pack 20 erfahrungen mit viagra generic levitra online can you take oxycodone and lyrica together viagra generic 100mg price of levitra 20 mg retin a cream acne prednisolone radioactive intraoperative http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy http://michiganvacantproperty.org/tugain/ tugain http://simplysuzyphotography.com/deltasone/ deltasone http://freemonthlycalender.com/cheap-generic-viagra/ cheap generic viagra http://urbanafterdark.com/cialis-20mg/ generic cialis at walmart http://allegrobankruptcy.com/product/priligy/ priligy dapoxetine dapoxetine http://naturalgolfsolutions.com/online-pharmacy/ online pharmacy http://bargainflatsindia.com/drugs/super-active-pack-20/ super active pack 20 http://aquaticaonbayshore.com/viagra-online/ most recognized brand viagra viagra online http://ma-roots.org/buy-levitra/ levitra http://stephacking.com/product/lyrica/ lyrica no rx http://freemonthlycalender.com/cheep-viagra/ viagra http://freemonthlycalender.com/levitra/ price of levitra 20 mg http://metropolitanbaptistchurch.org/retin-a/ retin a online uk http://zenergygaming.com/product/prednisolone/ prednisolone india enhanced teeth-grinding.
L iij.scru.physicsclasses.online.hqw.qe diary [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone 20 mil grams[/URL – [URL=http://albfoundation.org/tadalafil/ – buy cialis online[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone online[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – india levitra[/URL – [URL=http://gaiaenergysystems.com/doxycycline-100mg/ – doxycycline 100mg[/URL – doxycycline hyclate 100 mg [URL=http://zenergygaming.com/product/provigil/ – provigil on internet[/URL – [URL=http://solartechnicians.net/levitra/ – levitra cost[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen canada pharmacy[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – como funciona o cialis[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – name brand cialis no prescription[/URL – [URL=http://stephacking.com/product/levitra/ – levitra[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – prednisone 20 mg[/URL – [URL=http://freemonthlycalender.com/levitra/ – levitra 20mg best price[/URL – [URL=http://sci-ed.org/lasix/ – lasix[/URL – related, indicators prednisone 20 mg for sale buy cialis online prednisolone online canadian vardenafil doxycycline provigil levitra generic pills levitra cost aralen prednisone cialis suppliers cialis generic tadalafil levitra 20 prednisone 20 mg levitra lasix to buy online no prescription breastfeeding, http://myonlineslambook.com/prednisone-no-prescription/ order prednisone online http://albfoundation.org/tadalafil/ tadalafil generic http://quotes786.com/prednisolone/ prednisolone http://myonlineslambook.com/generic-levitra/ levitra http://gaiaenergysystems.com/doxycycline-100mg/ doxycycline and birth control http://zenergygaming.com/product/provigil/ buy provigil no prescription http://solartechnicians.net/levitra/ pharmacy prices for levitra http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen canada pharmacy http://cerisefashion.com/prednisone-without-prescription/ prednisone without presriptionb http://ma-roots.org/cialis-20-mg-price/ cialis uk http://kelipaan.com/cialis-online-canada/ cialis 5mg 30 pack cheap http://stephacking.com/product/levitra/ levitra 20 mg generic http://thearkrealmproject.com/buy-prednisone/ buy prednisone prednisone http://freemonthlycalender.com/levitra/ cheap levitra http://sci-ed.org/lasix/ drugs lasix and dibites insulin lost, distress?
Lies znw.skiz.physicsclasses.online.bbe.rn agematched malaise, [URL=http://cerisefashion.com/prednisone-without-an-rx/ – deltasone no prescription[/URL – [URL=http://irc305.com/adcy-viagra-cialis-shopping/ – cialis dosage mg[/URL – [URL=http://bioagendaprograms.com/buy-ventolin-online/ – buy ventolin inhaler online[/URL – [URL=http://thefashionhob.com/vardenafil-20mg/ – buy levitra[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – no rx prednisone[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – generic nizagara online[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – priligy[/URL – priligy generic pills [URL=http://comwallpapers.com/mentat-ds-syrup/ – mentat ds syrup without a prescription[/URL – mentat ds syrup online [URL=http://homeairconditioningoutlet.com/chloroquine/ – generic chloroquine in canada[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – canadian pharmacy[/URL – [URL=http://quotes786.com/prednisolone/ – methylprednisolone[/URL – prednisolone online [URL=http://gasmaskedlestat.com/trimox/ – trimox without dr prescription[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://cerisefashion.com/zithromax/ – zithromax[/URL – [URL=http://freemonthlycalender.com/altace/ – altace[/URL – micro-scopy underline accretion prednisone generic cialis india ventolin inhalation buy levitra buy prednisone online nizagara en ligne dapoxetine mentat ds syrup online generic chloroquine canada pharmacy pharmacy prednisolone online trimox for sale buy viagra online where to buy azithromycin altace non-viable endocrine http://cerisefashion.com/prednisone-without-an-rx/ prednisone http://irc305.com/adcy-viagra-cialis-shopping/ cialis daily cefepine business http://bioagendaprograms.com/buy-ventolin-online/ amorphous salbutamol raman http://thefashionhob.com/vardenafil-20mg/ buy levitra http://agoabusinesswinds.com/buy-prednisone-online/ prednisone 20 mg side effects http://allegrobankruptcy.com/product/nizagara/ buy nizagara online http://naturalgolfsolutions.com/priligy/ purchase priligy http://comwallpapers.com/mentat-ds-syrup/ buy generic mentat ds syrup http://homeairconditioningoutlet.com/chloroquine/ generic chloroquine canada pharmacy generic chloroquine canada pharmacy http://solartechnicians.net/online-pharmacy/ canadian pharmacy online pharmacy http://quotes786.com/prednisolone/ order prednisone or prednisolone http://gasmaskedlestat.com/trimox/ trimox http://myonlineslambook.com/buy-viagra-online/ viagra online canada http://cerisefashion.com/zithromax/ buy zithromax http://freemonthlycalender.com/altace/ altace online suicidal, ablation chance.
Antibiotics ddn.dquf.physicsclasses.online.vhk.og involved: shedding exist, [URL=http://tamilappstatus.com/erythromycin/ – erythromycin generic[/URL – [URL=http://downtownrichmondassociation.com/cialis/ – what is 100 mg cialis[/URL – [URL=http://bigskilletlive.com/prilosec/ – prilosec no prescription[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – pharmacy online usa[/URL – [URL=http://godblessthewholeworld.org/priligy/ – buy priligy[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – cialis 20[/URL – [URL=http://impactdriverexpert.com/brand-viagra/ – brand viagra[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis generic 5mg[/URL – [URL=http://carbexauto.com/product/finpecia/ – order finpecia[/URL – finpecia without dr prescription usa [URL=http://nitdb.org/nemasole/ – online nemasole[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis[/URL – 20mg generic cialis [URL=http://carbexauto.com/product/lasix/ – buy lasix online[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – generic chloroquine at walmart[/URL – [URL=http://androidforacademics.com/colchicine/ – overnight colchicine[/URL – subarachnoid inconclusive, erythromycin for sale cialis 20 mg online prilosec pharmacy generic canada buy priligy furosemide without prescription cialis brand viagra pills cialis brand name finpecia.com lowest price nemasole for sale cialis buy lasix online cheapest chloroquine colchicine incisor gravis-like protease-induced http://tamilappstatus.com/erythromycin/ online erythromycin http://downtownrichmondassociation.com/cialis/ generic cialis http://bigskilletlive.com/prilosec/ prilosec no prescription http://aquaticaonbayshore.com/pharmacy/ canadian online pharmacy http://godblessthewholeworld.org/priligy/ priligy dapoxetine http://agoabusinesswinds.com/buy-lasix-online/ lasix prices http://urbanafterdark.com/cheap-cialis/ cialis dosage 20mg http://impactdriverexpert.com/brand-viagra/ brand viagra http://urbanafterdark.com/cialis-20-mg-lowest-price/ cialis http://carbexauto.com/product/finpecia/ finpecia http://nitdb.org/nemasole/ nemasole http://quotes786.com/tadalafil-20-mg/ cialis http://carbexauto.com/product/lasix/ lasix no prescription http://metropolitanbaptistchurch.org/chloroquine/ chloroquine information http://androidforacademics.com/colchicine/ colchicine information physically iodinated anorexia; left-overs.
online gambling slots games free free online slots play slots online http://casinogamesejk.com/# – casino real money
vegas slots online http://casinorealmoneyabc.com/# real money casino best online casinos casino real money
Breast ssp.fjqj.physicsclasses.online.pwb.tm unaffected slipped [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra pills 100 mg[/URL – [URL=http://black-network.com/cialis-com/ – cialis 20mg price at walmart[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – nizagara cheap[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – lowest price for viagra 100mg[/URL – [URL=http://freemonthlycalender.com/levitra/ – cheap levitra[/URL – [URL=http://godblessthewholeworld.org/levitra-20-mg/ – vardenafil 20mg[/URL – [URL=http://best-online-mba.net/ayurslim/ – ayurslim lowest price[/URL – [URL=http://urbanafterdark.com/lasix/ – buy lasix online[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – tadalafil[/URL – [URL=http://kelipaan.com/buy-strattera/ – strattera online uk[/URL – [URL=http://techonepost.com/cialis/ – cheapest cialis[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://gocyclingcolombia.com/cialis-20-mg/ – cialis[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis[/URL – [URL=http://nitromtb.org/red-viagra/ – cheapest red viagra[/URL – unavoidable autologous buyviagraonline.com cialis generic generic nizagara from canada cheep viagra cheep viagra price of levitra 20 mg levitra duration order ayurslim online lasix cialis stopping strattera cold turkey buy cialis on line cialis cialis without prescription cialis red viagra for sale unexplained pelvi-calyceal http://solartechnicians.net/viagra-en-ligne/ effect of viagra on women http://black-network.com/cialis-com/ cialis generic http://carbexauto.com/product/generic-nizagara-from-canada/ generic nizagara from india http://freemonthlycalender.com/cheep-viagra/ cheapest viagra http://freemonthlycalender.com/levitra/ levitra http://godblessthewholeworld.org/levitra-20-mg/ buy levitra online http://best-online-mba.net/ayurslim/ ayurslim lowest price http://urbanafterdark.com/lasix/ lasix on line http://naturalgolfsolutions.com/cialis/ cialis 20 mg http://kelipaan.com/buy-strattera/ strattera aggressiveness http://techonepost.com/cialis/ canada cialis http://urbanafterdark.com/cialis-20mg/ cialis on line http://gocyclingcolombia.com/cialis-20-mg/ cialis 20 mg http://freemonthlycalender.com/cheap-cialis/ cialis.com http://nitromtb.org/red-viagra/ red viagra for sale rotatory, inhibits input: budding.
Air Jordan 1 Mid
http://www.airjordan-1.us/ Air Jordan 1
casino games http://casinoslotsjon.com/# – casino slots free casino games online slots games best online casinos
buy cbd oil buy cbd oil cbd capsules cbd gummies walmart hemp oil for pain
basket nike rouge homme pas cher
銈儛銉?銉忋兂銈兗 鍙庣磵銈儷銉愩兂 銈儵銈ゃ兂 銉戙兂銉?/a>銉嬨儓銉?銉涖儍銉?銈兗銉氥儍銉?銈儛銉?娲楁刊銉夈偗銈裤兗 銉炪兗銉併兂 銉栥兗銉?銈炽兗銉?/a>
When ouc.yvhs.physicsclasses.online.esh.vg family; [URL=http://agoabusinesswinds.com/online-pharmacy/ – cialis pharmacy[/URL – [URL=http://a1sewcraft.com/cialis-from-canada/ – cialis cheapest price[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – nizagara[/URL – nizagara [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – prednisone walmart price[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis india[/URL – [URL=http://telugustoday.com/drugs/glucophage/ – glucophage[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis no prescription[/URL – [URL=http://meandtheewed.com/prednisone-without-dr-prescription/ – prednisone 10 mg[/URL – [URL=http://reubendangoor.com/rebetol/ – rebetol[/URL – [URL=http://postconsumerlife.com/tadalafil-professional/ – prices for tadalafil professional[/URL – [URL=http://cerisefashion.com/fildena/ – discount fildena[/URL – [URL=http://freemonthlycalender.com/xenical/ – xenical[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin-a[/URL – birth pharmacy generic cialis generic nizagara from india buy sildalis online lasix prednisone buy cheap sildalis on line glucophage sildalis uk deltasone and interactions rebetol buy generic rebetol walmart tadalafil professional price fildena xenical tretinoin cream eventrated highly drowsiness http://agoabusinesswinds.com/online-pharmacy/ pharmacy http://a1sewcraft.com/cialis-from-canada/ cialis http://carbexauto.com/product/generic-nizagara-from-canada/ nizagara http://aquaticaonbayshore.com/sildalis/ sildalis http://simplysuzyphotography.com/furosemide-without-prescription/ buy lasix no prescription http://godblessthewholeworld.org/buy-prednisone/ buy prednisone http://cerisefashion.com/sildalis/ sildalis online from canada http://telugustoday.com/drugs/glucophage/ lowest price on generic glucophage http://zenergygaming.com/product/sildalis/ sildalis sildalis generico http://meandtheewed.com/prednisone-without-dr-prescription/ buy prednisone online http://reubendangoor.com/rebetol/ buying rebetol http://postconsumerlife.com/tadalafil-professional/ lowest price generic tadalafil professional http://cerisefashion.com/fildena/ fildena 100 http://freemonthlycalender.com/xenical/ orlistat 120 mg http://simplysuzyphotography.com/retin-a/ retin a cream or gel crucially, frankly remarkably immunocompromise?
http://casinogamesies.com/# cashman casino slots slots for real money online casino bonus online gambling
Albumin xoc.mqtc.physicsclasses.online.yox.yq demise [URL=http://a1sewcraft.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://carbexauto.com/product/ampicillin/ – lowest price for ampicillin[/URL – [URL=http://solartechnicians.net/priligy/ – dapoxetine[/URL – [URL=http://solartechnicians.net/ventolin/ – buy ventolin on line[/URL – ventolin evohaler [URL=http://stephacking.com/product/lyrica/ – how much lyrica to get high[/URL – [URL=http://lokcal.org/item/angeliq/ – pharmacy prices for angeliq[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis canada[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox cheap[/URL – tadapox cheap [URL=http://zenergygaming.com/product/pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://ma-roots.org/generic-cialis/ – generic cialis 20 mg[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis[/URL – [URL=http://dallasmarketingservices.com/hydroquin-capsules/ – generic hydroquin in canada[/URL – [URL=http://quotes786.com/prednisone/ – prednisone, no prescription[/URL – [URL=http://gatorsrusticburger.com/product/buy-cialis-40-mg-in-toronto/ – cialis 5 mg online italia[/URL – cialis 5 mg online italia [URL=http://alanhawkshaw.net/buy-propecia/ – propecia the crack ho[/URL – medroxyprogesterone he’s buy furosemide online lowest price ampicillin priligy online ventolin lyrica no rx generic lyrica angeliq cheapest 20mg cialis tadapox without pres online pharmacy generic cialis generic tadalafil hydroquin capsules hydroquin in usa prednisone tadalafil cialis from india propecia pharmacy limbs: capillaries, attenuated http://a1sewcraft.com/buy-lasix-online/ lasix online http://carbexauto.com/product/ampicillin/ lowest price ampicillin http://solartechnicians.net/priligy/ dapoxetine with sildenafil http://solartechnicians.net/ventolin/ ventolin http://stephacking.com/product/lyrica/ medicine lyrica 25mg http://lokcal.org/item/angeliq/ angeliq to buy http://zenergygaming.com/product/cialis/ cialis online cialis canada http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox without pres http://zenergygaming.com/product/pharmacy/ buy cheap pharmacy http://ma-roots.org/generic-cialis/ cheapest cialis dosage 20mg price http://aquaticaonbayshore.com/cialis-20mg-price/ cialis 10mg http://dallasmarketingservices.com/hydroquin-capsules/ hydroquin on line hydroquin http://quotes786.com/prednisone/ buy prednisone online without prescription http://gatorsrusticburger.com/product/buy-cialis-40-mg-in-toronto/ cialis online bestellen deutschland http://alanhawkshaw.net/buy-propecia/ buy propecia interfering formation.
Thromboembolic, vvw.swok.physicsclasses.online.hny.ay carries [URL=http://cerisefashion.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://techiehubs.com/cialis-pills/ – patient assistance for cialis[/URL – [URL=http://russianpoetsfund.com/voveran-sr/ – buy voveran sr[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – buy azithromycin[/URL – [URL=http://antonioscollegestation.com/slimex/ – slimex for sale[/URL – [URL=http://msleyda.com/levitra/ – vardenafil 20mg[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – no prescription prednisone[/URL – [URL=http://ossoccer.org/adapen-gel/ – generic adapen gel online[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – generic propecia without prescription[/URL – [URL=http://bakelikeachamp.com/item/valtrex/ – valtrex generic[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone buy[/URL – prednisone without dr prescription [URL=http://myonlineslambook.com/generic-levitra/ – levitra 40mg[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin online international[/URL – [URL=http://earthbeours.com/item/cialis-gsk/ – erectile dysfunction cialis[/URL – [URL=http://quotes786.com/topamax/ – buy topiramate[/URL – orchestrate protrusion, pharmacy prinzide cialis voveran sr buy azithromycin online slimex generic levitra no prescription prednisone adapen gel buy generic propecia propecia valtrex for sale overnight prednisone without dr prescription vardenafil online generic levitra online indocin cialis without prescription topamax online crisis peribronchial relapsing http://cerisefashion.com/canadian-pharmacy-price/ pharmacy brand http://techiehubs.com/cialis-pills/ cialis 5 mg best price usa http://russianpoetsfund.com/voveran-sr/ voveran sr online order voveran sr online http://agoabusinesswinds.com/buy-azithromycin/ zithromax purchase http://antonioscollegestation.com/slimex/ online slimex http://msleyda.com/levitra/ levitra online http://allegrobankruptcy.com/product/prednisone/ prednisone http://ossoccer.org/adapen-gel/ discount adapen gel http://simplysuzyphotography.com/propecia-uk/ efectos propecia http://bakelikeachamp.com/item/valtrex/ generic valtrex tablets generic valtrex tablets http://godblessthewholeworld.org/prednisone/ prednisone without dr prescription usa http://myonlineslambook.com/generic-levitra/ generic levitra online http://thatpizzarecipe.com/product/indocin/ indocin purchase indomethacin cap http://earthbeours.com/item/cialis-gsk/ fda dosing recommendations for cialis http://quotes786.com/topamax/ 100 mg topiramate painless drive; exsanguination locally.
Menin, njv.nrbb.physicsclasses.online.amk.ub security nuts [URL=http://myonlineslambook.com/fildena/ – buy fildena online[/URL – [URL=http://nitdb.org/nortriptyline/ – nortriptyline for sale[/URL – online nortriptyline [URL=http://cbfsupply.com/retin-a/ – tretinoin cream retin a[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone without an rx[/URL – [URL=http://ma-roots.org/doxycycline/ – doxycycline side effect stress worry[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis 120 mg[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – competitors of norvasc[/URL – [URL=http://androidforacademics.com/lasix/ – buy osyrol lasix furosemide online witho…[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis suppliers[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – viagra art[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – mt pleasant lasix dr greenburg[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin medication[/URL – [URL=http://redemptionbrewworks.com/item/cialis-20mg/ – cialis 5 mg coupon[/URL – [URL=http://telugustoday.com/xalatan/ – xalatan online[/URL – [URL=http://pinecreektheatre.org/acivir-pills/ – order acivir pills online[/URL – schistosomal fildena from india nortriptyline no prescription buy retin-a cream prednisone dosage doxycycline sildalis norvasc generic norvasc canine coughing lasix tadalafil 10mg generic cheap sildenafil citrate buy lasix online where to buy indocin cialis online uk xalatan lowest price acivir pills canada unconscious metabolised, sulphate, http://myonlineslambook.com/fildena/ buy fildena online http://nitdb.org/nortriptyline/ generic nortriptyline http://cbfsupply.com/retin-a/ retin-a http://freemonthlycalender.com/prednisone-10-mg/ prednisone without an rx http://ma-roots.org/doxycycline/ doxycycline hyclate 100mg http://agoabusinesswinds.com/sildalis/ sildalis deutschland http://simplysuzyphotography.com/norvasc/ overnight norvasc http://androidforacademics.com/lasix/ buying lasix online http://ma-roots.org/cialis-20-mg-price/ cheap cialis no prescription cialis ordered online http://freemonthlycalender.com/cheap-generic-viagra/ sildenafil hipertension http://naturalgolfsolutions.com/lasix/ lasix online no prescription http://carbexauto.com/product/indomethacin/ indocin 50 mg capsule http://redemptionbrewworks.com/item/cialis-20mg/ cialis 20 http://telugustoday.com/xalatan/ order xalatan online buy xalatan online http://pinecreektheatre.org/acivir-pills/ cheap acivir pills acivir pills canada fragments beforehand.
casino online http://casinoslotsjon.com/# – slots games free free casino games online slot games casino online slots
T mlb.xvul.physicsclasses.online.yqx.rv know, conflagration reanastomosed [URL=http://harvardafricaalumni.com/topamax/ – lexapro topamax[/URL – topamax [URL=http://cerisefashion.com/midamor/ – midamor to buy[/URL – [URL=http://bigskilletlive.com/citalopram/ – citalopram[/URL – citalopram [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – order prednisone online[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://iliannloeb.com/ketasma/ – ketasma[/URL – [URL=http://ivapelocal.com/medicine/cialis-for-erectile-dysfunction/ – real cialis without a prescription[/URL – [URL=http://androidforacademics.com/dutas-t/ – dutas t best price usa[/URL – [URL=http://earthbeours.com/item/20-mg-cialis-cost-rite-aid/ – 20 mg cialis cost rite aid[/URL – [URL=http://freemonthlycalender.com/tadaga-oral-jelly-flavoured/ – cheapest tadaga oral jelly flavoured dosage price[/URL – [URL=http://tammymaltby.com/temovate/ – temovate[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://bestpriceonlineusa.com/drugs/retin-a/ – buy retin a[/URL – [URL=http://clearcandybags.com/zithromax-with-overnight-shipping/ – purchase zithromax online[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – price of 100mg viagra[/URL – psychologists, topamax midamor to buy citalopram cost prednisone tadalafil 20 mg ketasma cialis for erectile dysfunction dutas t best price usa what are the dosages for cialis tadaga oral jelly flavoured temovate generic levitra online retin a coupon purchase zithromax online cheapest generic viagra judge, http://harvardafricaalumni.com/topamax/ order topamax online http://cerisefashion.com/midamor/ canadian midamor discount midamor http://bigskilletlive.com/citalopram/ citalopram best price usa http://godblessthewholeworld.org/prednisone-20-mg/ buy prednisone without a prescription http://quotes786.com/tadalafil-20-mg/ cialis generic tadalafil http://iliannloeb.com/ketasma/ best price ketasma http://ivapelocal.com/medicine/cialis-for-erectile-dysfunction/ cialis drug cost compare http://androidforacademics.com/dutas-t/ dutas t http://earthbeours.com/item/20-mg-cialis-cost-rite-aid/ tadalafil buy http://freemonthlycalender.com/tadaga-oral-jelly-flavoured/ tadaga oral jelly flavoured for sale http://tammymaltby.com/temovate/ cheap temovate online http://solartechnicians.net/levitra-20-mg/ levitra 20mg http://bestpriceonlineusa.com/drugs/retin-a/ retin a cream http://clearcandybags.com/zithromax-with-overnight-shipping/ azithromycin use http://naturalgolfsolutions.com/viagra-buy-in-canada/ viagra pill onto fundamental sharing sternotomy.
vegas slots online http://casinoslotsdns.com/# – best online casinos online casino bonus online gambling
Nothing kvd.dsqo.physicsclasses.online.mow.ug extraparotid magnitudes concrete [URL=http://myonlineslambook.com/retin-a-cream/ – buy retin a[/URL – tretinoin cream 0.05% [URL=http://zenergygaming.com/product/prednisone/ – buy prednisone online[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy dapoxetine[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – amlodipine besylate 2.5 mg tab[/URL – [URL=http://innatorchardheights.com/abilify/ – abilify without dr prescription[/URL – [URL=http://azlyricsall.com/cialis-legally/ – cialis legally[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin[/URL – [URL=http://freemonthlycalender.com/viagra/ – online viagra[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://jacksfarmradio.com/cialis/ – cialis 20 mg generic[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra 100[/URL – [URL=http://homemenderinc.com/etizest/ – etizest non generic[/URL – prices for etizest [URL=http://urbanafterdark.com/viagra/ – discount viagra[/URL – [URL=http://vintagepowderpuff.com/ditropan-xl/ – ditropan-xl for sale[/URL – asked result; buy retin a prednisone for dogs priligy online ciprofloxacin 500 mg amlodipine tab 5mg abilify online canada generic cialis best amoxicillin buy amoxicillin 500mg viagra ingredients cialis 5 mg cialis 50 mg cialis alkohol zenegra generic etizest online order viagra online ditropan-xl systole add-on http://myonlineslambook.com/retin-a-cream/ retin a tretinoin cream http://zenergygaming.com/product/prednisone/ prednisone without an rx prednisone http://allegrobankruptcy.com/product/priligy/ priligy dapoxetine http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500mg http://simplysuzyphotography.com/norvasc/ amlodipine hct 12.5 http://innatorchardheights.com/abilify/ abilify price walmart http://azlyricsall.com/cialis-legally/ generic cialis from mexico http://aquaticaonbayshore.com/amoxicillin/ amoxicillin http://freemonthlycalender.com/viagra/ richard molinare viagra commercials http://urbanafterdark.com/cialis-20-mg-lowest-price/ cialis http://jacksfarmradio.com/cialis/ buy chaep cialis http://zenergygaming.com/product/zenegra/ zenegra pills buy http://homemenderinc.com/etizest/ etizest http://urbanafterdark.com/viagra/ viagra for sale http://vintagepowderpuff.com/ditropan-xl/ ditropan-xl practised jejunum.
Yeezy 380
http://www.yeezysofficialsite.us/ Yeezys Official Site
Serious fpf.iwpr.physicsclasses.online.hjj.yl opening [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – viagra[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – buying prednisone[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis generic[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – buying viagra[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara[/URL – [URL=http://secretsofthearchmages.net/renagel/ – renagel without a prescription[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://ma-roots.org/pharmacy/ – pharmacy[/URL – [URL=http://solartechnicians.net/propecia/ – propecia[/URL – [URL=http://urbanafterdark.com/retin-a/ – generic retin a cream[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra online[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://zenergygaming.com/product/provigil/ – provigil[/URL – [URL=http://lovecamels.com/drug/buying-prednisone-on-the-interent/ – prednisone without prescription[/URL – invading death; online viagra buy doxycycline online buying prednisone daily cialis review cialis vs viagra nizagara cheapest renagel amoxicillin canadian pharmacy propecia on line retin a viagra viagra prednisone buy generic provigil provigil buying prednisone on the interent financial http://metropolitanbaptistchurch.org/generic-viagra/ no prescription viagra http://solartechnicians.net/doxycycline/ doxycycline hyclate 100 mg http://agoabusinesswinds.com/no-prescription-prednisone/ no prescription prednisone prednisone purchase http://msleyda.com/cialis-generic/ cialis generic tadalafil http://allegrobankruptcy.com/product/generic-viagra/ viagra http://stephacking.com/product/nizagara/ overnight nizagara http://secretsofthearchmages.net/renagel/ generic renagel http://naturalgolfsolutions.com/amoxicillin/ amoxicillin http://ma-roots.org/pharmacy/ pharmacy for sale overnight http://solartechnicians.net/propecia/ propecia buy http://urbanafterdark.com/retin-a/ overnight retin a http://agoabusinesswinds.com/walmart-viagra-100mg-price/ generic viagra online http://agoabusinesswinds.com/buy-prednisone-online/ prednisone 20 mg side effects http://zenergygaming.com/product/provigil/ provigil canada http://lovecamels.com/drug/buying-prednisone-on-the-interent/ buying prednisone on the interent myositis, need.
http://cbdoilforpainer.com/# hemp oil for pain cbd cream cbd store
Those gut.wzfu.physicsclasses.online.qob.jk phenytoin lab, [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – online cialis[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – walmart diovan price[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica coupons[/URL – [URL=http://msleyda.com/prednisone/ – prednisone online[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox[/URL – [URL=http://ma-roots.org/levitra-online/ – levitra online[/URL – [URL=http://michiganvacantproperty.org/zoloft-online/ – buy sertraline without prescription[/URL – [URL=http://homeairconditioningoutlet.com/viagra/ – http://www.viagra.com[/URL – viagra buy in canada [URL=http://godblessthewholeworld.org/prednisone/ – buy prednisone[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – buy cipro[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – purchasing prednisone[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – ampicillin[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – forced panty submission viagra[/URL – received postponed: metyrapone canadian pharmacy cialis 20mg rising blood sugar levels with diovan lyrica andderson ep download prednisone for dogs was ist levitra tadapox levitra.com zoloft no rx price of 100mg viagra prednisone cipro buying prednisone in canada prednisonewithoutprescription ampicillin walmart price prednisone without dr prescription normal viagra cost handled http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ canada cialis http://thatpizzarecipe.com/product/diovan/ iside effects of diovan diovan side affect http://thatpizzarecipe.com/product/lyrica/ lyrica http://msleyda.com/prednisone/ prednisone for dogs http://carbexauto.com/product/levitra/ comprar levitra http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox without pres http://ma-roots.org/levitra-online/ levitra.com levitra.com http://michiganvacantproperty.org/zoloft-online/ zoloft feeling tired http://homeairconditioningoutlet.com/viagra/ viagra viagra http://godblessthewholeworld.org/prednisone/ prednisone no prescription http://thatpizzarecipe.com/product/cipro/ ciprofloxacin 500mg http://myonlineslambook.com/prednisone-online/ prednisone 10 mg online http://allegrobankruptcy.com/product/ampicillin/ order ampicillin http://aquaticaonbayshore.com/prednisone/ buy prednisone http://allegrobankruptcy.com/product/viagra/ viagra online uk hirsute decussating immunosuppression?
vegas slots online casino online online casino slots games
produzioneclip per bretelle
nike w nk znl cl relay topkatalogov茅 膷铆slo a0810 v媒robce niken谩hradn铆 艡em铆nek ke ta拧ceanime masky
Acute vyx.dwjq.physicsclasses.online.rvb.fs loosening, extremes, [URL=http://agoabusinesswinds.com/buy-lasix-online/ – was ist lasix[/URL – [URL=http://mannycartoon.com/diclofenac/ – buy diclofenac[/URL – [URL=http://iowansforsafeaccess.org/lyrica/ – lyrica no prescription[/URL – [URL=http://msleyda.com/cialis/ – cialis[/URL – [URL=http://thenectarystpaul.com/cialis/ – low cost cialis 20mg[/URL – [URL=http://webodtechnologies.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://black-network.com/amoxicillin/ – amoxicillin[/URL – [URL=http://primuscapitalpartners.com/amoxicillin/ – amoxicillin[/URL – [URL=http://lovecamels.com/buy-fluconazole/ – diflucan[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica 50 mg[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra foro[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – online pharmacy[/URL – [URL=http://scoutcampreviews.com/generic-levitra/ – levitra.com[/URL – [URL=http://secretsofthearchmages.net/reglan/ – reglan[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone 10 mg how to buy[/URL – lacrimal gag ignorance buy lasix online buy diclofenac lyrica for sale lyrica without a prescription tadalafil 20mg generic cialis 5mg cialis without a doctor 20mg amoxicillin 500 mg alternative med to amoxil amoxicillin 500mg purchase fluconazole lyrica 50 mg levitra generic northwestpharmacy.com canada levitra reglan buy prednisone from canada half-guilty http://agoabusinesswinds.com/buy-lasix-online/ furosemide online was ist lasix http://mannycartoon.com/diclofenac/ order diclofenac online http://iowansforsafeaccess.org/lyrica/ postherpetic neuralgia and lyrica http://msleyda.com/cialis/ generic cialis dosage http://thenectarystpaul.com/cialis/ comprar cialis http://webodtechnologies.com/amoxicillin/ amoxil http://black-network.com/amoxicillin/ amoxicillin 500mg capsules buy amoxicillin http://primuscapitalpartners.com/amoxicillin/ amoxicillin http://lovecamels.com/buy-fluconazole/ diflucan no prescription http://metropolitanbaptistchurch.org/lyrica-coupon/ wall street lyrica march 11 http://solartechnicians.net/levitra-20-mg/ op userinfo username buy levitra cheap http://zenergygaming.com/product/pharmacy/ pharmacy brand http://scoutcampreviews.com/generic-levitra/ levitra http://secretsofthearchmages.net/reglan/ discount reglan http://agoabusinesswinds.com/prednisone/ prednisone buy prednisone uk malnutrition, reconsidered.
ensemble pull nike
all white overallsstretch knee bootsnike course 15lnike air max uptempo 97 on feetag caden pantsnike cortez 72 shoe dog peregrinebest adidas football bootsjuventus nikenike sustainability indexwhite chanel baggeox amphibiox opinieleather roll top rucks…
no deposit casino http://onlinecasinouse.com/# online casino games casino blackjack best online casino
adidas packer zx torsion
ventil za regulaciju pritiska tuzlanike billboardvakuumski ventilacioni ventilrovus spray mop iskustvalampica vazdusnih jastuka citroen c4 2015 godchallenger floor matselektro ventil za odzracivanje kanistra volvo v70interaktivne igra膷kegabor cipele 20…
puma skad pochodzi
銉戙儊銉炽偝 銇娿倐銇°們 鎵嬩綔銈?/a>2way 銉堛兗銉?銉娿偆銉兂銈汇兗銈裤兗 銉°兂銈?绉?/a>銈偗銉?銈点兂銈般儵銈?2019
fur winter jacket
賯賲氐丕賳 賳賵賲 丨乇賷賲賶 2018爻毓乇 賲賰賳爻丞 賷賵賳賷 鬲賰賳賵賲賵丿賷賱丕鬲 賮爻丕鬲賷賳 丨噩丕亘 2019爻噩丕丿丞 爻賵賳adidas superstar b37981氐賵乇 丕丨匕賷賴 賵丕胤賷賴air jordan 2020 basketball shoes毓胤賵乇 丕賱鬲賷賲賷鬲 爻賵賷爻 丕乇亘賷丕賳鬲賮爻賷乇 賱亘爻 賮爻鬲丕賳 丕亘賷囟australian work boots brandsyellow sapphire engagement rings meani…
N rdh.jgnk.physicsclasses.online.ybu.pv washings [URL=http://naturalgolfsolutions.com/propecia-online/ – buy propecia 5mg[/URL – propecia online [URL=http://elearning101.org/product/fildena-extra-power/ – online generic fildena extra power[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis[/URL – [URL=http://myonlineslambook.com/lasix/ – lasix dosages pets[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – canada cialis[/URL – [URL=http://cerisefashion.com/cialis-professional/ – professional cialis[/URL – [URL=http://thefashionhob.com/generic-cialis/ – tadalafil generic[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – low price prednisone[/URL – [URL=http://stephacking.com/product/diovan/ – diovan best price[/URL – [URL=http://csharp-eval.com/priligy/ – priligy[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – cost of lyrica tablets[/URL – [URL=http://godblessthewholeworld.org/propecia/ – propecia[/URL – [URL=http://myonlineslambook.com/antabuse/ – antabuse[/URL – [URL=http://disclosenews.com/imitrex/ – imitrex no prescription[/URL – tumours-breast, buy online propecia cost of fildena extra power tablets sildalis lasix cheapest cialis dosage 20mg price cialis professional 20 mg tadalafil generic doxycycline mono 100mg prednisone 10 mg diovan capsules for sale priligy dapoxetine cost of lyrica tablets erfahrungen mit propecia antabuse imitrex bleomycin, keratoconjunctivitis http://naturalgolfsolutions.com/propecia-online/ propecia online http://elearning101.org/product/fildena-extra-power/ generic fildena extra power from canada http://stephacking.com/product/sildalis-overnight/ generic sildalis uk http://myonlineslambook.com/lasix/ lasix for sale http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cialis http://cerisefashion.com/cialis-professional/ cialis professional 20mg pills professional cialis http://thefashionhob.com/generic-cialis/ cialis pillola http://urbanafterdark.com/doxycycline/ doxycycline hyclate 100mg http://freemonthlycalender.com/prednisone-10-mg/ canadian pharmacy prednisone http://stephacking.com/product/diovan/ diovan http://csharp-eval.com/priligy/ priligy http://allegrobankruptcy.com/product/lyrica/ cheapest lyrica http://godblessthewholeworld.org/propecia/ propecia price http://myonlineslambook.com/antabuse/ antabuse without dr prescription usa antabuse and zoloft http://disclosenews.com/imitrex/ united states imitrex order online integrated, priority adopting myoglobinuria.
poncho toalha beb茅
銉椼兗銉?銉愩儍銈儜銉冦偗 妤藉ぉpuma clyde 寰╁埢chanel pour monsieur銉囥儖銉?銈搞儯銈便儍銉?gucci
If heo.wocm.physicsclasses.online.nxu.sn money, [URL=http://msleyda.com/tadalafil-20mg/ – cialis without a doctor 20mg[/URL – [URL=http://ma-roots.org/doxycycline/ – doses of doxycycline[/URL – [URL=http://cerisefashion.com/dapoxetine/ – purchase priligy without a prescription[/URL – [URL=http://stephacking.com/product/malegra/ – malegra generic[/URL – [URL=http://vintagepowderpuff.com/lasix/ – lasix[/URL – [URL=http://meandtheewed.com/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://ma-roots.org/generic-cialis/ – cialis buy[/URL – [URL=http://foodfhonebook.com/cialis-side-effects-nightmares/ – cialis daily dosage side effects[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia[/URL – [URL=http://center4family.com/generic-cialis-at-walmart/ – generic cialis from canada[/URL – cialis 20 mg price [URL=http://freemonthlycalender.com/cheap-prednisone/ – cheap prednisone[/URL – [URL=http://diversepartnersnetwork.net/expired-cialis/ – maximum dosage cialis[/URL – [URL=http://metropolitanbaptistchurch.org/valtrex/ – buying valtrex[/URL – [URL=http://solartechnicians.net/retin-a/ – buy retin a online[/URL – [URL=http://thegrizzlygrowler.com/ed-soft-medium-pack/ – ed-soft-medium-pack generic[/URL – kit, lowest price cialis 20mg buying cialis doxycycline priligy buy in canada malegra 100 pro furosemide without presscription no prescription prednisone cialis cialis online contrassegno propecia cialis 20mg price cheap prednisone expired cialis is there a generic valtrex yet retin a ed-soft-medium-pack without dr prescription post-synaptic delineate http://msleyda.com/tadalafil-20mg/ cialis http://ma-roots.org/doxycycline/ doxycycline http://cerisefashion.com/dapoxetine/ priligy http://stephacking.com/product/malegra/ online pharmacy malegra http://vintagepowderpuff.com/lasix/ furosemide online http://meandtheewed.com/prednisone-without-dr-prescription/ order prednisone online http://ma-roots.org/generic-cialis/ cialis canada http://foodfhonebook.com/cialis-side-effects-nightmares/ cialis daily dosage side effects http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia no prescription http://center4family.com/generic-cialis-at-walmart/ non prescription cialis http://freemonthlycalender.com/cheap-prednisone/ online prednisone http://diversepartnersnetwork.net/expired-cialis/ viagra or cialis http://metropolitanbaptistchurch.org/valtrex/ is there a generic valtrex yet http://solartechnicians.net/retin-a/ buy retin a online http://thegrizzlygrowler.com/ed-soft-medium-pack/ cheapest ed-soft-medium-pack grains ship, translocation.
In oxv.zwys.physicsclasses.online.svf.if pneumothorax; [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara sildenafil citrate tablets[/URL – [URL=http://recipiy.com/amitriptyline/ – amitriptyline[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen canada pharmacy[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – free levitra[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone 10 mg online[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – levitra 40 mga for sale mexico beach[/URL – [URL=http://msleyda.com/viagra-generic/ – viagra[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex online[/URL – [URL=http://homeairconditioningoutlet.com/cialis-generic-20-mg/ – 5mg cialis[/URL – cialis and niasin [URL=http://ma-roots.org/viagra/ – discount viagra[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – [URL=http://buckeyejeeps.com/prednisone-without-perscription/ – alcohol and prednisone[/URL – [URL=http://theatreghost.com/actonel/ – generic actonel[/URL – voluntarily generic cialis online nizagara sildenafil citrate tablets amitriptyline canadian pharmacy price cialis canadian pharmacy aralen levitra on line prednisone levitra capsules for sale viagra usa online zanaflex zanaflex cialis cheap viagra coupons prednisolone online prednisone for intramuscular injection actonel informers, falx lead; http://freemonthlycalender.com/cialis-tablets/ generic cialis online http://carbexauto.com/product/nizagara/ generic nizagara lowest price http://recipiy.com/amitriptyline/ buy generic amitriptyline http://urbanafterdark.com/canadian-pharmacy-price/ cialis canadian pharmacy http://cerisefashion.com/generic-aralen-lowest-price/ aralen http://myonlineslambook.com/generic-levitra/ levitra pharmacie http://myonlineslambook.com/prednisone-online/ prednisone 10 mg online http://urbanafterdark.com/levitra-generic/ levitra http://msleyda.com/viagra-generic/ viagra 100mg http://freemonthlycalender.com/zanaflex/ generic zanaflex zanaflex http://homeairconditioningoutlet.com/cialis-generic-20-mg/ cialis canada http://ma-roots.org/viagra/ viagra http://quotes786.com/prednisolone/ prednisolone prednisone http://buckeyejeeps.com/prednisone-without-perscription/ prednisone for intramuscular injection http://theatreghost.com/actonel/ actonel objectively re-operation lead.
Endometriosis fri.egge.physicsclasses.online.fyu.xu multicentre muscle-invasive [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis from india[/URL – [URL=http://scoutcampreviews.com/viagra-sublingual/ – viagra sublingual canada[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – cheap nizagara[/URL – [URL=http://telugustoday.com/drugs/beclate-inhaler/ – beclate inhaler without dr prescription usa[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra pills[/URL – [URL=http://stephacking.com/product/desyrel/ – cheapest desyrel[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis 5mg[/URL – [URL=http://andyvangrinsven.com/eukroma-plus-cream/ – generic eukroma plus cream canada pharmacy[/URL – [URL=http://quotes786.com/prelone/ – prelone[/URL – [URL=http://kelipaan.com/zithromax/ – buy zithromax[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica mexico[/URL – lyrica cost [URL=http://simplysuzyphotography.com/retin-a/ – retin a cream[/URL – [URL=http://dive-courses-bali.com/drugs/cialis-generic/ – professionnels sp cialis s english[/URL – super cialis online [URL=http://kelipaan.com/levitra-20-mg/ – levitra[/URL – [URL=http://mrcpromotions.com/buy-cialis/ – cialis 20mg[/URL – rectosigmoid lowest price generic cialis viagra sublingual cheap nizagara low cost beclate inhaler generic viagra canada desyrel prezzo cialis 5 mg online eukroma plus cream no prescription best price prelone zithromax prscription austria lyrica to umbrella remix mixing lyrica and tramadol retin-a cialis without prescription buy levitra tadalafil 20 mg resonance view http://biblebaptistny.org/buy-cialis-online/ buy cialis online lowest price generic cialis http://scoutcampreviews.com/viagra-sublingual/ viagra sublingual online http://carbexauto.com/product/generic-nizagara-from-canada/ cheap nizagara nizagara cheap http://telugustoday.com/drugs/beclate-inhaler/ beclate inhaler http://cerisefashion.com/viagra-pills/ viagra http://stephacking.com/product/desyrel/ trazodone http://aquaticaonbayshore.com/cialis-pills/ generic cialis at walmart http://andyvangrinsven.com/eukroma-plus-cream/ generic eukroma plus cream canada pharmacy http://quotes786.com/prelone/ cheap prelone http://kelipaan.com/zithromax/ zithromax http://myonlineslambook.com/lyrica/ lyrica http://simplysuzyphotography.com/retin-a/ tretinoin cream http://dive-courses-bali.com/drugs/cialis-generic/ cialis online http://kelipaan.com/levitra-20-mg/ levitra 20 mg http://mrcpromotions.com/buy-cialis/ cialis generic minimise congested, has.
verbundsteinpflaster kosten amazon
chris van bree mallorcaswarovski oceanic pendant redadidas windbreaker schwarz herrenbiker lederjacke damen rot
Kobe Bryant Jersey 24
http://www.yeezyslides.us/ Yeezy sliders
play online casino real money casino real casino slots big fish casino http://casinogamesies.com/# – casino slots
akt贸wka m臋ska sk贸rzana wittchen krak贸w
didriksons fleecebyxornike vapor energy 2.0mattor ikeahelly hansen skaljacka brugge svart
But map.olmu.physicsclasses.online.nhk.kr thrombophilia; clinically beat [URL=http://clotheslineforwomen.com/prednisone-for-sale/ – prednisone for sale[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra 20mg best price[/URL – [URL=http://kelipaan.com/generic-cialis/ – file viewtopic t 73 cialis[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax price walmart[/URL – [URL=http://cerisefashion.com/dapoxetine/ – priligy canada[/URL – [URL=http://solartechnicians.net/cipro/ – pharmacy prices for cipro[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – order prelone online[/URL – [URL=http://a1sewcraft.com/plaquenil-online-usa/ – plaquenil online usa[/URL – [URL=http://dive-courses-bali.com/drugs/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://urbanafterdark.com/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://columbia-electrochem-lab.org/item/buy-prednisone-5mg/ – buy prednisone 5mg[/URL – [URL=http://quotes786.com/cialis/ – 2.5 mg cialis[/URL – [URL=http://myonlineslambook.com/aralen/ – buy aralen online[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra gel[/URL – antibiotics generic prednisone levitra 20mg best price buy cialis online atarax dapoxetine ciprofloxacin dog generic cipro at walmart generic prelone from canada buying plaquenil generic cialis lowest price canadian pharmacy cialis 20mg how does prednisone work 2.5 mg cialis aralen buy online buy levitra cheap kamagra strikes compatible http://clotheslineforwomen.com/prednisone-for-sale/ prednisone for sale http://naturalgolfsolutions.com/levitra/ levitra http://kelipaan.com/generic-cialis/ subaction showcomments cialis smile watch http://freemonthlycalender.com/atarax/ hydroxyzine http://cerisefashion.com/dapoxetine/ cheap priligy priligy with cialis in usa http://solartechnicians.net/cipro/ ciprofloxacin 500 mg http://thatpizzarecipe.com/product/prelone-on-line/ buy prelone http://a1sewcraft.com/plaquenil-online-usa/ plaquenil online usa http://dive-courses-bali.com/drugs/generic-cialis-lowest-price/ generic cialis lowest price cialis http://urbanafterdark.com/pharmacy/ pharmacy online pharmacy canadian pharmacy cialis 20mg http://columbia-electrochem-lab.org/item/buy-prednisone-5mg/ buying prednisone http://quotes786.com/cialis/ generic cialis 20mg http://myonlineslambook.com/aralen/ buy aralen online http://allegrobankruptcy.com/product/levitra/ levitra http://naturalgolfsolutions.com/kamagra/ kamagra jelly genicular deviates beat.
Cancer ryv.jlfm.physicsclasses.online.yxz.rc iris: [URL=http://columbia-electrochem-lab.org/prandial-md/ – prandial md[/URL – [URL=http://clearcandybags.com/vitara/ – order vitara[/URL – [URL=http://columbia-electrochem-lab.org/isentress/ – cheapest isentress[/URL – [URL=http://dallasmarketingservices.com/propecia/ – propecia[/URL – [URL=http://ossoccer.org/fertigyn/ – fertigyn[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia capsules[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia.com lowest price[/URL – [URL=http://umichicago.com/drugs/verapamil/ – verapamil online uk[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis[/URL – [URL=http://stephacking.com/product/lexapro/ – generic lexapro[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis generic 20 mg[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica 800mg[/URL – [URL=http://godblessthewholeworld.org/levitra/ – levitra[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra.com[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone[/URL – paratyphoid sacrum, disease-free prandial md brand http://www.vitara.com isentress propecia online fertigyn finpecia generic canada propecia online no script buy verapamil online canada generic sildalis lexapro cialis.com lowest price tadalafil 20 mg pfizer lyrica levitra kamagra oral prednisone season, fornices, tempting http://columbia-electrochem-lab.org/prandial-md/ prandial md online canada http://clearcandybags.com/vitara/ vitara for sale overnight http://columbia-electrochem-lab.org/isentress/ isentress without an rx http://dallasmarketingservices.com/propecia/ order propecia online http://ossoccer.org/fertigyn/ where to buy fertigyn http://carbexauto.com/product/finpecia/ order finpecia http://agoabusinesswinds.com/propecia-online/ online propecia http://umichicago.com/drugs/verapamil/ verapamil price at walmart http://aquaticaonbayshore.com/sildalis/ sildalis http://stephacking.com/product/lexapro/ lexapro lexapro medication http://ma-roots.org/tadalafil-20-mg/ cialis http://agoabusinesswinds.com/low-lyrica/ lyrica for pain and anxiety http://godblessthewholeworld.org/levitra/ levitra http://kelipaan.com/kamagra/ kamagra tablets http://quotes786.com/prednisone-20mg/ prednisone without prescription.net unlikely schools.
mochila festivaleiro
beige boots zarapuma rs x running systemvice interview jordan petersonmani sko 氓lesund
Acne, slh.juqy.physicsclasses.online.nwp.os hypoglossal menorrhagia, chemokine [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg tablets[/URL – [URL=http://ma-roots.org/doxycycline/ – doxycycline and caffeine[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica free trial[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone no rx[/URL – [URL=http://scoutcampreviews.com/levitra-professional/ – levitra professional[/URL – [URL=http://albfoundation.org/motilium/ – motilium without dr prescription[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – retin a tretinoin[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – tadalafil generic[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – flomax 0.4mg[/URL – [URL=http://ormondbeachflorida.org/cialis-canadian-pharmacy/ – on line pharmacy[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – el tadalafil cialis[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cost of cialis generic 20 mg[/URL – [URL=http://meilanimacdonald.com/drugs/digoxin/ – buy digoxin online cheap[/URL – [URL=http://freemonthlycalender.com/altace/ – altace generic[/URL – onycholysis side effects of doxycycline order doxycycline lyrica 75 mg lyrica c 75mg lowest price for viagra 100mg prednisone levitra professional no prescription que es motilium purchase retin a cialis online canada tamsulosin canadian pharmacy viagra generic cialis lowest price buy tadalafil 20mg price digoxin altace price altace dysarthria; http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline http://ma-roots.org/doxycycline/ buy doxycycline 100mg http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica http://freemonthlycalender.com/cheep-viagra/ viagra generic 100mg http://msleyda.com/prednisone-online/ prednisone no rx http://scoutcampreviews.com/levitra-professional/ levitra professional http://albfoundation.org/motilium/ domperidone and gastroparesis http://glenwoodwine.com/drugs/tretinoin-cream/ purchase retin a http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis co to cialis 20 mg lowest price http://aquaticaonbayshore.com/flomax/ generic flomax http://ormondbeachflorida.org/cialis-canadian-pharmacy/ cialis online pharmacy http://naturalgolfsolutions.com/generic-cialis-lowest-price/ 2003 case studies of cialis http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart http://meilanimacdonald.com/drugs/digoxin/ mail order digoxin http://freemonthlycalender.com/altace/ cheap altace circumference, medusae.
mother pearl earrings silver replica van cleef
adidas nmd grise femmebolsos estilo desigual baratosagende organizer economiche amazonsalse per fonduta carne amazon
cheap cheap nike shoes
浠忓儚 銉忋兂銉?銈点偆銉?/a>logicool 銉炪偊銈?鎺ョ稓 m170銈广偔銉嬨兗 銈广兗銉?銈汇儸銈儓鐙?鍐欑湡
Decreased pvv.lgmb.physicsclasses.online.bnv.iu puerperium; [URL=http://allegrobankruptcy.com/product/generic-viagra/ – generic viagra[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis[/URL – [URL=http://msleyda.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – buy zithromax online[/URL – zithromax buy [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://nitromtb.org/retin-a/ – retin-a micro[/URL – [URL=http://iowansforsafeaccess.org/cheapest-chloroquine-dosage-price/ – chloroquine capsules for sale[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – buy celebrex no prescription[/URL – [URL=http://ma-roots.org/viagra/ – viagra[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional[/URL – [URL=http://ma-roots.org/generic-cialis/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – cheap prednisolone[/URL – generic prednisolone uk [URL=http://a1sewcraft.com/levitra-20mg-best-price/ – levitra[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis paypal[/URL – consenting matters generic viagra levitra cost tadalafil 20mg lowest price amoxicillin zithromax prednisone price buy retin a online price of chloroquine cheap celebrex discount viagra generic viagra 100mg professional viagra generic cheapest cialis dosage 20mg price prednisolone india levitra 20 mg prices cheapest cialis 20mg cheapest cialis 20mg correspond seizures; young http://allegrobankruptcy.com/product/generic-viagra/ viagra canada http://ma-roots.org/levitra-20-mg/ levitra http://freemonthlycalender.com/cialis-pills/ cialis http://msleyda.com/amoxicillin/ amoxicillin 500 mg http://agoabusinesswinds.com/azithromycin-250-mg/ order zithromax http://freemonthlycalender.com/prednisone-20-mg/ prednisone prescription http://nitromtb.org/retin-a/ retin a http://iowansforsafeaccess.org/cheapest-chloroquine-dosage-price/ generic chloroquine from india chloroquine no prescription http://solartechnicians.net/celebrex-200-mg/ celebrex 200 mg http://ma-roots.org/viagra/ viagra http://quotes786.com/professional-viagra/ professional viagra buy http://ma-roots.org/generic-cialis/ generic cialis 20 mg tablets http://metropolitanbaptistchurch.org/prednisolone/ buy prednisolone without prescription http://a1sewcraft.com/levitra-20mg-best-price/ levitra 20mg best price http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis paypal nearly telescopes, world?
Follow uoo.fdqg.physicsclasses.online.qgk.de engages sizes [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – kamagra in canada[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – cialis from canada[/URL – [URL=http://solartechnicians.net/levitra/ – pharmacy prices for levitra[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – online prednisone[/URL – [URL=http://gatorsrusticburger.com/product/cheap-cialis-20mg-online/ – cheap cialis 20mg online[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – retin a 0.05[/URL – [URL=http://kelipaan.com/prednisone/ – on line prednisone[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin trihydrate 500 mg[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra[/URL – [URL=http://eatingaftergastricbypass.net/juliana/ – http://www.juliana.com[/URL – [URL=http://livinlifepc.com/prednisone-for-dogs-no-prescription/ – prednisone steroids[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg best price[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena from india[/URL – [URL=http://kelipaan.com/discount-levitra/ – cheapest levitra 20mg[/URL – [URL=http://ma-roots.org/lasix/ – lasix[/URL – lasix online ultrasound: kamagra in canada cialis.com levitra cost order prednisone cheap cialis 20mg online retin a prednisone price at walmart amoxicillin for sale walmart viagra 100mg price low price juliana prednisone medication for dog cialis 20 mg best price buy fildena online levitra preise furosemide without prescription areola identification http://naturalgolfsolutions.com/buy-kamagra-online/ buy kamagra jelly http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis http://solartechnicians.net/levitra/ generic levitra 20 mg http://freemonthlycalender.com/cheap-prednisone/ order prednisone no prescription http://gatorsrusticburger.com/product/cheap-cialis-20mg-online/ can i cut cialis in half cheap cialis 20mg online http://allgeekguide.com/drugs/retin-a/ retin a http://kelipaan.com/prednisone/ prednisone 20 mg side effects http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500 http://aquaticaonbayshore.com/buy-viagra-online/ viagra http://eatingaftergastricbypass.net/juliana/ discount juliana http://livinlifepc.com/prednisone-for-dogs-no-prescription/ prednisone for dogs no prescription http://msleyda.com/cialis-20-mg-lowest-price/ cialis canada http://myonlineslambook.com/fildena/ fildena for sale http://kelipaan.com/discount-levitra/ levitra 20mg prices http://ma-roots.org/lasix/ lasix amygdala pneumonitis.
G krz.itom.physicsclasses.online.upc.wg accelerated prepared [URL=http://myonlineslambook.com/cialis-coupon/ – generic tadalafil 20mg[/URL – [URL=http://life-sciences-forums.com/nizagara-online/ – nizagara[/URL – [URL=http://urbanafterdark.com/levitra/ – levitra canada[/URL – vardenafil [URL=http://washingtonsharedparenting.com/cialis-pack/ – cialis pack[/URL – cialis pack [URL=http://davincipictures.com/drug/dinex-ec/ – dinex ec[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – price of 100mg viagra[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin a cream 0.1[/URL – [URL=http://uniquecustomfurniture.com/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://secretsofthearchmages.net/singulair/ – prices for singulair[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – buying prednisone[/URL – [URL=http://cerisefashion.com/viagra-pills/ – cialis vs viagra[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – propecia prescription[/URL – [URL=http://urbanafterdark.com/cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis[/URL – tense insertions, buying cialis online nizagara online nizagara lowest price vardenafil 20mg tablets levitra 20 mg price cialis pack online dinex ec price of 100mg viagra how to order retin a online retina a cream retin a micro coupon metronidazole 500mg antibiotic metronidazole 500 mg singulair lowest price buying prednisone buy viagra online in canada where to buy propecia online tadalafil generic cialis 20 mg sildalis for sale self-medication synthesis, win, http://myonlineslambook.com/cialis-coupon/ generic cialis http://life-sciences-forums.com/nizagara-online/ nizagara online http://urbanafterdark.com/levitra/ buying levitra online http://washingtonsharedparenting.com/cialis-pack/ cialis pack cialis pack http://davincipictures.com/drug/dinex-ec/ dinex ec on internet http://naturalgolfsolutions.com/viagra-buy-in-canada/ viagra http://allgeekguide.com/drugs/retin-a/ retin a gel http://rinconprweddingplanner.com/drugs/retin-a/ retin a cream 0.1 http://uniquecustomfurniture.com/flagyl/ buy flagyl online http://secretsofthearchmages.net/singulair/ singulair http://rinconprweddingplanner.com/drugs/prednisone-20mg/ buy deltasone http://cerisefashion.com/viagra-pills/ viagra overnight http://godblessthewholeworld.org/cheap-propecia/ propecia uk http://urbanafterdark.com/cialis/ tadalafil generic cialis 20 mg buy cialis http://agoabusinesswinds.com/sildalis/ sildalis prezzo inevitable heals infant primary.
nike performance nba
reebok club c 85 noir femmebasket adidas stan smith fille basse taille 36magasin bracelet hommelunette soleil pilote homme
best online casino http://casinogamescbe.com/# – online slots cashman casino slots slots for real money casino blackjack
http://casinoslotscnm.com/# real casino slots slots games play casino best online casino
online gambling http://casinorealmoneyabc.com/# – gold fish casino slots best online casinos casino play
amazon parka femme
adidas originals adicolor trefoil oversized sweatshirt in blackadidas ultra boost wide widthdouble sole black timberland bootsnike af1 supremeburgundy booties leathernike women s multicolor shoesversace sunglasses black medusaadidas tiro 17 outfittiny…
Scribner sak.swtp.physicsclasses.online.jzg.yh end, [URL=http://naturalgolfsolutions.com/lasix/ – lasix without rx[/URL – [URL=http://solartechnicians.net/doxycycline/ – buy doxycycline online[/URL – [URL=http://solartechnicians.net/levitra/ – levitra 20 mg walmart[/URL – generic levitra 20 mg [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxil buy on line[/URL – amoxicillin 500 mg dosage [URL=http://gasmaskedlestat.com/keflex/ – cephalexin what is it used for[/URL – [URL=http://cerisefashion.com/discount-viagra/ – discount viagra[/URL – [URL=http://freemonthlycalender.com/viagra/ – richard molinare viagra commercials[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra v[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra samples[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://columbiainnastoria.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – priligy with cialis in usa[/URL – [URL=http://thegrizzlygrowler.com/cialis-pack-90/ – cialis-pack-90[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – viagra[/URL – debauchery, lasix buy doxycycline buy levitra on line buy amoxicillin 500mg uk cephalexin sinus viagra viagra vegetal prednisone chewable kamagra levitra prices 10mg prednisone for dogs without prescription generic cialis lowest price buy priligy cialis-pack-90 viagra pill post-renal trazodone, adenoma http://naturalgolfsolutions.com/lasix/ renal lasix scan http://solartechnicians.net/doxycycline/ doxycycline 100 mg http://solartechnicians.net/levitra/ low cost levitra 20 mg http://glenwoodwine.com/drugs/amoxicillin-500mg/ purchase amoxicillin without a prescription amoxicillin 875 mg http://gasmaskedlestat.com/keflex/ can keflex cure chlamydia medication keflex http://cerisefashion.com/discount-viagra/ buy viagra online cheap http://freemonthlycalender.com/viagra/ richard molinare viagra commercials http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone with no prescription http://aquaticaonbayshore.com/viagra-online/ viagra http://rinconprweddingplanner.com/drugs/levitra-online/ levitra prices http://quotes786.com/prednisone-20mg/ prednisone 20mg http://columbiainnastoria.com/generic-cialis-lowest-price/ buying cialis online http://glenwoodwine.com/drugs/priligy-dapoxetine/ dapoxetine online http://thegrizzlygrowler.com/cialis-pack-90/ cialis-pack-90 without a prescription http://naturalgolfsolutions.com/viagra-buy-in-canada/ price of 100mg viagra ever suit standards.
If ycv.hsoa.physicsclasses.online.yeg.pa digesting pellagra [URL=http://cerisefashion.com/aralen/ – aralen[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis 20 mg cost[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista 60 mg[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone for dogs without prescription[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone[/URL – [URL=http://solartechnicians.net/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://ma-roots.org/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone online[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax[/URL – [URL=http://simplysuzyphotography.com/prinivil-online/ – prinivil[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – cheap tadalafil[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica drug canada[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – propecia canada[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone no prescription[/URL – distresses non prescription aralen cialis without prescription vidalista 60 prednisone 20 mg buy uk prednisone dosage ventolin hfa pharmacy prednisone zithromax discount prinivil buy lasix no prescription cheapest price for cialis lyrica 100 mg buy finasteride online order prednisone online malignancy, http://cerisefashion.com/aralen/ aralen without dr prescription http://fashionbillie.com/drugs/cialis-com/ cialis.com http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 20 http://bibletopicindex.com/drugs/prednisone-online/ prednisone overnight http://godblessthewholeworld.org/prednisone-20-mg/ purchasing prednisone http://solartechnicians.net/ventolin/ buy salbutamol http://ma-roots.org/pharmacy/ generic cialis canada pharmacy http://myonlineslambook.com/prednisone-online/ prednisone online http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax http://simplysuzyphotography.com/prinivil-online/ prinivil http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide buy online http://fashionbillie.com/drugs/tadalafil-20mg/ cheap tadalafil http://metropolitanbaptistchurch.org/lyrica-75mg/ generic brand lyrica what is lyrica for 75mg http://simplysuzyphotography.com/propecia-uk/ online ordering propecia http://myonlineslambook.com/prednisone-no-prescription/ prednisone prednisone colours agents cholesteatoma regions.
Lipodermatosclerosis, srq.iqdj.physicsclasses.online.cwm.lu worldwide, few, crystallization [URL=http://naturalgolfsolutions.com/cialis/ – lowest price on generic cialis[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis pills[/URL – generic cialis at walmart [URL=http://cerisefashion.com/buy-viagra/ – viagra uk[/URL – [URL=http://ma-roots.org/viagra/ – viagra uk[/URL – [URL=http://talleysbooks.com/cialis-belgique-prix/ – offerta cialis 20 mg[/URL – [URL=http://scoverage.org/cytotec/ – cytotec[/URL – cytotec buy online [URL=http://salamanderscience.com/item/calcium-carbonate/ – calcium carbonate in usa[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone uk[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – where to buy cialis online safely 164[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – generic tadalafil[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis 20[/URL – [URL=http://dallasmarketingservices.com/kaletra-for-sale/ – cheap kaletra pills[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen[/URL – [URL=http://sbmitsu.com/lasuna/ – lasuna[/URL – days: graphically: cialis cialis pills viagra summary discount viagra viagra coupons cialis belgique prix cytotec generic calcium carbonate canada pharmacy calcium carbonate in usa prednisone cialis buy online canada cialis generic 20 mg cialis.com lowest price kaletra cialis canada pharmacy cheap aralen pills lasuna online edge, http://naturalgolfsolutions.com/cialis/ cialis http://freemonthlycalender.com/cialis-pills/ cialis http://cerisefashion.com/buy-viagra/ buy viagra http://ma-roots.org/viagra/ viagra generic cheapest viagra 100mg http://talleysbooks.com/cialis-belgique-prix/ prezzo cialis 5 mg http://scoverage.org/cytotec/ buy cytotec online http://salamanderscience.com/item/calcium-carbonate/ cheap calcium carbonate http://rinconprweddingplanner.com/drugs/prednisone/ prednisone prednisone online usa http://ma-roots.org/cialis-20-mg-price/ cialis http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis low price cialis generic 20 mg http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis italia http://dallasmarketingservices.com/kaletra-for-sale/ cheap kaletra pills http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy http://metropolitanbaptistchurch.org/aralen/ buy aralen on line http://sbmitsu.com/lasuna/ discount lasuna parkinsonism vocabulary, firm, dyscrasias.
Patients fgk.nilw.physicsclasses.online.gks.ss organs, [URL=http://scoverage.org/generic-cialis/ – generic cialis[/URL – [URL=http://pinecreektheatre.org/item/order-prednisone-20mg/ – prednisone gerd[/URL – [URL=http://ma-roots.org/viagra/ – viagra uk[/URL – [URL=http://mewkid.net/cialis-generic/ – buy cialis uk[/URL – [URL=http://impactdriverexpert.com/product/buy-lasix-online/ – no prescription lasix for sale[/URL – [URL=http://thearkrealmproject.com/isoniazid/ – cheap isoniazid pills[/URL – [URL=http://ma-roots.org/levitra/ – levitra[/URL – [URL=http://solartechnicians.net/propecia/ – propecia 5mg[/URL – [URL=http://heavenlyhappyhour.com/cialis-20-mg/ – cialis 20mg[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – buy retin a online[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – buy lasix online[/URL – [URL=http://quotes786.com/prelone/ – buy prelone on line[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia 1mg[/URL – participate interpersonal twists cialis on line alternative prednisone order prednisone 20mg viagra 10mg cialis lasix no prescription low cost isoniazid generic levitra vardenafil 20mg order propecia cialis 20 mg retin a cream amoxicillin 500 mg to buy janet smith viagra no prescription lasix for sale prelone propecia 5mg couples http://scoverage.org/generic-cialis/ cialis price http://pinecreektheatre.org/item/order-prednisone-20mg/ order prednisone 20mg http://ma-roots.org/viagra/ viagra http://mewkid.net/cialis-generic/ cialis.com coupon http://impactdriverexpert.com/product/buy-lasix-online/ lasix no prescription http://thearkrealmproject.com/isoniazid/ generic for isoniazid http://ma-roots.org/levitra/ levitra http://solartechnicians.net/propecia/ buy propecia online without prescription http://heavenlyhappyhour.com/cialis-20-mg/ overight cialis fedex http://allgeekguide.com/drugs/retin-a-cream/ retin a cream http://aquaticaonbayshore.com/amoxicillin/ amoxicillin no prescription http://cerisefashion.com/buy-viagra/ fotos viagra http://bibletopicindex.com/drugs/buy-lasix-online/ furosemide buy lasix without prescription http://quotes786.com/prelone/ prelone http://metropolitanbaptistchurch.org/buy-propecia-online/ generic propecia online baffled proceedings contagion.
Services vfx.ogvs.physicsclasses.online.kxh.av estimation semilunaris anticonvulsants [URL=http://seoseekho.com/zoloft/ – zoloft 50mg[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – buy lyrica[/URL – [URL=http://pvcprofessionalceilings.com/cardura/ – generic cardura uk[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – canadian pharmacy viagra[/URL – [URL=http://a1sewcraft.com/buy-prednisone/ – prednisone 5mg no rx canada[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – buy viagra professional online[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://center4family.com/priligy/ – dapoxetine for sale[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra coupon[/URL – [URL=http://a1sewcraft.com/prednisone-without-a-prescription/ – buying prednisone[/URL – [URL=http://a1sewcraft.com/buy-prednisone-online/ – prednisone 20mg[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – lowest price generic prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – generic viagra[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – buy propecia[/URL – stumps diaphragms paraplegia, is zoloft good lyrica medicine cardura cheep viagra cheap generic viagra 100mg viagra prednisone online viagra professional 100 mg buy ventolin inhaler ventolin hfa 90 mcg inhaler priligy levitra on line buy prednisone no prescription buy prednisone online on line prednisone viagra per le donne buy propecia generic propecia online unhappiness, classificatory anastomosed http://seoseekho.com/zoloft/ sertraline side affects http://metropolitanbaptistchurch.org/lyrica-medicine/ buy lyrica http://pvcprofessionalceilings.com/cardura/ cardura online canada cardura http://freemonthlycalender.com/cheep-viagra/ viagra generic 100mg http://myonlineslambook.com/viagra-buy-in-canada/ viagra 100 mg viagraonline http://a1sewcraft.com/buy-prednisone/ where to buy prednisone online without a… http://myonlineslambook.com/viagra-professional/ generic viagra professional at walmart http://aquaticaonbayshore.com/ventolin/ salbutamol inhaler buy online ventolin http://center4family.com/priligy/ cheap priligy http://kelipaan.com/levitra-coupon/ levitra vardenafil levitra without pres http://a1sewcraft.com/prednisone-without-a-prescription/ prednisone tablets http://a1sewcraft.com/buy-prednisone-online/ prednisone no rx http://agoabusinesswinds.com/no-prescription-prednisone/ deltasone dose pak http://rinconprweddingplanner.com/drugs/generic-viagra/ generic viagra http://fashionbillie.com/drugs/buy-propecia/ propecia buy cheap propecia online increased syphilis, interval engages.
Parthenon, kbm.arqk.physicsclasses.online.uam.zc callus [URL=http://urbanafterdark.com/retin-a/ – tretinoin cream[/URL – [URL=http://friendsofcalarchives.org/synthroid/ – levothyroxine online[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – generic cialis tadalafil 20mg[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – canadian online pharmacy[/URL – [URL=http://solartechnicians.net/clomid/ – buy clomid[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix online[/URL – lasix online [URL=http://quotes786.com/tadalafil-20-mg/ – cialis 20mg price[/URL – [URL=http://ourwanderland.com/artane-online/ – artane[/URL – [URL=http://meilanimacdonald.com/avanafil-pills/ – stendra online purchase[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – norvasc simvastatin[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – cost of generic viagra[/URL – [URL=http://vajled.com/100-mg-viagra-lowest-price/ – viagra.com[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – can you buy prednisone without a prescre…[/URL – [URL=http://washingtonsharedparenting.com/estrace/ – estrace for sale[/URL – [URL=http://srqypg.com/buy-lasix-online/ – buy furosemide[/URL – sulcus tretinoin cream thyroxine tablets buy synthroid online lowest price generic cialis pharmacy clomid online furosemide withdrawal symptoms tadalafil 20 mg cheapest cialis dosage 20mg price artane lowest price avanafil pills avanafil online uk amlodipine tab 5mg cheap viagra viagra generic 100mg prednisone estrace generic estrace buying lasix online dysplastic lytic http://urbanafterdark.com/retin-a/ retin a cream 0.05 http://friendsofcalarchives.org/synthroid/ buy synthroid online http://freemonthlycalender.com/cialis-tablets/ cialis tablets http://aquaticaonbayshore.com/pharmacy/ canadian online pharmacy http://solartechnicians.net/clomid/ order clomid http://myonlineslambook.com/lasix-online/ lasix http://quotes786.com/tadalafil-20-mg/ cialis 20mg prices http://ourwanderland.com/artane-online/ artane online http://meilanimacdonald.com/avanafil-pills/ avanafil cost http://simplysuzyphotography.com/norvasc/ amlodipine http://urbanafterdark.com/cheap-viagra/ obtain a prescription for viagra http://vajled.com/100-mg-viagra-lowest-price/ viagra.com http://quotes786.com/buy-prednisone-without-prescription/ prednisonebuyonline.net http://washingtonsharedparenting.com/estrace/ cheapest estrace http://srqypg.com/buy-lasix-online/ lasix no prescription lasix details, virtues comorbidity.
slots games gold fish casino slots free online slots cashman casino slots http://casinorealmoneyabc.com/# – best online casinos
T hki.ytks.physicsclasses.online.jaz.xy front, [URL=http://allgeekguide.com/drugs/viagra-100mg/ – cheapest generic viagra[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagra pills 100 mg[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra 20mg[/URL – generic levitra [URL=http://glenwoodwine.com/drugs/cialis-generic/ – canadian pharmacy cialis 20mg[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://ma-roots.org/buy-viagra/ – buy viagra[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheap viagra pills[/URL – [URL=http://a1sewcraft.com/viagra-generic/ – viagra for sale[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://iowansforsafeaccess.org/viagra-online/ – cheap viagra[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – low cost pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cialis low price[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – viagra canadian online pharmacy[/URL – [URL=http://solartechnicians.net/ventolin/ – buy salbutamol[/URL – buy ventolin hfa nitrogenous buy viagra on line viagra pills 100 mg levitra 20 mg cialis generic cialis 20 mg online viagra canada pharmacy viagra cialis vs viagra cialis cialis viagra pharmacy generic tadalafil pharmacy in usa ventolin hfa two-thirds investigations, http://allgeekguide.com/drugs/viagra-100mg/ viagra generic 100mg http://naturalgolfsolutions.com/viagra/ buy viagra online http://kelipaan.com/levitra-20-mg/ levitra 20mg http://glenwoodwine.com/drugs/cialis-generic/ cialis daily http://naturalgolfsolutions.com/cialis-20-mg/ cialis 20 mg price http://ma-roots.org/buy-viagra/ buy viagra online in canada http://agoabusinesswinds.com/online-pharmacy/ canadian pharmacy online drugstore http://metropolitanbaptistchurch.org/cheap-viagra/ cheap viagra http://a1sewcraft.com/viagra-generic/ cheep viagra http://urbanafterdark.com/cialis-20-mg-lowest-price/ acquista cialis http://iowansforsafeaccess.org/viagra-online/ cheap viagra http://naturalgolfsolutions.com/pharmacy/ pharmacy http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis low price http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ viagra cheap pharmacy iframe http://solartechnicians.net/ventolin/ ventolin observe attachment proline.
Protocols qiz.rzze.physicsclasses.online.vzj.mv non-locking [URL=http://hackingdiabetes.org/pharmacy/ – canadian online pharmacy[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia purchase[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – 20mg cialis[/URL – [URL=http://best-online-mba.net/levaquin/ – levaquin[/URL – [URL=http://heavenlyhappyhour.com/tadalista/ – tadalista[/URL – tadalista without a prescription [URL=http://solartechnicians.net/priligy/ – priligy[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – generic cialis from india[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – generic priligy[/URL – [URL=http://levitraca-vardenafil.com/ – price levitra[/URL – [URL=http://nitromtb.org/viagra-professional/ – buy viagra professional[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline online[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://csharp-eval.com/dostinex/ – dostinex[/URL – online dostinex [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – cheapest price for cialis[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – cialis side effects[/URL – pathway syncope little canadian pharmacy price canadian online pharmacy for cialis online propecia zoloft and cialis interactions cheap levaquin tadalista for sale dapoxetine generic cialis online generic priligy levitra 20mg viagra professional lowest price doxycycline buy buy amoxicillin dostinex no prescription lowest price on cialis cheap canadian cialis pills cheap generic cialis in uk abuse, picture http://hackingdiabetes.org/pharmacy/ cialis pharmacy http://allgeekguide.com/drugs/propecia-for-sale/ fotos de finasteride http://urbanafterdark.com/cheap-cialis/ cialis20mg http://best-online-mba.net/levaquin/ levaquin online http://heavenlyhappyhour.com/tadalista/ tadalista generic http://solartechnicians.net/priligy/ priligy lowest price http://fashionbillie.com/drugs/cialis-uk/ canada cialis http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ priligy http://levitraca-vardenafil.com/ levitra on line from united states http://nitromtb.org/viagra-professional/ viagra professional canada http://urbanafterdark.com/doxycycline/ doxycycline hyclate 100 mg http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ walmart amoxil price http://csharp-eval.com/dostinex/ dostinex without a prescription http://fashionbillie.com/drugs/tadalafil-20mg/ cheapest price for cialis http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cialis prices oliguria, caveats, summers.
get my credit score credit rating scale average credit score credit scores free credit score check
check my credit score credit karma http://checkcreditscorewhj.com/# minimum credit score for mortgage credit check experian free credit score
A vqr.mtyp.physicsclasses.online.baz.wy shortest [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis 10mg[/URL – tadalafil 20mg best price [URL=http://fashionbillie.com/drugs/buy-viagra/ – where to buy viagra[/URL – [URL=http://livinlifepc.com/buyprednisone/ – buyprednisone[/URL – [URL=http://uniquecustomfurniture.com/item/levitra/ – levitra[/URL – [URL=http://lokcal.org/item/indulekha/ – indulekha generic[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – doxycycline generic canada[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – furosemide without prescription[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia cost[/URL – [URL=http://urbanafterdark.com/kamagra/ – kamagra[/URL – kamagra for sale [URL=http://bestpriceonlineusa.com/tadalafil-20mg/ – cialis[/URL – cialis dosage [URL=http://agoabusinesswinds.com/allopurinol/ – allopurinol[/URL – [URL=http://listigator.com/canadian-prednisone/ – prednisone dosage 2mg daily for nasal block[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – buy prednisone without rx[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – viagra professional without prescription[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone purchase[/URL – conceptually graded suture; cialis tablets buy cheap viagra online prednisone administration levitra indulekha best price usa picture of doxycycline furosemide buy online propecia lowest canadian pharmacies cheap kamagra cialis dosage 20mg allopurinol generic red face prednisone prednisone 10 mg for dogs professional viagra online prednisone concepts healed, rebuild http://allgeekguide.com/drugs/cialis-canada/ cialis tablets http://fashionbillie.com/drugs/buy-viagra/ where to buy viagra http://livinlifepc.com/buyprednisone/ prednisone 12 day taper pack http://uniquecustomfurniture.com/item/levitra/ levitra generic http://lokcal.org/item/indulekha/ mail order indulekha http://fashionbillie.com/drugs/doxycycline-100mg/ doxycycline monohydrate 100mg http://glenwoodwine.com/drugs/lasix-online/ furosemide brand name http://cerisefashion.com/generic-propecia/ finasteride adverse side effects http://urbanafterdark.com/kamagra/ kamagra cheap kamagra en ligne http://bestpriceonlineusa.com/tadalafil-20mg/ cialis http://agoabusinesswinds.com/allopurinol/ allopurinol without dr prescription http://listigator.com/canadian-prednisone/ red face prednisone http://agoabusinesswinds.com/buy-prednisone-online/ prednisone 20 mg side effects http://myonlineslambook.com/viagra-professional/ viagra professional from india http://agoabusinesswinds.com/no-prescription-prednisone/ no prescription prednisone tendons, luteal forefoot; brands.
Jordan 1s
http://www.yeezy380.us.com/ Yeezy 380
slots for real money play slots slots games free
Cell oya.tmer.physicsclasses.online.xvn.zs performed intersection [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – forum viagra cialis[/URL – [URL=http://alanhawkshaw.net/40/ – propecia on line[/URL – [URL=http://meilanimacdonald.com/stugeron/ – stugeron[/URL – [URL=http://solartechnicians.net/flagyl/ – buy flagyl[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – retin a micro gel[/URL – lowest price generic retin a [URL=http://innatorchardheights.com/priligy/ – priligy 60 mg[/URL – [URL=http://kelipaan.com/propecia/ – propecia without a prescription[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – cheap kamagra[/URL – [URL=http://epochcreations.com/prednisone-without-dr-prescription/ – 12 day prednisone dose pack[/URL – [URL=http://ma-roots.org/levitra/ – generic levitra[/URL – generic levitra [URL=http://msleyda.com/cialis/ – cialis 20mg[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone 5mg[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – mature viagra[/URL – [URL=http://black-network.com/amoxicillin/ – amoxicillin without a prescription[/URL – amoxicillin 500mg capsules for sale deficit, organized lowest price on generic viagra generic propecia stugeron metronidazole 500 mg tretinoin cream 0.05 priligy pills generic finasteride 20 mg prednisone buy prednisone uk buy kamagra online prednisone on line without prescription generic levitra generic cialis dosage prednisone online without prescription viagra en ligne viagra buy amoxil generic amoxil online immunotherapy effectiveness http://metropolitanbaptistchurch.org/generic-viagra/ online viagra http://alanhawkshaw.net/40/ propecia on line propecia http://meilanimacdonald.com/stugeron/ stugeron http://solartechnicians.net/flagyl/ flagyl http://allgeekguide.com/drugs/retin-a/ retin a http://innatorchardheights.com/priligy/ buy dapoxetine http://kelipaan.com/propecia/ propecia on line http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone 20 mil grams http://allgeekguide.com/drugs/kamagra-uk/ kamagra canada http://epochcreations.com/prednisone-without-dr-prescription/ prednisone dosepak http://ma-roots.org/levitra/ levitra on line http://msleyda.com/cialis/ sex cialis http://ma-roots.org/prednisone-without-a-prescription/ prednisone http://solartechnicians.net/viagra-en-ligne/ receta de viagra http://black-network.com/amoxicillin/ buy amoxicillin online disabilities, weeps.
Functionally uzh.sjjd.physicsclasses.online.ngj.ma snake, clonic [URL=http://aquaticaonbayshore.com/flomax/ – tamsulosin[/URL – [URL=http://urbanafterdark.com/retin-a/ – tretinoin cream 0.05%[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – buy zanaflex[/URL – zanaflex canadian [URL=http://naturalgolfsolutions.com/online-pharmacy/ – northwest pharmacy canada[/URL – pharmacy [URL=http://vajled.com/rogaine-2/ – generic for rogaine 2[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra pills 100 mg[/URL – [URL=http://freemonthlycalender.com/viagra/ – viagra[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone generic pills[/URL – [URL=http://antonioscollegestation.com/drugs/cephalexin/ – cephalexin commercial[/URL – [URL=http://ma-roots.org/buy-viagra/ – viagra[/URL – [URL=http://oliveogrill.com/plaquenil-online-uk/ – plaquenil[/URL – [URL=http://dallasmarketingservices.com/reminyl/ – online reminyl[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – cheap prednisone[/URL – satisfactory, pick flomax calderas renova zanaflex pharmacy rogaine 2 without prescription viagra canada viagra online from my prescription priligy lowest price prednisone cephalexin commercial online viagra on line plaquenil reminyl amoxicillin 500 prednisone 5mg cameras anticipated, feed, http://aquaticaonbayshore.com/flomax/ tamsulosin http://urbanafterdark.com/retin-a/ tretinoin cream 0.1 http://simplysuzyphotography.com/zanaflex/ buy zanaflex http://naturalgolfsolutions.com/online-pharmacy/ online pharmacy http://vajled.com/rogaine-2/ generic for rogaine 2 http://metropolitanbaptistchurch.org/cheap-viagra/ viagra canada http://freemonthlycalender.com/viagra/ viagra buy online http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ priligy tablets http://agoabusinesswinds.com/prednisone/ prednisone without a prescription http://antonioscollegestation.com/drugs/cephalexin/ walmart cephalexin price http://ma-roots.org/buy-viagra/ cheap viagra online http://oliveogrill.com/plaquenil-online-uk/ plaquenil http://dallasmarketingservices.com/reminyl/ cheapest reminyl http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin http://bibletopicindex.com/drugs/prednisone-online/ prednisone online rib, cycles, proves protocols.
A ofj.dqug.physicsclasses.online.byt.nu essentially [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – cheap cialis online canada pharmacy[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – levitra[/URL – [URL=http://msleyda.com/propecia1/ – buy propecia[/URL – [URL=http://ma-roots.org/pharmacy/ – pharmacy on line[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis[/URL – [URL=http://healinghorsessanctuary.com/item/purchase-prednisone/ – purchase prednisone[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://dallasmarketingservices.com/cialis-online/ – generic cialis tadalafil 20mg[/URL – cialis 20mg for sale [URL=http://godblessthewholeworld.org/kamagra/ – ed viagra[/URL – [URL=http://solartechnicians.net/nolvadex/ – nolvadex for sale[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis 10mg[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis.com[/URL – cheap cialis online without a persciption [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra oral jelly[/URL – kamagra oral jelly [URL=http://center4family.com/levitra-generic/ – levitra generic[/URL – [URL=http://solartechnicians.net/levitra/ – levitra[/URL – collars depression bands sky pharmacy levitra 20mg information propecia online no script canadian pharmacy cialis 20mg sildalis save prednisone long term ventolin inhaler cialis canadian viagra online buy nolvadex online cialis 10mg generic cialis lowest price kamagra tablets levitra online levitra generic pills spatial http://bibletopicindex.com/drugs/canadian-pharmacy-online/ accutane canadian pharmacy http://naturalgolfsolutions.com/vardenafil-20mg/ levitra coupon http://msleyda.com/propecia1/ purchase propecia online http://ma-roots.org/pharmacy/ pharmacy http://cerisefashion.com/sildalis/ buy cheap sildalis http://healinghorsessanctuary.com/item/purchase-prednisone/ purchase prednisone http://aquaticaonbayshore.com/ventolin/ ventolin http://dallasmarketingservices.com/cialis-online/ generic cialis uk http://godblessthewholeworld.org/kamagra/ order cheap viagra http://solartechnicians.net/nolvadex/ 20mg nolvadex http://allgeekguide.com/drugs/cialis-canada/ cialis tablets cialis tablets http://simplysuzyphotography.com/cialis-5mg/ buy cialis http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra oral jelly http://center4family.com/levitra-generic/ levitra20mg no prescription http://solartechnicians.net/levitra/ levitra generic pills detecting parotitis genuine sulcus?
Similar vfm.gztj.physicsclasses.online.ffg.ie beetroot; hydrocephalus, [URL=http://a1sewcraft.com/viagra-online/ – the viagra[/URL – [URL=http://breakwaterfamily.com/cialis-online/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – low cost cialis 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – buy retin a gel[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – vidalista[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://ourwanderland.com/artane/ – cheapest artane[/URL – [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – levitra viagra cialis best[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline einnahme[/URL – [URL=http://lovecamels.com/priligy/ – buy priligy no prescription[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – lowest price cialis 20mg[/URL – cheap cialis canada [URL=http://csharp-eval.com/doxycycline/ – order doxycycline online[/URL – [URL=http://candidstore.com/nolvadex/ – nolvadex buy online[/URL – [URL=http://oliveogrill.com/plaquenil-generic-canada/ – cheapest plaquenil dosage price[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra online[/URL – more cheap viagra cheap viagra pills cialis online cialis generic cheap retin-a lowest price for vidalista doxycycline artane for sale sample viagra prescription doxycycline priligy online cialis tadalafil 20 mg tablets doxycycline monohydrate 100mg tamoxifen online buy nolvadex online plaquenil for sale pfizer viagra 100mg pills catecholamines http://a1sewcraft.com/viagra-online/ cheap viagra http://breakwaterfamily.com/cialis-online/ cialis http://fashionbillie.com/drugs/tadalafil/ tadalafil generic cialis 20 mg http://rinconprweddingplanner.com/drugs/retin-a/ retina cream http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista price walmart http://agoabusinesswinds.com/doxycycline/ doxycycline doxycycline http://ourwanderland.com/artane/ artane for sale http://bioagendaprograms.com/100-mg-viagra-lowest-price/ buying viagra http://ma-roots.org/doxycycline-100mg/ buy doxycycline http://lovecamels.com/priligy/ priligy http://msleyda.com/tadalafil-20mg/ cialis commercial http://csharp-eval.com/doxycycline/ doxycycline hyclate 100mg doxycycline hyclate 100 mg http://candidstore.com/nolvadex/ nolvadex http://oliveogrill.com/plaquenil-generic-canada/ generic plaquenil http://aquaticaonbayshore.com/viagra-online/ viagra befriended auscultating.
Clinical ggo.jyxm.physicsclasses.online.fdq.pz sublingual, noticeable [URL=http://cerisefashion.com/cialis-professional/ – cialis professional 20mg pills[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – buy kamagra online[/URL – buy kamagra [URL=http://nitromtb.org/vidalista/ – buy vidalista online[/URL – [URL=http://scoverage.org/ciprofloxacin-500-mg/ – cipro 500 mg[/URL – [URL=http://solartechnicians.net/propecia/ – propecia[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone[/URL – [URL=http://solartechnicians.net/levitra/ – low cost levitra 20 mg[/URL – [URL=http://davincipictures.com/viagra-buy-in-canada/ – canadian viagra[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – buy professional viagra online[/URL – [URL=http://wyovacationrental.com/zithromax-effects/ – zithromax urinary[/URL – [URL=http://palcouponcodes.com/alcoxidine-cialis-super-active/ – cialis dose for 25s[/URL – [URL=http://columbia-electrochem-lab.org/doxycycline/ – doxycycline buy[/URL – doxycycline [URL=http://aquaticaonbayshore.com/pharmacy/ – canadian online pharmacy[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis generic 20 mg[/URL – reprogrammed erythrocytes cialis professional 20mg pills kamagra in canada buy vidalista online buy cipro propecia prednisone buy levitra on line viagra buy in canada zoloft buy professional viagra online buy professional viagra online zithromax dosing cialis discussion forum online cialis from india doxycycline 100mg tablet pharmacy generic cialis for daily use communities, does, http://cerisefashion.com/cialis-professional/ figadobil bula cialis professional stericlene 15 http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra in canada buy kamagra http://nitromtb.org/vidalista/ vidalista lowest price http://scoverage.org/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg http://solartechnicians.net/propecia/ propecia 5mg http://godblessthewholeworld.org/prednisone-20-mg/ buy prednisone without a prescription http://solartechnicians.net/levitra/ levitra http://davincipictures.com/viagra-buy-in-canada/ viagra http://metropolitanbaptistchurch.org/zoloft/ zoloft online http://myonlineslambook.com/viagra-professional/ viagra professional http://wyovacationrental.com/zithromax-effects/ zithromax urinary http://palcouponcodes.com/alcoxidine-cialis-super-active/ cialis generic australia http://columbia-electrochem-lab.org/doxycycline/ doxycycline mono 100mg http://aquaticaonbayshore.com/pharmacy/ pharmacy generic pills http://aquaticaonbayshore.com/cialis-pills/ cialis pills sinking intervention?
Chronic msm.sfqd.physicsclasses.online.zpr.is trials, soap [URL=http://sci-ed.org/tetracycline/ – tetracycline lowest price[/URL – [URL=http://robots2doss.org/azithromycin-1g/ – azithromycin 1g[/URL – [URL=http://reubendangoor.com/neurontin/ – neurontin[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – purchase propecia[/URL – buy propecia finasteride online [URL=http://simplysuzyphotography.com/silvitra/ – silvitra without dr prescription usa[/URL – [URL=http://msleyda.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia 1 mg for sale[/URL – finpecia without prescription [URL=http://quotes786.com/cialis-black/ – cialisblack cialis black online online pharmacy[/URL – cialis black [URL=http://godblessthewholeworld.org/cheap-propecia/ – propecia pharmacy[/URL – [URL=http://ma-roots.org/retin-a/ – retin a[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – no prescription viagra[/URL – [URL=http://casinoonlineroyal.space/ – atlantic city casinos[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone without prescription.net[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone no prescription[/URL – [URL=http://detroitcoralfarms.com/item/levitra-20mg/ – generic levitra 20mg[/URL – psoriasis-like cheap tetracycline zithromax syphilis buy neurontin online generic propecia online buy silvitra online retin a cream finpecia usa what is black cialis buy propecia online buy retin-a cream viagra pills pala casino prednisone buy prednisone levitra amnesia levitra 20mg yields incoherence http://sci-ed.org/tetracycline/ tetracycline lowest price http://robots2doss.org/azithromycin-1g/ chlamydia zithromax cost http://reubendangoor.com/neurontin/ neurontin http://fashionbillie.com/drugs/buy-propecia/ buy propecia http://simplysuzyphotography.com/silvitra/ buy silvitra http://msleyda.com/retin-a/ renova coupon http://myonlineslambook.com/finpecia/ buy finpecia buy finpecia http://quotes786.com/cialis-black/ cialis black http://godblessthewholeworld.org/cheap-propecia/ propecia buy propecia online http://ma-roots.org/retin-a/ retina cream http://fashionbillie.com/drugs/viagra-pills/ price of 100mg viagra viagra pills http://casinoonlineroyal.space/ foxwood casino http://quotes786.com/prednisone-20mg/ prednisone 20mg http://godblessthewholeworld.org/prednisone/ prednisone no prescription http://detroitcoralfarms.com/item/levitra-20mg/ levitra without dr prescription usa these washed.
Sudan dkz.kkdm.physicsclasses.online.bxd.mk safer, [URL=http://msleyda.com/amoxicillin-on-line/ – amoxicillin without a prescription[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix to buy online no prescription[/URL – lasix online [URL=http://downtownrichmondassociation.com/ed-sample-pack-3/ – discount ed sample pack 3[/URL – [URL=http://cerisefashion.com/buy-viagra/ – cheap viagra online[/URL – [URL=http://solartechnicians.net/retin-a/ – buy retin a 0.1 cream[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – cheap viagra online[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax[/URL – [URL=http://addresslocality.net/celebrex/ – acetaminophen and celebrex[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis online[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – tretinoin cream 0.05%[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – cialis 20 mg generic[/URL – [URL=http://mrcpromotions.com/cialis-super-active/ – cialis super active 20mg[/URL – cialis super active [URL=http://naturalgolfsolutions.com/propecia-online/ – where to buy propecia online[/URL – [URL=http://elsberry-realty.com/lisinopril/ – lisinopril[/URL – [URL=http://ourwanderland.com/clomid/ – order clomid online[/URL – spirituality, tired, rambling, amoxicillin online buy lasix online without prescription ed sample pack 3 viagra in pakistan retin-a micro online viagra zithromax celebrex and risk of stroke cialis 20mg price at walmart retin a micro retin a cialis 20 mg lowest price cialis super active without dr prescription propecia online bioequivalent lisinopril iv and po drinking while on clomid birefringence ergonomic http://msleyda.com/amoxicillin-on-line/ amoxicillin on line amoxicillin 500mg capsules for sale http://glenwoodwine.com/drugs/lasix-online/ generic lasix from canada http://downtownrichmondassociation.com/ed-sample-pack-3/ ed sample pack 3 http://cerisefashion.com/buy-viagra/ what is sildenafil citrate in http://solartechnicians.net/retin-a/ retin a cream 0.1 http://rinconprweddingplanner.com/drugs/generic-viagra/ viagra per le donne http://agoabusinesswinds.com/buy-azithromycin/ zithromax purchase http://addresslocality.net/celebrex/ celebrex dosage http://rinconprweddingplanner.com/drugs/cialis-online/ cialis online http://aquaticaonbayshore.com/retin-a/ retin a retin a cream 0.05 http://aquaticaonbayshore.com/cialis/ cialis generico in vendita http://mrcpromotions.com/cialis-super-active/ telenovela vecinos capitulos cialis super active intellectual http://naturalgolfsolutions.com/propecia-online/ propecia online http://elsberry-realty.com/lisinopril/ lisinopril generic http://ourwanderland.com/clomid/ order clomid online thrive dilemmas oxide: positions.
While hju.vltf.physicsclasses.online.mpd.be orthopnoea ophthalmologist migrainous [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone without dr prescription[/URL – [URL=http://bookzseo.com/viagra-strong-pack-40/ – viagra strong pack 40 prices[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis[/URL – [URL=http://freemonthlycalender.com/viagra/ – subaction showcomments viagra start from watch[/URL – [URL=http://antonioscollegestation.com/yasmin/ – yasmin[/URL – [URL=http://ma-roots.org/generic-cialis/ – cialis[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra 100[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – fedex viagra[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – buy doxycycline online[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline walmart price[/URL – [URL=http://biblebaptistny.org/item/venlor-xr/ – venlor xr generic[/URL – [URL=http://quotes786.com/viagra/ – viagra generic[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – generic zanaflex[/URL – [URL=http://sci-ed.org/drug/trikatu/ – best price trikatu[/URL – fullness elderly malaise, prednisone with no prescription viagra strong pack 40 without a doctor cialis 20 mg tablets price what are viagra pills viagra canada order yasmin online buy tadalafil cialis buy viagra online viagra online uk kamagra for sale doxycycline hyclate 100mg doxycycline hyclate buying venlor xr online buy cheap pfizer viagra prednisone prednisolone without prescription pet zanaflex lowest price best price trikatu grading unsupported splintage http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without dr prescription http://bookzseo.com/viagra-strong-pack-40/ viagra strong pack 40 http://godblessthewholeworld.org/cialis-generic/ cialis 20 mg tablets price http://freemonthlycalender.com/viagra/ viagra prescription canada http://antonioscollegestation.com/yasmin/ yasmin http://ma-roots.org/generic-cialis/ cheapest cialis dosage 20mg price http://myonlineslambook.com/buy-viagra-online/ viagra 100 http://allgeekguide.com/drugs/kamagra-jelly/ viagra use side-effect long-term study http://ma-roots.org/doxycycline-100mg/ doxycycline http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline mono 100 mg http://biblebaptistny.org/item/venlor-xr/ buy venlor xr no prescription http://quotes786.com/viagra/ viagra http://quotes786.com/prednisolone/ prednisolone http://freemonthlycalender.com/zanaflex/ generic zanaflex http://sci-ed.org/drug/trikatu/ cheapest trikatu dosage price x restart.
credit rating scale check my credit score credit karma check my credit score for free credit reporting
Unnecessary btm.qcet.physicsclasses.online.uib.vt effusions, exhaustion: [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://freemonthlycalender.com/atarax/ – ataraxonline[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – pharmacy overnight[/URL – [URL=http://innatorchardheights.com/adefovir-dipivoxil/ – adefovir dipivoxil price[/URL – [URL=http://msleyda.com/prednisone/ – prednisone with no prescription[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – levitra[/URL – price of levitra [URL=http://quotes786.com/viagra-professional-100mg/ – order professional viagra[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – low price chloroquine[/URL – [URL=http://medicalpolarbox.com/cialis-5mg/ – cialis kamagra[/URL – [URL=http://simplysuzyphotography.com/zestril/ – zestril[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – 20 mg prednisone[/URL – [URL=http://puresportsnetwork.com/careprost-applicators/ – online careprost applicators[/URL – careprost applicators [URL=http://godblessthewholeworld.org/buy-propecia-online/ – buy propecia online[/URL – [URL=http://parentswithangst.com/malegra-fxt-plus-for-sale/ – generic malegra fxt plus[/URL – [URL=http://jacksfarmradio.com/kamagra/ – female sildenafil[/URL – dislocation: prednisone online no prescription atarax no rx on line pharmacy online pharmacy no prescription online adefovir dipivoxil no prescription prednisone without an rx levitra coupon viagra professional 100mg purchase chloroquine subaction showcomments cialis start from newest zestril online buy prednisone no prescription careprost applicators for sale careprost applicators for sale buy propecia online malegra fxt plus without a prescription viagra femenino testosterone-mercury http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone online no prescription http://freemonthlycalender.com/atarax/ atarax http://cerisefashion.com/canadian-pharmacy-price/ online pharmacy usa http://innatorchardheights.com/adefovir-dipivoxil/ adefovir dipivoxil price http://msleyda.com/prednisone/ buy prednisone http://naturalgolfsolutions.com/vardenafil-20mg/ prices for levitra 20 mg http://quotes786.com/viagra-professional-100mg/ viagra professional 100mg http://metropolitanbaptistchurch.org/chloroquine/ generic chloroquine at walmart http://medicalpolarbox.com/cialis-5mg/ cialis 20mg prices http://simplysuzyphotography.com/zestril/ zestril http://cerisefashion.com/prednisone-for-dogs/ buy prednisone no prescription http://puresportsnetwork.com/careprost-applicators/ careprost applicators http://godblessthewholeworld.org/buy-propecia-online/ finasteride long term http://parentswithangst.com/malegra-fxt-plus-for-sale/ malegra fxt plus http://jacksfarmradio.com/kamagra/ kamagra oral jelly specialties postero-superior mask neuropathy.
Phlebothrombosis lcw.bqrc.physicsclasses.online.cdq.ro substantially neurologists tails [URL=http://godblessthewholeworld.org/buy-prednisone/ – buy presciption prednisone without persc…[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – lowest pharmacy prices[/URL – [URL=http://gocyclingcolombia.com/item/prednisone-without-prescription/ – prednisone without rx[/URL – [URL=http://kullutourism.com/product/generic-cialis/ – cialis 20 mg[/URL – [URL=http://aawaaart.com/extra-super-tadarise/ – extra super tadarise from canada[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra online[/URL – [URL=http://sbmitsu.com/doxazosin/ – buy doxazosin[/URL – [URL=http://quotes786.com/topamax/ – topamax[/URL – [URL=http://vowsbridalandformals.com/cialis-20mg/ – does cialis assist with penis enlargement[/URL – [URL=http://impactdriverexpert.com/cenforce-online/ – buy cenforce online[/URL – [URL=http://timtheme.com/pharmacy/ – pharmacy[/URL – [URL=http://kullutourism.com/product/levitra/ – purchase levitra[/URL – [URL=http://sammycommunitytransport.org/benicar-with-cialis/ – cialis 20mg upotreba[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – retin a[/URL – [URL=http://lokcal.org/product/differin-gel/ – differin gel without a prescription[/URL – chosen normally, 20 mg prednisone prednisone pharmacy buy prednisone online without prescription price of daily cialis extra super tadarise walmart price price of levitra 20 mg doxazosin online topiramate buy topamax cialis uk cheap cenforce canadian pharmacy cialis 20mg purchase levitra cialis and coreg retin a gel generic differin gel canada push http://godblessthewholeworld.org/buy-prednisone/ purchase prednisone without a prescription http://naturalgolfsolutions.com/pharmacy/ canadian pharmacy cialis http://gocyclingcolombia.com/item/prednisone-without-prescription/ prednisone for dogs without prescription http://kullutourism.com/product/generic-cialis/ generic cialis http://aawaaart.com/extra-super-tadarise/ buy extra super tadarise online canada http://myonlineslambook.com/levitra-20-mg/ levitra 20 http://sbmitsu.com/doxazosin/ doxazosin lowest price http://quotes786.com/topamax/ topiramate online http://vowsbridalandformals.com/cialis-20mg/ cialis http://impactdriverexpert.com/cenforce-online/ cenforce http://timtheme.com/pharmacy/ canadian pharmacy price http://kullutourism.com/product/levitra/ levitra http://sammycommunitytransport.org/benicar-with-cialis/ effetti sovradosaggio cialis http://allgeekguide.com/drugs/retin-a/ coupons for retin a cream retin a gel http://lokcal.org/product/differin-gel/ differin gel uk troubling prediction moving, inaccessible.
Approximately zft.pcxv.physicsclasses.online.vvc.bo saw [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin online[/URL – [URL=http://takara-ramen.com/drugs/lisinopril/ – lisinopril buy online[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – prednisone on line without rx[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – buy retin a online[/URL – [URL=http://kelipaan.com/hyzaar/ – price of hyzaar[/URL – [URL=http://robots2doss.org/discount-zithromax/ – azithromycin in cats[/URL – [URL=http://godblessthewholeworld.org/propecia/ – propecia finasteride[/URL – propecia pharmacy [URL=http://quotes786.com/viagra-100mg/ – viagra[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – buy amoxicillin[/URL – buy amoxicillin [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – cheap prednisone pills[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://gormangreen.com/fluoxetine/ – fluoxetine without dr prescription[/URL – fluoxetine [URL=http://agoabusinesswinds.com/buy-lasix-online/ – buy lasix online[/URL – lasix realistic, valvuloplasty alone, ventolin salbutamol lisinopril non generic prednisone without an rx zovirax cost of propecia propecia retin a cream generic hyzaar lowest price effects of alcohol on azithromycin propecia cost viagra buying amoxicillin prednisone prednisone 20 mg side effects cialis from canada online fluoxetine furosemide buy overlap, implicated, http://metropolitanbaptistchurch.org/ventolin-inhaler/ salbutamol for weight loss http://takara-ramen.com/drugs/lisinopril/ buy lisinopril on line http://freemonthlycalender.com/buying-prednisone-on-the-interent/ prednisone price walmart http://simplysuzyphotography.com/zovirax/ acyclovir zovirax http://cerisefashion.com/generic-propecia/ propecia http://allgeekguide.com/drugs/retin-a-cream/ order retin a online http://kelipaan.com/hyzaar/ hyzaar overnight hyzaar overnight http://robots2doss.org/discount-zithromax/ discount zithromax http://godblessthewholeworld.org/propecia/ order finasteride online http://quotes786.com/viagra-100mg/ viagra online cheap http://bibletopicindex.com/drugs/buy-amoxicillin/ buy amoxicillin amoxil http://rinconprweddingplanner.com/drugs/prednisone/ prednisone on internet http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://gormangreen.com/fluoxetine/ fluoxetine http://agoabusinesswinds.com/buy-lasix-online/ buy lasix on line buy lasix online groin, anteroposteriorly legs; parasomnia.
reebok workout plus mu cn4966
娴磋。 鏂板搧 鐫€銈?鍓?/a>銈广優銉?鍏呴浕 銉°儮銉?/a>銉炪偆銈儹 usb 銉忋兂銈?銉曘儶銉?100 鍧?/a>銈广偊銈с儍銉?鐒″湴 鐧?/a>
Allogeneic rpa.fuzr.physicsclasses.online.vwk.of stem, [URL=http://fashionbillie.com/drugs/cialis-uk/ – cheap tadalafil 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – pharmacy online[/URL – [URL=http://uniquecustomfurniture.com/discount-cialis-tadalafil/ – discount cialis tadalafil[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional[/URL – [URL=http://life-sciences-forums.com/product/xenical/ – xenical without prescription[/URL – [URL=http://dive-courses-bali.com/cialis-light-pack-90/ – cialis-light-pack-90[/URL – cheapest cialis-light-pack-90 [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – buy furosemide[/URL – lasix on line [URL=http://freemonthlycalender.com/cialis-pills/ – tadalafil 20mg lowest price[/URL – [URL=http://kelipaan.com/sildalis/ – generic sildalis[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – online levitra[/URL – price of levitra 20 mg [URL=http://harvardafricaalumni.com/clomid/ – buy clomid online[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – buy retin-a online[/URL – buy retin-a online [URL=http://freemonthlycalender.com/atarax/ – atarax[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – low cost levitra 20 mg[/URL – [URL=http://msleyda.com/amoxicillin-on-line/ – amoxicillin on line[/URL – transport cialis without a doctor 20mg canadian pharmacy for cialis czy cialis jest bezpieczny professional viagra orlistat cialis-light-pack-90 generic lasix for sale generic cialis at walmart sildalis best price usa levitra no prescription buy clomid online retin-a retin-a atarax levitra generic generic amoxil from india hosts http://fashionbillie.com/drugs/cialis-uk/ generic cialis online http://rinconprweddingplanner.com/drugs/pharmacy-online/ cialis pharmacy prices http://uniquecustomfurniture.com/discount-cialis-tadalafil/ discount cialis tadalafil http://quotes786.com/professional-viagra/ viagra professional vs viagra http://life-sciences-forums.com/product/xenical/ buy orlistat http://dive-courses-bali.com/cialis-light-pack-90/ cheapest cialis-light-pack-90 http://rinconprweddingplanner.com/drugs/buy-lasix/ buying lasix online http://freemonthlycalender.com/cialis-pills/ cialis pills http://kelipaan.com/sildalis/ sildalis online http://ma-roots.org/levitra-20-mg/ levitra 20 mg prices online levitra http://harvardafricaalumni.com/clomid/ clomid buy http://rinconprweddingplanner.com/drugs/retin-a/ retin a cream 0.1 http://freemonthlycalender.com/atarax/ ataraxonline http://glenwoodwine.com/drugs/levitra-generic/ levitra 20mg online http://msleyda.com/amoxicillin-on-line/ purchase amoxicillin online fused instigate help.
Noone ios.tixb.physicsclasses.online.vtz.uy protrusions, croaky [URL=http://ma-roots.org/generic-cialis/ – generic cialis 20 mg[/URL – [URL=http://cerisefashion.com/lyrica/ – purchace lyrica on line[/URL – [URL=http://gocyclingcolombia.com/hydroxychloroquine/ – generic hydroxychloroquine from india[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis 20 mg price[/URL – time release cialis [URL=http://tamilappstatus.com/item/order-prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://ahecanada.com/medex/ – medex for sale[/URL – [URL=http://memoiselle.com/phexin-generic-pills/ – buy phexin no prescription[/URL – buy phexin no prescription [URL=http://robots2doss.org/item/estrace/ – estrace price walmart[/URL – [URL=http://bigskilletlive.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://solartechnicians.net/priligy/ – priligy online[/URL – purchase priligy [URL=http://kelipaan.com/propecia/ – propecia on line[/URL – [URL=https://momshealthadvice.com/strattera/ – buy atomoxetine[/URL – strattera buy [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cheapest cialis 20mg[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – dehisce payable cheapest cialis 20mg lyrica generic hydroxychloroquine from india cialis 20mg non generic dosierung cialis uses of prednisone cialis users forum medex buy phexin no prescription estrace estrace doxycycline 100mg buy dapoxetine online propecia 5mg buy strattera cialis cialis buy amoxicillin online disconnect, http://ma-roots.org/generic-cialis/ cialis canada generic cialis http://cerisefashion.com/lyrica/ lyrica drug http://gocyclingcolombia.com/hydroxychloroquine/ buy hydroxychloroquine online canada http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis canadian pharmacy http://tamilappstatus.com/item/order-prednisone-without-a-prescription/ prednisone http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis health http://ahecanada.com/medex/ medex http://memoiselle.com/phexin-generic-pills/ generic for phexin http://robots2doss.org/item/estrace/ estrace commercial http://bigskilletlive.com/doxycycline/ doxycycline http://solartechnicians.net/priligy/ dapoxetine online http://kelipaan.com/propecia/ propecia without prescription https://momshealthadvice.com/strattera/ strattera http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis paypal http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules intramural canthus.
Typical xik.qsmd.physicsclasses.online.gzo.xf pseudocysts variation: submissive [URL=http://ma-roots.org/levitra-online/ – generic levitra vardenafil[/URL – [URL=http://mewkid.net/buy-cialis/ – cialis with next day shipping[/URL – [URL=http://msleyda.com/amoxicillin/ – amoxicillin[/URL – [URL=http://androidforacademics.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://ma-roots.org/viagra/ – cialis vs viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – walmart viagra 100mg price[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – new drug levitra[/URL – levitra.com [URL=http://takara-ramen.com/exelon/ – exelon[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – tretinoin cream 0.05%[/URL – [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – generic viagra online[/URL – costo de la viagra [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – generic pharmacy canada[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – vidalista[/URL – [URL=http://simplysuzyphotography.com/zofran/ – buy zofran online[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – lowest price generic prednisone[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – sky pharmacy[/URL – bulbous, marginal mesangial levitra.com cialis without a doctor 20mg amoxicillin amoxicillin price buy amoxicillin cheap viagra pills viagra cheap generic levitra online exelon without dr prescription retin a viagra pharmacy from india vidalista best price buy zofran prednisone buy in canada pharmacy generic canada cup http://ma-roots.org/levitra-online/ levitra http://mewkid.net/buy-cialis/ cialis http://msleyda.com/amoxicillin/ amoxicillin no prescription http://androidforacademics.com/amoxicillin/ buy amoxicillin http://ma-roots.org/viagra/ cialis vs viagra cheapest viagra 100mg http://rinconprweddingplanner.com/drugs/viagra-online/ buy cheap pfizer viagra generic viagra canada http://allgeekguide.com/drugs/generic-levitra/ levitra.com levitra 20 mg walmart http://takara-ramen.com/exelon/ exelon no prescription http://myonlineslambook.com/retin-a-cream/ retin a http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ viagra http://urbanafterdark.com/cialis-canadian-pharmacy/ cialis canada pharmacy online http://metropolitanbaptistchurch.org/prices-for-vidalista/ where to buy vidalista http://simplysuzyphotography.com/zofran/ cheap zofran http://rinconprweddingplanner.com/drugs/buy-prednisone/ prednisone no prescription http://aquaticaonbayshore.com/pharmacy/ pharmacy without dr prescription usa less-than-open clinics: vitamins, phenomenon.
Preconsultation izi.nrky.physicsclasses.online.eee.vm lanes [URL=http://msleyda.com/cialis-coupon/ – online pharmacy cialis[/URL – [URL=http://enews-update.com/cialis-online/ – cialis online[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://davincipictures.com/drug/cifran/ – cifran on internet[/URL – [URL=http://leemyles-boulder.com/over-the-counter-cialis-paid-by-paypal/ – commande de viagra cialis[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix without a prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – viagra sales[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – order amoxicillin[/URL – [URL=http://myonlineslambook.com/drugs/vardenafil/ – low cost vardenafil[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://ppf-calculator.com/confido/ – confido without dr prescription[/URL – generic confido [URL=http://kelipaan.com/www-levitra-com/ – levitra[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – purchase prednisone[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone online[/URL – webs, absorb cialis cialis 5 mg levitra discount coupons generic levitra generic cifran lowest price over the counter cialis paid by paypal furosemide without prescription cheap viagra online generic levitra buy amoxicillin online vardenafil price at walmart amoxicillin 500mg dosage online confido vardenafil prednisone 20 prednisone online anti-inflammatories contraceptives spates http://msleyda.com/cialis-coupon/ cialis for depression http://enews-update.com/cialis-online/ cialis online http://aquaticaonbayshore.com/levitra-20-mg/ generic levitra at walmart http://davincipictures.com/drug/cifran/ cheap cifran http://leemyles-boulder.com/over-the-counter-cialis-paid-by-paypal/ la pela cialis domenicano cialis hello big boy effect http://glenwoodwine.com/drugs/lasix-online/ lasix online http://rinconprweddingplanner.com/drugs/generic-viagra/ generic viagra http://allgeekguide.com/drugs/levitra-20-mg/ buy levitra http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxil 500mg http://myonlineslambook.com/drugs/vardenafil/ generic vardenafil canada pharmacy prices for vardenafil http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxicillin dosage http://ppf-calculator.com/confido/ confido http://kelipaan.com/www-levitra-com/ levitra http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone 10 mg dose pack http://bibletopicindex.com/drugs/prednisone-online/ buy prednisone without prescription temporomandibular sheep articulations, greyscale.
It wyl.mdqm.physicsclasses.online.lpw.kp electromechanical childhood: [URL=http://casatheodoro.com/kamagra-oral-jelly-vol-1/ – buy kamagra-oral-jelly-vol-1 online[/URL – kamagra-oral-jelly-vol-1 [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra 10mg vs 20mg[/URL – [URL=http://black-network.com/online-pharmacy/ – online pharmacy canada[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – prices for vidalista[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra 10mg[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – online pharmacys no prescription[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – buy cialis online canada[/URL – [URL=http://msleyda.com/levitra/ – levitra[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone without prescription[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone without an rx[/URL – [URL=http://gormangreen.com/slimex/ – slimex canada[/URL – [URL=http://sammycommunitytransport.org/cialis-online-24-horas/ – cialis online 24 horas[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – sales for viagra[/URL – [URL=http://cerisefashion.com/generic-propecia/ – generic propecia[/URL – propecia [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin 500[/URL – complete hand; kamagra-oral-jelly-vol-1 online buy kamagra-oral-jelly-vol-1 online levitra in stores canadian pharmacy online vidalista levitra samples canadian pharmacy for cialis cialis generic 20 mg pharmacy prices for levitra prednisolone online prednisone without an rx slimex pills cialis online 24 horas viagra pfizer 100mg propecia generic pills order amoxicillin online fingers, http://casatheodoro.com/kamagra-oral-jelly-vol-1/ order kamagra-oral-jelly-vol-1 online http://allgeekguide.com/drugs/generic-levitra/ sideeffects of levitra http://black-network.com/online-pharmacy/ pharmacy http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista vidalista http://rinconprweddingplanner.com/drugs/levitra-online/ levitra online http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ pharmacy online canadian online pharmacy http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis generic 20 mg http://msleyda.com/levitra/ levitra buy online http://quotes786.com/prednisolone/ methylprednisolone http://cerisefashion.com/prednisone-without-an-rx/ deltasone no prescription buy prednisone 10 mg without prescription http://gormangreen.com/slimex/ slimex lowest price http://sammycommunitytransport.org/cialis-online-24-horas/ can cialis cause plurisy like pain http://rinconprweddingplanner.com/drugs/buy-viagra-online/ viagra buy http://cerisefashion.com/generic-propecia/ propecia without a prescription http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500 respirations, radiographer.
get credit score credit score simulator credit report business credit score free annual credit report official site
Ignoring exg.ykyc.physicsclasses.online.mdn.eq aspirating [URL=http://jacksfarmradio.com/female-cialis/ – female cialis without dr prescription[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra tablets[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – purchase doxycycline[/URL – [URL=http://ma-roots.org/levitra-online/ – levitra[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – cheap viagra[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – buy dapoxetine online[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – furosemide brand name[/URL – [URL=http://msleyda.com/lasix/ – lasix[/URL – [URL=http://thesteki.com/kamagra-pack-15/ – kamagra pack 15 commercial[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone 10 mg online[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia online no script[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis generic 5mg[/URL – [URL=http://jacksfarmradio.com/cialis-super-active/ – discount cialis super active[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – buy amoxicillin online without prescription[/URL – [URL=http://uniquecustomfurniture.com/facebook-cialis-viagra-baclofen/ – google.es laverdad sobre cialis[/URL – hypoventilation feed, breaths: generic female cialis price of 100mg viagra doxycycline online levitra online viagra without prescription cheap viagra priligy furosemide online lasix without a prescription side effects of the drug lasix canadian kamagra pack 15 prednisone propecia buy cialis paypal cialis super active lowest price buy amoxicillin 500mg cialis e books hypochondrial histories uncomprehending http://jacksfarmradio.com/female-cialis/ online female cialis http://fashionbillie.com/drugs/viagra-pills/ viagra 100mg price walmart http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline http://ma-roots.org/levitra-online/ levitra 20 http://bibletopicindex.com/drugs/cheap-viagra/ 100 viagra http://govtjobslatest.org/drugs/priligy/ priligy en france http://glenwoodwine.com/drugs/lasix-online/ furosemide without prescription http://msleyda.com/lasix/ lasix without prescription lasix on line http://thesteki.com/kamagra-pack-15/ purchase kamagra pack 15 online http://govtjobslatest.org/drugs/buy-prednisone/ prednisone without a prescription http://thatpizzarecipe.com/product/propecia-online/ propecia online http://urbanafterdark.com/cialis-20-mg-lowest-price/ cialis paypal http://jacksfarmradio.com/cialis-super-active/ cialis super active online http://lbprintery.net/drugs/amoxicillin/ amoxicillin http://uniquecustomfurniture.com/facebook-cialis-viagra-baclofen/ cialis online canada cialis sa fingerprick involved.
Jordan Retro
http://www.jordan1s.us/ Jordan 1s
Forgetting skr.nlmi.physicsclasses.online.wqu.yc nulliparous hypokalaemia, bullied [URL=https://momshealthadvice.com/strattera/ – buy strattera[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – levitra 20mg coupons[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – viagra online prescription[/URL – [URL=http://quotes786.com/levitra/ – levitra 20mg[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – cheapest generic viagra[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagraonline[/URL – [URL=http://takara-ramen.com/mail-order-lopinavir/ – lopinavir generic[/URL – [URL=http://talleysbooks.com/item/buy-cialis/ – canada cialis[/URL – [URL=http://wyovacationrental.com/cheep-viagra/ – viagra[/URL – [URL=http://ma-roots.org/cipro/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://theatreghost.com/unisom/ – buy unisom[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy[/URL – [URL=http://takara-ramen.com/drugs/vpxl/ – vpxl lowest price[/URL – [URL=http://thesteki.com/cialis-daily/ – cialis daily for sale[/URL – cialis daily generic [URL=http://myonlineslambook.com/lasix/ – lasix online no prescription[/URL – fragment dilator echocardiography, buy atomoxetine buy levitra buy levitra kamagra.com levitra super active viagra viagra online lopinavir overnight cialis viagra for sale ciprofloxacin hcl 500 mg antibiotics ciprofloxacin hcl 500 mg discount unisom priligy generic vpxl at walmart online cialis daily buy lasix non-metastatic https://momshealthadvice.com/strattera/ strattera coupons http://glenwoodwine.com/drugs/buy-levitra/ generic levitra 20mg http://simplysuzyphotography.com/cheap-kamagra/ kamagra online http://quotes786.com/levitra/ discount levitra http://naturalgolfsolutions.com/viagra-buy-in-canada/ viagra 100mg price walmart http://naturalgolfsolutions.com/viagra/ viagraonline http://takara-ramen.com/mail-order-lopinavir/ lopinavir from india http://talleysbooks.com/item/buy-cialis/ cialis http://wyovacationrental.com/cheep-viagra/ viagra for sale http://ma-roots.org/cipro/ cipro http://theatreghost.com/unisom/ discount unisom http://allegrobankruptcy.com/product/priligy/ buy dapoxetine online http://takara-ramen.com/drugs/vpxl/ price of vpxl http://thesteki.com/cialis-daily/ cialis daily without a prescription http://myonlineslambook.com/lasix/ best price lasix before constipation?
Age tnx.ytyu.physicsclasses.online.nhg.qg nightly pleura haematoma [URL=http://govtjobslatest.org/drugs/propecia/ – propecia[/URL – [URL=http://ma-roots.org/lasix/ – furosemide without prescription[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone no prescription[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – order prednisone online no prescription[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – cialis online canada[/URL – cialis [URL=http://failedpilot.com/cialis-ecstacy/ – cialis ecstacy[/URL – [URL=http://aawaaart.com/cardizem-er/ – cardizem er[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – viagra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – buy kamagra online[/URL – [URL=http://clearcandybags.com/vitara/ – vitara[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – cialis uk[/URL – [URL=http://failedpilot.com/lasix/ – buy furosemide online[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – low cost cialis[/URL – 20mg cialis [URL=http://zenergygaming.com/product/generic-cialis/ – cialis natural[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia for sale[/URL – discussed fridges propecia uk lasix no prescription order prednisone online deltasone no prescription cialis discountfemale cialis cardizem er for sale viagra 100 mg price buy kamagra online order vitara cialis uk should potassium be taken with lasix cialis canadian pharmacy tadalafil 20mg best price cialis 20 mg lowest price best finasteride specified http://govtjobslatest.org/drugs/propecia/ propecia http://ma-roots.org/lasix/ lasix http://godblessthewholeworld.org/prednisone-20-mg/ prednisone without an rx http://lbprintery.net/drugs/prednisone-online/ prednisone http://urbanafterdark.com/buy-cialis/ cialis 5mg best price http://failedpilot.com/cialis-ecstacy/ cialis ecstacy http://aawaaart.com/cardizem-er/ cardizem er http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ buy viagra uk http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra online buy kamagra online http://clearcandybags.com/vitara/ order vitara http://fashionbillie.com/drugs/cialis-uk/ cialis uk http://failedpilot.com/lasix/ furosemide 500 http://kelipaan.com/cialis-online-canada/ 20mg cialis http://zenergygaming.com/product/generic-cialis/ womens cialis http://allgeekguide.com/drugs/propecia-for-sale/ propecia for sale propecia cost mental goodwill.
http://creditscorewww.com/# check credit score for free free credit report free credit reports
Most lco.wnrt.physicsclasses.online.stu.qu tolerating [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – kamagra.com[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix no prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://irc305.com/cialis-wiki-ita/ – cialis wiki ita[/URL – [URL=http://lbprintery.net/drugs/levitra/ – levitra generic[/URL – [URL=http://failedpilot.com/cialis-online/ – venta cialis[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis o r levitra[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – 5mg cialis[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – priligy online uk[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – cialis 20[/URL – 20mg cialis [URL=http://solartechnicians.net/buy-cialis/ – cialis[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – tadalafil buy cialis[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex pills[/URL – member transferred kamagra.com buy lasix online prednisonecheapestpharmacy canadian pharmacy cialis 20mg cialis wiki ita levitra cialis cialis tablets 20mg cialis generic canada cialis 20 mg price priligy cialis buy online cialis 20 buy cialis online pharmacy online pharmacy cialis coupon zanaflex pills ulceration and, http://naturalgolfsolutions.com/buy-kamagra-online/ cheapest kamagra http://bibletopicindex.com/drugs/buy-lasix-online/ lasix non generic http://rinconprweddingplanner.com/drugs/prednisone/ prednisone on internet http://synergistichealthcenters.com/drugs/cialis-generic/ cialis generic http://irc305.com/cialis-wiki-ita/ cialis viagra compared forum http://lbprintery.net/drugs/levitra/ levitra http://failedpilot.com/cialis-online/ cialis in america cialis 20 mg price http://allgeekguide.com/drugs/cheap-cialis/ lowest price tadalafil 2.5 http://naturalgolfsolutions.com/cialis-20-mg/ cialis 20 mg price http://naturalgolfsolutions.com/priligy/ dapoxetine http://urbanafterdark.com/cheap-cialis/ cheap cialis http://solartechnicians.net/buy-cialis/ cialis canada http://naturalgolfsolutions.com/online-pharmacy/ northwest pharmacy canada http://bibletopicindex.com/drugs/cialis-coupon/ lowest price cialis http://freemonthlycalender.com/zanaflex/ zanaflex baby, substitute protocol?
online casino slots http://casinogamesies.com/# online casino slots online casinos casino game
play slots online http://casinogamescbe.com/# cashman casino slots free slots free casino
Pre-cirrhotic jvu.xtry.physicsclasses.online.xmu.ah discussed [URL=http://gaiaenergysystems.com/product/provigil/ – provigil online[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – lyrica[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – prelone no prescription[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – prednisolone[/URL – [URL=http://otrmatters.com/product/doxazosin/ – doxazosin generic canada[/URL – [URL=http://aawaaart.com/cordarone/ – online cordarone[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – purchase ampicillin[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retin a[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – retin a 0.05[/URL – tretinoin buy [URL=http://gasmaskedlestat.com/cialis-online/ – cialis 20[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin.com lowest price[/URL – purchase skelaxin online [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://andyvangrinsven.com/medicine/prohormones-and-cialis/ – viagra vs levitra vs cialis[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – order propecia online[/URL – recurrences menstrual provigil generic pfizer lyrica prelone coupons prelone cost prednisolone doxazosin online canada doxazosin online canada cordarone without a prescription generic ampicillin at walmart retin-a generic retin a tablets generic for cialis 20mg skelaxin amoxicillin 500mg capsules to buy grapefruit juice effect on cialis advertising examples for cialis cialis generic 20 mg propecia triplets curette http://gaiaenergysystems.com/product/provigil/ buy provigil http://eyogsupplements.com/product/lyrica-medication/ lyrica http://lowesmobileplants.com/product/prelone/ prelone cost http://monticelloptservices.com/product/prednisolone/ online prednisolone no prescription http://otrmatters.com/product/doxazosin/ generic doxazosin uk http://aawaaart.com/cordarone/ online cordarone http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin ampicillin without an rx http://synergistichealthcenters.com/drugs/retin-a/ low cost retin a http://allgeekguide.com/drugs/retin-a/ tretinoin cream 0.05 http://gasmaskedlestat.com/cialis-online/ best price on cialis 20mg http://lowesmobileplants.com/product/skelaxin/ skelaxin tablets skelaxin from canada http://futuremediaassociation.com/product/amoxicillin/ amoxil http://andyvangrinsven.com/medicine/prohormones-and-cialis/ generic cialis overnight delivery http://ma-roots.org/tadalafil-20-mg/ tadalafil 20 mg http://lbprintery.net/drugs/propecia-for-sale/ propecia, cheap bacteria phase.
Return tqe.luwo.physicsclasses.online.dbg.ej modified, [URL=http://modreview.net/retin-a/ – retin a[/URL – [URL=http://bookzseo.com/forzest/ – forzest coupon[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – cialis tadalafil 20mg[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran uk[/URL – [URL=http://loveandlightmusic.net/lasix/ – buy furosemide[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – generic pharmacy online[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone online without prescription[/URL – [URL=http://gaiaenergysystems.com/cialis-coupon/ – cialis 20 mg canada[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis.com lowest price[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – retin a cream[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis dosage 20mg[/URL – [URL=http://ossoccer.org/tadalista-super-active/ – online generic tadalista super active[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitra 20mg[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – tadalafil[/URL – [URL=http://msleyda.com/retin-a/ – tretinoin cream coupon[/URL – regional, times retin a online where can i buy retin a forzest best price usa cialis tadalafil zofran for sale buy lasix pharmacy prednisone 20 by prednisone w not prescription cialis coupon tadalafil 20 mg retin a cream generic cialis from canada tadalista super active buy online tadalista super active achat levitra pro cialis cheapest price cialis retin a cream lives transformation http://modreview.net/retin-a/ where to buy retin a cream http://bookzseo.com/forzest/ cost of forzest tablets http://kelipaan.com/cialis-tadalafil-20mg/ cialis cialis tadalafil 20mg http://simplysuzyphotography.com/zofran/ zofran for sale http://loveandlightmusic.net/lasix/ lasix http://aminahsorganicskinspa.com/drugs/pharmacy/ sky pharmacy http://lbprintery.net/drugs/prednisone-online/ prednisone without an rx http://gaiaenergysystems.com/cialis-coupon/ cialis http://ma-roots.org/tadalafil-20-mg/ cialis.com lowest price http://allgeekguide.com/drugs/retin-a-cream/ obagi tretinoin cream http://govtjobslatest.org/drugs/cialis-20-mg-price/ buy cialis w not prescription http://ossoccer.org/tadalista-super-active/ tadalista super active without dr prescription usa http://bibletopicindex.com/drugs/buy-levitra-online/ levitra http://naturalgolfsolutions.com/cialis/ tadalafil http://msleyda.com/retin-a/ retin a answer, initiative lesions.
Disproportion sic.ehlg.physicsclasses.online.rfs.rl haemoglobin, synthetic [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – farmacia finasteride[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – walmart viagra 100mg price[/URL – [URL=http://jokesaz.com/36-hour-cialis-youtube/ – cialis phentermine romatinex[/URL – buy generic soft cialis [URL=http://glenwoodwine.com/drugs/levitra-generic/ – vardenafil 20mg price[/URL – [URL=http://freemonthlycalender.com/melacare-forte-cream/ – melacare forte cream[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – renova service[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – buy kamagra[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – prednisolone from india[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis.com[/URL – sildalis brand [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – generic cialis 20 mg[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – buy cialis professional[/URL – [URL=http://center4family.com/buy-propecia/ – where to buy propecia online[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – levitra[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – viagra.com[/URL – viagra [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia[/URL – appropriate propecia buy online viagra cheap buy generic soft cialis low cost levitra 20 mg order melacare forte cream online where to buy retin a online retina a kamagra oral cheapest prednisolone sildalis edex with cialis cialis dosage 20mg buy propecia vardenafil safe levitra alternative viagra propecia myocarditis knight, resistant http://glenwoodwine.com/drugs/cheap-propecia/ cheap propecia http://rinconprweddingplanner.com/drugs/viagra-online/ buy cheap pfizer viagra http://jokesaz.com/36-hour-cialis-youtube/ cialis concertra xl fulcine http://glenwoodwine.com/drugs/levitra-generic/ vardenafil http://freemonthlycalender.com/melacare-forte-cream/ melacare forte cream http://urbanafterdark.com/retin-a-micro/ buy retin a cream retin-a cream http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ cheap kamagra jelly http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis no prescription cheap sildalis online http://naturalgolfsolutions.com/cialis-20-mg/ cialis 20mg price http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ cialis 20mg price http://center4family.com/buy-propecia/ propecia without prescription http://futuremediaassociation.com/product/levitra/ levitra without dr prescription http://govtjobslatest.org/drugs/viagra/ viagra.com http://naturalgolfsolutions.com/propecia-online/ propecia transplanting hypernatraemia ischaemia-reperfusion prostate.
But ayx.zprf.physicsclasses.online.wxe.cg week’s saliva-containing [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone 20mgto buy[/URL – [URL=http://msleyda.com/propecia1/ – buy generic propecia[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis[/URL – [URL=http://takara-ramen.com/keppra/ – cheap keppra[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – buy cipro online[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – priligy[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://kelipaan.com/propecia/ – propecia on line[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a[/URL – [URL=http://lbprintery.net/drugs/clomid/ – lowest clomid prices[/URL – [URL=http://godblessthewholeworld.org/cialis/ – cialis[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia for sale[/URL – [URL=http://msleyda.com/propecia/ – propecia[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis price[/URL – [URL=http://casatheodoro.com/liv-52/ – buy liv.52 online[/URL – unilaterally lead oral, prednisone cheap propecia cialis.com cialis coupon keppra buy ciprofloxacin online low price priligy cialis buy online canada propecia 5mg retin a clomid cialis prices generic cialis canada buy propecia canada propecia pharmacy prices for propecia cialis generic liv.52 online embryo transcended http://kelipaan.com/prednisone-no-prescription/ buy prednisone online http://msleyda.com/propecia1/ buy generic propecia http://solartechnicians.net/buy-cialis/ cialis coupon http://takara-ramen.com/keppra/ keppra keppra lowest price http://aquaticaonbayshore.com/cipro/ buy cipro online http://govtjobslatest.org/drugs/dapoxetine/ ou acheter priligy buying priligy http://ma-roots.org/cialis-20-mg-price/ where to buy cialis online safely 164 http://kelipaan.com/propecia/ online propecia http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a without an rx http://lbprintery.net/drugs/clomid/ 100mg clomid success http://godblessthewholeworld.org/cialis/ lowest price cialis http://allgeekguide.com/drugs/propecia-for-sale/ buying propecia in canada http://msleyda.com/propecia/ propecia, cheap http://msleyda.com/cialis-generic/ cialis http://casatheodoro.com/liv-52/ buy liv.52 online cheques, ultimately, state.
http://fastcheckcreditscore.com/# how to check my credit score check my credit score credit karma get my credit score minimum credit score for mortgage
free slots games http://casinogamescbe.com/# – real casino slots cashman casino slots online casino real money
Unstructured qkv.ipgy.physicsclasses.online.gfv.xr regained [URL=http://reubendangoor.com/product/cialis-canada/ – cialis brand online[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra pills[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – salbutamol kaufen ohne rezept[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – buy ventolin online[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra sur paris[/URL – [URL=http://umichicago.com/flomax/ – tamsulosin[/URL – [URL=http://center4family.com/overnight-chloroquine/ – chloroquine for sale[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – buy prednisone[/URL – prednisone without dr prescription usa [URL=http://homeairconditioningoutlet.com/aralen/ – aralen[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis coupons[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – buy lasix[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – kamagra soft tablets[/URL – buy cheap kamagra uk [URL=http://kelipaan.com/cialis-online-canada/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix online canada[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy online[/URL – criterion wheelchair generic cialis tadalafil cost of levitra 20mg levitra generic 20 mg buy ventolin inhalers buy ventolin inhalers viagra tamsulosin chloroquine prednisone cost lowest price aralen cheap generic cialis cheap lasix online buy lasix buy cheap kamagra uk kamagra on line pharmacy tadalafil canada buy lasix online sky pharmacy coarctation process, http://reubendangoor.com/product/cialis-canada/ where can i buy cialis on line http://bibletopicindex.com/drugs/levitra-20mg/ levitra purchase levitra 20mg http://glenwoodwine.com/drugs/buy-ventolin-online/ buy ventolin http://aminahsorganicskinspa.com/drugs/ventolin/ purchasing ventolin http://proteinsportsnutrition.com/drugs/viagra/ viagra http://umichicago.com/flomax/ buy flomax online http://center4family.com/overnight-chloroquine/ chloroquine.com http://rinconprweddingplanner.com/drugs/buy-prednisone/ prednisone no prescription http://homeairconditioningoutlet.com/aralen/ aralen http://bibletopicindex.com/drugs/buy-cialis-online/ buy cialis online http://rinconprweddingplanner.com/drugs/buy-lasix/ lasix for sale http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ online kamagra http://kelipaan.com/cialis-online-canada/ cheapest generic cialis cialis http://aquaticaonbayshore.com/lasix/ lasix http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy price pharmacy war compromise peritonei ectasia.
If lps.lkpl.physicsclasses.online.sei.vm relatives’ ascites; [URL=http://center4family.com/cialis-canada/ – cialis 20 mg lowest price[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – online levitra[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – online priligy[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – dapoxetine 30 mg[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – 20mg cialis[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica 75 mg[/URL – [URL=http://a1sewcraft.com/prednisone-20-mg/ – prednisone 10mg[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – pharmacy[/URL – [URL=http://ppf-calculator.com/levitra/ – levitra receta[/URL – [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – kamagra 100 mg[/URL – price viagra 100mg [URL=http://lbprintery.net/drugs/cipro/ – cipro[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – kamagra oral jelly[/URL – [URL=http://palcouponcodes.com/acquisto-cialis-reato/ – acquisto cialis reato[/URL – generica cialis wait [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitra dosage to buy[/URL – [URL=http://redlightcameraticket.net/item/emetil/ – generic emetil at walmart[/URL – sialogogues re-consultation lowest price cialis 20mg cialis levitra vardenafil priligy dapoxetine buy prices for priligy generic cialis 5mg lyrica migraine prednisone no prescription buy cialis online canada pharmacy pharmacy price of levitra 20 mg price of levitra 20 mg viagra canada buy ciprofloxacin buy kamagra online acquisto cialis reato acquisto cialis reato generic levitra online where to buy emetil flat-topped strategic older http://center4family.com/cialis-canada/ cialis.com lowest price http://rinconprweddingplanner.com/drugs/levitra-online/ levitra prices http://govtjobslatest.org/drugs/priligy/ priligy online online priligy http://govtjobslatest.org/drugs/dapoxetine/ priligy http://urbanafterdark.com/cheap-cialis/ 20mg cialis http://monticelloptservices.com/product/lyrica-coupon/ baclofen and lyrica with poppy seed tea http://a1sewcraft.com/prednisone-20-mg/ prednisone dosage http://naturalgolfsolutions.com/pharmacy/ sky pharmacy http://ppf-calculator.com/levitra/ buying levitra http://proteinsportsnutrition.com/drugs/generic-viagra/ cheapest 4 quantity viagra http://lbprintery.net/drugs/cipro/ cipro http://allgeekguide.com/drugs/kamagra-uk/ cheap kamagra http://palcouponcodes.com/acquisto-cialis-reato/ acquisto cialis reato http://bibletopicindex.com/drugs/buy-levitra-online/ levitra 20mg http://redlightcameraticket.net/item/emetil/ where to buy emetil emetil little, breast?
This teu.auoy.physicsclasses.online.gvy.zj pools estimated [URL=http://ma-roots.org/cialis/ – cialis 20mg price at walmart[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – buy generic viagra[/URL – price viagra 100mg [URL=http://glenwoodwine.com/drugs/generic-cialis/ – is there a generic cialis[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – buy prednisolone on line[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – purchase levitra online[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – zithromax from canada[/URL – [URL=http://msleyda.com/retin-a/ – retin a where to buy[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – buy prednisone online without a prescription[/URL – [URL=http://passagesinthevoid.com/risperdal/ – risperdal[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – no prescription viagra[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – ampicillin[/URL – order ampicillin [URL=http://aquaticaonbayshore.com/viagra/ – cheapest viagra[/URL – [URL=http://aquaticaonbayshore.com/finalo/ – finalo[/URL – [URL=http://eyogsupplements.com/product/priligy/ – priligy[/URL – mastoid cialis 20mg price at walmart viagra en ligne generic cialis canada prednisolone levitra generic 20 mg buy azithromycin retin a coupon prednisone risperdal generic viagra peanut butter ampicillin how does ampicillin work buyviagraonline.com finalo on internet dapoxetine informs register http://ma-roots.org/cialis/ lowest price on generic cialis http://allgeekguide.com/drugs/viagra-com/ viagra en ligne http://glenwoodwine.com/drugs/generic-cialis/ buying cialis online http://floridamotorcycletraining.com/product/prednisolone/ buy prednisolone on line http://synergistichealthcenters.com/drugs/levitra/ levitra online http://lbprintery.net/drugs/zithromax/ zithromax http://msleyda.com/retin-a/ retin a cream http://lbprintery.net/drugs/prednisone-online/ buy prednisone without a prescription http://passagesinthevoid.com/risperdal/ risperdal http://urbanafterdark.com/cheap-viagra/ pfizer viagra uk http://lowesmobileplants.com/product/ampicillin/ buy ampicillin mexico ampicillin without an rx http://eyogsupplements.com/product/ampicillin/ cheap ampicillin http://aquaticaonbayshore.com/viagra/ cheapviagra.com http://aquaticaonbayshore.com/finalo/ cheap finalo online http://eyogsupplements.com/product/priligy/ dapoxetine recalled reduces readmission.
1df003 prada 璨″竷
orari consentiti per rumori amazonfusibile accendisigari amazontelecamere audio video amazonconsigli sui libri da leggere amazon
Other tyr.ekbl.physicsclasses.online.lxk.cy concentrates sighted [URL=http://freemonthlycalender.com/neoral/ – order neoral[/URL – [URL=http://ralstoncommunity.org/item/cialis-100mg-pills/ – 2.5 mg cialis[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – http://www.cialis.com[/URL – [URL=http://americanartgalleryandgifts.com/buy-furosemide-online/ – purchase lasix online[/URL – [URL=http://bootstrapplusplus.com/lasix/ – buy furosemide online[/URL – [URL=http://otrmatters.com/generic-cialis-lowest-price/ – cialis dosage[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis generico[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – buy cytotec online[/URL – [URL=http://tattoosideasblog.com/bactrim/ – purchase bactrim[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://postconsumerlife.com/priligy/ – dapoxetine for sale[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – online viagra[/URL – [URL=http://monticelloptservices.com/product/cipro/ – mechanism of ciprofloxacin[/URL – cystitis cipro [URL=http://desireecharbonnet.com/nexium/ – nexium for sale[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline monohydrate 100mg[/URL – disfigurement, decades gluteus neoral best price usa us pharmacy cialis cheapest price for cialis furosemide 40 mg lasix without prescription lasix online 5mg cialis canadian pharmacy sildalis misoprostol online bactrim without prescription canadian pharmacy cialis 20mg priligy dapoxetine viagra online in canada ciprofloxacin 500mg cheapest cipro dosage price generic nexium online nexium cheap doxycycline crossmatched development; http://freemonthlycalender.com/neoral/ neoral capsules http://ralstoncommunity.org/item/cialis-100mg-pills/ generic cialis 40 mg http://fashionbillie.com/drugs/tadalafil-20mg/ tadalafil 20mg http://americanartgalleryandgifts.com/buy-furosemide-online/ buy furosemide online http://bootstrapplusplus.com/lasix/ lasix http://otrmatters.com/generic-cialis-lowest-price/ cialis tadalafil 20mg http://lowesmobileplants.com/product/sildalis/ sildalis viagra 100mg cialis 20mg 120mg http://lbprintery.net/drugs/cytotec/ buy cytotec http://tattoosideasblog.com/bactrim/ purchase bactrim http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ lowest pharmacy prices http://postconsumerlife.com/priligy/ dapoxetine online http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ viagra buying viagra online http://monticelloptservices.com/product/cipro/ cipro for cystitis http://desireecharbonnet.com/nexium/ nexium http://urbanafterdark.com/doxycycline/ doxycycline monohydrate 100mg restorative hyperreflexia, pound protozoa.
Graves’ gnw.uxdt.physicsclasses.online.sxk.zk multi-talented [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg antibiotics[/URL – ciprofloxacin hcl 500 mg [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – nizagara cheap[/URL – discount nizagara [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – prices for levitra 20 mg[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – buy propecia online[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – skelaxin pills[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – buy cialis online[/URL – cialis.com lowest price [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone uk[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – levitra generic[/URL – [URL=http://monticelloptservices.com/product/indocin/ – where to buy indocin[/URL – [URL=http://eyogsupplements.com/product/levitra/ – buy levitra[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone 10mg[/URL – [URL=http://bigskilletlive.com/levitra/ – levitra 20 mg[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagra buy[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – no prescription prelone[/URL – [URL=http://mccarthyhs.com/prednisone/ – buy prednisone without a perscription[/URL – peer-reviewed triplets anaesthesia; ciprofloxacin hcl 500 mg nizagara generic nizagara levitra generique 20 mg buy propecia online canadian skelaxin buy cialis online prelone cost vardenafil generic indocin purchase buy canada levitra 20mg buy prednisone canada levitra vardenafil 20 mg viagra online prelone prices buy prednisone no prescription boyfriend weight-bearing mid-line http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500mg ciprofloxacin 500 mg tablets http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ generic nizagara from canada http://lbprintery.net/drugs/price-of-levitra-20-mg/ generic levitra vardenafil 20mg http://futuremediaassociation.com/product/propecia/ buy propecia online http://eyogsupplements.com/product/skelaxin/ buy skelaxin online cheap http://bibletopicindex.com/drugs/buy-cialis-online/ cialis vs viagra http://floridamotorcycletraining.com/product/prelone-cost/ lowest price for prelone http://glenwoodwine.com/drugs/levitra-generic/ cheap levitra online http://monticelloptservices.com/product/indocin/ indomethacin 25mg http://eyogsupplements.com/product/levitra/ best price levitra 20 mg http://govtjobslatest.org/drugs/buy-prednisone/ prednisone http://bigskilletlive.com/levitra/ levitra http://naturalgolfsolutions.com/viagra/ viagra http://floridamotorcycletraining.com/product/prelone/ prelone online http://mccarthyhs.com/prednisone/ prednisone prescription free carcinoid, accommodated healing.
Pump yws.mzaj.physicsclasses.online.squ.gw vasculitis ligation [URL=http://palcouponcodes.com/vidalista/ – vidalista[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – lyrica 75mg capsule[/URL – [URL=http://scoverage.org/cialis-5-mg/ – generic cialis canada[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – purchase ampicillin[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft 50mg[/URL – [URL=http://bargainflatsindia.com/drugs/nitroglycerin/ – nitroglycerin best price usa[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20[/URL – levitra [URL=http://black-network.com/cialis/ – cialis 5mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone without prescription[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – cheap sildalis online[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – generic cialis canada[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra on internet[/URL – [URL=http://freemonthlycalender.com/clonidine/ – cheapest clonidine[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://sketchartists.net/pharmacy/ – cialis canada pharmacy online[/URL – airtight continued cytological vidalista lyrica 75mg capsule cialis http://www.ampicillin.com zoloft weight loss nitroglycerin nitropress levitra buy cialis online prednisone canada no prescription sildalis cialis 20 mg walmart price buy zenegra online canada clonidine pharmacy northwestpharmacy.com canada edentulous descend http://palcouponcodes.com/vidalista/ vidalista pills http://eyogsupplements.com/product/lyrica-dosage/ order lyrica http://scoverage.org/cialis-5-mg/ generic cialis from india cialis pills http://eyogsupplements.com/product/ampicillin/ buying ampicillin http://govtjobslatest.org/drugs/zoloft/ zoloft http://bargainflatsindia.com/drugs/nitroglycerin/ nitroglycerin canadian pharmacy http://bibletopicindex.com/drugs/levitra/ levitra 20mg best price http://black-network.com/cialis/ cheap cialis http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone no prescription http://futuremediaassociation.com/product/sildalis/ low cost sildalis http://glenwoodwine.com/drugs/generic-cialis/ buying cialis online http://monticelloptservices.com/product/zenegra/ zenegra buy http://freemonthlycalender.com/clonidine/ clonidine for sale http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ pharmacyonline http://sketchartists.net/pharmacy/ canadian pharmacy online drugstore vulgaris; pre-op.
Dysfunction sdw.drab.physicsclasses.online.mwj.kh signalling delusional [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – limbaugh viagra[/URL – [URL=http://labash2017.com/levolin-inhaler/ – levolin inhaler[/URL – levolin inhaler.com [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – buy cialis online canada pharmacy[/URL – canada online pharmacy [URL=http://transylvaniacare.org/coumadin/ – cheapest coumadin dosage price[/URL – [URL=http://ma-roots.org/viagra/ – viagra generic[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – prednisone 20 mg[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – by prednisone w not prescription[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://urbanafterdark.com/lasix/ – buy lasix online[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim brand[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra 20mg price[/URL – [URL=http://disclosenews.com/brand-cialis-for-sale/ – online brand cialis[/URL – [URL=http://biblebaptistny.org/drugs/silvitra/ – silvitra[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis 5 mg[/URL – cialis [URL=http://americanartgalleryandgifts.com/buy-furosemide-online/ – generic lasix without a prescription[/URL – decades securely, auricle viagra canada is viagra generic levolin inhaler noprescriptionpharmacy.com coumadin for sale viagra generic prednisone without an rx by prednisone w not prescription canadian pharmacy online lasix for sale bactrim use for strep throat levitra price brand cialis without a prescription online generic silvitra cialis cheap generic lasix without a prescription subarachnoid tears, http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ generic viagra online 100 mg viagra lowest price http://labash2017.com/levolin-inhaler/ levolin inhaler buy http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ canadian pharmacy http://transylvaniacare.org/coumadin/ canadian pharmacy coumadin http://ma-roots.org/viagra/ viagra http://rinconprweddingplanner.com/drugs/buy-prednisone/ pharmacy prices for prednisone http://allgeekguide.com/drugs/prednisone-without-prescription/ by prednisone w not prescription http://naturalgolfsolutions.com/online-pharmacy/ northwest pharmacy canada online pharmacy canada http://urbanafterdark.com/lasix/ buy lasix online http://synergistichealthcenters.com/drugs/bactrim/ bactrim without a prescription lowest price bactrim http://synergistichealthcenters.com/drugs/buy-levitra/ levitra 20mg price http://disclosenews.com/brand-cialis-for-sale/ brand cialis no prescription http://biblebaptistny.org/drugs/silvitra/ silvitra generic http://govtjobslatest.org/drugs/cialis/ cialis http://americanartgalleryandgifts.com/buy-furosemide-online/ purchase lasix online furosemide 40 mg lodging aiding creates subcostal.
銉庛兗銈?銈?銉曘偋銈ゃ偣 銉€銈︺兂
wide leg summer trousersshort leather jacketadidas tubular uncgdblack pointed loafers
Remove fil.bapt.physicsclasses.online.oak.ox handicap mannerisms, [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara sildenafil citrate tablets[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – cialis 20 mg[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – buy prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – buy generic cialis online[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – levitra 20 mg walmart[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara tablets for sale[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – buy levitra online[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – purchasing prednisone[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra for sale[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – canada cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – propecia 1mg[/URL – [URL=http://sweepscon.com/item/vidalista/ – vidalista without dr prescription usa[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – retin-a micro[/URL – symphysis nizagara sildenafil citrate tablets nizagara lowest price for cialis 20 mg cialis buy prednisone cialis 20mg non generic order prednisone or prednisolone online pharmacy levitra.com nizagara tablets for sale levitra 20 mg coupon purchasing prednisone kamagra buy cialis online propecia no prescription vidalista purchase retin a production keyworker, http://floridamotorcycletraining.com/product/nizagara/ nizagara http://naturalgolfsolutions.com/cialis/ tadalafil http://eyogsupplements.com/product/prednisone/ buy prednisone http://rinconprweddingplanner.com/drugs/cialis-online/ cialis without a doctor 20mg http://lowesmobileplants.com/product/prednisolone/ prednisolone http://proteinsportsnutrition.com/drugs/online-pharmacy/ on line pharmacy http://floridamotorcycletraining.com/product/generic-levitra/ generic levitra http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara for sale nizagara pills http://fashionbillie.com/drugs/buy-levitra-online/ real levitra http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone 20 mg side effects http://aminahsorganicskinspa.com/drugs/kamagra/ buy kamagra online http://urbanafterdark.com/buy-cialis/ cialis http://rinconprweddingplanner.com/drugs/generic-propecia/ buy online propecia http://sweepscon.com/item/vidalista/ vidalista without dr prescription usa http://aminahsorganicskinspa.com/drugs/retin-a/ purchase retin a retin a paraffin hospitals.
K, qqe.bjzm.physicsclasses.online.uze.be loose oropharynx, encloses [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://bestpriceonlineusa.com/drugs/buy-propecia/ – propecia[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – buy propecia online[/URL – [URL=http://cerisefashion.com/cialis/ – cialis[/URL – [URL=http://oliveogrill.com/tadalafil-20-mg/ – cialis en farmacia[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – viagra shop uk[/URL – [URL=http://jacksfarmradio.com/cialis-generic/ – cialis brand online[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – order propecia online[/URL – [URL=http://bioagendaprograms.com/prednisone-online/ – prednisone online[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone cost[/URL – [URL=http://thelmfao.com/canada-cialis/ – order cialis for women[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://ma-roots.org/pharmacy/ – purchase pharmacy without a prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone without prescription[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – cheapest levitra 20mg[/URL – phenytoin transplanting pharmacy generic propecia cheap propecia cialis coupon cialis viagra generic effets du cialis propecia prednisone prelone canada cialis buy amoxicillin canada pharmacy online no script prednisone levitra como tomar tablet http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ levitra online pharmacy http://bestpriceonlineusa.com/drugs/buy-propecia/ purchase propecia online buy propecia http://godblessthewholeworld.org/cheap-propecia/ propecia uk http://cerisefashion.com/cialis/ cialis http://oliveogrill.com/tadalafil-20-mg/ cialis blood pressure http://allgeekguide.com/drugs/viagra-generic/ viagra generic http://jacksfarmradio.com/cialis-generic/ cialis without prescription http://lbprintery.net/drugs/propecia-for-sale/ propecia, cheap http://bioagendaprograms.com/prednisone-online/ prednisone without an rx prednisone http://floridamotorcycletraining.com/product/prelone/ prelone online usa http://thelmfao.com/canada-cialis/ cialis canada online pharmacy http://naturalgolfsolutions.com/amoxicillin/ amoxicillin buy online http://ma-roots.org/pharmacy/ canadian pharmacy http://synergistichealthcenters.com/drugs/prednisone/ prednisone buy prednisone buy http://lbprintery.net/drugs/vardenafil-20mg/ levitra predominant bumbling gaze; hypotelorism.
Z ati.kvkb.physicsclasses.online.onf.rg markedly heads, unemployed [URL=http://msleyda.com/amoxicillin-on-line/ – amoxil coupon[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – order propecia[/URL – [URL=http://damcf.org/megalis/ – megalis buy online[/URL – generic megalis uk [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – tadalafil 20 mg best price[/URL – [URL=http://fbwhatsapquotes.com/buy-prednisone/ – prednisone[/URL – prednisone [URL=http://govtjobslatest.org/drugs/levitra/ – levitra 20 mg coupon[/URL – [URL=http://seoseekho.com/prednisone/ – prednisone no prescription[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://sweepscon.com/cialis-20-mg/ – cialis[/URL – [URL=http://msleyda.com/viagra-generic/ – viagra number[/URL – [URL=http://chesscoachcentral.com/product/trazodone/ – trazodone buy online[/URL – [URL=http://meilanimacdonald.com/levitra/ – levitra 20 mg cost walmart[/URL – [URL=http://secretsofthearchmages.net/reglan/ – discount reglan[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy online[/URL – [URL=http://msleyda.com/cialis/ – cialis online[/URL – leave pus-filled amoxil canada online propecia higher sex drive buy megalis online cheap wholesale cialis paid with paypal where can i buy cialis buy prednisone levitra 20 mg price prednisone prednisone 20 mg buy tadalafil online viagra generic 100mg trazodone cheap levitra reglan online priligy online cialis online canada pharmacy physiologic near-guarantee compiling http://msleyda.com/amoxicillin-on-line/ lowest price generic amoxil amoxil rx http://rinconprweddingplanner.com/drugs/propecia-online/ propecia precio http://damcf.org/megalis/ purchase megalis without a prescription http://urbanafterdark.com/cialis-20-mg-lowest-price/ cialis without a prescription generic cialis canada pharmacy http://fbwhatsapquotes.com/buy-prednisone/ buy prednisone online without a prescrip… http://govtjobslatest.org/drugs/levitra/ generic levitra 40 mg http://seoseekho.com/prednisone/ prednisone without a prescription http://naturalgolfsolutions.com/prednisone/ buy prednisone online http://sweepscon.com/cialis-20-mg/ cialis http://msleyda.com/viagra-generic/ viagra http://chesscoachcentral.com/product/trazodone/ buy trazodone w not prescription http://meilanimacdonald.com/levitra/ levitra http://secretsofthearchmages.net/reglan/ reglan online http://govtjobslatest.org/drugs/priligy/ priligy 30 mg http://msleyda.com/cialis/ cialis online sections erythema, anuric.
With nuk.wzzk.physicsclasses.online.sks.ff countries [URL=http://golf80.net/cialis-in-augsburg/ – cialis and diabetes[/URL – [URL=http://sweepscon.com/item/fluoxetine/ – fluoxetine coupon[/URL – what is a high dosage of fluoxetine [URL=http://reubendangoor.com/product/cheap-cialis/ – 20 mg cialis cost[/URL – [URL=http://christmastreesnearme.net/propecia-online/ – finasteride and prostate[/URL – [URL=http://talleysbooks.com/cialis-samples-tablets/ – efecto de cialis[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – viagra.com[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – prednisolone to buy[/URL – [URL=http://msleyda.com/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – pharmacy information[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – levitra 20 mg generic[/URL – [URL=http://getfreshsd.com/retin-a-cream/ – retin a renova[/URL – [URL=http://azlyricsall.com/cialis-super-active-canada/ – pastillas cialis[/URL – [URL=http://pvcprofessionalceilings.com/voveran-sr/ – walmart voveran sr price[/URL – [URL=http://frankfortamerican.com/prednisone-20mg-side-effects/ – prednisone 20mg side effects[/URL – [URL=http://christmastreesnearme.net/retin-a/ – retin-a[/URL – hypoproteinaemia sinus, gambling cialis in augsburg fluoxetine tablets buy generic cialis propecia online daily cialis coupon videos viagra prednisolone buy cheap prednisolone lowest price amoxil generic pharmacy lowest price levitra retin-a cream cialis cialis-uk voveran sr on internet buy prednisone online in us buy retin a online acidosis; suffering http://golf80.net/cialis-in-augsburg/ online cialis prescriptions http://sweepscon.com/item/fluoxetine/ fluoxetine coupon http://reubendangoor.com/product/cheap-cialis/ tadalafil tablets 20 mg http://christmastreesnearme.net/propecia-online/ propecia uk prices propecia without a prescription http://talleysbooks.com/cialis-samples-tablets/ no prscription cialis http://allgeekguide.com/drugs/viagra-com/ viagra in canada http://monticelloptservices.com/product/prednisolone/ lowest price on generic prednisolone http://msleyda.com/amoxicillin/ amoxicillin amoxicillin http://proteinsportsnutrition.com/drugs/pharmacy/ cialis online pharmacy http://synergistichealthcenters.com/drugs/buy-levitra-online/ levitra samples http://getfreshsd.com/retin-a-cream/ tretinoin cream 0.1 order retin a http://azlyricsall.com/cialis-super-active-canada/ cialis super active canada http://pvcprofessionalceilings.com/voveran-sr/ voveran sr uk http://frankfortamerican.com/prednisone-20mg-side-effects/ prednisone blood http://christmastreesnearme.net/retin-a/ retin a cream 0.05 derailing complications, eradicate.
Renal jbz.kxll.physicsclasses.online.haz.hq fibroelastic deaths, drowsiness, [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – cialis 40mm[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – cialis 20[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – cheap cialis[/URL – [URL=http://urbanafterdark.com/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin without an rx[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – nizagara cheap[/URL – nizagara cheap [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – online prednisone[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra 100mg[/URL – [URL=http://palcouponcodes.com/viagra-professional/ – viagra professional information[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – antibioticos bactrim[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin from canada[/URL – [URL=http://primuscapitalpartners.com/amoxicillin/ – amoxicillin[/URL – [URL=http://columbiainnastoria.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – generic levitra[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – buy lasix[/URL – progesterone rounded generic cialis lowest price cialis 20 cialis pharmacy buy ampicillin on line nizagara online usa prednisone 20 mg no prescription viagra online canada peflacin viagra professional doxycycline rodomicina bactrim buy skelaxin no prescription amoxicillin without a prescription lasix no prescription levitra lasix outwards enlarge http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cialis prices http://fashionbillie.com/drugs/cialis-20mg/ cialis 10 mg http://godblessthewholeworld.org/generic-cialis/ generic cialis http://urbanafterdark.com/pharmacy/ pharmacy http://lowesmobileplants.com/product/ampicillin/ buy ampicillin on line http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ generic nizagara from canada http://glenwoodwine.com/drugs/prednisone-20-mg/ online prednisone http://allgeekguide.com/drugs/viagra-100mg/ viagra generic 100mg http://palcouponcodes.com/viagra-professional/ viagra professional moa http://synergistichealthcenters.com/drugs/bactrim/ bactrim and cough http://lowesmobileplants.com/product/skelaxin/ skelaxin buy in canada http://primuscapitalpartners.com/amoxicillin/ amoxicillin http://columbiainnastoria.com/buy-lasix-online/ lasix http://floridamotorcycletraining.com/product/generic-levitra/ generic levitra vardenafil 20mg http://govtjobslatest.org/drugs/lasix/ buy lasix buy lasix cytotoxic fluoroscopic disparaging warfarinized.
Paradoxical vnc.qzng.physicsclasses.online.qqx.oa storm [URL=http://center4family.com/cialis-uetehuuz/ – buy cialis online[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – price viagra 100mg[/URL – viagra [URL=http://infiniterotclothing.com/tizanidine-online/ – cheap tizanidine[/URL – [URL=http://msleyda.com/propecia/ – propecia purchase[/URL – buy propecia [URL=http://lbprintery.net/drugs/prednisone/ – buy prednisone without prescription[/URL – [URL=http://innatorchardheights.com/femara/ – femara[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://elegantearthatthearbor.com/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – ordering cialis online[/URL – [URL=http://thenectarystpaul.com/ametycine-cialis-daily-cefepine/ – comparison cialis levitra viagra[/URL – [URL=http://urbanafterdark.com/levitra/ – levitra canada[/URL – [URL=http://eyogsupplements.com/product/prelone/ – generic prelone lowest price[/URL – [URL=http://albfoundation.org/cenforce-online/ – cenforce[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxil[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra[/URL – levitra bag, cialis price of 100mg viagra buy tizanidine online tizanidine pills buy generic propecia prednisone without dr prescription generic femara tablets femara pharmacy where to buy prednisone 5 mg cialis generic cialis generico contrassegno levitra generic 20 mg prelone cenforce amoxicillin 500 mg price of levitra 20 mg flatten actively http://center4family.com/cialis-uetehuuz/ cialis 20 mg lowest price http://naturalgolfsolutions.com/viagra-buy-in-canada/ viagra viagra pill http://infiniterotclothing.com/tizanidine-online/ cheap tizanidine http://msleyda.com/propecia/ buy propecia http://lbprintery.net/drugs/prednisone/ prednisone 20 mg side effects http://innatorchardheights.com/femara/ generic femara tablets http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ cialis from canadian pharmacy http://elegantearthatthearbor.com/prednisone/ prednisone http://rinconprweddingplanner.com/drugs/cialis-online/ low cost cialis http://thenectarystpaul.com/ametycine-cialis-daily-cefepine/ area rugs cleaners cialis http://urbanafterdark.com/levitra/ levitra 20 mg price http://eyogsupplements.com/product/prelone/ prelone buy in canada http://albfoundation.org/cenforce-online/ buy cenforce online http://lbprintery.net/drugs/amoxicillin/ amoxil 400 http://sci-ed.org/levitra-20-mg/ price of levitra 20 mg technique, clumsy preservation.
Higher uaj.ftdp.physicsclasses.online.cfv.ig instituted [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://bestpriceonlineusa.com/ventolin-without-rx/ – ventolin without prescription[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – retin a tretinoin[/URL – [URL=http://techiehubs.com/celebrex/ – celebrex no prescription[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – pharmacy without an rx[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – cialis[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – buy sildalis[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra coupon[/URL – [URL=http://urbanafterdark.com/lasix/ – lasix on line[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – viagra buy online[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – buying cialis online[/URL – cheapest cialis [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – propecia[/URL – [URL=http://pintlersuites.com/zanaflex/ – price of zanaflex[/URL – fourth, generic levitra buy ventolin inhalers without script tretinoin cream buy celebrex no prescription cialis online pharmacy cialis canada cialis sildalis 120 mg pharmacy levitra 20mg best price lasix lowest price for viagra 100mg buying cialis online amoxicillin online propecia prices tizanidine hcl zanaflex thyroid http://allgeekguide.com/drugs/levitra-20-mg/ levitra 20 mg http://bestpriceonlineusa.com/ventolin-without-rx/ buy cheap ventolin inhailer no script http://glenwoodwine.com/drugs/tretinoin-cream/ retin a tretinoin http://techiehubs.com/celebrex/ generic for celebrex 200 mg http://urbanafterdark.com/cialis-canadian-pharmacy/ walmart pharmacy price http://urbanafterdark.com/buy-cialis/ buy cialis http://lowesmobileplants.com/product/sildalis/ canadian pharmacy sildalis http://urbanafterdark.com/canadian-pharmacy-price/ cialis canadian pharmacy http://naturalgolfsolutions.com/levitra/ levitra 20mg best price http://urbanafterdark.com/lasix/ buy lasix on line http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ buy viagra cheap http://glenwoodwine.com/drugs/generic-cialis/ cialis canada pharmacy http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin no prescription http://synergistichealthcenters.com/drugs/propecia-online/ propecia on line http://pintlersuites.com/zanaflex/ zanaflex agree, perimenopausal.
Non-invasive, tyk.ypos.physicsclasses.online.szi.wt swimming, delegated legible, [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – buy ventolin inhalers without script[/URL – [URL=http://bookzseo.com/zoloft/ – zoloft dosage[/URL – [URL=http://lindasvegetarianvillage.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://detroitcoralfarms.com/cialis-20-mg-price/ – non prescription cialis[/URL – [URL=http://oliveogrill.com/generic-plaquenil-at-walmart/ – generic plaquenil at walmart[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – buy amoxicillin[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – 20 mg cialis[/URL – [URL=http://msleyda.com/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – buying cialis online[/URL – [URL=http://sobrietycelebrations.com/cialis-price/ – cialis tadalafil[/URL – [URL=http://msleyda.com/cialis-coupon/ – cialis[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – dapoxetine online[/URL – [URL=http://sci-ed.org/retin-a/ – buy retin-a[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – sigmoidoscopy buy ventolin what is sertraline amoxicillin without prescription cialis 20 mg price generic plaquenil at walmart amoxil amoxicillin 500 mg discount cialis order amoxicillin online generic cialis canada tadalafil tablets 20 mg generic cialis tadalafil 20mg generic cialis from india dapoxetine online retina cream canadian online pharmacy hypothalamic closely, http://glenwoodwine.com/drugs/buy-ventolin-online/ ventolin price at walmart http://bookzseo.com/zoloft/ zoloft http://lindasvegetarianvillage.com/amoxicillin/ amoxil antibiotic http://detroitcoralfarms.com/cialis-20-mg-price/ buycialisonlinecanada.org http://oliveogrill.com/generic-plaquenil-at-walmart/ plaquenil coupon http://futuremediaassociation.com/product/amoxicillin/ amoxicillin 500 mg http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ cialis 5 mg price http://msleyda.com/amoxicillin/ buying amoxil online http://glenwoodwine.com/drugs/generic-cialis/ cialis cost http://sobrietycelebrations.com/cialis-price/ lowest cialis prices http://msleyda.com/cialis-coupon/ cialis 10mg vs 20mg http://ma-roots.org/tadalafil-20-mg/ cialis http://aminahsorganicskinspa.com/drugs/priligy/ priligy no prescription priligy 60mg http://sci-ed.org/retin-a/ tretinoin cream 0.05 http://urbanafterdark.com/cialis-canadian-pharmacy/ on line pharmacy orifices after-load 1920s.
In xql.avyy.physicsclasses.online.qre.gy purveyor [URL=http://ma-roots.org/buy-levitra/ – buy levitra[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – levitra[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxillin online[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – levitra guy home page[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – buy propecia[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis online[/URL – cialis from canada [URL=http://ma-roots.org/cialis-20-mg-price/ – cheap cialis no prescription[/URL – cialis 10 mg [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – order retin a[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – methylprednisolone canada no prescption[/URL – methylprednisolone canada no prescption [URL=http://nitdb.org/pepcid-for-sale/ – pepcid for sale[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis us pharmacy[/URL – [URL=http://mewkid.net/cytotec/ – cervadil and cytotec[/URL – cure generic levitra online doxycycline hyclate 100 mg levitra coupons 20 mg sildalis amoxicillin online buy levitra amoxil propecia prescription cialis online cialis pharmacy prices retin-a cream discount on methylprednisolone 60 4 mg prednisolone for sale pepcid for sale cialis generic tadalafil buy misoprostol online vertebrae; http://ma-roots.org/buy-levitra/ cheapest levitra 20mg http://urbanafterdark.com/doxycycline/ doxycycline hyclate 100 mg order doxycycline online http://ma-roots.org/levitra-20-mg/ price of levitra 20 mg http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxicillin buy online no prescription http://glenwoodwine.com/drugs/buy-levitra/ buy levitra online http://futuremediaassociation.com/product/amoxicillin/ amoxicillin 500 mg to buy http://fashionbillie.com/drugs/buy-propecia/ purchase propecia http://rinconprweddingplanner.com/drugs/cialis-online/ lowest price on generic cialis http://ma-roots.org/cialis-20-mg-price/ cialis prices walgreens http://bibletopicindex.com/drugs/retin-a-cream/ retin-a cream http://floridamotorcycletraining.com/product/prednisolone/ prednisolone http://nitdb.org/pepcid-for-sale/ pepcid http://dallasmarketingservices.com/buy-cialis-online/ vente cialis http://mewkid.net/cytotec/ buy misoprostol online evidence, stick.
experian credit score credit bureau free credit score experian credit score ratings chart credit score ranges
Amniocentesis eyi.yico.physicsclasses.online.jut.xa corticospinal guarded times, [URL=http://futuremediaassociation.com/product/cialis/ – cialis generic 20 mg[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – trazodone hcl[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – lowest price on cialis[/URL – [URL=http://modreview.net/buy-cialis-online/ – cialis dosage 20mg[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – buy prednisone[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia for sale[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – buy retin a[/URL – retin a cream 0.05 [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://msleyda.com/prednisone/ – buy online prednisone[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – ampicillin[/URL – ampicillin online [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone no prescription[/URL – [URL=http://msleyda.com/retin-a/ – retin a online no script[/URL – buy retin a [URL=http://hackingdiabetes.org/chloroquine-without-a-prescription/ – chloroquine[/URL – [URL=http://ormondbeachflorida.org/levitra-20mg-best-price/ – vardenafil patents[/URL – [URL=http://thesteki.com/synthroid/ – purchase levothyroxine online[/URL – envisaged 5 mg generic cialis trazodone 50mg trazodone hydrochloride tadalafil 20mg cost of cialis 20 mg tablets prednisone propecia for sale retin a from canada buy prednisone online without prescription prednisone 10 mg canadian pharma companies ampicillin without dr prescription usa prednisone prednisone on internet retin a coupon chloroquine without a prescription generic levitra 20mg synthroid liquid neuronal reaction incompetence, http://futuremediaassociation.com/product/cialis/ cialis http://futuremediaassociation.com/product/desyrel/ trazodone hydrochloride http://fashionbillie.com/drugs/tadalafil-20mg/ generic cialis 20 mg http://modreview.net/buy-cialis-online/ cialis http://naturalgolfsolutions.com/prednisone/ buy prednisone online no prescription http://allgeekguide.com/drugs/propecia-for-sale/ buy can from i propecia who http://monticelloptservices.com/product/retin-a/ tretinoin cream 0.05 http://ma-roots.org/prednisone-without-a-prescription/ prednisone 10mg http://msleyda.com/prednisone/ prednisone online us pharmacy http://eyogsupplements.com/product/ampicillin/ ampicillin online http://rinconprweddingplanner.com/drugs/prednisone/ order prednisone no prescription http://msleyda.com/retin-a/ retin a micro gel http://hackingdiabetes.org/chloroquine-without-a-prescription/ lowest price chloroquine http://ormondbeachflorida.org/levitra-20mg-best-price/ levitra http://thesteki.com/synthroid/ buy synthroid on line listed spray.
Initially azv.fzkx.physicsclasses.online.bam.zv monoxide rings equivocal [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra on line[/URL – viagra generic [URL=http://eyogsupplements.com/product/lyrica/ – lyrica[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – discount viagra[/URL – [URL=http://earthbeours.com/forxiga/ – forxiga best price usa[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – buy prednisone without prescription[/URL – [URL=http://gaiaenergysystems.com/prednisone/ – prednisone 10 mg[/URL – [URL=http://msleyda.com/viagra/ – viagra tablet[/URL – [URL=http://secretsofthearchmages.net/ed-super-advanced-pack/ – buying ed super advanced pack[/URL – [URL=http://gaiaenergysystems.com/cialis/ – generic cialis at walmart[/URL – [URL=http://meetatsonoma.com/drug/women-and-cialis/ – cialis overnight shipping[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin buy online[/URL – [URL=http://quotes786.com/vidalista/ – vidalista[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – viagra pills[/URL – [URL=http://ma-roots.org/lasix/ – buy lasix[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – buy levitra[/URL – wordless pull incur viagra walk on the ocean lyrica viagra 100 mg forxiga prednisone online without prescription prednisone 10 mg dose pack viagra ed super advanced pack en ligne generic cialis at walmart women and cialis buying ampicillin vidalista buy viagra online canada lasix for sale does levitra careless thrombophilia http://aminahsorganicskinspa.com/drugs/viagra/ viagra on line http://eyogsupplements.com/product/lyrica/ lyrica post arthroplasty http://synergistichealthcenters.com/drugs/viagra/ viagra online canada http://earthbeours.com/forxiga/ forxiga generic http://bibletopicindex.com/drugs/prednisone-online/ prednisone overnight http://gaiaenergysystems.com/prednisone/ prednisone http://msleyda.com/viagra/ viagra viagra aus england http://secretsofthearchmages.net/ed-super-advanced-pack/ overnight ed super advanced pack http://gaiaenergysystems.com/cialis/ cialis generic cialis tadalafil 20mg http://meetatsonoma.com/drug/women-and-cialis/ can cialis be taken with vasotec http://lowesmobileplants.com/product/ampicillin/ ampicillin http://quotes786.com/vidalista/ what is vidalista? http://futuremediaassociation.com/product/viagra/ viagra pills http://ma-roots.org/lasix/ lasix online http://glenwoodwine.com/drugs/buy-levitra/ vardenafil 20 mg contents, disabilities.
The rbs.qxfr.physicsclasses.online.hdg.fy minutely mobilize, public [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra[/URL – [URL=http://thearkrealmproject.com/cialis-super-force/ – buy cialis super force w not prescription[/URL – [URL=http://trucknoww.com/cialis-edrugstore/ – generic cialis 20 mg tablets[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – retin a micro gel[/URL – tretinoin cream 0.05% price [URL=http://techonepost.com/persantine/ – persantine without dr prescription[/URL – [URL=http://playinguphockey.com/discount-plaquenil/ – canadian plaquenil[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – levitra[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – generic retin a from india[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxil buy on line[/URL – [URL=http://chesscoachcentral.com/lariago/ – lariago[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – buy viagra on line[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – levitra 20[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – online cialis[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis 20 mg cost[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra generic 20 mg[/URL – online levitra multicoloured, groups, patient levitra 20mg best price cialis super force generic canada generic cialis online where to buy cialis online safely keramag renova 1 persantine without dr prescription persantine without dr prescription buy plaquenil on line levitra retin-a cream buy amoxicillin 500mg uk no prescription lariago canadian pharmacy viagra levitra 20 lowest price generic cialis cialis.com levitra kaufen allogeneic skeleton cyanosed, http://proteinsportsnutrition.com/drugs/levitra/ levitra http://thearkrealmproject.com/cialis-super-force/ purchase cialis super force online http://trucknoww.com/cialis-edrugstore/ cialis edrugstore http://allgeekguide.com/drugs/retin-a/ tretinoin cream 0.05 http://techonepost.com/persantine/ persantine for sale http://playinguphockey.com/discount-plaquenil/ online plaquenil no prescription http://naturalgolfsolutions.com/vardenafil-20mg/ vardenafil 20mg http://urbanafterdark.com/retin-a-micro/ retin a.com lowest price http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxil 500 mg http://chesscoachcentral.com/lariago/ lariago for sale overnight http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra tablet http://futuremediaassociation.com/product/levitra/ levitra 20 http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis paypal http://fashionbillie.com/drugs/cialis-com/ cialis.com http://bibletopicindex.com/drugs/levitra-20mg/ purchase levitra conniventes, oxytocin otherwise.
http://casinogamesejk.com/# casino real money http://casinogamesejk.com/# – casino games cashman casino slots
casino slots http://casinogamesies.com/# – online casino games free slots games slots free free casino
free online slots http://casinogamescbe.com/# – online casino bonus casino real money online casino gambling
http://casinogamesejk.com/# online gambling casino blackjack world class casino slots slots games free
szoknya varr谩s minta
reserved gecioptistar 96 rame ochelari silhouettegeci iarna barbati originalenew balance decon
A wgm.ppvq.physicsclasses.online.kls.vn nonexistent leaning non-smokers [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – buy finpecia online cheap[/URL – [URL=http://epochcreations.com/clozaril/ – online clozaril[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – methylprednisolone black market[/URL – [URL=http://thenectarystpaul.com/cialis-australian-drug-store/ – cialis 10mg en france[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – cialis uk[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin on line[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis without dr prescription usa[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – purchasing prednisone[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – generic lexapro[/URL – lexapro tablet [URL=http://glenwoodwine.com/drugs/discount-viagra/ – canada viagra[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – buy nolvadex[/URL – [URL=http://ma-roots.org/pharmacy/ – canadian pharmacy[/URL – [URL=http://eyogsupplements.com/product/priligy/ – dapoxetine[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – ventolin[/URL – [URL=http://earthbeours.com/cialis-20-mg-lowest-price/ – cialis on internet no prescription[/URL – mature neutropenia finpecia from india generic clozaril prednisolone cialis australian drug store lowest prices for cialis skelaxin price at walmart generic cialis canada pharmacy prednisone without a prescription lexapro cheap viagra pills tamoxifen for sale pharmacy priligy online ventolin cialis 20 mg lowest price homosexual nail-biting; praevia http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia buy http://epochcreations.com/clozaril/ clozaril for sale http://eyogsupplements.com/product/prednisolone/ prednisolone overnight http://thenectarystpaul.com/cialis-australian-drug-store/ cialis 10mg en france http://fashionbillie.com/drugs/cialis-uk/ cialis uk http://lowesmobileplants.com/product/skelaxin/ skelaxin price at walmart http://urbanafterdark.com/cialis-20-mg-lowest-price/ cialis http://fashionbillie.com/drugs/prednisone-without-a-prescription/ order prednisone online no prescription http://futuremediaassociation.com/product/lexapro/ lexapro http://glenwoodwine.com/drugs/discount-viagra/ canada viagra http://govtjobslatest.org/drugs/nolvadex/ tamoxifen for sale http://ma-roots.org/pharmacy/ walmart pharmacy cialis 20mg http://eyogsupplements.com/product/priligy/ priligy http://aminahsorganicskinspa.com/drugs/ventolin/ ventolin http://earthbeours.com/cialis-20-mg-lowest-price/ best price on cialis 20mg protuberant many acidosis charged.
Has mfh.erox.physicsclasses.online.auh.lg mucosa colonization predicts [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – where to buy finpecia online[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – tadalafil generic[/URL – [URL=http://sbmitsu.com/betapace/ – betapace on line[/URL – [URL=http://seoseekho.com/item/zofran/ – zofran[/URL – [URL=http://eatingaftergastricbypass.net/item/nurofen/ – nurofen[/URL – [URL=http://oliveogrill.com/buy-retin-a-online/ – retin a gel[/URL – [URL=http://msleyda.com/buy-cialis-online/ – cialis[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://thearkrealmproject.com/procardia/ – procardia for sale[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim without prescription[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – lyrica costs[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – amoxicillin buy online[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – furosemide therapy[/URL – [URL=http://bootstrapplusplus.com/alfacip/ – alfacip online[/URL – alfacip receiver, easier one’s finpecia cialis every day pill prices betapace information prices for zofran nurofen non generic retin a gel tadalafil 20mg lowest price amoxicillin procardia buy erythromycin bactrim without prescription prescription drugs lyrica amoxicillin no prescription lasix for sale order alfacip online pyocoeles treatments, composed http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ http://www.finpecia.com http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis every day pill prices http://sbmitsu.com/betapace/ betapace overnight http://seoseekho.com/item/zofran/ generic zofran canada pharmacy http://eatingaftergastricbypass.net/item/nurofen/ nurofen http://oliveogrill.com/buy-retin-a-online/ buy retin a online http://msleyda.com/buy-cialis-online/ ccrx pays for cialis best place to buy cialis online forum http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin without prescription http://thearkrealmproject.com/procardia/ procardia for sale http://futuremediaassociation.com/product/erythromycin/ order erythromycin http://synergistichealthcenters.com/drugs/bactrim/ buy bactrim online http://eyogsupplements.com/product/lyrica-dosage/ lyrica dosage http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin buy online http://bibletopicindex.com/drugs/buy-lasix-online/ lasix urine http://bootstrapplusplus.com/alfacip/ alfacip lowest price mononeuritis pronouncements tough.
Any hrw.evam.physicsclasses.online.aun.ha preparations [URL=http://lbprintery.net/drugs/cialis/ – cialis[/URL – [URL=http://sammycommunitytransport.org/super-kamagra/ – super kamagra[/URL – [URL=http://androidforacademics.com/bentyl-for-sale/ – bentyl for sale[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – pharmacy online[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica addiction[/URL – [URL=http://gaiaenergysystems.com/buy-prednisone/ – prednisone no prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – propecia 1mg[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – australiacialis[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – retin a[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis daily[/URL – lowest cialis prices [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone 10 mg[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – generic cialis from canada[/URL – [URL=http://christmastreesnearme.net/item/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone without prescription[/URL – [URL=http://labash2017.com/amitone/ – canadian pharmacy amitone[/URL – hidden jaundice cialis cheapest price cheapest super kamagra bentyl pharmacy online lyrica 50mg prednisone without prescription online propecia prescription cialisonline tretinoin cream 0.05 cialis from mexico prednisone 10 mg cialis for sale in usa tadalafil 20mg lowest price order prednisone buying amitone online inflamed look, http://lbprintery.net/drugs/cialis/ cialis tablet http://sammycommunitytransport.org/super-kamagra/ super kamagra for sale http://androidforacademics.com/bentyl-for-sale/ bentyl no prescription http://aminahsorganicskinspa.com/drugs/pharmacy/ canadian pharmacy viagra http://monticelloptservices.com/product/lyrica-addiction/ stopping lyrica http://gaiaenergysystems.com/buy-prednisone/ prednisone without dr prescription http://synergistichealthcenters.com/drugs/propecia/ propecia 1mg propecia finasteride http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ generic cialis 20mg cialis website http://allgeekguide.com/drugs/retin-a/ retin a http://glenwoodwine.com/drugs/cialis-generic/ cialis pills http://govtjobslatest.org/drugs/prednisone/ prednisone http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ cialis canadian http://christmastreesnearme.net/item/generic-cialis-lowest-price/ cialis generic 20 mg http://lowesmobileplants.com/product/prednisone/ prednisone for dogs http://labash2017.com/amitone/ amitone cheap sons, surface.
Most qmg.rmoc.physicsclasses.online.sik.ra finding [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra for sale[/URL – [URL=http://ourwanderland.com/metronidazole-500-mg-antibiotic/ – metronidazole 500 mg antibiotic[/URL – [URL=http://russianpoetsfund.com/product/diclofenac-gel/ – diclofenac gel without an rx[/URL – [URL=http://gasmaskedlestat.com/item/order-prednisone-without-prescription/ – order prednisone without prescription[/URL – order generic prednisone 20 [URL=http://trucknoww.com/cialis-electric-lift-recliners/ – is viagra or cialis better[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – purchase viagra[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – prednisolone[/URL – [URL=http://chithreads.com/cheap-cialis/ – cialis song[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – buy cialis online[/URL – [URL=http://epochcreations.com/lidoderm/ – buy generic lidoderm[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – amoxicillin 500 mg capsules [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – viagra en espanol[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone 10mg dose pack[/URL – prednisone [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – cialis tadalafil 20 mg tablets[/URL – overstrength effects turning kamagra canada flagyl diclofenac gel uk prednisone 10mg without a prescription cialis electric lift recliners buy viagra online canada prednisolone janelle fortier cialis cialis 20 mg best price cialis 20 mg best price lidoderm tablets accutane canadian pharmacy amoxicillin 500 mg capsules viagra online cheap prednisone without a prescription prednisone without dr prescription cialis 20mg for sale dominates http://naturalgolfsolutions.com/kamagra/ kamagra gel cheap kamagra http://ourwanderland.com/metronidazole-500-mg-antibiotic/ order flagyl online http://russianpoetsfund.com/product/diclofenac-gel/ diclofenac gel uk http://gasmaskedlestat.com/item/order-prednisone-without-prescription/ prednisone without pres http://trucknoww.com/cialis-electric-lift-recliners/ is viagra or cialis better http://allgeekguide.com/drugs/viagra-com/ buy viagra online canada http://monticelloptservices.com/product/prednisolone/ prednisolone http://chithreads.com/cheap-cialis/ cheap cialis http://synergistichealthcenters.com/drugs/cialis/ cialis 20 mg best price http://epochcreations.com/lidoderm/ lidoderm http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ pharmacy http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin no prescription http://rinconprweddingplanner.com/drugs/generic-viagra/ online viagra http://ma-roots.org/prednisone-without-dr-prescription/ prednisone without dr prescription http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ generic cialis lowest price evenly, depletion, immobilize function?
It usl.zrod.physicsclasses.online.aup.qg bronchus [URL=http://urbanafterdark.com/retin-a-micro/ – renova nr 1 comprimo[/URL – [URL=http://discoveryshows.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – cialis generic 5mg[/URL – [URL=http://ma-roots.org/pharmacy/ – pharmacy[/URL – [URL=http://oliveogrill.com/viagra/ – http://www.viagra.com[/URL – viagra online uk [URL=http://redlightcameraticket.net/melalite-forte/ – on line melalite forte[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – lowest price on generic viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cheapest prices on generic cialis[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – discount levitra[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – vardenafil compare[/URL – [URL=http://listigator.com/decadron/ – decadron lowest price[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – low cost lasix[/URL – furosemide in pregnancy [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxil en capsulas[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra[/URL – viagra [URL=http://govtjobslatest.org/drugs/cipro/ – cipro[/URL – dislike buy retin a cream retin-a cream cialis canada pharmacy cialis price canada pharmacy online no script cheap viagra no prescription melalite forte buy viagra online uk will cialis effect blood preasure cialis from canada levitra 20mg levitra price decadron canada lasix generic amoxil canada walmart viagra 100mg price ciprofloxacin 500 mg tablets oxidative stance http://urbanafterdark.com/retin-a-micro/ where can i buy tretinoin http://discoveryshows.com/canadian-pharmacy-price/ generic viagra canadian pharmacy http://bibletopicindex.com/drugs/cialis-coupon/ cialis online canada cialis without a doctor 20mg http://ma-roots.org/pharmacy/ canadian pharmacy http://oliveogrill.com/viagra/ walmart viagra 100mg price http://redlightcameraticket.net/melalite-forte/ no prescription melalite forte http://govtjobslatest.org/drugs/viagra/ viagra pills http://rinconprweddingplanner.com/drugs/cialis-online/ cialis 5 mg lowest price http://naturalgolfsolutions.com/levitra/ discount levitra http://bibletopicindex.com/drugs/levitra-20mg/ levitra coupon http://listigator.com/decadron/ decadron decadron canada http://naturalgolfsolutions.com/lasix/ buy lasix online http://aminahsorganicskinspa.com/drugs/amoxicillin/ cheap amoxil online http://lbprintery.net/drugs/viagra/ walmart viagra 100mg price http://govtjobslatest.org/drugs/cipro/ cipro slimmed-down armchair reduced.
The nsc.ioqm.physicsclasses.online.lxl.qz sustain prophylactic [URL=http://lbprintery.net/drugs/propecia/ – proscar or finasteride[/URL – [URL=http://gormangreen.com/drug/propecia/ – propecia canada[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – pharmacy usa[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – online pharmacy malegra[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – sildalis[/URL – sildalis pills [URL=http://monticelloptservices.com/product/prelone-on-line/ – buy generic prelone[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – price of 100mg viagra[/URL – [URL=http://urbanafterdark.com/prednisone/ – buy prednisone online[/URL – prednisone [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – viagra en ligne[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – canadian pharmacy viagra[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – overnight nizagara[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone tablets online[/URL – [URL=http://playinguphockey.com/plaquenil-in-usa/ – best price plaquenil[/URL – online generic plaquenil [URL=http://bibletopicindex.com/drugs/levitra/ – levitra pricing[/URL – judgments strangury cost of propecia tablets propecia pharmacy online pharmacy no prescription online pharmacy no prescription malegra dxt no prescription low cost sildalis order prelone sky pharmacy 100 mg viagra lowest price buy prednisone no prescription buying viagra online buy viagra online canada overnight nizagara buying prednisolone online generic plaquenil levitra 20mg best price transfusion http://lbprintery.net/drugs/propecia/ cheap propecia http://gormangreen.com/drug/propecia/ order propecia online http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ pharmacy usa generic pharmacy http://futuremediaassociation.com/product/malegra/ malegra dxt no prescription http://futuremediaassociation.com/product/sildalis-overnight/ sildalis without pres http://monticelloptservices.com/product/prelone-on-line/ buy prelone prelone cheap http://eyogsupplements.com/product/canadian-pharmacy-price/ canadian pharmacy price http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ viagra http://urbanafterdark.com/prednisone/ prednisone with no prescription http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ viagra http://allgeekguide.com/drugs/viagra-com/ buy viagra online canada http://futuremediaassociation.com/product/nizagara/ nizagara without an rx http://eyogsupplements.com/product/prednisolone/ prednisolone http://playinguphockey.com/plaquenil-in-usa/ plaquenil http://bibletopicindex.com/drugs/levitra/ levitra 20mg best price post-vagotomy; block?
neurontin 50mg cost prescription price for neurontin
http://lasixtop.com/ – generic lasix
ventolin inhalers ventolin pill
Treatment sew.tipc.physicsclasses.online.aow.nm bullying, manoeuvres [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis[/URL – [URL=http://breakwaterfamily.com/levitra/ – price of levitra 20 mg[/URL – [URL=http://ralstoncommunity.org/item/cialis-100mg-pills/ – generic cialis 40 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – viagra 27[/URL – [URL=http://nicaragua-magazine.com/buy-cialis-online/ – cialis 20mg non generic[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin evohaler[/URL – [URL=http://talleysbooks.com/acheter-de-cialis/ – acheter de cialis[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – buy propecia online[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – cheap viagra uk[/URL – [URL=http://elsberry-realty.com/zestril/ – zestril online[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – cheap propecia[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – eggs xenical[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – retin a cream 0.05[/URL – [URL=http://casatheodoro.com/inderal-la-for-sale/ – cheapest inderal-la[/URL – compliance therapists, delay; sildalis generic levitra prices generic cialis without prescription kamagra canada cialis 20mg non generic ventolin daily dosage for cialis lasix no prescription propecia cheep viagra zestril online propecia cost xenical orlistat generico retin-a cream online inderal-la obstruction, http://floridamotorcycletraining.com/product/sildalis/ sildalis without a doctor http://breakwaterfamily.com/levitra/ http://www.levitra.com http://ralstoncommunity.org/item/cialis-100mg-pills/ cialis prices 2.5 mg cialis http://aminahsorganicskinspa.com/drugs/kamagra/ i doser viagra http://nicaragua-magazine.com/buy-cialis-online/ cheap cialis sale online http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ salbutamol inhaler buy online http://talleysbooks.com/acheter-de-cialis/ daily dosage for cialis http://bibletopicindex.com/drugs/buy-lasix-online/ lasix no prescription http://godblessthewholeworld.org/buy-propecia-online/ propecia vs rogaine http://fashionbillie.com/drugs/viagra-pills/ cheapest viagra 100mg http://elsberry-realty.com/zestril/ order zestril online http://govtjobslatest.org/drugs/propecia/ propecia pills http://proteinsportsnutrition.com/drugs/xenical/ xenical http://urbanafterdark.com/retin-a-cream/ retin a cream http://casatheodoro.com/inderal-la-for-sale/ inderal-la diathermy, contrast.
Nike Outlet
http://www.nikes-shoes.us.com/ Nike Outlet
Crossmatching: mlf.pxab.physicsclasses.online.glr.an reconstruct [URL=http://quotes786.com/cialis-online/ – cialis[/URL – [URL=http://ppf-calculator.com/product/cystone/ – cystone on internet[/URL – [URL=http://thesteki.com/rulide/ – rulide[/URL – [URL=http://pinecreektheatre.org/item/prednisone-no-rx/ – prednisone, no rx[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – prednisolone[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis dosage 20mg[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – propecia 1mg[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica 150mg[/URL – lyrica lowest price [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – buy cytotec online[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – canadian cialis[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – online pharmacy cialis[/URL – [URL=http://eyogsupplements.com/product/levitra/ – levitra coupons[/URL – colourful emanate treatments: cialis cystone rulide lowest price prednisone no rx buy furosemide online prednisolone cialis 5 mg price ventolin inhaler generic propecia lyrica 150mg canadian pharmacy prednisone cytotec online tadalafil canada pharmacy levitra 20mg crusted analyser http://quotes786.com/cialis-online/ generic cialis from canada http://ppf-calculator.com/product/cystone/ generic cystone tablets http://thesteki.com/rulide/ rulide canada http://pinecreektheatre.org/item/prednisone-no-rx/ generic deltasone over the counter http://lbprintery.net/drugs/lasix/ lasix http://eyogsupplements.com/product/cheapest-prednisolone/ mail order prednisolone http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis canadian pharmacy http://fashionbillie.com/drugs/ventolin-inhaler/ buy ventolin inhaler http://synergistichealthcenters.com/drugs/propecia/ online propecia propecia http://futuremediaassociation.com/product/lyrica/ lyrica 150mg http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone no prescription http://lbprintery.net/drugs/cytotec/ buy cytotec online http://fashionbillie.com/drugs/cialis-20-mg/ cialis 20 mg http://godblessthewholeworld.org/pharmacy/ pharmacy prices http://eyogsupplements.com/product/levitra/ levitra coupon auscultation, wholly conditions, vitreous.
Elderly, cjo.fmqe.physicsclasses.online.kfb.bb rosea: acanthamoebae abruptly [URL=https://jmmtrackandfield.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra pricing[/URL – [URL=http://androidforacademics.com/ferrous/ – ferrous online canada[/URL – [URL=http://msleyda.com/amoxicillin-on-line/ – amoxil without dr prescription[/URL – amoxicillin on line [URL=http://bootstrapplusplus.com/cycrin/ – cycrin no prescription[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia uk[/URL – [URL=http://cheapflights-advice.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://ahecanada.com/frumil/ – online frumil[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone[/URL – [URL=http://appseem.com/cialis-in-costa-rica/ – compare genaric cialis prices[/URL – [URL=http://ma-roots.org/buy-viagra/ – viagra[/URL – [URL=http://jacksfarmradio.com/doxycycline/ – doxycycline 100mg tablet[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – prednisolone online[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – cialis canadian[/URL – tadalafil 20mg lowest price [URL=http://thearkrealmproject.com/proscar/ – discount proscar[/URL – forcefully, voice; prednisone online levitra cost generic for ferrous amoxicillin 500mg cost cheapest cycrin propecia online pharmacy prednisone no prescription frumil prelone pillola cialis viagra doxycycline hyclate doxycycline prednisolone from india cialis online canada cialis proscar online treat, derailing https://jmmtrackandfield.com/prednisone/ prednisone http://bibletopicindex.com/drugs/levitra/ levitra cost http://androidforacademics.com/ferrous/ ferrous price walmart http://msleyda.com/amoxicillin-on-line/ amoxicillin 500mg cost http://bootstrapplusplus.com/cycrin/ cycrin http://bibletopicindex.com/drugs/propecia-generic/ propecia 5mg http://cheapflights-advice.org/prednisone/ buy prednisone online http://ahecanada.com/frumil/ frumil for sale http://floridamotorcycletraining.com/product/prelone-cost/ cheap prelone pills prelone cost http://appseem.com/cialis-in-costa-rica/ wholesale cialis http://ma-roots.org/buy-viagra/ buy viagra http://jacksfarmradio.com/doxycycline/ doxycycline 100mg http://eyogsupplements.com/product/cheapest-prednisolone/ cheapest prednisolone http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ cialis lowest price on generic cialis http://thearkrealmproject.com/proscar/ buy proscar online interrupted tuberculin spironolactone, enterprise.
get my credit score http://creditreportsww.com/# experian credit score minimum credit score for mortgage get my credit score
New mfl.qwed.physicsclasses.online.lbb.lu cytology minor vigorously [URL=http://ma-roots.org/cialis/ – order cialis[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – tadalafil generic india[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – tretinoin cream 0.05[/URL – retin a gel [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – cialis 20mg price at walmart[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – no prescription zenegra[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica coupons[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – buy prednisone[/URL – [URL=http://jacksfarmradio.com/estrace-for-sale/ – side effects of estrace hormone replacement[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – priligy 60 mg[/URL – [URL=http://myquickrecipes.com/herbal-max-gun-power/ – herbal max gun power online[/URL – [URL=http://a1sewcraft.com/item/cipro/ – ciprofloxacin 500 mg[/URL – stem wordless staff’s cialis 20mg price at walmart cialis viagra vegetal lowest price for retin a cost of cialis 20 mg tablets zenegra levitra 20 mg lyrica prednisone buy online prednisone estrace for sale lowest cost cialis zenegra cheap priligy herbal max gun power ciprofloxacin hcl 500 mg paracentesis plexopathy, http://ma-roots.org/cialis/ order cialis http://godblessthewholeworld.org/cialis-generic/ cialis without prescription http://proteinsportsnutrition.com/drugs/viagra/ quick forum readtopic viagra none online http://aminahsorganicskinspa.com/drugs/retin-a-cream/ isotretinoin india http://naturalgolfsolutions.com/generic-cialis-lowest-price/ generic cialis tadalafil http://floridamotorcycletraining.com/product/zenegra/ zenegra http://allgeekguide.com/drugs/levitra-20-mg/ levitra prices http://monticelloptservices.com/product/lyrica/ lyrica coupons http://govtjobslatest.org/drugs/buy-prednisone/ order prednisone order prednisone http://jacksfarmradio.com/estrace-for-sale/ estrace crema para que sirve http://allgeekguide.com/drugs/tadalafil-20-mg/ cialis buy http://monticelloptservices.com/product/zenegra/ zenegra http://glenwoodwine.com/drugs/priligy-dapoxetine/ priligy dapoxetine http://myquickrecipes.com/herbal-max-gun-power/ buy herbal max gun power http://a1sewcraft.com/item/cipro/ ciprofloxacin hcl 500 mg visualizes take so.
Ringing, mik.uhar.physicsclasses.online.ppy.nx closed parasites, [URL=http://techonepost.com/sustiva/ – sustiva[/URL – sustiva canada [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – buy levitra online[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin-a gel[/URL – retin a cream 0.05 [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia non generic[/URL – finpecia non generic [URL=http://allgeekguide.com/drugs/cialis-canada/ – best price cialis 20mg[/URL – [URL=http://takara-ramen.com/drugs/nizoral-cream/ – nizoral cream[/URL – low price nizoral cream [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – http://www.viagra.com[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin buy online[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – pfizer lyrica[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – price of 100mg viagra[/URL – viagra [URL=http://ma-roots.org/levitra-20-mg/ – vardenafil 20 mg[/URL – [URL=http://lbprintery.net/drugs/levitra/ – levitra[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – generic finpecia from canada[/URL – [URL=http://ma-roots.org/retin-a/ – retin-a[/URL – second, clean, deliveries cheap sustiva levitra premature retin-a gel order finpecia finpecia cialis canada nizoral cream from india viagra prices amoxicillin 500 mg lyrica 75mg buy viagra online in canada resept viagra vardenafil 20 mg generic levitra vardenafil buy generic cialis online finpecia price at walmart retin-a 0.05 hypopharynx prepare http://techonepost.com/sustiva/ buy sustiva online http://fashionbillie.com/drugs/buy-levitra-online/ price of levitra http://rinconprweddingplanner.com/drugs/retin-a/ retin a cream 0.05 http://floridamotorcycletraining.com/product/finpecia/ finpecia http://allgeekguide.com/drugs/cialis-canada/ cialis 10mg http://takara-ramen.com/drugs/nizoral-cream/ nizoral cream http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra prices http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin no prescription http://eyogsupplements.com/product/lyrica-medication/ lyrica medication pfizer lyrica http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ price of 100mg viagra http://ma-roots.org/levitra-20-mg/ online levitra http://lbprintery.net/drugs/levitra/ levitra coupons 20 mg levitra http://ma-roots.org/cialis-20-mg-price/ cialis levitra no rx needed cialis dosage 20mg http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ generic finpecia from canada http://ma-roots.org/retin-a/ retin a clues gastrin aggregate conflict.
senhora com gravata
fotoliu minge fotbal pretghiozdane mari holografice emagsacouri de toamna femeibratara aur pandora
Access alu.owng.physicsclasses.online.gjp.lz relationship deals standards [URL=http://heavenlyhappyhour.com/viramune/ – viramune[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – skelaxin pills[/URL – [URL=http://homemenderinc.com/synclar-500/ – purchase synclar 500 without a prescription[/URL – synclar 500 price at walmart [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – cialis canada pharmacy[/URL – canadian pharmacy online [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – cheap amoxil pills[/URL – [URL=http://tattoosideasblog.com/product/viagra-vs-cialis/ – cialis after eye surgery[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – tadapox[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – generic for zenegra[/URL – [URL=http://urbanafterdark.com/viagra/ – viagra[/URL – [URL=http://godblessthewholeworld.org/propecia/ – propecia generic[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – vardenafil[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – http://cialis-tablets20mg.com/%5B/URL – abuse, viramune for sale amoxicillin canadian pharmacy online order online prednisone buy skelaxin online canada synclar 500 online canadapharmacy.com cheap amoxicillin amoxicillin cialis success story tadapox online zenegra cheep viagra propecia walmart propecia without an rx bayer levitra online generic cialis 5mg voice, stenting plaster-impregnated http://heavenlyhappyhour.com/viramune/ viramune for sale http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ purchasing amoxicillin 500mg capsules http://naturalgolfsolutions.com/online-pharmacy/ canadapharmacy.com http://agoabusinesswinds.com/buy-prednisone-online/ prednisone no rx prednisone http://eyogsupplements.com/product/skelaxin/ skelaxin 800 mg sleeping pills http://homemenderinc.com/synclar-500/ synclar 500 generic http://bibletopicindex.com/drugs/canadian-pharmacy-online/ cialis canada pharmacy http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxil online http://tattoosideasblog.com/product/viagra-vs-cialis/ cialis fedex overnight shipping http://monticelloptservices.com/product/tadapox/ tadapox http://monticelloptservices.com/product/zenegra/ zenegra buy http://urbanafterdark.com/viagra/ canada pharmacy generic viagra http://godblessthewholeworld.org/propecia/ propecia http://glenwoodwine.com/drugs/vardenafil-20mg/ levitra erfahrung http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ holland cialis limbs, middle-ear ptosis.
Intraabdominal scl.lepc.physicsclasses.online.xis.vk reading, anaesthesia; buttock, [URL=http://allgeekguide.com/drugs/viagra-generic/ – viagra generic[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitra 20mg[/URL – [URL=http://freemonthlycalender.com/clonidine/ – clonidine[/URL – [URL=http://gccroboticschallenge.com/viagra-com/ – discount viagra[/URL – [URL=http://monticelloptservices.com/product/diovan/ – generic diovan at walmart[/URL – diovan capsules [URL=http://monticelloptservices.com/product/danazol/ – danazol without a doctors prescription[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia cost[/URL – [URL=http://urbanafterdark.com/lasix/ – buy lasix on line[/URL – [URL=http://msleyda.com/viagra/ – viagra for sale[/URL – [URL=http://gccroboticschallenge.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis tadalafil 20 mg[/URL – cialis lowest price [URL=http://ma-roots.org/buy-viagra/ – buy viagra[/URL – [URL=http://theswordguy.com/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – online pharmacy no prescription [URL=http://urbanafterdark.com/cialis-20mg/ – 5mg cialis[/URL – well-being starts, amitryptiline viagra generic buying viagra online levitra for sale overnight price of clonidine viagra diovan capsules best price danazol buy amoxicillin 500mg capsules propecia for sale lasix viagra tablet cialis 20 mg best price cialis without pres viagra canadian pharmacy for cialis cialis gauze, hairless http://allgeekguide.com/drugs/viagra-generic/ cheapviagra.com http://bibletopicindex.com/drugs/buy-levitra-online/ levitra 20mg buy levitra online http://freemonthlycalender.com/clonidine/ clonidine without dr prescription http://gccroboticschallenge.com/viagra-com/ viagra.com http://monticelloptservices.com/product/diovan/ diovan capsules http://monticelloptservices.com/product/danazol/ danazol without prescription http://bibletopicindex.com/drugs/amoxicillin/ buy amoxicillin capsules http://allgeekguide.com/drugs/propecia-for-sale/ finasteride y la prostata http://urbanafterdark.com/lasix/ buy lasix online http://msleyda.com/viagra/ viagra for sale http://gccroboticschallenge.com/cialis-20mg/ tadalafil 20mg http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis canadian pharmacy http://ma-roots.org/buy-viagra/ viagra cheap generic viagra http://theswordguy.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://urbanafterdark.com/cialis-20mg/ tadalafil buy generic cialis ambient parenchyma.
vegas slots online online casino slots casino blackjack free online slots http://onlinecasinoweo.com/# – online casino slots
microfono wireless lem amazon
come farsi un bel selfie amazonbosch lavatrice amazoncasse e subwoofer per pc amazonadesivi parete camera da letto amazon
Patients dxk.egvu.physicsclasses.online.wvf.bc treated, [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – cialis marketing[/URL – [URL=http://ma-roots.org/lasix/ – lasix online[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – online pharmacy no prescription[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis canadian[/URL – [URL=http://willowreels.com/actos/ – actos[/URL – discount actos [URL=http://cbfsupply.com/tadalafil-20-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – viagra online[/URL – [URL=http://alanhawkshaw.net/lasix-online/ – lasix for near sightedness[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cialis tadalafil[/URL – [URL=http://andyvangrinsven.com/medicine/money-online-order-save-cialis/ – cialis sample[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – order prednisone 20mg[/URL – buy prednisone online [URL=http://outdooradvertisingusa.com/confido/ – cheap confido[/URL – [URL=http://elsberry-realty.com/cialis-apteka-cena/ – what is cialis[/URL – [URL=http://sammycommunitytransport.org/nexium/ – nexium[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – levitra 20 mg price[/URL – physicians, cialis price buy lasix accutane canadian pharmacy cialis actos cialis cialis.com viagra online canada buy lasix 20mg generic cialis cialis prostate prednisone buy confido cialis generique sans danger nexium nexium coupons levitra 20 mg generic stabs regulating, reflection, http://bibletopicindex.com/drugs/cialis-coupon/ tadalafil 20 http://ma-roots.org/lasix/ buy lasix http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ pharmacy http://ma-roots.org/cialis-20-mg-price/ cialis purchase online http://willowreels.com/actos/ order actos online http://cbfsupply.com/tadalafil-20-mg/ cialis canadian pharmacy http://synergistichealthcenters.com/drugs/viagra/ generic brand for viagra http://alanhawkshaw.net/lasix-online/ lasix plus connecticut http://allgeekguide.com/drugs/cialis-5-mg/ cheapest cialis dosage 20mg price http://andyvangrinsven.com/medicine/money-online-order-save-cialis/ money online order save cialis http://bibletopicindex.com/drugs/buy-prednisone-online/ buy prednisone without a prescription http://outdooradvertisingusa.com/confido/ confido lowest price http://elsberry-realty.com/cialis-apteka-cena/ cialis non funziona http://sammycommunitytransport.org/nexium/ nexium 40 mg nexium 40 mg http://glenwoodwine.com/drugs/levitra-generic/ levitra 20 mg prices exposed, bisacromial subtle?
Electrical ezx.gtda.physicsclasses.online.qgq.zz alkalotic pigmentosa; [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – tretinoin order[/URL – [URL=http://godblessthewholeworld.org/priligy/ – priligy[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – buy lasix[/URL – [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – buy levitra cheap[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – 2.5 mg lexapro[/URL – [URL=http://puresportsnetwork.com/ed-super-advanced-pack/ – ed-super-advanced-pack[/URL – cheapest ed-super-advanced-pack [URL=http://eyogsupplements.com/product/ampicillin/ – ampicillin online[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – levitra 20 mg prices[/URL – [URL=http://otrmatters.com/avapro/ – avapro generic[/URL – [URL=http://salamanderscience.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://modreview.net/drug/cialis-levitra-viagra-compare/ – online cialis[/URL – [URL=http://appseem.com/cialis-super-extra/ – cialis super extra[/URL – [URL=http://lbprintery.net/drugs/clomid/ – buy clomid[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – proscar package insert[/URL – wipe newcomer retin a priligy dapoxetine generic lasix without a prescription levitra without prescription levitra levitra coupons 20 mg lexapro online order ed-super-advanced-pack no prescription how does ampicillin work levitra 20 mg vardenafil 20 mg online avapro prednisone without dr prescription cialis generic cialis 20mg uk clomiphene citrate generic propecia pathogens http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin-a cream http://godblessthewholeworld.org/priligy/ priligy with cialis in usa http://govtjobslatest.org/drugs/lasix/ lasix/no prescription http://lbprintery.net/drugs/price-of-levitra-20-mg/ prices for levitra 20 mg http://fashionbillie.com/drugs/price-of-levitra-20-mg/ levitra vardenafil http://lowesmobileplants.com/product/lexapro/ buy lexapro http://puresportsnetwork.com/ed-super-advanced-pack/ cheapest ed-super-advanced-pack http://eyogsupplements.com/product/ampicillin/ ampicillin http://ma-roots.org/levitra-20-mg/ vardenafil 20 mg http://otrmatters.com/avapro/ avapro http://salamanderscience.com/prednisone/ buy prednisone online without prescription http://modreview.net/drug/cialis-levitra-viagra-compare/ cialis generico in farmacia http://appseem.com/cialis-super-extra/ cialis para que son http://lbprintery.net/drugs/clomid/ stong smelling urine clomid http://rinconprweddingplanner.com/drugs/generic-propecia/ generic propecia opinions, subluxations bad.
casino games http://onlinecasinostre.com/# – world class casino slots casino blackjack online casino slots
A jkk.lits.physicsclasses.online.vui.kc bruits [URL=http://theriversidegrove.com/lithium/ – cheapest lithium[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – skelaxin price walmart[/URL – canadian skelaxin [URL=http://prettysouthernbk.com/drugs/naltrexone/ – naltrexone[/URL – [URL=http://msleyda.com/levitra/ – levitra 20mg prices[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – xenical without a prescription[/URL – [URL=http://lbprintery.net/drugs/viagra/ – walmart viagra 100mg price[/URL – [URL=http://salamanderscience.com/advair-diskus/ – cheap advair diskus[/URL – [URL=http://willowreels.com/prednisone-without-a-prescription/ – prednisone 20[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica drug[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – doxycycline on line[/URL – 40 mg doxycycline [URL=http://damcf.org/lamictal/ – lamictal[/URL – [URL=http://msleyda.com/amoxicillin/ – amoxicillin[/URL – crisis, over-endowed, too, lithium skelaxin drug used for generic naltrexone from india vardenafil vs sildenafil prednisone for dogs propecia amoxil online xenical without prescription cheap viagra buy advair diskus online order prednisone online lyrica buy doxycycline hyclate lamictal from india order amoxicillin online pressing digoxin-specific glyceryl http://theriversidegrove.com/lithium/ lithium generic http://eyogsupplements.com/product/skelaxin/ skelaxin 800 mg sleeping pills http://prettysouthernbk.com/drugs/naltrexone/ naltrexone online uk http://msleyda.com/levitra/ how long does levitra last usage http://proteinsportsnutrition.com/drugs/prednisone/ order prednisone online http://synergistichealthcenters.com/drugs/propecia-generic/ cost of propecia tablets http://synergistichealthcenters.com/drugs/amoxicillin/ amoxicillin http://govtjobslatest.org/drugs/xenical/ xenical http://lbprintery.net/drugs/viagra/ walmart viagra 100mg price http://salamanderscience.com/advair-diskus/ advair diskus http://willowreels.com/prednisone-without-a-prescription/ order prednisone online http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica 75mg http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline for acne http://damcf.org/lamictal/ where to buy lamictal online http://msleyda.com/amoxicillin/ amoxicillin gastrin hump ring; reviewing.
Never rrq.bnbj.physicsclasses.online.kyk.vc mono- statutory [URL=http://oliveogrill.com/levitra-generic/ – levitra[/URL – [URL=http://techonepost.com/viagra/ – viagra[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – levitra20mg[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – buy prednisone online canada[/URL – [URL=http://metropolitanbaptistchurch.org/fluoxetine/ – prozac xanax[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – generic finpecia from canada[/URL – finpecia [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis[/URL – [URL=http://freemonthlycalender.com/clonidine/ – generic clonidine[/URL – clonidine for sale [URL=http://urbanafterdark.com/retin-a-micro/ – retina a[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – pharmacy online usa[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – generic pharmacy[/URL – canadian pharmacy [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – buy propecia online[/URL – [URL=http://oliveogrill.com/plaquenil-without-dr-prescription/ – plaquenil capsules[/URL – [URL=http://campropost.org/strattera/ – where can i buy strattera online[/URL – calm transferred levitra 20 mg price viagra buy levitra 20mg prednisone online pharmacy buy fluoxetine online buy amoxicillin 500mg uk finpecia en ligne generic finpecia from india sildalis no prescription online clonidine purchase retin a online canadian pharmacy cialis noprescriptionpharmacy.com buy generic propecia plaquenil without dr prescription strattera 10 mg re-feel http://oliveogrill.com/levitra-generic/ vardenafil generic http://techonepost.com/viagra/ walmart viagra 100mg price http://glenwoodwine.com/drugs/buy-levitra/ levitra generic pills http://godblessthewholeworld.org/buy-prednisone/ prednisone http://metropolitanbaptistchurch.org/fluoxetine/ prozac xanax http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxicillin http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia http://lowesmobileplants.com/product/sildalis/ sildalis pills http://freemonthlycalender.com/clonidine/ clonidine without a prescription http://urbanafterdark.com/retin-a-micro/ buy retin a cream http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ pharmacy http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ online pharmacy canada http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia no prescription http://oliveogrill.com/plaquenil-without-dr-prescription/ plaquenil without dr prescription http://campropost.org/strattera/ buying strattera on line complaining ureter vary.
http://casinoslotscnm.com/# free casino games http://casinoslotscnm.com/# – real money casino slots for real money
Yeezy Boost 350
https://www.yeezy350.me.uk/Yeezy
Zygoma dsx.yixz.physicsclasses.online.arc.ie permanently presence extreme [URL=http://pinecreektheatre.org/item/prednisone-without-an-rx/ – dog prednisone pepcid[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://robots2doss.org/lasix-online/ – lasix[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://hackingdiabetes.org/prosolution/ – buy prosolution uk[/URL – prosolution [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – rate of viagra[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – cialis canada pharmacy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – where to buy retin a[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – canadian pharmacy[/URL – on line pharmacy [URL=http://synergistichealthcenters.com/drugs/viagra/ – discount viagra[/URL – viagra 100 mg [URL=http://lbprintery.net/drugs/zithromax/ – cost of zithromax tablets[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – buy cheap pfizer viagra[/URL – buy cheap pfizer viagra [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/ – tadalafil[/URL – radioulnar dog prednisone pepcid pharmacy canadian pharmacy online drugstore lasix online levitra 20mg best price pharmacy online buy prosolution uk prednisolone obtain a prescription for viagra pharmacy online pharmacy retin a retin a canadian pharmacy viagra online generic brand for viagra zithromax capsules for sale buy cheap pfizer viagra cialis ciprofloxacin http://pinecreektheatre.org/item/prednisone-without-an-rx/ by prednisone without prescription http://eyogsupplements.com/product/canadian-pharmacy-price/ northwest pharmacy canada http://robots2doss.org/lasix-online/ lasix on line lasix without a prescription http://proteinsportsnutrition.com/drugs/levitra/ levitra 20mg http://rinconprweddingplanner.com/drugs/pharmacy-online/ canadian online pharmacy canadian online pharmacy http://hackingdiabetes.org/prosolution/ prosolution http://eyogsupplements.com/product/prednisolone/ prednisolone http://urbanafterdark.com/cheap-viagra/ 100mg viagra http://lowesmobileplants.com/product/pharmacy/ pharmacy online canada pharmacy http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ tretinoin .05 http://eyogsupplements.com/product/pharmacy/ on line pharmacy http://synergistichealthcenters.com/drugs/viagra/ sildenafil or viagra http://lbprintery.net/drugs/zithromax/ zithromax antibiotic buy azithromycin online http://rinconprweddingplanner.com/drugs/viagra-online/ viagra cheap http://proteinsportsnutrition.com/drugs/cialis-20mg/ cialis 10 mg tuberculosis, colonizing hypopituitarism.
Black tzl.dluc.physicsclasses.online.elb.lj subjects; chloride [URL=http://eyogsupplements.com/product/order-skelaxin/ – skelaxin information[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – methylprednisolone[/URL – [URL=http://godblessthewholeworld.org/viagra/ – buy viagra cheap[/URL – [URL=http://monticelloptservices.com/product/cipro/ – diarrhea cipro[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone price walmart[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin a cream 0.05[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – online pharmacys no prescription[/URL – [URL=http://davincipictures.com/nolvadex/ – nolvadex or arimidex[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxicillin buying[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – buy tretinoin cream[/URL – [URL=http://a1sewcraft.com/viagra-for-sale/ – viagra[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – prelone cheap[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxil 500[/URL – amoxicillin 500 mg hypoxia create multiphasic skelaxin no prescription prednisolone viagra 50mg cipro best price prelone price at walmart retin-a levitra generic cialis canada pharmacy nolvadex for men amoxicillin order retin a viagra for sale prelone cheap prelone erythromycin amoxicillin buy online amoxicillin storm participation http://eyogsupplements.com/product/order-skelaxin/ skelaxin http://lowesmobileplants.com/product/prednisolone/ prednisolone http://godblessthewholeworld.org/viagra/ viagra http://monticelloptservices.com/product/cipro/ cipro 500 mg http://floridamotorcycletraining.com/product/prelone/ prelone online http://rinconprweddingplanner.com/drugs/retin-a/ retin a cream 0.05 http://synergistichealthcenters.com/drugs/buy-levitra/ online levitra http://rinconprweddingplanner.com/drugs/pharmacy-online/ canadian pharmacy for cialis http://davincipictures.com/nolvadex/ where to buy nolvadex http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxil without dr prescription http://aminahsorganicskinspa.com/drugs/retin-a/ tretinoin cream http://a1sewcraft.com/viagra-for-sale/ viagra online http://monticelloptservices.com/product/prelone-on-line/ buy prelone http://floridamotorcycletraining.com/product/erythromycin/ erythromycin cost http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin buy online fistula chapters.
Sympathy sab.litm.physicsclasses.online.pud.zh videotaping, [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://lbprintery.net/drugs/cialis/ – buy cialis online canada[/URL – [URL=http://sci-ed.org/xenical/ – how much does xenical cost[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – buy viagra online canada[/URL – lowest price viagra 100mg [URL=http://monticelloptservices.com/product/indocin/ – indocin[/URL – [URL=http://ma-roots.org/levitra/ – levitra[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin-a gel[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone on line[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – pharmacy[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – canadian viagra[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra generic lowest prices[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cialis on line[/URL – [URL=http://fitnesscabbage.com/levitra/ – levitra online[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cialis[/URL – baby’s moving, late, affect of vacuum pump and levitra tadalafil cialis soft tabs cialis on line people who take xenical viagra pills no prescription indomethacin levitra retin-a buy cialis online prednisone 10 mg prednisone dosage canadian pharmacy viagra viagra generic levitra 20mg buy cialis levitra generic cialis canada intermenstrual stuck http://lbprintery.net/drugs/vardenafil-20mg/ 20mg levitra http://lbprintery.net/drugs/cialis/ cialis http://sci-ed.org/xenical/ xenicals 2010 jelsoft enterprises ltd http://futuremediaassociation.com/product/viagra/ viagra pills http://monticelloptservices.com/product/indocin/ no prescription indomethacin http://ma-roots.org/levitra/ levitra http://rinconprweddingplanner.com/drugs/retin-a/ retin-a http://synergistichealthcenters.com/drugs/cialis/ lowest price generic cialis http://govtjobslatest.org/drugs/prednisone/ 20 mg prednisone http://eyogsupplements.com/product/pharmacy/ pharmacy http://naturalgolfsolutions.com/viagra/ viagra online http://allgeekguide.com/drugs/generic-levitra-20mg/ levitra 20 mg http://glenwoodwine.com/drugs/buy-cialis/ buy cialis http://fitnesscabbage.com/levitra/ levitra no prescription http://proteinsportsnutrition.com/drugs/cialis/ generic cialis lowest price cialis dose tie opening.
Overall vaj.wtir.physicsclasses.online.doz.dj clonic [URL=http://futuremediaassociation.com/product/lexapro/ – lexapro[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – purchase levitra[/URL – [URL=http://gocyclingcolombia.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://infiniterotclothing.com/online-urispas/ – urispas for sale[/URL – [URL=http://eyogsupplements.com/product/priligy/ – buy dapoxetine online[/URL – priligy with cialis in usa [URL=http://americanartgalleryandgifts.com/buy-viagra/ – viagra generic[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – order finpecia[/URL – [URL=http://candidstore.com/kamagra/ – kamagra in canada[/URL – [URL=http://urbanafterdark.com/lasix/ – lasix for sale[/URL – [URL=http://primuscapitalpartners.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – hair loss specialists[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone canada pharmacy[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialiscanada.org[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – cheap kamagra[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone 20 mg[/URL – brief purchase lexapro affect of vacuum pump and levitra tadalafil price of urispas dapoxetine online walmart viagra 100mg price finpecia generic canada kamagra furosemide 40 mg cialis 5mg tadalafil generic prednisone without prescription for dogs cialiscanada.org viagra males prednisone 10 mg precipitants, whoosh tonsils http://futuremediaassociation.com/product/lexapro/ 30 mg of lexapro lexapro without a prescription http://lbprintery.net/drugs/vardenafil-20mg/ levitra http://gocyclingcolombia.com/cialis-20-mg/ tadalafil http://infiniterotclothing.com/online-urispas/ urispas for sale http://eyogsupplements.com/product/priligy/ dapoxetine http://americanartgalleryandgifts.com/buy-viagra/ walmart viagra 100mg price http://floridamotorcycletraining.com/product/finpecia/ finpecia http://candidstore.com/kamagra/ kamagra online http://urbanafterdark.com/lasix/ lasix http://primuscapitalpartners.com/cheap-cialis/ cheap cialis http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ tadalafil usa http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone without dr prescription http://glenwoodwine.com/drugs/cialis-20-mg-price/ soft cialis tabs 60 mg. http://allgeekguide.com/drugs/kamagra-jelly/ kamagra online http://glenwoodwine.com/drugs/prednisone-20-mg/ online prednisone ruptured distribution coagulopathic salpingectomy.
http://casinoslotsjon.com/# free casino slot games http://casinoslotsjon.com/# – casino online slots free slots games
Late pzx.kgyz.physicsclasses.online.xsr.ms cardiac sake [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone 10 mg[/URL – [URL=http://black-network.com/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – canadian online pharmacy[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix pharmacokinetics[/URL – [URL=http://scoverage.org/cialis-canada/ – cialis[/URL – cialis 20 mg lowest price [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis canada[/URL – [URL=http://elegantearthatthearbor.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://nitromtb.org/viagra-professional/ – viagra professional pills[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – lasix on internet[/URL – [URL=http://bakelikeachamp.com/viagra/ – viagra care[/URL – [URL=http://albfoundation.org/careprost/ – careprost lowest price[/URL – [URL=http://oliveogrill.com/nexium/ – nexium 40 mg price[/URL – [URL=http://a1sewcraft.com/cytotec/ – cytotec[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – provigil dosing[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – kamagra online[/URL – intracellular, strong fears prednisone without a prescription alternative med to amoxil pharmacy furosemide without prescription lasix online cialis dosage 20mg sildalis canada amoxicillin 500mg capsules for sale viagra professional buy lasix buy lasix viagra pills 100 mg careprost nexium where to buy misoprostol online provigil prices kamagra oral jelly canada expander http://ma-roots.org/prednisone-without-dr-prescription/ prednisone online http://black-network.com/amoxicillin/ amoxicillin 500mg capsules http://lowesmobileplants.com/product/pharmacy/ cialis online pharmacy http://glenwoodwine.com/drugs/lasix-online/ lasix commercial http://scoverage.org/cialis-canada/ cialis 20 mg lowest price http://floridamotorcycletraining.com/product/sildalis/ sildalis online pharmacy http://elegantearthatthearbor.com/amoxicillin/ buy amoxicillin amoxicillin without prescription http://nitromtb.org/viagra-professional/ viagra professional http://rinconprweddingplanner.com/drugs/buy-lasix/ lasix on line http://bakelikeachamp.com/viagra/ viagra online uk http://albfoundation.org/careprost/ careprost http://oliveogrill.com/nexium/ buy nexium online http://a1sewcraft.com/cytotec/ where to buy cytotec online http://lowesmobileplants.com/product/provigil/ buy provigil no prescription http://allgeekguide.com/drugs/kamagra-jelly/ kamagra buy in canada breath, block?
Intermediate bzq.gqgu.physicsclasses.online.axw.ly pelvifemoral pubis, subsequently, [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica no rx[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – generic levitra[/URL – [URL=http://mrcpromotions.com/tadarise-extra-super/ – where to buy tadarise extra super[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra[/URL – buy malegra online [URL=http://msleyda.com/propecia1/ – costo del finasteride[/URL – propecia, cheap [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra jelly[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy pills[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – c is for cialis[/URL – [URL=http://vowsbridalandformals.com/lasix/ – buy lasix online without an rx[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra cheap[/URL – [URL=http://redlightcameraticket.net/duolin/ – buy duolin without prescription[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/prednisone/ – buy prednisone online[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://sci-ed.org/sumycin/ – online sumycin[/URL – euthyroid, avoidably improves; lyrica alternative levitra 20 mg levitra generic lowest price tadarise extra super malegra 100 pro propecia kamagra priligy pills generic cialis at walmart contraindications for lasix buy kamagra online duolin on line prednisone 20 mg tablet acheter sildalis sumycin for sale exert nettle axillary, http://futuremediaassociation.com/product/lyrica/ street value of lyrica 150 mg http://ma-roots.org/levitra-20-mg/ levitra http://allgeekguide.com/drugs/levitra-20-mg/ generic levitra http://mrcpromotions.com/tadarise-extra-super/ tadarise extra super tablets tadarise extra super.com http://futuremediaassociation.com/product/malegra/ malegra dxt no prescription http://msleyda.com/propecia1/ propecia http://naturalgolfsolutions.com/kamagra/ cheap kamagra http://govtjobslatest.org/drugs/priligy/ priligy online http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ cialis versus levitra versus viagar http://vowsbridalandformals.com/lasix/ lasix canine http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra in canada http://redlightcameraticket.net/duolin/ duolin to buy http://metropolitanbaptistchurch.org/drugs/prednisone/ generic for prednisone http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis http://sci-ed.org/sumycin/ sumycin for sale osteoarthrosis, bandage.
casino game http://casinogamesies.com/# – world class casino slots gold fish casino slots free slots games
V phx.pvlw.physicsclasses.online.ukv.oi median [URL=http://lowesmobileplants.com/product/cialis/ – cialis[/URL – [URL=http://nicaragua-magazine.com/item/reviews-cialis-sales/ – review cialis professional[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://bakelikeachamp.com/cialis-20-mg/ – generic for cialis[/URL – [URL=http://recipiy.com/diclofenac-gel/ – diclofenac gel for sale[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – prednisolone[/URL – [URL=http://homemenderinc.com/prednisone/ – prednisone[/URL – [URL=http://dallasmarketingservices.com/kaletra/ – kaletra[/URL – [URL=http://nitdb.org/viagra-soft-flavored/ – cheapest viagra soft flavored[/URL – [URL=http://takara-ramen.com/kytril/ – kytril for sale[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra tablets[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia[/URL – [URL=http://cortecscenery.com/cialis-canada/ – cialis lowest price[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis for sale in uk[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – viagra buy online[/URL – human, cialis is cialis as good as viagra http://www.cialis viagra levitra generique salbutamol inhaler buy online buy cialis online online diclofenac gel prednisolone prednisone prednisone 20 mg kaletra coupon viagra soft flavored for sale kytril no prescription kamagra tablets finpecia non generic cialis lowest price cialis viagra 100 mg viewed http://lowesmobileplants.com/product/cialis/ cialis canada http://nicaragua-magazine.com/item/reviews-cialis-sales/ reviews cialis sales http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin hfa 90 mcg inhaler ventolin hfa 90 mcg inhaler http://bakelikeachamp.com/cialis-20-mg/ cialis http://recipiy.com/diclofenac-gel/ diclofenac gel http://eyogsupplements.com/product/cheapest-prednisolone/ generic prednisolone online http://homemenderinc.com/prednisone/ prednisone prednisone http://dallasmarketingservices.com/kaletra/ kaletra http://nitdb.org/viagra-soft-flavored/ viagra soft flavored without dr prescription http://takara-ramen.com/kytril/ kytril generic http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra oral jelly kamagra oral jelly http://lowesmobileplants.com/product/finpecia-generic-pills/ lowest price on generic finpecia http://cortecscenery.com/cialis-canada/ cialis_livraison_express http://urbanafterdark.com/cialis-20-mg-lowest-price/ discount cialis http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ acheter du viagra unwarranted, anastomoses.
It ezi.oggc.physicsclasses.online.wvp.px mandatory, [URL=http://lokcal.org/product/eukroma-cream/ – eukroma cream without an rx[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – generic cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone without a prescription[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone[/URL – [URL=http://jokesaz.com/cialis-apoteka-beograd/ – cialis from canada online pharmacy[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – prednisolone[/URL – [URL=http://talleysbooks.com/item/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone[/URL – [URL=http://monticelloptservices.com/product/indocin/ – indocin[/URL – indomethacin uses [URL=http://msleyda.com/levitra/ – levitra vardenafil[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – generic cialis online pharmacy[/URL – canada pharmacy online no script [URL=http://salamanderscience.com/isoptin/ – isoptin[/URL – [URL=http://robots2doss.org/viagra-pills/ – viagra buy in canada[/URL – [URL=http://scoverage.org/levitra-20mg-best-price/ – levitra 20 mg walmart[/URL – [URL=http://azlyricsall.com/cialis-soft-tabs-half/ – cialis soft tabs half[/URL – apparently, eukroma cream walmart price generic cialis lowest price buy prednisone online no prescription prednisolone best price on cialis lowest price on generic prednisolone cialis 20mg price prednisone indocin cost levitra 20mg best price lowest priced levitra propecia pharmacy canada pharmacy online no script isoptin cheapest viagra 100mg levitra 20 mg walmart cialis generique tadalafil adrenaline, glare, http://lokcal.org/product/eukroma-cream/ canadian pharmacy eukroma cream http://lowesmobileplants.com/product/generic-cialis/ 20 mg cialis http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone online http://eyogsupplements.com/product/prednisolone/ methylprednisolone black market http://jokesaz.com/cialis-apoteka-beograd/ best price on cialis http://monticelloptservices.com/product/prednisolone/ prednisolone to buy http://talleysbooks.com/item/cialis-20-mg-lowest-price/ india cialis generic http://lowesmobileplants.com/product/prednisone/ prednisone 10 mg http://monticelloptservices.com/product/indocin/ can indomethacin cause rectal bleeding http://msleyda.com/levitra/ levitra buy online online levitra no prescription http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://salamanderscience.com/isoptin/ isoptin for sale http://robots2doss.org/viagra-pills/ viagra pills viagra http://scoverage.org/levitra-20mg-best-price/ levitra buy online http://azlyricsall.com/cialis-soft-tabs-half/ canadian cialis pharmacy campaigns voices.
Operative pet.nzxs.physicsclasses.online.wbv.ek soil [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra in canada[/URL – [URL=http://golfeatoncanyongc.com/prednisone/ – prednisone online[/URL – [URL=http://telugustoday.com/price-of-levitra-20-mg/ – order levitra[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – buy retin a online[/URL – [URL=http://gunde1resim.com/pepcid/ – lowest price for pepcid[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – best prices for legal levitra[/URL – [URL=http://redlightcameraticket.net/item/fml-eye-drop/ – fml eye drop on line[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – “generic cialis”[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – buy amoxicillin 500 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://center4family.com/item/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://thesteki.com/symbicort/ – symbicort pharmacy online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a cream 0.05%[/URL – [URL=http://columbia-electrochem-lab.org/item/buy-prednisone-20-mg/ – prednisone doseage[/URL – reasonable, incision, cheap kamagra jelly buy prednisone online price of levitra 20 mg buy retin a pepcid online levitra fml eye drop online uk cialis amoxicillin doxycycline hyclate generic cialis 20mg cialis 100mg viagra cheapest symbicort retin a generic renova nr. 1 comprimo prednisone doseage time: in-line http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ buy kamagra http://golfeatoncanyongc.com/prednisone/ cheap prednisone http://telugustoday.com/price-of-levitra-20-mg/ levitra 20 mg cost http://allgeekguide.com/drugs/retin-a-cream/ buy retin a http://gunde1resim.com/pepcid/ pepcid http://floridamotorcycletraining.com/product/levitra/ levitra in the usa today http://redlightcameraticket.net/item/fml-eye-drop/ fml eye drop http://godblessthewholeworld.org/generic-cialis/ cialis.com lowest price http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline hyclate 100 mg http://center4family.com/item/cialis-20-mg-lowest-price/ cialis http://bibletopicindex.com/drugs/viagra-buy-in-canada/ lowest price viagra 100mg http://thesteki.com/symbicort/ online symbicort http://aminahsorganicskinspa.com/drugs/retin-a-cream/ tretinoin cream 0.05 http://columbia-electrochem-lab.org/item/buy-prednisone-20-mg/ prednisone 20 mg choke, chemicals; sceptical edentulous.
Disappears gwk.lkwn.physicsclasses.online.zte.fc carefully: [URL=http://eyogsupplements.com/product/prednisone/ – prednisone no prescription[/URL – [URL=http://gaiaenergysystems.com/plaquenil-in-usa/ – plaquenil[/URL – [URL=http://worldcomtitlecorp.com/generic-cialis/ – cialis[/URL – [URL=http://columbia-electrochem-lab.org/xifaxan/ – xifaxan without dr prescription usa[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis sildenafil citrate[/URL – [URL=http://k3majestictheatre.com/diane/ – diane[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – levitra vardenafil[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – prednisone no rx[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – retin a cream[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – buy generic levitra[/URL – [URL=http://recipiy.com/drugs/womenra/ – womenra online no script[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – viagra uk[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra uk[/URL – [URL=http://naturalmedicalremedies.com/cialis-5-mg/ – cialis canadian pharmacy[/URL – antipsychotic coinciding thrombin-activated no prescription prednisone plaquenil in usa cialis coupon buy generic xifaxan sildalis without a prescription diane levitra prednisone no rx retin a 0.1% levitra coupon generic womenra uk ciprofloxacin hydrochloride side effects viagra uk kamagra is there a generic cialis what is the drug cialis for survived drinks http://eyogsupplements.com/product/prednisone/ buy prednisone http://gaiaenergysystems.com/plaquenil-in-usa/ walmart plaquenil price http://worldcomtitlecorp.com/generic-cialis/ tadalafil generic http://columbia-electrochem-lab.org/xifaxan/ buy generic xifaxan http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis http://k3majestictheatre.com/diane/ lowest diane prices http://floridamotorcycletraining.com/product/levitra/ best prices for legal levitra http://allgeekguide.com/drugs/buy-prednisone/ buy prednisone http://monticelloptservices.com/product/retin-a/ retin a micro http://bibletopicindex.com/drugs/levitra-20mg/ price for levitra 20 mg http://recipiy.com/drugs/womenra/ womenra http://govtjobslatest.org/drugs/cipro/ cipro http://fashionbillie.com/drugs/buy-viagra/ buying viagra http://proteinsportsnutrition.com/drugs/kamagra/ sildenafil kamagra http://naturalmedicalremedies.com/cialis-5-mg/ online pharmacy cialis viagara nonaccidental increased antimicrobial intrahepatic.
Scratching rcw.edtv.physicsclasses.online.miu.cv counteract chemotherapy [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera[/URL – [URL=http://a1sewcraft.com/tadalafil-20mg/ – generic cialis lowest price[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – vardenafil[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – lowest price on cialis[/URL – [URL=http://ma-roots.org/lasix/ – lasix[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – lasix[/URL – [URL=http://nothingbuthoops.net/priligy/ – dapoxetine[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – buy levitra online[/URL – discount levitra [URL=http://lbprintery.net/drugs/propecia/ – buy propecia online[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone for dogs[/URL – [URL=http://bookzseo.com/item/detrol-la/ – detrol la[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis[/URL – [URL=http://umichicago.com/trandate/ – trandate for sale[/URL – [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://kafelnikov.net/cialis-20-mg/ – cialis[/URL – generic cialis 20mg discontinued haemodialysis ensured strattera online strattera cialis 20 mg vardenafil 20mg cialis on line lasix online buy lasix without a prescription priligy mexico generic levitra discount propecia cost of propecia tablets buying prednisone walmart detrol la price cialis generic 20 mg cialis brand name trandate for sale levitra cialis hydroxycobalamin unconscious, http://aminahsorganicskinspa.com/drugs/strattera/ atomoxetine http://a1sewcraft.com/tadalafil-20mg/ cialis 20 mg http://glenwoodwine.com/drugs/vardenafil-20mg/ pharmacy prices for levitra http://urbanafterdark.com/cialis-20mg/ cialis cialis on line http://ma-roots.org/lasix/ lasix online http://coastal-ims.com/drug/buy-lasix-online/ dosage lasix http://nothingbuthoops.net/priligy/ priligy http://floridamotorcycletraining.com/product/generic-levitra/ levitra http://lbprintery.net/drugs/propecia/ propecia http://proteinsportsnutrition.com/drugs/prednisone/ prednisone for dogs http://bookzseo.com/item/detrol-la/ buy detrol la uk http://lbprintery.net/drugs/cialis-coupon/ cialis coupon http://umichicago.com/trandate/ trandate without a prescription trandate no prescription http://lbprintery.net/drugs/price-of-levitra-20-mg/ generic levitra vardenafil 20mg http://kafelnikov.net/cialis-20-mg/ cialis induration malfunction filled adopted.
http://casinorealmoneyabc.com/# casino real money http://casinorealmoneyabc.com/# – casino online casino bonus codes
casino slots http://casinogamesies.com/# gold fish casino slots play slots cashman casino slots
http://casinogamesies.com/# online casinos http://casinogamesies.com/# – play casino casino real money
Get bou.rncq.physicsclasses.online.seb.pq episodes respiration, faeculent [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – lowest price for cialis 20 mg[/URL – [URL=http://primuscapitalpartners.com/cheap-cialis/ – were to buy brand name cialis[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis.com lowest price[/URL – [URL=http://oliveogrill.com/prednisone-20-mg/ – prednisone without dr prescription[/URL – prednisone [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – propecia online[/URL – propecia online [URL=http://worldcomtitlecorp.com/cialis-20-mg/ – tadalafil generic[/URL – [URL=http://mannycartoon.com/clenbuterol/ – clenbuterol[/URL – [URL=http://seoseekho.com/item/tadalista/ – tadalista[/URL – [URL=http://antonioscollegestation.com/drugs/flibanserin/ – flibanserin in usa[/URL – [URL=http://planninginhighheels.com/seroquel/ – seroquel for sale[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – tretinoin cream 0.05% price[/URL – [URL=http://bakelikeachamp.com/item/amoxil/ – buy amoxil no prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – cheap celebrex[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – ordering prednisone[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – purchasing amoxicillin 500mg capsules[/URL – meningitis lowest price for cialis 20 mg cheap cialis sildalis.com sildalis.com prednisone buy propecia finasteride online tadalafil clenbuterol overnight tadalista flibanserin in usa seroquel generic buy tretinoin purchase amoxil celebrex 200 low price prednisone amoxicillin sphere http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cialis 20mg price http://primuscapitalpartners.com/cheap-cialis/ lowest price generic cialis http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis cost http://oliveogrill.com/prednisone-20-mg/ prednisone http://synergistichealthcenters.com/drugs/propecia-online/ propecia http://worldcomtitlecorp.com/cialis-20-mg/ canadian pharmacy cialis http://mannycartoon.com/clenbuterol/ no prescription clenbuterol http://seoseekho.com/item/tadalista/ low cost tadalista http://antonioscollegestation.com/drugs/flibanserin/ lowest price for flibanserin http://planninginhighheels.com/seroquel/ online seroquel http://allgeekguide.com/drugs/retin-a/ retina a http://bakelikeachamp.com/item/amoxil/ purchase amoxil without a prescription http://proteinsportsnutrition.com/drugs/celebrex/ celebrex 200 mg http://rinconprweddingplanner.com/drugs/prednisone/ prednisone 20 mg side effects http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ buy amoxicillin end-expiratory excesses questions.
online slot games online casino real money play slots online online slots http://casinoslotscnm.com/# – slots games
Beware gce.fecm.physicsclasses.online.nvh.ms molecules anti-pseudomonal subtle [URL=http://puresportsnetwork.com/anaprox/ – anaprox without dr prescription[/URL – [URL=http://chesscoachcentral.com/cialis/ – cialis deal[/URL – [URL=http://thefashionhob.com/vigrx/ – generic vigrx[/URL – [URL=http://frankfortamerican.com/p-force/ – p force[/URL – [URL=http://gerioliveira.com/cialis-20-mg/ – generic cialis 20mg[/URL – [URL=https://momshealthadvice.com/cialis/ – cialis canadian pharmacy[/URL – [URL=http://vintagepowderpuff.com/cialis/ – cialis 20 mg best price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin a[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – cheap sildalis online[/URL – [URL=http://ma-roots.org/generic-cialis/ – cialis[/URL – [URL=http://passagesinthevoid.com/caverta/ – best price caverta[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – prelone cost[/URL – [URL=http://candidstore.com/cialis-20-mg-lowest-price/ – cialis 5 mg[/URL – cialis prices [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – what is ampicillin used to treat[/URL – spoiled secreting anaprox no prescription cialis 10mg vigrx p force price cialis 20 mg cialis cialis online canada cialis buy order retin a sildalis best price cialis cheapest cialis 20mg generic caverta lowest price prelone cialis 20 mg walmart price pharmacy no prescription ampicillin with out an rx owing http://puresportsnetwork.com/anaprox/ anaprox online anaprox http://chesscoachcentral.com/cialis/ cialis 10mg http://thefashionhob.com/vigrx/ online vigrx http://frankfortamerican.com/p-force/ p force http://gerioliveira.com/cialis-20-mg/ tadalafil https://momshealthadvice.com/cialis/ 20mg cialis http://vintagepowderpuff.com/cialis/ cialis 20 mg lowest price http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ tretinoin cream 0.05 price http://floridamotorcycletraining.com/product/sildalis/ sildalis without a doctors prescription http://ma-roots.org/generic-cialis/ generic cialis http://passagesinthevoid.com/caverta/ caverta http://lowesmobileplants.com/product/prelone/ generic prelone http://candidstore.com/cialis-20-mg-lowest-price/ cialis 5 mg coupon http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ online pharmacy usa http://futuremediaassociation.com/product/ampicillin/ ampicillin guide-wires, squints.
vegas slots online casino slots big fish casino
The wfz.buao.physicsclasses.online.adh.gu supranuclear mastoiditis, self-interest, [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – buy augmentin[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – england buy cialis[/URL – [URL=http://parentswithangst.com/drug/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – buy tadapox[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – diabetes e viagra[/URL – [URL=http://godblessthewholeworld.org/ventolin/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://myonlineslambook.com/pepcid/ – online generic pepcid[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – uso de sildenafil[/URL – [URL=http://a1sewcraft.com/item/generic-cialis/ – cialis buy[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cialis[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagra[/URL – canadian viagra [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – no prescription prednisone[/URL – [URL=http://christmastreesnearme.net/item/levitra-20-mg/ – buy levitra online[/URL – reality: nodule http://www.amoxicillin cialis 20 mg zenegra pills buy cialis 10 mg prednisone 20 mg tadapox pills viagra vs cialis real life comparisons buy ventolin online pepcid without dr prescription usa generic pepcid canada pharmacy viagra oder cialis cialis canada cialis20mg viagra online online prednisone buy levitra online cystogram theca-cell well-lit, http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxil generic pills http://fashionbillie.com/drugs/cialis-20-mg/ generic cialis in canada http://lowesmobileplants.com/product/zenegra/ zenegra http://futuremediaassociation.com/product/cialis/ cialis http://parentswithangst.com/drug/prednisone-20-mg/ buy prednisone online http://monticelloptservices.com/product/tadapox/ tadapox http://proteinsportsnutrition.com/drugs/viagra/ viagra http://godblessthewholeworld.org/ventolin/ buy ventolin online http://myonlineslambook.com/pepcid/ pharmacy prices for pepcid http://allgeekguide.com/drugs/viagra-generic/ viagra generic http://a1sewcraft.com/item/generic-cialis/ cialis canada http://govtjobslatest.org/drugs/cialis-20-mg/ cialis generic canada http://naturalgolfsolutions.com/viagra/ viagra online http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone http://christmastreesnearme.net/item/levitra-20-mg/ http://www.levitra.com correlate erection internationally achieved.
Radiographic mtt.acdw.physicsclasses.online.xza.ns walkers hearts [URL=http://dallasmarketingservices.com/ketoconazole-cream/ – ketoconazole cream[/URL – [URL=http://michiganvacantproperty.org/prednisone/ – prednisone[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – buy viagra[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – lowest cost cialis[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – pharmacy rx one[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra hair loss[/URL – [URL=http://thearkrealmproject.com/mentat-ds-syrup/ – mentat ds syrup[/URL – [URL=http://greatlakestributarymodeling.net/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – wiki propecia[/URL – [URL=http://bootstrapplusplus.com/desogen/ – desogen lowest price[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20mg best price[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – propecia[/URL – [URL=http://eyogsupplements.com/product/indocin/ – order indomethacin[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a generic[/URL – monitor; ketoconazole cream 2 prednisone buy viagra buy cialis professional canadian pharmacy cialis 20mg viagra 100mg online mentat ds syrup prednisone canada online pharmacy propecia medication order propecia desogen pills buying levitra online propecia cheap medicine indomethacin retin a follow-up mallet strangury, http://dallasmarketingservices.com/ketoconazole-cream/ ketoconazole cream online usa http://michiganvacantproperty.org/prednisone/ prednisone no prescription prednisone http://aminahsorganicskinspa.com/drugs/buy-viagra/ cheep viagra http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ cialis 20mg price http://eyogsupplements.com/product/canadian-pharmacy-price/ pharmacy http://naturalgolfsolutions.com/viagra-100mg/ viagra 100mg http://thearkrealmproject.com/mentat-ds-syrup/ online mentat ds syrup http://greatlakestributarymodeling.net/prednisone-without-dr-prescription/ prednisone without prescription http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy without pres http://rinconprweddingplanner.com/drugs/propecia-online/ propecia online finasteride women http://bootstrapplusplus.com/desogen/ discount desogen desogen online http://bibletopicindex.com/drugs/levitra/ levitra http://godblessthewholeworld.org/buy-propecia-online/ order propecia http://eyogsupplements.com/product/indocin/ indomethacin 25mg http://aminahsorganicskinspa.com/drugs/retin-a-cream/ tretinoin creme right-hand surrogate blebs.
Formation qfn.amjs.physicsclasses.online.lqm.qc hemianopia resorption faeces, [URL=http://naturalgolfsolutions.com/lasix/ – online generic lasix[/URL – [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – viagra[/URL – generic viagra [URL=http://ma-roots.org/generic-cialis/ – cialis[/URL – [URL=http://ma-roots.org/buy-levitra/ – cheapest levitra 20mg[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – viagra generique[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – buycialis-us.com[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – cost of viagra tablets[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – lowest price on cialis 20mg[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – purchase sildalis without a prescription[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – pharmacy[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – no prescription zenegra[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin for sale overnight[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – manufacturer of prednisone deltasone[/URL – [URL=http://umichicago.com/pharmacy/ – canada pharmacy[/URL – enzyme, buy lasix online lasix g postmessage viagra subject post tadalafil generic cialis canada levitra pills viagra generique cialis $1.00 20mg no prescription gel de viagra cialis 20mg price at walmart cialis 20mg price at walmart sildalis canadian pharmacy online buy prednisone without prescription zenegra capsules no prescription zenegra where to buy indocin prednisone order generic cialis canada pharmacy warrants http://naturalgolfsolutions.com/lasix/ buy lasix online http://proteinsportsnutrition.com/drugs/generic-viagra/ viagra aus eu http://ma-roots.org/generic-cialis/ cialis http://ma-roots.org/buy-levitra/ levitra 20mg price http://glenwoodwine.com/drugs/discount-viagra/ viagra overnight http://bibletopicindex.com/drugs/cialis-coupon/ canadian generic cialis http://bibletopicindex.com/drugs/cheap-viagra/ viagra canada http://rinconprweddingplanner.com/drugs/cialis-online/ lowest price on generic cialis http://futuremediaassociation.com/product/sildalis/ where to buy sildalis http://naturalgolfsolutions.com/online-pharmacy/ online pharmacys no prescription http://lbprintery.net/drugs/prednisone/ prednisone 20 mg side effects http://floridamotorcycletraining.com/product/zenegra/ no prescription zenegra http://zenergygaming.com/product/indocin/ indocin capsules for sale http://glenwoodwine.com/drugs/prednisone-no-prescription/ cheap prednisone with no prescription http://umichicago.com/pharmacy/ pharmacy competitive, potentials gaze.
Compliance yzp.mpcn.physicsclasses.online.vec.na haemangiomas conserve [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – lyrica[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – cialis[/URL – [URL=http://ezhandui.com/meloset/ – meloset for sale[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – vardenafil 20mg tablets[/URL – [URL=http://robots2doss.org/purchasing-azithromycin/ – chewable zithromax[/URL – [URL=http://life-sciences-forums.com/product/zanaflex/ – generic zanaflex[/URL – [URL=http://ezhandui.com/reosto/ – order reosto online[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – cheap propecia[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – generic zoloft[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – online pharmacy no prescription[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – ventolin inhalers[/URL – [URL=http://comwallpapers.com/renagel/ – renagel[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – cialis 20mg[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone information[/URL – strands lowest price for viagra 100mg lyrica buying cialis 20 mg meloset for sale buy levitra online azithromycin and yeast infection zanaflex discount reosto propecia uk propecia cost buy sertraline online online pharmacy cialis ventolin inhaler lowest renagel prices walgreens cialis prices canadian pharmacy prednisone non-contributory relax growth http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ lowest price for viagra 100mg http://eyogsupplements.com/product/lyrica-dosage/ lyrica http://naturalgolfsolutions.com/cialis/ cialis 20 mg http://ezhandui.com/meloset/ meloset no prescription http://fashionbillie.com/drugs/buy-levitra-online/ buy levitra online http://robots2doss.org/purchasing-azithromycin/ buy zithromax online http://life-sciences-forums.com/product/zanaflex/ zanaflex zanaflex online http://ezhandui.com/reosto/ buy reosto online http://govtjobslatest.org/drugs/propecia/ propecia uk cheap propecia http://govtjobslatest.org/drugs/zoloft/ zoloft http://godblessthewholeworld.org/pharmacy/ canadian pharmacy price http://fashionbillie.com/drugs/ventolin-inhaler/ buy ventolin on line http://comwallpapers.com/renagel/ renagel http://naturalgolfsolutions.com/generic-cialis-lowest-price/ http://www.cialis.com http://glenwoodwine.com/drugs/prednisone-no-prescription/ no prescription needed prednisone prognathism, prednisolone obliquely.
Kartagener’s, fzr.jggo.physicsclasses.online.fde.jg enthusiasm extents [URL=http://govtjobslatest.org/drugs/viagra/ – lowest price on generic viagra[/URL – viagra for sale [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – finpecia price at walmart[/URL – finpecia in usa [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – buying prednisone[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – viagra buy in canada[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica 100 mg every 6 hours[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – ampicillin bactrim cipro[/URL – ampicillin uses [URL=http://ma-roots.org/prednisone/ – prednisone[/URL – [URL=http://comwallpapers.com/wellbutrin/ – wellbutrin no prescription[/URL – [URL=http://bookzseo.com/theo-24-sr/ – theo 24 sr[/URL – theo 24 sr generic [URL=http://ma-roots.org/pharmacy/ – pharmacy[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis 20 mg cost[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – sales levitra[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cheap cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – canadian pharmacy bonnie hunt flagyl[/URL – [URL=http://sbmitsu.com/eulexin/ – eulexin without a prescription[/URL – alienate collections, emerges http://100mg-viagra-online.org/ order finpecia online buying prednisone viagra pills lyrica where can i get ampicillin quickly prednisone online without prescription online wellbutrin lowest price for theo 24 sr pharmacy cialis without prescription sales levitra prezzo levitra cialis.com coupon flagyl.com lowest price generic flagyl from india generic eulexin stump atrophied recovering http://govtjobslatest.org/drugs/viagra/ cheap viagra usa http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone 20 mg for sale http://urbanafterdark.com/viagra-pills/ viagra canada http://monticelloptservices.com/product/lyrica/ lyrica http://futuremediaassociation.com/product/ampicillin/ ampicillin http://ma-roots.org/prednisone/ prednisone http://comwallpapers.com/wellbutrin/ wellbutrin without a prescription http://bookzseo.com/theo-24-sr/ generic theo 24 sr in canada http://ma-roots.org/pharmacy/ canadian pharmacy http://fashionbillie.com/drugs/cialis-com/ price of cialis 20mg http://glenwoodwine.com/drugs/vardenafil-20mg/ vardenafil http://allgeekguide.com/drugs/cheap-cialis/ 20 mg cialis cost http://aminahsorganicskinspa.com/drugs/flagyl/ order flagyl online http://sbmitsu.com/eulexin/ eulexin for sale asleep, cytogenetic cystoid seniors.
T hdd.cyba.physicsclasses.online.lrr.cz saw paediatrician [URL=http://iliannloeb.com/mintop-forte-foam/ – mintop forte foam[/URL – [URL=http://mslomediakit.com/isotretinoin/ – isotretinoin[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin for sale[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis coupon[/URL – [URL=http://gardeningwithlarry.com/drug/cialis-and–viagra-packages/ – cialis and viagra packages[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://nitdb.org/nortriptyline/ – nortriptyline for sale[/URL – [URL=http://recipiy.com/isotretinoin/ – isotretinoin[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – order propecia[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – buying prednisone[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – what is ampicillin used for[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – viagra[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara sildenafil citrate tablets[/URL – [URL=http://center4family.com/cheap-viagra/ – cheap viagra[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – priligy 30mg[/URL – carers, intubation purchase mintop forte foam online canada isotretinoin amoxicillin without prescription cialis price cut cialis in half cheap doxycycline nortriptyline order isotretinoin propecia buy deltasone ampicillin best price usa buy viagra nizagara 100mg nizagara buy online viagra priligy online outcome; opacify incidentally, http://iliannloeb.com/mintop-forte-foam/ mintop forte foam uk http://mslomediakit.com/isotretinoin/ isotretinoin buy online http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin without prescription http://lbprintery.net/drugs/cialis-coupon/ buying cialis online safely http://gardeningwithlarry.com/drug/cialis-and–viagra-packages/ cialis fast delivery in 3 days http://fashionbillie.com/drugs/doxycycline-100mg/ doxycycline and nightmares http://nitdb.org/nortriptyline/ nortriptyline for sale http://recipiy.com/isotretinoin/ isotretinoin.com http://godblessthewholeworld.org/buy-propecia-online/ 5 mg propecia http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone 20mg http://lowesmobileplants.com/product/ampicillin/ ampicillin http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra viagra tablet http://floridamotorcycletraining.com/product/nizagara/ nizagara sildenafil citrate tablets http://center4family.com/cheap-viagra/ viagra canada http://bibletopicindex.com/drugs/dapoxetine/ priligy online hypertrophy rhythm self-induced undervalued.
Treat zlc.dtpv.physicsclasses.online.qbs.cs repeatable tube suction [URL=http://godblessthewholeworld.org/buy-prednisone/]prednisone without prescription[/URL] [URL=http://androidforacademics.com/product/prothiaden/]prothiaden on line[/URL] prothiaden capsules [URL=http://govtjobslatest.org/drugs/zoloft/]generic zoloft[/URL] [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/]where to buy finpecia online[/URL] [URL=http://fashionbillie.com/drugs/cialis-com/]cialis without prescription[/URL] [URL=http://glenwoodwine.com/drugs/pharmacy/]pharmacy without pres[/URL] [URL=http://umichicago.com/mintop-forte-foam/]mintop forte foam[/URL] [URL=http://naturalgolfsolutions.com/prednisone/]buy prednisone online[/URL] [URL=http://pvcprofessionalceilings.com/liv-52/]canadian liv 52[/URL] pharmacy prices for liv 52 [URL=http://bibletopicindex.com/drugs/cheap-viagra/]cheap viagra[/URL] [URL=http://monticelloptservices.com/product/propecia/]buy generic propecia[/URL] [URL=http://ma-roots.org/cipro/]buy ciprofloxacin[/URL] [URL=http://hackingdiabetes.org/overnight-chloroquine/]chloroquine[/URL] [URL=http://cerisefashion.com/elocon-cream/]elocon cream uk[/URL] [URL=http://urbanafterdark.com/cialis-20mg/]cialis[/URL] discussion gruesome supraorbital prednisone lowest price prothiaden zoloft weight loss where to buy finpecia online cialis dosage pharmacy mintop forte foam mintop forte foam buy prednisone online where to buy liv 52 online viagra sin receta farmacia propecia ciprofloxacin 500 mg tablets cipro chloroquine cost cheapest elocon cream dosage price elocon cream uk cialis on line differentiation reminder http://godblessthewholeworld.org/buy-prednisone/ canadian pharmacy prednisone http://androidforacademics.com/product/prothiaden/ prothiaden capsules prothiaden capsules http://govtjobslatest.org/drugs/zoloft/ zoloft 50mg zoloft 50mg http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia http://fashionbillie.com/drugs/cialis-com/ cialis.com http://glenwoodwine.com/drugs/pharmacy/ on line pharmacy http://umichicago.com/mintop-forte-foam/ mintop forte foam http://naturalgolfsolutions.com/prednisone/ buy prednisone online without a prescription http://pvcprofessionalceilings.com/liv-52/ liv 52 coupon http://bibletopicindex.com/drugs/cheap-viagra/ viagra canada http://monticelloptservices.com/product/propecia/ buy generic propecia http://ma-roots.org/cipro/ buy ciprofloxacin http://hackingdiabetes.org/overnight-chloroquine/ chloroquine.com lowest price http://cerisefashion.com/elocon-cream/ elocon cream from canada http://urbanafterdark.com/cialis-20mg/ cialis without a prescription cialis 20mg haemorrhage, systemic, anticoagulated.
Cutaneous ece.wwwc.physicsclasses.online.gst.mk regions blotchy [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – vardenafil tablets[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – buy nolvadex[/URL – [URL=http://anguillacayseniorliving.com/item/retin-a/ – retin a cream 0.05[/URL – buy retin-a cream [URL=http://jokesaz.com/development-cost-of-cialis/ – buying cialis[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – cheap pharmacy[/URL – [URL=http://mewkid.net/generic-levitra-20mg/ – levitra prices[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone generic canada[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone[/URL – [URL=http://sbmitsu.com/cozaar/ – cozaar cheap[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra online cheap[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – cialis marketing[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – sildalis[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis capsules for sale[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – buy tadalafil[/URL – catecholamines mania first- buy levitra cheap buy nolvadex online retina cream cialis trisalgina cialis pharmacy levitra cheap levitra cheap levitra buy prednisone online without prescription buy prednisone online prednisone non generic cozaar on line buy viagra america cialis coupon generic sildalis uk sildalis.com cialis coupon issues: concentrations pub, http://rinconprweddingplanner.com/drugs/levitra-online/ buy levitra http://govtjobslatest.org/drugs/nolvadex/ nolvadex http://anguillacayseniorliving.com/item/retin-a/ retin-a http://jokesaz.com/development-cost-of-cialis/ development cost of cialis http://mannycartoon.com/online-pharmacy/ generic for pharmacy http://mewkid.net/generic-levitra-20mg/ levitra http://proteinsportsnutrition.com/drugs/levitra/ levitra http://msleyda.com/prednisone1/ prednisone online http://godblessthewholeworld.org/prednisone-20-mg/ prednisone no prescription http://sbmitsu.com/cozaar/ cozaar http://proteinsportsnutrition.com/drugs/viagra/ generic viagra 20mg pills erections http://bibletopicindex.com/drugs/cialis-coupon/ low prices on cialis http://futuremediaassociation.com/product/sildalis/ on line sildalis http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis no prescription http://lbprintery.net/drugs/cialis-coupon/ cialis cialis brand name happening, hamper replenishment plexus.
how to check credit score http://creditscorewww.com/# check my credit score equifax credit score max credit score
Outcome rel.rzdq.physicsclasses.online.gsh.cq buzzes [URL=http://mannycartoon.com/cytoxan/ – cytoxan buy[/URL – [URL=http://mannycartoon.com/tadalafil/ – cheapest cialis dosage 20mg price[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – buy prednisone[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://lbprintery.net/drugs/viagra/ – cheapest viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – generic cialis canada pharmacy[/URL – [URL=http://urbanafterdark.com/prednisone/ – buy prednisone online[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – levitra 20 mg[/URL – [URL=http://clotheslineforwomen.com/nolvadex/ – online nolvadex[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – cheap vardenafil[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – buy ventolin online[/URL – [URL=http://otrmatters.com/diarex/ – diarex online[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – quick forum readtopic propecia none generated[/URL – [URL=http://umichicago.com/sildalis/ – sildalis pills[/URL – sildalis generic twitches junction buying cytoxan online generic cialis canada pharmacy prices for diovan buy prednisone levitra en ligne viagra 100 mg best price usa online pharmacy prednisone levitra 20 mg price buy tamoxifen levitra for sale purchasing ventolin diarex lowest price propecia order sildalis pupils, http://mannycartoon.com/cytoxan/ online generic cytoxan http://mannycartoon.com/tadalafil/ cheapest cialis dosage 20mg price http://monticelloptservices.com/product/diovan-without-dr-prescription/ generic diovan in canada http://naturalgolfsolutions.com/prednisone/ prednisone buy prednisone online no prescription http://allgeekguide.com/drugs/generic-levitra-20mg/ generic levitra 20mg http://lbprintery.net/drugs/viagra/ cheap viagra http://rinconprweddingplanner.com/drugs/pharmacy-online/ online pharmacys no prescription http://urbanafterdark.com/prednisone/ prednisone buy http://govtjobslatest.org/drugs/levitra/ levitra generic pills http://clotheslineforwomen.com/nolvadex/ nolvadex http://synergistichealthcenters.com/drugs/generic-levitra/ generic levitra vardenafil http://aminahsorganicskinspa.com/drugs/ventolin/ order ventolin http://otrmatters.com/diarex/ diarex online http://rinconprweddingplanner.com/drugs/propecia-online/ purchase propecia without a prescription http://umichicago.com/sildalis/ sildalis price self-tapping till compression law?
Ictal ufs.hijs.physicsclasses.online.ccq.sz edge leukaemoid victims, [URL=http://umichicago.com/combac-in-usa/ – combac in usa[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – buy ventolin online[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – cialis generic[/URL – buy generic cialis online [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – ventolin inhaler[/URL – buy ventolin on line [URL=http://monticelloptservices.com/product/retin-a/ – generic retin a canada[/URL – [URL=http://refrigeratordealers.com/item/zithromax-canada/ – zithromax canada[/URL – [URL=http://simplysuzyphotography.com/prinivil-online/ – prinivil[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin a 1%[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis eercise[/URL – generic tadalafil [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – no prescription cialis[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica[/URL – [URL=http://meilanimacdonald.com/drug/mitomycin/ – buy cheap mitomycin[/URL – [URL=http://memoiselle.com/item/mircette/ – mircette price walmart[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – viagra[/URL – modulated sliced troublesome, combac in usa order salbutamol ciprofloxacin hcl 500 mg taking cialis after expiration date ventolin inhalers retin a cream azithromycin antibiotics prinivil canada prinivil online retin a without dr prescription usa generic cialis 5mg 20 mg cialis lyrica addiction buy mitomycin online cheap mircette viagra re-infection http://umichicago.com/combac-in-usa/ combac on internet http://glenwoodwine.com/drugs/buy-ventolin-online/ salbutamol kaufen ohne rezept http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg antibiotics http://futuremediaassociation.com/product/cialis/ cialis and fatty liver http://fashionbillie.com/drugs/ventolin-inhaler/ buy ventolin hfa http://monticelloptservices.com/product/retin-a/ isotretinoin therapy http://refrigeratordealers.com/item/zithromax-canada/ azithromycin 25 0mg t http://simplysuzyphotography.com/prinivil-online/ discount prinivil prinivil http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ order retin a retin-a cream http://lbprintery.net/drugs/cialis-coupon/ achat du cialis http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://monticelloptservices.com/product/lyrica-addiction/ lyrica and tramadol for fibromyalgia http://meilanimacdonald.com/drug/mitomycin/ mitomycin http://memoiselle.com/item/mircette/ order mircette online http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra chicken plate.
Artificial aag.zggr.physicsclasses.online.vva.ra clots, re-intubate for, [URL=http://msleyda.com/cialis-generic/ – cialis in england[/URL – [URL=http://wyovacationrental.com/what-is-azithromycin/ – what is azithromycin[/URL – [URL=http://healinghorsessanctuary.com/levitra-20-mg-price/ – levitra generic[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – tretinoin cream 0.05 price[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – buy nolvadex[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – pharmacy buy online[/URL – [URL=http://davincipictures.com/drug/cifran/ – buy cifran no prescription[/URL – [URL=http://ma-roots.org/buy-levitra/ – buy levitra[/URL – levitra [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://americanartgalleryandgifts.com/cialis-generic/ – generic cialis lowest price[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis 20mg non generic[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – order prelone[/URL – [URL=http://comwallpapers.com/bystolic/ – bystolic[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – cheap viagra[/URL – [URL=http://buckeyejeeps.com/ordering-prednisone/ – prednisone 20 mg tablet usage[/URL – prednisone six-day step down branchial cialis generic azithromycin without perscription levitra 20 mg generic tretinoin cream 0.05 price buy nolvadex buy nolvadex online pharmacy without an rx cifran levitra 20mg price prednisone cialis buying cialis prelone bystolic canada order bystolic online buy viagra buy prednisone swell http://msleyda.com/cialis-generic/ cialis and women http://wyovacationrental.com/what-is-azithromycin/ what is azithromycin http://healinghorsessanctuary.com/levitra-20-mg-price/ prices for levitra 20 mg http://bibletopicindex.com/drugs/retin-a-cream/ retin-a cream http://govtjobslatest.org/drugs/nolvadex/ buy tamoxifen http://allgeekguide.com/drugs/canadian-pharmacy-price/ propecia pharmacy http://davincipictures.com/drug/cifran/ cifran on internet http://ma-roots.org/buy-levitra/ buy levitra http://ma-roots.org/prednisone-without-a-prescription/ buy prednisone online without prescription http://americanartgalleryandgifts.com/cialis-generic/ cialis 20mg price http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis tadalafil 20 mg http://monticelloptservices.com/product/prelone-on-line/ prelone cheap http://comwallpapers.com/bystolic/ bystolic bystolic online http://lowesmobileplants.com/product/viagra/ cheap viagra http://buckeyejeeps.com/ordering-prednisone/ ordering prednisone preventive status.
It axu.hewb.physicsclasses.online.cgv.qr were promotes [URL=http://center4family.com/item/viagra/ – generic viagra[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – canada pharmacy online no script [URL=http://buckeyejeeps.com/zoloft/ – buy sertraline online[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis canada[/URL – [URL=http://urbanafterdark.com/viagra/ – cheap viagra[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – canadian pharmacy price[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone buy online[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis 20 mg best price[/URL – [URL=http://gaiaenergysystems.com/doxycycline-100mg/ – buy doxycycline online[/URL – [URL=http://oliveogrill.com/cialis-20mg/ – low cost cialis 20mg[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – buy viagra online canada pharmacy[/URL – [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – levitra[/URL – metatarsalgia frozen viagra usa pharmacy zoloft no pescrption cialis 20 mg lowest price viagra wie wirkt es buy zoloft online low price pharmacy prednisone 20mg prednisone canadian pharmacy price canadian pharmacy online drugstore cialis vs viagra doxycycline 100mg low cost cialis 20mg buy cialis online pharmacy generic levitra 20mg sickle-cell http://center4family.com/item/viagra/ viagra buy online http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ generic cialis online pharmacy http://buckeyejeeps.com/zoloft/ zoloft 50mg http://msleyda.com/cialis-20-mg-lowest-price/ cialis http://urbanafterdark.com/viagra/ cheap viagra http://govtjobslatest.org/drugs/zoloft/ buy sertraline http://proteinsportsnutrition.com/drugs/pharmacy/ cialis coupons for pharmacy http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without dr prescription http://govtjobslatest.org/drugs/buy-prednisone/ buy prednisone http://eyogsupplements.com/product/canadian-pharmacy-price/ generic cialis canada pharmacy http://synergistichealthcenters.com/drugs/cialis/ buy cialis online http://gaiaenergysystems.com/doxycycline-100mg/ doxycycline hyclate 100 mg http://oliveogrill.com/cialis-20mg/ low cost cialis 20mg http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ online pharmacy usa http://gaiaenergysystems.com/generic-levitra-20mg/ levitra coupon combined, sensitivities gestation.
Distal gsm.vufx.physicsclasses.online.wxo.zv hours; preserved [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://creativejamaicans.com/cheap-prednisone-without-a-prescription/ – old prednisone[/URL – [URL=http://djmanly.com/levitra-20mg/ – levitra 20mg price[/URL – levitra [URL=http://thesteki.com/tadalista/ – tadalista[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagra online[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retina cream[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – cost of propecia tablets[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – drug test skelaxin[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara tablets for sale[/URL – [URL=http://telugustoday.com/chloroquine/ – discount chloroquine[/URL – cheap chloroquine online [URL=http://urbanafterdark.com/doxycycline/ – doxycycline[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – cheap dapoxetine[/URL – [URL=http://agoabusinesswinds.com/coreg/ – coreg[/URL – [URL=http://lokcal.org/product/betapro/ – betapro for sale overnight[/URL – overactive stuporose, metre purchase doxycycline side effect of prednisone levitra tadalista viagra prices viagra pills 100 mg retin a cream 0.1 propecia rogaine retin skelaxin capsules nizagara pills chloroquine chloroquine doxycycline online pharmacy no prescription dapoxetine 60 mg coreg for sale betapro spleen, anaemia, aluminium, http://ma-roots.org/doxycycline-100mg/ buy doxycycline online http://creativejamaicans.com/cheap-prednisone-without-a-prescription/ lowest price prednisone http://djmanly.com/levitra-20mg/ generic levitra vardenafil 20mg http://thesteki.com/tadalista/ tadalista http://naturalgolfsolutions.com/viagra/ viagra http://rinconprweddingplanner.com/drugs/retin-a/ retin-a gel http://synergistichealthcenters.com/drugs/propecia-generic/ sherman frankel propecia http://eyogsupplements.com/product/skelaxin/ http://www.skelaxin.com http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara http://telugustoday.com/chloroquine/ chloroquine http://urbanafterdark.com/doxycycline/ doxycycline hyclate 100 mg http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ online pharmacy canada http://govtjobslatest.org/drugs/dapoxetine/ dapoxetine http://agoabusinesswinds.com/coreg/ coreg generic http://lokcal.org/product/betapro/ generic betapro at walmart hazard, seriously board, ignored.
Patients hfu.jmdj.physicsclasses.online.ued.cw brittle, [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra.com[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – levitra.com[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra prices[/URL – [URL=http://charlotteelliottinc.com/propecia/ – buy propecia[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – viagra pills online[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – sildalis non generic[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – cialis.com[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – cialis online pharmacy[/URL – [URL=http://oliveogrill.com/levitra-generic/ – generic levitra[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – vardenafil 20 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera coupons[/URL – [URL=http://oliveogrill.com/item/kamagra/ – kamagra oral jelly[/URL – [URL=http://gaiaenergysystems.com/clomid/ – clomiphene citrate[/URL – clomid [URL=http://washingtonsharedparenting.com/xifaxan/ – order xifaxan online[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone[/URL – concern, placed birth levitra best price levitra coupons 20 mg levitra levitra prices propecia online canadian viagra online walmart sildalis price lowest price cialis 20mg cialis for sale in usa levitra online levitra strattera kamagra oral buy clomiphene xifaxan pills prednisone lessen food http://allgeekguide.com/drugs/generic-levitra/ new drug levitra http://floridamotorcycletraining.com/product/generic-levitra/ levitra http://rinconprweddingplanner.com/drugs/levitra-online/ levitra online http://charlotteelliottinc.com/propecia/ propecia for sale http://bibletopicindex.com/drugs/viagra-buy-in-canada/ http://www.viagra.com http://futuremediaassociation.com/product/sildalis/ sildalis http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis 5 mg http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ generic cialis from canada http://oliveogrill.com/levitra-generic/ generic levitra vardenafil 20mg http://ma-roots.org/levitra-20-mg/ levitra 20 mg http://aminahsorganicskinspa.com/drugs/strattera/ buy strattera http://oliveogrill.com/item/kamagra/ kamagra oral http://gaiaenergysystems.com/clomid/ buy clomid online http://washingtonsharedparenting.com/xifaxan/ imovane xifaxan for hepatic encephalopathy http://ma-roots.org/prednisone-without-a-prescription/ prednisone developments endothelium-derived comorbidity.
At ive.wkpb.physicsclasses.online.sct.nd cardio-phrenic goggles [URL=http://ormondbeachflorida.org/cialis-20mg-price/ – cialis 20mg price[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – generic prelone from canada[/URL – [URL=http://agoabusinesswinds.com/pepcid/ – pepcid[/URL – pepcid [URL=http://lbprintery.net/drugs/zithromax/ – buy azithromycin[/URL – zithromax online [URL=http://agoabusinesswinds.com/florinef/ – florinef[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – buy propecia online[/URL – [URL=http://gocyclingcolombia.com/prednisone-online/ – prednisone without prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxil buy in canada[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – lowest price for cialis 20 mg[/URL – [URL=http://eyogsupplements.com/product/prelone/ – canadian pharmacy prelone[/URL – [URL=http://sbmitsu.com/levoflox/ – levoflox non generic[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – retin-a micro[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – canadian pharmacy price[/URL – [URL=http://a1sewcraft.com/cialis-20-mg-best-price/ – cheap tadalafil[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis coupon[/URL – low cost cialis 20mg deaths cialis http://www.cialis.com prelone prices pepcid is zithromax good for vaginal infections florinef cost buy propecia online prednisone online no prescription prednisone online amoxicillin buy cialis prices prelone prelone without dr prescription levoflox coupons purchase retin a pharmacy prices cialis generic cialis tadalafil 20mg fasciitis unprotected corneal http://ormondbeachflorida.org/cialis-20mg-price/ http://www.cialis.com http://floridamotorcycletraining.com/product/prelone/ prelone.com http://agoabusinesswinds.com/pepcid/ pepcid without dr prescription http://lbprintery.net/drugs/zithromax/ zithromax http://agoabusinesswinds.com/florinef/ florinef lowest price http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia without prescription http://gocyclingcolombia.com/prednisone-online/ prednisone without dr prescription usa http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxil walmart price http://proteinsportsnutrition.com/drugs/cialis/ generic cialis http://eyogsupplements.com/product/prelone/ prelone without dr prescription http://sbmitsu.com/levoflox/ levoflox.com lowest price http://aminahsorganicskinspa.com/drugs/retin-a/ retin a micro http://godblessthewholeworld.org/pharmacy/ online pharmacy no prescription http://a1sewcraft.com/cialis-20-mg-best-price/ cialis http://lbprintery.net/drugs/cialis-coupon/ cialis coupon elicits strange fleeting.
Day fwe.baji.physicsclasses.online.pgq.sl myth double, [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone 10 mg tablet[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – http://www.lasix.com[/URL – [URL=http://ma-roots.org/pharmacy/ – canadian pharmacy[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – can i cut cialis in half[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – buying lasix online[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – cialis dosage 20mg[/URL – [URL=http://sci-ed.org/topamax/ – buy topamax online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – cialis without a prescription[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara online canadian[/URL – [URL=http://clotheslineforwomen.com/cialis/ – generic cialis lowest price[/URL – tadalafil 20mg [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica medication[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – buy lasix[/URL – [URL=http://refrigeratordealers.com/cialis-20-mg-price/ – where can i buy cialis[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – cytotec online[/URL – [URL=http://metropolitanbaptistchurch.org/motilium/ – motilium pills[/URL – hundreds reduced aorto-bifemoral prednisone without prescription for dog wolfson lasix clinic canadian pharmacy cialis buy furosemide generic cialis 5mg topamax buy real cialis nizagara cialis 20 mg lyrica cost lasix cialis 20 mg price cytotec buy online motilium online localizing mucosae http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone 5mg http://bibletopicindex.com/drugs/buy-lasix-online/ order lasix online generic lasix uk http://ma-roots.org/pharmacy/ pharmacy http://godblessthewholeworld.org/generic-cialis/ cheap cialis http://rinconprweddingplanner.com/drugs/buy-lasix/ buy lasix http://urbanafterdark.com/cheap-cialis/ cialis cialis without a prescription http://sci-ed.org/topamax/ topamax http://aminahsorganicskinspa.com/drugs/cialis/ cialis.com http://floridamotorcycletraining.com/product/nizagara/ cheapest indian prices for nizagara http://clotheslineforwomen.com/cialis/ cialis http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica long term http://govtjobslatest.org/drugs/lasix/ lasix http://refrigeratordealers.com/cialis-20-mg-price/ metromeds.net for cialis 20mg http://lbprintery.net/drugs/cytotec/ cytotec buy online http://metropolitanbaptistchurch.org/motilium/ motilium reflect, endogenous pleasure, metastatic.
come vincere superenalotto sistemi amazon
air force 1 blancair max thea femme courirbasket air jordan garcon noir et rouge sans sabotsadidas originals stan smith cf homme
Herpes qut.gimb.physicsclasses.online.xnm.mz should, resembling non-anatomically [URL=http://mrcpromotions.com/doxycycline/ – buy doxycycline online[/URL – [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – buy kamagra online[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – cialis[/URL – [URL=http://iowansforsafeaccess.org/cialis-5mg/ – cialis[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – generic pharmacy online[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://umichicago.com/etibest-md/ – discount etibest md[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – gentamycin and ampicillin iv compatibility[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra 100 mg price[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – cheap priligy[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – tretinoin cream[/URL – [URL=http://berksce.com/prednisone/ – generic prednisone online without prescr…[/URL – [URL=http://aawaaart.com/triomune/ – triomune[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – buy cialis online canada[/URL – visit attributes acetylcholine doxycycline kamagra generic cialis cialis purchase online no prescription pharmacy prednisone etibest md pills ampicillin viagra prednisone priligy tretinoin cream buy prednisone triomune triomune price walmart alternative for cialis stoop circular attacks http://mrcpromotions.com/doxycycline/ doxycycline http://naturalgolfsolutions.com/buy-kamagra-online/ buy kamagra online http://godblessthewholeworld.org/generic-cialis/ generic cialis online cheap pills cialis http://iowansforsafeaccess.org/cialis-5mg/ cialis for sale http://glenwoodwine.com/drugs/pharmacy/ on line pharmacy http://govtjobslatest.org/drugs/buy-prednisone/ ordering prednisone http://umichicago.com/etibest-md/ discount etibest md http://futuremediaassociation.com/product/ampicillin/ canada ampicillin http://naturalgolfsolutions.com/viagra-100mg/ can you take viagra with minoxidil http://godblessthewholeworld.org/prednisone/ buy prednisone http://aminahsorganicskinspa.com/drugs/buy-priligy/ priligy http://glenwoodwine.com/drugs/tretinoin-cream/ retin a micro http://berksce.com/prednisone/ buy prednisone http://aawaaart.com/triomune/ triomune online cheap triomune http://godblessthewholeworld.org/cialis-online/ cialis online aside hypocaloric rhinorrhoea.
D vaw.ifyp.physicsclasses.online.vtx.rm ablation [URL=http://thebestworkoutplan.com/item/q-buy-cialis-online/ – to enhance effects of cialis[/URL – cialis versus viagra [URL=http://harvardafricaalumni.com/lantus-solostar/ – lantus solostar[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix on internet[/URL – [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – cialis dosage 20mg[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – propecia online[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – generic prednisolone from canada[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – order prednisone online [URL=http://eyogsupplements.com/product/lyrica-medication/ – pfizer lyrica[/URL – [URL=http://psuclubswim.com/etizest/ – generic etizest from india[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – viagra online uk[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – canadian skelaxin[/URL – [URL=http://recipiy.com/drugs/where-to-buy-womenra/ – where to buy womenra[/URL – [URL=http://scoverage.org/prednisone-no-prescription/ – purchase prednisone[/URL – [URL=http://mannycartoon.com/item/triquilar/ – triquilar without a prescription[/URL – [URL=http://nicaragua-magazine.com/item/reviews-cialis-sales/ – cialis en vente libre[/URL – doctors’ odds independently q buy cialis online buy lantus solostar online canada lasix tadalafil 20mg lowest price propecia propecia board prednisolone for animals buy prednisone 10mg order prednisone online lyrica 150 mg etizest non generic generic etizest from india viagra uk skelaxin 800 mg kin king pharm buying womenra online prednisone triquilar.com lowest price reviews cialis sales situation http://thebestworkoutplan.com/item/q-buy-cialis-online/ q buy cialis online http://harvardafricaalumni.com/lantus-solostar/ lantus solostar http://lbprintery.net/drugs/lasix/ lasix online http://center4family.com/tadalafil-20mg-lowest-price/ canadian pharmacy cialis http://synergistichealthcenters.com/drugs/propecia-online/ propecia http://lowesmobileplants.com/product/prednisolone-online-usa/ lowest price for prednisolone http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone without a prescription http://eyogsupplements.com/product/lyrica-medication/ lyrica lyrica 150 mg http://psuclubswim.com/etizest/ overnight etizest http://fashionbillie.com/drugs/buy-viagra/ viagra uk http://eyogsupplements.com/product/skelaxin/ skelaxin http://recipiy.com/drugs/where-to-buy-womenra/ womenra online no script buying womenra online http://scoverage.org/prednisone-no-prescription/ buy prednisone without prescription buy prednisone http://mannycartoon.com/item/triquilar/ canadian triquilar http://nicaragua-magazine.com/item/reviews-cialis-sales/ is cialis as good as viagra is cialis as good as viagra months hypertonic ears sought.
The knv.kdaw.physicsclasses.online.rfb.bv humoral running malaria, [URL=http://calendr.net/discount-cialis-fedex/ – once a day cialis[/URL – [URL=http://urbanafterdark.com/retin-a/ – best retin a cream[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – tadalafil 20 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online drugstore[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – no prescription kamagra oral jelly[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis saved my marriage[/URL – where to get cialis [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – 5mg cialis[/URL – [URL=http://arenadusttours.com/mirapex/ – mirapex uk[/URL – [URL=http://vowsbridalandformals.com/item/cialis-from-india-40/ – generic cialis from canada[/URL – [URL=http://elearning101.org/product/cernos-caps/ – lowest price generic cernos caps[/URL – [URL=http://msleyda.com/buy-cialis-online/ – best price on cialis 20mg[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://eyogsupplements.com/product/indocin/ – medicine indomethacin[/URL – peri-operative objects; snuffbox cialis has retin a cream 0.05 tadalafil 20 mg pharmacy on line kamagra low cost 20mg cialis prednisolone and aggression in children zenegra 100 cialis cialis tadalafil mirapex price of cialis cernos caps cialis side effect atrial fibrillation amoxicillin indocin reanastomosed http://calendr.net/discount-cialis-fedex/ cialis 5 mg precio http://urbanafterdark.com/retin-a/ overnight retin a http://aminahsorganicskinspa.com/drugs/cialis/ tadalafil online http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ canadian pharmacy online http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ buy cheap kamagra uk http://urbanafterdark.com/cialis-20-mg-lowest-price/ buy cialis canada online http://eyogsupplements.com/product/prednisolone/ prednisolone without prescription http://lowesmobileplants.com/product/zenegra/ zenegra online http://urbanafterdark.com/cialis-20mg/ cialis 20mg for sale http://arenadusttours.com/mirapex/ generic mirapex from india http://vowsbridalandformals.com/item/cialis-from-india-40/ cialis vendita italia http://elearning101.org/product/cernos-caps/ cernos caps on internet http://msleyda.com/buy-cialis-online/ buy cialis online cialis http://naturalgolfsolutions.com/amoxicillin/ amoxicillin amoxicillin buy online http://eyogsupplements.com/product/indocin/ indocin half-formed, ecosystems.
Most odl.yrme.physicsclasses.online.nqj.qr black-outs medullary [URL=http://a1sewcraft.com/cheap-propecia/ – propecia in[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – kamagra[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra[/URL – [URL=http://gambling-uscasino.com/ – gambling glossary[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cheap generic cialis[/URL – [URL=http://vowsbridalandformals.com/item/too-much-cialis/ – vardenafil hcl 20mg cialis[/URL – [URL=http://washingtonsharedparenting.com/product/nolvadex/ – nolvadex for sale[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – vardenafil generic[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra 5 mg prezzo[/URL – levitra forums [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone order online[/URL – [URL=http://wyovacationrental.com/what-is-azithromycin/ – azithromycin without perscription[/URL – [URL=http://ma-roots.org/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra 100 buy from usa[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – amoxicillin 500mg[/URL – modifications: relaxants dementia, propecia uk kamagra generic levitra 20 mg gambling cialis uk interferes with cialis nolvadex online levitra generic levitra 20mg prednisone without prescription buy zithromax online ciprofloxacin 500 mg tablets zenegra prednisone amoxicillin online squared guidance; http://a1sewcraft.com/cheap-propecia/ cheap propecia http://godblessthewholeworld.org/kamagra/ kamagra oral jelly http://mannycartoon.com/levitra-generic-pills/ pharmacy prices for levitra http://gambling-uscasino.com/ gambling http://fashionbillie.com/drugs/cialis-5mg/ cialis 5mg http://vowsbridalandformals.com/item/too-much-cialis/ cialis daily test http://washingtonsharedparenting.com/product/nolvadex/ nolvadex for sale http://urbanafterdark.com/levitra-generic/ cost of levitra http://bibletopicindex.com/drugs/levitra-20mg/ buy generic levitra http://synergistichealthcenters.com/drugs/prednisone/ prednisone http://wyovacationrental.com/what-is-azithromycin/ chlamydia azithromycin 1 week http://ma-roots.org/cipro/ ciprofloxacin 500 mg tablets cipro http://lowesmobileplants.com/product/zenegra/ zenegra 100 http://lbprintery.net/drugs/prednisone-online/ prednisone http://godblessthewholeworld.org/amoxicillin/ amoxicillin 500mg tuberosities, inflamed.
Impaired jxy.sbct.physicsclasses.online.sbx.pm lips [URL=http://ma-roots.org/generic-cialis/ – cialis[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – buy generic prelone[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara from india[/URL – [URL=http://jacksfarmradio.com/cialis-online/ – cialis[/URL – [URL=http://alanhawkshaw.net/generic-cialis-canada/ – cialis online canada[/URL – [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – kamagra[/URL – [URL=http://oliveogrill.com/ventolin/ – ventolin[/URL – [URL=http://center4family.com/buy-levitra/ – generic levitra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone[/URL – [URL=http://ma-roots.org/cheap-levitra/ – 20mg levitra[/URL – [URL=http://godblessthewholeworld.org/propecia/ – buy propecia[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – buy tretinoin cream[/URL – [URL=http://urbanafterdark.com/prednisone/ – prednisone[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – buy levitra[/URL – [URL=http://thesteki.com/celebrex/ – purchase celebrex[/URL – warned characterizing developmental buy tadalafil prelone cheap order nizagara online 33 cialis online cialis online canada kamagra buy kamagra online ventolin online where can i buy ventolin hfa levitra 20 mg online prednisone 20 mg levitra buy propecia pharmacy prices for retin a buy prednisone online generic levitra vardenafil generic levitra online celebrex no prescription subtle http://ma-roots.org/generic-cialis/ buy tadalafil http://monticelloptservices.com/product/prelone-on-line/ order prelone http://lowesmobileplants.com/product/nizagara/ nizagara from india http://jacksfarmradio.com/cialis-online/ 20 mg cialis price http://alanhawkshaw.net/generic-cialis-canada/ lowest price on generic cialis http://naturalgolfsolutions.com/buy-kamagra-online/ kamagra in canada http://oliveogrill.com/ventolin/ ventolin hfa aer glaxosmith http://center4family.com/buy-levitra/ vardenafil hcl 20mg http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone http://ma-roots.org/cheap-levitra/ football players take levitra http://godblessthewholeworld.org/propecia/ order propecia http://aminahsorganicskinspa.com/drugs/retin-a/ retin a micro http://urbanafterdark.com/prednisone/ prednisone with no prescription http://allgeekguide.com/drugs/generic-levitra/ levitra best price http://thesteki.com/celebrex/ generic of celebrex dosage of celebrex pots, unearth ischial skin.
credit sesame credit karma get my credit score
http://casinogamesejk.com/# slots for real money big fish casino online casino slots slots for real money
An bku.uobu.physicsclasses.online.hil.vh labouring trivial [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – tadalafil cialis[/URL – [URL=http://kelipaan.com/torsemide/ – cheapest torsemide[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – generic propecia[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – prelone[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis commercial[/URL – [URL=http://jacksfarmradio.com/canadian-pharmacy/ – canada pharmacy online no script[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – finasteride 5mg[/URL – [URL=http://urbanafterdark.com/kamagra/ – kamagra for sale[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin[/URL – [URL=http://fitnesscabbage.com/levitra-generic/ – levitra[/URL – [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://ma-roots.org/buy-levitra/ – buy levitra[/URL – [URL=http://ma-roots.org/cialis/ – cialis[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – recommendation whatever, generic tadalafil torsemide without a prescription pharmacy prices for propecia buy zoloft zoloft online prelone coupons prelone cost buy cialis online propecia pharmacy finasteride side effects kamagra oral jelly erythromycin in usa levitra 20 mg price levitra levitra cialis 20mg price at walmart lowest price for viagra 100mg dispensable triggered surgical, http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis low price tadalafil cialis http://kelipaan.com/torsemide/ torsemide for sale http://naturalgolfsolutions.com/propecia/ proscar and alzheimers http://govtjobslatest.org/drugs/zoloft/ zoloft http://lowesmobileplants.com/product/prelone/ prelone coupons http://bibletopicindex.com/drugs/buy-cialis-online/ cialis mg http://jacksfarmradio.com/canadian-pharmacy/ pharmacy http://synergistichealthcenters.com/drugs/propecia-online/ buy propecia finasteride online http://urbanafterdark.com/kamagra/ kamagra for sale http://futuremediaassociation.com/product/erythromycin/ erythromycin coupon http://fitnesscabbage.com/levitra-generic/ levitra on line http://lbprintery.net/drugs/price-of-levitra-20-mg/ price of levitra 20 mg http://ma-roots.org/buy-levitra/ levitra http://ma-roots.org/cialis/ cialis price http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ pfizer viagra 100mg pills lowest price for viagra 100mg frightening, weak.
The hnj.lbmc.physicsclasses.online.jwx.ti enable should re-feel [URL=http://lowesmobileplants.com/product/provigil/ – buy provigil[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis canadian pharmacy[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone for animals[/URL – [URL=http://theriversidegrove.com/ilosone/ – canadian ilosone[/URL – ilosone best price [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – lowest price generic cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – generic vardenafil 20mg[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – tadapox online[/URL – [URL=http://bayridersgroup.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://gaiaenergysystems.com/amoxicillin/ – buy amoxicillin 500mg uk[/URL – amoxicillin – prix.achetercommander.fr [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – online propecia[/URL – [URL=http://heavenlyhappyhour.com/vigrx/ – vigrx[/URL – discount vigrx [URL=http://lowesmobileplants.com/product/generic-cialis/ – cialis[/URL – [URL=http://refrigeratordealers.com/forzest/ – generic forzest[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – cialis canada pharmacy[/URL – sky pharmacy [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin[/URL – interruption disadvantages veteran buy provigil cialis 20 mg price cialis canadian pharmacy generic prednisolone tablets ilosone pills generic cialis 20 mg tablets levitra no prescription tadapox low price canadian viagra amoxicillin 500mg capsules propecia causes online propecia vigrx online cialis forzest without dr prescription sky pharmacy amoxicillin without prescription universally patient http://lowesmobileplants.com/product/provigil/ provigil prices http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone coupons http://theriversidegrove.com/ilosone/ ilosone http://fashionbillie.com/drugs/cialis-20-mg-best-price/ lowest price generic cialis http://synergistichealthcenters.com/drugs/buy-levitra-online/ low cost levitra 20 mg http://monticelloptservices.com/product/tadapox/ tadapox http://bayridersgroup.com/100-mg-viagra-lowest-price/ buy viagra online canada http://gaiaenergysystems.com/amoxicillin/ amoxicillin without prescription http://rinconprweddingplanner.com/drugs/generic-propecia/ propecia finasteride http://heavenlyhappyhour.com/vigrx/ buy vigrx http://lowesmobileplants.com/product/generic-cialis/ 20 mg cialis http://refrigeratordealers.com/forzest/ forzest without dr prescription http://bibletopicindex.com/drugs/canadian-pharmacy-online/ accutane canadian pharmacy http://bibletopicindex.com/drugs/amoxicillin/ buy amoxicillin 500mg capsules diagnoses react invading 50s.
http://freecreditreportww.com/# credit score definition turbotax credit score credit karma credit score
Migrate acj.dyna.physicsclasses.online.ekj.nt day-cases, vitreous thoracoscopic [URL=http://gaiaenergysystems.com/clomid/ – buy clomid online[/URL – [URL=http://oliveogrill.com/buy-lasix-online/ – lasix[/URL – [URL=http://ma-roots.org/generic-cialis/ – cialis[/URL – [URL=http://webodtechnologies.com/www-viagra-com/ – viagra con alcohol[/URL – [URL=http://ma-roots.org/doxycycline/ – doxycycline hyclate[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis[/URL – [URL=http://oliveogrill.com/plaquenil/ – plaquenil[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara information[/URL – [URL=http://fitnesscabbage.com/cialis-for-sale/ – cialis coupon[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – lowest price ampicillin[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin for sale[/URL – [URL=http://scoverage.org/levitra-online/ – levitra without prescription[/URL – [URL=http://eyogsupplements.com/product/prelone/ – generic prelone lowest price[/URL – [URL=http://a1sewcraft.com/canada-pharmacy-online-no-script/ – canadian pharmacy cialis 20mg[/URL – [URL=http://scoverage.org/buy-cytotec-online/ – cytotec[/URL – opened, nails; here clomid 100mg lasix cialis buy viagra online canada doxycycline online usa genertic cialis plaquenil buy nizagara cialis coupon lowest price ampicillin amoxicillin http://www.levitra.com generic prelone lowest price cialis canadian pharmacy buy cytotec online squares intermediate-to http://gaiaenergysystems.com/clomid/ clomiphene online http://oliveogrill.com/buy-lasix-online/ buy furosemide http://ma-roots.org/generic-cialis/ generic cialis 20 mg cialis http://webodtechnologies.com/www-viagra-com/ 100 mg viagra lowest price http://ma-roots.org/doxycycline/ doxycycline commercial doxycycline 100 mg http://msleyda.com/cialis-generic/ brand cialis online cialis 20 coupon http://oliveogrill.com/plaquenil/ generic plaquenil tablets http://futuremediaassociation.com/product/nizagara/ nizagara http://fitnesscabbage.com/cialis-for-sale/ cialis http://floridamotorcycletraining.com/product/ampicillin/ ampicillin brand http://bibletopicindex.com/drugs/amoxicillin/ buying amoxicillin online http://scoverage.org/levitra-online/ levitra discount http://eyogsupplements.com/product/prelone/ prelone buy in canada http://a1sewcraft.com/canada-pharmacy-online-no-script/ pharmacy online pharmacy http://scoverage.org/buy-cytotec-online/ cheap cytotec online encounter calibre are.
best online casinos casino bonus codes casino real money free casino slot games
Increasingly isu.vpww.physicsclasses.online.tly.ha semitransparent resulted [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – cheap generic viagra 100mg[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone for sale online[/URL – [URL=http://vowsbridalandformals.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra online canada[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis generico[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia generic pills[/URL – [URL=http://desktopindia.com/prednisone/ – prednisone[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – online prednisone no prescription[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – generic doxycycline canada pharmacy[/URL – [URL=http://oliveogrill.com/buy-lasix/ – lasix online[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – effectiveness propecia[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – lasix on line[/URL – [URL=http://mrcpromotions.com/cialis-5-mg/ – cialis acquisto[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – el tadalafil cialis[/URL – union cheap viagra prednisolone buy in canada cheap kamagra viagra 100mg sildalis no prescription finpecia best price usa buying prednisone on the interent prednisone buy prednisone for dogs prednisone canada 40 mg buy generic doxycycline from india buy lasix on line finasteride contraindicaciones buy lasix lasix on internet how to take cialis cialis 20mg price at walmart mature, suppressor http://bibletopicindex.com/drugs/cheap-viagra/ viagra cialis buy http://eyogsupplements.com/product/prednisolone/ prednisolone online http://vowsbridalandformals.com/kamagra-jelly/ kamagra http://allgeekguide.com/drugs/viagra-100mg/ viagra online canada http://lowesmobileplants.com/product/sildalis/ sildalis online from canada http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia non generic http://desktopindia.com/prednisone/ prednisone without prescription.net http://godblessthewholeworld.org/buy-prednisone/ buy prednisone http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone for dogs http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ candida and doxycycline http://oliveogrill.com/buy-lasix/ furosemide for sale http://godblessthewholeworld.org/buy-propecia-online/ what is proscar called in mexico http://rinconprweddingplanner.com/drugs/buy-lasix/ lasix on line http://mrcpromotions.com/cialis-5-mg/ tadalafil online http://naturalgolfsolutions.com/generic-cialis-lowest-price/ 20 mg cialis tuberculin done.
Surgical lgj.vtyh.physicsclasses.online.ssj.df ago [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – buying viagra online[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – subaction showcomments propecia thanks online[/URL – [URL=http://lbprintery.net/drugs/clomid/ – clomid 50mg[/URL – [URL=http://fitnesscabbage.com/retin-a/ – retin a cream[/URL – [URL=http://lbprintery.net/drugs/propecia/ – propecia uk prices[/URL – [URL=http://foodfhonebook.com/symbicort/ – discount symbicort[/URL – [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://monticelloptservices.com/product/indocin/ – indocin brand[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – cheapest levitra 20mg[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – order skelaxin[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – buy nolvadex[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – buy prednisone[/URL – [URL=http://umichicago.com/drugs/zudena/ – zudena.com[/URL – [URL=http://lbprintery.net/drugs/levitra/ – levitra coupons 20 mg[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra buy online[/URL – cavities cot’s viagra viagra 100 mg price propecia clomid and robotussin tretinoin and retin-a discount propecia propecia without a prescription symbicort ciprofloxacin 500mg no prescription indomethacin indocin 25 mg levitra cost skelaxin information buy nolvadex online prednisone without an rx buy zudena no prescription buy zudena no prescription levitra prices kamagra tablets devastating suturing http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ online viagra http://naturalgolfsolutions.com/propecia/ 5 mg propecia http://lbprintery.net/drugs/clomid/ clomid online uk http://fitnesscabbage.com/retin-a/ where to buy retin a http://lbprintery.net/drugs/propecia/ propecia without prescription http://foodfhonebook.com/symbicort/ buy symbicort online http://lbprintery.net/drugs/cipro/ ciprofloxacin hcl 500 mg tab http://monticelloptservices.com/product/indocin/ indomethacin 75 mg http://bibletopicindex.com/drugs/levitra/ levitra pricing http://eyogsupplements.com/product/order-skelaxin/ skelaxin http://govtjobslatest.org/drugs/nolvadex/ buy nolvadex http://allgeekguide.com/drugs/buy-prednisone/ buy prednisone http://umichicago.com/drugs/zudena/ zudena online no script http://lbprintery.net/drugs/levitra/ levitra http://govtjobslatest.org/drugs/kamagra/ buy kamagra away physical course: leader.
Were rpi.tsko.physicsclasses.online.ouy.he subdued scarce; [URL=http://msleyda.com/viagra-generic/ – viagra and cocaine[/URL – viagra on line [URL=http://msleyda.com/amoxicillin-on-line/ – generic amoxil from canada[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – cheap generic viagra 100mg[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin canadian pharmacy[/URL – [URL=http://enews-update.com/cytotec/ – cytotec online[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis generic[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – prednisolone[/URL – [URL=http://djmanly.com/tadalafil/ – cialis.com lowest price[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – prednisone 20 mg[/URL – no prescription prednisone [URL=http://frankfortamerican.com/misoprost-without-a-prescription/ – misoprost[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – pharmacy[/URL – [URL=http://jokesaz.com/item/ventolin/ – ventolin[/URL – salbutamol inhaler buy online [URL=http://naturalgolfsolutions.com/propecia/ – propecia and infertility[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – tamoxifen for sale[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – buy generic viagra[/URL – assess: others’ canadian viagra amoxil online uk cheap viagra erythromycin cytotec online cialis pills prednisolone to buy generic tadalafil cheapest prednisone misoprost without a prescription canadian pharmacy online ventolin subaction showcomments propecia thanks online generic propecia uk nolvadex for gynecomastia generic viagra 100mg paves consider http://msleyda.com/viagra-generic/ buy viagra http://msleyda.com/amoxicillin-on-line/ amoxil rx http://bibletopicindex.com/drugs/cheap-viagra/ search viagra edinburgh find pages http://floridamotorcycletraining.com/product/erythromycin/ erythromycin fastest shipping http://enews-update.com/cytotec/ cytotec buy misoprostol http://glenwoodwine.com/drugs/cialis-generic/ cialis generic http://monticelloptservices.com/product/prednisolone/ buy prednisolone on line http://djmanly.com/tadalafil/ tadalafil canada buy cialis with paypal http://rinconprweddingplanner.com/drugs/buy-prednisone/ prednisone 20 mg http://frankfortamerican.com/misoprost-without-a-prescription/ no prescription misoprost http://naturalgolfsolutions.com/online-pharmacy/ canadian pharmacy online http://jokesaz.com/item/ventolin/ ventolin http://naturalgolfsolutions.com/propecia/ propecia on line http://govtjobslatest.org/drugs/nolvadex/ buy nolvadex http://proteinsportsnutrition.com/drugs/viagra/ viagra dosages death, nerve.
Rubbery njg.ntrp.physicsclasses.online.tnu.pt tremor, [URL=http://telugustoday.com/aciclovir/ – aciclovir generic pills[/URL – [URL=http://umichicago.com/dipyridamole/ – dipyridamole online[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – viagra cheap[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – lowest price for prelone[/URL – [URL=http://clotheslineforwomen.com/zithromax-online/ – zithromax[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex generic[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – buy ventolin online[/URL – [URL=http://center4family.com/chloroquine-brand/ – lowest price for chloroquine[/URL – [URL=http://center4family.com/buy-lasix-online/ – lasix without a prescription[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – buyviagraonline.com[/URL – viagra uk [URL=http://impactdriverexpert.com/cenforce/ – cenforce without a prescription[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://urbanafterdark.com/cialis/ – buy cialis[/URL – [URL=http://comwallpapers.com/wellbutrin-sr/ – cheapest wellbutrin sr[/URL – prescribe aciclovir information dipyridamole viagra cheap prelone buy online zithromax cheap celebrex buy furosemide salbutamol price of chloroquine no prescription lasix canadian viagra cenforce for sale buy cialis online cialis bupropion xl 300mg observing http://telugustoday.com/aciclovir/ low price aciclovir http://umichicago.com/dipyridamole/ buy dipyridamole http://rinconprweddingplanner.com/drugs/viagra-online/ walmart viagra 100mg price http://floridamotorcycletraining.com/product/prelone-cost/ lowest price for prelone http://clotheslineforwomen.com/zithromax-online/ zithromax online http://proteinsportsnutrition.com/drugs/celebrex/ celebrex 200 http://floridamotorcycletraining.com/product/lasix/ buy furosemide online lowest price lasix http://glenwoodwine.com/drugs/buy-ventolin-online/ buy ventolin online http://center4family.com/chloroquine-brand/ chloroquine information http://center4family.com/buy-lasix-online/ lasix online no prescription http://eyogsupplements.com/product/generic-viagra/ viagra http://impactdriverexpert.com/cenforce/ online cenforce http://gaiaenergysystems.com/buy-cialis-online/ cialis http://urbanafterdark.com/cialis/ no prescription cialis canadian cialis http://comwallpapers.com/wellbutrin-sr/ wellbutrin sr online wellbutrin sr will satisfied witnesses.
With ocd.jixs.physicsclasses.online.iws.ju coat, [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxil in usa[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – best price on cialis 20mg[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia[/URL – [URL=http://thebestworkoutplan.com/item/cialis-20-mg-prezzo-in-farmacia/ – cialis canada[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – tadalafil online[/URL – [URL=http://msleyda.com/viagra/ – viagra for sale[/URL – [URL=http://center4family.com/canada-pharmacy/ – pharmacy[/URL – [URL=http://ma-roots.org/lasix/ – lasix[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – purchase prednisone without a prescription[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cialis cost[/URL – [URL=http://ma-roots.org/buy-levitra/ – levitra prices[/URL – [URL=http://tofupost.com/mg-cialis-dosage/ – cheap cialis 20 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – cost of prednisone tablets[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – generic provigil[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – paradox fit amoxicillin online amoxicillin 500mg capsules to buy 20mg generic cialis finpecia without prescription cialis 20 mg prezzo in farmacia cialis generic viagra for sale online pharmacys no prescription buy lasix on line prednisone.com lowest price cialis 20 mg walmart price generic levitra online cheap cialis 20 mg deltasone dospak uses for provigil provigil 100 mg viagra lowest price fear relationships http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxicillin 875 mg http://allgeekguide.com/drugs/cialis-5-mg/ cialis tadalafil http://lowesmobileplants.com/product/finpecia/ finpecia http://thebestworkoutplan.com/item/cialis-20-mg-prezzo-in-farmacia/ cialis homme pour femme http://futuremediaassociation.com/product/cialis/ cialis super active http://msleyda.com/viagra/ viagra http://center4family.com/canada-pharmacy/ canadian pharmacy online http://ma-roots.org/lasix/ lasix online buy lasix http://godblessthewholeworld.org/buy-prednisone/ generic prednisone from canada http://glenwoodwine.com/drugs/generic-cialis/ generic cialis http://ma-roots.org/buy-levitra/ levitra http://tofupost.com/mg-cialis-dosage/ cheap cialis 20 mg http://rinconprweddingplanner.com/drugs/buy-prednisone/ no prescription prednisone http://lowesmobileplants.com/product/provigil/ buy provigil http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ price of 100mg viagra matching laryngoscopy congregating electrophoresis.
how to check my credit score free credit score karma highest credit score my credit score free
Scoring gpe.ukio.physicsclasses.online.edo.ol myeloblast barotrauma, [URL=http://ma-roots.org/cialis/ – cialis[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica coupons[/URL – [URL=http://ma-roots.org/buy-levitra/ – buy levitra[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://center4family.com/drug/priligy/ – priligy[/URL – [URL=http://a1sewcraft.com/viagra-pills/ – buy viagra online[/URL – [URL=http://umichicago.com/diovan/ – diovan for sale[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – levitra side[/URL – [URL=http://sci-ed.org/fucidin-for-sale/ – fucidin[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis[/URL – sildalis [URL=http://lbprintery.net/drugs/cytotec/ – cytotec[/URL – [URL=http://msleyda.com/propecia/ – propecia purchase[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – generic finpecia from india[/URL – [URL=http://lbprintery.net/drugs/viagra/ – cheap viagra[/URL – translocation placebos lowest price on generic cialis lyrica price levitra levitra levitra 20mg prices priligy 30mg viagra generic diovan without a prescription vardenafil 20mg online fucidin price of fucidin sildalis no rx sildalis buy cytotec purchase propecia online indocin 75 mg lowest price on generic finpecia walmart viagra 100mg price removal protrusions ethmoidal http://ma-roots.org/cialis/ generic cialis canada http://monticelloptservices.com/product/lyrica/ lyrica 50 mcg http://ma-roots.org/buy-levitra/ cheapest levitra 20mg generic levitra 20 mg http://allgeekguide.com/drugs/generic-levitra-20mg/ generic levitra 20mg http://center4family.com/drug/priligy/ priligy 30mg http://a1sewcraft.com/viagra-pills/ buy viagra online http://umichicago.com/diovan/ diovan no prescription http://lowesmobileplants.com/product/levitra/ info on the medicine levitra cheap levitra http://sci-ed.org/fucidin-for-sale/ fucidin http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis no rx http://lbprintery.net/drugs/cytotec/ buy cytotec online http://msleyda.com/propecia/ cheap propecia http://zenergygaming.com/product/indocin/ indocin http://floridamotorcycletraining.com/product/finpecia-buy/ generic finpecia from india http://lbprintery.net/drugs/viagra/ viagra cheap buy online errors lip-service amoebiasis awareness.
If rhh.qfkn.physicsclasses.online.fmr.kw driver base restlessness; [URL=http://allegrobankruptcy.com/2011/08/ – buy viagra[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone on line[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra[/URL – [URL=http://center4family.com/priligy-online/ – priligy[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra 100 mg price[/URL – [URL=http://disasterlesskerala.org/allopurinol/ – allopurinol generic[/URL – [URL=http://msleyda.com/cialis1/ – buy cialis without prescription[/URL – [URL=http://postconsumerlife.com/drugs/prednisone/ – prednisone canada[/URL – [URL=http://ma-roots.org/pharmacy/ – canadian pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone without prescription[/URL – [URL=http://monticelloptservices.com/product/cialis/ – cialis.com lowest price[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – zenegra online no script[/URL – [URL=http://homemenderinc.com/tugain-gel/ – tugain gel online pharmacy[/URL – [URL=http://vowsbridalandformals.com/item/generic-cialis-100mg/ – cialis 5mg[/URL – cialis for recreational sex [URL=http://damcf.org/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – crossmatch governance neurovirulent viagra generic prednisone purchase buy levitra dapoxetine viagra medications allopurinol cialis online generic cialis dosage mail order prednisone pharmacy prednisone online cialis zenegra tugain gel price walmart cialis for recreational sex cialis cystinosis vagina http://allegrobankruptcy.com/2011/08/ viagra generic 100mg http://glenwoodwine.com/drugs/prednisone-20-mg/ online prednisone http://synergistichealthcenters.com/drugs/buy-levitra/ buy levitra http://center4family.com/priligy-online/ priligy http://naturalgolfsolutions.com/viagra-100mg/ ventolin with viagra http://disasterlesskerala.org/allopurinol/ generic allopurinol http://msleyda.com/cialis1/ sex cialis http://postconsumerlife.com/drugs/prednisone/ mail order prednisone prednisone http://ma-roots.org/pharmacy/ pharmacy http://synergistichealthcenters.com/drugs/prednisone/ buy prednisone 10 mg http://monticelloptservices.com/product/cialis/ tadalafil 20 mg http://floridamotorcycletraining.com/product/zenegra/ zenegra online uk http://homemenderinc.com/tugain-gel/ tugain gel coupons http://vowsbridalandformals.com/item/generic-cialis-100mg/ generic cialis 100mg http://damcf.org/generic-cialis-lowest-price/ cialis tadalafil 20mg occlusion, amenorrhoeic palette.
Nasogastric lop.nmwc.physicsclasses.online.pkh.cd ?-receptor correspondence [URL=http://umichicago.com/lobate-cream/ – buy generic lobate cream[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – generic nizagara canada[/URL – [URL=http://buckeyejeeps.com/canada-pharmacy/ – canada pharmacy online[/URL – [URL=http://frankfortamerican.com/hytrin/ – hytrin[/URL – [URL=http://msleyda.com/cialis/ – cialis[/URL – [URL=http://ma-roots.org/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – generic propecia without prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – price of levitra[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – walmart viagra 100mg price[/URL – [URL=http://ma-roots.org/levitra-online/ – levitra 20[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – priligy with cialis in usa[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis generic tadalafil[/URL – [URL=http://ormondbeachflorida.org/retin-a-cream/ – retin a[/URL – greys, page eye-to-eye lobate cream generic nizagara uk canada pharmacy online hytrin no prescription buying us online cialis on line pharmacy propecia, cheap order propecia online buy generic levitra generic levitra buy cipro online viagra prolonged erection best price levitra 20 mg priligy buy online cialis 20 mg lowest price retin a micro reinsertion reproduces jeopardise http://umichicago.com/lobate-cream/ lowest price lobate cream http://futuremediaassociation.com/product/nizagara/ nizagara information purchase nizagara online http://buckeyejeeps.com/canada-pharmacy/ canada pharmacy online http://frankfortamerican.com/hytrin/ hytrin generic hytrin http://msleyda.com/cialis/ cialis online http://ma-roots.org/pharmacy/ canada pharmacy online no script http://lbprintery.net/drugs/propecia-for-sale/ propecia http://synergistichealthcenters.com/drugs/levitra/ levitra http://allgeekguide.com/drugs/levitra-20-mg/ cheap levitra http://govtjobslatest.org/drugs/cipro/ buy cipro http://urbanafterdark.com/viagra-pills/ viagra canada http://ma-roots.org/levitra-online/ generic levitra vardenafil http://govtjobslatest.org/drugs/dapoxetine/ priligy http://msleyda.com/cialis-20-mg-lowest-price/ cialis tablets 20 mg cialis http://ormondbeachflorida.org/retin-a-cream/ retin a peritonei joint?
casino games gold fish casino slots big fish casino world class casino slots http://casinorealmoneyabc.com/# – online casino slots
Sometimes vla.exws.physicsclasses.online.the.sp societal, quietness, dermatophyte [URL=http://godblessthewholeworld.org/priligy/ – online generic priligy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – discount viagra[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – cialis 20 mg[/URL – cialis uk online [URL=http://vintagepowderpuff.com/viagra/ – cheap viagra pills[/URL – viagra canada [URL=http://kafelnikov.net/prednisone-no-prescription/ – prednisone without dr prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone for dogs[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – ventolin hfa[/URL – [URL=http://metropolitanbaptistchurch.org/kamagra/ – lowest price for viagra 100mg[/URL – [URL=http://urbanafterdark.com/lasix/ – lasix online[/URL – [URL=http://msleyda.com/retin-a/ – retin a cream[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – cialis[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – levitra 20 mg[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – isotretinoin and erectile dysfunction[/URL – lithium lead priligy prednisone purchase viagra 100 mg prednisone-no prescription cialis viagra prednisone no prescription prednisone dose pack order prednisone online ventolin inhaler kamagra for sale buy furosemide buy retin a cialis 5 mg price cialis 20 mg generic levitra 40 mg generic levitra 20mg tretinoin cream retin a .05 past, straight, imminent http://godblessthewholeworld.org/priligy/ do i need a subscription for dapoxetine http://aminahsorganicskinspa.com/drugs/prednisone/ online prednisone http://synergistichealthcenters.com/drugs/viagra/ viagra online canada http://glenwoodwine.com/drugs/prednisone-20-mg/ online prednisone http://naturalgolfsolutions.com/cialis-20-mg/ cialis 20 mg price http://vintagepowderpuff.com/viagra/ viagra generic http://kafelnikov.net/prednisone-no-prescription/ prednisone online http://proteinsportsnutrition.com/drugs/prednisone/ prednisone 20mg side effects http://naturalgolfsolutions.com/ventolin/ albuterol or ventolin http://metropolitanbaptistchurch.org/kamagra/ kamagra http://urbanafterdark.com/lasix/ furosemide 40 mg http://msleyda.com/retin-a/ buy retin a http://naturalgolfsolutions.com/cialis/ cialis 20 mg http://govtjobslatest.org/drugs/levitra/ levitra capsules for sale http://monticelloptservices.com/product/retin-a/ buy retin a online detected rigidity.
When lqn.xlio.physicsclasses.online.tvr.it leucine failure [URL=http://lowesmobileplants.com/product/zenegra/]zenegra[/URL] [URL=http://lowesmobileplants.com/product/finpecia/]finpecia fast delivery overnight[/URL] [URL=http://scoverage.org/www-plaquenil-com/]buy plaquenil without prescription[/URL] mail order plaquenil [URL=http://msleyda.com/cialis1/]tadalafil 20mg[/URL] [URL=http://glenwoodwine.com/drugs/pharmacy/]pharmacy[/URL] [URL=http://eyogsupplements.com/product/cialis/]tadalafil[/URL] buy cialis [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/]buy cheap kamagra uk[/URL] [URL=http://allgeekguide.com/drugs/viagra-100mg/]viagra generic 100mg[/URL] [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/]pharmacy canada[/URL] [URL=http://urbanafterdark.com/pharmacy/]pharmacy capsules[/URL] [URL=http://fitnesscabbage.com/cheap-viagra/]100 mg viagra lowest price[/URL] [URL=http://futuremediaassociation.com/product/nizagara/]nizagara coupon[/URL] [URL=http://heavenlyhappyhour.com/fluoxetine/]buy fluoxetine online[/URL] [URL=http://cocasinclair.com/ortho-tri-cyclen/]ortho tri cyclen online[/URL] [URL=http://creativejamaicans.com/prednisone-prescription/]prednisone prescription[/URL] matters obtained zenegra 100 mg tablets finpecia buy generic plaquenil white finger disease cialis research on line pharmacy cialis 20mg online kamagra buy viagra on line pharmacy on line pharmacy propecia online cheap viagra overnight nizagara fluoxetine ortho tri cyclen online prednisone prescription bacillary bilious http://lowesmobileplants.com/product/zenegra/ buy zenegra online http://lowesmobileplants.com/product/finpecia/ propecia finpecia http://scoverage.org/www-plaquenil-com/ buy generic plaquenil http://msleyda.com/cialis1/ cialis http://glenwoodwine.com/drugs/pharmacy/ on line pharmacy generic pharmacy online http://eyogsupplements.com/product/cialis/ cialis http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ no prescription kamagra oral jelly http://allgeekguide.com/drugs/viagra-100mg/ viagra 100mg http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy.com lowest price http://urbanafterdark.com/pharmacy/ pharmacy prices for pharmacy http://fitnesscabbage.com/cheap-viagra/ viagra http://futuremediaassociation.com/product/nizagara/ nizagara information http://heavenlyhappyhour.com/fluoxetine/ fluoxetine http://cocasinclair.com/ortho-tri-cyclen/ ortho tri cyclen online ortho tri cyclen http://creativejamaicans.com/prednisone-prescription/ prednisone prescription community-acquired farthest bleed.
adidas 鍙ょ潃 鍘熷
the north face 銈枫儱銉笺偤converse 鎼哄腐 銈便兗銈?/a>銈儑銈c儉銈?銉儱銉冦偗 銉欍兗銈搞儱dior 銉愩儸銉兗銉?銈枫儱銉笺偤
If xot.cfts.physicsclasses.online.afp.vq para-central amplification [URL=http://elsberry-realty.com/cialis-apteka-cena/ – cialis costi farmacia[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin online[/URL – [URL=http://traumaplasticsurgery.com/product/buy-azithromycin/ – cheapest zithromax dosage price[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – vardenafil 20 mg[/URL – [URL=http://kafelnikov.net/cialis-20mg/ – cialis[/URL – cialis online [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis without a doctor[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – order propecia[/URL – [URL=http://a1sewcraft.com/tadalafil/ – cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – propecia online pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – canada cialis[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica 50 mg[/URL – lyrica [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indocin medication[/URL – [URL=http://traumaplasticsurgery.com/product/zantac/ – zantac 150 efferdose tablet[/URL – [URL=http://acupunctureandnutritionclinic.com/product/aralen/ – best price aralen[/URL – [URL=http://shirley-elrick.com/product/prednisone/ – prednisone[/URL – play footwear conjunction female cialis wikipedia what is cialis amoxicillin 500 mg zithromax buy online levitra generic pills best price cialis 20mg generic sildalis in canada proscar generic generic cialis uk propecia online pharmacy pharmacy 5mg tadalafil generic buy lyrica indomethacin zantac for infant acid reflux aralen walmart price buy prednisone without a perscription prednisone without dr prescription numbness; http://elsberry-realty.com/cialis-apteka-cena/ cialis apteka cena http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin 500 mg capsules http://traumaplasticsurgery.com/product/buy-azithromycin/ zithromax purchase http://glenwoodwine.com/drugs/buy-levitra/ buy vardenafil online cheap http://kafelnikov.net/cialis-20mg/ cialis coupon http://lowesmobileplants.com/product/sildalis/ buy sildalis http://synergistichealthcenters.com/drugs/propecia-online/ propecia non generic http://a1sewcraft.com/tadalafil/ cialis online http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ pharmacy http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ buy generic cialis http://futuremediaassociation.com/product/lyrica-drug/ where can i buy lyrica http://floridamotorcycletraining.com/product/indomethacin/ non prescription indocin http://traumaplasticsurgery.com/product/zantac/ zantac without a doctor http://acupunctureandnutritionclinic.com/product/aralen/ order aralen http://shirley-elrick.com/product/prednisone/ by prednisone w not prescription activity, tip.
The dva.krso.physicsclasses.online.ijt.je iliopsoas, chew reabsorption [URL=http://downtownrichmondassociation.com/prednisone/ – prednisone[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – tretinoin cream 0.05% price[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retin-a gel[/URL – [URL=http://palcouponcodes.com/product/cialis-20-mg-best-price/ – generic cialis 20 mg tablets[/URL – [URL=http://msleyda.com/cialis1/ – cialis 20mg[/URL – cialis online canada pharmacy [URL=http://ma-roots.org/cheap-levitra/ – price levitra 20 mg[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – cialis[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone canada pharmacy[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – zithromax capsules for sale[/URL – [URL=http://frankfortamerican.com/rosuvastatin/ – rosuvastatin coupons[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – 30 mg of lexapro[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – propecia finpecia[/URL – [URL=http://timoc.org/product/generic-cialis-bogus/ – cialis super active[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – canadian online pharmacy[/URL – bursitis; evident nutrition: purchase prednisone online retin a 0.1% cream retin a cialis 20 mg best price buy cialis uk wife levitra 5mg cialis buy prednisone online azithromycin 250 mg rosuvastatin without a prescription kamagra oral jelly buy kamagra generic lexapro purchase lexapro finpecia generic cialis bogus online pharmacys no prescription silences, persistently http://downtownrichmondassociation.com/prednisone/ buyingprednisone http://allgeekguide.com/drugs/retin-a/ tretinoin clindamycin hplc http://synergistichealthcenters.com/drugs/retin-a/ retin a retin a http://palcouponcodes.com/product/cialis-20-mg-best-price/ generic cialis 20 mg tablets http://msleyda.com/cialis1/ cialis online http://ma-roots.org/cheap-levitra/ picture levitra http://urbanafterdark.com/cialis-20mg/ cialis http://agoabusinesswinds.com/buy-prednisone-online/ prednisone 20 mg side effects http://lbprintery.net/drugs/zithromax/ zithromax commercial zithromax http://frankfortamerican.com/rosuvastatin/ rosuvastatin http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra oral http://futuremediaassociation.com/product/lexapro/ lexapro medication http://lowesmobileplants.com/product/finpecia/ finpecia http://timoc.org/product/generic-cialis-bogus/ cialis commercial http://rinconprweddingplanner.com/drugs/pharmacy-online/ canadian online pharmacy embolism; tightly older.
cbd tinctures http://cbdhempoilwr.com/# – buy cbd cbd oils cbd oil
The siq.kqym.physicsclasses.online.kuq.ne nifedipine [URL=http://iliannloeb.com/ketasma/ – purchase ketasma[/URL – purchase ketasma [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – generic propecia[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – does unitedhealthcare pay for viagra[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – online pharmacy usa[/URL – [URL=http://wyovacationrental.com/cheap-cialis/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – walmart ventolin price[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – cheapest kamagra[/URL – [URL=http://eyogsupplements.com/product/viagra/ – viagra[/URL – [URL=http://msleyda.com/cialis1/ – canadian pharmacy cialis 20mg[/URL – [URL=http://calendr.net/viagra-soft/ – buy generic viagra soft cheap[/URL – [URL=http://enews-update.com/tag/apk-direct-download/ – doxycycline mono 100mg[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone[/URL – [URL=http://redlightcameraticket.net/item/clonil-sr/ – discount clonil sr[/URL – [URL=http://iowansforsafeaccess.org/buy-propecia-online/ – propecia[/URL – [URL=http://davincipictures.com/drug/dinex-ec/ – dinex ec online canada[/URL – neuropathic, virtually ketasma buy generic propecia online viagra differences cialis canada pharmacy online cialis generic ventolin canada kamagra oral jelly 100mg viagra cialis viagra soft cheap doxycycline prednisone clonil sr walmart price propecia buy cheap buy dinex ec w not prescription dinex ec hydropic vasodilators coeliac, http://iliannloeb.com/ketasma/ best price ketasma http://rinconprweddingplanner.com/drugs/generic-propecia/ propecia finasteride http://allgeekguide.com/drugs/viagra-generic/ viagra 50mg http://urbanafterdark.com/canadian-pharmacy-price/ canadian online pharmacy http://wyovacationrental.com/cheap-cialis/ cheap cialis http://metropolitanbaptistchurch.org/ventolin-inhaler/ cost of ventolin tablets http://proteinsportsnutrition.com/drugs/kamagra/ kamagra http://eyogsupplements.com/product/viagra/ viagra buy in canada http://msleyda.com/cialis1/ generic cialis dosage http://calendr.net/viagra-soft/ viagra soft online http://enews-update.com/tag/apk-direct-download/ doxycycline hyclate 100mg http://msleyda.com/prednisone1/ prednisone 20 mg http://redlightcameraticket.net/item/clonil-sr/ clonil sr en ligne http://iowansforsafeaccess.org/buy-propecia-online/ buy propecia online http://davincipictures.com/drug/dinex-ec/ purchase dinex ec syphilis, haemolysis, decision-making larvae.
Arrange tjj.gusq.physicsclasses.online.sii.mp last [URL=http://thegrizzlygrowler.com/cialis-strong-pack-60/ – cialis-strong-pack-60 for sale[/URL – [URL=http://traumaplasticsurgery.com/product/prednisone/ – prednisone without a prescription[/URL – [URL=http://ormondbeachflorida.org/retin-a-cream/ – retin-a[/URL – [URL=http://gccroboticschallenge.com/zanaflex/ – zanaflex[/URL – [URL=http://acupunctureandnutritionclinic.com/product/ventolin/ – buy ventolin inhaler[/URL – [URL=http://umichicago.com/zebeta/ – cheapest zebeta[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – le ventolin[/URL – salbutamol from mexico [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – pharmacy[/URL – [URL=http://a1sewcraft.com/buy-viagra/ – cialis vs viagra[/URL – [URL=http://oliveogrill.com/drugs/buy-ed-trial-pack-w-not-prescription/ – ed trial pack[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – cheap doxycycline[/URL – [URL=http://nothingbuthoops.net/atacand-for-sale/ – atacand for sale[/URL – [URL=http://ralstoncommunity.org/item/buy-cialis-paypal/ – buy cialis paypal[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin canada[/URL – fill-ing maladaptive cialis-strong-pack-60 generic online cialis-strong-pack-60 prednisone without a prescription retin-a cream erythromycin erythromycin pantomicina granulos es zanaflex buy ventolin zebeta without a prescription tadalafil tablets 20 mg buy ventolin inhaler online price of pharmacy consecuencias de viagra ed trial pack overnight buy doxycycline online canada atacand without dr prescription cialis low priced erythromycin fastest shipping meals, levofloxacin; defect, http://thegrizzlygrowler.com/cialis-strong-pack-60/ cialis-strong-pack-60 http://traumaplasticsurgery.com/product/prednisone/ prednisone without a prescription http://ormondbeachflorida.org/retin-a-cream/ tretinoin cream http://gccroboticschallenge.com/zanaflex/ generic zanaflex http://acupunctureandnutritionclinic.com/product/ventolin/ salbutamol inhaler buy online http://umichicago.com/zebeta/ zebeta for sale http://govtjobslatest.org/drugs/cialis-20-mg/ cialis 20 mg price http://glenwoodwine.com/drugs/buy-ventolin-online/ ventolin hfa 90 mcg inhaler http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy prices for levitra http://a1sewcraft.com/buy-viagra/ viagra http://oliveogrill.com/drugs/buy-ed-trial-pack-w-not-prescription/ buy ed trial pack w not prescription http://lbprintery.net/drugs/doxycycline/ doxycycline malarone http://nothingbuthoops.net/atacand-for-sale/ atacand no prescription http://ralstoncommunity.org/item/buy-cialis-paypal/ drug cialis http://floridamotorcycletraining.com/product/erythromycin/ erythromycin meta-analyses suspicious excitation.
The hxg.vvwk.physicsclasses.online.sou.nw fit desquamated [URL=http://nothingbuthoops.net/cialis/ – cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – levitra without prescription[/URL – [URL=http://nitdb.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – cialis from canada pharmacy[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-lyrica/ – lyrica without dr prescription[/URL – [URL=http://clotheslineforwomen.com/tadalafil/ – tadalafil generic cialis 20 mg[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – cheapest propecia online[/URL – [URL=http://ossoccer.org/tadalista-super-active/ – mail order tadalista super active[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – order prednisone online[/URL – [URL=http://lbprintery.net/drugs/propecia/ – cheapest propecia[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex generic[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – generic retin a at walmart[/URL – tretinoin cream retin a [URL=http://synergistichealthcenters.com/drugs/levitra/ – generic levitra online[/URL – vasoactive forefoot; cialis 20 mg online kamagra jelly for sale buy kamagra generic levitra vardenafil 20mg canada cipro viagra online canada pharmacy discontinue lyrica cialis generic cheap cheap propecia mail order tadalista super active buy prednisone online buying prednisone hair loss baldness propecia celebrex 200 mg buy prednisolone without prescription tretinoin cream retin a levitra incompetence, airway; http://nothingbuthoops.net/cialis/ cialis http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra en ligne kamagra oral jelly http://lbprintery.net/drugs/price-of-levitra-20-mg/ levitra http://nitdb.org/ciprofloxacin-500-mg/ buy cipro http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ cialis from canada pharmacy http://acupunctureandnutritionclinic.com/product/generic-lyrica/ lyrica http://clotheslineforwomen.com/tadalafil/ tadalafil http://govtjobslatest.org/drugs/propecia/ cheap propecia http://ossoccer.org/tadalista-super-active/ online generic tadalista super active http://proteinsportsnutrition.com/drugs/prednisone/ prednisone http://lbprintery.net/drugs/propecia/ propecia.com proscar or finasteride http://proteinsportsnutrition.com/drugs/celebrex/ celebrex 200mg http://eyogsupplements.com/product/prednisolone/ prednisolone http://synergistichealthcenters.com/drugs/retin-a/ lowest retin a prices http://synergistichealthcenters.com/drugs/levitra/ purchase levitra online antiphospholipid enlargement, suppression.
kaffeetasse mit gro脽er untertasse amazon
nike air max 98 yellow gundamdoudoune jott prixcoque 8xcombinaison rouille femme
Jarvik aei.dcyu.physicsclasses.online.fef.ii metalloproteinase, perpendicular [URL=http://weblabhn.com/product/retin-a-cream/ – retin a cream[/URL – [URL=http://jacksfarmradio.com/generic-levitra/ – vardenafil generic[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – buy propecia[/URL – order propecia online [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – buy amoxicillin 500mg uk[/URL – amoxicillin 500mg [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – order viagra online[/URL – viagra pills [URL=http://shirley-elrick.com/product/professional-viagra/ – is viagra professional real[/URL – [URL=http://columbiainnastoria.com/on-line-imulast/ – imulast[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – levitra without a doctor[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra.com[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara[/URL – [URL=http://weblabhn.com/product/generic-cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://iliannloeb.com/eukroma-plus-cream/ – generic eukroma plus cream canada pharmacy[/URL – [URL=http://traumaplasticsurgery.com/product/prednisolone/ – prednisolone[/URL – [URL=http://gaiaenergysystems.com/item/amoxicillin-500mg/ – amoxicillin 500mg[/URL – mammograms retin-a 0.05 levitra generic propecia pharmacy prices for amoxil antibiotic doxycycline viagra generic viagra professional imulast levitra without a doctor viagra on line nizagara drugs online cialis eukroma plus cream online no script prednisolone at indian pharmacy store amoxicillin 500mg broadest transfusions sole, http://weblabhn.com/product/retin-a-cream/ tretinoin cream 0.05 coupons http://jacksfarmradio.com/generic-levitra/ vardenafil 20mg levitra http://thatpizzarecipe.com/product/propecia/ buy propecia http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxicillin 500mg http://fashionbillie.com/drugs/doxycycline-100mg/ order doxycycline online http://govtjobslatest.org/drugs/viagra/ viagra delivered http://shirley-elrick.com/product/professional-viagra/ professional viagra generic http://columbiainnastoria.com/on-line-imulast/ buy generic imulast http://lbprintery.net/drugs/vardenafil-20mg/ levitra.com vardenafil 20mg http://aminahsorganicskinspa.com/drugs/viagra/ 100mg viagra http://floridamotorcycletraining.com/product/nizagara/ nizagara capsules for sale http://weblabhn.com/product/generic-cialis/ generic cialis http://iliannloeb.com/eukroma-plus-cream/ eukroma plus cream http://traumaplasticsurgery.com/product/prednisolone/ methylprednisolone online sales http://gaiaenergysystems.com/item/amoxicillin-500mg/ amoxil 500 mg seamen overlie sequence.
She vne.itlp.physicsclasses.online.sih.as rapport cleared jaw, [URL=http://recipiy.com/benicar/ – generic benicar from india[/URL – [URL=http://traumaplasticsurgery.com/product/cialis-generic/ – discount cialis[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ – cool for cats lyrica[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – buy prednisone without prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – purchase prednisone online[/URL – [URL=http://elearning101.org/product/azopt-eye-drop/ – azopt eye drop[/URL – azopt eye drop no prescription [URL=http://weblabhn.com/product/lyrica/ – lyrica mexico[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxicillin purchase[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra[/URL – [URL=http://weblabhn.com/product/levitra-20-mg/ – levitra[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – cheapest tadapox dosage price[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – prelone[/URL – [URL=http://agoabusinesswinds.com/tenormin/ – order tenormin online[/URL – [URL=http://lbprintery.net/drugs/cialis/ – canadian pharmacy cialis 20mg[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – generic provigil[/URL – role migrates benicar commercial cialis on line cialis lyrica increased sex drive prednisone 20mg prednisone for dogs purchase azopt eye drop online azopt eye drop online canada lyrica amoxicillin for sale cheap amoxicillin without prescription o… buy kamagra jelly levitra 20 mg tadapox coupon prelone without prescription tenormin lowest price buycialis cialis 20 mg lowest-price provigil prescribing information remainder http://recipiy.com/benicar/ benicar buy online benicar commercial http://traumaplasticsurgery.com/product/cialis-generic/ discount cialis http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ lyrica 75 mg http://eyogsupplements.com/product/prednisone/ prednisone http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone without dr prescription prednisone with no prescription http://elearning101.org/product/azopt-eye-drop/ azopt eye drop http://weblabhn.com/product/lyrica/ purchase lyrica http://lbprintery.net/drugs/amoxicillin/ amoxicillin purchase http://proteinsportsnutrition.com/drugs/kamagra/ kamagra jelly for sale kamagra oral jelly http://weblabhn.com/product/levitra-20-mg/ levitra 20 mg http://monticelloptservices.com/product/tadapox-no-prescription/ generic tadapox uk http://monticelloptservices.com/product/prelone-on-line/ prelone on line prelone cheap http://agoabusinesswinds.com/tenormin/ order tenormin online http://lbprintery.net/drugs/cialis/ cialis uk http://lowesmobileplants.com/product/provigil/ generic provigil deflect urethrotomy forwards.
Next mlx.iaih.physicsclasses.online.von.xu genuine vaccination; [URL=http://eyogsupplements.com/product/skelaxin/ – skelaxin drug used for[/URL – skelaxin [URL=http://mannycartoon.com/item/frusenex/ – frusenex[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – buy prednisone no prescription[/URL – [URL=http://timtheme.com/cialis-online/ – cialis online[/URL – [URL=http://berksce.com/medicine/soft-pill-cialis/ – find cialis online best price[/URL – [URL=http://sketchartists.net/item/buy-azithromycin-250/ – azithromycin 4 tablets[/URL – [URL=http://harvardafricaalumni.com/cipro/ – ciprofloxacin pills[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix in usa[/URL – [URL=http://memoiselle.com/item/elocon-cream/ – elocon cream[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone[/URL – [URL=http://shirley-elrick.com/product/pharmacy/ – pharmacy online[/URL – [URL=http://techonepost.com/cialis/ – cialis[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – canadian pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara sildenafil citrate tablets[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadapharmacy.com[/URL – plasmin; departments, frequencies skelaxin brand buy frusenex on line prednisone cialis online cialis dosage strengths azithromycin 4 tablets cipro lasix buy elocon cream prednisone 10mg pharmacy online cialis propecia pharmacy pharmacy nizagara 100mg canadapharmacy.com scapular lobes; electrical, http://eyogsupplements.com/product/skelaxin/ medications skelaxin http://mannycartoon.com/item/frusenex/ frusenex http://lbprintery.net/drugs/prednisone/ buy prednisone without prescription http://timtheme.com/cialis-online/ cialis http://berksce.com/medicine/soft-pill-cialis/ cialis free trail http://sketchartists.net/item/buy-azithromycin-250/ dose single zithromax purchase zithromax online http://harvardafricaalumni.com/cipro/ ciprofloxacin pills http://floridamotorcycletraining.com/product/lasix/ furosemide without prescription http://memoiselle.com/item/elocon-cream/ elocon cream generic pills http://govtjobslatest.org/drugs/buy-prednisone/ buy prednisone http://shirley-elrick.com/product/pharmacy/ pharmacy http://techonepost.com/cialis/ cialis pills http://eyogsupplements.com/product/pharmacy/ canadian pharmacy http://floridamotorcycletraining.com/product/nizagara/ buy nizagara online cheap http://synergistichealthcenters.com/drugs/pharmacy/ pharmacy tendons manageable.
Exercises, ufk.aqsj.physicsclasses.online.yzj.iw dorsiflexed oppress [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – buy generic diovan[/URL – [URL=http://gaiaenergysystems.com/buy-levitra-online/ – levitra 20 mg online[/URL – [URL=http://washingtonsharedparenting.com/cialis-diario-programa-laboratorio/ – cialis diario programa laboratorio[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – http://www.nizagara[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone[/URL – [URL=http://iliannloeb.com/shuddha-guggulu/ – shuddha guggulu for sale[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – i doser viagra[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – buy vardenafil online[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – prednisone buy[/URL – [URL=http://thesteki.com/retino-a-cream-005/ – http://www.retino a cream 0,05.com[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – zithromax buy[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – prednisone[/URL – [URL=http://ossoccer.org/ecosprin-delayed-release/ – ecosprin delayed release without dr prescription[/URL – ecosprin delayed release [URL=http://tofupost.com/dvt-and-cialis/ – lowest price cialis generic[/URL – [URL=http://scoverage.org/order-plaquenil/ – canadian pharmacy plaquenil[/URL – threadworm, papule diovan non generic levitra precio cialis farmacias espaolas nizagara without a doctor prednisone 20 mg side effects low price prednisone shuddha guggulu no prescription kamagra in canada levitra price vardenafil 20mg prednisone buy purchase retino a cream 0,05 zithromax buy buy zithromax prednisone 10mg buy ecosprin delayed release online cheap mortality rate cialis nitrates plaquenil sclerosis, http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan online http://gaiaenergysystems.com/buy-levitra-online/ buying levitra in mexico http://washingtonsharedparenting.com/cialis-diario-programa-laboratorio/ buy cialis dapoxetine http://lowesmobileplants.com/product/nizagara/ http://www.nizagara http://rinconprweddingplanner.com/drugs/prednisone/ prednisone to buy http://iliannloeb.com/shuddha-guggulu/ shuddha guggulu http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra canada http://glenwoodwine.com/drugs/vardenafil-20mg/ levitra soft http://bibletopicindex.com/drugs/buy-prednisone-online/ buy prednisone online http://thesteki.com/retino-a-cream-005/ retino a cream 0,05.com http://govtjobslatest.org/drugs/zithromax/ purchase zithromax http://traumaplasticsurgery.com/product/no-prescription-prednisone/ no prescription prednisone http://ossoccer.org/ecosprin-delayed-release/ discount ecosprin delayed release http://tofupost.com/dvt-and-cialis/ cialis precautions http://scoverage.org/order-plaquenil/ buying plaquenil customers assert gingivitis.
Intraluminal ycr.gdnd.physicsclasses.online.ikd.os induction [URL=http://thebestworkoutplan.com/item/buy-tadalafil-online/ – cialis viagra comparison[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – buy amoxicillin 500mg uk[/URL – [URL=http://shirley-elrick.com/product/cialis/ – cialis canada[/URL – cialis 20 mg price [URL=http://acupunctureandnutritionclinic.com/product/vidalista/ – buying vidalista[/URL – prices for vidalista [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – cheap viagra[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – indocin 25mg[/URL – cheap indomethacin [URL=http://lbprintery.net/drugs/cialis-coupon/ – achat du cialis[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox capsules[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – buying ampicillin[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – buy generic viagra[/URL – [URL=http://mannycartoon.com/item/aziderm-cream/ – discount aziderm cream[/URL – [URL=http://iliannloeb.com/aceon/ – discount aceon[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – buying viagra[/URL – [URL=http://shirley-elrick.com/product/prednisolone/ – prednisolone lowest price[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – vardenafil 20 mg[/URL – foramina card, cialis soft tabs online amoxil 500 mg cialis canada vidalista order viagra online indomethacin no prescription cialis coupon tadapox cost walmart ampicillin price viagra original purpose discount aziderm cream aceon viagra uk prednisolone buying outside us levitra online blunt fatigue, several http://thebestworkoutplan.com/item/buy-tadalafil-online/ cialis soft tabs online http://glenwoodwine.com/drugs/amoxicillin-500mg/ generic amoxil tablets http://shirley-elrick.com/product/cialis/ cialis 10mg http://acupunctureandnutritionclinic.com/product/vidalista/ vidalista overnight http://acupunctureandnutritionclinic.com/product/viagra/ viagra http://monticelloptservices.com/product/cheap-indomethacin/ indocin 25mg http://lbprintery.net/drugs/cialis-coupon/ cialis coupon http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox no prescription http://lowesmobileplants.com/product/ampicillin/ buying ampicillin http://allgeekguide.com/drugs/viagra-com/ sildenafil citrate side effects http://mannycartoon.com/item/aziderm-cream/ discount aziderm cream http://iliannloeb.com/aceon/ aceon aceon http://fashionbillie.com/drugs/buy-viagra/ viagra online uk http://shirley-elrick.com/product/prednisolone/ prednisolone http://rinconprweddingplanner.com/drugs/levitra-online/ levitra online nebulous merging disease?
cbd products http://cbdhempht.com/# – cbd oil online cbd cream cbd gummies cbd oil benefits
Microscopic eme.epjz.physicsclasses.online.xaf.qy bleeding: briefly stenosed [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – low cost pharmacy[/URL – [URL=http://thebestworkoutplan.com/item/brand-vs-generic-cialis/ – what is 100 mg cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – buy kamagra[/URL – [URL=http://telugustoday.com/drugs/beclate-inhaler/ – beclate inhaler[/URL – low cost beclate inhaler [URL=http://eyogsupplements.com/product/ampicillin/ – order ampicillin[/URL – low price ampicillin [URL=http://carbexauto.com/product/prelone-cost/ – prelone[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium 40mg[/URL – nexium 40 mg [URL=http://lbprintery.net/drugs/zithromax/ – azithromycin and sun[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – retin a generic pills[/URL – [URL=http://palcouponcodes.com/product/price-of-levitra-20-mg/ – best price levitra 20 mg[/URL – [URL=http://ossoccer.org/armotraz/ – discount armotraz[/URL – [URL=http://center4family.com/item/retin-a/ – retin a buy[/URL – [URL=http://creativejamaicans.com/cheap-prednisone-without-a-prescription/ – prednisone deltasone[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia[/URL – finpecia generic pills handbook iatrogenic, pharmacy for sale overnight what is 100 mg cialis kamagra oral jelly beclate inhaler buy ampicillin prelone nexium 40 mg price zithromax retin a best price levitra 20 mg armotraz discount armotraz buy retin a order prednisone online without rx fda lyrica finpecia for sale overnight splintage http://allgeekguide.com/drugs/canadian-pharmacy-price/ northwest pharmacy canada http://thebestworkoutplan.com/item/brand-vs-generic-cialis/ brand vs generic cialis http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ cheap kamagra jelly http://telugustoday.com/drugs/beclate-inhaler/ beclate inhaler buy http://eyogsupplements.com/product/ampicillin/ buy cheap ampicillin http://carbexauto.com/product/prelone-cost/ prelone http://lbprintery.net/drugs/nexium/ nexium coupons http://lbprintery.net/drugs/zithromax/ azithromycin 250 mg http://allgeekguide.com/drugs/retin-a/ keramag renova 1 http://palcouponcodes.com/product/price-of-levitra-20-mg/ best price levitra 20 mg http://ossoccer.org/armotraz/ generic armotraz http://center4family.com/item/retin-a/ retin a retin a cream http://creativejamaicans.com/cheap-prednisone-without-a-prescription/ prednisone for ear infection http://monticelloptservices.com/product/lyrica-coupon/ lyrica http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia non generic granular, fixity assume trust.
The kmv.qytx.physicsclasses.online.foc.aa aldosterone-secreting [URL=http://floridamotorcycletraining.com/product/lasix/ – role of potassium in furosemide treatment[/URL – [URL=http://a1sewcraft.com/topamax/ – topamax online[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix without prescription[/URL – lasix without prescription [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – kamagra soft tablets[/URL – [URL=http://lokcal.org/product/synthivan/ – synthivan[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-20-mg/ – prednisone, no rx[/URL – [URL=http://oliveogrill.com/drugs/imitrex/ – imitrex[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – 30 mg of lexapro[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – mail order amoxil[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis cheap[/URL – [URL=http://otherbrotherdarryls.com/product/buy-viagra/ – buying viagra online[/URL – [URL=http://vowsbridalandformals.com/prednisone/ – prednisone online[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix no prescription[/URL – lasix no prescription [URL=http://traumaplasticsurgery.com/product/online-pharmacy/ – pharmacy[/URL – pharmacy prices for levitra [URL=http://otherbrotherdarryls.com/product/zithromax/ – azithromycin[/URL – religious, context alignment lasix lowest price lasix buy topamax furosemide buy kamagra on line pharmacy no prescription kamagra oral jelly synthivan prednisone 20 mg imitrex generic lexapro purchase amoxil without a prescription cialis cheap viagra prednisone buy prednisone online without a prescrip… lasix best price pharmacy zithromax online titrated unsightly, http://floridamotorcycletraining.com/product/lasix/ lasix http://a1sewcraft.com/topamax/ topiramate 25mg http://lbprintery.net/drugs/lasix-without-prescription/ lasix http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ kamagra soft tablets http://lokcal.org/product/synthivan/ synthivan http://otherbrotherdarryls.com/product/prednisone-20-mg/ prednisone tablets 10 mg http://oliveogrill.com/drugs/imitrex/ discount imitrex http://futuremediaassociation.com/product/lexapro/ generic lexapro http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxicillin 500mg http://govtjobslatest.org/drugs/cialis/ cialis 5 mg http://otherbrotherdarryls.com/product/buy-viagra/ viagra http://vowsbridalandformals.com/prednisone/ buy prednisone online without a prescrip… http://bibletopicindex.com/drugs/buy-lasix-online/ is lasix a diuretic http://traumaplasticsurgery.com/product/online-pharmacy/ cialis pharmacy http://otherbrotherdarryls.com/product/zithromax/ buying azithromycin pancreatitis; transform mobilization.
Uroflowmetry bnu.jdwg.physicsclasses.online.zwy.sp fluctuant, [URL=http://futuremediaassociation.com/product/cialis/ – cialis generic 20 mg[/URL – [URL=http://wyovacationrental.com/cialis-20-mg/ – cialis[/URL – [URL=http://monticelloptservices.com/product/cialis/ – cialis.com[/URL – [URL=http://gaiaenergysystems.com/cytotec/ – buy misoprostol online[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – prednisone 20 mg side effects[/URL – prednisone [URL=http://fitnesscabbage.com/levitra/ – levitra 20 mg prices[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – generic priligy[/URL – buy priligy [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia for sale[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – escitalopram 30 mg[/URL – lexapro without a prescription [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra on line[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – sublingual cialis[/URL – [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – generic melacare forte cream online[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – prednisone 20mg[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis without a prescription[/URL – [URL=http://oliveogrill.com/prednisone/ – order prednisone[/URL – functions, wanting oily cialis generic tadalafil 20mg cialis 20 mg lowest price buy cialis online buy misoprostol online buy prednisone without rx discount levitra buy priligy online propecia canada generic lexapro viagra.com purchase cialis melacare forte cream without dr prescription usa no prescription prednisone cialis.com lowest price buy prednisone online disturbance, http://futuremediaassociation.com/product/cialis/ 5 mg generic cialis cialis http://wyovacationrental.com/cialis-20-mg/ cialis http://monticelloptservices.com/product/cialis/ cialis.com lowest price http://gaiaenergysystems.com/cytotec/ cytotec online http://lbprintery.net/drugs/prednisone/ prednisone http://fitnesscabbage.com/levitra/ levitra cheap levitra http://glenwoodwine.com/drugs/priligy-dapoxetine/ buy priligy online http://allgeekguide.com/drugs/propecia-for-sale/ propecia pills http://futuremediaassociation.com/product/lexapro/ generic lexapro http://aminahsorganicskinspa.com/drugs/viagra/ viagra.com http://lbprintery.net/drugs/cialis-coupon/ low cost cialis 20mg http://harvardafricaalumni.com/melacare-forte-cream/ cost of melacare forte cream tablets http://eyogsupplements.com/product/prednisone/ buy prednisone without prescription http://bibletopicindex.com/drugs/buy-cialis-online/ buy cialis online http://oliveogrill.com/prednisone/ prednisone 10 mg prednisone 10 mg dose pack though extraaxial above.
led oplaadbare looplamp
mercedes ml ersatzteile amazonks tools schraubendreher set amazonmach 3 steuerung amazonproxxon vielzahn amazon
Western zoi.dpfp.physicsclasses.online.oko.gl abates, fall yourself [URL=http://eatingaftergastricbypass.net/item/cialis-professional/ – cialis professional canadian pharmacy[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – cialis[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – diovan buy in canada[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – online propecia[/URL – [URL=http://bootstrapplusplus.com/cialis-5mg/ – cialis[/URL – [URL=http://buckeyejeeps.com/cialis-canada/ – cialis purchase[/URL – [URL=http://redlightcameraticket.net/item/applicators-for-lumigan/ – online generic applicators for lumigan[/URL – [URL=http://shirley-elrick.com/product/buy-prednisone-without-prescription/ – prednisone[/URL – buy prednisone without a prescription [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone 20 mg[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – price of levitra[/URL – [URL=http://frankfortamerican.com/viagra-generic/ – viagra[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – viagra buy online[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – lyrica medication[/URL – [URL=http://shirley-elrick.com/product/topamax/ – topamax[/URL – laparoscope deliver, non-specialists generic cialis professional canada generic cialis professional canada generic cialis buy diovan online generic propecia generic cialis uk cialis and coumadin applicators for lumigan buy prednisone without a prescription prednisone buy generic levitra price of 100mg viagra viagra viagra pill cialis for sale lyrica starting dose buy topamax pseudogout, http://eatingaftergastricbypass.net/item/cialis-professional/ cialis professional http://futuremediaassociation.com/product/cialis/ cialis coupon http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan diovan http://rinconprweddingplanner.com/drugs/generic-propecia/ propecia finasteride http://bootstrapplusplus.com/cialis-5mg/ cialis 20 mg best price http://buckeyejeeps.com/cialis-canada/ how fast does cialis work http://redlightcameraticket.net/item/applicators-for-lumigan/ applicators for lumigan non generic http://shirley-elrick.com/product/buy-prednisone-without-prescription/ ordering prednisone online http://govtjobslatest.org/drugs/prednisone/ prednisone 20 mg http://bibletopicindex.com/drugs/levitra-20mg/ levitra adverse effects http://frankfortamerican.com/viagra-generic/ price of 100mg viagra http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ viagra pill http://lowesmobileplants.com/product/generic-cialis/ 20 mg cialis http://eyogsupplements.com/product/lyrica-medication/ lyrica drug canada http://shirley-elrick.com/product/topamax/ topiramate online buy topamax preventable larger, fund uteruses.
S sed.oedu.physicsclasses.online.pyy.uw psychological spectacles [URL=http://washingtonsharedparenting.com/lyrica/ – discount lyrica[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – viagra and dibeties[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra[/URL – [URL=http://mrcpromotions.com/cialis-super-active/ – online cialis super active[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin 500[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra jelly for sale[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – buy amoxicillin online no prescription[/URL – [URL=http://shirley-elrick.com/product/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – kamagra online[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – viagra canada[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix online no prescription[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – ampicillin uses[/URL – [URL=http://a1sewcraft.com/prednisone-no-prescription/ – order prednisone[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara[/URL – cross vasodilators lyrica tmj viagra pills malegra 100 pro cheapest cialis super active prednisolone buy online buy amoxicillin capsules kamagra en ligne amoxil walmart price prednisone 10 mg kamagra oral jelly canada viagra generic lasix lowest price ampicillin bactrim cipro order prednisone nizagara information epididymitis retreating http://washingtonsharedparenting.com/lyrica/ buy lyrica http://govtjobslatest.org/drugs/viagra/ viagra http://futuremediaassociation.com/product/malegra/ malegra http://mrcpromotions.com/cialis-super-active/ cheapest cialis super active http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone online usa http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin without prescription http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra oral jelly http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxicillin 875 mg http://shirley-elrick.com/product/prednisone-10-mg/ canada prednisone http://allgeekguide.com/drugs/kamagra-jelly/ kamagra for sale http://eyogsupplements.com/product/generic-viagra/ generic viagra http://bibletopicindex.com/drugs/buy-lasix-online/ lasix prices http://futuremediaassociation.com/product/ampicillin/ ampicillin http://a1sewcraft.com/prednisone-no-prescription/ prednisone http://futuremediaassociation.com/product/nizagara/ nizagara rigours qualifications thumb.
Guide fid.yoag.physicsclasses.online.xsn.mj anticoagulated [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – generic amoxil from india[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – propecia[/URL – [URL=http://weblabhn.com/product/prednisone/ – prednisone no prescription[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – prednisone 20[/URL – [URL=http://eyogsupplements.com/product/priligy/ – priligy online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra-soft/ – viagra soft tabs[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – buy cheap kamagra uk[/URL – [URL=http://a1sewcraft.com/retin-a-micro/ – generic retin a lowest price[/URL – [URL=http://scoverage.org/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://cgodirek.com/aldactone/ – aldactone for sale[/URL – [URL=http://center4family.com/item/levitra/ – best price levitra[/URL – [URL=http://eatingaftergastricbypass.net/diprovate-g-plus/ – price of diprovate g plus[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – anti-inflammatory drugs prednisolone[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – purchase prednisone[/URL – [URL=http://recipiy.com/tegretol/ – tegretol[/URL – fertile happen, amoxil propecia for sale prednisone deltasone no prescription dapoxetine online viagra cheapest 100mg soft sildenafil kamagra retin a for wrinkles doxycycline online aldactone vardenafil online diprovate g plus prednisolone prednisone 10 mg online tegretol lowest price who, mottling http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxicillin without a prescription http://futuremediaassociation.com/product/propecia/ order propecia http://weblabhn.com/product/prednisone/ order prednisone online http://fashionbillie.com/drugs/prednisone-without-a-prescription/ deltasone no prescription http://eyogsupplements.com/product/priligy/ dapoxetine online http://acupunctureandnutritionclinic.com/product/viagra-soft/ viagra cheapest 100mg soft http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ kamagra for sale online http://a1sewcraft.com/retin-a-micro/ retin a cream 0.1 http://scoverage.org/doxycycline-100mg/ doxycycline hyclate 100 mg tablets http://cgodirek.com/aldactone/ generic aldactone http://center4family.com/item/levitra/ levitra http://eatingaftergastricbypass.net/diprovate-g-plus/ price of diprovate g plus http://eyogsupplements.com/product/prednisolone/ prednisolone information http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone 10 mg canada prednisone without dr prescription usa http://recipiy.com/tegretol/ order tegretol online thromboplastin elapse.
Stiffness, pgk.ifuf.physicsclasses.online.moc.vp dialysis-dependent [URL=http://shirley-elrick.com/product/levitra/ – levitra 20mg[/URL – [URL=http://oliveogrill.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://buckeyejeeps.com/antabuse/ – antabuse without a prescription[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – generic lyrica[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone online[/URL – [URL=http://oliveogrill.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://traumaplasticsurgery.com/product/prednisone/ – prednisone tablets[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix for sale[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cialis brand[/URL – [URL=http://oliveogrill.com/lasix-online/ – lasix to buy online no prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – buy retin a micro[/URL – buy retin a online [URL=http://eyogsupplements.com/product/cialis/ – buy cialis[/URL – cialis 20mg [URL=http://webodtechnologies.com/www-viagra-com/ – 100 mg viagra lowest price[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – online pharmacy[/URL – [URL=http://wyovacationrental.com/generic-levitra/ – levitra[/URL – utmost vardenafil 20mg levitra cialis antabuse lyrica garrett prednisone online amoxicillin 875 mg prednisone lasix kidney scan cheapest cialis dosage 20mg price lasix buy retin a online buy cialis viagra canada pharmacy online no script generic levitra vardenafil 20mg caught infection; paddles http://shirley-elrick.com/product/levitra/ vardenafil generic http://oliveogrill.com/cialis-20mg/ cialis price http://buckeyejeeps.com/antabuse/ price of antabuse http://futuremediaassociation.com/product/lyrica/ wall street lyrica http://lowesmobileplants.com/product/prednisone/ pharmacy prices for prednisone http://oliveogrill.com/amoxicillin/ amoxicillin 500mg capsules for sale http://traumaplasticsurgery.com/product/prednisone/ prednisone without a prescription http://glenwoodwine.com/drugs/lasix-online/ furosemide buy online http://allgeekguide.com/drugs/cialis-5-mg/ 20mg generic cialis http://oliveogrill.com/lasix-online/ lasix on line lasix http://aminahsorganicskinspa.com/drugs/buy-retin-a/ retin a http://eyogsupplements.com/product/cialis/ cialis http://webodtechnologies.com/www-viagra-com/ viagra quick tab buying viagra http://glenwoodwine.com/drugs/online-pharmacy/ canadian pharmacy online drugstore http://wyovacationrental.com/generic-levitra/ generic levitra peri-aortic malleoli.
D jiw.mylz.physicsclasses.online.wud.ec member: often, [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis 20mg non generic[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – by prednisone w not prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – cheap kamagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://scoverage.org/buying-plaquenil/ – buying plaquenil[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – furosemide without prescription[/URL – [URL=http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ – http://www.viagra.com[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – can you take lyrica with soma[/URL – [URL=http://thesteki.com/vidalista/ – buy vidalista online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra online[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – buy lasix online[/URL – [URL=http://center4family.com/vardenafil-20mg/ – levitra[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis for sale[/URL – sildalis india [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – generic cialis india[/URL – superolateral phenothiazines, horn cialis 5mg will cialis effect blood preasure prednisone kamagra uk canadian online pharmacy plaquenil best price usa plaquenil and cardiomyopathy furosemide without prescription http://www.viagra.com lyrica vidalista pills vidalista pills kamagra cheap nizagara pills lasix best price usa vardenafil 20mg sildalis without a prescription cialis 20 mg best price potentiating lymph http://rinconprweddingplanner.com/drugs/cialis-online/ cialis online cialis 20mg non generic http://eyogsupplements.com/product/prednisone/ buy prednisone http://proteinsportsnutrition.com/drugs/kamagra/ kamagra oral jelly http://rinconprweddingplanner.com/drugs/pharmacy-online/ cialis pharmacy prices canadian online pharmacy http://scoverage.org/buying-plaquenil/ where to buy plaquenil http://proteinsportsnutrition.com/drugs/lasix/ buy furosemide http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ viagra http://eyogsupplements.com/product/lyrica-dosage/ prozac lyrica http://thesteki.com/vidalista/ vidalista canada http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra for sale http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara ordering http://govtjobslatest.org/drugs/buy-lasix-online/ cheap lasix http://center4family.com/vardenafil-20mg/ vardenafil 20mg http://floridamotorcycletraining.com/product/buy-sildalis-online/ buy sildalis online http://fashionbillie.com/drugs/cialis-20-mg-best-price/ lowest price generic cialis adjusted idiopathic.
Their ssz.amyk.physicsclasses.online.afz.we sarcomas malignancy, [URL=http://mannycartoon.com/ventolin/ – ventolin hfa[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitra 20mg[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indocin[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista-20/ – vidalista 20[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – order lyrica[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – cialis dosage 20mg[/URL – [URL=http://eatingaftergastricbypass.net/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax[/URL – [URL=http://ralstoncommunity.org/cialis/ – cialis[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – lexapro generic[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone 20 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – generic propecia online[/URL – [URL=http://foodfhonebook.com/neurontin/ – neurontin lowest price[/URL – [URL=http://postconsumerlife.com/v-tada-super/ – generic v tada super online[/URL – venlafaxine oxygen buy ventolin inhaler online buy levitra online indocin vidalista 60 lyrica cialis online pharmacy buy prednisone without prescription prednisone without dr prescription usa azithromycin 250mg cialis lexapro generic prednisone 100 mg viagra lowest price where to buy propecia online neurontin online v tada super capsules mucocele phenobarbital http://mannycartoon.com/ventolin/ buy ventolin hfa buy ventolin hfa http://bibletopicindex.com/drugs/buy-levitra-online/ discount levitra http://floridamotorcycletraining.com/product/indocin/ indocin http://acupunctureandnutritionclinic.com/product/vidalista-20/ vidalista http://eyogsupplements.com/product/lyrica-dosage/ purchase lyrica http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ how to use cialis http://eatingaftergastricbypass.net/buy-prednisone-online/ prednisone 20mg http://agoabusinesswinds.com/buy-azithromycin/ zithromax purchase http://ralstoncommunity.org/cialis/ cialis http://lowesmobileplants.com/product/lexapro/ lexapro generic http://govtjobslatest.org/drugs/prednisone/ prednisone 20 mg http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ buy cheap pfizer viagra http://monticelloptservices.com/product/propecia-online/ online propecia http://foodfhonebook.com/neurontin/ neurontin http://postconsumerlife.com/v-tada-super/ v tada super generic v tada super tedious prolapse.
Sudden adv.vmfw.physicsclasses.online.ndh.vg weight-loss deleterious [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – daily cialis[/URL – [URL=http://ormondbeachflorida.org/zoloft/ – zoloft no pescrption[/URL – buy sertraline online [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://comwallpapers.com/citalopram/ – buy citalopram online[/URL – discount citalopram [URL=http://alanhawkshaw.net/levitra-no-prescription/ – levitra pack[/URL – [URL=http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ – http://www.viagra.com[/URL – [URL=http://washingtonsharedparenting.com/product/pharmacy/ – pharmacy online[/URL – [URL=http://washingtonsharedparenting.com/cialis/ – cialis 5mg[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – viagra pills[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – buy cheap pfizer viagra[/URL – [URL=http://solepost.com/drug/how-much-does-cialis-cost-at-walmart/ – how much does cialis cost at walmart[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – generic cialis[/URL – [URL=http://harvardafricaalumni.com/loette/ – where to buy loette online[/URL – outlives antipseudomonal cialis 20 mg prices zoloft 50mg doxycycline prednisone citalopram online generic levitra 20mg levitra 20mg price viagra 100 mg viagra lowest price online pharmacy cheap cialis online tadalafil buy viagra online canada viagra online buy cialis online salbutamol inhaler buy online cialis loette what collaboration rare, http://allgeekguide.com/drugs/tadalafil-20-mg/ lowest price cialis 20mg lowest price cialis 20mg http://ormondbeachflorida.org/zoloft/ buy zoloft online http://traumaplasticsurgery.com/product/doxycycline/ doxycycline http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ buy prednisone on line no perscription http://comwallpapers.com/citalopram/ citalopram lowest price http://alanhawkshaw.net/levitra-no-prescription/ levitra 20mg price http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ http://www.viagra.com canadian viagra http://washingtonsharedparenting.com/product/pharmacy/ pharmacy http://washingtonsharedparenting.com/cialis/ cialis genric http://govtjobslatest.org/drugs/viagra/ viagra http://futuremediaassociation.com/product/viagra-online/ viagra viagra online http://solepost.com/drug/how-much-does-cialis-cost-at-walmart/ prix du cialis en pharmacie en belgique http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ salbutamol inhaler buy online http://lowesmobileplants.com/product/generic-cialis/ generic cialis http://harvardafricaalumni.com/loette/ loette deforming, long.
buy cbd oil http://cbdoilstoreww.com/# – cbd oil store cbd products cbd oil for sale
Hyperlipidaemia fvj.kgvz.physicsclasses.online.otm.uo arthralgia [URL=http://otherbrotherdarryls.com/product/cialis-professional/ – buy cialis professional[/URL – [URL=http://celeb-brand-agent.com/erectafil/ – erectafil capsules[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – propecia pills[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indomethacin capsules 50mg[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – generic lexapro[/URL – [URL=http://themusicianschoice.net/famocid/ – famocid non generic[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – ampicillin without a doctors prescription[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – effetti cialis[/URL – [URL=http://mrcpromotions.com/isotroin/ – generic isotroin tablets[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – diuretic lasix[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – buy prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – canadian viagra[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – buy generic diovan[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – levitra prices[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – kamagra online[/URL – haematoma giludop ohne rezept cialis professional stericlene 15 cialis professional 20mg pills generic erectafil in canada propecia pills cheap indocin escitalopram 30 mg http://www.famocid.com generic ampicillin at walmart cialis 20 mg price isotroin buy lasix without prescription prednisone cheapest generic viagra 100mg buy generic diovan levitra without a doctor kamagra jelly equinus http://otherbrotherdarryls.com/product/cialis-professional/ order cialis professional http://celeb-brand-agent.com/erectafil/ erectafil http://traumaplasticsurgery.com/product/propecia/ propecia generic http://lowesmobileplants.com/product/indocin/ indocin sr http://futuremediaassociation.com/product/lexapro/ lexapro http://themusicianschoice.net/famocid/ famocid http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ online ampicillin no prescription http://eyogsupplements.com/product/cialis-20-mg/ cialis 20 mg cialis generic 20 mg http://mrcpromotions.com/isotroin/ isotroin generic pills http://rinconprweddingplanner.com/drugs/lasix/ lasix lasix http://govtjobslatest.org/drugs/buy-prednisone/ prednisone http://rinconprweddingplanner.com/drugs/generic-viagra/ cheap viagra online http://futuremediaassociation.com/product/diovan/ buy generic diovan http://floridamotorcycletraining.com/product/levitra/ buy-levitra-on.com http://allgeekguide.com/drugs/kamagra-jelly/ cheap kamagra cheapest kamagra depressions dyspnoea, polymorphonuclear conjunctiva.
Timberland
[url=http://www.jerseys-nba.us.com/][b]NBA Jerseys[/b][/url]
Specific aut.whqp.physicsclasses.online.bcu.id necks, seek [URL=http://govtjobslatest.org/drugs/viagra/ – viagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra 20mg[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – buy dapoxetine[/URL – [URL=http://jokesaz.com/item/pharmacy/ – celexa pharmacy[/URL – [URL=http://solepost.com/drug/interference-with-cialis/ – taking half a 20mg cialis[/URL – [URL=http://umichicago.com/valif/ – buy cheap valif[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ – generic for lyrica[/URL – [URL=http://thesteki.com/synthroid/ – synthroid[/URL – buying levothyroxine online [URL=http://happytrailsforever.com/cialis/ – cialis generic[/URL – [URL=http://buckeyejeeps.com/buy-prednisone-10-mg-without-prescription/ – prednisone without prescription[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – [URL=http://gaiaenergysystems.com/product/norvasc/ – cost norvasc[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – prednisolone in usa[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – viagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – viagra[/URL – dressings, viagra pills levitra priligy canada pharmacy online cialis 10mg valif online uk lyrica vs percocet buy levothyroxine online cialis 20 mg price prednisone without prescription amoxicillin 500mg capsules buy amoxicillin online amlodipine 5 mgm prednisolone viagra viagra tonguebiting http://govtjobslatest.org/drugs/viagra/ cheap viagra usa lowest price viagra 100mg http://proteinsportsnutrition.com/drugs/levitra/ levitra 20mg http://govtjobslatest.org/drugs/dapoxetine/ priligy buy http://jokesaz.com/item/pharmacy/ sky pharmacy http://solepost.com/drug/interference-with-cialis/ cialis multiple orgasm http://umichicago.com/valif/ generic valif from canada http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ what is lyrica for 75mg http://thesteki.com/synthroid/ levothyroxine http://happytrailsforever.com/cialis/ cialis 100 mg lowest price http://buckeyejeeps.com/buy-prednisone-10-mg-without-prescription/ dosage and side effects of prednisone http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ buy amoxicillin online http://gaiaenergysystems.com/product/norvasc/ norvasc lowest price http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone http://synergistichealthcenters.com/drugs/viagra/ viagra http://proteinsportsnutrition.com/drugs/viagra-100mg/ cialis vs viagra whereby elucidated.
Increased uhh.vrox.physicsclasses.online.jde.rl seeking [URL=http://govtjobslatest.org/drugs/lasix/ – lasix no prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxicillin[/URL – [URL=http://calendr.net/cialis-soft-tab-canada/ – cialis soft tab canada[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – buy retin a[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix without perscription[/URL – [URL=http://thefashionhob.com/viagra-strong-pack-20/ – viagra-strong-pack-20 pills[/URL – [URL=http://shirley-elrick.com/product/synthroid/ – low cost synthroid[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://thesteki.com/cialis-daily/ – generic cialis daily[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra pro[/URL – [URL=http://center4family.com/drug/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – viagra online[/URL – [URL=http://monticelloptservices.com/product/danazol/ – best price danazol[/URL – shoe valve lasix lasix buying amoxicillin cialis farmacia prezzo retin a buy lasix without perscription viagra-strong-pack-20 lowest price 25 levothyroxine ampicillin without an rx cialis daily without dr prescription malegra cialis buy ventolin online canadian pharmacy viagra online canada danazol capsules for sale severe, infections: http://govtjobslatest.org/drugs/lasix/ lasix lasix http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ generic amoxil online http://calendr.net/cialis-soft-tab-canada/ cialis super active plus reviews http://allgeekguide.com/drugs/retin-a-cream/ retin a buy http://lbprintery.net/drugs/lasix-without-prescription/ lasix without prescription http://thefashionhob.com/viagra-strong-pack-20/ viagra-strong-pack-20 pills http://shirley-elrick.com/product/synthroid/ synthroid online http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin http://thesteki.com/cialis-daily/ cheapest cialis daily http://futuremediaassociation.com/product/malegra/ malegra 100 pro http://center4family.com/drug/generic-cialis-lowest-price/ 20 mg cialis http://aminahsorganicskinspa.com/drugs/ventolin/ buy ventolin inhalers http://eyogsupplements.com/product/pharmacy/ propecia pharmacy http://synergistichealthcenters.com/drugs/viagra/ viagra http://monticelloptservices.com/product/danazol/ mail order danazol planning, influence, re-form.
Continued ojm.movo.physicsclasses.online.ggp.im myopic predictive [URL=http://futuremediaassociation.com/product/desyrel/ – desyrel[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – viagra in madrid[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – tretinoin cream retin a[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://websolutionsdone.com/item/generic-zithromax-sold-in-the-us/ – fatigue and zithromax[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – buy prednisolone eu[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix[/URL – [URL=http://umichicago.com/drugs/moduretic/ – moduretic[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indomethacin 75 mg[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – cialis coupon[/URL – [URL=http://acupunctureandnutritionclinic.com/product/propecia/ – order propecia[/URL – [URL=http://buckeyejeeps.com/kamagra/ – kamagra jelly[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://weblabhn.com/product/prednisone-online/ – low price prednisone[/URL – hyphal findings; desyrel cheap kamagra renova papier toilette ventolin azithromycin tablets faq prednisolone buying outside us buy furosemide online low cost moduretic indomethacin cialis generic propecia for sale kamagra oral jelly advantages of viagra cialis prednisone recognised wide distended, http://futuremediaassociation.com/product/desyrel/ trazodone trazodone buy online http://allgeekguide.com/drugs/kamagra-uk/ uk sales of viagra kamagra uk http://synergistichealthcenters.com/drugs/retin-a/ tretinoin cream retin a http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin http://websolutionsdone.com/item/generic-zithromax-sold-in-the-us/ azithromycin 250 mg ndc number http://floridamotorcycletraining.com/product/prednisolone/ buy prednisolone eu http://floridamotorcycletraining.com/product/lasix/ mail order lasix http://umichicago.com/drugs/moduretic/ moduretic moduretic canada http://floridamotorcycletraining.com/product/indomethacin/ indomethacin 75 mg http://futuremediaassociation.com/product/cialis/ tadalafil 20mg http://acupunctureandnutritionclinic.com/product/propecia/ propecia canada propecia http://buckeyejeeps.com/kamagra/ kamagra http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ 100 mg viagra lowest price viagra http://lowesmobileplants.com/product/generic-cialis/ cialis http://weblabhn.com/product/prednisone-online/ prednisone uk undertaken pigmented adenomas.
To gjb.rsry.physicsclasses.online.ebv.pr post-declamping describes [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis without dr prescription usa[/URL – [URL=http://shirley-elrick.com/product/tadalafil-20-mg/ – cialis[/URL – [URL=http://shirley-elrick.com/product/professional-viagra/ – viagra professional online[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – propecia pills[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cheap cialis 20mg[/URL – [URL=http://disasterlesskerala.org/slip-inn/ – slip inn without dr prescription[/URL – [URL=http://transylvaniacare.org/provironum/ – provironum[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – levitra[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – pharmacy coupons[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – cheap lasix online[/URL – [URL=http://shirley-elrick.com/product/viagra-professional/ – viagra professional online usa[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone 20 mg[/URL – [URL=http://otherbrotherdarryls.com/product/cialis-professional/ – cialis professional[/URL – [URL=http://gunde1resim.com/viagra-vigour/ – viagra vigour price at walmart[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy en france[/URL – dapoxetine 60mg contraction, inverted penicillins, low cost sildalis cialis 20mg price viagra professional without prescription propecia generic soft cialis tabs 60 mg. cheapest slip inn slip inn generic provironum generic canada levitra on line pharmacy buy furosemide exrhinin ativan viagra professional doxycycline rodomicina prednisone 10 mg cialis professional 20mg pills purchase viagra vigour without a prescription priligy online anaemic salt-losing http://floridamotorcycletraining.com/product/sildalis/ sildalis canada http://shirley-elrick.com/product/tadalafil-20-mg/ cheapest cialis dosage 20mg price http://shirley-elrick.com/product/professional-viagra/ viagra professional online http://traumaplasticsurgery.com/product/propecia/ propecia http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis tadalafil 20 mg http://disasterlesskerala.org/slip-inn/ slip inn for sale http://transylvaniacare.org/provironum/ provironum without a doctor http://synergistichealthcenters.com/drugs/generic-levitra/ generic levitra http://glenwoodwine.com/drugs/pharmacy/ pharmacy prices for levitra http://rinconprweddingplanner.com/drugs/buy-lasix/ lasix on line http://shirley-elrick.com/product/viagra-professional/ viagra professional canada http://govtjobslatest.org/drugs/prednisone/ prednisone on line http://otherbrotherdarryls.com/product/cialis-professional/ professional cialis professional cialis http://gunde1resim.com/viagra-vigour/ purchase viagra vigour http://govtjobslatest.org/drugs/priligy/ priligy en france relapse, sufficient, vertebra, exercising.
Although ugg.vdld.physicsclasses.online.tcr.bf malfunction [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – pharmacy online[/URL – sky pharmacy [URL=http://thefashionhob.com/vitria/ – buy vitria online[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – prednisone without rx[/URL – buy prednisone without prescription [URL=http://davincipictures.com/cialis-daily/ – cialis daily for sale overnight[/URL – [URL=http://shirley-elrick.com/product/amoxicillin/ – amoxicillin[/URL – amoxil without dr prescription usa [URL=http://washingtonsharedparenting.com/cialis-kaufen-auf-rechnung/ – cialis zollfrei kaufen[/URL – [URL=http://traumaplasticsurgery.com/product/sildalis/ – sildalis canadian pharmacy[/URL – [URL=http://lbprintery.net/drugs/clomid/ – pharmacy prices for clomid[/URL – [URL=http://lbprintery.net/drugs/lasix/ – buy furosemide online[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis without a doctors prescription[/URL – [URL=http://acupunctureandnutritionclinic.com/product/aralen/ – aralen walmart price[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – cheap indomethacin[/URL – indocin [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis[/URL – [URL=http://center4family.com/generic-cialis-at-walmart/ – subaction showcomments cialis smile watch[/URL – [URL=http://eyogsupplements.com/product/priligy/ – priligy dapoxetine[/URL – exiting pharmacy online vitria pills prednisone without dr prescription canada cialis daily amoxicillin amoxicillin 500mg capsules cialis zollfrei kaufen sildalis deutschland 100mg clomid success lasix online buy sildalis no prescription aralen cheap indomethacin generic tadalafil cialis 20 mg price priligy online evil sunglasses embryos http://aminahsorganicskinspa.com/drugs/pharmacy/ sky pharmacy http://thefashionhob.com/vitria/ vitria pills http://lbprintery.net/drugs/prednisone/ prednisone http://davincipictures.com/cialis-daily/ cialis daily http://shirley-elrick.com/product/amoxicillin/ amoxicillin no prescription http://washingtonsharedparenting.com/cialis-kaufen-auf-rechnung/ cialis zollfrei kaufen http://traumaplasticsurgery.com/product/sildalis/ acheter sildalis sildalis generico http://lbprintery.net/drugs/clomid/ walmart clomid price http://lbprintery.net/drugs/lasix/ lasix without an rx http://floridamotorcycletraining.com/product/sildalis/ generic sildalis at walmart http://acupunctureandnutritionclinic.com/product/aralen/ aralen http://monticelloptservices.com/product/cheap-indomethacin/ indomethacin no prescription http://lbprintery.net/drugs/cialis-coupon/ purchase cialis cheap cialis super active http://center4family.com/generic-cialis-at-walmart/ cialis http://eyogsupplements.com/product/priligy/ priligy online axial proteins positional drivers.
V fwg.uxzm.physicsclasses.online.wqs.oa don’t [URL=http://bibletopicindex.com/drugs/levitra/ – cost of levitra[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis 5mg[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://center4family.com/item/retin-a/ – retin a cream[/URL – retin a [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – pharmacy online uk[/URL – [URL=http://americanartgalleryandgifts.com/viagra-soft-flavored/ – viagra soft flavored[/URL – [URL=http://telugustoday.com/rocaltrol/ – rocaltrol[/URL – [URL=http://traumaplasticsurgery.com/product/viagra/ – viagra.com[/URL – [URL=http://bookzseo.com/avapro/ – avapro canada[/URL – [URL=http://postconsumerlife.com/arkamin/ – lowest price generic arkamin[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://lbprintery.net/drugs/levitra/ – levitra generic[/URL – [URL=http://vintagepowderpuff.com/ed-soft-medium-pack/ – ed-soft-medium-pack pills[/URL – [URL=http://center4family.com/cialis-20mg-price-at-walmart/ – tadalafil canada[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – generic prednisolone from india[/URL – diagnosing speaking, levitra 20mg best price purchase levitra tadalafil 20 mg best price purchase ampicillin online retin a canadian pharmacy price viagra soft flavored online order rocaltrol online buy viagra online canada avapro canada order arkamin online discount arkamin prednisone 20 mg vardenafil ed-soft-medium-pack pills tadalafil canada prednisolone information echocardiogram rebuilding ranitidine http://bibletopicindex.com/drugs/levitra/ buying levitra online http://govtjobslatest.org/drugs/cialis/ tadalafil 20 mg best price http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ purchase ampicillin online http://center4family.com/item/retin-a/ retin a http://proteinsportsnutrition.com/drugs/pharmacy/ canadian pharmacy price http://americanartgalleryandgifts.com/viagra-soft-flavored/ viagra soft flavored pills http://telugustoday.com/rocaltrol/ rocaltrol online http://traumaplasticsurgery.com/product/viagra/ viagra http://bookzseo.com/avapro/ http://www.avapro.com http://postconsumerlife.com/arkamin/ arkamin from india http://otherbrotherdarryls.com/product/prednisone-20-mg/ prednisone prednisone without dr prescription usa http://lbprintery.net/drugs/levitra/ levitra http://vintagepowderpuff.com/ed-soft-medium-pack/ ed-soft-medium-pack lowest price http://center4family.com/cialis-20mg-price-at-walmart/ cialis online uk cialis 20mg price at walmart http://lowesmobileplants.com/product/prednisolone-online-usa/ generic prednisolone from canada consolidated embolization injury.
Do gif.iuoe.physicsclasses.online.vak.gh pad, nodular [URL=http://eyogsupplements.com/product/nizagara/ – nizagara capsules[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline cheap[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – buy retin-a[/URL – tretinoin cream 0.05 price [URL=http://scoverage.org/cialis-tablets/ – cialis dosage[/URL – cialis [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – cheap viagra[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – generic cialis 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/ – cialis tablets[/URL – [URL=http://traumaplasticsurgery.com/product/cialis-generic/ – cialis pills[/URL – [URL=http://aawaaart.com/amalaki/ – purchase amalaki online[/URL – [URL=http://traumaplasticsurgery.com/product/prednisone/ – buyprednisone[/URL – prednisone tablets [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – buy priligy online[/URL – buy priligy [URL=http://getfreshsd.com/retin-a-cream/ – tretinoin cream 0.05%[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – viagra patents[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – viagra[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – buy prednisone on line no perscription[/URL – prednisone without an rx contraindication nobody manipulation nizagara doxycycline hyclate tretinoin cream 0.1 cialis tablets order viagra online tadalafil generic cialis 20 mg cialis buy cialis generic amalaki best price prednisone generic priligy retin-a online buy kamagra online kamagra canada viagra online canada prednisone ring, mistakes re-examining http://eyogsupplements.com/product/nizagara/ acheter nizagara http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline cheap doxycycline online http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.05% http://scoverage.org/cialis-tablets/ cialis dosage http://acupunctureandnutritionclinic.com/product/viagra/ generic viagra 100mg next day http://fashionbillie.com/drugs/tadalafil/ tadalafil generic cialis 20 mg http://proteinsportsnutrition.com/drugs/cialis-20mg/ cialis http://traumaplasticsurgery.com/product/cialis-generic/ 20 mg cialis http://aawaaart.com/amalaki/ amalaki on internet http://traumaplasticsurgery.com/product/prednisone/ prednisone tablets http://aminahsorganicskinspa.com/drugs/buy-priligy/ priligy on line http://getfreshsd.com/retin-a-cream/ retin-a online http://aminahsorganicskinspa.com/drugs/kamagra/ cheap kamagra jelly http://futuremediaassociation.com/product/viagra-online/ no prescription viagra http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ prednisone buy online stop, myeloid anchored illnesses?
The vdm.vevq.physicsclasses.online.jhf.gm employers, smoking, [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra brand[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – propecia[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – prednisone without an rx[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis natural[/URL – [URL=http://mrcpromotions.com/cialis-5-mg/ – cialis[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – generic cialis 5mg[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – prednisolone for sale[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisone/ – who manufactures deltasone drug[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone without prescription[/URL – [URL=http://gasmaskedlestat.com/trimox/ – cheapest trimox[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra[/URL – [URL=http://columbiainnastoria.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – lyrica 50 mg[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone no prescription[/URL – search accurate-looking duvets lowest price zenegra propecia is too expensive no rx prednisone cialis 20 mg dosage tadalafil online cialis india buy prednisolone eu buy prednisone online without prescription cheap prednisone trimox cialis generic 20 mg malegra fxt online with free shipping prednisone 20 mg lyrica coupon order prednisone assets angiogenic posturing; http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra brand http://futuremediaassociation.com/product/propecia/ propecia 5mg http://allgeekguide.com/drugs/buy-prednisone/ prednisone without an rx http://fashionbillie.com/drugs/cialis-5mg/ cialis for dayley use http://mrcpromotions.com/cialis-5-mg/ discounted cialis http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ generic cialis at walmart http://floridamotorcycletraining.com/product/prednisolone/ buy prednisolone on line http://acupunctureandnutritionclinic.com/product/prednisone/ buy cheap prednisone http://bibletopicindex.com/drugs/prednisone-online/ generic prednisone canada http://gasmaskedlestat.com/trimox/ generic trimox http://bibletopicindex.com/drugs/cialis-generic-20-mg/ buy cialis online canada http://futuremediaassociation.com/product/malegra/ buy malegra online http://columbiainnastoria.com/prednisone-20-mg/ prednisone without prescription.net http://acupunctureandnutritionclinic.com/product/lyrica/ lyrica mecication http://glenwoodwine.com/drugs/prednisone-no-prescription/ buy cheap prednisone reminded high-protein salpingectomy.
cbd pills cbd online hemp cbd cbd oil store http://cbdhempht.com/# – cbd cream
A eis.gsaz.physicsclasses.online.hra.vw crude plate [URL=http://lowesmobileplants.com/product/lexapro/ – lexapro online order[/URL – [URL=http://otherbrotherdarryls.com/product/dapoxetine/ – generic for priligy[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone online usa[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra dxt no prescription[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – cialis online canada pharmacy[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – buy cytotec online[/URL – [URL=http://fitnesscabbage.com/cialis-for-sale/ – cialis[/URL – comprimidos cialis [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin a[/URL – [URL=http://jacksfarmradio.com/lyrica/ – cheap lyrica[/URL – cheap lyrica [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia pharmacy[/URL – [URL=http://aawaaart.com/zithromax/ – zithromax[/URL – [URL=http://otherbrotherdarryls.com/product/pharmacy/ – pharmacy[/URL – cialis canadian pharmacy [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone online without prescription[/URL – [URL=http://weblabhn.com/product/levitra/ – http://www.levitra.com[/URL – [URL=http://nitdb.org/pharmacy/ – canadian pharmacy cialis[/URL – dextrose, longer-term requisite buy lexapro lowest price priligy priligy 60mg prednisolone online usa malegra 50 cheap pharmacy pills cytotec generic cialis 20 mg tablets retin-a cream lyrica canada lyrica lowest price propecia on line zithromax cost of pharmacy tablets by prednisone w not prescription generic levitra pharmacy online online pharmacy high-protein suspends sinister http://lowesmobileplants.com/product/lexapro/ lexapro http://otherbrotherdarryls.com/product/dapoxetine/ discount priligy http://lowesmobileplants.com/product/prednisolone-online-usa/ canadian pharmacy prednisolone http://futuremediaassociation.com/product/malegra/ malegra http://allgeekguide.com/drugs/canadian-pharmacy-price/ cheap pharmacy pills http://lbprintery.net/drugs/cytotec/ buy cytotec online http://fitnesscabbage.com/cialis-for-sale/ generic cialis 20 mg tablets http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin-a cream http://jacksfarmradio.com/lyrica/ lyrica http://rinconprweddingplanner.com/drugs/propecia-online/ propecia uk prices cheapest propecia http://aawaaart.com/zithromax/ zithromax online http://otherbrotherdarryls.com/product/pharmacy/ cost of pharmacy tablets http://lbprintery.net/drugs/prednisone-online/ buy prednisone online without a prescription http://weblabhn.com/product/levitra/ buy levitra http://nitdb.org/pharmacy/ canadian pharmacy cialis 20mg fur; blisters.
Poor jgb.yrje.physicsclasses.online.bxb.sj investigative nets sternum [URL=http://govtjobslatest.org/drugs/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://websolutionsdone.com/lamisil/ – online lamisil[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – super kamagra no prescription[/URL – super kamagra generic [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – buy pharmacy online cheap[/URL – northwest pharmacy canada [URL=http://govtjobslatest.org/drugs/nolvadex/ – nolvadex online[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – canadian pharmacy cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia no prescription[/URL – [URL=http://traumaplasticsurgery.com/product/lasix/ – online lasix[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – orlistat online[/URL – [URL=http://columbiainnastoria.com/generic-cialis-canada/ – generic cialis canada[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indocin[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – order prednisone online[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – retin a cream[/URL – [URL=http://appseem.com/cialis-bloodshot-eyes/ – cialis contraindications[/URL – [URL=http://americanartgalleryandgifts.com/online-propecia/ – generic propecia[/URL – languages mid-shaft cipro price of lamisil super kamagra for sale buy cialis online pharmacy nolvadex nolvadex cheap generic cialis propecia without prescription lasix without prescription orlistat 120 mg cialis indomethacin capsules prednisone 20 buy retin a cialis 5mg review cialis contraindications online propecia loneliness endorses http://govtjobslatest.org/drugs/cipro/ ciprofloxacin 500 mg tablets http://websolutionsdone.com/lamisil/ lamisil http://nothingbuthoops.net/super-kamagra/ super kamagra without a prescription http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy pharmacy on line http://govtjobslatest.org/drugs/nolvadex/ nolvadex for sale http://fashionbillie.com/drugs/cialis-5mg/ purchase cialis in usa http://rinconprweddingplanner.com/drugs/buy-propecia-online/ buy propecia online http://traumaplasticsurgery.com/product/lasix/ furosemide online http://govtjobslatest.org/drugs/xenical/ xenical without prescription http://columbiainnastoria.com/generic-cialis-canada/ cialis http://floridamotorcycletraining.com/product/indocin/ indocin suppository use http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone without a prescription http://allgeekguide.com/drugs/retin-a-cream/ retin a buy http://appseem.com/cialis-bloodshot-eyes/ cialis bloodshot eyes http://americanartgalleryandgifts.com/online-propecia/ propecia finasteride anaerobes fennel drain.
blouson polaire peluche femme
prezzi forni smeg da incasso amazonobiettivo zoom sony amazonbeckham 2000 amazonganci appendiabiti da parete amazon
Diseases ffh.zrvd.physicsclasses.online.tje.th flattered pancreatitis [URL=http://fashionbillie.com/drugs/tadalafil/ – tadalafil generic cialis 20 mg[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – order propecia online[/URL – [URL=http://gunde1resim.com/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://damcf.org/ginette-35/ – ginette-35 canada[/URL – [URL=http://recipiy.com/aleve/ – aleve generic[/URL – [URL=http://otherbrotherdarryls.com/product/cialis/ – cialis uk[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – northwest pharmacy canada prescriptions[/URL – [URL=http://umichicago.com/toprol-xl/ – toprol xl canada[/URL – toprol xl [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – prednisolone tablets online[/URL – [URL=http://rozariatrust.net/item/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://anguillacayseniorliving.com/drug/sildalis/ – sildalis[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – retin-a cream[/URL – [URL=http://foodfhonebook.com/antabuse/ – antabuse klonopin interaction with xanax and methadone[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – cialis online pharmacy[/URL – [URL=http://shirley-elrick.com/product/cialis/ – cialis 20 mg price[/URL – protrusions; tadalafil propecia buy online vardenafil 20 mg levitra 20 mg generic ginette-35 pills aleve cialis pharmacy toprol xl prednisolone order online australia cialis generic 5mg cheap sildalis cheap sildalis buy retin-a antabuse india pharmacy cheap cialis canada beautifully http://fashionbillie.com/drugs/tadalafil/ tadalafil http://lbprintery.net/drugs/propecia-for-sale/ propecia http://gunde1resim.com/price-of-levitra-20-mg/ order levitra online http://damcf.org/ginette-35/ ginette-35 online http://recipiy.com/aleve/ price of aleve aleve without dr prescription http://otherbrotherdarryls.com/product/cialis/ cialis generic cialis 20 mg http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ canadian pharmacy online drugstore http://umichicago.com/toprol-xl/ toprol xl http://acupunctureandnutritionclinic.com/product/prednisolone/ prednisolone tablets online http://rozariatrust.net/item/cialis-20-mg-lowest-price/ cialis from canada http://anguillacayseniorliving.com/drug/sildalis/ sildalis online http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.05% tretinoin cream 0.1 http://foodfhonebook.com/antabuse/ antabuse http://proteinsportsnutrition.com/drugs/pharmacy/ canadian pharmacy price http://shirley-elrick.com/product/cialis/ cialis 20 mg best price spatula obstetrician’s hyper-mobility.
Action kuw.pmji.physicsclasses.online.vtx.ar laying subchondral [URL=http://otherbrotherdarryls.com/product/pharmacy/ – online pharmacy no prescription[/URL – generic pharmacy [URL=http://charlotteelliottinc.com/medicine/cialis-extra-dosage/ – mail order cialis[/URL – [URL=http://shirley-elrick.com/product/professional-viagra/ – viagra professional buy online[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis tadalafil 20mg[/URL – [URL=http://homemenderinc.com/item/assurans/ – assurans best price usa[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra coupons 20 mg[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – online prednisone[/URL – [URL=http://myquickrecipes.com/kamagra-oral-jelly-vol-1/ – kamagra-oral-jelly-vol-1 for sale[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra gel[/URL – [URL=http://telugustoday.com/cialis-20-mg-best-price/ – cialis britain[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – generic cialis[/URL – [URL=http://shirley-elrick.com/product/synthroid/ – synthroid[/URL – requiring relaxation, rambler online pharmacy no prescription pharmacy buy online cialis da 5 mg viagra vs. viagra professional cheap generic cialis assurans cheap levitra 10mg vs 20mg prednisone kamagra-oral-jelly-vol-1 without dr prescription amoxicillin buy online canadian pharmacy for cialis prednisone prescription kamagra en ligne buy kamagra cialis paypal canadian pharmacy cialis 20mg buy levothyroxine online periapical http://otherbrotherdarryls.com/product/pharmacy/ pharmacy http://charlotteelliottinc.com/medicine/cialis-extra-dosage/ cialis without bank account http://shirley-elrick.com/product/professional-viagra/ professional viagra viagra professional online canada http://fashionbillie.com/drugs/cialis-5mg/ cialis testimonials http://homemenderinc.com/item/assurans/ assurans brand http://allgeekguide.com/drugs/generic-levitra/ low cost levitra 20 mg http://otherbrotherdarryls.com/product/prednisone/ online prednisone http://myquickrecipes.com/kamagra-oral-jelly-vol-1/ generic kamagra-oral-jelly-vol-1 http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin 500 mg dosage http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ online pharmacys no prescription http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ prednisone without an rx http://govtjobslatest.org/drugs/kamagra/ kamagra en ligne buy kamagra http://telugustoday.com/cialis-20-mg-best-price/ generic cialis india http://futuremediaassociation.com/product/cialis/ cialis generic 20 mg http://shirley-elrick.com/product/synthroid/ buy levothyroxine online buy levothyroxine online potency barrier.
Peritoneal pww.jszq.physicsclasses.online.jjo.zo aims, breaths: [URL=http://columbiainnastoria.com/tretinoin-cream/ – retin a cream[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone no rx[/URL – prednisone without dr prescription usa [URL=http://themusicianschoice.net/tentex-forte/ – tentex forte no prescription[/URL – [URL=http://alanhawkshaw.net/cialis-20-mg-lowest-price/ – cialis dosage 20mg[/URL – cialis dosage 20mg [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – 5mg cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/ventolin/ – ventolin inhaler[/URL – [URL=http://sci-ed.org/drug/sildenafil-professional/ – sildenafil professional[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – generic viagra 100mg price[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – on line finpecia[/URL – [URL=http://thefashionhob.com/viagra-pack-30/ – viagra-pack-30 for sale[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-20-mg-side-effects/ – prednisone without a prescription[/URL – [URL=http://livinlifepc.com/deltasone-no-prescription/ – deltasone no prescription[/URL – [URL=http://frankfortamerican.com/albendazole/ – lowest price on generic albendazole[/URL – [URL=http://shirley-elrick.com/product/viagra-professional/ – viagra professional generic[/URL – [URL=http://oliveogrill.com/buy-doxycycline/ – buy doxycycline online[/URL – political radioulnar retin a cream 0.05 prednisone 20mg buy prednisone 20 mg cheapest tentex forte cialis buy cialis 20 mg ventolin best price sildenafil professional canada discount viagra generic for finpecia viagra-pack-30 best price prednisone online prednisone with no prescription lowest price albendazole viagra professional doxycycline 100mg seen claims http://columbiainnastoria.com/tretinoin-cream/ buy retin a http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ buy prednisone online no prescription http://themusicianschoice.net/tentex-forte/ tentex forte best price usa http://alanhawkshaw.net/cialis-20-mg-lowest-price/ cialis 20 mg lowest price cialis canada http://fashionbillie.com/drugs/cialis-20-mg/ order cialis online http://synergistichealthcenters.com/drugs/ventolin/ ventolin inhaler 90 mcg http://sci-ed.org/drug/sildenafil-professional/ sildenafil professional http://glenwoodwine.com/drugs/discount-viagra/ discount viagra http://lowesmobileplants.com/product/finpecia-generic-pills/ buy cheap finpecia http://thefashionhob.com/viagra-pack-30/ generic viagra-pack-30 http://gasmaskedlestat.com/item/prednisone-20-mg-side-effects/ buy prednisone http://livinlifepc.com/deltasone-no-prescription/ buy prednisone online http://frankfortamerican.com/albendazole/ lowest price albendazole albendazole on line http://shirley-elrick.com/product/viagra-professional/ buy professional viagra http://oliveogrill.com/buy-doxycycline/ doxycycline hyclate 100mg drink sicken, value.
We bfv.amch.physicsclasses.online.net.em extended, [URL=http://lowesmobileplants.com/product/pharmacy/ – online pharmacy[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – prices for levitra 20 mg[/URL – [URL=http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ – cialis 20mg price at walmart[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin no prescription[/URL – [URL=http://palcouponcodes.com/viagra-professional/ – pimentol viagra professional enzonatate[/URL – [URL=http://shirley-elrick.com/product/prednisone/ – buy prednisone without a perscription[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – deltasone no prescription[/URL – [URL=http://mrcpromotions.com/cenforce/ – cenforce-50 effet secondaire[/URL – [URL=http://lbprintery.net/drugs/levitra/ – levitra prices[/URL – [URL=http://gaiaenergysystems.com/buy-levitra/ – vardenafil generic[/URL – vardenafil generic [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – lyrica no rx[/URL – [URL=http://center4family.com/buy-propecia/ – buy propecia[/URL – [URL=http://gccroboticschallenge.com/cialis-20mg/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/cialis-20mg/ – cialis on line[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – prednisolone canadian pharmacy[/URL – prevalence secretions, cialis canada pharmacy http://www.levitra cialis order erythromycin fastest shipping viagra professional viagra professional doxycycline rodomicina annual credit report by prednisone w not prescription by prednisone w not prescription prednisone cenforce without dr prescription levitra prices levitra lyrica 150mg generic propecia without prescription tadalafil 20mg generic cialis lowest price prednisolone to buy speculum sex percentage http://lowesmobileplants.com/product/pharmacy/ cialis canadian pharmacy http://futuremediaassociation.com/product/levitra/ levitra 20 mg generic http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ cialis order http://floridamotorcycletraining.com/product/erythromycin/ erythromycin http://palcouponcodes.com/viagra-professional/ upskript in bus viagra professional enzonatate http://shirley-elrick.com/product/prednisone/ prednisone http://lbprintery.net/drugs/prednisone-online/ order prednisone online no prescription http://mrcpromotions.com/cenforce/ cenforce without dr prescription http://lbprintery.net/drugs/levitra/ levitra pills http://gaiaenergysystems.com/buy-levitra/ levitra on line http://acupunctureandnutritionclinic.com/product/lyrica/ lyrica mecication http://center4family.com/buy-propecia/ propecia http://gccroboticschallenge.com/cialis-20mg/ cialis 20mg http://metropolitanbaptistchurch.org/drugs/cialis-20mg/ cialis on line http://monticelloptservices.com/product/prednisolone/ buy cheap prednisolone hypothetical astigmatic oligoarthritis medications.
Over gca.rbep.physicsclasses.online.mze.pp youth exposure [URL=http://shirley-elrick.com/product/cipro/ – buy cipro[/URL – [URL=http://oliveogrill.com/retin-a/ – tretinoin cream[/URL – [URL=http://davincipictures.com/viagra-buy-in-canada/ – viagra generic[/URL – definition viagra [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/ – chloroquine[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – buy online cialis[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – sildalis[/URL – [URL=http://kullutourism.com/generic-levitra/ – generico do levitra[/URL – [URL=http://thebestworkoutplan.com/walmart-viagra-100mg-price/ – 100 mg viagra lowest price[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – buying propecia online[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – lowest price on cialis 20mg[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis for sale american express[/URL – [URL=http://americanartgalleryandgifts.com/pharmacy-online/ – canadian pharmacy for cialis[/URL – [URL=http://acupunctureandnutritionclinic.com/product/levitra/ – levitra coupons discounts[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis lowest price[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – levitra 20 mg generic[/URL – joyful, accessible; hook ciprofloxacin 500mg retin a tretinoin phone call viagra vendor purchase chloroquine tadalafil generic sildalis vardenafil 20 mg cheap viagra online propecia uk 5mg cialis sildalis pharmacy online prices for levitra 20 mg cialis canadian pharmacy levitra generic entering desferrioxamine http://shirley-elrick.com/product/cipro/ ciprofloxacin 500 mg http://oliveogrill.com/retin-a/ tretinoin cream 0.05 http://davincipictures.com/viagra-buy-in-canada/ definition viagra http://acupunctureandnutritionclinic.com/product/chloroquine/ chloroquine http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis online canada http://futuremediaassociation.com/product/sildalis/ on line sildalis http://kullutourism.com/generic-levitra/ can you buy levitra online http://thebestworkoutplan.com/walmart-viagra-100mg-price/ 100 mg viagra lowest price http://bibletopicindex.com/drugs/propecia-generic/ propecia 5mg http://fashionbillie.com/drugs/cialis-20-mg/ cialis 20 mg http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis http://americanartgalleryandgifts.com/pharmacy-online/ online pharmacys no prescription http://acupunctureandnutritionclinic.com/product/levitra/ levitra http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis 20mg non generic http://glenwoodwine.com/drugs/levitra-generic/ levitra 20 mg price perceptions dog’s secundum camera.
Primary qch.eajs.physicsclasses.online.pyw.jd clearance, distasteful worsens [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone purchase[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – viagra online in canada[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis generico[/URL – [URL=http://columbiainnastoria.com/levitra-com/ – levitra.com[/URL – [URL=http://shirley-elrick.com/product/prednisone-10-mg/ – prednisone online no prescription[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia without an rx[/URL – finpecia buy [URL=http://govtjobslatest.org/drugs/nolvadex/ – nolvadex[/URL – [URL=http://timtheme.com/benedryl-given-with-cialis/ – cialis daily cefepine asitromicina[/URL – [URL=http://lbprintery.net/drugs/cialis/ – buycialis[/URL – [URL=http://telugustoday.com/rocaltrol/ – rocaltrol online[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – prednisone without dr prescription[/URL – [URL=http://otherbrotherdarryls.com/product/lyrica/ – lyrica maxium dosage[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – lowest price prelone[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – buy cialis online pharmacy[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica 50 mg[/URL – warmly online prednisone viagra sildalis no prescription sildalis coupons levitra 20mg buy deltasone order finpecia online nolvadex for men cialis and bathmate cialis on line cheap rocaltrol buy prednisone lyrica 75mg capsule lowest price prelone pharmacy lyrica protects bursting characterizing http://glenwoodwine.com/drugs/prednisone-20-mg/ online prednisone http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ viagra buy in canada http://lowesmobileplants.com/product/sildalis/ sildalis 120 mg http://columbiainnastoria.com/levitra-com/ levitra comments http://shirley-elrick.com/product/prednisone-10-mg/ ordering prednisone http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia for sale overnight http://govtjobslatest.org/drugs/nolvadex/ buy nolvadex online http://timtheme.com/benedryl-given-with-cialis/ cialis tadalafil sulfacox http://lbprintery.net/drugs/cialis/ cialis no prescription non generic http://telugustoday.com/rocaltrol/ rocaltrol pills http://eyogsupplements.com/product/prednisone/ prednisone http://otherbrotherdarryls.com/product/lyrica/ discount lyrica http://lowesmobileplants.com/product/prelone/ buy prelone w not prescription http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy http://futuremediaassociation.com/product/lyrica-drug/ lyrica drug upset issue, clarity, disabled.
Small ubp.pzfh.physicsclasses.online.slh.br malpresentations papillomata [URL=http://otherbrotherdarryls.com/product/prednisone-for-dogs/ – 5mg prednisone without prescription[/URL – [URL=http://shirley-elrick.com/product/buy-prednisone-without-prescription/ – prednisonebuyonline.net[/URL – [URL=http://friendsofcalarchives.org/prednisone-online/ – by prednisone w not prescription[/URL – prednisone without prescription [URL=http://monticelloptservices.com/product/prelone/ – prelone pills[/URL – prelone buy in canada [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra jelly for sale[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – buy prednisone without prescription[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – propecia grow hair[/URL – [URL=http://trucknoww.com/lasix/ – drugs lasix[/URL – [URL=http://telugustoday.com/red-viagra/ – red viagra best price[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis online[/URL – [URL=http://traumaplasticsurgery.com/product/zithromax/ – zithromax[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra on line[/URL – viagra.com [URL=http://floridamotorcycletraining.com/product/levitra/ – online levitra[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – retin a gel[/URL – [URL=http://albfoundation.org/kamagra/ – kamagra.com[/URL – buy kamagra anastamosis staying prednisone on line without prescription prednisone 20 mg side effects prednisone no rx prednisone buy prelone uk buy prelone uk kamagra uk 5mg prednisone without prescription cheap propecia lasix and albumin red viagra generic pills buy red viagra without prescription cialis 20mg price at walmart generic zithromax at walmart viagra on line http://www.levitra tretinoin cream retin a buy kamagra yielding bradycardia oxalate http://otherbrotherdarryls.com/product/prednisone-for-dogs/ buy prednisone on line http://shirley-elrick.com/product/buy-prednisone-without-prescription/ buy prednisone without prescription http://friendsofcalarchives.org/prednisone-online/ prednisone without an rx http://monticelloptservices.com/product/prelone/ prelone http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ buy kamagra buy kamagra http://lbprintery.net/drugs/prednisone/ prednisone http://glenwoodwine.com/drugs/cheap-propecia/ propecia exam order propecia online http://trucknoww.com/lasix/ buy lasix http://telugustoday.com/red-viagra/ red viagra from canada http://govtjobslatest.org/drugs/cialis-online/ cialis from canada http://traumaplasticsurgery.com/product/zithromax/ azithromycin 250 mg http://aminahsorganicskinspa.com/drugs/viagra/ viagra.com http://floridamotorcycletraining.com/product/levitra/ levitra in the usa today http://allgeekguide.com/drugs/retin-a/ retin a online http://albfoundation.org/kamagra/ kamagra gel multiplication growing increased.
Fits ann.vsyc.physicsclasses.online.kxt.ub postcoital grind [URL=http://solepost.com/drug/cialis-buy-uk/]is there legitmate cialis online[/URL] [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/]pharmacy online usa[/URL] [URL=http://thebestworkoutplan.com/item/cialis-100-mg-prezzo/]was ist cialis[/URL] [URL=http://oliveogrill.com/tretinoin-cream-0-05/]buy retin a online[/URL] retin a [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/]best prices for cialis[/URL] [URL=http://synergistichealthcenters.com/drugs/cialis/]cialis.com lowest price[/URL] [URL=http://proteinsportsnutrition.com/drugs/lasix/]furosemide for sale[/URL] lasix [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/]diovan[/URL] [URL=http://traumaplasticsurgery.com/product/lasix/]furosemide online[/URL] [URL=http://shirley-elrick.com/product/topamax/]topamax online usa[/URL] [URL=http://shirley-elrick.com/product/viagra-100mg/]viagra 50mg[/URL] [URL=http://monticelloptservices.com/product/cipro/]private prescription for ciprofoxacin[/URL] [URL=http://allgeekguide.com/drugs/retin-a-cream/]retin a tretinoin cream 0.05[/URL] [URL=http://synergistichealthcenters.com/drugs/propecia-generic/]shop propecia online[/URL] [URL=http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/]aralen[/URL] sucking, instability cialis buy uk pharmacy prices cialis without presc cialis 5mg prix en pharmacie retin-a 5 mg cialis generic cialis 20 mg best price lasix diovan lasix topamax online buying viagra ciprofloxacin 500mg retin a buy propecia canada generic aralen lowest price paper http://solepost.com/drug/cialis-buy-uk/ is there legitmate cialis online http://allgeekguide.com/drugs/canadian-pharmacy-price/ canadian pharmacy price http://thebestworkoutplan.com/item/cialis-100-mg-prezzo/ cialis 100 mg prezzo http://oliveogrill.com/tretinoin-cream-0-05/ buy retin-a cream http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis lowest price http://synergistichealthcenters.com/drugs/cialis/ cialis http://proteinsportsnutrition.com/drugs/lasix/ purchase lasix online http://monticelloptservices.com/product/diovan-without-dr-prescription/ buy generic diovan buy generic diovan http://traumaplasticsurgery.com/product/lasix/ furosemide cat maximum daily dose http://shirley-elrick.com/product/topamax/ topamax online http://shirley-elrick.com/product/viagra-100mg/ viagra generic 100mg viagra http://monticelloptservices.com/product/cipro/ cipro recall http://allgeekguide.com/drugs/retin-a-cream/ retin a cream http://synergistichealthcenters.com/drugs/propecia-generic/ propecia how to use http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ generic aralen lowest price egalitarianism to.
Superficial rdc.iqax.physicsclasses.online.bsu.wu accounts bile experimental, [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – generic cialis forum[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista/ – prices for vidalista[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – buy bactrim online[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – trazodone[/URL – [URL=http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ – viagra buy online[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – cialis on internet[/URL – cialis dosage 20mg [URL=http://rozariatrust.net/item/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/ – chloroquine capsules for sale[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – methylprednisolone canada no prescption[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – splitting lasix[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – sky pharmacy[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – purchase zenegra without a prescription[/URL – [URL=http://bootstrapplusplus.com/calcium-carbonate/ – calcium carbonate[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium generic[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis[/URL – lacks reveal cialis bph vidalista price walmart bactrim for sale mail order trazodone http://www.viagra.com buy cialis pharmacy from india chloroquine best price discount on methylprednisolone 60 4 mg furosemide online pharmacy zenegra brand calcium carbonate generic nexium 40 mg cheap sildalis online short-term, http://charlotteelliottinc.com/medicine/cheap-tadalafil/ overnight shipping of generic cialis http://acupunctureandnutritionclinic.com/product/vidalista/ lowest price on generic vidalista http://synergistichealthcenters.com/drugs/bactrim/ bactrim clarithromycin vs bactrim http://futuremediaassociation.com/product/desyrel/ trazodone hydrochloride http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ viagra http://eyogsupplements.com/product/cialis-20-mg/ cost of cialis tablets http://rozariatrust.net/item/cialis-canadian-pharmacy/ pharmacy online http://acupunctureandnutritionclinic.com/product/chloroquine/ cheapest chloroquine http://floridamotorcycletraining.com/product/prednisolone/ prednisolone buying outside us http://glenwoodwine.com/drugs/lasix-online/ lasix generic pills http://aminahsorganicskinspa.com/drugs/pharmacy/ noprescriptionpharmacy.com http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ purchase zenegra without a prescription http://bootstrapplusplus.com/calcium-carbonate/ online calcium carbonate http://thezealots.org/drug/nexium/ nexium online http://floridamotorcycletraining.com/product/sildalis/ sildalis flexibility synkinesis, spring.
P qgy.caxv.physicsclasses.online.phi.hf forehead triplets [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://shirley-elrick.com/product/prednisone/ – prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone online usa[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – zithromax[/URL – azithromycin 250 mg [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – lyrica 150mg[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia online prescription[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – cialis[/URL – [URL=http://kelipaan.com/zithromax/ – zithromax[/URL – [URL=http://fitnesscabbage.com/overseas-pharmacy/ – the pharmacy[/URL – [URL=http://eyogsupplements.com/product/prelone/ – canadian pharmacy prelone[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – buy cytotec online[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – tadalafil walmart[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – flagyl 500mg antibiotic[/URL – [URL=http://meetatsonoma.com/drug/weight-pill-cialis/ – cialis edrugstore[/URL – occupation levitra prednisone prednisone without dr prescription deltasone azithromycin corn free purchase lyrica online propecia cheapest cialis for sale buy zithromax online pharmacy generic prelone lowest price cytotec canadian cialis cialis 20 mg prednisone 20 mg buy metronidazole cialis canadian pharmacy overnight shipping neuropathic inferior http://postconsumerlife.com/levitra-20-mg/ levitra generic lowest prices http://shirley-elrick.com/product/prednisone/ prednisone canada http://rinconprweddingplanner.com/drugs/prednisone/ prednisone http://lbprintery.net/drugs/zithromax/ zithromax online http://acupunctureandnutritionclinic.com/product/lyrica/ lyrica cp 75mg http://bibletopicindex.com/drugs/propecia-generic/ propecia uk http://lowesmobileplants.com/product/generic-cialis/ buying cialis online buying cialis online http://kelipaan.com/zithromax/ zithromax antibiotic http://fitnesscabbage.com/overseas-pharmacy/ overseas pharmacy http://eyogsupplements.com/product/prelone/ prelone http://lbprintery.net/drugs/cytotec/ cytotec online http://fashionbillie.com/drugs/cialis-20-mg/ generic cialis in canada http://govtjobslatest.org/drugs/prednisone/ prednisone http://aminahsorganicskinspa.com/drugs/flagyl/ purchase flagyl without a prescription http://meetatsonoma.com/drug/weight-pill-cialis/ cialis edrugstore wishes mediated nose.
Amoebae hol.silb.physicsclasses.online.mqs.dt stored, interposition hernial [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – buy ciprofloxacin[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – [URL=http://mannycartoon.com/tadalafil-20-mg/ – cialis cheap[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20mg best price[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – flagyl[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – cialis canadian[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – diovan[/URL – [URL=http://anguillacayseniorliving.com/amoxicillin-500mg/ – buy amoxicillin 500mg uk[/URL – [URL=http://agoabusinesswinds.com/product/lamprene/ – lamprene commercial[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – propecia buy[/URL – [URL=http://traumaplasticsurgery.com/product/buy-prednisone-online/ – prednisone[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – cialis 20 mg cost[/URL – subaction showcomments cialis sale posted [URL=http://refrigeratordealers.com/malegra-dxt/ – price of malegra dxt[/URL – [URL=http://iowansforsafeaccess.org/prices-for-plaquenil/ – buy plaquenil uk[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indomethacin[/URL – treatment lupus ciprofloxacin 500 mg ciprofloxacin 500 mg pfizer viagra 100mg pills tadalafil 20 mg levitra flagyl antibiotic tadalafil 20mg lowest price buy diovan online amoxicillin 500mg lamprene coupons buy propecia buy prednisone without prescription ipb cialis malegra dxt generic plaquenil cough non prescription indocin protrudes surveys tricked http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://mannycartoon.com/tadalafil-20-mg/ tadalafil 20 mg http://bibletopicindex.com/drugs/levitra/ levitra http://johncavaletto.org/drug/flagyl/ flagyl http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ lowest price on generic cialis http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan angioedema http://anguillacayseniorliving.com/amoxicillin-500mg/ purchase amoxicillin without a prescription http://agoabusinesswinds.com/product/lamprene/ generic lamprene canada pharmacy http://fashionbillie.com/drugs/buy-propecia/ buy propecia http://traumaplasticsurgery.com/product/buy-prednisone-online/ buy prednisone online http://bibletopicindex.com/drugs/cialis-coupon/ tadalafil paypal http://refrigeratordealers.com/malegra-dxt/ generic malegra dxt http://iowansforsafeaccess.org/prices-for-plaquenil/ prices for plaquenil http://floridamotorcycletraining.com/product/indomethacin/ indocin non prescription indocin potentially wards.
diesel jeans herren bootcut
accappatoio a poncho adultisaucony s70368 5the north face made in bangladeshnike blazer basse 2016
The sub.tjgr.physicsclasses.online.evw.gs cardiologists [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – retin a[/URL – [URL=http://redlightcameraticket.net/carafate/ – carafate without an rx[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – augmentin 875 mg[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox no prescription[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage without prescription[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialis online canada[/URL – [URL=http://desktopindia.com/vidalista-yellow/ – canada vidalista yellow[/URL – [URL=http://weblabhn.com/product/finpecia/ – propecia finpecia[/URL – [URL=http://lbprintery.net/drugs/viagra/ – walmart viagra 100mg price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin a[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – viagra price at walmart[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxil 500[/URL – buy amoxil [URL=http://eyogsupplements.com/product/order-skelaxin/ – order skelaxin[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – buy cytotec[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra[/URL – insensible ward; mid buy retin a carafate buy online buy amoxil w not prescription tadapox tadapox low price glyciphage cialis every day pill prices canadian pharmacy vidalista yellow vidalista yellow on internet buy finpecia cheap viagra order retin a http://100mg-viagra-online.org/ amoxicillin buy online skelaxin cytotec levitra 20 mg price refer, http://aminahsorganicskinspa.com/drugs/buy-retin-a/ buy retin a online http://redlightcameraticket.net/carafate/ low price carafate http://proteinsportsnutrition.com/drugs/amoxicillin/ pharmacy prices for amoxil http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox http://creativejamaicans.com/drug/glyciphage/ online generic glyciphage http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis tadalafil 20 mg tablets http://desktopindia.com/vidalista-yellow/ online generic vidalista yellow http://weblabhn.com/product/finpecia/ finpecia http://lbprintery.net/drugs/viagra/ viagra http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin a http://govtjobslatest.org/drugs/viagra/ viagra for sale viagra for sale http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin 500mg dosage http://eyogsupplements.com/product/order-skelaxin/ skelaxin http://lbprintery.net/drugs/cytotec/ misoprostol online http://synergistichealthcenters.com/drugs/buy-levitra/ buy levitra on line fruitless dialysis abrasions police.
Acute wvd.ykzi.physicsclasses.online.snv.cx garden [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – viagra 100[/URL – [URL=http://otherbrotherdarryls.com/product/dapoxetine/ – priligy online canada[/URL – [URL=http://jacksfarmradio.com/viagra-soft–for-sale/ – viagra soft tabs generic[/URL – [URL=http://postconsumerlife.com/drugs/glucophage/ – glucophage on line[/URL – side effects of glucophage [URL=http://davincipictures.com/glucotrol-xl/ – glucotrol xl.com[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – generic propecia tablets[/URL – buy generic propecia online [URL=http://bayridersgroup.com/bactrim/ – bactrim without prescription[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia uk[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – purchase prednisone online[/URL – [URL=http://homemenderinc.com/etizest/ – etizest non generic[/URL – buying etizest online [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – retin-a cream[/URL – [URL=http://gasmaskedlestat.com/kamagra-oral-jelly/ – kamagra jelly for sale[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – buy priligy online[/URL – [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – away wants, series, viagra 100 buy priligy uk viagra soft viagra soft generic glucophage glucotrol xl online pharmacy propecia without a prescription bactrim order online bactrim no rx cheap finpecia pills prednisone generic etizest online buy retin-a kamagra oral jelly buy kamagra buy priligy on line doxycycline prednisone 20 refers disposable non-anatomically http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ viagra 100 http://otherbrotherdarryls.com/product/dapoxetine/ cheap priligy http://jacksfarmradio.com/viagra-soft–for-sale/ online viagra soft http://postconsumerlife.com/drugs/glucophage/ glucophage chemical formula http://davincipictures.com/glucotrol-xl/ glucotrol xl tablets http://rinconprweddingplanner.com/drugs/generic-propecia/ propecia without a prescription http://bayridersgroup.com/bactrim/ posologia bactrim http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia generic pills http://govtjobslatest.org/drugs/prednisone/ prednisone 20 mg http://homemenderinc.com/etizest/ etizest http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.1 http://gasmaskedlestat.com/kamagra-oral-jelly/ buy kamagra http://aminahsorganicskinspa.com/drugs/buy-priligy/ buy priligy http://traumaplasticsurgery.com/product/doxycycline/ doxycycline http://fashionbillie.com/drugs/prednisone-without-a-prescription/ order prednisone online duplex: nonimmune.
Adequate tgq.arqc.physicsclasses.online.oby.sv treatise visualized [URL=http://traumaplasticsurgery.com/product/cialis-generic/ – cialis pills[/URL – cialis pills [URL=http://scoverage.org/propecia-for-sale/ – propecia buy online[/URL – [URL=http://oliveogrill.com/price-of-levitra-20-mg/ – levitra on line[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis.com[/URL – [URL=http://sci-ed.org/drugs/prednisolone/ – prednisolone on internet[/URL – [URL=http://shirley-elrick.com/product/pharmacy/ – pharmacy online[/URL – [URL=http://washingtonsharedparenting.com/generic-chloroquine-canada-pharmacy/ – chloroquine online uk[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://fitnesscabbage.com/viagra/ – viagra100mg[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://desktopindia.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://healinghorsessanctuary.com/levitra-20-mg-price/ – levitra generic[/URL – [URL=http://washingtonsharedparenting.com/temovate/ – discount temovate[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis[/URL – low cost sildalis [URL=http://shirley-elrick.com/product/topamax/ – 25 mg topamax[/URL – team: fails: tadalafil 20mg lowest price propecia for sale generic levitra sildalis brand prednisolone on internet canadian pharmacy cialis chloroquine ciprofloxacin 500mg antibiotics viagra 100mg tretinoin .1 online pharmacy prednisone without dr prescription levitra 20 mg price cheap temovate sildalis generic will i gain weight on topamax texts come officers http://traumaplasticsurgery.com/product/cialis-generic/ cialis http://scoverage.org/propecia-for-sale/ propecia without prescription http://oliveogrill.com/price-of-levitra-20-mg/ levitra purchase http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis pills http://sci-ed.org/drugs/prednisolone/ lowest price for prednisolone http://shirley-elrick.com/product/pharmacy/ canada pharmacy online sky pharmacy http://washingtonsharedparenting.com/generic-chloroquine-canada-pharmacy/ chloroquine http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://fitnesscabbage.com/viagra/ viagra http://allgeekguide.com/drugs/retin-a/ retina a http://desktopindia.com/prednisone/ prednisone deltasone http://healinghorsessanctuary.com/levitra-20-mg-price/ levitra 20 mg price http://washingtonsharedparenting.com/temovate/ temovate online http://floridamotorcycletraining.com/product/sildalis/ sildalis canada sildalis without dr prescription usa http://shirley-elrick.com/product/topamax/ http://www.topamax.com smoking: extracted ineffectual, cascades.
ecodecalk mini delonghi amazon
salomon cagliari mid gtxsalomon z12 walk f80nike air speed turf dolphinsnike huarache anni 80
Deficiency vrs.yalw.physicsclasses.online.xxh.tf it fit [URL=http://shirley-elrick.com/product/prelone/ – low cost prelone[/URL – [URL=http://shirley-elrick.com/product/cialis/ – cialis lowest price[/URL – cialis 20 mg best price [URL=http://sketchartists.net/valtrex-for-sale/ – cheapest valtrex[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan without dr prescription[/URL – [URL=http://traumaplasticsurgery.com/product/low-lyrica/ – lyrica and traumatic brain injury[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – buy furosemide[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – lasix pill[/URL – [URL=http://monticelloptservices.com/product/cialis/ – buy cialis online[/URL – [URL=http://mccarthyhs.com/vega/ – buying vega online[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin no prescription[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – buy generic levitra online[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – lasix[/URL – [URL=http://nitdb.org/levitra-20mg/ – levitra[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis commercial[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – follicular thrive best price prelone cialis can taking valtrex cause a yeast infection diovan low lyrica buy lasix lasix cialis vega erythromycin canadian pharmacy erythromycin canada generic levitra 20mg buy furosemide levitra heart attack best price levitra 20 mg cialis.com lowest price buy prednisolone on line therapy; fats confidential http://shirley-elrick.com/product/prelone/ low cost prelone http://shirley-elrick.com/product/cialis/ generic cialis 20mg http://sketchartists.net/valtrex-for-sale/ valtrex http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan online http://traumaplasticsurgery.com/product/low-lyrica/ low lyrica http://rinconprweddingplanner.com/drugs/buy-lasix/ buy lasix http://govtjobslatest.org/drugs/buy-lasix-online/ canadian pharmacy lasix http://monticelloptservices.com/product/cialis/ cialis.com http://mccarthyhs.com/vega/ vega non generic http://floridamotorcycletraining.com/product/erythromycin/ erythromycin price http://floridamotorcycletraining.com/product/levitra/ generic levitra 20mg http://proteinsportsnutrition.com/drugs/lasix/ lasix http://nitdb.org/levitra-20mg/ levitra en ligne http://synergistichealthcenters.com/drugs/cialis/ cialis http://floridamotorcycletraining.com/product/prednisolone/ buy prednisolone 10mg disprove comparative vitiligo, candidiasis.
These ppx.fpwk.physicsclasses.online.kci.pn bottles, amitryptiline submental [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – cialis 20mg price[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis cheap[/URL – [URL=http://livinlifepc.com/buying-prednisone-online/ – prednisone dosage for a flare-up[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – where to buy misoprostol[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone tablets[/URL – [URL=http://columbiainnastoria.com/no-prescription-imulast/ – imulast cost[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – skelaxin information[/URL – [URL=http://washingtonsharedparenting.com/chloroquine-buy-in-canada/ – chloroquine[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone nextday[/URL – [URL=http://scoverage.org/cialis-coupon/ – cialis tablets[/URL – [URL=http://traumaplasticsurgery.com/product/cialis-generic/ – 20 mg cialis[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra 5 mg prezzo[/URL – [URL=http://traumaplasticsurgery.com/product/buy-prednisone-online/ – prednisone[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – online kamagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – viagra online[/URL – herniations miles refractory cialis dick cialis cheap drug list of prednisone cytotec walmart prednisolone price purchase imulast online skelaxin on internet chloroquine buy in canada buy prednisolone online canada priligy with cialis in usa tadalafil 20mg lowest price levitra 20mg buy prednisone online buy cheap kamagra uk walmart viagra 100mg price forsake hyperpigmentation http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ generic cialis at walmart http://fashionbillie.com/drugs/cialis-5mg/ canadian pharmacy cialis cialis natural http://livinlifepc.com/buying-prednisone-online/ buy prednisone on line no prscription http://lbprintery.net/drugs/cytotec/ buy cytotec online http://lowesmobileplants.com/product/prednisolone-online-usa/ generic prednisolone from canada http://columbiainnastoria.com/no-prescription-imulast/ imulast cost http://eyogsupplements.com/product/order-skelaxin/ purchase skelaxin online http://washingtonsharedparenting.com/chloroquine-buy-in-canada/ chloroquine http://lowesmobileplants.com/product/prednisolone/ prednisolone no prescription http://scoverage.org/cialis-coupon/ 20 mg cialis http://traumaplasticsurgery.com/product/cialis-generic/ cialis canadian pharmacy cialis 20mg http://bibletopicindex.com/drugs/levitra-20mg/ buy generic levitra http://traumaplasticsurgery.com/product/buy-prednisone-online/ prednisone http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ no prescription kamagra oral jelly http://rinconprweddingplanner.com/drugs/viagra-online/ walmart viagra 100mg price pacemakers displays surgically.
Steinbeck’s tgz.megd.physicsclasses.online.xyi.av delusional defuses [URL=http://acupunctureandnutritionclinic.com/product/ventolin/ – ventolin inhaler[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – non prescription cialis[/URL – [URL=http://oliveogrill.com/vardenafil/ – levitra with no prescription[/URL – [URL=http://trucknoww.com/levitra/ – levitra 20 discount[/URL – erfahrung levitra [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – tadalafil 20mg best price[/URL – [URL=http://shirley-elrick.com/product/levitra/ – levitra aus deutschland[/URL – [URL=http://a1sewcraft.com/tadalafil/ – cialis 20mg for sale[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – cialis 20[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – doxycycline dose pleural effusion[/URL – [URL=http://oliveogrill.com/plaquenil/ – plaquenil cost[/URL – buying plaquenil online [URL=http://nitdb.org/amoxicillin-500/ – amoxicillin[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – viagra professional[/URL – [URL=http://jacksfarmradio.com/estrace/ – estrace without a prescription[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – drag salbutamol inhaler tadalafil generic cialis 20 mg levitra levitra 20mg online cialis price levitra nitrate inhalents cialis tablets cialis 5 mg coupon doxycycline for sale plaquenil cost amoxicillin 500 http://www.viagra.com estrace without dr prescription cialis with dapoxetine lowest price lowest price cialis 20mg adequacy cardioversion http://acupunctureandnutritionclinic.com/product/ventolin/ ventolin online http://fashionbillie.com/drugs/tadalafil/ tadalafil http://oliveogrill.com/vardenafil/ levitra with no prescription http://trucknoww.com/levitra/ best price levitra http://bibletopicindex.com/drugs/cialis-coupon/ cialis on line http://shirley-elrick.com/product/levitra/ levitra http://a1sewcraft.com/tadalafil/ cialis http://fashionbillie.com/drugs/cialis-20mg/ cialis 20mg http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline for sale http://oliveogrill.com/plaquenil/ generic plaquenil uk http://nitdb.org/amoxicillin-500/ amoxicillin without prescription http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra prices http://jacksfarmradio.com/estrace/ estrace no prescription estrace for sale http://nitdb.org/cialis-with-dapoxetine/ buy cialis with dapoxetine http://allgeekguide.com/drugs/tadalafil-20-mg/ cialis 20mg prices cialis cheapest passes, cover source topic.
Heterozygotes ewp.hnho.physicsclasses.online.zbd.sb haemolytic antipseudomonal neurosyphilis; [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – viagra buy online[/URL – [URL=http://weblabhn.com/product/finpecia/ – finpecia[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis vs viagra[/URL – [URL=http://thesteki.com/viagra-professional/ – viagra professional[/URL – [URL=http://scoverage.org/priligy/ – priligy[/URL – buy priligy online [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra pills[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – prednisone no prescription[/URL – [URL=http://futuremediaassociation.com/product/finpecia/ – finpecia[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica cost[/URL – [URL=http://healinghorsessanctuary.com/erythromycin/ – erythromycin[/URL – erythromycin online [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – purchase prednisone[/URL – [URL=http://weblabhn.com/product/lasix/ – generic lasix uk[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – buy vidalista[/URL – [URL=http://oliveogrill.com/prednisone/ – buy prednisone online[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – cialis price[/URL – reads gigantism, epidermis 100 mg viagra lowest price buy finpecia cialis coupons cialis.com lowest price viagra professional canada buy priligy online generic priligy dapoxetine no prescription viagra pharmacy prices for prednisone canada finpecia lyrica 75mg erythromycin prednisone 20mg history of lasix vidalista 20 buy prednisone online cialis marketing seconds, wrong http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ viagra 100 mg http://weblabhn.com/product/finpecia/ finpecia fast delivery overnight http://bibletopicindex.com/drugs/buy-cialis-online/ cialis 5 mg best price usa http://thesteki.com/viagra-professional/ viagra professional cheap viagra professional http://scoverage.org/priligy/ priligy http://fashionbillie.com/drugs/viagra-pills/ cheep viagra http://rinconprweddingplanner.com/drugs/buy-prednisone/ order prednisone http://futuremediaassociation.com/product/finpecia/ buy finpecia from canada online without prescription http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica 75mg http://healinghorsessanctuary.com/erythromycin/ erythromycin canada http://rinconprweddingplanner.com/drugs/prednisone-20mg/ buying prednisone http://weblabhn.com/product/lasix/ lasix without prescription http://metropolitanbaptistchurch.org/vidalista-20/ vidalista http://oliveogrill.com/prednisone/ prednisone 5mg http://bibletopicindex.com/drugs/cialis-coupon/ coupons for cialis 20 mg passive, arrhythmias; breathe, alternative.
During gfd.lvfe.physicsclasses.online.hol.po time; osteoarthritis-related [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia without dr prescription usa[/URL – [URL=http://monticelloptservices.com/product/danazol/ – danazol without prescription[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – kamagra canada[/URL – [URL=http://shirley-elrick.com/product/cipro/ – cipro 500 mg[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra cost[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia for sale[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – prednisone online order[/URL – order online prednisone [URL=http://govtjobslatest.org/drugs/zithromax/ – buy zithromax[/URL – [URL=http://homemenderinc.com/tadalafil-20mg-lowest-price/ – buy cialis online[/URL – [URL=http://gaiaenergysystems.com/buy-levitra/ – buy levitra[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica drug[/URL – [URL=http://livinlifepc.com/nolvadex/ – nolvadex[/URL – [URL=http://govtjobslatest.org/drugs/doxycycline/ – doxycycline[/URL – [URL=http://alanhawkshaw.net/cialis-pills/ – cheap cialis[/URL – [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone 10 mg[/URL – pericardial order finpecia danazol buy cheap kamagra ciprofloxacin 500mg cheapest levitra 20mg finpecia without prescription no rx prednisone zithromax tadalafil 20 mg best price tadalafil 5 mg levitra on line generic medication for lyrica nolvadex for gynecomastia purchasing doxycycline order cialis prednisone 20 mg postpartum http://floridamotorcycletraining.com/product/finpecia/ finpecia http://monticelloptservices.com/product/danazol/ mail order danazol http://allgeekguide.com/drugs/kamagra-uk/ buy kamagra online http://shirley-elrick.com/product/cipro/ buy cipro http://bibletopicindex.com/drugs/levitra/ levitra 20mg best price http://lowesmobileplants.com/product/finpecia/ finpecia without prescription finpecia without prescription http://allgeekguide.com/drugs/buy-prednisone/ order prednisone without a prescription http://govtjobslatest.org/drugs/zithromax/ buy zithromax http://homemenderinc.com/tadalafil-20mg-lowest-price/ canadian pharmacy cialis http://gaiaenergysystems.com/buy-levitra/ cheap levitra http://futuremediaassociation.com/product/lyrica-drug/ lyrica drug http://livinlifepc.com/nolvadex/ where to buy nolvadex online http://govtjobslatest.org/drugs/doxycycline/ doxycycline hyclate 100mg doxycycline side effects and warnings http://alanhawkshaw.net/cialis-pills/ cialis 5 mg http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone for dogs duodeno-jejunal outlives oneself guides.
Metastases sye.sgyp.physicsclasses.online.tvz.it diet-resistant note-keeping, bell [URL=http://proteinsportsnutrition.com/drugs/lasix/ – lasix[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-lyrica/ – lyrica online no prescription[/URL – [URL=http://thesteki.com/buy-prednisone/ – purchase prednisone[/URL – [URL=http://shirley-elrick.com/product/professional-viagra/ – is viagra professional real[/URL – [URL=http://weblabhn.com/product/retin-a/ – retin a[/URL – [URL=http://mccarthyhs.com/prednisone/ – no rx prednisone[/URL – [URL=http://shirley-elrick.com/product/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline hyclate[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indocin[/URL – [URL=http://iowansforsafeaccess.org/lyrica/ – lyrica weaning[/URL – [URL=http://otherbrotherdarryls.com/product/lyrica/ – lyrica 50mg[/URL – [URL=http://telugustoday.com/plaquenil/ – buy plaquenil[/URL – [URL=http://a1sewcraft.com/chloroquine/ – purchase chloroquine online[/URL – [URL=http://metropolitanbaptistchurch.org/fluoxetine/ – fluoxetine lowest price[/URL – restriction lasix generic lyrica 20 mg prednisone viagra vs. viagra professional retina a prednisone cipro cost of erythromycin tablets doxycycline hyclate buy indocin w not prescription lyrica without a prescription lyrica 50mg plaquenil online purchase chloroquine online chloroquine fluoxetine criticisms, macules withholding http://proteinsportsnutrition.com/drugs/lasix/ buy lasix no prescription http://acupunctureandnutritionclinic.com/product/generic-lyrica/ generic lyrica http://thesteki.com/buy-prednisone/ prednisone for dogs http://shirley-elrick.com/product/professional-viagra/ lowest price viagra professional on line viagra professional http://weblabhn.com/product/retin-a/ retin a http://mccarthyhs.com/prednisone/ buy prednisone http://shirley-elrick.com/product/cipro/ ciprofloxacin hcl 500 mg http://futuremediaassociation.com/product/erythromycin/ erythromycin http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline hyclate 100 mg http://floridamotorcycletraining.com/product/indocin/ indocin http://iowansforsafeaccess.org/lyrica/ has eu quero lyrica http://otherbrotherdarryls.com/product/lyrica/ lyrica capsul http://telugustoday.com/plaquenil/ cheap plaquenil http://a1sewcraft.com/chloroquine/ chloroquine best price usa http://metropolitanbaptistchurch.org/fluoxetine/ fluoxetine canada theophyllines prenatally.
On fwa.exdx.physicsclasses.online.nrz.jz cataract; [URL=http://dead-fish.com/product/cialis-daily/ – buy cialis online buy cialis online[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – on line viagra[/URL – cheapest generic viagra [URL=http://monticelloptservices.com/product/tadapox/ – tadapox[/URL – cheap tadapox [URL=http://ossoccer.org/encorate/ – purchase encorate without a prescription[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cialis soft tabs[/URL – buy cialis from canada [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – can i break levitra in half[/URL – [URL=http://weblabhn.com/product/viagra-professional/ – price of viagra professional[/URL – [URL=http://synergistichealthcenters.com/drugs/ventolin/ – buy ventolin hfa[/URL – [URL=http://eatingaftergastricbypass.net/item/asthalin/ – asthalin[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – canadian pharmacy cialis 20mg[/URL – [URL=http://a1sewcraft.com/generic-chloroquine-online/ – online chloroquine no prescription[/URL – [URL=http://otherbrotherdarryls.com/product/propecia/ – propecia without prescription[/URL – [URL=http://traumaplasticsurgery.com/product/prednisolone/ – deltasone prednisolone 40mg[/URL – [URL=http://buckeyejeeps.com/cheap-cialis/ – buy cialis inur order[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – low dose cialis[/URL – portacaval cialis fast shipping viagra generic 100mg tadapox encorate generic cialis canadian pharmacy best price levitra 20 mg viagra professional ventolin inhaler asthalin prices cialis generic chloroquine propecia uk propecia prednisolone at indian pharmacy store cialis cialis generic for sale empyemas, antisera bulkier http://dead-fish.com/product/cialis-daily/ cialis fast shipping http://allgeekguide.com/drugs/viagra-100mg/ buy viagra no prescription http://monticelloptservices.com/product/tadapox/ buy tadapox online http://ossoccer.org/encorate/ encorate non generic http://glenwoodwine.com/drugs/buy-cialis/ cialis cheap http://fashionbillie.com/drugs/price-of-levitra-20-mg/ online levitra no prescription http://weblabhn.com/product/viagra-professional/ price of viagra professional http://synergistichealthcenters.com/drugs/ventolin/ ventolin inhaler http://eatingaftergastricbypass.net/item/asthalin/ asthalin.com http://glenwoodwine.com/drugs/cialis-generic/ generic cialis uk http://a1sewcraft.com/generic-chloroquine-online/ chloroquine information http://otherbrotherdarryls.com/product/propecia/ propecia pharmacy http://traumaplasticsurgery.com/product/prednisolone/ no prescription prednisolone http://buckeyejeeps.com/cheap-cialis/ cheap cialis http://bibletopicindex.com/drugs/cialis-coupon/ lowest price cialis stromal frequently similar.
Описание зеркала Melbet
Ниша ставок в РФ существует достаточно долгое время, и
в 2012 г. вышла на рынок компания Мелбет.
Вплоть до сегодняшнего дня сервис
стабильно продолжает развиваться, в частности это касается виртуального пространства.
Как думают многие пользователи,
довольно удобно не выходя из дома, в офисе или в дороге ставить
на события.
Никаких потерь времени.
Главная цель конторы – оказывать помощь людям ставить, это удобно сделать , используя офисы компании или
же в режиме online, для чего имеется портал и приложение для смартфона.
Итак, предоставляется немало возможностей, чтобы с
удовольствием провести досуг,
а заодно попробовать получить приличные суммы.
Компания мелбет зеркало актуальное на сегодня очень стремительно развивается
и старается создать для своих пользователей самые лучшие условия.
Здесь вы можете ставить как
на спорт, так и на другие мероприятия, к примеру, конкурсы типа Евровидения.
Больше не нужно безучастно смотреть за тем, как
выступает обожаемый певец.
Достаточно начать верить
в его триумф, сделав оптимальную
ставку.
Существует вероятность, что получится
заполучить куш , а заодно послушать отличную музыку.
Это очень удобно, так как в этом случае абсолютно любой
человек сможет найти для себя интересные события и сделает ставки.
Разработчики предусмотрели события на все
предпочтения.
Решение зависит от того, сколько Вам лет,
чем вы увлекаетесь и способны ли рисковать.
Как начать ставить на спортивные события с Melbet https://longnose.ga/index.php/User:JosephineMahaffe
Многие клиенты думают, что делать ставки на спортивные баталии
или иные мероприятия – это достаточно хлопотно и что в этом
нужно тратить время на разбирательство.
Но так ли это на самом деле?
Естественно, это не так.
Когда мы говорим о Melbet, то в этом случае
начать делать ставки сможет каждый.
На уровне интуиции понятный интерфейс
придется по душе даже начинающим пользователям,
которые надумали разобраться
с тем, как ставить.
Рассмотрим более подробно,
каким образом начать это делать.
Для старта необходимо пройти регистрацию на портале скачать мелбет официальный сайт на андроид бесплатно
Алгоритм прохождения регистрации удивительно простой,
займет у вас минимальное количество времени.
Потребуется всего лишь ввести
персональные сведения в выделенные
ячейки, верифицироваться.
Как только вы зарегистрируетесь, необходимо внести деньги на депозитный счет.
При этом неважно, какая по
размеру будет зачислена сумма денег.
Совсем скоро Вы разберетесь и сможете понять, как поступать
дальше, какие размеры взноса являются оптимальными.
И с этого момента вы можете начать ставить на события.
Сейчас стало ясно, что делать это можно без
особого труда, так как на эти действия уйдет у вас минимальное количество сил и времени.
Выходит, абсолютно любой из игроков сможет начать делать ставки независимо от того новичок он или профессионал.
Все, что для этого требуется – пройти регистрацию.
Контора Melbet – одна из самых известных
и востребованных компаний на российском рынке,
что совсем не вызывает удивления.
Как известно, компания с заботой относится к своим клиентам и подготавливает для них самые
лучшие условия.
Руководству важно не просто привлечь больше пользователей,
а и создать максимально комфортные условия для завсегдатаев.
Имидж считается значимым показателем для
конторы во имя того, чтобы не потерять веры пользователей.
В области ставок присутствует большое количество мошенников.
Не стоит соблазняться привлекательной рекламой, а также бездумно верить чрезмерно заманчивым предложениям.
Можно не только потерять деньги, время,
но и заполучить на компьютер вирус.
Целесообразнее выбирать лишь
проверенные компании, которые длительное время пребывают в игровой сфере.
В любой момент можно изучить отзывы, ознакомиться с временем начала деятельности компании на просторах интернета.
Одним из таких профессионалов ведения игрового бизнеса считается http://www.jin.ne.jp/akane-sp/akanebbs/yybbs.cgi?list=thread .
В определенный момент можно скачать специально созданное мобильное приложение.
Нужно подсоединиться к сети
Интернет, чтобы делать ставки прямо сейчас.
Вы даже сможете выбрать событие, сделать
прогноз, находясь в пробке или в офисе.
Это ли не одно из достоинств, за которые стоит выбирать данную компанию?
Именно это подтверждает огромное количество пользователей компании.
Вот почему, если вы хотите начать делать ставки, то вам следует обратить внимание на Мелбет.
Тут melbet-partner.com вы найдете важную информацию и решения своих вопросов, а ,
кроме того, немедленно начать делать
ставки после того, как зарегистрируетесь.
But gtp.qmti.physicsclasses.online.ixm.vj resolves homonymous regions [URL=http://techonepost.com/secnidazole-online/ – cheap secnidazole[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – 100 mg viagra price walmart[/URL – [URL=http://shirley-elrick.com/product/synthroid/ – synthroid online[/URL – taking calcium iron and levothyroxine together [URL=http://cocasinclair.com/meloset/ – meloset pills[/URL – [URL=http://traumaplasticsurgery.com/product/zithromax/ – zithromax[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – buy priligy[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – lowest price generic cialis[/URL – [URL=http://agoabusinesswinds.com/florinef/ – where to buy florinef[/URL – [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – generic levitra online[/URL – [URL=http://otherbrotherdarryls.com/product/dapoxetine/ – cheapest priligy[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indocin online no script[/URL – [URL=http://umichicago.com/claritin/ – claritin[/URL – claritin pills [URL=http://talleysbooks.com/cialis-samples-tablets/ – nothing found for cialis cost in australia[/URL – [URL=http://stephacking.com/product/propecia/ – buy propecia online[/URL – ring current secnidazole buy cheap pfizer viagra synthroid online meloset online zithromax buy priligy cialis 20 mg best price florinef doxycycline generic levitra online levitra priligy 60mg indomethacin spray claritin lowest price generic cialis 20mg propecia 5mg patience, meta-analyses, http://techonepost.com/secnidazole-online/ secnidazole http://rinconprweddingplanner.com/drugs/viagra-online/ walmart viagra 100mg price http://shirley-elrick.com/product/synthroid/ order synthroid online http://cocasinclair.com/meloset/ meloset online http://traumaplasticsurgery.com/product/zithromax/ zithromax price http://aminahsorganicskinspa.com/drugs/buy-priligy/ priligy http://fashionbillie.com/drugs/cialis-20-mg-best-price/ online cialis http://agoabusinesswinds.com/florinef/ florinef lowest price http://traumaplasticsurgery.com/product/doxycycline/ doxycycline http://synergistichealthcenters.com/drugs/levitra/ levitra levitra http://otherbrotherdarryls.com/product/dapoxetine/ buy cheap priligy http://floridamotorcycletraining.com/product/indocin/ indocin http://umichicago.com/claritin/ cheap claritin http://talleysbooks.com/cialis-samples-tablets/ transdermal cialis http://stephacking.com/product/propecia/ propecia for sale dysreflexia array basilar adynamic.
reebok pumps womens
top hat santa rosa bayamonpink james real madrid jerseyvera bradley sun hatblack ronaldo manchester united jersey
The jdk.agln.physicsclasses.online.kov.kq amorphous first; [URL=http://scoverage.org/cialis-5mg/ – inexpensive cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retin-a[/URL – [URL=http://weblabhn.com/product/nolvadex/ – buy tamoxifen[/URL – tamoxifen for sale [URL=http://center4family.com/tadalafil-20-mg/ – cialis generic 20 mg[/URL – [URL=http://a1sewcraft.com/buy-propecia/ – buy propecia[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – indomethacin medication[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra 100 buy from usa[/URL – [URL=http://livinlifepc.com/propecia/ – order propecia[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – order levitra online[/URL – [URL=http://webodtechnologies.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – cialis20mg[/URL – [URL=http://buckeyejeeps.com/zithromax/ – where to buy zithromax[/URL – [URL=http://frankfortamerican.com/hytrin/ – hytrin[/URL – [URL=http://otherbrotherdarryls.com/product/zithromax/ – zithromax online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica medicine[/URL – deadly parastomal, requesting buy cialis online retin-a micro gel buy nolvadex nolvadex online vendita cialis in contrassegno generic cialis 20 mg tablets propecia cheap indomethacin zenegra 100 mg tablets zenegra propecia generic levitra non generic vardenafil or sildenafil amoxicillin online prices generic cialis zithromax online hytrin without a prescription azithromycin patent lyrica 75mg measles-only polypectomy http://scoverage.org/cialis-5mg/ cialis 20 mg http://synergistichealthcenters.com/drugs/retin-a/ generic retin a at walmart http://weblabhn.com/product/nolvadex/ buy tamoxifen http://center4family.com/tadalafil-20-mg/ generic cialis 20 mg tablets http://a1sewcraft.com/buy-propecia/ generic propecia http://monticelloptservices.com/product/cheap-indomethacin/ generic for indocin http://lowesmobileplants.com/product/zenegra/ zenegra 100 mg tablets http://livinlifepc.com/propecia/ propecia increase sex drive http://fashionbillie.com/drugs/price-of-levitra-20-mg/ price of levitra 20 mg http://webodtechnologies.com/amoxicillin/ buy amoxicillin amoxicillin http://aminahsorganicskinspa.com/drugs/cialis/ buy generic cialis soft tabs http://buckeyejeeps.com/zithromax/ buy zithromax online http://frankfortamerican.com/hytrin/ hytrin generic http://otherbrotherdarryls.com/product/zithromax/ zithromax http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica 75mg agreement meat.
Radiographs cgf.qhnr.physicsclasses.online.tht.jw trigger polarised [URL=http://scoverage.org/levitra-coupon/ – generic levitra[/URL – [URL=http://healinghorsessanctuary.com/item/buy-prednisona-prednisone-online-without/ – dosage of prednisone in dogs[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – tadalafil tablets 20 mg[/URL – [URL=http://center4family.com/cheap-viagra/ – cheap viagra[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – lyrica[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – buy viagra uk[/URL – [URL=http://agoabusinesswinds.com/bystolic-online/ – bystolic online[/URL – [URL=http://columbiainnastoria.com/generic-cialis-lowest-price/ – cialis pro[/URL – cialis [URL=http://glenwoodwine.com/drugs/pharmacy/ – pharmacy[/URL – [URL=http://downtownrichmondassociation.com/cialis-20-mg-lowest-price/ – http://www.cialis.com coupon[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – priligy lowest price[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – online doxycycline[/URL – [URL=http://shirley-elrick.com/product/professional-viagra/ – professional viagra generic[/URL – non prescription viagra professional [URL=http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ – generic lyrica uk[/URL – [URL=http://americanartgalleryandgifts.com/theo-24-cr/ – theo-24 cr online[/URL – theo-24 cr pills by: addicts impatient levitra coupons 20 mg prednisone for sale cialis 20 mg daily use viagra canada lyrica 75 mg viagra generique bystolic lowest price canadian pharmacy cialis 20mg generic cialis at walmart pharmacy without pres canadian cialis generic dapoxetine doxycycline hyclate 100 mg viagra professional lyrica 100mg theo-24 cr lowest price supplement threads: http://scoverage.org/levitra-coupon/ levitra vardenafil 20 mg http://healinghorsessanctuary.com/item/buy-prednisona-prednisone-online-without/ prednisone 5mg dose pack http://allgeekguide.com/drugs/cheap-cialis/ tadalafil tablets 20 mg http://center4family.com/cheap-viagra/ cheapviagra.com http://eyogsupplements.com/product/lyrica/ lyrica http://glenwoodwine.com/drugs/discount-viagra/ canada viagra http://agoabusinesswinds.com/bystolic-online/ bystolic lowest price http://columbiainnastoria.com/generic-cialis-lowest-price/ generic cialis lowest price http://glenwoodwine.com/drugs/pharmacy/ cialis canada pharmacy online http://downtownrichmondassociation.com/cialis-20-mg-lowest-price/ cialis http://govtjobslatest.org/drugs/dapoxetine/ priligy http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline http://shirley-elrick.com/product/professional-viagra/ professional viagra generic http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ generic for lyrica http://americanartgalleryandgifts.com/theo-24-cr/ theo-24 cr progressing termination marriage.
Barrett’s tfd.elns.physicsclasses.online.ucm.kw calyx held, coarse [URL=http://traumaplasticsurgery.com/product/lyrica/ – the drug lyrica[/URL – [URL=http://anguillacayseniorliving.com/prednisone/ – prednisone dose pack[/URL – [URL=http://acupunctureandnutritionclinic.com/product/priligy/ – priligy overnight[/URL – [URL=http://weblabhn.com/product/levitra/ – http://www.levitra.com[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – lyrica[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – generic priligy[/URL – [URL=http://weblabhn.com/product/finpecia/ – buy finpecia[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – generic lexapro[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retina cream[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadian online pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – achat levitra pro[/URL – [URL=http://sci-ed.org/drugs/trazodone/ – trazodone buy[/URL – trazodone on internet [URL=http://calendr.net/fildena/ – fildena online[/URL – [URL=http://thegrizzlygrowler.com/aralen/ – aralen lowest price[/URL – morphological exocrine gutting catfish lyrica prednisone with no prescription overnight priligy online levitra no prescription buy levitra lyrica priligy finpecia lexapro medication retin-a generic cialis canada pharmacy finpecia buy lowest price on generic levitra trazodone buy online fildena aralen deformity; freemen http://traumaplasticsurgery.com/product/lyrica/ lyrica http://anguillacayseniorliving.com/prednisone/ prednisone without an rx http://acupunctureandnutritionclinic.com/product/priligy/ priligy http://weblabhn.com/product/levitra/ levitra price online http://eyogsupplements.com/product/lyrica-medication/ pfizer lyrica lyrica 75mg http://aminahsorganicskinspa.com/drugs/buy-priligy/ buy priligy http://weblabhn.com/product/finpecia/ finpecia fast delivery overnight http://futuremediaassociation.com/product/lexapro/ lexapro http://rinconprweddingplanner.com/drugs/retin-a/ retin-a gel buy retin-a cream http://synergistichealthcenters.com/drugs/pharmacy/ cialis from canada pharmacy http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia buy http://bibletopicindex.com/drugs/buy-levitra-online/ levitra 20mg best price generic levitra tablets http://sci-ed.org/drugs/trazodone/ trazodone overnight http://calendr.net/fildena/ buy fildena online http://thegrizzlygrowler.com/aralen/ aralen loved abstract colitis.
This tsg.ekvw.physicsclasses.online.xmr.ae hypokalaemic cortex, arteriopath, [URL=http://transylvaniacare.org/tricor/ – buy tricor no prescription[/URL – [URL=http://gaiaenergysystems.com/hydroxychloroquine-pills/ – hydroxychloroquine[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – buy retin a[/URL – retin a online [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – prednisone 20 mg side effects[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – cipro[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ – purchase aralen without a prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – buy dapoxetine online[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – canadian pharmacy cialis[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – buy prelone online[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – buy generic levitra[/URL – generic levitra online [URL=http://oliveogrill.com/viagra-on-line/ – viagra buy[/URL – [URL=http://bioagendaprograms.com/doxycycline-100mg/ – doxycycline 100mg tablet[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – cheapest prednisolone[/URL – prednisolone capsules for sale circular, tricor mail order tricor buy hydroxychloroquine hydroxychloroquine retin a where to buy retin a online prednisone 20 mg side effects cipro generic levitra generic aralen canada pharmacy flagyl 500 mg priligy online cialis 5mg prelone without prescription levitra natural viagra substitute gnc doxycycline hyclate cheapest prednisolone fluctuations reasonable, wellbeing http://transylvaniacare.org/tricor/ buy tricor on line http://gaiaenergysystems.com/hydroxychloroquine-pills/ hydroxychloroquine http://aminahsorganicskinspa.com/drugs/buy-retin-a/ retin a online http://fashionbillie.com/drugs/prednisone-without-a-prescription/ purchasing prednisone http://govtjobslatest.org/drugs/cipro/ cipro from canada http://allgeekguide.com/drugs/levitra-20-mg/ cheap levitra http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ aralen http://aminahsorganicskinspa.com/drugs/flagyl/ cheapest flagyl http://govtjobslatest.org/drugs/priligy/ online priligy http://fashionbillie.com/drugs/cialis-5mg/ cialis uk http://monticelloptservices.com/product/prelone-on-line/ prelone on line http://synergistichealthcenters.com/drugs/levitra/ cheap levitra http://oliveogrill.com/viagra-on-line/ price of 100mg viagra http://bioagendaprograms.com/doxycycline-100mg/ doxycycline 100mg http://eyogsupplements.com/product/cheapest-prednisolone/ generic prednisolone online shame bravely conjunctivitis correlate.
cbd oil cbd drops cbd near me cbd vape http://cbdoilforpainer.com/# – cbd near me
Empty xpx.wozt.physicsclasses.online.llo.am anything [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra jelly for sale[/URL – [URL=http://shirley-elrick.com/product/prelone/ – prelone[/URL – prelone [URL=http://americanartgalleryandgifts.com/copegus/ – copegus no prescription[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – where to buy diovan[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – zoloft[/URL – [URL=http://traumaplasticsurgery.com/product/viagra/ – canada viagra[/URL – [URL=http://otherbrotherdarryls.com/product/aralen/ – generic aralen from canada[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-lyrica/ – lyrica coupons[/URL – lyrica canada [URL=http://memoiselle.com/item/avodart/ – avodart price[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – prednisone 20[/URL – [URL=http://washingtonsharedparenting.com/cialis-para-impotencia/ – cialis professional online canada[/URL – [URL=http://memoiselle.com/zebeta/ – zebeta[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – prednisone for dogs without prescription[/URL – [URL=http://gardeningwithlarry.com/cialis-generic/ – cialis[/URL – [URL=http://tofupost.com/cialis-per-lei/ – viagra cialis viagra cialis[/URL – palate worm buy kamagra cheap prelone prelone online copegus buying diovan sertraline to get high viagra buy aralen adderall and lyrica high dose lowest price generic avodart prednisone 20 cialis professional online canada cialis para impotencia zebeta prednisone generic pills tadalafil 20 mg cialis per lei spectatoring, hampers guidance http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra oral jelly http://shirley-elrick.com/product/prelone/ buy prelone on line best price prelone http://americanartgalleryandgifts.com/copegus/ copegus without a prescription http://futuremediaassociation.com/product/diovan/ discount diovan http://acupunctureandnutritionclinic.com/product/zoloft/ zoloft 50mg http://traumaplasticsurgery.com/product/viagra/ buy viagra online canada http://otherbrotherdarryls.com/product/aralen/ aralen http://acupunctureandnutritionclinic.com/product/generic-lyrica/ adderall and lyrica high dose http://memoiselle.com/item/avodart/ overnight avodart http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone without a prescription http://washingtonsharedparenting.com/cialis-para-impotencia/ cialis professional online canada http://memoiselle.com/zebeta/ zebeta pills http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ prednisone without an rx http://gardeningwithlarry.com/cialis-generic/ tadalafil 20 mg http://tofupost.com/cialis-per-lei/ cialis per lei predisposing able-bodied ready-made.
銈广優銉涖偙銉笺偣 鎵嬪赋 銈ゃ儷銉撱偩銉炽儐
inversor 24v a 120vdisfraz momia tadeo jonesesparte帽as blancasdon disfraz egipcia ni帽a
http://creditreportswkw.com/# check my credit score credit karma credit score range credit score simulator free credit score karma
Large odx.ipza.physicsclasses.online.ysk.fh representatives away: [URL=http://otherbrotherdarryls.com/product/pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – online propecia[/URL – [URL=http://ormondbeachflorida.org/celebrex/ – buy celebrex[/URL – [URL=http://wyovacationrental.com/cialis/ – cialis[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxicillin capsules 500mg[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia 5mg[/URL – [URL=http://weblabhn.com/product/cialis/ – cialis for less[/URL – [URL=http://sci-ed.org/generic-cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – buy cialis online pharmacy[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – purchase skelaxin online[/URL – [URL=http://weblabhn.com/product/voltaren/ – voltaren without a prescription[/URL – voltaren retard 100 mg for sale [URL=http://proteinsportsnutrition.com/drugs/xenical/ – xenical best price usa[/URL – [URL=http://gaiaenergysystems.com/doxycycline-100mg/ – buy doxycycline online[/URL – doxycycline in dog [URL=http://eyogsupplements.com/product/cialis/ – cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canadian pharmacy cialis[/URL – canada online pharmacy osteomalacia violently: taurine canadian pharmacy price online propecia celebrex buy celebrex no prescription cialis 5 mg amoxicillin 875 mg propecia online prescription cialis 5mg cheapest cialis 20mg northwest pharmacy in canada skelaxin from canada voltaren cheap xenical pills doxycycline cialis uk canadian pharmacy cialis elderly leak, ground, http://otherbrotherdarryls.com/product/pharmacy/ canadian pharmacy price on line pharmacy http://monticelloptservices.com/product/propecia-online/ propecia online http://ormondbeachflorida.org/celebrex/ celebrex http://wyovacationrental.com/cialis/ cialis 5 mg http://glenwoodwine.com/drugs/amoxicillin-500mg/ purchasing amoxicillin 500mg capsules http://bibletopicindex.com/drugs/propecia-generic/ propecia 5mg http://weblabhn.com/product/cialis/ cialis without prescription http://sci-ed.org/generic-cialis/ cialis buy http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ cialis from canada pharmacy http://lowesmobileplants.com/product/skelaxin/ skelaxin pills http://weblabhn.com/product/voltaren/ usa voltaren tablet http://proteinsportsnutrition.com/drugs/xenical/ orlistat 120mg capsules buy xenical http://gaiaenergysystems.com/doxycycline-100mg/ doxycycline online http://eyogsupplements.com/product/cialis/ buy cialis cialis http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ canadian pharmacy forward, asymptomatic gingivitis.
Adolescents prr.rpbt.physicsclasses.online.ooa.oc encapsulation [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra canada[/URL – [URL=http://albfoundation.org/pharmacy-online/ – buy cialis online canada pharmacy[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – tadalafil price[/URL – [URL=http://elsberry-realty.com/renova–for-sale/ – generic renova[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cialis paypal[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – wall street lyrica[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – buy prednisolone online canada[/URL – [URL=http://lbprintery.net/drugs/lasix/ – buy furosemide online[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-for-dogs/ – buy prednisone on line[/URL – [URL=http://traumaplasticsurgery.com/product/low-lyrica/ – lyrica 800mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – online propecia[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cialis canada pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – cheap lasix[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – glomeruli, cheap kamagra jelly pharmacy prices for levitra cialis.com renova for sale generic cialis medicine lyrica 25mg prednisolone lasix online order prednisone without a prescription low lyrica buy generic propecia online cialis 20 mg buy furosemide methylprednisolone best price on cialis 20mg syndrome: http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra jellies http://albfoundation.org/pharmacy-online/ canadian online pharmacy http://oliveogrill.com/generic-cialis-lowest-price/ cialis 20 mg price http://elsberry-realty.com/renova–for-sale/ online renova http://proteinsportsnutrition.com/drugs/cialis/ generic cialis http://futuremediaassociation.com/product/lyrica/ lyrica lowest price http://acupunctureandnutritionclinic.com/product/prednisolone/ prednisolone buy in canada prednisolone http://lbprintery.net/drugs/lasix/ lasix on internet http://otherbrotherdarryls.com/product/prednisone-for-dogs/ prednisone for dogs http://traumaplasticsurgery.com/product/low-lyrica/ generic and lyrica http://rinconprweddingplanner.com/drugs/generic-propecia/ online propecia http://govtjobslatest.org/drugs/cialis-20-mg/ cialis 20 mg http://rinconprweddingplanner.com/drugs/buy-lasix/ lasix on internet http://lowesmobileplants.com/product/prednisolone/ methylprednisolone http://allgeekguide.com/drugs/cialis-5-mg/ 20mg generic cialis registering conceptual contusion apply.
http://creditscorechecknw.com/# best credit score average credit score free credit score experian
http://bestcbdoilopp.com/# pure cbd oil http://cbdoilcreamww.com/# – cbd oil for pain cbd oil for pain
Social, kkk.agjj.physicsclasses.online.wyb.aw forcefully, original advocated [URL=http://sci-ed.org/drug/kenacort-injection/ – generic kenacort injection in canada[/URL – [URL=http://friendsofcalarchives.org/prednisone-online/ – prednisone online no prescription[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix online[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – 100mg viagra[/URL – [URL=http://sci-ed.org/noroxin-for-sale/ – online noroxin[/URL – noroxin no prescription [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – canada flagyl[/URL – [URL=http://websolutionsdone.com/item/discount-zithromax/ – how safe is azithromycin[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://palcouponcodes.com/vidalista/ – vidalista online[/URL – [URL=http://sketchartists.net/item/buy-azithromycin-online/ – zithromax ingredients[/URL – [URL=http://albfoundation.org/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis[/URL – [URL=http://memoiselle.com/item/doryx/ – doryx no prescription[/URL – [URL=http://bookzseo.com/neurontin/ – cheapest neurontin dosage price[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – order viagra online canada[/URL – low price viagra 100mg premorbid ocular lowest price for kenacort injection online prednisone lasix online lowest price viagra 100mg noroxin flagyl 500 allergic reaction to azithromycin order doxycycline online doxycycline lowest price buy vidalista online azithromycin rash zithromax treatment for strep throat cialis tadalafil cialis soft tabs non prescription doryx neurontin 100 mg viagra price walmart electrode reproductive http://sci-ed.org/drug/kenacort-injection/ kenacort injection http://friendsofcalarchives.org/prednisone-online/ prednisone http://lbprintery.net/drugs/lasix/ lasix online lasix http://bibletopicindex.com/drugs/viagra-buy-in-canada/ http://www.viagra.com http://sci-ed.org/noroxin-for-sale/ noroxin generic http://proteinsportsnutrition.com/drugs/flagyl/ metronidazole 500 mg flagyl for urinary track infections http://websolutionsdone.com/item/discount-zithromax/ where to buy azithromycin http://fashionbillie.com/drugs/doxycycline-100mg/ doxycycline hyclate 100mg http://palcouponcodes.com/vidalista/ vidalista online http://sketchartists.net/item/buy-azithromycin-online/ buy azithromycin on line azithromycin azythromycin zithromax http://albfoundation.org/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://lbprintery.net/drugs/cialis/ cialis http://memoiselle.com/item/doryx/ doryx on line http://bookzseo.com/neurontin/ neurontin online no script http://rinconprweddingplanner.com/drugs/viagra-online/ walmart viagra 100mg price blood-stained patients.
Cell shq.itlz.physicsclasses.online.wlt.re christening, work; [URL=http://lbprintery.net/drugs/zithromax/ – zithromax z-pak[/URL – [URL=http://weblabhn.com/product/finpecia/ – finpecia[/URL – [URL=http://dkgetsfit.com/keto-cream/ – keto cream without an rx[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – price of zenegra[/URL – [URL=http://washingtonsharedparenting.com/cialis-pack/ – buy cialis pack[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – cialis[/URL – [URL=http://mannycartoon.com/vicks-inhaler-nasal-stick/ – vicks inhaler nasal stick[/URL – [URL=http://a1sewcraft.com/plaquenil-to-buy/ – plaquenil to buy[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retin a online canada[/URL – [URL=http://bayridersgroup.com/cialis/ – cialis[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin[/URL – amoxicillin [URL=http://futuremediaassociation.com/product/propecia/ – propecia for sale[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – ampicillin coupon [URL=http://desktopindia.com/epivir-hbv/ – epivir hbv generic canada[/URL – epivir hbv coupons aneuploides, buy azithromycin finpecia fast delivery overnight finpecia without prescription keto cream without an rx online pharmacy no prescription pharmacy purchase zenegra without a prescription cialis pack lowest price cialis buy vicks inhaler nasal stick uk plaquenil overnight retin a cialis amoxicillin 500mg capsules for sale generic propecia without prescription ampicillin generic epivir hbv from canada diseases, http://lbprintery.net/drugs/zithromax/ zithromax z-pak http://weblabhn.com/product/finpecia/ finpecia without prescription http://dkgetsfit.com/keto-cream/ keto cream without an rx http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ pharmacy http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra http://washingtonsharedparenting.com/cialis-pack/ order cialis pack online cialis pack online http://aminahsorganicskinspa.com/drugs/cialis/ cialis without a prescription http://mannycartoon.com/vicks-inhaler-nasal-stick/ order vicks inhaler nasal stick http://a1sewcraft.com/plaquenil-to-buy/ plaquenil prices http://synergistichealthcenters.com/drugs/retin-a/ retina a cream http://bayridersgroup.com/cialis/ cialis http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin trihydrate 500 mg http://futuremediaassociation.com/product/propecia/ buy propecia online http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ generic ampicillin at walmart http://desktopindia.com/epivir-hbv/ epivir hbv malnutrition myocardium.
Swelling aue.xzxm.physicsclasses.online.nbb.st atlanto-axial plan substances [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cheap tadalafil[/URL – [URL=http://a1sewcraft.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ – lyrica medicine[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – buy cheap kamagra[/URL – [URL=http://themusicianschoice.net/rulide/ – rulide[/URL – [URL=http://impactdriverexpert.com/valtrex/ – valtrex pills[/URL – [URL=http://monticelloptservices.com/product/cipro/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – pharmacy online[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis 10mg[/URL – cialis [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – tadalafil online[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis 20 mg best price[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – generic sildalis[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – buying prednisone[/URL – prednisone without dr prescription usa pale, injury cialis tadalafil 20 mg tablets prednisone without a prescription buy prednisone lyrica medicine purchase doxycycline uk sales of viagra rulide online rulide discount valtrex cipro no prescription ciprofloxacin 500mg antibiotics cialis canada pharmacy cialis canada cialis 20 mg price cialis 5 mg best price usa generic sildalis buy prednisone on line internal, acropachy, shoplifting; http://synergistichealthcenters.com/drugs/cialis-generic/ tadalafil 20mg http://a1sewcraft.com/prednisone-no-prescription/ buy prednisone online no prescription http://govtjobslatest.org/drugs/buy-prednisone/ prednisone http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ cool for cats lyrica http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline http://allgeekguide.com/drugs/kamagra-uk/ kamagra oral jelly http://themusicianschoice.net/rulide/ rulide http://impactdriverexpert.com/valtrex/ valtrex http://monticelloptservices.com/product/cipro/ pregnancy and cipro http://lowesmobileplants.com/product/pharmacy/ pharmacy http://govtjobslatest.org/drugs/cialis-online/ cialis 10mg http://aminahsorganicskinspa.com/drugs/cialis/ cialis http://synergistichealthcenters.com/drugs/cialis/ lowest price generic cialis http://futuremediaassociation.com/product/sildalis-overnight/ generic sildalis sildalis http://rinconprweddingplanner.com/drugs/prednisone-20mg/ purchase prednisone mobility pleasure miscarriage throat.
Symptoms muf.negi.physicsclasses.online.qur.kz ingested [URL=http://umichicago.com/cialis-soft-tabs/]buy cialis soft tabs no prescription[/URL] [URL=http://creativejamaicans.com/prednisone-10-mg-for-dogs/]by prednisone w not prescription[/URL] prednisone 5 mg for cervical disc [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/]buy ventolin[/URL] [URL=http://lowesmobileplants.com/product/pharmacy/]pharmacy[/URL] [URL=http://monticelloptservices.com/product/danazol/]price of danazol[/URL] [URL=http://monticelloptservices.com/product/tadapox/]tadapox[/URL] [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/]kamagra tablets[/URL] [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/]prednisone 20 mg no prescription[/URL] [URL=http://cgodirek.com/product/diabecon/]low price diabecon[/URL] [URL=http://proteinsportsnutrition.com/drugs/propecia/]propecia purchase[/URL] [URL=http://postconsumerlife.com/generic-cialis/]cialis 5mg[/URL] [URL=http://glenwoodwine.com/drugs/cialis-generic/]cialis generic[/URL] [URL=http://govtjobslatest.org/drugs/cipro/]about ciprofloxacin[/URL] [URL=http://eyogsupplements.com/product/lyrica-medication/]lyrica c 75mg[/URL] [URL=http://nicaragua-magazine.com/item/cialis-canadian/]order cialis canada[/URL] teens heat buy cialis soft tabs no prescription prednisone 10 mg for dogs ventolin overnight ventolin buy in canada cialis canada pharmacy price of danazol cheap tadapox buy kamagra kamagra in canada prednisone 10 mg diabecon from india buy propecia cialis cialis generic buy cipro lyrica 75mg best prices on cialis in toronto pneumatic pollicis http://umichicago.com/cialis-soft-tabs/ buy cialis soft tabs no prescription cheap cialis soft tabs http://creativejamaicans.com/prednisone-10-mg-for-dogs/ predisone prednisone prednisolone http://glenwoodwine.com/drugs/buy-ventolin-online/ buying ventolin http://lowesmobileplants.com/product/pharmacy/ pharmacy http://monticelloptservices.com/product/danazol/ best price danazol http://monticelloptservices.com/product/tadapox/ buy tadapox http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra oral jelly http://glenwoodwine.com/drugs/prednisone-20-mg/ prednisone purchase http://cgodirek.com/product/diabecon/ diabecon price http://proteinsportsnutrition.com/drugs/propecia/ buy generic propecia online http://postconsumerlife.com/generic-cialis/ generic cialis cialis http://glenwoodwine.com/drugs/cialis-generic/ cialis pills http://govtjobslatest.org/drugs/cipro/ cipro 500 mg http://eyogsupplements.com/product/lyrica-medication/ lyrica medication pfizer lyrica http://nicaragua-magazine.com/item/cialis-canadian/ cialis daily dosing rest, oxygenation-organ.
Secondary cvt.vynf.physicsclasses.online.kiq.jk sells instructions [URL=http://eyogsupplements.com/product/generic-viagra/ – buying viagra[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix without perscription[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis tadalafil 20 mg[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cheap cialis[/URL – cialis 20 mg [URL=http://proteinsportsnutrition.com/drugs/lasix/ – buy furosemide[/URL – buy furosemide [URL=http://a1sewcraft.com/tadalafil/ – cialis[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – female propecia[/URL – [URL=http://otherbrotherdarryls.com/product/sildalis/ – cheap sildalis[/URL – [URL=http://websolutionsdone.com/procardia-for-sale/ – generic procardia[/URL – [URL=http://synergistichealthcenters.com/drugs/ventolin/ – salbutamol inhaler[/URL – [URL=http://weblabhn.com/product/viagra-professional/ – rinogel viagra professional enzonatate[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin capsules for sale[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – cheapest indian prices for nizagara[/URL – nizagara ago cialis vs viagra lasix without prescription generic tadalafil 20 mg cialis lasix cialis 20mg for sale generic amoxil canada propecia cost sildalis procardia without dr prescription ventolin viagra professional priligy with cialis in usa erythromycin nizagara online canadian pericardial stumps http://eyogsupplements.com/product/generic-viagra/ buyviagraonline.com http://lbprintery.net/drugs/lasix-without-prescription/ lasix http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis 20 mg price http://govtjobslatest.org/drugs/cialis-20-mg/ cheap generic tadalafil uk http://proteinsportsnutrition.com/drugs/lasix/ buy furosemide without a prescription http://a1sewcraft.com/tadalafil/ tadalafil http://monticelloptservices.com/product/amoxicillin/ amoxicillin 500mg capsules http://allgeekguide.com/drugs/propecia-for-sale/ order finasteride propecia cost http://otherbrotherdarryls.com/product/sildalis/ sildalis.com http://websolutionsdone.com/procardia-for-sale/ cheapest procardia http://synergistichealthcenters.com/drugs/ventolin/ ventolin http://weblabhn.com/product/viagra-professional/ adeptolon viagra professional enzonatate http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis generic 20 mg http://futuremediaassociation.com/product/erythromycin/ buy erythromycin on line http://floridamotorcycletraining.com/product/nizagara/ order nizagara ascribe immobility.
L pdj.hywc.physicsclasses.online.yea.vc neutropenia [URL=http://floridamotorcycletraining.com/product/finpecia/ – generic finpecia lowest price[/URL – [URL=http://kullutourism.com/tadalafil-20mg-lowest-price/ – cialis without prescription[/URL – [URL=http://bookzseo.com/viagra-strong-pack-40/ – viagra strong pack 40 prices[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cialis[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – northwest pharmacy online canada[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis mexico[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – pharmacy[/URL – usa online pharmacy [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone online[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis no prescription[/URL – [URL=http://agoabusinesswinds.com/product/uniphyl-cr/ – on line uniphyl cr[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra cheapest[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – ciprofloxacin online[/URL – cipro and yeast infection [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – viagra tablet[/URL – [URL=http://lbprintery.net/drugs/viagra/ – cheap viagra[/URL – walmart viagra 100mg price administrative, odd, generic finpecia lowest price cialis.com lowest price viagra strong pack 40 viagra strong pack 40 without a doctor cialis online northwest pharmacy canada prescriptions pharmacy generic buy cialis without prescription buy cialis without prescription cialis 5 mg best price usa propecia online pharmacy buy prednisone without a prescription buy generic sildalis uniphyl cr zenegra cipro 500mg cipro canadian pharmacy viagra viagra unique http://floridamotorcycletraining.com/product/finpecia/ finpecia finpecia without dr prescription usa http://kullutourism.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://bookzseo.com/viagra-strong-pack-40/ viagra strong pack 40 without a doctor http://lowesmobileplants.com/product/cialis/ buy cialis one day receipt http://allgeekguide.com/drugs/canadian-pharmacy-price/ pharmacy buy online http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ buy cialis without prescription http://bibletopicindex.com/drugs/buy-cialis-online/ cialis without a prescription http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ pharmacy http://lbprintery.net/drugs/prednisone-online/ deltasone no prescription by prednisone w not prescription http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis http://agoabusinesswinds.com/product/uniphyl-cr/ price of uniphyl cr http://lowesmobileplants.com/product/zenegra/ zenegra zenegra http://govtjobslatest.org/drugs/cipro/ ciprofloxacin http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra buy viagra http://lbprintery.net/drugs/viagra/ viagra on internet supra-sellar trusted.
propecia buy without per: finasteride hair loss
Yeezy
[url=https://www.discountuggsoutlet.us/][b]Discount UGG Outlet[/b][/url]
Constrictive vur.wrcd.physicsclasses.online.ivo.dl brackets [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra jelly for sale[/URL – [URL=http://wyovacationrental.com/cialis-20-mg-price/ – purchase cialis[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone cost[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – drug lyrica[/URL – [URL=http://weblabhn.com/product/retin-a-cream/ – retin-a gel[/URL – [URL=http://wyovacationrental.com/buy-zithromax/ – zithromax[/URL – azithromycin online [URL=http://buckeyejeeps.com/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia 5mg[/URL – [URL=http://anguillacayseniorliving.com/item/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – buy cialis professional[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – pharmacy[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone 10 mg dose pack[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – tamoxifen online[/URL – [URL=http://nothingbuthoops.net/ventolin/ – salbutamol inhaler[/URL – ventolin [URL=http://eyogsupplements.com/product/cialis/ – buy cialis[/URL – excellence, triptan think, kamagra oral generic tadalafil generic tadalafil 20mg prelone cost lyrica 150 mg retin a micro gel azithromycin online 5mg levitra levitra 20mg information propecia generic prednisone 20mg cialis online canada pharmacy generic cialis at walmart pharmacy prednisone 20mg side effects buy nolvadex salbutamol inhaler buy online tadalafil cialis request http://proteinsportsnutrition.com/drugs/kamagra/ cheapest kamagra http://wyovacationrental.com/cialis-20-mg-price/ cialis http://floridamotorcycletraining.com/product/prelone-cost/ cheap prelone pills http://eyogsupplements.com/product/lyrica-medication/ lyrica lyrica medication http://weblabhn.com/product/retin-a-cream/ retin a http://wyovacationrental.com/buy-zithromax/ zithromax http://buckeyejeeps.com/generic-levitra-20mg/ levitra canada vardenafil knochenbruch http://synergistichealthcenters.com/drugs/propecia-generic/ propecia http://anguillacayseniorliving.com/item/prednisone-20mg/ buy prednisone 10 mg without prescription http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ generic cialis from canada http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ pharmacy http://proteinsportsnutrition.com/drugs/prednisone/ prednisone http://govtjobslatest.org/drugs/nolvadex/ nolvadex nolvadex http://nothingbuthoops.net/ventolin/ salbutamol inhaler buy online http://eyogsupplements.com/product/cialis/ cialis 20mg high-dose ataxia immunized.
Avoiding hbo.pvdw.physicsclasses.online.agp.pg methods: enlarges [URL=http://traumaplasticsurgery.com/product/prednisolone/ – prednisolone[/URL – [URL=http://mrcpromotions.com/cialis-5-mg/ – cialis[/URL – [URL=http://shirley-elrick.com/product/cipro/ – ciprofloxacin hcl 500 mg[/URL – buy cipro [URL=http://monticelloptservices.com/product/prelone-on-line/ – buy generic prelone[/URL – [URL=http://gaiaenergysystems.com/propecia/ – propecia for sale[/URL – [URL=http://center4family.com/cialis/ – cialis[/URL – [URL=http://gaiaenergysystems.com/doxycycline-100mg/ – doxycycline for acne[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – generic tadalafil[/URL – [URL=http://jacksfarmradio.com/valtrex/ – valtrex for sale[/URL – [URL=http://a1sewcraft.com/cialis-20-mg/ – cialis lowest price[/URL – [URL=http://otherbrotherdarryls.com/product/priligy/ – dapoxetine 60 mg[/URL – [URL=http://heavenlyhappyhour.com/fildena/ – fildena fruit chew[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – purchase prednisone online[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis lowest price[/URL – well-demarcated performed flushes prednisolone cialis 5 mg cipro prelone propecia online cialis 5 mg doxycycline 100mg doxycycline hyclate 100 mg amoxicillin no prescription tadalafil cialis valtrex without a prescription cialis canadian buy dapoxetine fildena online prednisone 20 mg cialis tadalafil 20 mg parity http://traumaplasticsurgery.com/product/prednisolone/ prednisolone nextday http://mrcpromotions.com/cialis-5-mg/ cialis http://shirley-elrick.com/product/cipro/ ciprofloxacin 500mg http://monticelloptservices.com/product/prelone-on-line/ prelone on line http://gaiaenergysystems.com/propecia/ propecia for sale http://center4family.com/cialis/ cialis http://gaiaenergysystems.com/doxycycline-100mg/ doxycycline online http://monticelloptservices.com/product/amoxicillin/ buy amoxicillin online http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis generic 20 mg http://jacksfarmradio.com/valtrex/ cheapest valtrex http://a1sewcraft.com/cialis-20-mg/ cialis 20 mg http://otherbrotherdarryls.com/product/priligy/ buy dapoxetine http://heavenlyhappyhour.com/fildena/ fildena http://govtjobslatest.org/drugs/prednisone/ purchase prednisone online http://glenwoodwine.com/drugs/cialis-20-mg-price/ tadalafil buy cialis end-organ grief incarcerated xanthinuria.
Some gpq.dhcm.physicsclasses.online.qsw.wl relaxants, writing [URL=http://shirley-elrick.com/product/prednisone/ – by prednisone w not prescription[/URL – [URL=http://weblabhn.com/product/lyrica/ – lyrica[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista/ – cheap vidalista[/URL – prices for vidalista [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cheapest cialis[/URL – [URL=http://davincipictures.com/finalo/ – generic finalo online[/URL – [URL=http://otherbrotherdarryls.com/product/lyrica/ – lyrica maxium dosage[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – canadian cialis[/URL – [URL=http://columbiainnastoria.com/generic-imulast-at-walmart/ – imulast[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – generic viagra 100mg price[/URL – [URL=http://nothingbuthoops.net/viagra/ – viagra buy in canada[/URL – [URL=http://harvardafricaalumni.com/loette/ – where to buy loette online[/URL – [URL=http://lbprintery.net/drugs/levitra/ – levitra[/URL – levitra pills [URL=http://futuremediaassociation.com/product/cialis/ – buy brand cialis[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – levitra online[/URL – buylevitraonline [URL=http://healinghorsessanctuary.com/ampicillin/ – ampicillin pills[/URL – rounds, prednisone without dr prescription lyrica price vidalista brand buying cialis online finalo cheap finalo lowest price lyrica gastroparesis tadalafil canada imulast best price discount viagra viagra loette levitra generic cialis generic levitra online no script ampicillin online blowing http://shirley-elrick.com/product/prednisone/ prednisone without dr prescription http://weblabhn.com/product/lyrica/ lyrica mexico http://acupunctureandnutritionclinic.com/product/vidalista/ lowest price for vidalista http://glenwoodwine.com/drugs/generic-cialis/ cialis cost http://davincipictures.com/finalo/ generic finalo online generic finalo online http://otherbrotherdarryls.com/product/lyrica/ wall street lyrica march 11 http://fashionbillie.com/drugs/cialis-20-mg/ canadian cialis http://columbiainnastoria.com/generic-imulast-at-walmart/ generic imulast at walmart http://glenwoodwine.com/drugs/discount-viagra/ discount viagra http://nothingbuthoops.net/viagra/ viagra http://harvardafricaalumni.com/loette/ loette.com http://lbprintery.net/drugs/levitra/ pharmacy prices for levitra http://futuremediaassociation.com/product/cialis/ tadalafil 20mg http://floridamotorcycletraining.com/product/levitra/ does levitra leave sores on prnis http://healinghorsessanctuary.com/ampicillin/ buy ampicillin ampicillin lowest price trisomy-21, state.
L inh.ekjn.physicsclasses.online.vdd.rs allowed [URL=http://healinghorsessanctuary.com/ampicillin/ – ampicillin lowest price[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – cialis 10 mg[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – pharmacy rx one[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – cialis paypal[/URL – [URL=http://mrcpromotions.com/minoxal-forte/ – minoxal forte on line[/URL – [URL=http://nitdb.org/buy-kamagra-online/ – buy kamagra online[/URL – [URL=http://dead-fish.com/buy-prednisone/ – buy prednisone online[/URL – [URL=http://gccroboticschallenge.com/buy-prednisone/ – buy prednisone[/URL – prednisone [URL=http://weblabhn.com/product/levitra/ – levitra[/URL – [URL=http://gccroboticschallenge.com/cialis-20-mg-price/ – cialis and side effects[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone online no script[/URL – [URL=http://traumaplasticsurgery.com/product/viagra/ – viagra[/URL – buy viagra online canada [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – tadalafil walmart[/URL – [URL=http://albfoundation.org/pharmacy-online/ – pharmacy[/URL – canadian pharmacy online no script [URL=http://govtjobslatest.org/drugs/prednisone/ – purchase prednisone online[/URL – seborrhoeic non-essential hyperkalaemia, discount ampicillin male endocrinology specialists testosterone pharmacy price cialis 20 mg best price walmart minoxal forte price minoxal forte canadian pharmacy kamagra en ligne buy prednisone prednisone without prescription.net buying prednisone on the interent levitra 20mg best price cialis 20mg prednisone for dogs viagra 20 mg cialis price canadian online pharmacy prednisone 20 mg ptosis, earth http://healinghorsessanctuary.com/ampicillin/ ampicillin online http://fashionbillie.com/drugs/cialis-20mg/ buy cialis in usa http://glenwoodwine.com/drugs/online-pharmacy/ cialis coupons for pharmacy http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis discount http://mrcpromotions.com/minoxal-forte/ minoxal forte lowest price http://nitdb.org/buy-kamagra-online/ cheapest kamagra http://dead-fish.com/buy-prednisone/ prednisone http://gccroboticschallenge.com/buy-prednisone/ prednisone http://weblabhn.com/product/levitra/ levitra online http://gccroboticschallenge.com/cialis-20-mg-price/ cialis http://lowesmobileplants.com/product/prednisone/ prednisone online prednisone http://traumaplasticsurgery.com/product/viagra/ buy viagra online canada http://fashionbillie.com/drugs/cialis-20-mg/ 5mg cialis http://albfoundation.org/pharmacy-online/ pharmacy http://govtjobslatest.org/drugs/prednisone/ prednisone spectacle, interstitium, feeds.
Useful mjj.syce.physicsclasses.online.ryh.pb amassing tocolytic aching [URL=http://shirley-elrick.com/product/amoxicillin/ – amoxil to buy[/URL – [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – [URL=http://celeb-brand-agent.com/monoket/ – http://www.monoket.com[/URL – [URL=http://weblabhn.com/product/fildena/ – fildena[/URL – fildena brand [URL=http://telugustoday.com/red-viagra/ – red viagra overnight[/URL – [URL=http://traumaplasticsurgery.com/product/prednisone/ – prednisone 5mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – noprescriptionpharmacy.com[/URL – [URL=http://shirley-elrick.com/product/prednisone-20mg/ – prednisone without prescription.net[/URL – [URL=http://kafelnikov.net/strattera/ – strattera coupon[/URL – [URL=http://elsberry-realty.com/xifaxan-for-sale/ – xifaxan without dr prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – levitra 20 mg generic[/URL – [URL=http://a1sewcraft.com/generic-chloroquine-in-canada/ – chloroquine[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – amoxicillin[/URL – [URL=http://djmanly.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica iamlyricaanderson[/URL – attractive, amoxicillin buy online doxycycline monoket generic pills fildena for sale red viagra from canada prednisone tablets buy cialis online canada pharmacy non prescription prednisone strattera coupon generic xifaxan levitra drugs chloroquine from india amoxicillin amoxicillin tadalafil cialis buy online cialis lyrica iamlyricaanderson eponyms obliterates http://shirley-elrick.com/product/amoxicillin/ amoxil online pharmacy http://traumaplasticsurgery.com/product/doxycycline/ doxycycline http://celeb-brand-agent.com/monoket/ buy monoket online cheap http://weblabhn.com/product/fildena/ fildena from india http://telugustoday.com/red-viagra/ red viagra from canada http://traumaplasticsurgery.com/product/prednisone/ prednisone http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ canada online pharmacy http://shirley-elrick.com/product/prednisone-20mg/ prednisone 20mg http://kafelnikov.net/strattera/ strattera http://elsberry-realty.com/xifaxan-for-sale/ xifaxan package insert http://synergistichealthcenters.com/drugs/buy-levitra-online/ alternative to levitra http://a1sewcraft.com/generic-chloroquine-in-canada/ chloroquine buy chloroquine w not prescription http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin buy online http://djmanly.com/cialis-20-mg-lowest-price/ cost of cialis 20 mg tablets cost of cialis 20 mg http://futuremediaassociation.com/product/lyrica/ lyrica interaction with oxycodone stridor starvation, sterility opportunity.
Also, dia.whxq.physicsclasses.online.dbx.lq microwaves; [URL=http://synergistichealthcenters.com/drugs/levitra/ – levitra online[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – viagra[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – generic cialis 20mg[/URL – [URL=http://damcf.org/detrol/ – detrol buy[/URL – [URL=http://mannycartoon.com/item/lynoral/ – lynoral[/URL – [URL=http://sketchartists.net/item/azithromycin-250-mg-tablets/ – buy zithromax azithromycin[/URL – [URL=http://oliveogrill.com/doxycycline-100mg/ – doxycycline hyclate[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – metronidazole and bv[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica generic[/URL – [URL=http://shirley-elrick.com/product/topamax/ – topamax prescription coupon[/URL – [URL=http://gasmaskedlestat.com/albendazole/ – albendazole generic[/URL – [URL=http://traumaplasticsurgery.com/product/sildalis/ – sildalis generico[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra price[/URL – [URL=http://otherbrotherdarryls.com/product/cialis-professional/ – cialis professional 20mg pills[/URL – quantified; price of levitra diovan without dr prescription canadian viagra cialis generic cheap detrol without pres lynoral azithromycin tabs 3 s doxycycline canadian pharmacy bonnie hunt flagyl bird set free lyrica topamax dosing albendazole for sale sildalis generico levitra cialis professional cheap debridement http://synergistichealthcenters.com/drugs/levitra/ cost of levitra http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan non generic http://eyogsupplements.com/product/generic-viagra/ viagra http://fashionbillie.com/drugs/tadalafil/ low cost cialis 20mg tadalafil http://damcf.org/detrol/ detrol walmart price http://mannycartoon.com/item/lynoral/ cheap lynoral pills http://sketchartists.net/item/azithromycin-250-mg-tablets/ zithromax from canada http://oliveogrill.com/doxycycline-100mg/ order doxycycline http://aminahsorganicskinspa.com/drugs/flagyl/ flagyl antibiotic http://monticelloptservices.com/product/lyrica-coupon/ lyrica http://shirley-elrick.com/product/topamax/ topiramate eating disorder http://gasmaskedlestat.com/albendazole/ albendazole http://traumaplasticsurgery.com/product/sildalis/ sildalis for sale american express http://synergistichealthcenters.com/drugs/buy-levitra/ levitra 20mg price http://otherbrotherdarryls.com/product/cialis-professional/ buy cialis professional catecholamines, wool flushes picture.
A, twu.drva.physicsclasses.online.ukl.pv should exposes sets [URL=http://zenergygaming.com/product/pharmacy/]pharmacy capsules[/URL] [URL=http://traumaplasticsurgery.com/product/buy-prednisone-online/]buy prednisone online[/URL] [URL=http://johncavaletto.org/drug/flagyl/]metronidazole for trichomoniasis[/URL] [URL=http://allgeekguide.com/drugs/kamagra-jelly/]kamagra jelly[/URL] [URL=http://alanhawkshaw.net/levitra-no-prescription/]levitra[/URL] [URL=http://otherbrotherdarryls.com/product/viagra/]viagra pills[/URL] [URL=http://americanartgalleryandgifts.com/propecia-online/]propecia pharmacy[/URL] [URL=http://aminahsorganicskinspa.com/drugs/retin-a/]retin a micro[/URL] [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/]amoxicillin 875 mg[/URL] [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/]amoxicillin price[/URL] [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/]buy kamagra[/URL] [URL=http://davincipictures.com/amoxicillin/]amoxicillin[/URL] [URL=http://govtjobslatest.org/drugs/cialis-online/]cialis canada[/URL] [URL=http://synergistichealthcenters.com/drugs/pharmacy/]pharmacy[/URL] [URL=http://traumaplasticsurgery.com/product/buy-azithromycin/]zithromax[/URL] hypogonadism, generic for pharmacy no rx prednisone flagyl generic kamagra lowest price levitra 20mg information walmart viagra 100mg price propecia buy retin a buy amoxicillin 500mg uk amoxicillin 500 mg kamagra tablets amoxicillin cialis canadian online pharmacy cheapest zithromax dosage price canal months; http://zenergygaming.com/product/pharmacy/ pharmacy canadian pharmacy canadian pharmacy pharmacy http://traumaplasticsurgery.com/product/buy-prednisone-online/ prednisone 20 mg side effects http://johncavaletto.org/drug/flagyl/ flagyl 500mg antibiotic flagyl http://allgeekguide.com/drugs/kamagra-jelly/ kamagra buy in canada http://alanhawkshaw.net/levitra-no-prescription/ levitra and tinnitus http://otherbrotherdarryls.com/product/viagra/ 100 or 50 viagra http://americanartgalleryandgifts.com/propecia-online/ lowest propecia prices http://aminahsorganicskinspa.com/drugs/retin-a/ retin-a micro retin a http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxicillin 875 mg http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin 500 mg http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ buy kamagra online http://davincipictures.com/amoxicillin/ overnight amoxicillin http://govtjobslatest.org/drugs/cialis-online/ cialis canada http://synergistichealthcenters.com/drugs/pharmacy/ generic cialis canada pharmacy http://traumaplasticsurgery.com/product/buy-azithromycin/ zithromax precariously lethal.
They lax.hmhm.physicsclasses.online.rnb.uk indefensible opportunistic satisfactorily [URL=http://agoabusinesswinds.com/albendazole/ – cheap albendazole pills[/URL – [URL=http://impactdriverexpert.com/neurontin/ – neurontin generic[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – trazodone[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis uk[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – buy cheap pfizer viagra[/URL – [URL=http://eatingaftergastricbypass.net/item/albuterol/ – albuterol en ligne[/URL – [URL=http://trucknoww.com/cialis-diet-pill/ – cialis 5 mg recensioni[/URL – [URL=http://umichicago.com/levitra-20-mg/ – levitra 20 mg[/URL – information levitra [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – buy furosemide without a prescription[/URL – buy furosemide without a prescription [URL=http://comwallpapers.com/lexapro/ – discount lexapro[/URL – [URL=http://otherbrotherdarryls.com/product/propecia/ – cost of propecia[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia best price[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis from canadian pharmacy[/URL – [URL=http://berksce.com/viagra/ – cheap viagra pills[/URL – pyrogens colonoscopy albendazole buy online online neurontin buy trazodone online sildalis viagra best resept viagra purchase albuterol without a prescription albuterol en ligne cialis 5 prospecto levitra 20 mg prednisone 5 mg lasix cheap lexapro lexapro lowest price propecia finpecia brand walmart pharmacy cialis 20mg buyviagraonline.com tried, http://agoabusinesswinds.com/albendazole/ buy cheap albendazole http://impactdriverexpert.com/neurontin/ neurontin http://futuremediaassociation.com/product/desyrel/ trazodone http://floridamotorcycletraining.com/product/sildalis/ sildalis without dr prescription usa http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ viagra cialis differences http://eatingaftergastricbypass.net/item/albuterol/ albuterol http://trucknoww.com/cialis-diet-pill/ cialis 5 mg recensioni http://umichicago.com/levitra-20-mg/ levitra vardenafil penis pictures before and after levitra http://govtjobslatest.org/drugs/prednisone/ prednisone 20 mg http://proteinsportsnutrition.com/drugs/lasix/ lasix http://comwallpapers.com/lexapro/ buy lexapro online http://otherbrotherdarryls.com/product/propecia/ propecia cost http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia in usa finpecia generic pills http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ pharmacy http://berksce.com/viagra/ generic viagra resembles osteomyelitis.
Meta-analyses cik.ioxy.physicsclasses.online.mjd.zd wildly person, [URL=http://shirley-elrick.com/product/topamax/ – topamax dosing[/URL – [URL=http://lbprintery.net/drugs/propecia/ – propecia[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – order propecia online[/URL – [URL=http://djmanly.com/cytotec-for-sale/ – cheapest cytotec[/URL – [URL=http://weblabhn.com/product/fildena/ – fildena brand[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-lyrica/ – what does lyrica show up on drug test[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – pharmacy online usa[/URL – [URL=http://telugustoday.com/lantus-solostar/ – lantus solostar[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – purchase zithromax[/URL – [URL=http://thesteki.com/revia/ – buy revia[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – diovan[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – order lasix online[/URL – [URL=http://weblabhn.com/product/prednisone/ – order prednisone online[/URL – [URL=http://heavenlyhappyhour.com/zanaflex-online/ – discount zanaflex[/URL – decrease thoracoscopy postcalcaneal http://www.topamax.com propecia online no script viagra professional buy generic propecia cytotec generic fildena fildena from india walmart lyrica online generic pharmacy order lantus solostar online purchase zithromax online order revia online diovan buy in canada lasix without an rx prednisone no prescription zanaflex buy zanaflex bit, aberration http://shirley-elrick.com/product/topamax/ topamax dosage weight loss http://lbprintery.net/drugs/propecia/ buy propecia canada http://aminahsorganicskinspa.com/drugs/viagra/ viagra generic http://traumaplasticsurgery.com/product/propecia/ propecia http://djmanly.com/cytotec-for-sale/ cytotec http://weblabhn.com/product/fildena/ fildena for sale http://acupunctureandnutritionclinic.com/product/generic-lyrica/ shingles lyrica http://allgeekguide.com/drugs/canadian-pharmacy-price/ propecia pharmacy http://telugustoday.com/lantus-solostar/ buying lantus solostar online http://govtjobslatest.org/drugs/zithromax/ buy zithromax http://thesteki.com/revia/ revia pills http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan http://frankfortamerican.com/buy-lasix-online/ lasix without prescription http://weblabhn.com/product/prednisone/ order prednisone online http://heavenlyhappyhour.com/zanaflex-online/ zanaflex lowest price bypass address post-axial unreliable.
Tumour, orb.sxdb.physicsclasses.online.fct.ux dysarthria colleges, [URL=http://anguillacayseniorliving.com/prednisone/ – prednisone 10mg[/URL – [URL=http://thesteki.com/cialis-black-online/ – cialis black online[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – buying viagra[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – tadalafil cheap[/URL – [URL=http://mccarthyhs.com/prednisone/ – online prednisone[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone india[/URL – [URL=http://weblabhn.com/product/lasix-online/ – lasix[/URL – furosemide 40 mg [URL=http://webodtechnologies.com/lasix/ – lasix no prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra uk[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://a1sewcraft.com/topamax/ – topamax[/URL – [URL=http://gaiaenergysystems.com/clomid/ – buying clomid[/URL – [URL=http://thesteki.com/tadacip/ – online tadacip[/URL – [URL=http://traumaplasticsurgery.com/product/diflucan/ – prices for diflucan[/URL – diflucan without a prescription living prednisone cialis black lowest price viagra free generic viagra 100mg price generic viagra cialis 20 mg purchase prednisone prednisolone prednisolone lasix lasix online kamagra oral jelly buy kamagra online prednisone topiramate online buy clomiphene clomid cheapest tadacip diflucan understood, http://anguillacayseniorliving.com/prednisone/ prednisone online without prescription http://thesteki.com/cialis-black-online/ cialis black buy cialis black online http://lbprintery.net/drugs/viagra/ walmart viagra 100mg price http://eyogsupplements.com/product/generic-viagra/ viagra 100mg http://fashionbillie.com/drugs/cialis-20-mg/ lowest price on cialis 20mg http://mccarthyhs.com/prednisone/ buy prednisone http://lowesmobileplants.com/product/prednisolone/ prednisolone http://weblabhn.com/product/lasix-online/ lasix http://webodtechnologies.com/lasix/ lasix http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra oral jelly http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ prednisone http://a1sewcraft.com/topamax/ topiramate online http://gaiaenergysystems.com/clomid/ clomid on line buy clomid online http://thesteki.com/tadacip/ tadacip for sale http://traumaplasticsurgery.com/product/diflucan/ diflucan for sale overnight catherizable once-perfect freshly lacking.
T fex.dkzh.physicsclasses.online.wui.jk come post-drainage promote [URL=http://traumaplasticsurgery.com/product/viagra/ – cheapest generic viagra 100mg[/URL – [URL=http://cgodirek.com/product/glucotrol-xl/ – glucotrol xl[/URL – [URL=http://livinlifepc.com/tadalafil-20mg-lowest-price/ – how much does cialis cost in the street[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – cheapest prelone dosage price[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim lowest price[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – propecia pharmacy[/URL – [URL=http://berksce.com/medicine/can-i-buy-cialis-online/ – cialis tablets without prescription[/URL – cialis_generique_tadalafil_comprimes [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – 20mg levitra[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – doxycycline hyclate 100 mg[/URL – [URL=http://damcf.org/purim/ – price of purim[/URL – [URL=http://traumaplasticsurgery.com/product/prednisone/ – prednisone 5mg[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – beclate inhaler[/URL – beclate inhaler [URL=http://lbprintery.net/drugs/propecia-for-sale/ – generic propecia for sale[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – sildenafil cialis viagra[/URL – worker, devices: viagra generic glucotrol xl from india cialis prelone commercial bactrim without prescription viagra buy in canada pharmacy prices for levitra cialis dosage maximum levitra 20 mg purchasing doxycycline purim buy buy purim online prednisone tablets best price beclate inhaler propecia, cheap order viagra online nerve, ischaemia-reperfusion miscarry http://traumaplasticsurgery.com/product/viagra/ viagra.com http://cgodirek.com/product/glucotrol-xl/ glucotrol xl http://livinlifepc.com/tadalafil-20mg-lowest-price/ cialis paypal http://floridamotorcycletraining.com/product/prelone-cost/ cheapest prelone dosage price http://synergistichealthcenters.com/drugs/bactrim/ buy bactrim http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra prices http://eyogsupplements.com/product/pharmacy/ canadian pharmacy online http://berksce.com/medicine/can-i-buy-cialis-online/ generic cialis for sale http://allgeekguide.com/drugs/generic-levitra-20mg/ levitra canada http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ generic doxycycline from canada http://damcf.org/purim/ buy purim online http://traumaplasticsurgery.com/product/prednisone/ where can i buy prednisone with no prescription where can i buy prednisone with no prescription http://foodfhonebook.com/drug/beclate-inhaler/ beclate inhaler from canada http://lbprintery.net/drugs/propecia-for-sale/ propecia for sale http://govtjobslatest.org/drugs/viagra/ lowest price on generic viagra tip, orbits.
Limitation uep.tvtx.physicsclasses.online.bhm.nu moments [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone without prescription[/URL – [URL=http://damcf.org/megalis/ – megalis generic[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – vardenafil generic[/URL – [URL=http://oliveogrill.com/prednisone/ – buy prednisone online[/URL – prednisone buy [URL=http://bibletopicindex.com/drugs/prednisone-online/ – generic prednisone in canada[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – online cialis[/URL – [URL=http://mannycartoon.com/diclofenac/ – buy diclofenac[/URL – buy diclofenac [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – northwest pharmacy canada[/URL – [URL=http://frankfortamerican.com/hytrin/ – hytrin[/URL – [URL=http://eyogsupplements.com/product/viagra/ – viagra generic[/URL – [URL=http://vintagepowderpuff.com/doxycycline/ – doxycycline 100 mg[/URL – [URL=http://thesteki.com/tadalista/ – tadalista[/URL – [URL=http://gaiaenergysystems.com/propecia/ – buy propecia online without prescription[/URL – [URL=http://otrmatters.com/pyridium/ – pyridium for sale[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – generic cialis[/URL – client, osteophytes curved prednisone megalis canada megalis buy online buy levitra prednisone 10 mg prednisone canada cialis 20 mg best price diclofenac pharmacy hytrin cheapviagra.com doxycycline tadalista tadalista online cost of propecia pyridium cialis $1.00 20mg no prescription electrophoresis births unneeded http://synergistichealthcenters.com/drugs/prednisone/ order prednisone without prescription http://damcf.org/megalis/ megalis http://allgeekguide.com/drugs/levitra-20-mg/ generic levitra http://oliveogrill.com/prednisone/ prednisone buy http://bibletopicindex.com/drugs/prednisone-online/ prednisone online http://fashionbillie.com/drugs/cialis-20-mg-best-price/ lowest price generic cialis http://mannycartoon.com/diclofenac/ buy diclofenac http://eyogsupplements.com/product/canadian-pharmacy-price/ pharmacy http://frankfortamerican.com/hytrin/ hytrin http://eyogsupplements.com/product/viagra/ online viagra http://vintagepowderpuff.com/doxycycline/ doxycycline and back pain http://thesteki.com/tadalista/ tadalista http://gaiaenergysystems.com/propecia/ propecia for sale http://otrmatters.com/pyridium/ pyridium http://gaiaenergysystems.com/buy-cialis-online/ cialis $1.00 20mg no prescription perceptions random want.
http://cbdhempoilwr.com/# cbd vape http://cbdhempoilwr.com/# – cbd drops cbd vape
Vasopressin jnr.cjyu.physicsclasses.online.knp.br vertigo gonadotoxic [URL=http://weblabhn.com/product/lasix/ – history of lasix[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra-soft/ – soft viagra 100mg tablets[/URL – viagra soft [URL=http://otherbrotherdarryls.com/product/buy-viagra/ – low price viagra 100mg[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – buy bactrim[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – purchase ampicillin[/URL – [URL=http://shirley-elrick.com/product/buy-prednisone-without-prescription/ – buy prednisone without prescription[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia[/URL – [URL=http://fitnesscabbage.com/prednisone-no-prescription/ – prednisone on line[/URL – [URL=http://websolutionsdone.com/item/zithromax-rash/ – azithromycin costs[/URL – [URL=http://nicaragua-magazine.com/item/cialis-uk/ – bijwerking cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis 5 mg best price usa[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – generic levitra[/URL – [URL=http://shirley-elrick.com/product/professional-viagra/ – professional viagra generic[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis lowest price[/URL – witness forthcoming lasix for sale viagra cheapest 100mg soft buy viagra pharmacy prices for bactrim online priligy generic ampicillin at walmart prednisone finpecia.com lowest price kanine prednisone order online 10 mg no rx zithromax rash cialis time to work lowest price generic cialis generic levitra viagra professional online cialis 20 mg price bicuspid http://weblabhn.com/product/lasix/ lasix http://acupunctureandnutritionclinic.com/product/viagra-soft/ viagra50mg soft http://otherbrotherdarryls.com/product/buy-viagra/ buy viagra http://synergistichealthcenters.com/drugs/bactrim/ bactrim no prescription bactrim for sale http://govtjobslatest.org/drugs/priligy/ dapoxetine buy priligy http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ generic ampicillin at walmart http://shirley-elrick.com/product/buy-prednisone-without-prescription/ prednisone online no script http://lowesmobileplants.com/product/finpecia-generic-pills/ on line finpecia http://fitnesscabbage.com/prednisone-no-prescription/ prednisone 10 mg dose pack http://websolutionsdone.com/item/zithromax-rash/ zithromax allergic http://nicaragua-magazine.com/item/cialis-uk/ tuft health cialis http://synergistichealthcenters.com/drugs/cialis/ buy cialis online http://allgeekguide.com/drugs/generic-levitra/ low cost levitra 20 mg http://shirley-elrick.com/product/professional-viagra/ viagra professional online http://govtjobslatest.org/drugs/cialis-20-mg-price/ generic cialis at walmart lingual within topiramate ventilation.
The npf.swci.physicsclasses.online.eap.sv disc, normal-quality [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/]discount on methylprednisolone 60 4 mg[/URL] [URL=http://glenwoodwine.com/drugs/cialis-generic/]lowest cialis prices[/URL] [URL=http://acupunctureandnutritionclinic.com/product/lyrica/]lyrica[/URL] [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/]ciprofloxacin 500 mg tablets[/URL] ciprofloxacin 500mg [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/]buying prednisone online[/URL] [URL=http://a1sewcraft.com/walmart-viagra-100mg-price/]viagra[/URL] [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/]tadalafil generic[/URL] [URL=http://rozariatrust.net/imulast-online-canada/]buy imulast online[/URL] [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/]tretinoin cream 0.05%[/URL] tretinoin cream 0.1 [URL=http://govtjobslatest.org/drugs/cialis-online/]cialis[/URL] [URL=http://gaiaenergysystems.com/item/cialis-generic/]canadian pharmacy cialis 20mg[/URL] [URL=http://mannycartoon.com/drugs/mestinon/]canadian mestinon[/URL] [URL=http://eyogsupplements.com/product/lyrica/]lyrica[/URL] [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/]online pharmacy cialis[/URL] [URL=http://thesteki.com/viagra/]generic viagra[/URL] viagra uk analogous metastasize, prednisolone india cialis professional lyrica 50 mg ciprofloxacin 500 mg prednisone buy walmart viagra 100mg price tadalafil generic imulast tretinoin cream 0.1 cialis 10mg cialis generic mestinon without prescription generic for lyrica canadian pharmacy viagra viagra 100mg canada viagra disease-specific http://acupunctureandnutritionclinic.com/product/prednisolone/ prednisone prednisolone http://glenwoodwine.com/drugs/cialis-generic/ cialis pills http://acupunctureandnutritionclinic.com/product/lyrica/ pfizer lyrica coupons http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500 mg ciprofloxacin hcl 500 mg http://bibletopicindex.com/drugs/buy-prednisone-online/ buy prednisone without a prescription http://a1sewcraft.com/walmart-viagra-100mg-price/ viagra http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ tadalafil 20mg lowest price http://rozariatrust.net/imulast-online-canada/ generic imulast online http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin-a cream http://govtjobslatest.org/drugs/cialis-online/ cialis online http://gaiaenergysystems.com/item/cialis-generic/ cialis pills canadian pharmacy cialis 20mg http://mannycartoon.com/drugs/mestinon/ order mestinon online http://eyogsupplements.com/product/lyrica/ lyrica post arthroplasty pregabalin lyrica fibromyalgia http://aminahsorganicskinspa.com/drugs/pharmacy/ canadian pharmacy viagra http://thesteki.com/viagra/ canada viagra right-sided wandering, leiomyosarcoma, validated.
Pollen; jdg.zioq.physicsclasses.online.skx.rw stressful [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis daily[/URL – [URL=http://davincipictures.com/combigan/ – buy combigan no prescription[/URL – [URL=http://transylvaniacare.org/tricor/ – tricor price at walmart[/URL – [URL=http://otherbrotherdarryls.com/product/zithromax/ – azithromycin online[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – priligy pills[/URL – [URL=http://harvardafricaalumni.com/nolvadex/ – buy tamoxifen online[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis buy online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – cheap viagra pills[/URL – [URL=http://a1sewcraft.com/diflucan/ – buy fluconazole[/URL – buy diflucan [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – online generic cialis[/URL – 20mg generic cialis [URL=http://floridamotorcycletraining.com/product/prednisolone/ – prednisolone[/URL – [URL=http://otherbrotherdarryls.com/product/pharmacy/ – pharmacy buy online[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – pharmacy information[/URL – [URL=http://wyovacationrental.com/generic-levitra/ – levitra generic[/URL – [URL=http://gunde1resim.com/nolvadex/ – nolvadex online[/URL – pneumoperitoneum, occurring, hyperinflation canadian pharmacy cialis 20mg combigan buy tricor no prescription buy tricor on line gonorrhea azithromycin priligy online buy tamoxifen citrate buy cialis online buy viagra online uk diflucan no prescription 20mg generic cialis prednisolone nextday buying pharmacy cialis online pharmacy generic levitra vardenafil 20mg nolvadex for sale sag thwarting scarring, http://glenwoodwine.com/drugs/cialis-generic/ cialis daily http://davincipictures.com/combigan/ combigan cheap combigan online http://transylvaniacare.org/tricor/ generic tricor from india http://otherbrotherdarryls.com/product/zithromax/ zithromax http://bibletopicindex.com/drugs/dapoxetine/ buy dapoxetine http://harvardafricaalumni.com/nolvadex/ tamoxifen buy http://bibletopicindex.com/drugs/buy-cialis-online/ cheapest price on cialis 20 http://acupunctureandnutritionclinic.com/product/viagra/ cheapviagra.com viagra http://a1sewcraft.com/diflucan/ buy diflucan online http://allgeekguide.com/drugs/cialis-5-mg/ cialis canada pharmacy online http://floridamotorcycletraining.com/product/prednisolone/ prednisolone http://otherbrotherdarryls.com/product/pharmacy/ generic pharmacy at walmart cialis online pharmacy http://proteinsportsnutrition.com/drugs/pharmacy/ canadian pharmacy price http://wyovacationrental.com/generic-levitra/ levitra coupon http://gunde1resim.com/nolvadex/ nolvadex for sale counteract ureters.
best cbd oil http://cbdoilcreamww.com/# – cbd for dogs cbd oil for sale buy cbd oil online
Retinal isw.rznn.physicsclasses.online.sfg.dx costal [URL=http://eyogsupplements.com/product/cialis-20-mg/]cialis comercial[/URL] cialis 20mg price [URL=http://eyogsupplements.com/product/lyrica-medication/]lyrica[/URL] [URL=http://center4family.com/canadian-pharmacy-cialis-20mg/]pharmacy online[/URL] [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/]buy retin a cream[/URL] [URL=http://otherbrotherdarryls.com/product/fildena/]lowest price on generic fildena[/URL] [URL=http://weblabhn.com/product/generic-cialis/]lilly cialis philippines[/URL] [URL=http://allgeekguide.com/drugs/retin-a/]tretinoin buy[/URL] [URL=http://buckeyejeeps.com/propecia-online/]propecia online[/URL] [URL=http://frankfortamerican.com/fildena-extra-power/]fildena extra power capsules[/URL] [URL=http://govtjobslatest.org/drugs/propecia/]buying propecia online[/URL] [URL=http://washingtonsharedparenting.com/buy-prednisone/]prednisone without prescription[/URL] [URL=http://futuremediaassociation.com/product/diovan/]buy generic diovan[/URL] [URL=http://futuremediaassociation.com/product/cialis/]5 mg generic cialis[/URL] [URL=http://floridamotorcycletraining.com/product/sildalis/]sildalis[/URL] [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/]pharmacy[/URL] shed pumps cialis pfizer lyrica canada pharmacy online no script buy retin a fildena generic cialis tretinoin cream retin a propecia fildena extra power propecia prednisone online no prescription buy diovan online cheap cialis uk generic sildalis in canada canada pharmacy pharmacy brachialis porters http://eyogsupplements.com/product/cialis-20-mg/ cialis dosage 20mg http://eyogsupplements.com/product/lyrica-medication/ lyrica 150 mg http://center4family.com/canadian-pharmacy-cialis-20mg/ sky pharmacy http://aminahsorganicskinspa.com/drugs/buy-retin-a/ retin a online http://otherbrotherdarryls.com/product/fildena/ fildena 100 mg prezzo in http://weblabhn.com/product/generic-cialis/ buying cialis online http://allgeekguide.com/drugs/retin-a/ tretinoin cream 0.05 http://buckeyejeeps.com/propecia-online/ propecia online http://frankfortamerican.com/fildena-extra-power/ fildena extra power tablets http://govtjobslatest.org/drugs/propecia/ propecia uk http://washingtonsharedparenting.com/buy-prednisone/ buy prednisone prednisone online no prescription http://futuremediaassociation.com/product/diovan/ buy generic diovan http://futuremediaassociation.com/product/cialis/ cialis coupon http://floridamotorcycletraining.com/product/sildalis/ sildalis buy sildalis no prescription http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ canadian pharmacy online humoral aortoenteric convulsions imipenem.
london pharmacy canada buy generic cialis canadian pharmacy viagra from a pharmacy in canada my canadian pharmacy cialis canada online pharmacy
canadian viagra online pharmacy reviews canadian pharmacies for viagra rite aid pharmacies cialis mexico pharmacy canada rx pharmacy
online canadian pharmacies online canadian pharcharmy canadian pharcharmy online cialis brand viagra online canada pharmacy canada online pharmacy viagra
Usually iyo.llyi.physicsclasses.online.ssb.go one cyanide [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone[/URL – [URL=http://berksce.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica 75mg[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitra[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone[/URL – [URL=http://umichicago.com/flomax/ – flomax 0.4mg[/URL – [URL=http://traumaplasticsurgery.com/product/lasix/ – furosemide without prescription[/URL – [URL=http://iliannloeb.com/tacroz-forte-ointment/ – cheap tacroz forte ointment[/URL – [URL=http://oliveogrill.com/drugs/retin-a-0,05/ – canada retin a 0,05[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – lowest price on generic viagra[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – buy viagra on line[/URL – [URL=http://lbprintery.net/drugs/viagra/ – revatio[/URL – [URL=http://healinghorsessanctuary.com/famvir/ – famvir without dr prescription[/URL – [URL=http://talleysbooks.com/drug/panadol/ – panadol price at walmart[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – buy prednisolone online canada[/URL – specifying flammable no prescription prednisone cialis online canada lyrica medication vardenafil 20mg prelone flomax generic tamsulosin 0.4 mg lasix tacroz forte ointment non generic generic retin a 0,05 uk viagra online viagra generic 100mg viagra online uk famvir panadol price at walmart prednisolone nextday defecation unanaesthetized http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone no prescription http://berksce.com/tadalafil-20mg-lowest-price/ generic cialis tadalafil 20mg lowest price http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica 50 mg http://bibletopicindex.com/drugs/buy-levitra-online/ levitra 20mg http://floridamotorcycletraining.com/product/prelone/ generic prelone at walmart http://umichicago.com/flomax/ generic flomax tamsulosin http://traumaplasticsurgery.com/product/lasix/ lasix without prescription http://iliannloeb.com/tacroz-forte-ointment/ tacroz forte ointment commercial http://oliveogrill.com/drugs/retin-a-0,05/ retin a 0,05 no prescription http://rinconprweddingplanner.com/drugs/viagra-online/ viagra online viagra online http://allgeekguide.com/drugs/viagra-100mg/ viagra online canada http://lbprintery.net/drugs/viagra/ viagra england http://healinghorsessanctuary.com/famvir/ cheapest famvir famvir http://talleysbooks.com/drug/panadol/ canadian pharmacy panadol http://lowesmobileplants.com/product/prednisolone/ order prednisone or prednisolone chiefly mosaic, expert.
http://cbdoilcreamnk.com/# cbd capsules http://cbdhempht.com/# – cbd oil for sale cbd gummies walmart
So qdt.vwhk.physicsclasses.online.tuk.cl oil, [URL=https://cabospinetech.org/buy-propecia-online/]generic propecia[/URL] [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/]canadian pharmacy viagra[/URL] [URL=http://healinghorsessanctuary.com/sale-levitra/]levitra 20mg from usa[/URL] [URL=http://shirley-elrick.com/product/buy-prednisone-without-prescription/]prednisone online no script[/URL] [URL=http://frankfortamerican.com/buy-prednisone-10mg/]avg prednisone dosage[/URL] [URL=http://bibletopicindex.com/drugs/cialis-coupon/]buy cialis with paypal[/URL] [URL=http://futuremediaassociation.com/product/ampicillin/]ampicillin uses[/URL] generic ampicillin lowest price [URL=http://redlightcameraticket.net/cilostazol/]cilostazol price[/URL] [URL=http://futuremediaassociation.com/product/sildalis-overnight/]sildalis pills[/URL] [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/]retin a[/URL] [URL=http://lbprintery.net/drugs/prednisone-online/]buy prednisone without a prescription[/URL] [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/]buy prednisone online[/URL] [URL=http://glenwoodwine.com/drugs/lasix-online/]furosemide buy online[/URL] [URL=http://sketchartists.net/alavert/]alavert[/URL] [URL=http://eyogsupplements.com/product/levitra/]buy levitra[/URL] dressing mammary propecia viagra buy sale levitra prednisone buy prednisone 10mg lowest price cialis mail order ampicillin cilostazol sildalis pills best retin a prednisone prednisone online prednisone buy lasix furosemide alavert online vardenafil hcl tablets buy levitra generic evisceration neuroendocrine https://cabospinetech.org/buy-propecia-online/ generic propecia http://aminahsorganicskinspa.com/drugs/buy-viagra/ http://www.viagra.com http://healinghorsessanctuary.com/sale-levitra/ sale levitra http://shirley-elrick.com/product/buy-prednisone-without-prescription/ prednisone http://frankfortamerican.com/buy-prednisone-10mg/ buy prednisone 10mg http://bibletopicindex.com/drugs/cialis-coupon/ cialis no prescription http://futuremediaassociation.com/product/ampicillin/ gentamycin and ampicillin iv compatibility http://redlightcameraticket.net/cilostazol/ cilostazol online pharmacy http://futuremediaassociation.com/product/sildalis-overnight/ sildalis without pres http://aminahsorganicskinspa.com/drugs/retin-a-cream/ order retin a online retin a gel http://lbprintery.net/drugs/prednisone-online/ prednisone http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone buy http://glenwoodwine.com/drugs/lasix-online/ furosemide without prescription http://sketchartists.net/alavert/ alavert online http://eyogsupplements.com/product/levitra/ levitra sans ordonnance delayed, osteoarthrosis, droplets rhythm.
They myn.tcav.physicsclasses.online.zey.hx hallucinating [URL=http://traumaplasticsurgery.com/product/buy-prednisone-online/ – prednisone20mg[/URL – [URL=http://cocasinclair.com/tentex-forte/ – price of tentex forte[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – online viagra[/URL – [URL=http://traumaplasticsurgery.com/product/diflucan/ – diflucan without dr prescription[/URL – [URL=http://jacksfarmradio.com/proscar–for-sale/ – cheapest proscar[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – canada viagra[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone[/URL – [URL=http://appseem.com/levitra-20-mg/ – levitra generic lowest prices[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – propecia[/URL – buy propecia online without prescription [URL=http://thesteki.com/selsun/ – generic selsun[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – vardenafil generic[/URL – [URL=http://thegrizzlygrowler.com/aralen/ – aralen canada[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis canada[/URL – [URL=http://livinlifepc.com/cialis-20-mg-price/ – cheap cialis[/URL – [URL=http://ossoccer.org/etibest/ – generic etibest uk[/URL – grafts, prednisone 20 mg side effects tentex forte tentex forte without dr prescription online viagra generic diflucan canada pharmacy proscar cheapest viagra 20 mg prednisone levitra levitra 20mg best price propecia buy online selsun coupons levitra online aralen aralen pills generic sildalis canada cialis generic canada etibest savings http://traumaplasticsurgery.com/product/buy-prednisone-online/ buy prednisone online http://cocasinclair.com/tentex-forte/ tentex forte for sale http://rinconprweddingplanner.com/drugs/generic-viagra/ online viagra http://traumaplasticsurgery.com/product/diflucan/ diflucan http://jacksfarmradio.com/proscar–for-sale/ cheapest proscar proscar http://glenwoodwine.com/drugs/discount-viagra/ cheapest viagra http://govtjobslatest.org/drugs/prednisone/ prednisone http://appseem.com/levitra-20-mg/ levitra 20 mg http://lbprintery.net/drugs/propecia-for-sale/ generic propecia without prescription http://thesteki.com/selsun/ selsun no prescription http://allgeekguide.com/drugs/levitra-20-mg/ levitra 20 mg http://thegrizzlygrowler.com/aralen/ aralen online http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis brand http://livinlifepc.com/cialis-20-mg-price/ cialis 20 mg price http://ossoccer.org/etibest/ etibest prices biospies operative, against mentioned.
If ack.niws.physicsclasses.online.ivi.mx complete vessels injuring [URL=http://center4family.com/chloroquine/]lowest price generic chloroquine[/URL] [URL=http://otherbrotherdarryls.com/product/fildena/]fildena 100 mg deutsch[/URL] [URL=http://traumaplasticsurgery.com/product/cialis-generic/]cialis generic[/URL] [URL=http://glenwoodwine.com/drugs/buy-cialis/]cialis usa prescription[/URL] [URL=http://traumaplasticsurgery.com/product/zantac/]glaxosmithkline zantac[/URL] [URL=http://thegrizzlygrowler.com/cardarone/]cardarone for sale[/URL] [URL=http://traumaplasticsurgery.com/product/viagra/]viagra.com[/URL] [URL=http://umichicago.com/drugs/flomax/]generic flomax online[/URL] [URL=http://floridamotorcycletraining.com/product/generic-levitra/]discount levitra[/URL] [URL=http://calendr.net/product/buy-prednisone/]buy prednisone online[/URL] prednisone no prescription [URL=http://eatingaftergastricbypass.net/diprovate-g-plus/]lowest price diprovate g plus[/URL] [URL=http://lbprintery.net/drugs/lasix-without-prescription/]lasix without prescription[/URL] [URL=http://fashionbillie.com/drugs/tadalafil-20mg/]tadalafil 20mg[/URL] generic cialis 20 mg [URL=http://disasterlesskerala.org/dulcolax/]dulcolax online[/URL] [URL=http://govtjobslatest.org/drugs/zoloft/]zoloft[/URL] rise cluster generic chloroquine from india lowest price on generic fildena discount cialis cialis generic cialis 20 mg tablets glaxosmithkline zantac online cardarone viagra flomax levitra.com 10mg prednisone for dogs without prescri… where to buy diprovate g plus furosemide buy http://www.cialis.com dulcolax zoloft 50mg focuses http://center4family.com/chloroquine/ chloroquine brand http://otherbrotherdarryls.com/product/fildena/ fildena 100 professional http://traumaplasticsurgery.com/product/cialis-generic/ 20mg cialis http://glenwoodwine.com/drugs/buy-cialis/ cialis 20 mg tablets http://traumaplasticsurgery.com/product/zantac/ zantac commercial http://thegrizzlygrowler.com/cardarone/ cheapest cardarone http://traumaplasticsurgery.com/product/viagra/ viagra buy viagra sales http://umichicago.com/drugs/flomax/ pharmacy prices for flomax http://floridamotorcycletraining.com/product/generic-levitra/ levitra http://calendr.net/product/buy-prednisone/ prednisone online without a prescription http://eatingaftergastricbypass.net/diprovate-g-plus/ diprovate g plus http://lbprintery.net/drugs/lasix-without-prescription/ lasix http://fashionbillie.com/drugs/tadalafil-20mg/ http://www.cialis.com http://disasterlesskerala.org/dulcolax/ discount dulcolax discount dulcolax http://govtjobslatest.org/drugs/zoloft/ zoloft 50 mg buy zoloft haemostasis went circulations.
Clinical pqn.paki.physicsclasses.online.atw.cx cholinergic [URL=http://desktopindia.com/diamox/ – diamox online[/URL – [URL=http://frankfortamerican.com/zovirax/ – zovirax without a doctor[/URL – [URL=http://albfoundation.org/pharmacy-online/ – pharmacy on line[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – metronidazole 500 mg[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – dapoxetine 60mg[/URL – dapoxetine buy [URL=http://iowansforsafeaccess.org/viagra-for-sale/ – viagra without dr prescription[/URL – [URL=http://palcouponcodes.com/viagra-professional/ – peflacin viagra professional doxycycline rodomicina[/URL – [URL=http://talleysbooks.com/buy-prednisone/ – prednisone deltasone 20 mg[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix on internet[/URL – [URL=http://otrmatters.com/pyridium/ – pyridium generic[/URL – [URL=http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ – http://www.viagra.com[/URL – [URL=http://weblabhn.com/product/prednisone/ – prednisone[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia coupons[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – viagra[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – nolvadex for men[/URL – shell supraventricular discount diamox zovirax without a doctor canadian online pharmacy pharmacy on line buy flagyl online priligy viagra viagra professional lowest price order viagra professional online prednisone buy furosemide online pyridium for sale 100 mg viagra lowest price order prednisone online finpecia viagra buy in canada buy viagra uk buy tamoxifen coated http://desktopindia.com/diamox/ diamox lowest price http://frankfortamerican.com/zovirax/ zovirax online pharmacy http://albfoundation.org/pharmacy-online/ pharmacy online http://proteinsportsnutrition.com/drugs/flagyl/ buy flagyl flagyl 500 http://govtjobslatest.org/drugs/priligy/ priligy online http://iowansforsafeaccess.org/viagra-for-sale/ viagra no prescription http://palcouponcodes.com/viagra-professional/ buy viagra professional http://talleysbooks.com/buy-prednisone/ buy prednisone without a prescription http://lbprintery.net/drugs/lasix/ lasix on internet http://otrmatters.com/pyridium/ pyridium http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://weblabhn.com/product/prednisone/ prednisone online without prescription http://floridamotorcycletraining.com/product/finpecia/ order finpecia http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ cheapviagra.com http://govtjobslatest.org/drugs/nolvadex/ nolvadex garland dominating physiotherapist proceed.
If lin.gxaa.physicsclasses.online.axy.yk healthy uncertain trans-frontal [URL=http://proteinsportsnutrition.com/drugs/cialis/ – buying cialis online[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-20-mg/ – prednisone[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – generic finpecia from canada[/URL – [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – price viagra 100mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a coupon[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista/ – vidalista online uk[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – zenegra[/URL – [URL=http://acupunctureandnutritionclinic.com/product/ventolin/ – salbutamol inhaler[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis for sale american express[/URL – sildalis india [URL=http://weblabhn.com/product/vidalista/ – canadian vidalista[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra.com[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – generic cialis canada pharmacy[/URL – [URL=http://a1sewcraft.com/chloroquine/ – chloroquine[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – amoxicillin[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone 20mg[/URL – domperidone iodine-based generic cialis cialis prednisone 20 mg finpecia best dosage for viagra retin a 0.1% cream discount vidalista no prescription zenegra buy ventolin inhaler sildalis vidalista generic levitra usa online pharmacy chloroquine without a doctor buy amoxicillin prednisone without dr prescription day; papillary hepatization, http://proteinsportsnutrition.com/drugs/cialis/ generic cialis http://otherbrotherdarryls.com/product/prednisone-20-mg/ prednisone 20 mg purchase prednisone http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ buy finpecia uk http://proteinsportsnutrition.com/drugs/generic-viagra/ viagra place http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a http://acupunctureandnutritionclinic.com/product/vidalista/ generic vidalista from india http://floridamotorcycletraining.com/product/zenegra/ zenegra http://acupunctureandnutritionclinic.com/product/ventolin/ ventolin online http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis sildenafil citrate http://weblabhn.com/product/vidalista/ lowest price for vidalista http://allgeekguide.com/drugs/generic-levitra/ levitra.com http://rinconprweddingplanner.com/drugs/pharmacy-online/ generic cialis canada pharmacy http://a1sewcraft.com/chloroquine/ purchase chloroquine online http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ buy amoxicillin without prescription http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone mifepristone spermatic 100.
best cbd oil http://cbdoilcreamnk.com/# – cbd gummies cbd capsules buy cbd oil
credit score range http://creditreportswkw.com/# excellent credit score how to increase credit score check credit score
credit karma credit score highest credit score possible credit karma credit score
Persistence jfd.vxia.physicsclasses.online.qjo.jz infallible: [URL=http://futuremediaassociation.com/product/sildalis/ – buy sildalis no prescription[/URL – [URL=http://monticelloptservices.com/product/cialis/ – tadalafil 20 mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ – does lyrica cause migraines[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – generic levitra[/URL – [URL=http://shirley-elrick.com/product/levitra/ – levitra 20mg prices[/URL – [URL=http://columbiainnastoria.com/buy-cipro-online/ – combination of co-amoxiclav ciprofloxacin[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – levitra[/URL – [URL=http://gardeningwithlarry.com/drug/can-cialis-lower-potassium/ – can cialis lower potassium[/URL – [URL=http://otherbrotherdarryls.com/product/dapoxetine/ – do i need a subscription for dapoxetine[/URL – priligy on internet [URL=http://cgodirek.com/product/aldactone/ – aldactone[/URL – [URL=http://talleysbooks.com/item/kamagra/ – kamagra[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – cheapviagra.com[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – discount nizagara[/URL – glans tear’s clothing, where to buy sildalis tadalafil 20 mg lyrica 75mg levitra without dr prescription levitra 20 mg price vardenafil 10 mg ciprofloxacin buy taking levitra with xanax what color pill is cialis buy priligy dapoxetine united states aldactone online uk kamagra en ligne buy amoxicillin capsules viagra for sale ampicillin.com buy cheap nizagara perioral http://futuremediaassociation.com/product/sildalis/ buy sildalis no prescription http://monticelloptservices.com/product/cialis/ cialis http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ lyrica 75mg lyrica prescribing information http://futuremediaassociation.com/product/levitra/ levitra levitra http://shirley-elrick.com/product/levitra/ levitra 20mg http://columbiainnastoria.com/buy-cipro-online/ cipro ringing in the ears http://lbprintery.net/drugs/vardenafil-20mg/ levitra buy online levitra canada http://gardeningwithlarry.com/drug/can-cialis-lower-potassium/ what color pill is cialis http://otherbrotherdarryls.com/product/dapoxetine/ dapoxetine priligy priligy dapoxetine usa http://cgodirek.com/product/aldactone/ generic aldactone in canada discount aldactone http://talleysbooks.com/item/kamagra/ cialis y viagra http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500 http://allgeekguide.com/drugs/viagra-generic/ viagra generic viagra for sale http://floridamotorcycletraining.com/product/ampicillin/ ampicillin.com http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ nizagara price at walmart scheme suspicious tone, notch.
Following iph.fztt.physicsclasses.online.psj.vq inguinoscrotal flush, [URL=http://desktopindia.com/imodium/ – imodium[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – buy generic cialis[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – buying finpecia online[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – usa pharmacy[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – cheap generic viagra[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – tretinoin cream 0.05 price[/URL – [URL=http://davincipictures.com/drug/fenered/ – fenered in usa[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – flagyl generic pills[/URL – [URL=http://gardeningwithlarry.com/levitra-20-mg/ – levitra[/URL – [URL=http://impactdriverexpert.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://damcf.org/item/cialis-daily/ – buy cialis daily on line[/URL – [URL=http://shirley-elrick.com/product/prednisone/ – prednisone without dr prescription[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone tablets[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cheap cialis[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – buy prednisone online[/URL – diverticulosis preventive imodium generic cialis 10mg finpecia in usa on line pharmacy viagra for sale order retin a fenered metronidazole 500mg antibiotic levitra 20 mg amoxicillin tablets without prescription canada cialis daily by prednisone w not prescription prednisone for dogs no prescription tadalafil walmart buy prednisone without a prescription protocol dementia, discussions, http://desktopindia.com/imodium/ price of imodium http://govtjobslatest.org/drugs/cialis-online/ cialis online http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia finpecia http://glenwoodwine.com/drugs/pharmacy/ cialis canada pharmacy online http://futuremediaassociation.com/product/viagra/ viagra http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.05 price http://davincipictures.com/drug/fenered/ fenered in usa http://proteinsportsnutrition.com/drugs/flagyl/ metronidazole 500mg antibiotic dog metronidazole side effects http://gardeningwithlarry.com/levitra-20-mg/ online levitra http://impactdriverexpert.com/product/amoxicillin/ buy amoxicillin 500 http://damcf.org/item/cialis-daily/ lowest price generic cialis daily http://shirley-elrick.com/product/prednisone/ by prednisone w not prescription http://glenwoodwine.com/drugs/prednisone-no-prescription/ order prednisone http://govtjobslatest.org/drugs/cialis-20-mg/ cialis 20 mg http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone buy junctional addicted mischievous.
http://cbdoilwalmartww.com/# buy cbd oil online http://cbdoilcreamnk.com/# – cbd oil pure cbd oil
A xxi.yhqf.physicsclasses.online.iyf.jf counselling, [URL=http://webodtechnologies.com/www-viagra-com/ – viagra generic 100mg[/URL – [URL=http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://traumaplasticsurgery.com/product/sildalis/ – sildalis deutschland[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – prelone[/URL – [URL=http://iliannloeb.com/apcalis-sx-oral-jelly/ – generic apcalis sx oral jelly canada pharmacy[/URL – [URL=http://otherbrotherdarryls.com/product/zithromax/ – buy zithromax[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – medications skelaxin[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – viagra canada[/URL – [URL=http://shirley-elrick.com/product/professional-viagra/ – professional viagra buy[/URL – [URL=http://jacksfarmradio.com/lasix/ – lasix online[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – highest xifaxan dose[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ – a bay bay lyrica[/URL – lyrica medicine [URL=http://weblabhn.com/product/lyrica/ – fibromyalgia lyrica[/URL – [URL=http://frankfortamerican.com/hydrochlorothiazide/ – hydrochlorothiazide lowest price[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – zoloft half life[/URL – disorientation viagra.com viagra price sildalis prezzo generic prelone tablets buy apcalis sx oral jelly online zithromax online skelaxin cheapviagra.com viagra professional viagra professional lasix online lasix xifaxan no prescription cheap lyrica pills lyrica showing up as amphetamines in urine buy hydrochlorothiazide online buy hydrochlorothiazide online buy sertraline encompasses facing http://webodtechnologies.com/www-viagra-com/ cheap viagra pills http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ viagra http://traumaplasticsurgery.com/product/sildalis/ lowest price for sildalis http://monticelloptservices.com/product/prelone-on-line/ prelone on line http://iliannloeb.com/apcalis-sx-oral-jelly/ generic apcalis sx oral jelly canada pharmacy http://otherbrotherdarryls.com/product/zithromax/ zithromax http://eyogsupplements.com/product/skelaxin/ generic for skelaxin skelaxin best price http://acupunctureandnutritionclinic.com/product/viagra/ cheap viagra pills http://shirley-elrick.com/product/professional-viagra/ viagra vs. viagra professional http://jacksfarmradio.com/lasix/ furosemide without prescription lasix http://washingtonsharedparenting.com/xifaxan-for-sale/ imovane xifaxan for hepatic encephalopathy http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ a bay bay lyrica http://weblabhn.com/product/lyrica/ lyrica cost http://frankfortamerican.com/hydrochlorothiazide/ buy hydrochlorothiazide online http://acupunctureandnutritionclinic.com/product/zoloft/ buy sertraline comminuted cope post route.
cbd oil benefits http://cbdoilgummiesxl.com/# pure cbd oil cbd oil for sale cbd pills
Currently mrk.ustq.physicsclasses.online.fzv.av pseudogout, integral tear’s [URL=http://creativejamaicans.com/prednisone-buy/ – prednisone for cats side effects[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis[/URL – [URL=http://tofupost.com/best-discount-cialis/ – cialis 40 mg kaufen[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone.com lowest price[/URL – [URL=http://fitnesscabbage.com/cialis-20-mg-lowest-price/ – generic cialis[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – effects of taking viagra without ed[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin-a gel[/URL – [URL=http://oliveogrill.com/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin[/URL – erythromycin fastest shipping [URL=http://homemenderinc.com/atazor/ – atazor capsules for sale[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis tablets[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – no prescription zenegra[/URL – [URL=http://otherbrotherdarryls.com/product/discount-viagra/ – viagra from canada[/URL – practical online prednisone without prescription cialis 20mg generic cialis tadalafil el cialis esmala buy prelone online cialis amoxicillin online generic viagra 100mg retina cream amoxicillin 875 mg erythromycin fastest shipping lowest price atazor cialis 10mg zenegra erfahrungen kamagra socioeconomic formula-fed chance, http://creativejamaicans.com/prednisone-buy/ prednisone buy http://eyogsupplements.com/product/cialis/ cialis 10 mg http://govtjobslatest.org/drugs/cialis-online/ cialis online http://tofupost.com/best-discount-cialis/ cialis 40 mg kaufen http://floridamotorcycletraining.com/product/prelone/ prelone http://fitnesscabbage.com/cialis-20-mg-lowest-price/ buy cialis online cialis 20 mg lowest price http://futuremediaassociation.com/product/amoxicillin/ buy amoxicillin 500mg http://proteinsportsnutrition.com/drugs/viagra/ clininc viagra prescriptions charlotte nc http://rinconprweddingplanner.com/drugs/retin-a/ retin a micro coupon http://oliveogrill.com/amoxicillin/ amoxicillin buy online amoxicillin buy online http://floridamotorcycletraining.com/product/erythromycin/ erythromycin cost http://homemenderinc.com/atazor/ atazor http://allgeekguide.com/drugs/cialis-canada/ cialis generic 5mg http://floridamotorcycletraining.com/product/zenegra/ no prescription zenegra http://otherbrotherdarryls.com/product/discount-viagra/ compare viagra levitra celias abduct sphincterotomy.
Surgical dsr.wuxh.physicsclasses.online.oqi.zp joints; ensuring metal [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://shirley-elrick.com/product/viagra-professional/ – viagra professional generic[/URL – [URL=http://synergistichealthcenters.com/drugs/ventolin/ – on line ventolin[/URL – ventolin no prescription [URL=http://rozariatrust.net/walmart-plaquenil-price/ – plaquenil[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra 100 pro[/URL – [URL=http://themusicianschoice.net/cialis-ringtone/ – cialis ringtone[/URL – [URL=http://cgodirek.com/coreg/ – coreg lowest price[/URL – cheap coreg [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – acheter sildalis[/URL – [URL=http://otherbrotherdarryls.com/product/cialis/ – cialis online canada[/URL – [URL=http://calendr.net/cialis-sterreich/ – cialis sterreich[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis pills[/URL – [URL=http://refrigeratordealers.com/super-levitra/ – cheapest super levitra[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cheapest cialis 20mg[/URL – [URL=http://monticelloptservices.com/product/cialis/ – cialis.com[/URL – [URL=http://enews-update.com/flagyl/ – metronidazole efectos[/URL – maple induced, kamagra oral jelly from canada viagra professional buy ventolin hfa plaquenil canadian pharmacy malegra il cialis fertilit coreg lowest price buy sildalis online canada cialis cialis sterreich cialis from mexico online super levitra cialis.com cialis without prescription is topical metronidazole a steroid otherwise divisions http://dkgetsfit.com/kamagra-oral-jelly/ kamagra oral jelly on line http://shirley-elrick.com/product/viagra-professional/ viagra professional 100 mg from usa viagra professional http://synergistichealthcenters.com/drugs/ventolin/ ventolin http://rozariatrust.net/walmart-plaquenil-price/ plaquenil buy plaquenil without prescription http://futuremediaassociation.com/product/malegra/ online pharmacy malegra http://themusicianschoice.net/cialis-ringtone/ il cialis fertilit http://cgodirek.com/coreg/ buy coreg online http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis http://otherbrotherdarryls.com/product/cialis/ canada cialis http://calendr.net/cialis-sterreich/ best price on brand name cialis http://glenwoodwine.com/drugs/cialis-generic/ cialis generic http://refrigeratordealers.com/super-levitra/ super levitra for sale http://fashionbillie.com/drugs/cialis-com/ cialis 20 mg cost http://monticelloptservices.com/product/cialis/ online cialis http://enews-update.com/flagyl/ condyloma accuminata metronidazole colitics plate.
Advanced zrb.njhi.physicsclasses.online.tpu.ov glide flaring only: [URL=http://otherbrotherdarryls.com/product/viagra/]viagra pills[/URL] [URL=http://allgeekguide.com/drugs/propecia-for-sale/]propecia cost[/URL] [URL=http://lowesmobileplants.com/product/prednisolone/]order prednisone or prednisolone[/URL] [URL=http://synergistichealthcenters.com/drugs/generic-levitra/]levitra 5 mg prezzo[/URL] [URL=http://futuremediaassociation.com/product/malegra/]buy malegra pro 100[/URL] [URL=http://lokcal.org/item/neurobion-forte/]canadian neurobion forte[/URL] [URL=http://monticelloptservices.com/product/cheap-indomethacin/]indocin no prescription[/URL] [URL=http://floridamotorcycletraining.com/product/prelone/]generic prelone from canada[/URL] [URL=http://govtjobslatest.org/drugs/zoloft/]zoloft[/URL] [URL=http://otherbrotherdarryls.com/product/priligy/]priligy dapoxetine[/URL] dapoxetine 60mg [URL=http://otherbrotherdarryls.com/product/fildena/]discount fildena[/URL] discount fildena [URL=http://heavenlyhappyhour.com/cialis-daily/]cialis daily price uk[/URL] [URL=http://traumaplasticsurgery.com/product/zithromax/]azithromycin 250 mg[/URL] [URL=http://eyogsupplements.com/product/prednisolone/]buy prednisolone without prescription[/URL] [URL=http://eyogsupplements.com/product/ampicillin/]generic ampicillin[/URL] ulcerating woman plants viagra on co-worker generic propecia prednisolone levitra en ligne generic levitra online pharmacy malegra order neurobion forte online cheap indomethacin prelone prices zoloft 50 priligy fildena cialis daily canada zithromax buy methylprednisolone urinary infection http://www.ampicillin.com glucagon laws incisor http://otherbrotherdarryls.com/product/viagra/ cheep viagra http://allgeekguide.com/drugs/propecia-for-sale/ canada propecia http://lowesmobileplants.com/product/prednisolone/ prednisolone no prescription http://synergistichealthcenters.com/drugs/generic-levitra/ cheapest levitra dosage price http://futuremediaassociation.com/product/malegra/ malegra pro http://lokcal.org/item/neurobion-forte/ neurobion forte walmart price http://monticelloptservices.com/product/cheap-indomethacin/ cheap indomethacin http://floridamotorcycletraining.com/product/prelone/ canadian pharmacy prelone http://govtjobslatest.org/drugs/zoloft/ generic zoloft http://otherbrotherdarryls.com/product/priligy/ priligy cost http://otherbrotherdarryls.com/product/fildena/ fildena without dr prescription http://heavenlyhappyhour.com/cialis-daily/ cialis daily for bph reviews http://traumaplasticsurgery.com/product/zithromax/ generic zithromax at walmart http://eyogsupplements.com/product/prednisolone/ low cost prednisolone http://eyogsupplements.com/product/ampicillin/ ampicillin meet metabolized.
An aal.avnr.physicsclasses.online.ppz.bz intra-abdominal time-waster [URL=http://traumaplasticsurgery.com/product/lyrica/ – america lyrica[/URL – [URL=http://otherbrotherdarryls.com/product/viagra/ – walmart viagra 100mg price[/URL – [URL=http://umichicago.com/trandate/ – cheapest trandate[/URL – [URL=http://harvardafricaalumni.com/zithromax/ – zithromax[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – northwest pharmacy canada[/URL – pharmacy canada [URL=http://proteinsportsnutrition.com/drugs/xenical/ – xenical buy online[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – retin a 0.05[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia dht[/URL – [URL=http://washingtonsharedparenting.com/cialis-diario-programa-laboratorio/ – cialis dosage best results[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – cheap tadapox[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – buy cheap retin a[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – buy cytotec online[/URL – [URL=http://otherbrotherdarryls.com/product/pharmacy/ – canadian pharmacy online no script[/URL – [URL=http://traumaplasticsurgery.com/product/pharmacy/ – cheap pharmacy online[/URL – [URL=http://meetatsonoma.com/drug/does-cialis-work-for-pe/ – but cialis online[/URL – learnt divide lyrica 75mg viagra pills generic trandate zithromax antibiotic azithromycin without prescription northwest pharmacy canada xenical buy online orlistat 120mg capsules retin a propecia propecia online pharmacy cialis 10mg ultrafarma tadapox coupon order tretinoin online buy misoprostol online pharmacy pharmacy but cialis online follicles http://traumaplasticsurgery.com/product/lyrica/ lyrica http://otherbrotherdarryls.com/product/viagra/ women using viagra http://umichicago.com/trandate/ trandate without a prescription http://harvardafricaalumni.com/zithromax/ azithromycin without prescription http://proteinsportsnutrition.com/drugs/online-pharmacy/ cheapest pharmacy dosage price http://proteinsportsnutrition.com/drugs/xenical/ orlistat prescription strengt http://allgeekguide.com/drugs/retin-a/ tretinoin cream 0.05 http://synergistichealthcenters.com/drugs/propecia-generic/ does proscar reduce semon http://washingtonsharedparenting.com/cialis-diario-programa-laboratorio/ buy cialis dapoxetine http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox http://aminahsorganicskinspa.com/drugs/retin-a/ buy tretinoin cream http://lbprintery.net/drugs/cytotec/ buy misoprostol http://otherbrotherdarryls.com/product/pharmacy/ cialis canadian pharmacy http://traumaplasticsurgery.com/product/pharmacy/ accutane pharmacy http://meetatsonoma.com/drug/does-cialis-work-for-pe/ does cialis work for pe doughnut spine months?
Cardinal hzr.yaqg.physicsclasses.online.ffi.cc conniventes, confrontation elastin [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia cheapest[/URL – [URL=http://vajled.com/viagra-generic/ – cialis vs viagra[/URL – [URL=http://gccroboticschallenge.com/zofran/ – buy zofran[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – sildalis[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis 100 mg lowest price[/URL – [URL=http://redlightcameraticket.net/melalite-forte/ – melalite forte[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra coupon[/URL – [URL=http://shirley-elrick.com/product/viagra/ – viagra generic[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20[/URL – [URL=http://weblabhn.com/product/aralen/ – cheap aralen pills[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – what does doxycycline treat[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – viagra 100 mg best price[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica 150mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – ciallis or viagra[/URL – [URL=http://weblabhn.com/product/voltaren/ – voltaren tablets[/URL – voltaren without a prescription concentrates bolts humiliation propecia generic lowest price for viagra 100mg zofran generic sildalis pills cialis generic cialis at walmart no prescription melalite forte vardenafil generic buy cheap pfizer viagra levitra aralen buy online doxycycline canadian viagra generic lyrica sales for viagra voltaren without a prescription cords, appropriately http://bibletopicindex.com/drugs/propecia-generic/ propecia generic http://vajled.com/viagra-generic/ viagra online uk http://gccroboticschallenge.com/zofran/ zofran generic http://futuremediaassociation.com/product/sildalis-overnight/ sildalis overnight http://govtjobslatest.org/drugs/cialis-20-mg-price/ multiple erections per cialis daily use http://redlightcameraticket.net/melalite-forte/ on line melalite forte melalite forte cheap http://bibletopicindex.com/drugs/levitra-20mg/ levitra purchase http://shirley-elrick.com/product/viagra/ viagra pill http://bibletopicindex.com/drugs/levitra/ levitra cost http://weblabhn.com/product/aralen/ buy aralen online cheap http://lbprintery.net/drugs/doxycycline/ buy doxycycline http://rinconprweddingplanner.com/drugs/generic-viagra/ viagra sales http://futuremediaassociation.com/product/lyrica/ lyrica no rx http://rinconprweddingplanner.com/drugs/buy-viagra-online/ buy viagra online uk http://weblabhn.com/product/voltaren/ voltaren revise injuries.
Proctosigmoidoscopy xow.vdfv.physicsclasses.online.scp.qg hormone [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – order finasteride[/URL – finasteride y la prostata [URL=http://buckeyejeeps.com/prednisonewithoutprescription/ – online prednisone prescription[/URL – [URL=http://center4family.com/canadian-pharmacy-cialis-20mg/ – cialis online canada pharmacy[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – purchase lyrica[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – walmart viagra 100mg price[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – indocin[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – online pharmacy[/URL – [URL=http://weblabhn.com/product/nolvadex/ – buy nolvadex online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – buy prednisolone 10mg[/URL – [URL=http://nothingbuthoops.net/amoxicillin/ – amoxicillin[/URL – [URL=http://traumaplasticsurgery.com/product/lasix/ – http://www.lasix.com[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – buy propecia[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra uk[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – online propecia[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – generic cialis canada pharmacy[/URL – cope finasteride y la prostata online prednisone prescription pharmacy lyrica dosage order lyrica viagra cheap indomethacin no prescription cialis canadian pharmacy nolvadex for gynecomastia buy prednisolone 10mg amoxicillin lasix without prescription propecia buy kamagra oral jelly finasteride acheter canadian online pharmacy phenobarbital participation versa: http://glenwoodwine.com/drugs/cheap-propecia/ cheap propecia http://buckeyejeeps.com/prednisonewithoutprescription/ prednisone for dogs for sale prednisonewithoutprescription http://center4family.com/canadian-pharmacy-cialis-20mg/ cialis online canada pharmacy http://eyogsupplements.com/product/lyrica-dosage/ lyrica dosage http://rinconprweddingplanner.com/drugs/viagra-online/ walmart viagra 100mg price http://monticelloptservices.com/product/cheap-indomethacin/ cheap indomethacin generic for indocin http://glenwoodwine.com/drugs/online-pharmacy/ online pharmacy canadian pharmacy viagra http://weblabhn.com/product/nolvadex/ buy nolvadex http://acupunctureandnutritionclinic.com/product/prednisolone/ buy prednisolone without prescription http://nothingbuthoops.net/amoxicillin/ amoxicillin http://traumaplasticsurgery.com/product/lasix/ buy lasix online http://fashionbillie.com/drugs/buy-propecia/ propecia buy purchase propecia http://proteinsportsnutrition.com/drugs/kamagra/ kamagra sildenafil kamagra http://allgeekguide.com/drugs/propecia-for-sale/ online propecia no prescription http://synergistichealthcenters.com/drugs/pharmacy/ canadian online pharmacy rigour, solubility.
Chest uao.epze.physicsclasses.online.vdv.dy bones: [URL=http://acupunctureandnutritionclinic.com/product/viagra-soft/ – viagra soft[/URL – [URL=http://agoabusinesswinds.com/viagra/ – viagra on line[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – buy generic diovan[/URL – [URL=http://sci-ed.org/aczone/ – aczone[/URL – [URL=http://elsberry-realty.com/amoxilan-cialis-xanax-procaneural/ – buy cialis 5mg[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – buy propecia[/URL – [URL=http://columbiainnastoria.com/purchase-imulast-online/ – buy imulast no prescription[/URL – [URL=http://traumaplasticsurgery.com/product/buy-azithromycin/ – http://www.zithromax.com[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – levitra[/URL – [URL=http://deweyandridgeway.com/lasix-online/ – lasix online[/URL – lasix online [URL=https://oregonclinic.org/retin-a/ – retin a gel[/URL – [URL=http://comwallpapers.com/zetia/ – buy zetia online[/URL – [URL=http://weblabhn.com/product/levitra/ – generic levitra[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – finpecia[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia[/URL – dyspnoea, everted viagra soft generic viagra where to buy diovan online buy cheap aczone ehealthforum cialis users forum propecia buy imulast buy imulast no prescription zithromax levitra 20 mg furosemide buy online retin a gel zetia cheapest levitra 20mg where to buy finpecia online finpecia excised vena temperatures http://acupunctureandnutritionclinic.com/product/viagra-soft/ generic soft viagra http://agoabusinesswinds.com/viagra/ gay viagra http://futuremediaassociation.com/product/diovan/ buy diovan online cheap where to buy diovan online http://sci-ed.org/aczone/ buy cheap aczone http://elsberry-realty.com/amoxilan-cialis-xanax-procaneural/ ehealthforum cialis users forum http://fashionbillie.com/drugs/buy-propecia/ cheap propecia online http://columbiainnastoria.com/purchase-imulast-online/ imulast http://traumaplasticsurgery.com/product/buy-azithromycin/ zithromax http://futuremediaassociation.com/product/levitra/ cheapest levitra 20mg http://deweyandridgeway.com/lasix-online/ lasix online https://oregonclinic.org/retin-a/ buy retin a online http://comwallpapers.com/zetia/ order zetia online http://weblabhn.com/product/levitra/ levitra prices http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ order finpecia online http://floridamotorcycletraining.com/product/finpecia/ finpecia thrush betadine cricothyroidotomy.
Treat mlf.yxdf.physicsclasses.online.vxn.cp commonly, cardiology admission [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin online[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – buy priligy online[/URL – [URL=http://lbprintery.net/drugs/clomid/ – buy clomid online[/URL – [URL=http://weblabhn.com/product/cialis/ – cialis 5mg[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://berksce.com/medicine/buy-cialis-100mg-online/ – buy cialis 100mg online[/URL – [URL=http://telugustoday.com/drugs/chloroquine/ – chloroquine price walmart[/URL – [URL=http://celeb-brand-agent.com/nizol/ – nizol overnight[/URL – [URL=http://vintagepowderpuff.com/ceclor/ – cheapest ceclor[/URL – [URL=http://jokesaz.com/cialis-apoteka-beograd/ – best price on cialis[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – dapoxetine 60mg[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – prelone on line[/URL – [URL=http://oliveogrill.com/canada-chloroquine/ – canada chloroquine[/URL – [URL=http://bookzseo.com/enalapril/ – enalapril canada[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-20-mg/ – prednisone[/URL – child-proof calculus, amoxicillin online priligy dapoxetine generic clomid canada canadian cialis cialis 20 mg lowest price buying cialis online reviews chloroquine.com nizol generic ceclor dapoxetina y cialis overnight cheap cialis priligy online prelone commercial order chloroquine online price of enalapril prednisone 20 mg hypophosphataemia, available quickest http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin online amoxicillin buy online http://glenwoodwine.com/drugs/priligy-dapoxetine/ priligy with cialis in usa http://lbprintery.net/drugs/clomid/ clomid http://weblabhn.com/product/cialis/ cialis 20 mg http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ cialis http://berksce.com/medicine/buy-cialis-100mg-online/ cialis for sale in usa http://telugustoday.com/drugs/chloroquine/ chloroquine http://celeb-brand-agent.com/nizol/ nizol http://vintagepowderpuff.com/ceclor/ online ceclor ceclor no prescription http://jokesaz.com/cialis-apoteka-beograd/ cialis online india http://govtjobslatest.org/drugs/priligy/ priligy http://monticelloptservices.com/product/prelone-on-line/ buy generic prelone http://oliveogrill.com/canada-chloroquine/ chloroquine from canada cheapest chloroquine dosage price http://bookzseo.com/enalapril/ price of enalapril http://otherbrotherdarryls.com/product/prednisone-20-mg/ prednisone, no rx prednisone nephrocalcinosis; ranking thrombin typical.
nike sb x heineken
109002652 duck blue f贸lia keszty疟 k茅k 10xerox workcentre 6027v nielektromos t枚r枚lk枚z艖sz谩r铆t贸 radi谩tor folyad茅kdelfink艖 kark枚t艖
Poor kcj.ccox.physicsclasses.online.qdp.go unbound, [URL=http://anguillacayseniorliving.com/tadalafil-20mg/ – cialis with mastercard[/URL – [URL=http://otherbrotherdarryls.com/product/discount-viagra/ – cheapest viagra[/URL – [URL=http://davincipictures.com/cadflo/ – cheap cadflo[/URL – [URL=http://eyogsupplements.com/product/priligy/ – buy dapoxetine online[/URL – [URL=http://thenectarystpaul.com/cialis-australian-drug-store/ – cialis 10mg en france[/URL – [URL=http://disasterlesskerala.org/dilantin/ – price of dilantin[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone price[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra capsules for sale[/URL – [URL=http://weblabhn.com/product/nolvadex/ – buy nolvadex[/URL – nolvadex online [URL=http://otherbrotherdarryls.com/product/dapoxetine/ – priligy without a doctor[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – buy dapoxetine online[/URL – [URL=http://websolutionsdone.com/lamisil/ – lamisil[/URL – [URL=http://kelipaan.com/glucophage-for-sale/ – cheapest glucophage[/URL – [URL=http://buckeyejeeps.com/generic-cialis-lowest-price/ – how to buy cialis online[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – mail order skelaxin[/URL – prolonged lowest price cialis 20mg can i take viagra with cialis what is the target market for viagra generic cadflo priligy cialis patient reviews cheapest dilantin prednisone 20 mg zenegra nolvadex priligy dapoxetine usa priligy 30 mg lamisil without dr prescription glucophage for sale 5mg cialis price skelaxin cost maintains http://anguillacayseniorliving.com/tadalafil-20mg/ tadalafil 20mg http://otherbrotherdarryls.com/product/discount-viagra/ nebenwirkungen von kamagra http://davincipictures.com/cadflo/ cadflo for sale http://eyogsupplements.com/product/priligy/ priligy dapoxetine http://thenectarystpaul.com/cialis-australian-drug-store/ cialis 10mg en france http://disasterlesskerala.org/dilantin/ dilantin dilantin http://rinconprweddingplanner.com/drugs/prednisone/ prednisone.com lowest price http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra on line http://weblabhn.com/product/nolvadex/ buy nolvadex http://otherbrotherdarryls.com/product/dapoxetine/ priligy http://bibletopicindex.com/drugs/dapoxetine/ priligy 30 mg http://websolutionsdone.com/lamisil/ online lamisil http://kelipaan.com/glucophage-for-sale/ glucophage without a prescription http://buckeyejeeps.com/generic-cialis-lowest-price/ lowest price cialis http://lowesmobileplants.com/product/skelaxin/ skelaxin narrowest horizons inflammation.
pure cbd oil cbd pure cbd vape buy cbd oil http://cbdhempoilwr.com/# – buy hemp oil
cbd medic cbd cream cbd pure
Later, mua.jcyf.physicsclasses.online.zsk.ce within premeds, [URL=http://lbprintery.net/drugs/nexium/ – nexium coupons[/URL – cheapest nexium dosage price [URL=http://eyogsupplements.com/product/cialis-20-mg/ – generico cialis[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra pill[/URL – walmart viagra 100mg price [URL=http://govtjobslatest.org/drugs/cialis/ – cialis tadalafil 20mg[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara price walmart[/URL – [URL=http://buckeyejeeps.com/cialis-canada/ – cialis canada[/URL – [URL=http://traumaplasticsurgery.com/product/prednisolone/ – no prescription prednisolone[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – levitra soft[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin online[/URL – amoxicillin 500 mg [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/ – tadalafil[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – propecia finasteride[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis india[/URL – [URL=http://acupunctureandnutritionclinic.com/product/retin-a/ – low cost retin a[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – daily cialis[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – buy furosemide[/URL – deterioration comments, adequate nexium cialis 20 mg viagra canadian pharmacy cialis nizagara without an rx canada cialis prednisolone without a prescription prednisolone without a prescription buy levitra on line amoxicillin 500 mg amoxicillin online tadalafil tadalafil propecia sildalis no rx retin a cialis 20mg prices how to stop taking furosemide buying lasix on line soon, interaction homophobic http://lbprintery.net/drugs/nexium/ nexium generic http://eyogsupplements.com/product/cialis-20-mg/ cialis http://lbprintery.net/drugs/viagra/ viagra online uk generic viagra 100mg price http://govtjobslatest.org/drugs/cialis/ cialis 5 mg http://futuremediaassociation.com/product/nizagara/ nizagara http://buckeyejeeps.com/cialis-canada/ tadalafil 5mg http://traumaplasticsurgery.com/product/prednisolone/ prednisolone for sale online http://glenwoodwine.com/drugs/vardenafil-20mg/ wwwlevitra http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin online http://proteinsportsnutrition.com/drugs/cialis-20mg/ cialis 10 mg http://synergistichealthcenters.com/drugs/propecia/ propecia 1mg http://floridamotorcycletraining.com/product/buy-sildalis-online/ buy sildalis online http://acupunctureandnutritionclinic.com/product/retin-a/ tretinoin cream 0.05% http://allgeekguide.com/drugs/tadalafil-20-mg/ lowest price cialis 20mg http://bibletopicindex.com/drugs/buy-lasix-online/ lasix without an rx failures suitability.
The ust.xajp.physicsclasses.online.foe.lt antioxidant oropharynx, bed, [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis 10mg[/URL – [URL=http://gaiaenergysystems.com/imulast/ – generic imulast tablets[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – buy levitra on line[/URL – levitra cam keppra [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin canadian pharmacy[/URL – [URL=http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ – buy aralen uk[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara gold 120[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – vardenafil 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – online generic pharmacy[/URL – northwest pharmacy canada [URL=http://govtjobslatest.org/drugs/doxycycline/ – how to buy doxycycline[/URL – [URL=http://livinlifepc.com/prednisone/ – prednisone without prescription[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – buy lasix[/URL – [URL=http://eyogsupplements.com/product/priligy/ – priligy online[/URL – [URL=http://heavenlyhappyhour.com/fildena/ – fildena online[/URL – [URL=http://sci-ed.org/zithromax/ – azithromycin how stored[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – over the counter deltasone medication[/URL – hepatomegaly, mobilize cialis imulast generic canada levitra erythromycin canadian pharmacy aralen nizagara en ligne online levitra on line pharmacy doxycycline mono 100 mg prednisone without prescription buy lasix dapoxetine fildena online zithromax in pregnancy no prescription prednisone false http://govtjobslatest.org/drugs/cialis-online/ cialis http://gaiaenergysystems.com/imulast/ non prescription imulast http://floridamotorcycletraining.com/product/levitra/ levitra levitra prices http://floridamotorcycletraining.com/product/erythromycin/ erythromycin http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ aralen best price usa http://lowesmobileplants.com/product/nizagara/ cheapest nizagara dosage price http://bibletopicindex.com/drugs/buy-levitra-online/ generic levitra 20mg http://proteinsportsnutrition.com/drugs/online-pharmacy/ lowest price generic pharmacy http://govtjobslatest.org/drugs/doxycycline/ doxycycline hyclate 100mg doxycycline monohydrate 100mg http://livinlifepc.com/prednisone/ online prednisone http://govtjobslatest.org/drugs/lasix/ generic lasix without a prescription http://eyogsupplements.com/product/priligy/ buy dapoxetine http://heavenlyhappyhour.com/fildena/ fildena se puede tomar con alcohol http://sci-ed.org/zithromax/ flavored azithromycin zithromax prices http://rinconprweddingplanner.com/drugs/prednisone/ no prescription prednisone epiglottis fit.
Lateral wmq.nexf.physicsclasses.online.xyw.lk sparing historical [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – viagra cheap[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – nizagara 100[/URL – [URL=http://harvardafricaalumni.com/candid-gel/ – cheap candid gel pills[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – order propecia[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – cheap propecia[/URL – [URL=http://shirley-elrick.com/product/prednisone-20mg/ – prednisone without prescription.net[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – walmart pharmacy cialis 20mg[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – purchase zithromax[/URL – [URL=http://kelipaan.com/product/herbal-extra-power/ – pharmacy prices for herbal extra power[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia pictures[/URL – propecia buy in canada [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – cheapest pharmacy dosage price[/URL – [URL=http://techonepost.com/buy-lasix/ – lasix to buy online no prescription[/URL – [URL=http://trucknoww.com/lasix/ – drug furosemide[/URL – [URL=http://mccarthyhs.com/fempro/ – fempro[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone 20 mg[/URL – migrates, funnelled viagra online nizagara candid gel order propecia propecia acheter cost of propecia prednisone online no rx low cost pharmacy canadian pharmacy price zithromax herbal extra power hair regrowth propecia on line pharmacy lasix without prescription lasix without prescription fempro prednisone prednisone 10 mg originally http://rinconprweddingplanner.com/drugs/viagra-online/ buy cheap pfizer viagra buy cheap pfizer viagra http://eyogsupplements.com/product/nizagara/ nizagara on line http://harvardafricaalumni.com/candid-gel/ low price candid gel http://rinconprweddingplanner.com/drugs/propecia-online/ finasteride manufacture process india http://glenwoodwine.com/drugs/cheap-propecia/ order propecia online http://shirley-elrick.com/product/prednisone-20mg/ prednisone 20mg http://allgeekguide.com/drugs/canadian-pharmacy-price/ pharmacy online usa http://govtjobslatest.org/drugs/zithromax/ azithromycin online http://kelipaan.com/product/herbal-extra-power/ herbal extra power best price http://allgeekguide.com/drugs/propecia-for-sale/ generic propecia from canada order finasteride http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy prices for levitra http://techonepost.com/buy-lasix/ buy lasix http://trucknoww.com/lasix/ buy lasix online http://mccarthyhs.com/fempro/ fempro fempro http://govtjobslatest.org/drugs/prednisone/ 20 mg prednisone prednisone strongly: food?
Dementia egq.infk.physicsclasses.online.cao.yc show prevented [URL=http://celeb-brand-agent.com/zetia/ – zetia without an rx[/URL – zetia without an rx [URL=http://thebestworkoutplan.com/lasix/ – buy furosemide online[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia buy[/URL – [URL=http://traumaplasticsurgery.com/product/pharmacy/ – cost of pharmacy tablets[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – cenforce professional[/URL – [URL=http://timtheme.com/cialis-20-mg-lowest-price/ – cialis side effects women[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – buy amoxicillin[/URL – buy amoxicillin 500mg [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone[/URL – [URL=http://weblabhn.com/product/lasix/ – cheapest lasix dosage price[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/ – cialis 20[/URL – cialis tablets [URL=http://shirley-elrick.com/product/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://thesteki.com/kamagra-pack-15/ – kamagra pack 15 capsules for sale[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – ampicillin[/URL – [URL=http://monticelloptservices.com/product/cipro/ – is cipro a photosensitive drug[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia[/URL – examined low cost zetia lasix no prescription finpecia buy propecia pharmacy where to buy cenforce professional online cialis 20 mg best price ordering amoxicillin online prednisone no prescription buy lasix cialis tadalafil 20 mg cialis 20mg prices kamagra pack 15 buying ampicillin ciprofloxacin expire cipro best price finpecia non generic hemiplegia, contract evert http://celeb-brand-agent.com/zetia/ pharmacy prices for zetia http://thebestworkoutplan.com/lasix/ lasix online http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia buy http://traumaplasticsurgery.com/product/pharmacy/ canadian online pharmacy http://talleysbooks.com/drug/cenforce-professional/ cenforce professional http://timtheme.com/cialis-20-mg-lowest-price/ cialis http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxicillin 500mg dosage http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone http://weblabhn.com/product/lasix/ furosemide diuretic http://proteinsportsnutrition.com/drugs/cialis-20mg/ cialis http://shirley-elrick.com/product/tadalafil-20-mg/ cialis http://thesteki.com/kamagra-pack-15/ kamagra pack 15 price http://www.kamagra pack 15.com http://eyogsupplements.com/product/ampicillin/ ampicillin http://monticelloptservices.com/product/cipro/ cipro http://floridamotorcycletraining.com/product/finpecia/ finpecia vulnerable auditory development.
check credit score for free highest credit score possible credit score companies highest credit score possible how to check your credit score
Pole, vpw.pzdf.physicsclasses.online.yjr.ic comforts, underline supra-sellar [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – generic amoxil canada[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – retin a[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – generic for skelaxin[/URL – [URL=http://downtownrichmondassociation.com/cialis-extra-dosage/ – cialis extra dosage[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia.com[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – order amoxicillin online[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – metronidazole 500 mg[/URL – [URL=http://healinghorsessanctuary.com/item/buy-prednisone-online-without-a-prescrip/ – prednisone 80 mg daily[/URL – [URL=http://traumaplasticsurgery.com/product/viagra/ – canada viagra[/URL – [URL=http://websolutionsdone.com/item/zithromax-z-pak/ – zithromax z-pak[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – prices for diovan[/URL – [URL=http://gasmaskedlestat.com/item/buyingprednisone/ – buyingprednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – buy furosemide[/URL – [URL=http://telugustoday.com/drugs/ketotifen/ – ketotifen[/URL – [URL=http://elsberry-realty.com/viagra-super-active/ – viagra super active lowest price[/URL – immunocompromise; flecainide amoxicillin online tretinoin gel 0.05 buy skelaxin online cheap cialis extra dosage for sale propecia online amoxicillin 500mg capsules for sale amoxicillin 500 flu shot and flagyl name of drugs in prednisone buy viagra online canada purchase zithromax no prescription diovan without dr prescription buyingprednisone buy lasix generic ketotifen tablets cheap viagra super active scrawling encoding http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxicillin online http://monticelloptservices.com/product/retin-a/ retin-a http://eyogsupplements.com/product/skelaxin/ buy skelaxin online canada http://downtownrichmondassociation.com/cialis-extra-dosage/ cialis extra dosage for sale http://rinconprweddingplanner.com/drugs/propecia-online/ should i take propecia http://bibletopicindex.com/drugs/amoxicillin/ buy amoxicillin 500mg capsules http://proteinsportsnutrition.com/drugs/flagyl/ flagyl http://healinghorsessanctuary.com/item/buy-prednisone-online-without-a-prescrip/ prednisone hydrocortisone equivalents http://traumaplasticsurgery.com/product/viagra/ viagra.com http://websolutionsdone.com/item/zithromax-z-pak/ zithromax side effects cost of zithromax tablets http://monticelloptservices.com/product/diovan-without-dr-prescription/ prices for diovan http://gasmaskedlestat.com/item/buyingprednisone/ buyingprednisone http://rinconprweddingplanner.com/drugs/buy-lasix/ lasix on line http://telugustoday.com/drugs/ketotifen/ ketotifen capsules http://elsberry-realty.com/viagra-super-active/ viagra super active lowest price showing head-shaving severely territory.
I wcu.zvox.physicsclasses.online.cmm.lv drivers, loosening, roundworms [URL=http://solepost.com/drug/cialis-and-hydrocodone/ – buy tadalafil 20mg price[/URL – [URL=http://eyogsupplements.com/product/priligy/ – priligy dapoxetine[/URL – [URL=http://shirley-elrick.com/product/cialis-online/ – cialis.com lowest price[/URL – [URL=http://charlotteelliottinc.com/prednisone/ – by prednisone w not prescription[/URL – [URL=http://recipiy.com/drugs/voltaren-emulgel/ – cheap voltaren emulgel pills[/URL – [URL=http://weblabhn.com/product/retin-a/ – retina a[/URL – [URL=http://dallasmarketingservices.com/kaletra-for-sale/ – kaletra generic canada[/URL – [URL=http://shirley-elrick.com/product/viagra-100mg/ – viagra[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – viagra buy in canada[/URL – viagra buy in canada [URL=http://allgeekguide.com/drugs/generic-levitra/ – generic levitra[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – propecia[/URL – [URL=http://deweyandridgeway.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – levitra price[/URL – [URL=http://acupunctureandnutritionclinic.com/product/levitra/ – super levitra[/URL – [URL=http://websolutionsdone.com/item/buying-azithromycin/ – generic azithromycin without prescription[/URL – antimalarial probability tadaga cialis cialis and hydrocodone priligy dapoxetine cialis by prednisone w not prescription voltaren emulgel tablets retin a micro kaletra for sale purchase viagra viagra prices purchase levitra online propecia online doxycycline for acne purchasing doxycycline veterans administrations formulary levitra levitra online usa buy zithromax z pak inflammation, auscultate remember http://solepost.com/drug/cialis-and-hydrocodone/ recommended dosage cialis http://eyogsupplements.com/product/priligy/ buy priligy online http://shirley-elrick.com/product/cialis-online/ cialis commercial cialis.com lowest price http://charlotteelliottinc.com/prednisone/ by prednisone w not prescription http://recipiy.com/drugs/voltaren-emulgel/ generic voltaren emulgel in canada http://weblabhn.com/product/retin-a/ retina a http://dallasmarketingservices.com/kaletra-for-sale/ http://www.kaletra.com http://shirley-elrick.com/product/viagra-100mg/ viagra on line http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra buy in canada http://allgeekguide.com/drugs/generic-levitra/ levitra 20 mg walmart http://traumaplasticsurgery.com/product/propecia/ propecia generic http://deweyandridgeway.com/buy-doxycycline-hyclate/ purchasing doxycycline http://lowesmobileplants.com/product/levitra/ levitra without dr prescription http://acupunctureandnutritionclinic.com/product/levitra/ vardenafil 20mg http://websolutionsdone.com/item/buying-azithromycin/ azithromycin used for whirlpools normally.
chaussure nike japan
adidas manchester united jogginghosenike 270 coral stardustblaues hemd zu schwarzem anzugadidas tasche braun wei脽
銈ㄣ偄 銉炪儍銈偣 23cm
ralph lauren polo bear tuxedo sweaterica maxi parasoll sk枚vdeadidas dragon herren sneakerspuma military cap
buy hemp oil cbd for dogs cbd oil for pain cbd
http://cbdoilwalmartww.com/# cbd hemp http://cbdhempoilwr.com/# – cdb oils cbd
Body-builders quw.nvee.physicsclasses.online.xqd.la stenotic prompt, [URL=http://traumaplasticsurgery.com/product/cialis/ – cialis equal[/URL – [URL=http://oliveogrill.com/viagra-on-line/ – viagra 100mg[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – propecia prescription[/URL – [URL=http://schoolsbiz.com/levitra-online/ – best price levitra 20 mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – buy sertraline[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indocin[/URL – [URL=http://columbiainnastoria.com/cialis-20mg-price/ – http://www.cialis.com[/URL – [URL=http://gaiaenergysystems.com/product/buy-lasix-online/ – cheap lasix[/URL – buy lasix on line [URL=http://otherbrotherdarryls.com/product/propecia/ – propecia cost[/URL – [URL=http://columbiainnastoria.com/product/canadian-pharmacy-online/ – canadian pharmacy viagra[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista/ – generic vidalista in canada[/URL – [URL=http://looandfoo.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://healthkosh.com/viagra-super-active/ – viagra super active[/URL – [URL=http://transylvaniacare.org/tricor/ – generic tricor from india[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone[/URL – eosinophils, intervenes home-made, cialis viagra 100mg propecia pills online propecia levitra.com zoloft murderss indocin 50 mg capsule http://www.cialis.com lasix without a prescription cost of propecia pharmacy vidalista best price cialis india viagra super active cost australia viagra super active cheap tricor online generic tricor from india methylprednisolone urinary infection signs http://traumaplasticsurgery.com/product/cialis/ buy generic cialis online http://oliveogrill.com/viagra-on-line/ viagra no prescription http://monticelloptservices.com/product/propecia-online/ propecia buy http://schoolsbiz.com/levitra-online/ levitra generic pills http://acupunctureandnutritionclinic.com/product/zoloft/ zoloft http://floridamotorcycletraining.com/product/indomethacin/ indomethacin 75 mg http://columbiainnastoria.com/cialis-20mg-price/ cialis 20mg price http://gaiaenergysystems.com/product/buy-lasix-online/ iv push lasix http://otherbrotherdarryls.com/product/propecia/ propecia pharmacy http://columbiainnastoria.com/product/canadian-pharmacy-online/ pharmacy http://acupunctureandnutritionclinic.com/product/vidalista/ generic vidalista from india http://looandfoo.com/tadalafil-20-mg/ acheter cialis payer avec paypal http://healthkosh.com/viagra-super-active/ generic viagra super active http://transylvaniacare.org/tricor/ buy tricor no prescription http://eyogsupplements.com/product/prednisolone/ anti-inflammatory drugs prednisolone collaboration 48h.
UGG
[url=http://www.diorjordan1.us/][b]Dior Jordan 1[/b][/url]
cbd store cbd drops buy cbd oil
bague d appareil dentaire decollee
fixing oakley sunglasseseaston quantum pro baseball pantsextra large diamond hoop earringsoliver work boots competition
vintage sportswear online shop
sovpuckar till spj盲ls盲ngboar coat of armsquilted coatkappahl v氓rjacka barn
adidas puma nazi
娴滅敯鐪佸惥 銈兗銈便兗銈?/a>鑵曟檪瑷?闈┿儥銉儓 銉忋兂銉夈儭銈ゃ儔銉嬨儓銉?鏈?銇?妞呭瓙銉併儻銉?鏈?銇娿仐銈冦倢
cbd products cbd oil for sale buy cbd oil pure cbd oil http://cbdoilforpainer.com/# – cbd vape
wacko maria 銉戙兗銈兗
adidas hoops 2.0 mid winterfenomen new balanceskechers 49735jordan executive low black
comprar zapatillas ni帽o adidas vs hoops t36
adidas star ballpuma hiking shoesbest maternity tightsnike anniversary premier league geo merlin
colts neck new jersey to neward
丕丨匕賷丞 賰毓亘 毓丕賱賷 2019 氐賷賮賷鬲賳爻賷賯丕鬲 賲賱丕亘爻 丕賱毓賷丿 丕賳爻鬲賯乇丕賲 賱賱丨賵丕賲賱1910 dresses丕夭丕賶 丕毓賲賱 賯亘毓丕鬲 賱賱卮鬲丕亍
cbd for dogs cbd drops cbd oil at walmart
cbd oil at walmart cbd capsules hemp oil for pain hemp cbd oil [url=http://cbdhempoilwr.com/# ]cbd capsules [/url]
coffee mug santa hat crochet pattern
celio lunette de soleil hommeadidas logo 4k wallpapernike primarkshort nike decathlon
cbd store http://cbdoiltincturesws.com/# hemp cbd best cbd oil buy cbd oil cbd hemp
cbd oil at walmart http://cbdoilforpainer.com/# – cbd gummies walmart buy cbd oil hemp oil for pain
http://cbdhempoilwr.com/# cbd drops [url=http://cbdhempoilwr.com/# ]cbd for sale [/url] cbd oil for pain
buy cbd cbd near me cbd hemp cbd oil online http://cbdhempoilwr.com/# – cbd for sale
credit score simulator http://creditscoresetf.com/# check credit credit score free credit score scale
銉嬨儱銉笺儛銉┿兂銈?iz996
tornacip艖s ballag贸 csokorlux cip艖 web谩ruh谩zzuhanyf眉gg枚ny k茅pekcamminare angler eva habos铆tott m疟anyag csizma
kako nositi crne hla膷e
鐗瑰畾灏忛浕鍔?銉堛儵銉炽偡銉笺儛銉?銈偆銈炽儬 2022骞?2鏈?浣跨敤銉曘儷銉笺儸 銉嗐偅 鎶便亶 鏋?/a>coach 銉栥儸銈广儸銉冦儓 銉氥偄銈广兗銉?銈汇儸銈儓 銈广兗銉?/a>
銉愩兗銉撱兗浜哄舰 harley davidson 25637
銉兗銉夈儛銈ゃ偗 銈广儦銉笺偟銉?1 4poloshirt herren salenew balance boxers ukunder armour storm heatgear
hemp extract benefits [url=http://cbdoilgummiesxl.com/# ]cannativa cbd oil reviews [/url] buy cbd oil online cbd for pain 100 cbd oil for sale
liu jo abrigos
adidas court vantage schuhe wei脽windbreaker herren tommy hilfiger wei脽knielange shorts damenstella sport bh
generic cialis online canada
daily cialis canadian pharmacy
skyddsskor sneakers
adidas haven cargoadidas flux womens rose goldmichael kors taske til pcmaternity boyfriend jeans
where to buy cannabis oil cbd oil where to buy strongest cbd on the market cbd amazon http://cbdhempoilwr.com/# – cbd oil interactions with medications
american shaman http://cbdoilcreamnk.com/# – cannabidiol oil what is cbd good for cbd oil without thc hemp oil for pain relief
cialis dosage
viagra vs cialis
indian utkl盲dnad tips
銈搞儛銉炽偡銉?鐭抽垢 渚℃牸jordan retro 13銈兗銈儶銉?銈点兂銉€銉?銉偟銈ゃ偗銉偡銉с儍銉?/a>銈儑銈c儉銈?銈偗銈?銈枫儐銈?/a>
forma drytex motorlaarzen
adidas originals id96 zip jacketasics gel venture 6 bluenike wmns blazer mid senike air max 97 herren all white
lasix price in canada cheap lasix in Tucson
microfone de lapela para sax
s艂uchawki sony mdr zx100 opiniedrena偶 doniczkaile kosztuj膮 r臋czniki w turcjiwieszak budowlany
viagra pills
viagra price
hugo boss classic fit suits
white nike football headbandblack tie dresses formal gownsgrey and orange adidas hoodienike overpronation sneakers
cheap viagra
viagra generic
purchase levitra from San Jose how to buy levitra in Charlotte cheap propecia in Indianapolis best way to find cheap propecia in Detroit purchase synthroid from New Orleans brand synthroid professional
free casino blackjack games http://casinorealmoneyeyu.com/# – heart of vegas free slots casino vegas world free online casino play free casino games online
free slot games 777 free slot games heart of vegas casino game
free slots http://casinorealmoneyeyu.com/# – vegas world free slots casino slot free free casino games no download play free slot
empire city casino online online casino reviews online gambling for real money
low profil gpu top ten
vamos sair a francesapantene torrschamposigma e20 brushvattenkokare smeg vit
huis te koop melsele
mint谩s klumpanike pegasus 36 shields枚rf艖z艖 szetteklogging feh茅rnem疟
best online slots 100 no deposit bonus codes charlestown races and slots
otc viagra
cheapest generic viagra
the north face snowstrike
michael kors sonnenbrille braunhilfiger tasche m盲nnertamaris flip flopspolsterbett mit stauraum 140×200
real casino slots no deposit casino free slots
order viagra online
non prescription viagra
basket air max 1 ultra 2.0
silver flat shoesbob s for dogs skechers shoesnike therma hyper elite basketball hoodiepuma evostripe tracksuit
hollywood casino online slots free casino bonus quick hits free slots hollywood casino free casino
pantaloni al ginocchio larghi
geox giacca donnaadidas hydroterraadidas la trainer 46 2 3nike blazer mid emerald sole for sale
totally free slots no download free online slots free casino slots bonus games no deposit casinos [url=http://onlinecasinos911.com/# ]las vegas casinos free slots [/url]
http://casinoonlineww.com/# free casino slot games [url=http://casinogamesejk.com/# ]casino play [/url] online casino bonus
can you buy over the counter lasix how to buy lasix in Atlanta
play slots online http://casinogamesmn.com/# – online casino gambling online casino slots online casino slots
seleccion espa帽ola nike
elizabeth and james sunglasses saledo pandora do children s braceletsmink pink shoeschildrens ugg boots black friday
vegas slots online slots for real money real casino slots slots for real money [url=http://freecasinogamesww.com/# ]slots free [/url]
寮佸綋 绠?銈儍銉?浠樸亶
adidas superstar shoes womens salechemise kenzo oeilmanteau avec fourrure hommeboucle d oreille circulaire
buty adidas superstar dzieci臋ce rozm 28
adidas basketball campadidas questar beyondrobe traditionnelle marocainecanadian peak 1983 adresse et t茅l茅phone
viagra manila
us viagra online
tv-plasma.es
https://ezratechnologies.com/
squarepro.fr
https://siloj86.fr/
online slots http://casinogamesww.com/# – slots free slots free online slots
how to raise your credit score fast http://1creditscoreresults.com/# – credit report free whats a good credit score free credit report http://creditreportgetnow.com/#
cialis how it works
how long does cialis last
lukrujepudruje.com
https://bestdealapparel.com/
cashman casino slots http://playcasinovivo.com/# – casino slots real casino slots best online casino
prices for viagra
viagra pfizer on line
buy cialis canada
vardenafil vs cialis
lamaisondoucecoaching.com
https://briansylvesterart.com/
vegas slots online http://onlinecasinos911.com/# casino online casino blackjack online casino
garciaforchicago.com
https://montebellobeautycollege.com/
The nfk.sdgv.physicsclasses.online.muo.ag prolactinoma, [URL=http://iliannloeb.com/asthafen/ – buy asthafen on line[/URL – [URL=http://cgodirek.com/aciphex/ – buy aciphex[/URL – [URL=http://frankfortamerican.com/viagra-com/ – viagra.com[/URL – [URL=http://aawaaart.com/danazol/ – danazol price walmart[/URL – [URL=http://iliannloeb.com/provigil/ – purchase provigil online[/URL – [URL=http://thegrizzlygrowler.com/generic-cialis-canada/ – cialis[/URL – [URL=http://homemenderinc.com/vidalista/ – vidalista cheap[/URL – [URL=http://lokcal.org/cipro/ – buy cipro[/URL – [URL=http://cgodirek.com/buy-levitra/ – levitra[/URL – levitra samples [URL=http://redlightcameraticket.net/item/fml-eye-drop/ – fml eye drop[/URL – [URL=http://cgodirek.com/ventolin/ – ventolin[/URL – [URL=http://stephacking.com/professional-cialis/ – cialis professional cheap[/URL – cialis professional [URL=http://mannycartoon.com/metronidazole-500mg-antibiotic/ – buy flagyl[/URL – [URL=http://eatingaftergastricbypass.net/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://anguillacayseniorliving.com/priligy-dapoxetine/ – buy priligy[/URL – non- assistant, generic asthafen canada pharmacy aciphex pills viagra generic danazol from canada danazol buy generic provigil generic cialis canada non prescription vidalista ciprofloxacin 500mg levitra fml eye drop uk buy ventolin inhaler professional cialis metronidazole 500mg generic ampicillin at walmart priligy dapoxetine risk-factors hormones, http://iliannloeb.com/asthafen/ where to buy asthafen http://cgodirek.com/aciphex/ aciphex online http://frankfortamerican.com/viagra-com/ viagra generic http://aawaaart.com/danazol/ danazol from india http://iliannloeb.com/provigil/ provigil http://thegrizzlygrowler.com/generic-cialis-canada/ cheapest cialis http://homemenderinc.com/vidalista/ lowest price for vidalista http://lokcal.org/cipro/ cipro http://cgodirek.com/buy-levitra/ generic levitra online http://redlightcameraticket.net/item/fml-eye-drop/ fml eye drop online generic fml eye drop http://cgodirek.com/ventolin/ ventolin ventolin inhaler http://stephacking.com/professional-cialis/ professional cialis http://mannycartoon.com/metronidazole-500mg-antibiotic/ flagyl http://eatingaftergastricbypass.net/generic-ampicillin-at-walmart/ online ampicillin no prescription purchase ampicillin online http://anguillacayseniorliving.com/priligy-dapoxetine/ priligy without dr prescription usa retreat coordinating likely.
cialis headache relief
wal mart pharmacy prices cialis
italy-hotels-holidays.co.uk
https://easy-tuto.fr/
jobbsverige.de
https://daswertvollste.at/
viagra prices
is there a viagra for women
cool-bricks.org
https://tomatowedding.com/
dapoxetine
purchase dapoxetine
priligy
銉娿偆銈?銈偊銈裤兗 銉偝銉偝
銉°兂銈?銉曘偂銉冦偡銉с兂銉栥儵銉炽儔 銉┿偝銈广儐 銉┿儷銉曘儹銉笺儸銉?/a>saint laurent factory store銉娿偆銈?銈ㄣ偄 銉炪儍銈偣 95 銈儸銉炽偢jr03 銉兗銈儷
buy cialis brand
Generic for sale
hdd銉偝銉笺儉銉?銈兂銉嗐儕 銈便兗銉栥儷
銉偆銈枫儯銉?澶?绱犳潗銈炽兗銉娿兂 浣滄キ 鐫€ 銈恒儨銉?/a>led 銉┿偆銉?鐓ф槑 鍣ㄥ叿鍒舵湇 銈兗銉囥偅銈兂 銉儑銈c兗銈?/a>
buy cialis canada
American health
http://paydayloanssfs.com/# installment loan http://loanonlineiuw.com/# – mortgages for bad credit payday installment loan help
careprost at cheapest prices https://carepro1st.com/
buy cialis
USA delivery
viagra 50mg canada
cheap generic viagra online
how to find clothes seen on tv shows uk
噩丕賳 亘賵賱 毓胤賵乇丕賱丿賮丕毓 丕賱賲丿賳賷 賮賷 丕賱丨夭丕賲 丕賱賲丿賷賳丞胤亘賱賴 卮乇賯賷 丕賲 亘賷 3賯賲氐丕賳 乇噩丕賱賷 爻賵賯
viagra in 3 days
viagra high blood pressure
銈儑銈c儉銈?銉儱銉冦偗 銉欍兗銈搞儱
璞?闆荤悆 灏傞杸 搴?abo銈炽兗銉囥儱銉偆 銉戙兂銉?銉偆銉?鐧?銈炽儍銉堛兂 銉戙兂銉?銉儑銈c兗銈?/a>銈嗐倠銈嗐倠 銉堛儍銉椼偣銈广儖銉笺偒銉?銉忋偆銈儍銉?銈炽兗銉?銉°兂銈?/a>
hydroxychloroquine for coronavirus https://hydroxychloroquine.webbfenix.com/
air max 270 react baskets basses white dynamic yelow
楂?鍙嶇櫤 鏋?妤藉ぉ浣?銇?銇勩亜 椋熴伖鐗?銉欍偣銉?10 2019銈汇儶銈?鎵囬ⅷ姗?銈儛銉?銉囥偅銈恒儖銉?/a>samsonite 銈点儬銈姐儕銈ゃ儓 debonair iv 銉囥儨銉嶃偄4 3way 銉栥儶銉笺儠銈便兗銈?2r
adidas superstar femme noir chaussure djherouan
cigarett忙nder adapteryoga bukser viscosebillige varme bluserlacoste mens deviation
銉堛儸銉笺儖銉炽偘 銈枫儱銉笺偤 閫氬
銉┿偆銉€銉笺偣 銈搞儯銈便儍銉?銈广儗銉笺儔cmos 銉°兗銈兗鐒″嵃 鑹搧 澶?鑹?銉氥兂銇嬨仱銈?浜?闊虫埜
stromectol usa https://ivermectin.mlsmalta.com/
order cialis without a prescription
cialis daily use review
mochilas de ataque desportivas
puma sf kart cat 3vans 銈儖銉炪儷 鏌?/a>銈偡銉冦偗銈?閲庣悆 銈广儜銈ゃ偗 銈点偆銈?/a>burberry the beat men 39
buy line viagra
order brand viagra
adidas 90 off
adidas superstar infoadidas id 96nike handschuhe wei脽clarks ukraine
vidalista dosage frequency https://vidalista40mg.mlsmalta.com/
rb2132 new wayfarer color mix 6054 85
faro 璨″竷 銉儑銈c兗銈?/a>銈枫儷銈?銈枫兗銉?銇婂湡鐢?/a>韪忋伩鍙?鏄囬檷 銈︺偐銉笺偔銉炽偘 銇┿仯銇?/a>澶櫧 鍏?銉愩儍銉嗐儶銉?鍏呴浕 鍣?/a>
No xby.kuqq.physicsclasses.online.rgu.ms anaemic, crack aggravating [URL=http://mannycartoon.com/cipro/ – kidney infection and cipro[/URL – [URL=http://center4family.com/plaquenil-for-sale-overnight/ – plaquenil[/URL – [URL=http://bioagendaprograms.com/viagra-avi/ – viagra[/URL – viagra en espanol [URL=http://homemenderinc.com/tenovate/ – tenovate[/URL – buy generic tenovate [URL=http://gaiaenergysystems.com/tadalafil-generic/ – cialis in australia[/URL – [URL=http://gccroboticschallenge.com/cialis-20-mg-price/ – cialis.com[/URL – [URL=http://foodfhonebook.com/propecia/ – nonprescription propecia au[/URL – [URL=http://impactdriverexpert.com/lyrica/ – lyrica mg[/URL – lyrica where to order [URL=http://theprettyguineapig.com/sildalis/ – sildalis prices[/URL – [URL=http://ossoccer.org/vardenafil/ – vardenafil[/URL – [URL=http://impactdriverexpert.com/order-nizagara-online-in-canada/ – order nizagara online in canada[/URL – [URL=http://thegrizzlygrowler.com/generic-viagra/ – viagra.com[/URL – [URL=http://davincipictures.com/viagra-com/ – viagra generic[/URL – [URL=http://themusicianschoice.net/amlip/ – online generic amlip[/URL – [URL=http://heavenlyhappyhour.com/fildena/ – fildena[/URL – sum buy ciprofloxacin plaquenil buy online viagra avi generic tenovate from canada cialis purchase online cialisextense get propecia without aprescription lyrica sildalis sell vardenafil pills legal sites cost of 25 mg nizagara kamagra fast viagra generic generic amlip lowest price fildena online testicular http://mannycartoon.com/cipro/ ciprofloxacin 500 mg http://center4family.com/plaquenil-for-sale-overnight/ cost of plaquenil tablets http://bioagendaprograms.com/viagra-avi/ low cost alternatives and viagra http://homemenderinc.com/tenovate/ tenovate best price http://gaiaenergysystems.com/tadalafil-generic/ generic cialis lowest price http://gccroboticschallenge.com/cialis-20-mg-price/ cialis http://foodfhonebook.com/propecia/ buying propecia online legal canada http://impactdriverexpert.com/lyrica/ genericos de lyrica http://theprettyguineapig.com/sildalis/ buying generic sildalis without prescription http://ossoccer.org/vardenafil/ vardenafil http://impactdriverexpert.com/order-nizagara-online-in-canada/ order nizagara online in canada http://thegrizzlygrowler.com/generic-viagra/ viagra viagra aus usa http://davincipictures.com/viagra-com/ viagra http://themusicianschoice.net/amlip/ amlip best price http://heavenlyhappyhour.com/fildena/ fildena pills asylum procreation cognition squints.
dapoxetine for sale in us https://ddapoxetine.com/
cialis free trial https://wisig.org/
chloroquine over the counter usa https://hydroxychloroquinee.com/
albuterol sulfate generic name
503 Service Unavailable