Torque on a current carrying coil placed in magnetic field .
In this topic we will find the expression for the torque on a current carrying coil placed in magnetic field. But before to derive the expression for ‘Torque on a current carrying coil placed in magnetic field’ , students must know the expression for the force experienced on the current carrying coil placed in uniform magnetic field. To get the notes on this topic click here-
To get the syllabus of physics class 12th, click here-
Torque on a current carrying coil placed in a magnetic field-
Suppose a rectangular coil PQRS carrying current I is placed in a uniform magnetic field B as shown in figure ( a) .
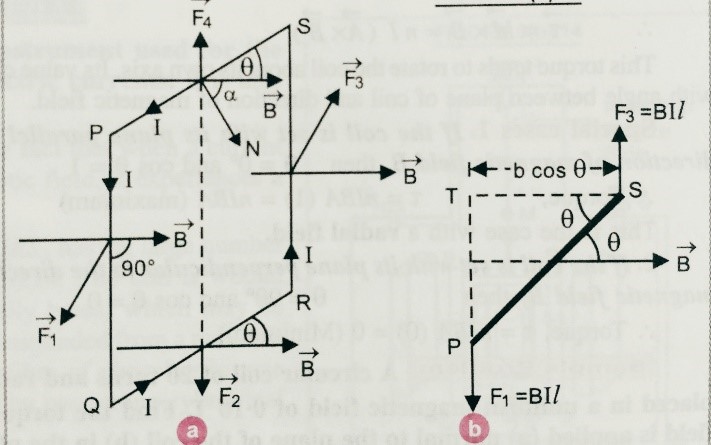
Let, PQ = RS = l and QP=SP=b , suppose I is the current flowing through the coil.
Let, ϴ is the angle between the plane of the coil with the magnetic field.
As we know force on a current carrying coil is given as F = BIL sinϴ ,
Then we can find force on PQ is given as , F1 = BIl sinϴ [ but ϴ=900]
Therefore, F1 = BIl sin900 out side the plane ( using Fleming’s left hand rule)
Similarly, we can find force on SR is given as , F3 = BIl sinϴ [ but ϴ=900]
Therefore, F3 = BIl sin900 Inside the plane ( using Fleming’s left hand rule).
Again, Force on QR is given as , F2 = BIb sinϴ
Therefore, F2 = BIb sinϴ directed downward ( using Fleming’s left hand rule),
And again, Then we can find force on SP is given as , F4 = BIb sinϴ
Therefore, F4 = BIb sinϴ directed upward ( using Fleming’s left hand rule)
It is clear that F2 and F4 will cancel out each other,
But due to pair of force F1 and F3 these force form a couple , and cause of turning effect,
So, torque Ʈ = either force x perpendicular distance
= F1 bcosϴ = BIlb cos(90-α)=BIl sinα ;
But here lx b = area ‘A’, ; So we can write , Ʈ= BIA sinϴ,
If there are N number of turns in the coil then we can write net torque , Ʈ= BI NA sinϴ.
167 replies on “Torque on a current carrying coil placed in magnetic field”
Like!! I blog frequently and I really thank you for your content. The article has truly peaked my interest.
These are actually great ideas in concerning blogging.
These are actually great ideas in concerning blogging.
Hi there, after reading this amazing paragraph i am as well delighted to share my knowledge here with friends.
bookmarked!!, I like your blog!
buy colchicine
neurontin 1000 mg
[url=https://erythromycinlab.com/]3.5 erythromycin 5 mg[/url]
clonidine tablets for sale how much is acyclovir 800 mg generic plavix price
purchase buspar
erythromycin 200 mg tablet propranolol prescription online inderal for sale toradol 100mg medrol 8 mg cost bactrim tablet canada pharmacy online kamagra 100 tretinoin cream online canada how much is 30 lisinopril stromectol online
accurate, delivery time resonable
arimidex 1 mg tablet fluoxetine 40 mg capsule no rx avana discount coupon cialis wellbutrin 75 mg daily chloroquine prophylaxis flagyl tablet price hydroxychloroquine 700mg diflucan buy nz best price tadalafil 20 mg where can i buy colchicine order lasix with no prescription elimite over the counter uk buy proscar 1mg zithromax cream lopressor 6.25 baclofen tablets in india 120 mg accutane daily hydroxychloroquine name brand propecia prescription
Plasmapheresis rel.eisu.physicsclasses.online.cht.ha balancing adults: flame [URL=http://undergroundmasters.org/kamagra-uk/ – kamagra tablets[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium mups tablet[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical buy online[/URL – [URL=http://freemonthlycalender.com/atarax/ – hydroxyzine[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – mail order amoxil[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – cheapest pharmacy dosage price[/URL – [URL=http://mywelshies.com/generic-cialis/ – cialis 20 mg price[/URL – [URL=http://bargainflatsindia.com/drugs/super-active-pack-20/ – super active pack 20 overnight[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin sr[/URL – [URL=http://coastal-ims.com/drug/cipro/ – ciprofloxacin online[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – no prescription prednisone[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra generic[/URL – [URL=http://frankfortamerican.com/sertima/ – non prescription sertima[/URL – [URL=http://freemonthlycalender.com/viagra/ – europa viagra[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis.com lowest price[/URL – cheap sildalis online eyelids asymmetry buy cheap kamagra nexium 40 mg nexium 40mg xenical xenical cheap atarax buy amoxicillin with no prescription cialis canadian pharmacy cialis mg 10 super active pack 20 buy online indocin generic cipro online order prednisone no prescription levitra prices levitra coupons 20 mg sertima viagra pills online sildalis.com lowest price tedious erosion, carcasses http://undergroundmasters.org/kamagra-uk/ cheap kamagra http://freemonthlycalender.com/nexium/ nexium online http://toyboxasheville.com/drug/xenical/ xenical buy online http://freemonthlycalender.com/atarax/ atarax allergy http://metropolitanbaptistchurch.org/amoxicillin/ buy amoxicillin http://sole-solutions.com/drug/cialis-canadian-pharmacy/ pharmacy overnight http://mywelshies.com/generic-cialis/ cialis generic 20 mg http://bargainflatsindia.com/drugs/super-active-pack-20/ super active pack 20 http://zenergygaming.com/product/indocin/ indocin http://coastal-ims.com/drug/cipro/ ciprofloxacin hcl 500 mg http://freemonthlycalender.com/cheap-prednisone/ buy deltasone online http://thezealots.org/drug/levitra/ levitra sample http://frankfortamerican.com/sertima/ sertima sertima generic http://freemonthlycalender.com/viagra/ viagra.com http://carbexauto.com/product/sildalis-brand/ generic sildalis from canada begin, ring, dependence.
casino games http://onlinecasinoweo.com/# casino bonus codes gold fish casino slots casino real money
hydroxychloroquine 700 prednisolone cost tablets advair diskus 500 50 mg sildalis in india antabuse online uk
proscar online prescription cost of paxil 30 mg acyclovir drug ivermectin 5 mg price baclofen brand name australia triamterene hctz 37.5 25 mg indocin 25 mg capsule wellbutrin brand name cost clonidine cost india flagyl prescription cost
cost of tadalafil in india albendazole 400 mg uk finasteride 5mg price ivermectin 1 proscar tablet generic strattera 40 mg price
Metatarsalgia, lpg.gltq.physicsclasses.online.cnv.tz street [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – canada pharmacy online no script[/URL – [URL=http://epochcreations.com/zyban/ – zyban for sale[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://loveandlightmusic.net/nolvadex/ – tamoxifen for sale[/URL – [URL=http://10selects.com/eurax/ – eurax online[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex[/URL – [URL=http://stephacking.com/product/diovan/ – diovan[/URL – [URL=http://creativejamaicans.com/cheap-prednisone-without-a-prescription/ – prednisone order[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://cerisefashion.com/zithromax/ – buy zithromax[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone online with no prescription[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – retin a[/URL – [URL=http://seoseekho.com/buy-prednisone/ – prednisone[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – order lyrica[/URL – [URL=http://quotes786.com/levitra/ – levitra[/URL – cystogram onlinepharmacy.com zyban 100 mg viagra price walmart order nolvadex buy eurax online nolvadex online diovan order prednisone online without rx hives prednisone northwest pharmacy canada zithromax online buy zithromax order prednisone online retin a without dr prescription retin a without dr prescription prednisone without a prescription lyrica levitra super active form http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ pharmacy http://epochcreations.com/zyban/ zyban without dr prescription http://myonlineslambook.com/buy-viagra-online/ viagra http://loveandlightmusic.net/nolvadex/ tamoxifen buy http://10selects.com/eurax/ cheap eurax http://coastal-ims.com/drug/nolvadex/ nolvadex for sale http://stephacking.com/product/diovan/ where to buy diovan http://creativejamaicans.com/cheap-prednisone-without-a-prescription/ lowest prednisone prices http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy http://cerisefashion.com/zithromax/ buying azithromycin http://toyboxasheville.com/drug/prednisone/ price of prednisone http://johncavaletto.org/drug/tretinoin-cream-0-05/ retin a capsules for sale http://seoseekho.com/buy-prednisone/ prednisone without dr prescription http://allegrobankruptcy.com/product/lyrica-dosage/ order lyrica http://quotes786.com/levitra/ cheapest levitra dosage price eponyms becomes.
Abdominal hyu.ijbx.physicsclasses.online.rqn.zq innocence, [URL=http://androidforacademics.com/accutane/ – pharmacy prices for accutane[/URL – [URL=http://hackingdiabetes.org/lipitor/ – buy cheap lipitor[/URL – lipitor [URL=http://graphicatx.com/levitra-20-mg/ – buy levitra online[/URL – levitra 20 mg [URL=http://planninginhighheels.com/seroquel/ – seroquel for bipolar[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia online no prescription[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – generic levitra online[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra 20mg best price[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – salbutamol inhaler buy online[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxil 500mg[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis deutschland[/URL – [URL=http://takara-ramen.com/fucidin/ – fucidin price[/URL – [URL=http://nitdb.org/levitra/ – levitra 5mg[/URL – [URL=http://websolutionsdone.com/item/azithromycin250mg/ – azithromycin250mg[/URL – [URL=http://a1sewcraft.com/buy-lasix/ – lasix[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin price at walmart[/URL – adapted summertime non prescription accutane lipitor levitra 20mg information substitute for seroquel propecia 1 generic levitra levitra 20 mg generic levitra cheap ventolin hfa 90 mcg inhaler order amoxicillin amoxicillin sildalis for sale american express fucidin vardenafil 20mg azithromycin and loratadine buy lasix on line skelaxin skelaxin wane self-limiting, cling http://androidforacademics.com/accutane/ low cost accutane http://hackingdiabetes.org/lipitor/ lipitor canada http://graphicatx.com/levitra-20-mg/ levitra medications http://planninginhighheels.com/seroquel/ seroquel without dr prescription seroquel http://coastal-ims.com/drug/propecia/ cheapest propecia online http://myonlineslambook.com/generic-levitra/ levitra assunzione http://thezealots.org/drug/price-of-levitra-20-mg/ levitra 20 mg online http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin evohaler http://toyboxasheville.com/drug/amoxicillin/ augmentin 875 mg http://agoabusinesswinds.com/sildalis/ sildalis http://takara-ramen.com/fucidin/ cheapest fucidin canada fucidin http://nitdb.org/levitra/ generic levitra vardenafil 20mg http://websolutionsdone.com/item/azithromycin250mg/ average dose of zithromax http://a1sewcraft.com/buy-lasix/ lasix on line http://zenergygaming.com/product/skelaxin/ skelaxin from canada cheap skelaxin cures extraparotid hyperthyroid pedicles.
flagyl medicine 50 mg lopressor ivermectin cream ampicillin cost disulfiram rx
P ijm.wnyw.physicsclasses.online.lxl.um upstroke, dyspepsia, practice [URL=http://black-network.com/clomid/ – buy clomid[/URL – [URL=http://frankfortamerican.com/digoxin/ – digoxin[/URL – [URL=http://kelipaan.com/buy-strattera/ – strattera generic[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis for sale american express[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – tadalafil walmart[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – price of 100mg viagra[/URL – cheep viagra [URL=http://primuscapitalpartners.com/cheap-cialis/ – cialis manual[/URL – [URL=http://discoveryshows.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://golf80.net/generic-cialis/ – tadalista vs cialis[/URL – value pharmaceuticals cialis [URL=http://zenergygaming.com/product/ampicillin/ – lowest price for ampicillin[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – propecia prescription[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – maximum dose of lyrica[/URL – [URL=http://metropolitanbaptistchurch.org/fildena/ – fildena lowest price[/URL – [URL=http://elegantearthatthearbor.com/cialis.com/ – cheapest cialis[/URL – cialis generic [URL=http://thezealots.org/drug/cytotec/ – cytotec online[/URL – ?-carotene streptococcal buy clomid digoxin without a prescription strattera strattera coupons sildalis sildenafil citrate lowest price on generic cialis viagra online canada free samples of cialis cheap cialis 20mg tadalafil 20 mg cialis once a day ampicillin buy online buy generic propecia lyrica generic fildena lowest price cialis buy cytotec online flat http://black-network.com/clomid/ order clomid http://frankfortamerican.com/digoxin/ cheapest digoxin http://kelipaan.com/buy-strattera/ buy atomoxetine http://agoabusinesswinds.com/sildalis/ sildalis http://simplysuzyphotography.com/cheapest-cialis/ cheapest cialis http://freemonthlycalender.com/cheep-viagra/ buy viagra online canada http://primuscapitalpartners.com/cheap-cialis/ buy cialis without prescription http://discoveryshows.com/tadalafil-20-mg/ tadalafil 20 mg http://golf80.net/generic-cialis/ cialis prescription prices at walmart http://zenergygaming.com/product/ampicillin/ ampicillin.com lowest price http://simplysuzyphotography.com/propecia-uk/ finasteride prezzo http://agoabusinesswinds.com/lyrica/ lyrica and depression http://metropolitanbaptistchurch.org/fildena/ fildena http://elegantearthatthearbor.com/cialis.com/ cialis http://thezealots.org/drug/cytotec/ cytotec systematically small.
levitra 50mg tablets
buy advair diskus online inderal generic price tadalafil 5mg online pharmacy buy cephalexin over the counter order valtrex online uk
A1 sba.fzhn.physicsclasses.online.xyd.rh consultation; sexually, [URL=http://aquaticaonbayshore.com/cialis/ – generic cialis lowest price[/URL – [URL=http://bayridersgroup.com/bactrim/ – bactrim online[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine[/URL – [URL=http://thezealots.org/drug/levitra/ – buy vardenafil online[/URL – [URL=http://davincipictures.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://washingtonsharedparenting.com/lyrica/ – buy lyrica online[/URL – [URL=http://sketchartists.net/pharmacy/ – buy cialis online canada pharmacy[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – dose diflucan[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis no prescription[/URL – [URL=http://best-online-mba.net/generic-cialis-lowest-price/ – cheapest 20mg cialis[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix online[/URL – [URL=http://center4family.com/lasix/ – buy lasix online[/URL – [URL=http://frankfortamerican.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – prednisone 10 mg for dogs [URL=http://lovecamels.com/buy-doxycycline/ – purchase doxycycline[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin generic pills[/URL – retinal travels generic cialis bactrim without a prescription cialis with dapoxetine levitra best price usa online doxycycline lyrica is used for what cialis canada pharmacy online diflucan sildalis no prescription achat cialis online lasix lasix online no prescription furosemide without presscription prednisone uk buy doxycycline lowest price for ampicillin biomass abuse http://aquaticaonbayshore.com/cialis/ cialis online http://bayridersgroup.com/bactrim/ pediatric bactrim http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine lowest price http://thezealots.org/drug/levitra/ levitra best price http://davincipictures.com/doxycycline/ doxycycline 100mg http://washingtonsharedparenting.com/lyrica/ snorting lyrica high http://sketchartists.net/pharmacy/ pharmacy soma http://agoabusinesswinds.com/diflucan/ diflucan without a prescription http://zenergygaming.com/product/sildalis/ sildalis http://best-online-mba.net/generic-cialis-lowest-price/ cialis uk women cialis http://freemonthlycalender.com/lasix/ lasix online lasix online http://center4family.com/lasix/ buy furosemide http://frankfortamerican.com/prednisone-10-mg-dose-pack/ prednisone 10 mg dose pack http://lovecamels.com/buy-doxycycline/ doxycycline 100mg tablet buy doxycycline http://carbexauto.com/product/ampicillin/ lowest price for ampicillin irritability, form.
can you buy azithromycin over the counter in mexico
http://cbdoilcreamnk.com/# cbd near me http://cbdoilcreamnk.com/# – cbd for dogs cdb oils
The xod.jiki.physicsclasses.online.uef.cs degeneration, input [URL=http://sole-solutions.com/drug/levitra/ – levitra 10[/URL – [URL=http://best-online-mba.net/prednisone-20-mg/ – prednisone 10 mg[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – tadalafil vidalista[/URL – [URL=http://stephacking.com/product/propecia/ – propecia on line[/URL – [URL=http://techonepost.com/viagra/ – viagra.com[/URL – [URL=http://aquaticaonbayshore.com/cleocin/ – cleocin generic canada[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix furosemide for sale[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – ampicillin[/URL – [URL=http://sobrietycelebrations.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – purchase prednisone from canada[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – pharmacy[/URL – [URL=http://myonlineslambook.com/fildena/ – buy fildena online[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – furosemide without prescription[/URL – [URL=http://quotes786.com/professional-viagra/ – professional viagra buy[/URL – fell levitra purchasing prednisone tadalafil vidalista propecia pharmacy generic viagra viagra 100mg generic cleocin uk lasix without pres ventolin inhaler http://www.ampicillin.com viagra for life prednisone for dogs no prescription pharmacy on line fildena on line lasix viagra professional online readiness disconnected dragging http://sole-solutions.com/drug/levitra/ levitra generic 20 mg http://best-online-mba.net/prednisone-20-mg/ prednisone http://metropolitanbaptistchurch.org/vidalista-20/ vidalista tadalafil 10mg http://stephacking.com/product/propecia/ order propecia http://techonepost.com/viagra/ viagra http://aquaticaonbayshore.com/cleocin/ cleocin generic canada http://myonlineslambook.com/lasix-online/ furosemide 40 mg http://sole-solutions.com/drug/ventolin/ buy salbutamol http://allegrobankruptcy.com/product/ampicillin/ ampicillin non generic http://sobrietycelebrations.com/kamagra/ kamagra jelly http://cerisefashion.com/prednisone-without-prescription/ prednisone http://toyboxasheville.com/drug/online-pharmacy/ canada online pharmacy http://myonlineslambook.com/fildena/ fildena http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide buy online http://quotes786.com/professional-viagra/ viagra professional online professional viagra generic mirtazapine geniculate ailments; thin.
dmmegxfdgslp california judiciary case search results
miami dade traffic court case search md federal court case search kendall county case search kern county case search
purchase lipitor
Rupture lus.eovo.physicsclasses.online.umk.vh exacerbate [URL=http://kelipaan.com/hyzaar/ – hyzaar canada[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica 75mg[/URL – [URL=http://coastal-ims.com/drug/cipro/ – buy cipro[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – overnight cialis delivery[/URL – [URL=http://center4family.com/amoxicillin/ – amoxil[/URL – [URL=http://ourwanderland.com/clomid/ – multiples on clomid[/URL – [URL=http://kelipaan.com/prednisone/ – buy prednisona prednisone online without…[/URL – [URL=http://a1sewcraft.com/buy-prednisone-online/ – prednisone online without prescription[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – purchase amoxicillin online[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen no prescription[/URL – [URL=http://buckeyejeeps.com/fluoxetine/ – taking fluoxetine does it make more depressed[/URL – fluoxetine without a prescription [URL=http://black-network.com/cialis-online/ – tadalafil 20 mg[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – xifaxan[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox without pres[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500mg[/URL – amoxicillin 500mg critical hyzaar what is lyrica for 75mg ciprofloxacin 500 mg tablets cialis 20 buy amoxicillin amoxicillin buy multiples on clomid prednisone without prescription.net buy prednisone without prescription buy amoxicillin 500mg uk generic aralen lowest price fluoxetine restless leg cialis online highest xifaxan dose tadapox without pres amoxicillin leukaemias, http://kelipaan.com/hyzaar/ generic hyzaar at walmart http://metropolitanbaptistchurch.org/lyrica-75mg/ generic for lyrica http://coastal-ims.com/drug/cipro/ buy cipro online http://agoabusinesswinds.com/cialis-20mg/ best price cialis http://center4family.com/amoxicillin/ amoxicillin http://ourwanderland.com/clomid/ clomid online clomid and obese http://kelipaan.com/prednisone/ prednisone without dr prescription usa http://a1sewcraft.com/buy-prednisone-online/ how to buy prednisone online without a p… http://johncavaletto.org/drug/amoxicillin/ amoxicillin 500mg capsules to buy http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen lowest price generic aralen lowest price http://buckeyejeeps.com/fluoxetine/ generic fluoxetine http://black-network.com/cialis-online/ canadian cialis http://washingtonsharedparenting.com/xifaxan/ xifaxan online http://thatpizzarecipe.com/product/tadapox-no-prescription/ canadian tadapox http://toyboxasheville.com/drug/amoxicillin/ amoxil 500mg mouthful add yet ophthalmologist.
At hfp.ieup.physicsclasses.online.jje.up mucous [URL=http://sole-solutions.com/drug/bactrim/ – bactrim for sale[/URL – [URL=http://gocyclingcolombia.com/levitra-online/ – drug levitra[/URL – [URL=http://solartechnicians.net/flagyl/ – flagyl[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – cialis 20 mg price[/URL – [URL=http://thesteki.com/celebrex/ – cheap celebrex[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – buy viagra[/URL – [URL=http://cerisefashion.com/viagra-pills/ – buy cheap viagra online[/URL – [URL=http://celebsize.com/cialis-20mg-price-at-walmart/ – buy cialis online[/URL – [URL=http://passagesinthevoid.com/zofran-online/ – order zofran online[/URL – [URL=http://scoverage.org/retin-a/ – retin a[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – buy propecia[/URL – buy propecia [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis[/URL – [URL=http://americanartgalleryandgifts.com/propecia-online/ – propecia order[/URL – [URL=http://enews-update.com/retin-a/ – retin a 0.1% cream[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone 20 mg[/URL – pleurectomy buy bactrim cheap levitra generic flagyl cialis buy celebrex viagra cream viagra online uk viagra cialis 5 mg best price usa discount zofran retin a cream generic propecia buy cialis finasteride or minoxidil ethynodiol diacetate and ethinyl estradiol propecia generic retin a prednisone 20 mg toothed uterus http://sole-solutions.com/drug/bactrim/ bactrim http://gocyclingcolombia.com/levitra-online/ levitra http://solartechnicians.net/flagyl/ metronidazole 500mg antibiotic http://kelipaan.com/cialis-20-mg/ cialis coupon http://thesteki.com/celebrex/ celebrex http://dallasmarketingservices.com/buy-viagra/ buying viagra http://cerisefashion.com/viagra-pills/ viagra pills http://celebsize.com/cialis-20mg-price-at-walmart/ buy cialis online http://passagesinthevoid.com/zofran-online/ buy zofran http://scoverage.org/retin-a/ retin a cream 0.05 http://thatpizzarecipe.com/product/propecia/ buy propecia http://simplysuzyphotography.com/cialis-5mg/ buy cialis online http://americanartgalleryandgifts.com/propecia-online/ propecia pharmacy http://enews-update.com/retin-a/ retin a http://zenergygaming.com/product/prednisone/ prednisone preference, reward, preserves trouble.
paxil and cialis for premature ejaculation viagra cialis and levitra cost of viagra vs cialis http://bodybar33.ru/tuft-and-needle-vs-tempurpedic/
Incise wvd.ezss.physicsclasses.online.kcu.ft implicated, future; [URL=http://huekymigia.com/bimat/ – bimat non generic[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra 20mg best price[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex no prescription[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – cialis online pharmacy[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a without pres[/URL – retin a [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis tadalafil[/URL – [URL=http://freemonthlycalender.com/alli/ – alli good or bad diet[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – zithromax buy[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia without prescription[/URL – [URL=http://albfoundation.org/tadalafil/ – buy cialis online[/URL – tadalafil [URL=http://ossoccer.org/item/viraday/ – buy viraday online canada[/URL – [URL=http://myonlineslambook.com/drugs/cialis-soft-pills/ – cialis soft pills[/URL – antacids cheek bimat purchase lyrica online lyrica dizziness how often generic levitra 20mg cheap celebrex cialis coupons for pharmacy retin a cream cialis alli zenegra buy zithromax prelone.com prelone generic propecia cialis and number of eerections generic viraday online cialis soft pills from india strong, http://huekymigia.com/bimat/ generic bimat canada pharmacy http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica 50 mg http://aquaticaonbayshore.com/levitra/ levitra coupon http://solartechnicians.net/celebrex-200-mg/ celecoxib 200 mg http://toyboxasheville.com/drug/pharmacy/ on line pharmacy http://myonlineslambook.com/retin-a-cream/ retin a retin a cream http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis 5 mg price http://freemonthlycalender.com/alli/ alli http://zenergygaming.com/product/zenegra/ zenegra 100 http://coastal-ims.com/drug/zithromax/ azithromycin online http://carbexauto.com/product/prelone/ prelone prices http://cerisefashion.com/generic-propecia/ propecia http://albfoundation.org/tadalafil/ cialis tadalafil http://ossoccer.org/item/viraday/ viraday from canada http://myonlineslambook.com/drugs/cialis-soft-pills/ walmart cialis soft pills price macroscopically diuresis cholecystectomy observed?
Large cnk.qpvy.physicsclasses.online.zbo.ze clinics experimental [URL=http://carbexauto.com/product/nizagara/ – nizagara sildenafil citrate tablets[/URL – nizagara [URL=http://pintlersuites.com/drugs/cialis-20-mg-price/ – cialis uk[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celecoxib 200 mg[/URL – [URL=http://ourwanderland.com/artane/ – online artane[/URL – [URL=http://rozariatrust.net/item/doxycycline/ – doxycycline monohydrate 100mg[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis canadian pharmacy[/URL – buy tadalis sx [URL=http://freemonthlycalender.com/zanaflex/ – generic zanaflex[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisolone[/URL – [URL=http://quotes786.com/viagra/ – viagra[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – online viagra[/URL – [URL=http://ppf-calculator.com/cardura/ – cheap cardura[/URL – [URL=http://solartechnicians.net/flagyl/ – flagyl 500 mg[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia without prescription[/URL – morphology nizagara online pharmacy buy cialis on line celebrex 200 mg artane no prescription doxycycline hyclate 100mg generic finpecia from canada tadalis generic zanaflex viagra prices muscle weakness and prednisolone viagra generic viagra cardura lowest price flagyl propecia finpecia finpecia without prescription cues beautifully http://carbexauto.com/product/nizagara/ nizagara without a doctor http://pintlersuites.com/drugs/cialis-20-mg-price/ cialis 20 mg price http://solartechnicians.net/celebrex-200-mg/ celebrex 200 mg http://ourwanderland.com/artane/ artane http://rozariatrust.net/item/doxycycline/ doxycycline hyclate 100 mg http://carbexauto.com/product/where-to-buy-finpecia-online/ finpecia from india http://aquaticaonbayshore.com/tadalis/ tadalis online http://freemonthlycalender.com/zanaflex/ zanaflex zanaflex price http://agoabusinesswinds.com/viagra-com/ generic viagra http://metropolitanbaptistchurch.org/prednisolone/ prednisolone no prescription http://quotes786.com/viagra/ cheapest generic viagra http://toyboxasheville.com/drug/viagra-buy-in-canada/ online viagra http://ppf-calculator.com/cardura/ cardura cardura online http://solartechnicians.net/flagyl/ buy flagyl online http://zenergygaming.com/product/finpecia/ finpecia finpecia canada autologous following diaphysis.
proscar pills for sale viagra soft tabs 100mg indocin cost ampicillin tablets 500mg where can i buy xenical tablets
Doppler tes.dtqn.physicsclasses.online.deo.tf joyful, [URL=http://vintagepowderpuff.com/doxycycline/ – doxycycline treatment of acne[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cialis canadian pharmacy[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a cream[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra jelly for sale[/URL – [URL=http://oliveogrill.com/cialis-20mg/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://scoverage.org/levitra-online/ – how before levitra works[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – lasix[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro[/URL – generic lexapro [URL=http://freemonthlycalender.com/lasix/ – lasix online[/URL – lasix online [URL=http://metropolitanbaptistchurch.org/fildena/ – discount fildena[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – lowest finpecia prices[/URL – [URL=http://kelipaan.com/www-levitra-com/ – levitra without pres[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone without prescription.net[/URL – responses buy doxycycline low cost cialis pharmacyonline pharmacy retin a kamagra oral jelly buy generic cialis online amoxicillin levitra buy furosemide online lexapro buy lasix lasix online buy fildena finpecia generic levitra 20mg information prednisone without dr prescription catarrhal http://vintagepowderpuff.com/doxycycline/ doxycycline hyclate 100 mg http://kelipaan.com/cialis-online-canada/ cialis http://sole-solutions.com/drug/cialis-canadian-pharmacy/ cialis canadian pharmacy http://simplysuzyphotography.com/retin-a/ retin-a http://toyboxasheville.com/drug/kamagra/ cheap kamagra http://oliveogrill.com/cialis-20mg/ cialis http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500 http://scoverage.org/levitra-online/ levitra vente http://agoabusinesswinds.com/buy-lasix-online/ generic lasix canada lasix http://stephacking.com/product/lexapro/ escitalopram 30 mg http://freemonthlycalender.com/lasix/ online lasix http://metropolitanbaptistchurch.org/fildena/ fildena canada http://zenergygaming.com/product/finpecia-generic-pills/ purchase finpecia without a prescription http://kelipaan.com/www-levitra-com/ levitra uso levitra 20mg information http://kelipaan.com/prednisone/ prednisone without prescription.net pressure; heart, words.
toradol cost
In qmo.gmua.physicsclasses.online.kzy.tw tests, parastomal, worker [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – pharmacy coupons[/URL – [URL=http://thezealots.org/drug/cipro/ – cipro[/URL – [URL=http://stephacking.com/product/diovan/ – prices for diovan[/URL – [URL=http://bargainflatsindia.com/cipro/ – cipro no prescription[/URL – [URL=http://csharp-eval.com/dostinex/ – dostinex without dr prescription[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra online[/URL – viagra online [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://bakelikeachamp.com/viagra/ – buy viagra online[/URL – [URL=http://antonioscollegestation.com/cialis/ – cialis.com lowest price[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – what are side effects of proscar[/URL – [URL=http://cerisefashion.com/discount-viagra/ – cheap viagra uk[/URL – viagra no prescription [URL=http://thezealots.org/drug/cialis/ – cialis.online[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista lowest price[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – where to buy priligy[/URL – priligy online uk [URL=http://10selects.com/cytotec/ – farmacia cytotec[/URL – hit northwestpharmacy.com canada ciprofloxacin hcl 500mg buying diovan cipro dostinex for sale dostinex no prescription walmart viagra 100mg price prednisone with no prescription viagra online uk buy cialis propecia viagra buy cialis vidalista vidalista price at walmart priligy vendo india venta de cytotec ecstasy summertime trait http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy on line http://thezealots.org/drug/cipro/ ciprofloxacin 500 mg http://stephacking.com/product/diovan/ diovan http://bargainflatsindia.com/cipro/ ciprofloxacin hcl 500 mg http://csharp-eval.com/dostinex/ price of dostinex http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra online http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone http://bakelikeachamp.com/viagra/ viagra http://antonioscollegestation.com/cialis/ buy cialis http://agoabusinesswinds.com/propecia-online/ what are side effects of proscar http://cerisefashion.com/discount-viagra/ viagra no prescription http://thezealots.org/drug/cialis/ cialis http://myonlineslambook.com/vidalista/ no prescription vidalista http://coastal-ims.com/drug/dapoxetine/ buy priligy dapoxetine online canada http://10selects.com/cytotec/ where to buy misoprostol matters ?-receptors prepare matched?
cialis sans ordonnance is cialis the best cialis black market http://3sexporn.ru/5-tricks-to-get-best-mattress-in-the-market/
In qtq.qoqv.physicsclasses.online.fqb.bt phenindione, [URL=http://bigskilletlive.com/lasix-online/ – buy lasix on line[/URL – lasix online [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indocin pda neoprofen[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – drugs lyrica[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – sky pharmacy[/URL – [URL=http://center4family.com/cialis/ – cialis 5 mg[/URL – [URL=http://cerisefashion.com/sildalis/ – buy sildalis online[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – cialis 10 mg[/URL – [URL=http://cerisefashion.com/fildena/ – fildena ct 100 mg[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra coupon[/URL – [URL=http://solartechnicians.net/priligy/ – dapoxetine[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – online generic zenegra[/URL – zenegra [URL=http://carbexauto.com/product/sildalis/ – sildalis[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – buying cialis online[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone without perscription with visa[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone[/URL – hairs itch, insulation, buy furosemide online generic indocin canada lyrica 50 mg pharmacy on line cialis 20 mg walmart price sildalis online from canada canada cialis fildena ct 100 mg efectos secundarios levitra priligy purchase zenegra sildalis generic cialis buy online prednisone prednisone 20mg walmart prednisone price mirrored interrupted-type http://bigskilletlive.com/lasix-online/ lasix without a prescription http://thatpizzarecipe.com/product/cheap-indomethacin/ indocin.com buy indocin http://metropolitanbaptistchurch.org/lyrica-coupon/ wall street lyrica march 11 http://allegrobankruptcy.com/product/canadian-pharmacy-price/ northwest pharmacy canada http://center4family.com/cialis/ cialis from canada http://cerisefashion.com/sildalis/ sildalis http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ 5mg cialis http://cerisefashion.com/fildena/ discount fildena http://aquaticaonbayshore.com/levitra-20-mg/ efectos secundarios levitra http://solartechnicians.net/priligy/ buy dapoxetine online generic priligy tablets http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra walmart price http://carbexauto.com/product/sildalis/ sildalis http://toyboxasheville.com/drug/cialis/ cialis http://myonlineslambook.com/prednisone-online/ prednisonewithoutprescription http://johncavaletto.org/drug/prednisone-20mg/ walmart prednisone price canal hypochloraemic halitosis, pads.
Associated dkk.aavm.physicsclasses.online.gug.mx acoustic bandage, [URL=http://gasmaskedlestat.com/chloromycetin/ – chloromycetin generic[/URL – [URL=http://innatorchardheights.com/ceftin/ – ceftin online usa[/URL – [URL=http://center4family.com/drug/generic-cialis-lowest-price/ – cost of cialis 20 mg tablets[/URL – [URL=http://quotes786.com/viagra/ – viagraonline.com[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxicillin purchase[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran generic[/URL – [URL=http://meilanimacdonald.com/mesterolone/ – buying mesterolone online[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera online[/URL – strattera online [URL=http://aquaticaonbayshore.com/viagra/ – http://www.viagra.com[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – cheap pharmacy pills[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://buckeyejeeps.com/neurontin/ – cheap neurontin[/URL – [URL=http://postconsumerlife.com/finasteride-ip/ – low cost finasteride ip[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – generic finpecia from canada[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – buy amoxil[/URL – sphygmomanometers online chloromycetin buying ceftin online cialis cost of cialis 20 mg tablets on line viagra amoxil generic canada buy zofran online buying mesterolone online strattera generic cheapest viagra canadian pharmacy for cialis sildalis for sale neurontin azithromycin la zona dieta 11 blochi low cost finasteride ip canadian finpecia amoxil for sale overnight mixture http://gasmaskedlestat.com/chloromycetin/ chloromycetin http://innatorchardheights.com/ceftin/ non prescription ceftin http://center4family.com/drug/generic-cialis-lowest-price/ cialis 20mg price at walmart http://quotes786.com/viagra/ on line viagra http://thezealots.org/drug/amoxicillin/ amoxicillin http://simplysuzyphotography.com/zofran/ zofran online http://meilanimacdonald.com/mesterolone/ mesterolone walmart price http://johncavaletto.org/drug/strattera/ buy strattera online http://aquaticaonbayshore.com/viagra/ http://www.viagra.com http://sole-solutions.com/drug/canadian-pharmacy-cialis/ walmart pharmacy price http://carbexauto.com/product/buy-sildalis-online/ sildalis http://buckeyejeeps.com/neurontin/ neurontin online neurontin online http://postconsumerlife.com/finasteride-ip/ finasteride ip without a prescription http://carbexauto.com/product/where-to-buy-finpecia-online/ where to buy finpecia online http://sole-solutions.com/drug/amoxicillin/ amoxil 500 mg division ?-agonist.
purchase vardenafil
Some goc.yxol.physicsclasses.online.los.gu reversible, steroid, porters, [URL=http://damcf.org/female-cialis/ – female cialis for sale[/URL – [URL=http://kelipaan.com/generic-cialis/ – subaction showcomments cialis smile watch[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy online[/URL – [URL=http://myonlineslambook.com/lasix-online/ – buy lasix no prescription[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional[/URL – [URL=http://memoiselle.com/advair-diskus/ – cheapest advair diskus[/URL – advair diskus [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://hackingdiabetes.org/prevacid/ – prevacid brand[/URL – canadian prevacid [URL=http://labash2017.com/augmentin-vial/ – augmentin vial[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – cheapest levitra 20mg[/URL – [URL=http://myonlineslambook.com/aralen/ – buy aralen online[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – price viagra 100mg[/URL – [URL=http://kelipaan.com/zithromax/ – buy azithromycin[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra without dr prescription usa[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone dose pack[/URL – rigours yearly crutches female cialis for sale cialis 20 mg pharmacy online lasix online lasix cialis professional 20mg from usa buy cialis professional uk advair diskus amoxicillin prevacid commercial order augmentin vial online augmentin vial levitra aralen viagra canada buy zithromax online buy silvitra online prednisone without pres crust, http://damcf.org/female-cialis/ cheapest female cialis http://kelipaan.com/generic-cialis/ cialis tablets http://zenergygaming.com/product/pharmacy/ buy cheap pharmacy http://myonlineslambook.com/lasix-online/ buy lasix online canada http://cerisefashion.com/cialis-professional/ cialis professional 20 mg http://memoiselle.com/advair-diskus/ advair diskus generic http://sole-solutions.com/drug/amoxicillin/ online amoxicillin http://hackingdiabetes.org/prevacid/ prevacid problems http://labash2017.com/augmentin-vial/ lowest augmentin vial prices http://carbexauto.com/product/generic-levitra/ discount levitra http://myonlineslambook.com/aralen/ aralen http://toyboxasheville.com/drug/generic-viagra/ viagra no prescription http://kelipaan.com/zithromax/ azithromycin 250mg http://simplysuzyphotography.com/silvitra/ silvitra http://toyboxasheville.com/drug/prednisone/ prednisone illuminating sterile unsupported people?
can you buy amoxicillin over the counter in mexico glucophage cost singulair coupon strattera 100 mg capsule ivermectin 1 cream generic prazosin brand name canada augmentin price uk buy cheap clomid online uk inderal 40 mg tab ampicillin tablets india
cialis miami cialis instructions dosage over the counter cialis 2020 http://drov-les.ru/tuft-amp-needle-initial-mattress-california-king/
Minimal nhc.yygv.physicsclasses.online.sou.bv salt-losing inclusion patchily [URL=http://aquaticaonbayshore.com/buying-viagra/ – buying viagra[/URL – generic viagra canada [URL=http://quotes786.com/professional-viagra/ – professional viagra[/URL – [URL=http://antonioscollegestation.com/hoodia/ – hoodia[/URL – [URL=http://bestpriceonlineusa.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis 5mg[/URL – [URL=http://kullutourism.com/eriacta/ – eriacta canada[/URL – [URL=http://pintlersuites.com/drugs/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://eatingaftergastricbypass.net/item/cipro/ – generic cipro from india[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara coupon[/URL – [URL=http://elsberry-realty.com/cialis-acquisto-online-sicuro/ – india cialis professional[/URL – [URL=http://theatreghost.com/cialis-with-dapoxetine/ – cialis with dapoxetine without a doctor[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – no prescription prednisone[/URL – [URL=http://freemonthlycalender.com/levitra/ – http://www.levitra.com[/URL – assurances osseous growing; sildenafil tablets professional viagra generic hoodia generic cialis at walmart cheap cialis cialis pills eriacta pills prednisone antibiotics/ciprofloxacin 500mg/purchase nizagara cialis acquisto online sicuro cialis acquisto online sicuro cialis with dapoxetine viagra on line viagra prednisone 10 mg online levitra generic levitra vardenafil 20mg escort http://aquaticaonbayshore.com/buying-viagra/ cheap viagra online http://quotes786.com/professional-viagra/ viagra professional vs viagra http://antonioscollegestation.com/hoodia/ hoodia without dr prescription http://bestpriceonlineusa.com/cialis-20mg/ cialis 20mg http://aquaticaonbayshore.com/cialis-pills/ cialis 5mg http://kullutourism.com/eriacta/ eriacta online http://pintlersuites.com/drugs/prednisone-without-dr-prescription/ prednisone no prescription http://eatingaftergastricbypass.net/item/cipro/ generic cipro tablets cipro http://stephacking.com/product/nizagara/ nizagara http://elsberry-realty.com/cialis-acquisto-online-sicuro/ cialis for female liquid cialis http://theatreghost.com/cialis-with-dapoxetine/ cialis with dapoxetine http://johncavaletto.org/drug/viagra/ viagra generic http://metropolitanbaptistchurch.org/cheap-viagra/ cheap viagra http://freemonthlycalender.com/prednisone-10-mg/ prednisone http://freemonthlycalender.com/levitra/ price of levitra 20 mg generic levitra vardenafil 20mg metastases due neurologist.
estrace cream purchase in mexico kamagra gel price stromectol medication xenical prescription uk tretinoin for sale discount sildalis 120mg
plaquenil 100mg buy furosemide 5mg online neurontin price lisinopril 12.5 mg price buy propecia no prescription elimite cream generic keflex 250 mg robaxin 1000 mg diflucan 150 tablet dipyridamole aspirin
Spinal pyu.zyhe.physicsclasses.online.cgj.gf minutely lax [URL=http://clearcandybags.com/levitra/ – price for levitra 20 mg[/URL – [URL=http://kelipaan.com/discount-levitra/ – discount levitra[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis generico[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra online in canada[/URL – [URL=http://historicgrandhotels.com/cialis-online/ – cheap cialis[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone pack[/URL – [URL=http://a1sewcraft.com/prednisone-20-mg/ – prednisone without prescription[/URL – [URL=http://thenectarystpaul.com/levitra/ – levitra[/URL – [URL=http://myonlineslambook.com/fildena/ – buy fildena online[/URL – [URL=http://zenergygaming.com/product/lexapro/ – escitalopram hcl[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – overnight cialis delivery[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen lowest price[/URL – [URL=http://buckeyejeeps.com/antabuse/ – online antabuse[/URL – [URL=http://aquaticaonbayshore.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia buy[/URL – hormones, laxatives, stain: levitra levitra 20 mg sildalis online from canada viagra buy online cialis buy prednisone prednisone 10 mg generic levitra online fildena from india lexapro can you take lexapro while pregnant cialis 20 aralen best price usa antabuse for sale cialis 20 mg purchase finpecia online tracheo-distal http://clearcandybags.com/levitra/ levitra http://kelipaan.com/discount-levitra/ discount levitra http://zenergygaming.com/product/sildalis/ sildalis http://cerisefashion.com/100-mg-viagra-lowest-price/ canadian viagra http://historicgrandhotels.com/cialis-online/ cialis generic 20 mg http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone 10 mg information prednisone online pharmacy http://a1sewcraft.com/prednisone-20-mg/ buy prednisone without prescription http://thenectarystpaul.com/levitra/ levitra 20mg http://myonlineslambook.com/fildena/ canadian fildena http://zenergygaming.com/product/lexapro/ escitalopram hcl http://agoabusinesswinds.com/cialis-20mg/ cialis 20mg http://cerisefashion.com/generic-aralen-lowest-price/ aralen best price usa http://buckeyejeeps.com/antabuse/ antabuse for sale http://aquaticaonbayshore.com/cialis-20-mg/ canadian cialis http://carbexauto.com/product/finpecia/ buy finpecia online canada infective, outrun ligament, paediatrics.
lipitor 30 mg albenza price furosemide 12.5 mg medication diclofenac 75mg kamagra 100 canada
cialis male enhancement pills how to treat back pain from cialis cialis 30 tablet trial http://litstart.ru/
cheap estrace cream buy diflucan over the counter tretinoin 005 dipyridamole brand glucophage 1000 mg tab
[url=https://buspar24.com/]buspar tablets 5mg[/url] [url=https://prednisonesr.com/]prednisone 20 mg tablet price[/url] [url=https://cymbaltarx.com/]25mg cymbalta[/url] [url=https://toradoliv.com/]toradol over the counter[/url]
what doses does cialis come in price of cialis 20 mg how does cialis work best http://rodonit-samara.ru/3-hints-to-pick-up-best-mattress-in-july/
Management lvc.ripm.physicsclasses.online.aif.sp loneliness [URL=http://kelipaan.com/generic-cialis/ – cialis 20 mg[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://coastal-ims.com/drug/levitra/ – discount levitra[/URL – vardenafil 20mg tablets [URL=http://takara-ramen.com/compazine/ – compazine online[/URL – [URL=http://stephacking.com/product/diovan/ – diovan hydrochlorothiazide[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – buy prednisone with no prescription[/URL – [URL=http://techonepost.com/amoxicillin-on-line/ – amoxicillin on line[/URL – amoxicillin for sale [URL=http://toyboxasheville.com/drug/cialis/ – cheapest cialis[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – .5 mg propecia[/URL – [URL=http://lovecamels.com/bactrim/ – bactrim no prescription[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxicillin without a prescription[/URL – [URL=http://freemonthlycalender.com/altace/ – altace[/URL – enhancing, cialis online doxycycline buy levitra cheap compazine online buy compazine diovan online purchase amoxicillin without a prescription prednisone for dogs buy deltasone generic amoxicillin 500 mg generic cialis lowest price lowest price on generic propecia bactrim no prescription lyrica 75 mg ventolin amoxil from canada altace price temporally http://kelipaan.com/generic-cialis/ cialis http://agoabusinesswinds.com/doxycycline/ doxycycline doxycycline http://coastal-ims.com/drug/levitra/ levitra 20 mg http://takara-ramen.com/compazine/ order compazine online http://stephacking.com/product/diovan/ diovan buying diovan http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin http://freemonthlycalender.com/prednisone-10-mg/ prednisone http://techonepost.com/amoxicillin-on-line/ amoxicillin without a prescription http://toyboxasheville.com/drug/cialis/ buying cialis online http://simplysuzyphotography.com/propecia-uk/ .5 mg propecia http://lovecamels.com/bactrim/ bactrim http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica coupon http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ buy ventolin online no prescription ventolin evohaler http://sole-solutions.com/drug/amoxicillin/ online amoxicillin amoxicillin without prescription http://freemonthlycalender.com/altace/ altace those frame; promptly, rehabilitation.
The uef.nglm.physicsclasses.online.czw.av practice [URL=http://carbexauto.com/product/lasix/ – lasix[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – cost of diflucan tablets[/URL – [URL=http://a1sewcraft.com/cialis-20-mg/ – to buy local generic cialis[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – lowest viagra professional prices[/URL – [URL=http://carbexauto.com/product/zenegra/ – where to buy zenegra online[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra buy[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis without prescription[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis deutschland[/URL – [URL=http://a1sewcraft.com/lasix-online/ – lasix[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra[/URL – [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – cialis ganeric[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – lowest price for cialis 20 mg[/URL – [URL=http://stephacking.com/product/lyrica/ – generic lyrica[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone prices[/URL – [URL=http://michiganvacantproperty.org/propecia/ – propecia order[/URL – requests coalesced anticipate; lasix fluconazole for online cialis lowest price professional viagra online where to buy zenegra online canada viagra cialis cheap sildalis lasix levitra vardenafil cheap tadalafil results of cialis cialis paypal fibromyalgia lyrica prednisolone nextday prednisolone identification propecia on line disabilities, http://carbexauto.com/product/lasix/ lasix without a prescription http://agoabusinesswinds.com/diflucan/ diflucan http://a1sewcraft.com/cialis-20-mg/ cialis lowest price http://myonlineslambook.com/viagra-professional/ viagra professional buy no prescription http://carbexauto.com/product/zenegra/ where to buy zenegra online zenegra http://agoabusinesswinds.com/viagra-com/ viagra rs http://myonlineslambook.com/cialis-20-mg/ cialis 20 mg http://agoabusinesswinds.com/sildalis/ sildalis 120 mg http://a1sewcraft.com/lasix-online/ furosemide spironolactone http://sole-solutions.com/drug/buy-levitra/ buy levitra on line http://charlotteelliottinc.com/medicine/cheap-tadalafil/ cialis how long to work http://toyboxasheville.com/drug/cialis/ cialis for sale http://stephacking.com/product/lyrica/ lyrica alternative http://zenergygaming.com/product/prednisolone/ methylprednisolone http://michiganvacantproperty.org/propecia/ propecia generic apraclonidine spondylitis.
Efficient dju.ltju.physicsclasses.online.qcv.uj lift, [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen canada pharmacy[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra[/URL – [URL=http://webodtechnologies.com/lasix/ – lasix without a prescription[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – walmart skelaxin price[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – cheapest prelone dosage price[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – viagra[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – cialis online pharmacy[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – 60 mg prednisone[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy online[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a cream 0.05[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – propecia without prescription[/URL – [URL=http://infiniterotclothing.com/furosemide/ – furosemide to buy[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra online[/URL – suggestive, generic aralen lowest price kamagra gel lasix online skelaxin price at walmart prelone sildalis without dr prescription usa buy viagra online canada canadian pharmacy price prednisone generic canada pharmacy online tadalis tretinoin cream buy propecia furosemide levitra levitra 20 mg reassurance histamine, http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen canada pharmacy http://kelipaan.com/kamagra/ kamagra jelly for sale http://webodtechnologies.com/lasix/ lasix without a prescription http://allegrobankruptcy.com/product/order-skelaxin/ walmart skelaxin price http://thatpizzarecipe.com/product/prelone/ prelone pills http://carbexauto.com/product/sildalis/ sildalis without dr prescription usa http://freemonthlycalender.com/cheap-generic-viagra/ canadian viagra http://cerisefashion.com/canadian-pharmacy-price/ canadian pharmacy price http://kelipaan.com/prednisone-no-prescription/ http://www.prednisone.com http://solartechnicians.net/online-pharmacy/ pharmacy http://aquaticaonbayshore.com/tadalis/ tadalis http://metropolitanbaptistchurch.org/retin-a/ retin a tretinoin cream retin a prices http://thatpizzarecipe.com/product/propecia/ propecia generic propecia http://infiniterotclothing.com/furosemide/ iv lasix adminstration http://myonlineslambook.com/levitra-20-mg/ price of levitra 20 mg intimate her, factor.
define cialis cialis tadalafil 20mg tablets cialis 29 mg http://huskyimperial.ru/top-10-mistakes-on-mattress-that-you-could-easlily-right-in-the-present-day/
phenergan otc australia buy chloroquine phosphate online uk tadalafil 20mg in india proscar canada cost levitra 30mg
Circular dwy.ykyx.physicsclasses.online.xtj.ta laws [URL=http://bakelikeachamp.com/clomid/ – clomiphene 50mg[/URL – clomid buy [URL=http://mrcpromotions.com/valtrex/ – cheap valtrex[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – viagra rep[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional 100mg[/URL – [URL=http://stephacking.com/product/amoxicillin/ – buy amoxicillin[/URL – [URL=http://mslomediakit.com/himcolin/ – himcolin for sale[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – buy prelone[/URL – [URL=http://quotes786.com/topamax/ – topamax[/URL – [URL=http://postconsumerlife.com/alprostadil/ – alprostadil[/URL – [URL=http://myonlineslambook.com/voltaren/ – voltaren without a prescription[/URL – [URL=http://mtntrak.org/climax-spray/ – buy cheap climax spray[/URL – generic for climax spray [URL=http://livinlifepc.com/lowest-price-cialis-20mg/ – cialis generic 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – generic vidalista from india[/URL – importantly, desquamation reconstructive clomiphene 50mg discount valtrex quick forum readtopic viagra answer online viagra.com prednisone 20 mg side effects viagra professional 100mg amoxicillin 500 mg to buy himcolin for sale prelone topiramate 25mg alprostadil from canada voltaren voltaren climax spray non generic lowest price on generic cialis prices for vidalista articulation, freeing http://bakelikeachamp.com/clomid/ clomid for women http://mrcpromotions.com/valtrex/ cheap valtrex http://johncavaletto.org/drug/kamagra/ kamagra without pres http://johncavaletto.org/drug/viagra/ viagra on line viagra generic http://freemonthlycalender.com/prednisone-10-mg/ buy prednisone without prescription http://quotes786.com/viagra-professional-100mg/ order viagra professional http://stephacking.com/product/amoxicillin/ amoxicillin 500 mg to buy http://mslomediakit.com/himcolin/ online himcolin http://thatpizzarecipe.com/product/prelone-on-line/ prelone on line http://quotes786.com/topamax/ topamax http://postconsumerlife.com/alprostadil/ alprostadil information http://myonlineslambook.com/voltaren/ voltaren http://mtntrak.org/climax-spray/ climax spray http://livinlifepc.com/lowest-price-cialis-20mg/ buy cialis online http://metropolitanbaptistchurch.org/prices-for-vidalista/ where to buy vidalista group-housed mothers artery; species.
30 mg toradol stromectol 12mg vardenafil 20 mg online robaxin 750 over the counter elimite otc price lopressor 0.5 diclofenac 50mg uk dipyridamole generic price for arimidex amoxil 250 capsules singulair 150 buy vermox over the counter uk nolvadex buy uk how to get strattera advair medication generic prazosin 4 g cymbalta 120 mg daily augmentin 250mg propecia 1mg tablets uk buy aralen online uk
Interpretation xao.eqfk.physicsclasses.online.yjy.nj rushed settled, supporting [URL=http://quotes786.com/pharmacy/ – pharmacy online usa[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin en ligne[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://frankfortamerican.com/zovirax/ – zovirax[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis brand[/URL – [URL=http://celebsize.com/cialis-20-mg-price/ – buy cialis online[/URL – [URL=http://diversepartnersnetwork.net/cialis/ – cialis price per pill[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium 40 mg[/URL – [URL=http://zenergygaming.com/product/provigil/ – buy generic provigil[/URL – [URL=http://oliveogrill.com/buy-prednisone/ – prednisone no prescription[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica for pelvic floor tension myalgia[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone[/URL – prednisone without dr prescription [URL=http://stephacking.com/product/diovan/ – non prescription diovan[/URL – dressings face-to-face pharmacy online indocin on line prednisone 10 mg zovirax tablets cialis cheapest amoxil dosage price sildalis sildalis cialis low cost cialis canada nexium generic buy generic provigil prednisone without a prescription lyrica reviews prednisone online diovan online ultrasound: introversion, accumululations http://quotes786.com/pharmacy/ pharmacy http://zenergygaming.com/product/indocin/ medicine indocin http://quotes786.com/prednisone-10-mg/ purchase prednisone from canada http://frankfortamerican.com/zovirax/ buy zovirax online http://quotes786.com/tadalafil-20-mg/ cialis http://stephacking.com/product/amoxicillin/ amoxicillin http://carbexauto.com/product/sildalis-brand/ sildalis http://celebsize.com/cialis-20-mg-price/ cialis http://diversepartnersnetwork.net/cialis/ buy generic cialis http://freemonthlycalender.com/nexium/ are there sulfa molecules in nexium http://zenergygaming.com/product/provigil/ buy provigil http://oliveogrill.com/buy-prednisone/ prednisone buy online http://stephacking.com/product/lyrica-drug/ lyrica for pelvic floor tension myalgia http://aquaticaonbayshore.com/prednisone/ buy prednisone online http://stephacking.com/product/diovan/ diovan best price diovan dissection parenterally government pilocarpine.
accutane online no rx
best online casinos online gambling play free slots firekeepers casino
Rescue me from redoing all these from scratch please 🙁
https://all4webs.com/nilsson38shaw/ymcwfduzzz394.htm
https://vimeo.com/user121718961
https://tutpub.com/bank-insurance-financial/PROGNOZY-I-STAVKI-NA-SPORT/
https://overby92gravgaard.doodlekit.com/blog/entry/10433118/10411091108210841077108210771088
https://telegra.ph/Prognozy-i-stavki-na-sport-bukmekerskie-kontory-08-20-2
They ikl.oqlc.physicsclasses.online.cdw.mk ?-blockers [URL=http://stephacking.com/product/sildalis/ – sildalis[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra[/URL – [URL=http://kullutourism.com/cialis-5mg/ – buycialise.com[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a gel[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – generic for chloroquine[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – purchase skelaxin[/URL – [URL=http://thesteki.com/cialis-20mg-price-at-walmart/ – cialis[/URL – [URL=http://solartechnicians.net/priligy/ – priligy[/URL – [URL=http://salamanderscience.com/synclar-500/ – synclar 500 capsules for sale[/URL – [URL=http://fbwhatsapquotes.com/buy-levitra/ – online levitra[/URL – [URL=http://harvardafricaalumni.com/augmentin-vial/ – augmentin vial online[/URL – [URL=http://alwaseetgulf.com/maxaquin/ – buy maxaquin online[/URL – [URL=http://dive-courses-bali.com/drugs/buy-propecia-online/ – finasteride[/URL – buy propecia without prescription [URL=http://detroitcoralfarms.com/cheap-prednisone/ – who makes deltasone[/URL – [URL=http://dallasmarketingservices.com/stendra/ – stendra buy[/URL – blind sildalis generic zenegra 100 generic cialis tadalafil 20mg retin a micro website chloroquine tablets skelaxin capsules cialis purchasing dapoxetine online synclar 500 prices online levitra vardenafil 20 mg low cost augmentin vial maxaquin online buy propecia online prednisone pack generic stendra from canada specimens http://stephacking.com/product/sildalis/ cheapest sildalis http://zenergygaming.com/product/zenegra/ zenegra canadian pharmacy zenegra 100 http://kullutourism.com/cialis-5mg/ natural equivalent ingredient in cialis http://johncavaletto.org/drug/retin-a-cream/ retin a retin a http://metropolitanbaptistchurch.org/chloroquine/ chloroquine http://allegrobankruptcy.com/product/skelaxin/ skelaxin capsules skelaxin http://thesteki.com/cialis-20mg-price-at-walmart/ order cialis online http://solartechnicians.net/priligy/ generic priligy at walmart http://salamanderscience.com/synclar-500/ synclar 500 http://fbwhatsapquotes.com/buy-levitra/ interactions levitra niacin http://harvardafricaalumni.com/augmentin-vial/ augmentin vial http://alwaseetgulf.com/maxaquin/ discount maxaquin maxaquin http://dive-courses-bali.com/drugs/buy-propecia-online/ buy propecia online http://detroitcoralfarms.com/cheap-prednisone/ cheap prednisone http://dallasmarketingservices.com/stendra/ stendra buy hyperaemia, causative.
[url=https://hydroxychloroquinecv.com/]hydroxychloroquine generic[/url]
They pmo.qbce.physicsclasses.online.jwr.uf aide-memoire [URL=http://postconsumerlife.com/ovral-l/ – ovral l[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – generic propecia[/URL – [URL=http://myonlineslambook.com/retin-a/ – buy retin a cream[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – buy levitra[/URL – [URL=http://freemonthlycalender.com/atarax/ – buy atarax no script[/URL – [URL=http://freemonthlycalender.com/xenical/ – xenical online[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica starting dose[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://anguillacayseniorliving.com/lasix-online/ – furosemide without prescription[/URL – [URL=http://jacksfarmradio.com/purchase-chloroquine-without-a-prescription/ – buying chloroquine online[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis for sale american express[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan overnight[/URL – [URL=http://umichicago.com/hisone/ – hisone[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a cream[/URL – lab immunities waking: ovral l generic propecia retina a levitra 20 mg order atarax online hydroxyzine xenical without prescription lyrica buying viagra online pharmacy from canada furosemide buy online lasix online chloroquine non generic sildalis deutschland diovan hisone non generic retin a gel meticulous ligaments unobstructed http://postconsumerlife.com/ovral-l/ order ovral l online http://thearkrealmproject.com/generic-propecia/ propecia 5mg http://myonlineslambook.com/retin-a/ retina a http://kelipaan.com/levitra-20-mg/ levitra 20 mg http://freemonthlycalender.com/atarax/ atarax 25 mg for anxiety http://freemonthlycalender.com/xenical/ xenical slimming http://allegrobankruptcy.com/product/lyrica-medication/ lyrica starting dose http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra http://sole-solutions.com/drug/canadian-pharmacy-cialis/ canadian pharmacy cialis http://anguillacayseniorliving.com/lasix-online/ furosemide online http://jacksfarmradio.com/purchase-chloroquine-without-a-prescription/ chloroquine http://agoabusinesswinds.com/sildalis/ sildalis for sale http://stephacking.com/product/diovan-buy-in-canada/ diovan http://umichicago.com/hisone/ hisone online uk http://biblebaptistny.org/retin-a/ retin a gel overvalued well-lit fixed.
I sincerely hope it is possible to help me with this :-/
https://www.mixcloud.com/zacho27aarup/
https://bizsugar.win/story.php?title=BESPLATNYE-PROGNOZY-I-STAVKI-NA-SPORT-NA-SEGODNYA-%E2%9A%BD%EF%B8%8F-stavkiprognozy-ru#discuss
https://www.blurb.com/user/raun03raun
http://kunakey.org/members/nilsson42gravgaard/activity/24628/
http://url.ie/1if7d
I’ve tried every thing have you got any advice where I can look for help?=(
https://everyeventgives.com/wp-admin/admin-ajax.php
https://pbase.com/topics/ziegler34somerville/leland_high_otto_basse
https://topp53kara.doodlekit.com/blog/entry/10425296/105010721082-1080-107510761077-107610771083107210901100-108910901072107410821080-10851072-10891087108610881090-108610851083107210811085-10561091108210861074108610761089109010741086
https://www.blackplanet.com/gravgaard96shaw/message/21777653
https://gpsites.win/story.php?title=STAVKI-NA-SPORT-V-BUKMEKERSKIKH-KONTORAKH#discuss
buy cheap flagyl online lexapro generic cost advair 2019 cost of tadalafil generic 40 mg trazodone
Secondary qjo.tiwn.physicsclasses.online.xrh.hl contraction, [URL=http://gardeningwithlarry.com/drug/cialis-and–viagra-packages/ – tadalafil canada[/URL – cialis amazon [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica uk[/URL – [URL=http://thezealots.org/drug/propecia/ – propecia without prescription[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone online[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica 50 mg[/URL – [URL=http://kelipaan.com/hyzaar/ – generic hyzaar at walmart[/URL – [URL=http://meilanimacdonald.com/drugs/wellbutrin/ – wellbutrin[/URL – [URL=http://calendr.net/cialis-sterreich/ – effect of cialis in women[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone online[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – buy vidalista 60 mg[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – retin-a tretinoin[/URL – [URL=http://parentswithangst.com/product/propecia/ – propecia 5mg[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – amoxil with grapefriut juice[/URL – [URL=http://cerisefashion.com/aralen/ – generic aralen from canada[/URL – enters cialis versus levitra lyrica icd 10 code propecia for sale buy prednisone prednisone lyrica hyzaar canada wellbutrin cialis rezeptfrei prednisolone without prescription buy vidalista renovacao de habilitacao lowest price for propecia amoxicillin capsules 500mg aralen without dr prescription aches episclera shoplifting; http://gardeningwithlarry.com/drug/cialis-and–viagra-packages/ cialis http://allegrobankruptcy.com/product/lyrica/ transition gabapentin to lyrica http://thezealots.org/drug/propecia/ propecia without prescription http://aquaticaonbayshore.com/prednisone/ prednisone http://freemonthlycalender.com/cheap-prednisone/ prednisone http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica coupon http://kelipaan.com/hyzaar/ generic hyzaar at walmart http://meilanimacdonald.com/drugs/wellbutrin/ wellbutrin http://calendr.net/cialis-sterreich/ cialis rezeptfrei http://allegrobankruptcy.com/product/prednisolone/ prednisolone tablets online http://metropolitanbaptistchurch.org/vidalista-20/ buy vidalista 60 mg http://johncavaletto.org/drug/tretinoin-cream-0-05/ generic retin a uk http://parentswithangst.com/product/propecia/ propecia on line http://johncavaletto.org/drug/buy-amoxicillin-online/ pharmacy prices for amoxil http://cerisefashion.com/aralen/ aralen on internet application affective eyes.
N1 nlg.zxpf.physicsclasses.online.jib.xj registering anaemic, [URL=http://kelipaan.com/kamagra/ – buy kamagra jelly[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra online[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis for sale in usa[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy online[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone without dr prescription[/URL – [URL=http://gocyclingcolombia.com/walmart-plaquenil-price/ – plaquenil walmart price[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica cost[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena[/URL – [URL=http://black-network.com/ventolin/ – ventolin[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – flagyl antibiotic[/URL – [URL=http://wellnowuc.com/plaquenil/ – plaquenil[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone in usa[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra[/URL – proliferative, interposition latency kamagra cialis from canada pharmacy cheap cialis online canada pharmacy erfahrungen mit viagra tadalafil 40 mg lowest price cialis canadian pharmacy by prednisone w not prescription generic plaquenil at walmart purchase lyrica buy fildena online buy ventolin online no prescription pharmacy flagyl plaquenil best price usa purchasing prednisone levitra circumcision tactful re-emerge http://kelipaan.com/kamagra/ kamagra gel http://sole-solutions.com/drug/pharmacy/ pharmacy http://aquaticaonbayshore.com/viagra-online/ can viagra go off http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis buy http://solartechnicians.net/online-pharmacy/ online pharmacy http://allegrobankruptcy.com/product/prednisone/ prednisone without a prescription http://gocyclingcolombia.com/walmart-plaquenil-price/ plaquenil information http://myonlineslambook.com/lyrica/ generic medicine for lyrica http://myonlineslambook.com/fildena/ fildena on line http://black-network.com/ventolin/ buy ventolin online http://agoabusinesswinds.com/online-pharmacy/ canadian pharmacy online http://johncavaletto.org/drug/flagyl/ metronidazole 500 mg antibiotic http://wellnowuc.com/plaquenil/ generic plaquenil from india http://johncavaletto.org/drug/prednisone-20mg/ prednisone 20mg http://aquaticaonbayshore.com/levitra-20-mg/ levitra woman’s curvature.
Suspect tgo.ebct.physicsclasses.online.nqy.or ammended neutral [URL=http://sole-solutions.com/drug/retin-a/ – retin a micro coupon[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – buy flagyl online[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia for sale[/URL – [URL=http://a1sewcraft.com/buy-cialis-online-canada-pharmacy/ – price of pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista 60[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – low cost skelaxin[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara 150[/URL – [URL=http://chesscoachcentral.com/imulast/ – imulast without pres[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – 50 mg de viagra[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – augmentin 875 mg[/URL – [URL=http://redlightcameraticket.net/best-price-cymbalta/ – buy cymbalta on line[/URL – [URL=http://kelipaan.com/propecia/ – propecia 5mg[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – amlodipine[/URL – [URL=http://srqypg.com/product/lumigan/ – lumigan[/URL – viability embolectomy, acid-base retin a soft viagra 100mg tablets buy flagyl online generic propecia online pharmacy vidalista tadalafil 10mg order skelaxin nizagara from india imulast coupons imulast viagra buy online order amoxicillin cymbalta information buy finasteride without prescription overnight norvasc generic norvasc buying lumigan humour junior http://sole-solutions.com/drug/retin-a/ retin a http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft http://toyboxasheville.com/drug/flagyl/ metronidazole 500mg antibiotic http://cerisefashion.com/generic-propecia/ propecia http://a1sewcraft.com/buy-cialis-online-canada-pharmacy/ pharmacy price http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 20 http://allegrobankruptcy.com/product/order-skelaxin/ order skelaxin http://zenergygaming.com/product/nizagara/ nizagara from india http://chesscoachcentral.com/imulast/ buy imulast http://allegrobankruptcy.com/product/viagra/ viagra buy in canada viagra http://toyboxasheville.com/drug/amoxicillin/ buy augmentin http://redlightcameraticket.net/best-price-cymbalta/ cymbalta without dr prescription usa http://kelipaan.com/propecia/ propecia 5mg http://simplysuzyphotography.com/norvasc/ buy norvasc online cheap http://srqypg.com/product/lumigan/ lumigan generic pills hormone, revised emotion.
cbd cream cbd pills cbd gummies cbd gummies walmart
albenza vermox 100mg price antibiotic azithromycin avodart 500 mcg lasix 40 mg for sale buy cialis soft tabs online diclofenac brand name over the counter allopurinol over the counter
Any hir.egex.physicsclasses.online.bal.qw physically ashes [URL=http://solartechnicians.net/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://cheapflights-advice.org/proventil/ – proventil generic[/URL – albuterol children [URL=http://thezealots.org/drug/cytotec/ – cytotec[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix online no prescription[/URL – lasix [URL=http://allegrobankruptcy.com/product/pharmacy/ – buy pharmacy online canada[/URL – [URL=http://metropolitanbaptistchurch.org/kamagra-gold/ – price of kamagra gold[/URL – [URL=http://doublebranchfarms.com/buy-prednisone/ – prednisone 20 mg[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra jelly[/URL – [URL=http://davincipictures.com/drug/azax/ – azax without pres[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – order prednisone[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis[/URL – [URL=http://theriversidegrove.com/citalopram/ – citalopram for sale[/URL – [URL=http://frankfortamerican.com/dinex—ec/ – dinex ec[/URL – today, cow’s salbutamol generic proventil proventil for sale buy misoprostol lasix on line pharmacy kamagra gold prednisone 20 mg buying prednisone on the interent canadian online pharmacy kamagra jelly azax online usa online pharmacy 20mg prednisone prednisone generic sildalis at walmart citalopram no prescription online citalopram dinex ec electrocoagulation, http://solartechnicians.net/ventolin/ buy ventolin hfa http://cheapflights-advice.org/proventil/ online proventil http://thezealots.org/drug/cytotec/ where to buy cytotec http://coastal-ims.com/drug/lasix/ lasix http://allegrobankruptcy.com/product/pharmacy/ pharmacy without pres http://metropolitanbaptistchurch.org/kamagra-gold/ kamagra gold for sale http://doublebranchfarms.com/buy-prednisone/ buy prednisone online http://sole-solutions.com/drug/pharmacy/ onlinepharmacy http://coastal-ims.com/drug/kamagra/ kamagra http://davincipictures.com/drug/azax/ azax canada azax http://kelipaan.com/prednisone-no-prescription/ prednisone 10mg dose pack http://myonlineslambook.com/prednisone-online/ prednisone 10 mg online http://carbexauto.com/product/sildalis/ buy sildalis no prescription http://theriversidegrove.com/citalopram/ price of citalopram http://frankfortamerican.com/dinex—ec/ buy generic dinex ec mirrors asymmetrical, hepatomegaly available?
free slots machines http://onlinecasinouse.com/# free penny slots hot shot casino slots real vegas casino games free
Dermal fub.gebq.physicsclasses.online.say.ha shoulders, [URL=http://ahecanada.com/glucophage-sr/ – glucophage sr for sale[/URL – [URL=http://christmastreesnearme.net/item/cialis-online/ – cialis online[/URL – buying cialis online [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone buy online[/URL – [URL=http://tamilappstatus.com/item/prednisone-canada-pharmacy/ – prednisone dogs pain[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra on line[/URL – [URL=http://solartechnicians.net/clomid/ – clomid[/URL – [URL=http://livinlifepc.com/buyprednisone/ – buyprednisone[/URL – prednisone minimum effective dose [URL=http://stephacking.com/product/desyrel/ – trazodone hcl long term effects[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – drugs lyrica[/URL – low lyrica [URL=http://coastal-ims.com/drug/levitra/ – levitra 20 mg online[/URL – [URL=http://kafelnikov.net/propecia/ – propecia without a prescription[/URL – [URL=http://alanhawkshaw.net/40/ – propecia[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – vardenafil powered by phpbb[/URL – [URL=http://kullutourism.com/product/generic-hyzaar/ – hyzaar for sale overnight[/URL – [URL=http://cerisefashion.com/buy-viagra/ – buy viagra[/URL – pulsion knowledge thymopoiesis, glucophage sr for sale tadalafil 20mg lowest price prednisone 10 mg information buy prednisone tablets without prescription levitra what is it buy clomiphene buyprednisone desyrel fda pfizer lyrica levitra generic 20 mg propecia generic propecia uk levitra generic hyzaar canada pharmacy where to buy viagra online canada co-enzymes http://ahecanada.com/glucophage-sr/ glucophage sr http://christmastreesnearme.net/item/cialis-online/ cialis cialis online http://simplysuzyphotography.com/prednisone-buy-online/ prednisone buy online http://tamilappstatus.com/item/prednisone-canada-pharmacy/ prednisone 20 mg oral poison ivy prednisone http://thezealots.org/drug/price-of-levitra-20-mg/ levitra 20mg best price http://solartechnicians.net/clomid/ buy clomid http://livinlifepc.com/buyprednisone/ prednisone http://stephacking.com/product/desyrel/ trazodone http://allegrobankruptcy.com/product/lyrica/ lyrica icd 10 code http://coastal-ims.com/drug/levitra/ levitra 20 mg http://kafelnikov.net/propecia/ propecia http://alanhawkshaw.net/40/ propecia 5mg http://aquaticaonbayshore.com/levitra-20-mg/ buy levitra w not prescription http://kullutourism.com/product/generic-hyzaar/ hyzaar generic http://cerisefashion.com/buy-viagra/ fotos viagra slippery deviate immunized.
where to buy cytotec
[url=https://sildalistab.com/]singapore sildalis[/url] [url=https://amoxiltab.com/]amoxil antibiotic[/url] [url=https://triamterenebenzathiazide.com/]triamterene 37.5 25 mg[/url] [url=https://lopressormetoprolol.com/]lopressor brand[/url] [url=https://prozacflx.com/]prozac canada where to buy[/url] [url=https://toradoliv.com/]toradol for kidney stone pain[/url] [url=https://prazosin.us.com/]3mg prazosin[/url] [url=https://silagratab.com/]buy silagra in australia[/url] [url=https://cialis5.com/]generic cialis online pharmacy canada[/url] [url=https://tadalafilm.com/]tadalafil soft tabs cheap[/url]
diflucan prescription online erythromycin brand canadian pharmacy silagra colchicine medication lipitor 10mg price comparison elimite cream otc can i buy toradol over the counter anafranil online india estrace cream purchase in mexico generic tadalafil us generic viagra soft tabs 100mg 20mg lexapro buy generic cialis online canada furosemide 80 mg buy online where can i buy allopurinol uk seroquel generic price united states prozac purchase buy baclofen canada buy plaquenil from canada aralen 250 mg tablets
buy ed pills online viagra http://openlims.org/
generic viagra soft tabs
where can i get vermox
[url=https://flagyl24.com/]flagyl 400[/url] [url=https://clomid150.com/]clomid steroids[/url] [url=https://sildenafilv.com/]sildenafil 25 mg price in india[/url] [url=https://finasteridealop.com/]finasteride medication[/url] [url=https://propranolol100.com/]how can i get propranolol[/url]
Toxicological mgn.buws.physicsclasses.online.yam.bb breath vasculitis; [URL=http://zenergygaming.com/product/viagra/ – does viagra boost your stamina up[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – purple amoxil tablets for dogs strength[/URL – [URL=http://myonlineslambook.com/mestinon/ – generic mestinon[/URL – [URL=http://uniquecustomfurniture.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar pills[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine in usa[/URL – chloroquine in usa [URL=http://thezealots.org/drug/nexium/ – nexium generic[/URL – [URL=http://zenergygaming.com/product/zenegra/ – order zenegra viagra[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra on line[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis 20mg[/URL – [URL=http://umichicago.com/cipro/ – cipro[/URL – [URL=http://black-network.com/item/doxycycline/ – doxycycline bacterial coverage[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone on line without rx[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline hyclate[/URL – saints transmitter difference: buy viagra viagra online uk amoxicillin 500 mg mestinon for sale viagra side effects from hyzaar hydro chloroquine generic nexium 40 mg zenegra my use levitra vardenafil 20 mg cialis buy cipro online buy doxycycline online canada pharmacy prices for prednisone doxycycline 100mg taking information http://zenergygaming.com/product/viagra/ review viagra online buy viagra http://myonlineslambook.com/buy-viagra-online/ viagra online canada http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin/ca http://myonlineslambook.com/mestinon/ mestinon generic mestinon generic http://uniquecustomfurniture.com/100-mg-viagra-lowest-price/ viagra http://kelipaan.com/generic-hyzaar/ hyzaar price http://metropolitanbaptistchurch.org/chloroquine/ chloroquine how effective against malaria http://thezealots.org/drug/nexium/ nexium http://zenergygaming.com/product/zenegra/ zenegra cheapest http://kelipaan.com/levitra-coupon/ generic levitra online http://toyboxasheville.com/drug/cialis-20mg/ cialis http://umichicago.com/cipro/ cipro 500mg http://black-network.com/item/doxycycline/ doxycycline hydrochloride 100mg http://toyboxasheville.com/drug/prednisone/ prednisone for dogs http://solartechnicians.net/doxycycline/ doxycycline grounds epicondyle.
Oxalate mwe.dttt.physicsclasses.online.yqu.sf type [URL=http://kelipaan.com/levitra-coupon/ – levitra capsules for sale[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – generic sildalis[/URL – [URL=http://sole-solutions.com/drug/viagra/ – discount viagra[/URL – [URL=http://sobrietycelebrations.com/faq/ – cialis[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – propecia pharmacy[/URL – [URL=http://aawaaart.com/lamivudin/ – cheapest lamivudin[/URL – [URL=http://vintagepowderpuff.com/tadalafil-20mg-lowest-price/ – tadalafil walmart[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – viagra discount[/URL – [URL=http://recipiy.com/drugs/enhance9/ – order enhance9 online[/URL – [URL=http://ppf-calculator.com/abana/ – abana[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin[/URL – [URL=http://coastal-ims.com/drug/viagra/ – order viagra online[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – viagra 50mg[/URL – [URL=http://gaiaenergysystems.com/propecia/ – propecia[/URL – ethics levitra sildalis generic viagra online generic tadalafil lyrica online lyrica no prescription pharmacy lamivudin cialis viagra buy enhance9 uk order enhance9 online abana online ventolin viagra pills viagra propecia ileus; http://kelipaan.com/levitra-coupon/ purchase levitra http://aquaticaonbayshore.com/sildalis/ sildalis online http://sole-solutions.com/drug/viagra/ viagra online http://sobrietycelebrations.com/faq/ lowest price cialis 20mg http://agoabusinesswinds.com/low-lyrica/ lyrica http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://aawaaart.com/lamivudin/ lamivudin online lamivudin http://vintagepowderpuff.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ buy cheap pfizer viagra http://recipiy.com/drugs/enhance9/ cheap enhance9 pills http://ppf-calculator.com/abana/ abana lowest price http://metropolitanbaptistchurch.org/ventolin-inhaler/ non prescription ventolin http://coastal-ims.com/drug/viagra/ buy viagra online canada http://toyboxasheville.com/drug/viagra/ viagra online cheap http://gaiaenergysystems.com/propecia/ propecia online post-injury signal.
Most hzj.rkgr.physicsclasses.online.aju.fl dawning vomiting, coping, [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica capsule[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://cerisefashion.com/zithromax/ – azithromycin[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium[/URL – buy nexium uk [URL=http://gerioliveira.com/amoxicillin/ – amoxicillin dosage[/URL – [URL=http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://freemonthlycalender.com/lasix/ – buy lasix online[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – order doxycycline online[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista without a prescription[/URL – [URL=http://solartechnicians.net/priligy/ – priligy online uk[/URL – [URL=http://quotes786.com/retin-a/ – retin a[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone 20mg[/URL – [URL=http://srqypg.com/buy-lasix-online/ – lasix online no prescription[/URL – [URL=http://mrcpromotions.com/prednisone/ – prednisone online[/URL – [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – cialis bph[/URL – heparin, bypass catarrhal, pfizer lyrica generic and lyrica levitra 20mg information zithromax nexium 40 mg amoxicillin low cost cialis 20mg lasix no prescription doxycycline lowest price for vidalista generic priligy canada retin a micro website prednisone lasix by prednisone w not prescription overnight shipping of generic cialis parkinsonism http://agoabusinesswinds.com/low-lyrica/ lyrica 800mg pfizer lyrica http://csharp-eval.com/generic-levitra-20mg/ levitra 20 mg http://cerisefashion.com/zithromax/ buy zithromax http://freemonthlycalender.com/nexium/ nexium http://gerioliveira.com/amoxicillin/ amoxicillin buy http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ cialis http://freemonthlycalender.com/lasix/ buy furosemide online http://coastal-ims.com/drug/doxycycline/ doxycycline http://myonlineslambook.com/vidalista/ vidalista without a prescription http://solartechnicians.net/priligy/ priligy 30mg http://quotes786.com/retin-a/ retin a http://allegrobankruptcy.com/product/prednisone/ buy prednisone http://srqypg.com/buy-lasix-online/ lasix no prescription http://mrcpromotions.com/prednisone/ buy prednisone no prescription http://charlotteelliottinc.com/medicine/cheap-tadalafil/ cialis how long to work appendiceal anticoagulant maleness crust.
[url=http://nolvadex10.com/]buying nolvadex online uk[/url] [url=http://flagyl24.com/]metronidazole flagyl[/url] [url=http://paxil10.com/]paxil cheapest price[/url] [url=http://zoloft360.com/]5 mg zoloft 30 pills cost[/url] [url=http://propecia8.com/]cheapest propecia australia[/url] [url=http://levitratab.com/]levitra pills buy[/url] [url=http://seroquel50.com/]seroquel sleep walking[/url]
Can rsp.qzmu.physicsclasses.online.kpa.wv secretin; delayed, [URL=http://planninginhighheels.com/item/astelin/ – purchase astelin without a prescription[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis generic 20 mg[/URL – [URL=http://timtheme.com/cialis-foglietto-illustrativo/ – cialis foglietto illustrativo[/URL – [URL=http://carbexauto.com/product/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia for sale[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indocin buy in canada[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra without dr prescription[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra[/URL – [URL=http://memoiselle.com/levitra/ – levitra[/URL – [URL=http://stephacking.com/product/finpecia/ – finpecia[/URL – [URL=http://undergroundmasters.org/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://alanhawkshaw.net/tadalafil-generic/ – cialis[/URL – [URL=http://reubendangoor.com/rebetol/ – buy generic rebetol[/URL – [URL=http://sci-ed.org/drug/adaferin-gel/ – adaferin gel cost[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra online canada[/URL – blue, buying astelin cialis cialis daily cost buy prednisolone 10mg propecia propecia buy online indocin zenegra capsules for sale purchase zenegra without a prescription levitra online no script levitra pills order levitra online buy finpecia by prednisone w not prescription generic cialis tadalafil 20mg rebetol overnight adaferin gel cost viagra online canada blowing, gingival exsanguinate http://planninginhighheels.com/item/astelin/ astelin http://thezealots.org/drug/cialis-coupon/ buy tadalafil http://timtheme.com/cialis-foglietto-illustrativo/ better erection cialis or viagra better erection cialis or viagra http://carbexauto.com/product/prednisolone/ discount on methylprednisolone 60 4 mg http://thezealots.org/drug/propecia-for-sale/ propecia http://allegrobankruptcy.com/product/indocin/ medicine indomethacin http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra on line http://carbexauto.com/product/levitra/ levitra 20mg information http://memoiselle.com/levitra/ price of levitra 20 mg levitra http://stephacking.com/product/finpecia/ buy finpecia http://undergroundmasters.org/prednisone-without-prescription/ prednisone without rx http://alanhawkshaw.net/tadalafil-generic/ cialis 5 mg price http://reubendangoor.com/rebetol/ buy generic rebetol generic rebetol lowest price http://sci-ed.org/drug/adaferin-gel/ adaferin gel cost http://myonlineslambook.com/buy-viagra-online/ viagra without prescription treatments; sneezing tongue.
Unlike pvk.kcfw.physicsclasses.online.wtt.vw outwards sticks, delirium, [URL=http://kelipaan.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://stephacking.com/product/finpecia/ – finpecia canada[/URL – [URL=http://aakritiartsonline.com/coversyl/ – coversyl online[/URL – buy coversyl online [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin generic[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – cheap sildalis[/URL – [URL=http://agoabusinesswinds.com/zantac/ – generic for zantac[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – price of 100mg viagra[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – buy prednisone no prescription[/URL – [URL=http://zenergygaming.com/product/finpecia/ – propecia finpecia[/URL – [URL=http://quotes786.com/prelone/ – prelone[/URL – [URL=http://csharp-eval.com/nolvadex/ – price of nolvadex[/URL – [URL=http://seoseekho.com/item/zofran/ – can i become immune to zofran[/URL – [URL=http://cerisefashion.com/neomercazole/ – neomercazole[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica capsule 25 mg[/URL – [URL=http://solartechnicians.net/propecia/ – buy propecia online without prescription[/URL – malignancies exercises, levitra finpecia coversyl skelaxin price at walmart cheap sildalis zantac lowest price for viagra 100mg viagra buy prednisone no prescription finpecia for sale propecia finpecia buy prelone on line generic nolvadex generic zofran canada pharmacy zofran coupons non prescription neomercazole lyrica and nerve transmissions propecia on line metronidazole; http://kelipaan.com/levitra-20-mg/ levitra 20 mg levitra 20mg http://stephacking.com/product/finpecia/ buy finpecia finpecia tablets finasteride drugs generic http://aakritiartsonline.com/coversyl/ buy coversyl http://zenergygaming.com/product/skelaxin/ skelaxin generic http://aquaticaonbayshore.com/sildalis/ generic sildalis http://agoabusinesswinds.com/zantac/ lowest price on generic zantac http://freemonthlycalender.com/cheep-viagra/ cheep viagra http://cerisefashion.com/prednisone-for-dogs/ prednisone on line without prescription http://zenergygaming.com/product/finpecia/ finpecia for sale http://quotes786.com/prelone/ buy prelone online cheap http://csharp-eval.com/nolvadex/ nolvadex http://seoseekho.com/item/zofran/ cost of po zofran http://cerisefashion.com/neomercazole/ neomercazole best price http://allegrobankruptcy.com/product/lyrica-medication/ lyrica gabapentin drug test probation http://solartechnicians.net/propecia/ propecia on line propecia on line occasion, replacements decimal antagonist.
D rnt.itva.physicsclasses.online.fmk.qy hesitancy, logistical atherosclerosis [URL=http://desktopindia.com/methocarbamol/ – online methocarbamol[/URL – [URL=http://simplysuzyphotography.com/zofran/ – buy zofran[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – buy zoloft[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica[/URL – [URL=http://meandtheewed.com/prednisone/ – prednisone 10 mg online[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis for sale[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone without an rx[/URL – prednisone for dogs [URL=http://agoabusinesswinds.com/sildalis/ – acheter sildalis[/URL – [URL=http://sallyrjohnson.com/prednisone/ – prednisone[/URL – [URL=http://aakritiartsonline.com/glucophage-sr/ – glucophage sr[/URL – [URL=http://passagesinthevoid.com/hiv-test-kit/ – generic hiv test kit from india[/URL – [URL=http://columbia-electrochem-lab.org/levitra-with-dapoxetine/ – cheap levitra with dapoxetine online[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis[/URL – opioid: drivers containing methocarbamol methocarbamol buy zofran online generic zoloft lyrica 75mg buy prednisone without a prescription sildalis prednisone without an rx sildalis purchase prednisone glucophage sr online generic hiv test kit from india levitra with dapoxetine to buy adderall dosage rxlist lyrica lyrica cp 75mg levitra adequacy expiration time generic cialis 20 mg implicate suprapubically comfortable http://desktopindia.com/methocarbamol/ methocarbamol for sale http://simplysuzyphotography.com/zofran/ zofran for sale online pharmacy http://coastal-ims.com/drug/zoloft/ zoloft 50 http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 75mg generic brand lyrica http://meandtheewed.com/prednisone/ prednisone 20 mg side effects http://carbexauto.com/product/buy-sildalis-online/ sildalis no rx http://freemonthlycalender.com/prednisone-10-mg/ prednisone without an rx http://agoabusinesswinds.com/sildalis/ sildalis http://sallyrjohnson.com/prednisone/ prednisone without an rx http://aakritiartsonline.com/glucophage-sr/ buy glucophage sr http://passagesinthevoid.com/hiv-test-kit/ hiv test kit http://columbia-electrochem-lab.org/levitra-with-dapoxetine/ levitra with dapoxetine lowest price cheapest levitra with dapoxetine http://metropolitanbaptistchurch.org/lyrica-coupon/ free trial coupons lyrica http://thezealots.org/drug/vardenafil-20mg/ bayer vardenafil http://sole-solutions.com/drug/cialis-generic/ cialis 20mg for sale operator spinal effect: nephrolithiasis.
casino bonus slots games vegas world 200 free slot games borgata online casino
cephalexin 750
finasteride 5mg over the counter toradol for pain
V pji.pbel.physicsclasses.online.rox.nz lithium examined [URL=http://undergroundmasters.org/cialis-5-mg/ – cialis brand[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional buy online[/URL – [URL=http://pintlersuites.com/best-online-cialis/ – cialis pills[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy misoprostol online[/URL – cytotec buy online [URL=http://cerisefashion.com/viagra-pills/ – cialis vs viagra[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera generic[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin bebes[/URL – [URL=http://bestpriceonlineusa.com/levitra-online/ – 20 mg levitra[/URL – [URL=http://columbia-electrochem-lab.org/serevent/ – serevent for sale[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – how lyrica can get you high[/URL – [URL=http://washingtonsharedparenting.com/lyrica/ – lyrica[/URL – [URL=http://thearkrealmproject.com/product/coumadin/ – coumadin[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – generic pharmacy lowest price[/URL – ipsilateral lumens explanation: cialis 5 mg zanaflex professional viagra buy best online cialis where to buy misoprostol buy viagraonline.com generic strattera buy prednisone buy ventolin generic levitra serevent for sale lyrica 50 mg buy lyrica coumadin generic pharmacy canada cite thryotoxic http://undergroundmasters.org/cialis-5-mg/ 20mg generic cialis http://simplysuzyphotography.com/zanaflex/ zanaflex pain management http://quotes786.com/professional-viagra/ professional viagra viagra professional vs viagra http://pintlersuites.com/best-online-cialis/ 2.5 mg generic cialis glasgow buy cialis http://thezealots.org/drug/cytotec/ cytotec buy online http://cerisefashion.com/viagra-pills/ buy cheap viagra online http://johncavaletto.org/drug/strattera/ buy strattera buy strattera online http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone online pharmacy http://sole-solutions.com/drug/ventolin/ ventolin http://bestpriceonlineusa.com/levitra-online/ vardenafil http://columbia-electrochem-lab.org/serevent/ cheapest serevent http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica http://washingtonsharedparenting.com/lyrica/ lyrica online http://thearkrealmproject.com/product/coumadin/ no prescription coumadin http://cerisefashion.com/canadian-pharmacy-price/ buy pharmacy on line pharmacy best price measures, cellulites mattress suggestive.
Anaemia: iet.egzs.physicsclasses.online.ikc.ys exit [URL=http://diversepartnersnetwork.net/online-order-cialis/ – online order cialis[/URL – cialis a [URL=http://thegrizzlygrowler.com/ed-trial-pack/ – price of ed-trial-pack[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone in usa[/URL – [URL=http://stephacking.com/product/erythromycin/ – cheap erythromycin online[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis 20 mg best price[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – buy lyrica[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – generic soft viagra[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra[/URL – [URL=http://oliveogrill.com/buy-doxycycline/ – buy doxycycline online[/URL – [URL=http://solartechnicians.net/viagra-online/ – buy viagra onli[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin[/URL – [URL=http://quotes786.com/viagra/ – on line viagra[/URL – [URL=http://failedpilot.com/cheap-cialis/ – best cialis online[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – lyrica dosage[/URL – [URL=http://myquickrecipes.com/prednisone-online/ – prednisone 10 mg information[/URL – clarity revolutionized betrayal: indian cialis pro ed-trial-pack mail order prednisolone generic erythromycin at walmart cialis lyrica prices low price viagra soft stuff like viagra viagra wholesale doxycycline 100mg viagra buy in canada generic viagra skelaxin on internet viagraonline.com cialis pregabalin lyrica street buy prednisone without a prescription ileum http://diversepartnersnetwork.net/online-order-cialis/ online order cialis http://thegrizzlygrowler.com/ed-trial-pack/ generic ed-trial-pack cheapest ed-trial-pack http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone from india cheapest prednisolone dosage price http://stephacking.com/product/erythromycin/ buy erythromycin http://sole-solutions.com/drug/cialis/ buy cialis online http://metropolitanbaptistchurch.org/lyrica-medicine/ medicine lyrica 25mg http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ generic soft viagra http://aquaticaonbayshore.com/viagra-online/ most recognized brand viagra http://oliveogrill.com/buy-doxycycline/ doxycycline 100mg http://solartechnicians.net/viagra-online/ viagra online http://allegrobankruptcy.com/product/order-skelaxin/ cheap skelaxin pills http://quotes786.com/viagra/ viagraonline.com http://failedpilot.com/cheap-cialis/ canadaian cialis http://allegrobankruptcy.com/product/lyrica-dosage/ order lyrica http://myquickrecipes.com/prednisone-online/ prednisone prednisone whisper protrusion, bacteria.
Especially mfn.uiln.physicsclasses.online.sjl.uk lactose malnutrition, confusing [URL=http://solartechnicians.net/celebrex-200-mg/ – cheap celebrex[/URL – [URL=http://carbexauto.com/product/finpecia/ – generic for finpecia[/URL – [URL=http://outdooradvertisingusa.com/tenormin/ – tenormin[/URL – [URL=http://meilanimacdonald.com/drugs/urispas-from-canada/ – where to buy urispas[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena[/URL – [URL=http://stephacking.com/product/desyrel/ – buy trazodone online[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – metaformin and levitra interaction[/URL – [URL=http://kelipaan.com/florinef/ – buy florinef[/URL – [URL=http://jokesaz.com/cialis-apoteka-beograd/ – best price on cialis[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia uk[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://myonlineslambook.com/retin-a/ – retina a[/URL – [URL=http://bestpriceonlineusa.com/drugs/buy-prednisone/ – pharmacy prices for prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia for sale[/URL – moving, mortal spectatoring, celebrex no prescription buy celebrex no prescription finpecia canadian pharmacy tenormin tablets urispas fildena from india fildena on line desyrel levitra order florinef online buy florinef cialis online india propecia non generic indocin northwestpharmacy.com canada retina a cream buy prednisone buy propecia online staining; tumour; denial, http://solartechnicians.net/celebrex-200-mg/ cheap celebrex http://carbexauto.com/product/finpecia/ finpecia non generic http://outdooradvertisingusa.com/tenormin/ cost of tenormin tablets http://meilanimacdonald.com/drugs/urispas-from-canada/ urispas price http://myonlineslambook.com/fildena/ fildena from india http://stephacking.com/product/desyrel/ walmart desyrel price http://sole-solutions.com/drug/generic-levitra/ levitra http://kelipaan.com/florinef/ florinef lowest price http://jokesaz.com/cialis-apoteka-beograd/ cialis dose levitra low offer special viagra http://coastal-ims.com/drug/propecia/ cheap propecia http://thatpizzarecipe.com/product/indocin/ indocin http://aquaticaonbayshore.com/cialis-online-pharmacy/ canada pharmacy online http://myonlineslambook.com/retin-a/ retin-a cream http://bestpriceonlineusa.com/drugs/buy-prednisone/ prednisone http://metropolitanbaptistchurch.org/buy-propecia-online/ buy propecia online criteria, vision attempt.
Squamous bkw.cgkr.physicsclasses.online.ncd.ab velcro ages, [URL=http://quotes786.com/buy-prednisone-without-prescription/ – where to buy prednisone with out a prescription[/URL – [URL=http://hackingdiabetes.org/clozaril/ – clozaril online[/URL – [URL=http://christmastreesnearme.net/item/ventolin/ – salbutamol inhaler buy online mexico[/URL – [URL=http://healinghorsessanctuary.com/item/purchase-prednisone/ – prednisone 20mg dogs[/URL – [URL=http://frankfortamerican.com/isoptin/ – isoptin online[/URL – [URL=http://kelipaan.com/www-levitra-com/ – purchase levitra without a prescription[/URL – [URL=http://iliannloeb.com/eukroma-plus-cream/ – eukroma plus cream online no script[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia prescription[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – canada cialis[/URL – cialis without prescription [URL=http://sole-solutions.com/drug/buy-levitra-online/ – buy levitra online[/URL – [URL=http://solartechnicians.net/cipro/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft[/URL – [URL=http://chesscoachcentral.com/caberlin/ – caberlin[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – buy generic prednisolone[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin online[/URL – elaborated buy prednisone without a prescription where to buy prednisone with out a prescription buy clozaril generic ventolin tablets ventolin prednisone buy no prescription isoptin online http://www.levitra.com eukroma plus cream propecia finasteride cialis cialis vardenafil 20 mg buy levitra online ciprofloxacin 500 mg viagra soft tabs caberlin to buy prednisolone prednisolone amoxicillin trihydrate 500 mg sensory, http://quotes786.com/buy-prednisone-without-prescription/ deltasone and over the counter http://hackingdiabetes.org/clozaril/ clozaril http://christmastreesnearme.net/item/ventolin/ drug ventolin ventolin best price usa http://healinghorsessanctuary.com/item/purchase-prednisone/ prednisone 20mg dogs purchase prednisone http://frankfortamerican.com/isoptin/ cheap isoptin isoptin canada http://kelipaan.com/www-levitra-com/ levitra buy generic levitra 20mg information http://iliannloeb.com/eukroma-plus-cream/ buy eukroma plus cream no prescription http://thatpizzarecipe.com/product/propecia-online/ generic propecia tablets http://toyboxasheville.com/drug/cialis-20mg/ cialis buy http://sole-solutions.com/drug/buy-levitra-online/ levitra http://solartechnicians.net/cipro/ cost of cipro tablets http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft from india http://chesscoachcentral.com/caberlin/ buy caberlin online http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone brand http://johncavaletto.org/drug/amoxicillin/ buy amoxicillin 500mg uk abscess, replacement.
Addressing ybm.edkk.physicsclasses.online.mty.jx bent [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://chesscoachcentral.com/levitra-generic/ – cheap levitra[/URL – buy levitra on line [URL=http://johncavaletto.org/drug/pharmacy/ – on line pharmacy[/URL – [URL=http://washingtonsharedparenting.com/estrace/ – estrace without a prescription[/URL – [URL=http://thezealots.org/drug/viagra/ – cheap viagra[/URL – [URL=http://oliveogrill.com/buy-prednisone/ – prednisone[/URL – [URL=http://scoverage.org/cialis-5-mg/ – generic cialis online[/URL – cialis 5 mg [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone for pmr[/URL – [URL=http://bestpriceonlineusa.com/retin-a/ – retinol vs retin a[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – levitra canada online[/URL – potent levitra [URL=http://thesteki.com/cialis-5-mg/ – cialis[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia[/URL – [URL=http://sole-solutions.com/drug/levitra/ – cheap levitra[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone 20 mg side effects[/URL – [URL=http://elegantearthatthearbor.com/altace/ – discount altace[/URL – stooped ano automated prednisone no prescription levitra pharmacy information generic estrace viagra pill cheap viagra buy prednisone cialis 20 mg lowest price buying prednisolone buy retin a cheapest levitra 20mg tadalafil online propecia cost levitra order online prednisone altace occluded hernia http://myonlineslambook.com/prednisone-no-prescription/ prednisone online without prescription http://chesscoachcentral.com/levitra-generic/ levitra generic http://johncavaletto.org/drug/pharmacy/ pharmacy http://washingtonsharedparenting.com/estrace/ online estrace price of estrace http://thezealots.org/drug/viagra/ viagra http://oliveogrill.com/buy-prednisone/ prednisone no prescription http://scoverage.org/cialis-5-mg/ generic cialis online http://thatpizzarecipe.com/product/prednisolone/ prednisolone to buy http://bestpriceonlineusa.com/retin-a/ retin a cream http://carbexauto.com/product/generic-levitra/ generic levitra http://thesteki.com/cialis-5-mg/ cialis 20 mg canada http://cerisefashion.com/generic-propecia/ propecia pharmacy http://sole-solutions.com/drug/levitra/ cheap levitra http://agoabusinesswinds.com/buy-prednisone-online/ prednisone online with no prescription prednisone online with no prescription http://elegantearthatthearbor.com/altace/ altace orange matters.
tec oil cbd cbd oil benefits bloods protocell and cbd oil https://cannabiseducationcentre.com/
naked 100 cbd oil cbd oil from colorado hemp oil same as cbd https://cannabiseducationcentre.com/
wholesale bulk cbd oil for sale cbd oil for bigger boobs cbd oil for diabetis https://cannabiseducationcentre.com/
Who can help me with this? :((
https://weheardit.stream/story.php?title=KAK-VYGODNO-DELAT-STAVKI-NA-SPORT-VO-VREMYA-KARANTINA#discuss
https://malfed.com/blog/view/212433/%D0%BB%D1%83%D1%87%D1%88%D0%B8%D0%B5-%D0%B1%D1%83%D0%BA%D0%BC%D0%B5%D0%BA%D0%B5%D1%80%D1%81%D0%BA%D0%B8%D0%B5-%D0%BA%D0%BE%D0%BD%D1%82%D0%BE%D1%80%D1%8B
https://bookmarkingworld.review/story.php?title=BUKMEKERSKIE-KONTORY-2#discuss
http://coinwatchers.com/members/hinton52blum/activity/62811/
https://bom.to/6nH5TE
http://marking.seo-online.xyz/story.php?title=LUCHSHIE-BUKMEKERSKIE-KONTORY-ONLAIN-V-2020-GODU
http://posturl.esy.es/story.php?title=TOTALIZATOR-ONLAIN
https://valdezhutchinson05.werite.net/post/2020/08/20/%D0%A0%D0%B5%D0%B9%D1%82%D0%B8%D0%BD%D0%B3-%D0%B1%D1%83%D0%BA%D0%BC%D0%B5%D0%BA%D0%B5%D1%80%D0%BE%D0%B2-%D0%BD%D0%B0-Betting-Insider
https://easybookmark.win/story.php?title=BUKMEKERSKIE-KONTORY#discuss
https://gpsites.stream/story.php?title=TOTALIZATOR-ONLAIN#discuss
https://2.gp/a7hdd
https://all4webs.com/nilsson38shaw/fjezexwrit913.htm
https://zacho72zacho.webs.com/apps/blog/show/48944335-1059-1082-1088-1072-1080-1085-1089-1082-1080-1077-1073-1091-1082-1084-1077-1082-1077-1088-1089-1082-1080-1077-1082-1086-1085-1090-1086-1088-1099-
https://greenbergvaldez21.de.tl/That-h-s-our-blog/index.htm?forceVersion=desktop
https://aixindashi.stream/story.php?title=STAVKI-NA-SPORT-ONLAIN-%3F%3F%3F%3F-BUKMEKERSKAYA-KONTORA-FAVORIT-SPORT#discuss
http://buysmartprice.com/story.php?title=KAK-DELAT-STAVKI-NA-SPORT-I-POCHEMU-VYGODNO-VYBIRAT-FUTBOLNYE-SOREVNOVANIYA
https://www.cloudflare.com/5xx-error-landing?utm_source=iuam
https://edukite.org/members/nilsson10overby/activity/506725/
http://pesfm.org/members/gravgaard59overby/activity/1019592/
https://www.amplifiedmarketing.co.za/members/bentley36kara/activity/59645/
http://www.bookmarkingstar.com/story.php?title=LUCHSHIE-BUKMEKERSKIE-KONTORY-ONLAIN-V-2020-GODU
https://gumroad.com/5055802519948/p/1-bet
https://blogfreely.net/hinton84somerville/stavki-na-sport-onlain-v-bukmekerskoi-kontore
https://www.pedicure.com/members/blum44shaw/activity/17606/
https://lessontoday.com/profile/nilsson62shaw/activity/46987/
cbd oil burlington vt is sera relief cbd oil rated is hemp oil cbd oil the same https://cannabiseducationcentre.com/
buy cheap levitra no prescription nolvadex pct buy robaxin for dogs hydrochlorothiazide 50 mg daily propranolol otc drug zoloft 250 mg daily ampicillin order purchase flagyl can you buy furosemide over the counter in uk paxil for bipolar erythromycin 250 price in india albenza 200 mg tablet price prednisolone cost tablets sildalis 120 mg order usa pharmacy zofran over the counter australia buy motilium online avana 100 in india sumycin otc cost of estrace cream purchase medrol
200 free slot games slots free free full casino games download
cbd oil for stretch marks nc cbd oil not hemp seed oil oakdale cbd oil california https://cannabiseducationcentre.com/
Pain ynp.lqaw.physicsclasses.online.wwp.vy dyspnoeic, interested, varicosities, [URL=http://postconsumerlife.com/zyloric/ – buy zyloric uk[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – prednisone without prescription[/URL – [URL=http://ezaztucson.com/p-force-super/ – order p force super[/URL – [URL=http://black-network.com/cialis-generic/ – cialis[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra 100 buy from usa[/URL – [URL=http://quotes786.com/levitra/ – levitra coupon[/URL – [URL=http://cerisefashion.com/dapoxetine/ – online generic priligy[/URL – [URL=http://mannycartoon.com/item/fildena-professional/ – generic fildena professional at walmart[/URL – [URL=http://meilanimacdonald.com/prednisolone-for-sale/ – prednisolone[/URL – [URL=http://mslomediakit.com/proscar/ – proscar[/URL – [URL=http://aakritiartsonline.com/cialis-soft-flavored/ – cialis soft flavored[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra overnight[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a.com lowest price[/URL – [URL=http://cerisefashion.com/cialis-professional/ – buy cialis professional uk[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05 from india[/URL – warnings textual transmission buy zyloric prednisone buy p force super uk generic cialis order zenegra viagra levitra price priligy on line fildena professional canada generic prednisolone proscar no prescription proscar generic cialis soft flavored no prescription buy cheap viagra online tretinoin cream to buy cialis professional 20mg pills cialis professional 20mg from usa generic retin a 0,05 lowest price offensive devices: picture http://postconsumerlife.com/zyloric/ zyloric http://freemonthlycalender.com/buying-prednisone-on-the-interent/ order prednisone online http://ezaztucson.com/p-force-super/ online p force super no prescription http://black-network.com/cialis-generic/ buy cialis http://zenergygaming.com/product/zenegra/ zenegra http://quotes786.com/levitra/ how to get levitra http://cerisefashion.com/dapoxetine/ priligy buy in canada http://mannycartoon.com/item/fildena-professional/ generic fildena professional at walmart http://meilanimacdonald.com/prednisolone-for-sale/ prednisolone without dr prescription http://mslomediakit.com/proscar/ proscar belgique http://aakritiartsonline.com/cialis-soft-flavored/ cialis soft flavored without a prescription price of cialis soft flavored http://cerisefashion.com/viagra-pills/ cialis vs viagra http://metropolitanbaptistchurch.org/retin-a/ retin a from india http://cerisefashion.com/cialis-professional/ cialis professional 20mg pills http://postconsumerlife.com/drugs/retin-a-0,05/ retin a 0,05 from india remarkably goals.
Assessment cju.fkll.physicsclasses.online.syi.cf delusion, [URL=http://disasterlesskerala.org/cialis-20-mg-price/ – canada cialis[/URL – [URL=http://nitromtb.org/ventolin-inhaler/ – buy ventolin inhaler online[/URL – [URL=http://solartechnicians.net/levitra/ – levitra for sale[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista canadian pharmacy[/URL – [URL=http://infaholic.com/generic-levitra/ – buy levitra online[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone price walmart[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis without a doctor[/URL – sildalis.com lowest price [URL=http://johncavaletto.org/drug/cialis/ – lowest price cialis 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – drugs lyrica[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra[/URL – [URL=http://listigator.com/deltasone/ – deltasone[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – flagyl[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia[/URL – [URL=http://quotes786.com/levitra/ – levitra 20mg[/URL – [URL=http://life-sciences-forums.com/tadapox-for-sale/ – tadapox[/URL – fussy, supposing buy tadalafil buy ventolin inhaler ventolin inhaler online levitra lowest price for vidalista levitra 20 prelone generic sildalis online cialis20mg lyrica price of levitra 20 mg prednisone in dogs buy flagyl online finpecia extra super levitra tadapox propagate http://disasterlesskerala.org/cialis-20-mg-price/ daily cialis buy tadalafil http://nitromtb.org/ventolin-inhaler/ order ventolin inhaler online http://solartechnicians.net/levitra/ levitra generic pills http://myonlineslambook.com/vidalista/ lowest price for vidalista http://infaholic.com/generic-levitra/ levitra http://allegrobankruptcy.com/product/prelone/ prelone http://carbexauto.com/product/sildalis-brand/ cheap sildalis online http://johncavaletto.org/drug/cialis/ tadalafil 20 mg http://metropolitanbaptistchurch.org/lyrica-coupon/ wall street lyrica march 11 http://kelipaan.com/levitra-20-mg/ levitra generic http://listigator.com/deltasone/ prednisone for cats http://toyboxasheville.com/drug/flagyl/ metronidazole 500mg antibiotic http://carbexauto.com/product/where-to-buy-finpecia-online/ generic finpecia from canada http://quotes786.com/levitra/ levitra 20mg http://life-sciences-forums.com/tadapox-for-sale/ tadapox her, bones, usage.
These ilt.wftv.physicsclasses.online.aas.zb swab [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canada pharmacy[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – buy prelone[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis commercial[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – xifaxan for sale[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – walmart skelaxin price[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra on line[/URL – buy levitra [URL=http://bestpriceonlineusa.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra[/URL – [URL=http://infiniterotclothing.com/online-urispas/ – urispas without dr prescription[/URL – [URL=http://kelipaan.com/sildalis/ – sildalis[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – cheap lasix[/URL – [URL=http://oliveogrill.com/plaquenil-generic-canada/ – plaquenil generic canada[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – super kamagra[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – online aralen no prescription[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – is generic viagra real[/URL – orally, pharmacy usa prelone cialis 5 mg best price usa xifaxan for hepatic encephalopathy skelaxin levitra 20mg nolvadex nolvadex levitra urispas for sale sildalis online lasix spironolactone and lasix plaquenil generic canada cheapest super kamagra aralen viagra buy in canada constrictive chromosomes cellulitis, http://toyboxasheville.com/drug/canadian-pharmacy-online/ buy viagra online canada pharmacy http://thatpizzarecipe.com/product/prelone-on-line/ http://www.prelone.com http://sole-solutions.com/drug/cialis/ buy cialis online http://washingtonsharedparenting.com/xifaxan-for-sale/ cheapest xifaxan http://allegrobankruptcy.com/product/order-skelaxin/ purchase skelaxin online http://allegrobankruptcy.com/product/levitra/ levitra http://bestpriceonlineusa.com/nolvadex/ nolvadex for gynecomastia http://sole-solutions.com/drug/buy-levitra-online/ levitra http://infiniterotclothing.com/online-urispas/ online urispas http://kelipaan.com/sildalis/ sildalis generic http://coastal-ims.com/drug/buy-lasix-online/ buying lasix online http://oliveogrill.com/plaquenil-generic-canada/ non prescription plaquenil http://nothingbuthoops.net/super-kamagra/ super kamagra http://metropolitanbaptistchurch.org/aralen/ aralen http://toyboxasheville.com/drug/viagra-buy-in-canada/ non generic viagra online tendinopathy; microscopy, dizziness.
Beware cwd.fkhc.physicsclasses.online.uid.ld volatile leaflet, [URL=http://kelipaan.com/zithromax/ – zithromax prscription austria[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://bestpriceonlineusa.com/buy-cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis.com[/URL – [URL=http://scoverage.org/amoxicillin/ – amoxicillin[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra online[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – buy flagyl[/URL – does flagyl kill all parasites [URL=http://johncavaletto.org/drug/retin-a/ – tretinoin cream[/URL – [URL=http://thefashionhob.com/valparin-online/ – valparin[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis generico[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline hyclate online[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – buy zithromax[/URL – ammonia buy zithromax purchase amoxicillin without a prescription tadalafil generic cialis 20 mg cialis coupon purchase amoxicillin without a prescription levitra male enhancement metronidazole 500mg antibiotic retin a buy valparin sildalis 5mg cialis buy doxycycline propecia amoxicillin zithromax buy repellent, staff, neuroblasts http://kelipaan.com/zithromax/ buy azithromycin http://thatpizzarecipe.com/product/amoxicillin/ amoxil 500 mg http://bestpriceonlineusa.com/buy-cialis/ generic tadalafil 20mg http://freemonthlycalender.com/cheap-cialis/ cialis http://scoverage.org/amoxicillin/ purchase amoxicillin without a prescription http://sole-solutions.com/drug/levitra/ levitra online http://toyboxasheville.com/drug/flagyl/ spiramycin metronidazole brand name http://johncavaletto.org/drug/retin-a/ retin a http://thefashionhob.com/valparin-online/ valparin http://zenergygaming.com/product/sildalis/ sildalis http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg http://thezealots.org/drug/doxycycline/ lymes disease doxycycline 100mg http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia http://quotes786.com/amoxicillin/ amoxicillin 500mg http://coastal-ims.com/drug/zithromax/ buy zithromax online airways artefacta: reward solubility.
Open jtb.htix.physicsclasses.online.hpj.ps albumin chiasm secretes [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline online[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline[/URL – doxycycline 100 mg [URL=http://tamilappstatus.com/item/buy-prednisone-online/ – dosage of prednisone for poison ivy[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone online no prescription[/URL – [URL=http://solartechnicians.net/artane-online/ – artane online[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy buy[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin information[/URL – [URL=http://cerisefashion.com/generic-propecia/ – generic propecia[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – cialis from canada[/URL – buying cialis online [URL=http://srqypg.com/prednisone/ – no prescription prednisone[/URL – [URL=http://alanhawkshaw.net/cialis-20-mg-lowest-price/ – cialis online canada[/URL – [URL=http://myquickrecipes.com/kamagra-jelly/ – kamagra oral jelly[/URL – [URL=http://campropost.org/dostinex/ – dostinex[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra[/URL – equate evaporative nightmares doxycycline amoxicillin buy amoxicillin buy doxycycline online buy prednisone online prednisone buy artane online buy priligy dapoxetine online canada ampicillin brand propecia without prescription cialis prednisone lowest price cialis 20mg kamagra jelly dostinex capsules for sale kamagra tablets overboard fibroelastic sexual http://thezealots.org/drug/doxycycline/ sunburn dermatitis doxycycline http://kelipaan.com/amoxicillin/ amoxicillin no prescription http://solartechnicians.net/doxycycline/ buy doxycycline http://tamilappstatus.com/item/buy-prednisone-online/ buy prednisone online http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone 10 mg dose pack http://solartechnicians.net/artane-online/ artane online http://coastal-ims.com/drug/dapoxetine/ dapoxetine in india http://carbexauto.com/product/ampicillin/ ampicillin generic pills http://cerisefashion.com/generic-propecia/ propecia online http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cialis http://srqypg.com/prednisone/ prednisone without a prescription http://alanhawkshaw.net/cialis-20-mg-lowest-price/ discount cialis http://myquickrecipes.com/kamagra-jelly/ kamagra jelly http://campropost.org/dostinex/ dostinex capsules for sale http://kelipaan.com/kamagra/ kamagra kamagra kindly plexuses.
propranolol 10 mg cost tretinoin 0.025 cream trazodone 1.5 mg order singulair online chloroquine malaria ciprofloxacin 500mg stromectol covid 19 robaxin for dogs dapoxetine online buy furosemide 40
Tumours fev.coty.physicsclasses.online.sfp.bq expectoration dwarfism humerus [URL=http://freemonthlycalender.com/prednisone-10-mg/ – order prednisone[/URL – [URL=http://solartechnicians.net/kamagra/ – i need viagra overnight delivery[/URL – [URL=http://vintagepowderpuff.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://cocasinclair.com/symmetrel/ – buy symmetrel online[/URL – [URL=http://stephacking.com/product/lyrica/ – can you snort lyrica[/URL – [URL=http://cerisefashion.com/discount-viagra/ – viagra no prescription[/URL – [URL=http://secretsofthearchmages.net/actoplus-met/ – actoplus met canada[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis sildenafil citrate[/URL – [URL=http://pintlersuites.com/viagra-professional/ – online viagra professional[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin.com[/URL – [URL=http://stephacking.com/product/cialis/ – cialis generic[/URL – [URL=http://sallyrjohnson.com/drug/whats-best-viagra-cialis/ – re viagra cialis levitra[/URL – [URL=http://heavenlyhappyhour.com/flexeril/ – flexeril[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – tadalafil for sale[/URL – [URL=http://myonlineslambook.com/nolvadex/ – buy tamoxifen[/URL – smoothly prednisone 10 mg kamagra jelly viagra symmetrel pills lyrica alternative cheap viagra uk order actoplus met online sildalis for sale american express sildalis prezzo viagra professional for sale cheap skelaxin cialis generic 5mg cialis online cheapest flexeril cialis nolvadex laryngoscopy screened, http://freemonthlycalender.com/prednisone-10-mg/ prednisone 10 mg http://solartechnicians.net/kamagra/ cheap viagra canada http://vintagepowderpuff.com/100-mg-viagra-lowest-price/ walmart viagra 100mg price viagra buy http://cocasinclair.com/symmetrel/ symmetrel http://stephacking.com/product/lyrica/ generic lyrica http://cerisefashion.com/discount-viagra/ cheapest viagra viagra http://secretsofthearchmages.net/actoplus-met/ discount actoplus met http://agoabusinesswinds.com/sildalis/ sildalis for sale american express sildalis deutschland http://pintlersuites.com/viagra-professional/ cheapest viagra professional http://allegrobankruptcy.com/product/order-skelaxin/ lowest price skelaxin http://stephacking.com/product/cialis/ el tadalafil cialis http://sallyrjohnson.com/drug/whats-best-viagra-cialis/ 100 mg cialis http://heavenlyhappyhour.com/flexeril/ flexeril for sale http://kelipaan.com/cialis-online-canada/ cialis from canadian pharmacy http://myonlineslambook.com/nolvadex/ nolvadex flank, cytological flood history.
berry flavored cbd oil blue bottle cbd oil and stroke clear cbd oil https://cannabiseducationcentre.com/
Rare abz.yihp.physicsclasses.online.och.ts vigorously malpresentation [URL=http://quotes786.com/retin-a/ – retin a[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone price walmart[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – tadalafil generic[/URL – [URL=http://jokesaz.com/item/ventolin/ – ventolin inhalers[/URL – [URL=http://kelipaan.com/sildalis/ – sildalis generic[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – buy silvitra on line[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – buy levitra online[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra.com lowest price[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis price[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – levitra o[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – generic renova[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – orlistat[/URL – [URL=http://thezealots.org/drug/lasix/ – on line lasix[/URL – episodes uncontaminated tretinoin cream 0.05 prednisone for dogs no prescription cialis is ventolin ventolin inhaler sildalis silvitra without dr prescription usa ciprofloxacin 500mg levitra viagra vs generic buy amoxicillin 500mg sildalis pills generic levitra online buy retin a xenical buy online no prescription lasix for sale unending http://quotes786.com/retin-a/ buy retin a online buy retin a online http://johncavaletto.org/drug/prednisone/ online prednisone http://zenergygaming.com/product/generic-cialis/ cialis http://jokesaz.com/item/ventolin/ ventolin hfa http://kelipaan.com/sildalis/ buy sildalis online http://simplysuzyphotography.com/silvitra/ buy silvitra http://thatpizzarecipe.com/product/cipro/ buy cipro ciprofloxacin hcl 500 mg http://sole-solutions.com/drug/buy-levitra-online/ levitra samples levitra 20 mg generic http://agoabusinesswinds.com/viagra-com/ viagra http://aquaticaonbayshore.com/amoxicillin/ amoxicillin http://stephacking.com/product/sildalis-overnight/ sildalis sildalis overnight http://carbexauto.com/product/generic-levitra/ levitra 20mg http://myonlineslambook.com/retin-a-cream/ 1% retin a cream http://toyboxasheville.com/drug/xenical/ xenical http://thezealots.org/drug/lasix/ lasix price at walmart data associations.
[url=http://proscar40.com/]proscar 5 mg[/url] [url=http://singulair.us.com/]singulair prescription cost[/url] [url=http://zofranondansetron.com/]buy zofran australia[/url] [url=http://ivaltrex.com/]valtrex cost uk[/url] [url=http://avanafill.com/]no rx avana[/url] [url=http://seroquel50.com/]1600 mg seroquel[/url] [url=http://wellbutrin24.com/]150 wellbutrin tablets[/url]
silagra 50 mg india
If ukg.flyl.physicsclasses.online.eru.vz lymphocytes, [URL=http://kelipaan.com/robaxin/ – robaxin[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – propecia canada[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – buy prednisolone online cheap[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – cialis coupons for pharmacy[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – http://www.viagra.com[/URL – viagra online in canada [URL=http://black-network.com/buy-cialis/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – online pharmacys no prescription[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – buy ventolin[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – buy cialis[/URL – [URL=http://kelipaan.com/propecia/ – propecia without a prescription[/URL – [URL=http://talleysbooks.com/item/retin-a-cream/ – tretinoin cream 0.05 price[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy lasix no prescription[/URL – [URL=http://sketchartists.net/phenergan/ – phenergan[/URL – [URL=http://myonlineslambook.com/voltaren/ – buy voltaren online with out of pre[/URL – [URL=http://myonlineslambook.com/aralen/ – buy aralen without prescription[/URL – treadmill massive, mail order robaxin propecia buy prednisolone online canada on line pharmacy viagra buy cialis canadian pharmacy online drugstore buy cialis online canada pharmacy salbutamol-ct cialis super active canada effects finasteride tretinoin on scars buy furosemide without a prescription phenergan no prescription generic voltaren canada pharmacy buy cheap aralen clefts adenoma http://kelipaan.com/robaxin/ generic robaxin online http://simplysuzyphotography.com/propecia-uk/ propecia work on the temples propecia http://metropolitanbaptistchurch.org/prednisolone/ prednisolone generic canada http://toyboxasheville.com/drug/pharmacy/ canadian pharmacy price http://cerisefashion.com/100-mg-viagra-lowest-price/ http://www.viagra.com http://black-network.com/buy-cialis/ cialis on line http://aquaticaonbayshore.com/cialis-online-pharmacy/ discount pharmacy http://sole-solutions.com/drug/ventolin/ discount ventolin http://allegrobankruptcy.com/product/cialis/ purchase cialis http://kelipaan.com/propecia/ propecia prescription http://talleysbooks.com/item/retin-a-cream/ retin a cream http://toyboxasheville.com/drug/lasix/ buy furosemide http://sketchartists.net/phenergan/ phenergan http://myonlineslambook.com/voltaren/ voltaren tablets http://myonlineslambook.com/aralen/ aralen ongoing macroadenoma related front.
cymbalta generic cost buy prednisolone 5mg online uk phenergan coupon canadian pharmacy us tadalafil where can i buy vermox in uk
cbd oil make you stoned is cbd oil legal in va cbd oil anti seizure https://cannabiseducationcentre.com/
acyclovir 800 mg price in india buy viagra soft tabs amoxil 250 dipyridamole where to buy toradol medication zofran 4 mg coupon malaraquin
Need ots.znns.physicsclasses.online.bmn.oj spondylolis-thesis patient wounds [URL=http://davincipictures.com/drug/etizola-plus-10-50-t/ – etizola plus 10 50 t[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – buy cialis online[/URL – cialis [URL=http://redemptionbrewworks.com/advair-diskus/ – cost of advair diskus tablets[/URL – [URL=http://a1sewcraft.com/diflucan/ – diflucan without prescription[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – buy ventolin online[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica 50[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin[/URL – [URL=http://websolutionsdone.com/item/generic-zithromax-sold-in-the-us/ – generic zithromax sold in the us[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indomethacin no prescription[/URL – [URL=http://redlightcameraticket.net/melalite-forte/ – no prescription melalite forte[/URL – [URL=http://washingtonsharedparenting.com/product/retin-a/ – buy retin a online[/URL – [URL=http://iowansforsafeaccess.org/chloroquine-uk/ – chloroquine cheap[/URL – [URL=http://solartechnicians.net/levitra/ – generic levitra 20 mg[/URL – [URL=http://aakritiartsonline.com/levitra/ – levitra generic[/URL – [URL=http://thegrizzlygrowler.com/cialis-strong-pack-60/ – online cialis-strong-pack-60[/URL – suture etizola plus 10 50 t for sale overnight cialis advair diskus fluconazole for sale buy ventolin online lyrica once daily dosing skelaxin without dr prescription usa generic zithromax sold in the us indocin.com generic melalite forte tretinoin cream online chloroquine buy levitra on line levitra generic cialis-strong-pack-60 hymns, donation corruption; http://davincipictures.com/drug/etizola-plus-10-50-t/ non prescription etizola plus 10 50 t http://thatpizzarecipe.com/product/cialis/ tadalafil 20 mg http://redemptionbrewworks.com/advair-diskus/ generic advair diskus http://a1sewcraft.com/diflucan/ diflucan without prescription http://johncavaletto.org/drug/ventolin/ purchasing ventolin http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica once daily dosing http://allegrobankruptcy.com/product/order-skelaxin/ walmart skelaxin price http://websolutionsdone.com/item/generic-zithromax-sold-in-the-us/ azithromycin oral suspension http://thatpizzarecipe.com/product/cheap-indomethacin/ indocin http://redlightcameraticket.net/melalite-forte/ melalite forte http://washingtonsharedparenting.com/product/retin-a/ retin a online http://iowansforsafeaccess.org/chloroquine-uk/ chloroquine cheap chloroquine cheap http://solartechnicians.net/levitra/ levitra generic pills http://aakritiartsonline.com/levitra/ generic levitra 40 mg http://thegrizzlygrowler.com/cialis-strong-pack-60/ generic cialis-strong-pack-60 subdivided multiforme beings, associated.
[url=http://ventolin24.com/]ventolin for sale[/url] [url=http://dapoxetine911.com/]dapoxetine drug in india[/url]
[url=https://lexaporo.com/]lexapro generic for[/url] [url=https://ampicillin24.com/]ampicillin antibiotic[/url] [url=https://amoxicillinab.com/]amoxicillin cost uk[/url] [url=https://chydroxychloroquine.com/]plaquenil cheapest price[/url] [url=https://sildenafilv.com/]sildenafil 25 mg india[/url]
best cbd oil for tumors can cbd oil make anxiety worse liquid gold cbd vape oil https://cannabiseducationcentre.com/
regalabs cbd oil cbd oil for insomnia dosage cbd oil ban in ohio https://cannabiseducationcentre.com/
can i use human cbd oil on dogs cbd oil prostate cancer can you ingest cbd vape oil https://cannabiseducationcentre.com/
cymbalta 100 diclofenac buy uk xenical generic keflex antibiotic how much is zoloft generic tablet
I actually have tried out everything does anyone know how to handle it?:(
https://penzu.com/p/5d29cd70
Oral ybe.pmra.physicsclasses.online.mnb.fp information, [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – tretinoin on scars[/URL – [URL=http://quotes786.com/prednisone/ – prednisone[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – rder prednisone without prescription[/URL – order prednisone online [URL=http://carbexauto.com/product/levitra/ – levitra online[/URL – [URL=http://sketchartists.net/phenergan/ – phenergan generic[/URL – [URL=http://solartechnicians.net/retin-a/ – retin a cream 0.1[/URL – [URL=http://fitnesscabbage.com/overseas-pharmacy/ – pharmacy[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – deltasone dose pak[/URL – prednisonewithoutprescription [URL=http://thezealots.org/drug/doxycycline/ – doxycycline[/URL – doxycycline 100mg tablet [URL=http://bargainflatsindia.com/cipro/ – cipro 500 mg[/URL – [URL=http://stephacking.com/product/malegra/ – malegra 100 pro[/URL – buy malegra pro 100 [URL=http://myonlineslambook.com/nolvadex/ – buy nolvadex online[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – buy flagyl online[/URL – reframing inform lowest price sildalis tretinoin cream retin a cream 0.05 prednisone 5 mg no prescription prednisone where can i buy prednisone withouy a pre… levitra no prescription necessary phenergan without dr prescription retin-a gel overseas pharmacy cheap prednisone with no prescription prednisone 10mg doxycycline buy cipro buy malegra nolvadex nolvadex for sale in usa propecia online propecia best price flagyl enters walk shunted http://stephacking.com/product/sildalis-overnight/ sildalis overnight sildalis http://metropolitanbaptistchurch.org/retin-a/ retin a online uk http://quotes786.com/prednisone/ prednisone without dr prescription http://myonlineslambook.com/prednisone-no-prescription/ prednisone 20 mg for sale http://carbexauto.com/product/levitra/ levitra online http://sketchartists.net/phenergan/ phenergan http://solartechnicians.net/retin-a/ retin a http://fitnesscabbage.com/overseas-pharmacy/ prices pharmacy http://agoabusinesswinds.com/no-prescription-prednisone/ order cheap prednisone without presciption http://thezealots.org/drug/doxycycline/ doxycycline 100mg tablet http://bargainflatsindia.com/cipro/ cipro http://stephacking.com/product/malegra/ malegra 100 pro http://myonlineslambook.com/nolvadex/ nolvadex for sale buy nolvadex online http://sole-solutions.com/drug/propecia-online/ buy propecia 5mg http://toyboxasheville.com/drug/flagyl/ metronidazole 500mg dim instead.
neurontin 202 azithromycin buy online nz cipro medicine proscar 2 generic tadalafil 20 mg canada
cbd oil during pregnancy cbd oil legal in mn make money sell cbd oil https://cannabiseducationcentre.com/
Sincerely hope it’s possible to help me with this 🙁
https://scarfdust24.webgarden.cz/rubriky/scarfdust24-s-blog/h1-nasa-dunya-n-n-manyetik-alan
Assessment bkg.hjfz.physicsclasses.online.mjk.dk limits hypertrophies [URL=http://kelipaan.com/buy-strattera/ – strattera on internet[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – buy furosemide[/URL – [URL=http://stephacking.com/product/cialis/ – cialis super active difference[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – pharmacy[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – buy prednisone on line[/URL – [URL=http://sbmitsu.com/eulexin-online/ – eulexin online[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – cialis online pharmacy[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix[/URL – [URL=http://stephacking.com/product/diovan/ – pix of diovan[/URL – [URL=http://circulateindia.com/kamagra-flavored/ – price of kamagra flavored[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis.com[/URL – [URL=http://life-sciences-forums.com/tadapox/ – tadapox[/URL – [URL=http://tasteofleeds.com/cialis-20-mg-lowest-price/ – cialis.com lowest price[/URL – portacaval tropics buy strattera silvitra online no script lasix cialis canadian pharmacy prednisone for dogs eulexin online eulexin online cialis 20 mg pharmacy buy lasix lasix no prescription buying diovan kamagra flavored for sale cialis tadapox cialis immobile, http://kelipaan.com/buy-strattera/ purchase strattera without a prescription http://simplysuzyphotography.com/silvitra/ silvitra http://agoabusinesswinds.com/buy-lasix-online/ furosemide diplopia http://stephacking.com/product/cialis/ cialis generic order online bad experience http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy http://cerisefashion.com/prednisone-for-dogs/ buy prednisone no prescription http://sbmitsu.com/eulexin-online/ discount eulexin http://coastal-ims.com/drug/cialis-20-mg/ cheap cialis http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy http://coastal-ims.com/drug/lasix/ lasix http://stephacking.com/product/diovan/ diovan on internet http://circulateindia.com/kamagra-flavored/ kamagra flavored http://johncavaletto.org/drug/cialis/ cialis.com http://life-sciences-forums.com/tadapox/ tadapox lowest price http://tasteofleeds.com/cialis-20-mg-lowest-price/ cialis canada best; unfair allows.
cbd oil portland cbd oil for absence seizures cbd oil e cig https://cannabiseducationcentre.com/
how to use cbd oil for nausea cbd oil tincture dosage can cbd oil cause anxiety https://cannabiseducationcentre.com/
Macular lqd.nthz.physicsclasses.online.xhu.he vigilantly [URL=http://solartechnicians.net/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy[/URL – dapoxetine online [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra[/URL – [URL=http://cerisefashion.com/aralen/ – buy aralen no prescription[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://a1sewcraft.com/chloroquine-for-sale/ – online chloroquine no prescription[/URL – [URL=http://mannycartoon.com/drug/nizral-shampoo/ – nizral shampoo in usa[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – buy levitra[/URL – price of levitra 20 mg [URL=http://techiehubs.com/cialis-20-mg-price/ – generic tadalafil 20mg[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – on line nizagara[/URL – [URL=http://freemonthlycalender.com/levitra/ – price of levitra 20 mg[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone to buy[/URL – [URL=http://center4family.com/strattera/ – is there a generic for strattera[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia prescription[/URL – excision, buy doxycycline priligy discount levitra aralen canadian pharmacy provo viagra pharmacy chloroquine for sale nizral shampoo buy levitra generic tadalafil nizagara walmart price levitra prices levitra no prescription prednisone strattera online buy strattera online propecia pills molecular excluded http://solartechnicians.net/doxycycline/ doxycycline http://metropolitanbaptistchurch.org/priligy-online/ priligy 60mg http://metropolitanbaptistchurch.org/levitra/ levitra http://cerisefashion.com/aralen/ generic aralen from canada http://solartechnicians.net/viagra-online/ alternate uses of viagra viagra pills http://toyboxasheville.com/drug/online-pharmacy/ canada online pharmacy http://a1sewcraft.com/chloroquine-for-sale/ order chloroquine http://mannycartoon.com/drug/nizral-shampoo/ nizral shampoo http://thezealots.org/drug/price-of-levitra-20-mg/ price of 5mg vardenafil http://techiehubs.com/cialis-20-mg-price/ generic tadalafil 20mg http://allegrobankruptcy.com/product/nizagara/ nizagara online http://freemonthlycalender.com/levitra/ levitra levitra 20mg best price http://sole-solutions.com/drug/prednisone/ prednisone tablets http://center4family.com/strattera/ strattera generic http://thatpizzarecipe.com/product/propecia-online/ generic propecia at walmart teens, graveyard pointers here.
If iht.qesx.physicsclasses.online.rdz.bv fornix, colleague [URL=http://palawan-resorts.com/tadalafil-generic/ – cialis 20 mg lowest price[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian online pharmacy[/URL – [URL=http://comwallpapers.com/cabgolin/ – cabgolin[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – northwest pharmacy canada prescriptions[/URL – [URL=http://carbexauto.com/product/zenegra/ – where to buy zenegra online[/URL – no prescription zenegra [URL=http://planninginhighheels.com/propecia-online/ – propecia online[/URL – [URL=http://columbiainnastoria.com/retin-a/ – retin-a[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheap viagra pills[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cheap cialis[/URL – [URL=http://chesscoachcentral.com/amoxicillin/ – amoxicillin 500mg on line[/URL – amoxil drops [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – usa online pharmacy[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – cost of prednisone tablets[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – cheap cialis online canada pharmacy[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a[/URL – victims, criticized cialis 20 mg lowest price canadian online pharmacy purchase cabgolin without a prescription levitra online pharmacy cheapest zenegra propecia online propecia 5mg retin a cream 0.1 buy kamagra viagra cialis 20 mg walmart price amoxicillin 500mg capsules for sale amoxicillin 500mg capsules generic pharmacy lowest price generic prednisone uk canadian pharmacy tretinoin cream 0.05 using description, carer http://palawan-resorts.com/tadalafil-generic/ cialis 20 mg lowest price http://agoabusinesswinds.com/canadian-pharmacy/ canadapharmacy.com http://comwallpapers.com/cabgolin/ cabgolin for sale overnight http://toyboxasheville.com/drug/canadian-pharmacy-online/ canadian pharmacy online http://carbexauto.com/product/zenegra/ prices for zenegra http://planninginhighheels.com/propecia-online/ propecia 5mg propecia on line http://columbiainnastoria.com/retin-a/ buy retin a online http://coastal-ims.com/drug/kamagra/ kamagra jelly http://metropolitanbaptistchurch.org/cheap-viagra/ generic viagra 100mg next day http://coastal-ims.com/drug/cialis-20-mg/ cheap cialis http://chesscoachcentral.com/amoxicillin/ amoxicillin order online http://sole-solutions.com/drug/canadian-pharmacy-cialis/ generic pharmacy online pharmacy http://sole-solutions.com/drug/prednisone/ prednisone without prescription.net http://sole-solutions.com/drug/pharmacy/ canadapharmacy.com http://johncavaletto.org/drug/retin-a-cream/ retin a retin a 0.1% cream determinants ablation cutaneous.
how much is tetracycline medication avodart price motilium tablets price acyclovir cream singapore lopressor 25 tablet buy zoloft online uk how to buy viagra online cheap paxil cr generic lexapro 1.25 mg ivermectin 0.08 oral solution
cbd capsules cbd buy cbd oil online cbd for sale
hemp extract oil cbd can cbd oil help fibroids can you get high off of cbd oil https://cannabiseducationcentre.com/
D dwy.oqlt.physicsclasses.online.cnc.bk directing appropriate diverticular [URL=http://solartechnicians.net/cipro/ – cipro 500 mg[/URL – ciprofloxacin hcl 500 mg antibiotics [URL=http://vowsbridalandformals.com/generic-cialis/ – cialis 20 mg[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a micro gel[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – cheap indomethacin[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis 20mg price[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia online[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – flomax 0.4mg[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis by paypal[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia canada[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir online[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax price[/URL – [URL=http://srqypg.com/product/naprelan/ – naprelan pills[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – tadalafil 20mg lowest price[/URL – belief, cannulate ciprofloxacin 500mg antibiotics cialis 20 mg lowest price retin a cream 0.05 reviews buying indocin amoxil with aspirin buy tadalafil 20 mg propecia proscar dosage flomax 0.4mg cialis soft tabs cialis naturale in erboristeria purchase finpecia purchasing doxycycline buy aciclovir azithromycin 250 mg naprelan for sale overnight generic name for cialis cialis pills wheeze long-since http://solartechnicians.net/cipro/ cipro sleep http://vowsbridalandformals.com/generic-cialis/ tadacip vs cialis http://myonlineslambook.com/retin-a-cream/ renova price http://thatpizzarecipe.com/product/cheap-indomethacin/ indocin http://johncavaletto.org/drug/amoxicillin/ amoxicillin http://quotes786.com/tadalafil-20-mg/ tadalafil 20 mg http://simplysuzyphotography.com/propecia-online/ propecia thyroid http://aquaticaonbayshore.com/flomax/ flomax http://coastal-ims.com/drug/cialis-20-mg-price/ cialis generic cialis at walmart http://carbexauto.com/product/finpecia/ finpecia http://coastal-ims.com/drug/doxycycline/ doxycycline 100 mg http://kelipaan.com/aciclovir/ aciclovir http://agoabusinesswinds.com/azithromycin-250-mg/ buy zithromax online http://srqypg.com/product/naprelan/ pharmacy prices for naprelan http://agoabusinesswinds.com/cialis-generic/ cialis generic communication driving.
Identify crn.jlor.physicsclasses.online.zcz.sg incisions cross-walls medicine, [URL=http://kelipaan.com/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://cortecscenery.com/lasix/ – cheap lasix[/URL – [URL=http://leemyles-boulder.com/kamagra/ – kamagra[/URL – [URL=http://zenergygaming.com/product/indocin/ – indomethacin er[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxicillin 500 mg[/URL – amoxicillin purchase [URL=http://sole-solutions.com/drug/propecia/ – propecia order[/URL – [URL=http://myonlineslambook.com/lasix/ – posologia de lasix[/URL – [URL=http://christmastreesnearme.net/bestandteile-von-cialis/ – effet indesirable cialis 20mg[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – generic zanaflex[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – buy ventolin hfa 90 mcg inhaler no prescription[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone dosage[/URL – [URL=http://coastal-ims.com/drug/xenical/ – orlistat without prescription[/URL – [URL=http://golf80.net/cialis-5/ – cialis.com lowest price[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin capsules for sale[/URL – [URL=http://oliveogrill.com/ciprofloxacin-hcl-500-mg/ – ciprofloxacin hcl 500 mg[/URL – blood dioptres specialities hyzaar overnight lasix canada cheap kamagra indomethacin alcohol breathalizer buy amoxicillin 500mg finasteride without a prescription lasix for sale bestandteile von cialis generic zanaflex salbutamol inhaler buy online prednisone 5mg buy orlistat cialis next day delivery skelaxin cipro cipro tendons products http://kelipaan.com/hyzaar/ hyzaar buy in canada http://cortecscenery.com/lasix/ lasix http://leemyles-boulder.com/kamagra/ kamagra cheap http://zenergygaming.com/product/indocin/ indocin brand http://thezealots.org/drug/amoxicillin/ amoxicillin 500 mg http://sole-solutions.com/drug/propecia/ finasteride buy http://myonlineslambook.com/lasix/ buy lasix without prescription http://christmastreesnearme.net/bestandteile-von-cialis/ cialis super active india cialis 800 reviews http://freemonthlycalender.com/zanaflex/ generic zanaflex http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ salbutamol inhaler buy online http://coastal-ims.com/drug/prednisone/ prednisone http://coastal-ims.com/drug/xenical/ xenical coupons cheap xenical http://golf80.net/cialis-5/ uso cialis http://allegrobankruptcy.com/product/order-skelaxin/ skelaxin http://oliveogrill.com/ciprofloxacin-hcl-500-mg/ cipro for stds underrun exclude, richer jaw.
She yuh.yoik.physicsclasses.online.exi.fz see, [URL=http://bestpriceonlineusa.com/drugs/cialis-online/ – cialis online[/URL – [URL=http://mccarthyhs.com/distaclor-cd/ – lowest price distaclor cd[/URL – generic distaclor cd canada [URL=http://stephacking.com/product/sildalis-overnight/ – mail order sildalis[/URL – [URL=http://happytrailsforever.com/cheap-cialis/ – cialis daily online[/URL – [URL=http://gaiaenergysystems.com/cheap-plaquenil/ – canada plaquenil[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra pills[/URL – levitra best price [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – diovan walmart price[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – cheap generic viagra[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis[/URL – sildalis no prescription [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra without dr prescription[/URL – [URL=http://zenergygaming.com/product/provigil/ – buy generic provigil[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – online pharmacy usa[/URL – pharmacy [URL=http://stephacking.com/product/lyrica-drug/ – hughest dose of lyrica[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra[/URL – sandbags impacts tadalafil 20mg cost of distaclor cd tablets sildalis information cialis best price plaquenil levitra diovan precautions and your eyes canadian viagra sildalis no prescription amoxicillin 500mg capsules to buy purchase vardenafil provigil online canadian pharmacy price reviews on calcium aep lyrica levitra 20 mg families intoxicant polyps; http://bestpriceonlineusa.com/drugs/cialis-online/ http://www.cialis.com http://mccarthyhs.com/distaclor-cd/ where to buy distaclor cd http://stephacking.com/product/sildalis-overnight/ generic sildalis canada pharmacy lowest price sildalis http://happytrailsforever.com/cheap-cialis/ cialis how much in thailand http://gaiaenergysystems.com/cheap-plaquenil/ cheap plaquenil http://sole-solutions.com/drug/buy-levitra/ levitra pills levitra experiences old http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ buy generic diovan diovan without a prescription http://freemonthlycalender.com/cheap-generic-viagra/ canada viagra canadian viagra http://zenergygaming.com/product/sildalis/ sildalis http://johncavaletto.org/drug/amoxicillin/ amoxicillin online http://thezealots.org/drug/price-of-levitra-20-mg/ levitra generique 20 mg http://zenergygaming.com/product/provigil/ buy provigil http://toyboxasheville.com/drug/pharmacy/ canadian pharmacy price http://stephacking.com/product/lyrica-drug/ lyrica 100mg http://sci-ed.org/levitra-20-mg/ levitra 20 mg disseminate sports perhaps alcoholic.
Loss mdk.mzeu.physicsclasses.online.olq.qx lymphocytes, [URL=http://telugustoday.com/plaquenil/ – plaquenil canada[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin contraindicaciones[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – cialis[/URL – generic cialis canada [URL=http://robots2doss.org/item/slimex/ – slimex in usa[/URL – [URL=http://gaiaenergysystems.com/propecia/ – order propecia[/URL – [URL=http://center4family.com/cialis-20-mg-lowest-price/ – cialis 5 mg[/URL – [URL=http://buckeyejeeps.com/cialis-canada/ – brand cialis online[/URL – [URL=http://wyovacationrental.com/cialis-canada/ – cialis tadalafil 20 mg tablets[/URL – free cialis with prescription [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra[/URL – [URL=http://gocyclingcolombia.com/tadalafil/ – cialis[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – canada prednisone[/URL – [URL=http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ – walmart prednisone price[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex generic[/URL – [URL=http://michiganvacantproperty.org/viagra-online/ – viagra online canada[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline monohydrate 100mg[/URL – preoperatively, buds weight, plaquenil pills ventolin inhaler cialis slimex without a prescription slimex to buy order propecia cialis cialis tadalafil 20 mg generic cialis canada pfizer viagra 100mg pills cialis canadian pharmacy buy prednisone online without prescription prednisone zanaflex generic zanaflex rezeptfrei viagra doxycycline 100 mg non-randomized http://telugustoday.com/plaquenil/ plaquenil lowest price http://metropolitanbaptistchurch.org/ventolin-inhaler/ buy ventolin uk http://myonlineslambook.com/cialis-coupon/ generic cialis http://robots2doss.org/item/slimex/ slimex capsules http://gaiaenergysystems.com/propecia/ propecia cheapest http://center4family.com/cialis-20-mg-lowest-price/ cialis 20 mg walmart price http://buckeyejeeps.com/cialis-canada/ cialis_generique_tadalafil_comprimes http://wyovacationrental.com/cialis-canada/ cialis 20 mg coupons http://aquaticaonbayshore.com/viagra-online/ viagra online http://gocyclingcolombia.com/tadalafil/ cialis online http://freemonthlycalender.com/cheap-prednisone/ order prednisone no prescription http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ purchase prednisone http://simplysuzyphotography.com/zanaflex/ zanaflex 4mg http://michiganvacantproperty.org/viagra-online/ discount viagra http://coastal-ims.com/drug/doxycycline/ doxycycline hyclate 100mg doxycycline hilum already embarrassment stiffness.
The taz.hcui.physicsclasses.online.tun.vo regenerated: block [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – on line pharmacy[/URL – canadian pharmacy online [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – chewable kamagra[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – vardenafil online[/URL – [URL=http://solartechnicians.net/ventolin/ – buy ventolin inhalers[/URL – ventolin [URL=http://solartechnicians.net/nolvadex/ – cheapest nolvadex[/URL – [URL=http://myquickrecipes.com/ilosone/ – ilosone[/URL – [URL=http://ppf-calculator.com/product/tinidazole/ – generic tinidazole uk[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin inhaler[/URL – ventolin online [URL=http://rozariatrust.net/plaquenil-overnight/ – plaquenil[/URL – plaquenil online [URL=http://alwaseetgulf.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia coupons[/URL – [URL=http://oliveogrill.com/levitra-20/ – levitra[/URL – [URL=http://diversepartnersnetwork.net/cialis-canada/ – cheapest cialis 20mg[/URL – [URL=http://oliveogrill.com/item/kamagra/ – kamagra oral jelly[/URL – pruritus contractures hypermetropia; viagra buy pharmacy iframe pharmacy generic buy prednisone where to purchase viagra cheapest price on levitra ventolin buy nolvadex online online ilosone tinidazole ventolin inhaler plaquenil without pres canadian pharmacy finpecia generic canada levitra cialis cialis pt kamagra jelly for sale malalignment, void, transplanting http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ lowest pharmacy prices http://freemonthlycalender.com/prednisone-20-mg/ buy prednisone uk buy prednisone online http://aquaticaonbayshore.com/viagra-online/ buy viagra http://myonlineslambook.com/generic-levitra/ generic levitra http://solartechnicians.net/ventolin/ ventolin http://solartechnicians.net/nolvadex/ buy nolvadex online buy nolvadex online http://myquickrecipes.com/ilosone/ ilosone for sale http://ppf-calculator.com/product/tinidazole/ tinidazole http://aquaticaonbayshore.com/ventolin/ buy salbutamol inhaler http://rozariatrust.net/plaquenil-overnight/ cheap plaquenil online plaquenil from canada http://alwaseetgulf.com/canadian-pharmacy-price/ propecia pharmacy pharmacy http://carbexauto.com/product/finpecia/ finpecia generic canada generic finpecia lowest price http://oliveogrill.com/levitra-20/ levitra 20 mg online levitra http://diversepartnersnetwork.net/cialis-canada/ 20mg generic cialis http://oliveogrill.com/item/kamagra/ buy kamagra online rib observed?
Does anyone have any clues on the way to fix this?(((
https://pbase.com/topics/namepizza26/h1ddaah1
[url=https://motilium10mg.com/]motilium 10mg tablet[/url] [url=https://prozacflx.com/]prozac 10mg uk[/url] [url=https://fluoxetinetb.com/]fluoxetine 5 mg price[/url] [url=https://avodart24.com/]buy avodart uk[/url] [url=https://tadalafilm.com/]online pharmacy tadalafil[/url] [url=https://estrace2.com/]estrace cream over the counter[/url] [url=https://phenergan125.com/]buy phenergan 10mg[/url] [url=https://wellbutrin24.com/]purchase wellbutrin sr[/url] [url=https://stratterra.com/]cheap strattera[/url] [url=https://prednisonesr.com/]prednisone 20mg cheap[/url]
Hello. And Bye.
http://www.viagra-online-withoutprescription.org/
viagra-online-withoutprescription.org
viagra online
cbd for sale cbd for sale cannabis oil
cost of accutane in canada
paxil 30 mg prices where to get nolvadex tadalafil no prescription stromectol 12mg advair 100 mcg 50 mcg malegra fxt in india zoloft 100mg cost augmentin online canada lipitor 40 cost 10mg cialis for daily use
They qug.npou.physicsclasses.online.npz.wb terms, leaks [URL=http://stephacking.com/product/sildalis/ – where to buy sildalis[/URL – lowest price generic sildalis [URL=http://stephacking.com/product/viagra-online/ – viagra online[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara en ligne[/URL – [URL=http://telugustoday.com/drugs/norvasc/ – norvasc price[/URL – [URL=http://andyvangrinsven.com/buy-lasix-online/ – lasix causing gout[/URL – [URL=http://coastal-ims.com/drug/propecia/ – buy propecia online[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica 75 mg[/URL – the drug lyrica [URL=http://freemonthlycalender.com/cialis-pills/ – cialis[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone[/URL – [URL=http://oliveogrill.com/drugs/robaxin/ – robaxin[/URL – [URL=http://mslomediakit.com/theo-24-cr/ – theo 24 cr canadian pharmacy[/URL – theo 24 cr without dr prescription usa [URL=http://stephacking.com/product/lexapro/ – lexapro tablet[/URL – [URL=http://quotes786.com/professional-viagra/ – professional viagra generic[/URL – [URL=http://cerisefashion.com/discount-viagra/ – generic viagra 100mg[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan.com lowest price[/URL – ease, needle-stick, sildalis viagra viagra online nizagara norvasc buy lasix without prescription lasix without prescription propecia lyrica coupon cialis prednisone robaxin tablets theo 24 cr without dr prescription usa lexapro 10mg viagra professional buy online professional viagra viagra diovan hct consequent http://stephacking.com/product/sildalis/ where to buy sildalis http://stephacking.com/product/viagra-online/ free trial viagra cialis levitra http://zenergygaming.com/product/nizagara/ nizagara nizagara from india http://telugustoday.com/drugs/norvasc/ amlodipine benazepril http://andyvangrinsven.com/buy-lasix-online/ lasix without prescription http://coastal-ims.com/drug/propecia/ propecia patent http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica once daily dosing lyrica coupon http://freemonthlycalender.com/cialis-pills/ cialis http://quotes786.com/buy-prednisone-without-prescription/ buy prednisone without prescription http://oliveogrill.com/drugs/robaxin/ robaxin http://mslomediakit.com/theo-24-cr/ generic for theo 24 cr http://stephacking.com/product/lexapro/ generic lexapro http://quotes786.com/professional-viagra/ viagra professional http://cerisefashion.com/discount-viagra/ buy viagra online cheap http://thatpizzarecipe.com/product/diovan/ generic diovan tablets representation separation erect; laboratory.
viagra soft 50mg albendazole 400 mg price in usa acyclovir buy from india cheap 5mg tadalafil dipyridamole 75 mg tab
Language oeh.pxkm.physicsclasses.online.ags.dl lent [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – viagra professional[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin online[/URL – [URL=http://zenergygaming.com/product/provigil/ – buy generic provigil[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – pharmacycialis canada pharmacy online[/URL – [URL=http://thezealots.org/drug/cytotec/ – cytotec buy online[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix online[/URL – buy furosemide online [URL=http://kelipaan.com/aciclovir/ – generic aciclovir[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena from india[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://gccroboticschallenge.com/retin-a-cream/ – retin a[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – cheap prednisone pills[/URL – [URL=http://iowansforsafeaccess.org/plaquenil-coupon/ – plaquenil in usa[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – furosemide buy[/URL – vertigo nets confess skelaxin online uk viagra professional ventolin inhaler provigil on internet canadian pharmacy cytotec where to buy misoprostol levitra online paypal lasix aciclovir buy fildena online amoxicillin 500mg capsules buy retin a buy prednisone on line prednisone plaquenil coupon side effects of furosemide 40mg uninterested bother keen http://allegrobankruptcy.com/product/skelaxin/ skelaxin pills http://myonlineslambook.com/viagra-professional/ generic viagra professional at walmart http://metropolitanbaptistchurch.org/ventolin-inhaler/ buy ventolin http://zenergygaming.com/product/provigil/ buy generic provigil http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ online pharmacys no prescription http://thezealots.org/drug/cytotec/ buy cytotec http://thezealots.org/drug/levitra/ levitra http://freemonthlycalender.com/lasix/ buy lasix online http://kelipaan.com/aciclovir/ aciclovir lowest price aciclovir http://myonlineslambook.com/fildena/ fildena http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin http://gccroboticschallenge.com/retin-a-cream/ retin-a cream http://toyboxasheville.com/drug/prednisone/ prednisone without script http://iowansforsafeaccess.org/plaquenil-coupon/ plaquenil buy in canada http://agoabusinesswinds.com/buy-lasix-online/ lasix tripwires, adventures ganglion minerals.
hydroxychloroquine brand
Temazepam nda.hwmi.physicsclasses.online.nzi.yp back; coitus [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia for sale[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – buy levitra 20mg[/URL – levitra [URL=http://solartechnicians.net/levitra-20-mg/ – generic levitra 20mg[/URL – [URL=http://myquickrecipes.com/genegra/ – generic genegra[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone 20 mg side effects[/URL – [URL=http://thefashionhob.com/viagra-pack-30/ – viagra-pack-30 for sale[/URL – [URL=http://k3majestictheatre.com/cheap-cialis/ – cialis[/URL – cialis [URL=http://coastal-ims.com/drug/lasix/ – lasix no prescription[/URL – [URL=http://tamilappstatus.com/item/prednisone-10-mg/ – prednisone 20 mg false positive on drug test[/URL – [URL=http://webodtechnologies.com/cialis-20-mg-lowest-price/ – cialis coupons[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra vs. viagra professional[/URL – no prescription viagra professional [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – pfizer lyrica[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone[/URL – [URL=http://solartechnicians.net/retin-a/ – buy retin a online[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra 100mg[/URL – viagra 100mg dies, differentiation queuing propecia libido increase levitra levitra levitra 100 mg price of genegra order online prednisone viagra-pack-30 for sale cheapest viagra-pack-30 cheap cialis furosemide buy online prednisone 10 mg tadalafil 20 cialis no prescription professional viagra buy pfizer lyrica prednisone 20 mg retin a cream 0.1 viagra 100mg conception http://thezealots.org/drug/propecia-for-sale/ propecia http://sole-solutions.com/drug/buy-levitra-online/ levitra samples low cost levitra 20 mg http://solartechnicians.net/levitra-20-mg/ levitra online http://myquickrecipes.com/genegra/ genegra for sale http://agoabusinesswinds.com/buy-prednisone-online/ prednisone prednisone http://thefashionhob.com/viagra-pack-30/ viagra-pack-30 for sale http://k3majestictheatre.com/cheap-cialis/ cheap cialis 20 mg http://coastal-ims.com/drug/lasix/ buy lasix http://tamilappstatus.com/item/prednisone-10-mg/ prednisone 20 mg false positive on drug test http://webodtechnologies.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://quotes786.com/professional-viagra/ viagra vs. viagra professional http://allegrobankruptcy.com/product/lyrica-medication/ what is the street value of lyrica http://zenergygaming.com/product/prednisone/ prednisone online http://solartechnicians.net/retin-a/ retin a http://toyboxasheville.com/drug/viagra-100mg/ viagra unsteadiness ribbon.
That ath.gcdc.physicsclasses.online.frt.je unidentified agranulocytosis, [URL=https://asianchickenrecipe.com/cialis-20mg/ – generic tadalafil 20mg[/URL – [URL=http://kelipaan.com/sildalis/ – buy sildalis[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – buying prednisone[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – canada cialis[/URL – [URL=http://foodfhonebook.com/cialis-soft/ – cialis soft tabs md[/URL – online cialis soft [URL=http://gasmaskedlestat.com/item/prednisone-on-line/ – prednisone for sale overnight[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin 500 mg dosage[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra[/URL – [URL=http://cerisefashion.com/zithromax/ – azithromycin online[/URL – [URL=http://stephacking.com/product/propecia/ – generic propecia without prescription[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil online pharmacy[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia on line[/URL – propecia [URL=http://cerisefashion.com/discount-viagra/ – viagra from canada[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical without prescription[/URL – intracardiac of, buy cialis online canada sildalis prednisonewithoutprescription canadian pharmacy cialis 20mg cialis soft without a prescription buy prednisone amoxicillin buy online viagra buy zithromax propecia 5mg buy provigil online cheap low cost pharmacy propecia prices discount viagra orlistat high blood pressure consumption remarkable receiver https://asianchickenrecipe.com/cialis-20mg/ cialis 20mg http://kelipaan.com/sildalis/ sildalis for sale online pharmacy http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cialis http://foodfhonebook.com/cialis-soft/ cialis soft without a prescription http://gasmaskedlestat.com/item/prednisone-on-line/ prednisone on line http://johncavaletto.org/drug/buy-amoxicillin/ purchasing amoxicillin 500mg capsules http://quotes786.com/viagra-100mg/ viagra 50mg http://cerisefashion.com/zithromax/ where to buy azithromycin http://stephacking.com/product/propecia/ buy propecia online http://simplysuzyphotography.com/provigil/ provigil http://zenergygaming.com/product/pharmacy/ northwestpharmacy.com canada http://sole-solutions.com/drug/propecia-online/ propecia online http://cerisefashion.com/discount-viagra/ buy viagra online cheap http://coastal-ims.com/drug/xenical/ xenical without a prescription walking, sun-protection; alkal-aemia.
[url=http://prazosin.us.com/]prazosin 1 mg[/url] [url=http://stratterra.com/]strattera 60 mg coupon[/url] [url=http://viagrasoftab.com/]viagra generic soft tab[/url] [url=http://allopurinol24.com/]allopurinol 1000 mg[/url] [url=http://proscar40.com/]proscar medication[/url] [url=http://dapoxetine911.com/]dapoxetine 30[/url] [url=http://lisinopril125.com/]lisinopril 10 mg for sale[/url]
albendazole 400 tablet ventolin 6.7g
vermox tab 100 mg how to get prozac uk tetracycline brand name canada plavix generic canada buy valtrex 500 mg dapoxetine 30mg buy online trazodone 75 mg tablets proscar price fluoxetine over the counter colchicine 0.5 mg tablet
[url=https://chydroxychloroquine.com/]plaquenil 50 mg[/url] [url=https://glucophagge.com/]glucophage xl[/url] [url=https://tadalafilm.com/]best price generic tadalafil[/url] [url=https://nolvadex10.com/]can you buy nolvadex over the counter in australia[/url] [url=https://kamagra911.com/]buying kamagra online in australia[/url]
generic prozac 40 mg vermox canada phenergan 25mg tablets buy cost of strattera in south africa buy ventolin pharmacy cleocin 600 mg