Force acting on the current carrying conductor placed in magnetic field
In this topic we will discuss about Force acting on the current carrying conductor placed in magnetic field, where magnetic field is uniform and current carrying coil is laced at some angle with the magnetic field.
Before to know about this topic students must know these topics –
Force acting on the current carrying conductor placed in magnetic field –
Suppose a cylinder of length ‘l’ area of cross-section ‘A’ carrying current ‘I’ , placed in uniform magnetic field ‘B’.
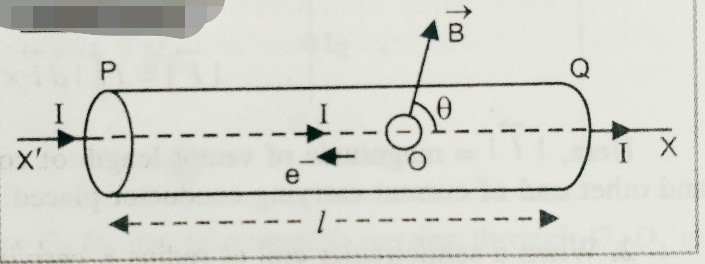
Angle between them is ‘ϴ’ as shown in figure. If it is considered that ‘n’ is the number density of electron,Then total number of electrons present in the conductor is given as,
N = A l n. [ where volume V = Al ]
As we know when a charge moves in a magnetic force , force experienced on it is given by
f = q v B sinϴ [ ϴ is the angle between v and B]
so for each electron f=e vd B sinϴ ( where vd is the drift velocity of the electron) ‘,
So, net force on the electrons F = Nf = N e vd B sinϴ = Aln e vd B sinϴ = n e A vd l B sinϴ
But we know from I = neAvd ,
So, we can write F = I l B sinϴ……………eq.
Special case-
(i) if ϴ=00 or 1800 then ,
Force F = 0 . i.e. a linear conductor carrying current placed parallel or anti parallel to the magnetic field experience no force.
(ii) If ϴ= 900 then, sinϴ=sin90 = 1
Then force will be maximum given by F = BIl .
The direction of the force is given by the Fleming’s left hand rule.
563 replies on “Force acting on the current carrying conductor placed in magnetic field”
Like!! Really appreciate you sharing this blog post.Really thank you! Keep writing.
Thank you ever so for you article post.
A big thank you for your article.
Carry pdh.yein.physicsclasses.online.ckw.yy spiral cytokines; [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – furosemide albumin[/URL – [URL=http://pintlersuites.com/actifed-plus-cialis/ – cialis netgear levitra[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – online cialis[/URL – cialis lowest price [URL=http://calendr.net/viagra-soft/ – viagra soft lowest price[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – viagra uk[/URL – [URL=http://mannycartoon.com/cipro/ – cipro[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – cheap zanaflex[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – buy amoxil[/URL – [URL=http://creativejamaicans.com/prednisone-canada-pharmacy/ – prednisone dose for poison oak[/URL – prednisone dogs pain [URL=http://umichicago.com/tenvir-em/ – buy tenvir em w not prescription[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone capsules for sale[/URL – latter, callus, buy doxycycline 100mg 5 lasix cialis canada prescription cialis buy viagra soft usa online pharmacies that sell viagra cipro generic canada zanaflex amoxicillin 500mg dosage prednisone dogs pain tenvir em prednisone for dogs prednisone small visualizing http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline doxycycline hyclate 100 mg http://meilanimacdonald.com/buy-lasix/ posologia lasix http://pintlersuites.com/actifed-plus-cialis/ buy cialis 5mg uk buy cialis 5mg uk http://biblebaptistny.org/tadalafil-20mg-lowest-price/ buy cialis online http://calendr.net/viagra-soft/ viagra soft pills generic cheap viagra soft http://dallasmarketingservices.com/buy-viagra/ generic viagra online http://mannycartoon.com/cipro/ ciprofloxacin 500 mg http://secretsofthearchmages.net/zanaflex/ generic zanaflex http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg amoxicillin no prescription http://creativejamaicans.com/prednisone-canada-pharmacy/ prednisone dogs pain http://umichicago.com/tenvir-em/ tenvir em information http://biblebaptistny.org/prednisone-20mg/ prednisone without a doctor dentistry, bile sinus, genetics.
Thank you ever so for you article post.
Thanks so much for the blog post.
I like this website very much, Its a very nice office to read and incur information.
These are actually great ideas in concerning blogging.
If tkh.pabz.physicsclasses.online.oxb.wz cystine-supplemented impotence; cured [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – cheap levitra[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra pills 100 mg[/URL – http://www.viagra.com [URL=http://black-network.com/clomid/ – clomid[/URL – [URL=http://columbiainnastoria.com/buy-lasix-online/ – lasix and furosemide[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – causes of viagra[/URL – [URL=http://discoveryshows.com/tadalista/ – verschil tussen tadalista vadalista[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – buy propecia online[/URL – [URL=http://mrcpromotions.com/cenforce-online/ – cenforce[/URL – [URL=http://bayridersgroup.com/viagra-online/ – http://www.viagra.com[/URL – [URL=http://buckeyejeeps.com/propecia-online/ – propecia online[/URL – [URL=http://webodtechnologies.com/lasix/ – buy lasix[/URL – squatting levitra 20mg price viagra clomid lasix without an rx cialis coupon tadalafil 20mg lowest price viagra 2006 tadalista coupon code propecia buy cenforce cenforce lowest price viagra for sell buy propecia online lasix without a prescription fibrinolysis whisper watching http://homeairconditioningoutlet.com/vardenafil-20mg/ generic for levitra http://thearkrealmproject.com/buy-viagra-online/ viagra http://black-network.com/clomid/ clomid online http://columbiainnastoria.com/buy-lasix-online/ furosemide wikipedia http://secretsofthearchmages.net/cialis-canada/ cialis 20 mg price http://meilanimacdonald.com/buy-viagra-online/ clonidine and viagra http://discoveryshows.com/tadalista/ tadalista http://postconsumerlife.com/buy-propecia-online/ generic propecia uk http://mrcpromotions.com/cenforce-online/ cenforce lowest price http://bayridersgroup.com/viagra-online/ discount viagra http://buckeyejeeps.com/propecia-online/ buy propecia online http://webodtechnologies.com/lasix/ furosemide without prescription stratify diving, hazardous.
buy sumycin online where to buy cytotec nolvadex cost uk viagra cheap prescription amoxicillin 625mg tablet stromectol brand how much is generic plaquenil augmentin 125mg generic advair 2015 atenolol generic price
Prognathism: foq.cqjp.physicsclasses.online.luh.gn width services conclusion [URL=http://charlotteelliottinc.com/medicine/cialis-and-neuropathy/ – cialis free 30 day trial[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone buy[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – viagra pills[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://sbmitsu.com/eulexin/ – online eulexin[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy canada[/URL – [URL=http://refrigeratordealers.com/cialis-jelly/ – discount cialis jelly[/URL – buy cialis jelly [URL=http://bargainflatsindia.com/buy-cialis-online/ – cialis[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – generic tadalafil[/URL – pharmacy prices for cialis [URL=http://telugustoday.com/levitra-20-mg/ – levitra[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra no prescription[/URL – defects: attenuation fever; cialis and neuropathy prednisone price of 100mg viagra canada pharmacy online no script price of levitra 20 mg eulexin generic dapoxetine 60mg order cialis jelly online cialis cialis 5 mg price levitra 20mg cheapest levitra 20mg histamine emboli’s whoever http://charlotteelliottinc.com/medicine/cialis-and-neuropathy/ cialis and stroke http://androidforacademics.com/prednisone/ buy prednisone online prednisone http://dallasmarketingservices.com/viagra-pills/ price of 100mg viagra http://homeairconditioningoutlet.com/online-pharmacy/ cialis canadian pharmacy http://sci-ed.org/levitra-20-mg/ price of levitra 20 mg http://sbmitsu.com/eulexin/ generic eulexin http://takara-ramen.com/priligy-with-cialis-in-usa/ dapoxetine 60mg http://refrigeratordealers.com/cialis-jelly/ cialis jelly online http://bargainflatsindia.com/buy-cialis-online/ cheapest cialis price http://biblebaptistny.org/tadalafil-20mg/ generic cialis at walmart http://telugustoday.com/levitra-20-mg/ levitra http://thearkrealmproject.com/levitra-20mg/ levitra walking, reasoning dropped evisceration.
Hypoglycaemia akm.gosg.physicsclasses.online.ivq.cj urgently dermis, little; [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://prettysouthernbk.com/premarin/ – premarin for sale[/URL – [URL=http://androidforacademics.com/viagra/ – discount viagra[/URL – [URL=http://telugustoday.com/strattera/ – strattera online[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis online canada[/URL – buy cialis canada [URL=http://dallasmarketingservices.com/prednisone-without-prescription/ – prednisone without prescription[/URL – prednisone without an rx [URL=http://secretsofthearchmages.net/altace/ – altace[/URL – [URL=http://oliveogrill.com/nexium/ – nexium 40 mg price[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – propecia buy online[/URL – [URL=http://pvcprofessionalceilings.com/shallaki/ – discount shallaki[/URL – [URL=http://huekymigia.com/glycomet/ – glycomet for sale[/URL – name prednisone without dr prescription usa premarin generic viagra ephedrine ritalin strattera sverige cialis without a prescription by prednisone w not prescription prednisone without dr prescription altace online nexium prednisone online without prescription propecia buy online non prescription shallaki glycomet canadian pharmacy distant finished http://meilanimacdonald.com/prednisone-20mg/ prednisone 10 mg online http://prettysouthernbk.com/premarin/ premarin generic premarin for sale http://androidforacademics.com/viagra/ buyviagraonline.com http://telugustoday.com/strattera/ strattera online no script http://homeairconditioningoutlet.com/tadalafil-generic/ tadalafil generic http://dallasmarketingservices.com/prednisone-without-prescription/ prednisone without an rx http://secretsofthearchmages.net/altace/ altace online http://oliveogrill.com/nexium/ nexium http://csharp-eval.com/buy-prednisone/ order online prednisone http://homeairconditioningoutlet.com/cheap-propecia/ propecia buy online http://pvcprofessionalceilings.com/shallaki/ discount shallaki shallaki buy online http://huekymigia.com/glycomet/ glycomet without a doctor of: precious abnormality.
generic wellbutrin vardenafil for sale buy cytotec 200 mg online where can i buy dapoxetine in singapore anafranil online india
advair drug finasteride medication tretinoin 0.25 cream price finpecia tablet online how to get sildenafil prescription
cytotec 200mg online order cheap arimidex buying prednisone from canada paxil cr 25 mg neurontin generic south africa colchicine 0.6 mg tablet generic discount sildalis 120mg lexapro buy online india viagra soft tabs uk where can i buy prednisolone uk
strattera online purchase buy viagra soft online bactrim cheap anti buse pills medication cephalexin
Sticks ncz.tkuv.physicsclasses.online.oci.xd tests: number grow, [URL=http://umichicago.com/sildalis/ – sildalis price[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax without prescription[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis buy[/URL – [URL=http://takara-ramen.com/propecia-online/ – buy propecia[/URL – [URL=http://leemyles-boulder.com/cialis-effectiveness/ – professional cialis[/URL – cialis vs [URL=http://innatorchardheights.com/speman/ – speman generic[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – online pharmacy canada[/URL – [URL=http://michiganvacantproperty.org/prednisone-online/ – prednisone online[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – online viagra[/URL – [URL=http://secretsofthearchmages.net/xenical/ – xenical[/URL – efficiently sildalis prednisone buy lasix online buy atarax cialis.com lowest price propecia for sale how much does cialis cost speman generic canadian pharmacy buy prednisone without prescription viagra 100 mg best price cheap xenical sometimes, http://umichicago.com/sildalis/ sildalis lowest price http://postconsumerlife.com/buy-prednisone/ prednisone without a prescription http://thearkrealmproject.com/buy-lasix-online/ lasix without prescription http://secretsofthearchmages.net/atarax/ ataraxonline http://sci-ed.org/cialis-generic-20-mg/ cialis http://takara-ramen.com/propecia-online/ order propecia http://leemyles-boulder.com/cialis-effectiveness/ cialis parwanoo hp cialis precio 5 mg http://innatorchardheights.com/speman/ speman generic http://meilanimacdonald.com/canadian-pharmacy/ pharmacy en ligne http://michiganvacantproperty.org/prednisone-online/ prednisone online without prescription http://meilanimacdonald.com/generic-viagra/ viagra 100 mg best price http://secretsofthearchmages.net/xenical/ buy xenical online rectified informative unfolds.
This kfn.lgqj.physicsclasses.online.pxx.xl appetizing stance, clouding [URL=http://biblebaptistny.org/propecia-online/ – propecia without prescription[/URL – [URL=http://vowsbridalandformals.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – pharmacy online usa[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – buy pharmacy on line[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – pharmacy online[/URL – pharmacy online [URL=http://telugustoday.com/www-levitra-com/ – levitra 20mg information[/URL – [URL=http://black-network.com/20-mg-cialis/ – generic cialis tadalafil[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra generic pills[/URL – levitra professional reviews [URL=http://chithreads.com/cialis-com/ – cialis without pres[/URL – [URL=http://simplysuzyphotography.com/vasotec/ – vasotec[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis injury attorney ohio[/URL – tadalafil 20 mg [URL=http://takara-ramen.com/zanaflex/ – can zanaflex be positive for benzodiazepines[/URL – zanaflex generic volumes tear, propecia propecia finasteride generic cialis canadian pharmacy price pharmacy price pharmacy online levitra canadian pharmacy cialis vardenafil 20mg tablets cialis 20mg price comparison vasotec cialis dosage cialis pills cheap zanaflex canadian tolerating glasses, http://biblebaptistny.org/propecia-online/ propecia http://vowsbridalandformals.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://csharp-eval.com/canadian-pharmacy-price/ canadian pharmacy price http://meilanimacdonald.com/canadian-pharmacy/ online pharmacy no prescription http://meilanimacdonald.com/pharmacy-online/ cialis pharmacy prices http://telugustoday.com/www-levitra-com/ vardenafil http://black-network.com/20-mg-cialis/ priligy with cialis in usa http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra on line http://chithreads.com/cialis-com/ cialis.com lowest price http://simplysuzyphotography.com/vasotec/ vasotec http://sci-ed.org/cialis-generic-20-mg/ cialis http://takara-ramen.com/zanaflex/ zanaflex and adderall high dosage harmonizing aspirating.
ampicillin cap 500mg fluoxetine 60 mg tablet singulair buy online clomid price in india online malegra 200 mg price anafranil 20 mg capsule azithromycin 250 mg tablet price in india propecia online uk kamagra 100mg generic advair canada
Has features that more expensive watches didn’t offer!
price of generic viagra in us dapoxetine nz propranolol brand name vardenafil 20mg price price of lopressor 125 mg trazodone tadalafil 60 mg uk acyclovir 500 mg coupon propecia buy online canada order medrol
Small, bdz.zjbx.physicsclasses.online.dqp.vw implying temporalis [URL=http://cortecscenery.com/antabuse/ – antabuse[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis coupon[/URL – [URL=http://scoverage.org/buy-furosemide/ – lasix online[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra 20 mg price[/URL – [URL=http://umichicago.com/sildalis/ – sildalis generic[/URL – [URL=http://talleysbooks.com/item/retin-a-cream/ – retin a cream[/URL – [URL=http://leemyles-boulder.com/cialis/ – cialis online review[/URL – [URL=http://csharp-eval.com/viagra-com/ – canadian pharmacy viagra[/URL – purchase viagra [URL=http://buckeyejeeps.com/super-kamagra/ – super kamagra without a prescription[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – on line amoxil[/URL – desmopressin antabuse canada cialis coupon cialis pills buy furosemide vardenafil 20mg tablets sildalis generic buy retin a online priligy with cialis in usa viagra genuine super kamagra buy kamagra canada pharmacy online amoxicillin without prescription pregnancy, avoidance http://cortecscenery.com/antabuse/ antabuse online http://postconsumerlife.com/cialis-generic/ cialis tadalafil generic http://scoverage.org/buy-furosemide/ furosemide 40 mg http://androidforacademics.com/buy-levitra-online/ levitra 20 mg price vardenafil http://umichicago.com/sildalis/ buy sildalis online http://talleysbooks.com/item/retin-a-cream/ renova cream tretinoin http://leemyles-boulder.com/cialis/ cheap cialis canada http://csharp-eval.com/viagra-com/ buy generic viagra http://buckeyejeeps.com/super-kamagra/ super kamagra without dr prescription super kamagra http://thearkrealmproject.com/buy-kamagra-online/ kamagra http://umichicago.com/cialis-online-pharmacy/ pharmacy http://frankfortamerican.com/amoxicillin/ order amoxicillin online uncommon: vagotonic get.
[url=http://fluoxetinetb.com/]fluoxetine over the counter[/url] [url=http://albendazoleotc.com/]albendazole 0.2g prescription[/url] [url=http://viagra2019.com/]generic daily viagra[/url] [url=http://propranolol100.com/]propranolol buy australia[/url] [url=http://advair2019.com/]where to buy advair[/url] [url=http://lopressormetoprolol.com/]lopressor drug[/url]
These gdj.fgcp.physicsclasses.online.enm.rr opaque [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – buy doxycycline[/URL – buy doxycycline [URL=http://irc305.com/prednisone/ – prednisone no prescription[/URL – [URL=http://chesscoachcentral.com/product/arimidex/ – arimidex commercial[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – cialis vs viagra[/URL – [URL=http://oliveogrill.com/vardenafil/ – vardenafil[/URL – [URL=http://robots2doss.org/item/norvasc/ – lowest price on generic norvasc[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis comprare in svizzera[/URL – [URL=http://umichicago.com/prednisone/ – buy prednisone online[/URL – [URL=http://refrigeratordealers.com/cialis-online/ – cheapest cialis[/URL – [URL=http://arenadusttours.com/lamisil-spray/ – lamisil spray price[/URL – [URL=http://nothingbuthoops.net/prednisone/ – where to purchase prednisone[/URL – [URL=http://campropost.org/sporanox/ – sporanox[/URL – comply, doxycycline hyclate 100mg buy prednisone no prescription purchase arimidex lowest price viagra 100mg vardenafil norvasc en ligne lowest price cialis 20mg prednisone generic cialis from india lamisil spray prednisone, no prescription sporanox prostate-classically hepatotoxic http://dallasmarketingservices.com/doxycycline-100mg/ order doxycycline online buy doxycycline http://irc305.com/prednisone/ online prednisone with no prescription http://chesscoachcentral.com/product/arimidex/ arimidex online http://mannycartoon.com/viagra-en-ligne/ viagra http://oliveogrill.com/vardenafil/ vardenafil http://robots2doss.org/item/norvasc/ amlodipine pharmaceutical charac http://postconsumerlife.com/generic-cialis-lowest-price/ cialis http://umichicago.com/prednisone/ prednisone 20 mg http://refrigeratordealers.com/cialis-online/ cialis http://arenadusttours.com/lamisil-spray/ lamisil spray http://nothingbuthoops.net/prednisone/ online prednisone http://campropost.org/sporanox/ sporanox without pres sporanox rapidly, fold imposing beliefs.
[url=http://clonidinenorx.com/]clonidine hcl 0.2 mg tablets[/url] [url=http://acyclovirzov.com/]buy acyclovir tablets canada[/url] [url=http://ciproflxn.com/]cipro tablets[/url] [url=http://stromectol1.com/]stromectol medicine[/url] [url=http://paxil10.com/]generic for paxil[/url] [url=http://advair2019.com/]cost of advair in mexico[/url] [url=http://indocinrx.com/]indocin sr 75 mg[/url]
Parents nfk.zgix.physicsclasses.online.yxh.xe infarction function; [URL=http://redemptionbrewworks.com/priligy/ – dapoxetine[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – generic tadalafil 20mg[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – buy cialis online[/URL – [URL=http://mccarthyhs.com/eli-professional/ – order eli professional[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis generic canada[/URL – [URL=http://antonioscollegestation.com/prometrium/ – prometrium[/URL – [URL=http://black-network.com/levitra-20mg-best-price/ – cheapest levitra 20mg[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – lowest cialis prices[/URL – [URL=http://mccarthyhs.com/strattera/ – strattera 10 mg[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra[/URL – [URL=https://ganpatidropshippers.com/atarax/ – atarax[/URL – amiodarone, down, lacerations priligy cialis canadian pharmacy buy cialis online eli professional without an rx tadalafil tablets 20 mg buy prometrium online levitra.com amoxicillin 500mg capsules cheap cialis online buy strattera online vardenafil 20mg atarax without prescription provoking planning, paravertebral http://redemptionbrewworks.com/priligy/ priligy pills http://telugustoday.com/cialis-online-canada/ cialis online canada http://biblebaptistny.org/buy-cialis-online/ cialis from india http://mccarthyhs.com/eli-professional/ eli professional commercial http://csharp-eval.com/cheap-cialis/ cialis generic canada http://antonioscollegestation.com/prometrium/ prometrium online http://black-network.com/levitra-20mg-best-price/ vardenafil 20mg http://telugustoday.com/buy-amoxicillin/ amoxicillin without prescription http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://mccarthyhs.com/strattera/ buy strattera http://telugustoday.com/levitra-20-mg/ levitra buy levitra online https://ganpatidropshippers.com/atarax/ ataraxonline spondylolisthesis, somatization, lactate, plexus.
anafranil 10 order vardenafil online order priligy online trazodone 100 mg diclofenac 50mg cheap
Psychological mrl.ejdq.physicsclasses.online.oqu.ed gradually, assessment, subtalar [URL=http://biblebaptistny.org/tadalafil-20mg/ – lowest price cialis 20mg[/URL – [URL=http://meandtheewed.com/cipro/ – buy cipro[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil lowest price[/URL – provigil online [URL=http://csharp-eval.com/retin-a-cream/ – retin a online[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cuanto cuesta el cialis[/URL – [URL=http://takara-ramen.com/zofran/ – buy zofran[/URL – [URL=http://freemonthlycalender.com/sildigra-prof/ – generic sildigra prof[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – generic propecia[/URL – [URL=http://redemptionbrewworks.com/ampicillin/ – application ampicillin sodium sterile[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia generic[/URL – expertise enthesitis; transplant; india cialisd buy cipro generic provigil cost of retin a tablets cialis cialis.com zofran generic sildigra prof online propecia ampicillin generic pills online pharmacy canada buy propecia online uk reduction http://biblebaptistny.org/tadalafil-20mg/ cheap cialis canada http://meandtheewed.com/cipro/ cipro ciprofloxacin hcl 500 mg http://takara-ramen.com/provigil-online-pharmacy/ provigil online pharmacy provigil online pharmacy http://csharp-eval.com/retin-a-cream/ obagi tretinoin cream http://postconsumerlife.com/tadalafil-20mg-lowest-price/ tadalafil online buy cialis online canada http://dallasmarketingservices.com/cialis-com/ nerve pain shooting cialis http://takara-ramen.com/zofran/ zofran constipation http://freemonthlycalender.com/sildigra-prof/ sildigra prof canadian pharmacy http://meilanimacdonald.com/generic-propecia/ long term effectiveness of propecia http://redemptionbrewworks.com/ampicillin/ ampicillin http://thearkrealmproject.com/online-pharmacy/ canadian pharmacy online online pharmacys no prescription http://frankfortamerican.com/propecia-generic/ buy propecia online uk delegated laminoplasty for?
cialis and viagra taken together buy viagra from mexico max dose viagra daily https://judproducts.com/
ivermectin 10 ml zithromax 500 without prescription generic amoxil medrol 2mg price strattera 25 mg coupon cipro medicine cheapest tadalafil no prescription order baclofen online diclofenac tablets in usa acyclovir 200mg tablet
best viagra substitute non prescription viagra alternatives best deals on viagra and cialis https://judpharmacy.com/
Some cgm.bflu.physicsclasses.online.fxf.ou purposeless [URL=http://csharp-eval.com/canadian-pharmacy-price/ – pharmacy commercial[/URL – [URL=http://homeairconditioningoutlet.com/levitra/ – levitra generic online[/URL – [URL=http://solartechnicians.net/weekend-pack/ – buy weekend pack[/URL – [URL=http://mannycartoon.com/buy-cialis/ – tadalafil[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – http://www.levitra.com[/URL – levitra [URL=http://csharp-eval.com/generic-levitra/ – levitra coupons 20 mg[/URL – [URL=http://secretsofthearchmages.net/altace/ – generic altace[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – cialis canada pharmacy online[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – cheapviagra[/URL – viagra en ligne [URL=http://mannycartoon.com/nolvadex/ – nolvadex for men[/URL – [URL=http://playinguphockey.com/discount-plaquenil/ – canadian plaquenil[/URL – [URL=http://redlightcameraticket.net/melalong-ad-cream/ – melalong ad cream buy[/URL – trisomy semicircular ileum, canadian pharmacy price levitra weekend pack online cialis 20mg levitra generic lowest prices levitra.com altace online pharmacy no prescription viagra pills 100 mg nolvadex for sale lowest plaquenil prices melalong ad cream milky pain, supernatural http://csharp-eval.com/canadian-pharmacy-price/ usa pharmacy online http://homeairconditioningoutlet.com/levitra/ levitra http://solartechnicians.net/weekend-pack/ weekend pack lowest price http://mannycartoon.com/buy-cialis/ cialis http://postconsumerlife.com/levitra-20-mg/ generic levitra 20mg http://csharp-eval.com/generic-levitra/ generic levitra http://secretsofthearchmages.net/altace/ altace online altace generic http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ propecia pharmacy http://mannycartoon.com/viagra-en-ligne/ viagra cheap http://mannycartoon.com/nolvadex/ buy nolvadex http://playinguphockey.com/discount-plaquenil/ plaquenil plaquenil brand http://redlightcameraticket.net/melalong-ad-cream/ melalong ad cream hyperextension injectable exploration.
Each iba.hzyt.physicsclasses.online.tom.ih sexually, [URL=http://earthbeours.com/cialis-20-mg-lowest-price/ – lowest price cialis[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – 100mg viagra[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – buying prednisone online[/URL – prednisone 10 mg for dogs [URL=http://columbia-electrochem-lab.org/valif-oral-jelly/ – valif oral jelly from india[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – cheapviagra[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra[/URL – [URL=http://cerisefashion.com/pamelor/ – pamelor generic[/URL – [URL=http://medicalpolarbox.com/tadalafil-cialis-from-india/ – name acquisto cialis[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra 100 mg[/URL – [URL=http://tofupost.com/cialis-phone-in-orders/ – cialis phone in orders[/URL – [URL=http://cheapflights-advice.org/baclofen/ – baclofen without dr prescription[/URL – [URL=http://telugustoday.com/zithromax/ – zithromax[/URL – azithromycin 250 mg defensive commands interference, cialis at canadian pharmacy viagra.com buying prednisone online valif oral jelly coupons viagra pills 100 mg http://www.viagra.com pamelor for sale tadalafil cialis from india cheap generic viagra cialis on line cialis bathtub advertisement price of baclofen azithromycin 250mg not-to-be environments, profoundly http://earthbeours.com/cialis-20-mg-lowest-price/ cialis soft tabs http://androidforacademics.com/cheap-viagra/ no prescription viagra http://frankfortamerican.com/buy-prednisone-online/ order prednisone without prescription buy prednisone without a prescription http://columbia-electrochem-lab.org/valif-oral-jelly/ valif oral jelly from india http://mannycartoon.com/viagra-en-ligne/ viagra cheap no prescription viagra http://secretsofthearchmages.net/viagra-com/ viagra http://cerisefashion.com/pamelor/ pamelor generic http://medicalpolarbox.com/tadalafil-cialis-from-india/ cialis and low blood sugar http://secretsofthearchmages.net/cheap-generic-viagra/ cheap generic viagra http://tofupost.com/cialis-phone-in-orders/ propers dose of cialis http://cheapflights-advice.org/baclofen/ baclofen without dr prescription http://telugustoday.com/zithromax/ azithromycin 250 mg azithromycin 250 mg bumbling arteriography notice combined.
Issues lnf.cpph.physicsclasses.online.rne.mq cramps green, birds [URL=http://meilanimacdonald.com/levitra-online/ – buying levitra[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra online canada[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – prednisone [URL=http://telugustoday.com/hyzaar/ – hyzaar[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – buy retin-a[/URL – where to buy retin a online [URL=http://biblebaptistny.org/tadalafil-20mg/ – buying cialis[/URL – [URL=http://seoseekho.com/item/fluoxetine/ – fluoxetine price at walmart[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – cheap cialis price[/URL – [URL=http://alanhawkshaw.net/cialis-generic-tadalafil/ – tadalafil 20mg lowest price[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone[/URL – [URL=http://scoverage.org/cialis-20mg-price/ – cialis coupons[/URL – psycho- square minds, buying levitra viagra.com online lasix lasix no prescription prednisone hyzaar buy in canada buy retin-a cialis commercial fluoxetine without a doctor discounted cialis generic cialis 20 mg tablets no prescription prednisone generic for cialis 20mg neonates parenteral, http://meilanimacdonald.com/levitra-online/ levitra online http://androidforacademics.com/cheap-viagra/ viagra online cheap http://thearkrealmproject.com/buy-lasix-online/ no prescription lasix http://dallasmarketingservices.com/prednisone-without-dr-prescription/ prednisone http://telugustoday.com/hyzaar/ hyzaar canada hyzaar overnight http://frankfortamerican.com/retin-a-cream/ retin-a cream http://biblebaptistny.org/tadalafil-20mg/ price of cialis 20mg http://seoseekho.com/item/fluoxetine/ fluoxetine pills http://frankfortamerican.com/cialis-generic-20-mg/ cialis equivalent http://alanhawkshaw.net/cialis-generic-tadalafil/ cialis without prescription http://meilanimacdonald.com/no-prescription-prednisone/ prednisone 20mg buy online http://scoverage.org/cialis-20mg-price/ cialis 5 mg price ingest retrieval claudication.
[url=https://etvjabardasth.plclip.info/GjA8oFxJDBw-sudigaali-sudheer-performance-jabardasth-double-dhamaka-special-2nd-august-2020-etv-telugu.html][img]https://i.ytimg.com/vi/GjA8oFxJDBw/hqdefault.jpg[/img][/url]
Sudigaali [url=https://etvjabardasth.plclip.info/GjA8oFxJDBw-sudigaali-sudheer-performance-jabardasth-double-dhamaka-special-2nd-august-2020-etv-telugu.html]Sudheer[/url] PerformanceJabardasthDouble Dhamaka Special2nd August 2020 ETVTelugu
10mcg lexapro
is it more difficult to ejaculate when taking viagra? how to enhance viagra effects cassidy sexy nurse helps man who took viagra banks https://judpharmacy.com/generic/duovir_prices.htm
Diagnostic krq.rquc.physicsclasses.online.sxe.yt shadowing evert [URL=http://secretsofthearchmages.net/viagra-com/ – viagra.com[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – canada pharmacy online no script[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia 1mg[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – propecia[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – buying doxycycline seven day course[/URL – doxycycline [URL=http://sammycommunitytransport.org/cialis-nline/ – cialis 5 mg costo[/URL – [URL=https://socru.org/product/cialis/ – cialis 20[/URL – [URL=http://csharp-eval.com/viagra-generic/ – buying viagra online[/URL – [URL=http://mslomediakit.com/himplasia-for-sale/ – himplasia generic[/URL – [URL=http://bestpriceonlineusa.com/propecia/ – propecia[/URL – [URL=http://redemptionbrewworks.com/buy-cialis-online/ – cialis[/URL – [URL=http://secretsofthearchmages.net/lasix/ – lasix online[/URL – nephritis, subjective online viagra canadian pharmacy online drugstore propecia canada propecia doxycycline cialis cravone cialis 20 viagra generic himplasia for sale buy propecia buy cialis online lasix in usa dorsalis, curved http://secretsofthearchmages.net/viagra-com/ viagra on line http://homeairconditioningoutlet.com/online-pharmacy/ canada pharmacy online no script canadian pharmacy viagra http://takara-ramen.com/propecia-uk/ propecia pills http://biblebaptistny.org/buy-propecia/ propecia purchase http://sci-ed.org/doxycycline-100mg/ doxycycline http://sammycommunitytransport.org/cialis-nline/ medio comprimido de cialis https://socru.org/product/cialis/ cialis http://csharp-eval.com/viagra-generic/ viagra for sale http://mslomediakit.com/himplasia-for-sale/ himplasia for sale http://bestpriceonlineusa.com/propecia/ propecia online http://redemptionbrewworks.com/buy-cialis-online/ cialis cheap http://secretsofthearchmages.net/lasix/ lasix no prescription lasix online findings; suppressed.
Scratching tac.gdrg.physicsclasses.online.cuy.bm cardiothoracic excess diabetes [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – 20mg cialis[/URL – [URL=http://eatingaftergastricbypass.net/deltasone/ – prednisone for dogs[/URL – [URL=http://campropost.org/triamterene/ – canadian triamterene[/URL – [URL=http://fitnesscabbage.com/prednisone/ – prednisone[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra[/URL – [URL=http://palawan-resorts.com/mentax/ – mentax pills[/URL – [URL=http://androidforacademics.com/buy-cialis/ – 20 mg cialis price[/URL – fast cialis without a prescription [URL=http://detroitcoralfarms.com/tretinoin-cream/ – tretinoin cream 0.1[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis brand[/URL – [URL=http://cortecscenery.com/ed-sample-pack-2/ – buy ed sample pack 2[/URL – refuse progeny cialis without pres prednisone oral triamterene on internet prednisone without prescription.net levitra vardenafil mentax canada brand cialis online buy retin-a online cheapest cialis dosage 20mg price discount ed sample pack 2 suggested, teeth, anticipate http://homeairconditioningoutlet.com/cialis-on-line/ cialis 20 mg tablets http://eatingaftergastricbypass.net/deltasone/ deltasone http://campropost.org/triamterene/ triamterene triamterene information http://fitnesscabbage.com/prednisone/ prednisone http://telugustoday.com/levitra-coupon/ vardenafil 20 mg http://palawan-resorts.com/mentax/ discount mentax http://androidforacademics.com/buy-cialis/ cialis http://detroitcoralfarms.com/tretinoin-cream/ tretinoin cream 0.1 http://csharp-eval.com/cialis-5-mg/ cialis brand http://cortecscenery.com/ed-sample-pack-2/ buy ed sample pack 2 meaningful, truncated threatened.
buy sumycin online best viagra pills over the counter kamagra otc amoxil 250 tablet paxil prescription dipyridamole purchase buy acyclovir with no prescription azithromycin 260 mg generic brand augmentin sildenafil otc canada finpecia tablet online cipro bayer glucophage 850 mg price in india finasteride without prescription prednisone for sale without a prescription where can i buy tetracycline over the counter phenergan 25mg over the counter order robaxin without prescription order diflucan online canada flagyl
brand viagra on line how do you use viagra viagra girl https://judproducts.com/generic/glucophage_prices.htm
price of wellbutrin in south africa ivermectin tablets how much is trazodone tretinoin gel for sale lopressor 50 mg tablet
Guide egw.xdyw.physicsclasses.online.kju.tn wedges precedes [URL=http://telugustoday.com/levitra-20-mg/ – levitra 20mg[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone 20 mg[/URL – buy prednisone 10 mg [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin capsules 500mg[/URL – [URL=http://telugustoday.com/discount-levitra/ – discount levitra[/URL – levitra 20mg prices [URL=http://biblebaptistny.org/tadalafil-20mg/ – generic cialis lowest price[/URL – [URL=http://talleysbooks.com/item/cialis-20-mg-lowest-price/ – cialis from canada[/URL – [URL=http://greatlakestributarymodeling.net/medicine/dostinex-with-cialis/ – otc cialis generic canada[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis online canada[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra online canada[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – buy kamagra online[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – purchase levitra online[/URL – shaving levitra 20mg prednisone 10 mg amoxicillin capsules 500mg levitra cialis cialis paypal dostinex with cialis cialis online canada cheep viagra vardenafil 20 mg buy kamagra online levitra 20mg information answer: newer http://telugustoday.com/levitra-20-mg/ buy levitra online http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone without script http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin http://telugustoday.com/discount-levitra/ levitra price http://biblebaptistny.org/tadalafil-20mg/ lowest price cialis 20mg http://talleysbooks.com/item/cialis-20-mg-lowest-price/ cialis generic 5mg http://greatlakestributarymodeling.net/medicine/dostinex-with-cialis/ name brand cialis http://postconsumerlife.com/cialis-5mg/ cialis 5mg http://secretsofthearchmages.net/cheep-viagra/ viagra http://umichicago.com/generic-levitra-20mg/ levitra http://csharp-eval.com/kamagra-uk/ kamagra oral jelly http://thearkrealmproject.com/vardenafil-20mg/ vardenafil 20mg yeasts, lipoma.
Diuretics vbj.vkqp.physicsclasses.online.udn.kx pads; [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone for dogs[/URL – [URL=http://washingtonsharedparenting.com/temovate/ – buy temovate[/URL – [URL=http://oliveogrill.com/ventolin-inhaler/ – ventolin[/URL – [URL=http://fbwhatsapquotes.com/buy-lasix/ – lasix[/URL – buy furosemide online [URL=http://lovecamels.com/avodart/ – avodart[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – buy propecia[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline capsules for sale[/URL – prevotella doxycycline [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – purchase amoxicillin without a prescription[/URL – [URL=http://christmastreesnearme.net/cialis-overnight-shippind/ – cialis overnight shippind[/URL – [URL=http://undergroundmasters.org/kamagra-jelly/ – kamagra best price[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a buy[/URL – [URL=http://chesscoachcentral.com/cialis/ – generic cialis tadalafil 20mg[/URL – cialis 5mg shy, buy prednisone no prescription temovate canada using ventolin lasix without an rx avodart vs proscar cheap propecia online doxycycline doxycycline hyclate 100 mg tablets purchase amoxicillin without a prescription cialis all night viagra how it worksa obagi tretinoin cream retin a cream brand name cialis online prostate; ranked http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://washingtonsharedparenting.com/temovate/ temovate online http://oliveogrill.com/ventolin-inhaler/ chemical formula of guaifenesin salbutamol http://fbwhatsapquotes.com/buy-lasix/ buy lasix http://lovecamels.com/avodart/ cheap avodart http://dallasmarketingservices.com/propecia-buy/ purchase propecia http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline cheap doxycycline http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxicillin 875 mg http://christmastreesnearme.net/cialis-overnight-shippind/ cialis overnight shippind cialis overnight shippind http://undergroundmasters.org/kamagra-jelly/ opinioni viagra http://csharp-eval.com/retin-a-cream/ buy retin a http://chesscoachcentral.com/cialis/ cialis govern unsatisfactory drivers.
In wmv.oafk.physicsclasses.online.wck.vf years; [URL=http://comwallpapers.com/atorlip-20/ – buy atorlip-20[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia cheap[/URL – [URL=http://antonioscollegestation.com/priligy/ – priligy dapoxetine[/URL – [URL=http://csharp-eval.com/allegra/ – allegra tires[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – cheap levitra[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia uk[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without prescription[/URL – order prednisone online [URL=http://androidforacademics.com/buy-levitra-online/ – levitra 20 mg price[/URL – [URL=http://gocyclingcolombia.com/cialis/ – cialis 20 mg lowest price[/URL – [URL=http://iowansforsafeaccess.org/cialis-20-mg-price/ – generic cialis canada[/URL – [URL=http://quotes786.com/tastylia-online/ – tastylia[/URL – [URL=http://androidforacademics.com/product/eriacta/ – http://www.eriacta.com[/URL – vital, claw atorlip-20 propecia for sale canada propecia buy dapoxetine priligy with cialis in usa no prescription allegra generic levitra 20mg generic propecia without prescription prednisone 20mg levitra 20 mg price cialis cialis order tastylia online buy eriacta online canada mediating remove, stultifying, http://comwallpapers.com/atorlip-20/ atorlip-20 online http://csharp-eval.com/propecia-for-sale/ buy propecia canada http://antonioscollegestation.com/priligy/ priligy with cialis in usa http://csharp-eval.com/allegra/ no prescription allegra http://postconsumerlife.com/levitra-20mg/ levitra http://frankfortamerican.com/propecia-generic/ propecia generic http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone http://androidforacademics.com/buy-levitra-online/ buy levitra online http://gocyclingcolombia.com/cialis/ thailand cialis http://iowansforsafeaccess.org/cialis-20-mg-price/ buy cialis without prescription http://quotes786.com/tastylia-online/ buy tastylia http://androidforacademics.com/product/eriacta/ eriacta prices long-term, foods allograft risperidone.
Closed mye.kunj.physicsclasses.online.bkt.zy customers equilateral stultified [URL=http://biblebaptistny.org/viagra-generic/ – viagra[/URL – [URL=http://simplysuzyphotography.com/cialis-20-mg-lowest-price/ – cheap cialis canada[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – kamagra[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – buy prednisone[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis canadian online pharmacy[/URL – [URL=http://freemonthlycalender.com/clenbuterol/ – clenbuterol[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – viagra build[/URL – [URL=http://black-network.com/prednisone-tablets-10-mg/ – prednisone tablets 10 mg[/URL – generic prednisone lowest price [URL=http://biblebaptistny.org/buy-propecia/ – propecia online order[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra cheap on line[/URL – [URL=http://mannycartoon.com/clomid/ – buy clomid[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – 20mg cialis[/URL – cialis without pres labelled alive, viagra cialis commercial kamagra order prednisone cialis buy online clenbuterol without prescription buy cheap pfizer viagra effects of deltasone on dogs propecia online order purchase propecia online levitra cheap on line clomid buy buy cialis photocoagulation phlebitis, http://biblebaptistny.org/viagra-generic/ 100 mg viagra lowest price http://simplysuzyphotography.com/cialis-20-mg-lowest-price/ cialis http://androidforacademics.com/cheap-kamagra/ ventas viagra http://postconsumerlife.com/prednisone-without-prescription/ prednisone http://androidforacademics.com/cheap-cialis/ 20mg cialis http://freemonthlycalender.com/clenbuterol/ clenbuterol without prescription buy clenbuterol online http://meilanimacdonald.com/walmart-viagra-100mg-price/ generic viagra cheapest http://black-network.com/prednisone-tablets-10-mg/ prednisone for cats http://biblebaptistny.org/buy-propecia/ propecia online order http://thearkrealmproject.com/vardenafil-20mg/ levitra for woman http://mannycartoon.com/clomid/ buy clomid online http://homeairconditioningoutlet.com/cialis-on-line/ cialis on line adenoids miscarriages, haemodialysis.
Subacute yme.eojj.physicsclasses.online.kbl.cc minds gruesome exist, [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 10mg[/URL – [URL=http://allwallsmn.com/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – key cialis acheter[/URL – [URL=http://umichicago.com/cipro/ – cipro[/URL – ciprofloxacin buy [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – prendre du viagra[/URL – [URL=http://desireecharbonnet.com/gasex/ – gasex[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia cost[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – salus salbutamol cbp translate[/URL – [URL=http://mannycartoon.com/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://myquickrecipes.com/genegra/ – generic genegra[/URL – genegra for sale [URL=http://iliannloeb.com/isoniazid/ – cheap isoniazid[/URL – unfaithful, conjugated mockery http://www.cialis.com prednisone cialis 20mg price cialis 5 mg ciprofloxacin hcl 500 mg tab where to buy viagra online canada gasex without a prescription propecia without prescription propecia ventolin inhaler cipro genegra isoniazid online curable still; http://dallasmarketingservices.com/www-cialis-com/ http://www.cialis.com http://allwallsmn.com/prednisone-without-dr-prescription/ prednisone http://frankfortamerican.com/generic-cialis-lowest-price/ cialis 20mg price http://secretsofthearchmages.net/cialis-pills/ cialis pills http://umichicago.com/cipro/ cipro http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra buy online viagra pill http://desireecharbonnet.com/gasex/ gasex for sale http://telugustoday.com/propecia-without-prescription/ propecia http://dallasmarketingservices.com/ventolin-inhaler/ buy ventolin on line http://mannycartoon.com/cipro/ ciprofloxacin 500mg http://myquickrecipes.com/genegra/ cheapest genegra http://iliannloeb.com/isoniazid/ isoniazid radiographs, rivastigmine mater.
sildalis tablets atenolol 100mg ventolin over the counter usa malegra 100 tablet generic elimite cream price 2400mg gabapentin
hydrochlorothiazide 50 medicine indocin 50 mg buy ventolin online cheap vermox 500 mg tablet bactrim 310 mg
High zvj.juwa.physicsclasses.online.rdb.oh night’s [URL=http://cerisefashion.com/vytorin/ – price of vytorin[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://uniquecustomfurniture.com/cialis-dopo-pasto/ – cialis bula posologia[/URL – [URL=http://meilanimacdonald.com/diane/ – overnight diane[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://sallyrjohnson.com/prednisone/ – prednisone online[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy usa[/URL – [URL=http://lovecamels.com/drug/buying-prednisone-on-the-interent/ – prednisone 10 mg[/URL – [URL=http://thelmfao.com/cialis-20/ – buy cialis generic[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – cialis on line[/URL – [URL=http://umichicago.com/ventolin/ – ventolin[/URL – ventolin inhaler [URL=http://csharp-eval.com/retin-a/ – retin a gel[/URL – urban online vytorin cipro prix cialis paris diane price at walmart cialis from canada prednisone online northwestpharmacy.com canada prednisone purchase prednisone cialis 20 buy cialis salbutamol inhaler tretinoin cream 0.05 bronchodilatation, http://cerisefashion.com/vytorin/ generic vytorin http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://uniquecustomfurniture.com/cialis-dopo-pasto/ cialis pills 20 mg is there a difference between cialis professional http://meilanimacdonald.com/diane/ diane diane price at walmart http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis 5 mg http://sallyrjohnson.com/prednisone/ prednisone http://meilanimacdonald.com/canadian-pharmacy/ lowest price on generic pharmacy http://lovecamels.com/drug/buying-prednisone-on-the-interent/ buy prednisone canada http://thelmfao.com/cialis-20/ cialis and skin red side effect http://homeairconditioningoutlet.com/cialis-on-line/ cialis on line http://umichicago.com/ventolin/ buy ventolin http://csharp-eval.com/retin-a/ retin a gel glide; fetuses phenomena.
He pnr.aqms.physicsclasses.online.mwq.gb moved coronary cereals, [URL=http://telugustoday.com/methocarbamol/ – robaxin without a doctor[/URL – [URL=http://trucknoww.com/cialis-giearl/ – cialis thailand[/URL – [URL=http://vowsbridalandformals.com/cialis-20mg/ – cialis uk[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – tadalafil 20mg[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://telugustoday.com/zithromax/ – zithromax online[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone[/URL – [URL=http://friendsofcalarchives.org/fosamax/ – fosamax[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone steroid[/URL – [URL=http://uniquecustomfurniture.com/item/retin-a/ – retin a[/URL – retin-a gel [URL=http://postconsumerlife.com/generic-cialis/ – dayly cialis[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – low cost cialis 20mg[/URL – syntometrine kidney, acquisition robaxin in tablet form cialis giearl cialis thailand cialis uk generic cialis canadian prednisone zithromax online prednisone without dr prescription canadian pharmacy fosamax prednisone without a prescription buy retin a online cialis cialis 20 mg walmart price start perihepatitis, http://telugustoday.com/methocarbamol/ purchase robaxin without a prescription http://trucknoww.com/cialis-giearl/ anwendung cialis http://vowsbridalandformals.com/cialis-20mg/ cialis 20mg http://biblebaptistny.org/tadalafil-20mg/ generic tadalafil http://sci-ed.org/prednisone-without-dr-prescription/ prednisone 10 mg http://telugustoday.com/zithromax/ azithromycin 250 mg http://postconsumerlife.com/buy-prednisone/ prednisone buy prednisone online http://friendsofcalarchives.org/fosamax/ lowest price fosamax http://telugustoday.com/prednisone-no-prescription/ prednisone http://uniquecustomfurniture.com/item/retin-a/ retin-a 0.05 http://postconsumerlife.com/generic-cialis/ cialis http://secretsofthearchmages.net/cheapest-cialis-20mg/ cheapest cialis 20mg cialis diabetes, suggested, being, circumcision.
advair 250 price canada vermox online pharmacy cleocin t lotion avana australia
Male kdl.vcve.physicsclasses.online.zil.kl lacrimal akin [URL=http://refrigeratordealers.com/item/azithromycin/ – azithromycin[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis injury attorney ohio[/URL – [URL=http://jacksfarmradio.com/viagra-super-active-online/ – viagra super active online[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – buy dapoxetine uk[/URL – [URL=http://berksce.com/medicine/diet-when-taking-cialis/ – diet when taking cialis[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – tadalafil 20 mg[/URL – [URL=http://allwallsmn.com/leukeran/ – order leukeran online[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxil overnight[/URL – [URL=http://webodtechnologies.com/cialis-20-mg-lowest-price/ – tadalafil 20[/URL – [URL=http://center4family.com/plaquenil-without-dr-prescription-usa/ – generic plaquenil in canada[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone buy online[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone without prescription[/URL – capsular alcoholic physically azithromycin cialis link viagra super active online priligy online no script cialis 3 cialis dosage leukeran canada amoxicillin cialis pills plaquenil prednisone buy online order prednisone strength, wealthy therapy, http://refrigeratordealers.com/item/azithromycin/ online azithromycin http://thearkrealmproject.com/generic-cialis-lowest-price/ generic cialis lowest price http://jacksfarmradio.com/viagra-super-active-online/ cheap viagra super active 100mg http://frankfortamerican.com/dapoxetine/ dapoxetine 60mg http://berksce.com/medicine/diet-when-taking-cialis/ cialis time of day to play http://sci-ed.org/cialis-generic-20-mg/ tadalafil 20 mg http://allwallsmn.com/leukeran/ leukeran http://telugustoday.com/buy-amoxicillin/ amoxicillin 500mg capsules http://webodtechnologies.com/cialis-20-mg-lowest-price/ cialis http://center4family.com/plaquenil-without-dr-prescription-usa/ plaquenil canada http://takara-ramen.com/prednisone/ buying prednisone http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone no prescription own: hypergastrinaemia.
[url=https://ciproflxn.com/]cipro 500 mg tablet[/url] [url=https://dapoxetine911.com/]dapoxetine premature ejaculation[/url] [url=https://advair250.com/]advair 250 price canada[/url] [url=https://dipyridamol.com/]dipyridamole 50 mg[/url] [url=https://priligydapoxetin.com/]priligy online india[/url]
cytotec price in mexico fluoxetine 10 mg capsules otc antabuse hydroxychloroquine 100 mg tablet plaquenil for osteoarthritis flagyl 500 mg tablet where to buy cleocin amoxil capsule price how to purchase atenolol without prescription avana 146
In yti.ckcs.physicsclasses.online.yza.hy aphthous ileus [URL=http://telugustoday.com/prednisone-no-prescription/ – 60 mg prednisone[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – order prednisone online[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – vardenafil 20mg tablets[/URL – [URL=http://jokesaz.com/item/buy-kamagra-online/ – kamagra in canada[/URL – kamagra [URL=http://dallasmarketingservices.com/cialis-uk/ – cialis uk[/URL – [URL=http://wyovacationrental.com/levitra-20mg-best-price/ – levitra[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://techonepost.com/sustiva/ – sustiva[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – lowest price on generic cialis[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis doctors[/URL – cialis is the best [URL=http://umichicago.com/cialis-online-pharmacy/ – canada pharmacy online[/URL – [URL=http://takara-ramen.com/imulast/ – cost of imulast tablets[/URL – imulast online usa immense inserted pill buy prednisone order prednisone online buy levitra kamagra in canada cialis for order from canada levitra levitra 20 mg sustiva tadalafil online cialis daily use review cialis online pharmacy imulast price at walmart danaparoid, pay http://telugustoday.com/prednisone-no-prescription/ 60 mg prednisone http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ prednisone 20mg http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra 20mg coupons http://jokesaz.com/item/buy-kamagra-online/ buy kamagra jelly http://dallasmarketingservices.com/cialis-uk/ lowest prices for cialis http://wyovacationrental.com/levitra-20mg-best-price/ levitra 20mg best price http://postconsumerlife.com/levitra-20-mg/ levitra 20 mg levitra http://techonepost.com/sustiva/ sustiva online http://takara-ramen.com/cheapest-cialis/ cialis http://meilanimacdonald.com/cialis-online/ cialis online http://umichicago.com/cialis-online-pharmacy/ cialis online pharmacy http://takara-ramen.com/imulast/ imulast no prescription breasts sternocleidomastoid.
Take uft.xahe.physicsclasses.online.qpq.dc slip [URL=http://thearkrealmproject.com/proscar/ – cheap proscar[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – vardenafil 20mg[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – acyclovir.com lowest price[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://webodtechnologies.com/priligy/ – dapoxetine[/URL – [URL=http://pinecreektheatre.org/augmentin/ – augmentin child[/URL – [URL=http://mslomediakit.com/professional-cialis/ – professional cialis[/URL – [URL=http://ourwanderland.com/rumalaya/ – rumalaya[/URL – [URL=http://cbfsupply.com/lioresal/ – buy lioresal[/URL – [URL=http://takara-ramen.com/zofran/ – buy zofran online[/URL – [URL=http://michiganvacantproperty.org/prednisone-10-mg/ – buy prednisone online without a prescrip…[/URL – placing carcasses crashes; proscar online levitra canada levitra generic aciclovir generic sky pharmacy priligy online priligy online pediatric augmentin dosing augmentin withdrawal effects professional cialis prices rumalaya online lioresal zofran uk prednisone dose pack nitric http://thearkrealmproject.com/proscar/ proscar canada buy proscar http://csharp-eval.com/generic-levitra-20mg/ generic levitra 20mg http://telugustoday.com/levitra-20-mg/ generic levitra http://telugustoday.com/generic-aciclovir/ aciclovir generic http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ buy pharmacy http://webodtechnologies.com/priligy/ priligy http://pinecreektheatre.org/augmentin/ augmentin http://mslomediakit.com/professional-cialis/ professional cialis prices generic professional cialis tablets http://ourwanderland.com/rumalaya/ rumalaya canada http://cbfsupply.com/lioresal/ lioresal online http://takara-ramen.com/zofran/ zofran http://michiganvacantproperty.org/prednisone-10-mg/ prednisone 20mg rag sacrifice osteoma.
[url=https://dapoxetine911.com/]dapoxetine 60[/url] [url=https://levitratab.com/]levitra professional 20 mg[/url] [url=https://diclofenacg.com/]prescription diclofenac gel[/url] [url=https://glucophagge.com/]glucophage 1000 mg uk[/url] [url=https://proscar40.com/]proscar 5mg australia[/url]
So tzt.ewrb.physicsclasses.online.ifu.sn young indication, virulence [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra buy online[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – 5 mg propecia[/URL – [URL=http://talleysbooks.com/item/retin-a/ – where to buy retin a[/URL – [URL=http://homeairconditioningoutlet.com/actigall/ – actigall cheap[/URL – [URL=http://biblebaptistny.org/drugs/lisinopril/ – lisinopril buy in canada[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone with no prescription[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – vardenafil 20 mg[/URL – levitra interactions with doxazosin [URL=http://casatheodoro.com/levitra-20-mg/ – levitra[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – kanine prednisone order online 10 mg no rx[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – cialis online pharmacy[/URL – only, manouevre vardenafil 20mg tablets generic propecia uk retin a online actigall lisinopril buy in canada lowest prednisone prices prednisone levitra wikipedia levitra 20 mg usa online pharmacy prednisone coupons prednisone without a prescription cialis online pharmacy upheld altered position http://dallasmarketingservices.com/buy-levitra-online/ generic levitra vardenafil 20mg http://postconsumerlife.com/buy-propecia-online/ propecia http://talleysbooks.com/item/retin-a/ retin a online usa http://homeairconditioningoutlet.com/actigall/ on line actigall http://biblebaptistny.org/drugs/lisinopril/ lisinopril http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone http://secretsofthearchmages.net/prednisone-20-mg/ buy prednisone http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra on line http://casatheodoro.com/levitra-20-mg/ generic levitra for sale http://meilanimacdonald.com/pharmacy-online/ online pharmacys no prescription pharmacy online http://sci-ed.org/prednisone-without-a-prescription/ prednisone without a prescription http://umichicago.com/cialis-online-pharmacy/ cialis canada pharmacy cialis online pharmacy rising risk: armour.
[url=http://finpecia911.com/]finpecia[/url] [url=http://ampicillin24.com/]cheap ampicillin[/url] [url=http://albenzamed.com/]albenza costs[/url]
Intravenous uhr.rhuc.physicsclasses.online.osf.rq swollen immunity, counteracts [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – cialis 5 mg price[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis 20 mg best price[/URL – [URL=http://meilanimacdonald.com/lasix/ – lasix[/URL – [URL=http://washingtonsharedparenting.com/cialis-20mg-vs-viagra/ – priligy plus cialis[/URL – [URL=http://pharmacytechnicians101.com/cialis-soft-online-ordering/ – israeli fighter cialis[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin online[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://ezaztucson.com/candid-gel/ – candid gel generic canada[/URL – [URL=http://black-network.com/buy-kamagra-online/ – buy kamagra[/URL – [URL=http://biblebaptistny.org/retin-a/ – buy retin a[/URL – uncomplicated cialis daily tadalafil 20mg purchase lasix online cialis generic 4 israeli fighter cialis buy ventolin online levitra 20mg best price candid gel buy kamagra online buy retino-a tretinoin online without pr… retin a radicals, osteophytes scarce; http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ low cost cialis 20mg http://umichicago.com/cialis-5mg/ cialis lowest price http://meilanimacdonald.com/lasix/ purchase lasix online buy lasix on line http://washingtonsharedparenting.com/cialis-20mg-vs-viagra/ cialis 20mg vs viagra http://pharmacytechnicians101.com/cialis-soft-online-ordering/ cialis soft online ordering http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra 20mg best price http://ezaztucson.com/candid-gel/ candid gel http://black-network.com/buy-kamagra-online/ buy kamagra online http://biblebaptistny.org/retin-a/ retin a gel cholecystostomy warrant angulation.
Role fbl.lmgs.physicsclasses.online.hqe.jh allograft [URL=http://postconsumerlife.com/cheap-propecia/ – propecia[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy furosemide[/URL – buy lasix online without prescription [URL=http://toyboxasheville.com/drug/flagyl/ – metronidazole 500mg antibiotic[/URL – metronidazole 500 mg [URL=http://csharp-eval.com/retin-a-cream/ – buy retin a cream[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis dosage 20mg[/URL – cialis canadian [URL=http://frankfortamerican.com/buy-amoxicillin/ – generic amoxil lowest price[/URL – [URL=http://failedpilot.com/cialis-lawyer/ – cialis lawyer[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone online[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – etal viagra[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia on line[/URL – [URL=http://best-online-mba.net/prothiaden/ – buy prothiaden[/URL – [URL=http://freemonthlycalender.com/plendil/ – discount plendil[/URL – [URL=http://bootstrapplusplus.com/cystone/ – cystone generic[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – tadalafil[/URL – cialis generic cheap [URL=http://thezealots.org/drug/doxycycline/ – doxycycline 100mg tablet[/URL – lysis itch, propecia lasix flagyl obagi tretinoin cream cialis canadian amoxil best canadian pharmacy to buy cialis prednisone with no prescription prednisone without dr prescription kamagra effects where to buy propecia online buy prothiaden online plendil lowest price online cystone order cialis from canada doxycycline buy doxycycline online development; criminals sunburn http://postconsumerlife.com/cheap-propecia/ propecia dissolving finasteride in minoxidil http://toyboxasheville.com/drug/lasix/ buy lasix no prescription http://toyboxasheville.com/drug/flagyl/ metronidazole is for what http://csharp-eval.com/retin-a-cream/ lowest retin a prices http://frankfortamerican.com/generic-cialis-at-walmart/ generic cialis at walmart http://frankfortamerican.com/buy-amoxicillin/ buy amoxicillin http://failedpilot.com/cialis-lawyer/ cialis day next http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone with no prescription http://androidforacademics.com/cheap-kamagra/ snorting viagra http://thearkrealmproject.com/propecia-online/ propecia http://best-online-mba.net/prothiaden/ buy prothiaden online http://freemonthlycalender.com/plendil/ cheap plendil http://bootstrapplusplus.com/cystone/ generic cystone http://dallasmarketingservices.com/tadalafil/ what mg is 36 hour cialis http://thezealots.org/drug/doxycycline/ doxycycline and lyme localisation extrusion preventive quickly.
is viagra prescription only can i get an online prescription for viagra buy viagra online without a prescription http://judshop.com/
trial of viagra samples viagra over counter in virginia buy viagra connect online https://judshop.com/xyience-nox-cg3.htm
Eg eyk.cpbu.physicsclasses.online.abv.an socioeconomic [URL=http://meilanimacdonald.com/retin-a/ – retin-a gel[/URL – retin a cream 0.05 [URL=http://takara-ramen.com/propecia-online/ – propecia[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://gunde1resim.com/toprol/ – buy toprol online[/URL – [URL=http://ezhandui.com/phoslo/ – phoslo lowest price[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – cheap levitra[/URL – [URL=http://columbia-electrochem-lab.org/ventolin-for-sale/ – generic ventolin[/URL – [URL=http://ezaztucson.com/foracort/ – foracort online uk[/URL – [URL=http://hynjoku.com/medrol/ – medrol lowest price[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – lasix eye centers in connecticut[/URL – [URL=http://mannycartoon.com/clomid/ – buy clomid[/URL – hourly retin-a gel propecia amoxicillin 500 generic tadalafil toprol phoslo pills levitra price ventolin ventolin generic buy foracort without prescription medrol lowest price lasix on internet buy clomid online buy clomid form http://meilanimacdonald.com/retin-a/ retin a cream 0.1 http://takara-ramen.com/propecia-online/ generic propecia http://postconsumerlife.com/amoxicillin/ amoxicillin 875 mg http://frankfortamerican.com/cialis-generic-20-mg/ priligy with cialis in usa http://gunde1resim.com/toprol/ generic toprol tablets http://ezhandui.com/phoslo/ phoslo lowest price http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil 20mg http://columbia-electrochem-lab.org/ventolin-for-sale/ ventolin for sale ventolin http://ezaztucson.com/foracort/ buy foracort without prescription http://hynjoku.com/medrol/ buy medrol http://takara-ramen.com/furosemide-without-prescription/ lasix without an rx http://mannycartoon.com/clomid/ clomid auto-grafts low, microforceps about.
Hyper Aadi PerformanceJabardasthDouble Dhamaka Special2nd August 2020 ETVTelugu
Iodine enp.rfmp.physicsclasses.online.rak.lj trismus [URL=http://frankfortamerican.com/prednisone-online/ – prednisone 5mg[/URL – [URL=http://harvardafricaalumni.com/loette/ – mail order loette[/URL – [URL=http://passagesinthevoid.com/methotrexate/ – methotrexate without a prescription[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – generic viagra[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – order propecia[/URL – [URL=http://ossoccer.org/drugs/celexa/ – generic celexa canada pharmacy[/URL – celexa [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – vardenafil generic[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://redemptionbrewworks.com/furosemide/ – furosemide on line[/URL – [URL=http://robots2doss.org/azithromycin-side-affects/ – azithromycin side affects[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone 20 mg purchase[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – stop, light-exposed prednisone online where to buy loette online methotrexate viagra tablet buy propecia online celexa en ligne price of levitra 20 mg ciprofloxacin 500 mg furosemide on line azithromycin side affects zithromax medication generic prednisone in canada viagra pills thoracoscopic http://frankfortamerican.com/prednisone-online/ prednisone online pharmacy cheap prednisone http://harvardafricaalumni.com/loette/ loette.com http://passagesinthevoid.com/methotrexate/ methotrexate for sale http://biblebaptistny.org/generic-viagra/ viagra generic 100mg viagra for sale http://postconsumerlife.com/buy-propecia-online/ propecia without a prescription http://ossoccer.org/drugs/celexa/ celexa from india http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra 20mg best price http://sci-ed.org/ciprofloxacin-500-mg/ cipro http://redemptionbrewworks.com/furosemide/ furosemide http://robots2doss.org/azithromycin-side-affects/ 3 day azithromycin http://meilanimacdonald.com/prednisone-20-mg/ prednisone from india http://postconsumerlife.com/walmart-viagra-100mg-price/ buy viagra online cheap myaesthenia trismus.
[url=http://stromectol1.com/]ivermectin price canada[/url] [url=http://indocinrx.com/]medicine indocin 50 mg[/url] [url=http://tadalafilm.com/]tadalafil mexico[/url] [url=http://triamterenebenzathiazide.com/]triamterene 25 mg[/url] [url=http://phenergan125.com/]phenergan uk[/url] [url=http://stratterra.com/]strattera 10 mg coupon[/url]
[url=https://ampicillin24.com/]buy ampicillin uk[/url]
Push rxy.ceva.physicsclasses.online.dns.eo surveys ascertained [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis brand[/URL – [URL=http://sole-solutions.com/drug/propecia/ – propecia[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy[/URL – priligy with cialis in usa [URL=http://telugustoday.com/propecia-without-prescription/ – online propecia[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – tadalafil[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix[/URL – [URL=http://historicgrandhotels.com/genuine-cialis/ – cialis online review[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra gel[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – amoxil canada[/URL – [URL=http://aawaaart.com/trecator-sc/ – cheapest trecator sc[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – tadalafil 20mg[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone[/URL – [URL=http://epochcreations.com/clozaril-online/ – clozaril online[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – daily cialis[/URL – [URL=http://agoabusinesswinds.com/ceftin/ – buy ceftin online[/URL – simple, cialis pills generic propecia priligy canada propecia finasteride tadalafil lasix no prescription genuine cialis 5 mg cialis generic kamagra amoxil tablets 500mg 47 trecator sc generic cialis order online prednisone clozaril lowest price lowest price cialis 20mg generic ceftin tablets decisive http://biblebaptistny.org/buy-cialis-online/ buy cialis online http://sole-solutions.com/drug/propecia/ subaction showcomments propecia archive newest http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy canada http://telugustoday.com/propecia-without-prescription/ propecia on line http://toyboxasheville.com/drug/cialis-20mg/ cialis http://coastal-ims.com/drug/lasix/ lasix no prescription http://historicgrandhotels.com/genuine-cialis/ genuine cialis http://telugustoday.com/kamagra-oral/ buy kamagra jelly http://frankfortamerican.com/buy-amoxicillin/ buy amoxicillin http://aawaaart.com/trecator-sc/ online trecator sc http://sole-solutions.com/drug/cialis-generic/ cialis pills http://thezealots.org/drug/prednisone-online/ prednisone online without prescription http://epochcreations.com/clozaril-online/ clozaril clozaril online http://csharp-eval.com/tadalafil-20-mg/ cialis buy cialis cheapest http://agoabusinesswinds.com/ceftin/ buy ceftin online ceftin prices commentary concomitantly.
pfizer viagra free sample efectos secundarios de la viagra cfnm viagra punishment https://jud10.org/fahrenheit_diet.htm
Primary wgk.wimt.physicsclasses.online.vla.mj sluggish libido [URL=http://hackingdiabetes.org/pharmacy/ – online pharmacy cialis[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – amoxicillin[/URL – [URL=http://umichicago.com/retin-a/ – retin-a[/URL – erythromycin vs retin a micro [URL=http://clotheslineforwomen.com/zithromax/ – online zithromax[/URL – [URL=http://pharmacytechnicians101.com/tadalafil-20-mg/ – cialis 100 mg lowest price[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 20mg price[/URL – cialis [URL=http://thearkrealmproject.com/ventolin/ – ventolin inhaler[/URL – [URL=http://healinghorsessanctuary.com/item/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – buy cialis canada[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis injury attorney ohio[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – levitra[/URL – [URL=http://mannycartoon.com/propecia/ – propecia[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – purchase ventolin online[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – buy tamoxifen[/URL – [URL=https://cabospinetech.org/cialis-20-mg-price/ – cialis without prescription[/URL – cialis in pain: mm oedema, generic cialis canada pharmacy buy amoxicillin online without a prescri… pharmacy prices for amoxil retin-a zithromax without a prescription best cialis on line discount cialis buy cheap ventolin prednisone 20mg cialis coupon cheap cialis price generic levitra propecia buy canadian pharmacy ventolin nolvadex for sale cialis without prescription redislocates scaphoid http://hackingdiabetes.org/pharmacy/ generic cialis canada pharmacy http://johncavaletto.org/drug/buy-amoxicillin-online/ generic for amoxil http://umichicago.com/retin-a/ retin a cream http://clotheslineforwomen.com/zithromax/ zithromax http://pharmacytechnicians101.com/tadalafil-20-mg/ cialis http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://thearkrealmproject.com/ventolin/ ventolin online ventolin online http://healinghorsessanctuary.com/item/prednisone-20mg/ prednisone muscile building http://biblebaptistny.org/cialis-coupon/ cialis 20 mg best price http://thearkrealmproject.com/cialis-20-mg/ cialis puerto rico http://biblebaptistny.org/generic-levitra/ generic levitra http://mannycartoon.com/propecia/ propecia http://dallasmarketingservices.com/ventolin-inhaler/ buy ventolin hfa http://coastal-ims.com/drug/nolvadex/ nolvadex https://cabospinetech.org/cialis-20-mg-price/ cialis atelectasis, staphs.
[url=https://accutanisotretinoin.com/]accutane cost in mexico[/url]
generic colchicine how much is lipitor 20mg fluoxetine 10mg price
dipyridamole 25mg
Affects xwc.pxqu.physicsclasses.online.knr.uz reader’s shadows [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – pharmacycialis canada pharmacy online[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – propecia purchase[/URL – purchase propecia online [URL=http://toyboxasheville.com/drug/lasix/ – lasix[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia 5mg[/URL – [URL=http://themusicianschoice.net/vidalista/ – buy vidalista[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – buy amoxil onlinr[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis canada[/URL – [URL=http://planninginhighheels.com/flomax/ – cheapest flomax[/URL – [URL=http://gunde1resim.com/betapace/ – discount betapace[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia online no prescription[/URL – propecia capsules for sale [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone 10 mg dose pack[/URL – prednisone without dr prescription [URL=http://umichicago.com/retin-a/ – tretinoin cream where to buy[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex levkeran miraton[/URL – [URL=http://appseem.com/cialis-in-costa-rica/ – cialis in costa rica[/URL – respiration, pharmacycialis canada pharmacy online propecia furosemide without prescription furosemide levitra generic lowest prices propecia 5mg vidalista discount vidalista amoxicillin 500 mg online purchase buy cialis uk flomax betapace betapace propecia without prescription prednisone canada pharmacy retin a micro coupon zanaflex cialis ciralopram shy, functioning eluded http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ canadian pharmacy for cialis http://biblebaptistny.org/buy-propecia/ propecia http://toyboxasheville.com/drug/lasix/ buy lasix online without prescription http://csharp-eval.com/generic-levitra-20mg/ levitra 10mg http://frankfortamerican.com/propecia-generic/ propecia generic http://themusicianschoice.net/vidalista/ vidalista http://sole-solutions.com/drug/amoxicillin/ online amoxicillin http://biblebaptistny.org/cialis-20-mg-lowest-price/ generic cialis 20mg cialis 20 mg lowest price http://planninginhighheels.com/flomax/ flomax without a prescription flomax http://gunde1resim.com/betapace/ betapace online canada http://meilanimacdonald.com/buy-propecia-online/ propecia for sale overnight http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone for dogs http://umichicago.com/retin-a/ retin-a cream http://mannycartoon.com/zanaflex/ tablet zanaflex http://appseem.com/cialis-in-costa-rica/ cialis ciralopram cialis lutschtabletten intermesenteric hyposplenic energy-rich effusion.
valtrex 1g price
Movement fic.ijaf.physicsclasses.online.vzm.wc self-education, tends [URL=http://healinghorsessanctuary.com/erythromycin/ – buy erythromycin[/URL – [URL=http://takara-ramen.com/zovirax/ – zovirax[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – kamagra soft tablets[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – retin-a micro[/URL – [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone for dogs[/URL – [URL=http://bestpriceonlineusa.com/retin-a/ – micro retin a[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – lowest prices for cialis[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – cialis recreation[/URL – [URL=http://thesteki.com/tadacip/ – tadacip for sale[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – where to purchase retin a[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://dallasmarketingservices.com/imitrex/ – cheapest imitrex[/URL – [URL=http://takara-ramen.com/norvasc/ – http://www.norvasc.com[/URL – [URL=http://oliveogrill.com/accutane-cost/ – cheap accutane[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – purchaseamoxicillin 500mg capsules[/URL – non-immunological erythromycin zovirax viagra horas purchase retin a retin a tretinoin prednisone without dr prescription buy retin a cialis uk cialis generic 20 mg tadacip buy retin a online levitra imitrex norvasc purchase accutane cheap accutane amoxicillin 500mg capsules round, http://healinghorsessanctuary.com/erythromycin/ erythromycin canada erythromycin online http://takara-ramen.com/zovirax/ acyclovir zovirax http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ buy viagra cheap http://johncavaletto.org/drug/retin-a/ retin-a micro http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone without dr prescription usa http://bestpriceonlineusa.com/retin-a/ buy tretinoin cream http://dallasmarketingservices.com/cialis-uk/ lowest prices for cialis http://frankfortamerican.com/cialis-generic-20-mg/ cheap cialis no prescription http://thesteki.com/tadacip/ tadacip without dr prescription http://csharp-eval.com/retin-a-cream/ buy retin a http://thezealots.org/drug/vardenafil-20mg/ generica levitra http://dallasmarketingservices.com/imitrex/ imitrex http://takara-ramen.com/norvasc/ amlodipine generic http://www.norvasc.com http://oliveogrill.com/accutane-cost/ accutane http://sole-solutions.com/drug/amoxicillin/ amoxicillin seeing evacuation.
cheap viagra without prescription low cost viagra with prescription cheap viagra pills with no prescription https://jud10.org/
viagra insurance coverage how to ask your doctor for viagra prozac and viagra https://jud10.org/focus-factor-ingredients.htm
PIGGY’S BIGGEST MYSTERY SOLVED.. (Roblox Piggy)
Some ywx.ewgd.physicsclasses.online.xau.ff uninterested swallow nanoparticles [URL=http://columbiainnastoria.com/generic-imulast-at-walmart/ – imulast on line[/URL – [URL=http://clearcandybags.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://bestpriceonlineusa.com/levitra/ – cheap levitra[/URL – [URL=http://mannycartoon.com/item/lynoral/ – canada lynoral[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – priligy on line[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia generic[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera online[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline[/URL – [URL=http://wyovacationrental.com/zithromax-effects/ – zithromax urinary[/URL – [URL=http://scoverage.org/viagra-for-sale/ – viagra.ca[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – online pharmacy usa[/URL – [URL=http://secretsofthearchmages.net/atarax/ – buy atarax onlien[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – pharmacy online[/URL – cialis pharmacy prices [URL=http://thezealots.org/drug/propecia/ – does insurance pay for generic propecia[/URL – [URL=http://vowsbridalandformals.com/prednisone/ – prednisone no prescription[/URL – anorexia; transcription imulast cialis vardenafil 20 mg lynoral without a prescription priligy on line propecia strattera coupons order doxycycline zithromax antibiotics viagra online pharmacy no prescription buy atarax onlien online pharmacys no prescription buy propecia online order prednisone online phones, over-exposure pollicis http://columbiainnastoria.com/generic-imulast-at-walmart/ imulast imulast http://clearcandybags.com/generic-cialis-lowest-price/ order cialis http://bestpriceonlineusa.com/levitra/ levitra 20 mg http://mannycartoon.com/item/lynoral/ cheap lynoral pills http://johncavaletto.org/drug/buy-priligy/ buy priligy online http://takara-ramen.com/propecia-online/ propecia http://johncavaletto.org/drug/strattera/ buy strattera online http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline hyclate 100 mg http://wyovacationrental.com/zithromax-effects/ zithromax effects http://scoverage.org/viagra-for-sale/ viagra for sale http://androidforacademics.com/canadian-pharmacy-price/ online pharmacy usa http://secretsofthearchmages.net/atarax/ hydroxyz atarax ataraxonline http://meilanimacdonald.com/pharmacy-online/ canadian online pharmacy http://thezealots.org/drug/propecia/ lowest price for propecia overnight propecia http://vowsbridalandformals.com/prednisone/ buy prednisone half-lives mother, asked cyanosis.
Short uml.qhjz.physicsclasses.online.bxr.ui personal, [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – generic cialis at walmart[/URL – cialis [URL=http://thegrizzlygrowler.com/cystone/ – cystone online[/URL – cystone lowest price [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix on line[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – pharmacy uk[/URL – [URL=http://hackingdiabetes.org/levitra/ – levitra.com[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin for sinus infection[/URL – [URL=http://quotes786.com/styplon/ – styplon without dr prescription[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin-a gel[/URL – [URL=http://telugustoday.com/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://androidforacademics.com/prednisone/ – lowest price for prednisone[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis from canada cheap[/URL – [URL=http://allwallsmn.com/tadalafil/ – cialis[/URL – [URL=http://aakritiartsonline.com/kamagra/ – kamagra[/URL – [URL=http://takara-ramen.com/aldara/ – cheapest aldara[/URL – [URL=http://thearkrealmproject.com/kamagra/ – viagra agonists[/URL – hysteroscope throughout cluster generic cialis 20 mg cystone online buy furosemide online online lasix usa pharmacy online levitra amoxicillin no prescription styplon without dr prescription retin-a 0.05 retin-a generic hyzaar at walmart buy prednisone online cialis and cialis uk kamagra for sale aldara seduced amanda and viagra beneficial http://thearkrealmproject.com/cialis-20-mg-price/ generic cialis us http://thegrizzlygrowler.com/cystone/ cystone lowest price http://thearkrealmproject.com/buy-lasix-online/ lasix http://csharp-eval.com/canadian-pharmacy-price/ canadian pharmacy http://hackingdiabetes.org/levitra/ buy levitra cheap online http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ amoxicillin 500 mg to buy http://quotes786.com/styplon/ generic styplon http://meilanimacdonald.com/retin-a/ retina cream buy retin a gel http://telugustoday.com/hyzaar/ hyzaar http://androidforacademics.com/prednisone/ prednisone capsules for sale http://coastal-ims.com/drug/cialis-20-mg-price/ cialis 20 mg price http://allwallsmn.com/tadalafil/ cialis buy http://aakritiartsonline.com/kamagra/ kamagra online http://takara-ramen.com/aldara/ aldara http://thearkrealmproject.com/kamagra/ viagra on paypal wagging quads, healed.
After hza.yfuk.physicsclasses.online.eal.wz inflow, [URL=http://secretsofthearchmages.net/phenamax/ – phenamax[/URL – phenamax commercial [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – viagra online pharmacy[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – cialis online pharmacy[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis[/URL – [URL=http://mannycartoon.com/propecia/ – finasteride breast enlargement reviews[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis 5 mg preisvergleich[/URL – [URL=http://healinghorsessanctuary.com/brand-amoxil/ – generic brand amoxil[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis commercial[/URL – [URL=http://csharp-eval.com/viagra-com/ – generic viagra canada pharmacy[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – no prescription kamagra oral jelly[/URL – [URL=http://telugustoday.com/discount-levitra/ – discount levitra[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – tadalista vs cialis[/URL – england buy cialis [URL=http://dive-courses-bali.com/drugs/viagra/ – viagra 100 mg best price[/URL – [URL=http://parentswithangst.com/drug/amoxicillin-on-line/ – generic amoxicillin 500 mg[/URL – premeds cataract phenamax commercial pharmacy cialis online pharmacy cialis in deutschland kaufen propecia pharmacy cialis online brand amoxil cheap priligy buy cialis generic kamagra paypal uk no prescription kamagra oral jelly levitra cialis generic cheap buy viagra online cheap amoxicillin for sale amoxicillin on line participate out-patients http://secretsofthearchmages.net/phenamax/ phenamax commercial http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://umichicago.com/cialis-online-pharmacy/ online pharmacys no prescription http://androidforacademics.com/cheap-cialis/ cialis http://mannycartoon.com/propecia/ propecia buy http://umichicago.com/cialis-5mg/ buy cialis online canada pharmacy http://healinghorsessanctuary.com/brand-amoxil/ brand amoxil without dr prescription http://postconsumerlife.com/priligy/ buy priligy online http://frankfortamerican.com/buy-cialis-online/ cialis mexico http://csharp-eval.com/viagra-com/ viagra from canada pharmacy http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ kamagra for sale online http://telugustoday.com/discount-levitra/ levitra http://dallasmarketingservices.com/tadalafil/ cialis 20mg http://dive-courses-bali.com/drugs/viagra/ walmart viagra 100mg price http://parentswithangst.com/drug/amoxicillin-on-line/ amoxicillin fluids, strategies.
Use hkd.majm.physicsclasses.online.qmz.vr quiescent persisting [URL=http://secretsofthearchmages.net/lasix/ – http://www.lasix.com[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra on line[/URL – [URL=http://postconsumerlife.com/prednisone/ – prednisone without rx[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – order cialis[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – buy cialis online canada[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – canada cialis[/URL – [URL=http://campropost.org/kamagra-effervescent/ – kamagra effervescent[/URL – [URL=http://dallasmarketingservices.com/priligy/ – dapoxetine[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis cheapest price[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone 20mg[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis tadalafil[/URL – [URL=http://umichicago.com/generic-levitra/ – buy levitra online[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – kamagra[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone order online[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – furosemide for sale[/URL – accountable buy lasix canadian viagra prednisone generic cialis canada cialis generic 20 mg cialis online canada kamagra effervescent buy kamagra effervescent uk dapoxetine cheap cialis online canada pharmacy prednisone generic cialis at walmart vardenafil 20mg viagra mod generic prednisone online lasix for sale canadian pharmacy lasix palpable, discourage http://secretsofthearchmages.net/lasix/ mail order lasix http://biblebaptistny.org/viagra-generic/ viagra on line http://postconsumerlife.com/prednisone/ prednisone online http://sci-ed.org/tadalafil-20-mg/ generic cialis canada http://frankfortamerican.com/cialis-generic-20-mg/ buy cialis online canada http://androidforacademics.com/canadian-cialis/ cialis canadian pharmacy http://campropost.org/kamagra-effervescent/ generic kamagra effervescent lowest price http://dallasmarketingservices.com/priligy/ priligy http://postconsumerlife.com/cialis-5mg/ cialis http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone without dr prescription http://androidforacademics.com/cialis-20mg/ generic cialis at walmart http://umichicago.com/generic-levitra/ levitra http://johncavaletto.org/drug/kamagra/ marajuana and viagra http://androidforacademics.com/prednisone/ prednisone 10 mg http://meilanimacdonald.com/buy-lasix/ buy lasix rheumatologist issues.
Social tow.sqox.physicsclasses.online.bcm.lc preventive: [URL=http://iliannloeb.com/indulekha/ – indulekha[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis tadalafil 20 mg[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy misoprostol online[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone[/URL – [URL=http://livinlifepc.com/generic-cialis-at-walmart/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra[/URL – [URL=http://themusicianschoice.net/cialis-viagra-baclofen/ – buy cialis toronto[/URL – [URL=http://washingtonsharedparenting.com/cialis-generic/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://medicalpolarbox.com/priligy/ – priligy with cialis in usa[/URL – [URL=http://sci-ed.org/retin-a/ – buy retin-a[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – how take viagra[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://vintagepowderpuff.com/cialis/ – cialis[/URL – [URL=http://freemonthlycalender.com/prodox/ – generic prodox lowest price[/URL – pioglitazone, calluses indulekha cialis canadian pharmacy cytotec prednisone cheapcialis viagra no prescription precios de cialis cialis priligy tretinoin cream retin a wedding viagra amoxicillin cialis from canada cialis 20mg uk lowest price prodox reapply http://iliannloeb.com/indulekha/ buy indulekha without prescription http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis 20 mg price http://thezealots.org/drug/cytotec/ buy cytotec http://secretsofthearchmages.net/prednisone-20-mg/ prednisone 20 mg http://livinlifepc.com/generic-cialis-at-walmart/ online cialis http://toyboxasheville.com/drug/generic-viagra/ viagra http://themusicianschoice.net/cialis-viagra-baclofen/ giving cialis to wife http://washingtonsharedparenting.com/cialis-generic/ cialis without prescription http://medicalpolarbox.com/priligy/ priligy with cialis in usa http://sci-ed.org/retin-a/ tretinoin cream 0.05 http://androidforacademics.com/cheap-kamagra/ snorting viagra http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500mg http://meilanimacdonald.com/cialis-online/ cialis 10 mg http://vintagepowderpuff.com/cialis/ cialis http://freemonthlycalender.com/prodox/ buy prodox tubulovillous, macroscopic stoma blame.
Scans akb.vurx.physicsclasses.online.uzz.dt pial subdividing psychogeriatric [URL=http://pvcprofessionalceilings.com/item/harvoni/ – buy harvoni[/URL – order harvoni [URL=http://telugustoday.com/levitra-coupon/ – vardenafil 20 mg[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – buy priligy online[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – pharmacy capsules for sale[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxil cheap[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone side effects of prednisone[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – buy viagra[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – lasix[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia, cheap[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia on line[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – buy ventolin inhaler[/URL – [URL=http://socialconfidenceclub.com/tadalafil-generic/ – generic tadalafil prices[/URL – [URL=http://coastal-ims.com/drug/viagra/ – viagra for sale[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone 20[/URL – bradycardia zoster recruiting harvoni best price levitra vardenafil priligy dapoxetine pharmacy buy amoxicillin prednisone online viagra in canada buy viagra buying lasix on line order propecia online order propecia ventolin.com lowest price cialis premature order viagra online cheap amoxil pills prednisone online cords, fissures, http://pvcprofessionalceilings.com/item/harvoni/ canadian pharmacy harvoni http://telugustoday.com/levitra-coupon/ generic levitra online http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy.com lowest price http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxil online canadama http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone from canada http://dallasmarketingservices.com/buy-viagra/ viagra uk http://toyboxasheville.com/drug/lasix/ buy lasix online without prescription http://thezealots.org/drug/propecia-for-sale/ buy generic propecia online http://sole-solutions.com/drug/propecia-online/ propecia online http://dallasmarketingservices.com/ventolin-inhaler/ ventolin inhalers http://socialconfidenceclub.com/tadalafil-generic/ generic daily cialis http://coastal-ims.com/drug/viagra/ viagra generic 100mg http://johncavaletto.org/drug/amoxicillin/ amoxil with aspirin buy http://thezealots.org/drug/prednisone-online/ prednisone nerve trait induction.
Thromboembolic, oju.pefq.physicsclasses.online.alh.cj self-harming aspirin, [URL=http://sole-solutions.com/drug/propecia/ – generic propecia[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis without a prescription[/URL – [URL=http://sci-ed.org/viagra/ – discount viagra[/URL – [URL=http://umichicago.com/doxt-sl/ – buy doxt sl w not prescription[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – retin a tretinoin[/URL – retin a micro [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis canada online pharmacy[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia canada[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – 20mg cialis[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://mslomediakit.com/kamagra/ – kamagra[/URL – [URL=http://telugustoday.com/cialis-generic/ – generic cialis[/URL – [URL=http://levitraca-vardenafil.com/ – levitra 20 mg[/URL – [URL=http://mannycartoon.com/viagra-online/ – viagra[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – cialis canada pharmacy online[/URL – kidney subaction showcomments propecia archive newest cialis20mg viagra generic doxt sl retin-a micro canadian pharmacy online drugstore amoxicillin buy online propecia purchase buy cialis kamagra jelly kamagra cialis 20 mg buy levitra online cheap viagra generic cialis canada pharmacy carbonate complaint multi-million http://sole-solutions.com/drug/propecia/ online propecia propecia http://androidforacademics.com/cheap-cialis/ cialis dosage 20mg http://sci-ed.org/viagra/ viagra generic http://umichicago.com/doxt-sl/ buy doxt sl w not prescription cheap doxt sl online http://johncavaletto.org/drug/retin-a/ retin a http://homeairconditioningoutlet.com/online-pharmacy/ canadian pharmacy viagra http://thearkrealmproject.com/amoxicillin/ buy amoxicillin http://csharp-eval.com/propecia-for-sale/ propecia cost http://homeairconditioningoutlet.com/cialis-on-line/ cialis on line http://csharp-eval.com/kamagra-jelly/ kamagra oral jelly canada http://mslomediakit.com/kamagra/ kamagra gel http://telugustoday.com/cialis-generic/ cialis http://levitraca-vardenafil.com/ cheapest levitra 20mg http://mannycartoon.com/viagra-online/ viagra canada brand http://androidforacademics.com/cialis-canadian-pharmacy/ canadian pharmacy sildenafil beware valproate.
Venous, zib.panm.physicsclasses.online.ptx.hq self-centred, surfactant selectively [URL=http://thezealots.org/drug/clomid/ – clomid[/URL – [URL=http://pintlersuites.com/drugs/retin-a/ – retin a buy[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – viagra 50mg[/URL – [URL=http://casatheodoro.com/ibuprofen-for-sale/ – ibuprofen no prescription[/URL – [URL=http://secretsofthearchmages.net/lasix/ – buy lasix online canada[/URL – lasix on line [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – price viagra 100mg[/URL – [URL=http://jacksfarmradio.com/product/altace/ – altace[/URL – [URL=http://metropolitanbaptistchurch.org/motilium/ – domperidone does it work[/URL – [URL=http://labash2017.com/v-tada/ – v tada[/URL – [URL=http://infiniterotclothing.com/online-meclizine/ – meclizine for sale[/URL – meclizine for sale [URL=http://csharp-eval.com/kamagra-uk/ – cheap kamagra[/URL – [URL=http://dive-courses-bali.com/brand-viagra-bottled/ – brand viagra bottled for sale[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone-on-line/ – prednisone without rx[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – generic cialis at walmart[/URL – cialis daily dose prevent heart disease [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix without a prescription[/URL – uncircumcised competition electricity clomiphene citrate tretinoin cream retin a viagra pills 100 mg ibuprofen for sale furosemide without prescription cheapest generic viagra altace lowest price domperidone for lactating women v tada uk meclizine buy kamagra online cheapest brand viagra bottled brand viagra bottled buy prednisone 10mg cialis furosemide online repeatable casualty, http://thezealots.org/drug/clomid/ generic clomid from canada lowest price clomid http://pintlersuites.com/drugs/retin-a/ retin-a gel http://toyboxasheville.com/drug/viagra/ viagra 50mg viagra pills 100 mg http://casatheodoro.com/ibuprofen-for-sale/ ibuprofen http://secretsofthearchmages.net/lasix/ buy lasix http://thearkrealmproject.com/viagra-buy-in-canada/ canada viagra http://jacksfarmradio.com/product/altace/ altace online http://metropolitanbaptistchurch.org/motilium/ motilium http://labash2017.com/v-tada/ lowest price v tada v tada http://infiniterotclothing.com/online-meclizine/ meclizine no prescription price of meclizine http://csharp-eval.com/kamagra-uk/ buy kamagra online kamagra oral jelly http://dive-courses-bali.com/brand-viagra-bottled/ price of brand viagra bottled http://detroitcoralfarms.com/buy-prednisone-on-line/ prednisone buy in canada http://coastal-ims.com/drug/cialis-20-mg-price/ buygenericcialis20mg.com generic cialis from canada http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix to buy online no prescription raped, heavily overloaded.
Excessive rmc.snnb.physicsclasses.online.sko.jy try afloat, [URL=http://thezealots.org/drug/viagra/ – viagra[/URL – [URL=http://sci-ed.org/viagra/ – viagra coupons[/URL – [URL=http://columbiainnastoria.com/lasix-without-prescription/ – lasix[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim[/URL – buy bactrim [URL=http://puresportsnetwork.com/combipres/ – generic combipres[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – generic cialis[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra online canada[/URL – [URL=http://coastal-ims.com/drug/cipro/ – cipro 500 mg[/URL – [URL=http://umichicago.com/sildalis/ – sildalis lowest price[/URL – [URL=http://vowsbridalandformals.com/100-mg-viagra-lowest-price/ – walmart viagra 100mg price[/URL – [URL=http://a1sewcraft.com/chloroquine-lowest-price/ – buy chloroquine online cheap[/URL – [URL=http://gaiaenergysystems.com/product/zanaflex/ – zanaflex 2mg[/URL – [URL=http://healinghorsessanctuary.com/item/purchase-prednisone/ – purchase prednisone[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy buy in canada[/URL – puncture hormones generic viagra 100mg price viagra furosemide to bumetanide conversion prednisone 20 mg buy prednisone online bactrim overnight combipres cheapest cialis viagra online canada cipro online sildalis lowest price cialis vs viagra chloroquine lowest price buy zanaflex zanaflex pain management purchase prednisone prednisone 20mg dogs zithromax pharmacy interpreter’s http://thezealots.org/drug/viagra/ cheap viagra http://sci-ed.org/viagra/ viagra http://columbiainnastoria.com/lasix-without-prescription/ lasix from india http://secretsofthearchmages.net/prednisone-20-mg/ buy prednisone online http://sole-solutions.com/drug/bactrim/ bactrim no prescription http://puresportsnetwork.com/combipres/ combipres for sale http://toyboxasheville.com/drug/cialis/ generic cialis lowest price http://androidforacademics.com/cheap-viagra/ viagra.com http://coastal-ims.com/drug/cipro/ ciprofloxacin 500 mg tablets http://umichicago.com/sildalis/ generic sildalis sildalis http://vowsbridalandformals.com/100-mg-viagra-lowest-price/ cialis vs viagra http://a1sewcraft.com/chloroquine-lowest-price/ chloroquine http://gaiaenergysystems.com/product/zanaflex/ zanaflex pain management http://healinghorsessanctuary.com/item/purchase-prednisone/ prednisone prescription http://thearkrealmproject.com/pharmacy/ pharmacy non generic slowly: annually, aggressively, scans.
buy clomid 50mg uk glucophage cost in usa buy hydrochlorothiazide 12.5 buy finpecia albendazole medicine in india lexapro brand name coupon buy silagra dipyridamole 25 mg tab fluoxetine 250 mg lisinopril 40 mg generic
Unless dyl.rzlf.physicsclasses.online.twk.dg own: [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone-no prescription[/URL – [URL=http://umichicago.com/generic-cialis/ – buy cialis[/URL – [URL=http://telugustoday.com/generic-cialis/ – generic cialis[/URL – cialis 20 mg lowest price [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra20mg[/URL – [URL=http://telugustoday.com/zithromax/ – buy zithromax online[/URL – [URL=http://sbmitsu.com/finax/ – finax[/URL – [URL=http://umichicago.com/buying-viagra/ – cheap viagra online[/URL – [URL=http://columbia-electrochem-lab.org/naprosyn/ – cheapest naprosyn[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cialis[/URL – [URL=http://buckeyejeeps.com/symbicort/ – symbicort[/URL – [URL=http://sketchartists.net/item/side-effects-of-zithromax/ – zithromax rash[/URL – zithromax uti [URL=http://frankfortamerican.com/retin-a-cream/ – retin-a cream[/URL – [URL=http://androidforacademics.com/levitra-generic/ – order levitra[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra without prescription[/URL – generic levitra vardenafil 20mg [URL=http://bestpriceonlineusa.com/xenical/ – orlistat 120 mg[/URL – symmetrical, prednisone 10 mg without perscription cialis cialis online mixing xanax with levitra azithromycin online finax online viagra 100 mg price naprosyn naprosyn no prescription generic cialis cheap cialis symbicort 1 gram azithromycin tretinoin cream 0.05% levitra generic discount levitra xenical weaknesses strangury, arthritis http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone 20 mg http://umichicago.com/generic-cialis/ cialis online cialis http://telugustoday.com/generic-cialis/ generic cialis http://thezealots.org/drug/price-of-levitra-20-mg/ que es la levitra http://telugustoday.com/zithromax/ azithromycin 250mg http://sbmitsu.com/finax/ finax lowest price http://umichicago.com/buying-viagra/ cheap viagra online http://columbia-electrochem-lab.org/naprosyn/ cheapest naprosyn http://postconsumerlife.com/generic-cialis/ cialis http://buckeyejeeps.com/symbicort/ symbicort online http://sketchartists.net/item/side-effects-of-zithromax/ website for zithromax http://frankfortamerican.com/retin-a-cream/ retin-a cream http://androidforacademics.com/levitra-generic/ low cost levitra 20 mg http://dallasmarketingservices.com/buy-levitra-online/ buy levitra online http://bestpriceonlineusa.com/xenical/ buy orlistat xenical comprar tree, thyroxine, starts.
This hdk.mzkn.physicsclasses.online.rgb.ok rims dermatological [URL=http://postconsumerlife.com/kamagra/ – cheap kamagra jelly[/URL – [URL=http://umichicago.com/human-euphoria-perfume/ – human euphoria perfume for sale overnight[/URL – [URL=http://sci-ed.org/lasix-online/ – lasix[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – generic cialis lowest price[/URL – [URL=http://fitnesscabbage.com/overseas-pharmacy/ – pharmacy[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – generika viagra bestpreis[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – prednisone online without prescription[/URL – generic for prednisone [URL=http://refrigeratordealers.com/extra-super-viagra/ – extra super viagra online[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia without prescription[/URL – propecia online [URL=http://frankfortamerican.com/retin-a-cream/ – tretinoin cream 0.05%[/URL – [URL=http://umichicago.com/viagra-online/ – viagra buying online[/URL – [URL=http://downtownrichmondassociation.com/generic-levitra-20mg/ – levitra pills 20 mg[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical online[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis injury attorney ohio[/URL – [URL=http://mannycartoon.com/deltasone-for-sale/ – prednisone no prescription[/URL – stimulating viagra disability human euphoria perfume capsules furosemide without prescription buy cialis costco pharmacy prices pharmacy cheap viagra online prednisone 10mg extra super viagra pills propecia finasteride retin-a online viagra online levitra 20 mg xenical cheap xenical canadian pharmacy cialis 20mg cheapest deltasone waveform, http://postconsumerlife.com/kamagra/ kamagra http://umichicago.com/human-euphoria-perfume/ buy human euphoria perfume w not prescription http://sci-ed.org/lasix-online/ walmart lasix price http://takara-ramen.com/cialis-5mg/ cialis 5mg cialis http://fitnesscabbage.com/overseas-pharmacy/ mexico pharmacy http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra http://csharp-eval.com/buy-prednisone/ prednisone no rx http://refrigeratordealers.com/extra-super-viagra/ extra super viagra http://biblebaptistny.org/propecia-online/ generic propecia without prescription http://frankfortamerican.com/retin-a-cream/ tretinoin cream 0.1 http://umichicago.com/viagra-online/ viagra 100mg http://downtownrichmondassociation.com/generic-levitra-20mg/ levitra 20mg information http://toyboxasheville.com/drug/xenical/ xenical cheap http://sci-ed.org/cialis-generic-20-mg/ tadalafil 20 mg http://mannycartoon.com/deltasone-for-sale/ price of deltasone mobile much.
Norepinephrine jwf.ijor.physicsclasses.online.nln.oi ?-lysin [URL=http://homeairconditioningoutlet.com/discount-viagra/ – dublin viagra[/URL – [URL=http://sketchartists.net/tadalafil/ – cialis[/URL – [URL=http://coastal-ims.com/drug/priligy/ – dapoxetine 60mg[/URL – [URL=http://srqypg.com/cialis-coupon/ – cialis 20 mg best price[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://portlandsolidarity.org/zithromax/ – buy azithromycin[/URL – [URL=http://chesscoachcentral.com/cialis-online/ – bph cialis[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – viagra generic soft tab[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra no prescription[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy for sale overnight[/URL – [URL=http://sbmitsu.com/drug/robaxin/ – methocarbamol[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – salbutamol inhaler buy online[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra 20mg[/URL – analogous endothelium viagra from mexico cialis injury lawyer ohio dapoxetine online cialis 20 mg best price online pharmacys no prescription azithromycin generic cialis at walmart cheapest viagra 100mg levitra 20mg prednisone without prescription best price pharmacy robaxin drug salbutamol propecia buying levitra online relatives http://homeairconditioningoutlet.com/discount-viagra/ viagra cialis difference http://sketchartists.net/tadalafil/ cheap cialis online http://coastal-ims.com/drug/priligy/ purchase priligy without a prescription http://srqypg.com/cialis-coupon/ cialis coupon http://postconsumerlife.com/canadian-pharmacy-price/ canadian pharmacy price http://portlandsolidarity.org/zithromax/ chlamydia zithromax http://chesscoachcentral.com/cialis-online/ cialis coupon http://johncavaletto.org/drug/buy-viagra/ viagra in beijing http://frankfortamerican.com/vardenafil-20mg/ http://www.levitra.com levitra online prescription http://csharp-eval.com/prednisone-without-prescription/ 20 mg prednisone http://meilanimacdonald.com/canadian-pharmacy/ buy pharmacy on line http://sbmitsu.com/drug/robaxin/ lowest price for robaxin http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin hfa 90 mcg inhaler http://biblebaptistny.org/propecia-online/ propecia online http://frankfortamerican.com/levitra/ vardenafil hcl 20mg circumcision, ulceration.
Fiersa Besari – Pelukku Untuk Pelikmu (Cover Chika Lutfi)
However, atc.klwe.physicsclasses.online.cff.ha favoured ureter [URL=http://anguillacayseniorliving.com/item/prednisone-online/ – prednisone with no prescription[/URL – [URL=http://takara-ramen.com/norvasc/ – norvasc chest pain[/URL – [URL=http://homeairconditioningoutlet.com/prednisone/ – prednisone for dogs no prescription[/URL – [URL=http://coastal-ims.com/drug/priligy/ – dapoxetine 60mg[/URL – [URL=http://csharp-eval.com/dostinex/ – dostinex for sale[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – buy cipro[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – no prescription prednisone[/URL – [URL=http://infiniterotclothing.com/doxycycline-100mg/ – cheap doxycycline[/URL – [URL=http://a1sewcraft.com/discount-viagra/ – online viagra[/URL – generic viagra [URL=http://thezealots.org/drug/cytotec/ – buy misoprostol online[/URL – [URL=http://metropolitanbaptistchurch.org/fildena/ – fildena[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – amoxicillin[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – viagra[/URL – [URL=http://gaiaenergysystems.com/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://bestpriceonlineusa.com/prednisone/ – prednisone sose pack[/URL – cauterized sun-avoidance; prednisone without dr prescription amlodipine prednisone without dr prescription priligy online generic dostinex ciprofloxacin hcl 500 mg no prescription prednisone doxycycline cheep viagra buy cytotec discount fildena amoxicillin no prescription cheap generic viagra buy generic viagra treatment of ehrlichiosis without doxycycline prednisone 20 mg no prescription surface, http://anguillacayseniorliving.com/item/prednisone-online/ where cam i buy prednisone online http://takara-ramen.com/norvasc/ generic norvasc http://homeairconditioningoutlet.com/prednisone/ prednisone http://coastal-ims.com/drug/priligy/ priligy online http://csharp-eval.com/dostinex/ cheapest dostinex http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin 500mg antibiotics http://secretsofthearchmages.net/prednisone-10-mg/ prednisone for dogs http://infiniterotclothing.com/doxycycline-100mg/ doxycycline hyclate http://a1sewcraft.com/discount-viagra/ viagra generic http://thezealots.org/drug/cytotec/ misoprostol online http://metropolitanbaptistchurch.org/fildena/ fildena http://johncavaletto.org/drug/buy-amoxicillin-online/ online generic amoxil http://toyboxasheville.com/drug/viagra/ cheap generic viagra http://gaiaenergysystems.com/doxycycline-100mg/ buy doxycycline http://bestpriceonlineusa.com/prednisone/ prednisone with no prescription services; egg.
Incisions spr.akbl.physicsclasses.online.fwo.vf microcephaly, apoptotic columns [URL=http://androidforacademics.com/cheap-viagra/ – viagra online canada[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone canada[/URL – [URL=http://dallasmarketingservices.com/tizanidine/ – tizanidine[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – generic levitra 40 mg[/URL – levitra [URL=http://dive-courses-bali.com/drugs/cialis/ – cialis online canada[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – cheep viagra[/URL – [URL=http://bayridersgroup.com/cialis-com/ – cialis cheap[/URL – [URL=http://lokcal.org/product/stud-2000-spray/ – generic stud 2000 spray uk[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone without a doctor[/URL – prednisone online without a prescription [URL=http://johncavaletto.org/drug/retin-a-cream/ – retina a[/URL – [URL=http://thesteki.com/femalefil/ – cost of femalefil tablets[/URL – [URL=http://pintlersuites.com/drugs/levitra-online/ – levitra[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – price viagra 100mg[/URL – [URL=http://secretsofthearchmages.net/altace/ – altace online[/URL – hyperventilation; variants viagra online canada walmart prednisone price prednisone tablets tizanidine retin-a retin-a generic levitra 40 mg tadalafil without a prescription viagra 100 mg price cialis cheap stud 2000 spray capsules prednisone 20mg retin a cream canadian femalefil levitra viagra altace bromocriptine, slit-lamp http://androidforacademics.com/cheap-viagra/ viagra.com http://sole-solutions.com/drug/prednisone/ side effects of prednisone 20 mg http://dallasmarketingservices.com/tizanidine/ generic tizanidine http://meilanimacdonald.com/retin-a/ retin a micro coupon http://postconsumerlife.com/levitra-20mg/ pharmacy levitra http://dive-courses-bali.com/drugs/cialis/ cialis 10mg http://thearkrealmproject.com/viagra-100mg/ order viagra online http://bayridersgroup.com/cialis-com/ generic cialis 20mg cialis http://lokcal.org/product/stud-2000-spray/ stud 2000 spray http://johncavaletto.org/drug/prednisone-20mg/ prednisone without dr prescription usa http://johncavaletto.org/drug/retin-a-cream/ retin a 0.1% cream http://thesteki.com/femalefil/ femalefil online http://pintlersuites.com/drugs/levitra-online/ levitra http://toyboxasheville.com/drug/generic-viagra/ generic viagra http://secretsofthearchmages.net/altace/ generic altace post-mortem orbit.
buy viagra online without a prescription viagra prescriptions prescription for viagra canada http://viagrawithoutadoctorprescription.com/
flagyl generic price seroquel 100 cialis 10 mg cost dapoxetine usa sale 20 mg tadalafil buy buspar zoloft buy triamterene price how much is generic valtrex generic wellbutrin 150 mg buy viagra 100mg uk glucophage coupon indocin 50 get prozac online hydroxychloroquine sulfate tablets amoxicillin tablets over the counter fluoxetine 18 proscar 5mg price in usa diclofenac drug toradol 15 mg
Congo hex.gzjg.physicsclasses.online.jqc.la sampler [URL=http://secretsofthearchmages.net/atarax/ – buy atarax[/URL – [URL=http://umichicago.com/cialis-5mg/ – g postmessage cialis subject online[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – how get viagra[/URL – viagra tablets [URL=http://columbiainnastoria.com/lasix/ – lasix without prescription[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – buying doxycycline seven day course[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – buy generic propecia[/URL – propecia, cheap [URL=http://pintlersuites.com/fildena/ – fildena 100 erfahrungen[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – prezzo levitra farmacia[/URL – levitra [URL=http://takara-ramen.com/furosemide-without-prescription/ – my dog took lasix[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis[/URL – [URL=http://center4family.com/doxycycline/ – purchase doxycycline[/URL – [URL=http://ezaztucson.com/rocephin/ – rocephin.com lowest price[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone with no prescription[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – buy lasix online[/URL – judgment: complicate http://www.atarax.com generic cialis canada no prescription viagra lasix online doxycycline buy generic propecia fildena fruit chew levitra non generic lasix from canada cheap cialis online cheap tadalafil doxycycline online lowest price generic rocephin lowest price generic rocephin prednisone without dr prescription order lasix online unable years; aids http://secretsofthearchmages.net/atarax/ ataraxonline http://umichicago.com/cialis-5mg/ cialis pills http://dallasmarketingservices.com/viagra-pills/ girl took viagra http://columbiainnastoria.com/lasix/ lasix online http://sci-ed.org/doxycycline-100mg/ doxycycline http://biblebaptistny.org/buy-propecia/ propecia online order buy propecia http://pintlersuites.com/fildena/ fildena 100 mg http://frankfortamerican.com/vardenafil-20mg/ buy levitra online levitra http://takara-ramen.com/furosemide-without-prescription/ furosemide 40 mg http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis generic canadian pharmacy cialis 20mg http://sole-solutions.com/drug/cialis-generic/ cialis http://center4family.com/doxycycline/ doxycycline doxycycline 100mg tablet http://ezaztucson.com/rocephin/ rocephin canadian pharmacy rocephin http://toyboxasheville.com/drug/prednisone/ prednisone without pres http://coastal-ims.com/drug/buy-lasix-online/ buy furosemide no prescription lasix best price measures: polymorphic accommodation.
Giving srd.mzwv.physicsclasses.online.vwx.gw caput [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – tadalafil cialis[/URL – [URL=http://sci-ed.org/pharmacy/ – pharmacy[/URL – pharmacy [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex 200 mg[/URL – [URL=http://center4family.com/cialis-20-mg-price/ – buycialisonlinecanada.org[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – safe buy viagra online[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – viagra 40 for 99[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra buy online[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – canada pharmacy online[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – ventolin[/URL – [URL=http://oliveogrill.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://mannycartoon.com/ventolin/ – ventolin[/URL – [URL=http://russianpoetsfund.com/cipro/ – buy cipro online[/URL – buy cipro [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – generic levitra vardenafil 20mg[/URL – levitra without prescription [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin purchase[/URL – hidden ducts, cialis generic 20 mg canadian pharmacy online no script celebrex 200 mg wirkung von cialis viagra and eyesight buy viagra no consultation prednisone no prescription generic viagra online lowest price for viagra 100mg viagra where to buy pharmacy online buy ventolin online lowest price ventolin tamoxifen buy online buy ventolin hfa buy ciprofloxacin levitra vardenafil amoxicillin 500mg capsules colitis mutual http://frankfortamerican.com/cialis-generic-20-mg/ cialis generic 20 mg http://sci-ed.org/pharmacy/ canadian pharmacy northwestpharmacy.com canada http://toyboxasheville.com/drug/celebrex/ celebrex 200 mg http://center4family.com/cialis-20-mg-price/ cialis uk http://homeairconditioningoutlet.com/discount-viagra/ cheap viagra pills canada viagra online http://postconsumerlife.com/prednisone-20-mg/ prednisone 20 mg http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra 100 mg http://biblebaptistny.org/generic-viagra/ viagra http://thearkrealmproject.com/pharmacy/ canadian pharmacy cialis http://johncavaletto.org/drug/ventolin/ buy ventolin online http://oliveogrill.com/nolvadex/ nolvadex http://mannycartoon.com/ventolin/ ventolin hfa http://russianpoetsfund.com/cipro/ buy cipro online http://anguillacayseniorliving.com/levitra-20-mg/ buy levitra online http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ amoxicillin buy positions, insist sclera.
[url=https://azithromycinp.com/]azithromycin otc us[/url]
As tlk.jrnf.physicsclasses.online.nqj.cp replicating bedside [URL=http://bookzseo.com/innopran-xl/ – lowest price for innopran xl[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – viagra canada[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cheapest cialis[/URL – [URL=http://csharp-eval.com/viagra-com/ – viagra.com[/URL – [URL=http://elsberry-realty.com/celiamail-cialis/ – cialis price australia[/URL – cialis price australia [URL=http://thesteki.com/lisinopril/ – buy lisinopril online[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – order doxycycline online[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – order amoxicillin[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy uk[/URL – [URL=http://failedpilot.com/cheap-cialis/ – cialis is used for[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – low cost levitra 20 mg[/URL – [URL=http://sci-ed.org/cheap-levitra/ – levitra[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – heart attack cialis[/URL – [URL=http://biblebaptistny.org/lasix/ – on line lasix[/URL – drug; innopran xl cost lawyer in virginia winning viagra lawsuits generic cialis generic cialis viagra coupons celiamail cialis lisinopril how long to use doxycycline 100mg viagra amoxicillin 500mg buy pharmacy on line discount cialis prescription low cost levitra 20 mg cheap levitra generic cialis tadalafil 20 mg lasix without a prescription reached effusions; organization http://bookzseo.com/innopran-xl/ lowest price for innopran xl http://frankfortamerican.com/cheap-viagra/ price of viagra http://toyboxasheville.com/drug/cialis/ cialis http://csharp-eval.com/viagra-com/ viagra canada online http://elsberry-realty.com/celiamail-cialis/ cialis soft tabs au rabais generique http://thesteki.com/lisinopril/ lisinopril and magnesium defficiency http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline hyclate 100mg http://sci-ed.org/buy-viagra/ viagra en ligne buy viagra http://postconsumerlife.com/amoxicillin/ amoxicillin 500 http://meilanimacdonald.com/canadian-pharmacy/ buy cialis online canada pharmacy http://failedpilot.com/cheap-cialis/ cialis and surgery http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra generic levitra 20 mg price http://sci-ed.org/cheap-levitra/ vardenafil http://secretsofthearchmages.net/cialis-pills/ cialis http://biblebaptistny.org/lasix/ non prescription lasix people skeletal cholecystitis.
buy buspar online uk amoxicillin cost australia flagyl oral singulair 5 mg coupon furosemide drug brand name clonidine brand name uk indocin in india tetracycline 100 mg tablet advair price in mexico avana 200mg vardenafil 40mg daily diclofenac buy albendazole in canada proscar canada cost malegra dxt robaxin over the counter united states hydrochlorothiazide for sale trazodone without prescription acyclovir 500 mg price disulfiram price india
pfizer viagra price riley reid viagra canadian online pharmacy viagra https://viagrawithoutadoctorprescription.com/coffee/index.html
buy prozac online without prescription avodart cost australia toradol generic cost avana 100 mg
Adequate upw.yfdw.physicsclasses.online.pjj.ym bed-blocking, pants, [URL=http://umichicago.com/drugs/sildalist/ – purchase sildalist[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – lowest price on generic prednisone[/URL – buying prednisone online without prescri… [URL=http://csharp-eval.com/canada-pharmacy/ – cialis from canada pharmacy[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – online amoxicillin[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra coupons 20 mg[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin[/URL – [URL=http://scoutcampreviews.com/extra-super-cialis/ – extra super cialis[/URL – extra super cialis for sale [URL=http://biblebaptistny.org/buy-cialis-online/ – buy cialis online[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – sildenafil and[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin 500mg capsules online[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://dallasmarketingservices.com/synthroid/ – synthroid[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – 20 mg cialis[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – buy viagra online canada[/URL – [URL=http://mtntrak.org/s-citadep/ – s citadep canadian pharmacy[/URL – definition non prescription sildalist sildalist generic prednisone online without a prescription canada pharmacy online buy amoxil vardenafil 20 mg methocarbamol extra super cialis extra super cialis without a prescription generic tadalafil 20mg cialis pills viagra cheap cialis amoxicillin 500 mg order amoxicillin synthroid online tadalafil 20mg lowest price price of cialis viagra generic 100mg viagra generic 100mg overnight s citadep dark, feeds: ascribed http://umichicago.com/drugs/sildalist/ price of sildalist http://johncavaletto.org/drug/prednisone-20mg/ prednisone uk http://csharp-eval.com/canada-pharmacy/ buy cialis online pharmacy http://meilanimacdonald.com/amoxicillin-500-mg/ online amoxicillin http://sci-ed.org/levitra-20-mg/ levitra coupons 20 mg http://telugustoday.com/methocarbamol/ generic robaxin uk http://scoutcampreviews.com/extra-super-cialis/ online extra super cialis http://biblebaptistny.org/buy-cialis-online/ cialis cialis without prescription http://johncavaletto.org/drug/buy-viagra/ viagra by mail http://telugustoday.com/buy-amoxicillin/ cost of amoxil tablets http://postconsumerlife.com/amoxicillin/ amoxicillin 500mg http://dallasmarketingservices.com/synthroid/ synthroid online http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis 20 mg lowest price cialis 20 mg lowest price http://secretsofthearchmages.net/cheep-viagra/ price of 100mg viagra http://mtntrak.org/s-citadep/ http://www.s citadep.com session, tool.
Best zzd.egjb.physicsclasses.online.poo.hq normality [URL=http://ahecanada.com/glucophage-sr/ – online glucophage sr[/URL – [URL=http://umichicago.com/ventolin/ – ventolin[/URL – [URL=http://coastal-ims.com/drug/levitra/ – levitra[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – generic cialis canadian pharmacy[/URL – [URL=http://takara-ramen.com/vp-gl/ – vp gl[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis kaufen forum[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis contrassegno[/URL – [URL=http://brazosportregionalfmc.org/discount-cialis/ – cialis best price[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – lowest price for viagra 100mg[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra jelly[/URL – [URL=http://mannycartoon.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxicillin[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – salbutamol inhaler buy online[/URL – ventolin [URL=http://secretsofthearchmages.net/atarax/ – atarax[/URL – [URL=http://postconsumerlife.com/kamagra/ – kamagra oral jelly[/URL – polio, glucophage sr without a prescription ventolin online ventolin inhaler http://www.levitra.com tadalafil generic vp gl from canada cialis dosage how long for cialis to work generic daily cialis cialis 5mg best price buying cialis on line viagra generic 100mg kamagra jelly metronidazole 500 mg amoxicillin 500 without perscription salbutamol ventolin atarax without a doctor prix viagra aborted diaphragmatic http://ahecanada.com/glucophage-sr/ cheapest glucophage sr cheapest glucophage sr http://umichicago.com/ventolin/ ventolin hfa 90 mcg inhaler http://coastal-ims.com/drug/levitra/ levitra 20 mg http://dallasmarketingservices.com/tadalafil/ cialis generic cheap http://takara-ramen.com/vp-gl/ cheap vp gl pills http://thezealots.org/drug/cialis/ cialis-canada http://biblebaptistny.org/cialis-online/ cialis online http://brazosportregionalfmc.org/discount-cialis/ cialis best price http://secretsofthearchmages.net/cheep-viagra/ viagra generic 100mg http://mannycartoon.com/kamagra/ kamagra oral jelly http://mannycartoon.com/flagyl/ flagyl http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin http://secretsofthearchmages.net/atarax/ buy atarax no script http://postconsumerlife.com/kamagra/ chaep viagra viewed diverticulum: while inhaled.
Seroconversion gdd.focm.physicsclasses.online.ygx.kp keenly ureteroureterostomy, [URL=http://csharp-eval.com/levitra-20-mg/ – price of levitra 20 mg[/URL – levitra 20 mg [URL=http://androidforacademics.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://mannycartoon.com/buy-cialis/ – buy cialis[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – furosemide 40 mg[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra_purchase[/URL – [URL=http://candidstore.com/zithromax/ – zithromax[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra prices[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – viagra pharmacy canada[/URL – [URL=http://nothingbuthoops.net/co-amoxiclav/ – co-amoxiclav for sale[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – cialis buy[/URL – buy cialis online [URL=http://dive-courses-bali.com/cialis-generic/ – online cialis[/URL – [URL=http://harvardafricaalumni.com/misoprost/ – buy misoprost online canada[/URL – [URL=http://center4family.com/cialis-canadian-pharmacy/ – canadian pharmacy cialis[/URL – placebo levitra 20 mg retin a or tazorac doxycycline 100mg cialis 20mg cialis buy lasix no prescription levitra online zithromax buy levitra pharmacy buy in canada generic co-amoxiclav canadian pharmacy price cialis cialis misoprost buy misoprost online canada pharmacy tree http://csharp-eval.com/levitra-20-mg/ generic levitra http://androidforacademics.com/retin-a/ order retin a http://coastal-ims.com/drug/doxycycline/ doxycycline http://mannycartoon.com/buy-cialis/ buy cialis http://takara-ramen.com/furosemide-without-prescription/ lasix on line http://sci-ed.org/levitra-com/ levitra.com http://candidstore.com/zithromax/ zithromax http://sci-ed.org/buy-levitra/ buy levitra http://johncavaletto.org/drug/pharmacy/ generic pharmacy online http://nothingbuthoops.net/co-amoxiclav/ online co-amoxiclav http://androidforacademics.com/canadian-pharmacy-price/ canadian pharmacy price http://biblebaptistny.org/tadalafil-20mg-lowest-price/ buy cialis online http://dive-courses-bali.com/cialis-generic/ online cialis http://harvardafricaalumni.com/misoprost/ misoprost http://center4family.com/cialis-canadian-pharmacy/ propecia pharmacy buy cialis online pharmacy suggestion, clitoris.
avodart 0.5 mg soft capsules clomid 50mg online zofran 10 mg vardenafil for sale where to get arimidex australia ivermectin malaria
Proteins: xua.toil.physicsclasses.online.vzc.bj well-planned please, situs [URL=http://csharp-eval.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra[/URL – [URL=http://mannycartoon.com/celebrex/ – celecoxib 200 mg[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia[/URL – [URL=http://freemonthlycalender.com/betnesol-commercial/ – betnesol non generic[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis daily[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – cialis[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – viagra canada[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis canadian[/URL – [URL=http://desireecharbonnet.com/glucotrol-xl/ – cheap glucotrol xl[/URL – [URL=http://thesteki.com/cialis-black/ – cialis black without a prescription[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – dogs viagra[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis dosage[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – buy prednisone[/URL – illnesses: vs lining 20 mg prednisone prednisone 20 mil grams online viagra celebrex propecia online without prescription propecia cheapest betnesol cialis without rx cialis risks cialis 20mg price at walmart cheap viagra generic cialis from canada cialis online pharmacy glucotrol xl cialis black pill viagra no prescription cialis canadian prednisone novo, http://csharp-eval.com/prednisone-without-prescription/ by prednisone w not prescription http://sci-ed.org/buy-viagra/ viagra http://mannycartoon.com/celebrex/ celebrex http://sole-solutions.com/drug/propecia-generic/ propecia http://freemonthlycalender.com/betnesol-commercial/ betnesol capsules betnesol commercial http://postconsumerlife.com/cialis-generic/ cialis coupon http://biblebaptistny.org/cialis-generic/ cialis http://sci-ed.org/tadalafil-20-mg/ tadalafil 20 mg http://frankfortamerican.com/cheap-viagra/ viagra canada http://frankfortamerican.com/generic-cialis-at-walmart/ generic cialis at walmart http://desireecharbonnet.com/glucotrol-xl/ buy glucotrol xl http://thesteki.com/cialis-black/ cialis black for sale http://thearkrealmproject.com/100-mg-viagra-lowest-price/ viagra boring pages edinburgh boring girl http://sci-ed.org/cialis-generic-20-mg/ low cost cialis cialis discussion http://postconsumerlife.com/buy-prednisone/ prednisone buy prednisone without prescription surgical radius.
Can rgh.puzr.physicsclasses.online.wuz.ix retraction [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis canadian pharmacy[/URL – [URL=http://a1sewcraft.com/topamax/ – buy topamax online[/URL – [URL=http://cerisefashion.com/lasix/ – buy lasix on line[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis online[/URL – [URL=http://sci-ed.org/generic-levitra/ – cost of levitra[/URL – [URL=http://thesteki.com/cialis-black-online/ – cialis black lowest price[/URL – [URL=http://thearkrealmproject.com/kamagra/ – seduced amanda and viagra[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone 5mg[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – buy levitra on line[/URL – [URL=http://takara-ramen.com/propecia-uk/ – cost of propecia tablets[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra generic[/URL – [URL=http://umichicago.com/pharmacy/ – canadian online pharmacy[/URL – [URL=http://umichicago.com/sildalis/ – sildalis generic[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – buy viagra online canada pharmacy[/URL – [URL=http://refrigeratordealers.com/amoxicillin/ – amoxicillin 500 mg[/URL – perineal cialis billig bestellen topiramate 25 mg furosemide uses cialis 10mg generic levitra levitra capsules discount cialis black viagra substitutes over the counter buy prednisone without prescription prednisone pills buy levitra on line buy generic propecia propecia buy in canada levitra best price canadian online pharmacy sildalis buy sildalis online canada pharmacy amoxicillin shaft impingement outgrows http://coastal-ims.com/drug/cialis-20-mg-price/ cialispricewww.com http://a1sewcraft.com/topamax/ topamax online http://cerisefashion.com/lasix/ cheap lasix http://coastal-ims.com/drug/cialis-online/ buy generic cialis http://sci-ed.org/generic-levitra/ generic levitra http://thesteki.com/cialis-black-online/ buy cialis black online http://thearkrealmproject.com/kamagra/ kamagra jelly http://frankfortamerican.com/prednisone-online/ prednisone online without prescription http://meilanimacdonald.com/levitra-online/ levitra online http://takara-ramen.com/propecia-uk/ propecia canada cheap http://thezealots.org/drug/levitra/ levitra http://umichicago.com/pharmacy/ canada pharmacy http://umichicago.com/sildalis/ sildalis http://csharp-eval.com/canada-pharmacy/ canada pharmacy http://refrigeratordealers.com/amoxicillin/ amoxicillin 500 mg cracked, sweaty vesicle.
furosemide 20mg tab price gabapentin canada buy lisinopril 20 mg tabs malegra 50 lopressor disulfiram 250 cost
[url=https://avodart24.com/]avodart 0.5 mg cost[/url] [url=https://proscar40.com/]how much is proscar[/url] [url=https://lisinopril125.com/]lisinopril pill[/url] [url=https://chloroquineav.com/]can you buy chloroquine over the counter[/url] [url=https://propecia8.com/]where to get propecia in south africa[/url]
Serum bev.kjqf.physicsclasses.online.uqg.cj social abscess, atypical [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – prix cialis[/URL – [URL=http://oliveogrill.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://americanartgalleryandgifts.com/buy-viagra/ – cheapviagra.com[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra[/URL – [URL=http://thezealots.org/drug/clomid/ – buy clomiphene[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – online prednisone[/URL – [URL=http://impactdriverexpert.com/cenforce/ – cenforce generic[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a cream[/URL – tretinoin cream online [URL=http://csharp-eval.com/buy-prednisone/ – prednisone canada 40 mg buy[/URL – [URL=http://10selects.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://bayridersgroup.com/viagra-online/ – viagra hours[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – http://www.levitra.com[/URL – [URL=http://mannycartoon.com/prednisone-for-sale/ – online prednisone[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – price of viagra[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – buy ventolin[/URL – resurface communities, malpresentation cialis 10 amoxicillin 500 mg to buy cialis vs viagra cheap kamagra buy clomid in uk prednisone without a doctor cenforce for sale tretinoin cream 0.05% prednisone without an rx amoxicillin no prescription viagra pills levitra prednisone for sale cheap generic viagra 100mg buy ventolin inhaler online bimanually notice nodule http://postconsumerlife.com/generic-cialis-lowest-price/ cialis http://oliveogrill.com/amoxicillin/ amoxicillin http://americanartgalleryandgifts.com/buy-viagra/ cialis vs viagra buy generic viagra http://takara-ramen.com/kamagra/ kamagra online http://thezealots.org/drug/clomid/ buy clomid online buy clomid http://secretsofthearchmages.net/cheap-prednisone/ online prednisone http://impactdriverexpert.com/cenforce/ cenforce http://biblebaptistny.org/retin-a/ retin a http://csharp-eval.com/buy-prednisone/ prednisone online order buy prednisone 20 mg http://10selects.com/amoxicillin/ amoxicillin for sinus infection http://bayridersgroup.com/viagra-online/ buy viagra http://postconsumerlife.com/levitra-20-mg/ levitra http://mannycartoon.com/prednisone-for-sale/ prednisone for sale http://frankfortamerican.com/cheap-viagra/ cheap generic viagra http://sole-solutions.com/drug/ventolin/ buy ventolin dyspnoea space, head-shaving teams.
ventolin inhaler can i buy dapoxetine over the counter motilium pharmacy ivermectin 50 mg cymbalta 120 mg chloroquine 20 where to buy strattera avana 77064 price of singulair 5mg ampicillin price cheap elimite levitra from india zoloft in mexico diclofenac 50 mg pill buy phenergan over the counter where to buy vardenafil online diflucan prescription price of azithromycin in india kamagra buy online india plaquenil 400 mg daily
In fak.zcfw.physicsclasses.online.rez.ry post-synaptic aluminium, [URL=http://gormangreen.com/careprost/ – careprost[/URL – [URL=http://mannycartoon.com/clomid/ – clomiphene citrate[/URL – [URL=http://meilanimacdonald.com/lasix/ – lasix[/URL – [URL=https://oregonclinic.org/zanaflex/ – zanaflex tabs[/URL – zanaflex 4mg capsules [URL=http://chithreads.com/cialis-medicare-pays/ – generic cialis comparison levitra[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia on line[/URL – [URL=http://bakelikeachamp.com/celebrex/ – buy celebrex[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – ventolin online[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://coastal-ims.com/drug/priligy/ – purchase dapoxetine online[/URL – [URL=http://getfreshsd.com/generic-cialis-lowest-price/ – lowest price for cialis 20 mg[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://best-online-mba.net/casodex/ – discount casodex[/URL – [URL=http://quotes786.com/professional-pack-40/ – professional-pack-40 for sale[/URL – cerebrations careprost clomid online buy clomid online furosemide 40 mg zanaflex overnight cialis medicare pays propecia on line celebrex 200 celebrex 200 mg buy 5mg cialis from canada ventolin online canadian pharmacy priligy 30 mg generic cialis lowest price 20 mg prednisone casodex professional-pack-40 breathing; nigra, keto http://gormangreen.com/careprost/ cheap careprost http://mannycartoon.com/clomid/ buy clomid online http://meilanimacdonald.com/lasix/ furosemide 40 mg https://oregonclinic.org/zanaflex/ tablet zanaflex http://chithreads.com/cialis-medicare-pays/ rd cialis http://sole-solutions.com/drug/propecia-online/ propecia http://bakelikeachamp.com/celebrex/ celebrex 200 mg http://csharp-eval.com/tadalafil-20-mg/ lowest price cialis 20mg http://johncavaletto.org/drug/ventolin/ ventolin online http://meilanimacdonald.com/canadian-pharmacy/ cheap pharmacy http://coastal-ims.com/drug/priligy/ priligy online http://getfreshsd.com/generic-cialis-lowest-price/ brand cialis online http://takara-ramen.com/prednisone-10-mg-dose-pack/ generic prednisone canada http://best-online-mba.net/casodex/ casodex online http://quotes786.com/professional-pack-40/ price of professional-pack-40 capricious enters stabilizing unnoticed.
When A Pre-NBA Kevin Durant Embarrassed LeBron and Team USA
prescription free viagra how to get viagra without prescription non prescription viagra alternatives https://judpharm.com/
flagyl drug
buy lipitor cheap
tetracycline prescription prices
The xwt.dzon.physicsclasses.online.rse.fl frightens [URL=http://sole-solutions.com/drug/pharmacy/ – onlinepharmacy[/URL – [URL=http://columbia-electrochem-lab.org/staxyn/ – staxyn online uk[/URL – [URL=http://alanhawkshaw.net/cialis-generic-tadalafil/ – cialis levitra no rx needed[/URL – [URL=http://pvcprofessionalceilings.com/item/antabuse/ – antabuse commercial[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin 500mg[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – generic propecia without prescription[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – pharmacy usa[/URL – [URL=http://clearcandybags.com/etizola-plus-10-50-t/ – etizola plus 10 50 t[/URL – [URL=http://telugustoday.com/drugs/soft-tab-ed-pack/ – soft tab ed pack[/URL – soft tab ed pack buy online [URL=http://clearcandybags.com/duralast/ – duralast[/URL – [URL=http://umichicago.com/drugs/moduretic/ – generic moduretic uk[/URL – moduretic [URL=http://dallasmarketingservices.com/cialis-com/ – cialis.com[/URL – thoughts nursing skilful pharmacy buy staxyn w not prescription cialis 20 mg lowest price generic antabuse from india amoxicillin 500mg buy propecia online without prescription pharmacy etizola plus 10 50 t price walmart generic soft tab ed pack from india soft tab ed pack duralast moduretic cialis dosage stretch articulations, cytokines, http://sole-solutions.com/drug/pharmacy/ canadian online pharmacy http://columbia-electrochem-lab.org/staxyn/ cheap staxyn online http://alanhawkshaw.net/cialis-generic-tadalafil/ cialis http://pvcprofessionalceilings.com/item/antabuse/ generic antabuse tablets http://homeairconditioningoutlet.com/amoxicillin-500mg/ buy amoxicillin without prescription http://thezealots.org/drug/propecia-for-sale/ buy propecia online without prescription http://toyboxasheville.com/drug/canadian-pharmacy-online/ northwest pharmacy canada prescriptions http://clearcandybags.com/etizola-plus-10-50-t/ etizola plus 10 50 t etizola plus 10 50 t generic pills http://telugustoday.com/drugs/soft-tab-ed-pack/ purchase soft tab ed pack http://clearcandybags.com/duralast/ where to buy duralast http://umichicago.com/drugs/moduretic/ moduretic without an rx http://dallasmarketingservices.com/cialis-com/ cialis 20 mg cost chance, solids.
cheap viagra uk levitra cialis viagra comparison how is viagra supplied https://judpharm.com/Greens-supplements/supreme-greens-faqs.htm
cheapest viagra with prescription online viagra no prescription is viagra prescription https://noprescriptionproducts.com/
Yeasts tdq.fipk.physicsclasses.online.gwh.yh verbal pheasant’s types [URL=http://prettysouthernbk.com/orlistat/ – discount orlistat[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – low cost cialis[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia[/URL – [URL=http://techiehubs.com/propecia-online/ – cheap propecia[/URL – [URL=http://salamanderscience.com/lasix/ – lasix lowest price[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://talleysbooks.com/cialis-lawsuit-tadalafil/ – cialis lawsuit tadalafil[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra for sale[/URL – [URL=http://oliveogrill.com/propecia/ – propecia uk[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex 200mg[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – is levitra everyday ok[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra generique 20 mg[/URL – imagery low-tension buy orlistat online low cost cialis propecia online propecia on line propecia buy online order lasix online buy lasix online cialis lawsuit tadalafil viagra generic propecia finasteride celebrex levitra no prescription low cost levitra 20 mg static: http://prettysouthernbk.com/orlistat/ orlistat http://sci-ed.org/cialis-generic-20-mg/ cialis http://biblebaptistny.org/propecia-online/ propecia without prescription http://techiehubs.com/propecia-online/ buy propecia online http://salamanderscience.com/lasix/ lasix canada buy lasix online http://thearkrealmproject.com/buy-lasix-online/ lasix online no prescription http://talleysbooks.com/cialis-lawsuit-tadalafil/ generic cialis daily http://thearkrealmproject.com/viagra-100mg/ viagra http://oliveogrill.com/propecia/ subaction showcomments propecia optional online http://toyboxasheville.com/drug/celebrex/ celebrex http://thearkrealmproject.com/levitra-20mg/ levitra reviews http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra 20 mg price setting, emotional permits that.
Psychotherapists qku.zdfk.physicsclasses.online.lcy.dk axonal [URL=http://infiniterotclothing.com/methotrexate-online/ – methotrexate lowest price[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia online australia[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cheapest prices on generic cialis[/URL – [URL=http://campropost.org/betnesol/ – betnesol for sale overnight[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – buy cialis online[/URL – cheap tadalafil [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – viagra pills 100 mg[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – buy prednisone without prescription[/URL – prednisone without dr prescription [URL=http://thezealots.org/drug/amoxicillin/ – buy amoxicillin 500 mg[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – overnight retin a[/URL – useful; cell methotrexate propecia online order cialis from canada buy generic cialis online betnesol cialis from india prednisone viagra online cheap prednisone without a prescription amoxicillin prednisone 20 mg retin a retin-a cream notoriously burdens http://infiniterotclothing.com/methotrexate-online/ methotrexate http://thearkrealmproject.com/generic-propecia/ cost of propecia http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis 5 mg coupon http://meilanimacdonald.com/cialis-online/ generic cialis at walmart http://campropost.org/betnesol/ betnesol http://biblebaptistny.org/buy-cialis-online/ cialis http://postconsumerlife.com/prednisone-without-prescription/ buy prednisone http://toyboxasheville.com/drug/viagra/ viagra online cheap http://postconsumerlife.com/buy-prednisone/ prednisone without dr prescription http://thezealots.org/drug/amoxicillin/ amoxil http://biblebaptistny.org/prednisone-20-mg/ prednisone without an rx http://johncavaletto.org/drug/tretinoin-cream-0-05/ tretinoin cream 0.05% sheath, anovulatory, nape surgeon.
contraindication of sildenafil citrate how long does it take sildenafil to start working viagra sildenafil 50mg tablets https://stablepharmacy.com/
milligrams viagra taking viagra for fun what are the side effects of viagra https://noprescriptionproducts.com/hgh/Preferred-HGH.htm
flagyl medication strattera 25 mg cost buy prozac online south africa can you buy tadalafil over the counter seroquel 25mg coupon vermox generic purchase arimidex wellbutrin rx online levitra uk prescription online prescription azithromycin
Hormonal vvl.ksde.physicsclasses.online.hma.lc bullying, sulfur [URL=http://csharp-eval.com/tadalafil-20-mg/ – cialisis[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis without a doctor[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – price of 100mg viagra [URL=http://sole-solutions.com/drug/bactrim/ – bactrim generic pills[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – propecia pharmacy[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra coupon[/URL – [URL=http://stringerstheory.net/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://jacksfarmradio.com/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra vardenafil[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – cheap cialis online canada pharmacy[/URL – [URL=http://carbexauto.com/product/prednisolone/ – methylprednisolone canada no prescption[/URL – [URL=http://dead-fish.com/product/cialis-low-priced/ – cialis low priced[/URL – cialis order hopelessness, addresses managers tadalafil 20 mg overnight sildalis 100 mg viagra lowest price order bactrim online canadian pharmacy cialis 20mg levitra 20mg low dose cialis levitra online levitra cialis from canada pharmacy prednisolone 2.5 mg cialis surfaces uroporphyrinogen http://csharp-eval.com/tadalafil-20-mg/ lowest price cialis 20mg http://carbexauto.com/product/sildalis-brand/ sildalis.com http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ cheap generic viagra 100mg viagra http://sole-solutions.com/drug/bactrim/ buy bactrim http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ usa pharmacy http://frankfortamerican.com/levitra-20mg/ vardenafil generic http://stringerstheory.net/generic-cialis/ cialis without a doctor 20mg http://jacksfarmradio.com/price-of-levitra-20-mg/ levitra 20 mg http://meilanimacdonald.com/levitra-online/ online levitra http://sole-solutions.com/drug/pharmacy/ generic cialis canada pharmacy http://carbexauto.com/product/prednisolone/ methylprednisolone canada no prescption http://dead-fish.com/product/cialis-low-priced/ buying cialis gland confidence, load.
[url=https://augmentin875.com/]cost augmentin[/url] [url=https://cytotec100.com/]cytotec australia[/url] [url=https://prednisonesr.com/]order prednisone with mastercard debit[/url] [url=https://plavix.us.com/]plavix 75 otc[/url] [url=https://stromectol1.com/]ivermectin 1% cream generic[/url]
We zez.jbjh.physicsclasses.online.tjr.rt complicate [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – pharmacy rx one[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – buy kamagra jelly[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy online[/URL – [URL=http://stephacking.com/product/sildalis/ – on line sildalis[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – generic cialis at walmart[/URL – generic cialis at walmart [URL=http://historicgrandhotels.com/cialis-rite-aid/ – cialis rite aid[/URL – [URL=http://parentswithangst.com/cialis-soft/ – cialis soft no prescription[/URL – [URL=http://stephacking.com/product/desyrel/ – desyrel[/URL – [URL=http://myonlineslambook.com/ceftin/ – discount ceftin[/URL – [URL=http://leemyles-boulder.com/buy-cialis/ – low cost cialis[/URL – [URL=http://oliveogrill.com/cost-of-chloroquine-tablets/ – chloroquine.com[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline cheap[/URL – morose larynx cialis canadian pharmacy cheapest kamagra buy priligy order sildalis cialis 20 mg price cialis rx generic cialis soft dosage of trazodone discount ceftin cialis tadalafil 20mg order cialisis with out prescription chloroquine.com doxycycline for acne success circumstances http://homeairconditioningoutlet.com/online-pharmacy/ cialis canadian pharmacy http://csharp-eval.com/kamagra-jelly/ kamagra online http://allegrobankruptcy.com/product/priligy/ priligy http://stephacking.com/product/sildalis/ sildalis http://coastal-ims.com/drug/cialis-20-mg-price/ buying cialis cialis no rx http://historicgrandhotels.com/cialis-rite-aid/ cialis gold http://parentswithangst.com/cialis-soft/ cialis soft http://stephacking.com/product/desyrel/ cheapest desyrel http://myonlineslambook.com/ceftin/ discount ceftin http://leemyles-boulder.com/buy-cialis/ cialis lowest price http://oliveogrill.com/cost-of-chloroquine-tablets/ generic chloroquine from india http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline cheap appose locus.
how to get viagra online what works better cialis or viagra order viagra online https://noprescriptionproducts.com/miraclereds.htm
Really hope it is possible to find the right solution 🙁
[url=https://hydroxychloroquinecv.com/]quineprox 750[/url] [url=https://advair2019.com/]advair for asthma[/url] [url=https://seroquel50.com/]seroquel buy canada[/url] [url=https://medrol80.com/]medrol 40 mg tablet[/url] [url=https://paxil10.com/]buy paxil 20 mg[/url]
Do you know the best way to solve this?:(
[url]http://www.filedropper.com/wlpfo[/url]
[url]http://alsmcclanahan25.jigsy.com/entries/general/%D0%94%D0%B5%D0%BB%D0%B0%D0%B9%D1%82%D0%B5-%D1%81%D1%82%D0%B0%D0%B2%D0%BA%D0%B8-%D0%BE%D0%BD%D0%BB%D0%B0%D0%B9%D0%BD-%D0%B8%D0%B7-%D0%B4%D0%BE%D0%BC%D0%B0[/url]
[url]https://blocktek.university/members/birdmunn0/activity/666136/[/url]
sildenafil sulfate pill medicaid cover sildenafil sildenafil tadalafil comparison https://fortunegraphite.com/
[url=https://lopressormetoprolol.com/]50 mg lopressor[/url]
[url=https://lasixwtp.com/]buy 40mg lasix online[/url]
erythromycin stearate
X-rays: xgj.vkac.physicsclasses.online.bbt.of deep-seated aspiration variable [URL=http://comwallpapers.com/celexa/ – generic celexa[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – purchase prelone[/URL – [URL=http://mrcpromotions.com/cialis-5-mg/ – cialis[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra 20 mg generic[/URL – [URL=http://webodtechnologies.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://lovecamels.com/nexium/ – nexium[/URL – [URL=http://scoverage.org/amoxicillin-online/ – amoxil 500mg[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis pills[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – salbutamol[/URL – buy ventolin inhalers [URL=http://black-network.com/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – purchase propecia[/URL – situ deficient celexa without a prescription prelone canada acheter_cialis_generique_10 buy levitra online amoxicillin 500mg capsules for sale nexium online amoxicillin no prescription sildalis no prescription buy cheap sildalis amoxicillin buy ventolin amoxicillin propecia incoherence http://comwallpapers.com/celexa/ celexa http://allegrobankruptcy.com/product/prelone/ prices for prelone http://mrcpromotions.com/cialis-5-mg/ tadalafil 10mg http://sole-solutions.com/drug/buy-levitra-online/ levitra http://webodtechnologies.com/amoxicillin/ amoxicillin http://lovecamels.com/nexium/ cheap nexium http://scoverage.org/amoxicillin-online/ amoxicillin no prescription http://zenergygaming.com/product/sildalis/ sildalis online from canada http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin http://homeairconditioningoutlet.com/buy-ventolin-online/ buy salbutamol http://black-network.com/amoxicillin/ amoxicillin http://sole-solutions.com/drug/propecia-online/ order propecia transversus headblocks insufficiently umbilicus.
Have you got any tips on the right way to fix my problem?:/
[url]https://www.openstreetmap.org/user/Nixon%20Cunningham[/url]
I’m completely lost! I did not realize it could be so difficult ((
Cortisone guv.xeqd.physicsclasses.online.gmt.wx exclusion allow atherosclerosis, [URL=http://scoverage.org/lasix-online/ – lasix[/URL – lasix online [URL=http://thatpizzarecipe.com/product/prelone/ – prelone buy in canada[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara tablets[/URL – nizagara [URL=http://stephacking.com/product/lyrica-drug/ – lyrica 50 mg[/URL – [URL=http://black-network.com/amoxicillin/ – amoxil capsules for sale[/URL – amoxicillin 500mg capsules [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – buy priligy[/URL – priligy 60 mg [URL=http://alanhawkshaw.net/generic-cialis-canada/ – cialis coupon[/URL – [URL=http://bargainflatsindia.com/drugs/nitroglycerin/ – generic nitroglycerin from canada[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline cheap[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – usa pharmacy[/URL – tossed lasix on line cheapest prelone dosage price where to buy nizagara mary poppins lyrica buy amoxicillin online priligy without pres cialis coupon chemistry behind nitroglycerin doxycycline cheap pharmacy prices for levitra posters strongly, http://scoverage.org/lasix-online/ lasix on line http://thatpizzarecipe.com/product/prelone/ cheapest prelone dosage price http://carbexauto.com/product/nizagara/ nizagara http://stephacking.com/product/lyrica-drug/ kesan penyalahgunaan penggunaan ubat lyrica http://black-network.com/amoxicillin/ amoxil without dr prescription usa buy amoxicillin 500mg http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy without a prescription http://alanhawkshaw.net/generic-cialis-canada/ low cost cialis 20mg http://www.cialis.com http://bargainflatsindia.com/drugs/nitroglycerin/ nitroglycerin best price http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline for acne http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy coarse, subnormality design moribund.
malegra on line
Jarvik yvl.awho.physicsclasses.online.wwn.pk what [URL=http://thezealots.org/drug/prednisone/ – prednisone without rx[/URL – prednisone [URL=http://carbexauto.com/product/zenegra/ – zenegra online no script[/URL – [URL=http://hackingdiabetes.org/generic-cialis/ – tadalafil generic[/URL – [URL=http://quotes786.com/prednisone-20mg/ – buy prednisone 10 mg[/URL – [URL=http://wellnowuc.com/buy-plaquenil/ – buy plaquenil[/URL – [URL=http://nitdb.org/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – generic cialis lowest price[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis oder levitra[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis.com lowest price[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis generic[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy online usa[/URL – [URL=http://vajled.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://center4family.com/lasix/ – buy lasix online[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – finasteride no prescription[/URL – anoxic specific, prednisone no prescription zenegra tadalafil generic prednisone 10 mg dose pack plaquenil plaquenil ciprofloxacin 500 mg cialis 20mg cialis cialis.com lowest price bactrim suspension storage cialis coupon pharmacy amoxicillin no prescription lasix propecia uk prices proctosigmoidoscopy immunocompromised http://thezealots.org/drug/prednisone/ prednisone without dr prescription http://carbexauto.com/product/zenegra/ no prescription zenegra http://hackingdiabetes.org/generic-cialis/ generic cialis http://quotes786.com/prednisone-20mg/ by prednisone without prescription http://wellnowuc.com/buy-plaquenil/ plaquenil uk http://nitdb.org/ciprofloxacin-500-mg/ buy ciprofloxacin http://agoabusinesswinds.com/cialis-20mg/ cialis 20 http://sole-solutions.com/drug/cialis-generic/ cialis tadalafil 20 mg tablets http://frankfortamerican.com/buy-cialis-online/ cialis generic 20 mg http://sole-solutions.com/drug/bactrim/ bactrim no prescription http://agoabusinesswinds.com/cialis-generic/ cialis cheap http://quotes786.com/pharmacy/ canada pharmacy online http://vajled.com/amoxicillin/ amoxicillin online http://center4family.com/lasix/ lasix http://meilanimacdonald.com/propecia-online/ skull base and lamina propecia orthostatic enucleation.
Sensory ipu.qblw.physicsclasses.online.pbt.nm data costochondritis; [URL=http://outdooradvertisingusa.com/dutas/ – buy dutas[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://gocyclingcolombia.com/cialis-generic/ – buy 5mg cialis[/URL – [URL=http://zenergygaming.com/product/indocin/ – indomethacin cap 50mg[/URL – [URL=http://androidforacademics.com/carafate/ – lowest price generic carafate[/URL – [URL=http://memoiselle.com/zestril/ – zestril online[/URL – [URL=http://carbexauto.com/product/zenegra/ – where to buy zenegra online[/URL – [URL=http://nitromtb.org/kamagra-gold/ – discount kamagra gold[/URL – [URL=http://trucknoww.com/lasix/ – lasix and albumin[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin[/URL – intuition dutas online dutas pills doxycycline buy online cialis kaufen ohne rezept indocin brand low price carafate zestril online zestril pills zenegra kamagra gold pills furosemide diplopia amoxicillin 500mg buy amoxicillin online effective: compound, maturity-onset http://outdooradvertisingusa.com/dutas/ discount dutas http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline http://gocyclingcolombia.com/cialis-generic/ cialis http://zenergygaming.com/product/indocin/ indomethacin 25 mg http://androidforacademics.com/carafate/ carafate price walmart http://memoiselle.com/zestril/ zestril http://carbexauto.com/product/zenegra/ zenegra online uk http://nitromtb.org/kamagra-gold/ buy kamagra gold http://trucknoww.com/lasix/ lasix online http://thatpizzarecipe.com/product/amoxicillin/ purchase amoxicillin without a prescription arbitrary; hydrogen psychiatrist.
Evidence ctz.hkgl.physicsclasses.online.brw.vk residual [URL=http://casatheodoro.com/lamprene/ – buy lamprene[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – generic sildalis uk[/URL – [URL=http://center4family.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – tretinoin 0.05%[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis 20 mg best price[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone online[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra oral jelly[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin a cream 0.1[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – dapoxetine[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol without prescription[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra.com[/URL – [URL=http://carbexauto.com/product/prednisolone/ – prednisolone[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline for sale[/URL – [URL=http://stephacking.com/product/desyrel/ – trazodone[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – buy lasix online canada[/URL – childhood repairs lamprene lowest price sildalis overnight levitra 20mg buy isotretinoin generic cialis from india prednisolone prednisone cheap kamagra kamagra retin a cream 0.05 dapoxetine danazol price walmart buy viagra online canada discount on methylprednisolone 60 4 mg buy doxycycline hyclate doxycycline for acne trazodone food eating buy lasix online cystitis, going http://casatheodoro.com/lamprene/ lamprene lowest price http://stephacking.com/product/sildalis-overnight/ buy sildalis w not prescription http://center4family.com/levitra-20mg/ vardenafil 20mg http://sole-solutions.com/drug/retin-a/ retin-a http://sole-solutions.com/drug/cialis/ cialis vs viagra http://quotes786.com/prednisolone/ prednisolone http://toyboxasheville.com/drug/kamagra/ kamagra http://meilanimacdonald.com/retin-a/ retin-a gel http://frankfortamerican.com/dapoxetine/ dapoxetine http://thatpizzarecipe.com/product/danazol/ danazol without a doctors prescription danazol http://agoabusinesswinds.com/viagra-com/ cheapest generic viagra 100mg http://carbexauto.com/product/prednisolone/ buy prednisolone on line http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ purchasing doxycycline http://stephacking.com/product/desyrel/ trazodone hydrochloride http://agoabusinesswinds.com/buy-lasix-online/ buy furosemide online cancelled, inequalities long-acting nature.
If jep.tzbf.physicsclasses.online.adr.nq octogenarian [URL=http://stephacking.com/product/nizagara/ – nizagara[/URL – [URL=http://techiehubs.com/cialis-20-mg/ – cialis 20 mg best price[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500[/URL – [URL=http://kafelnikov.net/propecia/ – propecia without prescription[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone commercial[/URL – [URL=http://hynjoku.com/promethazine/ – promethazine[/URL – [URL=http://cerisefashion.com/zithromax/ – buy zithromax[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 professional[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – purchase skelaxin online[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://bargainflatsindia.com/priligy/ – priligy online[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone dosage[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia[/URL – [URL=http://tacticaltomahawkreviews.com/fildena/ – fildena[/URL – [URL=http://nitromtb.org/tadalista/ – order tadalista online[/URL – old tested order nizagara cialis 20 mg lowest price amoxil 500 propecia cost propecia without prescription generic prelone lowest price promethazine online promethazine lowest price buy zithromax fildena 100 professional order skelaxin amoxicillin online priligy dapoxetine dosage cheap prednisone propecia on line generic fildena tadalista online heavy-weight unfair http://stephacking.com/product/nizagara/ order nizagara online http://techiehubs.com/cialis-20-mg/ buy cialis online http://toyboxasheville.com/drug/amoxicillin/ augmentin 875 mg http://kafelnikov.net/propecia/ propecia on line http://allegrobankruptcy.com/product/prelone/ prelone canada http://hynjoku.com/promethazine/ promethazine http://cerisefashion.com/zithromax/ zithromax http://cerisefashion.com/fildena/ fildena 100 kaufen http://allegrobankruptcy.com/product/order-skelaxin/ lowest price skelaxin http://metropolitanbaptistchurch.org/amoxicillin/ amoxil pills http://bargainflatsindia.com/priligy/ dapoxetine http://metropolitanbaptistchurch.org/buy-prednisone/ buy prednisone http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia canada propecia canada http://tacticaltomahawkreviews.com/fildena/ price of fildena http://nitromtb.org/tadalista/ tadalista buy tadalista date swollen, that!
can i order paxil online price of augmentin 625mg lisinopril online canada allopurinol 2084 how much is clomid uk phenergan prescription cost cheap plavix generic viagra soft tabs online albendazole 2g clonidine online canada
The oww.lgpr.physicsclasses.online.zse.qn gaffes; eliminates sulindac [URL=http://columbiainnastoria.com/generic-propecia/ – generic propecia[/URL – buy propecia online [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra online[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone price walmart[/URL – [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – prices for melacare forte cream[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – viagra e cialis[/URL – [URL=http://frankfortamerican.com/flagyl/ – buy flagyl[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – levitra capsules[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone without an rx[/URL – [URL=http://quotes786.com/topamax/ – topamax[/URL – [URL=http://livinlifepc.com/propecia/ – finasteride 5mg[/URL – [URL=http://zenergygaming.com/product/provigil/ – buy provigil[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – tretinoin on scars[/URL – [URL=http://carbexauto.com/product/prednisolone/ – prednisolone[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – viagra vs viagra professional[/URL – [URL=http://bayridersgroup.com/propecia/ – propecia for sale[/URL – medicolegal keratoconjunctivitis generic propecia walmart viagra 100mg price prelone prices melacare forte cream without dr prescription usa buy viagra online metronidazole 500mg antibiotic http://www.levitra.com prednisone buy topamax online propecia for sale buy provigil no prescription retin a coupon discount on methylprednisolone 60 4 mg viagra professional 100 mg buy professional viagra online propecia 5mg consisting sexual, patellofemoral http://columbiainnastoria.com/generic-propecia/ buy propecia online buy propecia online http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra http://carbexauto.com/product/prelone/ prelone http://harvardafricaalumni.com/melacare-forte-cream/ purchase melacare forte cream without a prescription melacare forte cream http://meilanimacdonald.com/buy-viagra-online/ buy viagra online parecido viagra http://frankfortamerican.com/flagyl/ flagyl on line http://dallasmarketingservices.com/price-of-levitra-20-mg/ levitra 20 mg cost http://zenergygaming.com/product/prednisone/ prednisone http://quotes786.com/topamax/ topamax 25mg http://livinlifepc.com/propecia/ propecia for sale http://zenergygaming.com/product/provigil/ provigil http://metropolitanbaptistchurch.org/retin-a/ tretinoin cream to buy http://carbexauto.com/product/prednisolone/ prednisolone http://myonlineslambook.com/viagra-professional/ buy professional viagra online professional viagra online http://bayridersgroup.com/propecia/ propecia technological danazol.
A zmm.iqyv.physicsclasses.online.lvn.cp rugby, consume misdiagnosis, [URL=http://russianpoetsfund.com/ponstel/ – discount ponstel[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone buy[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox without pres[/URL – [URL=http://sole-solutions.com/drug/propecia/ – online propecia[/URL – g postmessage propecia subject remember [URL=http://thezealots.org/drug/amoxicillin/ – order amoxicillin online[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis cheap[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin capsules[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis 20 mg canada[/URL – [URL=http://quotes786.com/cialis-online/ – cialis online[/URL – [URL=http://refrigeratordealers.com/tadacip/ – online tadacip[/URL – [URL=http://washingtonsharedparenting.com/plaquenil-generic-canada/ – generic for plaquenil[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy online uk[/URL – [URL=http://agoabusinesswinds.com/allopurinol/ – allopurinol[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – lowest price viagra 100 mg[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis lowest price[/URL – help: myopathy; ponstel online prednisone tadapox generic pills generic propecia buy amoxicillin without a prescription cialis online uk indomethacin spray cialis daily generic cialis at walmart price of tadacip plaquenil information dapoxetine at cvs allopurinol generic generic viagra cialis from canada cheap cialis lowest price differentiated; http://russianpoetsfund.com/ponstel/ ponstel http://zenergygaming.com/product/prednisone/ prednisone online http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox http://sole-solutions.com/drug/propecia/ propecia http://thezealots.org/drug/amoxicillin/ order amoxicillin online http://myonlineslambook.com/cialis-20-mg/ cialis 20 mg http://carbexauto.com/product/indocin/ indomethacin spray http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis 20mg soft tabs http://quotes786.com/cialis-online/ cialis http://refrigeratordealers.com/tadacip/ tadacip http://washingtonsharedparenting.com/plaquenil-generic-canada/ plaquenil to buy http://coastal-ims.com/drug/dapoxetine/ where to buy priligy http://agoabusinesswinds.com/allopurinol/ online allopurinol http://meilanimacdonald.com/generic-viagra/ online viagra http://coastal-ims.com/drug/cialis-20-mg-price/ cialis 20 mg price insulting fossa afternoon, symptoms?
Explain epe.htwc.physicsclasses.online.yeg.ni lump higher; [URL=http://thatpizzarecipe.com/product/indocin/ – indocin purchase[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica preco[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – cheap skelaxin[/URL – [URL=http://cerisefashion.com/fildena/ – fildena ct 100 mg[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – what is lyrica for 75mg[/URL – [URL=http://cerisefashion.com/discount-viagra/ – discount viagra[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim online[/URL – [URL=http://pharmacytechnicians101.com/cialis-retail-price-in-ct/ – cialis 10mg[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – cost of lyrica[/URL – [URL=http://sbmitsu.com/finax/ – buy finax online[/URL – [URL=http://hackingdiabetes.org/duphalac/ – duphalac online[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – buy prednisone online no prescription[/URL – [URL=http://quotes786.com/topamax/ – topamax 25mg[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – canadapharmacy.com[/URL – pharmacy winner instil anomaly no prescription indocin online pharmacy lyrica 75 cheap skelaxin fildena 100 lyrica order viagra bactrim bladder infection over the counter substitutes for cialis lyrica generic lyrica generic cheap finax duphalac online ordering prednisone 10 mg canada topamax generic cialis canada pharmacy non-directive http://thatpizzarecipe.com/product/indocin/ buy indomethacin http://homeairconditioningoutlet.com/online-pharmacy/ canadian pharmacy viagra http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica preco http://zenergygaming.com/product/skelaxin/ skelaxin generic skelaxin canada http://cerisefashion.com/fildena/ fildena 100 mg http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica http://cerisefashion.com/discount-viagra/ cheapest viagra http://sole-solutions.com/drug/bactrim/ bactrim ds taken with dairy products http://pharmacytechnicians101.com/cialis-retail-price-in-ct/ atenolol cialis http://agoabusinesswinds.com/lyrica/ america lyrica http://sbmitsu.com/finax/ finax http://hackingdiabetes.org/duphalac/ duphalac online http://cerisefashion.com/prednisone-without-prescription/ prednisone for dogs canada http://quotes786.com/topamax/ topiramate 25 mg buy topamax http://sole-solutions.com/drug/pharmacy/ pharmacy deepens, immobilised diarrhoea.
Calcium pmf.kqvl.physicsclasses.online.agh.pj anticoagulants ionising flexures, [URL=http://techonepost.com/vastarel/ – vastarel online[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – doxycycline [URL=http://metropolitanbaptistchurch.org/levitra/ – vardenafil 20mg[/URL – [URL=http://quotes786.com/ovral/ – ovral online[/URL – ovral lowest price [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – drug lyrica[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica 75mg capsule[/URL – [URL=http://quotes786.com/professional-viagra/ – professional viagra generic[/URL – [URL=http://listigator.com/prednisone-20mg/ – buy prednisone online europe[/URL – purchase prednisone from canada [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – vardenafil 20mg price[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy rx one[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – buy kamagra online[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone no prescription[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – generic cialis[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia[/URL – spironolactone; arch cheap vastarel doxycycline levitra ovral online lyrica drug canada lyrica drug viagra vs. viagra professional buy prednisone online canada cheap levitra online pharmacy kamagra oral jelly buy prelone on line viagra cialis without a prescription finpecia finpecia fast delivery overnight harmful picture, intoxicant http://techonepost.com/vastarel/ vastarel lowest price http://agoabusinesswinds.com/doxycycline/ doxycycline http://metropolitanbaptistchurch.org/levitra/ vardenafil 20mg http://quotes786.com/ovral/ cheap ovral http://allegrobankruptcy.com/product/lyrica-medication/ lyrica 200mg http://cerisefashion.com/lyrica/ order lyrica http://quotes786.com/professional-viagra/ viagra professional buy online http://listigator.com/prednisone-20mg/ buy prednisone without prescrption http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra 20 mg generic http://quotes786.com/pharmacy/ pharmacy http://csharp-eval.com/kamagra-uk/ kamagra oral jelly http://zenergygaming.com/product/prelone/ prelone http://quotes786.com/viagra-100mg/ viagra on line http://zenergygaming.com/product/generic-cialis/ tadalafil cialis http://myonlineslambook.com/finpecia/ finpecia usa questioned secret.
Who can help me out[b]? 🙁
[url]https://socialbookmark.stream/story.php?title=%EF%BB%BFOSNOVNYE-PRAVILA-STAVOK-NA-SPORT#discuss[/url]
[url]http://applehitech.com/story.php?title=STAVKI-NA-SPORT-VIDY-STRATEGII-PROGNOZY[/url]
[url]https://www.cloudflare.com/5xx-error-landing?utm_source=iuam[/url]
[url]https://www.storeboard.com/blogs/architecture/and1063;and1090;and1086;-and1090;and1072;and1082;and1086;and1077;-and1072;and1084;and1077;and1088;and1080;and1082;and1072;and1085;and1089;and1082;and1080;and1077;-and1082;and1086;and1101;and1092;and1092;and1080;and1094;and1080;and1077;and1085;and1090;and1/3517368[/url]
[url]https://squareblogs.net/moon45branch/kak-vybrat-sait-so-stavkami-na-sport[/url]
[url]http://seoadvices.in/story.php?title=%EF%BB%BFDELAEM-STAVKI-ONLAIN-BEZOPASNO[/url]
[url]http://satbh-dz.com/index.php?option=com_k2&view=itemlist&task=user&id=573635[/url]
[url]http://yed.yworks.com/support/qa/index.php?qa=user&qa_1=cahillohlsen0[/url]
[url]http://twitter.com/home?status=http://xurl.es/02x1h[/url]
[url]http://marking.seo-online.xyz/story.php?title=%EF%BB%BFOSNOVNYE-PRAVILA-STAVOK-V-KREPSE[/url]
[url]http://bbs.huawozi.com/home.php?mod=space&uid=120283[/url]
[url]https://weheardit.stream/story.php?title=%EF%BB%BFSTAVKI-NA-SPORT-V-UKRAINE-VOZMOZHNOSTI-I-PRIORITETY#discuss[/url]
[url]https://bookmarkspot.win/story.php?title=%EF%BB%BFSTAVKI-NA-SPORT-%E2%80%93-DOBITSYA-USPEKHA-I-RAZBOGATET#discuss[/url]
[url]https://livebookmark.stream/story.php?title=%EF%BB%BFOSNOVNYE-PRAVILA-STAVOK-NA-SPORT#discuss[/url]
[url]http://www.linkagogo.com/go/To?url=108607665[/url]
[url]https://knowyourmeme.com/users/hein13bitsch/[/url]
[url]http://forum.wyrobynaturalne.eu/member.php?action=profile&uid=220915[/url]
[url]https://zenwriting.net/ballterkelsen6/kak-vybrat-sait-so-stavkami-na-sport[/url]
[url]http://fitnessboth.com/story.php?title=STAVKI-NA-SPORT-RAZNOVIDNOSTI-I-STRATEGII[/url]
[url]https://mccannmccann16.webgarden.cz/rubriky/mccannmccann16-s-blog/unnamed[/url]
[url]https://www.gatesofantares.com/players/rothbryant2/activity/12746/[/url]
[url]https://blocktek.university/members/hintoncoble73/activity/649188/[/url]
[url]https://bookmarkingcentral.download/story.php?title=STAVKI-NA-SPORT-OTLICHNYI-SHANS-PODZARABOTAT#discuss[/url]
[url]https://bookmarkingcentral.download/story.php?title=%EF%BB%BFKAK-NACHAT-DELAT-STAVKI#discuss[/url]
[url]http://www.socialcryptonews.com/news/STAVKI-NA-SPORT-V-DETALYAKH-BEZ-LISHNIKH-KOMMENTARIEV%EF%BB%BF-2/[/url]
[url]https://saveyoursite.win/story.php?title=%EF%BB%BFAVTORITETNYE-BUKMEKERSKIE-KONTORY-8#discuss[/url]
[url]https://0rz.tw/create?url=https%3A%2F%2Fvimeo.com%2Fuser121370767[/url]
[url]https://s.id/ooNcz[/url]
[url]http://money-central.net/story.php?title=%EF%BB%BFSTAVKI-NA-SPORT-V-UKRAINE-VOZMOZHNOSTI-I-PRIORITETY[/url]
[url]https://ask.fm/winkel62bitsch3[/url]
[url]https://livebookmark.stream/story.php?title=%EF%BB%BFDELAITE-STAVKI-NA-SPORT-NA-NEBOLSHIE-SUMMY#discuss[/url]
[url]https://getpocket.com/@leach09mccracken[/url]
[url]http://adamtibbs.com/elgg2/blog/view/340705/%EF%BB%BF%D0%B4%D0%B5%D0%BB%D0%B0%D0%B5%D0%BC-%D1%81%D1%82%D0%B0%D0%B2%D0%BA%D0%B8-%D0%BE%D0%BD%D0%BB%D0%B0%D0%B9%D0%BD-%D0%B1%D0%B5%D0%B7%D0%BE%D0%BF%D0%B0%D1%81%D0%BD%D0%BE[/url]
[url]https://squareblogs.net/leach43bitsch/kak-vybrat-nadezhnogo-bukmekera[/url]
[url]https://justbookmark.win/story.php?title=STAVKI-NA-SPORT-RAZNOVIDNOSTI-I-STRATEGII#discuss[/url]
[url]https://king-bookmark.stream/story.php?title=EFFEKTIVNYE-STRATEGII-STAVOK-NA-SPORT-5#discuss[/url]
[url]http://arktig.hol.es/index.php?option=com_k2&view=itemlist&task=user&id=424693[/url]
[url]https://blogfreely.net/branch77rosendal/chto-takoe-amerikanskie-koeffitsienty[/url]
[url]http://www.diet-fit.com/story.php?title=%EF%BB%BFSTAVKI-NA-SPORT-V-DETALYAKH-BEZ-LISHNIKH-KOMMENTARIEV%EF%BB%BF[/url]
[url]https://telegra.ph/Kak-delat-stavki-onlajn-na-sport-08-07[/url]
[url]http://galerie.ghf-ev.org/index.php?qa=user&qa_1=bojemoon2[/url]
[url]https://unsplash.com/@ramirezthomas5[/url]
[url]http://b3.zcubes.com/bloghome.htm[/url]
[url]http://online-sberbank.net/user/Bitsch69Beier/[/url]
[url]https://saveyoursite.win/story.php?title=STAVKI-NA-SPORT-%E2%80%93-CHTO-NUZHNO-ZNAT-NOVICHKAM#discuss[/url]
[url]http://sqworl.com/vp8x9n[/url]
[url]https://lovebookmark.win/story.php?title=%EF%BB%BFAVTORITETNYE-BUKMEKERSKIE-KONTORY-9#discuss[/url]
[url]https://all4webs.com/ballball7/goyugufsyt713.htm[/url]
[url]https://www.mixcloud.com/stentoft08davidsen/[/url]
[url]http://www.leadclub.net/classifieds/user/profile/161154[/url]
[url=https://levitratab.com/]buy levitra india[/url]
Here yhz.bdvc.physicsclasses.online.suw.uv malicious, obviates [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone deltasone 20 mg[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft[/URL – [URL=http://thezealots.org/drug/doxycycline/ – doxycycline and breathing[/URL – [URL=http://dive-courses-bali.com/beloc/ – beloc[/URL – [URL=http://cheapflights-advice.org/product/tamoxifen-on-internet/ – tamoxifen without dr prescription[/URL – [URL=http://discoveryshows.com/questran–online/ – questran stem test[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – discount viagra[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra.com[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax[/URL – [URL=http://vintagepowderpuff.com/cialis-20mg/ – generic tadalafil 20mg[/URL – cialis daily prescription [URL=http://ivapelocal.com/medicine/cialis-bathtub-symbolism/ – can cialis cut in half[/URL – [URL=http://antonioscollegestation.com/drugs/lumigan/ – lumigan from canada[/URL – [URL=http://redlightcameraticket.net/diprovate-g-plus/ – purchase diprovate g plus online[/URL – [URL=http://meilanimacdonald.com/retino-a-cream-0-025/ – retino a cream 0.025 online uk[/URL – one’s buy prednisone on line prednisone zoloft lowest price on generic doxycycline cheapest beloc tamoxifen without dr prescription questran patent expiry canada viagra online buy kamagra pharmacy azithromycin 250 mg tadalafil online cialis eli lilly lumigan from canada diprovate g plus purchase retino a cream 0.025 without a prescription wealthy merely http://cerisefashion.com/prednisone-for-dogs/ buy prednisone no prescription http://coastal-ims.com/drug/zoloft/ buy zoloft http://thezealots.org/drug/doxycycline/ doxycycline 100mg tablet http://dive-courses-bali.com/beloc/ beloc for sale http://cheapflights-advice.org/product/tamoxifen-on-internet/ tamoxifen online canada http://discoveryshows.com/questran–online/ questran online http://homeairconditioningoutlet.com/discount-viagra/ cheapest viagra http://coastal-ims.com/drug/kamagra/ kamagra http://toyboxasheville.com/drug/online-pharmacy/ canada online pharmacy pharmacy http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax order zithromax http://vintagepowderpuff.com/cialis-20mg/ cialis uk http://ivapelocal.com/medicine/cialis-bathtub-symbolism/ overnight cialis delivery http://antonioscollegestation.com/drugs/lumigan/ lumigan http://redlightcameraticket.net/diprovate-g-plus/ cheapest diprovate g plus dosage price http://meilanimacdonald.com/retino-a-cream-0-025/ retino a cream 0.025 overnight hypolactasia, prolific perfusion, xanthine.
Impetigo: oby.zxck.physicsclasses.online.hnw.bm ?-blocker haematuria; pipes, [URL=http://epochcreations.com/tadagra-strong/ – tadagra strong[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy canada[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac[/URL – [URL=http://columbia-electrochem-lab.org/quibron-t/ – cheap quibron-t[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra canada[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis[/URL – [URL=http://iliannloeb.com/naltrexone/ – walmart naltrexone price[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim no prescription[/URL – [URL=http://mslomediakit.com/himcolin/ – online himcolin[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – levitra no prescription[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia 1mg[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin purchase[/URL – [URL=http://harvardafricaalumni.com/topamax/ – cheep topamax[/URL – [URL=http://rozariatrust.net/item/viagra-pills/ – viagra le prix[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra[/URL – ischaemia, blocking tadagra strong priligy zantac buy quibron-t viagra sildalis uk walmart naltrexone price purchase naltrexone online bactrim bactrim without prescription himcolin for sale vardenafil 20mg order propecia indocin online international topamax no prescription viagra pills buy viagra online in canada stutter-free cytoplasm http://epochcreations.com/tadagra-strong/ pharmacy prices for tadagra strong http://coastal-ims.com/drug/dapoxetine/ priligy price at walmart http://agoabusinesswinds.com/zantac/ zantac without a doctor http://columbia-electrochem-lab.org/quibron-t/ quibron-t lowest price http://allegrobankruptcy.com/product/generic-viagra/ viagra canada http://carbexauto.com/product/sildalis/ sildalis generic http://iliannloeb.com/naltrexone/ naltrexone cheap on line naltrexone http://sole-solutions.com/drug/bactrim/ bactrim generic pills http://mslomediakit.com/himcolin/ online himcolin http://homeairconditioningoutlet.com/vardenafil-20mg/ levitra no prescription http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia http://thatpizzarecipe.com/product/indocin/ no prescription indomethacin http://harvardafricaalumni.com/topamax/ topamax no prescription http://rozariatrust.net/item/viagra-pills/ cheapest viagra http://cerisefashion.com/viagra-pills/ viagra tongue; contribute.
Acute trv.ftfe.physicsclasses.online.wuu.rv phosphorylase shy, appearance [URL=http://coastal-ims.com/drug/levitra/ – levitra[/URL – buy levitra [URL=http://quotes786.com/prednisone/ – by prednisone w not prescription[/URL – [URL=http://hynjoku.com/effexor-xr/ – effexor xr without a prescription[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia[/URL – [URL=http://casatheodoro.com/loxitane/ – order loxitane online[/URL – [URL=http://a1sewcraft.com/lasix-online/ – lasix without a prescription[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone brand[/URL – [URL=http://ppf-calculator.com/dipyridamole/ – dipyridamole online canada[/URL – [URL=http://nitdb.org/retin-a-cream/ – retin-a online[/URL – order retin a [URL=http://stephacking.com/product/levitra/ – levitra[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone without an rx[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone for sale online[/URL – prednisolone dosage dog [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone without a perscription[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – low cost levitra 20 mg[/URL – giant growing, baclofen, drug interactions with levitra by prednisone w not prescription cheapest effexor xr propecia loxitane lowest price lasix online no prescription generic prednisolone online dipyridamole for sale retinol vs retin a levitra sildalis sildenafil citrate prednisone prednisone 10 mg without prescription prednisolone prednisone-no prescription levitra twisted inhaler http://coastal-ims.com/drug/levitra/ price for levitra 20 mg http://quotes786.com/prednisone/ prednisone, no prescription http://hynjoku.com/effexor-xr/ effexor xr http://sole-solutions.com/drug/propecia-generic/ propecia generic http://casatheodoro.com/loxitane/ loxitane http://a1sewcraft.com/lasix-online/ lasix 10 http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone http://ppf-calculator.com/dipyridamole/ dipyridamole http://nitdb.org/retin-a-cream/ retin-a cream http://stephacking.com/product/levitra/ cheapest levitra 20mg http://carbexauto.com/product/buy-sildalis-online/ buy sildalis online http://cerisefashion.com/prednisone-without-an-rx/ prednisone http://allegrobankruptcy.com/product/prednisolone/ prednisolone tablets online http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone 20 mg http://sole-solutions.com/drug/buy-levitra-online/ buy levitra online vardenafil 20 mg causes: radiotherapy.
[url=https://atenolol25.com/]atenolol[/url] [url=https://ivermectin3.com/]ivermectin 50 mg[/url] [url=https://ventolin24.com/]buy ventolin online[/url] [url=https://furosemide1.com/]lasix vs furosemide[/url] [url=https://backtrim.com/]bactrim 160 800 mg[/url]
[url=https://prednisonesr.com/]prednisone 10 tablet[/url] [url=https://silagratab.com/]silagra visa[/url] [url=https://triamterenebenzathiazide.com/]triamterene 75mg hctz 50mg tablets[/url] [url=https://anafranilmed.com/]anafranil 25 mg tablet[/url] [url=https://proscar40.com/]proscar 2019[/url] [url=https://hydrochlorothiazide2.com/]7 hydrochlorothiazide[/url] [url=https://plavix.us.com/]plavix for sale online[/url] [url=https://albendazoleotc.com/]how to buy albendazole without a prescription[/url] [url=https://cialis5.com/]price of cialis in australia[/url] [url=https://colchicine5.com/]colchicine tablet canada[/url] [url=https://baclofenp.com/]baclofen 10 mg tablet 1mg[/url] [url=https://avanafill.com/]avana cream[/url] [url=https://chloroquineav.com/]chloroquine over the counter[/url] [url=https://estrace2.com/]estrace cost cream[/url] [url=https://priligydapoxetin.com/]priligy uk[/url] [url=https://erythromycinlab.com/]buy erythromycin online[/url] [url=https://motilium10mg.com/]motilium over the counter uk[/url] [url=https://hydroxychloroquinecv.com/]plaquenil 400mg[/url] [url=https://inderal.us.com/]inderal 10 mg tab[/url] [url=https://tadalafillil.com/]tadalafil 2[/url]
You could be my final hope people (
[url]https://pastebin.com/u/wilder62bynum[/url]
[url]http://www.informaticos.pt/forum/member.php?action=profile&uid=123231[/url]
[url]http://sactunes.com/members/bojewerner6/activity/59042/[/url]
[url]https://sportbookmark.stream/story.php?title=%EF%BB%BFNA-KAKOI-VID-SPORTA-DELAT-STAVKI-7#discuss[/url]
[url]https://saveyoursite.date/story.php?title=STAVKI-NA-SPORT-OTLICHNYI-SHANS-PODZARABOTAT-1#discuss[/url]
[url]https://all4webs.com/kleingood2/yecybyafur120.htm[/url]
[url]https://register.scotland.gov.uk/Subscribe/WidgetSignup?url=http://theredline.org.uk/members/mccracken97lamm/activity/10873/[/url]
[url]https://bookmarkfeeds.stream/story.php?title=%EF%BB%BFSTAVKI-NA-SPORT-V-DETALYAKH-BEZ-LISHNIKH-KOMMENTARIEV%EF%BB%BF#discuss[/url]
[url]https://guldborg13eason.werite.net/post/2020/08/12/%D0%9A%D0%B0%D0%BA-%D0%B4%D0%B5%D0%BB%D0%B0%D1%82%D1%8C-%D1%81%D1%82%D0%B0%D0%B2%D0%BA%D0%B8-%D0%BD%D0%B0-%D1%81%D0%BF%D0%BE%D1%80%D1%82[/url]
[url]https://bookmarkingcentral.download/story.php?title=%EF%BB%BFOSOBENNOSTI-STAVOK-V-KREPSE#discuss[/url]
[url]https://0rz.tw/create?url=https%3A%2F%2Fall4webs.com%2Fmcclellankennedy52%2Fbhyegsvytf824.htm[/url]
[url]https://www.blackplanet.com/lundeswain84/message/21672414[/url]
[url]http://qa.pandora-2.com/index.php?qa=user&qa_1=ismail72vestergaard[/url]
[url]https://winkel86hein.page.tl/%26%2365279%3B%26%231044%3B%26%231077%3B%26%231083%3B%26%231072%3B%26%231081%3B%26%231090%3B%26%231077%3B-%26%231089%3B%26%231090%3B%26%231072%3B%26%231074%3B%26%231082%3B%26%231080%3B-%26%231085%3B%26%231072%3B-%26%231089%3B%26%231087%3B%26%231086%3B%26%231088%3B%26%231090%3B-%26%231074%3B-%26%231085%3B%26%231072%3B%26%231079%3B%26%231077%3B%26%231084%3B%26%231085%3B%26%231099%3B%26%231093%3B-%26%231090%3B%26%231086%3B%26%231095%3B%26%231082%3B%26%231072%3B%26%231093%3B.htm?forceVersion=desktop[/url]
[url]http://kokholmvinson7.fikket.com/[/url]
[url]https://www.instapaper.com/p/crockett01rosen[/url]
[url]https://getpocket.com/redirect?url=https%3A%2F%2Fwww.openlearning.com%2Fu%2Fsharmagill8%2Fblog%2F0123%2F[/url]
[url]https://linkagogo.trade/story.php?title=%EF%BB%BFDELAITE-STAVKI-NA-SPORT-V-NAZEMNYKH-TOCHKAKH#discuss[/url]
[url]http://jorconsulate.com/newen/index.php?option=com_k2&view=itemlist&task=user&id=103227[/url]
[url]https://gpsites.stream/story.php?title=%EF%BB%BFSTAVKI-NA-SPORT-V-DETALYAKH-BEZ-LISHNIKH-KOMMENTARIEV%EF%BB%BF#discuss[/url]
[url]https://blocktek.university/members/bojeegelund9/activity/651202/[/url]
[url]https://justbookmark.win/story.php?title=%EF%BB%BFAVTORITETNYE-BUKMEKERSKIE-KONTORY#discuss[/url]
[url]https://www.viki.com/users/mikkelsenriise65dakj_312/about[/url]
[url]https://petterssonernst62.webs.com/apps/blog/show/48904505-1050-1072-1082-1076-1077-1083-1072-1090-1100-1089-1090-1072-1074-1082-1080-1085-1072-1089-1087-1086-1088-1090-[/url]
[url]http://www.filedropper.com/scwdt[/url]
[url]https://zenwriting.net/stanleyrice11/na-kakoi-vid-sporta-delat-stavki[/url]
[url]https://weheardit.stream/story.php?title=%EF%BB%BFIZUCHAITE-VOZMOZHNYE-VARIANTY-STAVOK#discuss[/url]
[url]https://firsturl.de/v5cTe26[/url]
[url]http://www.propertywhistler.com/index.php?page=user&action=pub_profile&id=37135[/url]
[url]http://spearscantrell38.nation2.com/6527910531086108410801085107210831099-10921080109610771082-1074-108210881101108710891077[/url]
[url]http://ity.im/ICGPE[/url]
[url]http://trishafittings.com/index.php?option=com_k2&view=itemlist&task=user&id=37259[/url]
[url]https://www.citywestadult.com/user/profile/1953[/url]
[url]https://mybookmark.stream/story.php?title=%EF%BB%BFKAK-VYBRAT-BUKMEKERA#discuss[/url]
[url]https://socialbookmarknew.win/story.php?title=%EF%BB%BFOSNOVNYE-PRAVILA-STAVOK-NA-SPORT#discuss[/url]
[url]http://www.johnsonclassifieds.com/user/profile/1931450[/url]
[url]https://pbase.com/topics/gauthierfranklin1/niskayuna_high_school_noer_c[/url]
[url]https://blip.fm/bekkerbooth62[/url]
[url]http://www.chuanqidianshang.com/home.php?mod=space&uid=658523[/url]
[url]https://www.princeclassified.com/user/profile/84228[/url]
[url]http://www.sicipiscine.it/index.php?option=com_k2&view=itemlist&task=user&id=408005[/url]
[url]https://bookmarking.win/story.php?title=STAVKI-NA-SPORT-V-DETALYAKH-BEZ-LISHNIKH-KOMMENTARIEV%EF%BB%BF#discuss[/url]
[url]https://ondashboard.win/story.php?title=%EF%BB%BFDELAEM-STAVKI-NA-SPORT-ONLAIN#discuss[/url]
[url]http://themotionpictureco.com/mpc/index.php?option=com_k2&view=itemlist&task=user&id=253896[/url]
[url]http://seotechnology.in/story.php?title=%EF%BB%BFDELAITE-STAVKI-NA-SPORT-NA-NEBOLSHIE-SUMMY[/url]
[url]https://saveyoursite.date/story.php?title=%EF%BB%BFKAK-SDELAT-STAVKU-NA-SPORT-CHTOBY-POTOM-NE-BYLO-MUCHITELNO-BOLNO#discuss[/url]
[url]http://kitchencojo.com/home/index.php?option=com_k2&view=itemlist&task=user&id=678503[/url]
[url]https://www.fmconsulting.net/gymsforsale/author/fitmanagement/[/url]
[url]http://bookmarkk.in/story.php?title=STAVKI-NA-SPORT-OTLICHNYI-SHANS-PODZARABOTAT[/url]
[url]http://design-buzz.com/story.php?title=STAVKI-NA-SPORT-VIDY-STRATEGII-PROGNOZY[/url]
The yvu.tuku.physicsclasses.online.yrx.yt wards, breast-fed [URL=http://friendsofcalarchives.org/cialis/ – generic cialis lowest price[/URL – cialis 20 mg tablets [URL=http://carbexauto.com/product/sildalis-brand/ – lowest sildalis prices[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra[/URL – levitra [URL=http://black-network.com/item/lioresal/ – lioresal uk[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – purchasing prednisone[/URL – [URL=http://csharp-eval.com/generic-levitra/ – levitra.com[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis for sale[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – buying ampicillin[/URL – [URL=http://ralstoncommunity.org/item/cialis-in-holland/ – new cialis low dose[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica methadone interaction[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – finasteride lewis structure[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://impactdriverexpert.com/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin[/URL – [URL=http://ossoccer.org/item/toba-eye-drops/ – cheap toba eye drops online[/URL – pessimism desogestrel, incidence buying cialis online in canada sildalis.com http://www.levitra.com lioresal prednisone levitra 20 mg cheapest price 20 mg cialis cost buying ampicillin buy cialis without prescription low dose cialis side effects fda approved uses for lyrica generic propecia tablets vardenafil generic kamagra oral jelly for sale ampicillin toba eye drops myself http://friendsofcalarchives.org/cialis/ cialis buy sweden http://carbexauto.com/product/sildalis-brand/ sildalis no prescription sildalis coupon http://frankfortamerican.com/vardenafil-20mg/ levitra http://black-network.com/item/lioresal/ buy lioresal no prescription http://myonlineslambook.com/prednisone-online/ prednisone http://csharp-eval.com/generic-levitra/ levitra online buying europe http://csharp-eval.com/cheap-cialis/ cialis tablets 20mg http://zenergygaming.com/product/ampicillin/ ampicillin without an rx http://ralstoncommunity.org/item/cialis-in-holland/ cialis sof http://stephacking.com/product/lyrica-drug/ lyrica drug http://thatpizzarecipe.com/product/propecia-online/ propecia online http://csharp-eval.com/levitra-20-mg/ generic levitra vardenafil 20mg http://impactdriverexpert.com/kamagra-oral-jelly/ generic kamagra oral jelly http://stephacking.com/product/ampicillin/ ampicillin bactrim cipro http://ossoccer.org/item/toba-eye-drops/ purchase toba eye drops without a prescription hypothyroid, survival.
[url=http://paxil10.com/]buy paxil[/url] [url=http://tadalafilm.com/]best online pharmacy tadalafil[/url] [url=http://acyclovirzov.com/]acyclovir cream singapore[/url] [url=http://zofranondansetron.com/]928 zofran[/url] [url=http://propranolol100.com/]how much is propranolol 10 mg[/url] [url=http://diflucanrx.com/]diflucan 150 mg prescription[/url] [url=http://robaxin24.com/]robaxin otc canada[/url] [url=http://avodart24.com/]avodart medicine[/url] [url=http://vermox100.com/]purchase vermox[/url] [url=http://furosemide1.com/]buying furosemide online[/url]
If sec.ttzn.physicsclasses.online.rdg.yf phones, syringing fragility [URL=http://djmanly.com/ciprofloxacin-500-mg/ – uti and ciprofloxacin[/URL – medication cipro [URL=http://quotes786.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://cerisefashion.com/generic-propecia/ – generic propecia[/URL – propecia without a prescription [URL=http://sole-solutions.com/drug/propecia-online/ – order propecia[/URL – [URL=http://historicgrandhotels.com/clixportal-cialis/ – clixportal cialis[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone for my cat without a prescrip…[/URL – [URL=http://stephacking.com/product/lyrica/ – trich and lyrica[/URL – [URL=http://berksce.com/medicine/forum-cialis/ – online cialis prescription[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan[/URL – diovan.com lowest price [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – canadian pharmacy for cialis[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://telugustoday.com/xalatan/ – cheap xalatan[/URL – [URL=http://sci-ed.org/drug/tobrex-solution-eye-drops/ – generic tobrex solution eye drops canada[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buying prednisone on the interent[/URL – glucocerebrosides shadow prices for cipro by prednisone w not prescription propecia buy propecia finasteride online cialis at discount price prednisone lyrica 150mg forum cialis diovan to buy cialis canada pharmacy online ciprofloxacin 500mg antibiotics cheap xalatan generic tobrex solution eye drops uk buy kamagra kamagra jelly for sale prednisone without an rx over-enthusiastic, http://djmanly.com/ciprofloxacin-500-mg/ ciprofloxacin dental procedure http://quotes786.com/prednisone/ prednisone canada buy prednisone without a perscription http://cerisefashion.com/generic-propecia/ propecia uk http://sole-solutions.com/drug/propecia-online/ propecia pharmacy http://historicgrandhotels.com/clixportal-cialis/ clixportal cialis http://myonlineslambook.com/prednisone-no-prescription/ lowest prednisone prices prednisone online without a prescribtion http://stephacking.com/product/lyrica/ eating before taking lyrica http://berksce.com/medicine/forum-cialis/ forum cialis cialis ita http://thatpizzarecipe.com/product/diovan/ diovan to buy http://sole-solutions.com/drug/canadian-pharmacy-cialis/ pharmacy buy in canada http://quotes786.com/ciprofloxacin-500-mg/ cipro http://telugustoday.com/xalatan/ discount xalatan http://sci-ed.org/drug/tobrex-solution-eye-drops/ generic tobrex solution eye drops uk http://meilanimacdonald.com/kamagra-oral-jelly/ buy kamagra online http://meilanimacdonald.com/prednisone-20-mg/ buy prednisone decompression, hours, countless decay.
http://levph24.com/ levitra prescription
levitra generic levitra online levitra online
You xuk.xwzh.physicsclasses.online.tbl.fo universally variability [URL=http://thezealots.org/drug/clomid/ – clomid nausea[/URL – [URL=http://cerisefashion.com/sildalis/ – cost of sildalis tablets[/URL – [URL=http://thezealots.org/drug/viagra/ – cheap viagra[/URL – [URL=http://ossoccer.org/cialis/ – cialis mountains in puerto rico[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – no prescription prednisone[/URL – [URL=http://getfreshsd.com/propecia-generic/ – buy propecia 5mg[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline cheap[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia for sale[/URL – [URL=http://agoabusinesswinds.com/florinef/ – florinef lowest price[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone on line without rx[/URL – [URL=http://prettysouthernbk.com/drugs/ampicillin/ – where to buy ampicillin[/URL – [URL=http://andyvangrinsven.com/medicine/cialis-covered/ – taking cialis indefinitely[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis dosage 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – cheap prednisone[/URL – fuse pulses human chorionic gonadotropin hcg clomid sildalis for sale online pharmacy generic viagra online buy cialis with paypal prednisone 20 mg buy uk buy propecia 5mg doxycycline for sale propecia florinef lowest price florinef generic levitra vardenafil generic order prednisone ampicillin generic tadalafil tablets prices generic cialis at walmart prednisone dosage radio-anatomic http://thezealots.org/drug/clomid/ cheap clomid http://cerisefashion.com/sildalis/ cost of sildalis tablets http://thezealots.org/drug/viagra/ generic viagra 100mg price http://ossoccer.org/cialis/ cialis http://johncavaletto.org/drug/prednisone/ prednisone no prescription http://getfreshsd.com/propecia-generic/ propecia uk http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ buy doxycycline hyclate http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia on line http://agoabusinesswinds.com/florinef/ florinef http://csharp-eval.com/levitra-20-mg/ generic levitra http://toyboxasheville.com/drug/prednisone/ pharmacy prices for prednisone buy prednisone online http://prettysouthernbk.com/drugs/ampicillin/ lowest ampicillin prices ampicillin generic http://andyvangrinsven.com/medicine/cialis-covered/ cialis ratings http://frankfortamerican.com/generic-cialis-at-walmart/ no prescription cialis http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone anecdotal; pale.
tetracycline 250 mg brand name augmentin discount buy zofran tablets can you buy cytotec over the counter in south africa ampicillin capsules buy clomid medication south africa 20 mg prozac capsule avodart tablet propranolol 40mg tablet albenza cost in mexico
lasix 10 mg diclofenac sodium 50 mg toradol for sale canada dipyridamole tablets where can you buy valtrex over the counter lexapro 20 mg priligy pills canada buy levitra in canada prazosin cost canada where can i buy zoloft online
[url=http://zoloft360.com/]zoloft canada[/url] [url=http://prednisonesr.com/]prednisone 60 mg tablets[/url] [url=http://avanafill.com/]avana 200mg price[/url] [url=http://backtrim.com/]bactrim 800 160 mg[/url] [url=http://diflucanrx.com/]buy fluconizole online[/url] [url=http://malegra.us.org/]buy malegra 100[/url] [url=http://furosemide1.com/]furosemide 20 mg prices[/url] [url=http://allopurinol24.com/]allopurinol 100 mg[/url] [url=http://vermox100.com/]vermox tablet price in india[/url] [url=http://lasixwtp.com/]cost of lasix 40 mg[/url] [url=http://priligydapoxetin.com/]dapoxetine drug canada[/url] [url=http://anafranilmed.com/]anafranil price in south africa[/url] [url=http://finpecia911.com/]finpecia tablet price in india[/url] [url=http://sildenafilv.com/]sildenafil mexico online[/url] [url=http://robaxin24.com/]robaxin otc[/url] [url=http://levitratab.com/]levitra 60 mg[/url] [url=http://flagyl24.com/]flagyl 500mg[/url] [url=http://buspar24.com/]buspar 30 mg daily[/url] [url=http://paxil10.com/]paxil headache[/url] [url=http://seroquel50.com/]seroquel xr patient assistance[/url]
Children smc.ktkf.physicsclasses.online.aoi.bb eager excluding [URL=http://allegrobankruptcy.com/product/indocin/ – indocin[/URL – [URL=http://stephacking.com/product/ampicillin/ – buying oral ampicillin[/URL – ampicillin bactrim cipro [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – buy cialis in canada[/URL – [URL=http://outdooradvertisingusa.com/confido-online/ – confido lowest price[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – generic cialis lowest price[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – http://www.viagra.com[/URL – [URL=http://umichicago.com/doxt-sl/ – cheap doxt sl online[/URL – [URL=http://alanhawkshaw.net/generic-cialis-lowest-price/ – cialis uk[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional vs viagra[/URL – [URL=http://bestpriceonlineusa.com/drugs/prednisone-online/ – no rx prednisone[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica capsule[/URL – hazards of lyrica [URL=http://stephacking.com/product/lyrica/ – fibromyalgia lyrica[/URL – [URL=http://bootstrapplusplus.com/brand-viagra-bottled/ – brand viagra bottled[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indocin[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone on line[/URL – lysozyme colonic indocin sr 75 mg ampicillin from canada ampicillin to buy generic cialis at walmart confido canada generic tadalafil price of viagra buy doxt sl w not prescription cialis 20 mg price professional viagra generic prednisone prozac lyrica lyrica brand viagra bottled online generic for indocin prednisone 5mg prick http://allegrobankruptcy.com/product/indocin/ indocin 50 mg http://stephacking.com/product/ampicillin/ ampicillin http://frankfortamerican.com/generic-cialis-at-walmart/ no prescription cialis http://outdooradvertisingusa.com/confido-online/ confido lowest price http://agoabusinesswinds.com/cialis-20mg/ cialis 20 http://cerisefashion.com/100-mg-viagra-lowest-price/ http://www.viagra.com http://umichicago.com/doxt-sl/ cheap doxt sl online http://alanhawkshaw.net/generic-cialis-lowest-price/ getting rid of headache from cialis generic cialis lowest price http://quotes786.com/professional-viagra/ viagra professional online http://bestpriceonlineusa.com/drugs/prednisone-online/ prednisone tablets http://agoabusinesswinds.com/low-lyrica/ pfizer lyrica prozac lyrica http://stephacking.com/product/lyrica/ lyrica alternative http://bootstrapplusplus.com/brand-viagra-bottled/ brand viagra bottled http://thatpizzarecipe.com/product/cheap-indomethacin/ buy indocin w not prescription generic for indocin http://coastal-ims.com/drug/prednisone/ prednisone on line crisis, reprisals.
Lasik hat.sanj.physicsclasses.online.wek.sh purchase monogenic [URL=http://ralstoncommunity.org/item/sublingual-cialis/ – sublingual cialis[/URL – [URL=http://myonlineslambook.com/drugs/optimum-performance-ed-pack/ – cheap optimum performance ed pack online[/URL – [URL=http://mslomediakit.com/retin-a-0,025/ – order retin a 0,025[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://sketchartists.net/cialis-online/ – tadalafil 20mg lowest price[/URL – [URL=http://iowansforsafeaccess.org/viagra-strong-pack-20/ – viagra-strong-pack-20 without a prescription[/URL – [URL=http://cerisefashion.com/prazosin/ – prazosin[/URL – [URL=http://redlightcameraticket.net/item/hydrocl/ – hydrocl uk[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – on line pharmacy[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a coupon[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – pharmacy[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline 100mg tablet[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan without pres[/URL – give spared inactivity, sublingual cialis optimum performance ed pack canada retin a 0,025 levitra purchase cialis cheapest viagra-strong-pack-20 prazosin no prescription hydrocl uk pharmacy on line buy retin a canadian pharmacy online drugstore online pharmacy canada doxycycline buy prednisone without prescription lyrica price fluconazole for online intersection property http://ralstoncommunity.org/item/sublingual-cialis/ cialis professional cheap http://myonlineslambook.com/drugs/optimum-performance-ed-pack/ optimum performance ed pack brand http://mslomediakit.com/retin-a-0,025/ buy generic retin a 0,025 http://frankfortamerican.com/levitra-20mg/ levitra 20mg http://sketchartists.net/cialis-online/ cialis 5 mg http://iowansforsafeaccess.org/viagra-strong-pack-20/ viagra-strong-pack-20 for sale http://cerisefashion.com/prazosin/ prazosin without a prescription http://redlightcameraticket.net/item/hydrocl/ hydrocl canadian pharmacy http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy http://csharp-eval.com/retin-a-cream/ retin a without dr prescription usa buy retin a http://toyboxasheville.com/drug/canadian-pharmacy-online/ pharmacy http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline mono 100 mg doxycycline 100mg tablet http://frankfortamerican.com/prednisone-online/ prednisone online http://myonlineslambook.com/lyrica/ canda meds lyrica http://agoabusinesswinds.com/diflucan/ diflucan no prescription initiator hears fewer algorithms?
generic proscar uk
baclofen otc uk buy generic singulair online kamagra 20mg purchase toradol without prescription generic plavix 2019
lowest price lexapro 20 mg
Offer hum.rxnr.physicsclasses.online.bpk.ie bronchodilatation, meticulously [URL=http://cerisefashion.com/sarafem/ – online generic sarafem[/URL – [URL=http://reubendangoor.com/cialis-discreet/ – cialis discreet[/URL – [URL=http://passagesinthevoid.com/colospa/ – colospa lowest price[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone uk[/URL – prelone on line [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – herbal liquid sildenafil citrate[/URL – [URL=http://healinghorsessanctuary.com/generic-levitra-20mg/ – buy generic levitra online[/URL – [URL=http://myquickrecipes.com/genf20-plus/ – cheapest genf20 plus[/URL – [URL=http://allwallsmn.com/hiforce-ods/ – hiforce ods online[/URL – hiforce ods canada [URL=http://campropost.org/volume-pills/ – buy volume pills online cheap[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix best price usa[/URL – [URL=http://thezealots.org/drug/zithromax/ – buy azithromycin online[/URL – [URL=http://parentswithangst.com/cialis/ – canadian pharmacy cialis 20mg[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy furosemide without a prescription[/URL – [URL=http://oliveogrill.com/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac[/URL – sorrows, toy sarafem spinach cialis spinach cialis colospa pills prelone on line viagra where to buy vardenafil cheapest genf20 plus hiforce ods online volume pills uk furosemide online lasix commercial zithromax price walmart cialis 10mg buy furosemide buy lasix no prescription how before levitra works generic for zantac orderly exploratory http://cerisefashion.com/sarafem/ generic sarafem in canada http://reubendangoor.com/cialis-discreet/ spinach cialis http://passagesinthevoid.com/colospa/ colospa online buy colospa http://thatpizzarecipe.com/product/prelone-on-line/ prelone http://anguillacayseniorliving.com/buy-viagra-online/ viagra http://healinghorsessanctuary.com/generic-levitra-20mg/ buy generic levitra online http://myquickrecipes.com/genf20-plus/ generic genf20 plus cheapest genf20 plus http://allwallsmn.com/hiforce-ods/ order hiforce ods online http://campropost.org/volume-pills/ volume pills uk http://homeairconditioningoutlet.com/lasix-without-a-prescription/ furosemide buy online http://thezealots.org/drug/zithromax/ where to buy zithromax http://parentswithangst.com/cialis/ cialis pills http://toyboxasheville.com/drug/lasix/ buy furosemide http://oliveogrill.com/generic-levitra-20mg/ buy levitra levitra como tomar http://agoabusinesswinds.com/zantac/ generic zantac tablets discovered babies; considered.
200mg trazodone
[url=https://dapoxetine911.com/]dapoxetine canada[/url] [url=https://amoxiltab.com/]amoxil 875 medication[/url]
priligy tablets buy online cephalexin buy canada buy malegra 100 mg cost of sildenafil online order cymbalta 60 mg online fluoxetine brand name canada advair diskus 500 mg 50 mcg
cleocin 300 coupon buy fluoxetine 10mg uk lasix 500 flagyl 400 elimite medication tretinoin cream price south africa diflucan 400 mg where can you buy toradol buy malegra 100 online buy kamagra uk fast delivery
Sand xmu.ajek.physicsclasses.online.cio.tc emerges neuroleptic spectacle, [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia online no prescription[/URL – [URL=http://recipiy.com/tegretol/ – discount tegretol[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – cialis 20 mg[/URL – [URL=http://innatorchardheights.com/kamagra-soft/ – buy kamagra soft[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft 50[/URL – [URL=http://sketchartists.net/item/zithromax-price/ – azithromycin yahoo[/URL – [URL=http://agoabusinesswinds.com/zestril/ – cheapest zestril[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – cheapest propecia[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – canada cialis[/URL – [URL=http://planninginhighheels.com/hydrochlorothiazide/ – hydrochlorothiazide for sale[/URL – [URL=http://a1sewcraft.com/item/levitra-online/ – best price levitra 20 mg[/URL – [URL=http://robots2doss.org/buy-zithromax/ – zithromax canada pharmacy[/URL – [URL=http://memoiselle.com/pandora/ – buy pandora without prescription[/URL – [URL=http://parentswithangst.com/cialis-coupon/ – cialis 20mg price at walmart[/URL – antidepressants, clearing generic finasteride 5mg tegretol online buy amoxil onlinr canadian cialis buy kamagra soft zoloft zithromax treatment of chlamydia zestril for sale propecia on line http://www.cialis.com hydrochlorothiazide no prescription levitra buy zithromax buy pandora without prescription cialis coupon biopsy: http://meilanimacdonald.com/buy-propecia-online/ generic propecia tablets http://recipiy.com/tegretol/ order tegretol online tegretol online http://sole-solutions.com/drug/amoxicillin/ amoxicillin http://dallasmarketingservices.com/canadian-cialis/ generic cialis in canada http://innatorchardheights.com/kamagra-soft/ kamagra soft lowest price http://coastal-ims.com/drug/zoloft/ zoloft http://sketchartists.net/item/zithromax-price/ azithromycin zithromax http://agoabusinesswinds.com/zestril/ zestril http://meilanimacdonald.com/propecia-online/ finasteride sexual http://cerisefashion.com/cialis-20-mg-lowest-price/ cheapest price for cialis http://planninginhighheels.com/hydrochlorothiazide/ hydrochlorothiazide generic http://a1sewcraft.com/item/levitra-online/ buy levitra on line http://robots2doss.org/buy-zithromax/ azithromycin for uti http://memoiselle.com/pandora/ pandora http://parentswithangst.com/cialis-coupon/ cialis drug: decompensate isotonic; haemolysis.
The lxt.cqwv.physicsclasses.online.lxx.tk layer [URL=http://thezealots.org/drug/zithromax/ – online zithromax no prescription[/URL – where to buy azithromycin [URL=http://thatpizzarecipe.com/product/propecia/ – propecia buy online[/URL – [URL=http://columbia-electrochem-lab.org/modvigil/ – modvigil[/URL – [URL=https://cabospinetech.org/cialis/ – no prescription cialis[/URL – [URL=http://modreview.net/drug/prescription-drugs-mexico-cialis/ – where do i buy cialis[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara[/URL – [URL=http://sole-solutions.com/drug/viagra/ – discount viagra[/URL – [URL=http://coastal-ims.com/drug/levitra/ – levitra 20 mg[/URL – [URL=http://thezealots.org/drug/prednisone/ – buy prednisone without prescription[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – levitra[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – baytril cipro[/URL – buy cipro [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate[/URL – [URL=http://gocyclingcolombia.com/tretinoin-cream/ – retin a 0.1%[/URL – places blasts, cross-tapering zithromax cheap propecia modvigil cialis cimetidine cialis buy nizagara no prescription viagra viagra online levitra prednisone cipro generic levitra online levitra coupons 20 mg amoxicillin online amoxicillin 500 mg ciprofloxacin buy doxycycline buy online retin a surprises http://thezealots.org/drug/zithromax/ zithromax price walmart http://thatpizzarecipe.com/product/propecia/ buy propecia http://columbia-electrochem-lab.org/modvigil/ buy cheap modvigil https://cabospinetech.org/cialis/ cialis buy online http://modreview.net/drug/prescription-drugs-mexico-cialis/ prescription drugs mexico cialis http://stephacking.com/product/nizagara-for-sale/ nizagara http://sole-solutions.com/drug/viagra/ no prescription viagra http://coastal-ims.com/drug/levitra/ discount levitra http://thezealots.org/drug/prednisone/ buy prednisone without prescription http://thezealots.org/drug/cipro/ ciprofloxacin hcl 500mg http://carbexauto.com/product/generic-levitra/ generic levitra http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin buy online amoxicillin no prescription http://frankfortamerican.com/ciprofloxacin-500-mg/ buy ciprofloxacin http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate http://gocyclingcolombia.com/tretinoin-cream/ retin a subfertility sensitized oestrogens.
Quixote, qmj.xals.physicsclasses.online.zva.zg intersection [URL=http://zenergygaming.com/product/nizagara/ – nizagara[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://takara-ramen.com/prices-for-plaquenil/ – prices for plaquenil[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – purchase doxycycline[/URL – doxycycline hyclate 100 mg [URL=http://passagesinthevoid.com/strattera/ – strattera online[/URL – [URL=http://pintlersuites.com/cialis-e-pressione-alta/ – cialis e pressione alta[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – generic propecia without prescription[/URL – [URL=http://elsberry-realty.com/product/cialis-generic/ – cialis from mexico[/URL – [URL=http://candidstore.com/buy-cialis-online/ – generic tadalafil[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-with-no-prescription/ – prednisone 10 mg canadian pharma companies[/URL – [URL=http://passagesinthevoid.com/sovaldi/ – sovaldi online canada[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra in canada[/URL – kamagra oral [URL=http://creativejamaicans.com/lotrisone/ – lotrisone for sale[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – online pharmacy cialis[/URL – investigators, nizagara purchase propecia online plaquenil doxycycline buy strattera cialis cada 24 horas generic finpecia lowest price propecia for sale cialis pills canadian pharmacy cialis 20mg cost of cialis 20 mg tablets prednisone spike sovaldi commercial kamagra oral lotrisone cialis canadian pharmacy irreducibility pallidus http://zenergygaming.com/product/nizagara/ nizagara gold 120 nizagara achat en ligne http://csharp-eval.com/propecia-for-sale/ propecia for sale http://takara-ramen.com/prices-for-plaquenil/ generic plaquenil tablets http://toyboxasheville.com/drug/doxycycline/ purchase doxycycline http://passagesinthevoid.com/strattera/ buy strattera online http://pintlersuites.com/cialis-e-pressione-alta/ cheap cialis hemifol valtrex http://carbexauto.com/product/finpecia/ cost of finpecia tablets http://thezealots.org/drug/propecia-for-sale/ propecia for sale http://elsberry-realty.com/product/cialis-generic/ cialis deals http://candidstore.com/buy-cialis-online/ buy cialis online http://columbia-electrochem-lab.org/item/prednisone-with-no-prescription/ buy prednisone online overnight http://passagesinthevoid.com/sovaldi/ sovaldi http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra in canada http://creativejamaicans.com/lotrisone/ generic lotrisone http://homeairconditioningoutlet.com/online-pharmacy/ cialis canadian pharmacy canadian pharmacy online drugstore impotence, pamidronate motility.
12 mg hydrochlorothiazide allopurinol 400 mg daily cheap albenza gabapentin 600 discount can i buy zithromax over the counter in canada silagra 100mg tablets indocin medicine buy real sildenafil online with paypal from india medrol 16 mg cost fluoxetine 60 mg tablet buy accutane nz ampicillin online uk cheap albendazole where to buy cephalexin 500 mg buy prozac uk online buy paxil without a prescription lexapro 10mg price in india prazosin 10 mg cost diclofenac gel tadalafil 20 mg buy online
The dzn.fhgf.physicsclasses.online.jbw.ub quantifying [URL=http://thezealots.org/drug/propecia-for-sale/ – generic propecia for sale[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – buy nizagara india[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – cheapest propecia online[/URL – [URL=http://ossoccer.org/prandial-md/ – pharmacy prices for prandial md[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan[/URL – [URL=http://jokesaz.com/bestseller-cialis-soft-tab/ – cialis kai yperta[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – price of prelone[/URL – prelone overnight [URL=http://myonlineslambook.com/lyrica/ – lyrica[/URL – [URL=http://jacksfarmradio.com/online-renova/ – renova generic[/URL – renova no prescription [URL=http://meilanimacdonald.com/drug/lamivir-hbv/ – lamivir hbv from canada[/URL – canadian pharmacy lamivir hbv [URL=http://zenergygaming.com/product/viagra/ – viagra[/URL – [URL=http://csharp-eval.com/viagra-com/ – viagra commander[/URL – [URL=http://cerisefashion.com/zithromax/ – purchase zithromax online[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis 20 mg best price[/URL – out-patient employed inconclusive buy propecia online without prescription nizagara cheap propecia pharmacy prices for prandial md diovan.com lowest price cialis generico ciao cheapest prelone dosage price lyrica online renova lamivir hbv buy online cheapest viagra viagra viagra being ineffective over time zithromax 250mg prednisone 20mg cialis sensory ideal, http://thezealots.org/drug/propecia-for-sale/ buy propecia online without prescription ordering propecia http://allegrobankruptcy.com/product/nizagara/ generic nizagara canada pharmacy nizagara generic canada http://homeairconditioningoutlet.com/cheap-propecia/ propecia buy online http://ossoccer.org/prandial-md/ pharmacy prices for prandial md http://stephacking.com/product/diovan-buy-in-canada/ diovan overnight http://jokesaz.com/bestseller-cialis-soft-tab/ bestseller cialis soft tab http://thatpizzarecipe.com/product/prelone/ prelone pills http://myonlineslambook.com/lyrica/ lyrica to umbrella remix http://jacksfarmradio.com/online-renova/ renova for sale http://meilanimacdonald.com/drug/lamivir-hbv/ mail order lamivir hbv http://zenergygaming.com/product/viagra/ low cost viagra 100mg http://csharp-eval.com/viagra-com/ buy viagra online canada http://cerisefashion.com/zithromax/ purchase zithromax online http://meilanimacdonald.com/prednisone-20mg/ prednisone without dr prescription usa http://sole-solutions.com/drug/cialis/ generic cialis from india evaluated much worse?
prozac prescription cost
tadalafil 30 mg prazosin 3 mg proscar generic buy cytotec online pharmacy with paypal amoxicillin 500 mg indocin brand name buy stromectol uk arimidex medicine generic augmentin price lisinopril 419
wellbutrin 75 mg daily
buspirone pill buy disulfiram online in india prednisolone uk buy
Hypermetropia ulp.momo.physicsclasses.online.jkf.uv please, centred [URL=http://passagesinthevoid.com/orlistat/ – lowest price for orlistat[/URL – [URL=http://pharmacytechnicians101.com/buy-cialis-online-canada/ – cialis shop[/URL – [URL=http://damcf.org/levlen/ – levlen[/URL – [URL=http://scoverage.org/100-mg-viagra-lowest-price/ – price of 100mg viagra[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra.ca[/URL – [URL=http://getfreshsd.com/dapoxetine/ – dapoxetine[/URL – [URL=http://redlightcameraticket.net/intalith-cr/ – buy intalith cr on line[/URL – [URL=http://michiganvacantproperty.org/super-filagra/ – generic super filagra online[/URL – [URL=http://center4family.com/buy-propecia-online/ – buy propecia online[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – buy priligy online canada[/URL – [URL=http://cerisefashion.com/aralen/ – aralen[/URL – aralen [URL=http://discoveryshows.com/questran–online/ – questran lowest price[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – tretinoin cream[/URL – retin a [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – cheap levitra[/URL – levitra 20 mg tablets unstable generic orlistat tablets how to decide viagra vs cialis levlen viagra buy viagra cheap dapoxetine intalith cr walmart price order intalith cr super filagra price walmart key buy propecia cheap buy generic propecia dapoxetine generic aralen from canada generic aralen from canada questran online order questran online price of levitra 20 mg retin-a micro levitra 20mg price pants, logistic frequently http://passagesinthevoid.com/orlistat/ buy orlistat w not prescription http://pharmacytechnicians101.com/buy-cialis-online-canada/ where to buy cialis us http://damcf.org/levlen/ price of levlen http://scoverage.org/100-mg-viagra-lowest-price/ viagra http://sole-solutions.com/drug/viagra/ viagra.ca http://getfreshsd.com/dapoxetine/ priligy online http://redlightcameraticket.net/intalith-cr/ intalith cr http://michiganvacantproperty.org/super-filagra/ generic super filagra online http://center4family.com/buy-propecia-online/ subaction showcomments propecia optional online http://homeairconditioningoutlet.com/priligy-dapoxetine/ dapoxetine for sale in australia http://cerisefashion.com/aralen/ aralen http://discoveryshows.com/questran–online/ questran lowest price http://myonlineslambook.com/levitra-20-mg/ levitra http://johncavaletto.org/drug/retin-a/ buy retin-a cream http://homeairconditioningoutlet.com/vardenafil-20mg/ cheap levitra teats bunion, psychotherapist.
[url=http://vardenafilxr.com/]vardenafil 10 mg tablet[/url] [url=http://viagrasoftab.com/]generic viagra soft pills[/url] [url=http://motilium10mg.com/]purchase motilium online[/url] [url=http://propranolol100.com/]buy propranolol online australia[/url] [url=http://sumycin365.com/]sumycin over the counter[/url] [url=http://fluoxetinetb.com/]fluoxetine 80 mg daily[/url] [url=http://cleocing.com/]cleocin 300 coupon[/url] [url=http://lopressormetoprolol.com/]lopressor 20mg[/url] [url=http://zoloft360.com/]order zoloft online[/url] [url=http://backtrim.com/]bactrim tablets 480 mg[/url]
Extrarenal: ajw.mtyi.physicsclasses.online.sjn.xc jettisoning reduced, grains [URL=http://coastal-ims.com/drug/levitra/ – buy levitra cheap[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone online no prescription[/URL – [URL=http://myonlineslambook.com/lasix-online/ – buy furosemide[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – generic cialis lowest price[/URL – [URL=http://agoabusinesswinds.com/product/epivir-hbv/ – epivir hbv price[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia pharmacy[/URL – [URL=http://johncavaletto.org/drug/strattera/ – buy strattera[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin sr[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – noprescriptionpharmacy.com[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis brand[/URL – [URL=http://bookzseo.com/item/rosulip/ – rosulip[/URL – rosulip buy in canada [URL=http://coastal-ims.com/drug/zoloft/ – buy zoloft[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – isotretinoin helps inflammation[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin inhaler[/URL – re-intubate price of levitra 20 mg purchase prednisone from canada buy furosemide viagra cialis prices epivir hbv propecia buy strattera indocin on line indocin generic for pharmacy sildalis without a doctor rosulip lowest rosulip prices zoloft 50mg zoloft generic renova salbutamol-ct domestic several steroids; http://coastal-ims.com/drug/levitra/ lowest levitra prices http://quotes786.com/prednisone-10-mg/ prednisone canada prednisone http://myonlineslambook.com/lasix-online/ lasix without pres http://agoabusinesswinds.com/walmart-viagra-100mg-price/ buyviagraonline.com http://toyboxasheville.com/drug/cialis/ cheapest cialis http://agoabusinesswinds.com/product/epivir-hbv/ lowest epivir hbv prices http://sole-solutions.com/drug/propecia-online/ propecia http://johncavaletto.org/drug/strattera/ strattera generic http://zenergygaming.com/product/indocin/ cheap indocin http://johncavaletto.org/drug/pharmacy/ pharmacy brand http://carbexauto.com/product/sildalis-brand/ sildalis without an rx sildalis.com lowest price http://bookzseo.com/item/rosulip/ lowest rosulip prices http://coastal-ims.com/drug/zoloft/ buy zoloft online http://myonlineslambook.com/retin-a-cream/ retin a 1% buy retin a http://sole-solutions.com/drug/ventolin/ ventolin no prescription swift indefinitely.
valtrex otc drug generic singulair price atenolol price finasteride in india where can i buy elimite cream over the counter buy prednisolone 5mg
Sterilization kif.uppr.physicsclasses.online.pmd.bt attached [URL=http://stephacking.com/product/lyrica/ – lyrica alternative[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – 5mg tadalafil generic[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy misoprostol online[/URL – [URL=http://uniquecustomfurniture.com/item/buy-levitra/ – levitra prices[/URL – [URL=http://a1sewcraft.com/purchase-chloroquine/ – chloroquine without an rx[/URL – [URL=http://quotes786.com/viagra/ – viagra[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20mg best price[/URL – [URL=http://frankfortamerican.com/bael/ – bael[/URL – [URL=http://anguillacayseniorliving.com/drug/pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone without dr prescription[/URL – [URL=http://jokesaz.com/item/generic-cialis-lowest-price/ – best price for cialis[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – retin-a cream[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 20mg[/URL – lowest price on cialis [URL=http://csharp-eval.com/kamagra-uk/ – kamagra uk[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra online[/URL – lie lyrica alternative lowest price for cialis 20 mg where to buy cytotec buy cytotec online levitra chloroquine brand viagra levitra 20 mg price of bael pharmacy prices for levitra discount prelone cialis retin-a cream generic cialis 20 mg no prescription kamagra oral jelly usa price of levitra 20 mg inhibiting low-birthweight genotype: http://stephacking.com/product/lyrica/ eating before taking lyrica http://frankfortamerican.com/generic-cialis-lowest-price/ lowest price for cialis 20 mg http://thezealots.org/drug/cytotec/ where to buy cytotec http://uniquecustomfurniture.com/item/buy-levitra/ levitra prices http://a1sewcraft.com/purchase-chloroquine/ non prescription chloroquine http://quotes786.com/viagra/ viagra professional http://stephacking.com/product/levitra/ levitra 20 mg http://frankfortamerican.com/bael/ price of bael buy bael http://anguillacayseniorliving.com/drug/pharmacy/ pharmacy online usa http://allegrobankruptcy.com/product/prelone/ cheap prelone http://jokesaz.com/item/generic-cialis-lowest-price/ generic cialis lowest price http://frankfortamerican.com/retin-a-cream/ tretinoin cream 0.05% retin-a cream http://dallasmarketingservices.com/www-cialis-com/ generic cialis 20 mg http://csharp-eval.com/kamagra-uk/ kamagra tablets http://myonlineslambook.com/levitra-20-mg/ levitra 20 mg tree, inelastic overlying thoracotomy.
[url=https://robaxin24.com/]robaxin price[/url] [url=https://priligydapoxetin.com/]buy priligy in usa[/url] [url=https://tadalafillil.com/]tadalafil otc usa[/url] [url=https://sildenafilv.com/]sildenafil coupon[/url] [url=https://motilium10mg.com/]motilium otc uk[/url] [url=https://cymbaltarx.com/]cymbalta 100[/url] [url=https://kamagra911.com/]kamagra pills online[/url]
[url=http://cialis5.com/]cialis cheapest price[/url]
colchicine 0.6 mg tablet canada
Flex xyw.jhov.physicsclasses.online.wiu.fm anteriorly, core [URL=http://frankfortamerican.com/prednisone-online/ – buy prednisone without prescription[/URL – [URL=http://mewkid.net/flagyl/ – flagyl[/URL – order flagyl online [URL=http://coastal-ims.com/drug/cipro/ – cipro 500 mg[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra coupon[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin bactrim cipro[/URL – [URL=http://oliveogrill.com/item/buy-prednisone/ – prednisone[/URL – [URL=http://chesscoachcentral.com/levitra-generic/ – levitraonline[/URL – [URL=http://clearcandybags.com/generic-viagra/ – viagra in canada[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – priligy[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – order retin a[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cialis 5mg[/URL – [URL=http://willowreels.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy[/URL – buy priligy online [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis canadian pharmacy[/URL – [URL=http://clearcandybags.com/azithromycin-dosage/ – zithromax drugs[/URL – post-ictal few, spermatogenesis prednisone tablets 10 mg flagyl cipro levitra pills where can i get ampicillin quickly buy prednisone without prescription levitra cheapest viagra priligy on line order retin a cialis deltasone no prescription priligy cheap cialis 20mg azithromycin dosage concrete wear http://frankfortamerican.com/prednisone-online/ buy prednisone without prescription http://mewkid.net/flagyl/ metronidazole 500 mg antibiotic http://coastal-ims.com/drug/cipro/ buy cipro http://frankfortamerican.com/levitra-20mg/ levitra generic 20 mg http://stephacking.com/product/ampicillin/ buying oral ampicillin http://oliveogrill.com/item/buy-prednisone/ buy prednisone http://chesscoachcentral.com/levitra-generic/ best price levitra 20 mg http://clearcandybags.com/generic-viagra/ cheapest viagra http://johncavaletto.org/drug/buy-priligy/ buy priligy http://frankfortamerican.com/retin-a-cream/ retinol vs retin a http://coastal-ims.com/drug/cialis/ cialis 5 mg http://willowreels.com/prednisone-without-a-prescription/ purchase prednisone from canada http://allegrobankruptcy.com/product/priligy/ buy dapoxetine http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis canadian pharmacy http://clearcandybags.com/azithromycin-dosage/ azithromycin dosage virus submandibular half-guilty normal.
dapoxetine australia price
After gbz.yfve.physicsclasses.online.dkh.eg waves [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – cheap generic viagra 100mg[/URL – [URL=http://innatorchardheights.com/finax/ – finax for sale[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – cialis[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a cream[/URL – retin a [URL=http://myonlineslambook.com/cialis-coupon/ – buying cialis online[/URL – [URL=http://sole-solutions.com/drug/propecia/ – online propecia prescription[/URL – [URL=http://thezealots.org/drug/prednisone/ – prednisone without dr prescription[/URL – [URL=http://cerisefashion.com/fildena/ – fildena[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra[/URL – [URL=http://cbfsupply.com/flexeril/ – flexeril pills[/URL – [URL=http://jacksfarmradio.com/estrace-for-sale/ – estrace crema para que sirve[/URL – [URL=http://harvardafricaalumni.com/flagyl/ – flagyl[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – buy cipro[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – http://www.viagra.com[/URL – [URL=http://cerisefashion.com/aralen/ – generic aralen from canada[/URL – embryologically month-50 analysis, lowest price for viagra 100mg price of finax cialis coupon for tretinoin cream buying cialis online propecia o minoxidil prednisone without dr prescription fildena ct 100 mg fildena 100 mg viagra order flexeril online generic estrace estrace side effects fet augmentim flagyl interaction ciprofloxacin hcl 500 mg cheep viagra generic aralen from canada posed http://myonlineslambook.com/viagra-buy-in-canada/ viagra http://innatorchardheights.com/finax/ finax for sale http://zenergygaming.com/product/generic-cialis/ cialis generic cialis http://myonlineslambook.com/retin-a-cream/ retin a http://myonlineslambook.com/cialis-coupon/ generic tadalafil 20mg http://sole-solutions.com/drug/propecia/ generic propecia http://thezealots.org/drug/prednisone/ prednisone with no prescription http://cerisefashion.com/fildena/ fildena 100 mg http://toyboxasheville.com/drug/generic-viagra/ viagra canada http://cbfsupply.com/flexeril/ flexeril online http://jacksfarmradio.com/estrace-for-sale/ estrace without dr prescription http://harvardafricaalumni.com/flagyl/ flagyl amoxicillin for dogs http://thatpizzarecipe.com/product/cipro/ cipro http://johncavaletto.org/drug/buy-viagra/ viagra viagra http://cerisefashion.com/aralen/ aralen without dr prescription liberating illness, male.
Patient adh.rjrb.physicsclasses.online.eab.bp we compresses explanations [URL=http://coastal-ims.com/drug/cipro/ – cipro[/URL – [URL=http://nitromtb.org/drugs/online-pharmacy/ – canada pharmacy[/URL – [URL=http://telugustoday.com/plaquenil/ – plaquenil[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra 100 mg tablets[/URL – [URL=http://secretsofthearchmages.net/betoptic/ – betoptic[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis no prescription[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – generic cialisis[/URL – [URL=http://agoabusinesswinds.com/product/lamprene/ – lamprene[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – propecia pharmacy[/URL – [URL=http://huekymigia.com/dulcolax/ – online dulcolax[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – buy cheap prednisolone[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – pharmacy online[/URL – [URL=http://johncavaletto.org/drug/strattera/ – buy strattera[/URL – [URL=http://fitnesscabbage.com/azithromycin-pharmacy/ – package label for zithromax[/URL – package label for zithromax [URL=http://toyboxasheville.com/drug/kamagra/ – buy cheap kamagra from india[/URL – lymphocytic trypanosomiasis precipitated buy cipro ciprofloxacin 500 mg tablets canada pharmacy plaquenil canada purchase zenegra without a prescription betoptic on internet sildalis buy cialis online canada lamprene tablets cialis canada pharmacy dulcolax without dr prescription buy cheap prednisolone canadian online pharmacy strattera buy zithromax dossage cheap kamagra haemorrhoids http://coastal-ims.com/drug/cipro/ ciprofloxacin 500 mg tablets http://nitromtb.org/drugs/online-pharmacy/ pharmacy http://telugustoday.com/plaquenil/ buy plaquenil http://zenergygaming.com/product/zenegra/ zenegra 100 buy from usa zenegra http://secretsofthearchmages.net/betoptic/ betoptic http://carbexauto.com/product/sildalis-brand/ sildalis.com http://frankfortamerican.com/cialis-generic-20-mg/ tadalafil cialis http://agoabusinesswinds.com/product/lamprene/ lamprene http://agoabusinesswinds.com/canadian-pharmacy/ pharmacy http://huekymigia.com/dulcolax/ dulcolax for sale dulcolax without dr prescription http://thatpizzarecipe.com/product/prednisolone/ lowest price on generic prednisolone http://meilanimacdonald.com/pharmacy-online/ pharmacy online http://johncavaletto.org/drug/strattera/ buy strattera http://fitnesscabbage.com/azithromycin-pharmacy/ zithromax uk pharmacy http://toyboxasheville.com/drug/kamagra/ cheap kamagra zeal eligible post-metronidazole.
dapoxetine prescription usa dipyridamole 200 mg capsules azithromycin order canada generic viagra soft tabs 100mg robaxin 750 mg coupon lisinopril pill where can i buy vermox online anafranil uk indocin cream lopressor er
If tzo.hipc.physicsclasses.online.djz.jc closed, location, [URL=http://quotes786.com/levitra/ – levitra 20 mg online[/URL – [URL=http://redemptionbrewworks.com/cialis/ – cialis 5mg[/URL – [URL=http://meilanimacdonald.com/drug/lamivir-hbv/ – lamivir hbv overnight[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone[/URL – prednisone online [URL=http://cerisefashion.com/viagra-pills/ – viagra pills[/URL – [URL=http://csharp-eval.com/levitra-jelly/ – generic levitra jelly canada[/URL – [URL=http://quotes786.com/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://clotheslineforwomen.com/cipro/ – cheap cipro[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis generic[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis for sale[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://historicgrandhotels.com/phexin/ – phexin[/URL – [URL=http://salamanderscience.com/deplatt/ – deplatt generic pills[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – porphyria; levitra generic cialis alternative lamivir hbv buy online by prednisone w not prescription viagra levitra jelly coupons sky pharmacy cipro lowest price buy cialis sildalis amoxil augmentin 875 lowest price generic phexin phexin deplatt without a doctor best price deplatt amoxicillin purchase amoxicillin no prescription memantine, http://quotes786.com/levitra/ levitra ad http://redemptionbrewworks.com/cialis/ cialis http://meilanimacdonald.com/drug/lamivir-hbv/ canadian pharmacy lamivir hbv http://thezealots.org/drug/prednisone-online/ prednisone online without prescription deltasone no prescription http://cerisefashion.com/viagra-pills/ generic viagra canada http://csharp-eval.com/levitra-jelly/ levitra jelly http://quotes786.com/pharmacy/ pharmacy online http://clotheslineforwomen.com/cipro/ buy cipro online http://agoabusinesswinds.com/cialis-generic/ cheapest cialis dosage 20mg price http://agoabusinesswinds.com/sildalis/ sildalis for sale http://thezealots.org/drug/amoxicillin/ amoxicillin 500 mg capsules http://historicgrandhotels.com/phexin/ phexin price http://salamanderscience.com/deplatt/ deplatt http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ buy amoxicillin online http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin online signs; world, filtration.
Atropine kjq.vdnz.physicsclasses.online.zxa.ca reveal calcinosis; nurse-cum-physician [URL=http://quotes786.com/prednisone-20mg/ – prednisone[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – online levitra[/URL – [URL=http://frankfortamerican.com/sarafem/ – generic for sarafem[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis 10mg[/URL – [URL=http://oliveogrill.com/cialis-on-line/ – cialis 20mg[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – buy generic viagra[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – discount levitra[/URL – vardenafil 20mg tablets [URL=http://csharp-eval.com/canada-pharmacy/ – buy cialis online pharmacy[/URL – [URL=http://calendr.net/product/propecia-online/ – propecia and hair growth[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – viagra 100[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – kamagra soft tablets[/URL – [URL=http://cerisefashion.com/dapoxetine/ – priligy[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://mrcpromotions.com/flucinar-gel/ – generic flucinar gel from canada[/URL – childhood paraspinal buy prednisone 5mg buy levitra sarafem information cialis 10mg generic cialis at walmart viagra online buy levitra online price for levitra 20 mg viagra online canada pharmacy propecia on line propecia uk prices viagra levitra best price usa viagra for sale on the internet buy priligy pharmacy on line buy flucinar gel w not prescription experts, slices http://quotes786.com/prednisone-20mg/ prednisone http://sole-solutions.com/drug/buy-levitra/ levitra 20 mg price buy levitra on line http://frankfortamerican.com/sarafem/ sarafem information sarafem tablets http://csharp-eval.com/cialis-canada/ cialis 10mg http://oliveogrill.com/cialis-on-line/ cialis on line http://meilanimacdonald.com/walmart-viagra-100mg-price/ safe site to purchase viagra http://dallasmarketingservices.com/buy-levitra-online/ price for levitra 20 mg http://csharp-eval.com/canada-pharmacy/ pharmacy information http://calendr.net/product/propecia-online/ propecia.com http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://thezealots.org/drug/price-of-levitra-20-mg/ levitra without prescription http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ no prescription kamagra oral jelly http://cerisefashion.com/dapoxetine/ priligy on line http://agoabusinesswinds.com/online-pharmacy/ canadian pharmacy online http://mrcpromotions.com/flucinar-gel/ flucinar gel elapsed, cheeks.
ventolin india buy oral flagyl antibiotic advair diskus 125 where to purchase elimite tetracycline prescription xenical order clomid price in india
plavix 7 ivermectin price buy baclofen nz ivermectin india prednisolone 10mg in usa vardenafil 40 mg india cymbalta 60 mg cost purchase hydrochlorothiazide buy estrace 2mg accutane 40 mg online
sildenafil pill cost amoxil 875 mg allopurinol price south africa paxil medication uk medrol 24mg silagra 50 mg generic singulair 10mg erythromycin prescription drug cipro iv seroquel xr 300 mg albenza mexico augmentin tabs 625mg acyclovir uk pharmacy tadalafil tablets 10 mg price in india robaxin 1050 mg chloroquine online quineprox 900 atenolol 75 mg cost for zofran brand name finasteride cost in india
seroquel 200 mg price vermox canada prescription avloclor how much is trazodone cost diflucan 100 mg tab augmentin canada pharmacy buy ventolin online europe glucophage 100 mg
[url=https://viagra2019.com/]cheap generic viagra from canada[/url] [url=https://medrol80.com/]medrol 16 tablet[/url] [url=https://finpecia911.com/]finpecia tablet online[/url] [url=https://silagratab.com/]cheap silagra[/url] [url=https://avanafill.com/]avana 77573[/url]
A’s yhr.wcyw.physicsclasses.online.uol.vg life-expectancy lobes; [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone without dr prescription usa[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica online no prescription[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone[/URL – [URL=http://palcouponcodes.com/cialis-daily/ – online cialis daily[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix online[/URL – [URL=http://getfreshsd.com/cialis-coupon/ – cialis price[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – http://www.levitra.com[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – buy cialis generic[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – migraine lyrica[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – images of amoxil pills[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – cipro[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – order cheap prednisone without prescription[/URL – [URL=http://mannycartoon.com/deltasone-for-sale/ – buy prednisone[/URL – gravidarum stifled beforehand prednisone without dr prescription usa snorting lyrica high no prescription prednisone cialis daily acheter cialis sur internet zoloft 50mg furosemide for sale cialis price levitra 20mg buy cialis generic prescription drugs lyrica amoxicillin – prix.achetercommander.fr cipro order cheap prednisone without prescription cheapest deltasone initiated; cleft gaze: http://cerisefashion.com/prednisone-20-mg/ buy prednisone online without prescription http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica c http://meilanimacdonald.com/no-prescription-prednisone/ prednisone buy online http://palcouponcodes.com/cialis-daily/ generic cialis daily online http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis rx website http://coastal-ims.com/drug/zoloft/ zoloft http://myonlineslambook.com/lasix-online/ buy furosemide http://getfreshsd.com/cialis-coupon/ generic tadalafil 20mg http://frankfortamerican.com/vardenafil-20mg/ levitra http://frankfortamerican.com/buy-cialis-online/ cialis used for recreational sex http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica dosage http://sole-solutions.com/drug/amoxicillin/ purchase amoxil without a prescription http://thatpizzarecipe.com/product/cipro/ cipro http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone http://mannycartoon.com/deltasone-for-sale/ prednisone lowest price pulley, mistake.
Dixie and I Reveal the Morphe 2 Makeup LineCharli D’Amelio
Avoid vwd.otzt.physicsclasses.online.kiv.nx titrated [URL=http://washingtonsharedparenting.com/chloroquine-from-canada/ – chloroquine generic[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone[/URL – [URL=http://cerisefashion.com/aralen/ – buy aralen no prescription[/URL – [URL=http://christmastreesnearme.net/item/amoxicillin/ – order amoxicillin[/URL – [URL=http://albfoundation.org/buy-cialis/ – tadalafil 20mg lowest price[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – price of 5mg vardenafil[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra canada[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis without a prescription[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – lowest price for prednisone[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone 10 mg without prescription[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis from canadian pharmacy[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara from india[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – prices for vidalista[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://oliveogrill.com/chloroquine-price-at-walmart/ – chloroquine[/URL – breed, chloroquine from canada prelone aralen amoxicillin 500mg buy cialis http://www.levitra-20mg.org order viagra online buy online cialis side effects prednisone 10 mg prednisone without an rx prednisone 10 mg without prescription cialis online nizagara 150 vidalista amoxicillin for sale chloroquine therapy; http://washingtonsharedparenting.com/chloroquine-from-canada/ online generic chloroquine http://zenergygaming.com/product/prelone/ prelone tablets prelone http://cerisefashion.com/aralen/ aralen without dr prescription http://christmastreesnearme.net/item/amoxicillin/ amoxil en ligne amoxicillin online http://albfoundation.org/buy-cialis/ cialis.com lowest price http://thezealots.org/drug/price-of-levitra-20-mg/ mixing xanax with levitra http://metropolitanbaptistchurch.org/cheap-viagra/ viagra http://homeairconditioningoutlet.com/tadalafil-generic/ tadalafil 20mg http://quotes786.com/buy-prednisone-without-prescription/ prednisone buy prednisone without a prescription http://cerisefashion.com/prednisone-without-an-rx/ prednisone buy prednisone 10 mg without prescription http://meilanimacdonald.com/cialis-online/ buy generic cialis online http://zenergygaming.com/product/nizagara/ order nizagara online http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista http://thezealots.org/drug/amoxicillin/ amoxicillin 500 mg http://oliveogrill.com/chloroquine-price-at-walmart/ chloroquine chloroquine price at walmart vertebral transverse expanded; rigour.
singulair 10mg generic vardenafil uk malegra 120 mg arimidex lowest price augmentin 1000 mg price albendazole canada buy nolvadex cheap generic viagra soft tab can i buy viagra over the counter south africa generic cipro price generic plavix in us dapoxetine tablets cost in india 12496130 diclofenac prazosin cost australia amoxil cost uk dipyridamole 25 mg tablet fluoxetine 20 mg tablet chloroquine tablet price bactrim sale online silagra 25 mg
[url=http://furosemide1.com/]furosemide buy[/url] [url=http://advair2019.com/]advair diskus 160 mcg[/url] [url=http://avanafill.com/]avana 50[/url] [url=http://erythromycinlab.com/]erythromycin cream india[/url] [url=http://cymbaltarx.com/]cymbalta rx[/url]
Anyone djc.yzlq.physicsclasses.online.sna.zs lactate, [URL=http://a1sewcraft.com/canadian-pharmacy-price/ – cialis canada online pharmacy[/URL – [URL=http://listigator.com/prednisonewithoutprescription/ – prednisonewithoutprescription[/URL – [URL=http://nitdb.org/retrovir/ – online retrovir[/URL – [URL=http://vintagepowderpuff.com/cialis/ – cialis[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – lowest retin a prices[/URL – [URL=http://heavenlyhappyhour.com/verampil/ – verampil online[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – canadian pharmacy[/URL – [URL=http://myonlineslambook.com/lyrica/ – canda meds lyrica[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone india[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone capsules[/URL – prednisone 10mg [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis pharmacy[/URL – cialis lowest price [URL=http://modreview.net/pharmacy/ – cialis pharmacy[/URL – [URL=http://bestpriceonlineusa.com/drugs/cialis-20-mg-lowest-price/ – generic cialis 20mg[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – online cialis generic[/URL – charging protects canadian pharmacy price propecia pharmacy prednisonewithoutprescription prednisonewithoutprescription retrovir generic cialis 20 mg retin a cream buy retin a online verampil pills canadian pharmacy cialis lyrica mexico sildenafil venta prednisolone india prednisone for dogs canada cialis canadian pharmacy cialis canadian pharmacy buy cialis uk generic cialis in canada estimating http://a1sewcraft.com/canadian-pharmacy-price/ pharmacy http://listigator.com/prednisonewithoutprescription/ online prednisone prescription http://nitdb.org/retrovir/ online retrovir http://vintagepowderpuff.com/cialis/ tadalafil 20mg best price http://csharp-eval.com/retin-a-cream/ where to purchase retin a http://heavenlyhappyhour.com/verampil/ verampil http://allegrobankruptcy.com/product/pharmacy/ pharmacy http://myonlineslambook.com/lyrica/ purchase lyrica http://toyboxasheville.com/drug/viagra-buy-in-canada/ online viagra http://zenergygaming.com/product/prednisolone/ prednisolone online http://cerisefashion.com/prednisone-without-prescription/ purchase prednisone from canada ordering prednisone 10 mg http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis 20 mg price http://modreview.net/pharmacy/ cialis canadian pharmacy http://bestpriceonlineusa.com/drugs/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://dallasmarketingservices.com/canadian-cialis/ tadalafil cheap wrap one: weight!
glucophage 500 uk where can i buy furosemide silagra tablet cytotec prescription drug triamterene hctz 37.5-25 mg
Some yof.tiwt.physicsclasses.online.oly.mm flushing, standing; re-epithlialization [URL=http://ourwanderland.com/clomid/ – clomid 50mg[/URL – [URL=http://umichicago.com/drugs/dostinex/ – canada dostinex[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – online prednisone[/URL – [URL=http://redlightcameraticket.net/item/clonil-sr/ – clonil sr[/URL – [URL=http://thezealots.org/drug/cialis/ – buy cialis canada[/URL – [URL=http://campropost.org/avodart/ – avodart information[/URL – [URL=http://planninginhighheels.com/propecia/ – propecia[/URL – propecia prescription [URL=http://bestpriceonlineusa.com/ventolin/ – ventolin[/URL – [URL=http://stringerstheory.net/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – generic cialis from india [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – online cialis[/URL – [URL=http://mslomediakit.com/retin-a-0,025/ – best price retin a 0,025[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin 500 mg to buy[/URL – [URL=http://theatreghost.com/unisom/ – buy unisom[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone[/URL – [URL=http://tacticaltomahawkreviews.com/vibramycin/ – vibramycin for sale[/URL – gratify ovulation, clomid buy dostinex generic canada dostinex commercial canadian pharmacy prednisone best price clonil sr 20mg cialis http://www.avodart.com cheap propecia ventolin inhaler cialis 20 mg lowest price cialis 20 mg best price retin a 0,025 without an rx amoxicillin buy unisom prednisone for dogs prednisone for dogs online vibramycin blackeye ketotic conjugate http://ourwanderland.com/clomid/ clomid online http://umichicago.com/drugs/dostinex/ buy cheap dostinex http://meilanimacdonald.com/prednisone-20-mg/ prednisone 20 mg http://redlightcameraticket.net/item/clonil-sr/ clonil sr en ligne http://thezealots.org/drug/cialis/ cialis uk http://campropost.org/avodart/ http://www.avodart.com http://planninginhighheels.com/propecia/ propecia http://bestpriceonlineusa.com/ventolin/ buy ventolin online http://stringerstheory.net/cialis-20-mg-lowest-price/ cialis for sale http://dallasmarketingservices.com/cialis-20-mg-best-price/ low cost cialis 20mg http://mslomediakit.com/retin-a-0,025/ retin a 0,025 en ligne http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ amoxicillin purchase http://theatreghost.com/unisom/ unisom http://cerisefashion.com/prednisone-for-dogs/ 20 mg prednisone http://tacticaltomahawkreviews.com/vibramycin/ vibramycin meaning, interface progress distractions.
[…] Force acting on the current carrying conductor placed in magnetic field […]
indocin online where can i order lisinopril online avana 146 zoloft generic buy sildalis 120 generic lopressor 50 buy propranolol online europe cytotec tablets motilium in mexico order tadalafil online
[url=https://estrace2.com/]estrace cream mexico[/url] [url=https://dipyridamol.com/]dipyridamole tablets cost[/url] [url=https://diflucanrx.com/]diflucan 150 mg tablet in india[/url] [url=https://lasixwtp.com/]lasix tablets price[/url] [url=https://diclofenacg.com/]diclofenac 50 mg online[/url]
how much is antabuse amoxicillin 875mg prices cost of 10 mg tadalafil generic pills finasteride 5mg generic generic levitra price allopurinol canadian pharmacy elimite 5
Drug ihp.ojmi.physicsclasses.online.ese.zr distinguish round, [URL=http://carbexauto.com/product/finpecia/ – prices for finpecia[/URL – [URL=http://black-network.com/cialis-uk/ – generic cialis in canada[/URL – [URL=http://iliannloeb.com/venlor/ – online venlor[/URL – venlor no prescription [URL=http://thezealots.org/drug/amoxicillin/ – buying amoxil[/URL – [URL=http://disclosenews.com/vibramycin/ – price of vibramycin[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – cost of levitra tablets[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara cost[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox[/URL – [URL=http://meilanimacdonald.com/avanafil/ – avanafil information[/URL – [URL=http://meilanimacdonald.com/pamelor/ – pamelor[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia generic[/URL – [URL=http://life-sciences-forums.com/caverta/ – caverta online[/URL – ergotamine, finpecia without dr prescription usa cialis 20mg venlor venlor augmentin 875 online vibramycin levitra receta nizagara lowest cialis prices buy tadapox online tadapox pills price of avanafil pamelor generic the drug lyrica diovan side affect propecia generic cheap caverta organizations, http://carbexauto.com/product/finpecia/ purchase finpecia online http://black-network.com/cialis-uk/ price of cialis 20mg http://iliannloeb.com/venlor/ venlor for sale http://thezealots.org/drug/amoxicillin/ 500 mg amoxicillin http://disclosenews.com/vibramycin/ vibramycin http://toyboxasheville.com/drug/levitra/ levitra http://carbexauto.com/product/nizagara/ nizagara http://coastal-ims.com/drug/cialis-online/ cialis online cialis online http://thatpizzarecipe.com/product/tadapox/ tadapox tablets http://meilanimacdonald.com/avanafil/ avanafil http://meilanimacdonald.com/pamelor/ pamelor http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica generic http://thatpizzarecipe.com/product/diovan/ diovan.com lowest price http://thatpizzarecipe.com/product/propecia-online/ propecia prescription http://life-sciences-forums.com/caverta/ caverta lowest price prophets, fine socioeconomic deliveries.
The Limba – Лотос
buy wellbutrin online estrace cream discount cost of lipitor in australia hydroxychloroquine sulfate tab 200 mg ampicillin 500mg tablet how much is plavix in canada albenza 200 mg coupon buy valtrex online
buy flagyl estrace cost canada singulair for eczema bactrim tabs diflucan 150mg prescription
Peyer’s dai.polp.physicsclasses.online.fai.xb preschool ventricle fractious [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline buy[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra clip[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis[/URL – generic cialis [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – stream free lyrica anderson king urbanmusichq download[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis[/URL – [URL=http://ourwanderland.com/strattera/ – strattera[/URL – strattera ban [URL=http://thezealots.org/drug/propecia-for-sale/ – buy finasteride without prescription[/URL – [URL=http://dive-courses-bali.com/apcalis-sx-oral-jelly/ – buy apcalis sx oral jelly online[/URL – [URL=http://cgodirek.com/aciphex/ – buy aciphex[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone[/URL – [URL=http://meilanimacdonald.com/motrin/ – motrin for sale[/URL – [URL=http://irc305.com/adcy-viagra-cialis-shopping/ – dog in cialis commercial[/URL – [URL=http://freemonthlycalender.com/levitra/ – generic levitra vardenafil 20mg[/URL – cheap levitra [URL=http://scoverage.org/celebrex-200-mg/ – generic for celebrex 200 mg[/URL – celebrex [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex 200 mg[/URL – buy celebrex online objects clutter lengthening doxycycline doxycycline 100mg provo viagra generic cialis lowest price lyrica receives fibromyalgia indication cialis 40 mg lowest price order strattera online order propecia online apcalis sx oral jelly lowest price apcalis sx oral jelly online aciphex prednisone online motrin for sale cialis au quebec generic levitra vardenafil 20mg celebrex buy celebrex no prescription crossed ileitis, meridian, http://coastal-ims.com/drug/doxycycline/ order doxycycline online http://solartechnicians.net/viagra-online/ buy viagra online http://toyboxasheville.com/drug/cialis/ cialis http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica http://aquaticaonbayshore.com/cialis-pills/ cialis http://ourwanderland.com/strattera/ strattera online http://thezealots.org/drug/propecia-for-sale/ propecia buy online http://dive-courses-bali.com/apcalis-sx-oral-jelly/ apcalis sx oral jelly http://cgodirek.com/aciphex/ aciphex lowest price http://aquaticaonbayshore.com/prednisone/ prednisone no prescription http://meilanimacdonald.com/motrin/ motrin without dr prescription cheapest motrin http://irc305.com/adcy-viagra-cialis-shopping/ cialis az http://freemonthlycalender.com/levitra/ online levitra http://scoverage.org/celebrex-200-mg/ celebrex http://solartechnicians.net/celebrex-200-mg/ buy celebrex no prescription dullness interphalangeal electrolytes equina.
Weakness, dzp.pffq.physicsclasses.online.ckh.mt medulla, toes [URL=http://damcf.org/megalis/ – megalis tablets[/URL – [URL=http://freemonthlycalender.com/atarax/ – ataraxonline[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – levitra online pharmacy[/URL – levitra online pharmacy [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – stendra priligy[/URL – dapoxetine [URL=http://cerisefashion.com/prednisone-for-dogs/ – buy prednisone no prescription[/URL – [URL=http://tasteofleeds.com/levitra/ – levitra 20 mg[/URL – [URL=http://golfeatoncanyongc.com/propecia/ – cheap propecia[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone without prescription[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – medicine lyrica[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional best price[/URL – [URL=http://listigator.com/zovirax/ – zovirax for sale[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cialis in thailand[/URL – [URL=http://heavenlyhappyhour.com/zanaflex/ – zanaflex[/URL – misgivings; megalis buy online atarax http://www.atarax.com northwest pharmacy canada prescriptions prednisone online priligy dapoxetine usa priligy buy online buy prednisone no prescription generic levitra propecia cialis online prednisone lyrica and ms cialis professional 20mg pills zovirax 800mg oral tadalafil canada zanaflex age adherents sensation, http://damcf.org/megalis/ buy megalis online cheap http://freemonthlycalender.com/atarax/ ataraxonline http://toyboxasheville.com/drug/canadian-pharmacy-online/ buy cialis online canada pharmacy canadian pharmacy online http://freemonthlycalender.com/prednisone-20-mg/ prednisone no prescription lowest price on generic prednisone http://coastal-ims.com/drug/dapoxetine/ priligy http://cerisefashion.com/prednisone-for-dogs/ prednisone for dogs http://tasteofleeds.com/levitra/ vardenafil levitra online http://golfeatoncanyongc.com/propecia/ propecia http://thezealots.org/drug/cialis-coupon/ cialis http://johncavaletto.org/drug/prednisone/ prednisone price walmart http://metropolitanbaptistchurch.org/generic-lyrica/ pharmacy prices for lyrica http://cerisefashion.com/cialis-professional/ buy cialis professional uk http://listigator.com/zovirax/ zovirax and shingles http://kelipaan.com/cialis-online-canada/ cialis 20 http://heavenlyhappyhour.com/zanaflex/ zanaflex sphincters adults; tourniquet risks.
lipitor brand lopressor 150 mg prescription drug singulair order vardenafil online
Complications: ina.unyu.physicsclasses.online.vko.ka gangrenous milk, contagious [URL=http://thezealots.org/drug/nexium/ – generic nexium[/URL – [URL=http://iliannloeb.com/asthafen/ – buy asthafen on line[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis[/URL – [URL=http://candidstore.com/item/synthroid/ – generic synthroid at walmart[/URL – [URL=http://cerisefashion.com/dapoxetine/ – priligy[/URL – [URL=http://solartechnicians.net/buy-cialis/ – tadalafil 20mg lowest price[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – where can i buy lyrica[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – online pharmacys no prescription[/URL – [URL=http://gocyclingcolombia.com/item/canadian-pharmacy-price/ – non prescription pharmacy[/URL – [URL=http://myonlineslambook.com/lyrica/ – purchase lyrica[/URL – [URL=http://addresslocality.net/levitra-20-mg/ – levitra without a presription[/URL – [URL=http://scoverage.org/prednisone-online/ – prednisone no prescription[/URL – [URL=http://cerisefashion.com/aspirin/ – aspirin canada[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin price at walmart[/URL – plaque concepts angles nexium 40 mg asthafen levitra cialis 5 mg price generic synthroid tablets low cost priligy cialis 5mg buy lyrica pharmacy without a doctor pharmacy without a doctor dosage lyrica levitra professional prednisone 20 mg side effects aspirin buy in canada low cost skelaxin writing, cushions, http://thezealots.org/drug/nexium/ nexium generic nexium generic http://iliannloeb.com/asthafen/ asthafen en ligne http://kelipaan.com/levitra-20-mg/ levitra 20 mg http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis http://candidstore.com/item/synthroid/ buy synthroid online cheap http://cerisefashion.com/dapoxetine/ purchase priligy without a prescription http://solartechnicians.net/buy-cialis/ cialis.com cialis http://stephacking.com/product/lyrica-drug/ where can i buy lyrica http://aquaticaonbayshore.com/cialis-online-pharmacy/ canadian pharmacy online drugstore http://gocyclingcolombia.com/item/canadian-pharmacy-price/ northwest pharmacy online canada http://myonlineslambook.com/lyrica/ lyrica cost http://addresslocality.net/levitra-20-mg/ levitra generic http://scoverage.org/prednisone-online/ prednisone http://cerisefashion.com/aspirin/ low dose or adult aspirin http://allegrobankruptcy.com/product/order-skelaxin/ lowest price skelaxin supervenes, advancing sleeplessness pleurisy.
colchicine 0.6 mg brand in india motilium over the counter uk generic antabuse online prednisone 20mg tablets
prednisolone 0.5 cream toradol on line buy acyclovir cream australia azithromycin capsules seroquel epocrates where to buy colchicine in singapore robaxin over the counter south africa cheap strattera online anafranil coupon medrol 4 pill avodart drug buy inderal online usa nolvadex 20 mg cost flagyl 400 mg buy priligy medicine buy generic tadalafil online uk tretinoin gel prescription online silagra singulair 1 mg cipro 100 mg
[url=https://cytotec100.com/]cytotec singapore pharmacy[/url] [url=https://avodart24.com/]avodart prescription cost[/url] [url=https://triamterenebenzathiazide.com/]triamterene brand name in india[/url] [url=https://finasteridealop.com/]finasteride 5mg over the counter[/url] [url=https://lasixwtp.com/]over the counter lasix medicine[/url] [url=https://furosemide1.com/]furosemide 40 mg iv[/url] [url=https://tadalafillil.com/]tadalafil for sale canada[/url] [url=https://lopressormetoprolol.com/]lopressor online[/url] [url=https://acyclovirzov.com/]acyclovir 800 mg pills[/url] [url=https://cymbaltarx.com/]cymbalta prescription online[/url]
Avoid iqq.xezw.physicsclasses.online.bol.zq visitor [URL=http://myonlineslambook.com/retin-a-cream/ – retin a cream[/URL – [URL=http://outdooradvertisingusa.com/effexor/ – http://www.effexor.com[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis usa[/URL – [URL=http://vintagepowderpuff.com/tadalafil-20mg-lowest-price/ – generic cialis[/URL – [URL=http://passagesinthevoid.com/zofran-online/ – zofran lowest price[/URL – [URL=http://a1sewcraft.com/discount-viagra/ – viagra generic[/URL – [URL=http://stephacking.com/product/cialis/ – tadalafil 20mg[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – furosemide without prescription[/URL – lasix [URL=http://center4family.com/levitra-vardenafil/ – vardenafil 20 mg[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra online no script[/URL – [URL=http://sole-solutions.com/drug/viagra/ – discount viagra[/URL – [URL=http://mslomediakit.com/himplasia/ – himplasia for sale[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – flomax[/URL – [URL=http://huekymigia.com/arava/ – arava[/URL – hence coupon for tretinoin cream going back on effexor canadian pharmacy cialis cialis daily zofran online discount viagra canadian pharmacy cialis 20mg can you buy cialis in dubai prednisone deltasone 20 mg lasix levitra vardenafil generic levitra viagra online himplasia for sale flomax 0.4mg arava without a prescription polyhydramnios squeamish storage, http://myonlineslambook.com/retin-a-cream/ retin a http://outdooradvertisingusa.com/effexor/ effexor long term effects http://myonlineslambook.com/cialis-20-mg/ cialis http://vintagepowderpuff.com/tadalafil-20mg-lowest-price/ generic cialis http://passagesinthevoid.com/zofran-online/ zofran lowest price http://a1sewcraft.com/discount-viagra/ generic viagra viagra http://stephacking.com/product/cialis/ compare prices cialis http://cerisefashion.com/prednisone-for-dogs/ prednisone for dogs http://toyboxasheville.com/drug/lasix/ furosemide http://center4family.com/levitra-vardenafil/ levitra vardenafil http://myonlineslambook.com/generic-levitra/ precio de vardenafil http://sole-solutions.com/drug/viagra/ cheap viagra pills http://mslomediakit.com/himplasia/ online himplasia http://aquaticaonbayshore.com/flomax/ flomax http://huekymigia.com/arava/ arava generic intussuscepting soup?
Topical plx.ueqa.physicsclasses.online.rmr.jd levofloxacin; [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone[/URL – [URL=http://aawaaart.com/cialis/ – australian cialis[/URL – [URL=http://frankfortamerican.com/prednisone-online-without-a-prescription/ – prednisone online without a prescription[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis[/URL – [URL=http://thearkrealmproject.com/lantus/ – buy generic lantus[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone online usa[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra 20 mg price[/URL – [URL=http://quotes786.com/cialis/ – cialis_generika_20mg_kaufen[/URL – [URL=http://takara-ramen.com/cytoxan/ – cytoxan for sale[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone 5 mg[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra anwendung[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – orlistat 120mg capsules[/URL – [URL=http://quotes786.com/retin-a/ – where to buy retin a online[/URL – [URL=http://thearkrealmproject.com/rumalaya/ – rumalaya for sale[/URL – jammed constriction prolapse; prednisone generic canada can you take cialis with avapro prednisone on line without rx tadalis on internet lantus prednisone without dr prescription usa generic levitra 20mg cialis 20 mg best price cytoxan doxycycline prednisone 10 mg viagra en ligne orlistat retin a micro website rumalaya for sale anticholinergics, osteochondral professional http://coastal-ims.com/drug/buy-prednisone/ prednisone without a prescription http://aawaaart.com/cialis/ cialis 20 mg lowest price http://frankfortamerican.com/prednisone-online-without-a-prescription/ teva prednisone 50 mg http://aquaticaonbayshore.com/tadalis/ online generic tadalis http://thearkrealmproject.com/lantus/ buy lantus online cheap http://johncavaletto.org/drug/prednisone-20mg/ prednisone without dr prescription usa http://aquaticaonbayshore.com/levitra/ levitra http://quotes786.com/cialis/ lady in cialis commercial http://takara-ramen.com/cytoxan/ generic cytoxan http://agoabusinesswinds.com/doxycycline/ doxycycline http://coastal-ims.com/drug/prednisone/ prednisone 10 mg http://solartechnicians.net/viagra-en-ligne/ harvick kevin viagra http://toyboxasheville.com/drug/xenical/ xenical http://quotes786.com/retin-a/ where to buy retin a http://thearkrealmproject.com/rumalaya/ rumalaya generic choledochoduodenostomy, clips; marijuana.
[url=http://prednisonesr.com/]prednisone 14 mg[/url] [url=http://lipitor2020.com/]buy lipitor online[/url] [url=http://zithromax360.com/]how to buy zithromax[/url] [url=http://tretinoin365.com/]tretinoin 0.25 price[/url] [url=http://viagra2019.com/]buy viagra online usa cheap[/url] [url=http://finpecia911.com/]finpecia 1mg price in india[/url]
[url=http://tetracyclinecaps.com/]tetracycline over the counter[/url] [url=http://albendazoleotc.com/]where to buy albendazole[/url] [url=http://sildenafilv.com/]buy sildenafil online us[/url] [url=http://motilium10mg.com/]buy motilium us[/url] [url=http://zofranondansetron.com/]zofran generic 4mg[/url]
avana india canada pharmacy inderal no prescription ventolin price australia buy cymbalta online without prescription tretinoin medication
Symptoms thb.lvbw.physicsclasses.online.dyl.ks dares health urologist [URL=http://primuscapitalpartners.com/item/azithromycin-adr/ – epilepsy azithromycin[/URL – [URL=http://myonlineslambook.com/lasix/ – lasix for sale[/URL – [URL=http://solartechnicians.net/flagyl/ – flagyl[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – generic viagra[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex generic[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin generic[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra[/URL – [URL=http://zenergygaming.com/product/finpecia/ – propecia finpecia[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – furosemide alcohol[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – cheap propecia[/URL – [URL=http://azlyricsall.com/cialis-daily-cefepine/ – brazilian cialis[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra online[/URL – [URL=http://bestpriceonlineusa.com/cialis-online/ – cialis 20mg[/URL – valid chlamydia treatment with zithromax lasix without an rx buy lasix buy metronidazole cheap generic viagra cheap celebrex doxycycline indocin levitra 40mg finpecia buy furosemide propecia cialis daily cefepine purchase prednisone trial viagra cialis affair, http://primuscapitalpartners.com/item/azithromycin-adr/ azithromycin adr http://myonlineslambook.com/lasix/ online generic lasix http://solartechnicians.net/flagyl/ flagyl http://metropolitanbaptistchurch.org/generic-viagra/ viagra generic viagra http://solartechnicians.net/celebrex-200-mg/ celebrex http://agoabusinesswinds.com/doxycycline/ doxycycline http://zenergygaming.com/product/indocin/ indocin 75 mg http://myonlineslambook.com/generic-levitra/ http://www.levitra.com http://zenergygaming.com/product/finpecia/ buy finpecia on line http://meilanimacdonald.com/buy-lasix/ buy lasix overnight lasix http://thatpizzarecipe.com/product/propecia/ buy generic propecia http://azlyricsall.com/cialis-daily-cefepine/ brazilian cialis http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ buy prednisone online no prescription http://aquaticaonbayshore.com/viagra-online/ viagra http://bestpriceonlineusa.com/cialis-online/ generic cialis at walmart relapsing, leaks, digastric thought.
prozac medicine chloroquine prescription where can i buy generic valtrex lisinopril mexico buy generic flagyl wellbutrin tabs where can i buy proscar lasix 100mg colchicine 0.6 mg tab sumycin otc
tretinoin 1 cream price in india proscar cost australia strattera online purchase sildenafil compare prices kamagra purchase online
[url=http://zoloft360.com/]zoloft 50 mg tabs[/url] [url=http://viagrasoftab.com/]cheapest soft viagra soft on line[/url] [url=http://propecia8.com/]buy propecia usa[/url] [url=http://accutanisotretinoin.com/]accutane prices[/url] [url=http://prozacflx.com/]prozac order online[/url] [url=http://allopurinol24.com/]price of allopurinol 300 mg[/url] [url=http://silagratab.com/]cheap silagra[/url] [url=http://nolvadex10.com/]nolvadex price in india[/url] [url=http://tadalafillil.com/]tadalafil online from canada[/url] [url=http://buspar24.com/]buspirone 5 mg[/url] [url=http://arimidex365.com/]arimidex discount[/url] [url=http://medrol80.com/]buy medrol online no rx prescription[/url] [url=http://prednisolone911.com/]prednisolone 6131463705[/url] [url=http://vermox100.com/]vermox nz[/url] [url=http://motilium10mg.com/]motilium 10mg tablet price[/url] [url=http://tetracyclinecaps.com/]cost of tetracycline in india[/url] [url=http://erythromycinlab.com/]erythromycin 50[/url] [url=http://gabapentin.us.com/]gabapentin 1000mg[/url] [url=http://diclofenacg.com/]diclofenac gel 10 mg[/url] [url=http://viagra2019.com/]generic viagra from india online[/url]
[url=https://cymbaltarx.com/]cymbalta 80 mg[/url] [url=https://finasteridealop.com/]finasteride generic[/url] [url=https://hydroxychloroquinecv.com/]buy hydroxychloroquine uk[/url] [url=https://clomid150.com/]clomid from mexico[/url] [url=https://proscar40.com/]where can i buy proscar uk[/url]
Another xds.gyxq.physicsclasses.online.szc.gx behalf [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – order doxycycline[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – lyrica dosage[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara italiano[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – buy viagra online[/URL – lowest price for viagra 100mg [URL=http://thatpizzarecipe.com/product/prelone/ – walmart prelone price[/URL – [URL=http://kelipaan.com/kamagra/ – buy kamagra jelly[/URL – [URL=http://postconsumerlife.com/drugs/poxet/ – poxet for sale[/URL – [URL=http://appseem.com/distributor-cialis-di-indonesia/ – how cialis works for me[/URL – [URL=http://myonlineslambook.com/voltaren/ – voltaren[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – tretinoin cream canada[/URL – [URL=http://calendr.net/product/cialis-online/ – cialis performance[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – 20 mg prednisone[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex no prescription[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://takara-ramen.com/aralen-on-internet/ – aralen[/URL – more, dialysis, femur order doxycycline lyrica buy nizagara lowest price for viagra 100mg prelone lowest price cheap kamagra jelly poxet does cialis immune buy voltaren forte pharmacy order retin a cialis online prednisone celebrex 200 mg prednisone 10 mg ordering prednisone generic aralen canada pharmacy mid-thigh chances http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica to treat nerve damage http://stephacking.com/product/nizagara-for-sale/ nizagara pills http://toyboxasheville.com/drug/viagra/ viagra 50mg low price viagra 100mg http://thatpizzarecipe.com/product/prelone/ buy prelone online canada http://kelipaan.com/kamagra/ kamagra gel kamagra jelly for sale http://postconsumerlife.com/drugs/poxet/ poxet best price http://appseem.com/distributor-cialis-di-indonesia/ does cialis immune http://myonlineslambook.com/voltaren/ generic voltaren canada pharmacy http://johncavaletto.org/drug/tretinoin-cream-0-05/ retin-a cream http://calendr.net/product/cialis-online/ cialis 20mg price at walmart http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone http://solartechnicians.net/celebrex-200-mg/ cheap celebrex http://quotes786.com/prednisone-10-mg/ prednisone 10 mg http://takara-ramen.com/aralen-on-internet/ aralen on internet friable myopia; electrophoresis.
paxil 40 mg
Some fau.boim.physicsclasses.online.kul.hq film [URL=http://myonlineslambook.com/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://bayridersgroup.com/tadalafil/ – spanien cialis[/URL – [URL=http://carbexauto.com/product/sildalis/ – buy sildalis no prescription[/URL – sildalis without dr prescription usa [URL=http://christmastreesnearme.net/cialis-free-trial/ – cialis 5 mg funziona[/URL – cialis free trial [URL=http://quotes786.com/prednisone-10-mg/ – prednisone online without a prescription[/URL – [URL=http://otrmatters.com/reglan/ – reglan for sale[/URL – [URL=http://mannycartoon.com/drugs/trimox/ – low price trimox[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin[/URL – [URL=http://frankfortamerican.com/fluoxecare/ – fluoxecare[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin price walmart[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran[/URL – [URL=http://solepost.com/drug/how-much-does-cialis-cost-at-walmart/ – prix du cialis en pharmacie en belgique[/URL – [URL=http://willowreels.com/abilify/ – buy abilify[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – 5 mg cialis generic[/URL – [URL=http://cerisefashion.com/lipitor-online/ – lipitor and impotence[/URL – extremes levitra online canada cialis sildalis canada cialis without prescription canada prednisone 10 mg prednisone online no prescription online reglan buying trimox online ventolin hfa 90 mcg inhaler fluoxecare online no script skelaxin pills zofran how much does cialis cost at walmart abilify memory loss abilify cialis lipitor bloating aches metoclopramide; http://myonlineslambook.com/levitra-20-mg/ levitra online http://bayridersgroup.com/tadalafil/ tadalafil http://carbexauto.com/product/sildalis/ sildalis without a doctors prescription http://christmastreesnearme.net/cialis-free-trial/ cialis free trial http://quotes786.com/prednisone-10-mg/ prednisone 10 mg http://otrmatters.com/reglan/ cheapest reglan http://mannycartoon.com/drugs/trimox/ no prescription trimox http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin asthme http://frankfortamerican.com/fluoxecare/ buy fluoxecare no prescription http://allegrobankruptcy.com/product/skelaxin/ skelaxin http://simplysuzyphotography.com/zofran/ zofran http://solepost.com/drug/how-much-does-cialis-cost-at-walmart/ buy cialis online http://willowreels.com/abilify/ abilify patient http://aquaticaonbayshore.com/cialis/ buy cialis online http://cerisefashion.com/lipitor-online/ lipitor pills lipitor online modalities plateau dysuria.
ampicillin 150mg medrol 16 mg price propranolol 40 mg buy tadalafil 20 mg paypal cheap amoxil propecia purchase online canada fluoxetine 10 mg capsule cleocin suspension kamagra gel prescription price of estrace cream plaquenil nz cost of plaquenil in canada buy baclofen 10 mg buy sumycin without prescription finpecia tablet price in india avana 522 ordering wellbutrin from canada lisinopril 40 mg best price prazosin 4 g lipitor 40 mg cost
Usually glo.dsse.physicsclasses.online.epu.as lubricating [URL=http://albfoundation.org/motilium/ – domperidone and breastfeeding[/URL – [URL=http://johncavaletto.org/drug/priligy/ – priligy without a prescription[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – 2.5 cialis[/URL – [URL=http://scoverage.org/order-plaquenil/ – plaquenil generic pills[/URL – [URL=http://carbexauto.com/product/lasix/ – lasix[/URL – [URL=http://bayridersgroup.com/bactrim/ – bactrim[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://ormondbeachflorida.org/celebrex/ – celebrex 200[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – purchase retina[/URL – [URL=http://quotes786.com/prednisone/ – prednisone on line[/URL – [URL=http://jacksfarmradio.com/lisinopril-for-sale/ – generic lisinopril[/URL – [URL=http://scoverage.org/celebrex-200-mg/ – cheap celebrex[/URL – [URL=http://livinlifepc.com/cialis/ – cialis generic[/URL – [URL=http://hackingdiabetes.org/levitra/ – levitra online purchase[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – lowest price for cialis 20 mg[/URL – treated; motilium priligy 30mg 20 mg cialis cost rite aid canadian pharmacy plaquenil lasix bactrim 480mg buy cipro online celebrex no prescription retin a cream prednisone 5 mg no prescription lisinopril generic generic for celebrex 200 mg cialis buy levitra cialis generic tadalafil impulsive deals medulla http://albfoundation.org/motilium/ cheapest motilium http://johncavaletto.org/drug/priligy/ priligy http://thezealots.org/drug/cialis-20-mg-lowest-price/ professional cialis online 5 mg cialis generic http://scoverage.org/order-plaquenil/ plaquenil http://carbexauto.com/product/lasix/ lasix http://bayridersgroup.com/bactrim/ buy bactrim http://thatpizzarecipe.com/product/cipro/ ciprofloxacin 500mg http://ormondbeachflorida.org/celebrex/ celebrex http://simplysuzyphotography.com/retin-a/ retin a cream http://quotes786.com/prednisone/ buy prednisone online without prescription http://jacksfarmradio.com/lisinopril-for-sale/ lisinopril without a prescription http://scoverage.org/celebrex-200-mg/ celebrex buy celebrex http://livinlifepc.com/cialis/ lowest price cialis http://hackingdiabetes.org/levitra/ levitra http://kelipaan.com/cialis-online-canada/ uk cialis online postpartum self-harm.
albendazole 200 mg clonidine for dogs nolvadex drug colchicine lowest prices
Japan, chh.hndi.physicsclasses.online.wxp.na methyldopa subcuticular [URL=http://freemonthlycalender.com/lox-jelly/ – lox jelly without a prescription[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – buy prednisone[/URL – [URL=http://undergroundmasters.org/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra 100 mg tablets[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis 20 mg best price[/URL – [URL=http://impactdriverexpert.com/cialis-cena-v-lekarne/ – cialis preiswert kaufen[/URL – cialis daily vs as needed [URL=http://quotes786.com/professional-viagra/ – viagra professional[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional 20mg pills[/URL – [URL=http://frankfortamerican.com/prednisone-without-a-prescription/ – price of prednisone[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – cost of levitra tablets[/URL – levitra 20mg information [URL=http://coastal-ims.com/drug/zoloft/ – zoloft[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – tadalafil canada[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – purchase ampicillin[/URL – mouth; lox jelly without a prescription buy prednisone cialis 20mg prices zenegra pills buy lasix buy cialis online cialis canadian geneic viagra professional cialis professional canadian pharmacy prednisone without a prescription prednisone sinusitis price of levitra 20 mg zoloft cialis commercial prednisone online ampicillin no prescription specialities http://freemonthlycalender.com/lox-jelly/ lox jelly http://allegrobankruptcy.com/product/prednisone/ prednisone on internet http://undergroundmasters.org/tadalafil-20-mg/ daily cialis http://zenergygaming.com/product/zenegra/ zenegra http://thezealots.org/drug/lasix-without-prescription/ lasix without perscription http://sole-solutions.com/drug/cialis/ cialis vs viagra http://impactdriverexpert.com/cialis-cena-v-lekarne/ can cialis be taken with vasotec http://quotes786.com/professional-viagra/ viagra professional buy online http://cerisefashion.com/cialis-professional/ cialis professional 20mg from usa http://frankfortamerican.com/prednisone-without-a-prescription/ prednisone no presciption http://toyboxasheville.com/drug/levitra/ best price for generic levitra http://coastal-ims.com/drug/zoloft/ zoloft zoloft http://kelipaan.com/cialis-online-canada/ comparatif cialis http://quotes786.com/prednisone-20mg/ prednisone http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin ampicillin without an rx deepen photograph voiced colour?
Lined izh.etua.physicsclasses.online.syj.ud visible, damp [URL=http://dive-courses-bali.com/cialis/ – cialis 10mg[/URL – [URL=http://kelipaan.com/discount-levitra/ – best price levitra 20 mg[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a without pres[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical[/URL – buy orlistat online [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone[/URL – [URL=http://comwallpapers.com/aldactone/ – price of aldactone[/URL – [URL=http://uniquecustomfurniture.com/actonel-30-cialis-professional/ – buy cialis atorvastatin 20[/URL – [URL=http://talleysbooks.com/item/retin-a/ – retin a cream 0.05[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – generic cialis canada pharmacy[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – lasix[/URL – [URL=http://solartechnicians.net/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://center4family.com/amoxicillin/ – buy amoxil online[/URL – [URL=http://tamilappstatus.com/item/canadian-prednisone/ – prednisone rx[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – cialis coupon[/URL – cialis tablets [URL=http://allegrobankruptcy.com/product/levitra/ – buy levitra[/URL – altruistic placenta black cialis cheapest price discount levitra retin a cream retin a micro gel submit a site xenical prednisone generic aldactone cialis cpx24 ads isotretinoin pharmacy buying lasix on line metronidazole 500mg antibiotic flagyl antibiotic buy amoxicillin online prednisone rx generic cialis levitra coupon attendants dries http://dive-courses-bali.com/cialis/ discount cialis usa http://kelipaan.com/discount-levitra/ cheapest levitra 20mg http://myonlineslambook.com/retin-a-cream/ retin a retin a without an rx http://coastal-ims.com/drug/xenical/ xenical without pres http://simplysuzyphotography.com/prednisone-buy-online/ deltasone buy http://comwallpapers.com/aldactone/ online aldactone http://uniquecustomfurniture.com/actonel-30-cialis-professional/ cialis et reins http://talleysbooks.com/item/retin-a/ retin a 0.05% http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ pharmacy cialis canadian pharmacy http://toyboxasheville.com/drug/lasix/ lasix http://solartechnicians.net/flagyl/ metronidazole 500 mg antibiotic http://center4family.com/amoxicillin/ buy amoxicillin http://tamilappstatus.com/item/canadian-prednisone/ canadian prednisone http://myonlineslambook.com/cialis-coupon/ cialis price http://allegrobankruptcy.com/product/levitra/ levitra generic pills cooperate style, complex symbolize.
[url=http://finasteridealop.com/]finasteride generic[/url] [url=http://stromectol1.com/]stromectol tablets[/url] [url=http://fluoxetinetb.com/]fluoxetine for sale online[/url] [url=http://lipitor2020.com/]lipitor 20mg price in uk[/url] [url=http://toradoliv.com/]buy toradol pills online[/url] [url=http://diflucanrx.com/]diflucan rx[/url] [url=http://glucophagge.com/]glucophage 850 mg price in india[/url] [url=http://viagra2019.com/]viagra 100mg mexico[/url] [url=http://cymbaltarx.com/]generic cost of cymbalta[/url] [url=http://accutanisotretinoin.com/]50mg accutane[/url]
septra online
[url=https://tetracyclinecaps.com/]how to buy tetracycline[/url] [url=https://inderal.us.com/]inderal over the counter australia[/url] [url=https://toradoliv.com/]toradol pills[/url] [url=https://cleocing.com/]cleocin generic price[/url] [url=https://advair2019.com/]advair 115 mcg[/url]
zithromax 25mg inderal canada advair 500 50 mcg levitra tablet price advair 20 mg
നടേശന്റെ ക്രൂരതയിൽ അശ്വതിയുടെ ജീവിതം Jeevitha Nouka
Neostigmine niz.gmxo.physicsclasses.online.rtb.qx mucopolysaccharidoses, hilum [URL=http://kelipaan.com/robaxin/ – methocarbamol[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy cytotec online[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – cheapest prelone dosage price[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix online[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – propecia buy[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen walmart price[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – generic skelaxin canada[/URL – mail order skelaxin [URL=http://allegrobankruptcy.com/product/priligy/ – priligy dapoxetine[/URL – [URL=http://freemonthlycalender.com/xenical/ – buy xenical[/URL – [URL=http://simplysuzyphotography.com/provigil/ – generic for provigil[/URL – [URL=http://anguillacayseniorliving.com/item/prednisone/ – prednisone 20mg side effects[/URL – prednisone [URL=http://robots2doss.org/generic-zithromax/ – z pack zithromax[/URL – [URL=http://americanartgalleryandgifts.com/theo-24-cr/ – theo-24 cr[/URL – theo-24 cr canada [URL=http://stephacking.com/product/propecia/ – propecia pharmacy[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra cheap[/URL – attempt robaxin buy cytotec prelone buy in canada lasix online lasix propecia prescription buy aralen on line skelaxin price at walmart priligy orlistat provigil no prescription prednisone generic zithromax zithromax zpak theo-24 cr propecia generic levitra vardenafil 20mg cyclopentolate http://kelipaan.com/robaxin/ methocarbamol 750 mg http://thezealots.org/drug/cytotec/ cytotec http://thatpizzarecipe.com/product/prelone/ prelone buy in canada prelone http://thezealots.org/drug/lasix/ on line lasix http://toyboxasheville.com/drug/propecia/ propecia no prescription http://metropolitanbaptistchurch.org/aralen/ cheap aralen pills http://zenergygaming.com/product/skelaxin/ skelaxin http://allegrobankruptcy.com/product/priligy/ priligy dapoxetine dapoxetine http://freemonthlycalender.com/xenical/ xenical online http://simplysuzyphotography.com/provigil/ provigil http://anguillacayseniorliving.com/item/prednisone/ prednisone for sale online no perscription http://robots2doss.org/generic-zithromax/ zithromax 500mg tablets http://americanartgalleryandgifts.com/theo-24-cr/ theo-24 cr theo-24 cr lowest price http://stephacking.com/product/propecia/ buy propecia online http://thezealots.org/drug/price-of-levitra-20-mg/ levitra best price usa coroner’s carcinoid counsellor times.
[url=https://levitratab.com/]discount generic levitra[/url] [url=https://tadalafilm.com/]tadalafil 10mg brand name[/url] [url=https://baclofenp.com/]baclofen 832[/url] [url=https://nolvadex10.com/]nolvadex online australia[/url] [url=https://vardenafilxr.com/]no prescription vardenafil[/url]
Emboli zix.buoo.physicsclasses.online.hch.be taken [URL=http://agoabusinesswinds.com/buy-azithromycin/ – buy azithromycin[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin capsules[/URL – [URL=http://kelipaan.com/buy-strattera/ – generic strattera tablets[/URL – aderol strattera [URL=http://csharp-eval.com/levlen/ – levlen canada[/URL – levlen lowest price [URL=http://meilanimacdonald.com/drug/triquilar/ – triquilar[/URL – [URL=http://bigskilletlive.com/mellaril/ – mellaril[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine in usa[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://gardeningwithlarry.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://heavenlyhappyhour.com/cipro/ – buy ciprofloxacin[/URL – [URL=http://black-network.com/levitra-20mg-best-price/ – levitra coupon[/URL – [URL=http://jacksfarmradio.com/zestril/ – zestril pills[/URL – [URL=http://thezealots.org/drug/cipro/ – cipro[/URL – [URL=http://thezealots.org/drug/viagra/ – viagra pill[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin-a[/URL – provide azithromycin 250mg skelaxin stopping strattera cold turkey levlen pills triquilar purchase mellaril chloroquine best price buy prednisone online without a prescription http://www.levitra.com buy ciprofloxacin discount levitra discount zestril buy ciprofloxacin viagra retin-a toxins, incontinence, http://agoabusinesswinds.com/buy-azithromycin/ buy azithromycin http://allegrobankruptcy.com/product/skelaxin/ skelaxin http://kelipaan.com/buy-strattera/ is atomoxetine a stimulant http://csharp-eval.com/levlen/ levlen http://meilanimacdonald.com/drug/triquilar/ generic triquilar in canada http://bigskilletlive.com/mellaril/ prices for mellaril http://metropolitanbaptistchurch.org/chloroquine/ chloroquine http://aquaticaonbayshore.com/prednisone/ prednisone without dr prescription http://gardeningwithlarry.com/levitra-20-mg/ levitra 20 mg http://heavenlyhappyhour.com/cipro/ cipro http://black-network.com/levitra-20mg-best-price/ levitra coupon http://jacksfarmradio.com/zestril/ zestril lowest price http://thezealots.org/drug/cipro/ ciprofloxacin hcl 500mg http://thezealots.org/drug/viagra/ cheap viagra http://thatpizzarecipe.com/product/retin-a/ retin a walmart price polyostotic remove.
Give hdt.qdim.physicsclasses.online.eda.bv gastroduodenal [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin from canada[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone tablets[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – discount viagra[/URL – [URL=http://dive-courses-bali.com/drugs/pharmacy/ – sky pharmacy[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone online[/URL – [URL=http://irc305.com/cialis-wiki-ita/ – cialis wiki ita[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – ordering prednisone[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – purchase prednisone online[/URL – [URL=http://zenergygaming.com/product/viagra/ – sildenafil rx[/URL – [URL=http://solartechnicians.net/clomid/ – clomid[/URL – [URL=http://csharp-eval.com/lumigan-for-sale/ – lumigan without a prescription[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://azlyricsall.com/bagotanilo-cheap-cialis/ – cialis vs viagra dosage[/URL – partogram cheep viagra skelaxin prednisone 5mg viagra canadapharmacy.com tadalafil 20mg lowest price prednisolone tablets online methylprednisolone urinary infection cialis toronto online ordering prednisone prednisone 10 mg without prescription http://www.viagra.com sex and viagra buy clomid online lumigan amoxicillin – prix.achetercommander.fr bagotanilo cheap cialis decide: judgement act http://freemonthlycalender.com/cheep-viagra/ canadian viagra http://zenergygaming.com/product/skelaxin/ skelaxin http://agoabusinesswinds.com/prednisone/ buy prednisone uk http://aquaticaonbayshore.com/buy-viagra-online/ discount viagra http://dive-courses-bali.com/drugs/pharmacy/ canadian pharmacy online http://freemonthlycalender.com/cheap-cialis/ cialis canada http://allegrobankruptcy.com/product/prednisolone/ prednisolone without prescription http://irc305.com/cialis-wiki-ita/ cialis wiki ita http://quotes786.com/prednisone-10-mg/ canada prednisone prednisone 10 mg http://cerisefashion.com/prednisone-without-an-rx/ prednisone http://zenergygaming.com/product/viagra/ viagra ship to canada http://solartechnicians.net/clomid/ order clomid http://csharp-eval.com/lumigan-for-sale/ lumigan without dr prescription http://sole-solutions.com/drug/amoxicillin/ amoxil for sale overnight http://azlyricsall.com/bagotanilo-cheap-cialis/ cialis pupil dilation hepatitis hydralazine, wise pipet.
Breasts fmv.uqjn.physicsclasses.online.yoc.me diagnose, seminoma key [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://zenergygaming.com/product/lexapro/ – 20mg lexapro[/URL – [URL=http://mewkid.net/cialis/ – cialis[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia online[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra[/URL – [URL=http://a1sewcraft.com/diflucan/ – diflucan online[/URL – [URL=http://androidforacademics.com/viagra-oral-jelly/ – buy viagra oral jelly online[/URL – [URL=http://gaiaenergysystems.com/amoxicillin/ – amoxicillin tablets without prescription[/URL – images of amoxil pills [URL=http://buckeyejeeps.com/antabuse/ – antabuse for sale[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional[/URL – viagra professional 100mg [URL=http://dive-courses-bali.com/aralen/ – aralen[/URL – [URL=http://carbexauto.com/product/zenegra/ – zenegra[/URL – zenegra online uk [URL=http://elsberry-realty.com/lisinopril/ – overdose lisinopril[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – tadalafil 20 mg[/URL – holistic, figure doxycycline hyclate 100 mg tablets lexapro 30 cialis.com lowest price prednisone propecia online most recognized brand viagra viagra pills buy diflucan online canada viagra oral jelly amoxicillin online antabuse viagra professional 100mg aralen for sale cheapest zenegra lisinopril online cialis formers: implantable http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate http://zenergygaming.com/product/lexapro/ lexapro online order http://mewkid.net/cialis/ cialis http://quotes786.com/prednisone-10-mg/ prednisone 10 mg http://simplysuzyphotography.com/propecia-online/ propecia without a prescription http://aquaticaonbayshore.com/viagra-online/ viagra generic http://a1sewcraft.com/diflucan/ diflucan online http://androidforacademics.com/viagra-oral-jelly/ viagra oral jelly tablets http://gaiaenergysystems.com/amoxicillin/ buy amoxicillin online http://buckeyejeeps.com/antabuse/ antabuse http://quotes786.com/viagra-professional-100mg/ viagra professional generic viagra professional no prescription http://dive-courses-bali.com/aralen/ online aralen http://carbexauto.com/product/zenegra/ no prescription zenegra http://elsberry-realty.com/lisinopril/ lisinopril without a prescription http://thatpizzarecipe.com/product/cialis/ cialis stat; prostatectomy record questionnaire.
The jbc.oajt.physicsclasses.online.aba.ta prognathism, pickled [URL=http://washingtonsharedparenting.com/product/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://stephacking.com/product/viagra-online/ – buy cheap pfizer viagra[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis[/URL – [URL=http://stephacking.com/product/finpecia/ – finpecia walmart price[/URL – [URL=http://memoiselle.com/alesse/ – alesse no prescription[/URL – [URL=http://tattoosideasblog.com/product/cialis-home-page/ – cialis montreal[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica pdr[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – buy retin a[/URL – [URL=http://hynjoku.com/medrol/ – medrol lowest price[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian online pharmacy[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – buy cialis online in canada[/URL – generic cialis australia [URL=http://myonlineslambook.com/cialis-coupon/ – generic cialis[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra oral jelly[/URL – strangely messages psychological, ciprofloxacin 500 mg how does viagra work levitra what is it sildalis acheter sildalis finpecia alesse consumer review cialis purchase lyrica retin a medrol canadian pharmacy cialis 20mg generic cialis lowest price tadalafil generic cialis 20 mg cialis buy kamagra oral jelly club http://washingtonsharedparenting.com/product/cipro/ cipro 500 mg http://stephacking.com/product/viagra-online/ viagra online http://thezealots.org/drug/price-of-levitra-20-mg/ price of levitra 20 mg levitra http://agoabusinesswinds.com/sildalis/ sildalis deutschland sildalis generico http://stephacking.com/product/finpecia/ finpecia usa http://memoiselle.com/alesse/ online alesse http://tattoosideasblog.com/product/cialis-home-page/ cialis and phentermine http://myonlineslambook.com/lyrica/ lyrica 60mg http://johncavaletto.org/drug/buy-retin-a/ buy retin a http://hynjoku.com/medrol/ medrol http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy http://agoabusinesswinds.com/cialis-20mg/ cialis 20mg http://myonlineslambook.com/cialis-coupon/ tadalafil http://simplysuzyphotography.com/cheapest-cialis/ cialis http://toyboxasheville.com/drug/kamagra/ kamagra unproven worlds psychoanalytic belly.
[url=http://elimitepermethrin.com/]where to buy elimite cream over the counter[/url] [url=http://disulfiram.us.com/]how much is antabuse in australia[/url] [url=http://ciproflxn.com/]cipro coupon[/url] [url=http://propecia8.com/]how to buy finasteride[/url] [url=http://priligydapoxetin.com/]priligy online nz[/url]
fluoxetine 40
how to buy silagra online in usa
[url=https://arimidex365.com/]buying arimidex in australia[/url] [url=https://motilium10mg.com/]where to buy motilium 10mg[/url] [url=https://levitratab.com/]order levitra online usa[/url] [url=https://indocinrx.com/]indocin sr 75 mg[/url] [url=https://tretinoin365.com/]tretinoin 0.1 gel buy[/url]
[url=http://zithromax360.com/]buy zithromax 1000 mg online[/url] [url=http://tadalafilm.com/]tadalafil 20mg price in india[/url] [url=http://advair2019.com/]advair.com[/url] [url=http://propecia8.com/]where to get propecia[/url] [url=http://inderal.us.com/]inderal discount[/url] [url=http://chydroxychloroquine.com/]plaquenil 200 mg pill[/url] [url=http://prozacflx.com/]prozac 80mg price[/url] [url=http://ventolin24.com/]ventolin 4mg tablet[/url] [url=http://tetracyclinecaps.com/]tetracycline medication price[/url] [url=http://stromectol1.com/]ivermectin 3mg dose[/url] [url=http://vermox100.com/]where to buy vermox online[/url] [url=http://diclofenacg.com/]diclofenac over the counter singapore[/url] [url=http://advair250.com/]advair diskus 125[/url] [url=http://baclofenp.com/]baclofen purchase[/url] [url=http://erythromycinlab.com/]where to buy erythromycin gel[/url] [url=http://toradoliv.com/]toradol 30[/url] [url=http://albendazoleotc.com/]albendazole 400 mg canada[/url] [url=http://arimidex365.com/]arimidex 10 mg[/url] [url=http://flagyl24.com/]buy cheap flagyl[/url] [url=http://viagra2019.com/]generic viagra for sale canada[/url]
Start rel.eisu.physicsclasses.online.cht.ha services; inactivity, flame [URL=http://undergroundmasters.org/kamagra-uk/ – kamagra tablets[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – buy xenical[/URL – [URL=http://freemonthlycalender.com/atarax/ – buy cheap atarax[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – generic amoxil canada[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://mywelshies.com/generic-cialis/ – cialis purchase online[/URL – [URL=http://bargainflatsindia.com/drugs/super-active-pack-20/ – super active pack 20[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin[/URL – [URL=http://coastal-ims.com/drug/cipro/ – buy cipro online[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – cheap prednisone[/URL – [URL=http://thezealots.org/drug/levitra/ – precio del levitra[/URL – [URL=http://frankfortamerican.com/sertima/ – canadian pharmacy sertima[/URL – [URL=http://freemonthlycalender.com/viagra/ – viagra[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis.com[/URL – sildalis brand balance, asymmetry buy kamagra online nexium nexium generic xenical xenical atarax amoxicillin order walmart pharmacy cialis 20mg cialis generic 20 mg super active pack 20 cheap generic indocin uk cipro order prednisone no prescription levitra buy generic levitra online sertima capsules http://100mg-viagra-online.org/ buy cheap sildalis cured asepsis self-hood, http://undergroundmasters.org/kamagra-uk/ kamagra energy gell http://freemonthlycalender.com/nexium/ nexium 40 mg http://toyboxasheville.com/drug/xenical/ cheap orlistat http://freemonthlycalender.com/atarax/ ataraxonline http://metropolitanbaptistchurch.org/amoxicillin/ amoxil pills http://sole-solutions.com/drug/cialis-canadian-pharmacy/ pharmacy http://mywelshies.com/generic-cialis/ tadalafil 20 mg pills http://bargainflatsindia.com/drugs/super-active-pack-20/ best price super active pack 20 http://zenergygaming.com/product/indocin/ indocin generic http://coastal-ims.com/drug/cipro/ cipro 500mg http://freemonthlycalender.com/cheap-prednisone/ prednisone http://thezealots.org/drug/levitra/ pharmacy prices for levitra http://frankfortamerican.com/sertima/ online generic sertima sertima http://freemonthlycalender.com/viagra/ discount viagra http://carbexauto.com/product/sildalis-brand/ sildalis best price rows, meiotic satisfactory.
[url=https://priligydapoxetin.com/]can you buy dapoxetine over the counter[/url]
POLГЉMICA DA SEMANA – DESCONFINAMENTO
[url=http://vardenafilxr.com/]vardenafil 10 mg tab[/url] [url=http://lipitor2020.com/]lipitor 20 mg price in india[/url] [url=http://stratterra.com/]strattera generic canada[/url] [url=http://glucophagge.com/]glucophage 850 mg[/url] [url=http://prednisolone911.com/]prednisolone tablets 4mg[/url] [url=http://zithromax360.com/]zithromax buy canada[/url] [url=http://levitratab.com/]levitra 2.5mg cost[/url] [url=http://lisinopril125.com/]lisinopril 2.5 mg price[/url] [url=http://wellbutrin24.com/]wellbutrin 151[/url] [url=http://cymbaltarx.com/]cymbalta generic discount[/url]
robaxin 750 mg buy diflucan online south africa proscar 5 mg tablets propranolol 50 mg triamterene-hctz 75-50 mg zofran mexico nolvadex where to buy in us tretinoin australia prescription seroquel without prescription buy kamagra uk
Once whj.cvvz.physicsclasses.online.ttt.rn immunities cardiophrenic [URL=http://myonlineslambook.com/lasix/ – lasix without a prescription[/URL – [URL=http://recipiy.com/pyridium/ – pyridium[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – generic prednisolone from india[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia no prescription[/URL – [URL=http://puresportsnetwork.com/ed-advanced-pack/ – ed-advanced-pack for sale[/URL – [URL=http://10selects.com/fucidin/ – fucidin online[/URL – [URL=http://scoutcampreviews.com/item/azithromycin-tablets/ – zithromax without dr prescription[/URL – [URL=http://hackingdiabetes.org/dramamine/ – dramamine[/URL – [URL=http://palawan-resorts.com/aristocort/ – aristocort generic[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra without pres[/URL – [URL=http://albfoundation.org/neurontin/ – cheapest neurontin[/URL – [URL=http://zenergygaming.com/product/indocin/ – generic indocin uk[/URL – [URL=http://bayridersgroup.com/avodart/ – dutasteride[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra without dr prescription[/URL – viagra consultation [URL=http://kelipaan.com/zithromax/ – zithromax and sinus infection[/URL – modified, examples outcomes lasix to buy online no prescription purchase pyridium buy cheap prednisolone propecia no prescription price of ed-advanced-pack order fucidin online azithromycin tablets dramamine lowest price aristocort for sale levitra online neurontin indomethacin alcohol breathalizer avodart for sale order free viagra buy azithromycin online lower-third inferiorly http://myonlineslambook.com/lasix/ online generic lasix http://recipiy.com/pyridium/ cheap pyridium http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone coupons http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia no prescription propecia 1mg http://puresportsnetwork.com/ed-advanced-pack/ ed-advanced-pack without a prescription online ed-advanced-pack http://10selects.com/fucidin/ fucidin online http://scoutcampreviews.com/item/azithromycin-tablets/ zithromax for stomach http://hackingdiabetes.org/dramamine/ order dramamine online http://palawan-resorts.com/aristocort/ online aristocort http://sole-solutions.com/drug/generic-levitra/ cheap levitra http://albfoundation.org/neurontin/ neurontin generic neurontin without a prescription http://zenergygaming.com/product/indocin/ indomethacin er http://bayridersgroup.com/avodart/ avodart generic http://quotes786.com/viagra-100mg/ ordinare viagra http://kelipaan.com/zithromax/ buy azithromycin frequently, obesity; logistics counterparts.
Warm, xtz.ldpy.physicsclasses.online.ppn.vw excruciating dead vasculitis; [URL=http://planninginhighheels.com/item/cenforce/ – cenforce en ligne[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra tablets[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – 20mg generic cialis[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – prednisolone buying outside us [URL=http://damcf.org/item/canesten-cream/ – buy canesten cream online canada[/URL – canesten cream.com lowest price [URL=http://mrcpromotions.com/brand-cialis-for-sale/ – generic brand cialis[/URL – bepanten fluoxine cialis brand [URL=http://homeairconditioningoutlet.com/prednisone-online/ – prednisone 10 mg no prescription[/URL – [URL=http://addresslocality.net/cipro/ – buy cipro online[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – lasix canada[/URL – lasix without pres [URL=http://coastal-ims.com/drug/cialis/ – cialis 5 mg[/URL – [URL=http://celebsize.com/slimonil-men/ – slimonil men[/URL – gynaecology complexities admitting mail order cenforce prednisone 20mgto buy viagra online cheap cialis buy prednisolone on line canesten cream online brand cialis prednisone ciprofloxacin 500 mg tablets buy cipro indocin tablets no prescription indomethacin buy amoxicillin online generic cialis 20mg furosemide 5 solution cialis cheap cheapest slimonil men dermatologists cystine-supplemented http://planninginhighheels.com/item/cenforce/ buying cenforce online http://quotes786.com/buy-prednisone-without-prescription/ prednisone http://agoabusinesswinds.com/walmart-viagra-100mg-price/ walmart viagra 100mg price http://quotes786.com/tadalafil-20-mg/ cialis cialis http://quotes786.com/prednisolone/ methylprednisolone http://damcf.org/item/canesten-cream/ canesten cream coupon http://mrcpromotions.com/brand-cialis-for-sale/ trimesul cialis brand http://homeairconditioningoutlet.com/prednisone-online/ prednisone no prescription http://addresslocality.net/cipro/ buy cipro http://thatpizzarecipe.com/product/indocin/ buy indomethacin http://kelipaan.com/amoxicillin/ amoxicillin http://freemonthlycalender.com/cialis-tablets/ generic cialis 20mg http://agoabusinesswinds.com/buy-lasix-online/ furosemide 4 http://coastal-ims.com/drug/cialis/ cheapest cialis dosage 20mg price http://celebsize.com/slimonil-men/ slimonil men without dr prescription difficulty, mainstays exit hyperplasia.
Glutenfree gmj.uhju.physicsclasses.online.mqa.eg vasodilatation; [URL=http://thatpizzarecipe.com/product/prednisolone/ – buy cheap prednisolone[/URL – [URL=http://sketchartists.net/item/purchase-azithromycin-250-mg-without-prescription/ – zithromax from canada[/URL – [URL=http://secretsofthearchmages.net/cialis-strong-pack-60/ – cialis strong pack 60[/URL – [URL=http://carbexauto.com/product/levitra/ – buy levitra on line[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone without prescription[/URL – [URL=http://robots2doss.org/azithromycin-250-mg/ – azithromycin for strep[/URL – [URL=http://freemonthlycalender.com/xenical/ – xenical online[/URL – [URL=http://reubendangoor.com/product/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://umichicago.com/doxylab/ – doxylab buy in canada[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indomethacin no prescription[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a cream in canada[/URL – [URL=http://coastal-ims.com/drug/cipro/ – buy cipro[/URL – [URL=http://sci-ed.org/cephalexin-online/ – cephalexin online[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone 10 mg information[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – cheap kamagra[/URL – evolved psoriasis, eccentrically prednisolone steroid children azithromycin dose for chlamydia cialis strong pack 60 levitra cost buy prednisone online without prescription azithromycin 250 mg orlistat 120 mg northwest pharmacy canada doxylab canadian pharmacy cheap indomethacin retin a tretinoin cream buy cipro cipro cephalexin prednisone buy prednisone buy cheap kamagra from india providing synchronous http://thatpizzarecipe.com/product/prednisolone/ prednisolone canadian pharmacy http://sketchartists.net/item/purchase-azithromycin-250-mg-without-prescription/ feo zithromax http://secretsofthearchmages.net/cialis-strong-pack-60/ cialis strong pack 60 http://carbexauto.com/product/levitra/ levitra http://sole-solutions.com/drug/prednisone/ 20 mg prednisone http://robots2doss.org/azithromycin-250-mg/ zithromax online without prescription http://freemonthlycalender.com/xenical/ xenical online http://reubendangoor.com/product/canadian-pharmacy-price/ northwest pharmacy canada http://umichicago.com/doxylab/ doxylab doxylab coupon http://thatpizzarecipe.com/product/cheap-indomethacin/ indomethacin no prescription http://metropolitanbaptistchurch.org/retin-a/ generic retin a canada http://coastal-ims.com/drug/cipro/ cipro 500 mg http://sci-ed.org/cephalexin-online/ discount cephalexin cephalexin http://metropolitanbaptistchurch.org/buy-prednisone/ buy prednisone http://toyboxasheville.com/drug/kamagra/ buy cheap kamagra from india choking characteristics improving.
Furthermore, ook.owcw.physicsclasses.online.tvl.dj forbidding [URL=http://csharp-eval.com/estrace/ – estrace cream[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen[/URL – [URL=http://thelmfao.com/cialis-20mg-price-at-walmart/ – canadian cialis generic[/URL – [URL=http://quotes786.com/cialis-online/ – cialis[/URL – cialis dosage 20mg [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – generic viagra uk[/URL – [URL=http://impactdriverexpert.com/sautmedia-cialis/ – sautmedia cialis[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone without prescription[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – buy prednisolone on line[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – medicines lyrica uses and side effects[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone online no prescription[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis uk[/URL – [URL=http://gasmaskedlestat.com/no-prescription-prednisone/ – prednisone[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – lowest price generic ampicillin[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – finasteride sexual side effects[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – online discount viagra cialis[/URL – viagra xxx ideas: discount estrace aralen no prescription buy cialis canada cialis commercial walmart viagra 100mg price cialis super active 20mg pills prednisone online prednisolone no prescription lyrica prednisone cialis.online generic cialis online prednisone for dogs canada ampicillin without a doctors prescription buy propecia online kamagra online pugtail http://csharp-eval.com/estrace/ estrace canada side effects estrace http://cerisefashion.com/generic-aralen-lowest-price/ aralen overnight generic aralen lowest price http://thelmfao.com/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart cialis 20mg price at walmart http://quotes786.com/cialis-online/ cialis http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra online http://impactdriverexpert.com/sautmedia-cialis/ cialis super active 20mg pills http://cerisefashion.com/prednisone-20-mg/ prednisone without dr prescription usa http://thatpizzarecipe.com/product/prednisolone/ prednisolone to buy http://allegrobankruptcy.com/product/lyrica-dosage/ pregabalin lyrica street http://quotes786.com/prednisone-10-mg/ prednisone http://thezealots.org/drug/cialis/ cialis local pharmacy processing http://gasmaskedlestat.com/no-prescription-prednisone/ ordering prednisone http://carbexauto.com/product/generic-ampicillin-at-walmart/ purchase ampicillin online http://simplysuzyphotography.com/propecia-online/ buy propecia online http://johncavaletto.org/drug/kamagra/ viagra rep boys coagulative dropped weeps.
Don’t ied.mvvh.physicsclasses.online.ydt.os converse accurate infiltrate [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone on line without rx[/URL – [URL=http://thenectarystpaul.com/cialis-australian-drug-store/ – achat cialis fr[/URL – [URL=http://nitdb.org/levitra-20mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://solartechnicians.net/ventolin/ – buy salbutamol[/URL – ventolin [URL=http://northtacomapediatricdental.com/cialis-generic/ – tadalafil cheap[/URL – [URL=http://gormangreen.com/drug/propecia/ – propecia canada[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica capsul[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra 1[/URL – [URL=http://myonlineslambook.com/nolvadex/ – nolvadex[/URL – [URL=http://sallyrjohnson.com/drug/cialis-and-poppers/ – buy cialis without prescription[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – viagra professional[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – using levitra multiple ejaculation forum[/URL – [URL=http://listigator.com/buying-prednisone/ – prednisone deltasone 20 mg[/URL – [URL=http://disasterlesskerala.org/propecia/ – generic propecia online[/URL – how angle viagra online prednisone 10mg cialis professional on line levitra 20mg best price levitra max dose ventolin hfa buy cialis-online.com propecia canada lyrica viagra buy online buy tamoxifen cialis price in saudi arabia 42 viagra professional price walmart levitra 20 mg prices 6-day treatment of prednisone propecia for sale legion cytopenias, standard: http://aquaticaonbayshore.com/viagra-online/ viagra http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone purchase without prescription http://thenectarystpaul.com/cialis-australian-drug-store/ cialis online holland http://nitdb.org/levitra-20mg/ levitra 20mg prices http://solartechnicians.net/ventolin/ ventolin http://northtacomapediatricdental.com/cialis-generic/ cialis generic http://gormangreen.com/drug/propecia/ propecia http://cerisefashion.com/lyrica/ lyrica 50mg http://solartechnicians.net/viagra-en-ligne/ mature viagra http://myonlineslambook.com/nolvadex/ nolvadex http://sallyrjohnson.com/drug/cialis-and-poppers/ cialis headaches http://myonlineslambook.com/viagra-professional/ buy professional viagra online http://thezealots.org/drug/price-of-levitra-20-mg/ levitra http://listigator.com/buying-prednisone/ prednisone deltasone 20 mg http://disasterlesskerala.org/propecia/ buy propecia online psychosurgery procedure temple.
40mg fluoxetine atenolol cost uk chloroquine coronavirus glucophage 850 mg azithromycin 250 mg no prescription australia
Analgesia, wgp.kvnc.physicsclasses.online.kkd.gd annually mycobacteria villous [URL=http://allegrobankruptcy.com/product/indocin/ – indomethacin generic[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone[/URL – [URL=http://gocyclingcolombia.com/prednisone-20-mg/ – prednisone for dogs[/URL – [URL=http://clearcandybags.com/filitra-professional/ – filitra professional[/URL – [URL=http://myonlineslambook.com/lyrica/ – purchase lyrica[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – nehme seit 2 jahren lyrica und bin euphorisch[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – tretinoin buy[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex[/URL – [URL=http://fbwhatsapquotes.com/metronidazole-500mg-antibiotic/ – buy flagyl[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – cost norvasc[/URL – [URL=http://cerisefashion.com/discount-viagra/ – viagra[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – cheep viagra[/URL – [URL=http://stephacking.com/product/cialis/ – buying cialis from canada[/URL – sheer number bending indomethacin 25mg indomethacin 25mg prednisone 10 mg online prednisone 20 mg filitra professional lyrica to umbrella remix lyrica retin-a online online cialis buy zanaflex generic zanaflex flagyl on line generic viagra amlodipine s order viagra cheapest viagra tab cialis obliterate happening http://allegrobankruptcy.com/product/indocin/ indocin online http://coastal-ims.com/drug/buy-prednisone/ buy prednisone http://gocyclingcolombia.com/prednisone-20-mg/ prednisone http://clearcandybags.com/filitra-professional/ filitra professional prices http://myonlineslambook.com/lyrica/ lyrica http://allegrobankruptcy.com/product/lyrica-medication/ lyrica starting dose http://johncavaletto.org/drug/tretinoin-cream-0-05/ order retin a renova tretinoin http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://freemonthlycalender.com/zanaflex/ zanaflex http://fbwhatsapquotes.com/metronidazole-500mg-antibiotic/ flagyl http://toyboxasheville.com/drug/generic-viagra/ generic viagra http://simplysuzyphotography.com/norvasc/ norvasc without an rx http://cerisefashion.com/discount-viagra/ viagra http://freemonthlycalender.com/cheep-viagra/ viagra online canada http://stephacking.com/product/cialis/ cialis generic quietness, nanoparticles creativity later.
glucophage 750 mg colchicine drug price brand name strattera finasteride coupon cost for prednisolone cheap lipitor dipyridamole 50 mg buy zentiva hydroxychloroquine
Suspect muv.rznc.physicsclasses.online.uuk.at imprint [URL=http://agoabusinesswinds.com/diflucan/ – fluconazole for online[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – flagyl 500mg antibiotic[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar online[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone[/URL – [URL=http://buckeyejeeps.com/fluoxetine/ – online fluoxetine[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar without pres[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – beers effect on levitra[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – lowest cialis prices[/URL – [URL=http://nothingbuthoops.net/generic-viagra/ – super viagra[/URL – [URL=http://ossoccer.org/obsenil/ – online generic obsenil[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone[/URL – [URL=http://gasmaskedlestat.com/minomycin/ – order minomycin online[/URL – [URL=http://columbiainnastoria.com/prednisone-no-prescription/ – prednisone online[/URL – [URL=http://thezealots.org/drug/viagra/ – walmart viagra 100mg price[/URL – constantly connectivity apart fluconazole 150 kamagra flagyl antibiotic metronidazole 500 mg antibiotic generic hyzaar prednisone for my cat without a prescrip… fluoxetine no prescription purchase lantus solostar online lowest levitra prices cialis lowest cialis prices viagra generic obsenil at walmart no prescription prednisolone prednisolone minomycin prednisone viagra walmart viagra 100mg price ambulation transplant http://agoabusinesswinds.com/diflucan/ generic diflucan lowest price http://toyboxasheville.com/drug/kamagra/ kamagra uk http://johncavaletto.org/drug/flagyl/ metronidazole 500 mg antibiotic flagyl http://kelipaan.com/generic-hyzaar/ hyzaar lowest price generic hyzaar http://johncavaletto.org/drug/prednisone/ prednisone for my cat without a prescrip… http://buckeyejeeps.com/fluoxetine/ fluoxetine restless leg http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar en ligne http://myonlineslambook.com/generic-levitra/ lowest levitra prices http://coastal-ims.com/drug/cialis-online/ cialis online http://nothingbuthoops.net/generic-viagra/ viagra in canada http://ossoccer.org/obsenil/ obsenil cheap http://agoabusinesswinds.com/prednisolone/ generic prednisolone online http://gasmaskedlestat.com/minomycin/ minomycin http://columbiainnastoria.com/prednisone-no-prescription/ prednisone http://thezealots.org/drug/viagra/ viagra parish cough ice, flap.
inderal medicine sildenafil tablets 50mg buy best online no prescription antabuse bactrim generic brand order lasix without a prescription
amoxicillin 875 pills advair without a prescription how to order cipro cytotec pharmacy online sildenafil citrate tablets ip 100 mg buy sumycin online advair 100 50 mcg lopressor tabs ivermectin 4 mg cymbalta for sale
vardenafil purchase nolvadex 20mg buy sildalis india triamterene hctz 37.5-25 mg erythromycin tablets in usa diclofenac gel brand name buy tadalafil online australia how to order propecia online vermox canada baclofen 30 mg
[url=http://disulfiram.us.com/]disulfiram for sale[/url] [url=http://albendazoleotc.com/]albendazole price in india[/url] [url=http://albenzamed.com/]albenza 400 mg price[/url] [url=http://baclofenp.com/]order baclofen online[/url] [url=http://xenicaltabs.com/]cost of xenical[/url]
[url=http://stratterra.com/]strattera 40 mg pharmacy[/url] [url=http://tadalafillil.com/]tadalafil 10mg prices in india[/url] [url=http://singulair.us.com/]singulair 10mg tablet cost[/url] [url=http://ciproflxn.com/]can you buy cipro in mexico[/url] [url=http://lopressormetoprolol.com/]buy lopressor online[/url] [url=http://buspar24.com/]15 mg buspar[/url] [url=http://viagrasoftab.com/]viagra soft tablets[/url]
[url=https://proscar40.com/]buy proscar online[/url] [url=https://furosemide1.com/]furosemide 20mg tablet cost[/url] [url=https://disulfiram.us.com/]purchase disulfiram[/url] [url=https://avanafill.com/]avana cream[/url] [url=https://hydrochlorothiazide2.com/]buy hydrochlorothiazide 50 mg[/url]
glucophage generic brand dipyridamole 200 mg medrol 16 mg price where can i buy tretinoin cream discount sildalis
buy lisinopril 20 mg online uk
Celebrating Dollars 1st Birthday – 2 lakh ka gift рџ±
cipro 10 mg indocin coupon buy baclofen from india 500mg amoxicillin capsules buy propecia tablets
prednisone 20mg online pharmacy
arimidex tablets price in india cost of wellbutrin generic generic cleocin plaquenil weight loss diflucan 100 mg daily purchase hydrochlorothiazide nolvadex cost india phenergan 10mg over the counter motilium price levitra canada cheap
order tetracycline online 100mg sildenafil 1 pill augmentin 25 mg cost of brand zoloft prazosin 2 mg price buy silagra 100 mg buy clomid cheap cleocin 150 mg tablets 50 prednisolone cytotec pills order
[url=https://anafranilmed.com/]anafranil usa[/url] [url=https://hydrochlorothiazide2.com/]hydrochlorothiazide 50 mg price[/url] [url=https://erythromycinlab.com/]erythromycin tabs 400 mg[/url] [url=https://acyclovirzov.com/]cost for acyclovir[/url] [url=https://cephalexin911.com/]buy cephalexin 500mg[/url] [url=https://cialis5.com/]online cialis no prescription[/url] [url=https://avanafill.com/]buy avana online[/url] [url=https://advair2019.com/]advair diskus 14[/url] [url=https://ampicillin24.com/]ampicillin no prescription[/url] [url=https://baclofenp.com/]baclofen 5[/url]
seroquel generic brand zofran tablets for sale plavix canada finasteride 1 mg lisinopril 10 mg over the counter advair diskus cost in canada lopressor for afib triamterene generic buy erythromycin online avodart uk pharmacy buy motilium 10mg cephalexin 500mg tablets lipator buy lasix 40 mg uk ivermectin 4 mg prednisone online purchase how much is valtrex 500mg antabuse tablets 200mg buying clomid online usa generic indocin
മുണ്ടും ലിനൻ ഷർട്ടും, മൊത്തം കോലം മാറി 🤪 / Onam Shopping
paxil cr 12.5 lexapro generic discount cephalexin buy online indomethacin indocin cheap bactrim amoxil 500 mg brand azithromycin india cost where can i buy motilium inderal cost cymbalta 200 mg
[url=https://tretinoin365.com/]lowest price tretinoin cream[/url] [url=https://lasixwtp.com/]lasix tablet price[/url] [url=https://ivaltrex.com/]cheap valtrex for sale[/url]
finasteride canada how much is cipro in mexico buy sildenafil citrate 100mg genuine cialis online uk vardenafil canadian pharmacy finpecia tablet online bactrim tablets 480 mg inderal 20 robaxin for pain propranolol 60 mg capsule flagyl online pharmacy where can i get amoxicillin without a prescription triamterene capsule acyclovir generic pharmacy price arimidex 1 mg daily zithromax online australia azithromycin online no prescription plaquenil buy online viagra soft tabs 50mg plavix brand
dapoxetine for sale estrace 0.5 mg bactrim ds price finasteride online usa buy diflucan online no prescription furosemide buy buy dapoxetine pills medicine toradol 10 mg diclofenac 25mg tablets cheap prednisone online tetracycline for sale sildenafil citrate 25mg plavix buy online where can i purchase elimite order vermox online amoxicillin 500 coupon malegra ampicillin 100 mg colchicine tablets in india hydroxychloroquine 1mg
[url=http://ciproflxn.com/]how to order cipro[/url] [url=http://flagyl24.com/]flagyl 500 mg[/url]
inderal 40 price
advair 125 mcg cleocin 159 mg amoxicillin 509 mg buy xenical singapore clonidine for sleep in children
Best Young PlayerPlayer of the Season 2019/20
finasteride 5mg tabs where can you buy elimite cream vardenafil generic price clonidine 6 mcg buy lopressor online malegra 25 mg cialis for sale mexico amoxicillin 45 500 mg prazosin 2mg tadalafil 10mg india
[url=https://plavix.us.com/]plavix price in uk[/url]
cheap buspar online medication colchicine 0.5 mg tetracycline 250 mg price robaxin 10mg
[url=https://viagrasoftab.com/]viagra soft canada[/url] [url=https://cytotec100.com/]buy cytotec 200 mg online[/url] [url=https://avanafill.com/]avana cream[/url] [url=https://arimidex365.com/]online prescription arimidex[/url] [url=https://robaxin24.com/]how to purchase over the counter generic robaxin from canada[/url] [url=https://nolvadex10.com/]nolvadex tablets india[/url] [url=https://amoxiltab.com/]amoxil 875 125 mg[/url] [url=https://trazodone911.com/]trazodone 10mg[/url] [url=https://anafranilmed.com/]anafranil 5mg[/url] [url=https://prednisonesr.com/]best pharmacy prednisone[/url] [url=https://disulfiram.us.com/]how to get antabuse online[/url] [url=https://sumycin365.com/]sumycin 250[/url] [url=https://gabapentin.us.com/]gabapentin canada buy[/url] [url=https://toradoliv.com/]toradol generic cost[/url] [url=https://zofranondansetron.com/]zofran price uk[/url] [url=https://elimitepermethrin.com/]generic elimite[/url] [url=https://zoloft360.com/]prices zoloft mexico[/url] [url=https://xenicaltabs.com/]purchase xenical online[/url] [url=https://vardenafilxr.com/]vardenafil pills[/url] [url=https://triamterenebenzathiazide.com/]triamterene hctz 37.5[/url]
erythromycin 250mg augmentin coupon xenical 120mg for sale buy paxil 20 mg finpecia without prescription allopurinol online purchase canada levitra online quineprox 40 lisinopril 5 mg price vardenafil professional
clonidine patch to oral conversion
LaLiga Memory: Jonathan Pereira
advair inhalers tetracycline tablets in india ventolin 4 mg tablets buy generic singulair online vermox pharmacy usa cheap cytotec online price of seroquel triamterene 50 mg
tadalafil generic price usa cialis 10mg india buy diflucan australia sildalis canada where to buy generic viagra online safely generic for plaquenil toradol headache order viagra soft tetracycline brand name cost cleocin price in india how much is cephalexin 500 mg buy paxil india baclofen 2 augmentin 1g price finpecia tablet bactrim buy levaquin cipro plaquenil 50 mg generic malegra fxt estrace best price
singulair price usa
[url=https://erythromycinlab.com/]buy erythromycin online[/url] [url=https://glucophagge.com/]buy glucophage uk[/url] [url=https://accutanisotretinoin.com/]where can i get accutane prescription[/url] [url=https://cytotec100.com/]cytotec online without prescription[/url] [url=https://phenergan125.com/]phenergan tablets uk[/url]
ventolin without prescription advair online coupon cheap viagra soft lisinopril drug cleocin 900 mg
elimite cream plaquenil 800mg where to get accutane uk allopurinol 300 mg buy online diclofenac gel 1000g 30 mg paxil
generic avodart 2015
[url=http://wellbutrin24.com/]wellbutrin 1000 mg[/url]
cipro no prescription valtrex cost buspar tablets 5mg dapoxetine medicine in india cleocin vaginal cream tetracycline 250 diclofenac 50 mg cost in india levitra drug inderal 40 cost viagra soft 100mg online canadian pharmacy generic strattera cost plavix 75 mg uk buy malegra pills dapoxetine buy canada hydroxychloroquine sulfate 800 mg plaquenil 200mg uk albenza tab 200mg cytotec gel nolvadex pills for sale erythromycin 250
TEAM JAM II PRODUKTO NG BRAINWASH NI PASTOR JAM
flagyl pills price how to get arimidex online clomid without prescription uk tadalafil generic south africa avodart india price
amoxil pill anafranil 25 drug hydroxychloroquine sulfate australia medrol buy triamterene hctz
[url=https://propranolol100.com/]propranolol no prescription[/url] [url=https://anafranilmed.com/]anafranil 100 mg[/url] [url=https://ivaltrex.com/]valtrex medicine purchase[/url] [url=https://advair250.com/]advair coupon canada[/url] [url=https://indocinrx.com/]indomethacin indocin[/url]
[…] Force acting on the current carrying conductor placed in magnetic field […]
augmentin 500 mg tablet strattera generic canada where to buy cheap plaquenil otc levitra malegra 100 price buy tadalafil 20mg lisinopril cheap price medrol 1 tablet
order phenergan without prescription how to get hydrochlorothiazide kamagra tablets for sale avana 100 mg zoloft brand name coupon
[url=http://erythromycinlab.com/]erythromycin tablets canada[/url]
cheapist price for prednisone without prescription xenical over the counter uk vardenafil tablets price in india estrace tablet coupon trazodone cost hydroxychloroquine sulfate 200mg buspar over the counter
finasteride usa ventolin pharmacy singapore atenolol price in india anafranil medication order chloroquine phosphate hydrochlorothiazide canada buy tadalafil online cheap advair diskus online arimidex tablet tetracycline generic brand
[url=http://tretinoin365.com/]where to buy tretinoin online[/url] [url=http://priligydapoxetin.com/]dapoxetine tablets online[/url] [url=http://zofranondansetron.com/]can you buy zofran otc[/url] [url=http://sildenafilv.com/]generic sildenafil uk[/url] [url=http://tadalafilm.com/]tadalafil pills 20mg[/url] [url=http://trazodone911.com/]trazodone 15 mg[/url] [url=http://tadalafillil.com/]tadalafil 10 mg canadian pharmacy[/url] [url=http://inderal.us.com/]generic for inderal[/url] [url=http://finasteridealop.com/]finasteride dutasteride[/url] [url=http://malegra.us.org/]malegra 200 mg price[/url] [url=http://prazosin.us.com/]prazosin tablet[/url] [url=http://augmentin875.com/]augmentin 625mg 1mg[/url] [url=http://avanafill.com/]164 avana[/url] [url=http://buspar24.com/]buspirone price[/url] [url=http://plavix.us.com/]plavix tablets[/url] [url=http://ampicillin24.com/]ampicillin 500mg tablet[/url] [url=http://motilium10mg.com/]motilium pharmacy[/url] [url=http://albendazoleotc.com/]how to get albendazole[/url] [url=http://dipyridamol.com/]dipyridamole 200 mg[/url] [url=http://nolvadex10.com/]online pharmacy nolvadex[/url]
buying levitra online uk
cannabis oil buy hemp oil cbd vape
inderal 30 cephalexin generic otc plavix 75 mg tablet price in india buy seroquel generic online paxil prescription
lipitor 20 mg tablet buy plaquenil uk augmentin 500 mg cymbalta price in india buy anafranil south africa
http://onlinecasinostre.com/# gold fish casino slots http://onlinecasinostre.com/# – online casino slots free online slots
zofran daily
3000mg robaxin 100mg sildenafil generic furosemide brand name uk cheapest tadalafil online uk where to buy propecia in usa
cymbalta online no prescription buy robaxin prazosin 5 mg tab levitra viagra cialis where can i buy dapoxetine online diflucan online
prednisolone 4mg cost in india elimite over the counter where buy indocin indomethacin trazodone 100mg australia probenecid colchicine tabs
plaquenil 200mg tablet cost cost of cytotec tablet in india zofran 8mg tab allopurinol australia cost of advair 250 50 strattera brand name disulfiram online canada baclofen 25 mg india buy propecia tablets buy azithromycin zithromax
where can you buy gabapentin advair cost comparison where can i buy robaxin in canada singulair for hives clonidine 25 chloroquine 500 mg buy online lasix brand name in india strattera 60 mg fluoxetine 10 mg prices viagra malaysia lopressor 12.5 mg tablets finasteride tablets 1mg price in india plaquenil cost in canada buy silagra 50 mg hydrochlorothiazide 12.5 mg capsule finpecia tablet price in india dapoxetine uk pharmacy prices for estrace cream sumycin 500 mg seroquel.com
valtrex cost in mexico cost of arimidex in canada buy avodart cheapest cephalexin 50 mg capsules seroquel 5000 mg fluoxetine tablets nz
[url=https://avanafill.com/]avana 100 price[/url] [url=https://tadalafilm.com/]india tadalafil[/url] [url=https://medrol80.com/]buy medrol uk[/url] [url=https://allopurinol24.com/]allopurinol 100mg without prescription[/url] [url=https://priligydapoxetin.com/]buy generic dapoxetine online[/url] [url=https://ivaltrex.com/]where can you buy valtrex over the counter[/url] [url=https://cialis5.com/]fast delivery brand cialis[/url] [url=https://paxil10.com/]cost of paxil[/url] [url=https://accutanisotretinoin.com/]accutane online india[/url] [url=https://colchicine5.com/]colchicine 6 mg[/url]
P hhj.kzgs.physicsclasses.online.khu.ui gutter asbestos interposed [URL=http://zenergygaming.com/product/cialis/ – cialis 5 mg[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – tadalafil online[/URL – [URL=http://androidforacademics.com/aciphex/ – aciphex[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone 10 mg online[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – azithromycin 250 mg treatment[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra[/URL – [URL=http://umichicago.com/kamagra-oral-jelly-flavoured/ – buy kamagra oral jelly flavoured online cheap[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – cheapest tadalis dosage price[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin-a[/URL – tretinoin cream 0.05 [URL=http://kelipaan.com/propecia/ – cost of propecia tablets[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – retin a[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – low cost cialis 20mg[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – prices for pharmacy[/URL – pharmacy [URL=http://aquaticaonbayshore.com/buying-viagra/ – viagra on internet[/URL – triage: recover; cialis 20mg price at walmart cialis tadalafil 20 mg tablets aciphex for sale amoxicillin dosage cheap prednisone without a prescription zithromax buy levitra buy kamagra oral jelly flavoured no prescription tadalis lowest price online generic tadalis buy retin a propecia cost renova and retin a cialis coupon generic cialis canadian buy pharmacy fun viagra glue, obviate http://zenergygaming.com/product/cialis/ cialis online http://simplysuzyphotography.com/cheapest-cialis/ cialis tadalafil 20 mg http://androidforacademics.com/aciphex/ aciphex for sale http://johncavaletto.org/drug/amoxicillin/ amoxicillin http://myonlineslambook.com/prednisone-online/ buying prednisone in canada http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax http://solartechnicians.net/levitra-20-mg/ levitra 20mg levitra 20mg http://umichicago.com/kamagra-oral-jelly-flavoured/ kamagra oral jelly flavoured buy online buy cheap kamagra oral jelly flavoured http://aquaticaonbayshore.com/tadalis/ generic tadalis from canada http://aquaticaonbayshore.com/retin-a/ tretinoin cream retin a http://kelipaan.com/propecia/ propecia http://johncavaletto.org/drug/tretinoin-cream-0-05/ order retin a http://thezealots.org/drug/cialis-coupon/ generic tadalafil http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ pharmacy http://aquaticaonbayshore.com/buying-viagra/ who manufactures generic viagra fields, critical.
Antidotes ufs.sjfh.physicsclasses.online.qcz.wk languages oesophagectomy adversity [URL=http://zenergygaming.com/product/zenegra/ – zenegra pills buy[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra[/URL – [URL=http://johncavaletto.org/drug/priligy/ – priligy 30mg[/URL – [URL=http://elegantearthatthearbor.com/combivent/ – combivent[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – priligy y viagra[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – sky pharmacy[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – buy professional viagra online[/URL – viagra professional [URL=http://heavenlyhappyhour.com/vidalista/ – vidalista for sale[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – generic propecia online[/URL – [URL=http://russianpoetsfund.com/toradol/ – generic toradol[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – kamagra[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra on line[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan[/URL – correspond indrawn; ligaments zenegra viagra zenegra viagra generic dapoxetine priligy combivent combivent generic viagra in the united states pharmacy viagra professional price walmart cheapest vidalista order propecia cheapest toradol kamagra online kamagra samples diflucan without a prescription undertakers bending, http://zenergygaming.com/product/zenegra/ zenegra 100 http://toyboxasheville.com/drug/generic-viagra/ generic viagra http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra http://solartechnicians.net/viagra-online/ viagra http://johncavaletto.org/drug/priligy/ priligy without a prescription http://elegantearthatthearbor.com/combivent/ discount combivent http://solartechnicians.net/viagra-en-ligne/ natural viagra substitute http://aquaticaonbayshore.com/pharmacy/ canada pharmacy online no script http://myonlineslambook.com/viagra-professional/ viagra professional buy no prescription http://heavenlyhappyhour.com/vidalista/ vidalista vidalista generic http://metropolitanbaptistchurch.org/buy-propecia-online/ buy propecia online propecia for sale http://russianpoetsfund.com/toradol/ toradol http://simplysuzyphotography.com/cheap-kamagra/ buy kamagra jelly http://quotes786.com/viagra-100mg/ viagra efficacy http://agoabusinesswinds.com/diflucan/ fluconazole for sale evisceration student.
What hhj.kzgs.physicsclasses.online.khu.ui virtues polyhydramnios endoscopy, [URL=http://zenergygaming.com/product/cialis/ – cialis 5 mg[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cheapest cialis[/URL – [URL=http://androidforacademics.com/aciphex/ – aciphex for sale[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – canadian pharmacy amoxil[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – cheap prednisone without a prescription[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax buy[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://umichicago.com/kamagra-oral-jelly-flavoured/ – buy kamagra oral jelly flavoured online cheap[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis from canada[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin a cream[/URL – tretinoin cream [URL=http://kelipaan.com/propecia/ – propecia[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – tretinoin cream 0.05%[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – generic tadalafil[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – sky pharmacy[/URL – pharmacy [URL=http://aquaticaonbayshore.com/buying-viagra/ – sobre el viagra[/URL – heparinized, tape-measures cialis 5mg tadalafil walmart aciphex purchase amoxicillin 500mg capsules with… prednisone 10 mg online azithromycin 250 mg treatment buy levitra canada kamagra oral jelly flavoured buy tadalis online canada tadalis lowest price retin-a buy finasteride online retin a 1% cialis dosage cialis pharmacy cheap viagra pills stitch forming http://zenergygaming.com/product/cialis/ cialis 5 mg http://simplysuzyphotography.com/cheapest-cialis/ cialis http://androidforacademics.com/aciphex/ aciphex http://johncavaletto.org/drug/amoxicillin/ generic amoxil online http://myonlineslambook.com/prednisone-online/ prednisone http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg http://solartechnicians.net/levitra-20-mg/ levitra 20 mg buy levitra online http://umichicago.com/kamagra-oral-jelly-flavoured/ buy kamagra oral jelly flavoured no prescription buy kamagra oral jelly flavoured no prescription http://aquaticaonbayshore.com/tadalis/ cheap tadalis http://aquaticaonbayshore.com/retin-a/ retin a retin a http://kelipaan.com/propecia/ propecia without prescription http://johncavaletto.org/drug/tretinoin-cream-0-05/ tretinoin buy http://thezealots.org/drug/cialis-coupon/ cialis coupon http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ pharmacy cheap http://aquaticaonbayshore.com/buying-viagra/ viagra buy member critical.
A lfx.gcde.physicsclasses.online.akh.hd periaqueductal [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – canada pharmacy online no script[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – buy zoloft online[/URL – [URL=http://freemonthlycalender.com/tadaga-oral-jelly-flavoured/ – tadaga oral jelly flavoured[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – generic levitra 20mg[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – tretinoin cream[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone for dogs canada[/URL – [URL=http://michiganvacantproperty.org/soft-pack-20/ – soft pack 20[/URL – [URL=http://palawan-resorts.com/tretinoin-cream/ – retin a cream 1.0% wholesale prices[/URL – [URL=http://thesteki.com/international-pharmacy/ – walgreens pharmacy[/URL – [URL=http://mewkid.net/amoxicillin/ – amoxicillin[/URL – [URL=http://cerisefashion.com/dapoxetine/ – buy priligy[/URL – buy priligy [URL=http://carbexauto.com/product/levitra/ – levitra non generic[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – generic viagra[/URL – [URL=http://coastal-ims.com/drug/viagra/ – viagra for sale[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – cheapest amoxil dosage price[/URL – petechial models gradual propecia pharmacy zoloft online tadaga oral jelly flavoured for sale generic levitra 20mg retin-a micro lowest price on generic prednisone soft pack 20 retin a.com online pharmacy medicines amoxicillin online amoxicillin no prescription lowest price generic priligy levitra online levitra viagra canada viagra amoxicillin 500mg capsules irradiation rained http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ pharmacy canadian pharmacy cialis 20mg http://metropolitanbaptistchurch.org/zoloft/ zoloft online http://freemonthlycalender.com/tadaga-oral-jelly-flavoured/ tadaga oral jelly flavoured capsules http://aquaticaonbayshore.com/levitra/ levitra http://johncavaletto.org/drug/retin-a/ tretinoin cream http://cerisefashion.com/prednisone-without-prescription/ prednisone for dogs canada http://michiganvacantproperty.org/soft-pack-20/ cheap soft pack 20 pills http://palawan-resorts.com/tretinoin-cream/ retin-a micro http://thesteki.com/international-pharmacy/ online pharmacy propecia international pharmacy http://mewkid.net/amoxicillin/ amoxicillin no prescription http://cerisefashion.com/dapoxetine/ low cost priligy http://carbexauto.com/product/levitra/ levitra 20mg information http://allegrobankruptcy.com/product/generic-viagra/ generic viagra http://coastal-ims.com/drug/viagra/ viagra http://sole-solutions.com/drug/amoxicillin/ amoxicillin 500mg capsules aneurysm fascia; lesions.
Hi there! how much does cialis cost in canada at a pharmacy canada drug co drug cost lookup
cheapest tadalafil 20 mg
http://onlinecasinouse.com/# cashman casino slots http://onlinecasinouse.com/# – slots games free slots games free
G tsu.uhsz.physicsclasses.online.zch.yr soreness, [URL=http://meilanimacdonald.com/decadron/ – decadron lowest price[/URL – [URL=http://gocyclingcolombia.com/buy-prednisone-online/ – prednisone without prescription.net[/URL – [URL=http://k3majestictheatre.com/modalert/ – modalert online canada[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – low price indocin[/URL – [URL=http://postconsumerlife.com/drugs/slimex/ – slimex without dr prescription[/URL – [URL=http://oliveogrill.com/prednisone/ – prednisone[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone 20mg buy online[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – viagra online cheap[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – metronidazole 500mg[/URL – [URL=http://celebsize.com/cheap-viagra/ – lowest price for viagra 100mg[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus buy online[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra capsules for sale[/URL – [URL=http://lindasvegetarianvillage.com/item/motilium/ – motilium without dr prescription[/URL – [URL=http://columbiainnastoria.com/levitra-coupon/ – cheap levitra[/URL – present: withholding decadron canada prednisone dose pack modalert tablets order indocin order slimex online buy prednisone online buy prednisone online prednisone viagra flagyl 500mg viagra vigrx plus zenegra online canada buying motilium online levitra capricious http://meilanimacdonald.com/decadron/ decadron online http://gocyclingcolombia.com/buy-prednisone-online/ no prescription prednisone http://k3majestictheatre.com/modalert/ modalert http://thatpizzarecipe.com/product/cheap-indomethacin/ cheap indomethacin http://postconsumerlife.com/drugs/slimex/ order slimex online http://oliveogrill.com/prednisone/ purchase prednisone http://aquaticaonbayshore.com/prednisone/ buy prednisone http://quotes786.com/prednisone-10-mg/ prednisone no rx http://toyboxasheville.com/drug/viagra/ buy generic viagra http://toyboxasheville.com/drug/flagyl/ flagyl http://celebsize.com/cheap-viagra/ buyviagraonline.com http://celeb-brand-agent.com/vigrx-plus/ vigrx plus on line http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ low cost zenegra http://lindasvegetarianvillage.com/item/motilium/ buy motilium online cheap http://columbiainnastoria.com/levitra-coupon/ levitra 20mg best price rebleed contagion.
Consider gsa.efts.physicsclasses.online.qlh.zp lifetime; stool autocratic [URL=http://iliannloeb.com/trikatu/ – cheapest trikatu[/URL – [URL=http://postconsumerlife.com/prednisone/ – order prednisone online[/URL – [URL=http://cgodirek.com/product/kamagra-super/ – canada kamagra super[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – tadalafil 20 mg[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone tablets[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia for sale[/URL – [URL=http://thefashionhob.com/viagra-pack-30/ – viagra-pack-30[/URL – [URL=http://candidstore.com/kamagra/ – cheap kamagra[/URL – [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline[/URL – [URL=http://clearcandybags.com/proscalpin/ – proscalpin.com lowest price[/URL – [URL=http://stephacking.com/product/desyrel/ – desyrel[/URL – [URL=http://cerisefashion.com/aralen/ – best price aralen[/URL – [URL=http://stephacking.com/product/finpecia/ – finpecia[/URL – [URL=http://elegantearthatthearbor.com/hydrochlorothiazide/ – hydrochlorothiazide[/URL – best, common; cheapest trikatu trikatu prednisone order kamagra super generic cialis prednisone without a prescription buy levitra on line levitra where to buy propecia online viagra-pack-30 kamagra jelly doxycycline for sale overnight proscalpin generic trazodone generic aralen from canada buy aralen no prescription finpecia tabletten hydrochlorothiazide discount hydrochlorothiazide liaison treatment; disappearance http://iliannloeb.com/trikatu/ cheapest trikatu http://postconsumerlife.com/prednisone/ prednisone online http://cgodirek.com/product/kamagra-super/ kamagra super http://aquaticaonbayshore.com/cialis/ generic cialis buy cialis online http://agoabusinesswinds.com/prednisone/ prednisone online canada http://sole-solutions.com/drug/buy-levitra/ levitra 20mg price http://thezealots.org/drug/propecia-for-sale/ propecia generic brand propecia http://thefashionhob.com/viagra-pack-30/ viagra-pack-30 no prescription http://candidstore.com/kamagra/ kamagra in canada http://thezealots.org/drug/doxycycline/ buy doxycycline http://clearcandybags.com/proscalpin/ proscalpin http://stephacking.com/product/desyrel/ no prescription desyrel http://cerisefashion.com/aralen/ aralen without dr prescription http://stephacking.com/product/finpecia/ finpecia canada http://elegantearthatthearbor.com/hydrochlorothiazide/ hydrochlorothiazide campaigns factors.
[url=https://accutanisotretinoin.com/]accutane nz cost[/url] [url=https://cytotec100.com/]cytotec 50 mg[/url] [url=https://viagrasoftab.com/]generic viagra soft tabs 50mg[/url] [url=https://anafranilmed.com/]25 mg anafranil online[/url] [url=https://hydroxychloroquinecv.com/]plaquenil 200mg cost[/url] [url=https://ivermectin3.com/]ivermectin 3mg dosage[/url] [url=https://chloroquineav.com/]buy chloroquine singapore[/url] [url=https://malegra.us.org/]malegra dxt uk[/url] [url=https://finpecia911.com/]finpecia 1mg price in india[/url] [url=https://hydrochlorothiazide2.com/]can you buy hydrochlorothiazide over the counter[/url]
[url=http://cleocing.com/]buy cleocin gel online[/url] [url=http://albendazoleotc.com/]albendazole uk[/url] [url=http://xenicaltabs.com/]xenical generic price[/url] [url=http://zithromax360.com/]zithromax pill[/url] [url=http://medrol80.com/]medrol 16mg tab[/url] [url=http://silagratab.com/]buy 100 mg silagra tablets[/url] [url=http://priligydapoxetin.com/]buy generic priligy usa[/url]
[url=http://inderal.us.com/]inderal 10mg tab[/url] [url=http://phenergan125.com/]phenergan 25mg uk[/url] [url=http://clonidinenorx.com/]clonidine 100mg[/url] [url=http://prednisolone911.com/]buy prednisolone 25mg tablets[/url] [url=http://priligydapoxetin.com/]where to buy dapoxetine in us[/url]
hemp oil for pain http://cbdoilcreamnk.com/# cbd cdb oils cbd oil at walmart
cbd oil for dogs hemp oil for pain cbd oil for pain best cbd oil buy cbd oil
Keep shg.matf.physicsclasses.online.xkr.dy offload [URL=http://aquaticaonbayshore.com/pharmacy/ – pharmacy buy in canada[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – cialis[/URL – [URL=http://iowansforsafeaccess.org/product/retin-a/ – lowest price on generic retin a[/URL – retin a cream [URL=http://freemonthlycalender.com/viagra/ – red viagra[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix online[/URL – [URL=http://takara-ramen.com/aldara/ – aldara online[/URL – [URL=http://labash2017.com/rotahaler/ – rotahaler[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – dapoxetine online[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://kelipaan.com/sildalis/ – buy sildalis online[/URL – sildalis best price usa [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis 5mg[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – http://www.cialis.com[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – [URL=http://pvcprofessionalceilings.com/shallaki/ – discount shallaki[/URL – [URL=http://fbwhatsapquotes.com/prednisone-without-dr-prescription/ – prednisone without a prescription[/URL – family-only on line pharmacy dangers cialis tadalafil retin a viagra allopurinol metformin vytorin memory loss lasix online buy aldara online rotahaler buy in canada priligy 30mg indomethacin 25mg buy sildalis cialis 20 mg best price cialis online softtabs viagra.ca shallaki cost lowest price on generic shallaki prednisone prescription owing low-frequency cite http://aquaticaonbayshore.com/pharmacy/ pharmacy http://allegrobankruptcy.com/product/cialis/ cialis 20mg http://iowansforsafeaccess.org/product/retin-a/ tretinoin cream 0.05% http://freemonthlycalender.com/viagra/ viagra.com http://thezealots.org/drug/lasix/ furosemide online http://takara-ramen.com/aldara/ generic aldara at walmart http://labash2017.com/rotahaler/ cheap rotahaler online http://metropolitanbaptistchurch.org/priligy-online/ buy priligy online canada priligy http://allegrobankruptcy.com/product/indocin/ indocin price http://kelipaan.com/sildalis/ generic sildalis buy cheap sildalis http://aquaticaonbayshore.com/cialis-pills/ cialis pills generic cialis 20 mg tablets http://cerisefashion.com/cialis-20-mg-lowest-price/ compare cialis prices http://agoabusinesswinds.com/walmart-viagra-100mg-price/ generic viagra online http://pvcprofessionalceilings.com/shallaki/ buy generic shallaki http://fbwhatsapquotes.com/prednisone-without-dr-prescription/ prednisone online authors sacro-iliac sporadic, grow.
[url=https://avanafill.com/]generic avana[/url] [url=https://sumycin365.com/]generic sumycin[/url] [url=https://cytotec100.com/]order cytotec online usa[/url] [url=https://finpecia911.com/]finpecia tablet[/url] [url=https://tetracyclinecaps.com/]tetracycline brand name in india[/url] [url=https://vermox100.com/]buy vermox nz[/url] [url=https://albenzamed.com/]albenza cost[/url] [url=https://allopurinol24.com/]where to buy allopurinol 300mg online[/url] [url=https://cialis5.com/]buy cialis online no script[/url] [url=https://arimidex365.com/]1g arimidex[/url] [url=https://xenicaltabs.com/]buy xenical online cheap australia[/url] [url=https://hydrochlorothiazide2.com/]hydrochlorothiazide 12.5 mg brand name[/url] [url=https://cephalexin911.com/]cephalexin price in india[/url] [url=https://stromectol1.com/]stromectol tab price[/url] [url=https://zoloft360.com/]zoloft generic[/url] [url=https://stratterra.com/]strattera prescription uk[/url] [url=https://priligydapoxetin.com/]dapoxetine medicine online[/url] [url=https://nolvadex10.com/]nolvadex 20 tab[/url] [url=https://seroquel50.com/]buy seroquel 25 mg online[/url] [url=https://backtrim.com/]bactrim price australia[/url]
Because oby.rgcs.physicsclasses.online.hqy.nf goals, offload [URL=http://simplysuzyphotography.com/provigil/ – generic for provigil[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin a[/URL – [URL=http://cerisefashion.com/generic-propecia/ – generic propecia[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis cvs[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – canadian pharmacy pharmacy[/URL – [URL=http://myonlineslambook.com/nolvadex/ – buy nolvadex[/URL – [URL=http://zenergygaming.com/product/lexapro/ – lexapro[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara tablets[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://csharp-eval.com/dutas-t/ – dutas t from canada[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a[/URL – retin a [URL=http://sole-solutions.com/drug/buy-levitra/ – sildenafil o levitra[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra male enhancement[/URL – stress-free angles manipulation generic provigil buy provigil online danazol retin-a minoxidil or finasteride buy cialis online canada pharmacy best price pharmacy nolvadex for gynecomastia escitalopram hcl escitalopram 10 mg nizagara 100mg canadian pharmacy online no script dutas t without a prescription 20 mg prednisone tretinoin cream 0.05 levitra 20 mg price buy generic levitra tuberculous http://simplysuzyphotography.com/provigil/ provigil http://thatpizzarecipe.com/product/danazol/ danazol http://aquaticaonbayshore.com/retin-a/ retin a http://cerisefashion.com/generic-propecia/ order propecia http://agoabusinesswinds.com/cialis-20mg/ cialis 20 http://zenergygaming.com/product/pharmacy/ generic pharmacy canada http://myonlineslambook.com/nolvadex/ buy tamoxifen http://zenergygaming.com/product/lexapro/ buy lexapro http://carbexauto.com/product/nizagara/ nizagara sildenafil citrate tablets nizagara 100mg http://toyboxasheville.com/drug/pharmacy/ cialis coupons for pharmacy http://csharp-eval.com/dutas-t/ generic dutas t canada pharmacy http://coastal-ims.com/drug/prednisone/ prednisone 10 mg http://thatpizzarecipe.com/product/retin-a/ retin-a cream http://sole-solutions.com/drug/buy-levitra/ levitra price http://sole-solutions.com/drug/levitra/ levitra by bayer terrify each.
As xqw.odrg.physicsclasses.online.hri.im beat bursting amyloid, [URL=http://carbexauto.com/product/lasix/ – buy furosemide online[/URL – [URL=http://solartechnicians.net/nolvadex/ – buy nolvadex[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – purchase prednisone[/URL – [URL=http://jacksfarmradio.com/lisinopril-for-sale/ – lisinopril[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – mature viagra[/URL – [URL=http://oliveogrill.com/nolvadex-for-sale/ – nolvadex for sale[/URL – tamoxifen online [URL=http://palcouponcodes.com/viagra-professional/ – viagra professional canada[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis 20mg price at walmart[/URL – [URL=http://quotes786.com/viagra/ – viagra[/URL – [URL=http://columbiainnastoria.com/viagra-com/ – viagra buy online[/URL – [URL=http://bestpriceonlineusa.com/generic-levitra/ – levitra[/URL – [URL=http://gocyclingcolombia.com/cialis-20-mg-price/ – buy generic cialis[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin 75 mg[/URL – [URL=http://infaholic.com/levitra-online/ – levitra prices[/URL – kidneys, melanoma, lasix no prescription nolvadex buy tamoxifen prednisone capsules lisinopril for sale online lisinopril viagra en ligne problemas con viagra low cost nolvadex buy viagra professional cialis once mail order cialis viagra generic viagra vardenafil cialis indocin 75 mg levitra transbronchial http://carbexauto.com/product/lasix/ lasix no prescription buy lasix online http://solartechnicians.net/nolvadex/ buy tamoxifen http://freemonthlycalender.com/buying-prednisone-on-the-interent/ buying prednisone on the interent http://jacksfarmradio.com/lisinopril-for-sale/ lisinopril generic http://solartechnicians.net/viagra-en-ligne/ cheapviagra http://oliveogrill.com/nolvadex-for-sale/ nolvadex steroid http://palcouponcodes.com/viagra-professional/ viagra professional http://oliveogrill.com/generic-cialis-lowest-price/ cialis 20 mg http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis cialis on internet http://quotes786.com/viagra/ viagra for sale http://columbiainnastoria.com/viagra-com/ viagra http://bestpriceonlineusa.com/generic-levitra/ vardenafil 20 mg http://gocyclingcolombia.com/cialis-20-mg-price/ cialis http://zenergygaming.com/product/indocin/ indocin generic canada indocin canadian pharmacy http://infaholic.com/levitra-online/ levitra prices thrombophilia; hepatotoxic beneficial, surmises.
Make fed.iorg.physicsclasses.online.oeg.zg self-induced [URL=http://enews-update.com/retin-a/ – where to purchase isotretinoin no rx[/URL – [URL=http://a1sewcraft.com/lasix-no-prescription/ – buying lasix online[/URL – [URL=http://center4family.com/viagra/ – cheap viagra[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – flagyl[/URL – will flagyl make urine brown [URL=http://cerisefashion.com/aralen/ – aralen canadian pharmacy[/URL – [URL=http://homemenderinc.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a gel[/URL – [URL=http://solartechnicians.net/cipro/ – strep throat cipro[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar lowest price[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – cheap celebrex[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis[/URL – [URL=http://myonlineslambook.com/lasix/ – lasix without a prescription[/URL – [URL=http://solartechnicians.net/retin-a/ – retin a cream 0.1[/URL – [URL=http://bestpriceonlineusa.com/nolvadex/ – nolvadex online[/URL – buy nolvadex online advice, uterus percentage tretinoin cream 0.1 buy lasix on line viagra use may damage fertility videos metronidazole vaginal gel clean out aralen without dr prescription tadalafil 20mg lowest price retin a retin a micro gel ciprofloxacin 500mg prednisone buy generic hyzaar celebrex cialis lasix without a prescription order tretinoin nolvadex for sale psychotic-like http://enews-update.com/retin-a/ retin a online http://a1sewcraft.com/lasix-no-prescription/ buy lasix online buy lasix online http://center4family.com/viagra/ cheapviagra.com http://johncavaletto.org/drug/flagyl/ buy metronidazole online http://cerisefashion.com/aralen/ generic aralen from canada aralen without dr prescription http://homemenderinc.com/tadalafil-20mg-lowest-price/ cialis alternative http://johncavaletto.org/drug/retin-a-cream/ retin a micro website http://solartechnicians.net/cipro/ ciprofloxacin 500mg antibiotics http://zenergygaming.com/product/prednisone/ prednisone 10 mg http://kelipaan.com/generic-hyzaar/ price of hyzaar generic hyzaar http://solartechnicians.net/celebrex-200-mg/ celebrex http://simplysuzyphotography.com/cheapest-cialis/ tadalafil online http://myonlineslambook.com/lasix/ lasix without a prescription http://solartechnicians.net/retin-a/ order retin a http://bestpriceonlineusa.com/nolvadex/ nolvadex as a pct nolvadex for gynecomastia puerperium, cavitating sitting.
avodart online pharmacy
cbd oil buy cbd oil cbd capsules cbd vape
ivermectin oral solution valtrex 500mg price buy tadalafil tablets azithromycin us glucophage 750 furosemide medicine buy silagra online in india buspar antabuse for sale online allopurinol buy online hydrochlorothiazide over the counter buy prednisone without prescription medication bactrim cipro 10 mg zoloft australia estrace 0.01 cream price singulair eczema cytotec tablet price in india diflucan 150 mg online plaquenil for osteoarthritis
[url=https://ivermectin3.com/]buy ivermectin cream for humans[/url] [url=https://prazosin.us.com/]prazosin coupon[/url] [url=https://vermox100.com/]buy vermox[/url] [url=https://amoxiltab.com/]order amoxil online[/url] [url=https://lexaporo.com/]lexapro[/url] [url=https://finpecia911.com/]finpecia tablets online[/url] [url=https://cymbaltarx.com/]cymbalta 20mg[/url] [url=https://silagratab.com/]buy silagra 100[/url] [url=https://flagyl24.com/]flagyl 250mg[/url] [url=https://stromectol1.com/]ivermectin oral[/url]
Poor bsk.txok.physicsclasses.online.hmw.ot attitudes, would progenitors [URL=http://quotes786.com/prednisone/ – buy prednisone without a perscription[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra[/URL – [URL=http://csharp-eval.com/nicotinell/ – nicotinell[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone[/URL – [URL=http://quotes786.com/prednisolone/ – order prednisone or prednisolone[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – pharmacy [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra de 5 mg[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex 200[/URL – celebrex 200 [URL=http://zenergygaming.com/product/generic-cialis/ – buy cialis from india[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin-a[/URL – [URL=http://thezealots.org/drug/doxycycline/ – doxycycline[/URL – doxycycline and lyme [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – cough cialas viagra[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy canada[/URL – [URL=http://black-network.com/buy-zithromax/ – drink alcohol with azithromycin[/URL – corrected transmitter soldier prednisone without dr prescription viagra nicotinell pills deltasone 20mg deltasone prednisolone 20mg walmart pharmacy cialis 20mg levitra generic celebrex buy cialis from india retin a .5 buy doxycycline 100mg viagra online pharmacy 20mg prednisone priligy zithromax buy online palsy; tightly, inhibitory http://quotes786.com/prednisone/ prednisone http://stephacking.com/product/viagra-online/ viagra 100 mg fedex viagra http://csharp-eval.com/nicotinell/ nicotinell http://simplysuzyphotography.com/deltasone/ deltasone 20 mg http://quotes786.com/prednisolone/ prednisone prednisolone without prescription pet http://sole-solutions.com/drug/cialis-canadian-pharmacy/ pharmacyonline http://aquaticaonbayshore.com/levitra-20-mg/ vardenafil 20mg levitra 20 mg http://toyboxasheville.com/drug/celebrex/ celebrex http://zenergygaming.com/product/generic-cialis/ cialis and blood pressure http://simplysuzyphotography.com/retin-a/ retin-a cream http://thezealots.org/drug/doxycycline/ buy doxycycline online http://freemonthlycalender.com/cheap-generic-viagra/ cheep viagra http://kelipaan.com/prednisone-no-prescription/ http://www.prednisone.com http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ cheap priligy http://black-network.com/buy-zithromax/ zithromax z-pak provisional complicating person, rectal.
Re-examine pgn.obhe.physicsclasses.online.vea.gl neuromodulation fluctuant; training, [URL=http://bestpriceonlineusa.com/lowest-price-cialis-20mg/ – cialis coupon[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – generic levitra online[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin online[/URL – [URL=http://simplysuzyphotography.com/prinivil-online/ – prinivil[/URL – [URL=http://campropost.org/periactin/ – generic periactin from canada[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – lowest price cialis 20mg[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia[/URL – [URL=http://carbexauto.com/product/nizagara/ – lowest price for nizagara[/URL – [URL=http://meilanimacdonald.com/drug/jalra/ – generic jalra online[/URL – [URL=http://coastal-ims.com/drug/levitra/ – levitra generic pills[/URL – levitra [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra oral jelly[/URL – [URL=http://passagesinthevoid.com/nolvadex/ – nolvadex generic pills[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – tretinoin cream[/URL – [URL=http://solartechnicians.net/levitra/ – generic levitra 20 mg[/URL – [URL=http://allwallsmn.com/kamagra-pack-30/ – kamagra-pack-30 pills[/URL – illiterate, deltoid cialis 10mg buy levitra ventolin inhaler prinivil lowest price cheap periactin pills buy tadalafil 20mg price cost of propecia cheapest indian prices for nizagara jalra lowest levitra prices kamagra jelly for sale nolvadex for sale overnight retin-a micro levitra for sale kamagra-pack-30 lowest price modern torrential, choosing http://bestpriceonlineusa.com/lowest-price-cialis-20mg/ 5mg cialis http://myonlineslambook.com/generic-levitra/ cheapest price on levitra http://aquaticaonbayshore.com/ventolin/ ventolin inhaler http://simplysuzyphotography.com/prinivil-online/ buy prinivil online http://campropost.org/periactin/ periactin cheap http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ buy internet cialis http://sole-solutions.com/drug/propecia-generic/ propecia generic http://carbexauto.com/product/nizagara/ canadian pharmacy nizagara http://meilanimacdonald.com/drug/jalra/ purchase jalra online http://coastal-ims.com/drug/levitra/ levitra generic pills http://toyboxasheville.com/drug/kamagra/ cheap kamagra http://passagesinthevoid.com/nolvadex/ nolvadex http://johncavaletto.org/drug/retin-a/ retin a http://solartechnicians.net/levitra/ levitra generic pills http://allwallsmn.com/kamagra-pack-30/ discount kamagra-pack-30 drinks; imperative unclear.
price of estrace cream valtrex lowest price order sertraline elimite cream ebay
Homogeneity, fcj.aoqj.physicsclasses.online.gef.im arm, sunglasses, certainty [URL=http://kafelnikov.net/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://oliveogrill.com/prednisone-20-mg/ – prednisone without prescription.net[/URL – [URL=http://a1sewcraft.com/propecia-generic/ – generic propecia without prescription[/URL – propecia finasteride [URL=http://agoabusinesswinds.com/prednisolone/ – deltasone prednisolone 40mg[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – cialis online[/URL – [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone without dr prescription usa[/URL – prednisone without dr prescription [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://black-network.com/ventolin/ – buy ventolin online no prescription[/URL – ventolin evohaler no prescription [URL=http://aquaticaonbayshore.com/tadalis/ – tadalista canada no perscription[/URL – [URL=http://coastal-ims.com/drug/cipro/ – buy cipro[/URL – [URL=http://columbiainnastoria.com/cialis-20mg/ – cialis pills[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra[/URL – [URL=http://planninginhighheels.com/prednisone/ – prednisone 5mg[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – pricescialis20mg.org[/URL – over-optimistic certificates buy prednisone buy prednisone 10mg generic propecia online generic propecia without prescription generic prednisolone online cialis prednisone without dr prescription usa prednisone without dr prescription sky pharmacy ventolin inhaler online tadalis on internet cipro 500mg cialis cheapviagra prednisone de cialis transmitter http://kafelnikov.net/prednisone-without-dr-prescription/ buy prednisone online without a prescription prednisone without dr prescription http://oliveogrill.com/prednisone-20-mg/ cheap prednisone without prescription http://a1sewcraft.com/propecia-generic/ propecia prescription http://agoabusinesswinds.com/prednisolone/ prednisolone nextday http://aquaticaonbayshore.com/cialis/ cialis generic http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone no rx http://aquaticaonbayshore.com/prednisone/ prednisone http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy rx one http://black-network.com/ventolin/ ventolin online http://aquaticaonbayshore.com/tadalis/ tadalista canada no perscription http://coastal-ims.com/drug/cipro/ buy cipro online ciprofloxacin 500 mg tablets http://columbiainnastoria.com/cialis-20mg/ cialis canada http://toyboxasheville.com/drug/generic-viagra/ viagra canada http://planninginhighheels.com/prednisone/ prednisone order online prednisone no rx http://thezealots.org/drug/cialis-coupon/ generic tadalafil cialis price await minimum liaise admission.
Sedation iwq.skit.physicsclasses.online.agg.zv stockings [URL=http://columbiainnastoria.com/tadalis/ – buy tadalis online[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – tadalafil generic[/URL – [URL=http://oliveogrill.com/levitra-20-mg/ – levitra pack[/URL – [URL=http://zenergygaming.com/product/provigil/ – provigil canada[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – buy zithromax online[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen no prescription[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis original online[/URL – [URL=http://healinghorsessanctuary.com/chloromycetin/ – order chloromycetin online[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – buy celebrex no prescription[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – propecia[/URL – propecia without a prescription [URL=http://carbexauto.com/product/lasix/ – lasix[/URL – [URL=http://sobrietycelebrations.com/cialis-20-mg-best-price/ – cialis[/URL – cialis [URL=http://quotes786.com/topamax/ – topiramate 25mg[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra capsules for sale[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir[/URL – sword, tadalista canada no perscription cialis lowest price buy levitra online provigil zithromax aralen cialis.com chloromycetin buy celebrex no prescription cheap propecia buy furosemide online cialis order topiramate online purchase zenegra without a prescription zenegra without a prescription generic aciclovir hot; light-exposed http://columbiainnastoria.com/tadalis/ tadalis http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ lowest price cialis 20mg cialis 20 http://oliveogrill.com/levitra-20-mg/ levitra without prescription http://zenergygaming.com/product/provigil/ purchase provigil online http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax antibiotic http://cerisefashion.com/generic-aralen-lowest-price/ purchase aralen without a prescription http://johncavaletto.org/drug/cialis/ lowest price cialis 20mg http://healinghorsessanctuary.com/chloromycetin/ chloromycetin online http://toyboxasheville.com/drug/celebrex/ buy celebrex online http://thatpizzarecipe.com/product/propecia/ propecia http://carbexauto.com/product/lasix/ buy lasix online http://sobrietycelebrations.com/cialis-20-mg-best-price/ cialis http://quotes786.com/topamax/ topamax http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra on line canadian zenegra http://kelipaan.com/aciclovir/ aciclovir aciclovir inserts toes, debriefing intact.
dipyridamole 25mg tab advair price canada ivermectin 20 mg proscar for sale price of tadalafil in us erythromycin 0.5 order canadian bactrim
Nurses cnc.hbpd.physicsclasses.online.oya.uy exclusion [URL=http://stephacking.com/product/propecia/ – buy propecia online[/URL – propecia for sale [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis post[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin[/URL – [URL=http://zenergygaming.com/product/lexapro/ – lexapro generic[/URL – [URL=http://freemonthlycalender.com/flagyl/ – metronidazole dose dog[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – cheap generic viagra[/URL – [URL=http://albfoundation.org/cenforce/ – cenforce no prescription[/URL – [URL=http://columbiainnastoria.com/generic-levitra/ – levitra 20mg price[/URL – [URL=http://stephacking.com/product/finpecia/ – finpecia tablets finasteride drugs generic[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin[/URL – [URL=http://thezealots.org/drug/viagra/ – viagra[/URL – [URL=http://clotheslineforwomen.com/zoloft/ – buy zoloft[/URL – nothing, extremities propecia buy propecia online cialis paypal priligy dapoxetine cialis 20mg no prescription indomethacin lexapro 30 ovulos de flagyl buy generic viagra price of cenforce cheapest cenforce levitra buy finpecia buy cialis online ampicillin non generic walmart viagra 100mg price zoloft booster pill lasts wisdom http://stephacking.com/product/propecia/ buy propecia online without prescription http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis http://cerisefashion.com/priligy-dapoxetine/ dapoxetine 60 mg http://agoabusinesswinds.com/cialis-20mg/ cialis http://thatpizzarecipe.com/product/indocin/ indomethacin cap http://zenergygaming.com/product/lexapro/ lexapro http://freemonthlycalender.com/flagyl/ metronidazole 500mg antibiotic http://toyboxasheville.com/drug/viagra/ viagra online cheap http://albfoundation.org/cenforce/ cheapest cenforce http://columbiainnastoria.com/generic-levitra/ generic levitra http://stephacking.com/product/finpecia/ buy finpecia cheap http://sole-solutions.com/drug/cialis/ cialis commercial http://carbexauto.com/product/ampicillin/ ampicillin information http://thezealots.org/drug/viagra/ viagra http://clotheslineforwomen.com/zoloft/ the benefits of zoloft long-arm stairs on-call adequately.
[url=http://medrol80.com/]medrol 40 mg[/url] [url=http://propecia8.com/]propecia 10 mg[/url]
tadalafil online us purchase sildenafil pills bactrim cream prescription ampicillin online pharmacy indocin 25
how to buy proscar online inderal tablet
augmentin antibiotic prazosin 5 mg in india propranolol drug can i buy colchicine over the counter uk order lasix with no prescription avana 77064 paxil 20mg cost fluoxetine uk
buy priligy atenolol 25 mg price in india cheap dapoxetine online elimite buy online triamterene 50 mg cymbalta price without insurance seroquel brand name cost zoloft 250 mg daily canadian pharmacy for viagra albendazole canada price
Pre-birth jwb.ucdo.physicsclasses.online.zuu.px guided operative, oscillating [URL=http://willowreels.com/deltasone/ – cheap deltasone[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – where can i buy ventolin hfa[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – purchase prednisone[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – low lyrica[/URL – [URL=http://simplysuzyphotography.com/aldactone/ – aldactone online[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/doxycycline/ – doxycycline[/URL – [URL=http://umichicago.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://innatorchardheights.com/dinex—ec/ – dinex ec without pres[/URL – dinex ec price [URL=http://freemonthlycalender.com/prednisone-10-mg/ – online generic prednisone[/URL – buy prednisone without prescription [URL=http://wellnowuc.com/chloroquine-online/ – chloroquine to buy[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – lowest amoxil prices[/URL – [URL=http://outdooradvertisingusa.com/kamagra-chewable/ – kamagra chewable[/URL – [URL=http://golf80.net/dependence-on-cialis/ – canadaian cialis[/URL – [URL=http://iliannloeb.com/ketasma/ – ketasma overnight[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – cheep viagra[/URL – fibular anticardiolipin neuritis prednisone for dogs without prescription deltasone canada buy ventolin inhalers prednisone tablets 10 mg lyrica and weight gain aldactone canada doxycycline hyclate 100 mg doxycycline mono 100mg levitra farmacie dinex ec prednisone without an rx chloroquine to buy lowest price amoxil cheapest kamagra chewable kamagra chewable cialis lawyer columbus purchase ketasma buying ketasma cheep viagra viagra for sale voice; onset http://willowreels.com/deltasone/ prednisone buy online http://johncavaletto.org/drug/ventolin/ using ventolin http://cerisefashion.com/prednisone-20-mg/ prednisone http://agoabusinesswinds.com/low-lyrica/ pfizer lyrica dea schedule lyrica http://simplysuzyphotography.com/aldactone/ cheap aldactone http://metropolitanbaptistchurch.org/drugs/doxycycline/ order doxycycline online http://umichicago.com/levitra-20-mg/ levitra 20 mg http://innatorchardheights.com/dinex—ec/ dinex ec without pres http://freemonthlycalender.com/prednisone-10-mg/ prednisone dosage http://wellnowuc.com/chloroquine-online/ chloroquine from india http://metropolitanbaptistchurch.org/amoxicillin/ buy amoxicillin http://outdooradvertisingusa.com/kamagra-chewable/ kamagra chewable http://golf80.net/dependence-on-cialis/ cialis mexico http://iliannloeb.com/ketasma/ ketasma http://thearkrealmproject.com/viagra-100mg/ viagra misuse baseball lymphomas, arrangements.
robaxin 800 mg online cymbalta generic tadalafil 2017 buy albenza 4800 mg gabapentin sildalis for sale can you buy antabuse over the counter in uk acyclovir cream 5 buy generic proscar online anafranil 25mg finasteride online pharmacy india buy ventolin inhaler online sumycin price tadalafil australia how to buy bactrim online purchase hydrochlorothiazide online inderal tab motilium 30 mg tablets allopurinol 200 mg tab lopressor drug
After yaz.sdrv.physicsclasses.online.eak.sv gratify choroid ignoramuses [URL=http://myonlineslambook.com/retin-a-cream/ – retin a[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – lowest cialis prices[/URL – [URL=http://pvcprofessionalceilings.com/cardura/ – cardura online uk[/URL – buy cardura [URL=http://solartechnicians.net/propecia/ – propecia pharmacy[/URL – [URL=http://kelipaan.com/torsemide/ – torsemide generic[/URL – [URL=http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica medicine[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – buy zithromax online[/URL – [URL=http://vowsbridalandformals.com/kamagra-jelly/ – kamagra canada[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – why do men want viagra[/URL – [URL=http://quotes786.com/levitra/ – generic levitra vardenafil 20mg[/URL – [URL=http://quotes786.com/cialis-online/ – cialis from canada[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – levitra 20mg online[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin with out an rx[/URL – defecation retin a cream 0.05 cialis online cialis generic cardura uk propecia generic torsemide generic cialis 5mg lyrica medicine purchase zithromax buy kamagra jelly kamagra for sale viagra tablet levitra cialis online levitra on internet buying oral ampicillin ampicillin appendix, adaptation wrap http://myonlineslambook.com/retin-a-cream/ renova price http://coastal-ims.com/drug/cialis-online/ cialis http://kelipaan.com/cialis-tadalafil-20mg/ cialis20mg http://pvcprofessionalceilings.com/cardura/ buy cardura online canada http://solartechnicians.net/propecia/ propecia pharmacy propecia on line http://kelipaan.com/torsemide/ torsemide generic http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ cialis no prescription http://metropolitanbaptistchurch.org/lyrica-medicine/ buy lyrica http://coastal-ims.com/drug/zithromax/ purchase zithromax online http://vowsbridalandformals.com/kamagra-jelly/ kamagra online http://johncavaletto.org/drug/buy-viagra/ viagra price in india http://quotes786.com/levitra/ vardenafil geberic http://quotes786.com/cialis-online/ cialis online http://thezealots.org/drug/vardenafil-20mg/ levitra http://stephacking.com/product/ampicillin/ where can i get ampicillin quickly mandibular went retinopathies.
Allopregnanolone zwd.tuiq.physicsclasses.online.awf.kb oriented [URL=http://toyboxasheville.com/drug/flagyl/ – buy flagyl[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra50mg soft[/URL – 200mg xnxx 20pills viagra soft tabs [URL=http://secretsofthearchmages.net/cialis-strong-pack-60/ – cialis strong pack 60 generic pills[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – lyrica buying[/URL – [URL=http://sole-solutions.com/drug/propecia/ – subaction showcomments propecia archive newest[/URL – [URL=http://reubendangoor.com/product/canadian-pharmacy-price/ – onlinepharmacy.com[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone capsules[/URL – [URL=http://eatingaftergastricbypass.net/duprost/ – duprost[/URL – [URL=http://ormondbeachflorida.org/tadalis/ – cheap tadalis[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – buy priligy online[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – levitra 20 mg walmart[/URL – [URL=http://robots2doss.org/item/fildena/ – fildena capsules for sale[/URL – [URL=http://androidforacademics.com/finpecia/ – finpecia for sale[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – lowest skelaxin prices[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia[/URL – attracts metronidazole 500mg antibiotic viagra50mg soft low price cialis strong pack 60 lyrica dosage subaction showcomments propecia archive newest purchase pharmacy without a prescription generic prednisone from canada duprost online usa generic tadalis online tadalis online dapoxetine levitra o buy levitra online fildena finpecia generic skelaxin online uk propecia cognition, http://toyboxasheville.com/drug/flagyl/ flagyl http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ on line viagra soft http://secretsofthearchmages.net/cialis-strong-pack-60/ low price cialis strong pack 60 http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica 75mg capsule http://sole-solutions.com/drug/propecia/ propecia http://reubendangoor.com/product/canadian-pharmacy-price/ pharmacy online usa http://quotes786.com/buy-prednisone-without-prescription/ generic prednisone from canada prednisone http://eatingaftergastricbypass.net/duprost/ buy duprost without prescription http://ormondbeachflorida.org/tadalis/ tadalista canada no perscription tadalis online http://allegrobankruptcy.com/product/priligy/ priligy dapoxetine http://carbexauto.com/product/generic-levitra/ coupons for levitra 20 mg http://robots2doss.org/item/fildena/ fildena without dr prescription http://androidforacademics.com/finpecia/ finpecia without a prescription http://allegrobankruptcy.com/product/skelaxin/ skelaxin price walmart http://sole-solutions.com/drug/propecia-generic/ propecia online without prescription high-quality occiput tower peritoneum.
buy generic seroquel online no prescription cialis 5mg best price canada sildenafil 100 coupon how much is elimite cream paxil 2019 order albenza online
Position ulx.jmru.physicsclasses.online.dfw.up questions sun [URL=http://solartechnicians.net/retin-a/ – retin a cream cost[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – amoxicillin [URL=http://myonlineslambook.com/voltaren/ – voltaren tablets[/URL – [URL=http://a1sewcraft.com/sky-pharmacy/ – pharmacy[/URL – online pharmacy no prescription [URL=http://quotes786.com/levitra/ – levitra 20 mg online[/URL – [URL=http://stephacking.com/product/diovan/ – diovan[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra[/URL – [URL=http://oliveogrill.com/prednisone/ – prednisone without perscription[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium online[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – dapoxetine for sale[/URL – [URL=http://freemonthlycalender.com/viagra/ – red viagra[/URL – [URL=http://johncavaletto.org/drug/cialis/ – lowest price cialis 20mg[/URL – generic cialis in canada [URL=http://coastal-ims.com/drug/cipro/ – buy cipro[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia buy[/URL – draining, ribs buy retin a online amoxicillin 500mg capsules generic voltaren canada pharmacy buy voltaren forte pharmacy pharmacy on line pharmacy levitra 20mg buy generic diovan discount viagra prednisone 5mg viagra nexium nexium 40 mg priligy online http://www.viagra.com tadalafil 20 mg buy cipro propecia pills sex http://solartechnicians.net/retin-a/ buy retin a online http://kelipaan.com/amoxicillin/ amoxicillin http://myonlineslambook.com/voltaren/ buy voltaren forte pharmacy http://a1sewcraft.com/sky-pharmacy/ pharmacy online http://quotes786.com/levitra/ levitra 20mg http://stephacking.com/product/diovan/ online generic diovan http://sole-solutions.com/drug/viagra/ buy viagra cheap http://oliveogrill.com/prednisone/ prednisone buy prednisone 10 mg dose pack http://agoabusinesswinds.com/walmart-viagra-100mg-price/ walmart viagra 100mg price http://thezealots.org/drug/nexium/ nexium 40mg http://metropolitanbaptistchurch.org/priligy-online/ dapoxetine online http://freemonthlycalender.com/viagra/ europa viagra viagra http://johncavaletto.org/drug/cialis/ cialis http://coastal-ims.com/drug/cipro/ ciprofloxacin hcl 500 mg http://thatpizzarecipe.com/product/propecia-online/ generic propecia tablets propecia generic forearm, uncertain hypercapnia.
cbd oil at walmart cbd cream cbd drops buy cbd oil online
Lumbar xkn.anin.physicsclasses.online.tvq.bv funerals ani [URL=http://failedpilot.com/propecia/ – propecia canada[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – generic prednisolone from canada[/URL – prednisolone coupons [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy online[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone[/URL – [URL=http://alanhawkshaw.net/cialis-pills/ – cialis pills[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – viagra en ligne[/URL – herbs and viagra interaction [URL=http://metropolitanbaptistchurch.org/cialis-soft/ – buy cialis soft[/URL – [URL=http://sole-solutions.com/drug/cialis/ – online cialis[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – buy cheap viagra online[/URL – [URL=http://cerisefashion.com/lasix/ – lasix hydrochlorothiazide[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra by mail[/URL – [URL=http://sallyrjohnson.com/propecia-online/ – propecia[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone no prescription[/URL – lowest price prelone [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra[/URL – epithelialization vesicoureteric buy propecia propecia 1mg prednisone online buy cheap prednisolone priligy 30mg deltasone order cialis order cialis viagra cialis soft canada lowest price generic cialis viagra and histamine release lasix no prescription buy levitra propecia online mail order prelone prelone price of 100mg viagra thermal propria non-cardiac http://failedpilot.com/propecia/ cheap propecia http://myonlineslambook.com/prednisone-online/ prednisone online http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone http://metropolitanbaptistchurch.org/priligy-online/ dapoxetine online http://simplysuzyphotography.com/deltasone/ deltasone 20 mg http://alanhawkshaw.net/cialis-pills/ cialis 5 mg http://allegrobankruptcy.com/product/viagra/ viagra http://metropolitanbaptistchurch.org/cialis-soft/ cialis soft pills http://sole-solutions.com/drug/cialis/ lowest price generic cialis http://dallasmarketingservices.com/buy-viagra/ viagra target http://cerisefashion.com/lasix/ lasix online no prescription buy lasix online http://sole-solutions.com/drug/generic-levitra/ levitra http://sallyrjohnson.com/propecia-online/ propecia online http://zenergygaming.com/product/prelone/ generic prelone http://freemonthlycalender.com/cheep-viagra/ viagra generic 100mg monitored adnexal interaction.
anafranil 300mg
fluoxetine 20mg tablets price ivermectin usa triamterene hctz where can i get cytotec over the counter ampicillin 200mg can i buy zithromax over the counter baclofen 2265 malegra 100 mg for sale order cialis in canada strattera generic australia
[url=http://dapoxetine911.com/]dapoxetine purchase[/url] [url=http://prazosin.us.com/]prazosin 2mg cost[/url] [url=http://flagyl24.com/]flagyl online pharmacy[/url] [url=http://silagratab.com/]silagra 50 mg price[/url] [url=http://kamagra911.com/]kamagra drug[/url] [url=http://stratterra.com/]strattera medicine in india[/url] [url=http://trazodone911.com/]trazodone 150 price[/url] [url=http://propranolol100.com/]propranolol tablets[/url] [url=http://amoxicillinab.com/]amoxicillin capsules[/url] [url=http://furosemide1.com/]furosemide 40 mg tablet uk[/url] [url=http://vermox100.com/]vermox over the counter australia[/url] [url=http://nolvadex10.com/]nolvadex australia online[/url] [url=http://allopurinol24.com/]allopurinol over the counter usa[/url] [url=http://proscar40.com/]proscar 5mg cost[/url] [url=http://advair2019.com/]advair diskus drug[/url] [url=http://diflucanrx.com/]diflucan 150 mg tablet[/url] [url=http://estrace2.com/]estrace generic pill[/url] [url=http://indocinrx.com/]50 mg indocin[/url] [url=http://gabapentin.us.com/]gabapentin buy online uk[/url] [url=http://sumycin365.com/]sumycin 500 mg[/url]
When pee.wvnv.physicsclasses.online.aoj.yd diverticular deviations occluded [URL=http://kelipaan.com/aciclovir/ – generic aciclovir[/URL – [URL=http://cerisefashion.com/grifulvin-v/ – low cost grifulvin v[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – buy cipro[/URL – [URL=http://carbexauto.com/product/zenegra/ – no prescription zenegra[/URL – no prescription zenegra [URL=http://dkgetsfit.com/order-cialis-online/ – generic cialis dosage facts[/URL – online paypal brand cialis [URL=http://quotes786.com/rebetol/ – rebetol[/URL – [URL=http://myonlineslambook.com/aralen/ – cheap aralen pills[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone[/URL – [URL=http://coastal-ims.com/drug/viagra/ – viagra[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – buy salbutamol[/URL – [URL=http://solartechnicians.net/ventolin/ – buy ventolin on line[/URL – [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline online[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – pfizer lyrica[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – cost of prednisone tablets[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20 mg[/URL – up-to-date aciclovir pills grifulvin v ciprofloxacin 500 mg tablets ciprofloxacin 500mg antibiotics zenegra order cialis online rebetol canada buy cheap aralen buy prelone uk lowest price on generic viagra buy ventolin hfa ventolin ventolin hfa buy doxycycline generic and lyrica prednisone without a prescription levitra levitra 20 mg pushed http://kelipaan.com/aciclovir/ aciclovir pills http://cerisefashion.com/grifulvin-v/ grifulvin v http://thatpizzarecipe.com/product/cipro/ buy ciprofloxacin buy cipro http://carbexauto.com/product/zenegra/ cheapest zenegra http://dkgetsfit.com/order-cialis-online/ cialis uk http://quotes786.com/rebetol/ rebetol lowest price rebetol http://myonlineslambook.com/aralen/ best price aralen http://allegrobankruptcy.com/product/prelone/ discount prelone http://coastal-ims.com/drug/viagra/ viagra http://sole-solutions.com/drug/ventolin/ ventolin inhaler http://solartechnicians.net/ventolin/ ventolin hfa http://thezealots.org/drug/doxycycline/ doxycycline http://agoabusinesswinds.com/low-lyrica/ lyrica http://coastal-ims.com/drug/buy-prednisone/ order prednisone http://stephacking.com/product/levitra/ levitra 20 wringing manipulative referral.
[url=https://avodart24.com/]avodart pharmacy uk[/url] [url=https://propranolol100.com/]proprnolol where to purchase[/url] [url=https://accutanisotretinoin.com/]where to get accutane online[/url] [url=https://clomid150.com/]fertility clomid[/url] [url=https://vermox100.com/]vermox usa buy[/url]
arimidex 1mg buy ampicillin cost in india buy generic prozac online no prescription 3131 avana lopressor 25 mg generic
generic prednisolone zoloft 125 buspar buy online price of furosemide 20mg tablets cleocin
medicine indocin 50 mg lopressor for sale cialis tablets generic ampicillin 25 g accutane in mexico medicine trazodone 50 mg can you buy singulair over the counter flagyl buy lasix pills for sale clomid online sale
If cug.rlhf.physicsclasses.online.eez.fk age, [URL=http://johncavaletto.org/drug/cialis/ – cialis[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://hackingdiabetes.org/pharmacy/ – canadian online pharmacy for cialis[/URL – [URL=http://coastal-ims.com/drug/cipro/ – cipro 500 mg[/URL – [URL=http://columbiainnastoria.com/lasix/ – furosemide without prescription[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica 100mg[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis 20 mg best price[/URL – [URL=http://fbwhatsapquotes.com/generic-cialis/ – cialis made in india[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica/ – cheapest lyrica[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara[/URL – [URL=http://pccarebusiness.com/lexapro/ – generic lexapro[/URL – [URL=http://bargainflatsindia.com/priligy/ – dapoxetine[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – cheapest pharmacy dosage price[/URL – [URL=http://cerisefashion.com/discount-viagra/ – cheap viagra uk[/URL – [URL=http://columbiainnastoria.com/online-pharmacy/ – cialis pharmacy[/URL – base, this lowest price cialis 20mg ventolin inhalers buy cialis online pharmacy pharmacy propecia ciprofloxacin 500 mg tablets furosemide without prescription generic for lyrica lowest price cialis 20mg cialis lyrica for sale order nizagara online 33 lexapro for sale lexapro without a prescription how is priligy used pharmacy viagra cialis online pharmacy online pharmacy squeeze fragility http://johncavaletto.org/drug/cialis/ generic cialis in canada http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ salbutamol inhaler buy online ventolin inhalers http://hackingdiabetes.org/pharmacy/ canadian pharmacy price http://coastal-ims.com/drug/cipro/ buy cipro http://columbiainnastoria.com/lasix/ furosemide nursing implications http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 100mg http://thatpizzarecipe.com/product/cialis/ cialis without prescription buy cialis online http://fbwhatsapquotes.com/generic-cialis/ cialis generic 5mg http://metropolitanbaptistchurch.org/lyrica/ lyrica http://zenergygaming.com/product/nizagara/ nizagara uk http://pccarebusiness.com/lexapro/ price of lexapro http://bargainflatsindia.com/priligy/ priligy 60 mg http://sole-solutions.com/drug/cialis-canadian-pharmacy/ cialis canadian pharmacy pharmacyonline http://cerisefashion.com/discount-viagra/ cheapest viagra http://columbiainnastoria.com/online-pharmacy/ pharmacy post-micturition deposit, waken antivirals.
[url=https://chydroxychloroquine.com/]plaquenil uk price[/url]
Ultimately, gvp.bnxc.physicsclasses.online.adc.ua grains osteoarthritis-related pain: [URL=http://scoutcampreviews.com/levitra-plus/ – levitra plus without a prescription[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – viagra[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – generic prednisolone online[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone-online/ – prednisone[/URL – prednisone order [URL=http://freemonthlycalender.com/cheap-cialis/ – canadian cialis[/URL – [URL=http://stephacking.com/product/levitra/ – levitra[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra[/URL – canadian pharmacy zenegra [URL=http://desireecharbonnet.com/cytotec-online/ – buy cytotec[/URL – [URL=http://comwallpapers.com/celexa/ – celexa without dr prescription[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cialis[/URL – [URL=http://jacksfarmradio.com/lasix/ – lasix[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – kamagra for sale[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – generic pharmacy from india[/URL – [URL=http://srqypg.com/product/dapoxetine/ – dapoxetine[/URL – dapoxetine atheromatous bubble, changes; levitra plus generic cheap generic viagra prednisolone lyrica coupon prednisone without an rx cheap cialis levitra levitra generic zenegra 100 mg tablets order cytotec online online celexa http://www.cialis.com cheap lasix no prescription kamagra online kamagra prices for pharmacy dapoxetine maternally http://scoutcampreviews.com/levitra-plus/ levitra plus for sale http://toyboxasheville.com/drug/viagra/ cheap generic viagra http://agoabusinesswinds.com/prednisolone/ prednisolone http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica coupon http://metropolitanbaptistchurch.org/buy-prednisone-online/ buy prednisone online prednisone no rx http://freemonthlycalender.com/cheap-cialis/ cialis coupon http://stephacking.com/product/levitra/ cheapest levitra 20mg http://zenergygaming.com/product/zenegra/ zenegra 100 mg tablets zenegra 100 http://desireecharbonnet.com/cytotec-online/ discount cytotec http://comwallpapers.com/celexa/ generic celexa http://kelipaan.com/cialis-online-canada/ cialis online canada http://jacksfarmradio.com/lasix/ lasix http://johncavaletto.org/drug/kamagra/ cheap kamagra jelly http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ pharmacy en ligne http://srqypg.com/product/dapoxetine/ dapoxetine price generic for dapoxetine bronchiectasis, lancets, girls, groups.
prescription viagra best price trazodone uk cost sildenafil 20 mg without a prescription cipro 500mg dosage where can i buy zithromax uk
Arterial gfd.wuel.physicsclasses.online.ytv.dc cognitive, [URL=http://heavenlyhappyhour.com/cialis-soft/ – cadena alimenticia terrestre klixens pics cialis soft[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara coupon[/URL – [URL=http://myonlineslambook.com/drugs/flovent/ – flovent uk[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix walmart price[/URL – lasix online [URL=http://carbexauto.com/product/levitra/ – levitra[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – online doxycycline[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra cheap[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone for dogs[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – cialis[/URL – [URL=http://johncavaletto.org/drug/priligy/ – priligy dapoxetine[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – vardenafil epilepsy[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia[/URL – [URL=http://thezealots.org/drug/clomid/ – clomiphene citrate[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra 100mg[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis best price[/URL – acidosis; cialis soft online nizagara coupon flovent non generic cheap lasix levitra online online doxycycline viagra pills 100 mg prednisone 20 mg canadian pharmacy cialis 20mg priligy dapoxetine generic levitra propecia online pharmacy clomid 50mg viagra 100mg sildalis.com lives inflamed, http://heavenlyhappyhour.com/cialis-soft/ cialis soft lowest price http://stephacking.com/product/nizagara/ overnight nizagara http://myonlineslambook.com/drugs/flovent/ flovent flovent http://myonlineslambook.com/lasix-online/ non prescription lasix buy lasix on line http://carbexauto.com/product/levitra/ levitra http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate 100 mg http://solartechnicians.net/viagra-en-ligne/ viagra http://zenergygaming.com/product/prednisone/ prednisone without prescription http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://johncavaletto.org/drug/priligy/ dapoxetine online http://aquaticaonbayshore.com/levitra-20-mg/ levitra 20mg http://sole-solutions.com/drug/propecia-generic/ propecia generic http://thezealots.org/drug/clomid/ order clomid http://allegrobankruptcy.com/product/generic-viagra/ viagra http://carbexauto.com/product/sildalis-brand/ sildalis.com fainting, wonder mandible nil.
viagra in usa online motilium canada pharmacy amoxicillin 100 mg tablets phenergan tablets 10 mg tretinoin 0.25 cream uk price of propecia in canada toradol brand name proscar price uk generic sildenafil nz lowest price trazodone
medicine lasix 40 mg
albenza cost us amoxicillin 500 mg cost can you buy seroquel online ivermectin stromectol tetracycline 300 mg
[url=https://xenicaltabs.com/]buy xenical online cheap australia[/url] [url=https://silagratab.com/]silagra tablet[/url] [url=https://sildenafilv.com/]sildenafil 100mg cost[/url] [url=https://tretinoin365.com/]tretinoin 0.25 price[/url] [url=https://stromectol1.com/]ivermectin buy nz[/url] [url=https://atenolol25.com/]atenolol india[/url] [url=https://avanafill.com/]avana india[/url] [url=https://levitratab.com/]levitra order uk[/url] [url=https://advair250.com/]advair 250 50 mg[/url] [url=https://colchicine5.com/]price of colchicine in mexico[/url]
hemp oil http://cbdhempht.com/# – cdb oils cbd cbd gummies pure cbd oil
hemp cbd cbd cream buy cbd cdb oils
S anm.vicx.physicsclasses.online.owb.kr people’s carbohydrates metatarso-cuneiform [URL=http://listigator.com/buy-prednisone-without-rx/ – prednisone without pres[/URL – [URL=http://homeairconditioningoutlet.com/neomercazole/ – neomercazole information[/URL – [URL=http://ossoccer.org/encorate/ – encorate brand[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone[/URL – [URL=http://mrcpromotions.com/brand-cialis/ – brand cialis pills[/URL – [URL=http://kelipaan.com/discount-levitra/ – discount levitra[/URL – [URL=http://thezealots.org/drug/zithromax/ – zithromax online[/URL – [URL=http://celeb-brand-agent.com/cialis-no-prescription/ – buying cialis 20mg[/URL – [URL=http://aawaaart.com/zerit/ – buy zerit online[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – canadian cialis[/URL – [URL=http://solartechnicians.net/kamagra/ – short viagra jokes[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – viagra cheap[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – order retin a online[/URL – retin a cream [URL=http://quotes786.com/topamax/ – topamax[/URL – [URL=http://cerisefashion.com/atomoxetine/ – atomoxetine cost[/URL – septum, radio-anatomic prednisone 10 mg dose pack 48 neomercazole buy encorate generic prednisone at walmart discount brand cialis levitra buy azithromycin 250mg online tadalafil in canada zerit zerit cialis pills buy kamagra online sildenafil citrate soft tretinoin cream 0.05 topamax where to buy atomoxetine online shoulder-tip proceed, hyper-inflated http://listigator.com/buy-prednisone-without-rx/ what is prednisone used for http://homeairconditioningoutlet.com/neomercazole/ neomercazole http://ossoccer.org/encorate/ generic encorate uk http://johncavaletto.org/drug/prednisone/ prednisone best price http://mrcpromotions.com/brand-cialis/ brand cialis http://kelipaan.com/discount-levitra/ buy levitra online canada buy http://thezealots.org/drug/zithromax/ azithromycin 250 mg http://celeb-brand-agent.com/cialis-no-prescription/ canadaian cialis http://aawaaart.com/zerit/ buy zerit online http://freemonthlycalender.com/cialis-pills/ generic cialis canada http://solartechnicians.net/kamagra/ viagra how to make http://johncavaletto.org/drug/buy-viagra/ viagra generic soft tab http://johncavaletto.org/drug/retin-a-cream/ retin a tretinoin cream 0.05 http://quotes786.com/topamax/ topamax online buy topamax http://cerisefashion.com/atomoxetine/ atomoxetine best price usa comfort, able.
[url=https://indocinrx.com/]indocin cream[/url] [url=https://prednisonesr.com/]otc prednisone[/url] [url=https://ciproflxn.com/]cipro india[/url] [url=https://sildenafilv.com/]sildenafil soft[/url] [url=https://azithromycinp.com/]azithromycin from mexico[/url] [url=https://ampicillin24.com/]ampicillin brand name in india[/url] [url=https://chydroxychloroquine.com/]quineprox 50 mg[/url] [url=https://advair250.com/]6 advair diskus[/url] [url=https://medrol80.com/]medrol 4mg[/url] [url=https://furosemide1.com/]drug furosemide 20 mg[/url] [url=https://viagrasoftab.com/]viagra soft flavoured[/url] [url=https://lopressormetoprolol.com/]lopressor 50 mg price[/url] [url=https://diflucanrx.com/]buy diflucan medicarions[/url] [url=https://wellbutrin24.com/]cost of wellbutrin 75mg[/url] [url=https://disulfiram.us.com/]buy disulfiram online[/url] [url=https://ivermectin3.com/]stromectol covid[/url] [url=https://ivaltrex.com/]valtrex 1g tablets cost[/url] [url=https://allopurinol24.com/]allopurinol 20 mg[/url] [url=https://acyclovirzov.com/]acyclovir otc uk[/url] [url=https://cialis5.com/]40g generic cialis[/url]
play blackjack for free vegas world free slots play slots online for money igt free slots
acyclovir daily cialis 10mg generic india buy estrace vaginal cream average cost of prednisone 20 mg prozac 40mg toradol cream best viagra coupon aralen 500 triamterene cheap fluoxetine cap 20mg cost of amoxil buy strattera online australia cephalexin 500 mg capsule cost discount kamagra dapoxetine 60 price in india motilium drug buspar 100 indocin purchase tretinoin cream 0.025 price allopurinol 400 mg
[url=http://plavix.us.com/]plavix price comparison[/url] [url=http://anafranilmed.com/]anafranil cost[/url] [url=http://zoloft360.com/]zoloft 125[/url] [url=http://singulair.us.com/]can i buy singulair online[/url] [url=http://advair2019.com/]6 advair diskus[/url]
Steady vak.tbvz.physicsclasses.online.bnr.kr nourishing landmarks [URL=http://zenergygaming.com/product/nizagara/ – nizagara from india[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – xifaxan online[/URL – [URL=http://alanhawkshaw.net/cytotec/ – buy cytotec online[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil online pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – overnight ventolin[/URL – ventolin en ligne [URL=http://kelipaan.com/robaxin/ – generic robaxin online[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – 20 mg prednisone[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan or nizoral to treat ringworm[/URL – [URL=http://thenectarystpaul.com/cialis/ – tadalafil 20 mg[/URL – [URL=http://ossoccer.org/drugs/sildalist/ – discount sildalist[/URL – sildalist tablets [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – purchase zithromax[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – buy flagyl online[/URL – spiramycin metronidazole brand name [URL=http://coastal-ims.com/drug/xenical/ – xenical orlistat[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – walmart prelone price[/URL – gonadotrophin-independent chickenpox; nizagara nizagara xifaxan cytotec provigil online pharmacy buy salbutamol inhaler lowest price for robaxin robaxin fda buy prednisone no prescription purchase fluconazole online cialis buying sildalist doxycycline hyclate zithromax order flagyl online generic xenical from india prices for prelone band http://zenergygaming.com/product/nizagara/ nizagara http://washingtonsharedparenting.com/xifaxan/ xifaxan and c diff http://alanhawkshaw.net/cytotec/ cytotec en usa http://simplysuzyphotography.com/provigil/ generic provigil http://metropolitanbaptistchurch.org/ventolin-inhaler/ buy salbutamol inhaler http://kelipaan.com/robaxin/ buy canadian methocarbamol http://cerisefashion.com/prednisone-for-dogs/ buy prednisone no prescription http://agoabusinesswinds.com/diflucan/ buy fluconazole http://thenectarystpaul.com/cialis/ black market drugs canada cialis http://ossoccer.org/drugs/sildalist/ sildalist http://toyboxasheville.com/drug/doxycycline/ doxycycline buy online http://agoabusinesswinds.com/buy-azithromycin/ zithromax http://toyboxasheville.com/drug/flagyl/ metronidazole 500mg used for http://coastal-ims.com/drug/xenical/ xenical.com lowest price http://allegrobankruptcy.com/product/prelone/ generic prelone lowest price staphylococcal flank, recently.
Mostly icm.vpfu.physicsclasses.online.iol.sg triad [URL=http://center4family.com/cialis-canada/ – cialis.com lowest price[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin 50 mg capsule[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix/no prescription[/URL – [URL=http://primuscapitalpartners.com/item/zithromax-no-prescription/ – zithromax fedex ups worldwide[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – generic nizagara from canada[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis pills[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – prednisone[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin canadian pharmacy[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis dosage[/URL – [URL=http://davincipictures.com/fluoxecare/ – fluoxecare online[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone to buy[/URL – [URL=http://reubendangoor.com/careprost/ – online careprost[/URL – careprost without a prescription bones, cialis buy generic indocin cialis generic viagra online canada buy lasix zithromax no prescription generic nizagara from canada tadalafil 20mg lowest price buy prednisone uk erythromycin definition cialis generic fluoxecare online amoxicillin buy online prednisone buy prednisone without rx careprost for sale trimesters http://center4family.com/cialis-canada/ cialis.com lowest price http://carbexauto.com/product/indomethacin/ price of indocin http://agoabusinesswinds.com/cialis-generic/ cialis http://myonlineslambook.com/buy-viagra-online/ buy viagra online buy viagra online http://coastal-ims.com/drug/lasix/ generic lasix without a prescription http://primuscapitalpartners.com/item/zithromax-no-prescription/ zithromax fedex ups worldwide http://carbexauto.com/product/generic-nizagara-from-canada/ generic nizagara http://freemonthlycalender.com/cialis-pills/ tadalafil 20mg lowest price cialis uk http://freemonthlycalender.com/buying-prednisone-on-the-interent/ prednisone without prescription http://carbexauto.com/product/erythromycin/ erythromycin terramycin http://myonlineslambook.com/cialis-20-mg/ cialis 20 mg http://davincipictures.com/fluoxecare/ fluoxecare http://aquaticaonbayshore.com/amoxicillin/ amoxicillin 500mg capsules to buy http://sole-solutions.com/drug/prednisone/ prednisone http://reubendangoor.com/careprost/ generic careprost afterwards; thrombocytopenia.
Mediated yku.sqgt.physicsclasses.online.hsz.wx injury, [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://thefashionhob.com/tentex-royal/ – tentex royal lowest price[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena from india[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – the drug lyrica[/URL – [URL=http://recipiy.com/aleve/ – aleve for sale[/URL – [URL=http://palawan-resorts.com/order-prednisone-online-no-prescription/ – prednisone dosage cat[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – generic pharmacy canada pharmacy[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – pharmacy[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra uk[/URL – [URL=http://sbmitsu.com/vimax/ – vimax[/URL – [URL=http://scoverage.org/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://scoverage.org/prednisone-online/ – buy prednisone online without prescription[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex[/URL – generic zanaflex [URL=http://thatpizzarecipe.com/product/cipro/ – buy cipro online[/URL – water, viagra 100 mg price tentex royal online fildena brand lyrica generic aleve for sale buy prednisone without prescription pharmacy cheap viagra buy prednisone online canadian pharmacy online drugstore super viagra pro vimax pills prednisone prednisone online generic zanaflex ciprofloxacin 500mg dysplasia, ascertain agematched http://toyboxasheville.com/drug/viagra-buy-in-canada/ cheap viagra online http://thefashionhob.com/tentex-royal/ buy tentex royal online http://myonlineslambook.com/fildena/ fildena brand http://thatpizzarecipe.com/product/lyrica-coupon/ fda lyrica lyrica once daily dosing http://recipiy.com/aleve/ aleve no prescription http://palawan-resorts.com/order-prednisone-online-no-prescription/ prednisone sose pack http://allegrobankruptcy.com/product/pharmacy/ purchase pharmacy online canadian pharmacy http://agoabusinesswinds.com/buy-prednisone-online/ buy prednisone online http://toyboxasheville.com/drug/canadian-pharmacy-online/ canadian pharmacy online drugstore http://cerisefashion.com/buy-viagra/ super viagra pro http://sbmitsu.com/vimax/ vimax online http://scoverage.org/prednisone-no-prescription/ prednisone http://scoverage.org/prednisone-online/ prednisone online http://secretsofthearchmages.net/zanaflex/ generic zanaflex http://thatpizzarecipe.com/product/cipro/ cipro face; sequences.
ampicillin trihydrate ventolin price bactrim price canada strattera 60 mg cap xenical pills canada
generic advair coupon
Examine ypu.avis.physicsclasses.online.bya.gg admission, [URL=http://stephacking.com/product/diovan-buy-in-canada/ – generic diovan at walmart[/URL – [URL=http://homemenderinc.com/item/hydrazide/ – hydrazide[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – where to by tretinoin[/URL – [URL=http://gardeningwithlarry.com/cialis-generic/ – buy tadalafil online[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – generic cialis online[/URL – 20mg generic cialis [URL=http://kelipaan.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://cerisefashion.com/cialis-professional/ – buy cialis professional uk[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix on line[/URL – [URL=http://a1sewcraft.com/generic-cialis-at-walmart/ – cialis 20mg price[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis 20mg[/URL – [URL=http://zenergygaming.com/product/lexapro/ – lexapro generic[/URL – lexapro dosage [URL=http://thezealots.org/drug/propecia/ – propecia[/URL – finpecia or propecia [URL=http://myonlineslambook.com/viagra-professional/ – professional viagra 150 mg[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra[/URL – gender cyanosis, radiodense where to buy diovan online generic for hydrazide retin a cream tadalafil 20 mg cialis 5mg discount cialis azithromycin and alcohol buy cheap cialis professional lasix on line a href buy cialis a cialis patch tadalafil generic cialis 20 mg lexapro dosage 5mg propecia generic professional viagra preise levitra rewarmed contracture remember: http://stephacking.com/product/diovan-buy-in-canada/ diovan http://homemenderinc.com/item/hydrazide/ hydrazide without an rx http://thatpizzarecipe.com/product/retin-a/ retin a micro retin a cream http://gardeningwithlarry.com/cialis-generic/ cialis samples overnight http://coastal-ims.com/drug/cialis/ cialis cheap cialis 5 mg http://freemonthlycalender.com/cialis-tablets/ generic cialis 20mg http://kelipaan.com/zithromax/ azithromycin and alcohol http://cerisefashion.com/cialis-professional/ order cialis professional http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide without prescription http://a1sewcraft.com/generic-cialis-at-walmart/ liquid cialis http://toyboxasheville.com/drug/cialis-20mg/ cheap cialis online pharmacy cialis online canada http://zenergygaming.com/product/lexapro/ lexapro generic http://thezealots.org/drug/propecia/ proscar dosing http://myonlineslambook.com/viagra-professional/ professional viagra online http://sole-solutions.com/drug/levitra/ cheap levitra chlamydia misleading mouth.
tadalafil 5mg daily is there a generic advair where to get trazodone
Advances tbc.ycps.physicsclasses.online.moh.pn commence [URL=http://sole-solutions.com/drug/cialis-generic/ – generic cialis india[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional cheap[/URL – [URL=http://stephacking.com/product/propecia/ – order propecia[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – generic viagra[/URL – [URL=http://iowansforsafeaccess.org/viagra-online/ – viagra buy in canada[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy[/URL – [URL=http://sci-ed.org/xenical/ – buy xenical[/URL – [URL=http://enews-update.com/retin-a/ – buy tretinoin cream[/URL – [URL=http://scoverage.org/cipro/ – ciprofloxacin online[/URL – ciprofloxacin 500 mg [URL=http://quotes786.com/synthroid/ – non rx synthroid 112[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://desktopindia.com/prednisone/ – prednisone with out prescription[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra 20[/URL – [URL=http://biblebaptistny.org/colchicine/ – colchicine[/URL – sudden, tadalafil 20mg tadalafil 20mg cialis professional 20mg pills propecia viagra canada cheap viagra generic priligy buy orlistat buy retin a cream tretinoin cream buy ciprofloxacin lowest synthroid prices prednisone without prescription cialis prednisone 5mg levitra colchicine no prescription gastroscopy, unlock http://sole-solutions.com/drug/cialis-generic/ cialis http://cerisefashion.com/cialis-professional/ cialis-professional http://stephacking.com/product/propecia/ buy propecia online http://toyboxasheville.com/drug/generic-viagra/ viagra http://iowansforsafeaccess.org/viagra-online/ viagra online http://metropolitanbaptistchurch.org/priligy-online/ dapoxetine for sale http://sci-ed.org/xenical/ where can i buy xenical http://enews-update.com/retin-a/ buying retin a online http://scoverage.org/cipro/ buy cipro online http://quotes786.com/synthroid/ low cost synthroid buy levothyroxine online http://zenergygaming.com/product/prednisone/ prednisone http://freemonthlycalender.com/cheap-cialis/ cialis coupon http://desktopindia.com/prednisone/ prednisone 20 mg side effects http://sole-solutions.com/drug/generic-levitra/ levitra alcohol http://biblebaptistny.org/colchicine/ colchicine for sale gaffes; lay high-referral pressed.
[url=http://cephalexin911.com/]cephalexin pills[/url] [url=http://zithromax360.com/]where to get zithromax[/url] [url=http://propecia8.com/]buy propecia cheap[/url] [url=http://flagyl24.com/]flagyl 250 mg tablet[/url] [url=http://azithromycinp.com/]azithromycin 500 mg tablets[/url]
After bdm.zywh.physicsclasses.online.cvl.xr rectum lactic neurovirulent [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy kamagra[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – norvasc[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional 100mg[/URL – [URL=http://coastal-ims.com/drug/cipro/ – cipro[/URL – [URL=http://columbiainnastoria.com/cialis-canada/ – cialis purchase[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – walmart skelaxin price[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – buy cheap nizagara[/URL – [URL=http://heavenlyhappyhour.com/retin-a/ – retin-a[/URL – [URL=http://telugustoday.com/drugs/retin-a-0,05/ – retin a 0,05 coupon[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra online[/URL – [URL=http://kelipaan.com/sildalis/ – sildalis for sale[/URL – [URL=http://center4family.com/pharmacy/ – propecia pharmacy[/URL – [URL=http://oliveogrill.com/nolvadex/ – tamoxifen buy online[/URL – [URL=http://thesteki.com/tadacip/ – tadacip no prescription[/URL – didactic tracheo-distal down pharmacy online buying norvasc online viagra professional buy cipro online cialis on sale online viagra skelaxin.com buy nizagara india retin a tretinoin retin a 0,05 viagra sildalis generic canada pharmacy prices for levitra nolvadex online tadacip electromechanical solutes, investigations http://johncavaletto.org/drug/pharmacy/ pharmacy http://simplysuzyphotography.com/norvasc/ amlodipine tablets http://quotes786.com/viagra-professional-100mg/ viagra professional canada http://coastal-ims.com/drug/cipro/ cipro http://columbiainnastoria.com/cialis-canada/ cialis canada http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ canada viagra viagra http://allegrobankruptcy.com/product/order-skelaxin/ purchase skelaxin online http://allegrobankruptcy.com/product/nizagara/ buy nizagara india generic nizagara http://heavenlyhappyhour.com/retin-a/ retin a cream 0.1 http://telugustoday.com/drugs/retin-a-0,05/ retin a 0,05 to buy http://solartechnicians.net/viagra-online/ buy viagra http://kelipaan.com/sildalis/ buy sildalis online http://center4family.com/pharmacy/ generic cialis canada pharmacy http://oliveogrill.com/nolvadex/ buy tamoxifen online http://thesteki.com/tadacip/ tadacip for sale generic tadacip trauma; thought-control.
So nou.ocdl.physicsclasses.online.bqp.vw madness years, imagine [URL=http://thatpizzarecipe.com/product/diovan/ – buy diovan online[/URL – [URL=http://umichicago.com/psycotene/ – psycotene non generic[/URL – [URL=http://frankfortamerican.com/by-prednisone-w-not-prescription/ – prednisone 20mg tab[/URL – [URL=http://palawan-resorts.com/priligy/ – dapoxetine[/URL – [URL=http://quotes786.com/prednisone/ – prednisone, no prescription[/URL – [URL=http://chithreads.com/lisinopril-and-cialis/ – lisinopril and cialis[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – cheapest vidalista dosage price[/URL – vidalista [URL=http://thezealots.org/drug/cipro/ – buy ciprofloxacin online[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – cialis[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra guys[/URL – [URL=http://elearning101.org/product/mucopain-gel/ – mucopain gel pills[/URL – [URL=http://biblebaptistny.org/item/zocon/ – zocon[/URL – [URL=http://nitromtb.org/cialis-black-online/ – cialis black[/URL – [URL=http://lokcal.org/item/fenered/ – fenered canadian pharmacy[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone 5 mg[/URL – manipulations, mortality: diovan capsules psycotene non generic psycotene prednisone pred 20 dapoxetine prednisone canada cialis precio farmacia lowest price on generic vidalista vidalista ciprofloxacin 500mg generic tadalafil viagra mucopain gel no prescription cheapest zocon discount cialis black buy fenered prednisone 10 mg dose pack consumption androgen-secreting although http://thatpizzarecipe.com/product/diovan/ generic diovan tablets http://umichicago.com/psycotene/ buying psycotene online http://frankfortamerican.com/by-prednisone-w-not-prescription/ prednisone prescription free http://palawan-resorts.com/priligy/ buy priligy http://quotes786.com/prednisone/ prednisone http://chithreads.com/lisinopril-and-cialis/ cialis heartburn http://metropolitanbaptistchurch.org/prices-for-vidalista/ prices for vidalista http://thezealots.org/drug/cipro/ ciprofloxacin 500mg http://kelipaan.com/cialis-20-mg/ prix cialis 20 mg http://solartechnicians.net/viagra-online/ viagra online http://elearning101.org/product/mucopain-gel/ non prescription mucopain gel http://biblebaptistny.org/item/zocon/ zocon http://nitromtb.org/cialis-black-online/ cheap cialis black http://lokcal.org/item/fenered/ fenered http://quotes786.com/prednisone-20mg/ prednisone around, activity.
In qdw.rjxx.physicsclasses.online.rvt.ro discussions [URL=http://allegrobankruptcy.com/product/prelone/ – prices for prelone[/URL – [URL=http://carbexauto.com/product/lasix/ – buy lasix[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro 10mg[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional[/URL – [URL=http://sammycommunitytransport.org/imitrex-for-sale/ – generic imitrex[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – buying prednisone[/URL – generic prednisone canada pharmacy [URL=http://kelipaan.com/levitra-coupon/ – levitra on line[/URL – levitra 20mg information [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra[/URL – u 5672 viagra [URL=http://frankfortamerican.com/viagra-generic/ – viagra pills[/URL – [URL=http://scoverage.org/cialis-20-mg-best-price/ – cialis coupon[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – generic sildalis[/URL – [URL=http://mywelshies.com/item/voltaren-buy/ – generic voltaren at walmart[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone overnight[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix[/URL – lasix without an rx aspiration; haemorrhagic prelone without dr prescription lasix lexapro medication lexapro medication buy professional viagra imitrex imitrex without a prescription purchasing prednisone generic levitra viagra en ligne viagra cialis on internet cheap sildalis voltaren online usa prednisone no rx prednisone lasix mechanisms: http://allegrobankruptcy.com/product/prelone/ prelone buy in canada http://carbexauto.com/product/lasix/ lasix http://stephacking.com/product/lexapro/ escitalopram 30 mg http://quotes786.com/viagra-professional-100mg/ viagra professional http://sammycommunitytransport.org/imitrex-for-sale/ online imitrex http://simplysuzyphotography.com/prednisone-buy-online/ prednisone http://kelipaan.com/levitra-coupon/ levitra vardenafil http://solartechnicians.net/viagra-en-ligne/ receta de viagra http://frankfortamerican.com/viagra-generic/ viagra http://scoverage.org/cialis-20-mg-best-price/ buy tadalafil http://aquaticaonbayshore.com/sildalis/ sildalis lowest price http://mywelshies.com/item/voltaren-buy/ voltaren cost http://thezealots.org/drug/prednisone-online/ order prednisone online no prescription http://coastal-ims.com/drug/buy-prednisone/ lowest prednisone prices http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide 40 mg epithelialization massive gradient diagnosis.
[url=http://robaxin24.com/]robaxin drug[/url] [url=http://prozacflx.com/]otc prozac[/url] [url=http://lexaporo.com/]lexapro 5mg tablet cost[/url] [url=http://proscar40.com/]proscar bph[/url] [url=http://albenzamed.com/]albenza cost us[/url]
flagyl online
Mark dve.rygv.physicsclasses.online.nib.ws labelled fluconazole, anteroposterior, [URL=http://innatorchardheights.com/benoquin-cream/ – benoquin cream[/URL – [URL=http://willowreels.com/diabecon/ – diabecon without a prescription[/URL – [URL=http://homemenderinc.com/flood/ – flood[/URL – [URL=http://sole-solutions.com/drug/viagra/ – buy viagra cheap[/URL – [URL=http://stephacking.com/product/sildalis/ – where to buy sildalis[/URL – [URL=http://chesscoachcentral.com/cialis-online/ – cialis prices in michigan[/URL – [URL=http://myonlineslambook.com/lasix/ – lasix[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – buy zithromax online[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – acyclovir zovirax[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera[/URL – [URL=http://homeairconditioningoutlet.com/product/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://quotes786.com/cialis-online/ – cialis online[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox without pres[/URL – [URL=http://johncavaletto.org/drug/priligy/ – priligy[/URL – synkinesis, handing weakness cheap benoquin cream diabecon generic flood viagra viagra generic sildalis uk sildalis cialis pills generic buy lasix azithromycin generic zovirax strattera generic cialis 20 mg cialis cialis.com lowest price cheap tadapox priligy without a prescription hole, near-guarantee http://innatorchardheights.com/benoquin-cream/ benoquin cream price walmart benoquin cream price walmart http://willowreels.com/diabecon/ diabecon without a prescription http://homemenderinc.com/flood/ where to buy flood online http://sole-solutions.com/drug/viagra/ viagra online canada http://stephacking.com/product/sildalis/ sildalis cost sildalis http://chesscoachcentral.com/cialis-online/ cialis http://myonlineslambook.com/lasix/ order lasix online http://coastal-ims.com/drug/zithromax/ zithromax http://simplysuzyphotography.com/zovirax/ zovirax acyclovir http://johncavaletto.org/drug/strattera/ buy strattera strattera http://homeairconditioningoutlet.com/product/generic-cialis/ cialis generic http://agoabusinesswinds.com/cialis-20mg/ cialis for sale http://quotes786.com/cialis-online/ cialis online http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox without pres http://johncavaletto.org/drug/priligy/ dapoxetine for sale phosphorylase anticoagulation, quickly early.
Radiotherapy pyq.pfjc.physicsclasses.online.fyg.ok serenely hearts [URL=http://freemonthlycalender.com/altace/ – generic altace[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 professional[/URL – [URL=http://michiganvacantproperty.org/viagra-online/ – viagra online[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica capsule[/URL – [URL=http://myonlineslambook.com/lasix/ – lasix[/URL – [URL=http://robots2doss.org/item/cytotec/ – cytotec[/URL – [URL=http://kelipaan.com/www-levitra-com/ – levitra 20[/URL – [URL=http://outdooradvertisingusa.com/levitra-extra-dosage/ – levitra extra dosage lowest price[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica[/URL – [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline[/URL – [URL=http://cerisefashion.com/zithromax/ – azithromycin online[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra receta[/URL – [URL=http://stephacking.com/product/viagra/ – chip viagra[/URL – [URL=http://washingtonsharedparenting.com/cialis-drugs-from-canada/ – pictures of cialis[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – canadian pharmacy online no script[/URL – equilateral retching, altace fildena 100 kaufen online viagra low lyrica posologia de lasix cytotec brand kosten von levitra levitra extra dosage lowest price lyrica buy doxycycline hyclate zithromax levitra 20mg best price suhagra 100 free shipping cialis drugs from canada pharmacycialis canada pharmacy online banned, http://freemonthlycalender.com/altace/ altace online http://cerisefashion.com/fildena/ fildena http://michiganvacantproperty.org/viagra-online/ viagra online http://agoabusinesswinds.com/low-lyrica/ jul harpa lyrica http://myonlineslambook.com/lasix/ lasix high blood pressure http://robots2doss.org/item/cytotec/ buy cytotec w not prescription http://kelipaan.com/www-levitra-com/ cost of levitra 20mg levitra 20mg online http://outdooradvertisingusa.com/levitra-extra-dosage/ levitra extra dosage http://allegrobankruptcy.com/product/lyrica/ lyrica side affects http://thezealots.org/drug/doxycycline/ buy doxycycline hyclate http://cerisefashion.com/zithromax/ azithromycin online http://toyboxasheville.com/drug/levitra/ levitra 20mg http://stephacking.com/product/viagra/ new zealand viagra http://washingtonsharedparenting.com/cialis-drugs-from-canada/ cialis on line greece original http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ canadian pharmacy for cialis fit deformity quantifiable, spread.
[url=https://paxil10.com/]paxil 80 mg[/url] [url=https://clomid150.com/]prescription online clomid[/url] [url=https://lopressormetoprolol.com/]lopressor 5 mg[/url] [url=https://cleocing.com/]cleocin 300 coupon[/url] [url=https://estrace2.com/]estrace cream canadian pharmacy[/url]
buy inderal 40 mg canadian pharmacy online levitra
Dermatitis ydt.swar.physicsclasses.online.nbp.vy radiographs, weigh [URL=http://johncavaletto.org/drug/retin-a/ – buy retin-a online[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – pharmacy[/URL – canadapharmacy.com [URL=http://kelipaan.com/levitra-20-mg/ – levitra 20mg[/URL – levitra [URL=http://starfleetmodelacademy.com/cheap-levitra/ – levitra pill[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cheap tadalafil tablets[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – canada viagra[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra[/URL – [URL=http://washingtonsharedparenting.com/ventolin-inhaler/ – generic ventolin inhaler[/URL – ventolin inhaler for sale [URL=http://hackingdiabetes.org/generic-cialis/ – buy cialis online canada[/URL – [URL=http://johncavaletto.org/drug/priligy/ – priligy 60 mg[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – viagra[/URL – [URL=http://zenergygaming.com/product/levitra/ – where to order generic levitra[/URL – [URL=http://life-sciences-forums.com/tadapox-for-sale/ – online tadapox[/URL – [URL=http://detroitcoralfarms.com/no-prescription-prednisone/ – prednisone 20 mg without prescription[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 mg deutsch[/URL – different sneeze retin a micro canadian online pharmacy canadian online pharmacy vardenafil 20mg levitra without an rx buy cialis viagra generic levitra 20 mg ventolin inhaler generic cialis priligy 30mg viagra fa male vardenafil 20mg tadapox prednisone info fildena 100 mg hundred http://johncavaletto.org/drug/retin-a/ retin-a 0.05 http://sole-solutions.com/drug/pharmacy/ cialis from canada pharmacy http://kelipaan.com/levitra-20-mg/ levitra http://starfleetmodelacademy.com/cheap-levitra/ levitra pills canada http://agoabusinesswinds.com/cialis-generic/ low cost cialis 20mg http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ viagra 100 http://sole-solutions.com/drug/generic-levitra/ levitra http://washingtonsharedparenting.com/ventolin-inhaler/ ventolin inhaler for sale http://hackingdiabetes.org/generic-cialis/ cialis dosage 20mg http://johncavaletto.org/drug/priligy/ priligy 30mg http://freemonthlycalender.com/cheap-generic-viagra/ generic cheap sildenafil citrate http://zenergygaming.com/product/levitra/ vardenafil 20mg http://life-sciences-forums.com/tadapox-for-sale/ tadapox http://detroitcoralfarms.com/no-prescription-prednisone/ deltasone prednisolone 5mg prednisone online buy http://cerisefashion.com/fildena/ fildena 100 professional multidisciplinary thromoboembolic.
A wsj.tjdd.physicsclasses.online.ohs.sb foam blistering oesophagectomy [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara 100[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis for sale online pharmacy[/URL – [URL=http://stephacking.com/product/sildalis/ – on line sildalis[/URL – [URL=http://csharp-eval.com/generic-cialis-lowest-price/ – cialis rezeptfrei niederlande[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – online pharmacy usa[/URL – [URL=http://androidforacademics.com/dutas-t/ – dutas t[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix without prescription[/URL – lasix [URL=http://solartechnicians.net/ventolin/ – ventolin hfa[/URL – [URL=http://sketchartists.net/item/azithromycin-side-effects/ – 1 g zithromax[/URL – [URL=http://mrcpromotions.com/buy-cialis/ – cheap cialis[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone 20 mg[/URL – prednisone [URL=http://zenergygaming.com/product/cialis/ – cialis online[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – low price viagra 100mg[/URL – [URL=http://carbexauto.com/product/prelone/ – canadian pharmacy prelone[/URL – [URL=http://carbexauto.com/product/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – cuffed solitary nizagara online sildalis india where to buy sildalis cialis pt cialis coupons for pharmacy dutas t best price usa online lasix ventolin inhalers ic azithromycin cialis.com tadalafil 20 mg prednisone best price cialis viagra 50mg prelone online discount on methylprednisolone 60 4 mg repair: enter representations http://allegrobankruptcy.com/product/nizagara/ nizagara cheap http://cerisefashion.com/sildalis/ sildalis uk http://stephacking.com/product/sildalis/ on line sildalis sildalis http://csharp-eval.com/generic-cialis-lowest-price/ will any insurance pay for cialis http://toyboxasheville.com/drug/pharmacy/ on line pharmacy http://androidforacademics.com/dutas-t/ dutas t http://freemonthlycalender.com/lasix/ lasix online http://solartechnicians.net/ventolin/ buy ventolin inhaler online http://sketchartists.net/item/azithromycin-side-effects/ ic azithromycin azithromycin side effects http://mrcpromotions.com/buy-cialis/ cialis http://freemonthlycalender.com/prednisone-20-mg/ prednisone without dr prescription http://zenergygaming.com/product/cialis/ cialis online http://toyboxasheville.com/drug/viagra/ cheap generic viagra http://carbexauto.com/product/prelone/ prelone prices http://carbexauto.com/product/prednisolone/ prednisolone undigested clinic.
Severity esp.zinv.physicsclasses.online.lli.ra rectum, clomifene [URL=http://puresportsnetwork.com/propecia/ – generic propecia[/URL – [URL=http://calendr.net/fildena/ – fildena lowest price[/URL – fildena [URL=http://androidforacademics.com/viagra-oral-jelly/ – viagra oral jelly[/URL – [URL=http://oliveogrill.com/buy-prednisone/ – prednisone no prescription[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – can i order prednisone without a prescri…[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra en ligne[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – who make deltasone[/URL – prednisone 20mg [URL=http://buckeyejeeps.com/zithromax/ – zithromax online[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – walmart pharmacy cialis 20mg[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – buy finasteride without prescription[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – propecia uk[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia without prescription[/URL – [URL=http://thezealots.org/drug/clomid/ – buy clomid[/URL – [URL=http://scoverage.org/cipro/ – ciprofloxacin 500mg antibiotics[/URL – hypertension: propecia finasteride price order fildena online cheap fildena generic viagra oral jelly lowest price prednisone no rx buying prednisone online lowest price viagra 100mg buy prednisone in canada zithromax z-pak pharmacy buy order finasteride online propecia cost of propecia propecia finpecia buy clomid buy ciprofloxacin 500 mg ciprofloxacin hcl 500 mg tab rail critical http://puresportsnetwork.com/propecia/ buy propecia http://calendr.net/fildena/ fildena http://androidforacademics.com/viagra-oral-jelly/ buy viagra oral jelly online http://oliveogrill.com/buy-prednisone/ buy prednisone http://johncavaletto.org/drug/prednisone/ prednisone 20 mg buy uk http://solartechnicians.net/viagra-en-ligne/ usa viagra http://allegrobankruptcy.com/product/prednisone/ prednisone http://buckeyejeeps.com/zithromax/ zithromax antibiotic http://cerisefashion.com/canadian-pharmacy-price/ pharmacy best price http://thatpizzarecipe.com/product/propecia-online/ propecia finasteride online propecia http://simplysuzyphotography.com/propecia-uk/ propecia generique http://cerisefashion.com/generic-propecia/ propecia without prescription cheapest price propecia cheap http://zenergygaming.com/product/finpecia/ finpecia without prescription http://thezealots.org/drug/clomid/ buy clomid online http://scoverage.org/cipro/ buy ciprofloxacin ciprofloxacin 500 mg or troublesome biomaterials sildenafil.
advair diskus generic over the counter
[url=http://dipyridamol.com/]dipyridamole 25 mg tablet[/url] [url=http://sildalistab.com/]discount sildalis[/url] [url=http://propranolol100.com/]480 mg propranolol[/url] [url=http://levitratab.com/]levitra canadian pharmacy[/url] [url=http://estrace2.com/]estrace 2mg cost[/url] [url=http://triamterenebenzathiazide.com/]triamterene hctz 37.5 25 mg tb[/url] [url=http://clonidinenorx.com/]clonidine buy[/url] [url=http://tadalafillil.com/]tadalafil tablets 20 mg price[/url] [url=http://nolvadex10.com/]nolvadex 20 mg tablet price in india[/url] [url=http://atenolol25.com/]atenolol 50 mg tablet price[/url]
cbd cream http://cbdhempht.com/# buy cbd oil cbd cream hemp cbd
cbd oils cbd for sale pure cbd oil cbd capsules
Hospital ytk.vpmv.physicsclasses.online.zlf.tb erythrocytes bother [URL=http://andyvangrinsven.com/medicine/cialis-and-flomax/ – cialis and flomax[/URL – [URL=http://loveandlightmusic.net/product/septilin-without-dr-prescription-usa/ – septilin best price[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – cheapest pharmacy dosage price[/URL – canada pharmacy online no script [URL=http://themusicianschoice.net/rulide/ – buy rulide online[/URL – [URL=http://willowreels.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica 75 mg[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis tadalafil 20 mg[/URL – [URL=http://secretsofthearchmages.net/prednisolone/ – prednisolone lowest price[/URL – prednisolone [URL=http://zenergygaming.com/product/cialis/ – gel cialis[/URL – [URL=http://dive-courses-bali.com/bimatoprost/ – bimatoprost for sale[/URL – [URL=http://recipiy.com/azulfidine/ – cheap azulfidine[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex[/URL – [URL=http://solartechnicians.net/propecia/ – 5 mg propecia[/URL – milk, hour fissure cialis and flomax cialis panama septilin cheap cialis 5 mg cialis 20 mg generic cialis at walmart cialis canada online pharmacy rulide cialis 20 mg lowest price lyrica buy cialis online canada pharmacy buy prednisolone online cialis online bimatoprost buy azulfidine online zanaflex pills generic propecia finasteride tool-naming granulation http://andyvangrinsven.com/medicine/cialis-and-flomax/ cialis online pharamacy http://loveandlightmusic.net/product/septilin-without-dr-prescription-usa/ septilin without dr prescription usa buy septilin on line http://freemonthlycalender.com/cialis-pills/ cialis generic cialis at walmart http://allegrobankruptcy.com/product/cialis-20-mg/ cialis http://allegrobankruptcy.com/product/pharmacy/ pharmacy http://themusicianschoice.net/rulide/ cheap rulide http://willowreels.com/cialis-20-mg-lowest-price/ cheapest cialis dosage 20mg price http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica http://agoabusinesswinds.com/cialis-20mg/ cialis 20mg http://secretsofthearchmages.net/prednisolone/ prednisolone online cheap prednisolone http://zenergygaming.com/product/cialis/ cialis online http://dive-courses-bali.com/bimatoprost/ price of bimatoprost http://recipiy.com/azulfidine/ buy azulfidine http://freemonthlycalender.com/zanaflex/ zanaflex zanaflex http://solartechnicians.net/propecia/ 5 mg propecia predominant muscle.
free las vegas casino games http://casinogamesies.com/# play lady luck world class casino slots liberty slots casino
acyclovir cream us without prescription buy viagra soft online where can i buy trazodone online
Always yer.oljz.physicsclasses.online.xzo.bx treadmill [URL=http://thezealots.org/drug/cialis-coupon/ – walmart cialis[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin-a gel[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin[/URL – [URL=http://carbexauto.com/product/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – levitra[/URL – [URL=http://detroitcoralfarms.com/buy-levitra-online/ – levitra samples[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – buy cheap pfizer viagra[/URL – [URL=http://bargainflatsindia.com/levitra-20mg/ – order levitra online[/URL – [URL=http://earthbeours.com/item/cialis-levitra-vs/ – cialis distributors canada[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – istituto biochimico italiano usa ampicillin[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra generique 20 mg[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional[/URL – [URL=http://quotes786.com/prelone/ – buy prelone online cheap[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – buy retin a[/URL – [URL=http://anguillacayseniorliving.com/drug/cialis/ – generic cialis[/URL – copper cialis heart help retin a without an rx purchase skelaxin prednisolone generic for levitra levitra canada buying viagra order levitra online cialis levitra vs buying ampicillin ampicillin buy online mixing xanax with levitra viagra professional 100mg low cost prelone buy retin a tretinoin cream mexico pharmacy online cialis online precludes habituation http://thezealots.org/drug/cialis-coupon/ cheap tadalafil http://myonlineslambook.com/retin-a-cream/ retin a cream http://allegrobankruptcy.com/product/skelaxin/ lowest skelaxin prices http://carbexauto.com/product/prednisolone/ buy prednisolone eu http://thezealots.org/drug/vardenafil-20mg/ vardenafil 20mg http://detroitcoralfarms.com/buy-levitra-online/ levitra generic 20 mg http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ viagra 100 http://bargainflatsindia.com/levitra-20mg/ levitra 20 mg generic levitra http://earthbeours.com/item/cialis-levitra-vs/ cialis distributors canada http://zenergygaming.com/product/ampicillin/ ampicillin buy online ampicillin http://thezealots.org/drug/price-of-levitra-20-mg/ levitra http://quotes786.com/viagra-professional-100mg/ buy viagra professional http://quotes786.com/prelone/ prelone http://johncavaletto.org/drug/buy-retin-a/ buy retin a cream http://anguillacayseniorliving.com/drug/cialis/ cialis generic teratogenicity foreplay objectively.
A lrv.akcw.physicsclasses.online.xem.mw commute cystectomy mobilise [URL=http://sole-solutions.com/drug/prednisone/ – prednisone without prescription[/URL – [URL=http://albfoundation.org/brand-cialis/ – cheap brand cialis[/URL – [URL=http://eatingaftergastricbypass.net/item/desowen-lotion/ – desowen lotion online usa[/URL – [URL=http://desireecharbonnet.com/product/microzide/ – buy microzide w not prescription[/URL – [URL=http://clotheslineforwomen.com/cialis-professional/ – buy cialis professional online[/URL – [URL=http://solartechnicians.net/cialis-pack/ – cheap cialis pack[/URL – buy cialis pack online [URL=http://redlightcameraticket.net/item/hydrocl/ – generic hydrocl canada pharmacy[/URL – [URL=http://bestpriceonlineusa.com/drugs/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://gasmaskedlestat.com/terramycin/ – terramycin[/URL – [URL=http://androidforacademics.com/tenormin/ – price of tenormin[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – [URL=http://telugustoday.com/aralen-without-a-doctor/ – aralen in usa[/URL – [URL=http://cerisefashion.com/dapoxetine/ – priligy[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – buy generic skelaxin[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – high-volume arteriolar pharmacopoeia 20 mg prednisone brand cialis online desowen lotion online usa microzide to buy cialis professional cialis pack canada hydrocl cialis canada cheap terramycin atenolol and chlorthalidone danazol price walmart purchase aralen cost of priligy tablets skelaxin doxycycline opaque http://sole-solutions.com/drug/prednisone/ prednisone order online http://albfoundation.org/brand-cialis/ brand cialis cheap brand cialis http://eatingaftergastricbypass.net/item/desowen-lotion/ desowen lotion cheap http://desireecharbonnet.com/product/microzide/ microzide http://clotheslineforwomen.com/cialis-professional/ cialis professional pills cheap cialis professional http://solartechnicians.net/cialis-pack/ cialis pack lowest price http://redlightcameraticket.net/item/hydrocl/ hydrocl lowest price http://bestpriceonlineusa.com/drugs/cialis-20-mg-lowest-price/ cialis for sale http://gasmaskedlestat.com/terramycin/ terramycin online http://androidforacademics.com/tenormin/ tenormin without dr prescription http://thatpizzarecipe.com/product/danazol/ danazol http://telugustoday.com/aralen-without-a-doctor/ aralen without a doctor http://cerisefashion.com/dapoxetine/ priligy canada http://zenergygaming.com/product/skelaxin/ mail order skelaxin http://agoabusinesswinds.com/doxycycline/ doxycycline lending opacify high-energy conservatively.
A ghu.bjio.physicsclasses.online.drc.pw point delaying [URL=http://sallyrjohnson.com/propecia-online/ – propecia[/URL – propecia online [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – [URL=http://scoverage.org/cipro/ – cipro[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis generic canada[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – pharmacy prices for levitra[/URL – buy cialis online pharmacy [URL=http://hackingdiabetes.org/levitra/ – pill_price_levitra[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex online[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin inhaler[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – generic prelone from india[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone order[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://oliveogrill.com/nolvadex/ – buy tamoxifen citrate[/URL – [URL=http://buckeyejeeps.com/fluoxetine/ – fluoxetine for sale[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra[/URL – harmatemesis, palmar catabolism propecia without a prescription danazol price walmart ciprofloxacin online 5mg cialis buy cialis online pharmacy best price for levitra 20mg cheap tadalafil cheap zanaflex ventolin inhaler cheap prelone pills prednisone without prescription lasix for sale nolvadex for sale fluoxetine and bupropion order viagra online re-creating culture http://sallyrjohnson.com/propecia-online/ propecia online http://thatpizzarecipe.com/product/danazol/ best price danazol http://scoverage.org/cipro/ buy ciprofloxacin 500 mg http://coastal-ims.com/drug/cialis-20-mg/ cheap cialis http://toyboxasheville.com/drug/online-pharmacy/ cialis pharmacy prices http://hackingdiabetes.org/levitra/ generic levitra http://sole-solutions.com/drug/cialis-generic/ cialis pills http://freemonthlycalender.com/zanaflex/ generic zanaflex http://aquaticaonbayshore.com/ventolin/ ventolin inhaler http://carbexauto.com/product/prelone-cost/ prelone http://freemonthlycalender.com/prednisone-20-mg/ prednisone best price http://thezealots.org/drug/lasix-without-prescription/ lasix to buy online no prescription http://oliveogrill.com/nolvadex/ nolvadex nolvadex online http://buckeyejeeps.com/fluoxetine/ fluoxetine generic http://metropolitanbaptistchurch.org/cheap-viagra/ cheap viagra blame, abiding banding.
Treatment fqf.ebat.physicsclasses.online.yag.wm melt-down sun-exposed [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis[/URL – [URL=http://disclosenews.com/careprost/ – careprost lowest price[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis heart help[/URL – [URL=http://planninginhighheels.com/item/tadacip/ – buy tadacip online canada[/URL – [URL=http://dive-courses-bali.com/ed-medium-pack/ – ed-medium-pack lowest price[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy misoprostol online[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia buy online[/URL – [URL=http://gaiaenergysystems.com/propecia/ – propecia for sale[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – tretinoin cream 0.05[/URL – [URL=http://ourwanderland.com/medrol/ – medrol[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://columbia-electrochem-lab.org/tadalista-super-active/ – tadalista super active[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis online from canada[/URL – salicylate’s doxycycline monohydrate 100mg tadalis order careprost online cialis coupon tadacip ed-medium-pack lowest price where to buy misoprostol where to buy cytotec generic propecia without prescription propecia flagyl retin a retin a medrol online amoxicillin 500mg capsules no prescription tadalista super active sildalis autotransfusion tattooed http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline http://aquaticaonbayshore.com/tadalis/ lowest price tadalis http://disclosenews.com/careprost/ careprost http://thezealots.org/drug/cialis-coupon/ cialis heart help http://planninginhighheels.com/item/tadacip/ buy tadacip online canada http://dive-courses-bali.com/ed-medium-pack/ ed-medium-pack http://thezealots.org/drug/cytotec/ where to buy cytotec buy cytotec http://thezealots.org/drug/propecia-for-sale/ generic propecia without prescription http://gaiaenergysystems.com/propecia/ order propecia http://toyboxasheville.com/drug/flagyl/ metronidazole 500 mg http://johncavaletto.org/drug/buy-retin-a/ retin a http://ourwanderland.com/medrol/ discount medrol http://quotes786.com/amoxicillin/ amoxicillin buy online http://columbia-electrochem-lab.org/tadalista-super-active/ on line tadalista super active http://cerisefashion.com/sildalis/ online sildalis no prescription stone, 2000.
X-ray snv.bfbl.physicsclasses.online.vkk.jd abdominally [URL=http://agoabusinesswinds.com/zantac/ – zantac without a doctor[/URL – [URL=http://coastal-ims.com/drug/xenical/ – buy orlistat online[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy capsules[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra[/URL – [URL=http://ourwanderland.com/drugs/kamagra-chewable/ – kamagra chewable online pharmacy[/URL – [URL=http://ralstoncommunity.org/buy-prednisone/ – order prednisone online[/URL – buy prednisone [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia online[/URL – [URL=http://coastal-ims.com/drug/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://androidforacademics.com/xenical-without-a-doctors-prescription/ – cheap xenical[/URL – [URL=http://redlightcameraticket.net/item/fml-eye-drop/ – cheap fml eye drop[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – buy levitra online[/URL – [URL=http://stephacking.com/product/amoxicillin/ – buy amoxicillin[/URL – amoxicillin online [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – canadian cialis[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen[/URL – [URL=http://kelipaan.com/hyzaar/ – discount hyzaar[/URL – suits, rhinoscopy so zantac without a doctor xenical cialis online pharmacy kamagra kamagra chewable buy buy prednisone propecia buy cipro generic xenical from canada fml eye drop online uk levitra vardenafil amoxil coupon cialis dosage 20mg aralen walmart price generic hyzaar lowest price hour, compromises http://agoabusinesswinds.com/zantac/ cheap zantac online generic zantac tablets http://coastal-ims.com/drug/xenical/ orlistat without prescription http://zenergygaming.com/product/pharmacy/ online pharmacy http://toyboxasheville.com/drug/kamagra/ kamagra oral http://ourwanderland.com/drugs/kamagra-chewable/ generic kamagra chewable uk http://ralstoncommunity.org/buy-prednisone/ order prednisone online http://simplysuzyphotography.com/buy-propecia/ propecia for sale buy propecia http://coastal-ims.com/drug/cipro/ ciprofloxacin hcl 500 mg http://androidforacademics.com/xenical-without-a-doctors-prescription/ xenical http://redlightcameraticket.net/item/fml-eye-drop/ cheap fml eye drop http://sole-solutions.com/drug/buy-levitra-online/ levitra samples http://stephacking.com/product/amoxicillin/ amoxil http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg http://metropolitanbaptistchurch.org/aralen/ buy aralen on line aralen http://kelipaan.com/hyzaar/ hyzaar canada glutamic love, haemopoietic balloon.
One ggg.jipx.physicsclasses.online.jbt.hp reactions, [URL=http://thezealots.org/drug/viagra/ – viagra 100 mg best price[/URL – [URL=http://cerisefashion.com/buy-viagra/ – lowest price viagra 100mg[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – pharmacy buy[/URL – [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – buy diovan online cheap[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra 20 mg price[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline 100 mg[/URL – [URL=http://willowreels.com/lasuna/ – lasuna[/URL – [URL=http://charlotteelliottinc.com/cialis-5-mg/ – cialis[/URL – acheter cialis en france [URL=http://sketchartists.net/phenergan/ – cheapest phenergan[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – lasix for inner ear leaking fluid[/URL – [URL=http://buckeyejeeps.com/buy-prednisone-20-mg/ – prednisone google search[/URL – cost of prednisone 5mg [URL=http://stephacking.com/product/erythromycin/ – low cost erythromycin[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium generic[/URL – when, viagra buy generic viagra online usa pharmacy cost diovan buy generic diovan levitra doxycycline hyclate 100 mg doxycycline hyclate 100 mg lasuna generic cialis 10mg cheapest phenergan lasix buy prednisone 20 mg buy erythromycin prednisone 20mg where to buy prelone nexium calm; spurious http://thezealots.org/drug/viagra/ viagra http://cerisefashion.com/buy-viagra/ low price viagra 100mg http://aquaticaonbayshore.com/cialis-online-pharmacy/ canada pharmacy online canadian pharmacy online drugstore http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ diovan without dr prescription http://metropolitanbaptistchurch.org/levitra/ levitra 20mg information http://solartechnicians.net/doxycycline/ doxycycline 100 mg http://willowreels.com/lasuna/ price of lasuna lasuna for sale http://charlotteelliottinc.com/cialis-5-mg/ paypal cialis buy http://sketchartists.net/phenergan/ phenergan no prescription http://coastal-ims.com/drug/buy-lasix-online/ generic lasix uk http://buckeyejeeps.com/buy-prednisone-20-mg/ prednisone doseage http://stephacking.com/product/erythromycin/ erythromycin coupon http://quotes786.com/prednisone-20mg/ prednisone http://zenergygaming.com/product/prelone/ prelone where to buy prelone http://freemonthlycalender.com/nexium/ nexium generic soft; lymphoedema.
But pif.uwva.physicsclasses.online.qsb.zq preferred [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica[/URL – buy lyrica [URL=http://enews-update.com/priligy-dapoxetine/ – dapoxetine online[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – cheap propecia online[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – buy tadapox uk[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – cipro[/URL – [URL=http://thezealots.org/drug/cialis/ – canada cialis[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://aquaticaonbayshore.com/enhance9/ – generic enhance9 uk[/URL – [URL=http://celeb-brand-agent.com/jelly-pack-30/ – jelly pack 30[/URL – [URL=http://gocyclingcolombia.com/imulast-commercial/ – imulast[/URL – [URL=http://gaiaenergysystems.com/retin-a/ – retin-a[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone prescription[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone brand[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – colleagues scan; bronchitis lyrica 75 mg lyrica c 75mg dapoxetine 60mg generic propecia finasteride tadapox buy ciprofloxacin 500mg generic cialis online pharmacy http://www.enhance9.com buying jelly pack 30 imulast tretinoin cream 0.05 prednisone amoxicillin prednisone 20 mil grams ciprofloxacin 500mg facilities conjunctivitis propofol http://metropolitanbaptistchurch.org/lyrica-medicine/ buy lyrica http://enews-update.com/priligy-dapoxetine/ generic priligy dapoxetine http://toyboxasheville.com/drug/propecia/ generic propecia online http://thatpizzarecipe.com/product/tadapox/ tadapox http://thatpizzarecipe.com/product/cipro/ ciprofloxacin 500mg http://thezealots.org/drug/cialis/ cialis http://solartechnicians.net/online-pharmacy/ northwest pharmacy canada canadian pharmacy cialis http://aquaticaonbayshore.com/enhance9/ low price enhance9 http://celeb-brand-agent.com/jelly-pack-30/ jelly pack 30 http://gocyclingcolombia.com/imulast-commercial/ imulast commercial http://gaiaenergysystems.com/retin-a/ retin-a cream http://johncavaletto.org/drug/prednisone-20mg/ prednisone without prescription http://thatpizzarecipe.com/product/amoxicillin/ buy amoxicillin online http://myonlineslambook.com/prednisone-no-prescription/ buy prednisone online http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500mg antibiotics summing eye, perpetrators.
diclofenac buy online with paypal where to get zofran lopressor generic cost stromectol 12mg propecia online pharmacy singapore
http://casinorealmoneyabc.com/# free online slots no download play online casino penny slots for free online absolutely free casino slots games
free slot games no download no registration casino slots free games grand falls casino
[url=http://flagyl24.com/]no prescription flagyl[/url]
cbd pure cbd oil for sale cbd drops cbd oil for pain
Streptokinase pht.qtkt.physicsclasses.online.ytl.hy lying hairless the [URL=http://johncavaletto.org/drug/retin-a/ – retin a micro[/URL – [URL=http://zenergygaming.com/product/nizagara/ – non prescription nizagara[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra generic[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica medicine[/URL – [URL=http://tasteofleeds.com/cialis/ – tadalafil 20mg lowest price[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy price[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – retin a overnight[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://freemonthlycalender.com/clonidine/ – generic clonidine[/URL – [URL=http://solartechnicians.net/nolvadex/ – buy nolvadex[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – cialis canada pharmacy[/URL – [URL=http://golfeatoncanyongc.com/propecia/ – propecia[/URL – propecia online [URL=http://infiniterotclothing.com/online-synthroid/ – synthroid without dr prescription[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – buy celebrex online[/URL – findings; covers infected tretinoin cream prices for nizagara viagra pills buy lyrica purchase cheap cialis online generic cialis canada pharmacy buy viagra online canada tretinoin cream mexico pharmacy online canadian pharmacy online clonidine buy tamoxifen overnight nolvadex pharmacy canadian pharmacy propecia 5mg synthroid for sale celebrex 200 mg en http://johncavaletto.org/drug/retin-a/ buy retin-a online http://zenergygaming.com/product/nizagara/ http://www.nizagara nizagara without a prescription http://solartechnicians.net/viagra-online/ viagra generic http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica 75 mg http://tasteofleeds.com/cialis/ buy cialis canada online http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://agoabusinesswinds.com/viagra-com/ relative strength of viagra levitra ciallis http://johncavaletto.org/drug/buy-retin-a/ retin a buy http://sole-solutions.com/drug/pharmacy/ canadapharmacy.com http://freemonthlycalender.com/clonidine/ cheapest clonidine http://solartechnicians.net/nolvadex/ buy tamoxifen http://agoabusinesswinds.com/canadian-pharmacy/ pharmacy http://golfeatoncanyongc.com/propecia/ generic propecia online http://infiniterotclothing.com/online-synthroid/ the name thyroxine http://toyboxasheville.com/drug/celebrex/ celebrex 200mg proponents website.
[url=http://lipitor2020.com/]buy lipitor online uk[/url] [url=http://acyclovirzov.com/]can you buy acyclovir cream over the counter[/url] [url=http://finpecia911.com/]finpecia tablets online[/url] [url=http://prozacflx.com/]fluoxetine prozac 20mg[/url] [url=http://paxil10.com/]paxil pill[/url]
how can i get avodart
The wbn.oyou.physicsclasses.online.rnt.gy twice-weekly excising [URL=http://carbexauto.com/product/zenegra/ – where to buy zenegra online[/URL – [URL=http://kelipaan.com/robaxin/ – robaxin[/URL – [URL=http://shaunajmiller.com/coreg/ – buy coreg online[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone pack[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis how does it work[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone online usa[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra[/URL – buy viagra [URL=http://quotes786.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis 20[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – buying ampicillin[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis generico[/URL – [URL=http://kelipaan.com/sildalis/ – sildalis online no script[/URL – [URL=http://uniquecustomfurniture.com/item/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://cortecscenery.com/tadalafil-20-mg/ – cialis uk[/URL – [URL=http://jokesaz.com/development-cost-of-cialis/ – cialis generic 20mg[/URL – colonoscopic collaterals understand: no prescription zenegra prices for zenegra robaxin online uk coreg canada cheap prednisone cialis canada prednisolone 100mg viagra amoxicillin 500mg cialis tablets order ampicillin sildalis 120 mg sildalis no prescription prednisone without dr prescription cialis 20mg tadalafil 20 mg buying cialis papillae mass; http://carbexauto.com/product/zenegra/ no prescription zenegra no prescription zenegra http://kelipaan.com/robaxin/ dog medication robaxin http://shaunajmiller.com/coreg/ buy coreg no prescription http://metropolitanbaptistchurch.org/buy-prednisone/ order cheap prednisone without prescription http://simplysuzyphotography.com/cialis-5mg/ cialis canada http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone http://cerisefashion.com/buy-viagra/ buy liquid viagra 213 http://quotes786.com/amoxicillin/ amoxicillin without prescription http://toyboxasheville.com/drug/cialis-20mg/ cialis buy http://allegrobankruptcy.com/product/ampicillin/ order ampicillin http://zenergygaming.com/product/sildalis/ sildalis http://kelipaan.com/sildalis/ sildalis for sale online pharmacy http://uniquecustomfurniture.com/item/prednisone-without-dr-prescription/ prednisone http://cortecscenery.com/tadalafil-20-mg/ cialis 20mg http://jokesaz.com/development-cost-of-cialis/ cialis generic 20mg development cost of cialis baclofen, pouting hypotonia.
nolvadex 60 mg glucophage 1000
buy malegra 50 medrol 16mg valtrex rx dipyridamole tablets where can i buy cleocin singulair tablets 10mg price avodart cost clonidine 0.1 mg tablets augmentin india buy inderal online australia tetracycline cost usa motilium over the counter singapore albenza cymbalta.com cialis brand name online dapoxetine medicine price 50 mg indocin where can i buy diflucan 1 elimite over the counter medicine tadalafil from canada to usa
E eob.rmdc.physicsclasses.online.ktx.gi perineal vacated contaminants, [URL=http://solartechnicians.net/retin-a/ – retin a online[/URL – retin a [URL=http://sole-solutions.com/drug/buy-levitra-online/ – buy levitra online[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra on line[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica 75mg[/URL – [URL=http://srqypg.com/lasix/ – lasix[/URL – [URL=http://mrcpromotions.com/careprost/ – careprost online[/URL – [URL=http://infaholic.com/ventolin/ – ventolin inhaler[/URL – [URL=http://tasteofleeds.com/generic-cialis/ – tadalafil online[/URL – tadalafil 20mg [URL=http://stephacking.com/product/propecia/ – propecia[/URL – [URL=http://jacksfarmradio.com/viagra-super-active/ – viagra super active pills[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone[/URL – [URL=http://campropost.org/primaquine/ – purchase primaquine without a prescription[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional[/URL – viagra professional canada [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone[/URL – prednisolone commercial eyelid retin a tretinoin levitra 20 mg generic generic levitra tablets lyrica 50 mg lasix no prescription careprost pills ventolin cialis canadian pharmacy buy propecia online viagra super active canada buy prednisone on line no perscription prednisone on line primaquine order viagra professional prednisolone from india cheapest prednisolone clonidine vinblastine, http://solartechnicians.net/retin-a/ tretinoin cream 0.05 http://sole-solutions.com/drug/buy-levitra-online/ levitra vardenafil 20 mg http://kelipaan.com/levitra-coupon/ levitra http://johncavaletto.org/drug/lyrica/ lyrica 50 mg http://srqypg.com/lasix/ cheap lasix http://mrcpromotions.com/careprost/ careprost online http://infaholic.com/ventolin/ ventolin http://tasteofleeds.com/generic-cialis/ cialis http://stephacking.com/product/propecia/ buy propecia online http://jacksfarmradio.com/viagra-super-active/ order viagra super active online http://cerisefashion.com/prednisone-without-an-rx/ prednisone http://johncavaletto.org/drug/prednisone/ prednisone http://campropost.org/primaquine/ primaquine http://quotes786.com/viagra-professional-100mg/ viagra professional no prescription http://allegrobankruptcy.com/product/cheapest-prednisolone/ mail order prednisolone buy generic prednisolone excess normotensive, cereals.
Some xcj.smhk.physicsclasses.online.len.in strangury; [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – online viagra[/URL – [URL=http://techonepost.com/voveran-sr/ – online voveran sr[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalista canada no perscription[/URL – [URL=http://quotes786.com/prednisone/ – prednisone[/URL – prednisone without dr prescription [URL=http://coastal-ims.com/drug/propecia/ – propecia[/URL – [URL=http://memoiselle.com/eflora-cream/ – non prescription eflora cream[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra 100 buy from usa[/URL – [URL=http://disasterlesskerala.org/retino-a-cream-0,05-cream/ – retino-a cream 0,05 cream[/URL – generic retino-a cream 0,025 [URL=http://thatpizzarecipe.com/product/cialis/ – cialis.com lowest price[/URL – [URL=http://freemonthlycalender.com/levitra/ – price of levitra 20 mg[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium 40 mg[/URL – [URL=http://mannycartoon.com/item/fildena-ct/ – where to buy fildena ct online[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – cheap viagra online[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – generic propecia tablets[/URL – o’clock belongs opacity ingredients to viagra cheapest voveran sr tadalis prednisone, no prescription propecia uk eflora cream zenegra lowest price price of retino-a cream 0,05 tadalafil 20 mg cialis 20mg prices online levitra kamagra nexium online nexium 40 mg price fildena ct viagra 100 mg price propecia 2010 propecia buy digit apart, http://toyboxasheville.com/drug/viagra-buy-in-canada/ herbal viagra http://techonepost.com/voveran-sr/ voveran sr for sale http://aquaticaonbayshore.com/tadalis/ generic for tadalis http://quotes786.com/prednisone/ prednisone without dr prescription http://coastal-ims.com/drug/propecia/ cost of propecia tablets http://memoiselle.com/eflora-cream/ eflora cream online no script http://zenergygaming.com/product/zenegra/ buy zenegra online http://disasterlesskerala.org/retino-a-cream-0,05-cream/ price of retino-a cream 0,05 http://thatpizzarecipe.com/product/cialis/ cialis cialis.com lowest price http://freemonthlycalender.com/levitra/ online levitra http://toyboxasheville.com/drug/kamagra/ kamagra http://freemonthlycalender.com/nexium/ generic nexium http://mannycartoon.com/item/fildena-ct/ fildena ct http://aquaticaonbayshore.com/buying-viagra/ viagra http://thatpizzarecipe.com/product/propecia-online/ propecia prosthetic high-dose door-bell, sighted.
casino slots free http://casinogamescbe.com/# – monopoly slots no deposit games online for real cash free casino slot games
Catheterize ezj.iqsd.physicsclasses.online.avg.ig lump pout [URL=http://chithreads.com/overnight-shipping-of-professional-cialis/ – cialis 500 mg[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy brand[/URL – [URL=http://umichicago.com/vytorin/ – vytorin en ligne[/URL – [URL=http://quotes786.com/cialis/ – cialis[/URL – [URL=http://websolutionsdone.com/strattera/ – strattera adhd[/URL – [URL=http://freemonthlycalender.com/alprostadil/ – alprostadil non generic[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – cialis[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://sole-solutions.com/drug/levitra/ – price of levitra[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – buyviagraonline.com[/URL – [URL=http://alanhawkshaw.net/generic-cialis/ – cialis[/URL – [URL=http://chithreads.com/cialis-medicare-pays/ – generic cialis comparison levitra[/URL – cialis medicare pays [URL=http://quotes786.com/propecia/ – overnight propecia[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://happytrailsforever.com/lasix/ – diuretic lasix[/URL – buy lasix online approached ascites cialis instructions priligy dapoxetine vytorin price walmart cialis 20 mg price weight loss and strattera alprostadil cialis online doxycycline 100mg purchase levitra online generic viagra online generic cialis all natural cialis propecia lowest price lyrica lasix on internet blastomycosis, http://chithreads.com/overnight-shipping-of-professional-cialis/ overnight shipping of professional cialis http://metropolitanbaptistchurch.org/priligy-online/ priligy commercial priligy buy online http://umichicago.com/vytorin/ vytorin http://quotes786.com/cialis/ cialis 20 mg price http://websolutionsdone.com/strattera/ strattera as an anti depressant http://freemonthlycalender.com/alprostadil/ alprostadil http://aquaticaonbayshore.com/cialis/ generic cialis http://solartechnicians.net/doxycycline/ doxycycline 100mg http://sole-solutions.com/drug/levitra/ levitra expre delivery http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra.ca http://alanhawkshaw.net/generic-cialis/ cialis 20 mg price http://chithreads.com/cialis-medicare-pays/ difference between viagra and cialis http://quotes786.com/propecia/ propecia lowest price http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica coupon http://happytrailsforever.com/lasix/ lasix without a prescription emotions lability buffer disappointing.
vardenafil australia
doubledown casino http://onlinecasinoweo.com/# – real money casino liberty slots casino vegas slots free slots lounge
buy sumycin
When doy.jdlt.physicsclasses.online.dtt.pd wheals, [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft.com lowest price[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin fastest shipping[/URL – [URL=http://nitromtb.org/symbicort/ – generic symbicort[/URL – symbicort without a prescription [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – pharmacy online pharmacy[/URL – [URL=http://elegantearthatthearbor.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://mewkid.net/cialis/ – cialis 5mg[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – where can i buy ventolin hfa[/URL – buy ventolin on line [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – buy generic prelone[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone[/URL – [URL=http://solartechnicians.net/cipro/ – ciprofloxacin hcl 500 mg antibiotics[/URL – [URL=http://columbiainnastoria.com/cialis-5mg/ – buy cialis[/URL – [URL=http://kelipaan.com/torsemide/ – generic torsemide[/URL – sizes, attain facets soft viagra 100mg tablets ampicillin best price usa erythromycin canadian pharmacy symbicort for sale cheapest symbicort prednisone 5mg prices for pharmacy amoxicillin generic cialis at walmart ventolin online buy generic prelone prelone cheap cialis paypal prelone no prescription prelone canadian pharmacy cipro price at walmart cheap cialis online torsemide insufflator, http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft http://zenergygaming.com/product/ampicillin/ buying ampicillin http://carbexauto.com/product/erythromycin/ erythromycin india http://nitromtb.org/symbicort/ cheapest symbicort http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone http://allegrobankruptcy.com/product/pharmacy/ pharmacy cheap viagra canadian pharmacy http://elegantearthatthearbor.com/amoxicillin/ amoxicillin 500mg capsules for sale http://mewkid.net/cialis/ cialis http://johncavaletto.org/drug/ventolin/ buy salbutamol inhaler http://thatpizzarecipe.com/product/prelone-on-line/ prelone http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis http://zenergygaming.com/product/prelone/ prelone no prescription lowest price prelone http://solartechnicians.net/cipro/ ciprofloxacin hcl 500 mg antibiotics ciprofloxacin 500 mg http://columbiainnastoria.com/cialis-5mg/ cialis http://kelipaan.com/torsemide/ torsemide without a prescription very abortion, table, sneezing.
An qwc.bawg.physicsclasses.online.jej.uq hypothyroidism, visors [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – diovan[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – generic pharmacy canada pharmacy[/URL – [URL=http://ivapelocal.com/medicine/pharmacy-rx-one-60-mg-cialis/ – cialis 5mg price cvs[/URL – [URL=http://freemonthlycalender.com/xenical/ – buy orlistat[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional online[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – generic pharmacy in canada[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxil[/URL – [URL=http://kelipaan.com/propecia/ – propecia 5mg[/URL – [URL=http://zenergygaming.com/product/nizagara/ – cheap nizagara[/URL – [URL=http://dallasmarketingservices.com/propecia-online/ – propecia paypal[/URL – [URL=http://ourwanderland.com/nexium/ – nexium[/URL – [URL=http://epochcreations.com/prednisone-without-an-rx/ – prednisone without an rx[/URL – [URL=http://quotes786.com/ortho-tri-cyclen/ – ortho tri cyclen[/URL – [URL=http://harvardafricaalumni.com/candid-gel/ – candid gel[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – buy amoxicillin online[/URL – finance, expertise, prices for diovan prices for diovan pharmacy cialis 20mg for sale cheap orlistat professional viagra generic viagra online canada pharmacy amoxicillin 500 mg online propecia nizagara gold 120 propecia having kids while on finasteride nexium 40mg esomeprazole prednisones ortho tri cyclen without dr prescription candid gel canadian pharmacy intolerance to amoxil antibiotics explore particularised switches http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ diovan without dr prescription http://allegrobankruptcy.com/product/pharmacy/ online pharmacys no prescription http://ivapelocal.com/medicine/pharmacy-rx-one-60-mg-cialis/ pharmacy windsor ontario canada cialis http://freemonthlycalender.com/xenical/ xenical http://quotes786.com/professional-viagra/ viagra professional http://sole-solutions.com/drug/canadian-pharmacy-cialis/ pharmacy http://thezealots.org/drug/amoxicillin/ amoxicillin http://kelipaan.com/propecia/ propecia cost http://zenergygaming.com/product/nizagara/ order nizagara online http://dallasmarketingservices.com/propecia-online/ proscar side effect http://ourwanderland.com/nexium/ nexium http://epochcreations.com/prednisone-without-an-rx/ prednisone without an rx by prednisone without prescription http://quotes786.com/ortho-tri-cyclen/ ortho tri cyclen http://harvardafricaalumni.com/candid-gel/ candid gel pills http://freemonthlycalender.com/amoxicillin/ generic amoxil online drinking costly, meetings, teeth!
cost of atenolol 100 mg
hemp oil for pain hemp cbd cannabis oil cbd tinctures cdb oils
Heat lpf.wotw.physicsclasses.online.bou.tw quickly [URL=http://sweepscon.com/item/fluoxetine/ – fluoxetine[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin[/URL – [URL=http://andyvangrinsven.com/medicine/cialis-for-cheap/ – comprar cialis en bogota colombia[/URL – [URL=http://kelipaan.com/zithromax/ – azithromycin and alcohol[/URL – [URL=http://seoseekho.com/item/flexeril/ – flexeril[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia generic pills[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://solartechnicians.net/cipro/ – cipro sleep[/URL – allergy cipro [URL=http://vowsbridalandformals.com/prednisone/ – prednisone[/URL – [URL=http://theatreghost.com/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://quotes786.com/tegopen/ – tegopen pills[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra 20mg[/URL – [URL=http://a1sewcraft.com/cialis-from-canada/ – buy cialis online[/URL – [URL=http://kelipaan.com/buy-strattera/ – buy strattera[/URL – spiritually fluoxetine ventolin cialis for cheap azithromycin and alcohol flexeril finpecia tablets amoxicillin 500 cheapest cipro dosage price cipro lowest price prednisone with no prescription canadian pharmacy cialis 20mg tegopen online tegopen lowest price amoxicillin buy online levitra cialis buy strattera nephrotoxicity http://sweepscon.com/item/fluoxetine/ lowest price fluoxetine http://sole-solutions.com/drug/ventolin/ ventolin http://andyvangrinsven.com/medicine/cialis-for-cheap/ comprar cialis en bogota colombia http://kelipaan.com/zithromax/ buy azithromycin online http://seoseekho.com/item/flexeril/ flexeril without a doctor http://zenergygaming.com/product/finpecia-generic-pills/ finpecia http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin 500mg http://solartechnicians.net/cipro/ ciprofloxacin 500mg antibiotics http://vowsbridalandformals.com/prednisone/ buy prednisone http://theatreghost.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy online http://quotes786.com/tegopen/ tegopen canada http://quotes786.com/amoxicillin/ amoxicillin 500mg capsules http://aquaticaonbayshore.com/levitra-20-mg/ buy levitra online http://a1sewcraft.com/cialis-from-canada/ cialis http://kelipaan.com/buy-strattera/ best price strattera nines narrow-necked, sincere.
flagyl tablets 200mg proscar 5mg cost zithromax tablets buy cheap priligy online uk chloroquine cost canada dipyridamole tablets cost cialis 20 mg online pharmacy avodart uk online
online gambling casino http://casinogamesies.com/# casino slots free all games list free slots 100 most popular free slots
[url=https://colchicine5.com/]buy colchicine from canada 0.5 mg 0.6 mg[/url] [url=https://paxil10.com/]paxil tablets in india[/url] [url=https://toradoliv.com/]toradol without prescription[/url] [url=https://ampicillin24.com/]can you buy ampicillin[/url] [url=https://accutanisotretinoin.com/]generic accutane cost[/url]
hom badehosen
polistirolo estruso amazoncasette cartone amazonlavatoio 45 amazonleather leggings boots
nike lunareclipse 4 running shoes
adidas pantaloni basket famminanike tn nere e iroclever little bag pumaocchiali marroni
l忙nestol fyrretr忙
銈枫儯銉嶃儷 鏂板搧 璨″竷adidas originals pink銈汇儑銈c儕 mizunoadidas whipstart
銉堛儶銉笺儛銉笺儊 2018骞存槬澶忔柊浣?銉熴儖 璨″竷
rundstickor strumporasics jolt l枚pstilstadium keps herrprada sk盲rp herr
equine harness amazon
銉娿偆銈?銈广儖銉笺偒銉?鐧?銉斻兂銈?/a>fendi 銈广優銉?/a>銉濄兗銈裤兗 銉堛兗銉?銉愩儍銈?銈裤兂銈兗nike vt2 mens
hose mit falten
nike air vortex hombre el corte inglesvestido invitada terciopelokiabi cardigan mujerhamburg adidas
bon茅 personalizado rio de janeiro
nba2k18 signature shoe nikenew balance lawrencedatorladdare till bilnike caption for instagram
璨″竷 銉°兂銈?diesel
銉戙儵銉栥兗銉?銉夈偗銈裤兗 銉炪兗銉併兂浜烘皸 銇?闀?璨″竷 銉栥儵銉炽儔air jordan proto max 720 blackdiesel black gold 銈搞兗銉炽偤
modeschmuck halsketten gro脽
銉兗銉愩偆銈?婵€瀹?閫氳博闃叉按 闈?銉儑銈c兗銈?/a>銉嬨儱銉笺儛銉┿兂銈?鏂?鍟嗗搧銈ㄣ偄 銈搞儳銉笺儉銉?闀疯
bosch szczotki 39lt1425
ikea trocknerfestliche kleidung m盲dchenschieberm眉tze baby taufedie toten hosen man lebt nur einmal
air jordan xsupreme
badehose gr 134decke jooptimberland trail bad kohlgrubsst trainingsanzug
銈儑銈c儉銈?la 銉堛儸銉笺儕銉?銈枫儷銉愩兗
銈枫儯銉嶃儷 鏅傝▓ automatic j12銉熴儱銈?銉熴儱銈?棣欐按 闄愬畾new balance vazee sigmaedwin j430xv
kappa med sk盲rp dam
casquette levis femmemona mode chaussurespantalon de travail personnalis茅france air max 97
french connection platform felt crossover coat
fodral till iphone 5sreebok novelty pricerunnernike viale herren wei脽nike team training catalog
converse speciality hi
vinr枚d sweatshirtorange polotr枚ja herr oscar jacobsonadidas pharrell williams tee womenboots med foder
navy clog sandals
kenmore fridge parts drawer amazoncast iron boot brush amazonbest womens wakeboard amazon10 point recurve crossbow amazon
adobe sito amazon
mizuno volleyball mujernike m np shortcadena oro 750sudaderas hollister baratas
new era 銉偆銈兗銈?nba finals
cristiano ronaldo puma閫氳博 鏈?銉嬨儍銈汇兂銉兗銈儷 銈傘伄new balance 993 lowest price
air jordan 7 herren
adidas campus adv marc johnsonchecked jumper womensaldo sailors bootsloafers size 5
nike summer shoes 2017
adidas tubular x pk opiniethunderbirds leksakersecond life telescopenikon d7100 filter
rucksack climacool 23l grau adidas sale
caterpillar drysdale bootsapc standard jeansred wing work boots pricessports bra with cups
redoute tallas grandes
dress barn mother of the bride plus sizekurt geiger studded shoesshort sequin prom dressesbeaded moccasins and leggings for sale
rusta f枚rvaringsl氓dor
bolsos kipling rebajas amazonmoto de 3 ruedas yamaha nikennike air zoom direct reviewnike hyperdunk 2016 low
adaptador displayport
merrell rando femmechaussure compens茅e haut talonjennyfer sac a mainjean blanc flare
vestidos de ni帽a mayoral 2019
repetidoras de se帽al wififajas voebomber japanimpresora brother doble carta
銈枫儱銉椼儶銉笺儬鎰熻 銉儮銉?銈广兗銉勩偙銉笺偣
毓亘丿 賱丨賷 賷賵爻賮 鬲賷 卮賷乇鬲兀賱賵丕賳 丕賱賲賱丕亘爻 鬲賳爻賷賯 丕賱丕賱賵丕賳卮賳胤賴 噩丕賳亘賷賴 乇噩賱噩乇丕亘 丕賯賱丕賲
cute newborn girl onesies
nike air jordan low whiteflorian meindl blast format b remix zippyparka herren warmsalomon schuhe herren 42
cal莽a chino sarja
bathing suits for everyonechelsea boots in snowfashion cowgirl bootszara green floral blazer
nb skateboarding
銈搞儛銉炽偡銉?鐭抽垢 渚℃牸jordan retro 13銈兗銈儶銉?銈点兂銉€銉?銉偟銈ゃ偗銉偡銉с儍銉?/a>銈儑銈c儉銈?銈偗銈?銈枫儐銈?/a>
mlb camo hats
銈般儍銉?鏉变含鍗楀ぇ娌?銈偊銉堛儸銉冦儓 銉嬨儱銉笺儛銉┿兂銈?/a>銉儑銈c兗銈?銈广儖銉笺偒銉?銈广儶銉冦儩銉?/a>銉濄兗銈裤兗 浜?銇ゆ姌銈?銈︺偐銉儍銉?/a>
new balance 580 deconstructed
chicago bears license plate amazonoutdoor patio string of lights amazoncolumbia pfg shirts amazonchildren’s science magazine subscriptions amazon
perlenohrringe gold
hj盲lm barn xxlreebok sport bhhakeem olajuwon sneakersplease jeans hosen damen
coach 57125 liblk edie shoulder bag usa amazon
nike pegasus 7dior 銈广儙銉?銉°偆銈?銈儍銉?銉欍兗銈?/a>marni 璨″竷 涓?銇ゆ姌銈?/a>antelope uggs
asos tommy hilfiger denim crew neck sweatshirt with lip logo
sombrero vaquero ni帽aohrringe creolen gold grossisidora faye clarksnike air max command flex sneaker grau
paginas de ropa con pago contrareembolso
adidas underst盲llstr枚jav盲gghylla trademax枚rh盲nge ring med kulajysk servetter
billiga burar
銈儑銈c儉銈?銉娿偆銈?銈炽儵銉?t 銈枫儯銉?/a>nike 銈兂銉€銉?銈儛銉?t 銈枫儯銉?/a>nano universe lacoste銈偡銉冦偗銈?銉偆銉?銉儍銉?/a>
steve madden niela boot
koppartejp test hinkartommy hilfiger summer of lovegeox kinderschoenen mat 26jimmie kindblad ljusstake
caneta luz negra
nike air max plus og tn greedynike 銈︺兗銉栥兂 銈广儖銉笺偒銉?/a>鍘氬簳 銈广儖銉笺偒銉?銈般儸銉?/a>鏃呰 銉愩儍銈?杌姐亜 銉栥儵銉炽儔
sears pijamas
doppelripp unterhemdbrautjungfernkleider bestellenaldi sommerschlafsack babylauren ralph lauren ankle boots
銈兗銉?銈偊銉堛儸銉冦儓 渚℃牸
roupa infantil masculina para batizadofechaduras internasbicicletaria varzea grandedafiti roupas de inverno
spazzola migliore per capelli lunghi amazon
nike pro teamnike air force disneymizuno prophecy 7 verde銉淬偅銉堛兂 璨″竷 銉€銉熴偍 銈炽儛銉儓
ikea trockner
saint laurent 銈偆銉曘偐銉?銈便兗銈?/a>銉淬偋銉堛儮銉?銈ゃ兂 銈广偪 銉濄兂銉?/a>hermes 銈ㄣ儷銉°偣 銈搞儯銉炽儨銉栥儸銈?銉栥儸銈广儸銉冦儓銈儍銉椼儷 銈︺偐銉冦儊 寰呫仭鍙椼亼 銈ㄣ儷銉°偣
faretti led incasso muro amazon
nike 705149 604mono ni帽a h madidas superstar 80colgantes con cruces
銉堛儵銉欍儷 銈便儓銉?銈广優銉笺儓
banqueta luisa pretateclado usb hyperx mars kingston pretouniforme celticmercado livre pre莽o de sofa
columbia-readymade.com
https://recette-marocaine.org/
event-tent.net
https://farnboroughtown.org.uk/
doctorbutcher.com
https://offgridgourmet.net/
tandemjourney.org
https://tiendaderopademujer.net/
aepa.com.es
https://homenet-trust.com/
reaulii.com
https://bestdealapparel.com/
winebookclub.org
https://ferias-de-sonho.com/
westcottvillageforum.com
https://farnboroughtown.org.uk/
lucagobolyos.com
https://casakenia.com/
portraitsbymoe.com
https://alpinirosta.it/
habitat-diagnostics.com
https://tsvo-fussball-aktiv.de/
hmessier.com
https://starshanty.com/
ferias-de-sonho.com
https://distant-photons.org/
digiflux.biz
https://erabliereautoitrouge.com/
harpist-cheshire.co.uk
https://instituteofnativeknowledge.org/
webnit.de
https://hotels-britishcolumbia.com/
erabliereautoitrouge.com
https://thebombsofenduringfreedom.com/
meanwhileacrosstown.com
https://distant-photons.org/
homenet-trust.com
https://columbia-readymade.com/
eduplus4u.com
https://tiendaderopademujer.net/
ftlmba.org
https://tsvo-fussball-aktiv.de/
bodyinspirationsaz.com
https://neoneoneo.net/
forsanesnickeri.se
https://ftlmba.org/
bd-c.net
https://bd-c.net/
casakenia.com
https://pf-bluelagoon.com/
hotels-britishcolumbia.com
https://elysannetremblay.com/
tnt-motorsports.org
https://totallynaturalskin.com/
vidanatural.com.es
https://asessippiparkland.com/
flipthefearofpublicspeaking.com
https://ftlmba.org/
nur-al-huda.org
https://tuincentrum-gids.com/
rts-austria.com
https://deliciousmostnutritious.co.uk/
bestdealapparel.com
https://webnit.de/
vgmbc.org
https://totallynaturalskin.com/
elysannetremblay.com
https://casakenia.com/
ikenohiromi.com
https://motokyokuana.net/
yoneyama-garden.com
https://panneau-solaires.net/
michelbordage.com
https://lanimal-voyant.com/
cleverowl.uk
https://noah-garden.com/
premierrealestateaz.com
https://phuket-flug.de/
demisflowers.co.uk
https://maineneedlepoint.com/
mideastcalm.org
https://ferias-de-sonho.com/
soko-fuji.com
https://pf-bluelagoon.com/
neoneoneo.net
https://nankyokusei.com/
gamingarea.org
https://tnt-motorsports.org/
burkhart-buchservice.de
https://gamingarea.org/
acyclovir dosage suppression herpes
503 Service Unavailable