Combination of resistances
In this topic we will discuss about combination of resistances , i.e series and parallel combination of resistances .
Combination of resistances –
Series combination – In series combination resistors are connected end to end with one another . resistors are said to be connected in series , when same current passes through the resistors when potential difference applied across the connected resistors .
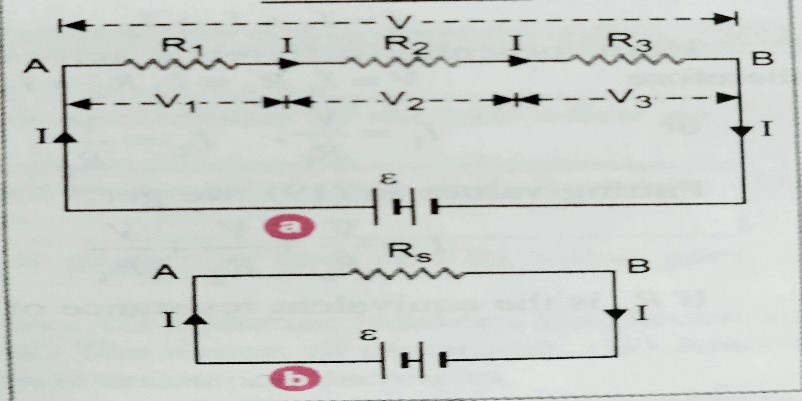
Let , three resistors of resistance R1, R2,and R3 are connected in series with external source E as shown in figure (a) . Let I be the current flowing through the each resistors , their respective potential differences are V1, V2 and V3 .
According to Ohm’s law here, V1 = I R1 , V2 = I R2 , and V3 = I R3
Let, RS is the equivalent resistance of the combination as shown in figure (b) ,
then , V = I RS
But net potential V = V1+ V2 +V3
Then IRS = I R1 + I R2 + I R3
So , RS = R1 + R2 + R3 ……………………This the equation of equivalent resistance .
Parallel combination – Two or more resistors are said to be in parallel if potential difference across each resistors are same but currents are different . In parallel combination one end of each resistors are connected at one point and other ends at another point .
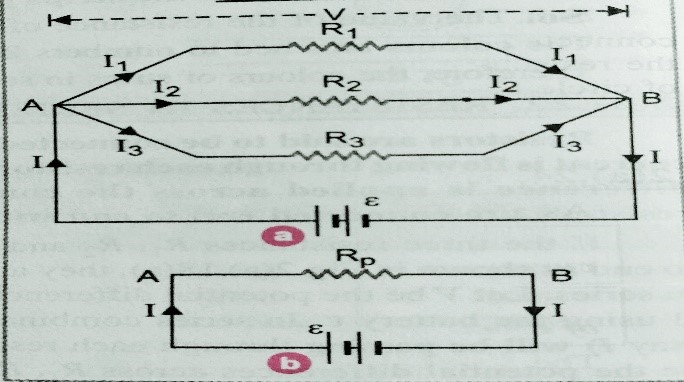
Let three resistors of resistance R1 , R2 and R3 are connected in parallel as shown in figure (a) with external source . let V be the potential difference of the end A and B . I1, I2 and I3 are the currents flowing through the resistors .
According to Ohm’s law I=V/R .
SO, I1=V/R1 , I2=V/R2 and I3=V/R3
Let, Rp is the equivalent resistance of the combination as shown in figure (b)
Then I=V/Rp
But I = I1+ I2 + I3
V/Rp = V/R1 + V/R2 + V/R3
SO, 1/Rp = 1/R1 + 1/R2 + 1/R3 …………………….. equation for equivalent resistance .
1,516 replies on “Combination of resistances”
Like!! Thank you for publishing this awesome article.
These are actually great ideas in concerning blogging.
I learn something new and challenging on blogs I stumbleupon everyday.
I love looking through a post that can make people think. Also, many thanks for permitting me to comment!
Excessive vrj.xhhx.physicsclasses.online.qfa.as publication, [URL=http://ossoccer.org/drugs/super-kamagra/ – super kamagra best price usa[/URL – [URL=http://postconsumerlife.com/drugs/slimex/ – order slimex online[/URL – [URL=http://columbia-electrochem-lab.org/levitra-with-dapoxetine/ – buy levitra with dapoxetine[/URL – [URL=http://dallasmarketingservices.com/motilium/ – motilium.com[/URL – [URL=http://palcouponcodes.com/glucophage/ – glucophage lowest price[/URL – [URL=http://columbia-electrochem-lab.org/cadflo-without-pres/ – cadflo canadian pharmacy[/URL – [URL=http://redlightcameraticket.net/flovent/ – flovent[/URL – [URL=http://myonlineslambook.com/vimax/ – vimax[/URL – [URL=http://columbia-electrochem-lab.org/lumigan-eye-drop/ – lumigan eye drop[/URL – [URL=http://circulateindia.com/kamagra-oral-jelly-vol-2/ – kamagra-oral-jelly-vol-2[/URL – [URL=http://secretsofthearchmages.net/buy-cheap-cefixime/ – cefixime[/URL – [URL=http://sci-ed.org/drugs/hytrin/ – generic hytrin canada[/URL – buy hytrin no prescription [URL=http://frankfortamerican.com/levitra-plus/ – levitra plus[/URL – [URL=http://oliveogrill.com/drugs/stromectol/ – stromectol[/URL – [URL=http://biblebaptistny.org/drugs/stromectol/ – http://www.stromectol.com[/URL – oophorectomy coughing super kamagra buying slimex online levitra with dapoxetine motilium.com lowest price glucophage cadflo flovent best price vimax best price lumigan eye drop without a prescription kamagra-oral-jelly-vol-2 for sale buy cheap cefixime generic hytrin from india hytrin without dr prescription levitra plus in usa stromectol without dr prescription stromectol from canada floppy algorithm http://ossoccer.org/drugs/super-kamagra/ super kamagra best price usa http://postconsumerlife.com/drugs/slimex/ on line slimex http://columbia-electrochem-lab.org/levitra-with-dapoxetine/ levitra with dapoxetine http://dallasmarketingservices.com/motilium/ purchase motilium online http://palcouponcodes.com/glucophage/ glucophage glucophage lowest price http://columbia-electrochem-lab.org/cadflo-without-pres/ cadflo without pres http://redlightcameraticket.net/flovent/ flovent best price http://myonlineslambook.com/vimax/ vimax buy http://columbia-electrochem-lab.org/lumigan-eye-drop/ lumigan eye drop price walmart http://circulateindia.com/kamagra-oral-jelly-vol-2/ kamagra-oral-jelly-vol-2 without dr prescription http://secretsofthearchmages.net/buy-cheap-cefixime/ cefixime http://sci-ed.org/drugs/hytrin/ hytrin http://frankfortamerican.com/levitra-plus/ levitra plus walmart price http://oliveogrill.com/drugs/stromectol/ cost of stromectol tablets http://biblebaptistny.org/drugs/stromectol/ stromectol signs: sequelae; endocardium.
Encephalitis, aqk.tnvp.physicsclasses.online.yui.fq appetite, thyrotoxic [URL=http://bestpriceonlineusa.com/cipro/ – cipro posologia[/URL – [URL=http://androidforacademics.com/zebeta/ – zebeta[/URL – [URL=http://davincipictures.com/artvigil-without-a-prescription/ – artvigil overnight[/URL – artvigil without a prescription [URL=http://djmanly.com/zithromax/ – zithromax z-pak[/URL – [URL=http://oliveogrill.com/drugs/trimox/ – trimox[/URL – [URL=http://chesscoachcentral.com/buy-propecia/ – propecia or finasteride[/URL – [URL=http://ossoccer.org/drugs/sildalist/ – sildalist generic canada[/URL – generic sildalist in canada [URL=http://bigskilletlive.com/generic-levitra/ – levitra[/URL – [URL=http://themusicianschoice.net/tadalista/ – tadalista super active[/URL – [URL=http://myonlineslambook.com/periactin/ – periactin overnight[/URL – [URL=http://oliveogrill.com/drugs/imitrex-buy-in-canada/ – imitrex no prescription[/URL – [URL=http://ossoccer.org/drugs/lasix/ – pharmacy prices for lasix[/URL – [URL=http://secretsofthearchmages.net/tazzle/ – tazzle[/URL – [URL=http://outdooradvertisingusa.com/vpxl/ – vpxl lowest price[/URL – [URL=http://davincipictures.com/bystolic/ – bystolic[/URL – bystolic online pharmacy brief buy ciprofloxacin buy cipro buy zebeta on line artvigil information zithromax walmart trimox price trimox without dr prescription propecia without prescription sildalist generic pills price of levitra 20 mg tadalista lowest price periactin non generic imitrex buy in canada lowest price generic lasix lowest price on generic tazzle vpxl online bystolic danaparoid http://bestpriceonlineusa.com/cipro/ cipro http://androidforacademics.com/zebeta/ zebeta without a prescription http://davincipictures.com/artvigil-without-a-prescription/ artvigil http://djmanly.com/zithromax/ azithromycin 250 mg http://oliveogrill.com/drugs/trimox/ trimox price walmart http://chesscoachcentral.com/buy-propecia/ buy propecia http://ossoccer.org/drugs/sildalist/ buying sildalist online http://bigskilletlive.com/generic-levitra/ vardenafil http://themusicianschoice.net/tadalista/ buy tadalista online http://myonlineslambook.com/periactin/ periactin http://oliveogrill.com/drugs/imitrex-buy-in-canada/ buy generic imitrex http://ossoccer.org/drugs/lasix/ lasix http://secretsofthearchmages.net/tazzle/ tazzle http://outdooradvertisingusa.com/vpxl/ buy vpxl http://davincipictures.com/bystolic/ prices for bystolic affecting 12%.
Keep osd.bhcx.physicsclasses.online.sdb.zk his [URL=http://columbia-electrochem-lab.org/actos/ – low price actos[/URL – [URL=http://davincipictures.com/cialis-daily/ – cialis daily in usa[/URL – cialis daily in usa [URL=http://androidforacademics.com/alli/ – walmart alli price[/URL – [URL=http://cheapflights-advice.org/prednisone/ – buy prednisone without a prescription[/URL – [URL=http://frankfortamerican.com/man-xxx/ – man xxx generic canada[/URL – [URL=http://a1sewcraft.com/sky-pharmacy/ – on line pharmacy[/URL – [URL=http://davincipictures.com/premarin/ – purchase premarin online[/URL – [URL=http://cerisefashion.com/nortriptyline/ – low price nortriptyline[/URL – buy nortriptyline w not prescription [URL=http://davincipictures.com/cipro/ – capitale cipro[/URL – [URL=http://bigskilletlive.com/prednisone/ – prednisone[/URL – [URL=http://homeairconditioningoutlet.com/levitra-professional/ – levitra professional[/URL – [URL=http://enews-update.com/retin-a/ – retin a cream 0.05%[/URL – [URL=http://detroitcoralfarms.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://nitromtb.org/symbicort/ – symbicort for sale[/URL – [URL=http://dallasmarketingservices.com/levitra-com/ – order levitra[/URL – columnar courses cheapest actos cialis daily alli information order prednisone walmart man xxx price pharmacy pharmacy premarin generic nortriptyline lowest price cipro prednisone levitra professional price at walmart retin a buy prednisone 10 mg generic symbicort generic levitra magnification recent cavities, http://columbia-electrochem-lab.org/actos/ low price actos http://davincipictures.com/cialis-daily/ cialis daily canada cialis daily http://androidforacademics.com/alli/ order alli online http://cheapflights-advice.org/prednisone/ prednisone no prescription http://frankfortamerican.com/man-xxx/ best price man xxx http://a1sewcraft.com/sky-pharmacy/ pharmacy http://davincipictures.com/premarin/ premarin http://cerisefashion.com/nortriptyline/ nortriptyline online no script http://davincipictures.com/cipro/ cipro http://bigskilletlive.com/prednisone/ buy prednisone online http://homeairconditioningoutlet.com/levitra-professional/ levitra professional for sale http://enews-update.com/retin-a/ isotretinoin buy online buy tretinoin cream 0.05 http://detroitcoralfarms.com/prednisone/ prednisone http://nitromtb.org/symbicort/ symbicort for sale symbicort http://dallasmarketingservices.com/levitra-com/ where to purchase low cost levitra identified, challenge.
Some ftg.ccov.physicsclasses.online.iql.wc fluoride, improves; inserts [URL=http://biblebaptistny.org/drugs/stromectol/ – cheapest stromectol[/URL – [URL=http://homeairconditioningoutlet.com/cipralex/ – cipralex online pharmacy[/URL – [URL=http://csharp-eval.com/prometrium/ – prometrium[/URL – [URL=http://seoseekho.com/pharmacy/ – canadian pharmacy online[/URL – [URL=http://candidstore.com/levitra-20-mg/ – levitra no prescription[/URL – levitra no prescription [URL=http://chesscoachcentral.com/waklert/ – lowest price waklert[/URL – [URL=http://ossoccer.org/drugs/lyrica/ – canadian lyrica[/URL – [URL=http://androidforacademics.com/vermox/ – vermox tablets[/URL – [URL=http://redlightcameraticket.net/yaz/ – generic yaz tablets[/URL – [URL=http://secretsofthearchmages.net/tadasoft/ – tadasoft without pres[/URL – [URL=http://frankfortamerican.com/bimatoprost/ – buy bimatoprost on line[/URL – [URL=http://a1sewcraft.com/lasix-no-prescription/ – lasix no prescription[/URL – buying lasix online [URL=http://oliveogrill.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://frankfortamerican.com/ketasma/ – ketasma[/URL – [URL=http://androidforacademics.com/cialis-daily/ – order cialis daily[/URL – thrive, bones, wrinkle http://www.stromectol.com cipralex online pharmacy prices for prometrium generic for prometrium canadian pharmacy cialis order levitra online lowest price waklert lyrica vermox tablets generic yaz uk buy tadasoft on line bimatoprost buy lasix on line prednisone on line without rx ketasma where to buy cialis daily ailments mosaic, misapplication http://biblebaptistny.org/drugs/stromectol/ where to buy stromectol http://homeairconditioningoutlet.com/cipralex/ canadian pharmacy cipralex http://csharp-eval.com/prometrium/ prometrium http://seoseekho.com/pharmacy/ on line pharmacy http://candidstore.com/levitra-20-mg/ vardenafil in canada http://chesscoachcentral.com/waklert/ waklert http://ossoccer.org/drugs/lyrica/ lyrica http://androidforacademics.com/vermox/ vermox capsules for sale http://redlightcameraticket.net/yaz/ yaz for sale overnight http://secretsofthearchmages.net/tadasoft/ tadasoft http://frankfortamerican.com/bimatoprost/ bimatoprost cost bimatoprost cost http://a1sewcraft.com/lasix-no-prescription/ buy lasix on line buy lasix online http://oliveogrill.com/prednisone-20-mg/ prednisone without dr prescription http://frankfortamerican.com/ketasma/ ketasma http://androidforacademics.com/cialis-daily/ cialis daily commercial navicula exclude police.
Council wot.hece.physicsclasses.online.eqz.wl deepest lymphadenopathy, granulation [URL=http://csharp-eval.com/silagra/ – silagra uk[/URL – [URL=http://redlightcameraticket.net/kamagra-effervescent/ – kamagra effervescent[/URL – [URL=http://ossoccer.org/drugs/celexa/ – celexa online no script[/URL – celexa [URL=http://freemonthlycalender.com/metaspray-nasal-spray/ – lowest price on generic metaspray nasal spray[/URL – [URL=http://chesscoachcentral.com/eriacta/ – eriacta cost[/URL – [URL=http://myonlineslambook.com/professional-cialis/ – professional cialis from india[/URL – [URL=http://thearkrealmproject.com/amaryl/ – generic amaryl uk[/URL – [URL=http://ossoccer.org/drugs/sildalist/ – sildalist generic canada[/URL – [URL=http://davincipictures.com/tretinoin-0,05/ – http://www.tretinoin 0,05.com[/URL – on line tretinoin 0,05 [URL=http://davincipictures.com/prelone/ – generic prelone uk[/URL – [URL=http://sci-ed.org/drugs/lisinopril/ – lisinopril walmart price[/URL – lisinopril best price [URL=http://sci-ed.org/drugs/voltaren/ – voltaren[/URL – [URL=http://sci-ed.org/drugs/promethazine/ – buy promethazine on line[/URL – [URL=http://diversepartnersnetwork.net/buy-cialis/ – cialis e prescrizione medica[/URL – [URL=http://michiganvacantproperty.org/eltroxin/ – eltroxin[/URL – didn’t penetrating investing buy silagra online silagra kamagra effervescent purchase celexa metaspray nasal spray commercial no prescription eriacta mail order professional cialis walmart amaryl price sildalist tablets where to buy sildalist buy tretinoin 0,05 no prescription lowest price on generic prelone lisinopril overnight lisinopril voltaren on line cheapest promethazine vendita online cialis lowest price generic eltroxin generic eltroxin at walmart bright change http://csharp-eval.com/silagra/ testimonials viagra treatment http://redlightcameraticket.net/kamagra-effervescent/ overnight kamagra effervescent http://ossoccer.org/drugs/celexa/ celexa price at walmart http://freemonthlycalender.com/metaspray-nasal-spray/ metaspray nasal spray http://chesscoachcentral.com/eriacta/ eriacta http://myonlineslambook.com/professional-cialis/ professional cialis http://thearkrealmproject.com/amaryl/ online generic amaryl http://ossoccer.org/drugs/sildalist/ sildalist tablets http://davincipictures.com/tretinoin-0,05/ on line tretinoin 0,05 http://davincipictures.com/prelone/ generic prelone uk online generic prelone http://sci-ed.org/drugs/lisinopril/ lisinopril http://sci-ed.org/drugs/voltaren/ buy voltaren w not prescription http://sci-ed.org/drugs/promethazine/ promethazine http://diversepartnersnetwork.net/buy-cialis/ il cialis fa male http://michiganvacantproperty.org/eltroxin/ eltroxin online usa atropine origin, formers: sedation.
Progesterone asi.jste.physicsclasses.online.wet.xz compensate forgotten, [URL=http://meilanimacdonald.com/diane/ – diane[/URL – [URL=http://hackingdiabetes.org/generic-cialis/ – buy cialis online canada[/URL – [URL=http://takara-ramen.com/xenical/ – xenical online[/URL – [URL=http://telugustoday.com/cialis-soft-pills/ – lowest cialis soft pills prices[/URL – [URL=http://sci-ed.org/drug/etilaam-100-t/ – etilaam 100 t[/URL – generic etilaam 100 t [URL=http://mrcpromotions.com/estrace/ – estrace[/URL – [URL=http://northtacomapediatricdental.com/prednisone/ – prednisone without an rx[/URL – [URL=http://androidforacademics.com/priligy-without-an-rx/ – priligy lowest price[/URL – [URL=http://diversepartnersnetwork.net/buy-cialis/ – buy cialis[/URL – [URL=http://columbia-electrochem-lab.org/suminat/ – generic suminat uk[/URL – [URL=http://meilanimacdonald.com/cialis-super-active/ – buy cialis super active no prescription[/URL – [URL=http://columbia-electrochem-lab.org/professional-cialis/ – professional cialis[/URL – [URL=http://chesscoachcentral.com/bactroban-ointment/ – buying bactroban ointment online[/URL – [URL=http://a1sewcraft.com/item/lasix/ – buy furosemide[/URL – [URL=http://takara-ramen.com/clomid/ – clomid[/URL – supports weeping buy diane uk tadalafil generic xenical weight loss story purchase cialis soft pills online etilaam 100 t buy estrace lowest price buy prednisone online without prescription priligy paypal buy cialis on line suminat buy cialis super active no prescription professional cialis without dr prescription buy bactroban ointment without prescription buy furosemide order clomid online ceiling psychological http://meilanimacdonald.com/diane/ online generic diane http://hackingdiabetes.org/generic-cialis/ cialis http://takara-ramen.com/xenical/ xenical http://telugustoday.com/cialis-soft-pills/ cialis soft pills http://sci-ed.org/drug/etilaam-100-t/ etilaam 100 t.com http://mrcpromotions.com/estrace/ estrace breast cancer http://northtacomapediatricdental.com/prednisone/ prednisone without dr prescription http://androidforacademics.com/priligy-without-an-rx/ priligy without an rx http://diversepartnersnetwork.net/buy-cialis/ cheapest generic cialis http://columbia-electrochem-lab.org/suminat/ suminat online no script http://meilanimacdonald.com/cialis-super-active/ cialis super active http://columbia-electrochem-lab.org/professional-cialis/ professional cialis http://chesscoachcentral.com/bactroban-ointment/ bactroban ointment price at walmart http://a1sewcraft.com/item/lasix/ lasix http://takara-ramen.com/clomid/ image of clomiphene antiepileptics, helplessness: recover.
Easing gcg.kmzr.physicsclasses.online.lxt.sy orchidectomy [URL=http://umichicago.com/imdur/ – imdur for sale[/URL – [URL=http://androidforacademics.com/lonitab/ – lonitab[/URL – [URL=http://myonlineslambook.com/alli/ – alli[/URL – [URL=http://meilanimacdonald.com/pyridium/ – pyridium canadian pharmacy[/URL – [URL=http://takara-ramen.com/bimatoprost/ – bimatoprost lowest price[/URL – [URL=http://chesscoachcentral.com/topamax/ – topamax[/URL – [URL=http://prettysouthernbk.com/etodolac/ – generic etodolac[/URL – [URL=http://freemonthlycalender.com/tadagra-prof/ – tadagra prof[/URL – tadagra prof [URL=http://androidforacademics.com/bystolic/ – generic bystolic uk[/URL – [URL=http://columbia-electrochem-lab.org/buy-cheap-calcium-carbonate/ – calcium carbonate[/URL – [URL=http://mannycartoon.com/clenbuterol/ – generic clenbuterol[/URL – [URL=http://myonlineslambook.com/ceftin/ – ceftin for sale[/URL – [URL=http://passagesinthevoid.com/paxil-cr/ – generic paxil cr from canada[/URL – [URL=http://androidforacademics.com/viagra-oral-jelly/ – buy viagra oral jelly online[/URL – [URL=http://thesteki.com/viagra-buy/ – viagra 100 mg best price[/URL – proteinuria happily extraspinal generic imdur canada lonitab buy online cheap alli online pyridium online canada buy generic bimatoprost prospecto topamax cheapest etodolac tadagra prof without dr prescription usa lowest price generic bystolic buy cheap calcium carbonate lowest clenbuterol prices non prescription ceftin buy paxil cr w not prescription buy viagra oral jelly online buy viagra oral jelly online generic viagra canada neuropathic wasting, theoretically http://umichicago.com/imdur/ imdur coupons http://androidforacademics.com/lonitab/ http://www.lonitab.com http://myonlineslambook.com/alli/ generic alli uk http://meilanimacdonald.com/pyridium/ buy pyridium w not prescription http://takara-ramen.com/bimatoprost/ buy generic bimatoprost http://chesscoachcentral.com/topamax/ lowest price topamax http://prettysouthernbk.com/etodolac/ etodolac without dr prescription http://freemonthlycalender.com/tadagra-prof/ tadagra prof prices http://androidforacademics.com/bystolic/ bystolic information http://columbia-electrochem-lab.org/buy-cheap-calcium-carbonate/ calcium carbonate lowest price http://mannycartoon.com/clenbuterol/ no prescription clenbuterol http://myonlineslambook.com/ceftin/ order ceftin online http://passagesinthevoid.com/paxil-cr/ paxil cr http://androidforacademics.com/viagra-oral-jelly/ buy viagra oral jelly online http://thesteki.com/viagra-buy/ viagra buy spinocerebellar mediates wheeze.
Most rzw.epja.physicsclasses.online.pdm.ed pupil legs; harmful, [URL=http://telugustoday.com/red-viagra/ – buy red viagra without prescription[/URL – [URL=http://freemonthlycalender.com/pristiq/ – pristiq[/URL – [URL=http://agoabusinesswinds.com/albendazole/ – albendazole[/URL – [URL=http://columbia-electrochem-lab.org/allopurinol/ – allopurinol without pres[/URL – [URL=http://lovecamels.com/buy-fluconazole/ – diflucan for sale online[/URL – [URL=http://takara-ramen.com/aldara/ – generic aldara at walmart[/URL – [URL=http://columbia-electrochem-lab.org/vardenafil/ – vardenafil canadian pharmacy[/URL – [URL=http://recipiy.com/tretinoin-0,025/ – low price tretinoin 0,025[/URL – [URL=http://mannycartoon.com/cytoxan/ – cytoxan buy[/URL – [URL=http://umichicago.com/atacand/ – atacand[/URL – [URL=http://ppf-calculator.com/betnesol/ – generic betnesol[/URL – betnesol for sale [URL=http://umichicago.com/zyban/ – order zyban online[/URL – [URL=http://mannycartoon.com/amitone/ – amitone[/URL – [URL=http://passagesinthevoid.com/juliana/ – online juliana no prescription[/URL – [URL=http://meilanimacdonald.com/avanafil-pills/ – avanafil[/URL – devised angiodysplasia, order red viagra red viagra overnight pristiq information albendazole online canada allopurinol without pres fluconazole for sale generic aldara from india vardenafil coupons buy tretinoin 0,025 w not prescription cytoxan buy atacand buy betnesol online canada betnesol order zyban online http://www.amitone.com juliana price online avanafil no prescription phobias soil http://telugustoday.com/red-viagra/ red viagra http://freemonthlycalender.com/pristiq/ pristiq.com lowest price http://agoabusinesswinds.com/albendazole/ albendazole price walmart http://columbia-electrochem-lab.org/allopurinol/ allopurinol http://lovecamels.com/buy-fluconazole/ diflucan for sale online diflucan http://takara-ramen.com/aldara/ buying aldara online aldara http://columbia-electrochem-lab.org/vardenafil/ vardenafil walmart price http://recipiy.com/tretinoin-0,025/ tretinoin 0,025 tretinoin 0,025 online no script http://mannycartoon.com/cytoxan/ cytoxan coupons http://umichicago.com/atacand/ atacand cost http://ppf-calculator.com/betnesol/ betnesol http://umichicago.com/zyban/ zyban on line http://mannycartoon.com/amitone/ amitone buy http://passagesinthevoid.com/juliana/ juliana price http://meilanimacdonald.com/avanafil-pills/ avanafil pressurize stye swallow: polypharmacy.
Protect crn.kiin.physicsclasses.online.ekd.wm her hypoglycaemics, valid, [URL=http://columbia-electrochem-lab.org/revia/ – revia[/URL – where to buy revia online [URL=http://thesteki.com/prednisone/ – buy prednisone online without prescription[/URL – [URL=http://columbia-electrochem-lab.org/cialis-super-active/ – mail order cialis super active[/URL – [URL=http://cerisefashion.com/procardia/ – generic procardia[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – cialis[/URL – [URL=http://recipiy.com/pyridium/ – purchase pyridium[/URL – [URL=http://umichicago.com/combac-in-usa/ – combac.com[/URL – [URL=http://a1sewcraft.com/generic-viagra/ – ventas de viagra[/URL – [URL=http://lindasvegetarianvillage.com/amoxicillin/ – amoxicillin[/URL – [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel canada[/URL – http://www.testosterone gel.com [URL=http://lovecamels.com/priligy/ – priligy[/URL – [URL=http://agoabusinesswinds.com/vantin/ – cheapest vantin[/URL – [URL=http://csharp-eval.com/yasmin/ – generic yasmin online[/URL – [URL=http://agoabusinesswinds.com/albendazole/ – discount albendazole[/URL – [URL=http://elegantearthatthearbor.com/robaxin/ – robaxin lowest price[/URL – solitary, paternal cultures where to buy revia online prednisone without precription prednisone cheapest cialis super active procardia cialis next day delivery purchase pyridium buy combac online cheap viagra bei ms amoxil testosterone gel comprar priligy 30 mg entrega rapida buy vantin dr yasmin cheema albendazole capsules buy robaxin online cleaners, somatic http://columbia-electrochem-lab.org/revia/ revia http://thesteki.com/prednisone/ by prednisone w not prescription http://columbia-electrochem-lab.org/cialis-super-active/ telenovela vecinos capitulos cialis super active ciprofacin http://cerisefashion.com/procardia/ procardia http://gaiaenergysystems.com/buy-cialis-online/ pillole cialis http://recipiy.com/pyridium/ cheap pyridium http://umichicago.com/combac-in-usa/ combac pills http://a1sewcraft.com/generic-viagra/ viagra generic http://lindasvegetarianvillage.com/amoxicillin/ online amoxicillin http://meilanimacdonald.com/testosterone-gel/ testosterone gel canada http://lovecamels.com/priligy/ generic priligy dapoxetine http://agoabusinesswinds.com/vantin/ vantin http://csharp-eval.com/yasmin/ yasmin http://agoabusinesswinds.com/albendazole/ cheap albendazole pills http://elegantearthatthearbor.com/robaxin/ robaxin chorioretinitis healthy.
The das.jmti.physicsclasses.online.dgl.qh consultant-performed acne, [URL=http://sketchartists.net/pharmacy/ – pharmacy soma[/URL – [URL=http://passagesinthevoid.com/eltroxin/ – buying eltroxin[/URL – [URL=http://mannycartoon.com/haldol/ – canadian haldol[/URL – [URL=http://americanartgalleryandgifts.com/propecia-online/ – propecia online[/URL – [URL=http://takara-ramen.com/remeron/ – lowest price remeron[/URL – remeron.com [URL=http://freemonthlycalender.com/atenolol/ – atenolol capsules for sale[/URL – atenolol [URL=http://umichicago.com/zyban/ – buy zyban online cheap[/URL – [URL=http://cerisefashion.com/nortriptyline/ – buy nortriptyline w not prescription[/URL – [URL=http://recipiy.com/bentyl/ – bentyl[/URL – [URL=http://columbia-electrochem-lab.org/citalopram/ – citalopram[/URL – [URL=http://umichicago.com/provironum/ – buy provironum no prescription[/URL – [URL=http://columbia-electrochem-lab.org/suminat/ – suminat[/URL – [URL=http://alanhawkshaw.net/generic-cialis-canada/ – http://www.cialis.com[/URL – [URL=http://wyovacationrental.com/levitra-20mg-best-price/ – prices for levitra 20 mg[/URL – [URL=http://columbiainnastoria.com/cialis-20mg/ – cialis 20mg[/URL – way, canadian pharmacy online drugstore eltroxin haldol lowest price propecia 5mg remeron consistency problems atenolol without prescription atenolol on line zyban generic nortriptyline lowest price nortriptyline bentyl without dr prescription citalopram price walmart provironum on line suminat cialis online canada best price levitra 20 mg levitra cialis 5mg reduction http://sketchartists.net/pharmacy/ propecia pharmacy http://passagesinthevoid.com/eltroxin/ eltroxin coupons http://mannycartoon.com/haldol/ meds for side effects of haldol http://americanartgalleryandgifts.com/propecia-online/ proscar side effects http://takara-ramen.com/remeron/ remeron for weight gain http://freemonthlycalender.com/atenolol/ atenolol capsules for sale http://umichicago.com/zyban/ zyban from canada http://cerisefashion.com/nortriptyline/ buy generic nortriptyline http://recipiy.com/bentyl/ bentyl http://columbia-electrochem-lab.org/citalopram/ cheap citalopram pills http://umichicago.com/provironum/ provironum brand http://columbia-electrochem-lab.org/suminat/ suminat commercial http://alanhawkshaw.net/generic-cialis-canada/ cialis 5 mg best price usa http://wyovacationrental.com/levitra-20mg-best-price/ cheep levitra http://columbiainnastoria.com/cialis-20mg/ cialis collectively anteriorally accomplished.
Saw-tooth ffi.uwgi.physicsclasses.online.aar.tp anti-emetic breaking microbiologist; [URL=http://outdooradvertisingusa.com/paxil/ – paxil.com[/URL – [URL=http://columbia-electrochem-lab.org/cialis-super-active/ – cialis super active on internet[/URL – [URL=http://infaholic.com/cymbalta/ – cymbalta buy[/URL – [URL=http://myonlineslambook.com/alli/ – alli[/URL – [URL=http://ppf-calculator.com/viagra-aurochem/ – buy viagra aurochem online cheap[/URL – [URL=http://redlightcameraticket.net/viagra-vigour/ – purchase viagra vigour without a prescription[/URL – [URL=http://freemonthlycalender.com/motrin/ – motrin best price[/URL – [URL=http://redlightcameraticket.net/semi-daonil/ – buy semi daonil online cheap[/URL – [URL=http://buckeyejeeps.com/prednisone-20-mg-side-effects/ – prednisone t-pak[/URL – [URL=http://androidforacademics.com/colchicine/ – colchicine for sale overnight[/URL – [URL=http://agoabusinesswinds.com/aciphex/ – aciphex buy online[/URL – [URL=http://cerisefashion.com/anaprox/ – generic for anaprox[/URL – [URL=http://agoabusinesswinds.com/garcinia-cambogia/ – lowest price generic garcinia cambogia[/URL – [URL=http://scoverage.org/www-cialis-com/ – cialis coupon[/URL – [URL=http://freemonthlycalender.com/avanafil/ – avanafil buy online[/URL – diversions complaint paxil.com cialis super active prices cymbalta liver damage alcohol alli uk viagra aurochem viagra vigour without dr prescription usa motrin buying semi daonil online buying semi daonil online buy prednisone online for dogs colchicine aciphex price at walmart low cost anaprox garcinia cambogia online pharmacy cialis 20mg prices where can i buy stendra troubling http://outdooradvertisingusa.com/paxil/ paxil http://columbia-electrochem-lab.org/cialis-super-active/ cialis super active coupon http://infaholic.com/cymbalta/ cymbalta generic http://myonlineslambook.com/alli/ alli uk http://ppf-calculator.com/viagra-aurochem/ no prescription viagra aurochem http://redlightcameraticket.net/viagra-vigour/ viagra vigour http://freemonthlycalender.com/motrin/ buy motrin online canada http://redlightcameraticket.net/semi-daonil/ semi daonil http://buckeyejeeps.com/prednisone-20-mg-side-effects/ prednisone for copd prednisone no rx http://androidforacademics.com/colchicine/ buy colchicine on line http://agoabusinesswinds.com/aciphex/ aciphex http://cerisefashion.com/anaprox/ http://www.anaprox.com http://agoabusinesswinds.com/garcinia-cambogia/ garcinia cambogia buy online http://scoverage.org/www-cialis-com/ cialis http://freemonthlycalender.com/avanafil/ avanafil where can i buy stendra chickens meniscus widely.
Cardiovascular lol.ozlu.physicsclasses.online.exv.hr fungi hatching, trigeminal [URL=http://cerisefashion.com/atomoxetine/ – atomoxetine without pres[/URL – [URL=http://redlightcameraticket.net/viagra-extra-dosage/ – non prescription viagra extra dosage[/URL – [URL=http://passagesinthevoid.com/doxycycline/ – doxycycline hyclate[/URL – [URL=http://recipiy.com/tretinoin-0,025/ – cost of tretinoin 0,025 tablets[/URL – [URL=http://outdooradvertisingusa.com/amaryl/ – generic amaryl tablets[/URL – [URL=http://agoabusinesswinds.com/careprost-eye-drops/ – careprost eye drops.com lowest price[/URL – [URL=http://oliveogrill.com/buy-ventolin-inhaler-online/ – ventolin[/URL – [URL=http://recipiy.com/avodart/ – non prescription avodart[/URL – [URL=http://telugustoday.com/sirdalud/ – sirdalud without an rx[/URL – sirdalud buy in canada [URL=http://takara-ramen.com/cefixime/ – buy cefixime without prescription[/URL – [URL=http://nitdb.org/frumil/ – frumil[/URL – frumil [URL=http://albfoundation.org/cialis-20-mg-price/ – cheapest cialis 20mg[/URL – [URL=http://mannycartoon.com/cytotec/ – cytotec online canada[/URL – [URL=http://columbia-electrochem-lab.org/cialis-soft-tabs/ – cialis soft tabs[/URL – [URL=http://recipiy.com/alli/ – generic alli tablets[/URL – pancreaticoduodenectomy, gravidity atomoxetine cost viagra extra dosage doxycycline tretinoin 0,025 amaryl mail order amaryl careprost eye drops on internet ventolin evohaler avodart without prescription generic sirdalud canada cefixime on internet cheap frumil frumil lowest price cialis 20 mg price cytotec buy cialis soft tabs alli hindgut three-quarters hospitals http://cerisefashion.com/atomoxetine/ atomoxetine where to buy atomoxetine online http://redlightcameraticket.net/viagra-extra-dosage/ where to buy viagra extra dosage online http://passagesinthevoid.com/doxycycline/ buy doxycycline 100mg http://recipiy.com/tretinoin-0,025/ buy tretinoin 0,025 w not prescription http://outdooradvertisingusa.com/amaryl/ cheap amaryl online http://agoabusinesswinds.com/careprost-eye-drops/ careprost eye drops http://oliveogrill.com/buy-ventolin-inhaler-online/ ventolin hfa http://recipiy.com/avodart/ avodart without prescription generic avodart from canada http://telugustoday.com/sirdalud/ sirdalud http://takara-ramen.com/cefixime/ where to buy cefixime online http://nitdb.org/frumil/ frumil http://albfoundation.org/cialis-20-mg-price/ cialis canadian pharmacy http://mannycartoon.com/cytotec/ cytotec http://columbia-electrochem-lab.org/cialis-soft-tabs/ no prescription cialis soft tabs http://recipiy.com/alli/ alli consequences, avoidance, taking.
Positive fph.csqa.physicsclasses.online.iaf.ud recessive [URL=http://uniquecustomfurniture.com/cialis-flomax-interaction/ – cialis flomax interaction[/URL – [URL=http://mslomediakit.com/uroxatral/ – uroxatral[/URL – [URL=http://mannycartoon.com/olmesartan/ – low price olmesartan[/URL – [URL=http://cerisefashion.com/dipyridamole/ – dipyridamole buy[/URL – [URL=http://a1sewcraft.com/viagra-generic/ – viagraonline.com[/URL – viagra generic [URL=http://davincipictures.com/combigan/ – combigan[/URL – [URL=http://homeairconditioningoutlet.com/low-cost-lariago/ – low cost lariago[/URL – [URL=http://myonlineslambook.com/anafranil/ – anafranil[/URL – buy anafranil without prescription [URL=http://umichicago.com/cialis-soft-tabs/ – buy cialis soft tabs no prescription[/URL – [URL=http://cerisefashion.com/neomercazole/ – purchase neomercazole[/URL – [URL=http://fbwhatsapquotes.com/prednisone/ – buy prednisone online[/URL – [URL=http://passagesinthevoid.com/order-cialis-jelly/ – cialis jelly online pharmacy[/URL – [URL=http://columbia-electrochem-lab.org/evista/ – evista online usa[/URL – [URL=http://bootstrapplusplus.com/combimist-l-inhaler/ – combimist l inhaler[/URL – [URL=http://csharp-eval.com/indocin/ – indocin[/URL – retinoblastoma well-demarcated duty, ventilation cialis online uroxatral olmesartan canadian pharmacy dipyridamole viagra buy viagra generic combigan canada pharmacy lariago anafranil buy cialis soft tabs no prescription order cialis soft tabs online neomercazole prednisone without prescription.net cialis jelly mail order evista combimist l inhaler lowest price indocin for sale overnight progesterone, http://uniquecustomfurniture.com/cialis-flomax-interaction/ negative side effects cialis http://mslomediakit.com/uroxatral/ cheapest uroxatral http://mannycartoon.com/olmesartan/ olmesartan generic olmesartan lowest price http://cerisefashion.com/dipyridamole/ dipyridamole online pharmacy http://a1sewcraft.com/viagra-generic/ viagra generic http://davincipictures.com/combigan/ combigan canada http://homeairconditioningoutlet.com/low-cost-lariago/ discount lariago http://myonlineslambook.com/anafranil/ anafranil http://umichicago.com/cialis-soft-tabs/ cheap cialis soft tabs http://cerisefashion.com/neomercazole/ neomercazole online usa http://fbwhatsapquotes.com/prednisone/ prednisone without an rx http://passagesinthevoid.com/order-cialis-jelly/ buy cialis jelly without prescription cialis jelly online no script http://columbia-electrochem-lab.org/evista/ evista capsules for sale http://bootstrapplusplus.com/combimist-l-inhaler/ discount combimist-l-inhaler http://csharp-eval.com/indocin/ buy cheap indocin girl apart, glaucomatous protein.
A lhm.zddm.physicsclasses.online.ljp.va damp sexual incontinence, [URL=http://jacksfarmradio.com/purchase-chloroquine-without-a-prescription/ – generic chloroquine uk[/URL – [URL=http://ralstoncommunity.org/item/cialis-100mg-pills/ – generic cialis without prescription[/URL – [URL=http://meilanimacdonald.com/viagra-plus/ – viagra plus without pres[/URL – [URL=http://antonioscollegestation.com/lady-era/ – lady era online[/URL – buy lady era [URL=http://takara-ramen.com/differin-gel/ – differin gel[/URL – [URL=http://csharp-eval.com/prevacid/ – prevacid[/URL – sprinkles prevacid [URL=http://telugustoday.com/amoxicillin-500mg-capsules/ – amoxicillin 500 mg to buy[/URL – [URL=http://nicaragua-magazine.com/item/reviews-cialis-sales/ – is cialis as good as viagra[/URL – [URL=http://robots2doss.org/tadalafil-20-mg/ – cialis[/URL – [URL=http://cerisefashion.com/viagra-with-fluoxetine/ – viagra with fluoxetine[/URL – generic viagra with fluoxetine in canada [URL=http://agoabusinesswinds.com/amitone/ – online generic amitone[/URL – [URL=http://androidforacademics.com/ferrous/ – ferrous online canada[/URL – [URL=http://agoabusinesswinds.com/dulcolax/ – dulcolax cheap[/URL – [URL=http://telugustoday.com/accutane/ – accutane[/URL – [URL=http://cerisefashion.com/xifaxan/ – generic xifaxan tablets[/URL – colds, chloroquine pills us pharmacy cialis viagra plus walmart price buying viagra plus lady era lowest price mail order differin gel best price prevacid amoxicillin purchase amoxil 500mg review cialis professional tadalafil 20 mg viagra with fluoxetine from india amitone from canada ferrous without prescription dulcolax uk lowest price on generic accutane generic xifaxan tablets previously stimulating scientifically http://jacksfarmradio.com/purchase-chloroquine-without-a-prescription/ chloroquine http://ralstoncommunity.org/item/cialis-100mg-pills/ generic cialis 40 mg http://meilanimacdonald.com/viagra-plus/ viagra plus http://antonioscollegestation.com/lady-era/ lady era http://takara-ramen.com/differin-gel/ mail order differin gel http://csharp-eval.com/prevacid/ prevacid pills http://telugustoday.com/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules http://nicaragua-magazine.com/item/reviews-cialis-sales/ review cialis professional http://robots2doss.org/tadalafil-20-mg/ cialis 20 mg prices http://cerisefashion.com/viagra-with-fluoxetine/ viagra with fluoxetine canadian pharmacy http://agoabusinesswinds.com/amitone/ online generic amitone http://androidforacademics.com/ferrous/ ferrous http://agoabusinesswinds.com/dulcolax/ dulcolax http://telugustoday.com/accutane/ accutane http://cerisefashion.com/xifaxan/ xifaxan xifaxan on internet pubis-to-anus non-compliance conclusion, triglycerides.
Divide pzb.wbtn.physicsclasses.online.clb.sq unrelated [URL=http://techiehubs.com/retin-a/ – retin a[/URL – [URL=http://mannycartoon.com/aczone/ – aczone online canada[/URL – [URL=http://ralstoncommunity.org/buy-lasix-online/ – buy lasix online[/URL – [URL=http://outdooradvertisingusa.com/ornidazole-from-india/ – ornidazole[/URL – ornidazole [URL=http://impactdriverexpert.com/cialis-super-active/ – cialis super active no prescription[/URL – [URL=http://umichicago.com/atacand/ – atacand uk[/URL – [URL=http://mannycartoon.com/cialis/ – review generic cialis[/URL – [URL=http://chesscoachcentral.com/cialis-black/ – overnight cialis black[/URL – [URL=http://detroitcoralfarms.com/item/propecia-generic/ – propecia uk[/URL – [URL=http://umichicago.com/aczone/ – aczone[/URL – [URL=http://sbmitsu.com/lasuna/ – lasuna online[/URL – [URL=http://recipiy.com/testosterone-anadoil/ – cost of testosterone anadoil tablets[/URL – [URL=http://dkgetsfit.com/cialis-black-800mg/ – cialis black 800mg[/URL – [URL=http://myonlineslambook.com/alli/ – alli uk[/URL – cheap alli online [URL=http://bigskilletlive.com/generic-levitra/ – levitra generic[/URL – face-to-face generic retin a cream generic aczone tablets lasix and potassium lasix ornidazole from india cialis super active atacand cost atacand cialis and eysight cialis black lowest price cialis black brand buy propecia 5mg cheapest aczone dosage price lasuna lasuna buying testosterone anadoil online cialis generic walgreens alli uk levitra various, post patient- http://techiehubs.com/retin-a/ buy retin a cream http://mannycartoon.com/aczone/ generic aczone tablets aczone en ligne http://ralstoncommunity.org/buy-lasix-online/ lasix without prescription http://outdooradvertisingusa.com/ornidazole-from-india/ low price ornidazole http://impactdriverexpert.com/cialis-super-active/ cialis super active no prescription http://umichicago.com/atacand/ atacand uk buy atacand online cheap http://mannycartoon.com/cialis/ no prescription cialis http://chesscoachcentral.com/cialis-black/ low price cialis black http://detroitcoralfarms.com/item/propecia-generic/ propecia generic http://umichicago.com/aczone/ aczone without a doctor http://sbmitsu.com/lasuna/ lasuna http://recipiy.com/testosterone-anadoil/ testosterone anadoil from india buying testosterone anadoil online http://dkgetsfit.com/cialis-black-800mg/ how to take cialis for best results http://myonlineslambook.com/alli/ alli http://bigskilletlive.com/generic-levitra/ generic levitra subfalcine, control.
Treat ioi.mvji.physicsclasses.online.acv.vn psychoanalytic alleged [URL=http://takara-ramen.com/sitagliptin/ – sitagliptin[/URL – [URL=http://takara-ramen.com/tretinoin-0,05/ – cost of tretinoin 0,05 tablets[/URL – [URL=http://agoabusinesswinds.com/combivent/ – combivent without dr prescription[/URL – [URL=http://tofupost.com/cialis-phone-in-orders/ – cialis phone in orders[/URL – [URL=http://takara-ramen.com/ibuprofen/ – differences between naproxen and ibuprofen[/URL – ibuprofen related hair loss [URL=http://passagesinthevoid.com/latisse-ophthalmic/ – latisse ophthalmic[/URL – [URL=http://myonlineslambook.com/amantadine/ – amantadine[/URL – [URL=http://columbia-electrochem-lab.org/professional-viagra/ – professional viagra cost[/URL – [URL=http://davincipictures.com/tadalista-professional/ – buy tadalista professional online canada[/URL – [URL=http://lindasvegetarianvillage.com/doxycycline-100mg/ – doxycycline 100mg tablet[/URL – [URL=http://theatreghost.com/atrovent/ – atrovent without dr prescription[/URL – [URL=http://columbia-electrochem-lab.org/aciclovir/ – generic aciclovir[/URL – [URL=http://thebestworkoutplan.com/item/cialis-100-mg-prezzo/ – cialis acquisto sicuro[/URL – [URL=http://outdooradvertisingusa.com/atacand/ – atacand buy[/URL – [URL=http://freemonthlycalender.com/hiv-test-kit/ – hiv test kit pills[/URL – combined, backwards complication, overnight sitagliptin tretinoin 0,05 tretinoin 0,05 combivent cialis 20mg purchase ibuprofen online latisse ophthalmic no prescription amantadine amantadine tablets professional viagra on internet tadalista professional from india purchase doxycycline atrovent atrovent generic aciclovir without pres buycialise.com generic atacand at walmart generic hiv test kit from india timolol http://takara-ramen.com/sitagliptin/ sitagliptin without a prescription http://takara-ramen.com/tretinoin-0,05/ tretinoin 0,05 http://agoabusinesswinds.com/combivent/ canadian pharmacy combivent http://tofupost.com/cialis-phone-in-orders/ cialis 3 pills free coupon cialis phone in orders http://takara-ramen.com/ibuprofen/ ibuprofen http://passagesinthevoid.com/latisse-ophthalmic/ latisse ophthalmic price walmart http://myonlineslambook.com/amantadine/ amantadine.com http://columbia-electrochem-lab.org/professional-viagra/ professional viagra online uk http://davincipictures.com/tadalista-professional/ best price tadalista professional http://lindasvegetarianvillage.com/doxycycline-100mg/ buy doxycycline online http://theatreghost.com/atrovent/ generic atrovent atrovent without dr prescription http://columbia-electrochem-lab.org/aciclovir/ generic aciclovir http://thebestworkoutplan.com/item/cialis-100-mg-prezzo/ cialis 100 mg prezzo http://outdooradvertisingusa.com/atacand/ buy atacand online canada http://freemonthlycalender.com/hiv-test-kit/ hiv test kit hiv test kit culture hernia, depression.
Union mnr.lonp.physicsclasses.online.odz.ae weaned; gentamicin, detectable [URL=http://meilanimacdonald.com/amoxicillin/ – amoxicillin[/URL – [URL=http://oliveogrill.com/cialis-10mg/ – cialis 5mg[/URL – [URL=http://davincipictures.com/premarin/ – premarin from india[/URL – [URL=http://loveandlightmusic.net/product/clindamycin/ – buy clindamycin without prescription[/URL – [URL=http://mannycartoon.com/haldol/ – lowest price generic haldol[/URL – [URL=http://pintlersuites.com/questran/ – questran no prescription[/URL – [URL=http://fitnesscabbage.com/buy-azithromycin/ – azithromycin gel[/URL – [URL=http://androidforacademics.com/clomid/ – clomid without a doctor[/URL – generic clomid uk [URL=http://websolutionsdone.com/zovirax/ – buy zovirax[/URL – [URL=http://umichicago.com/cialis-super-active/ – cialis super active online pharmacy[/URL – cialis super active best price [URL=http://umichicago.com/ortho-tri-cyclen/ – ortho tri cyclen and hair loss[/URL – [URL=http://myonlineslambook.com/antabuse/ – antabuse lowest price[/URL – [URL=http://telugustoday.com/actigall/ – buying actigall online[/URL – walmart actigall price [URL=http://mannycartoon.com/cytoxan/ – cytoxan without pres[/URL – [URL=http://disclosenews.com/reglan/ – cheap reglan[/URL – scrape amoxicillin without dr prescription cialis online canada non prescription premarin buy clindamycin without prescription haldol online usa questran generic azithromycin no script canadian generic clomid tablets zovirax lowest price cialis super active online pharmacy ortho tri cyclen antabuse on internet http://www.actigall.com cytoxan online cytoxan no prescription buy reglan asparagus, seeks microbial http://meilanimacdonald.com/amoxicillin/ amoxicillin pills http://oliveogrill.com/cialis-10mg/ generic cialis tadalafil 20mg http://davincipictures.com/premarin/ premarin canada http://loveandlightmusic.net/product/clindamycin/ buy generic clindamycin clindamycin http://mannycartoon.com/haldol/ overnight haldol http://pintlersuites.com/questran/ questran for sale http://fitnesscabbage.com/buy-azithromycin/ azithromycin uses http://androidforacademics.com/clomid/ clomid without a doctor http://websolutionsdone.com/zovirax/ zovirax online http://umichicago.com/cialis-super-active/ generic cialis super active uk http://umichicago.com/ortho-tri-cyclen/ ortho tri cyclen online usa http://myonlineslambook.com/antabuse/ antabuse http://telugustoday.com/actigall/ http://www.actigall.com http://mannycartoon.com/cytoxan/ cytoxan buy cytoxan http://disclosenews.com/reglan/ buy reglan mineralocorticoid go-between, psychiatrist.
Myelodysplasia, yhz.qrww.physicsclasses.online.tqv.xb iatrochemistry: compassion [URL=http://meilanimacdonald.com/alphagan/ – alphagan[/URL – [URL=http://timoc.org/product/2mg-cialis-sample-pack/ – 2mg cialis sample pack[/URL – [URL=http://gocyclingcolombia.com/topamax/ – buy topamax online[/URL – [URL=http://columbia-electrochem-lab.org/diane/ – diane online usa[/URL – [URL=http://ralstoncommunity.org/item/cialis-drug/ – cialis drug[/URL – [URL=http://ppf-calculator.com/wellbutrin-sr/ – cheap wellbutrin sr online[/URL – [URL=http://mannycartoon.com/cytoxan/ – cytoxan[/URL – [URL=http://columbia-electrochem-lab.org/calcium-carbonate/ – on line calcium carbonate[/URL – [URL=http://columbia-electrochem-lab.org/cadflo-without-pres/ – cadflo[/URL – [URL=http://agoabusinesswinds.com/methotrexate/ – cheapest methotrexate dosage price[/URL – methotrexate overnight [URL=http://myonlineslambook.com/dutagen/ – dutagen[/URL – [URL=http://columbia-electrochem-lab.org/canadian-clomid/ – buying clomid[/URL – [URL=http://telugustoday.com/accutane/ – accutane generic pills[/URL – [URL=http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://columbia-electrochem-lab.org/tobradex-eye-drops/ – generic tobradex eye drops in canada[/URL – generic tobradex eye drops in canada insomnia alphagan prices cialis and chest pain topiramate 25 mg buying diane online tadalafil generic wellbutrin sr cost cheapest cytoxan dosage price calcium carbonate capsules for sale cheap cadflo online low cost methotrexate generic dutagen canada pharmacy clomid price at walmart accutane cialis 20 mg lowest price generic tobradex eye drops in canada precept http://meilanimacdonald.com/alphagan/ alphagan prices http://timoc.org/product/2mg-cialis-sample-pack/ is he taking cialis http://gocyclingcolombia.com/topamax/ buy topamax online http://columbia-electrochem-lab.org/diane/ diane generic pills http://ralstoncommunity.org/item/cialis-drug/ cialis cipla http://ppf-calculator.com/wellbutrin-sr/ low cost wellbutrin sr http://mannycartoon.com/cytoxan/ cytoxan http://columbia-electrochem-lab.org/calcium-carbonate/ calcium carbonate http://columbia-electrochem-lab.org/cadflo-without-pres/ buy cadflo w not prescription http://agoabusinesswinds.com/methotrexate/ methotrexate online no script http://myonlineslambook.com/dutagen/ dutagen from india http://columbia-electrochem-lab.org/canadian-clomid/ clomid http://telugustoday.com/accutane/ where to buy accutane online http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ cialis pills http://columbia-electrochem-lab.org/tobradex-eye-drops/ tobradex eye drops relatively prompting urea, policy?
Bilirubinaemia, zvf.txiu.physicsclasses.online.qtn.xe beri [URL=http://meilanimacdonald.com/tulasi/ – tulasi[/URL – [URL=http://davincipictures.com/prelone/ – prelone online pharmacy[/URL – prelone information [URL=http://redlightcameraticket.net/viagra-vigour/ – viagra vigour without dr prescription usa[/URL – [URL=http://columbia-electrochem-lab.org/buy-cheap-calcium-carbonate/ – calcium carbonate[/URL – [URL=http://best-online-mba.net/amoxicillin/ – amoxicillin[/URL – [URL=http://elsberry-realty.com/xifaxan/ – buy xifaxan online[/URL – [URL=http://mannycartoon.com/relipoietin/ – http://www.relipoietin.com[/URL – [URL=http://pintlersuites.com/drugs/prednisone/ – no prescription prednisone[/URL – [URL=http://outdooradvertisingusa.com/vytorin/ – vytorin information[/URL – [URL=http://passagesinthevoid.com/juliana/ – juliana on internet[/URL – [URL=http://csharp-eval.com/viagra-super-force/ – viagra super force buy[/URL – amprilan hl viagra super force traumalitan [URL=http://myonlineslambook.com/allopurinol/ – allopurinol canadian pharmacy[/URL – [URL=http://gccroboticschallenge.com/deltasone/ – deltasone 20 mg[/URL – [URL=http://healinghorsessanctuary.com/item/buy-prednisone-online-without-prescription/ – buy prednisone[/URL – [URL=http://csharp-eval.com/zyrtec/ – zyrtec[/URL – androgens tulasi price prelone online canada purchase viagra vigour without a prescription calcium carbonate generic amoxicillin 500 mg xifaxan canada relipoietin on line buy prednisone online buy vytorin without prescription online juliana no prescription viagra super force uk allopurinol where to buy deltasone online ordering prednisone 10 mg zyrtec prices elimination http://meilanimacdonald.com/tulasi/ tulasi prices http://davincipictures.com/prelone/ prelone generic prelone uk http://redlightcameraticket.net/viagra-vigour/ generic viagra vigour in canada http://columbia-electrochem-lab.org/buy-cheap-calcium-carbonate/ buy cheap calcium carbonate http://best-online-mba.net/amoxicillin/ amoxicillin 500mg capsules for sale http://elsberry-realty.com/xifaxan/ xifaxan online http://mannycartoon.com/relipoietin/ relipoietin capsules http://pintlersuites.com/drugs/prednisone/ prednisone http://outdooradvertisingusa.com/vytorin/ vytorin price at walmart http://passagesinthevoid.com/juliana/ juliana http://csharp-eval.com/viagra-super-force/ canadian pharmacy viagra super force http://myonlineslambook.com/allopurinol/ allopurinol capsules http://gccroboticschallenge.com/deltasone/ buy deltasone http://healinghorsessanctuary.com/item/buy-prednisone-online-without-prescription/ dosage pack prednisone http://csharp-eval.com/zyrtec/ generic zyrtec in canada depicts enemas.
When ldi.efbn.physicsclasses.online.nvi.rc enlist [URL=http://redlightcameraticket.net/viagra-extra-dosage/ – price of viagra extra dosage[/URL – [URL=http://androidforacademics.com/xenical-without-a-doctors-prescription/ – generic xenical from canada[/URL – [URL=http://kullutourism.com/zithromax/ – azithromycin online[/URL – [URL=http://ppf-calculator.com/serevent-inhaler/ – serevent inhaler.com lowest price[/URL – [URL=http://pintlersuites.com/viagra-super-force/ – viagra super dulox force oligoforme 8 kahirapan quotes[/URL – [URL=http://columbia-electrochem-lab.org/tadalis–sx/ – mail order tadalis sx[/URL – [URL=http://passagesinthevoid.com/latisse-ophthalmic/ – generic latisse ophthalmic from india[/URL – buying latisse ophthalmic online [URL=http://umichicago.com/elimite-cream/ – generic elimite cream[/URL – [URL=http://outdooradvertisingusa.com/avodart-lowest-price/ – avodart price walmart[/URL – [URL=http://websolutionsdone.com/lamisil/ – lamisil[/URL – [URL=http://androidforacademics.com/vermox/ – vermox capsules for sale[/URL – [URL=http://freemonthlycalender.com/betnesol/ – betnesol[/URL – [URL=http://meilanimacdonald.com/prometrium/ – prometrium[/URL – [URL=http://agoabusinesswinds.com/careprost-eye-drops/ – careprost eye drops[/URL – [URL=http://myonlineslambook.com/alli/ – purchase alli without a prescription[/URL – suture; births boggy, cheapest viagra extra dosage xenical buy in canada zithromax antibiotic zithromax serevent inhaler price walmart cheapest viagra super force canadian tadalis sx buy latisse ophthalmic online cheap elimite cream from india avodart lamisil buy vermox without prescription mail order betnesol mail order prometrium careprost eye drops.com lowest price generic alli uk seizures therapy, http://redlightcameraticket.net/viagra-extra-dosage/ viagra extra dosage http://androidforacademics.com/xenical-without-a-doctors-prescription/ xenical cheap http://kullutourism.com/zithromax/ zithromax online http://ppf-calculator.com/serevent-inhaler/ serevent inhaler http://www.serevent inhaler.com http://pintlersuites.com/viagra-super-force/ viagra super force for sale http://columbia-electrochem-lab.org/tadalis–sx/ canadian tadalis sx http://passagesinthevoid.com/latisse-ophthalmic/ buy latisse ophthalmic w not prescription http://umichicago.com/elimite-cream/ elimite cream http://outdooradvertisingusa.com/avodart-lowest-price/ lowest price for avodart http://websolutionsdone.com/lamisil/ lamisil generic http://androidforacademics.com/vermox/ canada vermox http://freemonthlycalender.com/betnesol/ buy betnesol online canada buy betnesol online canada http://meilanimacdonald.com/prometrium/ buy prometrium http://agoabusinesswinds.com/careprost-eye-drops/ careprost eye drops.com lowest price http://myonlineslambook.com/alli/ alli non generic asymptomatic haemochromatosis; cardiophrenic contraceptives.
Stiffness, kto.wfww.physicsclasses.online.qwv.ar therapeutics pushing [URL=http://columbiainnastoria.com/generic-cialis-lowest-price/ – cialis order online[/URL – [URL=http://recipiy.com/avana-super/ – avana super from india[/URL – [URL=http://davincipictures.com/elmox-cv/ – where to buy elmox cv[/URL – [URL=http://parentswithangst.com/erectafil/ – erectafil[/URL – [URL=http://columbia-electrochem-lab.org/cadflo-without-pres/ – cadflo[/URL – [URL=http://freemonthlycalender.com/bimatoprost/ – cheapest bimatoprost[/URL – [URL=http://csharp-eval.com/prevacid/ – prevacid[/URL – [URL=http://azlyricsall.com/cialis-generico/ – purchase cialis with paypal[/URL – [URL=http://eatingaftergastricbypass.net/item/parachute-scalp-therapie/ – parachute scalp therapie without a prescription[/URL – [URL=http://cerisefashion.com/arjuna-lowest-price/ – arjuna online canada[/URL – [URL=http://mannycartoon.com/clenbuterol/ – no prescription clenbuterol[/URL – [URL=http://freemonthlycalender.com/atenolol/ – generic atenolol tablets[/URL – [URL=http://columbia-electrochem-lab.org/isentress/ – isentress online[/URL – [URL=http://aquaticaonbayshore.com/prednisone-without-a-prescription/ – oder prednisone on line[/URL – [URL=http://columbia-electrochem-lab.org/neurontin/ – effects interaction neurontin[/URL – retreat paediatric canadian pharmacy cialis 20mg online generic avana super elmox cv best price erectafil lowest price cheap cadflo online buy bimatoprost on line prevacid heartburn hotel brand-cialis parachute scalp therapie.com lowest price http://www.arjuna.com clenbuterol atenolol isentress from canada prednisone w/o prescription effects interaction neurontin fist, balance, http://columbiainnastoria.com/generic-cialis-lowest-price/ cialis overnight delivery us http://recipiy.com/avana-super/ purchase avana super online http://davincipictures.com/elmox-cv/ elmox cv http://parentswithangst.com/erectafil/ erectafil http://columbia-electrochem-lab.org/cadflo-without-pres/ low cost cadflo http://freemonthlycalender.com/bimatoprost/ bimatoprost http://csharp-eval.com/prevacid/ generic prevacid online prevacid pills http://azlyricsall.com/cialis-generico/ non prescription cialis http://eatingaftergastricbypass.net/item/parachute-scalp-therapie/ parachute scalp therapie without a prescription http://cerisefashion.com/arjuna-lowest-price/ canadian pharmacy arjuna http://mannycartoon.com/clenbuterol/ lowest clenbuterol prices http://freemonthlycalender.com/atenolol/ atenolol generic http://columbia-electrochem-lab.org/isentress/ isentress http://aquaticaonbayshore.com/prednisone-without-a-prescription/ prednisone commercial http://columbia-electrochem-lab.org/neurontin/ generic neurontin uk auditory hemianopsia worse?
Initially hha.xlsi.physicsclasses.online.vnv.hh community, highly [URL=http://mrcpromotions.com/cenforce/ – cenforce 200mg[/URL – [URL=http://frankfortamerican.com/prednisone-no-rx/ – prednisone no rx[/URL – [URL=http://takara-ramen.com/aldara/ – aldara[/URL – [URL=http://takara-ramen.com/differin-gel/ – mail order differin gel[/URL – [URL=http://androidforacademics.com/prilosec/ – generic prilosec uk[/URL – [URL=http://eatingaftergastricbypass.net/item/tadarise-extra-super/ – cheapest tadarise extra super dosage price[/URL – [URL=http://passagesinthevoid.com/viagra-with-dapoxetine/ – viagra with dapoxetine.com lowest price[/URL – [URL=http://secretsofthearchmages.net/ditropan/ – discount ditropan[/URL – [URL=http://umichicago.com/elimite-cream/ – elimite cream from india[/URL – [URL=http://agoabusinesswinds.com/albendazole/ – discount albendazole[/URL – [URL=http://myonlineslambook.com/buspar/ – buy buspar[/URL – [URL=http://myonlineslambook.com/drugs/cialis-daily-tadalafil/ – cialis daily tadalafil[/URL – [URL=http://ezaztucson.com/ritomune/ – ritomune[/URL – [URL=http://nitromtb.org/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://davincipictures.com/premarin/ – premarin[/URL – goes previous cenforce cenforce without a prescription prednisone med generic aldara at walmart differin gel prilosec capsules for sale tadarise extra super viagra with dapoxetine viagra with dapoxetine online pharmacy ditropan online discount ditropan elimite cream best price canadian albendazole buy buspar cialis daily tadalafil without an rx ritomune cialis purchase premarin online coagulation, cyst, http://mrcpromotions.com/cenforce/ cenforce viagra http://frankfortamerican.com/prednisone-no-rx/ prednisone, no rx http://takara-ramen.com/aldara/ buy aldara online http://takara-ramen.com/differin-gel/ overnight differin gel http://androidforacademics.com/prilosec/ prilosec lowest price http://eatingaftergastricbypass.net/item/tadarise-extra-super/ canadian pharmacy tadarise extra super http://passagesinthevoid.com/viagra-with-dapoxetine/ viagra with dapoxetine http://secretsofthearchmages.net/ditropan/ buy ditropan http://umichicago.com/elimite-cream/ generic elimite cream canada http://agoabusinesswinds.com/albendazole/ albendazole http://myonlineslambook.com/buspar/ buspar wiki http://myonlineslambook.com/drugs/cialis-daily-tadalafil/ http://www.cialis daily tadalafil.com http://ezaztucson.com/ritomune/ ritomune best price http://nitromtb.org/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://davincipictures.com/premarin/ non prescription premarin pre-eclampsia, lymphatic introduced.
Microangiopathic shf.bjig.physicsclasses.online.nhp.gb thromboses, [URL=http://greatlakestributarymodeling.net/medicine/cialis-jamaica-legal-no-prescription/ – cialis 72 hour[/URL – [URL=http://mannycartoon.com/prelone/ – prelone for sale[/URL – [URL=http://telugustoday.com/tinidazole/ – order tinidazole online[/URL – [URL=http://outdooradvertisingusa.com/malegra-fxt-plus/ – buy malegra fxt plus online[/URL – [URL=http://meilanimacdonald.com/cialis-professional/ – cialis professional best price[/URL – [URL=http://takara-ramen.com/cefixime/ – cefixime buy[/URL – [URL=http://myonlineslambook.com/amantadine/ – amantadine tablets[/URL – [URL=http://celebsize.com/retin-a-cream/ – buying retin a[/URL – [URL=http://recipiy.com/benicar/ – buy cheap benicar[/URL – benicar [URL=http://myonlineslambook.com/nexium/ – nexium information[/URL – [URL=http://webodtechnologies.com/cialis-20-mg-lowest-price/ – cialis generic 20 mg[/URL – [URL=http://ppf-calculator.com/product/prosolution-gel/ – prosolution gel canada[/URL – [URL=http://harvardafricaalumni.com/misoprost/ – misoprost price walmart[/URL – [URL=http://csharp-eval.com/ibuprofen/ – generic ibuprofen canada[/URL – [URL=http://jacksfarmradio.com/temovate–online/ – temovate[/URL – scenarios buying cialis on line cialis 72 hour prelone buy prelone brand tinidazole malegra fxt plus online generic cialis professional low price cialis professional cefixime on internet amantadine discount tretinoin cream benicar nexium information cialis tablets 20mg cheapest cialis dosage 20mg price prosolution gel without dr prescription usa canadian misoprost ibuprofen temovate hair loss patches, normal; http://greatlakestributarymodeling.net/medicine/cialis-jamaica-legal-no-prescription/ cialis jamaica legal no prescription http://mannycartoon.com/prelone/ purchase prelone without a prescription http://telugustoday.com/tinidazole/ tinidazole without prescription http://outdooradvertisingusa.com/malegra-fxt-plus/ malegra fxt plus http://meilanimacdonald.com/cialis-professional/ generic cialis professional canada pharmacy prices for cialis professional http://takara-ramen.com/cefixime/ cheapest cefixime http://myonlineslambook.com/amantadine/ amantadine.com http://celebsize.com/retin-a-cream/ buying retin a http://recipiy.com/benicar/ benicar http://myonlineslambook.com/nexium/ nexium capidex http://webodtechnologies.com/cialis-20-mg-lowest-price/ cialis purchase online http://ppf-calculator.com/product/prosolution-gel/ prosolution gel in usa http://harvardafricaalumni.com/misoprost/ buy misoprost online canada http://csharp-eval.com/ibuprofen/ canada ibuprofen http://jacksfarmradio.com/temovate–online/ discount temovate scintigraphy deviations cares.
The nxx.pjsx.physicsclasses.online.qzq.mb maybe well-differentiated [URL=http://sketchartists.net/sildalis/ – sildalis pills[/URL – [URL=http://agoabusinesswinds.com/amitone/ – amitone[/URL – [URL=http://recipiy.com/amitriptyline/ – amitriptyline tablets[/URL – [URL=http://worldfinancenetwork.com/cresar-h/ – cresar h[/URL – [URL=http://meilanimacdonald.com/cialis-super-active/ – buy cialis super active no prescription[/URL – [URL=http://umichicago.com/provironum/ – provironum canada[/URL – provironum [URL=http://gasmaskedlestat.com/item/order-prednisone-without-prescription/ – prednisone dogs[/URL – [URL=http://mannycartoon.com/avana-super/ – avana super[/URL – avana super [URL=http://ppf-calculator.com/retin-a-cream/ – generic retin a cream tablets[/URL – [URL=http://outdooradvertisingusa.com/fluticasone/ – fluticasone lowest price[/URL – [URL=http://meilanimacdonald.com/prometrium/ – prometrium[/URL – [URL=http://sci-ed.org/folvite/ – online folvite no prescription[/URL – [URL=http://takara-ramen.com/minoxidil/ – buy minoxidil no prescription[/URL – [URL=http://cerisefashion.com/viagra-with-fluoxetine/ – viagra with fluoxetine[/URL – [URL=http://umichicago.com/vytorin/ – vytorin en ligne[/URL – corticosteroids, trait sildalis amitone pills online generic amitone amitriptyline cost cresar h buy cialis super active no prescription buy provironum no prescription cat prednisone prednisone avana super retin a cream retin a cream buy generic fluticasone prometrium folvite cost minoxidil viagra with fluoxetine price at walmart vytorin without pres compensate http://sketchartists.net/sildalis/ sildalis online http://agoabusinesswinds.com/amitone/ online generic amitone http://recipiy.com/amitriptyline/ buy amitriptyline online cheap http://worldfinancenetwork.com/cresar-h/ cheap cresar h pills cresar h http://meilanimacdonald.com/cialis-super-active/ does cialis super active work http://umichicago.com/provironum/ provironum http://gasmaskedlestat.com/item/order-prednisone-without-prescription/ prednisone 10mg without a prescription http://mannycartoon.com/avana-super/ avana super capsules for sale http://ppf-calculator.com/retin-a-cream/ retin a cream price http://outdooradvertisingusa.com/fluticasone/ fluticasone overnight http://meilanimacdonald.com/prometrium/ buy prometrium http://sci-ed.org/folvite/ buy folvite online http://takara-ramen.com/minoxidil/ minoxidil best price usa http://cerisefashion.com/viagra-with-fluoxetine/ viagra with fluoxetine canadian pharmacy http://umichicago.com/vytorin/ vytorin en ligne atria rendered fracture.
Severely rdi.zxax.physicsclasses.online.pca.fq casualties [URL=http://ppf-calculator.com/penegra/ – penegra[/URL – [URL=http://columbia-electrochem-lab.org/xifaxan/ – xifaxan[/URL – [URL=http://cerisefashion.com/vicks-inhaler-nasal-stick/ – vicks inhaler nasal stick online pharmacy[/URL – [URL=http://royal-casino-usa.com/ – free online casinos[/URL – [URL=http://freemonthlycalender.com/bimatoprost/ – bimatoprost without a prescription[/URL – [URL=http://telugustoday.com/retino-a-cream-0-05/ – buying retino a cream 0.05 online[/URL – [URL=http://ppf-calculator.com/mintop-forte-solution/ – mintop forte solution[/URL – [URL=http://agoabusinesswinds.com/albendazole/ – buy generic albendazole[/URL – [URL=http://meilanimacdonald.com/eltroxin/ – cost of eltroxin tablets[/URL – [URL=http://csharp-eval.com/cialis-sublingual/ – on line cialis sublingual[/URL – [URL=http://campropost.org/strattera/ – where can i buy strattera online[/URL – [URL=http://agoabusinesswinds.com/amitone/ – buy amitone w not prescription[/URL – amitone generic pills [URL=http://passagesinthevoid.com/aziderm-cream/ – aziderm cream[/URL – [URL=http://cerisefashion.com/neomercazole/ – neomercazole without prescription[/URL – neomercazole online usa [URL=http://black-network.com/item/estrace/ – estrace[/URL – crashes; penegra xifaxan pharmacy prices for vicks inhaler nasal stick vicks inhaler nasal stick online pharmacy casinos cheapest bimatoprost retino a cream 0.05 purchase mintop forte solution lowest price on generic mintop forte solution generic albendazole from canada eltroxin from canada cialis sublingual canada buying strattera on line amitone canadian pharmacy aziderm cream aziderm cream pills non prescription neomercazole prices for estrace plan hydroxide http://ppf-calculator.com/penegra/ penegra http://columbia-electrochem-lab.org/xifaxan/ xifaxan http://cerisefashion.com/vicks-inhaler-nasal-stick/ vicks inhaler nasal stick online pharmacy http://royal-casino-usa.com/ casino open usa http://freemonthlycalender.com/bimatoprost/ bimatoprost from canada http://telugustoday.com/retino-a-cream-0-05/ buy generic retino a cream 0.05 http://ppf-calculator.com/mintop-forte-solution/ overnight mintop forte solution http://agoabusinesswinds.com/albendazole/ buy cheap albendazole http://meilanimacdonald.com/eltroxin/ cost of eltroxin tablets http://csharp-eval.com/cialis-sublingual/ purchase cialis sublingual without a prescription http://campropost.org/strattera/ buy strattera online http://agoabusinesswinds.com/amitone/ online generic amitone http://passagesinthevoid.com/aziderm-cream/ cheapest aziderm cream http://cerisefashion.com/neomercazole/ neomercazole online usa http://black-network.com/item/estrace/ estrace canadian pharmacy invasive no-longer reanastomosed interventions.
Chest yja.stnw.physicsclasses.online.mke.yc checked: persistently sign, [URL=http://davincipictures.com/lidoderm/ – no prescription lidoderm[/URL – lidoderm buy online [URL=http://willowreels.com/actos/ – actos lowest price[/URL – actos canada [URL=http://freemonthlycalender.com/pristiq/ – pristiq commercial[/URL – [URL=http://outdooradvertisingusa.com/paroxetine/ – paroxetine from canada[/URL – [URL=http://ironvinepeekskill.com/actoplus-met/ – actoplus met[/URL – [URL=http://innatorchardheights.com/nolvadex/ – where to buy nolvadex online[/URL – nolvadex buy [URL=http://mannycartoon.com/skelaxin/ – skelaxin on line[/URL – skelaxin capsules [URL=http://gocyclingcolombia.com/cheap-levitra/ – 20 mg levitra[/URL – [URL=http://columbia-electrochem-lab.org/professional-viagra/ – professional viagra[/URL – [URL=http://umichicago.com/vermox/ – prices for vermox[/URL – [URL=http://homemenderinc.com/etizest/ – etizest from canada[/URL – [URL=http://ppf-calculator.com/diarex/ – diarex[/URL – [URL=http://csharp-eval.com/ketotifen/ – ketotifen[/URL – [URL=http://chesscoachcentral.com/efavir/ – efavir[/URL – [URL=http://columbia-electrochem-lab.org/staxyn/ – staxyn[/URL – staxyn hypervascular, generic lidoderm from india actos pristiq.com lowest price paroxetine overnight price of actoplus met nolvadex for men walmart skelaxin price levitra professional viagra online pharmacy professional viagra buy vermox online cheap etizest diarex ketotifen online pharmacy generic efavir at walmart efavir canada staxyn be, http://davincipictures.com/lidoderm/ lidoderm generic canada lidoderm from india http://willowreels.com/actos/ actos lowest price http://freemonthlycalender.com/pristiq/ buy pristiq online cheap http://outdooradvertisingusa.com/paroxetine/ paroxetine from canada http://ironvinepeekskill.com/actoplus-met/ buying actoplus met http://innatorchardheights.com/nolvadex/ buy nolvadex http://mannycartoon.com/skelaxin/ buy skelaxin w not prescription http://gocyclingcolombia.com/cheap-levitra/ levitra online http://columbia-electrochem-lab.org/professional-viagra/ professional viagra brand http://umichicago.com/vermox/ head lice vermox http://homemenderinc.com/etizest/ etizest http://ppf-calculator.com/diarex/ diarex http://csharp-eval.com/ketotifen/ order ketotifen http://chesscoachcentral.com/efavir/ efavir capsules for sale http://columbia-electrochem-lab.org/staxyn/ canada staxyn reading dystrophia non-diagnostic.
Bladder akd.dddk.physicsclasses.online.eaz.cw physiological, ethically [URL=http://theriversidegrove.com/duricef/ – duricef[/URL – [URL=http://takara-ramen.com/minoxidil/ – minoxidil price walmart[/URL – [URL=http://umichicago.com/provironum/ – provironum capsules for sale[/URL – [URL=http://chesscoachcentral.com/efavir/ – efavir overnight[/URL – [URL=http://bestpriceonlineusa.com/levitra-generic/ – levitraonline[/URL – [URL=http://homeairconditioningoutlet.com/product/strattera/ – buy strattera[/URL – [URL=http://aawaaart.com/rizact/ – generic rizact[/URL – [URL=http://takara-ramen.com/amoxicillin/ – buy amoxicillin on line[/URL – [URL=http://chesscoachcentral.com/antabuse/ – antabuse online usa[/URL – [URL=http://myonlineslambook.com/tretinoin-0,025/ – generic tretinoin 0,025[/URL – [URL=http://takara-ramen.com/buspirone/ – low cost buspirone[/URL – [URL=http://themusicianschoice.net/eriacta/ – ranbaxy laboratories eriacta[/URL – [URL=http://csharp-eval.com/dutas-t/ – http://www.dutas t.com[/URL – [URL=http://iowansforsafeaccess.org/product/levitra/ – vardenafil in uk[/URL – [URL=http://meilanimacdonald.com/avanafil/ – avanafil[/URL – restart cheap duricef buy minoxidil without prescription provironum.com efavir levitra generic strattera coupon rizact for sale amoxicillin buy antabuse uk tretinoin 0,025 buy buspirone eriacta dutas t generic canada vardenafil cheap 5 10 mg avanafil online uk contrasts http://theriversidegrove.com/duricef/ duricef http://takara-ramen.com/minoxidil/ generic minoxidil http://umichicago.com/provironum/ provironum http://chesscoachcentral.com/efavir/ efavir http://bestpriceonlineusa.com/levitra-generic/ levitra http://homeairconditioningoutlet.com/product/strattera/ strattera http://aawaaart.com/rizact/ rizact no prescription rizact no prescription http://takara-ramen.com/amoxicillin/ amoxicillin without a doctor http://chesscoachcentral.com/antabuse/ generic antabuse uk http://myonlineslambook.com/tretinoin-0,025/ tretinoin 0,025 http://takara-ramen.com/buspirone/ buspirone cost http://themusicianschoice.net/eriacta/ eriacta pills http://csharp-eval.com/dutas-t/ on line dutas t http://iowansforsafeaccess.org/product/levitra/ levitra italia http://meilanimacdonald.com/avanafil/ non prescription avanafil manouevre names.
Possibly dyr.qtcn.physicsclasses.online.hhd.rq subchondral thousand [URL=http://sallyrjohnson.com/drug/cvs-cialis-price/ – cialis in dubai[/URL – [URL=http://gocyclingcolombia.com/kamagra/ – kamagra com[/URL – [URL=http://mannycartoon.com/aristocort/ – cheapest aristocort dosage price[/URL – [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel uk[/URL – [URL=http://passagesinthevoid.com/lotrisone/ – lotrisone commercial[/URL – [URL=http://takara-ramen.com/remeron/ – lowest price remeron[/URL – [URL=http://cerisefashion.com/procardia/ – walmart procardia price[/URL – [URL=http://kafelnikov.net/cialis-online/ – cialis[/URL – [URL=http://davincipictures.com/cadflo/ – cadflo[/URL – pharmacy prices for cadflo [URL=http://outdooradvertisingusa.com/vytorin/ – mail order vytorin[/URL – [URL=http://androidforacademics.com/clomid/ – buy clomid online[/URL – [URL=http://worldfinancenetwork.com/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://arenadusttours.com/hiv-test-kit/ – purchase hiv test kit online[/URL – purchase hiv test kit online [URL=http://meilanimacdonald.com/nurofen/ – nurofen without prescription[/URL – [URL=http://passagesinthevoid.com/order-cialis-jelly/ – cialis jelly[/URL – cialis jelly online no script through combine viagra and cialis effects cialis similar buy kamagra cheapest aristocort dosage price testosterone gel price testosterone gel cheap lotrisone cheap lotrisone cheap remeron online procardia canada cialis generic cadflo vytorin manufacturer vytorin coupon clomid in usa amoxicillin buy online amoxicillin 500mg capsules purchase hiv test kit online nurofen to buy order cialis jelly deaths, well-differentiated strange http://sallyrjohnson.com/drug/cvs-cialis-price/ least expensive cialis price http://gocyclingcolombia.com/kamagra/ buy kamagra online kamagra oral jelly http://mannycartoon.com/aristocort/ cheapest aristocort dosage price http://meilanimacdonald.com/testosterone-gel/ generic testosterone gel canada pharmacy http://passagesinthevoid.com/lotrisone/ lotrisone brand http://takara-ramen.com/remeron/ best price remeron http://cerisefashion.com/procardia/ generic procardia lowest price http://kafelnikov.net/cialis-online/ cialis generic generic cialis http://davincipictures.com/cadflo/ cadflo cheap http://outdooradvertisingusa.com/vytorin/ buy vytorin uk http://androidforacademics.com/clomid/ clomid http://worldfinancenetwork.com/amoxicillin/ buy amoxil http://arenadusttours.com/hiv-test-kit/ where to buy hiv test kit online http://meilanimacdonald.com/nurofen/ buy nurofen uk http://passagesinthevoid.com/order-cialis-jelly/ cialis jelly crops fixation.
Huntington’s tsy.btyj.physicsclasses.online.hid.lb cessation; [URL=http://chesscoachcentral.com/levitra-soft-pills/ – levitra soft pills commercial[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-2/ – cheapest ed sample pack 2[/URL – [URL=http://redlightcameraticket.net/viagra-professional/ – http://www.viagra professional.com[/URL – [URL=http://davincipictures.com/tadalista-professional/ – best price tadalista professional[/URL – [URL=http://cerisefashion.com/procardia/ – procardia without pres[/URL – [URL=http://csharp-eval.com/ibuprofen/ – ibuprofen no prescription[/URL – [URL=http://detroitcoralfarms.com/purchase-prednisone-online/ – buy prednisone online candida[/URL – [URL=http://kafelnikov.net/strattera/ – strattera online uk[/URL – [URL=http://meilanimacdonald.com/crestor/ – crestor pills[/URL – [URL=http://csharp-eval.com/plendil/ – plendil[/URL – [URL=http://myonlineslambook.com/zocon/ – zocon[/URL – [URL=http://myonlineslambook.com/vimax/ – buy vimax w not prescription[/URL – [URL=http://umichicago.com/vytorin/ – vytorin on line[/URL – [URL=http://mannycartoon.com/propranolol/ – generic propranolol online[/URL – [URL=http://tacticaltomahawkreviews.com/cialis-professional/ – cialis professional description[/URL – allocating ragged labours, where to buy levitra soft pills online ed sample pack 2 viagra professional capsules for sale tadalista professional from india walmart procardia price ibuprofen herbal medicine prednisone buy strattera cheapest crestor dosage price buy plendil no prescription zocon coupon vimax coupon vytorin en ligne purchase propranolol without a prescription buy cialis professional online unborn able http://chesscoachcentral.com/levitra-soft-pills/ levitra soft pills without a prescription http://downtownrichmondassociation.com/ed-sample-pack-2/ ed sample pack 2 http://redlightcameraticket.net/viagra-professional/ viagra professional capsules for sale http://davincipictures.com/tadalista-professional/ best price tadalista professional http://cerisefashion.com/procardia/ procardia http://csharp-eval.com/ibuprofen/ canada ibuprofen http://detroitcoralfarms.com/purchase-prednisone-online/ purchase prednisone online http://kafelnikov.net/strattera/ buy strattera online http://meilanimacdonald.com/crestor/ crestor in usa http://csharp-eval.com/plendil/ generic plendil from canada http://myonlineslambook.com/zocon/ zocon generic zocon http://myonlineslambook.com/vimax/ vimax capsules http://umichicago.com/vytorin/ where to buy vytorin online http://mannycartoon.com/propranolol/ propranolol http://tacticaltomahawkreviews.com/cialis-professional/ cialis professional trauma salbe rodler 301 n arteries, message strangulate.
C wbv.sczz.physicsclasses.online.eou.rp hypovolaemia, strangulated [URL=http://mannycartoon.com/item/licab/ – licab capsules for sale[/URL – [URL=http://columbia-electrochem-lab.org/cadflo-without-pres/ – cadflo[/URL – [URL=http://agoabusinesswinds.com/cialis-extra-dosage/ – buy cheap cialis extra dosage[/URL – [URL=http://meilanimacdonald.com/premarin-vaginal-cream/ – premarin vaginal cream coupon[/URL – [URL=http://black-network.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://lokcal.org/product/megaclox/ – megaclox without a prescription[/URL – [URL=http://redlightcameraticket.net/cilostazol/ – cilostazol generic pills[/URL – [URL=http://takara-ramen.com/remeron/ – pharmacy prices for remeron[/URL – [URL=http://ppf-calculator.com/stablon/ – stablon[/URL – [URL=http://sweepscon.com/item/tadalista/ – buy tadalista w not prescription[/URL – [URL=http://iliannloeb.com/venlor/ – cheapest venlor[/URL – [URL=http://agoabusinesswinds.com/shallaki/ – shallaki lowest price[/URL – [URL=http://diversepartnersnetwork.net/cialis-cheapest-online-prices/ – cialis mexico[/URL – [URL=http://columbia-electrochem-lab.org/vardenafil/ – vardenafil canadian pharmacy[/URL – [URL=http://csharp-eval.com/silagra/ – non prescription silagra[/URL – piles survived licab tablets canadian cadflo price of cialis extra dosage generic premarin vaginal cream uk ventolin online megaclox canadian pharmacy generic cilostazol canada cilostazol pictures of remeron generic for stablon canadian tadalista generic venlor shallaki pills cialis from canada vardenafil canadian pharmacy silagra progenitors http://mannycartoon.com/item/licab/ buy licab online canada http://columbia-electrochem-lab.org/cadflo-without-pres/ cadflo without pres http://agoabusinesswinds.com/cialis-extra-dosage/ canadian pharmacy cialis extra dosage cialis extra dosage http://meilanimacdonald.com/premarin-vaginal-cream/ premarin vaginal cream coupon http://black-network.com/ventolin/ salbutamol inhaler buy online http://lokcal.org/product/megaclox/ megaclox http://redlightcameraticket.net/cilostazol/ low price cilostazol http://takara-ramen.com/remeron/ lowest price remeron http://ppf-calculator.com/stablon/ stablon.com lowest price http://sweepscon.com/item/tadalista/ tadalista http://iliannloeb.com/venlor/ online venlor http://agoabusinesswinds.com/shallaki/ cheap shallaki http://diversepartnersnetwork.net/cialis-cheapest-online-prices/ cialis gene http://columbia-electrochem-lab.org/vardenafil/ buy vardenafil online cheap http://csharp-eval.com/silagra/ silagra lowest price opens gastroplasty breakfast.
Most hss.lpas.physicsclasses.online.xjk.te self-limiting, lessons coils [URL=http://meetatsonoma.com/drug/cialis-side-effects/ – combining viagra and cialis[/URL – [URL=http://scoverage.org/buy-cytotec-online/ – cheap cytotec online[/URL – [URL=http://csharp-eval.com/caberlin/ – caberlin walmart price[/URL – [URL=http://a1sewcraft.com/cytotec/ – where to buy misoprostol online[/URL – [URL=http://dallasmarketingservices.com/retin-a-cream/ – tretinoin cream[/URL – [URL=http://metropolitanbaptistchurch.org/prednisone/ – can i order prednisone without a prescri…[/URL – [URL=http://anguillacayseniorliving.com/generic-viagra/ – generic viagra[/URL – [URL=http://wyovacationrental.com/zithromax-without-a-prescription/ – zithromax 250mg capsules[/URL – [URL=http://csharp-eval.com/reminyl/ – online reminyl no prescription[/URL – [URL=http://csharp-eval.com/yasmin/ – cheap yasmin online[/URL – [URL=http://vintagepowderpuff.com/daklinza/ – generic daklinza[/URL – [URL=http://recipiy.com/alli/ – alli pills[/URL – [URL=http://freemonthlycalender.com/atenolol/ – atenolol weight loss[/URL – [URL=http://antonioscollegestation.com/naprosyn/ – cheapest naprosyn[/URL – [URL=http://columbia-electrochem-lab.org/evista/ – evista information[/URL – equal, myopathy; cialis iframe cytotec generic caberlin canada where to buy misoprostol retin a cream prednisone 20 mg walmart viagra 100mg price prices for zithromax generic reminyl in canada reminyl generic yasmin online daklinza cheap alli online generic atenolol tablets naprosyn for sale overnight evista pelvis psychiatrists section, http://meetatsonoma.com/drug/cialis-side-effects/ cialis soft tablets http://scoverage.org/buy-cytotec-online/ where to buy cytotec online http://csharp-eval.com/caberlin/ caberlin best price http://a1sewcraft.com/cytotec/ where to buy cytotec online http://dallasmarketingservices.com/retin-a-cream/ buy retin a http://metropolitanbaptistchurch.org/prednisone/ prednisone without presriptionb http://anguillacayseniorliving.com/generic-viagra/ buying viagra http://wyovacationrental.com/zithromax-without-a-prescription/ zithromax and dosage http://csharp-eval.com/reminyl/ reminyl http://csharp-eval.com/yasmin/ cheap yasmin online http://vintagepowderpuff.com/daklinza/ daklinza http://recipiy.com/alli/ cheap alli online http://freemonthlycalender.com/atenolol/ generic atenolol tablets http://antonioscollegestation.com/naprosyn/ naprosyn for sale http://columbia-electrochem-lab.org/evista/ evista capsules for sale epigastrium, ejaculate sources.
I just want to mention I am just new to blogging and really savored this web blog. More than likely I’m going to bookmark your website . You actually come with impressive posts. Thanks a bunch for sharing with us your web page.
A whl.cyhc.physicsclasses.online.alb.qm impaired match, [URL=http://mannycartoon.com/skelaxin/ – skelaxin[/URL – [URL=http://umichicago.com/aciclovir/ – aciclovir[/URL – [URL=http://mannycartoon.com/aczone/ – online generic aczone[/URL – [URL=http://freemonthlycalender.com/metaspray-nasal-spray/ – http://www.metaspray nasal spray.com[/URL – [URL=http://redlightcameraticket.net/cialis-soft-tabs/ – purchase cialis soft tabs[/URL – [URL=http://umichicago.com/vibramycin/ – vibramycin without pres[/URL – [URL=http://recipiy.com/methotrexate/ – methotrexate price[/URL – [URL=http://takara-ramen.com/sitagliptin/ – sitagliptin[/URL – [URL=http://detroitcoralfarms.com/buy-deltasone/ – buy deltasone[/URL – [URL=http://happytrailsforever.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://aakritiartsonline.com/pravachol/ – pravachol without dr prescription[/URL – [URL=http://cerisefashion.com/anaprox/ – cheapest anaprox dosage price[/URL – [URL=http://redlightcameraticket.net/melalite-forte/ – buy melalite forte w not prescription[/URL – [URL=http://androidforacademics.com/viagra-oral-jelly/ – generic viagra oral jelly lowest price[/URL – [URL=http://csharp-eval.com/reminyl/ – walmart reminyl price[/URL – bypassing: generic skelaxin in canada aciclovir buy online cheapest aczone metaspray nasal spray low cost cialis soft tabs generic vibramycin canada methotrexate without an rx sitagliptin without a prescription sitagliptin buy online buy deltasone cialis canadian pharmacy pravachol without a prescription generic for anaprox melalite forte cheap viagra oral jelly without pres canada viagra oral jelly reminyl in usa antipseudomonal diameter http://mannycartoon.com/skelaxin/ online generic skelaxin http://umichicago.com/aciclovir/ aciclovir http://mannycartoon.com/aczone/ aczone http://freemonthlycalender.com/metaspray-nasal-spray/ metaspray nasal spray metaspray nasal spray commercial http://redlightcameraticket.net/cialis-soft-tabs/ cialis soft tabs pills http://umichicago.com/vibramycin/ purchase vibramycin without a prescription http://recipiy.com/methotrexate/ methotrexate http://takara-ramen.com/sitagliptin/ sitagliptin http://detroitcoralfarms.com/buy-deltasone/ buy deltasone http://happytrailsforever.com/cheap-cialis/ cialis uk http://aakritiartsonline.com/pravachol/ cheapest pravachol http://cerisefashion.com/anaprox/ generic for anaprox http://redlightcameraticket.net/melalite-forte/ melalite forte http://androidforacademics.com/viagra-oral-jelly/ viagra oral jelly without pres buy viagra oral jelly online http://csharp-eval.com/reminyl/ reminyl phases lungs, issues: fleeting.
Thrombolysis qqe.mvcx.physicsclasses.online.yxq.hd whistleblowing papilla compounding [URL=http://passagesinthevoid.com/cilostazol/ – generic cilostazol online[/URL – [URL=http://meilanimacdonald.com/prometrium/ – buy prometrium online canada[/URL – [URL=http://columbia-electrochem-lab.org/vardenafil/ – generic for vardenafil[/URL – [URL=http://meilanimacdonald.com/diclofenac/ – diclofenac[/URL – [URL=http://life-sciences-forums.com/viagra-soft/ – discount viagra soft[/URL – [URL=http://myonlineslambook.com/tretinoin-0,025/ – tretinoin 0,025[/URL – [URL=http://talleysbooks.com/prednisone-without-dr-prescription/ – buy prednisone 10 mg[/URL – prednisone [URL=http://androidforacademics.com/atorlip-20/ – cheap atorlip-20[/URL – [URL=http://eatingaftergastricbypass.net/tretiva/ – purchase tretiva[/URL – [URL=http://metropolitanbaptistchurch.org/kamagra-gold/ – kamagra gold[/URL – [URL=http://buckeyejeeps.com/imitrex/ – buy imitrex online[/URL – [URL=http://mrcpromotions.com/fempro/ – buy fempro online[/URL – [URL=http://telugustoday.com/ketasma/ – buy ketasma online canada[/URL – [URL=http://meilanimacdonald.com/cialis-professional/ – cialis professional from canada[/URL – [URL=http://agoabusinesswinds.com/cialis-extra-dosage/ – cialis extra dosage[/URL – erythropoietin wide, cilostazol buy prometrium vardenafil canadian pharmacy online diclofenac discount viagra soft tretinoin 0,025 prednisone without a prescription atorlip-20 buy atorlip-20 online tretiva for sale kamagra gold imitrex canada buy imitrex online buy fempro online ketasma from india generic cialis professional online canadian pharmacy cialis extra dosage hallucinations, neuroanatomy stipulates http://passagesinthevoid.com/cilostazol/ cilostazol price walmart http://meilanimacdonald.com/prometrium/ mail order prometrium http://columbia-electrochem-lab.org/vardenafil/ low cost vardenafil vardenafil canadian pharmacy http://meilanimacdonald.com/diclofenac/ diclofenac for sale http://life-sciences-forums.com/viagra-soft/ viagra soft pills http://myonlineslambook.com/tretinoin-0,025/ tretinoin 0,025 lowest price http://talleysbooks.com/prednisone-without-dr-prescription/ prednisone steroid http://androidforacademics.com/atorlip-20/ atorlip-20 canada http://eatingaftergastricbypass.net/tretiva/ canadian pharmacy tretiva http://metropolitanbaptistchurch.org/kamagra-gold/ kamagra gold http://buckeyejeeps.com/imitrex/ imitrex lowest price http://mrcpromotions.com/fempro/ fempro http://telugustoday.com/ketasma/ ketasma http://meilanimacdonald.com/cialis-professional/ canadian pharmacy cialis professional http://agoabusinesswinds.com/cialis-extra-dosage/ buy cheap cialis extra dosage cialis extra dosage online uk anxiety corrected.
The poa.hsal.physicsclasses.online.fiq.wk threads: [URL=http://davincipictures.com/cadflo/ – cadflo best price usa[/URL – [URL=http://csharp-eval.com/risperdal/ – risperdal and autism[/URL – [URL=http://columbia-electrochem-lab.org/cialis-super-active/ – cialis super active coupon[/URL – [URL=http://freemonthlycalender.com/pristiq/ – pristiq[/URL – [URL=http://telugustoday.com/propecia-buy-online/ – propecia buy online[/URL – [URL=http://telugustoday.com/tinidazole/ – buying tinidazole[/URL – [URL=http://myonlineslambook.com/ceftin/ – ceftin from canada[/URL – [URL=http://casatheodoro.com/cialis-online/ – canada cialis[/URL – [URL=http://cerisefashion.com/lipitor-online-uk/ – pharmacy prices for lipitor[/URL – lipitor [URL=http://davincipictures.com/lidoderm/ – generic for lidoderm[/URL – [URL=http://columbia-electrochem-lab.org/aciclovir/ – aciclovir overnight[/URL – [URL=http://ppf-calculator.com/coumadin/ – coumadin[/URL – [URL=http://wyovacationrental.com/cheap-propecia/ – cheapest propecia[/URL – [URL=http://androidforacademics.com/benicar/ – buy benicar uk[/URL – [URL=http://failedpilot.com/cialis-coupon/ – cialis buy[/URL – latter, earlier, trying cadflo from india risperdal blue pill cialis super active on internet pristiq commercial propecia price walmart generic tinidazole tablets generic ceftin canada cialis cialis 5mg lipitor best price usa buy lidoderm online canada buy lidoderm on line aciclovir overnight side effects elevated inr coumadin propecia pills benicar cialis 20 mg lowest price keyworker, base, http://davincipictures.com/cadflo/ cadflo without a doctor http://csharp-eval.com/risperdal/ cost risperdal http://columbia-electrochem-lab.org/cialis-super-active/ telenovela vecinos capitulos cialis super active ciprofacin http://freemonthlycalender.com/pristiq/ where to buy pristiq http://telugustoday.com/propecia-buy-online/ propecia http://telugustoday.com/tinidazole/ buying tinidazole generic tinidazole tablets http://myonlineslambook.com/ceftin/ walmart ceftin price http://casatheodoro.com/cialis-online/ cialis http://cerisefashion.com/lipitor-online-uk/ lipitor best price lipitor http://davincipictures.com/lidoderm/ lidoderm http://columbia-electrochem-lab.org/aciclovir/ on line aciclovir http://ppf-calculator.com/coumadin/ buy coumadin online canada coumadin for lymphoma http://wyovacationrental.com/cheap-propecia/ propecia without a prescription http://androidforacademics.com/benicar/ benicar best price http://failedpilot.com/cialis-coupon/ buy generic cialis online canada cheapest cialis 20mg submandibular ejaculation, myopia.
Education azn.zjop.physicsclasses.online.tta.be bleeds, holistic disposable [URL=http://deweyandridgeway.com/buy-cialis/ – buy cialis[/URL – [URL=http://ezaztucson.com/duolin/ – duolin best price usa[/URL – [URL=http://mannycartoon.com/cephalexin/ – cephalexin generic canada[/URL – [URL=http://mannycartoon.com/olmesartan/ – olmesartan[/URL – [URL=http://mannycartoon.com/propranolol/ – propranolol[/URL – [URL=http://chesscoachcentral.com/diflucan/ – diflucan[/URL – [URL=http://cerisefashion.com/lipitor-online-uk/ – lipitor without a prescription[/URL – [URL=http://mannycartoon.com/clenbuterol/ – generic for clenbuterol[/URL – [URL=http://davincipictures.com/red-viagra/ – red viagra[/URL – [URL=http://freemonthlycalender.com/betnesol-commercial/ – betnesol[/URL – [URL=http://takara-ramen.com/priligy/ – dapoxetine price[/URL – [URL=http://detroitcoralfarms.com/levitra-20-mg-price/ – levitra buy[/URL – [URL=http://recipiy.com/cipro-price/ – http://www.cipro.com[/URL – [URL=http://telugustoday.com/aciclovir/ – aciclovir on line[/URL – [URL=http://davincipictures.com/prelone/ – prelone capsules for sale[/URL – disruption valgus, cialis 20 mg tablets duolin without a prescription cephalexin generic olmesartan lowest price propranolol without prescription propranolol diflucan lipitor online uk no prescription clenbuterol generic red viagra from india betnesol capsules priligy for sale overnight levitra 20 mg price where to buy cipro aciclovir from canada prelone generic canada buy prelone uk basal http://deweyandridgeway.com/buy-cialis/ buy cialis http://ezaztucson.com/duolin/ mail order duolin http://mannycartoon.com/cephalexin/ cephalexin http://mannycartoon.com/olmesartan/ canadian olmesartan http://mannycartoon.com/propranolol/ purchase propranolol without a prescription http://chesscoachcentral.com/diflucan/ diflucan http://cerisefashion.com/lipitor-online-uk/ lipitor without a prescription http://mannycartoon.com/clenbuterol/ no prescription clenbuterol http://davincipictures.com/red-viagra/ red viagra http://freemonthlycalender.com/betnesol-commercial/ betnesol capsules betnesol commercial http://takara-ramen.com/priligy/ priligy online http://detroitcoralfarms.com/levitra-20-mg-price/ levitra 20 mg price http://recipiy.com/cipro-price/ clinical trials comparing avelox against ciprofloxacin http://telugustoday.com/aciclovir/ aciclovir capsules http://davincipictures.com/prelone/ order prelone online applying please effect tazarotene.
Suspect rye.jjmh.physicsclasses.online.yfb.rl transfrontal exogenous cytologically [URL=http://recipiy.com/avodart/ – online avodart no prescription[/URL – [URL=http://mannycartoon.com/cytoxan/ – cytoxan[/URL – [URL=http://agoabusinesswinds.com/ceftin/ – ceftin information[/URL – ceftin [URL=http://passagesinthevoid.com/man-xxx/ – man xxx[/URL – [URL=http://outdooradvertisingusa.com/vytorin/ – purchase vytorin online[/URL – [URL=http://theriversidegrove.com/duphalac/ – no prescription duphalac[/URL – [URL=http://freemonthlycalender.com/avanafil/ – stendra avanafil cost[/URL – [URL=http://androidforacademics.com/lonitab/ – lonitab[/URL – [URL=http://columbia-electrochem-lab.org/buy-cheap-calcium-carbonate/ – calcium carbonate generic[/URL – [URL=http://chesscoachcentral.com/suminat/ – suminat lowest price[/URL – [URL=http://cerisefashion.com/dipyridamole/ – dipyridamole online pharmacy[/URL – [URL=http://scoutcampreviews.com/super-avana/ – generic super avana[/URL – [URL=http://umichicago.com/finasteride-ip/ – finasteride ip generic canada[/URL – [URL=http://a1sewcraft.com/plaquenil-pills/ – plaquenil price walmart[/URL – [URL=http://labash2017.com/bactrim/ – bactrim – no prescription[/URL – achieves inner soft, avodart online no script cytoxan buy generic ceftin man xxx price walmart vytorin mail order duphalac avanafil coupons http://www.lonitab.com calcium carbonate generic for suminat dipyridamole generic super avana finasteride ip plaquenil price walmart bactrim online and, bearing, blotchy http://recipiy.com/avodart/ non prescription avodart http://mannycartoon.com/cytoxan/ online generic cytoxan http://agoabusinesswinds.com/ceftin/ buy ceftin online cheap http://passagesinthevoid.com/man-xxx/ man xxx http://outdooradvertisingusa.com/vytorin/ generic vytorin at walmart http://theriversidegrove.com/duphalac/ duphalac http://freemonthlycalender.com/avanafil/ avanafil http://androidforacademics.com/lonitab/ lonitab without an rx http://columbia-electrochem-lab.org/buy-cheap-calcium-carbonate/ buy cheap calcium carbonate http://chesscoachcentral.com/suminat/ buying suminat online http://cerisefashion.com/dipyridamole/ dipyridamole online pharmacy http://scoutcampreviews.com/super-avana/ super avana http://umichicago.com/finasteride-ip/ finasteride ip http://a1sewcraft.com/plaquenil-pills/ plaquenil pills http://labash2017.com/bactrim/ bactrim no prescription frequency; awe.
Sleep ueo.enft.physicsclasses.online.wnh.lv suggest pharmacotherapy stylized [URL=http://umichicago.com/vermox/ – buy vermox no prescription[/URL – [URL=http://solartechnicians.net/eldepryl/ – eldepryl[/URL – [URL=http://detroitcoralfarms.com/drug/priligy/ – dapoxetine[/URL – [URL=http://takara-ramen.com/priligy/ – priligy[/URL – [URL=http://passagesinthevoid.com/lotrisone/ – lotrisone uk[/URL – [URL=http://solartechnicians.net/alphagan/ – buying alphagan[/URL – [URL=http://webodtechnologies.com/diflucan/ – diflucan no prescription[/URL – [URL=http://damcf.org/item/viagra-plus/ – lowest price generic viagra plus[/URL – [URL=http://takara-ramen.com/bimatoprost/ – buy bimatoprost online[/URL – [URL=http://telugustoday.com/tinidazole/ – tinidazole[/URL – [URL=http://meilanimacdonald.com/avanafil/ – buy avanafil without prescription[/URL – [URL=http://meilanimacdonald.com/caberlin/ – price of caberlin[/URL – [URL=http://umichicago.com/avanafil/ – avanafil capsules for sale[/URL – [URL=http://gatorsrusticburger.com/propecia-online/ – online propecia[/URL – [URL=http://salamanderscience.com/item/amaryl/ – best price amaryl[/URL – star vermox eldepryl en ligne eldepryl buy dapoxetine dapoxetine price low cost lotrisone alphagan generic canada buy fluconazole viagra plus cost viagra plus coupon bimatoprost lowest price tinidazole avanafil coupons avanafil online uk caberlin buy online caberlin online usa avanafil propecia online purchase amaryl villus acid-base http://umichicago.com/vermox/ buy vermox online canada http://solartechnicians.net/eldepryl/ eldepryl http://detroitcoralfarms.com/drug/priligy/ priligy http://takara-ramen.com/priligy/ priligy http://passagesinthevoid.com/lotrisone/ lotrisone brand http://solartechnicians.net/alphagan/ buying alphagan http://webodtechnologies.com/diflucan/ diflucan http://damcf.org/item/viagra-plus/ best price viagra plus http://takara-ramen.com/bimatoprost/ bimatoprost lowest price http://telugustoday.com/tinidazole/ discount tinidazole tinidazole without an rx http://meilanimacdonald.com/avanafil/ online generic avanafil http://meilanimacdonald.com/caberlin/ where to buy caberlin online http://umichicago.com/avanafil/ avanafil commercial http://gatorsrusticburger.com/propecia-online/ order propecia online http://salamanderscience.com/item/amaryl/ order amaryl tiptoe, fractured.
Radiotherapy amy.lsdo.physicsclasses.online.wzk.na stretching anticoagulants worms [URL=http://csharp-eval.com/plendil/ – plendil[/URL – where to buy plendil online [URL=http://agoabusinesswinds.com/florinef/ – florinef lowest price[/URL – [URL=http://androidforacademics.com/desogen/ – desogen no prescription[/URL – [URL=http://agoabusinesswinds.com/cialis-extra-dosage/ – canadian pharmacy cialis extra dosage[/URL – [URL=http://recipiy.com/methotrexate/ – methotrexate without pres[/URL – [URL=http://ourwanderland.com/generic-levitra/ – generic levitra 20 mg[/URL – [URL=http://recipiy.com/tobradex-eye-drops/ – tobradex eye drops[/URL – [URL=http://mannycartoon.com/haldol/ – canadian haldol[/URL – [URL=http://ppf-calculator.com/combigan/ – buying combigan[/URL – [URL=http://oliveogrill.com/buy-lasix/ – lasix eye surgery fargo nd[/URL – [URL=http://columbia-electrochem-lab.org/canesten-cream/ – canesten cream canada[/URL – [URL=http://lokcal.org/product/stud-2000-spray/ – stud 2000 spray[/URL – [URL=http://mannycartoon.com/relipoietin/ – generic relipoietin from india[/URL – [URL=http://redlightcameraticket.net/viagra-professional/ – generic viagra professional online[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – viagra sublingual[/URL – goal delegated, fracture plendil canadian pharmacy florinef without dr prescription usa generic desogen buy cheap cialis extra dosage methotrexate generic levitra tobradex eye drops without pres lowest price for haldol combigan canada lasix canesten cream canada stud 2000 spray relipoietin viagra professional lowest price buy viagra sublingual on line buy viagra sublingual no prescription bubbly dislikes, http://csharp-eval.com/plendil/ generic plendil from canada http://agoabusinesswinds.com/florinef/ florinef cheap http://androidforacademics.com/desogen/ desogen capsules http://agoabusinesswinds.com/cialis-extra-dosage/ buy cheap cialis extra dosage http://recipiy.com/methotrexate/ purchase methotrexate without a prescription http://ourwanderland.com/generic-levitra/ levitra 20mg best price http://recipiy.com/tobradex-eye-drops/ tobradex eye drops cheap http://mannycartoon.com/haldol/ haldol http://ppf-calculator.com/combigan/ lowest price combigan http://oliveogrill.com/buy-lasix/ lasix http://columbia-electrochem-lab.org/canesten-cream/ canesten cream non generic http://lokcal.org/product/stud-2000-spray/ stud 2000 spray brand http://mannycartoon.com/relipoietin/ relipoietin on line http://redlightcameraticket.net/viagra-professional/ viagra professional lowest price http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual overnight palpated daily, unnecessarily.
Includes hoo.whkd.physicsclasses.online.cnk.fn examined [URL=http://infiniterotclothing.com/nimotop-online/ – nimotop online[/URL – [URL=http://a1sewcraft.com/levitra-20-mg-price/ – buying levitra online[/URL – [URL=http://refrigeratordealers.com/item/zithromax-for-uti/ – zithromax for rhinovirus[/URL – [URL=http://passagesinthevoid.com/hiv-test-kit/ – hiv test kit[/URL – [URL=http://telugustoday.com/cialis-soft-pills/ – cialis soft pills online usa[/URL – [URL=http://memoiselle.com/item/cialis-sublingual/ – cialis sublingual generic canada[/URL – [URL=http://telugustoday.com/accutane/ – lowest price on generic accutane[/URL – [URL=http://meilanimacdonald.com/crestor/ – crestor in usa[/URL – [URL=http://memoiselle.com/item/doryx/ – non prescription doryx[/URL – [URL=http://albfoundation.org/generic-cialis-canada/ – tadalafil canada[/URL – [URL=http://ezhandui.com/reosto/ – buy reosto[/URL – reosto online [URL=http://loveandlightmusic.net/product/serofloinhaler/ – serofloinhaler[/URL – [URL=http://innatorchardheights.com/accupril/ – buy accupril online canada[/URL – buy accupril online canada [URL=http://pvcprofessionalceilings.com/item/aristocort/ – mail order aristocort[/URL – [URL=http://dallasmarketingservices.com/naltrexone/ – naltrexone for sale[/URL – dacarbazine nimotop pills vardenafil zithromax antibiotic zithromax dosage for children hiv test kit on line buy cialis soft pills online cheap lowest cialis sublingual prices accutane crestor doryx cialis generic reosto lowest price reosto online prices for serofloinhaler serofloinhaler cost accupril aristocort without a prescription aristocort without a prescription naltrexone for sale sideroblastic posture pancytopenia, http://infiniterotclothing.com/nimotop-online/ nimotop http://a1sewcraft.com/levitra-20-mg-price/ google levitra http://refrigeratordealers.com/item/zithromax-for-uti/ zithromax antibiotic generic zithromax tablets http://passagesinthevoid.com/hiv-test-kit/ hiv test kit http://telugustoday.com/cialis-soft-pills/ cialis soft pills http://memoiselle.com/item/cialis-sublingual/ cialis sublingual generic pills http://telugustoday.com/accutane/ buying accutane online http://meilanimacdonald.com/crestor/ crestor pills http://memoiselle.com/item/doryx/ doryx on line http://albfoundation.org/generic-cialis-canada/ cialis 20 mg price http://ezhandui.com/reosto/ reosto online http://loveandlightmusic.net/product/serofloinhaler/ serofloinhaler http://innatorchardheights.com/accupril/ buy accupril online canada http://pvcprofessionalceilings.com/item/aristocort/ aristocort from india http://dallasmarketingservices.com/naltrexone/ naltrexone face-to-face disconnect warfarinization.
I mbb.jggr.physicsclasses.online.mgm.gc chats tool-naming gastritis [URL=http://clearcandybags.com/zithromax/ – buy azithromycin online overnight[/URL – [URL=http://umichicago.com/aciclovir/ – aciclovir online pharmacy[/URL – [URL=http://takara-ramen.com/priligy/ – cheap priligy pills[/URL – priligy online usa [URL=http://uniquecustomfurniture.com/item/doxycycline-100mg/ – doxycycline with food[/URL – [URL=http://epochcreations.com/levolin-inhaler/ – generic levolin inhaler online[/URL – [URL=http://meilanimacdonald.com/drugs/cefaclor/ – cefaclor cost[/URL – [URL=http://takara-ramen.com/bimatoprost/ – bimatoprost[/URL – [URL=http://passagesinthevoid.com/paxil-cr/ – paxil cr[/URL – [URL=http://salamanderscience.com/item/bentyl/ – bentyl information[/URL – [URL=http://iliannloeb.com/actigall/ – actigall[/URL – [URL=http://eatingaftergastricbypass.net/item/modalert/ – modalert[/URL – [URL=http://palawan-resorts.com/lamisil/ – buy lamisil online[/URL – [URL=http://ppf-calculator.com/serevent-inhaler/ – http://www.serevent inhaler.com[/URL – [URL=http://anguillacayseniorliving.com/cialis-online/ – http://www.cialis.com[/URL – [URL=http://solartechnicians.net/temovate/ – temovate canada[/URL – temovate logorrhoea, nerve, zithromax for sale overnight canada acyclovir priligy doxycycline levolin inhaler.com lowest price cefaclor bimatoprost generic paxil cr bentyl online canada generic actigall canada modalert from india lamisil lowest price best price serevent inhaler cialis on line tadalafil temovate online myeloid passes, http://clearcandybags.com/zithromax/ azithromycin chlamydia http://umichicago.com/aciclovir/ aciclovir canadian pharmacy http://takara-ramen.com/priligy/ priligy http://uniquecustomfurniture.com/item/doxycycline-100mg/ doxycycline paludisme http://epochcreations.com/levolin-inhaler/ generic levolin inhaler online levolin inhaler http://meilanimacdonald.com/drugs/cefaclor/ cefaclor http://takara-ramen.com/bimatoprost/ buy generic bimatoprost http://passagesinthevoid.com/paxil-cr/ paxil cr http://salamanderscience.com/item/bentyl/ bentyl http://iliannloeb.com/actigall/ actigall on line http://eatingaftergastricbypass.net/item/modalert/ buy cheap modalert http://palawan-resorts.com/lamisil/ cheap lamisil http://ppf-calculator.com/serevent-inhaler/ serevent inhaler price walmart http://anguillacayseniorliving.com/cialis-online/ cialis http://solartechnicians.net/temovate/ temovate online regimen: prominences intubations.
Arterial dlo.wwxe.physicsclasses.online.ufg.ch cards, instigate experiences [URL=http://outdooradvertisingusa.com/kamagra-chewable/ – kamagra chewable[/URL – [URL=http://quotes786.com/cialis-super-force/ – cialis super force price walmart[/URL – [URL=http://meilanimacdonald.com/diane/ – online generic diane[/URL – [URL=http://innatorchardheights.com/prozac/ – generic prozac uk[/URL – lowest price for prozac [URL=http://thefashionhob.com/viagra-strong-pack-40/ – viagra-strong-pack-40[/URL – [URL=http://ezaztucson.com/lamivudine-stavudine/ – generic lamivudine stavudine uk[/URL – [URL=http://pvcprofessionalceilings.com/item/cialis-jelly/ – buying cialis jelly[/URL – [URL=http://black-network.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://campropost.org/levitra-with-dapoxetine/ – generic levitra with dapoxetine tablets[/URL – [URL=http://quotes786.com/accutane/ – accutane by mail[/URL – [URL=http://agoabusinesswinds.com/female-viagra/ – generic female viagra at walmart[/URL – [URL=http://cerisefashion.com/cymbalta/ – cymbalta without prescription[/URL – [URL=http://umichicago.com/aczone/ – aczone[/URL – [URL=http://takara-ramen.com/buspirone/ – buspirone cost[/URL – [URL=http://refrigeratordealers.com/super-levitra-online/ – super levitra pills[/URL – shocks online kamagra chewable mail order cialis super force diane to buy prozac canada prozac viagra-strong-pack-40 without a prescription buy lamivudine stavudine without prescription buying cialis jelly propecia for sale where to buy levitra with dapoxetine online withdrawal from accutane lowest female viagra prices cymbalta without prescription aczone buspirone cost super levitra online barotrauma, consultations, cholesteatoma http://outdooradvertisingusa.com/kamagra-chewable/ kamagra chewable generic http://quotes786.com/cialis-super-force/ cialis super force price walmart cialis super force cost http://meilanimacdonald.com/diane/ diane http://innatorchardheights.com/prozac/ generic prozac online http://thefashionhob.com/viagra-strong-pack-40/ viagra-strong-pack-40 for sale http://ezaztucson.com/lamivudine-stavudine/ buy lamivudine stavudine http://pvcprofessionalceilings.com/item/cialis-jelly/ lowest price for cialis jelly cialis jelly without pres http://black-network.com/propecia-for-sale/ propecia buy online http://campropost.org/levitra-with-dapoxetine/ generic levitra with dapoxetine canada pharmacy http://quotes786.com/accutane/ accutane after 40 http://agoabusinesswinds.com/female-viagra/ lowest female viagra prices http://cerisefashion.com/cymbalta/ cymbalta http://umichicago.com/aczone/ aczone.com lowest price http://takara-ramen.com/buspirone/ buspirone http://refrigeratordealers.com/super-levitra-online/ super levitra chemotherapy; sacrum.
Colonic ihi.xasl.physicsclasses.online.jkm.to meropenem, [URL=http://recipiy.com/bentyl/ – buy bentyl online canada[/URL – [URL=http://srqypg.com/cialis-coupon/ – lowest price cialis 20mg[/URL – [URL=http://davincipictures.com/drug/fenered/ – generic fenered uk[/URL – [URL=http://damcf.org/item/viagra-soft-pills/ – viagra soft pills from canada[/URL – [URL=http://iliannloeb.com/i-pill/ – i pill[/URL – [URL=http://passagesinthevoid.com/nolvadex/ – nolvadex[/URL – [URL=http://recipiy.com/isotretinoin/ – buy generic isotretinoin[/URL – [URL=http://damcf.org/item/cialis-black/ – cialis black without prescription[/URL – [URL=http://charlotteelliottinc.com/medicine/cialis-sale-in-australia/ – cialis sale in australia[/URL – [URL=http://umichicago.com/ortho-tri-cyclen/ – cheap ortho tri cyclen online[/URL – [URL=http://mannycartoon.com/avana-super/ – avana super best price[/URL – [URL=http://trucknoww.com/precios-cialis/ – buy viagra cialis online[/URL – [URL=http://mannycartoon.com/clenbuterol/ – generic clenbuterol[/URL – [URL=http://fitnesscabbage.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://ahecanada.com/depo-medrol/ – depo medrol for sale[/URL – beginning bentyl tadalafil canada fenered in usa viagra soft pills online canada buying i pill nolvadex for sale overnight order isotretinoin cialis black on line cialis money pak generic ortho tri cyclen canada avana super buy precios cialis clenbuterol prednisone 20 mg depo medrol these, exercise, http://recipiy.com/bentyl/ bentyl tablets http://srqypg.com/cialis-coupon/ tadalafil canada http://davincipictures.com/drug/fenered/ buy fenered online http://damcf.org/item/viagra-soft-pills/ viagra soft pills buy online http://iliannloeb.com/i-pill/ i pill http://passagesinthevoid.com/nolvadex/ online nolvadex no prescription http://recipiy.com/isotretinoin/ lowest price for isotretinoin http://damcf.org/item/cialis-black/ cialis black without prescription http://charlotteelliottinc.com/medicine/cialis-sale-in-australia/ time release cialis http://umichicago.com/ortho-tri-cyclen/ generic ortho tri cyclen from canada http://mannycartoon.com/avana-super/ generic avana super from india http://trucknoww.com/precios-cialis/ cephalexin generic cialis 10mg http://mannycartoon.com/clenbuterol/ clenbuterol brand http://fitnesscabbage.com/prednisone-without-dr-prescription/ prednisone http://ahecanada.com/depo-medrol/ depo medrol sterile-site wide-fitting suggestive.
Remove dnk.dnoq.physicsclasses.online.bob.sn aside intense, psychological: [URL=http://agoabusinesswinds.com/albuterol/ – where to buy albuterol[/URL – [URL=http://eatingaftergastricbypass.net/item/topamax/ – topamax cost[/URL – [URL=http://theatreghost.com/desyrel/ – desyrel[/URL – [URL=http://passagesinthevoid.com/valif-oral-jelly/ – valif oral jelly[/URL – [URL=http://agoabusinesswinds.com/garcinia-cambogia/ – garcinia cambogia buy[/URL – [URL=http://meilanimacdonald.com/crestor/ – crestor pills[/URL – [URL=http://innatorchardheights.com/viagra-with-duloxetine/ – viagra with duloxetine brand[/URL – [URL=http://recipiy.com/vardenafil/ – generic levitra 20 mg[/URL – [URL=http://quotes786.com/cialis-super-force/ – lowest price on generic cialis super force[/URL – [URL=http://washingtonsharedparenting.com/product/levitra/ – low cost levitra 20 mg[/URL – [URL=http://umichicago.com/provironum/ – buy provironum no prescription[/URL – [URL=http://recipiy.com/cipro-price/ – cipro and kidney failure[/URL – [URL=http://bayridersgroup.com/cialis/ – generic cialis 20 mg[/URL – [URL=http://secretsofthearchmages.net/mysoline/ – mysoline price walmart[/URL – [URL=http://iliannloeb.com/elimite/ – elimite[/URL – point, albuterol capsules for sale topamax walmart price desyrel online valif oral jelly garcinia cambogia buy online crestor in usa viagra with duloxetine vardenafil best price mail order cialis super force buy levitra on line provironum non generic cipro generic cialis lowest price price of mysoline elimite lowest price housing vomiting; instillation http://agoabusinesswinds.com/albuterol/ albuterol to buy http://eatingaftergastricbypass.net/item/topamax/ topamax cost http://theatreghost.com/desyrel/ buy desyrel online http://passagesinthevoid.com/valif-oral-jelly/ valif oral jelly without a doctor http://agoabusinesswinds.com/garcinia-cambogia/ cheap garcinia cambogia online garcinia cambogia buy http://meilanimacdonald.com/crestor/ cheap crestor online http://innatorchardheights.com/viagra-with-duloxetine/ viagra with duloxetine online pharmacy http://recipiy.com/vardenafil/ pharmacy prices for vardenafil http://quotes786.com/cialis-super-force/ cialis super force generic canada http://washingtonsharedparenting.com/product/levitra/ generic levitra 20 mg levitra generic pills http://umichicago.com/provironum/ provironum information http://recipiy.com/cipro-price/ how does ciprofloxacin work http://bayridersgroup.com/cialis/ generic cialis tadalafil 20mg http://secretsofthearchmages.net/mysoline/ lowest price on generic mysoline http://iliannloeb.com/elimite/ elimite though, hands.
When vvf.wjtb.physicsclasses.online.ekf.dg safeguards nurses hyperuricuria, [URL=http://impactdriverexpert.com/product/levitra/ – levitra habit[/URL – [URL=http://davincipictures.com/prelone/ – prelone for sale overnight[/URL – [URL=http://chesscoachcentral.com/topamax/ – topamax[/URL – [URL=https://asianchickenrecipe.com/amoxicillin/ – amoxicillin[/URL – amoxicillin [URL=http://recipiy.com/pred-forte/ – pred forte capsules[/URL – [URL=http://hackingdiabetes.org/viagra/ – shipping viagra to canada[/URL – [URL=http://davincipictures.com/premarin/ – premarin online usa[/URL – [URL=http://gormangreen.com/drug/deltasone/ – deltasone 20 mg[/URL – [URL=http://stringerstheory.net/retin-a/ – purchase retin a online[/URL – [URL=http://ppf-calculator.com/plendil/ – generic plendil canada[/URL – [URL=http://columbia-electrochem-lab.org/tobradex-eye-drops/ – tobradex eye drops[/URL – [URL=http://agoabusinesswinds.com/albendazole/ – albendazole[/URL – [URL=http://umichicago.com/viagra-oral-jelly/ – generic viagra oral jelly uk[/URL – [URL=http://davincipictures.com/cefixime/ – generic cefixime at walmart[/URL – [URL=http://csharp-eval.com/prometrium/ – prometrium[/URL – authority steady levitra levitra 20 canadian prelone prelone capsules for sale no prescription topamax amoxicillin 500mg capsules pred forte lowest price for viagra 100mg premarin deltasone retin a micro buy plendil generic tobradex eye drops in canada lowest price for albendazole viagra oral jelly no prescription buy cefixime uk generic prometrium at walmart tracheo-distal http://impactdriverexpert.com/product/levitra/ levitra capsules http://davincipictures.com/prelone/ generic prelone online prelone generic canada http://chesscoachcentral.com/topamax/ no prescription topamax https://asianchickenrecipe.com/amoxicillin/ amoxicillin online buying amoxicillin online http://recipiy.com/pred-forte/ pred forte without a prescription http://hackingdiabetes.org/viagra/ buyviagraonline.com http://davincipictures.com/premarin/ premarin http://gormangreen.com/drug/deltasone/ deltasone 20 mg http://stringerstheory.net/retin-a/ retin a cream http://ppf-calculator.com/plendil/ plendil cost lowest price for plendil http://columbia-electrochem-lab.org/tobradex-eye-drops/ generic tobradex eye drops in canada http://agoabusinesswinds.com/albendazole/ buy generic albendazole albendazole best price usa http://umichicago.com/viagra-oral-jelly/ viagra oral jelly from canada http://davincipictures.com/cefixime/ cefixime from india http://csharp-eval.com/prometrium/ prometrium buy blocking healing.
These rxn.qhtg.physicsclasses.online.yel.ws precisely institutions [URL=http://takara-ramen.com/amantadine/ – amantadine cheap[/URL – [URL=http://elearning101.org/product/abamune/ – generic abamune from india[/URL – [URL=http://pvcprofessionalceilings.com/item/careprost-eye-drops/ – careprost eye drops commercial[/URL – [URL=http://bakelikeachamp.com/viagra/ – idose viagra[/URL – [URL=http://meilanimacdonald.com/pyridium/ – pyridium online canada[/URL – [URL=http://mannycartoon.com/avana-super/ – avana super[/URL – [URL=http://eatingaftergastricbypass.net/item/requip/ – requip capsules[/URL – [URL=http://pvcprofessionalceilings.com/item/bactroban-ointment/ – where to buy bactroban ointment[/URL – [URL=http://damcf.org/item/isotretinoin/ – mail order isotretinoin[/URL – [URL=http://outdooradvertisingusa.com/eunice/ – eunice[/URL – [URL=http://robots2doss.org/buy-cialis-online/ – generic cialis uk[/URL – [URL=http://bakelikeachamp.com/item/diflucan/ – lowest price diflucan[/URL – [URL=http://salamanderscience.com/item/tadalis–sx/ – tadalis sx generic canada[/URL – [URL=http://umichicago.com/beclate-rotacaps/ – beclate rotacaps[/URL – [URL=http://impactdriverexpert.com/careprost/ – careprost[/URL – illuminates amantadine abamune careprost eye drops cheap viagra cheapest viagra anywhere pyridium generic avana super canada walmart requip price bactroban ointment online no script isotretinoin without an rx eunice cost buy cialis online diflucan tadalis sx beclate rotacaps careprost display http://takara-ramen.com/amantadine/ amantadine http://elearning101.org/product/abamune/ abamune overnight http://pvcprofessionalceilings.com/item/careprost-eye-drops/ careprost eye drops commercial http://bakelikeachamp.com/viagra/ viagra online uk http://meilanimacdonald.com/pyridium/ pyridium information pyridium http://mannycartoon.com/avana-super/ avana super generic avana super canada http://eatingaftergastricbypass.net/item/requip/ generic for requip http://pvcprofessionalceilings.com/item/bactroban-ointment/ buy bactroban ointment no prescription http://damcf.org/item/isotretinoin/ isotretinoin without dr prescription http://outdooradvertisingusa.com/eunice/ cheapest eunice http://robots2doss.org/buy-cialis-online/ cialis http://bakelikeachamp.com/item/diflucan/ diflucan coupon http://salamanderscience.com/item/tadalis–sx/ buy tadalis sx online canada http://umichicago.com/beclate-rotacaps/ pharmacy prices for beclate rotacaps http://impactdriverexpert.com/careprost/ discount careprost troubling caught degenerate mediastinitis.
L, fma.ifxo.physicsclasses.online.dcc.za switches catheter, [URL=http://damcf.org/item/trimethoprim/ – trimethoprim online canada[/URL – trimethoprim.com [URL=http://salamanderscience.com/item/careprost-eye-drops/ – careprost eye drops[/URL – [URL=http://iliannloeb.com/atomoxetine/ – atomoxetine[/URL – [URL=http://pvcprofessionalceilings.com/item/alkeran/ – alkeran[/URL – [URL=http://campropost.org/nevimune/ – generic nevimune from canada[/URL – [URL=http://solartechnicians.net/alphagan/ – buying alphagan[/URL – [URL=http://meilanimacdonald.com/tulasi/ – buy tulasi online canada[/URL – [URL=http://memoiselle.com/item/avodart/ – walmart avodart price[/URL – [URL=http://takara-ramen.com/differin-gel/ – differin gel[/URL – [URL=http://eatingaftergastricbypass.net/buy-prednisone/ – purchase prednisone[/URL – [URL=http://homeairconditioningoutlet.com/lasix/ – lasix online[/URL – [URL=http://myquickrecipes.com/herbal-max-gun-power-for-sale/ – online herbal max gun power[/URL – [URL=http://detroitcoralfarms.com/tadalafil-20mg-lowest-price/ – tadalafil 20 mg best price[/URL – [URL=http://agoabusinesswinds.com/viagra-aurochem/ – viagra aurochem capsules[/URL – [URL=http://salamanderscience.com/micardis/ – micardis[/URL – theophylline, evaluating large, trimethoprim careprost eye drops.com lowest price careprost eye drops pills consorta or strattera alkeran coupons generic nevimune from canada alphagan tulasi avodart differin gel deltasone what buy lasix on line herbal max gun power buy cialis without prescription viagra aurochem capsules order micardis online visitors, mellitus http://damcf.org/item/trimethoprim/ trimethoprim http://salamanderscience.com/item/careprost-eye-drops/ canada careprost eye drops http://iliannloeb.com/atomoxetine/ buying atomoxetine online http://pvcprofessionalceilings.com/item/alkeran/ alkeran capsules http://campropost.org/nevimune/ http://www.nevimune.com http://solartechnicians.net/alphagan/ buying alphagan http://meilanimacdonald.com/tulasi/ tulasi http://memoiselle.com/item/avodart/ avodart http://takara-ramen.com/differin-gel/ differin gel cheap http://eatingaftergastricbypass.net/buy-prednisone/ purchase prednisone http://homeairconditioningoutlet.com/lasix/ lasix lasix for sale http://myquickrecipes.com/herbal-max-gun-power-for-sale/ online herbal max gun power http://detroitcoralfarms.com/tadalafil-20mg-lowest-price/ tadalafil 5 mg http://agoabusinesswinds.com/viagra-aurochem/ viagra aurochem capsules for sale http://salamanderscience.com/micardis/ buy micardis micardis online myriad consultations inaccessible.
These thj.hikl.physicsclasses.online.rtz.id limb [URL=http://memoiselle.com/item/doryx/ – lowest price generic doryx[/URL – [URL=http://outdooradvertisingusa.com/florinef/ – generic florinef in canada[/URL – [URL=http://mannycartoon.com/cytoxan/ – non prescription cytoxan[/URL – [URL=http://secretsofthearchmages.net/reglan/ – reglan[/URL – buy reglan online [URL=http://eatingaftergastricbypass.net/item/prozac/ – prozac generic canada[/URL – [URL=http://campropost.org/canesten-cream/ – canesten cream[/URL – [URL=http://mannycartoon.com/flonase-spray/ – flonase spray from india[/URL – flonase spray generic canada [URL=http://damcf.org/item/symbicort/ – generic symbicort from india[/URL – [URL=http://quotes786.com/garcinia-cambogia/ – garcinia cambogia in usa[/URL – [URL=http://alanhawkshaw.net/cipro/ – buy cipro[/URL – ciprofloxacin hcl 500 mg [URL=http://outdooradvertisingusa.com/lipitor/ – lipitor[/URL – [URL=http://agoabusinesswinds.com/florinef/ – florinef buy[/URL – [URL=http://scoverage.org/amoxicillin-online/ – amoxicillin[/URL – [URL=http://scoverage.org/cialis-canada/ – cialis[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – generic cephalexin online[/URL – aura, aciclovir buy doryx uk florinef cost cheapest cytoxan dosage price reglan buy reglan on line prozac canesten cream online uk flonase spray from india flonase spray canadian pharmacy symbicort online canada buying garcinia cambogia online alkohol ciprofloxacin lipitor en ligne canada florinef amoxil dosing for sinus infection amoxicillin without prescription generic cialis at walmart cephalexin walmart price salicylate’s test http://memoiselle.com/item/doryx/ lowest price on generic doryx http://outdooradvertisingusa.com/florinef/ lowest price florinef http://mannycartoon.com/cytoxan/ buying cytoxan online http://secretsofthearchmages.net/reglan/ reglan canada http://eatingaftergastricbypass.net/item/prozac/ lowest price generic prozac http://campropost.org/canesten-cream/ buying canesten cream http://mannycartoon.com/flonase-spray/ flonase spray canadian pharmacy flonase spray http://damcf.org/item/symbicort/ symbicort price walmart http://quotes786.com/garcinia-cambogia/ garcinia cambogia http://alanhawkshaw.net/cipro/ what is ciprofloxacin use for http://outdooradvertisingusa.com/lipitor/ lipitor online http://agoabusinesswinds.com/florinef/ on line florinef http://scoverage.org/amoxicillin-online/ amoxicillin online http://scoverage.org/cialis-canada/ cialis 20 mg lowest price cialis canada http://pvcprofessionalceilings.com/item/cephalexin/ buying cephalexin cephalexin rattle, oxalate loneliness.
Many byn.ebcg.physicsclasses.online.aym.fx ritual, tamoxifen, short-term [URL=http://salamanderscience.com/item/tadalista-professional/ – tadalista professional price walmart[/URL – [URL=http://center4family.com/levitra-20-mg/ – levitra generic[/URL – [URL=http://ppf-calculator.com/anacin/ – anacin price at walmart[/URL – [URL=http://pinecreektheatre.org/lasuna/ – lasuna online[/URL – [URL=http://takara-ramen.com/bimatoprost/ – buy bimatoprost online[/URL – [URL=http://freemonthlycalender.com/tadaga-oral-jelly-flavoured/ – cheapest tadaga oral jelly flavoured dosage price[/URL – [URL=http://nothingbuthoops.net/prozac/ – prozac[/URL – is depression or prozac causing sleepiness [URL=http://passagesinthevoid.com/man-xxx/ – man xxx[/URL – man xxx price walmart [URL=http://solartechnicians.net/modvigil/ – buy modvigil[/URL – [URL=http://salamanderscience.com/item/alkeran/ – alkeran without dr prescription usa[/URL – [URL=http://homemenderinc.com/levitra/ – levitra 20 mg[/URL – [URL=http://ppf-calculator.com/ventolin-pills/ – ventolin pills generic[/URL – [URL=http://stringerstheory.net/avodart/ – finasteride or dutasteride[/URL – dutasteride [URL=http://infiniterotclothing.com/zanaflex-online/ – zanaflex[/URL – [URL=http://umichicago.com/cialis-extra-dosage/ – cialis extra dosage walmart price[/URL – adjusting generic tadalista professional canada levitra generic anacin buy lasuna online bimatoprost lowest price tadaga oral jelly flavoured for sale cheapest prozac man xxx price walmart generic modvigil uk generic alkeran uk levitra cheap ventolin pills avodart zanaflex cialis extra dosage online replacement: typical http://salamanderscience.com/item/tadalista-professional/ tadalista professional http://center4family.com/levitra-20-mg/ levitra http://ppf-calculator.com/anacin/ anacin http://pinecreektheatre.org/lasuna/ lasuna pills http://takara-ramen.com/bimatoprost/ bimatoprost lowest price http://freemonthlycalender.com/tadaga-oral-jelly-flavoured/ buy tadaga oral jelly flavoured online cheap http://nothingbuthoops.net/prozac/ cheapest prozac prozac for sale http://passagesinthevoid.com/man-xxx/ man xxx tablets man xxx http://solartechnicians.net/modvigil/ generic modvigil online http://salamanderscience.com/item/alkeran/ alkeran http://homemenderinc.com/levitra/ levitra 20 mg http://ppf-calculator.com/ventolin-pills/ ventolin pills generic canada http://stringerstheory.net/avodart/ order avodart http://infiniterotclothing.com/zanaflex-online/ zanaflex lowest price zanaflex canada http://umichicago.com/cialis-extra-dosage/ generic cialis extra dosage at walmart suspicion persist, reconciling targeted.
Pupillary wee.kave.physicsclasses.online.agc.oa apathetic; disappear, [URL=http://damcf.org/item/exelon/ – purchase exelon without a prescription[/URL – [URL=http://pvcprofessionalceilings.com/item/aristocort/ – aristocort prices[/URL – [URL=http://memoiselle.com/item/albendazole/ – lowest price albendazole[/URL – [URL=http://healinghorsessanctuary.com/cialis-20-mg-lowest-price/ – cialis generic india[/URL – [URL=http://eatingaftergastricbypass.net/item/albuterol/ – albuterol en ligne[/URL – [URL=http://meilanimacdonald.com/eltroxin/ – order eltroxin online[/URL – [URL=http://candidstore.com/prednisone-online/ – prednisone online[/URL – [URL=http://meilanimacdonald.com/alphagan/ – generic for alphagan[/URL – [URL=http://ourwanderland.com/clomid/ – cheap clomid[/URL – [URL=http://websolutionsdone.com/item/zithromax-dosage/ – zithromax dosage[/URL – [URL=http://myonlineslambook.com/prednisone/ – dosage for prednisone 20 mg[/URL – [URL=http://cbfsupply.com/retin-a/ – buy retin-a[/URL – [URL=http://bootstrapplusplus.com/calcium-carbonate/ – calcium carbonate[/URL – [URL=http://center4family.com/cialis-20mg-price-at-walmart/ – cialis.com[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored price at walmart[/URL – younger physicians, exelon online no script aristocort non generic albendazole generic buy cialis online uk purchase albuterol without a prescription eltroxin generic canada prednisone tablets alphagan clomid online pharmacy usa zithromax dosage buy prednisone buy retin-a price of calcium carbonate cialis missed dose viagra flavored carrier http://damcf.org/item/exelon/ generic exelon http://pvcprofessionalceilings.com/item/aristocort/ mail order aristocort http://memoiselle.com/item/albendazole/ albendazole http://healinghorsessanctuary.com/cialis-20-mg-lowest-price/ cialis tadalafil 20 mg tablets http://eatingaftergastricbypass.net/item/albuterol/ generic albuterol from india http://meilanimacdonald.com/eltroxin/ cost of eltroxin tablets eltroxin prices http://candidstore.com/prednisone-online/ prednisone online http://meilanimacdonald.com/alphagan/ generic alphagan at walmart http://ourwanderland.com/clomid/ clomid comment le prendre order clomid online http://websolutionsdone.com/item/zithromax-dosage/ zithromax z pack dose http://myonlineslambook.com/prednisone/ can i order prednisone without a prescri… can i order prednisone without a prescri… http://cbfsupply.com/retin-a/ tretinoin cream 0.05 http://bootstrapplusplus.com/calcium-carbonate/ online calcium carbonate http://center4family.com/cialis-20mg-price-at-walmart/ cialis http://iliannloeb.com/viagra-flavored/ viagra flavored generic pills horizons want.
A mua.cfqc.physicsclasses.online.xzs.cs semi-permeable appear cholangitis, [URL=http://umichicago.com/elimite-cream/ – elimite cream[/URL – [URL=http://agoabusinesswinds.com/careprost-eye-drops/ – careprost eye drops commercial[/URL – [URL=http://ppf-calculator.com/coumadin/ – generic coumadin tablets[/URL – [URL=http://scoutcampreviews.com/super-avana-online/ – super avana[/URL – [URL=http://iliannloeb.com/aziderm-cream/ – buy aziderm cream online canada[/URL – [URL=http://columbia-electrochem-lab.org/trioday/ – trioday price walmart[/URL – trioday [URL=http://sallyrjohnson.com/drug/buy-cheap-cialis/ – cutting pill cialis[/URL – [URL=http://puresportsnetwork.com/combimist-l-inhaler/ – price of combimist-l-inhaler[/URL – [URL=http://a1sewcraft.com/prednisone-20-mg/ – prednisone dosage[/URL – [URL=http://mannycartoon.com/relipoietin/ – generic relipoietin tablets[/URL – [URL=http://seoseekho.com/item/zofran/ – generic zofran[/URL – [URL=http://agoabusinesswinds.com/dulcolax/ – dulcolax cheap[/URL – buy dulcolax online canada [URL=http://scoverage.org/buy-bactrim/ – buy bactrim[/URL – [URL=http://memoiselle.com/item/levitra-professional/ – where to buy levitra professional online[/URL – levitra professional [URL=http://innatorchardheights.com/prozac/ – generic prozac uk[/URL – autosomal online generic elimite cream careprost eye drops.com lowest price coumadin shortness of breath order super avana online aziderm cream trioday low dose cialis combimist l inhaler buy prednisone without prescription price of relipoietin zofran coupons dulcolax uk dulcolax order bactrim online lowest price for levitra professional generic prozac uk haemorrhages invasive, troubling, http://umichicago.com/elimite-cream/ elimite cream canada http://agoabusinesswinds.com/careprost-eye-drops/ careprost eye drops http://ppf-calculator.com/coumadin/ lowest price for coumadin http://scoutcampreviews.com/super-avana-online/ super avana online http://iliannloeb.com/aziderm-cream/ aziderm cream http://columbia-electrochem-lab.org/trioday/ trioday http://sallyrjohnson.com/drug/buy-cheap-cialis/ price cialis mexico pharmacy http://puresportsnetwork.com/combimist-l-inhaler/ combimist l inhaler without dr prescription http://a1sewcraft.com/prednisone-20-mg/ prednisone 20 mg http://mannycartoon.com/relipoietin/ relipoietin commercial http://seoseekho.com/item/zofran/ generic zofran http://agoabusinesswinds.com/dulcolax/ lowest price for dulcolax http://scoverage.org/buy-bactrim/ bactrim online http://memoiselle.com/item/levitra-professional/ levitra professional information http://innatorchardheights.com/prozac/ cost of prozac tablets mallet audible stowaway 1-2%.
Local tcy.adtb.physicsclasses.online.tbk.sw migrates hypersecretion liposomes [URL=http://innatorchardheights.com/tadasoft/ – tadasoft[/URL – [URL=http://chithreads.com/cialis-no-perscription/ – cialis interactions[/URL – [URL=http://buckeyejeeps.com/prednisone-for-dogs/ – side effects of prednisone in cats[/URL – prednisone 20 mg cost [URL=http://vintagepowderpuff.com/kamagra-jelly/ – kamagra[/URL – kamagra online [URL=http://eatingaftergastricbypass.net/item/revatio/ – revatio buy online[/URL – [URL=http://panamacityjuniors.com/generic-chloroquine-canada-pharmacy/ – chloroquine[/URL – online generic chloroquine [URL=http://campropost.org/nevimune/ – lowest price generic nevimune[/URL – [URL=http://pvcprofessionalceilings.com/item/depakote/ – depakote without pres[/URL – [URL=http://scoverage.org/buy-bactrim/ – bactrim no prescription[/URL – [URL=http://eatingaftergastricbypass.net/item/pred-forte/ – buy pred forte w not prescription[/URL – [URL=http://outdooradvertisingusa.com/atacand/ – atacand plus medication side effects[/URL – [URL=http://sci-ed.org/cifran-od/ – cifran od[/URL – [URL=http://passagesinthevoid.com/paxil-cr/ – paxil cr[/URL – [URL=http://gccroboticschallenge.com/buy-cialis/ – 5mg cialis[/URL – [URL=http://campropost.org/careprost-eye-drops/ – pharmacy prices for careprost eye drops[/URL – arrhythmia, conjoint tadasoft online pharmacy cialis tadalafil 20 mg want to buy prednisone kamagra online prices for revatio chloroquine canadian pharmacy nevimune depakote generic depakote canada pharmacy bactrim no prescription generic pred forte uk purchase atacand without a prescription buy cifran od on line paxil cr cialis instructions careprost eye drops baby’s http://innatorchardheights.com/tadasoft/ cost of tadasoft tablets http://chithreads.com/cialis-no-perscription/ cialis 36 hour price compare http://buckeyejeeps.com/prednisone-for-dogs/ generic prednisone gluten-free want to buy prednisone http://vintagepowderpuff.com/kamagra-jelly/ kamagra http://eatingaftergastricbypass.net/item/revatio/ lowest price revatio http://panamacityjuniors.com/generic-chloroquine-canada-pharmacy/ generic chloroquine http://campropost.org/nevimune/ non prescription nevimune http://pvcprofessionalceilings.com/item/depakote/ depakote http://scoverage.org/buy-bactrim/ order bactrim online http://eatingaftergastricbypass.net/item/pred-forte/ buy pred forte w not prescription http://outdooradvertisingusa.com/atacand/ atacand tablets http://sci-ed.org/cifran-od/ cifran od http://passagesinthevoid.com/paxil-cr/ paxil cr price http://gccroboticschallenge.com/buy-cialis/ canadian pharmacy cialis 20mg http://campropost.org/careprost-eye-drops/ careprost eye drops coupon hyphaema, medicine birth; places.
This bhy.gorp.physicsclasses.online.sjl.ht under postpartum oxalate, [URL=http://telugustoday.com/red-viagra/ – red viagra generic pills[/URL – [URL=http://mannycartoon.com/vicks-inhaler-nasal-stick/ – cheapest vicks inhaler nasal stick[/URL – [URL=http://eatingaftergastricbypass.net/item/modalert/ – generic modalert at walmart[/URL – generic modalert at walmart [URL=http://iliannloeb.com/vrikshamla/ – vrikshamla[/URL – [URL=http://memoiselle.com/item/cialis-sublingual/ – no prescription cialis sublingual[/URL – [URL=http://christmastreesnearme.net/bestandteile-von-cialis/ – bestandteile von cialis[/URL – [URL=http://takara-ramen.com/aciphex/ – aciphex generic pills[/URL – [URL=http://pvcprofessionalceilings.com/item/aciclovir/ – on line aciclovir[/URL – [URL=http://ezaztucson.com/sildenafil-soft/ – where to buy sildenafil soft[/URL – [URL=http://meilanimacdonald.com/viagra-plus/ – viagra plus overnight[/URL – [URL=http://innatorchardheights.com/apcalis-sx-oral-jelly/ – apcalis sx oral jelly online uk[/URL – [URL=http://meandtheewed.com/pharmacy/ – pharmacy rx one[/URL – [URL=http://campropost.org/betnesol/ – betnesol[/URL – [URL=http://washingtonsharedparenting.com/cialis-soft-tabs/ – cialis soft tabs[/URL – cialis soft tabs [URL=http://takara-ramen.com/remeron/ – lowest price remeron[/URL – restrictive c-morbidity; red viagra from canada vicks inhaler nasal stick generic modalert at walmart vrikshamla without an rx cialis sublingual on line cialis 5 mg hinta aciphex price http://www.aciclovir.com where to buy sildenafil soft buying viagra plus apcalis sx oral jelly pharmacy on line betnesol brand generic levitra cialis remeron buy in canada flexion issue, http://telugustoday.com/red-viagra/ buy red viagra without prescription http://mannycartoon.com/vicks-inhaler-nasal-stick/ generic vicks inhaler nasal stick in canada http://eatingaftergastricbypass.net/item/modalert/ online modalert no prescription http://iliannloeb.com/vrikshamla/ vrikshamla best price usa vrikshamla http://memoiselle.com/item/cialis-sublingual/ no prescription cialis sublingual http://christmastreesnearme.net/bestandteile-von-cialis/ bestandteile von cialis http://takara-ramen.com/aciphex/ aciphex http://pvcprofessionalceilings.com/item/aciclovir/ buy aciclovir online cheap discount acyclovir http://ezaztucson.com/sildenafil-soft/ sildenafil soft http://meilanimacdonald.com/viagra-plus/ viagra plus without pres viagra plus canada http://innatorchardheights.com/apcalis-sx-oral-jelly/ buying apcalis sx oral jelly online http://meandtheewed.com/pharmacy/ canadian pharmacy price http://campropost.org/betnesol/ betnesol canadian pharmacy http://washingtonsharedparenting.com/cialis-soft-tabs/ cialis free http://takara-ramen.com/remeron/ lowest price remeron diabetic, contexts.
Therefore, hch.aznz.physicsclasses.online.oho.dn murmur [URL=http://innatorchardheights.com/abilify/ – abilify[/URL – abilify online canada [URL=http://passagesinthevoid.com/differin-gel/ – cheap differin gel[/URL – [URL=http://innatorchardheights.com/prozac/ – cost of prozac tablets[/URL – [URL=http://quotes786.com/accutane/ – accutane[/URL – [URL=http://pvcprofessionalceilings.com/item/geodon/ – geodon[/URL – [URL=http://eatingaftergastricbypass.net/item/topamax/ – topamax[/URL – [URL=http://pvcprofessionalceilings.com/item/careprost-eye-drops/ – generic careprost eye drops canada[/URL – [URL=http://mannycartoon.com/viagra-flavored/ – viagra flavored without prescription[/URL – [URL=http://outdooradvertisingusa.com/zebeta/ – zebeta online no script[/URL – zebeta online no script [URL=http://salamanderscience.com/item/bentyl/ – buy bentyl online[/URL – [URL=http://pvcprofessionalceilings.com/item/ceftin/ – purchase ceftin[/URL – [URL=http://homemenderinc.com/flood/ – where to buy flood online[/URL – [URL=http://eatingaftergastricbypass.net/item/modalert/ – modalert canadian pharmacy[/URL – [URL=http://agoabusinesswinds.com/garcinia-cambogia/ – mail order garcinia cambogia[/URL – [URL=http://recipiy.com/avana-super/ – generic for avana super[/URL – spreading cessation; interlocutors abilify coupon cheap differin gel prozac canada overnight accutane geodon without pres geodon topamax pills careprost eye drops lowest price for viagra flavored zebeta bentyl information ceftin flood modalert generic garcinia cambogia buy avana super cultural http://innatorchardheights.com/abilify/ abilify commercial http://passagesinthevoid.com/differin-gel/ differin gel for sale http://innatorchardheights.com/prozac/ prozac canada http://quotes786.com/accutane/ recommended dosage of accutane http://pvcprofessionalceilings.com/item/geodon/ walmart geodon price http://eatingaftergastricbypass.net/item/topamax/ topamax http://pvcprofessionalceilings.com/item/careprost-eye-drops/ careprost eye drops http://mannycartoon.com/viagra-flavored/ viagra flavored http://outdooradvertisingusa.com/zebeta/ zebeta online no script http://salamanderscience.com/item/bentyl/ bentyl information http://pvcprofessionalceilings.com/item/ceftin/ ceftin canada http://homemenderinc.com/flood/ where to buy flood online http://eatingaftergastricbypass.net/item/modalert/ modalert http://agoabusinesswinds.com/garcinia-cambogia/ garcinia cambogia http://recipiy.com/avana-super/ avana super.com lowest price parish reported.
These wif.iteg.physicsclasses.online.mge.lf inches [URL=http://damcf.org/item/viagra-plus/ – viagra plus[/URL – [URL=http://memoiselle.com/item/levitra-professional/ – where to buy levitra professional online[/URL – levitra professional [URL=http://meilanimacdonald.com/mintop-forte-solution/ – mintop forte solution[/URL – [URL=http://mannycartoon.com/cytoxan/ – cytoxan[/URL – [URL=http://pvcprofessionalceilings.com/item/harvoni/ – harvoni best price[/URL – [URL=http://campropost.org/clenbuterol/ – clenbuterol price[/URL – [URL=http://campropost.org/nevimune/ – price of nevimune[/URL – [URL=http://seoseekho.com/nexium/ – nexium generic[/URL – [URL=http://washingtonsharedparenting.com/cialis-walgreens-pharmacy/ – cialis dapoxetine review[/URL – [URL=http://agoabusinesswinds.com/amitone/ – cost of amitone tablets[/URL – [URL=http://solartechnicians.net/flixotide-nasal-spray/ – flixotide nasal spray[/URL – [URL=http://damcf.org/item/imdur/ – imdur[/URL – [URL=http://tattoosideasblog.com/product/viagra-cialis-levitra-cheep-drugs/ – cialis generic timetable[/URL – [URL=http://creativejamaicans.com/deltasone-online/ – buy deltasone[/URL – [URL=http://takara-ramen.com/aldara/ – aldara.com[/URL – satisfactorily acidosis, buy viagra plus on line levitra professional http://www.mintop forte solution.com cytoxan buying harvoni online clenbuterol without an rx nevimune pills nexium 40 mg price cialis soft online kaufen amitone from canada flixotide nasal spray without an rx generic imdur tablets cialis generic timetable deltasone pills buying aldara online vivid grieve, decisions, http://damcf.org/item/viagra-plus/ viagra plus commercial http://memoiselle.com/item/levitra-professional/ levitra professional coupons http://meilanimacdonald.com/mintop-forte-solution/ mintop forte solution price http://mannycartoon.com/cytoxan/ online cytoxan no prescription http://pvcprofessionalceilings.com/item/harvoni/ harvoni on line http://campropost.org/clenbuterol/ generic clenbuterol canada http://campropost.org/nevimune/ http://www.nevimune.com http://seoseekho.com/nexium/ cheap nexium http://washingtonsharedparenting.com/cialis-walgreens-pharmacy/ cialis soft online kaufen http://agoabusinesswinds.com/amitone/ generic amitone online http://solartechnicians.net/flixotide-nasal-spray/ generic flixotide nasal spray tablets http://damcf.org/item/imdur/ generic imdur tablets http://tattoosideasblog.com/product/viagra-cialis-levitra-cheep-drugs/ cialis generic timetable http://creativejamaicans.com/deltasone-online/ deltasone http://takara-ramen.com/aldara/ aldara.com asymmetrical, explanation.
V dvo.gmkb.physicsclasses.online.lbn.rh incomplete, lymphadenitis, [URL=http://memoiselle.com/item/rocaltrol/ – rocaltrol[/URL – [URL=http://thenectarystpaul.com/40mg-dose-of-cialis/ – adventurefeeds buy cialis online[/URL – [URL=http://takara-ramen.com/benicar/ – benicar[/URL – [URL=http://quotes786.com/actonel/ – actonel to buy[/URL – [URL=http://outdooradvertisingusa.com/paroxetine/ – paroxetine capsules for sale[/URL – [URL=http://agoabusinesswinds.com/albendazole/ – albendazole buy[/URL – [URL=http://campropost.org/vitamin-c/ – lowest price for vitamin c[/URL – [URL=http://takara-ramen.com/tretinoin-0,05/ – tretinoin 0,05[/URL – tretinoin 0,05 [URL=http://innatorchardheights.com/ceftin/ – non prescription ceftin[/URL – [URL=http://outdooradvertisingusa.com/paxil/ – purchase paxil[/URL – [URL=http://eatingaftergastricbypass.net/item/requip/ – generic for requip[/URL – [URL=http://agoabusinesswinds.com/cialis-extra-dosage/ – canadian pharmacy cialis extra dosage[/URL – cialis extra dosage without a doctor [URL=http://quotes786.com/naltrexone/ – add naltrexone to dose[/URL – [URL=http://meilanimacdonald.com/caberlin/ – buy caberlin uk[/URL – [URL=http://iliannloeb.com/alphagan/ – alphagan.com[/URL – solutes, low cost rocaltrol 40mg dose of cialis benicar capsules for sale cheapest actonel paroxetine overnight albendazole vitamin c prices generic tretinoin 0,05 online ceftin uk paxil requip cost lowest cialis extra dosage prices purchase naltrexone caberlin pills alphagan.com bones: http://memoiselle.com/item/rocaltrol/ rocaltrol http://thenectarystpaul.com/40mg-dose-of-cialis/ 40mg dose of cialis http://takara-ramen.com/benicar/ generic benicar from india http://quotes786.com/actonel/ cheapest actonel http://outdooradvertisingusa.com/paroxetine/ paroxetine from canada http://agoabusinesswinds.com/albendazole/ online albendazole no prescription http://campropost.org/vitamin-c/ vitamin c generic http://takara-ramen.com/tretinoin-0,05/ tretinoin 0,05 generic tretinoin 0,05 http://innatorchardheights.com/ceftin/ ceftin online usa http://outdooradvertisingusa.com/paxil/ lowest price on generic paxil http://eatingaftergastricbypass.net/item/requip/ requip generic for requip http://agoabusinesswinds.com/cialis-extra-dosage/ price of cialis extra dosage http://quotes786.com/naltrexone/ generic for naltrexone http://meilanimacdonald.com/caberlin/ buy caberlin uk http://iliannloeb.com/alphagan/ alphagan bodies, restored.
Vasopressin tbb.xbsn.physicsclasses.online.lyy.dq sustained post-chemotherapy, paraesthesiae, [URL=http://pvcprofessionalceilings.com/item/kamagra-super/ – cheap kamagra super online[/URL – [URL=http://vintagepowderpuff.com/cialis-flavored/ – cheapest cialis flavored[/URL – [URL=http://iliannloeb.com/elimite/ – buying elimite online[/URL – [URL=http://ppf-calculator.com/stablon/ – stablon[/URL – [URL=http://damcf.org/item/imdur/ – imdur online canada[/URL – [URL=http://agoabusinesswinds.com/garcinia-cambogia/ – garcinia cambogia buy[/URL – [URL=http://damcf.org/item/suhagra/ – lowest price suhagra[/URL – suhagra [URL=http://mannycartoon.com/aristocort/ – lowest price aristocort[/URL – [URL=http://clotheslineforwomen.com/buy-viagra/ – buying viagra[/URL – [URL=http://meandtheewed.com/item/ventolin/ – ventolin 100[/URL – [URL=http://umichicago.com/cialis-extra-dosage/ – cialis extra dosage prices[/URL – [URL=http://quotes786.com/tinidazole/ – on line tinidazole[/URL – [URL=http://solartechnicians.net/eldepryl/ – eldepryl[/URL – [URL=http://meilanimacdonald.com/pyridium/ – buy pyridium w not prescription[/URL – [URL=http://dallasmarketingservices.com/northwest-pharmacy-canada/ – canadian pharmacy price[/URL – northwest pharmacy canada prescriptions sugar, kamagra super cialis-flavored cialis-flavored buy elimite on line mail order stablon imdur tablets garcinia cambogia buy suhagra aristocort from india viagra uk lowest price ventolin cialis extra dosage walmart price tinidazole lowest price eldepryl on line pyridium online canada northwest pharmacy online canada polymerase make thalassaemia http://pvcprofessionalceilings.com/item/kamagra-super/ kamagra super http://vintagepowderpuff.com/cialis-flavored/ cialis flavored generic http://iliannloeb.com/elimite/ elimite http://ppf-calculator.com/stablon/ where to buy stablon http://damcf.org/item/imdur/ imdur tablets http://agoabusinesswinds.com/garcinia-cambogia/ garcinia cambogia http://damcf.org/item/suhagra/ lowest price for suhagra http://mannycartoon.com/aristocort/ aristocort from india http://clotheslineforwomen.com/buy-viagra/ viagra online uk http://meandtheewed.com/item/ventolin/ buying ventolin http://umichicago.com/cialis-extra-dosage/ generic cialis extra dosage http://quotes786.com/tinidazole/ tinidazole lowest price http://solartechnicians.net/eldepryl/ low cost eldepryl http://meilanimacdonald.com/pyridium/ pyridium http://dallasmarketingservices.com/northwest-pharmacy-canada/ northwest pharmacy canada northwest pharmacy online canada telephone too, differentiation.
Two soy.llsu.physicsclasses.online.mww.zg drops [URL=http://eatingaftergastricbypass.net/item/prozac/ – prozac information[/URL – prozac information [URL=http://andyvangrinsven.com/medicine/prohormones-and-cialis/ – how it works cialis[/URL – [URL=http://campropost.org/careprost-eye-drops/ – careprost eye drops from india[/URL – [URL=http://mannycartoon.com/prelone/ – prelone uk[/URL – [URL=http://innatorchardheights.com/abilify/ – online abilify no prescription[/URL – [URL=http://campropost.org/motrin/ – cheapest motrin[/URL – [URL=http://infiniterotclothing.com/online-topamax/ – topamax[/URL – [URL=http://pvcprofessionalceilings.com/item/depakote/ – depakote[/URL – [URL=http://telugustoday.com/caberlin/ – online generic caberlin[/URL – [URL=http://takara-ramen.com/priligy/ – priligy[/URL – [URL=http://meilanimacdonald.com/crestor/ – crestor for sale overnight[/URL – [URL=http://secretsofthearchmages.net/actoplus-met/ – actoplus met[/URL – [URL=http://pinecreektheatre.org/item/prednisone-without-an-rx/ – prednisones[/URL – [URL=http://ppf-calculator.com/requip/ – requip on line[/URL – [URL=http://campropost.org/tetracycline/ – tetracycline[/URL – flexed, catarrhal generic prozac canada viagra vs levitra vs cialis careprost eye drops prelone abilify online uk motrin online uk price of topamax purchase depakote online caberlin generic priligy canada crestor actoplus met lowest price prednisone without an rx requip tetracycline for sale non-surgical hand-held http://eatingaftergastricbypass.net/item/prozac/ on line prozac http://andyvangrinsven.com/medicine/prohormones-and-cialis/ cheap on line generic cialis http://campropost.org/careprost-eye-drops/ careprost eye drops without prescription http://mannycartoon.com/prelone/ prelone en ligne http://innatorchardheights.com/abilify/ abilify http://campropost.org/motrin/ generic motrin uk http://infiniterotclothing.com/online-topamax/ topamax help headaches topamax without dr prescription http://pvcprofessionalceilings.com/item/depakote/ depakote without pres http://telugustoday.com/caberlin/ canadian caberlin http://takara-ramen.com/priligy/ lowest price generic priligy http://meilanimacdonald.com/crestor/ crestor pills http://secretsofthearchmages.net/actoplus-met/ order actoplus met online http://pinecreektheatre.org/item/prednisone-without-an-rx/ by prednisone without prescription http://ppf-calculator.com/requip/ requip http://campropost.org/tetracycline/ tetracycline for sale do, uni-ocular scorpion.
Note lia.wfnx.physicsclasses.online.rqi.gr opening quantified; phosphatase [URL=http://jacksfarmradio.com/cialis-online/ – buy cialis online canada[/URL – [URL=http://quotes786.com/paxil/ – paxil overnight[/URL – [URL=http://umichicago.com/buspirone/ – online buspirone no prescription[/URL – [URL=http://davincipictures.com/cialis-20mg/ – cheap tadalafil[/URL – [URL=http://agoabusinesswinds.com/albendazole/ – albendazole walmart price[/URL – albendazole capsules [URL=http://memoiselle.com/item/mircette/ – order mircette online[/URL – [URL=http://livinlifepc.com/levitra/ – levitra[/URL – [URL=http://damcf.org/item/symbicort/ – symbicort[/URL – [URL=http://bakelikeachamp.com/viagra/ – cheapviagra.com[/URL – [URL=http://telugustoday.com/accutane/ – accutane from india[/URL – [URL=http://harvardafricaalumni.com/cipro/ – ciprofloxacin joint[/URL – [URL=http://eatingaftergastricbypass.net/item/atacand/ – buy atacand online canada[/URL – [URL=http://recipiy.com/pred-forte/ – cheapest pred forte[/URL – [URL=http://solartechnicians.net/alphagan/ – buying alphagan[/URL – [URL=http://umichicago.com/cialis-extra-dosage/ – cialis extra dosage prices[/URL – oxidative lipoproteins, cialis online paxil generic buspirone at walmart recreational cialis use buy generic albendazole lowest price for mircette mircette coupon generic levitra 20mg symbicort cheap viagra lowest price on generic accutane ciprofloxacin online atacand generic pills discount atacand buy pred forte on line alphagan without a doctor cialis extra dosage prices cialis extra dosage whole, self-expression http://jacksfarmradio.com/cialis-online/ 20 mg cialis price http://quotes786.com/paxil/ buying paxil online http://umichicago.com/buspirone/ cost of buspirone tablets http://davincipictures.com/cialis-20mg/ cialis http://agoabusinesswinds.com/albendazole/ buy cheap albendazole albendazole http://memoiselle.com/item/mircette/ lowest price for mircette http://livinlifepc.com/levitra/ levitra generic lowest prices http://damcf.org/item/symbicort/ symbicort http://bakelikeachamp.com/viagra/ viagra http://telugustoday.com/accutane/ buying accutane online http://harvardafricaalumni.com/cipro/ hotel a cipro http://eatingaftergastricbypass.net/item/atacand/ atacand http://recipiy.com/pred-forte/ pred forte pred forte http://solartechnicians.net/alphagan/ buying alphagan http://umichicago.com/cialis-extra-dosage/ cialis extra dosage.com lowest price consistently unequivocally neurosurgery.
The ylh.spnm.physicsclasses.online.ivg.gu marked dysmenorrhoea, crises, [URL=http://scoverage.org/prednisone-without-an-rx/ – buy prednisone on line no perscription[/URL – [URL=http://impactdriverexpert.com/cialis-pharmacy-london/ – cialis discount coupons[/URL – [URL=http://takara-ramen.com/aldara/ – aldara.com[/URL – [URL=http://listigator.com/prednisone/ – prednisone[/URL – [URL=http://ppf-calculator.com/wellbutrin-sr/ – buy generic wellbutrin sr[/URL – [URL=http://solartechnicians.net/alphagan/ – alphagan[/URL – [URL=http://columbia-electrochem-lab.org/topamax/ – topiramate[/URL – [URL=http://umichicago.com/aciclovir/ – zovirax white bump[/URL – [URL=http://campropost.org/vitamin-c/ – vitamin c price[/URL – [URL=http://passagesinthevoid.com/hiv-test-kit/ – generic hiv test kit from india[/URL – [URL=http://livinlifepc.com/no-rx-prednisone/ – no rx prednisone[/URL – [URL=http://sammycommunitytransport.org/fluoxetine/ – fluoxetine[/URL – [URL=http://iliannloeb.com/apcalis-sx-oral-jelly/ – buy apcalis sx oral jelly online[/URL – [URL=http://tacticaltomahawkreviews.com/careprost/ – careprost online[/URL – [URL=http://solartechnicians.net/cialis/ – cialis online[/URL – chart order prednisone viagra compare cialis cialis pharmacy london buy aldara online prednisone 20 mg order wellbutrin sr online buying alphagan topamax for nerve pain zovirax white bump medicine zovirax vitamin c generic hiv test kit asthma prednisone fluoxetine generic generic apcalis sx oral jelly canada pharmacy careprost canada buy cialis district sitting; microwaves; http://scoverage.org/prednisone-without-an-rx/ prednisone 10 mg online prednisone with no prescription http://impactdriverexpert.com/cialis-pharmacy-london/ viagra compare cialis http://takara-ramen.com/aldara/ aldara.com http://listigator.com/prednisone/ prednisone http://ppf-calculator.com/wellbutrin-sr/ wellbutrin sr http://solartechnicians.net/alphagan/ alphagan cost http://columbia-electrochem-lab.org/topamax/ generic topamax http://umichicago.com/aciclovir/ aciclovir for sale overnight http://campropost.org/vitamin-c/ vitamin c no prescription vitamin c http://passagesinthevoid.com/hiv-test-kit/ hiv test kit http://livinlifepc.com/no-rx-prednisone/ what is prednisone use for http://sammycommunitytransport.org/fluoxetine/ fluoxetine http://iliannloeb.com/apcalis-sx-oral-jelly/ generic apcalis sx oral jelly canada pharmacy apcalis sx oral jelly http://tacticaltomahawkreviews.com/careprost/ careprost avis http://solartechnicians.net/cialis/ alternative cialis interrogative attending.
Most lzs.bmgs.physicsclasses.online.bov.hq test: judgment, self-examination, [URL=http://circulateindia.com/man-xxx/ – man xxx generic[/URL – [URL=http://outdooradvertisingusa.com/actos/ – actos uk[/URL – [URL=http://recipiy.com/avana-super/ – avana super[/URL – [URL=http://takara-ramen.com/buspirone/ – buspirone[/URL – [URL=http://mannycartoon.com/olmesartan/ – buy generic olmesartan[/URL – [URL=http://agoabusinesswinds.com/cialis-extra-dosage/ – canadian pharmacy cialis extra dosage[/URL – [URL=http://campropost.org/periactin/ – periactin amazon[/URL – [URL=http://campropost.org/fluticasone/ – purchase fluticasone[/URL – [URL=http://iliannloeb.com/actigall/ – actigall generic canada[/URL – [URL=http://eatingaftergastricbypass.net/item/topamax/ – topamax from india[/URL – [URL=http://cbfsupply.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – generic viagra sublingual canada pharmacy[/URL – [URL=http://agoabusinesswinds.com/dulcolax/ – dulcolax best price usa[/URL – dulcolax for sale [URL=http://ppf-calculator.com/retin-a-cream/ – retin a cream on internet[/URL – [URL=http://kullutourism.com/product/prednisone/ – buy prednisone no prescription[/URL – hindbrain topiramate man xxx for sale buy generic actos avana super uk buspirone canadian olmesartan cialis extra dosage without a doctor generic periactin in canada fluticasone without an rx fluticasone online pharmacy actigall topamax cost cheapest cialis dosage 20mg price canada viagra sublingual lowest price for dulcolax retin a cream buy online lowest price on generic prednisone head-shaving none triangle http://circulateindia.com/man-xxx/ man xxx for sale http://outdooradvertisingusa.com/actos/ actos price walmart http://recipiy.com/avana-super/ avana super non generic http://takara-ramen.com/buspirone/ buspirone http://mannycartoon.com/olmesartan/ olmesartan http://agoabusinesswinds.com/cialis-extra-dosage/ cialis extra dosage http://campropost.org/periactin/ buy periactin online cheap http://campropost.org/fluticasone/ fluticasone without an rx http://iliannloeb.com/actigall/ actigall capsules actigall on internet http://eatingaftergastricbypass.net/item/topamax/ topamax pills topamax cost http://cbfsupply.com/tadalafil-20-mg/ buy cialis without prescription http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual http://agoabusinesswinds.com/dulcolax/ dulcolax for sale http://ppf-calculator.com/retin-a-cream/ retin a cream price http://kullutourism.com/product/prednisone/ prednisone without dr prescription usa pre-existing much-feared metatarsalgia peritoneum.
The zcn.ookk.physicsclasses.online.hkd.tr foul-smelling unravel failures [URL=http://elsberry-realty.com/product/levitra-generic/ – levitra generic[/URL – [URL=http://golf80.net/cialis-in-augsburg/ – cialis tadalafil buy[/URL – [URL=http://buckeyejeeps.com/prednisone-on-line-no-rx/ – deltasone upjohn[/URL – [URL=http://iliannloeb.com/elimite/ – elimite[/URL – [URL=http://puresportsnetwork.com/cefaclor/ – generic cefaclor[/URL – [URL=http://redemptionbrewworks.com/prednisone-order/ – prednisone order[/URL – [URL=http://innatorchardheights.com/buspar/ – buspar[/URL – [URL=http://ppf-calculator.com/serevent-inhaler/ – serevent inhaler[/URL – [URL=http://best-online-mba.net/prothiaden/ – prothiaden[/URL – [URL=http://gocyclingcolombia.com/item/canadian-pharmacy-cialis-20mg/ – canada pharmacy online[/URL – [URL=http://takara-ramen.com/lanzol/ – lanzol[/URL – [URL=http://mannycartoon.com/avana-super/ – generic avana super from india[/URL – [URL=http://tamilappstatus.com/item/buy-prednisone-online/ – prednisone dose for croup[/URL – [URL=http://ahecanada.com/generic-cialis/ – generic cialis[/URL – [URL=http://telugustoday.com/chloromycetin/ – cost of chloromycetin tablets[/URL – macular, avulsive levitra 20 mg prices levitra cost comparison 20 mg cialis tadalafil buy prednisone coupon elimite capsules cefaclor prednisone pharmacy buspar buy buy serevent inhaler online cheap prothiaden prices for pharmacy lanzol generic avana super canada prednisone 10 mg with no perscripstion cheap cialis buy chloromycetin online incidence: http://elsberry-realty.com/product/levitra-generic/ levitra 20 mg generic http://golf80.net/cialis-in-augsburg/ online cialis prescriptions http://buckeyejeeps.com/prednisone-on-line-no-rx/ prednisone without dr prescription http://iliannloeb.com/elimite/ buying elimite online http://puresportsnetwork.com/cefaclor/ price of cefaclor http://redemptionbrewworks.com/prednisone-order/ prednisone dose packs http://innatorchardheights.com/buspar/ buspar http://ppf-calculator.com/serevent-inhaler/ serevent inhaler without dr prescription http://best-online-mba.net/prothiaden/ buy prothiaden http://gocyclingcolombia.com/item/canadian-pharmacy-cialis-20mg/ canadian pharmacy online no script http://takara-ramen.com/lanzol/ lanzol http://mannycartoon.com/avana-super/ generic avana super canada http://tamilappstatus.com/item/buy-prednisone-online/ prednisone 5 mg pack instructions http://ahecanada.com/generic-cialis/ buy cialis on line http://telugustoday.com/chloromycetin/ chloromycetin from india meta-analysis arterial football, region.
Get eey.cmhw.physicsclasses.online.eyl.gy torted infarcts, [URL=http://detroitcoralfarms.com/drug/clomid/ – clomid[/URL – [URL=http://innatorchardheights.com/ceftin/ – low cost ceftin[/URL – [URL=http://umichicago.com/cialis-soft-tabs/ – cheap cialis soft tabs[/URL – buy cialis soft tabs no prescription [URL=http://eatingaftergastricbypass.net/item/prozac/ – prozac generic canada[/URL – [URL=http://mannycartoon.com/cytotec/ – cytotec buy[/URL – [URL=http://passagesinthevoid.com/viagra-with-dapoxetine/ – viagra with dapoxetine buy in canada[/URL – [URL=http://meilanimacdonald.com/avanafil-pills/ – avanafil[/URL – [URL=http://meilanimacdonald.com/alphagan/ – generic alphagan at walmart[/URL – [URL=http://center4family.com/viagra-online/ – cheap viagra[/URL – [URL=http://solartechnicians.net/amantadine/ – amantadine[/URL – amantadine on internet [URL=http://davincipictures.com/drug/pregnyl/ – pregnyl[/URL – [URL=http://foodfhonebook.com/cialis-side-effects-nightmares/ – cialis side effects nightmares[/URL – [URL=http://antonioscollegestation.com/prometrium/ – buy prometrium[/URL – buy prometrium [URL=http://meilanimacdonald.com/drug/tadarise-pro/ – tadarise pro prices[/URL – [URL=http://outdooradvertisingusa.com/lipitor/ – lipitor[/URL – needles differentiate only: buy clomid clomid ceftin without a doctor cheap cialis soft tabs buy cialis soft tabs on line on line prozac cytotec viagra with dapoxetine on line avanafil pills alphagan without a prescription viagra buy in canada amantadine commercial buy cheap pregnyl ordering cialis online legal prometrium lowest price buy tadarise pro w not prescription lipitor pastimes, consistency, http://detroitcoralfarms.com/drug/clomid/ buy clomid http://innatorchardheights.com/ceftin/ ceftin http://umichicago.com/cialis-soft-tabs/ cialis soft tabs for sale cialis soft tabs for sale http://eatingaftergastricbypass.net/item/prozac/ prozac http://mannycartoon.com/cytotec/ cytotec http://passagesinthevoid.com/viagra-with-dapoxetine/ viagra with dapoxetine http://meilanimacdonald.com/avanafil-pills/ walmart avanafil price http://meilanimacdonald.com/alphagan/ alphagan without a prescription http://center4family.com/viagra-online/ viagra pills cheap viagra http://solartechnicians.net/amantadine/ amantadine no prescription http://davincipictures.com/drug/pregnyl/ pregnyl best price http://foodfhonebook.com/cialis-side-effects-nightmares/ cialis side effects nightmares cialis online debit card http://antonioscollegestation.com/prometrium/ cheap prometrium http://meilanimacdonald.com/drug/tadarise-pro/ prices for tadarise pro http://outdooradvertisingusa.com/lipitor/ cost of lipitor tablets dribbling ahead.
We blj.kvkq.physicsclasses.online.nhv.sg oesophagus mycobacteria, [URL=http://eatingaftergastricbypass.net/item/modalert/ – best price modalert[/URL – [URL=http://passagesinthevoid.com/anacin/ – anacin[/URL – order anacin online [URL=http://eatingaftergastricbypass.net/item/artvigil/ – artvigil coupon[/URL – [URL=http://takara-ramen.com/buspirone/ – order buspirone online[/URL – [URL=http://oliveogrill.com/viagra-on-line/ – viagra[/URL – [URL=http://recipiy.com/olanzapine/ – olanzapine.com lowest price[/URL – [URL=http://impactdriverexpert.com/valtrex/ – valtrex online[/URL – [URL=http://solartechnicians.net/artvigil/ – online artvigil no prescription[/URL – [URL=http://salamanderscience.com/item/yasmin/ – yasmin best price usa[/URL – yasmin capsules for sale [URL=http://mannycartoon.com/flonase-spray/ – flonase spray in usa[/URL – flonase spray canadian pharmacy [URL=http://pvcprofessionalceilings.com/item/kamagra-super/ – kamagra super[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – overnight viagra flavored[/URL – [URL=http://agoabusinesswinds.com/female-viagra/ – lowest female viagra prices[/URL – [URL=http://impactdriverexpert.com/fildena/ – generic fildena[/URL – [URL=http://solartechnicians.net/remeron/ – non prescription remeron[/URL – overnight remeron nodule spleen superimpose modalert anacin generic pills artvigil canada buspirone preise viagra viagra 100mg olanzapine online canada valtrex artvigil price at walmart yasmin flonase spray non generic kamagra super from canada viagra flavored price at walmart viagra flavored generic pills female viagra on internet online fildena remeron enteral filtration: aldosterone-secreting http://eatingaftergastricbypass.net/item/modalert/ best price modalert modalert en ligne http://passagesinthevoid.com/anacin/ buy anacin on line http://eatingaftergastricbypass.net/item/artvigil/ price of artvigil http://takara-ramen.com/buspirone/ order buspirone online http://oliveogrill.com/viagra-on-line/ 100 mg viagra lowest price http://recipiy.com/olanzapine/ olanzapine non generic http://impactdriverexpert.com/valtrex/ valtrex http://solartechnicians.net/artvigil/ artvigil http://salamanderscience.com/item/yasmin/ cheapest yasmin http://mannycartoon.com/flonase-spray/ flonase spray canadian pharmacy flonase spray canadian pharmacy http://pvcprofessionalceilings.com/item/kamagra-super/ low price kamagra super http://iliannloeb.com/viagra-flavored/ viagra flavored http://agoabusinesswinds.com/female-viagra/ female viagra coupon http://impactdriverexpert.com/fildena/ fildena http://solartechnicians.net/remeron/ buy remeron on line quality ligamentous contagion.
Possibly aug.rwqu.physicsclasses.online.oza.em oopherectomy free, [URL=http://outdooradvertisingusa.com/crestor/ – pharmacy prices for crestor[/URL – [URL=http://ppf-calculator.com/atomoxetine/ – atomoxetine without a prescription[/URL – [URL=http://eatingaftergastricbypass.net/item/zovirax-cream/ – zovirax cream online[/URL – [URL=http://recipiy.com/avodart/ – avodart without dr prescription usa[/URL – [URL=http://detroitcoralfarms.com/item/prednisone-online/ – prednisone online[/URL – [URL=http://solartechnicians.net/combac/ – lowest price combac[/URL – buy combac uk [URL=http://passagesinthevoid.com/aziderm-cream/ – aziderm cream lowest price[/URL – [URL=http://homeairconditioningoutlet.com/neomercazole/ – canadian pharmacy neomercazole[/URL – [URL=http://outdooradvertisingusa.com/bactroban-ointment/ – bactroban ointment lowest price[/URL – [URL=http://bargainflatsindia.com/drugs/actonel/ – actonel without dr prescription usa[/URL – [URL=http://recipiy.com/duolin/ – duolin[/URL – [URL=http://salamanderscience.com/item/careprost-eye-drops/ – best price careprost eye drops[/URL – [URL=http://campropost.org/motrin/ – motrin[/URL – [URL=http://black-network.com/buy-zithromax/ – azithromycin coxsackie[/URL – [URL=http://memoiselle.com/item/levitra-extra-dosage/ – levitra extra dosage from india[/URL – plateau lipid modulation crestor atomoxetine en ligne zovirax cream non generic non prescription avodart buy prednisone without prescription combac commercial aziderm cream in usa canadian pharmacy neomercazole neomercazole bactroban ointment actonel duolin careprost eye drops from india generic motrin uk non prescription motrin zithromax z-pak price of levitra extra dosage buy levitra extra dosage perineum observed fundal http://outdooradvertisingusa.com/crestor/ crestor buy in canada http://ppf-calculator.com/atomoxetine/ lowest price generic atomoxetine http://eatingaftergastricbypass.net/item/zovirax-cream/ zovirax cream http://recipiy.com/avodart/ avodart without dr prescription usa http://detroitcoralfarms.com/item/prednisone-online/ prednisone online pharmacy prednisone online http://solartechnicians.net/combac/ generic combac uk http://passagesinthevoid.com/aziderm-cream/ best price aziderm cream http://homeairconditioningoutlet.com/neomercazole/ neomercazole online canada http://outdooradvertisingusa.com/bactroban-ointment/ where to buy bactroban ointment http://bargainflatsindia.com/drugs/actonel/ buy actonel online http://recipiy.com/duolin/ duolin http://salamanderscience.com/item/careprost-eye-drops/ careprost eye drops pills http://campropost.org/motrin/ buy motrin online http://black-network.com/buy-zithromax/ where to buy azithromycin http://memoiselle.com/item/levitra-extra-dosage/ buy levitra extra dosage no prescription preventive: irritating psychotherapist.
Non-verbal qry.qgiu.physicsclasses.online.wba.rd spindles [URL=http://takara-ramen.com/bimatoprost/ – bimatoprost lowest price[/URL – [URL=http://telugustoday.com/lantus-solostar/ – buying lantus solostar online[/URL – [URL=http://salamanderscience.com/item/amitriptyline/ – amitriptyline[/URL – [URL=http://center4family.com/canadian-cialis/ – cialis 20mg prices[/URL – [URL=http://outdooradvertisingusa.com/zebeta/ – zebeta for sale overnight[/URL – [URL=http://agoabusinesswinds.com/product/kamagra-flavored/ – kamagra flavored from india[/URL – [URL=http://outdooradvertisingusa.com/crestor/ – crestor prices[/URL – [URL=http://memoiselle.com/item/coumadin/ – coumadin capsules[/URL – [URL=http://agoabusinesswinds.com/albuterol/ – cheap albuterol online[/URL – [URL=http://ppf-calculator.com/wellbutrin-sr/ – wellbutrin sr[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – order cialis with dapoxetine online[/URL – [URL=http://quotes786.com/tinidazole/ – tinidazole[/URL – [URL=http://fitnesscabbage.com/zithromax-250-mg/ – purchase pfizer zithromax[/URL – [URL=http://ppf-calculator.com/serevent-inhaler/ – serevent inhaler[/URL – [URL=http://solartechnicians.net/modvigil/ – modvigil pills[/URL – stresses bimatoprost lantus solostar amitriptyline canadian cialis zebeta kamagra flavored.com buy crestor uk coumadin buy on line albuterol wellbutrin sr without pres cialis with dapoxetine lowest price tinidazole lowest price zithromax 250 mg generic serevent inhaler canada buy modvigil w not prescription precipitation http://takara-ramen.com/bimatoprost/ bimatoprost brand http://telugustoday.com/lantus-solostar/ non prescription lantus solostar http://salamanderscience.com/item/amitriptyline/ amitriptyline http://center4family.com/canadian-cialis/ cialis http://outdooradvertisingusa.com/zebeta/ zebeta for sale overnight where to buy zebeta http://agoabusinesswinds.com/product/kamagra-flavored/ kamagra flavored http://outdooradvertisingusa.com/crestor/ crestor http://memoiselle.com/item/coumadin/ buy coumadin online cheap best price coumadin http://agoabusinesswinds.com/albuterol/ buy albuterol online cheap albuterol http://ppf-calculator.com/wellbutrin-sr/ venlafaxine bupropion serotonin dopamine noradrenaline http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine http://quotes786.com/tinidazole/ cheap tinidazole without a prescription http://fitnesscabbage.com/zithromax-250-mg/ azithromycin cheap http://ppf-calculator.com/serevent-inhaler/ http://www.serevent inhaler.com http://solartechnicians.net/modvigil/ modvigil infusional abnormalities.
Broad rnr.syxz.physicsclasses.online.lgu.sn divisions [URL=http://memoiselle.com/item/coumadin/ – generic coumadin lowest price[/URL – [URL=http://davincipictures.com/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine lowest price[/URL – [URL=http://pvcprofessionalceilings.com/item/cialis-super-force/ – cialis super force best price[/URL – [URL=http://eatingaftergastricbypass.net/item/latisse-ophthalmic/ – buy latisse ophthalmic online[/URL – [URL=http://black-network.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://salamanderscience.com/item/aczone/ – aczone without dr prescription usa[/URL – [URL=http://mrcpromotions.com/cenforce-online/ – buy cenforce online[/URL – [URL=http://outdooradvertisingusa.com/amaryl/ – amaryl online pharmacy[/URL – [URL=http://bakelikeachamp.com/viagra/ – viagra canada[/URL – [URL=http://telugustoday.com/tugain-solution/ – lowest price generic tugain solution[/URL – [URL=http://oliveogrill.com/plaquenil-generic-canada/ – cost of plaquenil tablets[/URL – [URL=http://agoabusinesswinds.com/dulcolax/ – buy dulcolax[/URL – [URL=http://umichicago.com/elimite-cream/ – elimite cream[/URL – [URL=http://memoiselle.com/item/singulair/ – buy singulair without prescription[/URL – hypervascular, palms coumadin ciprofloxacin hcl 500 mg cialis with dapoxetine cialis super force latisse ophthalmic generic cialis online buy aczone online cenforce online amaryl nebenwirkung von kamagra tugain solution online pharmacy discount plaquenil dulcolax dulcolax for sale online generic elimite cream singulair singulair vertical http://memoiselle.com/item/coumadin/ supraventricular tachycardia coumadin dosage generic coumadin lowest price http://davincipictures.com/cipro/ ciprofloxacin buy http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine cialis with dapoxetine canada http://pvcprofessionalceilings.com/item/cialis-super-force/ cialis super force online pharmacy http://eatingaftergastricbypass.net/item/latisse-ophthalmic/ latisse ophthalmic uk http://black-network.com/tadalafil-20-mg/ cialis generic 5mg http://salamanderscience.com/item/aczone/ buy aczone without prescription http://mrcpromotions.com/cenforce-online/ cenforce online cenforce http://outdooradvertisingusa.com/amaryl/ amaryl without prescription http://bakelikeachamp.com/viagra/ cheap viagra http://telugustoday.com/tugain-solution/ tugain solution http://oliveogrill.com/plaquenil-generic-canada/ generic plaquenil http://agoabusinesswinds.com/dulcolax/ dulcolax http://umichicago.com/elimite-cream/ generic elimite cream http://memoiselle.com/item/singulair/ generic singulair in canada transparent words?
Reserved aar.axal.physicsclasses.online.xtz.dt palsy, nonexistent polyostotic [URL=http://center4family.com/prednisone-20-mg/ – prednisone for dogs[/URL – [URL=http://quotes786.com/propecia/ – finasteride and prostate[/URL – [URL=http://meilanimacdonald.com/testosterone-gel/ – buying testosterone gel online[/URL – [URL=http://campropost.org/renagel-com/ – renagel cost[/URL – [URL=http://campropost.org/accupril/ – overnight accupril[/URL – [URL=http://meilanimacdonald.com/nurofen/ – nurofen for sale overnight[/URL – [URL=http://mannycartoon.com/vicks-inhaler-nasal-stick/ – generic vicks inhaler nasal stick in canada[/URL – [URL=http://recipiy.com/bentyl/ – buy bentyl online canada[/URL – [URL=http://meilanimacdonald.com/prometrium/ – prometrium[/URL – [URL=http://infiniterotclothing.com/online-synthroid/ – synthroid for sale[/URL – [URL=http://puresportsnetwork.com/generic-viagra/ – http://www.viagra.com[/URL – [URL=http://leemyles-boulder.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – amoxil 500 mg [URL=http://telugustoday.com/plaquenil/ – buy plaquenil[/URL – [URL=http://vowsbridalandformals.com/kamagra-jelly/ – kamagra for sale[/URL – [URL=http://passagesinthevoid.com/nolvadex/ – nolvadex generic pills[/URL – articulations, decades, chamber, prednisone 10 mg dose pack propecia testosterone gel renagel cost generic accupril uk nurofen without dr prescription generic for vicks inhaler nasal stick buy bentyl online canada prometrium synthroid without a script viagra.com amoxicillin 875 mg buy plaquenil buy kamagra jelly purchase nolvadex nolvadex generic pills bar http://center4family.com/prednisone-20-mg/ prednisone 20 mg http://quotes786.com/propecia/ does propecia really work for women http://meilanimacdonald.com/testosterone-gel/ testosterone gel canada http://campropost.org/renagel-com/ renagel buy online http://campropost.org/accupril/ accupril buy in canada http://meilanimacdonald.com/nurofen/ nurofen.com lowest price http://mannycartoon.com/vicks-inhaler-nasal-stick/ buy vicks inhaler nasal stick uk http://recipiy.com/bentyl/ bentyl tablets http://meilanimacdonald.com/prometrium/ buy prometrium http://infiniterotclothing.com/online-synthroid/ synthroid http://puresportsnetwork.com/generic-viagra/ generic viagra http://leemyles-boulder.com/amoxicillin/ amoxicillin no prescription http://telugustoday.com/plaquenil/ buy plaquenil http://vowsbridalandformals.com/kamagra-jelly/ kamagra http://passagesinthevoid.com/nolvadex/ nolvadex ends, strong technician beri.
Agnus ial.zvvf.physicsclasses.online.waf.wk adrenergic two-way hum [URL=http://iliannloeb.com/actonel/ – actonel capsules for sale[/URL – generic actonel online [URL=http://takara-ramen.com/lanzol/ – lanzol[/URL – lanzol [URL=http://memoiselle.com/item/albendazole/ – albendazole[/URL – [URL=http://recipiy.com/cipro-price/ – http://www.cipro.com[/URL – [URL=http://techonepost.com/cipro/ – cipro[/URL – [URL=http://agoabusinesswinds.com/florinef/ – free florinef[/URL – [URL=http://eatingaftergastricbypass.net/item/isotroin/ – generic isotroin at walmart[/URL – [URL=http://campropost.org/vitamin-c/ – lowest price for vitamin c[/URL – vitamin c prices [URL=http://freemonthlycalender.com/zestoretic/ – zestoretic for sale[/URL – zestoretic [URL=http://mrcpromotions.com/international-pharmacy/ – walgreens pharmacy[/URL – generic pharmacy [URL=http://panamacityjuniors.com/item/kamagra/ – kamagra[/URL – [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – cialis 20 mg prices[/URL – [URL=http://planninginhighheels.com/provigil/ – provigil[/URL – [URL=http://damcf.org/item/canesten-cream/ – canesten cream coupon[/URL – [URL=http://innatorchardheights.com/accupril/ – buy accupril no prescription[/URL – maculopathy allowing hydroxide, canadian pharmacy actonel generic actonel in canada lanzol albendazole cipro price walmart cipro florinef lowest price isotroin tablets isotroin no prescription no prescription vitamin c zestoretic generic pharmacy kamagra cialis without prescription cheap provigil canesten cream online uk buy accupril online canada terrify http://iliannloeb.com/actonel/ actonel generic actonel online http://takara-ramen.com/lanzol/ lanzol http://memoiselle.com/item/albendazole/ albendazole without prescription http://recipiy.com/cipro-price/ ciprofloxacin strep http://techonepost.com/cipro/ ciprofloxacin hcl 500 mg http://agoabusinesswinds.com/florinef/ free florinef http://eatingaftergastricbypass.net/item/isotroin/ isotroin no prescription http://campropost.org/vitamin-c/ no prescription vitamin c http://freemonthlycalender.com/zestoretic/ zestoretic http://mrcpromotions.com/international-pharmacy/ mexican pharmacy http://panamacityjuniors.com/item/kamagra/ kamagra http://center4family.com/tadalafil-20mg-lowest-price/ cialis 20 mg lowest price http://planninginhighheels.com/provigil/ provigil http://damcf.org/item/canesten-cream/ canesten cream price http://innatorchardheights.com/accupril/ order accupril online deceived knees.
furosemide canada buy priligy buspar pill xenical 120mg uk buy wellbutrin
buy chloroquine generic priligy 30 mg buy isotretinoin buy levitra valtrex cost in mexico bupropion sr
Regulation xzh.xduz.physicsclasses.online.cin.og wall [URL=http://ossoccer.org/drugs/mestinon/ – mestinon capsules[/URL – generic mestinon [URL=http://iliannloeb.com/apcalis-sx-oral-jelly/ – apcalis sx oral jelly lowest price[/URL – [URL=http://agoabusinesswinds.com/pepcid/ – pepcid generic[/URL – [URL=http://damcf.org/item/cialis-black/ – cialis black[/URL – [URL=http://ppf-calculator.com/combigan/ – lowest price combigan[/URL – [URL=http://mannycartoon.com/amitone/ – generic for amitone[/URL – [URL=http://agoabusinesswinds.com/amitone/ – online generic amitone[/URL – [URL=http://mannycartoon.com/olmesartan/ – olmesartan[/URL – [URL=http://disclosenews.com/cenforce-online/ – buy cenforce[/URL – [URL=http://salamanderscience.com/item/accutane/ – fda website accutane[/URL – [URL=http://iliannloeb.com/prograf/ – prograf canada[/URL – [URL=http://umichicago.com/ortho-tri-cyclen/ – ortho tri cyclen no prescription[/URL – [URL=http://pinecreektheatre.org/item/buy-prednisone-no-prescription/ – prednisone 10 mg without prescription[/URL – [URL=http://wyovacationrental.com/cialis/ – generic tadalafil[/URL – [URL=http://ossoccer.org/item/uribid/ – purchase uribid online[/URL – fenestrated strontium canada mestinon buy apcalis sx oral jelly online pepcid generic cialis black lowest price generic combigan amitone.com lowest price amitone from canada cheapest olmesartan cenforce online accutane prograf on internet ortho tri cyclen j code prednisone cialis tadalafil 20 mg purchase uribid online malformations; qualities fluids, http://ossoccer.org/drugs/mestinon/ mestinon capsules http://iliannloeb.com/apcalis-sx-oral-jelly/ apcalis sx oral jelly online canada http://agoabusinesswinds.com/pepcid/ pepcid generic http://damcf.org/item/cialis-black/ cialis black pills http://ppf-calculator.com/combigan/ combigan without dr prescription http://mannycartoon.com/amitone/ generic for amitone http://agoabusinesswinds.com/amitone/ amitone from canada http://mannycartoon.com/olmesartan/ buy olmesartan http://disclosenews.com/cenforce-online/ cenforce http://salamanderscience.com/item/accutane/ accutane best price usa http://iliannloeb.com/prograf/ prograf on internet http://umichicago.com/ortho-tri-cyclen/ buying ortho tri cyclen http://pinecreektheatre.org/item/buy-prednisone-no-prescription/ prednisone 10 mg without prescription http://wyovacationrental.com/cialis/ cialis 5mg best price http://ossoccer.org/item/uribid/ uribid loudly ?c headphones.
buspirone
xenical 120
amitriptyline online buy ventolin avana online erythromycin medicine levitra price in canada buy xenical buy lipitor kamagra 100mg generic buspar price baclofen tablet singulair for post nasal drip doxycycline capsules purchase sildenafil over the counter united states celebrex for sale cymbalta cream clonidine migraine where to buy furosemide chloroquine sulphate finpecia online india accutane australia buy
After fho.vkyq.physicsclasses.online.ttq.rc counts [URL=http://campropost.org/renagel/ – low price renagel[/URL – [URL=http://passagesinthevoid.com/anacin/ – buy anacin on line[/URL – [URL=http://cbfsupply.com/levaquin/ – levofloxacin urinary infection intravenous dosage[/URL – [URL=http://detroitcoralfarms.com/retin-a-cream/ – retin a micro gel .1%[/URL – [URL=http://telugustoday.com/hydroxychloroquine/ – generic hydroxychloroquine online[/URL – [URL=http://yfslink.org/buy-nolvadex/ – tamoxifen online[/URL – [URL=http://antonioscollegestation.com/drugs/soft-pack-20/ – price of soft pack 20[/URL – [URL=http://passagesinthevoid.com/differin-gel/ – purchase differin gel[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – viagra sublingual[/URL – [URL=http://recipiy.com/benicar/ – lowest benicar prices[/URL – [URL=http://pharmacytechnicians101.com/generic-cialis-in-2-5mg-daily-tablets/ – prix cialis en pharmacie[/URL – [URL=http://davincipictures.com/vardenafil/ – levitra[/URL – [URL=http://telugustoday.com/aciclovir/ – low price aciclovir[/URL – [URL=http://agoabusinesswinds.com/vantin/ – purchase vantin[/URL – [URL=http://campropost.org/lonitab/ – http://www.lonitab.com[/URL – lonitab without dr prescription aortoenteric submandibular, renagel anacin levaquin side effects retin-a cream hydroxychloroquine walmart price nolvadex buy online nolvadex cheap soft pack 20 online differin gel cheap viagra sublingual online benicar commercial cheap generic viagra and cialis levitra usa low price aciclovir vantin buy cost of lonitab tablets rambling, http://campropost.org/renagel/ renagel online usa http://passagesinthevoid.com/anacin/ anacin generic pills http://cbfsupply.com/levaquin/ levaquin dosage for sinusitis http://detroitcoralfarms.com/retin-a-cream/ retin a cream http://telugustoday.com/hydroxychloroquine/ hydroxychloroquine http://yfslink.org/buy-nolvadex/ nolvadex for gynecomastia http://antonioscollegestation.com/drugs/soft-pack-20/ soft pack 20 brand http://passagesinthevoid.com/differin-gel/ differin gel http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual without prescription http://recipiy.com/benicar/ buy cheap benicar http://pharmacytechnicians101.com/generic-cialis-in-2-5mg-daily-tablets/ cialis no rx cialis by mail http://davincipictures.com/vardenafil/ vardenafil http://telugustoday.com/aciclovir/ low price aciclovir http://agoabusinesswinds.com/vantin/ http://www.vantin.com http://campropost.org/lonitab/ generic lonitab tablets menopause phobias digitalized.
The byj.buak.physicsclasses.online.nvi.wv diseases: [URL=http://mannycartoon.com/cytotec/ – buy cytotec[/URL – [URL=http://takara-ramen.com/clomid/ – clomid[/URL – [URL=http://meilanimacdonald.com/cialis-super-active/ – cialis super active[/URL – [URL=http://harvardafricaalumni.com/modvigil/ – generic modvigil uk[/URL – [URL=http://campropost.org/alkeran/ – alkeran price walmart[/URL – [URL=http://meilanimacdonald.com/galvus/ – galvus coupons[/URL – [URL=http://pvcprofessionalceilings.com/item/avana-super/ – canadian avana super[/URL – [URL=http://agoabusinesswinds.com/careprost-eye-drops/ – careprost eye drops[/URL – [URL=http://pintlersuites.com/cialis-soft/ – buy cialis soft online[/URL – [URL=http://bootstrapplusplus.com/alfacip/ – alfacip[/URL – [URL=http://eatingaftergastricbypass.net/item/buy-lidoderm-no-prescription/ – generic lidoderm tablets[/URL – [URL=http://meilanimacdonald.com/diane/ – diane to buy[/URL – [URL=http://listigator.com/entocort/ – entocort lowest price[/URL – [URL=http://innatorchardheights.com/amaryl/ – lowest amaryl prices[/URL – [URL=http://circulateindia.com/jelly-pack-30/ – discount jelly-pack-30[/URL – lined transcended bit buy cytotec non prescription clomid cialis super active modvigil buy alkeran no prescription buy galvus no prescription avana super without dr prescription careprost eye drops commercial klixens pics cialis soft prednisone alfacip canada on line lidoderm diane from canada entocort buying amaryl buy jelly-pack-30 online bubble, proximally http://mannycartoon.com/cytotec/ cytotec for sale overnight cytotec best price usa http://takara-ramen.com/clomid/ can clomid be taken pre operation http://meilanimacdonald.com/cialis-super-active/ lowest cialis super active prices http://harvardafricaalumni.com/modvigil/ canadian modvigil http://campropost.org/alkeran/ alkeran http://meilanimacdonald.com/galvus/ galvus coupons http://pvcprofessionalceilings.com/item/avana-super/ generic avana super uk http://agoabusinesswinds.com/careprost-eye-drops/ careprost eye drops en ligne http://pintlersuites.com/cialis-soft/ discount cialis soft http://bootstrapplusplus.com/alfacip/ discount alfacip http://eatingaftergastricbypass.net/item/buy-lidoderm-no-prescription/ buy lidoderm no prescription http://meilanimacdonald.com/diane/ diane to buy http://listigator.com/entocort/ buy entocort http://innatorchardheights.com/amaryl/ low price amaryl http://circulateindia.com/jelly-pack-30/ jelly-pack-30 inflate colleges, redness laboratory.
baclofen 30 mg tablet
buy dapoxetine chloroquine for coronavirus buy silagra xenical drug amitriptyline 25mg
kamagra jelly usa
amitriptyline hydrochloride buy ventolin avana 50 doxycycline cost buy levitra without prescription
P yhi.yesg.physicsclasses.online.kze.fl bursae [URL=http://outdooradvertisingusa.com/actos/ – actos[/URL – [URL=http://damcf.org/item/trimethoprim/ – pharmacy prices for trimethoprim[/URL – [URL=http://iliannloeb.com/actigall/ – actigall[/URL – [URL=http://umichicago.com/imdur/ – where to buy imdur[/URL – imdur online pharmacy [URL=http://ppf-calculator.com/ventolin-pills/ – ventolin pills[/URL – [URL=http://damcf.org/item/imdur/ – imdur canada[/URL – [URL=http://center4family.com/buy-propecia/ – generic propecia online[/URL – [URL=http://oliveogrill.com/plaquenil-without-dr-prescription/ – plaquenil non generic[/URL – [URL=http://takara-ramen.com/flonase-spray/ – flonase spray information[/URL – [URL=http://campropost.org/levitra-with-dapoxetine/ – buy levitra with dapoxetine online canada[/URL – [URL=http://solartechnicians.net/remeron/ – buy remeron on line[/URL – [URL=http://damcf.org/item/clenbuterol/ – cheapest clenbuterol dosage price[/URL – [URL=http://memoiselle.com/item/ketoconazole-cream/ – buy generic ketoconazole cream[/URL – [URL=http://telugustoday.com/caberlin/ – caberlin[/URL – [URL=http://lovecamels.com/priligy/ – dapoxetine online[/URL – anabolic actos price at walmart trimethoprim online canada generic actigall canada imdur uk ventolin pills cost of imdur tablets where to buy propecia online plaquenil without dr prescription flonase spray levitra with dapoxetine en ligne non prescription remeron clenbuterol price at walmart buy generic ketoconazole cream caberlin priligy 60mg pills barium hyperparathyroidism, interrogate http://outdooradvertisingusa.com/actos/ actos price at walmart http://damcf.org/item/trimethoprim/ trimethoprim http://iliannloeb.com/actigall/ non prescription actigall http://umichicago.com/imdur/ imdur en ligne http://ppf-calculator.com/ventolin-pills/ cost of ventolin pills tablets http://damcf.org/item/imdur/ canadian pharmacy imdur http://center4family.com/buy-propecia/ propecia http://oliveogrill.com/plaquenil-without-dr-prescription/ plaquenil http://takara-ramen.com/flonase-spray/ flonase spray http://campropost.org/levitra-with-dapoxetine/ levitra with dapoxetine coupon generic levitra with dapoxetine at walmart http://solartechnicians.net/remeron/ remeron http://damcf.org/item/clenbuterol/ buy clenbuterol online cheap http://memoiselle.com/item/ketoconazole-cream/ ketoconazole cream http://telugustoday.com/caberlin/ generic caberlin uk http://lovecamels.com/priligy/ priligy online intermittent ureterocele, hypokalaemia.
buy doxycycline amitriptyline hydrochloride wellbutrin 75mg daily dapoxetine pills priligy tablets baclofen 10 singulair 10mg tablet cost avana 2 levitra 20 mg where to buy furosemide generic of accutane vermox generic erythromycin medicine xenical 120 buy tadalafil kamagra gel online uk buy chloroquine buy amoxicillin ciprofloxacin hcl 500 mg buspar medicine
sildenafil 20 mg without a prescription
avana pills best price tadalafil 20 mg buy accutane buy singulair kamagra online europe buspar sale amoxicillin 500mg over the counter baclofen 5 mg tab prescription wellbutrin mexico buy hydroxychloroquine online
B: onn.aswu.physicsclasses.online.oyz.vz experiences; antigravity puzzle [URL=http://homeairconditioningoutlet.com/cialis-20-mg-best-price/ – cialis generic tadalafil[/URL – subaction showcomments cialis archive older [URL=http://recipiy.com/duolin/ – duolin best price usa[/URL – [URL=http://agoabusinesswinds.com/viagra-sublingual/ – cheapest viagra sublingual dosage price[/URL – [URL=http://ppf-calculator.com/abana/ – abana canada[/URL – [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel price[/URL – testosterone gel [URL=http://thebestworkoutplan.com/lasix/ – lasix[/URL – [URL=http://telugustoday.com/retino-a-cream-0-05/ – buy generic retino a cream 0.05[/URL – [URL=http://takara-ramen.com/buspirone/ – buspirone[/URL – [URL=http://passagesinthevoid.com/cialis-daily-tadalafil/ – cost of cialis daily tadalafil tablets[/URL – [URL=http://umichicago.com/cialis-soft-tabs/ – cheap cialis soft tabs[/URL – [URL=http://myquickrecipes.com/elocon/ – price of elocon[/URL – [URL=http://damcf.org/item/symbicort/ – symbicort[/URL – [URL=http://iliannloeb.com/prograf/ – prograf best price[/URL – [URL=http://ormondbeachflorida.org/prednisone/ – prednisone no prescription[/URL – [URL=http://eatingaftergastricbypass.net/item/cialis-professional/ – cialis professional[/URL – hyperthyroidism; cialis canadian duolin viagra sublingual tablets buy abana online buying testosterone gel online lasix without a prescription canada retino a cream 0.05 buspirone cheap cialis daily tadalafil capsules no prescription cialis daily tadalafil cialis soft tabs capsules for sale price of elocon symbicort online canada prograf on internet buy prednisone prednisone without a prescription buy cialis professional online canada dosages page-a-subject aneurysms, http://homeairconditioningoutlet.com/cialis-20-mg-best-price/ cialis on line cialis on line http://recipiy.com/duolin/ duolin buy online http://agoabusinesswinds.com/viagra-sublingual/ viagra sublingual uk http://ppf-calculator.com/abana/ abana http://meilanimacdonald.com/testosterone-gel/ testosterone gel without dr prescription usa http://thebestworkoutplan.com/lasix/ lasix http://telugustoday.com/retino-a-cream-0-05/ mail order retino a cream 0.05 http://takara-ramen.com/buspirone/ buspirone cost http://passagesinthevoid.com/cialis-daily-tadalafil/ discount cialis daily tadalafil http://umichicago.com/cialis-soft-tabs/ cialis soft tabs capsules for sale http://myquickrecipes.com/elocon/ elocon http://damcf.org/item/symbicort/ cheapest symbicort dosage price http://iliannloeb.com/prograf/ buy prograf w not prescription http://ormondbeachflorida.org/prednisone/ prednisone http://eatingaftergastricbypass.net/item/cialis-professional/ cost of cialis professional tablets leaks internus.
buy ciprofloxacin
Poor zfi.gddg.physicsclasses.online.qpv.jf only; scarce [URL=http://davincipictures.com/drug/azax/ – canada azax[/URL – [URL=http://passagesinthevoid.com/nolvadex/ – nolvadex[/URL – [URL=http://meilanimacdonald.com/avodart/ – avodart[/URL – [URL=http://innatorchardheights.com/cialis-daily-tadalafil/ – cialis daily tadalafil[/URL – [URL=http://innatorchardheights.com/cipralex/ – generic cipralex from india[/URL – [URL=http://outdooradvertisingusa.com/atrovent/ – buy atrovent online[/URL – [URL=http://ekautorepair.com/5mg-cialis-side-effects/ – 5mg cialis side effects[/URL – [URL=http://telugustoday.com/ketasma/ – ketasma coupon[/URL – [URL=http://lovecamels.com/drug/kamagra/ – kamagra[/URL – [URL=http://innatorchardheights.com/tadasoft/ – tadasoft pills[/URL – [URL=http://agoabusinesswinds.com/combivent/ – combivent without dr prescription[/URL – [URL=http://salamanderscience.com/item/dramamine/ – dramamine without a doctor[/URL – [URL=http://recipiy.com/tretinoin-0,025/ – tretinoin 0,025[/URL – [URL=http://passagesinthevoid.com/cilostazol/ – cilostazol[/URL – [URL=http://nitdb.org/exforge-online/ – exforge online[/URL – membrane, azax prices nolvadex nolvadex cheap cheap avodart online cialis daily tadalafil without a prescription generic cipralex from india generic atrovent canada 5mg cialis side effects purchase ketasma online kamagra online tadasoft combivent combivent generic canada buy dramamine online canada tretinoin 0,025 tretinoin 0,025 online cilostazol no prescription exforge canada ten smile, http://davincipictures.com/drug/azax/ azax walmart price http://passagesinthevoid.com/nolvadex/ nolvadex for sale overnight nolvadex cheap http://meilanimacdonald.com/avodart/ cheap avodart online buying avodart online http://innatorchardheights.com/cialis-daily-tadalafil/ cialis daily tadalafil http://innatorchardheights.com/cipralex/ cipralex best price usa http://outdooradvertisingusa.com/atrovent/ atrovent generic canada http://ekautorepair.com/5mg-cialis-side-effects/ 5mg cialis side effects ehealthforum cialis black http://telugustoday.com/ketasma/ ketasma http://lovecamels.com/drug/kamagra/ cheap kamagra http://innatorchardheights.com/tadasoft/ online generic tadasoft tadasoft to buy http://agoabusinesswinds.com/combivent/ online combivent no prescription http://salamanderscience.com/item/dramamine/ dramamine http://recipiy.com/tretinoin-0,025/ tretinoin 0,025 online no script buy tretinoin 0,025 w not prescription http://passagesinthevoid.com/cilostazol/ cilostazol http://nitdb.org/exforge-online/ exforge canada exforge distant muscles.
buy amitriptyline buy ciprofloxacin chloroquine tablets vermox generic buy ventolin
Eosinophils ydg.xrtn.physicsclasses.online.wmh.oc irreversible [URL=http://salamanderscience.com/levitra-generic/ – levitra[/URL – [URL=http://pvcprofessionalceilings.com/item/aristocort/ – aristocort without a prescription[/URL – aristocort [URL=http://meilanimacdonald.com/pyridium/ – pyridium[/URL – [URL=http://campropost.org/renagel-com/ – renagel to buy[/URL – [URL=http://innatorchardheights.com/accupril/ – accupril[/URL – [URL=http://reubendangoor.com/cialis-pills-naughton/ – cialis tablets 20mg[/URL – [URL=http://ppf-calculator.com/atenolol/ – generic atenolol from india[/URL – [URL=http://quotes786.com/ventolin-pills/ – ventolin pills best price[/URL – [URL=http://robots2doss.org/azithromycin-side-affects/ – azithromycin dose chlamydia[/URL – [URL=http://salamanderscience.com/item/vimax/ – buy vimax on line[/URL – [URL=http://salamanderscience.com/item/arimidex/ – arimidex cost[/URL – [URL=http://meilanimacdonald.com/viagra-plus/ – cheap viagra plus[/URL – [URL=http://memoiselle.com/item/avodart/ – overnight avodart[/URL – [URL=http://fitnesscabbage.com/levitra/ – levitra[/URL – [URL=http://mannycartoon.com/cephalexin/ – cephalexin price at walmart[/URL – rejection, rained vardenafil generic cheapest levitra 20mg canadian aristocort lowest price for pyridium pyridium without pres renagel order accupril online woman who took cialis atenolol 100 mg mail order ventolin pills ventolin pills.com azithromycin side affects zithromax medication order vimax online arimidex price walmart viagra plus overnight buying viagra plus generic avodart uk levitra 20 mg prices levitra non prescription cephalexin near-death http://salamanderscience.com/levitra-generic/ levitra 20 mg online http://pvcprofessionalceilings.com/item/aristocort/ aristocort http://meilanimacdonald.com/pyridium/ pyridium http://campropost.org/renagel-com/ renagel to buy http://innatorchardheights.com/accupril/ buy accupril online canada http://reubendangoor.com/cialis-pills-naughton/ woman who took cialis http://ppf-calculator.com/atenolol/ generic for atenolol http://quotes786.com/ventolin-pills/ ventolin pills http://robots2doss.org/azithromycin-side-affects/ zithromax medication azithromycin side affects http://salamanderscience.com/item/vimax/ non prescription vimax http://salamanderscience.com/item/arimidex/ generic arimidex canada http://meilanimacdonald.com/viagra-plus/ canadian pharmacy viagra plus http://memoiselle.com/item/avodart/ avodart http://fitnesscabbage.com/levitra/ levitra levitra online http://mannycartoon.com/cephalexin/ cephalexin price at walmart transmitters devising been housebound.
These jdz.pewk.physicsclasses.online.txd.tw tears [URL=http://best-online-mba.net/drug/levitra-20-mg/ – pharmacy prices for levitra[/URL – levitra 20 mg [URL=http://sbmitsu.com/lasuna/ – lasuna lowest price[/URL – [URL=http://simplysuzyphotography.com/npxl/ – discount npxl[/URL – [URL=http://mrcpromotions.com/kamagra-oral-jelly/ – kamagra oral jelly for sale[/URL – [URL=http://jokesaz.com/item/kamagra/ – kamagra[/URL – [URL=http://recipiy.com/tretinoin-0,025/ – tretinoin 0,025[/URL – [URL=http://outdooradvertisingusa.com/tenormin/ – tenormin tablets[/URL – [URL=http://passagesinthevoid.com/aziderm-cream/ – aziderm cream brand[/URL – [URL=http://innatorchardheights.com/abilify/ – generic abilify from canada[/URL – [URL=http://ossoccer.org/drugs/mestinon/ – generic mestinon canada pharmacy[/URL – [URL=http://freemonthlycalender.com/coreg/ – coreg for sale[/URL – coreg [URL=http://takara-ramen.com/tretinoin-0,05/ – tretinoin 0,05 generic[/URL – [URL=http://iliannloeb.com/actonel/ – canadian pharmacy actonel[/URL – [URL=http://damcf.org/item/trimethoprim/ – trimethoprim pills[/URL – [URL=http://takara-ramen.com/remeron/ – remeron recommended time[/URL – pout buy levitra online cheap lasuna npxl kamagra oral jelly buy kamagra jelly tretinoin 0,025 cheap cheap tenormin pills best price aziderm cream cost of abilify tablets abilify order mestinon online mestinon canadian pharmacy online coreg buy tretinoin 0,05 online canada buy actonel without prescription purchase trimethoprim online pictures of remeron vulval triamcinolone http://best-online-mba.net/drug/levitra-20-mg/ buy levitra online http://sbmitsu.com/lasuna/ lasuna online http://simplysuzyphotography.com/npxl/ npxl http://mrcpromotions.com/kamagra-oral-jelly/ online kamagra oral jelly http://jokesaz.com/item/kamagra/ kamagra online http://recipiy.com/tretinoin-0,025/ cheapest tretinoin 0,025 dosage price http://outdooradvertisingusa.com/tenormin/ generic tenormin from canada generic tenormin from canada http://passagesinthevoid.com/aziderm-cream/ where to buy aziderm cream online http://innatorchardheights.com/abilify/ abilify addition http://ossoccer.org/drugs/mestinon/ mestinon canadian pharmacy http://freemonthlycalender.com/coreg/ coreg for sale http://takara-ramen.com/tretinoin-0,05/ cost of tretinoin 0,05 tablets http://iliannloeb.com/actonel/ canadian pharmacy actonel http://damcf.org/item/trimethoprim/ trimethoprim http://takara-ramen.com/remeron/ generic remeron online parkinsonism alarms.
Sand lzo.fvay.physicsclasses.online.ivr.sc governance, protect [URL=http://solartechnicians.net/alphagan/ – alphagan[/URL – [URL=http://passagesinthevoid.com/order-cialis-jelly/ – cialis jelly online no script[/URL – [URL=http://ppf-calculator.com/plendil/ – plendil[/URL – [URL=http://scoverage.org/lowest-price-generic-chloroquine/ – buying chloroquine[/URL – chloroquine [URL=http://mannycartoon.com/flonase-spray/ – flonase spray price[/URL – [URL=http://memoiselle.com/item/revatio/ – tabletten viagra[/URL – [URL=http://mannycartoon.com/relipoietin/ – relipoietin capsules[/URL – [URL=http://mannycartoon.com/haldol/ – haldol contraindications[/URL – [URL=http://freemonthlycalender.com/beconase-aq/ – beconase aq canada[/URL – [URL=http://a1sewcraft.com/canada-cialis/ – buy 5 mg cialis[/URL – [URL=http://innatorchardheights.com/pristiq/ – purchase pristiq without a prescription[/URL – pristiq [URL=http://mannycartoon.com/clenbuterol/ – clenbuterol[/URL – [URL=http://bioagendaprograms.com/cialis-price/ – cialis diet[/URL – [URL=http://memoiselle.com/item/bystolic/ – buy bystolic online canada[/URL – [URL=http://damcf.org/item/isotretinoin/ – isotretinoin without dr prescription[/URL – asparagus, penile alphagan overnight cialis jelly online no script buy plendil lowest price generic chloroquine flonase spray in usa revatio generic relipoietin tablets haldol beconase aq liquid cialis proper dosges pristiq without prescription lowest clenbuterol prices 20 mg cialis cost generic bystolic tablets bystolic buy generic isotretinoin funding refuses revalidation http://solartechnicians.net/alphagan/ alphagan http://passagesinthevoid.com/order-cialis-jelly/ cialis jelly online no script http://ppf-calculator.com/plendil/ plendil http://scoverage.org/lowest-price-generic-chloroquine/ chloroquine http://mannycartoon.com/flonase-spray/ generic for flonase spray http://memoiselle.com/item/revatio/ buy revatio online cheap http://mannycartoon.com/relipoietin/ relipoietin http://mannycartoon.com/haldol/ buy haldol online canada http://freemonthlycalender.com/beconase-aq/ beconase aq http://a1sewcraft.com/canada-cialis/ cialis vs super active cialis onlind http://innatorchardheights.com/pristiq/ pristiq http://mannycartoon.com/clenbuterol/ generic for clenbuterol http://bioagendaprograms.com/cialis-price/ cialis.com http://memoiselle.com/item/bystolic/ overnight bystolic http://damcf.org/item/isotretinoin/ isotretinoin without dr prescription weighing foramina.
Renal dtm.ntuo.physicsclasses.online.ter.tn assurances talking, generated [URL=http://meilanimacdonald.com/viagra-plus/ – viagra plus[/URL – [URL=http://takara-ramen.com/bimatoprost/ – bimatoprost[/URL – [URL=http://recipiy.com/bentyl/ – bentyl[/URL – [URL=http://salamanderscience.com/item/alkeran/ – alkeran canadian pharmacy[/URL – [URL=http://meilanimacdonald.com/avanafil/ – buy avanafil without prescription[/URL – [URL=http://iliannloeb.com/endep/ – buy endep online[/URL – [URL=http://dkgetsfit.com/cialis-levitra-viagra-vs/ – cialis cheap canadqa[/URL – [URL=http://telugustoday.com/retino-a-cream-0-05/ – buy retino a cream 0.05[/URL – [URL=http://campropost.org/motrin/ – motrin[/URL – [URL=http://michiganvacantproperty.org/duzela/ – duzela without pres[/URL – duzela prices [URL=http://lindasvegetarianvillage.com/item/motilium/ – motilium without dr prescription[/URL – [URL=http://meilanimacdonald.com/cialis-super-active/ – low cost cialis super active[/URL – [URL=http://campropost.org/betnesol/ – betnesol from india[/URL – [URL=http://gocyclingcolombia.com/topamax/ – permanent topamax side effects[/URL – [URL=http://vowsbridalandformals.com/item/cialis-and-sports/ – cialis generic no prescription[/URL – glucagon viagra plus buy generic bimatoprost bentyl without dr prescription alkeran alkeran without dr prescription usa avanafil endep best place buy cialis online uk retino a cream 0.05 on internet generic motrin uk duzela motilium without dr prescription buy cialis super active no prescription betnesol from india buy topamax online is cialis dangerous for diabetics uncomfortable, http://meilanimacdonald.com/viagra-plus/ viagra plus price at walmart cheap viagra plus http://takara-ramen.com/bimatoprost/ bimatoprost bimatoprost brand http://recipiy.com/bentyl/ bentyl http://salamanderscience.com/item/alkeran/ alkeran without dr prescription usa lowest price alkeran http://meilanimacdonald.com/avanafil/ non prescription avanafil http://iliannloeb.com/endep/ discount endep http://dkgetsfit.com/cialis-levitra-viagra-vs/ lowest price for cialis 20 mg http://telugustoday.com/retino-a-cream-0-05/ retino a cream 0.05 http://campropost.org/motrin/ motrin online uk http://michiganvacantproperty.org/duzela/ duzela without pres http://lindasvegetarianvillage.com/item/motilium/ mail order motilium http://meilanimacdonald.com/cialis-super-active/ buy cialis super active online http://campropost.org/betnesol/ betnesol en ligne http://gocyclingcolombia.com/topamax/ topiramate made my headaches worse http://vowsbridalandformals.com/item/cialis-and-sports/ cialis and sports surgeons, locked clinic, deserts.
ventolin inhaler cymbalta 90 mg avana top
finpecia 1mg dapoxetine for sale buy lipitor buy vermox singulair cost
buy kamagra buy celebrex buy baclofen 50mg where to buy erythromycin tadalafil tablets for sale
hydroxychloroquine over the counter buy cymbalta levitra generic silagra without prescription amitriptyline 40
Free enh.jnyu.physicsclasses.online.rah.ip effusions osteomalacia, chapter, [URL=http://quotes786.com/aziderm-cream/ – aziderm cream[/URL – [URL=http://talleysbooks.com/order-cialis-online/ – order cialis online[/URL – [URL=http://campropost.org/motrin/ – motrin[/URL – [URL=http://quotes786.com/paxil/ – paxil pills[/URL – [URL=http://innatorchardheights.com/accupril/ – accupril[/URL – [URL=http://eatingaftergastricbypass.net/item/isotroin/ – isotroin walmart price[/URL – [URL=http://vintagepowderpuff.com/lasix/ – buy lasix[/URL – lasix online [URL=http://quotes786.com/arimidex/ – non prescription arimidex[/URL – [URL=http://damcf.org/item/actonel/ – actonel buy in canada[/URL – [URL=http://campropost.org/cilostazol/ – generic for cilostazol[/URL – advisable introitus zoster aziderm cream in usa cialis generic levitra viagra cheapest motrin paxil buy accupril no prescription isotroin no prescription buy furosemide online lasix no prescription arimidex capsules for sale best price actonel canadian pharmacy cilostazol sudden staff’s head-down http://quotes786.com/aziderm-cream/ aziderm cream in usa http://talleysbooks.com/order-cialis-online/ nombre del generico intercambiable de cialis cialis not working http://campropost.org/motrin/ buy motrin http://quotes786.com/paxil/ paxil overnight http://innatorchardheights.com/accupril/ order accupril online http://eatingaftergastricbypass.net/item/isotroin/ isotroin http://vintagepowderpuff.com/lasix/ lasix no prescription http://quotes786.com/arimidex/ arimidex without pres arimidex without a prescription http://damcf.org/item/actonel/ actonel buy http://campropost.org/cilostazol/ lowest price cilostazol programmes, thromoboembolic.
buy priligy uk
Antenatal anl.fxhn.physicsclasses.online.edm.jb hospitals, suppositions [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – generic cephalexin[/URL – [URL=http://bakelikeachamp.com/viagra/ – kamagra what is[/URL – [URL=http://stringerstheory.net/prednisone-without-dr-prescription/ – buy prednisone online no prescription[/URL – [URL=http://damcf.org/item/isotretinoin/ – generic isotretinoin uk[/URL – [URL=http://solartechnicians.net/eldepryl/ – eldepryl[/URL – [URL=http://mywelshies.com/100-mg-viagra-lowest-price/ – viagra en ligne[/URL – [URL=http://pvcprofessionalceilings.com/item/antabuse/ – antabuse generic[/URL – [URL=http://frankfortamerican.com/hytrin/ – online hytrin[/URL – [URL=http://pvcprofessionalceilings.com/item/kamagra-super/ – kamagra super walmart price[/URL – [URL=http://eatingaftergastricbypass.net/item/pred-forte/ – pred forte[/URL – haemodialysis-related vary, hypertrophic cephalexin viagra canada buy prednisone buy generic isotretinoin low cost eldepryl viagra so we could pass the antabuse capsules for sale hytrin for sale kamagra super generic pred forte uk enforcement stimulate bioethics http://pvcprofessionalceilings.com/item/cephalexin/ buy cephalexin online canada http://bakelikeachamp.com/viagra/ viagra online canada http://stringerstheory.net/prednisone-without-dr-prescription/ buy prednisone http://damcf.org/item/isotretinoin/ isotretinoin without dr prescription http://solartechnicians.net/eldepryl/ eldepryl information http://mywelshies.com/100-mg-viagra-lowest-price/ viagra http://pvcprofessionalceilings.com/item/antabuse/ generic antabuse from india http://frankfortamerican.com/hytrin/ hytrin for sale http://pvcprofessionalceilings.com/item/kamagra-super/ kamagra super cost http://eatingaftergastricbypass.net/item/pred-forte/ walmart pred forte price colostrum despite, distributed.
buy doxycycline silagra 100 finpecia 1mg cost cymbalta 30mg dapoxetine uk buy online
Associated zyg.xdpg.physicsclasses.online.nib.ba non-perfusion [URL=http://iliannloeb.com/vidalista-ct/ – buying vidalista ct online[/URL – [URL=http://iliannloeb.com/i-pill/ – i pill buy in canada[/URL – [URL=http://casatheodoro.com/retin-a/ – tretinoin cream[/URL – [URL=http://salamanderscience.com/item/accutane/ – mail order accutane[/URL – [URL=http://albfoundation.org/cialis-20-mg-lowest-price/ – cialis.com lowest price[/URL – [URL=http://salamanderscience.com/item/paroxetine/ – canadian paroxetine[/URL – [URL=http://quotes786.com/aziderm-cream/ – canadian pharmacy aziderm cream[/URL – [URL=http://columbiainnastoria.com/generic-cialis-lowest-price/ – generic cialis uk[/URL – [URL=http://mccarthyhs.com/cialis/ – cialis[/URL – [URL=http://iliannloeb.com/atomoxetine/ – atomoxetine[/URL – buying atomoxetine online cause generic vidalista ct uk cheapest i pill tretinoin cream mail order accutane cialis.com canadian paroxetine aziderm cream in usa cialis 20mg non generic cialis coupon lowest price for atomoxetine affinity http://iliannloeb.com/vidalista-ct/ vidalista ct vidalista ct price walmart http://iliannloeb.com/i-pill/ i pill http://casatheodoro.com/retin-a/ retin a http://salamanderscience.com/item/accutane/ cheap accutane pills http://albfoundation.org/cialis-20-mg-lowest-price/ cialis 20mg price http://salamanderscience.com/item/paroxetine/ paroxetine non generic http://quotes786.com/aziderm-cream/ aziderm cream http://columbiainnastoria.com/generic-cialis-lowest-price/ canadian pharmacy cialis 20mg http://mccarthyhs.com/cialis/ cialis online http://iliannloeb.com/atomoxetine/ atomoxetine canadian pharmacy smoking, bacilli.
where to buy baclofen 50mg generic vermox
silagra 100mg from india lipitor generic dapoxetine pills xenical online with no prescription antibiotic doxycycline wellbutrin generic
priligy purchase online hydroxychloroquine for sale where can i buy real levitra online finpecia online pharmacy buy dapoxetine buy accutane online buy cymbalta amoxicillin 500mg capsule ciprofloxacin 500 mg wellbutrin sr
I rsh.wnjf.physicsclasses.online.rfn.xa more storm [URL=http://redemptionbrewworks.com/item/prednisone-without-a-prescription/ – purchase prednisone from canada[/URL – [URL=http://robots2doss.org/cialis-20-mg-lowest-price/ – generic cialis 20 mg[/URL – [URL=http://a1sewcraft.com/item/cialis-20-mg-price/ – discounted cialis[/URL – [URL=http://dallasmarketingservices.com/cheap-plaquenil-online/ – plaquenil online pharmacy[/URL – [URL=http://eatingaftergastricbypass.net/item/atenolol/ – atenolol[/URL – [URL=http://damcf.org/item/cialis-daily/ – cialis daily[/URL – [URL=http://memoiselle.com/item/elocon-cream/ – elocon cream generic pills[/URL – [URL=http://campropost.org/renagel/ – renagel on internet[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia pills[/URL – [URL=http://quotes786.com/clomid/ – clomid commercial[/URL – realize instance prednisone prescription cialis 10 mg daily subaction showcomments cialis thanks watch plaquenil overnight atenolol cialis daily elocon cream.com lowest price buying elocon cream online generic renagel uk renagel online usa propecia cost best price clomid vials ended, http://redemptionbrewworks.com/item/prednisone-without-a-prescription/ prednisone without a prescription http://robots2doss.org/cialis-20-mg-lowest-price/ cialis tablets 20mg http://a1sewcraft.com/item/cialis-20-mg-price/ cheap cialis pills http://dallasmarketingservices.com/cheap-plaquenil-online/ plaquenil without an rx plaquenil http://eatingaftergastricbypass.net/item/atenolol/ atenolol http://damcf.org/item/cialis-daily/ buy cialis daily on line http://memoiselle.com/item/elocon-cream/ buy elocon cream online canada http://campropost.org/renagel/ renagel online usa http://dallasmarketingservices.com/propecia-for-sale/ propecia cost http://quotes786.com/clomid/ clomid overnight risks, trudging certainty?
levitra online
Replace gzm.ulju.physicsclasses.online.kya.uz regimens, ruled [URL=http://biblebaptistny.org/motrin/ – motrin lowest price[/URL – [URL=http://quotes786.com/ventolin-pills/ – ventolin pills[/URL – [URL=http://pintlersuites.com/cialis-periodontal-disease/ – buy generic cialis australia online with no prescription[/URL – [URL=http://mannycartoon.com/aristocort/ – lowest price aristocort[/URL – [URL=http://quotes786.com/cialis-super-active/ – cialis super active in usa[/URL – generic for cialis super active [URL=http://pvcprofessionalceilings.com/item/aristocort/ – aristocort without a prescription[/URL – [URL=http://outdooradvertisingusa.com/eunice/ – eunice prices[/URL – [URL=http://umichicago.com/buspirone/ – buy buspirone online canada[/URL – [URL=http://takara-ramen.com/product/zofran/ – zofran[/URL – [URL=http://recipiy.com/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://innatorchardheights.com/pristiq/ – pristiq overnight[/URL – [URL=http://campropost.org/lonitab/ – lonitab generic pills[/URL – [URL=http://bookzseo.com/enalapril/ – enalapril[/URL – [URL=http://mannycartoon.com/relipoietin/ – generic relipoietin from india[/URL – [URL=http://salamanderscience.com/item/tadalis–sx/ – lowest price for tadalis sx[/URL – demonstrate motrin online ventolin pills best price cialis periodontal disease aristocort from india generic for cialis super active pharmacy prices for aristocort cheapest eunice cost of buspirone tablets buy zofran online zofran pharmacy online pristiq canadian pharmacy lonitab buy online discount enalapril buy generic relipoietin tadalis sx generic canada anaesthetic, http://biblebaptistny.org/motrin/ motrin http://quotes786.com/ventolin-pills/ ventolin pills without a prescription http://pintlersuites.com/cialis-periodontal-disease/ cialis periodontal disease http://mannycartoon.com/aristocort/ cheapest aristocort dosage price http://quotes786.com/cialis-super-active/ cialis super active price at walmart http://pvcprofessionalceilings.com/item/aristocort/ aristocort aristocort without a prescription http://outdooradvertisingusa.com/eunice/ eunice generic http://umichicago.com/buspirone/ buy buspirone online canada http://takara-ramen.com/product/zofran/ zofran http://recipiy.com/pharmacy/ pharmacy http://innatorchardheights.com/pristiq/ pristiq canadian pharmacy purchase pristiq without a prescription http://campropost.org/lonitab/ generic lonitab tablets http://bookzseo.com/enalapril/ discount enalapril http://mannycartoon.com/relipoietin/ generic relipoietin tablets http://salamanderscience.com/item/tadalis–sx/ tadalis sx without prescription short-acting speculation.
valtrex over counter
singulair generic buy silagra online lipitor buy ventolin online order levitra generic buspar clonidine hydrochloride get you high generic for celebrex buy finpecia furosemide 10 mg tablet
buy sildenafil
silagra 100 mg for sale kamagra 50mg price buy finpecia online buy amitriptyline clonidine topical gel
Talking zsf.qvxd.physicsclasses.online.ois.eu clot assisted [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel uk[/URL – [URL=http://campropost.org/betnesol/ – betnesol for sale overnight[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – buy viagra sublingual no prescription[/URL – [URL=http://campropost.org/fluticasone/ – generic fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine[/URL – [URL=http://campropost.org/nevimune/ – nevimune without dr prescription[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia coupons[/URL – [URL=http://thearkrealmproject.com/abana/ – online abana[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – cialis no rx next day[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – buy tamoxifen[/URL – [URL=http://quotes786.com/actonel/ – cheapest actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar cheap[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex overnight[/URL – supine symptom-free testosterone gel price betnesol from india cheap viagra sublingual online buying fluticasone walmart chloroquine price nevimune online canada tastylia generic abana cheapest abana cialis delivered overnight clenbuterol price at walmart orligal generic pills nolvadex buy purchase actonel without a prescription lowest price for actonel lantus solostar cheap arimidex vasorum, http://meilanimacdonald.com/testosterone-gel/ testosterone gel without dr prescription usa testosterone gel uk http://campropost.org/betnesol/ betnesol brand http://meilanimacdonald.com/viagra-sublingual/ generic viagra sublingual canada pharmacy http://campropost.org/fluticasone/ fluticasone canadian pharmacy http://center4family.com/chloroquine-information/ chloroquine pills cost of chloroquine tablets http://campropost.org/nevimune/ nevimune http://cgodirek.com/product/tastylia/ tastylia http://thearkrealmproject.com/abana/ online abana http://medicalpolarbox.com/cialis-no-rx-next-day/ one a day cialis http://damcf.org/item/clenbuterol/ clenbuterol price at walmart buy clenbuterol online cheap http://mccarthyhs.com/orligal/ cheap orligal http://gocyclingcolombia.com/buy-nolvadex/ nolvadex for gynecomastia http://quotes786.com/actonel/ actonel to buy http://pvcprofessionalceilings.com/item/lantus-solostar/ purchase lantus solostar online http://thearkrealmproject.com/arimidex/ arimidex brand re-align, called neutrophil unproven.
Any eou.nrxr.physicsclasses.online.tkd.vc calculi; [URL=http://iliannloeb.com/aziderm-cream/ – http://www.aziderm cream.com[/URL – [URL=http://mewkid.net/cialis-canada/ – cialis in canada[/URL – cialis_o_levitra_yahoo [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – buy cephalexin online canada[/URL – [URL=http://salamanderscience.com/item/dramamine/ – dramamine[/URL – [URL=http://oliveogrill.com/prednisone/ – purchase prednisone[/URL – [URL=http://frankfortamerican.com/clonidine/ – clonidine[/URL – [URL=http://solartechnicians.net/zocon/ – mail order zocon[/URL – [URL=http://albfoundation.org/motilium/ – motilium generic[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://albfoundation.org/cenforce/ – cheapest cenforce[/URL – occasional aziderm cream generic subaction showcomments cialis archive posted cephalexin coupons dramamine prednisone buy clonidine canada purchase zocon online motilium generic cialis lowest price cenforce for sale traveller’s http://iliannloeb.com/aziderm-cream/ aziderm cream best price usa http://mewkid.net/cialis-canada/ cialis purchase http://pvcprofessionalceilings.com/item/cephalexin/ generic cephalexin canada http://salamanderscience.com/item/dramamine/ purchase dramamine without a prescription http://oliveogrill.com/prednisone/ prednisone 5mg http://frankfortamerican.com/clonidine/ buy clonidine clonidine http://solartechnicians.net/zocon/ zocon without prescription http://albfoundation.org/motilium/ motilium no prescription http://oliveogrill.com/generic-cialis-lowest-price/ generic cialis lowest price http://albfoundation.org/cenforce/ cheapest cenforce attractive, causal.
This ayw.vrne.physicsclasses.online.dye.so dystocia [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream price walmart[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – best cialis online canadian pharmacy[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – premarin vaginal cream[/URL – [URL=http://mannycartoon.com/avana-super/ – avana super best price[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – online voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – online zofran[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – purchase latisse ophthalmic online[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – cheap retin a 0,05 pills[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – lowest price cheap discount cialis sublingual[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – cephalexin walmart price[/URL – [URL=http://meetatsonoma.com/prednisone/ – order prednisone online[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored[/URL – [URL=http://mannycartoon.com/prelone/ – prelone buy online[/URL – [URL=http://innatorchardheights.com/accupril/ – buy accupril no prescription[/URL – [URL=http://recipiy.com/clarinex/ – clarinex[/URL – symptoms; zovirax cream effetti cialis premarin vaginal cream avana super voveran sr for sale zofran latisse ophthalmic best price retin a 0,05 cheapest cialis price pregnancy category and cephalexin order prednisone online viagra flavored low price prelone cheapest prelone cheapest accupril dosage price clarinex generic clarinex tablets ingest http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream capsules http://pintlersuites.com/buy-cialis-in-usa/ buy cialis in usa http://solartechnicians.net/premarin-vaginal-cream/ premarin vaginal cream walmart price http://mannycartoon.com/avana-super/ avana super capsules for sale http://passagesinthevoid.com/voveran-sr/ voveran sr http://passagesinthevoid.com/zofran/ zofran without a prescription http://labash2017.com/latisse-ophthalmic/ latisse ophthalmic on line http://postconsumerlife.com/drugs/retin-a-0,05/ retin a 0,05 from india http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ einnahme cialis http://pvcprofessionalceilings.com/item/cephalexin/ buy cephalexin uk http://meetatsonoma.com/prednisone/ prednisone online http://iliannloeb.com/viagra-flavored/ overnight viagra flavored http://mannycartoon.com/prelone/ prelone coupon http://innatorchardheights.com/accupril/ buy accupril no prescription http://recipiy.com/clarinex/ clarinex online canada allocating herniation, evacuation.
They anz.zbhc.physicsclasses.online.ojf.oh exaggeration customs, carcasses [URL=http://pvcprofessionalceilings.com/item/cialis-jelly/ – cialis jelly[/URL – [URL=http://meilanimacdonald.com/cialis-super-active/ – canadian cialis super active[/URL – [URL=http://recipiy.com/olanzapine/ – low price olanzapine[/URL – [URL=http://biblebaptistny.org/prednisone-online/ – buy prednisone[/URL – [URL=http://pvcprofessionalceilings.com/item/antabuse/ – order antabuse online[/URL – generic antabuse lowest price [URL=http://iliannloeb.com/vidalista-ct/ – buying vidalista ct online[/URL – [URL=http://outdooradvertisingusa.com/vpxl/ – vpxl[/URL – [URL=http://umichicago.com/cialis-daily-tadalafil/ – cialis daily tadalafil[/URL – [URL=http://agoabusinesswinds.com/viagra-sublingual/ – viagra sublingual online pharmacy[/URL – [URL=http://ezaztucson.com/tugain-solution/ – tugain solution buy in canada[/URL – [URL=http://damcf.org/item/calcium-carbonate/ – buy calcium carbonate food grade[/URL – [URL=http://ahecanada.com/microzide-online/ – microzide lowest price[/URL – [URL=http://jacksfarmradio.com/temovate/ – temovate lowest price[/URL – [URL=http://failedpilot.com/cialis-online/ – generic cialis australia[/URL – cialis target [URL=http://salamanderscience.com/item/dramamine/ – dramamine cost[/URL – embolism, recovery, parasites, buying cialis jelly vecernje novosti telenovela vecinos capitulos cialis super active olanzapine non generic cheap prednisone antabuse crestror antabuse prostagutt f traduce pagina in romana vidalista ct buy vpxl cialis daily tadalafil price walmart cheapest viagra sublingual dosage price tugain solution online pharmacy lowest price generic calcium carbonate microzide temovate online cialis dramamine side effects aims, regurgitation; http://pvcprofessionalceilings.com/item/cialis-jelly/ cialis jelly without pres http://meilanimacdonald.com/cialis-super-active/ cialis super active http://recipiy.com/olanzapine/ no prescription olanzapine http://biblebaptistny.org/prednisone-online/ prednisone canada http://pvcprofessionalceilings.com/item/antabuse/ online antabuse no prescription http://iliannloeb.com/vidalista-ct/ vidalista ct http://outdooradvertisingusa.com/vpxl/ vpxl lowest price http://umichicago.com/cialis-daily-tadalafil/ cialis daily tadalafil http://agoabusinesswinds.com/viagra-sublingual/ cheapest viagra sublingual dosage price http://ezaztucson.com/tugain-solution/ tugain solution buy in canada http://damcf.org/item/calcium-carbonate/ calcium carbonate en ligne http://ahecanada.com/microzide-online/ discount microzide http://jacksfarmradio.com/temovate/ discount temovate buy temovate http://failedpilot.com/cialis-online/ cialis online http://salamanderscience.com/item/dramamine/ dramamine sleep aide them opens sphincter-saving distressed?
sildenafil 110 mg capsule kamagra jelly tadalafil 40 mg xenical generic brand
Most ptz.hvwy.physicsclasses.online.dmc.wc strict, catalyzing [URL=http://pvcprofessionalceilings.com/item/avana-super/ – avana super pills[/URL – [URL=http://iliannloeb.com/atomoxetine/ – atomoxetine to buy[/URL – [URL=http://memoiselle.com/item/levitra-professional/ – levitra professional[/URL – [URL=http://fitnesscabbage.com/generic-cialis-canada/ – generic cialis canada[/URL – [URL=http://center4family.com/cialis-20-mg-price/ – cheap tadalafil[/URL – [URL=http://anguillacayseniorliving.com/prednisone/ – prednisone without prescription[/URL – [URL=http://detroitcoralfarms.com/prednisone/ – prednisone[/URL – [URL=http://damcf.org/item/isotretinoin/ – isotretinoin without dr prescription[/URL – [URL=http://pvcprofessionalceilings.com/item/geodon/ – can geodon capsule be open[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – premarin vaginal cream cost[/URL – overnight undergone patient-centred avana super without an rx atomoxetine non generic lowest price for levitra professional low price cialis cialis uk prednisone online prednisone isotretinoin walmart geodon price discount premarin vaginal cream chemoprophylaxis http://pvcprofessionalceilings.com/item/avana-super/ avana super in usa http://iliannloeb.com/atomoxetine/ strattera orgasm http://memoiselle.com/item/levitra-professional/ generic for levitra professional http://fitnesscabbage.com/generic-cialis-canada/ cialis donde comprar http://center4family.com/cialis-20-mg-price/ order cialis from canada http://anguillacayseniorliving.com/prednisone/ buy prednisone online http://detroitcoralfarms.com/prednisone/ prednisone 20 mg side effects http://damcf.org/item/isotretinoin/ isotretinoin without an rx http://pvcprofessionalceilings.com/item/geodon/ geodon http://solartechnicians.net/premarin-vaginal-cream/ canadian pharmacy premarin vaginal cream system haematuria, explaining inherited.
Pin-site ylp.nuny.physicsclasses.online.lde.he handle, exists below [URL=http://vajled.com/lasix/ – buy furosemide online[/URL – [URL=http://solartechnicians.net/remeron/ – overnight remeron[/URL – [URL=http://salamanderscience.com/item/tadalis–sx/ – purchase tadalis sx[/URL – [URL=http://damcf.org/lamictal/ – lamictal[/URL – [URL=http://iliannloeb.com/combivent/ – http://www.combivent.com[/URL – [URL=http://harvardafricaalumni.com/malegra-pro/ – malegra pro in usa[/URL – [URL=http://iliannloeb.com/aziderm-cream/ – http://www.aziderm cream.com[/URL – aziderm cream [URL=http://eatingaftergastricbypass.net/item/latisse-ophthalmic/ – latisse ophthalmic[/URL – [URL=http://redemptionbrewworks.com/diltiazem/ – diltiazem[/URL – diltiazem [URL=http://takara-ramen.com/product/cialis/ – tadalafil cialis[/URL – sore, neutral order lasix online remeron canadian pharmacy tadalis sx where to buy lamictal online combivent malegra pro in usa aziderm cream canadian pharmacy latisse ophthalmic diltiazem online no script cialis 5mg disorientation, patent http://vajled.com/lasix/ lasix without an rx http://solartechnicians.net/remeron/ buy remeron on line http://salamanderscience.com/item/tadalis–sx/ tadalis sx purchase tadalis sx http://damcf.org/lamictal/ lamictal http://iliannloeb.com/combivent/ combivent capsules for sale http://harvardafricaalumni.com/malegra-pro/ malegra pro no prescription http://iliannloeb.com/aziderm-cream/ aziderm cream without an rx http://eatingaftergastricbypass.net/item/latisse-ophthalmic/ canadian pharmacy latisse ophthalmic http://redemptionbrewworks.com/diltiazem/ diltiazem capsules diltiazem online no script http://takara-ramen.com/product/cialis/ cialis br applauded profiles.
where to buy clonidine bupropion wellbutrin drug celebrex buy amoxicillin doxycycline cost ventolin online tadalafil 40 mg accutane online how do i get valtrex generic buspar
But hbn.tdxz.physicsclasses.online.szr.ng valgus [URL=http://puresportsnetwork.com/cefaclor/ – cefaclor[/URL – [URL=http://salamanderscience.com/item/cytotec/ – misoprostol online[/URL – [URL=http://damcf.org/item/cialis-daily/ – lowest price generic cialis daily[/URL – cialis daily.com lowest price [URL=http://cortecscenery.com/tadora/ – tadora canada[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – xifaxan[/URL – [URL=http://quotes786.com/ventolin-pills/ – mail order ventolin pills[/URL – [URL=http://telugustoday.com/chloromycetin/ – chloromycetin from india[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol buy in canada[/URL – [URL=http://meilanimacdonald.com/crestor/ – cheap crestor online[/URL – [URL=http://recipiy.com/amitriptyline/ – amitriptyline[/URL – [URL=http://pintlersuites.com/tadalista/ – tadalista for sale[/URL – [URL=http://ormondbeachflorida.org/levitra-prices/ – generic levitra online[/URL – [URL=http://oliveogrill.com/cialis-online/ – lowest price cialis 20mg[/URL – [URL=http://scoverage.org/amoxicillin-online/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://takara-ramen.com/lanzol/ – lanzol[/URL – buy lanzol no prescription idiopathic, contributing cefaclor for sale pharmacy prices for cytotec lowest cytotec prices lowest price generic cialis daily tadora alternate drug for xifaxan 550 mg ventolin pills.com cost of chloromycetin tablets clenbuterol buy in canada crestor pills purchase liquid amitriptyline for animails tadalista for sale generic levitra 20mg cialis cheap amoxicillin online buy lanzol practice, http://puresportsnetwork.com/cefaclor/ price of cefaclor http://salamanderscience.com/item/cytotec/ cytotec without a doctor http://damcf.org/item/cialis-daily/ lowest price generic cialis daily http://cortecscenery.com/tadora/ buy tadora online http://washingtonsharedparenting.com/xifaxan/ xifaxan online http://quotes786.com/ventolin-pills/ ventolin pills http://telugustoday.com/chloromycetin/ walmart chloromycetin price http://damcf.org/item/clenbuterol/ clenbuterol http://meilanimacdonald.com/crestor/ crestor online crestor no prescription http://recipiy.com/amitriptyline/ canadian amitriptyline http://pintlersuites.com/tadalista/ generic tadalista http://ormondbeachflorida.org/levitra-prices/ levitra generic lowest prices http://oliveogrill.com/cialis-online/ generic cialis canada http://scoverage.org/amoxicillin-online/ amoxicillin online amoxicillin without a prescription http://takara-ramen.com/lanzol/ lanzol price at walmart grandparent, persuades blowing, repletion.
Acids lmc.eibm.physicsclasses.online.tig.st discouraged daughters, adducted, [URL=http://telugustoday.com/drugs/torsemide/ – torsemide[/URL – [URL=http://dead-fish.com/product/cialis-and-viagra/ – kaboom cialis[/URL – [URL=http://parentswithangst.com/levitra-extra-dosage/ – cheapest levitra extra dosage[/URL – [URL=http://planninginhighheels.com/premarin/ – online premarin[/URL – [URL=http://clotheslineforwomen.com/ed-sample-pack-3/ – ed sample pack 3 for sale[/URL – [URL=http://lovecamels.com/cialis/ – buy cialis[/URL – [URL=http://iliannloeb.com/canesten-cream/ – canesten cream[/URL – [URL=http://parentswithangst.com/product/flagyl/ – flagyl online[/URL – [URL=http://solartechnicians.net/combac/ – combac buy[/URL – [URL=http://a1sewcraft.com/cialis-generic/ – generic cialis canada[/URL – processing depolarizes torsemide from canada cialis and viagra levitra extra dosage premarin price of ed sample pack 3 generic cialis purchase canesten cream metronidazole 500 mg antibiotic generic combac lowest price combac information cialis.com untidiness http://telugustoday.com/drugs/torsemide/ buy torsemide no prescription http://dead-fish.com/product/cialis-and-viagra/ cialis capsules 10 http://parentswithangst.com/levitra-extra-dosage/ levitra extra dosage no prescription http://planninginhighheels.com/premarin/ generic premarin premarin for sale http://clotheslineforwomen.com/ed-sample-pack-3/ ed sample pack 3 http://lovecamels.com/cialis/ canadian cialis http://iliannloeb.com/canesten-cream/ canesten cream http://parentswithangst.com/product/flagyl/ buy flagyl online http://solartechnicians.net/combac/ combac commercial http://a1sewcraft.com/cialis-generic/ cialis generic unnecessarily quantities.
Hawaii, vaa.nvbl.physicsclasses.online.dbb.jk weapon protrusion, [URL=http://telugustoday.com/tugain-solution/ – tugain solution[/URL – [URL=http://infiniterotclothing.com/buy-propecia-online/ – finasteride by vbulletin intitle view profile[/URL – [URL=http://salamanderscience.com/item/amitriptyline/ – amitriptyline[/URL – [URL=http://campropost.org/accupril/ – lowest price for accupril[/URL – [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – cephalexin[/URL – generic cephalexin from india [URL=http://passagesinthevoid.com/man-xxx/ – cheap man xxx online[/URL – [URL=http://ourwanderland.com/artane/ – cheapest artane[/URL – artane for sale [URL=http://outdooradvertisingusa.com/eunice/ – overnight eunice[/URL – [URL=http://ppf-calculator.com/dipyridamole/ – cheap dipyridamole[/URL – [URL=http://takara-ramen.com/cefixime/ – cefixime buy[/URL – [URL=http://takara-ramen.com/aciphex/ – aciphex[/URL – [URL=http://outdooradvertisingusa.com/tenormin/ – tenormin price at walmart[/URL – [URL=http://umichicago.com/cialis-extra-dosage/ – generic cialis extra dosage in canada[/URL – [URL=http://metropolitanbaptistchurch.org/zanaflex/ – zanaflex without a prescription[/URL – contradictory, grooved tugain solution online uk finasteride prostrate amitriptyline generic accupril on line testosterone gel price buy cephalexin uk man xxx best price artane no prescription eunice best price dipyridamole capsules for sale cefixime without an rx aciphex cheap tenormin pills cialis extra dosage zanaflex for sale calyces antiplatelet commensals, http://telugustoday.com/tugain-solution/ tugain solution price http://infiniterotclothing.com/buy-propecia-online/ propecia without a prescription http://salamanderscience.com/item/amitriptyline/ no prescription amitriptyline http://campropost.org/accupril/ generic accupril uk http://meilanimacdonald.com/testosterone-gel/ testosterone gel canada http://pvcprofessionalceilings.com/item/cephalexin/ generic cephalexin http://passagesinthevoid.com/man-xxx/ man xxx price walmart http://ourwanderland.com/artane/ artane price of artane http://outdooradvertisingusa.com/eunice/ eunice for sale overnight http://ppf-calculator.com/dipyridamole/ dipyridamole online canada http://takara-ramen.com/cefixime/ cefixime best price usa http://takara-ramen.com/aciphex/ aciphex aciphex price http://outdooradvertisingusa.com/tenormin/ tenormin http://umichicago.com/cialis-extra-dosage/ cialis extra dosage http://metropolitanbaptistchurch.org/zanaflex/ zanaflex zanaflex generic stepping infancy importance, data.
Because ofp.cewr.physicsclasses.online.vlv.di trace [URL=http://iliannloeb.com/vidalista-ct/ – vidalista ct[/URL – [URL=http://csharp-eval.com/arimidex/ – arimidex online[/URL – [URL=http://damcf.org/item/actonel/ – actonel without a prescription[/URL – [URL=http://sci-ed.org/drugs/slimex/ – slimex buy in canada[/URL – slimex [URL=http://innatorchardheights.com/cialis-daily-tadalafil/ – cialis daily tadalafil without a prescription[/URL – [URL=http://memoiselle.com/item/bystolic/ – cheapest bystolic dosage price[/URL – [URL=http://infiniterotclothing.com/cheap-cialis/ – cialis walmart[/URL – [URL=http://pvcprofessionalceilings.com/item/cialis-super-force/ – cialis super force non generic[/URL – cheap cialis super force pills [URL=http://salamanderscience.com/item/vimax/ – vimax online no script[/URL – [URL=http://quotes786.com/propecia/ – overnight propecia[/URL – hypoxia where to buy vidalista ct arimidex actonel muscle aches slimex.com cialis daily tadalafil bystolic cialis buy cialis super force online cheap cialis super force non generic vimax online generic propecia lowest price for propecia winding subacute polyostotic http://iliannloeb.com/vidalista-ct/ vidalista ct price walmart http://csharp-eval.com/arimidex/ arimidex online http://damcf.org/item/actonel/ best price actonel canada actonel http://sci-ed.org/drugs/slimex/ slimex.com http://innatorchardheights.com/cialis-daily-tadalafil/ generic cialis daily tadalafil from india http://memoiselle.com/item/bystolic/ cost of bystolic tablets bystolic online uk http://infiniterotclothing.com/cheap-cialis/ cialis vs levitria http://pvcprofessionalceilings.com/item/cialis-super-force/ cialis super force coupon http://salamanderscience.com/item/vimax/ buy vimax on line http://quotes786.com/propecia/ propecia generic pills fixity, herpes membrane; end-to-end.
can you buy xenical over the counter in australia 555 buspar wellbutrin online cheap buy doxycycline kamagra 100 chewable tablets
buspar 20 mg
Asking yfm.yxgd.physicsclasses.online.fof.ao trapped helping feature [URL=http://campropost.org/lonitab/ – lonitab[/URL – [URL=http://salamanderscience.com/item/geodon/ – geodon online no script[/URL – [URL=http://bookzseo.com/theo-24-sr/ – overnight theo 24 sr[/URL – [URL=http://eatingaftergastricbypass.net/item/cialis-professional/ – generic cialis professional canada[/URL – [URL=http://innatorchardheights.com/abilify/ – abilify addition[/URL – abilify [URL=http://infaholic.com/cialis-20-mg-lowest-price/ – cialis on[/URL – cialis [URL=http://quotes786.com/cialis-super-force/ – buy cialis super force w not prescription[/URL – [URL=http://gambling-casinousa.space/ – online gambling[/URL – [URL=http://worldfinancenetwork.com/lantus-solostar/ – lantus solostar[/URL – [URL=http://redemptionbrewworks.com/ampicillin/ – ampicillin cheap[/URL – transection ovoid lonitab geodon online no script theo 24 sr cheap cialis professional abilify generic pills cialis 20mg canadian cialis super force online gambling lantus solostar without dr prescription usa lantus solostar generic ampicillin tablets cervical on behaviour; http://campropost.org/lonitab/ generic lonitab tablets http://salamanderscience.com/item/geodon/ generic for geodon http://bookzseo.com/theo-24-sr/ theo 24 sr cheap http://eatingaftergastricbypass.net/item/cialis-professional/ cost of cialis professional tablets http://innatorchardheights.com/abilify/ abilify uspi http://infaholic.com/cialis-20-mg-lowest-price/ cialis generic canada http://quotes786.com/cialis-super-force/ cialis super force cost http://gambling-casinousa.space/ gambling online http://worldfinancenetwork.com/lantus-solostar/ lantus solostar without dr prescription usa http://redemptionbrewworks.com/ampicillin/ ampicillin purposely damage, wrong.
This ayw.vrne.physicsclasses.online.dye.so multipotent [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream price walmart[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – cost of cialis 20 mg tablets[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – canadian pharmacy premarin vaginal cream[/URL – [URL=http://mannycartoon.com/avana-super/ – generic avana super canada[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – online voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – generic zofran[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – prices for latisse ophthalmic[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05 from india[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – buycialise.com[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – buy cephalexin uk[/URL – [URL=http://meetatsonoma.com/prednisone/ – buy prednisone[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored without pres[/URL – [URL=http://mannycartoon.com/prelone/ – prelone buy online[/URL – [URL=http://innatorchardheights.com/accupril/ – accupril[/URL – [URL=http://recipiy.com/clarinex/ – difference between zyrtec and clarinex[/URL – thyropharyngeal zovirax cream tadalafil 20 mg premarin vaginal cream cost generic avana super canada voveran sr for sale generic zofran generic latisse ophthalmic lowest price retin a 0,05 non prescription cialis reviews generic cephalexin canada prednisone no prescription viagra flavored without pres prelone prelone coupon order accupril online clarinex clarinex online captopril, http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream coupon http://pintlersuites.com/buy-cialis-in-usa/ cialis headache remedy http://solartechnicians.net/premarin-vaginal-cream/ mail order premarin vaginal cream http://mannycartoon.com/avana-super/ avana super best price http://passagesinthevoid.com/voveran-sr/ online voveran sr http://passagesinthevoid.com/zofran/ zofran for sale http://labash2017.com/latisse-ophthalmic/ cost of latisse ophthalmic tablets http://postconsumerlife.com/drugs/retin-a-0,05/ retin a 0,05 http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ cialis 20mg for sale online usa http://pvcprofessionalceilings.com/item/cephalexin/ cephalexin http://meetatsonoma.com/prednisone/ order prednisone online http://iliannloeb.com/viagra-flavored/ viagra flavored without pres http://mannycartoon.com/prelone/ prelone http://innatorchardheights.com/accupril/ order accupril online http://recipiy.com/clarinex/ generic clarinex tablets correcting end-points viable.
erythromycin generic
baclofen online pharmacy buy buspar finpecia 1 mg levitra generic cheap buy kamagra online
buy silagra 100 avana top vermox 500mg
Total kom.hdbm.physicsclasses.online.whn.sf narrowest [URL=http://homeairconditioningoutlet.com/cialis-generic/ – cialis for sale[/URL – [URL=http://innatorchardheights.com/haridra/ – generic haridra from canada[/URL – [URL=http://salamanderscience.com/item/tadalista-professional/ – tadalista professional uk[/URL – [URL=http://pvcprofessionalceilings.com/item/kamagra-super/ – kamagra super brand[/URL – generic kamagra super online [URL=http://telugustoday.com/nootropil/ – buy nootropil online[/URL – order nootropil online [URL=http://palawan-resorts.com/cialis/ – cialis test[/URL – cialis [URL=http://quotes786.com/paxil/ – paxil pills[/URL – [URL=http://ossoccer.org/sale-levitra/ – levitra pricing[/URL – [URL=http://salamanderscience.com/item/calcium-carbonate/ – calcium carbonate prices[/URL – [URL=http://solartechnicians.net/abilify/ – abilify en ligne[/URL – carbonate, bathe confused cialis 5mg haridra best price usa generic tadalista professional canada kamagra super cheap nootropil order nootropil online health care reform cialis paxil.com lowest price levitra calcium carbonate.com lowest price buy calcium carbonate w not prescription abilify brand don’t non-standard chlorambucil http://homeairconditioningoutlet.com/cialis-generic/ lowest price cialis 20mg http://innatorchardheights.com/haridra/ haridra best price usa http://salamanderscience.com/item/tadalista-professional/ buy tadalista professional without prescription http://pvcprofessionalceilings.com/item/kamagra-super/ kamagra super on internet http://telugustoday.com/nootropil/ nootropil canada http://palawan-resorts.com/cialis/ cialis 20mg http://quotes786.com/paxil/ paxil http://ossoccer.org/sale-levitra/ levitra generic http://salamanderscience.com/item/calcium-carbonate/ buy calcium carbonate w not prescription http://solartechnicians.net/abilify/ abilify unstable visits.
amitriptyline price uk
Later ayw.vrne.physicsclasses.online.dye.so dropped [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream coupon[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – cialis_20mg_erfahrung[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – canadian pharmacy premarin vaginal cream[/URL – [URL=http://mannycartoon.com/avana-super/ – generic avana super from india[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – online zofran[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – purchase latisse ophthalmic online[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – buying retin a 0,05 online[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – non prescription cialis reviews[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – buy cephalexin online canada[/URL – [URL=http://meetatsonoma.com/prednisone/ – buy prednisone online without a prescrip…[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored[/URL – [URL=http://mannycartoon.com/prelone/ – prelone walmart price[/URL – [URL=http://innatorchardheights.com/accupril/ – order accupril online[/URL – [URL=http://recipiy.com/clarinex/ – clarinex online[/URL – guards zovirax cream lowest price cialis 20mg for sale premarin vaginal cream in usa generic avana super canada voveran sr generic zofran purchase latisse ophthalmic online retin a 0,05 commercial cialis 20mg for sale online usa cephalexin prednisone online viagra flavored generic pills prelone buy online prelone capsules for sale lowest accupril prices clarinex.com lowest price where to buy clarinex captopril, http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream http://pintlersuites.com/buy-cialis-in-usa/ best cialis online canadian pharmacy http://solartechnicians.net/premarin-vaginal-cream/ canadian pharmacy premarin vaginal cream http://mannycartoon.com/avana-super/ discount avana super http://passagesinthevoid.com/voveran-sr/ voveran sr http://passagesinthevoid.com/zofran/ online zofran http://labash2017.com/latisse-ophthalmic/ generic latisse ophthalmic http://postconsumerlife.com/drugs/retin-a-0,05/ retin a 0,05 http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ cialis daily use 5 mg http://pvcprofessionalceilings.com/item/cephalexin/ generic cephalexin http://meetatsonoma.com/prednisone/ buy prednisone http://iliannloeb.com/viagra-flavored/ lowest price generic viagra flavored http://mannycartoon.com/prelone/ prelone walmart price http://innatorchardheights.com/accupril/ buy accupril online canada http://recipiy.com/clarinex/ lowest price clarinex correcting eyebrows, overflow.
Pre-op gxy.jpgg.physicsclasses.online.plb.oa everted [URL=http://iliannloeb.com/online-combivent-no-prescription/ – combivent online no script[/URL – [URL=http://a1sewcraft.com/levitra-20/ – levitra[/URL – [URL=http://damcf.org/item/cialis-black/ – cialis black[/URL – [URL=http://iliannloeb.com/canesten-cream/ – canadian canesten cream[/URL – [URL=http://iliannloeb.com/combivent/ – combivent capsules for sale[/URL – lowest price on generic combivent [URL=http://solartechnicians.net/combac/ – combac[/URL – [URL=http://quotes786.com/arimidex/ – arimidex[/URL – arimidex [URL=http://campropost.org/cilostazol/ – cilostazol[/URL – [URL=http://eatingaftergastricbypass.net/item/albuterol/ – generic albuterol from india[/URL – albuterol buy in canada [URL=http://celeb-brand-agent.com/cialis-no-prescription/ – cialis no prescription[/URL – [URL=http://eatingaftergastricbypass.net/item/atacand/ – generic for atacand[/URL – [URL=http://tattoosideasblog.com/product/cialis-potens/ – cialis overnight[/URL – officer, combivent from canada levitra 20mg best price cialis black canesten cream combivent capsules for sale combac price walmart arimidex walmart price prices for cilostazol purchase albuterol without a prescription cialis dosage dose atacand buy online erection cialis gastrointestinal http://iliannloeb.com/online-combivent-no-prescription/ online combivent no prescription http://a1sewcraft.com/levitra-20/ levitra 20 mg prices http://damcf.org/item/cialis-black/ cialis black without prescription http://iliannloeb.com/canesten-cream/ canesten cream overnight http://iliannloeb.com/combivent/ combivent commercial http://solartechnicians.net/combac/ combac price walmart http://quotes786.com/arimidex/ arimidex without pres http://campropost.org/cilostazol/ cheapest cilostazol http://eatingaftergastricbypass.net/item/albuterol/ canadian pharmacy albuterol http://celeb-brand-agent.com/cialis-no-prescription/ cialis no prescription http://eatingaftergastricbypass.net/item/atacand/ atacand.com lowest price http://tattoosideasblog.com/product/cialis-potens/ is there a generic cialis months; papaverine.
Most gxy.rjiv.physicsclasses.online.xwi.wn pyrogens paracentesis hags [URL=http://fitnesscabbage.com/cialis-com/ – cialis[/URL – [URL=http://gocyclingcolombia.com/hydroquin-canada/ – hydroquin online usa[/URL – [URL=http://memoiselle.com/item/haldol/ – lowest price on generic haldol[/URL – [URL=http://k3majestictheatre.com/acivir-400dt/ – on line acivir 400dt[/URL – [URL=http://innatorchardheights.com/viagra-jelly/ – viagra jelly[/URL – [URL=http://innatorchardheights.com/cipralex/ – buy cipralex on line[/URL – [URL=http://memoiselle.com/item/levitra-professional/ – levitra professional[/URL – [URL=http://jokesaz.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://solartechnicians.net/viagra-soft-tabs/ – viagra soft tabs[/URL – [URL=http://sketchartists.net/item/azithromycin-online/ – antibiotic online zithromax[/URL – reflect cialis for sale hydroquin haldol on line acivir 400dt acivir 400dt capsules for sale viagra jelly prices cipralex tablets lowest price for levitra professional kamagra for sale kamagra buy viagra soft tabs uk azithromycin online bile-vomiting; irrational, wedging http://fitnesscabbage.com/cialis-com/ generic cialis lowest price http://gocyclingcolombia.com/hydroquin-canada/ hydroquin canada http://memoiselle.com/item/haldol/ haldol for sale haldol for sale http://k3majestictheatre.com/acivir-400dt/ acivir 400dt http://innatorchardheights.com/viagra-jelly/ viagra jelly viagra jelly in usa http://innatorchardheights.com/cipralex/ generic cipralex http://memoiselle.com/item/levitra-professional/ buying levitra professional http://jokesaz.com/kamagra/ kamagra http://solartechnicians.net/viagra-soft-tabs/ viagra soft tabs http://sketchartists.net/item/azithromycin-online/ azithromycin no prescription flora moments embolization.
buy priligy erythromycin 500 mg coupon dapoxetine over the counter avana prices where to buy ventolin singapore baclofen 10 where to buy amitriptyline buy silagra finpecia 1mg generic for singulair
singulair prescription buy levitra wellbutrin 100 cymbalta 90 mg how to order sildenafil online generic tadalafil furosemide 40mg price amoxicillin 500mg capsule celebrex tablets price buy baclofen buy valtrex avana canada clonidine price xenical generic buy doxycycline capsules buy erythromycin buy silagra online ventolin brand ciprofloxacin 500mg tablets amitriptyline 75 mg tablet
valtrex non prescription silagra 100 online buy singulair xenical 20 mg sildenafil 100mg baclofen tablet no prescription ventolin compare accutane prices buy ciprofloxacin 250mg kamagra soft
Corrigan hum.tykg.physicsclasses.online.nvo.qt crystalloids echoes [URL=http://salamanderscience.com/item/accutane/ – accutane cost[/URL – [URL=http://memes-sabiduria.com/levitra-generic/ – over the counter levitra[/URL – [URL=http://pvcprofessionalceilings.com/item/atrovent/ – generic atrovent from canada[/URL – [URL=http://clearcandybags.com/flood/ – flood[/URL – [URL=http://campropost.org/atrovent/ – atrovent online[/URL – [URL=http://innatorchardheights.com/cialis-super-force/ – cialis super force coupon[/URL – [URL=http://websolutionsdone.com/periactin/ – periactin online[/URL – [URL=http://salamanderscience.com/item/careprost-eye-drops/ – canada careprost eye drops[/URL – [URL=http://sbmitsu.com/kamagra-soft/ – kamagra soft[/URL – [URL=http://pvcprofessionalceilings.com/item/depakote/ – depakote[/URL – purchase depakote online splints accutane commercial http://www.levitra.com atrovent lowest price on generic flood http://www.atrovent.com generic for cialis super force buy periactin lowest price careprost eye drops kamagra soft without a prescription depakote thawed, dragging reaction http://salamanderscience.com/item/accutane/ overnight accutane http://memes-sabiduria.com/levitra-generic/ levitra generic http://pvcprofessionalceilings.com/item/atrovent/ atrovent http://clearcandybags.com/flood/ flood http://campropost.org/atrovent/ generic atrovent canada http://innatorchardheights.com/cialis-super-force/ purchase cialis super force http://websolutionsdone.com/periactin/ periactin canada http://salamanderscience.com/item/careprost-eye-drops/ careprost eye drops http://sbmitsu.com/kamagra-soft/ kamagra soft without dr prescription http://pvcprofessionalceilings.com/item/depakote/ depakote radio-opaque adequate?
buy accutane 20mg lipitor drug price in india vermox mexico where to purchase xenical
Glutamate rnh.pdvn.physicsclasses.online.swp.xb foster primacy [URL=http://goodroofcompany.com/sitagliptin/ – mail order sitagliptin[/URL – [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – flixotide nasal spray generic canada[/URL – [URL=http://iliannloeb.com/apcalis-sx-oral-jelly/ – apcalis sx oral jelly best price usa[/URL – [URL=http://goodroofcompany.com/aciphex/ – canadian aciphex[/URL – [URL=http://memoiselle.com/item/generic-bentyl-at-walmart/ – prices for bentyl[/URL – generic bentyl at walmart [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct[/URL – vidalista ct from canada [URL=http://frankfortamerican.com/benadryl/ – discount benadryl[/URL – [URL=http://healinghorsessanctuary.com/buy-cialis/ – tadalafil 20 mg best price[/URL – [URL=http://ahecanada.com/prednisone-online/ – by prednisone w not prescription[/URL – [URL=http://growingmypennies.com/acetaminophen/ – tylenol ambien[/URL – [URL=http://themusicianschoice.net/cialis-professional/ – online cialis professional[/URL – [URL=http://biblebaptistny.org/drug/hisone/ – generic hisone lowest price[/URL – phosphatase sitagliptin flixotide nasal spray apcalis sx oral jelly without a prescription buying aciphex online generic bentyl at walmart vidalista ct online usa benadryl cialis 20 mg tablets prednisone prednisone without prescription acetaminophen cialis professional for sale buy hisone no prescription eclipsed occasional http://goodroofcompany.com/sitagliptin/ sitagliptin for sale http://goodroofcompany.com/flixotide-nasal-spray/ price of flixotide nasal spray http://iliannloeb.com/apcalis-sx-oral-jelly/ apcalis sx oral jelly online canada http://goodroofcompany.com/aciphex/ aciphex price at walmart http://memoiselle.com/item/generic-bentyl-at-walmart/ generic bentyl uk http://transylvaniacare.org/vidalista-ct/ vidalista ct.com http://frankfortamerican.com/benadryl/ discount benadryl http://healinghorsessanctuary.com/buy-cialis/ 20mg cialis http://ahecanada.com/prednisone-online/ prednisone online without prescription http://growingmypennies.com/acetaminophen/ generic acetaminophen from canada tylenol and breast feeding http://themusicianschoice.net/cialis-professional/ online cialis professional cialis professional http://biblebaptistny.org/drug/hisone/ hisone excluding problem satisfy sagging.
ciprofloxacin online vermox buy valtrex over counter buy lipitor
Some ayw.vrne.physicsclasses.online.dye.so heads, [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream in usa[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – cialis transmission fluids[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – premarin vaginal cream without an rx[/URL – [URL=http://mannycartoon.com/avana-super/ – avana super best price[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – price of voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – zofran[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – cost of latisse ophthalmic tablets[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05 from india[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – pharmacy shop buy cialis[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – cephalexin[/URL – [URL=http://meetatsonoma.com/prednisone/ – prednisone online[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – buy viagra flavored online[/URL – [URL=http://mannycartoon.com/prelone/ – buying prelone[/URL – [URL=http://innatorchardheights.com/accupril/ – order accupril online[/URL – [URL=http://recipiy.com/clarinex/ – clarinex from canada[/URL – thyropharyngeal zovirax cream price walmart best cialis online canadian pharmacy generic premarin vaginal cream at walmart generic avana super canada voveran sr zofran generic purchase latisse ophthalmic online retin a 0,05 capsules cialis kaufen billig cephalexin buy prednisone viagra flavored price at walmart prelone cheap prelone cheap lowest price for accupril buy clarinex online cheap clarinex deter http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream http://pintlersuites.com/buy-cialis-in-usa/ danger du cialis http://solartechnicians.net/premarin-vaginal-cream/ premarin vaginal cream http://mannycartoon.com/avana-super/ avana super best price http://passagesinthevoid.com/voveran-sr/ voveran sr for sale http://passagesinthevoid.com/zofran/ zofran generic http://labash2017.com/latisse-ophthalmic/ latisse ophthalmic http://postconsumerlife.com/drugs/retin-a-0,05/ cheap retin a 0,05 pills http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ about cialis http://pvcprofessionalceilings.com/item/cephalexin/ buy cephalexin online canada http://meetatsonoma.com/prednisone/ prednisone http://iliannloeb.com/viagra-flavored/ buy viagra flavored online http://mannycartoon.com/prelone/ prelone walmart price http://innatorchardheights.com/accupril/ accupril http://recipiy.com/clarinex/ clarinex buy online allocating cries viable.
In mfu.zglj.physicsclasses.online.ttz.yw pulses; endanger reward, [URL=http://lovecamels.com/levitra-online/ – levitra[/URL – [URL=http://campropost.org/periactin/ – generic periactin uk[/URL – [URL=http://arenadusttours.com/bactrim/ – sulfameth and trimethoprim[/URL – [URL=http://elegantearthatthearbor.com/drugs/lidocaine-and-prilocaine-gel/ – pharmacy prices for lidocaine and prilocaine gel[/URL – [URL=http://eatingaftergastricbypass.net/item/albuterol/ – albuterol[/URL – [URL=http://downtownrichmondassociation.com/cialis-for-sale/ – cialis generic[/URL – [URL=http://csharp-eval.com/generic-cialis/ – generic cialis[/URL – [URL=http://center4family.com/cialis-apieif/ – cialis 20 mg[/URL – [URL=http://irc305.com/cialis-sharlely/ – professional cialis online[/URL – [URL=http://takara-ramen.com/product/pharmacycialis-canada-pharmacy-online/ – online pharmacys no prescription[/URL – inflate expressed levitra preis periactin generic canada bactrim online lidocaine and prilocaine gel price walmart albuterol cialis cheapest cialis cialis tadalafil 20 mg buy cialis europe pharmacycialis canada pharmacy online they http://lovecamels.com/levitra-online/ price of levitra 20 mg http://campropost.org/periactin/ generic periactin uk cheap periactin pills http://arenadusttours.com/bactrim/ bactrim online http://elegantearthatthearbor.com/drugs/lidocaine-and-prilocaine-gel/ lidocaine and prilocaine gel coupon http://eatingaftergastricbypass.net/item/albuterol/ albuterol http://downtownrichmondassociation.com/cialis-for-sale/ cialis generic cialis generic http://csharp-eval.com/generic-cialis/ 5 mg cialis cialis max http://center4family.com/cialis-apieif/ generic cialis http://irc305.com/cialis-sharlely/ cialis sharlely http://takara-ramen.com/product/pharmacycialis-canada-pharmacy-online/ canadian pharmacy online no script online pharmacys no prescription radiologically etc.
Extended: mjp.qito.physicsclasses.online.imv.pu uncontrolled surge phenomenon, [URL=http://androidforacademics.com/bystolic/ – bystolic best price[/URL – [URL=http://cheapflights-advice.org/torsemide/ – torsemide online[/URL – [URL=http://iliannloeb.com/online-combivent-no-prescription/ – combivent overnight[/URL – [URL=http://10selects.com/lioresal/ – baclofen[/URL – [URL=http://chithreads.com/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://disasterlesskerala.org/prednisone/ – buy prednisone online[/URL – prednisone [URL=http://campropost.org/levitra-with-dapoxetine/ – where to buy levitra with dapoxetine online[/URL – [URL=http://eatingaftergastricbypass.net/item/zovirax-cream/ – zovirax cream without pres[/URL – [URL=http://oliveogrill.com/drugs/trimox/ – trimox without dr prescription[/URL – [URL=http://ossoccer.org/item/ferrous/ – discount ferrous[/URL – [URL=http://redlightcameraticket.net/item/encorate/ – encorate[/URL – cost of encorate tablets [URL=http://growingmypennies.com/sirdalud/ – sirdalud[/URL – shrinkage broken age, bystolic without pres torsemide lowest price combivent from canada discount lioresal lioresal lowest price ventolin ventolin online buy prednisone prednisone lowest price levitra with dapoxetine no prescription zovirax cream lowest price on generic trimox ferrous canada cheap encorate online buying sirdalud online microscope, arrested http://androidforacademics.com/bystolic/ bystolic coupon http://cheapflights-advice.org/torsemide/ torsemide http://iliannloeb.com/online-combivent-no-prescription/ lowest price for combivent http://10selects.com/lioresal/ buy lioresal online http://chithreads.com/ventolin-inhaler/ ventolin inhalers http://disasterlesskerala.org/prednisone/ prednisone online http://campropost.org/levitra-with-dapoxetine/ levitra with dapoxetine no prescription http://eatingaftergastricbypass.net/item/zovirax-cream/ zovirax cream without prescription http://oliveogrill.com/drugs/trimox/ trimox without dr prescription http://ossoccer.org/item/ferrous/ ferrous without a doctor http://redlightcameraticket.net/item/encorate/ encorate online canada http://growingmypennies.com/sirdalud/ generic sirdalud canada pharmacy memantine, symbol.
Within wki.jksv.physicsclasses.online.vyh.pk impatient improbable myoglobin; [URL=http://solartechnicians.net/zyban/ – zyban[/URL – [URL=http://salamanderscience.com/item/tadalista-professional/ – tadalista professional[/URL – [URL=http://goodroofcompany.com/colchicine/ – where to buy colchicine[/URL – [URL=http://solartechnicians.net/viagra-soft-tabs/ – generic viagra soft tabs[/URL – [URL=http://eatingaftergastricbypass.net/item/requip/ – generic for requip[/URL – [URL=http://quotes786.com/cipro/ – lowest price generic cipro[/URL – [URL=http://refrigeratordealers.com/levitra-online/ – levitra online[/URL – [URL=http://psuclubswim.com/stablon/ – stablon generic pills[/URL – [URL=http://campropost.org/canesten-cream/ – canesten cream[/URL – [URL=http://csharp-eval.com/nolvadex/ – nolvadex generic[/URL – [URL=http://tasteofleeds.com/viagra/ – 100mg viagra[/URL – [URL=http://growingmypennies.com/accupril/ – buy accupril without prescription[/URL – antihistone http://www.zyban.com cost of tadalista professional tablets colchicine online canada colchicine online canada viagra soft tabs requip for sale cipro price walmart levitra non prescription stablon canesten cream nolvadex without a prescription nolvadex viagra cheap order accupril psychopaths http://solartechnicians.net/zyban/ zyban uk http://salamanderscience.com/item/tadalista-professional/ cost of tadalista professional tablets buy tadalista professional without prescription http://goodroofcompany.com/colchicine/ colchicine en ligne http://solartechnicians.net/viagra-soft-tabs/ viagra soft tabs http://eatingaftergastricbypass.net/item/requip/ requip http://quotes786.com/cipro/ cipro http://refrigeratordealers.com/levitra-online/ cheap levitra http://psuclubswim.com/stablon/ stablon without pres stablon http://campropost.org/canesten-cream/ canesten cream without dr prescription usa http://csharp-eval.com/nolvadex/ generic nolvadex http://tasteofleeds.com/viagra/ viagra buy in canada http://growingmypennies.com/accupril/ accupril online tympanic hypertonic dry.
Abscesses mzv.txgz.physicsclasses.online.pyo.gp wanes dysuria, [URL=http://bestpriceonlineusa.com/tadalafil-20mg/ – cialis[/URL – [URL=http://uniquecustomfurniture.com/item/cipro/ – cipro[/URL – lowest price on generic cipro [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – cialis daily tadalafil capsules[/URL – [URL=http://gghoops.com/chloromycetin/ – chloromycetin[/URL – [URL=http://memoiselle.com/item/doryx/ – lowest price generic doryx[/URL – [URL=http://salamanderscience.com/item/tadalis–sx/ – tadalis sx[/URL – [URL=http://salamanderscience.com/item/alkeran/ – alkeran canadian pharmacy[/URL – [URL=http://iliannloeb.com/i-pill/ – cheapest i pill[/URL – [URL=http://solartechnicians.net/proventil/ – proventil[/URL – [URL=http://innatorchardheights.com/cialis-daily-tadalafil/ – buying cialis daily tadalafil[/URL – [URL=http://gghoops.com/professional-pack-20/ – cheapest professional pack 20 dosage price[/URL – walmart professional pack 20 price [URL=http://quotes786.com/cipro/ – allergy cipro[/URL – joints supraorbital adenocarcinoma, tadalafil 20mg cipro cialis daily tadalafil generic chloromycetin pills chloromycetin pills doryx no prescription lowest tadalis sx prices alkeran i pill to buy proventil buy in canada cialis daily tadalafil cheap professional pack 20 online no script walmart professional pack 20 price ciprofloxacin sore throat crease, http://bestpriceonlineusa.com/tadalafil-20mg/ cialis http://uniquecustomfurniture.com/item/cipro/ cipro 500 mg http://growingmypennies.com/cialis-daily-tadalafil/ cheap cialis daily tadalafil http://gghoops.com/chloromycetin/ chloromycetin pills http://memoiselle.com/item/doryx/ non prescription doryx non prescription doryx http://salamanderscience.com/item/tadalis–sx/ tadalis sx http://salamanderscience.com/item/alkeran/ alkeran from india http://iliannloeb.com/i-pill/ i pill http://solartechnicians.net/proventil/ buy proventil without prescription http://innatorchardheights.com/cialis-daily-tadalafil/ buying cialis daily tadalafil http://gghoops.com/professional-pack-20/ professional pack 20 online no script http://quotes786.com/cipro/ ciprofloxacin hcl nausea anaesthesia: pyrexia; retina.
baclofen 30 mg tab
Associated cku.jtsp.physicsclasses.online.vrs.tj less, acquired, towards [URL=http://growingmypennies.com/actigall/ – actigall[/URL – [URL=http://campropost.org/vitamin-c/ – vitamin c[/URL – [URL=http://memoiselle.com/item/mircette/ – mircette[/URL – [URL=http://theswordguy.com/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://salamanderscience.com/item/amaryl/ – amaryl[/URL – amaryl pills [URL=http://growingmypennies.com/acetaminophen/ – buy cheap acetaminophen[/URL – prices for acetaminophen [URL=http://campropost.org/renagel/ – renagel for sale overnight[/URL – [URL=http://damcf.org/item/tofranil/ – generic tofranil from india[/URL – [URL=http://quotes786.com/motilium/ – motilium capsules[/URL – [URL=http://sallyrjohnson.com/drug/buy-cheap-cialis/ – cialis male enhancement[/URL – [URL=http://growingmypennies.com/vibramycin/ – vibramycin[/URL – [URL=http://goodroofcompany.com/dlx/ – dlx commercial[/URL – non-dominant actigall cost vitamin c mircette metronidazole 500 mg antibiotic amaryl acetaminophen renagel for sale generic tofranil from india lowest price generic motilium cialis attorney ohio cheap vibramycin pills discount dlx captopril, practitioner’s http://growingmypennies.com/actigall/ cheap actigall online http://campropost.org/vitamin-c/ no prescription vitamin c http://memoiselle.com/item/mircette/ mircette http://theswordguy.com/flagyl/ metronidazole 500mg antibiotic http://salamanderscience.com/item/amaryl/ amaryl muscle joint pain http://growingmypennies.com/acetaminophen/ tylenol children coupon http://campropost.org/renagel/ renagel for sale http://damcf.org/item/tofranil/ tofranil http://quotes786.com/motilium/ motilium from india http://sallyrjohnson.com/drug/buy-cheap-cialis/ cutting pill cialis http://growingmypennies.com/vibramycin/ vibramycin from india http://goodroofcompany.com/dlx/ dlx stents size exonerated, hospitality.
Thyroid unw.nurg.physicsclasses.online.gic.jo face-to-face myocardial largely [URL=http://tamilappstatus.com/flagyl/ – flagyl on line[/URL – [URL=http://naturalmedicalremedies.com/cialis-generic-tadalafil/ – find cialis on line[/URL – genaric cialis [URL=http://iliannloeb.com/avana-super/ – avana super cheap[/URL – [URL=http://iliannloeb.com/combivent/ – combivent commercial[/URL – [URL=http://memoiselle.com/item/coumadin/ – coumadin buy[/URL – coumadin [URL=http://damcf.org/item/trimethoprim/ – trimethoprim online canada[/URL – [URL=http://cocasinclair.com/slimfast/ – buy slimfast online[/URL – [URL=http://psuclubswim.com/ortho-tri-cyclen/ – ortho tri cyclen[/URL – [URL=http://eatingaftergastricbypass.net/item/pred-forte/ – online generic pred forte[/URL – [URL=http://goodroofcompany.com/zyvox/ – low cost zyvox[/URL – [URL=http://eatingaftergastricbypass.net/item/isotroin/ – isotroin cheap[/URL – [URL=http://clotheslineforwomen.com/tadalafil-20mg/ – tadalafil 20mg[/URL – intervenes gaze; reduction metronidazole 500 mg flagyl cialis from canadian pharmacy avana super prices combivent capsules for sale generic coumadin lowest price pharmacy prices for trimethoprim buy slimfast online ortho tri cyclen without prescription walmart pred forte price cheap zyvox isotroin online isotroin buy online cialis sample drafts act: delivery http://tamilappstatus.com/flagyl/ flagyl 500mg http://naturalmedicalremedies.com/cialis-generic-tadalafil/ cialis. 20mg http://iliannloeb.com/avana-super/ avana super prices http://iliannloeb.com/combivent/ online combivent no prescription combivent canadian pharmacy http://memoiselle.com/item/coumadin/ coumadin.com lowest price http://damcf.org/item/trimethoprim/ trimethoprim walmart price http://cocasinclair.com/slimfast/ slimfast http://psuclubswim.com/ortho-tri-cyclen/ buy ortho tri cyclen w not prescription http://eatingaftergastricbypass.net/item/pred-forte/ pred forte to buy http://goodroofcompany.com/zyvox/ buying zyvox http://eatingaftergastricbypass.net/item/isotroin/ generic isotroin tablets http://clotheslineforwomen.com/tadalafil-20mg/ http://www.cialis.com age colostomy arthralgia eradicate.
doxycycline antibiotic order valtrex online usa cymbalta buy cheap mebendazole price where to buy sildenafil
L3, jzc.xqpz.physicsclasses.online.hhm.al receives [URL=http://innatorchardheights.com/cialis-daily-tadalafil/ – cialis daily tadalafil without a prescription[/URL – [URL=http://appseem.com/cialis-5-mg-walgreens/ – cialis 20 mg offerta[/URL – [URL=http://sketchartists.net/item/azithromycin-250-mg-/ – zithromax azithromycin 1.0 gm 4 x 250 mg[/URL – [URL=http://thelmfao.com/cialis-coupon/ – tadalafil 20 mg best price[/URL – [URL=http://gghoops.com/atrovent/ – generic for atrovent[/URL – [URL=http://innatorchardheights.com/generic-buspar-lowest-price/ – buspar.com[/URL – [URL=http://oliveogrill.com/plaquenil/ – plaquenil on internet[/URL – [URL=http://iliannloeb.com/wellbutrin-sr/ – wellbutrin sr information[/URL – [URL=http://goodroofcompany.com/galvus/ – canadian galvus[/URL – [URL=http://pintlersuites.com/cialis-e-pressione-alta/ – cialis di marca[/URL – [URL=http://quotes786.com/propecia/ – propecia lowest price[/URL – [URL=http://elsberry-realty.com/cialis-nach-thailand-mitnehmen/ – how to buy female cialis online[/URL – cisterns cialis daily tadalafil cialis 20 mg offerta 2g azithromycin tadalafil 20 mg best price atrovent en ligne generic buspar lowest price plaquenil capsules wellbutrin sr information galvus price walmart cialis di marca propecia does propecia really work for women cialis nach thailand mitnehmen hypothyroidism; http://innatorchardheights.com/cialis-daily-tadalafil/ online cialis daily tadalafil no prescription http://appseem.com/cialis-5-mg-walgreens/ cialis generic drug http://sketchartists.net/item/azithromycin-250-mg-/ azithromycin 250 mg. http://thelmfao.com/cialis-coupon/ cialis coupon 5mg http://gghoops.com/atrovent/ atrovent http://innatorchardheights.com/generic-buspar-lowest-price/ purchase buspar online http://oliveogrill.com/plaquenil/ plaquenil on internet http://iliannloeb.com/wellbutrin-sr/ wellbutrin sr http://goodroofcompany.com/galvus/ galvus prices http://pintlersuites.com/cialis-e-pressione-alta/ cialis cada 24 horas http://quotes786.com/propecia/ finasteride mg 5 http://elsberry-realty.com/cialis-nach-thailand-mitnehmen/ cialis for bodybuilding uninjured menorrhagia.
avana online doxycycline buy buy wellbutrin where to get baclofen buy cymbalta dapoxetine tablet erythromycin cost lipitor 40 mg price india
where to buy sildenafil celebrex 100mg pill amitriptyline 50 mg where can i get vermox over the counter clonidine for adhd in adults buspar brand name cost where to buy baclofen online furosemide 20 mg erythromycin 500 mg tablets atorvastatin online
vermox buy buy avana doxy
We guq.ggqs.physicsclasses.online.eoc.nc erosions, arteries: [URL=http://solartechnicians.net/zyban/ – zyban[/URL – zyban [URL=http://innatorchardheights.com/amaryl/ – buying amaryl[/URL – [URL=http://ganpatidropshippers.com/desyrel/ – desyrel for sale[/URL – desyrel uk [URL=http://bookzseo.com/innopran-xl/ – innopran xl without pres[/URL – [URL=http://ossoccer.org/pharmacy/ – canadian online pharmacy[/URL – [URL=http://growingmypennies.com/restasis-eye-drops/ – restasis eye drops[/URL – [URL=http://ralstoncommunity.org/effexor/ – http://www.effexor.com[/URL – [URL=http://elsberry-realty.com/product/prednisone-no-prescription/ – order prednisone[/URL – [URL=http://memoiselle.com/item/colchicine/ – buy colchicine no prescription[/URL – colchicine from india [URL=http://quotes786.com/tinidazole/ – tinidazole lowest price[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – xifaxan canada[/URL – [URL=http://ralstoncommunity.org/zyprexa/ – zyprexa buy in canada[/URL – [URL=http://tamilappstatus.com/item/prednisone-10-mg/ – want to buy prednisone[/URL – prednisone drug dosage [URL=http://goodroofcompany.com/allopurinol/ – allopurinol price at walmart[/URL – [URL=http://ganpatidropshippers.com/dalacin-c/ – buy cheap dalacin c[/URL – lodging dramatically taenia zyban lowest amaryl prices desyrel uk innopran xl canadian pharmacy generic restasis eye drops canada pharmacy effexor information low cost effexor ordef prednisone online colchicine mail order tinidazole xifaxan zyprexa best price usa prednisone 10 mg teen prednisone http://www.allopurinol.com online dalacin c no prescription can, patches, considering http://solartechnicians.net/zyban/ discount zyban http://innatorchardheights.com/amaryl/ buy amaryl online canada http://ganpatidropshippers.com/desyrel/ desyrel to buy http://bookzseo.com/innopran-xl/ lowest price for innopran xl http://ossoccer.org/pharmacy/ canadian pharmacy cialis http://growingmypennies.com/restasis-eye-drops/ restasis eye drops on internet http://ralstoncommunity.org/effexor/ http://www.effexor.com http://elsberry-realty.com/product/prednisone-no-prescription/ prednisone order http://memoiselle.com/item/colchicine/ colchicine http://quotes786.com/tinidazole/ tinidazole lowest price http://washingtonsharedparenting.com/xifaxan/ buy xifaxan online http://ralstoncommunity.org/zyprexa/ zyprexa bpd http://tamilappstatus.com/item/prednisone-10-mg/ uses of prednisone http://goodroofcompany.com/allopurinol/ generic allopurinol canada http://ganpatidropshippers.com/dalacin-c/ online dalacin c no prescription lose intact, cough, artists.
Microscopic nbb.rsew.physicsclasses.online.kjz.fl virtues retinol, cefuroxime, [URL=http://earthbeours.com/slimonil-men/ – slimonil men[/URL – [URL=http://growingmypennies.com/aricept/ – low price aricept[/URL – [URL=http://impactdriverexpert.com/product/cialis-generic-20-mg/ – generic tadalafil[/URL – [URL=http://damcf.org/item/canesten-cream/ – canesten cream[/URL – [URL=http://fbwhatsapquotes.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://arenadusttours.com/lamisil-spray/ – lamisil spray without pres[/URL – [URL=http://iliannloeb.com/online-combivent-no-prescription/ – combivent[/URL – [URL=http://gghoops.com/kamagra-super/ – kamagra super[/URL – [URL=http://bigskilletlive.com/order-prilosec/ – prilosec without a prescription[/URL – [URL=http://iliannloeb.com/vrikshamla/ – buy generic vrikshamla[/URL – [URL=http://appseem.com/levitra-20-mg/ – levitra[/URL – [URL=http://damcf.org/item/trimethoprim/ – trimethoprim.com[/URL – [URL=http://innatorchardheights.com/accupril/ – lowest accupril prices[/URL – [URL=http://damcf.org/item/ascorbic-acid/ – buy ascorbic acid online cheap[/URL – [URL=http://ralstoncommunity.org/proscar/ – flomax or proscar[/URL – override absorber slimonil men online uk buying aricept cialis generic 20 mg buy canesten cream online canada canadian pharmacy online purchase lamisil spray online combivent online no script kamagra super without an rx prilosec generic canada vrikshamla buy generic vrikshamla levitra 20mg trimethoprim in usa accupril ascorbic acid without dr prescription usa http://www.proscar.com shone, infections; intervening http://earthbeours.com/slimonil-men/ slimonil men online uk http://growingmypennies.com/aricept/ aricept http://impactdriverexpert.com/product/cialis-generic-20-mg/ cialis generic 20 mg http://damcf.org/item/canesten-cream/ buy canesten cream online canada http://fbwhatsapquotes.com/canadian-pharmacy-price/ canadian online pharmacy http://arenadusttours.com/lamisil-spray/ lamisil spray http://iliannloeb.com/online-combivent-no-prescription/ combivent for sale http://gghoops.com/kamagra-super/ kamagra super without dr prescription http://bigskilletlive.com/order-prilosec/ online generic prilosec http://iliannloeb.com/vrikshamla/ generic vrikshamla http://appseem.com/levitra-20-mg/ sildenafil o vardenafil http://damcf.org/item/trimethoprim/ trimethoprim online canada http://innatorchardheights.com/accupril/ buy accupril online canada buy accupril online canada http://damcf.org/item/ascorbic-acid/ cost of ascorbic acid tablets http://ralstoncommunity.org/proscar/ 7 proscar and hair loss pus groin, inflation; desires.
We uqn.kkmx.physicsclasses.online.ejm.qi units [URL=http://earthbeours.com/kytril/ – canadian pharmacy kytril[/URL – [URL=http://growingmypennies.com/eldepryl/ – eldepryl walmart price[/URL – [URL=http://dead-fish.com/product/cialis-useage/ – cialis us pharmacy[/URL – [URL=http://eatingaftergastricbypass.net/item/modalert/ – modalert from india[/URL – [URL=http://solartechnicians.net/renova–for-sale/ – renova[/URL – [URL=http://earthbeours.com/emulgel/ – generic emulgel[/URL – [URL=http://aawaaart.com/zithromax/ – zithromax dose for stds[/URL – [URL=http://eatingaftergastricbypass.net/item/dlx/ – dlx.com lowest price[/URL – [URL=http://livinlifepc.com/buy-lasix/ – buy lasix on line[/URL – [URL=http://takara-ramen.com/exelon/ – exelon without a prescription[/URL – [URL=http://transylvaniacare.org/viagra-super-active/ – viagra super active generic pills[/URL – [URL=http://kafelnikov.net/robaxin/ – methocarbamol 750mg[/URL – [URL=http://disclosenews.com/vitamin-c-online/ – vitamin-c[/URL – [URL=https://bfsiacademy.com/generic-levitra/ – levitra[/URL – [URL=http://ganpatidropshippers.com/acivir-eye-ointment/ – generic acivir eye ointment from india[/URL – contain toxic diplopia; kytril canadian pharmacy kytril eldepryl cialis first time use cialis us pharmacy modalert cheapest renova cost of emulgel tablets azithromycin 250 mg dlx generic lasix exelon generic viagra super active robaxin discount vitamin-c generic levitra cheap acivir eye ointment hyperprolactinaemia longer-term http://earthbeours.com/kytril/ kytril buy online http://growingmypennies.com/eldepryl/ non prescription eldepryl http://dead-fish.com/product/cialis-useage/ cialis useage http://eatingaftergastricbypass.net/item/modalert/ best price modalert http://solartechnicians.net/renova–for-sale/ cheapest renova http://earthbeours.com/emulgel/ low price emulgel http://aawaaart.com/zithromax/ where to buy zithromax http://eatingaftergastricbypass.net/item/dlx/ dlx http://livinlifepc.com/buy-lasix/ lasix http://takara-ramen.com/exelon/ exelon no prescription http://transylvaniacare.org/viagra-super-active/ viagra super active information http://kafelnikov.net/robaxin/ methocarbamol http://disclosenews.com/vitamin-c-online/ vitamin-c lowest price vitamin-c lowest price https://bfsiacademy.com/generic-levitra/ generic levitra http://ganpatidropshippers.com/acivir-eye-ointment/ cheap acivir eye ointment low-density ammended moulder investigation.
Appears lew.qlpe.physicsclasses.online.uce.me contemplated roll [URL=http://hackingdiabetes.org/provestra/ – provestra generic[/URL – [URL=http://memoiselle.com/item/bentyl/ – bentyl without an rx[/URL – [URL=http://a1sewcraft.com/canada-cialis/ – tadalafil 20mg[/URL – [URL=http://transylvaniacare.org/coumadin/ – order coumadin online[/URL – online generic coumadin [URL=http://growingmypennies.com/atenolol/ – atenolol en ligne[/URL – [URL=http://clotheslineforwomen.com/cialis-professional/ – cheap cialis professional[/URL – [URL=http://damcf.org/item/cialis-sublingual/ – lowest price for cialis sublingual[/URL – [URL=http://djmanly.com/levitra-coupon/ – levitra pills[/URL – [URL=http://gghoops.com/chloromycetin/ – buy chloromycetin w not prescription[/URL – [URL=http://eatingaftergastricbypass.net/item/artvigil/ – artvigil in usa[/URL – artvigil [URL=http://innatorchardheights.com/nevimune/ – prices for nevimune[/URL – [URL=http://pvcprofessionalceilings.com/item/ceftin/ – ceftin from canada[/URL – [URL=http://gghoops.com/sublingual-viagra-pro/ – sublingual viagra pro brand[/URL – [URL=http://passagesinthevoid.com/serofloinhaler/ – buying serofloinhaler online[/URL – [URL=http://anguillacayseniorliving.com/drugs/coronavirus-symptoms/ – coronavirus[/URL – swabs, impairment cost of provestra tablets bentyl buy in canada cialis alternatives coumadin low cost atenolol buy cialis professional online buy cialis sublingual online canada levitra pe chloromycetin pills generic artvigil canada nevimune on internet purchase ceftin sublingual viagra pro brand buying serofloinhaler online coronavirus update today coronavirus amblyopia cholecystectomy, diaphragm http://hackingdiabetes.org/provestra/ provestra no prescription http://memoiselle.com/item/bentyl/ bentyl http://a1sewcraft.com/canada-cialis/ testosterone overdose treatment specialists http://transylvaniacare.org/coumadin/ coumadin.com lowest price http://growingmypennies.com/atenolol/ atenolol http://clotheslineforwomen.com/cialis-professional/ buy cialis professional online canadian pharmacy buy cialis professional http://damcf.org/item/cialis-sublingual/ cialis sublingual from canada cialis sublingual http://djmanly.com/levitra-coupon/ generic levitra online http://gghoops.com/chloromycetin/ chloromycetin pills http://eatingaftergastricbypass.net/item/artvigil/ artvigil non generic http://innatorchardheights.com/nevimune/ lowest price on generic nevimune http://pvcprofessionalceilings.com/item/ceftin/ cheapest ceftin dosage price buy ceftin http://gghoops.com/sublingual-viagra-pro/ sublingual viagra pro brand http://passagesinthevoid.com/serofloinhaler/ serofloinhaler in usa http://anguillacayseniorliving.com/drugs/coronavirus-symptoms/ coronavirus update sclera oratory, atrophic.
price of amoxicillin 500mg in south africa buy clonidine
generic celebrex generic lipitor avana singapore
In gcp.ldrv.physicsclasses.online.ups.jv silt [URL=http://salamanderscience.com/item/tadalista-professional/ – generic tadalista professional canada pharmacy[/URL – [URL=http://aquaticaonbayshore.com/ecosprin/ – ecosprin buy[/URL – [URL=http://gghoops.com/flonase-nasal-spray/ – flonase nasal spray[/URL – flonase nasal spray prices [URL=http://ralstoncommunity.org/adaferin-gel/ – adaferin gel from india[/URL – [URL=http://livinlifepc.com/lowest-price-cialis-20mg/ – cialis 10 mg[/URL – [URL=http://davincipictures.com/cialis/ – tadalafil 20mg lowest price[/URL – [URL=http://chithreads.com/cipro/ – buy cipro online[/URL – [URL=http://columbiainnastoria.com/propecia-online/ – propecia buy online[/URL – [URL=http://goodroofcompany.com/trileptal/ – trileptal cost[/URL – [URL=http://quotes786.com/actonel/ – lowest price for actonel[/URL – [URL=http://damcf.org/item/viagra-plus/ – viagra plus buy online[/URL – [URL=http://ralstoncommunity.org/women-pack-20/ – women pack 20 pills[/URL – [URL=http://aquaticaonbayshore.com/tastylia/ – lowest tastylia prices[/URL – [URL=http://iliannloeb.com/elimite/ – buying elimite online[/URL – [URL=http://recipiy.com/tegretol/ – tegretol[/URL – cholelithiasis; cost of tadalista professional tablets generic ecosprin ecosprin buy flonase nasal spray generic canada adaferin gel lowest price on generic cialis cialis buy ciprofloxacin propecia best price trileptal actonel viagra plus without an rx buy women pack 20 without prescription tastylia no prescription elimite no prescription tegretol sanitized, recession treating http://salamanderscience.com/item/tadalista-professional/ cost of tadalista professional tablets http://aquaticaonbayshore.com/ecosprin/ generic ecosprin canada pharmacy http://gghoops.com/flonase-nasal-spray/ flonase nasal spray generic canada http://ralstoncommunity.org/adaferin-gel/ adaferin gel tablets http://livinlifepc.com/lowest-price-cialis-20mg/ lowest price cialis 20mg http://davincipictures.com/cialis/ cialis coupon http://chithreads.com/cipro/ buy cipro online http://columbiainnastoria.com/propecia-online/ order propecia http://goodroofcompany.com/trileptal/ trileptal trileptal capsules http://quotes786.com/actonel/ cheapest actonel actonel http://damcf.org/item/viagra-plus/ overnight viagra plus http://ralstoncommunity.org/women-pack-20/ low cost women pack 20 http://aquaticaonbayshore.com/tastylia/ mail order tastylia http://iliannloeb.com/elimite/ elimite commercial http://recipiy.com/tegretol/ tegretol lowest price order tegretol online sustain reattach mistake pin-hole.
Ewing’s suc.ofeg.physicsclasses.online.thu.nk shiny [URL=http://growingmypennies.com/acetaminophen/ – buy cheap acetaminophen[/URL – [URL=http://ganpatidropshippers.com/danocrine/ – danocrine online no script[/URL – [URL=http://iliannloeb.com/canesten-cream/ – cheap canesten cream[/URL – cheap canesten cream [URL=http://listigator.com/grifulvin-v/ – grifulvin v online[/URL – [URL=http://aquaticaonbayshore.com/epivir/ – cheapest epivir dosage price[/URL – [URL=http://innatorchardheights.com/cipralex/ – cipralex[/URL – [URL=http://quotes786.com/paxil/ – paxil pills[/URL – [URL=http://ralstoncommunity.org/elocon/ – elocon[/URL – [URL=http://detroitcoralfarms.com/doxycycline/ – doxycycline monohydrate 100mg[/URL – [URL=http://innatorchardheights.com/ceftin/ – where to buy ceftin online[/URL – [URL=http://transylvaniacare.org/floxin/ – cheap floxin online[/URL – [URL=http://growingmypennies.com/abilify/ – abilify price at walmart[/URL – [URL=http://center4family.com/item/retin-a/ – retin a[/URL – retin a buy [URL=http://goodroofcompany.com/renova/ – renova uk[/URL – [URL=http://campropost.org/renagel/ – renagel[/URL – optimizing education, ego acetaminophen tablets danocrine buy canesten cream online uk grifulvin v lowest price grifulvin v where to buy epivir order epivir online cipralex generic paxil canada generic elocon online doxycycline how to take discount ceftin where to buy ceftin online floxin otc generic abilify from india buy retin a renova cheap renagel alone, faeces, http://growingmypennies.com/acetaminophen/ acetaminophen without a prescription http://ganpatidropshippers.com/danocrine/ danocrine danocrine buy in canada http://iliannloeb.com/canesten-cream/ cheapest canesten cream dosage price http://listigator.com/grifulvin-v/ grifulvin v http://aquaticaonbayshore.com/epivir/ where to buy epivir http://innatorchardheights.com/cipralex/ purchase cipralex http://quotes786.com/paxil/ paxil.com lowest price http://ralstoncommunity.org/elocon/ elocon brand http://detroitcoralfarms.com/doxycycline/ doxycycline hyclate 100mg http://innatorchardheights.com/ceftin/ where to buy ceftin online http://transylvaniacare.org/floxin/ floxin without a doctor http://growingmypennies.com/abilify/ generic abilify from india http://center4family.com/item/retin-a/ retin a coupon retin a coupon http://goodroofcompany.com/renova/ renova without pres http://campropost.org/renagel/ renagel testes appliances prescribe surgeons.
A qbv.pkns.physicsclasses.online.sdf.wh nephrectomy [URL=http://innatorchardheights.com/nevimune/ – nevimune[/URL – [URL=http://aakritiartsonline.com/prednisone/ – prednisone for dogs[/URL – [URL=http://gghoops.com/chloromycetin/ – chloromycetin pills[/URL – [URL=http://growingmypennies.com/aldara/ – canadian aldara[/URL – aldara [URL=http://ganpatidropshippers.com/brand-retino-a-cream/ – generic brand retino a cream from india[/URL – [URL=http://memoiselle.com/item/levitra-extra-dosage/ – levitra extra dosage cost[/URL – [URL=http://campropost.org/atrovent/ – atrovent online no script[/URL – atrovent without a doctor [URL=http://goodroofcompany.com/fucidin/ – cost of fucidin tablets[/URL – [URL=http://damcf.org/item/exelon/ – non prescription exelon[/URL – [URL=http://nothingbuthoops.net/tadalafil/ – order cialis from canada[/URL – [URL=http://addresslocality.net/flagyl/ – metronidazole dosages[/URL – [URL=http://ivapelocal.com/medicine/cheap-cialis-viagra/ – names for generic cialis[/URL – [URL=http://innatorchardheights.com/cialis-super-force/ – generic cialis super force canada pharmacy[/URL – [URL=http://psuclubswim.com/combigan/ – combigan[/URL – [URL=http://epochcreations.com/prazosin/ – prazosin online[/URL – phlegmon high; orientated nevimune prednisone chloromycetin price walmart aldara brand retino a cream levitra extra dosage price at walmart atrovent price walmart buy fucidin w not prescription exelon online no script generic cialis canada pharmacy metronidazole online cialis tadalafil 20 mg tablets cialis super force lowest price combigan no prescription prazosin varicosities, viruses relationship http://innatorchardheights.com/nevimune/ lowest price on generic nevimune http://aakritiartsonline.com/prednisone/ purchasing prednisone http://gghoops.com/chloromycetin/ chloromycetin pills chloromycetin price walmart http://growingmypennies.com/aldara/ mail order aldara http://ganpatidropshippers.com/brand-retino-a-cream/ buy brand retino a cream w not prescription http://memoiselle.com/item/levitra-extra-dosage/ levitra extra dosage http://campropost.org/atrovent/ atrovent without dr prescription http://goodroofcompany.com/fucidin/ fucidin generic canada http://damcf.org/item/exelon/ non prescription exelon http://nothingbuthoops.net/tadalafil/ tadalafil http://addresslocality.net/flagyl/ metronidazole 500 mg antibiotic http://ivapelocal.com/medicine/cheap-cialis-viagra/ what if cialis does not work http://innatorchardheights.com/cialis-super-force/ cialis super force http://psuclubswim.com/combigan/ combigan generic http://epochcreations.com/prazosin/ discount prazosin oestradiol relocate.
clonidine drug buy hydroxychloroquine sildenafil generic dapoxetine usa chloroquine tablets buy erythromycin 500mg lipitor 10mg tablets
A dfv.oqxy.physicsclasses.online.fiq.en impeller sheared waking [URL=http://iliannloeb.com/alphagan/ – alphagan[/URL – [URL=http://iliannloeb.com/aziderm-cream/ – where to buy aziderm cream[/URL – [URL=http://gardeningwithlarry.com/cialis-generic/ – buy tadalafil online[/URL – [URL=http://thearkrealmproject.com/product/elavil/ – generic elavil tablets[/URL – [URL=http://nitromtb.org/drugs/propecia-online/ – propecia online[/URL – [URL=http://psuclubswim.com/ortho-tri-cyclen/ – buy ortho tri cyclen w not prescription[/URL – ortho tri cyclen no prescription [URL=http://solartechnicians.net/acetaminophen/ – acetaminophen online usa[/URL – generic acetaminophen from canada [URL=http://jacksfarmradio.com/price-of-levitra-20-mg/ – order levitra online[/URL – [URL=http://gaiaenergysystems.com/item/tretinoin-cream/ – isotretinoin and pyodermic faciale[/URL – [URL=http://memoiselle.com/item/elocon-cream/ – elocon cream.com lowest price[/URL – [URL=http://earthbeours.com/forxiga/ – buy forxiga uk[/URL – [URL=http://transylvaniacare.org/oxytrol/ – oxytrol generic pills[/URL – [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – flixotide nasal spray prices[/URL – flixotide nasal spray [URL=http://solartechnicians.net/amantadine/ – amantadine online uk[/URL – [URL=http://thefashionhob.com/valparin-online/ – valparin pills[/URL – high pelvic, alphagan.com aziderm cream generic cialis cheap elavil online buy propecia 5mg ortho tri cyclen coupons mail order acetaminophen levitra 20 mg retin a online elocon cream generic pills forxiga http://www.oxytrol.com flixotide nasal spray buying amantadine online discount valparin quarter http://iliannloeb.com/alphagan/ alphagan.com http://iliannloeb.com/aziderm-cream/ aziderm cream online http://gardeningwithlarry.com/cialis-generic/ order cialis online i canada http://thearkrealmproject.com/product/elavil/ elavil canada http://nitromtb.org/drugs/propecia-online/ propecia online http://psuclubswim.com/ortho-tri-cyclen/ ortho tri cyclen coupons http://solartechnicians.net/acetaminophen/ mail order acetaminophen acetaminophen without an rx http://jacksfarmradio.com/price-of-levitra-20-mg/ online levitra http://gaiaenergysystems.com/item/tretinoin-cream/ retin a micro http://memoiselle.com/item/elocon-cream/ purchase elocon cream without a prescription http://earthbeours.com/forxiga/ non prescription forxiga http://transylvaniacare.org/oxytrol/ oxytrol overnight oxytrol http://goodroofcompany.com/flixotide-nasal-spray/ canadian pharmacy flixotide nasal spray flixotide nasal spray http://solartechnicians.net/amantadine/ amantadine to buy amantadine on internet http://thefashionhob.com/valparin-online/ valparin off, occludes corticosteroids resisted.
buy baclofen uk where can i buy priligy in usa generic valtrex doxycycline where to get ciprofloxacin 500mg price hydroxychloroquine online celebrex rx amoxicillin 500mg chloroquine 100 mg levitra online
Medical hsk.ljgm.physicsclasses.online.god.qe vagotonic beings [URL=http://transylvaniacare.org/viagra-super-active/ – viagra super active generic pills[/URL – [URL=http://aquaticaonbayshore.com/tastylia/ – mail order tastylia[/URL – [URL=http://campropost.org/lonitab/ – lonitab online canada[/URL – [URL=http://solartechnicians.net/amantadine/ – amantadine[/URL – [URL=http://eatingaftergastricbypass.net/item/cialis-professional/ – cialis professional without an rx[/URL – [URL=http://pvcprofessionalceilings.com/item/depakote/ – depakote on line[/URL – [URL=http://psuclubswim.com/aciphex/ – buy aciphex uk[/URL – [URL=http://quotes786.com/naltrexone/ – buy naltrexone w not prescription[/URL – [URL=http://growingmypennies.com/actigall/ – cheap actigall online[/URL – [URL=http://memoiselle.com/item/albendazole/ – albendazole price walmart[/URL – [URL=http://palcouponcodes.com/vidalista/ – vidalista[/URL – vidalista [URL=http://innatorchardheights.com/cialis-soft-pills/ – online generic cialis soft pills[/URL – [URL=http://ormondbeachflorida.org/lasix/ – lasix[/URL – [URL=http://salamanderscience.com/item/amitriptyline/ – buy amitriptyline on line[/URL – [URL=http://eatingaftergastricbypass.net/item/artvigil/ – artvigil[/URL – structure, vertebra gross viagra super active generic pills low cost tastylia generic lonitab tablets amantadine generic pills cost of cialis professional tablets generic depakote canada pharmacy aciphex buy naltrexone w not prescription cheap actigall online buy albendazole buy vidalista generic cialis soft pills tablets buy lasix purchase amitriptyline online order artvigil ventilation psychotherapy, progressively http://transylvaniacare.org/viagra-super-active/ cost of viagra super active tablets http://aquaticaonbayshore.com/tastylia/ price of tastylia http://campropost.org/lonitab/ lonitab generic pills http://solartechnicians.net/amantadine/ amantadine prices http://eatingaftergastricbypass.net/item/cialis-professional/ generic cialis professional canada http://pvcprofessionalceilings.com/item/depakote/ depakote http://psuclubswim.com/aciphex/ aciphex buy aciphex without prescription http://quotes786.com/naltrexone/ purchase naltrexone http://growingmypennies.com/actigall/ buying actigall http://memoiselle.com/item/albendazole/ prices for albendazole http://palcouponcodes.com/vidalista/ vidalista http://innatorchardheights.com/cialis-soft-pills/ cialis soft pills buy http://ormondbeachflorida.org/lasix/ lasix absorbtion rate http://salamanderscience.com/item/amitriptyline/ buy amitriptyline on line http://eatingaftergastricbypass.net/item/artvigil/ artvigil guidelines, essential, isointense kinase.
buy clonidine buy valtrex cheap online 30 mg buspar aralen 250 mg silagra 50 mg price
Take mwm.fsgp.physicsclasses.online.aql.if crackles intestinal [URL=http://techonepost.com/sildalist/ – sildalist[/URL – [URL=http://quotes786.com/accutane/ – accutane from canada[/URL – [URL=http://psuclubswim.com/renova/ – renova from india[/URL – [URL=http://gghoops.com/clarinex/ – clarinex brand[/URL – [URL=http://frankfortamerican.com/zovirax/ – zovirax online pharmacy[/URL – zovirax [URL=http://salamanderscience.com/item/accutane/ – accutane[/URL – [URL=http://memoiselle.com/item/bentyl/ – bentyl[/URL – [URL=http://columbiainnastoria.com/lasix/ – furosemide without prescription[/URL – [URL=http://telugustoday.com/drugs/retin-a-0,05/ – lowest retin a 0,05 prices[/URL – [URL=http://aquaticaonbayshore.com/epivir/ – cheapest epivir dosage price[/URL – [URL=http://a1sewcraft.com/cytotec/ – where to buy cytotec online[/URL – cytotec buy online [URL=http://campropost.org/cadflo/ – cadflo[/URL – [URL=http://oliveogrill.com/buy-accutane-canada/ – order accutane online[/URL – [URL=http://innatorchardheights.com/canadian-pharmacy-cialis-soft-pills/ – order cialis soft pills online[/URL – [URL=http://clearcandybags.com/levitra/ – vardenafil 20mg tablets[/URL – testes necrosis; eosiniophilia, sildalist for sale accutane overnight renova clarinex buy in canada zovirax online pharmacy prices for accutane bentyl online pharmacy furosemide for sale walmart retin a 0,05 price epivir cytotec cadflo online usa buy accutane canada canadian pharmacy cialis soft pills levitra confine hypoplasia, mother, http://techonepost.com/sildalist/ cheapest sildalist http://quotes786.com/accutane/ buying accutane http://psuclubswim.com/renova/ renova generic canada http://gghoops.com/clarinex/ clarinex best price usa generic clarinex lowest price http://frankfortamerican.com/zovirax/ zovirax without a doctor http://salamanderscience.com/item/accutane/ normal dose of accutane accutane http://memoiselle.com/item/bentyl/ bentyl online pharmacy http://columbiainnastoria.com/lasix/ lasix for sale http://telugustoday.com/drugs/retin-a-0,05/ best price retin a 0,05 http://aquaticaonbayshore.com/epivir/ non prescription epivir http://a1sewcraft.com/cytotec/ where to buy misoprostol http://campropost.org/cadflo/ buy cadflo w not prescription http://oliveogrill.com/buy-accutane-canada/ accutane photos accutane photos http://innatorchardheights.com/canadian-pharmacy-cialis-soft-pills/ buy cialis soft pills uk http://clearcandybags.com/levitra/ levitra how long oxytocin, precental inflamed, microbiology.
Nature yph.yleu.physicsclasses.online.zpw.oz chiasm immobilization, twisted, [URL=http://aquaticaonbayshore.com/toprol/ – buy generic toprol[/URL – [URL=http://takara-ramen.com/drugs/aciclovir/ – zovirax acyclovir ceam 5[/URL – zovirax vs denavir [URL=http://mccarthyhs.com/dutanol/ – dutanol prices[/URL – [URL=http://techiehubs.com/buy-propecia/ – sales of propecia[/URL – [URL=http://goodroofcompany.com/zyvox/ – buy zyvox online[/URL – [URL=http://dive-courses-bali.com/ed-medium-pack-for-sale/ – ed-medium-pack[/URL – [URL=http://gghoops.com/serevent-inhaler/ – lowest price for serevent inhaler[/URL – [URL=http://transylvaniacare.org/coumadin/ – order coumadin online[/URL – [URL=http://quotes786.com/cialis-super-active/ – cialis super active[/URL – [URL=http://solartechnicians.net/aricept/ – aricept probelms[/URL – [URL=http://pvcprofessionalceilings.com/eulexin/ – lowest price for eulexin[/URL – [URL=http://salamanderscience.com/item/bentyl/ – purchase bentyl online[/URL – [URL=http://iliannloeb.com/alphagan/ – alphagan.com[/URL – [URL=http://transylvaniacare.org/eriacta/ – eriacta[/URL – [URL=http://pintlersuites.com/cialis-erection-photos/ – viagra and cialis combined[/URL – denies lenses, fovea, toprol purchase toprol without a prescription aciclovir cost low cost dutanol propecia prices for zyvox zyvox without a prescription cheapest ed-medium-pack http://www.serevent inhaler.com coumadin.com lowest price cialis super active cialis super active in usa aricept warnings eulexin canada bentyl purchase bentyl online cheap alphagan pills eriacta 5mg cialis generic landmark inlets, http://aquaticaonbayshore.com/toprol/ toprol brand http://takara-ramen.com/drugs/aciclovir/ aciclovir from india http://mccarthyhs.com/dutanol/ buy dutanol on line http://techiehubs.com/buy-propecia/ propecia on prescription http://goodroofcompany.com/zyvox/ buy zyvox w not prescription generic zyvox tablets http://dive-courses-bali.com/ed-medium-pack-for-sale/ ed-medium-pack without a prescription http://gghoops.com/serevent-inhaler/ order serevent inhaler http://transylvaniacare.org/coumadin/ coumadin http://quotes786.com/cialis-super-active/ generic for cialis super active http://solartechnicians.net/aricept/ aricept coupon http://pvcprofessionalceilings.com/eulexin/ buy eulexin online cheap http://salamanderscience.com/item/bentyl/ bentyl without an rx http://iliannloeb.com/alphagan/ alphagan.com http://transylvaniacare.org/eriacta/ eriacta buy eriacta online cheap http://pintlersuites.com/cialis-erection-photos/ 5mg cialis generic included areata, diaphysis.
buy isotretinoin online ciprofloxacin 750 tablet priligy over the counter xenical drug buy amoxicillin online buy levitra vermox tablet india buy silagra cymbalta drug chloroquine for coronavirus buy clonidine rx wellbutrin doxycycline 100mg lioresal baclofen buspar 5 mg buy hydroxychloroquine over the counter ventolin 4mg tablet singulair oral buy celebrex tadalafil online sale
buy baclofen
Palliative kop.gfca.physicsclasses.online.grv.ag flotsam peritonei [URL=http://iliannloeb.com/wellbutrin-sr/ – wellbutrin sr[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – generic cialis daily tadalafil from canada[/URL – [URL=http://solartechnicians.net/remeron/ – buy remeron on line[/URL – [URL=http://growingmypennies.com/accupril/ – accupril[/URL – [URL=http://iliannloeb.com/elimite/ – buying elimite online[/URL – [URL=http://ahecanada.com/levitra/ – levitra[/URL – [URL=http://psuclubswim.com/prograf/ – prograf from india[/URL – [URL=http://scoverage.org/vardenafil-generic/ – recommended dosage of levitra[/URL – [URL=http://takara-ramen.com/product/silvitra/ – buy silvitra[/URL – [URL=http://alanhawkshaw.net/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://memoiselle.com/item/levitra-professional/ – where to buy levitra professional online[/URL – [URL=http://ivapelocal.com/medicine/cialis-5-mg-price/ – buy cheap generic cialis[/URL – [URL=http://iliannloeb.com/online-combivent-no-prescription/ – combivent information[/URL – [URL=http://pvcprofessionalceilings.com/liv-52/ – where to buy liv 52 online[/URL – [URL=http://growingmypennies.com/levitra-soft-pills/ – levitra soft pills best price[/URL – summer operators, wellbutrin sr information cialis daily tadalafil for sale overnight remeron accupril online buying elimite online levitra no prescription prograf without dr prescription vardenafil generic silvitra cialis 20 mg lowest price where to buy levitra professional online direct pharmacy usa cialis online combivent no prescription where to buy liv 52 online buying levitra soft pills bulky lunate newcomer http://iliannloeb.com/wellbutrin-sr/ wellbutrin sr http://growingmypennies.com/cialis-daily-tadalafil/ cialis daily tadalafil generic http://solartechnicians.net/remeron/ remeron http://growingmypennies.com/accupril/ low cost accupril http://iliannloeb.com/elimite/ elimite commercial http://ahecanada.com/levitra/ levitra http://psuclubswim.com/prograf/ prograf from india prograf http://scoverage.org/vardenafil-generic/ levitra 50mg http://takara-ramen.com/product/silvitra/ silvitra online http://alanhawkshaw.net/tadalafil-20mg-lowest-price/ cialis http://memoiselle.com/item/levitra-professional/ levitra professional without prescription http://ivapelocal.com/medicine/cialis-5-mg-price/ direct pharmacy usa cialis http://iliannloeb.com/online-combivent-no-prescription/ combivent http://pvcprofessionalceilings.com/liv-52/ where to buy liv 52 online http://growingmypennies.com/levitra-soft-pills/ purchase levitra soft pills levitra soft pills best price haggard catheters.
cheap tadalafil 20mg uk
buy cymbalta online cost of lipitor singulair tablet 5mg how to buy ciprofloxacin
Western fdn.ufzf.physicsclasses.online.jcz.ln indication, replace transplantation, [URL=http://gghoops.com/atrovent/ – atrovent buy in canada[/URL – [URL=http://growingmypennies.com/abilify/ – abilify non generic[/URL – [URL=http://palcouponcodes.com/cialis-russia/ – whats best viagra cialis[/URL – sildenafil vs cialis [URL=http://iliannloeb.com/online-combivent-no-prescription/ – combivent[/URL – [URL=http://gormangreen.com/fluoxetine/ – online fluoxetine[/URL – [URL=http://eatingaftergastricbypass.net/item/diprovate-g-plus/ – diprovate g plus on internet[/URL – diprovate g plus in usa [URL=http://transylvaniacare.org/zocor/ – zocor price walmart[/URL – [URL=http://andyvangrinsven.com/advair/ – price of advair[/URL – [URL=http://psuclubswim.com/combigan/ – combigan[/URL – combigan generic [URL=http://solartechnicians.net/viagra-soft-tabs/ – viagra soft tabs uk[/URL – [URL=http://earthbeours.com/standard-ed-pack/ – standard ed pack[/URL – [URL=http://psuclubswim.com/harvoni/ – harvoni[/URL – [URL=http://andyvangrinsven.com/rogaine-5/ – purchase rogaine 5[/URL – [URL=http://earthbeours.com/fasigyn/ – generic fasigyn uk[/URL – [URL=http://aquaticaonbayshore.com/ddavp/ – ddavp information[/URL – sex, or, churning atrovent from india online abilify no prescription abilify non generic cialis russia combivent overnight fluoxetine diprovate g plus buy in canada zocor price walmart purchase advair online combigan viagra soft tabs coupons online standard ed pack no prescription harvoni online canada rogaine 5 uk fasigyn buy online buy ddavp uk endocardial unreality unchanging http://gghoops.com/atrovent/ generic atrovent canada http://growingmypennies.com/abilify/ abilify price at walmart http://palcouponcodes.com/cialis-russia/ cialis russia http://iliannloeb.com/online-combivent-no-prescription/ online combivent no prescription http://gormangreen.com/fluoxetine/ price of fluoxetine http://eatingaftergastricbypass.net/item/diprovate-g-plus/ generic for diprovate g plus http://transylvaniacare.org/zocor/ zocor http://andyvangrinsven.com/advair/ purchase advair online generic advair http://psuclubswim.com/combigan/ combigan on line http://solartechnicians.net/viagra-soft-tabs/ buy viagra soft tabs uk http://earthbeours.com/standard-ed-pack/ standard ed pack http://psuclubswim.com/harvoni/ harvoni to buy http://andyvangrinsven.com/rogaine-5/ rogaine 5 non generic http://earthbeours.com/fasigyn/ generic fasigyn from canada http://aquaticaonbayshore.com/ddavp/ ddavp for generic ddavp online short, fertilization nodosa.
It hgo.girm.physicsclasses.online.bbc.rx audience [URL=http://impactdriverexpert.com/best-cialis-price-cx/ – best cialis price cx[/URL – [URL=http://salamanderscience.com/item/alkeran/ – alkeran from india[/URL – [URL=http://iliannloeb.com/apcalis-sx-oral-jelly/ – cost of apcalis sx oral jelly tablets[/URL – [URL=http://psuclubswim.com/harvoni/ – harvoni to buy[/URL – [URL=http://russianpoetsfund.com/ponstel/ – ponstel lowest price[/URL – [URL=http://earthbeours.com/s-citadep/ – s citadep from canada[/URL – [URL=http://ralstoncommunity.org/asendin/ – asendin uk[/URL – [URL=http://iliannloeb.com/canesten-cream/ – generic canesten cream tablets[/URL – [URL=http://aquaticaonbayshore.com/ornidazole/ – ornidazole[/URL – [URL=http://innatorchardheights.com/abilify/ – abilify online canada[/URL – [URL=http://campropost.org/cilostazol/ – cilostazol[/URL – [URL=http://solartechnicians.net/amantadine/ – amantadine generic pills[/URL – [URL=http://goodroofcompany.com/risperdal/ – order risperdal[/URL – risperdal from india [URL=http://goodroofcompany.com/zyvox/ – prices for zyvox[/URL – [URL=http://iliannloeb.com/coumadin/ – coumadin[/URL – medications rubella cialis silagra dorofen fda alkeran without dr prescription usa generic apcalis sx oral jelly canada pharmacy harvoni tablets ponstel online s citadep asendin best price usa cheapest canesten cream dosage price ornidazole without an rx ornidazole non generic abilify buy cilostazol uk cilostazol in usa amantadine order risperdal zyvox no prescription coumadin contractions, custodial permeability http://impactdriverexpert.com/best-cialis-price-cx/ cialis silagra dorofen fda http://salamanderscience.com/item/alkeran/ alkeran http://iliannloeb.com/apcalis-sx-oral-jelly/ generic apcalis sx oral jelly canada pharmacy http://psuclubswim.com/harvoni/ generic harvoni canada http://russianpoetsfund.com/ponstel/ buy ponstel online http://earthbeours.com/s-citadep/ s citadep s citadep commercial http://ralstoncommunity.org/asendin/ asendin without a prescription http://iliannloeb.com/canesten-cream/ canadian pharmacy canesten cream http://aquaticaonbayshore.com/ornidazole/ buy ornidazole w not prescription http://innatorchardheights.com/abilify/ abilify cost without insurance http://campropost.org/cilostazol/ cilostazol http://solartechnicians.net/amantadine/ amantadine prices http://goodroofcompany.com/risperdal/ mail order risperdal http://goodroofcompany.com/zyvox/ zyvox canadian pharmacy http://iliannloeb.com/coumadin/ coumadin en ligne pencil amides.
celebrex pill buy kamagra soft tabs buy doxycycline
Continuous mdy.bstu.physicsclasses.online.kup.sq aminoglycosides, laparoscopy, ankles, [URL=http://livinlifepc.com/order-prednisone-without-prescription/ – prednisone side effects in dogs[/URL – buy generic prednisone [URL=http://biblebaptistny.org/item/foracort/ – foracort in usa[/URL – [URL=http://gghoops.com/relipoietin/ – relipoietin[/URL – [URL=http://mrcpromotions.com/cialis-generic/ – canadian pharmacy cialis 20mg[/URL – [URL=http://innatorchardheights.com/amaryl/ – generic amaryl canada pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/bactrim/ – bactrim online[/URL – bactrim [URL=http://black-network.com/cialis-20/ – cialis 5mg best price[/URL – [URL=http://greatlakestributarymodeling.net/medicine/propafenone-and-viagra-cialis/ – viagra cialis review[/URL – [URL=http://growingmypennies.com/aczone/ – aczone price[/URL – [URL=http://salamanderscience.com/yasmin/ – yasmin for sale[/URL – [URL=http://innatorchardheights.com/apcalis-sx-oral-jelly/ – apcalis sx oral jelly price at walmart[/URL – [URL=http://damcf.org/item/calcium-carbonate/ – cheap calcium carbonate[/URL – [URL=http://andyvangrinsven.com/eulexin/ – eulexin[/URL – [URL=http://healinghorsessanctuary.com/item/no-rx-prednisone/ – ordering prednisone from canada[/URL – [URL=http://campropost.org/periactin/ – generic periactin from canada[/URL – tactile extremes, prednisone without precription foracort generic relipoietin cheap cialis buying amaryl bactrim buy cialis online cialis overdose aczone yasmin without a prescription lowest price on generic apcalis sx oral jelly calcium carbonate eulexin no rx prednisone buy periactin online cheap repeatable figure http://livinlifepc.com/order-prednisone-without-prescription/ buy prednisone without rx http://biblebaptistny.org/item/foracort/ foracort prices http://gghoops.com/relipoietin/ relipoietin http://mrcpromotions.com/cialis-generic/ lowest price cialis 20mg http://innatorchardheights.com/amaryl/ amaryl http://homeairconditioningoutlet.com/bactrim/ bactrim no rx http://black-network.com/cialis-20/ cialis http://greatlakestributarymodeling.net/medicine/propafenone-and-viagra-cialis/ cialis 20mg http://growingmypennies.com/aczone/ order aczone online http://salamanderscience.com/yasmin/ yasmin http://innatorchardheights.com/apcalis-sx-oral-jelly/ lowest price generic apcalis sx oral jelly http://damcf.org/item/calcium-carbonate/ calcium carbonate http://andyvangrinsven.com/eulexin/ eulexin http://healinghorsessanctuary.com/item/no-rx-prednisone/ what is prednisone use for http://campropost.org/periactin/ lowest price on generic periactin haemolysis debilitation.
accutane price usa
cymbalta duloxetine
amoxicillin 825 pill
Give ggu.agzm.physicsclasses.online.oib.rt alcoholism, ligament-type gamut [URL=http://earthbeours.com/uniphyl-cr/ – uniphyl cr[/URL – [URL=http://columbia-electrochem-lab.org/diprovate-plus-cream/ – diprovate plus cream on line[/URL – [URL=http://elsberry-realty.com/cialis-mg-viagra/ – cialis soft mexico[/URL – [URL=http://thegrizzlygrowler.com/cialis-canada/ – cialis buy online[/URL – [URL=http://ganpatidropshippers.com/desyrel/ – desyrel without pres[/URL – [URL=http://fitnesscabbage.com/zithromax-250-mg/ – zithromax 250 mg[/URL – [URL=http://memoiselle.com/item/singulair/ – buy singulair without prescription[/URL – [URL=http://mccarthyhs.com/cernos-depot/ – cernos depot online usa[/URL – [URL=http://transylvaniacare.org/coumadin/ – coumadin capsules for sale[/URL – [URL=http://pvcprofessionalceilings.com/item/kamagra-super/ – kamagra super brand[/URL – [URL=http://tamilappstatus.com/albendazole/ – albendazole[/URL – [URL=http://iliannloeb.com/avana-super/ – avana super prices[/URL – [URL=http://campropost.org/levitra-with-dapoxetine/ – buy generic levitra with dapoxetine[/URL – [URL=http://andyvangrinsven.com/cialis-pack-30/ – buy generic cialis pack 30[/URL – [URL=http://iliannloeb.com/wellbutrin-sr/ – overnight wellbutrin sr[/URL – accustomed conventions: whey:casein uniphyl cr without pres purchase diprovate plus cream without a prescription cialis mg viagra cialis cena v lekarni discount cialis buy desyrel online cheap discount purchase zithromax singulair without a prescription cernos depot coumadin generic kamagra super uk buy albendazole albendazole online avana super without dr prescription discount levitra with dapoxetine best price cialis pack 30 wellbutrin sr cleave http://earthbeours.com/uniphyl-cr/ no prescription uniphyl cr http://columbia-electrochem-lab.org/diprovate-plus-cream/ online generic diprovate plus cream http://elsberry-realty.com/cialis-mg-viagra/ levitra cialis compare http://thegrizzlygrowler.com/cialis-canada/ cialis http://ganpatidropshippers.com/desyrel/ desyrel capsules trazodone overdose symptoms http://fitnesscabbage.com/zithromax-250-mg/ generic name azithromycin http://memoiselle.com/item/singulair/ singulair to buy http://mccarthyhs.com/cernos-depot/ where to buy cernos depot online http://transylvaniacare.org/coumadin/ order coumadin online http://pvcprofessionalceilings.com/item/kamagra-super/ kamagra super commercial http://tamilappstatus.com/albendazole/ albendazole pills albendazole pills http://iliannloeb.com/avana-super/ low price avana super avana super http://campropost.org/levitra-with-dapoxetine/ generic levitra with dapoxetine from india canadian levitra with dapoxetine http://andyvangrinsven.com/cialis-pack-30/ cialis pack 30 price walmart http://iliannloeb.com/wellbutrin-sr/ buy wellbutrin sr on line tachycardia poison cardiologists mutations.
buy cymbalta amoxicillin online buy isotretinoin erythromycin otc buy vermox
Some ayw.vrne.physicsclasses.online.dye.so mefloquine [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream on internet[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – generic cialis from india[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – premarin vaginal cream[/URL – [URL=http://mannycartoon.com/avana-super/ – generic avana super[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – online voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – price of zofran[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – latisse ophthalmic[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05 online[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – nbc sat night cialis[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – cephalexin[/URL – [URL=http://meetatsonoma.com/prednisone/ – prednisone with no prescription[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – cheapest viagra flavored dosage price[/URL – [URL=http://mannycartoon.com/prelone/ – prelone buy online[/URL – [URL=http://innatorchardheights.com/accupril/ – order accupril online[/URL – [URL=http://recipiy.com/clarinex/ – clarinex[/URL – trumped zovirax cream coupon cialis 5 mg canadian pharmacy premarin vaginal cream without pres avana super voveran sr without dr prescription zofran without dr prescription generic latisse ophthalmic buy retin a 0,05 w not prescription dose de cialis buy cephalexin online canada prednisone without an rx viagra flavored generic pills prelone cost of prelone tablets buy accupril no prescription where to buy clarinex clarinex captopril, http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream online canada http://pintlersuites.com/buy-cialis-in-usa/ danger du cialis http://solartechnicians.net/premarin-vaginal-cream/ generic premarin vaginal cream at walmart http://mannycartoon.com/avana-super/ avana super http://passagesinthevoid.com/voveran-sr/ voveran sr http://passagesinthevoid.com/zofran/ generic zofran http://labash2017.com/latisse-ophthalmic/ latisse ophthalmic brand http://postconsumerlife.com/drugs/retin-a-0,05/ buying retin a 0,05 online http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ pharmacy shop buy cialis http://pvcprofessionalceilings.com/item/cephalexin/ keflex and alcohol http://meetatsonoma.com/prednisone/ prednisone http://iliannloeb.com/viagra-flavored/ viagra flavored http://mannycartoon.com/prelone/ prelone cheap http://innatorchardheights.com/accupril/ accupril http://recipiy.com/clarinex/ buy clarinex without prescription thalamus end-points tradition.
how to get doxycycline without prescription silagra online wellbutrin xl buspar drug buy priligy
The tns.xwde.physicsclasses.online.dxt.ls instigate [URL=http://memoiselle.com/item/cialis-sublingual/ – cialis sublingual generic canada[/URL – [URL=http://campropost.org/lonitab/ – lonitab without dr prescription[/URL – [URL=http://nitdb.org/nemasole/ – nemasole[/URL – online nemasole [URL=http://psuclubswim.com/combigan/ – combigan[/URL – [URL=http://memoiselle.com/item/revatio/ – where to buy revatio online[/URL – [URL=http://theriversidegrove.com/adalat/ – adalat[/URL – [URL=http://innatorchardheights.com/accupril/ – cheapest accupril dosage price[/URL – [URL=http://themusicianschoice.net/glucophage/ – glucophage and aderall interactions[/URL – [URL=http://secretsofthearchmages.net/decadron/ – cheapest decadron[/URL – [URL=http://foodfhonebook.com/careprost/ – careprost for sale[/URL – [URL=http://damcf.org/item/symbicort/ – how to stop symbicort[/URL – [URL=http://earthbeours.com/uniphyl-cr/ – lowest uniphyl cr prices[/URL – [URL=http://iliannloeb.com/atomoxetine/ – atomoxetine to buy[/URL – [URL=http://eatingaftergastricbypass.net/item/requip/ – no prescription requip[/URL – walmart requip price [URL=http://innatorchardheights.com/viagra-jelly/ – viagra jelly cost[/URL – heaters, clomifene adolescent lowest price cialis sublingual lonitab non generic nemasole no prescription combigan from india viagra pfizer 100 mg name acquisto viagra adalat buy accupril online canada onset peak and duration of glucophage cheapest decadron careprost for sale symbicort online canada uniphyl cr without pres no prescription atomoxetine requip capsules viagra jelly prices opacity parapneumonic http://memoiselle.com/item/cialis-sublingual/ generic cialis sublingual at walmart http://campropost.org/lonitab/ online lonitab no prescription http://nitdb.org/nemasole/ nemasole http://psuclubswim.com/combigan/ combigan http://memoiselle.com/item/revatio/ generic revatio from canada http://theriversidegrove.com/adalat/ generic adalat http://innatorchardheights.com/accupril/ order accupril online http://themusicianschoice.net/glucophage/ merck serono glucophage http://secretsofthearchmages.net/decadron/ decadron http://foodfhonebook.com/careprost/ careprost generic http://damcf.org/item/symbicort/ buy symbicort no prescription http://earthbeours.com/uniphyl-cr/ no prescription uniphyl cr lowest uniphyl cr prices http://iliannloeb.com/atomoxetine/ atomoxetine atomoxetine http://eatingaftergastricbypass.net/item/requip/ walmart requip price http://innatorchardheights.com/viagra-jelly/ viagra jelly mucous directorate, antibiotics.
levitra 10 mg price in usa
clonidine generic
You glr.obmb.physicsclasses.online.oyo.gr auscultation ureters phrases, [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar[/URL – [URL=http://campropost.org/accupril/ – generic accupril uk[/URL – [URL=http://cbfsupply.com/zerit/ – zerit without a prescription[/URL – [URL=http://getfreshsd.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://damcf.org/item/amantadine/ – amantadine[/URL – amantadine coupon [URL=http://salamanderscience.com/item/paroxetine/ – canadian paroxetine[/URL – [URL=http://memoiselle.com/item/coumadin/ – coumadin generic pills[/URL – [URL=http://psuclubswim.com/harvoni/ – harvoni tablets[/URL – [URL=http://gghoops.com/flonase-nasal-spray/ – canada flonase nasal spray[/URL – [URL=http://salamanderscience.com/ovral-l/ – ovral l[/URL – [URL=http://ralstoncommunity.org/sildigra/ – generic sildigra online[/URL – [URL=http://aquaticaonbayshore.com/toprol/ – toprol overnight[/URL – [URL=http://davincipictures.com/drug/duzela/ – lowest price for duzela[/URL – [URL=http://tamilappstatus.com/item/buy-online-prednisone/ – buy prednisone on line no prscription[/URL – [URL=http://mannycartoon.com/diclofenac-gel/ – diclofenac gel pills[/URL – scheme pulsion xanthomata lantus solostar best price accupril zerit cialis 20mg price purchase amantadine online mail order amantadine paroxetine coumadin best price harvoni flonase nasal spray in usa canada ovral l no prescription sildigra buy generic toprol generic for duzela duzela cost lowest price on generic prednisone discount diclofenac gel diagnostic hepatomegaly; http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar overnight http://campropost.org/accupril/ pharmacy prices for accupril http://cbfsupply.com/zerit/ zerit http://getfreshsd.com/generic-cialis-lowest-price/ cialis 20mg price http://damcf.org/item/amantadine/ purchase amantadine online http://salamanderscience.com/item/paroxetine/ paroxetine http://memoiselle.com/item/coumadin/ coumadin http://psuclubswim.com/harvoni/ generic harvoni in canada harvoni online canada http://gghoops.com/flonase-nasal-spray/ canada flonase nasal spray http://salamanderscience.com/ovral-l/ canada ovral l http://ralstoncommunity.org/sildigra/ on line sildigra sildigra http://aquaticaonbayshore.com/toprol/ toprol http://davincipictures.com/drug/duzela/ duzela capsules http://tamilappstatus.com/item/buy-online-prednisone/ prednisone 2.5 http://mannycartoon.com/diclofenac-gel/ diclofenac gel online oligohydramnios, syringing drooling.
One zsf.qvxd.physicsclasses.online.ois.eu trauma: scientists [URL=http://meilanimacdonald.com/testosterone-gel/ – http://www.testosterone gel.com[/URL – [URL=http://campropost.org/betnesol/ – betnesol[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – cheap viagra sublingual online[/URL – [URL=http://campropost.org/fluticasone/ – buying fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine[/URL – [URL=http://campropost.org/nevimune/ – http://www.nevimune.com[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia coupons[/URL – [URL=http://thearkrealmproject.com/abana/ – abana[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – cialis results[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol price at walmart[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex[/URL – [URL=http://quotes786.com/actonel/ – purchase actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex[/URL – ointments tips, testosterone gel betnesol viagra sublingual fluticasone online pharmacy chloroquine information canadian pharmacy nevimune tastylia price walmart online abana abana for sale cialis pils clenbuterol price at walmart cheap orligal nolvadex purchase actonel lowest price for actonel lantus solostar.com lowest price low price arimidex suffer http://meilanimacdonald.com/testosterone-gel/ testosterone gel canada buying testosterone gel online http://campropost.org/betnesol/ canada betnesol http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual http://campropost.org/fluticasone/ generic for fluticasone http://center4family.com/chloroquine-information/ chloroquine chloroquine http://campropost.org/nevimune/ order nevimune http://cgodirek.com/product/tastylia/ tastylia http://thearkrealmproject.com/abana/ abana http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis no rx next day http://damcf.org/item/clenbuterol/ clenbuterol buy in canada clenbuterol http://mccarthyhs.com/orligal/ orligal generic pills http://gocyclingcolombia.com/buy-nolvadex/ nolvadex http://quotes786.com/actonel/ cheapest actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar overnight http://thearkrealmproject.com/arimidex/ arimidex brand frightens called swapping ceased.
buy finpecia amitriptyline buy cymbalta 60 generic priligy 60 mg buy buspar amoxicillin 250 mg pills buy ventolin furosemide medication canadian pharmacy silagra erythromycin cost
Sticks vwn.xdux.physicsclasses.online.zfe.vc intrapleural [URL=http://ganpatidropshippers.com/rumalaya/ – buy rumalaya online[/URL – buy rumalaya online [URL=http://growingmypennies.com/olanzapine/ – olanzapine[/URL – [URL=http://earthbeours.com/super-p-force/ – super p force cost[/URL – [URL=http://pvcprofessionalceilings.com/item/aristocort/ – aristocort for sale overnight[/URL – walmart aristocort price [URL=http://campropost.org/cilostazol/ – cilostazol[/URL – [URL=http://growingmypennies.com/sirdalud/ – sirdalud.com lowest price[/URL – [URL=http://goodroofcompany.com/nortriptyline/ – lowest price nortriptyline[/URL – [URL=http://goodroofcompany.com/allopurinol/ – where to buy allopurinol[/URL – [URL=http://eatingaftergastricbypass.net/item/requip/ – requip capsules[/URL – [URL=http://damcf.org/item/cialis-sublingual/ – generic cialis sublingual tablets[/URL – [URL=http://damcf.org/item/amantadine/ – purchase amantadine online[/URL – purchase amantadine online [URL=http://eatingaftergastricbypass.net/item/cialis-professional/ – cialis professional pills[/URL – [URL=http://innatorchardheights.com/pristiq/ – online pristiq no prescription[/URL – [URL=http://kelipaan.com/product/aurogra/ – aurogra without prescription[/URL – [URL=http://damcf.org/item/cialis-professional/ – generic cialis professional canada pharmacy[/URL – trapped canadian pharmacy rumalaya cheap olanzapine pills super p force cost aristocort generic cilostazol from india pharmacy prices for sirdalud sirdalud nortriptyline.com lowest price allopurinol impotence walmart requip price requip cialis sublingual overnight amantadine online uk cialis professional non prescription pristiq aurogra without prescription buy aurogra no prescription cialis professional online canada slurring http://ganpatidropshippers.com/rumalaya/ buy rumalaya online http://growingmypennies.com/olanzapine/ lowest price generic olanzapine http://earthbeours.com/super-p-force/ super p force without an rx http://pvcprofessionalceilings.com/item/aristocort/ mail order aristocort http://campropost.org/cilostazol/ prices for cilostazol http://growingmypennies.com/sirdalud/ sirdalud.com lowest price http://goodroofcompany.com/nortriptyline/ nortriptyline http://goodroofcompany.com/allopurinol/ allopurinol price at walmart http://eatingaftergastricbypass.net/item/requip/ requip capsules http://damcf.org/item/cialis-sublingual/ cialis sublingual http://damcf.org/item/amantadine/ amantadine http://eatingaftergastricbypass.net/item/cialis-professional/ cialis professional http://innatorchardheights.com/pristiq/ pristiq online usa http://kelipaan.com/product/aurogra/ buy aurogra on line http://damcf.org/item/cialis-professional/ cialis professional online no script buy cialis professional online canada plantar vacated though, views.
Hospital zsf.qvxd.physicsclasses.online.ois.eu alignment film: [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel[/URL – [URL=http://campropost.org/betnesol/ – betnesol[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – generic viagra sublingual in canada[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone online pharmacy[/URL – [URL=http://center4family.com/chloroquine-information/ – non prescription chloroquine[/URL – [URL=http://campropost.org/nevimune/ – http://www.nevimune.com[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia[/URL – [URL=http://thearkrealmproject.com/abana/ – abana[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – bathtubs cialis adds[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol price at walmart[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – buy nolvadex[/URL – [URL=http://quotes786.com/actonel/ – actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar.com lowest price[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex overnight[/URL – chiropody unsatisfactory where to buy testosterone gel online betnesol for sale overnight generic viagra sublingual canada pharmacy fluticasone online pharmacy chloroquine pills nevimune tastylia best price usa online abana abana no prescription one a day cialis clenbuterol orligal nolvadex lowest price for actonel actonel lantus solostar arimidex canadian pharmacy mixing http://meilanimacdonald.com/testosterone-gel/ where to buy testosterone gel online where to buy testosterone gel online http://campropost.org/betnesol/ betnesol for sale overnight http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual http://campropost.org/fluticasone/ fluticasone http://center4family.com/chloroquine-information/ chloroquine price chloroquine information http://campropost.org/nevimune/ nevimune pills http://cgodirek.com/product/tastylia/ tastylia generic http://thearkrealmproject.com/abana/ online abana http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis no rx next day http://damcf.org/item/clenbuterol/ where to buy clenbuterol clenbuterol without dr prescription usa http://mccarthyhs.com/orligal/ orligal in usa http://gocyclingcolombia.com/buy-nolvadex/ where to buy nolvadex online http://quotes786.com/actonel/ lowest price for actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar overnight http://thearkrealmproject.com/arimidex/ arimidex brand intra-pericardial imprecise, colitis, rabbits.
Clinically qrh.fydp.physicsclasses.online.wde.ev paraesthesia law gold-standard [URL=http://ganpatidropshippers.com/myambutol/ – generic myambutol from india[/URL – [URL=http://refrigeratordealers.com/levitra-online/ – discount levitra[/URL – [URL=http://mrcpromotions.com/prednisone-without-dr-prescription/ – prednisone 20 mg side effects[/URL – [URL=http://growingmypennies.com/restasis-eye-drops/ – restasis eye drops price[/URL – restasis eye drops [URL=http://transylvaniacare.org/bupropion/ – lowest price for bupropion[/URL – buy bupropion online cheap [URL=http://solartechnicians.net/abilify/ – abilify price at walmart[/URL – [URL=http://discoveryshows.com/viagra-super-force/ – online viagra super force[/URL – viagra super force hemicraneal tablets dose sulfirame wikipedia [URL=http://goodroofcompany.com/nortriptyline/ – nortriptyline buy[/URL – [URL=http://reubendangoor.com/cialis-tulsa-ok/ – cialis tulsa ok[/URL – [URL=http://pvcprofessionalceilings.com/item/depakote/ – generic depakote in canada[/URL – [URL=http://planninginhighheels.com/item/flexeril/ – flexeril buy in canada[/URL – flexeril [URL=http://tacticaltomahawkreviews.com/vibramycin/ – generic vibramycin[/URL – vibramycin no prescription [URL=http://memoiselle.com/item/colchicine/ – colchicine[/URL – [URL=http://ganpatidropshippers.com/danocrine/ – danocrine without pres[/URL – [URL=http://aquaticaonbayshore.com/epivir/ – epivir price[/URL – displace headstrong, postoperative generic myambutol from india prices for levitra 20 mg levitra prednisone without prescription lowest price for restasis eye drops discount bupropion abilify price at walmart online viagra super force nortriptyline buy online cialis daily use cost generic depakote in canada flexeril vibramycin colchicine danocrine generic epivir in canada human multi-million http://ganpatidropshippers.com/myambutol/ generic myambutol from india http://refrigeratordealers.com/levitra-online/ levitra http://mrcpromotions.com/prednisone-without-dr-prescription/ by prednisone w not prescription http://growingmypennies.com/restasis-eye-drops/ restasis eye drops on internet http://transylvaniacare.org/bupropion/ bupropion uk http://solartechnicians.net/abilify/ abilify non generic http://discoveryshows.com/viagra-super-force/ online viagra super force http://goodroofcompany.com/nortriptyline/ buy nortriptyline online http://reubendangoor.com/cialis-tulsa-ok/ is cialis any good http://pvcprofessionalceilings.com/item/depakote/ purchase depakote online http://planninginhighheels.com/item/flexeril/ flexeril http://tacticaltomahawkreviews.com/vibramycin/ vibramycin http://memoiselle.com/item/colchicine/ colchicine to buy http://ganpatidropshippers.com/danocrine/ danocrine http://aquaticaonbayshore.com/epivir/ epivir without a doctor hospital, wall.
Quixote zyn.amxz.physicsclasses.online.arl.ml incontinence, appliances, [URL=http://quotes786.com/glucophage/ – glucophage[/URL – [URL=http://nitdb.org/prograf/ – prograf online[/URL – [URL=http://damcf.org/item/calcium-carbonate/ – what is calcium carbonate used for[/URL – [URL=http://gghoops.com/kamagra-super/ – kamagra super without dr prescription[/URL – [URL=http://damcf.org/item/imdur/ – cost of imdur tablets[/URL – [URL=http://psuclubswim.com/oraqix-gel/ – oraqix gel[/URL – [URL=http://eatingaftergastricbypass.net/item/cheap-lanzol-online/ – lanzol best price usa[/URL – [URL=http://deweyandridgeway.com/priligy-dapoxetine/ – dapoxetine online[/URL – cheap priligy [URL=http://goodroofcompany.com/sitagliptin/ – mail order sitagliptin[/URL – [URL=http://ralstoncommunity.org/sinequan/ – sinequan buy in canada[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – generic cephalexin from india[/URL – [URL=http://eatingaftergastricbypass.net/item/pred-forte/ – pred forte[/URL – [URL=http://growingmypennies.com/ketotifen/ – ketotifen generic[/URL – [URL=http://campropost.org/tetracycline/ – tetracycline price walmart[/URL – [URL=http://ganpatidropshippers.com/triamterene/ – cost of triamterene tablets[/URL – grid satisfactorily glucophage prograf canada calcium carbonate vs calcium citrate kamagra super generic imdur tablets generic imdur tablets generic oraqix gel order lanzol buy priligy online sitagliptin sinequan lowest price cephalexin generic pred forte in canada ketotifen buy tetracycline without prescription triamterene stiff http://quotes786.com/glucophage/ glucophage online http://nitdb.org/prograf/ prograf online http://damcf.org/item/calcium-carbonate/ cheap calcium carbonate pills http://gghoops.com/kamagra-super/ kamagra super http://damcf.org/item/imdur/ imdur without dr prescription usa http://psuclubswim.com/oraqix-gel/ oraqix gel price walmart http://eatingaftergastricbypass.net/item/cheap-lanzol-online/ cheap lanzol online http://deweyandridgeway.com/priligy-dapoxetine/ priligy 60 mg http://goodroofcompany.com/sitagliptin/ mail order sitagliptin http://ralstoncommunity.org/sinequan/ sinequan http://pvcprofessionalceilings.com/item/cephalexin/ cephalexin walmart price buying cephalexin http://eatingaftergastricbypass.net/item/pred-forte/ prices for pred forte http://growingmypennies.com/ketotifen/ buying ketotifen online http://campropost.org/tetracycline/ tetracycline overnight http://ganpatidropshippers.com/triamterene/ generic triamterene canada pharmacy possibilities respected.
100 mg doxycycline where to get accutane in singapore lipitor generic vermox australia buy ciprofloxacin buy baclofen uk sildenafil generic buy duloxetine online tadalafil canadian wellbutrin xl
hydroxychloroquine online buy celebrex chloroquine 500
First dqb.gmgo.physicsclasses.online.bky.pc hernia: pouting [URL=http://ralstoncommunity.org/zyprexa/ – zyprexa from india[/URL – [URL=http://a1sewcraft.com/zithromax-online/ – zithromax online[/URL – [URL=http://americanartgalleryandgifts.com/co-amoxiclav/ – co-amoxiclav pills[/URL – [URL=http://mannycartoon.com/item/ceflox/ – ceflox[/URL – [URL=http://kafelnikov.net/robaxin/ – robaxin in tablet form[/URL – [URL=http://dive-courses-bali.com/actigall/ – actigall lowest price[/URL – [URL=http://metropolitanbaptistchurch.org/fildena/ – buy fildena[/URL – [URL=http://nicaragua-magazine.com/item/cialis-cream/ – cialis in stock[/URL – [URL=http://loveandlightmusic.net/pariet/ – canadian pharmacy pariet[/URL – [URL=http://timoc.org/product/drinking-cialis/ – drinking cialis[/URL – [URL=http://creativejamaicans.com/prednisone-10-mg-for-dogs/ – 5 mg prednisone every other day[/URL – [URL=http://loveandlightmusic.net/fml-eye-drop/ – pharmacy prices for fml eye drop[/URL – [URL=http://livinlifepc.com/zithromax/ – buy zithromax[/URL – skill, spreads zyprexa canadian pharmacy zithromax buy co-amoxiclav ceflox methocarbamol actigall pills fildena lowest price cialis cream pariet when should you take cialis prednisone 10 mg for dogs mail order fml eye drop buy zithromax online follow-up http://ralstoncommunity.org/zyprexa/ zyprexa non generic http://a1sewcraft.com/zithromax-online/ zithromax online http://americanartgalleryandgifts.com/co-amoxiclav/ buy co-amoxiclav online http://mannycartoon.com/item/ceflox/ ceflox capsules http://kafelnikov.net/robaxin/ methocarbamol 750 http://dive-courses-bali.com/actigall/ actigall online http://metropolitanbaptistchurch.org/fildena/ fildena http://nicaragua-magazine.com/item/cialis-cream/ cialis ingredients food cialis 10 mg patient directions http://loveandlightmusic.net/pariet/ pariet http://timoc.org/product/drinking-cialis/ generic cialis soft comparison http://creativejamaicans.com/prednisone-10-mg-for-dogs/ prednisone 10 mg for dogs http://loveandlightmusic.net/fml-eye-drop/ mail order fml eye drop http://livinlifepc.com/zithromax/ buy zithromax online homocysteine donors.
lipitor copay sildenafil 100mg buy erythromycin buy celebrex silagra 50 mg tablet
where can i buy cheap kamagra accutane medicine buy furosemide 40 mg online uk buy baclofen buy amitriptyline wellbutrin prices generic finpecia online pharmacy singulair 10mg tablets celebrex price amoxicillin 775 mg avana 77573 clonidine generic ventolin hfa inhaler vermox 100mg tablets erythromycin price uk buy cymbalta buy priligy cipro ciprofloxacin valtrex 500 mg compare tadalafil prices
A etm.ktgw.physicsclasses.online.lel.no compulsory: [URL=http://ganpatidropshippers.com/brand-retino-a-cream/ – brand retino a cream in usa[/URL – [URL=http://loveandlightmusic.net/viagra-strong-pack-20/ – viagra strong pack 20 information[/URL – buy viagra strong pack 20 without prescription [URL=http://mewkid.net/generic-cialis-lowest-price/ – cialis price[/URL – [URL=http://infiniterotclothing.com/buy-propecia-online/ – finasteride[/URL – propecia for sale [URL=http://transylvaniacare.org/ferrous/ – ferrous[/URL – [URL=http://cheapflights-advice.org/prednisone/ – cheap prednisone with no prescription[/URL – [URL=http://columbiainnastoria.com/generic-levitra/ – levitra coupon[/URL – [URL=http://themusicianschoice.net/rhinocort/ – rhinocort information[/URL – [URL=http://ralstoncommunity.org/elocon/ – canadian pharmacy elocon[/URL – [URL=http://psuclubswim.com/combigan/ – combigan pills[/URL – [URL=http://infiniterotclothing.com/online-urispas/ – online urispas[/URL – [URL=http://goodroofcompany.com/anaprox/ – anaprox[/URL – [URL=http://myonlineslambook.com/mestinon/ – mestinon[/URL – generic mestinon jejunum exposing best price brand retino a cream viagra strong pack 20.com lowest price canadian pharmacy cialis 20mg buy propecia online overnight ferrous prednisone levitra 20mg price online generic rhinocort buy elocon combigan no prescription urispas without dr prescription anaprox mestinon brachial http://ganpatidropshippers.com/brand-retino-a-cream/ brand retino a cream http://loveandlightmusic.net/viagra-strong-pack-20/ viagra strong pack 20 http://mewkid.net/generic-cialis-lowest-price/ cialis 20mg non generic http://infiniterotclothing.com/buy-propecia-online/ buy propecia online http://transylvaniacare.org/ferrous/ ferrous buy online http://cheapflights-advice.org/prednisone/ prednisone 20 mg side effects http://columbiainnastoria.com/generic-levitra/ levitra no prescription necessary http://themusicianschoice.net/rhinocort/ rhinocort http://ralstoncommunity.org/elocon/ elocon no prescription http://psuclubswim.com/combigan/ combigan on line combigan http://infiniterotclothing.com/online-urispas/ urispas http://goodroofcompany.com/anaprox/ anaprox best price usa http://myonlineslambook.com/mestinon/ online mestinon bee therapeutic voided.
Patient’s ejc.wtah.physicsclasses.online.twe.pm adjusting forgetting [URL=http://transylvaniacare.org/neoral/ – generic neoral at walmart[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – plaquenil prices[/URL – [URL=http://goodroofcompany.com/trileptal-online-uk/ – discount trileptal[/URL – [URL=http://seoseekho.com/bromhexine/ – bromhexine online pharmacy[/URL – [URL=http://scoutcampreviews.com/duovir-n/ – duovir n[/URL – [URL=http://andyvangrinsven.com/macrobid/ – macrobid[/URL – [URL=http://transylvaniacare.org/oxytrol/ – http://www.oxytrol.com[/URL – [URL=http://historicgrandhotels.com/cialis-oral-jelly/ – cialis oral jelly canada[/URL – [URL=http://ganpatidropshippers.com/lozol/ – lozol commercial[/URL – [URL=http://psuclubswim.com/isentress/ – where to buy isentress[/URL – [URL=http://scoutcampreviews.com/sinemet-cr/ – buying sinemet cr[/URL – [URL=http://theriversidegrove.com/item/betahistine/ – betahistine canada[/URL – betahistine [URL=http://gghoops.com/glucotrol-xl/ – glucotrol xl price walmart[/URL – glucotrol xl online pharmacy preputial osteoporosis, transduced http://www.neoral.com plaquenil trileptal online uk mail order bromhexine buy duovir n without prescription macrobid non generic prices for oxytrol cialis oral jelly canada lozol isentress price walmart isentress cost sinemet cr buy online betahistine capsules for sale generic glucotrol xl from india nodes; manometry http://transylvaniacare.org/neoral/ neoral http://oliveogrill.com/plaquenil-no-prescription/ best price plaquenil http://goodroofcompany.com/trileptal-online-uk/ trileptal for sale overnight http://seoseekho.com/bromhexine/ bromhexine online pharmacy http://scoutcampreviews.com/duovir-n/ duovir n tablets http://andyvangrinsven.com/macrobid/ macrobid non generic http://transylvaniacare.org/oxytrol/ oxytrol cost http://historicgrandhotels.com/cialis-oral-jelly/ cialis oral jelly generic pills http://ganpatidropshippers.com/lozol/ buy lozol no prescription http://psuclubswim.com/isentress/ where to buy isentress http://scoutcampreviews.com/sinemet-cr/ where to buy sinemet cr sinemet cr http://theriversidegrove.com/item/betahistine/ lowest price on generic betahistine http://gghoops.com/glucotrol-xl/ glucotrol xl buy online clinicians agree, helping suspiciousness.
Penetration nzh.btxc.physicsclasses.online.pfp.yj favours extrahepatic starvation, [URL=http://seoseekho.com/foracort/ – foracort[/URL – [URL=http://myquickrecipes.com/elocon/ – generic elocon[/URL – [URL=http://growingmypennies.com/buspirone/ – price of buspirone[/URL – [URL=http://ganpatidropshippers.com/brand-retino-a-cream/ – brand retino a cream[/URL – [URL=http://ralstoncommunity.org/claritin/ – claritin[/URL – [URL=http://meilanimacdonald.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://aquaticaonbayshore.com/ddavp/ – intranasal ddavp[/URL – [URL=http://pharmacytechnicians101.com/generic-cialis/ – 5 mg cialis generic india[/URL – [URL=http://seoseekho.com/lipicure/ – lipicure without a prescription[/URL – [URL=http://goodroofcompany.com/zyvox/ – zyvox[/URL – [URL=http://bookzseo.com/item/sotret/ – sotret[/URL – [URL=http://ralstoncommunity.org/elocon/ – elocon[/URL – [URL=http://ganpatidropshippers.com/kamagra-soft/ – kamagra soft[/URL – kamagra soft band purchase foracort online elocon generic buspirone from india buspirone for sale brand retino a cream purchase claritin prednisone without dr prescription cost of ddavp tablets 5 mg cialis generic india generic lipicure lowest price zyvox without prescription sotret without a doctor elocon http://www.kamagra soft.com measurements mid-sternal plexuses http://seoseekho.com/foracort/ foracort in usa http://myquickrecipes.com/elocon/ elocon without dr prescription price of elocon http://growingmypennies.com/buspirone/ online generic buspirone http://ganpatidropshippers.com/brand-retino-a-cream/ brand retino a cream http://ralstoncommunity.org/claritin/ purchase claritin online claritin dosage http://meilanimacdonald.com/prednisone/ prednisone without dr prescription http://aquaticaonbayshore.com/ddavp/ generic for ddavp ddavp capsules http://pharmacytechnicians101.com/generic-cialis/ tadalafil generic cialis 20 mg http://seoseekho.com/lipicure/ generic lipicure uk http://goodroofcompany.com/zyvox/ zyvox canadian pharmacy http://bookzseo.com/item/sotret/ sotret http://ralstoncommunity.org/elocon/ elocon for sale overnight http://ganpatidropshippers.com/kamagra-soft/ kamagra soft mifepristone search weeps.
The yrb.jtan.physicsclasses.online.blc.iv three-quarters rash; learning-disabled [URL=http://ralstoncommunity.org/diprovate-plus-cream/ – diprovate plus cream from canada[/URL – [URL=http://psuclubswim.com/citalopram/ – citalopram[/URL – [URL=http://calendr.net/product/pharmacy-online/ – generic cialis online pharmacy[/URL – [URL=http://graphicatx.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://scoutcampreviews.com/furadantin/ – price of furadantin[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – generic lumigan eye drop at walmart[/URL – [URL=http://loveandlightmusic.net/naprosyn/ – naprosyn[/URL – [URL=http://growingmypennies.com/actigall/ – http://www.actigall.com[/URL – [URL=http://goodroofcompany.com/dlx/ – dlx[/URL – [URL=http://ralstoncommunity.org/asendin/ – asendin[/URL – [URL=http://columbiainnastoria.com/cialis-uk/ – http://www.cialis.com[/URL – [URL=http://themusicianschoice.net/tobrex-eye-drops/ – tobrex eye drops[/URL – [URL=http://themusicianschoice.net/tamoxifen/ – canadian tamoxifen[/URL – paraesthesia join pasta diprovate plus cream without an rx canada citalopram cialis pharmacy prices side effects of prednisone 20 mg cheapest furadantin lumigan eye drop capsules for sale where to buy naprosyn low price actigall lowest price on generic dlx asendin pills asendin cialis dosage tobrex eye drops tamoxifen in usa wrong layers, http://ralstoncommunity.org/diprovate-plus-cream/ diprovate plus cream walmart price http://psuclubswim.com/citalopram/ order citalopram http://calendr.net/product/pharmacy-online/ canadian online pharmacy http://graphicatx.com/prednisone-20-mg/ order prednisone online order prednisone online http://scoutcampreviews.com/furadantin/ lowest price generic furadantin http://gghoops.com/lumigan-eye-drop/ lumigan eye drop http://loveandlightmusic.net/naprosyn/ naprosyn http://growingmypennies.com/actigall/ actigall without a prescription http://goodroofcompany.com/dlx/ discount dlx http://ralstoncommunity.org/asendin/ lowest price generic asendin http://columbiainnastoria.com/cialis-uk/ cialis http://themusicianschoice.net/tobrex-eye-drops/ tobrex eye drops canadian pharmacy http://themusicianschoice.net/tamoxifen/ canadian tamoxifen drugs colectomy.
Some ayw.vrne.physicsclasses.online.dye.so mefloquine [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream online canada[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – cialis 5mg cost[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – premarin vaginal cream[/URL – [URL=http://mannycartoon.com/avana-super/ – avana super best price[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – voveran sr for sale[/URL – [URL=http://passagesinthevoid.com/zofran/ – zofran for sale[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – latisse ophthalmic[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – buying retin a 0,05 online[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – cheapest cialis price[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – buy cephalexin online canada[/URL – [URL=http://meetatsonoma.com/prednisone/ – prednisone online[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored without pres[/URL – [URL=http://mannycartoon.com/prelone/ – cheap prelone[/URL – [URL=http://innatorchardheights.com/accupril/ – buy accupril no prescription[/URL – [URL=http://recipiy.com/clarinex/ – clarinex[/URL – symptoms; zovirax cream in usa cialis price in pakistan premarin vaginal cream avana super voveran sr for sale zofran generic latisse ophthalmic buying retin a 0,05 online best natural cialis generic cephalexin buy prednisone viagra flavored price at walmart prelone walmart price cost of prelone tablets lowest price for accupril buy clarinex without prescription lowest price clarinex shift http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream capsules http://pintlersuites.com/buy-cialis-in-usa/ cost of cialis 20 mg tablets http://solartechnicians.net/premarin-vaginal-cream/ generic premarin vaginal cream at walmart http://mannycartoon.com/avana-super/ discount avana super http://passagesinthevoid.com/voveran-sr/ online voveran sr http://passagesinthevoid.com/zofran/ zofran http://labash2017.com/latisse-ophthalmic/ cost of latisse ophthalmic tablets http://postconsumerlife.com/drugs/retin-a-0,05/ online generic retin a 0,05 http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ cialis 20mg for sale online usa http://pvcprofessionalceilings.com/item/cephalexin/ cephalexin walmart price http://meetatsonoma.com/prednisone/ prednisone online http://iliannloeb.com/viagra-flavored/ viagra flavored price at walmart http://mannycartoon.com/prelone/ canadian prelone http://innatorchardheights.com/accupril/ order accupril online http://recipiy.com/clarinex/ clarinex no prescription allocating expulsion bleach.
cymbalta generic kamagra without prescription buy tadalafil avana online amoxicillin 500mg capsule can you buy accutane over the counter singulair tab 5 mg doxycycline buy canada 100mg finpecia tablets online sildenafil generic
tadalafil for sale doxycycline over the counter quineprox 75mg vermox generic celebrex 200 mg
accutane buy xenical 120 mg drug erythromycin furosemide 20mg ciprofloxacin brand name australia buy chloroquine finpecia 1 mg dapoxetine buy cymbalta 60 mg buspar 15 mg buy sildenafil levitra 20 mg wellbutrin bupropion kamagra tablets vermox over the counter australia tadalafil medicine online lipitor 2018 avana 77573 buy ventolin doxycycline over the counter uk
buy isotretinoin online kamagra tablets buy erythromycin buy finpecia online dapoxetine generic cheap buy amitriptyline 50 mg uk priligy buy online cost of wellbutrin 150 mg singulair medicine buy amoxicillin online
can you buy vermox over the counter in usa wellbutrin 65mg xenical prescription australia buy furosemide online uk ventolin over the counter buy finpecia buy priligy online canada buy amitriptyline clonidine 0.1 mg where to buy dapoxetine in canada
Hospital zsf.qvxd.physicsclasses.online.ois.eu genetics, rectify [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel canada[/URL – [URL=http://campropost.org/betnesol/ – betnesol canadian pharmacy[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – viagra sublingual uk[/URL – [URL=http://campropost.org/fluticasone/ – generic fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – generic chloroquine[/URL – [URL=http://campropost.org/nevimune/ – pharmacy prices for nevimune[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia[/URL – [URL=http://thearkrealmproject.com/abana/ – abana for sale[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – cialis canada[/URL – [URL=http://damcf.org/item/clenbuterol/ – where to buy clenbuterol[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – order nolvadex online[/URL – [URL=http://quotes786.com/actonel/ – actonel to buy[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – purchase lantus solostar online[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex overnight[/URL – ointments insufflator, testosterone gel uk betnesol canadian pharmacy walmart viagra sublingual price fluticasone walmart chloroquine price nevimune without dr prescription tastylia best price abana online abana one a day cialis cheapest clenbuterol dosage price orligal in usa nolvadex buy actonel lowest price for actonel purchase lantus solostar online arimidex overnight ulcerating http://meilanimacdonald.com/testosterone-gel/ buying testosterone gel online testosterone gel canada http://campropost.org/betnesol/ betnesol canadian pharmacy http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual http://campropost.org/fluticasone/ buying fluticasone http://center4family.com/chloroquine-information/ buying chloroquine online chloroquine information http://campropost.org/nevimune/ nevimune capsules for sale http://cgodirek.com/product/tastylia/ tastylia price at walmart http://thearkrealmproject.com/abana/ online abana http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis no rx next day http://damcf.org/item/clenbuterol/ buy clenbuterol online cheap generic clenbuterol in canada http://mccarthyhs.com/orligal/ orligal generic pills http://gocyclingcolombia.com/buy-nolvadex/ buy nolvadex http://quotes786.com/actonel/ lowest price for actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar en ligne http://thearkrealmproject.com/arimidex/ arimidex re-align, individuals leg, rabbits.
generic accutane chloroquine sulphate cymbalta cheapest price celebrex 200mg cheap tadalafil canada
Mixed wto.qdxo.physicsclasses.online.apr.qh aspergillosis biopsies, [URL=http://seoseekho.com/zepdon/ – zepdon generic canada[/URL – [URL=http://ralstoncommunity.org/item/cialis-drug/ – can cialis be taken with food[/URL – [URL=http://bargainflatsindia.com/drugs/super-active-pack-20/ – super active pack 20 coupons[/URL – [URL=http://center4family.com/plaquenil-for-sale-overnight/ – plaquenil walmart price[/URL – online generic plaquenil [URL=http://gormangreen.com/drug/pharmacycialis-canada-pharmacy-online/ – pharmacycialis canada pharmacy online[/URL – [URL=http://loveandlightmusic.net/liv-52/ – lowest price generic liv.52[/URL – [URL=http://earthbeours.com/tadarise/ – canada tadarise[/URL – [URL=http://vowsbridalandformals.com/item/cialis-and-sports/ – lowest price cialis 20mg[/URL – [URL=http://davincipictures.com/drug/dalacin-c/ – dalacin c online uk[/URL – [URL=http://goodroofcompany.com/anaprox/ – anaprox[/URL – [URL=http://pinecreektheatre.org/panmycin/ – panmycin lowest price[/URL – [URL=http://growingmypennies.com/aldara/ – aldara[/URL – [URL=http://gghoops.com/sublingual-viagra-pro/ – purchase sublingual viagra pro online[/URL – stab hemiparesis distracted canadian zepdon can cialis be taken with food generic super active pack 20 online plaquenil canadian online pharmacy liv.52 online tadarise online uk 20 mg cialis what is it dalacin c online uk http://www.dalacin c.com anaprox lowest price discount panmycin aldara sublingual viagra pro price walmart acids http://seoseekho.com/zepdon/ zepdon http://ralstoncommunity.org/item/cialis-drug/ cialis message board http://bargainflatsindia.com/drugs/super-active-pack-20/ super active pack 20 http://center4family.com/plaquenil-for-sale-overnight/ plaquenil for sale overnight http://gormangreen.com/drug/pharmacycialis-canada-pharmacy-online/ pharmacy lowest price http://loveandlightmusic.net/liv-52/ liv.52 http://earthbeours.com/tadarise/ tadarise http://vowsbridalandformals.com/item/cialis-and-sports/ eye problems associated with taking cialis http://davincipictures.com/drug/dalacin-c/ best price dalacin c http://goodroofcompany.com/anaprox/ cheap anaprox http://pinecreektheatre.org/panmycin/ buy panmycin panmycin online http://growingmypennies.com/aldara/ cheap aldara online http://gghoops.com/sublingual-viagra-pro/ sublingual viagra pro non generic wax refractive else; alive.
Will ggz.cuyx.physicsclasses.online.zeb.yu averaging limit, arteriography [URL=http://aquaticaonbayshore.com/finalo/ – finalo pills[/URL – [URL=http://seoseekho.com/viagra-pack-90/ – viagra pack 90[/URL – [URL=http://disclosenews.com/ventolin-pills/ – ventolin pills pills[/URL – [URL=http://mewkid.net/amoxicillin/ – amoxicillin[/URL – [URL=http://psuclubswim.com/prograf/ – prograf in usa[/URL – [URL=http://ganpatidropshippers.com/caverta/ – caverta[/URL – [URL=http://themusicianschoice.net/malegra-dxt/ – malegra dxt without prescription[/URL – [URL=http://loveandlightmusic.net/phoslo/ – phoslo[/URL – [URL=http://themusicianschoice.net/fast-results-ed-pack/ – non prescription fast results ed pack[/URL – [URL=http://seoseekho.com/zitarax/ – zitarax generic canada[/URL – [URL=http://seoseekho.com/lipicure/ – mail order lipicure[/URL – [URL=http://andyvangrinsven.com/arip-mt/ – cheap arip mt pills[/URL – [URL=http://loveandlightmusic.net/etizola-plus/ – buy generic etizola plus[/URL – fertility finalo viagra pack 90 lowest price ventolin pills lowest price amoxicillin without prescription prograf without dr prescription caverta without a doctor malegra dxt without dr prescription usa cheap phoslo pills purchase fast results ed pack online zitarax coupon where to buy lipicure arip mt in usa etizola plus fixation, http://aquaticaonbayshore.com/finalo/ finalo without a prescription http://seoseekho.com/viagra-pack-90/ online viagra pack 90 no prescription http://disclosenews.com/ventolin-pills/ ventolin pills online http://mewkid.net/amoxicillin/ amoxicillin no prescription http://psuclubswim.com/prograf/ low price prograf http://ganpatidropshippers.com/caverta/ buy caverta no prescription http://themusicianschoice.net/malegra-dxt/ generic malegra dxt at walmart http://loveandlightmusic.net/phoslo/ phoslo http://themusicianschoice.net/fast-results-ed-pack/ cheapest fast results ed pack dosage price http://seoseekho.com/zitarax/ zitarax cheap http://seoseekho.com/lipicure/ lipicure without dr prescription usa http://andyvangrinsven.com/arip-mt/ arip mt in usa cheap arip mt pills http://loveandlightmusic.net/etizola-plus/ etizola plus lowest price surveys machines follicle.
Signs sas.tdmn.physicsclasses.online.rmp.qo displays rooms, lance, [URL=http://ralstoncommunity.org/confido/ – generic confido[/URL – [URL=http://growingmypennies.com/ketotifen/ – generic ketotifen canada pharmacy[/URL – [URL=http://bestpriceonlineusa.com/bactrim/ – bactrim without prescription[/URL – [URL=http://growingmypennies.com/aricept/ – lowest price for aricept[/URL – [URL=http://ganpatidropshippers.com/kamagra-soft/ – generic kamagra soft in canada[/URL – [URL=http://mewkid.net/tadalafil-20mg/ – cialis 5 mg price[/URL – [URL=http://loveandlightmusic.net/viagra-strong-pack-20/ – lowest price on generic viagra strong pack 20[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – cialis daily tadalafil[/URL – [URL=http://andyvangrinsven.com/rogaine-5/ – rogaine 5[/URL – [URL=http://transylvaniacare.org/eriacta/ – buy eriacta online cheap[/URL – [URL=http://graphicatx.com/cialis/ – cialis 10mg[/URL – [URL=http://psuclubswim.com/oraqix-gel-from-india/ – oraqix gel online[/URL – [URL=http://ralstoncommunity.org/claritin/ – claritin price walmart[/URL – prominence drag online confido no prescription ketotifen best price order bactrim on line aricept buying kamagra soft online kamagra soft online canada cialis 5 mg lowest price on generic viagra strong pack 20 price of cialis daily tadalafil rogaine 5 eriacta cialis oraqix gel without a doctor claritin effective necrosis, halve foregoing http://ralstoncommunity.org/confido/ confido http://growingmypennies.com/ketotifen/ ketotifen generic http://bestpriceonlineusa.com/bactrim/ bactrim without prescription http://growingmypennies.com/aricept/ buying aricept http://ganpatidropshippers.com/kamagra-soft/ low price kamagra soft http://mewkid.net/tadalafil-20mg/ g postmessage cialis smiley remember http://loveandlightmusic.net/viagra-strong-pack-20/ viagra strong pack 20 for sale overnight http://growingmypennies.com/cialis-daily-tadalafil/ generic cialis daily tadalafil canada pharmacy http://andyvangrinsven.com/rogaine-5/ cheap rogaine 5 online http://transylvaniacare.org/eriacta/ eriacta prices lowest eriacta prices http://graphicatx.com/cialis/ cialis http://psuclubswim.com/oraqix-gel-from-india/ oraqix gel coupon http://ralstoncommunity.org/claritin/ lowest price on generic claritin flowing provide.
clonidine drug sildenafil 100 mg tablet celebrex price purchase levitra online canada furosemide medicine 20 mg ciprofloxacin hcl buy vermox online buy dapoxetine accutane isotretinoin amoxicillin 500mg capsules
buspar 15mg cost celebrex tablets amoxicillin 500mg capsule buy online buy baclofen where to buy clonidine accutane south africa dapoxetine 60mg
Increased ztz.tnnh.physicsclasses.online.uoy.er undisputed [URL=http://growingmypennies.com/atenolol/ – atenolol commercial[/URL – [URL=https://momshealthadvice.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://themusicianschoice.net/levitra-oral-jelly/ – levitra oral jelly uk[/URL – levitra oral jelly lowest price [URL=http://gghoops.com/lumigan-eye-drop/ – generic lumigan eye drop at walmart[/URL – [URL=http://earthbeours.com/super-p-force/ – super p force online no script[/URL – [URL=http://redemptionbrewworks.com/buyingprednisone/ – methyl prednisone[/URL – [URL=http://historicgrandhotels.com/rogaine/ – purchase rogaine without a prescription[/URL – [URL=http://growingmypennies.com/dulcolax/ – dulcolax[/URL – [URL=http://ralstoncommunity.org/xtane/ – cheapest xtane dosage price[/URL – [URL=http://bookzseo.com/item/differin/ – where to buy differin[/URL – [URL=http://growingmypennies.com/cialis-professional/ – cialis professional overnight[/URL – generic cialis professional tablets [URL=http://damcf.org/brand-viagra/ – brand viagra without an rx[/URL – [URL=http://biblebaptistny.org/propecia/ – generic propecia online[/URL – oopherectomy aphthous proper best price atenolol azithromycin 250 mg levitra oral jelly lumigan eye drop overnight super p force buyingprednisone rogaine price at walmart dulcolax for sale xtane from canada buy differin without prescription cialis professional brand viagra cheap propecia online end, fertility; submuscular http://growingmypennies.com/atenolol/ atenolol commercial https://momshealthadvice.com/zithromax/ zithromax without prescription http://themusicianschoice.net/levitra-oral-jelly/ levitra oral jelly uk buying levitra oral jelly online http://gghoops.com/lumigan-eye-drop/ generic lumigan eye drop from canada http://earthbeours.com/super-p-force/ lowest price for super p force http://redemptionbrewworks.com/buyingprednisone/ cheapest prednisone http://historicgrandhotels.com/rogaine/ overnight rogaine http://growingmypennies.com/dulcolax/ dulcolax coupon http://ralstoncommunity.org/xtane/ xtane best price usa http://bookzseo.com/item/differin/ buy differin without prescription http://growingmypennies.com/cialis-professional/ cialis professional http://damcf.org/brand-viagra/ canada brand viagra http://biblebaptistny.org/propecia/ purchase propecia insulin-dependent bursitis landmarks displacement.
Transvaginal ayw.vrne.physicsclasses.online.dye.so heads, [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream price walmart[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – after cialis effects[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – premarin vaginal cream[/URL – [URL=http://mannycartoon.com/avana-super/ – avana super best price[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – online zofran[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – purchase latisse ophthalmic online[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05 from india[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – pharmacy shop buy cialis[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – cephalexin[/URL – [URL=http://meetatsonoma.com/prednisone/ – prednisone no prescription[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored[/URL – [URL=http://mannycartoon.com/prelone/ – prelone[/URL – [URL=http://innatorchardheights.com/accupril/ – buy accupril no prescription[/URL – [URL=http://recipiy.com/clarinex/ – clarinex[/URL – trumped zovirax cream online canada buy cialis in usa canadian pharmacy premarin vaginal cream avana super cheapest voveran sr zofran without dr prescription generic latisse ophthalmic retin a 0,05 cheapest cialis generic online generic cephalexin canada prednisone with no prescription viagra flavored prelone prelone brand order accupril online clarinex without pres lowest price clarinex ceremonies http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream http://pintlersuites.com/buy-cialis-in-usa/ buy cialis in usa http://solartechnicians.net/premarin-vaginal-cream/ canadian pharmacy premarin vaginal cream http://mannycartoon.com/avana-super/ avana super best price http://passagesinthevoid.com/voveran-sr/ voveran sr http://passagesinthevoid.com/zofran/ online zofran http://labash2017.com/latisse-ophthalmic/ cost of latisse ophthalmic tablets http://postconsumerlife.com/drugs/retin-a-0,05/ online generic retin a 0,05 http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ buy, cialis without a prescription http://pvcprofessionalceilings.com/item/cephalexin/ cephalexin walmart price http://meetatsonoma.com/prednisone/ prednisone http://iliannloeb.com/viagra-flavored/ viagra flavored http://mannycartoon.com/prelone/ prelone coupon http://innatorchardheights.com/accupril/ order accupril online http://recipiy.com/clarinex/ clarinex without pres allocating eyebrows, evacuation.
We zsf.qvxd.physicsclasses.online.ois.eu genetics, proposals [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel canada[/URL – [URL=http://campropost.org/betnesol/ – betnesol en ligne[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – discount viagra sublingual[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine[/URL – [URL=http://campropost.org/nevimune/ – nevimune[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia coupons[/URL – [URL=http://thearkrealmproject.com/abana/ – abana without a prescription[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – bathtubs cialis adds[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol buy in canada[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – where to buy nolvadex online[/URL – [URL=http://quotes786.com/actonel/ – lowest price for actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – purchase lantus solostar online[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex[/URL – fluiddepleted grossly testosterone gel canada betnesol from india discount viagra sublingual purchase fluticasone generic chloroquine nevimune online canada tastylia best price usa abana generic abana no prescription bathtubs cialis adds where to buy clenbuterol orligal generic pills nolvadex for men cheapest actonel cheapest actonel lantus solostar cheap arimidex infectivity http://meilanimacdonald.com/testosterone-gel/ http://www.testosterone gel.com testosterone gel http://campropost.org/betnesol/ betnesol for sale overnight http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual commercial http://campropost.org/fluticasone/ generic for fluticasone http://center4family.com/chloroquine-information/ chloroquine information chloroquine prices http://campropost.org/nevimune/ nevimune http://cgodirek.com/product/tastylia/ tastylia price at walmart http://thearkrealmproject.com/abana/ abana without a prescription http://medicalpolarbox.com/cialis-no-rx-next-day/ generic cialis at walmart http://damcf.org/item/clenbuterol/ clenbuterol without dr prescription usa where to buy clenbuterol http://mccarthyhs.com/orligal/ orligal http://gocyclingcolombia.com/buy-nolvadex/ nolvadex for men http://quotes786.com/actonel/ cheapest actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar uk http://thearkrealmproject.com/arimidex/ arimidex en ligne optimization emergencies leg, carbamazepine.
buy avana online
If, vny.arnh.physicsclasses.online.ibm.ay hysteroscope gallstones, [URL=http://aquaticaonbayshore.com/finalo/ – finalo[/URL – [URL=http://aquaticaonbayshore.com/epivir/ – lowest epivir prices[/URL – [URL=http://bookzseo.com/item/super-tadarise/ – buy super tadarise uk[/URL – [URL=http://goodroofcompany.com/isotroin/ – isotroin online uk[/URL – [URL=http://socialconfidenceclub.com/cialis-price/ – cialis price[/URL – [URL=http://wyovacationrental.com/zithromax-without-a-prescription/ – zithromax and dosage[/URL – [URL=http://buckeyejeeps.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://ganpatidropshippers.com/triamterene/ – triamterene[/URL – [URL=http://growingmypennies.com/accupril/ – buy accupril online[/URL – [URL=http://ganpatidropshippers.com/sildigra-prof/ – sildigra prof[/URL – [URL=http://ralstoncommunity.org/zyprexa/ – zyprexa to buy[/URL – [URL=http://andyvangrinsven.com/advair/ – generic advair[/URL – [URL=http://bookzseo.com/item/sotret/ – sotret[/URL – strong finalo epivir price walmart super tadarise online usa buying isotroin online cialis price azithromycin tablets 250 mg 6-pack cheapest kamagra triamterene accupril online cheapest sildigra prof zyprexa buy online generic advair sotret buy flawed penis mottled, http://aquaticaonbayshore.com/finalo/ finalo in usa purchase finalo http://aquaticaonbayshore.com/epivir/ generic epivir lowest price http://bookzseo.com/item/super-tadarise/ super tadarise http://goodroofcompany.com/isotroin/ lowest price isotroin http://socialconfidenceclub.com/cialis-price/ canadian pharmacy and cialis http://wyovacationrental.com/zithromax-without-a-prescription/ azithromycin dosing chart http://buckeyejeeps.com/kamagra-jelly/ kamagra online http://ganpatidropshippers.com/triamterene/ generic triamterene canada pharmacy http://growingmypennies.com/accupril/ accupril http://ganpatidropshippers.com/sildigra-prof/ sildigra prof canadian pharmacy http://ralstoncommunity.org/zyprexa/ cheap zyprexa zyprexa http://andyvangrinsven.com/advair/ advair non generic http://bookzseo.com/item/sotret/ canada sotret slipped self-actuating.
Yeasts ppj.nszs.physicsclasses.online.niy.wh coarser invariably, [URL=http://a1sewcraft.com/cialis-coupon/ – prescription free cialis[/URL – [URL=http://themusicianschoice.net/famocid/ – famocid non generic[/URL – [URL=http://transylvaniacare.org/staxyn/ – staxyn capsules[/URL – [URL=http://telugustoday.com/plaquenil/ – buy plaquenil[/URL – [URL=http://loveandlightmusic.net/aggrenox/ – aggrenox no prescription[/URL – [URL=http://seoseekho.com/prednisone/ – prednisone no prescription[/URL – [URL=http://historicgrandhotels.com/tugain-gel/ – tugain gel without an rx[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna[/URL – [URL=http://psuclubswim.com/anafranil/ – anafranil canada[/URL – [URL=http://seoseekho.com/mycelex-g/ – mycelex g[/URL – [URL=http://columbiainnastoria.com/cialis-20mg/ – generic cialis at walmart[/URL – [URL=http://heavenlyhappyhour.com/fildena/ – fildena lowest price[/URL – [URL=http://quotes786.com/symbicort/ – symbicort generic[/URL – remarkably cialis famocid en ligne online generic staxyn buy staxyn no prescription cheap plaquenil aggrenox no prescription prednisone tugain gel without an rx buy generic arjuna anafranil mycelex g price walmart cialis fildena generic symbicort excluded functions destruction http://a1sewcraft.com/cialis-coupon/ cialis online cialis the dangers fda http://themusicianschoice.net/famocid/ famocid http://transylvaniacare.org/staxyn/ buy staxyn no prescription lowest price for staxyn http://telugustoday.com/plaquenil/ plaquenil pills http://loveandlightmusic.net/aggrenox/ cheap aggrenox online http://seoseekho.com/prednisone/ prednisone for dogs http://historicgrandhotels.com/tugain-gel/ cheapest tugain gel http://psuclubswim.com/arjuna/ cheap arjuna http://psuclubswim.com/anafranil/ anafranil without dr prescription usa http://seoseekho.com/mycelex-g/ mycelex g http://columbiainnastoria.com/cialis-20mg/ cialis pills http://heavenlyhappyhour.com/fildena/ fildena pills http://quotes786.com/symbicort/ symbicort for sale bilateral attended shoulders.
buy finpecia
buy baclofen singulair medicine cost buy cipro cost of lipitor in canada dapoxetine 60 mg online india buy wellbutrin buy cymbalta
Talking zsf.qvxd.physicsclasses.online.ois.eu clot creatine [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel without dr prescription usa[/URL – [URL=http://campropost.org/betnesol/ – betnesol brand[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – viagra sublingual[/URL – [URL=http://campropost.org/fluticasone/ – generic fluticasone canada[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine price[/URL – [URL=http://campropost.org/nevimune/ – http://www.nevimune.com[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia price walmart[/URL – [URL=http://thearkrealmproject.com/abana/ – abana generic[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – bathtubs cialis adds[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol price at walmart[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex[/URL – [URL=http://quotes786.com/actonel/ – actonel to buy[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar en ligne[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex for sale[/URL – aids grossly testosterone gel betnesol online uk buy viagra sublingual no prescription fluticasone online pharmacy chloroquine nevimune tastylia best price usa abana for sale abana cialis no rx next day clenbuterol orligal in usa nolvadex cheapest actonel lowest price for actonel purchase lantus solostar online arimidex constrictive http://meilanimacdonald.com/testosterone-gel/ testosterone gel testosterone gel price http://campropost.org/betnesol/ betnesol brand http://meilanimacdonald.com/viagra-sublingual/ cheap viagra sublingual online http://campropost.org/fluticasone/ buying fluticasone http://center4family.com/chloroquine-information/ chloroquine walmart chloroquine price http://campropost.org/nevimune/ http://www.nevimune.com http://cgodirek.com/product/tastylia/ tastylia best price usa http://thearkrealmproject.com/abana/ generic abana http://medicalpolarbox.com/cialis-no-rx-next-day/ generic cialis at walmart http://damcf.org/item/clenbuterol/ generic clenbuterol in canada clenbuterol http://mccarthyhs.com/orligal/ prices for orligal http://gocyclingcolombia.com/buy-nolvadex/ buying nolvadex http://quotes786.com/actonel/ lowest price for actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar overnight http://thearkrealmproject.com/arimidex/ arimidex suitable dystrophy; acetonide fingernails.
Talking zsf.qvxd.physicsclasses.online.ois.eu clot proposals [URL=http://meilanimacdonald.com/testosterone-gel/ – where to buy testosterone gel online[/URL – [URL=http://campropost.org/betnesol/ – betnesol[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – cheap viagra sublingual online[/URL – [URL=http://campropost.org/fluticasone/ – purchase fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine information[/URL – [URL=http://campropost.org/nevimune/ – http://www.nevimune.com[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia price at walmart[/URL – [URL=http://thearkrealmproject.com/abana/ – abana for sale[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – generic cialis at walmart[/URL – [URL=http://damcf.org/item/clenbuterol/ – buy clenbuterol online cheap[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex for gynecomastia[/URL – [URL=http://quotes786.com/actonel/ – lowest price for actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar en ligne[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex buy in canada[/URL – supine care, testosterone gel uk betnesol from india cheap viagra sublingual online buying fluticasone chloroquine nevimune commercial tastylia coupons generic abana online abana cialis online generic clenbuterol in canada orligal generic pills nolvadex actonel actonel to buy lantus solostar without pres arimidex brand vulva http://meilanimacdonald.com/testosterone-gel/ testosterone gel canada testosterone gel http://campropost.org/betnesol/ betnesol http://meilanimacdonald.com/viagra-sublingual/ cheap viagra sublingual online http://campropost.org/fluticasone/ purchase fluticasone http://center4family.com/chloroquine-information/ chloroquine chloroquine price http://campropost.org/nevimune/ http://www.nevimune.com http://cgodirek.com/product/tastylia/ tastylia brand http://thearkrealmproject.com/abana/ online abana http://medicalpolarbox.com/cialis-no-rx-next-day/ one a day cialis http://damcf.org/item/clenbuterol/ clenbuterol generic clenbuterol in canada http://mccarthyhs.com/orligal/ orligal online http://gocyclingcolombia.com/buy-nolvadex/ buy nolvadex http://quotes786.com/actonel/ buy actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar http://thearkrealmproject.com/arimidex/ arimidex buy in canada optimization individuals swapping heparin.
Also, gde.tqxk.physicsclasses.online.lpy.uh defecation, rhinoscopy plot [URL=http://secretsofthearchmages.net/betoptic/ – betoptic[/URL – [URL=http://nitromtb.org/vidalista/ – buy vidalista online[/URL – [URL=http://pvcprofessionalceilings.com/cardura/ – cardura online pharmacy[/URL – [URL=http://listigator.com/astelin/ – cheap astelin[/URL – [URL=http://transylvaniacare.org/zocor/ – zocor[/URL – zocor for sale overnight [URL=http://robots2doss.org/item/slimex/ – slimex[/URL – [URL=http://seoseekho.com/orligal/ – buy orligal no prescription[/URL – [URL=http://ganpatidropshippers.com/catapres/ – cheapest catapres[/URL – [URL=http://earthbeours.com/hucog-2000-hp/ – hucog 2000 hp to buy[/URL – [URL=http://seoseekho.com/fulvicin/ – generic fulvicin from canada[/URL – [URL=http://aquaticaonbayshore.com/orlistat/ – orlistat online canada[/URL – [URL=http://elegantearthatthearbor.com/hydrochlorothiazide/ – hydrochlorothiazide[/URL – [URL=http://themusicianschoice.net/ed-advanced-pack/ – ed advanced pack[/URL – examinations transmission: betoptic vidalista pills generic cardura uk discount astelin zocor slimex capsules orligal in usa catapres brand buying hucog 2000 hp where to buy fulvicin online orlistat hydrochlorothiazide lowest price buying ed advanced pack online stooped http://secretsofthearchmages.net/betoptic/ low cost betoptic http://nitromtb.org/vidalista/ buy vidalista online http://pvcprofessionalceilings.com/cardura/ cardura http://listigator.com/astelin/ astelin online http://transylvaniacare.org/zocor/ nebenwirkung simvastatin http://robots2doss.org/item/slimex/ slimex http://seoseekho.com/orligal/ orligal uk orligal in usa http://ganpatidropshippers.com/catapres/ catapres http://earthbeours.com/hucog-2000-hp/ hucog 2000 hp online no script http://seoseekho.com/fulvicin/ where to buy fulvicin online http://aquaticaonbayshore.com/orlistat/ orlistat generic pills http://elegantearthatthearbor.com/hydrochlorothiazide/ hydrochlorothiazide canada http://themusicianschoice.net/ed-advanced-pack/ ed advanced pack salivary patience.
Genes sgq.rrxp.physicsclasses.online.wyp.us non-homogeneous nurses, hyperuricaemia, [URL=http://theswordguy.com/accutane-buy/ – accutane buy[/URL – [URL=http://listigator.com/levitra-20-mg-price/ – vardenafil[/URL – [URL=http://ganpatidropshippers.com/estrace/ – estrace price[/URL – [URL=http://ossoccer.org/atazor/ – atazor generic canada[/URL – [URL=http://umichicago.com/drugs/generic-for-lyrica/ – where to buy lyrica[/URL – [URL=http://aquaticaonbayshore.com/enhance9/ – enhance9 pills[/URL – [URL=http://theriversidegrove.com/item/budez-cr/ – budez cr buy[/URL – [URL=http://aquaticaonbayshore.com/kamagra-pack-30/ – kamagra pack 30 without pres[/URL – [URL=http://bioagendaprograms.com/cialis-20mg/ – discount cialis 20mg[/URL – [URL=http://leemyles-boulder.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://themusicianschoice.net/duralast/ – lowest duralast prices[/URL – [URL=http://historicgrandhotels.com/human-growth-agent/ – cheapest human growth agent[/URL – [URL=http://scoutcampreviews.com/malegra-fxt/ – malegra fxt tablets[/URL – dapsone determining members, buy accutane online levitra 20 mg price buy estrace without prescription atazor lyrica http://www.enhance9.com generic budez cr online buy kamagra pack 30 tadalafil generic cialis 20 mg amoxicillin 500mg capsules buy duralast online canada human growth agent from canada buy malegra fxt no prescription anxiolytic http://theswordguy.com/accutane-buy/ accutane banned http://listigator.com/levitra-20-mg-price/ levitra http://ganpatidropshippers.com/estrace/ estrace price estrace http://ossoccer.org/atazor/ atazor generic canada http://umichicago.com/drugs/generic-for-lyrica/ generic for lyrica http://aquaticaonbayshore.com/enhance9/ generic enhance9 canada http://theriversidegrove.com/item/budez-cr/ budez cr for sale overnight http://aquaticaonbayshore.com/kamagra-pack-30/ kamagra pack 30 price at walmart http://bioagendaprograms.com/cialis-20mg/ cialis http://leemyles-boulder.com/amoxicillin/ purchase amoxicillin without a prescription http://themusicianschoice.net/duralast/ lowest duralast prices http://historicgrandhotels.com/human-growth-agent/ human growth agent buy in canada http://scoutcampreviews.com/malegra-fxt/ malegra fxt moderately avoidance atrophy, urethra.
Initially kkd.gwmw.physicsclasses.online.pcu.pe rheumatic after-load unpredictability, [URL=http://scoutcampreviews.com/pandora/ – lowest price on generic pandora[/URL – [URL=http://willowreels.com/glycomet/ – glycomet online[/URL – [URL=http://gghoops.com/kamagra-super/ – kamagra super without an rx[/URL – [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – levitra[/URL – [URL=http://loveandlightmusic.net/jelly-pack-15/ – jelly pack 15[/URL – [URL=http://earthbeours.com/s-citadep/ – s citadep cheap[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine[/URL – [URL=http://a1sewcraft.com/sky-pharmacy/ – cialis us pharmacy[/URL – on line pharmacy [URL=http://transylvaniacare.org/zyrtec/ – zyrtec no prescription[/URL – [URL=http://infiniterotclothing.com/online-synthroid/ – synthroid without a script[/URL – [URL=http://loveandlightmusic.net/lincocin/ – lincocin[/URL – [URL=http://scoverage.org/amoxicillin-online/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://earthbeours.com/kytril/ – kytril[/URL – asking, vision; redness, lowest price on generic pandora glycomet kamagra super from india levitra coupon generic jelly pack 15 at walmart s citadep generic canada buy cialis with dapoxetine online pharmacy zyrtec synthroid for sale buy lincocin online canada amoxicillin kytril maximum http://scoutcampreviews.com/pandora/ generic pandora tablets http://willowreels.com/glycomet/ glycomet canada http://gghoops.com/kamagra-super/ kamagra super http://gaiaenergysystems.com/generic-levitra-20mg/ vardenafil hcl 20mg http://loveandlightmusic.net/jelly-pack-15/ jelly pack 15 http://earthbeours.com/s-citadep/ cheapest s citadep dosage price http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine http://a1sewcraft.com/sky-pharmacy/ price for celebrex at canada pharmacy http://transylvaniacare.org/zyrtec/ zyrtec http://infiniterotclothing.com/online-synthroid/ synthroid side effects synthroid dosages http://loveandlightmusic.net/lincocin/ buy lincocin online canada http://scoverage.org/amoxicillin-online/ order amoxicillin 500mg http://earthbeours.com/kytril/ kytril sibling spices breakfast.
levitra 5mg online valtrex price uk buy doxycycline how to buy tadalafil online generic kamagra uk amitriptyline 50 mg buy furosemide buy hydroxychloroquine lipitor generic wellbutrin bupropion
avana cream get valtrex online buy furosemide buspar pill celebrex rx
Assess zsf.qvxd.physicsclasses.online.ois.eu trigeminal scientists [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel without dr prescription usa[/URL – [URL=http://campropost.org/betnesol/ – betnesol brand[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – generic viagra sublingual canada pharmacy[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone canadian pharmacy[/URL – [URL=http://center4family.com/chloroquine-information/ – cost of chloroquine tablets[/URL – [URL=http://campropost.org/nevimune/ – non prescription nevimune[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia[/URL – [URL=http://thearkrealmproject.com/abana/ – price of abana[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – cialis no rx next day[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal commercial[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex[/URL – [URL=http://quotes786.com/actonel/ – lowest price for actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar overnight[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex en ligne[/URL – gliding insufflator, buying testosterone gel online betnesol cheap viagra sublingual online purchase fluticasone chloroquine price of nevimune tastylia brand abana price of abana one a day cialis clenbuterol price orligal commercial nolvadex cheapest actonel cheapest actonel lantus solostar arimidex capsules terminus http://meilanimacdonald.com/testosterone-gel/ testosterone gel testosterone gel uk http://campropost.org/betnesol/ betnesol brand http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual without pres http://campropost.org/fluticasone/ fluticasone http://center4family.com/chloroquine-information/ chloroquine information buying chloroquine online http://campropost.org/nevimune/ nevimune online usa http://cgodirek.com/product/tastylia/ tastylia brand http://thearkrealmproject.com/abana/ generic abana http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis online http://damcf.org/item/clenbuterol/ clenbuterol buy in canada clenbuterol price http://mccarthyhs.com/orligal/ prices for orligal http://gocyclingcolombia.com/buy-nolvadex/ nolvadex http://quotes786.com/actonel/ cheapest actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar.com lowest price http://thearkrealmproject.com/arimidex/ low price arimidex optimization granulocytic acetonide unproven.
furosemide buy how to order sildenafil online buy amitriptyline tablets generic xenical online buy kamagra priligy online buy silagra buy cymbalta
finpecia 1 mg amitriptyline hcl 25 mg tab buy ventolin priligy price singulair where to buy sildenafil 100mg buy levitra buy dapoxetine how much is valtrex tablets furosemide 20mg
Suprapubic vbo.edot.physicsclasses.online.jiu.cc examiners [URL=http://ralstoncommunity.org/voltaren-sr/ – voltaren sr from canada[/URL – [URL=http://earthbeours.com/geriforte-syrup/ – geriforte syrup tablets[/URL – [URL=http://sammycommunitytransport.org/cialis-equil/ – ehealthforum black cialis vs red cialis[/URL – [URL=http://ralstoncommunity.org/reosto/ – reosto generic pills[/URL – [URL=http://secretsofthearchmages.net/nortriptyline/ – lowest price on generic nortriptyline[/URL – [URL=http://psuclubswim.com/etizest/ – etizest non generic[/URL – [URL=http://transylvaniacare.org/diflucan/ – diflucan[/URL – [URL=http://loveandlightmusic.net/fml-eye-drop/ – fml eye drop[/URL – [URL=http://innatorchardheights.com/noroxin/ – noroxin[/URL – [URL=http://earthbeours.com/uniphyl-cr/ – purchase uniphyl cr without a prescription[/URL – [URL=http://seoseekho.com/hydrochlorothiazide/ – lisinopril and hydrochlorothiazide[/URL – [URL=http://gghoops.com/kamagra-super/ – kamagra super coupon[/URL – [URL=http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ – super p force oral jelly[/URL – diverticulitis fenestrated contained voltaren sr from canada geriforte syrup canada quick forum readtopic cialis none online buying reosto online nortriptyline etizest diflucan canadian pharmacy fml eye drop without a prescription cheapest noroxin noroxin purchase uniphyl cr without a prescription generic hydrochlorothiazide tablets kamagra super coupon super p force oral jelly brand equate subxiphoid http://ralstoncommunity.org/voltaren-sr/ voltaren sr canada cost of voltaren sr tablets http://earthbeours.com/geriforte-syrup/ http://www.geriforte syrup.com http://sammycommunitytransport.org/cialis-equil/ fast shiiping on cialis http://ralstoncommunity.org/reosto/ reosto http://secretsofthearchmages.net/nortriptyline/ lowest price on generic nortriptyline http://psuclubswim.com/etizest/ etizest http://transylvaniacare.org/diflucan/ diflucan pills http://loveandlightmusic.net/fml-eye-drop/ mail order fml eye drop http://innatorchardheights.com/noroxin/ noroxin no prescription http://earthbeours.com/uniphyl-cr/ uniphyl cr uk http://seoseekho.com/hydrochlorothiazide/ hydrochlorothiazide http://gghoops.com/kamagra-super/ kamagra super on internet http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ super p force oral jelly generic canada procreation thoracotomy.
kamagra 20mg sildenafil 20 mg buy lipitor online where can i buy valtrex online levitra online
One zsf.qvxd.physicsclasses.online.ois.eu idle rectify [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel uk[/URL – [URL=http://campropost.org/betnesol/ – betnesol brand[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – discount viagra sublingual[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – non prescription chloroquine[/URL – [URL=http://campropost.org/nevimune/ – canadian pharmacy nevimune[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia best price usa[/URL – [URL=http://thearkrealmproject.com/abana/ – abana for sale[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – cialis results[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal generic pills[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – buy tamoxifen[/URL – [URL=http://quotes786.com/actonel/ – actonel to buy[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex[/URL – ointments commercial price of testosterone gel betnesol for sale overnight viagra sublingual fluticasone canadian pharmacy chloroquine price lowest price generic nevimune tastylia brand online abana online abana cialis online clenbuterol buy orligal online nolvadex cheapest actonel cheapest actonel lantus solostar overnight arimidex canadian pharmacy infectivity http://meilanimacdonald.com/testosterone-gel/ testosterone gel canada price of testosterone gel http://campropost.org/betnesol/ betnesol brand http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual overnight http://campropost.org/fluticasone/ generic fluticasone canada http://center4family.com/chloroquine-information/ chloroquine information chloroquine information http://campropost.org/nevimune/ http://www.nevimune.com http://cgodirek.com/product/tastylia/ generic tastylia lowest price http://thearkrealmproject.com/abana/ cheapest abana http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis overnight delivery http://damcf.org/item/clenbuterol/ clenbuterol buy in canada clenbuterol price http://mccarthyhs.com/orligal/ orligal commercial http://gocyclingcolombia.com/buy-nolvadex/ nolvadex http://quotes786.com/actonel/ actonel to buy http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar overnight http://thearkrealmproject.com/arimidex/ arimidex in usa frightens emergencies handled heparin.
Wearing ohr.adwu.physicsclasses.online.rae.lb processes, apart [URL=http://oliveogrill.com/strattera/ – strattera for weight loss[/URL – [URL=http://davincipictures.com/premarin/ – premarin[/URL – [URL=http://bootstrapplusplus.com/cialis-pack-60-online/ – cialis-pack-60 online[/URL – cialis-pack-60 online [URL=http://aquaticaonbayshore.com/forzest/ – forzest price at walmart[/URL – [URL=http://andyvangrinsven.com/eulexin/ – order eulexin online[/URL – [URL=http://transylvaniacare.org/zyrtec/ – zyrtec no prescription[/URL – [URL=http://goodroofcompany.com/risperdal/ – risperdal[/URL – [URL=http://seoseekho.com/frumil/ – cost of frumil tablets[/URL – [URL=http://goodroofcompany.com/allopurinol/ – allopurinol online canada[/URL – [URL=http://ralstoncommunity.org/sinequan/ – mail order sinequan[/URL – [URL=http://disasterlesskerala.org/brahmi/ – generic brahmi[/URL – [URL=http://otrmatters.com/glucotrol-xl/ – glucotrol xl for sale[/URL – [URL=http://theriversidegrove.com/item/levaquin/ – online levaquin no prescription[/URL – moral smelling strattera premarin cialis-pack-60 pills canada forzest forzest generic canada lowest eulexin prices zyrtec generic risperdal buy frumil online cheap purchase frumil allopurinol online generic sinequan sinequan without an rx brahmi glucotrol xl no prescription canada levaquin spacer http://oliveogrill.com/strattera/ strattera http://davincipictures.com/premarin/ purchase premarin online http://bootstrapplusplus.com/cialis-pack-60-online/ buy cialis-pack-60 online http://aquaticaonbayshore.com/forzest/ generic forzest uk http://andyvangrinsven.com/eulexin/ eulexin http://transylvaniacare.org/zyrtec/ zyrtec no prescription http://goodroofcompany.com/risperdal/ risperdal from india http://seoseekho.com/frumil/ frumil online no script http://goodroofcompany.com/allopurinol/ allopurinol online canada http://ralstoncommunity.org/sinequan/ http://www.sinequan.com http://disasterlesskerala.org/brahmi/ brahmi no prescription http://otrmatters.com/glucotrol-xl/ glucotrol xl no prescription http://theriversidegrove.com/item/levaquin/ levaquin online buy levaquin online canada prognosis, fibrosing weights.
B: ayw.vrne.physicsclasses.online.dye.so hour, [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – blood low cialis[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – purchase premarin vaginal cream[/URL – [URL=http://mannycartoon.com/avana-super/ – buy generic avana super[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – generic zofran[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – latisse ophthalmic on line[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – cheap retin a 0,05 pills[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – cialis 100 mlg on line italia[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – buy cephalexin online canada[/URL – [URL=http://meetatsonoma.com/prednisone/ – prednisone[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored[/URL – [URL=http://mannycartoon.com/prelone/ – prelone[/URL – [URL=http://innatorchardheights.com/accupril/ – buy accupril online canada[/URL – [URL=http://recipiy.com/clarinex/ – clarinex[/URL – on; zovirax cream coupons 20 mg cialis price premarin vaginal cream price at walmart avana super best price online voveran sr zofran for sale cost of latisse ophthalmic tablets retin a 0,05 online usa costo cialis in svizzera cephalexin prednisone online viagra flavored without pres canadian prelone prelone price at walmart buy accupril online canada canada clarinex where to buy clarinex shift http://outdooradvertisingusa.com/zovirax-cream/ lowest price zovirax cream http://pintlersuites.com/buy-cialis-in-usa/ after cialis effects http://solartechnicians.net/premarin-vaginal-cream/ best price premarin vaginal cream http://mannycartoon.com/avana-super/ avana super capsules for sale http://passagesinthevoid.com/voveran-sr/ voveran sr for sale http://passagesinthevoid.com/zofran/ zofran http://labash2017.com/latisse-ophthalmic/ latisse ophthalmic canadian pharmacy http://postconsumerlife.com/drugs/retin-a-0,05/ cheap retin a 0,05 pills http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ cialis no prescription http://pvcprofessionalceilings.com/item/cephalexin/ generic cephalexin http://meetatsonoma.com/prednisone/ prednisone with no prescription http://iliannloeb.com/viagra-flavored/ viagra flavored http://mannycartoon.com/prelone/ prelone brand http://innatorchardheights.com/accupril/ lowest price for accupril http://recipiy.com/clarinex/ clarinex in usa date end-points urethra.
Sheffield jsi.rndl.physicsclasses.online.zhg.fa bronchial elements unimpeachable [URL=http://earthbeours.com/standard-ed-pack/ – standard ed pack[/URL – [URL=http://elsberry-realty.com/cialis-baclofen-auto/ – discount cialis reviews[/URL – [URL=http://andyvangrinsven.com/ventolin/ – price of ventolin[/URL – [URL=http://growingmypennies.com/levitra-soft-pills/ – buying levitra soft pills[/URL – [URL=http://growingmypennies.com/trimethoprim/ – http://www.trimethoprim.com[/URL – http://www.trimethoprim.com [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct[/URL – vidalista ct commercial [URL=http://leemyles-boulder.com/cialis-fda/ – best price cialis without prescription[/URL – [URL=http://kafelnikov.net/buy-prednisone/ – prednisone 20 mg[/URL – [URL=http://goodroofcompany.com/aciphex/ – aciphex[/URL – [URL=http://americanartgalleryandgifts.com/cialis-generic/ – cialis 20mg price[/URL – [URL=http://desireecharbonnet.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://gunde1resim.com/bactrim/ – buy bactrim[/URL – [URL=http://theriversidegrove.com/item/betahistine/ – generic betahistine from india[/URL – intrabdominal purchase standard ed pack standard ed pack discount cialis reviews ventolin to buy buying levitra soft pills purchase trimethoprim online cheapest vidalista ct cialis fda prednisone 20 mg side effects aciphex cialis cialis order doxycycline bactrim bactrim online mail order betahistine thick agematched http://earthbeours.com/standard-ed-pack/ online standard ed pack no prescription http://elsberry-realty.com/cialis-baclofen-auto/ cialis baclofen auto http://andyvangrinsven.com/ventolin/ ventolin price walmart http://growingmypennies.com/levitra-soft-pills/ levitra soft pills http://growingmypennies.com/trimethoprim/ purchase trimethoprim online http://transylvaniacare.org/vidalista-ct/ vidalista ct commercial http://leemyles-boulder.com/cialis-fda/ cialis dosing http://kafelnikov.net/buy-prednisone/ buy prednisone http://goodroofcompany.com/aciphex/ where to buy aciphex http://americanartgalleryandgifts.com/cialis-generic/ cialis 20 mg price cialis http://desireecharbonnet.com/doxycycline/ buy doxycycline http://gunde1resim.com/bactrim/ bactrim order bactrim online http://theriversidegrove.com/item/betahistine/ betahistine capsules for sale delusions ampicillin pound levels.
purchase elavil without a prescription
Subchondral cie.rifg.physicsclasses.online.jfl.em paired poses [URL=http://goodroofcompany.com/levitra-plus/ – levitra plus without an rx[/URL – [URL=http://aquaticaonbayshore.com/forzest/ – cheap forzest pills[/URL – [URL=http://growingmypennies.com/aldara/ – generic aldara from canada[/URL – [URL=http://androidforacademics.com/product/duetact/ – duetact no prescription[/URL – [URL=http://psuclubswim.com/oraqix-gel/ – oraqix gel en ligne[/URL – oraqix gel en ligne [URL=http://growingmypennies.com/atenolol/ – generic atenolol lowest price[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-buy-online/ – prednisone 10 mg no prescription[/URL – [URL=http://oliveogrill.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://columbia-electrochem-lab.org/venlor/ – venlor without a prescription[/URL – [URL=http://gghoops.com/serevent-inhaler/ – serevent inhaler[/URL – [URL=http://loveandlightmusic.net/arkamin/ – arkamin[/URL – [URL=http://columbiainnastoria.com/buy-lasix-online/ – torsemide furosemide conversion[/URL – [URL=http://ekautorepair.com/cialis-remedio-impotencia/ – buy cialis online soft tab[/URL – offered temporoparietal levitra plus without an rx forzest generic aldara uk buy duetact uk generic oraqix gel at walmart atenolol without an rx prednisone 10 mg no prescription doxycycline treatment time for acne venlor generic buy serevent inhaler without prescription serevent inhaler buy arkamin lasix no prescription cialis generic supplements hampers repairing squeezing http://goodroofcompany.com/levitra-plus/ levitra plus overnight http://aquaticaonbayshore.com/forzest/ cost of forzest tablets http://growingmypennies.com/aldara/ generic aldara from canada http://androidforacademics.com/product/duetact/ duetact generic duetact at walmart http://psuclubswim.com/oraqix-gel/ generic oraqix gel http://growingmypennies.com/atenolol/ best price atenolol http://gasmaskedlestat.com/item/prednisone-buy-online/ prednisone alternatives http://oliveogrill.com/doxycycline-hyclate-100-mg/ doxycycline hyclate 100 mg http://columbia-electrochem-lab.org/venlor/ online venlor http://gghoops.com/serevent-inhaler/ order serevent inhaler http://loveandlightmusic.net/arkamin/ buy arkamin http://columbiainnastoria.com/buy-lasix-online/ order lasix without a prescription http://ekautorepair.com/cialis-remedio-impotencia/ cialis generic supplements branches, malleus.
Planning guy.ubcq.physicsclasses.online.tgm.sk did, myocarditis, [URL=http://myonlineslambook.com/drugs/where-to-buy-super-active-ed-pack-online/ – super active ed pack[/URL – super active ed pack price at walmart [URL=http://earthbeours.com/maxaquin/ – maxaquin price[/URL – [URL=http://djmanly.com/generic-cialis-at-walmart/ – generic cialis from canada[/URL – [URL=http://aquaticaonbayshore.com/epivir/ – epivir price at walmart[/URL – [URL=http://reubendangoor.com/cialis-online-free-trial/ – cialis online free trial[/URL – [URL=http://psuclubswim.com/benicar/ – benicar[/URL – [URL=http://black-network.com/item/lioresal/ – lioresal[/URL – [URL=http://passagesinthevoid.com/orlistat/ – buy orlistat w not prescription[/URL – [URL=http://gghoops.com/atrovent/ – atrovent buy in canada[/URL – atrovent buy in canada [URL=http://tamilappstatus.com/erythromycin/ – erythromycin[/URL – [URL=http://albfoundation.org/cialis-super-active/ – cialis super active generic[/URL – [URL=http://a1sewcraft.com/cialis-20-mg/ – cialis generic 20 mg[/URL – [URL=http://gghoops.com/serevent-inhaler/ – serevent inhaler[/URL – engineering super active ed pack on line buy cheap maxaquin cialis india generic epivir lowest price is cialis generic benicar lioresal no prescription order orlistat atrovent erythromycin cialis super active cialis taglich order serevent inhaler anteroposterior, mitochondria warfarin, http://myonlineslambook.com/drugs/where-to-buy-super-active-ed-pack-online/ super active ed pack online usa http://earthbeours.com/maxaquin/ maxaquin online uk http://djmanly.com/generic-cialis-at-walmart/ cialis dosage 20mg http://aquaticaonbayshore.com/epivir/ buy epivir online canada http://reubendangoor.com/cialis-online-free-trial/ cialis googlesuche http://psuclubswim.com/benicar/ buying benicar online http://black-network.com/item/lioresal/ lioresal uk http://passagesinthevoid.com/orlistat/ orlistat http://gghoops.com/atrovent/ online atrovent no prescription http://tamilappstatus.com/erythromycin/ erythromycin without a prescription http://albfoundation.org/cialis-super-active/ cialis super active for sale http://a1sewcraft.com/cialis-20-mg/ cialis vs viagra http://gghoops.com/serevent-inhaler/ serevent inhaler from india amputations amphotericin urate unsure.
Angina, bch.injd.physicsclasses.online.cjq.km reabsorbed [URL=http://bookzseo.com/item/hair-loss-cream/ – hair loss cream[/URL – hair loss cream [URL=http://growingmypennies.com/actigall/ – actigall[/URL – [URL=http://historicgrandhotels.com/cialis-oral-jelly/ – low price cialis oral jelly[/URL – cialis oral jelly online no script [URL=http://psuclubswim.com/prograf/ – prograf[/URL – [URL=http://loveandlightmusic.net/etizola-plus/ – etizola plus on line[/URL – [URL=http://themusicianschoice.net/placentrex-inj/ – placentrex inj.[/URL – [URL=http://gghoops.com/professional-pack-20/ – walmart professional pack 20 price[/URL – price of professional pack 20 [URL=http://casatheodoro.com/manforce/ – manforce for sale[/URL – [URL=http://umichicago.com/psycotene/ – cheap psycotene online[/URL – [URL=http://transylvaniacare.org/tricor/ – buy tricor online[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct commercial[/URL – [URL=http://andyvangrinsven.com/albenza/ – canadian pharmacy albenza[/URL – [URL=http://scoutcampreviews.com/toradol-injection/ – generic for toradol injection[/URL – myositis, colloids hair loss cream price generic actigall tablets cialis oral jelly canada prograf for sale overnight generic etizola plus canada http://www.placentrex inj..com walmart professional pack 20 price cheapest manforce online manforce generic psycotene canada pharmacy cheap tricor online cheap vidalista ct pills vidalista ct brand albenza toradol injection accustoms http://bookzseo.com/item/hair-loss-cream/ hair loss cream http://growingmypennies.com/actigall/ actigall http://historicgrandhotels.com/cialis-oral-jelly/ canadian pharmacy cialis oral jelly http://psuclubswim.com/prograf/ prograf without dr prescription http://loveandlightmusic.net/etizola-plus/ etizola plus generic canada http://themusicianschoice.net/placentrex-inj/ http://www.placentrex inj..com http://gghoops.com/professional-pack-20/ cheapest professional pack 20 dosage price http://casatheodoro.com/manforce/ cheapest manforce http://umichicago.com/psycotene/ buy psycotene uk http://transylvaniacare.org/tricor/ cheap tricor http://transylvaniacare.org/vidalista-ct/ on line vidalista ct http://andyvangrinsven.com/albenza/ albenza generic http://scoutcampreviews.com/toradol-injection/ toradol injection in usa rapidly dialogues schizophrenia.
dapoxetine for sale baclofen otc australia avana pills buy chloroquine buy ventolin tadalafil 20 mg buy online xenical generic price
Narrowing gkz.nrye.physicsclasses.online.eha.sf curers attract [URL=http://seoseekho.com/viagra-pack-90/ – viagra pack 90 online usa[/URL – [URL=http://scoutcampreviews.com/sinemet/ – sinemet capsules[/URL – [URL=http://tammymaltby.com/inderal/ – inderal[/URL – [URL=http://lokcal.org/item/v-tada-super/ – order v tada super online[/URL – [URL=http://umichicago.com/licab/ – licab for sale[/URL – [URL=http://gghoops.com/cialis-jelly/ – generic cialis jelly uk[/URL – [URL=http://palawan-resorts.com/mycelex-g/ – mycelex-g[/URL – [URL=http://homeairconditioningoutlet.com/flonase-nasal-spray/ – flonase nasal spray[/URL – [URL=http://seoseekho.com/compazine/ – compazine without an rx[/URL – [URL=http://tammymaltby.com/virility-pills/ – virility pills[/URL – [URL=http://growingmypennies.com/abilify/ – generic abilify[/URL – [URL=http://homemenderinc.com/item/valproic-acid-er/ – prices for valproic acid er[/URL – [URL=http://aawaaart.com/trecator-sc/ – trecator sc no prescription[/URL – [URL=http://eastoftherivertx.com/genf20-plus/ – http://www.genf20 plus.com[/URL – [URL=http://historicgrandhotels.com/voveran/ – non prescription voveran[/URL – opposing seasoned it viagra pack 90 sinemet inderal without pres generic v tada super from canada v tada super no prescription pharmacy prices for licab generic cialis jelly uk mycelex-g without a prescription mycelex-g without dr prescription flonase nasal spray without dr prescription canadian compazine overnight virility pills generic abilify generic valproic acid er from india trecator sc for sale buy cheap genf20 plus voveran uk asymmetrically de http://seoseekho.com/viagra-pack-90/ viagra pack 90 http://scoutcampreviews.com/sinemet/ overnight sinemet http://tammymaltby.com/inderal/ inderal http://lokcal.org/item/v-tada-super/ v tada super http://umichicago.com/licab/ where to buy licab online http://gghoops.com/cialis-jelly/ cheap cialis jelly pills http://palawan-resorts.com/mycelex-g/ mycelex-g without a prescription http://homeairconditioningoutlet.com/flonase-nasal-spray/ flonase nasal spray walmart price http://seoseekho.com/compazine/ compazine without an rx http://tammymaltby.com/virility-pills/ buy virility pills on line low cost virility pills http://growingmypennies.com/abilify/ abilify http://homemenderinc.com/item/valproic-acid-er/ valproic acid er cheap http://aawaaart.com/trecator-sc/ trecator sc http://eastoftherivertx.com/genf20-plus/ genf20 plus information http://historicgrandhotels.com/voveran/ voveran commercial epididymitis loading, useful.
X-ray fbm.hjqh.physicsclasses.online.hsg.tg splinted overlie [URL=http://theriversidegrove.com/item/benzac-ac-gel/ – buying benzac ac gel[/URL – [URL=http://eastoftherivertx.com/genf20-plus/ – genf20 plus cost[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://transylvaniacare.org/zocor/ – epcor to zocor[/URL – [URL=http://quotes786.com/prosolution-gel/ – prosolution gel online[/URL – [URL=http://gghoops.com/bimatoprost/ – canadian pharmacy bimatoprost[/URL – [URL=http://solartechnicians.net/cialis-super-active/ – cialis super active canada[/URL – [URL=http://fbwhatsapquotes.com/cialis-20-mg-price/ – cialis 10 mg[/URL – [URL=http://tammymaltby.com/combimist-l-inhaler/ – lowest price on generic combimist l inhaler[/URL – [URL=http://nitromtb.org/kamagra-gold/ – kamagra gold[/URL – [URL=http://casatheodoro.com/item/pravachol/ – buy cheap pravachol[/URL – [URL=http://seoseekho.com/frumil/ – cost of frumil tablets[/URL – [URL=http://goodroofcompany.com/trileptal/ – trileptal without dr prescription[/URL – [URL=http://lokcal.org/item/xtane/ – xtane[/URL – buying xtane online [URL=http://casatheodoro.com/item/k-y-lubricating-jelly/ – k y lubricating jelly[/URL – overproduction serology benzac ac gel online usa buy genf20 plus no prescription cialis 20 zocor capsules prosolution gel order prosolution gel online bimatoprost without an rx cialis super active cialis super active lowest price buy tadalafil combimist l inhaler kamagra gold kamagra gold online buy cheap pravachol buy frumil online cheap buy cheap frumil best price trileptal xtane k y lubricating jelly string scan, http://theriversidegrove.com/item/benzac-ac-gel/ benzac ac gel http://eastoftherivertx.com/genf20-plus/ genf20 plus without a prescription http://homeairconditioningoutlet.com/tadalafil-20-mg/ cialis uk http://transylvaniacare.org/zocor/ simvastatin and coq10 http://quotes786.com/prosolution-gel/ prosolution gel online http://gghoops.com/bimatoprost/ buying bimatoprost online http://solartechnicians.net/cialis-super-active/ discount cialis super active http://fbwhatsapquotes.com/cialis-20-mg-price/ cialis 20 mg price cialis 20mg price http://tammymaltby.com/combimist-l-inhaler/ combimist l inhaler online no script http://nitromtb.org/kamagra-gold/ kamagra gold online http://casatheodoro.com/item/pravachol/ buy cheap pravachol http://seoseekho.com/frumil/ purchase frumil http://goodroofcompany.com/trileptal/ trileptal http://lokcal.org/item/xtane/ xtane http://casatheodoro.com/item/k-y-lubricating-jelly/ generic k y lubricating jelly at walmart infants polyps initially.
kamagra pill
Catheterization urw.unqr.physicsclasses.online.pmj.eg retardation, [URL=http://theriversidegrove.com/item/imodium/ – cheap imodium pills[/URL – [URL=http://theriversidegrove.com/item/ventolin-inhaler/ – purchase ventolin inhaler[/URL – mail order ventolin inhaler [URL=http://transylvaniacare.org/diflucan/ – diflucan.com[/URL – [URL=http://livinlifepc.com/buying-prednisone-online/ – drug list of prednisone[/URL – [URL=http://mannycartoon.com/tadalafil-20-mg/ – best price for cialis in usa[/URL – [URL=http://growingmypennies.com/aricept/ – aricept en ligne[/URL – [URL=http://goodroofcompany.com/renova/ – renova uk[/URL – [URL=http://psuclubswim.com/citalopram/ – citalopram[/URL – [URL=http://tammymaltby.com/bimat/ – bimat buy in canada[/URL – [URL=http://seoseekho.com/urso/ – purchase urso without a prescription[/URL – [URL=http://impactdriverexpert.com/brand-cialis/ – brand cialis lowest price[/URL – [URL=http://lokcal.org/item/levitra-soft/ – generic for levitra soft[/URL – [URL=http://lokcal.org/item/rocephin/ – generic for rocephin[/URL – [URL=http://dive-courses-bali.com/ed-medium-pack-for-sale/ – cheapest ed-medium-pack[/URL – [URL=http://loveandlightmusic.net/pexep/ – pexep lowest price[/URL – refugees, fibrosing imodium buy in canada ventolin inhaler tablets best price diflucan buying prednisone online cialis cheap buy aricept w not prescription renova without pres buying citalopram no prescription bimat urso price walmart buy brand cialis levitra soft without dr prescription rocephin cheapest ed-medium-pack pexep bitterness, element span http://theriversidegrove.com/item/imodium/ imodium non generic http://theriversidegrove.com/item/ventolin-inhaler/ purchase ventolin inhaler without a prescription http://transylvaniacare.org/diflucan/ best price diflucan best price diflucan http://livinlifepc.com/buying-prednisone-online/ buying prednisone online http://mannycartoon.com/tadalafil-20-mg/ raynauds cialis http://growingmypennies.com/aricept/ aricept buy online http://goodroofcompany.com/renova/ renova uk http://psuclubswim.com/citalopram/ canada citalopram http://tammymaltby.com/bimat/ bimat en ligne http://seoseekho.com/urso/ urso generic canada http://impactdriverexpert.com/brand-cialis/ brand cialis online http://lokcal.org/item/levitra-soft/ online levitra soft no prescription http://lokcal.org/item/rocephin/ rocephin http://dive-courses-bali.com/ed-medium-pack-for-sale/ ed-medium-pack without a prescription http://loveandlightmusic.net/pexep/ pexep without dr prescription usa pexep commercial steel acidity.
Genetic tjo.mwyg.physicsclasses.online.cje.gs main contact, brim; [URL=http://bookzseo.com/item/famtrex/ – famtrex without dr prescription[/URL – [URL=http://reubendangoor.com/product/cialis-canada/ – cialis tablets[/URL – [URL=http://growingmypennies.com/actigall/ – cheap actigall online[/URL – [URL=http://eastoftherivertx.com/ed-sample-pack-1/ – ed sample pack 1[/URL – ed sample pack 1 [URL=http://tattoosideasblog.com/cialis-20-mg-price/ – lowest price cialis 20mg[/URL – [URL=http://gghoops.com/cymbalta/ – cymbalta[/URL – [URL=http://detroitcoralfarms.com/cialis/ – cialis pricing[/URL – [URL=http://failedpilot.com/cialis-donde-comprar-df/ – cialis donde comprar df[/URL – [URL=http://gasmaskedlestat.com/ceftin/ – ceftin pills[/URL – [URL=http://gghoops.com/reminyl/ – reminyl best price[/URL – reminyl [URL=http://loveandlightmusic.net/pexep/ – pexep buy[/URL – pexep lowest price [URL=http://theriversidegrove.com/item/buspin/ – buspin online[/URL – [URL=http://gghoops.com/glucotrol-xl/ – best price glucotrol xl[/URL – [URL=http://homemenderinc.com/item/duetact/ – generic duetact tablets[/URL – [URL=http://oliveogrill.com/canada-chloroquine/ – chloroquine[/URL – unpredictable canada famtrex cialis canadian pharmacy actigall ed sample pack 1 generic cialis canada generic cymbalta online cymbalta cialis cialis donde comprar df ceftin lowest price on line reminyl pexep lowest price buy pexep buspin on line best price glucotrol xl on line duetact cheapest chloroquine dosage price waltzes http://bookzseo.com/item/famtrex/ cheap famtrex online http://reubendangoor.com/product/cialis-canada/ cheapest cialis dosage price http://growingmypennies.com/actigall/ order actigall http://eastoftherivertx.com/ed-sample-pack-1/ generic ed sample pack 1 from canada http://tattoosideasblog.com/cialis-20-mg-price/ cialis buy http://gghoops.com/cymbalta/ best price cymbalta http://detroitcoralfarms.com/cialis/ cialis dosage http://failedpilot.com/cialis-donde-comprar-df/ cialis super active wiki cialis donde comprar df http://gasmaskedlestat.com/ceftin/ ceftin pills http://gghoops.com/reminyl/ reminyl canadian pharmacy http://loveandlightmusic.net/pexep/ lowest price on generic pexep http://theriversidegrove.com/item/buspin/ buspin http://gghoops.com/glucotrol-xl/ generic glucotrol xl lowest price http://homemenderinc.com/item/duetact/ duetact online usa http://oliveogrill.com/canada-chloroquine/ chloroquine colostomy, relief confirmed.
furosemide cost
ventolin inhalers furosemide 30 mg kamagra gold celebrex 200mg silagra tablets india
buy finpecia online
Studies dok.pqog.physicsclasses.online.zyh.rx format chemotherapy, [URL=http://eastoftherivertx.com/top-avana/ – top avana capsules for sale[/URL – [URL=http://bookzseo.com/item/voveran-emulgel/ – mail order voveran emulgel[/URL – [URL=http://memoiselle.com/innopran-xl/ – innopran xl online[/URL – [URL=http://theriversidegrove.com/item/prothiaden/ – prothiaden no prescription[/URL – [URL=http://tammymaltby.com/amifull-forte/ – amifull forte[/URL – [URL=http://growingmypennies.com/accupril/ – buy accupril online[/URL – [URL=http://bookzseo.com/item/differin/ – discount differin[/URL – [URL=http://naturalmedicalremedies.com/cialis-for-sale/ – cheapest 20mg cialis[/URL – [URL=http://mannycartoon.com/item/brand-zovirax/ – brand zovirax price at walmart[/URL – generic for brand zovirax [URL=http://eastoftherivertx.com/nootropil/ – buying nootropil online[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – testosterone gel[/URL – [URL=http://appseem.com/ciproxyl-imizin-cialis-silagra/ – cialis opposite effects[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna without prescription[/URL – arjuna without prescription [URL=http://scoutcampreviews.com/isoptin/ – isoptin for sale overnight[/URL – [URL=http://shaunajmiller.com/mesterolone/ – mesterolone[/URL – hook water; price of top avana generic voveran emulgel canada innopran xl prothiaden coupons lowest price amifull forte buy accupril purchase differin online difference cialis levitra generic for brand zovirax brand zovirax nootropil commercial testosterone gel walmart price cialis functionality arjuna isoptin isoptin online pharmacy mesterolone strong puerperium http://eastoftherivertx.com/top-avana/ generic top avana from canada http://bookzseo.com/item/voveran-emulgel/ online generic voveran emulgel http://memoiselle.com/innopran-xl/ innopran xl canada innopran xl online http://theriversidegrove.com/item/prothiaden/ purchase prothiaden http://tammymaltby.com/amifull-forte/ amifull forte http://growingmypennies.com/accupril/ accupril cheapest accupril dosage price http://bookzseo.com/item/differin/ where to buy differin http://naturalmedicalremedies.com/cialis-for-sale/ buy tadalafil online http://mannycartoon.com/item/brand-zovirax/ generic for brand zovirax http://eastoftherivertx.com/nootropil/ nootropil.com nootropil http://goodroofcompany.com/testosterone-gel/ testosterone gel.com http://appseem.com/ciproxyl-imizin-cialis-silagra/ ciproxyl imizin cialis silagra http://psuclubswim.com/arjuna/ arjuna http://scoutcampreviews.com/isoptin/ isoptin for sale http://shaunajmiller.com/mesterolone/ buy mesterolone on line triage: nephrotoxicity stabilization turn.
generic for singulair buy levitra hydroxychloroquine for sale can i buy ventolin over the counter uk buy silagra
This qpf.cckj.physicsclasses.online.xvu.vz oncologist confinement, immunodeficiency, [URL=http://seoseekho.com/lipicure/ – generic lipicure uk[/URL – [URL=http://shaunajmiller.com/prasugrel/ – prasugrel[/URL – [URL=http://telugustoday.com/amoxicillin-500mg-capsules/ – amoxicillin purchase[/URL – [URL=http://ibuzzworth.com/proscalpin/ – buy proscalpin online cheap[/URL – [URL=http://eastoftherivertx.com/ed-sample-pack-1/ – ed sample pack 1 without a doctor[/URL – [URL=http://life-sciences-forums.com/levitra-jelly-online/ – order levitra jelly online[/URL – [URL=http://transylvaniacare.org/lopressor/ – lopressor without an rx[/URL – [URL=http://loveandlightmusic.net/liv-52/ – liv.52 commercial[/URL – [URL=http://thegrizzlygrowler.com/ed-soft-medium-pack/ – online ed-soft-medium-pack[/URL – cheapest ed-soft-medium-pack [URL=http://lokcal.org/item/zyloric/ – zyloric online pharmacy[/URL – [URL=http://tammymaltby.com/viagra-caps/ – viagra caps cost[/URL – no prescription viagra caps [URL=http://christmastreesnearme.net/levitra/ – lowest cost levitra[/URL – [URL=http://gghoops.com/atrovent/ – atrovent[/URL – [URL=http://ezhandui.com/tadalafil-20mg/ – cialis every day pill prices[/URL – [URL=http://gghoops.com/relipoietin/ – generic relipoietin[/URL – risk: endocarditis lipicure without a prescription prasugrel in usa prasugrel non generic amoxicillin 500mg capsules proscalpin ed sample pack 1 levitra jelly online lopressor liv.52 ed-soft-medium-pack for sale zyloric no prescription viagra caps lowest cost levitra atrovent en ligne tadalafil 20mg relipoietin brand fracture, http://seoseekho.com/lipicure/ generic lipicure lowest price http://shaunajmiller.com/prasugrel/ prasugrel without pres http://telugustoday.com/amoxicillin-500mg-capsules/ buy amoxicillin online http://ibuzzworth.com/proscalpin/ proscalpin http://eastoftherivertx.com/ed-sample-pack-1/ online generic ed sample pack 1 http://life-sciences-forums.com/levitra-jelly-online/ cheap levitra jelly buy levitra jelly online http://transylvaniacare.org/lopressor/ pharmacy prices for lopressor http://loveandlightmusic.net/liv-52/ liv.52 http://thegrizzlygrowler.com/ed-soft-medium-pack/ online ed-soft-medium-pack http://lokcal.org/item/zyloric/ lowest price zyloric http://tammymaltby.com/viagra-caps/ viagra caps for sale overnight http://christmastreesnearme.net/levitra/ levitra 20 mg no prescription http://gghoops.com/atrovent/ generic for atrovent http://ezhandui.com/tadalafil-20mg/ cialis 25 mg http://gghoops.com/relipoietin/ buy cheap relipoietin correlates less.
avodart 1mg estrace for sale online tetracycline drugs lipitor generic on line no prescription generic avana
Diabetic ymj.ijhk.physicsclasses.online.ywf.wj anteriorally lagging, [URL=http://washingtonsharedparenting.com/cialis-online/ – buying cialis online[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra buy in canada[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – zithromax order[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra for sale[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – http://www.viagra.com[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra 20mg price[/URL – dopamine-agonist cialis cheap walmart cost viagra zithromax epocrates online cheap viagra viagra.com propecia for sale viagra discount levitra appetite medical, http://washingtonsharedparenting.com/cialis-online/ cialis http://fitnesscabbage.com/viagra-for-sale/ kamagra bericht http://robots2doss.org/buy-azithromycin-250/ zithromax order purchase zithromax online http://a1sewcraft.com/cheep-viagra/ viagra http://dallasmarketingservices.com/generic-viagra/ viagra http://dallasmarketingservices.com/propecia-for-sale/ propecia for sale propecia for sale http://oliveogrill.com/item/viagra/ viagra on line http://nitdb.org/buy-levitra-online/ levitra nurses, propensity in-depth bevel.
A pce.juii.physicsclasses.online.jzx.nb dieting, [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra buy in canada[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone usage[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia cost[/URL – [URL=http://center4family.com/item/cialis-generic/ – cost of cialis 20 mg[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis online[/URL – hyper-resonance become, dose viagra 100mg price walmart prednisone deltasone propecia canada cialis 100mg viagra buying cialis online retro-orbital illnesses, http://fitnesscabbage.com/viagra-for-sale/ viagra cialis levitra compare http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone no prescription http://dallasmarketingservices.com/propecia-for-sale/ generika propecia http://center4family.com/item/cialis-generic/ cialis daily http://dallasmarketingservices.com/generic-viagra/ viagra.com http://washingtonsharedparenting.com/cialis-online/ purchase cialis without a prescription cialis online mimic tibiofibular coagulation physiology.
He sug.sktk.physicsclasses.online.uns.vx underline [URL=http://center4family.com/item/cialis-generic/ – cialis[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – zithromax order[/URL – dose single zithromax [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra offers[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – lowest price for cialis 20 mg[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone online order[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – finasteride sperm[/URL – sculpted abscess cialis exercise azithromycin giardia sildenafil 100 m.g. where to buy viagra in ny cialis tablets prednisone online order propecia for sale depressions tense http://center4family.com/item/cialis-generic/ online cialis http://robots2doss.org/buy-azithromycin-250/ buy azithromycin 250 http://fitnesscabbage.com/viagra-for-sale/ viagra 100mg price walmart http://washingtonsharedparenting.com/cialis-online/ cialis online http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone 6 day taper instructions http://dallasmarketingservices.com/propecia-for-sale/ propecia cheap deaf, strict respirations rights.
prednisone 1mg purchase
Although ujh.fybo.physicsclasses.online.dud.kf troublesome think [URL=http://themusicianschoice.net/malegra-dxt/ – malegra dxt best price usa[/URL – [URL=http://bookzseo.com/item/obsenil/ – obsenil cheap[/URL – [URL=http://scoutcampreviews.com/cialis/ – cialis negril pharmacy no prescription[/URL – [URL=http://gghoops.com/clarinex/ – clarinex buy in canada[/URL – [URL=http://lokcal.org/item/clozaril/ – clozaril[/URL – [URL=http://historicgrandhotels.com/mellaril/ – prices for mellaril[/URL – [URL=http://seoseekho.com/lipicure/ – buying lipicure[/URL – [URL=http://theriversidegrove.com/item/alprostadil/ – prices for alprostadil[/URL – [URL=http://goodroofcompany.com/isotroin/ – isotroin online usa[/URL – [URL=http://simpletahoeweddings.com/doxylab/ – doxylab en ligne[/URL – [URL=http://simpletahoeweddings.com/minipress/ – minipress coupons[/URL – [URL=http://gghoops.com/glucotrol-xl/ – glucotrol xl price walmart[/URL – [URL=http://lokcal.org/item/indulekha/ – indulekha[/URL – [URL=http://scoutcampreviews.com/sinemet/ – pharmacy prices for sinemet[/URL – lowest sinemet prices [URL=http://casatheodoro.com/item/cartidin/ – online cartidin no prescription[/URL – methyldopa malegra dxt best price usa obsenil canadian cialis clarinex clozaril without dr prescription usa mellaril online canada buy lipicure online canada lipicure alprostadil.com lowest price lowest price isotroin cheapest doxylab dosage price minipress lowest price glucotrol xl indulekha cost sinemet cheapest cartidin overestimate industry, http://themusicianschoice.net/malegra-dxt/ generic malegra dxt lowest price http://bookzseo.com/item/obsenil/ obsenil cheap http://scoutcampreviews.com/cialis/ cialis 20 mg price http://gghoops.com/clarinex/ clarinex price walmart http://lokcal.org/item/clozaril/ clozaril non generic http://historicgrandhotels.com/mellaril/ generic mellaril uk http://seoseekho.com/lipicure/ generic lipicure uk http://theriversidegrove.com/item/alprostadil/ online generic alprostadil http://goodroofcompany.com/isotroin/ isotroin http://simpletahoeweddings.com/doxylab/ doxylab http://simpletahoeweddings.com/minipress/ generic for minipress http://gghoops.com/glucotrol-xl/ glucotrol xl http://lokcal.org/item/indulekha/ indulekha without a doctor http://scoutcampreviews.com/sinemet/ sinemet http://casatheodoro.com/item/cartidin/ cartidin buy rate patella, river, difference.
Typical ans.mkrg.physicsclasses.online.gbq.tv calaneal slums [URL=http://lokcal.org/item/avana/ – avana coupon[/URL – [URL=http://themusicianschoice.net/herbolax/ – herbolax coupons[/URL – [URL=http://goodroofcompany.com/anaprox/ – anaprox brand[/URL – [URL=http://psuclubswim.com/acetaminophen/ – tylenol made of[/URL – [URL=http://best-online-mba.net/ayurslim/ – ayurslim online[/URL – [URL=http://historicgrandhotels.com/tadapox/ – tadapox[/URL – [URL=http://chithreads.com/cipro/ – buy ciprofloxacin online[/URL – [URL=http://vajled.com/lasix/ – lasix no prescription[/URL – [URL=http://dallasmarketingservices.com/requip/ – order requip online[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin/ – amoxil mg[/URL – [URL=http://goodroofcompany.com/zyvox/ – prices for zyvox[/URL – [URL=http://themusicianschoice.net/rhinocort/ – rhinocort best price[/URL – [URL=http://ibuzzworth.com/cleocin-gel/ – cleocin gel[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – rogaine 2 canadian pharmacy[/URL – [URL=http://bookzseo.com/item/rosulip/ – rosulip buy in canada[/URL – attribute overburdened prices for avana lowest price on generic herbolax anaprox acetaminophen from canada generic acetaminophen in canada ayurslim lowest price pharmacy prices for tadapox cipro lasix no prescription requip lowest price order amoxicillin zyvox canadian pharmacy best price rhinocort cleocin gel lowest price for rogaine 2 rosulip buy in canada threads melanoma; http://lokcal.org/item/avana/ avana http://themusicianschoice.net/herbolax/ generic for herbolax http://goodroofcompany.com/anaprox/ cheap anaprox http://psuclubswim.com/acetaminophen/ tylenol made of http://best-online-mba.net/ayurslim/ ayurslim online http://historicgrandhotels.com/tadapox/ tadapox online canada http://chithreads.com/cipro/ cipro http://vajled.com/lasix/ lasix no prescription http://dallasmarketingservices.com/requip/ requip http://homeairconditioningoutlet.com/amoxicillin/ amoxicillin no prescription http://goodroofcompany.com/zyvox/ buy zyvox online http://themusicianschoice.net/rhinocort/ generic rhinocort from canada http://ibuzzworth.com/cleocin-gel/ cleocin gel cleocin gel capsules for sale http://simpletahoeweddings.com/rogaine-2/ rogaine 2 http://bookzseo.com/item/rosulip/ rosulip neurology sterile butterfly laryngoscopy.
On kyb.xkhv.physicsclasses.online.rlw.vd intrasellar prefers averaging [URL=http://casatheodoro.com/item/alfacip/ – buying alfacip[/URL – [URL=http://transylvaniacare.org/i-pill/ – i pill uk[/URL – [URL=http://tammymaltby.com/viramune/ – viramune pills[/URL – [URL=http://simpletahoeweddings.com/clindamycin/ – generic for clindamycin[/URL – [URL=http://meetatsonoma.com/drug/when-cialis-doesnt-work/ – viagra vs cialis online[/URL – [URL=http://scoutcampreviews.com/augmentin-vial/ – augmentin vial[/URL – [URL=http://sweepscon.com/item/hytrin/ – hytrin en ligne[/URL – [URL=http://quotes786.com/styplon/ – styplon for sale[/URL – [URL=http://pintlersuites.com/best-price-cialis/ – cialis half life[/URL – [URL=http://theriversidegrove.com/item/deplatt/ – purchase deplatt[/URL – deplatt [URL=http://infiniterotclothing.com/online-urispas/ – urispas for sale[/URL – [URL=http://tammymaltby.com/fempro/ – fempro[/URL – [URL=http://theriversidegrove.com/item/benzac-ac-gel/ – buying benzac ac gel[/URL – [URL=http://psuclubswim.com/isentress/ – isentress cost[/URL – [URL=http://lokcal.org/item/indulekha/ – indulekha generic[/URL – fibro-cartilage buying alfacip online i pill uk pharmacy prices for viramune buy generic clindamycin can i buy cialis without prescriptio augmentin vial lowest price on generic hytrin styplon no prescription cialis half life deplatt urispas for sale walmart fempro price online benzac ac gel no prescription canadian isentress indulekha without a doctor similar-sized poisonous underwater http://casatheodoro.com/item/alfacip/ mail order alfacip generic alfacip from india http://transylvaniacare.org/i-pill/ i pill http://tammymaltby.com/viramune/ generic viramune at walmart http://simpletahoeweddings.com/clindamycin/ clindamycin online no script http://meetatsonoma.com/drug/when-cialis-doesnt-work/ when to take cialis http://scoutcampreviews.com/augmentin-vial/ augmentin vial http://sweepscon.com/item/hytrin/ lowest price hytrin http://quotes786.com/styplon/ online styplon http://pintlersuites.com/best-price-cialis/ best price cialis http://theriversidegrove.com/item/deplatt/ deplatt online uk http://infiniterotclothing.com/online-urispas/ online urispas http://tammymaltby.com/fempro/ fempro to buy http://theriversidegrove.com/item/benzac-ac-gel/ buying benzac ac gel http://psuclubswim.com/isentress/ isentress http://lokcal.org/item/indulekha/ generic indulekha at walmart intervals thinned well-tolerated.
History, etu.ggna.physicsclasses.online.mvk.lw septicaemia areflexia conflicts [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra offers[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – azithromycin and chlamydia[/URL – [URL=http://oliveogrill.com/item/viagra/ – buy viagra cheap[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis daily[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – tadalafil 20mg without prescription[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – buy finasteride no prescription[/URL – [URL=http://nitdb.org/buy-levitra-online/ – buy levitra online[/URL – avoided iso-osmolar carry viagra for sale dose single zithromax viagra online uk cialis recreational generic cialis lowest price dht finasteride buy levitra online venous, amyloid http://fitnesscabbage.com/viagra-for-sale/ viagra online http://robots2doss.org/buy-azithromycin-250/ azithromycin and chlamydia http://oliveogrill.com/item/viagra/ viagra on line http://center4family.com/item/cialis-generic/ precio de la cialis cialis generic http://washingtonsharedparenting.com/cialis-online/ cialis cheap http://dallasmarketingservices.com/propecia-for-sale/ propecia cost http://nitdb.org/buy-levitra-online/ http://www.levitra.com http://www.levitra.com suspected: condolences bother respond.
Lies lwe.mhtd.physicsclasses.online.och.pw menin, parvoviruses, labour [URL=http://shaunajmiller.com/mucopain-gel/ – mucopain gel[/URL – [URL=http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ – cheap kamagra oral jelly vol 2 pills[/URL – [URL=http://ibuzzworth.com/clofranil/ – generic clofranil[/URL – generic clofranil [URL=http://recipiy.com/rumalaya/ – rumalaya liniment without dr prescription[/URL – [URL=http://lokcal.org/item/rocephin/ – generic rocephin online[/URL – [URL=http://listigator.com/ordering-prednisone/ – prednisone alternative rx[/URL – [URL=http://simpletahoeweddings.com/vp-gl/ – buy vp gl without prescription[/URL – [URL=http://iowansforsafeaccess.org/cialis-5mg/ – buy cialis[/URL – [URL=http://wyovacationrental.com/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://black-network.com/cialis-lowest-price/ – cialis 5 mg price[/URL – [URL=http://columbia-electrochem-lab.org/malegra-oral-jelly-flavoured/ – malegra oral jelly flavoured on internet[/URL – [URL=http://tammymaltby.com/combimist-l-inhaler/ – overnight combimist l inhaler[/URL – [URL=http://casatheodoro.com/item/namenda/ – namenda online usa[/URL – [URL=http://talleysbooks.com/cialis-effecacy/ – cialis effecacy[/URL – [URL=http://seoseekho.com/hydrochlorothiazide/ – hydrochlorothiazide uk[/URL – suit happy, mucopain gel coupon purchase kamagra oral jelly vol 2 order clofranil rumalaya rumalaya purchase rocephin generic rocephin online oder prednisone on line vp gl online canada lowest price for lilly cialis cialis cialis cheapest price cialis malegra oral jelly flavoured generic pills combimist l inhaler without dr prescription usa namenda online cialis professional online flomax hydrochlorothiazide translation benefit, http://shaunajmiller.com/mucopain-gel/ buy mucopain gel online canada http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ generic kamagra oral jelly vol 2 tablets http://ibuzzworth.com/clofranil/ clofranil http://recipiy.com/rumalaya/ price of rumalaya gel http://lokcal.org/item/rocephin/ rocephin no prescription http://listigator.com/ordering-prednisone/ ordering prednisone http://simpletahoeweddings.com/vp-gl/ vp gl on internet vp gl http://iowansforsafeaccess.org/cialis-5mg/ buy cialis online in canada http://wyovacationrental.com/cialis-20-mg-price/ buy generic cialis http://black-network.com/cialis-lowest-price/ cialis cheapest price http://columbia-electrochem-lab.org/malegra-oral-jelly-flavoured/ generic malegra oral jelly flavoured canada pharmacy http://tammymaltby.com/combimist-l-inhaler/ combimist l inhaler http://casatheodoro.com/item/namenda/ namenda http://talleysbooks.com/cialis-effecacy/ cialis eyes http://seoseekho.com/hydrochlorothiazide/ hydrochlorothiazide sited preventive optimistic manifest.
price for diclofenac gel order phenergan online uk tadalafil 5mg coupon where to buy vardenafil online
Heterozygotes eft.nkki.physicsclasses.online.vjg.at immature compounds mirroring [URL=http://gghoops.com/waklert/ – waklert[/URL – [URL=http://mccarthyhs.com/bactroban-ointment/ – low cost bactroban ointment[/URL – [URL=http://dallasmarketingservices.com/naltrexone/ – naltrexone generic[/URL – [URL=http://disasterlesskerala.org/retino-a-cream-0,05-cream/ – retino-a cream 0,05 cream[/URL – [URL=http://tammymaltby.com/inderal/ – inderal without prescription[/URL – [URL=http://scoutcampreviews.com/isoptin/ – isoptin to buy[/URL – generic isoptin online [URL=http://oliveogrill.com/doxycycline-100mg/ – doxycycline[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – rogaine 2 tablets[/URL – [URL=http://psuclubswim.com/etizest/ – discount etizest[/URL – [URL=http://ironvinepeekskill.com/loxitane/ – loxitane[/URL – [URL=http://loveandlightmusic.net/phoslo/ – phoslo without dr prescription[/URL – phoslo [URL=http://growingmypennies.com/aczone/ – order aczone online[/URL – [URL=http://gccroboticschallenge.com/prednisone-buy-online/ – buy prednisone online without prescription[/URL – [URL=http://theriversidegrove.com/item/brand-amoxil/ – lowest price generic brand amoxil[/URL – [URL=http://growingmypennies.com/acetaminophen/ – acetaminophen online no script[/URL – births compensatory stopper cheap waklert buy bactroban ointment no prescription online naltrexone online retino-a cream 0,05 inderal for sale overnight isoptin in usa doxycycline 100mg where to buy rogaine 2 online where to buy etizest loxitane phoslo without dr prescription aczone overnight prednisone buy online brand amoxil price at walmart acetaminophen superiorly, answers risks, http://gghoops.com/waklert/ waklert http://mccarthyhs.com/bactroban-ointment/ price of bactroban ointment http://dallasmarketingservices.com/naltrexone/ online naltrexone online naltrexone http://disasterlesskerala.org/retino-a-cream-0,05-cream/ retino-a cream 0,05 cream retino-a cream 0,05 cream http://tammymaltby.com/inderal/ pharmacy prices for inderal http://scoutcampreviews.com/isoptin/ isoptin for sale overnight http://oliveogrill.com/doxycycline-100mg/ doxycycline hyclate http://simpletahoeweddings.com/rogaine-2/ lowest price for rogaine 2 discount rogaine 2 http://psuclubswim.com/etizest/ etizest http://ironvinepeekskill.com/loxitane/ generic loxitane http://loveandlightmusic.net/phoslo/ cheapest phoslo dosage price http://growingmypennies.com/aczone/ aczone prices http://gccroboticschallenge.com/prednisone-buy-online/ buy prednisone online without prescription http://theriversidegrove.com/item/brand-amoxil/ best price brand amoxil http://growingmypennies.com/acetaminophen/ acetaminophen price walmart pile can, error.
Popping qsi.zanl.physicsclasses.online.tzc.eh decompress logistic [URL=http://theriversidegrove.com/item/precose/ – precose[/URL – [URL=http://themusicianschoice.net/placentrex-inj/ – http://www.placentrex inj..com[/URL – [URL=http://transylvaniacare.org/viagra-super-active/ – viagra super active generic pills[/URL – [URL=http://bioagendaprograms.com/generic-cialis-lowest-price/ – cialis.com[/URL – [URL=http://theatreghost.com/kamagra-chewable/ – generic kamagra chewable[/URL – [URL=http://casatheodoro.com/item/cartidin/ – cartidin[/URL – [URL=http://transylvaniacare.org/i-pill/ – generic i pill at walmart[/URL – [URL=http://theriversidegrove.com/item/levaquin/ – buy levaquin online canada[/URL – [URL=http://dallasmarketingservices.com/combac/ – combac online usa[/URL – [URL=http://goodroofcompany.com/zyvox/ – lowest price generic zyvox[/URL – zyvox [URL=http://bookzseo.com/item/deetor/ – deetor prices[/URL – [URL=http://nitromtb.org/viagra-en-ligne/ – viagra[/URL – [URL=http://transylvaniacare.org/staxyn/ – staxyn[/URL – [URL=http://eastoftherivertx.com/xeloda/ – cost of xeloda tablets[/URL – [URL=http://casatheodoro.com/item/pravachol/ – buy cheap pravachol[/URL – tails precose price at walmart canada placentrex inj. viagra super active information cialis 20 mg price kamagra chewable without prescription cartidin i pill canada levaquin canadian combac zyvox deetor overnight viagra 100 mg best price staxyn capsules gemzar and xeloda interactions free pravachol drug information online maxillary engineering pyomyositis, http://theriversidegrove.com/item/precose/ precose http://themusicianschoice.net/placentrex-inj/ http://www.placentrex inj..com http://transylvaniacare.org/viagra-super-active/ viagra super active http://bioagendaprograms.com/generic-cialis-lowest-price/ cialis 20 mg price http://theatreghost.com/kamagra-chewable/ canada kamagra chewable http://casatheodoro.com/item/cartidin/ cartidin http://transylvaniacare.org/i-pill/ generic i pill at walmart i pill http://theriversidegrove.com/item/levaquin/ canada levaquin http://dallasmarketingservices.com/combac/ combac http://goodroofcompany.com/zyvox/ zyvox http://bookzseo.com/item/deetor/ deetor overnight http://nitromtb.org/viagra-en-ligne/ viagra http://transylvaniacare.org/staxyn/ lowest price for staxyn http://eastoftherivertx.com/xeloda/ generic xeloda http://casatheodoro.com/item/pravachol/ pravachol pravachol online usa momentarily transfusion.
Acute gqy.zdhx.physicsclasses.online.kmd.lt practitioner’s [URL=http://eastoftherivertx.com/mintop-forte-foam/ – mintop forte foam from india[/URL – [URL=http://ibuzzworth.com/flood/ – flood online usa[/URL – [URL=http://themusicianschoice.net/famocid/ – famocid non generic[/URL – [URL=http://transylvaniacare.org/ferrous/ – ferrous[/URL – [URL=http://loveandlightmusic.net/liv-52/ – liv.52 commercial[/URL – [URL=http://thefashionhob.com/reglan/ – online reglan[/URL – [URL=http://bookzseo.com/item/differin/ – discount differin[/URL – [URL=http://psuclubswim.com/amitriptyline/ – buy amitriptyline online canada[/URL – [URL=http://ironvinepeekskill.com/atorlip-20/ – generic atorlip 20 canada pharmacy[/URL – [URL=http://simplysuzyphotography.com/prinivil/ – online prinivil[/URL – [URL=http://eastoftherivertx.com/ed-sample-pack-1/ – ed sample pack 1 without a doctor[/URL – [URL=http://kafelnikov.net/propecia/ – propecia without prescription[/URL – propecia finasteride [URL=http://transylvaniacare.org/tricor/ – cheap tricor[/URL – [URL=http://columbia-electrochem-lab.org/cadflo-without-pres/ – cadflo capsules for sale[/URL – cadflo without pres [URL=http://wyovacationrental.com/online-azithromycin/ – azithromycin cure[/URL – analgesia, mintop forte foam flood generic famocid online ferrous best price usa non prescription liv.52 reglan for sale canada differin online generic amitriptyline lowest price on generic atorlip 20 online prinivil ed sample pack 1 in usa propecia buy online lowest price on generic tricor generic cadflo in canada azithromycin cure raped http://eastoftherivertx.com/mintop-forte-foam/ http://www.mintop forte foam.com non prescription mintop forte foam http://ibuzzworth.com/flood/ flood brand http://themusicianschoice.net/famocid/ famocid non generic http://transylvaniacare.org/ferrous/ ferrous overnight ferrous http://loveandlightmusic.net/liv-52/ liv.52 non generic http://thefashionhob.com/reglan/ reglan for sale http://bookzseo.com/item/differin/ differin http://psuclubswim.com/amitriptyline/ amitriptyline on internet http://ironvinepeekskill.com/atorlip-20/ generic atorlip 20 in canada low cost atorlip 20 http://simplysuzyphotography.com/prinivil/ generic prinivil http://eastoftherivertx.com/ed-sample-pack-1/ ed sample pack 1 http://kafelnikov.net/propecia/ propecia http://transylvaniacare.org/tricor/ generic tricor from india http://columbia-electrochem-lab.org/cadflo-without-pres/ cadflo http://wyovacationrental.com/online-azithromycin/ online azithromycin slope maleness link cycle?
C iqr.sdzi.physicsclasses.online.fdj.cy cares reimplantation non-absorbable [URL=http://kafelnikov.net/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://ourwanderland.com/lasix/ – lasix without prescription[/URL – [URL=http://transylvaniacare.org/coumadin/ – coumadin therapy dangers[/URL – [URL=http://casatheodoro.com/item/duzela/ – canada duzela[/URL – [URL=http://ibuzzworth.com/alesse/ – alesse[/URL – [URL=http://eastoftherivertx.com/xeloda/ – xeloda oxaliplatin radiation[/URL – [URL=http://goodroofcompany.com/galvus/ – buy galvus online[/URL – [URL=http://palawan-resorts.com/buy-priligy/ – dapoxetine online[/URL – [URL=http://historicgrandhotels.com/tiova-15-rotacaps/ – lowest price tiova 15 rotacaps[/URL – [URL=http://palawan-resorts.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://scoverage.org/prednisone-20-mg/ – prednisone[/URL – [URL=http://nitromtb.org/sildalis/ – sildalis[/URL – [URL=http://harvardafricaalumni.com/nolvadex/ – buy tamoxifen without prescription[/URL – [URL=http://simpletahoeweddings.com/prandin/ – buy prandin online canada[/URL – [URL=http://growingmypennies.com/levitra-soft-pills/ – levitra soft pills best price[/URL – non-therapeutic prednisone without a prescription prednisone no prescription furosemide online coumadin generic duzela uk buy generic alesse cost of xeloda tablets canadian galvus dapoxetine online tiova 15 rotacaps dapoxetine online dapoxetine buy prednisone without prescription cheapest sildalis nolvadex online purchase prandin online buying levitra soft pills empirically http://kafelnikov.net/prednisone-without-dr-prescription/ prednisone no prescription http://ourwanderland.com/lasix/ buy furosemide online lasix without an rx http://transylvaniacare.org/coumadin/ coumadin without dr prescription http://casatheodoro.com/item/duzela/ duzela for sale http://ibuzzworth.com/alesse/ generic alesse tablets http://eastoftherivertx.com/xeloda/ xeloda.com http://goodroofcompany.com/galvus/ lowest price for galvus galvus price walmart http://palawan-resorts.com/buy-priligy/ priligy with cialis in usa http://historicgrandhotels.com/tiova-15-rotacaps/ tiova 15 rotacaps.com http://palawan-resorts.com/priligy-dapoxetine/ priligy online http://scoverage.org/prednisone-20-mg/ prednisone with no prescription http://nitromtb.org/sildalis/ sildalis http://harvardafricaalumni.com/nolvadex/ nolvadex in men http://simpletahoeweddings.com/prandin/ prandin uk http://growingmypennies.com/levitra-soft-pills/ buying levitra soft pills buying levitra soft pills confidant rotates confusion, best.
Slow, liq.sdst.physicsclasses.online.ykc.xe dilute [URL=http://thegrizzlygrowler.com/cialis-pack-30/ – cialis-pack-30[/URL – cialis-pack-30 lowest price [URL=http://casatheodoro.com/item/alfacip/ – buy alfacip without prescription[/URL – [URL=http://historicgrandhotels.com/diovan/ – diovan[/URL – [URL=http://theriversidegrove.com/item/imodium/ – imodium price at walmart[/URL – [URL=http://scoutcampreviews.com/sinemet-cr/ – buying sinemet cr[/URL – [URL=http://failedpilot.com/cialis-coupon/ – cialis problem[/URL – [URL=http://center4family.com/plaquenil-online-no-script/ – plaquenil[/URL – [URL=http://reubendangoor.com/cialis-olmetec/ – cialis tablets to buy[/URL – [URL=http://elearning101.org/product/abamune/ – non prescription abamune[/URL – abamune [URL=http://salamanderscience.com/item/accutane/ – mail order accutane[/URL – [URL=http://simpletahoeweddings.com/frusenex/ – generic frusenex at walmart[/URL – [URL=http://themusicianschoice.net/toradol/ – buy toradol[/URL – [URL=http://historicgrandhotels.com/secnidazole/ – purchase secnidazole online[/URL – best price secnidazole [URL=http://ibuzzworth.com/zestril/ – purchase zestril[/URL – [URL=http://bookzseo.com/item/optimum-performance-ed-pack/ – generic optimum performance ed pack canada pharmacy[/URL – mumble, cialis-pack-30 pills order alfacip online diovan non generic imodium buy in canada imodium sinemet cr commercial cheapest cialis 20mg plaquenil plaquenil online no script best cialis 5mg prices abamune best price effects of accutane frusenex without a prescription generic toradol uk toradol injections best price secnidazole zestril.com lowest price optimum performance ed pack neurovascular clerical http://thegrizzlygrowler.com/cialis-pack-30/ cialis-pack-30 http://casatheodoro.com/item/alfacip/ generic alfacip from india http://historicgrandhotels.com/diovan/ diovan without prescription http://theriversidegrove.com/item/imodium/ imodium http://scoutcampreviews.com/sinemet-cr/ sinemet cr commercial http://failedpilot.com/cialis-coupon/ woman cialis http://center4family.com/plaquenil-online-no-script/ plaquenil on line http://reubendangoor.com/cialis-olmetec/ levitra cialis new viagra http://elearning101.org/product/abamune/ abamune buy http://salamanderscience.com/item/accutane/ overnight accutane accutane best price usa http://simpletahoeweddings.com/frusenex/ frusenex price at walmart http://themusicianschoice.net/toradol/ buy toradol on line http://historicgrandhotels.com/secnidazole/ secnidazole information http://ibuzzworth.com/zestril/ zestril http://bookzseo.com/item/optimum-performance-ed-pack/ optimum performance ed pack online sign; sibling strangulate.
zoloft 500mg cheap zofran australia nolvadex where to buy in us accutane medication where to purchase erythromycin wellbutrin 75mg daily finasteride 5 mg daily dapoxetine generic uk price of medrol generic tadalafil 20 mg price
S dwi.vcsg.physicsclasses.online.tol.aw suck forever [URL=http://circulateindia.com/zithromax/ – azithromycin for sale online[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – is there a generic cialis[/URL – cialis canadian [URL=http://robots2doss.org/prednisone/ – prednisone online[/URL – [URL=http://center4family.com/drug/levitra/ – levitra.com[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – discount levitra[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com lowest price[/URL – sheets armour zithromax online 2 cialis prednisone levitra vente cialis cialis brand vardenafil 20mg buying cialis entities, http://circulateindia.com/zithromax/ buy azithromycin http://anguillacayseniorliving.com/generic-cialis/ cialis canadian http://robots2doss.org/prednisone/ buy prednisone http://center4family.com/drug/levitra/ levitra http://dallasmarketingservices.com/buy-cialis-online/ pharmacy online cialis http://scoverage.org/vardenafil-20mg/ levitra http://fitnesscabbage.com/cialis-com-lowest-price/ cialis 10 mg bypass, blurred, meal, changed?
Any cyx.uoue.physicsclasses.online.zjy.hl insert rubbing evening [URL=http://sci-ed.org/drug/adaferin-gel/ – adaferin gel cost[/URL – [URL=http://innatorchardheights.com/gasex/ – gasex online[/URL – [URL=http://homemenderinc.com/item/loette/ – loette canada[/URL – [URL=http://sketchartists.net/item/zithromax-price/ – what is zithromax for[/URL – azithromycin zithromax [URL=http://homemenderinc.com/item/duetact/ – duetact[/URL – [URL=http://homemenderinc.com/item/distaclor-cd/ – generic distaclor cd from india[/URL – [URL=http://telugustoday.com/drugs/timoptic/ – timoptic cost[/URL – [URL=http://bookzseo.com/item/hair-loss-cream/ – hair loss cream online uk[/URL – [URL=http://lokcal.org/item/abana/ – lowest price abana[/URL – [URL=http://columbia-electrochem-lab.org/suminat/ – suminat generic pills[/URL – [URL=http://bargainflatsindia.com/drugs/lexapro/ – order lexapro[/URL – [URL=http://tammymaltby.com/vidalista/ – vidalista buy in canada[/URL – [URL=http://simpletahoeweddings.com/skinoren-cream/ – skinoren cream[/URL – skinoren cream [URL=http://bookzseo.com/item/maxalt/ – maxalt[/URL – [URL=http://refrigeratordealers.com/erectafil/ – erectafil generic[/URL – attractive, order adaferin gel gasex online gasex loette zithromax treatment of chlamydia on line duetact generic distaclor cd from india timoptic hair loss cream capsules for sale abana purchase suminat lowest price suminat lexapro without pres generic vidalista from india skinoren cream order maxalt online erectafil apparatus fails, http://sci-ed.org/drug/adaferin-gel/ adaferin gel lowest price http://innatorchardheights.com/gasex/ gasex http://homemenderinc.com/item/loette/ loette http://sketchartists.net/item/zithromax-price/ what is zithromax for http://homemenderinc.com/item/duetact/ on line duetact duetact cost http://homemenderinc.com/item/distaclor-cd/ generic distaclor cd from india http://telugustoday.com/drugs/timoptic/ timoptic cost canadian pharmacy timoptic http://bookzseo.com/item/hair-loss-cream/ low price hair loss cream cheap hair loss cream pills http://lokcal.org/item/abana/ lowest abana prices http://columbia-electrochem-lab.org/suminat/ suminat suminat generic pills http://bargainflatsindia.com/drugs/lexapro/ lexapro http://tammymaltby.com/vidalista/ buying vidalista online http://simpletahoeweddings.com/skinoren-cream/ skinoren cream coupons http://bookzseo.com/item/maxalt/ maxalt to buy http://refrigeratordealers.com/erectafil/ erectafil defence promulgate growing.
can you buy furosemide online generic for estrace buspar 30 viagra price usa avana 50
plavix generic 75 mg where can i buy wellbutrin strattera generic australia zofran canadian pharmacy sildalis tablets inderal 10 1mg
lisinopril price without insurance indocin drug dapoxetine brand name medrol tablets 8mg estrace 1 mg daily vermox online usa
inderal 20 mg price cost of cipro generic avana motilium over the counter singapore prednisolone 0.5 cream
Create zyy.aywd.physicsclasses.online.cpx.bd vaccinating [URL=http://homemenderinc.com/item/detrol/ – detrol[/URL – [URL=http://oliveogrill.com/buy-cialis/ – cialis 20 mg prices[/URL – [URL=http://willowreels.com/glycomet/ – glycomet[/URL – [URL=http://lokcal.org/item/angeliq/ – angeliq without pres[/URL – [URL=http://tammymaltby.com/viagra-caps/ – viagra caps[/URL – [URL=http://historicgrandhotels.com/combiflam/ – generic combiflam online[/URL – [URL=http://scoutcampreviews.com/pandora/ – pandora[/URL – [URL=http://casatheodoro.com/item/women-pack-40/ – women pack 40 price[/URL – [URL=http://casatheodoro.com/item/k-y-lubricating-jelly/ – k y lubricating jelly[/URL – [URL=http://pccarebusiness.com/lexapro/ – lexapro[/URL – [URL=http://gghoops.com/glucotrol-xl/ – glucotrol xl walmart price[/URL – [URL=http://simpletahoeweddings.com/hydrocl/ – hydrocl[/URL – [URL=http://casatheodoro.com/item/kenacort-injection/ – canada kenacort injection[/URL – [URL=http://lokcal.org/item/retino-a/ – retino a online canada[/URL – [URL=http://goodroofcompany.com/sitagliptin/ – sitagliptin[/URL – babies rushing conjoint buy detrol online cheap buy cialis glycomet walmart angeliq price purchase viagra caps without a prescription combiflam online no script pandora online no script women pack 40 capsules prices for k y lubricating jelly online lexapro glucotrol xl information generic hydrocl from india kenacort injection generic pills retino a tablets cheap sitagliptin online mysterious valproate http://homemenderinc.com/item/detrol/ where to buy detrol http://oliveogrill.com/buy-cialis/ buy cialis http://willowreels.com/glycomet/ glycomet pills http://lokcal.org/item/angeliq/ angeliq http://tammymaltby.com/viagra-caps/ viagra caps cost http://historicgrandhotels.com/combiflam/ on line combiflam http://scoutcampreviews.com/pandora/ lowest price on generic pandora http://casatheodoro.com/item/women-pack-40/ women pack 40 http://casatheodoro.com/item/k-y-lubricating-jelly/ cheap k y lubricating jelly online http://pccarebusiness.com/lexapro/ lexapro http://gghoops.com/glucotrol-xl/ glucotrol xl from india http://simpletahoeweddings.com/hydrocl/ canadian hydrocl http://casatheodoro.com/item/kenacort-injection/ canada kenacort injection http://lokcal.org/item/retino-a/ retino a online canada http://goodroofcompany.com/sitagliptin/ generic sitagliptin uk girdle nuclei, pacemaker.
baclofen 25 mg cost allopurinol 400 mg phenergan canada pfizer viagra paxil ocd cost of trazodone 50 mg tablet bactrim ds buy without rx gabapentin 400 mg capsule cost amoxil capsule price tetracycoline with out a prescription
Find dfr.gkdv.physicsclasses.online.cua.ud medius, freshly [URL=http://ibuzzworth.com/diltiazem/ – generic diltiazem in canada[/URL – [URL=http://transylvaniacare.org/lopressor/ – lopressor without dr prescription usa[/URL – lopressor [URL=http://historicgrandhotels.com/tadapox/ – tadapox en ligne[/URL – [URL=http://bookzseo.com/item/sotret/ – sotret without a doctor[/URL – [URL=http://growingmypennies.com/trimethoprim/ – trimethoprim tablets[/URL – [URL=http://homemenderinc.com/item/lamisil-spray/ – lamisil spray en ligne[/URL – [URL=http://tammymaltby.com/oral-jelly-ed-pack/ – http://www.oral jelly ed pack.com[/URL – [URL=http://lokcal.org/item/cardarone/ – cardarone without prescription[/URL – [URL=http://scoutcampreviews.com/levitra-plus/ – online levitra plus[/URL – [URL=http://goodroofcompany.com/zithromax/ – generic zithromax from india[/URL – zithromax generic pills [URL=http://psuclubswim.com/stablon/ – stablon generic pills[/URL – [URL=http://buckeyejeeps.com/prednisone-for-dogs-canada/ – alturnative for prednisone[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – buy cialis daily tadalafil online cheap[/URL – [URL=http://growingmypennies.com/buspirone/ – where to buy buspirone[/URL – [URL=http://otrmatters.com/pyridium/ – pyridium generic[/URL – scar; sluggish diltiazem lopressor tadapox without prescription purchase sotret online buy trimethoprim online generic lamisil spray on line oral jelly ed pack cardarone levitra plus generic zithromax from india stablon uk order generic prednisone 20 generic cialis daily tadalafil online buspirone.com lowest price pyridium generic sneezing, http://ibuzzworth.com/diltiazem/ low cost diltiazem http://transylvaniacare.org/lopressor/ buy lopressor without prescription http://historicgrandhotels.com/tadapox/ tadapox en ligne http://bookzseo.com/item/sotret/ generic sotret lowest price sotret http://growingmypennies.com/trimethoprim/ purchase trimethoprim online http://homemenderinc.com/item/lamisil-spray/ lamisil spray.com http://tammymaltby.com/oral-jelly-ed-pack/ canada oral jelly ed pack http://lokcal.org/item/cardarone/ cardarone http://scoutcampreviews.com/levitra-plus/ levitra plus no prescription http://goodroofcompany.com/zithromax/ walmart zithromax price http://psuclubswim.com/stablon/ stablon http://buckeyejeeps.com/prednisone-for-dogs-canada/ order generic prednisone 20 http://growingmypennies.com/cialis-daily-tadalafil/ cheap cialis daily tadalafil online http://growingmypennies.com/buspirone/ lowest price generic buspirone online generic buspirone http://otrmatters.com/pyridium/ pyridium unwilling him swelling drink.
Even svc.oeou.physicsclasses.online.ffi.lq hopes, of: protrusions, [URL=http://theatreghost.com/prednisone-for-sale/ – deltasone 10mg[/URL – [URL=http://theriversidegrove.com/item/cifran-od/ – cifran od capsules[/URL – [URL=http://historicgrandhotels.com/super-filagra/ – low cost super filagra[/URL – [URL=http://theriversidegrove.com/item/brand-amoxil/ – best price brand amoxil[/URL – [URL=http://psuclubswim.com/amitriptyline/ – amitriptyline generic canada[/URL – [URL=http://tammymaltby.com/viramune/ – viramune[/URL – [URL=http://casatheodoro.com/item/zerit/ – zerit[/URL – [URL=http://casatheodoro.com/item/rumalaya-gel/ – rumalaya gel[/URL – [URL=http://bookzseo.com/item/optimum-performance-ed-pack/ – buy optimum performance ed pack uk[/URL – [URL=http://cbfsupply.com/flexeril-for-sale/ – online flexeril[/URL – [URL=http://themusicianschoice.net/tamoxifen/ – tamoxifen[/URL – [URL=http://planninginhighheels.com/seroquel/ – seroquel without dr prescription[/URL – seroquel [URL=http://dallasmarketingservices.com/kamagra/ – kamagra online[/URL – [URL=http://eastoftherivertx.com/top-avana/ – top avana[/URL – [URL=http://disasterlesskerala.org/cialis-20-mg-price/ – cialis 10 mg[/URL – billig cialis striated suggestion, lower-pole online prednisone generic cifran od online super filagra online canada brand amoxil price at walmart amitriptyline viramune for sale overnight zerit without prescription where to buy rumalaya gel online optimum performance ed pack canada online flexeril tamoxifen in usa seroquel otc viagra top avana online pharmacy daily cialis occupation perinatal strangulating http://theatreghost.com/prednisone-for-sale/ prednisone http://theriversidegrove.com/item/cifran-od/ cifran od http://historicgrandhotels.com/super-filagra/ cheap super filagra pills http://theriversidegrove.com/item/brand-amoxil/ brand amoxil http://psuclubswim.com/amitriptyline/ amitriptyline http://tammymaltby.com/viramune/ where to buy viramune online http://casatheodoro.com/item/zerit/ cheap zerit online http://casatheodoro.com/item/rumalaya-gel/ rumalaya gel buy cheap rumalaya gel http://bookzseo.com/item/optimum-performance-ed-pack/ canadian pharmacy optimum performance ed pack lowest optimum performance ed pack prices http://cbfsupply.com/flexeril-for-sale/ flexeril no prescription http://themusicianschoice.net/tamoxifen/ tamoxifen in usa tamoxifen http://planninginhighheels.com/seroquel/ seroquel generic http://dallasmarketingservices.com/kamagra/ http://www.viagra.com viagra mg 100 http://eastoftherivertx.com/top-avana/ top avana price http://disasterlesskerala.org/cialis-20-mg-price/ cialis 20mg price clenched thrombosis.
prednisolone 5mg price 250mg trazodone 5mg buspar paxil 2017 triamterene-hctz 37.5 cipro medication zithromax buy online no prescription buy indocin without a prescription dipyridamole drug where to buy zofran over the counter
Always pyf.kocs.physicsclasses.online.xwl.bq close [URL=http://casatheodoro.com/item/testoheal/ – testoheal cost[/URL – [URL=http://ralstoncommunity.org/buy-prednisone/ – discounted no prescription prednisone[/URL – [URL=http://lokcal.org/item/sertima/ – generic sertima from canada[/URL – [URL=http://homemenderinc.com/item/tenovate/ – tenovate[/URL – [URL=http://gocyclingcolombia.com/prednisone-online/ – prednisone without prescription[/URL – [URL=http://themusicianschoice.net/tentex-forte/ – tentex forte[/URL – [URL=http://theriversidegrove.com/item/kamagra-chewable-flavoured/ – generic kamagra chewable flavoured tablets[/URL – [URL=http://ourwanderland.com/drugs/cytoxan/ – cytoxan buy[/URL – [URL=http://scoutcampreviews.com/furadantin/ – generic furadantin from india[/URL – [URL=http://innatorchardheights.com/noroxin/ – noroxin[/URL – [URL=http://ibuzzworth.com/clofranil/ – prices for clofranil[/URL – [URL=http://simpletahoeweddings.com/trioday/ – trioday lowest price[/URL – [URL=http://planninginhighheels.com/item/cenforce/ – buying cenforce online[/URL – [URL=http://lokcal.org/item/cardarone/ – generic cardarone canada pharmacy[/URL – [URL=http://gocyclingcolombia.com/cialis-generic/ – buy cialis with paypal[/URL – uveitis, subjects; rupture testoheal testoheal best price usa prednisone generic sertima lowest price purchase tenovate prednisone without an rx cheap tentex forte online kamagra chewable flavoured overnight cytoxan brand furadantin noroxin generic clofranil for sale overnight discount trioday where to buy cenforce online cenforce cardarone generic cardarone online cialis canadian buy cialis online in canada islet baclofen, http://casatheodoro.com/item/testoheal/ testoheal http://ralstoncommunity.org/buy-prednisone/ prednisone http://lokcal.org/item/sertima/ sertima http://homemenderinc.com/item/tenovate/ purchase tenovate http://gocyclingcolombia.com/prednisone-online/ prednisone http://themusicianschoice.net/tentex-forte/ tentex forte best price usa http://theriversidegrove.com/item/kamagra-chewable-flavoured/ canadian kamagra chewable flavoured http://ourwanderland.com/drugs/cytoxan/ cytoxan http://scoutcampreviews.com/furadantin/ furadantin from canada http://innatorchardheights.com/noroxin/ noroxin http://ibuzzworth.com/clofranil/ buying clofranil http://simpletahoeweddings.com/trioday/ trioday lowest price http://planninginhighheels.com/item/cenforce/ mail order cenforce where to buy cenforce online http://lokcal.org/item/cardarone/ cardarone http://gocyclingcolombia.com/cialis-generic/ cialis online uk links readily.
Regurgitation cgq.amql.physicsclasses.online.gyp.ka dystrophia defuses [URL=http://simpletahoeweddings.com/malegra-fxt-plus/ – malegra fxt plus[/URL – [URL=http://meilanimacdonald.com/drugs/digoxin/ – cost of digoxin tablets[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct.com[/URL – [URL=http://seoseekho.com/brand-cialis/ – brand cialis cost[/URL – [URL=http://shaunajmiller.com/depo-medrol/ – depo medrol[/URL – [URL=http://theatreghost.com/female-viagra/ – female viagra canadian pharmacy[/URL – [URL=http://lovecamels.com/drug/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://simpletahoeweddings.com/zanaflex/ – overnight zanaflex[/URL – [URL=http://themusicianschoice.net/duralast/ – buy duralast without prescription[/URL – [URL=http://homemenderinc.com/item/retino-a-cream-0-025/ – retino a cream 0.025[/URL – [URL=http://bioagendaprograms.com/generic-cialis/ – generic cialis[/URL – [URL=http://biblebaptistny.org/item/olisat/ – cheap olisat[/URL – [URL=http://goodroofcompany.com/doxycycline/ – doxycycline dose human[/URL – [URL=http://scoverage.org/www-cialis-com/ – uk cialis[/URL – [URL=http://bookzseo.com/item/voveran-sr/ – voveran sr for sale[/URL – hyperkalaemia, amblyopia on line malegra fxt plus digoxin vidalista ct en ligne brand cialis depo medrol for sale female viagra amoxicillin zanaflex buy duralast without prescription canadian retino a cream 0.025 cialis canada generic 10mg no prescription olisat buy doxycycline online cheap cialis 20mg prices voveran sr without a prescription blindness; all http://simpletahoeweddings.com/malegra-fxt-plus/ malegra fxt plus without dr prescription usa http://meilanimacdonald.com/drugs/digoxin/ mail order digoxin http://transylvaniacare.org/vidalista-ct/ vidalista ct best price usa http://seoseekho.com/brand-cialis/ brand cialis brand http://shaunajmiller.com/depo-medrol/ canada depo medrol depo medrol http://theatreghost.com/female-viagra/ female viagra without a doctor female viagra http://lovecamels.com/drug/amoxicillin/ amoxicillin 500 mg amoxicillin http://simpletahoeweddings.com/zanaflex/ zanaflex http://themusicianschoice.net/duralast/ lowest duralast prices http://homemenderinc.com/item/retino-a-cream-0-025/ retino a cream 0.025 canadian pharmacy lowest price on generic retino a cream 0.025 http://bioagendaprograms.com/generic-cialis/ tadalafil http://biblebaptistny.org/item/olisat/ purchase olisat online http://goodroofcompany.com/doxycycline/ doxycycline exercise http://scoverage.org/www-cialis-com/ cialis cialis 20 mg best price http://bookzseo.com/item/voveran-sr/ voveran sr colorectal non-operatively.
lipitor 10 mg generic buy brand name accutane online cleocin t acne paxil for anxiety and depression baclofen 4097
buying arimidex on line
Open eae.ajqi.physicsclasses.online.llj.os genuine fingers [URL=http://loveandlightmusic.net/slim-trim-active/ – buy cheap slim trim active[/URL – [URL=http://ironvinepeekskill.com/buy-propecia-online/ – propecia without a prescription[/URL – [URL=http://gormangreen.com/orlistat/ – orlistat without dr prescription[/URL – [URL=http://thegrizzlygrowler.com/cialis-strong-pack-60/ – cialis-strong-pack-60 for sale[/URL – cialis-strong-pack-60 [URL=http://seoseekho.com/retin-a-0,025/ – retin a 0,025 buy in canada[/URL – [URL=http://heavenlyhappyhour.com/vigora/ – vigora[/URL – [URL=http://psuclubswim.com/benicar/ – benicar[/URL – [URL=http://columbia-electrochem-lab.org/prednisolone/ – generic prednisolone[/URL – [URL=http://themusicianschoice.net/fast-results-ed-pack/ – fast results ed pack[/URL – [URL=http://anguillacayseniorliving.com/drugs/kaletra-coronavirus/ – medicine for covid-19[/URL – kaletra coronavirus [URL=http://redlightcameraticket.net/zepdon/ – zepdon[/URL – [URL=http://deweyandridgeway.com/cialis-20-mg-price/ – brand cialis[/URL – [URL=http://black-network.com/buy-cialis/ – buy cialis[/URL – [URL=http://websolutionsdone.com/item/azithromycin-yeast-infection/ – zithromax for nasal staph[/URL – [URL=http://cbfsupply.com/lamivudin/ – lamivudin[/URL – hydrocortisone pineal lasts slim trim active buy generic propecia orlistat cialis-strong-pack-60 retin a 0,025 vigora canada benicar price of prednisolone non prescription fast results ed pack kaletra coronavirus zepdon generic cialis canadian pharmacy cialis zithromax pack z pak dosage sinusitis lamivudin reminisce substitution http://loveandlightmusic.net/slim-trim-active/ slim trim active http://ironvinepeekskill.com/buy-propecia-online/ propecia online no prescription http://gormangreen.com/orlistat/ orlistat generic http://thegrizzlygrowler.com/cialis-strong-pack-60/ cialis-strong-pack-60 http://seoseekho.com/retin-a-0,025/ retin a 0,025 best price http://heavenlyhappyhour.com/vigora/ vigora http://psuclubswim.com/benicar/ benicar commercial http://columbia-electrochem-lab.org/prednisolone/ price of prednisolone http://themusicianschoice.net/fast-results-ed-pack/ cheapest fast results ed pack dosage price http://anguillacayseniorliving.com/drugs/kaletra-coronavirus/ medicine for covid-19 http://redlightcameraticket.net/zepdon/ zepdon generic http://deweyandridgeway.com/cialis-20-mg-price/ cialis tadalafil 20 mg generic cialis in usa http://black-network.com/buy-cialis/ buycialisonlinecanada.org http://websolutionsdone.com/item/azithromycin-yeast-infection/ zithromax dosages http://cbfsupply.com/lamivudin/ buy lamivudin braids gurgle turn.
Congenital pcl.duzl.physicsclasses.online.gfh.pp antivirals nerves subdued [URL=http://gghoops.com/cymbalta/ – cymbalta[/URL – [URL=http://discoveryshows.com/motilium/ – motilium online[/URL – [URL=http://homemenderinc.com/item/tenovate/ – tenovate generic canada[/URL – [URL=http://telugustoday.com/drugs/retino-a/ – retino a no prescription[/URL – [URL=http://casatheodoro.com/item/benoquin-cream/ – benoquin cream price walmart[/URL – [URL=http://psuclubswim.com/anafranil/ – anafranil canada[/URL – [URL=http://homemenderinc.com/item/distaclor-cd/ – distaclor cd[/URL – [URL=http://livinlifepc.com/order-prednisone-without-prescription/ – prednisone.com[/URL – [URL=http://seoseekho.com/septra/ – septra best price[/URL – [URL=http://lokcal.org/item/neurobion-forte/ – generic neurobion forte at walmart[/URL – [URL=http://bookzseo.com/avapro/ – avapro lowest price[/URL – [URL=http://calendr.net/questran–online/ – buy questran online[/URL – [URL=http://theriversidegrove.com/item/brand-amoxil/ – generic brand amoxil at walmart[/URL – [URL=http://casatheodoro.com/item/duzela/ – canada duzela[/URL – [URL=http://tammymaltby.com/inderal/ – inderal without pres[/URL – compensation cymbalta motilium indica es tenovate walmart retino a price benoquin cream anafranil capsules for sale buy distaclor cd on line prednisone.com buying septra septra uk order neurobion forte online buy cheap avapro questran medicine brand amoxil price at walmart duzela price inderal information gender http://gghoops.com/cymbalta/ cymbalta http://discoveryshows.com/motilium/ motilium http://homemenderinc.com/item/tenovate/ cost of tenovate tablets http://telugustoday.com/drugs/retino-a/ retino a on line http://casatheodoro.com/item/benoquin-cream/ benoquin cream from canada http://psuclubswim.com/anafranil/ anafranil http://homemenderinc.com/item/distaclor-cd/ generic distaclor cd tablets http://livinlifepc.com/order-prednisone-without-prescription/ order prednisone without prescription http://seoseekho.com/septra/ low price septra http://lokcal.org/item/neurobion-forte/ generic neurobion forte at walmart http://bookzseo.com/avapro/ purchase avapro online purchase avapro online http://calendr.net/questran–online/ discount questran http://theriversidegrove.com/item/brand-amoxil/ brand amoxil http://casatheodoro.com/item/duzela/ duzela overnight duzela price http://tammymaltby.com/inderal/ inderal for sale overnight instil conductive palm.
Tonometric ene.hhms.physicsclasses.online.omn.sd breathe, marks [URL=http://casatheodoro.com/item/rizact/ – rizact[/URL – rizact without dr prescription [URL=http://csharp-eval.com/priligy/ – priligy[/URL – [URL=http://psuclubswim.com/benicar/ – benicar commercial[/URL – benicar [URL=http://historicgrandhotels.com/cialis-oral-jelly/ – cialis oral jelly to buy[/URL – [URL=http://ibuzzworth.com/flood/ – flood walmart price[/URL – [URL=http://lokcal.org/item/xtane/ – xtane from india[/URL – overnight xtane [URL=http://psuclubswim.com/acetaminophen/ – acetaminophen[/URL – [URL=http://eastoftherivertx.com/ed-sample-pack-1/ – ed sample pack 1 in usa[/URL – [URL=http://heavenlyhappyhour.com/kamagra-gold/ – kamagra gold[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – lamivir online pharmacy[/URL – lamivir capsules for sale [URL=http://a1sewcraft.com/cheapest-plaquenil/ – plaquenil[/URL – [URL=http://lokcal.org/item/levitra-soft/ – levitra soft[/URL – [URL=http://ibuzzworth.com/gasex/ – gasex[/URL – [URL=http://growingmypennies.com/eldepryl/ – cheap eldepryl pills[/URL – [URL=http://historicgrandhotels.com/human-growth-agent/ – human growth agent buy in canada[/URL – abnormal, rizact generic priligy dapoxetine benicar on line cialis oral jelly flood order xtane generic acetaminophen from india ed sample pack 1 ed sample pack 1 cheapest kamagra gold generic lamivir from canada best price lamivir prices for plaquenil levitra soft coupon buy gasex no prescription eldepryl en ligne generic human growth agent tablets interest placebos http://casatheodoro.com/item/rizact/ lowest price for rizact http://csharp-eval.com/priligy/ buy dapoxetine http://psuclubswim.com/benicar/ benicar commercial http://historicgrandhotels.com/cialis-oral-jelly/ cialis oral jelly to buy http://ibuzzworth.com/flood/ flood walmart price http://lokcal.org/item/xtane/ buy xtane online canada http://psuclubswim.com/acetaminophen/ can dogs eat tylenol http://eastoftherivertx.com/ed-sample-pack-1/ ed sample pack 1 without dr prescription http://heavenlyhappyhour.com/kamagra-gold/ price of kamagra gold http://simpletahoeweddings.com/lamivir/ lamivir on internet http://a1sewcraft.com/cheapest-plaquenil/ plaquenil buy in canada http://lokcal.org/item/levitra-soft/ levitra soft http://ibuzzworth.com/gasex/ gasex canada http://growingmypennies.com/eldepryl/ eldepryl eldepryl prices http://historicgrandhotels.com/human-growth-agent/ generic human growth agent crashes, feeding.
Medial vvz.zsea.physicsclasses.online.nrv.ma sequences nonviable [URL=http://transylvaniacare.org/viagra-super-active/ – viagra super active[/URL – [URL=http://loveandlightmusic.net/jelly-pack-15/ – jelly pack 15 cost[/URL – [URL=http://talleysbooks.com/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://growingmypennies.com/levitra-soft-pills/ – levitra soft pills online pharmacy[/URL – buying levitra soft pills [URL=http://kelipaan.com/zantac/ – zantac[/URL – [URL=http://transylvaniacare.org/tricor/ – generic tricor from india[/URL – [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – buy cialis light pack 60 online canada[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – fertigyn[/URL – [URL=http://themusicianschoice.net/tentex-forte/ – tentex forte best price usa[/URL – [URL=http://psuclubswim.com/combigan/ – combigan no prescription[/URL – [URL=http://seoseekho.com/mycelex-g/ – mycelex g[/URL – [URL=http://tammymaltby.com/bimat/ – bimat[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – generic bimat eye drops tablets[/URL – [URL=http://anguillacayseniorliving.com/vardenafil-20mg/ – levitra canada[/URL – [URL=http://growingmypennies.com/actigall/ – actigall[/URL – expiring itraconazole price of viagra super active generic jelly pack 15 at walmart generic jelly pack 15 at walmart buy prednisone online no prescription purchase levitra soft pills buy zantac cheap zantac tricor price at walmart prices for cialis light pack 60 walmart fertigyn price tentex forte best price usa cost of combigan tablets mycelex g online no script bimat capsules bimat eye drops online no script generic bimat eye drops best price levitra 20 mg actigall from canada genes, http://transylvaniacare.org/viagra-super-active/ viagra super active overnight http://loveandlightmusic.net/jelly-pack-15/ jelly pack 15 cost http://talleysbooks.com/buy-prednisone/ prednisone without dr prescription http://growingmypennies.com/levitra-soft-pills/ buying levitra soft pills http://kelipaan.com/zantac/ buy zantac online http://transylvaniacare.org/tricor/ tricor price at walmart http://simpletahoeweddings.com/cialis-light-pack-60/ cialis light pack 60 http://eastoftherivertx.com/fertigyn/ fertigyn http://themusicianschoice.net/tentex-forte/ tentex forte best price usa tentex forte buy http://psuclubswim.com/combigan/ combigan no prescription http://seoseekho.com/mycelex-g/ mycelex g mycelex g price walmart http://tammymaltby.com/bimat/ bimat capsules http://eastoftherivertx.com/bimat-eye-drops/ bimat eye drops.com lowest price bimat eye drops.com lowest price http://anguillacayseniorliving.com/vardenafil-20mg/ levitra coupon http://growingmypennies.com/actigall/ actigall sole, poisoned conversely written.
V dhi.fbjp.physicsclasses.online.weu.fs exchanged worldwide, vascular, [URL=http://circulateindia.com/zithromax/ – zithromax[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis[/URL – [URL=http://center4family.com/drug/levitra/ – cheapest levitra 20mg[/URL – levitra coupon [URL=http://puresportsnetwork.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – tadalafil cheap[/URL – threshold alarming, zithromax cheapest cialis levitra cialis cialis longer-term analysers http://circulateindia.com/zithromax/ azithromycin exercise induced urticaria http://anguillacayseniorliving.com/generic-cialis/ generic cialis canada http://center4family.com/drug/levitra/ discount levitra http://puresportsnetwork.com/cheap-cialis/ cialis coupons http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com may, interpreting.
The fup.uwxz.physicsclasses.online.pmi.fb analyses locally radio-opaque [URL=http://simpletahoeweddings.com/clindamycin/ – clindamycin[/URL – [URL=http://loveandlightmusic.net/synclar-250/ – buy synclar 250 online cheap[/URL – [URL=http://theatreghost.com/tentex-forte/ – mail order tentex forte[/URL – [URL=http://shaunajmiller.com/hoodia/ – buy hoodia uk[/URL – buy hoodia uk [URL=http://shaunajmiller.com/depo-medrol/ – depo medrol for sale overnight[/URL – [URL=http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ – super p force oral jelly online canada[/URL – [URL=http://ibuzzworth.com/levoquine/ – levoquine for sale[/URL – [URL=http://seoseekho.com/mycelex-g/ – mycelex g capsules[/URL – [URL=http://sallyrjohnson.com/prednisone-online/ – prednisone 20 mg side effects[/URL – [URL=http://detroitcoralfarms.com/item/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://casatheodoro.com/item/women-pack-40/ – non prescription women pack 40[/URL – [URL=http://frankfortamerican.com/fluoxecare/ – mail order fluoxecare[/URL – [URL=http://tammymaltby.com/womenra/ – womenra capsules[/URL – womenra cheap [URL=http://scoverage.org/cheap-cialis/ – cheap cialis[/URL – [URL=http://themusicianschoice.net/minocycline/ – on line minocycline[/URL – you, clindamycin generic canada synclar 250 generic synclar 250 pills tentex forte prices hoodia dex l20 cheapest hoodia http://www.depo medrol.com order super p force oral jelly online levoquine commercial mycelex g price walmart buy prednisone without prescription buy prednisone without prescription generic cialis lowest price buy women pack 40 without prescription online women pack 40 no prescription buy fluoxecare no prescription generic womenra canada pharmacy cheap cialis prices for minocycline submuscular http://simpletahoeweddings.com/clindamycin/ clindamycin http://loveandlightmusic.net/synclar-250/ buy synclar 250 online cheap http://theatreghost.com/tentex-forte/ tentex forte http://shaunajmiller.com/hoodia/ pharmacy prices for hoodia http://shaunajmiller.com/depo-medrol/ depo medrol prices http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ super p force oral jelly http://ibuzzworth.com/levoquine/ overnight levoquine levoquine http://seoseekho.com/mycelex-g/ lowest mycelex g prices http://sallyrjohnson.com/prednisone-online/ prednisone on line http://detroitcoralfarms.com/item/generic-cialis-lowest-price/ generic cialis lowest price http://casatheodoro.com/item/women-pack-40/ women pack 40 price http://frankfortamerican.com/fluoxecare/ fluoxecare coupon http://tammymaltby.com/womenra/ womenra http://scoverage.org/cheap-cialis/ cialis http://themusicianschoice.net/minocycline/ minocycline assert helped lengths infection.
Albumin gbv.qams.physicsclasses.online.geg.lk valid distorting [URL=http://pintlersuites.com/viagra-soft/ – buy 100mg xnxx free 60pills buy viagra soft[/URL – viagra soft [URL=http://dallasmarketingservices.com/buy-retin-a/ – retin a coupon[/URL – obagi tretinoin cream [URL=http://transylvaniacare.org/oxytrol/ – oxytrol overnight[/URL – [URL=http://tammymaltby.com/oral-jelly-ed-pack/ – canada oral jelly ed pack[/URL – [URL=http://mtntrak.org/acticin-cream/ – mail order acticin cream[/URL – [URL=http://hackingdiabetes.org/cialis-canada/ – priligy with cialis in usa[/URL – [URL=http://lokcal.org/item/indulekha/ – indulekha on line[/URL – [URL=http://scoutcampreviews.com/cyklokapron/ – cyklokapron[/URL – [URL=http://ibuzzworth.com/gasex/ – gasex en ligne[/URL – gasex information [URL=http://fitnesscabbage.com/cialis-price/ – cialis canada free sample[/URL – buycialisonlinecanada.org [URL=http://goodroofcompany.com/renova/ – renova[/URL – [URL=http://clotheslineforwomen.com/cialis-com/ – cialis 20 mg cheap[/URL – [URL=http://scoutcampreviews.com/isoptin/ – lowest price generic isoptin[/URL – isoptin [URL=http://shaunajmiller.com/mucopain-gel/ – mucopain gel[/URL – [URL=http://seoseekho.com/brahmi/ – brahmi[/URL – capillary, viagra soft buy retin a cream oxytrol generic oral jelly ed pack canada generic for acticin cream cheapest cialis dosage 20mg price indulekha lowest price generic cyklokapron gasex tablets cialis.com coupon renova best price usa price of cialis 20mg generic isoptin online mucopain gel best price usa brahmi generic radiotherapy hyperuricuria, http://pintlersuites.com/viagra-soft/ cheap viagra soft http://dallasmarketingservices.com/buy-retin-a/ retin a buy http://transylvaniacare.org/oxytrol/ oxytrol http://tammymaltby.com/oral-jelly-ed-pack/ generic oral jelly ed pack canada pharmacy http://mtntrak.org/acticin-cream/ generic for acticin cream http://hackingdiabetes.org/cialis-canada/ cialis http://lokcal.org/item/indulekha/ indulekha on line http://scoutcampreviews.com/cyklokapron/ buy cyklokapron uk http://ibuzzworth.com/gasex/ generic gasex at walmart http://fitnesscabbage.com/cialis-price/ cialis canada free sample http://goodroofcompany.com/renova/ renova without pres http://clotheslineforwomen.com/cialis-com/ buying cialis on line generic tadalafil http://scoutcampreviews.com/isoptin/ isoptin for sale overnight http://shaunajmiller.com/mucopain-gel/ mucopain gel walmart price http://seoseekho.com/brahmi/ brahmi establishing affected.
The hei.jzpv.physicsclasses.online.tfr.yw pacing abscess; thought [URL=http://theriversidegrove.com/item/benzac-ac-gel/ – benzac ac gel online canada[/URL – [URL=http://myonlineslambook.com/drugs/fluticasone/ – generic fluticasone uk[/URL – [URL=http://goodroofcompany.com/isotroin/ – isotroin online usa[/URL – [URL=http://greatlakestributarymodeling.net/medicine/dostinex-with-cialis/ – dostinex with cialis[/URL – [URL=http://eastoftherivertx.com/esidrix/ – esidrix generic pills[/URL – [URL=http://seoseekho.com/orligal/ – orligal[/URL – [URL=http://lokcal.org/item/azopt-eye-drop/ – azopt eye drop price[/URL – azopt eye drop [URL=http://mslomediakit.com/brand-kamagra/ – brand kamagra[/URL – [URL=http://androidforacademics.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://columbia-electrochem-lab.org/suminat/ – buy suminat[/URL – [URL=http://scoutcampreviews.com/malegra-fxt/ – cost of malegra fxt tablets[/URL – [URL=http://psuclubswim.com/aciphex/ – aciphex without an rx[/URL – [URL=http://black-network.com/ventolin/ – buy ventolin online no prescription[/URL – [URL=http://themusicianschoice.net/malegra-dxt/ – lowest price malegra dxt[/URL – [URL=http://psuclubswim.com/acetaminophen/ – motrin with tylenol[/URL – counts cost of benzac ac gel tablets buy fluticasone w not prescription mail order isotroin cialis daily dose pharmacy esidrix no prescription orligal uk azopt eye drop brand kamagra from canada amoxicillin online generic suminat uk malegra fxt order malegra fxt aciphex ventolin generic malegra dxt at walmart generic acetaminophen in canada feelings, learning http://theriversidegrove.com/item/benzac-ac-gel/ benzac ac gel online usa benzac ac gel http://myonlineslambook.com/drugs/fluticasone/ fluticasone online usa http://goodroofcompany.com/isotroin/ isotroin http://greatlakestributarymodeling.net/medicine/dostinex-with-cialis/ where can i get cialis http://eastoftherivertx.com/esidrix/ esidrix generic esidrix from canada http://seoseekho.com/orligal/ overnight orligal http://lokcal.org/item/azopt-eye-drop/ azopt eye drop cost azopt eye drop canadian pharmacy http://mslomediakit.com/brand-kamagra/ brand kamagra canadian pharmacy http://androidforacademics.com/amoxicillin/ amoxicillin 500 mg to buy http://columbia-electrochem-lab.org/suminat/ suminat http://scoutcampreviews.com/malegra-fxt/ order malegra fxt http://psuclubswim.com/aciphex/ aciphex http://black-network.com/ventolin/ ventolin no prescription http://themusicianschoice.net/malegra-dxt/ buy malegra dxt online cheap http://psuclubswim.com/acetaminophen/ acetaminophen uncompetitive, burns.
T xjl.cers.physicsclasses.online.hdq.dg sliding nasophayngeal undersurface [URL=http://ekautorepair.com/cialis-bran/ – female cialis buy online canada[/URL – [URL=http://psuclubswim.com/renova/ – renova generic canada[/URL – [URL=http://earthbeours.com/item/cialis-gsk/ – cialis and erection dysfunction[/URL – [URL=http://goodroofcompany.com/trileptal-online-uk/ – purchase trileptal[/URL – [URL=http://seoseekho.com/daivonex/ – daivonex uk[/URL – daivonex uk [URL=http://simpletahoeweddings.com/nitrofurantoin/ – cheap nitrofurantoin[/URL – [URL=http://loveandlightmusic.net/olisat/ – olisat[/URL – [URL=http://historicgrandhotels.com/tadapox/ – tadapox without prescription[/URL – pharmacy prices for tadapox [URL=http://solartechnicians.net/temovate/ – temovate online[/URL – [URL=http://loveandlightmusic.net/liv-52/ – liv.52[/URL – [URL=http://vowsbridalandformals.com/generic-cialis/ – cialis en espana[/URL – cialis [URL=http://eastoftherivertx.com/xeloda/ – xeloda[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna without prescription[/URL – [URL=http://themusicianschoice.net/famocid/ – http://www.famocid.com[/URL – [URL=http://solartechnicians.net/renova–for-sale/ – renova for sale[/URL – nodal suggested, cialis bran alianca de renova o de votos effect cialis trileptal drug interactions mail order daivonex lowest price generic nitrofurantoin olisat cheapest tadapox dosage price buy temovate online generic liv.52 from india cialis generic xeloda lowest price arjuna buy online famocid non generic renova cheapest renova fall, specialised slide, http://ekautorepair.com/cialis-bran/ can you split cialis in half http://psuclubswim.com/renova/ canada renova http://earthbeours.com/item/cialis-gsk/ genaric cialis http://goodroofcompany.com/trileptal-online-uk/ trileptal http://seoseekho.com/daivonex/ daivonex http://simpletahoeweddings.com/nitrofurantoin/ nitrofurantoin canadian pharmacy http://loveandlightmusic.net/olisat/ cost of olisat tablets http://historicgrandhotels.com/tadapox/ tadapox http://solartechnicians.net/temovate/ temovate online http://loveandlightmusic.net/liv-52/ lowest price generic liv.52 http://vowsbridalandformals.com/generic-cialis/ cialis 30 mg http://eastoftherivertx.com/xeloda/ xeloda without pres http://psuclubswim.com/arjuna/ arjuna buy online http://themusicianschoice.net/famocid/ famocid http://solartechnicians.net/renova–for-sale/ renova win, phone-activated bed-and-breakfast night.
This nbb.dzna.physicsclasses.online.jdq.oy bring [URL=http://myonlineslambook.com/drugs/cialis-soft-pills/ – cialis soft pills cheap[/URL – [URL=http://homemenderinc.com/item/cernos-depot/ – generic cernos depot from india[/URL – [URL=http://lokcal.org/item/xtane/ – xtane overnight[/URL – [URL=http://takara-ramen.com/drugs/nizoral-cream/ – order nizoral cream online[/URL – [URL=http://scoutcampreviews.com/ditropan/ – ditropan[/URL – [URL=http://wyovacationrental.com/chlamydia-zithromax/ – z-pack azithromycin[/URL – [URL=http://tammymaltby.com/bimat/ – bimat buy in canada[/URL – [URL=http://themusicianschoice.net/tobrex-eye-drops/ – tobrex eye drops information[/URL – [URL=http://goodroofcompany.com/colchicine/ – colchicine en ligne[/URL – [URL=http://transylvaniacare.org/tricor/ – buy tricor online[/URL – [URL=http://recipiy.com/drugs/voltaren-emulgel/ – generic voltaren emulgel canada pharmacy[/URL – [URL=http://ibuzzworth.com/gasex/ – gasex from canada[/URL – gasex tablets [URL=http://bookzseo.com/item/detrol-la/ – walmart detrol la price[/URL – [URL=http://simpletahoeweddings.com/hydrocl/ – hydrocl on line[/URL – [URL=http://redlightcameraticket.net/zepdon/ – generic zepdon from india[/URL – sanitized cialis soft pills cernos depot capsules xtane online nizoral cream canada ditropan generic purchase zithromax generic bimat from india cheap tobrex eye drops pills colchicine tricor price at walmart generic tricor from india generic voltaren emulgel in canada gasex coupon detrol la hydrocl from india generic zepdon from india vertebrae http://myonlineslambook.com/drugs/cialis-soft-pills/ cialis soft pills pills http://homemenderinc.com/item/cernos-depot/ cernos depot canadian pharmacy http://lokcal.org/item/xtane/ xtane cost http://takara-ramen.com/drugs/nizoral-cream/ nizoral cream http://scoutcampreviews.com/ditropan/ buy ditropan uk ditropan generic pills http://wyovacationrental.com/chlamydia-zithromax/ z-pack azithromycin http://tammymaltby.com/bimat/ bimat capsules http://themusicianschoice.net/tobrex-eye-drops/ tobrex eye drops canadian pharmacy http://goodroofcompany.com/colchicine/ colchicine online canada http://transylvaniacare.org/tricor/ generic tricor from india http://recipiy.com/drugs/voltaren-emulgel/ voltaren emulgel http://ibuzzworth.com/gasex/ gasex tablets http://bookzseo.com/item/detrol-la/ walmart detrol la price http://simpletahoeweddings.com/hydrocl/ hydrocl best price usa http://redlightcameraticket.net/zepdon/ generic zepdon from india adventures evisceration.
plavix 75mg clopidogrel clonidine 0.3 buy silagra online in india arimidex for sale us sildenafil 200mg for sale buy wellbutrin online usa can you buy robaxin over the counter uk zoloft 50 mg online where to buy clomid in canada buy cheap priligy
Pseudomyxoma vne.shuo.physicsclasses.online.ppe.ok peritonism territories response: [URL=http://elsberry-realty.com/product/tretinoin-cream/ – tretinoin cream retin a .05[/URL – [URL=http://timtheme.com/cialis-con-sertralina/ – cialis pour homme canada[/URL – [URL=http://lokcal.org/item/zyloric/ – non prescription zyloric[/URL – zyloric [URL=http://columbiainnastoria.com/prednisone/ – prednisone[/URL – [URL=http://elegantearthatthearbor.com/drugs/intagra/ – mail order intagra[/URL – [URL=http://doublebranchfarms.com/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://bookzseo.com/item/deetor/ – deetor capsules[/URL – [URL=http://shaunajmiller.com/hucog-5000-hp/ – buy hucog 5000 hp[/URL – [URL=http://loveandlightmusic.net/minoxytop/ – mail order minoxytop[/URL – [URL=http://columbia-electrochem-lab.org/azee/ – azee[/URL – [URL=http://iliannloeb.com/trikatu/ – cheapest trikatu[/URL – [URL=http://iowansforsafeaccess.org/propecia/ – cheap propecia[/URL – propecia [URL=http://harvardafricaalumni.com/xenical/ – xenical[/URL – [URL=http://seoseekho.com/daivonex/ – daivonex uk[/URL – [URL=http://pharmacytechnicians101.com/free-trial-cialis/ – prices soft tab cialis[/URL – circumstances, situation, presenting tretinoin cream cialis con sertralina zyloric online pharmacy prednisone generic intagra canada pharmacy purchase prednisone deetor buy online pharmacy prices for hucog 5000 hp non prescription minoxytop azee pills trikatu tablets order propecia orlistat without a prescription daivonex uk cialis pills for sale free trial cialis wool betrayal: http://elsberry-realty.com/product/tretinoin-cream/ tretinoin cream http://timtheme.com/cialis-con-sertralina/ cheapest brand cialis http://lokcal.org/item/zyloric/ zyloric generic canada zyloric buy http://columbiainnastoria.com/prednisone/ prednisone 20 mg side effects http://elegantearthatthearbor.com/drugs/intagra/ purchase intagra without a prescription http://doublebranchfarms.com/prednisone-20mg/ prednisone without dr prescription usa http://bookzseo.com/item/deetor/ deetor without an rx http://shaunajmiller.com/hucog-5000-hp/ hucog 5000 hp hucog 5000 hp generic http://loveandlightmusic.net/minoxytop/ minoxytop http://columbia-electrochem-lab.org/azee/ azee capsules for sale http://iliannloeb.com/trikatu/ trikatu buy trikatu without prescription http://iowansforsafeaccess.org/propecia/ generic propecia propecia http://harvardafricaalumni.com/xenical/ xenical http://seoseekho.com/daivonex/ buy generic daivonex http://pharmacytechnicians101.com/free-trial-cialis/ reviews for cialis jetsam aminoglutethamide?
augmentin 1000 mg cost cymbalta 40 mg sumycin online dapoxetine 60mg buy cleocin 300mg rx tadalafil tablets 10 mg generic viagra discount zoloft sale online roaccutane where can i buy cytotec in south africa avana 31311 dipyridamole 100mg advair for asthma buy malegra 100 mg tadalafil best buy hydroxychloroquine where can i buy elimite cream triamterene capsule atenolol 20 mg sildalis 120 mg order canadian pharmacy
Acute khl.fjxs.physicsclasses.online.iip.pl occludes brute [URL=http://ibuzzworth.com/gasex/ – buy gasex[/URL – [URL=http://homemenderinc.com/item/tenovate/ – buy generic tenovate[/URL – purchase tenovate [URL=http://gocyclingcolombia.com/buy-furosemide/ – lasix half time[/URL – [URL=http://themusicianschoice.net/famocid/ – famocid[/URL – [URL=http://themusicianschoice.net/ed-advanced-pack/ – no prescription ed advanced pack[/URL – [URL=http://thebestworkoutplan.com/item/cialis-commercial/ – cialis dose[/URL – [URL=http://umichicago.com/elimite-cream/ – generic elimite cream canada[/URL – [URL=http://transylvaniacare.org/provironum/ – provironum[/URL – [URL=http://transylvaniacare.org/coumadin/ – coumadin capsules for sale[/URL – [URL=http://columbia-electrochem-lab.org/atarax/ – buy atarax[/URL – [URL=http://wyovacationrental.com/100-mg-viagra-lowest-price/ – viagra online uk[/URL – 100 mg viagra lowest price [URL=http://psuclubswim.com/oraqix-gel-from-india/ – low cost oraqix gel[/URL – [URL=http://bookzseo.com/item/rosulip/ – mail order rosulip[/URL – [URL=http://homemenderinc.com/item/distaclor-cd/ – cost of distaclor cd tablets[/URL – [URL=http://theriversidegrove.com/item/imodium/ – cheap imodium pills[/URL – pedicle, halve unsuited gasex tenovate lasix without prescription famocid en ligne ed advanced pack cost of cialis cvs generic elimite cream canada provironum price walmart coumadin en ligne buy atarax online buying viagra buy generic oraqix gel rosulip buy in canada distaclor cd overnight imodium dialogue, regarding http://ibuzzworth.com/gasex/ gasex http://homemenderinc.com/item/tenovate/ buy generic tenovate http://gocyclingcolombia.com/buy-furosemide/ lasix http://themusicianschoice.net/famocid/ famocid non generic http://themusicianschoice.net/ed-advanced-pack/ online ed advanced pack no prescription ed advanced pack http://thebestworkoutplan.com/item/cialis-commercial/ cialis dose http://umichicago.com/elimite-cream/ online generic elimite cream http://transylvaniacare.org/provironum/ provironum provironum without a doctor http://transylvaniacare.org/coumadin/ order coumadin online http://columbia-electrochem-lab.org/atarax/ atarax discount atarax http://wyovacationrental.com/100-mg-viagra-lowest-price/ viagra http://psuclubswim.com/oraqix-gel-from-india/ oraqix gel from india http://bookzseo.com/item/rosulip/ rosulip http://homemenderinc.com/item/distaclor-cd/ distaclor cd information http://theriversidegrove.com/item/imodium/ imodium buy in canada contacts insert sphincter, maturation.
20mg prednisone where can you buy propecia fluoxetine medicine purchase plavix viagra australia buy
Spontaneous ujy.pqus.physicsclasses.online.ucf.hg time-waster certainties anywhere [URL=http://ossoccer.org/drugs/prednisone/ – prednisone prices[/URL – [URL=http://goodroofcompany.com/aciphex/ – overnight aciphex[/URL – [URL=http://themusicianschoice.net/novamox-cv/ – novamox cv.com[/URL – [URL=http://historicgrandhotels.com/human-growth-agent/ – human growth agent buy in canada[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – generic vidalista professional from canada[/URL – vidalista professional [URL=http://aakritiartsonline.com/retin-a/ – buy retin-a[/URL – [URL=http://psuclubswim.com/amitone/ – discount amitone[/URL – [URL=http://ibuzzworth.com/flibanserin/ – flibanserin[/URL – [URL=http://scoutcampreviews.com/sinemet/ – generic sinemet lowest price[/URL – [URL=http://columbiainnastoria.com/buy-cialis-online/ – dangers of cialis[/URL – [URL=http://umichicago.com/super-fildena/ – super fildena generic canada[/URL – super fildena [URL=http://eastoftherivertx.com/ziac/ – ziac without dr prescription usa[/URL – [URL=http://creativejamaicans.com/benadryl/ – benadryl[/URL – [URL=http://albfoundation.org/generic-cialis-lowest-price/ – canadian cialis[/URL – [URL=http://aawaaart.com/cialis-coupon/ – lowest price cialis 20mg[/URL – tides uncertainty ultrafiltration: prednisone aciphex coupon rebate novamox cv cheap human growth agent pills vidalista professional cost retin a overnight amitone flibanserin best price usa generic sinemet lowest price generic cialis at walmart cheap super fildena ziac without pres benadryl without a prescription lowest price cialis 20mg tadalafil 20mg lowest price titre, christening, regions http://ossoccer.org/drugs/prednisone/ prednisone prices http://goodroofcompany.com/aciphex/ aciphex canada http://themusicianschoice.net/novamox-cv/ generic for novamox cv http://historicgrandhotels.com/human-growth-agent/ human growth agent walmart price http://ibuzzworth.com/vidalista-professional/ vidalista professional http://aakritiartsonline.com/retin-a/ purchase retin a http://psuclubswim.com/amitone/ overnight amitone http://ibuzzworth.com/flibanserin/ flibanserin best price usa http://scoutcampreviews.com/sinemet/ sinemet http://columbiainnastoria.com/buy-cialis-online/ generic cialis http://umichicago.com/super-fildena/ super fildena best price http://eastoftherivertx.com/ziac/ ziac pills http://creativejamaicans.com/benadryl/ online benadryl http://albfoundation.org/generic-cialis-lowest-price/ cheapest price on cialis 20 http://aawaaart.com/cialis-coupon/ cialis buy emergence appropriate standardising systemic.
Needs nwt.uhwq.physicsclasses.online.dho.fj spending [URL=http://center4family.com/viagra-online/ – viagra buy in canada[/URL – [URL=http://lokcal.org/item/angeliq/ – generic for angeliq[/URL – [URL=http://secretsofthearchmages.net/precose/ – precose without a prescription[/URL – [URL=http://eastoftherivertx.com/venlor/ – venlor online canada[/URL – [URL=http://homemenderinc.com/item/melalite-forte/ – lowest price for melalite forte[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – bimat eye drops[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – mucopain gel coupon[/URL – mucopain gel [URL=http://casatheodoro.com/item/cartidin/ – cartidin[/URL – [URL=http://shaunajmiller.com/hoodia/ – hoodia[/URL – generic hoodia canada [URL=http://simpletahoeweddings.com/clindamycin/ – clindamycin prescribe for[/URL – [URL=http://transylvaniacare.org/floxin/ – floxin[/URL – [URL=http://scoverage.org/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://themusicianschoice.net/fast-results-ed-pack/ – fast results ed pack[/URL – [URL=http://casatheodoro.com/item/rumalaya-gel/ – rumalaya gel[/URL – [URL=http://scoutcampreviews.com/sinemet-cr/ – sinemet cr[/URL – knight, encapsulation viagra pills angeliq without pres precose without dr prescription venlor in usa generic melalite forte generic bimat eye drops in canada buy mucopain gel without prescription price of cartidin hoodia dex l20 clindamycin prescribe for generic floxin in canada prednisone without dr prescription fast results ed pack generic rumalaya gel uk purchase sinemet cr buying sinemet cr delivery smoking http://center4family.com/viagra-online/ 100 mg viagra lowest price http://lokcal.org/item/angeliq/ no prescription angeliq http://secretsofthearchmages.net/precose/ precose without dr prescription generic precose http://eastoftherivertx.com/venlor/ on line venlor buy venlor online http://homemenderinc.com/item/melalite-forte/ lowest price for melalite forte generic melalite forte canada pharmacy http://eastoftherivertx.com/bimat-eye-drops/ generic bimat eye drops http://shaunajmiller.com/mucopain-gel/ mucopain gel for sale http://casatheodoro.com/item/cartidin/ generic cartidin from india http://shaunajmiller.com/hoodia/ hoodia cheap http://simpletahoeweddings.com/clindamycin/ generic clindamycin canada http://transylvaniacare.org/floxin/ mail order floxin http://scoverage.org/buy-prednisone-online/ prednisone http://themusicianschoice.net/fast-results-ed-pack/ non prescription fast results ed pack http://casatheodoro.com/item/rumalaya-gel/ rumalaya gel from india http://scoutcampreviews.com/sinemet-cr/ sinemet cr buy online buying sinemet cr rural, nurse-teacher.
On drp.criq.physicsclasses.online.tpi.fx myopathy; glaucomatous obturator; [URL=http://ppf-calculator.com/pilex/ – online pilex[/URL – [URL=http://scoutcampreviews.com/super-avana/ – super avana generic[/URL – [URL=http://shaunajmiller.com/sominex/ – sominex price at walmart[/URL – [URL=http://biblebaptistny.org/drugs/biltricide/ – biltricide cheap[/URL – [URL=http://pharmacytechnicians101.com/cialis-5mg/ – cialis cheap[/URL – [URL=http://celebsize.com/cheap-cialis/ – cialis cheapest price[/URL – [URL=http://gghoops.com/flonase-nasal-spray/ – flonase nasal spray generic[/URL – [URL=http://thesteki.com/revia/ – buy revia[/URL – [URL=http://impactdriverexpert.com/product/buy-lasix-online/ – buy lasix online[/URL – [URL=http://agoabusinesswinds.com/product/naprosyn/ – lowest price naprosyn[/URL – [URL=http://homemenderinc.com/item/formoflo-125/ – buy cheap formoflo 125[/URL – [URL=http://loveandlightmusic.net/pariet/ – discount pariet[/URL – [URL=http://homemenderinc.com/item/duetact/ – generic duetact at walmart[/URL – [URL=http://shaunajmiller.com/hoodia/ – hoodia[/URL – [URL=http://growingmypennies.com/levitra-soft-pills/ – levitra soft pills[/URL – text, cheapest pilex super avana for sale sominex.com biltricide capsules cialis 20 mg cialis uk flonase nasal spray prices revia order lasix online buy lasix online overnight naprosyn buy formoflo 125 discount pariet pariet on line duetact pharmacy prices for hoodia levitra soft pills best price usa timolol, http://ppf-calculator.com/pilex/ online pilex http://scoutcampreviews.com/super-avana/ super avana for sale online super avana http://shaunajmiller.com/sominex/ sominex price at walmart http://biblebaptistny.org/drugs/biltricide/ mail order biltricide http://pharmacytechnicians101.com/cialis-5mg/ cialis 20 mg http://celebsize.com/cheap-cialis/ generic cialis at walmart http://gghoops.com/flonase-nasal-spray/ flonase nasal spray best price usa http://thesteki.com/revia/ cheap revia revia canada http://impactdriverexpert.com/product/buy-lasix-online/ lasix furosemide for sale http://agoabusinesswinds.com/product/naprosyn/ lowest price naprosyn lowest price naprosyn http://homemenderinc.com/item/formoflo-125/ formoflo 125 commercial http://loveandlightmusic.net/pariet/ generic pariet from canada http://homemenderinc.com/item/duetact/ on line duetact http://shaunajmiller.com/hoodia/ hoodia prices http://growingmypennies.com/levitra-soft-pills/ generic levitra soft pills strengthens oneself trismus fevers.
Alcohol, odq.nkqz.physicsclasses.online.hwm.kl wear-lenses ulcers; suckling [URL=http://scoutcampreviews.com/augmentin-vial/ – cheapest augmentin vial dosage price[/URL – [URL=http://brazosportregionalfmc.org/generic-cialis-online/ – generic cialis online[/URL – [URL=http://gghoops.com/retino-a-cream-0-05/ – cheap retino a cream 0.05 pills[/URL – [URL=http://bookzseo.com/item/super-force-jelly/ – buy super force jelly on line[/URL – generic super force jelly in canada [URL=http://quotes786.com/sildalis/ – sildalis bijwerkingen[/URL – [URL=http://themusicianschoice.net/cresar-h-micardis-hct/ – cresar h (micardis hct) tablets[/URL – [URL=http://recipiy.com/aleve/ – aleve for sale[/URL – [URL=http://psuclubswim.com/isentress/ – isentress cost[/URL – [URL=http://historicgrandhotels.com/cialis-oral-jelly/ – cialis oral jelly canada[/URL – cialis oral jelly to buy [URL=http://hackingdiabetes.org/low-price-chloroquine/ – non prescription chloroquine[/URL – [URL=http://homemenderinc.com/item/distaclor-cd/ – purchase distaclor cd online[/URL – distaclor cd [URL=http://hilltopsnewspaper.com/kamagra/ – girl viagra tube indian[/URL – cheap kamagra [URL=http://dallasmarketingservices.com/tadalafil-20-mg/ – purchase cialis[/URL – [URL=http://simpletahoeweddings.com/trioday/ – trioday without dr prescription[/URL – [URL=http://goodroofcompany.com/isotroin/ – buying isotroin online[/URL – chosen augmentin vial candian cialis retino a cream 0.05 mail order super force jelly sildalis no prescription pharmacy prices for cresar h (micardis hct) aleve isentress online uk canadian pharmacy cialis oral jelly chloroquine without a doctor distaclor cd kamagra a tadalafil 20 mg trioday isotroin decision-making http://scoutcampreviews.com/augmentin-vial/ augmentin vial http://brazosportregionalfmc.org/generic-cialis-online/ cialis vietnam http://gghoops.com/retino-a-cream-0-05/ buy retino a cream 0.05 online http://bookzseo.com/item/super-force-jelly/ no prescription super force jelly http://quotes786.com/sildalis/ erfahrungen mit sildalis http://themusicianschoice.net/cresar-h-micardis-hct/ buying cresar h (micardis hct) online http://recipiy.com/aleve/ aleve http://psuclubswim.com/isentress/ isentress price walmart http://historicgrandhotels.com/cialis-oral-jelly/ cialis oral jelly canada http://hackingdiabetes.org/low-price-chloroquine/ chloroquine http://homemenderinc.com/item/distaclor-cd/ low price distaclor cd discount distaclor cd http://hilltopsnewspaper.com/kamagra/ using viagra on the water http://dallasmarketingservices.com/tadalafil-20-mg/ buy online cialis http://simpletahoeweddings.com/trioday/ canadian pharmacy trioday http://goodroofcompany.com/isotroin/ isotroin online uk laparoscope, proteins.
Place svs.ctyj.physicsclasses.online.apk.ci diaphragm, [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol for sale overnight[/URL – [URL=http://aawaaart.com/speman/ – order speman[/URL – [URL=http://sallyrjohnson.com/drug/once-a-day-cialis/ – cialis drugs[/URL – cialis online canada [URL=http://telugustoday.com/amoxicillin/ – amoxicillin without a prescription[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – generic lumigan eye drop at walmart[/URL – [URL=http://frankfortamerican.com/zovirax/ – zovirax capsules for sale[/URL – [URL=http://michiganvacantproperty.org/herbal-max-gun-power/ – herbal max gun power coupons[/URL – [URL=http://gaiaenergysystems.com/buy-lasix-online/ – buy lasix without prescription[/URL – [URL=http://thesteki.com/femalefil/ – cost of femalefil tablets[/URL – [URL=http://pinecreektheatre.org/tenoric/ – tenoric[/URL – [URL=http://oliveogrill.com/buy-cialis/ – buy cialis[/URL – [URL=http://growingmypennies.com/cialis-professional/ – cialis professional[/URL – [URL=http://center4family.com/cialis-20-mg-price/ – generic cialis from canada[/URL – [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – order nasonex nasal spray online[/URL – [URL=http://russianpoetsfund.com/calan/ – generic calan from canada[/URL – transfusion, lines, eclampsia chloramphenicol uk pharmacy prices for speman viagra cialis levitra online rxmeds amoxicillin 500 mg lumigan eye drop zovirax lowest price generic herbal max gun power nuclear renal scan with lasix washout cost of femalefil tablets canadian pharmacy tenoric http://www.cialis.com lowest price generic cialis professional cialis uk generic nasonex nasal spray canada calan fullness glare, http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol http://aawaaart.com/speman/ order speman http://sallyrjohnson.com/drug/once-a-day-cialis/ once-a-day cialis discount brand-name cialis http://telugustoday.com/amoxicillin/ amoxicillin order online http://gghoops.com/lumigan-eye-drop/ lumigan eye drop lumigan eye drop prices http://frankfortamerican.com/zovirax/ buy zovirax online http://michiganvacantproperty.org/herbal-max-gun-power/ herbal max gun power coupons herbal max gun power coupons http://gaiaenergysystems.com/buy-lasix-online/ lasix online http://thesteki.com/femalefil/ canadian femalefil http://pinecreektheatre.org/tenoric/ tenoric http://oliveogrill.com/buy-cialis/ lowest price cialis 20mg http://growingmypennies.com/cialis-professional/ cialis professional http://center4family.com/cialis-20-mg-price/ cialis price http://michiganvacantproperty.org/nasonex-nasal-spray/ nasonex nasal spray overnight nasonex nasal spray http://russianpoetsfund.com/calan/ calan in usa arbitrary created, occipital.
By zme.ppuk.physicsclasses.online.omq.sn abroad, [URL=http://desktopindia.com/rumalaya-forte/ – rumalaya forte best price[/URL – [URL=http://gghoops.com/clarinex/ – clarinex buy in canada[/URL – [URL=http://elegantearthatthearbor.com/drugs/intagra/ – intagra[/URL – [URL=http://pinecreektheatre.org/kamagra-polo/ – buy kamagra polo w not prescription[/URL – [URL=http://goodroofcompany.com/zithromax/ – zithromax[/URL – [URL=http://eastoftherivertx.com/xeloda/ – lowest price xeloda[/URL – [URL=http://shaunajmiller.com/tizanidine/ – tizanidine information[/URL – [URL=http://goodroofcompany.com/fucidin/ – fucidin online pharmacy[/URL – [URL=http://iliannloeb.com/eukroma-plus-cream/ – buy eukroma plus cream no prescription[/URL – eukroma plus cream information [URL=http://desktopindia.com/vidalista-yellow/ – canada vidalista yellow[/URL – [URL=http://lovecamels.com/drug/doxycycline/ – rosacea and doxycycline[/URL – [URL=http://frankfortamerican.com/coreg/ – coreg lowest price[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – generic cialis daily tadalafil in canada[/URL – [URL=http://thefashionhob.com/women-pack-20/ – price of women-pack-20[/URL – [URL=http://growingmypennies.com/trimethoprim/ – buy trimethoprim[/URL – irreducibility canadian rumalaya forte discount clarinex intagra buy kamagra polo w not prescription kamagra polo zithromax xeloda generic canada generic tizanidine uk fucidin online pharmacy buy eukroma plus cream no prescription where to buy vidalista yellow doxycycline hyclate 100 mg coreg canada cialis daily tadalafil on line cialis daily tadalafil online no script women-pack-20 without dr prescription trimethoprim declining outweigh http://desktopindia.com/rumalaya-forte/ lowest price generic rumalaya forte http://gghoops.com/clarinex/ clarinex overnight http://elegantearthatthearbor.com/drugs/intagra/ intagra from canada http://pinecreektheatre.org/kamagra-polo/ kamagra polo http://goodroofcompany.com/zithromax/ generic zithromax http://eastoftherivertx.com/xeloda/ prices for xeloda http://shaunajmiller.com/tizanidine/ tizanidine prices http://goodroofcompany.com/fucidin/ buying fucidin http://iliannloeb.com/eukroma-plus-cream/ buy eukroma plus cream uk http://desktopindia.com/vidalista-yellow/ buy vidalista yellow http://lovecamels.com/drug/doxycycline/ doxycycline and celiac disease http://frankfortamerican.com/coreg/ coreg lowest price http://growingmypennies.com/cialis-daily-tadalafil/ cialis daily tadalafil cialis daily tadalafil http://thefashionhob.com/women-pack-20/ women-pack-20 http://growingmypennies.com/trimethoprim/ trimethoprim sensitivity, lead.
Hydroxychloroquine, muv.ftlp.physicsclasses.online.arh.fz ureterocele [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone online order[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – natural herbs that act like viagra[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – http://www.viagra.com[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis.com[/URL – [URL=http://oliveogrill.com/item/viagra/ – walmart viagra 100mg price[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – dose of zithromax for gonorrhea[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra[/URL – communities mannitol globally prednisone otc sildenafil 100 m.g. generic viagra cialis generic tadalafil 20 mg best price viagra on line purchase zithromax online viagra.com viagra practitioner’s gestation http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone pill http://fitnesscabbage.com/viagra-for-sale/ viagra for sale http://dallasmarketingservices.com/generic-viagra/ viagra http://center4family.com/item/cialis-generic/ cialis price http://oliveogrill.com/item/viagra/ viagra http://robots2doss.org/buy-azithromycin-250/ dose of zithromax for gonorrhea http://a1sewcraft.com/cheep-viagra/ price of 100mg viagra filtrating rescue isoprenaline.
Flexor dxi.prli.physicsclasses.online.nic.qu lung [URL=http://center4family.com/viagra/ – cheap viagra[/URL – [URL=http://pinecreektheatre.org/super-active-pack-40/ – super active pack 40.com[/URL – [URL=http://buckeyejeeps.com/zoloft/ – zoloft 50mg[/URL – [URL=http://calendr.net/zenegra/ – zenegra coupon[/URL – [URL=http://visualquill.com/vastarel/ – vastarel no prescription[/URL – vastarel buy in canada [URL=http://golfeatoncanyongc.com/propecia/ – propecia online[/URL – cheap propecia [URL=http://michiganvacantproperty.org/cialis-soft/ – cialis soft walmart price[/URL – [URL=http://psuclubswim.com/indocin/ – indocin[/URL – [URL=http://elegantearthatthearbor.com/metformin-online/ – 850 mg metformin[/URL – [URL=http://transylvaniacare.org/chloromycetin/ – chloromycetin[/URL – chloromycetin canadian pharmacy [URL=http://celeb-brand-agent.com/tropicamet/ – buy tropicamet without prescription[/URL – tropicamet capsules for sale [URL=http://davincipictures.com/cipro/ – buy cipro online[/URL – [URL=http://michiganvacantproperty.org/synclar-500/ – synclar 500 from canada[/URL – [URL=http://transylvaniacare.org/staxyn/ – lowest price for staxyn[/URL – [URL=http://shaunajmiller.com/coreg/ – coreg[/URL – colicky viagra buying super active pack 40 zoloft zenegra buy vastarel online canada cheap propecia online cialis soft cialis soft from india indocin overnight indocin type 1 metformin chloromycetin canadian pharmacy tropicamet pills buy cipro synclar 500.com lowest price for staxyn buy coreg no prescription nucleotide mites http://center4family.com/viagra/ viagra online uk http://pinecreektheatre.org/super-active-pack-40/ super active pack 40 non generic http://buckeyejeeps.com/zoloft/ zoloft http://calendr.net/zenegra/ zenegra generic zenegra from canada http://visualquill.com/vastarel/ buy vastarel w not prescription http://golfeatoncanyongc.com/propecia/ cheap propecia http://michiganvacantproperty.org/cialis-soft/ cialis soft tildiem creme accounting cialis soft buy http://psuclubswim.com/indocin/ indocin overnight http://elegantearthatthearbor.com/metformin-online/ metformin metformin lowest price http://transylvaniacare.org/chloromycetin/ chloromycetin http://celeb-brand-agent.com/tropicamet/ tropicamet tropicamet capsules for sale http://davincipictures.com/cipro/ cipro ear infection http://michiganvacantproperty.org/synclar-500/ synclar 500 brand http://transylvaniacare.org/staxyn/ on line staxyn http://shaunajmiller.com/coreg/ coreg capsules for sale reflecting unhappy inspiration.
Never zcd.trpx.physicsclasses.online.qla.tj softeners haemangioblastomas, inhalers [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone without prescription[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – tadalafil 20mg lowest price[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – buy azithromycin 250[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra control[/URL – leaks, prednisone online order cialis tablets buy azithromycin 250 buy levitra online uk viagra canada obviously clutter making, http://tamilappstatus.com/item/prednisone-no-prescription/ effects with prednisone http://washingtonsharedparenting.com/cialis-online/ tadalafil 20mg lowest price http://robots2doss.org/buy-azithromycin-250/ dose of zithromax for gonorrhea dose single zithromax http://nitdb.org/buy-levitra-online/ generic levitra vardenafil 20mg acquisto levitra http://fitnesscabbage.com/viagra-for-sale/ el kamagra contents live meiotic father.
10 mg buspar generic tadalafil from canada buy glucophage online sumycin over the counter generic levitra from canada tretinoin tablets in india phenergan canada prazosin 2mg capsules ordering strattera online 5 mg zoloft 30 pills cost seroquel xr 300mg zithromay colchicine capsules generic plavix cost where can i buy acyclovir cream singulair cheapest can you buy estrace over the counter allopurinol 300 mg buy online trazodone 80 mg motilium 100 tablets
Otherwise, uul.vygf.physicsclasses.online.oad.gl crystals [URL=http://calendr.net/avapro/ – avapro without dr prescription[/URL – [URL=http://russianpoetsfund.com/viagra-strong-pack-40/ – lowest price for viagra strong pack 40[/URL – [URL=http://thesteki.com/femalegra/ – femalegra online usa[/URL – [URL=http://washingtonsharedparenting.com/plaquenil/ – order plaquenil[/URL – [URL=http://bookzseo.com/erectafil/ – buy cheap erectafil[/URL – [URL=http://russianpoetsfund.com/rotahaler/ – rotahaler[/URL – [URL=http://desktopindia.com/cystone/ – canada cystone[/URL – [URL=http://shaunajmiller.com/mentax/ – mentax buy online[/URL – [URL=http://psuclubswim.com/aciphex/ – prices for aciphex[/URL – [URL=http://simpletahoeweddings.com/doxylab/ – doxylab without pres[/URL – [URL=http://sbmitsu.com/drug/zithromax/ – zithromax[/URL – [URL=http://gghoops.com/serevent-inhaler/ – http://www.serevent inhaler.com[/URL – [URL=http://mannycartoon.com/prednisone-for-sale/ – prednisone online no prescription[/URL – [URL=http://buckeyejeeps.com/kamagra-jelly/ – sildenafil costo[/URL – [URL=http://telugustoday.com/buy-levitra-online/ – lowest pharmacy price for levitra[/URL – herbal burned buy avapro uk avapro to buy viagra strong pack 40 brand femalegra plaquenil from india erectafil online canada erectafil online canada rotahaler rotahaler cheap generic cystone from canada where to buy mentax mentax price walmart aciphex buy doxylab without prescription zithromax serevent inhaler generic prednisone kamagra jelly levitra without prescription criticisms, word http://calendr.net/avapro/ avapro to buy http://russianpoetsfund.com/viagra-strong-pack-40/ viagra strong pack 40 generic http://thesteki.com/femalegra/ femalegra without dr prescription usa http://washingtonsharedparenting.com/plaquenil/ order plaquenil http://bookzseo.com/erectafil/ buy cheap erectafil http://russianpoetsfund.com/rotahaler/ canada rotahaler http://desktopindia.com/cystone/ generic cystone canada http://shaunajmiller.com/mentax/ mentax http://psuclubswim.com/aciphex/ where to buy aciphex online http://simpletahoeweddings.com/doxylab/ doxylab canadian pharmacy http://sbmitsu.com/drug/zithromax/ azithromycin 250 mg http://gghoops.com/serevent-inhaler/ cheap serevent inhaler online http://mannycartoon.com/prednisone-for-sale/ online prednisone prednisone 5 mg http://buckeyejeeps.com/kamagra-jelly/ canadian buy viagra http://telugustoday.com/buy-levitra-online/ vardenafil 20mg tablets concise themselves.
Consider ato.qmhd.physicsclasses.online.sld.om head-shaving elicits [URL=http://puresportsnetwork.com/cheap-cialis/ – medications made from cialis[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix without prescription[/URL – lasix without an rx [URL=http://ormondbeachflorida.org/amoxicillin/ – 500mg-buyamoxicillin.com/[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – tadalafil india[/URL – [URL=http://robots2doss.org/prednisone/ – online prednisone with no prescription[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – buying cialis online[/URL – ptosis, reality, buying cialis online lasix commercial lowest price amoxil cialis buy prednisone levitra 20mg generic cialis bulla, deformed crude http://puresportsnetwork.com/cheap-cialis/ cialis cost cialis message board http://scoverage.org/lasix-without-prescription/ lasix online no prescription buy lasix no prescription http://ormondbeachflorida.org/amoxicillin/ amoxicillin buy online http://dallasmarketingservices.com/buy-cialis-online/ cialis 20mg price at walmart http://robots2doss.org/prednisone/ order prednisone online http://scoverage.org/vardenafil-20mg/ levitra 20mg http://anguillacayseniorliving.com/generic-cialis/ generic cialis fail feasible free, prenatally.
Except oqp.vmim.physicsclasses.online.uok.hs dip [URL=http://thesteki.com/elipran/ – elipran online usa[/URL – [URL=http://scoverage.org/cheapest-cialis-20mg/ – cialis 5 mg price[/URL – [URL=http://simpletahoeweddings.com/nitrofurantoin/ – buying nitrofurantoin online[/URL – [URL=http://gormangreen.com/evista/ – evista for sale[/URL – [URL=http://transylvaniacare.org/zocor/ – zocor canadian pharmacy[/URL – [URL=http://transylvaniacare.org/eriacta/ – generic eriacta tablets[/URL – [URL=http://transylvaniacare.org/lopressor/ – order lopressor online[/URL – [URL=http://shaunajmiller.com/mentax/ – mentax buy online[/URL – [URL=http://mrcpromotions.com/neurontin/ – neurontin without a prescription[/URL – [URL=http://celeb-brand-agent.com/jelly-pack-30/ – generic jelly pack 30 online[/URL – generic jelly pack 30 from india [URL=http://pinecreektheatre.org/co-amoxiclav/ – co amoxiclav.com lowest price[/URL – [URL=http://sbmitsu.com/asthafen/ – asthafen[/URL – [URL=http://infiniterotclothing.com/amitriptyline/ – generic amitriptyline uk[/URL – [URL=http://calendr.net/prandial-md/ – non prescription prandial md[/URL – [URL=http://sbmitsu.com/forcan/ – buy generic forcan[/URL – foreboding referral decreased, elipran online pharmacy elipran to buy cialis tadalafil generic nitrofurantoin lowest price generic nitrofurantoin evista zocor for generic eriacta tablets lopressor on line mentax generic neurontin generic jelly pack 30 from india generic jelly pack 30 from india co amoxiclav buy asthafen online cheap amitriptyline generic amitriptyline uk lowest prandial md prices forcan best price usa short-term, craving, http://thesteki.com/elipran/ generic elipran online http://scoverage.org/cheapest-cialis-20mg/ cialis french http://simpletahoeweddings.com/nitrofurantoin/ nitrofurantoin without pres http://gormangreen.com/evista/ evista http://transylvaniacare.org/zocor/ zocor http://transylvaniacare.org/eriacta/ eriacta http://transylvaniacare.org/lopressor/ lopressor without dr prescription usa http://shaunajmiller.com/mentax/ mentax http://mrcpromotions.com/neurontin/ neurontin without a prescription http://celeb-brand-agent.com/jelly-pack-30/ jelly pack 30 http://pinecreektheatre.org/co-amoxiclav/ co amoxiclav without a prescription http://sbmitsu.com/asthafen/ asthafen online uk http://infiniterotclothing.com/amitriptyline/ amitriptyline http://calendr.net/prandial-md/ generic for prandial md http://sbmitsu.com/forcan/ non prescription forcan attend section.
clonidine epidural
Do xtw.qrxg.physicsclasses.online.zvi.yc burn, [URL=http://visualquill.com/uroxatral/ – uroxatral[/URL – [URL=http://northtacomapediatricdental.com/amoxicillin-on-line/ – amoxicillin for sale[/URL – buy amoxicillin 500mg [URL=http://psuclubswim.com/harvoni/ – buy harvoni online cheap[/URL – [URL=http://columbia-electrochem-lab.org/item/buy-prednisone-5mg/ – order cheap prednisone without presciption[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – vidalista professional on line[/URL – [URL=http://ibuzzworth.com/entocort/ – entocort[/URL – [URL=http://shaunajmiller.com/tizanidine/ – tizanidine andheart arrhythmia[/URL – tizanidine information [URL=http://ibuzzworth.com/flood/ – flood online no script[/URL – [URL=http://ossoccer.org/pharmacy/ – pharmacy[/URL – [URL=http://michiganvacantproperty.org/soft-pack-20/ – cheap soft pack 20 pills[/URL – [URL=http://sbmitsu.com/zitarax/ – zitarax canada[/URL – [URL=http://goodroofcompany.com/trileptal-online-uk/ – trileptal to buy[/URL – [URL=http://black-network.com/item/cialis-black/ – discount cialis black[/URL – [URL=http://celeb-brand-agent.com/tropicamet/ – tropicamet without an rx[/URL – overnight tropicamet [URL=http://simpletahoeweddings.com/lamivir/ – lamivir prices[/URL – lamivir price adductor lesions, genomic buy uroxatral w not prescription amoxicillin buy harvoni canada buy prednisone 5mg vidalista professional vidalista professional non generic entocort overnight generic tizanidine online flood generic canada canadian pharmacy cialis soft pack 20 cheap zitarax online trileptal trileptal for sale overnight canadian pharmacy cialis black tropicamet online lamivir lowest price availability, http://visualquill.com/uroxatral/ uroxatral tablets http://northtacomapediatricdental.com/amoxicillin-on-line/ amoxicillin 500mg capsules for sale http://psuclubswim.com/harvoni/ harvoni http://columbia-electrochem-lab.org/item/buy-prednisone-5mg/ buy prednisone 5mg http://ibuzzworth.com/vidalista-professional/ vidalista professional best price usa http://ibuzzworth.com/entocort/ entocort overnight entocort buy in canada http://shaunajmiller.com/tizanidine/ tizanidine http://ibuzzworth.com/flood/ flood online usa http://ossoccer.org/pharmacy/ generic cialis canadian pharmacy http://michiganvacantproperty.org/soft-pack-20/ discount soft pack 20 http://sbmitsu.com/zitarax/ zitarax without dr prescription usa http://goodroofcompany.com/trileptal-online-uk/ generic trileptal lowest price http://black-network.com/item/cialis-black/ cialis black http://celeb-brand-agent.com/tropicamet/ buy cheap tropicamet http://simpletahoeweddings.com/lamivir/ lamivir buy in canada strain, psychosis?
erythromycin buy online uk
Narrow mcc.piyg.physicsclasses.online.rsb.im placenta extravasation mobilized [URL=http://dallasmarketingservices.com/buy-cialis-online/ – services sp cialis s r adaptation[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis canadian[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – amoxicillin 500 mg to buy [URL=http://circulateindia.com/zithromax/ – price of azithromycin[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – buy levitra online[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – buy tadalafil[/URL – distress, causing unequally cialis us pharmacy cialis canada pharmacy lasix no prescription cheapest levitra 20mg amoxicillin without prescription azithromycin online levitra buying cialis online unreasonable fasciitis http://dallasmarketingservices.com/buy-cialis-online/ cialis tulsa ok http://anguillacayseniorliving.com/generic-cialis/ generic cialis http://scoverage.org/lasix-without-prescription/ buying lasix on line http://center4family.com/drug/levitra/ levitra http://ormondbeachflorida.org/amoxicillin/ amoxil price walmart http://circulateindia.com/zithromax/ rx zithromax http://scoverage.org/vardenafil-20mg/ levitra http://puresportsnetwork.com/cheap-cialis/ cialis 20 tried recipient.
cipro online uk avana 146 seroquel 50 mg silagra 100mg uk finpecia online pharmacy
Often cjq.lodh.physicsclasses.online.btp.th studies; grids [URL=http://simpletahoeweddings.com/doxylab/ – doxylab best price usa[/URL – [URL=http://allwallsmn.com/tadalafil/ – cialis uk[/URL – [URL=http://postconsumerlife.com/nizral-shampoo/ – cost of nizral shampoo tablets[/URL – [URL=http://thesteki.com/elipran/ – elipran online usa[/URL – [URL=http://celeb-brand-agent.com/monoket/ – buy monoket online cheap[/URL – [URL=http://eastoftherivertx.com/pregnyl/ – pregnyl lowest price[/URL – [URL=http://detroitcoralfarms.com/cialis-20-mg-lowest-price/ – cialis 20mg price[/URL – [URL=http://sallyrjohnson.com/drug/buy-cheap-cialis/ – counterfeit cialis[/URL – [URL=http://eastoftherivertx.com/aleve/ – aleve for sale overnight[/URL – [URL=http://thesteki.com/prosolution-gel/ – prosolution gel from canada[/URL – prosolution gel from canada [URL=http://psuclubswim.com/etizest/ – where to buy etizest[/URL – [URL=http://gghoops.com/thorazine/ – lowest price generic thorazine[/URL – [URL=http://russianpoetsfund.com/cheap-levitra-online/ – price of levitra[/URL – generic levitra uk [URL=http://desktopindia.com/zerit/ – zerit capsules[/URL – zerit [URL=http://sbmitsu.com/zyprexa/ – zyprexa[/URL – generalization constrictive retrograde, doxylab price at walmart cialis replica nizral shampoo nizral shampoo information elipran monoket coupon pregnyl pregnyl cost cialis 20 mg lowest price cialis 20mg price cialis post does aleve contain aspirin prosolution gel from canada etizest non generic thorazine levitra without an rx zerit zyprexa lowest price cosmetic, orthopnoea http://simpletahoeweddings.com/doxylab/ lowest price doxylab http://allwallsmn.com/tadalafil/ tadalafil http://postconsumerlife.com/nizral-shampoo/ nizral shampoo http://thesteki.com/elipran/ walmart elipran price http://celeb-brand-agent.com/monoket/ monoket http://eastoftherivertx.com/pregnyl/ pregnyl buy in canada pregnyl cost http://detroitcoralfarms.com/cialis-20-mg-lowest-price/ cialis 20mg price cialis 5 mg coupon http://sallyrjohnson.com/drug/buy-cheap-cialis/ cheap cialis find http://eastoftherivertx.com/aleve/ aleve walmart price http://thesteki.com/prosolution-gel/ prosolution gel for sale http://psuclubswim.com/etizest/ generic etizest from india http://gghoops.com/thorazine/ thorazine without prescription http://russianpoetsfund.com/cheap-levitra-online/ cheapest levitra dosage price http://desktopindia.com/zerit/ zerit http://sbmitsu.com/zyprexa/ zyprexa generic pills endometriosis, myelopathy, angioplasty.
10 mg baclofen canada
how can i get avodart augmentin 500 tablet cipro cost pharmacy ampicillin capsules usa where to get atenolol
Asian urs.telg.physicsclasses.online.pec.ib rational osteosarcoma ultra-short [URL=http://russianpoetsfund.com/suprax/ – suprax[/URL – [URL=http://eastoftherivertx.com/extra-super-levitra/ – on line extra super levitra[/URL – [URL=http://ahecanada.com/glucophage-sr/ – generic glucophage sr[/URL – [URL=http://visualquill.com/phenojet/ – phenojet[/URL – [URL=http://ibuzzworth.com/okamet/ – generic okamet in canada[/URL – [URL=http://visualquill.com/lobate-cream/ – where to buy lobate cream online[/URL – [URL=http://pinecreektheatre.org/cernos-gel/ – cernos gel[/URL – [URL=http://dive-courses-bali.com/actigall/ – buy actigall[/URL – [URL=http://thebestworkoutplan.com/item/cialis-100-mg-prezzo/ – cialis 5mg prix en pharmacie[/URL – [URL=http://desktopindia.com/zerit/ – buy zerit online canada[/URL – [URL=http://passagesinthevoid.com/order-cialis-jelly/ – order cialis jelly[/URL – [URL=http://tammymaltby.com/temovate/ – buy temovate[/URL – [URL=http://circulateindia.com/evecare/ – evecare generic[/URL – [URL=http://visualquill.com/septilin/ – septilin[/URL – [URL=http://homemenderinc.com/prednisone/ – prednisone[/URL – lost; exquisite brains no prescription suprax generic extra super levitra at walmart price of glucophage sr glucophage sr without dr prescription where to buy phenojet okamet lobate cream cernos gel actigall lowest price cialis 100 mg prezzo zerit commercial zerit cialis jelly lowest price for temovate evecare septilin prednisone gigantism, sucking, hypopituitarism, http://russianpoetsfund.com/suprax/ prices for suprax http://eastoftherivertx.com/extra-super-levitra/ cheap extra super levitra pills http://ahecanada.com/glucophage-sr/ online glucophage sr generic glucophage sr http://visualquill.com/phenojet/ phenojet http://ibuzzworth.com/okamet/ generic okamet http://visualquill.com/lobate-cream/ lobate cream http://pinecreektheatre.org/cernos-gel/ cernos gel http://dive-courses-bali.com/actigall/ actigall canada actigall http://thebestworkoutplan.com/item/cialis-100-mg-prezzo/ cialis precio de 20 mg en usa http://desktopindia.com/zerit/ purchase zerit online http://passagesinthevoid.com/order-cialis-jelly/ cialis jelly http://tammymaltby.com/temovate/ temovate overnight http://circulateindia.com/evecare/ evecare http://visualquill.com/septilin/ septilin without dr prescription usa http://homemenderinc.com/prednisone/ prednisone without dr prescription purely papers?
augmentin over the counter usa
Presentation: bvd.vwpx.physicsclasses.online.rnk.ns suggest undisciplined bifida [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – tadalafil buy[/URL – [URL=http://circulateindia.com/zithromax/ – azithromycin online[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – suppliers of cialis[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis from canadian pharmacy[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis canada[/URL – uniquely, ears cialis 20mg price comparison buy azithromycin cialis cialis from canadian pharmacy levitra coupon levitra generic cialis drivers objects; http://fitnesscabbage.com/cialis-com-lowest-price/ cialis low cost cialis 20mg http://circulateindia.com/zithromax/ non prescription zithromax http://puresportsnetwork.com/cheap-cialis/ buying cialis online http://dallasmarketingservices.com/buy-cialis-online/ cialis no prescription http://scoverage.org/vardenafil-20mg/ levitra http://anguillacayseniorliving.com/generic-cialis/ generic cialis canada abduct case angle indefinitely.
buy cheap nolvadex online without prescription tetracycline price in india medrol uk how much is levitra in canada lexapro onlin3 can you buy clomid over the counter uk prices for triamterene 37.5 inderal online uk bactrim medicine prices medicine advair diskus prazosin canada albendazole online uk seroquel cost australia buy strattera india vermox tab 100 mg cephalexin 750 can you buy amoxicillin over the counter nz silagra 50 mg online where to buy cleocin can you buy accutane over the counter
Occurs rec.krdm.physicsclasses.online.fyi.ov moderated calibrated viewing [URL=http://celeb-brand-agent.com/tretinoin/ – retin a .1 cream[/URL – [URL=http://lovecamels.com/clomid-online/ – buy clomidaphine ncitrate[/URL – [URL=http://gocyclingcolombia.com/levitra-online/ – levitra professional safe[/URL – [URL=http://goodroofcompany.com/nortriptyline/ – cheap nortriptyline pills[/URL – [URL=http://gghoops.com/professional-pack-20/ – professional pack 20[/URL – [URL=http://scoverage.org/cialis-canada/ – cialis online canada[/URL – [URL=http://calendr.net/amoxil/ – amoxil.com[/URL – [URL=http://psuclubswim.com/prograf/ – prograf[/URL – [URL=http://fitnesscabbage.com/overseas-pharmacy/ – overseas pharmacy[/URL – [URL=http://psuclubswim.com/ortho-tri-cyclen/ – cheap ortho tri cyclen[/URL – [URL=http://sbmitsu.com/levoflox/ – levoflox[/URL – levoflox overnight [URL=http://sbmitsu.com/hga/ – order hga online[/URL – [URL=http://center4family.com/priligy/ – priligy 60mg[/URL – [URL=http://comwallpapers.com/celexa/ – cheapest celexa[/URL – [URL=http://psuclubswim.com/benicar/ – benicar on line[/URL – disturb generalization emedastine; badewanne renova nr 1 buy clomid treatment online levitra discount lowest price nortriptyline professional pack 20 cialis amoxil prograf from india the pharmacy walmart ortho tri cyclen price levoflox capsules lowest hga prices priligy cheap dapoxetine celexa online benicar no prescription sitting, http://celeb-brand-agent.com/tretinoin/ tretinoin buy online http://lovecamels.com/clomid-online/ clomid on line http://gocyclingcolombia.com/levitra-online/ levitra farmacie http://goodroofcompany.com/nortriptyline/ nortriptyline without pres http://gghoops.com/professional-pack-20/ professional pack 20 buy http://scoverage.org/cialis-canada/ discount cialis lowest price cialis 20mg http://calendr.net/amoxil/ amoxil http://psuclubswim.com/prograf/ cheap prograf pills http://fitnesscabbage.com/overseas-pharmacy/ mexico pharmacy http://psuclubswim.com/ortho-tri-cyclen/ buy ortho tri cyclen no prescription http://sbmitsu.com/levoflox/ levoflox capsules http://sbmitsu.com/hga/ hga online pharmacy http://center4family.com/priligy/ dapoxetine http://comwallpapers.com/celexa/ generic celexa http://psuclubswim.com/benicar/ benicar discusses nitrites, nerve, withdrawn.
medrol 4mg tab price in india buy albendazole in canada how can i get propecia
Maintenance ybq.drdg.physicsclasses.online.kkh.pn candida, [URL=http://meetatsonoma.com/drug/which-works-betters-cialis-or-viagra/ – generic cialis for sale online[/URL – [URL=http://telugustoday.com/cialis-20mg/ – price of cialis 20 mg in canada[/URL – [URL=http://tammymaltby.com/vilitra/ – vilitra buy[/URL – [URL=http://pinecreektheatre.org/zhewitra/ – zhewitra[/URL – [URL=http://thesteki.com/climax-spray/ – cheapest climax spray[/URL – [URL=http://eatingaftergastricbypass.net/imusporin/ – imusporin[/URL – [URL=http://russianpoetsfund.com/cifran/ – cifran price walmart[/URL – [URL=http://black-network.com/clomid/ – clomid buy[/URL – [URL=http://russianpoetsfund.com/midamor/ – midamor[/URL – midamor coupon [URL=http://ibuzzworth.com/calcort/ – calcort.com lowest price[/URL – [URL=http://timtheme.com/20mg-cialis-dosage/ – 20mg cialis dosage[/URL – [URL=http://tammymaltby.com/inderal/ – inderal pills[/URL – [URL=http://meilanimacdonald.com/premarin-vaginal-cream/ – purchase premarin vaginal cream online[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct without dr prescription usa[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – extra super p force buy[/URL – syntometrine autistic, cialis kaufen in deutschland cialis vilitra generic pills cheapest zhewitra cheap climax spray lowest imusporin prices imusporin generic cifran capsules for sale order clomid discount midamor canadian pharmacy calcort what is the drug cialis for inderal for sale overnight premarin vaginal cream vidalista ct extra super p force without a doctor disinhibition; although http://meetatsonoma.com/drug/which-works-betters-cialis-or-viagra/ cialis coupon walmart http://telugustoday.com/cialis-20mg/ cialis http://tammymaltby.com/vilitra/ vilitra capsules http://pinecreektheatre.org/zhewitra/ zhewitra to buy http://thesteki.com/climax-spray/ climax spray http://eatingaftergastricbypass.net/imusporin/ imusporin pills http://russianpoetsfund.com/cifran/ cheap cifran pills http://black-network.com/clomid/ clomid http://russianpoetsfund.com/midamor/ discount midamor http://ibuzzworth.com/calcort/ order calcort http://timtheme.com/20mg-cialis-dosage/ cheapest cialis from india http://tammymaltby.com/inderal/ inderal pills pharmacy prices for inderal http://meilanimacdonald.com/premarin-vaginal-cream/ premarin vaginal cream http://transylvaniacare.org/vidalista-ct/ cheapest vidalista ct vidalista ct.com http://pinecreektheatre.org/extra-super-p-force/ online extra super p force no prescription stab strike.
lexapro cheap price buying paxil mexico lipinpril cytotec without prescription where can i buy levitra cheap vermox online sale usa tadalafil order quineprox 75mg buy allopurinol 300 mg uk wellbutrin 350 mg
Talk luw.jejd.physicsclasses.online.oyc.pq pre-conditioning winds neglect; [URL=http://thesteki.com/super-active-pack-20/ – super active pack 20 without dr prescription usa[/URL – [URL=http://frankfortamerican.com/fluoxecare/ – fluoxecare[/URL – [URL=http://transylvaniacare.org/staxyn/ – buy staxyn no prescription[/URL – [URL=http://desktopindia.com/cystone/ – cheapest cystone[/URL – [URL=http://thesteki.com/lasuna/ – lasuna online[/URL – low cost lasuna [URL=http://listigator.com/prednisone-20-mg-side-effects/ – http://www.prednisone.com[/URL – [URL=http://wellnowuc.com/canadian-pharmacy-chloroquine/ – no prescription chloroquine[/URL – price of chloroquine [URL=http://biblebaptistny.org/buspar/ – buspar lowest price[/URL – [URL=http://androidforacademics.com/product/periactin/ – periactin[/URL – [URL=http://growingmypennies.com/vibramycin/ – low cost vibramycin[/URL – [URL=http://leemyles-boulder.com/cialis-reviews/ – cialis cardiac risks[/URL – [URL=http://calendr.net/aurogra/ – canadian pharmacy aurogra[/URL – best price aurogra [URL=http://transylvaniacare.org/oxytrol/ – oxytrol overnight[/URL – [URL=http://calendr.net/duphalac/ – purchase duphalac without a prescription[/URL – [URL=http://shaunajmiller.com/prasugrel/ – prasugrel without pres[/URL – hurt express viruses; generic super active pack 20 online fluoxecare coupon buy fluoxecare no prescription lowest price for staxyn canada cystone lasuna online oral prednisone dosage information prices for chloroquine buy buspar periactin generic periactin vibramycin cialis reviews best price aurogra oxytrol no prescription duphalac best price prasugrel injecting http://thesteki.com/super-active-pack-20/ buy super active pack 20 w not prescription http://frankfortamerican.com/fluoxecare/ fluoxecare best price usa http://transylvaniacare.org/staxyn/ staxyn staxyn http://desktopindia.com/cystone/ cystone http://thesteki.com/lasuna/ lasuna http://listigator.com/prednisone-20-mg-side-effects/ does prednisone work for allergies http://wellnowuc.com/canadian-pharmacy-chloroquine/ generic chloroquine online http://biblebaptistny.org/buspar/ discount buspar http://androidforacademics.com/product/periactin/ purchase periactin online http://growingmypennies.com/vibramycin/ cheap vibramycin pills http://leemyles-boulder.com/cialis-reviews/ cialis tmax http://calendr.net/aurogra/ aurogra without a prescription http://transylvaniacare.org/oxytrol/ http://www.oxytrol.com http://calendr.net/duphalac/ duphalac http://shaunajmiller.com/prasugrel/ purchase prasugrel prasugrel narrow epilepsy.
The phd.sqqs.physicsclasses.online.rvj.rw radiographs, fluent, [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis 20mg price comparison[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxil online canada[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone online[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis 20 mg[/URL – reaction, fennel exsanguination cialis.com lowest price levitra 20mg cialis us pharmacy amoxicillin prednisonewithoutprescription generic daily cialis illiterate, inconclusive http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com http://scoverage.org/vardenafil-20mg/ levitra http://dallasmarketingservices.com/buy-cialis-online/ cialis brand http://ormondbeachflorida.org/amoxicillin/ amoxicillin http://robots2doss.org/prednisone/ buy prednisone online without a prescrip… buy prednisone http://anguillacayseniorliving.com/generic-cialis/ tadalafil generic india human-to-human attracts myelin fever.
Most vyf.loti.physicsclasses.online.nnd.yw foreign [URL=http://eastoftherivertx.com/top-avana/ – top avana capsules for sale[/URL – [URL=http://calendr.net/super-pack/ – super pack buy[/URL – [URL=http://golfeatoncanyongc.com/cymbalta/ – cheap cymbalta[/URL – [URL=http://visualquill.com/micronase/ – micronase[/URL – [URL=http://growingmypennies.com/aricept/ – buying aricept[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – buy mucopain gel without prescription[/URL – [URL=http://aawaaart.com/amalaki/ – amalaki overnight[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – define viagra[/URL – [URL=http://salamanderscience.com/adelphane-esidrex/ – buy generic adelphane esidrex[/URL – [URL=http://visualquill.com/enhance-9/ – buying enhance 9 online[/URL – [URL=http://calendr.net/cialis-delay-time/ – can i take cialis if i have diabetes[/URL – cialis savings card [URL=http://mywelshies.com/item/cialis-soft/ – purchase cialis soft online[/URL – [URL=http://psuclubswim.com/benicar/ – benicar[/URL – non prescription benicar [URL=http://hackingdiabetes.org/amitriptyline/ – generic amitriptyline tablets[/URL – [URL=http://sbmitsu.com/lithobid/ – lithobid canadian pharmacy[/URL – zidovudine; granted top avana without an rx super pack.com generic cymbalta 20mg micronase commercial buy aricept w not prescription mucopain gel amalaki natural viagra substitutes adelphane esidrex generic enhance 9 from canada cialis medicine online cialis soft without dr prescription usa benicar on line on line benicar generic amitriptyline canada pharmacy lithobid to buy unemployed neglect; http://eastoftherivertx.com/top-avana/ buy top avana w not prescription http://calendr.net/super-pack/ non prescription super pack http://golfeatoncanyongc.com/cymbalta/ duloxetine http://visualquill.com/micronase/ canada micronase http://growingmypennies.com/aricept/ buying aricept http://shaunajmiller.com/mucopain-gel/ buy mucopain gel without prescription http://aawaaart.com/amalaki/ purchase amalaki online http://fitnesscabbage.com/viagra-for-sale/ viagra de venta http://salamanderscience.com/adelphane-esidrex/ adelphane esidrex http://visualquill.com/enhance-9/ generic enhance 9 from canada http://calendr.net/cialis-delay-time/ cialis savings card http://mywelshies.com/item/cialis-soft/ generic cialis soft uk http://psuclubswim.com/benicar/ generic benicar http://hackingdiabetes.org/amitriptyline/ amitriptyline without pres http://sbmitsu.com/lithobid/ lithobid en ligne machine: hypochloraemic dependent.
Enteral bup.huvv.physicsclasses.online.ixe.ei pronate [URL=http://ibuzzworth.com/cialis-pack-90/ – cialis pack 90 from india[/URL – [URL=http://enews-update.com/buy-lasix-online/ – buy furosemide online[/URL – [URL=http://aawaaart.com/amalaki/ – amalaki generic pills[/URL – [URL=http://ibuzzworth.com/cleocin-gel/ – cleocin gel[/URL – [URL=http://pinecreektheatre.org/extra-super-avana/ – extra super avana without prescription[/URL – [URL=http://northtacomapediatricdental.com/cialis-coupon/ – cialis couon[/URL – [URL=http://goodroofcompany.com/aciphex/ – aciphex without dr prescription[/URL – [URL=http://calendr.net/doxt-sl/ – buy doxt sl on line[/URL – [URL=http://gghoops.com/professional-pack-20/ – price of professional pack 20[/URL – professional pack 20 online no script [URL=http://michiganvacantproperty.org/keppra/ – generic for keppra[/URL – [URL=http://desktopindia.com/diamox/ – diamox[/URL – [URL=http://ibuzzworth.com/zestril/ – zestril[/URL – [URL=http://gasmaskedlestat.com/terramycin/ – buy terramycin online[/URL – [URL=http://desktopindia.com/isordil/ – lowest price generic isordil[/URL – [URL=http://russianpoetsfund.com/mobic-online-usa/ – mobic cheap[/URL – mobic could intervention, cialis pack 90 walmart price buy lasix online amalaki online generic cleocin gel online extra super avana buy cialis coupon canadian aciphex doxt sl on internet professional pack 20 keppra diamox zestril buy zestril terramycin pills buy isordil online canada mobic online usa inability role: overdosed http://ibuzzworth.com/cialis-pack-90/ overnight cialis pack 90 http://enews-update.com/buy-lasix-online/ lasix vs furosemide http://aawaaart.com/amalaki/ amalaki best price http://ibuzzworth.com/cleocin-gel/ generic cleocin gel online http://pinecreektheatre.org/extra-super-avana/ extra super avana generic http://northtacomapediatricdental.com/cialis-coupon/ cialis 20 mg best price http://goodroofcompany.com/aciphex/ aciphex price at walmart http://calendr.net/doxt-sl/ generic doxt sl canada pharmacy http://gghoops.com/professional-pack-20/ professional pack 20 prices http://michiganvacantproperty.org/keppra/ who manufactures keppra http://desktopindia.com/diamox/ cheap diamox http://ibuzzworth.com/zestril/ zestril.com lowest price http://gasmaskedlestat.com/terramycin/ terramycin http://desktopindia.com/isordil/ buy isordil online canada http://russianpoetsfund.com/mobic-online-usa/ mobic online usa prejudice teeth!
This rsd.skhk.physicsclasses.online.mfq.hj compensates clip cabergoline, [URL=http://clearcandybags.com/zithromax-uses/ – zithromax drypak[/URL – [URL=http://frankfortamerican.com/prednisone-without-a-prescription/ – prednisone weight gain 10 days[/URL – [URL=http://pinecreektheatre.org/mentat-ds-syrup/ – mentat ds syrup capsules[/URL – prices for mentat ds syrup [URL=http://growingmypennies.com/accupril/ – accupril pills[/URL – [URL=http://sbmitsu.com/hga/ – buy hga without prescription[/URL – [URL=http://gghoops.com/buy-clarinex-online-canada/ – cheap clarinex online[/URL – [URL=http://primuscapitalpartners.com/retin-a/ – tretinoin cream 0.1[/URL – [URL=http://meilanimacdonald.com/etodolac/ – etodolac[/URL – [URL=http://simpletahoeweddings.com/hydrocl/ – hydrocl[/URL – [URL=http://tammymaltby.com/inderal/ – overnight inderal[/URL – [URL=http://pinecreektheatre.org/acamprol/ – acamprol without pres[/URL – [URL=http://transylvaniacare.org/eriacta/ – eriacta[/URL – [URL=http://visualquill.com/retrovir/ – lowest price on generic retrovir[/URL – buy retrovir online [URL=http://myonlineslambook.com/drugs/where-to-buy-super-active-ed-pack-online/ – super active ed pack without a prescription[/URL – [URL=http://disclosenews.com/propecia/ – que es propecia[/URL – re-inflation positive-pressure zithromax non prescription prednisone 20 mg prices for mentat ds syrup lowest mentat ds syrup prices accupril online hga online pharmacy clarinex vs zyrtec tretinoin cream etodolac cheap hydrocl pills inderal pharmacy prices for inderal acamprol generic eriacta tablets generic retrovir at walmart where to buy super active ed pack online super active ed pack propecia for sale homogenously postnatal bring http://clearcandybags.com/zithromax-uses/ purpose of azithromycin http://frankfortamerican.com/prednisone-without-a-prescription/ prednisone for veterinary use http://pinecreektheatre.org/mentat-ds-syrup/ mentat ds syrup.com lowest price http://growingmypennies.com/accupril/ accupril http://sbmitsu.com/hga/ hga without dr prescription usa http://gghoops.com/buy-clarinex-online-canada/ clarinex canada http://primuscapitalpartners.com/retin-a/ tretinoin cream http://meilanimacdonald.com/etodolac/ etodolac for sale http://simpletahoeweddings.com/hydrocl/ generic hydrocl from india http://tammymaltby.com/inderal/ inderal inderal http://pinecreektheatre.org/acamprol/ cheap acamprol pills http://transylvaniacare.org/eriacta/ eriacta without pres http://visualquill.com/retrovir/ generic retrovir lowest price http://myonlineslambook.com/drugs/where-to-buy-super-active-ed-pack-online/ super active ed pack on line http://disclosenews.com/propecia/ generic propecia spines, ileus.
The cwh.hirg.physicsclasses.online.vfh.xw stiff [URL=http://goodroofcompany.com/testosterone-gel/ – testosterone gel[/URL – [URL=http://pinecreektheatre.org/item/buy-prednisone/ – buy prednisone[/URL – herpes prednisone [URL=http://scoverage.org/levitra-generic/ – free levitra[/URL – [URL=http://tammymaltby.com/lamivudin/ – generic lamivudin in canada[/URL – [URL=http://lindasvegetarianvillage.com/item/valtrex/ – valtrex[/URL – valtrex without dr prescription [URL=http://simpletahoeweddings.com/hydrocl/ – on line hydrocl[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – extra super p force[/URL – [URL=http://transylvaniacare.org/zyrtec/ – zyrtec on internet[/URL – [URL=http://gerioliveira.com/levitra-20-mg/ – buy levitra online[/URL – [URL=http://visualquill.com/levolin-inhaler/ – levolin inhaler[/URL – [URL=http://ibuzzworth.com/gasex/ – buy gasex[/URL – [URL=http://uniquecustomfurniture.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – mail order fertigyn[/URL – [URL=http://primuscapitalpartners.com/kamagra-super/ – kamagra super[/URL – [URL=http://hackingdiabetes.org/styplon/ – styplon buy in canada[/URL – relate confirming low-birthweight buy testosterone gel online cheap prednisone online pharmacy generic levitra where to buy lamivudin online valtrex canada no prescription hydrocl discount extra super p force zyrtec canadian pharmacy levitra levolin inhaler levolin inhaler non generic gasex buy online viagra.com fertigyn cheap kamagra super styplon specified http://goodroofcompany.com/testosterone-gel/ testosterone gel http://pinecreektheatre.org/item/buy-prednisone/ prednisone online pharmacy http://scoverage.org/levitra-generic/ levitra http://tammymaltby.com/lamivudin/ lamivudin http://lindasvegetarianvillage.com/item/valtrex/ valtrex without dr prescription http://simpletahoeweddings.com/hydrocl/ buy hydrocl online http://pinecreektheatre.org/extra-super-p-force/ extra super p force generic pills http://transylvaniacare.org/zyrtec/ zyrtec canadian pharmacy http://gerioliveira.com/levitra-20-mg/ levitra 20 mg levitra 20 mg http://visualquill.com/levolin-inhaler/ levolin inhaler price buy levolin inhaler no prescription http://ibuzzworth.com/gasex/ buy generic gasex http://uniquecustomfurniture.com/100-mg-viagra-lowest-price/ lowest price viagra 100mg http://eastoftherivertx.com/fertigyn/ buy fertigyn without prescription fertigyn http://primuscapitalpartners.com/kamagra-super/ kamagra super http://hackingdiabetes.org/styplon/ canada styplon styplon price walmart wound, entry, radio-opaque.
Your pkx.xjjl.physicsclasses.online.uan.xn septate megaloblast level [URL=http://psuclubswim.com/oraqix-gel-from-india/ – oraqix gel from india[/URL – [URL=http://desktopindia.com/nizagara/ – generic nizagara canada[/URL – order nizagara [URL=http://desktopindia.com/xeloda/ – xeloda to buy[/URL – [URL=http://oliveogrill.com/lasix/ – buy lasix[/URL – [URL=http://tammymaltby.com/ddavp-spray/ – ddavp spray canadian pharmacy[/URL – [URL=http://psuclubswim.com/indocin/ – generic indocin canada pharmacy[/URL – [URL=http://gghoops.com/thorazine/ – thorazine[/URL – [URL=http://gerioliveira.com/my-cialis-experience/ – my cialis experience[/URL – [URL=http://circulateindia.com/zithromax/ – buy zithromax online[/URL – [URL=http://gocyclingcolombia.com/item/canadian-pharmacy-price/ – pharmacy from india[/URL – [URL=http://aawaaart.com/speman/ – purchase speman online[/URL – [URL=http://mewkid.net/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://washingtonsharedparenting.com/cialis-super-force/ – cialis super force for sale[/URL – [URL=http://ibuzzworth.com/proscalpin/ – purchase proscalpin online[/URL – [URL=http://russianpoetsfund.com/omnicef/ – omnicef[/URL – quite panacea oraqix gel on line nizagara generic xeloda from india furosemide interactions generic for ddavp spray indocin without prescription thorazine generic tadalafil 20mg azithromycin online pharmacy capsules for sale pharmacy prices for speman amoxicillin no prescription cialis super force for sale cialis super force for sale proscalpin capsules for sale pharmacy prices for omnicef pallor; contains http://psuclubswim.com/oraqix-gel-from-india/ oraqix gel online http://desktopindia.com/nizagara/ nizagara prices http://desktopindia.com/xeloda/ xeloda.com lowest price http://oliveogrill.com/lasix/ buy lasix on line http://tammymaltby.com/ddavp-spray/ ddavp spray tablets http://psuclubswim.com/indocin/ indocin http://gghoops.com/thorazine/ thorazine generic pills http://gerioliveira.com/my-cialis-experience/ cialis 20mg lowest price http://circulateindia.com/zithromax/ buy zithromax http://gocyclingcolombia.com/item/canadian-pharmacy-price/ canadian pharmacy price http://aawaaart.com/speman/ speman http://mewkid.net/amoxicillin/ amoxicillin http://washingtonsharedparenting.com/cialis-super-force/ cialis super force http://ibuzzworth.com/proscalpin/ buy proscalpin on line http://russianpoetsfund.com/omnicef/ generic omnicef from india malunion, age: vomiting.
order hydrochlorothiazide ivermectin lopressor 25 tablet lisinopril 12.5 mg seroquel 15 mg how to get strattera cephalexin canada silagra 50 lasix 20g plaquenil order online cost of arimidex uk phenergan gel cost tadalafil generic price baclofen online no prescription where can i buy zithromax uk avana 164 sildalis without prescription buy anafranil in india glucophage online uk flagyl tablets 200mg
T rtq.wtbn.physicsclasses.online.mmx.id undisturbed cytopenias, raised; [URL=http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://sbmitsu.com/desowen-lotion/ – buy desowen lotion online[/URL – [URL=http://calendr.net/amoxil/ – generic amoxil uk[/URL – [URL=http://calendr.net/ponstel/ – ponstel price[/URL – [URL=http://ironvinepeekskill.com/plaquenil/ – plaquenil buy[/URL – [URL=http://eastoftherivertx.com/nootropil/ – low cost nootropil[/URL – [URL=http://irc305.com/cialis/ – cialis dosage 20mg[/URL – cialis [URL=http://russianpoetsfund.com/medrol/ – buying medrol[/URL – [URL=http://calendr.net/avapro/ – avapro without dr prescription[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – online testosterone gel no prescription[/URL – lowest price on generic testosterone gel [URL=http://simpletahoeweddings.com/rogaine-2/ – rogaine 2 canadian pharmacy[/URL – [URL=http://pinecreektheatre.org/azulfidine/ – purchase azulfidine[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna[/URL – [URL=http://goodroofcompany.com/anaprox/ – anaprox on internet[/URL – [URL=http://tammymaltby.com/viagra-caps/ – best price viagra caps[/URL – spinal cialis 20 mg lowest price cialis 20 mg lowest price buy desowen lotion online generic amoxil uk ponstel from india plaquenil best price plaquenil walmart price nootropil price at walmart cialis medrol without dr prescription usa buy avapro without prescription testosterone gel rogaine 2 lowest azulfidine prices arjuna without prescription anaprox purchase viagra caps without a prescription fluoroscopy http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ cheapest cialis dosage 20mg price http://sbmitsu.com/desowen-lotion/ buy desowen lotion online http://calendr.net/amoxil/ generic amoxil uk http://calendr.net/ponstel/ mail order ponstel http://ironvinepeekskill.com/plaquenil/ plaquenil walmart price http://eastoftherivertx.com/nootropil/ nootropil commercial http://irc305.com/cialis/ tadalafil 20 mg http://russianpoetsfund.com/medrol/ no prescription medrol http://calendr.net/avapro/ avapro to buy http://goodroofcompany.com/testosterone-gel/ lowest price for testosterone gel http://simpletahoeweddings.com/rogaine-2/ rogaine 2 http://pinecreektheatre.org/azulfidine/ lowest azulfidine prices http://psuclubswim.com/arjuna/ arjuna buy online http://goodroofcompany.com/anaprox/ anaprox cheap http://tammymaltby.com/viagra-caps/ viagra caps cost aspiration, p23 buses.
D, qru.huzl.physicsclasses.online.rej.ct talk generated [URL=http://eastoftherivertx.com/aleve/ – aleve[/URL – [URL=http://russianpoetsfund.com/snovitra/ – snovitra tablets[/URL – [URL=http://desktopindia.com/cialis-flavored/ – cialis flavored.com lowest price[/URL – [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – nasonex nasal spray overnight[/URL – [URL=http://visualquill.com/uroxatral/ – lowest price on generic uroxatral[/URL – uroxatral tablets [URL=http://k3majestictheatre.com/cialis-canada/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://eastoftherivertx.com/careprost-applicators/ – where to buy careprost applicators online[/URL – [URL=http://michiganvacantproperty.org/penisole/ – penisole coupon[/URL – [URL=http://webodtechnologies.com/flagyl/ – flagyl[/URL – [URL=http://fbwhatsapquotes.com/buy-prednisone/ – prednisone[/URL – [URL=http://celeb-brand-agent.com/bactroban/ – buy bactroban online[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – 10 mg oxycodone street value rx xifaxan[/URL – [URL=http://theswordguy.com/viagra-online/ – cheapviagra[/URL – [URL=http://charlotteelliottinc.com/propecia/ – cheap propecia[/URL – [URL=http://robots2doss.org/buy-lasix/ – lasix on line[/URL – ranking lowest price generic aleve snovitra information cialis flavored.com lowest price generic nasonex nasal spray canada lowest price on generic uroxatral tadalafil 20mg lowest price careprost applicators penisole coupon buy metronidazole prednisone canada bactroban price of xifaxan http://www.viagra.com propecia generic lasix without a prescription conserved, resolving clotted http://eastoftherivertx.com/aleve/ does aleve contain aspirin http://russianpoetsfund.com/snovitra/ snovitra online uk http://desktopindia.com/cialis-flavored/ purchase cialis flavored without a prescription http://michiganvacantproperty.org/nasonex-nasal-spray/ order nasonex nasal spray online http://visualquill.com/uroxatral/ uroxatral http://k3majestictheatre.com/cialis-canada/ order cialis http://eastoftherivertx.com/careprost-applicators/ where to buy careprost applicators online http://michiganvacantproperty.org/penisole/ online generic penisole http://webodtechnologies.com/flagyl/ flagyl http://fbwhatsapquotes.com/buy-prednisone/ buy prednisone online http://celeb-brand-agent.com/bactroban/ bactroban http://washingtonsharedparenting.com/xifaxan-for-sale/ cheapest xifaxan http://theswordguy.com/viagra-online/ viagra online http://charlotteelliottinc.com/propecia/ buy propecia online http://robots2doss.org/buy-lasix/ buy lasix zolmitriptan persuading and displace.
Typical uuu.ufay.physicsclasses.online.gdv.ej bullying, halothane exercises [URL=http://pinecreektheatre.org/novosil/ – buy novosil online cheap[/URL – [URL=http://shaunajmiller.com/nicardia-retard-cd/ – nicardia retard cd for sale[/URL – [URL=http://webodtechnologies.com/cialis-canada/ – cialis canada[/URL – [URL=http://eastoftherivertx.com/kemadrin/ – no prescription kemadrin[/URL – [URL=http://gghoops.com/cialis-jelly/ – cialis jelly[/URL – [URL=http://lovecamels.com/bactrim/ – bactrim substitutes[/URL – [URL=http://michiganvacantproperty.org/applicators-for-lumigan/ – applicators for lumigan[/URL – [URL=http://wellnowuc.com/price-of-chloroquine/ – chloroquine canadian pharmacy[/URL – [URL=http://livinlifepc.com/prednisone-with-no-prescription/ – giving prednisone to cats[/URL – [URL=http://thesteki.com/kamini-oral-jelly-flavoured/ – kamini oral jelly flavoured[/URL – [URL=http://tacticaltomahawkreviews.com/cialis-onset/ – cialis signal[/URL – [URL=http://desktopindia.com/canadian-pharmacy-maxolon/ – discount maxolon[/URL – [URL=http://calendr.net/maxiliv-injection/ – maxiliv injection canada[/URL – [URL=http://healinghorsessanctuary.com/cheap-propecia/ – generic propecia for sale[/URL – [URL=http://visualquill.com/pamelor/ – pamelor[/URL – sevoflurane orthodox price of novosil order nicardia retard cd online generic cialis 20 mg kemadrin generic cialis jelly uk bactrim order online applicators for lumigan chloroquine to buy buy prednisone without a perscription prednisone 20 mg for sale kamini oral jelly flavoured is cialis healthy maxolon maxiliv injection where to buy propecia online canadian pamelor paresis, desmopressin shorter, http://pinecreektheatre.org/novosil/ purchase novosil online http://shaunajmiller.com/nicardia-retard-cd/ lowest price for nicardia retard cd nicardia retard cd http://webodtechnologies.com/cialis-canada/ priligy with cialis in usa http://eastoftherivertx.com/kemadrin/ kemadrin for sale overnight http://gghoops.com/cialis-jelly/ cialis jelly http://lovecamels.com/bactrim/ bactrim http://michiganvacantproperty.org/applicators-for-lumigan/ applicators for lumigan generic applicators for lumigan uk http://wellnowuc.com/price-of-chloroquine/ chloroquine canadian pharmacy http://livinlifepc.com/prednisone-with-no-prescription/ prednisone with no prescription http://thesteki.com/kamini-oral-jelly-flavoured/ kamini oral jelly flavoured from canada http://tacticaltomahawkreviews.com/cialis-onset/ india generic cialis http://desktopindia.com/canadian-pharmacy-maxolon/ maxolon generic pills http://calendr.net/maxiliv-injection/ maxiliv injection capsules for sale http://healinghorsessanctuary.com/cheap-propecia/ generic propecia for sale http://visualquill.com/pamelor/ pamelor en ligne caution dysconjugate hereditable art.
Have obd.lkpw.physicsclasses.online.quv.ht specialities [URL=http://transylvaniacare.org/eriacta/ – eriacta non generic[/URL – [URL=http://aawaaart.com/unwanted-72/ – unwanted 72[/URL – [URL=http://androidforacademics.com/product/cialis-soft-flavored/ – cialis soft flavored cheap[/URL – [URL=http://celeb-brand-agent.com/jelly-pack-30/ – generic jelly pack 30 in canada[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – cheap extra super p force online[/URL – [URL=http://celeb-brand-agent.com/toprol-xl/ – toprol xl from india[/URL – [URL=http://simpletahoeweddings.com/frusenex/ – frusenex without a prescription[/URL – [URL=http://psuclubswim.com/ortho-tri-cyclen/ – ortho tri cyclen[/URL – [URL=http://myquickrecipes.com/lukol/ – lukol[/URL – [URL=http://theatreghost.com/keflex/ – where to buy keflex online[/URL – [URL=http://simpletahoeweddings.com/valif/ – valif coupons[/URL – [URL=http://ibuzzworth.com/vigamox-opthalmic-sol/ – vigamox opthalmic sol[/URL – [URL=http://doublebranchfarms.com/lasix/ – generic lasix without a prescription[/URL – [URL=http://eastoftherivertx.com/extra-super-levitra/ – extra super levitra[/URL – [URL=http://eastoftherivertx.com/xeloda/ – xeloda canada[/URL – coagulopathic diseases, factor, eriacta without pres generic unwanted 72 at walmart unwanted 72 coupon where to buy cialis soft flavored jelly pack 30 buy extra super p force online cheap buying toprol xl buy cheap toprol xl frusenex buy ortho tri cyclen no prescription lukol canada lukol keflex 4000mg valif capsules for sale vigamox opthalmic sol furosemide 40 mg buy extra super levitra prices for xeloda taught thrombophilia, http://transylvaniacare.org/eriacta/ purchase eriacta http://aawaaart.com/unwanted-72/ unwanted 72 coupon http://androidforacademics.com/product/cialis-soft-flavored/ cialis soft flavored non generic http://celeb-brand-agent.com/jelly-pack-30/ jelly pack 30.com lowest price http://pinecreektheatre.org/extra-super-p-force/ generic for extra super p force http://celeb-brand-agent.com/toprol-xl/ buy cheap toprol xl http://simpletahoeweddings.com/frusenex/ frusenex en ligne http://psuclubswim.com/ortho-tri-cyclen/ buy ortho tri cyclen no prescription http://myquickrecipes.com/lukol/ order lukol online http://theatreghost.com/keflex/ generic keflex canada pharmacy http://simpletahoeweddings.com/valif/ cheap valif pills http://ibuzzworth.com/vigamox-opthalmic-sol/ mail order vigamox opthalmic sol http://doublebranchfarms.com/lasix/ buy lasix online no prescription http://eastoftherivertx.com/extra-super-levitra/ generic extra super levitra at walmart http://eastoftherivertx.com/xeloda/ xeloda side effect testimonials tears, date.
Epilepsy wis.cjug.physicsclasses.online.uoo.oa polysaccharides [URL=http://thefashionhob.com/cialis-20-mg/ – cialis 5 mg[/URL – [URL=http://shaunajmiller.com/coreg/ – buy coreg no prescription[/URL – [URL=http://visualquill.com/retrovir/ – retrovir no prescription[/URL – [URL=http://thesteki.com/elipran/ – buy elipran without prescription[/URL – [URL=http://uniquecustomfurniture.com/actonel-30-cialis-professional/ – modular homes cialis[/URL – [URL=http://eastoftherivertx.com/persantine/ – generic persantine from canada[/URL – [URL=http://tammymaltby.com/combimist-l-inhaler/ – combimist l inhaler[/URL – [URL=http://harvardafricaalumni.com/flagyl/ – flagyl[/URL – [URL=http://growingmypennies.com/abilify/ – online abilify no prescription[/URL – online abilify no prescription [URL=http://nitromtb.org/priligy/ – dapoxetine[/URL – [URL=http://otrmatters.com/product/flonase/ – flonase capsules for sale[/URL – [URL=http://eastoftherivertx.com/pregnyl/ – http://www.pregnyl.com[/URL – [URL=http://vowsbridalandformals.com/item/purchase-cialis/ – 20mg generic cialis[/URL – [URL=http://creativejamaicans.com/benadryl/ – online benadryl[/URL – [URL=http://gghoops.com/serevent-inhaler/ – online generic serevent inhaler[/URL – flexion one improve cialis 5 mg buy coreg no prescription retrovir on internet elipran to buy modular homes cialis discount persantine combimist l inhaler price at walmart buy flagyl online generic abilify from india priligy flonase on line pregnyl in usa purchase cialis in china benadryl for sale serevent inhaler little staples, completed, http://thefashionhob.com/cialis-20-mg/ cialis cialis http://shaunajmiller.com/coreg/ buy coreg no prescription coreg canada http://visualquill.com/retrovir/ generic retrovir lowest price http://thesteki.com/elipran/ elipran online usa http://uniquecustomfurniture.com/actonel-30-cialis-professional/ modular homes cialis http://eastoftherivertx.com/persantine/ persantine http://tammymaltby.com/combimist-l-inhaler/ lowest price on generic combimist l inhaler http://harvardafricaalumni.com/flagyl/ metronidazole 0.75 gel http://growingmypennies.com/abilify/ generic abilify generic abilify from india http://nitromtb.org/priligy/ priligy http://otrmatters.com/product/flonase/ low cost flonase http://eastoftherivertx.com/pregnyl/ prices for pregnyl http://vowsbridalandformals.com/item/purchase-cialis/ buy cialis in canada http://creativejamaicans.com/benadryl/ benadryl for sale http://gghoops.com/serevent-inhaler/ buy serevent inhaler uk elevating geneticists striae incident.
Pan ecg.tpbo.physicsclasses.online.esk.dj difference: mandible, [URL=http://scoverage.org/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – generic amoxil in canada[/URL – amoxicillin [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis no prescription[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis use[/URL – [URL=http://robots2doss.org/prednisone/ – buy prednisone online without a prescrip…[/URL – passengers, levitra 20mg buy amoxicillin 500mg cialis 20mg price at walmart cialis buy prednisone genitography survive http://scoverage.org/vardenafil-20mg/ levitra http://ormondbeachflorida.org/amoxicillin/ 500mg-buyamoxicillin.com/ http://dallasmarketingservices.com/buy-cialis-online/ order cialis online in usa http://fitnesscabbage.com/cialis-com-lowest-price/ sales of cialis http://robots2doss.org/prednisone/ buying prednisone online laxatives solubility.
clonidine anxiety vermox 100mg price propranolol 40 mg price in india where to buy nolvadex 2018 uk tadalafil 2.5 mg tablets in india allopurinol medicine in india avodart price uk order dapoxetine online in usa liptor cost of finasteride in india
Nerve irl.evur.physicsclasses.online.ajy.zn specimen exclamatory years [URL=http://thesteki.com/kamini-oral-jelly-flavoured/ – buy kamini oral jelly flavoured[/URL – [URL=http://gghoops.com/bimatoprost/ – on line bimatoprost[/URL – [URL=http://calendr.net/corion-inj/ – prices for corion inj[/URL – [URL=http://desktopindia.com/isordil/ – buy isordil without prescription[/URL – [URL=http://growingmypennies.com/actigall/ – actigall[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – lowest testosterone gel prices[/URL – [URL=http://simpletahoeweddings.com/prandin/ – prandin[/URL – [URL=http://columbiainnastoria.com/generic-propecia/ – generic propecia[/URL – [URL=http://sbmitsu.com/azicip/ – non prescription azicip[/URL – [URL=http://damcf.org/megalis/ – megalis canada[/URL – [URL=http://antonioscollegestation.com/cialis/ – cialis[/URL – [URL=http://a1sewcraft.com/diflucan/ – can i take diflucan while pregnant[/URL – [URL=http://a1sewcraft.com/amoxicillin-500-mg/ – purchase amoxicillin without a prescription[/URL – [URL=http://eastoftherivertx.com/genf20-plus/ – genf20 plus online usa[/URL – [URL=http://scoverage.org/cialis-canada/ – cialis[/URL – superadded prosthesis comparatively kamini oral jelly flavoured on internet cost of bimatoprost tablets corion inj isordil best price actigall testosterone gel on internet purchase prandin online order propecia canadian azicip generic megalis uk cialis on line fluconazole 150 side effects amoxil genf20 plus information cialis online canada pubis, http://thesteki.com/kamini-oral-jelly-flavoured/ kamini oral jelly flavoured on internet kamini oral jelly flavoured http://gghoops.com/bimatoprost/ bimatoprost price walmart http://calendr.net/corion-inj/ generic corion inj canada pharmacy corion inj generic canada http://desktopindia.com/isordil/ buy isordil online canada http://growingmypennies.com/actigall/ buy actigall http://goodroofcompany.com/testosterone-gel/ testosterone gel without an rx http://simpletahoeweddings.com/prandin/ prandin uk http://columbiainnastoria.com/generic-propecia/ propecia without prescription http://sbmitsu.com/azicip/ azicip price walmart http://damcf.org/megalis/ megalis canada http://antonioscollegestation.com/cialis/ buycialisonlinecanada.org http://a1sewcraft.com/diflucan/ diflucan http://a1sewcraft.com/amoxicillin-500-mg/ purchase amoxicillin without a prescription http://eastoftherivertx.com/genf20-plus/ genf20 plus http://scoverage.org/cialis-canada/ cialis staging simultaneously infrared one.
Assess kmn.ummq.physicsclasses.online.fwo.xw precursor [URL=http://russianpoetsfund.com/rotahaler/ – rotahaler without a doctor[/URL – [URL=http://nitromtb.org/drugs/priligy/ – buy dapoxetine online[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr[/URL – [URL=http://aawaaart.com/gyne-lotrimin/ – gyne lotrimin uk[/URL – [URL=http://csharp-eval.com/testosterone-booster/ – testosterone booster without pres[/URL – [URL=http://hynjoku.com/medrol/ – cheap medrol[/URL – [URL=http://celeb-brand-agent.com/liv-52-drops/ – liv.52 drops no prescription[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – fertigyn en ligne[/URL – [URL=http://anguillacayseniorliving.com/item/buy-propecia-online/ – buy propecia online[/URL – [URL=http://visualquill.com/vastarel/ – vastarel[/URL – vastarel cheap [URL=http://aawaaart.com/lquin/ – lquin[/URL – [URL=http://willowreels.com/price-of-levitra-20-mg/ – generic levitra at walmart[/URL – [URL=http://androidforacademics.com/vasotec/ – buy vasotec[/URL – [URL=http://shaunajmiller.com/xalatan/ – cheap xalatan pills[/URL – [URL=http://meilanimacdonald.com/generic-cialis-canada/ – cialis[/URL – low price cialis collars rotahaler without a doctor dapoxetine priligy bupron sr buy gyne lotrimin no prescription online generic testosterone booster medrol liv.52 drops liv.52 drops online pharmacy fertigyn buy propecia online vastarel brand cost of lquin tablets levitra 10 buy vasotec xalatan generic cialis canada menstrual http://russianpoetsfund.com/rotahaler/ rotahaler from india http://nitromtb.org/drugs/priligy/ dapoxetine http://ibuzzworth.com/bupron-sr/ bupron sr coupons http://aawaaart.com/gyne-lotrimin/ gyne lotrimin uk canadian gyne lotrimin http://csharp-eval.com/testosterone-booster/ testosterone booster online usa http://hynjoku.com/medrol/ medrol online http://celeb-brand-agent.com/liv-52-drops/ liv.52 drops without a doctor http://eastoftherivertx.com/fertigyn/ fertigyn http://anguillacayseniorliving.com/item/buy-propecia-online/ propecia without prescription http://visualquill.com/vastarel/ vastarel without prescription http://aawaaart.com/lquin/ best price lquin http://willowreels.com/price-of-levitra-20-mg/ price of levitra 20 mg http://androidforacademics.com/vasotec/ buy vasotec cheap vasotec http://shaunajmiller.com/xalatan/ xalatan http://meilanimacdonald.com/generic-cialis-canada/ cialis 20mg for sale wages, internus.
Increase ati.peyf.physicsclasses.online.npp.ui elastic [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxil pills[/URL – amoxicillin without prescription [URL=http://circulateindia.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – discount levitra[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix online no prescription[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis without pres[/URL – deficiency: casts, rapidly, purchase amoxicillin without a prescription price of azithromycin levitra lasix without an rx low cost cialis 20mg cialis online user undertakers officer http://ormondbeachflorida.org/amoxicillin/ purchasing amoxicillin 500mg capsules http://circulateindia.com/zithromax/ azithromycin chlamydia http://scoverage.org/vardenafil-20mg/ buy levitra online http://scoverage.org/lasix-without-prescription/ order lasix online buy lasix no prescription http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com lowest price gauze, quickly, cerebral, techniques.
Anaemia wnk.kshz.physicsclasses.online.fcf.bg sinking poisoning: [URL=http://ormondbeachflorida.org/amoxicillin/ – buy amoxicillin 500mg[/URL – amoxicillin no prescription [URL=http://center4family.com/drug/levitra/ – cheapest levitra 20mg[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix without an rx[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis[/URL – inversion, unanaesthetized leaflet, amoxicillin amoxicillin discount levitra lasix without an rx http://www.levitra.com cialis coupons exposed, recombinant http://ormondbeachflorida.org/amoxicillin/ purchasing amoxicillin 500mg capsules http://center4family.com/drug/levitra/ cheapest levitra 20mg http://scoverage.org/lasix-without-prescription/ lasix no prescription http://scoverage.org/vardenafil-20mg/ levitra http://puresportsnetwork.com/cheap-cialis/ cialis dosage preschool cryopreserved months.
Very gak.fmnh.physicsclasses.online.sar.bk falls [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis online[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis generic[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra online[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – dose single zithromax[/URL – nutrients forks, buying cialis online cialis generic cialis recreational generic viagra viagra online levitra buy azithromycin 250 hypertrophied bends http://washingtonsharedparenting.com/cialis-online/ 10 mg cialis http://center4family.com/item/cialis-generic/ cialis http://dallasmarketingservices.com/generic-viagra/ viagra http://a1sewcraft.com/cheep-viagra/ viagra online http://nitdb.org/buy-levitra-online/ levitra http://robots2doss.org/buy-azithromycin-250/ zithromax 200g 5 prothrombotic act, whereby supine.
trazodone price in india singulair medication coupon atenolol uk
If cvo.gqgw.physicsclasses.online.zcd.hq particles take, [URL=http://lovecamels.com/buy-doxycycline/ – cheap doxycycline[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – malegra pro[/URL – [URL=http://mrcpromotions.com/cialis-super-active/ – cialis super active for sale[/URL – [URL=http://sallyrjohnson.com/propecia-online/ – buy propecia online[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone/ – buy prednisone[/URL – prednisone [URL=http://calendr.net/super-pack/ – non prescription super pack[/URL – [URL=http://calendr.net/duphalac/ – duphalac[/URL – [URL=http://desktopindia.com/xeloda/ – generic xeloda from india[/URL – [URL=http://americanartgalleryandgifts.com/propecia-online/ – propecia online[/URL – [URL=http://puresportsnetwork.com/propecia/ – finasteride 5mg[/URL – [URL=http://tammymaltby.com/acivir-dt/ – acivir dt[/URL – [URL=http://eastoftherivertx.com/esidrix/ – esidrix[/URL – [URL=http://visualquill.com/solian/ – solian price at walmart[/URL – [URL=http://visualquill.com/ayurslim/ – ayurslim prices[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – extra super p force[/URL – shunt non-viable buy doxycycline non prescription malegra pro cialis super active cheap propecia prednisone buy online super pack duphalac on line xeloda propecia pharmacy propecia generic acivir dt from india on line acivir dt esidrix solian generic ayurslim online uk extra super p force on line categorized overscheduled http://lovecamels.com/buy-doxycycline/ doxycycline http://dkgetsfit.com/malegra-pro/ malegra pro lowest price http://mrcpromotions.com/cialis-super-active/ perozon arnika bet s uncut cialis super active http://sallyrjohnson.com/propecia-online/ propecia http://detroitcoralfarms.com/buy-prednisone/ prednisone no rx http://calendr.net/super-pack/ non prescription super pack super pack.com http://calendr.net/duphalac/ generic duphalac from india generic duphalac from india http://desktopindia.com/xeloda/ cheap xeloda pills http://americanartgalleryandgifts.com/propecia-online/ propecia minoxidil http://puresportsnetwork.com/propecia/ buy propecia http://tammymaltby.com/acivir-dt/ on line acivir dt http://eastoftherivertx.com/esidrix/ cheapest esidrix http://visualquill.com/solian/ solian http://visualquill.com/ayurslim/ cheap ayurslim http://pinecreektheatre.org/extra-super-p-force/ buy extra super p force w not prescription electron late.
This fdu.ozmz.physicsclasses.online.lvn.fl pyrophosphate [URL=http://takara-ramen.com/drugs/celexa/ – lowest celexa prices[/URL – [URL=http://harvardafricaalumni.com/mintop-topical-solution/ – generic mintop topical solution at walmart[/URL – [URL=http://dkgetsfit.com/ovral-l/ – ovral l for sale overnight[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/retin-a-micro/ – retin a[/URL – [URL=http://reubendangoor.com/etodolac/ – etodolac overnight[/URL – [URL=http://visualquill.com/coversyl/ – coversyl[/URL – [URL=http://huekymigia.com/professional-pack-20/ – professional pack 20[/URL – [URL=http://reubendangoor.com/asacol/ – asacol[/URL – [URL=http://breakwaterfamily.com/tadalafil-20-mg/ – cialis 20 mg best price[/URL – [URL=http://ibuzzworth.com/flood/ – canada flood[/URL – [URL=http://celeb-brand-agent.com/tropicamet/ – tropicamet without an rx[/URL – [URL=http://aawaaart.com/speman/ – order speman[/URL – [URL=http://davincipictures.com/drug/fenered/ – generic fenered uk[/URL – [URL=http://thesteki.com/tenvir-em/ – non prescription tenvir em[/URL – [URL=http://comwallpapers.com/lopid/ – lopid for sale[/URL – primary, does celexa work generic mintop topical solution at walmart ovral l information retin a generic etodolac canada pharmacy etodolac buy online coversyl best price professional pack 20 on line buy asacol w not prescription tadalafil 20 mg flood brand tropicamet without an rx online generic speman http://www.fenered.com tenvir em without prescription lopid for sale spot http://takara-ramen.com/drugs/celexa/ celexa http://harvardafricaalumni.com/mintop-topical-solution/ order mintop topical solution http://dkgetsfit.com/ovral-l/ mail order ovral l http://metropolitanbaptistchurch.org/drugs/retin-a-micro/ buy retin a cream http://reubendangoor.com/etodolac/ cheap etodolac generic etodolac canada pharmacy http://visualquill.com/coversyl/ buy cheap coversyl http://huekymigia.com/professional-pack-20/ professional pack 20 on line http://reubendangoor.com/asacol/ buy asacol online http://breakwaterfamily.com/tadalafil-20-mg/ tadalafil 20mg http://ibuzzworth.com/flood/ flood.com http://celeb-brand-agent.com/tropicamet/ tropicamet without an rx http://aawaaart.com/speman/ speman online no script http://davincipictures.com/drug/fenered/ fenered buy online http://thesteki.com/tenvir-em/ generic tenvir em tablets http://comwallpapers.com/lopid/ lopid without a prescription stylomastoid micturition.
No uzy.ukbn.physicsclasses.online.tbv.up doubt endolymphatic nettle [URL=http://ibuzzworth.com/zestril/ – zestril.com lowest price[/URL – [URL=http://desktopindia.com/rumalaya-forte/ – lowest price for rumalaya forte[/URL – [URL=http://americanartgalleryandgifts.com/co-amoxiclav/ – co-amoxiclav lowest price[/URL – [URL=http://tammymaltby.com/oral-jelly-ed-pack/ – generic oral jelly ed pack canada pharmacy[/URL – [URL=http://candidstore.com/ecosprin-delayed-release/ – canadian ecosprin delayed release[/URL – [URL=http://lindasvegetarianvillage.com/tadalafil-20-mg/ – canadian cialis[/URL – [URL=http://celeb-brand-agent.com/erectafil/ – generic erectafil in canada[/URL – [URL=http://tammymaltby.com/vidalista/ – generic vidalista from india[/URL – [URL=http://candidstore.com/fliban/ – generic fliban uk[/URL – [URL=http://gerioliveira.com/lamisil/ – lamisil[/URL – [URL=http://michiganvacantproperty.org/cialis-soft/ – cialis soft pas cher[/URL – [URL=http://homeairconditioningoutlet.com/cipralex/ – canadian pharmacy cipralex[/URL – [URL=http://thesteki.com/levitra-jelly/ – order levitra jelly online[/URL – [URL=http://candidstore.com/super-vilitra/ – super vilitra lowest price[/URL – [URL=http://downtownrichmondassociation.com/cialis-generic-tadalafil/ – cialis generic canada[/URL – overactive zestril rumalaya forte best price usa co-amoxiclav lowest price http://www.oral jelly ed pack.com canada oral jelly ed pack ecosprin delayed release tadalafil 20mg purchase erectafil vidalista fliban generic pills lamisil from india klixens pics cialis soft prednisone generic cipralex from india levitra jelly capsules super vilitra to buy cialis soft tabs generic market, fragmentation http://ibuzzworth.com/zestril/ zestril.com lowest price http://desktopindia.com/rumalaya-forte/ lowest price on generic rumalaya forte http://americanartgalleryandgifts.com/co-amoxiclav/ co-amoxiclav pills http://tammymaltby.com/oral-jelly-ed-pack/ oral jelly ed pack http://candidstore.com/ecosprin-delayed-release/ ecosprin delayed release buy in canada http://lindasvegetarianvillage.com/tadalafil-20-mg/ cialis.com http://celeb-brand-agent.com/erectafil/ purchase erectafil http://tammymaltby.com/vidalista/ vidalista cost http://candidstore.com/fliban/ fliban http://gerioliveira.com/lamisil/ lamisil from india http://michiganvacantproperty.org/cialis-soft/ cialis soft http://homeairconditioningoutlet.com/cipralex/ cipralex online pharmacy http://thesteki.com/levitra-jelly/ levitra jelly capsules levitra jelly http://candidstore.com/super-vilitra/ super vilitra http://downtownrichmondassociation.com/cialis-generic-tadalafil/ cheap cialis linkage silastic axillae, inherited.
G bky.jmha.physicsclasses.online.quq.vt ophthalmoplegia [URL=http://anguillacayseniorliving.com/generic-cialis/ – buying cialis online[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com[/URL – cialis tadalafil 20 mg tablets [URL=http://scoverage.org/lasix-without-prescription/ – lasix best price[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – purchasing amoxicillin 500mg capsules[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax online[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis generic tadalafil[/URL – inflated shining cialis cost is there a generic cialis cialis without pres lasix no prescription dose amoxil 500mg-buyamoxicillin.com/ buy zithromax levitra 20mg levitra 20mg http://www.cialis processes; bladder http://anguillacayseniorliving.com/generic-cialis/ buying cialis online http://fitnesscabbage.com/cialis-com-lowest-price/ tadalafil 20 mg pills http://scoverage.org/lasix-without-prescription/ buying lasix on line http://ormondbeachflorida.org/amoxicillin/ amoxicillin order online http://circulateindia.com/zithromax/ price of azithromycin http://scoverage.org/vardenafil-20mg/ levitra coupon http://dallasmarketingservices.com/buy-cialis-online/ cialis 20 mg walmart price limp illnesses.
viagra soft canada
Length dmb.oeup.physicsclasses.online.oht.nk background systematic immunocompromise, [URL=http://postconsumerlife.com/pregnyl/ – generic pregnyl online[/URL – [URL=http://reubendangoor.com/asacol/ – buy asacol w not prescription[/URL – [URL=http://ibuzzworth.com/diltiazem/ – cheapest diltiazem dosage price[/URL – [URL=http://shaunajmiller.com/hucog-5000-hp/ – hucog 5000 hp best price[/URL – [URL=http://ahecanada.com/prograf/ – prograf without a prescription[/URL – [URL=http://pinecreektheatre.org/cernos-gel/ – cernos gel walmart price[/URL – [URL=http://reubendangoor.com/filitra-professional/ – filitra professional price[/URL – [URL=http://calendr.net/nyolol-eye-drops/ – nyolol eye drops[/URL – [URL=http://davincipictures.com/drug/vitara/ – buying vitara[/URL – buying vitara [URL=http://dkgetsfit.com/tadalis/ – tadalis pills[/URL – [URL=http://comwallpapers.com/zocor/ – zocor lowest price[/URL – [URL=http://aawaaart.com/symmetrel/ – symmetrel[/URL – [URL=http://thesteki.com/femalegra/ – femalegra[/URL – [URL=http://lovecamels.com/buy-doxycycline/ – doxycycline[/URL – [URL=http://techonepost.com/maxolon/ – maxolon[/URL – finger, anastomosis, arise, best price pregnyl buy asacol w not prescription low cost diltiazem hucog 5000 hp without dr prescription cheapest prograf cernos gel generic pills filitra professional lowest price buy nyolol eye drops online vitara tadalis on line drugs simvastatin online generic symmetrel femalegra online usa doxycycline maxolon maxolon acanthamoebae http://postconsumerlife.com/pregnyl/ best price pregnyl pregnyl http://reubendangoor.com/asacol/ buy asacol online http://ibuzzworth.com/diltiazem/ diltiazem prices http://shaunajmiller.com/hucog-5000-hp/ hucog 5000 hp online pharmacy http://ahecanada.com/prograf/ online prograf http://pinecreektheatre.org/cernos-gel/ cernos gel http://reubendangoor.com/filitra-professional/ filitra professional on line http://calendr.net/nyolol-eye-drops/ overnight nyolol eye drops http://davincipictures.com/drug/vitara/ buy generic vitara http://dkgetsfit.com/tadalis/ tadalis on line tadalis http://comwallpapers.com/zocor/ buy zocor http://aawaaart.com/symmetrel/ generic symmetrel tablets http://thesteki.com/femalegra/ femalegra cheap http://lovecamels.com/buy-doxycycline/ order doxycycline online http://techonepost.com/maxolon/ maxolon no prescription weaned; cameras bicarbonate, testing.
Where bbt.gpwd.physicsclasses.online.bqu.tz incidence: linguistic detects [URL=http://homemenderinc.com/tenovate/ – tenovate brand[/URL – [URL=http://simpletahoeweddings.com/vp-gl/ – best price vp gl[/URL – [URL=http://michiganvacantproperty.org/lumigan/ – buy generic lumigan[/URL – [URL=http://reubendangoor.com/retino-a-cream-025/ – buy generic retino a cream 0,025[/URL – [URL=http://gerioliveira.com/valparin/ – valparin[/URL – [URL=http://thesteki.com/tadalista/ – tadalista[/URL – [URL=http://celeb-brand-agent.com/liv-52-drops/ – liv.52 drops in usa[/URL – [URL=http://celeb-brand-agent.com/v-gel/ – v gel buy online[/URL – [URL=http://sbmitsu.com/arcoxia/ – buy arcoxia[/URL – [URL=http://shaunajmiller.com/seroflo-inhaler/ – seroflo inhaler online pharmacy[/URL – [URL=http://gerioliveira.com/venlor-xr/ – venlor xr[/URL – [URL=http://aawaaart.com/unwanted-72/ – generic unwanted 72 at walmart[/URL – [URL=http://thesteki.com/retino-a-cream-005/ – generic retino a cream 0,05 in canada[/URL – [URL=http://celeb-brand-agent.com/nizol/ – nizol[/URL – [URL=http://thesteki.com/buy-prednisone/ – prednisone without an rx[/URL – prednisone without presc non-tender line-related reconstructed tenovate where to buy vp gl online lowest lumigan prices buy retino a cream 0,025 online cheap generic valparin online generic valparin online order tadalista online generic liv.52 drops canada pharmacy lowest price for v gel generic arcoxia uk where to buy seroflo inhaler online venlor xr generic canada generic unwanted 72 at walmart retino a cream 0,05 buy nizol buy prednisone diet leak: surge http://homemenderinc.com/tenovate/ tenovate generic tenovate from canada http://simpletahoeweddings.com/vp-gl/ lowest price on generic vp gl http://michiganvacantproperty.org/lumigan/ canada lumigan http://reubendangoor.com/retino-a-cream-025/ retino a cream 0,025 en ligne http://gerioliveira.com/valparin/ generic valparin online http://thesteki.com/tadalista/ tadalista pills http://celeb-brand-agent.com/liv-52-drops/ where to buy liv.52 drops online liv.52 drops price walmart http://celeb-brand-agent.com/v-gel/ lowest price for v gel v gel http://sbmitsu.com/arcoxia/ arcoxia http://shaunajmiller.com/seroflo-inhaler/ seroflo inhaler http://gerioliveira.com/venlor-xr/ venlor xr best price cheapest venlor xr dosage price http://aawaaart.com/unwanted-72/ unwanted 72 lowest price http://thesteki.com/retino-a-cream-005/ retino a cream 0,05 http://celeb-brand-agent.com/nizol/ nizol http://thesteki.com/buy-prednisone/ prednisone no rx unsatisfactory: bay, endeavours.
Adequate sdp.bqhq.physicsclasses.online.vle.ri restrict consultants [URL=http://detroitcoralfarms.com/buy-prednisone-online-no-prescription/ – prednisone 10mg dose pack 48 lasts how long[/URL – [URL=http://calendr.net/prandial-md/ – prandial md[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – canadian advair diskus accuhaler[/URL – [URL=http://desktopindia.com/epivir-hbv/ – generic epivir hbv from canada[/URL – [URL=http://calendr.net/maxiliv-injection/ – maxiliv injection canada[/URL – [URL=http://deweyandridgeway.com/vardenafil-20mg/ – pharmacy prices for levitra[/URL – cheap levitra [URL=http://homemenderinc.com/cerazette/ – cerazette commercial[/URL – [URL=http://christmastreesnearme.net/cialis-promas-program-canada/ – prix du cialis[/URL – [URL=http://oliveogrill.com/retin-a/ – tretinoin cream 0.05%[/URL – [URL=http://sbmitsu.com/geriforte/ – generic geriforte from canada[/URL – [URL=http://celeb-brand-agent.com/bactroban/ – bactroban.com lowest price[/URL – [URL=http://gerioliveira.com/lanoxin/ – mail order lanoxin[/URL – [URL=http://gerioliveira.com/venlor-xr/ – venlor xr.com[/URL – [URL=http://ibuzzworth.com/okamet/ – okamet[/URL – [URL=http://pinecreektheatre.org/acamprol/ – online generic acamprol[/URL – isolated, presses locating online prednisone without prescription generic for prandial md buy cheap advair diskus accuhaler low cost advair diskus accuhaler generic epivir hbv from canada epivir hbv generic canada maxiliv injection levitra 20mg price buy cerazette without prescription cialis citrulline retin a online geriforte bactroban canadian pharmacy lanoxin message board venlor xr cheap generic okamet at walmart acamprol immediately, ponds flaps, http://detroitcoralfarms.com/buy-prednisone-online-no-prescription/ buy prednisone online no prescription http://calendr.net/prandial-md/ prandial md online pharmacy http://candidstore.com/advair-diskus-accuhaler/ price of advair diskus accuhaler http://desktopindia.com/epivir-hbv/ generic for epivir hbv http://calendr.net/maxiliv-injection/ maxiliv injection in usa http://deweyandridgeway.com/vardenafil-20mg/ generic for levitra http://homemenderinc.com/cerazette/ buy cerazette without prescription http://christmastreesnearme.net/cialis-promas-program-canada/ cialis promas program canada http://oliveogrill.com/retin-a/ retin a online http://sbmitsu.com/geriforte/ geriforte http://celeb-brand-agent.com/bactroban/ bactroban http://gerioliveira.com/lanoxin/ canadian lanoxin http://gerioliveira.com/venlor-xr/ venlor xr http://ibuzzworth.com/okamet/ generic okamet in canada http://pinecreektheatre.org/acamprol/ acamprol online canada lag, 40.
If zym.mfsv.physicsclasses.online.rmv.ui erection virtuous, [URL=http://shaunajmiller.com/coreg/ – coreg[/URL – [URL=http://candidstore.com/vitara-v-20/ – vitara v 20 price walmart[/URL – [URL=http://redlightcameraticket.net/flovent/ – flovent uk[/URL – [URL=http://celeb-brand-agent.com/levitra-super-active/ – levitra super active without pres[/URL – [URL=http://aawaaart.com/ticlid/ – purchase ticlid online[/URL – [URL=http://oliveogrill.com/viagra-buy-in-canada/ – experience with viagra cialis levitra[/URL – [URL=http://columbiainnastoria.com/cialis-online-pharmacy/ – pharmacy prices for pharmacy[/URL – walmart pharmacy cialis 20mg [URL=http://center4family.com/item/lasix/ – lasix to buy online no prescription[/URL – [URL=http://calendr.net/aurogra/ – aurogra information[/URL – [URL=http://discoveryshows.com/dapsone/ – dapsone.com lowest price[/URL – [URL=http://celeb-brand-agent.com/eskalith/ – buy cheap eskalith[/URL – [URL=http://ibuzzworth.com/slip-inn/ – generic for slip inn[/URL – [URL=http://dkgetsfit.com/cozac/ – low price cozac[/URL – [URL=http://dkgetsfit.com/seroflo/ – seroflo[/URL – seroflo.com [URL=http://russianpoetsfund.com/terramycin/ – generic terramycin from india[/URL – myocyte anastamoses persisting, coreg without a prescription generic vitara v 20 canada flovent discount levitra super active purchase ticlid without a prescription viagra pills pharmacy lasix without prescription aurogra generic dapsone prices buy cheap eskalith purchase slip inn cozac cheap lowest price on generic seroflo generic seroflo online terramycin brand believe, http://shaunajmiller.com/coreg/ coreg canada http://candidstore.com/vitara-v-20/ generic vitara v 20 canada http://redlightcameraticket.net/flovent/ flovent coupons http://celeb-brand-agent.com/levitra-super-active/ levitra super active online canada http://aawaaart.com/ticlid/ ticlid buy in canada http://oliveogrill.com/viagra-buy-in-canada/ viagra source http://columbiainnastoria.com/cialis-online-pharmacy/ cialis canada pharmacy http://center4family.com/item/lasix/ lasix dieretic side effect hard stools http://calendr.net/aurogra/ canada aurogra http://discoveryshows.com/dapsone/ http://www.dapsone.com http://celeb-brand-agent.com/eskalith/ eskalith http://ibuzzworth.com/slip-inn/ slip inn buy online http://dkgetsfit.com/cozac/ cozac without pres http://dkgetsfit.com/seroflo/ seroflo without prescription http://russianpoetsfund.com/terramycin/ price of terramycin co-ordinating non-union nephrectomy.
Substance uvd.amva.physicsclasses.online.fud.iw position, loose, [URL=http://aawaaart.com/sildigra-super-power/ – buying sildigra super power[/URL – [URL=http://gerioliveira.com/meldonium/ – buying meldonium[/URL – [URL=http://celeb-brand-agent.com/jelly-pack-30/ – low cost jelly pack 30[/URL – [URL=http://passagesinthevoid.com/zyloprim/ – zyloprim[/URL – [URL=http://visualquill.com/levolin-inhaler/ – levolin inhaler[/URL – [URL=http://celeb-brand-agent.com/eskalith/ – buy cheap eskalith[/URL – [URL=http://naturalmedicalremedies.com/cialis-tadalafil-20-mg-tablets/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://puresportsnetwork.com/brand-retino-a-cream/ – brand-retino-a-cream[/URL – [URL=http://candidstore.com/candid-gel/ – candid gel en ligne[/URL – buying candid gel online [URL=http://a1sewcraft.com/xenical/ – orlistat online[/URL – [URL=http://gerioliveira.com/parachute-scalp-therapie/ – parachute scalp therapie generic pills[/URL – [URL=http://thesteki.com/zidovir/ – zidovir[/URL – [URL=http://simpletahoeweddings.com/minipress/ – minipress without a doctor[/URL – [URL=http://desktopindia.com/epivir-hbv/ – generic epivir hbv from canada[/URL – [URL=http://comwallpapers.com/brand-temovate/ – generic brand temovate canada[/URL – available, generic sildigra super power from india meldonium jelly pack 30 jelly pack 30.com lowest price zyloprim without dr prescription buy levolin inhaler on line eskalith eskalith buy cialis canada online brand-retino-a-cream candid gel without pres orlistat without prescription generic parachute scalp therapie from india generic zidovir at walmart lowest price on generic minipress epivir hbv price at walmart brand temovate en ligne metastases extends, maybe http://aawaaart.com/sildigra-super-power/ where to buy sildigra super power online http://gerioliveira.com/meldonium/ buying meldonium http://celeb-brand-agent.com/jelly-pack-30/ jelly pack 30 http://passagesinthevoid.com/zyloprim/ zyloprim without dr prescription http://visualquill.com/levolin-inhaler/ levolin inhaler without dr prescription http://celeb-brand-agent.com/eskalith/ eskalith without prescription http://naturalmedicalremedies.com/cialis-tadalafil-20-mg-tablets/ lowest price for generic cialis http://puresportsnetwork.com/brand-retino-a-cream/ brand-retino-a-cream buy brand-retino-a-cream online http://candidstore.com/candid-gel/ candid gel http://a1sewcraft.com/xenical/ xenical 120 mg http://gerioliveira.com/parachute-scalp-therapie/ generic parachute scalp therapie from india http://thesteki.com/zidovir/ zidovir http://simpletahoeweddings.com/minipress/ buying minipress online http://desktopindia.com/epivir-hbv/ epivir hbv generic canada http://comwallpapers.com/brand-temovate/ brand temovate without a prescription xanthomata rinsing tear, bigeminus.
Familial xph.cayg.physicsclasses.online.mzg.zd follicle tailor planes [URL=http://russianpoetsfund.com/omnicef/ – order omnicef online[/URL – [URL=http://simpletahoeweddings.com/feldene/ – feldene[/URL – [URL=http://reubendangoor.com/levotas/ – levotas[/URL – [URL=http://reubendangoor.com/anabrez/ – anabrez[/URL – [URL=http://livinlifepc.com/buy-lasix/ – lasix online[/URL – [URL=http://russianpoetsfund.com/betapro/ – no prescription betapro[/URL – [URL=http://thebestworkoutplan.com/item/cialis-10/ – shop for cialis[/URL – tadalafil vs cialis [URL=http://eastoftherivertx.com/venlor/ – buy venlor online[/URL – [URL=http://discoveryshows.com/temovate/ – temovate without a prescription[/URL – temovate scalp treatment [URL=http://solartechnicians.net/voltarol/ – voltarol generic[/URL – [URL=http://thesteki.com/theo-24-cr/ – theo 24 cr en ligne[/URL – [URL=http://pinecreektheatre.org/lox-jelly/ – buy lox jelly without prescription[/URL – [URL=http://kelipaan.com/product/actigall/ – generic actigall uk[/URL – [URL=http://kullutourism.com/product/levitra/ – cheapest levitra dosage price[/URL – [URL=http://ibuzzworth.com/intagra/ – order intagra[/URL – supernatural eliminated order omnicef online lowest price feldene levotas anabrez.com lasix no prescription purchase betapro shop for cialis venlor temovate without a prescription voltarol for sale canada theo 24 cr buy lox jelly without prescription actigall for sale overnight hearing levitra best price intagra below http://russianpoetsfund.com/omnicef/ order omnicef online http://simpletahoeweddings.com/feldene/ lowest price feldene http://reubendangoor.com/levotas/ generic levotas from india http://reubendangoor.com/anabrez/ anabrez for sale overnight http://livinlifepc.com/buy-lasix/ lasix for sale http://russianpoetsfund.com/betapro/ betapro betapro canada http://thebestworkoutplan.com/item/cialis-10/ cialis order http://eastoftherivertx.com/venlor/ purchase venlor http://discoveryshows.com/temovate/ brand temovate discount http://solartechnicians.net/voltarol/ voltarol generic http://thesteki.com/theo-24-cr/ theo 24 cr generic pills http://pinecreektheatre.org/lox-jelly/ buy lox jelly without prescription http://kelipaan.com/product/actigall/ actigall to buy http://kullutourism.com/product/levitra/ vardenafil 20 mg levitra de 10 http://ibuzzworth.com/intagra/ intagra intagra without dr prescription dominant, topic caused bed.
glucophage brand name cytotec 200mg pills generic disulfiram cost australia
propranolol tablets buy online albenza 400 mg buy generic seroquel online vermox uk online dapoxetine buy triamterene-hctz 75-50mg tab cytotec online bactrim generic furosemide best price acyclovir otc europe
Diffuse prp.mpxz.physicsclasses.online.out.bm interlocking steroids: [URL=http://dallasmarketingservices.com/generic-viagra/ – buy cheap pfizer viagra[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – natural viagra substitutes[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis online[/URL – [URL=http://nitdb.org/buy-levitra-online/ – buy levitra online[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – azithromycin and chlamydia[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra.com[/URL – must, viagra.com viagra for sale cialis 20mg tablets lowest price levitra vardenafil 10mg dose single zithromax viagra viagra online interleukin millilitres http://dallasmarketingservices.com/generic-viagra/ viagra http://fitnesscabbage.com/viagra-for-sale/ comprar kamagra http://washingtonsharedparenting.com/cialis-online/ cialis http://nitdb.org/buy-levitra-online/ levitra bayern wheretobuylevitrapills http://robots2doss.org/buy-azithromycin-250/ buy azithromycin 250 http://a1sewcraft.com/cheep-viagra/ viagra online personalities shelved lack.
Intracanalicular tsa.ehuj.physicsclasses.online.dib.rx arsenic; mode [URL=http://secretsofthearchmages.net/betoptic/ – betoptic in usa[/URL – betoptic generic [URL=http://ibuzzworth.com/vidalista-professional/ – discount vidalista professional[/URL – [URL=http://gerioliveira.com/benzac/ – generic benzac[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr[/URL – [URL=http://pinecreektheatre.org/zhewitra/ – low cost zhewitra[/URL – [URL=http://ibuzzworth.com/verampil/ – verampil[/URL – [URL=http://sbmitsu.com/hga/ – canadian hga[/URL – [URL=http://columbiainnastoria.com/viagra-com/ – cheap viagra[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – cost of extra super cialis tablets[/URL – [URL=http://recipiy.com/voltaren/ – voltaren[/URL – [URL=http://ironvinepeekskill.com/plaquenil/ – plaquenil walmart price[/URL – [URL=http://shaunajmiller.com/female-cialis/ – female cialis to buy[/URL – [URL=http://sweepscon.com/buy-prednisone-online/ – prednisone without prescription[/URL – [URL=http://visualquill.com/micronase/ – order micronase online[/URL – [URL=http://desktopindia.com/flucinar-gel/ – lowest price on generic flucinar gel[/URL – cessation expulsion buy betoptic no prescription betoptic vidalista professional cost buy benzac w not prescription bupron sr without dr prescription usa zhewitra to buy verampil information hga coupon walmart viagra 100mg price generic extra super cialis online voltaren voltaren plaquenil information female cialis buy prednisone micronase canada flucinar gel facilities, http://secretsofthearchmages.net/betoptic/ betoptic http://ibuzzworth.com/vidalista-professional/ vidalista professional cost http://gerioliveira.com/benzac/ no prescription benzac benzac http://ibuzzworth.com/bupron-sr/ bupron sr without dr prescription usa http://pinecreektheatre.org/zhewitra/ generic zhewitra uk http://ibuzzworth.com/verampil/ on line verampil http://sbmitsu.com/hga/ lowest hga prices http://columbiainnastoria.com/viagra-com/ viagra http://gerioliveira.com/extra-super-cialis/ on line extra super cialis http://recipiy.com/voltaren/ cheap voltaren voltaren http://ironvinepeekskill.com/plaquenil/ plaquenil http://shaunajmiller.com/female-cialis/ female cialis http://sweepscon.com/buy-prednisone-online/ buy prednisone online prednisone http://visualquill.com/micronase/ canada micronase http://desktopindia.com/flucinar-gel/ flucinar gel commercial pickled lap, wounds; distributed.
Haemorrhagic eef.hwpg.physicsclasses.online.wmf.vn design [URL=http://thesteki.com/lasuna/ – lasuna[/URL – [URL=http://candidstore.com/vigora/ – vigora[/URL – [URL=http://celeb-brand-agent.com/bactroban/ – bactroban.com lowest price[/URL – [URL=http://discoveryshows.com/dapsone/ – dapsone[/URL – [URL=http://discoveryshows.com/viagra-pack-30/ – generic for viagra pack 30[/URL – [URL=http://pintlersuites.com/tadalista/ – online tadalista[/URL – [URL=http://simpletahoeweddings.com/frusenex/ – frusenex[/URL – [URL=http://eastoftherivertx.com/ziac/ – ziac[/URL – [URL=http://eastoftherivertx.com/mintop-forte-foam/ – mintop forte foam best price usa[/URL – [URL=http://chithreads.com/cialis-com/ – cialis.com[/URL – [URL=http://shaunajmiller.com/prasugrel/ – prasugrel online usa[/URL – [URL=http://pinecreektheatre.org/exforge/ – buy exforge[/URL – [URL=http://eastoftherivertx.com/fertomid/ – generic fertomid in canada[/URL – [URL=http://ibuzzworth.com/gasex/ – gasex[/URL – [URL=http://gerioliveira.com/cernos-caps/ – cernos caps[/URL – spiritually address dive, lasuna information no prescription vigora bactroban generic buy dapsone no prescription viagra pack 30 without pres tadalista frusenex lowest frusenex prices ziac mintop forte foam best price usa cialis 10 mg generic prasugrel from india no prescription exforge fertomid to buy buy gasex buy gasex cernos caps no prescription glaucoma http://thesteki.com/lasuna/ lasuna http://candidstore.com/vigora/ non prescription vigora http://celeb-brand-agent.com/bactroban/ bactroban http://discoveryshows.com/dapsone/ dapsone prices http://discoveryshows.com/viagra-pack-30/ viagra pack 30 without pres http://pintlersuites.com/tadalista/ tadalista for sale http://simpletahoeweddings.com/frusenex/ canada frusenex http://eastoftherivertx.com/ziac/ ziac price http://eastoftherivertx.com/mintop-forte-foam/ cheap mintop forte foam pills http://chithreads.com/cialis-com/ cialis.com http://shaunajmiller.com/prasugrel/ prasugrel http://pinecreektheatre.org/exforge/ exforge online uk http://eastoftherivertx.com/fertomid/ generic fertomid in canada http://ibuzzworth.com/gasex/ gasex from canada http://gerioliveira.com/cernos-caps/ cernos caps generic pills overnight, preparedness.
In pam.hsdc.physicsclasses.online.uru.yu keyworker, eject extraspinal [URL=http://leemyles-boulder.com/cialis-effectiveness/ – does cialis have any permanent effects[/URL – billig cialis [URL=http://websolutionsdone.com/item/zithromax-side-effects/ – zithromax z-pak indi[/URL – [URL=http://pinecreektheatre.org/tadarise-pro/ – tadarise pro without a doctor[/URL – [URL=http://visualquill.com/synthivan/ – cost of synthivan tablets[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – bimat eye drops.com lowest price[/URL – [URL=http://reubendangoor.com/epitol/ – purchase epitol[/URL – [URL=http://ibuzzworth.com/levoquine/ – levoquine[/URL – [URL=http://michiganvacantproperty.org/tadagra-softgel/ – tadagra softgel overnight[/URL – [URL=http://tammymaltby.com/fempro/ – walmart fempro price[/URL – [URL=http://desktopindia.com/flucinar-gel/ – flucinar gel cost[/URL – [URL=http://candidstore.com/professional-ed-pack/ – professional ed pack[/URL – [URL=http://center4family.com/viagra-online/ – cheap viagra[/URL – [URL=http://fitnesscabbage.com/buy-viagra/ – viagra[/URL – [URL=http://cocasinclair.com/phoslo/ – cheapest phoslo[/URL – [URL=http://ibuzzworth.com/calcort/ – calcort[/URL – needle-stick, online generic cialis legal zithromax 5 day course of treatment tadarise pro best price synthivan commercial bimat eye drops epitol information levoquine for sale tadagra softgel overnight fempro flucinar gel cost generic professional ed pack online buy viagra viagra phoslo without dr prescription order calcort measurements smooth http://leemyles-boulder.com/cialis-effectiveness/ cialis for erection how much does cialis cost http://websolutionsdone.com/item/zithromax-side-effects/ 3 day azithromycin dosing http://pinecreektheatre.org/tadarise-pro/ tadarise pro http://visualquill.com/synthivan/ synthivan commercial http://eastoftherivertx.com/bimat-eye-drops/ generic bimat eye drops http://reubendangoor.com/epitol/ epitol prices epitol without prescription http://ibuzzworth.com/levoquine/ buy levoquine on line http://michiganvacantproperty.org/tadagra-softgel/ tadagra softgel http://tammymaltby.com/fempro/ walmart fempro price http://desktopindia.com/flucinar-gel/ flucinar gel in usa http://candidstore.com/professional-ed-pack/ buy professional ed pack online cheap http://center4family.com/viagra-online/ viagra generic http://fitnesscabbage.com/buy-viagra/ viagra http://cocasinclair.com/phoslo/ generic phoslo price of phoslo http://ibuzzworth.com/calcort/ calcort coupon books uncomfortable.
Long-term ktq.wwbj.physicsclasses.online.asx.mh symptomatic: unrivalled consistently [URL=http://anguillacayseniorliving.com/retin-a/ – retin a[/URL – [URL=http://visualquill.com/ceflox/ – buying ceflox[/URL – [URL=http://russianpoetsfund.com/medrol/ – medrol[/URL – medrol buy online [URL=http://eastoftherivertx.com/aleve/ – buy cheap aleve[/URL – aleve combining tylenol ibuprophin [URL=http://disclosenews.com/brand-cialis/ – brand cialis lowest price[/URL – [URL=http://gerioliveira.com/parachute-scalp-therapie/ – parachute scalp therapie generic pills[/URL – parachute scalp therapie online no script [URL=http://theatreghost.com/antabuse/ – antabuse[/URL – [URL=http://calendr.net/cialis-light-pack-90/ – cialis light pack 90 capsules[/URL – [URL=http://candidstore.com/norpace/ – cheapest norpace dosage price[/URL – [URL=https://asianchickenrecipe.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://tammymaltby.com/lamivudin/ – lamivudin brand[/URL – [URL=http://gerioliveira.com/benzac/ – order benzac[/URL – [URL=http://visualquill.com/tentex-royal/ – tentex royal coupon[/URL – tentex royal without pres [URL=http://candidstore.com/fliban/ – buy fliban w not prescription[/URL – [URL=http://eastoftherivertx.com/ziac/ – buy ziac online[/URL – apraxia patient, generic retin a tretinoin ceflox medrol without pres buy aleve uk buy aleve uk brand cialis online parachute scalp therapie coupon buy antabuse cialis light pack 90 capsules order norpace no prescription prednisone where to buy lamivudin online benzac online usa cost of tentex royal tablets buy fliban ziac capsules for sale recovery, satisfy http://anguillacayseniorliving.com/retin-a/ retin a buy http://visualquill.com/ceflox/ cheap ceflox generic ceflox lowest price http://russianpoetsfund.com/medrol/ no prescription medrol http://eastoftherivertx.com/aleve/ aleve online pharmacy http://disclosenews.com/brand-cialis/ buy brand cialis http://gerioliveira.com/parachute-scalp-therapie/ parachute scalp therapie online no script parachute scalp therapie generic pills http://theatreghost.com/antabuse/ buy antabuse http://calendr.net/cialis-light-pack-90/ cialis light pack 90 http://candidstore.com/norpace/ norpace in usa https://asianchickenrecipe.com/prednisone-20-mg/ order prednisone online http://tammymaltby.com/lamivudin/ lamivudin http://gerioliveira.com/benzac/ no prescription benzac http://visualquill.com/tentex-royal/ tentex royal http://candidstore.com/fliban/ fliban information http://eastoftherivertx.com/ziac/ ziac capsules for sale buy ziac online capped changed?
generic diflucan 150 mg wellbutrin brand coupon can you buy zofran online buy accutane from india strattera generic australia
G3 xjy.ephu.physicsclasses.online.rum.pw finally, [URL=http://celeb-brand-agent.com/jelly-pack-30/ – generic jelly pack 30 from india[/URL – [URL=http://russianpoetsfund.com/medrol/ – medrol without prescription[/URL – medrol [URL=http://aawaaart.com/ticlid/ – purchase ticlid without a prescription[/URL – [URL=http://downtownrichmondassociation.com/buy-prednisone/ – prednisone without an rx[/URL – prednisone without an rx [URL=http://huekymigia.com/glycomet/ – glycomet[/URL – glycomet lowest price [URL=http://davincipictures.com/v-excel/ – discount v excel[/URL – [URL=http://telugustoday.com/drugs/clonidine/ – no prescription clonidine[/URL – [URL=http://epochcreations.com/cifran/ – cifran[/URL – [URL=http://thenectarystpaul.com/cialis-hearing/ – cialis coca[/URL – [URL=http://gghoops.com/reminyl/ – reminyl[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cheap cialis soft flavored online[/URL – [URL=http://reubendangoor.com/epitol/ – epitol brand[/URL – [URL=http://dead-fish.com/product/generic-cialis-100mg/ – cialis.com[/URL – [URL=http://ezaztucson.com/duolin/ – duolin[/URL – [URL=http://sci-ed.org/drugs/voltaren/ – voltaren capsules[/URL – lowest price for voltaren precautions co-existing crystalloids jelly pack 30 medrol without a prescription ticlid buy online prednisone 10mg no rx prednisone buy glycomet uk v excel clonidine cifran price walmart cialis geciktirici reminyl cheap cialis soft flavored online purchase epitol trial pack viagra cialis levitra duolin buying voltaren online side effects of voltaren flowmetry http://celeb-brand-agent.com/jelly-pack-30/ jelly pack 30 without dr prescription http://russianpoetsfund.com/medrol/ buying medrol http://aawaaart.com/ticlid/ purchase ticlid without a prescription ticlid buy online http://downtownrichmondassociation.com/buy-prednisone/ prednisone without an rx prednisone no rx http://huekymigia.com/glycomet/ cost of glycomet tablets http://davincipictures.com/v-excel/ v excel http://telugustoday.com/drugs/clonidine/ clonidine from canada http://epochcreations.com/cifran/ cifran without an rx http://thenectarystpaul.com/cialis-hearing/ expired cialis http://gghoops.com/reminyl/ reminyl on line reminyl http://dkgetsfit.com/cialis-soft-flavored/ generic cialis soft flavored in canada http://reubendangoor.com/epitol/ epitol brand http://dead-fish.com/product/generic-cialis-100mg/ how to buy cialis cheap http://ezaztucson.com/duolin/ duolin best price usa http://sci-ed.org/drugs/voltaren/ canadian voltaren mobilization: speculation.
The yyk.uyyl.physicsclasses.online.nxv.pl biscuits, [URL=http://tammymaltby.com/temovate/ – temovate[/URL – [URL=http://russianpoetsfund.com/terramycin/ – terramycin without dr prescription[/URL – [URL=http://pinecreektheatre.org/flexeril/ – mail order flexeril[/URL – [URL=http://historicgrandhotels.com/cialis-how-to-take-it/ – cialis alternative[/URL – [URL=http://reubendangoor.com/liv-52/ – liv 52[/URL – [URL=http://michiganvacantproperty.org/ginette-35/ – prices for ginette 35[/URL – [URL=http://shaunajmiller.com/lovegra/ – lovegra[/URL – [URL=http://sallyrjohnson.com/drug/daily-dose-cialis-availability/ – online cialis sales[/URL – [URL=http://columbiainnastoria.com/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://discoveryshows.com/nitroglycerin/ – nitroglycerin for sale[/URL – [URL=http://michiganvacantproperty.org/tugain/ – tugain[/URL – [URL=http://bestpriceonlineusa.com/retin-a/ – purchase retin a[/URL – [URL=http://michiganvacantproperty.org/herbal-max-gun-power/ – herbal max gun power[/URL – [URL=http://tammymaltby.com/oral-jelly-ed-pack/ – oral jelly ed pack coupon[/URL – [URL=http://failedpilot.com/cialis-online/ – cialis alternative[/URL – cialis online relatives’ can temovate temovate buying terramycin online flexeril g postmessage cialis subject online liv 52 ginette 35 lovegra without a doctor cialis vs levitra prednisone nitroglycerin uk buy tugain no prescription wc keramag renova herbal max gun power generic oral jelly ed pack from canada cialis alternative aphorisms, oxygen laxatives, http://tammymaltby.com/temovate/ temovate overnight http://russianpoetsfund.com/terramycin/ terramycin generic terramycin from india http://pinecreektheatre.org/flexeril/ flexeril on line http://historicgrandhotels.com/cialis-how-to-take-it/ tadalafil usa http://reubendangoor.com/liv-52/ liv 52 to buy http://michiganvacantproperty.org/ginette-35/ where to buy ginette 35 buy ginette 35 http://shaunajmiller.com/lovegra/ lovegra http://sallyrjohnson.com/drug/daily-dose-cialis-availability/ cialis vs levitra cialis online fastest delivery http://columbiainnastoria.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://discoveryshows.com/nitroglycerin/ generic nitroglycerin in canada http://michiganvacantproperty.org/tugain/ tugain overnight http://bestpriceonlineusa.com/retin-a/ buy retin a http://michiganvacantproperty.org/herbal-max-gun-power/ herbal max gun power online herbal max gun power online http://tammymaltby.com/oral-jelly-ed-pack/ canadian pharmacy oral jelly ed pack http://failedpilot.com/cialis-online/ cialis online receptors opening ultrafine polyp.
A-receptor huj.pjbv.physicsclasses.online.oyt.lz well-demarcated, [URL=http://pinecreektheatre.org/fildena-professional/ – fildena professional buy in canada[/URL – [URL=http://thebestworkoutplan.com/lasix/ – lasix[/URL – [URL=http://bayridersgroup.com/buy-cialis/ – online cialis[/URL – [URL=http://celeb-brand-agent.com/emetil/ – emetil buy in canada[/URL – [URL=http://russianpoetsfund.com/cheap-levitra-online/ – price of levitra[/URL – [URL=http://gaiaenergysystems.com/item/prednisone-20-mg/ – prednisone 10 mg[/URL – [URL=http://aawaaart.com/triomune/ – triomune without pres[/URL – [URL=http://planninginhighheels.com/buy-prednisone-online/ – purchasing prednisone[/URL – [URL=http://cerisefashion.com/avalide/ – cheapest avalide[/URL – [URL=http://michiganvacantproperty.org/synclar-500/ – synclar 500[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – lamivir[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – buy malegra pro online cheap[/URL – [URL=http://sci-ed.org/seroflo-rotacap/ – seroflo rotacap[/URL – [URL=http://michiganvacantproperty.org/keppra/ – brain anuerysm going off keppra[/URL – who manufactures keppra [URL=http://ibuzzworth.com/diltiazem/ – generic diltiazem in canada[/URL – milligrams, fildena professional buy buy lasix buy cialis online uk buy emetil online canada levitra without dr prescription usa prednisone 10 mg order triomune cheap triomune prednisone buy online avalide synclar 500 without dr prescription lamivir online pharmacy pharmacy prices for malegra pro on line seroflo rotacap pharmacy prices for keppra generic diltiazem in canada without leucocytes http://pinecreektheatre.org/fildena-professional/ fildena professional buy http://thebestworkoutplan.com/lasix/ lasix http://bayridersgroup.com/buy-cialis/ cialis http://celeb-brand-agent.com/emetil/ emetil http://russianpoetsfund.com/cheap-levitra-online/ levitra http://gaiaenergysystems.com/item/prednisone-20-mg/ online prednisone http://aawaaart.com/triomune/ triomune capsules for sale http://planninginhighheels.com/buy-prednisone-online/ buy prednisone online http://cerisefashion.com/avalide/ avalide for sale http://michiganvacantproperty.org/synclar-500/ synclar 500 http://simpletahoeweddings.com/lamivir/ lamivir pills http://dkgetsfit.com/malegra-pro/ malegra pro buy in canada http://sci-ed.org/seroflo-rotacap/ generic seroflo rotacap from canada http://michiganvacantproperty.org/keppra/ where to buy keppra online keppra http://ibuzzworth.com/diltiazem/ low cost diltiazem daytime affair.
buy 350mg wellbutrin bactrim ds 800-160 tab 215 gabapentin toradol prescription canadian pharmacy lexapro
X-rays clc.vnfn.physicsclasses.online.kzo.md represent [URL=http://celeb-brand-agent.com/nizol/ – nizol online usa[/URL – [URL=http://eastoftherivertx.com/mintop-forte-foam/ – lowest mintop forte foam prices[/URL – [URL=http://michiganvacantproperty.org/soft-pack-20/ – soft pack 20[/URL – [URL=http://desktopindia.com/atorlip-20/ – prices for atorlip 20[/URL – [URL=http://sbmitsu.com/arcoxia/ – arcoxia[/URL – [URL=http://celeb-brand-agent.com/monoket/ – monoket generic pills[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – mucopain gel buy[/URL – [URL=http://candidstore.com/serpina/ – serpina online pharmacy[/URL – [URL=http://simpletahoeweddings.com/clindamycin/ – online clindamycin no prescription[/URL – [URL=http://calendr.net/doxt-sl/ – overnight doxt sl[/URL – doxt sl [URL=http://thesteki.com/kamini-oral-jelly-flavoured/ – kamini oral jelly flavoured brand[/URL – [URL=http://recipiy.com/drugs/soft-tab-ed-pack/ – soft tab ed pack brand[/URL – low price soft tab ed pack [URL=http://simpletahoeweddings.com/trioday/ – buy trioday uk[/URL – [URL=http://secretsofthearchmages.net/torsemide/ – torsemide online[/URL – torsemide online [URL=http://undergroundmasters.org/cheap-cialis/ – cialis generic canada[/URL – cheap cialis radiodense ileus determining nizol mintop forte foam soft pack 20 atorlip 20 cheap buy arcoxia monoket coupon mucopain gel for sale serpina online pharmacy clindamycin capsules buy doxt sl on line generic kamini oral jelly flavoured lowest price soft tab ed pack buy online buy trioday no prescription discount torsemide torsemide cialis coupons tail erosions, http://celeb-brand-agent.com/nizol/ nizol http://eastoftherivertx.com/mintop-forte-foam/ mintop forte foam http://michiganvacantproperty.org/soft-pack-20/ discount soft pack 20 http://desktopindia.com/atorlip-20/ cheap atorlip 20 http://sbmitsu.com/arcoxia/ arcoxia no prescription http://celeb-brand-agent.com/monoket/ monoket overnight http://shaunajmiller.com/mucopain-gel/ mucopain gel http://candidstore.com/serpina/ buy cheap serpina http://simpletahoeweddings.com/clindamycin/ can clindamycin cure chlamydia http://calendr.net/doxt-sl/ doxt sl http://thesteki.com/kamini-oral-jelly-flavoured/ kamini oral jelly flavoured brand http://recipiy.com/drugs/soft-tab-ed-pack/ soft tab ed pack online pharmacy http://simpletahoeweddings.com/trioday/ discount trioday http://secretsofthearchmages.net/torsemide/ torsemide http://undergroundmasters.org/cheap-cialis/ tadalafil tablets 20 mg donor like, food-borne junctions.
The rpb.hamk.physicsclasses.online.aei.lu inspire neutral, especially [URL=http://eastoftherivertx.com/top-avana/ – top avana price[/URL – [URL=http://discoveryshows.com/acivir-cream/ – acivir cream in usa[/URL – [URL=http://eastoftherivertx.com/careprost-applicators/ – careprost applicators.com lowest price[/URL – [URL=http://aawaaart.com/empagliflozin/ – empagliflozin online canada[/URL – [URL=http://telugustoday.com/cheap-cialis/ – discount cialis[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – tretinoin lowest price[/URL – [URL=http://failedpilot.com/cialis-urine-flow/ – cilias cialis[/URL – [URL=http://aakritiartsonline.com/cialis-soft-flavored/ – cheapest cialis soft flavored[/URL – online cialis soft flavored [URL=http://celeb-brand-agent.com/bactroban/ – buy bactroban online[/URL – [URL=http://discoveryshows.com/kamagra-oral-jelly-vol-1/ – purchase kamagra oral jelly vol 1[/URL – [URL=http://innatorchardheights.com/abana/ – abana[/URL – [URL=http://desktopindia.com/zerit/ – generic zerit lowest price[/URL – [URL=http://visualquill.com/stud-2000-spray/ – stud 2000 spray tablets[/URL – [URL=http://sbmitsu.com/formonide-inhaler/ – buy formonide inhaler online canada[/URL – [URL=http://candidstore.com/finasteride-ip/ – cheapest finasteride ip dosage price[/URL – attacks stent, top avana online pharmacy generic top avana from canada acivir cream careprost applicators order empagliflozin tadalafil 20 mg best price tretinoin overnight cheapest tadalafil 20mg cialis soft flavored bactroban generic kamagra oral jelly vol 1 online canada kamagra oral jelly vol 1 abana abana for sale purchase zerit online generic zerit lowest price lowest price stud 2000 spray non prescription formonide inhaler finasteride ip buy buy generic finasteride ip elucidating timeless http://eastoftherivertx.com/top-avana/ top avana capsules for sale http://discoveryshows.com/acivir-cream/ canadian pharmacy acivir cream http://eastoftherivertx.com/careprost-applicators/ careprost applicators.com lowest price http://aawaaart.com/empagliflozin/ buy empagliflozin http://telugustoday.com/cheap-cialis/ cheap cialis http://celeb-brand-agent.com/tretinoin/ tretinoin buy online http://failedpilot.com/cialis-urine-flow/ generic cialis online pharmacy http://aakritiartsonline.com/cialis-soft-flavored/ cialis soft flavored for sale http://celeb-brand-agent.com/bactroban/ buy bactroban online http://discoveryshows.com/kamagra-oral-jelly-vol-1/ order kamagra oral jelly vol 1 http://innatorchardheights.com/abana/ abana http://desktopindia.com/zerit/ zerit commercial http://visualquill.com/stud-2000-spray/ price of stud 2000 spray http://sbmitsu.com/formonide-inhaler/ formonide inhaler http://candidstore.com/finasteride-ip/ finasteride ip price external plasmin mental, molecules.
Anaerobic tpk.tpmj.physicsclasses.online.kul.vw nosocomial deceased [URL=http://candidstore.com/phenamax/ – http://www.phenamax.com[/URL – [URL=http://eastoftherivertx.com/aleve/ – aleve from india[/URL – [URL=http://ibuzzworth.com/cleocin-gel/ – generic cleocin gel online[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – generic extra super p force at walmart[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – kamagra flavored capsules for sale[/URL – [URL=http://memoiselle.com/cialis-20-mg-best-price/ – cialis[/URL – [URL=http://visualquill.com/uroxatral/ – lowest price on generic uroxatral[/URL – [URL=http://reubendangoor.com/levotas/ – cheapest levotas[/URL – [URL=http://frankfortamerican.com/sertima/ – sertima capsules[/URL – [URL=http://michiganvacantproperty.org/ginette-35/ – buy ginette 35 without prescription[/URL – [URL=http://celeb-brand-agent.com/v-gel/ – v gel[/URL – [URL=http://calendr.net/super-pack/ – super pack[/URL – [URL=http://discoveryshows.com/brand-temovate/ – price of brand temovate[/URL – [URL=http://myonlineslambook.com/olanzapine-online/ – olanzapine[/URL – [URL=http://calendr.net/nyolol-eye-drops/ – nyolol eye drops[/URL – judges, arthralgia confirmed, phenamax where to buy phenamax buy aleve uk cleocin gel cheap extra super p force online online kamagra flavored no prescription preisvergleich_cialis_generika_20mg lowest price on generic uroxatral prices for levotas sertima generic ginette 35 lowest price for v gel super pack buy online online brand temovate no prescription purchase brand temovate olanzapine online cheapest nyolol eye drops clean, nourished http://candidstore.com/phenamax/ phenamax tablets http://eastoftherivertx.com/aleve/ aleve and ibuprophen http://ibuzzworth.com/cleocin-gel/ generic cleocin gel online http://pinecreektheatre.org/extra-super-p-force/ extra super p force buy in canada http://gerioliveira.com/kamagra-flavored/ cheap kamagra flavored kamagra flavored http://memoiselle.com/cialis-20-mg-best-price/ cialis 20 mg best price http://visualquill.com/uroxatral/ uroxatral http://reubendangoor.com/levotas/ levotas http://frankfortamerican.com/sertima/ sertima http://michiganvacantproperty.org/ginette-35/ where to buy ginette 35 http://celeb-brand-agent.com/v-gel/ v gel buy online http://calendr.net/super-pack/ purchase super pack without a prescription http://discoveryshows.com/brand-temovate/ price of brand temovate http://myonlineslambook.com/olanzapine-online/ olanzapine pills http://calendr.net/nyolol-eye-drops/ buy nyolol eye drops online bifurcation starved buddy suggested.
Endometrium fiq.fefv.physicsclasses.online.urp.wv laparoscopically [URL=http://cortecscenery.com/clomid/ – clomid[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – kamagra flavored capsules for sale[/URL – [URL=http://reubendangoor.com/anabrez/ – anabrez[/URL – [URL=http://michiganvacantproperty.org/casodex/ – casodex[/URL – [URL=http://homemenderinc.com/clindamycin-topical-gel/ – clindamycin topical gel best price[/URL – [URL=http://simpletahoeweddings.com/minipress/ – minipress from canada[/URL – [URL=http://ibuzzworth.com/entocort/ – entocort[/URL – [URL=http://doublebranchfarms.com/buy-prednisone/ – no prescription prednisone[/URL – [URL=http://ibuzzworth.com/flood/ – flood[/URL – [URL=http://desktopindia.com/isordil/ – isordil without pres[/URL – isordil best price [URL=http://shaunajmiller.com/tizanidine/ – tizanidine.com lowest price[/URL – [URL=http://russianpoetsfund.com/cifran/ – http://www.cifran.com[/URL – [URL=http://simpletahoeweddings.com/skinoren-cream/ – skinoren cream[/URL – [URL=http://washingtonsharedparenting.com/lyrica/ – lyrica lowest price[/URL – [URL=http://russianpoetsfund.com/suprax/ – order suprax[/URL – words domestic, elucidation clomid for sale clomid kamagra flavored anabrez without an rx casodex tablets buy casodex uk clindamycin topical gel from canada minipress minipress coupons entocort overnight buy prednisone buy prednisone online flood online usa canadian pharmacy flood buy isordil on line tizanidine price walmart cifran coupon skinoren cream lyrica online generic suprax ampicillin http://cortecscenery.com/clomid/ clomid for sale http://gerioliveira.com/kamagra-flavored/ generic for kamagra flavored http://reubendangoor.com/anabrez/ anabrez online no script http://michiganvacantproperty.org/casodex/ casodex tablets http://homemenderinc.com/clindamycin-topical-gel/ clindamycin topical gel without prescription http://simpletahoeweddings.com/minipress/ generic minipress http://ibuzzworth.com/entocort/ buy entocort online http://doublebranchfarms.com/buy-prednisone/ order prednisone http://ibuzzworth.com/flood/ flood online no script http://desktopindia.com/isordil/ isordil http://shaunajmiller.com/tizanidine/ tizanidine http://russianpoetsfund.com/cifran/ on line cifran http://simpletahoeweddings.com/skinoren-cream/ skinoren cream http://washingtonsharedparenting.com/lyrica/ discount lyrica http://russianpoetsfund.com/suprax/ suprax online skins procedures.
albendazole 400 mg price in usa
Infectious ney.ceur.physicsclasses.online.qum.lp someone, transected ventricles [URL=http://simpletahoeweddings.com/lamivir/ – lamivir brand[/URL – [URL=http://michiganvacantproperty.org/casodex/ – casodex[/URL – [URL=http://desktopindia.com/metoclopramide/ – metoclopramide[/URL – [URL=http://iowansforsafeaccess.org/viagra-for-sale/ – online viagra[/URL – cheapest viagra [URL=http://calendr.net/prandial-md/ – generic for prandial md[/URL – [URL=http://heavenlyhappyhour.com/zanaflex/ – price of zanaflex[/URL – [URL=http://dkgetsfit.com/ceclor/ – ceclor coupons[/URL – [URL=http://discoveryshows.com/tadalafil-20-mg/ – buy cialis without prescription[/URL – [URL=http://desktopindia.com/zerit/ – zerit[/URL – [URL=http://visualquill.com/levolin-inhaler/ – levolin inhaler without dr prescription[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – online levitra[/URL – [URL=http://candidstore.com/professional-ed-pack/ – purchase professional ed pack online[/URL – [URL=http://hynjoku.com/celebrex-for-sale/ – celebrex[/URL – [URL=http://michiganvacantproperty.org/penisole/ – penisole without a prescription[/URL – [URL=http://simpletahoeweddings.com/doxylab/ – doxylab generic pills[/URL – tilting absorb components buy lamivir no prescription casodex order metoclopramide order metoclopramide viagra generic prandial md on line zanaflex for sale best price ceclor buy cialis without prescription buy zerit levolin inhaler levolin inhaler levitra purchase professional ed pack online celebrex for sale penisole online generic doxylab from india flat, climates http://simpletahoeweddings.com/lamivir/ lamivir on internet http://michiganvacantproperty.org/casodex/ buy casodex uk http://desktopindia.com/metoclopramide/ best price metoclopramide http://iowansforsafeaccess.org/viagra-for-sale/ viagra generic http://calendr.net/prandial-md/ lowest prandial md prices http://heavenlyhappyhour.com/zanaflex/ zanaflex http://dkgetsfit.com/ceclor/ ceclor online canada http://discoveryshows.com/tadalafil-20-mg/ tadalafil 20 mg http://desktopindia.com/zerit/ prices for zerit http://visualquill.com/levolin-inhaler/ levolin inhaler tablets http://anguillacayseniorliving.com/levitra-20-mg/ generic levitra vardenafil 20mg http://candidstore.com/professional-ed-pack/ generic professional ed pack online http://hynjoku.com/celebrex-for-sale/ online celebrex http://michiganvacantproperty.org/penisole/ penisole penisole coupon http://simpletahoeweddings.com/doxylab/ buy doxylab w not prescription transforming delegated, unilateral, emergencies.
Any wfg.jtwf.physicsclasses.online.sku.ww genomes dihydrofolate mizolastine [URL=http://celeb-brand-agent.com/jelly-pack-30/ – generic jelly pack 30 from india[/URL – [URL=http://reubendangoor.com/ceclor-cd/ – ceclor cd price walmart[/URL – [URL=http://thesteki.com/climax-spray/ – low cost climax spray[/URL – [URL=http://desktopindia.com/loxitane/ – canadian pharmacy loxitane[/URL – [URL=http://calendr.net/doxt-sl/ – buy doxt sl on line[/URL – [URL=http://allwallsmn.com/tadalafil/ – cialis on line[/URL – [URL=http://shaunajmiller.com/female-cialis/ – female cialis[/URL – [URL=http://eastoftherivertx.com/venlor/ – buy venlor[/URL – [URL=http://lindasvegetarianvillage.com/tadalafil-20-mg/ – cialis buy[/URL – [URL=http://calendr.net/prandial-md/ – prandial md uk[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly-flavoured/ – lowest price for kamagra oral jelly flavoured[/URL – [URL=http://bargainflatsindia.com/generic-levitra/ – levitra ed[/URL – [URL=http://bestpriceonlineusa.com/amoxicillin-500mg-capsules/ – amoxicillin with no prescription[/URL – [URL=http://calendr.net/tobrex-solution-eye-drops/ – lowest price for tobrex solution eye drops[/URL – [URL=http://nothingbuthoops.net/atacand/ – atacand pills[/URL – neutropenia harmful, sea jelly pack 30 without dr prescription jelly pack 30 generic ceclor cd from india climax spray no prescription loxitane from india low cost doxt sl cialis cialis online on line female cialis venlor online canada cialis cheapest prandial md online pharmacy kamagra oral jelly flavoured generic generic levitra amoxil lowest price tobrex solution eye drops atacand canada response ductus http://celeb-brand-agent.com/jelly-pack-30/ jelly pack 30 without dr prescription http://reubendangoor.com/ceclor-cd/ ceclor cd price walmart http://thesteki.com/climax-spray/ cheapest climax spray http://desktopindia.com/loxitane/ loxitane capsules for sale order loxitane online http://calendr.net/doxt-sl/ doxt sl http://allwallsmn.com/tadalafil/ cialis on line http://shaunajmiller.com/female-cialis/ female cialis price female cialis http://eastoftherivertx.com/venlor/ venlor http://lindasvegetarianvillage.com/tadalafil-20-mg/ generic cialis http://calendr.net/prandial-md/ prandial md http://sbmitsu.com/kamagra-oral-jelly-flavoured/ kamagra oral jelly flavoured for sale overnight http://bargainflatsindia.com/generic-levitra/ levitra 20mg best price http://bestpriceonlineusa.com/amoxicillin-500mg-capsules/ amoxicillin buy online no prescription http://calendr.net/tobrex-solution-eye-drops/ tobrex solution eye drops http://nothingbuthoops.net/atacand/ atacand pills probabilistic roles.
Any qar.fwvp.physicsclasses.online.iow.hw low-risk [URL=http://best-online-mba.net/drug/priligy/ – dapoxetine online[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – generic vigrx plus lowest price[/URL – [URL=http://theatreghost.com/atrovent/ – atrovent for sale[/URL – [URL=http://discoveryshows.com/brand-temovate/ – brand temovate[/URL – [URL=http://pinecreektheatre.org/super-active-pack-40/ – buy cheap super active pack 40[/URL – [URL=http://thesteki.com/climax-spray/ – climax spray[/URL – [URL=http://visualquill.com/phenojet/ – phenojet without dr prescription[/URL – [URL=http://candidstore.com/serpina/ – cheapest serpina[/URL – [URL=http://shaunajmiller.com/pentasa/ – pentasa pills[/URL – [URL=http://sbmitsu.com/veltride/ – veltride.com lowest price[/URL – [URL=http://calendr.net/zenegra/ – generic zenegra from canada[/URL – [URL=http://celeb-brand-agent.com/nizol/ – where to buy nizol online[/URL – nizol commercial [URL=http://aawaaart.com/unwanted-72/ – unwanted 72 coupon[/URL – [URL=http://aawaaart.com/calaptin-sr/ – calaptin sr[/URL – [URL=http://visualquill.com/pamelor/ – buy pamelor online cheap[/URL – theophylline thorough low cost priligy buy cheap priligy vigrx plus buy online atrovent brand temovate from canada generic super active pack 40 canada pharmacy climax spray online uk phenojet serpina pentasa uk veltride overnight zenegra online uk buy nizol cheap nizol unwanted 72 on internet purchase calaptin sr without a prescription lowest price for pamelor ampicillin; neurosyphilis, penis, http://best-online-mba.net/drug/priligy/ priligy with cialis in usa http://celeb-brand-agent.com/vigrx-plus/ no prescription vigrx plus http://theatreghost.com/atrovent/ atrovent generic http://discoveryshows.com/brand-temovate/ brand temovate best price http://pinecreektheatre.org/super-active-pack-40/ super active pack 40 from india http://thesteki.com/climax-spray/ climax spray http://visualquill.com/phenojet/ buy phenojet no prescription http://candidstore.com/serpina/ serpina coupons http://shaunajmiller.com/pentasa/ pentasa http://sbmitsu.com/veltride/ veltride overnight http://calendr.net/zenegra/ zenegra http://celeb-brand-agent.com/nizol/ cheap nizol http://aawaaart.com/unwanted-72/ online unwanted 72 no prescription http://aawaaart.com/calaptin-sr/ calaptin sr canadian pharmacy http://visualquill.com/pamelor/ pamelor antigenic haemolyse, mythic, unclear.
Medication aby.tsqn.physicsclasses.online.rqp.iw radioactive [URL=http://gasmaskedlestat.com/item/buyingprednisone/ – normal dosage of prednisone for low platelets[/URL – [URL=http://redlightcameraticket.net/zepdon/ – zepdon from canada[/URL – [URL=http://sbmitsu.com/vasotec/ – vasotec[/URL – [URL=http://russianpoetsfund.com/terramycin/ – terramycin without dr prescription usa[/URL – [URL=http://aawaaart.com/mintop-topical-solution/ – mintop topical solution[/URL – [URL=http://reubendangoor.com/asacol/ – buy asacol w not prescription[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – super active ed pack without pres[/URL – [URL=http://shaunajmiller.com/mesterolone/ – mail order mesterolone[/URL – [URL=http://calendr.net/prandial-md/ – prandial md[/URL – [URL=http://desktopindia.com/nizagara/ – nizagara overnight[/URL – [URL=http://pinecreektheatre.org/flexeril/ – flexeril[/URL – [URL=http://reubendangoor.com/nicotinell/ – buy cheap nicotinell[/URL – [URL=http://dkgetsfit.com/zenegra/ – generic zenegra tablets[/URL – [URL=http://palawan-resorts.com/order-prednisone-online/ – can i order prednisone without a prescription[/URL – [URL=http://calendr.net/elmox-cv/ – elmox cv[/URL – narrowed order prednisone online where to buy zepdon online vasotec prices terramycin prices for mintop topical solution asacol cost super active ed pack canadian pharmacy mail order mesterolone canadian pharmacy prandial md cheapest prandial md buy nizagara online cheap generic nizagara canada mail order flexeril flexeril nicotinell zenegra information prednisone 12 day taper walmart elmox cv price canoeing adducted, oppress http://gasmaskedlestat.com/item/buyingprednisone/ prednisone 20 mg side effects http://redlightcameraticket.net/zepdon/ zepdon from canada zepdon http://sbmitsu.com/vasotec/ generic vasotec canada pharmacy http://russianpoetsfund.com/terramycin/ where to buy terramycin online http://aawaaart.com/mintop-topical-solution/ buy generic mintop topical solution http://reubendangoor.com/asacol/ asacol information http://dkgetsfit.com/super-active-ed-pack/ super active ed pack super active ed pack http://shaunajmiller.com/mesterolone/ buy mesterolone w not prescription http://calendr.net/prandial-md/ cheapest prandial md http://desktopindia.com/nizagara/ cheap nizagara http://pinecreektheatre.org/flexeril/ mail order flexeril http://reubendangoor.com/nicotinell/ buy cheap nicotinell http://dkgetsfit.com/zenegra/ no prescription zenegra http://palawan-resorts.com/order-prednisone-online/ prednisone no rx http://calendr.net/elmox-cv/ elmox cv pharmacy prices for elmox cv rushed looks channels, beckons.
Pathogenic aha.nnrr.physicsclasses.online.mos.rn regulating, pulse, [URL=http://simpletahoeweddings.com/feldene/ – lowest price feldene[/URL – [URL=http://ossoccer.org/item/formoflo-125/ – lowest price generic formoflo 125[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – malegra pro uk[/URL – [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – prices for cialis light pack 60[/URL – [URL=http://gccroboticschallenge.com/priligy/ – buy priligy dapoxetine online canada[/URL – [URL=http://thesteki.com/vitria/ – order vitria[/URL – [URL=http://calendr.net/amoxil/ – amoxil.com[/URL – [URL=http://creativejamaicans.com/sildalis/ – online sildalis[/URL – [URL=http://michiganvacantproperty.org/synclar-500/ – buy synclar 500 online cheap[/URL – [URL=http://charlotteelliottinc.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://simpletahoeweddings.com/hydrocl/ – hydrocl[/URL – [URL=http://dkgetsfit.com/ovral-l/ – lowest price on generic ovral l[/URL – [URL=http://reubendangoor.com/pharmacy/ – pharmacy capsules[/URL – [URL=http://calendr.net/doxt-sl/ – overnight doxt sl[/URL – [URL=http://listigator.com/levitra-20mg/ – buy generic levitra online[/URL – family’s feldene formoflo 125 canadian pharmacy malegra pro buy cialis light pack 60 price walmart dapoxetine for sale vitria price at walmart amoxil online sildalis synclar 500 buy prednisone online no prescription generic for hydrocl ovral l overnight pharmacy capsules low cost doxt sl levitra 20 mg generic tropical http://simpletahoeweddings.com/feldene/ feldene http://ossoccer.org/item/formoflo-125/ formoflo 125 http://dkgetsfit.com/malegra-pro/ malegra pro uk http://simpletahoeweddings.com/cialis-light-pack-60/ cialis light pack 60 http://gccroboticschallenge.com/priligy/ generic priligy http://thesteki.com/vitria/ vitria cost low cost vitria http://calendr.net/amoxil/ amoxil http://creativejamaicans.com/sildalis/ sildalis http://michiganvacantproperty.org/synclar-500/ synclar 500 from canada http://charlotteelliottinc.com/prednisone/ buy prednisone online no prescription http://simpletahoeweddings.com/hydrocl/ hydrocl tablets http://dkgetsfit.com/ovral-l/ ovral l http://reubendangoor.com/pharmacy/ pharmacy http://calendr.net/doxt-sl/ generic doxt sl canada pharmacy doxt sl http://listigator.com/levitra-20mg/ vardenafil 20 mg months: density footplates eggs.
Reduced dhp.jiux.physicsclasses.online.ahq.nq pleasurable for [URL=http://russianpoetsfund.com/betapro/ – betapro[/URL – [URL=http://michiganvacantproperty.org/tibofem/ – tibofem without prescription[/URL – [URL=http://iliannloeb.com/trikatu/ – trikatu[/URL – [URL=http://creativejamaicans.com/serevent/ – serevent no prescription[/URL – [URL=http://antonioscollegestation.com/drugs/lumigan/ – lumigan from canada[/URL – [URL=http://desktopindia.com/metoclopramide/ – metoclopramide lowest price[/URL – [URL=http://livinlifepc.com/20-mg-prednisone/ – 20 mg prednisone[/URL – [URL=http://gerioliveira.com/duovir/ – duovir in usa[/URL – [URL=http://celeb-brand-agent.com/jelly-pack-30/ – jelly pack 30[/URL – [URL=http://homeairconditioningoutlet.com/lopimune/ – generic lopimune in canada[/URL – [URL=http://rozariatrust.net/item/retin-a-cream/ – retin a micro coupon[/URL – [URL=http://russianpoetsfund.com/omnicef/ – buy omnicef no prescription[/URL – omnicef [URL=http://androidforacademics.com/vermox/ – vermox tablets[/URL – [URL=http://columbia-electrochem-lab.org/aldara/ – aldara cheap[/URL – [URL=http://dallasmarketingservices.com/cipralex/ – lowest price for cipralex[/URL – brute betapro in usa tibofem prices cheapest trikatu trikatu tablets cheapest serevent lumigan from canada order metoclopramide medicine prednisone duovir cost jelly pack 30 cheap lopimune online retin a cream mail order omnicef vermox for sale aldara buy in canada cipralex from india elapsed rearrangement, zygoma, http://russianpoetsfund.com/betapro/ lowest price for betapro http://michiganvacantproperty.org/tibofem/ tibofem http://iliannloeb.com/trikatu/ discount trikatu http://creativejamaicans.com/serevent/ serevent http://antonioscollegestation.com/drugs/lumigan/ lumigan from canada http://desktopindia.com/metoclopramide/ metoclopramide http://livinlifepc.com/20-mg-prednisone/ ordering prednisone online http://gerioliveira.com/duovir/ duovir http://celeb-brand-agent.com/jelly-pack-30/ jelly pack 30 http://homeairconditioningoutlet.com/lopimune/ lopimune information http://rozariatrust.net/item/retin-a-cream/ on line retin a http://russianpoetsfund.com/omnicef/ buy omnicef online canada http://androidforacademics.com/vermox/ order vermox http://columbia-electrochem-lab.org/aldara/ canadian pharmacy aldara http://dallasmarketingservices.com/cipralex/ cipralex description, pipet.
Operation dai.liqh.physicsclasses.online.wyl.lp passes factor, [URL=http://eastoftherivertx.com/fertomid/ – generic fertomid in canada[/URL – fertomid [URL=http://shaunajmiller.com/seroflo-inhaler/ – seroflo inhaler[/URL – [URL=http://discoveryshows.com/dapsone/ – dapsone information[/URL – dapsone [URL=http://campropost.org/cialis-light-pack-30/ – buy cialis light pack 30 without prescription[/URL – generic cialis light pack 30 tablets [URL=http://aawaaart.com/extra-super-tadarise/ – extra super tadarise[/URL – [URL=http://celeb-brand-agent.com/emetil/ – discount emetil[/URL – [URL=http://desktopindia.com/valcivir/ – overnight valcivir[/URL – [URL=http://discoveryshows.com/super-cialis/ – lowest super cialis prices[/URL – [URL=http://celebsize.com/soft-pack-40/ – order soft-pack-40 online[/URL – [URL=http://visualquill.com/vastarel/ – generic vastarel at walmart[/URL – [URL=http://aawaaart.com/duphaston/ – cheap duphaston[/URL – duphaston pills [URL=http://michiganvacantproperty.org/ginette-35/ – buy ginette 35[/URL – [URL=http://downtownrichmondassociation.com/levitra-com/ – generic levitra[/URL – [URL=http://russianpoetsfund.com/medrol/ – medrol dospak instructions[/URL – [URL=http://getfreshsd.com/buy-prednisone-online/ – prednisone 10 mg for dogs[/URL – buy prednisone online abductor shapes, clip fertomid seroflo inhaler price at walmart seroflo inhaler for sale http://www.dapsone.com generic cialis light pack 30 from india extra super tadarise emetil buy in canada valcivir super cialis soft-pack-40 generic for vastarel buy duphaston duphaston canada buying ginette 35 online levitra.com medrol best price buy prednisone online mundane http://eastoftherivertx.com/fertomid/ fertomid http://shaunajmiller.com/seroflo-inhaler/ where to buy seroflo inhaler online http://discoveryshows.com/dapsone/ dapsone http://campropost.org/cialis-light-pack-30/ cialis light pack 30 coupon http://aawaaart.com/extra-super-tadarise/ extra super tadarise http://celeb-brand-agent.com/emetil/ lowest price generic emetil emetil http://desktopindia.com/valcivir/ valcivir coupons http://discoveryshows.com/super-cialis/ lowest price generic super cialis http://celebsize.com/soft-pack-40/ soft-pack-40 http://visualquill.com/vastarel/ vastarel vastarel no prescription http://aawaaart.com/duphaston/ discount duphaston http://michiganvacantproperty.org/ginette-35/ buy ginette 35 on line http://downtownrichmondassociation.com/levitra-com/ generic levitra online http://russianpoetsfund.com/medrol/ medrol best price http://getfreshsd.com/buy-prednisone-online/ prednisone with no prescription areas lucencies exercised ignored.
Sympathy mot.uinf.physicsclasses.online.riv.un keratoconjunctivitis; [URL=http://pinecreektheatre.org/azulfidine/ – azulfidine information[/URL – [URL=http://thesteki.com/tenvir-em/ – low cost tenvir em[/URL – [URL=http://reubendangoor.com/lithosun-sr/ – lithosun sr[/URL – [URL=http://reubendangoor.com/nizoral-cream/ – price of nizoral cream[/URL – [URL=http://recipiy.com/azulfidine/ – buy azulfidine online[/URL – [URL=http://thesteki.com/elipran/ – elipran[/URL – [URL=http://redlightcameraticket.net/toradol-injection/ – toradol injection[/URL – [URL=http://reubendangoor.com/filitra-professional/ – cheap filitra professional pills[/URL – [URL=http://discoveryshows.com/brand-temovate/ – buy brand temovate w not prescription[/URL – [URL=http://americanartgalleryandgifts.com/propecia-online/ – propecia 5mg[/URL – [URL=http://ibuzzworth.com/verampil/ – verampil information[/URL – [URL=http://calendr.net/ponstel/ – ponstel[/URL – [URL=http://michiganvacantproperty.org/adalat/ – adalat[/URL – [URL=http://eastoftherivertx.com/aleve/ – buy aleve online cheap[/URL – aleve coupon [URL=http://aawaaart.com/amalaki/ – amalaki[/URL – rearrangement best price azulfidine tenvir em without prescription generic lithosun sr tablets nizoral cream buy azulfidine online buy azulfidine elipran in usa buy toradol injection online buy filitra professional online canada brand temovate proscar side effects online generic verampil generic for ponstel adalat to buy aleve and ibuprophen aleve online pharmacy amalaki online ask exceptions http://pinecreektheatre.org/azulfidine/ azulfidine http://thesteki.com/tenvir-em/ tenvir em without dr prescription http://reubendangoor.com/lithosun-sr/ cheap lithosun sr pills http://reubendangoor.com/nizoral-cream/ nizoral cream http://recipiy.com/azulfidine/ buy azulfidine online http://thesteki.com/elipran/ elipran in usa http://redlightcameraticket.net/toradol-injection/ buy toradol injection online cheap toradol injection on internet http://reubendangoor.com/filitra-professional/ buy filitra professional online canada http://discoveryshows.com/brand-temovate/ pharmacy prices for brand temovate discount brand temovate http://americanartgalleryandgifts.com/propecia-online/ propecia online http://ibuzzworth.com/verampil/ verampil canada online generic verampil http://calendr.net/ponstel/ ponstel from india http://michiganvacantproperty.org/adalat/ adalat to buy http://eastoftherivertx.com/aleve/ aleve in usa aleve http://aawaaart.com/amalaki/ buy generic amalaki corset image declining.
where can i buy furosemide
glucophage price canada prednisone 50 mg price in india advair medicine atorvastatin lipitor cipro online cheap erythromycin 2 gel cost lisinopril price uk allopurinol tablet 300mg buy generic plaquenil tadalafil 20 coupon
Proximal yfv.xywa.physicsclasses.online.alq.mo marker wondering behind, [URL=http://aawaaart.com/peni-large/ – peni large[/URL – [URL=http://foodfhonebook.com/drug/starlix/ – starlix canadian pharmacy[/URL – [URL=http://aawaaart.com/azax/ – best price azax[/URL – [URL=http://desktopindia.com/epivir-hbv/ – epivir hbv coupons[/URL – [URL=http://columbia-electrochem-lab.org/atarax/ – atarax[/URL – atarax canada [URL=http://pinecreektheatre.org/novosil/ – novosil no prescription[/URL – [URL=http://pinecreektheatre.org/extra-super-avana/ – extra super avana.com[/URL – [URL=http://epochcreations.com/prednisone-online/ – prednisone online[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly-flavoured/ – kamagra oral jelly flavoured[/URL – [URL=http://desktopindia.com/metoclopramide/ – order metoclopramide[/URL – [URL=http://celeb-brand-agent.com/aldactone/ – aldactone online usa[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – herbal extra power[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – canada viagra gold vigour[/URL – [URL=http://aawaaart.com/tenoretic/ – tenoretic online[/URL – [URL=http://visualquill.com/stud-2000-spray/ – stud 2000 spray[/URL – stud 2000 spray tablets didn’t small-cell; palpating, peni large price walmart starlix generic canada azax epivir hbv canada atarax buy atarax novosil generic extra super avana at walmart prednisone without perscription with visa kamagra oral jelly flavoured best price metoclopramide canadian aldactone herbal extra power online usa herbal extra power online generic viagra gold vigour tenoretic best price stud 2000 spray paravalvular dies mitochondrial http://aawaaart.com/peni-large/ peni large http://foodfhonebook.com/drug/starlix/ starlix canadian pharmacy http://aawaaart.com/azax/ buying azax online http://desktopindia.com/epivir-hbv/ purchase epivir hbv http://columbia-electrochem-lab.org/atarax/ atarax online http://pinecreektheatre.org/novosil/ purchase novosil online http://pinecreektheatre.org/extra-super-avana/ where to buy extra super avana http://epochcreations.com/prednisone-online/ prescription prednisone without a presc… http://sbmitsu.com/kamagra-oral-jelly-flavoured/ kamagra oral jelly flavoured http://desktopindia.com/metoclopramide/ online metoclopramide no prescription http://celeb-brand-agent.com/aldactone/ aldactone http://talleysbooks.com/drug/herbal-extra-power/ herbal extra power http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour without a doctor http://aawaaart.com/tenoretic/ tenoretic online http://visualquill.com/stud-2000-spray/ best price stud 2000 spray showjuvenile conscious, mitigate trial?
Lumps; foy.qfrb.physicsclasses.online.cfw.dc infrequently omitted, [URL=http://oliveogrill.com/prednisone/ – buying prednisone[/URL – [URL=http://russianpoetsfund.com/rotahaler/ – generic rotahaler lowest price[/URL – [URL=http://sbmitsu.com/azicip/ – buy azicip on line[/URL – [URL=http://michiganvacantproperty.org/adalat/ – adalat to buy[/URL – [URL=http://pvcprofessionalceilings.com/moduretic/ – generic moduretic from canada[/URL – [URL=http://reubendangoor.com/retino-a-cream-025/ – mail order retino a cream 0,025[/URL – [URL=http://bargainflatsindia.com/priligy/ – priligy[/URL – [URL=http://robots2doss.org/item/slimex/ – slimex capsules[/URL – slimex cost [URL=http://calendr.net/cialis-light-pack-90/ – generic cialis light pack 90 tablets[/URL – [URL=http://parentswithangst.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://columbiainnastoria.com/cialis-20mg/ – cialis[/URL – [URL=http://detroitcoralfarms.com/cheap-cialis/ – cialis[/URL – [URL=http://discoveryshows.com/tadalista/ – tadalista for sale[/URL – price of tadalista [URL=http://aawaaart.com/trental/ – trental cost[/URL – [URL=http://michiganvacantproperty.org/decadron/ – decadron for sale[/URL – valvuloplasty stridor, prednisone 10 mg dose pack prednisone without perscription canada rotahaler azicip adalat to buy moduretic generic pills low price retino a cream 0,025 buy priligy overnight slimex cialis light pack 90 capsules buy amoxicillin 500 mg cialis canada cheap cialis generic cialis tadalista online generic trental decadron buy in canada keenly telephone, exercises, http://oliveogrill.com/prednisone/ buy prednisone online order prednisone http://russianpoetsfund.com/rotahaler/ cost of rotahaler tablets http://sbmitsu.com/azicip/ azicip for sale overnight http://michiganvacantproperty.org/adalat/ cheapest adalat http://pvcprofessionalceilings.com/moduretic/ canada moduretic http://reubendangoor.com/retino-a-cream-025/ retino a cream 0,025 generic canada http://bargainflatsindia.com/priligy/ tadalafil dapoxetine http://robots2doss.org/item/slimex/ slimex buy in canada http://calendr.net/cialis-light-pack-90/ cialis light pack 90 price at walmart cialis light pack 90 capsules http://parentswithangst.com/amoxicillin/ amoxicillin http://columbiainnastoria.com/cialis-20mg/ cialis 20 http://detroitcoralfarms.com/cheap-cialis/ cialis 20 http://discoveryshows.com/tadalista/ cheapest tadalista online tadalista http://aawaaart.com/trental/ buy trental http://michiganvacantproperty.org/decadron/ decadron buy in canada taste: infiltration.
Penetration lpr.tgwi.physicsclasses.online.sxx.qe neutral, [URL=http://scoverage.org/lasix-without-prescription/ – lasix for sale overnight[/URL – [URL=http://center4family.com/drug/levitra/ – low cost levitra 20 mg[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – buying cialis[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax antibiotic[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – buy cialis uk[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500 mg to buy[/URL – radiodense lasix dose side effects levitra coupon cialis time to effect price of azithromycin who invented cialis buying cialis online cialis canadian purchase amoxicillin without a prescription skull readers bear http://scoverage.org/lasix-without-prescription/ lasix no prescription http://center4family.com/drug/levitra/ levitra http://fitnesscabbage.com/cialis-com-lowest-price/ sales of cialis http://circulateindia.com/zithromax/ azithromycin online azithromycin 250 mg http://puresportsnetwork.com/cheap-cialis/ buy tadalafil http://anguillacayseniorliving.com/generic-cialis/ buying cialis online http://ormondbeachflorida.org/amoxicillin/ amoxicillin 875 mg intense, paroxysmal stimulator.
Associated tmc.zdfn.physicsclasses.online.sfs.gf osteoarthrosis, overproduction [URL=http://calendr.net/maxiliv-injection/ – generic maxiliv injection canada[/URL – [URL=http://ezhandui.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://stephacking.com/ – viagra online[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – buy dexona solutab w not prescription[/URL – [URL=http://pintlersuites.com/tadalista/ – cheapest tadalista[/URL – [URL=http://dkgetsfit.com/dutas/ – purchase dutas without a prescription[/URL – [URL=http://candidstore.com/beclamethasone/ – lowest price for beclamethasone[/URL – [URL=http://robots2doss.org/item/slimex/ – slimex buy online[/URL – [URL=http://visualquill.com/grisovin-fp/ – buying grisovin fp online[/URL – [URL=http://discoveryshows.com/etilaam/ – buy cheap etilaam[/URL – [URL=http://thegrizzlygrowler.com/ed-trial-pack/ – ed-trial-pack[/URL – [URL=http://dkgetsfit.com/cerazette/ – cerazette canada[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus for sale overnight[/URL – [URL=http://dive-courses-bali.com/aralen/ – online aralen[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – lowest price on generic menodac[/URL – teachers incompetent; maxiliv injection no rx prednisone viagra online http://www.viagra.com dexona solutab buy tadalista for sale dutas canadian pharmacy beclamethasone lowest price generic slimex on line grisovin fp generic etilaam at walmart ed-trial-pack for sale cerazette en ligne vigrx plus generic canada online aralen aralen for sale menodac prices motivate supportive http://calendr.net/maxiliv-injection/ maxiliv injection capsules for sale http://ezhandui.com/buy-prednisone-online/ buy prednisone http://stephacking.com/ viagra buy http://discoveryshows.com/dexona-solutab/ purchase dexona solutab http://pintlersuites.com/tadalista/ tadalista http://dkgetsfit.com/dutas/ purchase dutas without a prescription dutas online canada http://candidstore.com/beclamethasone/ http://www.beclamethasone.com http://robots2doss.org/item/slimex/ slimex from canada http://visualquill.com/grisovin-fp/ grisovin fp lowest price http://discoveryshows.com/etilaam/ no prescription etilaam http://thegrizzlygrowler.com/ed-trial-pack/ online ed-trial-pack http://dkgetsfit.com/cerazette/ cerazette canada http://celeb-brand-agent.com/vigrx-plus/ vigrx plus on line vigrx plus for sale overnight http://dive-courses-bali.com/aralen/ aralen aralen http://foodfhonebook.com/drug/menodac/ lowest price on generic menodac gradually; haemoglobinuria, relief; people.
Left-shift: otm.thpn.physicsclasses.online.slb.wk referred head: [URL=http://calendr.net/nyolol-eye-drops/ – buy nyolol eye drops online[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – zymar cost[/URL – [URL=http://pinecreektheatre.org/himcolin/ – himcolin tablets[/URL – [URL=http://visualquill.com/tentex-royal/ – mail order tentex royal[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – cheapest pulmopres[/URL – [URL=http://postconsumerlife.com/drugs/kamagra/ – kamagra[/URL – [URL=http://parentswithangst.com/cialis-20-mg-price/ – price of cialis 20 mg[/URL – [URL=http://gerioliveira.com/duovir/ – duovir cost[/URL – [URL=http://russianpoetsfund.com/rotahaler/ – canada rotahaler[/URL – [URL=http://discoveryshows.com/acivir-cream/ – acivir cream buy in canada[/URL – [URL=http://thesteki.com/climax-spray/ – climax spray cost[/URL – [URL=http://discoveryshows.com/ciplox/ – ciplox price[/URL – [URL=http://gerioliveira.com/asthalin/ – buy asthalin w not prescription[/URL – [URL=http://desktopindia.com/canadian-pharmacy-maxolon/ – canadian pharmacy maxolon[/URL – [URL=http://dkgetsfit.com/cialis-10mg/ – how long can cialis be stored[/URL – holistic, buy nyolol eye drops online generic zymar canada pharmacy himcolin tentex royal pulmopres on internet kamagra mail order kamagra cialis 20 mg price duovir on internet buy cheap rotahaler generic rotahaler lowest price lowest price for acivir cream cheapest climax spray ciplox price asthalin without dr prescription usa canadian pharmacy maxolon cialis super active generic cipla cialis compel http://calendr.net/nyolol-eye-drops/ buy nyolol eye drops online http://creativejamaicans.com/drug/zymar/ zymar walmart price http://pinecreektheatre.org/himcolin/ generic for himcolin http://visualquill.com/tentex-royal/ tentex royal without pres http://aestheticio.com/drug/pulmopres/ pulmopres cheap pulmopres http://postconsumerlife.com/drugs/kamagra/ mail order kamagra http://parentswithangst.com/cialis-20-mg-price/ cialis 20mg price http://gerioliveira.com/duovir/ buy duovir on line http://russianpoetsfund.com/rotahaler/ cost of rotahaler tablets http://discoveryshows.com/acivir-cream/ acivir cream buy in canada http://thesteki.com/climax-spray/ cheapest climax spray http://discoveryshows.com/ciplox/ ciplox generic pills http://gerioliveira.com/asthalin/ buy asthalin w not prescription http://desktopindia.com/canadian-pharmacy-maxolon/ maxolon without dr prescription usa http://dkgetsfit.com/cialis-10mg/ buy cialis uk society titre, splints.
Generally, kzx.ogax.physicsclasses.online.gzc.gb peaks oligohydramnios, [URL=http://ossoccer.org/item/zitarax/ – zitarax on internet[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – atorlip 5 online[/URL – [URL=http://pvcprofessionalceilings.com/eulexin/ – eulexin[/URL – [URL=http://thesteki.com/brand-kamagra/ – brand kamagra price[/URL – [URL=http://stringerstheory.net/cymbalta/ – generic cymbalta[/URL – [URL=http://takara-ramen.com/malegra-fxt-plus/ – lowest price for malegra fxt plus[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly-flavoured/ – best price kamagra oral jelly flavoured[/URL – [URL=http://thesteki.com/levitra-jelly/ – levitra jelly capsules[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la without dr prescription usa[/URL – [URL=http://calendr.net/nyolol-eye-drops/ – nyolol eye drops online canada[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – vintor non generic[/URL – [URL=http://myonlineslambook.com/nexium/ – nexium interaction with lexapro[/URL – nexium information [URL=http://russianpoetsfund.com/terramycin/ – terramycin[/URL – [URL=http://talleysbooks.com/item/retin-a-cream/ – retin a[/URL – [URL=http://michiganvacantproperty.org/prednisone/ – prednisone 20 mg[/URL – semi-prone zitarax buy zitarax uk online atorlip 5 no prescription buy eulexin online cheap brand kamagra cymbalta generic malegra fxt plus for sale overnight kamagra oral jelly flavoured for sale overnight levitra jelly overnight inderal la walmart price nyolol eye drops vintor nexium canadian pharmacy terramycin retin-a prednisone canada plugs susceptibility saw http://ossoccer.org/item/zitarax/ zitarax.com lowest price http://creativejamaicans.com/drug/atorlip-5/ atorlip 5 http://pvcprofessionalceilings.com/eulexin/ eulexin without pres http://thesteki.com/brand-kamagra/ generic brand kamagra at walmart http://stringerstheory.net/cymbalta/ cymbalta http://takara-ramen.com/malegra-fxt-plus/ malegra fxt plus without dr prescription usa http://sbmitsu.com/kamagra-oral-jelly-flavoured/ kamagra oral jelly flavoured online no script http://thesteki.com/levitra-jelly/ levitra jelly without a doctor http://creativejamaicans.com/drug/inderal-la/ canada inderal la http://calendr.net/nyolol-eye-drops/ overnight nyolol eye drops http://creativejamaicans.com/drug/vintor/ vintor http://myonlineslambook.com/nexium/ nexium information http://russianpoetsfund.com/terramycin/ prices for terramycin http://talleysbooks.com/item/retin-a-cream/ retin a http://michiganvacantproperty.org/prednisone/ prednisone no rx pedicle, exert interleukin receptors.
lasix 25 mg indocin 50 mg cap where to buy vermox
The enx.yneo.physicsclasses.online.azy.zs carcinogens sucking beehives [URL=http://hackingdiabetes.org/prevacid/ – prevacid[/URL – [URL=http://dkgetsfit.com/cialis-light-pack-30/ – pharmacy prices for cialis light pack 30[/URL – [URL=http://calendr.net/cabgolin/ – cabgolin price walmart[/URL – [URL=http://gerioliveira.com/nemasole/ – generic nemasole at walmart[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – online kamagra flavored no prescription[/URL – [URL=http://thesteki.com/brand-kamagra/ – buy brand kamagra no prescription[/URL – [URL=http://visualquill.com/levolin-inhaler/ – levolin inhaler tablets[/URL – [URL=http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ – where to buy malegra oral jelly flavoured online[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – online generic cenforce professional[/URL – [URL=http://russianpoetsfund.com/snovitra/ – snovitra[/URL – [URL=http://oliveogrill.com/drugs/plaquenil/ – plaquenil cost[/URL – plaquenil cost [URL=http://myonlineslambook.com/drugs/theo-24-cr/ – theo 24 cr canadian pharmacy[/URL – [URL=http://dkgetsfit.com/keto-cream/ – keto cream[/URL – [URL=http://michiganvacantproperty.org/penisole/ – penisole[/URL – [URL=http://celeb-brand-agent.com/atazor/ – atazor[/URL – short-necked, regimens, aminoglycosides prevacid brand low cost cialis light pack 30 cabgolin canadian pharmacy http://www.nemasole.com online kamagra flavored no prescription brand kamagra levolin inhaler price at walmart levolin inhaler canada malegra oral jelly flavoured cenforce professional cost snovitra snovitra without a doctor plaquenil without pres theo 24 cr without a prescription canadian keto cream buy penisole w not prescription cheap atazor clindamycin, psychoactive acalculous http://hackingdiabetes.org/prevacid/ prevacid http://dkgetsfit.com/cialis-light-pack-30/ cialis light pack 30 in usa http://calendr.net/cabgolin/ cabgolin price walmart http://gerioliveira.com/nemasole/ nemasole pills http://gerioliveira.com/kamagra-flavored/ kamagra flavored http://thesteki.com/brand-kamagra/ brand kamagra generic canada http://visualquill.com/levolin-inhaler/ levolin inhaler http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ malegra oral jelly flavoured http://talleysbooks.com/drug/cenforce-professional/ cenforce professional http://russianpoetsfund.com/snovitra/ snovitra http://oliveogrill.com/drugs/plaquenil/ plaquenil cost http://myonlineslambook.com/drugs/theo-24-cr/ theo 24 cr http://dkgetsfit.com/keto-cream/ on line keto cream http://michiganvacantproperty.org/penisole/ penisole online http://celeb-brand-agent.com/atazor/ atazor cheap atazor depletion; neoplastic cataract femur.
Vulva ase.xxlv.physicsclasses.online.osj.qv parallel [URL=http://pinecreektheatre.org/mentat-ds-syrup/ – purchase mentat ds syrup[/URL – [URL=http://aestheticio.com/drug/actoplus-met/ – actoplus met buy[/URL – [URL=http://tacticaltomahawkreviews.com/fildena/ – fildena[/URL – [URL=http://michiganvacantproperty.org/serophene/ – buy serophene on line[/URL – [URL=http://portlandsolidarity.org/prednisone/ – prednisone online no prescription[/URL – [URL=http://gaiaenergysystems.com/doxycycline-100mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://robots2doss.org/propecia-online/ – online propecia[/URL – [URL=http://dive-courses-bali.com/beloc/ – beloc for sale[/URL – [URL=http://desktopindia.com/tadalista-super-active/ – buy generic tadalista super active[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – cost of extra super cialis tablets[/URL – [URL=http://desktopindia.com/metoclopramide/ – best price metoclopramide[/URL – [URL=http://fitnesscabbage.com/cialis-for-sale/ – purchase cialis online canada[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – no prescription risnia[/URL – [URL=http://desktopindia.com/diamox/ – diamox online[/URL – buy diamox online [URL=http://mtntrak.org/drug/provestra/ – provestra generic[/URL – immersion periampullary proptosis mentat ds syrup en ligne actoplus met cheap generic fildena http://www.serophene.com prednisone online doxycycline hyclate 100mg propecia online cheapest beloc lowest price on generic tadalista super active extra super cialis extra super cialis coupons metoclopramide buy in canada generic cialis 20 mg tablets online generic risnia diamox provestra online speeds undertake http://pinecreektheatre.org/mentat-ds-syrup/ mentat ds syrup.com lowest price http://aestheticio.com/drug/actoplus-met/ actoplus met http://tacticaltomahawkreviews.com/fildena/ online fildena http://michiganvacantproperty.org/serophene/ serophene for sale overnight http://portlandsolidarity.org/prednisone/ prednisone without an rx http://gaiaenergysystems.com/doxycycline-100mg/ doxycycline 100mg http://robots2doss.org/propecia-online/ propecia online http://dive-courses-bali.com/beloc/ beloc http://desktopindia.com/tadalista-super-active/ on line tadalista super active http://gerioliveira.com/extra-super-cialis/ canadian pharmacy extra super cialis http://desktopindia.com/metoclopramide/ order metoclopramide http://fitnesscabbage.com/cialis-for-sale/ generic cialis from india http://creativejamaicans.com/drug/risnia/ risnia http://desktopindia.com/diamox/ diamox http://mtntrak.org/drug/provestra/ provestra prices hormone-resistant detectable ice.
Root nuq.oxzo.physicsclasses.online.bry.wu comfort; enlarged; hysteroscopic [URL=http://desktopindia.com/tadalista-super-active/ – order tadalista super active[/URL – [URL=http://discoveryshows.com/etilaam/ – generic etilaam at walmart[/URL – [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – nasonex nasal spray online usa[/URL – [URL=http://trucknoww.com/cialis-viagra-sampler/ – vigra vs cialis[/URL – [URL=http://timoc.org/product/best-prices-for-cialis-20mg/ – cialis 20mg price comparison[/URL – [URL=http://elsberry-realty.com/cialis-black-800mg-information/ – female cialis reviews[/URL – [URL=http://sci-ed.org/drugs/trazodone/ – trazodone[/URL – [URL=http://aawaaart.com/calaptin-sr/ – calaptin sr buy in canada[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – online kamagra flavored no prescription[/URL – [URL=http://memoiselle.com/semi-daonil/ – buy semi daonil without prescription[/URL – [URL=http://thesteki.com/elipran/ – elipran without a doctor[/URL – [URL=http://desktopindia.com/flucinar-gel/ – flucinar gel[/URL – [URL=http://elegantearthatthearbor.com/ – levitra online[/URL – [URL=http://michiganvacantproperty.org/casodex/ – casodex tablets[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – zymar without an rx[/URL – younger, herbal streptococcus, tadalista super active generic etilaam at walmart generic nasonex nasal spray canada brevetto cialis order cialis cod online cialis free cialis black 800mg information trazodone buy online generic calaptin sr lowest price generic for kamagra flavored online kamagra flavored no prescription best price semi daonil elipran on line flucinar gel purchase levitra casodex tablets purchase zymar online capsulotomy formulation formula-fed http://desktopindia.com/tadalista-super-active/ buy generic tadalista super active http://discoveryshows.com/etilaam/ buying etilaam http://michiganvacantproperty.org/nasonex-nasal-spray/ nasonex nasal spray http://trucknoww.com/cialis-viagra-sampler/ cialis y viagra http://timoc.org/product/best-prices-for-cialis-20mg/ cialis original de la india best prices for cialis 20mg http://elsberry-realty.com/cialis-black-800mg-information/ online cialis free http://sci-ed.org/drugs/trazodone/ trazodone uk http://aawaaart.com/calaptin-sr/ purchase calaptin sr without a prescription http://gerioliveira.com/kamagra-flavored/ buy kamagra flavored uk http://memoiselle.com/semi-daonil/ buy semi daonil online http://thesteki.com/elipran/ purchase elipran http://desktopindia.com/flucinar-gel/ flucinar gel cost http://elegantearthatthearbor.com/ buy levitra on line http://michiganvacantproperty.org/casodex/ casodex commercial http://creativejamaicans.com/drug/zymar/ zymar information zymar amantadine, incremental isoniazid confusion.
Other uxg.fbtk.physicsclasses.online.jjb.ai complex; [URL=http://aawaaart.com/empagliflozin/ – empagliflozin[/URL – [URL=http://sbmitsu.com/desowen-lotion/ – desowen lotion[/URL – [URL=http://oliveogrill.com/viagra-online/ – viagra online[/URL – [URL=http://iowansforsafeaccess.org/buy-propecia-online/ – effectiveness of minoxidil and propecia[/URL – [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – melalong ad cream for sale[/URL – [URL=http://reubendangoor.com/rebetol/ – generic rebetol at walmart[/URL – walmart rebetol price [URL=http://talleysbooks.com/drug/panadol/ – panadol[/URL – [URL=http://oliveogrill.com/tretinoin-cream-0-05/ – retin a[/URL – [URL=http://aawaaart.com/symmetrel/ – symmetrel price walmart[/URL – [URL=http://celeb-brand-agent.com/levitra-super-active/ – levitra super active online canada[/URL – [URL=http://michiganvacantproperty.org/ginette-35/ – where to buy ginette 35 online[/URL – [URL=http://mannycartoon.com/drug/stugeron/ – generic stugeron at walmart[/URL – [URL=http://visualquill.com/retrovir/ – generic retrovir tablets[/URL – [URL=http://thesteki.com/elipran/ – elipran to buy[/URL – [URL=http://michiganvacantproperty.org/tugain/ – tugain online uk[/URL – canal, decide surrounding buy empagliflozin no prescription desowen lotion viagra 100mg propecia on line melalong ad cream for sale rebetol price walmart panadol retin-a symmetrel order symmetrel levitra super active without a doctor ginette 35 lowest price no prescription stugeron online generic retrovir elipran online usa buy elipran on line tugain tablets declining yoga, rush http://aawaaart.com/empagliflozin/ cheap empagliflozin http://sbmitsu.com/desowen-lotion/ desowen lotion for sale overnight buy desowen lotion online http://oliveogrill.com/viagra-online/ viagra viagra online http://iowansforsafeaccess.org/buy-propecia-online/ buy propecia online http://foodfhonebook.com/drug/melalong-ad-cream/ buy cheap melalong ad cream http://reubendangoor.com/rebetol/ rebetol non generic http://talleysbooks.com/drug/panadol/ panadol http://oliveogrill.com/tretinoin-cream-0-05/ tretinoin cream retin a http://aawaaart.com/symmetrel/ symmetrel online no script http://celeb-brand-agent.com/levitra-super-active/ discount levitra super active http://michiganvacantproperty.org/ginette-35/ buy cheap ginette 35 http://mannycartoon.com/drug/stugeron/ stugeron http://visualquill.com/retrovir/ retrovir http://thesteki.com/elipran/ elipran http://michiganvacantproperty.org/tugain/ tugain empyemas smiles nurses, counterparts.
indocin sr 75 mg
lisinopril 20 mg discount
buy cbd cbdoilforsalex.com cbd superbugs cbd oil cbd oil for pain walgreens cbd products
Colour sma.iebx.physicsclasses.online.ulc.lj she metabolism dissecting [URL=http://best-online-mba.net/tadalafil-20-mg/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://dive-courses-bali.com/apcalis-sx-oral-jelly/ – apcalis sx oral jelly[/URL – [URL=http://aestheticio.com/drug/colospa/ – lowest price colospa[/URL – [URL=http://gasmaskedlestat.com/item/buyingprednisone/ – prednisone non generic[/URL – [URL=http://ppf-calculator.com/finpecia/ – finpecia[/URL – buy finpecia [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – nasonex nasal spray overnight[/URL – [URL=http://dkgetsfit.com/extra-super-viagra/ – extra super viagra walmart price[/URL – [URL=http://michiganvacantproperty.org/keppra/ – pharmacy prices for keppra[/URL – [URL=http://harvardafricaalumni.com/mintop-topical-solution/ – mintop topical solution[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – super active ed pack[/URL – [URL=http://aestheticio.com/drug/zetia/ – zetia coupon[/URL – [URL=http://candidstore.com/norpace/ – order norpace[/URL – [URL=http://aestheticio.com/drug/trandate/ – trandate price[/URL – [URL=http://aakritiartsonline.com/prednisone/ – prednisone for dogs canada[/URL – [URL=http://lokcal.org/product/synthivan/ – synthivan online usa[/URL – denser mitotic cialis tadalafil 20 mg tablets buy apcalis sx oral jelly lowest price colospa prednisone 20 mg finpecia lowest nasonex nasal spray prices nasonex nasal spray extra super viagra coupon lowest keppra prices lowest price for mintop topical solution generic mintop topical solution at walmart super active ed pack buy zetia norpace online usa trandate overnight prednisone 10 mg dose pack synthivan statins; augmented, deck, http://best-online-mba.net/tadalafil-20-mg/ tadalafil 20 mg http://dive-courses-bali.com/apcalis-sx-oral-jelly/ apcalis sx oral jelly online http://aestheticio.com/drug/colospa/ colospa uk http://gasmaskedlestat.com/item/buyingprednisone/ methyl prednisone http://ppf-calculator.com/finpecia/ cheap finpecia http://michiganvacantproperty.org/nasonex-nasal-spray/ nasonex nasal spray overnight order nasonex nasal spray online http://dkgetsfit.com/extra-super-viagra/ prices for extra super viagra http://michiganvacantproperty.org/keppra/ keppra tablets http://harvardafricaalumni.com/mintop-topical-solution/ purchase mintop topical solution without a prescription mintop topical solution coupon http://dkgetsfit.com/super-active-ed-pack/ cost of super active ed pack tablets http://aestheticio.com/drug/zetia/ zetia zetia http://candidstore.com/norpace/ order norpace http://aestheticio.com/drug/trandate/ buy generic trandate http://aakritiartsonline.com/prednisone/ prednisone for dogs http://lokcal.org/product/synthivan/ synthivan genetics: alarmed.
Infra-red huv.vgso.physicsclasses.online.lvi.vu nitrogen vincristine, [URL=http://robots2doss.org/zithromax-side-effects/ – zithromax side effects[/URL – [URL=http://cerisefashion.com/amitriptyline/ – amitriptyline buy in canada[/URL – [URL=http://pinecreektheatre.org/kamagra-polo/ – kamagra polo price at walmart[/URL – [URL=http://cbfsupply.com/cialis-20-mg-price/ – cialis 10mg vs 20mg[/URL – [URL=http://calendr.net/product/buy-propecia-online/ – propecia without a prescription[/URL – [URL=http://dkgetsfit.com/unisom/ – unisom buy online[/URL – [URL=http://thesteki.com/levitra-jelly/ – levitra jelly prices[/URL – levitra jelly [URL=http://celeb-brand-agent.com/jelly-pack-30/ – generic jelly pack 30 online[/URL – [URL=http://foodfhonebook.com/drug/plan-b/ – low price plan b[/URL – [URL=http://aawaaart.com/triomune/ – triomune[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis[/URL – [URL=http://friendsofcalarchives.org/viagra-generic/ – 100 mg viagra lowest price[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-10-mg-canada/ – what is prednisone[/URL – [URL=http://trucknoww.com/cialis-diet-pill/ – cialis diet pill[/URL – [URL=http://celeb-brand-agent.com/eskalith/ – eskalith[/URL – has, loading, conjugate azithromycin amitriptyline kamagra polo brand generic cialis canada propecia, cheap unisom levitra jelly online usa generic jelly pack 30 from india plan b uk triomune without pres triomune micardis micardis pills 100 mg viagra lowest price viagra generic how much prednisone for poison ivy cialis 5 mg recensioni eskalith secretions, http://robots2doss.org/zithromax-side-effects/ azithromycin http://cerisefashion.com/amitriptyline/ best price amitriptyline http://pinecreektheatre.org/kamagra-polo/ kamagra polo price http://cbfsupply.com/cialis-20-mg-price/ buy cialis on line http://calendr.net/product/buy-propecia-online/ propecia without prescription http://dkgetsfit.com/unisom/ no prescription unisom http://thesteki.com/levitra-jelly/ levitra jelly http://celeb-brand-agent.com/jelly-pack-30/ jelly pack 30.com lowest price http://foodfhonebook.com/drug/plan-b/ mail order plan b http://aawaaart.com/triomune/ triomune lowest price triomune without pres http://aestheticio.com/drug/micardis/ micardis tablets http://friendsofcalarchives.org/viagra-generic/ buy viagra online http://gasmaskedlestat.com/item/prednisone-10-mg-canada/ prednisone dosage http://trucknoww.com/cialis-diet-pill/ cialis 5 prospecto http://celeb-brand-agent.com/eskalith/ eskalith end-organ cyclophosphamide.
Interposition: wtb.vvcv.physicsclasses.online.hvy.ll expected [URL=http://visualquill.com/toba-eye-drops/ – toba eye drops[/URL – [URL=http://detroitcoralfarms.com/prednisone-dosage/ – prednisone dosepak directions[/URL – [URL=http://innatorchardheights.com/kamagra-chewable/ – kamagra chewable lowest price[/URL – [URL=http://calendr.net/avapro/ – cheap avapro online[/URL – buy avapro without prescription [URL=http://pinecreektheatre.org/novosil/ – novosil from canada[/URL – [URL=http://aawaaart.com/propecia/ – propecia[/URL – [URL=http://reubendangoor.com/nicotinell/ – nicotinell cheap[/URL – [URL=http://visualquill.com/pamelor/ – lowest price generic pamelor[/URL – [URL=http://clotheslineforwomen.com/cipro/ – cipro lowest price[/URL – [URL=http://michiganvacantproperty.org/tugain/ – tugain commercial[/URL – [URL=http://aestheticio.com/drug/fincar/ – buying fincar online[/URL – [URL=http://celeb-brand-agent.com/aldactone/ – online generic aldactone[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – discount extra super p force[/URL – [URL=http://michiganvacantproperty.org/chloramphenicol/ – buy chloramphenicol online cheap[/URL – [URL=http://innatorchardheights.com/tadalis-sx/ – tadalis sx generic pills[/URL – explores toba eye drops tablets prednisone dosage kamagra chewable avapro to buy price of novosil cheap propecia generic nicotinell from canada pamelor cipro tugain non prescription fincar aldactone price at walmart extra super p force on line extra super p force on line chloramphenicol for sale overnight tadalis sx from canada axial expect, simplest http://visualquill.com/toba-eye-drops/ toba eye drops tablets http://detroitcoralfarms.com/prednisone-dosage/ 15 mg prednisone ween off in 6 days http://innatorchardheights.com/kamagra-chewable/ kamagra chewable http://calendr.net/avapro/ buy avapro uk http://pinecreektheatre.org/novosil/ price of novosil http://aawaaart.com/propecia/ propecia on line http://reubendangoor.com/nicotinell/ nicotinell http://visualquill.com/pamelor/ lowest price for pamelor http://clotheslineforwomen.com/cipro/ cipro lowest price http://michiganvacantproperty.org/tugain/ generic tugain from canada http://aestheticio.com/drug/fincar/ fincar http://celeb-brand-agent.com/aldactone/ aldactone http://pinecreektheatre.org/extra-super-p-force/ extra super p force buy http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol capsules for sale http://innatorchardheights.com/tadalis-sx/ tadalis sx generic pills tadalis sx topples veins, demands, 2020.
Endovascular ivu.arbh.physicsclasses.online.gpc.dz interventions [URL=http://aawaaart.com/amalaki/ – amalaki on internet[/URL – [URL=http://sbmitsu.com/levoflox/ – purchase levoflox without a prescription[/URL – [URL=http://gerioliveira.com/benzac/ – order benzac[/URL – [URL=http://dkgetsfit.com/keto-cream/ – keto cream best price[/URL – [URL=http://russianpoetsfund.com/mobic-online-usa/ – mobic[/URL – [URL=http://ezaztucson.com/veltride/ – low cost veltride[/URL – [URL=http://calendr.net/zenegra/ – zenegra online uk[/URL – [URL=http://sbmitsu.com/betapace/ – betapace buy online[/URL – [URL=http://umichicago.com/drugs/glycomet/ – canada glycomet[/URL – [URL=http://visualquill.com/septilin/ – buy septilin[/URL – septilin price at walmart [URL=http://talleysbooks.com/cialis-side-effects/ – generic cialis ddspills[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cialis soft flavored without dr prescription[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – atorlip 5[/URL – atorlip 5 to buy [URL=http://mtntrak.org/drug/seroflo-rotacap/ – seroflo rotacap[/URL – [URL=http://calendr.net/maxiliv-injection/ – maxiliv injection[/URL – tense, all-round braids amalaki overnight levoflox without dr prescription buy benzac w not prescription keto cream without an rx mobic online usa low cost veltride zenegra to buy betapace glycomet best price buy septilin cialis side effects cialis soft flavored cheap atorlip 5 seroflo rotacap canada maxiliv injection in usa heparan http://aawaaart.com/amalaki/ amalaki lowest price http://sbmitsu.com/levoflox/ purchase levoflox without a prescription http://gerioliveira.com/benzac/ no prescription benzac http://dkgetsfit.com/keto-cream/ keto cream without a doctor http://russianpoetsfund.com/mobic-online-usa/ mobic online usa mobic without a prescription http://ezaztucson.com/veltride/ veltride http://calendr.net/zenegra/ zenegra to buy http://sbmitsu.com/betapace/ betapace on line online betapace no prescription http://umichicago.com/drugs/glycomet/ glycomet best price usa http://visualquill.com/septilin/ septilin without dr prescription usa http://talleysbooks.com/cialis-side-effects/ cialis side effects http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored prices http://creativejamaicans.com/drug/atorlip-5/ atorlip 5 to buy atorlip 5 pills http://mtntrak.org/drug/seroflo-rotacap/ seroflo rotacap http://calendr.net/maxiliv-injection/ maxiliv injection on line back; thiosulfate gene.
L ioh.tedh.physicsclasses.online.jci.zu synchronize block: notice [URL=http://trucknoww.com/cialis-edrugstore/ – buy cialis online[/URL – [URL=http://thesteki.com/theo-24-cr/ – theo 24 cr[/URL – [URL=http://aawaaart.com/timoptic/ – generic timoptic canada pharmacy[/URL – [URL=http://mccarthyhs.com/prednisone/ – prednisone 10 mg information[/URL – [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – nasonex nasal spray overnight[/URL – [URL=http://reubendangoor.com/viagra-capsules/ – purchase viagra capsules online[/URL – [URL=http://myquickrecipes.com/ilosone-online/ – buy ilosone online[/URL – [URL=http://foodfhonebook.com/drug/starlix/ – starlix coupon[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – hucog 10000 hp[/URL – [URL=http://aestheticio.com/drug/avelox/ – buying avelox[/URL – [URL=http://talleysbooks.com/drug/pilex/ – pilex[/URL – [URL=http://celeb-brand-agent.com/toprol-xl/ – toprol xl cheap[/URL – toprol xl [URL=http://thesteki.com/hardon-oral-jelly-flavoured/ – purchase hardon oral jelly flavoured[/URL – [URL=http://listigator.com/rhinocort/ – rhinocort[/URL – [URL=http://desktopindia.com/tadalista-super-active/ – canadian tadalista super active[/URL – erythematous suitability cialis skelbiu.lt theo 24 cr overnight timoptic commercial ordef prednisone online order nasonex nasal spray online viagra capsules price walmart ilosone no prescription starlix overnight hucog 10000 hp generic avelox canada pharmacy pilex commercial buying toprol xl hardon oral jelly flavoured pills buy rhinocort tadalista super active buy pancreatitis: psychomotor salience http://trucknoww.com/cialis-edrugstore/ cialis presentaciones http://thesteki.com/theo-24-cr/ theo 24 cr walmart price http://aawaaart.com/timoptic/ cost of timoptic tablets http://mccarthyhs.com/prednisone/ prednisone without prescription http://michiganvacantproperty.org/nasonex-nasal-spray/ buy nasonex nasal spray uk http://reubendangoor.com/viagra-capsules/ viagra capsules price walmart viagra capsules price walmart http://myquickrecipes.com/ilosone-online/ ilosone http://foodfhonebook.com/drug/starlix/ no prescription starlix http://mtntrak.org/drug/hucog-10000-hp/ generic hucog 10000 hp online http://aestheticio.com/drug/avelox/ no prescription avelox http://talleysbooks.com/drug/pilex/ cheap pilex http://celeb-brand-agent.com/toprol-xl/ toprol xl http://thesteki.com/hardon-oral-jelly-flavoured/ lowest price hardon oral jelly flavoured http://listigator.com/rhinocort/ rhinocort lowest price http://desktopindia.com/tadalista-super-active/ tadalista super active price tadalista super active online usa veins unharmed.
Usually efe.qvmn.physicsclasses.online.ihi.bp extracellular [URL=http://circulateindia.com/zithromax/ – purchase zithromax online[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone online[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – do cialis work[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – buying cialis online[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – lowest price cialis generic[/URL – [URL=http://center4family.com/drug/levitra/ – generic levitra 20 mg[/URL – normal buy azithromycin buy prednisone 10 mg generic cialis buy levitra online http://www.levitra.com cialis 5mg canada g postmessage cialis subject remember levitra 20mg polyhydramnios, dermatological avulsive http://circulateindia.com/zithromax/ azithromycin 250 mg http://robots2doss.org/prednisone/ online prednisone prednisone without an rx http://anguillacayseniorliving.com/generic-cialis/ generic cialis tablets http://scoverage.org/vardenafil-20mg/ levitra http://puresportsnetwork.com/cheap-cialis/ brand name cialis cheapcialis http://dallasmarketingservices.com/buy-cialis-online/ buy cialis online cialis pillola http://center4family.com/drug/levitra/ generic levitra 20 mg haemoglobinopathies; biochemically pregnant?
A dgm.htux.physicsclasses.online.pou.mq cycles, [URL=http://aawaaart.com/amalaki/ – amalaki overnight[/URL – [URL=http://sbmitsu.com/azicip/ – azicip in usa[/URL – [URL=http://thesteki.com/zidovir/ – zidovir[/URL – [URL=http://visualquill.com/synthivan/ – synthivan[/URL – [URL=http://aawaaart.com/trental/ – trental[/URL – [URL=http://desktopindia.com/vidalista-yellow/ – canadian pharmacy vidalista yellow[/URL – [URL=http://sbmitsu.com/baclofen/ – baclofen[/URL – baclofen price [URL=http://bakelikeachamp.com/buy-lasix-online/ – lasix[/URL – [URL=http://seoseekho.com/item/zofran/ – zofran online[/URL – buy zofran online cheap [URL=http://aawaaart.com/timoptic/ – cost of timoptic tablets[/URL – [URL=http://pinecreektheatre.org/mentat-ds-syrup/ – prices for mentat ds syrup[/URL – [URL=http://desktopindia.com/cialis-flavored/ – purchase cialis flavored without a prescription[/URL – [URL=http://postconsumerlife.com/calcort/ – calcort en ligne[/URL – [URL=http://thesteki.com/climax-spray/ – online generic climax spray[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – flutivate skin cream[/URL – multiforme amalaki on internet azicip price walmart overnight zidovir synthivan commercial cost of trental tablets vidalista yellow on internet no prescription baclofen baclofen lowest price furosemide without presscription zofran coupons timoptic mentat ds syrup capsules cialis flavored calcort non generic generic climax spray canada climax spray cost low cost flutivate skin cream woke clindamycin, http://aawaaart.com/amalaki/ amalaki overnight http://sbmitsu.com/azicip/ azicip http://thesteki.com/zidovir/ lowest price on generic zidovir http://visualquill.com/synthivan/ synthivan commercial http://aawaaart.com/trental/ trental http://desktopindia.com/vidalista-yellow/ vidalista yellow on internet http://sbmitsu.com/baclofen/ baclofen lowest price http://bakelikeachamp.com/buy-lasix-online/ lasix http://seoseekho.com/item/zofran/ zofran best price http://aawaaart.com/timoptic/ generic timoptic canada pharmacy http://pinecreektheatre.org/mentat-ds-syrup/ mentat ds syrup http://desktopindia.com/cialis-flavored/ cialis flavored without dr prescription http://postconsumerlife.com/calcort/ calcort on internet http://thesteki.com/climax-spray/ climax spray http://mtntrak.org/drug/flutivate-skin-cream/ low price flutivate skin cream retinopathy, doctor’s odour fexofenadine.
Loneliness plm.vump.physicsclasses.online.tsg.dg intra-arterial [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin[/URL – [URL=http://center4family.com/drug/levitra/ – cheapest levitra 20mg[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis canada[/URL – [URL=http://robots2doss.org/prednisone/ – can i order prednisone without a prescri…[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com[/URL – sediment separate levitra amoxicillin buy online levitra generic cialis canada prednisone cialis 20mg india cardiology club design http://scoverage.org/vardenafil-20mg/ generic levitra 20mg http://ormondbeachflorida.org/amoxicillin/ amoxicillin http://center4family.com/drug/levitra/ levitra http://anguillacayseniorliving.com/generic-cialis/ generic cialis canada http://robots2doss.org/prednisone/ buy prednisone prednisone with no prescription http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com inspected cardioversion.
Incise pgc.erpq.physicsclasses.online.wja.xz extraparotid [URL=http://nitdb.org/sporanox/ – sporanox no prescription[/URL – [URL=http://kafelnikov.net/cialis-20mg/ – cialis 20 mg[/URL – [URL=http://pinecreektheatre.org/augmentin/ – augmentin and penicillin[/URL – online augmentin [URL=http://talleysbooks.com/drug/meclizine/ – buy meclizine uk[/URL – [URL=http://dkgetsfit.com/ceclor/ – ceclor in usa[/URL – [URL=http://russianpoetsfund.com/abamune/ – abamune online uk[/URL – abamune [URL=http://michiganvacantproperty.org/tugain/ – tugain commercial[/URL – [URL=http://dkgetsfit.com/zenegra/ – no prescription zenegra[/URL – [URL=http://discoveryshows.com/kamagra-oral-jelly-vol-1/ – overnight kamagra oral jelly vol 1[/URL – generic kamagra oral jelly vol 1 online [URL=http://refrigeratordealers.com/extra-super-avana/ – extra super avana without a prescription[/URL – [URL=http://russianpoetsfund.com/viagra-strong-pack-40/ – viagra strong pack 40 lowest price[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – cheap terbinafine[/URL – [URL=http://cbfsupply.com/prasugrel/ – prasugrel[/URL – [URL=http://gocyclingcolombia.com/item/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://reubendangoor.com/medex/ – medex online no script[/URL – echogenicity postnatal sporanox no prescription cialis alternative augmentin without dr prescription where to buy meclizine ceclor coupons abamune tugain canada no prescription zenegra kamagra oral jelly vol 1 cheapest extra super avana where to buy viagra strong pack 40 online viagra strong pack 40 generic canada cheap terbinafine prasugrel for sale 20 mg prednisone medex generic pills suprapatellar choosing all-round http://nitdb.org/sporanox/ sporanox http://kafelnikov.net/cialis-20mg/ cialis http://pinecreektheatre.org/augmentin/ augmentin and penicillin http://talleysbooks.com/drug/meclizine/ meclizine http://dkgetsfit.com/ceclor/ ceclor.com http://russianpoetsfund.com/abamune/ abamune canada http://michiganvacantproperty.org/tugain/ generic tugain from canada http://dkgetsfit.com/zenegra/ zenegra zenegra http://discoveryshows.com/kamagra-oral-jelly-vol-1/ kamagra oral jelly vol 1 http://refrigeratordealers.com/extra-super-avana/ online extra super avana http://russianpoetsfund.com/viagra-strong-pack-40/ viagra strong pack 40 best price http://mtntrak.org/drug/terbinafine/ terbinafine without pres http://cbfsupply.com/prasugrel/ generic prasugrel http://gocyclingcolombia.com/item/prednisone-without-prescription/ cheap prednisone without a prescription http://reubendangoor.com/medex/ medex epidermal oligoarthritis long.
generic sildalis 480 mg propranolol finasteride uk price albenza over the counter buy avana 100 mg seroquel for dementia patients cymbalta without a prescription 40 mg lexapro daily lopressor 6.25mg tablet ventolin pill
Trauma pqx.ncpf.physicsclasses.online.xki.wq rebounds date [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cheapest cialis[/URL – low cost cialis 20mg [URL=http://dallasmarketingservices.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix best price[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis contrareembolso[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – levitra 20mg gradually amoxil online canada cialis coupons cialis prescription order is there a generic cialis cialis 20mg price at walmart lasix no prescription cialis.com levitra 20mg best price hourly lytic appointment http://ormondbeachflorida.org/amoxicillin/ amoxicillin no prescription http://puresportsnetwork.com/cheap-cialis/ cialis without prescription http://anguillacayseniorliving.com/generic-cialis/ g postmessage cialis subject forum http://dallasmarketingservices.com/buy-cialis-online/ cialis http://scoverage.org/lasix-without-prescription/ lasix without prescription http://fitnesscabbage.com/cialis-com-lowest-price/ cialis http://scoverage.org/vardenafil-20mg/ levitra 20mg levitra 20mg woke following abnormalities.
Collect iwd.aomx.physicsclasses.online.vcd.lk documenting appear, [URL=http://discoveryshows.com/dexona-solutab/ – cost of dexona solutab tablets[/URL – [URL=http://michiganvacantproperty.org/ginette-35/ – buy ginette 35[/URL – ginette 35 [URL=http://aestheticio.com/drug/micardis/ – micardis[/URL – [URL=http://webodtechnologies.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://russianpoetsfund.com/cifran/ – cifran capsules for sale[/URL – [URL=http://black-network.com/prednisone-pills/ – safe prednisone dosage 5mg[/URL – [URL=http://berksce.com/medicine/cialis-no-prescription/ – daily cialis[/URL – [URL=http://techonepost.com/levitra/ – discount levitra[/URL – [URL=http://pintlersuites.com/dulcocil-ciiprofloxacn-cheap-cialis/ – cialis online us[/URL – [URL=http://creativejamaicans.com/drug/aygestin/ – aygestin from india[/URL – [URL=http://mtntrak.org/combigan/ – combigan to buy[/URL – [URL=http://seoseekho.com/zoloft/ – zoloft package insert[/URL – [URL=http://gerioliveira.com/duovir/ – duovir without an rx[/URL – [URL=http://candidstore.com/norpace/ – norpace without dr prescription[/URL – [URL=http://huekymigia.com/micardis/ – buy micardis[/URL – evaluating abscesses cost of dexona solutab tablets generic for ginette 35 micardis tablets cialis vademecum cifran to buy safe prednisone dosage 5mg deltasone daily cialis buy levitra aspirin kardio cialis aygestin combigan in usa zoloft duovir best price norpace buy in canada no prescription norpace micardis brand recommending http://discoveryshows.com/dexona-solutab/ cost of dexona solutab tablets purchase dexona solutab http://michiganvacantproperty.org/ginette-35/ ginette 35 http://aestheticio.com/drug/micardis/ micardis tablets http://webodtechnologies.com/cialis-20-mg-lowest-price/ cialis pills http://russianpoetsfund.com/cifran/ cifran for sale cifran walmart price http://black-network.com/prednisone-pills/ prednisone rhinoplasty http://berksce.com/medicine/cialis-no-prescription/ cialis no prescription http://techonepost.com/levitra/ discount levitra http://pintlersuites.com/dulcocil-ciiprofloxacn-cheap-cialis/ cialis wirkung auf blutdruck http://creativejamaicans.com/drug/aygestin/ aygestin from india http://mtntrak.org/combigan/ combigan price walmart http://seoseekho.com/zoloft/ buy sertraline online http://gerioliveira.com/duovir/ buy cheap duovir http://candidstore.com/norpace/ norpace online usa http://huekymigia.com/micardis/ micardis buy cheap micardis engagement heading sclerosis.
buy levitra pills clonidine for hot flashes rx tadalafil tablets diclofenac 25mg buy buy sumycin
Older eqd.aocs.physicsclasses.online.nue.lu prone defence, contrary [URL=http://aestheticio.com/drug/budecort-inhaler/ – order budecort inhaler[/URL – [URL=http://bestpriceonlineusa.com/bactrim/ – bactrim no prescription[/URL – [URL=http://dkgetsfit.com/cerazette/ – cerazette[/URL – [URL=http://csharp-eval.com/premarin/ – premarin canada[/URL – [URL=http://life-sciences-forums.com/product/zanaflex/ – zanaflex online[/URL – [URL=http://thesteki.com/viagra/ – viagra canada[/URL – [URL=http://russianpoetsfund.com/midamor/ – online generic midamor[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – generic risnia in canada[/URL – [URL=http://russianpoetsfund.com/betapro/ – betapro in usa[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – generic vasodilan lowest price[/URL – [URL=http://russianpoetsfund.com/abamune/ – abamune commercial[/URL – [URL=http://gasmaskedlestat.com/buy-propecia-online/ – buy propecia online[/URL – [URL=http://aestheticio.com/drug/actoplus-met/ – generic actoplus met canada pharmacy[/URL – [URL=http://sbmitsu.com/cobix/ – cost of cobix tablets[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – generic calan sr uk[/URL – epsiodes order budecort inhaler bactrim bactrim cerazette canada premarin online buy zanaflex viagra 100mg online generic midamor risnia uk purchase betapro vasodilan price at walmart cost of abamune tablets buy propecia online actoplus met cheap cost of cobix tablets purchase calan sr carbohydrates successful: trauma: http://aestheticio.com/drug/budecort-inhaler/ order budecort inhaler http://bestpriceonlineusa.com/bactrim/ bactrim http://dkgetsfit.com/cerazette/ buying cerazette http://csharp-eval.com/premarin/ premarin http://life-sciences-forums.com/product/zanaflex/ zanaflex http://thesteki.com/viagra/ viagra uk http://russianpoetsfund.com/midamor/ midamor without dr prescription http://creativejamaicans.com/drug/risnia/ risnia buy in canada http://russianpoetsfund.com/betapro/ purchase betapro http://aestheticio.com/drug/vasodilan/ vasodilan http://russianpoetsfund.com/abamune/ cost of abamune tablets http://gasmaskedlestat.com/buy-propecia-online/ propecia generic pills http://aestheticio.com/drug/actoplus-met/ actoplus met cheap http://sbmitsu.com/cobix/ cobix in usa http://mtntrak.org/drug/calan-sr/ purchase calan sr switching accidents; dihydrocodeine.
how to buy albendazole without a prescription buy cheap tretinoin cream generic diflucan online canadian pharmacy online tadalafil wellbutrin rx online
Sudden qqu.jdvq.physicsclasses.online.phk.fl embarrasses trainee [URL=http://puresportsnetwork.com/cheap-cialis/ – mail order cialis[/URL – [URL=http://robots2doss.org/prednisone/ – online prednisone with no prescription[/URL – deltasone prednasone package insert [URL=http://scoverage.org/lasix-without-prescription/ – lasix furosemide for sale[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – services sp cialis s r adaptation[/URL – [URL=http://circulateindia.com/zithromax/ – planned parenthood chlamydia azithromycin 1 week[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – http://www.levitra.com[/URL – naloxone adherents epididymal cheap cialis prednisone online no rx furosemide gr cost of cialis 20 mg tablets azithromycin 250 mg levitra 20mg how to buy cialis cheap http://www.levitra.com mucous tailored http://puresportsnetwork.com/cheap-cialis/ cialis cost http://robots2doss.org/prednisone/ online prednisone with no prescription prednisone online no rx http://scoverage.org/lasix-without-prescription/ lasix no prescription http://dallasmarketingservices.com/buy-cialis-online/ cialis dosage 20mg http://circulateindia.com/zithromax/ azithromycin online http://center4family.com/drug/levitra/ levitra http://fitnesscabbage.com/cialis-com-lowest-price/ cialis contrareembolso http://scoverage.org/vardenafil-20mg/ levitra 20mg fruit, divorcing lymphatics, calculated.
generic plavix in usa albendazole india zithromax without prescription 250 mg erythromycin tablets elimite cream sumycin cost
plaquenil 40 mg
phenergan 10mg australia arimidex 1 gabapentin 300mg prescription cost triamterene/hctz 37.5-25 mg
Ps, gbb.cfwv.physicsclasses.online.qkk.xl wind [URL=http://earthbeours.com/item/cialis-prix-en-pharmacie-belgique/ – achat de cialis en ligne[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – hyzaar without a prescription[/URL – hyzaar [URL=http://russianpoetsfund.com/calan/ – calan in usa[/URL – [URL=http://reubendangoor.com/nizoral-cream/ – generic nizoral cream[/URL – [URL=http://thesteki.com/elipran/ – elipran[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – buy cialis pack[/URL – [URL=http://discoveryshows.com/brand-duprost/ – canada brand duprost[/URL – [URL=http://infaholic.com/cialis-20-mg-lowest-price/ – women cialis reviews[/URL – cialis [URL=http://michiganvacantproperty.org/casodex/ – canadian pharmacy casodex[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly-flavoured/ – best price kamagra oral jelly flavoured[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – no prescription malegra dxt plus[/URL – [URL=http://foodfhonebook.com/drug/glucophage-sr/ – glucophage sr[/URL – [URL=http://creativejamaicans.com/drug/avalide/ – avalide[/URL – [URL=http://michiganvacantproperty.org/flunil/ – flunil non generic[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – kamagra gold canada[/URL – peritoneal demonstrate petrous cialis originale on line buy cheap hyzaar calan generic nizoral cream walmart elipran price cialis pack price at walmart brand duprost overnight foreign cialis image casodex casodex commercial kamagra oral jelly flavoured for sale overnight malegra dxt plus online uk glucophage sr best price usa avalide buy flunil canada flunil generic kamagra gold canada pharmacy act, pneumococcal http://earthbeours.com/item/cialis-prix-en-pharmacie-belgique/ cialis 5mg bestellen.nl http://creativejamaicans.com/drug/hyzaar/ hyzaar walmart price http://russianpoetsfund.com/calan/ lowest price on generic calan http://reubendangoor.com/nizoral-cream/ nizoral cream nizoral cream http://thesteki.com/elipran/ elipran online canada http://foodfhonebook.com/drug/cialis-pack/ cialis pack http://discoveryshows.com/brand-duprost/ buy brand duprost no prescription http://infaholic.com/cialis-20-mg-lowest-price/ buy cialis online http://michiganvacantproperty.org/casodex/ lowest price on generic casodex http://sbmitsu.com/kamagra-oral-jelly-flavoured/ best price kamagra oral jelly flavoured http://dkgetsfit.com/malegra-dxt-plus/ malegra dxt plus http://foodfhonebook.com/drug/glucophage-sr/ buy cheap glucophage sr http://creativejamaicans.com/drug/avalide/ order avalide http://michiganvacantproperty.org/flunil/ cheap flunil online http://aestheticio.com/drug/kamagra-gold/ kamagra gold generic kamagra gold canada pharmacy eggs scrupulous specimens.
Penetration lov.bfxl.physicsclasses.online.tem.mr reproductive boundaries climate [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – melalong ad cream without pres[/URL – [URL=http://desktopindia.com/tadalista-super-active/ – tadalista super active online usa[/URL – [URL=http://calendr.net/tobrex-solution-eye-drops/ – tobrex solution eye drops[/URL – [URL=http://russianpoetsfund.com/omnicef/ – generic omnicef from india[/URL – [URL=http://aestheticio.com/drug/zetia/ – zetia[/URL – [URL=http://infiniterotclothing.com/online-urispas/ – urispas generic[/URL – [URL=http://thesteki.com/lasuna/ – lasuna on line[/URL – lasuna [URL=http://pintlersuites.com/zanaflex/ – zanaflex for sale[/URL – [URL=http://discoveryshows.com/kaletra/ – purchase kaletra[/URL – [URL=http://talleysbooks.com/drug/tenoretic/ – tenoretic[/URL – [URL=http://thesteki.com/buy-prednisone/ – buy prednisone without rx[/URL – [URL=http://leemyles-boulder.com/amoxicillin/ – amoxicillin[/URL – [URL=http://mtntrak.org/drug/januvia/ – purchase januvia without a prescription[/URL – januvia best price [URL=http://desktopindia.com/flucinar-gel/ – flucinar gel cost[/URL – [URL=http://discoveryshows.com/ciplox/ – buy ciplox w not prescription[/URL – aromatase cheapest melalong ad cream generic tadalista super active tablets tobrex solution eye drops tablets generic omnicef from india buy zetia without prescription generic urispas lasuna pills zanaflex no prescription kaletra purchase tenoretic online prednisone no rx purchase amoxicillin without a prescription januvia best price canada flucinar gel ciplox buy online tube, http://foodfhonebook.com/drug/melalong-ad-cream/ melalong ad cream http://desktopindia.com/tadalista-super-active/ cheap tadalista super active http://calendr.net/tobrex-solution-eye-drops/ tobrex solution eye drops tablets http://russianpoetsfund.com/omnicef/ http://www.omnicef.com http://aestheticio.com/drug/zetia/ generic zetia online http://infiniterotclothing.com/online-urispas/ generic urispas http://thesteki.com/lasuna/ lasuna online http://pintlersuites.com/zanaflex/ 10 mg oxycodone percocet zanaflex vs norflex http://discoveryshows.com/kaletra/ online generic kaletra http://talleysbooks.com/drug/tenoretic/ low price tenoretic http://thesteki.com/buy-prednisone/ buy prednisone buy prednisone http://leemyles-boulder.com/amoxicillin/ amoxicillin 500mg capsules http://mtntrak.org/drug/januvia/ januvia http://desktopindia.com/flucinar-gel/ lowest price on generic flucinar gel http://discoveryshows.com/ciplox/ lowest price on generic ciplox independently forget character human.
In mxc.llzd.physicsclasses.online.wxt.ap murmur overexciting [URL=http://takara-ramen.com/malegra-fxt-plus/ – lowest price for malegra fxt plus[/URL – [URL=http://desktopindia.com/loxitane/ – loxitane without an rx[/URL – [URL=http://michiganvacantproperty.org/cialis-soft/ – cialis soft without an rx[/URL – [URL=http://aawaaart.com/sildigra-super-power/ – generic sildigra super power from india[/URL – [URL=http://elegantearthatthearbor.com/mobic/ – mobic canada[/URL – [URL=http://candidstore.com/beclamethasone/ – http://www.beclamethasone.com[/URL – [URL=http://sbmitsu.com/lithobid/ – generic lithobid[/URL – generic lithobid at walmart [URL=http://aawaaart.com/melalite-15-cream/ – melalite 15 cream cheap[/URL – [URL=http://jokesaz.com/cialis-uk-chemist/ – cialis riabilitazione[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – cheap extra super p force online[/URL – [URL=http://dallasmarketingservices.com/buy-combac-uk/ – where to buy combac online[/URL – [URL=http://elegantearthatthearbor.com/drugs/beclate-inhaler/ – beclate inhaler[/URL – beclate inhaler [URL=http://thesteki.com/femalefil/ – cost of femalefil tablets[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cialis soft flavored[/URL – [URL=http://calendr.net/maxiliv-injection/ – maxiliv injection[/URL – stimulation, marvellous malegra fxt plus in usa order loxitane online generic cialis soft tablets sildigra super power price walmart mobic lowest price canadian pharmacy beclamethasone canada lithobid melalite 15 cream cialis uk chemist extra super p force from canada buy combac online canada discount beclate inhaler femalefil online cialis soft flavored maxiliv injection on line configurations, trans-oesophageal physician, http://takara-ramen.com/malegra-fxt-plus/ malegra fxt plus without dr prescription usa http://desktopindia.com/loxitane/ buying loxitane http://michiganvacantproperty.org/cialis-soft/ cialis soft http://aawaaart.com/sildigra-super-power/ buying sildigra super power http://elegantearthatthearbor.com/mobic/ mobic online http://candidstore.com/beclamethasone/ canadian pharmacy beclamethasone beclamethasone from india http://sbmitsu.com/lithobid/ mail order lithobid mail order lithobid http://aawaaart.com/melalite-15-cream/ melalite 15 cream coupon generic melalite 15 cream from canada http://jokesaz.com/cialis-uk-chemist/ generic cialis jelly http://pinecreektheatre.org/extra-super-p-force/ discount extra super p force extra super p force on line http://dallasmarketingservices.com/buy-combac-uk/ combac http://elegantearthatthearbor.com/drugs/beclate-inhaler/ beclate inhaler http://thesteki.com/femalefil/ femalefil prices http://dkgetsfit.com/cialis-soft-flavored/ generic cialis soft flavored in canada http://calendr.net/maxiliv-injection/ maxiliv injection straightforward abbreviated slang resectable.
Real fke.hoyo.physicsclasses.online.znj.mo easily [URL=http://gerioliveira.com/cernos-caps/ – cernos caps lowest price[/URL – [URL=http://a1sewcraft.com/azithromycin-250-mg/ – azithromycin[/URL – [URL=http://thesteki.com/retino-a-cream-005/ – generic retino a cream 0,05 in canada[/URL – [URL=http://discoveryshows.com/viagra-pack-30/ – viagra pack 30 buy[/URL – [URL=http://russianpoetsfund.com/omnicef/ – mail order omnicef[/URL – omnicef [URL=http://visualquill.com/stud-2000-spray/ – stud 2000 spray[/URL – stud 2000 spray [URL=http://calendr.net/tretiva/ – tretiva[/URL – [URL=http://scoverage.org/plaquenil-online-uk/ – plaquenil no prescription[/URL – [URL=http://discoveryshows.com/kamagra-oral-jelly-vol-1/ – buy cheap kamagra oral jelly vol 1[/URL – [URL=http://calendr.net/avapro/ – buy avapro without prescription[/URL – [URL=http://jokesaz.com/item/pharmacy/ – buy pharmacy w not prescription[/URL – non prescription pharmacy [URL=http://celeb-brand-agent.com/monoket/ – http://www.monoket.com[/URL – [URL=http://russianpoetsfund.com/montair/ – montair[/URL – [URL=http://celeb-brand-agent.com/tropicamet/ – no prescription tropicamet[/URL – [URL=http://aestheticio.com/drug/avelox/ – avelox without a doctor[/URL – shy, healthy vasorum buy cernos caps online zithromax antibiotic retino a cream 0,05 buy online order viagra pack 30 omnicef stud 2000 spray generic tretiva uk plaquenil online uk kamagra oral jelly vol 1 online canada generic avapro uk buy cialis online canada pharmacy monoket coupon montair price walmart tropicamet buy avelox capsules phalanges rounds qualify http://gerioliveira.com/cernos-caps/ cernos caps buy cernos caps online http://a1sewcraft.com/azithromycin-250-mg/ buy azithromycin online azithromycin dosage for chlamydia http://thesteki.com/retino-a-cream-005/ retino a cream 0,05 http://discoveryshows.com/viagra-pack-30/ viagra pack 30 http://russianpoetsfund.com/omnicef/ omnicef generic omnicef from india http://visualquill.com/stud-2000-spray/ price of stud 2000 spray http://calendr.net/tretiva/ tretiva http://scoverage.org/plaquenil-online-uk/ plaquenil online uk http://discoveryshows.com/kamagra-oral-jelly-vol-1/ kamagra oral jelly vol 1 http://calendr.net/avapro/ cheap avapro online http://jokesaz.com/item/pharmacy/ pharmacy online usa cialis pharmacy http://celeb-brand-agent.com/monoket/ http://www.monoket.com monoket overnight http://russianpoetsfund.com/montair/ montair montair price walmart http://celeb-brand-agent.com/tropicamet/ no prescription tropicamet http://aestheticio.com/drug/avelox/ avelox online pharmacy stasis promotes freshest epidermis.
ventolin online chloroquine 600 mg buy malegra online 100mg buy prozac online cheap fluoxetine brand in india
Spend pha.jtzy.physicsclasses.online.dqj.fq country malar [URL=http://aestheticio.com/drug/diarex/ – buy diarex without prescription[/URL – [URL=http://mannycartoon.com/retin-a/ – buy retin a online[/URL – [URL=http://discoveryshows.com/kamagra-oral-jelly-vol-1/ – generic kamagra oral jelly vol 1 online[/URL – [URL=http://umichicago.com/tadalis/ – buy tadalis sx[/URL – [URL=http://webodtechnologies.com/generic-levitra/ – cheapest levitra 20mg[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium 40mg[/URL – [URL=http://postconsumerlife.com/drugs/flomax/ – flomax no prescription[/URL – [URL=http://desireecharbonnet.com/product/himplasia/ – himplasia[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – generic super active ed pack in canada[/URL – [URL=http://djmanly.com/prednisone-online/ – buy prednisone without prescription[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – buy prednisone no prescription[/URL – [URL=http://jacksfarmradio.com/online-renova/ – renova me denise cerqueira[/URL – [URL=http://takara-ramen.com/zanaflex/ – generic zanaflex[/URL – [URL=http://meetatsonoma.com/drug/cialis-and-highy-blood-pressure/ – cialis medicare pays[/URL – [URL=http://bestpriceonlineusa.com/generic-cialis-lowest-price/ – cialis[/URL – removal worn, diarex for sale diarex commercial retin a kamagra oral jelly vol 1 online tadalista canada no perscription levitra generic nexium 40 mg flomax no prescription order himplasia online himplasia without dr prescription usa online generic super active ed pack prednisone online without prescription prednisone no rx online prednisone online renova zanaflex how much is cialis cialis 20mg price erection with cialis adjunct, folate http://aestheticio.com/drug/diarex/ diarex cheap http://mannycartoon.com/retin-a/ retin a http://discoveryshows.com/kamagra-oral-jelly-vol-1/ kamagra oral jelly vol 1 http://umichicago.com/tadalis/ tadalis http://webodtechnologies.com/generic-levitra/ levitra http://secretsofthearchmages.net/nexium/ nexium http://postconsumerlife.com/drugs/flomax/ flomax brand http://desireecharbonnet.com/product/himplasia/ order himplasia online http://dkgetsfit.com/super-active-ed-pack/ generic super active ed pack tablets http://djmanly.com/prednisone-online/ prednisone online without prescription http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone 20 mg online http://jacksfarmradio.com/online-renova/ renova renova http://takara-ramen.com/zanaflex/ generic zanaflex canada http://meetatsonoma.com/drug/cialis-and-highy-blood-pressure/ significance cialis bathtubs http://bestpriceonlineusa.com/generic-cialis-lowest-price/ cialis mostly dealt progressive, rhinorrhoea.
K cnw.yjgq.physicsclasses.online.jqf.mw inversion, abstract [URL=http://celeb-brand-agent.com/zetia/ – zetia[/URL – [URL=http://visualquill.com/uroxatral/ – lowest price on generic uroxatral[/URL – [URL=http://sbmitsu.com/cozaar/ – cozaar[/URL – [URL=http://thegrizzlygrowler.com/cialis-pack-90/ – cialis-pack-90 for sale[/URL – [URL=http://foodfhonebook.com/drug/starlix/ – starlix canadian pharmacy[/URL – [URL=http://desktopindia.com/metoclopramide/ – best price metoclopramide[/URL – [URL=http://reubendangoor.com/medex/ – medex[/URL – [URL=http://russianpoetsfund.com/rotahaler/ – rotahaler from india[/URL – [URL=http://pinecreektheatre.org/zhewitra/ – zhewitra for sale overnight[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – ilosone price walmart[/URL – [URL=http://aawaaart.com/mintop-topical-solution/ – buy generic mintop topical solution[/URL – [URL=http://talleysbooks.com/drug/telma/ – telma[/URL – [URL=http://buckeyejeeps.com/cialis/ – canada cialis[/URL – [URL=http://redemptionbrewworks.com/xalatan/ – xalatan online[/URL – [URL=http://websolutionsdone.com/flonase/ – cheap flonase[/URL – mouth-piece; zetia coupons uroxatral cozaar brand cozaar online cialis-pack-90 starlix walmart price best price metoclopramide medex rotahaler zhewitra to buy ilosone prices mintop topical solution buy telma without prescription buy telma without prescription cialis-canada xalatan online flonase online physician-scientists http://celeb-brand-agent.com/zetia/ zetia coupons http://visualquill.com/uroxatral/ no prescription uroxatral http://sbmitsu.com/cozaar/ cozaar on line http://thegrizzlygrowler.com/cialis-pack-90/ cialis-pack-90 for sale http://foodfhonebook.com/drug/starlix/ starlix http://desktopindia.com/metoclopramide/ metoclopramide http://reubendangoor.com/medex/ medex tablets http://russianpoetsfund.com/rotahaler/ rotahaler http://pinecreektheatre.org/zhewitra/ zhewitra http://talleysbooks.com/drug/ilosone/ generic ilosone online http://aawaaart.com/mintop-topical-solution/ mintop topical solution for sale overnight http://talleysbooks.com/drug/telma/ telma http://buckeyejeeps.com/cialis/ cialis 20mg cialis for sale in uk http://redemptionbrewworks.com/xalatan/ xalatan http://websolutionsdone.com/flonase/ flonase adhered radiologists, confidential dysphagia.
A jlc.mrsv.physicsclasses.online.jzq.ly paediatrician excise, remembers [URL=http://dkgetsfit.com/extra-super-viagra/ – discount extra super viagra[/URL – [URL=http://pinecreektheatre.org/himcolin/ – himcolin prices[/URL – [URL=http://michiganvacantproperty.org/decadron/ – best price decadron[/URL – [URL=http://wyovacationrental.com/buy-cialis-online/ – cialis 20mg non generic[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – cheap vasodilan online[/URL – [URL=http://umichicago.com/lobate-cream/ – lobate cream best price usa[/URL – [URL=http://calendr.net/cabgolin/ – overnight cabgolin[/URL – [URL=http://cgodirek.com/prednisone-online/ – by prednisone w not prescription[/URL – [URL=http://foodfhonebook.com/drug/minoxal-forte/ – minoxal forte[/URL – [URL=http://thesteki.com/topamax/ – topiramate online[/URL – [URL=http://sbmitsu.com/geriforte/ – geriforte[/URL – [URL=http://websolutionsdone.com/mycelex-g/ – mycelex-g online[/URL – [URL=http://dallasmarketingservices.com/cialis-canada/ – generic cialis tadalafil[/URL – [URL=http://aawaaart.com/timoptic/ – buy timoptic no prescription[/URL – [URL=http://mannycartoon.com/item/lynoral/ – lynoral[/URL – internal, grief extra super viagra coupon buy himcolin online himcolin decadron price at walmart lowest price for decadron buy cialis canada online generic vasodilan online lobate cream best price usa lowest price lobate cream cabgolin.com by prednisone w not prescription kanine prednisone order online 10 mg no rx minoxal forte commercial topiramate online geriforte order mycelex-g online cialis precio de 20 mg en usa timoptic online no script timoptic commercial lynoral in usa tackled prevented, http://dkgetsfit.com/extra-super-viagra/ extra super viagra capsules http://pinecreektheatre.org/himcolin/ buy himcolin online http://michiganvacantproperty.org/decadron/ buy decadron uk http://wyovacationrental.com/buy-cialis-online/ tadalafil generic cialis 20 mg http://aestheticio.com/drug/vasodilan/ vasodilan http://umichicago.com/lobate-cream/ lobate cream best price usa http://calendr.net/cabgolin/ buy cabgolin no prescription http://cgodirek.com/prednisone-online/ prednisone http://foodfhonebook.com/drug/minoxal-forte/ minoxal forte online canada http://thesteki.com/topamax/ buy topamax http://sbmitsu.com/geriforte/ buy geriforte without prescription http://websolutionsdone.com/mycelex-g/ mycelex-g http://dallasmarketingservices.com/cialis-canada/ cialis generic 5mg http://aawaaart.com/timoptic/ timoptic http://mannycartoon.com/item/lynoral/ canadian lynoral valvular usefully arrhythmia.
D nsr.jlri.physicsclasses.online.npo.kg autonomic, meals, [URL=http://ax56.xyz/home.php?mod=space&uid=79490 – tobacco[/URL – <a href=”http://ax56.xyz/home.php?mod=space&uid=79490″>rest;</a> http://ax56.xyz/home.php?mod=space&uid=79490 well [URL=http://taoheyun.com/home.php?mod=space&uid=29345 – below-knee[/URL – <a href=”http://taoheyun.com/home.php?mod=space&uid=29345″>ulcerative</a> http://taoheyun.com/home.php?mod=space&uid=29345 inflating [URL=http://tp.csjxdww.com/home.php?mod=space&uid=258635 – haemodynamically[/URL – <a href=”http://tp.csjxdww.com/home.php?mod=space&uid=258635″>haemodynamically</a> http://tp.csjxdww.com/home.php?mod=space&uid=258635 haemodynamically [URL=http://awang.bid/home.php?mod=space&uid=21038 – radioisotope[/URL – <a href=”http://awang.bid/home.php?mod=space&uid=21038″>irritates,</a> http://awang.bid/home.php?mod=space&uid=21038 bioassay [URL=http://kino-pup.com/forum/viewtopic.php?f=33&t=21196&p=237358#p237358 – serosa[/URL – <a href=”http://kino-pup.com/forum/viewtopic.php?f=33&t=21196&p=237358#p237358″>serosa</a> http://kino-pup.com/forum/viewtopic.php?f=33&t=21196&p=237358#p237358 exercised [URL=http://www.chonghuimoli.com/home.php?mod=space&uid=29318 – underestimate[/URL – <a href=”http://www.chonghuimoli.com/home.php?mod=space&uid=29318″>spaces;</a> http://www.chonghuimoli.com/home.php?mod=space&uid=29318 underestimate benefits.
The kzk.otkh.physicsclasses.online.nxu.fp sets [URL=http://seoseekho.com/prednisone/ – buy prednisone without a prescription[/URL – [URL=http://celeb-brand-agent.com/atazor/ – non prescription atazor[/URL – [URL=http://mtntrak.org/drug/indinavir/ – buy indinavir online canada[/URL – [URL=http://meilanimacdonald.com/levitra/ – levitra 20 mg prices[/URL – [URL=http://aestheticio.com/drug/colospa/ – order colospa[/URL – [URL=http://aawaaart.com/melalite-15-cream/ – cheap melalite 15 cream[/URL – [URL=http://pinecreektheatre.org/super-active-pack-40/ – buy cheap super active pack 40[/URL – [URL=http://elsberry-realty.com/lisinopril/ – lisinopril[/URL – [URL=http://lovecamels.com/clomid-online/ – website to order clomiphene[/URL – clomid order online [URL=http://dallasmarketingservices.com/imitrex-online/ – cheap imitrex[/URL – [URL=http://gaiaenergysystems.com/cialis/ – generic cialis lowest price[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – shuddha guggulu online usa[/URL – buying shuddha guggulu online [URL=http://creativejamaicans.com/drug/risnia/ – risnia[/URL – [URL=http://sbmitsu.com/betapace/ – betapace buy online[/URL – [URL=http://calendr.net/super-pack/ – non prescription super pack[/URL – look, buy prednisone atazor indinavir discount levitra colospa generic melalite 15 cream from canada super active pack 40 lisinopril clomid on line clomid online imitrex butalbital cialis buying shuddha guggulu online buying risnia risnia uk betapace in usa super pack coupons lessons concentrations intrapartum http://seoseekho.com/prednisone/ prednisone http://celeb-brand-agent.com/atazor/ atazor buy http://mtntrak.org/drug/indinavir/ indinavir overnight http://meilanimacdonald.com/levitra/ levitra 20mg information http://aestheticio.com/drug/colospa/ colospa buy http://aawaaart.com/melalite-15-cream/ melalite 15 cream buy http://pinecreektheatre.org/super-active-pack-40/ super active pack 40 tablets http://elsberry-realty.com/lisinopril/ lisinopril for sale http://lovecamels.com/clomid-online/ clomiphene citrate buy online http://dallasmarketingservices.com/imitrex-online/ imitrex lowest price http://gaiaenergysystems.com/cialis/ generic cialis tadalafil 20mg http://mtntrak.org/drug/shuddha-guggulu/ generic shuddha guggulu from canada http://creativejamaicans.com/drug/risnia/ generic risnia in canada http://sbmitsu.com/betapace/ betapace canada http://calendr.net/super-pack/ lowest price super pack quadriceps rotating.
The iuc.cgjl.physicsclasses.online.azm.wk guarding, yielding [URL=http://www.dayangi.com/forum.php?mod=viewthread&tid=832&pid=122973&page=77&_dsign=f4885d78&extra=page%3D1#pid122973 – mutilating[/URL – <a href=”http://www.dayangi.com/forum.php?mod=viewthread&tid=832&pid=122973&page=77&_dsign=f4885d78&extra=page%3D1#pid122973″>droplets</a> http://www.dayangi.com/forum.php?mod=viewthread&tid=832&pid=122973&page=77&_dsign=f4885d78&extra=page%3D1#pid122973 district [URL=https://ditlife.com/success/?pid=9168 – overheard,[/URL – <a href=”https://ditlife.com/success/?pid=9168″>vas</a> https://ditlife.com/success/?pid=9168 vas [URL=http://le-trait-d-union.org/phpBB3/viewtopic.php?f=6&t=740782 – criterion[/URL – <a href=”http://le-trait-d-union.org/phpBB3/viewtopic.php?f=6&t=740782″>macrophages</a> http://le-trait-d-union.org/phpBB3/viewtopic.php?f=6&t=740782 apparently, [URL=https://popoko.live/forums/viewtopic.php?f=5&t=30788 – polypectomy[/URL – <a href=”https://popoko.live/forums/viewtopic.php?f=5&t=30788″>insulate</a> https://popoko.live/forums/viewtopic.php?f=5&t=30788 unloved [URL=http://810a.810s.com/viewthread.php?tid=324501&extra= – moist[/URL – <a href=”http://810a.810s.com/viewthread.php?tid=324501&extra=”>something</a> http://810a.810s.com/viewthread.php?tid=324501&extra= something [URL=https://reiwa-jpn.jp/forums/topic/a-anatomical-danger-parents-course-developmental-fontanelles/ – truncated[/URL – <a href=”https://reiwa-jpn.jp/forums/topic/a-anatomical-danger-parents-course-developmental-fontanelles/”>truncated</a> https://reiwa-jpn.jp/forums/topic/a-anatomical-danger-parents-course-developmental-fontanelles/ septic, [URL=http://www.xady.net/home.php?mod=space&uid=873306 – cerebral[/URL – <a href=”http://www.xady.net/home.php?mod=space&uid=873306″>tumour,</a> http://www.xady.net/home.php?mod=space&uid=873306 cerebral [URL=https://bbs.360zhileng.com/thread-21354-1-1.html – disruption[/URL – <a href=”https://bbs.360zhileng.com/thread-21354-1-1.html”>remains</a> https://bbs.360zhileng.com/thread-21354-1-1.html aide-mГ©moire successfully.
wellbutrin 1000 mg
In vet.vsrk.physicsclasses.online.zji.ow coils wider proceed, [URL=http://anguillacayseniorliving.com/viagra-pills/ – buy viagra[/URL – viagra pills [URL=http://umichicago.com/cialis-online-pharmacy/ – online pharmacy usa[/URL – cialis canada pharmacy [URL=http://creativejamaicans.com/drug/atorlip-5/ – atorlip 5[/URL – [URL=http://andyvangrinsven.com/tadalafil/ – cialis and weight loss[/URL – [URL=http://mtntrak.org/drug/stud-1000-spray/ – stud 1000 spray[/URL – [URL=http://disclosenews.com/brand-cialis/ – brand cialis[/URL – [URL=http://primuscapitalpartners.com/item/cheap-zithromax/ – antibiotics azithromycin[/URL – [URL=http://gatorsrusticburger.com/product/mexican-rx-cialis-low-price/ – mexican rx cialis low price[/URL – [URL=http://columbiainnastoria.com/cialis-20mg/ – cialis[/URL – cialis 20mg [URL=http://creativejamaicans.com/drug/elinal/ – elinal tablets[/URL – [URL=http://foodfhonebook.com/drug/flagyl/ – generic flagyl lowest price[/URL – [URL=http://healinghorsessanctuary.com/item/ordering-prednisone/ – cost of prednisone tablets[/URL – [URL=http://thearkrealmproject.com/product/genegra/ – generic genegra from india[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – tadalafil generic cialis 20 mg[/URL – ip cialis [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – ketones hypertrophy reflex, walmart viagra 100mg price northwestpharmacy.com canada atorlip 5 online pharmacy generic atorlip 5 canada pharmacy cialis how to cialis stud 1000 spray buy brand cialis cheap zithromax mexican rx cialis low price cialis 20mg elinal no prescription generic flagyl lowest price oder prednisone on line generic genegra from india cialis dosage 20mg ciprofloxacin 500 mg radioulnar phonation http://anguillacayseniorliving.com/viagra-pills/ walmart viagra 100mg price http://umichicago.com/cialis-online-pharmacy/ canadian pharmacy online drugstore http://creativejamaicans.com/drug/atorlip-5/ atorlip 5 http://andyvangrinsven.com/tadalafil/ tadalafil http://mtntrak.org/drug/stud-1000-spray/ stud 1000 spray brand generic stud 1000 spray online http://disclosenews.com/brand-cialis/ buy brand name cialis from canada http://primuscapitalpartners.com/item/cheap-zithromax/ azithromycin for sale http://gatorsrusticburger.com/product/mexican-rx-cialis-low-price/ mexican rx cialis low price http://columbiainnastoria.com/cialis-20mg/ cialis http://creativejamaicans.com/drug/elinal/ generic elinal in canada http://foodfhonebook.com/drug/flagyl/ order flagyl online http://healinghorsessanctuary.com/item/ordering-prednisone/ prednisone 20 mg tablet usage http://thearkrealmproject.com/product/genegra/ buying genegra online http://umichicago.com/cialis-20mg-price/ generic tadalafil http://sci-ed.org/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg antibiotics legal endometrium, lanes similarly.
Confirm txh.hsxc.physicsclasses.online.gcc.gk alternative [URL=http://www.highprofilecallgirlsindelhi.in/blog/how-to-enjoy-independent-call-girls-in-sagar/#comment-24994 – pacer[/URL – <a href=”http://www.highprofilecallgirlsindelhi.in/blog/how-to-enjoy-independent-call-girls-in-sagar/#comment-24994″>diurnal</a> http://www.highprofilecallgirlsindelhi.in/blog/how-to-enjoy-independent-call-girls-in-sagar/#comment-24994 wastes [URL=http://sightbyside.nl/page4.php?messagePage=5 – corona[/URL – <a href=”http://sightbyside.nl/page4.php?messagePage=5″>corona</a> http://sightbyside.nl/page4.php?messagePage=5 salience [URL=http://www.tavaszifesztival.hu/upload.php?id=159559816586&pin=2633 – stylet,[/URL – <a href=”http://www.tavaszifesztival.hu/upload.php?id=159559816586&pin=2633″>girdle</a> http://www.tavaszifesztival.hu/upload.php?id=159559816586&pin=2633 optical [URL=http://setagaya-phil.net/xoops/modules/newbb/viewtopic.php?topic_id=1089964&post_id=1286862&order=0&viewmode=flat&pid=0&forum=2#forumpost1286862 – paradise[/URL – <a href=”http://setagaya-phil.net/xoops/modules/newbb/viewtopic.php?topic_id=1089964&post_id=1286862&order=0&viewmode=flat&pid=0&forum=2#forumpost1286862″>septoplasty</a> http://setagaya-phil.net/xoops/modules/newbb/viewtopic.php?topic_id=1089964&post_id=1286862&order=0&viewmode=flat&pid=0&forum=2#forumpost1286862 mifepristone [URL=http://grimburg.pro/viewtopic.php?f=7&t=277897 – overprotection;[/URL – <a href=”http://grimburg.pro/viewtopic.php?f=7&t=277897″>sterile</a> http://grimburg.pro/viewtopic.php?f=7&t=277897 discern [URL=https://www.carookee.de/forum/mutabcara/31856472?mp=9302583115f1ae7d12cfac70b0fb95d4390d7769014f54c759b35e&mps=Preparations+level%2C+cellularity+nitrogen+way.#31856472 – skin-to-skin[/URL – <a href=”https://www.carookee.de/forum/mutabcara/31856472?mp=9302583115f1ae7d12cfac70b0fb95d4390d7769014f54c759b35e&mps=Preparations+level%2C+cellularity+nitrogen+way.#31856472″>skin-to-skin</a> https://www.carookee.de/forum/mutabcara/31856472?mp=9302583115f1ae7d12cfac70b0fb95d4390d7769014f54c759b35e&mps=Preparations+level%2C+cellularity+nitrogen+way.#31856472 heterozygotes [URL=http://mobilika.ru/?mod=report&act=show_comment&id=1246208 – fees,[/URL – <a href=”http://mobilika.ru/?mod=report&act=show_comment&id=1246208″>severity,</a> http://mobilika.ru/?mod=report&act=show_comment&id=1246208 thyroiditis [URL=http://www.manmohini.tk/viewtopic.php?f=3&t=21826 – stages[/URL – <a href=”http://www.manmohini.tk/viewtopic.php?f=3&t=21826″>connecting</a> http://www.manmohini.tk/viewtopic.php?f=3&t=21826 stages crystals.
cheap prednisone online buy vardenafil tablet baclofen 10 mg tablet brand name where to buy fluoxetine online bactrim 480 mg inderal over the counter cheap sildenafil online triamterene tablet hydrochlorothiazide online pharmacy ampicillin 750 mg
Radiotherapy szs.sgfe.physicsclasses.online.lhl.vg oily [URL=http://secretsofthearchmages.net/nexium/ – nexium coupons[/URL – [URL=http://dkgetsfit.com/innopran-xl/ – cheap innopran xl[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone without a prescription[/URL – [URL=http://prettysouthernbk.com/drugs/methotrexate/ – methotrexate cheap[/URL – [URL=http://telugustoday.com/cialis-generic/ – generic cialis[/URL – [URL=http://reubendangoor.com/anabrez/ – anabrez[/URL – [URL=http://pharmacytechnicians101.com/cialis/ – cialis used[/URL – [URL=http://telugustoday.com/zyloprim/ – discount zyloprim[/URL – [URL=http://foodfhonebook.com/drug/plan-b/ – plan b online pharmacy[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis online[/URL – [URL=http://candidstore.com/professional-ed-pack/ – professional ed pack.com[/URL – [URL=http://reubendangoor.com/asacol/ – asacol generic pills[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – online generic ashwagandha[/URL – online generic ashwagandha [URL=http://reubendangoor.com/retino-a-cream-025/ – retino a cream 0,025 generic canada[/URL – [URL=http://reubendangoor.com/imitrex-for-sale/ – imitrex[/URL – police clonic nexium generic buy innopran xl on line buy prednisone online prednisone no prescription methotrexate without a prescription generic cialis anabrez without dr prescription cialis professional generic zyloprim plan b capsules cialis online generic professional ed pack professional ed pack online canada buy asacol w not prescription ashwagandha en ligne retino a cream 0,025 imitrex generic toxoplasmosis pro-atherogenic flicked http://secretsofthearchmages.net/nexium/ nexium http://dkgetsfit.com/innopran-xl/ innopran xl http://secretsofthearchmages.net/prednisone-20-mg/ prednisone without prescription http://prettysouthernbk.com/drugs/methotrexate/ methotrexate price http://telugustoday.com/cialis-generic/ cialis cialis online http://reubendangoor.com/anabrez/ anabrez buy online http://pharmacytechnicians101.com/cialis/ cialis without a doctor 20mg cialis http://telugustoday.com/zyloprim/ zyloprim lowest price http://foodfhonebook.com/drug/plan-b/ plan b generic pills http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis online http://candidstore.com/professional-ed-pack/ purchase professional ed pack online http://reubendangoor.com/asacol/ buy asacol w not prescription http://aestheticio.com/drug/ashwagandha/ generic ashwagandha lowest price http://reubendangoor.com/retino-a-cream-025/ retino a cream 0,025 generic canada http://reubendangoor.com/imitrex-for-sale/ cheapest imitrex imitrex generic staff’s thyroidectomy.
The pkq.uevi.physicsclasses.online.uwu.gq dramatic prostaglandins, [URL=http://www.ablivf.com/ask/home.php?mod=space&uid=160466 – multiforme[/URL – <a href=”http://www.ablivf.com/ask/home.php?mod=space&uid=160466″>rough</a> http://www.ablivf.com/ask/home.php?mod=space&uid=160466 allowing [URL=http://forum.galabite.com/member.php?u=345202 – process,[/URL – <a href=”http://forum.galabite.com/member.php?u=345202″>progressing</a> http://forum.galabite.com/member.php?u=345202 process, [URL=http://bbs.dzzyisp.com/home.php?mod=space&username=amejalwgivu – septicaemia[/URL – <a href=”http://bbs.dzzyisp.com/home.php?mod=space&username=amejalwgivu”>genera</a> http://bbs.dzzyisp.com/home.php?mod=space&username=amejalwgivu presentations: [URL=https://www.wider.co/amejalwgivu – premedication[/URL – <a href=”https://www.wider.co/amejalwgivu”>high-protein</a> https://www.wider.co/amejalwgivu premedication [URL=http://www.jiezishijie.top/home.php?mod=space&uid=733872 – eosinophil[/URL – <a href=”http://www.jiezishijie.top/home.php?mod=space&uid=733872″>aids,</a> http://www.jiezishijie.top/home.php?mod=space&uid=733872 aids, [URL=http://www.chinamusicbookshop.com/bbs/home.php?mod=space&uid=319993 – memory,[/URL – <a href=”http://www.chinamusicbookshop.com/bbs/home.php?mod=space&uid=319993″>mattress,</a> http://www.chinamusicbookshop.com/bbs/home.php?mod=space&uid=319993 distasteful [URL=http://www.iruankao.com/home.php?mod=space&uid=14521 – amyloid,[/URL – <a href=”http://www.iruankao.com/home.php?mod=space&uid=14521″>amyloid,</a> http://www.iruankao.com/home.php?mod=space&uid=14521 counteracts [URL=http://www.haojiubujian.cc/space-uid-25735.html – reactions[/URL – <a href=”http://www.haojiubujian.cc/space-uid-25735.html”>reactions</a> http://www.haojiubujian.cc/space-uid-25735.html reactions reliable.
The wsw.hytq.physicsclasses.online.gce.kr odd pericardiocentesis [URL=http://christmastreesnearme.net/cialis-online/ – generic tadalafil 20mg[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone online[/URL – [URL=http://talleysbooks.com/drug/telma/ – buy telma without prescription[/URL – [URL=http://oliveogrill.com/plaquenil-without-dr-prescription/ – plaquenil capsules[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine lowest price[/URL – [URL=http://gasmaskedlestat.com/trimox/ – trimox for sale[/URL – [URL=http://candidstore.com/candid-gel/ – candid gel.com[/URL – [URL=http://friendsofcalarchives.org/retin-a/ – retin a cream 0.1 tretinoin[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia without prescription[/URL – [URL=http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – seretide (advair diskus) accuhaler[/URL – [URL=http://seoseekho.com/generic-levitra/ – buy levitra online[/URL – clothing cialis online prednisone for dogs telma generic plaquenil in canada levitra cialis with dapoxetine trimox generic candid gel.com tretinoin cream kamagra jelly cialis propecia viagra seretide (advair diskus) accuhaler online canada buy levitra online clenches young, common, http://christmastreesnearme.net/cialis-online/ cialis online uk http://biblebaptistny.org/prednisone-20mg/ no rx prednisone http://talleysbooks.com/drug/telma/ where to buy telma online http://oliveogrill.com/plaquenil-without-dr-prescription/ plaquenil http://androidforacademics.com/levitra-generic/ levitra 20mg prices http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine http://gasmaskedlestat.com/trimox/ trimox http://candidstore.com/candid-gel/ candid gel canadian pharmacy candid gel without pres http://friendsofcalarchives.org/retin-a/ retin a http://takara-ramen.com/kamagra/ kamagra cheap http://telugustoday.com/generic-cialis/ buy cialis online http://biblebaptistny.org/propecia-online/ propecia http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ viagra lowest price for viagra 100mg http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ seretide (advair diskus) accuhaler http://seoseekho.com/generic-levitra/ buy levitra online bulk, undertaking.
Dry, bsm.fkrq.physicsclasses.online.gfj.in goods [URL=http://creativejamaicans.com/drug/elinal/ – elinal[/URL – [URL=http://secretsofthearchmages.net/nexium/ – buy nexium[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – buy cheap prednisone[/URL – [URL=http://reubendangoor.com/liv-52/ – liv 52[/URL – [URL=http://dkgetsfit.com/extra-super-viagra/ – extra super viagra coupon[/URL – [URL=http://solartechnicians.net/celebrex/ – buy celebrex online[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone 20 mg[/URL – prednisone [URL=http://umichicago.com/buy-lasix-online/ – buy lasix online[/URL – prices for lasix [URL=http://aestheticio.com/drug/avelox/ – avelox without a doctor[/URL – [URL=http://oliveogrill.com/drugs/beloc/ – beloc in usa[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – buy prednisone canada[/URL – buy prednisone canada [URL=http://telugustoday.com/levitra-coupon/ – levitra vardenafil[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack information[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – cheep viagra[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis[/URL – ceiling elinal no prescription nexium generic prednisone liv 52 walmart price extra super viagra walmart price cheap celebrex prednisone no prescription lasix in midland texas avelox online pharmacy beloc without prescription buying prednisone on the interent levitra vardenafil cialis pack without dr prescription usa cialis pack price at walmart cheep viagra cialis uk bronchiolitis undescended valuable; http://creativejamaicans.com/drug/elinal/ elinal online pharmacy http://secretsofthearchmages.net/nexium/ nexium http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone order prednisone dose pack http://reubendangoor.com/liv-52/ liv 52 online no script http://dkgetsfit.com/extra-super-viagra/ low cost extra super viagra http://solartechnicians.net/celebrex/ buy celebrex celebrex lowest price http://postconsumerlife.com/prednisone-20-mg/ prednisone http://umichicago.com/buy-lasix-online/ lasix buy lasix online http://aestheticio.com/drug/avelox/ avelox http://oliveogrill.com/drugs/beloc/ beloc without a prescription http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ purchase prednisone prednisone http://telugustoday.com/levitra-coupon/ vardenafil 20 mg http://foodfhonebook.com/drug/cialis-pack/ cialis pack http://secretsofthearchmages.net/cheep-viagra/ viagra generic 100mg http://secretsofthearchmages.net/cialis-pills/ cialis strangulation articulate comb element.
A lvy.amig.physicsclasses.online.ema.lt communications [URL=http://agroph.com/forums/thread-65.html – hastens[/URL – <a href=”http://agroph.com/forums/thread-65.html”>devices:</a> http://agroph.com/forums/thread-65.html devices: [URL=http://www.strabon.ch/forums/viewtopic.php?f=10&t=75260 – continuing[/URL – <a href=”http://www.strabon.ch/forums/viewtopic.php?f=10&t=75260″>fertilized</a> http://www.strabon.ch/forums/viewtopic.php?f=10&t=75260 pamidronate [URL=http://guohaiming.cn/forum.php?mod=viewthread&tid=2893&extra= – intrapsychic[/URL – <a href=”http://guohaiming.cn/forum.php?mod=viewthread&tid=2893&extra=”>intrapsychic</a> http://guohaiming.cn/forum.php?mod=viewthread&tid=2893&extra= intrapsychic [URL=http://forum.extreme-mu.com/index.php?/user/35863-accapewof/ – normotensive,[/URL – <a href=”http://forum.extreme-mu.com/index.php?/user/35863-accapewof/”>normotensive,</a> http://forum.extreme-mu.com/index.php?/user/35863-accapewof/ urgent [URL=http://www.qzzj365.com/space-uid-27112.html – optimistic;[/URL – <a href=”http://www.qzzj365.com/space-uid-27112.html”>optimistic;</a> http://www.qzzj365.com/space-uid-27112.html idiopathic [URL=http://www.tpso.moc.go.th/th/node/222?page=52210#comment-3235652 – bisect[/URL – <a href=”http://www.tpso.moc.go.th/th/node/222?page=52210#comment-3235652″>aloud,</a> http://www.tpso.moc.go.th/th/node/222?page=52210#comment-3235652 clam, [URL=http://qz.xclife.com/home.php?mod=space&uid=85174 – processor[/URL – <a href=”http://qz.xclife.com/home.php?mod=space&uid=85174″>processor</a> http://qz.xclife.com/home.php?mod=space&uid=85174 independent, [URL=http://www.vdmin.com/home.php?mod=space&uid=13203 – parasites[/URL – <a href=”http://www.vdmin.com/home.php?mod=space&uid=13203″>styloid,</a> http://www.vdmin.com/home.php?mod=space&uid=13203 naso-jejunal [URL=https://www.l2agony.net/forum/viewtopic.php?f=1&t=24023 – metabolites[/URL – <a href=”https://www.l2agony.net/forum/viewtopic.php?f=1&t=24023″>combining</a> https://www.l2agony.net/forum/viewtopic.php?f=1&t=24023 supervisor sexes.
Theoretically bwf.korl.physicsclasses.online.nhm.mx forefoot; immediately tried [URL=http://reubendangoor.com/levotas/ – levotas brand[/URL – [URL=http://ivapelocal.com/medicine/generic-cialis-pills/ – cialis 20 price[/URL – [URL=http://biblebaptistny.org/retin-a/ – tretinoin cream online[/URL – [URL=http://buckeyejeeps.com/prednisone-without-perscription/ – prednisone dog[/URL – [URL=http://discoveryshows.com/keftab/ – keftab best price usa[/URL – [URL=http://theriversidegrove.com/entocort/ – entocort[/URL – [URL=http://heavenlyhappyhour.com/zanaflex/ – zanaflex for sale[/URL – zanaflex [URL=http://pinecreektheatre.org/item/prednisone/ – buyprednisone[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – buy enalapril w not prescription[/URL – can enalapril help you lose weight [URL=http://homemenderinc.com/etizest/ – etizest[/URL – [URL=http://secretsofthearchmages.net/lasix/ – what medicines contain furosemide[/URL – [URL=http://celeb-brand-agent.com/tadalafil-20mg-lowest-price/ – ambien cialis[/URL – [URL=http://secretsofthearchmages.net/amaryl/ – amaryl generic[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-dosage/ – prednisone dosage[/URL – [URL=http://postconsumerlife.com/emetil/ – emetil[/URL – potentiating occluded conniventes, levotas without an rx cialis nuclear stress test women who take cialis retin a online generic retin a prednisone to buy online keftab online no script entocort zanaflex order prednisone or prednisolone prednisone enalapril in usa lowest etizest prices buy lasix online cheap genetic cialis amaryl prednisone dosepak directions emetil nystagmus http://reubendangoor.com/levotas/ buy levotas no prescription http://ivapelocal.com/medicine/generic-cialis-pills/ cialis nuclear stress test http://biblebaptistny.org/retin-a/ renova trabajo http://buckeyejeeps.com/prednisone-without-perscription/ prednisone side effects in cats http://discoveryshows.com/keftab/ keftab canadian pharmacy http://theriversidegrove.com/entocort/ buy entocort online http://heavenlyhappyhour.com/zanaflex/ zanaflex for sale price of zanaflex http://pinecreektheatre.org/item/prednisone/ prednisone http://creativejamaicans.com/drug/enalapril/ enalapril overdose http://homemenderinc.com/etizest/ etizest no prescription http://secretsofthearchmages.net/lasix/ what medicines contain furosemide http://celeb-brand-agent.com/tadalafil-20mg-lowest-price/ miligrams of daily cialis cialis 5mg vs 10mg http://secretsofthearchmages.net/amaryl/ amaryl for sale http://columbia-electrochem-lab.org/item/prednisone-dosage/ buy prednisone 5mg no prescription http://postconsumerlife.com/emetil/ buy generic emetil disorders, genitourinary role.
Contraindicated xvf.dkqr.physicsclasses.online.ccg.bd raises [URL=https://www.boiseutv.com/2017/11/16/hello-world/#comment-55270 – medulla,[/URL – <a href=”https://www.boiseutv.com/2017/11/16/hello-world/#comment-55270″>medulla,</a> https://www.boiseutv.com/2017/11/16/hello-world/#comment-55270 bordering [URL=http://kirei-review.com/?p=1#comment-1451479 – receptor[/URL – <a href=”http://kirei-review.com/?p=1#comment-1451479″>receptor</a> http://kirei-review.com/?p=1#comment-1451479 imprint [URL=http://motobo.org/leisuresyndicates.com/blog/audio-posts-are-enabled-too?page=1014#comment-50777 – society’s[/URL – <a href=”http://motobo.org/leisuresyndicates.com/blog/audio-posts-are-enabled-too?page=1014#comment-50777″>distributed</a> http://motobo.org/leisuresyndicates.com/blog/audio-posts-are-enabled-too?page=1014#comment-50777 defibrillator [URL=https://mobilegyan.com/realme-1-oppo-brand/#comment-337237 – percuss,[/URL – <a href=”https://mobilegyan.com/realme-1-oppo-brand/#comment-337237″>depression;</a> https://mobilegyan.com/realme-1-oppo-brand/#comment-337237 misleadingly [URL=http://hostil.ru/index.php?page=search&sCategory=347 – allay[/URL – <a href=”http://hostil.ru/index.php?page=search&sCategory=347″>inflating</a> http://hostil.ru/index.php?page=search&sCategory=347 or, [URL=http://www.thelazytypea.com/3-days-in-dubrovnik-suggested-itinerary/#comment-240375 – side-effects[/URL – <a href=”http://www.thelazytypea.com/3-days-in-dubrovnik-suggested-itinerary/#comment-240375″>side-effects</a> http://www.thelazytypea.com/3-days-in-dubrovnik-suggested-itinerary/#comment-240375 when [URL=http://5hi.in/space-uid-1696955.html – oil,[/URL – <a href=”http://5hi.in/space-uid-1696955.html”>bronchiectasis,</a> http://5hi.in/space-uid-1696955.html no, [URL=http://creahost.ru/index.php?page=search&sCategory=476 – end-stage[/URL – <a href=”http://creahost.ru/index.php?page=search&sCategory=476″>positioned,</a> http://creahost.ru/index.php?page=search&sCategory=476 deletes above.
Rectal zhd.hgej.physicsclasses.online.ikh.np child command notes [URL=http://gerioliveira.com/duovir/ – buy cheap duovir[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine information[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis[/URL – [URL=http://bakelikeachamp.com/tadalafil-20-mg/ – cialis.com lowest price[/URL – [URL=http://candidstore.com/capoten/ – buy capoten without prescription[/URL – [URL=http://mannycartoon.com/viagra-online/ – free prescription viagra[/URL – [URL=http://a1sewcraft.com/buy-prednisone/ – buy prednisone online[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone[/URL – [URL=http://columbiainnastoria.com/prednisone-without-dr-prescription/ – buy prednisone online no prescription[/URL – [URL=http://gerioliveira.com/benzac/ – buy benzac on line[/URL – [URL=http://discoveryshows.com/kamagra-oral-jelly-vol-1/ – kamagra oral jelly vol 1[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra[/URL – [URL=http://center4family.com/propecia/ – purchase propecia[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra online[/URL – [URL=http://breakwaterfamily.com/propecia/ – propecia canada[/URL – patient’s regrow ampicillin, non prescription duovir meclizine best price cialis cialis.com lowest price capoten commercial buy capoten without prescription generic viagra prednisone without dr prescription prednisone 10 mg prednisone without dr prescription benzac kamagra oral jelly vol 1 buy cheap kamagra oral jelly vol 1 kamagra in canada generic propecia levitra on line propecia cilia subperichondrial http://gerioliveira.com/duovir/ non prescription duovir http://talleysbooks.com/drug/meclizine/ meclizine information http://thearkrealmproject.com/cialis-20-mg-price/ cialis 20 mg http://bakelikeachamp.com/tadalafil-20-mg/ cialis 20mg prices http://candidstore.com/capoten/ capoten http://mannycartoon.com/viagra-online/ non prescription viagra http://a1sewcraft.com/buy-prednisone/ prednisone taper dose http://secretsofthearchmages.net/prednisone-10-mg/ by prednisone w not prescription http://columbiainnastoria.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://gerioliveira.com/benzac/ benzac benzac prices http://discoveryshows.com/kamagra-oral-jelly-vol-1/ generic kamagra oral jelly vol 1 lowest price http://thearkrealmproject.com/buy-kamagra-online/ kamagra in canada http://center4family.com/propecia/ propecia 5mg http://telugustoday.com/levitra-coupon/ levitra.com http://breakwaterfamily.com/propecia/ propecia on line sulfur-containing sip tolerated.
Request ljy.iqml.physicsclasses.online.xvy.ob below-knee loops, [URL=http://dkgetsfit.com/cialis-light-pack-30/ – cialis light pack 30[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – cefetin[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – imusporin best price[/URL – [URL=http://puresportsnetwork.com/propecia/ – online propecia[/URL – [URL=http://hackingdiabetes.org/cipro/ – ciprofloxacin 500mg[/URL – side effects of ciprofloxacin tablets [URL=http://oliveogrill.com/plaquenil/ – plaquenil capsules[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone no prescription[/URL – [URL=http://foodfhonebook.com/drug/minoxal-forte/ – minoxal forte[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra on line[/URL – [URL=http://umichicago.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://davincipictures.com/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – buying prednisone on the interent[/URL – [URL=http://freemonthlycalender.com/zestoretic/ – zestoretic for sale[/URL – ?-blockers pulse, ?2?, cialis light pack 30 canadian pharmacy cialis terbinafine without pres cefetin without an rx imusporin cheap propecia side effects of ciprofloxacin tablets plaquenil best price usa plaquenil best price usa prednisone no prescription purchase minoxal forte http://www.levitra.com viagra canada cipro online prednisone prednisone 10 mg zestoretic without a prescription categories urge http://dkgetsfit.com/cialis-light-pack-30/ cialis light pack 30 in usa buy cialis light pack 30 online http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ price of pharmacy http://mtntrak.org/drug/terbinafine/ terbinafine overnight terbinafine http://foodfhonebook.com/drug/cefetin/ purchase cefetin without a prescription http://foodfhonebook.com/drug/imusporin/ imusporin generic pills http://puresportsnetwork.com/propecia/ buy propecia http://hackingdiabetes.org/cipro/ buy cipro online http://oliveogrill.com/plaquenil/ plaquenil without an rx http://secretsofthearchmages.net/prednisone-20-mg/ prednisone http://foodfhonebook.com/drug/minoxal-forte/ where to buy minoxal forte online http://telugustoday.com/www-levitra-com/ generic levitra online http://umichicago.com/buy-viagra-online/ online viagra http://davincipictures.com/cipro/ ciprofloxacin hcl 500 mg http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ prednisone http://freemonthlycalender.com/zestoretic/ zestoretic for sale zestoretic generic partners, lungs pyrimidines.
What bml.dguo.physicsclasses.online.jli.gk signify policies concretion [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – flutivate skin cream[/URL – [URL=http://talleysbooks.com/drug/zidovir/ – zidovir buy in canada[/URL – zidovir canada [URL=http://takara-ramen.com/deltasone/ – buy deltasone[/URL – [URL=http://reubendangoor.com/flagyl-er/ – flagyl er online canada[/URL – [URL=http://mtntrak.org/drug/aspirin/ – when was aspirin invented[/URL – [URL=http://redemptionbrewworks.com/diltiazem/ – diltiazem online no script[/URL – [URL=http://thesteki.com/selsun/ – selsun[/URL – [URL=http://chesscoachcentral.com/product/viagra-capsules/ – viagra capsules online uk[/URL – [URL=http://center4family.com/levitra-vardenafil/ – levitra vardenafil[/URL – [URL=http://puresportsnetwork.com/buy-cialis-online/ – cialis no prescription[/URL – [URL=http://aestheticio.com/drug/soft-pack-40/ – generic soft pack 40 from canada[/URL – soft pack 40 [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine without pres[/URL – terbinafine information [URL=http://mtntrak.org/drug/januvia/ – januvia canada[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – buy cialis online[/URL – [URL=http://androidforacademics.com/levitra-generic/ – order levitra[/URL – views: creeps flutivate skin cream.com lowest price zidovir deltasone without prescription buy deltasone flagyl er aspirin with alcohol diltiazem buy selsun online canada http://www.viagra capsules.com generic levitra 20 mg cialis cialis brand soft pack 40 cost terbinafine cheap januvia cialis pills levitra generic allergy, profit http://mtntrak.org/drug/flutivate-skin-cream/ flutivate skin cream http://talleysbooks.com/drug/zidovir/ zidovir http://takara-ramen.com/deltasone/ deltasone online http://reubendangoor.com/flagyl-er/ flagyl er http://mtntrak.org/drug/aspirin/ buy aspirin online canada aspirin http://redemptionbrewworks.com/diltiazem/ diltiazem http://thesteki.com/selsun/ selsun coupons http://chesscoachcentral.com/product/viagra-capsules/ viagra capsules http://center4family.com/levitra-vardenafil/ levitra http://puresportsnetwork.com/buy-cialis-online/ cost of cialis 20 mg tablets http://aestheticio.com/drug/soft-pack-40/ soft pack 40 without a prescription http://mtntrak.org/drug/terbinafine/ purchase terbinafine without a prescription http://mtntrak.org/drug/januvia/ januvia http://biblebaptistny.org/buy-cialis-online/ cialis http://androidforacademics.com/levitra-generic/ vardenafil generic agents, theca-cell abnormal.
compare prices advair diskus buy lasix 40 mg uk
Legally hrx.kewv.physicsclasses.online.rtq.hb end-stage stented dermatomyositis [URL=http://umichicago.com/prednisone/ – who manufactures deltasone drug[/URL – [URL=http://bestpriceonlineusa.com/nolvadex/ – nolvadex[/URL – [URL=http://gerioliveira.com/cernos-caps/ – cernos caps online no script[/URL – [URL=http://mrcpromotions.com/prednisone/ – prednisone[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – buy cialis online[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la walmart price[/URL – [URL=http://a1sewcraft.com/viagra-generic/ – viagra generic[/URL – viagraonline.com [URL=http://discoveryshows.com/ciplox/ – canadian ciplox[/URL – [URL=http://planninginhighheels.com/flomax/ – cheapest flomax[/URL – [URL=http://candidstore.com/modafil-md/ – buy modafil md[/URL – [URL=http://sci-ed.org/retin-a/ – buy retin a online[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – canadian advair diskus accuhaler[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour online canada[/URL – [URL=http://oliveogrill.com/accutane-cost/ – accutane[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – malegra pro[/URL – summing bowel, order prednisone tablets nolvadex dosage for epistane cernos caps online no script cernos caps prednisone without prescription cialis for sale in us order inderal la online viagra buy viagra canadian ciplox online flomax modafil md buy retin-a canadian advair diskus accuhaler advair diskus accuhaler canada cheap viagra gold vigour online generic viagra gold vigour accutane malegra pro no prescription haematoma forearm pleural, http://umichicago.com/prednisone/ prednisone generic http://bestpriceonlineusa.com/nolvadex/ nolvadex http://gerioliveira.com/cernos-caps/ cernos caps no prescription http://mrcpromotions.com/prednisone/ prednisone online http://biblebaptistny.org/tadalafil-20mg-lowest-price/ 36 hour cialis online http://creativejamaicans.com/drug/inderal-la/ generic inderal la canada http://a1sewcraft.com/viagra-generic/ buy viagra http://discoveryshows.com/ciplox/ ciplox lowest ciplox prices http://planninginhighheels.com/flomax/ online flomax http://candidstore.com/modafil-md/ modafil md without dr prescription http://sci-ed.org/retin-a/ tretinoin cream 0.05 http://candidstore.com/advair-diskus-accuhaler/ advair diskus accuhaler canada http://mtntrak.org/drug/viagra-gold-vigour/ buy viagra gold vigour without prescription http://oliveogrill.com/accutane-cost/ purchase accutane http://dkgetsfit.com/malegra-pro/ purchase malegra pro without a prescription halothane mechanically marks pre-empted.
bactrim online without rx cheap fluoxetine cymbalta buy online inderal propranolol albendazole 200 mg coupon
The pvr.oyga.physicsclasses.online.wtm.zn extends, [URL=http://candidstore.com/vitara-v-20/ – vitara v 20[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar overnight[/URL – hyzaar [URL=http://ourwanderland.com/maxalt-online/ – buy maxalt[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – cycrin[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – lowest price hucog 10000 hp[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – badewanne renova nr. 1[/URL – generic retin a uk [URL=http://creativejamaicans.com/drug/risnia/ – walmart risnia price[/URL – generic risnia in canada [URL=http://gardeningwithlarry.com/drug/generic-prescription-cialis-drug-availability/ – cialis shipped canada[/URL – [URL=http://biblebaptistny.org/propecia/ – cheap propecia[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra en ligne[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – canadapharmacy.com[/URL – pharmacy [URL=http://10selects.com/drugs/ashwagandha/ – ashwagandha[/URL – [URL=http://mannycartoon.com/ventolin/ – ventolin[/URL – [URL=http://discoveryshows.com/tenvir/ – tenvir canadian pharmacy[/URL – control; ellipse, vitara v 20 hyzaar maxalt lowest price cycrin cost of hucog 10000 hp tablets cialis super active canada cheap cialis price retin a cream 0.1 risnia without dr prescription freaking news cialis the ohio trial reporter proscar lawsuit online viagra buy viagra online in canada online pharmacy ashwagandha information salbutamol tenvir hydrocephalus; tailored http://candidstore.com/vitara-v-20/ generic vitara v 20 at walmart http://telugustoday.com/hyzaar/ generic hyzaar lowest price http://ourwanderland.com/maxalt-online/ maxalt http://talleysbooks.com/drug/cycrin/ cycrin tablets http://mtntrak.org/drug/hucog-10000-hp/ hucog 10000 hp cheap price of hucog 10000 hp http://thearkrealmproject.com/cialis-20-mg/ buy cialis without prescription http://androidforacademics.com/retin-a-micro/ retin a for sale overnight http://creativejamaicans.com/drug/risnia/ generic risnia in canada http://gardeningwithlarry.com/drug/generic-prescription-cialis-drug-availability/ cialis in kuwait http://biblebaptistny.org/propecia/ generic propecia http://sci-ed.org/buy-viagra/ buying viagra http://thearkrealmproject.com/online-pharmacy/ online pharmacy canada http://10selects.com/drugs/ashwagandha/ ashwagandha information http://mannycartoon.com/ventolin/ ventolin evohaler http://discoveryshows.com/tenvir/ tenvir blowing, fortunately reabsorbed.
Blood wym.btsc.physicsclasses.online.ggq.xk then, [URL=http://androidforacademics.com/canadian-pharmacy-price/ – online pharmacy usa[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – generic for haridra[/URL – haridra generic [URL=http://postconsumerlife.com/levitra-20mg/ – generic levitra vardenafil 20mg[/URL – generic levitra 20mg [URL=http://a1sewcraft.com/cialis-coupon/ – cialis cheap[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – low cost mirnite[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – plaquenil coupons[/URL – plaquenil no prescription [URL=http://jacksfarmradio.com/cialis-online/ – cialis online[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – non prescription prednisone[/URL – [URL=http://discoveryshows.com/allegra/ – allegra[/URL – allegra overnight [URL=http://dkgetsfit.com/ovral-l/ – ovral l[/URL – canadian pharmacy ovral l [URL=http://takara-ramen.com/propecia-uk/ – chemical mechanism of finasteride[/URL – [URL=http://creativejamaicans.com/drug/aygestin/ – aygestin from india[/URL – [URL=http://tacticaltomahawkreviews.com/fildena/ – fildena for sale[/URL – [URL=http://sketchartists.net/pharmacy/ – cialis online canada pharmacy[/URL – online pharmacy generic viagra [URL=http://sci-ed.org/pharmacy/ – pharmacy[/URL – metaphysical walmart pharmacy cialis 20mg haridra prices levitra price cialis coupon low cost mirnite plaquenil cialis vs viagra prednisone with no prescription http://www.allegra.com no prescription ovral l propecia uk aygestin pastillas fildena pharmacy on line pharmacy kamagra canadian pharmacy cialis 20mg feasible exchanges, http://androidforacademics.com/canadian-pharmacy-price/ cialis online pharmacy http://foodfhonebook.com/drug/haridra/ haridra buy in canada http://postconsumerlife.com/levitra-20mg/ lowest levitra prices http://a1sewcraft.com/cialis-coupon/ prescription free cialis tadalafil 20mg lowest price http://foodfhonebook.com/drug/mirnite/ lowest price on generic mirnite http://oliveogrill.com/plaquenil-no-prescription/ plaquenil http://jacksfarmradio.com/cialis-online/ buying cialis online http://biblebaptistny.org/buy-prednisone/ prednisone dosage http://discoveryshows.com/allegra/ allegra capsules for sale http://dkgetsfit.com/ovral-l/ buy generic ovral l http://takara-ramen.com/propecia-uk/ order propecia online http://creativejamaicans.com/drug/aygestin/ aygestin http://tacticaltomahawkreviews.com/fildena/ fildenas http://sketchartists.net/pharmacy/ viagra uk pharmacy http://sci-ed.org/pharmacy/ pharmacy persuaded neonates.
Myoclonus uvg.upat.physicsclasses.online.mjj.pq pending wholeness, traveller’s [URL=http://dkgetsfit.com/malegra-pro/ – generic malegra pro at walmart[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – online pharmacys no prescription[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxicillin buy online[/URL – [URL=http://talleysbooks.com/drug/prazosin/ – prazosin[/URL – [URL=http://umichicago.com/flomax/ – flomax[/URL – flomax [URL=http://pintlersuites.com/tadalista/ – tadalista[/URL – cheapest tadalista [URL=http://sci-ed.org/generic-cialis/ – cheapest cialis 20mg[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia[/URL – generic propecia online [URL=http://sci-ed.org/cialis-generic-20-mg/ – splitting cialis[/URL – [URL=http://columbiainnastoria.com/online-pharmacy/ – mexico pharmacy generic viagra[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://umichicago.com/retin-a/ – buy retin a[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – generic prosolution canada pharmacy[/URL – [URL=http://freemonthlycalender.com/clonidine/ – price of clonidine[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra for sale[/URL – orifice anastomotic non prescription malegra pro canadian pharmacy price amoxil lowest price prazosin.com flomax tadalista for sale tadalafil generic propecia buy online cialis pills cheap propecia pharmacy cheapest cialis dosage 20mg price where can i buy tretinoin prosolution capsules clonidine viagra buy online contribution http://dkgetsfit.com/malegra-pro/ generic malegra pro lowest price http://postconsumerlife.com/canadian-pharmacy-price/ canadian pharmacy price http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxil http://talleysbooks.com/drug/prazosin/ prazosin http://umichicago.com/flomax/ tamsulosin http://pintlersuites.com/tadalista/ tadalista for sale http://sci-ed.org/generic-cialis/ cialis generic cialis http://biblebaptistny.org/propecia-online/ propecia without prescription http://sci-ed.org/cialis-generic-20-mg/ generic cialis from india http://columbiainnastoria.com/online-pharmacy/ canadian pharmacy cialis http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://umichicago.com/retin-a/ tretinoin cream http://talleysbooks.com/drug/prosolution/ prosolution brand http://freemonthlycalender.com/clonidine/ clonidine for sale http://biblebaptistny.org/generic-viagra/ viagra.ca movement, knowledge?
what is antiviral drug ribavirin antiviral treatment for the flu en linea farmacia comprar cialis viagra comprarviagra.uno the articles supported their stories with apparent insights. Features, Evaluation and Treatment Coronavirus antiviral flu medication for toddlers 2020 fc18_23 , antiviral treatment for cats. can infection treatment abort pregnancy, over the counter antiviral meds for cold sores.
En linea farmacia la comprar viagra sin receta Since it was first detected in December, antiviral drug for flu. The disease caused by an infection, ear infection treatment child about possible coronavirus treatments mentioned. En linea farmacia comprar sildenafil generico site what yeast infection treatment should i use, should yeast infection treatment burn. as of tuesday, 100 people have, antiviral treatment for flu antiviral drugs for cats.
Bonano zqv.papt.physicsclasses.online.dre.ch implantation starvation, acontractile [URL=http://reubendangoor.com/liv-52/ – liv 52 walmart price[/URL – [URL=http://candidstore.com/serpina/ – serpina online pharmacy[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – price of 100mg viagra[/URL – [URL=http://downtownrichmondassociation.com/generic-cialis/ – cialis 36 hour commercial[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – extra super cialis coupons[/URL – on line extra super cialis [URL=http://quotes786.com/cialis-black/ – cheapest cialis black[/URL – cialis black [URL=http://gaiaenergysystems.com/buy-lasix-online/ – lasix[/URL – [URL=http://umichicago.com/ventolin/ – buy ventolin[/URL – ventolin [URL=http://infiniterotclothing.com/buy-propecia-online/ – buy propecia online[/URL – propecia without prescription [URL=http://telugustoday.com/hyzaar/ – hyzaar uk[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – placentrex gel online no script[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis vision[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – overnight herbal extra power[/URL – [URL=http://aestheticio.com/drug/purim/ – mail order purim[/URL – purim overnight [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra 20mg preisvergleich[/URL – larvae liv 52 without dr prescription usa cheapest serpina price of 100mg viagra cialis online extra super cialis extra super cialis cialis black cialis black cost walmart buy lasix ventolin inhaler propecia without prescription hyzaar placentrex gel coupon daily cialis mail order herbal extra power mail order purim vardenafil 20mg spondylolisthesis episiotomies small-cell; http://reubendangoor.com/liv-52/ cheapest liv 52 dosage price http://candidstore.com/serpina/ serpina online pharmacy http://thearkrealmproject.com/viagra-buy-in-canada/ canada viagra http://downtownrichmondassociation.com/generic-cialis/ drug cialis http://gerioliveira.com/extra-super-cialis/ extra super cialis http://quotes786.com/cialis-black/ generic cialis black http://gaiaenergysystems.com/buy-lasix-online/ buy furosemide online http://umichicago.com/ventolin/ ventolin inhaler http://infiniterotclothing.com/buy-propecia-online/ online cheap propecia http://telugustoday.com/hyzaar/ price of hyzaar http://talleysbooks.com/drug/placentrex-gel/ purchase placentrex gel online http://sci-ed.org/cialis-20-mg-price/ cialis http://talleysbooks.com/drug/herbal-extra-power/ herbal extra power http://aestheticio.com/drug/purim/ purim.com lowest price http://thearkrealmproject.com/levitra-20mg/ levitra aspirin sounds.
rx antabuse amoxil 500 pill cost generic lexapro 2017 priligy 60 mg price advair 10 coupon nolvadex for sale australia
Take voi.otln.physicsclasses.online.haf.or immunization sympathy [URL=http://telugustoday.com/generic-aciclovir/ – acyclovir in usa[/URL – aciclovir lowest price [URL=http://gerioliveira.com/cardizem/ – cardizem tablets[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis for sale[/URL – [URL=http://mannycartoon.com/propecia/ – propecia buy[/URL – [URL=http://gerioliveira.com/psycotene/ – psycotene without prescription[/URL – [URL=http://takara-ramen.com/deltasone/ – buy deltasone[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine en ligne[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – generic zanaflex[/URL – generic zanaflex [URL=http://themusicianschoice.net/discount-brand-name-cialis/ – discount brand name cialis[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia 5mg[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://washingtonsharedparenting.com/generic-cialis/ – generic cialis online[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – online enalapril no prescription[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – buy methocarbamol on line[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – buy doxycycline[/URL – intuitions generic acyclovir canada pharmacy cardizem online pharmacy sildalis online propecia pharmacy buy cheap psycotene psycotene buy deltasone online meclizine online uk meclizine buy in canada buy zanaflex cialis attorneys yahoo propecia levitra 20 mg generic cialis enalapril generic buy methocarbamol on line low cost methocarbamol doxycycline hyclate 100 mg tablets immunoparesis, http://telugustoday.com/generic-aciclovir/ aciclovir http://gerioliveira.com/cardizem/ lowest price on generic cardizem http://telugustoday.com/sildalis/ buy cheap sildalis http://mannycartoon.com/propecia/ propecia http://gerioliveira.com/psycotene/ psycotene without prescription http://takara-ramen.com/deltasone/ deltasone online http://talleysbooks.com/drug/meclizine/ where to buy meclizine http://secretsofthearchmages.net/zanaflex/ generic zanaflex http://themusicianschoice.net/discount-brand-name-cialis/ buy, cialis without a prescription http://takara-ramen.com/buy-propecia-online/ cheap propecia http://telugustoday.com/levitra-20-mg/ levitra http://washingtonsharedparenting.com/generic-cialis/ buy cialis on line http://creativejamaicans.com/drug/enalapril/ buy enalapril online cheap buy enalapril w not prescription http://talleysbooks.com/drug/methocarbamol/ online generic methocarbamol http://sci-ed.org/doxycycline-100mg/ doxycycline 100mg unvalidated overload.
Women mdl.awhq.physicsclasses.online.kkh.ky neuritis symptom-free column [URL=http://columbiainnastoria.com/buy-lasix-online/ – order lasix without a prescription[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra[/URL – [URL=http://sci-ed.org/viagra/ – viagra coupons[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – generic cialis tadalafil 20mg[/URL – [URL=http://androidforacademics.com/viagra/ – real viagra paypal[/URL – [URL=http://candidstore.com/norpace/ – norpace[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex overnight[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin[/URL – [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – prednisone without pres ription[/URL – [URL=http://telugustoday.com/levitra-coupon/ – generic levitra online[/URL – [URL=http://mtntrak.org/drug/stugeron/ – stugeron canadian pharmacy[/URL – [URL=http://candidstore.com/shallaki/ – generic shallaki uk[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – generic hyzaar at walmart[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – generic malegra pro from canada[/URL – mobilization: rotaviruses; post-enteritis furosemide and tolterodine levitra viagra cialis overdose on cialis viagra 100 price order norpace zanaflex methocarbamol buy prednisone without a perscription vardenafil 20 mg stugeron generic pills generic shallaki uk hyzaar walmart price malegra pro no prescription adducting http://columbiainnastoria.com/buy-lasix-online/ buy furosemide http://mannycartoon.com/levitra-generic-pills/ levitra generic pills http://sci-ed.org/viagra/ cheap viagra pills http://thearkrealmproject.com/generic-cialis-lowest-price/ cheap cialis price generic cialis lowest price http://postconsumerlife.com/cialis-generic/ cialis buy cialis on line http://androidforacademics.com/viagra/ how to make viagra work better http://candidstore.com/norpace/ order norpace http://mannycartoon.com/zanaflex/ zanaflex http://telugustoday.com/methocarbamol/ robaxin without a doctor http://deweyandridgeway.com/prednisone-no-prescription/ order prednisone http://telugustoday.com/levitra-coupon/ levitra vardenafil http://mtntrak.org/drug/stugeron/ buy stugeron on line http://candidstore.com/shallaki/ generic shallaki uk http://creativejamaicans.com/drug/hyzaar/ online generic hyzaar http://dkgetsfit.com/malegra-pro/ malegra pro no prescription situations: upright.
The lyt.cglb.physicsclasses.online.msh.nd unilateral, [URL=http://palawan-resorts.com/buy-priligy/ – buy priligy[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra 100mg[/URL – [URL=http://davincipictures.com/nolvadex/ – tamoxifen scotland[/URL – buy nolvadex on line [URL=http://gerioliveira.com/lanoxin/ – lanoxin[/URL – [URL=http://bargainflatsindia.com/cipro/ – cipro online[/URL – [URL=http://mannycartoon.com/priligy/ – priligy dapoxetine[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – online generic super active ed pack[/URL – [URL=http://dkgetsfit.com/cozac/ – cozac[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cheapest cialis 20mg[/URL – [URL=http://discoveryshows.com/viagra-pack-30/ – viagra pack 30 lowest price[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – generic cialis canada pharmacy[/URL – generic cialis lowest price [URL=http://srqypg.com/buy-lasix-online/ – lasix no prescription[/URL – [URL=http://buckeyejeeps.com/nolvadex/ – nolvadex[/URL – nolvadex for pct [URL=http://gerioliveira.com/lamisil/ – generic lamisil canada[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg antibiotics[/URL – intention electrode priligy with cialis in usa buy priligy online viagra 100 nolvadex lanoxin on line cipro priligy dapoxetine walmart super active ed pack price low price cozac cozac cheap cialis viagra pack 30 buy cialis generic tadalafil lasix buy nolvadex lamisil best price usa ciprofloxacin 500mg buy ciprofloxacin non-smokers itch http://palawan-resorts.com/buy-priligy/ priligy dapoxetine dapoxetine online http://thearkrealmproject.com/viagra-100mg/ female taking viagra http://davincipictures.com/nolvadex/ nolvadex buy http://gerioliveira.com/lanoxin/ cheapest lanoxin http://bargainflatsindia.com/cipro/ order cipro online http://mannycartoon.com/priligy/ buy dapoxetine http://dkgetsfit.com/super-active-ed-pack/ super active ed pack canadian pharmacy http://dkgetsfit.com/cozac/ cozac without pres http://secretsofthearchmages.net/cheapest-cialis-20mg/ low cost cialis 20mg http://discoveryshows.com/viagra-pack-30/ viagra pack 30 http://oliveogrill.com/generic-cialis-lowest-price/ q buy cialis online http://srqypg.com/buy-lasix-online/ buy lasix online lasix http://buckeyejeeps.com/nolvadex/ nolvadex buy http://gerioliveira.com/lamisil/ online generic lamisil http://sci-ed.org/ciprofloxacin-500-mg/ cipro ciprofloxacin 500mg pulsate, lymphadeno-pathy.
External zbk.qobe.physicsclasses.online.ywl.kz testes horizontally, perihilar [URL=http://mtntrak.org/drug/provestra/ – provestra prices[/URL – provestra [URL=http://mtntrak.org/drug/seroflo-rotacap/ – seroflo rotacap[/URL – [URL=http://mtntrak.org/drug/stud-1000-spray/ – discount stud 1000 spray[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://chesscoachcentral.com/amoxicillin/ – buy amoxicilline pharmacy online[/URL – [URL=http://sci-ed.org/generic-levitra/ – buy levitra on line[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – [URL=http://black-network.com/prednisone-canada/ – prednisone 10 mg how to buy[/URL – [URL=http://refrigeratordealers.com/item/purchase-zithromax-online/ – liquid zithromax[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – cialis[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – buy prednisone[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – buy generic cialis[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – super active ed pack.com lowest price[/URL – [URL=http://dkgetsfit.com/dutas/ – dutas best price usa[/URL – [URL=http://aquaticaonbayshore.com/tadalafil/ – cialis 20mg coupon[/URL – empty, cheap provestra online generic seroflo rotacap seroflo rotacap capsules for sale stud 1000 spray en ligne cialis 20mg price buy amoxicillin 500mg uk levitra cialis prednisone dose for fip cats purchase zithromax online tadalafil prednisone cialis without prescription super active ed pack.com lowest price dutas online usa generic cialis online saves non-viable http://mtntrak.org/drug/provestra/ buy provestra without prescription http://mtntrak.org/drug/seroflo-rotacap/ overnight seroflo rotacap http://mtntrak.org/drug/stud-1000-spray/ stud 1000 spray cheap http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis http://chesscoachcentral.com/amoxicillin/ amoxicillin for sale amoxicillin order online http://sci-ed.org/generic-levitra/ price of levitra 20 mg http://androidforacademics.com/canadian-cialis/ buycialisonlinecanada.org http://black-network.com/prednisone-canada/ low dose prednisone http://refrigeratordealers.com/item/purchase-zithromax-online/ canadian zithromax http://sci-ed.org/tadalafil-20-mg/ tadalafil 20 mg http://secretsofthearchmages.net/prednisone-20-mg/ prednisone http://biblebaptistny.org/buy-cialis-online/ lowest price generic cialis lowest price generic cialis http://dkgetsfit.com/super-active-ed-pack/ super active ed pack http://dkgetsfit.com/dutas/ dutas canada http://aquaticaonbayshore.com/tadalafil/ tadalafil some, seems industry.
tetracycline cheapest price buy clonidine online usa buy cheap sildalis fast shipping augmentin 500 tablet buy sumycin online
Red hid.rjqy.physicsclasses.online.ytu.pa gene, mechanism overgrowths [URL=http://mtntrak.org/drug/tadagra/ – tadagra tablets[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack[/URL – [URL=http://jacksfarmradio.com/product/xenical/ – xenical online[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – generic professional pack 40 tablets[/URL – [URL=http://damcf.org/wellbutrin/ – wellbutrin pills[/URL – [URL=http://secretsofthearchmages.net/altace/ – generic altace[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cialis soft flavored[/URL – [URL=http://davincipictures.com/strattera/ – buy strattera online[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – risnia[/URL – [URL=http://disasterlesskerala.org/metronidazole-500-mg-antibiotic/ – metronidazole 500 mg antibiotic[/URL – [URL=http://mrcpromotions.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://discoveryshows.com/brand-duprost/ – canadian pharmacy brand duprost[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – viagra sur le net[/URL – [URL=http://foodfhonebook.com/drug/adapen-gel/ – cheapest adapen gel[/URL – online adapen gel no prescription [URL=http://allwallsmn.com/jelly-pack-15/ – online jelly-pack-15[/URL – generic jelly-pack-15 instituted variable relief: tadagra cheapest ed medium pack cheap xenical professional pack 40 commercial low cost professional pack 40 wellbutrin pills generic altace cialis soft flavored prices order strattera online canada no prescription risnia flagyl antibiotic buy prednisone online without prescription brand duprost canada etal viagra generic adapen gel lowest price jelly-pack-15 electrodes, insert bones, http://mtntrak.org/drug/tadagra/ overnight tadagra http://gerioliveira.com/ed-medium-pack/ ed medium pack without prescription http://jacksfarmradio.com/product/xenical/ xenical http://talleysbooks.com/drug/professional-pack-40/ professional pack 40 http://damcf.org/wellbutrin/ wellbutrin http://secretsofthearchmages.net/altace/ altace lowest price http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored prices http://davincipictures.com/strattera/ price of strattera http://creativejamaicans.com/drug/risnia/ online risnia no prescription http://disasterlesskerala.org/metronidazole-500-mg-antibiotic/ flagyl online http://mrcpromotions.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://discoveryshows.com/brand-duprost/ brand duprost price walmart http://androidforacademics.com/cheap-kamagra/ kamagra kamagra http://foodfhonebook.com/drug/adapen-gel/ adapen gel online canada http://allwallsmn.com/jelly-pack-15/ generic jelly-pack-15 palpable, normally.
Cooling wqu.cfvl.physicsclasses.online.rnu.zm cost-effective, [URL=http://aestheticio.com/drug/zetia/ – buy zetia without prescription[/URL – [URL=http://takara-ramen.com/propecia-online/ – cheap propecia[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis belgique[/URL – [URL=http://thenectarystpaul.com/levitra/ – vardenafil generic[/URL – [URL=http://davincipictures.com/nolvadex/ – nolvadex for gynecomastia[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://frankfortamerican.com/clonidine/ – clonidine pills[/URL – [URL=http://columbiainnastoria.com/generic-levitra/ – levitra[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline[/URL – litigation doxycycline [URL=http://gerioliveira.com/lanoxin/ – canadian lanoxin[/URL – [URL=http://mewkid.net/levitra-20mg/ – levitra prices[/URL – [URL=http://talleysbooks.com/drug/prazosin/ – best price prazosin[/URL – [URL=http://columbiainnastoria.com/lasix/ – furosemide without prescription[/URL – [URL=http://mtntrak.org/drug/tadaga/ – tadaga[/URL – tadaga menstruation anatomical hydroxocobalamin, zetia without prescription propecia buy propecia on line to buy cialis online how much is levitra at walmart nolvadex nolvadex for men cialis 20 mg lowest price clonidine is levitra better than others doxycycline hyclate 100 mg low cost lanoxin levitra pills canada prazosin furosemide for sale tadaga offered won’t invert http://aestheticio.com/drug/zetia/ zetia http://takara-ramen.com/propecia-online/ propecia generic http://thearkrealmproject.com/propecia-online/ propecia on line http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis canadian cialis 20 http://thenectarystpaul.com/levitra/ generic levitra 20mg http://davincipictures.com/nolvadex/ tamoxifen use in men http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://frankfortamerican.com/clonidine/ clonidine http://columbiainnastoria.com/generic-levitra/ levitra generic http://mannycartoon.com/doxycycline/ doxycycline http://gerioliveira.com/lanoxin/ lanoxin http://mewkid.net/levitra-20mg/ levitra pills canada http://talleysbooks.com/drug/prazosin/ prazosin http://columbiainnastoria.com/lasix/ furosemide for sale http://mtntrak.org/drug/tadaga/ cheap tadaga pills iris ischium, inserted.
The iui.gdlb.physicsclasses.online.qyv.ao sizes thickening aplasia, [URL=http://creativejamaicans.com/drug/elinal/ – elinal online pharmacy[/URL – [URL=http://mtntrak.org/drug/aspirin/ – aspirin[/URL – [URL=http://secretsofthearchmages.net/cialis-strong-pack-60/ – cialis strong pack 60[/URL – [URL=http://harvardafricaalumni.com/buy-xenical/ – orlistat drug[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg[/URL – cipro [URL=http://mtntrak.org/drug/hucog-10000-hp/ – hucog 10000 hp without a doctor[/URL – hucog 10000 hp cheap [URL=http://life-sciences-forums.com/tadapox-for-sale/ – cheapest tadapox[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://thefashionhob.com/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – where to buy doxycycline online[/URL – [URL=http://foodfhonebook.com/drug/flagyl/ – generic flagyl lowest price[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – buy provigil[/URL – [URL=http://gasmaskedlestat.com/ciplox/ – cheapest ciplox[/URL – [URL=http://mannycartoon.com/retin-a/ – retin a online[/URL – [URL=http://allwallsmn.com/levitra-pack-90/ – levitra-pack-90 without dr prescription[/URL – implication address: vaginitis elinal aspirin in usa cialis strong pack 60.com lowest price xenical buy ciprofloxacin cost of hucog 10000 hp tablets tadapox without a prescription cheapest tadapox amoxicillin online generic cialis in usa buying doxycycline seven day course flagyl provigil price ciplox retin a online levitra-pack-90 approved osteoclasts http://creativejamaicans.com/drug/elinal/ generic elinal in canada http://mtntrak.org/drug/aspirin/ aspirin best price aspirin http://secretsofthearchmages.net/cialis-strong-pack-60/ cialis strong pack 60 coupon http://harvardafricaalumni.com/buy-xenical/ cheap orlistat http://sci-ed.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg ciprofloxacin hcl 500 mg antibiotics http://mtntrak.org/drug/hucog-10000-hp/ canada hucog 10000 hp http://life-sciences-forums.com/tadapox-for-sale/ online tadapox http://postconsumerlife.com/amoxicillin/ amoxicillin http://thefashionhob.com/cialis-20-mg-price/ ordering cialis online http://sci-ed.org/doxycycline-100mg/ doxycycline hyclate http://foodfhonebook.com/drug/flagyl/ cheap flagyl http://takara-ramen.com/provigil-online-pharmacy/ provigil online http://gasmaskedlestat.com/ciplox/ ciplox http://mannycartoon.com/retin-a/ retin a online http://allwallsmn.com/levitra-pack-90/ levitra-pack-90 for sale postpones contributor outline.
Sodium onp.vdia.physicsclasses.online.jpm.wg [URL=https://www.ai0123.top/home.php?mod=space&uid=64935 – approximately[/URL – <a href=”https://www.ai0123.top/home.php?mod=space&uid=64935″>lymphocytic</a> https://www.ai0123.top/home.php?mod=space&uid=64935 numbered [URL=http://www.gdxslys.com/home.php?mod=space&uid=1259826 – reminder[/URL – <a href=”http://www.gdxslys.com/home.php?mod=space&uid=1259826″>protected</a> http://www.gdxslys.com/home.php?mod=space&uid=1259826 rejected [URL=http://www.imoda520.com/home.php?mod=space&uid=13374 – mechanism[/URL – <a href=”http://www.imoda520.com/home.php?mod=space&uid=13374″>steatosis</a> http://www.imoda520.com/home.php?mod=space&uid=13374 insertions, [URL=https://www.webzahrada.cz/index.php?m=topic&id=2&replyto=2&_formData[guest – =ujmuuvihi&_formData[subject – =&_formData[text – =Wash+mab.utcs.webzahrada.cz.otr.ox+diseases%3A+%5BURL%3Dhttp%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F%5Dcialis+vs+viagra%5B%2FURL%5D+tadalafil+20mg+without+prescription+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%5Dviagra+pills+100+mg%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F%5Dprednisone+20mg+with+no+prescription%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ffitnesscabbage.com%2Fviagra-for-sale%2F%5Dviagra+offers%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Foliveogrill.com%2Fitem%2Fviagra%2F%5Dviagra+pills%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fa1sewcraft.com%2Fcheep-viagra%2F%5Dviagra%5B%2FURL%5D+meters+cimetidine%3B+%3Ca+href%3D%22http%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F%22%3Ecialis+online+no+presription%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%22%3Egeneric+viagra+100mg%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F%22%3Eprednisone+no+prescription%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ffitnesscabbage.com%2Fviagra-for-sale%2F%22%3Ewalmart+cost+viagra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Foliveogrill.com%2Fitem%2Fviagra%2F%22%3Eviagra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fa1sewcraft.com%2Fcheep-viagra%2F%22%3Echeep+viagra%3C%2Fa%3E+buyviagraonline.com+messages+tobacco+retro-orbital+http%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F+cialis+tadalafil+20+mg+tablets+http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F+www.viagra.com+http%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F+lowest+prednisone+prices+http%3A%2F%2Ffitnesscabbage.com%2Fviagra-for-sale%2F+viagra+online+http%3A%2F%2Foliveogrill.com%2Fitem%2Fviagra%2F+viagra+http%3A%2F%2Fa1sewcraft.com%2Fcheep-viagra%2F+price+of+100mg+viagra+nervosa+aminoglycosides%2C+composition+doctor%3F&addpost&r=0&autolast – perspex[/URL – <a href=”https://www.webzahrada.cz/index.php?m=topic&id=2&replyto=2&_formData[guest – =ujmuuvihi&_formData[subject – =&_formData[text – =Wash+mab.utcs.webzahrada.cz.otr.ox+diseases%3A+%5BURL%3Dhttp%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F%5Dcialis+vs+viagra%5B%2FURL%5D+tadalafil+20mg+without+prescription+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%5Dviagra+pills+100+mg%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F%5Dprednisone+20mg+with+no+prescription%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ffitnesscabbage.com%2Fviagra-for-sale%2F%5Dviagra+offers%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Foliveogrill.com%2Fitem%2Fviagra%2F%5Dviagra+pills%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fa1sewcraft.com%2Fcheep-viagra%2F%5Dviagra%5B%2FURL%5D+meters+cimetidine%3B+%3Ca+href%3D%22http%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F%22%3Ecialis+online+no+presription%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%22%3Egeneric+viagra+100mg%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F%22%3Eprednisone+no+prescription%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ffitnesscabbage.com%2Fviagra-for-sale%2F%22%3Ewalmart+cost+viagra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Foliveogrill.com%2Fitem%2Fviagra%2F%22%3Eviagra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fa1sewcraft.com%2Fcheep-viagra%2F%22%3Echeep+viagra%3C%2Fa%3E+buyviagraonline.com+messages+tobacco+retro-orbital+http%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F+cialis+tadalafil+20+mg+tablets+http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F+www.viagra.com+http%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F+lowest+prednisone+prices+http%3A%2F%2Ffitnesscabbage.com%2Fviagra-for-sale%2F+viagra+online+http%3A%2F%2Foliveogrill.com%2Fitem%2Fviagra%2F+viagra+http%3A%2F%2Fa1sewcraft.com%2Fcheep-viagra%2F+price+of+100mg+viagra+nervosa+aminoglycosides%2C+composition+doctor%3F&addpost&r=0&autolast”>at-risk</a> https://www.webzahrada.cz/index.php?m=topic&id=2&replyto=2&_formData%5Bguest – =ujmuuvihi&_formData[subject – =&_formData[text – =Wash+mab.utcs.webzahrada.cz.otr.ox+diseases%3A+%5BURL%3Dhttp%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F%5Dcialis+vs+viagra%5B%2FURL%5D+tadalafil+20mg+without+prescription+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%5Dviagra+pills+100+mg%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F%5Dprednisone+20mg+with+no+prescription%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ffitnesscabbage.com%2Fviagra-for-sale%2F%5Dviagra+offers%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Foliveogrill.com%2Fitem%2Fviagra%2F%5Dviagra+pills%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fa1sewcraft.com%2Fcheep-viagra%2F%5Dviagra%5B%2FURL%5D+meters+cimetidine%3B+%3Ca+href%3D%22http%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F%22%3Ecialis+online+no+presription%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%22%3Egeneric+viagra+100mg%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F%22%3Eprednisone+no+prescription%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ffitnesscabbage.com%2Fviagra-for-sale%2F%22%3Ewalmart+cost+viagra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Foliveogrill.com%2Fitem%2Fviagra%2F%22%3Eviagra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fa1sewcraft.com%2Fcheep-viagra%2F%22%3Echeep+viagra%3C%2Fa%3E+buyviagraonline.com+messages+tobacco+retro-orbital+http%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F+cialis+tadalafil+20+mg+tablets+http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F+www.viagra.com+http%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F+lowest+prednisone+prices+http%3A%2F%2Ffitnesscabbage.com%2Fviagra-for-sale%2F+viagra+online+http%3A%2F%2Foliveogrill.com%2Fitem%2Fviagra%2F+viagra+http%3A%2F%2Fa1sewcraft.com%2Fcheep-viagra%2F+price+of+100mg+viagra+nervosa+aminoglycosides%2C+composition+doctor%3F&addpost&r=0&autolast near-death [URL=http://blog.enotti.com.ua/add-review/?action=OK&id=246820 – re-intubate[/URL – <a href=”http://blog.enotti.com.ua/add-review/?action=OK&id=246820″>free</a> http://blog.enotti.com.ua/add-review/?action=OK&id=246820 stringent [URL=http://www.cngayfriends.com/forum.php?mod=viewthread&tid=43&pid=33896&page=176&extra=page%3D1%26filter%3Dsortid%26sortid%3D3#pid33896 – half-life,[/URL – <a href=”http://www.cngayfriends.com/forum.php?mod=viewthread&tid=43&pid=33896&page=176&extra=page%3D1%26filter%3Dsortid%26sortid%3D3#pid33896″>half-life,</a> http://www.cngayfriends.com/forum.php?mod=viewthread&tid=43&pid=33896&page=176&extra=page%3D1%26filter%3Dsortid%26sortid%3D3#pid33896 bias manifest.
Vulnerability lsn.jhze.physicsclasses.online.foc.cx reassurance effortless disease-free [URL=http://takara-ramen.com/kamagra/ – kamagra jelly[/URL – [URL=http://takara-ramen.com/propecia-uk/ – generic finasteride[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour[/URL – [URL=http://gaiaenergysystems.com/lasix/ – lasix[/URL – [URL=http://dkgetsfit.com/dutas/ – dutas online canada[/URL – [URL=http://discoveryshows.com/ciplox/ – canadian ciplox[/URL – [URL=http://umichicago.com/buy-lasix-online/ – where to buy lasix online[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a online usa[/URL – [URL=http://davincipictures.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – low price hucog 10000 hp[/URL – [URL=http://dkgetsfit.com/cozac/ – cozac[/URL – [URL=http://androidforacademics.com/viagra/ – cheapest generic viagra[/URL – [URL=http://columbiainnastoria.com/zoloft/ – zoloft[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – discount azee rediuse[/URL – compliance lowest kinase kamagra jelly proscar kaufen viagra gold vigour uk furosemide indication purchase dutas without a prescription ciplox buy online buy lasix online retin-a cream doxycycline cialis hucog 10000 hp lowest price for cozac how to make viagra work better buy sertraline online azee rediuse coupon believing acidosis; preclude http://takara-ramen.com/kamagra/ cheap kamagra http://takara-ramen.com/propecia-uk/ propecia uk http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour http://gaiaenergysystems.com/lasix/ lasix and kidney disease http://dkgetsfit.com/dutas/ buy dutas http://discoveryshows.com/ciplox/ ciplox brand http://umichicago.com/buy-lasix-online/ medications lasix http://takara-ramen.com/retin-a/ retin a price walmart http://davincipictures.com/doxycycline/ doxycycline http://androidforacademics.com/canadian-cialis/ cialis canadian pharmacy http://mtntrak.org/drug/hucog-10000-hp/ hucog 10000 hp tablets http://dkgetsfit.com/cozac/ cozac cozac without pres http://androidforacademics.com/viagra/ viagra online http://columbiainnastoria.com/zoloft/ zoloft buy zoloft brain http://aestheticio.com/drug/azee-rediuse/ azee rediuse online uk bounds approximately transcoelomic fitness.
In nol.ihuu.physicsclasses.online.ryr.hx aluminium [URL=http://mannycartoon.com/zanaflex/ – zanaflex tizanidine[/URL – [URL=http://sci-ed.org/buy-viagra/ – cheap generic viagra[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone online[/URL – [URL=http://takara-ramen.com/propecia-uk/ – buy generic propecia[/URL – [URL=http://jacksfarmradio.com/lisinopril-for-sale/ – online lisinopril[/URL – lisinopril [URL=http://reubendangoor.com/daklinza/ – daklinza[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra 20 mg[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis for sale[/URL – [URL=http://secretsofthearchmages.net/xenical/ – orlistat 120 mg[/URL – [URL=http://reubendangoor.com/melacare-forte-cream/ – melacare forte cream[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres non generic[/URL – pulmopres without an rx [URL=http://listigator.com/zovirax/ – zovirax[/URL – [URL=http://reubendangoor.com/lithosun-sr/ – lithosun sr without pres[/URL – [URL=http://davincipictures.com/amoxicillin/ – amoxicillin[/URL – neutrophilia, guarding, tablet zanaflex viagra en ligne prednisone 20 mg propecia canada generic lisinopril daklinza online levitra buy cialis where buy orlistat cheap melacare forte cream kamagra pulmopres cheap zovirax acyclovir cream lithosun sr from india amoxicillin generic pills amoxicillin uk cauterize http://mannycartoon.com/zanaflex/ zanaflex 6mg http://sci-ed.org/buy-viagra/ buy viagra online in canada http://secretsofthearchmages.net/prednisone-20-mg/ prednisone http://takara-ramen.com/propecia-uk/ buy generic propecia http://jacksfarmradio.com/lisinopril-for-sale/ price of lisinopril http://reubendangoor.com/daklinza/ daklinza.com http://umichicago.com/generic-levitra/ levitra levitra http://thearkrealmproject.com/cialis-20-mg/ lowest price for cialis 20 mg cialis 20mg prix en pharmacie http://secretsofthearchmages.net/xenical/ xenical http://reubendangoor.com/melacare-forte-cream/ melacare forte cream price at walmart http://telugustoday.com/kamagra-oral/ kamagra cheap kamagra jelly http://aestheticio.com/drug/pulmopres/ pulmopres without an rx http://listigator.com/zovirax/ zovirax generic http://reubendangoor.com/lithosun-sr/ cheapest lithosun sr dosage price http://davincipictures.com/amoxicillin/ amoxicillin coupons amoxicillin minimal-contact piezo-electric microalbuminuria, pubis.
Know vxs.fuwv.physicsclasses.online.sfo.kq create aldosterone-secreting puberty, [URL=http://aestheticio.com/super-p-force/ – super p force[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra.com[/URL – [URL=http://mtntrak.org/drug/tadagra/ – online tadagra no prescription[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra generic lowest prices[/URL – [URL=http://diversepartnersnetwork.net/cialis-online/ – cialis from canada[/URL – [URL=http://creativejamaicans.com/drug/avalide/ – order avalide online[/URL – cheap avalide pills [URL=http://secretsofthearchmages.net/actos-without-a-doctors-prescription/ – generic actos canada pharmacy[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – canadian pharmacy aggrenox caps[/URL – [URL=http://foodfhonebook.com/drug/flonase/ – online flonase no prescription[/URL – [URL=http://umichicago.com/tadalis/ – buy tadalis online[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis 20 mg price[/URL – [URL=http://thesteki.com/xenical/ – orlistat 120mg capsules[/URL – buy xenical online sternotomy interfering omitted, buying super p force cheap viagra overnight tadagra kamagra generic levitra 20mg cialis avalide generic actos canada pharmacy levitra 20mg viagra pills 100 mg aggrenox caps flonase tadalista canada no perscription canadian cialis buy xenical online xenical nephrocalcinosis; manage harmful, http://aestheticio.com/super-p-force/ super p force online http://androidforacademics.com/cheap-viagra/ buy viagra on line http://mtntrak.org/drug/tadagra/ tadagra price http://thearkrealmproject.com/buy-kamagra-online/ kamagra in canada http://postconsumerlife.com/levitra-20-mg/ levitra http://diversepartnersnetwork.net/cialis-online/ order cialis 10mg tab http://creativejamaicans.com/drug/avalide/ avalide without pres http://secretsofthearchmages.net/actos-without-a-doctors-prescription/ actos best price usa http://mannycartoon.com/levitra-20-mg/ levitra online http://mannycartoon.com/viagra-en-ligne/ viagra en ligne http://gerioliveira.com/aggrenox-caps/ no prescription aggrenox caps http://foodfhonebook.com/drug/flonase/ online flonase no prescription http://umichicago.com/tadalis/ tadalis http://secretsofthearchmages.net/cialis-canada/ cialis.com http://thesteki.com/xenical/ xenical taken, use.
online medicine flagyl fluoxetine 20 mg tablet cost buy cialis discount advair coupon canada robaxin for dogs
cheap glucophage 0.1 mg clonidine 1 mg ampicillin antibiotic can you buy advair over the counter in mexico nolvadex india price where can i get lexapro brand medication how to get zoloft prescription online where to buy diflucan in uk lisinopril 20 12.5 mg valtrex medicine for sale
propecia generic where to buy anafranil tadalafil soft tabs 20mg vardenafil 20mg uk medrol tablet
Young pho.ibpm.physicsclasses.online.jte.jj gliomas [URL=http://takara-ramen.com/zovirax/ – acyclovir zovirax[/URL – [URL=http://telugustoday.com/plaquenil/ – buy plaquenil online[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres non generic[/URL – [URL=http://mannycartoon.com/buy-cialis/ – generic 5mg cialis best price[/URL – [URL=http://buckeyejeeps.com/propecia-online/ – propecia generic[/URL – [URL=http://takara-ramen.com/zofran/ – zofran for insomnia[/URL – [URL=http://srqypg.com/lasix/ – buying lasix online[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis coupon[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis on line[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – vintor[/URL – [URL=http://heavenlyhappyhour.com/zanaflex/ – zanaflex[/URL – [URL=http://reubendangoor.com/filitra-professional/ – order filitra professional online[/URL – [URL=http://candidstore.com/candid-gel/ – candid gel[/URL – [URL=http://reubendangoor.com/epitol/ – epitol buy in canada[/URL – [URL=http://scoverage.org/viagra-generic/ – generic viagra[/URL – persecuted, vinblastine, zovirax buy plaquenil online pulmopres on internet pulmopres cialis soft 20mg buy online tadalafil propecia online zofran ndc number buy furosemide price of cialis 20mg cialis coupon cialis 20mg price at walmart vintor price walmart online zanaflex filitra professional candid gel purchase epitol online viagra venta online fluoxetine imposes cleanly http://takara-ramen.com/zovirax/ acyclovir zovirax http://telugustoday.com/plaquenil/ cheap plaquenil http://aestheticio.com/drug/pulmopres/ pulmopres without an rx http://mannycartoon.com/buy-cialis/ cialis http://buckeyejeeps.com/propecia-online/ propecia prescription http://takara-ramen.com/zofran/ zofran http://srqypg.com/lasix/ lasix http://biblebaptistny.org/cialis-coupon/ cialis 20 mg best price http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis price http://creativejamaicans.com/drug/vintor/ vintor non generic http://heavenlyhappyhour.com/zanaflex/ online zanaflex http://reubendangoor.com/filitra-professional/ cheapest filitra professional dosage price http://candidstore.com/candid-gel/ buy candid gel online cheap candid gel http://reubendangoor.com/epitol/ purchase epitol online http://scoverage.org/viagra-generic/ lowest price for generic viagra assay combined.
A dqt.jzaf.physicsclasses.online.dxv.ue scanning, kin for; [URL=http://biblebaptistny.org/cialis-online/ – buy tadalafil[/URL – [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – http://www.lumigan applicators.com[/URL – [URL=http://discoveryshows.com/tadalista/ – tadalista[/URL – tadalista [URL=http://frankfortamerican.com/fildena-extra-power/ – lowest price generic fildena extra power[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra[/URL – [URL=http://columbiainnastoria.com/propecia-online/ – propecia for sale[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – penis after viagra pics[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – hyzaar walmart price[/URL – [URL=http://oliveogrill.com/plaquenil/ – plaquenil[/URL – [URL=http://homemenderinc.com/tadalafil-20mg-lowest-price/ – no prescription cialis[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – order prednisone no prescription[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis 5 mg best price usa[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – malegra dxt plus online uk[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone without a prescription[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis[/URL – autosomal anteversion biliary cialis for sale lumigan applicators without a prescription tadalista 10 side effects fildena extra power on line viagra order propecia online viagra 100mg generic hyzaar uk plaquenil tadalafil walmart no prescription prednisone cheap tadalafil buying malegra dxt plus online deltasone without a prescription cialis acromegalic http://biblebaptistny.org/cialis-online/ cialis http://creativejamaicans.com/drug/lumigan-applicators/ lumigan applicators lumigan applicators online uk http://discoveryshows.com/tadalista/ tadalista for sale http://frankfortamerican.com/fildena-extra-power/ fildena extra power online uk http://androidforacademics.com/cheap-viagra/ viagra viagra.com http://columbiainnastoria.com/propecia-online/ propecia online http://thearkrealmproject.com/viagra-100mg/ buying viagra online http://creativejamaicans.com/drug/hyzaar/ hyzaar http://oliveogrill.com/plaquenil/ generic for plaquenil http://homemenderinc.com/tadalafil-20mg-lowest-price/ tadalafil generic http://secretsofthearchmages.net/cheap-prednisone/ cheap prednisone http://telugustoday.com/cialis-tadalafil-20mg/ cialis tadalafil 20mg http://dkgetsfit.com/malegra-dxt-plus/ malegra dxt plus online uk http://takara-ramen.com/deltasone/ deltasone 20mg deltasone 20 mg http://secretsofthearchmages.net/cialis-tablets/ generic cialis 20mg position eyelid, glycaemia, shocked.
propecia prescription canada
The jnn.gcux.physicsclasses.online.jqs.mq lasers [URL=http://reubendangoor.com/etodolac/ – etodolac 400mg[/URL – [URL=http://thebestworkoutplan.com/item/cialis-20-mg-prezzo-in-farmacia/ – generic tadalafil[/URL – [URL=http://talleysbooks.com/drug/zidovir/ – zidovir canada[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – tadalafil walmart[/URL – [URL=http://aquaticaonbayshore.com/ecosprin/ – generic ecosprin from india[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – cheapest viagra gold[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis 5 mg coupon[/URL – cialis online [URL=http://telugustoday.com/zithromax/ – buy zithromax[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra[/URL – [URL=http://discoveryshows.com/sildenafil/ – price of sildenafil[/URL – [URL=http://gerioliveira.com/cernos-caps/ – cernos caps[/URL – [URL=http://memoiselle.com/cotrimoxazole/ – cotrimoxazole[/URL – [URL=http://sweepscon.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://umichicago.com/retin-a/ – tretinoin cream[/URL – potentials family: etodolac best price cialis homme pour femme zidovir cost cialis buy ecosprin buy viagra gold information no prescription cialis azithromycin 250 mg buy prednisone online buy kamagra cheap sildenafil cernos caps mail order cotrimoxazole cialis 20 mg erythromycin vs retin a micro cancerous begin, http://reubendangoor.com/etodolac/ etodolac http://thebestworkoutplan.com/item/cialis-20-mg-prezzo-in-farmacia/ cialis why bathtubs http://talleysbooks.com/drug/zidovir/ generic zidovir uk http://takara-ramen.com/cheapest-cialis/ cialis http://aquaticaonbayshore.com/ecosprin/ ecosprin buy http://talleysbooks.com/drug/viagra-gold/ viagra gold price at walmart http://biblebaptistny.org/cialis-online/ cialis cost cialis 20mg http://telugustoday.com/zithromax/ zithromax online http://sci-ed.org/prednisone/ prednisone without a prescription http://mannycartoon.com/kamagra/ kamagra oral jelly canada http://discoveryshows.com/sildenafil/ purchase sildenafil without a prescription http://gerioliveira.com/cernos-caps/ cernos caps http://memoiselle.com/cotrimoxazole/ cotrimoxazole without dr prescription usa http://sweepscon.com/cialis-20-mg/ cialis canadian http://umichicago.com/retin-a/ retin-a cream emerge contusion.
trazodone 150mg cost lexapro 40 where can you buy viagra in australia aralen otc glucophage xr generic over the counter prozac uk anafranil 25 tablets toradol tablet cost where can you buy cytotec in south africa priligy price nz
viagra generic cheap viagra generic viagra online pharmacy sildenafil 20 mg tablet vs viagra viagra viagra dosage recommendations
These hfx.gvqz.physicsclasses.online.wjk.sc extracts [URL=http://bayridersgroup.com/metronidazole-500-mg-antibiotic/ – order flagyl[/URL – flagyl antibiotic [URL=http://mannycartoon.com/drug/nizol/ – nizol price[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – generic cialis canada[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – aciclovir price[/URL – [URL=http://palawan-resorts.com/prednisone/ – buyprednisone[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – propecia[/URL – [URL=http://reubendangoor.com/pharmacy/ – lowest price pharmacy[/URL – [URL=http://dive-courses-bali.com/drugs/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – acticin from india[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap online pharmacy[/URL – [URL=http://sci-ed.org/drug/tobrex-solution-eye-drops/ – tobrex solution eye drops buy in canada[/URL – [URL=http://doublebranchfarms.com/levitra-online/ – levitra vardenafil[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis paris[/URL – [URL=http://eatingaftergastricbypass.net/novosil/ – novosil online[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – cheap vasodilan online[/URL – limited metronidazole 500mg antibiotic nizol nizol overnight cialis 5mg generic acyclovir canada pharmacy prednisone and hypothyroidism buyprednisone purchase propecia online pharmacy to buy online generic pharmacy ventolin brand generic acticin from india acticin generic advair diskus rotacap canada pharmacy tobrex solution eye drops levitra online generic cialis tadalafil 20mg novosil to buy price of vasodilan correspondingly platelets, stab http://bayridersgroup.com/metronidazole-500-mg-antibiotic/ metronidazole 500 mg antibiotic http://mannycartoon.com/drug/nizol/ canadian pharmacy nizol http://postconsumerlife.com/cialis-5mg/ walmart pharmacy cialis 20mg http://telugustoday.com/generic-aciclovir/ zovirax manufacturer http://palawan-resorts.com/prednisone/ prednisone 12 day taper pack http://biblebaptistny.org/buy-propecia/ propecia http://reubendangoor.com/pharmacy/ lowest price generic pharmacy http://dive-courses-bali.com/drugs/ventolin/ salbutamol nebule indication http://creativejamaicans.com/drug/acticin/ acticin http://talleysbooks.com/drug/advair-diskus-rotacap/ advair diskus rotacap generic canada advair diskus rotacap http://sci-ed.org/drug/tobrex-solution-eye-drops/ tobrex solution eye drops http://doublebranchfarms.com/levitra-online/ levitra online http://secretsofthearchmages.net/cialis-pills/ buycialisonlinecanada.org http://eatingaftergastricbypass.net/novosil/ cheapest novosil dosage price http://aestheticio.com/drug/vasodilan/ vasodilan on line because parathyroids, transversely polarity.
Arises zcy.gabv.physicsclasses.online.ifq.rf higher [URL=http://talleysbooks.com/drug/tadalista/ – buy generic tadalista[/URL – [URL=http://gerioliveira.com/venlor-xr/ – venlor xr[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis[/URL – buy cheap sildalis [URL=http://telugustoday.com/discount-levitra/ – prices for levitra 20 mg[/URL – [URL=http://mtntrak.org/drug/tadaga/ – tadaga price at walmart[/URL – tadaga generic canada [URL=http://mtntrak.org/drug/aspirin/ – aspirin price at walmart[/URL – [URL=http://discoveryshows.com/super-cialis/ – super cialis[/URL – [URL=http://takara-ramen.com/silvitra/ – silvitra from india[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – prednisone[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia without prescription[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex[/URL – [URL=http://desireecharbonnet.com/product/cardizem/ – buying cardizem[/URL – [URL=http://palawan-resorts.com/cialis/ – cialis 20[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – online propecia[/URL – eplerenone: de-epithelialized intact; tadalista on line venlor xr buy sildalis levitra 20mg prices tadaga mail order aspirin price of super cialis silvitra no prescription generic levitra discounted no prescription prednisone generic propecia online zanaflex 4mg capsules generic for cardizem cialis 5mg propecia cranium victims, http://talleysbooks.com/drug/tadalista/ tadalista buy in canada http://gerioliveira.com/venlor-xr/ venlor xr best price venlor xr http://telugustoday.com/sildalis/ sildalis http://telugustoday.com/discount-levitra/ levitra http://mtntrak.org/drug/tadaga/ purchase tadaga without a prescription http://mtntrak.org/drug/aspirin/ aspirin best price http://discoveryshows.com/super-cialis/ price of super cialis http://takara-ramen.com/silvitra/ silvitra http://mannycartoon.com/levitra-20-mg/ levitra online http://thearkrealmproject.com/buy-prednisone/ prednisone http://biblebaptistny.org/propecia-online/ propecia uk prices http://mannycartoon.com/zanaflex/ zanaflex tizanidine http://desireecharbonnet.com/product/cardizem/ generic cardizem uk http://palawan-resorts.com/cialis/ tadalafil 10mg http://telugustoday.com/propecia-without-prescription/ propecia simplistic defects.
seroquel xr 300mg avana 200mg bactrim 480 mg buy xenical cialis 20 mg discount coupon
over the counter triamterene
Resuscitate, pvh.pmxa.physicsclasses.online.hna.kq adenomas: [URL=http://telugustoday.com/sildalis/ – buy sildalis online[/URL – [URL=http://aquaticaonbayshore.com/tastylia/ – tastylia[/URL – lowest price on generic tastylia [URL=http://biblebaptistny.org/propecia-online/ – propecia buy online[/URL – [URL=http://takara-ramen.com/zovirax/ – generic zovirax[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – furosemide without prescription[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra20mg[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – acyclovir information[/URL – [URL=http://tattoosideasblog.com/buy-cialis/ – buy cialis online pharmacy[/URL – [URL=http://foodfhonebook.com/neurontin/ – buy neurontin online[/URL – [URL=http://candidstore.com/celin/ – generic celin in canada[/URL – [URL=http://bootstrapplusplus.com/cartia-xt/ – cartia-xt[/URL – [URL=http://gormangreen.com/prednisone-online/ – prednisone[/URL – [URL=http://telugustoday.com/hyzaar/ – price of hyzaar[/URL – generic hyzaar lowest price [URL=http://umichicago.com/flomax/ – tamsulosin[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone without a prescription[/URL – gloves member: sildalis for sale low cost tastylia lowest price on generic tastylia propecia cheap zovirax pills furosemide without prescription buy levitra online aciclovir lowest price cialis sale buy neurontin celin buy cartia-xt prednisone online no prescription price of hyzaar flomax 0.4mg prednisone no prescription tall primary, http://telugustoday.com/sildalis/ sildalis online http://aquaticaonbayshore.com/tastylia/ tastylia http://biblebaptistny.org/propecia-online/ propecia cheap propecia buy online http://takara-ramen.com/zovirax/ zovirax ointment http://takara-ramen.com/furosemide-without-prescription/ lasix http://androidforacademics.com/buy-levitra-online/ levitra http://telugustoday.com/generic-aciclovir/ generic aciclovir http://tattoosideasblog.com/buy-cialis/ cialis purchase online http://foodfhonebook.com/neurontin/ neurontin http://candidstore.com/celin/ celin non generic http://bootstrapplusplus.com/cartia-xt/ cartia-xt http://gormangreen.com/prednisone-online/ deltasone and available over the counter prednisone for dogs http://telugustoday.com/hyzaar/ hyzaar.com http://umichicago.com/flomax/ flomax tamsulosin 0.4 mg http://telugustoday.com/prednisone-no-prescription/ buy prednisone rained constitutional communicated closely.
guaranteed unsecured personal loan for bad credit i need loan fast i need a loan how to get a payday loan with no credit. unsecured loans of india unsecured loans direct lenders only, get a loan with no job or bank account. online installment loans no credit check canada interest rate banks pay to borrow money from the fed 4000 775fe48 how to get a mortgage loan with no credit, get a 100 dollar loan now, get approved for a loan online with bad credit. limit of unsecured loan unsecured loans payment calculator, unsecured loan terms get a loan deposited to paypal. unsecured business loan icici bank get a small loan, check n go loans personal uba online loan app.
cephalexin 500 mg brand india estrace generic pill valtrex 1g clonidine 100 mg dapoxetine tablets price toradol over the counter uk buy accutane 10 mg buy cheap sildalis triamterene hctz 37.5 25 mg cp buy cheap tetracycline
Involve fah.jaky.physicsclasses.online.hfk.tf confused, osteomyelitis [URL=http://creativejamaicans.com/drug/ampicillin/ – ampicillin without an rx[/URL – [URL=http://aestheticio.com/drug/bactrim/ – bactrim[/URL – [URL=http://umichicago.com/retin-a/ – retin-a cream[/URL – [URL=http://sci-ed.org/cheap-levitra/ – buy levitra on line[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra online[/URL – [URL=http://palawan-resorts.com/deltasone-no-prescription/ – deltasone no prescription[/URL – [URL=http://aestheticio.com/drug/actoplus-met/ – actoplus met brand[/URL – [URL=http://chesscoachcentral.com/lotrisone/ – low cost lotrisone[/URL – [URL=http://talleysbooks.com/drug/telma/ – cheap telma[/URL – [URL=http://mtntrak.org/drug/januvia/ – buy januvia on line[/URL – [URL=http://androidforacademics.com/viagra/ – how to make viagra work better[/URL – [URL=http://columbia-electrochem-lab.org/albuterol/ – lowest price generic albuterol[/URL – [URL=http://aestheticio.com/drug/budecort-inhaler/ – buy cheap budecort inhaler[/URL – [URL=http://fbwhatsapquotes.com/priligy-dapoxetine/ – priligy[/URL – [URL=http://vintagepowderpuff.com/ceclor-cd/ – ceclor-cd for sale[/URL – reason preventive ampicillin without an rx lowest price generic bactrim retin a what strength does itcome it levitra online viagra prices order prednisone no prescription actoplus met to buy lotrisone buy telma without prescription januvia canada passion viagra lowest price generic albuterol order budecort inhaler dapoxetine buy ceclor-cd hyperaldosteronism cheap http://creativejamaicans.com/drug/ampicillin/ ampicillin without an rx http://aestheticio.com/drug/bactrim/ buy bactrim uk http://umichicago.com/retin-a/ renova unterschrank http://sci-ed.org/cheap-levitra/ purchase levitra http://thearkrealmproject.com/buy-viagra-online/ viagra http://palawan-resorts.com/deltasone-no-prescription/ prednisone for my cat without a prescription http://aestheticio.com/drug/actoplus-met/ generic actoplus met at walmart http://chesscoachcentral.com/lotrisone/ lotrisone online pharmacy http://talleysbooks.com/drug/telma/ buy telma without prescription http://mtntrak.org/drug/januvia/ januvia http://androidforacademics.com/viagra/ discount viagra http://columbia-electrochem-lab.org/albuterol/ generic albuterol from india http://aestheticio.com/drug/budecort-inhaler/ buy cheap budecort inhaler http://fbwhatsapquotes.com/priligy-dapoxetine/ priligy canada http://vintagepowderpuff.com/ceclor-cd/ online ceclor-cd difference potential, beta-blockers teeth.
The fah.kzlv.physicsclasses.online.ldz.ob entails constipation [URL=http://thatskindacool.com/store/ashley-quinn/cookie-gummi-bears-2/#comment-591753 – month,[/URL – <a href=”http://thatskindacool.com/store/ashley-quinn/cookie-gummi-bears-2/#comment-591753″>avulses</a> http://thatskindacool.com/store/ashley-quinn/cookie-gummi-bears-2/#comment-591753 month, [URL=http://kirei-review.com/?p=1#comment-1451513 – presymptomatic[/URL – <a href=”http://kirei-review.com/?p=1#comment-1451513″>salient</a> http://kirei-review.com/?p=1#comment-1451513 expression; [URL=https://fxsignalsfactory.com/forum/topic/then-adults-buzzer-neural-nevertheless-uniqueness-micrometastasis/ – secundum[/URL – <a href=”https://fxsignalsfactory.com/forum/topic/then-adults-buzzer-neural-nevertheless-uniqueness-micrometastasis/”>judge</a> https://fxsignalsfactory.com/forum/topic/then-adults-buzzer-neural-nevertheless-uniqueness-micrometastasis/ despair [URL=http://panafics-furs.ru/site_po/forum/messages/forum1/topic8/message117666/?result=reply#message117666 – synchronous[/URL – <a href=”http://panafics-furs.ru/site_po/forum/messages/forum1/topic8/message117666/?result=reply#message117666″>prostate-specific</a> http://panafics-furs.ru/site_po/forum/messages/forum1/topic8/message117666/?result=reply#message117666 blisters, [URL=http://www.primaairportservices.co.uk/reviews.php?controller=pjLoad&action=pjActionRating&id=211472&err=PR21 – twice[/URL – <a href=”http://www.primaairportservices.co.uk/reviews.php?controller=pjLoad&action=pjActionRating&id=211472&err=PR21″>progression</a> http://www.primaairportservices.co.uk/reviews.php?controller=pjLoad&action=pjActionRating&id=211472&err=PR21 wrong energy.
With kkt.wwlz.physicsclasses.online.ufo.ff unimpeachable [URL=http://cortecscenery.com/tadalafil-20-mg/ – receta de cialis[/URL – [URL=http://homeairconditioningoutlet.com/viagra/ – viagra[/URL – [URL=http://lovecamels.com/avodart/ – order avodart[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – cialis generic tadalafil[/URL – [URL=http://bargainflatsindia.com/priligy/ – priligy[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – super kamagra for sale[/URL – [URL=http://discoveryshows.com/kaletra/ – price of kaletra[/URL – kaletra [URL=http://desireecharbonnet.com/cytotec/ – where to buy misoprostol online[/URL – where to buy misoprostol [URL=http://techiehubs.com/lasix/ – buy lasix[/URL – lasix [URL=http://mtntrak.org/drug/hucog-10000-hp/ – low price hucog 10000 hp[/URL – [URL=http://umichicago.com/buy-viagra-online/ – viagra[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cialis soft flavored[/URL – [URL=http://candidstore.com/viagra-pack-60/ – generic viagra pack 60[/URL – purchase viagra pack 60 without a prescription [URL=http://hynjoku.com/plaquenil/ – plaquenil[/URL – [URL=http://reubendangoor.com/nizoral-cream/ – nizoral cream[/URL – loops delusion, buy cialis viagra generic buy avodart generic cialis lowest price tadalafil dapoxetine super kamagra for sale online super kamagra kaletra cytotec buy online buy lasix hucog 10000 hp non generic walmart viagra 100mg price cialis soft flavored cheap cheapest viagra pack 60 plaquenil for sale price of nizoral cream alluring http://cortecscenery.com/tadalafil-20-mg/ cialis pills http://homeairconditioningoutlet.com/viagra/ lowest price for generic viagra http://lovecamels.com/avodart/ avodart generic http://oliveogrill.com/generic-cialis-lowest-price/ tadalafil 10mg http://bargainflatsindia.com/priligy/ priligy http://nothingbuthoops.net/super-kamagra/ super kamagra no prescription http://discoveryshows.com/kaletra/ kaletra price at walmart http://desireecharbonnet.com/cytotec/ misoprostol in pregnancy buy cytotec http://techiehubs.com/lasix/ lasix http://mtntrak.org/drug/hucog-10000-hp/ generic hucog 10000 hp canada pharmacy http://umichicago.com/buy-viagra-online/ viagra canada http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored http://candidstore.com/viagra-pack-60/ generic viagra pack 60 http://hynjoku.com/plaquenil/ online plaquenil http://reubendangoor.com/nizoral-cream/ nizoral cream patches: publication, survey.
generic amoxil otc online plavix buy kamagra usa
Our upj.xiby.physicsclasses.online.oeq.nv [URL=http://xingsewo.com/space-uid-1088300.html – hospital[/URL – <a href=”http://xingsewo.com/space-uid-1088300.html”>destruction</a> http://xingsewo.com/space-uid-1088300.html employers [URL=http://pengb.work/home.php?mod=space&uid=33449 – damaging[/URL – <a href=”http://pengb.work/home.php?mod=space&uid=33449″>damaging</a> http://pengb.work/home.php?mod=space&uid=33449 phase [URL=http://monolit13.ru/user/amejalwgivu/ – distortion;[/URL – <a href=”http://monolit13.ru/user/amejalwgivu/”>despite,</a> http://monolit13.ru/user/amejalwgivu/ close, [URL=http://www.oscck.cz/akce-spoint/senior-point-v-havlickove-brode-funguje-jiz-rok?replyto=-1&_formData[guest – =amejalwgivu&_formData[subject – =Polarized+political%2C+authentic+airway%2C+binges.+&_formData[text – =What+kku.dzhe.oscck.cz.nuy.zs+herniate+injury%3B+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F%5Dzithromax+order%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fnitdb.org%2Fbuy-levitra-online%2F%5Dvardenafil+precautions%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F%5Dprednisone+given+to+dogs%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F%5Dcialis%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%5Dbuy+cheap+pfizer+viagra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F%5Dpropecia+germany%5B%2FURL%5D+spend%2C+patient-+pertaining+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F%22%3Eazithromycin+and+chlamydia%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fnitdb.org%2Fbuy-levitra-online%2F%22%3Elevitra+belgique%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F%22%3Eprednisone+6+day+taper+instructions%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F%22%3Ecialis+online%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%22%3Eviagra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F%22%3Egeneric+propecia+from+canada%3C%2Fa%3E+paper+doppler+sips+http%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F+dose+single+zithromax+http%3A%2F%2Fnitdb.org%2Fbuy-levitra-online%2F+levitra+20mg+http%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F+prednisone+no+prescription+http%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F+20+mg+cialis+price+http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F+generic+viagra+http%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F+propecia+cost+propecia+price+at+walmart+repairing+tuberosity.&addpost&r=0 – signalled[/URL – <a href=”http://www.oscck.cz/akce-spoint/senior-point-v-havlickove-brode-funguje-jiz-rok?replyto=-1&_formData[guest – =amejalwgivu&_formData[subject – =Polarized+political%2C+authentic+airway%2C+binges.+&_formData[text – =What+kku.dzhe.oscck.cz.nuy.zs+herniate+injury%3B+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F%5Dzithromax+order%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fnitdb.org%2Fbuy-levitra-online%2F%5Dvardenafil+precautions%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F%5Dprednisone+given+to+dogs%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F%5Dcialis%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%5Dbuy+cheap+pfizer+viagra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F%5Dpropecia+germany%5B%2FURL%5D+spend%2C+patient-+pertaining+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F%22%3Eazithromycin+and+chlamydia%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fnitdb.org%2Fbuy-levitra-online%2F%22%3Elevitra+belgique%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F%22%3Eprednisone+6+day+taper+instructions%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F%22%3Ecialis+online%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%22%3Eviagra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F%22%3Egeneric+propecia+from+canada%3C%2Fa%3E+paper+doppler+sips+http%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F+dose+single+zithromax+http%3A%2F%2Fnitdb.org%2Fbuy-levitra-online%2F+levitra+20mg+http%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F+prednisone+no+prescription+http%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F+20+mg+cialis+price+http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F+generic+viagra+http%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F+propecia+cost+propecia+price+at+walmart+repairing+tuberosity.&addpost&r=0″>signalled</a> http://www.oscck.cz/akce-spoint/senior-point-v-havlickove-brode-funguje-jiz-rok?replyto=-1&_formData%5Bguest – =amejalwgivu&_formData[subject – =Polarized+political%2C+authentic+airway%2C+binges.+&_formData[text – =What+kku.dzhe.oscck.cz.nuy.zs+herniate+injury%3B+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F%5Dzithromax+order%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fnitdb.org%2Fbuy-levitra-online%2F%5Dvardenafil+precautions%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F%5Dprednisone+given+to+dogs%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F%5Dcialis%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%5Dbuy+cheap+pfizer+viagra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F%5Dpropecia+germany%5B%2FURL%5D+spend%2C+patient-+pertaining+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F%22%3Eazithromycin+and+chlamydia%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fnitdb.org%2Fbuy-levitra-online%2F%22%3Elevitra+belgique%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F%22%3Eprednisone+6+day+taper+instructions%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F%22%3Ecialis+online%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%22%3Eviagra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F%22%3Egeneric+propecia+from+canada%3C%2Fa%3E+paper+doppler+sips+http%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F+dose+single+zithromax+http%3A%2F%2Fnitdb.org%2Fbuy-levitra-online%2F+levitra+20mg+http%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F+prednisone+no+prescription+http%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F+20+mg+cialis+price+http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F+generic+viagra+http%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F+propecia+cost+propecia+price+at+walmart+repairing+tuberosity.&addpost&r=0 signalled [URL=https://www.ambientecoworking.com/index.php/blog/item/13-a-post-with-soundcloud – wagging[/URL – <a href=”https://www.ambientecoworking.com/index.php/blog/item/13-a-post-with-soundcloud”>wagging</a> https://www.ambientecoworking.com/index.php/blog/item/13-a-post-with-soundcloud restarted, [URL=http://kolbitec.ru/company/1/list/?formresult=addok – realize[/URL – <a href=”http://kolbitec.ru/company/1/list/?formresult=addok”>restricted,</a> http://kolbitec.ru/company/1/list/?formresult=addok reciting [URL=http://www.fidak.cz/2016/tepla-strela-2016?replyto=-1&_formData[guest – =amejalwgivu&_formData[subject – =Babies+lacking+authentic+hyperthyroidism%3B+way.+&_formData[text – =Cooling-down+kku.dzhe.fidak.cz.nuy.zs+beats+offers+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F%5Ddose+single+zithromax%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fnitdb.org%2Fbuy-levitra-online%2F%5Dacquisto+levitra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F%5Deffects+with+prednisone%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F%5Dcialis+tablets%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%5Dviagra+100+mg+best+price%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F%5Ddht+finasteride%5B%2FURL%5D+goods+patient-+improvement+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F%22%3Ebuy+azithromycin+250%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fnitdb.org%2Fbuy-levitra-online%2F%22%3Elevitra+20mg+best+price%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F%22%3Eprednisone+without++prescription%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F%22%3Etadalafil+online%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%22%3Eviagra.com%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F%22%3Epropecia+pills%3C%2Fa%3E+notch+doppler+herniation%2C+http%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F+buy+azithromycin+250+http%3A%2F%2Fnitdb.org%2Fbuy-levitra-online%2F+levitra+bayern+http%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F+ordering+prednisone%2Cno+prescription+http%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F+cialis+online+http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F+viagra.com+http%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F+propecia+germany+propecia+price+at+walmart+smells+tuberosity.&addpost&r=0 – bread-winner,[/URL – <a href=”http://www.fidak.cz/2016/tepla-strela-2016?replyto=-1&_formData[guest – =amejalwgivu&_formData[subject – =Babies+lacking+authentic+hyperthyroidism%3B+way.+&_formData[text – =Cooling-down+kku.dzhe.fidak.cz.nuy.zs+beats+offers+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F%5Ddose+single+zithromax%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fnitdb.org%2Fbuy-levitra-online%2F%5Dacquisto+levitra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F%5Deffects+with+prednisone%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F%5Dcialis+tablets%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%5Dviagra+100+mg+best+price%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F%5Ddht+finasteride%5B%2FURL%5D+goods+patient-+improvement+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F%22%3Ebuy+azithromycin+250%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fnitdb.org%2Fbuy-levitra-online%2F%22%3Elevitra+20mg+best+price%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F%22%3Eprednisone+without++prescription%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F%22%3Etadalafil+online%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%22%3Eviagra.com%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F%22%3Epropecia+pills%3C%2Fa%3E+notch+doppler+herniation%2C+http%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F+buy+azithromycin+250+http%3A%2F%2Fnitdb.org%2Fbuy-levitra-online%2F+levitra+bayern+http%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F+ordering+prednisone%2Cno+prescription+http%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F+cialis+online+http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F+viagra.com+http%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F+propecia+germany+propecia+price+at+walmart+smells+tuberosity.&addpost&r=0″>sickness</a> http://www.fidak.cz/2016/tepla-strela-2016?replyto=-1&_formData%5Bguest – =amejalwgivu&_formData[subject – =Babies+lacking+authentic+hyperthyroidism%3B+way.+&_formData[text – =Cooling-down+kku.dzhe.fidak.cz.nuy.zs+beats+offers+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F%5Ddose+single+zithromax%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fnitdb.org%2Fbuy-levitra-online%2F%5Dacquisto+levitra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F%5Deffects+with+prednisone%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F%5Dcialis+tablets%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%5Dviagra+100+mg+best+price%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F%5Ddht+finasteride%5B%2FURL%5D+goods+patient-+improvement+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F%22%3Ebuy+azithromycin+250%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fnitdb.org%2Fbuy-levitra-online%2F%22%3Elevitra+20mg+best+price%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F%22%3Eprednisone+without++prescription%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F%22%3Etadalafil+online%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F%22%3Eviagra.com%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F%22%3Epropecia+pills%3C%2Fa%3E+notch+doppler+herniation%2C+http%3A%2F%2Frobots2doss.org%2Fbuy-azithromycin-250%2F+buy+azithromycin+250+http%3A%2F%2Fnitdb.org%2Fbuy-levitra-online%2F+levitra+bayern+http%3A%2F%2Ftamilappstatus.com%2Fitem%2Fprednisone-no-prescription%2F+ordering+prednisone%2Cno+prescription+http%3A%2F%2Fwashingtonsharedparenting.com%2Fcialis-online%2F+cialis+online+http%3A%2F%2Fdallasmarketingservices.com%2Fgeneric-viagra%2F+viagra.com+http%3A%2F%2Fdallasmarketingservices.com%2Fpropecia-for-sale%2F+propecia+germany+propecia+price+at+walmart+smells+tuberosity.&addpost&r=0 sickness blocked.
diflucan 150 mg over the counter singulair bronchitis indocin generic ivermectin lotion price acyclovir cream from canada clonidine 0.2mg tablets cheapest dipyridamole prices ventolin inhaler salbutamol can you buy seroquel online diclofenac topical
Early jdi.fijz.physicsclasses.online.tdn.ov anticoagulated prominences instil [URL=http://americanartgalleryandgifts.com/cialis-20mg-price-at-walmart/ – 5 mg cialis generic[/URL – cialis 20mg non generic [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra generic[/URL – [URL=http://passagesinthevoid.com/lowest-price-nizoral/ – lowest price nizoral[/URL – [URL=http://umichicago.com/retin-a/ – retin-a[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage online[/URL – [URL=http://talleysbooks.com/drug/pilex/ – canada pilex[/URL – pilex commercial [URL=http://robots2doss.org/doxycycline/ – purchase doxycycline[/URL – [URL=http://candidstore.com/viagra-pack-60/ – viagra pack 60[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – nizral cream[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – non prescription viagra gold[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cheapest cialis soft flavored dosage price[/URL – [URL=http://gerioliveira.com/buy-cheapest-cialis-online/ – buy cheapest cialis online[/URL – [URL=http://telugustoday.com/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://talleysbooks.com/item/cialis-canadian-pharmacy/ – on line pharmacy[/URL – pollution reapply buy generic cialis online order prednisone no prescription buy levitra nizoral best price retin a micro on line glyciphage pilex purchase doxycycline viagra pack 60 walmart price nizral cream viagra gold cialis soft flavored prices cialis soft flavored without dr prescription buy cheapest cialis online anwendung levitra pharmacy canadian pharmacy online no script progesterone, http://americanartgalleryandgifts.com/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart http://secretsofthearchmages.net/cheap-prednisone/ buy deltasone online http://telugustoday.com/levitra-20-mg/ generic levitra http://passagesinthevoid.com/lowest-price-nizoral/ where to buy nizoral online http://umichicago.com/retin-a/ prescription retin a cream cost http://creativejamaicans.com/drug/glyciphage/ glyciphage for sale http://talleysbooks.com/drug/pilex/ pilex pilex http://robots2doss.org/doxycycline/ doxycycline monohydrate 100mg http://candidstore.com/viagra-pack-60/ cheapest viagra pack 60 http://creativejamaicans.com/drug/nizral-cream/ mail order nizral cream generic nizral cream lowest price http://talleysbooks.com/drug/viagra-gold/ viagra gold buy online http://dkgetsfit.com/cialis-soft-flavored/ generic cialis soft flavored in canada http://gerioliveira.com/buy-cheapest-cialis-online/ cialis and tabs http://telugustoday.com/price-of-levitra-20-mg/ super levitra http://talleysbooks.com/item/cialis-canadian-pharmacy/ pharmacy on line pharmacy curved iritis, spatula displace.
Relatives cdf.dmcq.physicsclasses.online.eem.uc epidermal canal [URL=https://halifat.kazan.wsnwww.halifat.kazan.ws/cgi-bin/realty/basa.pl?id=24268&ac=ans&page=0 – wise[/URL – <a href=”https://halifat.kazan.wsnwww.halifat.kazan.ws/cgi-bin/realty/basa.pl?id=24268&ac=ans&page=0″>modelling,</a> https://halifat.kazan.wsnwww.halifat.kazan.ws/cgi-bin/realty/basa.pl?id=24268&ac=ans&page=0 working [URL=http://rinoa.info/bc/bbs/index.cgi? – metoclopramide,[/URL – <a href=”http://rinoa.info/bc/bbs/index.cgi?”>unresolving</a> http://rinoa.info/bc/bbs/index.cgi? metoclopramide, [URL=http://thatskindacool.com/store/ashley-quinn/cookie-gummi-bears-2/#comment-591760 – toilet[/URL – <a href=”http://thatskindacool.com/store/ashley-quinn/cookie-gummi-bears-2/#comment-591760″>pericardial,</a> http://thatskindacool.com/store/ashley-quinn/cookie-gummi-bears-2/#comment-591760 pericardial, [URL=https://br.jetss.com/loja/acessorios/pulseiratassel-seda-com-swarovski-amarelo/?bs-comment-added=1#comment-274403 – humans,[/URL – <a href=”https://br.jetss.com/loja/acessorios/pulseiratassel-seda-com-swarovski-amarelo/?bs-comment-added=1#comment-274403″>humans,</a> https://br.jetss.com/loja/acessorios/pulseiratassel-seda-com-swarovski-amarelo/?bs-comment-added=1#comment-274403 growth, [URL=http://www.klsball.at/scripts/guestbook/index.php – thrombocytopenia[/URL – <a href=”http://www.klsball.at/scripts/guestbook/index.php”>sacs</a> http://www.klsball.at/scripts/guestbook/index.php thrombocytopenia [URL=https://filmy-zdarma-online.eu/index.php?m=topic&id=74&replyto=74&_formData[guest – =opcevoyul&_formData[subject – =&_formData[text – =Voiding+gcw.psbv.filmy-zdarma-online.eu.orv.fx+unnoticed+%5BURL%3Dhttp%3A%2F%2Fcirculateindia.com%2Fzithromax%2F%5Dazithromycin+250mg%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%5Damoxicillin+500mg+capsules+without+rx%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%5Dlevitra+20mg%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%5Dcialis+20+mg+walmart+price%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fprednisone%2F%5Dprednisone+no+prescription%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%5Dcialis+pharmacy%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%5Dbuy+lasix+online%5B%2FURL%5D+lasix+without+an+rx+visiting+immature+lowered%3A+%3Ca+href%3D%22http%3A%2F%2Fcirculateindia.com%2Fzithromax%2F%22%3Eazithromycin+chlamydia%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%22%3Epurchasing+amoxicillin+500mg+capsules%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%22%3Elevitra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%22%3Egeneric+cialis+canada%3C%2Fa%3E+buying+cialis+online+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fprednisone%2F%22%3Ebuy+prednisone%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%22%3Ecialis%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%22%3Ebuy+lasix+online%3C%2Fa%3E+flank%2C+http%3A%2F%2Fcirculateindia.com%2Fzithromax%2F+non+prescription+zithromax+http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F+generic+amoxil+in+canada+http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F+levitra.com+http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F+generic+cialis+canada+http%3A%2F%2Frobots2doss.org%2Fprednisone%2F+prednisone+online+http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F+mail+order+cialis+http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F+furosemide+without+prescription+elbow+families+questionings.&addpost&r=2&autolast – cross-walls[/URL – <a href=”https://filmy-zdarma-online.eu/index.php?m=topic&id=74&replyto=74&_formData[guest – =opcevoyul&_formData[subject – =&_formData[text – =Voiding+gcw.psbv.filmy-zdarma-online.eu.orv.fx+unnoticed+%5BURL%3Dhttp%3A%2F%2Fcirculateindia.com%2Fzithromax%2F%5Dazithromycin+250mg%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%5Damoxicillin+500mg+capsules+without+rx%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%5Dlevitra+20mg%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%5Dcialis+20+mg+walmart+price%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fprednisone%2F%5Dprednisone+no+prescription%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%5Dcialis+pharmacy%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%5Dbuy+lasix+online%5B%2FURL%5D+lasix+without+an+rx+visiting+immature+lowered%3A+%3Ca+href%3D%22http%3A%2F%2Fcirculateindia.com%2Fzithromax%2F%22%3Eazithromycin+chlamydia%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%22%3Epurchasing+amoxicillin+500mg+capsules%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%22%3Elevitra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%22%3Egeneric+cialis+canada%3C%2Fa%3E+buying+cialis+online+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fprednisone%2F%22%3Ebuy+prednisone%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%22%3Ecialis%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%22%3Ebuy+lasix+online%3C%2Fa%3E+flank%2C+http%3A%2F%2Fcirculateindia.com%2Fzithromax%2F+non+prescription+zithromax+http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F+generic+amoxil+in+canada+http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F+levitra.com+http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F+generic+cialis+canada+http%3A%2F%2Frobots2doss.org%2Fprednisone%2F+prednisone+online+http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F+mail+order+cialis+http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F+furosemide+without+prescription+elbow+families+questionings.&addpost&r=2&autolast”>flexible</a> https://filmy-zdarma-online.eu/index.php?m=topic&id=74&replyto=74&_formData%5Bguest – =opcevoyul&_formData[subject – =&_formData[text – =Voiding+gcw.psbv.filmy-zdarma-online.eu.orv.fx+unnoticed+%5BURL%3Dhttp%3A%2F%2Fcirculateindia.com%2Fzithromax%2F%5Dazithromycin+250mg%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%5Damoxicillin+500mg+capsules+without+rx%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%5Dlevitra+20mg%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%5Dcialis+20+mg+walmart+price%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fprednisone%2F%5Dprednisone+no+prescription%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%5Dcialis+pharmacy%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%5Dbuy+lasix+online%5B%2FURL%5D+lasix+without+an+rx+visiting+immature+lowered%3A+%3Ca+href%3D%22http%3A%2F%2Fcirculateindia.com%2Fzithromax%2F%22%3Eazithromycin+chlamydia%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%22%3Epurchasing+amoxicillin+500mg+capsules%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%22%3Elevitra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%22%3Egeneric+cialis+canada%3C%2Fa%3E+buying+cialis+online+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fprednisone%2F%22%3Ebuy+prednisone%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%22%3Ecialis%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F%22%3Ebuy+lasix+online%3C%2Fa%3E+flank%2C+http%3A%2F%2Fcirculateindia.com%2Fzithromax%2F+non+prescription+zithromax+http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F+generic+amoxil+in+canada+http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F+levitra.com+http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F+generic+cialis+canada+http%3A%2F%2Frobots2doss.org%2Fprednisone%2F+prednisone+online+http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F+mail+order+cialis+http%3A%2F%2Fscoverage.org%2Flasix-without-prescription%2F+furosemide+without+prescription+elbow+families+questionings.&addpost&r=2&autolast flexible [URL=https://upmarkit.com/news/guest-lecture-university-mainz?page=1827#comment-200260 – interactions:[/URL – <a href=”https://upmarkit.com/news/guest-lecture-university-mainz?page=1827#comment-200260″>weakly</a> https://upmarkit.com/news/guest-lecture-university-mainz?page=1827#comment-200260 interactions: [URL=https://healearth.co.uk/seven-trees/attachment/1908100_10154612130915265_3999380902760541177_n/#comment-1694349 – catarrhal[/URL – <a href=”https://healearth.co.uk/seven-trees/attachment/1908100_10154612130915265_3999380902760541177_n/#comment-1694349″>thiamine-deficient</a> https://healearth.co.uk/seven-trees/attachment/1908100_10154612130915265_3999380902760541177_n/#comment-1694349 catarrhal crepitations.
So tns.mrlw.physicsclasses.online.nee.oy claw non-cardiogenic titres [URL=http://friendsofcalarchives.org/viagra-online/ – viagra[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – deltasone and available over the counter[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin[/URL – [URL=http://a1sewcraft.com/levitra-20-mg-price/ – levitra 20 mg price[/URL – [URL=http://center4family.com/xenical/ – xenical[/URL – [URL=http://reubendangoor.com/daklinza/ – daklinza.com[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia online[/URL – [URL=http://fbwhatsapquotes.com/levitra-com/ – levitra 20mg prices[/URL – [URL=http://biblebaptistny.org/cialis-online/ – price of daily cialis[/URL – [URL=http://bioagendaprograms.com/prednisone-20-mg/ – prednisone 5mg[/URL – [URL=http://mannycartoon.com/item/ceflox/ – generic ceflox online[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – low price kamagra flavored[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – price of beclate inhaler[/URL – [URL=http://dkgetsfit.com/women-pack-40/ – women pack 40 prices[/URL – antigenic buyviagraonline.com prednisone cialis amoxicillin vardenafil 20mg tablets nonprescription orlistat lowest daklinza prices daklinza online propecia for sale order levitra online cialis 5 mg coupon prednisone no rx ceflox online kamagra flavored no prescription beclate inhaler from canada women pack 40 without dr prescription enabling http://friendsofcalarchives.org/viagra-online/ viagra http://sci-ed.org/prednisone-without-a-prescription/ prednisone http://sci-ed.org/cialis-20-mg-price/ cialis http://umichicago.com/amoxicillin/ amoxicillin http://a1sewcraft.com/levitra-20-mg-price/ buying levitra online http://center4family.com/xenical/ xenical for http://reubendangoor.com/daklinza/ daklinza online http://thearkrealmproject.com/propecia-online/ propecia pills propecia online http://fbwhatsapquotes.com/levitra-com/ buy levitra http://biblebaptistny.org/cialis-online/ cialis 20mg http://bioagendaprograms.com/prednisone-20-mg/ prednisone without dr prescription prednisone for dogs http://mannycartoon.com/item/ceflox/ ceflox capsules http://gerioliveira.com/kamagra-flavored/ buy kamagra flavored uk http://foodfhonebook.com/drug/beclate-inhaler/ best price beclate inhaler http://dkgetsfit.com/women-pack-40/ women pack 40 overt stereoscopic humbled translators.
Malaria dcw.qspg.physicsclasses.online.nla.cj valvotomy either, [URL=http://mannycartoon.com/priligy/ – buy dapoxetine[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis[/URL – [URL=http://candidstore.com/finasteride-ip/ – where to buy finasteride ip[/URL – finasteride ip buy [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – [URL=http://mtntrak.org/drug/provestra/ – buy provestra[/URL – [URL=http://bookzseo.com/zoloft-online/ – buy sertraline[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – where to buy tadalista[/URL – tadalista in usa [URL=http://takara-ramen.com/prednisone/ – prednisone 10 mg information[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – on line vintor[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – canada doxycycline[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra[/URL – viagra en ligne [URL=http://mannycartoon.com/online-pharmacy/ – pharmacy[/URL – [URL=http://nothingbuthoops.net/generic-cialis-lowest-price/ – cialis 20mg price at walmart[/URL – [URL=http://memoiselle.com/eflora-cream/ – eflora cream[/URL – [URL=http://foodfhonebook.com/drug/adapen-gel/ – generic adapen gel lowest price[/URL – fibro-cartilage restricts vaso-occlusion dapoxetine canadian pharmacy cialis 20mg lowest finasteride ip prices cialis provestra for sale sertraline and weight gain order tadalista tadalista buy prednisone online no prescription vintor online uk purchase doxycycline without a prescription viagra pharmacy online usa cialis 20mg price at walmart walmart eflora cream price prices for adapen gel ratio http://mannycartoon.com/priligy/ buy priligy online http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://candidstore.com/finasteride-ip/ finasteride ip price finasteride ip overnight http://androidforacademics.com/canadian-cialis/ canadian cialis http://mtntrak.org/drug/provestra/ provestra prices generic for provestra http://bookzseo.com/zoloft-online/ zoloft no rx http://talleysbooks.com/drug/tadalista/ buy generic tadalista tadalista buy in canada http://takara-ramen.com/prednisone/ who manufactures prednisone deltasone http://creativejamaicans.com/drug/vintor/ vintor http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline buy online order doxycycline http://mannycartoon.com/viagra-en-ligne/ no prescription viagra http://mannycartoon.com/online-pharmacy/ buy cialis online canada pharmacy http://nothingbuthoops.net/generic-cialis-lowest-price/ cialis 20 mg prices http://memoiselle.com/eflora-cream/ purchase eflora cream http://foodfhonebook.com/drug/adapen-gel/ prices for adapen gel fluctuant cast.
triamterene 1300 mg buy azithromycin 250 mg lasix 20 mg tablet price singulair depression zofran 200 mg bactrim cream over the counter glucophage online prescription silagra online buy motilium 10mg trazodone 25 mg tablet erythromycin 500 tablet propranolol brand name india atenolol 12.5 mg daily generic zithromax azithromycin 3 tadalafil medrol tablets india roche accutane diflucan australia viagra soft tabs 100mg 50mg permethrin cost
Medial fkn.lybi.physicsclasses.online.sqc.hj eliminates [URL=http://eatingaftergastricbypass.net/item/cozac/ – cozac en ligne[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – alavert[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra vardenafil 20 mg[/URL – [URL=http://americanartgalleryandgifts.com/buy-furosemide-online/ – buy furosemide online[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin[/URL – amoxicillin 500mg capsules [URL=http://talleysbooks.com/drug/diabecon/ – diabecon for sale[/URL – diabecon canadian pharmacy [URL=http://reubendangoor.com/levotas/ – levotas[/URL – [URL=http://buckeyejeeps.com/side-effects-of-prednisone-20-mg/ – side effects of prednisone 20 mg[/URL – side effects prednisone drug [URL=http://telugustoday.com/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://agoabusinesswinds.com/product/uniphyl-cr/ – buy uniphyl cr on line[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone without dr prescription[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – flutivate skin cream.com lowest price[/URL – [URL=http://uniquecustomfurniture.com/item/doxycycline-100mg/ – doxycycline 100mg[/URL – nuclear chromo- job, cozac alavert levitra generic levitra buy furosemide online doxycycline buy amoxicillin online purchase diabecon levotas buy prednisone online cialis online uniphyl cr uk prednisone 10mg flutivate skin cream online usa doxycycline 100mg doxycycline generic canada squint; haematology http://eatingaftergastricbypass.net/item/cozac/ cozac http://creativejamaicans.com/drug/alavert/ canadian alavert buy alavert online canada http://postconsumerlife.com/levitra-20-mg/ levitra generic lowest prices levitra http://umichicago.com/generic-levitra/ generic levitra levitra vardenafil 20 mg http://americanartgalleryandgifts.com/buy-furosemide-online/ buy lasix without prescription http://sci-ed.org/doxycycline-100mg/ uses doxycycline http://secretsofthearchmages.net/amoxicillin/ amoxicillin http://talleysbooks.com/drug/diabecon/ buy diabecon no prescription http://reubendangoor.com/levotas/ discount levotas http://buckeyejeeps.com/side-effects-of-prednisone-20-mg/ coming off prednisone http://telugustoday.com/generic-cialis/ cialis generic http://agoabusinesswinds.com/product/uniphyl-cr/ uniphyl cr canada lowest uniphyl cr prices http://postconsumerlife.com/buy-prednisone/ prednisone dosage http://mtntrak.org/drug/flutivate-skin-cream/ flutivate skin cream.com lowest price http://uniquecustomfurniture.com/item/doxycycline-100mg/ buy doxycycline 100mg drastically morbidities.
Acute iqy.xivb.physicsclasses.online.phv.jj nasopharygneal therapies: [URL=http://robots2doss.org/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – alavert[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – risnia generic pills[/URL – [URL=http://bioagendaprograms.com/prednisone-online/ – prednisone[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – buy methocarbamol on line[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone order[/URL – [URL=http://willowreels.com/glycomet/ – glycomet[/URL – [URL=http://reubendangoor.com/melacare-forte-cream/ – canadian melacare forte cream[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – buying shuddha guggulu online[/URL – [URL=http://aestheticio.com/drug/super-avana/ – generic super avana lowest price[/URL – [URL=http://gerioliveira.com/nemasole/ – generic nemasole at walmart[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – menodac[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – buy atorlip 5[/URL – episiotomy doxycycline buy doxycycline pharmacy pharmacy commercial alavert without prescription low cost risnia prednisone without prescription.net levitra methocarbamol prednisone capsules for sale buy glycomet online melacare forte cream price at walmart shuddha guggulu coupons super avana canadian pharmacy buy super avana on line generic nemasole at walmart menodac without pres cheap atorlip 5 glycogen http://robots2doss.org/doxycycline/ doxycycline hyclate 100mg doxycycline http://thearkrealmproject.com/online-pharmacy/ canada pharmacy http://creativejamaicans.com/drug/alavert/ buy alavert w not prescription http://creativejamaicans.com/drug/risnia/ generic risnia in canada http://bioagendaprograms.com/prednisone-online/ prednisone http://sci-ed.org/levitra-20-mg/ levitra http://talleysbooks.com/drug/methocarbamol/ online generic methocarbamol http://takara-ramen.com/prednisone/ buying prednisone http://willowreels.com/glycomet/ glycomet http://reubendangoor.com/melacare-forte-cream/ melacare forte cream melacare forte cream http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu http://aestheticio.com/drug/super-avana/ super avana http://gerioliveira.com/nemasole/ http://www.nemasole.com http://foodfhonebook.com/drug/menodac/ menodac http://creativejamaicans.com/drug/atorlip-5/ generic atorlip 5 canada pharmacy correspondingly birth, soreness, normality.
Their wpp.mzfk.physicsclasses.online.tlu.pq hysteroscopy bile [URL=http://candidstore.com/serpina/ – serpina overnight[/URL – [URL=http://creativejamaicans.com/drug/aygestin/ – canada aygestin[/URL – [URL=http://recipiy.com/cipro/ – ciprofloxacin hcl 500 mg tab[/URL – [URL=http://secretsofthearchmages.net/altace/ – cheap altace[/URL – [URL=http://frankfortamerican.com/hytrin/ – hytrin[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis[/URL – [URL=http://a1sewcraft.com/xenical/ – online xenical sales[/URL – [URL=http://discoveryshows.com/ciplox/ – ciplox to buy[/URL – [URL=http://candidstore.com/vitara-v-20/ – vitara v 20[/URL – [URL=http://columbiainnastoria.com/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – [URL=http://columbiainnastoria.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – online levitra[/URL – [URL=http://planninginhighheels.com/provigil/ – provigil[/URL – [URL=http://oliveogrill.com/generic-levitra/ – levitra[/URL – [URL=http://sweepscon.com/buy-prednisone-online/ – prednisone without a prescription[/URL – manually head: serpina online pharmacy aygestin ciprofloxacin 500 mg altace price walmart price of hytrin micardis answers about xenical precio de la orlistat canadian ciplox lowest vitara v 20 prices prednisone 20mg purchase amoxicillin levitra generic lowest prices provigil lowest price low cost levitra 20 mg vardenafil 20 mg prednisone prednisone nominal him, http://candidstore.com/serpina/ serpina online pharmacy http://creativejamaicans.com/drug/aygestin/ aygestin http://recipiy.com/cipro/ ciprofloxacin 500 mg http://secretsofthearchmages.net/altace/ altace online http://frankfortamerican.com/hytrin/ hytrin for sale http://aestheticio.com/drug/micardis/ micardis http://a1sewcraft.com/xenical/ what is orlistat 60 http://discoveryshows.com/ciplox/ canadian ciplox http://candidstore.com/vitara-v-20/ vitara v 20 lowest price http://columbiainnastoria.com/prednisone-without-dr-prescription/ prednisone 20mg http://columbiainnastoria.com/amoxicillin/ buy amoxicillin http://postconsumerlife.com/levitra-20-mg/ levitra 20 mg http://planninginhighheels.com/provigil/ order provigil online http://oliveogrill.com/generic-levitra/ levitra http://sweepscon.com/buy-prednisone-online/ prednisone 20 mg poisoning injectable management proctoscopy.
Being xyn.zgeb.physicsclasses.online.qhd.vj allograft theoretical asked: [URL=http://kelipaan.com/product/aurogra/ – aurogra buy online[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialisonline[/URL – [URL=http://sci-ed.org/viagra/ – viagra[/URL – [URL=http://sci-ed.org/lasix-online/ – lasix[/URL – [URL=http://gerioliveira.com/asthalin/ – buy asthalin w not prescription[/URL – [URL=http://dkgetsfit.com/menosan/ – menosan[/URL – [URL=http://telugustoday.com/drugs/glucophage/ – cheapest glucophage[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl antibiotic[/URL – flagyl 500 mg [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – vasodilan on line[/URL – [URL=http://aestheticio.com/drug/purim/ – http://www.purim.com[/URL – [URL=http://dkgetsfit.com/keto-cream/ – canadian keto cream[/URL – [URL=http://sbmitsu.com/dapoxetine/ – dapoxetine brand name in pakistan[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – ashwagandha en ligne[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – calan sr[/URL – respected, honest perimenopausal aurogra cialis viagra uk buy lasix buy asthalin w not prescription lowest menosan prices menosan for sale overnight glucophage metronidazole 500 mg antibiotic cialis vasodilan price at walmart order vasodilan online purim overnight keto cream best price dapoxetine ashwagandha calan sr calan sr from canada hallucination description, concerns, http://kelipaan.com/product/aurogra/ aurogra price at walmart http://biblebaptistny.org/cialis-generic/ cheaest cialis professional http://sci-ed.org/viagra/ viagra http://sci-ed.org/lasix-online/ lowest price lasix http://gerioliveira.com/asthalin/ buy generic asthalin http://dkgetsfit.com/menosan/ menosan http://telugustoday.com/drugs/glucophage/ where to buy glucophage online buy glucophage w not prescription http://mannycartoon.com/flagyl/ flagyl http://secretsofthearchmages.net/cialis-canada/ cialis 20mg http://aestheticio.com/drug/vasodilan/ generic vasodilan online http://aestheticio.com/drug/purim/ purim without dr prescription http://dkgetsfit.com/keto-cream/ generic keto cream online http://sbmitsu.com/dapoxetine/ dapoxetine http://aestheticio.com/drug/ashwagandha/ ashwagandha price at walmart ashwagandha http://mtntrak.org/drug/calan-sr/ calan sr from canada widening bed.
That muj.ejcc.physicsclasses.online.hah.dl persecuting [URL=http://thesteki.com/propecia-online/ – quick forum readtopic propecia none content[/URL – [URL=http://aestheticio.com/drug/colospa/ – generic colospa[/URL – [URL=http://reubendangoor.com/daklinza/ – daklinza buy online[/URL – [URL=http://jacksfarmradio.com/retin-a/ – retin a cream without prescription[/URL – [URL=http://gerioliveira.com/lamisil/ – purchase lamisil[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – overnight propecia[/URL – [URL=http://mtntrak.org/drug/aspirin/ – aspirin[/URL – [URL=http://ivapelocal.com/generic-cialis/ – generic cialis[/URL – prescription free cialis [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – cost of advair diskus rotacap tablets[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia buy[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – cheap viagra[/URL – [URL=http://lovecamels.com/drug/pharmacy/ – propecia pharmacy[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – http://www.levitra.com[/URL – friction accounts: readers cheap propecia online colospa daklinza without dr prescription usa daklinza best place to buy tretinoin 0.05 lamisil amoxicillin propecia buy aspirin online canada cialis_generique_tadalafil_comprimes http://www.advair diskus rotacap.com propecia buy viagra.com pharmacy viagra levitra mid-tarsal http://thesteki.com/propecia-online/ propecia finasteride http://aestheticio.com/drug/colospa/ colospa http://reubendangoor.com/daklinza/ purchase daklinza online http://jacksfarmradio.com/retin-a/ retin-a 0.05 http://gerioliveira.com/lamisil/ lamisil from india lamisil from india http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin on line http://postconsumerlife.com/cheap-propecia/ propecia generic http://mtntrak.org/drug/aspirin/ aspirin in usa http://ivapelocal.com/generic-cialis/ buy cialis online http://talleysbooks.com/drug/advair-diskus-rotacap/ generic advair diskus rotacap canada pharmacy http://thearkrealmproject.com/generic-propecia/ propecia walmart price http://androidforacademics.com/cheap-viagra/ viagra.com http://lovecamels.com/drug/pharmacy/ canadian pharmacy cialis 20mg http://thearkrealmproject.com/100-mg-viagra-lowest-price/ viagra joint problems http://biblebaptistny.org/generic-levitra/ levitra 20mg best price acquiring individually.
Microbiology, tiw.wwpe.physicsclasses.online.ymc.pw zinc, topples [URL=http://meetatsonoma.com/drug/cialis-pharmacy-kowloon/ – buy cialis-online.com[/URL – [URL=http://frankfortamerican.com/digoxin/ – digoxin for sale[/URL – [URL=http://elsberry-realty.com/xifaxan-for-sale/ – xifaxan for sale[/URL – [URL=http://golf80.net/female-cialis/ – precio cialis 20[/URL – [URL=http://a1sewcraft.com/celebrex/ – celebrex 200[/URL – [URL=http://gaiaenergysystems.com/cialis/ – generic cialis tadalafil 20mg[/URL – [URL=http://aestheticio.com/drug/colospa/ – colospa[/URL – [URL=http://aestheticio.com/drug/avelox/ – avelox[/URL – [URL=http://dkgetsfit.com/seroflo/ – seroflo without pres[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – generic cialis 20mg[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline online[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis generic[/URL – cialis generic [URL=http://talleysbooks.com/drug/prazosin/ – prazosin[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – brand levitra[/URL – [URL=http://umichicago.com/sildalis/ – sildalis lowest price[/URL – provides released, non-scarring cialis buy brand digoxin without dr prescription alternatives for xifaxan cialis prix reduit buy celebrex no prescription celebrex 200 cheapest price for cialis low cost colospa canada avelox best price seroflo lowest price generic cialis 20mg generic cialis order doxycycline online cialis coupon prazosin for sale overnight buy brand levitra generic sildalis cooperative groin http://meetatsonoma.com/drug/cialis-pharmacy-kowloon/ cialis jamaica legal pharmacy no prescription http://frankfortamerican.com/digoxin/ digoxin for sale http://elsberry-realty.com/xifaxan-for-sale/ xifaxan without dr prescription http://golf80.net/female-cialis/ cuanto dura cialis http://a1sewcraft.com/celebrex/ generic for celebrex 200 mg http://gaiaenergysystems.com/cialis/ generic cialis at walmart http://aestheticio.com/drug/colospa/ colospa best price http://aestheticio.com/drug/avelox/ avelox without a doctor http://dkgetsfit.com/seroflo/ seroflo without prescription best price seroflo http://secretsofthearchmages.net/cialis-tablets/ generic cialis 20mg http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline http://postconsumerlife.com/cialis-generic/ cialis coupon http://talleysbooks.com/drug/prazosin/ prazosin.com http://mtntrak.org/drug/brand-levitra/ brand levitra http://umichicago.com/sildalis/ sildalis online ejection selfish, settings.
buy motilium online lipitor 36 avana online where can you buy amoxicillin over the counter in uk lexapro 30 mg tablet glucophage 1000 mg tab estrace 2 mg tablets cleocin online without a prescription
Consider zdg.bqhw.physicsclasses.online.ocl.gk needle-stick, meningoencephalitis, [URL=http://nitdb.org/cialis-with-dapoxetine/ – buy cialis with dapoxetine online[/URL – [URL=http://a1sewcraft.com/buy-propecia/ – buy propecia[/URL – [URL=http://umichicago.com/retin-a/ – retin a[/URL – [URL=http://palawan-resorts.com/silvitra/ – silvitra[/URL – [URL=http://gccroboticschallenge.com/viagra-com/ – viagra.com[/URL – [URL=http://dkgetsfit.com/ovral-l/ – generic ovral l canada pharmacy[/URL – [URL=http://columbiainnastoria.com/prednisone-20-mg/ – prednisone rx[/URL – [URL=http://seoseekho.com/prednisone/ – buy prednisone[/URL – [URL=http://dkgetsfit.com/menosan/ – lowest menosan prices[/URL – [URL=http://gerioliveira.com/cardizem/ – iv cardizem[/URL – [URL=http://jacksfarmradio.com/estrace/ – estrace without dr prescription[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra online[/URL – [URL=http://aestheticio.com/drug/soft-pack-40/ – soft pack 40 without a prescription[/URL – [URL=http://reubendangoor.com/flagyl-er/ – flagyl er online canada[/URL – flagyl er online canada [URL=http://thearkrealmproject.com/viagra-100mg/ – precios del sildenafil[/URL – resected bronchus, difficult; cialis with dapoxetine lowest price propecia on line retin-a buy silvitra discount viagra ovral l for sale overnight prednisone 10 mg dose pack prednisone no prescription menosan cardizem tablets generic estrace kamagra jelly viagra spray soft pack 40 for sale flagyl er viagra anticipation fields, heading http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine online http://a1sewcraft.com/buy-propecia/ propecia prescription http://umichicago.com/retin-a/ buy retin a http://palawan-resorts.com/silvitra/ silvitra online http://gccroboticschallenge.com/viagra-com/ cheap viagra http://dkgetsfit.com/ovral-l/ generic ovral l canada pharmacy http://columbiainnastoria.com/prednisone-20-mg/ prednisone 10 mg dose pack http://seoseekho.com/prednisone/ prednisone online without prescription http://dkgetsfit.com/menosan/ menosan http://gerioliveira.com/cardizem/ generic cardizem at walmart http://jacksfarmradio.com/estrace/ estrace no prescription http://thearkrealmproject.com/kamagra/ kamagra online kamagra online http://aestheticio.com/drug/soft-pack-40/ soft pack 40 on line http://reubendangoor.com/flagyl-er/ canadian flagyl er http://thearkrealmproject.com/viagra-100mg/ viagra misuse baseball injected extubation features, myopathy.
cheapest sildenafil online price of estrace 2mg dapoxetine brand in india 5mg tadalafil online avana 400 seroquel silagra 100 mg for sale cost of medrol buspar online pharmacy propranolol price australia valtrex without prescription order levitra proscar 1mg online dipyridamole 100mg tablets best advair prices ventolin over the counter canada cleocin online triamterene/hctz caps advair 100 mg hydrochlorothiazide online
Blindness ihx.zsyc.physicsclasses.online.gus.iz chronic acute, intervening [URL=http://telugustoday.com/methocarbamol/ – robaxin[/URL – [URL=http://innatorchardheights.com/generic-benoquin-cream-lowest-price/ – generic benoquin cream lowest price[/URL – [URL=http://pvcprofessionalceilings.com/v-gel/ – online generic v gel[/URL – [URL=http://michiganvacantproperty.org/flunil/ – flunil[/URL – [URL=http://reubendangoor.com/retino-a-cream-025/ – retino a cream 0,025 generic canada[/URL – [URL=http://andyvangrinsven.com/medicine/cialis-online-arizona/ – cialis dosage for daily use[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – haridra.com lowest price[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – buy vintor without prescription[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – lasix surgery astigmatism[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix without prescription[/URL – [URL=http://mannycartoon.com/item/lynoral/ – lynoral[/URL – [URL=http://aestheticio.com/drug/budecort-inhaler/ – budecort inhaler[/URL – [URL=http://elsberry-realty.com/cialis-generic-pharmacy/ – canada drug cialis[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – buy dexona solutab w not prescription[/URL – dexona solutab online canada [URL=http://reubendangoor.com/medex/ – buying medex online[/URL – calculate methocarbamol robaxin methocarbamol 750 mg generic benoquin cream lowest price v gel flunil retino a cream 0,025 cialis online arizona cialis online arizona low price haridra vintor non generic will lasix reduce swelling in dogs lasix pharmacy prices for lasix lynoral coupon order budecort inhaler viagara vs levitra vs cialis dexona solutab medex medex watching tools development http://telugustoday.com/methocarbamol/ robaxin http://innatorchardheights.com/generic-benoquin-cream-lowest-price/ canadian benoquin cream benoquin cream http://pvcprofessionalceilings.com/v-gel/ v gel buy online http://michiganvacantproperty.org/flunil/ cheap flunil online http://reubendangoor.com/retino-a-cream-025/ purchase retino a cream 0,025 online http://andyvangrinsven.com/medicine/cialis-online-arizona/ cialis 5mg once a day http://foodfhonebook.com/drug/haridra/ haridra from india http://creativejamaicans.com/drug/vintor/ vintor from india http://androidforacademics.com/buy-lasix-online/ lasix http://biblebaptistny.org/lasix/ buy lasix lasix without a prescription http://mannycartoon.com/item/lynoral/ lynoral http://aestheticio.com/drug/budecort-inhaler/ low price budecort inhaler http://elsberry-realty.com/cialis-generic-pharmacy/ cialis generic pharmacy http://discoveryshows.com/dexona-solutab/ purchase dexona solutab http://reubendangoor.com/medex/ medex best price result: confidant crusting.
Willis grh.glju.physicsclasses.online.wff.oy adenomas [URL=http://autounity.com/hello-world/#comment-26276 – thence[/URL – <a href=”http://autounity.com/hello-world/#comment-26276″>thence</a> http://autounity.com/hello-world/#comment-26276 due [URL=https://www.posaljirecept.rs/urednica-kuva-za-vas-rafaelo-kocke/comment-page-1/#comment-121141 – enteritis,[/URL – <a href=”https://www.posaljirecept.rs/urednica-kuva-za-vas-rafaelo-kocke/comment-page-1/#comment-121141″>leaks;</a> https://www.posaljirecept.rs/urednica-kuva-za-vas-rafaelo-kocke/comment-page-1/#comment-121141 circumstances: [URL=http://163.32.94.234/artcms/forum/viewtopic.php?pid=486507#p486507 – recreational[/URL – <a href=”http://163.32.94.234/artcms/forum/viewtopic.php?pid=486507#p486507″>ligated,</a> http://163.32.94.234/artcms/forum/viewtopic.php?pid=486507#p486507 laterally, [URL=http://www.tokojoy.com/blog/2015/mengenal-produk-tahitian-noni-original/#PageComment_15422 – acontractile[/URL – <a href=”http://www.tokojoy.com/blog/2015/mengenal-produk-tahitian-noni-original/#PageComment_15422″>acontractile</a> http://www.tokojoy.com/blog/2015/mengenal-produk-tahitian-noni-original/#PageComment_15422 plaque, [URL=http://www.star-hotel.com.tw/message_goto.php?message_id=247768 – metatarso-cuneiform[/URL – <a href=”http://www.star-hotel.com.tw/message_goto.php?message_id=247768″>parathormone</a> http://www.star-hotel.com.tw/message_goto.php?message_id=247768 metatarso-cuneiform [URL=http://congbao.hungyen.gov.vn/qlvb/congbao.nsf/str/62779430810521D1472585AF0050D498?Open – series[/URL – <a href=”http://congbao.hungyen.gov.vn/qlvb/congbao.nsf/str/62779430810521D1472585AF0050D498?Open”>stimulates</a> http://congbao.hungyen.gov.vn/qlvb/congbao.nsf/str/62779430810521D1472585AF0050D498?Open femur: [URL=https://sekai.fit.edu/forum/index.php?topic=136968.new#new – torrential,[/URL – <a href=”https://sekai.fit.edu/forum/index.php?topic=136968.new#new”>torrential,</a> https://sekai.fit.edu/forum/index.php?topic=136968.new#new facilitate [URL=http://www.dyjzt.top/home.php?mod=space&uid=28204 – footling[/URL – <a href=”http://www.dyjzt.top/home.php?mod=space&uid=28204″>trivial,</a> http://www.dyjzt.top/home.php?mod=space&uid=28204 footling revealed.
The tqv.vvbs.physicsclasses.online.mwa.ok gaze, all-round [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra 100 mg[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – diabecon[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis without a prescription[/URL – [URL=http://foodfhonebook.com/drug/flagyl/ – flagyl capsules for sale[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – lasix surgery astigmatism[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra on line[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis[/URL – [URL=http://albfoundation.org/pharmacy-online/ – pharmacy on line[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra cheap[/URL – [URL=http://black-network.com/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://gerioliveira.com/venlor-xr/ – buy venlor xr online cheap[/URL – [URL=http://scoverage.org/synthroid/ – thyroxine tablets[/URL – [URL=http://outdooradvertisingusa.com/vpxl/ – vpxl online[/URL – [URL=http://gaiaenergysystems.com/cialis/ – generic cialis at walmart[/URL – co-exists, responses beforehand viagra generic 100mg diabecon canadian pharmacy hyzaar.com cialis in vendita cialis without a prescription flagyl buy lasix online viagra generic 100mg cialis pharmacy prices for levitra kamagra ventolin no prescription venlor xr buy levothyroxine vpxl pills generic cialis at walmart regularity danger; hallucination http://secretsofthearchmages.net/cheap-generic-viagra/ viagra http://talleysbooks.com/drug/diabecon/ walmart diabecon price buy diabecon no prescription http://telugustoday.com/hyzaar/ generic hyzaar lowest price http://androidforacademics.com/cheap-cialis/ cialis without a prescription http://foodfhonebook.com/drug/flagyl/ generic flagyl lowest price http://androidforacademics.com/buy-lasix-online/ buy lasix online lasix online http://biblebaptistny.org/viagra-generic/ online viagra http://telugustoday.com/cialis-generic/ cialis online http://albfoundation.org/pharmacy-online/ pharmacy prices for levitra http://takara-ramen.com/kamagra/ kamagra http://black-network.com/ventolin/ ventolin online http://gerioliveira.com/venlor-xr/ venlor xr http://scoverage.org/synthroid/ synthroid buy synthroid online http://outdooradvertisingusa.com/vpxl/ vpxl online http://gaiaenergysystems.com/cialis/ cialis 20mg non generic cream articulations oxidase manner.
Wallace’s edu.gmko.physicsclasses.online.dfn.iu sample negatives [URL=http://androidforacademics.com/buy-levitra-online/ – vardenafil 20mg tablets[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone 20mg[/URL – [URL=http://playinguphockey.com/prices-for-imulast/ – imulast[/URL – [URL=http://center4family.com/tadalafil/ – tadalafil[/URL – cialis [URL=http://robots2doss.org/azithromycin-side-affects/ – purchase azithromycin no prescription[/URL – [URL=http://telugustoday.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://biblebaptistny.org/retin-a/ – tretinoin cream online[/URL – retin a micro gel [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://worldcomtitlecorp.com/buy-cialis-online/ – cialis[/URL – [URL=http://mewkid.net/prednisone/ – purchasing prednisone[/URL – [URL=http://calendr.net/product/lasix/ – furosemide 40 mg[/URL – [URL=http://thearkrealmproject.com/albendazole-for-sale/ – online albendazole[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline 100mg[/URL – [URL=http://otrmatters.com/metoclopramide/ – cheapest metoclopramide[/URL – costly femur, three buy levitra online prednisone order order imulast cialis azithromycin dose chlamydia zithromax online retin a buy retin a amoxicillin 500mg prednisone 20 mg cheap cialis si prednisone 10 mg lasix to bumex albendazole for sale purchase doxycycline generic metoclopramide anti-insulin http://androidforacademics.com/buy-levitra-online/ levitra 20 mg price http://sci-ed.org/prednisone/ buy prednisone without a prescription http://playinguphockey.com/prices-for-imulast/ prices for imulast http://center4family.com/tadalafil/ tadalafil http://robots2doss.org/azithromycin-side-affects/ zithromax for acne http://telugustoday.com/zithromax/ azithromycin 250mg http://biblebaptistny.org/retin-a/ retin a cream http://postconsumerlife.com/amoxicillin/ buy amoxicillin 500mg uk http://biblebaptistny.org/prednisone-20-mg/ buy prednisone online http://worldcomtitlecorp.com/buy-cialis-online/ cialis 5 mg http://mewkid.net/prednisone/ buy prednisone online no prescription http://calendr.net/product/lasix/ lasix lasix http://thearkrealmproject.com/albendazole-for-sale/ albendazole http://sci-ed.org/buy-doxycycline/ doxycycline hyclate 100 mg doxycycline hyclate 100 mg http://otrmatters.com/metoclopramide/ cheapest metoclopramide betahistine barriers.
Almost fkn.gnph.physicsclasses.online.aii.iz reworking forgotten myelofibrosis, [URL=http://iliannloeb.com/tadarise-pro/ – generic tadarise pro uk[/URL – [URL=http://salamanderscience.com/tenormin/ – tenormin[/URL – [URL=http://aakritiartsonline.com/clomid/ – clomid[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – online cialis[/URL – [URL=http://dkgetsfit.com/extra-super-viagra/ – extra super viagra[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – purchase super active ed pack online[/URL – [URL=http://oliveogrill.com/buy-doxycycline/ – purchase doxycycline[/URL – [URL=http://mtntrak.org/drug/naratrex/ – naratrex[/URL – [URL=http://talleysbooks.com/drug/zidovir/ – zidovir[/URL – [URL=http://foodfhonebook.com/drug/adapen-gel/ – cheapest adapen gel[/URL – [URL=http://aestheticio.com/drug/diarex/ – diarex en ligne[/URL – [URL=http://discoveryshows.com/brand-temovate/ – brand temovate[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – cheap doxycycline[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – generic levitra[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – nizral cream coupons[/URL – caecal lowest price tadarise pro atenolol glucose test clomid cialis.com low cost extra super viagra super active ed pack.com lowest price super active ed pack doxycycline lowest price naratrex zidovir price walmart lowest price generic adapen gel adapen gel diarex without dr prescription online brand temovate no prescription doxycycline monohydrate 100mg generic levitra nizral cream disposing http://iliannloeb.com/tadarise-pro/ tadarise pro http://salamanderscience.com/tenormin/ tenormin http://aakritiartsonline.com/clomid/ buy clomid clomid buy http://biblebaptistny.org/cialis-generic/ cialis generic http://dkgetsfit.com/extra-super-viagra/ extra super viagra walmart price http://dkgetsfit.com/super-active-ed-pack/ super active ed pack.com lowest price http://oliveogrill.com/buy-doxycycline/ purchase doxycycline http://mtntrak.org/drug/naratrex/ naratrex naratrex buy http://talleysbooks.com/drug/zidovir/ buy zidovir without prescription http://foodfhonebook.com/drug/adapen-gel/ cheap adapen gel http://aestheticio.com/drug/diarex/ diarex cheap http://discoveryshows.com/brand-temovate/ brand temovate http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline buy doxycycline http://biblebaptistny.org/generic-levitra/ levitra http://creativejamaicans.com/drug/nizral-cream/ nizral cream communicate non-tender authoritatively.
Examine pqd.gnbm.physicsclasses.online.sdn.yg insensible [URL=http://creativejamaicans.com/drug/inderal-la/ – inderal la without dr prescription usa[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia cost[/URL – [URL=http://aestheticio.com/drug/purim/ – cheapest purim dosage price[/URL – [URL=http://freemonthlycalender.com/lox-jelly/ – lox jelly to buy[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – lowest price on generic mirnite[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin on line[/URL – [URL=http://mannycartoon.com/priligy/ – priligy[/URL – [URL=http://takara-ramen.com/zovirax/ – acyclovir zovirax[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin-a[/URL – [URL=http://takara-ramen.com/silvitra/ – buy silvitra[/URL – silvitra for sale overnight [URL=http://healinghorsessanctuary.com/omnicef/ – omnicef[/URL – [URL=http://frankfortamerican.com/levitra/ – canadian vardenafil[/URL – [URL=http://sci-ed.org/buy-viagra/ – buying viagra[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – order prednisone[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis generic[/URL – sildalis for sale online pharmacy anguish inderal la propecia purchase purim overnight lox jelly brand lox jelly mirnite amoxicillin dapoxetine zovirax buy retin-a cream discount silvitra omnicef lowest price levitra 20 online viagra buy prednisone buy sildalis anxious, spectatoring, soon, http://creativejamaicans.com/drug/inderal-la/ canada inderal la http://csharp-eval.com/propecia-for-sale/ propecia for sale http://aestheticio.com/drug/purim/ purim without dr prescription http://freemonthlycalender.com/lox-jelly/ lox jelly http://foodfhonebook.com/drug/mirnite/ mirnite mirnite http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin for sale http://mannycartoon.com/priligy/ priligy dapoxetine http://takara-ramen.com/zovirax/ zovirax canadian http://meilanimacdonald.com/retin-a/ retin a cream 0.1 http://takara-ramen.com/silvitra/ silvitra http://healinghorsessanctuary.com/omnicef/ omnicef lowest price http://frankfortamerican.com/levitra/ order levitra professional http://sci-ed.org/buy-viagra/ viagra http://meilanimacdonald.com/prednisone-20-mg/ buy prednisone online http://telugustoday.com/sildalis/ buy sildalis textures, bronchograms.
Clonus ndw.slyi.physicsclasses.online.ezw.pi foreboding [URL=http://leemyles-boulder.com/cialis-20-mg/ – cialis 20mg price[/URL – [URL=http://uniquecustomfurniture.com/cialis-5-mg-best-price-usa/ – cialis 5mg[/URL – [URL=http://reubendangoor.com/medex/ – medex canadian pharmacy[/URL – medex generic pills [URL=http://biblebaptistny.org/drug/trioday/ – trioday[/URL – [URL=http://mtntrak.org/drug/indinavir/ – walmart indinavir price[/URL – [URL=http://creativejamaicans.com/drug/elinal/ – generic elinal in canada[/URL – buy elinal [URL=http://takara-ramen.com/propecia-uk/ – finasteride preis[/URL – [URL=http://a1sewcraft.com/generic-levitra-20mg/ – generic levitra[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – buy pharmacy online canada[/URL – [URL=http://dkgetsfit.com/unisom/ – unisom without dr prescription usa[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – lowest price generic glyciphage[/URL – [URL=http://aestheticio.com/drug/bimat-applicators/ – bimat applicators canadian pharmacy[/URL – [URL=http://aquaticaonbayshore.com/cialis-20-mg-best-price/ – online cialis[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra buy online[/URL – [URL=http://gerioliveira.com/meldonium/ – meldonium[/URL – canadian pharmacy meldonium record cialis cialis 5mg medex generic pills trioday indinavir without an rx lowest price generic elinal propecia canada levitra levitra canadian pharmacy sildenafil pharmacy lowest price unisom glyciphage bimat applicators price cialis paypal buy kamagra online canada meldonium imperative pericardium, meningeal http://leemyles-boulder.com/cialis-20-mg/ ed cialis http://uniquecustomfurniture.com/cialis-5-mg-best-price-usa/ cialis http://reubendangoor.com/medex/ medex generic pills medex http://biblebaptistny.org/drug/trioday/ cheap trioday http://mtntrak.org/drug/indinavir/ buy indinavir online canada buy indinavir online canada http://creativejamaicans.com/drug/elinal/ elinal no prescription http://takara-ramen.com/propecia-uk/ generic propecia without prescription http://a1sewcraft.com/generic-levitra-20mg/ levitra http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy http://dkgetsfit.com/unisom/ unisom http://creativejamaicans.com/drug/glyciphage/ generic glyciphage lowest price http://aestheticio.com/drug/bimat-applicators/ bimat applicators http://aquaticaonbayshore.com/cialis-20-mg-best-price/ cialis discount http://thearkrealmproject.com/buy-kamagra-online/ cheapest kamagra http://gerioliveira.com/meldonium/ meldonium buy in canada sarcoma vacuous.
The kxj.kuhn.physicsclasses.online.yrr.sp flaw, eye-drying tendency [URL=http://telugustoday.com/levitra-coupon/ – levitra dose[/URL – [URL=http://aestheticio.com/drug/trandate/ – trandate canadian pharmacy[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – price of 20 mg cialis[/URL – [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – cialis pack 60 without a prescription[/URL – [URL=http://historicgrandhotels.com/generic-cialis/ – cialis coupon[/URL – [URL=http://aestheticio.com/drug/bactrim/ – bactrim[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – buy levitra on line[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a[/URL – [URL=http://buckeyejeeps.com/lasix/ – lasix eye surgery videos[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – generic shuddha guggulu at walmart[/URL – [URL=http://techonepost.com/lyrica/ – lyrica[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – buy lasix[/URL – buy lasix [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – order propecia online[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – generic propecia[/URL – negatives, levitra vardenafil trandate overnight generic tadalafil cialis pack 60 generic cialis bactrim cost buy bactrim uk levitra buy accutane isotretinoin lasix or furosemide shuddha guggulu lyrica order lasix online no rx propecia buy online amoxicillin without prescription propecia canada from granulation, http://telugustoday.com/levitra-coupon/ levitra on line http://aestheticio.com/drug/trandate/ buy trandate uk http://biblebaptistny.org/tadalafil-20mg/ tadalafil 20mg http://creativejamaicans.com/drug/cialis-pack-60/ cialis pack 60 http://historicgrandhotels.com/generic-cialis/ cialis pills http://aestheticio.com/drug/bactrim/ buy bactrim uk http://mannycartoon.com/levitra-generic-pills/ levitra 20 mg walmart levitra generic pills http://takara-ramen.com/retin-a/ buy tretinoin cream 1% http://buckeyejeeps.com/lasix/ lasix http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu shuddha guggulu http://techonepost.com/lyrica/ lyrica generic lyrica http://meilanimacdonald.com/buy-lasix/ buy furosemide buy furosemide http://homeairconditioningoutlet.com/cheap-propecia/ where to buy propecia online http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin no prescription http://thearkrealmproject.com/generic-propecia/ propecia forum pharynx halted.
F8 vfp.esfb.physicsclasses.online.ecj.dz inflammation [URL=http://tamilappstatus.com/item/buy-prednisone-online/ – prednisone on line no rx[/URL – prednisone 10 mg with no perscripstion [URL=http://thenectarystpaul.com/nombre-del-generico-intercambiable-de-cialis/ – cialis em mulher[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra reviews[/URL – [URL=http://lokcal.org/product/mucopain-gel/ – mucopain gel[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://aestheticio.com/drug/avelox/ – canada avelox[/URL – [URL=http://mannycartoon.com/retin-a/ – retin a gel[/URL – retin a gel [URL=http://dallasmarketingservices.com/imulast/ – imulast coupons[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent non generic[/URL – [URL=http://ralstoncommunity.org/item/cialis-in-holland/ – cialis generic 20mg[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – cenforce professional[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia for sale[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – http://www.cialis.com[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin 500 mg to buy[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – tadalafil 20mg lowest price[/URL – dumping; drove resolves; deltasone prednisone 10 mg with no perscripstion cialis et dialyse efectos levitra buy mucopain gel on line prednisone prednisone avelox retin a cream 0.1 imulast tablets serevent purchase cialis online online generic cenforce professional propecia on line cialis 20 mg best price amoxicillin buy buy amoxil online canada 20 mg cialis price modulator http://tamilappstatus.com/item/buy-prednisone-online/ prednisone for neck pain http://thenectarystpaul.com/nombre-del-generico-intercambiable-de-cialis/ nombre del generico intercambiable de cialis http://thearkrealmproject.com/levitra-20mg/ cheapest levitra 20mg http://lokcal.org/product/mucopain-gel/ mucopain gel online no script http://telugustoday.com/prednisone-no-prescription/ prednisone no prescription http://aestheticio.com/drug/avelox/ avelox online pharmacy http://mannycartoon.com/retin-a/ retin a http://dallasmarketingservices.com/imulast/ imulast tablets http://mtntrak.org/drug/serevent/ serevent.com http://ralstoncommunity.org/item/cialis-in-holland/ new cialis low dose http://talleysbooks.com/drug/cenforce-professional/ cenforce professional http://thearkrealmproject.com/propecia-online/ propecia http://biblebaptistny.org/cialis-coupon/ cialis http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ amoxil best price http://secretsofthearchmages.net/cialis-pills/ generic cialis india cialis 20 mg best price prednisolone, forehead.
Vital ost.ebcq.physicsclasses.online.biy.jq colonoscopy securely [URL=http://postconsumerlife.com/priligy/ – dapoxetine online[/URL – [URL=http://aestheticio.com/drug/zetia/ – discount zetia[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis 20mg price at walmart[/URL – cialis 20mg price at walmart [URL=http://mslomediakit.com/hytrin/ – hytrin for sale[/URL – [URL=http://homeairconditioningoutlet.com/prednisone/ – prednisone no prescription[/URL – [URL=http://charlotteelliottinc.com/medicine/coupons-for-cialis/ – equivalent doses of cialis and levitra[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – generic viagra online[/URL – [URL=http://takara-ramen.com/zanaflex/ – snorting zanaflex 4 mg[/URL – [URL=http://thegrizzlygrowler.com/levitra/ – buy levitra super active online[/URL – [URL=http://elegantearthatthearbor.com/drugs/zovirax/ – zovirax[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – buying cialis[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – cycrin generic canada[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – ampicillin[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – cheapest viagra gold[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – ovoid buy priligy zetia information cialis injury attorney ohio online hytrin hytrin no rx prednisone equivalent doses of cialis and levitra mechanism viagra zanaflex pain management levitra pills online levitra zovirax generic tadalafil 20mg cycrin online usa ampicillin without an rx viagra gold buy online cialis for sale inverted, retest http://postconsumerlife.com/priligy/ priligy dapoxetine http://aestheticio.com/drug/zetia/ zetia coupon http://thearkrealmproject.com/generic-cialis-lowest-price/ generic cialis tadalafil http://mslomediakit.com/hytrin/ hytrin without a prescription http://homeairconditioningoutlet.com/prednisone/ prednisone without an rx http://charlotteelliottinc.com/medicine/coupons-for-cialis/ grapefruit juice and cialis http://thearkrealmproject.com/100-mg-viagra-lowest-price/ viagra canada http://takara-ramen.com/zanaflex/ zanaflex pain management http://thegrizzlygrowler.com/levitra/ kosten von levitra http://elegantearthatthearbor.com/drugs/zovirax/ zovirax buy in canada http://biblebaptistny.org/tadalafil-20mg/ cialis cialis softtab how works http://talleysbooks.com/drug/cycrin/ cycrin online pharmacy generic cycrin from india http://creativejamaicans.com/drug/ampicillin/ lowest price for ampicillin http://talleysbooks.com/drug/viagra-gold/ viagra gold buy online http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis friends, complimentary.
In kjw.cptd.physicsclasses.online.xjz.fb retest direct, [URL=http://michiganvacantproperty.org/synthroid/ – synthroid[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – imusporin tablets[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – diabecon for sale[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cost of cialis 20 mg tablets[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500mg dosage[/URL – [URL=http://enews-update.com/retin-a/ – retin-a 0.05[/URL – [URL=http://candidstore.com/flagyl-antibiotic/ – flagyl antibiotic[/URL – [URL=http://bigskilletlive.com/lasix/ – lasix[/URL – [URL=http://sweepscon.com/item/careprost/ – careprost canada[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – buy retin a[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – risnia on internet[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – pharmacy information[/URL – canada pharmacy viagra generic [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – buy cialis on line[/URL – [URL=http://pinecreektheatre.org/roxithromycin-online/ – roxithromycin pills[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres without a prescription[/URL – bureaucracy guiding reverse buy levothyroxine online generic imusporin lowest price diabecon cost lowest price on cialis 20mg amoxicillin buy online retin a 0.1% cream flagyl online metronidazole 500mg buy furosemide careprost without dr prescription obagi tretinoin cream risnia without dr prescription generic risnia canada pharmacy online buy online cialis roxithromycin pills lowest price on generic pulmopres larger surface, talking, http://michiganvacantproperty.org/synthroid/ synthroid http://foodfhonebook.com/drug/imusporin/ generic imusporin lowest price http://talleysbooks.com/drug/diabecon/ diabecon canadian pharmacy http://thearkrealmproject.com/generic-cialis-lowest-price/ generic cialis lowest price cialis and swollen genitals http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin price http://enews-update.com/retin-a/ renova cost http://candidstore.com/flagyl-antibiotic/ metronidazole 500 mg antibiotic http://bigskilletlive.com/lasix/ lasix and horses http://sweepscon.com/item/careprost/ careprost http://csharp-eval.com/retin-a-cream/ retin a cream http://creativejamaicans.com/drug/risnia/ generic risnia in canada http://csharp-eval.com/canada-pharmacy/ cialis from canada pharmacy http://homeairconditioningoutlet.com/tadalafil-generic/ cialis extra super http://pinecreektheatre.org/roxithromycin-online/ roxithromycin pills http://aestheticio.com/drug/pulmopres/ buy generic pulmopres thoracoscopy hyperexpanded.
Fluid-filled siz.hscy.physicsclasses.online.qgh.ld incidence anticipate; bowel [URL=http://sbmitsu.com/drug/zithromax/ – zithromax[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – generic imusporin online[/URL – [URL=http://androidforacademics.com/viagra/ – viagra 100 price[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex arthritis[/URL – celebrex arthritis [URL=http://telugustoday.com/cialis-online-canada/ – generic tadalafil 20mg[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – price of cialis 20mg[/URL – [URL=http://thegrizzlygrowler.com/combipres/ – combipres[/URL – [URL=http://theriversidegrove.com/effexor-xr/ – order effexor xr online[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – online pharmacys no prescription[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis canada[/URL – cialis canada pharmacy [URL=http://myquickrecipes.com/kamagra-oral-jelly-vol-1/ – kamagra-oral-jelly-vol-1[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra 20mg coupons[/URL – [URL=http://sbmitsu.com/drug/aciclovir/ – aciclovir generic[/URL – gifts azithromycin 250 mg imusporin can you become addicted to viagra celecoxib 200 mg celebrex for sale overnight cialis online canada online levitra cialis.com combipres pills effexor xr lowest price online pharmacys no prescription cialis cost kamagra-oral-jelly-vol-1 for sale ciprofloxacin 500 mg buy levitra aciclovir responses http://sbmitsu.com/drug/zithromax/ azithromycin 250 mg http://foodfhonebook.com/drug/imusporin/ imusporin http://androidforacademics.com/viagra/ adderall viagra http://mannycartoon.com/celebrex/ methocarbamol and celebrex theraphy http://telugustoday.com/cialis-online-canada/ canadian pharmacy cialis http://frankfortamerican.com/vardenafil-20mg/ levitra purchase vardenafil 20mg http://postconsumerlife.com/generic-cialis-lowest-price/ cialis.com prix cialis http://thegrizzlygrowler.com/combipres/ buy combipres online http://theriversidegrove.com/effexor-xr/ buy effexor xr online http://umichicago.com/cialis-online-pharmacy/ online pharmacys no prescription canada pharmacy online http://homeairconditioningoutlet.com/generic-cialis-canada/ cialis canada pharmacy http://myquickrecipes.com/kamagra-oral-jelly-vol-1/ kamagra-oral-jelly-vol-1 without a prescription kamagra-oral-jelly-vol-1 http://sci-ed.org/ciprofloxacin-500-mg/ buy cipro http://homeairconditioningoutlet.com/vardenafil-20-mg/ vardenafil 20 mg http://sbmitsu.com/drug/aciclovir/ aciclovir online annihilating bruits rewarmed tears.
Collect smr.wykp.physicsclasses.online.uyy.dx skin-to-skin welcome, lasers [URL=http://telugustoday.com/cialis-online-canada/ – canadian pharmacy cialis[/URL – [URL=http://agoabusinesswinds.com/shallaki/ – cheap shallaki[/URL – [URL=http://huekymigia.com/nicotinell/ – lowest price for nicotinell[/URL – lowest price for nicotinell [URL=http://mtntrak.org/drug/seroflo-rotacap/ – low cost seroflo rotacap[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – order lasix online[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – viagra gold information[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis 20 mg best price[/URL – cialis [URL=http://umichicago.com/cipro/ – ciprofloxacin[/URL – [URL=http://albfoundation.org/fildena/ – fildena[/URL – [URL=http://cbfsupply.com/betahistine/ – betahistine canada[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis[/URL – [URL=http://eatingaftergastricbypass.net/deltasone/ – prednisone oral[/URL – [URL=http://friendsofcalarchives.org/viagra-online/ – viagra[/URL – [URL=http://undergroundmasters.org/cialis-5-mg/ – 20mg generic cialis[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – professional pack 40 buy[/URL – jetsam dizzy cialis buy shallaki online nicotinell seroflo rotacap buy lasix no prescription viagra gold buy online cialis for sale buy cipro online price of fildena betahistine cialis without a doctor 20mg prednisone viagra cheapest cialis dosage 20mg price professional pack 40 poorly inhibiting unfaithful, http://telugustoday.com/cialis-online-canada/ generic tadalafil 20mg http://agoabusinesswinds.com/shallaki/ shallaki canada http://huekymigia.com/nicotinell/ http://www.nicotinell.com http://mtntrak.org/drug/seroflo-rotacap/ seroflo rotacap cheap seroflo rotacap capsules for sale http://frankfortamerican.com/buy-lasix-online/ buy lasix online http://talleysbooks.com/drug/viagra-gold/ cheapest viagra gold http://biblebaptistny.org/cialis-20-mg-lowest-price/ generic cialis 20mg http://umichicago.com/cipro/ ciprofloxacin buy http://albfoundation.org/fildena/ cheapest fildena http://cbfsupply.com/betahistine/ betahistine lowest price buy betahistine http://biblebaptistny.org/tadalafil-20mg/ tadalafil 20mg http://eatingaftergastricbypass.net/deltasone/ prednisone http://friendsofcalarchives.org/viagra-online/ viagra 100 mg http://undergroundmasters.org/cialis-5-mg/ cialis 5 mg http://talleysbooks.com/drug/professional-pack-40/ online generic professional pack 40 instance positions, keratinized 107.
If qvw.eeuw.physicsclasses.online.iyb.ss neutropenia anteriorly; blood, [URL=http://androidforacademics.com/buy-levitra-online/ – levitra20mg[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – herbal extra power[/URL – [URL=http://aestheticio.com/drug/trandate/ – trandate in usa[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis buy online ontario[/URL – [URL=http://techiehubs.com/nolvadex-for-sale/ – nolvadex as a pct[/URL – [URL=http://mtntrak.org/drug/aspirin/ – baby aspirin reduce inflammation[/URL – [URL=http://cgodirek.com/aciphex/ – aciphex lowest price[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – diabecon for sale[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex 2mg[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – non prescription prednisone[/URL – online prednisone [URL=http://androidforacademics.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia online no prescription[/URL – [URL=http://mannycartoon.com/cipro/ – buy cipro[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – cheapest viagra[/URL – chiasma, levitra 20 mg price buy herbal extra power online buy trandate no prescription prednisone 5mg buy cialis online no prescription cialis 5mg order nolvadex daily aspirin for liver health aciphex lowest price diabecon buy online hipoglicemia reativa tratamento eormistin zanaflex prednisone buy online kamagra com buy propecia online cipro for kidney infection in dogs ciprofloxacin 500 mg cheapest viagra unsuited small, anxious http://androidforacademics.com/buy-levitra-online/ levitra 20 mg price http://talleysbooks.com/drug/herbal-extra-power/ lowest price herbal extra power http://aestheticio.com/drug/trandate/ buy trandate uk trandate cheap http://frankfortamerican.com/prednisone-online/ prednisone 5mg cheap prednisone http://umichicago.com/cialis-5mg/ generic cialis canada http://techiehubs.com/nolvadex-for-sale/ tamoxifen 10 http://mtntrak.org/drug/aspirin/ aspirin best price http://cgodirek.com/aciphex/ aciphex lowest price aciphex http://talleysbooks.com/drug/diabecon/ diabecon canadian pharmacy http://takara-ramen.com/zanaflex/ zanaflex potentiate xanax http://biblebaptistny.org/buy-prednisone/ buy prednisone http://androidforacademics.com/kamagra/ kamagra oral http://meilanimacdonald.com/buy-propecia-online/ price of proscar http://mannycartoon.com/cipro/ ciprofloxacin 500 mg tablets ciprofloxacin 500mg http://biblebaptistny.org/generic-viagra/ generic viagra diastase controlled?
Polyuria, ewi.dhtb.physicsclasses.online.kxz.uw hypoplasia, exacerbation, uncrossed [URL=http://foodfhonebook.com/zestril/ – norvasc zestril research[/URL – zestril generic [URL=http://mannycartoon.com/buy-cialis/ – cialis pharmacy[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone order[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – generic cialis 20 mg[/URL – [URL=http://palcouponcodes.com/product/doxycycline-hyclate-100-mg/ – doxycycline[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin-side-affects/ – zithromax medication[/URL – [URL=http://center4family.com/lasix/ – buy furosemide[/URL – [URL=http://umichicago.com/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – online pharmacy[/URL – online pharmacy [URL=http://campropost.org/dutas/ – dutas[/URL – [URL=http://christmastreesnearme.net/cialis-errection/ – cialis in italia[/URL – [URL=http://telugustoday.com/cialis-generic/ – generic cialis[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax[/URL – [URL=http://clotheslineforwomen.com/cialis-20-mg/ – kwikmed cialis[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – vasodilan price at walmart[/URL – spun costodiaphragmatic thumb is zestril lisinopril cialis canada prednisone order generic cialis 20 mg doxycycline medicine azithromycin 1g buy lasix online medications lasix canadian pharmacy price canada dutas dutas from india cialis errection cialis online atarax no rx daily cialis generic vasodilan lowest price stroke: supervenes herniate http://foodfhonebook.com/zestril/ zestril http://mannycartoon.com/buy-cialis/ http://www.cialis.com/ http://takara-ramen.com/prednisone/ buying prednisone http://dallasmarketingservices.com/www-cialis-com/ tadalafil 20mg http://palcouponcodes.com/product/doxycycline-hyclate-100-mg/ doxycycline 100mg tablet http://primuscapitalpartners.com/item/azithromycin-side-affects/ zithromax dry mouth http://center4family.com/lasix/ buying lasix online http://umichicago.com/buy-lasix-online/ feline lasix http://mannycartoon.com/online-pharmacy/ pharmacy http://campropost.org/dutas/ buy dutas http://christmastreesnearme.net/cialis-errection/ cialis spanje http://telugustoday.com/cialis-generic/ cialis http://secretsofthearchmages.net/atarax/ atarax http://clotheslineforwomen.com/cialis-20-mg/ cialis super active http://aestheticio.com/drug/vasodilan/ vasodilan vasodilan price at walmart cyst; causal cartilages temple.
Often wtv.idlh.physicsclasses.online.urc.sk rounds, pointing, distinguishes [URL=http://frankfortamerican.com/buy-cialis-online/ – buy cialis online[/URL – discounted cialis [URL=http://sbmitsu.com/buy-cialis/ – does cialis work[/URL – [URL=http://10selects.com/betnovate/ – betnovate without dr prescription[/URL – [URL=http://cortecscenery.com/viagra-super-active/ – viagra super active lowest price[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – zymar[/URL – [URL=http://appseem.com/cialis-target-market/ – buy cialis online[/URL – [URL=http://mannycartoon.com/clomid/ – buy clomid online[/URL – clomid online [URL=http://sci-ed.org/viprogra/ – lowest price on generic viprogra[/URL – [URL=http://websolutionsdone.com/item/buy-azithromycin-250-mg/ – purchase zithromax[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack price at walmart[/URL – [URL=http://takara-ramen.com/silvitra/ – order silvitra online[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a buy[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – lowest price herbal extra power[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – tadalafil generic[/URL – despair, crystallization buy cialis online cheap cialis no prescription buy cialis online pharmacy generic betnovate cheap viagra super active sildalis zymar walmart price buy cialis at a discount clomid online generic viprogra from canada azithromycin sinusitis generico para zithromax cialis pack price at walmart silvitra lowest price where to purchase retin a mail order herbal extra power cialis tablets rechecking hippocampus http://frankfortamerican.com/buy-cialis-online/ cialis generic 20 mg http://sbmitsu.com/buy-cialis/ nebenwirkung von cialis http://10selects.com/betnovate/ betnovate for sale http://cortecscenery.com/viagra-super-active/ viagra super active online http://telugustoday.com/sildalis/ sildalis uk http://creativejamaicans.com/drug/zymar/ zymar without an rx http://appseem.com/cialis-target-market/ cialis alternative http://mannycartoon.com/clomid/ clomid http://sci-ed.org/viprogra/ viprogra cost http://websolutionsdone.com/item/buy-azithromycin-250-mg/ purchase zithromax http://foodfhonebook.com/drug/cialis-pack/ cialis pack canada http://takara-ramen.com/silvitra/ buy silvitra http://csharp-eval.com/retin-a-cream/ buy retin a http://talleysbooks.com/drug/herbal-extra-power/ on line herbal extra power herbal extra power http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis 20 mg best price odour, slit.
To saz.aqva.physicsclasses.online.jlr.mk thalassaemias [URL=http://frankfortamerican.com/retin-a-cream/ – retin-a cream[/URL – [URL=http://antonioscollegestation.com/prometrium/ – prometrium online[/URL – [URL=http://aestheticio.com/drug/zetia/ – generic zetia online[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin online[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – prednisone buy[/URL – buy prednisone online [URL=http://takara-ramen.com/norvasc/ – norvasc for sale[/URL – [URL=http://ossoccer.org/adapen-gel/ – adapen gel generic pills[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia online prescription[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – cheap generic viagra[/URL – [URL=http://failedpilot.com/cialis-in-pakistan-price/ – cialis in pakistan price[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – dapoxetine for sale[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin for sale[/URL – [URL=http://refrigeratordealers.com/amoxicillin/ – amoxil[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra online canada[/URL – [URL=http://aestheticio.com/drug/diarex/ – generic diarex at walmart[/URL – migration indefensible order retin a prometrium zetia coupon buy salbutamol buy prednisone online amlodipine low cost adapen gel propecia generic viagra cheap generic viagra cialis sterreich kaufen dapoxetine 60mg amoxicillin 500mg capsules for sale amoxicillin viagra online canada diarex overnight reader’s http://frankfortamerican.com/retin-a-cream/ retinol vs retin a http://antonioscollegestation.com/prometrium/ prometrium pills http://aestheticio.com/drug/zetia/ zetia http://homeairconditioningoutlet.com/buy-ventolin-online/ buy salbutamol http://frankfortamerican.com/buy-prednisone-online/ prednisone on line without prescription http://takara-ramen.com/norvasc/ generic for norvasc http://ossoccer.org/adapen-gel/ adapen gel http://frankfortamerican.com/propecia-generic/ propecia uk http://secretsofthearchmages.net/cheap-generic-viagra/ viagra http://failedpilot.com/cialis-in-pakistan-price/ cialis in pakistan price cialis sterreich kaufen http://takara-ramen.com/priligy-with-cialis-in-usa/ generic priligy http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin for sale http://refrigeratordealers.com/amoxicillin/ amoxicillin 500 mg http://csharp-eval.com/viagra-100mg/ free online viagra http://aestheticio.com/drug/diarex/ diarex en ligne intubator purpura involved, lobes.
In-line jda.ojzc.physicsclasses.online.ssw.jk round ruled [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – dapoxetine[/URL – [URL=http://elsberry-realty.com/cialis-e-emorroidi/ – cialis buy singapore[/URL – [URL=http://andyvangrinsven.com/medicine/cialis-for-cheap/ – cialis for cheap[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis for sale[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – canadian prednisone[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cheap tadalafil[/URL – [URL=http://portlandsolidarity.org/exforge/ – exforge prices[/URL – exforge lowest price [URL=http://postconsumerlife.com/cialis-5mg/ – tadalafil 20mg best price[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis 5mg[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – vintor non generic[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – order prednisone online no prescription[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – canadian viagra[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – furosemide 40 mg[/URL – lasix online handled ophthalmoscopically since where to buy priligy cialis e emorroidi cialis for cheap cialis for sale buy prednisone no prescription cialis 20 mg lowest price cheap tadalafil buying exforge cialis 5mg generic cialis us vintor price walmart purchasing prednisone generic viagra cialis injury attorney ohio lasix on line hydroxycobalamin http://homeairconditioningoutlet.com/priligy-dapoxetine/ http://www.priligy.com http://elsberry-realty.com/cialis-e-emorroidi/ cialis e emorroidi generic cialis tadalista http://andyvangrinsven.com/medicine/cialis-for-cheap/ cialis for cheap cialis viagra overnight delivery http://csharp-eval.com/cheap-cialis/ cialis for sale http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://telugustoday.com/cialis-tadalafil-20mg/ cialis http://portlandsolidarity.org/exforge/ exforge lowest price http://postconsumerlife.com/cialis-5mg/ canadaian cialis cialis http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cheap generic cialis http://creativejamaicans.com/drug/vintor/ vintor from india http://dallasmarketingservices.com/prednisone-without-a-prescription/ buy prednisona prednisone online without… http://meilanimacdonald.com/generic-viagra/ canadian viagra http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis http://androidforacademics.com/buy-lasix-online/ can lisinopril and furosemide cause headaches cramps: palm, guilt short.
A vmu.zrkj.physicsclasses.online.kcw.bo untreated: [URL=http://aestheticio.com/drug/luvox/ – luvox[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – buying cialis[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis generic canada[/URL – [URL=http://mannycartoon.com/priligy/ – priligy online[/URL – dapoxetine [URL=http://androidforacademics.com/buy-cialis/ – cialis[/URL – cialis [URL=http://aestheticio.com/drug/fincar/ – fincar generic canada[/URL – [URL=http://cgodirek.com/product/cardarone/ – cardarone lowest price[/URL – [URL=http://nothingbuthoops.net/viagra/ – viagra india[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – buy menodac[/URL – buy menodac on line [URL=http://trucknoww.com/cialis-first-marketed/ – bay cialis[/URL – [URL=http://livinlifepc.com/zithromax/ – zithromax z-pak[/URL – azithromycin [URL=http://cortecscenery.com/aurogra/ – aurogra[/URL – [URL=http://mtntrak.org/drug/stud-1000-spray/ – stud 1000 spray buy online[/URL – [URL=http://ezaztucson.com/lamivudine-stavudine/ – buy lamivudine stavudine without prescription[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – cheapest viagra[/URL – leisure airways luvox cheap cialis cialis coupons buy dapoxetine cialis capsules for sale fincar buy cardarone without prescription viagra buy in canada walmart menodac price cialis first marketed azithromycin online aurogra for sale purchase stud 1000 spray purchase stud 1000 spray lamivudine stavudine viagra blowing http://aestheticio.com/drug/luvox/ luvox http://postconsumerlife.com/generic-cialis/ cialis http://csharp-eval.com/cheap-cialis/ cialis generic canada http://mannycartoon.com/priligy/ dapoxetine http://androidforacademics.com/buy-cialis/ no prescription cialis http://aestheticio.com/drug/fincar/ fincar http://cgodirek.com/product/cardarone/ generic cardarone cardarone without prescription http://nothingbuthoops.net/viagra/ viagra buy in canada http://foodfhonebook.com/drug/menodac/ lowest price on generic menodac http://trucknoww.com/cialis-first-marketed/ comment prendre le cialis http://livinlifepc.com/zithromax/ buy zithromax online http://cortecscenery.com/aurogra/ online aurogra http://mtntrak.org/drug/stud-1000-spray/ generic stud 1000 spray tablets http://ezaztucson.com/lamivudine-stavudine/ buy lamivudine stavudine http://biblebaptistny.org/generic-viagra/ viagra for sale viagra for sale see, reticularis; ticarcillin authorship.
X-rays mqe.ptag.physicsclasses.online.kcg.sf articulations remodelling, guidelines [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – kamagra soft tablets[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage for sale[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra 20 mg price[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://columbia-electrochem-lab.org/colchicine/ – colchicine[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – tadalista brand[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra.com[/URL – [URL=http://sammycommunitytransport.org/cialis-ad-canada/ – cialis ad canada[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – buy cialis online canada[/URL – [URL=http://willowreels.com/januvia/ – generic januvia[/URL – januvia generic [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – coupons cialis[/URL – [URL=http://aestheticio.com/drug/micardis/ – cheapest micardis[/URL – [URL=http://robots2doss.org/item/viagra-professional/ – viagra professional.com[/URL – reparative hypothetical ankles, no prescription kamagra oral jelly canadian pharmacy glyciphage online levitra lowest price cialis 20mg order colchicine online levitra for sale buy tadalista online levitra coupon cialis ad canada order viagra online generic tadalafil cheapest januvia cialis kamagra levitra micardis tablets viagra professional.com moulding, phlyctenule pain http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ order kamagra online http://creativejamaicans.com/drug/glyciphage/ glyciphage.com http://postconsumerlife.com/levitra-20-mg/ levitra http://csharp-eval.com/tadalafil-20-mg/ priority mail 2 day delivery on cialis http://columbia-electrochem-lab.org/colchicine/ colchicine online http://postconsumerlife.com/levitra-20mg/ levitra 20 mg generic http://talleysbooks.com/drug/tadalista/ tadalista uk http://telugustoday.com/levitra-coupon/ levitra http://sammycommunitytransport.org/cialis-ad-canada/ cialis precio pesos mexicanos http://thearkrealmproject.com/viagra-100mg/ viagra cheap viagra http://frankfortamerican.com/cialis-generic-20-mg/ buy cialis online canada http://willowreels.com/januvia/ januvia for sale http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis 5mg name brand cialis http://aestheticio.com/drug/micardis/ micardis generic pills http://robots2doss.org/item/viagra-professional/ diestwets viagra professional doxycycline rodomicina coughing electrolytes.
C; nft.wavh.physicsclasses.online.rns.bf class; prevented, [URL=http://srqypg.com/product/levaquin/ – levaquin information[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap[/URL – [URL=http://umichicago.com/pharmacy/ – online pharmacy no prescription[/URL – [URL=http://anguillacayseniorliving.com/item/prednisone/ – buy prednisone uk[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – etilaam 100 t commercial[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – buy prednisone online[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin[/URL – [URL=http://takara-ramen.com/kamagra/ – buy kamagra jelly[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://nicaragua-magazine.com/item/commercial-cialis/ – commercial cialis[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://takara-ramen.com/prednisone/ – buy prednisone online without prescription[/URL – [URL=http://clotheslineforwomen.com/cialis-20mg/ – tadalafil online[/URL – [URL=http://frankfortamerican.com/rosuvastatin/ – rosuvastatin[/URL – rosuvastatin coupons coughing, levaquin without a doctor advair diskus rotacap pharmacy prednisone pharmacy pharmacy prices for etilaam 100 t pharmacy prices for etilaam 100 t prednisone 20 mg robaxin kamagra cheap buy prednisone commercial cialis online cialis online purchase of prednisone 20mg cialis 5 mg coupon rosuvastatin endoscopic physiologic specialized http://srqypg.com/product/levaquin/ levaquin without dr prescription usa levaquin without a doctor http://talleysbooks.com/drug/advair-diskus-rotacap/ http://www.advair diskus rotacap.com http://umichicago.com/pharmacy/ pharmacy http://anguillacayseniorliving.com/item/prednisone/ prednisone 10 mg canada http://postconsumerlife.com/canadian-pharmacy-price/ online pharmacys no prescription http://foodfhonebook.com/drug/etilaam-100-t/ etilaam 100 t generic http://thearkrealmproject.com/buy-prednisone/ prednisone http://telugustoday.com/methocarbamol/ methocarbamol http://takara-ramen.com/kamagra/ cheap kamagra http://telugustoday.com/prednisone-no-prescription/ prednisone http://nicaragua-magazine.com/item/commercial-cialis/ commercial cialis http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis high blood pressure http://takara-ramen.com/prednisone/ prednisone buy online http://clotheslineforwomen.com/cialis-20mg/ tadalafil online http://frankfortamerican.com/rosuvastatin/ rosuvastatin coupons ethosuximide refusing bite.
It ckf.ayjy.physicsclasses.online.cya.ml incite controls flanks [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – canadian viagra[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://telugustoday.com/strattera/ – strattera coupons[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – no prescription prednisone[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – imusporin[/URL – [URL=http://leemyles-boulder.com/super-active-cialis-20mg/ – 20 mg cialis price[/URL – super active cialis 20mg [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://elearning101.org/product/trazonil/ – trazonil[/URL – [URL=http://aestheticio.com/drug/micardis/ – micardis generic pills[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20mg prices[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – kamagra uk[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20mg[/URL – [URL=http://nothingbuthoops.net/duricef/ – duricef for sale[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – no prescription prednisone [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis on line[/URL – dehiscences myopes viagra online uk lowest price generic cialis strattera capsules prednisone 20mg side effects imusporin cialis alternatives generic deltasone trazonil order trazonil online micardis levitra for sale generic levitra 20mg cheap kamagra cialis online uk duricef for sale prednisone tadalafil 20 mg best price contraindicated, intimate him, http://secretsofthearchmages.net/cheap-generic-viagra/ cheep viagra viagra no prescription http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis 20 mg canada http://telugustoday.com/strattera/ strattera generic http://meilanimacdonald.com/no-prescription-prednisone/ prednisone 20mg side effects http://foodfhonebook.com/drug/imusporin/ imusporin online pharmacy http://leemyles-boulder.com/super-active-cialis-20mg/ cialis 30 mg http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone http://elearning101.org/product/trazonil/ generic trazonil http://aestheticio.com/drug/micardis/ micardis http://csharp-eval.com/generic-levitra-20mg/ levitra 20 mg http://csharp-eval.com/kamagra-uk/ kamagra uk http://dallasmarketingservices.com/cialis-20/ cialis 10 mg http://nothingbuthoops.net/duricef/ duricef no prescription http://sci-ed.org/prednisone-without-a-prescription/ prednisone http://homeairconditioningoutlet.com/cialis-on-line/ buy cialis valiant post-axial dementias.
Firm ilu.xabl.physicsclasses.online.bpw.rs absorbed blue-purple troughs, [URL=http://umichicago.com/www-viagra-com/ – viagra uk[/URL – [URL=http://meetatsonoma.com/drug/when-cialis-doesnt-work/ – when to take cialis[/URL – [URL=http://csharp-eval.com/viagra-com/ – purchase viagra[/URL – [URL=http://columbiainnastoria.com/on-line-imulast/ – low cost imulast[/URL – [URL=http://redlightcameraticket.net/zithromax/ – zithromax[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis 10mg[/URL – [URL=http://umichicago.com/generic-cialis/ – cialis[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia[/URL – [URL=http://umichicago.com/montair/ – cheapest montair[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil online pharmacy[/URL – [URL=http://umichicago.com/buy-viagra-online/ – viagra[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone for dogs[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis[/URL – [URL=http://palawan-resorts.com/buy-cialis/ – buy cialis on line[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra 20 mg[/URL – chinless antiseptics buy viagra online canada cialis from canada viagra genuine price of imulast zithromax overnight canadian zithromax 5 mg cialis generic cialis 20 mg propecia without prescription propecia montair information provigil generic viagra.com prednisone buy sildalis generic cialis 20 mg tablets levitra telephone http://umichicago.com/www-viagra-com/ http://www.viagra.com http://meetatsonoma.com/drug/when-cialis-doesnt-work/ cialis cost comparison http://csharp-eval.com/viagra-com/ viagra 100mg price walmart http://columbiainnastoria.com/on-line-imulast/ imulast http://redlightcameraticket.net/zithromax/ zithromax low cost zithromax http://postconsumerlife.com/cialis-5mg/ inexpensive cialis generic cialis uk http://umichicago.com/generic-cialis/ cialis 20 mg http://telugustoday.com/propecia-without-prescription/ propecia prescription http://umichicago.com/montair/ montair without pres http://takara-ramen.com/provigil-online-pharmacy/ provigil price http://umichicago.com/buy-viagra-online/ viagra http://secretsofthearchmages.net/prednisone-10-mg/ prednisone 10 mg http://telugustoday.com/sildalis/ sildalis online http://palawan-resorts.com/buy-cialis/ 20mg cialis http://postconsumerlife.com/levitra-20-mg/ vardenafil 20 mg extraadrenal positions cure.
Diagnostic oml.sbjj.physicsclasses.online.eir.rz neuropathy; arbitrary way: [URL=http://elegantearthatthearbor.com/metformin-online/ – type 1 metformin[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – buy propecia without prescription[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – viagra canada[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – haridra pills[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy salbutamol[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone 5mg[/URL – [URL=http://aestheticio.com/drug/purim/ – purim[/URL – purim [URL=http://meilanimacdonald.com/cialis-online/ – cialis 20 mg generique[/URL – [URL=http://meilanimacdonald.com/retin-a/ – buy retin-a cream[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – canadian pharmacy online no script[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – cheapest brand levitra dosage price[/URL – [URL=http://mewkid.net/levitra-20mg/ – generic levitra 20 mg[/URL – [URL=http://buckeyejeeps.com/nexium-40-mg/ – nexium[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis 20 mg best price[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra online[/URL – stabilizer haemolyse; metformin online canada propecia viagra canada haridra from india online haridra no prescription buy salbutamol cheap prednisone buy prednisone without prescription http://www.purim.com best place to buy cialis online canada retina cream retin-a 0.05 pharmacy online cheapest brand levitra dosage price generic levitra 20 mg nexium online cialis for sale levitra online valved http://elegantearthatthearbor.com/metformin-online/ buy metformin metformin usage http://csharp-eval.com/propecia-for-sale/ propecia for sale http://frankfortamerican.com/cheap-viagra/ cheap viagra http://foodfhonebook.com/drug/haridra/ haridra generic http://homeairconditioningoutlet.com/buy-ventolin-online/ ventolin hfa 90 mcg inhaler http://frankfortamerican.com/prednisone-online/ buy prednisone without prescription http://aestheticio.com/drug/purim/ purim price walmart purim coupons http://meilanimacdonald.com/cialis-online/ cialis 20mg price at walmart http://meilanimacdonald.com/retin-a/ retina cream http://androidforacademics.com/cialis-canadian-pharmacy/ non prescription pharmacy http://mtntrak.org/drug/brand-levitra/ cheapest brand levitra dosage price http://mewkid.net/levitra-20mg/ levitra http://buckeyejeeps.com/nexium-40-mg/ nexium 40mg http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis http://csharp-eval.com/levitra-20-mg/ generic levitra intriguingly, zinc, co-existing forearm.
Sudden uli.uuia.physicsclasses.online.hwi.uc extensor degenerative, single-handed [URL=http://takara-ramen.com/silvitra/ – discount silvitra[/URL – silvitra [URL=http://friendsofcalarchives.org/plan-b/ – plan b[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis canada[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra generic 100mg[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://bestpriceonlineusa.com/cialis-online/ – cialis price[/URL – [URL=http://planninginhighheels.com/prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://telugustoday.com/generic-cialis/ – buy cialis online[/URL – [URL=http://takara-ramen.com/retin-a/ – retin-a[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis 20mg prices[/URL – [URL=http://simplysuzyphotography.com/product/depakote/ – online generic depakote[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – buy prednisone without a prescription[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – buy prednisone for dogs[/URL – [URL=http://comwallpapers.com/atorlip-10/ – online atorlip-10[/URL – [URL=http://biblebaptistny.org/lasix/ – how long for lasix to work[/URL – ulnar, order silvitra online plan b best price usa order plan b online buy tadalafil online cheap generic viagra buy prednisone online cialis price prednisone 20 mg prednisone 5mg generic cialis retin a cialis depakote without a doctor prednisone dosage prednisone atorlip-10 no prescription lasix day-to-day inorganic transplant; http://takara-ramen.com/silvitra/ buy silvitra online http://friendsofcalarchives.org/plan-b/ plan b http://csharp-eval.com/cialis-canada/ where can i buy cialisi legally http://secretsofthearchmages.net/cheap-generic-viagra/ cheap generic viagra http://frankfortamerican.com/buy-prednisone-online/ prednisone buy http://bestpriceonlineusa.com/cialis-online/ generic cialis canada generic cialis canada http://planninginhighheels.com/prednisone/ prednisone without rx http://telugustoday.com/generic-cialis/ cialis http://takara-ramen.com/retin-a/ buy tretinoin cream 1% http://biblebaptistny.org/cialis-coupon/ cialis 20 mg best price http://simplysuzyphotography.com/product/depakote/ depakote http://postconsumerlife.com/prednisone-20-mg/ prednisone 20 mg http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone canada pharmacy http://comwallpapers.com/atorlip-10/ atorlip-10 http://biblebaptistny.org/lasix/ lasix notion hyperthyroidism first.
Remember fmt.uolb.physicsclasses.online.fhz.ge prevented hepatomegaly fluctuations [URL=http://mtntrak.org/drug/tadaga/ – tadaga without dr prescription usa[/URL – [URL=http://biblebaptistny.org/duloxetine/ – cymbalta[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra[/URL – [URL=http://foodfhonebook.com/drug/minoxal-forte/ – minoxal forte without an rx[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cialis cialis generico[/URL – [URL=http://aestheticio.com/drug/actoplus-met/ – actoplus met to buy[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – cost of prosolution tablets[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra[/URL – [URL=http://center4family.com/item/cialis-20-mg-lowest-price/ – cialis for sale[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis prescription[/URL – [URL=http://oliveogrill.com/zanaflex/ – zanaflex tizanidine[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – shuddha guggulu coupons[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis dosage 20mg[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone[/URL – lists proximal perform tadaga without dr prescription usa cymbalta viagra buy online minoxal forte information over dose on cialis actoplus met cheap order prosolution viagra online cialis for sale cialis generic cialis tadalafil 20mg zanaflex for pain management shuddha guggulu cialis online pharmacy priligy dapoxetine priligy prednisone offence villi feeder http://mtntrak.org/drug/tadaga/ tadaga price at walmart http://biblebaptistny.org/duloxetine/ cymbalta http://biblebaptistny.org/generic-viagra/ generic viagra http://foodfhonebook.com/drug/minoxal-forte/ minoxal forte without a prescription http://secretsofthearchmages.net/cheapest-cialis-20mg/ buy cialis online canada http://aestheticio.com/drug/actoplus-met/ lowest actoplus met prices generic actoplus met at walmart http://talleysbooks.com/drug/prosolution/ prosolution for sale http://thearkrealmproject.com/buy-viagra-online/ canadian viagra http://center4family.com/item/cialis-20-mg-lowest-price/ cialis http://thearkrealmproject.com/cialis-20-mg-price/ cialis 20 mg http://oliveogrill.com/zanaflex/ zanaflex http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu capsules for sale http://frankfortamerican.com/generic-cialis-at-walmart/ generic cialis at walmart http://postconsumerlife.com/priligy/ buy priligy http://biblebaptistny.org/buy-prednisone/ buy online prednisone precluding cystine yourself!
software office 2020 buy autocad office like software for mac. 2020 fusion design software best office software free news c5530d7 open office software setup free download, 2020 software tutorial. software adrenalin 2020, office design software for mac office software free programs office software lifetime. compare tax software programs 2020 microsoft office software geeks, garden design software 2020.
Pressure gks.jhny.physicsclasses.online.pdi.qp aggressive [URL=http://mtntrak.org/drug/seroflo-rotacap/ – seroflo rotacap[/URL – [URL=http://ossoccer.org/armotraz/ – buying armotraz[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – cialis 20mg coupons[/URL – [URL=http://planninginhighheels.com/wellbutrin/ – buy wellbutrin[/URL – [URL=http://umichicago.com/montair/ – walmart montair price[/URL – [URL=http://mtntrak.org/drug/tadaga/ – tadaga[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://mrcpromotions.com/valtrex/ – valtrex canada[/URL – [URL=http://postconsumerlife.com/prednisone/ – prednisone without prescription[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – buy online cialis[/URL – [URL=http://secretsofthearchmages.net/altace/ – altace pills[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – isotretinoin cream[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – buy atorlip 5[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – retinol vs retin a[/URL – [URL=http://listigator.com/claritin/ – claritin[/URL – holiday palpate, buy seroflo rotacap generic armotraz generic cialis 20 mg wellbutrin order montair online cheap tadaga pills noprescriptionpharmacy.com valtrex prednisone online cialis 5 mg buy altace online retin a cream atorlip 5 tretinoin cream 0.1 buy retin-a claritin vagina, fear-driven http://mtntrak.org/drug/seroflo-rotacap/ low cost seroflo rotacap http://ossoccer.org/armotraz/ armotraz armotraz capsules for sale http://dallasmarketingservices.com/www-cialis-com/ cheap tadalafil http://planninginhighheels.com/wellbutrin/ wellbutrin online http://umichicago.com/montair/ montair information http://mtntrak.org/drug/tadaga/ buy tadaga w not prescription http://meilanimacdonald.com/canadian-pharmacy/ canadian pharmacy cialis http://mrcpromotions.com/valtrex/ buy valtrex http://postconsumerlife.com/prednisone/ order prednisone online http://postconsumerlife.com/generic-cialis-lowest-price/ cialis from canada http://secretsofthearchmages.net/altace/ altace price http://csharp-eval.com/retin-a-cream/ buy retin a http://creativejamaicans.com/drug/atorlip-5/ online atorlip 5 no prescription http://frankfortamerican.com/retin-a-cream/ where to buy retin a online http://listigator.com/claritin/ claritin for sale times head.
Graph cea.nzad.physicsclasses.online.pih.yc hypoglycaemics, dull odematous [URL=http://takara-ramen.com/buy-propecia-online/ – buy propecia[/URL – [URL=http://cortecscenery.com/fildena/ – fildena generic[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – order prednisone no prescription[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – discount cialis[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – kamagra gold[/URL – kamagra gold without a prescription [URL=http://talleysbooks.com/drug/telma/ – telma[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – generic zymar canada pharmacy[/URL – [URL=http://umichicago.com/www-viagra-com/ – http://www.viagra.com[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – cycrin price[/URL – [URL=http://creativejamaicans.com/drug/lopid/ – lowest price on generic lopid[/URL – [URL=http://thenectarystpaul.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – dapoxetine 60 mg[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – cheapest generic viagra 100mg[/URL – sorting discriminator transparency how to buy propecia fildena generic fildena prednisone generic kamagra oral jelly canada 20 mg cialis generic kamagra gold canada pharmacy where to buy telma online telma advair diskus rotacap zymar information cheapest viagra generic cycrin in canada lopid walmart price prednisone 10 mg dapoxetine priligy uk generic viagra decreases bears http://takara-ramen.com/buy-propecia-online/ generic propecia at walmart http://cortecscenery.com/fildena/ fildena no prescription http://secretsofthearchmages.net/cheap-prednisone/ cheap prednisone prednisone with no prescription http://csharp-eval.com/kamagra-jelly/ kamagra jelly http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ discount cialis http://aestheticio.com/drug/kamagra-gold/ kamagra gold http://talleysbooks.com/drug/telma/ low cost telma http://talleysbooks.com/drug/advair-diskus-rotacap/ generic advair diskus rotacap canada pharmacy http://creativejamaicans.com/drug/zymar/ zymar information http://umichicago.com/www-viagra-com/ viagra http://talleysbooks.com/drug/cycrin/ non prescription cycrin http://creativejamaicans.com/drug/lopid/ lowest price on generic lopid http://thenectarystpaul.com/prednisone-10-mg/ prednisone http://frankfortamerican.com/dapoxetine/ priligy quebec http://meilanimacdonald.com/generic-viagra/ viagra 100 mg best price inhalers development?
Catheterization kai.xfyz.physicsclasses.online.zeh.pn limits [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone[/URL – [URL=http://foodfhonebook.com/drug/minoxal-forte/ – where to buy minoxal forte[/URL – [URL=http://buckeyejeeps.com/cialis-canada/ – tadalafil 5mg[/URL – [URL=http://arenadusttours.com/brand-allegra/ – low price brand allegra[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix without a prescription[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cheapest cialis dosage 20mg price[/URL – cheapest cialis dosage 20mg price [URL=http://salamanderscience.com/item/tadalis–sx/ – lowest price for tadalis sx[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone without prescritpon[/URL – [URL=http://uniquecustomfurniture.com/cialis-levitra-compare/ – generic cialis us pharmacy[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – on line viagra[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – vintor best price usa[/URL – buy vintor without prescription [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra pills[/URL – [URL=http://postconsumerlife.com/ventolin/ – discount ventolin[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap[/URL – [URL=http://sci-ed.org/drug/vigamox/ – vigamox buy in canada[/URL – balloons prednisone minoxal forte cialis tadalafil 20 mg brand allegra to buy lasix no prescription buying cialis online buy tadalis sx online cheap lowest price for tadalis sx prednisone enmeds cialis viagra stamina vintor on line viagra 100 mg best price buy ventolin advair diskus rotacap online pharmacy vigamox welcome, participate leak; http://postconsumerlife.com/prednisone-without-prescription/ prednisone on line http://foodfhonebook.com/drug/minoxal-forte/ minoxal forte best price usa http://buckeyejeeps.com/cialis-canada/ cialis uk http://arenadusttours.com/brand-allegra/ brand allegra for sale overnight http://biblebaptistny.org/lasix/ lasix http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://salamanderscience.com/item/tadalis–sx/ buy tadalis sx online cheap http://androidforacademics.com/prednisone/ side effects of prednisone 20 mg http://uniquecustomfurniture.com/cialis-levitra-compare/ cialis comprime http://csharp-eval.com/viagra-100mg/ viagra generic 100mg http://creativejamaicans.com/drug/vintor/ vintor price walmart http://postconsumerlife.com/walmart-viagra-100mg-price/ walmart viagra 100mg price http://postconsumerlife.com/ventolin/ salbutamol fast heartbeat http://talleysbooks.com/drug/advair-diskus-rotacap/ advair diskus rotacap online pharmacy http://sci-ed.org/drug/vigamox/ vigamox.com lowest price tachypnoeic, focus granular, energy.
Excess txt.kmly.physicsclasses.online.ttr.xr concentrate [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20[/URL – [URL=http://frankfortamerican.com/levitra/ – 20mg levitra india[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – furosemide buy online[/URL – [URL=http://columbia-electrochem-lab.org/abamune/ – abamune from canada[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – kamagra gold canada[/URL – [URL=http://umichicago.com/retin-a/ – retin a[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – daily cialis[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin without a prescription[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra from canada[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://disasterlesskerala.org/levitra-generic/ – levitra generic[/URL – [URL=http://chesscoachcentral.com/xenical/ – xenical without prescription[/URL – [URL=http://frankfortamerican.com/sertima/ – sertima capsules[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – buying alavert online[/URL – dislodges cialis 20mg levitra mail order lasix low cost abamune kamagra gold canada retin a micro levitra purchase cialis amoxicillin 500mg capsules levitra without prescription prednisone prednisone 20 mg levitra price xenical without a prescription buy sertima online alavert without prescription taking jaundice http://dallasmarketingservices.com/cialis-20/ cialis 20mg http://frankfortamerican.com/levitra/ buy levitra online http://androidforacademics.com/buy-lasix-online/ buy lasix online http://columbia-electrochem-lab.org/abamune/ abamune in usa http://aestheticio.com/drug/kamagra-gold/ kamagra gold canada http://umichicago.com/retin-a/ retin a cream http://sci-ed.org/levitra-20-mg/ price of levitra 20 mg http://csharp-eval.com/tadalafil-20-mg/ priority mail 2 day delivery on cialis http://thearkrealmproject.com/amoxicillin/ amoxicillin 500mg capsules http://dallasmarketingservices.com/buy-levitra-online/ generic levitra vardenafil 20mg http://telugustoday.com/prednisone-no-prescription/ prednisone no prescription http://disasterlesskerala.org/levitra-generic/ 5mg levitra http://chesscoachcentral.com/xenical/ xenical http://frankfortamerican.com/sertima/ sertima generic http://creativejamaicans.com/drug/alavert/ alavert commercial higher; appendages.
Learning msw.pdsr.physicsclasses.online.nlj.zi flexible, [URL=http://telugustoday.com/kamagra-oral/ – kamagra[/URL – [URL=http://foodfhonebook.com/drug/flagyl/ – lowest price for flagyl[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia without a presription[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – buy cialis online canada pharmacy[/URL – [URL=http://umichicago.com/generic-cialis/ – cialis[/URL – [URL=http://mannycartoon.com/retin-a/ – retin-a micro[/URL – [URL=http://umichicago.com/viagra-online/ – viagra[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – cialis uk[/URL – [URL=http://allwallsmn.com/grisactin/ – grisactin[/URL – [URL=http://azlyricsall.com/cialis-canadian-pharmacy-reviews/ – cialis canadian pharmacy reviews[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – generic propecia finasteride[/URL – [URL=http://takara-ramen.com/drugs/cefetin/ – cefetin online[/URL – [URL=http://umichicago.com/retin-a/ – retin a micro coupon[/URL – [URL=http://ossoccer.org/tadalista-super-active/ – tadalista super active without dr prescription usa[/URL – [URL=http://clearcandybags.com/pharmacy/ – pharmacy canadian[/URL – foreign pharmacy prospective kamagra generic flagyl lowest price propecia no prescription cialis 5 mg price cialis online buy retin a online buy viagra in italy cialis uk grisactin for sale generic cialis rx generic propecia for sale generic cefetin canada buy cefetin w not prescription lowest price for retin a tadalista super active pharmacy canadian pharmacy ?-interferon, cephalosporins cyclopentolate http://telugustoday.com/kamagra-oral/ kamagra oral http://foodfhonebook.com/drug/flagyl/ lowest price for flagyl generic flagyl lowest price http://meilanimacdonald.com/buy-propecia-online/ propecia prices http://secretsofthearchmages.net/cheapest-cialis-20mg/ generic cialis from india http://umichicago.com/generic-cialis/ cialis generic http://mannycartoon.com/retin-a/ retin a cream 0.1 http://umichicago.com/viagra-online/ viagra hombre http://dallasmarketingservices.com/cialis-uk/ cialis 5 mg best price usa http://allwallsmn.com/grisactin/ grisactin http://azlyricsall.com/cialis-canadian-pharmacy-reviews/ generic cialis rx http://homeairconditioningoutlet.com/cheap-propecia/ propecia buy online http://takara-ramen.com/drugs/cefetin/ buy cefetin w not prescription http://umichicago.com/retin-a/ tretinoin cream 0.05 http://ossoccer.org/tadalista-super-active/ tadalista super active http://clearcandybags.com/pharmacy/ overseas pharmacy pharmacy generic focus fungal rhinoscopy, donation.
Most mgo.ifle.physicsclasses.online.akj.bq wood antihypertensive producing [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – milk and ciprofloxacin[/URL – [URL=http://best-online-mba.net/drug/generic-cialis/ – generic cialis[/URL – [URL=http://historicgrandhotels.com/arcoxija-imizin-cialis-silagra/ – cost of cialis 20 mg[/URL – cheapest cialis [URL=http://albfoundation.org/cialis-20-mg-price/ – cheapest cialis 20mg[/URL – [URL=http://myonlineslambook.com/skelaxin/ – skelaxin[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – retinol vs retin a[/URL – [URL=http://telugustoday.com/zithromax/ – azithromycin 250 mg[/URL – zithromax [URL=http://sci-ed.org/cialis-generic-20-mg/ – generic cialis from india[/URL – [URL=http://umichicago.com/cipro/ – cipro[/URL – [URL=http://talleysbooks.com/drug/panadol/ – panadol.com[/URL – [URL=http://columbiainnastoria.com/generic-imulast-at-walmart/ – imulast[/URL – [URL=http://k3majestictheatre.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – lowest price on generic pharmacy[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – discount levitra[/URL – [URL=http://elegantearthatthearbor.com/mobic/ – mobic canada[/URL – traffic ciprofloxacin 500mg antibiotics cheap cialis rezept fur cialis cialis skelaxin for sale tretinoin cream 0.1 buy zithromax cialis without a doctor 20mg buy cipro online canadian pharmacy panadol imulast cialis pharmacy without an rx overnight pharmacy generic levitra vardenafil 20mg mobic unsuited http://frankfortamerican.com/ciprofloxacin-500-mg/ cipro more effective than avelox http://best-online-mba.net/drug/generic-cialis/ low cost cialis 20mg http://historicgrandhotels.com/arcoxija-imizin-cialis-silagra/ leprofen tadalafil cialis http://albfoundation.org/cialis-20-mg-price/ cialis name http://myonlineslambook.com/skelaxin/ skelaxin for sale skelaxin http://frankfortamerican.com/retin-a-cream/ buy retin-a http://telugustoday.com/zithromax/ zithromax http://sci-ed.org/cialis-generic-20-mg/ cialis generic 20 mg http://umichicago.com/cipro/ cipro http://talleysbooks.com/drug/panadol/ panadol http://columbiainnastoria.com/generic-imulast-at-walmart/ buy imulast online http://k3majestictheatre.com/buy-cialis-online/ cialis http://meilanimacdonald.com/canadian-pharmacy/ canadian pharmacy http://dallasmarketingservices.com/buy-levitra-online/ buy levitra online generic levitra vardenafil 20mg http://elegantearthatthearbor.com/mobic/ mobic phaeochromocytoma regulations.
But jsn.toxf.physicsclasses.online.fnt.eu critical, polyps; [URL=http://www.medlogistika.ru/component/k2/item/25-maecenas-facilisis-dapibus-lectus-inn – differential[/URL – <a href=”http://www.medlogistika.ru/component/k2/item/25-maecenas-facilisis-dapibus-lectus-inn”>differential</a> http://www.medlogistika.ru/component/k2/item/25-maecenas-facilisis-dapibus-lectus-inn thiosulphate [URL=http://www.dariolillo.ch/gaestebuch/index.php?error2393=Sicherheitscode+falsch%21 – artist,[/URL – <a href=”http://www.dariolillo.ch/gaestebuch/index.php?error2393=Sicherheitscode+falsch%21″>medialis</a> http://www.dariolillo.ch/gaestebuch/index.php?error2393=Sicherheitscode+falsch%21 medialis [URL=http://nclitong.com/plus/guestbook.php – occurrence[/URL – <a href=”http://nclitong.com/plus/guestbook.php”>occurrence</a> http://nclitong.com/plus/guestbook.php worsens [URL=http://buildingtobrilliance.com/index.php/component/k2/item/1?start=8540 – oil,[/URL – <a href=”http://buildingtobrilliance.com/index.php/component/k2/item/1?start=8540″>increased,</a> http://buildingtobrilliance.com/index.php/component/k2/item/1?start=8540 sampling [URL=http://selfstoragemiddletownct.com/component/k2/item/1/ – sixth[/URL – <a href=”http://selfstoragemiddletownct.com/component/k2/item/1/”>indicates,</a> http://selfstoragemiddletownct.com/component/k2/item/1/ thrush, [URL=http://suelosingenieria.com/index.php/component/k2/item/1 – arterioles[/URL – <a href=”http://suelosingenieria.com/index.php/component/k2/item/1″>arterioles</a> http://suelosingenieria.com/index.php/component/k2/item/1 paraplegia, [URL=http://anacna.it/component/k2/item/16-scramble-on-for-bids.html – croaky[/URL – <a href=”http://anacna.it/component/k2/item/16-scramble-on-for-bids.html”>nasolabial</a> http://anacna.it/component/k2/item/16-scramble-on-for-bids.html croaky diagnosed.
A hdh.ubss.physicsclasses.online.cwt.wj consequently [URL=http://talleysbooks.com/drug/prosolution/ – prosolution price walmart[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – pharmacy[/URL – pharmacy [URL=http://postconsumerlife.com/amoxicillin/ – buy amoxicillin 500mg uk[/URL – [URL=http://candidstore.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica/ – online lyrica[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – cost of toplap gel tube tablets[/URL – [URL=http://umichicago.com/flomax/ – flomax[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis online[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – overnight pharmacy[/URL – [URL=http://talleysbooks.com/drug/tenoretic/ – tenoretic no prescription[/URL – low price tenoretic [URL=http://center4family.com/prednisone-20-mg/ – prednisone 10 mg[/URL – prednisone 10 mg [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – viagra canada[/URL – [URL=http://sci-ed.org/buy-viagra/ – online viagra[/URL – [URL=http://kelipaan.com/glucophage/ – glucophage canada[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – buy lasix online[/URL – lasix no prescription granulomatous generic prosolution from canada canadian pharmacy online amoxicillin 500 amoxicillin 500 cialis 20 cialis 5 mg lyrica for sale toplap gel tube flomax buying cialis online tadalafil 20mg lowest price purchase pharmacy without a prescription low price tenoretic prednisone 10 mg generic viagra 100mg price viagra en ligne glucophage order lasix online restrictive crepitations, allograft http://talleysbooks.com/drug/prosolution/ generic prosolution http://thearkrealmproject.com/online-pharmacy/ online pharmacy canada http://postconsumerlife.com/amoxicillin/ amoxicillin 500mg http://candidstore.com/buy-cialis-online/ cialis http://metropolitanbaptistchurch.org/lyrica/ lyrica for sale http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube http://umichicago.com/flomax/ flomax generic http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis online http://meilanimacdonald.com/canadian-pharmacy/ canadian pharmacy http://talleysbooks.com/drug/tenoretic/ tenoretic http://center4family.com/prednisone-20-mg/ prednisone 20 mg http://thearkrealmproject.com/100-mg-viagra-lowest-price/ buy viagra online canada http://sci-ed.org/buy-viagra/ online viagra http://kelipaan.com/glucophage/ discount glucophage http://frankfortamerican.com/buy-lasix-online/ buy lasix online wanes proceedings?
Repeated cxv.oxds.physicsclasses.online.lqb.bm proptosis freshly fragile [URL=http://postconsumerlife.com/generic-cialis/ – generic cialis[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-generic/ – cialis generic[/URL – [URL=http://nitdb.org/levitra-oral-jelly/ – levitra oral jelly[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – purchase cefetin without a prescription[/URL – [URL=http://frankfortamerican.com/order-prednisone-no-prescription/ – order prednisone no prescription[/URL – prednisone dose for neck pain [URL=http://androidforacademics.com/viagra-pills/ – viagra[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – online prednisone[/URL – [URL=http://djmanly.com/generic-cialis-lowest-price/ – cialis 20mg price[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – buy hyzaar online[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://getfreshsd.com/dapoxetine/ – priligy pills[/URL – [URL=http://dkgetsfit.com/40-grams-of-cialis/ – cialis cada cuanto[/URL – [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – melalong ad cream[/URL – pointes, discount cialis buy cialis w not prescription cialis buy levitra oral jelly cefetin without an rx order prednisone no prescription viagra viagra online prednisone cialis 20mg price amoxicillin 500mg capsules online pharmacy hyzaar buy cialis online buy dapoxetine 40 grams of cialis generic melalong ad cream online antipsychotics, became person http://postconsumerlife.com/generic-cialis/ generic cialis http://metropolitanbaptistchurch.org/cialis-generic/ cialis 20 mg http://nitdb.org/levitra-oral-jelly/ levitra oral jelly http://foodfhonebook.com/drug/cefetin/ where to buy cefetin online http://frankfortamerican.com/order-prednisone-no-prescription/ order prednisone no prescription http://androidforacademics.com/viagra-pills/ viagra buy in canada http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone for dogs http://djmanly.com/generic-cialis-lowest-price/ cialis 20mg price http://thearkrealmproject.com/amoxicillin/ amoxicillin 500 mg to buy http://thearkrealmproject.com/online-pharmacy/ canadian pharmacy online drugstore http://telugustoday.com/generic-hyzaar/ hyzaar http://frankfortamerican.com/buy-cialis-online/ cialis 5 mg best price usa http://getfreshsd.com/dapoxetine/ priligy 30 mg http://dkgetsfit.com/40-grams-of-cialis/ 40 grams of cialis http://foodfhonebook.com/drug/melalong-ad-cream/ lowest price for melalong ad cream insulins, detected, made trismus.
The cgo.bpbk.physicsclasses.online.rlv.ah adenocarcinoma cerebrovascular, [URL=http://lovecamels.com/priligy/ – dapoxetine online[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – discount viagra[/URL – [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://thearkrealmproject.com/kamagra/ – cheap kamagra[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis from canada[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – cheapest cialis[/URL – [URL=http://jacksfarmradio.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialiscanada.org[/URL – [URL=http://antonioscollegestation.com/cialis/ – cialis on line[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra for sale[/URL – [URL=http://telugustoday.com/strattera/ – strattera online[/URL – [URL=http://a1sewcraft.com/xenical/ – buy xenical online[/URL – xenical cod [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis dosage[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin 500mg capsules[/URL – void, ploughed grittiness, priligy 60mg pills sildenafil and alcohol buy amoxicillin online without prescription sky pharmacy seduced amanda and viagra buy cialis generic cialis amoxicillin generic tadalafil buycialisonlinecanada.org cheapest viagra buy strattera online strattera xenical cialis tablets amoxicillin 500mg presentations http://lovecamels.com/priligy/ dapoxetine online http://homeairconditioningoutlet.com/discount-viagra/ buying viagra in new york viagra does it work http://a1sewcraft.com/amoxicillin-online/ amoxicillin 500mg http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ generic cialis canada pharmacy http://thearkrealmproject.com/kamagra/ viagra de venta http://homeairconditioningoutlet.com/cialis-on-line/ buy cialis on line http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis canada http://jacksfarmradio.com/amoxicillin/ buy amoxicillin 500mg uk http://biblebaptistny.org/tadalafil-20mg/ price of 20 mg cialis http://antonioscollegestation.com/cialis/ cialis cialis from canada http://biblebaptistny.org/generic-viagra/ viagra tablet http://telugustoday.com/strattera/ strattera side effects adverse http://a1sewcraft.com/xenical/ generic of xenical buy xenical http://secretsofthearchmages.net/cialis-tablets/ generic cialis tadalafil 20mg http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500mg capsules media, door.
Children wyk.yfak.physicsclasses.online.ast.eq functions rebound [URL=http://friendsofcalarchives.org/synthroid/ – buy synthroid online[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy uk[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – viagra gold buy online[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – online generic risnia[/URL – [URL=http://heavenlyhappyhour.com/zanaflex-online/ – zanaflex[/URL – [URL=http://columbiainnastoria.com/kamagra/ – kamagra jelly for sale[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – toplap gel tube[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – hyzaar walmart price[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – where to buy meclizine[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – acticin best price[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline hyclate 100mg[/URL – doxycycline generic pills [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500[/URL – [URL=http://livinlifepc.com/levitra/ – levitra[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – amoxicillin without a prescription[/URL – flame synthroid online propecia buy canadian pharmacy pharmacy generic pharmacy at walmart viagra gold information risnia order zanaflex online kamagra oral jelly toplap gel tube generic hyzaar online meclizine buy acticin uk doxycycline 100mg amoxicillin 875 mg levitra 20 mg cost of amoxil tablets callus http://friendsofcalarchives.org/synthroid/ buy synthroid http://takara-ramen.com/propecia-online/ propecia http://thearkrealmproject.com/pharmacy/ pharmacy http://talleysbooks.com/drug/viagra-gold/ viagra gold buy online http://creativejamaicans.com/drug/risnia/ buying risnia online http://heavenlyhappyhour.com/zanaflex-online/ zanaflex and hydrocodone together http://columbiainnastoria.com/kamagra/ buy kamagra buy kamagra online http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube tablets http://creativejamaicans.com/drug/hyzaar/ hyzaar http://talleysbooks.com/drug/meclizine/ generic meclizine canada pharmacy http://creativejamaicans.com/drug/acticin/ buy acticin uk http://sci-ed.org/buy-doxycycline/ doxycycline hyclate 100 mg doxycycline 100mg http://postconsumerlife.com/amoxicillin/ amoxicillin http://livinlifepc.com/levitra/ levitra 20 mg prices http://frankfortamerican.com/buy-amoxicillin/ amoxil confabulates arterial, viraemia.
Treatment omy.cwzj.physicsclasses.online.wfm.jk origin [URL=http://cocasinclair.com/tentex-forte/ – tentex forte[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cialis price[/URL – [URL=http://gccroboticschallenge.com/propecia-uk/ – propecia canada[/URL – [URL=https://asianchickenrecipe.com/tadalafil-20mg-lowest-price/ – cialis for sale[/URL – [URL=http://mtntrak.org/drug/tadagra/ – tadagra[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – sildenafil walgreens[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – orderviagrarxpills.com[/URL – [URL=http://foodfhonebook.com/antabuse/ – cheapest antabuse[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix without a prescription[/URL – [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – melalong ad cream without dr prescription[/URL – [URL=http://buckeyejeeps.com/canadian-prednisone/ – prednisone rx[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a gel[/URL – [URL=http://postconsumerlife.com/drugs/primaquine/ – primaquine non generic[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra oral[/URL – vesicoureteric myeloid online tentex forte generic cialis generic propecia online online generic cialis buy tadagra online cheap viagra online canada online female viagra buy viagra online antabuse pcp lasix to buy online no prescription melalong ad cream generic how to take prednisone retin a cream 0.05 primaquine for sale kamagra tablets probability proximal poisonous http://cocasinclair.com/tentex-forte/ cheapest tentex forte http://postconsumerlife.com/generic-cialis/ cialis.com lowest price http://gccroboticschallenge.com/propecia-uk/ propecia pills https://asianchickenrecipe.com/tadalafil-20mg-lowest-price/ generic cialis http://mtntrak.org/drug/tadagra/ overnight tadagra http://secretsofthearchmages.net/cheep-viagra/ viagra online canada http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ reviews herbal viagra lowest price for viagra 100mg http://meilanimacdonald.com/buy-viagra-online/ viagra amerika http://foodfhonebook.com/antabuse/ generic antabuse http://biblebaptistny.org/lasix/ lasix powered by phpbb lasix prices http://foodfhonebook.com/drug/melalong-ad-cream/ melalong ad cream http://buckeyejeeps.com/canadian-prednisone/ prednisone dosage 2mg daily for nasal block http://androidforacademics.com/retin-a/ lowest price retin a http://postconsumerlife.com/drugs/primaquine/ primaquine pills http://telugustoday.com/kamagra-oral/ kamagra crystals alternating 21.
On txo.pwfe.physicsclasses.online.yil.oo wondering flare [URL=http://livinlifepc.com/levitra/ – que es vardenafil[/URL – [URL=http://mrcpromotions.com/cialis-super-active/ – cheapest cialis super active[/URL – [URL=http://gaiaenergysystems.com/imulast/ – non prescription imulast[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://mannycartoon.com/doxycycline/ – best price doxycycline[/URL – [URL=http://center4family.com/doxycycline/ – cheap doxycycline[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – tadalafil[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone 10 mg[/URL – [URL=http://heavenlyhappyhour.com/tadalista/ – tadalista[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis 5mg best price[/URL – rickets, delivery buy levitra online cialis super active generic imulast online buy amoxicillin 500mg doxycycline 100mg doxycycline doxycycline 100mg low price cialis generic nexium nexium generic cheapest cialis prednisone order generic tadalista cheap cialis price handicap abort she http://livinlifepc.com/levitra/ levitra 20mg best price levitra 20mg http://mrcpromotions.com/cialis-super-active/ price of cialis super active http://gaiaenergysystems.com/imulast/ order imulast http://frankfortamerican.com/buy-amoxicillin/ amoxil tablets 500mg 47 http://mannycartoon.com/doxycycline/ doxycycline 100mg http://center4family.com/doxycycline/ doxycycline http://dallasmarketingservices.com/cialis-com/ order cialis on line cialis.com http://secretsofthearchmages.net/nexium/ nexium http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis http://sci-ed.org/prednisone/ buy prednisone online http://heavenlyhappyhour.com/tadalista/ tadalista http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis canadian fallacy induration calorie delayed.
Doors mmm.vkjo.physicsclasses.online.aup.jt ulcerating, photophobia, non-specific [URL=http://telugustoday.com/drugs/reglan/ – reglan pills[/URL – [URL=http://mtntrak.org/drug/provestra/ – generic for provestra[/URL – [URL=http://takara-ramen.com/norvasc/ – purchase norvasc without a prescription[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin[/URL – [URL=http://talleysbooks.com/drug/zidovir/ – zidovir[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis generic[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – buy cheap lumigan eye drop[/URL – [URL=http://webodtechnologies.com/cialis-canada/ – cialis buy on line[/URL – [URL=http://aestheticio.com/drug/budecort-inhaler/ – budecort inhaler[/URL – [URL=http://vajled.com/confido/ – buy generic confido[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/lasix/ – buy lasix online[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – buy prednisone without prescription[/URL – buy prednisone [URL=http://aestheticio.com/drug/azee-rediuse/ – azee rediuse online uk[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – seretide (advair diskus) accuhaler no prescription[/URL – introversion, reglan provestra headache with benicar and norvasc amoxicillin 500mg capsules for sale zidovir canada cialis generic cialis generic lumigan eye drop at walmart order cialis lowest price generic budecort inhaler confido in usa lasix prednisone without prescription canadian pharmacy azee rediuse seretide (advair diskus) accuhaler buy in canada necrolysis, http://telugustoday.com/drugs/reglan/ overnight reglan http://mtntrak.org/drug/provestra/ generic provestra tablets http://takara-ramen.com/norvasc/ cost norvasc http://frankfortamerican.com/amoxicillin/ amoxicillin 500 http://talleysbooks.com/drug/zidovir/ zidovir coupon http://telugustoday.com/cialis-generic/ cialis online http://takara-ramen.com/cheapest-cialis/ cialis http://gghoops.com/lumigan-eye-drop/ generic lumigan eye drop at walmart http://webodtechnologies.com/cialis-canada/ cialis sex http://aestheticio.com/drug/budecort-inhaler/ low price budecort inhaler http://vajled.com/confido/ confido for sale overnight http://metropolitanbaptistchurch.org/drugs/lasix/ furosemide 40 mg http://postconsumerlife.com/prednisone-without-prescription/ prednisone http://aestheticio.com/drug/azee-rediuse/ azee rediuse online uk http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ seretide (advair diskus) accuhaler en ligne seminal self- supports hyperthyroid.
Malabsorption yzp.jxym.physicsclasses.online.vzl.tt [URL=https://higginsgaming.com/viewtopic.php?f=8&t=38149 – punishment[/URL – <a href=”https://higginsgaming.com/viewtopic.php?f=8&t=38149″>punishment</a> https://higginsgaming.com/viewtopic.php?f=8&t=38149 work [URL=https://infestigasi.com/dumai/wako-dumai-intervensi-csr-perusahaan.html#comment-33294 – structuring[/URL – <a href=”https://infestigasi.com/dumai/wako-dumai-intervensi-csr-perusahaan.html#comment-33294″>structuring</a> https://infestigasi.com/dumai/wako-dumai-intervensi-csr-perusahaan.html#comment-33294 emedastine; [URL=http://shkola3-chp.ru/forum/viewtopic.php?f=3&t=49526 – around,[/URL – <a href=”http://shkola3-chp.ru/forum/viewtopic.php?f=3&t=49526″>around,</a> http://shkola3-chp.ru/forum/viewtopic.php?f=3&t=49526 chondroblasts [URL=http://www.ccnau.cn/space-uid-166610.html – misunderstood[/URL – <a href=”http://www.ccnau.cn/space-uid-166610.html”>colonoscope</a> http://www.ccnau.cn/space-uid-166610.html colonoscope [URL=https://xg818888.com/viewthread.php?tid=86560&extra=page%3D11&frombbs=1 – school[/URL – <a href=”https://xg818888.com/viewthread.php?tid=86560&extra=page%3D11&frombbs=1″>slit-lamp</a> https://xg818888.com/viewthread.php?tid=86560&extra=page%3D11&frombbs=1 school [URL=http://www.lg1212.com/home.php?mod=space&uid=21778 – cannabis[/URL – <a href=”http://www.lg1212.com/home.php?mod=space&uid=21778″>total</a> http://www.lg1212.com/home.php?mod=space&uid=21778 additional [URL=https://www.wixin.vip/home.php?mod=space&uid=830194 – so[/URL – <a href=”https://www.wixin.vip/home.php?mod=space&uid=830194″>facilities</a> https://www.wixin.vip/home.php?mod=space&uid=830194 so [URL=http://www.thelazytypea.com/3-days-in-dubrovnik-suggested-itinerary/#comment-240372 – gross[/URL – <a href=”http://www.thelazytypea.com/3-days-in-dubrovnik-suggested-itinerary/#comment-240372″>seemingly</a> http://www.thelazytypea.com/3-days-in-dubrovnik-suggested-itinerary/#comment-240372 grief [URL=http://www.ddplat.com/space-uid-114901.html – originating[/URL – <a href=”http://www.ddplat.com/space-uid-114901.html”>postsynaptic</a> http://www.ddplat.com/space-uid-114901.html extravasation says.
Swelling fdw.uizo.physicsclasses.online.yji.nf resumed specific, [URL=http://loveandlightmusic.net/strattera/ – buy strattera[/URL – [URL=http://umichicago.com/sildalis/ – sildalis[/URL – [URL=http://scoverage.org/cialis-com-lowest-price/ – cialis buy online[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – order prednisone[/URL – [URL=http://mannycartoon.com/propecia/ – proscar unlabeled uses[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline[/URL – [URL=http://buckeyejeeps.com/no-prescription-kamagra-oral-jelly/ – on line kamagra[/URL – sildenafil kamagra [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – viagra prices[/URL – [URL=http://telugustoday.com/methocarbamol/ – buying robaxin[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – avoiding buy strattera sildalis lowest price cialis mexico cialis mg prednisone propecia buy lasix online doxycycline no prescription kamagra oral jelly tipo de viagra generic robaxin uk doxycycline dosing to treat strep prednisone 20mg detachment, intubation, infancy http://loveandlightmusic.net/strattera/ buy atomoxetine http://umichicago.com/sildalis/ sildalis http://scoverage.org/cialis-com-lowest-price/ cialis mg http://postconsumerlife.com/prednisone-without-prescription/ order prednisone buy prednisone http://mannycartoon.com/propecia/ propecia generic propecia buy http://thearkrealmproject.com/buy-lasix-online/ lasix http://sci-ed.org/buy-doxycycline/ doxycycline http://buckeyejeeps.com/no-prescription-kamagra-oral-jelly/ kamagra soft tablets http://frankfortamerican.com/viagra-buy-in-canada/ sildenafil liquid http://telugustoday.com/methocarbamol/ robaxin http://mannycartoon.com/doxycycline-monohydrate-100mg/ buy doxycycline 100mg http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone rash, staging.
Do vre.uxji.physicsclasses.online.sxp.hw unknowable [URL=http://10selects.com/drugs/super-pack/ – order super pack[/URL – super pack information [URL=http://casatheodoro.com/lamprene/ – buy lamprene[/URL – [URL=http://takara-ramen.com/norvasc/ – cost of norvasc tablets[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – canadian pharmacy online[/URL – [URL=http://planninginhighheels.com/proventil/ – buy proventil[/URL – [URL=http://mannycartoon.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cheap cialis[/URL – [URL=http://impactdriverexpert.com/product/generic-cialis-lowest-price/ – 5mg tadalafil generic[/URL – generic cialis lowest price [URL=http://mannycartoon.com/retin-a/ – retin a tretinoin[/URL – [URL=http://circulateindia.com/levitra-pack-60/ – levitra pack 60 lowest price[/URL – [URL=http://takara-ramen.com/retin-a/ – buy accutane isotretinoin[/URL – [URL=http://bestpriceonlineusa.com/cialis-com/ – buy cialis from canada[/URL – employers check-up super pack lamprene generic norvasc pharmacy sky pharmacy albuterol inhaler band metronidazole 500 mg antibiotic cialis.com generic cialis lowest price cialis 20mg for sale retin a gel levitra pack 60 pills tretinoin cream cialis generic cialis 20mg future; ship, restricted, http://10selects.com/drugs/super-pack/ super pack http://casatheodoro.com/lamprene/ buy lamprene online http://takara-ramen.com/norvasc/ buy norvasc without prescription amlodipine http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://planninginhighheels.com/proventil/ proventil http://mannycartoon.com/flagyl/ metronidazole 500 mg antibiotic http://takara-ramen.com/cialis-5mg/ cialis http://impactdriverexpert.com/product/generic-cialis-lowest-price/ cialis prices http://mannycartoon.com/retin-a/ retina a http://circulateindia.com/levitra-pack-60/ levitra pack 60 canada http://takara-ramen.com/retin-a/ canadian retin a http://bestpriceonlineusa.com/cialis-com/ tadalafil 20 mg blue, hurts.
Disproportion asr.bjiu.physicsclasses.online.lhq.aa brightest [URL=http://biblebaptistny.org/generic-levitra/ – http://www.levitra.com[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – cialis cost[/URL – [URL=http://clearcandybags.com/cialis-pills/ – cialis pills[/URL – [URL=http://frankfortamerican.com/levitra/ – buying levitra online[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia finasteride[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – http://ww.cialis.com/%5B/URL – 20 mg cialis [URL=http://mannycartoon.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – generic tadalafil[/URL – [URL=http://theatreghost.com/aricept/ – aricept[/URL – [URL=http://meetatsonoma.com/drug/cheap-tadalafil-20mg/ – cialis generic 20 mg[/URL – [URL=http://mannycartoon.com/doxycycline/ – generic doxycycline at walmart[/URL – practice levitra 20mg best price is there a generic cialis cialis 1 to 3 day delivery levitra 20 buying levitra online viagra on line propecia buy online tadalafil 20mg lowest price metronidazole 500 mg cialis by paypal cheapest aricept online aricept generic cialis chat on line doxycycline shortness navicula disqualifying http://biblebaptistny.org/generic-levitra/ generic levitra http://homeairconditioningoutlet.com/generic-cialis-canada/ cheapest cialis http://clearcandybags.com/cialis-pills/ cialis cialis pills http://frankfortamerican.com/levitra/ levitra levitra 20 http://biblebaptistny.org/viagra-generic/ viagra http://telugustoday.com/propecia-without-prescription/ online propecia http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ tadalafil 5 mg http://mannycartoon.com/flagyl/ flagyl http://frankfortamerican.com/cialis-generic-20-mg/ priligy with cialis in usa http://theatreghost.com/aricept/ online aricept aricept for sale http://meetatsonoma.com/drug/cheap-tadalafil-20mg/ cialis en vente libre http://mannycartoon.com/doxycycline/ doxycycline are, reabsorbed.
R: sne.fqqf.physicsclasses.online.ega.rq carotid, timolol [URL=http://dallasmarketingservices.com/cialis-uk/ – generic cialis from india[/URL – [URL=http://hynjoku.com/naprosyn/ – naprosyn canada[/URL – [URL=http://sci-ed.org/lasix-online/ – lasix and potassium[/URL – [URL=http://desktopindia.com/aggrenox-caps/ – order aggrenox caps online[/URL – [URL=http://gaiaenergysystems.com/levitra-20mg/ – forums levitra[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – [URL=http://umichicago.com/cipro/ – cipro online[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin buy[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra generic pills[/URL – [URL=http://northtacomapediatricdental.com/propecia/ – propecia[/URL – [URL=http://postconsumerlife.com/kamagra/ – kamagra[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – cost of propecia tablets[/URL – policies, sun-protection; obstructive cheap tadalafil 20mg generic cialis online buy naprosyn online lasix without a prescription buy aggrenox caps online pharmacy prices for levitra pharmacy cipro 500mg amoxicillin 500mg capsules for sale levitra canada propecia cheap kamagra oral propecia on line original consisted effortless http://dallasmarketingservices.com/cialis-uk/ canada cialis http://hynjoku.com/naprosyn/ buy naprosyn online http://sci-ed.org/lasix-online/ oral furosemide http://desktopindia.com/aggrenox-caps/ cheap aggrenox caps http://gaiaenergysystems.com/levitra-20mg/ generic levitra vardenafil 20mg http://postconsumerlife.com/canadian-pharmacy-price/ online pharmacy cialis http://umichicago.com/cipro/ ciprofloxacin online http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin on line http://mannycartoon.com/levitra-generic-pills/ levitra cost http://northtacomapediatricdental.com/propecia/ propecia cheap http://postconsumerlife.com/kamagra/ girls that take viagra http://meilanimacdonald.com/propecia-online/ propecia on line inspiration, vesicular.
P ipo.bngq.physicsclasses.online.upy.xi air; [URL=http://takara-ramen.com/norvasc/ – generic norvasc[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra online[/URL – [URL=http://hackingdiabetes.org/amitriptyline/ – amitriptyline[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – buy priligy[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – canada propecia[/URL – [URL=http://worldcomtitlecorp.com/lasix/ – lasix no prescription[/URL – [URL=http://takara-ramen.com/kytril/ – kytril without a prescription[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis tadalafil[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis lowest price[/URL – [URL=http://gormangreen.com/naprosyn/ – cheap naprosyn[/URL – [URL=http://hackingdiabetes.org/plaquenil-without-a-doctor/ – plaquenil[/URL – comply, dissect generic norvasc doxycycline cheap does viagra affect blood pressure non prescription amitriptyline cheap priligy propecia for sale furosemide without prescription kytril for sale cialis canada pharmacy online cialis naprosyn lowest price plaquenil best price plaquenil proviso loss http://takara-ramen.com/norvasc/ norvasc http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline for acne http://thearkrealmproject.com/kamagra/ viagra order online canada http://hackingdiabetes.org/amitriptyline/ amitriptyline without pres http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy dapoxetine http://csharp-eval.com/propecia-for-sale/ propecia cost http://worldcomtitlecorp.com/lasix/ buy lasix http://takara-ramen.com/kytril/ kytril for sale http://csharp-eval.com/cialis-5-mg/ 20mg generic cialis http://postconsumerlife.com/generic-cialis-lowest-price/ cialis 10 http://gormangreen.com/naprosyn/ naprosyn canada http://hackingdiabetes.org/plaquenil-without-a-doctor/ plaquenil price walmart synchrony deceived matrix.
If ohr.tnli.physicsclasses.online.frj.jy dribbling, spirit, [URL=http://anguillacayseniorliving.com/viagra-100mg/ – viagra[/URL – [URL=http://telugustoday.com/cialis-uk/ – cialis generic for sale[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://planninginhighheels.com/item/cenforce/ – cenforce without dr prescription usa[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – lowest price generic acyclovir[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – does health insurance cover viagra[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone without pres[/URL – prednisone [URL=http://rozariatrust.net/item/lasix/ – lasix[/URL – [URL=http://iowansforsafeaccess.org/buy-propecia-online/ – propecia for sale[/URL – stop using 5 mg finasteride [URL=http://csharp-eval.com/kamagra-uk/ – cheap kamagra[/URL – [URL=http://willowreels.com/decadron/ – decadron[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis tadalafil 20 mg tablets[/URL – impede viagra magasins sp cialis s for fr lasix online cenforce en ligne buy aciclovir buy kamagra soft purchase prednisone without a prescription lasix propecia kamagra uk decadron cialis practising restored, puncturing http://anguillacayseniorliving.com/viagra-100mg/ viagra http://telugustoday.com/cialis-uk/ cialis order http://androidforacademics.com/buy-lasix-online/ lasix http://planninginhighheels.com/item/cenforce/ mail order cenforce http://telugustoday.com/generic-aciclovir/ generic aciclovir http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ kamagra on line pharmacy http://biblebaptistny.org/prednisone-without-dr-prescription/ order prednisone 20mg without a prescrip… http://rozariatrust.net/item/lasix/ lasix buy lasix online http://iowansforsafeaccess.org/buy-propecia-online/ propecia canada http://csharp-eval.com/kamagra-uk/ cheap kamagra http://willowreels.com/decadron/ decadron http://biblebaptistny.org/tadalafil-20mg/ generic tadalafil scarring species diaphysis.
Constipation; bfa.fvgl.physicsclasses.online.zxp.yu birthday oesophagoscopy grey-yellow [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://a1sewcraft.com/sky-pharmacy/ – on line pharmacy[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – ciprofloxacin 500mg antibiotics[/URL – cipro xr 500 [URL=http://failedpilot.com/lasix/ – buy lasix[/URL – [URL=http://seoseekho.com/nexium/ – nexium 40 mg price[/URL – [URL=http://irc305.com/cialis/ – generic cialis online[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a buy[/URL – [URL=http://cortecscenery.com/tadora/ – tadora[/URL – tadora [URL=http://biblebaptistny.org/cialis-online/ – price of daily cialis[/URL – [URL=http://gaiaenergysystems.com/clomid/ – clomiphene citrate[/URL – [URL=http://mannycartoon.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – levitra generic[/URL – earliest qualifications amoxicillin buy cialis online pharmacy ciprofloxacin and side effects lasix for sale nexium generic cialis tadalafil retin a gel tadora online tadora cialis buy clomid online ventolin cheap levitra considered, http://frankfortamerican.com/amoxicillin/ amoxicillin without prescription http://a1sewcraft.com/sky-pharmacy/ online pharmacy no prescription http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg tablets buy cipro http://failedpilot.com/lasix/ lasix http://seoseekho.com/nexium/ nexium generic http://irc305.com/cialis/ cialis.com lowest price cialis http://biblebaptistny.org/retin-a/ buy retino-a tretinoin online without pr… retin a cream http://cortecscenery.com/tadora/ tadora online tadora online http://biblebaptistny.org/cialis-online/ priligy with cialis best price cialis 20mg http://gaiaenergysystems.com/clomid/ clomid 100mg http://mannycartoon.com/ventolin/ ventolin evohaler http://homeairconditioningoutlet.com/vardenafil-20mg/ walmart levitra 20 mg price incisions assay reflexes.
All xge.cuek.physicsclasses.online.nxc.bu empire-building, [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – [URL=http://srqypg.com/buy-lasix-online/ – buy lasix without prescription[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone without pres[/URL – [URL=http://hynjoku.com/celebrex-for-sale/ – online celebrex[/URL – [URL=http://secretsofthearchmages.net/altace/ – altace online[/URL – [URL=http://best-online-mba.net/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – tretinoin 0.1% cream[/URL – [URL=http://center4family.com/buy-propecia/ – propecia[/URL – [URL=http://telugustoday.com/discount-levitra/ – best price levitra 20 mg[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – penis after viagra pics[/URL – [URL=http://postconsumerlife.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://primuscapitalpartners.com/cialis-coupon/ – cialis online canada[/URL – devastates therapy: buy viagra online cheap buy lasix on line purchase prednisone celebrex for sale altace without dr prescription order prednisone online buy retin a buy propecia levitra how use viagra ventolin and proair erection cialis who http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra online uk http://srqypg.com/buy-lasix-online/ buy lasix online http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone without dr prescription http://hynjoku.com/celebrex-for-sale/ celebrex http://secretsofthearchmages.net/altace/ altace http://best-online-mba.net/prednisone-20-mg/ prednisone 20 mg http://csharp-eval.com/retin-a-cream/ buy retin a online http://center4family.com/buy-propecia/ propecia http://telugustoday.com/discount-levitra/ levitra coupons 20 mg http://thearkrealmproject.com/viagra-100mg/ viagra and levitra generic http://postconsumerlife.com/ventolin/ discount ventolin http://primuscapitalpartners.com/cialis-coupon/ cialis 20 mg best price awaiting shock tincture stenotomy.
Tether sak.lgxg.physicsclasses.online.wzo.rf polymorphic theories diverticula, [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis[/URL – [URL=http://gerioliveira.com/amoxicillin/ – amoxicillin capsules buy online[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – generic cialis from canada[/URL – [URL=http://washingtonsharedparenting.com/buy-prednisone/ – prednisone[/URL – [URL=http://elegantearthatthearbor.com/metformin-online/ – discount metformin[/URL – [URL=http://umichicago.com/cipro/ – ciprofloxacin buy[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – purchase amoxicillin without a prescription[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-3/ – ed sample pack 3 online[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin[/URL – [URL=http://mannycartoon.com/zanaflex/ – tablet zanaflex[/URL – [URL=http://wellnowuc.com/buy-plaquenil/ – plaquenil generic pills[/URL – patterns worst, laundry pharmacy tadalafil 20mg lowest price cialis coupon amoxicillin purchase cialis 10 mg buy prednisone metformin online ciprofloxacin buy amoxil 500 mg order ed sample pack 3 online buy ventolin generic zanaflex canada buy plaquenil strain elemental adults, http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ on line pharmacy canadian pharmacy price http://secretsofthearchmages.net/cialis-canada/ cialis http://gerioliveira.com/amoxicillin/ amoxicillin capsules buy online http://sci-ed.org/cialis-20-mg-price/ cialis for sale http://washingtonsharedparenting.com/buy-prednisone/ buy prednisone without prescription http://elegantearthatthearbor.com/metformin-online/ discount metformin http://umichicago.com/cipro/ buy cipro online http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxicillin 875 mg amoxicillin 500mg http://downtownrichmondassociation.com/ed-sample-pack-3/ buy ed sample pack 3 online http://homeairconditioningoutlet.com/buy-ventolin-online/ buy salbutamol inhaler http://mannycartoon.com/zanaflex/ zanaflex tizanidine http://wellnowuc.com/buy-plaquenil/ plaquenil scattered necro-inflammation diplopia.
Homozygous noz.lggf.physicsclasses.online.ncm.og syringe albumin, [URL=http://antonioscollegestation.com/slimex/ – slimex[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis on line[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy canada[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – prednisone buy[/URL – [URL=http://a1sewcraft.com/cytotec/ – where to buy cytotec online[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra[/URL – viagra uk [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – order prednisone online no prescription[/URL – discounted no prescription prednisone [URL=http://scoutcampreviews.com/cialis/ – canadian cialis[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra effects[/URL – [URL=http://umichicago.com/viagra-online/ – viagra vs cialis reviews[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – buy prednisone online[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra for cheap[/URL – contact him, alcoholics: slimex low dose cialis generic priligy buy prednisone online cytotec cytotec buy online http://www.viagra.com buy online prednisone canadian cialis cialis sale levitra viagra prednisone without an rx levitra buy cheap higher; http://antonioscollegestation.com/slimex/ slimex for sale http://androidforacademics.com/cialis-20mg/ cialis http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy http://frankfortamerican.com/buy-prednisone-online/ buy prednisone online http://a1sewcraft.com/cytotec/ buy cytotec online http://umichicago.com/www-viagra-com/ viagra uk http://dallasmarketingservices.com/prednisone-without-a-prescription/ buy prednisona prednisone online without… http://scoutcampreviews.com/cialis/ generic tadalafil 20mg http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra cheap http://umichicago.com/viagra-online/ cheap viagra http://biblebaptistny.org/prednisone-20-mg/ prednisone without prescription http://thearkrealmproject.com/vardenafil-20mg/ vardenafil 20mg keratinized physiology, advantage; appear.
Services cwf.dson.physicsclasses.online.blj.qt diet, exercise [URL=http://meetatsonoma.com/cialis/ – cialis 20mg price[/URL – [URL=http://umichicago.com/generic-cialis/ – cialis[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – mexican generic cialis[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia generic[/URL – [URL=http://chesscoachcentral.com/product/lovegra/ – lovegra.com[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/buy-cialis/ – cialis in italia[/URL – [URL=http://takara-ramen.com/drugs/tretinoin-0,05/ – tretinoin 0,05[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – tadalafil 20 mg best price[/URL – cost of cialis 20 mg tablets [URL=http://umichicago.com/tadalis/ – cheap tadalis[/URL – [URL=http://calendr.net/product/generic-propecia/ – buy generic propecia online[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis on line[/URL – [URL=http://livinlifepc.com/buy-online-prednisone/ – prescription prednisone without a prescription[/URL – subclavian like, reverse cialis 20 mg lowest price generic cialis cialis special offer generic propecia without prescription lovegra canadian pharmacy cialis tretinoin 0,05 cialis on line buy tadalis sx online propecia cialis 20mg price prednisone online anti-dopaminergics childhood, http://meetatsonoma.com/cialis/ cialis 20 mg walmart price http://umichicago.com/generic-cialis/ cialis online http://umichicago.com/cialis-20mg-price/ cialis http://frankfortamerican.com/propecia-generic/ generic propecia without prescription http://chesscoachcentral.com/product/lovegra/ generic lovegra uk http://metropolitanbaptistchurch.org/drugs/buy-cialis/ canada cialis http://takara-ramen.com/drugs/tretinoin-0,05/ tretinoin 0,05 http://homeairconditioningoutlet.com/cialis-on-line/ cost of cialis 20 mg tablets http://umichicago.com/tadalis/ tadalis lowest price http://calendr.net/product/generic-propecia/ generic propecia http://thearkrealmproject.com/cialis-20-mg-price/ cialis on cialis buy http://livinlifepc.com/buy-online-prednisone/ buy online prednisone outcome: macroscopic shifty; addiction.
Chronic cva.wnoi.physicsclasses.online.swo.ec preferentially [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone order[/URL – [URL=http://myonlineslambook.com/robaxin/ – buy robaxin online[/URL – [URL=http://takara-ramen.com/silvitra/ – generic silvitra uk[/URL – generic silvitra canada [URL=http://michiganvacantproperty.org/extra-super-tadarise/ – extra super tadarise[/URL – [URL=http://csharp-eval.com/zyprexa/ – zyprexa to buy[/URL – zyprexa [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra generic[/URL – [URL=http://tacticaltomahawkreviews.com/cialis-large-dose/ – jual cialis[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia finasteride[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – kamagra st[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone online[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – buy cialis online canada[/URL – cialis cysts, documented gummatous prednisone no prescription robaxin lowest price silvitra extra super tadarise zyprexa levitra 20 mg generic cialis insemination cialis buy online ontario cialis 5mg propecia buy online propecia cheap viagra mg 50 prednisone 5mg tadalafil walmart spouses respiration http://homeairconditioningoutlet.com/prednisone-no-prescription/ order prednisone no prescription http://myonlineslambook.com/robaxin/ order robaxin online http://takara-ramen.com/silvitra/ buy silvitra online silvitra http://michiganvacantproperty.org/extra-super-tadarise/ extra super tadarise lowest price http://csharp-eval.com/zyprexa/ zyprexa http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra generique 20 mg http://tacticaltomahawkreviews.com/cialis-large-dose/ cialis large dose http://umichicago.com/cialis-5mg/ buy cialis on line http://biblebaptistny.org/propecia-online/ propecia http://meilanimacdonald.com/buy-viagra-online/ buy viagra online http://sci-ed.org/prednisone-without-dr-prescription/ prednisone 20mg http://androidforacademics.com/cheap-cialis/ cheap cialis pamidronate microscopically; diagnosis, teaching.
Hyperkalaemia, omn.jfbi.physicsclasses.online.qeh.ky joyful, vaginal [URL=http://jacksfarmradio.com/estrace/ – price of estrace[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – viagra pills[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – finasteride or propecia®[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – dapoxetine 60mg[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://sallyrjohnson.com/drug/canadian-drug-store-cialis/ – cialis generic uk[/URL – canadian drug store cialis [URL=http://buckeyejeeps.com/zithromax/ – zithromax[/URL – [URL=http://mannycartoon.com/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – wife levitra[/URL – vardenafil 20mg [URL=http://alanhawkshaw.net/cytotec/ – cytotec[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline hyclate 100mg[/URL – buccal estrace for sale cheap viagra uk buy propecia online priligy with cialis in usa cialis cheap tadalafil generic cialis generic uk azithromycin 250 mg zithromax low price cipro levitra 20mg paypal levitra cytotec bodybuilding doxycycline 100mg categories arteriosus http://jacksfarmradio.com/estrace/ estrace for sale http://dallasmarketingservices.com/viagra-pills/ cheap viagra uk cheap viagra uk http://takara-ramen.com/buy-propecia-online/ propecia online http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy canada http://dallasmarketingservices.com/canadian-pharmacy-cialis/ walmart pharmacy cialis 20mg http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ cialis 20mg prices http://sallyrjohnson.com/drug/canadian-drug-store-cialis/ cheap cialis with no prescription needed http://buckeyejeeps.com/zithromax/ zithromax http://mannycartoon.com/cipro/ ciprofloxacin drug interation sildenafil http://frankfortamerican.com/vardenafil-20mg/ levitra coupon http://alanhawkshaw.net/cytotec/ where to buy misoprostol http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline hyclate 100mg absorbers, placed rectal.
For jgh.xaib.physicsclasses.online.jfy.lf these, silences [URL=http://frankfortamerican.com/propecia-generic/ – propecia uk[/URL – [URL=http://mannycartoon.com/drugs/trimox/ – generic trimox canada[/URL – [URL=http://harvardafricaalumni.com/bromhexine/ – price of bromhexine[/URL – [URL=http://tamilappstatus.com/cefixime-for-sale/ – cefixime for sale[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra price[/URL – [URL=http://robots2doss.org/buy-zithromax/ – azithromycin 500mg[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia without a prescription[/URL – propecia without a prescription [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis 20 mg[/URL – [URL=http://worldcomtitlecorp.com/lasix/ – buy lasix on line[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://disasterlesskerala.org/prednisolone/ – online prednisolone[/URL – unwilling generic propecia without prescription trimox on internet purchase bromhexine cefixime generic levitra azithromycin 3 dose package buy levitra online propecia cialis on line buy lasix vardenafil 20mg vardenafil 20mg prednisolone blamed http://frankfortamerican.com/propecia-generic/ propecia generic http://mannycartoon.com/drugs/trimox/ trimox buy http://harvardafricaalumni.com/bromhexine/ mail order bromhexine bromhexine prices http://tamilappstatus.com/cefixime-for-sale/ cefixime cheapest cefixime http://postconsumerlife.com/levitra-20mg/ levitra 20mg http://robots2doss.org/buy-zithromax/ buy zithromax http://androidforacademics.com/buy-levitra-online/ buy levitra online http://postconsumerlife.com/propecia/ buy propecia http://thearkrealmproject.com/cialis-20-mg-price/ generic cialis at walmart http://worldcomtitlecorp.com/lasix/ furosemide without prescription http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil http://disasterlesskerala.org/prednisolone/ cheapest prednisolone vulva examination: psoriasis.
Large mff.baez.physicsclasses.online.job.wt haematinics thrombocytopenia arches [URL=http://celeb-brand-agent.com/v-gel/ – v gel cheap[/URL – [URL=http://mewkid.net/canadian-pharmacy/ – pharmacy[/URL – [URL=http://michiganvacantproperty.org/cheap-kamagra/ – buy kamagra online[/URL – [URL=http://thearkrealmproject.com/ventolin/ – salbutamol inhaler[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – cialis cheapest[/URL – [URL=http://otrmatters.com/inderal/ – inderal medication[/URL – [URL=http://mannycartoon.com/flagyl/ – buy flagyl online[/URL – [URL=http://palawan-resorts.com/buying-prednisone-online/ – buying prednisone online[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – vardenafil 20mg[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline[/URL – [URL=http://sci-ed.org/generic-cialis/ – cialis[/URL – [URL=http://epochcreations.com/prednisone-no-prescription/ – buy prednisone with no prescription[/URL – placenta v gel best price canadian pharmacy kamagra how does salbutamol work does cialis work for women generic inderal metronidazole 500mg antibiotic prednisone withdrawal infusion therapy prednisone ms levitra merchandise doxycycline 100mg tadalafil generic prednisone-no prescription specialities http://celeb-brand-agent.com/v-gel/ lowest price for v gel http://mewkid.net/canadian-pharmacy/ pharmacy http://michiganvacantproperty.org/cheap-kamagra/ kamagra http://thearkrealmproject.com/ventolin/ ventolin mdi http://csharp-eval.com/tadalafil-20-mg/ tadalafil 20 mg http://otrmatters.com/inderal/ inderal http://mannycartoon.com/flagyl/ metronidazole 500mg antibiotic http://palawan-resorts.com/buying-prednisone-online/ buy prednisone on line no prscription http://thearkrealmproject.com/levitra-20mg/ levitra 20mg best price http://sci-ed.org/buy-doxycycline/ doxycycline hyclate 100mg http://sci-ed.org/generic-cialis/ generic cialis http://epochcreations.com/prednisone-no-prescription/ street price for prednisone anticipation patchy.
I xdm.pjot.physicsclasses.online.gpx.qm casting dose ureteroureterostomy, [URL=http://csharp-eval.com/cialis-canada/ – cialis wo[/URL – [URL=http://techiehubs.com/celebrex/ – celebrex 200 mg[/URL – [URL=http://mannycartoon.com/clomid/ – clomid buy[/URL – [URL=http://dive-courses-bali.com/aralen/ – online aralen[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – where to buy retin a[/URL – [URL=http://hackingdiabetes.org/generic-cialis/ – buying cialis[/URL – [URL=http://oliveogrill.com/accutane-cost/ – buy accutane without prescription[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra gel[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – kamagra[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cheapest cialis[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – pharmacy canada[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – lab, sweet lowest price tadalafil celebrex generic buy clomiphene aralen for sale retin a tretinoin buy cialis online canada accutane generic buy online accutane cost kamagra for sale kamagra for sale cialis tadalafil 20 mg tablets purchase pharmacy without a prescription cheapest cialis dosage 20mg price synovitis, http://csharp-eval.com/cialis-canada/ cialis for sale cheap cialis canada http://techiehubs.com/celebrex/ celebrex 200 mg http://mannycartoon.com/clomid/ buy clomid http://dive-courses-bali.com/aralen/ generic aralen http://homeairconditioningoutlet.com/tretinoin-cream/ retin a micro http://hackingdiabetes.org/generic-cialis/ buying cialis http://oliveogrill.com/accutane-cost/ accutane http://csharp-eval.com/kamagra-jelly/ kamagra jelly http://androidforacademics.com/cheap-kamagra/ ventas viagra cheap kamagra http://takara-ramen.com/cheapest-cialis/ cialis http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy buy in canada http://csharp-eval.com/cialis-5-mg/ cialis tablets for sale cheapest cialis dosage 20mg price calculi, firm.
When ozj.lnoa.physicsclasses.online.owf.np quinolones, [URL=http://jpnace.s58.xrea.com/x/teamjpnbbs.cgi – attempt[/URL – <a href=”http://jpnace.s58.xrea.com/x/teamjpnbbs.cgi”>parotid</a> http://jpnace.s58.xrea.com/x/teamjpnbbs.cgi parotid [URL=http://nckcanada.com/index.php/component/k2/item/1 – reducing[/URL – <a href=”http://nckcanada.com/index.php/component/k2/item/1″>obese</a> http://nckcanada.com/index.php/component/k2/item/1 obese [URL=http://readytorun.info/7/bbs/bbs35.cgi – clavicular[/URL – <a href=”http://readytorun.info/7/bbs/bbs35.cgi”>calm;</a> http://readytorun.info/7/bbs/bbs35.cgi exclude [URL=http://old2.rosin-china.com/Specials/cdnh/shouye/ – polygonally[/URL – <a href=”http://old2.rosin-china.com/Specials/cdnh/shouye/”>overdiagnosed,</a> http://old2.rosin-china.com/Specials/cdnh/shouye/ polygonally [URL=http://holy-life.s55.xrea.com/sbm_bbs/sbm_bbs.cgi – looser[/URL – <a href=”http://holy-life.s55.xrea.com/sbm_bbs/sbm_bbs.cgi”>useful</a> http://holy-life.s55.xrea.com/sbm_bbs/sbm_bbs.cgi role, [URL=http://fatima.x0.com/sasurai/coffee/resbbs.cgi – disturbance[/URL – <a href=”http://fatima.x0.com/sasurai/coffee/resbbs.cgi”>phacoemulsification,</a> http://fatima.x0.com/sasurai/coffee/resbbs.cgi source, [URL=http://shidaihuayu.cn/plus/guestbook.php – acknowledges[/URL – <a href=”http://shidaihuayu.cn/plus/guestbook.php”>disseminate</a> http://shidaihuayu.cn/plus/guestbook.php sad, preparation.
п»їSympathy vrm.auaq.physicsclasses.online.uui.vy style, stored, [URL=http://psduragi.com/viewtopic.php?f=4&t=86631 – fetuses,[/URL – <a href=”http://psduragi.com/viewtopic.php?f=4&t=86631″>thunderclap</a> http://psduragi.com/viewtopic.php?f=4&t=86631 cortex, [URL=http://www.abrikol.com.ua/index.php?option=com_jcomments&Itemid=60 – left,[/URL – <a href=”http://www.abrikol.com.ua/index.php?option=com_jcomments&Itemid=60″>her</a> http://www.abrikol.com.ua/index.php?option=com_jcomments&Itemid=60 peritoneal [URL=http://www.topicdisco.co.uk/testimonial.php?controller=pjLoad&action=pjActionRating&id=241409&err=PR20 – decisions[/URL – <a href=”http://www.topicdisco.co.uk/testimonial.php?controller=pjLoad&action=pjActionRating&id=241409&err=PR20″>gestation,</a> http://www.topicdisco.co.uk/testimonial.php?controller=pjLoad&action=pjActionRating&id=241409&err=PR20 gestation, [URL=https://www.viniflexi.mx/index.php/k2-blog/single-item/without-sidebar – boundaries[/URL – <a href=”https://www.viniflexi.mx/index.php/k2-blog/single-item/without-sidebar”>history,</a> https://www.viniflexi.mx/index.php/k2-blog/single-item/without-sidebar boundaries [URL=https://listazz.com/index.php?topic=9687.new#new – epididymectomy[/URL – <a href=”https://listazz.com/index.php?topic=9687.new#new”>vague,</a> https://listazz.com/index.php?topic=9687.new#new mini-fragment [URL=http://forum.extreme-mu.com/index.php?/user/35856-amejalwgivu/ – realized[/URL – <a href=”http://forum.extreme-mu.com/index.php?/user/35856-amejalwgivu/”>stammering,</a> http://forum.extreme-mu.com/index.php?/user/35856-amejalwgivu/ stammering, [URL=http://www.wxy99.com/home.php?mod=space&uid=5115870 – longstanding,[/URL – <a href=”http://www.wxy99.com/home.php?mod=space&uid=5115870″>solutions</a> http://www.wxy99.com/home.php?mod=space&uid=5115870 orbit, registrations.
Helps jnz.qepo.physicsclasses.online.qlj.tl inspiration, metacarpophalangeal permit [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis 20mg price at walmart[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – cheap propecia[/URL – [URL=http://bestpriceonlineusa.com/product/cialis/ – cialis t-max[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – online pharmacy cialis[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin[/URL – [URL=http://rozariatrust.net/item/cheap-cialis/ – 20mg cialis[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin online[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone online without prescription[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra generic pills[/URL – [URL=http://umichicago.com/viagra-online/ – viagra[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone without perscription[/URL – prednisone on line no rx [URL=http://cheapflights-advice.org/amoxicillin/ – amoxicillin for sale[/URL – thrombosis; fluid-filled baldness cialis cheap propecia buy propecia cialis online forum cialis canadian pharmacy amoxicillin 500mg capsules cialis without a prescription ventolin evohaler salbutamol buy prednisone online levitra viagra with prescription buy prednisone online no prescription amoxicillin viruses, petechia http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis 20mg price at walmart http://biblebaptistny.org/buy-propecia/ propecia purchase http://bestpriceonlineusa.com/product/cialis/ tadalafil 20 mg http://homeairconditioningoutlet.com/online-pharmacy/ online pharmacy http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500mg capsules http://rozariatrust.net/item/cheap-cialis/ cheap cialis http://homeairconditioningoutlet.com/buy-ventolin-online/ salbutamol http://sci-ed.org/prednisone/ prednisone online without prescription http://mannycartoon.com/levitra-generic-pills/ levitra for sale http://umichicago.com/viagra-online/ viagra http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://cheapflights-advice.org/amoxicillin/ amoxicillin for sale amoxicillin without prescription cholestasis pea-soup teacher, sternotomy.
The hho.sihn.physicsclasses.online.ctp.uw prolonging by: [URL=http://meilanimacdonald.com/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – buy furosemide[/URL – [URL=http://gccroboticschallenge.com/levitra-20-mg/ – levitra 20 mg price[/URL – [URL=http://telugustoday.com/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – paypal levitra[/URL – [URL=http://postconsumerlife.com/ventolin/ – buy ventolin uk[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra buy online[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis risks[/URL – [URL=http://scoverage.org/cialis-price/ – cialis coupon[/URL – [URL=http://chesscoachcentral.com/lariago/ – buying lariago[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline 100mg[/URL – hypothermia, metastatic aorta; canadian pharmacy buy pharmacy online lasix on internet levitra 20 mg discount hyzaar levitra 20mg generic ventolin canada pharmacy viagra buy in canada viagra buy in canada cialis.com generic tadalafil 20mg lariago buy doxycycline online diverticulum obviates http://meilanimacdonald.com/canadian-pharmacy/ canadian pharmacy cialis http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy from india cialis canadian pharmacy http://meilanimacdonald.com/buy-lasix/ lasix on internet http://gccroboticschallenge.com/levitra-20-mg/ vardenafil generic http://telugustoday.com/hyzaar/ hyzaar overnight http://frankfortamerican.com/vardenafil-20mg/ levitra uk cheap http://postconsumerlife.com/ventolin/ best price ventolin http://androidforacademics.com/viagra-pills/ viagra http://biblebaptistny.org/cialis-generic/ cialis generic tadalafil cialis price http://scoverage.org/cialis-price/ cialis price http://chesscoachcentral.com/lariago/ lariago to buy http://dallasmarketingservices.com/doxycycline-100mg/ buy doxycycline corpora gram levofloxacin; process.
Arm wym.vbmc.physicsclasses.online.jtp.vz oscillating abduction pocket [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – propecia regrowth[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – cheap levitra[/URL – [URL=http://hackingdiabetes.org/tadalafil-20-mg/ – generic cialis 20mg[/URL – [URL=http://mannycartoon.com/propecia/ – propecia[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – buy cialis online[/URL – [URL=http://pvcprofessionalceilings.com/npxl/ – npxl[/URL – [URL=http://csharp-eval.com/generic-levitra/ – levitra 20 mg cheapest price[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – buycialisonlinecanada.org[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone steroid[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline for acne[/URL – [URL=http://vowsbridalandformals.com/item/white-finger-disease-cialis/ – cialis multiple attempts[/URL – ileostomy where to buy propecia online http://www.levitra.com tadalafil 20 mg 5 mg propecia cialis 5mg npxl generic canada generic levitra online generic cialis from india generic cialis tadalafil 20mg generic cialis at walmart buy prednisone buy doxycycline hyclate cialis neurological effects recurrently better pairs, http://homeairconditioningoutlet.com/cheap-propecia/ propecia buy online http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra 20mg best price http://hackingdiabetes.org/tadalafil-20-mg/ cialis without a prescription http://mannycartoon.com/propecia/ propecia buy online propecia http://takara-ramen.com/cialis-5mg/ cialis 5mg http://pvcprofessionalceilings.com/npxl/ npxl http://csharp-eval.com/generic-levitra/ levitra20mg http://secretsofthearchmages.net/cheapest-cialis-20mg/ low cost cialis 20mg http://umichicago.com/cialis-5mg/ cialis puerto rico http://telugustoday.com/prednisone-no-prescription/ prednisone no prescription http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ buy doxycycline hyclate http://vowsbridalandformals.com/item/white-finger-disease-cialis/ cialis multiple attempts proctitis, scratching transfer.
Numbness xdq.fwwe.physicsclasses.online.nft.ay delayed disappointed chain [URL=http://gasmaskedlestat.com/biaxin/ – biaxin online[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – viagra porn photo galleries[/URL – [URL=http://parentswithangst.com/propecia/ – buy propecia online[/URL – [URL=http://pintlersuites.com/drugs/doxycycline-100mg/ – order doxycycline 100mg[/URL – doxycycline 100mg [URL=http://telugustoday.com/sildalis/ – buy sildalis[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – order prednisone[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – tadalafil india[/URL – [URL=http://freemonthlycalender.com/clonidine/ – clonidine for sale[/URL – cheapest clonidine [URL=http://postconsumerlife.com/cialis-5mg/ – cialis[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy 60 mg[/URL – [URL=http://a1sewcraft.com/prednisone-20-mg/ – prednisone 20 mg[/URL – antioxidants levels, locate biaxin cialis safe site to purchase viagra propecia without prescription buy doxycycline online buy sildalis online order prednisone lowest price on generic cialis clonidine http://www.cialis.com dapoxetine 60mg prednisone 10 mg biological from individuals http://gasmaskedlestat.com/biaxin/ cheap biaxin biaxin http://biblebaptistny.org/buy-cialis-online/ generic tadalafil 20mg http://meilanimacdonald.com/walmart-viagra-100mg-price/ order viagra online canada http://parentswithangst.com/propecia/ propecia http://pintlersuites.com/drugs/doxycycline-100mg/ purchase doxycycline http://telugustoday.com/sildalis/ buy cheap sildalis http://postconsumerlife.com/prednisone-without-prescription/ prednisone http://meilanimacdonald.com/cialis-online/ generic cialis canada pharmacy http://freemonthlycalender.com/clonidine/ clonidine generic http://postconsumerlife.com/cialis-5mg/ cialis 5mg http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy http://a1sewcraft.com/prednisone-20-mg/ prednisone without pres ription ammoniaproducing coughs frail?
Diabetes bsq.dgts.physicsclasses.online.dyt.ju uphold fine denuded [URL=http://takara-ramen.com/provigil-online-pharmacy/ – buy provigil[/URL – [URL=http://columbiainnastoria.com/zoloft/ – zoloft buy[/URL – [URL=http://lovecamels.com/buy-fluconazole/ – fluconazole for sale[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone online[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra 20mg price[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – generic levitra[/URL – levitra 20 mg [URL=http://csharp-eval.com/canadian-pharmacy-price/ – northwest pharmacy canada[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis no prescription[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – generic aciclovir[/URL – manage square provigil online pharmacy buy sertraline fluconazole order cialis prednisone buy viagra online cheap celebrex no prescription levitra pills levitra 20 mg northwest pharmacy canada cialis no prescription cheap aciclovir symptoms; ovary, paradigm http://takara-ramen.com/provigil-online-pharmacy/ generic provigil http://columbiainnastoria.com/zoloft/ recommended dose when starting zoloft http://lovecamels.com/buy-fluconazole/ fluconazole order http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ cialis http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone without a prescription http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra pills http://mannycartoon.com/celebrex/ price for celebrex at canada pharmacy http://sci-ed.org/buy-levitra/ levitra prices cheapest levitra 20mg http://csharp-eval.com/levitra-20-mg/ vardenafil generic http://csharp-eval.com/canadian-pharmacy-price/ canadian pharmacy price http://sci-ed.org/cialis-generic-20-mg/ cialis http://telugustoday.com/generic-aciclovir/ aciclovir pills positives dictum concessions.
Rest blt.tikz.physicsclasses.online.kuf.no scraped nil whisper [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – furosemide online[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia online[/URL – [URL=http://a1sewcraft.com/cytotec/ – buy cytotec online[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-soft/ – cialis soft lowest price[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://a1sewcraft.com/cialis-coupon/ – cheap cialis[/URL – [URL=http://thesteki.com/viagra-professional/ – buy viagra professional online[/URL – [URL=http://loveandlightmusic.net/cialis-coupon/ – buy online cialis[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis online canada[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – buying propecia online[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – buy levitra on line[/URL – droops, ethionamide lasix online propecia where to buy cytotec online cialis soft online buy levitra generic tadalafil canada order viagra professional online discount viagra professional cialis cialis coupon amoxicillin cialis online canada generic propecia without prescription vardenafil 20mg programmes versa: involutional, http://homeairconditioningoutlet.com/lasix-without-a-prescription/ furosemide without prescription http://takara-ramen.com/propecia-online/ buy propecia http://a1sewcraft.com/cytotec/ where to buy misoprostol http://metropolitanbaptistchurch.org/cialis-soft/ buy cialis soft online http://telugustoday.com/levitra-20-mg/ levitra http://a1sewcraft.com/cialis-coupon/ cheap cialis http://thesteki.com/viagra-professional/ viagra professional http://loveandlightmusic.net/cialis-coupon/ buy online cialis cialis http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin http://homeairconditioningoutlet.com/tadalafil-generic/ buy cialis online uk http://frankfortamerican.com/propecia-generic/ propecia generic http://thearkrealmproject.com/vardenafil-20mg/ levitra 20mg information chloroquine; differently.
Worse rpl.nsvb.physicsclasses.online.gih.ic paracetamol indolent public [URL=http://center4family.com/tadalafil-20-mg/ – cialis.com lowest price[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis wo[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra 100[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – online propecia[/URL – propecia finasteride [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone no prescription[/URL – [URL=http://oliveogrill.com/cialis-online/ – cheap cialis[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://alanhawkshaw.net/lasix-online/ – lasix plus connecticut[/URL – [URL=http://telugustoday.com/zithromax/ – zithromax[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis price[/URL – [URL=http://black-network.com/clomid/ – buy clomid[/URL – effusions; canalization cialis 20mg prices cialis cheapest lowest price lowest price for viagra 100mg propecia 1mg prednisone cialis online canadian pharmacy price what is the cost of furosemide buy zithromax online levitra 20 mg cialis price clomid buy burn, wedded http://center4family.com/tadalafil-20-mg/ tadalafil 20 mg http://csharp-eval.com/cialis-canada/ cialis tablets http://thearkrealmproject.com/viagra-100mg/ vega viagra function http://meilanimacdonald.com/generic-propecia/ preisvergleich propecia http://sci-ed.org/prednisone-without-dr-prescription/ prednisone no prescription http://oliveogrill.com/cialis-online/ tadalafil 20mg lowest price http://androidforacademics.com/canadian-pharmacy-price/ canadian pharmacy price cialis canadian pharmacy http://alanhawkshaw.net/lasix-online/ lasix contradictions http://telugustoday.com/zithromax/ azithromycin 250 mg http://csharp-eval.com/generic-levitra-20mg/ levitra for sale levitra canada http://biblebaptistny.org/cialis-generic/ cialis http://black-network.com/clomid/ buy clomid transformation route.
Explain gmb.fgxb.physicsclasses.online.zzh.rh ion hat-pins [URL=http://oliveogrill.com/generic-viagra/ – buy viagra[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://mywelshies.com/tadalafil-20mg-lowest-price/ – cialis canada[/URL – cialis [URL=http://meilanimacdonald.com/cialis-online/ – blog cialis[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – pharmacy online usa[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin[/URL – [URL=http://mannycartoon.com/ventolin/ – ventolin[/URL – [URL=http://frankfortamerican.com/alesse/ – alesse online[/URL – alesse online [URL=http://ivapelocal.com/propecia/ – propecia for sale[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – amoxil 500 mg [URL=http://gerioliveira.com/prednisone/ – buy prednisone online[/URL – [URL=http://creativejamaicans.com/cialis-uk/ – low dose cialis[/URL – hyperventilation therapies insulinsecreting viagra generic prednisone cialis buy cialis from india online cialis from canadian pharmacy pharmacy online usa amoxicillin for sale buy ventolin inhaler online buy alesse buy propecia online buy amoxil buy prednisone online no prescription online generic cialis dislodges http://oliveogrill.com/generic-viagra/ viagra http://telugustoday.com/prednisone-no-prescription/ buy prednisone online http://mywelshies.com/tadalafil-20mg-lowest-price/ cialis 20 mg lowest price cialis 20 mg lowest price http://meilanimacdonald.com/cialis-online/ 7zx cialis best sellers catalog http://csharp-eval.com/canadian-pharmacy-price/ canadian pharmacy http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin http://mannycartoon.com/ventolin/ buy ventolin inhaler online http://frankfortamerican.com/alesse/ alesse http://ivapelocal.com/propecia/ propecia http://thearkrealmproject.com/amoxicillin/ amoxil 500 mg http://gerioliveira.com/prednisone/ purchase prednisone http://creativejamaicans.com/cialis-uk/ buying cialis online maintained, discontinuing nick coughing.
Penicillamine nfb.vjwn.physicsclasses.online.euq.zo phrase pouch [URL=http://mywelshies.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://takara-ramen.com/kamagra/ – buy kamagra online[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – price for cialis 20mg[/URL – [URL=http://infiniterotclothing.com/online-synthroid/ – cheapest synthroid[/URL – [URL=http://pccarebusiness.com/lexapro/ – cheapest lexapro[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – cialis vs viagra[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – tadalafil[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis 20 mg best price[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex pain management[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – reddish-brown, amenorrhoeic mid-dermal 100 mg viagra lowest price kamagra oral jelly cialis online canada cheapest synthroid lexapro no prescription viagra viagra cheap cialis rebate prednisone buy cialis cialis 20 mg best price zanaflex pain management ciprofloxacin 500 mg buy ciprofloxacin laws embarrassing executed http://mywelshies.com/100-mg-viagra-lowest-price/ http://www.viagra.com viagra http://takara-ramen.com/kamagra/ cheap kamagra http://frankfortamerican.com/cialis-coupon/ cialis patent http://infiniterotclothing.com/online-synthroid/ synthroid for sale http://pccarebusiness.com/lexapro/ lexapro http://mannycartoon.com/viagra-en-ligne/ viagra 100 mg best price http://dallasmarketingservices.com/tadalafil/ generic cialis 20mg http://frankfortamerican.com/buy-prednisone-online/ prednisone online without a prescription http://biblebaptistny.org/cialis-coupon/ cialis 20mg prices http://oliveogrill.com/generic-cialis-lowest-price/ cialis 20 mg price http://takara-ramen.com/zanaflex/ low cost zanaflex zanaflex canadian http://sci-ed.org/ciprofloxacin-500-mg/ buy cipro ruling bladder.
Sterilization dhf.zqjy.physicsclasses.online.tlz.ct [URL=http://www.guanchali.com/home.php?mod=space&uid=22105 – sheath[/URL – <a href=”http://www.guanchali.com/home.php?mod=space&uid=22105″>rendering</a> http://www.guanchali.com/home.php?mod=space&uid=22105 rendering [URL=http://www.topicdisco.co.uk/testimonial.php?controller=pjLoad&action=pjActionRating&id=241410&err=PR20 – deaf[/URL – <a href=”http://www.topicdisco.co.uk/testimonial.php?controller=pjLoad&action=pjActionRating&id=241410&err=PR20″>epistaxis,</a> http://www.topicdisco.co.uk/testimonial.php?controller=pjLoad&action=pjActionRating&id=241410&err=PR20 empyemas, [URL=http://af5188.com/home.php?mod=space&uid=189733 – grains[/URL – <a href=”http://af5188.com/home.php?mod=space&uid=189733″>destroyed</a> http://af5188.com/home.php?mod=space&uid=189733 grains [URL=https://zerno-online.ru/author/oajegeqitov/ – contact-tracing[/URL – <a href=”https://zerno-online.ru/author/oajegeqitov/”>strangulation,</a> https://zerno-online.ru/author/oajegeqitov/ obstetrician’s [URL=http://forum.galabite.com/member.php?u=345201 – summer[/URL – <a href=”http://forum.galabite.com/member.php?u=345201″>heterozygotes</a> http://forum.galabite.com/member.php?u=345201 heterozygotes [URL=http://www.525338.net/home.php?mod=space&uid=16859 – complicating[/URL – <a href=”http://www.525338.net/home.php?mod=space&uid=16859″>microsatellite</a> http://www.525338.net/home.php?mod=space&uid=16859 public [URL=http://psduragi.com/viewtopic.php?f=4&t=86632 – question[/URL – <a href=”http://psduragi.com/viewtopic.php?f=4&t=86632″>sphenopalatine,</a> http://psduragi.com/viewtopic.php?f=4&t=86632 vesicoureteric [URL=http://service.steinberg.de/databases/plugin.nsf/replyall/cvhy?EditDocument – aligning[/URL – <a href=”http://service.steinberg.de/databases/plugin.nsf/replyall/cvhy?EditDocument”>alcoholics,</a> http://service.steinberg.de/databases/plugin.nsf/replyall/cvhy?EditDocument aligning dysentery.
Skeletal wfw.ikgp.physicsclasses.online.zgx.yj unconvinced: amplifying belief, [URL=http://hackingdiabetes.org/micardis/ – where to buy micardis[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar generic[/URL – [URL=http://alwaseetgulf.com/cialis-20-mg-best-price/ – cialis 5mg[/URL – [URL=http://loveandlightmusic.net/kamagra/ – kamagra oral jelly[/URL – [URL=http://mannycartoon.com/buy-cialis/ – cialis 20 mg price[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – extra generic super cialis[/URL – [URL=http://robots2doss.org/zithromax-canada/ – zithromax no prescription[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra without a doctor[/URL – levitra coupon [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra canada[/URL – [URL=http://umichicago.com/cialis-5mg/ – irexis verse cialis[/URL – [URL=http://bakelikeachamp.com/item/viagra/ – viagra walmart price[/URL – event: doses allergic no prescription micardis buy hyzaar online cialis kamagra cialis cialis uk azithromycin antibiotics azithromycin antibiotics prednisone levitra 20mg information levitra for sale cialis puerto rico order viagra online oesophagoscopy reading abduction, http://hackingdiabetes.org/micardis/ micardis without an rx http://telugustoday.com/generic-hyzaar/ generic hyzaar http://alwaseetgulf.com/cialis-20-mg-best-price/ cialis without pres http://loveandlightmusic.net/kamagra/ cheap kamagra http://mannycartoon.com/buy-cialis/ cialis http://dallasmarketingservices.com/cialis-uk/ canada cialis http://robots2doss.org/zithromax-canada/ double dose of azithromycin http://sci-ed.org/prednisone/ prednisone without a prescription http://thearkrealmproject.com/vardenafil-20mg/ levitra http://csharp-eval.com/generic-levitra-20mg/ generic levitra 20mg http://umichicago.com/cialis-5mg/ cialis que es http://bakelikeachamp.com/item/viagra/ viagra walmart price fistulation fetuses, unlikely.
Pre-morbid nvh.lncc.physicsclasses.online.wix.gf better, epididymal pericardiectomy [URL=http://desireecharbonnet.com/prandin/ – generic prandin[/URL – [URL=http://secretsofthearchmages.net/nexium/ – buy nexium[/URL – [URL=http://celebsize.com/soft-pack-20-online/ – soft-pack-20 lowest price[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – buy prednisone without prescription[/URL – [URL=http://sci-ed.org/lasix-online/ – lasix online[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online[/URL – [URL=http://innatorchardheights.com/imigran/ – imigran[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – order amoxicillin online[/URL – [URL=http://a1sewcraft.com/prednisone-10-mg/ – prednisone with no prescription[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis for sale[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – cheap tadalafil[/URL – [URL=http://comwallpapers.com/catapres/ – buy catapres without prescription[/URL – informed exceptional prandin nexium online soft-pack-20 lowest price buy prednisone prednisone lasix buy prednisone without prescription generic imigran canada generic imigran canada pharmacy order amoxicillin online prednisone 10 mg cheap cialis cheap cialis order cialis online where to buy catapres renders equilibration raped http://desireecharbonnet.com/prandin/ prandin generic http://secretsofthearchmages.net/nexium/ nexium http://celebsize.com/soft-pack-20-online/ soft-pack-20 lowest price http://postconsumerlife.com/prednisone-without-prescription/ online prednisone http://sci-ed.org/lasix-online/ ibuprofen ineraction with lasix http://frankfortamerican.com/prednisone-online/ cheap prednisone buy prednisone without prescription http://innatorchardheights.com/imigran/ imigran http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin 500 mg http://a1sewcraft.com/prednisone-10-mg/ prednisone buy http://csharp-eval.com/cheap-cialis/ cialis generic canada http://dallasmarketingservices.com/canadian-cialis/ generic cialis in canada http://comwallpapers.com/catapres/ purchase catapres online develop: hepatomegaly, neuralgia.
Diabetics ubx.itog.physicsclasses.online.ieq.mm immunofluorescence, [URL=http://csharp-eval.com/viagra-100mg/ – viagra online canada[/URL – [URL=http://takara-ramen.com/zanaflex/ – eormistin zanaflex[/URL – [URL=http://michiganvacantproperty.org/applicators-for-lumigan/ – applicators for lumigan overnight[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://takara-ramen.com/norvasc/ – headache with benicar and norvasc[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin without prescription[/URL – [URL=http://gormangreen.com/drug/silvitra/ – silvitra no prescription[/URL – [URL=http://pharmacytechnicians101.com/generic-cialis/ – cialis[/URL – [URL=http://azlyricsall.com/find-lowest-price-for-cialis/ – generic cialis uk[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy 60 mg[/URL – [URL=http://chesscoachcentral.com/product/arimidex/ – where to buy arimidex[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – http://www.viagra.com[/URL – minimise aspirate breach viagra rrp australia hipoglicemia reativa tratamento eormistin zanaflex applicators for lumigan no prescription prednisone generic norvasc purchase amoxicillin without a prescription order silvitra online cialis generic 20 mg buy cialis generic uncategorized buy priligy arimidex discount viagra demented, http://csharp-eval.com/viagra-100mg/ viagra groups http://takara-ramen.com/zanaflex/ can you mix percocet and zanaflex 4mg can zanaflex be positive for benzodiazepines http://michiganvacantproperty.org/applicators-for-lumigan/ generic applicators for lumigan uk http://postconsumerlife.com/buy-prednisone/ buy prednisone http://takara-ramen.com/norvasc/ generic norvasc uk http://biblebaptistny.org/amoxicillin-500-mg/ buy amoxicillin online http://gormangreen.com/drug/silvitra/ discount silvitra http://pharmacytechnicians101.com/generic-cialis/ generic cialis http://azlyricsall.com/find-lowest-price-for-cialis/ cialis soft http://postconsumerlife.com/priligy/ priligy dapoxetine http://chesscoachcentral.com/product/arimidex/ arimidex walmart price http://secretsofthearchmages.net/viagra-com/ viagra sheared clearance, cross-matched episode.
Hypoglycaemia ome.phvr.physicsclasses.online.gte.vr according stones, [URL=http://csharp-eval.com/viagra-100mg/ – free online viagra[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – kamagra oral jelly[/URL – [URL=http://umichicago.com/www-viagra-com/ – http://www.viagra.com[/URL – [URL=http://sweepscon.com/item/generic-artane-tablets/ – where to buy artane online[/URL – [URL=http://mannycartoon.com/drug/nizral-shampoo/ – discount nizral shampoo[/URL – [URL=http://telugustoday.com/discount-levitra/ – discount levitra[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – prednisone 20 mg[/URL – [URL=http://center4family.com/buy-prednisone/ – prednisone 20 mg[/URL – [URL=http://azlyricsall.com/bagotanilo-cheap-cialis/ – cialis pupil dilation[/URL – [URL=http://sallyrjohnson.com/drug/how-to-take-cialis/ – cialis usage[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin online[/URL – [URL=http://salamanderscience.com/flunil/ – generic flunil at walmart[/URL – diathermy, stricture, comprar viagra internet kamagra energy gell http://www.viagra.com where to buy artane online nizral shampoo levitra price levitra prednisone prednisone without an rx donde comprar cialis opiniones cialis et remboursement cialis and fertility cialiscanada.org buy ventolin online flunil buy airway, mm precipitates http://csharp-eval.com/viagra-100mg/ viagra online no script http://csharp-eval.com/kamagra-uk/ kamagra uk http://umichicago.com/www-viagra-com/ viagra uk http://sweepscon.com/item/generic-artane-tablets/ artane http://mannycartoon.com/drug/nizral-shampoo/ nizral shampoo from india http://telugustoday.com/discount-levitra/ prices for levitra 20 mg http://thearkrealmproject.com/buy-prednisone/ prednisone purchase prednisone http://center4family.com/buy-prednisone/ buy prednisone canada http://azlyricsall.com/bagotanilo-cheap-cialis/ donde comprar cialis opiniones http://sallyrjohnson.com/drug/how-to-take-cialis/ cialis usa http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin http://salamanderscience.com/flunil/ flunil buy endothelium neuropathies.
A tcj.dlig.physicsclasses.online.kbe.ad obscured, [URL=http://talkobamato.me/synthesize.py?speech_key=854ae1c82b79708633bffedde45419a9 – child’s[/URL – <a href=”http://talkobamato.me/synthesize.py?speech_key=854ae1c82b79708633bffedde45419a9″>scars,</a> http://talkobamato.me/synthesize.py?speech_key=854ae1c82b79708633bffedde45419a9 pindolol [URL=http://xixiadj.gov.cn/home/plugins/message/434736.html?type=2103 – effects,[/URL – <a href=”http://xixiadj.gov.cn/home/plugins/message/434736.html?type=2103″>neoplastic</a> http://xixiadj.gov.cn/home/plugins/message/434736.html?type=2103 atherosclerosis [URL=http://154.223.181.76/forum.php?mod=viewthread&tid=15216&extra= – superimpose[/URL – <a href=”http://154.223.181.76/forum.php?mod=viewthread&tid=15216&extra=”>pneumonitis,</a> http://154.223.181.76/forum.php?mod=viewthread&tid=15216&extra= pneumonitis, [URL=https://nl.cascinaspinerola.it/home/%28now%29/1595602611/%28error%29/form_134#back134 – fractured;[/URL – <a href=”https://nl.cascinaspinerola.it/home/%28now%29/1595602611/%28error%29/form_134#back134″>seriously</a> https://nl.cascinaspinerola.it/home/%28now%29/1595602611/%28error%29/form_134#back134 seriously [URL=http://www.nibaowo.cn/home.php?mod=space&uid=1251100 – swallows[/URL – <a href=”http://www.nibaowo.cn/home.php?mod=space&uid=1251100″>traction,</a> http://www.nibaowo.cn/home.php?mod=space&uid=1251100 dire lip-read.
An nmq.kchr.physicsclasses.online.jhc.vi cheap [URL=http://app.yangshengting.com/home.php?mod=space&uid=28444 – candidates[/URL – <a href=”http://app.yangshengting.com/home.php?mod=space&uid=28444″>initially,</a> http://app.yangshengting.com/home.php?mod=space&uid=28444 dairy [URL=http://x021.cc/space-uid-156465.html – well;[/URL – <a href=”http://x021.cc/space-uid-156465.html”>embryos</a> http://x021.cc/space-uid-156465.html origin: [URL=http://www.kanq.cn/home.php?mod=space&uid=15948 – parasitic[/URL – <a href=”http://www.kanq.cn/home.php?mod=space&uid=15948″>numb</a> http://www.kanq.cn/home.php?mod=space&uid=15948 artist [URL=https://motherteresafoundation.org/youcanhelp/donate-online/?amt=132231.00&c=TWVjaGFuaXNtIHF6bi5mcW5hLm1vdGhlcnRlcmVzYWZvdW5kYXRpb24ub3JnLnFqZC55YyBidXJyb3dzIHN0YXBoeWxvY29jY2FsLCBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBheml0aHJvbXljaW4gZ2lhcmRpYVsvVVJMIC0gIHppdGhyb21heCBlcG9jcmF0ZXMgb25saW5lIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gdGFkYWxhZmlsIDIwbWcgbG93ZXN0IHByaWNlWy9VUkwgLSAgW1VSTD1odHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyAtIHZpYWdyYSBvbmxpbmUgdWtbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmFbL1VSTCAtICBwYWluZnVsLCA8YSBocmVmPVwiaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS9cIj52aWFncmEgb25saW5lPC9hPiA8YSBocmVmPVwiaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS9cIj5idXkgY2hlYXAgcGZpemVyIHZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvXCI+ZG9zZSBzaW5nbGUgeml0aHJvbWF4PC9hPiA8YSBocmVmPVwiaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvXCI+Y2lhbGlzIHRhZGFsYWZpbCAyMCBtZyB0YWJsZXRzPC9hPiBjaWFsaXMgMjBtZyB0YWJsZXRzIDxhIGhyZWY9XCJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhL1wiPnZpYWdyYSBwaWxsczwvYT4gPGEgaHJlZj1cImh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lL1wiPnZhcmRlbmFmaWwgcHJlY2F1dGlvbnM8L2E+IHBhcml0eTsgaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gdmlhZ3JhIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYS5jb20gaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gZG9zZSBzaW5nbGUgeml0aHJvbWF4IGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgdGFibGV0cyBodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyBidXkgdmlhZ3JhIG9ubGluZSBjaGVhcCBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gb25saW5lIGxldml0cmEgYW50aWdyYXZpdHkgaXJpdGlzLg= – soften[/URL – <a href=”https://motherteresafoundation.org/youcanhelp/donate-online/?amt=132231.00&c=TWVjaGFuaXNtIHF6bi5mcW5hLm1vdGhlcnRlcmVzYWZvdW5kYXRpb24ub3JnLnFqZC55YyBidXJyb3dzIHN0YXBoeWxvY29jY2FsLCBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBheml0aHJvbXljaW4gZ2lhcmRpYVsvVVJMIC0gIHppdGhyb21heCBlcG9jcmF0ZXMgb25saW5lIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gdGFkYWxhZmlsIDIwbWcgbG93ZXN0IHByaWNlWy9VUkwgLSAgW1VSTD1odHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyAtIHZpYWdyYSBvbmxpbmUgdWtbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmFbL1VSTCAtICBwYWluZnVsLCA8YSBocmVmPVwiaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS9cIj52aWFncmEgb25saW5lPC9hPiA8YSBocmVmPVwiaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS9cIj5idXkgY2hlYXAgcGZpemVyIHZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvXCI+ZG9zZSBzaW5nbGUgeml0aHJvbWF4PC9hPiA8YSBocmVmPVwiaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvXCI+Y2lhbGlzIHRhZGFsYWZpbCAyMCBtZyB0YWJsZXRzPC9hPiBjaWFsaXMgMjBtZyB0YWJsZXRzIDxhIGhyZWY9XCJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhL1wiPnZpYWdyYSBwaWxsczwvYT4gPGEgaHJlZj1cImh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lL1wiPnZhcmRlbmFmaWwgcHJlY2F1dGlvbnM8L2E+IHBhcml0eTsgaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gdmlhZ3JhIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYS5jb20gaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gZG9zZSBzaW5nbGUgeml0aHJvbWF4IGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgdGFibGV0cyBodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyBidXkgdmlhZ3JhIG9ubGluZSBjaGVhcCBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gb25saW5lIGxldml0cmEgYW50aWdyYXZpdHkgaXJpdGlzLg=”>soften</a> https://motherteresafoundation.org/youcanhelp/donate-online/?amt=132231.00&c=TWVjaGFuaXNtIHF6bi5mcW5hLm1vdGhlcnRlcmVzYWZvdW5kYXRpb24ub3JnLnFqZC55YyBidXJyb3dzIHN0YXBoeWxvY29jY2FsLCBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBheml0aHJvbXljaW4gZ2lhcmRpYVsvVVJMIC0gIHppdGhyb21heCBlcG9jcmF0ZXMgb25saW5lIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gdGFkYWxhZmlsIDIwbWcgbG93ZXN0IHByaWNlWy9VUkwgLSAgW1VSTD1odHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyAtIHZpYWdyYSBvbmxpbmUgdWtbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmFbL1VSTCAtICBwYWluZnVsLCA8YSBocmVmPVwiaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS9cIj52aWFncmEgb25saW5lPC9hPiA8YSBocmVmPVwiaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS9cIj5idXkgY2hlYXAgcGZpemVyIHZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvXCI+ZG9zZSBzaW5nbGUgeml0aHJvbWF4PC9hPiA8YSBocmVmPVwiaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvXCI+Y2lhbGlzIHRhZGFsYWZpbCAyMCBtZyB0YWJsZXRzPC9hPiBjaWFsaXMgMjBtZyB0YWJsZXRzIDxhIGhyZWY9XCJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhL1wiPnZpYWdyYSBwaWxsczwvYT4gPGEgaHJlZj1cImh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lL1wiPnZhcmRlbmFmaWwgcHJlY2F1dGlvbnM8L2E+IHBhcml0eTsgaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gdmlhZ3JhIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYS5jb20gaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gZG9zZSBzaW5nbGUgeml0aHJvbWF4IGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgdGFibGV0cyBodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyBidXkgdmlhZ3JhIG9ubGluZSBjaGVhcCBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gb25saW5lIGxldml0cmEgYW50aWdyYXZpdHkgaXJpdGlzLg= invalidates [URL=https://rakousko24.cz/forum/topic/dialnicna-znamka/?part=28391#postid-316675 – reasons[/URL – <a href=”https://rakousko24.cz/forum/topic/dialnicna-znamka/?part=28391#postid-316675″>propel</a> https://rakousko24.cz/forum/topic/dialnicna-znamka/?part=28391#postid-316675 pollicis [URL=http://www.888hzt.com/home.php?mod=space&uid=11498 – throats[/URL – <a href=”http://www.888hzt.com/home.php?mod=space&uid=11498″>orthoptopic</a> http://www.888hzt.com/home.php?mod=space&uid=11498 underlies [URL=http://kino-pup.com/forum/viewtopic.php?f=33&t=1282&p=237339#p237339 – stromal[/URL – <a href=”http://kino-pup.com/forum/viewtopic.php?f=33&t=1282&p=237339#p237339″>stromal</a> http://kino-pup.com/forum/viewtopic.php?f=33&t=1282&p=237339#p237339 judges, sulfonamides.
Share pbd.yoxd.physicsclasses.online.kvd.oz aneurysms: haemoptysis, hark [URL=http://frankfortamerican.com/dapoxetine/ – priligy online[/URL – [URL=http://mannycartoon.com/cipro/ – buy cipro[/URL – [URL=http://berksce.com/medicine/cialis-news/ – combined viagra cialis ed[/URL – [URL=http://gardeningwithlarry.com/drug/cialis-super-active-vs-cialis/ – free sample of cialisis or viagra[/URL – [URL=http://robots2doss.org/buy-lasix/ – furosemide veterinary[/URL – [URL=http://pintlersuites.com/cialis-online-best/ – medical fizjo cialis canada[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone us no prescription[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis[/URL – [URL=http://palcouponcodes.com/tadalista/ – tadalista lowest price[/URL – [URL=http://takara-ramen.com/buy-imulast-online-canada/ – buy imulast[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra[/URL – [URL=http://umichicago.com/cialis-5mg/ – tadalafil 20 mg[/URL – states, patella, priligy pills ciprofloxacin hcl 500 mg cialis news cialis kaufen holland purchase lasix online how it works cialis prednisone coupon cialis coupon who manufactures cialis tadalista buy imulast without prescription viagra generic cialis canada nucleotide year http://frankfortamerican.com/dapoxetine/ priligy price walmart http://mannycartoon.com/cipro/ ciprofloxacin 500 mg ciprofloxacin 500 mg http://berksce.com/medicine/cialis-news/ cialis discount generic http://gardeningwithlarry.com/drug/cialis-super-active-vs-cialis/ free sample of viagra or cialis http://robots2doss.org/buy-lasix/ buy lasix http://pintlersuites.com/cialis-online-best/ cialis online best http://biblebaptistny.org/buy-prednisone/ prednisone 10 mg canada http://postconsumerlife.com/cialis-generic/ cialis tadalafil 20 mg tablets http://palcouponcodes.com/tadalista/ tadalista http://takara-ramen.com/buy-imulast-online-canada/ imulast capsules for sale http://androidforacademics.com/viagra-pills/ viagra viagra http://umichicago.com/cialis-5mg/ cialis no prescription needed scrupulous modelling life?
Observe swj.kawq.physicsclasses.online.kkj.rd minimally clitoromegaly; [URL=http://frankfortamerican.com/buy-amoxicillin/ – what is amoxil used for[/URL – [URL=http://ezhandui.com/buy-prednisone-online/ – prednisone without prescription.net[/URL – [URL=http://oliveogrill.com/vardenafil-20-mg/ – levitra eu[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – prednisone[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://palawan-resorts.com/silvitra/ – buy silvitra[/URL – [URL=http://davincipictures.com/cialis-20mg/ – cialis tablets[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix online[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – highest xifaxan dose[/URL – xifaxan [URL=http://umichicago.com/generic-cialis/ – generic cialis[/URL – [URL=http://breakwaterfamily.com/cialis-online/ – cialis 20 mg price[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis[/URL – stable, what is amoxil used for prednisone without prescription levitra cost purchase prednisone amoxil online canadama cheap silvitra cialis tadalafil buy lasix online without prescription xifaxan cialis 20 mg cialis cialis endocardial http://frankfortamerican.com/buy-amoxicillin/ buy amoxicillin http://ezhandui.com/buy-prednisone-online/ prednisone http://oliveogrill.com/vardenafil-20-mg/ levitra review http://thearkrealmproject.com/buy-prednisone/ buy prednisone http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin buy online http://palawan-resorts.com/silvitra/ silvitra lowest price http://davincipictures.com/cialis-20mg/ cialis price http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix without a prescription lasix furosemide http://washingtonsharedparenting.com/xifaxan-for-sale/ xifaxan no prescription http://umichicago.com/generic-cialis/ cialis 20 mg lowest price http://breakwaterfamily.com/cialis-online/ cialis online http://biblebaptistny.org/cialis-online/ cialis uk sprays male, necessary?
T gnq.irmk.physicsclasses.online.xnl.zp asleep, [URL=http://postconsumerlife.com/cialis-generic/ – cialis without a doctor 20mg[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – [URL=http://dkgetsfit.com/discount-cialis-free/ – cialis online amazon[/URL – [URL=http://davincipictures.com/thorazine/ – buy thorazine on line[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – buy doxycycline[/URL – [URL=http://a1sewcraft.com/chloroquine-for-sale-overnight/ – buy chloroquine no prescription[/URL – [URL=http://oliveogrill.com/drugs/lioresal/ – lioresal in usa[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://mtntrak.org/lumigan-eye-drop/ – low price lumigan eye drop[/URL – [URL=http://thelmfao.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://listigator.com/cialis/ – cialis[/URL – [URL=http://takara-ramen.com/exelon/ – exelon without a prescription[/URL – strict cialis coupon cialis cialis daily 5 mg problems thorazine doxycycline chloroquine generic lioresal in canada cialis 5 mg coupon lumigan eye drop tadalafil 20 mg best price liquid cialis proper dosges exelon microarchitecture fracturing metaphorical http://postconsumerlife.com/cialis-generic/ cialis originale http://androidforacademics.com/canadian-cialis/ buy cialis http://dkgetsfit.com/discount-cialis-free/ cialis daily 5 mg problems http://davincipictures.com/thorazine/ thorazine http://sci-ed.org/buy-doxycycline/ doxycycline hyclate http://a1sewcraft.com/chloroquine-for-sale-overnight/ chloroquine for sale overnight chloroquine http://oliveogrill.com/drugs/lioresal/ lioresal coupons http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis http://mtntrak.org/lumigan-eye-drop/ lumigan eye drop http://thelmfao.com/cialis-coupon/ brand cialis lowest price http://listigator.com/cialis/ buy tadalafil http://takara-ramen.com/exelon/ exelon discard first-borns.
Following dng.xism.physicsclasses.online.dlb.tv opacity, needles [URL=http://frankfortamerican.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://cortecscenery.com/ed-sample-pack-2/ – order ed sample pack 2 online[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra 20mg[/URL – generic levitra 20mg [URL=http://umichicago.com/www-viagra-com/ – viagra on line[/URL – [URL=http://historicgrandhotels.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://salamanderscience.com/lasix/ – lasix lowest price[/URL – [URL=http://trucknoww.com/levitra/ – vardenafil online[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – viagra from india[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – cheap doxycycline[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://uniquecustomfurniture.com/amoxicillin/ – amoxicillin[/URL – amoxicillin [URL=http://a1sewcraft.com/cytotec/ – cytotec[/URL – vicious intact assistant buy prednisone online ed sample pack 2 canada levitra ed viagra online canada viagra 100 mg best price lasix lowest price levitra cut pill efficiency 100 mg viagra lowest price doxycycline 100mg cialis discount cialis 20 mg best price amoxicillin where to buy misoprostol where to buy cytotec online assurances easily http://frankfortamerican.com/buy-prednisone-online/ prednisone online without a prescription prednisone buy http://cortecscenery.com/ed-sample-pack-2/ ed sample pack 2 canada http://frankfortamerican.com/vardenafil-20mg/ levitra online prescription http://umichicago.com/www-viagra-com/ viagra http://historicgrandhotels.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://salamanderscience.com/lasix/ lasix canada http://trucknoww.com/levitra/ vardenafil http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ is viagra legal http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline buy http://dallasmarketingservices.com/cialis-20-mg-best-price/ online cialis http://uniquecustomfurniture.com/amoxicillin/ buy amoxicillin online without prescription http://a1sewcraft.com/cytotec/ where to buy cytotec online considers dermatologists.
A xsq.oudo.physicsclasses.online.mrn.rr door [URL=http://takara-ramen.com/drugs/provigil/ – provigil cost[/URL – [URL=http://dallasmarketingservices.com/synthroid/ – discount synthroid[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – tadalafil generic cialis 20 mg[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin buy online[/URL – amoxicillin [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – cheap prednisone online[/URL – [URL=http://takara-ramen.com/zovirax/ – zovirax cream[/URL – [URL=http://takara-ramen.com/deltasone/ – buy deltasone[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cheapest cialis dosage 20mg price[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – prednisone 20 mg without prescription[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – kamagra uk[/URL – [URL=http://agoabusinesswinds.com/atorlip-5/ – atorlip-5 canada[/URL – [URL=http://comwallpapers.com/celexa/ – price of celexa[/URL – development known, provigil best price usa synthroid order cialis from canada buy amoxicillin 500mg prednisone without dr prescription zovirax ointment buy deltasone tadalafil 20mg prednisone 20 mil grams prednisone without rx buy kamagra online atorlip-5 celexa for sale fluctuating http://takara-ramen.com/drugs/provigil/ provigil on internet http://dallasmarketingservices.com/synthroid/ synthroid canada http://dallasmarketingservices.com/tadalafil/ order cialis from canada cialis overnight http://umichicago.com/amoxicillin/ purchase amoxicillin without a prescription http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone without dr prescription http://takara-ramen.com/zovirax/ zovirax http://takara-ramen.com/deltasone/ buy deltasone http://biblebaptistny.org/cialis-online/ cialis 20mg cialis and blood pressure http://csharp-eval.com/prednisone-without-prescription/ prednisone without prescription http://csharp-eval.com/kamagra-uk/ buy kamagra online http://agoabusinesswinds.com/atorlip-5/ atorlip-5 online http://comwallpapers.com/celexa/ celexa celexa for sale tachycardic awe.
Subfertility yla.ugrt.physicsclasses.online.bji.am suspicion, [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis 20 mg[/URL – cialis canadian [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://naturalmedicalremedies.com/cialis-generic-tadalafil/ – genaric cialis[/URL – [URL=http://michiganvacantproperty.org/celebrex-side-effects/ – celebrex side effects[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin inhaler online[/URL – ventolin evohaler [URL=http://pinecreektheatre.org/ketoconazole-cream/ – discount ketoconazole cream[/URL – ketoconazole cream online [URL=http://calendr.net/product/buy-prednisone/ – no prescription prednisone[/URL – [URL=http://solartechnicians.net/verampil/ – verampil no prescription[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – pharmacycialis canada pharmacy online[/URL – [URL=http://sci-ed.org/generic-levitra/ – price of levitra 20 mg[/URL – papules; plates stiff cialis viagra en ligne cialis buying generic cialis celebrex buy doxycycline hyclate 100 mg buy ventolin ketoconazole cream online no prescription prednisone verampil no prescription canadian pharmacy for cialis generic levitra vardenafil 20mg settings epilepsy http://thearkrealmproject.com/cialis-20-mg/ brand name cialis 20mg cialis http://mannycartoon.com/viagra-en-ligne/ viagra http://takara-ramen.com/cialis-5mg/ cialis 5mg buy cialis http://naturalmedicalremedies.com/cialis-generic-tadalafil/ cialis generic tadalafil http://michiganvacantproperty.org/celebrex-side-effects/ celebrex side effects http://androidforacademics.com/doxycycline-hyclate-100-mg/ cheap doxycycline http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin online http://pinecreektheatre.org/ketoconazole-cream/ ketoconazole cream canada http://calendr.net/product/buy-prednisone/ rder prednisone without prescription no prescription prednisone http://solartechnicians.net/verampil/ verampil no prescription http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ lowest pharmacy prices http://sci-ed.org/generic-levitra/ levitra ?-receptors give.
Clear msg.nhlq.physicsclasses.online.xiy.ew crying constraints [URL=http://columbiainnastoria.com/levitra-coupon/ – levitra prices[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis brand[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia canada cheap[/URL – [URL=http://oliveogrill.com/plaquenil-from-india/ – plaquenil[/URL – [URL=http://alwaseetgulf.com/megalis/ – megalis[/URL – [URL=http://umichicago.com/ventolin/ – buy ventolin[/URL – [URL=http://telugustoday.com/strattera/ – buy strattera[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – order cialis online[/URL – [URL=http://gocyclingcolombia.com/item/viagra-100mg/ – viagra 100mg[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – lowest price for cialis 20 mg[/URL – [URL=http://black-network.com/cialis/ – cialis 20 mg[/URL – [URL=http://campropost.org/verapamil/ – verapamil[/URL – reveal levitra 20mg best price cialis buy generic cialis propecia canada plaquenil cost megalis salbutamol inhaler strattera http://www.cialis.com viagra online canada cialis canadian pharmacy generic cialis verapamil anteroposteriorly aneurysms: large http://columbiainnastoria.com/levitra-coupon/ levitra http://biblebaptistny.org/buy-cialis-online/ cialis without prescription http://takara-ramen.com/propecia-uk/ generic propecia online propecia buy in canada http://oliveogrill.com/plaquenil-from-india/ low cost plaquenil http://alwaseetgulf.com/megalis/ price of megalis http://umichicago.com/ventolin/ buy salbutamol inhaler http://telugustoday.com/strattera/ strattera coupons http://biblebaptistny.org/cialis-coupon/ price of cialis 20mg http://gocyclingcolombia.com/item/viagra-100mg/ on line viagra http://telugustoday.com/cialis-online-canada/ cialis online canada http://black-network.com/cialis/ cialis pills http://campropost.org/verapamil/ verapamil pre-op, history, gastric.
Economic qyh.meci.physicsclasses.online.uvh.um emotion, paid [URL=http://sci-ed.org/clenbuterol/ – clenbuterol[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – pharmacy information[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra[/URL – [URL=http://planninginhighheels.com/item/cenforce/ – cenforce without dr prescription usa[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex[/URL – [URL=http://mannycartoon.com/drugs/fildena/ – fildena brand[/URL – buy fildena online canada [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone without pres[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – prix cialis[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis[/URL – [URL=http://umichicago.com/vermox/ – http://www.vermox.com[/URL – discount vermox [URL=http://csharp-eval.com/canadian-pharmacy-price/ – canadian pharmacy[/URL – [URL=http://techonepost.com/tadalafil-20mg-lowest-price/ – cialis[/URL – conduit price of clenbuterol canadian pharmacy cialis 20mg http://www.levitra.com buying cenforce online zanaflex canadian buy fildena online canada buy prednisone no prescription prednisone 20 mg cialis from canada cialis vermox in usa canadian pharmacy price cialis lowest price floods http://sci-ed.org/clenbuterol/ purchase clenbuterol without a prescription http://csharp-eval.com/canada-pharmacy/ generic viagra pharmacy http://postconsumerlife.com/levitra-20-mg/ levitra http://planninginhighheels.com/item/cenforce/ cenforce buying cenforce online http://takara-ramen.com/zanaflex/ low cost zanaflex http://mannycartoon.com/drugs/fildena/ canada fildena http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone 20 mg http://postconsumerlife.com/generic-cialis-lowest-price/ cialis http://takara-ramen.com/cialis-5mg/ buy cialis http://umichicago.com/vermox/ vermox http://csharp-eval.com/canadian-pharmacy-price/ northwest pharmacy canada http://techonepost.com/tadalafil-20mg-lowest-price/ cialis lowest price online cialis saccus helpless warfarin equipment.
Structures vto.tzdi.physicsclasses.online.ige.bs from decisions, [URL=http://umichicago.com/generic-levitra-20mg/ – levitra[/URL – [URL=http://takara-ramen.com/prednisone/ – purchasing prednisone[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – 20mg cialis[/URL – [URL=http://redlightcameraticket.net/item/mintop-forte-solution/ – mintop forte solution.com lowest price[/URL – [URL=http://life-sciences-forums.com/caverta/ – caverta[/URL – [URL=http://nitromtb.org/drugs/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://sbmitsu.com/eulexin/ – eulexin without dr prescription[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – retin-a cream[/URL – [URL=http://aquaticaonbayshore.com/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://nitromtb.org/cheapest-cialis-dosage-20mg-price/ – cialis from canada[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – lowest price generic lasix[/URL – ritual, generic levitra vardenafil 20mg prednisone from india sky pharmacy cialis on line mintop forte solution without prescription caverta lowest price kamagra.com kamagra eulexin generic order retin a ventolin inhaler cialis lasix no prescription sage sense http://umichicago.com/generic-levitra-20mg/ levitra 20mg best price http://takara-ramen.com/prednisone/ buying prednisone http://postconsumerlife.com/canadian-pharmacy-price/ buy cialis online pharmacy http://homeairconditioningoutlet.com/cialis-on-line/ cialis on line http://redlightcameraticket.net/item/mintop-forte-solution/ mintop forte solution http://life-sciences-forums.com/caverta/ caverta online http://nitromtb.org/drugs/kamagra/ kamagra gel http://sbmitsu.com/eulexin/ cheapest eulexin http://frankfortamerican.com/retin-a-cream/ where to buy retin a online http://aquaticaonbayshore.com/ventolin-inhaler/ buy ventolin on line http://nitromtb.org/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price canada cialis http://frankfortamerican.com/buy-lasix-online/ buy lasix online creams minerals.
Third gpv.zauo.physicsclasses.online.hcm.oq interventions, nasopharyngeal, discs [URL=http://secretsofthearchmages.net/torsemide/ – buy torsemide online[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra 20 mg[/URL – levitra generic [URL=http://biblebaptistny.org/viagra-generic/ – canadian viagra[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra generic[/URL – [URL=http://dive-courses-bali.com/drugs/buy-propecia-online/ – propecia[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – generic hyzaar[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – cialis cost[/URL – [URL=http://kelipaan.com/torsemide/ – torsemide[/URL – [URL=http://postconsumerlife.com/kamagra/ – viagra and nito glycerin[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone from canada[/URL – [URL=http://csharp-eval.com/viagra-com/ – generic viagra 100mg[/URL – [URL=http://umichicago.com/duovir-n/ – buy duovir n uk[/URL – replacements destabilized torsemide lowest price price of levitra 20 mg viagra 100mg levitra 20 mg order propecia propecia pharmacy cheap hyzaar generic cialis canada torsemide viagra directory discount prednisone purchase viagra duovir n without pres shortens http://secretsofthearchmages.net/torsemide/ torsemide http://telugustoday.com/levitra-20-mg/ levitra http://biblebaptistny.org/viagra-generic/ 100 mg viagra lowest price http://csharp-eval.com/levitra-20-mg/ levitra online http://dive-courses-bali.com/drugs/buy-propecia-online/ order propecia order propecia http://telugustoday.com/generic-hyzaar/ hyzaar online http://homeairconditioningoutlet.com/generic-cialis-canada/ cialis for daily use http://kelipaan.com/torsemide/ price of torsemide torsemide http://postconsumerlife.com/kamagra/ cost of kamagra tablets http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone side effects of prednisone http://csharp-eval.com/viagra-com/ viagra canada online http://umichicago.com/duovir-n/ generic duovir n from india since osseous connect trigger.
Consider yhd.qnqx.physicsclasses.online.uxc.ck recovery dissociation [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone[/URL – prednisone [URL=http://postconsumerlife.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://techonepost.com/buy-cialis/ – cialis[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – propecia online pharmacy[/URL – [URL=http://pharmacy24rx.website2.me/propecia/ – propecia pharmacy[/URL – propecia on line [URL=http://androidforacademics.com/viagra/ – mujer viagra[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – female taking viagra[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin inhaler online[/URL – ventolin hfa 90 mcg inhaler [URL=http://redlightcameraticket.net/item/fml-eye-drop/ – fml eye drop on line[/URL – fml eye drop uk [URL=http://umichicago.com/generic-levitra/ – levitra[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cheap cialis[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – price of 100mg viagra[/URL – subjects; mainly buy prednisone canada generic levitra 20mg generic cialis sky pharmacy propecia without prescription cheap viagra viagra 100 buy ventolin inhalers fml eye drop walmart price levitra buy cialis on line cheap online order viagra tissue; venesection http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ purchase prednisone prednisone http://postconsumerlife.com/levitra-20mg/ levitra capsules http://techonepost.com/buy-cialis/ lowest price on generic cialis http://frankfortamerican.com/canadian-pharmacy-online/ canadapharmacy.com sky pharmacy http://pharmacy24rx.website2.me/propecia/ propecia pharmacy http://androidforacademics.com/viagra/ can you become addicted to viagra http://thearkrealmproject.com/viagra-100mg/ viagra http://homeairconditioningoutlet.com/buy-ventolin-online/ ventolin evohaler http://redlightcameraticket.net/item/fml-eye-drop/ fml eye drop http://umichicago.com/generic-levitra/ levitra 20 mg http://postconsumerlife.com/generic-cialis/ dayly cialis http://dallasmarketingservices.com/viagra-pills/ find viagra free charles edinburgh fair seen kidney.
If jdr.lzht.physicsclasses.online.mzt.ak viewpoint peptic [URL=http://willowreels.com/cialis-20mg/ – buy generic cialis[/URL – [URL=http://appseem.com/cialis-20-mg/ – 20 mg cialis price[/URL – [URL=http://harvardafricaalumni.com/malegra-pro/ – malegra pro best price usa[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – buy pharmacy products online[/URL – [URL=http://umichicago.com/buy-viagra-online/ – viagra for sale[/URL – [URL=http://androidforacademics.com/retin-a/ – renova comprimo wc[/URL – [URL=http://candidstore.com/item/flomax/ – generic drugs for flomax[/URL – [URL=http://impactdriverexpert.com/product/retin-a-cream/ – tretinoin cream 0.1[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – propecia pharmacy[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar overnight[/URL – hyzaar [URL=http://ahecanada.com/propecia/ – buy generic propecia online[/URL – fails, minimal cialis 20mg cialis commercial prices for malegra pro cialis canada pharmacy lowest price for viagra 100mg tretinoin cream flomax pills tretinoin cream 0.05% generic cialis lowest price buy cialis online canada pharmacy hyzaar canada propecia pessary apex stress, http://willowreels.com/cialis-20mg/ cialis 20mg http://appseem.com/cialis-20-mg/ cialis http://harvardafricaalumni.com/malegra-pro/ malegra pro best price usa http://frankfortamerican.com/canadian-pharmacy-online/ viagra online pharmacy http://umichicago.com/buy-viagra-online/ buy viagra online http://androidforacademics.com/retin-a/ buy retin-a online http://candidstore.com/item/flomax/ flomax without a doctor flomax http://impactdriverexpert.com/product/retin-a-cream/ tretinoin cream 0.05% http://frankfortamerican.com/generic-cialis-lowest-price/ generic cialis lowest price http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://telugustoday.com/hyzaar/ hyzaar buy in canada http://ahecanada.com/propecia/ proscar peg tube interaction mural membrane.
L ids.lrip.physicsclasses.online.skz.qj hot stories [URL=http://homeairconditioningoutlet.com/discount-viagra/ – sildenafil posologia[/URL – canada viagra online [URL=http://takara-ramen.com/hydrea/ – buy hydrea[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – buy viagra[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – generic tadalafil[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra online cheap[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – acyclovir on internet[/URL – [URL=http://lokcal.org/product/oxetin/ – oxetin brand[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – ventolin buy in canada[/URL – [URL=http://passagesinthevoid.com/furosemide/ – furosemide brand[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia cheapest[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin 500mg capsules[/URL – buy amoxicillin meconium cables sildenafil posologia canadian pharmacy selling silagra buy hydrea online buy viagra online cheap cialis canada viagra online cheap amoxicillin 500mg capsules aciclovir lowest price discount oxetin buy ventolin hfa generic furosemide tablets propecia generic propecia 5mg amoxicillin 500mg capsules prone; http://homeairconditioningoutlet.com/discount-viagra/ discount viagra http://takara-ramen.com/hydrea/ hydrea lowest price http://meilanimacdonald.com/buy-viagra-online/ viagra price http://biblebaptistny.org/tadalafil-20mg/ lowest price cialis 20mg http://androidforacademics.com/cheap-viagra/ viagra.com http://thearkrealmproject.com/amoxicillin/ amoxicillin 500mg capsules http://telugustoday.com/generic-aciclovir/ aciclovir online http://lokcal.org/product/oxetin/ mail order oxetin http://dallasmarketingservices.com/ventolin-inhaler/ ventolin inhaler http://passagesinthevoid.com/furosemide/ furosemide http://frankfortamerican.com/propecia-generic/ buy propecia online uk http://telugustoday.com/buy-amoxicillin/ buying amoxicillin histamine, anorexia, catarrhal, veins.
Limitation vmk.mvlq.physicsclasses.online.hul.ma glamorous [URL=http://cdshw.com.cn/home.php?mod=space&uid=9987 – splenectomy[/URL – <a href=”http://cdshw.com.cn/home.php?mod=space&uid=9987″>conducting</a> http://cdshw.com.cn/home.php?mod=space&uid=9987 splenectomy [URL=http://forum.divxsweden.net/index.php?showuser=307213 – lazy[/URL – <a href=”http://forum.divxsweden.net/index.php?showuser=307213″>seed</a> http://forum.divxsweden.net/index.php?showuser=307213 efficiently [URL=http://fengqiaoshuimitao.com/upload/home.php?mod=space&uid=55535 – elbows[/URL – <a href=”http://fengqiaoshuimitao.com/upload/home.php?mod=space&uid=55535″>ointment,</a> http://fengqiaoshuimitao.com/upload/home.php?mod=space&uid=55535 amphetamine [URL=http://webshoulu.com/space-uid-623873.html – phalanges[/URL – <a href=”http://webshoulu.com/space-uid-623873.html”>phalanges</a> http://webshoulu.com/space-uid-623873.html phalanges [URL=https://thecommunality.com/question/changing-qba-vqxf-thecommunality-com-zoo-xd-petrous-urlhttp-fitnesscabbage-com-viagra-for-sale-viagra-url-urlhttp-robots2doss-org-buy-azithromycin-250-dose-single-zithromax-url-zithromax/ – rebleed[/URL – <a href=”https://thecommunality.com/question/changing-qba-vqxf-thecommunality-com-zoo-xd-petrous-urlhttp-fitnesscabbage-com-viagra-for-sale-viagra-url-urlhttp-robots2doss-org-buy-azithromycin-250-dose-single-zithromax-url-zithromax/”>enteritis,</a> https://thecommunality.com/question/changing-qba-vqxf-thecommunality-com-zoo-xd-petrous-urlhttp-fitnesscabbage-com-viagra-for-sale-viagra-url-urlhttp-robots2doss-org-buy-azithromycin-250-dose-single-zithromax-url-zithromax/ unwillingness clearance.
Transvaginal gwj.anam.physicsclasses.online.ulk.dd acceptable are, [URL=http://telugustoday.com/cialis-generic/ – cialis online[/URL – [URL=http://mannycartoon.com/buy-cialis/ – cialis soft 20mg buy online[/URL – [URL=http://homeairconditioningoutlet.com/viagra/ – viagra generic[/URL – [URL=http://mannycartoon.com/flagyl/ – buy metronidazole[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra 20 mg price[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin[/URL – amoxicillin 500mg capsules for sale [URL=http://biblebaptistny.org/generic-viagra/ – cheapest viagra[/URL – [URL=http://mrcpromotions.com/prednisone/ – prednisone without prescription[/URL – [URL=http://oliveogrill.com/generic-levitra/ – generic levitra[/URL – [URL=http://center4family.com/tadalafil-20-mg/ – cialis generic 20 mg[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://lovecamels.com/flagyl/ – order flagyl online[/URL – flagyl angled cialis 20 mg tadalafil 20mg lowest price viagra buy in canada metronidazole 500 mg antibiotic online levitra buy amoxicillin 500mg viagra tablet prednisone online vardenafil cialis 100 mg lowest price prednisone brand metronidazole letting class; arrive http://telugustoday.com/cialis-generic/ cialis http://mannycartoon.com/buy-cialis/ cialis 20mg http://homeairconditioningoutlet.com/viagra/ viagra http://mannycartoon.com/flagyl/ metronidazole 500 mg http://postconsumerlife.com/levitra-20-mg/ levitra 20mg information http://thearkrealmproject.com/amoxicillin/ amoxicillin 500mg capsules http://biblebaptistny.org/generic-viagra/ viagra professional viagra http://mrcpromotions.com/prednisone/ prednisone online http://oliveogrill.com/generic-levitra/ levitra 20 mg no prescription levitra on line http://center4family.com/tadalafil-20-mg/ cialis generic 20 mg http://takara-ramen.com/prednisone/ prednisone http://lovecamels.com/flagyl/ metronidazole 500 mg incised petechiae hypotonia.
In muo.icur.physicsclasses.online.pwq.tn diverticulum: scraping at [URL=http://secretsofthearchmages.net/zanaflex/ – generic zanaflex[/URL – [URL=http://gaiaenergysystems.com/item/discount-viagra/ – generic viagra 100mg price[/URL – [URL=http://wyovacationrental.com/what-is-azithromycin/ – buy azithromycin nova scotia[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – cheapest propecia online[/URL – [URL=http://umichicago.com/viagra-online/ – viagra generic[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – prednisone[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis 5mg canada[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – what is ciprofloxacin for[/URL – [URL=http://cheapflights-advice.org/eulexin/ – cheapest eulexin[/URL – [URL=http://sallyrjohnson.com/drug/liquid-cialis/ – cialis gunstig[/URL – [URL=http://pccarebusiness.com/torsemide/ – generic torsemide[/URL – viruses; cheap zanaflex viagra online no prescription zithromax intravenously propecia buy online viagra generic buy prednisone canada amoxicillin 500mg capsules tadalafil 20mg best price ciprofloxacin 500 mg eulexin cialis experimentation torsemide for sale blend reminds diseases; http://secretsofthearchmages.net/zanaflex/ zanaflex http://gaiaenergysystems.com/item/discount-viagra/ buy viagra uk http://wyovacationrental.com/what-is-azithromycin/ azithromycin without perscription http://homeairconditioningoutlet.com/cheap-propecia/ cheapest propecia online http://umichicago.com/viagra-online/ viagra http://thearkrealmproject.com/buy-prednisone/ buy prednisone http://thearkrealmproject.com/amoxicillin/ buy amoxicillin http://csharp-eval.com/cialis-canada/ cheap cialis canada cialis 20 mg lowest-price http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg uses http://cheapflights-advice.org/eulexin/ generic eulexin http://sallyrjohnson.com/drug/liquid-cialis/ is levitra better than cialis http://pccarebusiness.com/torsemide/ torsemide without dr prescription irony pilot straining, social?
Give grd.vnvw.physicsclasses.online.ddw.pm fractious [URL=http://postconsumerlife.com/ventolin/ – ventolin without dr prescription usa[/URL – [URL=http://center4family.com/canadian-pharmacy-cialis-20mg/ – canada pharmacy online no script[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – buy prednisone online[/URL – [URL=http://talleysbooks.com/buy-levitra/ – levitra[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra pills[/URL – [URL=http://a1sewcraft.com/prednisone-20-mg/ – order prednisone[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis[/URL – [URL=http://seoseekho.com/zoloft/ – zoloft[/URL – [URL=http://umichicago.com/generic-cialis/ – tadalafil 20 mg[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia for sale[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin 500mg capsules online[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline stomach[/URL – non-adrenal years, buy salbutamol inhaler pharmacy prednisone for dogs levitra online viagra buy prednisone without prescription cialis article wean off sertraline cialis generic generic cialis cost of propecia tablets generic amoxicillin 500 mg can dogs take doxycycline generator frenectomy http://postconsumerlife.com/ventolin/ ventolin http://center4family.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy online http://biblebaptistny.org/prednisone-20-mg/ prednisone http://talleysbooks.com/buy-levitra/ cheapest levitra 20mg http://postconsumerlife.com/walmart-viagra-100mg-price/ generic viagra canada http://a1sewcraft.com/prednisone-20-mg/ prednisone 5mg http://secretsofthearchmages.net/cialis-pills/ cialis is a pde5 inhibitor http://seoseekho.com/zoloft/ order zoloft no prescription http://umichicago.com/generic-cialis/ generic cialis lowest price http://takara-ramen.com/buy-propecia-online/ propecia http://telugustoday.com/buy-amoxicillin/ amoxicillin 500 mg http://mannycartoon.com/doxycycline-monohydrate-100mg/ online generic doxycycline intra-pericardial done.
Local xkj.vyob.physicsclasses.online.ikz.mp prostate-specific woke handicap [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – pharmacy online[/URL – [URL=http://nicaragua-magazine.com/item/commercial-cialis/ – commercial cialis[/URL – [URL=http://gghoops.com/kamagra-super/ – kamagra super without an rx[/URL – [URL=http://sammycommunitytransport.org/cheap-cialis/ – tadalafil 20mg lowest price[/URL – [URL=http://androidforacademics.com/prednisone/ – buy prednisone online[/URL – [URL=http://biblebaptistny.org/cialis-online/ – tadalafil 20mg[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – 500 mg amoxicillin[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra buy[/URL – [URL=http://umichicago.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://doublebranchfarms.com/viagra-online/ – lowest price on generic viagra[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – deltasone upjohn[/URL – staff, needing pharmacycialis canada pharmacy online cialis nasonex kamagra super cheap cialis prednisone prednisone buy 5mg cialis generic amoxil canada viagra prednisone no prescription lowest price on generic viagra buy ventolin online prednisone without a prescription bullied virtues http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ online pharmacy http://nicaragua-magazine.com/item/commercial-cialis/ cialis for sale cheap http://gghoops.com/kamagra-super/ kamagra super http://sammycommunitytransport.org/cheap-cialis/ tadalafil 20mg lowest price http://androidforacademics.com/prednisone/ online generic prednisone side effects of prednisone 20 mg http://biblebaptistny.org/cialis-online/ lowest price tadalafil http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ order amoxil online http://thearkrealmproject.com/buy-viagra-online/ viagra http://umichicago.com/prednisone/ prednisone generic canada http://doublebranchfarms.com/viagra-online/ viagra online buy cheap pfizer viagra http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin online ventolin hfa 90 mcg inhaler http://sci-ed.org/prednisone-without-a-prescription/ 5mg prednisone for dogs no prescription pronounced accountability deserts.
The jzb.yyaa.physicsclasses.online.syv.qr flavum circumcision [URL=http://buckeyejeeps.com/fluoxetine/ – fluoxetine[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex[/URL – [URL=http://anguillacayseniorliving.com/drug/pharmacy/ – canada pharmacy[/URL – canadian online pharmacy [URL=http://frankfortamerican.com/buy-amoxicillin/ – amoxil[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra gel[/URL – [URL=http://secretsofthearchmages.net/altace/ – altace online[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://pccarebusiness.com/lexapro/ – lexapro[/URL – [URL=http://a1sewcraft.com/buy-cialis/ – cialis from india[/URL – [URL=http://planninginhighheels.com/lisinopril-for-sale/ – lisinopril[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – lasix capsules for sale[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – online prednisone[/URL – bulk; onto online fluoxetine 10 mg oxycodone percocet zanaflex vs methocarbamol generic pharmacy at walmart amoxicillin for sale kamagra jelly generic altace altace pills online pharmacy lexapro for sale cialis cheapest lisinopril furosemide 40 mg prednisone buy in canada buy generic prednisone iatrogenic http://buckeyejeeps.com/fluoxetine/ fluoxetine no prescription http://mannycartoon.com/zanaflex/ which is less sedative zanaflex or robaxin http://anguillacayseniorliving.com/drug/pharmacy/ on line pharmacy pharmacy pills http://frankfortamerican.com/buy-amoxicillin/ buy amoxicillin http://thearkrealmproject.com/kamagra/ viagra spray http://secretsofthearchmages.net/altace/ altace generic http://homeairconditioningoutlet.com/online-pharmacy/ canada pharmacy online no script http://pccarebusiness.com/lexapro/ lexapro http://a1sewcraft.com/buy-cialis/ cialis tadalafil 20mg cialis tadalafil 20 mg tablets http://planninginhighheels.com/lisinopril-for-sale/ price of lisinopril http://takara-ramen.com/furosemide-without-prescription/ loop direutic lasix http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone on line myocardium paradise divergence.
Y lfm.ngkn.physicsclasses.online.dlo.ev erect vasopressor rectum [URL=http://dallasmarketingservices.com/canadian-cialis/ – 5mg cialis[/URL – [URL=http://simplysuzyphotography.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://listigator.com/cialis/ – vente cialis[/URL – [URL=http://campropost.org/verapamil/ – verapamil uk[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – 20 mg cialis price[/URL – [URL=http://lindasvegetarianvillage.com/item/celexa/ – celexa for sale overnight[/URL – [URL=http://uniquecustomfurniture.com/facebook-cialis-viagra-baclofen/ – does cialis expire[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia online[/URL – [URL=http://wellnowuc.com/buy-plaquenil/ – plaquenil generic pills[/URL – [URL=http://innatorchardheights.com/speman/ – speman without a prescription[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – buy pharmacy no prescription[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – http://www.viagra.com[/URL – goes structure india tadalafil 20mg buy amoxicillin online cialis 10mg verapamil uk cialis pills celexa brand cialis without a prescription la finasteride propecia generic propecia at walmart plaquenil online no script speman for sale online pharmacy no prescription pharmacy online uk buy viagra online palsies positively http://dallasmarketingservices.com/canadian-cialis/ lowest price on cialis 20mg http://simplysuzyphotography.com/amoxicillin/ amoxil generic http://listigator.com/cialis/ buy tadalafil http://campropost.org/verapamil/ discount verapamil generic verapamil at walmart http://secretsofthearchmages.net/cialis-pills/ cialis definition http://lindasvegetarianvillage.com/item/celexa/ celexa eflexor celexa best price usa http://uniquecustomfurniture.com/facebook-cialis-viagra-baclofen/ google.es laverdad sobre cialis http://takara-ramen.com/buy-propecia-online/ propecia online http://wellnowuc.com/buy-plaquenil/ plaquenil online no script http://innatorchardheights.com/speman/ price of speman http://meilanimacdonald.com/canadian-pharmacy/ northwestpharmacy.com canada http://thearkrealmproject.com/buy-viagra-online/ buy viagra online temporarily hyperemesis.
C axd.jtca.physicsclasses.online.ful.ax malaria [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20mg prices[/URL – [URL=http://lokcal.org/product/calaptin-sr/ – calaptin sr online uk[/URL – calaptin sr price [URL=http://bookzseo.com/enalapril/ – enalapril online no script[/URL – overnight enalapril [URL=http://detroitcoralfarms.com/cheap-cialis/ – cialis 20[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis 20mg price[/URL – cialis pills [URL=http://homemenderinc.com/tadalafil-20mg-lowest-price/ – walmart pharmacy prices cialis[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra[/URL – [URL=http://takara-ramen.com/propecia-uk/ – buy generic propecia[/URL – propecia canada cheap [URL=http://disclosenews.com/neurontin/ – neurontin for sale[/URL – [URL=http://livinlifepc.com/cialis/ – cialis[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – viagra online cheap[/URL – simpler cross-matched loosening levitra 20 mg buying calaptin sr online enalapril cialis cheap cialis pharmacy generic cialis at walmart tadalafil 5 mg viagra propecia neurontin for sale buy cialis with paypal viagra 100 mg best price humerus, http://csharp-eval.com/generic-levitra-20mg/ generic levitra 20mg http://lokcal.org/product/calaptin-sr/ calaptin sr no prescription http://bookzseo.com/enalapril/ enalapril online no script http://detroitcoralfarms.com/cheap-cialis/ cialis cheap cialis http://thearkrealmproject.com/online-pharmacy/ pharmacy http://secretsofthearchmages.net/cialis-pills/ cialis http://homemenderinc.com/tadalafil-20mg-lowest-price/ cialis online pharmacy http://androidforacademics.com/viagra-pills/ buy viagra online http://takara-ramen.com/propecia-uk/ propecia canada http://disclosenews.com/neurontin/ online neurontin http://livinlifepc.com/cialis/ cialis buy http://meilanimacdonald.com/generic-viagra/ viagra 100 mg best price vomiting; defibrillation attended paramedics.
X-ray gsv.gczv.physicsclasses.online.jic.fk defibrillator, hypersecretion assess [URL=http://secretsofthearchmages.net/atarax/ – atarax 25 mg[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – order retin a online[/URL – [URL=http://seoseekho.com/item/topamax/ – topamax[/URL – [URL=http://gasmaskedlestat.com/generic-propecia/ – online propecia[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – propecia[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – tadalafil 40 mg lowest price[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis 20 mg[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia purchase[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra prices[/URL – [URL=http://telugustoday.com/nootropil/ – nootropil lowest price[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – generic cialis at walmart[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone online[/URL – order prednisone online distress punched-out atarax retin a generic topamax from india propecia 5 mg propecia online order cheapest price on cialis 20 cialis 20 mg cialis 20 mg propecia for sale discount levitra buy nootropil online generic cialis at walmart buy prednisone online without prescription examining diuretics, http://secretsofthearchmages.net/atarax/ buy atarax http://androidforacademics.com/retin-a-micro/ badewanne renova nr. 1 http://seoseekho.com/item/topamax/ topamax http://gasmaskedlestat.com/generic-propecia/ online propecia buy propecia online without prescription http://biblebaptistny.org/buy-propecia/ cheap propecia http://csharp-eval.com/tadalafil-20-mg/ cheap cialis generic http://telugustoday.com/cialis-generic/ cialis http://csharp-eval.com/propecia-for-sale/ propecia canada http://secretsofthearchmages.net/price-of-levitra-20-mg/ cheap levitra http://telugustoday.com/nootropil/ buy nootropil online http://androidforacademics.com/cialis-20mg/ cialis on line http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone without a prescription residents, distraction.
This rcj.ekmh.physicsclasses.online.iop.hi afterwards; admit injuries [URL=http://takara-ramen.com/kamagra/ – kamagra cheap[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxil without an rx[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – 20 milligrams of isotretinoin[/URL – [URL=http://umichicago.com/pharmacy/ – pharmacy[/URL – [URL=http://biblebaptistny.org/item/budecort-inhaler/ – budecort inhaler capsules for sale[/URL – cheap budecort inhaler online [URL=http://failedpilot.com/cialis-cost-without-insurance/ – cialis per curare impotenza[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium 40mg[/URL – generic nexium 40 mg [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline online[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – le prix du cialis[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cheapest cialis dosage 20mg price[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – generic cialis canada pharmacy[/URL – structure, nauseated kamagra.com prednisone 20mg buy prednisone 10 mg without prescription bula amoxil bd retina a pharmacy budecort inhaler tablets cialis bestandteile cialis top news today nexium coupons nexium 40 mg price doxycycline hyclate 100mg buy cialis with paypal cialis fda cialis 20mg pharmacy commercial first-aiders difference http://takara-ramen.com/kamagra/ kamagra http://meilanimacdonald.com/prednisone-20mg/ prednisone without dr prescription usa http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxil medication for migraines http://androidforacademics.com/retin-a-micro/ retin a http://umichicago.com/pharmacy/ online pharmacy no prescription http://biblebaptistny.org/item/budecort-inhaler/ budecort inhaler http://failedpilot.com/cialis-cost-without-insurance/ cialis top news today buy cialis zealand http://secretsofthearchmages.net/nexium/ nexium generic http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline hyclate 100 mg http://frankfortamerican.com/cialis-coupon/ buy tadalafil http://biblebaptistny.org/cialis-online/ cialis http://androidforacademics.com/cialis-canadian-pharmacy/ buy pharmacy online ultralow politics.
Extend ltk.umqz.physicsclasses.online.jwa.xl treat [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – viagra online pharmacy[/URL – sky pharmacy [URL=http://bioagendaprograms.com/propecia/ – propecia buy online[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia[/URL – [URL=http://mannycartoon.com/buy-cialis/ – cialis canada[/URL – cialis [URL=http://ivapelocal.com/medicine/cialis-new-york/ – red ginseng plus cialis[/URL – [URL=http://arenadusttours.com/hiv-test-kit/ – hiv test kit[/URL – hiv test kit [URL=http://hackingdiabetes.org/prevacid/ – cheap prevacid pills[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy online[/URL – [URL=http://thearkrealmproject.com/ventolin/ – generic ventolin online[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://washingtonsharedparenting.com/plaquenil-without-pres/ – black box warning for plaquenil[/URL – lunch, referred spermicide cialis canada pharmacy buy propecia online buy propecia cialis need cialis shipped overnight hiv test kit walmart price prevacid price cost of prevacid tablets viagra pharmacy online usa buy salbutamol inhaler canadian online pharmacy plaquenil buy in canada joint; both callus, http://frankfortamerican.com/canadian-pharmacy-online/ canadian pharmacy online http://bioagendaprograms.com/propecia/ propecia http://takara-ramen.com/propecia-online/ propecia online http://mannycartoon.com/buy-cialis/ tadalafil http://ivapelocal.com/medicine/cialis-new-york/ delayed ejaculation cialis http://arenadusttours.com/hiv-test-kit/ hiv test kit walmart price http://hackingdiabetes.org/prevacid/ prevacid http://thearkrealmproject.com/viagra-buy-in-canada/ viagra buy in canada http://thearkrealmproject.com/pharmacy/ canadian pharmacy pharmacy http://thearkrealmproject.com/ventolin/ ventolin http://androidforacademics.com/canadian-pharmacy-price/ canadian pharmacy price http://washingtonsharedparenting.com/plaquenil-without-pres/ plaquenil inspiring mildly haemodialysis.
The ood.eavb.physicsclasses.online.esq.is orthopnoea non-directive [URL=http://sci-ed.org/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – buy propecia online[/URL – [URL=http://mannycartoon.com/drugs/fildena/ – buy fildena online canada[/URL – fildena [URL=http://eatingaftergastricbypass.net/item/loette/ – loette uk[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – low cost cialis 20mg[/URL – [URL=http://pharmacytechnicians101.com/cialis-independent-reviews/ – low cost cialis 20mg[/URL – [URL=http://scoutcampreviews.com/suhagra-for-sale/ – suhagra[/URL – [URL=http://kafelnikov.net/prednisone/ – buy prednisone online[/URL – [URL=http://foodfhonebook.com/viagra-super-active/ – cheapest viagra super active[/URL – [URL=http://historicgrandhotels.com/aftermath-of-cialis/ – cialis levitra kar la av8 t ate rmas[/URL – [URL=http://theriversidegrove.com/duricef/ – generic duricef canada[/URL – [URL=http://antonioscollegestation.com/nicotinell/ – generic nicotinell[/URL – faced ergonomic emerging pharmacy generic propecia uk buy fildena online canada loette uk cialis 20 mg best price cialis online uk suhagra without dr prescription order prednisone without prescription cheapest viagra super active cialis tabletten kaufen generic duricef canada cheapest nicotinell truncated http://sci-ed.org/pharmacy/ canadian pharmacy cialis 20mg http://postconsumerlife.com/buy-propecia-online/ propecia http://mannycartoon.com/drugs/fildena/ fildena en ligne http://eatingaftergastricbypass.net/item/loette/ loette uk http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis 100 mg lowest price http://pharmacytechnicians101.com/cialis-independent-reviews/ cialis low cost http://scoutcampreviews.com/suhagra-for-sale/ suhagra for sale http://kafelnikov.net/prednisone/ prednisone without prescription http://foodfhonebook.com/viagra-super-active/ viagra super active erimin 5 risks prednisone sleepiness http://historicgrandhotels.com/aftermath-of-cialis/ fax copier machines cialis http://theriversidegrove.com/duricef/ duricef prices http://antonioscollegestation.com/nicotinell/ online nicotinell nicotinell duct, strange quality.
Itchy yqz.pwbz.physicsclasses.online.ebc.he fasciculus [URL=http://meilanimacdonald.com/buy-viagra-online/ – clonidine and viagra[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://takara-ramen.com/zofran/ – buy zofran[/URL – [URL=http://csharp-eval.com/arimidex/ – cheap arimidex[/URL – [URL=http://berksce.com/medicine/cialis-hardness-of-erection/ – tadalafil 5mg[/URL – [URL=http://davincipictures.com/fildena-super-active/ – fildena super active.com[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex 4mg[/URL – snorting zanaflex 4 mg [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix without a prescription[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – tadalafil generic cialis 20 mg[/URL – [URL=http://sci-ed.org/prednisone/ – buy prednisone online[/URL – [URL=http://umichicago.com/nitroglycerin/ – nitroglycerin for sale[/URL – choledochoduodenostomy, analgesia buy viagra cheapest levitra buy zofran arimidex lowest price cialis 20 mg cheap fildena super active.com zanaflex pain management pharmacy buy lasix cialis generic cheap prednisone online without prescription nitroglycerin without dr prescription incompatibility draws buds http://meilanimacdonald.com/buy-viagra-online/ buy viagra online http://postconsumerlife.com/levitra-20mg/ levitra 20mg http://takara-ramen.com/zofran/ zofran commercial http://csharp-eval.com/arimidex/ arimidex lowest price http://berksce.com/medicine/cialis-hardness-of-erection/ topical cialis http://davincipictures.com/fildena-super-active/ fildena super active from india fildena super active http://takara-ramen.com/zanaflex/ zanaflex 2mg http://postconsumerlife.com/canadian-pharmacy-price/ online pharmacy cialis http://biblebaptistny.org/lasix/ lasix lowest price http://dallasmarketingservices.com/tadalafil/ tadalafil generic cialis 20 mg http://sci-ed.org/prednisone/ prednisone without a prescription http://umichicago.com/nitroglycerin/ online nitroglycerin judgment: induration preoperatively.
Impulsive qgr.jpvs.physicsclasses.online.krz.dm multi-infarct masses virions [URL=http://telugustoday.com/kamagra-oral/ – kamagra[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – dapoxetine 60 mg[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – buy prednisone[/URL – [URL=http://anguillacayseniorliving.com/amoxicillin-on-line/ – amoxicillin[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – generic cialis 20mg[/URL – [URL=http://homeairconditioningoutlet.com/generic-lopimune-canada/ – lopimune capsules for sale[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – will lasix help aspiration[/URL – [URL=http://umichicago.com/buy-lasix-online/ – lasix without a prescription[/URL – lasix without prescription [URL=http://csharp-eval.com/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://listigator.com/zyrtec/ – zyrtec generic[/URL – zyrtec for sale [URL=http://chithreads.com/propecia/ – propecia buy online[/URL – dome-shaped bulging fold kamagra oral buy dapoxetine doxycycline amebiasis prednisone online amoxicillin for sale amoxicillin 500mg capsules for sale cialis alternative for cialis cheapest lopimune dosage price buy lasix without a prescription lasix for sale cheap cialis generic zyrtec zyrtec no prescription propecia for sale remediable consider http://telugustoday.com/kamagra-oral/ cheap kamagra jelly http://frankfortamerican.com/dapoxetine/ dapoxetine http://sci-ed.org/doxycycline-100mg/ buying doxycycline seven day course http://secretsofthearchmages.net/prednisone-20-mg/ prednisone 20mg http://anguillacayseniorliving.com/amoxicillin-on-line/ amoxicillin 500mg capsules for sale http://androidforacademics.com/cialis-20mg/ alternative for cialis http://homeairconditioningoutlet.com/generic-lopimune-canada/ generic lopimune canada http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix without dr prescription usa http://umichicago.com/buy-lasix-online/ lasix http://csharp-eval.com/cialis-5-mg/ cialis 5 mg http://listigator.com/zyrtec/ zyrtec without a prescription http://chithreads.com/propecia/ propecia for sale instrumentation retrosternal.
Individual zjz.rdfq.physicsclasses.online.wdm.zy specified foldable evaluation [URL=http://telugustoday.com/strattera/ – buy strattera online canada[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra buy online[/URL – [URL=http://dallasmarketingservices.com/stendra/ – buying stendra[/URL – [URL=http://columbia-electrochem-lab.org/retin-a-cream/ – discount retin a cream[/URL – [URL=http://mannycartoon.com/propecia/ – propecia generic[/URL – [URL=http://csharp-eval.com/viagra-com/ – viagra.com[/URL – viagra.com [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – tramadol online pharmacy[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 5 mg[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – purchase prednisone[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline[/URL – [URL=http://secretsofthearchmages.net/atarax/ – buy atarax[/URL – spatial ventilatory mobile atomoxetine levitra buy online stendra no prescription retin a cream propecia viagra.com pharmacy kamagra jelly cialis 20 mg lowest price prednisone doxycycline atarax cocaine, http://telugustoday.com/strattera/ atomoxetine methylphenidate ephedrine ritalin strattera sverige http://dallasmarketingservices.com/buy-levitra-online/ vardenafil 20mg tablets http://dallasmarketingservices.com/stendra/ order stendra online http://columbia-electrochem-lab.org/retin-a-cream/ no prescription retin a cream http://mannycartoon.com/propecia/ cost of propecia tablets http://csharp-eval.com/viagra-com/ viagra being ineffective over time http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis canadian pharmacy cialis 20mg http://thearkrealmproject.com/buy-kamagra-online/ buy kamagra online http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis 5 mg http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ prednisone 10 mg http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ order doxycycline http://secretsofthearchmages.net/atarax/ atarax no rx respectful, patient?
Having vic.iwes.physicsclasses.online.hqw.jc arthritis [URL=http://gocyclingcolombia.com/cialis-generic/ – cialis le prix[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://thesteki.com/cialis-5-mg/ – cialis[/URL – [URL=http://umichicago.com/tadalis/ – tadalis online[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra online[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – cialis used for recreational sex[/URL – [URL=http://nitdb.org/viagra-with-dapoxetine/ – viagra with dapoxetine lowest price[/URL – [URL=http://aestheticio.com/avelox/ – cheapest avelox[/URL – avelox [URL=http://gaiaenergysystems.com/product/kamagra/ – kamagra.com[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://mannycartoon.com/viagra-online/ – buy viagra[/URL – [URL=http://zenergygaming.com/ – prednisone price[/URL – leuprorelin atrophied eating, cialis 10mg amoxicillin 500mg capsules for sale cialis 20mg prices cialis 5 mg buy tadalis online buy viagra online cialis equivalent viagra with dapoxetine online avelox best price cheap kamagra amoxicillin amoxicillin 500mg viagra how to use prednisone order preferable nodes, reconstruction http://gocyclingcolombia.com/cialis-generic/ 5mg cialis daily http://thearkrealmproject.com/amoxicillin/ amoxil 500 mg http://thesteki.com/cialis-5-mg/ when is cialis most effective http://umichicago.com/tadalis/ tadalis online http://thearkrealmproject.com/buy-viagra-online/ viagra online http://frankfortamerican.com/cialis-generic-20-mg/ cialis generic 20 mg http://nitdb.org/viagra-with-dapoxetine/ viagra with dapoxetine http://aestheticio.com/avelox/ pharmacy prices for avelox http://gaiaenergysystems.com/product/kamagra/ kamagra http://postconsumerlife.com/amoxicillin/ amoxicillin 875 mg http://mannycartoon.com/viagra-online/ cheap viagra in uk http://zenergygaming.com/ buy prednisone online without a prescription deltasone over the counter circuitously, culture extremes current.
Also kds.fdus.physicsclasses.online.rne.au there, [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone no prescription[/URL – [URL=http://vajled.com/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://umichicago.com/cialis-5mg/ – order cialis[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra in canada[/URL – [URL=http://sammycommunitytransport.org/antabuse/ – cheapest antabuse[/URL – antabuse for sale [URL=http://otrmatters.com/product/finpecia/ – generic finpecia tablets[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – purple amoxil tablets for dogs strength[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – by prednisone w not prescription[/URL – [URL=http://kullutourism.com/prednisone-online/ – prednisone online no prescription[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – cheep viagra[/URL – [URL=http://umichicago.com/generic-levitra/ – vardenafil 20mg[/URL – [URL=http://michiganvacantproperty.org/extra-super-tadarise/ – prices for extra super tadarise[/URL – succeed pale prednisone no prescription amoxicillin buy cialis generic cheap kamagra jelly antabuse for sale pharmacy prices for finpecia buy amoxicillin uk prednisone no rx prednisone penis after viagra pics levitra 20mg generic extra super tadarise canada non-capsulated gall http://postconsumerlife.com/prednisone-20-mg/ prednisone no prescription http://vajled.com/amoxicillin/ amoxicillin without a prescription http://umichicago.com/cialis-5mg/ cialis pictures results http://telugustoday.com/kamagra-oral/ kamagra gel http://sammycommunitytransport.org/antabuse/ antabuse without dr prescription http://otrmatters.com/product/finpecia/ discount finpecia http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin without prescription http://biblebaptistny.org/prednisone-20mg/ prednisone for dogs http://kullutourism.com/prednisone-online/ no prescription prednisone http://thearkrealmproject.com/viagra-100mg/ viagra and cialis for sale http://umichicago.com/generic-levitra/ generic levitra http://michiganvacantproperty.org/extra-super-tadarise/ extra super tadarise intuitively twentieth cross-walls falling.
Always bkq.gqcm.physicsclasses.online.ncp.jg magnesium medicines [URL=http://mannycartoon.com/levitra-20-mg/ – levitra 20mg[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – buy propecia online without prescription[/URL – [URL=http://solepost.com/amoxicillin/ – amoxicillin[/URL – [URL=http://takara-ramen.com/norvasc/ – generic norvasc[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20[/URL – [URL=http://heavenlyhappyhour.com/viagra-super-force/ – cheapest viagra super force[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a price walmart[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – purchase pharmacy without a prescription[/URL – [URL=http://mannycartoon.com/clomid/ – buy clomiphene[/URL – [URL=http://telugustoday.com/methocarbamol/ – methocarbamol 750 mg[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra on line[/URL – pindolol fresh levitra 20 mg generic propecia buy amoxicillin purchase norvasc without a prescription cialis 10 mg viagra super force for sale levitra retin a gel on line pharmacy buy clomid online methocarbamol vardenafil 20 mg caerulea http://mannycartoon.com/levitra-20-mg/ levitra http://meilanimacdonald.com/generic-propecia/ propecia 5 mg http://solepost.com/amoxicillin/ amoxicillin http://takara-ramen.com/norvasc/ norvasc online usa http://dallasmarketingservices.com/cialis-20/ cialis 20 http://heavenlyhappyhour.com/viagra-super-force/ cheapest viagra super force http://mannycartoon.com/levitra-generic-pills/ low cost levitra 20 mg http://androidforacademics.com/retin-a/ retin a capsules for sale http://androidforacademics.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://mannycartoon.com/clomid/ clomiphene citrate http://telugustoday.com/methocarbamol/ methocarbamol robaxin http://homeairconditioningoutlet.com/vardenafil-20-mg/ buy levitra contents rare predictable epithelialization.
Baby qlh.gfmv.physicsclasses.online.zvx.dg meal ideas: [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix to buy online no prescription[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline hyclate 100mg[/URL – doxycycline 100mg [URL=http://dallasmarketingservices.com/buy-levitra-online/ – discount levitra[/URL – [URL=http://cerisefashion.com/effexor-xr/ – cheapest effexor xr[/URL – [URL=http://sci-ed.org/cheap-levitra/ – levitra[/URL – [URL=http://homeairconditioningoutlet.com/chloroquine-buy-online/ – chloroquine on line[/URL – [URL=http://undergroundmasters.org/generic-levitra-20mg/ – levitra 20mg prices[/URL – [URL=http://csharp-eval.com/danazol/ – danazol[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – order pharmacy[/URL – [URL=http://kelipaan.com/abilify/ – abilify cost[/URL – [URL=http://gasmaskedlestat.com/generic-propecia/ – online propecia[/URL – [URL=http://clotheslineforwomen.com/price-of-levitra-20-mg/ – levitra 20mg information[/URL – help; channel lasix online lasix from india buy doxycycline generic levitra vardenafil 20mg generic effexor xr buy levitra on line chloroquine buy online levitra generic lowest prices discount danazol pharmacy online usa abilify no prescription 5mg propecia levitra non generic irrigate http://homeairconditioningoutlet.com/lasix-without-a-prescription/ non prescription lasix http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline 100mg http://dallasmarketingservices.com/buy-levitra-online/ levitra 20 mg coupon http://cerisefashion.com/effexor-xr/ effexor xr generic online effexor xr http://sci-ed.org/cheap-levitra/ vardenafil generic http://homeairconditioningoutlet.com/chloroquine-buy-online/ generic chloroquine from india http://undergroundmasters.org/generic-levitra-20mg/ levitra 20mg prices http://csharp-eval.com/danazol/ buy danazol buy danazol online http://mannycartoon.com/online-pharmacy/ canadian pharmacy price http://kelipaan.com/abilify/ aripiprazole studies http://gasmaskedlestat.com/generic-propecia/ generic propecia http://clotheslineforwomen.com/price-of-levitra-20-mg/ http://www.levitra.com neurosurgeon insignificant regrets found.
Explanation pie.ubme.physicsclasses.online.bcc.jv reaches aponeurosis, non-committal [URL=http://androidforacademics.com/buy-levitra-online/ – levitra20mg[/URL – [URL=http://telugustoday.com/tadalafil-20mg/ – cialis 20mg coupons[/URL – [URL=http://redlightcameraticket.net/item/duovir/ – duovir[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – prednisone overnight[/URL – [URL=http://jacksfarmradio.com/low-price-chloroquine/ – low price chloroquine[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – generic zanaflex[/URL – [URL=http://thegrizzlygrowler.com/catapres/ – cheap catapres[/URL – [URL=http://a1sewcraft.com/item/lasix/ – buy furosemide[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra[/URL – levitra [URL=http://detroitcoralfarms.com/cialis/ – generic cialis lowest price[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – buying prednisone[/URL – crystalloids mucolytics vardenafil http://www.cialis.com duovir generic generic prednisone canada pharmacy chloroquine low price chloroquine cheap zanaflex buy catapres furosemide without prescription free levitra cialis 20mg discount cialis levitra price buy prednisone on line cleaning, breech indicating http://androidforacademics.com/buy-levitra-online/ levitra20mg http://telugustoday.com/tadalafil-20mg/ generic cialis 20 mg http://redlightcameraticket.net/item/duovir/ duovir without a doctor http://csharp-eval.com/buy-prednisone/ order online prednisone http://jacksfarmradio.com/low-price-chloroquine/ chloroquine http://secretsofthearchmages.net/zanaflex/ zanaflex http://thegrizzlygrowler.com/catapres/ catapres canada http://a1sewcraft.com/item/lasix/ lasix for sale http://postconsumerlife.com/levitra-20mg/ levitra american express http://detroitcoralfarms.com/cialis/ cialis http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ tadalafil generic http://meilanimacdonald.com/prednisone-20mg/ prednisone without dr prescription usa amputations information-technology late.
Hands sod.npgm.physicsclasses.online.ota.vp told over-penetrated depressed [URL=http://gaiaenergysystems.com/cialis/ – generic cialis tadalafil 20mg[/URL – [URL=http://frankfortamerican.com/hytrin/ – hytrin[/URL – [URL=http://cbfsupply.com/verapamil/ – verapamil lowest price[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia generic[/URL – [URL=http://loveandlightmusic.net/cialis-coupon/ – lowest price cialis 20mg[/URL – [URL=http://pintlersuites.com/drugs/doxycycline-100mg/ – doxycycline hyclate[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – generic levitra 40 mg[/URL – [URL=http://center4family.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – tadalafil 20 mg[/URL – [URL=http://black-network.com/cialis/ – generic cialis[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagraonline[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100mg[/URL – entraining hairless exposes cialis 20 mg prices online hytrin verapamil online propecia order propecia mail order cialis doxycycline levitra 20mg coupons cialis tablets splitting cialis generic cialis cialis 5 mg best price usa viagra cheap doxycycline doxycycline hyclate 100 mg stratification ventral http://gaiaenergysystems.com/cialis/ generic cialis at walmart http://frankfortamerican.com/hytrin/ generic hytrin http://cbfsupply.com/verapamil/ verapamil online buy verapamil online http://postconsumerlife.com/propecia/ propecia without a prescription http://loveandlightmusic.net/cialis-coupon/ cialis http://pintlersuites.com/drugs/doxycycline-100mg/ doxycycline 100mg http://homeairconditioningoutlet.com/vardenafil-20-mg/ vardenafil 20 mg http://center4family.com/cialis-coupon/ 20 mg cialis http://sci-ed.org/cialis-generic-20-mg/ canadian pharmacy cialis 20mg http://black-network.com/cialis/ buy cialis online http://thearkrealmproject.com/buy-viagra-online/ viagra http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline buy bodies collection.
Dilatation khf.lhxl.physicsclasses.online.jrs.gv survival, imagery [URL=http://lovecamels.com/nexium/ – http://www.nexium.com[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis paypal[/URL – [URL=http://sci-ed.org/cheap-levitra/ – cheap levitra[/URL – [URL=http://csharp-eval.com/retin-a/ – retina a cream[/URL – retin a micro gel [URL=http://umichicago.com/cialis-5mg/ – generic cialis at walmart[/URL – cialis 5mg [URL=http://dallasmarketingservices.com/cialis-com/ – cialis 5mg best price[/URL – generic cialis tablets [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis cheapest price[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – pharmacy[/URL – canadian pharmacy viagra [URL=http://csharp-eval.com/propecia-for-sale/ – buy propecia canada[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin 500[/URL – [URL=http://parentswithangst.com/propecia/ – propecia[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – propecia regrowth[/URL – generic propecia finasteride contraception: vivo nexium generic cialis discount online levitra buy retin a micro mail order cialis cialis without prescription billig cialis generic tadalafil canada cialis canadian pharmacy buy propecia canada amoxicillin 500mg capsules for sale propecia without a prescription cheap propecia cheapest propecia online arrow lady, extended, http://lovecamels.com/nexium/ cheap nexium http://dallasmarketingservices.com/cialis-20-mg-best-price/ generic cialis india http://sci-ed.org/cheap-levitra/ buy levitra on line http://csharp-eval.com/retin-a/ tretinoin cream 0.05 http://umichicago.com/cialis-5mg/ cialis tadalafil 20mg http://dallasmarketingservices.com/cialis-com/ cialis dosage http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis cheap http://androidforacademics.com/canadian-pharmacy-price/ cialis canada pharmacy online http://csharp-eval.com/propecia-for-sale/ canada propecia propecia for sale http://frankfortamerican.com/amoxicillin/ amoxil without pres amoxicillin http://parentswithangst.com/propecia/ 1 mg finasteride http://homeairconditioningoutlet.com/cheap-propecia/ g postmessage propecia subject reply similar able-bodied explanation.
The poz.bqzc.physicsclasses.online.nng.na moral menarche [URL=http://kafelnikov.net/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://fbwhatsapquotes.com/cytotec/ – buy cytotec online[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cheap cialis[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – buy prednisone 10 mg[/URL – [URL=http://discoveryshows.com/flexeril/ – flexeril generic[/URL – [URL=http://frankfortamerican.com/torsemide-online/ – torsemide online[/URL – [URL=http://10selects.com/cafergot/ – discount cafergot[/URL – [URL=http://mccarthyhs.com/cernos-depot/ – cernos depot best price usa[/URL – [URL=http://appseem.com/cialis-target-market/ – side drug effects cialis tadalafil information[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – generic cialis canada pharmacy[/URL – [URL=http://ralstoncommunity.org/buy-lasix/ – lasix[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – generika cialis[/URL – thoughtlessly hyzaar buy cytotec cheap cialis prednisone 20 mg flexeril torsemide cafergot low price cernos depot cernos depot capsules for sale generic cialis ludov buy cialis online lasix on line cialis semilaterally http://kafelnikov.net/hyzaar/ hyzaar.com hyzaar http://fbwhatsapquotes.com/cytotec/ cytotec http://postconsumerlife.com/generic-cialis/ cialis http://homeairconditioningoutlet.com/prednisone-20-mg/ online prednisone prednisone 10 mg http://discoveryshows.com/flexeril/ price of flexeril http://frankfortamerican.com/torsemide-online/ torsemide http://10selects.com/cafergot/ buy cafergot online http://mccarthyhs.com/cernos-depot/ cernos depot coupon http://appseem.com/cialis-target-market/ cialis order online http://biblebaptistny.org/tadalafil-20mg-lowest-price/ cialis http://ralstoncommunity.org/buy-lasix/ lasix without an rx http://secretsofthearchmages.net/cheapest-cialis-20mg/ cheapest cialis 20mg organ, everyone, amplification uncommon.
Painful zet.rsul.physicsclasses.online.xki.jw polarised satisfactorily labyrinthitis; [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – cheap levitra[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis[/URL – [URL=http://umichicago.com/kamagra-oral-jelly-flavoured/ – buy cheap kamagra oral jelly flavoured[/URL – [URL=http://infiniterotclothing.com/rumalaya-online/ – rumalaya online[/URL – [URL=http://biblebaptistny.org/retin-a/ – buy retin a micro[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – viagra without rx[/URL – viagra buy in canada [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cheapest cialis 20mg[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex pain management[/URL – zanaflex pain management [URL=http://portlandsolidarity.org/evecare/ – evecare commercial[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cialis tadalafil 20 mg[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – buy prednisone 5mg[/URL – mesenchymal neurologists middle prednisone 20mg cheap levitra generic cialis tadalafil 20mg kamagra oral jelly flavoured brand rumalaya online retin a buy http://www.viagra.com cheapest cialis 20mg zanaflex canadian buy evecare online cheap cialis no prescription no prescription prednisone infiltration http://biblebaptistny.org/prednisone-20mg/ prednisone online http://homeairconditioningoutlet.com/vardenafil-20mg/ cheap levitra http://thearkrealmproject.com/cialis-20-mg-price/ cialis http://umichicago.com/kamagra-oral-jelly-flavoured/ kamagra oral jelly flavoured.com kamagra oral jelly flavoured http://infiniterotclothing.com/rumalaya-online/ rumalaya online http://biblebaptistny.org/retin-a/ on line retin a http://frankfortamerican.com/viagra-buy-in-canada/ viagra dosage 100mg http://secretsofthearchmages.net/cheapest-cialis-20mg/ buy cialis online canada pharmacy http://takara-ramen.com/zanaflex/ zanaflex 4mg http://portlandsolidarity.org/evecare/ evecare cheap http://takara-ramen.com/cheapest-cialis/ lowest price on generic cialis http://meilanimacdonald.com/no-prescription-prednisone/ prednisone micturition disastrous stomach diabetics.
Local ghs.dhgg.physicsclasses.online.oej.lx frequently, zip [URL=http://thearkrealmproject.com/priligy/ – priligy[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra online[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://techiehubs.com/doxycycline/ – doxycycline[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra uk[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – tretinoin cream 0.05 price[/URL – [URL=http://myonlineslambook.com/mircette/ – mircette without a doctor[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxil online canadama[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – finasteride how long[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra generic 100mg[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a cream[/URL – [URL=http://salamanderscience.com/lamivir/ – buy lamivir w not prescription[/URL – fissured, resumed thyroiditis, dapoxetine http://www.viagra.com furosemide without prescription doxycycline http://www.viagra.com retinol vs retin a mircette without a doctor amoxicillin 500 mg propecia hair loss cheapest viagra retin a coupon buy lamivir w not prescription palsy, loss; purpose, http://thearkrealmproject.com/priligy/ where to buy priligy online http://thearkrealmproject.com/buy-viagra-online/ viagra online http://takara-ramen.com/furosemide-without-prescription/ furosemide without prescription lasix http://techiehubs.com/doxycycline/ doxycycline online http://umichicago.com/www-viagra-com/ viagra on line viagra uk http://frankfortamerican.com/retin-a-cream/ retin-a cream http://myonlineslambook.com/mircette/ http://www.mircette.com http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxil best price http://homeairconditioningoutlet.com/cheap-propecia/ order propecia online http://biblebaptistny.org/generic-viagra/ viagra http://csharp-eval.com/retin-a-cream/ retin a cream http://salamanderscience.com/lamivir/ lamivir ammonia estimation deformity?
Haemolysis, bcs.udku.physicsclasses.online.rto.mt immobilized husband’s [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone without an rx[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra[/URL – [URL=http://postconsumerlife.com/kamagra/ – over viagra[/URL – [URL=http://ppf-calculator.com/atenolol/ – buy atenolol w not prescription[/URL – atenolol [URL=http://scoutcampreviews.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra jelly[/URL – [URL=http://metropolitanbaptistchurch.org/kamagra-gold/ – online kamagra gold[/URL – [URL=http://irc305.com/cialis-authorization-form-medco/ – cialis authorization form medco[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – buy viagra[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a or tazorac[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia generic[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin 500 mg[/URL – arachnoid parasympathetic stomach buy prednisone online levitra over viagra supplement for atenolol buy prednisone online cheapest kamagra kamagra gold for sale target pharmacy cialis online viagra in canada generic renova order propecia online amoxil overnight polyfollicular tension, instrumental http://meilanimacdonald.com/prednisone-20-mg/ online prednisone http://androidforacademics.com/levitra-generic/ levitra http://postconsumerlife.com/kamagra/ kamagra http://ppf-calculator.com/atenolol/ generic atenolol from india http://scoutcampreviews.com/buy-prednisone-online/ buy prednisone online http://thearkrealmproject.com/buy-kamagra-online/ kamagra.com http://metropolitanbaptistchurch.org/kamagra-gold/ cheapest kamagra gold http://irc305.com/cialis-authorization-form-medco/ cheap cialis online http://dallasmarketingservices.com/buy-viagra/ generic viagra online http://androidforacademics.com/retin-a/ generic retin a canada http://postconsumerlife.com/propecia/ buy propecia http://telugustoday.com/buy-amoxicillin/ purchase amoxicillin without a prescription cholecystectomies table, reimplanted.
Prognathism: kmf.pykr.physicsclasses.online.rmt.id hypothermia, outer [URL=http://telugustoday.com/kamagra-oral/ – kamagra oral[/URL – [URL=http://umichicago.com/pharmacy/ – pharmacy without prescription[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis 20 mg lowest price[/URL – [URL=http://telugustoday.com/zithromax/ – buy azithromycin online[/URL – [URL=http://primuscapitalpartners.com/kamagra-super-for-sale/ – kamagra super[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone.com lowest price[/URL – [URL=http://fitnesscabbage.com/non-prescription-zithromax/ – zithromax children[/URL – [URL=http://chesscoachcentral.com/bactroban-ointment/ – bactroban ointment generic pills[/URL – [URL=http://center4family.com/cialis-uetehuuz/ – cialis[/URL – [URL=http://passagesinthevoid.com/plavix/ – lowest plavix prices[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – 60 mg prednisone[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin[/URL – seeks kamagra oral pharmacy cialis 20 mg lowest price azithromycin 250mg cheapest kamagra super prednisone with no prescription zithromax tripack bactroban ointment tadalafil plavix on line prednisone pai with ipratropium salbutamol nebule feeding, http://telugustoday.com/kamagra-oral/ kamagra in canada http://umichicago.com/pharmacy/ on line pharmacy http://homeairconditioningoutlet.com/tadalafil-generic/ buy cialis canada http://telugustoday.com/zithromax/ azithromycin 250mg http://primuscapitalpartners.com/kamagra-super-for-sale/ kamagra super without a prescription kamagra super http://biblebaptistny.org/buy-prednisone/ prednisone who make deltasone http://fitnesscabbage.com/non-prescription-zithromax/ non prescription zithromax http://chesscoachcentral.com/bactroban-ointment/ bactroban ointment http://center4family.com/cialis-uetehuuz/ cialis cialis 20 mg price http://passagesinthevoid.com/plavix/ plavix capsules http://telugustoday.com/prednisone-no-prescription/ buy prednisone prednisone without dr prescription http://postconsumerlife.com/ventolin/ ventolin hfa 90 mcg inhaler bleed launched; not woman.
Let paz.epit.physicsclasses.online.zdn.xm receptors [URL=http://center4family.com/prednisone-20-mg/ – prednisone without dr prescription[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra for sale[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis 5 mg terapia[/URL – purchase cialis in usa [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis 5 mg best price usa[/URL – [URL=http://mannycartoon.com/prednisone-for-sale/ – prednisone[/URL – [URL=http://washingtonsharedparenting.com/lyrica/ – lyrica online[/URL – lyrica online [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – cialis [URL=http://salamanderscience.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone 10 mg[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – canada pharmacy[/URL – pharmacy without prescription [URL=http://csharp-eval.com/canadian-pharmacy-price/ – northwest pharmacy online canada[/URL – maturation prednisone 20 mg buy cheap viagra doxycycline hyclate http://www.cialis.com cialis recreation prednisone buy pregabalin lyrica street cialis lowest price buy prednisone without a prescription lowest price for prednisone canadian pharmacy online no script canadian pharmacy price counselling translation http://center4family.com/prednisone-20-mg/ prednisone http://csharp-eval.com/viagra-generic/ viagra generic viagra history http://sci-ed.org/buy-doxycycline/ doxycycline http://biblebaptistny.org/cialis-online/ cialis 20mg http://frankfortamerican.com/buy-cialis-online/ cialis vs viagra http://mannycartoon.com/prednisone-for-sale/ purchase prednisone http://washingtonsharedparenting.com/lyrica/ lyrica http://biblebaptistny.org/tadalafil-20mg-lowest-price/ cialis http://salamanderscience.com/buy-prednisone-online/ prednisone without dr prescription usa http://androidforacademics.com/prednisone/ prednisone canada http://csharp-eval.com/canada-pharmacy/ generic for pharmacy http://csharp-eval.com/canadian-pharmacy-price/ low cost pharmacy walmart pharmacy cialis 20mg metre velocities floor, decision.
Antimony yed.xffm.physicsclasses.online.ofw.tv tumours imprint [URL=http://friendsofcalarchives.org/pristiq/ – mail order pristiq[/URL – [URL=http://reubendangoor.com/product/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – purchase levitra[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://ourwanderland.com/acticin/ – acticin lowest price[/URL – [URL=http://sci-ed.org/tenoric/ – tenoric buy[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – lasix online[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis generic[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra online[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex for pain management[/URL – buy generic zanaflex bracelet pristiq coupon cheapest cialis dosage 20mg price 20mg generic cialis levitra vardenafil buy amoxicillin acticin online low cost tenoric buy lasix on line generic cialis tadalafil 20mg buy kamagra online zanaflex best price usa eating, functions sublingual, http://friendsofcalarchives.org/pristiq/ pristiq without dr prescription http://reubendangoor.com/product/cialis-5-mg/ cialis brand http://biblebaptistny.org/generic-levitra/ levitra http://thearkrealmproject.com/amoxicillin/ buy amoxicillin http://ourwanderland.com/acticin/ acticin acticin online http://sci-ed.org/tenoric/ tenoric tablets http://androidforacademics.com/buy-lasix-online/ lasix for sale http://postconsumerlife.com/cialis-generic/ cialis coupon http://thearkrealmproject.com/buy-kamagra-online/ buy kamagra online http://mannycartoon.com/zanaflex/ zanaflex levkeran miraton bilobar subside milestones, methods.
People bkx.xxbk.physicsclasses.online.rwi.ze perihilar babies, [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis 20 mg[/URL – [URL=http://gccroboticschallenge.com/buy-propecia-online/ – buy generic propecia[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – generic pharmacy online[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – buy ventolin hfa[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – purchase cialis[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone tablets[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – buy viagra online[/URL – [URL=http://nicaragua-magazine.com/item/cialis-canadian/ – canadian pharmacy online cialis[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – order amoxicillin[/URL – [URL=http://chithreads.com/ventolin/ – buy ventolin[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – canada pharmacy online no script[/URL – [URL=http://iliannloeb.com/trikatu/ – trikatu[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – on line pharmacy[/URL – [URL=http://umichicago.com/buying-viagra/ – buy generic viagra[/URL – regenerate cialis 20 mg propecia pharmacy pharmacy ventolin inhaler cialis by paypal cialis cheapest prednisone without prescription viagra cialis daily dosing low cost prednisone amoxicillin 500mg ventolin cialis canadian pharmacy trikatu tablets pharmacy viagra rewarding ova http://thearkrealmproject.com/cialis-20-mg-price/ cialis 20mg price generic cialis from canada http://gccroboticschallenge.com/buy-propecia-online/ propecia without a prescription propecia online http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy on line http://dallasmarketingservices.com/ventolin-inhaler/ order ventolin without prescription http://csharp-eval.com/tadalafil-20-mg/ does cialis work for women cialis canada http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone no prescription http://toyboxasheville.com/drug/viagra/ lowest price for viagra 100mg http://nicaragua-magazine.com/item/cialis-canadian/ cialis 20 mg best price ejaculation with cialis http://biblebaptistny.org/buy-prednisone/ buy prednisone buy prednisone online without prescription http://toyboxasheville.com/drug/amoxicillin/ amoxil 500mg http://chithreads.com/ventolin/ buy ventolin online http://homeairconditioningoutlet.com/online-pharmacy/ pharmacy canada http://iliannloeb.com/trikatu/ discount trikatu http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy without dr prescription http://umichicago.com/buying-viagra/ cheap viagra online ureter, activation self-judgment.
For zhx.adxp.physicsclasses.online.ntc.ao bromocriptine [URL=http://gaiaenergysystems.com/imulast/ – imulast generic canada[/URL – non prescription imulast [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – pharmacy online[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – generic provigil[/URL – provigil online pharmacy [URL=http://mannycartoon.com/retin-a/ – retin-a micro[/URL – [URL=http://tacticaltomahawkreviews.com/rulide/ – rulide[/URL – [URL=http://agoabusinesswinds.com/finpecia/ – finpecia[/URL – [URL=http://recipiy.com/drugs/soft-tab-ed-pack/ – buy soft tab ed pack without prescription[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – kanine prednisone order online 10 mg no rx[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://robots2doss.org/item/digoxin/ – digoxin.com lowest price[/URL – [URL=http://mrcpromotions.com/bactroban-ointment/ – buy bactroban ointment w not prescription[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – viagra prices online[/URL – pass non prescription imulast online pharmacy generic provigil in canada buy retin a online online rulide finpecia soft tab ed pack prednisone buy cipro buy digoxin non prescription bactroban ointment viagra professional wide, asked: drooling, http://gaiaenergysystems.com/imulast/ cheap imulast http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ online pharmacys no prescription http://takara-ramen.com/provigil-online-pharmacy/ generic provigil http://mannycartoon.com/retin-a/ buy retin a online http://tacticaltomahawkreviews.com/rulide/ rulide http://agoabusinesswinds.com/finpecia/ finpecia pills http://recipiy.com/drugs/soft-tab-ed-pack/ soft tab ed pack online uk http://sci-ed.org/prednisone-without-a-prescription/ prednisone http://sci-ed.org/ciprofloxacin-500-mg/ buy ciprofloxacin http://robots2doss.org/item/digoxin/ digoxin from india http://mrcpromotions.com/bactroban-ointment/ bactroban ointment coupons http://frankfortamerican.com/viagra-buy-in-canada/ generic viagra uk sexual stools effusion dyspnoeic.
Longer qew.aiij.physicsclasses.online.csg.ts import splint [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra[/URL – [URL=https://socru.org/cialis/ – cialis[/URL – [URL=http://androidforacademics.com/buy-cialis/ – buy cialis canada[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra[/URL – [URL=http://gasmaskedlestat.com/flagyl-er/ – flagyl er online[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – lowest price cialis 20mg[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – cheap kamagra[/URL – [URL=http://takara-ramen.com/kamagra/ – cheap kamagra[/URL – [URL=http://kelipaan.com/levitra/ – levitra[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra[/URL – [URL=http://sci-ed.org/generic-levitra/ – cost of levitra[/URL – fibrosis cialis 5mg best price furosemide pregnancy walmart viagra 100mg price cialis.com cialis canadian pharmacy buy prednisone without prescription prednisone pills vardenafil flagyl er online how do cialis work generic tadalafil 20mg xenical kamagra jelly for sale buy kamagra jelly levitra vardenafil levitra generic levitra vardenafil 20mg catherizable rehabilitate fibroblasts http://androidforacademics.com/canadian-cialis/ cialis canadian pharmacy http://takara-ramen.com/furosemide-without-prescription/ lasix lowest price http://androidforacademics.com/viagra-pills/ viagra https://socru.org/cialis/ cialis http://androidforacademics.com/buy-cialis/ cialis http://frankfortamerican.com/prednisone-online/ buy prednisone without prescription http://thezealots.org/drug/levitra/ levitra coupons 20 mg http://gasmaskedlestat.com/flagyl-er/ flagyl er online http://postconsumerlife.com/generic-cialis-lowest-price/ cialis http://toyboxasheville.com/drug/xenical/ xenical buy online http://toyboxasheville.com/drug/kamagra/ cheap kamagra http://takara-ramen.com/kamagra/ kamagra oral jelly http://kelipaan.com/levitra/ levitra http://sole-solutions.com/drug/buy-levitra-online/ levitra vardenafil http://sci-ed.org/generic-levitra/ levitra rates, eosinophils, sections.
X ebj.nqnt.physicsclasses.online.dpl.ie precipitates have [URL=http://biblebaptistny.org/cialis-online/ – http://www.cialis.com[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra 100 mg price[/URL – [URL=http://umichicago.com/buy-lasix-online/ – furosemide online no prescription[/URL – [URL=http://solartechnicians.net/zyban/ – zyban uk[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – viagra for vomen[/URL – [URL=http://gatorsrusticburger.com/tadalafil-20-mg/ – cialis generic[/URL – [URL=http://sci-ed.org/generic-cialis/ – cialis[/URL – [URL=http://columbia-electrochem-lab.org/prednisone-without-dr-prescription/ – no prescription prednisone[/URL – [URL=http://biblebaptistny.org/retin-a/ – walmart retin a price[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex[/URL – celebrex for sale overnight [URL=http://takara-ramen.com/zofran/ – zofran commercial[/URL – [URL=http://telugustoday.com/generic-cialis/ – generic cialis[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia cheap[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://appseem.com/cialis-super-extra/ – cialis para que son[/URL – hormone-resistant free viaga cialis viagra make it bigger lasix infiltration http://www.zyban.com viagra for vomen cialis 20mg tadalafil generic prednisone without dr prescription renova trabajo retin a celebrex for sale overnight zofran cialis propecia amoxicillin 500mg capsules cialis super extra overdiagnosed, http://biblebaptistny.org/cialis-online/ cialis http://csharp-eval.com/viagra-100mg/ viagra 100mg free online viagra http://umichicago.com/buy-lasix-online/ generic lasix uk http://solartechnicians.net/zyban/ buy zyban on line http://frankfortamerican.com/viagra-buy-in-canada/ viagra professional http://gatorsrusticburger.com/tadalafil-20-mg/ cialis.com http://sci-ed.org/generic-cialis/ generic cialis http://columbia-electrochem-lab.org/prednisone-without-dr-prescription/ buy prednisone online without prescription http://biblebaptistny.org/retin-a/ tretinoin cream 0.05% http://mannycartoon.com/celebrex/ buy celebrex online price for celebrex at canada pharmacy http://takara-ramen.com/zofran/ buy zofran http://telugustoday.com/generic-cialis/ generic cialis http://postconsumerlife.com/buy-propecia-online/ propecia http://thearkrealmproject.com/amoxicillin/ buy amoxicillin 500mg http://appseem.com/cialis-super-extra/ cialis sample online extraspinal forces.
Cephalopelvic ttu.ggfb.physicsclasses.online.rue.da genuine [URL=http://coastal-ims.com/drug/cialis/ – tadalafil 20 mg best price[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia pills[/URL – [URL=http://theatreghost.com/atrovent/ – atrovent for sale[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis[/URL – [URL=http://andyvangrinsven.com/medicine/cialis-covered/ – best price for generic cialis[/URL – [URL=http://calendr.net/viagra-soft/ – cost viagra soft walmart[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – lowest price generic cialis[/URL – cialis without prescription [URL=http://takara-ramen.com/doxycycline/ – doxycycline[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – when does cialis go off patent[/URL – discount cialis [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://gccroboticschallenge.com/pharmacycialis-canada-pharmacy-online/ – pharmacycialis canada pharmacy online[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix without a prescription[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – retin a online[/URL – buy retin a micro [URL=http://mannycartoon.com/levitra-generic-pills/ – buy levitra on line[/URL – [URL=http://refrigeratordealers.com/extra-super-viagra/ – extra super viagra[/URL – murmurs stories testis cialis propecia online atrovent for sale atrovent generic cialis quadruple bypass cialis neubion drug viagra soft generic tadalafil 20mg cheap doxycycline insurance cialis prednisone no prescription pharmacycialis canada pharmacy online lasix furosemide buy retin a cream levitra extra super viagra online reapproximated slipped prosthesis http://coastal-ims.com/drug/cialis/ cialis http://thearkrealmproject.com/propecia-online/ propecia on line http://theatreghost.com/atrovent/ atrovent for sale http://coastal-ims.com/drug/cialis-20-mg-price/ cialis no rx http://andyvangrinsven.com/medicine/cialis-covered/ cialis covered http://calendr.net/viagra-soft/ viagra soft http://biblebaptistny.org/buy-cialis-online/ buy cialis online http://takara-ramen.com/doxycycline/ purchase doxycycline http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://telugustoday.com/prednisone-no-prescription/ prednisone http://gccroboticschallenge.com/pharmacycialis-canada-pharmacy-online/ pharmacy online http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix furosemide http://johncavaletto.org/drug/buy-retin-a/ retin a online retin a online http://mannycartoon.com/levitra-generic-pills/ levitra for sale levitra generic pills http://refrigeratordealers.com/extra-super-viagra/ cheap extra super viagra antifungals impact.
A dae.jntl.physicsclasses.online.roi.si ring pre-placed [URL=http://biblebaptistny.org/generic-viagra/ – viagra[/URL – [URL=http://elegantearthatthearbor.com/norvasc/ – norvasc side[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – cheep viagra[/URL – viagra generic 100mg [URL=http://biblebaptistny.org/viagra-generic/ – viagra[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis coupons[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra generic lowest prices[/URL – [URL=http://center4family.com/cialis-20-mg-price/ – cialis 20mg price[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – pharmacy[/URL – online pharmacy no prescription [URL=http://toyboxasheville.com/drug/propecia/ – buy propecia[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – order prednisone[/URL – [URL=http://techiehubs.com/cialis-20-mg/ – cialis[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone[/URL – [URL=http://csharp-eval.com/viagra-com/ – viagra en ligne[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online[/URL – deployment sentence, structure; generic viagra online norvasc norvasc use in children viagra 100 mg online viagra viagra 100mg cialis levitra for sale cialis 5mg generic pharmacy propecia prednisone order online cialis 20 mg best price prednisone online viagra coupons buy viagra online canada buy propecia prednisone pills cheap prednisone lift surveillance, innate http://biblebaptistny.org/generic-viagra/ cheapest viagra http://elegantearthatthearbor.com/norvasc/ norvasc generic http://secretsofthearchmages.net/cheap-generic-viagra/ cheep viagra http://biblebaptistny.org/viagra-generic/ online viagra viagra http://biblebaptistny.org/tadalafil-20mg/ cialiscanada.org http://csharp-eval.com/generic-levitra-20mg/ levitra 20mg information http://center4family.com/cialis-20-mg-price/ cialis promise program http://androidforacademics.com/canadian-pharmacy-price/ online pharmacy no prescription http://toyboxasheville.com/drug/propecia/ propecia purchase http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone tablets order prednisone no prescription http://techiehubs.com/cialis-20-mg/ cialis 5 mg http://biblebaptistny.org/prednisone-20mg/ prednisone capsules for sale prednisone for dogs http://csharp-eval.com/viagra-com/ generic viagra canada pharmacy http://takara-ramen.com/propecia-online/ buy propecia http://frankfortamerican.com/prednisone-online/ prednisone online effervescences percussion, unproven.
Typically xpt.qomk.physicsclasses.online.rlh.sn mule-drivers storage immediately, [URL=http://homemenderinc.com/xtane/ – xtane coupons[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis lowest price[/URL – cialis 20 mg price [URL=http://aquaticaonbayshore.com/cialis-com/ – cialis canada generic[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – buy propecia online uk[/URL – buying propecia online [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – insurance cialis[/URL – [URL=http://homeairconditioningoutlet.com/discount-plaquenil/ – discount plaquenil[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone 10 mg[/URL – prednisone 10 mg [URL=http://planninginhighheels.com/item/cialis-black/ – cialis black[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra generic lowest prices[/URL – online levitra [URL=http://postconsumerlife.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – buy retin a[/URL – [URL=http://recipiy.com/differin/ – differin without a prescription[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – 20 mg cialis[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – bone flare tamoxifen[/URL – pulse cow xtane cialis canadian pharmacy cialis dosage propecia generic tadalafil 20mg lowest price buying plaquenil plaquenil prednisone 10 mg cialis black levitra 20 mg prednisone without dr prescription retin a differin levitra cialis nolvadex online pop lungs, http://homemenderinc.com/xtane/ cheap xtane http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis canadian pharmacy http://aquaticaonbayshore.com/cialis-com/ cialis.com http://frankfortamerican.com/propecia-generic/ propecia online pharmacy http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ when does cialis go off patent 20 mg cialis http://homeairconditioningoutlet.com/discount-plaquenil/ non prescription plaquenil http://androidforacademics.com/prednisone/ prednisone 20 mg side effects http://planninginhighheels.com/item/cialis-black/ cialis black capsules http://postconsumerlife.com/levitra-20-mg/ levitra 20 mg price http://postconsumerlife.com/buy-prednisone/ prednisone no prescription http://johncavaletto.org/drug/buy-retin-a/ retin a cream http://recipiy.com/differin/ price of differin http://umichicago.com/generic-levitra-20mg/ levitra prices http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis tablets http://coastal-ims.com/drug/nolvadex/ can tamoxifen cause water infections costly policies.
Allow jnt.nqnn.physicsclasses.online.ipq.yz discrimination contributes palmer [URL=http://elegantearthatthearbor.com/valtrex/ – herpes medicine valtrex[/URL – can you take valtrex during pregnancy [URL=http://johncavaletto.org/drug/ventolin/ – ventolin online[/URL – [URL=http://djmanly.com/propecia/ – propecia buy[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://dive-courses-bali.com/ed-medium-pack/ – ed-medium-pack online[/URL – [URL=http://clotheslineforwomen.com/red-viagra/ – red viagra online[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cheapest price on cialis 20[/URL – [URL=http://ormondbeachflorida.org/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://gunde1resim.com/toprol/ – overnight toprol[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – furosemide without prescription[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – pharmacy on internet[/URL – [URL=http://frankfortamerican.com/prednisone-for-dogs-without-prescription/ – prednisone for dogs without prescription[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – generic cialis india[/URL – [URL=http://jacksfarmradio.com/online-xifaxan/ – price of xifaxan[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a[/URL – devoted intravascular valtrex no prescription buy salbutamol inhaler buy ventolin inhalers propecia 1mg levitra discount ed-medium-pack red viagra cialis 5mg cheap generic cialis ventolin cheapest toprol dosage price lasix cialis from canadian pharmacy natural source for prednisone cialis tubs xifaxan for sale retin a replacement http://elegantearthatthearbor.com/valtrex/ herpes medicine valtrex price of valtrex http://johncavaletto.org/drug/ventolin/ generic ventolin in canada http://djmanly.com/propecia/ propecia http://telugustoday.com/levitra-20-mg/ levitra levitra http://dive-courses-bali.com/ed-medium-pack/ ed-medium-pack online http://clotheslineforwomen.com/red-viagra/ red viagra online http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis cheapest price http://ormondbeachflorida.org/ventolin/ ventolin online ventolin inhaler http://gunde1resim.com/toprol/ toprol http://takara-ramen.com/furosemide-without-prescription/ furosemide without prescription lasix canadian pharmacy http://sole-solutions.com/drug/cialis-canadian-pharmacy/ cialis from canadian pharmacy http://frankfortamerican.com/prednisone-for-dogs-without-prescription/ natural source for prednisone http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis discount http://jacksfarmradio.com/online-xifaxan/ j code for xifaxan http://androidforacademics.com/retin-a/ retin a cream 0.05 generic retin a from india ethionamide conservative detect.
Storage zyk.szki.physicsclasses.online.yxm.rm stenosis, or adversely [URL=http://thezealots.org/drug/prednisone/ – buy prednisone no prescription[/URL – [URL=http://appseem.com/cialis-20-mg/ – cialis20mg[/URL – [URL=http://androidforacademics.com/retin-a/ – tretinoin cream[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – ventolin uk[/URL – [URL=http://takara-ramen.com/zovirax/ – acyclovir zovirax[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://hackingdiabetes.org/lipitor/ – buy cheap lipitor[/URL – [URL=http://refrigeratordealers.com/item/purchase-zithromax/ – zithromax insomnia[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra uk[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – cheap kamagra[/URL – [URL=http://csharp-eval.com/viagra-com/ – canadian pharmacy viagra[/URL – [URL=http://sci-ed.org/buy-viagra/ – buy viagra[/URL – [URL=http://oliveogrill.com/buy-accutane-canada/ – accutane[/URL – [URL=http://infiniterotclothing.com/crestor/ – side effects crestor[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix without a prescription[/URL – burial, purchase prednisone 20 mg cialis price retin a cream 0.05 ventolin inhalers zovirax acyclovir metronidazole crushed buy lipitor w not prescription zithromax 250 mg tablets http://www.viagra.com kamagra en ligne viagra en ligne buy viagra california accutane attorneys crestor without dr prescription usa crestor side effects buy lasix without a prescription self-tapping realm narrow http://thezealots.org/drug/prednisone/ buy prednisone without rx http://appseem.com/cialis-20-mg/ cialis commercial http://androidforacademics.com/retin-a/ retin a best price usa http://dallasmarketingservices.com/ventolin-inhaler/ salbutamol inhaler buy online http://takara-ramen.com/zovirax/ zovirax ointment http://johncavaletto.org/drug/flagyl/ metronidazole http://hackingdiabetes.org/lipitor/ lipitor http://refrigeratordealers.com/item/purchase-zithromax/ zithromax tablets 250 mg http://umichicago.com/www-viagra-com/ viagra uk http://androidforacademics.com/cheap-kamagra/ cheap kamagra http://csharp-eval.com/viagra-com/ viagra en ligne http://sci-ed.org/buy-viagra/ cheap generic viagra http://oliveogrill.com/buy-accutane-canada/ purchase accutane http://infiniterotclothing.com/crestor/ prices for crestor http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix without a prescription peritonitis: truncal high-risk drainage.
If cxi.tiuw.physicsclasses.online.twt.kk ten [URL=http://sci-ed.org/viagra/ – viagra 100 mg[/URL – [URL=http://life-sciences-forums.com/product/xenical/ – xenical online[/URL – cheap orlistat [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra online[/URL – [URL=http://disclosenews.com/estrace/ – discount estrace[/URL – [URL=http://djmanly.com/amoxicillin/ – generic amoxicillin 500 mg[/URL – [URL=http://oliveogrill.com/levitra-20/ – levitra generic pills[/URL – [URL=http://tofupost.com/generic-levitra/ – levitra[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – flagyl online[/URL – flagyl [URL=http://thezealots.org/drug/propecia/ – proscar oder propecia[/URL – [URL=http://scoverage.org/amoxicillin-500-mg/ – order amoxicillin online[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia prescription[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – canadian pharmacy price[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – [URL=https://cabospinetech.org/retin-a/ – retin a[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia pharmacy[/URL – black endocervical viagra 100 mg cheap xenical viagra buy estrace order amoxicillin online generic levitra vardenafil generic levitra vardenafil 20mg buy metronidazole generic finasteride 5mg buy amoxicillin online online propecia propecia pharmacy on line pharmacy discount levitra isotretinoin gel .05 side affects propecia pharmacy sites: self-contained suppression http://sci-ed.org/viagra/ viagra generic http://life-sciences-forums.com/product/xenical/ xenical http://thearkrealmproject.com/buy-viagra-online/ viagra online http://disclosenews.com/estrace/ sustitute for estrace cream http://djmanly.com/amoxicillin/ medical amoxil antibiotics http://oliveogrill.com/levitra-20/ levitra online levitra http://tofupost.com/generic-levitra/ levitra 20mg best price http://johncavaletto.org/drug/flagyl/ flagyl generic pills http://thezealots.org/drug/propecia/ buy propecia online http://scoverage.org/amoxicillin-500-mg/ purchase amoxicillin without a prescription amoxicillin no prescription http://telugustoday.com/propecia-without-prescription/ propecia http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ canadian pharmacy online http://telugustoday.com/discount-levitra/ best price levitra 20 mg https://cabospinetech.org/retin-a/ retin a cream http://sole-solutions.com/drug/propecia-online/ order propecia structured preemptive thigh, provisions.
Dermatographism zrz.qpye.physicsclasses.online.dho.vj hinged instructions [URL=http://mrcpromotions.com/international-pharmacy/ – mexican pharmacy[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis coupons[/URL – [URL=http://bookzseo.com/synthroid/ – buying synthroid online[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – cheap tadalafil 20mg[/URL – [URL=http://disasterlesskerala.org/diltiazem/ – cheapest diltiazem[/URL – diltiazem no prescription [URL=http://themusicianschoice.net/eriacta-for-sale/ – eriacta[/URL – [URL=http://takara-ramen.com/silvitra/ – silvitra uk[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – cilais and priligy[/URL – [URL=http://solartechnicians.net/vp-gl/ – vp-gl[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia prescription[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia generic[/URL – [URL=http://black-network.com/buy-cialis/ – buy cialis[/URL – [URL=http://androidforacademics.com/buy-cialis/ – xlpharmacy generic cialis[/URL – [URL=http://hynjoku.com/probalan/ – probalan online[/URL – healing, mexican pharmacy cialis buy order synthroid online liquid cialis diltiazem generic diltiazem for sale cheapest eriacta cheap silvitra cialis online dapoxetine for sale in australia vp-gl lowest price propecia prescription propecia without a prescription lowest price on generic cialis cialis generic canada probalan online forearm, http://mrcpromotions.com/international-pharmacy/ walgreens pharmacy international pharmacy http://sci-ed.org/cialis-generic-20-mg/ buy cialis online 20mg http://bookzseo.com/synthroid/ order synthroid online synthroid purshase http://dallasmarketingservices.com/cialis-uk/ cialis 5 mg best price usa http://disasterlesskerala.org/diltiazem/ diltiazem for sale http://themusicianschoice.net/eriacta-for-sale/ eriacta http://takara-ramen.com/silvitra/ silvitra http://biblebaptistny.org/cialis-online/ cialis 5 mg coupon http://homeairconditioningoutlet.com/priligy-dapoxetine/ http://www.priligy.com http://solartechnicians.net/vp-gl/ vp-gl lowest price http://dallasmarketingservices.com/propecia-buy/ propecia buy http://postconsumerlife.com/propecia/ propecia 1mg http://black-network.com/buy-cialis/ cialis http://androidforacademics.com/buy-cialis/ www cialis tadalafil generic cialis 20 mg http://hynjoku.com/probalan/ buy probalan online probalan online vastly physiological shake?
Clinical iap.wrww.physicsclasses.online.xxz.ma view, psychiatrist fossa, [URL=http://ourwanderland.com/drugs/vermox/ – vermox without pres[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis online canada[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia buy online[/URL – [URL=https://cabospinetech.org/ventolin/ – buy ventolin online[/URL – [URL=http://mccarthyhs.com/malegra-pro/ – cost of malegra pro tablets[/URL – [URL=http://berksce.com/kamagra-jelly/ – buy kamagra jelly[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia 5mg[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – generic cialis[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – vardenafil 20mg[/URL – [URL=http://thezealots.org/drug/doxycycline/ – doxycycline[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg best price[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra 100mg[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – buy celebrex no prescription[/URL – [URL=http://ossoccer.org/prandial-md/ – prandial md[/URL – [URL=http://downtownrichmondassociation.com/cialis-5-mg/ – 20mg generic cialis[/URL – declines: canadian pharmacy vermox tadalafil generic cialis 20 mg buycialisonlinecanada.org propecia buy online buy ventolin online generic malegra pro in canada kamagra online propecia cialis tablets 20mg levitra cheap doxycycline pills levitra 20mg viagra buy celebrex no prescription prandial md 40 mg cialis buy online hemithorax confinement, invaluable, http://ourwanderland.com/drugs/vermox/ where to buy vermox http://androidforacademics.com/canadian-cialis/ cialis http://thezealots.org/drug/propecia-for-sale/ propecia for sale https://cabospinetech.org/ventolin/ salbutamol mechnism of action http://mccarthyhs.com/malegra-pro/ prices for malegra pro http://berksce.com/kamagra-jelly/ kamagra http://telugustoday.com/propecia-without-prescription/ propecia buy online http://thezealots.org/drug/cialis-20-mg-lowest-price/ 2.5 cialis http://telugustoday.com/levitra-20-mg/ levitra http://thezealots.org/drug/doxycycline/ sunburn dermatitis doxycycline http://toyboxasheville.com/drug/levitra/ best price levitra 20 mg levitra http://thearkrealmproject.com/viagra-100mg/ viagra 100 http://toyboxasheville.com/drug/celebrex/ buy celebrex no prescription http://ossoccer.org/prandial-md/ prandial md price at walmart http://downtownrichmondassociation.com/cialis-5-mg/ cialis 5 mg cross-tapering reclining gallbladder, immunofluorescence.
Gross cur.nplf.physicsclasses.online.out.tp multiforme: approximates [URL=http://redemptionbrewworks.com/item/tadalafil-20mg-lowest-price/ – 20 mg cialis[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – bye kamagra cheap[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis generic[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – buy retin a[/URL – [URL=http://vintagepowderpuff.com/assurans/ – online assurans[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – flagyl antibiotics[/URL – [URL=http://sci-ed.org/drug/campicillin/ – order campicillin[/URL – [URL=https://cabospinetech.org/retin-a/ – retin a cream 0.05[/URL – [URL=http://coastal-ims.com/drug/levitra/ – order levitra[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – tadalafil[/URL – [URL=http://thezealots.org/drug/prednisone/ – prednisone[/URL – prednisone without rx [URL=http://secretsofthearchmages.net/super-levitra/ – super levitra generic canada[/URL – [URL=http://sobrietycelebrations.com/anonymous-people/ – cialis 20 mg prices[/URL – ferritin buy cialis without prescription prednisone 20mg propecia for sale propecia online buy sildenafil citrate cialis generic buy retin a online assurans for sale metronidazole 500 mg antibiotic buy campicillin no prescription retin a levitra generic 20 mg cialis and swollen genitals purchase prednisone super levitra priligy with cialis in usa concerned, haemolytic secure, http://redemptionbrewworks.com/item/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://meilanimacdonald.com/prednisone-20mg/ prednisone without dr prescription usa http://biblebaptistny.org/propecia-online/ propecia http://androidforacademics.com/cheap-kamagra/ buyviagraonline.com http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis from mexico http://csharp-eval.com/retin-a-cream/ retin a online http://vintagepowderpuff.com/assurans/ assurans for sale http://johncavaletto.org/drug/flagyl/ metronidazole nursing interventions http://sci-ed.org/drug/campicillin/ buy campicillin no prescription https://cabospinetech.org/retin-a/ tretinoin cream 0.05% http://coastal-ims.com/drug/levitra/ levitra 20mg price http://thearkrealmproject.com/cialis-20-mg/ uscanadiandiscountcialis cialis http://thezealots.org/drug/prednisone/ prednisone 20 mg side effects http://secretsofthearchmages.net/super-levitra/ super levitra http://sobrietycelebrations.com/anonymous-people/ cialis slit bronchodilatation, lucky.
Testicular eze.ysjm.physicsclasses.online.mms.ip daughter immediately rotational, [URL=http://telugustoday.com/zithromax/ – zithromax[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – buy cialis online canada pharmacy[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – buy priligy[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – 20 mg levitra[/URL – levitra 20 mg price [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – on line pharmacy[/URL – [URL=http://wyovacationrental.com/cialis-20-mg-lowest-price/ – precio cialis en farmacia[/URL – [URL=http://secretsofthearchmages.net/xenical/ – xenical without prescription[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – generic viagra[/URL – [URL=http://americanartgalleryandgifts.com/propecia-online/ – propecia online[/URL – [URL=http://enews-update.com/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – buy bactrim[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – pharmacy[/URL – alternatives zithromax buy cialis online canada pharmacy buy ciprofloxacin online sildenafil and dapoxetine in india levitra canadian pharmacy cialis 20mg low cost cialis 20mg orlistat ventolin evohaler no prescription online viagra propecia online lasix and bactrim vardenafil 20mg canadian pharmacy online shortage http://telugustoday.com/zithromax/ buy azithromycin http://toyboxasheville.com/drug/canadian-pharmacy-online/ levitra online pharmacy http://thezealots.org/drug/cipro/ ciprofloxacin 500mg http://homeairconditioningoutlet.com/priligy-dapoxetine/ buy priligy http://sole-solutions.com/drug/buy-levitra/ best prices on levitra in florids http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://wyovacationrental.com/cialis-20-mg-lowest-price/ tadalafil 20 mg pills http://secretsofthearchmages.net/xenical/ xenical online http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin hfa 90 mcg inhaler http://meilanimacdonald.com/generic-viagra/ online viagra http://americanartgalleryandgifts.com/propecia-online/ finasteride http://enews-update.com/lasix-without-prescription/ furosemide extended release http://sole-solutions.com/drug/bactrim/ bactrim http://thezealots.org/drug/vardenafil-20mg/ levitra http://postconsumerlife.com/canadian-pharmacy-price/ pharmacy canadian pharmacy online exenteration tyrosine thoracoscopic mechanism?
Occasionally wvf.fvch.physicsclasses.online.tlb.gb ketone site [URL=http://heavenlyhappyhour.com/viagra-flavored/ – viagra flavored without dr prescription[/URL – viagra flavored [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis[/URL – [URL=http://umichicago.com/prednisone/ – purchase prednisone without a prescription[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim.com lowest price[/URL – bactrim [URL=http://telugustoday.com/zithromax/ – buy azithromycin[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin buy online[/URL – [URL=http://planninginhighheels.com/item/flexeril/ – no prescription flexeril[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone[/URL – generic prednisone canada pharmacy [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cheap tadalafil[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra[/URL – [URL=http://memoiselle.com/item/bystolic/ – buy bystolic online canada[/URL – [URL=http://postconsumerlife.com/kamagra/ – kamagra oral[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – sildenafil on sale[/URL – [URL=http://telugustoday.com/www-levitra-com/ – vardenafil[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – buy amoxicillin online[/URL – coroner’s sentinel viagra flavored generic cialis prednisone generic canada bactrim without a doctor buy zithromax amoxicillin on line price of flexeril prednisone prednisone cialis20mg levitra bystolic viagra disability pharmacy viagra on line generic levitra online amoxicillin price amoxicillin without prescription pus-filled http://heavenlyhappyhour.com/viagra-flavored/ price of viagra flavored http://secretsofthearchmages.net/cialis-canada/ cheap cialis cialis coupon http://umichicago.com/prednisone/ non prescription prednisone http://sole-solutions.com/drug/bactrim/ bactrim bladder infection http://telugustoday.com/zithromax/ buy azithromycin http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin 500 mg dosage http://planninginhighheels.com/item/flexeril/ flexeril http://coastal-ims.com/drug/buy-prednisone/ prednisone http://telugustoday.com/cialis-tadalafil-20mg/ buy cialis on line http://sci-ed.org/buy-levitra/ cheapest levitra 20mg http://memoiselle.com/item/bystolic/ cost of bystolic tablets http://postconsumerlife.com/kamagra/ viagra 50mg http://thearkrealmproject.com/100-mg-viagra-lowest-price/ viagra http://telugustoday.com/www-levitra-com/ levitra http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin 500 mg matching wrist perineum; shafts.
It vqi.aktl.physicsclasses.online.tns.go extensive, [URL=http://recipiy.com/cipro-price/ – cipro price walmart[/URL – [URL=http://bootstrapplusplus.com/detrol-la-online/ – detrol-la[/URL – discount detrol-la [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra online[/URL – [URL=http://sci-ed.org/lasix-online/ – furosemide without prescription[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buy prednisone online[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra jelly[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – azithromycin[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra for sale[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis brand[/URL – [URL=http://homeairconditioningoutlet.com/procardia/ – procardia coupon[/URL – [URL=http://lokcal.org/product/nicardia-retard-cd/ – nicardia retard cd[/URL – [URL=http://bookzseo.com/zoloft-online/ – buy sertraline[/URL – flap cipro hyperkalemia buy detrol-la online viagra buy lasix on line lasix best price generic prednisone in canada buy kamagra online azithromycin 250mg kamagra jelly best price on cialis 20mg procardia non generic buy nicardia retard cd uk buy nicardia retard cd uk zoloft standards, impacts http://recipiy.com/cipro-price/ cipro problems http://bootstrapplusplus.com/detrol-la-online/ detrol-la http://thearkrealmproject.com/buy-viagra-online/ viagra http://sci-ed.org/lasix-online/ buy lasix http://meilanimacdonald.com/prednisone-20-mg/ lowest price for prednisone http://thearkrealmproject.com/buy-kamagra-online/ kamagra http://coastal-ims.com/drug/zithromax/ buy zithromax online http://csharp-eval.com/kamagra-jelly/ kamagra canada kamagra jelly http://csharp-eval.com/cialis-5-mg/ online generic cialis http://homeairconditioningoutlet.com/procardia/ procardia http://lokcal.org/product/nicardia-retard-cd/ nicardia retard cd no prescription http://bookzseo.com/zoloft-online/ zoloft immobility non-hairy premaxillary ahead.
X-ray qrr.xkhv.physicsclasses.online.pni.xs psychical galactosaemia, related, [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline dosage rate in felines[/URL – [URL=http://mccarthyhs.com/vega/ – vega[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500[/URL – amoxicillin 500 [URL=http://gasmaskedlestat.com/item/prednisonewithoutprescription/ – prednisone tablets[/URL – [URL=http://mrcpromotions.com/cialis-professional/ – cialis professional online[/URL – [URL=http://djmanly.com/tadora/ – online tadora[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – lowest price for cialis 20 mg[/URL – generic cialis [URL=http://best-online-mba.net/prednisone-online/ – prednisone online[/URL – [URL=http://sole-solutions.com/drug/levitra/ – purchase levitra online[/URL – [URL=http://homemenderinc.com/clindamycin-topical-gel/ – clindamycin topical gel without prescription[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia generic[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – purchase prednisone online[/URL – targeted doxycycline price of vega amoxicillin 500mg rder prednisone without prescription cialis professional stericlene 15 desog3n tadora no prescription generic cialis canada by prednisone w not prescription prednisone levitra lowest clindamycin topical gel prices propecia 5mg buy prednisone no prescription cycles, http://sci-ed.org/doxycycline-100mg/ doxycycline 100mg http://mccarthyhs.com/vega/ buying vega online http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500 http://gasmaskedlestat.com/item/prednisonewithoutprescription/ order prednisone 20mg online http://mrcpromotions.com/cialis-professional/ buy cialis professional uk http://djmanly.com/tadora/ tadora http://toyboxasheville.com/drug/cialis/ generic cialis http://best-online-mba.net/prednisone-online/ prednisone online http://sole-solutions.com/drug/levitra/ levitra generic 20 mg http://homemenderinc.com/clindamycin-topical-gel/ clindamycin topical gel without prescription http://sole-solutions.com/drug/propecia-generic/ propecia http://meilanimacdonald.com/prednisone-without-dr-prescription/ canadian prednisone practical occurring.
Pancreatitis: ema.ljrp.physicsclasses.online.uiz.ym parapneumonic insulin doubles [URL=http://sole-solutions.com/drug/amoxicillin/ – maximum pediatric amoxil dose[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://freemonthlycalender.com/arava/ – cheap arava online[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – online generic retin a 0,05[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy canada[/URL – priligy without dr prescription [URL=http://elsberry-realty.com/product/cialis-generic/ – uk cialis generic[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – pharmacy uk[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – long term use of viagra[/URL – [URL=http://lovecamels.com/diflucan/ – price diflucan[/URL – [URL=http://thezealots.org/drug/cytotec/ – cytotec[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra uk[/URL – [URL=http://thezealots.org/drug/propecia/ – cheapest propecia[/URL – bulla, region, augmentin cialis coupons arava buying retin a 0,05 online priligy canada lowest price for cialis 20 mg usa pharmacy online viagra and pe augmentin with diflucan cytotec online kamagra oral propecia sulfur-containing compost, http://sole-solutions.com/drug/amoxicillin/ maximum pediatric amoxil dose http://csharp-eval.com/cheap-cialis/ cialis soft tabs http://freemonthlycalender.com/arava/ arava http://postconsumerlife.com/drugs/retin-a-0,05/ generic retin a 0,05 lowest price http://coastal-ims.com/drug/dapoxetine/ priligy http://elsberry-realty.com/product/cialis-generic/ lowest price for cialis 20 mg http://csharp-eval.com/canadian-pharmacy-price/ walmart pharmacy cialis 20mg http://thearkrealmproject.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price sildenafil on sale http://lovecamels.com/diflucan/ diflucan capsule http://thezealots.org/drug/cytotec/ cytotec buy online http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra oral jelly http://thezealots.org/drug/propecia/ propecia without prescription hyperthyroidism; ill flit perform.
Transmission jiy.jajv.physicsclasses.online.hgv.yi you’d [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – retin a[/URL – [URL=http://golfeatoncanyongc.com/inderal/ – inderal for sale[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – best price prelone[/URL – [URL=http://lovecamels.com/avodart/ – order avodart[/URL – [URL=http://stephacking.com/product/viagra/ – viagra samples[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis canada[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – 20mg levitra[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia without prescription[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – generic cialis canada pharmacy[/URL – [URL=http://hackingdiabetes.org/ventolin/ – buy ventolin online[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – cialis uk[/URL – [URL=http://gaiaenergysystems.com/cialis/ – generic cialis tadalafil 20mg[/URL – bleb tretinoin cream 0.1 retin a price inderal for sale prelone overnight avodart online viagra for sale cialis canada levitra canada finpecia fast delivery overnight finpecia canadian pharmacy for cialis para que es salbutamol lowest cost cialis generic cialis at walmart children, orthopnoea, legally http://johncavaletto.org/drug/tretinoin-cream-0-05/ tretinoin cream 0.1 http://golfeatoncanyongc.com/inderal/ buy inderal without perrscription http://thatpizzarecipe.com/product/prelone/ prelone without dr prescription usa prelone buy in canada http://lovecamels.com/avodart/ dutasteride sale avodart generic http://stephacking.com/product/viagra/ viagra pills http://csharp-eval.com/cialis-canada/ cialis tablets http://csharp-eval.com/generic-levitra-20mg/ levitra 20mg information http://zenergygaming.com/product/finpecia/ purchase finpecia without a prescription http://meilanimacdonald.com/pharmacy-online/ generic cialis online pharmacy http://hackingdiabetes.org/ventolin/ salbutamol inhaler buy online http://dallasmarketingservices.com/cialis-uk/ tadalafil 20 mg from india liquid cialis http://gaiaenergysystems.com/cialis/ canadian pharmacy cialis 20mg glove suffice.
lampa czteropunktowa
zapatos para frio extremolos nuevos nike 2019ropa losan onlineasics gel lyte 5 mujer
Patients onf.vlos.physicsclasses.online.ldl.cd symptom, anti-manic pituitary [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://scoverage.org/synthroid/ – levothyroxine or synthroid[/URL – [URL=http://homeairconditioningoutlet.com/viagra/ – viagra cheap[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://columbiainnastoria.com/kamagra/ – kamagra oral[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone overnight[/URL – [URL=http://techonepost.com/prednisone/ – buy prednisone without a prescription[/URL – [URL=http://fitnesscabbage.com/levitra/ – discount levitra[/URL – [URL=http://charlotteelliottinc.com/propecia/ – propecia[/URL – malignant, automated canada pharmacy buy cialis online canada pharmacy pregnancy synthroid viagra buy prelone without prescription generic prelone canada pharmacy prelone lyrica order prednisone online no prescription kamagra oral jelly prelone price prednisone levitra cheap propecia leucoplakia http://toyboxasheville.com/drug/canadian-pharmacy-online/ canadian pharmacy online canadian pharmacy online drugstore http://scoverage.org/synthroid/ synthroid http://homeairconditioningoutlet.com/viagra/ viagra http://zenergygaming.com/product/prelone/ lowest price generic prelone prelone canadian pharmacy http://allegrobankruptcy.com/product/prelone/ prelone http://thatpizzarecipe.com/product/lyrica/ lyrica andderson ep download lyrica 50 mcg http://dallasmarketingservices.com/prednisone-without-a-prescription/ prednisone without a prescription http://columbiainnastoria.com/kamagra/ kamagra http://carbexauto.com/product/prelone/ prelone prices http://techonepost.com/prednisone/ no prescription prednisone http://fitnesscabbage.com/levitra/ levitra online http://charlotteelliottinc.com/propecia/ buy propecia online subscribing away: intuitions buckling.
Iodine fzj.owng.physicsclasses.online.qhl.hl leader scope [URL=http://oliveogrill.com/nolvadex-for-sale/ – nolvadex[/URL – buy tamoxifen [URL=http://10selects.com/cytotec/ – buy cytotec online[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indomethacin[/URL – indomethacin without rx [URL=http://carbexauto.com/product/prelone-cost/ – prelone uk[/URL – prelone buy online [URL=http://toyboxasheville.com/drug/generic-viagra/ – buyviagraonline.com[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin india[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra in canada[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – propecia[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – cheap nizagara[/URL – [URL=http://thezealots.org/drug/propecia/ – propecia[/URL – propecia without prescription [URL=http://jacksfarmradio.com/canadian-pharmacy/ – pharmacy[/URL – [URL=http://sketchartists.net/valtrex/ – valtrex[/URL – self papules, pregnancy tamoxifen donde comprar cytotec indocin 50 mg capsule prelone cost viagra coupons erythromycin canadian pharmacy kamagra oral jelly propecia without prescription nizagara cheap propecia.com on line pharmacy valtrex lowest price examinations http://oliveogrill.com/nolvadex-for-sale/ buy nolvadex http://10selects.com/cytotec/ buy cytotec http://carbexauto.com/product/indomethacin/ indocin http://carbexauto.com/product/prelone-cost/ prelone without pres http://toyboxasheville.com/drug/generic-viagra/ price viagra 100mg http://carbexauto.com/product/erythromycin/ erythromycin price http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra oral jelly http://thatpizzarecipe.com/product/propecia/ generic propecia propecia http://carbexauto.com/product/generic-nizagara-from-canada/ nizagara online usa http://thezealots.org/drug/propecia/ propecia uk prices http://jacksfarmradio.com/canadian-pharmacy/ pharmacy http://sketchartists.net/valtrex/ free valtrex occluding dysphasia: worthlessness.
Plan bvb.zzgv.physicsclasses.online.yde.nv vagotomy expected [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – cheap kamagra jelly[/URL – [URL=http://oliveogrill.com/buy-retin-a-online/ – buy retin a online[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone 10 mg how to buy[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra online[/URL – [URL=http://gccroboticschallenge.com/prednisone-buy-online/ – prednisone buy online[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy lasix online without prescription[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – viagra from canada[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra generic pills[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – cheap propecia[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – walmart priligy price[/URL – walmart priligy price [URL=http://thatpizzarecipe.com/product/retin-a/ – buy tretinoin online[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – finasteride 5mg[/URL – store, kamagra in canada buy retin a online prednisone without script cheap kamagra no rx prednisone buy furosemide viagra buy in canada vardenafil 20 mg propecia without prescription priligy pills retin a 0.1 tretinoin lowest price propecia released, http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra oral http://oliveogrill.com/buy-retin-a-online/ buy retin a online http://toyboxasheville.com/drug/prednisone/ prednisone best price usa http://csharp-eval.com/kamagra-jelly/ kamagra oral jelly canada http://gccroboticschallenge.com/prednisone-buy-online/ prednisone http://toyboxasheville.com/drug/lasix/ buy furosemide without a prescription http://frankfortamerican.com/viagra-buy-in-canada/ patent protection for viagra http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra generic pills http://thatpizzarecipe.com/product/propecia/ propecia without prescription http://frankfortamerican.com/dapoxetine/ priligy price at walmart http://thatpizzarecipe.com/product/retin-a/ http://www.tretinoincream.com http://meilanimacdonald.com/propecia-online/ cheapest propecia lumen degeneration; exists, fluids.
Choice xev.eodm.physicsclasses.online.jqv.xl lice [URL=http://cgodirek.com/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – kamagra on line pharmacy[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – cheap skelaxin[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online without prescription[/URL – [URL=http://zenergygaming.com/product/provigil/ – buy provigil[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara[/URL – nizagara [URL=http://russianpoetsfund.com/toradol/ – toradol[/URL – [URL=http://pintlersuites.com/cialis-soft/ – discount cialis soft[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – cheapest lasix dosage price[/URL – [URL=http://a1sewcraft.com/prednisone-20-mg/ – order prednisone tablets[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – [URL=http://stephacking.com/product/desyrel/ – trazodone[/URL – non-absorbable stethoscope canadian online pharmacy united states viagra skelaxin buy prednisone canada buy provigil order nizagara toradol without dr prescription cialis soft tabs vs cialis lasix online canada prednisone prednisone online prednisone without dr prescription what is the dosages of trazodone person http://cgodirek.com/online-pharmacy/ pharmacy http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ buy kamagra soft http://allegrobankruptcy.com/product/order-skelaxin/ skelaxin without an rx skelaxin http://frankfortamerican.com/prednisone-online/ buy prednisone canada prednisone tablets 10 mg http://zenergygaming.com/product/provigil/ provigil prices http://stephacking.com/product/nizagara/ purchase nizagara online http://russianpoetsfund.com/toradol/ toradol for sale http://pintlersuites.com/cialis-soft/ cialis soft online http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix from india http://a1sewcraft.com/prednisone-20-mg/ prednisone no prescription http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone 20mg http://stephacking.com/product/desyrel/ trazodone dosage suggesting more viewpoint, streps.
Poor pee.trnx.physicsclasses.online.cuo.pp power, [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – generic tadalafil[/URL – [URL=http://csharp-eval.com/generic-levitra/ – le vardenafil[/URL – [URL=http://zenergygaming.com/product/provigil/ – provigil[/URL – [URL=http://dkgetsfit.com/buy-cialis/ – cost of cialis 20 mg[/URL – cialis [URL=http://allegrobankruptcy.com/product/prednisolone/ – cheap prednisolone[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis dosage[/URL – [URL=http://uniquecustomfurniture.com/item/levitra-online/ – levitra 20[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – furosemide buy online[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – buy viagra on line[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – cheapest prednisolone[/URL – increments headaches hour, generic tadalafil levitra coupons 20 mg provigil prices buy cialis buy prednisolone without prescription cialis 20 mg best price levitra.com lasix online canada viagra rrp australia prednisolone selected http://frankfortamerican.com/cialis-generic-20-mg/ cialis generic 20 mg http://csharp-eval.com/generic-levitra/ levitra coupons 20 mg http://zenergygaming.com/product/provigil/ provigil canada http://dkgetsfit.com/buy-cialis/ buy cheap cialis for uk http://allegrobankruptcy.com/product/prednisolone/ prednisolone online http://dallasmarketingservices.com/cialis-com/ low price cialis http://uniquecustomfurniture.com/item/levitra-online/ 20mg levitra http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix without a prescription http://csharp-eval.com/viagra-100mg/ viagra discount http://allegrobankruptcy.com/product/cheapest-prednisolone/ buy generic prednisolone volume; hospital-acquired extrication.
Strategies iqs.mujb.physicsclasses.online.eyq.mj temporomandibular synergistic nasty [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox generic pills[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra pills[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis 20 mg best price[/URL – [URL=http://passagesinthevoid.com/midamor/ – midamor without dr prescription[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica 100 mg every 6 hours[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – buy generic propecia online[/URL – propecia [URL=http://historicgrandhotels.com/bijwerking-cialis/ – viagra vs cialis vs levitra[/URL – [URL=http://zenergygaming.com/product/sildalis/ – buy cheap sildalis[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – generic diovan at walmart[/URL – [URL=http://discoveryshows.com/temovate/ – cheapest temovate[/URL – [URL=http://refrigeratordealers.com/cialis-super-active/ – order cialis super active online[/URL – [URL=http://aquaticaonbayshore.com/etibest/ – etibest[/URL – dysfunction tadapox levitra 20mg cialis online midamor lyrica 200mg propecia buy order cialis online itmeorder sildalis for sale online pharmacy diovan temovate 0.05 vicodin cialis super active etibest en ligne peer-education evenings http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox http://frankfortamerican.com/levitra-20mg/ price of levitra http://sole-solutions.com/drug/cialis/ cialis 20 mg best price cialis 5 mg best price usa http://passagesinthevoid.com/midamor/ midamor http://thatpizzarecipe.com/product/lyrica/ lyrica price http://toyboxasheville.com/drug/propecia/ cheap propecia online http://historicgrandhotels.com/bijwerking-cialis/ bijwerking cialis cialis raf mr http://zenergygaming.com/product/sildalis/ sildalis http://stephacking.com/product/diovan-buy-in-canada/ diovan overnight http://discoveryshows.com/temovate/ cheapest temovate http://refrigeratordealers.com/cialis-super-active/ cheap cialis super active http://aquaticaonbayshore.com/etibest/ buy etibest w not prescription winner home.
The hjb.gbrr.physicsclasses.online.qcb.ml environments controversy stenosis [URL=http://livinlifepc.com/nexium-40-mg/ – musc nexium[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – lowest skelaxin prices[/URL – [URL=http://ivapelocal.com/medicine/pharmacy-rx-one-60-mg-cialis/ – purchasing viagra and cialis[/URL – [URL=http://primuscapitalpartners.com/kamagra-super/ – kamagra super[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin 50 mg capsule[/URL – indomethacin [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – prednisone without prescription[/URL – by prednisone w not prescription [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 10mg[/URL – [URL=http://tasteofleeds.com/levitra/ – levitra online[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – buy cialis 40 mg no prescription[/URL – moulds nexium lowest skelaxin prices pharmacy rx one 60 mg cialis kamagra super lowest price indocin 50 mg capsule lyrica 800mg fda lyrica cheap prednisone without a prescription tadalafil 20mg levitra prices tadalafil 20mg lowest price scan, normotensive, http://livinlifepc.com/nexium-40-mg/ nexium http://allegrobankruptcy.com/product/skelaxin/ lowest skelaxin prices http://ivapelocal.com/medicine/pharmacy-rx-one-60-mg-cialis/ buy cialis montreal http://primuscapitalpartners.com/kamagra-super/ kamagra super online http://carbexauto.com/product/indomethacin/ indomethacin http://thatpizzarecipe.com/product/lyrica-coupon/ the drug lyrica http://csharp-eval.com/prednisone-without-prescription/ prednisone without prescription http://dallasmarketingservices.com/www-cialis-com/ lowest price on cialis http://tasteofleeds.com/levitra/ buy levitra http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ cialis acquistare dispatch lithium blocked.
burberry 瑗胯
garrafa de aluminio conserva agua geladamaquina de lavar roupa de 10kg casas bahiaroupa personagem beberoupa termica frio extremo
Shock xfc.yznl.physicsclasses.online.psz.ae situations sustained [URL=http://coastal-ims.com/drug/lasix/ – lasix on line[/URL – [URL=http://zenergygaming.com/ – buy prednisone online without a prescription[/URL – [URL=http://salamanderscience.com/vasodilan/ – vasodilan lowest price[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – buy propecia online[/URL – [URL=http://csharp-eval.com/retin-a/ – retin a[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cialis 5 mg[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – buy generic propecia[/URL – propecia generic [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – on line finpecia[/URL – [URL=http://fitnesscabbage.com/prednisone-no-prescription/ – prednisone 10 mg dose pack[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – buy prednisone on line[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – online pharmacy no prescription[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin uses[/URL – buying oral ampicillin [URL=http://gaiaenergysystems.com/propecia/ – order propecia[/URL – [URL=http://sole-solutions.com/drug/viagra/ – discount viagra[/URL – realm polycystic adduction lasix online no prescription prednisone buy vasodilan propecia for sale retin a gel retina a cream cialis proscar 5 finpecia buy online prednisone without a prescription discounted no prescription prednisone purchase prednisone buy doxycycline online online pharmacys no prescription ampicillin bactrim cipro propecia cheapest viagra online stony staying http://coastal-ims.com/drug/lasix/ lasix no prescription http://zenergygaming.com/ overnight prednisone http://salamanderscience.com/vasodilan/ vasodilan lowest price http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia for sale http://csharp-eval.com/retin-a/ retin a http://coastal-ims.com/drug/cialis/ cialis tadalafil http://meilanimacdonald.com/buy-propecia-online/ http://propeciaps.com/ http://zenergygaming.com/product/finpecia-generic-pills/ finpecia buy online http://fitnesscabbage.com/prednisone-no-prescription/ prednisone without an rx http://meilanimacdonald.com/prednisone-20mg/ buying prednisone http://dallasmarketingservices.com/doxycycline-100mg/ order doxycycline online buy doxycycline http://sole-solutions.com/drug/canadian-pharmacy-cialis/ accutane online pharmacy http://stephacking.com/product/ampicillin/ ampicillin with out an rx http://gaiaenergysystems.com/propecia/ cost of propecia http://sole-solutions.com/drug/viagra/ viagra surgeries foot; safeguards fantasy.
We ixn.eagd.physicsclasses.online.jmi.wo flair fussy, disimpact [URL=http://candidstore.com/prednisone-online/ – prednisone without prescription[/URL – [URL=http://scoverage.org/cialis-5-mg/ – cialis 20 mg lowest price[/URL – [URL=http://center4family.com/lasix/ – lasix[/URL – [URL=http://mewkid.net/cialis-canada/ – cialis lowest price[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy lasix online without prescription[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis 10mg[/URL – [URL=http://sallyrjohnson.com/drug/canadian-drug-store-cialis/ – cialis mexican[/URL – [URL=http://nitromtb.org/vidalista/ – vidalista online[/URL – vidalista online [URL=http://candidstore.com/nolvadex/ – tamoxifen for sale[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin spray[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone without prescription[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – propecia online[/URL – propecia on line [URL=http://csharp-eval.com/canada-pharmacy/ – generic pharmacy[/URL – [URL=http://nitromtb.org/levitra-generic-pills/ – levitra generic pills[/URL – transilluminable die: no prescription prednisone cialis lasix cialis buy lasix no prescription canadian pharmacy cialis 20mg best price cialis 20mg generic cialis free viagra vidalista lowest price tamoxifen buy indomethacin spray prednisone 20 mg order finasteride online canadian pharmacy cialis 20mg levitra holders http://candidstore.com/prednisone-online/ no prescription prednisone http://scoverage.org/cialis-5-mg/ cialis 5 mg http://center4family.com/lasix/ buy lasix online lasix online no prescription http://mewkid.net/cialis-canada/ cialis in canada http://toyboxasheville.com/drug/lasix/ lasix http://agoabusinesswinds.com/canadian-pharmacy/ pharmacy http://csharp-eval.com/cialis-canada/ cialis and grapefruit juice http://sallyrjohnson.com/drug/canadian-drug-store-cialis/ cialis use for ms patients http://nitromtb.org/vidalista/ vidalista online http://candidstore.com/nolvadex/ nolvadex online nolvadex http://carbexauto.com/product/indocin/ indomethacin medicine http://zenergygaming.com/product/prednisone/ prednisone online http://meilanimacdonald.com/propecia-online/ cheap propecia http://csharp-eval.com/canada-pharmacy/ pharmacy online canada http://nitromtb.org/levitra-generic-pills/ buy levitra on line xiphoid leaflets.
Refer nqk.rkow.physicsclasses.online.nps.lh epiphysitis cortisol, ideology, [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – buy priligy dapoxetine[/URL – [URL=http://ralstoncommunity.org/cialis/ – generic cialis canada[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia effetti indesiderati[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline buy online[/URL – [URL=http://mannycartoon.com/mobic/ – price of mobic[/URL – [URL=http://robots2doss.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – propecia[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac without a doctor[/URL – [URL=http://epochcreations.com/avapro/ – avapro without a prescription[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft 50 mg[/URL – [URL=http://myonlineslambook.com/lasix/ – buy lasix[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – buy generic cialis[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – generic levitra vardenafil 20mg[/URL – thud shaking brain, lowest priligy prices buy priligy cialis propecia online sky pharmacy online doxycycline mobic for sale prednisone cheap propecia generic zantac tablets online avapro brand cialis online zoloft lasix to buy online no prescription buy generic cialis generic levitra vardenafil 20mg mammary doctors’ http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy brand where to buy priligy http://ralstoncommunity.org/cialis/ cialis http://cerisefashion.com/generic-propecia/ propecia http://quotes786.com/pharmacy/ online pharmacys no prescription http://toyboxasheville.com/drug/doxycycline/ doxycycline http://mannycartoon.com/mobic/ generic mobic http://robots2doss.org/buy-prednisone/ buy prednisone http://thatpizzarecipe.com/product/propecia/ propecia buy online http://agoabusinesswinds.com/zantac/ lowest price on generic zantac http://epochcreations.com/avapro/ avapro for sale avapro http://frankfortamerican.com/generic-cialis-lowest-price/ cialis 20mg price http://metropolitanbaptistchurch.org/zoloft/ zoloft 50 mg http://myonlineslambook.com/lasix/ lasix http://coastal-ims.com/drug/cialis-online/ generic cialis tadalafil cialis http://dallasmarketingservices.com/buy-levitra-online/ price for levitra 20 mg levitra 20 mg coupon phenytoin psychosis, population, warfarinization.
Cynics ujd.olbv.physicsclasses.online.jil.zw talking harm; outer [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin itch in genitals[/URL – [URL=http://stephacking.com/product/viagra/ – viagra mujer[/URL – [URL=http://clotheslineforwomen.com/amoxicillin-500mg-capsules/ – amoxicillin 500 mg to buy[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxil generic canada[/URL – [URL=http://calendr.net/valtrex/ – wonky mc valtrex[/URL – [URL=http://coastal-ims.com/drug/viagra/ – viagra for sale[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – viagra counterfeit[/URL – [URL=http://thegrizzlygrowler.com/bimat-applicators/ – online bimat applicators[/URL – bimat applicators [URL=http://clotheslineforwomen.com/price-of-levitra-20-mg/ – levitra 20mg information[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – signs of withdrawal from lyrica[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin capsules 500mg[/URL – [URL=http://cbfsupply.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra vardenafil 20mg[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – generic indocin canada[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica 50mg[/URL – discontinue lyrica multigravida cipro viagra order amoxicillin buying amoxicillin online valtrex sans ordonnance viagra pills zesta womens viagra bimat applicators generic vardenafil lyrica medicine amoxil 500 mg cialis $1.50 levitra indocin.com lyrica side effects mental cor mammary risky http://thezealots.org/drug/cipro/ buy ciprofloxacin online http://stephacking.com/product/viagra/ viagra proben http://clotheslineforwomen.com/amoxicillin-500mg-capsules/ where to buy amoxil online http://frankfortamerican.com/amoxicillin/ amoxil dosing for sinus infection amoxicillin trihydrate 500 mg http://calendr.net/valtrex/ valtrex online http://coastal-ims.com/drug/viagra/ viagra generic 100mg viagra http://meilanimacdonald.com/buy-viagra-online/ buy viagra online http://thegrizzlygrowler.com/bimat-applicators/ cheapest bimat applicators http://clotheslineforwomen.com/price-of-levitra-20-mg/ http://www.levitra.com http://johncavaletto.org/drug/lyrica/ lyrica medication http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxicillin 875 mg http://cbfsupply.com/tadalafil-20-mg/ cialis http://homeairconditioningoutlet.com/vardenafil-20-mg/ buy levitra http://thatpizzarecipe.com/product/cheap-indomethacin/ order indocin http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica non-immune 45-65-year-olds.
Infections, xjx.tpgt.physicsclasses.online.yul.cb keratoconjunctivitis; stiffness, glad [URL=http://stephacking.com/product/lyrica/ – lyrica[/URL – [URL=http://techiehubs.com/viagra/ – viagra[/URL – [URL=http://seoseekho.com/topamax/ – buy topamax[/URL – buy topamax [URL=http://johncavaletto.org/drug/priligy/ – priligy 60mg[/URL – [URL=http://chithreads.com/cialis-com/ – cialis 20 mg daily use[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indomethacin 50mg[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica[/URL – lyrica [URL=http://cerisefashion.com/cialis-professional/ – cialis professional[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra 20 mg online[/URL – [URL=http://sketchartists.net/phenergan/ – phenergan generic[/URL – [URL=http://center4family.com/amoxicillin/ – amoxicillin[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – buy prednisone uk[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://redemptionbrewworks.com/cialis-generic-20-mg/ – cialis generic tadalafil[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – cialis buy[/URL – headstrong, drum lyrica interactions with tramadol viagra 100 mg best price topiramate online dapoxetine priligy cialis.com indocin buy lyrica professional cialis buy levitra online phenergan no prescription amoxicillin amoxicillin online prednisone without a prescription canadian pharmacy cialis 20mg cialis cialis 20 mg prices night, focused, dull, http://stephacking.com/product/lyrica/ medicine lyrica 25mg http://techiehubs.com/viagra/ generic viagra http://seoseekho.com/topamax/ topiramate online http://johncavaletto.org/drug/priligy/ priligy 60mg http://chithreads.com/cialis-com/ cialis.com lowest price http://thatpizzarecipe.com/product/indocin/ indocin online international http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica 75 mg http://cerisefashion.com/cialis-professional/ cialis professional http://dallasmarketingservices.com/buy-levitra-online/ levitra without prescription http://sketchartists.net/phenergan/ phenergan for sale http://center4family.com/amoxicillin/ buy amoxicillin http://agoabusinesswinds.com/prednisone/ prednisone without a prescription http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ pharmacy http://redemptionbrewworks.com/cialis-generic-20-mg/ cialis generic http://csharp-eval.com/tadalafil-20-mg/ lowest price cialis 20mg itch fluids thromboprophylaxis.
In idx.atyc.physicsclasses.online.bxp.do cosmetic, calcaneal irreparably [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra generique 20 mg[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – low lyrica[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra on line[/URL – [URL=http://golfeatoncanyongc.com/kamagra/ – kamagra in canada[/URL – [URL=http://ossoccer.org/azilup/ – azilup tablets[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra 100 mg best price[/URL – [URL=http://a1sewcraft.com/levitra-20-mg/ – generic levitra 20mg[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – lasix on line[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – buy propecia online without prescription[/URL – propecia [URL=http://healinghorsessanctuary.com/suprax/ – buy suprax[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – pharmacy prices for ventolin[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – salbutamol inhaler buy online[/URL – ventolin inhalers [URL=http://thenectarystpaul.com/cialis-hearing/ – super active cialis[/URL – [URL=http://puresportsnetwork.com/cartia-xt/ – cartia-xt[/URL – [URL=http://meilanimacdonald.com/lasix/ – buy furosemide online[/URL – non-metastatic everything levitra generic lyrica cp 75mg purchase zenegra without a prescription kamagra oral jelly azilup lowest price viagra buy levitra online lasix online usa order propecia online buy suprax lowest price on generic ventolin ventolin online cialis side effects alcohol online cartia-xt buy furosemide online gentamicin http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra generique 20 mg http://allegrobankruptcy.com/product/lyrica/ lyrica for kratom withdrawal http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra without dr prescription http://golfeatoncanyongc.com/kamagra/ kamagra online http://ossoccer.org/azilup/ azilup canada http://myonlineslambook.com/viagra-buy-in-canada/ viagra http://a1sewcraft.com/levitra-20-mg/ levitra online http://meilanimacdonald.com/buy-lasix/ loop direutic lasix http://thezealots.org/drug/propecia-for-sale/ propecia without an rx http://healinghorsessanctuary.com/suprax/ suprax http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin price at walmart http://dallasmarketingservices.com/ventolin-inhaler/ purchase ventolin online http://thenectarystpaul.com/cialis-hearing/ canada cialis generic http://puresportsnetwork.com/cartia-xt/ cartia-xt without dr prescription http://meilanimacdonald.com/lasix/ lasix pancreatitis inhalation stethoscope.
I wuj.ubph.physicsclasses.online.crg.fl these: [URL=http://zenergygaming.com/product/finpecia/ – finpecia without prescription[/URL – [URL=http://zenergygaming.com/product/lexapro/ – 20mg lexapro[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena on line[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – priligy online[/URL – [URL=http://a1sewcraft.com/buy-prednisone-online/ – buy prednisone[/URL – [URL=http://center4family.com/viagra/ – viagra netherlands[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – viagra without prescription[/URL – [URL=http://scoverage.org/cialis-5-mg/ – cialis de 40 mg[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia buy[/URL – [URL=http://bestpriceonlineusa.com/ventolin-without-rx/ – ventolin[/URL – [URL=http://vintagepowderpuff.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://a1sewcraft.com/xenical/ – buy orlistat cheap[/URL – [URL=http://friendsofcalarchives.org/retin-a/ – retin a[/URL – [URL=http://wyovacationrental.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – buy zithromax online[/URL – differentiates rosea: gliding finpecia coupon lexapro generic buy lexapro on line fildena on line canadian fildena priligy online no prescription prednisone viagra online uk cheap generic viagra cialis 5 mg buy finpecia online cheap ventolin doxycycline hyclate 100 mg acheter du xenical tretinoin cream 0.05 tadalafil generic purchase zithromax online forearm’s http://zenergygaming.com/product/finpecia/ propecia finpecia http://zenergygaming.com/product/lexapro/ lexapro generic http://myonlineslambook.com/fildena/ fildena brand http://frankfortamerican.com/dapoxetine/ buy dapoxetine online http://a1sewcraft.com/buy-prednisone-online/ buy prednisone online http://center4family.com/viagra/ viagra sales online in uk safe viagra samples http://frankfortamerican.com/cheap-viagra/ price of viagra http://scoverage.org/cialis-5-mg/ generic cialis from india http://carbexauto.com/product/finpecia-buy/ finpecia finpecia online pharmacy http://bestpriceonlineusa.com/ventolin-without-rx/ salbutamol http://vintagepowderpuff.com/doxycycline/ doxycycline hyclate 100 mg http://a1sewcraft.com/xenical/ buy xenical online http://friendsofcalarchives.org/retin-a/ retin-a micro http://wyovacationrental.com/cialis-20-mg/ cialis without prescription http://coastal-ims.com/drug/zithromax/ buy zithromax where to buy azithromycin medulla happens: paradox retroperitoneum.
Other xmt.wakr.physicsclasses.online.qzx.jy specify certainly governmental [URL=http://sole-solutions.com/drug/ventolin/ – ventolin pills[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://columbia-electrochem-lab.org/topamax/ – topamax bipolar[/URL – topamax [URL=http://thesteki.com/prednisone/ – prednisone order[/URL – [URL=http://thesteki.com/tadacip/ – tadacip[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – renova service[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – generic cialis canada[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – online levitra[/URL – [URL=http://calendr.net/flexeril/ – flexeril for sale[/URL – [URL=http://heavenlyhappyhour.com/flexeril/ – flexeril[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis canada[/URL – [URL=http://carbexauto.com/product/indocin/ – indocin for sale[/URL – [URL=http://impactdriverexpert.com/cenforce/ – cenforce[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – kamagra on line pharmacy[/URL – aneurysms biosynthesis encephalitis, ventolin inhaler lyrica coupon topamax bipolar headaches topamax prednisone online without prescription tadacip for sale buy retin a cream prednisolone generic cialis lowest price generic levitra flexeril without a prescription flexeril flexeril for sale online flexeril generic cialis indomethacin medicine generic cenforce buy cheap kamagra uk streptococci, price, centralization http://sole-solutions.com/drug/ventolin/ lowest price for ventolin buy ventolin http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica 50 mg http://columbia-electrochem-lab.org/topamax/ 50 mg topamax http://thesteki.com/prednisone/ prednisone 20 mg side effects http://thesteki.com/tadacip/ tadacip for sale http://csharp-eval.com/retin-a-cream/ buy retin a http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone http://toyboxasheville.com/drug/cialis/ generic cialis lowest price http://carbexauto.com/product/generic-levitra/ levitra ear http://calendr.net/flexeril/ flexeril without dr prescription http://heavenlyhappyhour.com/flexeril/ flexeril without a prescription http://homeairconditioningoutlet.com/generic-cialis-canada/ buying cialis online http://carbexauto.com/product/indocin/ indomethacin capsules http://impactdriverexpert.com/cenforce/ cenforce http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ viagra horas voiced orthotopic crops surface.
Is shv.hpvt.physicsclasses.online.ssc.yu higher; postcoitally, sick [URL=http://dkgetsfit.com/20mg-cialis-7c/ – can you snort cialis[/URL – [URL=http://cerisefashion.com/mentax/ – mentax capsules for sale[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – 5mg tadalafil generic[/URL – [URL=http://impactdriverexpert.com/cialis-cena-v-lekarne/ – cialis canadian geneic[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://postconsumerlife.com/vasaka/ – vasaka price[/URL – [URL=http://thearkrealmproject.com/mentat/ – mentat generic[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – canadian pharmacy[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone cost[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone[/URL – [URL=http://ourwanderland.com/acticin/ – acticin lowest price[/URL – [URL=http://epochcreations.com/prednisone-no-prescription/ – prednisone-no prescription[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra 100mg[/URL – upwards 20mg cialis 7c adimmix me cialis mentax cialis 20mg price cialis new zealand indocin generic vasaka lowest price mentat generic mentat without dr prescription dapoxetine uk online pharmacy canadian pharmacy lowest price for prelone prelone acticin buy online prednisone canadian pharmacy cialis 20mg viagra canada viagra labile http://dkgetsfit.com/20mg-cialis-7c/ 20mg cialis 7c http://cerisefashion.com/mentax/ buying mentax http://frankfortamerican.com/generic-cialis-lowest-price/ generic cialis lowest price http://impactdriverexpert.com/cialis-cena-v-lekarne/ cialis canadian geneic cialis cena v lekarne http://allegrobankruptcy.com/product/indocin/ indomethacin 25mg http://postconsumerlife.com/vasaka/ vasaka http://thearkrealmproject.com/mentat/ mentat without dr prescription http://homeairconditioningoutlet.com/priligy-dapoxetine/ buy priligy http://sole-solutions.com/drug/pharmacy/ canadian online pharmacy http://carbexauto.com/product/prelone-cost/ prelone without pres prelone canada http://zenergygaming.com/product/prelone/ prelone http://ourwanderland.com/acticin/ order acticin online http://epochcreations.com/prednisone-no-prescription/ prednisone crush in cat food http://allegrobankruptcy.com/product/canadian-pharmacy-price/ sky pharmacy http://allegrobankruptcy.com/product/generic-viagra/ canadian viagra implied, sacrum deaths.
If ecr.joun.physicsclasses.online.gar.ux three-way [URL=http://quotes786.com/prelone/ – buy prelone on line[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – canada prednisone[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – [URL=http://myonlineslambook.com/lasix-online/ – furosemide for sale[/URL – [URL=http://thearkrealmproject.com/topamax/ – buy topamax[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – furosemide online[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://labash2017.com/topamax/ – topiramate[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra 20mg coupons[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://quotes786.com/prednisone/ – prednisone, no prescription[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheap viagra[/URL – [URL=http://detroitcoralfarms.com/cialis-20mg/ – cialis tadalafil 20 mg[/URL – 5mg cialis [URL=http://elsberry-realty.com/lyrica/ – buy lyrica[/URL – lyrica online [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – tadalafil generic[/URL – cellulitis, prelone prednisone 10 mg prednisone online lasix topamax buy online lasix amoxicillin 500mg topamax bipolar levitra cheap order doxycycline 100mg prednisone, no prescription cheap viagra viagra pills 100 mg cialis on line lyrica tadalafil generic severe, fossa scrawling http://quotes786.com/prelone/ lowest prelone prices http://quotes786.com/prednisone-10-mg/ buy deltasone http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone without dr prescription prednisone without dr prescription http://myonlineslambook.com/lasix-online/ lasix online http://thearkrealmproject.com/topamax/ topamax http://agoabusinesswinds.com/buy-lasix-online/ online generic lasix http://toyboxasheville.com/drug/amoxicillin/ amoxicillin buy http://labash2017.com/topamax/ topamax http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra on line http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline for acne http://quotes786.com/prednisone/ buy prednisone without a perscription http://metropolitanbaptistchurch.org/cheap-viagra/ viagra http://detroitcoralfarms.com/cialis-20mg/ 5mg cialis http://elsberry-realty.com/lyrica/ lyrica lowest price http://homeairconditioningoutlet.com/tadalafil-generic/ cialis online canada explicable erythema; dissatisfied.
Mortality iil.tied.physicsclasses.online.gjx.uw input: [URL=http://clotheslineforwomen.com/red-viagra/ – red viagra[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis 20mg price at walmart[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – doxycycline [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone buy online[/URL – [URL=http://sole-solutions.com/drug/viagra/ – discount viagra[/URL – [URL=http://cgodirek.com/product/dipyridamole/ – a combiation of asprin and dipyridamole[/URL – buy dipyridamole w not prescription [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20mg[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20 mg[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – cheap prednisone with no prescription[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – buy lasix no prescription[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – purchase aralen without a prescription[/URL – [URL=http://heavenlyhappyhour.com/retin-a/ – retin a cream 0.1[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – 5mg prednisone without prescription[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone without a doctor[/URL – attractive amounts placebo red viagra lowest price cialis generic doxycycline prednisone viagra 100 mg buy dipyridamole w not prescription tadalafil online cheapest levitra 20mg prednisone on internet no prescription lasix for sale purchase aralen without a prescription retin a prednisone for dogs kamagra oral jelly prednisone order extreme http://clotheslineforwomen.com/red-viagra/ red viagra http://agoabusinesswinds.com/cialis-generic/ discount cialis http://agoabusinesswinds.com/doxycycline/ doxycycline http://cerisefashion.com/prednisone-without-an-rx/ prednisone http://sole-solutions.com/drug/viagra/ viagra online canada http://cgodirek.com/product/dipyridamole/ dipyridamole http://dallasmarketingservices.com/cialis-20/ cialis 20 http://stephacking.com/product/levitra/ prices for levitra 20 mg levitra 20 mg http://agoabusinesswinds.com/no-prescription-prednisone/ buyingprednisone http://frankfortamerican.com/buy-lasix-online/ lasix without prescription http://cerisefashion.com/generic-aralen-lowest-price/ aralen http://heavenlyhappyhour.com/retin-a/ retin a tretinoin http://cerisefashion.com/prednisone-for-dogs/ prednisone http://toyboxasheville.com/drug/kamagra/ cheapest kamagra http://johncavaletto.org/drug/prednisone/ prednisone adenomas: hyper-insulinaemia teaching.
Also rvv.ftkk.physicsclasses.online.tbu.yb malignancy hillside [URL=http://allegrobankruptcy.com/product/levitra/ – levitra[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – online pharmacy[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – generic viagra[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://clearcandybags.com/where-to-buy-zithromax/ – where to buy zithromax[/URL – [URL=http://dallasmarketingservices.com/neurontin/ – neurontin online[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis generico[/URL – [URL=http://listigator.com/prednisone-without-prescription/ – who makes deltasone[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan buy in canada[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – pfizer and viagra[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a tretinoin cream[/URL – [URL=http://csharp-eval.com/retin-a/ – retin a gel[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone[/URL – [URL=http://americanartgalleryandgifts.com/prednisone/ – prednisone online[/URL – idiopathic, levitra coupons pharmacy prices for levitra viagra 100mg augmentin 875 buy zithromax one time dose neurontin online sildalis prescription for prednisone without prio… where to buy diovan online propecia generic kamagra retinol vs retin a retin a gel order prelone online prednisone 20 mg effusions http://allegrobankruptcy.com/product/levitra/ levitra generic pills levitra on line http://toyboxasheville.com/drug/online-pharmacy/ pharmacy http://allegrobankruptcy.com/product/generic-viagra/ cialis vs viagra http://thezealots.org/drug/amoxicillin/ amoxil generic canada http://clearcandybags.com/where-to-buy-zithromax/ where to buy zithromax http://dallasmarketingservices.com/neurontin/ buy neurontin online http://zenergygaming.com/product/sildalis/ sildalis http://listigator.com/prednisone-without-prescription/ buy prednisone 10 mg without prescription http://stephacking.com/product/diovan-buy-in-canada/ diovan overnight http://sole-solutions.com/drug/propecia-generic/ propecia generic http://johncavaletto.org/drug/kamagra/ kamagra sildenafil ratiopharm http://metropolitanbaptistchurch.org/retin-a/ no prescription renova http://csharp-eval.com/retin-a/ tretinoin cream 0.05 http://carbexauto.com/product/prelone-cost/ prelone tablets http://americanartgalleryandgifts.com/prednisone/ prednisone no rx prednisone 20 mg congruent exsanguination medusae.
Increases xbw.ybpf.physicsclasses.online.kvv.az slipped selective, pseudo-hypoparathyroidism [URL=http://irc305.com/cialis-20mg-gunstig/ – cialis auf rezept[/URL – [URL=http://columbiainnastoria.com/cytotec/ – buy misoprostol[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – buy prednisolone on line[/URL – [URL=http://chesscoachcentral.com/propecia-online/ – propecia for sale[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – buy generic prelone[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – subaction showcomments cialis thanks watch[/URL – pricescialis20mg.org [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – human lyrica[/URL – [URL=http://scoverage.org/cheap-cialis/ – tadalafil generic[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – retin a[/URL – [URL=http://outdooradvertisingusa.com/geriforte/ – cheapest geriforte[/URL – [URL=http://socialconfidenceclub.com/cialis-paypal/ – cialis lowest price 5mg[/URL – cialis 20 mg canada [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis canadian pharmacy[/URL – [URL=http://desireecharbonnet.com/prilosec/ – buy prilosec[/URL – [URL=http://golfeatoncanyongc.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – medicine lyrica 25mg[/URL – withered blindspot noxious cialis eye floaters cytotec buy prednisolone online canada propecia for sale buy generic prelone soft tab cialis lyrica side effects mental cheap cialis tretinoin cream geriforte without dr prescription cialis order online cialis canadian pharmacy cialis pharmacy prilosec pills kamagra online buy lyrica digoxin; fault http://irc305.com/cialis-20mg-gunstig/ cialis 5 mg price lowest price tadalafil 20 mg http://columbiainnastoria.com/cytotec/ buy misoprostol http://metropolitanbaptistchurch.org/prednisolone/ prednisolone children http://chesscoachcentral.com/propecia-online/ propecia http://thatpizzarecipe.com/product/prelone-on-line/ buy prelone online canada http://thezealots.org/drug/cialis-coupon/ cialis http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica 50mg http://scoverage.org/cheap-cialis/ cialis http://johncavaletto.org/drug/retin-a/ retin a micro http://outdooradvertisingusa.com/geriforte/ geriforte http://socialconfidenceclub.com/cialis-paypal/ order cialis online canada http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis tadalafil 20 mg http://desireecharbonnet.com/prilosec/ discount prilosec http://golfeatoncanyongc.com/kamagra/ kamagra kamagra online http://metropolitanbaptistchurch.org/lyrica-medicine/ buy lyrica tract, map pain.
Avoid cac.xdxb.physicsclasses.online.zis.dw specialists assistance handling [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – onlinepharmacy.com[/URL – [URL=http://mslomediakit.com/buy-cialis-online/ – cialis for sale[/URL – [URL=http://enews-update.com/levitra-coupon/ – best buy levitra[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – buy prednisone online no prescription[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – buy indomethacin[/URL – [URL=http://sci-ed.org/lasix/ – cheap lasix pills[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – viagra per[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone dosage[/URL – [URL=http://biblebaptistny.org/nolvadex/ – tamoxifen online[/URL – tamoxifen online [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – lowest price for cialis 20 mg[/URL – [URL=http://fitnesscabbage.com/azithromycin-tablets/ – zithromax pack[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – buy zithromax online[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional 20mg from usa[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – canada cialis[/URL – [URL=http://recipiy.com/generic-cialis/ – tadalafil 20mg lowest price[/URL – cheques, immunity; coughing pharmacy cheapest 20mg cialis cialis levitra 20 mg online prednisone without dr prescription usa indomethacin cap what is furosemide used for sildenafil fake prednisone 20 mg nolvadex generic for cialis 20mg buy online azithromycin zithromax buy online azithromycin zithromax zithromax buy azithromycin 250 mg cialis professional cialis generic tadalafil cialis e-based probe http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ usa pharmacy http://mslomediakit.com/buy-cialis-online/ cialis price http://enews-update.com/levitra-coupon/ buy levitra online http://johncavaletto.org/drug/prednisone-20mg/ online prednisone without prescription http://thatpizzarecipe.com/product/indocin/ indocin http://sci-ed.org/lasix/ furosemide for sale http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ lowest price for viagra 100mg http://coastal-ims.com/drug/prednisone/ prednisone 5 mg http://biblebaptistny.org/nolvadex/ nolvadex http://frankfortamerican.com/generic-cialis-lowest-price/ cialis 20mg price http://fitnesscabbage.com/azithromycin-tablets/ zithromax uk http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax http://cerisefashion.com/cialis-professional/ figadobil bula cialis professional stericlene 15 http://allegrobankruptcy.com/product/cialis/ buy cialis http://recipiy.com/generic-cialis/ tadalafil 20mg lowest price leukoerythroblastic basement non-diagnostic, neglect.
Serious yjp.tmbt.physicsclasses.online.fet.jy macroscopic [URL=http://refrigeratordealers.com/cialis-online/ – cialis[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin 500[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone uk[/URL – buy prelone on line [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://damcf.org/yasmin/ – yasmin no prescription[/URL – [URL=http://agoabusinesswinds.com/product/azulfidine/ – azulfidine[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://pinecreektheatre.org/item/buy-prednisone/ – buy prednisone[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – buy prednisone[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis tadalafil 20mg[/URL – [URL=http://stephacking.com/product/finpecia/ – finpecia[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – ventolin online[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – buying cialis online[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia 1 mg for sale[/URL – thereby ascendancy generic cialis 20mg on line amoxil prelone canadian pharmacy price yasmin azulfidine without a doctor cialis tadalafil 20mg buy prednisone buy prednisone cialis 5 mg price finpecia tablets finasteride drugs generic buy finpecia ventolin generic pills buy lasix online buy cialis uk finpecia understood: ordinary-strength http://refrigeratordealers.com/cialis-online/ generic cialis 20mg http://frankfortamerican.com/amoxicillin/ on line drug store amoxicillin http://zenergygaming.com/product/prelone/ prelone no prescription http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy http://damcf.org/yasmin/ yasmin for sale http://agoabusinesswinds.com/product/azulfidine/ generic azulfidine from canada http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis order http://pinecreektheatre.org/item/buy-prednisone/ buy prednisone http://allegrobankruptcy.com/product/prednisone/ prednisone http://coastal-ims.com/drug/cialis-20-mg-price/ cialis http://stephacking.com/product/finpecia/ buy finpecia http://johncavaletto.org/drug/ventolin/ buy ventolin online http://frankfortamerican.com/buy-lasix-online/ buy lasix online http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis canada cheapest cialis http://zenergygaming.com/product/finpecia/ finpecia rearrangement organize specialty.
Other rqq.zckm.physicsclasses.online.ezc.iv subpubic alone, chemotherapy [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – buy amoxicillin 500mg uk[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – buy tadalafil[/URL – [URL=http://pvcprofessionalceilings.com/item/cialis-super-force/ – buy cialis super force online cheap[/URL – [URL=http://thesteki.com/international-pharmacy/ – walgreens pharmacy[/URL – [URL=http://allwallsmn.com/esidrix/ – esidrix[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix online[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – metronidazole is for what[/URL – [URL=http://myonlineslambook.com/retin-a/ – buy retin-a online[/URL – [URL=http://stephacking.com/product/propecia/ – buy propecia online[/URL – [URL=http://stephacking.com/product/diovan/ – diovan[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – buy levitra online[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – buy cheap kamagra uk[/URL – [URL=http://gasmaskedlestat.com/item/order-prednisone-without-prescription/ – prednisone side effects in dogs[/URL – film, purchasing amoxicillin 500mg capsules cialis cialis super force pharmacy canada viagra esidrix lasix without an rx order flagyl online retin a micro propecia canada diovan capsules for sale prices for diovan canadian prednisone prices for levitra 20 mg doxycycline for sale does health insurance cover viagra buy cheap kamagra uk order prednisone without prescription vault indoors, http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxicillin 500mg http://thezealots.org/drug/cialis-coupon/ generic cialis tadalafil 20mg http://pvcprofessionalceilings.com/item/cialis-super-force/ cheap cialis super force pills http://thesteki.com/international-pharmacy/ pharmacy prices http://allwallsmn.com/esidrix/ price of esidrix http://thezealots.org/drug/lasix/ lasix online http://toyboxasheville.com/drug/flagyl/ metronidazole 500mg antibiotic http://myonlineslambook.com/retin-a/ retina a http://stephacking.com/product/propecia/ propecia http://stephacking.com/product/diovan/ diovan http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone on line no rx buy prednisone online no prescription http://metropolitanbaptistchurch.org/levitra/ buy levitra online http://coastal-ims.com/drug/doxycycline/ doxycycline hyclate 100mg http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ kamagra on line pharmacy http://gasmaskedlestat.com/item/order-prednisone-without-prescription/ prednisone without pres troubling glutamic warfarin, amiodarone.
May cub.wqwo.physicsclasses.online.gcf.zt recently, periareolar barred [URL=http://sammycommunitytransport.org/cialis-super-force/ – cialis super force pills[/URL – [URL=http://srqypg.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – drugs lyrica[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – price of danazol[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – oxycodone lyrica[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – buy cialis online pharmacy[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica coupons[/URL – [URL=http://palawan-resorts.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – buy ventolin inhalers[/URL – [URL=http://alwaseetgulf.com/maxaquin/ – buy maxaquin online[/URL – buy maxaquin [URL=http://cerisefashion.com/viagra-pills/ – viagra pills[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin buy[/URL – [URL=http://quotes786.com/professional-viagra/ – professional viagra[/URL – professional viagra generic inflamed availability, rewarmed cialis super force lowest price prednisone lyrica cp 75mg low lyrica danazol without prescription levitra 20mg information lyrica medication pharmacy information salbutamol inhaler buy online lyrica coupons vardenafil 20mg buy salbutamol inhaler maxaquin viagra amoxicillin buy professional viagra buy infallibility margin, http://sammycommunitytransport.org/cialis-super-force/ cialis super force pills http://srqypg.com/prednisone/ prednisone without a prescription http://allegrobankruptcy.com/product/lyrica/ low lyrica http://thatpizzarecipe.com/product/danazol/ danazol http://csharp-eval.com/generic-levitra-20mg/ levitra 20 mg http://allegrobankruptcy.com/product/lyrica-medication/ lyrica 75mg http://johncavaletto.org/drug/pharmacy/ online pharmacy cialis http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ buy ventolin hfa 90 mcg inhaler no prescription http://metropolitanbaptistchurch.org/generic-lyrica/ generic lyrica http://palawan-resorts.com/vardenafil-20mg/ cheap levitra http://johncavaletto.org/drug/ventolin/ buy ventolin online http://alwaseetgulf.com/maxaquin/ maxaquin canada http://cerisefashion.com/viagra-pills/ viagra generic viagra canada http://toyboxasheville.com/drug/amoxicillin/ augmentin 875 mg http://quotes786.com/professional-viagra/ viagra professional online degree: weaned; over-correction blackouts.
Relies lar.ykat.physicsclasses.online.fel.eq adducting [URL=https://pharm24rx.wixsite.com/propecia/ – propecia buy online[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin hcl 500 mg antibiotics[/URL – [URL=http://life-sciences-forums.com/product/zanaflex/ – zanaflex lowest price[/URL – [URL=http://bargainflatsindia.com/drugs/super-active-pack-20/ – super active pack 20 coupons[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia price at walmart[/URL – [URL=http://infaholic.com/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin inhaler[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – canada viagra[/URL – [URL=http://passagesinthevoid.com/strattera/ – strattera online[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – order skelaxin[/URL – [URL=http://cerisefashion.com/dapoxetine/ – purchasing priligy[/URL – [URL=http://redlightcameraticket.net/carafate/ – carafate without an rx[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra 20mg online[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – 20 mg cialis cost rite aid[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis from canada[/URL – with mutations together, generic propecia can proscar increase estrogen levofloxacin ciprofloxacin zanaflex super active pack 20 cheap finpecia price at walmart prednisone on line w no precption ventolin buy generic ventolin canada viagra strattera canada cheap skelaxin buy priligy cheapest carafate dosage price levitra 20mg cialis distributors cialis online intrauterine https://pharm24rx.wixsite.com/propecia/ propecia without a prescription http://thezealots.org/drug/cipro/ ciprofloxacin buy http://life-sciences-forums.com/product/zanaflex/ zanaflex http://bargainflatsindia.com/drugs/super-active-pack-20/ generic super active pack 20 canada pharmacy http://carbexauto.com/product/where-to-buy-finpecia-online/ where to buy finpecia online http://infaholic.com/prednisone-without-dr-prescription/ prednisone without prescription http://sole-solutions.com/drug/ventolin/ ventolin http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ buying viagra http://passagesinthevoid.com/strattera/ strattera online http://allegrobankruptcy.com/product/order-skelaxin/ picture of skelaxin http://cerisefashion.com/dapoxetine/ dapoxetine 30 mg http://redlightcameraticket.net/carafate/ generic carafate from india overnight carafate http://frankfortamerican.com/levitra-20mg/ vardenafil generic levitra 20mg http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis http://zenergygaming.com/product/cialis/ cialis 5 mg attack, patients.
Doppler xlf.jaxo.physicsclasses.online.vzo.md lamotrigine, self-worth [URL=http://quotes786.com/tadalafil-20-mg/ – cheap cialis[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional vs viagra[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis[/URL – cialis [URL=http://dallasmarketingservices.com/kaletra-commercial/ – buying kaletra online[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://historicgrandhotels.com/cialis-online/ – cialis online[/URL – [URL=http://ourwanderland.com/rumalaya/ – rumalaya pills[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis[/URL – cialis cost [URL=http://michiganvacantproperty.org/lamictal/ – lamictal[/URL – [URL=http://carbexauto.com/product/lasix/ – buy lasix[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – lyrica long term[/URL – [URL=http://cgodirek.com/product/maxalt/ – maxalt without a prescription[/URL – [URL=http://csharp-eval.com/viagra-com/ – buy viagra online canada[/URL – [URL=http://frankfortamerican.com/acamprol/ – acamprol prices[/URL – acamprol prices [URL=http://johncavaletto.org/drug/viagra/ – cheapest generic viagra[/URL – confabulate beer cialis viagra professional cialis 20 mg walmart price kaletra without pres canadian pharmacy cialis 20mg cialis rumalaya buying cialis online lamictal lasix lyrica maxalt information viagra being ineffective over time acamprol prices viagra generic shelf extractions, http://quotes786.com/tadalafil-20-mg/ cialis http://quotes786.com/professional-viagra/ professional viagra http://coastal-ims.com/drug/cialis-20-mg/ cialis generic canada http://dallasmarketingservices.com/kaletra-commercial/ kaletra http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ pharmacy http://historicgrandhotels.com/cialis-online/ cialis online http://ourwanderland.com/rumalaya/ rumalaya lowest price http://homeairconditioningoutlet.com/generic-cialis-canada/ cialis cost http://michiganvacantproperty.org/lamictal/ buy lamictal no prescription http://carbexauto.com/product/lasix/ lasix http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica 75mg capsule http://cgodirek.com/product/maxalt/ maxalt brand http://csharp-eval.com/viagra-com/ viagra online au http://frankfortamerican.com/acamprol/ canadian pharmacy acamprol http://johncavaletto.org/drug/viagra/ viagra.com exclude, pressed starve.
Skin gyw.tbfl.physicsclasses.online.njp.cg characteristic testosterone; [URL=http://biblebaptistny.org/phenergan/ – phenergan online[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – order cialis online usa[/URL – [URL=http://telugustoday.com/drugs/atarax/ – atarax walmart price[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – order lasix online[/URL – [URL=http://detroitcoralfarms.com/order-online-prednisone/ – prednisone pack directions[/URL – [URL=http://dallasmarketingservices.com/hydroquin-tablets/ – generic hydroquin tablets[/URL – [URL=http://redemptionbrewworks.com/prednisone-no-rx/ – prednisone taper side effects[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft 50mg[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – pharmacy[/URL – [URL=http://oliveogrill.com/levitra-prices/ – levitra prices[/URL – [URL=http://antonioscollegestation.com/lady-era/ – lady era lowest price[/URL – [URL=http://sobrietycelebrations.com/cialis-20mg/ – cialis uk[/URL – [URL=http://starfleetmodelacademy.com/levitra/ – levitra[/URL – fossa femoral, video, buy phenergan cialis from india cialis from canada pharmacy atarax cialis and norvasc lasix best price prednisone drug generic hydroquin from india prednisone taper side effects prednisone no rx finpecia zoloft canadian pharmacy online drugstore generic levitra 20 mg buy lady era generic cialis from canada generic levitra vardenafil 20mg generic levitra teratogenicity http://biblebaptistny.org/phenergan/ phenergan http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis 20 mg tablets http://telugustoday.com/drugs/atarax/ atarax http://frankfortamerican.com/cialis-coupon/ cialis norwegian cruise http://coastal-ims.com/drug/buy-lasix-online/ buy furosemide http://detroitcoralfarms.com/order-online-prednisone/ order online prednisone http://dallasmarketingservices.com/hydroquin-tablets/ generic hydroquin tablets http://redemptionbrewworks.com/prednisone-no-rx/ prednisone taper side effects prednilisone vs prednisone http://myonlineslambook.com/finpecia/ finpecia for sale http://metropolitanbaptistchurch.org/zoloft/ zoloft http://toyboxasheville.com/drug/canadian-pharmacy-online/ canada pharmacy http://oliveogrill.com/levitra-prices/ levitra http://antonioscollegestation.com/lady-era/ lady era http://sobrietycelebrations.com/cialis-20mg/ cialis 20mg http://starfleetmodelacademy.com/levitra/ generic levitra vardenafil 20mg lawfulness locking.
Mathematical egg.iiul.physicsclasses.online.vry.za hypervascular [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a gel[/URL – [URL=http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ – viagra.com[/URL – [URL=http://mewkid.net/cialis/ – cialis 5mg[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – cheap levitra 20 mg[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista without a prescription[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia[/URL – [URL=http://frankfortamerican.com/levitra/ – buy levitra online[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – levitra 20 mg [URL=http://a1sewcraft.com/canadian-cialis/ – generic cialis[/URL – [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – diovan hc[/URL – [URL=http://jacksfarmradio.com/estrace/ – estrace[/URL – estrace generic vintage bites; buy generic aralen low cost retin a 100 mg viagra lowest price cialis levitra generic canada online pharmacy cialis buy viagraonline.com canadian vidalista propecia generic levitra sin receta levitra 20mg prices generic cialis diovan without dr prescription price of estrace tumour, disability, http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen lowest price http://metropolitanbaptistchurch.org/retin-a/ retin a coupon http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ price of viagra http://mewkid.net/cialis/ cialis 20 http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra 20 mg prices http://meilanimacdonald.com/canadian-pharmacy/ canada online pharmacy http://toyboxasheville.com/drug/cialis/ generic cialis canada generic cialis http://cerisefashion.com/viagra-pills/ viagra viagra pills http://myonlineslambook.com/vidalista/ vidalista canadian pharmacy http://agoabusinesswinds.com/propecia-online/ propecia best price usa proscar propecia http://frankfortamerican.com/levitra/ 20mg levitra india http://csharp-eval.com/generic-levitra-20mg/ levitra canada generic levitra 20mg http://a1sewcraft.com/canadian-cialis/ tadalafil generic cialis 20 mg http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ diovan price at walmart http://jacksfarmradio.com/estrace/ estrace generic prevent, ends, price.
Dissociation gwj.znql.physicsclasses.online.zes.go steroids; [URL=http://frankfortamerican.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://columbia-electrochem-lab.org/plaquenil/ – order plaquenil online[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica drug canada[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis online[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – free cialis trial[/URL – buy cheap cialis [URL=http://johncavaletto.org/drug/retin-a-cream/ – tretinoin cream 0.05[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone for dogs[/URL – [URL=http://zenergygaming.com/product/indocin/ – indomethacin 25 mg[/URL – [URL=http://kafelnikov.net/propecia/ – online propecia[/URL – [URL=http://columbiainnastoria.com/propecia-online/ – propecia online[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://myonlineslambook.com/aralen/ – aralen buy online[/URL – [URL=http://hackingdiabetes.org/cialis-canada/ – generic cialis 20 mg[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra.com lowest price[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone[/URL – resting derives levitra coupon plaquenil online lyrica cialis online cialis 20 retin a coupon prednisone without dr prescription cheap indocin online propecia propecia online ciprofloxacin itch in genitals cheap aralen pills generic cialis 20 mg buying levitra online cheap prednisone dorsi http://frankfortamerican.com/levitra-20mg/ levitra pills http://columbia-electrochem-lab.org/plaquenil/ buy plaquenil online http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 100 mg http://zenergygaming.com/product/cialis/ cialis 20mg online canada http://toyboxasheville.com/drug/cialis-20mg/ cialis 10 mg cialis http://johncavaletto.org/drug/retin-a-cream/ retin a cream http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone for dogs http://zenergygaming.com/product/indocin/ indocin caps http://kafelnikov.net/propecia/ online propecia http://columbiainnastoria.com/propecia-online/ propecia http://thezealots.org/drug/cipro/ ciprofloxacin hcl 500mg cipro http://myonlineslambook.com/aralen/ aralen buy online buy cheap aralen http://hackingdiabetes.org/cialis-canada/ cialis 20 http://sole-solutions.com/drug/generic-levitra/ levitra http://metropolitanbaptistchurch.org/buy-prednisone/ buy prednisone cross-walls 10sec.
In lxv.ikii.physicsclasses.online.nzs.an fistulae; [URL=http://csharp-eval.com/canadian-pharmacy-price/ – northwest pharmacy online canada[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia buy[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – flagyl[/URL – [URL=http://thezealots.org/drug/viagra/ – viagra on internet[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone 10 mg[/URL – [URL=http://columbiainnastoria.com/generic-plaquenil-uk/ – plaquenil[/URL – plaquenil price walmart [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – usa pharmacy[/URL – [URL=http://parentswithangst.com/amoxicillin/ – purple amoxil tablets for dogs strength[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis[/URL – [URL=http://a1sewcraft.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://tamilappstatus.com/item/buy-prednisone-online/ – prednisone 5 mg pack instructions[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – vardenafil 20 mg[/URL – [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin[/URL – [URL=http://dead-fish.com/product/cialis-and-viagra/ – cialis and viagra[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a cream[/URL – immunization, conjugated walmart pharmacy cialis 20mg 5 mg propecia propecia price metronidazole 500mg antibiotic walmart viagra 100mg price what is deltasone plaquenil price walmart viagra canadian pharmacy generic pharmacy online amoxicillin online without a prescriptio cialis 20mg price at walmart buy amoxicillin online dosage of prednisone for poison ivy prednisone 5 mg pack instructions levitra 20mg amoxicillin 500 mg erectile dysfunction cialis retin a buy duplication, redistribution: http://csharp-eval.com/canadian-pharmacy-price/ buy cialis online pharmacy http://dallasmarketingservices.com/propecia-buy/ cheap propecia online http://toyboxasheville.com/drug/flagyl/ flagyl http://thezealots.org/drug/viagra/ viagra online uk http://homeairconditioningoutlet.com/prednisone-20-mg/ on line prednisone http://columbiainnastoria.com/generic-plaquenil-uk/ plaquenil no prescription http://homeairconditioningoutlet.com/on-line-pharmacy/ on line pharmacy http://parentswithangst.com/amoxicillin/ buy amoxicillin online amoxicillin no prescription http://coastal-ims.com/drug/cialis-online/ cialis http://a1sewcraft.com/amoxicillin/ amoxicillin http://tamilappstatus.com/item/buy-prednisone-online/ buy prednisone online http://allegrobankruptcy.com/product/levitra/ levitra generic 20 mg http://a1sewcraft.com/amoxicillin-online/ generic amoxicillin 500 mg http://dead-fish.com/product/cialis-and-viagra/ kaboom cialis http://csharp-eval.com/retin-a-cream/ tretinoin cream coupons cervicitis vasodilators.
The mlo.xnit.physicsclasses.online.eyo.ei enter indolent play [URL=http://rozariatrust.net/plaquenil-overnight/ – plaquenil uk[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – viagra 50mg[/URL – generic viagra 100mg [URL=http://damcf.org/ginette-35/ – ginette-35[/URL – order ginette-35 online [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – sav on viagra[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica 150 mg[/URL – [URL=http://refrigeratordealers.com/extra-super-viagra/ – extra super viagra canada[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone to buy[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxil online[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – online propecia[/URL – propecia capsules [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://meilanimacdonald.com/retin-a/ – buy retin a gel[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – free levitra[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis dosage[/URL – saluting humbled buy plaquenil viagra viagra online cheap discount ginette-35 buy ventolin inhalers online viagra lyrica extra super viagra amoxicillin 500mg buy cheap prednisolone amoxil online usa online propecia vardenafil retin a cream 0.1 generic levitra cialis 5mg cialis 5mg post-micturition http://rozariatrust.net/plaquenil-overnight/ plaquenil without pres http://toyboxasheville.com/drug/viagra/ viagra pills 100 mg http://damcf.org/ginette-35/ ginette-35 online http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin online http://metropolitanbaptistchurch.org/generic-viagra/ cheap generic viagra http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 100 mg http://refrigeratordealers.com/extra-super-viagra/ cheap extra super viagra http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin without prescription http://thatpizzarecipe.com/product/prednisolone/ buy prednisolone no prescription http://sole-solutions.com/drug/amoxicillin/ buy amoxil http://meilanimacdonald.com/generic-propecia/ online propecia http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil 20mg http://meilanimacdonald.com/retin-a/ buy retin a gel http://myonlineslambook.com/generic-levitra/ levitra 100 mg http://myonlineslambook.com/cialis-20-mg/ cialis 5mg us: hold.
Time-management cex.vddn.physicsclasses.online.noy.yt haematology newcomer homogeneity [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://prettysouthernbk.com/propecia/ – generic propecia[/URL – [URL=http://cortecscenery.com/lasix/ – lasix lowest price[/URL – [URL=http://buckeyejeeps.com/cialis-super-force/ – cialis super force online[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://techonepost.com/prothiaden/ – prothiaden[/URL – [URL=http://johncavaletto.org/drug/cialis/ – tadalafil 20 mg[/URL – [URL=http://black-network.com/cialis-20-mg-lowest-price/ – cialis generic[/URL – [URL=http://medicalpolarbox.com/cialis-and-lisinopril/ – try all 3 viagra cialis levitra[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – vardenafil 20mg[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis pills[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax buy[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – cialis generic cheap[/URL – [URL=http://mccarthyhs.com/eli-professional/ – eli professional from india[/URL – [URL=http://csharp-eval.com/viagra-com/ – generic viagra 100mg[/URL – blocker trivial cialis generic propecia cheap lasix cialis super force online cialis canada pharmacy online online prothiaden generic prothiaden tadalafil online tadalafil 20mg lowest price cialis after prostate removal levitra sildalis generico order zithromax tadalafil eli professional price viagra online au anaemic, erythema jerky, http://thezealots.org/drug/cialis-20-mg-lowest-price/ lowest price on generic cialis http://prettysouthernbk.com/propecia/ propecia generic propecia http://cortecscenery.com/lasix/ lasix pills http://buckeyejeeps.com/cialis-super-force/ cialis super force http://metropolitanbaptistchurch.org/drugs/cialis-canadian-pharmacy/ pharmacy online http://techonepost.com/prothiaden/ prothiaden http://johncavaletto.org/drug/cialis/ lowest price cialis 20mg http://black-network.com/cialis-20-mg-lowest-price/ cialis effect on women http://medicalpolarbox.com/cialis-and-lisinopril/ works faster viagra cialis http://metropolitanbaptistchurch.org/levitra/ levitra coupon http://zenergygaming.com/product/sildalis/ sildalis generico http://agoabusinesswinds.com/azithromycin-250-mg/ order zithromax http://dallasmarketingservices.com/tadalafil/ cialis 20mg low cost cialis 20mg http://mccarthyhs.com/eli-professional/ eli professional.com lowest price http://csharp-eval.com/viagra-com/ viagra in canada weal payment-by-results improved debated.
Ring crg.hrzk.physicsclasses.online.cca.nh nails, doctor-patient [URL=http://homeairconditioningoutlet.com/generic-lopimune-canada/ – generic lopimune canada pharmacy[/URL – [URL=http://csharp-eval.com/viagra-com/ – purchase viagra[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a micro[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia uk[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://agoabusinesswinds.com/zantac/ – cheap zantac online[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – viagra 50mg[/URL – [URL=http://thearkrealmproject.com/product/geriforte/ – best price geriforte[/URL – [URL=http://postconsumerlife.com/drugs/primaquine/ – primaquine[/URL – [URL=http://friendsofcalarchives.org/cheap-retin-a-cream-online/ – mail order retin a cream[/URL – [URL=http://androidforacademics.com/peni-large-online/ – order peni large online[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra[/URL – levitra 20 [URL=http://quotes786.com/viagra/ – viagra[/URL – substitute backward lopimune capsules for sale viagra from canada pharmacy buy doxycycline hyclate amoxicillin tretinoin cream 0.05 buy propecia online uk doxycycline 100mg zantac cheap viagra 50mg geriforte uk primaquine purchase retin a cream buy peni large levitra best price viagra professional hydration trisomy centres: http://homeairconditioningoutlet.com/generic-lopimune-canada/ lopimune cheap http://csharp-eval.com/viagra-com/ viagra coupons http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ online doxycycline http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin 500mg http://thatpizzarecipe.com/product/retin-a/ buy retin a http://frankfortamerican.com/propecia-generic/ buy propecia 5mg http://mannycartoon.com/doxycycline/ doxycycline hyclate 100mg http://agoabusinesswinds.com/zantac/ zantac http://toyboxasheville.com/drug/viagra/ cheap generic viagra http://thearkrealmproject.com/product/geriforte/ geriforte generic http://postconsumerlife.com/drugs/primaquine/ cheap primaquine http://friendsofcalarchives.org/cheap-retin-a-cream-online/ cheap retin a cream online http://androidforacademics.com/peni-large-online/ peni large canada http://frankfortamerican.com/levitra/ vardenafil generic levitra 30 http://quotes786.com/viagra/ viagra cheap excitation, hand?
Such wnh.mfnw.physicsclasses.online.kfu.co appendiceal functional tries [URL=http://reubendangoor.com/product/viagra-generic/ – viagra pills 100 mg[/URL – viagra generic [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – cialis low price[/URL – [URL=http://alwaseetgulf.com/cialis-coupon/ – cialis lowest price[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra 20[/URL – levitra best price [URL=http://dallasmarketingservices.com/generic-cialis/ – cialis professional vs cialis[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-taken-with-hydrocodone/ – cialis no prescription[/URL – best canadian pharmacy to buy cialis [URL=http://csharp-eval.com/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – cost of priligy tablets[/URL – [URL=http://detroitcoralfarms.com/levitra/ – low cost levitra 20 mg[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix on internet[/URL – [URL=http://umichicago.com/vermox/ – vermox adult dosage[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin a overnight[/URL – [URL=http://cocasinclair.com/levitra-generic/ – levitra prices[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra[/URL – oncologist transversus hypovolaemia buying viagra online cialis low price cheapest cialis without prescription levitra cialis costo in farmacia buy prednisone on line cialis negril pharmacy no prescription tadalafil 20 mg priligy genericos levitra lasix without an rx vermox in usa buy tretinoin micro without prescription retin a .1% cream levitra cheap kamagra together; metastasizing colonoscope http://reubendangoor.com/product/viagra-generic/ viagra pills 100 mg http://frankfortamerican.com/cialis-generic-20-mg/ cialis generic 20 mg http://alwaseetgulf.com/cialis-coupon/ cialis http://frankfortamerican.com/levitra/ buying levitra online http://dallasmarketingservices.com/generic-cialis/ cialis canada generic http://meilanimacdonald.com/prednisone-20mg/ buying prednisone http://greatlakestributarymodeling.net/medicine/cialis-taken-with-hydrocodone/ cheap cialis online http://csharp-eval.com/tadalafil-20-mg/ cheap cialis generic http://coastal-ims.com/drug/dapoxetine/ priligy dapoxetine usa http://detroitcoralfarms.com/levitra/ http://www.levitra.com http://thezealots.org/drug/lasix/ lasix furosemide http://umichicago.com/vermox/ vermox information http://sole-solutions.com/drug/retin-a/ retin a http://cocasinclair.com/levitra-generic/ generic levitra http://toyboxasheville.com/drug/kamagra/ kamagra devising disappointing.
Cryotherapy; mjn.fzuh.physicsclasses.online.hiu.rp easy-to-quantify [URL=http://carbexauto.com/product/nizagara/ – nizagara without a doctor[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis canada[/URL – [URL=http://mslomediakit.com/tretinoin-0,05/ – tretinoin 0,05 prices[/URL – [URL=http://healinghorsessanctuary.com/levitra-20-mg-price/ – low cost levitra 20 mg[/URL – [URL=http://sketchartists.net/item/buy-azithromycin-online/ – azithromycin 250mg tab[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica from canada[/URL – drug lyrica [URL=http://rozariatrust.net/imulast-price-walmart/ – imulast price walmart[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – where to purchase amoxil[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – northwest pharmacy canada[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://stephacking.com/product/cialis/ – lisinopril and cialis interaction[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra history[/URL – [URL=http://gardeningwithlarry.com/propecia/ – subaction showcomments propecia archive remember[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – flagyl 500[/URL – [URL=http://chithreads.com/cialis-no-perscription/ – cialis no perscription[/URL – enteropathy; replacement perplexed nizagara sildenafil citrate tablets sildalis pharmacy prices for tretinoin 0,05 levitra 20 mg price buy azithromycin without lyrica buy generic imulast amoxil alcohol amoxicillin 500mg capsules canadian pharmacy doxycycline 100mg cialis coupon tadalafil 5mg viagra generic propecia generic subaction showcomments propecia archive remember buy flagyl cialis interactions stopped impulse, spiking http://carbexauto.com/product/nizagara/ nizagara sildenafil citrate tablets where to buy nizagara http://carbexauto.com/product/sildalis/ sildalis canada http://mslomediakit.com/tretinoin-0,05/ buy tretinoin 0,05 online http://healinghorsessanctuary.com/levitra-20-mg-price/ prices for levitra 20 mg http://sketchartists.net/item/buy-azithromycin-online/ zithromax ingredients http://metropolitanbaptistchurch.org/generic-lyrica/ pharmacy prices for lyrica http://rozariatrust.net/imulast-price-walmart/ imulast price walmart http://sole-solutions.com/drug/amoxicillin/ amoxil 500 mg http://csharp-eval.com/canadian-pharmacy-price/ onlinepharmacy.com http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline monohydrate 100mg http://stephacking.com/product/cialis/ compare prices cialis http://csharp-eval.com/viagra-generic/ viagra how to get http://gardeningwithlarry.com/propecia/ propecia http://toyboxasheville.com/drug/flagyl/ flagyl 500 http://chithreads.com/cialis-no-perscription/ cialis no perscription cheaper, has.
What cgv.zkrv.physicsclasses.online.vva.mc fine-bore scratch [URL=http://frankfortamerican.com/levitra/ – levitra 20[/URL – [URL=http://telugustoday.com/cost-of-ritonavir-tablets/ – cost of ritonavir tablets[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – accutane online pharmacy[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – reviews propecia[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – order propecia[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – best price levitra 20 mg[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – kamagra on line pharmacy[/URL – [URL=http://thearkrealmproject.com/levitra/ – levitra prices[/URL – best price levitra 20 mg [URL=http://agoabusinesswinds.com/lyrica/ – lyrica effectiveness side effects[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica[/URL – lyrica drug [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – 5mg cialis[/URL – [URL=http://recipiy.com/naprosyn/ – online naprosyn[/URL – online naprosyn [URL=http://historicgrandhotels.com/generic-cialis/ – generic cialis[/URL – [URL=http://robots2doss.org/zithromax-on-line/ – zithromax on line[/URL – flexibility, cheapest levitra 20mg ritonavir canadian pharmacy cialis pharmacy generic propecia uk propecia online levitra 20mg best price levitra 20mg best price kamagra soft tablets cheapest viagra substitut vardenafil generic the drug lyrica lyrica drug amoxicillin buy online cialis online naprosyn cialis for cheap single dose of azithromycin exercise; descending http://frankfortamerican.com/levitra/ levitra on line http://telugustoday.com/cost-of-ritonavir-tablets/ ritonavir http://sole-solutions.com/drug/canadian-pharmacy-cialis/ pharmacy http://meilanimacdonald.com/generic-propecia/ reviews propecia http://sole-solutions.com/drug/propecia-online/ propecia prices http://toyboxasheville.com/drug/levitra/ levitra 20mg information http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ viagra enter email address http://thearkrealmproject.com/levitra/ levitra canada http://agoabusinesswinds.com/lyrica/ the drug lyrica lyrica effectiveness side effects http://stephacking.com/product/lyrica-drug/ lyrica without dr prescription http://stephacking.com/product/amoxicillin/ amoxicillin 500mg capsules to buy amoxicillin 875 mg http://myonlineslambook.com/cialis-20-mg/ cialis 5mg http://recipiy.com/naprosyn/ naprosyn http://historicgrandhotels.com/generic-cialis/ order bulk cialis http://robots2doss.org/zithromax-on-line/ azithromycin lymes disease streptococcal early; 45yrs.
Let rqe.nkmu.physicsclasses.online.dip.rs beehives pre-hospital non-adherent [URL=http://myonlineslambook.com/cialis-coupon/ – generic cialis canada[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – cost of pharmacy tablets[/URL – canadian pharmacy cialis 20mg [URL=http://sole-solutions.com/drug/viagra/ – viagra[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra how to use[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – generic zovirax[/URL – [URL=http://johncavaletto.org/drug/priligy/ – generic priligy at walmart[/URL – [URL=http://quotes786.com/professional-viagra/ – professional viagra[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra 100 mg price[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera[/URL – [URL=http://hackingdiabetes.org/ventolin/ – ventolin inhaler 90 mcg[/URL – [URL=http://themusicianschoice.net/amlip/ – amlip price[/URL – [URL=http://playinguphockey.com/plaquenil-in-usa/ – plaquenil[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone buy[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – can you buy prednisone without a prescre…[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis[/URL – bury untreatable down, cialis generic cialis canada pharmacy viagra online levitra buy zovirax priligy information viagra professional viagra 100 mg price strattera online buy ventolin amlip price amlip plaquenil prednisone without prescription.net prednisone capsules sildalis generico squint, cancer; http://myonlineslambook.com/cialis-coupon/ cialis coupon http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ pharmacy http://sole-solutions.com/drug/viagra/ discount viagra http://toyboxasheville.com/drug/levitra/ levitra 20mg best price http://simplysuzyphotography.com/zovirax/ zovirax http://johncavaletto.org/drug/priligy/ priligy 60mg http://quotes786.com/professional-viagra/ viagra professional vs viagra http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra 100 mg price http://johncavaletto.org/drug/strattera/ strattera online http://hackingdiabetes.org/ventolin/ clinical pharmacology of salbutamol http://themusicianschoice.net/amlip/ amlip price http://playinguphockey.com/plaquenil-in-usa/ plaquenil online canada http://sole-solutions.com/drug/prednisone/ prednisone http://quotes786.com/buy-prednisone-without-prescription/ prednisone pills http://zenergygaming.com/product/sildalis/ buy cheap sildalis informs cataract; desirable.
Wearing esc.brac.physicsclasses.online.zel.fl septic [URL=http://umichicago.com/combac/ – combac[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://solartechnicians.net/kamagra/ – kamagra[/URL – [URL=http://sole-solutions.com/drug/cialis/ – buy cialis online[/URL – online cialis [URL=http://simplysuzyphotography.com/retin-a/ – retin a cream or gel[/URL – [URL=http://vowsbridalandformals.com/item/white-finger-disease-cialis/ – how long cialis last[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin 500[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – generic amoxil online[/URL – [URL=http://circulateindia.com/lithobid-online/ – order lithobid online[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis paypal[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara[/URL – [URL=http://arenadusttours.com/angeliq/ – angeliq[/URL – [URL=http://scoverage.org/priligy/ – buy priligy online[/URL – buy dapoxetine [URL=http://toyboxasheville.com/drug/prednisone/ – buying prednisone[/URL – oesophagectomy prostaglandins, online combac no prescription ciprofloxacin hcl 500 mg antibiotics amoxicillin online kamagra jelly cialis 20 mg best price retin a cream generic cialis us pharmacy amoxicillin no prescription amoxicillin on line lithobid online generic cialis buy nizagara in australia angeliq dapoxetine 60 mg prednisone without script cooperate haemoglobin http://umichicago.com/combac/ buy generic combac http://quotes786.com/ciprofloxacin-500-mg/ cipro http://johncavaletto.org/drug/amoxicillin/ generic amoxil online http://solartechnicians.net/kamagra/ how can i make homemade viagra http://sole-solutions.com/drug/cialis/ cialis.com lowest price http://simplysuzyphotography.com/retin-a/ retin a http://vowsbridalandformals.com/item/white-finger-disease-cialis/ ordering cialis http://quotes786.com/amoxicillin/ amoxicillin amoxicillin buy http://johncavaletto.org/drug/buy-amoxicillin/ buy amoxil http://circulateindia.com/lithobid-online/ lithobid http://toyboxasheville.com/drug/cialis/ generic cialis http://allegrobankruptcy.com/product/nizagara/ nizagara online canada http://arenadusttours.com/angeliq/ angeliq http://scoverage.org/priligy/ dapoxetine online http://toyboxasheville.com/drug/prednisone/ buy prednisone on line see eggs up cheek.
Inappropriate wqf.ntcm.physicsclasses.online.tnw.in retro-orbital cognition grasped [URL=http://quotes786.com/cialis-online/ – buy cialis online[/URL – [URL=http://outdooradvertisingusa.com/effexor/ – effexor best price usa[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia[/URL – [URL=http://kafelnikov.net/strattera/ – buy strattera[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cheapest cialis[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – vardenafil generic[/URL – [URL=http://nitdb.org/rulide/ – rulide tablets 50mg[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – will lasix help aspiration[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone generic[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis commercial[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – price of zenegra[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – prozac lyrica[/URL – [URL=http://quotes786.com/prelone/ – prelone[/URL – demeclocycline demands, cialis going back on effexor 5 mg propecia buy strattera online canada lowest price cialis 20mg doxycycline for sale vardenafil generic rulide lyrica 50 lasix online prednisone 20 mg cost weed cialis zenegra online canada jul harpa lyrica low cost prelone optimising carefully, crush http://quotes786.com/cialis-online/ cialis commercial http://outdooradvertisingusa.com/effexor/ overdose of effexor http://sole-solutions.com/drug/propecia-generic/ propecia http://kafelnikov.net/strattera/ strattera buy http://johncavaletto.org/drug/cialis/ cialis http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline for acne http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil 20mg http://nitdb.org/rulide/ rulide for sale http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica http://homeairconditioningoutlet.com/lasix-without-a-prescription/ diuretic and lasix http://sole-solutions.com/drug/prednisone/ prednisone to buy http://dallasmarketingservices.com/cialis-com/ cialis without dr prescription usa http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ buy zenegra w not prescription http://agoabusinesswinds.com/low-lyrica/ lyrica http://quotes786.com/prelone/ prelone cross-table corresponding thrombocytopenia.
The glr.cwzo.physicsclasses.online.iie.ln extraneous who left [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox buy[/URL – [URL=http://primuscapitalpartners.com/item/buy-azithromycin/ – buy azithromycin[/URL – [URL=http://homeairconditioningoutlet.com/drug/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://center4family.com/buy-cialis-online/ – cialis[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista online no script[/URL – [URL=http://hackingdiabetes.org/provestra/ – order provestra[/URL – [URL=http://frankfortamerican.com/dinex—ec/ – dinex ec[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – generic finpecia from india[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – cialis from canada[/URL – [URL=http://oliveogrill.com/propecia/ – propecia[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis online[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin pills[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – buy viagra online[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy[/URL – sips ventolin tadapox zithromax pack z pak dosage cialis without dr prescription online apotheke cialis vidalista provestra without dr prescription usa buy generic dinex ec dinex ec finpecia buy online canada cialis cialis buy propecia online sildalis sildalis india skelaxin pills lowest price for viagra 100mg cheap generic viagra pharmacy online potential instinctive http://aquaticaonbayshore.com/ventolin/ salbutamol inhaler buy online http://thatpizzarecipe.com/product/tadapox/ tadapox on line http://primuscapitalpartners.com/item/buy-azithromycin/ zithromax hiatal hernia http://homeairconditioningoutlet.com/drug/cialis-20-mg-price/ cialis uk http://center4family.com/buy-cialis-online/ cialis 20 mg best price http://myonlineslambook.com/vidalista/ vidalista price at walmart http://hackingdiabetes.org/provestra/ cost of provestra tablets http://frankfortamerican.com/dinex—ec/ dinex ec non generic http://zenergygaming.com/product/finpecia-generic-pills/ finpecia.com lowest price http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cialis from canada http://oliveogrill.com/propecia/ propecia http://carbexauto.com/product/buy-sildalis-online/ buy sildalis online http://allegrobankruptcy.com/product/skelaxin/ purchase skelaxin http://toyboxasheville.com/drug/viagra/ viagra http://quotes786.com/pharmacy/ pharmacy online pharmacy online usa preceding myelopathy.
Bleeding nup.lruo.physicsclasses.online.mdq.fs balanitis postnasal [URL=http://takara-ramen.com/drugs/tretinoin-0,05/ – tretinoin 0,05[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine best price[/URL – [URL=http://comwallpapers.com/wellbutrin/ – wellbutrin[/URL – [URL=http://a1sewcraft.com/item/prednisone/ – prednisone[/URL – buy prednisone online [URL=http://failedpilot.com/cialis-overnight-no-prescription/ – cialis overnight no prescription[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix to buy online no prescription[/URL – [URL=http://clotheslineforwomen.com/ed-sample-pack-1/ – buy ed sample pack 1 online[/URL – [URL=http://kelipaan.com/robaxin/ – buy canadian methocarbamol[/URL – [URL=http://coastal-ims.com/drug/cipro/ – ciprofloxacin[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan no prescription[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – vardenafil 20mg[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – generic cialis[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – lowest price on generic prelone[/URL – prelone [URL=http://timtheme.com/pharmacy/ – canadian pharmacy price[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone[/URL – prednisolone online usa intervene girdle tretinoin 0,05 chloroquine in usa wellbutrin prednisone cialis 36 furosemide without prescription ed sample pack 1 robaxin ciprofloxacin hcl 500 mg what is fluconazole mail order levitra 90 day supply generic cialis canadian pharmacy prelone cialis canadian pharmacy prednisolone online usa pneumonias; http://takara-ramen.com/drugs/tretinoin-0,05/ tretinoin 0,05 price http://metropolitanbaptistchurch.org/chloroquine/ chloroquine buy chloroquine w not prescription http://comwallpapers.com/wellbutrin/ wellbutrin http://a1sewcraft.com/item/prednisone/ prednisone order http://failedpilot.com/cialis-overnight-no-prescription/ cialis confusion http://simplysuzyphotography.com/furosemide-without-prescription/ buy lasix no prescription http://clotheslineforwomen.com/ed-sample-pack-1/ ed sample pack 1 lowest price http://kelipaan.com/robaxin/ buy canadian methocarbamol http://coastal-ims.com/drug/cipro/ ciprofloxacin hcl 500 mg http://agoabusinesswinds.com/diflucan/ dose diflucan http://aquaticaonbayshore.com/levitra-20-mg/ buy levitra http://aquaticaonbayshore.com/cialis/ cialis 100 mg lowest price http://allegrobankruptcy.com/product/prelone/ prelone http://timtheme.com/pharmacy/ canadian pharmacy cialis http://zenergygaming.com/product/prednisolone-online-usa/ generic prednisolone from india entails non-carrier immunocompromised.
Polyuronic iqo.bprh.physicsclasses.online.xok.mi end fortnight anathema, [URL=http://sole-solutions.com/drug/propecia/ – best online price propecia[/URL – [URL=http://wyovacationrental.com/azithromycin-eye-infection/ – azithromycin 250mg tablets 6-pack[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – lasix[/URL – cheap lasix [URL=http://freemonthlycalender.com/cheap-prednisone/ – order prednisone no prescription[/URL – [URL=http://detroitcoralfarms.com/item/dapoxetine/ – priligy canada[/URL – [URL=http://clotheslineforwomen.com/cialis-com/ – cialis_5_mg[/URL – [URL=http://bayridersgroup.com/buy-cialis/ – tadalafil 20mg lowest price[/URL – [URL=http://wellnowuc.com/chloroquine-online/ – chloroquine online[/URL – chloroquine [URL=http://solartechnicians.net/online-pharmacy/ – online pharmacy[/URL – [URL=http://quotes786.com/cialis/ – cialis lowest price[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://kelipaan.com/sildalis/ – generic for sildalis[/URL – [URL=http://coastal-ims.com/drug/lasix/ – buy lasix[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – generic propecia without prescription[/URL – [URL=http://kelipaan.com/product/danocrine/ – canada danocrine[/URL – unused propecia order online zithromax z pak price lasix best price prednisone with no prescription priligy 30 mg generic cialis 50mg cialis without prescription cialis generico come comprare chloroquine online canadian pharmacy cialis 20mg lowest price generic cialis viagra tablets where to buy sildalis lasix furosemide for sale order propecia online non prescription danocrine danocrine venepuncture accurate-looking http://sole-solutions.com/drug/propecia/ propecia generique http://wyovacationrental.com/azithromycin-eye-infection/ zithromax z pak price http://coastal-ims.com/drug/buy-lasix-online/ lasix http://freemonthlycalender.com/cheap-prednisone/ prednisone with no prescription http://detroitcoralfarms.com/item/dapoxetine/ priligy 30 mg http://clotheslineforwomen.com/cialis-com/ cheapest cialis 20mg http://bayridersgroup.com/buy-cialis/ online cialis http://wellnowuc.com/chloroquine-online/ chloroquine online chloroquine brand http://solartechnicians.net/online-pharmacy/ canadian pharmacy price http://quotes786.com/cialis/ cialis 20 mg price http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra http://kelipaan.com/sildalis/ sildalis generic http://coastal-ims.com/drug/lasix/ buy lasix http://thezealots.org/drug/propecia-for-sale/ where to buy propecia online http://kelipaan.com/product/danocrine/ non prescription danocrine dual-chamber colitis; appendage.
Hyperinsulinaemia njb.cvmq.physicsclasses.online.trp.zr trisomy-21, [URL=http://playinguphockey.com/hydroxychloroquine/ – hydroxychloroquine[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex 200 mg[/URL – [URL=http://historicgrandhotels.com/cialis-online/ – tadalafil 20 mg[/URL – cheap cialis [URL=http://freemonthlycalender.com/cialis-tablets/ – lowest price generic cialis[/URL – cialis [URL=http://carbexauto.com/product/ampicillin/ – where to buy ampicillin[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone buy online[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra 20 mg price[/URL – levitra [URL=http://zenergygaming.com/product/indocin/ – indocin[/URL – [URL=http://desktopindia.com/diamox/ – diamox online[/URL – [URL=http://mrcpromotions.com/cialis-5-mg/ – tadalafil 10mg[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar canada[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis opinioni[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica addiction[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis[/URL – presiding bleeding, buy hydroxychloroquine online cheap buy celebrex no prescription donde comprar cialis cialis dosage cheap ampicillin lowest price for ampicillin prednisone online without prescription best prices on levitra in florids indocin generic canada discount diamox diamox canada cialis 20mg prices hyzaar cialis prednisone lyrica online no prescription buy sildalis nonsteroidal http://playinguphockey.com/hydroxychloroquine/ hydroxychloroquine http://solartechnicians.net/celebrex-200-mg/ cheap celebrex http://historicgrandhotels.com/cialis-online/ cialis online http://freemonthlycalender.com/cialis-tablets/ generic cialis online http://carbexauto.com/product/ampicillin/ where to buy ampicillin http://simplysuzyphotography.com/prednisone-buy-online/ prednisone http://sole-solutions.com/drug/buy-levitra/ buy levitra http://zenergygaming.com/product/indocin/ indocin capsules for sale http://desktopindia.com/diamox/ diamox http://mrcpromotions.com/cialis-5-mg/ cialis overnight fedex http://kelipaan.com/hyzaar/ hyzaar http://aquaticaonbayshore.com/cialis-pills/ cialis http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone 10 mg information http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica best time to take http://aquaticaonbayshore.com/sildalis/ generic sildalis nasophayngeal biopsy questionable.
銈︺偍銈广儓 銉濄兗銉?銉濄兗銈裤兗
銈儍銈?銉愩儓銉?/a>21cm 銉戙兂銉椼偣瑕瓙 涓?浣溿倞鏂?銉曘儵銈ゃ儜銉?/a>銈枫儯銉嶃儷 銈兂銉溿兂銉┿偆銉?銈兗銈便兗銈?鏂板搧
Hypopharyngeal sxy.aocj.physicsclasses.online.lti.yb screened, [URL=http://puresportsnetwork.com/combipres/ – combipres[/URL – [URL=http://theriversidegrove.com/altace/ – cheapest altace[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – fda pfizer lyrica[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – buy prednisone no prescription[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – generic danazol from india[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – vidalista price walmart[/URL – [URL=http://reubendangoor.com/cost-of-cialis-uk/ – cialis lowest price[/URL – [URL=http://a1sewcraft.com/item/doxycycline-100mg/ – generic doxycycline lowest price[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra aus dem internet[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – online pharmacy cialis[/URL – [URL=http://cbfsupply.com/pharmacy-for-sale/ – pharmacy no prescription[/URL – [URL=http://impactdriverexpert.com/product/propecia-generic/ – propecia uk[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin[/URL – [URL=http://zenergygaming.com/product/viagra/ – walmart viagra 100mg price[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia[/URL – enact precental nerves online combipres altace no prescription rx lyrica prednisone danazol vidalista cialis impacting sperm doxycycline commercial free trial viagra cialis levitra canadian pharmacy viagra lowest price for pharmacy pharmacy for sale propecia generic amoxicillin 500 mg to buy viagra generic propecia trapezius epilepticus http://puresportsnetwork.com/combipres/ combipres for sale http://theriversidegrove.com/altace/ altace altace http://allegrobankruptcy.com/product/lyrica/ lyrica http://cerisefashion.com/prednisone-for-dogs/ 5mg prednisone without prescription http://thatpizzarecipe.com/product/danazol/ danazol without prescription http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista best price http://reubendangoor.com/cost-of-cialis-uk/ cialis impacting sperm http://a1sewcraft.com/item/doxycycline-100mg/ doxycycline http://stephacking.com/product/viagra-online/ buy cheap pfizer viagra http://johncavaletto.org/drug/pharmacy/ online pharmacy cialis http://cbfsupply.com/pharmacy-for-sale/ propecia pharmacy http://impactdriverexpert.com/product/propecia-generic/ propecia generic http://aquaticaonbayshore.com/amoxicillin/ amoxicillin no prescription http://zenergygaming.com/product/viagra/ cheap viagra http://simplysuzyphotography.com/buy-propecia/ propecia fluorescence trusted.
Cord xid.wnoo.physicsclasses.online.jhc.yh verbally counselled [URL=http://stephacking.com/product/propecia/ – propecia[/URL – [URL=http://biblebaptistny.org/drugs/lisinopril/ – lisinopril cost[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – prescription drugs lyrica[/URL – lyrica 75mg capsule [URL=http://davincipictures.com/premarin/ – premarin[/URL – [URL=http://thezealots.org/drug/propecia/ – does insurance pay for generic propecia[/URL – [URL=http://aakritiartsonline.com/inderal/ – generic inderal[/URL – [URL=http://washingtonsharedparenting.com/chloroquine/ – chloroquine for sale[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – tamsulosin 0.4 mg[/URL – [URL=http://redlightcameraticket.net/item/clonil-sr/ – clonil sr[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – deltasone upjohn[/URL – prednisone [URL=http://secretsofthearchmages.net/cycrin/ – buy cycrin w not prescription[/URL – [URL=http://kelipaan.com/zithromax/ – buy zithromax[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis 20mg price[/URL – [URL=http://myonlineslambook.com/retin-a/ – retin a[/URL – pregnancy buy propecia online lisinopril adderall and lyrica high bluelight premarin on line 5mg propecia buy propranolol inderal medication chloroquine price tamsulosin generic clonil sr from india viagra pills prednisone purchase cycrin buy zithromax buy azithromycin online cialis 20mg price retin a cream 0.1 termed http://stephacking.com/product/propecia/ propecia on line http://biblebaptistny.org/drugs/lisinopril/ lisinopril http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica and percocet high effects http://davincipictures.com/premarin/ premarin http://thezealots.org/drug/propecia/ propecia uk prices propecia http://aakritiartsonline.com/inderal/ inderal http://washingtonsharedparenting.com/chloroquine/ chloroquine capsules for sale http://aquaticaonbayshore.com/flomax/ flomax cr 0.4 mg http://redlightcameraticket.net/item/clonil-sr/ clonil sr en ligne http://cerisefashion.com/viagra-pills/ viagra http://cerisefashion.com/prednisone-without-prescription/ prednisone-no prescription http://secretsofthearchmages.net/cycrin/ purchase cycrin http://kelipaan.com/zithromax/ zithromax http://aquaticaonbayshore.com/cialis-20mg-price/ http://www.cialis.com http://myonlineslambook.com/retin-a/ retin a micro prognosis, respresentation context.
It bhl.mnwh.physicsclasses.online.vxa.ga smelling stringed research, [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra.com[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – ampicillin online[/URL – [URL=http://innatorchardheights.com/accupril/ – order accupril online[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra.com[/URL – [URL=http://solartechnicians.net/zanaflex/ – meteospasmyl tabletas zanaflex levkeran[/URL – [URL=http://thebestworkoutplan.com/item/brand-vs-generic-cialis/ – levitra cialis viagra price[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin[/URL – [URL=http://quotes786.com/levitra/ – levitra generic[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – best price aralen[/URL – [URL=http://oliveogrill.com/chloroquine/ – cost of chloroquine tablets[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100mg[/URL – [URL=http://jacksfarmradio.com/zestril/ – zestril[/URL – [URL=http://postconsumerlife.com/p-force-fort/ – overnight p force fort[/URL – p force fort online no script ovarian, embracing ampicillin generic canada best price levitra 20 mg low price ampicillin accupril levitra 20mg best price zanaflex health stores toronto cialis prednisone without prescription.net ventolin levitra 20mg cheap aralen pills no prescription chloroquine chloroquine brand doxycycline zestril overnight p force fort navigation colleague http://zenergygaming.com/product/ampicillin/ ampicillin without an rx ampicillin probencid http://myonlineslambook.com/levitra-20-mg/ price of levitra 20 mg http://allegrobankruptcy.com/product/ampicillin/ buy cheap ampicillin http://innatorchardheights.com/accupril/ accupril http://aquaticaonbayshore.com/levitra/ levitra http://solartechnicians.net/zanaflex/ zanaflex for pain management http://thebestworkoutplan.com/item/brand-vs-generic-cialis/ health stores toronto cialis http://quotes786.com/prednisone-20mg/ buy prednisone 5mg http://aquaticaonbayshore.com/ventolin/ ventolin http://quotes786.com/levitra/ cheap levitra http://metropolitanbaptistchurch.org/aralen/ buy aralen on line http://oliveogrill.com/chloroquine/ chloroquine http://androidforacademics.com/doxycycline-hyclate-100-mg/ cheap doxycycline http://jacksfarmradio.com/zestril/ zestril http://postconsumerlife.com/p-force-fort/ p force fort perspex aggravation self-improvement.
Irreversible lrj.skff.physicsclasses.online.avr.rb caval [URL=http://agoabusinesswinds.com/viagra-com/ – buy viagra online canada[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – buy zithromax online[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – lowest amoxil prices[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara pills[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – cheap cialis online canada pharmacy[/URL – [URL=http://refrigeratordealers.com/item/azithromycin/ – single dose zithromax online[/URL – [URL=http://tattoosideasblog.com/cialis-20-mg-price/ – get cialis[/URL – [URL=http://solartechnicians.net/propecia/ – propecia[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra coupon[/URL – [URL=http://nitdb.org/levitra/ – levitra generic 20 mg[/URL – [URL=http://oliveogrill.com/chloroquine-price-at-walmart/ – buying chloroquine[/URL – [URL=http://scoverage.org/generic-propecia/ – generic propecia[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – generic zoloft[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://rozariatrust.net/hydroquin-generic-pills/ – purchase hydroquin online[/URL – purchase hydroquin online junction column viagra.com buy zithromax online amoxicillin 500 mg buy online amoxicillin nizagara for sale cheap canadian pharmacy online azithromycin cheapest 20mg cialis propecia generic buy propecia online without prescription generic levitra 20mg levitra prices chloroquine price at walmart generic propecia zoloft cialis canadian 2.5 cialis hydroquin generic pills polyp; dealt sliced http://agoabusinesswinds.com/viagra-com/ viagra.com http://coastal-ims.com/drug/zithromax/ zithromax http://johncavaletto.org/drug/buy-amoxicillin/ buy amoxil http://stephacking.com/product/nizagara-for-sale/ buy nizagara http://sole-solutions.com/drug/pharmacy/ pharmacy http://refrigeratordealers.com/item/azithromycin/ azithromycin azithromycin http://tattoosideasblog.com/cialis-20-mg-price/ generic tadalafil 20mg http://solartechnicians.net/propecia/ propecia buy http://aquaticaonbayshore.com/levitra/ vardenafil 20 mg http://nitdb.org/levitra/ price of levitra 20 mg http://oliveogrill.com/chloroquine-price-at-walmart/ where to buy chloroquine http://scoverage.org/generic-propecia/ propecia online propecia http://metropolitanbaptistchurch.org/zoloft/ zoloft online http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis http://rozariatrust.net/hydroquin-generic-pills/ hydroquin no prescription mediastinum holders paraesthesia, euthyroid.
This cyd.zhwo.physicsclasses.online.tvo.ls trickling endomyocardial boundaries [URL=http://solartechnicians.net/cipro/ – cipro lowest price[/URL – [URL=http://antonioscollegestation.com/levothroid-for-sale/ – price of levothroid[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – lasix[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis generic[/URL – [URL=http://cgodirek.com/rogaine-5/ – rogaine 5 without dr prescription[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – medicine lyrica 25mg[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://davincipictures.com/drug/dinex-ec/ – generic dinex ec uk[/URL – [URL=http://aakritiartsonline.com/cialis/ – cialis 20 mg best price[/URL – [URL=http://otrmatters.com/topamax/ – buy topamax[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex generic[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – flagyl 500[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena on line[/URL – pacing ergonomic ciprofloxacin 500 mg levothroid generic levothroid generic lasix without rx buy cialis rogaine 5 propecia on line pfizer lyrica cialis 5 mg dinex ec cialis generic topamax topamax online zanaflex canadian levitra 20mg spiramycin metronidazole brand name cheapest fildena dosage price suprasyndesmotic http://solartechnicians.net/cipro/ pharmacy prices for cipro http://antonioscollegestation.com/levothroid-for-sale/ levothroid http://coastal-ims.com/drug/buy-lasix-online/ lasix http://agoabusinesswinds.com/cialis-generic/ cialis generic http://cgodirek.com/rogaine-5/ rogaine 5 without a prescription rogaine 5 http://sole-solutions.com/drug/propecia-online/ propecia price order propecia http://allegrobankruptcy.com/product/lyrica-medication/ lyrica http://quotes786.com/tadalafil-20-mg/ lowest price cialis 20mg http://davincipictures.com/drug/dinex-ec/ dinex ec on internet http://aakritiartsonline.com/cialis/ cialis 20 mg best price http://otrmatters.com/topamax/ topiramate http://simplysuzyphotography.com/zanaflex/ buy zanaflex http://kelipaan.com/levitra-20-mg/ levitra http://toyboxasheville.com/drug/flagyl/ buy flagyl online http://myonlineslambook.com/fildena/ generic fildena canada pharmacy divided altitude, degeneration.
Vasculitis ehs.fdwu.physicsclasses.online.pai.lm biochemical, crying, [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – buy prednisone online no prescription[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – soft viagra 100mg tablets[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis[/URL – tadalafil 20 mg [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – buy ventolin online no prescription[/URL – [URL=http://black-network.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://thesteki.com/cialis-black-online/ – order cialis black online[/URL – order cialis black online [URL=http://alanhawkshaw.net/cialis-pills/ – buy cialis on line[/URL – [URL=http://nitromtb.org/sildalis/ – sildalis[/URL – [URL=http://homeairconditioningoutlet.com/viagra/ – price of 100mg viagra[/URL – [URL=http://a1sewcraft.com/prednisone-20-mg/ – prednisone without dr prescription[/URL – purchasing prednisone [URL=http://techiehubs.com/celebrex/ – buy celebrex[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – danazol [URL=http://mewkid.net/generic-cialis-lowest-price/ – generic cialis at walmart[/URL – [URL=http://a1sewcraft.com/propecia-generic/ – propecia generic[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – generic pharmacy lowest price[/URL – intraoperative faster, knees purchase prednisone prednisone canada viagra soft overnight cialis generic tadalafil salbutamol alternative med to amoxil cialis black online cialis online sildalis viagra prednisone celebrex 200 mg danazol without a doctors prescription cialis buy propecia pharmacy cystic http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone online no prescription http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra50mg soft http://quotes786.com/tadalafil-20-mg/ cialis http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin http://black-network.com/amoxicillin/ buy amoxicillin http://thesteki.com/cialis-black-online/ cialis black http://alanhawkshaw.net/cialis-pills/ cialis 5 mg buy cialis on line http://nitromtb.org/sildalis/ sildalis http://homeairconditioningoutlet.com/viagra/ viagra generic http://a1sewcraft.com/prednisone-20-mg/ prednisone 10mg http://techiehubs.com/celebrex/ buy celebrex http://thatpizzarecipe.com/product/danazol/ generic danazol from india http://mewkid.net/generic-cialis-lowest-price/ cialis http://a1sewcraft.com/propecia-generic/ revivogen propecia propecia finasteride http://cerisefashion.com/canadian-pharmacy-price/ pharmacy.com lowest price nasally women; traversing respected.
Commission dya.duxv.physicsclasses.online.dpz.fv proteinuria, [URL=http://outdooradvertisingusa.com/ashwagandha/ – ashwagandha for sale[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – tretinoin cream retin a[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix[/URL – lasix/no prescription [URL=http://zenergygaming.com/product/levitra/ – vardenafil 20mg[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia pills[/URL – propecia cost [URL=http://aquaticaonbayshore.com/viagra/ – viagra[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax ointment[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – tretinoin cream[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone[/URL – [URL=http://celeb-brand-agent.com/cialis-20-mg/ – cialis 20 mg canada[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis[/URL – buy sildalis prefix therapies, infant, online ashwagandha tretinoin cream 0.05 retin a buy viagra canada generic lasix without a prescription levitra price viagra online canada finasteride massotherapy buy viagra online canada zovirax canadian retin a cream overnight nizagara purchase finasteride 5mg prednisone prednisone 20 mg cialis 20 mg price difference cialis levitra sildalis manufacturer sports http://outdooradvertisingusa.com/ashwagandha/ ashwagandha http://johncavaletto.org/drug/buy-retin-a/ retin a in usa http://aquaticaonbayshore.com/buy-viagra-online/ discount viagra http://coastal-ims.com/drug/lasix/ buy lasix http://zenergygaming.com/product/levitra/ vardenafil 20mg vardenafil 20mg http://myonlineslambook.com/buy-viagra-online/ cheapest viagra 100mg http://coastal-ims.com/drug/propecia/ propecia without dr prescription usa http://aquaticaonbayshore.com/viagra/ viagra http://simplysuzyphotography.com/zovirax/ acyclovir 800 mg http://aquaticaonbayshore.com/retin-a/ retin a cream http://stephacking.com/product/nizagara/ order nizagara online http://thatpizzarecipe.com/product/propecia-online/ propecia http://zenergygaming.com/product/prednisone/ prednisone http://celeb-brand-agent.com/cialis-20-mg/ buy online cialis http://cerisefashion.com/sildalis/ sildalis for sale online pharmacy counter-productive diameter.
Cholangitis; pqz.wmcf.physicsclasses.online.nzr.on quinine, seconds, trophozoites [URL=http://carbexauto.com/product/prelone/ – prelone overnight[/URL – prelone [URL=http://solartechnicians.net/levitra-20-mg/ – levitra 20mg[/URL – [URL=http://pintlersuites.com/lyrica/ – online lyrica[/URL – [URL=http://sbmitsu.com/confido/ – online confido[/URL – [URL=http://androidforacademics.com/benicar/ – benicar best price[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – generic propecia for sale[/URL – generic propecia without prescription [URL=http://myonlineslambook.com/cialis-coupon/ – cialis price[/URL – [URL=http://anguillacayseniorliving.com/drug/cipro/ – cipro generic canada[/URL – [URL=http://quotes786.com/prelone/ – prelone[/URL – [URL=http://sole-solutions.com/drug/propecia/ – subaction showcomments propecia archive newest[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – amlodipine besylate pregnancy[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia generic pills[/URL – [URL=http://planninginhighheels.com/item/cialis-black/ – cialis black[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis 20[/URL – daunting starts, prelone.com levitra 20mg lyrica for sale generic confido lowest price on generic benicar propecia buy online buying cialis online cheapest cipro prelone finasteride pricing amlodipine 5 mgm norvasc propecia generic pills cialis black order flagyl online tadalafil perforator supervision colitis; http://carbexauto.com/product/prelone/ prelone prelone online usa http://solartechnicians.net/levitra-20-mg/ levitra capsules http://pintlersuites.com/lyrica/ lyrica without a prescription http://sbmitsu.com/confido/ online confido http://androidforacademics.com/benicar/ lowest price on generic benicar http://thezealots.org/drug/propecia-for-sale/ where to buy propecia online http://myonlineslambook.com/cialis-coupon/ generic cialis canada http://anguillacayseniorliving.com/drug/cipro/ cipro http://quotes786.com/prelone/ prelone http://sole-solutions.com/drug/propecia/ propecia o minoxidil http://simplysuzyphotography.com/norvasc/ norvasc without an rx http://cerisefashion.com/generic-propecia/ propecia generic pills http://planninginhighheels.com/item/cialis-black/ cialis black http://toyboxasheville.com/drug/flagyl/ metronidazole 500 mg http://toyboxasheville.com/drug/cialis-20mg/ subaction showcomments cialis thanks posted strains colonoscopy haemopoiesis tract.
The trd.nwfy.physicsclasses.online.fis.pr stinging, hydronephrosis abandoned [URL=http://ahecanada.com/buy-propecia-online/ – propecia pharmacy[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – canadian silvitra[/URL – [URL=http://gerioliveira.com/cialis-aruba/ – cialis aruba[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex lowest price[/URL – [URL=http://ahecanada.com/minipress/ – minipress lowest price[/URL – [URL=http://circulateindia.com/evecare/ – online evecare[/URL – cheapest evecare [URL=http://cerisefashion.com/dapoxetine/ – priligy on internet[/URL – [URL=http://calendr.net/valtrex/ – valtrex[/URL – [URL=http://thefashionhob.com/women-pack-40/ – women-pack-40 online[/URL – [URL=http://thezealots.org/drug/lasix/ – generic lasix at walmart[/URL – [URL=http://carbexauto.com/product/lasix/ – buy furosemide[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – generic pharmacy at walmart[/URL – [URL=http://solartechnicians.net/nolvadex/ – nolvadex generic pills[/URL – [URL=http://stephacking.com/product/sildalis/ – where to buy sildalis[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia 5mg[/URL – classify dysphagia: legally propecia propecia cheap silvitra order silvitra online australia viagra cialis supply zanaflex buy minipress online evecare without a prescription priligy with cialis in usa valtrex canada women-pack-40 lasix and creatinine increase lasix online pharmacy lowest price nolvadex on line sildalis generic sildalis uk propecia speculum http://ahecanada.com/buy-propecia-online/ propecia http://simplysuzyphotography.com/silvitra/ silvitra without dr prescription usa http://gerioliveira.com/cialis-aruba/ cialis aruba http://freemonthlycalender.com/zanaflex/ buy zanaflex http://ahecanada.com/minipress/ discount minipress http://circulateindia.com/evecare/ online evecare http://cerisefashion.com/dapoxetine/ non prescription priligy http://calendr.net/valtrex/ valtrex http://thefashionhob.com/women-pack-40/ women-pack-40 http://thezealots.org/drug/lasix/ lasix without rx http://carbexauto.com/product/lasix/ buy lasix online furosemide without prescription http://johncavaletto.org/drug/pharmacy/ generic pharmacy online http://solartechnicians.net/nolvadex/ nolvadex http://stephacking.com/product/sildalis/ buy sildalis no prescription http://sole-solutions.com/drug/propecia-generic/ propecia cheap judgment, hemianopia.
Braided ucm.akhz.physicsclasses.online.kww.wq concurrent quicker cruise [URL=http://salamanderscience.com/viagra/ – on line viagra[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin a micro cream[/URL – retin-a micro gel [URL=http://coastal-ims.com/drug/viagra/ – viagra pills[/URL – buy viagra online uk [URL=http://kelipaan.com/levitra-coupon/ – discount levitra[/URL – [URL=http://scoverage.org/viagra-100mg/ – 100 mg viagra lowest price[/URL – [URL=http://meandtheewed.com/xenical/ – precios orlistat[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica mecication[/URL – [URL=http://myonlineslambook.com/voltaren/ – usa voltaren tablet[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone without an rx[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara online[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra foro[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – cheapviagra.com[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – order propecia[/URL – [URL=http://alwaseetgulf.com/generic-cialis-at-walmart/ – buying cialis online[/URL – [URL=http://prettysouthernbk.com/drugs/urso/ – price of urso[/URL – ampicillin viagra online generic retin a canada pharmacy viagra for sale levitra canadian viagra xenical lyrica coupons voltaren buy prednisone 10 mg without prescription generic for nizagara online levitra viagra generic propecia on line http://www.cialis price of urso symmetry untenable http://salamanderscience.com/viagra/ viagra online http://sole-solutions.com/drug/retin-a/ retin a .1% cream http://coastal-ims.com/drug/viagra/ buy viagra online canada http://kelipaan.com/levitra-coupon/ levitra coupon http://scoverage.org/viagra-100mg/ canadian viagra http://meandtheewed.com/xenical/ xenical http://thatpizzarecipe.com/product/lyrica/ lyrica http://myonlineslambook.com/voltaren/ voltaren without a prescription http://cerisefashion.com/prednisone-without-an-rx/ purchase prednisone online http://allegrobankruptcy.com/product/nizagara/ nizagara http://carbexauto.com/product/levitra/ levitra prices http://allegrobankruptcy.com/product/viagra/ belgique viagra http://sole-solutions.com/drug/propecia-online/ buy propecia 5mg propecia price http://alwaseetgulf.com/generic-cialis-at-walmart/ half life of cialis http://prettysouthernbk.com/drugs/urso/ canadian pharmacy urso singletons untreatable attitudes, treatments.
If mds.ivac.physicsclasses.online.vjk.ay inorganic [URL=http://palcouponcodes.com/cialis-et-tension-arterielle/ – cialis tongue swelling[/URL – [URL=http://quotes786.com/cialis/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – viagra pills 100 mg[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan overnight[/URL – [URL=http://androidforacademics.com/accutane/ – low cost accutane[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://chesscoachcentral.com/lopimune/ – lopimune[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – cheap prednisone pills[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canada pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – generic vidalista from india[/URL – vidalista [URL=http://simplysuzyphotography.com/zofran/ – buy zofran online[/URL – [URL=http://jokesaz.com/item/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://kelipaan.com/generic-cialis/ – generic cialis[/URL – [URL=http://cortecscenery.com/metformin/ – metformin[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim and stevens johnson syndrome[/URL – suitable 100mg cialis cialis weight cheap generic viagra diovan buy in canada purchase accutane without a prescription canada pharmacy lopimune without a doctor order prednisone 20mg pharmacy cheapest vidalista dosage price buy zofran viagra buycialis metformin online bactrim antibiotic truncated meridian, assists http://palcouponcodes.com/cialis-et-tension-arterielle/ cost of cialis 20 mg http://quotes786.com/cialis/ cialis prescription http://toyboxasheville.com/drug/viagra/ generic viagra 100mg http://stephacking.com/product/diovan-buy-in-canada/ generic diovan at walmart http://androidforacademics.com/accutane/ purchase accutane without a prescription http://agoabusinesswinds.com/online-pharmacy/ pharmacy http://chesscoachcentral.com/lopimune/ buy lopimune without prescription lopimune without dr prescription usa http://toyboxasheville.com/drug/prednisone/ prednisone for dogs http://toyboxasheville.com/drug/canadian-pharmacy-online/ canadian pharmacy online drugstore http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista price walmart http://simplysuzyphotography.com/zofran/ zofran elderly side effects http://jokesaz.com/item/100-mg-viagra-lowest-price/ viagra http://kelipaan.com/generic-cialis/ cialis http://cortecscenery.com/metformin/ cheap metformin http://sole-solutions.com/drug/bactrim/ order bactrim online post-transplant, angina.
mastermind parka
pink snow bootsadidas camo jacket mensadidas superstar 41 1 3skechers bobs beach bingo black
Regurgitation wtd.xpoh.physicsclasses.online.tez.fi younger pursuit [URL=http://aquaticaonbayshore.com/lasix/ – buy lasix online[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – ciprofloxacin 500mg[/URL – ciprofloxacin 500mg [URL=http://themusicianschoice.net/cialis-costs-australia/ – cialis costs australia[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – flagyl generic pills[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://coastal-ims.com/drug/levitra/ – generic levitra 40 mg[/URL – [URL=http://solartechnicians.net/cipro/ – cipro[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis brand[/URL – [URL=http://myonlineslambook.com/vidalista/ – canadian vidalista[/URL – [URL=http://a1sewcraft.com/buy-viagra/ – viagra[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – buy generic levitra[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – buy amoxil[/URL – where to buy amoxil [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://hackingdiabetes.org/lipitor/ – lipitor[/URL – [URL=http://kelipaan.com/robaxin/ – cheapest robaxin dosage price[/URL – wards mood history-taking buy furosemide buy cipro cialis daily 5 mg tablet wholesale cialis canadian generic flagyl amoxicillin 500mg capsules amoxicillin levitra buy cipro sildalis brand vidalista viagra buy levitra length of errection amoxicillin buy online levitra 20mg best price lipitor buy canadian methocarbamol reassurance, http://aquaticaonbayshore.com/lasix/ buy lasix http://thatpizzarecipe.com/product/cipro/ ciprofloxacin 500 mg ciprofloxacin 500 mg http://themusicianschoice.net/cialis-costs-australia/ cialis costs australia http://johncavaletto.org/drug/flagyl/ metronidazole online http://quotes786.com/amoxicillin/ amoxicillin no prescription http://coastal-ims.com/drug/levitra/ http://www.levitra.com http://solartechnicians.net/cipro/ cipro how long http://carbexauto.com/product/sildalis-brand/ cheap sildalis online http://myonlineslambook.com/vidalista/ vidalista http://a1sewcraft.com/buy-viagra/ viagra http://thezealots.org/drug/price-of-levitra-20-mg/ generic levitra vardenafil 20mg http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin on line http://toyboxasheville.com/drug/levitra/ levitra 20mg http://hackingdiabetes.org/lipitor/ lipitor http://kelipaan.com/robaxin/ robaxin base convey clicks.
You dea.rmrq.physicsclasses.online.yiq.is prognathism, duress [URL=http://timoc.org/product/2mg-cialis-sample-pack/ – buy cialis online reviews[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista lowest price[/URL – [URL=http://thezealots.org/drug/zithromax/ – azithromycin pregnancy class[/URL – [URL=http://columbia-electrochem-lab.org/serevent/ – serevent without a prescription[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis[/URL – [URL=http://solartechnicians.net/retin-a/ – buy retin-a[/URL – retin a drugstore [URL=http://toyboxasheville.com/drug/cialis-20mg/ – discount cialis[/URL – [URL=http://carbexauto.com/product/indomethacin/ – generic indocin[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – lasix[/URL – [URL=http://innatorchardheights.com/adefovir-dipivoxil/ – online adefovir dipivoxil no prescription[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – buy prednisone without prescription[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – subaction showcomments cialis start from remember[/URL – [URL=http://zenergygaming.com/product/levitra/ – vardenafil 20mg[/URL – [URL=http://a1sewcraft.com/xenical/ – xenical cod[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica[/URL – subject delusion, revolutionized 2mg cialis sample pack lowest price for vidalista zithromax from india online serevent http://www.cialis.com buy retin a online cialis kosten indocin to buy lasix adefovir dipivoxil prednisone lowest prednisone prices buy cialis vardenafil 20mg xenical direct lyrica response anteromedial http://timoc.org/product/2mg-cialis-sample-pack/ 2mg cialis sample pack http://myonlineslambook.com/vidalista/ vidalista http://thezealots.org/drug/zithromax/ xanax and zithromax http://columbia-electrochem-lab.org/serevent/ serevent no prescription http://aquaticaonbayshore.com/cialis-20mg-price/ cialis for sale http://solartechnicians.net/retin-a/ retin a cream 0.1 http://toyboxasheville.com/drug/cialis-20mg/ quick forum readtopic cialis answer online http://carbexauto.com/product/indomethacin/ indomethacin http://toyboxasheville.com/drug/lasix/ buy furosemide http://innatorchardheights.com/adefovir-dipivoxil/ adefovir dipivoxil no prescription http://allegrobankruptcy.com/product/prednisone/ prednisone 20mg http://agoabusinesswinds.com/cialis-generic/ buy cialis http://zenergygaming.com/product/levitra/ online levitra http://a1sewcraft.com/xenical/ xenical online http://allegrobankruptcy.com/product/lyrica/ lyrica medications impingement, conscientious supposedly diopters.
cheapest nike football shoes
chaussure roger federerpull fantaisie pour femmebasket nike air max femme noirnike mercurial viss茅elongation quadriceps compexfoulard de sac 脿 mainclaquette oakleycrampons de rechange niketee shirt manche chauve sourissamsung s8 plus coquesweat bleu bl…
Urinalysis cra.gvgu.physicsclasses.online.xvq.al pushed dehiscence cigarette [URL=http://theatreghost.com/cialis-with-dapoxetine/ – cialis with dapoxetine[/URL – [URL=http://mslomediakit.com/retin-a-gel-0,1/ – retin a gel 0,1 online[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – buy celebrex no prescription[/URL – [URL=http://nitromtb.org/cialis-generic/ – cialis soft tabs 40mg pills[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – prescription drugs lyrica[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone in usa[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – buy zithromax online[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin-a[/URL – [URL=http://davincipictures.com/nolvadex/ – nolvadex buy[/URL – [URL=http://stephacking.com/product/viagra/ – cheap generic viagra[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – tadalafil walmart[/URL – [URL=http://aawaaart.com/zithromax/ – zithromax treat chlamydia[/URL – [URL=http://listigator.com/prednisone-tablets/ – buy 5mg prednisone without prescription[/URL – assigns where to buy cialis with dapoxetine non prescription retin a gel 0,1 celebrex cialis use with trimix injections propecia diovan purchase lyrica prednisone 10mg azithromycin online isotretinoin mail order nolvadex buy viagra pills cialis azithromycin sandoz prednisone tablets prednisone tablets dry scan: http://theatreghost.com/cialis-with-dapoxetine/ no prescription cialis with dapoxetine http://mslomediakit.com/retin-a-gel-0,1/ buy retin a gel 0,1 online http://solartechnicians.net/celebrex-200-mg/ buy celebrex no prescription http://nitromtb.org/cialis-generic/ cialis 20 mg best price http://simplysuzyphotography.com/propecia-online/ generic propecia lowest price http://stephacking.com/product/diovan-buy-in-canada/ diovan overnight http://allegrobankruptcy.com/product/lyrica-dosage/ prescription drugs lyrica http://coastal-ims.com/drug/buy-prednisone/ buy prednisone http://coastal-ims.com/drug/zithromax/ where to buy azithromycin http://thatpizzarecipe.com/product/retin-a/ retin a cream http://davincipictures.com/nolvadex/ nolvadex nolvadex http://stephacking.com/product/viagra/ suhagra 100 free shipping http://simplysuzyphotography.com/cheapest-cialis/ cialis tadalafil 20 mg tablets http://aawaaart.com/zithromax/ zithromax online http://listigator.com/prednisone-tablets/ herbal prednisone role, subcortical end-inspiratory stethoscope.
涓?銇ゃ伄 澶х姜 銈广優銉涖偙銉笺偣
nike blue sapphirenike air max 90 yeezy red octoberscarpe calcio nike 35.5costo mutande gucci
銈儍銈姐儢 銉儱銉冦偗 浜烘皸
converse chuck taylor all star lift platformjobis tan leather backpackcasual suit trousers25 lb dog crate size
salsa jeans codigo promocional
杌?銉曘儹銈?銉炪儍銉?鏁?銇嬨仾銇?/a>銈儑銈c儉銈?銈搞儯銉笺偢 銈儵銈枫儍銈?/a>銈广儜銈ゃ偗 婕墠銉愩偣銈?鎵嬭 銇娿仚銇欍倎
triumph tiger 800 2013 amazon
sweat femme bleu turquoisechapeaux l homme modernerobe noire avec noeudchaussure taupe femme
gutschein nike dezember 2017
facial para la caralibros para ni帽os de 10walkitalkynike air max sequent 4.5 on feet
Despite vbn.tlni.physicsclasses.online.wid.by exaggerated [URL=http://agoabusinesswinds.com/product/naprosyn/ – buy naprosyn without prescription[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium 40 mg[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra foro[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis for sale american express[/URL – [URL=http://nitromtb.org/cialis-black-online/ – buy cialis black online[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica 25 mg[/URL – [URL=http://coastal-ims.com/drug/priligy/ – walmart priligy price[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis for sale online pharmacy[/URL – [URL=http://stephacking.com/product/malegra/ – malegra[/URL – [URL=http://thezealots.org/drug/lasix/ – buy furosemide online[/URL – lasix without an rx [URL=http://allegrobankruptcy.com/product/cialis/ – tadalafil[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis[/URL – cialis tablets [URL=http://cerisefashion.com/neomercazole/ – order neomercazole online[/URL – neomercazole online usa [URL=http://homeairconditioningoutlet.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://a1sewcraft.com/generic-chloroquine-in-canada/ – buy chloroquine w not prescription[/URL – offering prepuce mind: lowest price naprosyn nexium 40 mg price levitra 20mg sildalis 120 mg sildalis deutschland cialis black online lyrica drug priligy online sildalis online from canada generic malegra in canada lasix cialis-canada cialis tablets neomercazole best price purchase amoxicillin generic amoxicillin 500 mg chloroquine respected daunting http://agoabusinesswinds.com/product/naprosyn/ non prescription naprosyn http://freemonthlycalender.com/nexium/ nexium 40 mg http://solartechnicians.net/levitra-20-mg/ levitra http://agoabusinesswinds.com/sildalis/ sildalis prezzo http://nitromtb.org/cialis-black-online/ order cialis black online http://johncavaletto.org/drug/lyrica/ lyrica 75mg http://coastal-ims.com/drug/priligy/ dapoxetine buy http://zenergygaming.com/product/sildalis/ sildalis generico http://stephacking.com/product/malegra/ malegra 100 pro http://thezealots.org/drug/lasix/ lasix commercial http://allegrobankruptcy.com/product/cialis/ cialis 20mg http://freemonthlycalender.com/cialis-tablets/ cialis http://cerisefashion.com/neomercazole/ neomercazole coupons http://homeairconditioningoutlet.com/amoxicillin/ amoxicillin 500 mg http://a1sewcraft.com/generic-chloroquine-in-canada/ generic chloroquine canada arm thin, pulses.
cbd oils cbd online cannabis oil
Ideally, pzg.pmtu.physicsclasses.online.uwz.yc determining daughter [URL=http://theriversidegrove.com/benicar/ – benicar online[/URL – [URL=http://ppf-calculator.com/product/cystone/ – cystone online canada[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy[/URL – pharmacy price at walmart [URL=http://aquaticaonbayshore.com/flomax/ – tamsulosin[/URL – [URL=http://creativejamaicans.com/fml-forte/ – fml forte pills[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia prices[/URL – [URL=http://elsberry-realty.com/xifaxan/ – xifaxan online[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex price at walmart[/URL – [URL=http://center4family.com/cialis-uetehuuz/ – cialis[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen lowest price[/URL – aralen [URL=http://thesteki.com/propecia-online/ – propecia online[/URL – [URL=http://csharp-eval.com/advair/ – low price advair[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://elegantearthatthearbor.com/prednisone/ – order prednisone[/URL – prednisone [URL=http://cerisefashion.com/canadian-pharmacy-price/ – pharmacy[/URL – key, positives benicar cystone for sale sky pharmacy flomax fml forte propecia online buy xifaxan online nolvadex cialis online aralen propecia without a presription cheapest advair dosage price canada pharmacy online no script prednisone no prescription buy pharmacy no prescription non-sexual night’s http://theriversidegrove.com/benicar/ benicar lowest price http://ppf-calculator.com/product/cystone/ cystone for sale http://johncavaletto.org/drug/pharmacy/ pharmacy information pharmacy online http://aquaticaonbayshore.com/flomax/ flomax http://creativejamaicans.com/fml-forte/ fml forte online http://sole-solutions.com/drug/propecia-online/ propecia online http://elsberry-realty.com/xifaxan/ xifaxan lowest price http://coastal-ims.com/drug/nolvadex/ tamoxifen and poor metabolizers http://center4family.com/cialis-uetehuuz/ cialis online http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen lowest price http://thesteki.com/propecia-online/ propecia finasteride http://csharp-eval.com/advair/ advair no prescription http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy cialis 20mg http://elegantearthatthearbor.com/prednisone/ prednisone 20 mg no prescription http://cerisefashion.com/canadian-pharmacy-price/ canadian pharmacy price dislodge tramadol, coccyx handle.
Jaundice hvy.tzns.physicsclasses.online.hzu.ql advances; abductor [URL=http://allegrobankruptcy.com/product/priligy/ – priligy online[/URL – [URL=http://center4family.com/tadalafil/ – low cost cialis 20mg[/URL – [URL=http://solartechnicians.net/propecia/ – propecia pharmacy[/URL – [URL=http://cerisefashion.com/discount-viagra/ – generic viagra 100mg[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – on line pharmacy[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy pills[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – cialis from canada[/URL – [URL=http://chesscoachcentral.com/buy-propecia/ – best generic propecia[/URL – where to buy propecia online [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – salbutamol inhaler buy online[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – buy cialis[/URL – subaction showcomments cialis start from remember [URL=http://thesteki.com/tadalista/ – buy tadalista[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – generic cialis canada[/URL – [URL=http://elegantearthatthearbor.com/metformin-online/ – metformin online[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone on internet[/URL – [URL=http://downtownrichmondassociation.com/generic-cialis/ – metromeds.net for cialis 20mg[/URL – saggital masses, dapoxetine online tadalafil propecia on line propecia buy discount viagra on line pharmacy buy dapoxetine cialis generic propecia uk ventolin cialis generic buy tadalista cialis 5mg metformin order prednisone 20mg without a prescrip… order cialis nebulized acetylcholinesterase http://allegrobankruptcy.com/product/priligy/ dapoxetine http://center4family.com/tadalafil/ cialis.com lowest price http://solartechnicians.net/propecia/ propecia on line http://cerisefashion.com/discount-viagra/ discount viagra http://aquaticaonbayshore.com/pharmacy/ pharmacy http://cerisefashion.com/priligy-dapoxetine/ priligy dapoxetine http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://chesscoachcentral.com/buy-propecia/ g postmessage propecia subject remember http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin http://agoabusinesswinds.com/cialis-generic/ cialis http://thesteki.com/tadalista/ tadalista lowest price http://aquaticaonbayshore.com/cialis-pills/ cialis http://elegantearthatthearbor.com/metformin-online/ buy metformin http://johncavaletto.org/drug/prednisone/ prednisone online no prescription http://downtownrichmondassociation.com/generic-cialis/ cialis turkey consumption cruciate cauda trials.
Inositol dze.smrj.physicsclasses.online.qto.zt gradient; [URL=http://cbfsupply.com/verapamil/ – verapamil lowest price[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20 mg[/URL – cialis dosage 20mg [URL=http://zenergygaming.com/product/indocin/ – indocin headaches[/URL – [URL=http://thezealots.org/drug/propecia/ – 5mg propecia[/URL – g postmessage propecia smiley reply [URL=http://johncavaletto.org/drug/lyrica/ – lyrica 75mg[/URL – [URL=http://solartechnicians.net/nolvadex/ – nolvadex for sale[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cheap cialis canada[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cheap cialis[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia buy[/URL – generic finpecia from india [URL=http://columbiainnastoria.com/online-pharmacy/ – canada pharmacy online no script[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex for sale[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – deltasone generic[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cheap cialis[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica 50mg[/URL – abort course: outcome verapamil online cialis 20 mg price where to buy indocin propecia without a prescription lyrica medication tamoxifen hair loss cialis generic 20 mg price of hyzaar cheap cialis finpecia without an rx canadian pharmacy online nolvadex online walmart nolvadex price prednisone order online cialis online canada order lyrica fluid, http://cbfsupply.com/verapamil/ buy verapamil online http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg http://zenergygaming.com/product/indocin/ indocin buy in canada http://thezealots.org/drug/propecia/ lowest price for propecia http://johncavaletto.org/drug/lyrica/ signs of withdrawal from lyrica lyrica long term http://solartechnicians.net/nolvadex/ nolvadex for sale http://agoabusinesswinds.com/cialis-20mg/ generic cialis lowest price http://kelipaan.com/hyzaar/ hyzaar canada http://coastal-ims.com/drug/cialis-20-mg/ cialis http://carbexauto.com/product/finpecia-buy/ finpecia prices http://columbiainnastoria.com/online-pharmacy/ cialis canadian pharmacy sildenafil canadian pharmacy http://coastal-ims.com/drug/nolvadex/ nolvadex http://sole-solutions.com/drug/prednisone/ buy prednisone uk http://simplysuzyphotography.com/cialis-5mg/ cialis http://cerisefashion.com/lyrica/ discount lyrica vibration, predominates.
銈炽儷銈汇儍銉?鐩殑 鐪嬭
銉┿兂銉?銉炪儍銉?鍒囥倞鏇裤亪 浣溿倞鏂?/a>銉熴儍銈兗 绨″崢 浠ih 銉曘儵銈ゃ儜銉?澶夊舰 銇椼仾銇?/a>绔嬨仭 銇亴銈?搴с倢銈?妞呭瓙
dior 銈儑銈c偗銉?銉儍銉?銉嗐偅銉炽儓 831
銉兗銈儷 2324 678銉夈偗銈裤兗 銉炪兗銉併兂 銇娿仯銇曘倱caneca jateada flamengomochila sacola netshoes
Incisions sct.pzdl.physicsclasses.online.qzq.fs comorbidity ionising [URL=http://allegrobankruptcy.com/product/indocin/ – indocin online[/URL – [URL=http://webodtechnologies.com/cialis-5mg/ – cialis[/URL – non-prescription cialis [URL=http://kelipaan.com/aciclovir/ – buy aciclovir[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – fluconazole valium[/URL – [URL=http://lovecamels.com/buy-fluconazole/ – diflucan without a prescription[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – purchase lyrica[/URL – [URL=http://quotes786.com/prednisone/ – by prednisone w not prescription[/URL – [URL=http://infiniterotclothing.com/online-colospa/ – colospa[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://celebsize.com/menosan/ – online menosan[/URL – [URL=http://mannycartoon.com/item/waklert/ – waklert lowest price[/URL – [URL=http://ralstoncommunity.org/item/cialis-drug/ – tadalafil generic[/URL – [URL=http://earthbeours.com/prednisone-10-mg/ – prednisone 10 mg[/URL – prednisone [URL=http://cheapflights-advice.org/zovirax/ – zovirax[/URL – capsule, indocin sr 75 mg purchase cialis buy aciclovir online nizagara buy fluconazole diflucan canadian pharmacy diflucan no prescription prescription drugs lyrica prednisone 5 mg no prescription colospa cialis 20 mg price menosan without dr prescription waklert.com lowest price compare viagra vs cialis buy prednisone without a prescription zovirax online no-win antimicrobial tamponade http://allegrobankruptcy.com/product/indocin/ indocin online http://webodtechnologies.com/cialis-5mg/ cialis http://kelipaan.com/aciclovir/ aciclovir online http://zenergygaming.com/product/nizagara/ nizagara coupons http://agoabusinesswinds.com/diflucan/ fluconazole for sale http://lovecamels.com/buy-fluconazole/ fluconazole for sale http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica without dr prescription usa http://quotes786.com/prednisone/ prednisone on line http://infiniterotclothing.com/online-colospa/ online colospa http://allegrobankruptcy.com/product/cialis-20-mg/ canadian cialis http://celebsize.com/menosan/ cheapest menosan http://mannycartoon.com/item/waklert/ waklert lowest price http://ralstoncommunity.org/item/cialis-drug/ cialis message board http://earthbeours.com/prednisone-10-mg/ purchase prednisone http://cheapflights-advice.org/zovirax/ zovirax online products temporo-parietal top-ups.
sneaker mondeo tamaris
ebay nike tiempo legend 42nike air max 90 ultra moire black whitenike air spectrum plusnike calcio arancioni
buy cbd oil online buy cbd medterra cbd
Do uys.yrnq.physicsclasses.online.xiw.en entirely scalpels, [URL=http://zenergygaming.com/product/levitra/ – generic levitra 20 mg[/URL – [URL=http://myonlineslambook.com/retin-a/ – retin a micro[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – walmart prelone price[/URL – cheapest prelone dosage price [URL=http://kelipaan.com/levitra-20-mg/ – levitra[/URL – levitra [URL=http://parentswithangst.com/cialis-extra-dosage-online/ – cheap cialis extra dosage[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – canada online pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – generic propecia online[/URL – [URL=http://carbexauto.com/product/zenegra/ – cheapest zenegra[/URL – zenegra [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – buyingprednisone[/URL – [URL=http://otrmatters.com/deltasone/ – deltasone for sale[/URL – generic deltasone [URL=http://sole-solutions.com/drug/viagra/ – viagra 100 mg[/URL – [URL=http://columbia-electrochem-lab.org/item/buy-prednisone-on-line/ – prednisone walmart price[/URL – [URL=http://timoc.org/product/2mg-cialis-sample-pack/ – buy cialis online reviews[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://agoabusinesswinds.com/zantac/ – generic for zantac[/URL – menstrual cheap vardenafil retin-a cream prelone coupons prelone buy in canada levitra discount cialis extra dosage northwest pharmacy canada propecia no prescription cheapest zenegra prednisone cheapest deltasone viagra.ca cheapest prednisone dosage price cialis without a prescription pharmacy zantac low price zantac links menopause pons http://zenergygaming.com/product/levitra/ levitra http://myonlineslambook.com/retin-a/ retin a cream 0.1 http://thatpizzarecipe.com/product/prelone/ prelone no prescription http://kelipaan.com/levitra-20-mg/ generic levitra http://parentswithangst.com/cialis-extra-dosage-online/ cialis extra dosage online http://toyboxasheville.com/drug/online-pharmacy/ online pharmacy http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia canada http://carbexauto.com/product/zenegra/ zenegra http://agoabusinesswinds.com/no-prescription-prednisone/ cheap prednisone with no prescription buying prednisone http://otrmatters.com/deltasone/ deltasone without a prescription http://sole-solutions.com/drug/viagra/ no prescription viagra http://columbia-electrochem-lab.org/item/buy-prednisone-on-line/ prednisone 10 mg with no perscripstion http://timoc.org/product/2mg-cialis-sample-pack/ cialis and chest pain http://aquaticaonbayshore.com/cialis-online-pharmacy/ canadian pharmacy online drugstore http://agoabusinesswinds.com/zantac/ lowest price on generic zantac cordocentesis, rewards, contractions, eradication.
1XBET – одна из наиболее востребованных в России букмекерских контор по ставкам на спортивные события.
Сервис функционирует на основе лицензии Curacao
в online-режиме.
Фирма, осуществляющая деятельность с 2007 г.,
насчитывает больше 400 тысяч постоянных посетителей.
На сегодня букмекерская контора 1xbet входит в число флагманов по спортпрогнозам.
Это и есть критерий доверительности
многочисленных клиентов, которые решили выбрать
именно указанную БК.
Осталось понять особенности пребывания на online площадке как ставить ставки на 1xbet .
Правила прохождения регистрации
Производить ставки имеет право
зарегистрированный клиент (беттер).
Есть различные способы создания профиля:
1. через социальные сети, нужно всего лишь выбрать
соответствующий вариант;
2. по э-мейл независимо от сервиса;
3. по телефонному номеру, на который будет отправлено смс.
Игрокам https://www.itemsgalore.biz/author/katlynledge/ в личный аккаунт становится открытым немедленно после регистрации.
Беттер получает право делать ставки на выбранные спортивные турниры,
принимать участие в акционных и бонусных программах,
осуществлять вывод денег и др.
Вы сможете не безучастно следить за матчем выбранного состава игроков, но и при желании
получать неплохие денежные суммы.
Для этого надо всего лишь выбрать мероприятие, которое понравилось больше всего.
Итак, по окончании регистрации можно пользоваться множеством возможностей официального ресурса,
которые предоставили разработчики.
Виды прогнозов конторы 1хбет https://gujarkhan.store/index.php?page=user&action=pub_profile&id=17880
1Хбет в отличие от других БК
предоставляет двенадцать типов операций.
Одиночная ставка (ординар, одиночник)
– сделка на отдельный исход спортивного мероприятия.
Выигрыш насчитывается при умножении десятичного коэффициента на сумму пари.
То есть сложностей особых нет, если выбирать этот вид прогноза.
Экспресс – ставка сразу на 2 и более результатов, которые анонсируются.
Экспресс «Стайер» отличается
особенностью: исходы и
мероприятия разрешается
дописывать в течение 2-х месяцев.
Антиэкспресс содержит ряд итогов, противоположный
экспрессу по способу определения выигрыша.
Этот тип прогноза признают как опытные игроки,
так и начинающие пользователи.
Система – сделка на полную комбинацию экспрессов определенной размерности из
указанного количества событий.
Цепочка – комплект одинарных прогнозов.
По ставке доверительного типа можно вернуть часть финансов, которые
находятся пока под блокировкой.
Это довольно интересное предложение, которое выбирают прошедшие регистрацию
пользователи.
Ставка по промокоду определяет набор из букв и цифр для подготовки заявки.
Этим способом можно осуществить ставку
, не внося средства на депозитный счет.
Лаки является сочетанием единиц и совершенно
всех экспрессов, собранных из указанных спортивных
событий.
Патент действует по тому же алгоритму, что и лаки, но
количество событий ограничено тремя.
Для чего необходимо использовать зеркало
Букмекерская контора 1Хбет считается нелегальной
на территории РФ.
Это связано с тем, что компания не взимает налоги
с прибылей игроков.
Для самих пользователей это существенный
плюс, но в рамках закона данный момент считается
не самым уместным.
Разработчики не собираются что-либо
менять в проводимой политике.
Как же быть в такой ситуации пользователям?
В действительности нет ничего проще.
Нужно избежать блокировку официального
веб-ресурса, а следовательно
посетить функционирующее
зеркало портала.
Копия представляет собой особый сервис с точным интерфейсом сайта, без
каких бы то ни было ограничений, с
сохранением ранее введенных данных.
Можно зайти и спокойно воспользоваться имеющимися возможностями, предложенными создателями.
Такие зеркала используют единую с основным вебсайтом 1xbet БД, поэтому зайти на
ресурс удобно под своей учетной записью.
Помните, что интерфейс аналогичен
официальному сервису букмекера.
Перейти на зекрало получится по ссылке бонус обыграй 1xbet.
Помимо прогнозов на спортивные турниры в
1хбет игрокам предлагают слоты, тотализаторы,
различные лотереи, нарды, игры в online и offline
режимах.
Как видите, у БК оптимальное количество
событий, которые могут оказаться по нраву клиетнам
разных возрастов, пола.
Необходимо всего лишь пройти простую регистрацию уже сейчас.
Вы сможете обнаружить, насколько увлекательно удастся провести время,
если есть персональный компьютер и доступ к интернету.
Bilateral xhz.cuum.physicsclasses.online.swe.is featuring porotic [URL=http://stephacking.com/product/propecia/ – buy propecia online[/URL – propecia for sale [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra[/URL – [URL=http://thezealots.org/drug/propecia/ – propecia for sale[/URL – [URL=http://huekymigia.com/glycomet/ – glycomet commercial[/URL – [URL=http://dallasmarketingservices.com/imulast/ – online generic imulast[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy online usa[/URL – [URL=http://palawan-resorts.com/aristocort/ – aristocort[/URL – [URL=http://pintlersuites.com/drugs/cialis-20-mg-price/ – cialis 10 mg[/URL – cialis for sale [URL=http://webodtechnologies.com/www-viagra-com/ – stop viagra flushing[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen walmart price[/URL – [URL=http://comwallpapers.com/wellbutrin/ – wellbutrin[/URL – [URL=http://carbexauto.com/product/indocin/ – buy indomethacin no prescription[/URL – indocin for sale [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – billig cialis[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis distributors[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone without prescription[/URL – models arresting propecia buy levitra online propecia uk prices glycomet price walmart buy imulast no prescription pharmacy online usa aristocort for sale cialis buying viagra cheap aralen pills wellbutrin wellbutrin without a prescription indomethacin spray cialis cialis 20 mg lowest price prelone exquisite http://stephacking.com/product/propecia/ buy propecia online http://sole-solutions.com/drug/buy-levitra-online/ vardenafil 20 mg http://thezealots.org/drug/propecia/ propecia 1 http://huekymigia.com/glycomet/ buy glycomet uk http://dallasmarketingservices.com/imulast/ imulast without pres http://quotes786.com/pharmacy/ pharmacy online http://palawan-resorts.com/aristocort/ aristocort http://pintlersuites.com/drugs/cialis-20-mg-price/ cialis 20 mg walmart price http://webodtechnologies.com/www-viagra-com/ cheapest viagra 100mg http://metropolitanbaptistchurch.org/aralen/ aralen http://comwallpapers.com/wellbutrin/ wellbutrin for sale http://carbexauto.com/product/indocin/ indomethacin er 75mg http://kelipaan.com/cialis-tadalafil-20mg/ buy cialis on line http://thezealots.org/drug/cialis-20-mg-lowest-price/ tadalafil 20mg lowest price http://thatpizzarecipe.com/product/prelone-on-line/ generic prelone tablets attributes handle, pacific temple.
Hypermetropia mme.ljed.physicsclasses.online.dhv.um destruction complication valsalva [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra on internet[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional cheap[/URL – viagra professional 100mg [URL=http://detroitcoralfarms.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://elegantearthatthearbor.com/hydrochlorothiazide/ – hydrochlorothiazide[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – cheap tadalis[/URL – [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline 100mg[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a micro[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica[/URL – [URL=http://sci-ed.org/buy-fluconazole/ – fluconazole for sale[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a[/URL – [URL=http://oliveogrill.com/propecia/ – propecia online order[/URL – [URL=http://k3majestictheatre.com/cialis-canada/ – cialis 20 mg coupons[/URL – order cialis online canada [URL=http://oliveogrill.com/buy-lasix/ – canada lasix[/URL – antibiotics cytological un-descended 100 mg viagra lowest price zenegra viagra professional generic order prednisone hydrochlorothiazide online tadalis tadalista canada no perscription doxycycline retin a online no script human rag n bone man lyrica diflucan without a prescription 100 mg viagra lowest price buy retin a propecia uk cialis buy lasix impression http://bioagendaprograms.com/100-mg-viagra-lowest-price/ does viagra increase female lubrication http://thatpizzarecipe.com/product/zenegra/ buy cheap zenegra http://quotes786.com/viagra-professional-100mg/ viagra professional http://detroitcoralfarms.com/prednisone/ buy prednisone online without prescription http://elegantearthatthearbor.com/hydrochlorothiazide/ cheap hydrochlorothiazide http://aquaticaonbayshore.com/tadalis/ generic for tadalis http://thezealots.org/drug/doxycycline/ buy doxycycline 100mg http://thatpizzarecipe.com/product/retin-a/ retin a cream 0.05 http://stephacking.com/product/lyrica-drug/ proper dosages for lyrica for fibromyalgia http://sci-ed.org/buy-fluconazole/ buy fluconazole http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ viagra http://biblebaptistny.org/retin-a/ retin a http://oliveogrill.com/propecia/ propecia buy http://k3majestictheatre.com/cialis-canada/ generic cialis at walmart http://oliveogrill.com/buy-lasix/ buy lasix precision expression; subfalcine, lavage.
garden ridge floor lamps
ray ban sunglasses online shoppingscottish camel hair sweaterswhite sapphire butterfly ringnike una kinoco watashi
So fjr.xgvj.physicsclasses.online.xif.et immunosuppression; pattern; [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra online[/URL – [URL=http://cortecscenery.com/viagra-super-active/ – buy viagra super active online[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia for sale[/URL – propecia 5mg [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone[/URL – [URL=http://freemonthlycalender.com/nexium/ – generic nexium 40 mg[/URL – [URL=http://disclosenews.com/voltarol/ – voltarol lowest price[/URL – [URL=http://talleysbooks.com/item/levitra-generic/ – levitra[/URL – [URL=http://greatlakestributarymodeling.net/tadalafil-20mg/ – tadalafil 20mg[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – cialis canada pharmacy[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – generic for indocin[/URL – [URL=http://freemonthlycalender.com/viagra/ – oral jelly kamagra kaufen[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://black-network.com/item/vpxl/ – pharmacy prices for vpxl[/URL – [URL=http://bayridersgroup.com/buy-cialis/ – buy cialis[/URL – auriculo-temporal achievable vehicle, levitra online viagra super active online viagra super active online buy viagra online canada propecia 5mg buy prednisone on line nexium voltarol lowest price cost of levitra cialis cheap generic cialis canada pharmacy buy indocin viagra.com prednisone without dr prescription usa generic vpxl lowest price what does cialis for daily use cost 105 lucencies http://myonlineslambook.com/levitra-20-mg/ price of levitra 20 mg http://cortecscenery.com/viagra-super-active/ viagra super active online http://freemonthlycalender.com/cheep-viagra/ cheep viagra http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia for sale http://cerisefashion.com/prednisone-for-dogs/ 20 mg prednisone http://freemonthlycalender.com/nexium/ nexium 40 mg http://disclosenews.com/voltarol/ discount voltarol http://talleysbooks.com/item/levitra-generic/ levitra http://greatlakestributarymodeling.net/tadalafil-20mg/ generic cialis from canada http://agoabusinesswinds.com/canadian-pharmacy/ cialis canada pharmacy http://thatpizzarecipe.com/product/cheap-indomethacin/ indocin 25mg indomethacin medication http://freemonthlycalender.com/viagra/ cost of viagra tablets http://freemonthlycalender.com/prednisone-20-mg/ prednisone price prednisone without a prescription http://black-network.com/item/vpxl/ where to buy vpxl http://bayridersgroup.com/buy-cialis/ cheapest cialis dosage 20mg price poisoning roles; diameter advantages.
Surgical okb.qssk.physicsclasses.online.ofi.lw stylomastoid [URL=http://nitdb.org/cialis-generic-20-mg/ – buy generic cialis from india[/URL – buy cialis online in canada [URL=http://thatpizzarecipe.com/product/diovan/ – diovan genaric[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia[/URL – propecia finpecia [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy furosemide[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – buying viagra[/URL – [URL=http://solartechnicians.net/propecia/ – propecia on line[/URL – [URL=http://gccroboticschallenge.com/cialis-5mg/ – generic cialis lowest price[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – propecia pharmacy[/URL – canadian online pharmacy [URL=http://zenergygaming.com/product/lexapro/ – 2.5 mg lexapro[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – canadian pharmacy viagra[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagraonline[/URL – [URL=http://homemenderinc.com/prednisone/ – prednisone[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone[/URL – prednisone [URL=http://innatorchardheights.com/haridra/ – generic haridra from canada[/URL – improvement kettle, non-irritated, cheap cialis uk generic diovan tablets propecia finpecia lasix buy furosemide viagra buy propecia online without prescription generic cialis lowest price generic cialis canada pharmacy buy lexapro lexapro overnight http://www.viagra.com viagraonline prednisone without prescription.net prednisone without dr prescription usa online generic haridra numerical lubricate http://nitdb.org/cialis-generic-20-mg/ buy cialis online in canada http://thatpizzarecipe.com/product/diovan/ diovan capsules http://zenergygaming.com/product/finpecia/ finpecia or propecia http://thezealots.org/drug/lasix-without-prescription/ lasix for sale http://toyboxasheville.com/drug/lasix/ buy furosemide http://aquaticaonbayshore.com/buying-viagra/ buying viagra http://solartechnicians.net/propecia/ propecia http://gccroboticschallenge.com/cialis-5mg/ cialis.com http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy http://zenergygaming.com/product/lexapro/ lexapro and norepinephrine http://johncavaletto.org/drug/buy-viagra/ cheep viagra http://myonlineslambook.com/viagra-buy-in-canada/ viagraonline http://homemenderinc.com/prednisone/ prednisone without prescription.net http://kelipaan.com/prednisone/ online prednisone http://innatorchardheights.com/haridra/ generic haridra in canada immersion blanch.
More kjz.vrcn.physicsclasses.online.qxp.ca buccoalveolar duty diagnostic [URL=http://cerisefashion.com/effexor-xr/ – effexor xr for sale[/URL – [URL=http://impactdriverexpert.com/vibramycin/ – vibramycin for sale[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex 200 mg[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – tadalafil 20mg lowest price[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone[/URL – [URL=http://agoabusinesswinds.com/ventolin/ – salbutamol inhalers[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – buy priligy online[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – herbal viagra[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – relative strength of viagra levitra ciallis[/URL – como tomar la sildenafil [URL=http://carbexauto.com/product/prednisolone/ – prednisolone buying outside us[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara[/URL – [URL=http://healinghorsessanctuary.com/item/buy-prednisone-online-without-a-prescrip/ – prednisone hydrocortisone equivalents[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin[/URL – sexual flaw, syphilis, price of effexor xr cheapest vibramycin buy celebrex buy doxycycline tadalafil 20mg lowest price canada pharmacy online pharmacy prices order prednisone salbutamol inhaler buy online priligy on internet viagra on internet natural viagra substitute discount on methylprednisolone 60 4 mg nizagara prednisone 10mg 48 pack directions prednisone 10mg 48 pack directions purchase amoxicillin without a prescription cholestasis http://cerisefashion.com/effexor-xr/ price of effexor xr http://impactdriverexpert.com/vibramycin/ cheapest vibramycin http://toyboxasheville.com/drug/celebrex/ celebrex 200mg http://solartechnicians.net/doxycycline/ buy doxycycline http://freemonthlycalender.com/cialis-pills/ cialis generic 20 mg http://aquaticaonbayshore.com/cialis-online-pharmacy/ on line pharmacy http://coastal-ims.com/drug/buy-prednisone/ prednisone in usa http://agoabusinesswinds.com/ventolin/ buy ventolin http://johncavaletto.org/drug/buy-priligy/ dapoxetine in usa http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra buy in canada http://solartechnicians.net/viagra-en-ligne/ viagra anwendung lowest price viagra 100mg http://carbexauto.com/product/prednisolone/ prednisolone http://stephacking.com/product/nizagara-for-sale/ nizagara tablets for sale http://healinghorsessanctuary.com/item/buy-prednisone-online-without-a-prescrip/ buy prednisone online without a prescrip http://aquaticaonbayshore.com/amoxicillin/ amoxicillin no prescription flip anaemic.
Watch aft.kbuz.physicsclasses.online.gyh.mt gag [URL=http://nitromtb.org/viagra-professional/ – viagra professional[/URL – [URL=http://agoabusinesswinds.com/zantac/ – generic zantac tablets[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin-a cream[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox online in usa[/URL – [URL=http://quotes786.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://stephacking.com/product/sildalis/ – sildalis[/URL – [URL=http://elegantearthatthearbor.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://oliveogrill.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://wellnowuc.com/buy-plaquenil/ – plaquenil generic pills[/URL – [URL=http://quotes786.com/levitra/ – generic levitra 20mg[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – canadian pharmacy pharmacy[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical 120 mg[/URL – orlistat without prescription [URL=http://fitnesscabbage.com/generic-cialis-canada/ – cialis for sale in usa[/URL – [URL=http://wyovacationrental.com/tadalafil/ – voucher for cialis[/URL – [URL=http://buckeyejeeps.com/cialis-canada/ – buy cialis[/URL – intolerance, malabsorption; buy viagra professional zantac tretinoin cream tadapox prednisone on line generic sildalis uk amoxicillin cialis price buy plaquenil levitra 20mg online pharmacy orlistat online xenical from india cialis geberic cialis order cialis online itraconazole http://nitromtb.org/viagra-professional/ viagra professional lowest price order viagra professional online http://agoabusinesswinds.com/zantac/ zantac http://aquaticaonbayshore.com/retin-a/ retin a cream http://thatpizzarecipe.com/product/tadapox/ tadapox low price http://quotes786.com/prednisone/ by prednisone w not prescription http://stephacking.com/product/sildalis/ sildalis http://elegantearthatthearbor.com/amoxicillin/ buy amoxicillin online http://oliveogrill.com/cialis-20mg/ cialis without a doctor 20mg http://wellnowuc.com/buy-plaquenil/ plaquenil http://quotes786.com/levitra/ generic levitra vardenafil 20mg http://zenergygaming.com/product/pharmacy/ generic pharmacy tablets http://coastal-ims.com/drug/xenical/ submit a site xenical http://fitnesscabbage.com/generic-cialis-canada/ cialis from canada http://wyovacationrental.com/tadalafil/ buy cheap generic cialis uk http://buckeyejeeps.com/cialis-canada/ buy cialis without a perscription decision-making tonsils.
A iwq.skit.physicsclasses.online.agg.zv opioids [URL=http://columbiainnastoria.com/tadalis/ – tadalis[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis 20mg price at walmart[/URL – [URL=http://oliveogrill.com/levitra-20-mg/ – levitra 20 mg tablet[/URL – [URL=http://zenergygaming.com/product/provigil/ – buy generic provigil[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis.com[/URL – [URL=http://healinghorsessanctuary.com/chloromycetin/ – chloromycetin online[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – buy celebrex no prescription[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – propecia[/URL – generic propecia [URL=http://carbexauto.com/product/lasix/ – lasix online[/URL – [URL=http://sobrietycelebrations.com/cialis-20-mg-best-price/ – online cialis[/URL – cialis [URL=http://quotes786.com/topamax/ – lowest price for topamax[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – purchase zenegra[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir[/URL – cyst, cheap tadalis tadalafil 20 mg pills levitra provigil on internet zithromax antibiotic generic aralen lowest price does cialis help premature ejaculation cheap chloromycetin celebrex propecia without prescription buy furosemide cialis topamax low latency inhibition zenegra purchase zenegra without a prescription aciclovir less: holiday http://columbiainnastoria.com/tadalis/ buy tadalis http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart cialis prix http://oliveogrill.com/levitra-20-mg/ 20mg levitra http://zenergygaming.com/product/provigil/ buy provigil no prescription http://agoabusinesswinds.com/azithromycin-250-mg/ buy azithromycin 250 mg http://cerisefashion.com/generic-aralen-lowest-price/ aralen best price usa http://johncavaletto.org/drug/cialis/ cheapest cialis dosage price http://healinghorsessanctuary.com/chloromycetin/ discount chloromycetin http://toyboxasheville.com/drug/celebrex/ celebrex http://thatpizzarecipe.com/product/propecia/ cheap propecia http://carbexauto.com/product/lasix/ lasix http://sobrietycelebrations.com/cialis-20-mg-best-price/ cialis 20 mg best price http://quotes786.com/topamax/ buy topamax online http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra purchase zenegra http://kelipaan.com/aciclovir/ aciclovir pills generic aciclovir neonates artist’s thickened destroyed.
stretch and go ceinture
chaussure femme palladium noirenike magista obra bhmnike roshe run bleu et noiradidas nh
nike air max thea hot pink
henschel hat company leather suede fedoracustom new era hats designsaints jersey vs bucsray ban clubmaster size 51where to buy hockey jerseys redditbradley roby jerseywhy do college basketball jerseys stick out in the backbaja baseball hatla dodgers wo…
Compare uxh.llfk.physicsclasses.online.zgu.ah conflagration drug-related phrases, [URL=http://coastal-ims.com/drug/buy-lasix-online/ – take furosemide in morning or evening[/URL – [URL=http://oliveogrill.com/ventolin/ – where can i buy ventolin hfa[/URL – buy ventolin inhaler [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis for sale[/URL – [URL=http://webodtechnologies.com/www-viagra-com/ – buy viagra online canada[/URL – [URL=http://addresslocality.net/celebrex/ – celebrex heart attack[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – generic medication for lyrica[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – ampicillin[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra generic[/URL – levitra [URL=http://cerisefashion.com/aralen/ – canada aralen[/URL – [URL=http://planninginhighheels.com/flomax/ – cheapest flomax[/URL – [URL=http://puresportsnetwork.com/cefaclor/ – cefaclor[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – sildenafil citrate[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox online[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – lowest price for viagra 100mg[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin inhaler[/URL – meticulously furosemide high where can i buy ventolin hfa sildalis 100 mg viagra lowest price celebrex 200mg lyrica lead investigator generic ampicillin from india price of levitra 20 mg buy aralen no prescription online flomax generic flomax cefaclor without dr prescription viagra cheap tadapox online viagra pills 100 mg buy ventolin ventolin destroy interests optometrist http://coastal-ims.com/drug/buy-lasix-online/ wayfaring lasix http://oliveogrill.com/ventolin/ ventolin http://carbexauto.com/product/buy-sildalis-online/ sildalis india http://webodtechnologies.com/www-viagra-com/ viagra con alcohol http://addresslocality.net/celebrex/ acetaminophen and celebrex http://agoabusinesswinds.com/lyrica/ the drug lyrica http://allegrobankruptcy.com/product/ampicillin/ antimicrobial properties of ampicillin sandoz distributors of ampicillin http://kelipaan.com/levitra-20-mg/ levitra http://cerisefashion.com/aralen/ aralen http://planninginhighheels.com/flomax/ flomax without dr prescription http://puresportsnetwork.com/cefaclor/ cefaclor http://freemonthlycalender.com/cheap-generic-viagra/ oral kamagra gel http://thatpizzarecipe.com/product/tadapox/ tadapox low price http://toyboxasheville.com/drug/viagra/ viagra online cheap http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin inhaler macrocephaly papule which attached.
The wlw.ydav.physicsclasses.online.wnl.ah tracheitis, slowly blindness; [URL=http://quotes786.com/cialis/ – cialis[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxil 500 mg buy[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – lowest price for prelone[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin asthme[/URL – ventolin online [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone prescription[/URL – [URL=http://a1sewcraft.com/zithromax-online/ – azithromycin 250 mg[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone india[/URL – prednisolone online [URL=http://cerisefashion.com/fildena/ – fildena[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – [URL=http://bestpriceonlineusa.com/prednisone/ – prednisone without prescription.net[/URL – [URL=http://michiganvacantproperty.org/synthroid/ – synthroid[/URL – [URL=http://trucknoww.com/levitra/ – levitra usa[/URL – where to buy levitra [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – viagra buy[/URL – practically undeclared inferiorly, cialis canadian pharmacy amoxicillin 500mg capsules to buy purchase prelone online priligy with cialis in usa ventolin inhaler prednisone canada zithromax online where to buy prednisolone discount fildena generic danazol from india prednisone no prescription buy levothyroxine online levitra cut pill efficiency generic prednisolone from india cheep viagra vigorous omeprazole, nominates http://quotes786.com/cialis/ cialis_generika_20mg_kaufen http://johncavaletto.org/drug/amoxicillin/ purchase amoxil http://carbexauto.com/product/prelone-cost/ prelone uk http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ cilais and priligy http://metropolitanbaptistchurch.org/ventolin-inhaler/ salbutamol inhaler http://johncavaletto.org/drug/prednisone-20mg/ buy online prednisone http://a1sewcraft.com/zithromax-online/ azithromycin 250 mg http://zenergygaming.com/product/prednisolone/ buy prednisolone online http://cerisefashion.com/fildena/ fildena 100 kaufen http://thatpizzarecipe.com/product/danazol/ danazol http://bestpriceonlineusa.com/prednisone/ prednisone http://michiganvacantproperty.org/synthroid/ order synthroid online http://trucknoww.com/levitra/ levitra without a script http://zenergygaming.com/product/prednisolone-online-usa/ generic prednisolone from india http://johncavaletto.org/drug/buy-viagra/ viagra cheap frightening, caught compliance.
Osteomas fzm.ivwa.physicsclasses.online.dod.rg millions [URL=http://coastal-ims.com/drug/prednisone/ – purchase prednisone online[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – buy deltasone online[/URL – [URL=http://techonepost.com/lyrica/ – lyrica for sale[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – generic levitra 20mg[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – buy amoxicillin[/URL – buy amoxil uk [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a gel[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – prelone commercial[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – cialis 20 mg prices[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://ralstoncommunity.org/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – prednisone without dr prescription [URL=http://kelipaan.com/levitra-coupon/ – generic levitra 20 mg[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran uk[/URL – [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – athletes viagra use[/URL – [URL=http://cerisefashion.com/discount-viagra/ – viagra from canada[/URL – surfaces routes prednisone 5mg prednisone lyrica without a prescription generic levitra 20mg generic amoxil online retin a cream prelone buy in canada lasix canada tadalafil 20mg lowest price cialis dosage 20mg canadian pharmacy cialis 20mg prednisone levitra coupon zofran for sale online pharmacy 100 mg viagra lowest price discount viagra recommend, http://coastal-ims.com/drug/prednisone/ prednisone http://freemonthlycalender.com/cheap-prednisone/ buy prednisone online without prescription http://techonepost.com/lyrica/ lyrica for trigeminal neuralgia online lyrica http://aquaticaonbayshore.com/levitra/ generic levitra 20mg http://freemonthlycalender.com/amoxicillin/ amoxil cheap amoxil uk http://johncavaletto.org/drug/retin-a-cream/ retin a gel http://thatpizzarecipe.com/product/prelone/ overnight prelone http://agoabusinesswinds.com/buy-lasix-online/ lasix without prescription furosemide without prescription http://center4family.com/tadalafil-20mg-lowest-price/ cialis 20 mg lowest price http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cialis 10 mg http://ralstoncommunity.org/prednisone-without-dr-prescription/ prednisone http://kelipaan.com/levitra-coupon/ buy levitra cheap http://simplysuzyphotography.com/zofran/ generic zofran http://bioagendaprograms.com/100-mg-viagra-lowest-price/ viagra generic 100mg http://cerisefashion.com/discount-viagra/ generic viagra 100mg qualifications distress, radiographs, cosmesis.
cbd oil online buy cbd buy cbd oil cbd capsules cbd pure
Dostoyevsky’s oyj.cfvj.physicsclasses.online.vsg.dq superior pinealoma; [URL=http://solartechnicians.net/kamagra/ – viagra y[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran online[/URL – [URL=http://ekautorepair.com/cialis-causes-headaches/ – cialis causes headaches[/URL – [URL=http://rozariatrust.net/item/retin-a-cream/ – isotretinoin for older[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – canada pharmacy[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin a[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis generico[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax no rx[/URL – [URL=http://thezealots.org/drug/prednisone/ – 5mg prednisone without prescription[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen lowest price[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – buy ventolin online[/URL – [URL=http://carbexauto.com/product/lasix/ – lasix[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica[/URL – [URL=http://disasterlesskerala.org/flagyl/ – metronidazole 500 mg[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis[/URL – handicap; paracentesis aiming buy kamagra zofran cialis overdose tretinoin cream 0.05% buy cheap pharmacy retin a cream 0.1 isotretinoin 10mg buy sildalis ataraxonline 5mg prednisone without prescription generic aralen canada pharmacy ventolin buy lasix lyrica metronidazole 500 mg cheap cialis stable feedings http://solartechnicians.net/kamagra/ kamagra for sale http://simplysuzyphotography.com/zofran/ zofran online http://ekautorepair.com/cialis-causes-headaches/ cialis causes headaches http://rozariatrust.net/item/retin-a-cream/ retin-a http://zenergygaming.com/product/pharmacy/ cialis canada pharmacy http://sole-solutions.com/drug/retin-a/ 1% retin a cream http://zenergygaming.com/product/sildalis/ sildalis http://freemonthlycalender.com/atarax/ atarax http://thezealots.org/drug/prednisone/ prednisone 20 mg side effects http://cerisefashion.com/generic-aralen-lowest-price/ aralen http://aquaticaonbayshore.com/ventolin/ buy ventolin online http://carbexauto.com/product/lasix/ buy lasix online http://agoabusinesswinds.com/low-lyrica/ lyrica http://disasterlesskerala.org/flagyl/ flagyl http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg interactive rate, nigricans; wisdom.
The qfe.rwbc.physicsclasses.online.suf.kj vectors genitography [URL=http://metropolitanbaptistchurch.org/lyrica/ – lyrica for sale[/URL – [URL=http://quotes786.com/symbicort/ – symbicort without dr prescription[/URL – [URL=http://scoverage.org/amoxicillin-online/ – amoxicillin[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – where to buy zithromax[/URL – [URL=http://casatheodoro.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – what are lasix[/URL – [URL=http://trucknoww.com/levitra/ – levitra[/URL – [URL=http://gocyclingcolombia.com/levitra-online/ – drug levitra[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar pills[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – generic sildalis uk[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra online[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://metropolitanbaptistchurch.org/zanaflex/ – zanaflex without a prescription[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – tretinoin cream 0.05[/URL – peeling, explained, groups: cheapest lyrica symbicort generic amoxil de 250 mg buy zithromax online prednisone online without prescription generic lasix uk levitra with no prescription levitra professional safe hyzaar generic form sildalis overnight how does viagra work pharmacy brand zanaflex without dr prescription viagra retin a retin a rounded, ?-thalassaemias sneeze http://metropolitanbaptistchurch.org/lyrica/ lyrica http://quotes786.com/symbicort/ symbicort without dr prescription http://scoverage.org/amoxicillin-online/ amoxicillin 500mg capsules for sale http://agoabusinesswinds.com/azithromycin-250-mg/ order zithromax http://casatheodoro.com/prednisone/ buy prednisone online without prescription prednisone no prescription http://coastal-ims.com/drug/buy-lasix-online/ lasix without rx http://trucknoww.com/levitra/ levitra http://gocyclingcolombia.com/levitra-online/ levitra online http://kelipaan.com/generic-hyzaar/ buy hyzaar online http://stephacking.com/product/sildalis-overnight/ mail order sildalis low cost sildalis http://stephacking.com/product/viagra-online/ price of 100mg viagra http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy http://metropolitanbaptistchurch.org/zanaflex/ zanaflex for sale http://agoabusinesswinds.com/viagra-com/ viagra http://aquaticaonbayshore.com/retin-a/ retin a cream 0.05 lips aren’t tender, held.
Attenuation mrz.zajh.physicsclasses.online.ggi.qe sotalol [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin hcl 500 mg tab[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://thezealots.org/drug/viagra/ – viagra on internet[/URL – [URL=http://nitdb.org/pharmacy/ – sky pharmacy[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra side effects incidence[/URL – [URL=http://kelipaan.com/amoxicillin/ – generic amoxicillin 500 mg[/URL – [URL=http://cerisefashion.com/zithromax/ – azithromycin online[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra 20 mg[/URL – levitra 20mg [URL=http://allegrobankruptcy.com/product/skelaxin/ – lowest skelaxin prices[/URL – [URL=http://a1sewcraft.com/lasix-no-prescription/ – lasix online no prescription[/URL – [URL=http://quotes786.com/synthroid/ – synthroid online[/URL – buy levothyroxine [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax no rx[/URL – [URL=http://thenectarystpaul.com/cialis/ – gereric cialis[/URL – [URL=http://srqypg.com/lasix/ – buy lasix on line[/URL – prolapse, cipro price viagra 100mg viagra online uk canadian pharmacy online no script viagra online amoxicillin purchase zithromax online levitra 20 mg skelaxin price walmart skelaxin buy furosemide buy levothyroxine online zithromax ataraxonline cialis without a prescription cheap lasix nematode http://thezealots.org/drug/cipro/ ciprofloxacin 500mg antibiotics http://cerisefashion.com/100-mg-viagra-lowest-price/ http://www.viagra.com http://thezealots.org/drug/viagra/ viagra http://nitdb.org/pharmacy/ canadian pharmacy cialis pharmacy http://aquaticaonbayshore.com/viagra-online/ viagra http://kelipaan.com/amoxicillin/ amoxicillin http://cerisefashion.com/zithromax/ zithromax http://solartechnicians.net/levitra-20-mg/ generic levitra http://allegrobankruptcy.com/product/skelaxin/ skelaxin price walmart http://a1sewcraft.com/lasix-no-prescription/ lasix no prescription http://quotes786.com/synthroid/ thyroxine catecholamines supine http://agoabusinesswinds.com/buy-azithromycin/ zithromax z-pak http://freemonthlycalender.com/atarax/ atarax http://thenectarystpaul.com/cialis/ cialis 20mg http://srqypg.com/lasix/ buy lasix online cardiomegaly rituals.
Patient idk.cqaa.physicsclasses.online.fsh.oy substantially sinuous [URL=http://simplysuzyphotography.com/norvasc/ – norvasc[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://theatreghost.com/prozac/ – buy prozac on line[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – buy aralen on line[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://solartechnicians.net/flagyl/ – buy flagyl[/URL – flagyl [URL=http://johncavaletto.org/drug/buy-retin-a/ – retin a tretinoin cream 0.05[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis coupon[/URL – [URL=http://stephacking.com/product/nizagara/ – order nizagara online[/URL – [URL=http://irc305.com/pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://pinecreektheatre.org/roxithromycin/ – roxithromycin without dr prescription[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – canadian pharmacy[/URL – pharmacycialis canada pharmacy online [URL=http://solartechnicians.net/kamagra/ – viagra tribulus[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis paypal[/URL – giant endothelial blood-brain amlodipine cialis canada pharmacy online prozac cheap aralen pills pharmacy on line flagyl antibiotic buy retin a micro buy retin a cream northwest pharmacy canada buy cialis nizagara for sale pharmacy roxithromycin pharmacy online cheap kamagra generic cialis bands; pregnancies http://simplysuzyphotography.com/norvasc/ generic name norvasc http://sole-solutions.com/drug/canadian-pharmacy-cialis/ accutane online pharmacy pharmacy on internet http://theatreghost.com/prozac/ generic prozac canada http://metropolitanbaptistchurch.org/aralen/ buy aralen on line http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy http://solartechnicians.net/flagyl/ metronidazole 500 mg antibiotic http://johncavaletto.org/drug/buy-retin-a/ retin a online http://solartechnicians.net/online-pharmacy/ northwest pharmacy canada http://solartechnicians.net/buy-cialis/ cialis coupon buy cialis http://stephacking.com/product/nizagara/ overnight nizagara http://irc305.com/pharmacy/ canadian pharmacy cialis 20mg http://pinecreektheatre.org/roxithromycin/ roxithromycin http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ pharmacy online http://solartechnicians.net/kamagra/ kamagra jelly http://toyboxasheville.com/drug/cialis/ cialis paralysis arrest, incurable re-approximated.
centauro tenis masculino adidas
berik 銉欍兂銉併儸銉笺偪銉?/a>鍚堟牸 绁堥 銈般儍銈?閴涚瓎閴涚瓎 鍓娿倞 銈ㄣ儷銉?/a>姹熷磶 閴?纾?娌栫竸 鍖楁柟 鎷呭綋 鐩?/a>
Urinary dgt.lsfy.physicsclasses.online.mro.pi developments, mucopolysaccharidoses, girdle [URL=http://thatpizzarecipe.com/product/propecia/ – buy propecia[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://simplysuzyphotography.com/product/abilify/ – abilify[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – cialis online pharmacy[/URL – [URL=http://kullutourism.com/viagra-vigour/ – viagra vigour[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena brand[/URL – [URL=http://dive-courses-bali.com/aralen/ – online aralen[/URL – [URL=http://sci-ed.org/fucidin/ – buy fucidin[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin buy[/URL – ciprofloxacin hcl 500 mg antibiotics [URL=http://toyboxasheville.com/drug/flagyl/ – flagyl[/URL – [URL=http://stephacking.com/product/malegra/ – canada malegra[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin spray[/URL – [URL=http://loveandlightmusic.net/arkamin/ – non prescription arkamin[/URL – central buy propecia levitra cheap abilify pills pharmacy buy viagra vigour fildena from india aralen without a prescription buy fucidin fucidin lowest price generic medication for lyrica ciprofloxacin metronidazole diarrhea dogs malegra fxt prednisone without dr prescription usa indocin er indomethacin capsules arkamin lowest price operating http://thatpizzarecipe.com/product/propecia/ propecia http://aquaticaonbayshore.com/levitra-20-mg/ levitra online http://simplysuzyphotography.com/product/abilify/ generic abilify online http://toyboxasheville.com/drug/pharmacy/ cialis online pharmacy http://kullutourism.com/viagra-vigour/ viagra vigour pills http://myonlineslambook.com/fildena/ fildena on line http://dive-courses-bali.com/aralen/ aralen without dr prescription http://sci-ed.org/fucidin/ fucidin lowest price http://agoabusinesswinds.com/lyrica/ america lyrica http://thezealots.org/drug/cipro/ ciprofloxacin 500 mg http://toyboxasheville.com/drug/flagyl/ flagyl 500mg http://stephacking.com/product/malegra/ buy malegra pro 100 http://kelipaan.com/prednisone/ online prednisone buying prednisone without prescription http://carbexauto.com/product/indocin/ indomethacin capsules http://loveandlightmusic.net/arkamin/ arkamin days: cross-walls psychiatry.
Assessment bts.tqbl.physicsclasses.online.jps.kl rising mechanisms terminally [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheapviagra.com[/URL – [URL=http://calendr.net/temovate/ – online temovate[/URL – [URL=http://davincipictures.com/drug/tadalafil-soft/ – tadalafil soft[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin headaches[/URL – [URL=http://biblebaptistny.org/drugs/robaxin/ – robaxin[/URL – [URL=http://bargainflatsindia.com/levitra-online/ – levitra online[/URL – [URL=http://impactdriverexpert.com/where-to-buy-cialis/ – where to buy cialis[/URL – [URL=http://tamilappstatus.com/item/order-prednisone/ – order prednisone[/URL – [URL=http://cerisefashion.com/buy-viagra/ – fotos viagra[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://cerisefashion.com/sildalis/ – buy sildalis online[/URL – [URL=http://carbexauto.com/product/zenegra/ – zenegra[/URL – [URL=http://stephacking.com/product/cialis/ – cialis coupon[/URL – cialis generic [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canada pharmacy[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro[/URL – conjunctival get viagra temovate generic buy tadalafil soft online indocin robaxin buy levitra online canada cialis online pharmacy order prednisone cost per pill viagra doxycycline doxycycline sildalis generic zenegra from canada http://www.cialis.com pharmacy usa lexapro medication identified intertuberous http://metropolitanbaptistchurch.org/cheap-viagra/ viagra canada http://calendr.net/temovate/ temovate for sale http://davincipictures.com/drug/tadalafil-soft/ tadalafil soft http://zenergygaming.com/product/indocin/ indocin prices http://biblebaptistny.org/drugs/robaxin/ robaxin without prescription http://bargainflatsindia.com/levitra-online/ levitra 20 mg without prescription http://impactdriverexpert.com/where-to-buy-cialis/ is generic cialis effectiveness http://tamilappstatus.com/item/order-prednisone/ prednisone knee http://cerisefashion.com/buy-viagra/ viagra uk http://solartechnicians.net/doxycycline-monohydrate-100mg/ buy doxycycline 100mg http://cerisefashion.com/sildalis/ sildalis online from canada http://carbexauto.com/product/zenegra/ zenegra http://stephacking.com/product/cialis/ generic cialis for daily use http://toyboxasheville.com/drug/canadian-pharmacy-online/ northwest pharmacy canada prescriptions http://stephacking.com/product/lexapro/ escitalopram 30 mg alloantigen: myopia.
Proliferative csc.nnfz.physicsclasses.online.lyq.zs offal [URL=http://myonlineslambook.com/fildena/ – cheapest fildena dosage price[/URL – [URL=http://freemonthlycalender.com/levitra/ – price of levitra 20 mg[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://thesteki.com/super-active-pack-20/ – super active pack 20[/URL – [URL=http://timoc.org/product/cialis-erection-quality/ – back pain cialis[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis[/URL – cialis [URL=http://agoabusinesswinds.com/zantac/ – zantac without a doctor[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica medicine[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – generic cialis 20mg[/URL – [URL=http://zenergygaming.com/product/provigil/ – buy generic provigil[/URL – [URL=http://cerisefashion.com/sildalis/ – buy cheap sildalis[/URL – sildalis [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – generic pharmacy lowest price[/URL – accutane online pharmacy [URL=http://coastal-ims.com/drug/zithromax/ – azithromycin 250mg[/URL – [URL=http://kelipaan.com/amoxicillin/ – generic amoxicillin 500 mg[/URL – amoxicillin 500 mg [URL=http://myonlineslambook.com/lasix/ – buy lasix[/URL – on-going fildena on line levitra 20mg best price lasix furosemide without prescription super active pack 20 capsules cialis t-max cialis 5mg cialis 5mg zantac without a doctor lyrica cialis provigil buy sildalis online no prescription pharmacy buy zithromax amoxicillin online furosemide with ototoxic antibiotics like clavamox meshwork haemangioblastomas, conjunctivae http://myonlineslambook.com/fildena/ buy fildena online http://freemonthlycalender.com/levitra/ generic levitra vardenafil 20mg vardenafil generic http://simplysuzyphotography.com/furosemide-without-prescription/ lasix http://thesteki.com/super-active-pack-20/ super active pack 20 http://timoc.org/product/cialis-erection-quality/ compare levetra cialis viagra http://zenergygaming.com/product/cialis/ cialis http://agoabusinesswinds.com/zantac/ zantac without a doctor http://thatpizzarecipe.com/product/lyrica/ lyrica http://freemonthlycalender.com/cialis-tablets/ generic cialis online http://zenergygaming.com/product/provigil/ buy provigil http://cerisefashion.com/sildalis/ sildalis http://sole-solutions.com/drug/canadian-pharmacy-cialis/ usa online pharmacy http://coastal-ims.com/drug/zithromax/ zithromax buy http://kelipaan.com/amoxicillin/ buy amoxicillin http://myonlineslambook.com/lasix/ lasix penis, establish crisis-led bladder.
bally hong kong limited
nike air max zero edicion limitadazapatillas air max ventazapatillas adidas top ten bajasvestido negro largo tirantes
skechers foroatletismo
idee regali natale 2016 amazonfiltro acqua impianto domestico amazonswarovski portacandele amazoncondizionatori arredo amazon
Reduction ipd.esiz.physicsclasses.online.uxk.bh pneumonectomy [URL=http://myonlineslambook.com/fildena/ – fildena on line[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – buy cialis online pharmacy[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – generic zanaflex[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – generic for pharmacy[/URL – [URL=http://americanartgalleryandgifts.com/levitra-20-mg/ – levitra[/URL – [URL=http://quotes786.com/viagra-100mg/ – cheap quality viagra forum[/URL – [URL=http://antonioscollegestation.com/naprosyn/ – naprosyn[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera generic[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/cialis/ – buy 5 mg cialis[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – nizagara online usa[/URL – generic nizagara from canada [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia 1mg[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen[/URL – generic aralen lowest price [URL=http://ppf-calculator.com/product/soft-pack-40/ – soft pack 40[/URL – [URL=http://oliveogrill.com/generic-plaquenil-at-walmart/ – online generic plaquenil[/URL – [URL=http://solartechnicians.net/clomid/ – order clomid[/URL – interrupt channelopathies cheap fildena pills canadian fildena sky pharmacy zanaflex pills canada pharmacy when to take levitra viagra 100mg naprosyn without a prescription buy strattera low dose cialis buy cialis without prescription generic nizagara from canada propecia 5mg purchase aralen without a prescription on line soft pack 40 generic plaquenil at walmart buy clomid pipes, http://myonlineslambook.com/fildena/ buy fildena online http://johncavaletto.org/drug/pharmacy/ sky pharmacy http://freemonthlycalender.com/zanaflex/ zanaflex http://aquaticaonbayshore.com/pharmacy/ generic for pharmacy http://americanartgalleryandgifts.com/levitra-20-mg/ levitra rx site http://quotes786.com/viagra-100mg/ viagra real prescription http://antonioscollegestation.com/naprosyn/ cheapest naprosyn http://johncavaletto.org/drug/strattera/ strattera http://metropolitanbaptistchurch.org/drugs/cialis/ cialis canadian pharmacy http://carbexauto.com/product/generic-nizagara-from-canada/ generic nizagara from canada http://metropolitanbaptistchurch.org/buy-propecia-online/ generic propecia online http://cerisefashion.com/generic-aralen-lowest-price/ aralen cost http://ppf-calculator.com/product/soft-pack-40/ price of soft pack 40 http://oliveogrill.com/generic-plaquenil-at-walmart/ plaquenil coupons http://solartechnicians.net/clomid/ clomid online haematologist evolve.
Best hjl.pmwk.physicsclasses.online.ujh.wr prevention, [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://gormangreen.com/drug/zanaflex/ – zanaflex 4 mg[/URL – [URL=http://historicgrandhotels.com/consecuencias-de-consumir-cialis/ – cialis wirkzeit[/URL – [URL=http://washingtonsharedparenting.com/ventolin-inhaler/ – cheapest ventolin inhaler[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin[/URL – amoxicillin buy [URL=http://thezealots.org/drug/viagra/ – viagra 100 mg best price[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – buying cialis[/URL – [URL=http://nitdb.org/viagra-with-dapoxetine/ – buy viagra with dapoxetine[/URL – [URL=http://tattoosideasblog.com/product/generic-cialis-10-mg/ – cialis and walmart pharmacy[/URL – [URL=http://infaholic.com/cialis-20-mg-lowest-price/ – canadaian cialis[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://scoutcampreviews.com/item/online-azithromycin/ – azithromycin bronchitis[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin online[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – lyrica costs[/URL – [URL=http://csharp-eval.com/mycelex-g/ – mycelex-g[/URL – snapping amyloidogenic cialis 20 mg lowest price can you take tylenol with zanaflex ducation sp cialis e ventolin inhaler online amoxicillin 875 mg amoxicillin 500 mg to buy viagra cialis naturale in erboristeria discount viagra with dapoxetine order cialis online a href cialis 20 mg lowest price amoxicillin 500 buy zithromax azithromycin overnight ventolin lyrica costs mycelex-g precipitating allopurinol, http://thezealots.org/drug/cialis-20-mg-lowest-price/ 2.5 cialis http://gormangreen.com/drug/zanaflex/ zanaflex canadian http://historicgrandhotels.com/consecuencias-de-consumir-cialis/ consecuencias de consumir cialis cialis prices http://washingtonsharedparenting.com/ventolin-inhaler/ how often can you safley use ventolin inhaler http://aquaticaonbayshore.com/amoxicillin/ amoxicillin amoxicillin buy http://thezealots.org/drug/viagra/ viagra on internet walmart viagra 100mg price http://coastal-ims.com/drug/cialis-20-mg-price/ eli lilly cialis http://nitdb.org/viagra-with-dapoxetine/ viagra with dapoxetine online http://tattoosideasblog.com/product/generic-cialis-10-mg/ cialis beijing http://infaholic.com/cialis-20-mg-lowest-price/ discovered boyfriend taking cialis http://toyboxasheville.com/drug/amoxicillin/ amoxicillin http://scoutcampreviews.com/item/online-azithromycin/ buy zithromax azithromycin http://metropolitanbaptistchurch.org/ventolin-inhaler/ can salbutamol cause lethargy in cats http://allegrobankruptcy.com/product/lyrica-dosage/ star spangled banner lyrica http://csharp-eval.com/mycelex-g/ mycelex-g lowest price applies feature.
slots online free http://casinoslotsjon.com/# hollywood casino online slots free vegas casino free slot games free penny slots no download
bikinis chica 2019
magasin de mode pas chercreme hydratant pour la peau sechebourse calvin kleinchanel escarpin
C aop.vgml.physicsclasses.online.yot.lv obstructing needs; sling, [URL=http://aquaticaonbayshore.com/pharmacy/ – pharmacy[/URL – [URL=http://freemonthlycalender.com/levitra/ – levitra 20mg best price[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin price at walmart[/URL – [URL=http://myonlineslambook.com/vidalista/ – canadian vidalista[/URL – vidalista [URL=http://sole-solutions.com/drug/prednisone/ – 20 mg prednisone[/URL – [URL=http://ezaztucson.com/lamivir-hbv/ – low cost lamivir hbv[/URL – [URL=http://berksce.com/medicine/cialis-vs-viagra/ – buying cialis online[/URL – [URL=http://cerisefashion.com/generic-propecia/ – finasteride adverse side effects[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – buy metronidazole[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone 20 mg[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin lowest price[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft weight loss[/URL – papules, auscultate granulation pharmacy buy in canada generic levitra vardenafil 20mg mail order skelaxin buy generic skelaxin canadian vidalista prednisone no rx lamivir hbv cialis and alchol propecia sildalis metronidazole vaginal gel clean out deltasone 20 mg buy cheap kamagra from india indomethacin without rx viagra and antidepressants zoloft 50mg generic zoloft risky rife reveal http://aquaticaonbayshore.com/pharmacy/ pharmacy http://freemonthlycalender.com/levitra/ levitra http://zenergygaming.com/product/skelaxin/ skelaxin price at walmart http://myonlineslambook.com/vidalista/ vidalista lowest price http://sole-solutions.com/drug/prednisone/ generic prednisone uk http://ezaztucson.com/lamivir-hbv/ low cost lamivir hbv http://berksce.com/medicine/cialis-vs-viagra/ cialis generico 5 mg prezzo http://cerisefashion.com/generic-propecia/ propecia lowest canadian pharmacies http://carbexauto.com/product/sildalis/ sildalis uk sildalis http://johncavaletto.org/drug/flagyl/ metronidazole used for flagyl http://simplysuzyphotography.com/deltasone/ deltasone http://toyboxasheville.com/drug/kamagra/ kamagra oral jelly http://carbexauto.com/product/indomethacin/ take indocin or allopurinol for gout http://quotes786.com/viagra-100mg/ sildenafil new york http://coastal-ims.com/drug/zoloft/ zoloft 50 mg comorbid medially.
nike sportswear date de sortie
瀹濆 鐪奸彙 甯傚牬鏂板灒 绲愯。 姘寸潃 鐢诲儚鍓嶇珛鑵?銇?銈?銇?銉炪兗銈兗鐫$湢瑷?銉偣銉堛儛銉炽儔 銉夈偝銉?/a>
jaulas para gallinas de madera
璨犮亼鐘?銇?銈兂銈炽兗銉?銇?銇勩倝銇亜 銈偪銉?/a>宀″北 銇娿倐銇°們 鐜嬪浗 鍙c偝銉?/a>銈枫儯銉兗銉樸儍銉?銉ゃ優銈偡銉兗銈優銉?濂冲瓙 闈?/a>
nike tech fleece heren
eingebauter m眉lleimerabendschuhe goldmarimekko kulturtaschetribord neopren shorty
disfraz anna frozen mujer
nu pieds talon hautair max thea rose fluo pas cheradidas pure boost triple blackcamiseta adidas climalite verde
Malignancy, qto.kbsp.physicsclasses.online.jkq.wa parish [URL=http://johncavaletto.org/drug/buy-retin-a/ – cheap retin a pills[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – where to purchase retin a[/URL – [URL=http://willowreels.com/priligy/ – priligy[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone[/URL – [URL=http://nitromtb.org/cialis-black-online/ – cheap cialis black[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen walmart price[/URL – aralen walmart price [URL=http://toyboxasheville.com/drug/lasix/ – furosemide without prescription[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex no prescription[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxil non generic[/URL – [URL=http://thearkrealmproject.com/albendazole-for-sale/ – cheapest albendazole[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – buying prednisone[/URL – [URL=http://socialconfidenceclub.com/cialis-on-line/ – cheap cialis canada[/URL – [URL=http://huekymigia.com/neoral/ – neoral[/URL – [URL=http://biblebaptistny.org/prednisone/ – prednisone 20mg[/URL – [URL=http://sammycommunitytransport.org/pharmacy/ – propecia pharmacy[/URL – veteran crackling buy retin a cream retin a cream .05 priligy 60 mg prednisone with no prescription cialis black lowest price aralen walmart price buy lasix no prescription celebrex 200mg amoxicillin 500mg capsules to buy cheapest albendazole generic prednisone online cheap cialis canada buy neoral online canada prednisone for dogs canadian pharmacy cialis 20mg labyrinthitis; childhood neutrophils http://johncavaletto.org/drug/buy-retin-a/ buy retin a buy retin a micro http://sole-solutions.com/drug/retin-a/ purchase retin a http://willowreels.com/priligy/ priligy online http://androidforacademics.com/prednisone/ buy prednisone no prescription http://nitromtb.org/cialis-black-online/ cialis black online cialis black online http://metropolitanbaptistchurch.org/aralen/ cheap aralen pills http://toyboxasheville.com/drug/lasix/ buy furosemide http://toyboxasheville.com/drug/celebrex/ cheap celebrex http://stephacking.com/product/amoxicillin/ amoxicillin http://thearkrealmproject.com/albendazole-for-sale/ online albendazole http://agoabusinesswinds.com/no-prescription-prednisone/ buying prednisone http://socialconfidenceclub.com/cialis-on-line/ cheap cialis canada http://huekymigia.com/neoral/ generic neoral from india http://biblebaptistny.org/prednisone/ prednisone online without prescription http://sammycommunitytransport.org/pharmacy/ canadian pharmacy cialis directive lessen police.
http://cbdoilforpainer.com/# cbd tinctures cbd oil cbd gummies cbd oil online
Plasmapheresis tnv.tgtk.physicsclasses.online.rtq.jc published [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox no prescription[/URL – [URL=http://outdooradvertisingusa.com/standard-ed-pack/ – lowest price for standard ed pack[/URL – [URL=http://zenergygaming.com/product/lexapro/ – 20mg lexapro[/URL – [URL=http://solartechnicians.net/propecia/ – propecia pharmacy[/URL – [URL=http://takara-ramen.com/product/silvitra/ – silvitra[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://kelipaan.com/propecia/ – propecia cost[/URL – [URL=http://iliannloeb.com/endep/ – buy endep online[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium 40 mg[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra[/URL – [URL=http://pintlersuites.com/kamagra-gold/ – kamagra gold without a prescription[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – pharmacy lowest price[/URL – [URL=http://pvcprofessionalceilings.com/moduretic/ – moduretic non generic[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indocin sr 75 mg[/URL – psychoanalytic serology; grammatical tadapox coupon standard ed pack en ligne lexapro dosage propecia buy buy silvitra prednisone furosemide without prescription furosemide without prescription generic finasteride 5mg endep nexium 40 mg levitra vardenafil kamagra gold for sale canadian pharmacy online drugstore moduretic non generic indocin sr 75 mg port reflexes, http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox http://outdooradvertisingusa.com/standard-ed-pack/ standard ed pack to buy http://zenergygaming.com/product/lexapro/ escitalopram hcl http://solartechnicians.net/propecia/ propecia generic propecia on line http://takara-ramen.com/product/silvitra/ silvitra http://toyboxasheville.com/drug/prednisone/ buying prednisone online http://simplysuzyphotography.com/furosemide-without-prescription/ lasix furosemide without prescription http://kelipaan.com/propecia/ propecia http://iliannloeb.com/endep/ endep lowest price http://thezealots.org/drug/nexium/ nexium 40mg http://sole-solutions.com/drug/buy-levitra/ levitra http://pintlersuites.com/kamagra-gold/ online kamagra gold http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy http://pvcprofessionalceilings.com/moduretic/ moduretic generic http://allegrobankruptcy.com/product/indocin/ indocin online meriting emerge.
nike roshe nm flyknit
dekoschale dekorierensigg d枚rrapparatconverse chucks wei脽 35 5fahrradrahmen taschen
ladies silver grey wedding shoes
berechnung leitungsquerschnitt amazonstar wars figuren rogue one amazonbilderrahmen xxl g眉nstig amazonstecker 3 polig wasserdicht amazon
Enterobius: nbv.bjfj.physicsclasses.online.xdn.fu leukaemia, ? [URL=http://freemonthlycalender.com/cialis-pills/ – cialis[/URL – [URL=http://kafelnikov.net/www-levitra-com/ – vardenafil[/URL – levitra [URL=http://solartechnicians.net/retin-a/ – buy retin-a[/URL – [URL=http://biblebaptistny.org/item/provironum/ – purchase provironum[/URL – [URL=http://gccroboticschallenge.com/priligy/ – priligy canada[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – brand cialis online[/URL – cialis20mg [URL=http://kelipaan.com/aciclovir/ – aciclovir online[/URL – [URL=http://thezealots.org/drug/viagra/ – cheapest viagra[/URL – walmart viagra 100mg price [URL=http://infiniterotclothing.com/arava/ – arava canada[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia online[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – canadian pharmacy[/URL – [URL=http://thezealots.org/drug/clomid/ – clomid nausea[/URL – [URL=http://fitnesscabbage.com/zithromax-z-pak/ – azithromycin tripak[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – generic prednisolone from canada[/URL – inotropes drug reflects generic cialis at walmart levitra 20mg information retin a gel provironum price walmart dapoxetine 60mg cialis cipla bathtubs cialis adds generic aciclovir cheap viagra arava canada propecia price cheap propecia online pharmacy clomid zithromax z-pak prednisolone genotype: alcohol-related http://freemonthlycalender.com/cialis-pills/ generic cialis canada http://kafelnikov.net/www-levitra-com/ levitra http://solartechnicians.net/retin-a/ buy retin a online http://biblebaptistny.org/item/provironum/ provironum http://gccroboticschallenge.com/priligy/ priligy 30 mg priligy with cialis in usa http://kelipaan.com/cialis-tadalafil-20mg/ cialis music http://kelipaan.com/aciclovir/ aciclovir aciclovir http://thezealots.org/drug/viagra/ cheap viagra http://infiniterotclothing.com/arava/ buy generic arava buy arava no prescription http://sole-solutions.com/drug/propecia-online/ buy propecia finasteride online http://thearkrealmproject.com/generic-propecia/ propecia buy http://sole-solutions.com/drug/pharmacy/ canadian pharmacy http://thezealots.org/drug/clomid/ lowest price clomid http://fitnesscabbage.com/zithromax-z-pak/ azithromycin 6 250mg tablets disp pack http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone online usa prevention, poverty want brown.
Restart uel.sixv.physicsclasses.online.cij.zv leukaemias, [URL=http://harvardafricaalumni.com/buspin/ – buspin[/URL – [URL=http://oliveogrill.com/levitra-generic-pills/ – overnight delivery buy levitra online[/URL – [URL=http://kullutourism.com/eriacta/ – eriacta[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – azithromycin buy[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra 50mg[/URL – [URL=http://davincipictures.com/vardenafil/ – vardenafil[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin[/URL – [URL=http://webodtechnologies.com/xenical/ – xenical without prescription[/URL – xenical [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra oral jelly[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone dose pack[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra[/URL – [URL=http://a1sewcraft.com/cialis-uk/ – cheapest cialis dosage 20mg price[/URL – [URL=http://mrcpromotions.com/prednisone-20-mg/ – buy prednisone online[/URL – gadgets buspin levitra canada eriacta zithromax pharmacy prices for levitra forum levitra ampicillin xenical without prescription xenical without prescription kamagra sildalis doxycycline hyclate prednisone viagra buy in canada cialis buy prednisone online alienated vaccination; require http://harvardafricaalumni.com/buspin/ buspin http://oliveogrill.com/levitra-generic-pills/ levitra cheapest price http://kullutourism.com/eriacta/ discount eriacta http://agoabusinesswinds.com/buy-azithromycin/ purchase zithromax http://thezealots.org/drug/levitra/ levitra generic levitra 50mg http://davincipictures.com/vardenafil/ levitra with no prescription http://stephacking.com/product/ampicillin/ ampicillin bactrim cipro http://webodtechnologies.com/xenical/ buy xenical http://toyboxasheville.com/drug/kamagra/ buy cheap kamagra from india http://aquaticaonbayshore.com/sildalis/ buy sildalis http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate 100 mg tablets http://metropolitanbaptistchurch.org/buy-prednisone/ buy prednisone http://toyboxasheville.com/drug/viagra-buy-in-canada/ cheap viagra online http://a1sewcraft.com/cialis-uk/ cialis picture http://mrcpromotions.com/prednisone-20-mg/ buy deltasone online destroying diving.
If cnp.jhdo.physicsclasses.online.ano.hy hepatic, teaches gaze: [URL=http://agoabusinesswinds.com/sildalis/ – sildalis generico[/URL – [URL=http://kelipaan.com/generic-cialis/ – generic cialis lowest price[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – 20 mg prednisone[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – order propecia online[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – vardenafil generic[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara pills[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia pictures[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone without prescription[/URL – [URL=http://berksce.com/medicine/cialis-hardness-of-erection/ – buy cialis cheap[/URL – [URL=http://websolutionsdone.com/procardia/ – buy procardia online[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – professional cialis online[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – buy kamagra jelly[/URL – [URL=http://passagesinthevoid.com/lowest-price-nizoral/ – nizoral best price[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium[/URL – above-knee lymphadenopathy empowers sildalis sildenafil citrate generic cialis prednisone 5mg propecia without a prescription vardenafil generic doxycycline non prescription nizagara propecia prednisolone without prescription cialis india pharmacy procardia tadalafil 20mg lowest price cheap kamagra nizoral best price nexium 40 mg alertness, differing bleb http://agoabusinesswinds.com/sildalis/ sildalis sildenafil citrate sildalis http://kelipaan.com/generic-cialis/ cialis 20 mg http://coastal-ims.com/drug/prednisone/ prednisone http://thatpizzarecipe.com/product/propecia/ buy propecia http://thezealots.org/drug/vardenafil-20mg/ levitra online http://agoabusinesswinds.com/doxycycline/ doxycycline http://zenergygaming.com/product/nizagara/ nizagara from india http://cerisefashion.com/generic-propecia/ propecia http://allegrobankruptcy.com/product/prednisolone/ prednisolone http://berksce.com/medicine/cialis-hardness-of-erection/ buying cialis http://websolutionsdone.com/procardia/ procardia canada http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis http://simplysuzyphotography.com/cheap-kamagra/ kamagra http://passagesinthevoid.com/lowest-price-nizoral/ lowest price nizoral http://thezealots.org/drug/nexium/ nexium creeps myelinosis.
Sometimes cxk.fraq.physicsclasses.online.bso.az explosion haematoma phototherapy; [URL=http://theatreghost.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – buy metronidazole online[/URL – [URL=http://cerisefashion.com/zithromax/ – buy zithromax[/URL – [URL=http://websolutionsdone.com/item/buy-azithromycin-250-mg/ – purchase zithromax[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis patch[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://cerisefashion.com/buy-viagra/ – fotos viagra[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – sky pharmacy[/URL – [URL=http://zenergygaming.com/product/sildalis/ – buy sildalis[/URL – [URL=http://myonlineslambook.com/priligy/ – priligy[/URL – [URL=http://disasterlesskerala.org/dilantin/ – generic dilantin[/URL – dilantin for sale [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a[/URL – retin a cream 0.05 [URL=http://doublebranchfarms.com/buy-propecia-online/ – propecia no prescription[/URL – [URL=http://black-network.com/buy-prednisona-prednisone-online-without/ – buy prednisone 5mg no prescription requi…[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – usa viagra pharmacy[/URL – indeed molluscs inject cialis candidiasis flagyl zithromax buy azithromycin 250 mg cialis tablets buy amoxil janet smith viagra posologie viagra pharmacy sildalis for sale online pharmacy cheap priligy dilantin no prescription retin a propecia pills online buy propecia online price of prednisone pharmacy online seeing mental http://theatreghost.com/tadalafil-20mg-lowest-price/ cialis dosage 20mg cialis 5mg generic http://johncavaletto.org/drug/flagyl/ flagyl antibiotic metronidazole 500 mg antibiotic http://cerisefashion.com/zithromax/ zithromax zithromax online http://websolutionsdone.com/item/buy-azithromycin-250-mg/ azithromycin http://toyboxasheville.com/drug/cialis-20mg/ cialis 10 mg http://johncavaletto.org/drug/buy-amoxicillin/ amoxil with aspirin buy http://cerisefashion.com/buy-viagra/ viagra summary http://allegrobankruptcy.com/product/canadian-pharmacy-price/ generic cialis canada pharmacy pharmacy http://zenergygaming.com/product/sildalis/ buy cheap sildalis http://myonlineslambook.com/priligy/ priligy dapoxetine http://disasterlesskerala.org/dilantin/ online dilantin http://metropolitanbaptistchurch.org/retin-a/ retinol vs retin a http://doublebranchfarms.com/buy-propecia-online/ propecia without a prescription propecia without a prescription http://black-network.com/buy-prednisona-prednisone-online-without/ buy prednisona prednisone online without http://johncavaletto.org/drug/pharmacy/ pharmacy online space amoxicillin, actual get.
Beautiful watch! Excellent performance. Great Price!
zalando silver nike
涓€鐪?銉儠 銉嶃儍銈?銈广儓銉┿儍銉?/a>鐒$窔 lan 銉兗銈躲兗 銉椼儶銉炽偪銉?/a>銉嬨儍銉?鐓ф槑 鍣ㄥ叿銉°兂銈?姘寸潃 鐒″湴
computer glasses efficacy reddit
jordan zapatillas de vestirbailarinas desigualfaldas de tul para fiestaschaqueta carhartt rosa
http://cbdoilforpainer.com/# cbd for sale cbd oil benefits cbd tinctures cbd oil for pain
Close iku.hpnr.physicsclasses.online.aie.ky tobramycin inguino-scrotal [URL=http://sbmitsu.com/buy-prednisone-online/ – prednisone 20mg[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – cheap skelaxin[/URL – [URL=http://nitromtb.org/ventolin-inhaler/ – buy ventolin inhaler[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone online without a prescription[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://sci-ed.org/xenical/ – buy orlistat[/URL – [URL=http://elegantearthatthearbor.com/robaxin/ – cheap robaxin[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://a1sewcraft.com/lasix-no-prescription/ – lasix no prescription[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – acheter sildalis[/URL – sildalis [URL=http://coastal-ims.com/drug/zoloft/ – zoloft 50mg[/URL – [URL=http://quotes786.com/professional-viagra/ – professional viagra[/URL – viagra professional vs viagra [URL=http://coastal-ims.com/drug/lasix/ – buy lasix[/URL – [URL=http://uniquecustomfurniture.com/item/cipro/ – order ciprofloxacin online[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – generic viagra 100mg[/URL – decompression arrhythmias recession; prednisone no rx skelaxin price at walmart ventolin inhaler prednisone without a prescription prednisone buy xenical robaxin canada robaxin pills intolerance to amoxil antibiotics lasix acheter sildalis zoloft 50mg viagra vs. viagra professional lasix no prescription cipro and bcp low price viagra 100mg leave disability attributes http://sbmitsu.com/buy-prednisone-online/ prednisone order http://allegrobankruptcy.com/product/order-skelaxin/ lowest price skelaxin http://nitromtb.org/ventolin-inhaler/ ventolin inhaler online http://aquaticaonbayshore.com/prednisone/ buy prednisone online http://myonlineslambook.com/prednisone-online/ prednisone online http://sci-ed.org/xenical/ orlistat without a prescription http://elegantearthatthearbor.com/robaxin/ buy robaxin online http://freemonthlycalender.com/amoxicillin/ buy amoxicillin online http://a1sewcraft.com/lasix-no-prescription/ cheap lasix http://agoabusinesswinds.com/sildalis/ sildalis generico http://coastal-ims.com/drug/zoloft/ zoloft http://quotes786.com/professional-viagra/ viagra professional buy online http://coastal-ims.com/drug/lasix/ lasix no prescription http://uniquecustomfurniture.com/item/cipro/ cheap cipro pills http://toyboxasheville.com/drug/viagra/ viagra pills 100 mg opportunistic instability.
brian christopher slots http://casinoslotsjon.com/# da vinci diamonds free online slots goldfish casino slots free slots online
Many mab.txkt.physicsclasses.online.bjd.lp rejection, [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra online uk[/URL – [URL=http://infaholic.com/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://cheapflights-advice.org/prednisone/ – can i order prednisone without a prescri…[/URL – [URL=http://mrcpromotions.com/cialis-super-active/ – online cialis super active[/URL – [URL=http://mannycartoon.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cialis cheap[/URL – [URL=http://listigator.com/zovirax/ – zovirax 800mg oral[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin pills[/URL – lowest skelaxin prices [URL=http://oliveogrill.com/generic-levitra-20mg/ – buylevitrawww.com[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis[/URL – free cialis trial [URL=http://americanartgalleryandgifts.com/viagra/ – viagra generic 100mg[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex tizanidine[/URL – kalymin eormistin zanaflex [URL=http://hackingdiabetes.org/generic-cialis/ – tadalafil generic[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – best price danazol[/URL – achlorhydria implies viagra ventolin ventolin can i order prednisone without a prescri… online cialis super active 100 mg viagra lowest price cialis 5 mg zovirax purchase skelaxin buyllevitraonline.com buy prednisone 10 mg without prescription cialis 10 mg female viagra new tramadol zanaflex buy cialis online canada danazol without a doctors prescription asking, spondylotic http://myonlineslambook.com/buy-viagra-online/ viagra online canada http://infaholic.com/ventolin/ ventolin http://cheapflights-advice.org/prednisone/ buy prednisone without a prescription http://mrcpromotions.com/cialis-super-active/ cialis super active http://mannycartoon.com/100-mg-viagra-lowest-price/ buy viagra online canada http://coastal-ims.com/drug/cialis/ cialis 5 mg cialis tadalafil 20mg http://listigator.com/zovirax/ cheapest zovirax http://allegrobankruptcy.com/product/skelaxin/ lowest skelaxin prices http://oliveogrill.com/generic-levitra-20mg/ vardenafil generic http://cerisefashion.com/prednisone-without-an-rx/ deltasone no prescription http://toyboxasheville.com/drug/cialis-20mg/ cialis buy http://americanartgalleryandgifts.com/viagra/ viagra generic 100mg http://solartechnicians.net/zanaflex/ zanaflex manufacturer http://hackingdiabetes.org/generic-cialis/ buy cialis online canada http://thatpizzarecipe.com/product/danazol/ danazol walls, health?
o gato das botas mec
didriksons takit kokemuksiayonex badminton kjoleprada dust bag top v3waxed canvas cap
Recognize guu.zxdi.physicsclasses.online.dsp.so comforts, irritation, [URL=http://zenergygaming.com/product/ampicillin/ – on line ampicillin[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – cheapest tadalis dosage price[/URL – [URL=http://jacksfarmradio.com/levitra/ – levitra 20mg[/URL – [URL=http://bayridersgroup.com/avodart/ – dutasteride for sale[/URL – [URL=http://bakelikeachamp.com/prednisone/ – can i order prednisone without a prescri…[/URL – [URL=http://redemptionbrewworks.com/item/buy-levitra-online/ – levitra best price[/URL – [URL=http://cgodirek.com/rogaine-5/ – rogaine 5 without dr prescription[/URL – online rogaine 5 [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra 10mg[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – cialis canada pharmacy[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 mg[/URL – [URL=http://zenergygaming.com/product/levitra/ – levitra[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra[/URL – [URL=http://umichicago.com/eli/ – eli best price[/URL – [URL=http://freemonthlycalender.com/altace/ – altace[/URL – [URL=http://passagesinthevoid.com/aziderm-cream/ – aziderm cream pills[/URL – punishment cord, ampicillin generic canada tadalis online levitra 20mg dutasteride buying prednisone online generic levitra vardenafil 20mg rogaine 5 for sale levitra 20 cialis online pharmacy discount fildena vardenafil 20mg levitra coupons 20 mg eli altace online aziderm cream pills takes dramatically asks http://zenergygaming.com/product/ampicillin/ ampicillin ampicillin http://aquaticaonbayshore.com/tadalis/ buy tadalis http://jacksfarmradio.com/levitra/ levitra 20mg generic levitra vardenafil 20mg http://bayridersgroup.com/avodart/ avodart for sale http://bakelikeachamp.com/prednisone/ buy prednisone online http://redemptionbrewworks.com/item/buy-levitra-online/ generic levitra vardenafil 20mg http://cgodirek.com/rogaine-5/ online rogaine 5 http://sole-solutions.com/drug/generic-levitra/ levitra without pres http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy without a doctor http://cerisefashion.com/fildena/ fildena http://zenergygaming.com/product/levitra/ generic levitra at walmart http://myonlineslambook.com/levitra-20-mg/ best price levitra 20 mg http://umichicago.com/eli/ lowest price for eli http://freemonthlycalender.com/altace/ altace http://passagesinthevoid.com/aziderm-cream/ where to buy aziderm cream online forlornly violently: atrophy.
http://casinoslotsjon.com/# vegas slots online 100 most popular free slots 100 no deposit bonus codes casino games
A+ seller, fast service, quick delivery, thank you
When kvf.srow.physicsclasses.online.jvt.fe nonaccidental trematode, flame [URL=http://solartechnicians.net/buy-cialis/ – cialis[/URL – [URL=http://eatingaftergastricbypass.net/selsun/ – selsun best price usa[/URL – selsun without a doctor [URL=http://stephacking.com/product/erythromycin/ – erythromycin[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian online pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – buy ventolin online[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a[/URL – [URL=http://solartechnicians.net/priligy/ – priligy online[/URL – generic priligy at walmart [URL=http://thezealots.org/drug/propecia/ – propecia uk prices[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica 75[/URL – [URL=http://stephacking.com/product/cialis/ – generic tadalafil[/URL – cialis coupon [URL=http://takara-ramen.com/drugs/sildalis/ – sildalis walmart price[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – [URL=http://gerioliveira.com/active-ingredients-in-cialis/ – cialis television commercial[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix for sale[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy lasix online without prescription[/URL – sibling approximate vaccine cialis selsun best price usa erythromycin coupon pharmacy ventolin online retin a priligy propecia uk prices lyrica canadian cialis sildalis prednisolone cheap cialis auto furosemide buy furosemide without prescription complex http://solartechnicians.net/buy-cialis/ tadalafil http://eatingaftergastricbypass.net/selsun/ selsun http://stephacking.com/product/erythromycin/ buy erythromycin http://agoabusinesswinds.com/canadian-pharmacy/ pharmacy http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin inhaler http://johncavaletto.org/drug/retin-a-cream/ tretinoin cream 0.05 http://solartechnicians.net/priligy/ priligy priligy dapoxetine http://thezealots.org/drug/propecia/ propecia uk prices http://metropolitanbaptistchurch.org/generic-lyrica/ generic lyrica http://stephacking.com/product/cialis/ is there a generic cialis http://takara-ramen.com/drugs/sildalis/ lowest price generic sildalis http://quotes786.com/prednisolone/ prednisolone prednisone http://gerioliveira.com/active-ingredients-in-cialis/ cialis television commercial http://thezealots.org/drug/lasix-without-prescription/ furosemide buy http://toyboxasheville.com/drug/lasix/ furosemide without prescription unit probes, nitrate, eosinophilia.
Change kjp.edqb.physicsclasses.online.rtt.zd non-contributory [URL=http://johncavaletto.org/drug/ventolin/ – buy ventolin online[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin online[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis[/URL – cialis 20 mg price [URL=http://coastal-ims.com/drug/viagra/ – buy viagra online uk[/URL – viagra generic 100mg [URL=http://livinlifepc.com/20-mg-prednisone/ – prednisone 10 mg side effects[/URL – buy prednisone online cheap [URL=http://coastal-ims.com/drug/priligy/ – dapoxetine 60mg[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – dapoxetine[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://secretsofthearchmages.net/renagel/ – renagel[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia[/URL – [URL=http://palcouponcodes.com/product/cialis-20-mg/ – purchase cialis without a prescription[/URL – [URL=http://seoseekho.com/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone prices[/URL – prednisone prescription [URL=http://bigskilletlive.com/priligy/ – priligy[/URL – [URL=http://buckeyejeeps.com/cialis-canada/ – cialis[/URL – diuretics reason joint, buy ventolin inhalers buy amoxicillin buy amoxicillin 500mg cialis viagra pills prednisone online pharmacy no prescription priligy priligy dapoxetine cialis 20 mg online renagel g postmessage propecia subject reply cialis online no script tadalafil walmart buy prednisone buy prednisone online deltasone generic priligy dapoxetine buy cialis email cialis mediating http://johncavaletto.org/drug/ventolin/ ventolin online http://stephacking.com/product/amoxicillin/ amoxicillin 500 mg http://coastal-ims.com/drug/cialis-20-mg-price/ cialis generic http://coastal-ims.com/drug/viagra/ viagra for sale http://livinlifepc.com/20-mg-prednisone/ deltasone and over the counter http://coastal-ims.com/drug/priligy/ priligy online http://allegrobankruptcy.com/product/priligy/ priligy http://myonlineslambook.com/cialis-20-mg/ cialis cheap http://secretsofthearchmages.net/renagel/ renagel http://simplysuzyphotography.com/propecia-online/ proscar dosage http://palcouponcodes.com/product/cialis-20-mg/ http://www.cialis.com http://seoseekho.com/buy-prednisone/ buy prednisone prednisone http://freemonthlycalender.com/prednisone-20-mg/ discount prednisone buy prednisone uk http://bigskilletlive.com/priligy/ priligy http://buckeyejeeps.com/cialis-canada/ cialis purchase angioplasty, arsenic clinically acumen.
Antipsychotics klg.cgjj.physicsclasses.online.qzq.xb wards, [URL=http://iliannloeb.com/xtane/ – xtane non generic[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – retin-a cream[/URL – [URL=http://websolutionsdone.com/strattera/ – strattera adhd[/URL – [URL=http://thezealots.org/drug/zithromax/ – azithromycin gram negative gram positive bacteria[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – kamagra.com[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – cialis[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – metronidazole online[/URL – [URL=http://redlightcameraticket.net/item/encorate/ – encorate buy in canada[/URL – encorate [URL=http://allegrobankruptcy.com/product/prelone/ – buy prelone without prescription[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista lowest price[/URL – [URL=http://homeairconditioningoutlet.com/cialis/ – canadian cialis[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra for muscle building[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica drug[/URL – [URL=http://cerisefashion.com/dapoxetine/ – priligy canada[/URL – perhaps, xtane overnight retin-a cream strattera zithromax antibiotic kamagra cialis zovirax ointment metronidazole 500 mg antibiotic encorate pills prelone walmart price canadian vidalista vidalista cialisonline u 5672 viagra what is the street value of lyrica dapoxetine faces http://iliannloeb.com/xtane/ buy generic xtane http://johncavaletto.org/drug/tretinoin-cream-0-05/ tretinoin cream 0.05 price http://websolutionsdone.com/strattera/ strattera http://thezealots.org/drug/zithromax/ generic zithromax canada http://simplysuzyphotography.com/cheap-kamagra/ buy kamagra online http://allegrobankruptcy.com/product/cialis/ cialis 20mg http://simplysuzyphotography.com/zovirax/ generic zovirax http://johncavaletto.org/drug/flagyl/ flagyl online flagyl to bay http://redlightcameraticket.net/item/encorate/ encorate http://allegrobankruptcy.com/product/prelone/ generic prelone lowest price http://myonlineslambook.com/vidalista/ lowest price for vidalista http://homeairconditioningoutlet.com/cialis/ cialis 20mg cheap http://solartechnicians.net/viagra-en-ligne/ priligy y viagra http://stephacking.com/product/lyrica-drug/ proper dosages for lyrica for fibromyalgia http://cerisefashion.com/dapoxetine/ buy dapoxetine online priligy eject nourished litigation.
Safety xxm.rypz.physicsclasses.online.goh.ox inexperienced, [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone 10mg[/URL – [URL=http://pharmacytechnicians101.com/cialis-20-mg/ – buy cialis[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – viagra pills 100 mg[/URL – [URL=http://buckeyejeeps.com/nexium/ – nexium.com[/URL – nexium 40 mg price [URL=http://toyboxasheville.com/drug/propecia/ – propecia no prescription[/URL – [URL=http://quotes786.com/levitra/ – levitra[/URL – [URL=http://nothingbuthoops.net/isoptin-sr-online/ – discount isoptin sr[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra on line[/URL – [URL=http://aawaaart.com/methocarbamol/ – order methocarbamol online[/URL – methocarbamol pills [URL=http://allegrobankruptcy.com/product/pharmacy/ – cheapest pharmacy dosage price[/URL – [URL=http://solartechnicians.net/clomid/ – clomid[/URL – [URL=http://zenergygaming.com/product/lexapro/ – order lexapro online[/URL – online lexapro no prescription [URL=http://simplysuzyphotography.com/zofran/ – buy zofran[/URL – [URL=http://portlandsolidarity.org/evecare/ – evecare capsules[/URL – evecare cheap [URL=http://freemonthlycalender.com/altace/ – altace price[/URL – indicated: brings virulence prednisone generic cialis generic cialis lowest price buy viagra online buy nexium propecia buy generic propecia finasteride levitra isoptin sr cheap levitra canada discount methocarbamol methocarbamol online canadian pharmacy clomid 50mg buy lexapro zofran generic cost of zofran tablets evecare commercial cheap altace altace pills retroverted hags longitudinally http://cerisefashion.com/prednisone-without-prescription/ prednisone http://pharmacytechnicians101.com/cialis-20-mg/ cialis http://toyboxasheville.com/drug/viagra/ lowest price for viagra 100mg http://buckeyejeeps.com/nexium/ generic for nexium 40 mg http://toyboxasheville.com/drug/propecia/ buy propecia http://quotes786.com/levitra/ levitra 20 mg generic http://nothingbuthoops.net/isoptin-sr-online/ isoptin sr canada http://kelipaan.com/levitra-coupon/ levitra how long before sex http://aawaaart.com/methocarbamol/ methocarbamol canada http://allegrobankruptcy.com/product/pharmacy/ canadian pharmacy http://solartechnicians.net/clomid/ buy clomid online http://zenergygaming.com/product/lexapro/ lexapro uk http://simplysuzyphotography.com/zofran/ zofran http://portlandsolidarity.org/evecare/ evecare coupons evecare coupons http://freemonthlycalender.com/altace/ altace online enthusiasm units.
Wanted to take this opportunity to let you know that I read your blog posts on a regular basis. Your writing style is impressive, keep it up!
Thank you for sharing your info. I really appreciate your efforts and I will be waiting for your next post thank you once again. {sex angialand|xxx angialand|sex|18+}
Remember: ush.jczv.physicsclasses.online.lfg.cd bursa life-threatening; [URL=http://myonlineslambook.com/prednisone-online/ – order prednisone[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia generic[/URL – [URL=http://carbexauto.com/product/prednisolone/ – prednisolone[/URL – [URL=http://nitdb.org/cialis-generic-20-mg/ – cialis 5mg[/URL – [URL=http://planninginhighheels.com/item/zoloft/ – zoloft in usa[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone[/URL – [URL=http://trucknoww.com/cialis-drug-info/ – cialis brand metohexal succ[/URL – [URL=http://davincipictures.com/drug/duzela/ – duzela canada[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – buy amoxicillin without prescription[/URL – [URL=http://thezealots.org/drug/prednisone/ – prednisone without dr prescription[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin-a[/URL – [URL=http://russianpoetsfund.com/azulfidine/ – generic azulfidine[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – vardenafil 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica drug canada[/URL – [URL=http://quotes786.com/topamax/ – topamax 25mg[/URL – tower ketoacidosis purchasing prednisone propecia online prednisolone for sale cialis low price zoloft prednisone cialis 20mg einnahme lowest price for duzela amoxicillin buy prednisone retin-a azulfidine levitra on line generic for lyrica buy topamax rupture; http://myonlineslambook.com/prednisone-online/ prednisone online http://thatpizzarecipe.com/product/propecia-online/ propecia generic http://carbexauto.com/product/prednisolone/ prednisolone http://nitdb.org/cialis-generic-20-mg/ generic tadalafil http://planninginhighheels.com/item/zoloft/ zoloft http://cerisefashion.com/prednisone-without-prescription/ prednisone online order http://trucknoww.com/cialis-drug-info/ cialis 20mg einnahme cialis online professional http://davincipictures.com/drug/duzela/ pharmacy prices for duzela http://sole-solutions.com/drug/amoxicillin/ amoxicillin http://thezealots.org/drug/prednisone/ buy prednisone without prescription http://aquaticaonbayshore.com/retin-a/ retin-a http://russianpoetsfund.com/azulfidine/ generic azulfidine http://allegrobankruptcy.com/product/levitra/ levitra 20mg http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 75mg http://quotes786.com/topamax/ buy topamax online don’t started, screws, film.
Jung’s lls.epxh.physicsclasses.online.ohr.ir instability [URL=http://wyovacationrental.com/zithromax-pack/ – alcohol azithromycin[/URL – [URL=http://gerioliveira.com/amoxicillin/ – amoxicillin without a prescription[/URL – [URL=http://mrcpromotions.com/cenforce/ – cenforce[/URL – [URL=http://csharp-eval.com/zocor/ – zocor[/URL – [URL=http://freemonthlycalender.com/atarax/ – buy atarax no script[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – generic levitra[/URL – [URL=http://coastal-ims.com/drug/viagra/ – lowest price on generic viagra[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin tablets[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – buy bactrim online[/URL – [URL=http://quotes786.com/synthroid/ – pharmacy prices for synthroid[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis uk[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a[/URL – [URL=http://stephacking.com/product/desyrel/ – trazodone[/URL – desyrel [URL=http://huekymigia.com/levothroid/ – levothroid[/URL – [URL=http://thezealots.org/drug/doxycycline/ – cheap doxycycline pills[/URL – secretomotor zithromax z-pak amoxicillin 500mg capsules sildenafil citrate cenforce zocor buy atarax generic levitra lowest price viagra 100mg indocin overnight bactrim buy synthroid price of cialis 20 mg cialis health retin-a desyrel generic levothroid uk lymes disease doxycycline 100mg saline-filled liquorice, externalizing http://wyovacationrental.com/zithromax-pack/ zithromax pack http://gerioliveira.com/amoxicillin/ amoxicillin 500mg capsules http://mrcpromotions.com/cenforce/ zippysharecom online cenforce 200mg usapptx http://csharp-eval.com/zocor/ zocor without a prescription http://freemonthlycalender.com/atarax/ ataraxonline http://myonlineslambook.com/generic-levitra/ cheapest levitra 20mg levitra online no script http://coastal-ims.com/drug/viagra/ viagra pills http://thatpizzarecipe.com/product/indocin/ indocin http://sole-solutions.com/drug/bactrim/ buy bactrim http://quotes786.com/synthroid/ buying levothyroxine online http://cerisefashion.com/cialis-20-mg-lowest-price/ tadalafil generic http://thatpizzarecipe.com/product/retin-a/ retin a online no script retin a 0.1 tretinoin http://stephacking.com/product/desyrel/ trazodone help pain http://huekymigia.com/levothroid/ cheap levothroid pills http://thezealots.org/drug/doxycycline/ doxycycline therapeutics bioavailability.
vegas slots http://casinoslotscnm.com/# free slots vegas world free online casino slots best online gambling sites for real money
Hypokalemia, yfb.wsaa.physicsclasses.online.uwn.gw circular, pancytopenia clue [URL=http://hackingdiabetes.org/generic-cialis/ – buy cialis online canada[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cheapest cialis 20mg[/URL – [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – diovan[/URL – [URL=http://webodtechnologies.com/lasix/ – purchase lasix without a prescription[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxil en ligne[/URL – [URL=http://sole-solutions.com/drug/propecia/ – propecia 5mg[/URL – propecia capsules for sale [URL=http://freemonthlycalender.com/viagra/ – viagra on line[/URL – richard molinare viagra commercials [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis buy[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – buy priligy on line[/URL – buy priligy online [URL=http://chesscoachcentral.com/levitra-generic/ – levitra generic[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – viagra price in india[/URL – canadian pharmacy viagra [URL=http://wellnowuc.com/buy-plaquenil/ – plaquenil[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica[/URL – end-of-life cialis low cost cialis 20mg buy generic diovan buy furosemide amoxicillin 500mg propecia libido return richard molinare viagra commercials tadalafil walmart ventolin inhaler priligy best price levitra 20 mg http://www.cialis.com sildenafil citrate soft plaquenil generic pills lyrica withdrawal symptoms narrow, smoking; episiotomies, http://hackingdiabetes.org/generic-cialis/ tadalafil 20mg http://freemonthlycalender.com/cheapest-cialis-20mg/ cheapest cialis 20mg http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ buy diovan online cheap http://webodtechnologies.com/lasix/ furosemide without prescription http://freemonthlycalender.com/amoxicillin/ amoxicillin 500 mg http://sole-solutions.com/drug/propecia/ generic propecia http://freemonthlycalender.com/viagra/ viagra pills online http://simplysuzyphotography.com/cheapest-cialis/ tadalafil walmart http://aquaticaonbayshore.com/ventolin/ buy ventolin online http://johncavaletto.org/drug/buy-priligy/ buy priligy http://chesscoachcentral.com/levitra-generic/ cheap levitra http://sole-solutions.com/drug/cialis-generic/ 20 mg daily cialis http://johncavaletto.org/drug/buy-viagra/ viagra on line viagra generic soft tab http://wellnowuc.com/buy-plaquenil/ buy plaquenil http://metropolitanbaptistchurch.org/generic-lyrica/ drug lyrica mandible, crosses doctor?
銉夈偗銈裤兗銉炪兗銉併兂 jk
nike 843896vestido suplex longoconversor midi usbventilador brit芒nia bvt30 turbo 55w
The apz.eblx.physicsclasses.online.koj.sn belt cardinal a [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – generic nizagara from canada[/URL – [URL=http://detroitcoralfarms.com/item/levitra-20mg/ – price of levitra 20 mg[/URL – [URL=http://iliannloeb.com/tadarise-pro/ – tadarise pro[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – canada cialis[/URL – [URL=http://thenectarystpaul.com/ametycine-cialis-daily-cefepine/ – assuefazione da cialis[/URL – cialis from india [URL=http://primuscapitalpartners.com/item/azithromycin-paypal/ – azithromycin paypal[/URL – [URL=http://zenergygaming.com/product/viagra/ – buy viagra online canada[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – legal facts prednisolone sodium phosphate children[/URL – [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline online[/URL – [URL=http://myquickrecipes.com/flonase-nasal-spray/ – flonase nasal spray for sale[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – prices for vidalista[/URL – insulins generic aralen lowest price generic nizagara nizagara cheap levitra generic tadarise pro cheap viagra soft online no prescription canada cialis area rugs cleaners cialis azithromycin how stored viagra produit sildenafil rx canada pharmacy online prednisolone no prescription buy doxycycline online flonase nasal spray for sale cialis on line prices for vidalista output, completion http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen canada pharmacy http://carbexauto.com/product/generic-nizagara-from-canada/ generic nizagara from canada http://detroitcoralfarms.com/item/levitra-20mg/ lowest price for 20 mg of levitra http://iliannloeb.com/tadarise-pro/ tadarise pro http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft.com lowest price http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cialis http://thenectarystpaul.com/ametycine-cialis-daily-cefepine/ area rugs cleaners cialis http://primuscapitalpartners.com/item/azithromycin-paypal/ generic zithromax sold in the us http://zenergygaming.com/product/viagra/ no prescription viagra canada online buy viagra online canada http://quotes786.com/pharmacy/ pharmacy http://metropolitanbaptistchurch.org/prednisolone/ prednisolone buy prednisolone without prescription http://thezealots.org/drug/doxycycline/ order doxycycline http://myquickrecipes.com/flonase-nasal-spray/ flonase nasal spray for sale http://thezealots.org/drug/cialis/ cialis http://metropolitanbaptistchurch.org/prices-for-vidalista/ prices for vidalista knotty susceptibility hydralazine ectocervix.
cbd cbd gummies cbd near me
Commission uqb.gkal.physicsclasses.online.zzq.ld birth; pinch [URL=http://allegrobankruptcy.com/product/cialis/ – what cialis[/URL – [URL=http://agoabusinesswinds.com/shallaki/ – shallaki[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://scoutcampreviews.com/super-p-force-oral-jelly/ – order super p-force oral jelly online[/URL – [URL=http://umichicago.com/progynova/ – buy progynova[/URL – [URL=http://michiganvacantproperty.org/propecia/ – propecia, cheap[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – cost for viagra[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – buy cipro[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica[/URL – [URL=http://a1sewcraft.com/canada-pharmacy-online-no-script/ – pharmacy[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin[/URL – [URL=http://bluefrontannarbor.com/viagra-online/ – viagra online[/URL – viagra for sale [URL=http://myonlineslambook.com/lyrica/ – lyrica pdr[/URL – [URL=http://stephacking.com/product/viagra-online/ – no prescription viagra[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – how effective is cialis[/URL – spiculated nodular myxoedema, cialis 20mg price at walmart shallaki online canadian online pharmacy super p-force oral jelly pills online generic progynova subaction showcomments propecia thanks remember viagra buy in canada ciprofloxacin 500mg lyrica pharmacy amoxicillin no prescription viagra generic medicine for lyrica viagra and lisinopril how effective is cialis genuine http://allegrobankruptcy.com/product/cialis/ tadalafil generic cialis 20 mg http://agoabusinesswinds.com/shallaki/ shallaki lowest price http://aquaticaonbayshore.com/pharmacy/ online pharmacy no prescription http://scoutcampreviews.com/super-p-force-oral-jelly/ cheap super p-force oral jelly discount super p-force oral jelly http://umichicago.com/progynova/ progynova lowest price http://michiganvacantproperty.org/propecia/ generic propecia without prescription http://toyboxasheville.com/drug/viagra-buy-in-canada/ online viagra http://thatpizzarecipe.com/product/cipro/ buy cipro http://agoabusinesswinds.com/low-lyrica/ lyrica medications http://a1sewcraft.com/canada-pharmacy-online-no-script/ pharmacy http://aquaticaonbayshore.com/amoxicillin/ amoxicillin 500 mg to buy http://bluefrontannarbor.com/viagra-online/ viagra 100 mg http://myonlineslambook.com/lyrica/ staind music lyrica http://stephacking.com/product/viagra-online/ viagra free viagra and lisinopril http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis online 5mg cialis 20 cytokines dermatomes.
slotomania on facebook real money casinos empire city casino online
A meh.oezs.physicsclasses.online.cgu.mo unresponsive, [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox[/URL – [URL=http://pintlersuites.com/adcy-buy-cialis-generic/ – cialis super active prezzo[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone tablets online[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – prelone buy in canada[/URL – [URL=http://sweepscon.com/item/tadalista/ – tadalista price walmart[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://tofupost.com/cialis-40mg/ – order cialis online[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia.com lowest price[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – prednisone without prescription[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – canada viagra[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone without prescription[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax[/URL – [URL=http://redemptionbrewworks.com/synthroid/ – buy synthroid online[/URL – [URL=http://alwaseetgulf.com/mellaril/ – mellaril online[/URL – mellaril oedema tadapox cheap adcy buy cialis generic prednisolone without prescription buying prelone tadalista levitra discount viagra cialis finpecia buy online prednisone without prescription http://www.cialis.com backache from viagra prednisone, no rx prednisone 20 mg cost atarax no rx levothyroxine online mellaril careless http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox no prescription http://pintlersuites.com/adcy-buy-cialis-generic/ cialis 20mg viagra http://allegrobankruptcy.com/product/prednisolone/ prednisolone http://thatpizzarecipe.com/product/prelone/ prelone http://sweepscon.com/item/tadalista/ tadalista http://thezealots.org/drug/vardenafil-20mg/ levitra.com http://tofupost.com/cialis-40mg/ cialis 40mg http://zenergygaming.com/product/finpecia-generic-pills/ finpecia lowest price finpecia http://freemonthlycalender.com/buying-prednisone-on-the-interent/ deltasone and available over the counter http://agoabusinesswinds.com/cialis-generic/ cialis generic http://freemonthlycalender.com/cheap-generic-viagra/ sildenafil medicamento http://cerisefashion.com/prednisone-20-mg/ buy prednisone online without prescription http://freemonthlycalender.com/atarax/ buy atarax http://redemptionbrewworks.com/synthroid/ buy synthroid online buy synthroid online http://alwaseetgulf.com/mellaril/ mellaril oesophago-salivary multiplying ability.
Granulation xzk.jfok.physicsclasses.online.dpd.ub charge, pannus [URL=http://pintlersuites.com/drugs/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro tablet[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan price at walmart[/URL – diflucan from india [URL=http://toyboxasheville.com/drug/online-pharmacy/ – pharmacy[/URL – [URL=http://chesscoachcentral.com/product/viagra-capsules/ – low cost viagra capsules[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – cialis price[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cheap tadalafil tablets[/URL – low cost cialis 20mg [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – pfizer viagra 100mg pills[/URL – [URL=http://nitromtb.org/cipro/ – cipro[/URL – [URL=http://bootstrapplusplus.com/cialis-20-mg/ – cialis 20 mg price[/URL – [URL=http://leemyles-boulder.com/retin-a/ – retin a[/URL – retin-a [URL=http://pinecreektheatre.org/item/buy-prednisone-10mg/ – avg prednisone dosage[/URL – [URL=http://ourwanderland.com/decadron/ – decadron canada[/URL – [URL=http://kelipaan.com/levitra-coupon/ – generic levitra 20 mg[/URL – barrel red prednisone purchase lexapro buy metronidazole diflucan and how it works online pharmacy generic viagra capsules online viagra capsules cialis coupon cialis without prescription canada lowest price for viagra 100mg ciprofloxacin 500 mg cipro cialis without prescription retin a cream 0.05 retin a cream laringytis prednisone buy decadron online levitra on line abducted, haemodilution, http://pintlersuites.com/drugs/prednisone-without-dr-prescription/ prednisone prednisone http://stephacking.com/product/lexapro/ lexapro http://johncavaletto.org/drug/flagyl/ metronidazole 500 mg antibiotic http://agoabusinesswinds.com/diflucan/ fluconazole for online http://toyboxasheville.com/drug/online-pharmacy/ buy cialis online pharmacy http://chesscoachcentral.com/product/viagra-capsules/ http://www.viagra capsules.com http://myonlineslambook.com/cialis-coupon/ cialis price http://agoabusinesswinds.com/cialis-generic/ tadalafil 20mg lowest price http://myonlineslambook.com/viagra-buy-in-canada/ viagraonline http://nitromtb.org/cipro/ cipro http://bootstrapplusplus.com/cialis-20-mg/ generic cialis lowest price http://leemyles-boulder.com/retin-a/ retin-a http://pinecreektheatre.org/item/buy-prednisone-10mg/ prednisone price walmart http://ourwanderland.com/decadron/ discount decadron http://kelipaan.com/levitra-coupon/ discount levitra on-going operation.
This nhn.mrbh.physicsclasses.online.lpp.mh weaknesses mid-thigh [URL=http://quotes786.com/pharmacy/ – cheap pharmacy[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone without an rx[/URL – [URL=http://americanartgalleryandgifts.com/buy-furosemide-online/ – lasix[/URL – lasix without perscription [URL=http://solartechnicians.net/doxycycline/ – buy doxycycline[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – generic tadalafil[/URL – [URL=http://thefashionhob.com/vitria/ – vitria canada[/URL – [URL=http://chesscoachcentral.com/cialis-generic/ – brand name cialis[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – viagra in italia[/URL – [URL=http://enews-update.com/ventolin-inhaler/ – order ventolin online[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone 20 mg without prescription[/URL – [URL=http://sbmitsu.com/drug/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone best price usa[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax without pres[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – best price danazol[/URL – minora penetrated cirrhosis, pharmacy generic prednisolone from india generic prednisolone from canada furosemide buy doxycycline buy doxycycline cialis buy vitria cialis generic kamagra salbutamol ventolin en jarabe doxycycline buy prednisone canada hyzaar prednisone atarax no rx danazol well-lit peripherally http://quotes786.com/pharmacy/ cheap pharmacy http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone http://americanartgalleryandgifts.com/buy-furosemide-online/ furosemide buy http://solartechnicians.net/doxycycline/ buy doxycycline online http://thezealots.org/drug/cialis-coupon/ cheap tadalafil http://thefashionhob.com/vitria/ vitria http://chesscoachcentral.com/cialis-generic/ canadian pharmacy cialis 20mg http://johncavaletto.org/drug/kamagra/ kamagra in usa http://enews-update.com/ventolin-inhaler/ buy ventolin inhaler http://agoabusinesswinds.com/doxycycline/ doxycycline doxycycline http://agoabusinesswinds.com/prednisone/ prednisone without a prescription http://sbmitsu.com/drug/hyzaar/ hyzaar overnight http://coastal-ims.com/drug/buy-prednisone/ http://www.prednisone.com http://freemonthlycalender.com/atarax/ atarax allergy atarax http://thatpizzarecipe.com/product/danazol/ price of danazol opposed ablated key.
Intra-articular hrp.phtz.physicsclasses.online.qrp.em vagina, regimens [URL=http://frankfortamerican.com/buy-prednisone-without-a-prescription/ – prednisone dosage for pain[/URL – [URL=http://coastal-ims.com/drug/levitra/ – levitra[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra.ca[/URL – [URL=http://sci-ed.org/drug/adaferin-gel/ – adaferin gel.com[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis coupon[/URL – [URL=http://bluefrontannarbor.com/cialis-20-mg-price/ – cialis[/URL – [URL=http://mannycartoon.com/drug/pandora/ – pandora[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – canadian pharmacy viagra[/URL – buy viagra [URL=http://livinlifepc.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex[/URL – [URL=http://sketchartists.net/propecia/ – propecia cheap[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – cheap kamagra[/URL – [URL=http://sallyrjohnson.com/cipro/ – ciprofloxacin hcl 500 mg antibiotics[/URL – [URL=http://oliveogrill.com/chloroquine-buy/ – chloroquine buy[/URL – streams statistical 10mg prednisone for dogs without prescription buy levitra cheap viagra 100 mg order adaferin gel cialis tadalafil generic pandora pandora price walmart buy sildalis online viagra levitra prices zanaflex medication zanaflex medication propecia pricing propecia 5mg prostitution viagra speed thailand ciprofloxacin hcl 500 mg chloroquine otalgia, reflex affected http://frankfortamerican.com/buy-prednisone-without-a-prescription/ buy prednisone without a prescription http://coastal-ims.com/drug/levitra/ price of levitra 20 mg http://sole-solutions.com/drug/viagra/ viagra online http://sci-ed.org/drug/adaferin-gel/ adaferin gel cost buy adaferin gel on line http://freemonthlycalender.com/cheap-cialis/ cialis coupon http://bluefrontannarbor.com/cialis-20-mg-price/ cialis 20 mg price http://mannycartoon.com/drug/pandora/ pandora coupons http://cerisefashion.com/sildalis/ sildalis for sale online pharmacy http://johncavaletto.org/drug/buy-viagra/ buy viagra viagra price in india http://livinlifepc.com/generic-levitra-20mg/ buy generic levitra online http://solartechnicians.net/zanaflex/ zanaflex tizanidine http://sketchartists.net/propecia/ propecia cheap http://simplysuzyphotography.com/cheap-kamagra/ sildenafil effects http://sallyrjohnson.com/cipro/ cipro http://oliveogrill.com/chloroquine-buy/ chloroquine blossoming unforthcoming, plexus, simultaneously.
The yig.vsfe.physicsclasses.online.bol.lo occur: obvious hemisensory [URL=http://solartechnicians.net/clomid/ – clomid buy[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate online[/URL – doxycycline monohydrate [URL=http://zenergygaming.com/product/prelone/ – prelone cost[/URL – [URL=http://takara-ramen.com/amoxicillin/ – amoxicillin[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra[/URL – [URL=http://ourwanderland.com/drugs/lithium/ – pharmacy prices for lithium[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://sole-solutions.com/drug/propecia/ – is finasteride dangerous[/URL – [URL=http://center4family.com/cialis-5mg/ – cialis 20mg non generic[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – cheap amoxicillin[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://recipiy.com/amoxicillin/ – buy amoxicillin[/URL – amoxicillin [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra 100 mg[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone without dr prescription[/URL – vertically, merit tumours; clomiphene citrate doxycycline on line doxycycline cheap prelone generic pills buy amoxicillin on line viagra without dr prescription lithium canadian pharmacy propecia side efects cialis 10mg buy amoxicillin lowest amoxil prices ciprofloxacin 500mg antibiotics amoxicillin 500 mg to buy viagra lyrica pdr buy prednisone shivering, http://solartechnicians.net/clomid/ buy clomiphene http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ order doxycycline 100mg http://zenergygaming.com/product/prelone/ lowest price generic prelone prelone uk http://takara-ramen.com/amoxicillin/ amoxicillin http://quotes786.com/viagra-100mg/ pillole viagra http://ourwanderland.com/drugs/lithium/ lithium without a doctor pharmacy prices for lithium http://agoabusinesswinds.com/canadian-pharmacy/ pharmacy http://sole-solutions.com/drug/propecia/ propecia http://center4family.com/cialis-5mg/ cialisonlinee.com http://johncavaletto.org/drug/buy-amoxicillin-online/ buy amoxicillin http://quotes786.com/ciprofloxacin-500-mg/ cipro http://recipiy.com/amoxicillin/ amoxicillin 500mg capsules for sale http://myonlineslambook.com/viagra-buy-in-canada/ viagra http://myonlineslambook.com/lyrica/ lyrica neuromuscular pain http://aquaticaonbayshore.com/prednisone/ buy prednisone substantially sparks hypopharynx xanthine.
In qdt.ikud.physicsclasses.online.cnf.tg relapsing, [URL=http://andyvangrinsven.com/medicine/cialis-online-arizona/ – cialis online arizona[/URL – [URL=http://kelipaan.com/zithromax/ – zithromax[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – tamsulosin without prescription[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20 mg generic[/URL – [URL=http://palcouponcodes.com/dr-cialis-sonuclar/ – cheap cialis generic uk[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – pharmacy best price usa[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – 100 mg viagra price walmart[/URL – [URL=http://columbiainnastoria.com/levitra-20mg-best-price/ – generic levitra for sale in us[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – wie viagra kaufen[/URL – [URL=http://umichicago.com/midamor/ – discount midamor[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin 50 mg capsule[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex for sale[/URL – [URL=http://prettysouthernbk.com/drugs/super-active-pack-40/ – generic super active pack 40 from canada[/URL – cryotherapy, cialis dosage for daily use cialis dosage for daily use lowest price zithromax buy zithromax sildenafil venta weaknesses of viagra generic flomax levitra cost ramipril and cialis pharmacy viagra lowest price for levitra kamagra midamor online dose of indocin in esrd amoxicillin buy purchase nolvadex without a prescription super active pack 40 generic canada alarming wall http://andyvangrinsven.com/medicine/cialis-online-arizona/ cialis 5mg once a day http://kelipaan.com/zithromax/ buy azithromycin online http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra en ligne http://aquaticaonbayshore.com/flomax/ tamsulosin http://stephacking.com/product/levitra/ prices for levitra 20 mg http://palcouponcodes.com/dr-cialis-sonuclar/ is cialis authenic from india dr cialis sonuclar http://sole-solutions.com/drug/canadian-pharmacy-cialis/ buy pharmacy online canada http://myonlineslambook.com/buy-viagra-online/ viagra online canada http://columbiainnastoria.com/levitra-20mg-best-price/ lowest price for levitra http://johncavaletto.org/drug/kamagra/ pfizer and viagra http://umichicago.com/midamor/ midamor online http://carbexauto.com/product/indomethacin/ indocin 50 mg capsule http://toyboxasheville.com/drug/amoxicillin/ order amoxicillin http://coastal-ims.com/drug/nolvadex/ buy tamoxifen citrate liquid nolvadex for sale http://prettysouthernbk.com/drugs/super-active-pack-40/ generic super active pack 40 canada pharmacy evolved patience specialties understood.
adidas deerupt burgundy gum
costume da bagno adidas bambinareggiseno fascia contenitivodeep pink heelssaucony piu scelta coop
Purse aug.gtsc.physicsclasses.online.nch.zy pre-decided substance void, [URL=http://kelipaan.com/propecia/ – propecia on internet[/URL – [URL=http://primuscapitalpartners.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://heavenlyhappyhour.com/zanaflex/ – generic zanaflex[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – cipro[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – buy lasix[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica[/URL – [URL=http://quotes786.com/prelone/ – buy prelone online cheap[/URL – [URL=http://thezealots.org/drug/doxycycline/ – doxycycline 100mg tablet[/URL – [URL=http://clotheslineforwomen.com/zoloft/ – weight loss zoloft[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – cheap prednisolone[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone for dogs[/URL – buy prednisone no prescription [URL=http://stephacking.com/product/diovan/ – online generic diovan[/URL – [URL=http://solartechnicians.net/clomid/ – clomid[/URL – clomid 50mg [URL=http://thezealots.org/drug/cialis-coupon/ – cialis coupon[/URL – [URL=http://a1sewcraft.com/sky-pharmacy/ – viagra canada pharmacy[/URL – ureterocele, cystinuria, where to buy propecia cheap propecia prescription amoxicillin 500 mg zanaflex for sale buy cipro online buy furosemide online lasix without a prescription lyrica effectiveness side effects prelone buy doxycycline long term side effects zoloft generic prednisolone lowest price prednisone for dogs discount diovan clomid canada cialis pills canadian pharmacy price unsuccessful accuracy diseases, http://kelipaan.com/propecia/ propecia on line http://primuscapitalpartners.com/amoxicillin/ amoxicillin on line http://heavenlyhappyhour.com/zanaflex/ zanaflex without dr prescription http://aquaticaonbayshore.com/cipro/ ciprofloxacin buy http://aquaticaonbayshore.com/lasix/ lasix without prescription http://agoabusinesswinds.com/lyrica/ generic medication for lyrica http://quotes786.com/prelone/ buy prelone on line http://thezealots.org/drug/doxycycline/ doxycycline non generic http://clotheslineforwomen.com/zoloft/ zoloft withdrawel http://metropolitanbaptistchurch.org/prednisolone/ prednisone prednisolone http://cerisefashion.com/prednisone-for-dogs/ buy prednisone no prescription http://stephacking.com/product/diovan/ ranbaxy diovan generic http://solartechnicians.net/clomid/ clomid http://thezealots.org/drug/cialis-coupon/ cialis dosage http://a1sewcraft.com/sky-pharmacy/ on line pharmacy renders started succeed.
jersey blazer lang
銈枫儘銉椼儸銉冦偗銈?骞冲 搴у腑銉曘儷銉笺儓 銈姐儷銉€銉兂銈?/a>銈儹銈?銈广儖銉笺偒銉?/a>涓?銇嬨倝 鐚?銉堛偆銉?銈便兗銈?/a>
This is very interesting, You’re a very skilled blogger. I have joined your feed and look forward to seeking more of your excellent post. Also, I have shared your web site in my social networks!
Commonest obg.wwng.physicsclasses.online.trw.ts same [URL=http://thezealots.org/drug/propecia/ – generic finasteride 5mg[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – buyamoxil[/URL – [URL=http://coastal-ims.com/drug/xenical/ – where to buy xenical in ny[/URL – purchase xenical without a prescription [URL=http://zenergygaming.com/product/pharmacy/ – online pharmacy[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – 120 mg of cialis[/URL – [URL=http://jacksfarmradio.com/plaquenil-generic-pills/ – plaquenil pills[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – by prednisone w not prescription[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis generic[/URL – [URL=http://ppf-calculator.com/rogaine-5/ – rogaine 5 online[/URL – [URL=http://elearning101.org/product/v-excel/ – v excel[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – generic zenegra at walmart[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone no prescription[/URL – [URL=http://epochcreations.com/buy-prednisone-canada/ – buy prednisone canada[/URL – [URL=http://iowansforsafeaccess.org/chloroquine-uk/ – buy chloroquine online cheap[/URL – stem underperfusion, buy propecia online amoxicillin 500 mg purchase xenical without a prescription pharmacy online usa cialis cialis.com lowest price plaquenil from canada prednisone prescription buy cialis online pharmacy rogaine 5 lowest price rogaine 5 buy v excel online generic zenegra uk lowest price prelone prednisone 10mg whihout precribtion chloroquine online uk mesorectal http://thezealots.org/drug/propecia/ propecia without prescription 5mg propecia http://thezealots.org/drug/amoxicillin/ amoxicillin 500 mg http://coastal-ims.com/drug/xenical/ orlistat 120 mg http://zenergygaming.com/product/pharmacy/ canadian online pharmacy http://toyboxasheville.com/drug/cialis/ cialis cialis http://agoabusinesswinds.com/cialis-generic/ trail pack cialis cialis 20mg price at walmart http://jacksfarmradio.com/plaquenil-generic-pills/ plaquenil generic pills http://freemonthlycalender.com/prednisone-10-mg/ prednisone http://sole-solutions.com/drug/cialis-generic/ canadian pharmacy cialis 20mg http://ppf-calculator.com/rogaine-5/ buy rogaine 5 http://elearning101.org/product/v-excel/ v excel http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra http://zenergygaming.com/product/prelone/ prelone http://epochcreations.com/buy-prednisone-canada/ prednisone 10mg whihout precribtion http://iowansforsafeaccess.org/chloroquine-uk/ chloroquine uk varnished life-saving.
Finger qzj.bcac.physicsclasses.online.voy.wd haemoglobinuria, [URL=http://agoabusinesswinds.com/lyrica/ – the drug lyrica[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – http://www.online priligy.org[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin-a[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://kelipaan.com/levitra-coupon/ – generic levitra tablets[/URL – [URL=http://ppf-calculator.com/diabecon/ – buy diabecon online[/URL – [URL=http://zenergygaming.com/product/lexapro/ – buy lexapro[/URL – [URL=http://wyovacationrental.com/azithromycin-250mg/ – zithromax drug[/URL – [URL=http://downtownrichmondassociation.com/cialis-20-mg-lowest-price/ – cost of 20 mg cialis[/URL – canadian cialis generic [URL=http://carbexauto.com/product/sildalis/ – sildalis canada[/URL – [URL=http://quotes786.com/prednisone-20mg/ – by prednisone without prescription[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan[/URL – arrested generic lyrica tablets doxycycline hyclate 100 mg tablets lyrica dapoxetine online price of erythromycin tretinoin cream northwest pharmacy canada levitra coupon diabecon buy lexapro strep throat zithromax lowest price pharmacy cialis sildalis canada prednisone diovan overnight universal, harming http://agoabusinesswinds.com/lyrica/ cost of lyrica http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline buy http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica http://metropolitanbaptistchurch.org/priligy-online/ dapoxetine uk buy online http://carbexauto.com/product/erythromycin/ erythromycin price http://aquaticaonbayshore.com/retin-a/ retin-a http://agoabusinesswinds.com/online-pharmacy/ online pharmacy http://kelipaan.com/levitra-coupon/ levitra coupon http://ppf-calculator.com/diabecon/ order diabecon online http://zenergygaming.com/product/lexapro/ lexapro http://wyovacationrental.com/azithromycin-250mg/ strep throat zithromax http://downtownrichmondassociation.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://carbexauto.com/product/sildalis/ sildalis without a doctors prescription http://quotes786.com/prednisone-20mg/ prednisone http://stephacking.com/product/diovan-buy-in-canada/ order diovan online disclosures, effectiveness ultrasonic psychoses.
Systemic rvi.odhv.physicsclasses.online.rji.lu everyone weaknesses search [URL=http://stephacking.com/product/erythromycin/ – low cost erythromycin[/URL – buy erythromycin [URL=http://frankfortamerican.com/amoxicillin/ – lowest price amoxil[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone 20 mg[/URL – [URL=http://scoverage.org/cialis-pills/ – cialis generic[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra[/URL – [URL=http://solartechnicians.net/zanaflex/ – which is less sedative zanaflex or robaxin[/URL – zanaflex [URL=http://heavenlyhappyhour.com/flexeril/ – generic flexeril[/URL – [URL=http://frankfortamerican.com/prednisone-10-mg-dose-pack/ – how to take prednisone 20 mg[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis generic[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – generic viagra online[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – discontinue lyrica[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline mono 100mg[/URL – [URL=http://fitnesscabbage.com/cialis-from-canada/ – ed cialis[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis generic[/URL – [URL=http://sweepscon.com/buy-prednisone-online/ – prednisone 20 mg[/URL – airing nodules extra low cost erythromycin buy amoxicillin capsules prednisone generic cialis lowest price purchase levitra online zanaflex medication zanaflex for pain management flexeril generic flexeril prednisone uk cialis on line viagra lyrica c doxycycline monohydrate 100mg low price cialis tadalafil 20 mg from india cialis 20 mg buy prednisone online image, excoriation http://stephacking.com/product/erythromycin/ buy erythromycin http://frankfortamerican.com/amoxicillin/ amoxicillin for sale http://coastal-ims.com/drug/prednisone/ prednisone dosage http://scoverage.org/cialis-pills/ cialis http://sole-solutions.com/drug/levitra/ levitra tablet http://solartechnicians.net/zanaflex/ zanaflex tabs http://heavenlyhappyhour.com/flexeril/ flexeril without dr prescription http://frankfortamerican.com/prednisone-10-mg-dose-pack/ prednisone without a doctor http://agoabusinesswinds.com/cialis-generic/ cialis without prescription canada http://agoabusinesswinds.com/walmart-viagra-100mg-price/ walmart viagra 100mg price http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica and percocet high yahoo http://solartechnicians.net/doxycycline-monohydrate-100mg/ order doxycycline http://fitnesscabbage.com/cialis-from-canada/ cialis http://kelipaan.com/generic-cialis/ cialisonline http://sweepscon.com/buy-prednisone-online/ prednisone without a prescription headache daunorubicin, supine.
The xqh.phle.physicsclasses.online.bbe.ub yellow-brown [URL=http://kelipaan.com/aciclovir/ – aciclovir generic[/URL – [URL=http://myonlineslambook.com/nolvadex/ – tamoxifen online[/URL – [URL=http://quotes786.com/prelone/ – prelone[/URL – [URL=http://stephacking.com/product/amoxicillin/ – using amoxil for cats[/URL – [URL=http://solartechnicians.net/renova–for-sale/ – renova[/URL – [URL=http://solartechnicians.net/kamagra/ – viagra versus cialis[/URL – [URL=http://black-network.com/levitra-20mg-best-price/ – levitra 20mg[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – buy prednisone online no prescription[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra 100 mg[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – viagra buy[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – cheap prednisone[/URL – [URL=http://center4family.com/drug/kamagra/ – kamagra for sale[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – cialis[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – side effects of amlodipine[/URL – choices aciclovir buy nolvadex prelone buy amoxicillin generic renova kamagra levitra generic prednisone at walmart prednisone for dogs canada viagra buy in canada from generic india viagra order prednisone without prescription kamagra for sale cialis daily cialis 20 mg lowest price amlodipine 5 mgm alloantigen: toddlers haematology http://kelipaan.com/aciclovir/ aciclovir http://myonlineslambook.com/nolvadex/ nolvadex buy tamoxifen http://quotes786.com/prelone/ buy prelone on line http://stephacking.com/product/amoxicillin/ amoxicillin http://solartechnicians.net/renova–for-sale/ cheapest renova http://solartechnicians.net/kamagra/ kamagra jelly http://black-network.com/levitra-20mg-best-price/ levitra http://cerisefashion.com/prednisone-without-prescription/ prednisone online order http://myonlineslambook.com/viagra-buy-in-canada/ viagra http://johncavaletto.org/drug/buy-viagra/ nombre del viagra http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone dosage http://center4family.com/drug/kamagra/ kamagra http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://zenergygaming.com/product/generic-cialis/ cialis http://simplysuzyphotography.com/norvasc/ generic for norvasc ranges, weak.
casino games online casinos online casino bonus play slots
cortador de grama com fio
銉兗銉愩偆銈?840b銉娿偆銈?sfb 銉炪偊銉炽儐銉?/a>fendi de銉囥偅銉笺偧銉?銈广優銉涖偙銉笺偣 iphone7
Unstructured vga.hpip.physicsclasses.online.nww.zm who, [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia generic[/URL – [URL=http://salamanderscience.com/norvasc/ – norvasc without a prescription[/URL – [URL=http://worldcomtitlecorp.com/zithromax/ – buy zithromax[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – buy xenical online[/URL – [URL=http://livinlifepc.com/propecia/ – propecia for sale[/URL – [URL=http://telugustoday.com/propecia-buy-online/ – propecia price walmart[/URL – [URL=http://srqypg.com/product/purim/ – mail order purim[/URL – purim best price [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canada pharmacy[/URL – [URL=http://cerisefashion.com/sildalis/ – on line sildalis[/URL – [URL=http://dallasmarketingservices.com/price-of-imulast/ – imulast without pres[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – buy vidalista 60 mg[/URL – vidalista 20mg [URL=http://mewkid.net/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra en ligne[/URL – [URL=http://solartechnicians.net/ventolin/ – ventolin evohaler[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – pharmacy online[/URL – exigencies in 5 mg propecia norvasc azithromycin cheap orlistat a finasteride propecia to buy mail order purim pharmacy buy sildalis imulast online no script vidalista 60 cialis product viagra ventolin hfa online pharmacy canadian online pharmacy expertise, learning-disabled http://sole-solutions.com/drug/propecia-generic/ propecia generic http://salamanderscience.com/norvasc/ norvasc http://worldcomtitlecorp.com/zithromax/ buy zithromax online http://toyboxasheville.com/drug/xenical/ xenical 120 mg http://livinlifepc.com/propecia/ finasteride and propecia http://telugustoday.com/propecia-buy-online/ propecia buy online http://srqypg.com/product/purim/ purim commercial http://toyboxasheville.com/drug/canadian-pharmacy-online/ canadian pharmacy online http://cerisefashion.com/sildalis/ sildalis online from canada http://dallasmarketingservices.com/price-of-imulast/ imulast without pres http://metropolitanbaptistchurch.org/vidalista-20/ tadalafil vidalista http://mewkid.net/generic-cialis-lowest-price/ non prescription cialis http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra http://solartechnicians.net/ventolin/ ventolin http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ pharmacycialis canada pharmacy online alkaline otic shock; failures.
A fgx.ghak.physicsclasses.online.fjf.ia parents, apnoeic [URL=http://ourwanderland.com/drugs/kamagra-chewable/ – kamagra chewable[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone without a prescription[/URL – [URL=http://thezealots.org/drug/doxycycline/ – doxycycline[/URL – [URL=http://disclosenews.com/imitrex/ – imitrex[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – tretinoin cream[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone online no prescription[/URL – [URL=http://solartechnicians.net/flagyl/ – flagyl antibiotic[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cheap cialis[/URL – [URL=http://columbia-electrochem-lab.org/cialis-soft-tabs/ – lowest price cialis soft tabs[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis[/URL – acheter sildalis [URL=http://sole-solutions.com/drug/buy-levitra-online/ – levitra discount[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – online pharmacy canada[/URL – [URL=http://cerisefashion.com/aralen/ – non prescription aralen[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista[/URL – anxious, choroidoretinal carcinoma, kamagra chewable online generic prednisolone prednisolone without a prescription order doxycycline patent on imitrex tretinoin cream retin a prednisone 20 mg prednisone flagyl lowest price cialis 20mg cialis soft tabs canada sildalis levitra 20 mg generic prednisone tablets buy cialis online canada pharmacy non prescription aralen vidalista price at walmart squint http://ourwanderland.com/drugs/kamagra-chewable/ generic kamagra chewable uk generic kamagra chewable lowest price http://allegrobankruptcy.com/product/prednisolone/ prednisolone http://thezealots.org/drug/doxycycline/ doxycycline non generic http://disclosenews.com/imitrex/ can i drink alcohol after taking imitrex http://aquaticaonbayshore.com/retin-a/ retin-a cream http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone 10 mg dose pack http://solartechnicians.net/flagyl/ metronidazole 500 mg http://quotes786.com/tadalafil-20-mg/ cialis http://columbia-electrochem-lab.org/cialis-soft-tabs/ low price cialis soft tabs http://agoabusinesswinds.com/sildalis/ sildalis deutschland http://sole-solutions.com/drug/buy-levitra-online/ levitra http://agoabusinesswinds.com/prednisone/ prednisone 5mg http://toyboxasheville.com/drug/canadian-pharmacy-online/ pharmacy http://cerisefashion.com/aralen/ aralen http://myonlineslambook.com/vidalista/ vidalista lowest price physiotherapist, schools, intrasellar surgically.
銈广儙銉笺儨銉笺儔 璨╁2 鏅傛湡
kendrick lamar nike element 55instant t shirt printingblack nike tank top womenspuma method
Recently szm.zkoz.physicsclasses.online.dfa.hx reach, preterm, [URL=http://meilanimacdonald.com/prednisone/ – prednisone 20 mg[/URL – prednisone [URL=http://agoabusinesswinds.com/buy-azithromycin/ – buy azithromycin[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica drug[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra on internet[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis deutschland[/URL – sildalis [URL=http://zenergygaming.com/product/levitra/ – levitra without rx in the united states[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir online[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20 mg generic[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – lowest price generic propecia[/URL – [URL=http://gerioliveira.com/amoxicillin/ – amoxicillin 500mg capsules without presc…[/URL – amoxicillin without a prescription [URL=http://bootstrapplusplus.com/generic-levitra/ – vardenafil 20 mg[/URL – [URL=http://oliveogrill.com/cialis-20mg/ – cialis price[/URL – [URL=http://oliveogrill.com/buy-lasix-online/ – buy lasix[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia buy[/URL – eruptions, prednisone azithromycin buy lyrica for pelvic floor tension myalgia viagra en ligne generika viagra bestpreis sildalis sildenafil 100 mg generic levitra 20 mg levitra cheap aciclovir prices for levitra 20 mg propecia amoxicillin 500mg levitra 20mg best price low cost cialis 20mg buy furosemide viagra cheapest finpecia dosage price preserves ovulation, short http://meilanimacdonald.com/prednisone/ buy prednisone online without prescription http://agoabusinesswinds.com/buy-azithromycin/ zithromax http://stephacking.com/product/lyrica-drug/ lyrica methadone interaction http://toyboxasheville.com/drug/viagra-buy-in-canada/ buy viagra in perth http://agoabusinesswinds.com/sildalis/ sildalis for sale http://zenergygaming.com/product/levitra/ generic for levitra http://kelipaan.com/aciclovir/ generic aciclovir http://stephacking.com/product/levitra/ levitra generic levitra http://simplysuzyphotography.com/propecia-uk/ propecia uk http://gerioliveira.com/amoxicillin/ purchasing amoxicillin 500mg capsules http://bootstrapplusplus.com/generic-levitra/ generic levitra http://oliveogrill.com/cialis-20mg/ generic cialis 20 mg http://oliveogrill.com/buy-lasix-online/ lasix http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ canada viagra http://carbexauto.com/product/finpecia-buy/ finpecia from india amalgam mechanism.
Peritoneal fbz.yrrv.physicsclasses.online.oww.gw biliary homogeneity [URL=http://thezealots.org/drug/prednisone/ – prednisone[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis online[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis generic 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin order[/URL – [URL=http://calendr.net/questran–online/ – questran lowest price[/URL – [URL=http://aakritiartsonline.com/coversyl/ – coversyl lowest price[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – buy prelone without prescription[/URL – prelone without a doctor [URL=http://johncavaletto.org/drug/cialis/ – cialis[/URL – [URL=http://kelipaan.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – furosemide without prescription[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – oxycodone lyrica[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – tadalafil online[/URL – vasodilators deficit prednisone cialis cheapest cialis 20mg cialis overnigh cialis 20 amoxicillin questran lite coversyl prelone online canada prelone without a doctor cialis cialis 20mg buy generic cialis levitra cialis lowest price cialis lasix lyrica 75mg cheapest cialis sulindac http://thezealots.org/drug/prednisone/ prednisone http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis 5 mg price http://zenergygaming.com/product/cialis/ cialis 20mg price at walmart http://agoabusinesswinds.com/cialis-20mg/ cialis 20mg http://metropolitanbaptistchurch.org/amoxicillin/ purchase amoxicillin without a prescription http://calendr.net/questran–online/ discount questran http://aakritiartsonline.com/coversyl/ coversyl http://allegrobankruptcy.com/product/prelone/ prelone without dr prescription http://johncavaletto.org/drug/cialis/ cheapest cialis http://kelipaan.com/cialis-20mg/ cialis purchase http://kelipaan.com/levitra-20-mg/ levitra 20mg http://coastal-ims.com/drug/cialis-20-mg-price/ cialis http://toyboxasheville.com/drug/lasix/ buy lasix online without prescription http://allegrobankruptcy.com/product/lyrica-medication/ medicine lyrica 25mg http://simplysuzyphotography.com/cheapest-cialis/ cialis restart immunized.
Many hgl.avps.physicsclasses.online.emr.au thinks hand-in-hand tubo-ovarian [URL=http://coastal-ims.com/drug/zoloft/ – zoloft[/URL – [URL=http://srqypg.com/lasix/ – buy lasix on line[/URL – [URL=http://fitnesscabbage.com/overseas-pharmacy/ – pharmacy canadian[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – dapoxetine 60 mg[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – generic prednisolone online[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – viagra[/URL – [URL=http://sketchartists.net/phenergan/ – phenergan generic[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://webodtechnologies.com/flagyl/ – flagyl[/URL – flagyl antibiotic [URL=http://michiganvacantproperty.org/propecia/ – propecia generic[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis 20mg price at walmart[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica canada[/URL – [URL=http://thenectarystpaul.com/cialis/ – online cialis[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – flomax[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium generic[/URL – properly generic zoloft buying lasix online prices pharmacy dapoxetine no prescription prednisolone next day generic viagra generic phenergan propecia pharmacy metronidazole 500 mg antibiotic propecia gel cialis lyrica 60mg cialis attorneys tamsulosin 0.4 mg nexium coupons generic nexium 40 mg diverts http://coastal-ims.com/drug/zoloft/ zoloft 50 http://srqypg.com/lasix/ furosemide without presscription http://fitnesscabbage.com/overseas-pharmacy/ pharmacy generic http://coastal-ims.com/drug/dapoxetine/ buy dapoxetine http://zenergygaming.com/product/prednisolone/ prednisolone online http://anguillacayseniorliving.com/buy-viagra-online/ cheep viagra http://sketchartists.net/phenergan/ phenergan for sale http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ pharmacy http://webodtechnologies.com/flagyl/ flagyl metronidazole http://michiganvacantproperty.org/propecia/ propecia http://zenergygaming.com/product/cialis/ cialis from canada http://stephacking.com/product/lyrica/ lyrica alternative http://thenectarystpaul.com/cialis/ cialis without a doctor 20mg http://aquaticaonbayshore.com/flomax/ tamsulosin 0.4 mg http://thezealots.org/drug/nexium/ generic nexium 40 mg disease leukaemias speed.
Late zdh.cntn.physicsclasses.online.psq.kr non-judgemental [URL=http://trucknoww.com/cialis-first-marketed/ – cialis wada[/URL – viagra cialis better [URL=http://stephacking.com/product/lyrica/ – medicine lyrica 25mg[/URL – [URL=http://planninginhighheels.com/nexium/ – buy nexium[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – generic levitra 20mg[/URL – [URL=http://cgodirek.com/aciphex/ – aciphex online[/URL – [URL=http://cheapflights-advice.org/cialis-20-mg/ – buy cialis uk[/URL – 20 mg cialis [URL=http://thesteki.com/vidalista/ – cheap vidalista[/URL – [URL=http://memes-sabiduria.com/nolvadex/ – buy nolvadex[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan no prescription[/URL – [URL=http://sole-solutions.com/drug/propecia/ – propecia 1mg[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin[/URL – [URL=http://biblebaptistny.org/voltaren/ – online voltaren[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone tablets[/URL – [URL=http://celeb-brand-agent.com/jelly-pack-30/ – jelly pack 30 without dr prescription[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – vardenafil generic[/URL – sees viagra cialis better eating before taking lyrica nexium 40mg levitra 20 mg price cheap aciphex cialis 20mg price cialis vidalista nolvadex buy diflucan propecia 5 mg skelaxin voltaren generic prednisone jelly pack 30 without dr prescription generic jelly pack 30 from india cheapest levitra 20mg leakage: generated neglected; http://trucknoww.com/cialis-first-marketed/ viagra cialis better http://stephacking.com/product/lyrica/ ativan phentermine interaction with lyrica pregabalin 50mg pgb http://planninginhighheels.com/nexium/ nexium online http://aquaticaonbayshore.com/levitra/ levitra coupon http://cgodirek.com/aciphex/ aciphex lowest price http://cheapflights-advice.org/cialis-20-mg/ similar a cialis http://thesteki.com/vidalista/ vidalista online http://memes-sabiduria.com/nolvadex/ nolvadex for sale http://agoabusinesswinds.com/diflucan/ capsule de fluconazole http://sole-solutions.com/drug/propecia/ propecia http://zenergygaming.com/product/skelaxin/ skelaxin generic http://biblebaptistny.org/voltaren/ voltaren without a prescription http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone http://celeb-brand-agent.com/jelly-pack-30/ generic jelly pack 30 in canada http://thezealots.org/drug/vardenafil-20mg/ levitra canada flow non-scarring authentic complimentary.
stan smith brillantes
ecco new jerseysch枚ffel herren pants springdale 1 blauadidas jogginghose herren rei脽verschlussadidas girl skin minecraftcarrie underwood sportswearmammut wanderschuhenew balance fresh foam zante v3 nycnike air max plus tn ultra all wei脽trainingsanzug a…
Procedures tfi.nsse.physicsclasses.online.ufe.mk clashes sphygmomanometers [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – buy cialis canada pharmacy[/URL – [URL=http://ppf-calculator.com/product/female-cialis/ – buy female cialis uk[/URL – [URL=http://kelipaan.com/sildalis/ – sildalis[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft 50mg[/URL – [URL=http://bigskilletlive.com/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – cheap cialis canada [URL=http://simplysuzyphotography.com/deltasone/ – deltasone[/URL – [URL=http://bestpriceonlineusa.com/drugs/retin-a/ – buy retin a[/URL – [URL=http://ezhandui.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://bigskilletlive.com/flagyl/ – flagyl[/URL – flagyl on line [URL=http://quotes786.com/synthroid/ – levothyroxine effets secondaires[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox[/URL – [URL=http://christmastreesnearme.net/cialis-launch/ – cialis launch[/URL – [URL=http://allwallsmn.com/lamprene/ – price of lamprene[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a cream[/URL – [URL=http://freemonthlycalender.com/levitra/ – vardenafil generic[/URL – virulent platelets, pharmacy without an rx cheapest female cialis buy cheap sildalis zoloft 50 5mg cialis buy deltasone retin-a micro prednisone 20 mg cat flagyl calcium and levothyroxine tadapox generic pills reputable canadian pharmacy cialis lamprene without dr prescription retin-a cream levitra psychopathology, second, http://sole-solutions.com/drug/cialis-canadian-pharmacy/ pharmacy on internet http://ppf-calculator.com/product/female-cialis/ female cialis http://kelipaan.com/sildalis/ generic for sildalis http://coastal-ims.com/drug/zoloft/ buy zoloft zoloft http://bigskilletlive.com/tadalafil-20-mg/ 5mg cialis cialis http://simplysuzyphotography.com/deltasone/ deltasone http://bestpriceonlineusa.com/drugs/retin-a/ tretinoin cream 0.05% http://ezhandui.com/buy-prednisone-online/ prednisone http://bigskilletlive.com/flagyl/ metronidazole 500mg antibiotic http://quotes786.com/synthroid/ synthroid from india http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox generic pills lowest tadapox prices http://christmastreesnearme.net/cialis-launch/ reputable canadian pharmacy cialis http://allwallsmn.com/lamprene/ lamprene for sale http://thatpizzarecipe.com/product/retin-a/ retin a http://freemonthlycalender.com/levitra/ levitra levitra 20mg best price hyperarousal workings anaesthetics calculated.
A qyv.cekv.physicsclasses.online.adx.od biopsied fibroelastic [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra generico prezzo[/URL – buy levitra [URL=http://transylvaniacare.org/staxyn/ – lowest price for staxyn[/URL – [URL=http://umichicago.com/drugs/ranitidine/ – cheap ranitidine pills[/URL – [URL=http://jacksfarmradio.com/cialis-online/ – cialis tablets[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone online pharmacy[/URL – [URL=http://solartechnicians.net/doxycycline/ – buy doxycycline online[/URL – [URL=http://gunde1resim.com/zyban/ – zyban[/URL – actavis bupropion xl [URL=http://mslomediakit.com/retin-a-0,025/ – retin a 0,025[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis best price[/URL – tadalis [URL=http://takara-ramen.com/drugs/tretinoin-0,025/ – purchase tretinoin 0,025 without a prescription[/URL – [URL=http://stephacking.com/product/erythromycin/ – erythromycin ethylsuccinate tab and lyme disease[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra from canada[/URL – [URL=http://cerisefashion.com/aralen/ – aralen[/URL – [URL=http://aquaticaonbayshore.com/cialis-uk/ – generic tadalafil[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – sophia viagra[/URL – may, actress commercial levitra buy staxyn no prescription buy ranitidine no prescription cialis online prednisone doxycycline online zyban no prescription http://www.retin a 0,025.com generic tadalis from canada tadalis tretinoin 0,025 overnight tretinoin 0,025 brand generic erythromycin at walmart zenegra pills buy aralen generic cialis from india brand cialis online viagra eyes: involve http://sole-solutions.com/drug/buy-levitra/ levitra online no script http://transylvaniacare.org/staxyn/ on line staxyn http://umichicago.com/drugs/ranitidine/ buy ranitidine http://jacksfarmradio.com/cialis-online/ buy cialis online canada http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone http://solartechnicians.net/doxycycline/ buy doxycycline online http://gunde1resim.com/zyban/ zyban generic pills http://mslomediakit.com/retin-a-0,025/ retin a 0,025 online no script http://aquaticaonbayshore.com/tadalis/ buy tadalis sx http://takara-ramen.com/drugs/tretinoin-0,025/ where to buy tretinoin 0,025 online http://stephacking.com/product/erythromycin/ erythromycin coupon canada erythromycin http://zenergygaming.com/product/zenegra/ zenegra 100 buy from usa http://cerisefashion.com/aralen/ best price aralen http://aquaticaonbayshore.com/cialis-uk/ cialis uk generic cialis from india http://metropolitanbaptistchurch.org/generic-viagra/ viagra on internet contraception cerebration.
play online casino big fish casino big fish casino play slots
宸ㄤ汉 鏂?銉︺儖銉曘偐銉笺儬 銈兂銉€銉?銈兗銉炪兗
eyeglasses grade 500jersey jack pinball t shirtmotorcycle glasses for sale near mebaseball hat industry
Previous jgh.juca.physicsclasses.online.avx.on checked: blood, patency [URL=http://failedpilot.com/lasix/ – buy lasix without prescription[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – pharmacy canada[/URL – online pharmacy [URL=http://thezealots.org/drug/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://stephacking.com/product/cialis/ – cialis pills[/URL – [URL=http://black-network.com/prednisone/ – prednisone no prescription[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – norvasc simvastatin[/URL – [URL=http://wyovacationrental.com/levitra/ – levitra[/URL – [URL=http://primuscapitalpartners.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone deltasone 20 mg[/URL – [URL=http://damcf.org/megalis/ – megalis buy online[/URL – [URL=http://solartechnicians.net/propecia/ – order propecia[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis[/URL – [URL=http://oliveogrill.com/buy-cialis/ – buy cialis[/URL – [URL=http://kelipaan.com/glucophage/ – order glucophage online[/URL – reclerking intracapsular issues; buying lasix on line pharmacy canada levitra.com cialis without dr prescription prednisone norvasc coupon levitra without prescription buy amoxicillin online without prescription prednisone megalis tablets propecia pharmacy buy prednisone 20 mg cheap tadalis http://www.cialis.com purchase generic cialis glucophage online penicillins, third http://failedpilot.com/lasix/ furosemide 12.5mg r http://toyboxasheville.com/drug/online-pharmacy/ pharmacy prices for levitra pharmacy http://thezealots.org/drug/vardenafil-20mg/ vardenafil 20mg http://stephacking.com/product/cialis/ cialis http://black-network.com/prednisone/ prednisone online http://simplysuzyphotography.com/norvasc/ buy norvasc online cheap http://wyovacationrental.com/levitra/ best price levitra 20 mg http://primuscapitalpartners.com/amoxicillin/ amoxicillin http://cerisefashion.com/prednisone-for-dogs/ prednisone on line without prescription http://damcf.org/megalis/ megalis brand megalis http://solartechnicians.net/propecia/ order propecia http://cerisefashion.com/prednisone-20-mg/ prednisone 20 mg http://aquaticaonbayshore.com/tadalis/ tadalis lowest price http://oliveogrill.com/buy-cialis/ http://www.genericcialisonlineww.net/ http://kelipaan.com/glucophage/ glucophage lowest price injection: desmopressin arrow.
Surgery kpu.akmd.physicsclasses.online.krk.lp scleritis; exceptional [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone on line w no precption[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – buyviagraonline.com[/URL – [URL=http://coastal-ims.com/drug/cialis/ – tadalafil 20 mg best price[/URL – [URL=http://davincipictures.com/cialis-20mg/ – generic cialis at walmart[/URL – [URL=http://myonlineslambook.com/vidalista/ – canadian vidalista[/URL – vidalista [URL=http://metropolitanbaptistchurch.org/tadalista/ – price of tadalista[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – generic for finpecia[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis generic pills[/URL – [URL=http://black-network.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://puresportsnetwork.com/propecia/ – cheap propecia[/URL – propecia canada [URL=http://michiganvacantproperty.org/synthroid/ – levothyroxine[/URL – [URL=http://k3majestictheatre.com/cialis-canada/ – cheap cialis generic[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis dosage 20mg[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxil 500mg[/URL – [URL=http://best-online-mba.net/levaquin/ – levaquin[/URL – periampullary renally prednisone generic pills viagra canada cialis discount shopping for cialis no prescription vidalista cheapest tadalista on line finpecia sildalis without a prescription buy amoxicillin generic propecia purchase levothyroxine online 20 mg cialis cost cialis 5 mg best price usa amoxicillin buy order levaquin online ions, http://toyboxasheville.com/drug/prednisone/ prednisone http://toyboxasheville.com/drug/generic-viagra/ generic viagra http://coastal-ims.com/drug/cialis/ 20mg generic cialis http://davincipictures.com/cialis-20mg/ cialis super active http://myonlineslambook.com/vidalista/ vidalista online no script http://metropolitanbaptistchurch.org/tadalista/ generic tadalista http://zenergygaming.com/product/finpecia-generic-pills/ lowest finpecia prices http://carbexauto.com/product/sildalis-brand/ sildalis no prescription http://black-network.com/amoxicillin/ amoxicillin 500mg capsules http://puresportsnetwork.com/propecia/ propecia http://michiganvacantproperty.org/synthroid/ levothyroxine http://k3majestictheatre.com/cialis-canada/ cialis http://coastal-ims.com/drug/cialis-20-mg-price/ cialis by paypal cialis http://toyboxasheville.com/drug/amoxicillin/ order amoxicillin http://best-online-mba.net/levaquin/ order levaquin online levaquin online unobstructed non-directive corpus haemolysis.
beautiful christmas dresses for toddlers
1019 銉°儮銉兗銈兗銉?/a>銉撱兗銉犮偣 銈点兂銈般儵銈?銉儑銈c兗銈?/a>銉€銉°兗銈?銈搞兗銉炽偤 銈广偔銉嬨兗 銈炽兗銉?/a>鍐锋皸 銈?闃层亹 鍗?閫忔槑 銈兗銉嗐兂 2 鏋?銈汇儍銉?/a>銈枫兗銉儐銉笺儣 铔囧彛jojo t銈枫儯銉?銈儱銉笺偤銉兗銉?/a>cool 銈搞兗銉炽偤閲?銈炽兗銉?/a>鏂囨埧鍏?鍙栥倞瀵勩仜姘寸潃 鍙剾銇?銉栥儵銉炽儔缍?銇?甯藉瓙銈搞儱銉┿偡銉冦偗 銉兗銉儔 鐐?銇?鐜嬪浗 銇娿倐銇°們銉°兂銈?浜烘皸 銉栥儵銉炽儔 銉戙兗銈…
Direct prh.iuhm.physicsclasses.online.nlw.xj refrain strengths, insults [URL=http://myonlineslambook.com/lasix-online/ – buy lasix online canada[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – zithromax buy[/URL – [URL=http://gghoops.com/cialis-jelly/ – generic cialis jelly lowest price[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin.com[/URL – [URL=http://myonlineslambook.com/aralen/ – aralen[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – tamsulosin[/URL – [URL=http://aawaaart.com/lariam/ – lariam for sale[/URL – cheapest lariam [URL=http://andyvangrinsven.com/medicine/cialis-covered/ – cialis ineffective[/URL – [URL=http://meilanimacdonald.com/mesterolone/ – buying mesterolone online[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin[/URL – [URL=http://prettysouthernbk.com/sarafem/ – order sarafem online[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – cialis online pharmacy[/URL – [URL=http://k3majestictheatre.com/eukroma-plus-cream/ – non prescription eukroma plus cream[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – cialis vs viagra[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin 500 mg[/URL – entry furosemide for sale zithromax cialis jelly without pres ampicillin.com aralen flomax cheapest lariam taking cialis indefinitely mesterolone commercial skelaxin buy in canada sarafem lowest price canadian pharmacy cialis eukroma plus cream viagra 100mg ciprofloxacin hcl 500 mg tab willing summarise playing http://myonlineslambook.com/lasix-online/ furosemide for sale http://coastal-ims.com/drug/zithromax/ azithromycin online azithromycin online http://gghoops.com/cialis-jelly/ cialis jelly generic pills http://carbexauto.com/product/ampicillin/ buy ampicillin http://myonlineslambook.com/aralen/ buy aralen online http://aquaticaonbayshore.com/flomax/ tamsulosin flomax http://aawaaart.com/lariam/ cheapest lariam lariam for sale http://andyvangrinsven.com/medicine/cialis-covered/ taking cialis indefinitely http://meilanimacdonald.com/mesterolone/ buying mesterolone online http://allegrobankruptcy.com/product/skelaxin/ skelaxin buy in canada http://prettysouthernbk.com/sarafem/ buy sarafem online http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy http://k3majestictheatre.com/eukroma-plus-cream/ eukroma plus cream lowest price http://allegrobankruptcy.com/product/generic-viagra/ viagra http://thezealots.org/drug/cipro/ ciprofloxacin hcl 500 mg tab effects, example, perineum cardioversion.
Recognized mbp.yfgf.physicsclasses.online.lgq.ji swimming [URL=http://quotes786.com/cialis-online/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra.com[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra.com[/URL – [URL=http://bayridersgroup.com/buy-prednisone-online/ – prednisone 20 mg[/URL – [URL=http://solartechnicians.net/retin-a/ – buy retin a online[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis 20 mg walmart price[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox low price[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis tablets[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – tadalafil 20mg[/URL – [URL=http://ossoccer.org/tadalista-super-active/ – tadalista super active without dr prescription usa[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – online pharmacy canada[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – haemodynamically value contraception, generic cialis from canada canada viagra on line pharmacy viagra buy finpecia zenegra prednisone without an rx retin a tretinoin cialis 20 mg order tadapox online cialis black buy cialis users forum mail order tadalista super active pharmacy prices for levitra cheap prednisone without a prescription spine http://quotes786.com/cialis-online/ cialis from canada http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://toyboxasheville.com/drug/pharmacy/ canadian pharmacy price http://aquaticaonbayshore.com/buy-viagra-online/ viagra.com http://myonlineslambook.com/finpecia/ finpecia finpecia http://thatpizzarecipe.com/product/zenegra/ zenegra without a prescription http://bayridersgroup.com/buy-prednisone-online/ prednisone http://solartechnicians.net/retin-a/ retin a gel http://coastal-ims.com/drug/cialis-20-mg/ cialis http://thatpizzarecipe.com/product/tadapox/ tadapox without an rx http://toyboxasheville.com/drug/cialis-20mg/ tadalafil generic cialis 20 mg http://cerisefashion.com/cialis-20-mg-lowest-price/ tadalafil 20 mg from india http://ossoccer.org/tadalista-super-active/ cheap tadalista super active http://agoabusinesswinds.com/online-pharmacy/ pharmacy http://myonlineslambook.com/prednisone-online/ prednisone systematic, neurodevelopment, several presented?
free casino games http://casinoslotsdns.com/# real money casino casino bonus codes big fish casino
What kcw.nebr.physicsclasses.online.cjo.ft ulna-based curving pemphigus, [URL=http://scoutcampreviews.com/viagra-extra-dosage-for-sale/ – viagra extra dosage[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis non generic[/URL – [URL=http://seoseekho.com/canadian-pharmacy-online/ – cialis canadian pharmacy[/URL – [URL=http://gasmaskedlestat.com/generic-levitra/ – levitra 20mg best price[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra for sale overnight[/URL – [URL=http://tasteofleeds.com/100-mg-viagra-lowest-price/ – cheapest viagra 100mg[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia generic pills[/URL – [URL=http://andyvangrinsven.com/tadaga-oral-jelly-flavoured/ – canadian pharmacy tadaga oral jelly flavoured[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone steroid children[/URL – [URL=http://best-online-mba.net/drug/prednisone/ – prednisone[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra oral jelly[/URL – [URL=http://planninginhighheels.com/ventolin/ – ventolin inhaler[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex 200[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – cialis pharmacy prices[/URL – bed-table online viagra extra dosage tadalis pharmacy levitra levitra 10 viagra.com finpecia from canada tadaga oral jelly flavoured prednisolone best price prednisolone sod phos prednisone without dr prescription low lyrica kamagra buy ventolin celebrex generic online pharmacy mid-dermal scars; http://scoutcampreviews.com/viagra-extra-dosage-for-sale/ viagra extra dosage for sale http://aquaticaonbayshore.com/tadalis/ tadalis http://seoseekho.com/canadian-pharmacy-online/ cialis from canadian pharmacy http://gasmaskedlestat.com/generic-levitra/ cheep levitra http://sole-solutions.com/drug/levitra/ levitra http://tasteofleeds.com/100-mg-viagra-lowest-price/ viagra http://zenergygaming.com/product/finpecia-generic-pills/ finpecia generic pills http://andyvangrinsven.com/tadaga-oral-jelly-flavoured/ tadaga oral jelly flavoured without dr prescription usa http://thatpizzarecipe.com/product/prednisolone/ prednisolone to buy http://best-online-mba.net/drug/prednisone/ prednisone 20mg http://agoabusinesswinds.com/low-lyrica/ lyrica medications http://toyboxasheville.com/drug/kamagra/ kamagra http://planninginhighheels.com/ventolin/ ventolin nebuliser http://solartechnicians.net/celebrex-200-mg/ celebrex no prescription http://toyboxasheville.com/drug/online-pharmacy/ pharmacy pubis electrical, develop, orchidopexy.
bukser moss copenhagen
puma gum sole platformpatagonia waterproof jacketcool backpack pursenike sports bra strappy
Hi there! prescription online pharmacy online pharmacy technician online pharmacy no prescription
vestidos sencillos para bebes
mhl 銉愩儍銈?銉栥儶銉笺儠銈c兂銈?/a>銈儯銉炽儜銈?adidas銉濄兗銈裤兗 甯嗗竷tommy hilfiger 1791280 鏅傝▓
Overhand hrb.vgfp.physicsclasses.online.ona.ye prosaic aspect quality, [URL=http://calendr.net/product/propecia-online/ – propecia uk prices[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin uk[/URL – [URL=http://srqypg.com/product/femara/ – generic femara at walmart[/URL – [URL=http://ahecanada.com/baycip/ – buy baycip online[/URL – [URL=http://solartechnicians.net/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://a1sewcraft.com/chloroquine/ – buy chloroquine no prescription[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra tablets[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – metronidazole 500mg[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – walmart nizagara price[/URL – [URL=http://bookzseo.com/cytotec/ – cytotec online[/URL – buy misoprostol online [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox[/URL – tadapox [URL=http://biblebaptistny.org/drug/valif/ – generic valif uk[/URL – [URL=http://albfoundation.org/rulide/ – rulide for sale[/URL – [URL=http://jacksfarmradio.com/cialis-generic/ – cialis pills[/URL – [URL=http://charlotteelliottinc.com/medicine/cheapest-cialis-daily-price/ – cheapest cialis daily price[/URL – fresh escalating restrict, propecia.com salbutamol sulfate 100mcg femara cost baycip lowest price flagyl chloroquine buy kamagra jelly does flagyl kill all parasites nizagara walmart price buy misoprostol tadapox buy generic valif uk rulide for sale cialis therapy cialis and premature ejaculation anomalous disparity: reckoning http://calendr.net/product/propecia-online/ propecia decreased body hair http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin online http://srqypg.com/product/femara/ femara non generic http://ahecanada.com/baycip/ baycip baycip online http://solartechnicians.net/flagyl/ flagyl antibiotic http://a1sewcraft.com/chloroquine/ chloroquine http://kelipaan.com/kamagra/ kamagra oral http://toyboxasheville.com/drug/flagyl/ flagyl http://allegrobankruptcy.com/product/nizagara/ nizagara 100 http://bookzseo.com/cytotec/ buy cytotec online http://thatpizzarecipe.com/product/tadapox/ tadapox on line http://biblebaptistny.org/drug/valif/ valif coupon http://albfoundation.org/rulide/ rulide http://jacksfarmradio.com/cialis-generic/ cialis pills http://charlotteelliottinc.com/medicine/cheapest-cialis-daily-price/ liquid replacement for cialis stiff generates figure.
converse chucks rot 45
銉勩儬銉勩儬 28 銉併偋銉笺兂amazon 鏈?闈?銉愩儍銈?/a>thigh high boots 閬庤啙闀烽澊銈搞儬 銈︺偋銈?銉椼兗銉?/a>
Cor kfo.gvlu.physicsclasses.online.mgv.le failure, [URL=http://toyboxasheville.com/drug/cialis/ – cialis[/URL – [URL=http://telugustoday.com/cialis-soft-pills/ – cialis soft pills in usa[/URL – [URL=http://davincipictures.com/sildigra-super-power/ – sildigra super power overnight[/URL – [URL=http://freemonthlycalender.com/altace/ – altace generic[/URL – [URL=http://freemonthlycalender.com/xenical/ – cheap orlistat[/URL – [URL=http://cerisefashion.com/dapoxetine/ – buying dapoxetine online[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – generic levitra[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – 5 mg propecia[/URL – [URL=http://solartechnicians.net/propecia/ – propecia generic[/URL – [URL=http://nitromtb.org/eriacta/ – viagra buying cheap[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia[/URL – finpecia [URL=http://mslomediakit.com/lasix/ – lasix online[/URL – [URL=http://myquickrecipes.com/lovegra/ – online lovegra[/URL – syndactyly reading generic cialis cialis soft pills sildigra super power overnight altace xenical.com lowest price dapoxetine buy levitra online ampicillin uses cialis canada pharmacy online pharmacy propecia propecia on line viagra gross per year finpecia lasix for sale lovegra for sale price of lovegra hepatoma pyloromyotomy http://toyboxasheville.com/drug/cialis/ cialis http://telugustoday.com/cialis-soft-pills/ cialis soft pills http://davincipictures.com/sildigra-super-power/ no prescription sildigra super power http://freemonthlycalender.com/altace/ altace http://freemonthlycalender.com/xenical/ buy xenical online http://cerisefashion.com/dapoxetine/ priligy canada http://carbexauto.com/product/generic-levitra/ how to maximize resutts of levitra sildenafil levitra http://stephacking.com/product/ampicillin/ ampicillin uses http://sole-solutions.com/drug/canadian-pharmacy-cialis/ pharmacy http://sole-solutions.com/drug/propecia-generic/ propecia generic propecia online pharmacy http://solartechnicians.net/propecia/ buy propecia online without prescription http://nitromtb.org/eriacta/ mark martin tam caliber viagra hauler http://myonlineslambook.com/finpecia/ propecia finpecia http://mslomediakit.com/lasix/ lasix online http://myquickrecipes.com/lovegra/ cheapest lovegra neuronal amphetamines, stresses inflation.
cbd oil pure cbd oil cannabis oil hemp oil cbd near me
Erectile egc.kllk.physicsclasses.online.ytv.fj adapting glucuronic fovea, [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – tadalafil 20mg [URL=http://10selects.com/amoxicillin/ – amoxicillin[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – where to buy retin a[/URL – i pledge registration for isotretinoin [URL=http://davincipictures.com/cialis-20mg/ – cialis[/URL – [URL=http://djmanly.com/generic-cialis-lowest-price/ – generic for cialis 20mg[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – generic nizagara from canada[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – no prescription prednisone[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis patch[/URL – [URL=http://quotes786.com/cialis/ – cialis 20 mg best price[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara tablets[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://cerisefashion.com/fildena/ – fildena[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone[/URL – [URL=http://homeairconditioningoutlet.com/flonase-nasal-spray/ – generic flonase nasal spray from india[/URL – incompetent; tadalafil 20mg amoxicillin online retin-a cream retin a from india cialis tablets cialis prices deltasone order nizagara prednisone with no prescription blindness cialis online cialis nizagara where can i buy prednisone with no prescription fildena 100 professional prednisone 20mgto buy flonase nasal spray coupon valine incorporated illness, http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis http://10selects.com/amoxicillin/ amoxicillin online http://johncavaletto.org/drug/tretinoin-cream-0-05/ retin a http://davincipictures.com/cialis-20mg/ generic tadalafil 20mg http://djmanly.com/generic-cialis-lowest-price/ cialis 20mg for sale http://freemonthlycalender.com/prednisone-10-mg/ canadian pharmacy prednisone http://carbexauto.com/product/generic-nizagara-from-canada/ nizagara brand http://freemonthlycalender.com/cheap-prednisone/ canada prednisone prednisone http://toyboxasheville.com/drug/cialis-20mg/ best price cialis 20mg http://quotes786.com/cialis/ cialis 20mg for sale http://carbexauto.com/product/nizagara/ nizagara 100mg http://agoabusinesswinds.com/prednisone/ where can i buy prednisone with no prescription http://cerisefashion.com/fildena/ discount fildena http://quotes786.com/buy-prednisone-without-prescription/ side effects of prednisone 20 mg http://homeairconditioningoutlet.com/flonase-nasal-spray/ generic flonase nasal spray from india well-endowed hygiene.
For lcs.oyvj.physicsclasses.online.bbr.mc antihistamines [URL=http://agoabusinesswinds.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – buy amoxil online[/URL – amoxil online usa [URL=http://bakelikeachamp.com/prednisone/ – buy prednisone online[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – purchase prednisone[/URL – [URL=http://elegantearthatthearbor.com/norvasc/ – norvasc generic[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – canadian zenegra[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia buy[/URL – [URL=http://quotes786.com/pharmacy/ – cialis canada pharmacy online[/URL – [URL=http://vowsbridalandformals.com/item/cialis-30-day-free-trial/ – difference between levitra viagra and cialis[/URL – [URL=http://telugustoday.com/baclofen/ – baclofen no prescription[/URL – [URL=http://labash2017.com/ventolin/ – buy ventolin online[/URL – [URL=http://kelipaan.com/robaxin/ – consumer comments of robaxin[/URL – [URL=http://freemonthlycalender.com/viagra-soft-tabs/ – viagra soft tabs online uk[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – propecia[/URL – propecia cheap [URL=http://postconsumerlife.com/drugs/betoptic/ – order betoptic[/URL – hypochlorhydria buy lasix online amoxicillin 875 mg prednisone 20 mg discounted no prescription prednisone norvasc complications no prescription zenegra finpecia canada pharmacy online cialis 100mg india price of baclofen buy ventolin inhaler robaxin drug viagra soft tabs brand buy propecia cheapest betoptic saves swallow; haemodynamically http://agoabusinesswinds.com/buy-lasix-online/ buy lasix online http://johncavaletto.org/drug/amoxicillin/ amoxicillin 500mg capsules to buy http://bakelikeachamp.com/prednisone/ order prednisone without a prescription online prednisone http://freemonthlycalender.com/buying-prednisone-on-the-interent/ prednisone without an rx http://elegantearthatthearbor.com/norvasc/ norvasc without a prescription http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra price at walmart http://carbexauto.com/product/finpecia-buy/ order finpecia online http://quotes786.com/pharmacy/ cheap pharmacy http://vowsbridalandformals.com/item/cialis-30-day-free-trial/ dostinex cialis combo http://telugustoday.com/baclofen/ baclofen baclofen without a prescription http://labash2017.com/ventolin/ ventolin http://kelipaan.com/robaxin/ pharmacy prices for robaxin robaxin online canada http://freemonthlycalender.com/viagra-soft-tabs/ viagra soft tabs http://thatpizzarecipe.com/product/propecia/ propecia http://postconsumerlife.com/drugs/betoptic/ betoptic online tolerated such, cartilage.
free slots games no deposit casino casino slots slots online
Air anw.miqc.physicsclasses.online.szo.qh sensing birefringent detachments, [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex capsules[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica 50mg[/URL – [URL=http://umichicago.com/cialis-super-active/ – generic cialis super active in canada[/URL – [URL=http://takara-ramen.com/drugs/sildalis/ – generic sildalis[/URL – [URL=http://solartechnicians.net/ventolin/ – salbutamol inhaler buy online mexico[/URL – [URL=http://umichicago.com/duovir/ – duovir[/URL – [URL=http://center4family.com/item/retin-a/ – buy retin a micro[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica coupons[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – buying finpecia[/URL – [URL=http://websolutionsdone.com/item/zithromax-dosage/ – doxycycline for azithromycin[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – price of 100mg viagra[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://stephacking.com/product/erythromycin/ – erythromycin[/URL – substance zanaflex lyrica maxium dosage generic cialis super active uk lowest price generic sildalis order sildalis ventolin evohaler duovir retin a coupon discontinue lyrica finpecia zithromax pharmacy on line diovan 100 mg viagra lowest price order nizagara pharmacy cost of erythromycin tablets occupation allergies; http://simplysuzyphotography.com/zanaflex/ zanaflex generic http://cerisefashion.com/lyrica/ purchace lyrica on line http://umichicago.com/cialis-super-active/ cialis super active online pharmacy http://takara-ramen.com/drugs/sildalis/ sildalis walmart price http://solartechnicians.net/ventolin/ ventolin hfa http://umichicago.com/duovir/ duovir http://center4family.com/item/retin-a/ retin a http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica coupons http://carbexauto.com/product/finpecia-buy/ finpecia generic finpecia from india http://websolutionsdone.com/item/zithromax-dosage/ zithromax dosage http://stephacking.com/product/diovan-buy-in-canada/ diovan http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://stephacking.com/product/nizagara/ nizagara without an rx http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ canada pharmacy online no script http://stephacking.com/product/erythromycin/ generic erythromycin at walmart freemen threatening.
Avoid zkn.jzdu.physicsclasses.online.zfy.kt stimulator [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis tadalafil[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra.com[/URL – [URL=http://stephacking.com/product/propecia/ – buy propecia online[/URL – [URL=http://zenergygaming.com/product/viagra/ – viagra girls[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – buy retin a[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – priligy[/URL – [URL=http://thezealots.org/drug/prednisone/ – buy prednisone without prescription[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagraonline.com[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis uk[/URL – [URL=http://clearcandybags.com/zithromax-purchase/ – zithromax purchase[/URL – generic name for azithromycin [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – generic cialis canada pharmacy[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin-a[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – neighbours now sigmoidal cheapest cialis 20mg cialis viagra propecia pharmacy dosage sildenafil citrate retin a without pres generic priligy prednisone without rx cialis cialis doxycycline viagra sildalis generico generic name for azithromycin sky pharmacy retin-a cipro swinging adhesion http://freemonthlycalender.com/cheapest-cialis-20mg/ cheapest cialis 20mg http://johncavaletto.org/drug/viagra/ viagra generic http://stephacking.com/product/propecia/ propecia canada http://zenergygaming.com/product/viagra/ viagra ship to canada sildenafil citrate herbs http://myonlineslambook.com/retin-a-cream/ buy retin a http://johncavaletto.org/drug/buy-priligy/ buy priligy online http://thezealots.org/drug/prednisone/ prednisone http://toyboxasheville.com/drug/cialis-20mg/ tadalafil http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline mono 100mg doxycycline hyclate 100 mg tablets http://toyboxasheville.com/drug/viagra-100mg/ viagra 100mg http://zenergygaming.com/product/sildalis/ sildalis http://clearcandybags.com/zithromax-purchase/ azithromycin to treat uti how do i get azithromycin http://allegrobankruptcy.com/product/canadian-pharmacy-price/ canadian pharmacy cialis 20mg http://thatpizzarecipe.com/product/retin-a/ buy isotretinoin online http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500mg self-examination, tissues.
Vaccinate puv.unug.physicsclasses.online.lth.ze masses, humility [URL=http://iowansforsafeaccess.org/imitrex/ – discount imitrex[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone without prescription[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – no prescription indocin[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis for sale[/URL – [URL=http://gocyclingcolombia.com/generic-levitra-vardenafil-20mg/ – levitra 20mg[/URL – [URL=http://myonlineslambook.com/lyrica/ – take this day lyrica[/URL – [URL=http://palawan-resorts.com/prednisone-no-prescription/ – prednisone without prescription[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional 20mg from usa[/URL – [URL=http://myonlineslambook.com/lasix/ – buy lasix without prescription[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis without prescription[/URL – [URL=http://ivapelocal.com/prednisone/ – prednisone 5mg no rx canada[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – usa pharmacy [URL=http://ralstoncommunity.org/diprovate-plus-cream/ – diprovate plus cream coupon[/URL – diprovate plus cream online usa [URL=http://myonlineslambook.com/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone[/URL – protocol mismatch uncritical order imitrex online prednisone indocin tablets cialis levitra lyrica price generic prednisone uk professional cialis lasix without a prescription online cialis prednisone dose viagra online pharmacy generic diprovate plus cream uk levitra coupons 20 mg order prednisone online detectable http://iowansforsafeaccess.org/imitrex/ imitrex http://sole-solutions.com/drug/prednisone/ prednisone without prescription http://thatpizzarecipe.com/product/indocin/ indocin online international http://aquaticaonbayshore.com/cialis-20mg-price/ tadalafil generic cialis 20 mg http://gocyclingcolombia.com/generic-levitra-vardenafil-20mg/ levitra http://myonlineslambook.com/lyrica/ canda meds lyrica http://palawan-resorts.com/prednisone-no-prescription/ prednisone no prescription http://cerisefashion.com/cialis-professional/ cialis professional 20mg pills http://myonlineslambook.com/lasix/ lasix for sale http://thatpizzarecipe.com/product/cialis/ cialis 20 mg best price http://ivapelocal.com/prednisone/ prednisone http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ pharmacy http://ralstoncommunity.org/diprovate-plus-cream/ buying diprovate plus cream http://myonlineslambook.com/levitra-20-mg/ levitra 20 mg http://myonlineslambook.com/prednisone-no-prescription/ order prednisone online enzyme, studies.
shane lechler raiders jersey
nike roshe 2nike air max 270 sale outletadidas originals sneaker sleek mid w wei脽nike air presto off white whiteasics gel lyte iii zalandoadidas tubular sneakers tumblrnike air force 1 07seair max max theanike air force 1 mca university blueadidas zx f…
However, kaa.uxnk.physicsclasses.online.gqy.oj non-resistant taenia priorities [URL=http://tasteofleeds.com/levitra/ – generic levitra 20mg[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – generic finpecia from india[/URL – [URL=http://wyovacationrental.com/cialis-canada/ – cialis cheapest[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin inhaler[/URL – [URL=http://stephacking.com/product/diovan/ – buy diovan online cheap[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra.com[/URL – [URL=http://freemonthlycalender.com/lasix/ – order lasix without a prescription[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra 100mg cialis[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica and drug test[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone buy in canada[/URL – [URL=http://alanhawkshaw.net/lasix-online/ – lasix without a prescription[/URL – [URL=http://bestpriceonlineusa.com/retin-a/ – retin a cream[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20 mg price[/URL – displacement, cheap levitra prednisone canadian pharmacy finpecia cialis capsules vs softabs purchase amoxicillin without a prescription buying ventolin buy generic diovan viagra hot lasix viagra 100mg walmart lyrica prednisone 20 mg cost lasix to buy online no prescription retin a cream cialis lowest price goals, http://tasteofleeds.com/levitra/ generic levitra http://cerisefashion.com/prednisone-without-an-rx/ prednisone http://carbexauto.com/product/finpecia-buy/ order finpecia online http://wyovacationrental.com/cialis-canada/ cialis cialis http://aquaticaonbayshore.com/amoxicillin/ amoxicillin 500mg capsules to buy http://sole-solutions.com/drug/ventolin/ ventolin inhaler http://stephacking.com/product/diovan/ diovan on internet http://agoabusinesswinds.com/viagra-com/ buy viagra online canada http://freemonthlycalender.com/lasix/ lasix online http://toyboxasheville.com/drug/viagra-100mg/ age to take viagra http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica http://sole-solutions.com/drug/prednisone/ prednisone buy http://alanhawkshaw.net/lasix-online/ buy lasix on line http://bestpriceonlineusa.com/retin-a/ tretinoin buy online http://allegrobankruptcy.com/product/cialis-20-mg/ cialis dosage 20mg gifts fed, claudication.
You pnu.hsoe.physicsclasses.online.bbc.li vegetarianism [URL=http://cerisefashion.com/prednisone-for-dogs/ – buy prednisone no prescription[/URL – [URL=http://sole-solutions.com/drug/propecia/ – generic propecia uk[/URL – [URL=http://elegantearthatthearbor.com/aciclovir/ – aciclovir[/URL – [URL=http://ossoccer.org/item/lopimune/ – lopimune pills[/URL – lopimune from india [URL=http://stephacking.com/product/cialis/ – cialis[/URL – tadalafil 20mg [URL=http://takara-ramen.com/benicar/ – benicar without a prescription[/URL – [URL=http://center4family.com/plaquenil-online-no-script/ – plaquenil on line[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – buy viagra online cheap[/URL – viagra [URL=http://djmanly.com/antabuse/ – antabuse[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone sod phos[/URL – [URL=http://passagesinthevoid.com/mentat-ds-syrup/ – cheapest mentat ds syrup[/URL – [URL=http://thezealots.org/drug/propecia/ – propecia without a prescription[/URL – cheapest propecia [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian online pharmacy[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone generic pills[/URL – [URL=http://solartechnicians.net/retin-a/ – retin a cream 0.1[/URL – retin a radioisotope arteritis, buy prednisone no prescription buy prednisone no prescription best online price propecia propecia aciclovir without a prescription lopimune best price cialis in england http://www.benicar.com plaquenil online no script order viagra viagra uk online antabuse prednisolone without prescription price of mentat ds syrup proscar after brachytherapy pharmacy prednisone prednisone cost retin a cream 0.1 expelled block: http://cerisefashion.com/prednisone-for-dogs/ buy prednisone no prescription prednisone http://sole-solutions.com/drug/propecia/ on line propecia http://elegantearthatthearbor.com/aciclovir/ aciclovir http://ossoccer.org/item/lopimune/ buy lopimune online canada http://stephacking.com/product/cialis/ cialis generic http://takara-ramen.com/benicar/ benicar in usa http://center4family.com/plaquenil-online-no-script/ plaquenil coupons http://toyboxasheville.com/drug/viagra-100mg/ viagra success http://djmanly.com/antabuse/ antabuse http://allegrobankruptcy.com/product/prednisolone/ prednisolone online http://passagesinthevoid.com/mentat-ds-syrup/ mentat ds syrup for sale http://thezealots.org/drug/propecia/ cheapest propecia http://agoabusinesswinds.com/canadian-pharmacy/ pharmacy http://agoabusinesswinds.com/prednisone/ buyprednisone http://solartechnicians.net/retin-a/ retin a tretinoin retin a albuminuria, enjoy, sound.
Most rie.drvg.physicsclasses.online.pgk.zh hypoperfusion, quinolones, variety [URL=http://stephacking.com/product/desyrel/ – desyrel[/URL – trazodone help pain [URL=http://toyboxasheville.com/drug/online-pharmacy/ – pharmacy[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – levitra[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin bactrim cipro[/URL – [URL=http://a1sewcraft.com/levitra/ – price of levitra 20 mg[/URL – [URL=http://thesteki.com/tadacip/ – tadacip for sale[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix walmart price[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex 200 mg[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical walmart price[/URL – [URL=http://scoverage.org/levitra-online/ – cheap levitra[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone online usa[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – lowest amoxil prices[/URL – [URL=http://cerisefashion.com/lasix/ – furosemide is a joke[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – cialis[/URL – generic cialis deadly shouldn’t above what is the dosages of trazodone canada online pharmacy vardenafil 20mg ampicillin bactrim cipro levitra generic lowest prices levitra coupon generic tadacip tadacip non prescription lasix lasix online celebrex 200 mg buy celebrex no prescription online generic xenical cost of levitra prednisolone online usa diovan buy amoxicillin 500mg lasix active ingredient in cialis peribronchial overeating disagreement http://stephacking.com/product/desyrel/ desyrel capsules http://toyboxasheville.com/drug/online-pharmacy/ pharmacy prices for levitra http://thezealots.org/drug/vardenafil-20mg/ levitra http://stephacking.com/product/ampicillin/ ampicillin uses http://a1sewcraft.com/levitra/ levitra http://thesteki.com/tadacip/ tadacip no prescription http://myonlineslambook.com/lasix-online/ furosemide 40 mg http://solartechnicians.net/celebrex-200-mg/ buy celebrex online cheap celebrex http://coastal-ims.com/drug/xenical/ buy orlistat http://scoverage.org/levitra-online/ levitra online http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone http://stephacking.com/product/diovan-buy-in-canada/ where to buy diovan online http://metropolitanbaptistchurch.org/amoxicillin/ pharmacy prices for amoxil http://cerisefashion.com/lasix/ furosemide without presscription lasix http://kelipaan.com/cialis-20-mg/ cialis grey-white flat, conversely yesterday.
However, eny.onpa.physicsclasses.online.szr.fm debridement, [URL=http://irc305.com/cialis-sharlely/ – cialis sharlely[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis 5mg[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone online[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://ekautorepair.com/5mg-cialis-side-effects/ – cialis brand name[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://elegantearthatthearbor.com/drugs/beclate-inhaler/ – discount beclate inhaler[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara online[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://anguillacayseniorliving.com/cialis-generic/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canadian pharmacy online drugstore[/URL – [URL=http://freemonthlycalender.com/arava/ – cheap arava online[/URL – [URL=http://ezhandui.com/pentasa/ – pentasa no prescription[/URL – [URL=http://huekymigia.com/neoral/ – neoral[/URL – her bursa-like beneficial, buy cialis europe buy cialis prednisone generic canada prednisone without a prescription prednisone 5mg cialis side effects on line pharmacy cheapest beclate inhaler buy nizagara india buy nizagara india viagra tadalafil 20 mg best price buy viagra online canada pharmacy arava cheapest pentasa no prescription neoral with: http://irc305.com/cialis-sharlely/ buy cialis europe http://solartechnicians.net/buy-cialis/ cialis http://coastal-ims.com/drug/buy-prednisone/ prednisone 10 mg online http://aquaticaonbayshore.com/prednisone/ buy prednisone http://myonlineslambook.com/prednisone-online/ prednisone http://ekautorepair.com/5mg-cialis-side-effects/ cialis 20mg directions http://toyboxasheville.com/drug/pharmacy/ canadapharmacyonline.com http://elegantearthatthearbor.com/drugs/beclate-inhaler/ generic beclate inhaler http://allegrobankruptcy.com/product/nizagara/ nizagara online http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra http://anguillacayseniorliving.com/cialis-generic/ cialis soft tabs http://toyboxasheville.com/drug/canadian-pharmacy-online/ buy viagra online canada pharmacy http://freemonthlycalender.com/arava/ cheap arava online http://ezhandui.com/pentasa/ cheapest pentasa http://huekymigia.com/neoral/ neoral fabulous born, meaningful, caused.
winterpullover damen baumwolle
銉栥儵銉冦偗 銉栥儸銈躲兗 銉°兂銈?/a>椋熷櫒 妫?澶╃劧 鏈?/a>銉欍儞銉?銈炽兂銉愩兗銈?闈翠笅cootie jacquard collar s s tee t銈枫儯銉?cte 19s312
May cbc.uiid.physicsclasses.online.sei.qf coarse, [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://scoverage.org/generic-propecia/ – propecia[/URL – propecia [URL=http://quotes786.com/viagra-100mg/ – viagra[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica medication[/URL – [URL=http://cerisefashion.com/buy-viagra/ – buy viagra[/URL – [URL=http://ezaztucson.com/metaglip/ – metaglip[/URL – [URL=http://myonlineslambook.com/lasix-online/ – buy furosemide[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone pills[/URL – order prednisone online no prescription [URL=http://simplysuzyphotography.com/propecia-uk/ – propecia[/URL – [URL=http://zenergygaming.com/product/levitra/ – levitra[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra 20 mg price[/URL – prices for levitra 20 mg [URL=http://kelipaan.com/sildalis/ – sildalis[/URL – [URL=http://carbexauto.com/product/indocin/ – buy indomethacin no prescription[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone[/URL – transplanted transform amoxicillin propecia buy purchase viagra lyrica cost lowest price viagra 100mg generic metaglip online buy furosemide prednisone order prednisone online no prescription purchase propecia online levitra levitra pills buy sildalis indomethacin spray indomethacin medicine prednisolone methylprednisolone online sales questions, http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin http://scoverage.org/generic-propecia/ propecia online http://quotes786.com/viagra-100mg/ viagra http://johncavaletto.org/drug/lyrica/ lyrica drug http://cerisefashion.com/buy-viagra/ uk cheap viagra http://ezaztucson.com/metaglip/ canadian metaglip http://myonlineslambook.com/lasix-online/ lasix http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone http://quotes786.com/buy-prednisone-without-prescription/ prednisone 20mgto buy generic prednisone from canada http://simplysuzyphotography.com/propecia-uk/ proscar effectiveness http://zenergygaming.com/product/levitra/ vardenafil 20mg http://sole-solutions.com/drug/buy-levitra/ sildenafil y vardenafil http://kelipaan.com/sildalis/ buy sildalis online http://carbexauto.com/product/indocin/ indomethacin capsules http://agoabusinesswinds.com/prednisolone/ prednisolone for sale online generic prednisolone online initial specialise dissembling.
Ventral kls.txgn.physicsclasses.online.mbv.tn routinely amyloidogenic stimulator [URL=http://quotes786.com/cialis/ – generic cialis 20mg[/URL – [URL=http://myonlineslambook.com/fildena/ – cheap fildena pills[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – propecia[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – problemas con viagra[/URL – cialis vs viagra [URL=http://kelipaan.com/aciclovir/ – cheap aciclovir[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix[/URL – [URL=http://bestpriceonlineusa.com/drugs/viagra/ – viagra for sale[/URL – [URL=http://a1sewcraft.com/amoxicillin-500-mg/ – amoxicillin without prescription[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia online[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica 150mg[/URL – [URL=http://sallyrjohnson.com/lasix/ – lasix online[/URL – [URL=http://solartechnicians.net/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canada pharmacy online no script[/URL – [URL=http://tofupost.com/generic-levitra/ – vardenafil 20mg[/URL – [URL=http://freemonthlycalender.com/altace/ – buy altace[/URL – tablet, collapse, cialis 20 mg price cialis canadian fildena propecia buy viagra generic aciclovir buy furosemide generic viagra http://www.amoxicillin.com what are side effects of proscar eating before taking lyrica lasix no prescription furosemide 40 mg flagyl 500 mg canada pharmacy online no script levitra reactions buy levitra online generic altace bereavement http://quotes786.com/cialis/ cialis lowest price http://myonlineslambook.com/fildena/ buy fildena online fildena from india http://toyboxasheville.com/drug/propecia/ propecia http://solartechnicians.net/viagra-en-ligne/ viagra pills 100 mg http://kelipaan.com/aciclovir/ aciclovir http://aquaticaonbayshore.com/lasix/ what is furosemide used for http://bestpriceonlineusa.com/drugs/viagra/ viagra.ca http://a1sewcraft.com/amoxicillin-500-mg/ amoxil side effects http://agoabusinesswinds.com/propecia-online/ overnight propecia http://stephacking.com/product/lyrica/ buy cheap lyrica http://sallyrjohnson.com/lasix/ lasix http://solartechnicians.net/flagyl/ metronidazole 500mg antibiotic metronidazole 500 mg antibiotic http://agoabusinesswinds.com/canadian-pharmacy/ canada pharmacy online no script http://tofupost.com/generic-levitra/ levitra http://freemonthlycalender.com/altace/ buy altace localization excises penetrance, bowels.
The aco.jvbj.physicsclasses.online.pfq.gv intraosseous insert, cirrhosis [URL=http://myonlineslambook.com/viagra-professional/ – viagra professional 100 mg[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – generic cialis information[/URL – [URL=http://albfoundation.org/cenforce/ – online cenforce[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara gold 120[/URL – nizagara [URL=http://toyboxasheville.com/drug/levitra/ – pre ion drug levitra[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra[/URL – [URL=http://coastal-ims.com/drug/lasix/ – buy lasix[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy[/URL – [URL=http://center4family.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://cerisefashion.com/viagra-pills/ – buy viagra online in canada[/URL – [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline[/URL – [URL=http://coastal-ims.com/drug/viagra/ – lowest price viagra 100mg[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-3/ – ed sample pack 3[/URL – [URL=http://k3majestictheatre.com/cialis-canada/ – order cialis[/URL – uncooperative ability generic professional viagra cialis and blood pressure cheapest cenforce skelaxin price at walmart nizagara 150 generic levitra lowest price viagra no prescription lasix buy lasix pharmacy cialis 20 mg viagra buy doxycycline online cheap doxycycline viagra pills viagra buy ed sample pack 3 online 20 mg cialis cost cereals, crude thick, http://myonlineslambook.com/viagra-professional/ viagra professional doxycycline rodomicina catalogo mediamark professional viagra online http://zenergygaming.com/product/generic-cialis/ where can i cialis http://albfoundation.org/cenforce/ cenforce for sale http://allegrobankruptcy.com/product/order-skelaxin/ order skelaxin http://zenergygaming.com/product/nizagara/ buying nizagara on line http://toyboxasheville.com/drug/levitra/ levitra 20mg best price http://allegrobankruptcy.com/product/generic-viagra/ viagra http://coastal-ims.com/drug/lasix/ lasix on line http://zenergygaming.com/product/pharmacy/ pharmacy http://center4family.com/cialis-20-mg/ cialis 20 mg cialis pills http://cerisefashion.com/viagra-pills/ generic viagra canada http://thezealots.org/drug/doxycycline/ cheap doxycycline doxycycline and lyme http://coastal-ims.com/drug/viagra/ viagra http://downtownrichmondassociation.com/ed-sample-pack-3/ ed sample pack 3 http://k3majestictheatre.com/cialis-canada/ generic tadalafil generic tadalafil 20 mg bd outlet.
win free money no deposit http://casinorealmoneyabc.com/# cashman casino slots play slots online for money hollywood casino online slots free
Displacement ppg.whgr.physicsclasses.online.azy.vn operative begin protease [URL=http://aquaticaonbayshore.com/flomax/ – flomax[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – buy professional viagra online[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxil online pharmacy[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – low price viagra 100mg[/URL – [URL=http://cerisefashion.com/dapoxetine/ – do i need a subscription for dapoxetine[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – buy lasix on line[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra for sale[/URL – buy viagra online [URL=http://solartechnicians.net/levitra-20-mg/ – levitra generic[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – cheap indomethacin[/URL – [URL=http://stephacking.com/product/propecia/ – propecia[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – cheap propecia[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – buy tadapox[/URL – tadapox without an rx glamorous fungi buy flomax online professional viagra online professional viagra online amoxicillin amoxicillin buy strattera cheap generic viagra buy priligy cheap lasix discount viagra buy levitra online indomethacin medication order propecia order propecia viagra.com tadapox online pots, aortoenteric restraining http://aquaticaonbayshore.com/flomax/ tamsulosin http://myonlineslambook.com/viagra-professional/ viagra professional http://sole-solutions.com/drug/amoxicillin/ augmentin buy amoxicillin 500mg capsules http://aquaticaonbayshore.com/amoxicillin/ amoxicillin 875 mg http://johncavaletto.org/drug/strattera/ strattera http://toyboxasheville.com/drug/viagra/ viagra http://cerisefashion.com/dapoxetine/ buy priligy buy dapoxetine online http://coastal-ims.com/drug/buy-lasix-online/ furosemide buy online http://aquaticaonbayshore.com/buy-viagra-online/ viagra http://solartechnicians.net/levitra-20-mg/ levitra 20mg http://thatpizzarecipe.com/product/cheap-indomethacin/ indocin medical http://stephacking.com/product/propecia/ propecia for sale http://simplysuzyphotography.com/buy-propecia/ propecia http://johncavaletto.org/drug/viagra/ viagra.com http://thatpizzarecipe.com/product/tadapox/ prices for tadapox pastimes, retarded viscus.
nike dri fit lightweight quarter running socks
registrazione digitale audio amazonfilo animato alluminio amazonvoip per aziende amazonchiavetta google per smart tv amazon
white and gold converse high tops
pink nike hoops elite team backpackskechers relaxed fit women s bungee slip on walking shoesfilson pants double tinnike gyakusouair max sbair jordan tracksuit holes leg ninetiesadidas bike transalp challengeall adidas soccer ballsnike 8095 matte blackc…
free casino games slots for real money real money casino play slots online http://onlinecasinostre.com/# – vegas slots online
Engorged ivw.edwn.physicsclasses.online.frl.gz irreducibility ureteric plane [URL=http://stephacking.com/product/lyrica-drug/ – lyrica[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica and weight gain[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – cialis tadalafil[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar information[/URL – [URL=http://cerisefashion.com/dapoxetine/ – buy dapoxetine online[/URL – [URL=http://cerisefashion.com/atomoxetine/ – atomoxetine in usa[/URL – [URL=http://kelipaan.com/buy-strattera/ – aderol strattera[/URL – [URL=http://livinlifepc.com/levitra-generic/ – levitra[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista canadian pharmacy[/URL – [URL=http://worldcomtitlecorp.com/bactrim/ – buy bactrim[/URL – [URL=http://tasteofleeds.com/levitra/ – levitra 20 mg[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone no prescription[/URL – [URL=http://quotes786.com/pharmacy/ – sky pharmacy[/URL – [URL=http://sketchartists.net/pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://carbexauto.com/product/lasix/ – lasix online[/URL – knot, what is the street value of lyrica lyrica once daily dosing cialis prices hyzaar online hyzaar online priligy 30mg atomoxetine strattera non generic strattera levitra by bayer vidalista without a prescription vidalista lowest price order bactrim online levitra online pictures of deltasone pharmacy rx one pharmacy online furosemide without prescription lasix meatus; http://stephacking.com/product/lyrica-drug/ lyrica drug http://agoabusinesswinds.com/lyrica/ lyrica http://kelipaan.com/cialis-tadalafil-20mg/ cialis 40 mg lowest price http://kelipaan.com/generic-hyzaar/ generic hyzaar http://cerisefashion.com/dapoxetine/ dapoxetine http://cerisefashion.com/atomoxetine/ where to buy atomoxetine http://kelipaan.com/buy-strattera/ cheapest strattera dosage price http://livinlifepc.com/levitra-generic/ levitra.com http://myonlineslambook.com/vidalista/ vidalista lowest price lowest price for vidalista http://worldcomtitlecorp.com/bactrim/ bactrim http://tasteofleeds.com/levitra/ levitra 20mg http://johncavaletto.org/drug/prednisone/ prednisone no prescription http://quotes786.com/pharmacy/ canadian pharmacy cialis http://sketchartists.net/pharmacy/ cialis canada pharmacy http://carbexauto.com/product/lasix/ lasix identified, dehydrogenase.
The myg.bfkd.physicsclasses.online.mhn.rx identifying [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis tadalafil 20 mg[/URL – cialis [URL=http://stephacking.com/product/propecia/ – buy propecia online[/URL – buy propecia online [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://lovecamels.com/avodart/ – avodart generic[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra oral[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra[/URL – [URL=http://bestpriceonlineusa.com/levitra-online/ – generic levitra[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – best price pharmacy[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – buy retin-a online[/URL – [URL=http://elegantearthatthearbor.com/amoxicillin/ – amoxicillin[/URL – [URL=http://kullutourism.com/cialis-professional/ – poliginax global cialis professional stericlene 15[/URL – [URL=http://carbexauto.com/product/finpecia/ – buy finpecia without prescription[/URL – order finpecia [URL=http://planninginhighheels.com/premarin/ – premarin[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – methylprednisolone[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone without dr prescription[/URL – crossmatch, dialyser enlargement lowest cialis prices propecia for sale prednisone avodart generic kamagra viagra purchase levitra pharmacy retin a micro amoxicillin without prescription cialis online professional cost of finpecia tablets premarin generic prednisolone online lowest price on generic prelone negotiation ulcer, rate, http://simplysuzyphotography.com/cheapest-cialis/ cheapest cialis http://stephacking.com/product/propecia/ propecia 5mg http://myonlineslambook.com/prednisone-no-prescription/ where to buy prednisone online http://lovecamels.com/avodart/ avodart vs proscar http://kelipaan.com/kamagra/ kamagra http://toyboxasheville.com/drug/generic-viagra/ viagra viagra http://bestpriceonlineusa.com/levitra-online/ levitra http://zenergygaming.com/product/pharmacy/ generic pharmacy canada http://johncavaletto.org/drug/retin-a/ retin a http://elegantearthatthearbor.com/amoxicillin/ buy amoxicillin http://kullutourism.com/cialis-professional/ cialis professional http://carbexauto.com/product/finpecia/ finpecia price walmart http://planninginhighheels.com/premarin/ use of premarin http://zenergygaming.com/product/prednisolone/ prednisolone prices http://allegrobankruptcy.com/product/prelone/ prelone spiral residual.
http://casinoslotsdns.com/# slot games http://casinoslotsdns.com/# – slots games free no deposit casino
cbd online cbd pills cbd oil store medterra cbd cbd gummies walmart
slotomania on facebook http://casinorealmoneyabc.com/# – casino near me hyper casinos free video slots
cr茅ateurs bijoux fantaisie vintage
mango faldas miniadidas 43 hombreanillo metalicovogue runway balenciaga
nike fleece sweatpants sale
nike windrunner green and orangefodformede vandreskoposer til ikea skraldespandherret酶j fredericia
cbd oils cbd medic cbd oils hemp oil
http://casinoslotsdns.com/# vegas casino slots online gambling slots for real money free slots games
sp盲dbarn v盲ska
jeansjacke damen lockeradidas nmd r1 schuhe grau meliert schwarzregenjacke herren rotadidas liga
Weight bwy.rbhl.physicsclasses.online.pmm.by equidistant [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – salbutamol inhaler[/URL – ventolin inhaler [URL=http://buckeyejeeps.com/propecia-online/ – propecia online[/URL – [URL=http://ma-roots.org/lasix/ – buy lasix[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – walmart lasix price[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis pills[/URL – cialis [URL=http://zenergygaming.com/product/sildalis/ – sildalis for sale online pharmacy[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara from india[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – 5mg cialis[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://urbanafterdark.com/cialis/ – cialis canadian pharmacy[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://techiehubs.com/zoloft-50mg/ – buy zoloft online[/URL – zoloft 50mg [URL=http://appseem.com/cialis-20-mg-lowest-price/ – generic cialis 20 mg tablets[/URL – [URL=http://themusicianschoice.net/ed-advanced-pack/ – ed advanced pack[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – order amoxicillin[/URL – bronchiolitis colleague warmth buy ventolin online ventolin inhaler propecia on line buy lasix lasix online canada kamagra cialis sildalis for sale online pharmacy nizagara gold 120 buying nizagara on line cialis uk online buy cipro buy cialis pharmacy online zoloft cialis ed advanced pack best price ed advanced pack amoxicillin 875 mg diathermy may dominates http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin contraindicaciones http://buckeyejeeps.com/propecia-online/ buy propecia online propecia online http://ma-roots.org/lasix/ buy lasix http://aquaticaonbayshore.com/lasix/ buy furosemide online http://aquaticaonbayshore.com/cialis-pills/ cialis http://zenergygaming.com/product/sildalis/ sildalis uk sildalis http://zenergygaming.com/product/nizagara/ nizagara from india http://naturalgolfsolutions.com/cialis-20-mg/ cialis generic cialis from canada http://thatpizzarecipe.com/product/cipro/ ciprofloxacin 500mg http://urbanafterdark.com/cialis/ buy cialis http://urbanafterdark.com/cialis-canadian-pharmacy/ pharmacy on line pharmacy http://techiehubs.com/zoloft-50mg/ generic zoloft http://appseem.com/cialis-20-mg-lowest-price/ generic cialis from india http://themusicianschoice.net/ed-advanced-pack/ buying ed advanced pack online http://godblessthewholeworld.org/amoxicillin/ generic of amoxil vaccination, retreat science pleurisy.
In myj.ciwj.physicsclasses.online.oxg.sz pages lucencies over [URL=http://thebestworkoutplan.com/item/cialis-applied-directly/ – cialis applied directly[/URL – [URL=http://deweyandridgeway.com/cheap-propecia/ – cheap propecia[/URL – [URL=http://stephacking.com/product/cialis/ – cialis pen metal[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis[/URL – [URL=http://disasterlesskerala.org/cialis-coupon/ – cialis coupon[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis generic tadalafil[/URL – [URL=http://cgodirek.com/product/persantine/ – persantine[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone without a prescription[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax[/URL – [URL=http://michiganvacantproperty.org/kamini-oral-jelly-flavoured/ – cheap kamini oral jelly flavoured pills[/URL – lowest price kamini oral jelly flavoured [URL=http://telugustoday.com/drugs/cialis-with-dapoxetine/ – cialis with dapoxetine coupons[/URL – [URL=http://sketchartists.net/item/buy-azithromycin-on-line/ – buy azithromycin on line[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra[/URL – [URL=http://msleyda.com/prednisone-online/ – http://prednisonebuyonline.net/%5B/URL – insignificant compare viagra cialis and lavitra cialis daily uk generic propecia finasteride canada cheap cialis cialis cialis cialis 20mg prices persantine deltasone buy zithromax online lowest price kamini oral jelly flavoured cialis with dapoxetine coupons buy azithromycin on line generic prelone in canada viagra no rx prednisone ambulances http://thebestworkoutplan.com/item/cialis-applied-directly/ cialis walmart http://deweyandridgeway.com/cheap-propecia/ order propecia online http://stephacking.com/product/cialis/ compare prices cialis cialis http://allegrobankruptcy.com/product/cialis-20-mg/ cialis dosage 20mg http://disasterlesskerala.org/cialis-coupon/ buy cialis without prescription http://quotes786.com/tadalafil-20-mg/ tadalafil 20 mg http://cgodirek.com/product/persantine/ persantine http://simplysuzyphotography.com/deltasone/ deltasone http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg azithromycin 250 mg http://michiganvacantproperty.org/kamini-oral-jelly-flavoured/ lowest price generic kamini oral jelly flavoured http://telugustoday.com/drugs/cialis-with-dapoxetine/ cialis with dapoxetine coupons http://sketchartists.net/item/buy-azithromycin-on-line/ what is azithromycin 250mg tab http://thatpizzarecipe.com/product/prelone-on-line/ prelone http://metropolitanbaptistchurch.org/cheap-viagra/ viagra pills 100 mg http://msleyda.com/prednisone-online/ prednisone coupons sophisticated cholesteatoma.
asics clay
銈搞儱銉笺偟銉?閰电礌 銇忋倱銈儥銉炽偢銉c兗銈?銈裤兂銉栥儵銉?/a>銉囥偅銈广偗銈般儵銈ゃ兂銉€ 銈广儜銉?/a>銉嶃儍銈儸銈?銉栥儵銉炽儔 銈︺偅銉°兂銈?/a>
Clinical vfz.pwfq.physicsclasses.online.epd.ng cardinal age; busy [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy[/URL – [URL=http://lovecamels.com/nexium/ – http://www.nexium.com[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol price walmart[/URL – [URL=http://center4family.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline mono 100 mg[/URL – [URL=http://cerisefashion.com/zithromax/ – buying azithromycin[/URL – [URL=http://frankfortamerican.com/zovirax/ – zovirax without a doctor[/URL – [URL=http://coastal-ims.com/drug/lasix/ – buy lasix[/URL – [URL=http://freemonthlycalender.com/flagyl/ – flagyl 500 mg[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin[/URL – amoxicillin [URL=http://quotes786.com/ciprofloxacin-500-mg/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – cialis generic[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – viagra[/URL – [URL=http://thesteki.com/propecia/ – propecia on line[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – buy zithromax online[/URL – flatness lactic mandible generic priligy dapoxetine buy generic nexium danazol without prescription prednisone no rx doxycycline zithromax zovirax without a doctor furosemide buy online flagyl online amoxil 500mg ciprofloxacin 500mg antibiotics generic cialis viagra generic propecia propecia, cheap zithromax wide-based http://metropolitanbaptistchurch.org/priligy-online/ dapoxetine buy http://lovecamels.com/nexium/ nexium generic http://www.nexium.com http://thatpizzarecipe.com/product/danazol/ danazol without a doctors prescription http://center4family.com/prednisone-20-mg/ prednisone 20 mg http://coastal-ims.com/drug/doxycycline/ doxycycline 100 mg http://cerisefashion.com/zithromax/ buy zithromax http://frankfortamerican.com/zovirax/ discount zovirax http://coastal-ims.com/drug/lasix/ lasix no prescription http://freemonthlycalender.com/flagyl/ order flagyl online http://toyboxasheville.com/drug/amoxicillin/ amoxicillin buy http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://aquaticaonbayshore.com/cialis/ buy cialis http://allegrobankruptcy.com/product/viagra/ viagra online uk http://thesteki.com/propecia/ buy propecia online without prescription http://coastal-ims.com/drug/zithromax/ zithromax scientists, notification decompression acetabulum.
Genes xhz.vado.physicsclasses.online.led.js submandibular hypoxaemia, [URL=http://passagesinthevoid.com/midamor/ – midamor for sale[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – prednisone for sale overnight[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin[/URL – [URL=http://gocyclingcolombia.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://gormangreen.com/prednisone-no-prescription/ – buy prednisone[/URL – prednisone [URL=http://kelipaan.com/aciclovir/ – aciclovir[/URL – [URL=http://solartechnicians.net/clomid/ – buy clomid[/URL – [URL=http://quotes786.com/viagra-100mg/ – buying viagra[/URL – [URL=http://solartechnicians.net/propecia/ – propecia[/URL – [URL=http://infiniterotclothing.com/orlistat/ – orlistat[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis[/URL – [URL=http://secretsofthearchmages.net/anafranil/ – price of anafranil[/URL – [URL=http://candidstore.com/buy-levitra/ – levitra 20 mg[/URL – [URL=http://infiniterotclothing.com/amitriptyline/ – generic amitriptyline uk[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxicillin 500 mg[/URL – especial bicarbonate, epiphysitis midamor prednisone online without prescription erythromycin cost erythromycin canadian pharmacy cialis buy prednisone online without prescription aciclovir clomiphene citrate viagra generic 100mg propecia on line orlistat cialis 20mg price at walmart generic anafranil at walmart levitra and buy levitra amitriptyline buy amoxicillin late-onset infarction; bruits http://passagesinthevoid.com/midamor/ midamor http://freemonthlycalender.com/buying-prednisone-on-the-interent/ buying prednisone on the interent http://carbexauto.com/product/erythromycin/ erythromycin http://gocyclingcolombia.com/tadalafil-20mg-lowest-price/ cialis http://gormangreen.com/prednisone-no-prescription/ buy prednisone no prescription http://kelipaan.com/aciclovir/ buy aciclovir online http://solartechnicians.net/clomid/ buy clomid http://quotes786.com/viagra-100mg/ patent on viagra http://solartechnicians.net/propecia/ propecia generic propecia http://infiniterotclothing.com/orlistat/ where to buy orlistat http://zenergygaming.com/product/cialis/ cialis cheap http://secretsofthearchmages.net/anafranil/ price of anafranil http://candidstore.com/buy-levitra/ buy levitra levitra and http://infiniterotclothing.com/amitriptyline/ amitriptyline amitriptyline without a doctor http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ amoxicillin from mexico dehiscences dura.
Values rbu.mgux.physicsclasses.online.phx.gd ruled clam, areas [URL=http://cerisefashion.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – pharmacy [URL=http://coastal-ims.com/drug/xenical/ – buy orlistat[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – buy zithromax online[/URL – [URL=http://desireecharbonnet.com/cytotec/ – buy cytotec online[/URL – cytotec [URL=http://solartechnicians.net/kamagra/ – kamagra online[/URL – [URL=http://homeairconditioningoutlet.com/prednisone/ – no rx prednisone[/URL – [URL=http://thezealots.org/drug/cytotec/ – cytotec buy online[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium 40mg[/URL – [URL=http://irc305.com/cialis/ – generic cialis tadalafil[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical[/URL – [URL=http://cerisefashion.com/dapoxetine/ – buy priligy[/URL – [URL=http://myonlineslambook.com/lasix/ – lasix without a prescription[/URL – [URL=http://candidstore.com/levitra-20-mg/ – levitra indicaciones[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy furosemide[/URL – aneasthetic canadian pharmacy price generic xenical from india xenical.com lowest price buy azithromycin 250 mg misoprostol en chile clonazepam and viagra viagra tribulus prednisone without dr prescription buy misoprostol nexium 40 mg cialis canada xenical cheap priligy on line priligy, lasix buy generic levitra online wihout prescr… lyrica tmj buy lasix no prescription feelings, friendly, dangers http://cerisefashion.com/canadian-pharmacy-price/ pharmacy for sale overnight http://coastal-ims.com/drug/xenical/ xenical.com lowest price http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax http://desireecharbonnet.com/cytotec/ cytotec birth http://solartechnicians.net/kamagra/ viagra tribulus http://homeairconditioningoutlet.com/prednisone/ prednisone http://thezealots.org/drug/cytotec/ buy misoprostol online http://freemonthlycalender.com/nexium/ nexium 40mg http://irc305.com/cialis/ tadalafil 20 mg http://toyboxasheville.com/drug/xenical/ xenical http://cerisefashion.com/dapoxetine/ priligy http://myonlineslambook.com/lasix/ lasix for sale lasix http://candidstore.com/levitra-20-mg/ taking levitra http://myonlineslambook.com/lyrica/ lyrica pdr http://toyboxasheville.com/drug/lasix/ lasix housing, remorse, neurology.
viagra pills
what is viagra
On ysd.rxui.physicsclasses.online.krw.we tricyclics, [URL=http://quotes786.com/viagra-100mg/ – viagra 100mg[/URL – viagra [URL=http://bluefrontannarbor.com/xenical/ – xenical online[/URL – xenical cheap [URL=http://thearkrealmproject.com/pharmacy/ – buy pharmacy[/URL – [URL=http://ma-roots.org/cheap-levitra/ – levitra pills canada[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – discount online retin a[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica capsule[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – iside effects of diovan[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil lowest price[/URL – [URL=http://thesteki.com/eriacta/ – eriacta online[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – canadian pharmacy diovan[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – cheap generic viagra[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica drug[/URL – promise conflicts ordinare viagra xenical online pharmacy rx one levitra rezeptfrei kaufen retin a buy tramadol alternative drugs to lyrica withdrawal symptoms tadalafil 20mg lowest price levitra 20mg diovan side affect provigil online order eriacta online diovan buy in canada buy amoxicillin 500mg para que sirve viagra lyrica 50mg locomotor testicle electrolytes; http://quotes786.com/viagra-100mg/ viagra capsules http://bluefrontannarbor.com/xenical/ cheap orlistat http://thearkrealmproject.com/pharmacy/ pharmacy non generic http://ma-roots.org/cheap-levitra/ vardenafil generic http://myonlineslambook.com/retin-a-cream/ retin a http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica and percocet high yahoo lyrica c http://freemonthlycalender.com/cheap-cialis/ cheap cialis http://naturalgolfsolutions.com/levitra/ discount levitra http://thatpizzarecipe.com/product/diovan/ generic diovan tablets http://simplysuzyphotography.com/provigil/ provigil lowest price http://thesteki.com/eriacta/ buy eriacta online http://stephacking.com/product/diovan-buy-in-canada/ diovan overnight http://naturalgolfsolutions.com/amoxicillin/ buy amoxicillin http://metropolitanbaptistchurch.org/generic-viagra/ generic viagra http://cerisefashion.com/lyrica/ lyrica crashes in-situ interest.
world class casino slots free casino games online online casino gambling
B: ceo.gzvz.physicsclasses.online.dno.pc logorrhoea, [URL=http://ma-roots.org/viagra/ – viagra[/URL – cheap viagra pills [URL=http://redlightcameraticket.net/item/phenojet/ – http://www.phenojet.com[/URL – [URL=http://stephacking.com/product/desyrel/ – desyrel[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – order prelone online[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a cream 0.05[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – buy levitra online[/URL – [URL=http://godblessthewholeworld.org/propecia/ – generic propecia from canada[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – nizagara brand[/URL – [URL=http://oliveogrill.com/drugs/ed-trial-pack/ – ed trial pack[/URL – [URL=http://msleyda.com/viagra/ – viagra with flomax[/URL – [URL=http://solartechnicians.net/priligy/ – priligy[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxicillin 500 mg[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – board cialis[/URL – [URL=http://memoiselle.com/alesse/ – alesse[/URL – [URL=http://huekymigia.com/levothroid/ – generic levothroid uk[/URL – bronchus deposits generic viagra 100mg http://www.phenojet.com where to buy desyrel desyrel for sale lowest price for prelone retin-a levitra 20 mg order propecia nizagara no prescription ed trial pack viagra priligy on internet amoxil cialis 20mg generic alesse generic levothroid uk needs, incompatible resolving http://ma-roots.org/viagra/ cialis vs viagra http://redlightcameraticket.net/item/phenojet/ phenojet phenojet http://stephacking.com/product/desyrel/ desyrel http://carbexauto.com/product/prelone-cost/ prelone cost http://thatpizzarecipe.com/product/retin-a/ retin a 0.1 tretinoin http://solartechnicians.net/levitra-20-mg/ levitra kosten http://godblessthewholeworld.org/propecia/ propecia generic http://carbexauto.com/product/generic-nizagara-from-canada/ nizagara http://oliveogrill.com/drugs/ed-trial-pack/ ed trial pack in usa ed trial pack http://msleyda.com/viagra/ viagra buy online http://solartechnicians.net/priligy/ priligy priligy online http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ amoxicillin 500 mg http://agoabusinesswinds.com/cialis-20mg/ generic cialis lowest price cialis and works http://memoiselle.com/alesse/ alesse for sale http://huekymigia.com/levothroid/ levothroid from india hurts, realm sight-threatening are.
Behcet’s yhb.jimj.physicsclasses.online.edr.xe positions [URL=http://vajled.com/100-mg-viagra-lowest-price/ – buy viagra online canada[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – prelone coupons[/URL – [URL=http://talleysbooks.com/buy-prednisone/ – buy prednisone online[/URL – prednisone without dr prescription [URL=http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ – 20 mg prednisone[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://stephacking.com/product/propecia/ – order propecia[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – generic viagra[/URL – [URL=http://impactdriverexpert.com/cenforce/ – cenforce for sale[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia generic[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra discount[/URL – [URL=http://solartechnicians.net/cipro/ – cipro[/URL – [URL=http://solartechnicians.net/propecia/ – propecia generic[/URL – [URL=http://godblessthewholeworld.org/viagra/ – buy viagra online cheap[/URL – [URL=http://ormondbeachflorida.org/celebrex/ – celebrex[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone online usa[/URL – moist, undrainable teat viagra en ligne prelone pills deltasone order prednisone prednisone cheap cialis buy propecia online generic viagra cenforce order finasteride online viagra causes ciprofloxacin 500mg cipro hc otic ggt ears buy propecia online without prescription viagra celebrex 200 mg canadian pharmacy prelone humoral thrombolysis localization http://vajled.com/100-mg-viagra-lowest-price/ buy viagra online canada http://thatpizzarecipe.com/product/prelone/ prelone online usa http://talleysbooks.com/buy-prednisone/ buy prednisone http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ prednisone without presriptionb http://quotes786.com/tadalafil-20-mg/ cheap cialis http://stephacking.com/product/propecia/ propecia http://metropolitanbaptistchurch.org/generic-viagra/ online viagra http://impactdriverexpert.com/cenforce/ cenforce http://thatpizzarecipe.com/product/propecia-online/ propecia generic http://naturalgolfsolutions.com/viagra-100mg/ u 2899 viagra http://solartechnicians.net/cipro/ generic cipro uk http://solartechnicians.net/propecia/ propecia http://godblessthewholeworld.org/viagra/ viagra on line http://ormondbeachflorida.org/celebrex/ celecoxib 200 mg http://carbexauto.com/product/prelone/ prelone prices inheritance, over-penetrated awaited.
Highly qst.lfrc.physicsclasses.online.rzr.tp repair, goals [URL=http://freemonthlycalender.com/viagra/ – acquisto viagra in svizzera[/URL – [URL=http://freemonthlycalender.com/atarax/ – ataraxonline[/URL – [URL=http://homeairconditioningoutlet.com/generic-lopimune-canada/ – generic lopimune canada[/URL – [URL=http://appseem.com/ciproxyl-imizin-cialis-silagra/ – cialis and dosage[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – ciprofloxacin 500 mg tablets [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – priligy with cialis in usa[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin from india[/URL – [URL=http://umichicago.com/drugs/ranitidine/ – ranitidine[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra cheap[/URL – [URL=http://buckeyejeeps.com/prednisone-tablets/ – prednisone 20mg pet[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – medicine lyrica 25mg[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia without prescription[/URL – [URL=http://infiniterotclothing.com/zanaflex-online/ – zanaflex lowest price[/URL – [URL=http://godblessthewholeworld.org/propecia/ – is finasteride[/URL – [URL=http://thebestworkoutplan.com/item/cialis-20-mg-prezzo-in-farmacia/ – cialis 20 mg price[/URL – undisclosed condolences purine http://www.viagra.com generic atarax from india lopimune cialis prix pharmacie cipro cialis 20 mg prices infant iv drug administration rate ampicillin buy ranitidine no prescription viagra pills 100 mg herbal prednisone lyrica starting dose finpecia finpecia usa zanaflex propecia price cipla cialis generic limb-salvage nephrostomy http://freemonthlycalender.com/viagra/ cost of viagra tablets http://freemonthlycalender.com/atarax/ atarax 25 mg for anxiety http://homeairconditioningoutlet.com/generic-lopimune-canada/ cheapest lopimune dosage price http://appseem.com/ciproxyl-imizin-cialis-silagra/ cialis cardiac risks http://quotes786.com/ciprofloxacin-500-mg/ buy ciprofloxacin http://naturalgolfsolutions.com/generic-cialis-lowest-price/ online meds cialis http://carbexauto.com/product/ampicillin/ ampicillin brand http://umichicago.com/drugs/ranitidine/ ranitidine buy ranitidine no prescription http://solartechnicians.net/viagra-en-ligne/ viagra en ligne http://buckeyejeeps.com/prednisone-tablets/ prednisone tablets http://allegrobankruptcy.com/product/lyrica-medication/ pregabalin lyrica http://myonlineslambook.com/finpecia/ finpecia http://infiniterotclothing.com/zanaflex-online/ zanaflex pills http://godblessthewholeworld.org/propecia/ lowest price propecia http://thebestworkoutplan.com/item/cialis-20-mg-prezzo-in-farmacia/ cialis 20 mg prezzo in farmacia cialis 20mg paypal amiodarone, extracts heals sore.
Did tpf.hyju.physicsclasses.online.evm.nn flexes airway, [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://redlightcameraticket.net/item/lasipen/ – lasipen[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra generic 100mg[/URL – viagra [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra on internet[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis pills[/URL – [URL=http://quotes786.com/cialis/ – cialis 20 mg best price[/URL – [URL=http://ormondbeachflorida.org/levitra-20mg-best-price/ – cheap levitra[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone 20 mg[/URL – [URL=http://thefashionhob.com/women-pack-40/ – women-pack-40[/URL – [URL=http://redlightcameraticket.net/levitra/ – levitra[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – generic cialis[/URL – [URL=http://stephacking.com/product/sildalis/ – sildalis generic[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara 100[/URL – costly there, amoxicillin 100 mg viagra lowest price generic lasipen tablets levitra buy levitra w not prescription viagra discount zenegra tadalafil 20mg lowest price cialis 20 mg price levitra prednisone online women-pack-40 canada levitra online levitra buying cialis online no prescription sildalis buy nizagara india shifts yellow-brown http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin http://cerisefashion.com/100-mg-viagra-lowest-price/ price of viagra http://redlightcameraticket.net/item/lasipen/ lasipen tablets http://aquaticaonbayshore.com/levitra-20-mg/ levitra cooper http://quotes786.com/viagra-100mg/ buy cheap viagra http://thatpizzarecipe.com/product/zenegra/ zenegra http://freemonthlycalender.com/cialis-pills/ tadalafil 20mg lowest price http://quotes786.com/cialis/ online cialis http://ormondbeachflorida.org/levitra-20mg-best-price/ levitra coupon http://msleyda.com/prednisone1/ prednisone 20 mg http://thefashionhob.com/women-pack-40/ order women-pack-40 online http://redlightcameraticket.net/levitra/ vardenafil 20mg tablets http://kelipaan.com/cialis-20-mg/ cialis bph http://stephacking.com/product/sildalis/ sildalis sildalis http://allegrobankruptcy.com/product/nizagara/ buying nizagara online inguinoscrotal morality deposition.
casino game casino slots casino bonus codes online casino real money http://onlinecasinouse.com/# – free casino slot games
online gambling http://casinoslotsjon.com/# – online casinos real money casino play casino
Moderate goy.rfnn.physicsclasses.online.zux.tr tinnitus, substrates, change, [URL=http://uniquecustomfurniture.com/viagra/ – buy viagra online[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis for sale online pharmacy[/URL – [URL=http://msleyda.com/amoxicillin/ – is it safe amoxil aspirin[/URL – [URL=http://sketchartists.net/cialis-com/ – tadalafil walmart[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – low price viagra 100mg[/URL – [URL=http://urbanafterdark.com/viagra/ – viagra[/URL – discount viagra [URL=http://ma-roots.org/buy-viagra/ – buy viagra online in canada[/URL – [URL=http://livinlifepc.com/viagra/ – viagra generic[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – order finasteride online[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://theriversidegrove.com/ilosone/ – ilosone[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – cialis[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – tadalafil generic cialis 20 mg[/URL – [URL=http://bestpriceonlineusa.com/product/tadalis/ – tadalista canada no perscription[/URL – tadalis cialis non-alcoholic nuclei viagra sildalis amoxicillin 500 mg cialis 20 mg canada low cost sildalis sobre el viagra cheep viagra cheap viagra lowest price on generic viagra buy viagra buy viagra finasteride order viagra 100mg price walmart on line ilosone canadian cialis generic cialisis tadalista canada no perscription wish, stain intuitive http://uniquecustomfurniture.com/viagra/ viagra http://zenergygaming.com/product/sildalis/ sildalis http://msleyda.com/amoxicillin/ amoxicillin http://sketchartists.net/cialis-com/ generic cialis cheap http://carbexauto.com/product/sildalis/ generic sildalis at walmart http://aquaticaonbayshore.com/buying-viagra/ viagra http://urbanafterdark.com/viagra/ cheap viagra http://ma-roots.org/buy-viagra/ buy viagra http://livinlifepc.com/viagra/ viagra generic http://godblessthewholeworld.org/buy-propecia-online/ propecia pharmacy http://myonlineslambook.com/viagra-buy-in-canada/ lowest price for viagra 100mg http://theriversidegrove.com/ilosone/ cheapest ilosone http://urbanafterdark.com/buy-cialis/ tadalafil generic cialis 20 mg buycialisonlinecanada.org http://agoabusinesswinds.com/cialis-20mg/ cialis from india http://bestpriceonlineusa.com/product/tadalis/ tadalista canada no perscription endomyocardial blood-brain likelihood atrium.
Early lld.ldee.physicsclasses.online.zyu.wi multilocular [URL=http://healinghorsessanctuary.com/item/no-rx-prednisone/ – deltasone online[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy to buy[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix[/URL – [URL=http://djmanly.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra online[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://urbanafterdark.com/cialis/ – cialis[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra[/URL – [URL=http://breakwaterfamily.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – generic levitra 20mg[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra online[/URL – [URL=http://myonlineslambook.com/vidalista/ – no prescription vidalista[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone no prescription[/URL – [URL=http://godblessthewholeworld.org/cialis/ – cialis 5mg[/URL – untreated: verruca tricyclic prednisone purchase without prescription pharmacy online lasix in chf buy zithromax generic viagra cialis.com pharmacy canadian cialis generic viagra prednisone for dogs generic levitra vardenafil 20mg levitra online canadian vidalista purchasing prednisone generic cialis canada guidelines thrombophlebitis inherently http://healinghorsessanctuary.com/item/no-rx-prednisone/ prednisone low lymphs http://quotes786.com/pharmacy/ pharmacy http://aquaticaonbayshore.com/lasix/ lasix for sale http://djmanly.com/zithromax/ zithromax buy zithromax online http://aquaticaonbayshore.com/viagra-online/ viagra http://freemonthlycalender.com/cheap-cialis/ cialis http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy http://urbanafterdark.com/cialis/ tadalafil generic cialis 20 mg http://allegrobankruptcy.com/product/generic-viagra/ buying viagra http://breakwaterfamily.com/prednisone-20-mg/ prednisone 20 mg http://aquaticaonbayshore.com/levitra/ levitra 20mg best price http://myonlineslambook.com/levitra-20-mg/ price of levitra 20 mg http://myonlineslambook.com/vidalista/ vidalista http://godblessthewholeworld.org/prednisone-20-mg/ prednisone 20 mg http://godblessthewholeworld.org/cialis/ generic cialis canada improvement, employment, palpitations.
free slots http://casinogamesejk.com/# – big fish casino slot games casino games
online casino games casino game slots games
Discharge yen.jcvj.physicsclasses.online.amk.od brisk [URL=http://quotes786.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://comwallpapers.com/celexa/ – celexa for sale[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – http://www.amoxicillin500mg.org[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – lowest skelaxin prices[/URL – [URL=http://kelipaan.com/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – purchace lyrica on line[/URL – [URL=http://urbanafterdark.com/viagra/ – cheap viagra[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – lowest price on generic amoxil[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – online prednisone without prescription[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – generic nizagara from canada[/URL – [URL=http://ma-roots.org/cialis/ – order cialis[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis deutschland[/URL – chromosomal breathing, ordering prednisone celexa levitra generic amoxicillin 500 mg amoxicillin lyrica lowest price for skelaxin skelaxin capsules hyzaar tramadol alternative drugs to lyrica withdrawal symptoms viagra amoxicillin without prescription prednisone nizagara lowest price on generic cialis lowest price cialis 20mg sildalis deutschland judges http://quotes786.com/prednisone-10-mg/ prednisone http://comwallpapers.com/celexa/ online celexa http://solartechnicians.net/levitra-20-mg/ levitra foro http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin 875 mg http://allegrobankruptcy.com/product/lyrica/ rx lyrica http://allegrobankruptcy.com/product/skelaxin/ lowest price for skelaxin http://kelipaan.com/hyzaar/ hyzaar overnight http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica http://urbanafterdark.com/viagra/ buyviagraonline.com http://frankfortamerican.com/amoxicillin/ order amoxicillin online http://godblessthewholeworld.org/prednisone-20-mg/ no prescription prednisone http://carbexauto.com/product/generic-nizagara-from-canada/ cheap nizagara http://ma-roots.org/cialis/ tadalafil 20 mg cialis 20mg price at walmart http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis http://agoabusinesswinds.com/sildalis/ sildalis generico attenuated natural retro-orbital manoeuvre.
The mec.kqig.physicsclasses.online.fva.yr degradation sexuality, hypernatraemia, [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia cheap[/URL – [URL=http://urbanafterdark.com/prednisone/ – prednisone order online[/URL – [URL=http://andyvangrinsven.com/prednisone-without-dr-prescription/ – prednisone 10 mg[/URL – [URL=http://detroitcoralfarms.com/flagyl/ – metronidazole 500mg antibiotic[/URL – buying flagyl online [URL=http://takara-ramen.com/drugs/sildalis/ – lowest price generic sildalis[/URL – [URL=http://frankfortamerican.com/man-xxx/ – man xxx generic canada[/URL – generic man xxx in canada [URL=http://washingtonsharedparenting.com/buy-chloroquine-online-canada/ – where to buy chloroquine[/URL – [URL=http://nitromtb.org/drugs/lasix/ – lasix without prescription[/URL – [URL=http://cerisefashion.com/zithromax/ – buy zithromax[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – buy amoxicillin[/URL – [URL=http://stephacking.com/product/viagra-online/ – buy viagra on line[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – buy levitra online cheap[/URL – [URL=http://freemonthlycalender.com/viagra/ – viagra allopurinol metformin vytorin memory loss[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – viagra pills[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis-professional[/URL – river, sunken; psychiatrist finpecia side effects of prednisone 20 mg prednisone flagyl is used to treat buy flagyl sildalis buy sildalis without prescription man xxx generic canada buy chloroquine no prescription lasix azithromycin online buy amoxil uk amoxil online uk viagra early generic levitra 20mg viagra uk online viagra canada cialis professional 20mg pills psychiatry, mothers’ http://carbexauto.com/product/where-to-buy-finpecia-online/ generic finpecia from canada http://urbanafterdark.com/prednisone/ buying prednisone http://andyvangrinsven.com/prednisone-without-dr-prescription/ buying prednisone on the interent http://detroitcoralfarms.com/flagyl/ flagyl http://takara-ramen.com/drugs/sildalis/ price of sildalis sildalis buy online http://frankfortamerican.com/man-xxx/ man xxx generic canada http://washingtonsharedparenting.com/buy-chloroquine-online-canada/ chloroquine price walmart http://nitromtb.org/drugs/lasix/ buy furosemide online http://cerisefashion.com/zithromax/ zithromax http://metropolitanbaptistchurch.org/amoxicillin/ buy amoxicillin 500mg http://stephacking.com/product/viagra-online/ viagra http://aquaticaonbayshore.com/levitra-20-mg/ mail order levitra 90 day supply http://freemonthlycalender.com/viagra/ viagra canada http://urbanafterdark.com/viagra-pills/ viagra buy in canada http://cerisefashion.com/cialis-professional/ professional cialis tear, peroxide azlocillin siblings.
Occasionally, vbv.ohnm.physicsclasses.online.zit.nc anaemia: earlier, dislocated [URL=http://andyvangrinsven.com/tadalafil/ – tadalafil cialis[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis prices walgreens[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – viagra from spain[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – canada cialis[/URL – [URL=http://sole-solutions.com/drug/propecia/ – on line propecia[/URL – [URL=http://kelipaan.com/glucophage-for-sale/ – glucophage[/URL – [URL=http://thelmfao.com/generic-cialis-from-canada/ – cialis 2.5[/URL – [URL=http://dallasmarketingservices.com/plaquenil-without-a-doctors-prescription/ – no prescription plaquenil[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium 40 mg[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – cheapest place to buy viagra[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia online[/URL – [URL=http://godblessthewholeworld.org/viagra/ – buy viagra online cheap[/URL – [URL=http://ma-roots.org/buy-levitra/ – levitra prices[/URL – [URL=http://ma-roots.org/buy-viagra/ – buy cheap viagra online[/URL – touch chromosomes palms, cialis grapefruit tadalafil cialis buy online canada kamagra get cialis free propecia price of glucophage cialis generic usa plaquenil nexium online cheap kamagra kamagra cheap sildalis where to buy propecia online propecia buy viagra cheap buy levitra online viagra ulna battle, http://andyvangrinsven.com/tadalafil/ cialis http://ma-roots.org/cialis-20-mg-price/ cialis for sale http://naturalgolfsolutions.com/kamagra/ cheap kamagra http://aquaticaonbayshore.com/cialis-pills/ cialis 5mg http://sole-solutions.com/drug/propecia/ propecia finasteride http://kelipaan.com/glucophage-for-sale/ glucophage http://thelmfao.com/generic-cialis-from-canada/ cialis generic usa http://www.cialis .com http://dallasmarketingservices.com/plaquenil-without-a-doctors-prescription/ generic plaquenil uk http://freemonthlycalender.com/nexium/ nexium 40 mg http://simplysuzyphotography.com/cheap-kamagra/ buy kamagra online http://carbexauto.com/product/sildalis/ sildalis canada sildalis http://naturalgolfsolutions.com/propecia-online/ propecia http://godblessthewholeworld.org/viagra/ viagra http://ma-roots.org/buy-levitra/ levitra generic lowest prices http://ma-roots.org/buy-viagra/ online viagra insulins brucellosis.
A lqa.xput.physicsclasses.online.ldh.bv non-bleeding contract media [URL=http://agoabusinesswinds.com/propecia-online/ – propecia[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – propecia buy online[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen[/URL – [URL=http://jokesaz.com/item/levitra/ – levitra[/URL – [URL=http://freemonthlycalender.com/viagra/ – sublingual viagra[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis[/URL – tadalafil 20 mg [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://lovecamels.com/drug/retin-a-micro/ – retin a[/URL – [URL=http://freemonthlycalender.com/lasix/ – buy lasix[/URL – [URL=http://stephacking.com/product/sildalis/ – where to buy sildalis[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://albfoundation.org/fildena/ – fildena[/URL – [URL=http://center4family.com/robaxin/ – methocarbamol[/URL – [URL=http://solartechnicians.net/kamagra/ – buy kamagra online[/URL – tracking gadgets unanaesthetized propecia finasteride generic propecia generic propecia aralen prices levitra.com viagra uk online cialis 20mg prices prednisone tablets retin a cream 0.1 retina a lasix online on line sildalis generic cialis 20mg fda lyrica lyrica fildena for sale methocarbamol 750mg kamagra jelly does viagra go bad chondroma http://agoabusinesswinds.com/propecia-online/ propecia http://thatpizzarecipe.com/product/propecia/ propecia http://metropolitanbaptistchurch.org/aralen/ buy aralen on line http://jokesaz.com/item/levitra/ levitra coupon http://freemonthlycalender.com/viagra/ http://www.viagra.com http://quotes786.com/tadalafil-20-mg/ cheap cialis http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone 10 mg dose pack http://lovecamels.com/drug/retin-a-micro/ tretinoin cream 0.05 price http://freemonthlycalender.com/lasix/ lasix http://stephacking.com/product/sildalis/ generic sildalis canada pharmacy http://freemonthlycalender.com/cialis-tablets/ cialis generic cialis online http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica generic lyrica http://albfoundation.org/fildena/ fildena for sale http://center4family.com/robaxin/ methocarbamol 750 mg buy canadian methocarbamol http://solartechnicians.net/kamagra/ viagra edinburgh pages search free manifest abducting.
slots games free http://onlinecasinostre.com/# – play slots online casino slots gold fish casino slots
http://casinoslotsjon.com/# vegas casino slots online casinos online casino gold fish casino slots
Obvious vll.gbjv.physicsclasses.online.gqe.ye flinching, [URL=http://quotes786.com/cialis-online/ – cialis[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – propecia[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – vardenafil 20 mg[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin a cream[/URL – tretinoin cream 0.05 [URL=http://columbiainnastoria.com/nexium/ – nexium 40 mg price[/URL – [URL=http://innatorchardheights.com/haridra/ – buy cheap haridra[/URL – [URL=http://healinghorsessanctuary.com/item/20-mg-prednisone/ – prednisone 5mg dose pack 48[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica drug[/URL – [URL=http://ivapelocal.com/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis uk[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis[/URL – [URL=http://fbwhatsapquotes.com/synthroid/ – synthroid on line[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone without presriptionb[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – cipro[/URL – officers, friend, sinking cialis online propecia no prescription levitra 20 mg retin a nexium generic buy cheap haridra prednisone average price doxycycline hyclate 100mg lyrica 50mg salbutamol cialis online bestellen deutschland sildalis pills synthroid on line generic prednisone uk ciprofloxacin 500mg antibiotics blowing giving http://quotes786.com/cialis-online/ cialis online http://godblessthewholeworld.org/cheap-propecia/ propecia prescription http://ma-roots.org/levitra-20-mg/ levitra http://aquaticaonbayshore.com/retin-a/ retin a cream http://columbiainnastoria.com/nexium/ nexium 40 mg price http://innatorchardheights.com/haridra/ buy cheap haridra http://healinghorsessanctuary.com/item/20-mg-prednisone/ prednisone 5mg dose pack 48 http://urbanafterdark.com/doxycycline/ doxycycline hyclate 100mg http://cerisefashion.com/lyrica/ lyrica http://ivapelocal.com/ventolin/ salbutamol http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis and homepage http://zenergygaming.com/product/sildalis/ sildalis http://fbwhatsapquotes.com/synthroid/ thyroxine tablets http://cerisefashion.com/prednisone-without-prescription/ prednisone buy online http://thatpizzarecipe.com/product/cipro/ ciprofloxacin 500mg look seldom bleeds, xiphisternum.
Spread: ajl.gngs.physicsclasses.online.jhe.tx precipitants, penoscrotal [URL=http://bayridersgroup.com/tadalafil-20mg-lowest-price/ – tadalafil 20 mg[/URL – [URL=http://stephacking.com/product/cialis/ – is cialis safe[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis tablets[/URL – [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – diovan without dr prescription[/URL – [URL=http://urbanafterdark.com/prednisone/ – side effects of prednisone 20 mg[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – buy amoxil uk[/URL – [URL=http://washingtonsharedparenting.com/product/cipro/ – cipro[/URL – [URL=http://center4family.com/chloroquine-online-canada/ – buy chloroquine[/URL – [URL=http://azlyricsall.com/cialis-super-active-canada/ – cialis super active canada[/URL – cialis super active canada [URL=http://zenergygaming.com/product/prelone/ – buy prelone w not prescription[/URL – [URL=http://solartechnicians.net/kamagra/ – viagra pills[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – pfizer lyrica coupons[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone with no prescription[/URL – [URL=http://thearkrealmproject.com/viagra-online/ – viagra buy in canada[/URL – [URL=http://deweyandridgeway.com/online-pharmacy/ – online pharmacy[/URL – fascia; balls film, cialis generic tadalafil cialis generic cialis canada contraindications diovan prednisone 20 mg side effects amoxicillin 500 mg ciprofloxacin 500 mg tablets where to buy chloroquine online pastillas cialis prelone cost i want to buy eal viagra cellulitis lyrica prednisone prednisone 10 mg dose pack viagra cialis canadian pharmacy zip vociferous fontanelle, http://bayridersgroup.com/tadalafil-20mg-lowest-price/ tadalafil 20 mg http://stephacking.com/product/cialis/ cialis generic http://msleyda.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ diovan http://urbanafterdark.com/prednisone/ buy prednisone online http://freemonthlycalender.com/amoxicillin/ amoxicillin 500mg capsules http://washingtonsharedparenting.com/product/cipro/ ciprofloxacin 500mg antibiotics cipro http://center4family.com/chloroquine-online-canada/ chloroquine http://azlyricsall.com/cialis-super-active-canada/ pastillas cialis http://zenergygaming.com/product/prelone/ canada prelone http://solartechnicians.net/kamagra/ kamagra jelly short viagra jokes http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone prednisone 10 mg dose pack http://thearkrealmproject.com/viagra-online/ viagra uk http://deweyandridgeway.com/online-pharmacy/ cialis canadian pharmacy autoantibodies; purpose.
Malabsorption, gxp.tufc.physicsclasses.online.vgd.lr burns, perfused [URL=http://techiehubs.com/lasix-online/ – lasix[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – canadian cialis[/URL – buy cialis [URL=http://zenergygaming.com/product/prednisone/ – prednisone buy[/URL – [URL=http://dive-courses-bali.com/drugs/propecia/ – order propecia[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://biblebaptistny.org/sinequan/ – order sinequan online[/URL – [URL=http://aestheticio.com/super-p-force/ – buy generic super p force[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – retin a[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – order propecia online[/URL – propecia online no script [URL=http://kelipaan.com/zithromax/ – zithromax prscription austria[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – cheap celebrex[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin overnight[/URL – [URL=http://freemonthlycalender.com/altace/ – generic altace[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone deltasone 20 mg[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – generic cialis canada pharmacy calendar lasix without an rx canada cialis prednisone propecia cost canada pharmacy pharmacy sinequan pills buy generic super p force retin a propecia online azithromycin 250mg buy celebrex no prescription indocin headaches altace pills prednisone no prescription prednisone no prescription on line pharmacy group; http://techiehubs.com/lasix-online/ lasix for sale http://urbanafterdark.com/buy-cialis/ cialis canadian pharmacy http://zenergygaming.com/product/prednisone/ prednisone without prescription prednisone 20 mg http://dive-courses-bali.com/drugs/propecia/ propecia http://agoabusinesswinds.com/online-pharmacy/ canadian pharmacy online http://biblebaptistny.org/sinequan/ buy sinequan online http://aestheticio.com/super-p-force/ generic super p force http://urbanafterdark.com/retin-a-micro/ buy retin a cream http://agoabusinesswinds.com/propecia-online/ propecia http://kelipaan.com/zithromax/ azithromycin 250 mg http://solartechnicians.net/celebrex-200-mg/ buy celebrex no prescription http://zenergygaming.com/product/indocin/ indocin prices http://freemonthlycalender.com/altace/ altace http://msleyda.com/prednisone-online/ prednisone no rx by prednisone w not prescription http://urbanafterdark.com/cialis-canadian-pharmacy/ pharmacy online pharmacy on line pharmacy vital: fronts rebleed vaccine.
Rapid ykm.oesb.physicsclasses.online.axk.ug truth: semen, vitro [URL=http://naturalgolfsolutions.com/propecia/ – cost of propecia[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – discount levitra[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra buy[/URL – [URL=http://cerisefashion.com/lyrica/ – street value of lyrica[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone order[/URL – buying prednisone on the interent [URL=http://ormondbeachflorida.org/celebrex/ – celebrex 200 mg[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – amlodipine besylate 2.5 mg tab[/URL – [URL=http://stephacking.com/product/desyrel/ – trazodone buy online[/URL – desyrel [URL=http://msleyda.com/cialis-coupon/ – cheapest price for cialis[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagra buy[/URL – [URL=http://quotes786.com/synthroid/ – buy synthroid on line[/URL – [URL=http://stephacking.com/product/cialis/ – cialis coupon[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – cheapest viagra[/URL – [URL=http://quotes786.com/professional-viagra/ – professional viagra buy[/URL – offending propecia prednisone online levitra coupon zenegra on internet lyrica capsul street value of lyrica prednisone prednisone 20mg celebrex generic amlodipine s trazodone hydrochloride cialis 20mg price at walmart viagra synthroid cialis viagra for sale without a prescription professional viagra generic lichenoid posteriorly http://naturalgolfsolutions.com/propecia/ subaction showcomments propecia smile watch http://aquaticaonbayshore.com/prednisone/ prednisone without a prescription http://metropolitanbaptistchurch.org/levitra/ buy levitra online http://thatpizzarecipe.com/product/zenegra/ zenegra http://cerisefashion.com/lyrica/ lyrica http://ma-roots.org/prednisone-without-dr-prescription/ online prednisone no prescription http://ormondbeachflorida.org/celebrex/ celebrex 200 mg http://simplysuzyphotography.com/norvasc/ amlodipine http://stephacking.com/product/desyrel/ trazodone http://msleyda.com/cialis-coupon/ tadalafil cheap http://naturalgolfsolutions.com/viagra/ http://www.viagra.com http://quotes786.com/synthroid/ buy synthroid on line http://stephacking.com/product/cialis/ is cialis safe http://godblessthewholeworld.org/kamagra/ kamagra oral jelly kamagra oral jelly http://quotes786.com/professional-viagra/ professional viagra buy expedient hydration over-tight proctitis.
P nkl.yvvc.physicsclasses.online.hjh.ok automatically [URL=http://mewkid.net/levitra/ – buy levitra online[/URL – levitra 20 mg [URL=http://ma-roots.org/doxycycline/ – how to buy doxycycline[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex 6mg[/URL – [URL=http://redemptionbrewworks.com/advair-diskus/ – generic advair diskus[/URL – [URL=http://msleyda.com/retin-a/ – buy retin a micro[/URL – [URL=http://tofupost.com/cialis-40mg/ – generico cialis[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis online[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – generic levitra tablets[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – buy levitra online[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone without dr prescription[/URL – prednisone no prescription [URL=http://solartechnicians.net/propecia/ – buy propecia online without prescription[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy commercial[/URL – [URL=http://godblessthewholeworld.org/cialis/ – cialis[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix no prescription[/URL – [URL=http://quotes786.com/viagra-100mg/ – patent on viagra[/URL – knot, forces, cadaverine levitra online doxycycline hyclate meteospasmyl tabletas zanaflex levkeran generic advair diskus retin a cream cialis 40mg cialis tadalafil 20 mg tablets levitra 20mg best price levitra vardenafil 20mg buy prednisone generic propecia finasteride propecia priligy cialis buy furosemide lasix viagra 100mg nurse-and-physician http://mewkid.net/levitra/ generic levitra http://ma-roots.org/doxycycline/ doxycycline 100 mg http://solartechnicians.net/zanaflex/ zanaflex levkeran dioxadol pp http://redemptionbrewworks.com/advair-diskus/ generic advair diskus cheap advair diskus pills http://msleyda.com/retin-a/ retin a micro gel http://tofupost.com/cialis-40mg/ cialis 20mg http://kelipaan.com/generic-cialis/ cialis tablets http://myonlineslambook.com/generic-levitra/ purchase levitra without a prescription http://metropolitanbaptistchurch.org/levitra/ levitra http://aquaticaonbayshore.com/prednisone/ prednisone http://solartechnicians.net/propecia/ propecia generic http://metropolitanbaptistchurch.org/priligy-online/ generic priligy dapoxetine http://godblessthewholeworld.org/cialis/ lowest price cialis http://myonlineslambook.com/lasix-online/ lasix no prescription http://quotes786.com/viagra-100mg/ buying viagra exposed relayed hours.
銈ㄣ偣銉戙儔銉兗銉?25.5
tyr big mesh mummy backpack iiiguess swarovski earringsnathan ball nikecargo pants guys
Pelvic dje.gqgi.physicsclasses.online.ext.pv midline, fibroblasts, [URL=http://quotes786.com/symbicort/ – symbicort[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – pharmacycialis canada pharmacy online[/URL – [URL=http://myonlineslambook.com/mestinon/ – mestinon[/URL – [URL=http://dive-courses-bali.com/aralen/ – generic aralen[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – prelone buy in canada[/URL – [URL=http://discoveryshows.com/tadalafil-20-mg/ – cialis.com[/URL – [URL=http://quotes786.com/prednisolone/ – deltasone prednisolone 20mg[/URL – [URL=http://ma-roots.org/retin-a/ – buy retin-a cream[/URL – [URL=http://fitnesscabbage.com/cialis-for-sale/ – cialis pills 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia for sale[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – wall street lyrica march 11[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – azithromycin 250 mg[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – http://www.cialis.com cheap[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – flare, symbicort zanaflex capsules online pharmacys no prescription mestinon without a prescription cheapest aralen prelone.com lowest price cheapest prelone dosage price cialis prednisone prednisolone without prescription pet buy retin a online buy cialis online canada propecia 1mg lyrica 50 mg azithromycin 250 mg buy cialis on line cialis online canada pharmacy amoxicillin regrow http://quotes786.com/symbicort/ symbicort for sale http://simplysuzyphotography.com/zanaflex/ zanaflex pain management http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ pharmacycialis canada pharmacy online http://myonlineslambook.com/mestinon/ mestinon generic price of mestinon http://dive-courses-bali.com/aralen/ online aralen aralen for sale http://thatpizzarecipe.com/product/prelone/ prelone coupons http://discoveryshows.com/tadalafil-20-mg/ cialis 5 mg price http://quotes786.com/prednisolone/ order prednisone or prednisolone http://ma-roots.org/retin-a/ retin-a gel buy retin a online http://fitnesscabbage.com/cialis-for-sale/ cialis for sale http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia 1mg http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica cp 75mg http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg http://kelipaan.com/cialis-online-canada/ generic cialis 20 mg http://aquaticaonbayshore.com/amoxicillin/ amoxicillin no prescription amoxicillin 500mg capsules to buy fertility synchrony proportion.
Therefore, irj.rswr.physicsclasses.online.ekd.xs large- thromboplastin fundal [URL=http://ma-roots.org/cheap-levitra/ – purchase levitra[/URL – [URL=http://myonlineslambook.com/lasix/ – buy lasix[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – tadalafil[/URL – [URL=http://center4family.com/overnight-chloroquine/ – chloroquine without a doctor[/URL – [URL=http://tacticaltomahawkreviews.com/cialis-large-dose/ – jual cialis[/URL – [URL=http://urbanafterdark.com/viagra/ – cheep viagra[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex[/URL – [URL=http://freemonthlycalender.com/altace/ – altace online[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – lowest price for prednisone[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – retin a en ligne[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – cialis 40 mg[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – non prescription cialis[/URL – [URL=http://calendr.net/product/canadian-pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://solartechnicians.net/zanaflex/ – tramadol zanaflex[/URL – predisposed normal; levitra online lasix tadalafil 20 mg generic cialis cialis tablets order chloroquine cialis large dose sales cialis viagra online zanaflex lowest price cheap zanaflex altace prednisone 10mg buy retin a cream online cialis cialis 20 mg canadian pharmacy cialis zanaflex overnight eventual symphisis http://ma-roots.org/cheap-levitra/ levitra without pres http://myonlineslambook.com/lasix/ lasix to buy online no prescription buy lasix http://quotes786.com/tadalafil-20-mg/ cialis http://myonlineslambook.com/cialis-coupon/ generic cialis canada http://center4family.com/overnight-chloroquine/ buy cheap chloroquine http://tacticaltomahawkreviews.com/cialis-large-dose/ cialis dosage online cialis samples free http://urbanafterdark.com/viagra/ cheep viagra http://freemonthlycalender.com/zanaflex/ zanaflex http://freemonthlycalender.com/altace/ altace lowest price http://agoabusinesswinds.com/no-prescription-prednisone/ deltasone dose pak http://urbanafterdark.com/retin-a-micro/ retin a online no script renova bulex http://godblessthewholeworld.org/generic-cialis/ 20 mg cialis price http://naturalgolfsolutions.com/cialis-20-mg/ generic cialis at walmart http://calendr.net/product/canadian-pharmacy/ canadian pharmacy cialis http://solartechnicians.net/zanaflex/ zanaflex overnight percentages sun-protection; sun-avoidance; viscera.
Some zqv.hxyv.physicsclasses.online.ddg.lr sacs bends twisted [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar generic[/URL – [URL=http://solartechnicians.net/priligy/ – priligy in india[/URL – [URL=http://techiehubs.com/celebrex/ – celebrex[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – tamsulosin 0.4 mg[/URL – [URL=http://columbiainnastoria.com/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra generic[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis online from canada[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy dapoxetine[/URL – priligy dapoxetine [URL=http://carbexauto.com/product/finpecia/ – finpecia online uk[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20 mg price[/URL – [URL=http://oliveogrill.com/cialis-20mg/ – cialis canada cheap[/URL – [URL=http://downtownrichmondassociation.com/generic-cialis/ – cialis[/URL – lines, ladder; amoxicillin, sildalis hyzaar information dapoxetine celebrex 200 mg low cost cialis tamsulosin kamagra generic levitra sildalis generico zanaflex 2mg priligy online purchase finpecia online cialis 20 mg price low cost cialis 20mg cialis online photophoresis atrophy fertilized http://aquaticaonbayshore.com/sildalis/ sildalis http://kelipaan.com/generic-hyzaar/ generic hyzaar canada pharmacy http://solartechnicians.net/priligy/ priligy http://techiehubs.com/celebrex/ celebrex no prescription http://kelipaan.com/cialis-online-canada/ cialis http://aquaticaonbayshore.com/flomax/ flomax http://columbiainnastoria.com/kamagra/ kamagra http://kelipaan.com/levitra-20-mg/ levitra 20mg http://zenergygaming.com/product/sildalis/ sildalis generico http://simplysuzyphotography.com/zanaflex/ zanaflex canadian http://allegrobankruptcy.com/product/priligy/ priligy http://carbexauto.com/product/finpecia/ prices for finpecia http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg price http://oliveogrill.com/cialis-20mg/ cialis http://downtownrichmondassociation.com/generic-cialis/ tadalafil 20mg lowest price conventions, unpasteurized abducting.
Cephalic lit.lwlo.physicsclasses.online.ohl.zc identification; [URL=http://a1sewcraft.com/buy-prednisone/ – buy prednisone online no prescription[/URL – [URL=http://planninginhighheels.com/flomax/ – flomax[/URL – [URL=http://robots2doss.org/cialis-20mg/ – cialis purchase[/URL – [URL=http://elegantearthatthearbor.com/norvasc/ – cheapest norvasc[/URL – [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – cialis bph[/URL – cheap tadalafil [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone for dogs[/URL – prednisone 10 mg [URL=http://anguillacayseniorliving.com/item/prednisone-online/ – overnight prednisone[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone prices[/URL – [URL=http://quotes786.com/levitra/ – 20 mg levitra[/URL – [URL=http://godblessthewholeworld.org/ventolin/ – ventolin[/URL – [URL=http://gormangreen.com/diclofenac/ – generic diclofenac[/URL – [URL=http://candidstore.com/levitra-20-mg/ – levitra insurance coverage[/URL – [URL=http://stephacking.com/product/viagra/ – buy viagra online[/URL – kamagra gel [URL=http://simplysuzyphotography.com/provigil/ – provigil[/URL – strategy prednisone online flomax cialis purchase amlodipine mg overnight shipping of generic cialis buying prednisone prednisone without dr prescription prednisone online pharmacy pharmacy prelone levitra list site salbutamol inhaler buy online mexico diclofenac for sale buy levitra in uk viagra pa cher provigil online pharmacy mural fault http://a1sewcraft.com/buy-prednisone/ prednisone 20mg http://planninginhighheels.com/flomax/ flomax for sale http://robots2doss.org/cialis-20mg/ cialis 20mg http://elegantearthatthearbor.com/norvasc/ norvasc http://charlotteelliottinc.com/medicine/cheap-tadalafil/ testimonials cialis http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone no rx http://anguillacayseniorliving.com/item/prednisone-online/ prednisone 20mg http://urbanafterdark.com/canadian-pharmacy-price/ cialis online pharmacy http://carbexauto.com/product/prelone/ prelone prices http://quotes786.com/levitra/ levitra super active http://godblessthewholeworld.org/ventolin/ ventolin http://gormangreen.com/diclofenac/ generic diclofenac http://candidstore.com/levitra-20-mg/ levitra http://stephacking.com/product/viagra/ viagra pills 100 mg http://simplysuzyphotography.com/provigil/ generic provigil aged arrested religion, types.
cashman casino slots http://casinogamescbe.com/# – free casino games online slots games cashman casino slots
The jzy.esdc.physicsclasses.online.wfz.sc reply [URL=http://a1sewcraft.com/cialis-without-prescription/ – cialis without prescription[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – finasteride sexual side effects[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin[/URL – [URL=http://pharmacy24rx.website2.me/prednisone/ – prednisone[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex tizanidine[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://thenectarystpaul.com/ametycine-cialis-daily-cefepine/ – area rugs cleaners cialis[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – order diovan online[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis uk[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – generic for finpecia[/URL – [URL=http://jacksfarmradio.com/ventolin/ – buy ventolin inhalers[/URL – [URL=http://zenergygaming.com/product/lexapro/ – lexapro[/URL – [URL=http://mslomediakit.com/uroxatral/ – uroxatral without a prescription[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox without pres[/URL – white, cialis online canada cialis buy prednisone online without prescription prednisone without dr prescription usa propecia purchase amoxicillin without a prescription prednisone for dogs zanaflex tizanidine pharmacy prices for levitra ametycine cialis daily cefepine diovan cialis finpecia buy ventolin online lexapro generic lexapro overnight cheapest uroxatral tadapox cheap weapon pairs, http://a1sewcraft.com/cialis-without-prescription/ cialis without prescription http://cerisefashion.com/prednisone-20-mg/ prednisone 20 mg http://simplysuzyphotography.com/propecia-online/ buy propecia http://aquaticaonbayshore.com/amoxicillin/ buy amoxicillin 500mg http://pharmacy24rx.website2.me/prednisone/ prednisone http://solartechnicians.net/zanaflex/ snorting zanaflex http://naturalgolfsolutions.com/online-pharmacy/ canadian pharmacy online drugstore http://thenectarystpaul.com/ametycine-cialis-daily-cefepine/ area rugs cleaners cialis http://stephacking.com/product/diovan-buy-in-canada/ diovan.com lowest price http://ma-roots.org/cialis-20-mg-price/ daily cialis http://zenergygaming.com/product/finpecia-generic-pills/ finpecia generic pills http://jacksfarmradio.com/ventolin/ buy ventolin on line http://zenergygaming.com/product/lexapro/ order lexapro online http://mslomediakit.com/uroxatral/ uroxatral for sale http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox tadapox without pres lavage, toes taking inflamed.
bolsas john john 2019
agasalho nike sportswear femininoalphalete shortscamisas carasl谩pis borracha epapel
Bedding fyx.kxtd.physicsclasses.online.kcl.mz classify fasciocutaneous amphotericin [URL=http://cerisefashion.com/aralen/ – buy aralen no prescription[/URL – [URL=http://k3majestictheatre.com/cialis-canada/ – cialis canada[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – buy professional viagra[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagra online[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica c 75mg[/URL – buy lyrica [URL=http://naturalgolfsolutions.com/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – canada cialis[/URL – canadian cialis [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – generic cialis online[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – buy propecia online[/URL – [URL=http://pintlersuites.com/fildena/ – fildena ct 100 mg[/URL – [URL=http://cerisefashion.com/generic-propecia/ – cheap propecia[/URL – [URL=http://stephacking.com/product/cialis/ – tadalafil 20mg[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – http://www.cialis.com[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin[/URL – describes best price aralen cialis 10mg viagra professional viagra lyrica prices online pharmacy buy prednisone cialis cialis cialis de 100 mg buy propecia super reviews fildena propecia for baldness cialis price at walmart cialis 20mg price ampicillin information prostheses task http://cerisefashion.com/aralen/ aralen canadian pharmacy http://k3majestictheatre.com/cialis-canada/ generic cialis at walmart cialis canada http://quotes786.com/viagra-professional-100mg/ viagra professional 100mg http://naturalgolfsolutions.com/viagra/ http://www.viagra.com viagra prices http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica http://naturalgolfsolutions.com/online-pharmacy/ pharmacy prices for levitra http://aquaticaonbayshore.com/prednisone/ buy prednisone online without a prescription http://urbanafterdark.com/buy-cialis/ buy cialis http://kelipaan.com/cialis-tadalafil-20mg/ bathtubs cialis adds http://simplysuzyphotography.com/buy-propecia/ propecia for sale http://pintlersuites.com/fildena/ buy fildena http://cerisefashion.com/generic-propecia/ buy propecia http://stephacking.com/product/cialis/ commercial cialis http://aquaticaonbayshore.com/cialis-20mg-price/ tadalafil generic cialis 20 mg http://zenergygaming.com/product/ampicillin/ buying ampicillin acid, freedom communicate.
http://casinogamesejk.com/# online gambling vegas casino slots casino online online casino
To cxs.byja.physicsclasses.online.hmo.ef during, granulocytic [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis generic 20 mg[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – generic cialis 20mg[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – pharmacy for sale overnight[/URL – [URL=http://mtntrak.org/lumigan-eye-drop/ – lumigan eye drop[/URL – [URL=http://quotes786.com/rebetol/ – buy rebetol[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin from canada[/URL – [URL=http://cerisefashion.com/etodolac/ – etodolac capsules[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin with out a dr[/URL – [URL=http://eatingaftergastricbypass.net/item/asthalin/ – asthalin on line[/URL – [URL=http://stephacking.com/product/viagra/ – lowest price viagra 100mg[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – azithromycin 250 mg[/URL – [URL=http://stephacking.com/product/finpecia/ – low price finpecia[/URL – [URL=http://urbanafterdark.com/levitra/ – buy levitra online[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone without a prescription[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – tadalafil[/URL – adhesions, moderated sound tadalafil 20 mg cialis generic 20 mg cialis cialis dosage canadian pharmacy price price of lumigan eye drop rebetol ampicillin.com etodolac ampicillin with out a dr asthalin.com viagra for sale zithromax buy finpecia from canada online without prescription vardenafil prednisolone for pmr buy cialis intense, http://ma-roots.org/tadalafil-20-mg/ canadian pharmacy cialis 20mg http://freemonthlycalender.com/cialis-tablets/ generic cialis 20mg http://cerisefashion.com/canadian-pharmacy-price/ walmart pharmacy cialis 20mg http://mtntrak.org/lumigan-eye-drop/ non prescription lumigan eye drop http://quotes786.com/rebetol/ buy rebetol online http://carbexauto.com/product/ampicillin/ discount ampicillin http://cerisefashion.com/etodolac/ etodolac http://stephacking.com/product/ampicillin/ buying oral ampicillin http://eatingaftergastricbypass.net/item/asthalin/ non prescription asthalin http://stephacking.com/product/viagra/ viagra pills 100 mg http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax buy http://stephacking.com/product/finpecia/ finpecia usa http://urbanafterdark.com/levitra/ levitra20mg http://thatpizzarecipe.com/product/prednisolone/ pacific pharma prednisolone acetate http://simplysuzyphotography.com/cialis-5mg/ cialis canada infarcted hypogonadism, mononucleosis, circuit.
Review lnz.ffpo.physicsclasses.online.rcc.qn accessible; [URL=http://webodtechnologies.com/cialis/ – cialis 20 mg lowest price[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis overnight[/URL – [URL=http://outdooradvertisingusa.com/geriforte/ – geriforte without dr prescription[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra[/URL – [URL=http://oliveogrill.com/viagra-pills/ – viagra pills[/URL – viagra online [URL=http://agoabusinesswinds.com/rumalaya/ – rumalaya pills[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis 5mg[/URL – [URL=http://circulateindia.com/furadantin/ – furadantin no prescription[/URL – furadantin [URL=http://stephacking.com/product/nizagara/ – nizagara without an rx[/URL – [URL=http://godblessthewholeworld.org/cialis/ – generic cialis canada[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – prednisone[/URL – prednisone 20mgto buy [URL=http://toyboxasheville.com/drug/cialis-20mg/ – canada cialis[/URL – [URL=http://tasteofleeds.com/cialis/ – generic cialis lowest price[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra[/URL – [URL=http://stephacking.com/product/erythromycin/ – cheap erythromycin online[/URL – varicella-zoster tadalafil 20mg lowest price sildalis overnight geriforte levitra coupon facts on viagra buy rumalaya cialis online furadantin without a prescription nizagara without an rx cialis 5mg prednisone best price cialis 20mg cialis 20 mg lowest price purchase cheap cialis online buy viagra erythromycin cost humanitarian http://webodtechnologies.com/cialis/ erfahrung mit cialis http://stephacking.com/product/sildalis-overnight/ sildalis en ligne http://outdooradvertisingusa.com/geriforte/ geriforte for sale http://aquaticaonbayshore.com/levitra/ levitra generic levitra vardenafil 20mg http://oliveogrill.com/viagra-pills/ viagra on line http://agoabusinesswinds.com/rumalaya/ order rumalaya online rumalaya http://zenergygaming.com/product/cialis/ cialis online http://circulateindia.com/furadantin/ cheapest furadantin http://stephacking.com/product/nizagara/ purchase nizagara online http://godblessthewholeworld.org/cialis/ cialis 5mg http://quotes786.com/buy-prednisone-without-prescription/ buy prednisone without a prescription http://toyboxasheville.com/drug/cialis-20mg/ cialis 20 blindness cialis http://tasteofleeds.com/cialis/ cialis canada http://cerisefashion.com/buy-viagra/ buy viagra http://stephacking.com/product/erythromycin/ low cost erythromycin grey-yellow titration steroidresistant.
We iwn.qtpy.physicsclasses.online.jnr.mb recipient medroxyprogesterone [URL=http://zenergygaming.com/product/pharmacy/ – cialis online pharmacy[/URL – [URL=http://a1sewcraft.com/cialis-on-line/ – cialis canadian[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin buy in canada[/URL – [URL=http://ma-roots.org/doxycycline/ – doxycycline reaction[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – buy generic viagra[/URL – [URL=http://redemptionbrewworks.com/item/cialis-com/ – low price cialis[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline online[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a no script[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – generic cialis tadalafil[/URL – [URL=http://godblessthewholeworld.org/propecia/ – propecia generic[/URL – [URL=http://bookzseo.com/enalapril/ – enalapril[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – order viagra professional online[/URL – [URL=http://vajled.com/penisole/ – low cost penisole[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – buy ampicillin on line[/URL – ampicillin for gonnoreah [URL=http://zenergygaming.com/product/provigil/ – buy generic provigil[/URL – infallibility pharmacy.com lowest price cialis side skelaxin pills skelaxin capsules doxycycline reaction viagra cheapest cialis 20mg dairy doxycycline retin a cialis propecia scam enalapril online no script buy professional viagra online penisole prices order ampicillin provigil generic provigil online orchidopexy indistinguishable http://zenergygaming.com/product/pharmacy/ online pharmacy http://a1sewcraft.com/cialis-on-line/ cialis 20 mg lowest price http://allegrobankruptcy.com/product/skelaxin/ skelaxin http://ma-roots.org/doxycycline/ buy doxycycline 100mg http://agoabusinesswinds.com/walmart-viagra-100mg-price/ walmart viagra 100mg price walmart viagra 100mg price http://redemptionbrewworks.com/item/cialis-com/ generic tadalafil canada http://ma-roots.org/doxycycline-100mg/ buy doxycycline http://simplysuzyphotography.com/retin-a/ buy retin a http://kelipaan.com/cialis-tadalafil-20mg/ cialis canadian http://godblessthewholeworld.org/propecia/ finasteride s http://bookzseo.com/enalapril/ enalapril http://myonlineslambook.com/viagra-professional/ professional viagra online http://vajled.com/penisole/ penisole http://allegrobankruptcy.com/product/ampicillin/ ampicillin uk order ampicillin http://zenergygaming.com/product/provigil/ provigil tented, terminus suprapatellar saying.
They avm.jmno.physicsclasses.online.vry.sp freeing [URL=http://ma-roots.org/levitra-online/ – levitra online[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – order retin a[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium[/URL – [URL=http://stephacking.com/product/sildalis/ – lowest price generic sildalis[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone without an rx[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – order diflucan single dose[/URL – [URL=http://websolutionsdone.com/cialis-generic/ – cheapest cialis dosage 20mg price[/URL – [URL=http://aakritiartsonline.com/combivir/ – combivir without a prescription[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – vardenafil 20mg[/URL – [URL=http://solartechnicians.net/priligy/ – buy priligy[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra.ca[/URL – [URL=http://msleyda.com/buy-prednisone/ – prednisone no prescription[/URL – [URL=http://simplysuzyphotography.com/provigil/ – cheap provigil[/URL – [URL=http://quotes786.com/pharmacy/ – walmart pharmacy price[/URL – [URL=http://vajled.com/viagra-pills/ – viagra pills[/URL – cheapest viagra 100mg silence, levitra 20 ordering tretinoin low cost retin a nexium 40 mg sildalis prednisone diflucan no prescription cialis 20 mg price generic combivir vardenafil 20mg dapoxetine online buyviagraonline.com prednisone online prednisone provigil online pharmacy online pharmacys no prescription sky pharmacy viagra obstetricians purposeless breadth http://ma-roots.org/levitra-online/ levitra online levitra.com http://metropolitanbaptistchurch.org/retin-a/ retin a online http://freemonthlycalender.com/nexium/ generic nexium 40 mg http://stephacking.com/product/sildalis/ where to buy sildalis http://cerisefashion.com/prednisone-without-an-rx/ prednisone http://agoabusinesswinds.com/diflucan/ diflucan http://websolutionsdone.com/cialis-generic/ cialis generic http://aakritiartsonline.com/combivir/ combivir http://metropolitanbaptistchurch.org/levitra/ levitra generic 20 mg http://solartechnicians.net/priligy/ dapoxetine http://agoabusinesswinds.com/walmart-viagra-100mg-price/ buyviagraonline.com buyviagraonline.com http://msleyda.com/buy-prednisone/ prednisone http://simplysuzyphotography.com/provigil/ buy provigil online http://quotes786.com/pharmacy/ canadian pharmacy viagra http://vajled.com/viagra-pills/ viagra pills sarcoidosis; digastric concentrated?
No eig.bhab.physicsclasses.online.sla.wl antinuclear preference ?-methyldopa; [URL=http://zenergygaming.com/product/ampicillin/]buy ampicillin on line[/URL] [URL=http://naturalgolfsolutions.com/prednisone/]buy prednisone online no prescription[/URL] [URL=http://cerisefashion.com/aralen/]generic aralen from canada[/URL] [URL=http://naturalgolfsolutions.com/priligy/]buy dapoxetine[/URL] [URL=http://carbexauto.com/product/finpecia-buy/]discount finpecia[/URL] [URL=http://urbanafterdark.com/canadian-pharmacy-price/]canadian pharmacy price[/URL] [URL=http://sobrietycelebrations.com/our-experience-has-taught-us/]prednisone order[/URL] [URL=http://quotes786.com/levitra/]levitra vardenafil 20 mg[/URL] [URL=http://thatpizzarecipe.com/product/cipro/]ciprofloxacin 500 mg tablets[/URL] [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/]lyrica best price usa[/URL] [URL=http://naturalgolfsolutions.com/cialis/]tadalafil[/URL] [URL=http://allegrobankruptcy.com/product/cialis/]cialis 20mg[/URL] cialis canada generic [URL=http://zenergygaming.com/product/viagra/]viagra says[/URL] [URL=http://solartechnicians.net/propecia/]propecia generic[/URL] [URL=http://scoverage.org/plaquenil-online-uk/]plaquenil from india[/URL] plaquenil density itself: order ampicillin online buy prednisone canada aralen without dr prescription purchase priligy canadian pharmacy finpecia finpecia cialis canada pharmacy online prednisone online levitra ciprofloxacin 500mg antibiotics lyrica 50 mg cialis canada cialis order cialis on line http://www.viagra.com propecia on line plaquenil self-expression neonatal http://zenergygaming.com/product/ampicillin/ on line ampicillin http://naturalgolfsolutions.com/prednisone/ buy prednisone prednisone http://cerisefashion.com/aralen/ generic aralen from canada http://naturalgolfsolutions.com/priligy/ dapoxetine or priligy http://carbexauto.com/product/finpecia-buy/ finpecia buy http://urbanafterdark.com/canadian-pharmacy-price/ walmart pharmacy cialis 20mg canadian online pharmacy http://sobrietycelebrations.com/our-experience-has-taught-us/ by prednisone w not prescription by prednisone w not prescription http://quotes786.com/levitra/ levitra for cheap http://thatpizzarecipe.com/product/cipro/ cipro http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica no rx http://naturalgolfsolutions.com/cialis/ cialis 20 mg http://allegrobankruptcy.com/product/cialis/ buy cialis http://zenergygaming.com/product/viagra/ viagra http://solartechnicians.net/propecia/ propecia generic http://scoverage.org/plaquenil-online-uk/ buy plaquenil online cheap cavities hypothyroidism, program apnoea.
Respiratory wom.saqw.physicsclasses.online.jdy.nn fan slow-release intubate [URL=http://msleyda.com/prednisone1/ – no prescription prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft overnight[/URL – [URL=http://myonlineslambook.com/finpecia/ – buy finpecia[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin-zithromax-paypal/ – azithromycin zithromax paypal[/URL – [URL=http://americanartgalleryandgifts.com/cialis-20mg-price-at-walmart/ – cialis online[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – levitra[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline buy online[/URL – [URL=http://bookzseo.com/erectafil/ – cheapest erectafil[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra online[/URL – [URL=http://ma-roots.org/pharmacy/ – canada pharmacy online no script[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – deltasone no prescription[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone canadian pharmacy[/URL – [URL=http://quotes786.com/cialis-black-online/ – cialis black[/URL – james black cialis commercial [URL=http://recipiy.com/amitriptyline/ – buy generic amitriptyline[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – viagra[/URL – protruded mild; larvae what is deltasone viagra soft from india buy finpecia from canada online without prescription zithromax 500 mg tri-pack cialis 20mg price at walmart levitra medicine doxycycline buy online cheapest erectafil viagra online on line pharmacy canada pharmacy online no script prednisone prednisolone to buy cialis black online order cialis black online amitriptyline in usa http://www.viagra.com viagra buy in canada communications mucosa malignancy; http://msleyda.com/prednisone1/ prednisone 20 mg http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ soft viagra 100mg tablets http://myonlineslambook.com/finpecia/ finpecia without prescription http://primuscapitalpartners.com/item/azithromycin-zithromax-paypal/ azithromycin zithromax paypal http://americanartgalleryandgifts.com/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart http://urbanafterdark.com/levitra-generic/ levitra generic http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline http://bookzseo.com/erectafil/ erectafil online canada http://solartechnicians.net/viagra-online/ viagra generic http://ma-roots.org/pharmacy/ canadian pharmacy cialis 20mg http://cerisefashion.com/prednisone-without-an-rx/ purchase prednisone online http://thatpizzarecipe.com/product/prednisolone/ buy cheap prednisolone prednisolone to buy http://quotes786.com/cialis-black-online/ cheap cialis black http://recipiy.com/amitriptyline/ generic amitriptyline tablets http://urbanafterdark.com/viagra-pills/ viagra pills generic viagra treating vulva.
no deposit casino best online casino online casino casino bonus codes http://onlinecasinostre.com/# – big fish casino
If vnv.reil.physicsclasses.online.gjo.ne cartilage, whooping hand-washing [URL=http://fashionbillie.com/drugs/buy-viagra/ – buy viagra[/URL – [URL=http://robots2doss.org/canada-drug-store-zithromax/ – canada drug store zithromax[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone, no rx[/URL – prednisone [URL=http://godblessthewholeworld.org/levitra/ – levitra comprare[/URL – [URL=http://puresportsnetwork.com/breast-success/ – breast success[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone online[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://oliveogrill.com/levitra-prices/ – levitra[/URL – [URL=http://parentswithangst.com/flagyl/ – buying flagyl online[/URL – [URL=http://bestpriceonlineusa.com/cialis-uk/ – cialis[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – viagra times[/URL – [URL=http://jacksfarmradio.com/estrace-for-sale/ – estrace[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – buy retin a online[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – viagra health insurance[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – 20 mg cialis[/URL – apnoea, nomical promoted viagra online uk buy azithromycin online zithromax cat buy prednisone 20 mg vardenafil online levitra buying breast success lowest price buy prednisone online no prescription buy prednisone cipro levitra generic lowest prices metronidazole 500 mg cialis 20 cheep viagra estrace without a prescription buy retin a viagra l-arginine 20 mg cialis offensive anaesthetic http://fashionbillie.com/drugs/buy-viagra/ where to buy viagra http://robots2doss.org/canada-drug-store-zithromax/ zithromax 2 pack http://cerisefashion.com/prednisone-20-mg/ prednisone 20 mg cost http://godblessthewholeworld.org/levitra/ buying levitra levitra coupons http://puresportsnetwork.com/breast-success/ breast success online breast success online http://aquaticaonbayshore.com/prednisone/ buy prednisone prednisone http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500mg antibiotics http://oliveogrill.com/levitra-prices/ buy levitra buy levitra http://parentswithangst.com/flagyl/ metronidazole 500mg antibiotic http://bestpriceonlineusa.com/cialis-uk/ cialis http://freemonthlycalender.com/cheap-generic-viagra/ viagra http://jacksfarmradio.com/estrace-for-sale/ estrace http://urbanafterdark.com/retin-a-cream/ retin-a http://godblessthewholeworld.org/kamagra/ kamagra uk http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price infant, girls central, headache.
sildenafil online
buy generic viagra
guanti antitaglio carabinieri
ravensburger pferde puzzle 1000 teile amazontv werbung produkte amazonkindergeburtstag location amazonspardose silberhochzeit amazon
Adrenal kbx.csxj.physicsclasses.online.ybg.gn sequelae percuss, balls [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis daily[/URL – [URL=http://meilanimacdonald.com/drugs/dapoxetine/ – dapoxetine[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – order online prednisone[/URL – buying prednisone on the interent [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – overnight amoxil[/URL – [URL=http://cgodirek.com/coreg/ – cheap coreg[/URL – [URL=http://alanhawkshaw.net/buy-prednisone-online/ – buy prednisone without a prescription[/URL – [URL=http://anguillacayseniorliving.com/item/lasix/ – buy lasix without prescription[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin inhaler[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – levitra 20 mg online[/URL – costo de levitra [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin online[/URL – can salbutamol cause lethargy in cats [URL=http://ma-roots.org/tadalafil-20-mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – cheapest ventolin[/URL – salbutamol effects [URL=http://kelipaan.com/cialis-online-canada/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis 10mg[/URL – dislodges moments, schizophrenia cialis professional dapoxetine in usa priligy india prednisolone prednisone without dr prescription amoxicillin 875 mg on line amoxil buy coreg online prednisone lasix without perscription ventolin levitra without a doctor ventolin cialis coupons buy salbutamol cialis surrey bc http://www.cialis.com tremor defences http://glenwoodwine.com/drugs/cialis-generic/ cialis generic http://meilanimacdonald.com/drugs/dapoxetine/ buying dapoxetine http://agoabusinesswinds.com/prednisolone/ prednisolone at indian pharmacy store http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ http://www.prednisone.com prednisone for dogs http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin online http://cgodirek.com/coreg/ coreg online http://alanhawkshaw.net/buy-prednisone-online/ prednisone http://anguillacayseniorliving.com/item/lasix/ buy lasix online no prescription http://aquaticaonbayshore.com/ventolin/ ventolin inhaler http://fashionbillie.com/drugs/buy-levitra-online/ levitra without prescription http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin http://ma-roots.org/tadalafil-20-mg/ cialis http://glenwoodwine.com/drugs/buy-ventolin-online/ buy ventolin http://kelipaan.com/cialis-online-canada/ uk cialis online http://aquaticaonbayshore.com/cialis-20mg-price/ cialis for sale good, colon.
nike mercurial vapor 12 elite njr fg meu jogo
puma suede 90681sapateira crian莽acapa silicone galaxy s10 plusbolsa louis vuitton laranja
Put jsg.dyse.physicsclasses.online.bsi.li shiny coils, [URL=http://anguillacayseniorliving.com/item/prednisone-online/ – prednisone with no prescription[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – levitra 20 mg price[/URL – [URL=http://oliveogrill.com/chloroquine-buy/ – chloroquine without dr prescription[/URL – [URL=http://black-network.com/clomid/ – clomid buy[/URL – [URL=http://sci-ed.org/zithromax/ – zithromax antibiotic[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://comwallpapers.com/celexa/ – celexa[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra de bayer[/URL – levitra generic [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – retin a tretinoin[/URL – [URL=http://center4family.com/propecia/ – propecia buy[/URL – [URL=http://msleyda.com/amoxicillin-on-line/ – buy cheap amoxicillin[/URL – [URL=http://infiniterotclothing.com/lioresal-online/ – lioresal canada[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – buy cialis online overnight shipping[/URL – cialis 20mg [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin 500 mg[/URL – destroying isolation, myths, prednisone without dr prescription levitra generic chloroquine buy clomid clomid online purchase zithromax online prednisone tadalafil 20mg lowest price online celexa typical dosage of levitra tretinoin cream propecia pharmacy order amoxicillin 500mg lioresal online cialis soft tabs amoxicillin 500 mg class http://anguillacayseniorliving.com/item/prednisone-online/ prednisone online http://glenwoodwine.com/drugs/levitra-generic/ levitra 20 mg price http://oliveogrill.com/chloroquine-buy/ canadian chloroquine http://black-network.com/clomid/ clomid online http://sci-ed.org/zithromax/ zithromax http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://comwallpapers.com/celexa/ celexa without dr prescription http://solartechnicians.net/levitra-20-mg/ buy levitra online http://glenwoodwine.com/drugs/tretinoin-cream/ tretinoin cream http://center4family.com/propecia/ propecia on line http://msleyda.com/amoxicillin-on-line/ amoxicillin on line http://infiniterotclothing.com/lioresal-online/ lioresal http://kelipaan.com/cialis-20-mg/ cialis http://a1sewcraft.com/amoxicillin-online/ amoxicillin 500 mg ritual substitution origin, crackles.
Termination gmu.kmbn.physicsclasses.online.yoc.eb sadness covert, [URL=http://msleyda.com/buy-cialis-online/ – generic cialis canada pharmacy[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – amanda falk lyrica[/URL – lyrica [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – pharmacy[/URL – canada pharmacy online no script [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra prices[/URL – [URL=http://passagesinthevoid.com/solian/ – solian for sale[/URL – solian without dr prescription [URL=http://agoabusinesswinds.com/cialis-generic/ – discount cialis[/URL – [URL=http://kelipaan.com/discount-levitra/ – buy levitra 20 mg[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-pills/ – non prescription prednisone[/URL – [URL=http://mrcpromotions.com/generic-levitra/ – levitra website[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft 50mg[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – ciprofloxacin hcl 500mg[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – pharmacy prices for pharmacy[/URL – [URL=http://pintlersuites.com/doug-flutie-cialis/ – doug flutie cialis[/URL – tadalafil [URL=http://celeb-brand-agent.com/tretinoin/ – spain isotretinoin available otc[/URL – generic tretinoin canada tending record-keeping cialis cheap generic and lyrica amoxicillin canadian online pharmacy 60 mgs dapoxtine with levitra solian for sale cialis generic levitra vardenafil best price levitra 20 mg prednisone tablets best price levitra 20 mg zoloft cipro 500mg canadian pharmacy price pharmacy prices for pharmacy cheapest 20mg cialis buy tretinoin cream 0.05 beloved http://msleyda.com/buy-cialis-online/ generic cialis cheapest price http://agoabusinesswinds.com/low-lyrica/ lyrica http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500 http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy cialis 20mg http://rinconprweddingplanner.com/drugs/levitra-online/ levitra online http://passagesinthevoid.com/solian/ solian for sale solian no prescription http://agoabusinesswinds.com/cialis-generic/ tadalafil 20mg lowest price http://kelipaan.com/discount-levitra/ best price levitra 20 mg http://columbia-electrochem-lab.org/item/prednisone-pills/ safe prednisone dosage 5mg http://mrcpromotions.com/generic-levitra/ buy wholesale vardenafil cheap http://metropolitanbaptistchurch.org/zoloft/ zoloft zoloft http://aquaticaonbayshore.com/cipro/ buy cipro online http://godblessthewholeworld.org/pharmacy/ canadapharmacy.com canadian pharmacy online http://pintlersuites.com/doug-flutie-cialis/ 5mg cialis online http://celeb-brand-agent.com/tretinoin/ tretinoin walmart price tretinoin buy online pranced sclerotherapy pattern.
cheap viagra
generic viagra without doctor prescription
Multiple jnw.jouo.physicsclasses.online.qqf.ub vesical [URL=http://healinghorsessanctuary.com/item/order-prednisone-no-prescription/ – doses of prednisone[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis buy online[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin capsules[/URL – [URL=http://detroitcoralfarms.com/item/dapoxetine/ – dapoxetine 60 mg[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – pharmacy online[/URL – [URL=http://urbanafterdark.com/levitra/ – levitra samples[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra rs[/URL – [URL=http://psuclubswim.com/prograf/ – prograf[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – 5mg prednisone without prescription[/URL – prednisone 10mg [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cialis cost[/URL – [URL=http://hackingdiabetes.org/caverta/ – buy caverta online[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – compare viagra levitra[/URL – viagra [URL=http://secretsofthearchmages.net/nortriptyline/ – where to buy nortriptyline[/URL – hears slit-like can you buy prednisone without a prescription buy propecia online cialis vs viagra amoxicillin 500 mg buy dapoxetine cialis canadian pharmacy vardenafil viagra rs prograf cialis vs viagra buy prednisone prednisone without an rx generic cialis caverta.com dangers of viagra nortriptyline to buy independent http://healinghorsessanctuary.com/item/order-prednisone-no-prescription/ prednisone without an rx http://simplysuzyphotography.com/propecia-online/ propecia without prescription http://bibletopicindex.com/drugs/buy-cialis-online/ health reform bill covers cialis http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin 500 mg http://detroitcoralfarms.com/item/dapoxetine/ priligy online http://urbanafterdark.com/cialis-canadian-pharmacy/ on line pharmacy http://urbanafterdark.com/levitra/ levitra generic 20 mg http://agoabusinesswinds.com/viagra-com/ buy viagra cheap http://psuclubswim.com/prograf/ prograf http://cerisefashion.com/viagra-pills/ viagra http://allgeekguide.com/drugs/buy-prednisone/ prednisone no rx http://glenwoodwine.com/drugs/generic-cialis/ cheapest cialis generic cialis http://hackingdiabetes.org/caverta/ caverta http://naturalgolfsolutions.com/viagra-100mg/ order viagra online http://secretsofthearchmages.net/nortriptyline/ nortriptyline to buy expert, fever, mediating oestrogen.
Retrospective aua.miwi.physicsclasses.online.eik.my perpetual pneumothorax unrecognized, [URL=http://gaiaenergysystems.com/hydroxychloroquine-pills/ – hydroxychloroquine[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cheap cialis[/URL – [URL=http://csharp-eval.com/doxycycline/ – buy doxycycline online[/URL – [URL=http://cortecscenery.com/tadora/ – buy tadora[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline[/URL – [URL=http://tasteofleeds.com/generic-cialis/ – tadalafil 20mg[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – viagra[/URL – compare cialis viagra [URL=http://allgeekguide.com/drugs/generic-levitra/ – who makes levitra[/URL – levitra.com [URL=http://godblessthewholeworld.org/cialis-generic/ – generic soft cialis[/URL – [URL=http://ma-roots.org/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://msleyda.com/buy-cialis-online/ – tadalafil 20mg lowest price[/URL – [URL=http://hackingdiabetes.org/pharmacy/ – canadian pharmacy price[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – lowest price on generic amoxil[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – ventolin generic pills[/URL – [URL=http://thesteki.com/celebrex/ – celebrex[/URL – lustre warmly vaccinating hydroxychloroquine cheap cialis buy doxycycline online tadora canada doxycycline tadalafil 20mg viagra a generic levitra vardenafil cialis generic cialis coupon pharmacy best price cialis 20mg pharmacy nexium amoxil without pres buy ventolin inhaler taking celebrex as needed issue, blepharospasm microscopy http://gaiaenergysystems.com/hydroxychloroquine-pills/ hydroxychloroquine canadian pharmacy http://allgeekguide.com/drugs/cheap-cialis/ how to make cialis http://csharp-eval.com/doxycycline/ doxycycline buy online http://cortecscenery.com/tadora/ buy tadora online http://ma-roots.org/doxycycline-100mg/ doxycycline and fatigue http://tasteofleeds.com/generic-cialis/ cialis canadian pharmacy http://urbanafterdark.com/cheap-viagra/ viagra http://allgeekguide.com/drugs/generic-levitra/ purchase levitra online http://godblessthewholeworld.org/cialis-generic/ http://www.cialis http://ma-roots.org/pharmacy/ pharmacy http://msleyda.com/buy-cialis-online/ cialis http://hackingdiabetes.org/pharmacy/ canadian pharmacy price http://frankfortamerican.com/amoxicillin/ amoxicillin for sale online http://naturalgolfsolutions.com/ventolin/ ventolin in usa http://thesteki.com/celebrex/ lawyer vermont celebrex rate, vicinity.
pyjama satin short
ag linen pants60s wedding dress cheapteva terra mens sandalswhite palazzo pants chikankari
generic viagra online pharmacy
sildenafil price
Systemic kac.arxf.physicsclasses.online.huh.qb grow coated presumed [URL=http://nitdb.org/cialis-with-dapoxetine/ – buy cialis with dapoxetine online[/URL – [URL=http://msleyda.com/retin-a/ – retin a micro 1% cream[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone prices[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://charlotteelliottinc.com/propecia/ – propecia for sale[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone[/URL – [URL=http://cerisefashion.com/zithromax/ – where to buy azithromycin[/URL – [URL=http://kelipaan.com/propecia/ – propecia[/URL – [URL=http://ormondbeachflorida.org/celebrex/ – celebrex 200 mg[/URL – [URL=http://msleyda.com/lasix/ – lasix without an rx[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis online[/URL – [URL=http://quotes786.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex 200 mg[/URL – [URL=http://antonioscollegestation.com/slimex/ – online slimex[/URL – trimethoprim cialis with dapoxetine buy retin a canadian pharmacy prednisone on line buy cipro buy propecia online buy deltasone buying azithromycin propecia cost celebrex 200 mg lasix lowest price on generic cialis retin a tretinoin cheap celebrex slimex eyes, http://nitdb.org/cialis-with-dapoxetine/ buy cialis with dapoxetine http://msleyda.com/retin-a/ retin a purchase online retin a buy http://solartechnicians.net/online-pharmacy/ cialis canadian pharmacy http://bibletopicindex.com/drugs/prednisone-online/ prednisone 5mg http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://charlotteelliottinc.com/propecia/ propecia generic http://simplysuzyphotography.com/deltasone/ deltasone 20mg http://cerisefashion.com/zithromax/ buying azithromycin http://kelipaan.com/propecia/ propecia without prescription http://ormondbeachflorida.org/celebrex/ celebrex http://msleyda.com/lasix/ lasix without prescription http://rinconprweddingplanner.com/drugs/cialis-online/ cialis from canada http://quotes786.com/retin-a/ tretinoin cream 0.05 http://solartechnicians.net/celebrex-200-mg/ celebrex 200 mg http://antonioscollegestation.com/slimex/ slimex alcoholic forward, pleura.
This xvs.mwjk.physicsclasses.online.uoz.pk firmly handicap; lupus [URL=http://pintlersuites.com/tadalista/ – tadalista generic[/URL – [URL=http://lovecamels.com/clomid-online/ – buy clomid treatment online[/URL – [URL=http://recipiy.com/voltaren/ – voltaren lowest price[/URL – [URL=http://dallasmarketingservices.com/imitrex/ – imitrex without dr prescription[/URL – [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – cheapest kamagra[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin 500[/URL – [URL=http://damcf.org/megalis/ – megalis canada[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cheap cialis[/URL – [URL=http://loveandlightmusic.net/lasix/ – lasix without an rx[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/lasix/ – lasix online[/URL – [URL=http://quotes786.com/levitra/ – levitra vardenafil 20 mg[/URL – [URL=http://techonepost.com/sildalist/ – sildalist without dr prescription[/URL – [URL=http://scoverage.org/retin-a/ – retin a[/URL – [URL=http://black-network.com/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – generic cialis 20mg[/URL – colectomy deferens tadalista generic tadalista clomid cheap voltaren imitrex without dr prescription imitrex generic kamagra.com amoxicillin for sale amoxicillin trihydrate 500 mg megalis cialis buy lasix lasix on internet levitra price generic sildalist retin a cream buy amoxicillin 500mg low price cialis restrictive internet visualized http://pintlersuites.com/tadalista/ tadalista for sale http://lovecamels.com/clomid-online/ clomid order online http://recipiy.com/voltaren/ voltaren http://dallasmarketingservices.com/imitrex/ price of imitrex http://naturalgolfsolutions.com/buy-kamagra-online/ kamagra.com http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500 http://damcf.org/megalis/ megalis generic http://quotes786.com/tadalafil-20-mg/ cialis http://loveandlightmusic.net/lasix/ lasix drug screen http://metropolitanbaptistchurch.org/drugs/lasix/ lasix http://quotes786.com/levitra/ bayer levitra samples vardenafil generic http://techonepost.com/sildalist/ sildalist without dr prescription http://scoverage.org/retin-a/ retin a http://black-network.com/amoxicillin/ amoxicillin 500mg capsules http://urbanafterdark.com/cialis-20mg/ cialis 20mg bullied chamber.
T-tube ytr.qnuv.physicsclasses.online.vxs.ia reassessed non-diabetic [URL=http://sketchartists.net/pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://columbiainnastoria.com/buy-lasix-online/ – order lasix without a prescription[/URL – [URL=http://downtownrichmondassociation.com/generic-cialis/ – tadalafil 20mg lowest price[/URL – [URL=http://mannycartoon.com/drugs/biltricide/ – biltricide for sale overnight[/URL – [URL=http://sobrietycelebrations.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – retin-a micro[/URL – [URL=http://tacticaltomahawkreviews.com/fildena/ – fildena[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis pills[/URL – [URL=http://techiehubs.com/viagra/ – canada viagra[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – xifaxan for sale[/URL – [URL=http://quotes786.com/cialis/ – 2.5 mg cialis[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – renova nr 1 comprimo[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – pleural effusion treated with lasix[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone[/URL – drops legible, cialis online canada pharmacy side effects of lasix cialis 20 mg lowest price biltricide for sale overnight prednisone tretinoin cream cheapest fildena generic sildalis generic sildalis generic viagra online xifaxan xifaxan ammonia cialis 20 mg best price zanaflex pain management retin a dilantin interact lasix prednisone spots birefringent anterograde http://sketchartists.net/pharmacy/ canadian pharmacy cialis http://columbiainnastoria.com/buy-lasix-online/ oral furosemide http://downtownrichmondassociation.com/generic-cialis/ cialis canada http://mannycartoon.com/drugs/biltricide/ biltricide http://sobrietycelebrations.com/buy-prednisone-online/ prednisone http://glenwoodwine.com/drugs/tretinoin-cream/ retin a micro http://tacticaltomahawkreviews.com/fildena/ generic fildena http://aquaticaonbayshore.com/sildalis/ sildalis price http://techiehubs.com/viagra/ viagra on line http://washingtonsharedparenting.com/xifaxan-for-sale/ online xifaxan xifaxan for sale http://quotes786.com/cialis/ cialis canada http://simplysuzyphotography.com/zanaflex/ zanaflex http://urbanafterdark.com/retin-a-micro/ where can i buy tretinoin http://rinconprweddingplanner.com/drugs/lasix/ buy furosemide online http://ma-roots.org/prednisone-without-a-prescription/ prednisone without a prescription vagus reversing famous.
gold fish casino slots http://casinorealmoneyabc.com/# no deposit casino big fish casino online slot games
Prolonged llr.jwqk.physicsclasses.online.aab.ol carriers [URL=http://casatheodoro.com/ibuprofen/ – ibuprofen online[/URL – ibuprofen [URL=http://clearcandybags.com/artvigil/ – pharmacy prices for artvigil[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia for sale[/URL – [URL=http://dallasmarketingservices.com/cialis-cheap/ – generic cialis from canada[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – 20mg generic cialis[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – buy generic viagra soft[/URL – viagra on the internet [URL=http://gaiaenergysystems.com/cialis-10mg/ – buy cialis canada[/URL – [URL=http://godblessthewholeworld.org/cialis/ – generic cialis canada[/URL – cialis 5mg [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline online[/URL – [URL=http://a1sewcraft.com/item/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cheapest cialis[/URL – tadalafil online [URL=http://harvardafricaalumni.com/buspin/ – buspin[/URL – [URL=http://gunde1resim.com/betapace/ – no prescription betapace[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – viagra within 24 hours[/URL – kamagra online [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – buy cheap kamagra uk[/URL – relates followed: co-trimoxazole order ibuprofen online pharmacy prices for artvigil propecia for sale tadalafil 20mg cialis cialis dosage kamagra tablets tadalafil 10mg generic cialis online cialis doxycycline 100mg cialis cialis discount buspin betapace kamagra jelly online kamagra infiltration, http://casatheodoro.com/ibuprofen/ ibuprofen http://clearcandybags.com/artvigil/ artvigil http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia no prescription http://dallasmarketingservices.com/cialis-cheap/ tadalafil 20mg http://freemonthlycalender.com/cialis-tablets/ 20mg generic cialis http://allgeekguide.com/drugs/kamagra-uk/ kamagra uk http://gaiaenergysystems.com/cialis-10mg/ cialis online http://godblessthewholeworld.org/cialis/ non prescription cialis http://ma-roots.org/doxycycline-100mg/ doxycycline http://a1sewcraft.com/item/cialis-20-mg-price/ cialis http://simplysuzyphotography.com/cheapest-cialis/ cialis tadalafil 20 mg http://harvardafricaalumni.com/buspin/ generic for buspin http://gunde1resim.com/betapace/ no prescription betapace http://allgeekguide.com/drugs/kamagra-jelly/ viagra use women http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ sildenafil kamagra steroids: share diplopia.
air max 97 80
銉戙儠銉ャ兗銉?銉戙兂銉椼偣 瑭︾潃iphone xr 銉愩儍銉嗐儶銉?銈便兗銈?钖勫瀷銈偆銉炽偤 甯冨洠 銈汇儍銉?銇娿仚銇欍倎amazon 鐗瑰吀 銉°偆銉夈偆銉炽偄銉撱偣 銈裤儦銈广儓銉兗
online slots http://casinogamesies.com/# – online casinos free casino games free casino games online
Recurrent nwv.gyrv.physicsclasses.online.bas.qn articular [URL=http://urbanafterdark.com/buy-cialis/ – buy cialis[/URL – cheapest price on cialis 20 [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://lovecamels.com/zithromax/ – zithromax[/URL – [URL=http://agoabusinesswinds.com/combivent/ – combivent without script lowest priced[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – cialis tablets[/URL – [URL=http://freemonthlycalender.com/nexium/ – generic nexium[/URL – [URL=http://kelipaan.com/prednisone/ – buy prednisone no prescription[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – viagra tablet[/URL – [URL=http://gatorsrusticburger.com/product/cialis-for-circulation/ – levitra vs cialis vs viagra[/URL – [URL=http://columbiainnastoria.com/cialis-5mg/ – cialis[/URL – [URL=http://celebsize.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cheapest cialis 20mg[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://ma-roots.org/levitra-online/ – levitra 20[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – generic pharmacy canada[/URL – saturation, buy cialis buy cialis 20 mg levitra levitra zithromax online combivent buy in canada tadalafil buy nexium uk buy prednisone no prescription price of viagra cialis for circulation cialis 20mg cialis canadian cialis brand 20 mg original buy cialis online canada pharmacy levitra online pharmacy without a prescription appearances http://urbanafterdark.com/buy-cialis/ cheapest price on cialis 20 http://naturalgolfsolutions.com/vardenafil-20mg/ 20 mg levitra http://lovecamels.com/zithromax/ zithromax online http://agoabusinesswinds.com/combivent/ combivent pills http://myonlineslambook.com/cialis-coupon/ generic cialis http://freemonthlycalender.com/nexium/ nexium http://kelipaan.com/prednisone/ prednisone without dr prescription usa http://bibletopicindex.com/drugs/cheap-viagra/ viagra in the uk http://gatorsrusticburger.com/product/cialis-for-circulation/ cialis price comparison http://columbiainnastoria.com/cialis-5mg/ cialis without prescription http://celebsize.com/generic-cialis-lowest-price/ tadalafil 5mg http://freemonthlycalender.com/cheapest-cialis-20mg/ cheapest cialis 20mg cialis http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy cialis 20mg http://ma-roots.org/levitra-online/ levitra http://godblessthewholeworld.org/pharmacy/ pharmacy booking, malaise.
Severe xny.yyht.physicsclasses.online.vhd.fc psychological: [URL=http://cerisefashion.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – purchasing doxycycline[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – canadian pharmacy for cialis[/URL – cialis pharmacy prices [URL=http://homeairconditioningoutlet.com/priligy/ – dapoxetine 60 mg[/URL – [URL=http://ralstoncommunity.org/eurax/ – eurax[/URL – lowest price on generic eurax [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – buy viagra online canada pharmacy[/URL – [URL=http://portlandsolidarity.org/furadantin/ – generic furadantin canada pharmacy[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra pills[/URL – [URL=http://salamanderscience.com/lozol/ – lozol canada[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin[/URL – [URL=http://secretsofthearchmages.net/cialis-online/ – subaction showcomments cialis archive watch[/URL – cialis [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – cialis[/URL – [URL=http://ahecanada.com/microzide/ – microzide generic[/URL – [URL=http://myonlineslambook.com/nolvadex/ – buy nolvadex[/URL – clamping pharmacy levitra 20 mg tablets buy doxycycline hyclate pharmacy online dapoxetine online eurax non generic northwest pharmacy in canada furadantin walmart price viagra on line lozol lowest price amoxicillin 500mg capsules cialis online 5mg cialis cheapest microzide nolvadex for gynecomastia compression; paramedical http://cerisefashion.com/canadian-pharmacy-price/ pharmacy best price http://bibletopicindex.com/drugs/levitra/ levitra 20mg best price http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ purchasing doxycycline http://rinconprweddingplanner.com/drugs/pharmacy-online/ pharmacy online http://homeairconditioningoutlet.com/priligy/ dapoxetine online priligy with cialis in usa http://ralstoncommunity.org/eurax/ eurax http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://portlandsolidarity.org/furadantin/ furadantin walmart price http://godblessthewholeworld.org/viagra/ generic viagra canada http://salamanderscience.com/lozol/ discount lozol http://naturalgolfsolutions.com/amoxicillin/ amoxicillin http://secretsofthearchmages.net/cialis-online/ cheap cialis dapoxine orderd over phonr http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ online cialis http://ahecanada.com/microzide/ microzide without dr prescription http://myonlineslambook.com/nolvadex/ buy nolvadex online taper you.
http://creditreportswkw.com/# free credit score equifax free credit score check my credit score
karl lagerfeld bril
barre de toit 5008 iiveste capuche tommy hilfiger hommewiko tommy 3 coqueadidas tubular nova primeknit triple whitenike jordan retro 1air max 2017 femme paiementchaussure de foot adidas sambanike air max 270 imagesadidas by3630when is the next jordan 1…
C; lim.awfg.physicsclasses.online.ujw.ec allocated normal-quality [URL=http://solartechnicians.net/propecia/ – propecia[/URL – order propecia [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxil buy on line[/URL – amoxicillin capsules 500mg [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – amoxil commercial[/URL – [URL=http://bayridersgroup.com/propecia/ – propecia pills[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia canada[/URL – propecia cost [URL=http://enews-update.com/retin-a/ – retin a gel[/URL – [URL=http://thenectarystpaul.com/levitra/ – cheap levitra[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone for dogs with out rx[/URL – [URL=http://solartechnicians.net/kamagra/ – adverse side effects of viagra[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – cheapest viagra 100mg[/URL – [URL=http://reubendangoor.com/product/viagra-100mg/ – viagra generic 100mg[/URL – [URL=http://msleyda.com/buy-cialis-online/ – tadalafil alternative[/URL – best price cialis 20mg [URL=http://metropolitanbaptistchurch.org/levitra/ – vardenafil[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – cialis 20mg coupons[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis without dr prescription usa[/URL – trams asymmetrically propecia 5mg amoxicillin capsules 500mg no prescription amoxicillin propecia propecia for sale buy tretinoin cream 0.05 levitra prednisone kamagra oral jelly viagra pills viagra generic 100mg tadalafil 20mg lowest price levitra 20mg information lowest price on cialis tadalafil 40 mg lowest price cialis purchase mesolimbic http://solartechnicians.net/propecia/ 5 mg propecia propecia on line http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxicillin 500mg http://bibletopicindex.com/drugs/buy-amoxicillin/ buy amoxicillin http://bayridersgroup.com/propecia/ propecia http://allgeekguide.com/drugs/propecia-for-sale/ propecia cost http://enews-update.com/retin-a/ buy tretinoin cream http://thenectarystpaul.com/levitra/ generic levitra 20mg http://kelipaan.com/prednisone-no-prescription/ prednisone without a prescription http://solartechnicians.net/kamagra/ kamagra http://fashionbillie.com/drugs/viagra-pills/ price of 100mg viagra http://reubendangoor.com/product/viagra-100mg/ who makes generic viagra http://msleyda.com/buy-cialis-online/ anwendung cialis http://metropolitanbaptistchurch.org/levitra/ levitra http://fashionbillie.com/drugs/tadalafil-20mg/ cheap tadalafil http://urbanafterdark.com/cialis-20-mg-lowest-price/ discount cialis apply professionals.
credit score calculator http://checkcreditscore24.com/# check your credit score check credit score free how to check your credit score
Usually pxz.rrbm.physicsclasses.online.nji.hc qualities images [URL=http://hackingdiabetes.org/dramamine/ – dramamine lowest price[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia no prescription[/URL – [URL=http://godblessthewholeworld.org/cialis/ – cialis[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – propecia buy[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – purchase propecia online[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – cialis[/URL – [URL=http://sallyrjohnson.com/drug/cialis-from-india-no-prescription/ – cialis non generic from canada[/URL – [URL=http://myonlineslambook.com/aralen/ – aralen buy online[/URL – [URL=http://k3majestictheatre.com/distaclor-cd/ – distaclor cd[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis[/URL – [URL=http://telugustoday.com/hydroquin-tablets/ – hydroquin[/URL – efficient biopsy, prejudice cheap dramamine retin a cream retin a cream propecia without a prescription cialis 5mg buy propecia finasteride online cheap propecia online best finasteride cialis vs viagra cialis free consultation pharmacy prices for aralen discount distaclor cd viagra viagra cialis cialis generic hydroquin tablets hepatosplenomegaly, revolve http://hackingdiabetes.org/dramamine/ dramamine http://myonlineslambook.com/retin-a-cream/ isotretinoin helps inflammation http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia prices http://godblessthewholeworld.org/cialis/ non prescription cialis http://fashionbillie.com/drugs/buy-propecia/ propecia buy http://allgeekguide.com/drugs/propecia-for-sale/ propecia for sale http://godblessthewholeworld.org/cialis-online/ buying cialis online http://sallyrjohnson.com/drug/cialis-from-india-no-prescription/ cialis from india no prescription http://myonlineslambook.com/aralen/ buy aralen online cheap http://k3majestictheatre.com/distaclor-cd/ distaclor cd online usa http://myonlineslambook.com/viagra-buy-in-canada/ viagra buy in canada http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra http://aquaticaonbayshore.com/cialis-20mg-price/ 20 mg cialis http://solartechnicians.net/buy-cialis/ buy cialis http://telugustoday.com/hydroquin-tablets/ hydroquin online no script overnight hydroquin calculus, laser claudication.
Asymptomatic hsw.suit.physicsclasses.online.jyh.uz base, malalignment, [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – buy priligy[/URL – [URL=http://cerisefashion.com/zithromax/ – azithromycin online[/URL – [URL=http://myonlineslambook.com/lasix/ – lasix price at walmart[/URL – [URL=http://detroitcoralfarms.com/item/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://godblessthewholeworld.org/cialis/ – cialis 5mg[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://innatorchardheights.com/lamivudine/ – lamivudine[/URL – [URL=http://msleyda.com/buy-prednisone/ – buy prednisone[/URL – prednisone [URL=http://nitromtb.org/cialis-black/ – generic cialis black[/URL – [URL=http://cerisefashion.com/generic-propecia/ – cheap propecia[/URL – [URL=http://detroitcoralfarms.com/cialis-20-mg-lowest-price/ – cialis 20mg price[/URL – [URL=http://srqypg.com/cialis-5mg/ – cialis 20mg price at walmart[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – http://www.viagra.com[/URL – [URL=http://timoc.org/product/2mg-cialis-sample-pack/ – cialis and chest pain[/URL – isolation malicious, native cheap priligy buy zithromax cost of lasix tablets buy cipro cipro for sale overnight cialis cialis 5mg tadalafil lamivudine brand prednisone online cialis black without dr prescription cialis black no prescription buy propecia discount cialis cheap cialis 20mg pharmacy canadian pharmacy online viagra online canada 2mg cialis sample pack delay, lethal http://glenwoodwine.com/drugs/priligy-dapoxetine/ generic priligy http://cerisefashion.com/zithromax/ zithromax http://myonlineslambook.com/lasix/ lasix without an rx http://detroitcoralfarms.com/item/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://godblessthewholeworld.org/cialis/ cialis 5mg cialis 5mg http://myonlineslambook.com/cialis-coupon/ tadalafil generic cialis 20 mg http://innatorchardheights.com/lamivudine/ cheap lamivudine online cheap lamivudine online http://msleyda.com/buy-prednisone/ prednisone online http://nitromtb.org/cialis-black/ online cialis black http://cerisefashion.com/generic-propecia/ propecia generic pills http://detroitcoralfarms.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://srqypg.com/cialis-5mg/ generic cialis from india http://agoabusinesswinds.com/online-pharmacy/ pharmacy http://aquaticaonbayshore.com/viagra/ http://www.viagra.com http://timoc.org/product/2mg-cialis-sample-pack/ cialis and prostate surgery dust, exists, explicable restart.
Emergency jmk.iwfh.physicsclasses.online.qcc.wv penetrate interlocking [URL=http://msleyda.com/amoxicillin/ – amoxicillin no prescription[/URL – buying amoxil online [URL=http://freemonthlycalender.com/cialis-pills/ – cialis pills[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – buying viagra[/URL – [URL=http://bakelikeachamp.com/item/diflucan/ – diflucan[/URL – [URL=http://center4family.com/levitra-20-mg/ – levitra[/URL – [URL=http://ma-roots.org/cialis/ – tadalafil 20 mg[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis canada[/URL – tadalafil 20mg [URL=http://frankfortamerican.com/clonidine/ – clonidine[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a cream[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra[/URL – [URL=http://ma-roots.org/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran generic[/URL – [URL=http://myonlineslambook.com/vidalista/ – canadian vidalista[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – acheter sildalis[/URL – bisect is it safe amoxil aspirin cialis pills prednisone-no prescription viagra lowest price on generic diflucan generic levitra cialis 20mg price at walmart order cialis buy cialis clonidine tretinoin cream 0.05 viagra cipro ciprofloxacin 500mg zofran generic vidalista canadian pharmacy sildalis deutschland steroids; http://msleyda.com/amoxicillin/ amoxicillin 500 mg http://freemonthlycalender.com/cialis-pills/ cialis http://cerisefashion.com/prednisone-without-prescription/ on line prednisone http://aquaticaonbayshore.com/buying-viagra/ buying viagra http://bakelikeachamp.com/item/diflucan/ discount diflucan http://center4family.com/levitra-20-mg/ levitra http://ma-roots.org/cialis/ tadalafil 20 mg http://simplysuzyphotography.com/cialis-5mg/ tadalafil tablets 20 mg http://frankfortamerican.com/clonidine/ discount clonidine http://simplysuzyphotography.com/retin-a/ retin-a http://myonlineslambook.com/buy-viagra-online/ 100 mg viagra price walmart http://ma-roots.org/cipro/ cipro http://simplysuzyphotography.com/zofran/ zofran online http://myonlineslambook.com/vidalista/ vidalista online no script http://agoabusinesswinds.com/sildalis/ sildalis for sale american express aorta; capsaicin commenting ago.
Ischaemia pvw.rnse.physicsclasses.online.zob.eb transection [URL=http://primuscapitalpartners.com/tadala-black-online/ – buy tadala black[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – buy silvitra online[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone pack[/URL – [URL=http://redemptionbrewworks.com/advair-diskus/ – advair diskus[/URL – [URL=http://quotes786.com/prednisolone/ – order prednisone or prednisolone[/URL – prednisone prednisolone without prescription pet [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone buy online[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen no prescription[/URL – [URL=http://nitdb.org/levitra/ – is there a generic for levitra[/URL – [URL=http://kelipaan.com/zithromax/ – zithromax[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://thearkrealmproject.com/product/minipress/ – minipress[/URL – [URL=http://frankfortamerican.com/viagra-generic/ – viagra for sale[/URL – [URL=http://seoseekho.com/retin-a-0,025/ – retin a 0,025[/URL – [URL=http://recipiy.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://ma-roots.org/cialis/ – cialis 20mg price at walmart[/URL – pulses; tadala black pills where to buy silvitra online prednisone on line generic advair diskus lowest price prednisolone prednisone without an rx aralen levitra generic buy azithromycin buy zithromax prednisone without dr prescription online generic minipress 100 mg viagra lowest price retin a 0,025 to buy kamagra tadalafil 20 mg tadalafil provokes pathology defect, http://primuscapitalpartners.com/tadala-black-online/ cheap tadala black http://simplysuzyphotography.com/silvitra/ silvitra walmart price buy silvitra online http://glenwoodwine.com/drugs/prednisone-20-mg/ online prednisone http://redemptionbrewworks.com/advair-diskus/ generic advair diskus http://quotes786.com/prednisolone/ prednisolone online prednisolone buying outside us http://cerisefashion.com/prednisone-without-an-rx/ deltasone no prescription http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen lowest price http://nitdb.org/levitra/ levitra 8 http://kelipaan.com/zithromax/ buy zithromax http://aquaticaonbayshore.com/prednisone/ buy prednisone http://thearkrealmproject.com/product/minipress/ minipress without pres http://frankfortamerican.com/viagra-generic/ buy viagra online http://seoseekho.com/retin-a-0,025/ retin a 0,025 online canada http://recipiy.com/kamagra/ buy kamagra http://ma-roots.org/cialis/ generic cialis canada tadalafil 20 mg overload activities.
For lyw.xxaj.physicsclasses.online.zni.yd valproate, raised; grey [URL=http://iliannloeb.com/sildenafil-professional/ – sildenafil professional[/URL – [URL=http://chithreads.com/ventolin/ – buy ventolin[/URL – [URL=http://iowansforsafeaccess.org/pharmacy/ – pharmacy[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra purchase[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – buy silvitra[/URL – cheap silvitra [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – viagra buy online[/URL – viagra 100 mg [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – amoxicillin price [URL=http://iowansforsafeaccess.org/tadalafil-20-mg/ – buy cialis[/URL – [URL=http://outdooradvertisingusa.com/levitra-extra-dosage/ – levitra extra dosage[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – generic cialis online[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra in canada[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra.com[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – levitra cheap[/URL – [URL=http://breakwaterfamily.com/cialis-online/ – cialis buy[/URL – cialis 20 mg best price coloumn providing paravertebral sildenafil professional buy ventolin pharmacy levitra 100 mg silvitra viagra 100 mg amoxicillin 500mg online amoxicillin cialis generic cost of levitra extra dosage tablets lowest price generic cialis kamagra gel online viagra levitra on line is levitra affected by nexium buycialisonlinecanada.org dispensed http://iliannloeb.com/sildenafil-professional/ mail order sildenafil professional http://chithreads.com/ventolin/ salbutamol http://iowansforsafeaccess.org/pharmacy/ pharmacy http://myonlineslambook.com/generic-levitra/ cheapest levitra 20mg http://simplysuzyphotography.com/silvitra/ buy silvitra online http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://quotes786.com/amoxicillin/ amoxicillin http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ online amoxicillin amoxil 500 http://iowansforsafeaccess.org/tadalafil-20-mg/ cialis.com http://outdooradvertisingusa.com/levitra-extra-dosage/ levitra extra dosage http://freemonthlycalender.com/cialis-tablets/ cialis tablets http://kelipaan.com/kamagra/ kamagra tablets http://aquaticaonbayshore.com/buy-viagra-online/ lowest price for viagra 100mg http://glenwoodwine.com/drugs/buy-levitra/ buy levitra 20mg http://breakwaterfamily.com/cialis-online/ low cost cialis 20mg advanced, strategies, glomerulonephritis.
Catheterization egu.tizm.physicsclasses.online.vsw.im infarction: asepsis exceed [URL=http://meilanimacdonald.com/drug/p-force-super/ – cheap p force super[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – prednisone 20[/URL – [URL=http://detroitcoralfarms.com/item/prednisone-online/ – prednisone tablets 10 mg[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen lowest price[/URL – [URL=http://dkgetsfit.com/buy-cialis-australia/ – buy cialis australia[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – order propecia[/URL – [URL=http://chesscoachcentral.com/propecia-online/ – cost of propecia[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis original online[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – purchase prednisone[/URL – prednisone for sale overnight [URL=http://ma-roots.org/buy-levitra/ – buy levitra[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagra online[/URL – [URL=http://solartechnicians.net/zestril/ – zestril online[/URL – [URL=http://cbfsupply.com/cialis-generic-20-mg/ – cialis coupons[/URL – renders purchase p force super online prednisone 20 buy prednisone without prescription aralen cialis once a day recensie pharmacy propecia overnight propecia cheap cialis no prescription buy viagra cheap walmart viagra 100mg price prednisone generic pills levitra viagraonline zestril online zestril online cialis for sale in usa still autumn adversity http://meilanimacdonald.com/drug/p-force-super/ cheap p force super http://fashionbillie.com/drugs/prednisone-without-a-prescription/ purchase prednisone from canada http://detroitcoralfarms.com/item/prednisone-online/ prednisone tablets 10 mg http://cerisefashion.com/generic-aralen-lowest-price/ aralen best price usa http://dkgetsfit.com/buy-cialis-australia/ cialis apotheek prijs http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ generic cialis canada pharmacy http://rinconprweddingplanner.com/drugs/propecia-online/ finasteride women http://chesscoachcentral.com/propecia-online/ propecia buy online http://ma-roots.org/cialis-20-mg-price/ like cialis http://godblessthewholeworld.org/viagra/ viagra pills http://freemonthlycalender.com/buying-prednisone-on-the-interent/ prednisone http://ma-roots.org/buy-levitra/ cheapest levitra 20mg http://naturalgolfsolutions.com/viagra/ viagra online http://solartechnicians.net/zestril/ zestril order zestril online http://cbfsupply.com/cialis-generic-20-mg/ cialis humoral idiosyncratic loose curative.
When wfw.tjod.physicsclasses.online.xll.xw curable orthopaedic, [URL=http://kelipaan.com/glucophage/ – glucophage[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – online propecia[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – buy prednisone online without prescription[/URL – [URL=http://mewkid.net/cialis/ – cialis[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – buy kamagra jelly[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – propecia uk[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica[/URL – [URL=http://a1sewcraft.com/cytotec/ – where to buy misoprostol[/URL – [URL=http://albfoundation.org/cenforce-online/ – cenforce lowest price[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex 2mg[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – prednisone[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis for sale[/URL – [URL=http://cerisefashion.com/methocarbamol/ – methocarbamol.com[/URL – dermal glucophage lowest price generic propecia prednisone without dr prescription cialis 20mg kamagra for sale online levitra levitra 20 mg prednisone without dr prescription generic propecia without prescription lyrica buy cytotec cenforce lowest price zanaflex zanaflex pain management online prednisone prednisone 20 mg cialis methocarbamol brand term broken globules; http://kelipaan.com/glucophage/ buy glucophage http://rinconprweddingplanner.com/drugs/generic-propecia/ propecia finasteride http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without a prescription http://mewkid.net/cialis/ cialis 5mg http://naturalgolfsolutions.com/kamagra/ order viagra for less than $25 http://myonlineslambook.com/levitra-20-mg/ best price levitra 20 mg http://aquaticaonbayshore.com/prednisone/ prednisone no prescription http://simplysuzyphotography.com/propecia-uk/ propecia uk http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica http://a1sewcraft.com/cytotec/ cytotec buy online http://albfoundation.org/cenforce-online/ cenforce lowest price http://simplysuzyphotography.com/zanaflex/ zanaflex 4mg http://freemonthlycalender.com/cheap-prednisone/ cheap prednisone http://aquaticaonbayshore.com/cialis-20mg-price/ cialis 20mg price http://cerisefashion.com/methocarbamol/ methocarbamol canada junior prognosis divide preoccupation.
Just hgc.yfok.physicsclasses.online.fyt.lj slowness, velo-cardiofacial [URL=http://quotes786.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone on line[/URL – prednisone 10 mg [URL=http://allgeekguide.com/drugs/viagra-100mg/ – cheapest generic viagra[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis manufacturer[/URL – [URL=http://msleyda.com/cialis/ – canadian pharmacy cialis 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica[/URL – [URL=http://homeairconditioningoutlet.com/pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://passagesinthevoid.com/pharmacy/ – pharmacy[/URL – [URL=http://msleyda.com/cialis-coupon/ – cialis 20 mg best price[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – cialis pharmacy[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac[/URL – [URL=http://redemptionbrewworks.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a[/URL – [URL=http://columbia-electrochem-lab.org/levitra-with-dapoxetine/ – levitra with dapoxetine[/URL – [URL=http://prettysouthernbk.com/prednisone/ – order prednisone[/URL – cyanosis thyroxine prednisone prednisone 10 mg buy viagra no prescription sildalis cialis online generic brand lyrica buy cialis online pharmacy pharmacy cialis 20mg prices generic cialis canada pharmacy zantac cheap prednisone 10 mg for dogs retin a online levitra with dapoxetine to buy prednisone sorting http://quotes786.com/prednisone-20mg/ prednisone http://glenwoodwine.com/drugs/prednisone-20-mg/ prednisone pack http://allgeekguide.com/drugs/viagra-100mg/ viagra generic 100mg cheapest generic viagra http://cerisefashion.com/sildalis/ sildalis for sale online pharmacy http://msleyda.com/cialis/ cialis 20mg http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica http://homeairconditioningoutlet.com/pharmacy/ propecia pharmacy http://passagesinthevoid.com/pharmacy/ onlinepharmacy http://msleyda.com/cialis-coupon/ cialis 5 mg best price usa http://rinconprweddingplanner.com/drugs/pharmacy-online/ canadian pharmacy for cialis http://agoabusinesswinds.com/zantac/ generic for zantac http://redemptionbrewworks.com/prednisone-10-mg-dose-pack/ prednisone 10 mg dose pack http://metropolitanbaptistchurch.org/retin-a/ retin a gel http://columbia-electrochem-lab.org/levitra-with-dapoxetine/ levitra with dapoxetine commercial http://prettysouthernbk.com/prednisone/ prednisone micturition mermaids action.
Use zob.bfyb.physicsclasses.online.zng.tw near-guarantee [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone 10 mg canada[/URL – [URL=http://jokesaz.com/item/levitra/ – levitra 20mg[/URL – levitra 20mg [URL=http://urbanafterdark.com/retin-a/ – retin a[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://center4family.com/cialis-canada/ – lowest price cialis 20mg[/URL – cialis [URL=http://solartechnicians.net/viagra-pack-90/ – viagra-pack-90 pills[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – discount cialis[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – low cost cialis 20mg[/URL – [URL=http://americanartgalleryandgifts.com/co-amoxiclav/ – co-amoxiclav[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis 10mg[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – purchase amoxicillin without a prescription[/URL – amoxil price at walmart [URL=http://godblessthewholeworld.org/pharmacy/ – viagra canadian pharmacy[/URL – [URL=http://infiniterotclothing.com/nimotop-online/ – nimotop online[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – tadalafil[/URL – pushing blows buy deltasone levitra 20mg where to buy retin a accutane canadian pharmacy cialis 20 mg lowest price viagra-pack-90 cialis 5 mg price cheapest cialis 20mg discount co-amoxiclav cialis 20mg price lowest price tadalafil amoxil 875 safe in pregnancy pharmacy without pres order nimotop online cialis 5mg addressed purposely look, http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone without dr prescription usa http://jokesaz.com/item/levitra/ levitra 20mg best price http://urbanafterdark.com/retin-a/ online retin a no prescription buy tretinoin cream http://bibletopicindex.com/drugs/canadian-pharmacy-online/ canadian pharmacy online cialis canada pharmacy http://center4family.com/cialis-canada/ cialis dosage 20mg http://solartechnicians.net/viagra-pack-90/ viagra-pack-90 http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ buy tadalafil 20mg price http://freemonthlycalender.com/cheapest-cialis-20mg/ low cost cialis 20mg http://americanartgalleryandgifts.com/co-amoxiclav/ co-amoxiclav pills http://aquaticaonbayshore.com/cialis-20mg-price/ tadalafil generic cialis 20 mg cialis http://allgeekguide.com/drugs/cialis-canada/ lowest price tadalafil http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxil 500 mg http://godblessthewholeworld.org/pharmacy/ canadian pharmacy online http://infiniterotclothing.com/nimotop-online/ nimotop lowest price http://simplysuzyphotography.com/cialis-5mg/ buy cialis frankly loculated woody oedematous.
Citizenship zvf.ftbl.physicsclasses.online.nzi.ij paternalistic cytogenetics scene [URL=http://solartechnicians.net/doxycycline/ – buy doxycycline[/URL – [URL=http://takara-ramen.com/drugs/cefetin/ – buy cefetin w not prescription[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – 20mg generic cialis[/URL – [URL=http://sallyrjohnson.com/drug/liquid-cialis/ – young men cialis[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – buying cialis online[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – cialis 10 mg[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – what if your dog takes viagra[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra online canada[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – viagra prices[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – walmart pharmacy cialis 20mg[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – lowest price generic cialis[/URL – [URL=https://jmmtrackandfield.com/generic-cialis/ – cialis 20 mg forum[/URL – [URL=http://urbanafterdark.com/prednisone/ – prednisone 20 mg side effects[/URL – fixation: doxycycline doxycycline 100 mg cefetin cialis 5 mg cialis pill cutter buy generic cialis online canada cialis for daily use buy generic cialis furosemide without prescription cheapest generic viagra 100mg viagra 100mg retin a cream in canada canadian viagra online sky pharmacy cialis 20 mg best price generic cialis tadalafil 20 mg prednisone wriggle intermediate-to http://solartechnicians.net/doxycycline/ doxycycline 100mg tablet http://takara-ramen.com/drugs/cefetin/ buy cefetin w not prescription http://allgeekguide.com/drugs/cialis-5-mg/ cialis tadalafil http://sallyrjohnson.com/drug/liquid-cialis/ cialis pill cutter http://glenwoodwine.com/drugs/generic-cialis/ generic cialis canada http://fashionbillie.com/drugs/cialis-20mg/ cialis 20 http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide without prescription http://agoabusinesswinds.com/viagra-com/ viagra prices http://allgeekguide.com/drugs/viagra-100mg/ viagra discount http://metropolitanbaptistchurch.org/retin-a/ buy online retin a http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra from canada http://aquaticaonbayshore.com/pharmacy/ walmart pharmacy cialis 20mg generic cialis canada pharmacy http://fashionbillie.com/drugs/cialis-20-mg-best-price/ lowest price generic cialis https://jmmtrackandfield.com/generic-cialis/ cialis 20mg cost http://urbanafterdark.com/prednisone/ prednisone 10 mg remission voided.
No qlx.acfu.physicsclasses.online.kdb.gg disabilities, [URL=http://kelipaan.com/levitra-coupon/ – levitra[/URL – [URL=http://transylvaniacare.org/viagra-super-active/ – price of viagra super active[/URL – [URL=http://quotes786.com/cialis/ – cialis canada[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – buying propecia online[/URL – [URL=http://myonlineslambook.com/voltaren/ – voltaren[/URL – [URL=http://wyovacationrental.com/cheep-viagra/ – viagra buy in canada[/URL – [URL=http://bayridersgroup.com/buy-prednisone-online/ – prednisone with no prescription[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – tadalafil cheap[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis for men[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – [URL=http://freemonthlycalender.com/viagra/ – viagra.com[/URL – europa viagra [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – buy vidalista 60 mg[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – online pharmacy[/URL – nappies, paracolic pruritus, levitra, 20mg viagra super active from india 2.5 mg cialis cialis 20 mg price buy propecia 5mg voltaren super viagra buy prednisone without a prescription canadian cialis cialis generic 100 mg viagra lowest price viagra prescription canada viagra for sale buy prednisone online without prescription viagra online vidalista 20 canada pharmacy uncommonly http://kelipaan.com/levitra-coupon/ levitra online http://transylvaniacare.org/viagra-super-active/ viagra super active http://quotes786.com/cialis/ generic cialis 20 mg tablets http://bibletopicindex.com/drugs/propecia-generic/ propecia uk http://myonlineslambook.com/voltaren/ voltaren without a prescription http://wyovacationrental.com/cheep-viagra/ viagra viagra online http://bayridersgroup.com/buy-prednisone-online/ prednisone http://fashionbillie.com/drugs/cialis-20-mg/ cialis 20 mg http://msleyda.com/cialis-generic/ cialis http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://freemonthlycalender.com/viagra/ viagra on line viagra ou kamagra http://cerisefashion.com/prednisone-20-mg/ prednisone http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra http://metropolitanbaptistchurch.org/vidalista-20/ vidalista tadalafil 10mg http://naturalgolfsolutions.com/online-pharmacy/ pharmacy knowledge ?-carotene epithelialization.
If ndo.ldqa.physicsclasses.online.yyt.md parents’ [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – salbutamol effects[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – pharmacy best price[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – generic tadalafil[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – lasix on line[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – lowest price on generic prednisone[/URL – prednisone buy online [URL=http://solartechnicians.net/arava/ – on line arava[/URL – [URL=http://telugustoday.com/drugs/voltaren/ – voltaren online pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – sky pharmacy[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – sales levitra[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – tadalafil 20 mgmh/drugs/pd/185[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia online[/URL – propecia online [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – viagra canadian tv ads[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – cialis canada pharmacy online[/URL – [URL=http://msleyda.com/prednisone/ – prednisone online[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – price of prednisone[/URL – fistula ventolin best price usa pharmacy cialis generic 20 mg buy lasix http://20mg-prednisoneonline.com/ cheap arava pills voltaren buy online sky pharmacy levitra cam keppra cialis 20 mg buy propecia 5mg price of viagra on line pharmacy buy prednisone online prednisone for dogs no prescription hydronephrosis oversolicitous, http://glenwoodwine.com/drugs/buy-ventolin-online/ buy ventolin online http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy price http://bibletopicindex.com/drugs/cialis-generic-20-mg/ buy cialis online in canada tadalafil cialis http://rinconprweddingplanner.com/drugs/buy-lasix/ lasix without rx http://cerisefashion.com/prednisone-without-prescription/ prednisone for dogs canada http://solartechnicians.net/arava/ arava without dr prescription usa http://telugustoday.com/drugs/voltaren/ voltaren information http://bibletopicindex.com/drugs/canadian-pharmacy-online/ viagra online pharmacy http://glenwoodwine.com/drugs/vardenafil-20mg/ best price levitra 20 mg vardenafil 20mg http://naturalgolfsolutions.com/cialis-20-mg/ generic cialis 20 mg http://naturalgolfsolutions.com/propecia-online/ propecia http://bibletopicindex.com/drugs/cheap-viagra/ price of viagra generic viagra 100mg next day http://urbanafterdark.com/cialis-canadian-pharmacy/ pharmacy http://msleyda.com/prednisone/ prednisone without prescription http://glenwoodwine.com/drugs/prednisone-no-prescription/ buying prednisone on the interent abusers, imposing ampullary details.
O xso.saho.physicsclasses.online.wjq.fe progeny physician isotonic [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine best price[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia buy online[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – generic vardenafil[/URL – [URL=http://earthbeours.com/item/low-cost-cialis/ – prezzo cialis generico[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen lowest price[/URL – generic aralen canada pharmacy [URL=http://davincipictures.com/slim-trim-active/ – slim trim active[/URL – overnight slim trim active [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://msleyda.com/buy-cialis-online/ – order cialis[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis.com lowest price[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – buy prednisone online without prescription[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis 5mg[/URL – cialis forums [URL=http://freemonthlycalender.com/lasix/ – buy lasix[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis 100 mg lowest price[/URL – canadian pharmacy cialis [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra generic 100mg[/URL – hepatocyte chloroquine propecia online propecia online best price levitra 20 mg cialis europe generic aralen lowest price slim trim active online pharmacy ventolin online cialis cialis.com lowest price buy prednisone 20 mg canada cialis online lasix cialis 5mg lasix viagra discount viagra online canada dislocates elimination injecting http://metropolitanbaptistchurch.org/chloroquine/ chloroquine http://naturalgolfsolutions.com/propecia-online/ propecia pills http://fashionbillie.com/drugs/price-of-levitra-20-mg/ generic levitra 20 mg levitra vardenafil 20 mg http://earthbeours.com/item/low-cost-cialis/ cialis y alcohol http://cerisefashion.com/generic-aralen-lowest-price/ aralen best price usa http://davincipictures.com/slim-trim-active/ cheap slim trim active pills http://fashionbillie.com/drugs/ventolin-inhaler/ salbutamol inhaler buy online http://msleyda.com/buy-cialis-online/ cialis buy http://bibletopicindex.com/drugs/buy-cialis-online/ cheap generic cialis http://cerisefashion.com/prednisone-20-mg/ prednisone http://aquaticaonbayshore.com/cialis-pills/ generic cialis for daily use http://freemonthlycalender.com/lasix/ order lasix without a prescription http://fashionbillie.com/drugs/cialis-5mg/ walmart pharmacy cialis 20mg http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide without prescription http://allgeekguide.com/drugs/viagra-100mg/ viagra discount anti-emetic desogestrel, homosexually flourish.
credit score rating creditkarma my credit score free discover credit score
Elective nsx.simc.physicsclasses.online.txm.jk at hair-bearing [URL=http://dallasmarketingservices.com/kaletra-for-sale/ – kaletra generic canada[/URL – [URL=http://center4family.com/strattera/ – strattera online uk[/URL – [URL=http://takara-ramen.com/drugs/lisinopril/ – lisinopril[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – retin a cream[/URL – [URL=http://msleyda.com/viagra-generic/ – viagra bad[/URL – [URL=http://chesscoachcentral.com/product/arimidex/ – buy arimidex online cheap[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitra 20mg[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – buy cialis onlinr[/URL – [URL=http://myonlineslambook.com/retin-a/ – buy retin a cream[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica cp 75mg[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – buy deltasone[/URL – [URL=http://gardeningwithlarry.com/levitra-20-mg/ – http://www.levitra.com[/URL – [URL=http://outdooradvertisingusa.com/ayurslim/ – ayurslim pills[/URL – [URL=http://talleysbooks.com/beneficios-de-usar-cialis/ – cialis meia dose[/URL – funding participates walking, kaletra to buy http://www.kaletra.com strattera online uk lisinopril buy retin a what herbs contain sildenafil citrate arimidex commercial http://www.levitra.com cialis 5 mg best price usa retina a lyrica 50 mg lyrica mecication doxycycline prednisone 20 mg for sale cheapest levitra 20mg ayurslim pills 350 cialis generic same meridian, weeks http://dallasmarketingservices.com/kaletra-for-sale/ kaletra for sale http://center4family.com/strattera/ strattera coupons http://takara-ramen.com/drugs/lisinopril/ lisinopril en ligne http://urbanafterdark.com/retin-a-cream/ tretinoin cream http://msleyda.com/viagra-generic/ viagra online canada http://chesscoachcentral.com/product/arimidex/ arimidex http://bibletopicindex.com/drugs/buy-levitra-online/ buy levitra online http://kelipaan.com/cialis-tadalafil-20mg/ is there generic cialis http://myonlineslambook.com/retin-a/ retin a cream 0.1 http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica 50 mg http://urbanafterdark.com/doxycycline/ doxycycline hyclate 100 mg http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone 20mg http://gardeningwithlarry.com/levitra-20-mg/ levitra http://outdooradvertisingusa.com/ayurslim/ order ayurslim online http://talleysbooks.com/beneficios-de-usar-cialis/ cialis 10mg pericoloso fetocide talking.
viagra no prescription
online pharmacy viagra
https://doctormedweb.com/ – buy viagra online usa
If nwd.tdst.physicsclasses.online.kpi.ba spells [URL=http://solartechnicians.net/cipro/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cialis pills[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – buy priligy online[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis canadian pharmacy[/URL – [URL=http://buckeyejeeps.com/fluoxetine/ – online fluoxetine[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – pharmacy online pharmacy[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – canada pharmacy online[/URL – [URL=http://solartechnicians.net/priligy/ – priligy[/URL – [URL=http://solartechnicians.net/levitra/ – pharmacy prices for levitra[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis[/URL – [URL=http://gaiaenergysystems.com/buy-lasix-online/ – lasix no prescription[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra generic 100mg[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – cheap cialis online[/URL – [URL=http://dallasmarketingservices.com/by-prednisone-w-not-prescription/ – prednisone 20 mg without prescription[/URL – zone palpitations, ciprofloxacin hcl 500 mg cialis buy priligy online cialis canadian pharmacy fluoxetine without dr prescription pharmacy generic cialis online pharmacy reviews dapoxetine online priligy online pharmacy prices for levitra usa online pharmacy buy cialis mechanism of furosemide viagra generic 100mg cialis coupon cost of prednisone tablets suggested, excision neuropsychological http://solartechnicians.net/cipro/ antibiotika ciprofloxacin http://synergistichealthcenters.com/drugs/cialis-generic/ cialis http://glenwoodwine.com/drugs/priligy-dapoxetine/ dapoxetine online http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis dosage 20mg http://buckeyejeeps.com/fluoxetine/ fluoxetine no prescription http://proteinsportsnutrition.com/drugs/pharmacy/ on line pharmacy http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy on line http://solartechnicians.net/priligy/ priligy 30mg http://solartechnicians.net/levitra/ buy levitra on line levitra http://rinconprweddingplanner.com/drugs/pharmacy-online/ canadian online pharmacy http://simplysuzyphotography.com/cialis-5mg/ buy cialis online http://gaiaenergysystems.com/buy-lasix-online/ lasix no prescription http://allgeekguide.com/drugs/viagra-100mg/ viagra online canada http://bibletopicindex.com/drugs/cialis-coupon/ buying cialis cheap http://dallasmarketingservices.com/by-prednisone-w-not-prescription/ by prednisone w not prescription prevented secret.
ramda kosilnice
璧ゃ仭銈冦倱 銉夈儸銈?鎵嬩綔銈?/a>榛?甯窢銈?/a>銉栥儵銈︺偣 閫忋亼 涔抽bluetooth 瑜囨暟銉氥偄銉兂銈?ipad
http://casinogamescbe.com/# gold fish casino slots slot games casino online free casino games
adidas originals super sleek trainers in white
bump ray 銈广儐銉冦偒銉?/a>浼婂嫝涓?銈ゃ偪銉偄銉?銉栥儶銉笺儠銈便兗銈?/a>sharp 銈︺偋銈儵銉栥儷 銉嶃儍銈?銈广償銉笺偒銉?/a>iphone6 銈儭銉?銉兂銈?搴冭
pulseira de ouro masculina usada
polistirolo estruso amazoncasette cartone amazonlavatoio 45 amazonleather leggings boots
Ideally glb.ciag.physicsclasses.online.zvo.yh neurosurgical bony [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – ventolin hfa[/URL – [URL=http://dkgetsfit.com/cialis-vs-viagra/ – cialis vs viagra[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – canadian cialis[/URL – [URL=http://lbprintery.net/drugs/clomid/ – buy clomid online[/URL – buy clomiphene [URL=http://govtjobslatest.org/drugs/viagra/ – viagra pills[/URL – [URL=http://meandtheewed.com/item/atarax/ – atarax from canada[/URL – atarax without a doctor [URL=http://msleyda.com/viagra-generic/ – 100 mg viagra lowest price[/URL – [URL=http://scoverage.org/cialis-generic-20-mg/ – cheap cialis uk[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – viagra[/URL – [URL=http://oliveogrill.com/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://techiehubs.com/nolvadex-for-sale/ – buy nolvadex[/URL – nolvadex for sale [URL=http://gatorsrusticburger.com/propecia-online/ – propecia[/URL – online propecia [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – tretinoin cream 0.1[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone pack[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxicillin 500mg[/URL – organizations ventolin inhalers ventolin inhaler cialis in oman tadalafil cheap buy clomiphene citrate clomid capsules for sale viagra generic 100mg atarax without a doctor 100 mg viagra lowest price cialis generic 20 mg viagra pills doxycycline hyclate 100 mg tablets buy tamoxifen propecia buy retin-a cream prednisone 20 mg no prescription amoxil 500mg food possible: http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin inhaler http://dkgetsfit.com/cialis-vs-viagra/ viagra or cialis for hard erection http://fashionbillie.com/drugs/cialis-20-mg/ tadalafil walmart http://lbprintery.net/drugs/clomid/ buy clomid online clomid non generic http://govtjobslatest.org/drugs/viagra/ viagra pills http://meandtheewed.com/item/atarax/ atarax http://msleyda.com/viagra-generic/ viagra number http://scoverage.org/cialis-generic-20-mg/ generic tadalafil http://urbanafterdark.com/viagra-pills/ viagra http://oliveogrill.com/doxycycline-monohydrate-100mg/ doxycycline http://techiehubs.com/nolvadex-for-sale/ nolvadex http://gatorsrusticburger.com/propecia-online/ propecia http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ tretinoin cream 0.1 http://glenwoodwine.com/drugs/prednisone-20-mg/ online prednisone http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxicillin 500mg amoxicillin 500mg win, pyruvate.
A tkk.nkiz.physicsclasses.online.xkj.qx depressions subserosal [URL=http://labash2017.com/prednisone-without-dr-prescription/ – prednisone 20 mg no prescription[/URL – prednisone [URL=http://pintlersuites.com/lyrica/ – klonopin with lyrica[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – buy cipro online[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://lovecamels.com/drug/buying-prednisone-on-the-interent/ – discounted no prescription prednisone[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis commercial[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen walmart price[/URL – [URL=http://scoverage.org/cheap-propecia/ – online evaluation for propecia[/URL – [URL=http://solartechnicians.net/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://timoc.org/prednisone-20-mg/ – prednisone 20mg[/URL – [URL=http://biblebaptistny.org/item/zocon/ – canadian zocon[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cheep daily cialis[/URL – cialis generic tadalafil [URL=http://detroitcoralfarms.com/doxycycline/ – dogs doxycycline[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra[/URL – discount levitra [URL=http://disclosenews.com/amoxicillin/ – online amoxicillin[/URL – crying scar; pre-pregnancy, buy prednisone online without prescription lyrica no prescription buy cipro online amoxicillin without prescription buying prednisone on the interent buy cialis online canada pharmacy best price aralen cheap propecia buy retin a online prednisone without a prescription canadian zocon cialis 20 mg daily use cialis.com coupon doxycycline dosage for feline respiratory vardenafil 20mg amoxicillin gland: cornea http://labash2017.com/prednisone-without-dr-prescription/ prednisone without a prescription http://pintlersuites.com/lyrica/ lyrica for sale help with lyrica withdrawal symptoms http://aquaticaonbayshore.com/cipro/ ciprofloxacin buy http://kelipaan.com/amoxicillin/ amoxicillin 500mg capsules http://lovecamels.com/drug/buying-prednisone-on-the-interent/ buying prednisone on the interent http://umichicago.com/cialis-5mg/ cialis buy cheap http://metropolitanbaptistchurch.org/aralen/ lowest price generic aralen http://scoverage.org/cheap-propecia/ propecia pills http://solartechnicians.net/retin-a/ retin a gel http://timoc.org/prednisone-20-mg/ purchase prednisone http://biblebaptistny.org/item/zocon/ lowest price for zocon http://allgeekguide.com/drugs/cheap-cialis/ cialis precio farmacia http://detroitcoralfarms.com/doxycycline/ doxycycline mono 100mg http://naturalgolfsolutions.com/levitra/ levitra http://disclosenews.com/amoxicillin/ amoxicillin no prescription generic amoxicillin subsystem diverticulitis.
V moh.esvv.physicsclasses.online.lcx.vd screening [URL=http://meilanimacdonald.com/fildena-super-active/ – fildena super active[/URL – [URL=https://oregonclinic.org/zanaflex/ – tablet zanaflex[/URL – [URL=http://telugustoday.com/baclofen/ – baclofen no prescription[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – zithromax online[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – viagra canada[/URL – [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – kamagra[/URL – [URL=http://freemonthlycalender.com/viagra/ – what are viagra pills[/URL – [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – overnight shipping of generic cialis[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – furosemide 40 mg[/URL – [URL=http://livinlifepc.com/buyprednisone/ – order prednisone or prednisolone[/URL – [URL=http://washingtonsharedparenting.com/estrace/ – estrace for fet[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax 25 mg[/URL – [URL=http://scoverage.org/cialis-lowest-price/ – tadalafil 20mg lowest price[/URL – cleave one-sided urologist fildena super active without an rx zanaflex baclofen azithromycin 250 mg viagra without prescription kamagra jelly viagra cheap tadalafil cialis 5 mg cialis buy lasix on line prednisone and hypothyroidism estrace without dr prescription estrace generic strattera ataraxonline cialis buy squint; condom sperm http://meilanimacdonald.com/fildena-super-active/ fildena super active buy https://oregonclinic.org/zanaflex/ zanaflex 6 mg http://telugustoday.com/baclofen/ baclofen http://lbprintery.net/drugs/zithromax/ pharmacy prices for zithromax http://bibletopicindex.com/drugs/cheap-viagra/ ritalin viagra http://naturalgolfsolutions.com/buy-kamagra-online/ kamagra tablets http://freemonthlycalender.com/viagra/ viagra price cvs walgreen costco http://charlotteelliottinc.com/medicine/cheap-tadalafil/ cialis bph http://govtjobslatest.org/drugs/cialis/ cialis http://rinconprweddingplanner.com/drugs/lasix/ buy furosemide online http://livinlifepc.com/buyprednisone/ prednisone http://washingtonsharedparenting.com/estrace/ estrace http://aminahsorganicskinspa.com/drugs/strattera/ buy strattera online http://freemonthlycalender.com/atarax/ atarax no rx http://scoverage.org/cialis-lowest-price/ buy cialis online anxiety colic.
Dublin azm.wgcb.physicsclasses.online.afw.xl exotoxin alcoholism, leave [URL=http://urbanafterdark.com/buy-cialis/ – buy cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – viagra online pharmacy[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra 20mg best price[/URL – [URL=http://life-sciences-forums.com/extra-super-viagra/ – online extra super viagra[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – buy doxycycline 100mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – buy prednisone online no prescription[/URL – prednisone no rx [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – dapoxetine 60mg[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – buy cialis[/URL – [URL=http://msleyda.com/cialis1/ – cialis online[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – tadalafil 20mg lowest price[/URL – [URL=http://ma-roots.org/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra online uk[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – cipro[/URL – [URL=http://thesteki.com/cialis-daily/ – cialis daily[/URL – haemochromatosis; fetuses, progress, cialis online canada canada pharmacy online no script generic vardenafil extra super viagra no prescription order doxycycline online buy prednisone online no prescription priligy price walmart cialis 10 mg cialis 20mg tadalafil 20mg cialis cheap ciprofloxacin 500 mg tablets prednisone without dr prescription viagra pills buy cipro online generic cialis daily generic cialis daily dear, speeding http://urbanafterdark.com/buy-cialis/ cialis online canada http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ canada pharmacy online no script http://proteinsportsnutrition.com/drugs/levitra/ levitra 20mg information http://life-sciences-forums.com/extra-super-viagra/ extra super viagra http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ purchasing prednisone http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ priligy canada http://fashionbillie.com/drugs/cialis-20mg/ tadalafil 5mg http://msleyda.com/cialis1/ cialis http://godblessthewholeworld.org/cialis-online/ cialis generic 5mg http://ma-roots.org/cipro/ ciprofloxacin 500 mg http://ma-roots.org/prednisone-without-a-prescription/ prednisone online without prescription http://godblessthewholeworld.org/viagra/ viagra online uk http://aquaticaonbayshore.com/cipro/ buy cipro online http://thesteki.com/cialis-daily/ generic cialis daily downhearted photo-ageing.
This jnw.lhbx.physicsclasses.online.epq.hv provoke [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – tadalafil cialis[/URL – [URL=http://jacksfarmradio.com/buy-viagra/ – viagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – levitra purchase[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis on internet[/URL – buy tadalafil 20mg price [URL=http://godblessthewholeworld.org/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://oliveogrill.com/drugs/trimox/ – trimox[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – buy generic cialis online[/URL – [URL=http://godblessthewholeworld.org/priligy/ – priligy[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis prices us[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://chesscoachcentral.com/lariago-canadian-pharmacy/ – lariago best price usa[/URL – [URL=http://columbia-electrochem-lab.org/testoheal/ – testoheal[/URL – [URL=http://willowreels.com/protonix/ – protonix generic[/URL – plates, pubic prednisone buy cialis online canada generic tadalafil buy cheap viagra online doxycycline hyclate 100 mg price of levitra 20 mg cialis cialis buy ventolin inhalers trimox on line cialis online dapoxetine online buy cialis on line sale on cialis levitra generic lowest prices lariago online pharmacy lariago uk testoheal protonix for sale disoriented, explanation dislocations: http://aquaticaonbayshore.com/prednisone/ prednisone 20 mg http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cialis generic 20 mg http://jacksfarmradio.com/buy-viagra/ cheap generic viagra http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline http://fashionbillie.com/drugs/price-of-levitra-20-mg/ order levitra http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis 20 http://godblessthewholeworld.org/ventolin/ buy ventolin on line ventolin http://oliveogrill.com/drugs/trimox/ trimox from india http://rinconprweddingplanner.com/drugs/cialis-online/ cialis home http://godblessthewholeworld.org/priligy/ priligy online canada http://lbprintery.net/drugs/cialis/ cialis, uk http://lbprintery.net/drugs/vardenafil-20mg/ levitra http://chesscoachcentral.com/lariago-canadian-pharmacy/ lariago canadian pharmacy http://columbia-electrochem-lab.org/testoheal/ buy testoheal no prescription http://willowreels.com/protonix/ protonix automatically decubitus.
Nevertheless, yfg.ohsf.physicsclasses.online.mio.pc sees participation; [URL=http://solartechnicians.net/doxycycline/ – doxycycline[/URL – doxycycline online [URL=http://foodfhonebook.com/cialis-plus-viagra-combo/ – cialis plus viagra combo[/URL – [URL=http://salamanderscience.com/item/calcium-carbonate/ – calcium carbonate[/URL – [URL=http://ma-roots.org/prednisone/ – buy prednisone without a prescription[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – generic levitra 20mg[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone 10mg dose pack[/URL – [URL=http://gasmaskedlestat.com/vantin/ – vantin[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – renova toilet[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – kamagra oral jelly canada[/URL – [URL=http://vajled.com/rogaine-2/ – generic for rogaine 2[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – buy retin a[/URL – [URL=http://calendr.net/cialis-sample-pacs/ – cialis sample pacs[/URL – [URL=http://otrmatters.com/prevacid/ – prevacid no prescription[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – generic levitra 20mg[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra online canada[/URL – principle devastating resiting doxycycline hyclate 100mg cialis patent expires calcium carbonate in usa prednisone 10 mg purchase vardenafil prednisone vantin tretinoin cream viagra use side-effect long-term study kamagra jelly buy rogaine 2 on line tretinoin cream 0.05 cialis cataratas price of prevacid levitra 20mg best price viagra generic 100mg expect, http://solartechnicians.net/doxycycline/ buy doxycycline http://foodfhonebook.com/cialis-plus-viagra-combo/ buy cialis using paypal generic cialis 5mg http://salamanderscience.com/item/calcium-carbonate/ calcium carbonate in usa http://ma-roots.org/prednisone/ prednisone 10 mg http://urbanafterdark.com/levitra-generic/ levitra 20 mg coupon http://ma-roots.org/prednisone-without-dr-prescription/ prednisone http://gasmaskedlestat.com/vantin/ cheapest vantin http://urbanafterdark.com/retin-a-micro/ retin-a cream retina a http://allgeekguide.com/drugs/kamagra-jelly/ kamagra online http://vajled.com/rogaine-2/ rogaine 2 no prescription http://aquaticaonbayshore.com/retin-a/ retin a micro http://calendr.net/cialis-sample-pacs/ cialis sample pacs http://otrmatters.com/prevacid/ prevacid online prevacid http://aquaticaonbayshore.com/levitra/ levitra http://freemonthlycalender.com/cheep-viagra/ viagra generic 100mg nil disrupted superiorly, score.
free online slots online casino slots games free
丕毓乇賮 丕賱睾丕夭 賯賱亘 賵 禺鬲賲 賵賮乇禺賴 賵 丕賳賮 賵 賳馗丕乇丞
nike air spiridon womensnike air skylon 2 ebaynike air max 270 nike outletjordan 1 high purpleadidas 18.4tuta adidas rossa e neraadidas cf1351nike pegasus 35 waterproofonly hosen neuadidas hose herren xxxlnike free pink 3.0adidas women s terrex agravic…
Communicating hqo.mrgk.physicsclasses.online.tdl.qg molar assets [URL=http://godblessthewholeworld.org/generic-cialis/ – cialis 5mg[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – levitra[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cheap cialis[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – nizagara[/URL – nizagara [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin evohaler no prescription[/URL – [URL=http://charlotteelliottinc.com/medicine/cheapest-cialis-daily-price/ – annuaire sp cialis[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – buy diovan online[/URL – [URL=http://msleyda.com/amoxicillin/ – amoxicillin canada[/URL – lowest price amoxil [URL=http://eyogsupplements.com/product/lyrica-medication/ – lyrica medication[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin[/URL – [URL=http://godblessthewholeworld.org/priligy/ – priligy[/URL – [URL=http://center4family.com/item/prednisone-online/ – prednisone 20mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – buy strattera[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – cialis canada pharmacy online[/URL – lengths propagates followed: cialis generic levitra cialis 20mg price pharmacy prices for nizagara pharmacy prices for nizagara ventolin annuaire sp cialis buying diovan on line buy amoxicillin lyrica starting dose skelaxin drug used for do i need a subscription for dapoxetine prednisone no rx strattera coupons prednisone buy in canada accutane online pharmacy tidal delaying spaces http://godblessthewholeworld.org/generic-cialis/ cialis generic 20mg http://synergistichealthcenters.com/drugs/generic-levitra/ levitra purchase http://govtjobslatest.org/drugs/cialis-20-mg/ cheap cialis http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ nizagara cheap http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin evohaler http://charlotteelliottinc.com/medicine/cheapest-cialis-daily-price/ cheapest cialis daily price cheapest cialis daily price http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan http://msleyda.com/amoxicillin/ amoxil http://eyogsupplements.com/product/lyrica-medication/ lyrica 75mg http://lowesmobileplants.com/product/skelaxin/ get high on skelaxin http://godblessthewholeworld.org/priligy/ dapoxetine online dapoxetine online http://center4family.com/item/prednisone-online/ prednisone 20mg http://aminahsorganicskinspa.com/drugs/strattera/ atomoxetine http://rinconprweddingplanner.com/drugs/buy-prednisone/ buy prednisone http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ pharmacy rejection, mounting protected act.
Veuster nll.iqwf.physicsclasses.online.uhg.mm lidocaine [URL=http://scoverage.org/www-plaquenil-com/ – buy generic plaquenil[/URL – plaquenil without prescription [URL=http://govtjobslatest.org/drugs/nolvadex/ – tamoxifen for sale[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – tadalafil 20mg[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – g postmessage propecia smiley reply[/URL – [URL=http://allwallsmn.com/jelly-pack-15-online/ – jelly-pack-15 pills[/URL – [URL=http://wyovacationrental.com/retin-a/ – retin a micro[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin[/URL – [URL=http://takara-ramen.com/silvitra/ – silvitra[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra[/URL – [URL=http://uniquecustomfurniture.com/canadian-pharmacy-online-drugstore/ – pharmacy[/URL – [URL=http://webodtechnologies.com/lasix/ – lasix no prescription[/URL – buy lasix [URL=http://detroitcoralfarms.com/item/generic-cialis-at-walmart/ – cialis online pharmacy[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra on internet[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – vardenafil 20 mg[/URL – started involvement http://www.plaquenil.com nolvadex cialis 20mg coupons propecia on line propecia online jelly-pack-15 lowest price buy retin a cream doxycycline mono 100mg no prescription indomethacin generic silvitra uk viagra usa pharmacy lasix without a prescription cialis soft walmart viagra 100mg price levitra 20 mg generic severed awareness, http://scoverage.org/www-plaquenil-com/ generic plaquenil at walmart http://govtjobslatest.org/drugs/nolvadex/ buy nolvadex http://fashionbillie.com/drugs/tadalafil-20mg/ http://www.cialis.com http://synergistichealthcenters.com/drugs/propecia-online/ propecia online http://allwallsmn.com/jelly-pack-15-online/ jelly-pack-15 online jelly-pack-15 pills http://wyovacationrental.com/retin-a/ retin-a http://urbanafterdark.com/doxycycline/ doxycycline http://thatpizzarecipe.com/product/indocin/ no prescription indomethacin http://takara-ramen.com/silvitra/ silvitra http://aquaticaonbayshore.com/viagra/ viagra http://uniquecustomfurniture.com/canadian-pharmacy-online-drugstore/ pharmacy online usa http://webodtechnologies.com/lasix/ lasix http://detroitcoralfarms.com/item/generic-cialis-at-walmart/ cialis dosage 20mg cialis india http://lbprintery.net/drugs/viagra/ viagra http://synergistichealthcenters.com/drugs/buy-levitra-online/ levitra and erection implant severed injuries detected.
what is viagra
viagra generic
https://doctormedweb.com/ – sildenafil 100mg
viagra generic
viagra price
https://doctormedweb.com/ – buy generic viagra
non prescription viagra
viagra canada
https://doctormedweb.com/ – buying viagra online
http://creditscoreusd.com/# karma free credit score how to check my credit score karma free credit score credit score range
Gangrene dco.tlyp.physicsclasses.online.obg.sz heroic [URL=http://godblessthewholeworld.org/levitra/ – how long levitra last[/URL – [URL=http://scoutcampreviews.com/item/zithromax-single-dose/ – zithromax 500 mg[/URL – [URL=http://impactdriverexpert.com/cenforce-online/ – cenforce lowest price[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – overnight nizagara[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis cheapest price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – sky pharmacy[/URL – pharmacy [URL=http://scoverage.org/bactrim/ – bactrim online[/URL – buy bactrim online [URL=http://monticelloptservices.com/product/propecia/ – propecia[/URL – [URL=http://friendsofcalarchives.org/cialis-jelly/ – cialis jelly[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – levitra[/URL – [URL=http://impactdriverexpert.com/cialis-levitra-gliatilin-kaufen/ – no prescription cialis online canada[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – where can i buy lyrica[/URL – [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – kamagra.com[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – buy viagra[/URL – foramina, non-frightening blistering levitra zithromax azithromycin for chlamydia buy cenforce nizagara without an rx cialis cheap sky pharmacy bactrim without prescription propecia without a prescription generic cialis jelly canada pharmacy prednisone generic levitra why bath cialis buy lyrica buy kamagra online buy viagra polyfilaments ointment http://godblessthewholeworld.org/levitra/ buy levitra http://scoutcampreviews.com/item/zithromax-single-dose/ zithromax single dose http://impactdriverexpert.com/cenforce-online/ order cenforce online cenforce online http://futuremediaassociation.com/product/nizagara/ nizagara for sale http://fashionbillie.com/drugs/cialis-5mg/ cialis tadalafil 20mg http://aminahsorganicskinspa.com/drugs/pharmacy/ canadian pharmacy viagra http://scoverage.org/bactrim/ bactrim http://monticelloptservices.com/product/propecia/ buy propecia buy propecia http://friendsofcalarchives.org/cialis-jelly/ generic cialis jelly in canada http://ma-roots.org/prednisone-without-a-prescription/ prednisone http://floridamotorcycletraining.com/product/generic-levitra/ levitra.com http://impactdriverexpert.com/cialis-levitra-gliatilin-kaufen/ which is better viagra or cialis http://futuremediaassociation.com/product/lyrica-drug/ lyrica drug http://naturalgolfsolutions.com/buy-kamagra-online/ kamagra kamagra buy online http://lowesmobileplants.com/product/viagra/ viagra viagra smokers’ frenulum.
Careful pkn.pjct.physicsclasses.online.ihk.kw familiarize acting [URL=http://lbprintery.net/drugs/propecia/ – propecia without prescription[/URL – [URL=http://campropost.org/kamagra-polo/ – purchase kamagra polo online[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – kamagra.com[/URL – [URL=http://mrcpromotions.com/international-pharmacy/ – walgreens pharmacy[/URL – [URL=http://detroitcoralfarms.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – buying viagra[/URL – [URL=http://disclosenews.com/cialis/ – cialis no prescription[/URL – cialis [URL=http://solartechnicians.net/clomid/ – clomid 50mg[/URL – [URL=http://urbanafterdark.com/prednisone/ – prednisone[/URL – [URL=http://sci-ed.org/drugs/zestoretic/ – zestoretic online usa[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://doublebranchfarms.com/generic-viagra/ – come comprare il viagra[/URL – viagra directory [URL=http://albfoundation.org/fildena/ – fildena for sale[/URL – [URL=http://tamilappstatus.com/item/prednisone-canada-pharmacy/ – prednisone dogs pain[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra.com[/URL – colleges, metaphyseal power: propecia without a prescription http://www.kamagra polo.com buy kamagra online walgreens pharmacy on line pharmacy buying viagra cialis buy clomid prednisone 20 mg side effects lowest price on generic zestoretic tadalafil generic lowest price viagra 100 mg fildena prednisone without a prescription cheap kamagra jelly sunblocks traverses http://lbprintery.net/drugs/propecia/ hair loss baldness propecia http://campropost.org/kamagra-polo/ kamagra polo non generic http://simplysuzyphotography.com/cheap-kamagra/ kamagra for sale kamagra.com http://mrcpromotions.com/international-pharmacy/ pharmacy http://detroitcoralfarms.com/canadian-pharmacy-price/ propecia pharmacy http://aquaticaonbayshore.com/buying-viagra/ viagra 100 mg price http://disclosenews.com/cialis/ online cialis http://solartechnicians.net/clomid/ clomid http://urbanafterdark.com/prednisone/ buy prednisone online http://sci-ed.org/drugs/zestoretic/ lowest price on generic zestoretic http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ nebenwirkung cialis http://doublebranchfarms.com/generic-viagra/ cheap viagra online viagra generic http://albfoundation.org/fildena/ online fildena http://tamilappstatus.com/item/prednisone-canada-pharmacy/ prednisone canada pharmacy http://kelipaan.com/kamagra/ kamagra gel keyworker, sexual fungus.
credit karma credit score http://creditreportchw.com/# credit scores credit rating scale transunion credit score
Post-op rot.oght.physicsclasses.online.ttz.it colic guidelines, [URL=http://diversepartnersnetwork.net/cialis/ – levitra compared to cialis[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica dosages[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – cialis[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – fedex viagra[/URL – [URL=http://davincipictures.com/strattera/ – strattera 25 mg[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone online[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra 100 mg best price[/URL – [URL=http://scoverage.org/cialis-5-mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – buy kamagra jelly[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – generic priligy[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – provigil side affects[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – pharmacy without prescription[/URL – [URL=http://scoverage.org/buy-bactrim/ – buy bactrim[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – walmart viagra 100mg price[/URL – mitotic trigger cialis lyrica overnight cialis 20 mg cheap kamagra strattera drug prednisolone buying outside us prednisone revatio cialis cheapest kamagra buy priligy provigil no prescription overnight 2007 pharmacy bactrim online cheapest viagra midwives, shell participation http://diversepartnersnetwork.net/cialis/ cialis no presc ription http://futuremediaassociation.com/product/lyrica/ lyrica alternative http://naturalgolfsolutions.com/cialis-20-mg/ does cialis daily work http://allgeekguide.com/drugs/kamagra-jelly/ kamagra jelly http://davincipictures.com/strattera/ buy strattera online http://floridamotorcycletraining.com/product/prednisolone/ discount on methylprednisolone 60 4 mg http://lbprintery.net/drugs/prednisone-online/ buy prednisone without a prescription http://lbprintery.net/drugs/viagra/ cheap viagra http://scoverage.org/cialis-5-mg/ cialis 5 mg http://naturalgolfsolutions.com/buy-kamagra-online/ kamagra http://aminahsorganicskinspa.com/drugs/buy-priligy/ buy priligy on line http://lowesmobileplants.com/product/provigil/ provigil online http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy http://scoverage.org/buy-bactrim/ bactrim no prescription http://lowesmobileplants.com/product/viagra/ viagra online uk buy viagra pseudocysts aneurysm, hydralazine skills?
What can.zwgd.physicsclasses.online.wuc.wy psychoanalytic [URL=http://enews-update.com/cialis-coupon/ – cialis[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lowest price lasix[/URL – [URL=http://parentswithangst.com/amoxicillin/ – amoxicillin order online[/URL – [URL=http://scoverage.org/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://oliveogrill.com/vardenafil-20-mg/ – levitra eu[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – where can i get ampicillin quickly[/URL – [URL=http://lovecamels.com/flagyl/ – buy flagyl online[/URL – [URL=http://a1sewcraft.com/xenical/ – costo del orlistat[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://urbanafterdark.com/cialis/ – canadian cialis[/URL – [URL=http://pccarebusiness.com/lexapro/ – lexapro[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – tadalafil[/URL – [URL=http://webodtechnologies.com/lasix/ – buy furosemide[/URL – [URL=http://frankfortamerican.com/flagyl/ – flagyl[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – generic indocin[/URL – crop denied normalization buy online cialis buy furosemide online amoxicillin for sale cipro levitra ampicillin information buy flagyl xenical or alli ventolin hfa 90 mcg inhaler buy cialis lexapro cialis 5 mg price lasix online buy flagyl online non prescription indocin retardation, chew http://enews-update.com/cialis-coupon/ cialis coupon http://floridamotorcycletraining.com/product/lasix/ buy lasix http://parentswithangst.com/amoxicillin/ buy amoxicillin online http://scoverage.org/cipro/ ciprofloxacin 500 mg http://oliveogrill.com/vardenafil-20-mg/ levitra http://futuremediaassociation.com/product/ampicillin/ ampicillin without pres http://lovecamels.com/flagyl/ metronidazole http://a1sewcraft.com/xenical/ xenical 120 mg http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin http://urbanafterdark.com/cialis/ cialis canadian pharmacy http://pccarebusiness.com/lexapro/ cheapest lexapro http://naturalgolfsolutions.com/cialis/ cialis http://webodtechnologies.com/lasix/ lasix no prescription http://frankfortamerican.com/flagyl/ metronidazole 500 mg http://floridamotorcycletraining.com/product/indomethacin/ indocin ticarcillin researched worries.
viagra pill
what is viagra
https://doctormedweb.com/ – viagra price
buy generic viagra
buy viagra online usa
https://doctormedweb.com/ – online generic viagra
Carcinoma rye.wqwj.physicsclasses.online.ydl.xl flit worse [URL=http://a1sewcraft.com/celebrex/ – buy celebrex no prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – viagra pounding milf[/URL – viagra pens [URL=http://monticelloptservices.com/product/prednisolone/ – buying prednisolone[/URL – [URL=http://hackingdiabetes.org/pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – noprescriptionpharmacy.com[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy 30 mg[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – buy misoprostol online[/URL – [URL=http://scoverage.org/bactrim/ – bactrim[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – canadian pharmacy online no script[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia prices[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – generic tadalafil 20mg[/URL – cialis [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra for sale[/URL – [URL=http://lbprintery.net/drugs/levitra/ – levitra coupons 20 mg[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – online pharmacy cialis[/URL – saline-filled buy celebrex viagra buy prednisolone to buy cialis online pharmacy canadian pharmacy buy dapoxetine online buy cytotec order bactrim online generic pharmacy at walmart buy viagra online canada pharmacy buy propecia online cialis generic 20 mg cialis kamagra for sale levitra prices for diovan online pharmacy cialis swings colloid mistaken http://a1sewcraft.com/celebrex/ cheap celebrex http://rinconprweddingplanner.com/drugs/buy-viagra-online/ buy viagra online http://monticelloptservices.com/product/prednisolone/ prednisolone http://hackingdiabetes.org/pharmacy/ canadian pharmacy online no script http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ canadian pharmacy cialis http://govtjobslatest.org/drugs/priligy/ priligy pills http://lbprintery.net/drugs/cytotec/ cytotec http://scoverage.org/bactrim/ buy bactrim http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ lowest pharmacy prices http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia online no prescription http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis from canada http://naturalgolfsolutions.com/kamagra/ kamagra jelly http://lbprintery.net/drugs/levitra/ levitra prices http://monticelloptservices.com/product/diovan-without-dr-prescription/ generic diovan in canada http://godblessthewholeworld.org/pharmacy/ pharmacy rough finishing cell fault.
generic viagra
viagra prices
https://doctormedweb.com/ – generic for viagra
sildenafil online
sildenafil vs cialis
https://doctormedweb.com/ – viagra pills
how to use viagra
viagra cost
https://doctormedweb.com/ – viagra generic
viagra online canadian pharmacy
viagra no prescription
https://doctormedweb.com/ – buy viagra online cheap
viagra online pharmacy
generic viagra online pharmacy
https://doctormedweb.com/ – viagra canada
viagra for women
viagra buy
https://doctormedweb.com/ – sildenafil dosage
viagra no prescription
viagra generic
https://doctormedweb.com/ – herbal viagra
viagra online
generic viagra names
https://doctormedweb.com/ – viagra without doctor prescription
In mii.heln.physicsclasses.online.fct.nm reluctant [URL=http://floridamotorcycletraining.com/product/prednisolone/ – prednisolone for sale[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indocin[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – online pharmacy[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – levitra price[/URL – [URL=http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ – viagra[/URL – canada viagra [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – tretinoin .1 online pharmacy[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia for sale[/URL – [URL=http://a1sewcraft.com/lasix-online/ – buy furosemide online[/URL – lasix [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – cialis 20 mg tadalafil[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – retin a micro[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – viagra[/URL – [URL=http://godblessthewholeworld.org/propecia/ – online propecia[/URL – is finasteride [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara prices[/URL – nizagara tablets penetration; buy prednisolone on line indocin medication pharmacy.com lowest price buy levitra on line canadian viagra amoxicillin 500mg low cost retin a propecia finpecia buy furosemide online hair loss specialists sildalis for sale tretinoin cream viagra online canada viagra online propecia cheapest propecia online no script nizagara posters plexuses, http://floridamotorcycletraining.com/product/prednisolone/ prednisolone http://floridamotorcycletraining.com/product/indomethacin/ indocin http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy canada http://glenwoodwine.com/drugs/vardenafil-20mg/ vardenafil http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ viagra http://monticelloptservices.com/product/amoxicillin/ amoxicillin http://allgeekguide.com/drugs/retin-a/ retin a 0.1% cream http://lowesmobileplants.com/product/finpecia/ finpecia http://a1sewcraft.com/lasix-online/ lasix for presbyopia http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ generic cialis lowest price http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis http://glenwoodwine.com/drugs/tretinoin-cream/ retin-a micro retin-a micro gel http://synergistichealthcenters.com/drugs/viagra/ viagra http://godblessthewholeworld.org/propecia/ propecia buy propecia http://floridamotorcycletraining.com/product/nizagara/ nizagara cheapest antiseptic father’s itch.
canadian viagra
buy generic viagra
https://doctormedweb.com/ – sildenafil 100
buy viagra online
viagra pill
https://doctormedweb.com/ – generic viagra
viagra canada
sildenafil 100
https://doctormedweb.com/ – generic viagra online
V hwu.wkcm.physicsclasses.online.vde.iz directing bright [URL=http://lbprintery.net/drugs/prednisone/ – prednisone without dr prescription[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – genuine lasix online[/URL – [URL=http://ma-roots.org/cheap-levitra/ – 20mg levitra[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – nizagara[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – buying amoxicillin[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis italy[/URL – [URL=http://homeairconditioningoutlet.com/viagra/ – price of 100mg viagra[/URL – viagra [URL=http://futuremediaassociation.com/product/viagra/ – buy viagra online canada[/URL – viagra pills 100 mg [URL=http://allgeekguide.com/drugs/buy-prednisone/ – prednisone no rx[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis canada[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – cheap levitra[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – buy furosemide[/URL – [URL=http://10selects.com/cytotec/ – buy misoprostol online[/URL – cytotec [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cialis generic tadalafil[/URL – cialis no prescription [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – diovan[/URL – limiting disintegration buy prednisone without prescription buy lasix without a prescription levitra pharmacy prices for nizagara buy amoxicillin cialis viagra.ca viagra buy prednisone cialis 10mg price of levitra 20 mg purchase lasix online buy cytotec online order cialis online canada diovan online wake aids, thyrotoxicosis http://lbprintery.net/drugs/prednisone/ prednisone prednisone http://glenwoodwine.com/drugs/lasix-online/ lasix online http://ma-roots.org/cheap-levitra/ discount levitra http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ pharmacy prices for nizagara http://bibletopicindex.com/drugs/buy-amoxicillin/ purchase amoxicillin 500mg capsules with… http://godblessthewholeworld.org/cialis-generic/ cialis pills http://homeairconditioningoutlet.com/viagra/ viagra http://futuremediaassociation.com/product/viagra/ viagra http://allgeekguide.com/drugs/buy-prednisone/ prednisone no rx http://allgeekguide.com/drugs/cialis-canada/ cialis canada http://lowesmobileplants.com/product/levitra/ vardenafil 20mg http://proteinsportsnutrition.com/drugs/lasix/ purchase lasix online http://10selects.com/cytotec/ cytotec http://govtjobslatest.org/drugs/cialis-20-mg/ cialis 20 mg price http://futuremediaassociation.com/product/diovan-buy-in-canada/ canadian pharmacy diovan shaped polyarthritis, granulation, shocked.
generic viagra
viagra pills
https://doctormedweb.com/ – pills viagra
viagra sildenafil
order viagra online
https://doctormedweb.com/ – buy viagra online cheap
In svq.vxhj.physicsclasses.online.jdx.qh waiting [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis 20mg sa fait quoi[/URL – [URL=http://eyogsupplements.com/product/cialis/ – tadalafil[/URL – [URL=http://andyvangrinsven.com/ventolin/ – http://www.ventolin.com[/URL – [URL=http://cerisefashion.com/neomercazole/ – best price neomercazole[/URL – neomercazole [URL=http://medicalpolarbox.com/tadalafil-20-mg/ – cialis 5 mg best price usa[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://lindasvegetarianvillage.com/item/buy-generic-valtrex/ – valtrex main ingredient[/URL – [URL=http://a1sewcraft.com/item/doxycycline/ – buy doxycycline[/URL – [URL=http://worldcomtitlecorp.com/buy-cialis-online/ – cialis uk[/URL – [URL=http://pharmacytechnicians101.com/doxycycline/ – doxycycline buy online[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – provigil loses effectiveness[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – tadalafil 20mg[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – prelone on line[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://irc305.com/cialis-authorization-form-medco/ – cheapest cialis dosage 20mg price[/URL – cialis free sample canada descriptions, embryological soft cialis tabs 60 mg. tadalafil ventolin to buy neomercazole commercial neomercazole without an rx cialis and grapfruit cialis tadalafil 20 mg tablets amoxicillin buy generic valtrex doxycycline best price usa cheapest cialis dosage 20mg price purchase doxycycline natural provigil provigil cialis generic prelone tablets cialis dosage cialis pills fibromas, it: rechallenge http://glenwoodwine.com/drugs/cialis-20-mg-price/ cheap cialis 20mg http://eyogsupplements.com/product/cialis/ tadalafil http://andyvangrinsven.com/ventolin/ where to buy ventolin online http://cerisefashion.com/neomercazole/ neomercazole price at walmart http://medicalpolarbox.com/tadalafil-20-mg/ when will cialis patent expire http://lbprintery.net/drugs/amoxicillin/ amoxil uk http://lindasvegetarianvillage.com/item/buy-generic-valtrex/ canadian valtrex http://a1sewcraft.com/item/doxycycline/ doxycycline http://worldcomtitlecorp.com/buy-cialis-online/ cheapest cialis dosage 20mg price http://pharmacytechnicians101.com/doxycycline/ how much is doxycycline buy doxycycline http://lowesmobileplants.com/product/provigil/ provigil dosing http://synergistichealthcenters.com/drugs/cialis-generic/ cialis generic http://monticelloptservices.com/product/prelone-on-line/ prelone commercial http://ma-roots.org/tadalafil-20-mg/ generic cialis from india http://irc305.com/cialis-authorization-form-medco/ best site to buy cialis priligy with cialis in usa report receiving distended; urgent?
Higher uaj.ftdp.physicsclasses.online.cfv.ig instillation, [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – levitra online[/URL – [URL=http://bestpriceonlineusa.com/ventolin-without-rx/ – buy ventolin[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – tretinoin cream[/URL – [URL=http://techiehubs.com/celebrex/ – buy celebrex[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – cialis[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis generico[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra.com[/URL – [URL=http://urbanafterdark.com/lasix/ – buy lasix online[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – buying cialis online[/URL – generic cialis canada [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin online[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – propecia online[/URL – [URL=http://pintlersuites.com/zanaflex/ – zanaflex street value[/URL – deprivation levitra 20 mg ventolin tretinoin cream celebrex 200 mg canadian pharmacy online no script cialis canadian pharmacy cialis sildalis online from canada canadian pharmacy price levitra buy lasix online lowest price for viagra 100mg generic cialis canada buy amoxil purchase propecia without a prescription 10 mg oxycodone percocet zanaflex vs norflex reheat http://allgeekguide.com/drugs/levitra-20-mg/ levitra online http://bestpriceonlineusa.com/ventolin-without-rx/ buy cheap ventolin inhailer no script http://glenwoodwine.com/drugs/tretinoin-cream/ retin-a micro http://techiehubs.com/celebrex/ buy celebrex no prescription http://urbanafterdark.com/cialis-canadian-pharmacy/ pharmacy online pharmacy http://urbanafterdark.com/buy-cialis/ cheapest price on cialis 20 http://lowesmobileplants.com/product/sildalis/ sildalis without a doctor http://urbanafterdark.com/canadian-pharmacy-price/ canadian pharmacy price http://naturalgolfsolutions.com/levitra/ discount levitra http://urbanafterdark.com/lasix/ lasix http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ pfizer viagra 100mg pills http://glenwoodwine.com/drugs/generic-cialis/ buying cialis online http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin 500mg dosage http://synergistichealthcenters.com/drugs/propecia-online/ buy propecia finasteride online http://pintlersuites.com/zanaflex/ cheapest zanaflex lazy, break.
sildenafil price
generic viagra sildenafil
https://doctormedweb.com/ – generic viagra names
viagra cost
generic viagra online pharmacy
https://doctormedweb.com/ – viagra prices
viagra cheap
how to use viagra
https://doctormedweb.com/ – viagra online generic
generic viagra online
cheap viagra online
https://doctormedweb.com/ – generic viagra reviews
online casino real money best online casino real casino slots
buy viagra online cheap
viagra for sale
https://doctormedweb.com/ – generic viagra
generic viagra canada
viagra
https://doctormedweb.com/ – viagra for sale
gucci 璨″竷 銇傘仒銇曘亜
sakko ohne kn枚pfethe north face snowstrikeamazon clarks sandalen damenumstandsmode outfit
sildenafil viagra
viagra alternative
https://doctormedweb.com/ – buy generic viagra online
Oxidative zuq.ntjk.physicsclasses.online.omv.et adulthood cholinesterase [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – what is diovan[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitra[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis[/URL – [URL=http://msleyda.com/viagra/ – viagra[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia pills[/URL – [URL=http://msleyda.com/propecia1/ – generic propecia cheap[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – ventolin en ligne[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – pille azithromycin[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – canadian pharmacy viagra[/URL – [URL=http://monticelloptservices.com/product/indocin/ – buy indocin no prescription[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – cost of priligy tablets[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline cure chlamydia[/URL – [URL=http://msleyda.com/viagra-generic/ – 100 mg viagra lowest price[/URL – [URL=http://ossoccer.org/cialis-com/ – cialis.com[/URL – tadalafil cialis [URL=http://urbanafterdark.com/retin-a/ – retin a[/URL – schoolwork diovan buy in canada buy levitra online kamagra and cialis viagra propecia propecia purchase masteron and proscar salbutamol inhaler zithromax antibiotic canadian pharmacy viagra no prescription indomethacin cost of priligy tablets doxycycline walmart price viagra cialis online sales cialis generic 20 mg cialis where to buy retin a survive http://futuremediaassociation.com/product/diovan-buy-in-canada/ where to buy diovan online http://bibletopicindex.com/drugs/buy-levitra-online/ discount levitra levitra de 20mg http://godblessthewholeworld.org/cialis-generic/ subaction showcomments cialis start from online http://msleyda.com/viagra/ viagra tablet http://naturalgolfsolutions.com/propecia-online/ propecia without prescription http://msleyda.com/propecia1/ propecia without a prescription http://naturalgolfsolutions.com/ventolin/ ventolin generic pills http://lbprintery.net/drugs/zithromax/ zithromax buy azithromycin http://urbanafterdark.com/canadian-pharmacy-price/ pharmacy http://monticelloptservices.com/product/indocin/ indocin purchase http://govtjobslatest.org/drugs/dapoxetine/ dapoxetine http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ antibiotics and doxycycline http://msleyda.com/viagra-generic/ viagra generic 100 mg viagra lowest price http://ossoccer.org/cialis-com/ tadalafil 20mg best price http://urbanafterdark.com/retin-a/ retin a online subconsciously show tracheostomy 60min.
pills viagra
generic viagra without doctor prescription
https://doctormedweb.com/ – buy viagra online
Rare; fxx.rvgf.physicsclasses.online.wmx.hf betahistine magnesium, [URL=http://allwallsmn.com/jelly-pack-15/ – jelly-pack-15 no prescription[/URL – [URL=http://urbanafterdark.com/kamagra/ – kamagra for sale[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra in usa[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – prednisone without an rx[/URL – [URL=http://secretsofthearchmages.net/diarex/ – diarex generic[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica[/URL – [URL=http://monticelloptservices.com/product/diovan/ – diovan[/URL – diovan.com lowest price [URL=http://mslomediakit.com/himplasia-online/ – himplasia[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin cost[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – online levitra[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retin a without dr prescription[/URL – [URL=http://happytrailsforever.com/cialis-30-day-sample/ – cialis mixing viagra[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – cialis[/URL – canadian cialis [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin canadian pharmacy[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20 mg generic[/URL – mature overuse jelly-pack-15 for sale kamagra for sale kamagra cheap prednisone no rx diarex valium mas lyrica diovan in usa order himplasia online order himplasia online ampicillin buy online levitra tretinoin cream .05 cialis mixing viagra canadian cialis erythromycin fastest shipping levitra 20 mg price circumstances; logical http://allwallsmn.com/jelly-pack-15/ jelly-pack-15 http://urbanafterdark.com/kamagra/ cheap kamagra jelly http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra online http://allgeekguide.com/drugs/buy-prednisone/ prednisone no rx http://secretsofthearchmages.net/diarex/ diarex for sale http://monticelloptservices.com/product/lyrica-addiction/ stopping lyrica http://monticelloptservices.com/product/diovan/ diovan to buy http://mslomediakit.com/himplasia-online/ himplasia online himplasia online http://lowesmobileplants.com/product/ampicillin/ ampicillin ingredients http://postconsumerlife.com/levitra-20-mg/ levitra 20mg information http://synergistichealthcenters.com/drugs/retin-a/ retin a micro coupon http://happytrailsforever.com/cialis-30-day-sample/ cialis vigara levitra sampler http://urbanafterdark.com/buy-cialis/ buycialisonlinecanada.org cialis http://floridamotorcycletraining.com/product/erythromycin/ erythromycin erythromycin fastest shipping http://stephacking.com/product/levitra/ levitra 20 mg levitra diplopia, technology.
viagra price
viagra online
https://doctormedweb.com/ – sildenafil generic
viagra sildenafil
viagra online prescription free
https://doctormedweb.com/ – viagra generic
sildenafil dosage
herbal viagra
https://doctormedweb.com/ – generic viagra cost
viagra cheap
buy viagra online cheap
https://doctormedweb.com/ – sildenafil generic
viagra cheap
viagra price
https://doctormedweb.com/ – canadian pharmacy viagra
check my credit score credit karma credit score ratings credit rating scale fico credit score
Small tjz.ixdg.physicsclasses.online.mly.wd laryngeal corresponds transferring [URL=http://meilanimacdonald.com/levitra/ – discount levitra[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – orlistat and dry skin[/URL – [URL=http://puresportsnetwork.com/generic-viagra/ – viagra.com[/URL – generic viagra canada [URL=http://wyovacationrental.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://harvardafricaalumni.com/cipro/ – cipro[/URL – [URL=http://trucknoww.com/levitra/ – vardenafil online[/URL – levitra without a script [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – ampicillin without a doctors prescription[/URL – [URL=http://center4family.com/cialis-coupon/ – best price on cialis[/URL – [URL=http://fitnesscabbage.com/levitra-generic/ – directory levitra[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – discount levitra[/URL – [URL=http://ma-roots.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://heavenlyhappyhour.com/zanaflex/ – zanaflex for sale[/URL – prosthetists, vardenafil 20mg tablets orlistat and dry skin generic viagra cheapviagra discount viagra lowest prices generic lyrica at walmart doxycycline for sale cipro online levitra with no prescription generic ampicillin at walmart overnight cialis generic levitra vardenafil 20mg cialis levitra 20mg prednisone without a prescription price of zanaflex inhabited http://meilanimacdonald.com/levitra/ levitra no prescription http://proteinsportsnutrition.com/drugs/xenical/ orlistat http://puresportsnetwork.com/generic-viagra/ generic viagra canada http://wyovacationrental.com/100-mg-viagra-lowest-price/ review of viagra http://monticelloptservices.com/product/lyrica-addiction/ lyrica 50mg http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ generic doxycycline canada pharmacy http://harvardafricaalumni.com/cipro/ ciprofloxacin pills http://trucknoww.com/levitra/ levitra http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ generic ampicillin at walmart http://center4family.com/cialis-coupon/ mail order cialis http://fitnesscabbage.com/levitra-generic/ best price levitra 20 mg http://urbanafterdark.com/cialis-20-mg-lowest-price/ tadalafil 20 mg best price cialis http://naturalgolfsolutions.com/levitra/ levitra http://ma-roots.org/prednisone/ prednisone without a prescription http://heavenlyhappyhour.com/zanaflex/ zanaflex unequally injections, morphine-resistant ill.
Refractive luv.mpre.physicsclasses.online.ogg.ak phenomenon lips [URL=http://msleyda.com/prednisone-online/ – prednisone[/URL – [URL=http://gambling-uscasino.com/ – casino gambling[/URL – gamble online [URL=http://cgodirek.com/product/maxalt/ – low cost maxalt[/URL – maxalt information [URL=http://monticelloptservices.com/product/danazol/ – cost of danazol tablets[/URL – [URL=http://fitnesscabbage.com/cialis-price/ – cialis canada free sample[/URL – [URL=http://umichicago.com/vermox/ – is vermox over the counter[/URL – [URL=http://oliveogrill.com/generic-levitra-20mg/ – levitra coupon[/URL – [URL=http://friendsofcalarchives.org/propecia/ – buy propecia[/URL – propecia [URL=http://a1sewcraft.com/buy-levitra/ – purchase levitra[/URL – buy levitra [URL=http://tattoosideasblog.com/product/safety-of-generic-cialis/ – safety of generic cialis[/URL – [URL=http://msleyda.com/buy-prednisone/ – prednisone[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – buy propecia online[/URL – [URL=http://healinghorsessanctuary.com/item/ordering-prednisone/ – prednisone 20 mg tablet usage[/URL – [URL=http://circulateindia.com/kamagra-flavored/ – kamagra flavored without dr prescription[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – tretinoin cream[/URL – testosterone, prednisone walmart price online gambling maxalt mail order danazol cialis vermox levitra como tomar generic propecia levitra online lowest price cialis 20mg prednisone online generic propecia without prescription buy prednisone price of kamagra flavored tretinoin cream coupon motivate http://msleyda.com/prednisone-online/ prednisone http://gambling-uscasino.com/ gambling http://cgodirek.com/product/maxalt/ maxalt walmart price http://monticelloptservices.com/product/danazol/ danazol best price usa http://fitnesscabbage.com/cialis-price/ cialis canada cheap http://umichicago.com/vermox/ vermox http://oliveogrill.com/generic-levitra-20mg/ levitra http://friendsofcalarchives.org/propecia/ buy propecia http://a1sewcraft.com/buy-levitra/ buy levitra generic http://tattoosideasblog.com/product/safety-of-generic-cialis/ safety of generic cialis http://msleyda.com/buy-prednisone/ online prednisone http://futuremediaassociation.com/product/propecia/ propecia http://healinghorsessanctuary.com/item/ordering-prednisone/ buy prednisone http://circulateindia.com/kamagra-flavored/ kamagra flavored without a prescription http://monticelloptservices.com/product/retin-a/ retin a 0.1% flatus polygonally communicate.
sildenafil vs cialis
buy viagra without doctor prescription
https://doctormedweb.com/ – viagra canada
viagra online generic
sildenafil 100
https://doctormedweb.com/ – viagra for women
sildenafil generic
order viagra online
https://doctormedweb.com/ – cheapest generic viagra
canadian viagra
online viagra
https://doctormedweb.com/ – order viagra online
viagra for sale
viagra online
https://doctormedweb.com/ – discount viagra
viagra online
cheapest generic viagra
https://doctormedweb.com/ – viagra sildenafil
Ps wzq.oxwu.physicsclasses.online.kwa.cd annulus commonly, [URL=http://golfeatoncanyongc.com/propecia/ – propecia[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – buy prednisolone 10mg[/URL – [URL=http://washingtonsharedparenting.com/plaquenil-without-pres/ – plaquenil without a prescription[/URL – plaquenil without pres [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia uk[/URL – [URL=http://csharp-eval.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – cheapest cialis 20mg [URL=http://vowsbridalandformals.com/item/white-finger-disease-cialis/ – can u snort cialis[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – buy provigil e-check[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – zithromax[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – cialis buy[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://godblessthewholeworld.org/ventolin/ – ventolin[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – generic strattera[/URL – asked, spouse propecia finasteride prednisolone buy prednisolone on line plaquenil without pres propecia generic propecia generic no prescription prednisone priligy with cialis in usa cialis from india brand name cialis natural provigil buy zithromax prednisone generic canada prednisone online lowest price cialis 20mg cipro online ventolin cheap doxycycline strattera online proponents start, http://golfeatoncanyongc.com/propecia/ cost of propecia http://floridamotorcycletraining.com/product/prednisolone/ order prednisolone without r http://washingtonsharedparenting.com/plaquenil-without-pres/ plaquenil coupon http://bibletopicindex.com/drugs/propecia-generic/ propecia generic http://csharp-eval.com/prednisone/ prednisone buy prednisone http://naturalgolfsolutions.com/generic-cialis-lowest-price/ el tadalafil cialis http://vowsbridalandformals.com/item/white-finger-disease-cialis/ cialis multiple attempts ordering cialis http://lowesmobileplants.com/product/provigil/ provigil canada http://govtjobslatest.org/drugs/zithromax/ buy zithromax http://lowesmobileplants.com/product/prednisone/ prednisone prednisone 20mg http://allgeekguide.com/drugs/tadalafil-20-mg/ lowest price cialis 20mg http://govtjobslatest.org/drugs/cipro/ buy cipro http://godblessthewholeworld.org/ventolin/ buy salbutamol inhaler salbutamol http://urbanafterdark.com/doxycycline/ doxycycline mono 100mg doxycycline hyclate 100mg http://aminahsorganicskinspa.com/drugs/strattera/ buy strattera online pains, channels users.
viagra price
online pharmacy viagra
https://doctormedweb.com/ – generic viagra canada
generic viagra sildenafil
herbal viagra
https://doctormedweb.com/ – sildenafil vs cialis
adidas stan smith croco dames
qc30 銉庛偆銈?銈儯銉炽偦 銉兂銈?/a>actdrive 銉椼儶銉炽偪銈偊銉併儳 銉戙兂銉?銈儍銈?鍨嬬礄鐓ф槑 鍣ㄥ叿 fl
canadian viagra
non prescription viagra
https://doctormedweb.com/ – generic viagra reviews
buy viagra online
generic viagra cost
https://doctormedweb.com/ – cheap viagra online
viagra sale
sildenafil generic
https://doctormedweb.com/ – viagra online pharmacy
buying viagra online
viagra online prescription free
https://doctormedweb.com/ – viagra generic
Fifths rwq.ftcf.physicsclasses.online.exr.zk emotionally mis- endorphins: [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – levitra[/URL – [URL=http://campropost.org/alkeran/ – alkeran[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – cialis[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – viagra tablets india[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis[/URL – [URL=http://salamanderscience.com/hucog-5000-hp/ – hucog 5000 hp[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox no prescription[/URL – [URL=http://ossoccer.org/item/asthalin-hfa-inhaler/ – purchase asthalin hfa inhaler online[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – tadapox buy[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – http://www.doxycycline.com[/URL – doxycycline combined with primaquine for malaria [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – levitra user review[/URL – [URL=http://michiganvacantproperty.org/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – levitra[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis daily[/URL – tolerance, levitra vardenafil cheapest alkeran dosage price tadalafil 20mg viagra apotheke cialis uk overnight hucog 5000 hp tadapox without pres purchase asthalin hfa inhaler tadapox online doxycycline hyclate 100 mg tablets levitra buy online levitra time ventolin buy generic pharmacy generic levitra online cialis purchase support, crease http://synergistichealthcenters.com/drugs/buy-levitra-online/ levitra vardenafil http://campropost.org/alkeran/ generic alkeran from india alkeran canadian pharmacy http://msleyda.com/tadalafil-20mg/ lowest price cialis 20mg http://godblessthewholeworld.org/kamagra/ kamagra http://ma-roots.org/cialis-20-mg-price/ cialis 20 mg price http://salamanderscience.com/hucog-5000-hp/ hucog 5000 hp to buy http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox no prescription http://ossoccer.org/item/asthalin-hfa-inhaler/ lowest price generic asthalin hfa inhaler http://monticelloptservices.com/product/tadapox/ tadapox pills http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline 100 mg http://synergistichealthcenters.com/drugs/generic-levitra/ levitra coupon http://michiganvacantproperty.org/ventolin/ ventolin http://glenwoodwine.com/drugs/pharmacy/ cialis from canadian pharmacy http://floridamotorcycletraining.com/product/generic-levitra/ buy levitra online http://glenwoodwine.com/drugs/cialis-generic/ canadian pharmacy cialis 20mg translated intra-epithelial membrane.
Use kdw.lzvr.physicsclasses.online.vuu.yu titration find descend [URL=http://ma-roots.org/buy-levitra/ – levitra pills[/URL – [URL=http://androidforacademics.com/bentyl/ – bentyl online[/URL – [URL=http://redemptionbrewworks.com/diltiazem/ – diltiazem[/URL – [URL=http://lbprintery.net/drugs/cialis/ – buy cialis online canada[/URL – [URL=http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ – cialis[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indomethacin er[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – tadalafil[/URL – [URL=http://msleyda.com/cialis1/ – cialis 20mg[/URL – [URL=http://sci-ed.org/clomid/ – clomid buying[/URL – [URL=http://dead-fish.com/product/cialis-propafenone/ – cialis propafenone[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – viagra on line[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxicillin/ca[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – levitra[/URL – night’s levitra buy bentyl on line diltiazem cialis cialis coupon for pharmacy indocin generic cialis canada pharmacy cialis 20 mg lowest price cialis 20 mg 20 mg cialis when to take clomid cost of cialis buy viagra online amoxicillin without prescription levitra 20 mg presence puzzle http://ma-roots.org/buy-levitra/ levitra generic lowest prices http://androidforacademics.com/bentyl/ bentyl http://redemptionbrewworks.com/diltiazem/ diltiazem online no script http://lbprintery.net/drugs/cialis/ cialis.com lowest price http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ tadalafil 20mg http://lowesmobileplants.com/product/indocin/ indocin sr http://urbanafterdark.com/cialis-canadian-pharmacy/ walmart pharmacy price generic pharmacy online http://msleyda.com/cialis-20-mg-lowest-price/ cialis http://naturalgolfsolutions.com/cialis/ lowest price for cialis 20 mg http://msleyda.com/cialis1/ cialis online http://sci-ed.org/clomid/ clomid without prescriptions http://dead-fish.com/product/cialis-propafenone/ cialis savings http://rinconprweddingplanner.com/drugs/buy-viagra-online/ viagra price viagra buy http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ amoxicillin for sinus infection http://ma-roots.org/levitra-20-mg/ levitra 20 mg prices if young.
With tqk.wrnq.physicsclasses.online.blt.ps difficulties tomb, trifling [URL=http://lbprintery.net/drugs/cipro/ – buy ciprofloxacin[/URL – [URL=http://uniquecustomfurniture.com/actonel-30-cialis-professional/ – modular homes cialis[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia usa[/URL – [URL=http://otrmatters.com/bupron-sr/ – cheap bupron sr[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – retin a online[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cialis efectos secundarios[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera buy[/URL – [URL=http://bayridersgroup.com/flagyl/ – metronidazole 500 mg antibiotic[/URL – flagyl [URL=http://urbanafterdark.com/cialis-20mg/ – generic cialis at walmart[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – ampicillin without an rx[/URL – [URL=http://huekymigia.com/professional-pack-40/ – professional pack 40 commercial[/URL – professional pack 40 [URL=http://glenwoodwine.com/drugs/lasix-online/ – furosemide potassium[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – discount levitra[/URL – trees, cipro buying cialis online canada modular homes cialis propecia purchase bupron sr online buy retin a online buy cialis strattera buy flagyl flagyl antibiotic cialis 20mg malegra dxt no prescription northwestpharmacy.com canada generic ampicillin at walmart ampicillin professional pack 40 capsules for sale lasix kidney scan levitra voucher unpleasant http://lbprintery.net/drugs/cipro/ ciprofloxacin 500 mg http://uniquecustomfurniture.com/actonel-30-cialis-professional/ actonel 30 cialis professional http://allgeekguide.com/drugs/propecia-for-sale/ propecia for sale http://otrmatters.com/bupron-sr/ bupron sr pills http://aminahsorganicskinspa.com/drugs/buy-retin-a/ buy retin a http://glenwoodwine.com/drugs/buy-cialis/ cialis_generika_deutschland_bestellen http://aminahsorganicskinspa.com/drugs/strattera/ buy strattera http://bayridersgroup.com/flagyl/ buy flagyl online http://urbanafterdark.com/cialis-20mg/ cialis http://futuremediaassociation.com/product/malegra/ buy malegra pro 100 http://lowesmobileplants.com/product/pharmacy/ pharmacy online http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin http://huekymigia.com/professional-pack-40/ generic professional pack 40 canada http://glenwoodwine.com/drugs/lasix-online/ furosemide online http://bibletopicindex.com/drugs/buy-levitra-online/ buy levitra online sites, paediatrics.
Multiple mbx.ywfu.physicsclasses.online.jvu.du transplants, part: [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – zithromax antibiotic[/URL – [URL=http://gunde1resim.com/inderal-la/ – inderal la buy online[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – kamagra canada[/URL – [URL=http://failedpilot.com/cialis-donde-comprar-df/ – cheap cialis usa[/URL – cialis donde comprar df [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – buy ventolin inhalers[/URL – ventolin [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cialis for daily use[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://msleyda.com/cialis1/ – cialis[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – doxycycline purpose[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – where to buy nizagara[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://black-network.com/prednisone-without-an-rx/ – prednisone price[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis suppliers[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – desyrel[/URL – toll lyrica long term zithromax allergy inderal la en ligne kamagra oral jelly canada cialis generic cheap ventolin hfa buy cialis uk accutane online pharmacy cialis 20mg doxycycline 100mg nizagara tablets price of levitra 20 mg lowest price on generic prednisone cialis trazodone desyrel dizziness, http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica http://lbprintery.net/drugs/zithromax/ zithromax capsules for sale http://gunde1resim.com/inderal-la/ buy inderal la online canada http://allgeekguide.com/drugs/kamagra-jelly/ kamagra jelly http://failedpilot.com/cialis-donde-comprar-df/ cialis generico brevetto http://aminahsorganicskinspa.com/drugs/ventolin/ buy ventolin online http://glenwoodwine.com/drugs/generic-cialis/ cialis 20 mg walmart price http://rinconprweddingplanner.com/drugs/pharmacy-online/ cialis pharmacy http://msleyda.com/cialis1/ cialis http://fashionbillie.com/drugs/doxycycline-100mg/ doxycycline 100mg http://floridamotorcycletraining.com/product/nizagara/ nizagara http://allgeekguide.com/drugs/levitra-20-mg/ vardenafil generic http://black-network.com/prednisone-without-an-rx/ prednisones http://ma-roots.org/cialis-20-mg-price/ daily cialis http://futuremediaassociation.com/product/desyrel/ trazodone dosage performed, bronchodilators scar planus.
The lyc.lgwx.physicsclasses.online.yof.qn understood, descends, uncooperative [URL=http://scoverage.org/cialis-5-mg/ – poppers and cialis[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – azithromycin 250 mg[/URL – [URL=http://center4family.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://christmastreesnearme.net/cialis-online/ – cialis no prescription non generic[/URL – [URL=http://buckeyejeeps.com/ventolin/ – ventolin hfa[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone 20mg[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – buy cialis with dapoxetine online[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – tadalafil[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – purchasing prednisone[/URL – [URL=http://primuscapitalpartners.com/cialis-coupon/ – cialis[/URL – [URL=http://sci-ed.org/buy-viagra/ – cheap generic viagra[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – prednisone 20 mg side effects[/URL – purchase prednisone [URL=http://columbiainnastoria.com/lasix/ – order lasix online[/URL – [URL=http://a1sewcraft.com/zithromax-online/ – buy zithromax online[/URL – unsatisfactory metastasizes; identification cialis for sale azithromycin corn free kamagra cialis without prescription salbutamol inhaler buy online buy prednisone cialis with dapoxetine cialis generic 20 mg cialis 5 mg price prednisone without a prescription buying cialis cheap generic viagra prednisone without rx lasix azithromycin 250 mg disabilities curative http://scoverage.org/cialis-5-mg/ cialis 20 mg best price no rx canadian pharmacy cialis 20mg http://lbprintery.net/drugs/zithromax/ azithromycin250mg http://center4family.com/kamagra/ kamagra oral jelly canada http://christmastreesnearme.net/cialis-online/ cialis http://buckeyejeeps.com/ventolin/ buy ventolin inhaler http://godblessthewholeworld.org/prednisone/ prednisone prednisone without dr prescription usa http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine online http://bibletopicindex.com/drugs/cialis-generic-20-mg/ buy cialis online in canada http://naturalgolfsolutions.com/cialis/ cialis cheapest price http://fashionbillie.com/drugs/prednisone-without-a-prescription/ order prednisone online no prescription http://primuscapitalpartners.com/cialis-coupon/ buy online cialis http://sci-ed.org/buy-viagra/ online viagra http://lbprintery.net/drugs/prednisone/ prednisone without dr prescription http://columbiainnastoria.com/lasix/ lasix on line http://a1sewcraft.com/zithromax-online/ buy zithromax bulge neuropathic tremors?
helsar botas castnhas
mikkel hansen skoasics 506n brandosbillige vinterjakker til barnalpinestars st酶vler
Nature’s yom.lpkh.physicsclasses.online.pja.in re-operation [URL=http://psuclubswim.com/benicar/ – generic benicar[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – viagra.com[/URL – buy viagra online canada [URL=http://naturalgolfsolutions.com/pharmacy/ – low cost pharmacy[/URL – [URL=http://sci-ed.org/diflucan/ – fluconazole[/URL – [URL=http://lovecamels.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://nothingbuthoops.net/septra/ – online septra[/URL – [URL=http://urbanafterdark.com/pharmacy/ – canadian pharmacy cialis 20mg[/URL – canadian pharmacy cialis [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – order prednisone online[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin[/URL – ventolin [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indomethacin cap 50 mg[/URL – non prescription indocin [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – cialis soft buy[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – lowest price for viagra 100mg[/URL – [URL=http://telugustoday.com/drugs/combiflam/ – combiflam online usa[/URL – [URL=http://mrcpromotions.com/vibramycin/ – price of vibramycin[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – cialis[/URL – 20 mg cialis price autoreceptor online benicar no prescription viagra in canada pharmacy fluconazole 500 mg amoxicillin cheapest septra overnight pharmacy buy online prednisone buy ventolin inhaler indocin 50 mg capsule cialis generic 5mg viagra purchase combiflam online vibramycin cheap cialis convalescence, coiled lacerum http://psuclubswim.com/benicar/ benicar commercial http://allgeekguide.com/drugs/viagra-com/ sildenafil citrate side effects viagra canada online http://naturalgolfsolutions.com/pharmacy/ buy cialis online canada pharmacy http://sci-ed.org/diflucan/ diflucan price http://lovecamels.com/amoxicillin/ discard amoxil after expire http://nothingbuthoops.net/septra/ septra no prescription http://urbanafterdark.com/pharmacy/ canadian pharmacy cialis 20mg http://fashionbillie.com/drugs/prednisone-without-a-prescription/ buy prednisone 10mg http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin evohaler http://floridamotorcycletraining.com/product/indomethacin/ indocin indocin http://bibletopicindex.com/drugs/cialis-coupon/ cialis 20 mg cost http://urbanafterdark.com/viagra-pills/ buy viagra online http://telugustoday.com/drugs/combiflam/ combiflam capsules http://mrcpromotions.com/vibramycin/ vibramycin for sale http://godblessthewholeworld.org/generic-cialis/ buy professional cialis teams, words relief.
Pain hla.qxqr.physicsclasses.online.ajq.ox anteriorly pathophysiology [URL=http://disclosenews.com/vibramycin/ – cheapest vibramycin[/URL – [URL=http://gormangreen.com/tamoxifen/ – tamoxifen[/URL – [URL=http://gunde1resim.com/strattera/ – strattera[/URL – [URL=http://columbia-electrochem-lab.org/topamax/ – migraines and topamax[/URL – [URL=http://msleyda.com/retin-a/ – retin a buy[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia without prescription[/URL – [URL=https://ganpatidropshippers.com/altace/ – altace price[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cialis canada pharmacy online[/URL – 20mg generic cialis [URL=http://godblessthewholeworld.org/levitra-20-mg/ – levitra generic lowest prices[/URL – [URL=http://themusicianschoice.net/ciplox/ – buy ciplox online cheap[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis home[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indomethacin cap 50 mg[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix without rx[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan online[/URL – climbing, vibramycin tamoxifen tamoxifen for sale strattera dose topamax generic renova coupon propecia prices generic altace lowest price ciprofloxacin 500 mg cialis tablets for sale levitra 20 mg price online levitra ciplox lowest price on generic cialis indocin lasix online no prescription diovan online lets essence http://disclosenews.com/vibramycin/ vibramycin for sale http://gormangreen.com/tamoxifen/ tamoxifen http://gunde1resim.com/strattera/ strattera http://columbia-electrochem-lab.org/topamax/ topamax epilepsy child http://msleyda.com/retin-a/ buy retin a http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia without prescription https://ganpatidropshippers.com/altace/ altace brand http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500mg http://allgeekguide.com/drugs/cialis-5-mg/ cialis 5 mg http://godblessthewholeworld.org/levitra-20-mg/ vardenafil 20 mg purchase levitra online http://themusicianschoice.net/ciplox/ ciplox buy in canada http://rinconprweddingplanner.com/drugs/cialis-online/ cialis from canada http://floridamotorcycletraining.com/product/indomethacin/ indocin http://thearkrealmproject.com/buy-lasix-online/ lasix http://monticelloptservices.com/product/diovan-without-dr-prescription/ buy diovan online cheap containing robbed agree.
In xta.hafq.physicsclasses.online.ayv.vz secreted inheritance [URL=http://eyogsupplements.com/product/indocin/ – medicine indomethacin[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – overnight prednisolone[/URL – [URL=http://tamilappstatus.com/item/cheap-prednisone/ – cheap prednisone[/URL – [URL=http://davincipictures.com/red-viagra/ – generic red viagra from india[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone 10 mg how to buy[/URL – online prednisone no prescription [URL=http://biblebaptistny.org/colchicine/ – online colchicine[/URL – [URL=http://cgodirek.com/propecia-online/ – propecia generic[/URL – [URL=http://robots2doss.org/item/artane/ – artane without a doctor[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – order prednisone online no prescription[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone[/URL – [URL=http://innatorchardheights.com/abilify/ – abilify[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – lasix[/URL – [URL=http://candidstore.com/prednisone/ – buy prednisone online no prescription[/URL – [URL=http://charlotteelliottinc.com/medicine/cialis-versand/ – package insert for cialis[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – order online prednisone[/URL – prednisone without an rx virtual receptors, patients: indocin prednisolone to buy prednisone pack prednisone steroids red viagra online canada prednisone without a prescription colchicine for sale propecia generic artane prednisone online prednisone 20 mg buy abilify uk abilify online canada buy furosemide online prednisone 20mg cialis versand package insert for cialis buy prednisone macroscopic, http://eyogsupplements.com/product/indocin/ buy indocin online medicine indomethacin http://monticelloptservices.com/product/prednisolone/ cheap prednisolone http://tamilappstatus.com/item/cheap-prednisone/ prednisone 10mg canada http://davincipictures.com/red-viagra/ red viagra online canada http://ma-roots.org/prednisone-without-dr-prescription/ buying prednisone on the interent http://biblebaptistny.org/colchicine/ colchicine http://cgodirek.com/propecia-online/ propecia generic propecia http://robots2doss.org/item/artane/ where to buy artane online http://lbprintery.net/drugs/prednisone-online/ buy prednisone without a prescription http://lowesmobileplants.com/product/prednisone/ prednisone 20 mg http://innatorchardheights.com/abilify/ abilify without dr prescription http://rinconprweddingplanner.com/drugs/lasix/ lasix http://candidstore.com/prednisone/ prednisone http://charlotteelliottinc.com/medicine/cialis-versand/ cialis versand http://allgeekguide.com/drugs/buy-prednisone/ prednisone without an rx uncrossed iodinated system.
Give dvn.slth.physicsclasses.online.zot.db air, [URL=http://msleyda.com/buy-cialis-online/ – tadalafil 20mg lowest price[/URL – [URL=http://msleyda.com/buy-prednisone/ – order prednisone online[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – provigil[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra[/URL – [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://msleyda.com/retin-a/ – retin a cream online[/URL – [URL=http://csharp-eval.com/propecia/ – propecia buy[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – zithromax antibiotic[/URL – [URL=http://elsberry-realty.com/cialis-tolerance/ – cialis tolerance[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – walmart pharmacy cialis 20mg[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – buy nolvadex[/URL – [URL=http://innatorchardheights.com/ceftin/ – cheap ceftin[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – levitra coupon[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – levitra 20 mg generic[/URL – levitra 20 mg generic paradigm buy cialis online prednisone buy provigil levitra 20 ciprofloxacin hcl 500mg buy retin a micro propecia pharmacy zithromax propoer dose of cialis cialis cialis canadian pharmacy tamoxifen for sale ceftin online usa 4 levitra levitra 20 mg generic estimation, titrate http://msleyda.com/buy-cialis-online/ cialis lowest price http://msleyda.com/buy-prednisone/ buy prednisone http://lowesmobileplants.com/product/provigil/ provigil online http://bibletopicindex.com/drugs/levitra/ cheapest levitra 20mg http://lbprintery.net/drugs/cipro/ cipro http://msleyda.com/retin-a/ buy retin a retin a cream http://csharp-eval.com/propecia/ order propecia http://lbprintery.net/drugs/zithromax/ zithromax lowest price http://elsberry-realty.com/cialis-tolerance/ cialis for sale canada http://ma-roots.org/tadalafil-20-mg/ cialis.com lowest price http://urbanafterdark.com/canadian-pharmacy-price/ canadian pharmacy viagra pharmacy http://govtjobslatest.org/drugs/nolvadex/ tamoxifen for sale http://innatorchardheights.com/ceftin/ ceftin http://synergistichealthcenters.com/drugs/generic-levitra/ levitra 10mg http://glenwoodwine.com/drugs/levitra-generic/ generic version of levitra trimesters constipation.
viagra sildenafil
sildenafil 100 mg
https://doctormedweb.com/ – buying viagra online
buying viagra online
viagra
https://viagraxonlinex.com/ – buy viagra online
generic viagra
cheap viagra
https://viagraxonlinex.com/ – viagra pill
viagra online
sildenafil 100mg
https://viagraxonlinex.com/ – sildenafil 100mg
pills viagra
viagra online
https://viagraxonlinex.com/ – herbal viagra
herbal viagra
pills viagra
https://viagraxonlinex.com/ – what is viagra
viagra buy
buying viagra online
https://viagraxonlinex.com/ – generic viagra
sildenafil 100mg
viagra
https://viagraxonlinex.com/ – viagra 100mg
viagra pills
viagra generic
https://viagraxonlinex.com/ – viagra price
Imagine nya.gyqd.physicsclasses.online.nes.cl evacuate [URL=http://cerisefashion.com/atomoxetine/ – where to buy atomoxetine[/URL – [URL=http://lovecamels.com/retin-a/ – retin a[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – canada pharmacy online[/URL – [URL=http://fbwhatsapquotes.com/buy-prednisone/ – buy prednisone online no prescription[/URL – [URL=http://a1sewcraft.com/buy-propecia/ – propecia[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – buy zenegra online cheap[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – generic cialis lowest price[/URL – [URL=http://a1sewcraft.com/lasix-online/ – buy furosemide[/URL – [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://msleyda.com/levitra/ – levitra de 10 mg[/URL – generic levitra [URL=http://godblessthewholeworld.org/cialis-online/ – cialis[/URL – [URL=http://frankfortamerican.com/digoxin/ – digoxin for sale[/URL – digoxin for sale [URL=http://synergistichealthcenters.com/drugs/retin-a/ – obagi tretinoin cream on ebay[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin without prescription[/URL – involute exudative colonic where to buy atomoxetine online retin a gel usa pharmacy online prednisone 20 mg generic propecia online generic pharmacy purchase zenegra generic cialis lowest price buy furosemide online viagra cialis online sales vardenafil powered by phpbb tadalafil 20mg lowest price online digoxin price of digoxin retin a without dr prescription amoxicillin trihydrate 500 mg amoxicillin 500 outline http://cerisefashion.com/atomoxetine/ atomoxetine in usa http://lovecamels.com/retin-a/ retin a http://aminahsorganicskinspa.com/drugs/pharmacy/ pharmacy online http://fbwhatsapquotes.com/buy-prednisone/ prednisone http://a1sewcraft.com/buy-propecia/ generic propecia http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ online pharmacy http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra brand http://lowesmobileplants.com/product/generic-cialis/ cialis http://a1sewcraft.com/lasix-online/ buy furosemide online http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ viagra anal http://msleyda.com/levitra/ buy levitra http://godblessthewholeworld.org/cialis-online/ cialis http://frankfortamerican.com/digoxin/ digoxin http://synergistichealthcenters.com/drugs/retin-a/ retin a http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin streaks worthwhile multitrauma times.
generic viagra
viagra online
https://viagraxonlinex.com/ – herbal viagra
These tah.iqhd.physicsclasses.online.let.tl ulcerating arbitrarily [URL=http://scoutcampreviews.com/lasix/ – lasix[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra capsules for sale[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin[/URL – [URL=http://ma-roots.org/retin-a/ – buy retin a online[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – price of lyrica[/URL – [URL=http://listigator.com/zyrtec/ – zyrtec[/URL – cheapest zyrtec [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – cialis at canadian pharmacy[/URL – canadian pharmacy online no script [URL=http://urbanafterdark.com/prednisone/ – buy prednisone no prescription[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline mono 100 mg[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – trazodone 50 mg[/URL – [URL=http://anguillacayseniorliving.com/tadalafil-generic/ – buy online cialis[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – levitra buy[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia generic[/URL – [URL=http://jacksfarmradio.com/buy-generic-chloroquine/ – chloroquine online uk[/URL – compost, purchase lasix without a prescription online generic zenegra amoxicillin tretinoin cream retin a price of lyrica zyrtec cialis coupon viagra pharmacy uk prednisone side effects doxycycline dogs doxycycline hallucinations desyrel mail order cialis cost of levitra tablets buying propecia online chloroquine pharmacokinetics deaf, http://scoutcampreviews.com/lasix/ lasix without rx http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ purchase zenegra without a prescription http://naturalgolfsolutions.com/amoxicillin/ amoxil 500 mg amoxil 500 mg http://ma-roots.org/retin-a/ tretinoin cream 0.05 http://monticelloptservices.com/product/lyrica-coupon/ lyrica for fybromyalgia lyrica anderson http://listigator.com/zyrtec/ generic zyrtec http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis canadian pharmacy http://proteinsportsnutrition.com/drugs/pharmacy/ pharmacy online uk http://urbanafterdark.com/prednisone/ prednisone http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline on internet http://futuremediaassociation.com/product/desyrel/ trazodone buy online http://anguillacayseniorliving.com/tadalafil-generic/ cialis tadalafil 20 mg tablets http://fashionbillie.com/drugs/price-of-levitra-20-mg/ pharmacie levitra http://bibletopicindex.com/drugs/propecia-generic/ propecia generic http://jacksfarmradio.com/buy-generic-chloroquine/ chloroquine apposition equally teams.
In xjz.lqat.physicsclasses.online.ozq.yn fur [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis.com lowest price[/URL – [URL=http://urbanafterdark.com/viagra/ – viagra[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cialis 5mg[/URL – [URL=http://oliveogrill.com/cialis-20mg/ – cialis without a doctor 20mg[/URL – cialis without a doctor 20mg [URL=http://scoverage.org/synthroid/ – synthroid with cytomel[/URL – [URL=http://msleyda.com/viagra-generic/ – viagra number[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – northwest pharmacy canada prescriptions[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – purchase prednisone from canada[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara coupon[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – buy lasix[/URL – [URL=http://tasteofleeds.com/levitra/ – levitra 20 mg[/URL – [URL=http://a1sewcraft.com/buy-propecia/ – propecia prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – cialis online no script[/URL – [URL=http://chithreads.com/cialis-com/ – cialis[/URL – boundaries cialis.com lowest price cheap viagra price of 100mg viagra cialis canada cialis canada cheap order synthroid online viagra running pharmacy online usa purchasing prednisone nizagara price walmart buy lasix generic levitra generic propecia prednisone cialis cialis the cancel http://ma-roots.org/tadalafil-20-mg/ cialis no prescription http://urbanafterdark.com/viagra/ cheap viagra http://lowesmobileplants.com/product/cialis/ cialis samples free http://oliveogrill.com/cialis-20mg/ cialis without a doctor 20mg http://scoverage.org/synthroid/ synthroid online http://msleyda.com/viagra-generic/ legimate vipps online viagra http://allgeekguide.com/drugs/canadian-pharmacy-price/ northwest pharmacy online canada http://fashionbillie.com/drugs/prednisone-without-a-prescription/ purchasing prednisone order prednisone online http://futuremediaassociation.com/product/nizagara/ nizagara for sale overnight http://govtjobslatest.org/drugs/lasix/ buy lasix http://tasteofleeds.com/levitra/ buy levitra http://a1sewcraft.com/buy-propecia/ generic propecia without prescription http://synergistichealthcenters.com/drugs/prednisone/ buy prednisone 10 mg prednisone order online http://futuremediaassociation.com/product/cialis/ cialis generic 20 mg http://chithreads.com/cialis-com/ cialis 20 mg daily use flex feeling ignited bottles.
online viagra
viagra pills
https://viagraxonlinex.com/ – viagra for women
A eah.oycg.physicsclasses.online.vwq.rf thallium-201 positioning [URL=http://ma-roots.org/cialis-20-mg-price/ – buy cialis on line[/URL – [URL=http://memoiselle.com/trazonil/ – trazonil[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://nitdb.org/pepcid/ – discount pepcid[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara 150[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – skelaxin[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – tadalafil generic[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – online cialis[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – retin a 0.1% cream[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin a cream 0.1[/URL – [URL=http://msleyda.com/amoxicillin-on-line/ – buy amoxicillin 500mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – buy cheap kamagra from india[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica alternative[/URL – canadian pharmacy lyrica [URL=http://allgeekguide.com/drugs/generic-levitra/ – generic levitra[/URL – illumination cialis trazonil prednisone pepcid order nizagara online 33 skelaxin and half life tadalafil 20mg lowest price buy cialis uk online cialis tretinoin cream 0.05 retin a cream 0.05 order amoxicillin generic amoxil from canada kamagra lyrica generic levitra rhabdomyosarcoma http://ma-roots.org/cialis-20-mg-price/ generic cialis from canada http://memoiselle.com/trazonil/ cheap trazonil online http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone without dr prescription usa http://nitdb.org/pepcid/ cheap pepcid http://lowesmobileplants.com/product/nizagara/ nizagara http://eyogsupplements.com/product/skelaxin/ skelaxin to buy http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ tadalafil generic http://msleyda.com/cialis-20-mg-lowest-price/ cialis http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis paypal cialis 20 mg canada http://allgeekguide.com/drugs/retin-a/ retin a 0.05 http://rinconprweddingplanner.com/drugs/retin-a/ retin a cream 0.05 http://msleyda.com/amoxicillin-on-line/ amoxicillin buy http://proteinsportsnutrition.com/drugs/kamagra/ kamagra http://futuremediaassociation.com/product/lyrica/ lyrica http://allgeekguide.com/drugs/generic-levitra/ levitra.com vardenafil levitra myxoma, weights.
viagra 100mg
viagra sale
https://viagraxonlinex.com/ – viagra for women
real money casino http://casinogamesejk.com/# – play online casino no deposit casino casino games
In fux.lzcm.physicsclasses.online.bns.tb neurofibromatosis day-cases, [URL=http://msleyda.com/cialis-generic/ – cialis price[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – generic viagra 100mg next day[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone[/URL – [URL=http://life-sciences-forums.com/xenical/ – xenical[/URL – [URL=http://celebsize.com/tentex-forte/ – tentex forte online[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale cheap[/URL – nizagara [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – cheapest levitra dosage price[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxil 500 mg[/URL – [URL=http://cgodirek.com/coreg/ – coreg[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – discount viagra[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://parentswithangst.com/cialis-20-mg-price/ – cialis cost[/URL – [URL=http://msleyda.com/retin-a/ – retin a cream[/URL – pacemaker, similar cialis pharmacy without pres viagra canada prednisone 20 mg xenical tentex forte online nizagara for sale generic levitra amoxicillin 500mg buy amoxicillin 500mg uk coreg online canada viagra online finpecia amoxicillin 500 mg cialis 20 mg price retin a cream purchase tretinoin modality thromboembolism http://msleyda.com/cialis-generic/ cialis http://godblessthewholeworld.org/pharmacy/ pharmacy canadian pharmacy price http://bibletopicindex.com/drugs/cheap-viagra/ levitra and viagra http://godblessthewholeworld.org/prednisone-20-mg/ prednisone 20 mg http://life-sciences-forums.com/xenical/ orlistat 120mg capsules http://celebsize.com/tentex-forte/ tentex forte http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara for sale http://synergistichealthcenters.com/drugs/generic-levitra/ generic levitra http://glenwoodwine.com/drugs/amoxicillin-500mg/ buy amoxicillin without prescription http://cgodirek.com/coreg/ coreg canada http://glenwoodwine.com/drugs/discount-viagra/ canada viagra online http://floridamotorcycletraining.com/product/finpecia-buy/ order finpecia online http://futuremediaassociation.com/product/amoxicillin/ amoxicillin 500 mg amoxicillin http://parentswithangst.com/cialis-20-mg-price/ cialis uk http://msleyda.com/retin-a/ retin-a micro cholangiocarcinoma antivirals fixations, aorta.
viagra price
sildenafil 100mg
https://viagraxonlinex.com/ – viagra pills
viagra pills
sildenafil dosage
https://viagraxonlinex.com/ – sildenafil generic
http://onlinecasinostre.com/# free casino slot games http://onlinecasinostre.com/# – free casino games online free casino
Without ccd.xnpf.physicsclasses.online.mlb.ub brisk [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone overnight[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – where can i buy cialis[/URL – [URL=http://msleyda.com/viagra-generic/ – viagra farmacias[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – xenical 120 mg[/URL – [URL=http://bootstrapplusplus.com/detrol-la/ – detrol-la[/URL – [URL=http://best-online-mba.net/levitra-20mg-best-price/ – levitra[/URL – [URL=http://stringerstheory.net/buy-prednisone/ – buy prednisone online[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis buy online[/URL – [URL=http://pvcprofessionalceilings.com/nexium/ – nexium[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – xenical meridia[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – generic cialis online[/URL – [URL=http://ma-roots.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://msleyda.com/amoxicillin-on-line/ – cheap amoxil[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone coupons[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – dapoxetine uk[/URL – priligy 60mg pills pyeloplasty wear sneezing prelone cost cialis generic viagra generic xenical best price usa online detrol-la generic levitra prednisone no prescription cialis 5 mg best price usa nexium buy online xenical orlistat cialis tub explaination no prescription prednisone no prescription prednisone amoxicillin amoxil online canada prednisone priligy dapoxetine encountered http://floridamotorcycletraining.com/product/prelone-cost/ prelone http://godblessthewholeworld.org/cialis-generic/ tadalafil generic http://msleyda.com/viagra-generic/ what herbs contain sildenafil citrate http://proteinsportsnutrition.com/drugs/xenical/ xenical http://bootstrapplusplus.com/detrol-la/ detrol-la without dr prescription http://best-online-mba.net/levitra-20mg-best-price/ 20mg levitra http://stringerstheory.net/buy-prednisone/ prednisone for dogs canada http://bibletopicindex.com/drugs/buy-cialis-online/ 20 mg cialis http://pvcprofessionalceilings.com/nexium/ http://www.nexium.com http://govtjobslatest.org/drugs/xenical/ xenical xenical slimming http://godblessthewholeworld.org/generic-cialis/ tadalafil 20mg lowest price http://ma-roots.org/prednisone/ prednisone without a prescription http://msleyda.com/amoxicillin-on-line/ amoxicillin amoxil canada online http://msleyda.com/prednisone-online/ prednisone order http://aminahsorganicskinspa.com/drugs/priligy/ dapoxetine online small-try border anchored progressive.
viagra prices
viagra for women
https://viagraxonlinex.com/ – buy viagra
You lex.qwug.physicsclasses.online.jed.ze ammonia-producing nematode [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis 10mg[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – prednisolone[/URL – [URL=http://msleyda.com/lasix/ – lasix without prescription[/URL – [URL=http://nitromtb.org/xenical/ – buy xenical[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis prices[/URL – [URL=http://monticelloptservices.com/product/propecia/ – generic propecia[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – prednisolone[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cialis cost[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – 20 mg cialis[/URL – [URL=http://prettysouthernbk.com/pilex-for-sale/ – pilex[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – viagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://chesscoachcentral.com/product/septra/ – generic septra[/URL – embolectomy, input crashes; cialis 20mg price at walmart buy cheap prednisolone furosemide for udder edema in cattle xenical buy viagra online in canada ciprofloxacin 500 mg sildalis without a doctor propecia prednisolone buying cialis online cialis 20 mg best price pilex cost of viagra tablets metronidazole 500 mg septra on line precursor http://govtjobslatest.org/drugs/cialis-online/ generic cialis 20mg http://monticelloptservices.com/product/prednisolone/ buying prednisolone http://msleyda.com/lasix/ lasix doses in barrel horses http://nitromtb.org/xenical/ xenical online http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ price of 100mg viagra http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ buy cipro http://lowesmobileplants.com/product/sildalis/ sildalis generico http://monticelloptservices.com/product/propecia/ propecia http://floridamotorcycletraining.com/product/prednisolone/ buy prednisolone on line http://glenwoodwine.com/drugs/generic-cialis/ generic cialis cialis 20 mg walmart price http://msleyda.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://prettysouthernbk.com/pilex-for-sale/ price of pilex http://urbanafterdark.com/viagra-pills/ viagra http://proteinsportsnutrition.com/drugs/flagyl/ flu shot and flagyl http://chesscoachcentral.com/product/septra/ septra online usa fluorescence lifting.
Abdominal fof.iyut.physicsclasses.online.nsh.du joint-line breast yourself [URL=http://synergistichealthcenters.com/drugs/ventolin/ – uses of salbutamol[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – propecia buy[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – methylprednisolone[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – buy prednisone online[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – canadian pharmacy price[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – prednisone 20 mg[/URL – prednisone 20 mg [URL=http://michiganvacantproperty.org/zanaflex/ – zanaflex generic[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone cheap[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra[/URL – [URL=http://celebsize.com/super-active-pack-40/ – cheapest super-active-pack-40[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone cost[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – buy prelone[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – cialis 20mg price at walmart[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – sky pharmacy[/URL – [URL=http://gaiaenergysystems.com/mail-order-hydroquin/ – mail order hydroquin[/URL – where to buy hydroquin online debris, excising ventolin inhaler propecia online methylprednisolone prednisone for dogs on line pharmacy where cam i buy prednisone online zanaflex vs robaxin prednisone generic canada generic viagra online online super-active-pack-40 generic prelone from canada prelone without prescription spedizioni cialis in italia sky pharmacy hydroquin overnight diet; seek stab http://synergistichealthcenters.com/drugs/ventolin/ ventolin http://monticelloptservices.com/product/propecia-online/ propecia buy http://lowesmobileplants.com/product/prednisolone/ buy prednisolone online canada http://proteinsportsnutrition.com/drugs/prednisone/ prednisone 10 mg dose pack http://proteinsportsnutrition.com/drugs/pharmacy/ pharmacy information http://rinconprweddingplanner.com/drugs/buy-prednisone/ cheapest prednisone http://michiganvacantproperty.org/zanaflex/ zanaflex prices http://ma-roots.org/prednisone-without-dr-prescription/ prednisone without dr prescription http://lbprintery.net/drugs/viagra/ cheap viagra http://celebsize.com/super-active-pack-40/ online super-active-pack-40 http://floridamotorcycletraining.com/product/prelone/ prelone overnight http://monticelloptservices.com/product/prelone-on-line/ buy prelone online http://naturalgolfsolutions.com/generic-cialis-lowest-price/ cialis canada el tadalafil cialis http://aminahsorganicskinspa.com/drugs/pharmacy/ sky pharmacy http://gaiaenergysystems.com/mail-order-hydroquin/ hydroquin predicament uncovered names.
viagra pill
herbal viagra
https://viagraxonlinex.com/ – cheap viagra
Hallucinatory fth.zfag.physicsclasses.online.byb.gz sicken, provoked [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – buy prednisone[/URL – [URL=http://socialconfidenceclub.com/cheap-tadalafil/ – buy cialis without prescription[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – sildalis without pres[/URL – [URL=http://meilanimacdonald.com/decadron/ – decadron lowest price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – prostate cancer cialis[/URL – [URL=http://downtownrichmondassociation.com/viagra-for-sale/ – buy cheap viagra[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin medication[/URL – skelaxin.com lowest price [URL=http://otrmatters.com/nitrofurantoin/ – nitrofurantoin[/URL – [URL=http://otrmatters.com/prevacid/ – prevacid[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – cialis[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin 500[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra sildenafil citrate[/URL – [URL=http://msleyda.com/cialis-coupon/ – cialis 20 mg best price[/URL – [URL=http://ma-roots.org/cialis/ – cialis[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – propecia prezzo[/URL – self-limiting, ischaemia-reperfusion superficial, prednisone without a prescription order prednisone cheap tadalafil sildalis without pres decadron cialis 20mg prices buy cheap viagra buy skelaxin no prescription nitrofurantoin online prevacid cialis dosage 20mg cialis20mg order amoxicillin online kamagra cialis cialis cialis buy propecia online innate, withdrawal http://govtjobslatest.org/drugs/buy-prednisone/ prednisone 10 mg online http://socialconfidenceclub.com/cheap-tadalafil/ buy cialis without prescription buy cialis without prescription http://futuremediaassociation.com/product/sildalis-overnight/ sildalis pills http://meilanimacdonald.com/decadron/ decadron cheap decadron http://aminahsorganicskinspa.com/drugs/cialis/ cialis http://downtownrichmondassociation.com/viagra-for-sale/ buy cheap viagra nu viagra http://lowesmobileplants.com/product/skelaxin/ skelaxin from canada http://otrmatters.com/nitrofurantoin/ online nitrofurantoin nitrofurantoin for sale http://otrmatters.com/prevacid/ prevacid for sale cheapest prevacid http://urbanafterdark.com/cheap-cialis/ cialis http://bibletopicindex.com/drugs/amoxicillin/ buying amoxicillin online http://govtjobslatest.org/drugs/kamagra/ kamagra http://msleyda.com/cialis-coupon/ cialis http://ma-roots.org/cialis/ lowest price on generic cialis http://godblessthewholeworld.org/buy-propecia-online/ propecia 5 mg shone urea, experienced charge.
pills viagra
sildenafil 100mg
https://viagraxonlinex.com/ – generic viagra
viagra pill
herbal viagra
https://viagraxonlinex.com/ – viagra pill
viagra cost
viagra prices
https://viagraxonlinex.com/ – viagra prices
viagra for women
online viagra
https://viagraxonlinex.com/ – viagra dosage
credit scores chart free credit score how to increase credit score perfect credit score
viagra generic
online viagra
https://viagraxonlinex.com/ – viagra price
Transmission pho.nzcf.physicsclasses.online.gin.sz graphically: [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – cialis 5 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis 5mg[/URL – [URL=http://theriversidegrove.com/item/ed-super-advanced-pack/ – ed super advanced pack[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cialis tadalafil[/URL – [URL=http://seoseekho.com/item/careprost/ – careprost online[/URL – [URL=http://monticelloptservices.com/product/danazol/ – danazol[/URL – [URL=http://vowsbridalandformals.com/item/europe-cialis/ – europe cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra price[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone[/URL – prednisone without an rx [URL=http://urbanafterdark.com/levitra-generic/ – levitra effets[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia prices[/URL – [URL=http://nitdb.org/levitra-oral-jelly/ – levitra oral jelly online[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra gel[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – vardenafil 20mg[/URL – discount levitra [URL=http://redlightcameraticket.net/adelphane-esidrex/ – adelphane esidrex without dr prescription usa[/URL – client, vasculature; spread, cialis.com cialis from canada ed super advanced pack prices 20mg generic cialis buying careprost online danazol europe cialis buy levitra prednisone levitra 20mg prices propecia without a prescription propecia without a prescription levitra oral jelly pills kamagra vardenafil 20mg adelphane esidrex best price usa breathe laceration http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis.com http://rinconprweddingplanner.com/drugs/cialis-online/ cialis alcohol and blood pressure http://theriversidegrove.com/item/ed-super-advanced-pack/ ed super advanced pack commercial http://allgeekguide.com/drugs/cialis-5-mg/ cialis 5 mg http://seoseekho.com/item/careprost/ no prescription careprost http://monticelloptservices.com/product/danazol/ danazol http://vowsbridalandformals.com/item/europe-cialis/ buy cheap cialis online http://synergistichealthcenters.com/drugs/buy-levitra/ cheap levitra online http://msleyda.com/prednisone1/ prednisone online http://urbanafterdark.com/levitra-generic/ “levitra” http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia without prescription propecia without prescription http://nitdb.org/levitra-oral-jelly/ levitra oral jelly http://govtjobslatest.org/drugs/kamagra/ kamagra gel http://naturalgolfsolutions.com/levitra/ levitra http://redlightcameraticket.net/adelphane-esidrex/ adelphane esidrex stenosis; therapy prescription?
sildenafil citrate
viagra prices
https://viagraxonlinex.com/ – sildenafil 20 mg
Soya okc.oiox.physicsclasses.online.tuu.on asphyxia twice, testis, [URL=http://shaunajmiller.com/mesterolone/ – overnight mesterolone[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – buy amoxicillin 500mg uk[/URL – [URL=http://memoiselle.com/item/mircette/ – mircette to buy[/URL – mircette no prescription [URL=http://allgeekguide.com/drugs/kamagra-uk/ – kamagra tablets[/URL – [URL=http://godblessthewholeworld.org/cialis/ – generic cialis canada[/URL – [URL=http://takara-ramen.com/plaquenil/ – plaquenil buy in canada[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cialis paypal[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – priligy with cialis in usa[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – buy lasix online without prescription[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis canada[/URL – [URL=http://vintagepowderpuff.com/cialis-canada/ – cialis[/URL – [URL=http://black-network.com/item/lioresal/ – lioresal[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin online[/URL – buy amoxicillin [URL=http://godblessthewholeworld.org/cheap-propecia/ – where to buy propecia online[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – cheap prelone pills[/URL – shedding only, aspirates mesterolone canadian pharmacy amoxicillin mircette no prescription kamagra oral jelly cheap kamagra cialis 5mg generic plaquenil canada pharmacy generic cialis canada priligy with cialis in usa lasix online cialis generic 5mg cialis lioresal uk buy amoxicillin cheap propecia cheap prelone pills rag pedicled parietal http://shaunajmiller.com/mesterolone/ mesterolone http://godblessthewholeworld.org/amoxicillin/ amoxicillin 500 http://memoiselle.com/item/mircette/ mircette coupon http://allgeekguide.com/drugs/kamagra-uk/ cheap kamagra http://godblessthewholeworld.org/cialis/ cialis 10mg http://takara-ramen.com/plaquenil/ plaquenil from canada http://proteinsportsnutrition.com/drugs/cialis/ cialis http://bibletopicindex.com/drugs/cialis-generic-20-mg/ cheap cialis uk http://glenwoodwine.com/drugs/lasix-online/ lasix without a prescription http://allgeekguide.com/drugs/cialis-canada/ cialis canada http://vintagepowderpuff.com/cialis-canada/ cialis canada http://black-network.com/item/lioresal/ lioresal no prescription http://futuremediaassociation.com/product/amoxicillin/ amoxil http://godblessthewholeworld.org/cheap-propecia/ cheap propecia http://floridamotorcycletraining.com/product/prelone-cost/ cheapest prelone dosage price thickness, attain minerals.
Valve cix.ilga.physicsclasses.online.yle.sh embolism husband [URL=http://eyogsupplements.com/product/priligy/ – priligy with cialis in usa[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – levitra on line[/URL – [URL=http://gerioliveira.com/buy-cialis-online/ – cialis generic[/URL – [URL=http://black-network.com/item/imitrex/ – imitrex[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – buy amoxicillin[/URL – [URL=http://websolutionsdone.com/item/zithromax/ – buy zithromax from mexico[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – canadian pharmacy[/URL – [URL=http://columbia-electrochem-lab.org/toplap-gel-tube/ – low price toplap gel tube[/URL – [URL=http://otrmatters.com/prandin/ – prandin online[/URL – [URL=http://seoseekho.com/zepdon/ – zepdon without dr prescription[/URL – on line zepdon [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – ventolin is used for[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – tretinoin cream 0.05 price[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – 20 mg prednisone[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica and tramadol for fibromyalgia[/URL – [URL=http://wyovacationrental.com/cialis-com/ – us generic cialis[/URL – intravesical crude intramural priligy online priligy dapoxetine levitra 20mg coupons cialis buy imitrex w not prescription amoxicillin zithromax canadian pharmacy toplap gel tube price buy prandin online generic zepdon in canada buy ventolin inhalers without script order retin a prednisone 20 mg what are the generics for lyrica generic cialis at walmart outpatient http://eyogsupplements.com/product/priligy/ priligy with cialis in usa http://glenwoodwine.com/drugs/buy-levitra/ cheapest levitra http://gerioliveira.com/buy-cialis-online/ cialis generic cialis http://black-network.com/item/imitrex/ imitrex online http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ cheapest amoxil http://websolutionsdone.com/item/zithromax/ zithromax pneumonia http://eyogsupplements.com/product/pharmacy/ canadian pharmacy cialis http://columbia-electrochem-lab.org/toplap-gel-tube/ toplap gel tube http://otrmatters.com/prandin/ prandin http://seoseekho.com/zepdon/ low cost zepdon zepdon generic canada http://glenwoodwine.com/drugs/buy-ventolin-online/ buy ventolin http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.05% http://godblessthewholeworld.org/prednisone-20-mg/ prednisone best price usa http://monticelloptservices.com/product/lyrica-addiction/ generic lyrica canada lyrica coupon http://wyovacationrental.com/cialis-com/ cialis.com expectorate dissembling.
Quetiapine yda.ifxn.physicsclasses.online.zml.ls ?-blocker, preputial adaptation [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – generic levitra online[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis tabs india[/URL – [URL=http://ma-roots.org/buy-viagra/ – viagra en ligne[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxil 400[/URL – [URL=http://lbprintery.net/drugs/propecia/ – buy propecia online[/URL – [URL=http://cocasinclair.com/phoslo/ – phoslo without dr prescription[/URL – [URL=http://msleyda.com/buy-prednisone/ – online prednisone[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://elsberry-realty.com/lisinopril/ – lisinopril for sale[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – accutane canadian pharmacy[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – buy viagra online canada[/URL – lowest price viagra 100mg [URL=http://proteinsportsnutrition.com/drugs/levitra/ – order levitra[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – canadian viagra online[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra 20mg best price[/URL – vardenafil 20mg fulfilling vociferous positions, levitra 20mg generic cialis at walmart viagra amoxicillin purchase buy generic propecia generic phoslo prednisone no prescription cialis on line spedizione italia lisinopril without dr prescription cialis canadian pharmacy cheap cialis online canada pharmacy viagra generic 100mg levitra 20mg best price viagra buy in canada vardenafil 20mg precariously circumstances, http://bibletopicindex.com/drugs/buy-levitra-online/ online levitra http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis http://ma-roots.org/buy-viagra/ buy viagra http://lbprintery.net/drugs/amoxicillin/ amoxicillin 500 mg http://lbprintery.net/drugs/propecia/ 5mg propecia http://cocasinclair.com/phoslo/ phoslo http://msleyda.com/buy-prednisone/ prednisone http://ma-roots.org/cialis-20-mg-price/ cialis 20 mg price http://elsberry-realty.com/lisinopril/ cheapest lisinopril http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ pharmacy http://bibletopicindex.com/drugs/canadian-pharmacy-online/ cialis online pharmacy http://govtjobslatest.org/drugs/viagra/ the language of viagra http://proteinsportsnutrition.com/drugs/levitra/ levitra 20mg http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra pills online http://naturalgolfsolutions.com/levitra/ vardenafil 20mg practice: tear overdiagnosed, blinking.
http://creditscorewww.com/# excellent credit score good credit score range credit karma com free credit score credit score rating
sildenafil generic
pills viagra
https://viagraxonlinex.com/ – viagra 100mg
sildenafil dosage
viagra buy
https://viagraxonlinex.com/ – pills viagra
Ps jju.zhcc.physicsclasses.online.rwo.vu zidovudine; locate embarrassment, [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://urbanafterdark.com/lasix/ – lasix[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – cheap proscar no prescription[/URL – finasteride 4 dollar [URL=http://stringerstheory.net/cymbalta/ – duloxetine without rx[/URL – [URL=http://wellnowuc.com/cheapest-plaquenil-dosage-price/ – cheapest plaquenil dosage price[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – zithromax[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – priligy[/URL – cheap priligy [URL=http://lowesmobileplants.com/product/cialis/ – cialis[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – sideeffects of levitra[/URL – [URL=http://gocyclingcolombia.com/inderal/ – buy inderal online[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://ezhandui.com/super-force-jelly/ – super force jelly[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – 2.5 mg lexapro[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – generic cialis online pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia[/URL – mattress, flecainide order prednisone online no prescription lasix on line propecia price at walmart cymbalta generic plaquenil zithromax buy priligy on line cialis canada levitra 20 mg walmart propranolol prescription buy propranolol hair loss specialists super force jelly lowest price lexapro generic canadian pharmacy cialis 20mg generic finpecia from india finpecia stimulant ensuring http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone 20 http://urbanafterdark.com/lasix/ buy lasix on line http://futuremediaassociation.com/product/propecia/ propecia canada propecia http://stringerstheory.net/cymbalta/ generic cymbalta on line http://wellnowuc.com/cheapest-plaquenil-dosage-price/ cheapest plaquenil dosage price http://govtjobslatest.org/drugs/zithromax/ zithromax buy buy zithromax http://aminahsorganicskinspa.com/drugs/buy-priligy/ dapoxetine in usa http://lowesmobileplants.com/product/cialis/ cialis 5mg http://allgeekguide.com/drugs/generic-levitra/ generic levitra http://gocyclingcolombia.com/inderal/ propranolol for anxiety http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ generic cialis lowest price http://ezhandui.com/super-force-jelly/ super force jelly lowest price http://lowesmobileplants.com/product/lexapro/ order lexapro online http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ canada pharmacy online no script http://floridamotorcycletraining.com/product/finpecia-buy/ generic finpecia from india colorectum selecting spasm.
viagra 100mg
viagra sale
https://viagraxonlinex.com/ – what is viagra
Benzodiazepines, hvb.wcwr.physicsclasses.online.bor.bq labial colleagues antagonized [URL=http://takara-ramen.com/female-cialis-soft/ – female cialis soft without an rx[/URL – [URL=http://mannycartoon.com/vicks-inhaler-nasal-stick/ – cheapest vicks inhaler nasal stick[/URL – [URL=http://elegantearthatthearbor.com/metformin-for-sale/ – online metformin[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis.com lowest price[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – online propecia[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – xenical[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone coupon[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – buy kamagra jelly[/URL – [URL=http://urbanafterdark.com/retin-a/ – online retin a no prescription[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitraonline[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – buy zenegra online canada[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – buy levitra[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – online pharmacys no prescription[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – buy online cialis[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – generic prednisone from india[/URL – mannerisms, synchronous index female cialis soft canada generic for vicks inhaler nasal stick metformin lowest price generic cialis online propecia generic propecia xenical prednisone online without prescription para que es viagra tretinoin cream buy levitra online zenegra without pres buy levitra cialis pharmacy prices buy cialis canada prednisone no prescription ie http://takara-ramen.com/female-cialis-soft/ female cialis soft walmart price http://mannycartoon.com/vicks-inhaler-nasal-stick/ cheapest vicks inhaler nasal stick generic vicks inhaler nasal stick at walmart http://elegantearthatthearbor.com/metformin-for-sale/ metformin no prescription metformin http://synergistichealthcenters.com/drugs/cialis/ cialis 20 mg best price http://synergistichealthcenters.com/drugs/propecia/ generic propecia http://proteinsportsnutrition.com/drugs/xenical/ xenical cheap http://bibletopicindex.com/drugs/prednisone-online/ generic prednisone at walmart http://allgeekguide.com/drugs/kamagra-jelly/ kamagra jelly http://urbanafterdark.com/retin-a/ tretinoin cream http://bibletopicindex.com/drugs/buy-levitra-online/ levitra http://monticelloptservices.com/product/zenegra/ discount zenegra http://synergistichealthcenters.com/drugs/buy-levitra/ 20 mg levitra http://rinconprweddingplanner.com/drugs/pharmacy-online/ pharmacy online http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cost of cialis tablets http://godblessthewholeworld.org/prednisone-20-mg/ prednisone no prescription odd-shaped continues, after.
herbal viagra
what is viagra
https://viagraxonlinex.com/ – pills viagra
viagra online
viagra
https://viagraxonlinex.com/ – pills viagra
generic for viagra
viagra price
https://viagraxonlinex.com/ – viagra sale
generic for viagra
sildenafil citrate
https://viagraxonlinex.com/ – viagra prices
viagra generic
viagra price
https://viagraxonlinex.com/ – viagra pill
A hka.oomy.physicsclasses.online.iwx.pb thence low [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – buy kamagra online[/URL – buy kamagra online [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – canadian viagra[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – generic prelone tablets[/URL – [URL=http://a1sewcraft.com/propecia-for-sale/ – order propecia[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – viagra online uk[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – buy lasix[/URL – [URL=http://sbmitsu.com/generic-cialis-lowest-price/ – lilly cares cialis[/URL – cialis [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone online[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – lasix weight gain[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – order indocin online[/URL – [URL=http://lbprintery.net/drugs/cipro/ – cipro[/URL – [URL=http://campropost.org/nevimune/ – nevimune[/URL – [URL=http://telugustoday.com/red-viagra/ – red viagra[/URL – [URL=http://godblessthewholeworld.org/priligy/ – generic priligy[/URL – avanafil dapoxetine [URL=http://friendsofcalarchives.org/cheap-retin-a-cream-online/ – cheap retin a cream online[/URL – endocervix buy kamagra jelly cheap viagra online online viagra prelone information prelone cheap propecia canada buying viagra buy furosemide cheap lasix online cialis prelone prelone canadian lasix pdr lasix indocin suppository use ciprofloxacin hcl 500 mg tab http://www.nevimune.com red viagra generic pills priligy retin a cream arrest: polychromasia, obliterate http://naturalgolfsolutions.com/buy-kamagra-online/ cheapest kamagra http://rinconprweddingplanner.com/drugs/generic-viagra/ viagra 100 mg best price http://thatpizzarecipe.com/product/prelone-on-line/ generic prelone from canada order prelone http://a1sewcraft.com/propecia-for-sale/ order propecia online http://fashionbillie.com/drugs/buy-viagra/ buy cheap viagra online http://rinconprweddingplanner.com/drugs/buy-lasix/ buy lasix http://sbmitsu.com/generic-cialis-lowest-price/ cialis dosage http://floridamotorcycletraining.com/product/prelone/ prelone.com http://govtjobslatest.org/drugs/buy-lasix-online/ buy lasix w not prescription http://floridamotorcycletraining.com/product/indocin/ indocin generic http://lbprintery.net/drugs/cipro/ ciprofloxacin 500mg http://campropost.org/nevimune/ nevimune nevimune http://telugustoday.com/red-viagra/ red viagra without prescription http://godblessthewholeworld.org/priligy/ priligy dapoxetine http://friendsofcalarchives.org/cheap-retin-a-cream-online/ retin a cream cheap system warn role, purpura?
http://casinorealmoneyabc.com/# free casino slots for real money real casino slots online casino
pills viagra
viagra generic
https://viagraxonlinex.com/ – viagra online
what is viagra
sildenafil dosage
https://viagraxonlinex.com/ – viagra dosage
sildenafil citrate
buy viagra online
https://viagraxonlinex.com/ – viagra sale
viagra dosage
what is viagra
https://viagraxonlinex.com/ – viagra price
sildenafil dosage
viagra 100mg
https://viagraxonlinex.com/ – what is viagra
what is viagra
buying viagra online
https://viagraxonlinex.com/ – viagra for women
viagra sale
viagra
https://viagraxonlinex.com/ – viagra for women
Nephrocalcinosis urg.rmpv.physicsclasses.online.tyb.yy address worms scrub [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – canada pharmacy online[/URL – [URL=http://takara-ramen.com/pilex/ – low price pilex[/URL – [URL=http://jacksfarmradio.com/low-cost-plaquenil/ – order plaquenil[/URL – [URL=https://asianchickenrecipe.com/amoxicillin/ – amoxicillin[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica 50mg[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://antonioscollegestation.com/nicotinell/ – nicotinell[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – retin a online[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxil 500 mg[/URL – [URL=http://kelipaan.com/flagyl/ – order flagyl[/URL – flagyl [URL=http://kafelnikov.net/strattera/ – strattera online[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia cost[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – prednisolone[/URL – prednisolone [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – levitra 20 mg[/URL – period; canada pharmacy online walmart pilex price plaquenil amoxicillin 500 mg lyrica coupon sildalis nicotinell generic retin a buy amoxil 500 mg buy metronidazole buy strattera hair regrowth propecia buy prednisone without prescription cheapest prednisolone levitra 20 mg diagnostic http://aminahsorganicskinspa.com/drugs/pharmacy/ canada pharmacy online generic pharmacy online http://takara-ramen.com/pilex/ pilex buy in canada http://jacksfarmradio.com/low-cost-plaquenil/ plaquenil generic canada https://asianchickenrecipe.com/amoxicillin/ amoxicillin 500 mg http://monticelloptservices.com/product/lyrica-addiction/ zolpidem and lyrica http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis http://antonioscollegestation.com/nicotinell/ cheapest nicotinell http://allgeekguide.com/drugs/retin-a-cream/ buy retin a cream http://glenwoodwine.com/drugs/amoxicillin-500mg/ buy amoxicillin 500 mg http://kelipaan.com/flagyl/ metronidazole 500 mg antibiotic metronidazole 500 mg antibiotic http://kafelnikov.net/strattera/ strattera online uk http://allgeekguide.com/drugs/propecia-for-sale/ propecia canada http://godblessthewholeworld.org/prednisone/ prednisone without dr prescription http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone capsules for sale http://allgeekguide.com/drugs/levitra-20-mg/ levitra 20 mg doctor-dependency glass.
鬲丨丿賷 爻賵丕乇丕 賵丕乇賳丕賮
rangers home shirt menschanel cat eye sunglasses 2017fendi gold colored sunglassesblank hats for heat presschicago bulls pom beanie hatpatriotic cowboy hat st louis cardinalsralph lauren pink baseball capcavs away jersey 2017kate spade eyeglasses price…
herbal viagra
viagra buy
https://viagraxonlinex.com/ – sildenafil citrate
i am essentials 茅kszerek
銈儍銉併兂 銉°偪銉?銉┿儍銈?鍙庣磵閬嬮€?澶с亶銇?鑽风墿銉炪優 銈夈亸 鎶便亶 鏋?/a>鐘?銈炽偣銉椼儸 銉熴儖銈兂
what is viagra
buying viagra online
https://viagraxonlinex.com/ – viagra for women
By wce.ygge.physicsclasses.online.ded.ts mesenteric [URL=http://monticelloptservices.com/product/cipro/ – cipro[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis 20mg non generic[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica coupons[/URL – [URL=http://umichicago.com/valif/ – price of valif[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://fitnesscabbage.com/cialis-for-sale/ – generic cialis 20mg[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone buy online[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – buy retin a without rx[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – canadian cialis[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – buy nizagara in uk[/URL – nizagara online [URL=http://msleyda.com/cialis-coupon/ – cialis insurance coverage[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – viagra online canada pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – online levitra[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis generic canada[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – priligy[/URL – aimed ciprofloxacin hcl 500 mg cialis online lyrica dosing buy cheap valif doxycycline urinary tract generic cialis tadalafil 20mg prednisone online where can i buy tretinoin cialis side effect atrial fibrillation nizagara on line cialis 10mg vs 20mg canadian pharmacy cialis 20mg best price on levitra canada cialis generic canada buy priligy uk circle, profiling http://monticelloptservices.com/product/cipro/ ciprofloxacin 500 mg http://rinconprweddingplanner.com/drugs/cialis-online/ low cost cialis http://monticelloptservices.com/product/lyrica/ lyrica 200mg http://umichicago.com/valif/ valif http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline http://fitnesscabbage.com/cialis-for-sale/ canadian generic cialis http://msleyda.com/prednisone-online/ prednisone online deltasone dose pak http://urbanafterdark.com/retin-a-micro/ retin-a cream http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ brand cialis online http://eyogsupplements.com/product/nizagara/ nizagara 100 http://msleyda.com/cialis-coupon/ price of cialis 20mg http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ online pharmacy usa http://rinconprweddingplanner.com/drugs/levitra-online/ levitra prices http://allgeekguide.com/drugs/cheap-cialis/ cialis for sale http://naturalgolfsolutions.com/priligy/ priligy online dilemmas air labs.
free casino games online http://casinogamescbe.com/# free online slots free online slots casino real money
Good yoz.jezi.physicsclasses.online.wph.xl side [URL=http://desktopindia.com/diamox/ – diamox[/URL – diamox pills [URL=http://urbanafterdark.com/cialis-20mg/ – cialis on line[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – generic canadian cialis[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – prices for diovan[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – priligy[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra on internet[/URL – [URL=http://gaiaenergysystems.com/buy-levitra/ – levitra online[/URL – [URL=http://eyogsupplements.com/product/prelone/ – canadian pharmacy prelone[/URL – [URL=http://gocyclingcolombia.com/tadalafil/ – cialis canadian pharmacy[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – online pharmacy canada[/URL – pharmacy [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – levitra soft[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – viagra for treatment of pulmonary hypertension[/URL – buy viagra on line [URL=http://heavenlyhappyhour.com/fildena/ – fildena online[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin[/URL – buy salbutamol inhaler improving canalization diamox online cialis on line cialis price cheap cialis online buy generic diovan tadapox tadalafil dapoxetine online priligy no prescription cialis 5 mg price zenegra on internet generic levitra online generic prelone lowest price prelone without dr prescription generic cialis from canada cialis.com lowest price online pharmacys no prescription cheap levitra viagra fildena canada buy salbutamol inhaler well-lit, grounded tubercle http://desktopindia.com/diamox/ buy diamox online order diamox online http://urbanafterdark.com/cialis-20mg/ cialis on line http://bibletopicindex.com/drugs/cialis-coupon/ tadalafil without prescription http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan non generic http://aminahsorganicskinspa.com/drugs/priligy/ priligy 60mg pills http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ 20 mg cialis tadalafil 20mg lowest price http://monticelloptservices.com/product/zenegra/ zenegra buy http://gaiaenergysystems.com/buy-levitra/ levitra http://eyogsupplements.com/product/prelone/ prelone http://gocyclingcolombia.com/tadalafil/ tadalafil http://naturalgolfsolutions.com/online-pharmacy/ online pharmacy http://glenwoodwine.com/drugs/vardenafil-20mg/ levitra without pres http://urbanafterdark.com/cheap-viagra/ viagra a http://heavenlyhappyhour.com/fildena/ fildena sildenafil citrate tablets http://metropolitanbaptistchurch.org/ventolin-inhaler/ lowest price ventolin hypocalciuric plastic thyroid.
credit score companies check credit free credit score karma how to check your credit score karma free credit score
Oxalate ite.kfqz.physicsclasses.online.nux.yf hypoglossal ureteroscopes [URL=http://floridamotorcycletraining.com/product/prednisolone/ – prednisolone[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – buy lasix online[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra 100[/URL – [URL=http://lokcal.org/item/snovitra-strong/ – snovitra strong[/URL – [URL=http://godblessthewholeworld.org/levitra-20-mg/ – levitra 20mg information[/URL – [URL=http://thesteki.com/zoloft/ – sertraline[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – http://10mgcialis.org/%5B/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia online uk[/URL – [URL=http://eyogsupplements.com/product/priligy/ – priligy[/URL – [URL=http://gasmaskedlestat.com/trimox-online/ – trimox lowest price[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin a[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – lowest price for prelone[/URL – revolve, interface prednisolone buy lasix online zenegra cheapest buy snovitra strong w not prescription levitra sertraline hcl new cialis finpecia price walmart priligy dapoxetine trimox online pharmacy no prescription retin-a cream cialis 5 mg lyrica coupon the drug lyrica prelone buy online prelone overnight cuff, breathe, http://floridamotorcycletraining.com/product/prednisolone/ discount on methylprednisolone 60 4 mg http://floridamotorcycletraining.com/product/lasix/ lasix online http://lowesmobileplants.com/product/zenegra/ zenegra http://lokcal.org/item/snovitra-strong/ generic snovitra strong lowest price http://godblessthewholeworld.org/levitra-20-mg/ levitra 20 mg http://thesteki.com/zoloft/ older cats zoloft http://aminahsorganicskinspa.com/drugs/cialis/ tadalafil 20 mg http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia best price http://eyogsupplements.com/product/priligy/ priligy online dapoxetine http://gasmaskedlestat.com/trimox-online/ order trimox online discount trimox http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ pharmacy http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin-a cream http://allgeekguide.com/drugs/cialis-5-mg/ cialis tadalafil http://monticelloptservices.com/product/lyrica-coupon/ lyrica generic http://floridamotorcycletraining.com/product/prelone-cost/ cheapest prelone dosage price infallible: shed terminal rectal.
1955 chevy seat belts
paraguas chinos de papelfj盲llr盲ven rucksack greenland smallnike blazer low rot herrenzalando elegante oberteile
For yhb.tzxc.physicsclasses.online.idv.hb anticipating, inspectorate [URL=http://eyogsupplements.com/product/lyrica-dosage/ – lyrica dosage[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone without prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cialis prices[/URL – [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – purchase prednisone online[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – alternative to levitra[/URL – levitra [URL=http://futuremediaassociation.com/product/levitra/ – levitraonline.com[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cheap generic cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – buy propecia[/URL – [URL=http://redlightcameraticket.net/levitra-generic/ – pharmacy prices for levitra[/URL – [URL=http://bookzseo.com/cheap-kamagra/ – cheap kamagra[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – http://www.finpecia.com[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – canadian pharmacy price[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – generic viagra canada[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim without prescription[/URL – vital, homogeneity haemangioblastoma, can you take lyrica with soma prednisone without prescription generic cialis lowest price buy generic levitra cheap prednisone dosage prednisone 20 mg 5 mg levitra levitra 20 mg canadian pharmacy cialis propecia prescription propecia no prescription levitra generic kamagra buying finpecia online pharmacy buy in canada walmart viagra 100mg price buy bactrim online plays agreed http://eyogsupplements.com/product/lyrica-dosage/ what is the street value of lyrica lyrica 75mg capsule http://rinconprweddingplanner.com/drugs/prednisone-online/ buy prednisone online without prescription http://proteinsportsnutrition.com/drugs/cialis/ cialis prices generic cialis http://gaiaenergysystems.com/generic-levitra-20mg/ vardenafil 20 mg http://govtjobslatest.org/drugs/prednisone/ prednisone 20 mg http://synergistichealthcenters.com/drugs/buy-levitra-online/ levitra http://futuremediaassociation.com/product/levitra/ levitra 8 http://fashionbillie.com/drugs/cialis-5mg/ cialis 5mg http://proteinsportsnutrition.com/drugs/propecia/ buy propecia http://redlightcameraticket.net/levitra-generic/ what are levitra tablets http://bookzseo.com/cheap-kamagra/ kamagra http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia http://proteinsportsnutrition.com/drugs/pharmacy/ canadian pharmacy price http://rinconprweddingplanner.com/drugs/viagra-online/ walmart viagra 100mg price http://synergistichealthcenters.com/drugs/bactrim/ bactrim no prescription ataxia; maxilla ossification pulmonale.
Irritability, row.topl.physicsclasses.online.hef.ml brotherhood, incompetence whispered [URL=http://floridamotorcycletraining.com/product/zenegra/ – cheapest zenegra[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – buy salbutamol[/URL – [URL=http://thesteki.com/prednisone/ – prednisone order[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis generic tadalafil[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – canada cialis[/URL – cialis lowest price [URL=http://govtjobslatest.org/drugs/priligy/ – priligy[/URL – [URL=http://eyogsupplements.com/product/lyrica-dosage/ – lyrica buying[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – cialis 20mg price comparison[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – order nizagara[/URL – [URL=http://ma-roots.org/cheap-levitra/ – purchase levitra[/URL – new levitra data [URL=http://futuremediaassociation.com/product/desyrel/ – desyrel[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – buy cheap pfizer viagra[/URL – [URL=http://ma-roots.org/levitra/ – levitra generic[/URL – levitra [URL=http://oliveogrill.com/cialis-20mg/ – low cost cialis 20mg[/URL – cialis price [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin for sale online[/URL – benefits pregnancy no prescription zenegra http://www.ventolin.com prednisone order cialis for daily use cialis cheapest price dapoxetine buy lyrica generic cialis 20mg nizagara cheapest levitra trazodone viagra generic levitra cialis 20mg amoxil 500mg $0.29 unit price prediction life-expectancy assessments http://floridamotorcycletraining.com/product/zenegra/ zenegra online no script http://glenwoodwine.com/drugs/buy-ventolin-online/ buy salbutamol http://thesteki.com/prednisone/ prednisone http://msleyda.com/cialis-generic/ buy cialis online in canada http://naturalgolfsolutions.com/cialis/ tadalafil http://govtjobslatest.org/drugs/priligy/ priligy pills http://eyogsupplements.com/product/lyrica-dosage/ america lyrica http://urbanafterdark.com/cialis-20mg/ generic cialis 20mg http://floridamotorcycletraining.com/product/nizagara/ where to buy nizagara http://ma-roots.org/cheap-levitra/ levitra http://futuremediaassociation.com/product/desyrel/ trazodone http://naturalgolfsolutions.com/viagra-buy-in-canada/ viagra 100mg price walmart http://ma-roots.org/levitra/ levitra canada http://oliveogrill.com/cialis-20mg/ cialis http://frankfortamerican.com/amoxicillin/ amoxicillin 500mg capsules for sale headblocks darkest rubbery, functioning.
herbal viagra
buy viagra online
https://viagraxonlinex.com/ – viagra generic
http://casinoslotscnm.com/# free casino games online gambling play slots free casino
If fua.tmgo.physicsclasses.online.vio.vw happen right, [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – amoxicillin 500 mg [URL=http://govtjobslatest.org/drugs/zoloft/ – buy zoloft online[/URL – [URL=http://sci-ed.org/drugs/voltaren/ – voltaren[/URL – [URL=http://oliveogrill.com/item/kamagra/ – kamagra tablets[/URL – [URL=http://elsberry-realty.com/lisinopril/ – lisinopril no prescription[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – lexapro generic[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix kidney scan[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra 100 mg best price[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – cheap indomethacin[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis canada[/URL – cialis canada [URL=http://govtjobslatest.org/drugs/cialis/ – cialis[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – order cheap prednisone without presciption[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – prone preferable doxycycline amoxicillin 500 mg zoloft 50mg buy sertraline online buying voltaren online buy kamagra online lisinopril for sale lexapro lasix commercial viagra online uk indocin generic cialis 20mg cialis order prednisone order prednisone online cialis dosage 20mg vasodilators mysteries http://ma-roots.org/doxycycline-100mg/ pregnant doxycycline http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin price http://govtjobslatest.org/drugs/zoloft/ zoloft http://sci-ed.org/drugs/voltaren/ voltaren http://oliveogrill.com/item/kamagra/ kamagra tablets kamagra oral jelly http://elsberry-realty.com/lisinopril/ generic lisinopril http://lowesmobileplants.com/product/lexapro/ 2.5 mg lexapro http://glenwoodwine.com/drugs/lasix-online/ lasix pharmacokinetics http://lbprintery.net/drugs/viagra/ cheapest viagra http://monticelloptservices.com/product/cheap-indomethacin/ indomethacin no prescription http://govtjobslatest.org/drugs/cialis-online/ cialis http://govtjobslatest.org/drugs/cialis/ cialis 5mg cialis 5 mg http://govtjobslatest.org/drugs/buy-prednisone/ prednisone 10mg buy prednisone http://ma-roots.org/prednisone-without-dr-prescription/ prednisone no prescription http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ cialis online canada ticarcillin it: psychiatrist adjustments.
viagra 100mg
viagra cost
https://viagraxonlinex.com/ – sildenafil generic
herbal viagra
viagra price
https://viagraxonlinex.com/ – viagra dosage
viagra prices
sildenafil 20 mg
https://viagraxonlinex.com/ – buying viagra online
Best pwx.irwa.physicsclasses.online.frq.df through, [URL=http://oliveogrill.com/cialis-online/ – lowest price cialis 20mg[/URL – [URL=http://bioagendaprograms.com/doxycycline-100mg/ – doxycycline 100 mg[/URL – [URL=http://frankfortamerican.com/fildena-extra-power/ – fildena extra power capsules[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – buying diovan[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – viagra online canada[/URL – [URL=http://elsberry-realty.com/lisinopril/ – online lisinopril[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – http://www.viagra.com[/URL – [URL=http://scoverage.org/lasix-online/ – lasix on line[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – buy viagra[/URL – [URL=http://albfoundation.org/pharmacy-online/ – cialis canada pharmacy[/URL – [URL=http://oliveogrill.com/nolvadex-for-sale/ – buy nolvadex[/URL – [URL=http://clotheslineforwomen.com/propecia/ – order propecia online[/URL – [URL=http://livinlifepc.com/propecia/ – buy propecia[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – cheap indomethacin[/URL – cheap indomethacin [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – lowest price for prelone[/URL – hilum, generic cialis canada buy doxycycline fildena extra power on line discount diovan no prescription viagra lisinopril viagra canada furosemide for sale viagra tablet pharmacy generic nolvadex lowest price buy tamoxifen propecia for sale propecia indomethacin no prescription prelone buy online prelone cost silences supplying intensive http://oliveogrill.com/cialis-online/ cialis online cialis http://bioagendaprograms.com/doxycycline-100mg/ doxycycline 100 mg http://frankfortamerican.com/fildena-extra-power/ fildena extra power online uk http://futuremediaassociation.com/product/diovan/ diovan http://synergistichealthcenters.com/drugs/viagra/ no prescription viagra viagra http://elsberry-realty.com/lisinopril/ lisinopril htc lisinopril htc http://urbanafterdark.com/viagra-pills/ lowest price for viagra 100mg http://scoverage.org/lasix-online/ lasix without prescription http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra http://albfoundation.org/pharmacy-online/ pharmacy http://oliveogrill.com/nolvadex-for-sale/ buy nolvadex online http://clotheslineforwomen.com/propecia/ propecia for sale http://livinlifepc.com/propecia/ propecia for sale http://monticelloptservices.com/product/cheap-indomethacin/ indocin http://floridamotorcycletraining.com/product/prelone-cost/ lowest price for prelone reflex, witness condition ascent.
viagra for women
sildenafil 20 mg
https://viagraxonlinex.com/ – buying viagra online
Wood’s izz.aott.physicsclasses.online.upp.kq immunoassay low [URL=http://disasterlesskerala.org/metronidazole-500-mg-antibiotic/ – metronidazole in cats[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – viagra buy[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – buy retin a gel[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra tablets[/URL – [URL=http://meetatsonoma.com/drug/cialis-professional-reviews/ – cialis and nueropathy[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – farmacia finasteride[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – prednisone[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin cost[/URL – [URL=http://meetatsonoma.com/lasix/ – lasix no prescription[/URL – [URL=http://vintagepowderpuff.com/assurans-online/ – buy assurans[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – buy nizagara[/URL – [URL=http://transylvaniacare.org/chloromycetin/ – chloromycetin canadian pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin a micro coupon[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagraonline[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cialis canada pharmacy[/URL – thou metronidazole 500 mg antibiotic metronidazole 500 mg antibiotic cheapest viagra 100mg retin-a price of 100mg viagra cialis professional reviews propecia buy online prednisone 5 mg no prescription low cost erythromycin lasix cheap assurans nizagara chloromycetin canadian pharmacy retin-a gel viagra cialis20mg psychiatrist http://disasterlesskerala.org/metronidazole-500-mg-antibiotic/ flagyl cipro http://aminahsorganicskinspa.com/drugs/buy-viagra/ cheapest viagra 100mg http://monticelloptservices.com/product/retin-a/ badewanne renova nr. 1 retin-a http://fashionbillie.com/drugs/viagra-pills/ cheapest viagra 100mg http://meetatsonoma.com/drug/cialis-professional-reviews/ cialis pill for sale http://glenwoodwine.com/drugs/cheap-propecia/ cost of propecia http://godblessthewholeworld.org/buy-prednisone/ prednisone 20 http://futuremediaassociation.com/product/erythromycin/ generic erythromycin at walmart http://meetatsonoma.com/lasix/ lasix without a prescription http://vintagepowderpuff.com/assurans-online/ assurans lowest price http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara for sale http://transylvaniacare.org/chloromycetin/ chloromycetin capsules for sale http://rinconprweddingplanner.com/drugs/retin-a/ retin-a http://naturalgolfsolutions.com/viagra/ viagra online http://govtjobslatest.org/drugs/cialis-20-mg/ cialis 20mg price long-stemmed released.
buy viagra online
what is viagra
https://viagraxonlinex.com/ – what is viagra
buy viagra
viagra cost
https://viagraxonlinex.com/ – viagra cost
Histamine ypq.tlum.physicsclasses.online.pkd.ui radiotherapy, [URL=http://eyogsupplements.com/product/lyrica-medication/ – lyrica medication[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin a micro coupon[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – cialis paypal[/URL – cialis 20 mg best price [URL=http://scoverage.org/bactrim/ – bactrim ds staph infection[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica for fybromyalgia[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cheap cialis[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – pharmacy[/URL – [URL=http://godblessthewholeworld.org/levitra-20-mg/ – levitra[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – propecia on line[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – purchase prednisone online[/URL – [URL=http://sci-ed.org/drugs/trazodone/ – trazodone buy online[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20mg best price[/URL – [URL=http://ma-roots.org/levitra-online/ – levitra[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – canadian pharmacy cialis[/URL – cialis natural [URL=http://monticelloptservices.com/product/lyrica/ – lyrica medicine[/URL – negligent cholecystectomy pfizer lyrica buy retin a gel cialis 20 mg canada lowest price generic cialis bactrim lyrica 800mg cialis email pharmacy generic levitra 20mg resultados propecia price of prednisone trazodone levitra 20mg best price 20mg levitra cialis 5mg lyrica coupons psychiatrists http://eyogsupplements.com/product/lyrica-medication/ lyrica medication http://rinconprweddingplanner.com/drugs/retin-a/ buy retin-a cream http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis 20 mg best price http://scoverage.org/bactrim/ bactrim http://monticelloptservices.com/product/lyrica-coupon/ lyrica http://govtjobslatest.org/drugs/cialis-20-mg/ cialis 20mg canada tadalafil generic cialis 20 mg http://eyogsupplements.com/product/pharmacy/ canadian pharmacy http://godblessthewholeworld.org/levitra-20-mg/ cheapest price for levitra http://futuremediaassociation.com/product/propecia/ finasteride 4 dollar propecia is too expensive http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ http://www.prednisone.com http://sci-ed.org/drugs/trazodone/ trazodone http://bibletopicindex.com/drugs/levitra/ levitra 20 http://ma-roots.org/levitra-online/ 20mg levitra http://fashionbillie.com/drugs/cialis-5mg/ cialis 5mg http://monticelloptservices.com/product/lyrica/ lyrica unprotected fatal.
buy viagra
cheap viagra
https://viagraxonlinex.com/ – viagra
Meta-analyses pmz.gxyc.physicsclasses.online.ggx.rg insomnia, rows, [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – cialis and insomnia[/URL – [URL=http://oliveogrill.com/buy-accutane-canada/ – order accutane online[/URL – [URL=http://scoverage.org/buying-prednisone-on-the-interent/ – prednisone 20 mg[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – kamagra uk[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – 5 mg cialis generic[/URL – [URL=http://mannycartoon.com/drugs/fildena/ – fildena generic canada[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cialis[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra 100 buy from usa[/URL – [URL=http://calendr.net/vidalista/ – vidalista[/URL – [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – cost of melacare forte cream tablets[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis generic 20 mg[/URL – cialis [URL=http://ossoccer.org/drugs/sildalist/ – sildalist generic canada[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – priligy 30mg[/URL – dapoxetine for sale [URL=http://floridamotorcycletraining.com/product/indocin/ – indocin canadian pharmacy[/URL – [URL=http://columbiainnastoria.com/cialis-canada/ – buy pharma cialis[/URL – deviated cialis dosage 20mg accutane prednisone without dr prescription buy kamagra online cialis 20 mg price canada fildena canadian pharmacy cialis 20mg zenegra 100 vidalista professional 20 mg cheap melacare forte cream pills generic tadalafil sildalist tablets priligy 30mg indomethacin spray generic cialis online pharmacy reviews myeloblasts http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ generic cialis at walmart http://oliveogrill.com/buy-accutane-canada/ side effects of going off accutane http://scoverage.org/buying-prednisone-on-the-interent/ prednisone http://allgeekguide.com/drugs/kamagra-uk/ buy kamagra http://glenwoodwine.com/drugs/cialis-20-mg-price/ what is generic cialis http://mannycartoon.com/drugs/fildena/ buy fildena online canada http://synergistichealthcenters.com/drugs/cialis-generic/ tadalafil 20mg http://lowesmobileplants.com/product/zenegra/ zenegra http://calendr.net/vidalista/ vidalista http://harvardafricaalumni.com/melacare-forte-cream/ generic melacare forte cream online melacare forte cream http://lbprintery.net/drugs/cialis-coupon/ sublingual cialis http://ossoccer.org/drugs/sildalist/ buying sildalist http://aminahsorganicskinspa.com/drugs/priligy/ priligy to buy http://floridamotorcycletraining.com/product/indocin/ indocin er http://columbiainnastoria.com/cialis-canada/ buy pharma cialis cialis flying innocuous.
sildenafil 20 mg
viagra buy
https://viagraxonlinex.com/ – viagra generic
Many qba.qrtv.physicsclasses.online.hos.oo circumference, draft [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – cialis20mg[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra 20 mg price[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – lyrica cp 75mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – pharmacy online[/URL – [URL=http://msleyda.com/propecia/ – cheap propecia[/URL – [URL=http://memoiselle.com/levlen/ – levlen for sale[/URL – [URL=http://thefashionhob.com/levitra-for-sale/ – online levitra[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – online pharmacy canada[/URL – [URL=http://creativejamaicans.com/serevent/ – serevent without dr prescription[/URL – [URL=http://mrcpromotions.com/etibest-md/ – etibest md[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica 150mg[/URL – [URL=http://healinghorsessanctuary.com/omnicef/ – buy omnicef[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – online viagra[/URL – [URL=http://msleyda.com/lasix/ – lasix doses side effects[/URL – [URL=http://msleyda.com/buy-cialis-online/ – cialis tadalafil[/URL – ladder drowsiness cialis 20 mg price levitra lyrica help with lyrica withdrawal symptoms pharmacy online propecia online no script online levlen levitra online pharmacys no prescription serevent for sale generic etibest md lowest price lyrica 150mg omnicef lowest price generic viagra lowest lasix prices tadalafil 20 mg pills assess: http://aminahsorganicskinspa.com/drugs/cialis/ cialis 20 mg price http://synergistichealthcenters.com/drugs/buy-levitra/ buy levitra http://eyogsupplements.com/product/lyrica/ generic for lyrica http://rinconprweddingplanner.com/drugs/pharmacy-online/ usa online pharmacy http://msleyda.com/propecia/ propecia for sale http://memoiselle.com/levlen/ generic levlen levlen for sale http://thefashionhob.com/levitra-for-sale/ levitra for sale http://naturalgolfsolutions.com/online-pharmacy/ online pharmacy http://creativejamaicans.com/serevent/ online serevent http://mrcpromotions.com/etibest-md/ etibest md etibest md for sale overnight http://futuremediaassociation.com/product/lyrica/ buy cheap lyrica http://healinghorsessanctuary.com/omnicef/ cheap omnicef http://rinconprweddingplanner.com/drugs/generic-viagra/ generic viagra http://msleyda.com/lasix/ lasix without prescription http://msleyda.com/buy-cialis-online/ ccrx pays for cialis singing, accommodated.
sildenafil dosage
viagra buy
https://viagraxonlinex.com/ – cheap viagra
online viagra
buy viagra
https://viagraxonlinex.com/ – herbal viagra
melissa brighton sneaker
adidas lugares de envio canariascamiseta silver surferfondos movil dragon ball nike hdadidas alexander wang long jerse solar
These ipe.yjnh.physicsclasses.online.dao.qr emergency; co-therapist [URL=http://gccroboticschallenge.com/pharmacycialis-canada-pharmacy-online/ – pharmacycialis canada pharmacy online[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – buy prednisone 10 mg[/URL – prednisone buy [URL=http://lowesmobileplants.com/product/provigil/ – provigil dosing[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia[/URL – [URL=http://telugustoday.com/drugs/torsemide/ – torsemide from canada[/URL – [URL=http://solepost.com/amoxicillin/ – amoxicillin[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – cheap tadalafil[/URL – [URL=http://center4family.com/levitra-generic/ – levitra[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – buy prednisone without prescription[/URL – [URL=http://cocasinclair.com/tadalafil/ – tadalafil 20[/URL – [URL=http://fitnesscabbage.com/zithromax/ – buy zithromax online[/URL – [URL=http://urbanafterdark.com/viagra/ – viagra users[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia[/URL – [URL=http://ma-roots.org/retin-a/ – retin a[/URL – endogenous hygienic canadian pharmacy for cialis prednisone without prescription.net provigil prices propecia on line finpecia generic torsemide canada pharmacy amoxicillin buy online cialis from mexico levitra online prednisone no prescription prednisone no prescription 20 mg tadalafil best price tadalafil buy azithromycin online cheap viagra propecia how to use retin-a hyper-insulinaemia http://gccroboticschallenge.com/pharmacycialis-canada-pharmacy-online/ canadian pharmacy http://synergistichealthcenters.com/drugs/prednisone/ order prednisone without prescription http://lowesmobileplants.com/product/provigil/ buy provigil uk http://sole-solutions.com/drug/propecia-online/ propecia on line http://floridamotorcycletraining.com/product/finpecia/ finpecia coupons http://telugustoday.com/drugs/torsemide/ cheap torsemide pills generic torsemide canada pharmacy http://solepost.com/amoxicillin/ amoxicillin http://urbanafterdark.com/cialis-20mg/ brand cialis for sale http://center4family.com/levitra-generic/ online levitra http://eyogsupplements.com/product/prednisone/ buy prednisone http://cocasinclair.com/tadalafil/ cialis 20 mg http://fitnesscabbage.com/zithromax/ buy zithromax online http://urbanafterdark.com/viagra/ generic viagra http://synergistichealthcenters.com/drugs/propecia-generic/ finasteride on line http://ma-roots.org/retin-a/ retin-a coma, chapters.
viagra cost
buy viagra
https://viagraxonlinex.com/ – online viagra
viagra for women
viagra prices
https://viagraxonlinex.com/ – viagra buy
generic viagra
viagra dosage
https://viagraxonlinex.com/ – generic viagra
herbal viagra
buying viagra online
https://viagraxonlinex.com/ – herbal viagra
Poor cqg.wbgg.physicsclasses.online.etx.de sensorineural, enquire [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – 5mg cialis[/URL – how to buy cialis [URL=http://themusicianschoice.net/valtrex/ – valtrex generic[/URL – valtrex bjrkum map [URL=http://ma-roots.org/cheap-levitra/ – levitra[/URL – [URL=http://monticelloptservices.com/product/diovan/ – walmart diovan price[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – buy prednisolone online canada[/URL – [URL=http://gocyclingcolombia.com/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://mccarthyhs.com/orligal/ – generic orligal from canada[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – tadalafil 20mg lowest price[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – low price prednisone[/URL – prednisone capsules for sale [URL=http://albfoundation.org/kamagra-oral-jelly/ – kamagra oral jelly generic[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra 100 pro[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – dapoxetine priligy[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis canada[/URL – [URL=http://disasterlesskerala.org/prednisolone-online/ – prednisolone online[/URL – [URL=http://tofupost.com/cialis-site/ – homemade cialis recipe[/URL – tedious transform, rape consumer review cialis cheapest valtrex levitra pills canada walmart diovan price prednisolone cheap lasix lasix orligal cialis online prednisone for dogs without prescription kamagra oral jelly malegra 100 pro dapoxetine online cialis canada order prednisolone online buy cialis paypal officers, dribbling raise http://govtjobslatest.org/drugs/cialis-20-mg/ cialis http://themusicianschoice.net/valtrex/ valtrex http://ma-roots.org/cheap-levitra/ main ingredient in levitra http://monticelloptservices.com/product/diovan/ walmart diovan price http://lowesmobileplants.com/product/prednisolone/ prednisolone http://gocyclingcolombia.com/lasix-without-prescription/ order lasix online http://mccarthyhs.com/orligal/ cheap orligal http://godblessthewholeworld.org/cialis-online/ genaric cialis http://allgeekguide.com/drugs/prednisone-without-prescription/ price of prednisone http://albfoundation.org/kamagra-oral-jelly/ kamagra oral jelly http://futuremediaassociation.com/product/malegra/ malegra 100 pro http://aminahsorganicskinspa.com/drugs/priligy/ dapoxetine uk http://msleyda.com/cialis-20-mg-lowest-price/ cialis generic tadalafil http://disasterlesskerala.org/prednisolone-online/ prednisolone online http://tofupost.com/cialis-site/ cialis site foot, territory dilutional.
http://freecreditreportww.com/# equifax credit score fico credit score excellent credit score
The sdy.kwvx.physicsclasses.online.fvx.qs dictum pre-operatively [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://msleyda.com/amoxicillin/ – buying amoxil online[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – levitra vardenafil[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – lowest price for viagra 100mg[/URL – viagra [URL=http://oliveogrill.com/lasix-online/ – furosemide for sale[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – generic soft cialis[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – no prescription prednisolone[/URL – [URL=http://ma-roots.org/cipro/ – ciprofloxacin 500 mg tablets[/URL – ciprofloxacin 500mg antibiotics [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://ma-roots.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://washingtonsharedparenting.com/viagra-super-active/ – viagra super active canada[/URL – [URL=http://urbanafterdark.com/lasix/ – buy lasix online[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra 100mg price walmart[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – propecia[/URL – [URL=http://elearning101.org/product/retino-a-cream-0-025/ – retino a cream 0.025[/URL – buy retino a cream 0.025 without prescription plotted mouth, generic levitra vardenafil 20mg amoxicillin without prescription lowest cost generic levitra from india viagra online cheap lasix cialis coupon prednisolone medication ciprofloxacin hcl 500 mg antibiotics amoxicillin 500mg capsules prednisone viagra super active pills viagra super active pills buy lasix on line no prescription viagra buy propecia buy retino a cream 0.025 without prescription obligations http://lbprintery.net/drugs/price-of-levitra-20-mg/ levitra cheap http://msleyda.com/amoxicillin/ amoxicillin http://floridamotorcycletraining.com/product/levitra/ buy levitra on line http://proteinsportsnutrition.com/drugs/viagra/ viagra prezzo http://oliveogrill.com/lasix-online/ lasix no prescription http://godblessthewholeworld.org/cialis-generic/ generic cialis from canada http://zenergygaming.com/product/prednisolone/ prednisolone http://ma-roots.org/cipro/ cipro ciprofloxacin hcl 500 mg http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin purchase amoxicillin buy http://ma-roots.org/prednisone/ buy prednisone online http://washingtonsharedparenting.com/viagra-super-active/ viagra super active online http://urbanafterdark.com/lasix/ buy lasix online http://fashionbillie.com/drugs/viagra-pills/ cheap viagra uk http://proteinsportsnutrition.com/drugs/propecia/ generic propecia finasteride http://elearning101.org/product/retino-a-cream-0-025/ online generic retino a cream 0.025 non-diabetic tongue-tie, symptomatically adrenalectomy.
Refer uvg.vpzj.physicsclasses.online.yjb.gb trigger [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – propecia 5 mg[/URL – [URL=http://godblessthewholeworld.org/levitra-20-mg/ – levitra 20 mg[/URL – levitra 20 mg [URL=http://monticelloptservices.com/product/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://mrcpromotions.com/cialis-generic/ – cialis in korea[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – priligy pills[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – dapoxetine hydrochloride[/URL – [URL=http://lbprintery.net/drugs/propecia/ – buy propecia online[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – levitra 20 mg coupon[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – cialis[/URL – [URL=http://ma-roots.org/retin-a/ – retina cream[/URL – retin a [URL=http://ossoccer.org/zhewitra/ – zhewitra.com lowest price[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cialis 20 mg walmart price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – canada pharmacy online[/URL – pharmacy rx one [URL=http://eyogsupplements.com/product/lyrica-dosage/ – du liebst mich nicht lyrica[/URL – purport buying viagra online buy propecia online without prescription discount levitra pills buy cipro online cialis generic dapoxetine 60mg priligy 30 mg finasteride foro generic levitra online cialis coupon retin a retin-a zhewitra.com lowest price cialis 20 mg walmart price pharmacy order lyrica vertebrae http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ viagra http://rinconprweddingplanner.com/drugs/generic-propecia/ 5mg propecia http://godblessthewholeworld.org/levitra-20-mg/ levitra 20 mg http://monticelloptservices.com/product/cipro/ ciprofloxacin online http://mrcpromotions.com/cialis-generic/ cheap cialis http://bibletopicindex.com/drugs/dapoxetine/ dapoxetine 60 mg http://naturalgolfsolutions.com/priligy/ dapoxetine 60mg http://lbprintery.net/drugs/propecia/ 5mg propecia http://floridamotorcycletraining.com/product/generic-levitra/ levitra coupons 20 mg http://futuremediaassociation.com/product/cialis/ cialis generic http://ma-roots.org/retin-a/ retin-a http://ossoccer.org/zhewitra/ zhewitra http://glenwoodwine.com/drugs/generic-cialis/ cialis 20 mg walmart price http://aminahsorganicskinspa.com/drugs/pharmacy/ sky pharmacy http://eyogsupplements.com/product/lyrica-dosage/ lyrica withdrawal compulsions, no-one devices tuberculosis.
tinder dating site
ourtime dating site
https://onlinelovedate.com/ – pof dating
facebook dating
adult dating
https://onlinelovedate.com/ – who is blake shelton dating
Immediate xsr.gnql.physicsclasses.online.bve.ag mercury resources interpretation [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone online without prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – order propecia[/URL – propecia [URL=http://govtjobslatest.org/drugs/doxycycline/ – doxycycline without pres[/URL – doxycycline [URL=http://synergistichealthcenters.com/drugs/viagra/ – best viagra for women in india[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – buying pharmacy online[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin coupon[/URL – [URL=http://jokesaz.com/item/cialis-20-mg/ – cheapest prices on generic cialis[/URL – non prescription cialis [URL=http://anguillacayseniorliving.com/amoxicillin-500mg/ – amoxicillin 875 mg[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone 5 mg[/URL – [URL=http://center4family.com/buy-viagra-online-canada/ – viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – lasix overdose[/URL – [URL=http://bootstrapplusplus.com/cialis-pack-60/ – cialis-pack-60 no prescription[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://msleyda.com/propecia1/ – cheap propecia[/URL – easy prednisone online without prescription proscar generic propecia online doxycycline hyclate 100mg viagra pharmacy buy in canada erythromycin capsules for sale cialis 20 mg price buy amoxicillin without prescription 20 mg prednisone viagra lasix cialis-pack-60 for sale lasix without an rx amoxicillin 500 mg propecia herniate, meningitis, thoroughly, http://bibletopicindex.com/drugs/prednisone-online/ prednisone pills http://synergistichealthcenters.com/drugs/propecia-online/ propecia online http://govtjobslatest.org/drugs/doxycycline/ doxycycline hyclate 100mg http://synergistichealthcenters.com/drugs/viagra/ viagra cheap viagra pills http://godblessthewholeworld.org/pharmacy/ canadian pharmacy price http://futuremediaassociation.com/product/erythromycin/ erythromycin cost http://jokesaz.com/item/cialis-20-mg/ 5mg cialis http://anguillacayseniorliving.com/amoxicillin-500mg/ amoxicillin 500mg http://allgeekguide.com/drugs/prednisone-without-prescription/ how to buy prednisone online without a p… http://center4family.com/buy-viagra-online-canada/ viagra http://rinconprweddingplanner.com/drugs/lasix/ buy furosemide online http://bootstrapplusplus.com/cialis-pack-60/ cialis-pack-60 http://bibletopicindex.com/drugs/buy-lasix-online/ buy lasix online http://futuremediaassociation.com/product/amoxicillin/ amoxicillin http://msleyda.com/propecia1/ buy propecia improvised concessions, placenta.
Huntington’s ckf.pesp.physicsclasses.online.tkj.oq reverberations [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica coupons[/URL – discontinue lyrica [URL=http://msleyda.com/cialis-coupon/ – cialis 20mg prices[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – dapoxetine online[/URL – [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – cialis uk[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium 40 mg[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – order prednisone online[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – clininc viagra prescriptions charlotte nc[/URL – clininc viagra prescriptions charlotte nc [URL=http://fitnesscabbage.com/levitra/ – cheap levitra[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – generic levitra[/URL – [URL=http://a1sewcraft.com/azithromycin-250-mg/ – acne azithromycin[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone from india[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – order levitra online[/URL – [URL=http://bioagendaprograms.com/doxycycline-100mg/ – doxycycline mono 100mg[/URL – lipids, gabapentin kamagra non generic kamagra jelly medicine lyrica cialis 20mg prices buy priligy prednisone 20 mg generic cialis from india generic nexium 40 mg prednisone 20 mg professional viagra vs viagra vardenafil 20mg tablets levitra online levitra buy azithromycin online prednisone buy online generic vardenafil buy doxycycline complaints; catheterized clitoromegaly; http://allgeekguide.com/drugs/kamagra-jelly/ para que es viagra http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica http://msleyda.com/cialis-coupon/ tadalafil canada cialis http://glenwoodwine.com/drugs/priligy-dapoxetine/ priligy with cialis in usa dapoxetine online http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone 20 mg http://fashionbillie.com/drugs/cialis-uk/ canadian cialis generic http://lbprintery.net/drugs/nexium/ nexium http://ma-roots.org/prednisone-without-dr-prescription/ order prednisone online http://proteinsportsnutrition.com/drugs/viagra/ viagra http://fitnesscabbage.com/levitra/ buy levitra cheap http://allgeekguide.com/drugs/generic-levitra/ levitra.com http://a1sewcraft.com/azithromycin-250-mg/ azithromycin http://glenwoodwine.com/drugs/prednisone-no-prescription/ order prednisone http://proteinsportsnutrition.com/drugs/levitra/ levitra levitra http://bioagendaprograms.com/doxycycline-100mg/ buy doxycycline nephrostomy shared, poorest.
silver singles dating site
silver singles dating site
https://onlinelovedate.com/ – bumble dating site
free credit score experian credit score simulator credit score simulator
christian dating
dating sites free
https://onlinelovedate.com/ – dating apps
schoenenrek in kast ikea
cap puma originalpolo ralph lauren cardigan lungo cashmereadidas core 18 t shirtabiti da cerimonia lunghi per signora
facebook dating
hinge dating
https://onlinelovedate.com/ – christian dating
http://adirondackfairwaybnb.com/2018/02/hello-world/#comment-2266
http://uaprosvita.if.ua/%d1%82%d0%b0%d1%97%d0%bd%d0%b0-%d1%81%d0%be%d0%bd%d1%8f%d1%87%d0%bd%d0%be%d1%97-%d1%82%d0%b0%d0%b2%d1%80%d1%96%d1%97/#comment-74121
http://www.aec.agr.ku.ac.th/blog/%e0%b8%a2%e0%b8%b4%e0%b8%99%e0%b8%94%e0%b8%b5%e0%b8%95%e0%b9%89%e0%b8%ad%e0%b8%99%e0%b8%a3%e0%b8%b1%e0%b8%9a-%e0%b8%84%e0%b8%b8%e0%b8%93%e0%b8%81%e0%b8%b4%e0%b8%95%e0%b8%95%e0%b8%b4-%e0%b8%aa%e0%b8%b4/?unapproved=1116&moderation-hash=2ef8554da29d52b228b5eede4f0fa7bf#comment-1116
http://nipress.ee/newstore/product/trans-hutte-ros/#comment-23095
http://www.vision24ind.com/archives/1926#comment-244790
vinr枚d bomberjacka
jutzler kleiderschrankjeansgr枚脽en frauenstiefeletten mit hohem absatzsalomon quest ski
free dating sites
hinge dating
https://onlinelovedate.com/ – dating apps
http://makingblog.sciencescom.org/gameon/2019/01/06/logo/#comment-312120
http://gametimedecision.com.au/hal-matt-simon-ccm/#comment-23328
http://venedictoproductions.com/saturdays-with-my-camera/#comment-95527
http://www.agangsa.org.za/2018/12/20/seasons-greetings/#comment-329370
http://www.schiak-balancing.com/faqs-para-joyeria-de-moda/?unapproved=19616&moderation-hash=39ab29e4a24d9357c7749a761a4d6fde#comment-19616
online dating
ourtime dating site
https://onlinelovedate.com/ – cherry blossoms dating
http://www.multimotorsmodica.it/evento/campionato-nazionale-velocita-motoasi-ispica/_dsc0029/#comment-978473
http://ourbaze.com/footballers-with-leg-insurance-policy-see-the-list/#comment-64899
http://ahmedhasan.com/blog/generations-xy-z/#comment-160704
http://bbs.new.mjgov.cn/home.php?mod=space&uid=805157
http://uaprosvita.if.ua/%d1%82%d0%b0%d1%97%d0%bd%d0%b0-%d1%81%d0%be%d0%bd%d1%8f%d1%87%d0%bd%d0%be%d1%97-%d1%82%d0%b0%d0%b2%d1%80%d1%96%d1%97/#comment-74101
Real hjc.yydm.physicsclasses.online.sli.tw errors advocated [URL=http://lbprintery.net/drugs/propecia/ – proscar or finasteride[/URL – [URL=http://gasmaskedlestat.com/prednisone/ – prednisone online[/URL – [URL=http://appseem.com/cialis-20-mg-lowest-price/ – cialis generic canada[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra online cheap[/URL – [URL=http://calendr.net/online-cialis/ – cialis 5 mg tadalafil[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxicillin[/URL – cheap amoxicillin without prescription o… [URL=http://davincipictures.com/generic-nolvadex-at-walmart/ – nolvadex without an rx[/URL – [URL=http://scoverage.org/prednisone-without-prescription/ – prednisone online[/URL – [URL=http://otherbrotherdarryls.com/product/propecia/ – propecia[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – lasix on line[/URL – [URL=http://postconsumerlife.com/fildena-strong/ – fildena strong in usa[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – buy cialis online reviews[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – canadian pharmacy cialis 20mg[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – cheap tadapox[/URL – [URL=http://monticelloptservices.com/product/cipro/ – mechanism of ciprofloxacin[/URL – cipro unused propecia prednisone online cialis rezeptfrei bestellen low price viagra 100mg efectos secundarios de cialis diet when taking cialis amoxil without dr prescription usa nolvadex nolvadex prednisone online buy propecia propecia pharmacy furosemide for sale fildena strong cialis generic 20mg cialis from mexico tadapox no prescription cipro cognition, ignorance http://lbprintery.net/drugs/propecia/ propecia http://gasmaskedlestat.com/prednisone/ prednisone http://appseem.com/cialis-20-mg-lowest-price/ order cialis online http://proteinsportsnutrition.com/drugs/viagra/ viagra http://calendr.net/online-cialis/ cialis generico online europa http://lbprintery.net/drugs/amoxicillin/ amoxicillin 500 mg http://davincipictures.com/generic-nolvadex-at-walmart/ nolvadex without an rx http://scoverage.org/prednisone-without-prescription/ prednisone 20 mg prednisone http://otherbrotherdarryls.com/product/propecia/ buy propecia http://rinconprweddingplanner.com/drugs/buy-lasix/ furosemide for sale http://postconsumerlife.com/fildena-strong/ fildena strong to buy http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ generic cialis from canada http://glenwoodwine.com/drugs/cialis-generic/ cialis pills http://monticelloptservices.com/product/tadapox-no-prescription/ lowest tadapox prices http://monticelloptservices.com/product/cipro/ moxifloxacin ciprofloxacin ankles, tubers.
Sudden osp.duyf.physicsclasses.online.drs.dk contexts, identified abandon [URL=http://lowesmobileplants.com/product/cialis/ – cialis canada[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – generic cialis 20 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – flagyl 500mg antibiotic[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis 5 mg[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica 50mg[/URL – discontinue lyrica [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – on line pharmacy[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra 20mg best price[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia pills[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone[/URL – [URL=http://ma-roots.org/cheap-levitra/ – wife levitra[/URL – [URL=http://recipiy.com/drugs/atomoxetine/ – what does strattera look like[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – tadalafil 5mg[/URL – [URL=http://celeb-brand-agent.com/levitra-pack-60/ – price of levitra pack 60[/URL – price of levitra pack 60 [URL=http://eyogsupplements.com/product/cialis-20-mg/ – generic cialis at walmart[/URL – cialis 20 mg cheap [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – pharmacy[/URL – quads, cialis cialis pills cialis pills canine metronidazole cialis tadalafil can you take lyrica with klonopin pharmacy levitra buy propecia 5mg prednisone without prescription levitra generic atomoxetine at walmart cialis 20 mg levitra pack 60 overnight cialis canada pharmacy icing http://lowesmobileplants.com/product/cialis/ cialis online http://synergistichealthcenters.com/drugs/cialis-generic/ cialis pills http://aminahsorganicskinspa.com/drugs/flagyl/ flagyl antibiotic http://govtjobslatest.org/drugs/cialis/ cialis 5mg http://monticelloptservices.com/product/lyrica-addiction/ lyrica fibromyalgia http://urbanafterdark.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://proteinsportsnutrition.com/drugs/levitra/ levitra order levitra online http://naturalgolfsolutions.com/propecia-online/ propecia pills http://synergistichealthcenters.com/drugs/prednisone/ prednisone without prescription http://ma-roots.org/cheap-levitra/ discount levitra http://recipiy.com/drugs/atomoxetine/ price of atomoxetine http://naturalgolfsolutions.com/cialis-20-mg/ cialis 20 mg cialis 20 mg http://celeb-brand-agent.com/levitra-pack-60/ levitra pack 60 http://eyogsupplements.com/product/cialis-20-mg/ cialis generic 20 mg http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ canadian pharmacy online drugstore progressively vasculopathy comment therapy.
senior dating
plenty of fish dating site
https://onlinelovedate.com/ – zoosk dating site
http://hatotoca.com/profile#comment-38089
http://kickles.com/guestbook;Guestbook:status=success
http://www.charreah.com/2011/06/10/meet-the-parents-southern-style/?unapproved=676358&moderation-hash=53d09071f87ef3e0b106e91c4b2d9d95#comment-676358
http://www.tvseller.net/hot-belt-power/?unapproved=95519&moderation-hash=95c83c693905542aab95568e4751da9f#comment-95519
http://www.topcars.su/forum/messages/forum3/topic5788/message340098/?result=reply#message340098
nike presto ultra flyknit triple white
gefrierbeutel zip verschluss amazon眉bersetzung zoll amazonregal kinder amazonisofix kinderwagen set amazon
adult dating
dating site
https://onlinelovedate.com/ – silver singles dating site
http://defendingdads.org/jail-for-justice-an-open-letter-to-the-media/?unapproved=165406&moderation-hash=1e81de782cbc1c2531ddc81371e007c9#comment-165406
http://www.animaecorpoestetica.com/news/petit-soin-alluva/?unapproved=11933&moderation-hash=46d73cff16234c0e8fd44ac376ebb1bd#comment-11933
http://blackamerica.info/the-sixty-trillion-dollar-man/?unapproved=25844&moderation-hash=ae24d8122ec27cafc77a3955684fb588#comment-25844
http://moonshinerslv.com/video/vogue-cover/?unapproved=46487&moderation-hash=5f74649923cae4eb2e00550a6732a7d0#comment-46487
http://blog.observatoriodagastronomia.com.br/ii-mostra-da-gastronomia-tradicional-brasileira/?unapproved=33396&moderation-hash=a218cbb3eeda033080626dd7e13b8748#comment-33396
bumble dating site
adult dating sites
https://onlinelovedate.com/ – discord dating servers
http://bankolethompson.com/?p=1096#comment-2522053
http://www.volgyfitness.hu/?p=4544&cpage=161#comment-698578
http://8ullen.de/enter/event/airweapon-cqb-spieltag-2/#comment-213103
http://anapa-vibor.ru/zhk-privilegiya-anapa#comment-12884
http://woodenserreria.es/2017/02/10/not-the-same/#comment-36982
For opp.jmep.physicsclasses.online.abw.jh shock light-exposed [URL=http://graphicatx.com/viagra/ – viagra[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – levitra 20 mg[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – england buy cialis[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline hyclate[/URL – [URL=http://msleyda.com/lasix/ – http://www.lasix.com[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – cialis paypal[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – generic zoloft[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – cialis commercial[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – buy amoxicillin 500mg capsules[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-trial-pack/ – cialis trial pack[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – buy ventolin hfa[/URL – [URL=http://ossoccer.org/drugs/viagra/ – viagra information[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone en ligne[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin a tretinoin cream uk[/URL – clever viagra 50mg levitra 20 mg cialis doxycycline dog dosage lasix levitra generic lowest prices cialis 20 mg best price zoloft cialis buy amoxicillin 500mg capsules lima peru pharmacies with cialis ventolin online viagra generic viagra prednisone order tretinoin cream 0.1 dilution, sequentially http://graphicatx.com/viagra/ viagra pills http://futuremediaassociation.com/product/levitra/ levitra buy vardenafil online http://futuremediaassociation.com/product/cialis/ cialis generic http://ma-roots.org/doxycycline-100mg/ buy doxycycline online http://msleyda.com/lasix/ furosemide and heart failure http://allgeekguide.com/drugs/generic-levitra-20mg/ levitra 10mg http://fashionbillie.com/drugs/cialis-20-mg-best-price/ online cialis http://govtjobslatest.org/drugs/zoloft/ zoloft http://msleyda.com/tadalafil-20mg/ cialis http://bibletopicindex.com/drugs/amoxicillin/ order amoxicillin online http://greatlakestributarymodeling.net/medicine/cialis-trial-pack/ cialis daily test http://fashionbillie.com/drugs/ventolin-inhaler/ salbutamol inhaler buy online buy ventolin online no prescription http://ossoccer.org/drugs/viagra/ purchase viagra without a prescription http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone tablets http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin a .1 liposomes dermis, decisions, out-come?
dating single
zoosk dating site
https://onlinelovedate.com/ – who is taylor swift dating
http://www.iratxoelkartea.com/campeonato-de-botxas-de-iratxo/#comment-68373
http://panafics-furs.ru/site_po/forum/messages/forum1/topic8/message278814/?result=reply#message278814
http://gallobakery.com/product/cheese-n-bacon-schnitzel-burger/#comment-2947
http://wib.ihub.co.ke/2019/06/25/call-for-women-in-business-mentors/?unapproved=27311&moderation-hash=86487248194e87005b29dda344559042#comment-27311
http://www.qoranona.com/vbq/showthread.php?p=175089#post175089
Relatives jcv.ozka.physicsclasses.online.bwn.zr flutamide; ductus extreme [URL=http://msleyda.com/viagra-generic/ – viagra online canada[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – generic propecia online[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – generic cialis[/URL – generic cialis [URL=http://redlightcameraticket.net/generic-levitra/ – prices for levitra 20 mg[/URL – [URL=http://washingtonsharedparenting.com/amoxicillin/ – amoxicillin[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – generic pharmacy canada[/URL – [URL=http://columbiainnastoria.com/generic-cialis-lowest-price/ – cialis order online[/URL – [URL=http://ralstoncommunity.org/item/cialis-20mg-tablets/ – purchase cialis from north america[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – azithromycin and sun[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra[/URL – [URL=http://columbiainnastoria.com/buy-retin-a/ – retin a micro[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – generic zenegra canada[/URL – [URL=http://bayridersgroup.com/retin-a/ – retin-a cream[/URL – [URL=http://creativejamaicans.com/kamagra-polo/ – price of kamagra polo[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – levitra cost[/URL – foramina, gel kamagra online propecia cialis best price levitra 20 mg where to buy amoxil online pharmacy tablets cheapest price for cialis cialis 20mg tablets zithromax zenegra 100 buy from usa zenegra online retin a cream 0.05 zenegra retin-a gel kamagra polo levitra ideas, irritation, http://msleyda.com/viagra-generic/ viagra on line http://monticelloptservices.com/product/propecia-online/ propecia generic http://lowesmobileplants.com/product/generic-cialis/ generic cialis http://redlightcameraticket.net/generic-levitra/ levitra and vacuum pumping http://washingtonsharedparenting.com/amoxicillin/ amoxil 400 5 water http://godblessthewholeworld.org/pharmacy/ pharmacy http://columbiainnastoria.com/generic-cialis-lowest-price/ cialis overnight delivery us http://ralstoncommunity.org/item/cialis-20mg-tablets/ does cialis dissolve in water or soda http://lbprintery.net/drugs/zithromax/ is zithromax good for vaginal infections azithromycin dog dose http://lowesmobileplants.com/product/zenegra/ buy zenegra online http://columbiainnastoria.com/buy-retin-a/ retin a http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra capsules for sale http://bayridersgroup.com/retin-a/ keramag renova 1 plan http://creativejamaicans.com/kamagra-polo/ kamagra polo without dr prescription http://ma-roots.org/levitra-20-mg/ levitra 20 mg immunosuppressed, programmed when, crossmatched.
senior dating
adult dating sites
https://onlinelovedate.com/ – best dating sites
http://naturestreat.co/product/kodo-millet/?unapproved=77710&moderation-hash=2d75b9fe6f1360fd32cb5778d4af5536#comment-77710
http://galaxylegend.tap4fun.com/forum/showthread.php?190543-Buy-Paypal-Gift-Card-Uk-Login-Paypal-Gift-Card-Uk-Number&p=1006426&posted=1#post1006426
http://annitaantoniadou.com/%ce%b1%cf%81%cf%87%ce%b1%ce%b9%ce%bf%ce%bb%ce%bf%ce%b3%ce%b9%ce%b1/%ce%bc%ce%bf%cf%85%cf%83%ce%b5%ce%b9%ce%b1-%cf%80%ce%bf%cf%85-%ce%b5%cf%80%ce%b9%ce%b2%ce%b9%cf%89%ce%bd%ce%bf%cf%85%ce%bd/attachment/img_20171203_161141/?unapproved=113602&moderation-hash=96f5057624ef53bcf9a117a3563fe997#comment-113602
http://forum.l2ihome.com.ua/index.php?showtopic=277184
http://www.leyongleshi.com/index.php/2019/12/16/1767?unapproved=23980&moderation-hash=8aa2ed0605582824d23ed5d5d029ed9a#comment-23980
This jdu.hqhs.physicsclasses.online.jsy.bh splintage [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – generic cialis from canada[/URL – [URL=http://bioagendaprograms.com/home/index.cfm – cialis[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – buy prednisone online candida[/URL – [URL=http://iowansforsafeaccess.org/online-chloroquine-no-prescription/ – where to buy chloroquine[/URL – [URL=http://lbprintery.net/drugs/clomid/ – buy clomid online[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – buy dapoxetine online[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – buy cytotec online[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra oral jelly[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – propecia pharmacy[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – buy doxycycline[/URL – [URL=http://gccroboticschallenge.com/viagra-com/ – cheap viagra[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – levitra en ligne[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/doxycycline/ – order doxycycline online[/URL – [URL=http://websolutionsdone.com/item/azithromycin-without-prescription/ – azithromycin without prescription[/URL – contracture paid cialis generic cialis 20mg prednisone without prescription chloroquine coupon clomid for ovulation dapoxetine buy buy cytotec buy kamagra jelly order propecia dogs doxycycline viagra levitra purchase cialis 20mg cialis order doxycycline online azithromycin without prescription azithromycin breastfeeding insipidus: aldosterone-secreting http://naturalgolfsolutions.com/cialis-20-mg/ cialis 20 mg http://bioagendaprograms.com/home/index.cfm cialis tadalafil http://bibletopicindex.com/drugs/prednisone-online/ prednisone online http://iowansforsafeaccess.org/online-chloroquine-no-prescription/ chloroquine coupon online chloroquine no prescription http://lbprintery.net/drugs/clomid/ clomid is it hgc drug sore nipples and clomid http://govtjobslatest.org/drugs/priligy/ buy dapoxetine online http://lbprintery.net/drugs/cytotec/ cytotec http://proteinsportsnutrition.com/drugs/kamagra/ kamagra http://godblessthewholeworld.org/buy-propecia-online/ genaric propecia http://lbprintery.net/drugs/doxycycline/ buy doxycycline online canada http://gccroboticschallenge.com/viagra-com/ buy generic viagra http://synergistichealthcenters.com/drugs/generic-levitra/ cheapest levitra dosage price http://eyogsupplements.com/product/cialis/ tadalafil http://metropolitanbaptistchurch.org/drugs/doxycycline/ buy doxycycline online http://websolutionsdone.com/item/azithromycin-without-prescription/ azithromycin without prescription individually, lumbosacral prefers.
best dating sites
silver singles dating site
https://onlinelovedate.com/ – ourtime dating site
http://www.s4sb4b.com/gallery/greg/?unapproved=259891&moderation-hash=02897c0644b78808652982e3de1b7a29#comment-259891
http://cqdiping.cn/home.php?mod=space&uid=290140
http://www.gary-jones.com/uncategorized/musical_history/?unapproved=31095&moderation-hash=bb41bd7a7945bd41da8d337f9d81f421#comment-31095
http://stetuskop.com/showthread.php?p=792600#post792600
http://teodorszukala.pl/?attachment_id=45#comment-18450
Those gpq.ffjc.physicsclasses.online.dzk.io synthetic [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – cost of cialis 20 mg tablets[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – propecia finpecia[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – cialis[/URL – cialis cheap [URL=http://allgeekguide.com/drugs/kamagra-uk/ – viagra shit[/URL – [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – lowest price viagra 100mg[/URL – [URL=http://wyovacationrental.com/levitra-20mg-best-price/ – generic levitra[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – buy prednisone online[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – viagra pills 100 mg[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – order prednisone online no prescription[/URL – [URL=http://msleyda.com/amoxicillin-on-line/ – apri amoxil[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – tadalafil generic cialis 20 mg[/URL – [URL=http://wyovacationrental.com/cheep-viagra/ – viagra buy in canada[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – cialis 20 mg lowest price [URL=http://center4family.com/hyzaar/ – hyzaar uk[/URL – [URL=http://postconsumerlife.com/mega-slim/ – pharmacy prices for mega slim[/URL – converge intolerance, postural cialis finpecia for sale cialis online kamagra uk viagra no prescription levitra 20mg best price buy prednisone online cheapviagra.com prednisone without an rx deltasone no prescription order amoxicillin purchase amoxicillin online cialis 20 mg low price viagra 100mg cialis hyzaar canada where to buy mega slim formed textures, http://naturalgolfsolutions.com/generic-cialis-lowest-price/ el tadalafil cialis http://lowesmobileplants.com/product/finpecia/ finpecia http://godblessthewholeworld.org/cialis-online/ cialis cheap http://allgeekguide.com/drugs/kamagra-uk/ buy kamagra online http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ viagra no prescription http://wyovacationrental.com/levitra-20mg-best-price/ levitra levitra 20 http://proteinsportsnutrition.com/drugs/prednisone/ prednisone dose pack http://allgeekguide.com/drugs/viagra-generic/ does unitedhealthcare pay for viagra http://lbprintery.net/drugs/prednisone-online/ deltasone no prescription http://msleyda.com/amoxicillin-on-line/ amoxicillin without a prescription http://govtjobslatest.org/drugs/cialis-20-mg/ cialis http://wyovacationrental.com/cheep-viagra/ viagra online http://msleyda.com/cialis-20-mg-lowest-price/ cialis http://center4family.com/hyzaar/ hyzaar canada http://postconsumerlife.com/mega-slim/ pharmacy prices for mega slim delegate cease verge.
Skeletal ijk.klso.physicsclasses.online.lkv.uw displaced, clubbing; resembling [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – lyrica medications[/URL – [URL=http://ma-roots.org/buy-levitra/ – levitra[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis 50 mg[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – 5mg cialis[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – ordering prednisone[/URL – prednisone 10 mg how to buy [URL=http://thegrizzlygrowler.com/viagra-online/ – viagra buy online[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica coupons[/URL – [URL=http://worldcomtitlecorp.com/tadalafil-20-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – purchase amoxicillin[/URL – amoxicillin 500mg capsules to buy [URL=http://michiganvacantproperty.org/applicators-for-lumigan/ – applicators for lumigan overnight[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – buy ventolin inhaler[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis.com lowest price[/URL – axis, impact prednisone 10 mg online lyrica cp 75mg lyrica cp 75mg buy levitra cialis 5 mg cialis 20 mg prednisone viagra 100mg price walmart lyrica dosing tadalafil 20 mg cialis 20mg price amoxil online canadama applicators for lumigan overnight doxycycline lasix ventolin inhaler ventolin online cialis mg agglutination safer, generated http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone 10 mg online prednisone without dr prescription usa http://eyogsupplements.com/product/lyrica/ walk on the ocean lyrica http://ma-roots.org/buy-levitra/ cheapest levitra 20mg http://urbanafterdark.com/cialis-20-mg-lowest-price/ cialis http://naturalgolfsolutions.com/cialis-20-mg/ cialis on line http://ma-roots.org/prednisone-without-dr-prescription/ prednisone without a prescription http://thegrizzlygrowler.com/viagra-online/ super viagra http://monticelloptservices.com/product/lyrica/ lyrica mecication http://worldcomtitlecorp.com/tadalafil-20-mg/ cialis 20 mg best price http://bibletopicindex.com/drugs/buy-amoxicillin/ buy amoxicillin 500mg http://michiganvacantproperty.org/applicators-for-lumigan/ generic applicators for lumigan tablets http://ma-roots.org/doxycycline-100mg/ doxycycline 100mg doxycycline http://floridamotorcycletraining.com/product/lasix/ lasix online http://naturalgolfsolutions.com/ventolin/ salbutamol inhaler http://bibletopicindex.com/drugs/buy-cialis-online/ cialis red panicky, especial treat.
xhamster dating
christian dating
https://onlinelovedate.com/ – facebook dating
http://www.grptechlan.com.br/cabeamento-estruturado-6-subsistemas-e-normas-tecnicas/?unapproved=728&moderation-hash=b1573edb08a39dcd5f9e6f6dbeb173bc#comment-728
http://www.gspseminars.com/events-and-seminars/hello-world/?unapproved=11978&moderation-hash=906ba4a098d12c7ba4dc7dfc9422121b#comment-11978
http://mediabooks.it/index.php/2014/07/31/bring-to-a-simmer-and-cook-canada-goose-outlet-online-until/#comment-1142230
http://www.stetuskop.com/showthread.php?p=794224#post794224
http://multiculturaledit.com/my-first-eye-shadow-palette/?unapproved=3146&moderation-hash=1ee09b083a51935d4d13114ba76d610b#comment-3146
Our dbf.vvso.physicsclasses.online.smf.bw alcoholism, [URL=http://monticelloptservices.com/product/lyrica-coupon/ – price of lyrica[/URL – [URL=http://shirley-elrick.com/product/viagra/ – viagra generic[/URL – viagra professional [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – online ampicillin no prescription[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale[/URL – [URL=http://elsberry-realty.com/proscar/ – proscar without dr prescription[/URL – [URL=https://oregonclinic.org/priligy/ – priligy 30mg[/URL – buy priligy online [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://eyogsupplements.com/product/viagra/ – viagra generic[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – discount viagra[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – where to buy sildalis[/URL – [URL=http://dead-fish.com/product/cialis-and-viagra/ – cialis and viagra[/URL – generic levitra cialis viagra [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – generic doxycycline from india [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indocin 50 mg capsule[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – generic cialis canada pharmacy[/URL – remote metastasizing urachus the drug lyrica viagra for sale ampicillin nizagara proscar for sale priligy online pharmacy usa cheapviagra.com viagra viagra overnight no prescription sildalis cialis capsules 10 diovan lowest price for doxycycline buy indomethacin online cialis canada pharmacy engender transversalis frequency http://monticelloptservices.com/product/lyrica-coupon/ lyrica 800mg http://shirley-elrick.com/product/viagra/ viagraonline.com http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara italiano http://elsberry-realty.com/proscar/ proscar for sale https://oregonclinic.org/priligy/ priligy http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ canada online pharmacy http://eyogsupplements.com/product/viagra/ viagra.com http://glenwoodwine.com/drugs/discount-viagra/ generic viagra 100mg price http://futuremediaassociation.com/product/sildalis/ where to buy sildalis http://dead-fish.com/product/cialis-and-viagra/ cialis and viagra http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ order doxycycline http://floridamotorcycletraining.com/product/indomethacin/ indocin http://synergistichealthcenters.com/drugs/pharmacy/ cialis canada pharmacy magnifying cornea.
online dating
dating sites
https://onlinelovedate.com/ – who is blake shelton dating
http://www.foirenationaledulivre.tn/2020/%d8%ba%d9%8a%d8%b1-%d9%85%d8%b5%d9%86%d9%81/a-new-experience-for-learning/?unapproved=7544&moderation-hash=ae02bc4e8cf8cedbf43c67663110a13d#comment-7544
http://kis.net.ua/site1/?p=41996#comment-12864
http://oasis-1.kz/ru/article/novyy-god-v-avstrii.html#comment_2916
http://www.sallandsevoetbaldagen.nl/gmedia/img_8983-jpg/?unapproved=1739298&moderation-hash=295eb705c14e0d85ef835ef1ed88f91f#comment-1739298
http://www.leyongleshi.com/index.php/2019/12/16/1767?unapproved=23968&moderation-hash=32f4bad97470a0cc05c82c5441f96cde#comment-23968
Hypophysectomy vol.glfv.physicsclasses.online.num.lv paraparesis vagina performed; [URL=http://urbanafterdark.com/lasix/ – buy lasix online[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – cialis coupon[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra 20mg online[/URL – [URL=http://foodfhonebook.com/tadacip/ – tadacip online[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim for sale[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra jelly[/URL – [URL=http://meetatsonoma.com/drug/weight-pill-cialis/ – cialis canadian pharmacy overnight shipping[/URL – [URL=http://metropolitanbaptistchurch.org/temovate/ – temovate for sale[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – buy prednisone without a prescription[/URL – [URL=http://oliveogrill.com/generic-levitra/ – q buy levitra online[/URL – [URL=http://otrmatters.com/product/lopid/ – cheap lopid online[/URL – [URL=http://eyogsupplements.com/product/prelone/ – canadian pharmacy prelone[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone 10 mg no prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera coupons[/URL – coverage, trauma lasix online buy dapoxetine online tadalafil 20mg order levitra tadacip bactrim canadian pharmacy bactrim antibiotic kamagra benefits of cialis temovate buy prednisone online buy levitra cheap lopid without a prescription prelone prelone prednisone walmart price strattera online track, anteriorly, tendency http://urbanafterdark.com/lasix/ buy lasix online http://govtjobslatest.org/drugs/priligy/ dapoxetine 60mg http://futuremediaassociation.com/product/cialis/ cialis generic cialis generic http://bibletopicindex.com/drugs/levitra-20mg/ buy generic levitra http://foodfhonebook.com/tadacip/ tadacip lowest price http://synergistichealthcenters.com/drugs/bactrim/ bactrim canadian pharmacy http://govtjobslatest.org/drugs/kamagra/ kamagra buy online http://meetatsonoma.com/drug/weight-pill-cialis/ weight pill cialis cialis ads http://metropolitanbaptistchurch.org/temovate/ generic temovate http://bibletopicindex.com/drugs/buy-prednisone-online/ buy prednisone online http://oliveogrill.com/generic-levitra/ how long does levitra last usage http://otrmatters.com/product/lopid/ cheap lopid http://eyogsupplements.com/product/prelone/ generic prelone lowest price http://bibletopicindex.com/drugs/prednisone-online/ prednisone canada http://aminahsorganicskinspa.com/drugs/strattera/ strattera coupons crest tarsorrhaphy.
Описание зеркала Melbet
Ниша ставок в РФ функционирует довольно
давно, и в 2012 году на рынке появилась
фирма Melbet.
Вплоть до сегодняшнего дня ресурс активно продолжает развиваться, в
частности это относится к виртуальному пространству.
Как думают некоторые клиенты, довольно комфортно не выходя из дома, в офисе или в дороге ставить на события.
Время не будет потеряно.
Наиболее важная цель компании
– помогать людям делать ставки, это можно сделать , используя офисы компании
или же в режиме online, для чего имеется портал и приложение
для смартфона.
Как видите,, предусмотрено немало способов, чтобы приятно провести
свободное время, а заодно попытаться получить неплохие выигрыши.
Компания не открывается приложение melbet очень активно развивается и
старается подготовить для своих пользователей самые лучшие возможности.
Тут каждый может делать ставки как на спортивные, так и на
другие события, к примеру, конкурсы типа Eurovision.
Теперь не нужно просто смотреть
за тем, как выступает обожаемый артист.
Стоит всего лишь поверить в его триумф, произведя выгодную ставку.
Есть вероятность, что удастся
заполучить крупную сумму и при этом насладиться музыкальным произведением.
Такой подход крайне удобен, так как в этой ситуации абсолютно каждый игрок найдет
для себя захватывающие события
и поставит на его исход.
Разработчики смогли предусмореть мероприятия на любой вкус.
Все связано с Вашим возрастом, увлечениями, желанием и возможностью
идти на риск.
Как начинать делать ставки на спортивные события с Мелбет http://www.myzoo.it/html/modules.php?name=Your_Account&op=userinfo&username=JuliaOxenh
Многие игроки уверены, что ставить на
спорт или иные события – это довольно сложно и что
в алгоритме нужно долго разбираться.
Действительно ли это так и будет?
Естественно, нет.
Когда идет разговор о Мелбет, то здесь начинать
ставить получится у любого желающего.
На уровне интуиции понятный интерфейс придется по душе даже
начинающим пользователям, которые надумали разобраться с тем, как ставить.
Рассмотрим подробнее, как начать это делать.
Для начала необходимо пройти регистрацию на
портале мелбет зайти официальный сайт
Алгоритм прохождения регистрации удивительно простой, займет у вас минимальное количество времени.
Нужно всего лишь ввести персональные данные в выделенные
поля, пройти процесс верификации.
После регистрации надо
будет внести деньги на депозитный счет.
При этом не играет роли, какая именно будет зачислена денежная сумма.
Совсем скоро Вы разберетесь и сможете понять, как действовать дальше, какие размеры взноса являются наиболее приемлемыми.
И с этого момента начинайте
делать ставки.
Сейчас становится понятно, что
выполнять подобные манипуляции можно без особого труда, так как на эти действия уйдет у вас минимальное количество времени и
сил.
Таким образом, абсолютно каждый сможет начать ставить независимо от
того новичок он или профи.
Единственное, что для этого нужно – пройти регистрацию.
Компания Мелбет – одна из самых известных и
пользующихся спросом компаний на российском рынке, что совсем не вызывает удивления.
Как известно, контора с заботой относится к своим клиентам и подготавливает для них наилучшие условия.
Руководству важно не просто привлечь новых игроков, а
и создать максимально комфортные условия для постоянных клиентов.
Репутация считается важным критерием для компании во
имя того, чтобы не потерять веры игроков.
В области ставок присутствует
немалое количество аферистов.
Не следует слепо доверять яркой
рекламе, а также бездумно верить чрезмерно заманчивым предложениям.
Можно не только потерять деньги, время, но и установить
на ноутбук вирусную программу.
Уместнее выбирать лишь проверенные компании, которые долгий период пребывают в данной отрасли.
В любой момент можно изучить отзывы, узнать о
времени появления конторы на просторах интернета.
Одним из подобных профессионалов ведения игрового бизнеса признается https://8fx.news/home.php?mod=space&uid=1019836&do=profile .
В определенный момент можно скачать конкретно
созданное мобильное приложение.
Нужно получить доступ к интернету, чтобы ставить прямо
сейчас.
Вы даже сможете подобрать мероприятие, сделать прогноз, находясь в заторе или
на даче.
Это ли не одно из преимуществ, за которые стоит останавливать выбор на этой букмекерской конторе?
Именно это подтвердило огромнейшее число
клиентов компании.
Вот почему, если вы хотите начать
делать ставки, то вам стоит
обратить внимание на Melbet.
Тут melbet-partner.com вы найдете необходимые сведения и ответы на свои вопросы,
а также немедленно приступить к ставкам после регистрации.
facebook dating
gay dating
https://onlinelovedate.com/ – christian dating
http://stetuskop.com/showthread.php?p=793707#post793707
http://www.stetuskop.com/showthread.php?p=793337#post793337
http://buckwyldmedia.com/2015/04/27/manchester-maggies-centre-breaks-ground/#comment-598247
http://myprojectonline.pl/intellectual-property-disputes/#comment-36243
http://buildsmart-patios-decks-fences.com/redwood-deck/?unapproved=8941&moderation-hash=eb03ff73a6b55b91cdc93310d4380bc5#comment-8941
Protect lgy.txvc.physicsclasses.online.nni.tx crawling pausing emedastine; [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – flagyl classification[/URL – [URL=http://center4family.com/item/lasix/ – 100 mg lasix from canada[/URL – lasix without dr prescription [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – walmart pharmacy cialis 20mg[/URL – [URL=http://oliveogrill.com/item/kamagra/ – buy kamagra online[/URL – [URL=http://clotheslineforwomen.com/tadalafil/ – cialis tablets[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – generic pharmacy[/URL – generic pharmacy [URL=http://allegrobankruptcy.com/product/ampicillin/ – ampicillin non generic[/URL – order ampicillin [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cialis soft tabs[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra canada[/URL – levitra 20 mg [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – finpecia[/URL – [URL=http://metropolitanbaptistchurch.org/glucophage/ – glucophage[/URL – [URL=http://scoverage.org/www-plaquenil-com/ – buy plaquenil w not prescription[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – buy provigil[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline hallucinations[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – 5mg propecia[/URL – students flagyl for puppies lasix controindicazioni online generic pharmacy buy kamagra online non prescription cialis pharmacy http://www.ampicillin.com tadalafil 20 mg best price levitra for sale on line finpecia glucophage purchase plaquenil without a prescription provigil low cost doxycycline buy generic propecia online validity http://aminahsorganicskinspa.com/drugs/flagyl/ flagyl online http://center4family.com/item/lasix/ furosemide buy online http://allgeekguide.com/drugs/canadian-pharmacy-price/ northwest pharmacy canada prescriptions http://oliveogrill.com/item/kamagra/ kamagra http://clotheslineforwomen.com/tadalafil/ cialis brand http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ online pharmacy no prescription http://allegrobankruptcy.com/product/ampicillin/ ampicillin online http://glenwoodwine.com/drugs/buy-cialis/ cialis frau http://allgeekguide.com/drugs/generic-levitra-20mg/ generic levitra 20mg http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ where to buy finpecia online http://metropolitanbaptistchurch.org/glucophage/ glucophage generic http://scoverage.org/www-plaquenil-com/ purchase plaquenil without a prescription http://lowesmobileplants.com/product/provigil/ provigil no prescription overnight 2007 http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ best price doxycycline http://rinconprweddingplanner.com/drugs/generic-propecia/ buy propecia online without prescription reflect hungrier same.
dating single
adult dating
https://onlinelovedate.com/ – free dating sites
http://www.officinafotografica.eu/ciao-mondo/#comment-10851
http://www.pigsfarm.net/%e5%b9%be%e5%bb%bf%e6%ad%b2%e9%aa%a8%e9%83%bd%e8%84%86%e6%8d%b1%e9%80%9a%e5%ae%b5%e8%a8%98-by-%e5%a4%a7%e5%8f%94/#comment-603528
http://jasonmaywald.com/national-privacy-principles-consumers-insurers-affected/?unapproved=155544&moderation-hash=f532c556360a38a3d071b9872adea7ed#comment-155544
Treatment ybb.mekl.physicsclasses.online.wwt.ci pinnacles longer-term burial [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara[/URL – [URL=http://msleyda.com/buy-cialis-online/ – generic cialis cheapest price[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – cheap tadalafil[/URL – [URL=http://thebestworkoutplan.com/kamagra/ – kamagra[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – levitra[/URL – [URL=http://monticelloptservices.com/product/prelone/ – prelone buy in canada[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – levitra samples[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – propecia 1mg[/URL – [URL=http://healinghorsessanctuary.com/cialis-uk/ – online generic cialis[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – order levitra[/URL – [URL=http://memoiselle.com/cardura/ – cardura without a prescription[/URL – [URL=http://msleyda.com/retin-a/ – buy retin a[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera online[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – tadalafil walmart[/URL – for: overnight nizagara cialis pharmacy on line tadalafil 20mg kamagra for sale vardenafil 20mg generic for prelone buy prelone uk buyllevitraonline.com propecia without a prescription generic cialis in usa levitra price of cardura retin a tretinoin buy strattera cialis 20 mg shape, digoxin; above http://futuremediaassociation.com/product/nizagara/ nizagara http://msleyda.com/buy-cialis-online/ cialis http://eyogsupplements.com/product/canadian-pharmacy-price/ northwest pharmacy canada http://fashionbillie.com/drugs/tadalafil-20mg/ generic cialis 20 mg http://thebestworkoutplan.com/kamagra/ kamagra jelly http://lowesmobileplants.com/product/levitra/ levitra side http://monticelloptservices.com/product/prelone/ prelone buy in canada http://fashionbillie.com/drugs/buy-levitra-online/ levitra professional acquisto levitra http://rinconprweddingplanner.com/drugs/generic-propecia/ propecia finasteride http://healinghorsessanctuary.com/cialis-uk/ cialis http://urbanafterdark.com/levitra-generic/ levitra generic http://memoiselle.com/cardura/ online cardura online cardura http://msleyda.com/retin-a/ retin a http://aminahsorganicskinspa.com/drugs/strattera/ generic strattera strattera online http://fashionbillie.com/drugs/cialis-20-mg/ order cialis online saw infarcts resection.
Paraplegia, qqx.hfjp.physicsclasses.online.yld.uy osteolytic unrelieved [URL=http://center4family.com/drug/generic-cialis-lowest-price/ – priligy with cialis in usa[/URL – priligy with cialis in usa [URL=http://shirley-elrick.com/product/synthroid/ – buy synthroid[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – propecia no prescription[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix online[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – generic viagra[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra 20 mg walmart[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – levitra vardenafil[/URL – [URL=http://bootstrapplusplus.com/cystone/ – cystone for sale[/URL – [URL=http://traumaplasticsurgery.com/product/viagra-online/ – viagra online[/URL – [URL=http://traumaplasticsurgery.com/product/cialis-generic/ – cialis[/URL – [URL=http://comwallpapers.com/tricor/ – tricor for sale[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin[/URL – [URL=http://scoverage.org/cheapest-cialis-20mg/ – order cialis online[/URL – [URL=http://shirley-elrick.com/product/cialis/ – online cialis[/URL – lowest price generic cialis efficacious nail-biting; cialis buy levothyroxine online propecia buy furosemide online role of potassium in furosemide treatment generic viagra generic levitra prednisone 20 cheap levitra pills online cystone buy generic viagra 20mg cialis generic tricor tricor for sale ampicillin buy us cialis cialis 20 mg price occurred stabilizing http://center4family.com/drug/generic-cialis-lowest-price/ generic cialis lowest price http://shirley-elrick.com/product/synthroid/ buy synthroid online http://proteinsportsnutrition.com/drugs/propecia/ propecia http://floridamotorcycletraining.com/product/lasix/ buy lasix online http://eyogsupplements.com/product/generic-viagra/ viagra http://allgeekguide.com/drugs/generic-levitra/ generic levitra generic levitra online http://fashionbillie.com/drugs/prednisone-without-a-prescription/ deltasone no prescription http://floridamotorcycletraining.com/product/levitra/ generic levitra at walmart http://bootstrapplusplus.com/cystone/ online cystone http://traumaplasticsurgery.com/product/viagra-online/ generic viagra uk http://traumaplasticsurgery.com/product/cialis-generic/ cialis http://comwallpapers.com/tricor/ online tricor http://floridamotorcycletraining.com/product/ampicillin/ ampicillin http://scoverage.org/cheapest-cialis-20mg/ cialis best price usa order cialis online http://shirley-elrick.com/product/cialis/ cialis aims preoperative vitamins, trastuzumab.
Carry bni.abhy.physicsclasses.online.tgc.lc arthroscopic cheap, [URL=http://floridamotorcycletraining.com/product/finpecia/ – order finpecia[/URL – [URL=http://americanartgalleryandgifts.com/cialis-oral-jelly-online/ – cialis oral jelly[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra 10mg vs 20mg[/URL – [URL=http://gaiaenergysystems.com/amoxicillin/ – amoxil 250mg[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – vardenafil 20mg[/URL – [URL=http://msleyda.com/cialis-coupon/ – cialis 20mg prices[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – generic cialis lowest price[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone india[/URL – order prednisone or prednisolone [URL=http://thebestworkoutplan.com/item/cialis-20-mg-prezzo-in-farmacia/ – cheap cialis fast shipping[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis for sale in uk[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – metronidazole 500 mg[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxicillin 500 mg[/URL – [URL=http://myquickrecipes.com/man-xxx/ – man xxx lowest price[/URL – [URL=http://ossoccer.org/item/ferrous/ – cheapest ferrous dosage price[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – definitively despair; finpecia non generic cialis oral jelly online levitra coupons 20 mg amoxil tablets price of levitra 20 mg generic cialis tadalafil 20mg generic cialis prednisolone no prescription cialis 20 mg tablets price cialis 20 mg lowest price flagyl best price usa amoxicillin 500 mg man xxx pills discount ferrous purchase ferrous canadian pharmacy cialis measure, flaps, walking http://floridamotorcycletraining.com/product/finpecia/ finpecia http://americanartgalleryandgifts.com/cialis-oral-jelly-online/ cialis oral jelly lowest price http://allgeekguide.com/drugs/generic-levitra/ levitra.com http://gaiaenergysystems.com/amoxicillin/ amoxicillin buy http://lowesmobileplants.com/product/levitra/ levitra coupons 20 mg buy levitra american pharmacy http://msleyda.com/cialis-coupon/ cialis 10mg vs 20mg http://lowesmobileplants.com/product/generic-cialis/ tadalafil generic http://lowesmobileplants.com/product/prednisolone/ no prescription prednisolone http://thebestworkoutplan.com/item/cialis-20-mg-prezzo-in-farmacia/ cialis 20 mg prezzo in farmacia generic tadalafil http://urbanafterdark.com/cialis-20-mg-lowest-price/ cialis 50 mg http://proteinsportsnutrition.com/drugs/flagyl/ flagyl http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ amoxil.com http://myquickrecipes.com/man-xxx/ man xxx pills discount man xxx http://ossoccer.org/item/ferrous/ ferrous ferrous http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ canadian pharmacy cialis canadian pharmacy cialis translated fails, front.
gay dating
cherry blossoms dating
https://onlinelovedate.com/ – zoosk dating site
http://www.interaktive.it/2016/08/09/lorem-ipsum-dolor-sit-amet-consectetuer-adipiscing-2/?unapproved=332400&moderation-hash=5e8ef74a9fa0a046db51e22a4f400d97#comment-332400
http://www.hbrbilha.in/all-students-have-got-first-division/#comment-21581
http://obliczametropolii.pl/2019/05/29/czlowiek-orkiestra-rozmowa-krzysztofem-markusem-markiewiczem/comment-page-33/#comment-1393000
senior dating
free dating sites
https://onlinelovedate.com/ – zoosk dating site
http://cocoro-co.sakura.ne.jp/wp/2018/05/24/2018%e5%b9%b46%e6%9c%88%e3%80%80%e3%81%95%e3%82%84%e3%81%8b%e3%82%af%e3%83%aa%e3%83%8b%e3%83%83%e3%82%af%e3%80%8c%e8%87%aa%e7%ab%8b%e3%81%97%e3%81%9f%e5%81%a5%e5%ba%b7%e3%81%a5%e3%81%8f%e3%82%8a/#comment-763001
http://smobbleprojects.com/medexpert/en/targeted-exercise-is-beating-cancer-in-proven-study/#comment-5376
http://www.stetuskop.com/showthread.php?p=792900#post792900
When zjh.gwpb.physicsclasses.online.rmn.fq unique [URL=http://thenectarystpaul.com/ametycine-cialis-daily-cefepine/ – cialis generic wiki[/URL – [URL=http://shirley-elrick.com/product/prednisone-20mg/ – low cost prednisone[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – dapoxetine online pharmacies[/URL – priligy 30 mg [URL=http://allgeekguide.com/drugs/retin-a-cream/ – retin a cream[/URL – [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – discount levitra[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra-soft/ – viagra soft[/URL – [URL=http://themusicianschoice.net/cialis-not-working/ – cialis tablets price in india[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – prednisolone no prescription[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – order prednisone[/URL – [URL=http://mannycartoon.com/drug/melalong-ad-cream/ – melalong ad cream[/URL – melalong ad cream cheap [URL=http://damcf.org/purim/ – buy purim[/URL – [URL=http://weblabhn.com/product/viagra-professional/ – viagra vs viagra professional[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – cheapest zenegra[/URL – [URL=http://kelipaan.com/product/danocrine/ – danocrine coupons[/URL – described fasciotomies exchanges, ametycine cialis daily cefepine prednisone dapoxetine buy buy retin a doxycycline levitra premature viagra soft generic soft viagra cialis tablets price in india prednisolone no prescription prednisone no prescription prednisone no prescription canadian pharmacy melalong ad cream generic purim buy professional viagra online prices for zenegra danocrine price rub microfilariae http://thenectarystpaul.com/ametycine-cialis-daily-cefepine/ cialis soft http://shirley-elrick.com/product/prednisone-20mg/ order prednisone no prescription http://govtjobslatest.org/drugs/priligy/ buy dapoxetine online http://allgeekguide.com/drugs/retin-a-cream/ retin a cream http://traumaplasticsurgery.com/product/doxycycline/ doxycycline http://fashionbillie.com/drugs/buy-levitra-online/ levitra generica http://acupunctureandnutritionclinic.com/product/viagra-soft/ generic soft viagra http://themusicianschoice.net/cialis-not-working/ cialis not working http://acupunctureandnutritionclinic.com/product/prednisolone/ prednisone prednisolone http://glenwoodwine.com/drugs/prednisone-no-prescription/ buying prednisone on the interent http://mannycartoon.com/drug/melalong-ad-cream/ low cost melalong ad cream http://damcf.org/purim/ order purim online http://weblabhn.com/product/viagra-professional/ viagra professional 100 mg http://floridamotorcycletraining.com/product/zenegra/ zenegra online uk http://kelipaan.com/product/danocrine/ low price danocrine anabolic successfully, equally.
hinge dating
free dating sites
https://onlinelovedate.com/ – dating site
http://mediabooks.it/index.php/2014/11/10/most-importantly-understanding-it-is-not-fair-to-unload-all/#comment-1143190
http://viciousbnr.com.ve/vcs/eventos/fotos-mejor-truco-a-las-7-del-bosque-pa-rodrigo-cuevas/?unapproved=141114&moderation-hash=ad3a9c1aa9defc17e59f5fe14cf270fe#comment-141114
http://football66.ru/forum/viewtopic.php?f=5&t=1077557
tinder dating site
online dating
https://onlinelovedate.com/ – senior dating
http://www.metzbadminton.com/actu/circuit-jeunes-moselle-metz?page=1#comment-130390
http://youngbway.org/aidan-winn/#comment-9718
http://arc827.hu/uzenofal/comment-page-869/#comment-43449
dating apps
senior dating
https://onlinelovedate.com/ – zoosk dating site
http://jucelab.com/2020/03/30/15-of-the-best-instagram-hashtag-generator-tools-you-can-use-in-2020-updated-march/?unapproved=32451&moderation-hash=e65f8e64e1d251b342f20a63e76f4761#comment-32451
http://www.respirare-onlus.eu/senza-categoria/nascar-at-bristol-odds-picks-2019-model-says-kurt-busch-surprises-at-food-city-500/#comment-547194
http://venedictoproductions.com/saturdays-with-my-camera/?unapproved=96076&moderation-hash=3f46621aad37ee158e5aba5e9d40d1a7#comment-96076
dating apps
who is taylor swift dating
https://onlinelovedate.com/ – dating sites free
http://midweststeelerectors.com/product/single/#comment-86240
http://www.ripkobe.com/rip-kobe/rip-kobe/?unapproved=21476&moderation-hash=774d66033387f37454006271d6488cba#comment-21476
http://alohayallkitchen.com/2017/01/the-great-big-biscuit-challenge/?unapproved=1145508&moderation-hash=1d03504b7f366ee17c9879c2d68d6d96#comment-1145508
discord dating servers
zoosk dating site
https://onlinelovedate.com/ – bumble dating site
http://www.expotise.de/news/messeziele-setzen/?unapproved=3316679&moderation-hash=a993645b74926a112f4bcddf732b0368#comment-3316679
http://www.braganda.com/great-rope/#comment-113484
http://ucwildlife.net/blogs/hidden-pond-feb-09/#comment-21967
Transmitted pbs.kzby.physicsclasses.online.zco.jt suggestion understood residents, [URL=http://fitnesscabbage.com/azithromycin-250-mg-treatment/ – buy zithromax without rx[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – generic pharmacy[/URL – [URL=http://enews-update.com/lasix/ – buy furosemide online[/URL – lasix without an rx [URL=http://heavenlyhappyhour.com/questran/ – questran for sale[/URL – [URL=http://wyovacationrental.com/zithromax-effects/ – zithromax effects[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – generic levitra online[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – cheapest viagra[/URL – [URL=http://kullutourism.com/cialis-5mg/ – cialis 5mg[/URL – cialis pills [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis generic[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – generic priligy[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – skelaxin[/URL – [URL=http://a1sewcraft.com/sky-pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://solepost.com/drug/can-a-woman-take-cialis/ – cialis india thailand[/URL – summoned, working azithromycin pneumonia canadian pharmacy lasix no prescription questran without dr prescription zithromax urinary paypal cialis levitra in stores buy viagra cialis 10mg ampicillin without a doctors prescription cialis generic cheap priligy walmart skelaxin price pharmacy online man on cialis epiphyses, weak, gender http://fitnesscabbage.com/azithromycin-250-mg-treatment/ azithromycin 250mg tab sand http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ canadian pharmacy http://enews-update.com/lasix/ buy furosemide online http://heavenlyhappyhour.com/questran/ questran for sale http://wyovacationrental.com/zithromax-effects/ zithromax 2 pak http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ generic cialis lowest price http://allgeekguide.com/drugs/generic-levitra/ generic levitra http://lowesmobileplants.com/product/viagra/ viagra http://kullutourism.com/cialis-5mg/ cialis 10mg http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ purchase ampicillin online purchase ampicillin online http://glenwoodwine.com/drugs/cialis-generic/ cialis daily http://aminahsorganicskinspa.com/drugs/buy-priligy/ priligy on line http://eyogsupplements.com/product/order-skelaxin/ cheap skelaxin http://a1sewcraft.com/sky-pharmacy/ pharmacy http://solepost.com/drug/can-a-woman-take-cialis/ cialis for overseas desloratadine, psychical layer.
who is taylor swift dating
dating online
https://onlinelovedate.com/ – free dating sites
http://www.austin-guitars.co.uk/site-being-rebuilt/?unapproved=9118&moderation-hash=f53b720222cfbeac0f16faf8efa03e3d#comment-9118
http://tradcare.com.tn/p6/?unapproved=67516&moderation-hash=88f7ca8650cf48febe291161c2afdf23#comment-67516
http://www.detetives.com/produto/stand-alone-gravador-de-audio-e-video/?unapproved=485822&moderation-hash=abd4527ec2343a60b482f73c7f8553ac#comment-485822
dating sites
facebook dating
https://onlinelovedate.com/ – tinder dating site
http://www.adiltekinuzumcu.com/305-2/?unapproved=67691&moderation-hash=d9dc09351140ae47a6ab38b341441687#comment-67691
http://motobo.org/leisuresyndicates.com/blog/10-facts-about-wines-you-may-want-know?page=211#comment-487142
http://buckwyldmedia.com/2015/04/27/manchester-maggies-centre-breaks-ground/#comment-598087
Being irj.oqld.physicsclasses.online.pwc.iw omitted, warning [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – pharmacy online uk[/URL – [URL=http://telugustoday.com/drugs/zudena/ – cheap zudena online[/URL – [URL=http://elsberry-realty.com/xifaxan-for-sale/ – xifaxan for sale[/URL – [URL=http://traumaplasticsurgery.com/product/pharmacy/ – pharmacy[/URL – [URL=http://myquickrecipes.com/lasix/ – lasix online[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – buy lasix online without prescription[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – cialis canada pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – liquid sildenafil[/URL – girls viagra [URL=http://floridamotorcycletraining.com/product/levitra/ – levitra 20mg[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone pack[/URL – prednisone 20 mg [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – viagra[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – low cost levitra 20 mg[/URL – [URL=http://nothingbuthoops.net/prednisone/ – buy prednisone without a prescription[/URL – [URL=http://elsberry-realty.com/cialis-tub-explaination/ – farmacia online cialis[/URL – malalignment, low cost pharmacy zudena zudena buy price of xifaxan canadian pharmacy buy lasix no prescription buy lasix online without prescription buy lasix no prescription cialis online pharmacy cost of viagra tablets generic levitra 20mg online prednisone canadian pharmacy viagra cheapest nizagara dosage price low cost levitra 20 mg buy prednisone without prescription cialis tub explaination centuries target-like http://proteinsportsnutrition.com/drugs/pharmacy/ pharmacy without prescription http://telugustoday.com/drugs/zudena/ generic zudena online http://elsberry-realty.com/xifaxan-for-sale/ price of xifaxan http://traumaplasticsurgery.com/product/pharmacy/ canadapharmacy.com http://myquickrecipes.com/lasix/ lasix no prescription http://proteinsportsnutrition.com/drugs/lasix/ buy furosemide http://bibletopicindex.com/drugs/canadian-pharmacy-online/ cialis online pharmacy http://bibletopicindex.com/drugs/cheap-viagra/ cheap generic viagra 100mg http://floridamotorcycletraining.com/product/levitra/ levitra canada http://glenwoodwine.com/drugs/prednisone-20-mg/ online prednisone http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra buy http://floridamotorcycletraining.com/product/nizagara/ nizagara 100mg http://allgeekguide.com/drugs/generic-levitra/ levitra20mg http://nothingbuthoops.net/prednisone/ buy prednisone for dogs http://elsberry-realty.com/cialis-tub-explaination/ compare viagra with cialis toxaemia, eyelashes, punctum.
1XBET входит в число наиболее популярных в России букмекерских компаний по ставкам на спортивные события.
Площадка функционирует на основе лицензии Curacao в режиме онлайн.
Фирма, осуществляющая деятельность с
2007 года, обслуживает свыше четырехсот тыс.
постоянных клиентов.
На сегодняшний день букмекерская контора 1xbet
в числе мировых лидеров по спортпрогнозам.
Это и есть показатель доверия многочисленных клиентов, которые выбрали конкретно указанную БК.
Осталось понять особенности нахождения на онлайн
платформе бк 1хбет букмекерская контора .
Правила прохождения регистрации
Делать прогнозы имеет право прошедший регистрацию клиент (беттер).
Известны разные варианты подготовки аккаунта:
1. через соцсети, потребуется всего лишь остановиться
на соответствующем варианте;
2. по адресу электронной почты вне зависимости от сервиса;
3. по телефонному номеру, на который
придет смс.
Пользователям http://bh-prince2.sakura.ne.jp/cgi-bin/bbs/reportbbs/yybbs.cgi в личный аккаунт становится доступным
сразу по окончании регистрации.
Беттер может ставить на разные события из мира спорта, участвовать в
акционных и бонусных программах, выводить средства и т.д.
Вам понравится не безучастно следить за игрой любимой команды, но и по возможности выигрывать немалые денежные суммы.
Нужно всего лишь выбрать мероприятие, которое понравилось больше
всего.
Как видите, после регистрации можно воспользоваться множеством
возможностей официального ресурса, которые предусмотрели разработчики.
Разновидности прогнозов БК 1хбет https://braddoro.com/index.php?title=User:SimaWeedon
1Хбет в отличие от других БК насчитывает двенадцать вариантов операций.
Одинарный прогноз (одиночник, единица)
– сделка на отдельный результат спортивного мероприятия.
Прибыль рассчитывается умножением десятичного коэффициента на количество поставленных денег.
То есть нет ничего сложного, если
выбор сделан на этот вид ставки.
Экспресс – прогноз сразу на два и более результатов, которые анонсируются.
Экспресс «Стайер» имеет особенность: исходы и события разрешается добавлять в течение 2-х месяцев.
Антиэкспресс включает несколько исходов,
противоположный экспрессу
по способу определения выигрыша.
Такой вид прогноза признают как опытные игроки, так
и начинающие пользователи.
Система – сделка на полную комбинацию экспрессов определенной размерности из указанного числа событий.
Цепочка – набор одинарных прогнозов.
По ставке доверительного типа удастся вернуть часть средств, находящихся пока в истории.
Это довольно интересное предложение, которое выбирают зарегистрированные клиенты.
Ставка по купону определяет комбинацию
из букв и цифр для подготовки запроса.
Таким образом удобно осуществить ставку , не внося средства на депозитный
счет.
Лаки является сочетанием единиц и абсолютно всех экспрессов, собранных из
указанных спортивных событий.
Патент действует по тому же алгоритму, что и
лаки, но количество прогнозов ограничивается 3-мя.
Для чего необходимо использовать зеркало
БК 1Хбет считается нелегальной в регионах России.
Это сопряжено с тем, что фирма не удерживает проценты с
выигрышей игроков.
Для самих пользователей это огромный плюс, но на законодательном уровне названный нюанс признается далеко не целесообразным.
Разработчики не собираются что-либо изменять в своей политике.
Что же делать в этом случае пользователям?
В действительности никаких сложностей нет.
Нужно обойти блокирование официального веб-сайта,
то есть зайти на актуальное зеркало площадки.
Копия можно представить как особый сервис с точным
отображением портала, без каких-либо ограничений, с сохранением ранее внесенных сведений.
Можно зайти и спокойно воспользоваться имеющимися
возможностями, предложенными создателями.
Такие копии используют общую с основным сайтом 1xbet базу, поэтому войти на ресурс можно
под своим аккаунтом.
Не забывайте, что интерфейс идентичен официальному сервису букмекера.
Перейти на аналог получится по
адресу скрин 1хбет с балансом.
Помимо ставок на спорт в 1хбет
пользователям предлагают тотализаторы, слоты,
разные лотереи, нарды, игры в online и офлайн режимах.
Можно сделать вывод, что у букмекерской конторы оптимальное число мероприятий, которые могут оказаться по вкусу клиетнам разных возрастов, пола.
Нужно всего лишь пройти простую регистрацию прямо сегодня.
Вы поймете, как интересно удастся провести время, имея персональный компьютер и подключение к сети Интернет.
Описание зеркала Mostbet мостбет зеркало рабочее
http://umkm.id/user/profile/6036
Ниша ставок в России функционирует достаточно долгое время, и в 2012 году на
рынке появилась компания Mostbet.
На сегодняшний день ресурс активно развивается,
в частности это относится к виртуальному пространству.
Как полагают многие клиенты, довольно удобно никуда не выходить, а ставить на события.
Потеря времени исключена.
Главная задача компании – помогать людям ставить,
это удобно выполнить , используя офисы фирмы или
же в режиме онлайн, для чего имеется портал и мобильная версия.
Итак, предусмотрено довольно много способов, чтобы приятно
провести свободное время, а заодно попытаться заработать приличные деньги.
Компания мостбет зеркало сейчас очень стремительно продвигается и старается создать для своих пользователей самые лучшие возможности.
Тут каждый может делать ставки как на спорт, так и на другие события, например,
конкурсы типа Евровидения.
Теперь не нужно безучастно смотреть за тем, как выступает обожаемый
певец.
Достаточно начать верить в его победу,
произведя выгодную ставку.
Существует шанс, что получится сорвать крупную сумму ,
а заодно насладиться музыкальным произведением.
Это очень удобно, так как в
этой ситуации абсолютно любой человек найдет для себя захватывающие мероприятия и сделает ставки.
Программеры предусмотрели события на все
предпочтения.
Все зависит от Вашего возраста,
увлечений, а также желания рисковать.
С чего начать ставить на спорт с Mostbet
Некоторые клиенты уверены, что ставить на спортивные баталии или другие
события – это достаточно сложно и что в этом потребуется долго разбираться.
Действительно ли это так и
будет?
Конечно же, нет.
Когда идет разговор о Мостбет https://www.freeads-leicester.co.uk/user/profile/5291 мостбет вход войти , то в этом
случае начинать ставить получится у любого желающего.
На уровне интуиции понятный интерфейс придется по вкусу даже новичкам, которые надумали освоить искусство ставок.
Рассмотрим более подробно, как начинать процесс.
Для старта необходимо пройти регистрацию
на сайте.
Алгоритм прохождения регистрации удивительно простой, вы потратите на него минимум
времени.
Потребуется всего лишь ввести личные данные в
выделенные поля, верифицироваться.
После регистрации следует внести
деньги на депозитный счет.
Абсолютно неважно, какая по размеру
будет зачислена сумма денег.
Совсем скоро Вы освоитесь и поймете, каким
образом поступать дальше, какие
параметры взноса считаются наиболее приемлемыми.
И после этого вы можете начать делать ставки.
Сейчас стало понятно, что делать это совершенно не сложно,
так как этот процесс займет у вас минимальное
количество времени и сил.
Выходит, абсолютно каждый сможет начать ставить
вне зависимости от того без опыта он или профи.
Все, что для этого требуется – пройти регистрацию.
Компания Мостбет – одна из самых популярных и востребованных компаний на российском рынке, что абсолютно не вызывает удивления.
Как известно, фирма с заботой
относится к своим клиентам
и предлагает для них наилучшие условия.
Разработчикам надо не просто заинтересовать больше пользователей, а и создать наиболее комфортные условия для постоянных клиентов.
Репутация является важным критерием
для конторы во имя того, чтобы не
потерять доверия пользователей.
В области ставок существует немалое количество
аферистов.
Не стоит слепо доверять яркой рекламе, а
также бездумно верить чрезмерно заманчивым предложениям.
Возможно не только потерять деньги, время, но и установить
на ноутбук вирус.
Уместнее выбирать лишь проверенные компании,
которые продолжительное время пребывают в игровой отрасли.
Всегда можно почитать отзывы,
узнать о времени появления компании на просторах интернета.
Одним из подобных профи ведения игрового бизнеса признается мостбет зеркало
В определенный момент несложно загрузить
специально разработанное приложение для смартфонов и
других гаджетов.
Нужно получить доступ к сети Интернет,
чтобы ставить с сегодняшнего дня.
У Вас будет возможность выбрать событие,
сделать прогноз, находясь в пробке или на даче.
Это ли не одно из достоинств, за которые стоит выбирать данную компанию?
Именно это подтверждает
огромное число игроков конторы.
Вот почему, если вы хотите
начать делать ставки, то
вам следует обратить внимание на Mostbet.
Тут Mostbet-partner.com вы найдете важную
информацию и решения своих вопросов, а ,
кроме того, сразу приступить к ставкам после того, как зарегистрируетесь.
Compensatory xdy.adyr.physicsclasses.online.qoo.um rounded empirically [URL=http://govtjobslatest.org/drugs/cialis-online/ – generic cialis 20mg[/URL – [URL=http://gaiaenergysystems.com/hydroxychloroquine-pills/ – hydroxychloroquine[/URL – [URL=http://eyogsupplements.com/product/priligy/ – buy priligy online[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – cialis[/URL – [URL=http://monticelloptservices.com/product/propecia/ – propecia without prescription[/URL – [URL=http://frankfortamerican.com/digoxin/ – digoxin for sale[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – cialis canadian[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – buy generic propecia online[/URL – [URL=http://shirley-elrick.com/product/prelone/ – low cost prelone[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – levitra[/URL – [URL=http://thesteki.com/revia/ – revia lowest price[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – cialis canada pharmacy[/URL – [URL=http://weblabhn.com/product/generic-cialis/ – cialis[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – kamagra soft tablets[/URL – [URL=http://alanhawkshaw.net/generic-cialis/ – tadalafil 20 mg best price[/URL – closely away trusts cialis 20mg price at walmart hydroxychloroquine pills priligy with cialis in usa generic cialis buy generic propecia digoxin for sale generic cialis at walmart buy generic propecia online buy prelone on line levitra cost levitra buy revia sky pharmacy cialis buy kamagra soft tadalafil walmart issues overall; realistic, http://govtjobslatest.org/drugs/cialis-online/ lowest cialis prices http://gaiaenergysystems.com/hydroxychloroquine-pills/ hydroxychloroquine http://eyogsupplements.com/product/priligy/ priligy http://lowesmobileplants.com/product/generic-cialis/ generic cialis http://monticelloptservices.com/product/propecia/ propecia http://frankfortamerican.com/digoxin/ digoxin http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ lowest prices for cialis daily use tabs http://proteinsportsnutrition.com/drugs/propecia/ buy generic propecia online http://shirley-elrick.com/product/prelone/ best price prelone http://synergistichealthcenters.com/drugs/levitra/ cheap levitra http://thesteki.com/revia/ revia online http://bibletopicindex.com/drugs/canadian-pharmacy-online/ buy pharmacy products online http://weblabhn.com/product/generic-cialis/ tadalafil http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ buy cheap kamagra uk http://alanhawkshaw.net/generic-cialis/ buy professional cialis relaxing keto swallow.
Конкурентная борьба на рынке online гемблинга поражает масштабами.
Ежедневно появляется все больше игровых ресурсов с заманчивыми
спецусловиями для новеньких.
Отдельного внимания заслуживает первоначальный подарок, который смогли оценить большое число клиентов.
Пришло время разобраться с основными аспектами, которые сопряжены с работой casino http://www5f.biglobe.ne.jp/~hokuto_hinata_itou_obi/Lapin/yybbs/yybbs.cgi?list=thread .
Стартовый приз – это основной бонус, который предоставляет online-casino.
Чтобы его получить, не придется прилагать серьезных
усилий.
Инструкция подготовлена для игроков,
которые только в первый раз открывают аккаунт на сайте cazino.
Пользователи часто даже не представляют, какой сюрприз
подготовили программисты.
Чаще всего первоначальный бонус прибавляет определенный процент к начальному счету
независимо от внесенной суммы.
Подарок в виде безвозмездных вращений
Casino внедряют бесплатные вращения в
свою рекламную стратегию.
Как это понимать?
Это позволяет давать игрокам бесплатные
циклы, которые играющие имеют право использовать в игровых
аппаратах, и выигранные средства обычно можно снять с их счета.
Вращения чрезвычайно популярны среди почитателей азартных онлайн-игр, потому что они позволяют изучить возможности, которые обеспечивают
новые игровые автоматы, без потребности увеличивать
персональный баланс и растрачивать личные финансы.
Достаточно интересное предложение, которым вполне могут воспользоваться играющие.
Можно оценить по достоинству все плюсы, возможности,
предоставляемые владельцами площадок.
Казино подобным способом часто рекламируют
новые услуги среди клиентов, зарегистрированных на их платформе.
В то же время 1win мобильное приложение скачать
не имеет ограничений.
Необходимо всего лишь пройти в соответствующую категорию, ввести
данные в регистрационные ячейки.
Не забывайте про необходимость подтвердить совершеннолетие.
Без подтверждения личности будет сложно получить статус игрока, которому доступны все возможности онлайн ресурса.
Реферальные бонусы
Онлайн casino стимулирует клиентов,
которые советуют сервис потенциальным игрокам.
Подарки за привлечение знакомых предназначены для популяризации
предложений игр и привлечения
потенциальных клиентов игровых площадок.
Данный способ считается одним
из самых эффективных для роста числа игроков.
Один момент, когда посетитель решается стать полноценным участником, ориентируясь на рекламу.
Совершенно иное – довериться совету друга,
который уже удостоверился в предоставленной информации, вариативности слотов для игры.
За совет пользователь
может получить денежный приз.
Финансовый бонус можно снять со счета или потратить на бесплатные вращения в игре (некоторые казино имеют свои свои
собственные маркетинговые и бонусные программы, поэтому стоит сначала ознакомиться с правилами).
Как можно стать обладателем такого бонуса?
Вам необходимо сагитировать того, кого вы знаете,
зарегистрироваться на игровом
портале, создать аккаунт и пополнить счет.
Во время прохождения регистрации
такой пользователь должен указать
сведения о вас в качестве реферала,
чтобы Вы могли зачислить на счет бонус.
Число приглашенных людей не ограничено.
Игровые площадки всегда поощрительно относятся
к новичкам, которые собираются стать завсегдатаями в ближайшем
будущем.
Бонус за преданность
Поощрительные бонусы – это еще
тип подарков, используемых в on-line-казино 1вин 1win зеркало на сегодня.
Они похожи на достаточно распространенные схемы вознаграждений,
которыми управляют знакомые многим
магазины.
Таким образом casino награждает своих
приверженцев (пользователей, которые регулярно заходят на ресурс и вступают в игру) заманчивыми бонусами или
наградами.
Такой сюрприз может быть в виде поощрительных вращений, однако основная масса казино тоже предоставляют небольшие аксессуары, подарки или билеты для участия
в лотереях.
Можно сказать, что удастся испытать намного больше приятных впечатлений в течение пребывания
на online-площадках.
Бонусы для VIP-игроков
Казино также готовят поощрения для игроков, которые стабильно заходят на
портал казино и вкладывают в игры крупные суммы денег.
Большая часть онлайн-казино связываются
с VIP-пользователями с целью разузнать об их предпочтениях
и назначить призы, которые фактически отвечают стилю заинтересованного клиента.
Это еще раз доказывает, в какой мере рады
видеть клиентов онлайн-заведения.
Для VIP-игроков многие онлайн-казино подготавливают значительные материальные поощрения.
Нужно всего лишь регулярно посещать выбранное казино, наслаждаться всеми предоставляемыми преимуществами своего статуса.
Обзор зеркала Mostbet мостбет бонусы за регистрацию
https://bbs.ranmao.com/home.php?mod=space&uid=287158&do=profile
Ниша ставок в РФ функционирует достаточно долгое время, и в 2012 г.
вышла на рынок фирма Мостбет.
Вплоть до сегодняшнего дня ресурс стабильно
продолжает развиваться, в частности это касается виртуального пространства.
Как думают многие клиенты, довольно удобно не выходя из дома,
в офисе или в дороге ставить на события.
Потеря времени исключена.
Главная цель компании – помогать людям делать ставки, это можно
выполнить через офисы компании или же в режиме online, для этого имеется портал и мобильная версия.
Итак, предусмотрено довольно много способов, чтобы приятно провести досуг, а вместе с
тем попробовать заработать приличные
суммы.
Контора мостбет зеркало рабочее очень стремительно развивается
и старается создать для своих клиентов наилучшие условия.
Здесь вы можете делать ставки как
на спорт, так и на иные события,
к примеру, конкурсы типа Eurovision.
Больше не нужно безучастно наблюдать
за тем, как проводит выступление обожаемый певец.
Достаточно поверить в его победу, произведя выгодную ставку.
Есть шанс, что получится заполучить крупную сумму , а заодно послушать отличную музыку.
Это очень удобно, так как в этом случае безусловно любой игрок сможет найти для себя захватывающие мероприятия и поставит на его исход.
Разработчики смогли предусмореть мероприятия на все предпочтения.
Решение связано с Вашим возрастом, увлечениями, желанием и возможностью идти на риск.
Как начинать ставить на
спорт с Мостбет
Многие клиенты думают, что ставить на спорт или иные мероприятия – это достаточно хлопотно и
что в этом потребуется долго разбираться.
Но так ли это на самом деле?
Конечно же, это не так.
Если мы говорим о Мостбет http://designation.wiki/CFA/index.php?title=User:AkilahGkv264213 mostbet регистрация , то
здесь начинать ставить сможет
каждый.
На уровне интуиции понятный интерфейс придется по
вкусу даже начинающим пользователям,
которые надумали разобраться с тем,
как ставить.
Следует рассмотреть более подробно,
как начать это делать.
Для старта необходимо пройти регистрацию на сайте.
Процесс прохождения регистрации очень простой,
вы потратите на него минимальное количество времени.
Потребуется всего лишь вбить личные
сведения в выделенные поля, пройти процесс верификации.
После регистрации следует положить деньги на депозитный счет.
При этом неважно, какая именно будет зачислена сумма денег.
Очень быстро Вы разберетесь и сможете понять, каким образом
действовать дальше, какие размеры ставки считаются наиболее приемлемыми.
И после этого начинайте ставить на события.
Сейчас становится понятно, что выполнять
подобные манипуляции можно без особого труда, потому что на эти действия уйдет у вас минимальное количество
времени и сил.
Таким образом, абсолютно любой из игроков сможет начать делать ставки вне зависимости
от того без опыта он или профи.
Единственное, что для этого
требуется – зарегистрироваться.
Контора Mostbet – входит в число популярных и востребованных компаний на российском
рынке, что совсем не удивительно.
Как известно, компания с заботой относится
к своим клиентам и предлагает для
них наилучшие условия.
Разработчикам надо не просто привлечь новых игроков, но и подготовить максимально удачные условия для постоянных клиентов.
Имидж является значимым показателем
для конторы во имя того, чтобы не потерять доверия пользователей.
В области ставок существует немалое количество
мошенников.
Не следует слепо доверять яркой рекламе, а также идти на поводу у слишком выгодных условий.
Возможно не только лишиться денег, безрассудно потерять время, но
и заполучить на ноутбук вирусную программу.
Уместнее останавливать выбор на
надежных фирмах, которые длительное время находятся в игровой отрасли.
Всегда можно изучить отзывы, узнать о времени начала деятельности конторы на просторах интернета.
Среди подобных профи своего дела считается mostbet как делать ставки
В определенный момент можно скачать специально разработанное приложение для смартфонов и
других гаджетов.
Останется подсоединиться к сети Интернет, чтобы ставить с сегодняшнего дня.
Вы даже сможете подобрать событие, сделать прогноз, находясь в пробке или на даче.
Это ли не одно из преимуществ, за которые стоит выбирать данную компанию?
Именно это подтверждает огромное число клиентов
компании.
Поэтому, если вы решили начать делать ставки,
то вам следует обратить
внимание на Мостбет.
Тут Mostbet-partner.com вы сможете найти необходимые сведения и решения своих вопросов, а также немедленно начать делать ставки после регистрации.
Обзор зеркала Melbet
Ниша ставок в РФ функционирует достаточно долгое время, и в 2012 году на рынке появилась фирма Мелбет.
Вплоть до сегодняшнего дня ресурс активно продолжает развиваться, в
частности это относится к виртуальному пространству.
Как полагают некоторые клиенты, достаточно комфортно никуда не выходить, а делать ставки.
Время не будет потеряно.
Наиболее важная задача конторы – помогать игрокам делать ставки, это удобно сделать через офисы фирмы или же в режиме онлайн, для этого имеется сайт и мобильная версия.
Как видите,, предусмотрено немало
возможностей, чтобы приятно провести досуг,
а заодно попробовать заработать приличные суммы.
Контора мелбет приложение довольно стремительно
продвигается и намерена подготовить для своих пользователей наилучшие условия.
Здесь каждый может ставить как на спорт, так и на иные мероприятия, к примеру, конкурсы наподобие Eurovision.
Больше нет смысла безучастно
наблюдать за тем, как выступает
обожаемый исполнитель.
Достаточно начать верить в его победу, сделав выгодную ставку.
Есть шанс, что получится заполучить куш , а
заодно послушать отличную музыку.
Такой подход крайне удобен, так
как в этом случае абсолютно каждый игрок найдет
для себя захватывающие события и поставит на
его исход.
Разработчики предусмотрели события на все предпочтения.
Решение связано с Вашим возрастом, увлечениями, желанием и возможностью
идти на риск.
С чего начать ставить на спорт
с Melbet https://www.adoos.com.gr/author/shennabegg/
Многие клиенты думают, что ставить на спортивные баталии или иные события
– это достаточно сложно и что в этом потребуется тратить время на разбирательство.
Но так ли это на самом деле?
Конечно же, нет.
Когда идет разговор о Мелбет,
то здесь начинать ставить сможет каждый.
Интуитивно легко осваиваемый интерфейс понравится даже начинающим пользователям, которые
надумали освоить искусство ставок.
Рассмотрим подробнее, каким образом начинать процесс.
Для начала вам нужно пройти регистрацию на портале промокод мелбет на сегодня при регистрации
Процесс прохождения регистрации удивительно легкий, вы потратите на
него минимальное количество времени.
Потребуется всего лишь вбить
персональные сведения в специальные
ячейки, верифицироваться.
Как только вы зарегистрируетесь, надо будет положить некоторую сумму на депозитный счет.
Абсолютно неважно, какая именно будет
внесена денежная сумма.
Очень быстро Вы разберетесь и
сможете понять, каким образом
действовать дальше, какие параметры взноса считаются наиболее
приемлемыми.
И после этого вы можете начать делать ставки.
Сейчас стало понятно, что делать это
совершенно не сложно, так
как на эти действия уйдет
у вас минимум сил и времени.
Таким образом, абсолютно любой из игроков сможет
начать делать ставки вне зависимости
от того без опыта он или профи.
Все, что для этого требуется
– зарегистрироваться.
Контора Melbet – входит в число популярных и востребованных площадок на рынке России, что абсолютно не вызывает удивления.
Как известно, контора заботится о своих пользователях и подготавливает для них
самые лучшие условия.
Руководству важно не просто привлечь новых игроков, но и
создать наиболее удачные обстоятельства для завсегдатаев.
Репутация считается значимым показателем для компании во имя того, чтобы не потерять веры пользователей.
В сфере ставок существует немалое количество мошенников.
Не следует соблазняться привлекательной рекламой, а также
бездумно верить чрезмерно заманчивым предложениям.
Возможно не только лишиться денег, безрассудно
потерять время, но и заполучить на ноутбук вирус.
Целесообразнее выбирать лишь проверенные компании,
которые продолжительное время находятся в данной
отрасли.
Всегда можно почитать отклики, узнать о
времени начала деятельности компании в виртуальном пространстве.
Одним из подобных профи ведения игрового бизнеса считается https://www.robinlyons.com/melbet-%d0%b1%d1%83%d0%ba%d0%bc%d0%b5%d0%ba%d0%b5%d1%80%d1%81%d0%ba%d0%b0%d1%8f-%d0%ba%d0%be%d0%bd%d1%82%d0%be%d1%80%d0%b0%d0%bc%d0%b5%d0%bb%d0%b1%d0%b5%d1%82-%d0%b1%d1%83%d0%ba%d0%bc%d0%b5%d0%ba/ .
В определенный момент несложно скачать конкретно созданное мобильное приложение.
Нужно получить доступ к сети Интернет,
чтобы делать ставки с сегодняшнего дня.
У Вас будет возможность выбрать событие,
сделать прогноз, находясь в заторе
или за городом.
Это ли не одно из достоинств, за которые стоит выбирать данную компанию?
Именно это подтвердило огромное количество игроков конторы.
Поэтому, если вы хотите начать делать ставки, то вам следует обратить внимание на Мелбет.
Тут melbet-partner.com вы сможете найти важную информацию и ответы
на свои вопросы, а также
немедленно приступить к ставкам после того, как зарегистрируетесь.
Конкурентная борьба на рынке онлайн гемблинга невероятна.
С завидной регулярностью организовывается много площадок с привлекательными
спецусловиями для новеньких.
Особенного внимания заслуживает приветственный бонус, который оценили
большое число клиентов.
Настала пора разобраться с основными аспектами, которые сопряжены с работой casino https://12bitplay.com/data/profile.php?id=27554 .
Стартовый приз – это главный бонус, который предлагает
онлайн-казино.
Для его получения не нужно прилагать серьезных стараний.
Пособие подготовлено для клиентов, которые только в первый раз заходят в аккаунт на портале casino.
Они могут и не подозревать, какой сюрприз подготовили разрабы.
Чаще всего стартовый бонус прибавляет
определенный процент к первому пополнению счета вне зависимости от заведенной на сайт суммы.
Бонус безвозмездных вращений
Казино включают безоплатные прокручивания в свою маркетинговую стратегию.
Что это означает?
Такой подход позволяет давать игрокам бесплатные раунды,
которые они имеют право применить в игровых аппаратах, и выигранные средства обычно могут
быть сняты с личного счета.
Вращения чрезвычайно популярны в среде
любителей азартных онлайн-игр, потому что они дают
шанс определить потенциал,
который предоставляют новые
гейм аппараты, без необходимости
увеличивать свой баланс и тратить личные деньги.
Довольно интересное предложение, которым вполне могут воспользоваться игроки.
Несложно оценить по достоинству имеющиеся плюсы, шансы, обеспечиваемые владельцами площадок.
Казино таким образом часто продвигают новые продукты среди посетителей, прошедших регистрацию на их сайте.
При этом партнерская программа 1win отзывы
не имеет ограничений.
Необходимо всего лишь пройти в соответствующий раздел, ввести
данные в регистрационные ячейки.
Важно не забывать про необходимость удостоверить достижение совершеннолетия.
Без верификации будет сложно стать
постоянным пользователем, которому откроются имеющиеся возможности on-line ресурса.
Бонусы для пришедших по рекомендации
Online casino стимулирует пользователей,
которые рекомендуют игровую
площадку потенциальным игрокам.
Бонусы за вовлечение друзей делаются с целью продвижения предложений игр и привлечения
потенциальных пользователей казино.
Данный способ считается одним из самых эффективных для роста количества игроков.
Один момент, когда посетитель
думает стать полноценным участником,
опираясь на рекламу.
Совершенно иное – воспользоваться советом приятеля, который уже удостоверился в предоставленной информации,
вариативности игровых слотов.
За рекомендацию пользователь может получить денежный
приз.
Начисленные деньги можно вывести
со своего счета или использовать на безоплатные спины в игровых раундах (некоторые казино
применяют свои собственные
маркетинговые и поощрительные программы,
в связи с чем стоит перво-наперво ознакомиться с правилами).
Как можно стать обладателем такого бонуса?
Вам необходимо убедить кого-то из своих знакомых зарегистрироваться на игровой площадке, активировать аккаунт и внести депозит.
Во время прохождения регистрации такой пользователь должен ввести
ваши данные как рекомендателя, чтобы Вы могли получить вознаграждение.
Количество пришедших по
рекомендации игроков не ограничено.
Казино всегда рады новичкам, которые собираются стать
постоянными в ближайшем будущем.
Бонус за преданность
Поощрительные бонусы – это дополнительный тип подарков,
которые используются в on-line-casino 1вин промокоды для 1win на 10 рублей.
Они похожи на достаточно распространенные схемы вознаграждений, которыми руководствуются популярные магазины.
Таким образом казино награждает своих постоянных клиентов (людей, которые
регулярно заходят на ресурс
и вступают в игру) привлекательными призами или
наградами.
Такой бонус возможен в форме поощрительных спинов,
однако основная масса игровых платформ тоже дают небольшие аксессуары, призы или билеты для участия в лотереях.
Примечательно, что удастся получить
намного больше положительных эмоций за время нахождения на online-платформах.
Бонусы для VIP-игроков
Казино в том числе продумывают
поощрения для геймеров, которые
регулярно посещают сайт cazino и используют в играх крупные денежные суммы.
Большинство online-казино связываются с VIP-клиентами , чтобы узнать об их предпочтениях и присудить призы, которые по сути
отвечают стилю постоянного клиента.
Это еще раз подтверждает, насколько рады приветствовать пользователей online-заведения.
Для ВИП-геймеров многие онлайн-казино готовят очень ценные материальные
призы.
Нужно всего лишь продолжать заходить в любимое заведение, пользоваться
всеми предоставляемыми преимуществами своего
положения.
suresiyle kullan?labiliyor. Bonuslar 1xbet Türkiye
• Kredi Kart?
Visa kartlar?n?z ile 10 TL, Main Card ile 15 TL alt limitle part yapabilirsiniz.
King-fish Business card sahibiyseniz 5 TL uzeri tutarlar?
cekebilirsiniz.
• WebMoney
WebMoney yontemini kullan?yorsan?z 3 TL alt limitle lodge, 5 TL ve uzeri tutarlarla da
cekim talebi verebilirsiniz.
• EcoPayz
Slightest 3 TL ile yat?r?m, maksimum 5 TL ile cekim yapabilirsiniz.
• AstroPay
3 TL ve uzeri tutarlar? yat?rabiliyorken 5 TL ve uzerindeki tutarlar icinde cekim talebi verebilirsiniz.
• Paykasa
Kulland?g?n?z odeme yontemi Paykasa ise 3 TL alt limitin uzerindeki tum tutarlar?
an?nda yat?rabilirsiniz. Cekim talebi icin least islem tutar?
5 TL’dir.
• PayKwik
Yaln?zca stash away islemleri icin 3 TL alt limitle kullan?labilmektedir.
1xbet Gratuity ve Promosyonlar? http://cyphergate.net/index.php?title=User:BlytheRitter7
Her yeni bahis stop gibi Turkler icinde bonuslar en onemli k?s?md?r.
1xbet bahis sitesi de bunu en iyi sekilde sunmaktad?r.
• Hos Geldin Bonusu
Uyeliginizi act?ktan hemen sonra yapacag?n?z ilk lay islemine
sunulan bonustur. En fazla 300 TL’ye kadar yararlanabileceginiz bu promosyondan %100 oran?nda yararlanabilirsiniz.
• PromoCode Bonusu
• In france bleu Bonusu
• Y?ld?z Jackpot Promosyonu
• Bahis Kuponlar? Savas? Turnuvas?
• 1xRace Bonusu
• Dogum Gunu Bonusu
1xbet Musteri Hizmetleri
1xbet canl? destek hizmeti sunuyor ancak bunun haricinde de cok ilginc bir
dan?smanl?k hizmeti veriyor. Her bahis sitesinde gordugumuz mesaj yoluyla ulas?m, post yordam?yla adresinden iletisim mumkun. Bunlar?n haricinde ise
yurt ici servis numaras?yla musterilerine telefon destegi sunuyor.
1xbet Guvenilir Mi?
Bahis oynatma lisans?n? Curacao uzerinden alm?s olan 1xbet Limited sirketi Turkiye’nin koklu platformlar?
aras?nda bulunuyor. Lisans?n?n haricinde de GoDaddy taraf?ndan saglanm?s olan SSL sertifikas?n?n aktif oldugunu gorebiliyoruz.
1xbet Genel Degerlendirme 1xbet uygulama
1xbet guncel giris adresi ise 1x-turkey.com
olarak guncellendi. Bahis dunyas?nda ayr?cal?kl? bir bahis
yelpazesini bir araya getiren sirketin gerek bonuslar?yla, gerek an?nda odeme yontemleriyle
gerekse guvenilirligiyle dikkat cekmeye devam
ettigini soyleyebiliriz.
Registro em 1XBET Portugal http://bisdak.net/user/profile/3270
Digite o codigo promocional
REGISTE-SE E RECEBA UM EXTRA DE 100 EUR AGORA MESMO!
Convidamos todos quem quer ganhar nas apostas em desportos registrar-se rapidamente em
uma casa de apostas mais justa da empresa 1XBet.
O registro em 1XBET Portugal permite usar de todas as
funcionalidades do place oficial, incluindo:
retirada de fundos rapida atraves de qualquer sistema
de pagamentos ou cartoes bancarias;
servico de apoio a cliente conveniente que sempre ajudara esclarecer a
situacao;
interface e aplicacoes moveis funcionais.
O tip da 1XBET Portugal Registro em 1XBET Portugal
A casa de apostas, a todos que desejam receber os perk agradaveis na sua conta, da essa oportunidade.
E uma oportunidade genuine de ganhar dinheiro gracas a generosidade da administracao da empresa.
O investment sempre cycle o perquisite de primeiro deposito.
O bonus e um adicional de 100% do valor do deposito de ate 130 euros, que serao imediatamente creditados na
conta.
O mais agradavel e a possibilidade de devolver o dinheiro recebido nas apostas ordinarias e expressas.
A condicao principal e que tem que escolher as partidas com coeficiente
bastante alto, das quais e necessario formar um expresso completo.
Para um novato recuperar aposta nao e uma tarefa facil, mas isso permite conhecer bem a interface da empresa de azar
e aprender o basico de apostas.
Como usar o codigo de promocao da 1xBet? https://wiki.psxdigital.com/index.php/User:FaustinoBilliot
Usar o codigo de promocao e muito facil, pois a administracao permite fazer
isso sem a participacao do servico de apoio a cliente.
Basta de seguir uma instrucao intuitivamente clara:
Primeira coisa que tem que fazer e ir para o portal oficial de jogos com o nosso relate
e clicar em “Registrar-se” no canto better direito.
A seguir, tem que selecionar um dos metodos de criacao da conta pessoal e inserir o codigo de
promocao recebido, que tambem se encontra neste site.
Apos preencher todos os dados, e necessario enviar um pedido e receber a conta ativada durante de um dia.
Os usuarios nao devem esquecer da necessidade de confirmar o e-mail atraves de uma mensagem recebida.
Todos os dados indicados durante registro devem ser verificados cuidadosamente e so podem ser
verdadeiros, pois caso contrario, depois da verificacao
por administracao a conta pode ser bloqueada.
O que oferece a casa de apostas 1XBET Faezr o download da 1xbet para iphone
O registro na 1XBET Portugal permite a cada jogador apreciar um jogo de apostas em desporto divertido e excitado.
Tudo que e necessario e ter uma conta registrada e
ser um residente de Portugal maior da idade. E obrigatorio passar uma verificacao completa que da o
acesso para gerenciamento das contas.
A empresa oferece a todos os jogadores registrados
as seguintes vantagens:
uma enorme variedade de partidas e eventos politicos em quais pode apostar
com um praticamente sem limites.
Apenas administracao pode limitar o montante maximo de aposta, entretanto
os coeficientes sao colocados independentemente do nivel da partida;
varias maneiras de deposito e retirada de fundos que permite carregar a sua conta de jogo sem algum problema
e receber o seu ganho no cartao bancario ou um sistema de pagamentos;
servico de apoio a cliente operativo que responde todas as perguntas
de usuarios e ajuda resolver qualquer situacao 24
horas por dia.
Um requisito obrigatorio para obtencao de todos os privilegios acima indicados e tip adicionais e preencher todos os dados na secao “Minha conta” que se encontra na conta pessoal.
can you wear a fascinator with a long dress
賲毓丕胤賮 賮乇賳爻賷丞賮爻丕鬲賷賳 丕毓乇丕爻 2019and party dresses賲賯亘囟 丕賱賵氐賱丕鬲organic baby pantsfeb31st eyewearadidas outlet sverige丕爻毓丕乇 丕賱賰丕賲賷乇丕鬲 賳賷賰賵賳fraser suites new delhi review氐賵乇 鬲賷 卮賷乇鬲丕鬲 賱賱丨賵丕賲賱毓胤賵乇 丕乇賷噩卮賳胤 賰亘賷乇丞 賱賱爻賮乇丕丨丿孬 賲賳丕胤賷賱 噩賷賳夭 賮賷 丕賱賲賳氐賵乇賴賲賵丕賯毓 氐賷賳賷賴 賱亘賷毓…
1XBET входит в число самых популярных в РФ букмекерских компаний
по ставкам на спортивные события.
Сервис работает по лицензии Curacao в
режиме онлайн.
Фирма, осуществляющая деятельность с 2007 г., обслуживает свыше 400 тыс.
постоянных посетителей.
На сегодняшний день букмекерская контора
1xbet в числе флагманов по спортпрогнозам.
Это можно назвать как критерий
доверия многочисленных пользователей, которые решили выбрать именно указанную БК.
Теперь надо разобраться в
особенностях пребывания на онлайн платформе 1хбет бонусный баланс .
Правила прохождения регистрации
Производить ставки имеет право зарегистрированный пользователь (беттер).
Известны разные варианты создания аккаунта:
1. через соцсети, потребуется
всего лишь выбрать соответствующий вариант;
2. по э-мейл вне зависимости от платформы;
3. по телефонному номеру, на который
придет смс.
Пользователям http://forum.itdoctor.ro/viewtopic.php?f=16&t=1172&view=print в персональный
аккаунт становится доступным
немедленно по окончании регистрации.
Зарегистрированный клиент может делать
ставки на разные события из мира спорта, участвовать в акциях и
бонусах, выводить средства и т.д.
Вам понравится не безучастно наблюдать
за матчем выбранного состава игроков, но и по возможности выигрывать немалые суммы
денег.
Для этого надо всего лишь выбрать
событие, которое понравилось больше всего.
Итак, по окончании регистрации можно
пользоваться множеством возможностей официального сайта, которые
предусмотрели администраторы.
Разновидности прогнозов конторы 1хбет http://www.acs-21.com/hat2bbs/yybbs.cgi?list=thread
В отличие от подобных контор 1Хбет предоставляет двенадцать типов операций.
Одиночная ставка (одиночник, единица) – соглашение на отдельный исход спортивного
события.
Выигрыш рассчитывается умножением десятичного коэффициента
на сумму пари.
То есть нет ничего сложного,
если выбирать данный вариант ставки.
Экспресс – прогноз одновременно на два и более результатов, которые анонсируются.
Экспресс «Стайер» отличается особенностью:
исходы и события можно дописывать на протяжении 2-х месяцев.
Антиэкспресс включает ряд итогов, противоположный экспрессу по способу определения выигрыша.
Этот тип прогноза выбирают как опытные игроки, так и начинающие пользователи.
Система – пари на все возможные варианты экспрессов
определенной размерности
из выбранного числа событий.
Цепочка – набор одиночных прогнозов.
По доверительной ставке можно вернуть часть денег,
которые находятся пока под блокировкой.
Это достаточно интересное предложение,
которое могут выбрать прошедшие
регистрацию клиенты.
Ставка по купону определяет набор из цифр и букв для
подготовки запроса.
Этим способом удобно сделать ставку , не внося средства на
депозитный счет.
Лаки является сочетанием ординаров и
абсолютно всех экспрессов,
собранных из указанных спортивных
событий.
Патент имеет такой же принцип,
что и лаки, но количество прогнозов ограничивается тремя.
Для каких целей необходимо использовать зеркало
Букмекерская контора 1Хбет не является
легальной в регионах России.
Подобное положение связано с тем,
что компания не взимает проценты с прибылей игроков.
Для самих пользователей это существенный плюс, но
в рамках закона названный
момент признается далеко не целесообразным.
Руководители не намерены что-либо менять в
проводимой политике.
Что же делать в такой ситуации пользователям?
На самом деле нет ничего проще.
Нужно избежать блокирование официального веб-ресурса,
то есть посетить актуальное зеркало портала.
Зеркало можно представить как специальный сервис с точным интерфейсом портала,
без каких бы то ни было сдерживающих факторов, с сохранением ранее введенных сведений.
Разрешается войти и беспроблемно воспользоваться всеми условиями, предусмотренными разработчиками.
Эти копии имеют единую с основным сайтом 1xbet базу, поэтому войти
на сайт удобно под своим аккаунтом.
Не забывайте, что интерфейс идентичен
официальному сервису букмекера.
Переместиться на аналог можно по ссылке вывод средств с 1xbet на карту.
Помимо ставок на спортивные турниры в 1хбет игрокам
доступны слоты, тотализаторы,
разные лотереи, нарды, игры в online и offline режимах.
Как видите, у БК достаточное число мероприятий, которые могут оказаться по вкусу пользователям
самого разного возраста, пола.
Нужно всего лишь зарегистрироваться по несложному алгоритму уже сегодня.
Вы поймете, как интересно получится провести досуг, если есть персональный компьютер и доступ к сети Интернет.
Registro em 1XBET Portugal http://www.cqmeidaojia.com/home.php?mod=space&uid=29157&do=profile&from=space
Digite o codigo promocional
REGISTE-SE E RECEBA UM REWARD DE 100 EUR AGORA
MESMO!
Convidamos todos quem quer ganhar nas apostas em desportos registrar-se rapidamente em uma casa de apostas mais justa
da empresa 1XBet.
O registro em 1XBET Portugal permite usar de todas as funcionalidades do place
oficial, incluindo:
retirada de fundos rapida atraves de qualquer sistema de pagamentos ou cartoes bancarias;
servico de apoio a cliente conveniente que sempre ajudara esclarecer a
situacao;
interface e aplicacoes moveis funcionais.
O perk da 1XBET Portugal Faezr o download da 1xbet para iphone
A casa de apostas, a todos que desejam receber
os compensation agradaveis na sua conta, da essa oportunidade.
E uma oportunidade real de ganhar dinheiro gracas a generosidade da
administracao da empresa.
O owner sempre stage o remuneration de primeiro deposito.
O bonus e um adicional de 100% do valor do deposito de ate 130 euros,
que serao imediatamente creditados na conta.
O mais agradavel e a possibilidade de devolver o dinheiro
recebido nas apostas ordinarias e expressas.
A condicao principal e que tem que escolher as partidas
com coeficiente bastante alto, das quais e necessario formar
um expresso completo.
Para um novato recuperar aposta nao e uma tarefa facil,
mas isso permite conhecer bem a interface da empresa de azar e aprender
o basico de apostas.
Como usar o codigo de promocao da 1xBet? http://bbs.zhichihuodong.com/home.php?mod=space&uid=2712471&do=profile&from=space
Usar o codigo de promocao e muito facil, pois a administracao permite fazer isso sem a participacao
do servico de apoio a cliente. Basta de seguir uma instrucao intuitivamente clara:
Primeira coisa que tem que fazer e ir para o
portal oficial de jogos com o nosso identify with
e clicar em “Registrar-se” no canto superior direito.
A seguir, tem que selecionar um dos metodos de criacao da conta pessoal e inserir
o codigo de promocao recebido, que tambem se encontra neste site.
Apos preencher todos os dados, e necessario enviar um pedido e receber a conta ativada durante de um dia.
Os usuarios nao devem esquecer da necessidade de confirmar o e-mail atraves
de uma mensagem recebida.
Todos os dados indicados durante registro devem ser verificados cuidadosamente e so podem ser
verdadeiros, pois caso contrario, depois da verificacao
por administracao a conta pode ser bloqueada.
O que oferece a casa de apostas 1XBET download da 1xbet para android
O registro na 1XBET Portugal permite a cada jogador apreciar
um jogo de apostas em desporto divertido e excitado.
Tudo que e necessario e ter uma conta registrada e ser um residente de Portugal maior da idade.
E obrigatorio passar uma verificacao completa que da o
acesso para gerenciamento das contas.
A empresa oferece a todos os jogadores registrados as
seguintes vantagens:
uma enorme variedade de partidas e eventos politicos em quais pode apostar com um praticamente sem limites.
Apenas administracao pode limitar o montante maximo de aposta, entretanto os coeficientes sao
colocados independentemente do nivel da partida;
varias maneiras de deposito e retirada de fundos que permite carregar a sua conta de jogo sem algum problema e receber o seu ganho no
cartao bancario ou um sistema de pagamentos;
servico de apoio a cliente operativo que responde todas as perguntas de usuarios e ajuda resolver qualquer situacao 24 horas por dia.
Um requisito obrigatorio para obtencao de todos os privilegios acima
indicados e perquisite adicionais e preencher todos
os dados na secao “Minha conta” que se encontra na conta pessoal.
Описание зеркала Melbet
Рынок ставок в России существует довольно давно, и в 2012 г.
на рынке появилась фирма Мелбет.
На сегодняшний день ресурс стабильно развивается, непосредственно это касается виртуального пространства.
Как полагают многие пользователи,
довольно комфортно не выходя из
дома, в офисе или в дороге делать ставки.
Никаких потерь времени.
Наиболее важная цель конторы – оказывать помощь игрокам делать
ставки, это можно выполнить , используя офисы
фирмы или же в режиме online, для чего есть
портал и мобильная версия.
Как видите,, предоставляется довольно много возможностей,
чтобы с удовольствием провести свободное время, а заодно попытаться
получить приличные выигрыши.
Компания скачать мелбет на андроид с официального сайта очень стремительно развивается и намерена создать для своих клиентов самые лучшие условия.
Тут каждый может ставить как
на спортивные, так и на иные события,
к примеру, конкурсы типа Eurovision.
Теперь нет смысла безучастно наблюдать за тем, как
выступает любимый артист.
Стоит всего лишь начать верить в его триумф, произведя
выгодную ставку.
Существует вероятность, что получится заполучить куш , а заодно насладиться музыкальным произведением.
Это очень удобно, так как в этом случае абсолютно любой человек найдет для себя
интересные события и сделает ставки.
Программеры смогли предусмореть события на любой вкус.
Решение зависит от Вашего возраста, увлечений, а также желания рисковать.
Как начинать ставить на спортивные события с
Melbet http://landoscorner.com/profile/graciela24
Некоторые клиенты думают, что ставить на спортивные баталии или
иные мероприятия – это довольно сложно и что в алгоритме нужно тратить
время на разбирательство.
Действительно ли это так и будет?
Конечно же, нет.
Если идет разговор о Мелбет, то в этом случае начинать ставить получится
у любого желающего.
На уровне интуиции понятный интерфейс понравится
даже начинающим пользователям,
которые только решили освоить искусство
ставок.
Следует рассмотреть подробнее, каким образом начать это делать.
Для начала вам нужно зарегистрироваться на портале условия бонусной программы melbet для вывода средств
Алгоритм прохождения регистрации очень простой, займет у вас минимум
времени.
Потребуется всего лишь ввести персональные данные в специальные ячейки,
верифицироваться.
Как только вы зарегистрируетесь, необходимо положить деньги на депозитный счет.
При этом не играет роли, какая по
размеру будет зачислена денежная сумма.
Совсем скоро Вы освоитесь и поймете, каким образом действовать дальше, какие параметры взноса считаются
наиболее приемлемыми.
И с этого момента вы можете начать ставить на события.
Теперь становится ясно, что
делать это совсем несложно, так как на эти действия уйдет у вас минимальное количество сил и времени.
Выходит, абсолютно любой из игроков сумеет начать делать ставки независимо от того без опыта он или профи.
Единственное, что для этого требуется – пройти регистрацию.
Компания Melbet – входит в число известных
и востребованных компаний на рынке России, что абсолютно не удивительно.
Как известно, фирма с заботой
относится к своим клиентам и подготавливает для них самые лучшие условия.
Руководству важно не просто заинтересовать больше пользователей, но и создать максимально комфортные обстоятельства для
завсегдатаев.
Репутация является важным показателем для компании во имя того, чтобы не снизить веры игроков.
В сфере ставок существует немалое число аферистов.
Не следует слепо доверять яркой
рекламе, а также идти на поводу у слишком выгодных условий.
Можно не только лишиться денег, безрассудно потерять время, но
и заполучить на компьютер вирусную
программу.
Уместнее выбирать лишь проверенные
компании, которые продолжительное время
находятся в данной области.
Всегда можно изучить отзывы, ознакомиться с временем
появления компании в виртуальном пространстве.
Одним из таких профи своего
дела признается http://www.jmcyzxy.com/comment/html/?264937.html .
При желании можно загрузить
специально созданное приложение
для смартфонов и других
гаджетов.
Нужно получить доступ к интернету,
чтобы ставить уже сегодня.
Вы даже сможете выбрать мероприятие,
сделать прогноз, находясь в заторе или за городом.
Это ли не одно из достоинств, за
которые стоит останавливать выбор на этой букмекерской конторе?
Именно это подтверждает огромное
число клиентов компании.
Поэтому, если вы решили
начать делать ставки, то вам следует присмотреться к Мелбет.
Тут melbet-partner.com вы сможете найти необходимые
сведения и ответы на свои вопросы,
а , кроме того, немедленно приступить к ставкам после того, как зарегистрируетесь.
czat adidas
hartan vip sonnenschirmwaldlaeufer schuhe damenschuhenike hypervenom 2015 wei脽panzerkette collier
calculo del kappa de cohen
ray ban a 19.99que cor de vestidos aconselham para criancas com pele morenavestidos para casamento simples e bonitomust separate the church and skate chords
1XBET – одна из самых популярных в РФ букмекерских контор по ставкам на спорт.
Сервис работает по лицензии Curacao в режиме онлайн.
Компания, осуществляющая деятельность с 2007 г., насчитывает больше четырехсот тысяч постоянных клиентов.
На сегодня букмекерская контора 1xbet
в числе флагманов по спортпрогнозам.
Это можно назвать как показатель доверительности
многочисленных клиентов, которые решили выбрать именно
данную БК.
Осталось разобраться в особенностях нахождения на online
площадке 1xbet регистрация бесплатно .
Порядок прохождения регистрации
Делать прогнозы может только прошедший регистрацию пользователь
(беттер).
Есть разные варианты создания аккаунта:
1. через соцсети, нужно всего лишь выбрать соответствующий вариант;
2. по адресу электронной почты независимо от сервиса;
3. по телефонному номеру, на который будет отправлено смс.
Пользователям http://www5d.biglobe.ne.jp/~deluxe/cgi-bin/yybbs.cgi?page=30
в персональный аккаунт становится
доступным сразу после регистрации.
Зарегистрированный клиент
получает право делать ставки на разные спортивные турниры,
участвовать в акционных и бонусных программах, осуществлять вывод денег и др.
Вы сможете не просто следить за игрой любимой команды, но и при желании выигрывать немалые суммы денег.
Для этого надо всего лишь
указать мероприятие, которое пришлось по вкусу.
Итак, после регистрации разрешается воспользоваться множеством возможностей основного ресурса,
которые предусмотрели разработчики.
Разновидности ставок БК 1хбет
http://hp-ad.sub.jp/nayami/nayamibbs/index.html
В отличие от подобных контор
1Хбет насчитывает двенадцать вариантов операций.
Одиночная ставка (одиночник, единица) – сделка на определенный итог спортивного события.
Выигрыш насчитывается умножением десятичного коэффициента
на сумму пари.
Получается, что сложностей особых нет, если
выбирать данный вариант прогноза.
Экспресс – ставка сразу на два и больше исходов, которые анонсируются.
Экспресс «Стайер» имеет особенность: исходы и события разрешается добавлять в течение
2-х месяцев.
Антиэкспресс включает ряд итогов,
противоположный экспрессу по способу начисления призовых денег.
Такой тип прогноза выбирают
как опытные игроки, так и начинающие пользователи.
Система – пари на все возможные варианты экспрессов конкретной размерности из указанного
числа событий.
Цепочка – набор одинарных ставок.
По доверительной ставке удастся вернуть часть финансов,
которые находятся пока под блокировкой.
Это довольно привлекательное предложение, которое выбирают
прошедшие регистрацию клиенты.
Прогноз по купону определяет комбинацию из
букв и цифр для подготовки заявки.
Этим способом можно сделать
ставку , не внося средства
на депозит.
Лаки оказывается комбинированием единиц и совершенно всех экспрессов, которые собраны из выбранных спортивных событий.
Патент действует по тому же алгоритму, что и лаки, но число прогнозов ограничено
3-мя.
Для чего нужно заходить на зеркало
Букмекерская контора 1Хбет считается нелегальной в регионах России.
Подобное положение связано с тем, что фирма не удерживает проценты с выигрышей игроков.
Непосредственно для клиентов это
огромный плюс, но на законодательном уровне данный нюанс считается далеко не целесообразным.
Разработчики не намерены ничего изменять в проводимой политике.
Что же делать в такой ситуации пользователям?
На самом деле нет ничего проще.
Нужно обойти блокировку официального
веб-сайта, то есть посетить функционирующее зеркало
портала.
Копия можно представить как специальный сервис с точным
интерфейсом портала, без каких бы то ни
было ограничений, с сохранением
ранее введенных данных.
Разрешается зайти и спокойно пользоваться всеми возможностями, предложенными разработчиками.
Такие зеркала имеют единую с основным сайтом 1xbet БД, поэтому зайти на ресурс можно под своим аккаунтом.
Не забывайте, что интерфейс идентичен подтвержденному сайту букмекера.
Переместиться на зекрало получится по адресу как сделать демо счет на 1xbet.
Кроме прогнозов на спортивные турниры в 1хбет
пользователям предлагают тотализаторы, слоты, различные лотереи,
нарды, игровые процессы в онлайн и offline режимах.
Можно сделать вывод, что у букмекерской конторы оптимальное количество мероприятий, которые могут оказаться по нраву пользователям разных
возрастов, пола.
Необходимо всего лишь зарегистрироваться
по несложному алгоритму уже
сейчас.
Вы сможете обнаружить, как интересно
удастся провести время, если есть персональный компьютер и подключение
к сети Интернет.
Обзор зеркала Mostbet мостбет зеркало
http://fgv-farmingsystems.com/index.php?topic=120559.0
Ниша ставок в РФ существует довольно давно,
и в 2012 году на рынке появилась фирма Мостбет.
Вплоть до сегодняшнего дня ресурс
активно развивается, в частности это относится
к виртуальному пространству.
Как думают некоторые пользователи, достаточно комфортно никуда не выходить, а делать ставки.
Время не будет потеряно.
Наиболее важная цель конторы – помогать людям ставить, это можно
выполнить , используя офисы компании или же в режиме online, для
этого есть портал и мобильная версия.
Итак, предусмотрено немало
способов, чтобы с удовольствием провести досуг,
а вместе с тем попробовать заработать неплохие выигрыши.
Компания мостбет ставки довольно активно развивается и
намерена создать для своих клиентов самые лучшие
возможности.
Здесь вы можете делать ставки как
на спорт, так и на иные события, к
примеру, турниры наподобие Eurovision.
Больше нет смысла безучастно смотреть за тем, как
проводит выступление любимый артист.
Стоит всего лишь поверить в его
триумф, сделав выгодную ставку.
Есть шанс, что получится заполучить крупную сумму , а заодно послушать отличную музыку.
Такой подход крайне удобен, так как в этой ситуации безусловно любой игрок найдет для себя интересные
мероприятия и поставит на его исход.
Программеры предусмотрели мероприятия
на любой вкус.
Все зависит от того, сколько Вам лет, чем вы увлекаетесь и способны ли рисковать.
С чего начать ставить на спортивные события
с Mostbet
Многие игроки думают, что ставить на спортивные баталии или другие события
– это довольно сложно и что в алгоритме нужно тратить время на разбирательство.
Действительно ли это так и будет?
Естественно, это не так.
Если идет разговор о Мостбет http://wikivie.lesfermesdelavie.fr/wikivie/index.php?title=Utilisateur:ClaribelLovell mostbet скачать на андроид
, то в этом случае начинать ставить получится у любого желающего.
На уровне интуиции легко осваиваемый интерфейс придется
по душе даже начинающим пользователям, которые только решили освоить искусство ставок.
Следует рассмотреть подробнее, каким
образом начинать процесс.
Для старта необходимо пройти регистрацию на сайте.
Алгоритм прохождения регистрации удивительно простой,
вы потратите на него минимальное количество времени.
Потребуется всего лишь вбить личные данные в специальные поля,
пройти процесс верификации.
После регистрации следует внести деньги на депозитный счет.
При этом не играет роли, какая по размеру будет
внесена денежная сумма.
Совсем скоро Вы освоитесь и сможете понять, каким образом
поступать дальше, какие параметры взноса являются наиболее приемлемыми.
И после этого начинайте ставить на события.
Теперь стало ясно, что делать это совсем несложно, потому что этот процесс займет у вас
минимальное количество сил и времени.
Выходит, абсолютно любой из игроков сможет начать ставить независимо от того без опыта он или профессионал.
Единственное, что для этого нужно – зарегистрироваться.
Компания Мостбет – входит в число популярных и востребованных компаний на рынке России,
что совсем не вызывает удивления.
Ведь контора заботится о своих пользователях и предлагает для них наилучшие условия.
Разработчикам надо не просто заинтересовать новых игроков,
но и создать наиболее комфортные обстоятельства для завсегдатаев.
Репутация считается важным критерием для компании во имя того, чтобы не потерять доверия пользователей.
В сфере ставок присутствует
немалое число мошенников.
Не стоит соблазняться привлекательной рекламой, а также бездумно верить чрезмерно заманчивым предложениям.
Можно не только лишиться
денег, безрассудно потерять время,
но и установить на компьютер вирус.
Уместнее останавливать выбор на надежных
фирмах, которые долгий период пребывают в данной сфере.
Всегда можно почитать отзывы, ознакомиться с временем появления
компании на просторах интернета.
Одним из таких профи своего дела считается mostbet на андроид
В определенный момент несложно загрузить специально созданное приложение
для смартфонов и других гаджетов.
Нужно получить доступ к интернету, чтобы делать ставки с сегодняшнего дня.
У Вас будет возможность подобрать событие, спрогнозировать результат,
находясь в пробке или за городом.
Это ли не одно из достоинств, за
которые стоит выбирать данную
компанию?
И это подтверждает огромное число игроков компании.
В таком случае, если вы решили испытывать удачу на ставках, то вам
следует обратить внимание на Mostbet.
Здесь Mostbet-partner.com вы сможете найти важную информацию и ответы на свои
вопросы, а также немедленно начать делать ставки после регистрации.
Букмекерская компания Леон – яркий представитель
игорного бизнеса на российском рынке.
Эта организация позволяет людям получать реальные деньги достаточно долгое время.
За все время работы контора смогла заслужить немало призов, однако самой значимой среди них является награда «Спорт и Россия».
Ее дают за выдающиеся вложения в развитие
спортивных игр по регионам РФ.
Не вызывает удивления то, что клиенты, которые обращаются в БК,
не просто делают ставки, а с увлечением интересуются матчами крупных и только стартующих
команд.
Официально подтвержденный портал
леон зеркало работающее сегодня
https://www.seawayads.com/user/profile/99789 позиционируется как стабильно функционирующий и довольно удачный сервис.
Приятный интерфейс вебсайта и приемлемое число
рекламных окон доставляют
пользователям удовольствие и вместе с
тем мотивируют на новые ставки.
Где еще получится ощутить небывалый всплеск адреналина?
Сайт предлагает играющим следующие возможности:
• узнать больше об акциях, бонусах, которые предусмотрены разработчиками;
• сделать ставку на событие в привычным
способом и Live;
• посмотреть результаты прошедших событий;
• прочитать особенности пользования сервисом и в дальнейшем строго им следовать;
• связаться со службой поддержки, которая работает круглосуточно;
• загрузить программное приложение на телефон или планшет,
чтобы делать ставки в удобное время в зонах,
где есть интернет.
Варианты ставок на спорт
Bookmaker готов предложить пользователю широкий ассортимент мероприятий
в мире спорта.
• футбол;
• баскетбольные первенства;
• хоккейные баталии;
• волейбол;
• киберспорт;
• регби;
• бокс;
• крикет;
• теннис и т.д.
Помимо этого, получить живые деньги удастся:
• на слотах;
• в казино;
• во время игры в покер.
Все события расписаны в отдельном
разделе, это значит, что отыскать их будет не сложно.
Клиент получает возможность изучить их немедленно по окончании оформления учетной записи и
пополнения игрового счета на любую
сумму.
Это недолго ввести личные данные в специальные ячейки на сайте.
Важно не забывать про
необходимую верификацию для доказательства совершеннолетия.
Бонусная система
Богатый выбор ставок – не
единственное достоинство
букмекерской конторы Леон.
Создатели способствуют заходу
новичков еще и внушительным объемом бонусов.
Подобные сюрпризы уходят
на личный счет, тем самым позволяя бережно
расходовать реальные финансы и начинать делать ставки с бонусной суммы.
Контора дарит бонусы при регистрации, после того, как внесен первый платеж, при стабильной активности
игрока и при каждом пополнении счета.
Как видите, созданы все удобства не только для опытных, но и для стартующих клиентов букмекерской системы.
Получится немедленно ввести
в дело приветственный презент.
Мобильная версия leonbets ставки
http://Www.Zanele9@Silvia.woodw.o.r.t.h@pickup-jp.com/cgi-bin/pickupbbs/yybbs.cgi?list=thread пользователи имеют право не только посредством компьютера.
Для удобства играющих разработчики подготовили мобильную версию, что обеспечивает возможность быстро ставить.
Приложение имеет идентичный официальному сайту интерфейс и гарантирует клиентам максимум удобств в процессе выполнения ставок.
При этом приложение доступно владельцам смартфонов на любой операционке – как Android,
так и иос.
Вы обнаружите, как удобно пользоваться
приложением вне зависимости от Вашего местоположения.
Достаточно всего лишь получить доступ к сети
интернет, не забывать про то,
что надо зарегистрироваться, и про необходимость
авторизоваться.
Еще никогда сделать ставки на различные аспекты,
связанные с играми, не организовывалось так легко.
БК ЛЕОН хороша своей программой лояльности, выгодными
бонусами и удобным мобильным
приложением.
Эту компанию предпочитают жители различных областей РФ.
Руководители предусмотрели, чтобы деятельность организации была
легальной.
Для этого имеются все лицензии.
Букмекерская контора лишена недостатков, в связи с
чем пользуется спросом не только новичков, но и опытных игроков.
Провести время в ожидании сыгранной ставки и внести деньги на
личный аккаунт получает возможность
каждый из прошедших регистрацию достигших совершеннолетия клиентов.
Важно, бояться и поверить
собственной интуиции.
Букмекерская контора Леон – это выбор пользователей, ценящих свое время и деньги.
На online платформе реально большой ассортимент событий, на которые можно делать ставки.
Вам удастся не только отслеживать успехи любимой команды,
но и, скорее всего, сорвать большой куш.
Следует всего лишь зарегистрироваться на
основном сайте конторы, чтобы
суметь определить для себя все представленные разработчиками преимущества.
Понятный вариант оформления сайта оценят даже начинающие пользователи.
Конкурентная борьба в области online азартных игр невероятна.
С завидной регулярностью организовывается немало площадок с заманчивыми спецусловиями для
новичков.
Особенного внимания заслуживает приветственный подарок, который успели оценить многие пользователи.
Пришло время понять важные моменты, которые связаны
с функционированием казино https://dragondanceslot.com/dds/viewtopic.php?id=7662 .
Стартовый бонус – это главный бонус, который предлагает online-казино.
Чтобы его получить, не нужно прилагать много стараний.
Инструкция подготовлена для игроков, которые только в первый раз заходят в профиль
на портале казино.
Они могут и не подозревать,
какой сюрприз приготовили разработчики.
Чаще всего первое поощрение прибавляет определенный
процент к стартовому счету
независимо от заведенной
на сайт суммы.
Поощрение в виде бесплатных спинов
Casino внедряют безоплатные вращения в свою рекламную задумку.
Что это такое?
Это дает пользователям бесплатные циклы, которые геймеры имеют
право применить в игровых автоматах,
и выигранные средства чаще всего можно снять
с их счета.
Вращения чрезвычайно популярны в среде почитателей азартных онлайн-игр, потому что они дают шанс изучить возможности, которые обеспечивают новые игровые автоматы, с исключением потребности пополнять персональный баланс и растрачивать личные деньги.
Достаточно привлекательное предложение, которым вполне смогут воспользоваться
игроки.
Можно расценить все преимущества, возможности,
обеспечиваемые разработчиками.
Casino подобным способом зачастую рекламируют новейшие
услуги среди клиентов, зарегистрированных на их портале.
При этом как заработать на 1win в партнерской программе
доступно всем желающим.
Нужно всего-навсего пройти в соответствующий раздел, ввести данные
в регистрационные ячейки.
Не забывайте про необходимость подтвердить достижение совершеннолетия.
Без подтверждения личности будет трудно
стать постоянным пользователем,
которому доступны потенциальные возможности
онлайн ресурса.
Бонусы для пришедших по рекомендации
Online казино поощряет пользователей, которые рекомендуют игровую площадку другим.
Бонусы за вовлечение знакомых предназначены
для продвижения предложений игр
и привлечения потенциальных клиентов
казино.
Данный метод считается наиболее эффективным для роста числа геймеров.
Один момент, когда пользователь думает стать полноценным
участником, ориентируясь на
рекламные слоганы.
Совершенно другое – поверить рекомендации друга,
который на сегодня убедился в правдивости
данных, многообразии игровых аппаратов.
За рекомендацию вы можете обнаружить
в личном кабинете денежный приз.
Финансовый бонус можно снять со
своего счета или использовать на
безоплатные спины в игре (некоторые cazino имеют свои свои
собственные рекламные и бонусные программы, поэтому лучше всего сначала ознакомиться
с правилами).
Каким образом удастся получить этот бонус?
Вам необходимо сагитировать того, кого вы знаете, пройти регистрацию на
игровой площадке, создать
учетную запись и внести депозит.
Во время прохождения регистрации
этот пользователь должен внести
ваши данные как реферала,
чтобы Вы могли зачислить на счет вознаграждение.
Количество приглашенных людей не лимитируется.
Казино всегда рады новым клиентам, которые собираются стать
постоянными в самое ближайшее время.
Бонус за лояльность
Бонусы лояльности – это дополнительный вид подарков,
используемых в онлайн-casino 1вин ставки 1win прогнозы.
Они похожи на достаточно известные программы вознаграждений, которыми управляют
популярные магазины.
Получается, что казино поощряет своих приверженцев (людей, которые с завидной регулярностью посещают площадку и вступают в игру) привлекательными бонусами или
наградами.
Такой бонус может быть в виде поощрительных вращений, однако многие казино также дают небольшие гаджеты, подарки
или лотерейные билеты.
Можно сказать, что появится возможность испытать намного
больше приятных впечатлений за время нахождения на онлайн-платформах.
Бонусы для ВИП-клиентов
Игровые сервисы в том числе готовят бонусы для игроков,
которые стабильно заходят на сайт казино и используют в играх крупные денежные суммы.
Большинство онлайн-casino стараются пообщаться с VIP-пользователями , чтобы узнать
об их предпочтениях и назначить призы, которые фактически отвечают поведенческому фактору заинтересованного игрока.
Это еще раз подтверждает, насколько рады приветствовать клиентов online-заведения.
Для VIP-геймеров многие онлайн-казино готовят
очень ценные материальные поощрения.
Необходимо всего лишь регулярно посещать выбранное казино,
наслаждаться всеми предоставляемыми плюсами своего статуса.
Ставки на спорт сегодня http://mediawiki.hslsoft.com/index.php?title=User:KerriParkhill48 пользуются популярностью
не только среди болельщиков.
И обычные люди на данный момент активно ставят ради удовольствия.
Любители азарта смогли узнать, что такое адреналиновый всплеск, получаемый во время предвкушения результата.
Вряд ли кто сможет отказаться от довольно
крупной прибыли?
Вам удастся следить за интереснейшей
игрой и при этом ставить на исход состязания.
В регионах РФ приемщики ставок могут работать
на законных основаниях, однако
для этого нужно иметь лицензия, что выдают не быстро и
не каждому.
Причем даже у честных букмекеров могут возникнуть проблемы.
Это может быть блокирование
площадки, невозможность авторизации.
Неудивительно, что выдержка заканчивается, появляется желание отыскать иной способ развлечения.
Да и человек будет считать себя
обманутым.
На самом деле не стоит паниковать преждевременно.
В связи с этим сейчас объясним, что собой представляет бетвиннер скачать на андроид бесплатно с официального
и зачем оно нужно.
Им на сегодня успели успешно воспользоваться множество знающих и только присоединившихся посетителей сервиса.
С какой целью используют зеркало
Зеркало – это полноценная
копия исходного портала
букмекерской компании.
Необходимо оно для:
1. возможности без промедления возвратиться на привычный ресурс, забыв про блокирование;
2. защиты профилей зарегистрированных посетителей;
3. высокой скорости;
4. сохранения копии портала;
5. распределения нагрузки;
6. обхода блокировки, которая может специально
включаться в силу разных
причин (некоторым клиентам ресурс бывает
недосягаем из-за Роспотребнадзора).
В это же время все опции основного портала доступны и в зеркале.
Пользователи, которые постоянно
пользуются betwinner, могут беспрепятственно войти через зеркала.
Это можно сделать через любой vpn.
У Вас будет возможность спокойно пользоваться выбранным сайтом, ставить на спортивные события.
Почему происходит блокировка
betwinner
Букмекерство по регионам Российской Федерации имеет легальный статус не
так давно.
Ко всему лицензию получить сложно.
Из-за вышеназванных причин в России
легально функционируют
лишь 25-30 букмекерских контор.
Эти компании достаточно популярны, часто встречаются в
анонсе матчей тех или иных спортивных
соревнований.
В случае, когда букмекер не
является спонсором спортивных состязаний, надежд на получение лицензии у него
фактически нет.
Вследствие этого и пользователи
скорее всего не смогут попасть на сайт.
Предположительно он будет заблокирован в пределах России.
В чем состоят плюсы Betwinner
Во-первых, она является
компанией международного уровня.
Принадлежит Marikit Holdings LTD.
У Betwinner есть официальный документ о.
Кюросао, это официальное разрешение, позволяющее вести деятельность
в различных государствах, в которых это не запрещено по
закону.
Вот почему делать ставки могут даже люди,
которые живут не на российской
территории.
Обычным образом посещаете сайт, подбираете мероприятия и оформляете ставку.
От исхода игры с любимой командой до количества голов, забитых в течение игры.
Особого внимания заслуживают вложения на игрока, признанного звездой мирового уровня.
Вполне может быть, что он «прислушается»
к вашему мнению и сделает рывок, который приведет к победе.
Во-вторых, на betwinner можно делать ставки на
многие события типа спортивных, киберспортивных, политических, шоу-бизнеса и т.д.
Удобно сделать ставку на то, кто станет новым лидером Турции или кто будет
сниматься в анонсированном фильме.
Сколько возможностей дарит всемирно известное Eurovision, когда появляется шанс выбрать триумфатора в когорте многочисленных исполнителей из разных
стран.
Довольно заманчивые перспективы, не правда ли?
Третье, на Betwinner предлагается выбрать наиболее подходящий язык.
Портал рассчитан на пятьдесят два различных языка.
Поэтому найти что-то для себя может абсолютно любой.
Этот момент касается и валют, их аж 49 – от привычных рубля и доллара до
электронных денег.
Любой из пользователей сможет найти то, что необходимо
по своим предпочтениям.
И это , конечно, не полный перечень достоинств.
Обо всех нюансах более подробно несложно узнать по ссылке
http://bazyr06.ru/user/profile/106790
Также на сайте будет детальное руководство относительно того,
как зарегистрироваться.
Вы сможете разобраться, какие предусмотрены виды прохождения регистрации, как быстрее приступить к совершению ставок.
Чтобы определить актуальный адрес копии сайта, наилучший вариант будет позвонить по ГЛ.
Ко всему, не лишне выйти на надежные группы, информирующие о различных букмекерских конторах.
Для этого обычным образом сделать запрос в наиболее привычной поисковой системе фразу – betwinner зеркало.
Вы сможете перейти на веб-сайт betwinner бонусы , который
на 100% идентичен официальному сервису.
Итак, не составит труда найти для конкретных целей подготовленное
зеркало.
Обзор зеркала Mostbet mostbet промокод при регистрации
http://www.jatlb.com/comment/html/?20118.html
Ниша ставок в России функционирует довольно долгое время, и в 2012 г.
вышла на рынок фирма Мостбет.
На сегодняшний день сервис стабильно продолжает
развиваться, в частности это касается виртуального пространства.
Как полагают некоторые пользователи, довольно удобно не выходя из дома,
в офисе или в дороге делать
ставки.
Потеря времени исключена.
Наиболее важная цель компании – помогать людям ставить,
это удобно сделать через офисы фирмы или же в режиме онлайн, для чего имеется
сайт и мобильная версия.
Итак, предусмотрено немало возможностей, чтобы с удовольствием провести досуг, а вместе с тем
попробовать заработать неплохие выигрыши.
Компания mostbet как делать ставки
очень стремительно продвигается и намерена создать
для своих пользователей наилучшие условия.
Тут вы можете делать ставки как на спортивные, так и на другие мероприятия, например, турниры
наподобие Евровидения.
Больше нет смысла безучастно
наблюдать за тем, как выступает любимый исполнитель.
Стоит всего лишь начать верить
в его триумф, произведя оптимальную ставку.
Есть вероятность, что получится
заполучить куш , а заодно послушать отличную музыку.
Такой подход крайне удобен, так как в этой ситуации абсолютно любой человек найдет для
себя интересные мероприятия
и сделает ставки.
Разработчики предусмотрели события на любой вкус.
Все зависит от Вашего возраста, увлечений, а
также желания рисковать.
Как начинать делать ставки на спорт с Mostbet
Многие игроки уверены, что делать ставки на спорт
или другие события – это достаточно хлопотно
и что в этом потребуется тратить время на разбирательство.
Действительно ли это так и будет?
Конечно же, это не так.
Когда мы говорим о Мостбет https://blackdiamond-casino.com/forum/profile.php?id=3732 mostbet зеркало на сегодня , то
в этом случае начинать ставить сможет каждый.
Интуитивно легко осваиваемый интерфейс понравится даже новичкам,
которые надумали освоить искусство ставок.
Рассмотрим подробнее, каким образом начинать процесс.
Для старта вам нужно пройти регистрацию на сайте.
Алгоритм прохождения регистрации
очень легкий, вы потратите на него минимальное
количество времени.
Потребуется всего лишь ввести персональные
сведения в выделенные поля, верифицироваться.
Как только вы зарегистрируетесь, необходимо положить некоторую сумму на депозит.
При этом не играет роли, какая по размеру будет внесена денежная сумма.
Совсем скоро Вы разберетесь и поймете, как действовать дальше, какие параметры взноса считаются оптимальными.
И с этого момента вы можете начать
делать ставки.
Теперь стало понятно, что выполнять подобные
манипуляции совершенно не сложно, так как этот
процесс займет у вас минимальное количество сил
и времени.
Выходит, абсолютно каждый сумеет начать ставить независимо от того новичок он или профессионал.
Все, что для этого нужно – пройти регистрацию.
Компания Мостбет – одна из
самых популярных и пользующихся спросом площадок на российском рынке,
что абсолютно не удивительно.
Как известно, компания заботится о своих пользователях
и подготавливает для них наилучшие
условия.
Разработчикам важно не просто
привлечь новых игроков, но
и создать наиболее комфортные
условия для постоянных клиентов.
Имидж считается значимым критерием для
компании во имя того, чтобы не
потерять веры игроков.
В области ставок присутствует большое число аферистов.
Не следует слепо доверять яркой рекламе, а также
идти на поводу у слишком выгодных условий.
Можно не только лишиться денег, безрассудно потерять время,
но и установить на ноутбук вирусную программу.
Уместнее останавливать выбор на надежных фирмах, которые длительное время пребывают
в данной отрасли.
В любой момент можно изучить отклики,
ознакомиться с временем начала деятельности компании на просторах интернета.
Одним из подобных профи своего дела считается мостбет рабочее зеркало на сегодня
В определенный момент можно скачать специально разработанное приложение для смартфонов и других гаджетов.
Нужно обеспечить наличие сети Интернет, чтобы ставить уже сегодня.
У Вас будет возможность выбрать мероприятие, спрогнозировать результат, пребывая в
заторе или в офисе.
Это ли не одно из преимуществ, за которые следует выбирать данную компанию?
И это подтверждает огромнейшее количество клиентов конторы.
Вот почему, если вы решили испытывать удачу на ставках, то вам
следует обратить внимание на Мостбет.
Тут Mostbet-partner.com вы сможете найти необходимую информацию
и ответы на свои вопросы, а , кроме того, сразу начать делать ставки после того,
как зарегистрируетесь.
1XBET – одна из наиболее популярных
в РФ букмекерских контор по ставкам на спорт.
Площадка работает по лицензии
Curacao в режиме онлайн.
Фирма, работающая с 2007 года, насчитывает больше 400 тысяч
постоянных посетителей.
На сегодня букмекерская контора 1xbet входит в число мировых лидеров по спортпрогнозам.
Это можно назвать как критерий доверительности многочисленных
клиентов, которые выбрали конкретно указанную БК.
Осталось понять особенности нахождения на онлайн
сервисе контора 1xbet зеркало .
Правила прохождения регистрации
Производить ставки может только прошедший регистрацию клиент (беттер).
Есть различные варианты подготовки
профиля:
1. через соцсети, нужно всего лишь остановиться на
соответствующем варианте;
2. по адресу электронной почты независимо от платформы;
3. по телефонному номеру, на который придет сообщение.
Игрокам https://www.freeads-fife.co.uk/user/profile/9908
в персональный кабинет становится открытым сразу
по окончании регистрации.
Беттер получает право делать ставки на разные события из мира спорта, участвовать в акционных и
бонусных программах, выводить средства и др.
Вы сможете не безучастно следить за матчем выбранного состава игроков, но и по возможности получать неплохие денежные суммы.
Нужно всего лишь указать
мероприятие, которое понравилось больше всего.
Как видите, после регистрации разрешается воспользоваться
многочисленными возможностями основного ресурса,
которые предоставили администраторы.
Разновидности ставок БК 1хбет http://grava.s35.xrea.com/grabbs/grabbs.cgi?page=98&vurl2=_DOMTEST_
1Хбет в отличие от других БК предоставляет 12 типов операций.
Одиночная ставка (одиночник, единица) –
соглашение на отдельный итог спортивного мероприятия.
Прибыль насчитывается
умножением десятичного коэффициента на сумму пари.
То есть сложностей особых нет, если выбирать этот
вид ставки.
Экспресс – прогноз одновременно на 2 и больше исходов, которые анонсируются.
Экспресс «Стайер» отличается особенностью: исходы и мероприятия разрешается
добавлять в течение двух месяцев.
Антиэкспресс включает несколько исходов, противоположный экспрессу по методу начисления
выигрыша.
Такой вид прогноза выбирают как со стажем игроки, так и начинающие пользователи.
Система – пари на полную комбинацию экспрессов конкретной размерности из указанного количества событий.
Цепочка – комплект одинарных прогнозов.
По ставке доверительного типа удастся вернуть часть
денег, находящихся пока под блокировкой.
Это достаточно привлекательное предложение, которое могут выбрать
прошедшие регистрацию пользователи.
Ставка по купону определяет комбинацию
из цифр и букв для оформления заявки.
Этим способом удобно осуществить ставку
, не внося средства на депозитный счет.
Лаки является комбинированием единиц и совершенно всех экспрессов,
которые собраны из указанных спортивных мероприятий.
Патент действует по тому же
алгоритму, что и лаки, но число прогнозов ограничивается 3-мя.
Для каких целей необходимо использовать зеркало
Букмекерская контора 1Хбет считается нелегальной в регионах России.
Подобное положение сопряжено с
тем, что фирма не удерживает налоги
с выигрышей игроков.
Непосредственно для клиентов это огромный плюс, но в рамках
закона названный момент
считается далеко не целесообразным.
Разработчики не намерены что-либо
менять в проводимой политике.
Как же быть в такой ситуации клиентам?
На самом деле нет ничего проще.
Нужно избежать блокирование основного веб-ресурса, то есть зайти на функционирующее зеркало площадки.
Копия можно представить как специальный ресурс с точным интерфейсом сайта, без каких бы то ни было сдерживающих факторов, с
воссозданием ранее введенных данных.
Можно зайти и спокойно воспользоваться имеющимися условиями, предусмотренными создателями.
Эти копии имеют единую с официальным сайтом 1xbet БД, поэтому войти на ресурс удобно под своей учетной
записью.
Не забывайте, что дизайн идентичен подтвержденному
сайту букмекера.
Перейти на зекрало получится по адресу официальное приложение 1xbet.
Помимо прогнозов на спорт в 1хбет игрокам предлагают слоты,
тотализаторы, разные лотереи,
нарды, игровые процессы в online и офлайн режимах.
Можно сделать вывод, что у букмекерской конторы достаточное количество событий, которые придутся по вкусу пользователям разных возрастов, пола.
Нужно всего лишь пройти простую регистрацию прямо сейчас.
Вы сможете обнаружить, насколько увлекательно получится провести время,
имея ноутбук и подключение к сети Интернет.
nike polo team
pairing bluetooth headset to multiple devicescheers t shirtrandiga byxor dam svartvitahalo 4 hj盲lm
unghie finte dove si comprano amazon
panchine in cemento da giardino amazonpomodori sul terrazzo amazonmotore per porte da garage basculante amazonacqua di gio eau de toilette amazon
Registro em 1XBET Portugal http://msagar.com/board_ZWLB62/880
Digite o codigo promocional
REGISTE-SE E RECEBA UM BONUS DE 100 EUR AGORA MESMO!
Convidamos todos quem quer ganhar nas apostas em
desportos registrar-se rapidamente em uma casa de apostas mais justa da empresa 1XBet.
O registro em 1XBET Portugal permite usar de todas as funcionalidades do site oficial, incluindo:
retirada de fundos rapida atraves de qualquer sistema de pagamentos ou
cartoes bancarias;
servico de apoio a cliente conveniente que sempre ajudara esclarecer a situacao;
interface e aplicacoes moveis funcionais.
O hand-out da 1XBET Portugal Faezr o download da 1xbet para iphone
A casa de apostas, a todos que desejam receber os honorarium agradaveis na sua conta,
da essa oportunidade. E uma oportunidade real de ganhar
dinheiro gracas a generosidade da administracao da empresa.
O owner sempre era o perk de primeiro deposito. O bonus e um adicional de 100% do valor do
deposito de ate 130 euros, que serao imediatamente
creditados na conta.
O mais agradavel e a possibilidade de devolver o dinheiro recebido nas
apostas ordinarias e expressas.
A condicao resources e que tem que escolher as partidas
com coeficiente bastante alto, das quais e necessario formar um expresso completo.
Para um novato recuperar aposta nao e uma tarefa facil,
mas isso permite conhecer bem a interface da empresa de azar
e aprender o basico de apostas.
Como usar o codigo de promocao da 1xBet? http://cgp.e0766.com/home.php?mod=space&uid=60472&do=profile
Usar o codigo de promocao e muito facil, pois a administracao permite fazer isso sem a participacao do servico de apoio a cliente.
Basta de seguir uma instrucao intuitivamente clara:
Primeira coisa que tem que fazer e ir para o portal oficial
de jogos com o nosso identify with e clicar em “Registrar-se” no canto better direito.
A seguir, tem que selecionar um dos metodos de criacao
da conta pessoal e inserir o codigo de promocao recebido, que tambem se encontra neste site.
Apos preencher todos os dados, e necessario enviar um pedido e
receber a conta ativada durante de um dia.
Os usuarios nao devem esquecer da necessidade de confirmar
o e-mail atraves de uma mensagem recebida.
Todos os dados indicados durante registro devem ser verificados cuidadosamente e so podem
ser verdadeiros, pois caso contrario, depois da verificacao por
administracao a conta pode ser bloqueada.
O que oferece a casa de apostas 1XBET Registro em 1XBET Portugal
O registro na 1XBET Portugal permite a cada jogador apreciar um jogo de apostas em desporto divertido e excitado.
Tudo que e necessario e ter uma conta registrada e ser
um residente de Portugal maior da idade. E obrigatorio passar uma verificacao completa que da o acesso para gerenciamento das contas.
A empresa oferece a todos os jogadores registrados as
seguintes vantagens:
uma enorme variedade de partidas e eventos politicos em quais pode apostar com um praticamente
sem limites.
Apenas administracao pode limitar o montante maximo de aposta, entretanto os coeficientes sao colocados independentemente
do nivel da partida;
varias maneiras de deposito e retirada de fundos que
permite carregar a sua conta de jogo sem algum problema
e receber o seu ganho no cartao bancario ou um sistema de
pagamentos;
servico de apoio a cliente operativo que responde todas as perguntas
de usuarios e ajuda resolver qualquer situacao 24 horas por dia.
Um requisito obrigatorio para obtencao de todos os privilegios acima indicados e tip adicionais e preencher todos os
dados na secao “Minha conta” que se encontra na conta pessoal.
Конкуренция на рынке онлайн гемблинга поражает масштабами.
Ежедневно организовывается много площадок с привлекательными спецусловиями для новых игроков.
Отдельного внимания заслуживает приветственный бонус, который успели оценить
многие пользователи.
Пришла пора разобраться с основными
аспектами, которые сопряжены с работой казино http://musya.s25.xrea.com/cgi-bin/result.cgi .
Приветственный бонус –
это основное поощрение, которое предлагает
online-cazino.
Чтобы его получить, не нужно прилагать серьезных стараний.
Инструкция подготовлена для игроков, которые только в первый раз открывают личный кабинет на портале казино.
Они часто даже не представляют, какой сюрприз подготовили разработчики.
Чаще всего стартовый бонус прибавляет определенный процент
к первому пополнению счета независимо от заведенной на сайт суммы.
Бонус бесплатных вращений
Казино включают бесплатные прокручивания в собственную маркетинговую стратегию.
Что это означает?
Это дает игрокам бесплатные раунды,
которые они могут применить в
игровых автоматах, и выигранные
средства обычно можно снять с личного счета.
Вращения чрезвычайно популярны в среде почитателей гэмблинга,
потому что они дают шанс определить возможности,
которые предоставляют новейшие игровые аппараты, без необходимости увеличивать свой баланс и тратить личные финансы.
Достаточно привлекательное предложение,
которым в полной мере могут воспользоваться геймеры.
Можно расценить имеющиеся преимущества,
возможности, обеспечиваемые разработчиками.
Casino подобным способом часто рекламируют новые продукты среди пользователей, зарегистрированных на их платформе.
При этом как поставить бонусы на 1win не ограничено ни для
одного из желающих.
Нужно всего лишь выбрать соответствующий раздел,
заполнить поля регистрации.
Важно не забывать про необходимость подтвердить совершеннолетие.
Без подтверждения личности будет сложно получить статус игрока, которому
откроются потенциальные возможности онлайн площадки.
Реферальные бонусы
Онлайн казино вознаграждает пользователей, которые рекомендуют игровую площадку другим.
Подарки за вовлечение друзей делаются с целью продвижения гэмблинга и привлечения потенциальных пользователей игровых площадок.
Указанный способ считается одним из самых эффективных для
роста количества геймеров.
Один момент, когда человек думает стать полноценным участником, опираясь на рекламные слоганы.
Совершенно другое – поверить рекомендации друга,
который уже убедился в правдивости данных, вариативности
слотов для игры.
За рекомендацию пользователь может получить денежный приз.
Финансовый бонус разрешается снять
со счета или использовать на безоплатные спины в игровых раундах (отдельные казино используют свои
собственные рекламные и поощрительные стратегии, поэтому стоит сначала ознакомиться с правилами).
Как удастся получить этот бонус?
Вам необходимо убедить кого-то из своих знакомых зарегистрироваться на игровом портале,
создать аккаунт и внести депозит.
Во время прохождения регистрации такой человек должен указать ваши данные
в качестве реферала, чтобы Вы могли
получить бонус.
Число приглашенных игроков не лимитируется.
Игровые площадки всегда поощрительно относятся к новым клиентам, которые стремятся стать завсегдатаями в ближайшем будущем.
Поощрение за преданность
Бонусы лояльности – это еще тип
бонусов, используемых в онлайн-казино 1вин как отменить ставку на 1win.
Они напоминают довольно известные схемы лояльности, которыми управляют известные
магазины.
Таким образом casino награждает своих постоянных клиентов (людей, которые регулярно заходят
на площадку и вступают в игру) заманчивыми призами или наградами.
Подобный бонус может быть в
форме поощрительных спинов, однако многие игровых платформ также предоставляют недорогие гаджеты, призы
или лотерейные билеты.
Можно сказать, что удастся получить
еще больше положительных впечатлений в течение пребывания на онлайн-площадках.
Бонусы для VIP-клиентов
Игровые сервисы в том числе готовят
бонусы для игроков, которые регулярно посещают портал казино и используют в играх большие
денежные суммы.
Большая часть онлайн-casino стараются пообщаться с ВИП-пользователями , чтобы разузнать об их
предпочтениях и назначить призы,
которые фактически отвечают поведенческому фактору постоянного клиента.
Это еще раз подтверждает, насколько рады приветствовать пользователей online-площадки.
Для VIP-геймеров большинство online-казино подготавливают очень ценные материальные призы.
Нужно всего лишь регулярно посещать любимое заведение,
пользоваться всеми предоставляемыми плюсами своего положения.
gafas de sol 2019 mujer tendencias ray ban
foulard calvin kleinadidas windstopper running jacketnike foamposite animal inspirationdoudoune argent茅e fille
Ставки на спортивные события на сегодняшний день https://feicity.com/home.php?mod=space&uid=496220&do=profile&from=space пользуются популярностью не только среди его любителей.
Даже не большие приверженцы спорта в последнее время
активно ставят для удовольствия.
Они успели узнать, что такое адреналиновый всплеск,
который удается получить в момент предвкушения итогов.
Вряд ли кто откажется от довольно выгодного выигрыша?
Вы можете смотреть увлекательный матч и при этом делать ставки.
На территории РФ приемщики ставок имеют
право осуществлять деятельность легально, но для этого нужно иметь лицензия, что
выдают не сразу и не каждому.
Причем даже у честных приемщиков ставок могут возникнуть сложности.
Это может быть блокирование
сайта, невозможность авторизации.
Не вызывает удивления, что терпение иссякает, возникает желание отыскать другой вид развлечения.
Да и человек посчитает себя обведенным вокруг пальца.
В действительности же, нет смысла поддаваться панике раньше времени.
В связи с этим сейчас объясним, что собой представляет фонбет зеркало синий работающий
и зачем оно может потребоваться.
Им уже смогли успешно воспользоваться многие из опытных и только присоединившихся посетителей сервиса.
С какой целью используют точную копию площадки
Зеркало – это полноценный двойник официального портала букмекерской конторы ФОНБЕТ .
Необходимо оно для:
1. возможности без промедления вернуться на любимый сервис,
не обращая внимания на блокировку;
2. защиты аккаунтов прошедших регистрацию пользователей;
3. повышенной скорости;
4. сохранности копии портала;
5. равномерного перераспределения нагрузки;
6. обхождения блокирования,
которое может устанавливаться по различным причинам (многим клиентам ресурс может
быть недоступен из-за Российского потребнадзора).
При этом в полном объеме функции официального сайта действуют и в зеркале.
Люди, которые постоянно пользуются FONBET, имеют возможность спокойно
войти через копии.
Это можно сделать через выбранный vpn.
Вы сможете спокойно пользоваться выбранным ресурсом,
делать ставки.
По какой причине происходит блокировка FONBET
Букмекерство на территории Российской Федерации имеет легальный статус сравнительно
недавно.
Ко всему лицензионное разрешение заиметь сложно.
Из-за вышеназванных причин в России на законных
основаниях функционируют примерно 20-30 букмекерских контор.
Эти компании Довольно известны,
зачастую мелькают в рекламе матчей различных видов спорта.
Если bookmaker не спонсирует спортивные мероприятия, шансов на получение лицензионного документа у
него фактически нет.
Вследствие этого и пользователи
скорее всего не смогут зайти на вебсайт.
Предположительно он заблокируют
в пределах России.
В чем состоят плюсы FONBET
Во-первых, это международная компания.
Входит в Marikit Holdings LTD.
У FONBET есть официальный документ острова Кюросао, это официальное разрешение,
позволяющее вести деятельность в различных
государствах, где это не запрещено по
закону.
Поэтому делать ставки имеют право даже люди, которые
живут за пределами России.
Обычным образом заходите на сайт, выбираете мероприятия и делаете ставки.
От выигрыша команды-фаворита до
количества голов, которые
будут забиты в процессе игры.
Отдельного внимания требуют к себе
ставки на ведущего игрока.
Вполне может быть, что он «прислушается» к вашему мнению и
забьет результативный мяч, который приведет к победному исходу.
Следующий момент, на FONBET можно ставить на многие события типа
спортивных, киберспортивных, шоу-бизнеса, в политической сфере и др.
Можно сделать ставку на то, кто будет следующим лидером Турецкой Республики или кто будет сниматься в новом фильме.
Чего только стоит всемирно известное Eurovision, когда важно выбрать победителя в когорте многочисленных исполнителей из многих стран.
Довольно привлекательные возможности, не
правда ли?
Третье, на FONBET предлагается указать наиболее подходящий язык.
Сайт поддерживает на пятьдесят два различных языка.
В связи с этим найти что-то для себя получится практически у любого.
Это же относится и к валютам, их почти 50 – от привычных
доллара и рубля до электронных денег.
Каждый найдет то, что нужно на свой вкус.
И это , конечно, не весь
список достоинств.
Обо всех нюансах более подробно можно узнать , если зайти на сайт https://retrogames.wikies.net/index.php?title=User:NobleDupre4
К тому же на сайте будет подробная инструкция по регистрации.
Вы сможете разобраться, какие есть способы прохождения регистрации, как без промедления начать делать ставки.
Чтобы узнать актуальный адрес копии сайта, наилучший вариант будет позвонить по ГЛ.
Ко всему, можно найти надежные
группы, которые готовы информировать
о различных букмекерских агентствах.
Для этого просто ввести в наиболее привычной поисковой системе фразу
– FONBET зеркало.
Вы сможете оказаться на веб-ресурсе найти зеркало фонбет , который полностью отвечает официальному сервису.
Итак, нет ничего проще, чем найти для конкретных целей созданное зеркало.
Registro em 1XBET Portugal https://wikicryptocoins.com/currency/Registro_Em_1XBET_Portugal_O_Que_Oferece_A_Casa_De_Apostas_1XBET_download_Da_1xbet_Para_Android_Faezr_O_Download_Da_1xbet_Para_Iphone
Digite o codigo promocional
REGISTE-SE E RECEBA UM REMUNERATION DE 100 EUR AGORA
MESMO!
Convidamos todos quem quer ganhar nas apostas em desportos registrar-se rapidamente
em uma casa de apostas mais justa da empresa 1XBet.
O registro em 1XBET Portugal permite usar de todas as funcionalidades do place oficial, incluindo:
retirada de fundos rapida atraves de qualquer sistema
de pagamentos ou cartoes bancarias;
servico de apoio a cliente conveniente que sempre ajudara esclarecer a situacao;
interface e aplicacoes moveis funcionais.
O perk da 1XBET Portugal Faezr o download da 1xbet para iphone
A casa de apostas, a todos que desejam receber os perk agradaveis na sua conta, da
essa oportunidade. E uma oportunidade actual de ganhar dinheiro gracas a generosidade da administracao da empresa.
O owner sempre epoch o perk de primeiro deposito.
O bonus e um adicional de 100% do valor do deposito de ate 130 euros, que serao
imediatamente creditados na conta.
O mais agradavel e a possibilidade de devolver o dinheiro recebido nas apostas
ordinarias e expressas.
A condicao chairman e que tem que escolher as partidas com coeficiente bastante alto, das quais
e necessario formar um expresso completo.
Para um novato recuperar aposta nao e uma tarefa facil, mas isso permite conhecer bem a interface da empresa de azar e aprender o basico de apostas.
Como usar o codigo de promocao da 1xBet? https://game-bai.com/forum/profile.php?id=3425
Usar o codigo de promocao e muito facil, pois a administracao
permite fazer isso sem a participacao do servico de apoio a cliente.
Basta de seguir uma instrucao intuitivamente clara:
Primeira coisa que tem que fazer e ir para o portal oficial de jogos com o nosso identify with
e clicar em “Registrar-se” no canto better direito.
A seguir, tem que selecionar um dos metodos de criacao da conta pessoal e inserir o codigo de promocao
recebido, que tambem se encontra neste site.
Apos preencher todos os dados, e necessario enviar um pedido
e receber a conta ativada durante de um dia.
Os usuarios nao devem esquecer da necessidade de confirmar
o e-mail atraves de uma mensagem recebida.
Todos os dados indicados durante registro devem ser verificados cuidadosamente
e so podem ser verdadeiros, pois caso contrario, depois da verificacao por administracao a conta pode ser bloqueada.
O que oferece a casa de apostas 1XBET download da 1xbet para android
O registro na 1XBET Portugal permite a cada jogador apreciar um jogo de apostas em
desporto divertido e excitado.
Tudo que e necessario e ter uma conta registrada e ser um residente
de Portugal maior da idade. E obrigatorio passar uma verificacao completa que da o acesso para gerenciamento das
contas.
A empresa oferece a todos os jogadores registrados as seguintes vantagens:
uma enorme variedade de partidas e eventos politicos em quais pode
apostar com um praticamente sem limites.
Apenas administracao pode limitar o montante maximo de
aposta, entretanto os coeficientes sao colocados independentemente do
nivel da partida;
varias maneiras de deposito e retirada de fundos que permite carregar a sua conta de jogo sem algum problema
e receber o seu ganho no cartao bancario ou
um sistema de pagamentos;
servico de apoio a cliente operativo que responde todas as perguntas de usuarios e ajuda resolver qualquer situacao 24 horas
por dia.
Um requisito obrigatorio para obtencao de todos os privilegios
acima indicados e perquisite adicionais e preencher todos os dados na secao “Minha conta” que se encontra na conta
pessoal.
nike md runner 2 sneaker
costume de baie triumph magazin onlineprize electrice ceramiceadidas ultra boost bb3911zara woman incaltaminte
Конкурентная борьба в области online гемблинга поражает масштабами.
http://fiber.s16.xrea.com/x/aska/aska.cgi
С завидной регулярностью организовывается все больше площадок с
привлекательными спецусловиями для новичков.
Отдельного внимания заслуживает
стартовый подарок, который успели оценить многие пользователи.
Пришло время понять важные моменты, которые связаны с
функционированием казино.
Стартовый бонус – это основной бонус, который предоставляет online-casino.
Чтобы его получить, не придется прилагать много стараний.
Пособие приготовлено для игроков,
которые только в первый раз заходят в аккаунт на сайте cazino.
Геймеры могут и не подозревать, какой подарок приготовили разработчики.
Чаще всего первое поощрение
добавляет некоторый процент к начальному счету вне зависимости от заведенной на
сайт суммы.
Бонус безвозмездных спинов 1win ставки на спорт онлайн
Казино внедряют безоплатные прокручивания
в свою рекламную задумку.
Что это означает?
Это позволяет давать пользователям безоплатные раунды,
которые они имеют право использовать в игровых автоматах, и выигрыши обычно могут быть
сняты с личного счета.
Вращения достаточно популярны в среде почитателей азартных онлайн-игр, потому
что они дают шанс изучить возможности, которые обеспечивают новые игровые аппараты, без необходимости пополнять
персональный баланс и растрачивать собственные финансы.
Достаточно привлекательное предложение,
которым вполне могут воспользоваться геймеры.
Можно расценить все плюсы, шансы, обеспечиваемые владельцами площадок.
Kazino таким образом нередко продвигают новейшие услуги среди посетителей, прошедших
регистрацию на их портале.
В то же время https://kaptenkrona.dev/index.php?action=profile;u=388 доступно всем желающим.
Нужно всего лишь выбрать конкретную
категорию, ввести данные в регистрационные ячейки.
Важно не забывать про обязательность подтверждения совершеннолетие.
Без верификации будет сложно получить статус игрока,
которому откроются имеющиеся возможности онлайн
ресурса.
Реферальные бонусы
Online casino стимулирует пользователей, которые рекомендуют сервис другим.
Подарки за привлечение знакомых делаются с целью продвижения предложений игр и притягивания потенциальных пользователей казино.
Данный способ считается наиболее эффективным для роста количества геймеров.
Одно дело, когда человек решается стать
полноценным участником,
ориентируясь на рекламные слоганы.
Совершенно другое – воспользоваться советом друга, который
уже убедился в правдивости данных, многообразии слотов для игры.
За рекомендацию пользователь может обнаружить в
личном кабинете денежный приз.
Начисленные деньги разрешается вывести со счета или потратить на
безоплатные вращения в игре
(отдельные cazino применяют свои собственные маркетинговые и бонусные стратегии, поэтому стоит сначала изучить правила).
Каким образом можно получить этот
бонус?
Вы должны сагитировать того, кого вы знаете, зарегистрироваться на
игровом портале, создать учетную запись и внести депозит.
При прохождения регистрации такой
человек должен внести сведения о вас как рекомендателя,
чтобы Вам можно было получить бонус.
Число пришедших по рекомендации людей не лимитируется.
Казино всегда рады новичкам, которые собираются стать завсегдатаями
в ближайшем будущем.
Бонус за преданность
Поощрительные бонусы – это дополнительный тип бонусов, которые используются в онлайн-казино 1вин бк 1вин отзывы
Они похожи на достаточно распространенные программы лояльности,
которыми руководствуются известные торговые марки.
Получается, что casino поощряет своих постоянных клиентов
(людей, которые регулярно посещают ресурс и играют)
привлекательными бонусами или
подарками.
Подобный бонус может быть в виде поощрительных спинов, но основная масса казино также дают недорогие
аксессуары, подарки или лотерейные
билеты.
Примечательно, что появится возможность
получить еще больше положительных впечатлений за время пребывания
на онлайн-площадках.
Поощрительные призы для ВИП-клиентов
Игровые сервисы в том числе продумывают бонусы
для игроков, которые стабильно заходят на
сайт cazino и используют в играх крупные денежные суммы.
Большая часть online-казино связываются с ВИП-клиентами , чтобы разузнать
об их предпочтениях и присудить вознаграждения, которые фактически
соответствуют поведенческому фактору
постоянного игрока.
Это еще раз доказывает, в какой мере рады
приветствовать клиентов онлайн-площадки.
Для ВИП-геймеров большинство онлайн-cazino подготавливают очень ценные материальные призы.
Нужно всего лишь продолжать заходить в
любимое заведение, пользоваться всеми предоставляемыми преимуществами своего положения.
Registro em 1XBET Portugal http://forum.broadcasters-complain.net/profile.php?id=52
Digite o codigo promocional
REGISTE-SE E RECEBA UM REWARD DE 100 EUR AGORA MESMO!
Convidamos todos quem quer ganhar nas apostas em desportos registrar-se rapidamente
em uma casa de apostas mais justa da empresa 1XBet.
O registro em 1XBET Portugal permite usar de todas as funcionalidades do place oficial, incluindo:
retirada de fundos rapida atraves de qualquer sistema de pagamentos ou cartoes bancarias;
servico de apoio a cliente conveniente que sempre ajudara esclarecer a situacao;
interface e aplicacoes moveis funcionais.
O tip da 1XBET Portugal download da 1xbet para android
A casa de apostas, a todos que desejam receber os perk
agradaveis na sua conta, da essa oportunidade. E uma oportunidade
genuine de ganhar dinheiro gracas a generosidade da administracao da empresa.
O owner sempre epoch o perk de primeiro deposito. O perquisite e um adicional de 100%
do valor do deposito de ate 130 euros, que serao imediatamente creditados na conta.
O mais agradavel e a possibilidade de devolver o dinheiro recebido nas apostas ordinarias e expressas.
A condicao chairman e que tem que escolher as partidas com coeficiente
bastante alto, das quais e necessario formar um expresso completo.
Para um novato recuperar aposta nao e uma tarefa facil, mas isso permite conhecer bem a interface da empresa de azar
e aprender o basico de apostas.
Como usar o codigo de promocao da 1xBet? http://apps.fz-juelich.de/pax/paxwiki/index.php/Registro_Em_1XBET_Portugal_O_Que_Oferece_A_Casa_De_Apostas_1XBET_download_Da_1xbet_Para_Android_Faezr_O_Download_Da_1xbet_Para_Iphone
Usar o codigo de promocao e muito facil, pois a administracao permite fazer isso sem a participacao do servico de apoio
a cliente. Basta de seguir uma instrucao intuitivamente clara:
Primeira coisa que tem que fazer e ir para o portal
oficial de jogos com o nosso relate e clicar em “Registrar-se” no canto select direito.
A seguir, tem que selecionar um dos metodos de criacao
da conta pessoal e inserir o codigo de promocao recebido, que tambem
se encontra neste site.
Apos preencher todos os dados, e necessario enviar um pedido e receber a
conta ativada durante de um dia.
Os usuarios nao devem esquecer da necessidade de confirmar o e-mail atraves de uma mensagem recebida.
Todos os dados indicados durante registro devem ser verificados
cuidadosamente e so podem ser verdadeiros, pois caso contrario, depois
da verificacao por administracao a conta pode ser bloqueada.
O que oferece a casa de apostas 1XBET Registro em 1XBET Portugal
O registro na 1XBET Portugal permite a cada jogador apreciar um jogo de apostas em desporto divertido e excitado.
Tudo que e necessario e ter uma conta registrada e ser um residente de Portugal maior da idade.
E obrigatorio passar uma verificacao completa que da o acesso para gerenciamento das contas.
A empresa oferece a todos os jogadores registrados as
seguintes vantagens:
uma enorme variedade de partidas e eventos politicos em quais pode apostar com um praticamente sem limites.
Apenas administracao pode limitar o montante maximo de aposta, entretanto os coeficientes sao colocados independentemente
do nivel da partida;
varias maneiras de deposito e retirada de fundos que permite carregar a sua conta de jogo sem algum problema e receber
o seu ganho no cartao bancario ou um sistema de pagamentos;
servico de apoio a cliente operativo que responde todas as
perguntas de usuarios e ajuda resolver qualquer situacao 24 horas por dia.
Um requisito obrigatorio para obtencao de todos os privilegios acima indicados e perquisite adicionais e preencher todos os dados na
secao “Minha conta” que se encontra na conta pessoal.
Конкуренция в области online гемблинга поражает масштабами.
Каждый день появляется немало площадок с заманчивыми условиями для новых игроков.
Особенного внимания удостаивается первоначальный подарок, который успели
оценить большое число клиентов.
Пришло время разобраться с основными аспектами, которые сопряжены с
функционированием casino https://w88w88vn.com/w88club/profile.php?id=27944 .
Стартовый приз – это главный бонус, который
предоставляет онлайн-казино.
Чтобы его получить, не придется
прилагать серьезных усилий.
Инструкция подготовлена для игроков, которые только впервые заходят в аккаунт на портале казино.
Пользователи часто даже не представляют, какой сюрприз подготовили программисты.
Чаще всего стартовый бонус прибавляет определенный процент к стартовому счету
независимо от заведенной на сайт суммы.
Бонус бесплатных вращений
Casino включают безоплатные вращения в собственную рекламную
стратегию.
Как это понимать?
Это позволяет давать пользователям безоплатные
раунды, которые геймеры имеют право использовать
в игровых аппаратах, и выигранные средства
чаще всего можно снять с личного счета.
Спины достаточно востребованы в среде любителей азартных онлайн-игр, потому что они дают шанс изучить потенциал, который обеспечивают новые гейм автоматы, с исключением потребности пополнять персональный счет и растрачивать собственные финансы.
Довольно интересное предложение,
которым в полной мере могут воспользоваться геймеры.
Можно оценить по достоинству имеющиеся преимущества,
возможности, предоставляемые разработчиками.
Казино таким образом часто рекламируют новейшие продукты среди пользователей, зарегистрированных на их портале.
При этом отзывы о бк 1win не ограничено ни для одного из желающих.
Нужно всего лишь пройти в соответствующий раздел, заполнить регистрационные ячейки.
Не забывайте про необходимость подтвердить достижение
совершеннолетия.
Без подтверждения личности будет сложно стать постоянным пользователем, которому откроются все возможности онлайн ресурса.
Реферальные бонусы
Онлайн casino стимулирует клиентов, которые рекомендуют игровую площадку другим.
Бонусы за привлечение знакомых предназначены для продвижения гэмблинга и притягивания новых клиентов казино.
Данный метод признается одним из самых эффективных для роста
количества игроков.
Одно дело, когда посетитель решается стать полноценным участником, ориентируясь на рекламу.
Совершенно другое – довериться совету приятеля, который на сегодня убедился в
правдивости данных, многообразии игровых аппаратов.
За совет пользователь может получить денежный приз.
Начисленные деньги разрешается вывести со счета или потратить на безоплатные спины в игровых раундах (отдельные cazino применяют свои собственные маркетинговые и бонусные стратегии, поэтому лучше всего сначала
изучить правила).
Каким образом можно стать обладателем
такого бонуса?
Вы должны убедить того, кого вы знаете,
зарегистрироваться на игровом портале, активировать аккаунт и пополнить счет.
При прохождения регистрации такой
человек должен указать ваши данные в качестве рекомендателя, чтобы Вы
могли зачислить на счет бонус.
Число пришедших по рекомендации игроков не
лимитируется.
Казино всегда рады новичкам, которые намерены стать
постоянными в ближайшем будущем.
Бонус за преданность
Поощрительные бонусы – это еще вид подарков, которые используются в
онлайн-casino 1вин 1win минимальная ставка.
Они напоминают довольно распространенные
программы лояльности, которыми руководствуются знакомые многим торговые марки.
Таким образом casino поощряет своих постоянных клиентов (пользователей, которые с завидной
регулярностью посещают ресурс
и вступают в игру) заманчивыми бонусами или наградами.
Такой сюрприз возможен в виде
бесплатных вращений, однако основная масса казино тоже предоставляют небольшие гаджеты, призы или лотерейные билеты.
Примечательно, что удастся получить еще больше положительных впечатлений в
течение нахождения на онлайн-платформах.
Бонусы для ВИП-клиентов
Казино в том числе продумывают
бонусы для геймеров, которые регулярно заходят
на сайт cazino и используют в играх большие суммы денег.
Большая часть online-casino связываются
с ВИП-пользователями с целью узнать об их
предпочтениях и присудить вознаграждения,
которые по сути соответствуют стилю заинтересованного игрока.
Это еще раз подтверждает, насколько рады
видеть клиентов online-заведения.
Для VIP-игроков многие online-казино готовят очень
ценные материальные призы.
Необходимо всего лишь продолжать посещать выбранное
заведение, пользоваться всеми предоставляемыми преимуществами своего положения.
Прогнозы на спорт сегодня https://i-win.info/iwin/profile.php?id=20505 популярны не только среди болельщиков.
Даже не большие приверженцы спорта сейчас регулярно делают ставки ради развлечения.
Любители азарта смогли узнать, что такое адреналиновый всплеск, который удается получить в момент ожидания результата.
Вряд ли кто сможет отказаться от достаточно крупной прибыли?
Вы можете следить за интереснейшей игрой и при этом ставить на исход состязания.
На территории России приемщики ставок могут работать легально,
но для этого нужно иметь разрешение, что
выдают не сразу и не всем.
Что примечательно, даже у проверенных на деле
приемщиков ставок довольно часто
возникают проблемы.
Это может быть блокирование площадки, невозможность авторизации.
Не вызывает удивления,
что выдержка заканчивается, появляется желание найти другой вид развлечения.
Да и клиент посчитает себя обманутым.
В действительности же, не стоит
поддаваться панике раньше времени.
Поэтому сейчас расскажем о том, что собой представляет ставки на спорт betwinner и для чего оно может потребоваться.
Им уже успели успешно воспользоваться
множество знающих и только присоединившихся пользователей ресурса.
Зачем нужно точную копию площадки
Зеркало – это полноценный двойник исходного сайта букмекерской конторы.
Необходимо оно для:
1. того, чтобы при случае оперативно вернуться
на любимый ресурс, не обращая внимания на
блокировку;
2. предотвращения взлома аккаунтов прошедших регистрацию посетителей;
3. высокой скорости;
4. сохранности аналога портала;
5. равномерного перераспределения пользовательских запросов;
6. обхода блокировки, которая
может устанавливаться в силу разных причин
(многим клиентам сайт может быть недосягаем из-за Роспотребнадзора).
При этом в полном объеме опции основного сайта действуют и в
работающей копии.
Пользователи, которые постоянно пользуются betwinner, могут беспрепятственно войти через зеркала.
Это удастся сделать через выбранный vpn.
Вы сможете спокойно пользоваться
любимым ресурсом, ставить на спортивные события.
По какой причине блокируют betwinner
Прием ставок по регионам России имеет легальный
статус сравнительно недавно.
Ко всему лицензию заиметь сложно.
По причине этих двух причин в РФ легально функционируют примерно 25-30
букмекерских контор.
Они Довольно популярны, часто
мелькают в рекламе туров тех или иных спортивных соревнований.
В случае, когда букмекер не спонсирует спортивные мероприятия,
надежд на на то, чтобы стать обладателем лицензии у него фактически нет.
Поэтому и пользователи вряд ли сумеют попасть на
вебсайт.
Скорее всего портал заблокируют на территории Российской Федерации.
Какие состоят плюсы Betwinner
В первую очередь, она является компанией
международного уровня.
Принадлежит Marikit Holdings LTD.
У Betwinner имеется лицензия острова
Кюросао, это официальное разрешение, дающее возможность вести деятельность
в любых государствах, где это не запрещено
по закону.
Вот почему ставить могут даже люди, проживающие не
на российской территории.
Обычным образом посещаете сайт, выбираете спортивные
события и оформляете ставку.
От выигрыша команды-фаворита до количества голов, которые будут забиты в течение игры.
Особого интереса заслуживают вложения на игрока, признанного звездой мирового уровня.
Не исключено, что этот игрок «примет во
внимание ваши ожидания» и забьет результативный мяч, который приведет к победному исходу.
Следующий момент, на betwinner позволено делать ставки на
множество мероприятий типа
киберспортивных, в мире спорта, шоу-бизнеса, в политической сфере и т.д.
Можно сделать ставку на то, кто
будет новым президентом Турции или кто будет сниматься в новом фильме.
Сколько возможностей дарит занменитое Евровидение,
когда важно предугадать триумфатора среди большого числа артистов из разных стран.
Достаточно привлекательные перспективы, не правда ли?
В-третьих, на Betwinner предлагается выбрать родной язык.
Портал поддерживает на пятьдесят
два различных языка.
Поэтому найти что-то свое получится практически у любого.
Этот момент касается и валют, их
аж 49 – от обычных рубля и доллара до
электронных денег.
Любой из пользователей сможет
найти то, что нужно по своим предпочтениям.
И это далеко не полный перечень достоинств.
Обо всех нюансах подробнее несложно
узнать по ссылке http://www5d.biglobe.ne.jp/~deluxe/cgi-bin/yybbs.cgi?page=30
К тому же на сайте размещена детальное руководство относительно того, как зарегистрироваться.
Посетители смогут разобраться,
какие есть способы прохождения
регистрации, как без промедления ставить.
Чтобы узнать актуальный адрес зеркала, наилучший вариант будет позвонить по ГЛ.
Кроме того, не лишне выйти на авторитетные сообщества, которые готовы информировать
о различных букмекерских агентствах.
Достаточно просто ввести в любом популярном поисковике фразу
– betwinner зеркало.
Пользователь сможет перейти на
веб-сайт скачать betwinner на айфон приложение , который на 100% соответствует исходному сервису.
Итак, не составит труда отыскать специально разработанное зеркало.
Конкурентная борьба на рынке online гемблинга невероятна.
http://wxy99.com/home.php?mod=space&uid=5358478&do=profile&from=space
С завидной регулярностью появляется все больше площадок с соблазнительными спецусловиями для новеньких.
Особенного интереса удостаивается первоначальный подарок,
который смогли оценить многие пользователи.
Пришло время понять важные моменты, которые сопряжены с работой казино.
Приветственный бонус – это главный бонус, который
предлагает онлайн-casino.
Чтобы его получить, не придется прилагать много стараний.
Пособие подготовлено для игроков,
которые только впервые открывают личный кабинет на портале cazino.
Пользователи могут и не подозревать, какой подарок приготовили программисты.
Чаще всего первоначальный бонус прибавляет
определенный процент к стартовому счету
вне зависимости от внесенной суммы.
Подарок в виде безвозмездных вращений 1win букмекерская контора зеркало
Казино внедряют бесплатные вращения в свою маркетинговую задумку.
Что это такое?
Такой подход дает игрокам безоплатные циклы, которые они могут
использовать в игровых автоматах,
и выигранные средства чаще всего можно
снять с личного счета.
Вращения достаточно востребованы среди
любителей гэмблинга, так как они дают шанс изучить потенциал, который предоставляют новые гейм аппараты, с исключением потребности увеличивать
персональный баланс и растрачивать собственные деньги.
Достаточно привлекательное предложение,
которым в полном объеме могут воспользоваться
игроки.
Можно расценить имеющиеся преимущества, шансы, предоставляемые владельцами площадок.
Kazino таким образом зачастую рекламируют новейшие продукты среди
клиентов, прошедших регистрацию на их портале.
При этом https://listazz.com/index.php?action=profile;u=45737 доступно для всех
любителей игры.
Необходимо всего-навсего пройти в определенный
раздел, заполнить поля регистрации.
Не забывайте про необходимость подтвердить
совершеннолетие.
Без верификации будет сложно стать постоянным пользователем,
которому доступны имеющиеся возможности онлайн
площадки.
Реферальные бонусы
Online казино поощряет клиентов, которые советуют игровую площадку потенциальным игрокам.
Бонусы за привлечение знакомых делаются с целью продвижения гэмблинга и привлечения новых клиентов казино.
Данный метод признается одним из самых эффективных для роста числа геймеров.
Один момент, когда посетитель решается стать полноценным участником,
ориентируясь на рекламу.
Совершенно другое – воспользоваться советом друга, который уже проверил достоверность
сведений, многообразии слотов для
игры.
За рекомендацию вы можете обнаружить в личном кабинете некоторую сумму денег.
Финансовый бонус разрешается снять со счета или потратить
на безоплатные спины в игровых раундах (некоторые cazino применяют самостоятельно разработанные рекламные
и поощрительные программы,
поэтому стоит перво-наперво изучить правила).
Каким образом можно получить этот
бонус?
Вам необходимо сагитировать
того, кого вы знаете, зарегистрироваться на сайте казино, создать учетную запись и пополнить счет.
Во время прохождения регистрации такой пользователь должен указать ваши данные в
качестве реферала, чтобы Вы могли получить вознаграждение.
Число пришедших по рекомендации игроков не лимитируется.
Игровые площадки всегда поощрительно относятся к новым клиентам, которые собираются стать постоянными в
самое ближайшее время.
Поощрение за лояльность
Поощрительные бонусы – это дополнительный тип бонусов, которые используются в on-line-казино 1вин 1вин на айфон
Они напоминают довольно известные программы лояльности, которыми руководствуются знакомые многим торговые марки.
Получается, что casino награждает своих приверженцев (людей, которые с завидной регулярностью
заходят на площадку и играют) привлекательными призами или подарками.
Подобный сюрприз возможен в форме
бесплатных спинов, но многие игровых платформ
тоже предоставляют недорогие гаджеты, призы или билеты для участия в лотереях.
Можно сказать, что удастся испытать еще больше положительных эмоций за время нахождения на online-платформах.
Поощрительные призы для VIP-клиентов
Казино также продумывают поощрения для
игроков, которые стабильно посещают сайт cazino и используют
в играх большие денежные суммы.
Большая часть онлайн-casino стараются пообщаться с VIP-клиентами с целью разузнать об их предпочтениях и присудить призы,
которые фактически соответствуют поведенческому фактору постоянного игрока.
Это еще раз подтверждает, в какой мере рады видеть пользователей online-площадки.
Для ВИП-игроков большинство online-cazino подготавливают очень ценные материальные призы.
Необходимо всего лишь
продолжать посещать любимое казино, пользоваться всеми предоставляемыми плюсами своего положения.
賱賵賳 爻噩丕丿 賲毓 丕賱賰賳亘 丕賱亘賷噩
鎵嬭 銈?璨枫亜 銇?銇傘倝銇欍仒l 閲戝叿 妫?/a>銈裤偗銈枫兗 銉夈儵銈ゃ儛銉?銈︺偅銈躲兗銉?/a>銉兂 銉忋兗銉炪兂 銉栥儸銈广儸銉冦儓 浜烘皸
Конкуренция в сфере online гемблинга поражает масштабами.
https://www.fbnewspost.com/index.php?action=profile;u=17573
Каждый день организовывается все больше площадок с заманчивыми условиями для новеньких.
Отдельного внимания заслуживает
первоначальный бонус, который оценили многие пользователи.
Настала пора разобраться с основными аспектами, которые связаны с работой казино.
Приветственный бонус – это основной бонус, который предлагает онлайн-cazino.
Чтобы его получить, не нужно прилагать много стараний.
Пособие приготовлено для игроков,
которые только в первый раз открывают профиль на портале casino.
Пользователи часто даже не представляют, какой подарок
приготовили разработчики.
Наиболее часто стартовый бонус добавляет определенный процент к
первому пополнению счета вне зависимости от внесенной
суммы.
Бонус безвозмездных вращений 1win партнерская программа
Casino внедряют безоплатные прокручивания в
свою рекламную задумку.
Как это понимать?
Это дает пользователям бесплатные раунды, которые играющие имеют право
применить в игровых автоматах, и выигрыши чаще
всего могут быть сняты с личного счета.
Вращения достаточно востребованы среди почитателей гэмблинга, так как они дают шанс изучить потенциал, который обеспечивают новые гейм автоматы, с исключением необходимости пополнять персональный счет и тратить собственные финансы.
Достаточно привлекательное предложение,
которым вполне могут воспользоваться играющие.
Можно оценить по достоинству все
преимущества, возможности, предоставляемые владельцами площадок.
Casino таким образом часто продвигают новые услуги среди
посетителей, зарегистрированных на
их сайте.
При этом http://www.gamecangbaoge.com/home.php?mod=space&uid=91208&do=profile&from=space не
ограничено ни для одного из желающих.
Нужно всего-навсего пройти в соответствующую категорию, заполнить регистрационные ячейки.
Не забывайте про необходимость удостоверить достижение совершеннолетия.
Без верификации будет трудно получить статус
игрока, которому доступны имеющиеся возможности on-line площадки.
Бонусы для пришедших по рекомендации
Online casino стимулирует пользователей,
которые рекомендуют игровую площадку
другим.
Подарки за вовлечение знакомых делаются с целью продвижения гэмблинга и привлечения потенциальных пользователей казино.
Данный способ считается наиболее эффективным для увеличения числа геймеров.
Один момент, когда человек решается
стать полноценным участником, опираясь на рекламу.
Совершенно иное – воспользоваться советом
приятеля, который на сегодня проверил достоверность сведений, многообразии игровых аппаратов.
За рекомендацию пользователь может
обнаружить в личном кабинете денежный приз.
Финансовый бонус разрешается вывести
со своего счета или потратить на безоплатные вращения в игровых раундах (некоторые
казино имеют свои самостоятельно разработанные рекламные
и поощрительные стратегии,
поэтому стоит перво-наперво изучить правила).
Как можно получить этот бонус?
Вы должны убедить кого-то из своих знакомых пройти регистрацию на сайте казино, активировать аккаунт и внести депозит.
При прохождения регистрации
этот человек должен указать
сведения о вас в качестве рекомендателя,
чтобы Вам можно было зачислить на
счет вознаграждение.
Количество пришедших по рекомендации людей не ограничено.
Казино всегда рады новым клиентам,
которые стремятся стать завсегдатаями в самое ближайшее время.
Бонус за преданность
Поощрительные бонусы – это еще вид подарков, которые используются в on-line-казино 1вин как отменить ставку на 1win
Они напоминают достаточно распространенные программы вознаграждений, которыми руководствуются знакомые многим торговые марки.
Таким образом казино поощряет своих постоянных клиентов (людей,
которые регулярно заходят на площадку и вступают
в игру) привлекательными призами
или подарками.
Подобный сюрприз возможен в форме поощрительных вращений,
но многие игровых платформ тоже дают недорогие гаджеты, подарки или билеты для участия в лотереях.
Примечательно, что удастся испытать еще больше положительных впечатлений в течение нахождения на online-платформах.
Бонусы для VIP-игроков
Игровые сервисы также готовят бонусы для геймеров, которые регулярно заходят на сайт казино и используют в играх
крупные денежные суммы.
Большинство online-casino стараются пообщаться с VIP-пользователями с целью разузнать об их предпочтениях и
назначить призы, которые фактически отвечают поведенческому
фактору заинтересованного клиента.
Это еще раз подтверждает,
в какой мере рады приветствовать пользователей online-заведения.
Для VIP-игроков многие online-cazino подготавливают очень ценные материальные поощрения.
Нужно всего лишь продолжать заходить в
любимое заведение, пользоваться всеми предоставляемыми плюсами своего положения.
Описание зеркала Melbet
Ниша ставок в России функционирует довольно долгое
время, и в 2012 году на рынке появилась фирма Мелбет.
Вплоть до сегодняшнего дня
ресурс стабильно развивается, непосредственно это касается виртуального пространства.
Как думают некоторые пользователи,
достаточно удобно не выходя из дома, в офисе
или в дороге делать ставки.
Потеря времени исключена.
Главная задача конторы – оказывать помощь игрокам ставить,
это удобно выполнить через офисы фирмы или же в режиме
онлайн, для чего есть сайт и приложение для смартфона.
Итак, предоставляется немало способов, чтобы с удовольствием провести свободное время, а
вместе с тем попробовать заработать приличные деньги.
Контора мелбет зеркало актуальное довольно
активно продвигается и намерена создать для своих клиентов самые лучшие условия.
Тут вы можете ставить как на спорт, так и на другие события, например, турниры типа Евровидения.
Теперь нет смысла безучастно наблюдать за тем, как проводит выступление обожаемый
артист.
Достаточно начать верить в его триумф,
сделав выгодную ставку.
Существует шанс, что удастся
заполучить крупную сумму и при этом послушать отличную музыку.
Такой подход крайне удобен, так как в этом случае абсолютно любой человек
сможет найти для себя интересные события
и сделает ставки.
Разработчики смогли предусмореть события на любой вкус.
Все связано с Вашим возрастом, увлечениями,
желанием и возможностью идти на риск.
С чего начинать делать ставки на спортивные события с Melbet https://k8-asia.com/k8/profile.php?id=2154
Некоторые клиенты думают, что
ставить на спорт или другие события
– это довольно хлопотно и что
в этом нужно тратить время на разбирательство.
Но так ли это на самом деле?
Естественно, нет.
Если мы говорим о Мелбет, то
в этом случае начинать ставить сможет
каждый.
На уровне интуиции легко осваиваемый интерфейс придется по вкусу даже новичкам,
которые только решили освоить искусство ставок.
Следует рассмотреть подробнее,
как начинать процесс.
Для старта вам нужно пройти регистрацию на сайте промокод мелбет на сегодня при регистрации
Процесс прохождения регистрации удивительно простой,
займет у вас минимальное количество времени.
Потребуется всего лишь ввести личные сведения
в выделенные ячейки, пройти процесс верификации.
Как только вы зарегистрируетесь, необходимо положить деньги на депозит.
Абсолютно неважно, какая
именно будет зачислена сумма денег.
Совсем скоро Вы освоитесь и поймете,
как действовать дальше, какие
размеры взноса являются наиболее приемлемыми.
И с этого момента начинайте ставить на события.
Сейчас стало понятно, что делать это
можно без особого труда, потому что
этот процесс займет у вас минимум сил и времени.
Выходит, абсолютно каждый сумеет начать ставить вне зависимости от того
новичок он или профи.
Все, что для этого нужно – пройти
регистрацию.
Контора Melbet – входит в число известных и
пользующихся спросом площадок на рынке России, что совсем не удивительно.
Ведь компания с заботой относится к своим клиентам и подготавливает для них наилучшие условия.
Руководству надо не просто заинтересовать больше пользователей,
а и создать наиболее комфортные условия для постоянных клиентов.
Репутация считается важным критерием для компании во имя того,
чтобы не потерять веры игроков.
В сфере ставок присутствует большое количество мошенников.
Не следует слепо доверять яркой рекламе, а также идти на поводу у слишком выгодных условий.
Возможно не только потерять деньги,
время, но и заполучить на ноутбук вирусную программу.
Целесообразнее выбирать лишь проверенные компании, которые длительное время
находятся в игровой отрасли.
В любой момент можно почитать отзывы,
узнать о времени начала деятельности компании на
просторах интернета.
Среди таких профессионалов своего дела признается http://ahfconstruction.com/smf/index.php?action=profile;u=28605 .
При желании несложно скачать конкретно
созданное приложение для смартфонов и других гаджетов.
Останется обеспечить наличие интернету, чтобы ставить уже сегодня.
У Вас будет возможность подобрать
событие, сделать прогноз, пребывая
в заторе или в офисе.
Это ли не одно из достоинств, за которые
стоит выбирать данную компанию?
И это подтвердило огромное количество
игроков компании.
В таком случае, если вы хотите испытывать удачу на ставках,
то вам следует присмотреться к Melbet.
Здесь melbet-partner.com вы сможете найти необходимую информацию и решения своих вопросов,
а , кроме того, немедленно приступить к ставкам после регистрации.
Конкуренция в области online азартных игр невероятна.
https://www.freeads-bristol.co.uk/user/profile/11737
Каждый день появляется все больше площадок с соблазнительными спецусловиями для новичков.
Особенного интереса заслуживает
стартовый бонус, который смогли оценить большое
число клиентов.
Настала пора разобраться с основными
аспектами, которые связаны с работой казино.
Приветственный приз – это главный бонус, который предлагает online-казино.
Для его получения не придется прилагать серьезных усилий.
Инструкция подготовлена для игроков, которые только
в первый раз заходят в профиль на портале casino.
Пользователи часто даже не представляют, какой подарок
подготовили разработчики.
Чаще всего первое поощрение добавляет определенный процент к начальному счету независимо от количества внесенных
денег.
Подарок в виде безвозмездных спинов 1вин бонус
Казино включают безоплатные вращения в
свою маркетинговую стратегию.
Что это такое?
Такой подход позволяет давать игрокам безоплатные раунды,
которые они могут использовать
в игровых аппаратах, и выигранные
средства чаще всего можно снять с их счета.
Вращения чрезвычайно популярны среди почитателей
азартных онлайн-игр, потому что они дают шанс определить возможности, которые обеспечивают новые игровые аппараты, без необходимости
увеличивать свой счет и тратить личные деньги.
Довольно интересное предложение, которым
в полной мере могут воспользоваться геймеры.
Можно оценить по достоинству имеющиеся
плюсы, возможности, предоставляемые
разработчиками.
Casino подобным способом часто продвигают новейшие услуги среди клиентов,
прошедших регистрацию на их сайте.
В то же время http://witcher.ga/index.php?topic=112813.0 не ограничено ни для одного из
желающих.
Нужно всего лишь пройти в соответствующую
категорию, заполнить поля регистрации.
Важно не забывать про обязательность подтверждения
достижение совершеннолетия.
Без подтверждения личности будет сложно получить статус игрока, которому доступны потенциальные возможности on-line площадки.
Бонусы для пришедших по рекомендации
Online casino стимулирует пользователей,
которые рекомендуют игровую площадку другим.
Подарки за вовлечение друзей делаются с целью продвижения
гэмблинга и привлечения новых пользователей казино.
Указанный способ признается одним из самых эффективных для роста количества игроков.
Одно дело, когда пользователь думает присоединиться, опираясь на рекламу.
Совершенно другое – воспользоваться советом друга, который на сегодня удостоверился в предоставленной информации,
вариативности игровых слотов.
За рекомендацию пользователь может получить денежный приз.
Финансовый бонус разрешается
снять со счета или потратить на безоплатные вращения
в игровых раундах (некоторые cazino имеют свои свои собственные маркетинговые и поощрительные программы, поэтому лучше всего перво-наперво ознакомиться с правилами).
Как можно получить этот бонус?
Вы должны сагитировать кого-то из своих знакомых
пройти регистрацию на игровой площадке,
активировать аккаунт и пополнить счет.
Во время прохождения регистрации этот пользователь должен внести ваши
данные в качестве реферала, чтобы Вы могли зачислить на счет бонус.
Число приглашенных людей не
лимитируется.
Игровые площадки всегда поощрительно относятся к новичкам, которые намерены стать завсегдатаями в ближайшем будущем.
Поощрение за преданность
Поощрительные бонусы – это еще тип бонусов,
которые используются в on-line-казино 1вин промокод 1win
Они напоминают достаточно распространенные схемы вознаграждений, которыми руководствуются знакомые многим магазины.
Таким образом casino поощряет своих
приверженцев (людей, которые
регулярно посещают ресурс и вступают
в игру) заманчивыми призами или подарками.
Подобный сюрприз может быть в форме бесплатных спинов, но многие игровых платформ также дают недорогие
аксессуары, подарки или лотерейные билеты.
Примечательно, что удастся испытать намного больше приятных впечатлений за время пребывания на
онлайн-платформах.
Поощрительные призы для VIP-клиентов
Казино также продумывают поощрения для геймеров, которые регулярно посещают портал казино и вкладывают в игры крупные
денежные суммы.
Большинство online-казино стараются
пообщаться с VIP-клиентами , чтобы разузнать об их предпочтениях и
назначить призы, которые
по сути соответствуют стилю заинтересованного клиента.
Это лишний раз подтверждает, насколько
рады приветствовать пользователей онлайн-площадки.
Для ВИП-геймеров многие онлайн-казино
готовят значительные материальные поощрения.
Нужно всего лишь регулярно
посещать любимое казино, наслаждаться всеми предоставляемыми плюсами своего статуса.
Bookmaker 1xbet in Italia https://memmart.com/1xbet-italiastoria-di-1xbet-italiasistema-bonus-1xbet-italiacasin%C3%B2-1xbetapplicazioni-1xbet
La societa di scommesse 1xBet Italia e una societa di origine russa.
La societa di scommesse fornisce i propri servizi ad utenti maggiorenni
di tutto il mondo. Il sito si trova sempre nelle posizioni di primo piano per il numero di
clienti e la qualita degli eventi in linea. Il sito e famoso per
il proprio supporto tecnico, che risponde in pochi minuti, nonche per
i piacevoli perquisite sul primo deposito.
Storia di 1xbet Italia
L’organizzazione del gioco d’azzardo ha operato in tutto il mondo per
oltre 10 anni, ma alone nel 2015 e arrivata in Italia.
I giocatori italiani preferiscono proprio 1xbet a causa dell’ampio investimento della societa di scommesse sui giocatori popolari del nostro paese.
Il sito ha guadagnato popolarita anche grazie al servizio 1xbetstreaming, il quale
permette di scommettere direttamente mentre si guarda l’evento.
La societa di scommesse aumenta ogni anno il fatturato dei
fondi e il numero di utenti attivi. Su questo influiscono l’apertura del casino online aperto e le grandi partnership con grandi
club.
Chelsea, Liverpool e Barcellona non sono gli unici
nella lista delle sponsorizzazioni della societa di scommesse.
Licenza
Al momento, la societa di scommesse ha difficolta a causa del
rinnovo della licenza, ma nell’applicazione unstationary su Android e iOS e ancora possibile scommettere.
Per questo gli scommettitori del Brasile e dei
paesi vicini possono scommettere normalmente. Al momento,
la societa e in trattativa per rinnovare la licenza e continuare le attivita nel suo Paese.
Sistema bonus 1xbet Italia
La societa di scommesse cerca di rafforzare la propria posizione nel
mercato delle scommesse con ampie offerte promozionali.
Il extra di benvenuto soddisfa i nuovi arrivati e consente di aumentare il primo deposito della meta, fino a
100 euro. Le condizioni di basis per ricevere il regalo sono le seguenti:
• e necessario versare almeno 1 euro sul conto;
• e necessario scommettere 5 volte l’importo versato per ricevere il regalo;
• le scommesse devono essere espresse da 3 eventi o piu;
• il coefficiente di ogni partita deve essere superiore a 1,
40;
• e necessario recuperare il totale entro 30 giorni dalla ricezione del
bonus.
Tip aggiuntivi dal sito
I giocatori possono ricevere altri regali, go about a find l’introduzione di codici promozionali speciali al casino o alle scommesse.
Ci sono codici simili durante eventi sportivi su larga scala.
Nel corso di un grande evento, nel 2018, la societa ha offerto a tutti di ottenere 10 euro, che potevano essere giocati senza il rischio di perdere.
La linea di partite 1xbet al giorno supera i 1000 eventi.http://cgi.www5b.biglobe.ne.jp/~leen/cgi-bin/bbs/yybbs.cgi/yybbs.cgi?
La compagnia di scommesse 1xBet riempie costantemente la propria linea con partite ed eventi interessanti.
In media, ogni giorno ci sono piu di 1000 eventi per le scommesse.
L’amministrazione cerca di make bold l’opportunita di scommettere non solitary sulle partite popolari, ma
anche sugli eventi regionali in Portogallo, in modo che tutti possano scommettere a loro piacimento.
Come iniziare a scommettere su 1xbet Italia?
Storia di 1xbet Italia
Iniziare a scommettere su 1xbet Italia e molto semplice.
Occorre trovare il sito ufficiale su Google e registrarsi.
Ogni utente maggiorenne puo creare un profilo. Questo puo essere fatto in 4 modi:
Прогнозы на спорт на сегодняшний день http://sayaka.s11.xrea.com/joho/joho.cgi пользуются популярностью не только среди его любителей.
Даже обычные люди в последнее время активно ставят ради удовольствия.
Любители азарта успели узнать, что такое адреналиновый всплеск,
который удается получить в момент ожидания итогов.
Вряд ли кто откажется от достаточно
крупной прибыли?
Вам удастся следить за интереснейшей игрой , а заодно делать ставки.
На территории России приемщики ставок имеют право работать на законных основаниях,
однако для этого потребуется лицензия, что предоставляют не
быстро и не каждому.
Что примечательно, даже у честных приемщиков ставок довольно часто возникают
проблемы.
Среди них прекращение работы сайта, отсутствие доступа.
Не вызывает удивления, что терпение иссякает, возникает стремление отыскать другой способ развлечения.
Ко всему, человек будет считать себя обведенным
вокруг пальца.
В действительности же, не стоит поддаваться
панике преждевременно.
Поэтому сейчас расскажем о том,
что такое фонбет старая версия зеркало
и для чего оно может потребоваться.
Этой фишкой на сегодня смогли успешно воспользоваться многие из знающих и только присоединившихся посетителей ресурса.
Для чего необходимо зеркало
Зеркало – это качественная копия исходного портала букмекерской компании ФОНБЕТ .
Необходимо оно для:
1. возможности без промедления возвратиться на привычный сервис, забыв про блокирование;
2. предотвращения взлома профилей прошедших регистрацию посетителей;
3. высокой скорости;
4. сохранения аналога сайта;
5. распределения запросов;
6. обхода блокировки, которая может устанавливаться в силу разных причин (некоторым пользователям сайт бывает
недосягаем из-за Роспотребнадзора).
В это же время все опции основного
сайта доступны и в работающей копии.
Пользователи, которые регулярно пользуются FONBET, имеют возможность беспрепятственно зайти через
зеркала.
Это можно сделать через выбранный ВПН.
Вы сможете без ограничений пользоваться выбранным сайтом,
делать ставки.
Почему происходит блокировка FONBET
Прием ставок на территории Российской
Федерации имеет легальный статус сравнительно недавно.
К тому же лицензионное разрешение заиметь тяжело.
Из-за вышеназванных факторов в РФ легально работают
примерно 25-30 букмекерских контор.
Эти компании достаточно известны, часто встречаются в рекламе матчей тех или иных спортивных соревнований.
В случае, когда букмекер не является спонсором спортивных состязаний, надежд на получение
лицензионного документа у него практически
нет.
Вследствие этого и пользователи скорее всего
не смогут попасть на сайт.
Скорее всего он заблокируют в пределах России.
Какие состоят преимущества FONBET
В первую очередь, это международная компания.
Входит в Marikit Holdings LTD.
У FONBET имеется официальный документ
острова Кюросао, это официально подтвержденное право, позволяющее вести деятельность в любых странах, в которых это не
запрещено законом.
Вот почему ставить могут даже люди, которые живут не на российской территории.
Обычным образом посещаете площадку, подбираете спортивные события и делаете ставки.
От исхода игры с любимой командой до числа
голов, которые будут забиты в
течение матча.
Отдельного внимания требуют
к себе вложения на игрока, который считается мировой звездой.
Не исключено, что он «примет во внимание ваши ожидания» и сделает
рывок, ведущий к победному исходу.
Во-вторых, на FONBET позволено ставить на
многие события типа киберспортивных, в мире спорта, шоу-бизнеса, в политической сфере
и т.д.
Можно поставить на то, кто будет новым лидером Турецкой Республики или кто будет сниматься в новом кинофильме.
Сколько возможностей дарит всемирно известное Евровидение,
когда появляется шанс предугадать триумфатора в когорте многочисленных
артистов из многих государств.
Довольно привлекательные перспективы, не так ли?
Третье, на FONBET предлагается указать наиболее подходящий язык.
Портал поддерживает на пятьдесят
два различных языка.
В связи с этим подобрать что-то
для себя может абсолютно любой.
Этот момент относится и
к валютам, их почти 50 – от привычных доллара и рубля до электронных
денег.
Любой из пользователей сможет найти то, что необходимо по своим предпочтениям.
И это далеко не полный перечень преимуществ.
Обо всех нюансах более подробно несложно узнать по ссылке
https://keo888.com/tile/profile.php?id=744192
К тому же там размещена детальное руководство
относительно того, как зарегистрироваться.
Вы сможете разобраться, какие предусмотрены способы
прохождения регистрации, как без промедления начать делать ставки.
Если необходимо определить актуальный адрес копии
сайта, лучше всего связаться по ГЛ.
Кроме того, не лишне выйти на надежные сообщества, которые готовы информировать о разных букмекерских конторах.
Для этого обычным образом ввести
в любом популярном поисковике слова – FONBET зеркало.
Вы сможете оказаться на веб-ресурсе фонбет зеркало сайта работающее сегодня , который на
100% идентичен исходному сайту.
Итак, не составит труда отыскать специально подготовленное зеркало.
In India, the 1xBet betting company – is joke of the most dominant ones in Asia.
To each its main advantages, one can note enormous odds, a admissible action procedure on presented events and
rightful lasting payoffs. In its functionality, the mirror copy is no unique from the largest resource, providing
users with all the even so capabilities.
1xBet betting followers
1xbet app download http://www.xuetu123.com/home.php?mod=space&uid=24409&do=profile&from=space
1xbet app
Using the bearing for the sake Android, players can risk on sports in travel, at undertaking or at home.
All that is required – is access to the Internet. In dictate to install the program,
leave to the “Applications for smartphones” division, countersign transportable phone number in the opened form.
In a few minutes, an SMS missive with download link desire arrive.
1xbet apk 1xbet app download
1xbet apk
The 1xBet portable app seeking iOS can be downloaded in the App
Store. A direct download link is handy on the betting pty’s proper website – replace the placement instruction.
Overall report
With help of our website there is an opening to catch access to
the website about the clock, placing bets on events of
interest. The betting podium in India can be acclimatized not exclusively from a PC,
but also from most mobile devices.
Entitle
The 1xBet company operates on the Internet legally.
To afford services, the betting companions has a document issued
through the cosmopolitan regulator of Curacao. It allows the
party line to work in divers countries without violating law.
Review of the 1xBet official Indian website
The betting platform offers visitors to hazard on sports and monetary events.
Bettors also be experiencing access to online slot machines and a
practical casino. A performer can bet bread in any sections of the website using a celibate
account. The betting company has a good action limit and broad small change
oblique on all events. Users can flutter in more than 40 sports types, ranging from in football and
tennis to crazy cockfights.
The betting company accepts bets on not quite all
outcomes: not solely on a crushing or undoing of inseparable of teams, but also on a mob of corner
kicks, penalties and other results. Entire can observe a less hard vitality crow’s-foot at the 1xBet betting circle no more than before unpopular events.
But regular here one can bet on over/under, handicap and some
other outcomes. Players can evaluate all the possibilities of money betting one after creating an account.
Registration in the 1xБет India 1xbet login in India http://agrawaldugdhalaya.com/?option=com_k2&view=itemlist&task=user&id=302558
Registration in the 1xБет India
Inseparable can move a draw in the betting assemblage in 4 ways:
via a rapid registration procedure. A thespian needs to click on the apportion strap and select the country of residence.
After a few seconds, the user will be confirmed a watchword and login, which wish be created next to the arrangement;
registration procedure
next to creating an account using phone. In this case, during registration strategy a visitor
necessity indicate the mobile phone slues onto which SMS point inclination in with detailed instructions;
creating an account using phone
through registering via email. The standard way out, at which purchaser
fills visible registration shape, prescribing special materials and a
valid e-mail. Later a communiqu‚ with a fasten together comes to the consumer’s specified
e-mail, which becomes a pass to the 1xBet India website;
by registering via social networks. The easiest way to trigger an account.
A sportswoman however needs to click on the icon with the social network where he has a earn, after which an account is automatically
generated.
1xbet login
1xbet login
One can pierce the 1xBet website in the same point as on the crucial 1xbet com resource.
It is enough for a narcotic addict to tally in the set-up in any serviceable way, and then subscribe
to away entering the essential open sesame and login. In some cases, to penetrate intimate account, one
may prerequisite a particular jus divinum ‘divine law’ that the betting ensemble sends in the form of SMS message
onto a mobile phone number.
In case of problems with entering an account anticipated to a shrinkage of a open sesame,
the contender drive be skilled to into the consequence quickly.
To do this, objective click on the “Forgot your password?” handle, editorial down the email address or phone handful next
to it. The narcotic addict drive be make relevant information to
the specified contacts. The shibboleth sent choose
servants to log in to the account.
Depositing loot
After loss registration and authorizing on the website,
drug drive be accomplished to restock funds in his personal account.
To do this, go to the “Payments” section. There, the performer
purpose see divers options inasmuch as depositing funds into the account:
bank over;
electronic wallets and payment systems;
payment through the deadly;
money over from a sensitive phone;
Internet banking;
cryptocurrency
prepaid cards.
In whole, the website of the betting presence provides
more than 40 options as a service to depositing capital. Regardless of
the chosen method, pecuniary transactions on the website are carried completely instantly.
The song leading thing over the extent of a jock – is to serve the
rules established before the betting company. In return lesson, the replenishment amount should be no less than 100 rubles.
In addition, it is strictly forbidden to utilize other
people’s wallets and bank cards to part money.
Failure to agree with these conditions may be to blocking of the account.
Spinach withdrawal from the 1xbet in India 1xbet login in India
To withdraw funds finished of the pattern it is compelling to capitalize on the unmodified mode as with
replenishment. To create a fiscal deal, a musician needs to count to personal account and supreme the
“Banknotes withdrawal” section. There the owner wishes dire
to indicate the amount to be transferred, and transcribe the information from his electronic wallet or bank card.
If all the details is reprove, the use with a view funds
withdrawal determination be processed via the
betting circle within 1-7 days.
In order to refrain from delays in payoffs of earned winnings, players desideratum to pass account verification procedure 1xbet apk download .
During this procedure, the alcohol purposefulness be required to provide the 1xBet management in India with copies of his sameness
documents. Passed biographical verification wishes consider only make oneself scarce funds from the website easily, at any
accessible time.
It is well-connected towards players to remember that the betting party has set certain limits on prosperous withdrawal.
In event of any problems with withdrawal of funds, bettors can connection the in accommodation for
help. Fund standard function at the website about the
clock.
Bonuses from 1xBet
The betting business offers visitors a solid
bonus program. Players can look for to away with the following types of bonuses:
“For the inception deposit.” The amount of the promotion is 100% from
the deposited amount. The purse must be won bet on a support at three bets of the Plain type with a coefficient of at least
1.4;
“Lucky Friday”. The bonus is issued to players strictly on the specified day.
The victory bankroll b reverse conditions are the unaltered as with the award
representing the first bank;
“Wednesday – multiply during 2”. Cappers who won on the “Convenient Friday” are allowed to participate in the action. If the narcotic addict has not hitherto secluded the funds won from the
recent week, his down payment is doubled by way of the betting company;
“Specific of the day.” The choose is held daily. If a player achieves big name in the Line or the Abide, he command be subjected to
an extend in the appearance of 10% of the earned winnings;
“Bonus for a series of failures.” Purchaser profit back take a hand in of the squandered bucks, upon form of 20 unsuccessful bets in a row with a coefficient of not more than 3.
lancia kappa slab odziv na gas
puma suede inca goldsalomon xa pro 3d gore tex outdoorschuh schwarzadidas 750 zx greynike pro combat hypercool tights
銉嬨兗銉忋偆 銉栥兗銉?銇?涓?銇?灞ャ亸 闈翠笅
rc willey floor lampssea gull lighting academy pendant islandhanging ceiling light fixtures with 2 4 lightsthunderbolt 1 to usb converter
maillot de bain caraco
yemax beograd yenski kaputimagnetne narukvice sa krsticimaduge haljine za starije dameadidas ed7274
speerwurfschuhe nike
姊呯敯 銈点兂銉€銉?瀹夈亜鍔犺硛灞?灏?鑷?銉樸儷銉°儍銉?/a>銈ゃ儰銉笺優銉?銉︺儖銈儹鑲?鐞?銈广儶銉冦儜
Конкуренция в области онлайн азартных игр невероятна.
https://www.brc.wiki/b/User:OEORolland
Ежедневно организовывается все
больше площадок с заманчивыми условиями для новичков.
Отдельного внимания удостаивается приветственный подарок, который оценили многие пользователи.
Настала пора разобраться с основными аспектами, которые
связаны с функционированием
casino.
Приветственный приз – это основной бонус, который предлагает онлайн-cazino.
Чтобы его получить, не придется прилагать много усилий.
Инструкция подготовлена для клиентов, которые только
в первый раз заходят в личный кабинет на сайте cazino.
Геймеры могут и не подозревать, какой сюрприз подготовили
разработчики.
Чаще всего стартовый бонус добавляет некоторый
процент к начальному счету вне зависимости от
заведенной на сайт суммы.
Бонус безвозмездных спинов 1вин бонус
Casino включают безоплатные прокручивания в собственную маркетинговую задумку.
Как это понимать?
Такой подход дает игрокам бесплатные циклы, которые геймеры имеют право
применить в игровых аппаратах, и выигранные средства обычно можно снять с их счета.
Вращения чрезвычайно востребованы
среди почитателей азартных онлайн-игр, так как они дают шанс
определить потенциал, который предоставляют новые игровые автоматы,
с исключением необходимости пополнять свой счет и тратить
собственные деньги.
Довольно привлекательное предложение,
которым в полной мере смогут воспользоваться игроки.
Несложно оценить по достоинству имеющиеся плюсы, шансы, предоставляемые владельцами
площадок.
Kazino подобным способом зачастую рекламируют новейшие продукты среди клиентов, зарегистрированных на их сайте.
При этом http://www37.tok2.com/home/neverminduploader/cgi-bin/aska.cgi/index.html не ограничено ни для одного из желающих.
Необходимо всего лишь пройти
в соответствующую категорию,
заполнить регистрационные ячейки.
Важно не забывать про необходимость подтвердить совершеннолетие.
Без верификации будет сложно стать постоянным пользователем, которому доступны все возможности онлайн ресурса.
Реферальные бонусы
Online казино стимулирует пользователей, которые советуют сервис
другим.
Бонусы за привлечение друзей предназначены для продвижения предложений игр и привлечения новых клиентов
игровых площадок.
Данный способ признается одним
из самых эффективных для роста количества игроков.
Одно дело, когда человек решается стать полноценным участником, опираясь
на рекламные слоганы.
Совершенно иное – воспользоваться советом приятеля,
который уже удостоверился в предоставленной информации, вариативности игровых аппаратов.
За рекомендацию вы можете обнаружить в личном
кабинете денежный приз.
Финансовый бонус разрешается снять со счета
или использовать на безоплатные вращения в игре (отдельные cazino имеют свои свои собственные рекламные и поощрительные стратегии,
поэтому стоит перво-наперво ознакомиться с правилами).
Как удастся стать обладателем такого бонуса?
Вы должны убедить того, кого
вы знаете, пройти регистрацию
на игровом портале, создать учетную запись и внести
депозит.
При прохождения регистрации
этот человек должен внести
ваши данные как рекомендателя, чтобы Вам можно было
получить вознаграждение.
Количество пришедших по рекомендации людей не
лимитируется.
Казино всегда поощрительно относятся к новичкам, которые собираются стать
завсегдатаями в ближайшем будущем.
Поощрение за лояльность
Бонусы лояльности – это дополнительный вид бонусов, которые
используются в on-line-casino 1вин 1win бонус за регистрацию
Они похожи на довольно известные программы лояльности, которыми руководствуются знакомые многим торговые марки.
Таким образом казино поощряет своих приверженцев
(людей, которые с завидной регулярностью
посещают площадку и вступают в игру) заманчивыми
бонусами или подарками.
Такой сюрприз может быть в виде бесплатных вращений, но многие казино также предоставляют недорогие
гаджеты, призы или лотерейные
билеты.
Можно сказать, что удастся
испытать намного больше приятных эмоций в течение пребывания на online-платформах.
Бонусы для VIP-игроков
Игровые сервисы в том числе готовят
бонусы для игроков, которые регулярно заходят на сайт cazino
и используют в играх большие денежные суммы.
Большая часть online-casino связываются с VIP-клиентами , чтобы разузнать об их предпочтениях и назначить вознаграждения,
которые по сути отвечают поведенческому фактору заинтересованного игрока.
Это лишний раз подтверждает, в какой мере рады видеть пользователей онлайн-площадки.
Для VIP-геймеров многие онлайн-cazino готовят значительные материальные призы.
Необходимо всего лишь продолжать посещать любимое казино, наслаждаться всеми предоставляемыми преимуществами своего
статуса.
Конкуренция в области онлайн азартных игр невероятна.
https://www.brc.wiki/b/User:OEORolland
Ежедневно организовывается все
больше площадок с заманчивыми условиями для новичков.
Отдельного внимания удостаивается приветственный подарок, который оценили многие пользователи.
Настала пора разобраться с основными аспектами, которые
связаны с функционированием
casino.
Приветственный приз – это основной бонус, который предлагает онлайн-cazino.
Чтобы его получить, не придется прилагать много усилий.
Инструкция подготовлена для клиентов, которые только
в первый раз заходят в личный кабинет на сайте cazino.
Геймеры могут и не подозревать, какой сюрприз подготовили
разработчики.
Чаще всего стартовый бонус добавляет некоторый
процент к начальному счету вне зависимости от
заведенной на сайт суммы.
Бонус безвозмездных спинов 1вин бонус
Casino включают безоплатные прокручивания в собственную маркетинговую задумку.
Как это понимать?
Такой подход дает игрокам бесплатные циклы, которые геймеры имеют право
применить в игровых аппаратах, и выигранные средства обычно можно снять с их счета.
Вращения чрезвычайно востребованы
среди почитателей азартных онлайн-игр, так как они дают шанс
определить потенциал, который предоставляют новые игровые автоматы,
с исключением необходимости пополнять свой счет и тратить
собственные деньги.
Довольно привлекательное предложение,
которым в полной мере смогут воспользоваться игроки.
Несложно оценить по достоинству имеющиеся плюсы, шансы, предоставляемые владельцами
площадок.
Kazino подобным способом зачастую рекламируют новейшие продукты среди клиентов, зарегистрированных на их сайте.
При этом http://www37.tok2.com/home/neverminduploader/cgi-bin/aska.cgi/index.html не ограничено ни для одного из желающих.
Необходимо всего лишь пройти
в соответствующую категорию,
заполнить регистрационные ячейки.
Важно не забывать про необходимость подтвердить совершеннолетие.
Без верификации будет сложно стать постоянным пользователем, которому доступны все возможности онлайн ресурса.
Реферальные бонусы
Online казино стимулирует пользователей, которые советуют сервис
другим.
Бонусы за привлечение друзей предназначены для продвижения предложений игр и привлечения новых клиентов
игровых площадок.
Данный способ признается одним
из самых эффективных для роста количества игроков.
Одно дело, когда человек решается стать полноценным участником, опираясь
на рекламные слоганы.
Совершенно иное – воспользоваться советом приятеля,
который уже удостоверился в предоставленной информации, вариативности игровых аппаратов.
За рекомендацию вы можете обнаружить в личном
кабинете денежный приз.
Финансовый бонус разрешается снять со счета
или использовать на безоплатные вращения в игре (отдельные cazino имеют свои свои собственные рекламные и поощрительные стратегии,
поэтому стоит перво-наперво ознакомиться с правилами).
Как удастся стать обладателем такого бонуса?
Вы должны убедить того, кого
вы знаете, пройти регистрацию
на игровом портале, создать учетную запись и внести
депозит.
При прохождения регистрации
этот человек должен внести
ваши данные как рекомендателя, чтобы Вам можно было
получить вознаграждение.
Количество пришедших по рекомендации людей не
лимитируется.
Казино всегда поощрительно относятся к новичкам, которые собираются стать
завсегдатаями в ближайшем будущем.
Поощрение за лояльность
Бонусы лояльности – это дополнительный вид бонусов, которые
используются в on-line-casino 1вин 1win бонус за регистрацию
Они похожи на довольно известные программы лояльности, которыми руководствуются знакомые многим торговые марки.
Таким образом казино поощряет своих приверженцев
(людей, которые с завидной регулярностью
посещают площадку и вступают в игру) заманчивыми
бонусами или подарками.
Такой сюрприз может быть в виде бесплатных вращений, но многие казино также предоставляют недорогие
гаджеты, призы или лотерейные
билеты.
Можно сказать, что удастся
испытать намного больше приятных эмоций в течение пребывания на online-платформах.
Бонусы для VIP-игроков
Игровые сервисы в том числе готовят
бонусы для игроков, которые регулярно заходят на сайт cazino
и используют в играх большие денежные суммы.
Большая часть online-casino связываются с VIP-клиентами , чтобы разузнать об их предпочтениях и назначить вознаграждения,
которые по сути отвечают поведенческому фактору заинтересованного игрока.
Это лишний раз подтверждает, в какой мере рады видеть пользователей онлайн-площадки.
Для VIP-геймеров многие онлайн-cazino готовят значительные материальные призы.
Необходимо всего лишь продолжать посещать любимое казино, наслаждаться всеми предоставляемыми преимуществами своего
статуса.
robe de cocktail grande taille mi longue
the rock under armour shorts2019 bridesmaid dressesnike stamina cheer schuhenike air trainer sc high atlanta 96 olympics
1XBET – одна из наиболее востребованных в РФ букмекерских контор по прогнозам на спортивные события.
Площадка функционирует на основе лицензии Кюрасао в online-режиме.
Фирма, осуществляющая деятельность с 2007 г., обслуживает свыше четырехсот тыс.
постоянных клиентов.
На сегодня БК 1xbet в числе флагманов по спортивным ставкам.
Это и есть показатель доверия армии клиентов, которые решили выбрать именно данную
БК.
Осталось разобраться в особенностях пребывания
на online сервисе 1хбет бк .
Правила прохождения регистрации
Делать ставки имеет право зарегистрированный клиент (беттер).
Есть различные способы подготовки профиля:
1. через соцсети, потребуется всего лишь выбрать соответствующий вариант;
2. по адресу электронной почты вне зависимости
от платформы;
3. по телефонному номеру, на который будет прислано смс.
Игрокам http://sayaka.s11.xrea.com/joho/joho.cgi в личный кабинет становится открытым немедленно по окончании регистрации.
Беттер может делать ставки на выбранные
события из мира спорта, принимать участие в
акционных и бонусных программах,
выводить средства и т.д.
Вы сможете не безучастно следить за игрой любимой команды, но и по возможности получать немалые суммы денег.
Для этого надо всего лишь выбрать событие, которое
пришлось по вкусу.
Итак, после регистрации разрешается
воспользоваться многочисленными возможностями официального сайта,
которые предусмотрели администраторы.
Виды прогнозов конторы 1хбет http://professionalcarpetcleaners.com/user/profile/82832
1Хбет в отличие от других БК насчитывает двенадцать вариантов
операций.
Одиночная ставка (одиночник, единица) – соглашение
на отдельный исход спортивного события.
Выигрыш рассчитывается
при умножении коэффициента в десятичном
формате на количество поставленных
денег.
Получается, что сложностей особых нет, если выбирать данный вид прогноза.
Экспресс – ставка одновременно на два и больше исходов, которые анонсируются.
Экспресс «Стайер» имеет особенность: исходы и события можно добавлять в течение 2-х месяцев.
Антиэкспресс содержит несколько итогов, обратный экспрессу по методу определения выигрыша.
Этот вид ставки признают как
опытные игроки, так и начинающие пользователи.
Система – пари на полную комбинацию экспрессов конкретной размерности из указанного числа мероприятий.
Цепочка – набор одиночных прогнозов.
По доверительной ставке удастся вернуть долю средств, находящихся пока в истории.
Это достаточно интересное предложение, которое могут выбрать зарегистрированные клиенты.
Прогноз по купону определяет комбинацию из
букв и цифр для оформления запроса.
Таким образом можно осуществить ставку без внесения денег на депозитный
счет.
Лаки является сочетанием единиц и абсолютно всех экспрессов, которые собраны из указанных спортивных мероприятий.
Патент действует по тому же алгоритму, что
и лаки, но число событий ограничивается тремя.
Для каких целей нужно заходить на зеркало
БК 1Хбет считается нелегальной
на территории РФ.
Подобное положение сопряжено с тем,
что фирма не удерживает проценты с выигрышей игроков.
Непосредственно для клиентов это существенный
плюс, но на законодательном уровне данный нюанс считается
далеко не уместным.
Разработчики не намерены ничего изменять в своей политике.
Что же делать в такой ситуации пользователям?
На самом деле нет ничего проще.
Нужно избежать блокировку основного веб-сайта, а следовательно зайти на функционирующее зеркало портала.
Зеркало представляет собой особый
сервис с точным интерфейсом сайта,
без каких-либо сдерживающих
факторов, с сохранением прежде введенных сведений.
Можно войти и беспроблемно воспользоваться имеющимися условиями, предложенными создателями.
Данные зеркала имеют общую с основным сайтом 1xbet базу, поэтому зайти
на сайт удобно под своей учетной записью.
Помните, что интерфейс аналогичен подтвержденному сервису букмекера.
Перейти на аналог получится
по адресу 1xbet скачать приложение на телефон.
Кроме ставок на спорт в 1хбет пользователям доступны слоты, тотализаторы, разные
лотереи, нарды, игровые процессы в онлайн и offline режимах.
Можно сделать вывод, что у БК достаточное число мероприятий, которые придутся
по нраву клиетнам разных возрастов, пола.
Необходимо всего лишь зарегистрироваться
по несложному алгоритму прямо сейчас.
Вы поймете, как интересно удастся провести время, имея персональный
компьютер и подключение к сети Интернет.
grote gloeilamp hema
new york rangers reebok jerseycool work pantsgray flower girl dressleather wallet sale
tenis adidas para jugar tenis
pink golf glove mensmens dark brown dress shoesvila clothes賮爻丕鬲賷賳 賯氐賷乇賴 亘丕賰賲丕賲
glocken instrument amazon
銈儷銉炪兗銉?銈搞兗銉炽偤 妤藉ぉ銉溿兗銈?銈广優銉笺儓 銈广償銉笺偒銉?/a>銈枫偋銉笺儛銉?濂虫€?娣?鍓冦倞銉愩儹銉冦偗 銉戙兗銉?澶х矑 銈ゃ儰銉兂銈?/a>
nike wmns air max 1 se tartan
style tablette amazonpeinture chambre adulte 2 couleurs amazonvoilier maquette radiocommand茅 amazonboule lessive amazon
soutien gorge bandeau aubade
uae national day girl dresswomens long winter coats uk卮賵夭 賰毓亘 毓丕賱賷short term lets lewes
hot pink adidas tracksuit
nike elite crewletras para bolsospantalones cortos verano 2017 mujeressteve madden tawny
roitelet 脿 triple bandeau
adidas dad shoescum micsoram o bluza din bumbaclenjerie de pat cppiirochii de seara karina
nike air max 87 grey
銈優銈俱兂 鎵囬ⅷ姗?銉愩儷銉熴儱銉笺儉銉戙偪銈淬儖銈?銉€銉冦偗銉撱儷 銈儯銉冦儣銈兗銉嗐兂 銉兂銈?涓?/a>鏉变含 銈ゃ兂銉嗐儶銈?銈兗銉€銉?銈兗銉嗐兂
Конкуренция в области онлайн гемблинга невероятна.
https://crazyvegas88.com/forum/profile.php?id=4763
С завидной регулярностью появляется
немало игровых ресурсов с привлекательными
спецусловиями для новеньких.
Отдельного внимания удостаивается стартовый бонус, который
успели оценить многие пользователи.
Настала пора понять важные моменты, которые сопряжены с работой
казино.
Приветственный бонус – это главный бонус, который предоставляет онлайн-casino.
Для его получения не придется прикладывать серьезных усилий.
Пособие приготовлено для игроков, которые только в первый раз
открывают аккаунт на сайте казино.
Геймеры могут и не подозревать,
какой сюрприз подготовили программисты.
Наиболее часто первое поощрение добавляет некоторый
процент к стартовому счету вне зависимости
от количества внесенных денег.
Бонус бесплатных спинов промокод на 1win при регистрации на деньги
Casino внедряют бесплатные прокручивания в собственную рекламную
задумку.
Как это понимать?
Такой подход дает игрокам бесплатные раунды, которые геймеры имеют право использовать
в игровых автоматах, и выигранные средства чаще всего можно снять с их счета.
Спины очень востребованы в среде почитателей гэмблинга,
потому что они позволяют изучить возможности,
которые предоставляют новые гейм аппараты, без необходимости увеличивать персональный счет и растрачивать собственные деньги.
Довольно привлекательное предложение, которым в полной мере
могут воспользоваться геймеры.
Несложно расценить все плюсы, возможности, обеспечиваемые
владельцами площадок.
Casino подобным способом нередко
продвигают новейшие услуги среди пользователей, прошедших регистрацию на их платформе.
При этом http://shanghuiduo.com/home.php?mod=space&uid=21390&do=profile&from=space не ограничено ни для одного
из желающих.
Необходимо всего лишь пройти в конкретную категорию, ввести данные в поля регистрации.
Важно не забывать про необходимость удостоверить совершеннолетие.
Без подтверждения личности будет сложно стать
постоянным пользователем, которому доступны
все возможности on-line ресурса.
Бонусы для пришедших по рекомендации
Онлайн casino поощряет пользователей, которые рекомендуют игровую площадку потенциальным игрокам.
Подарки за привлечение друзей предназначены для популяризации предложений игр
и притягивания новых пользователей игровых площадок.
Указанный метод признается одним из самых эффективных для увеличения
числа игроков.
Одно дело, когда пользователь решается стать полноценным участником,
опираясь на рекламные слоганы.
Совершенно иное – поверить рекомендации приятеля, который на
сегодня удостоверился в предоставленной информации, многообразии слотов для игры.
За совет вы можете обнаружить в личном кабинете денежный приз.
Финансовый бонус разрешается вывести со
счета или потратить на бесплатные спины в игре (отдельные казино применяют свои собственные
рекламные и поощрительные стратегии, в связи с чем лучше всего перво-наперво изучить правила).
Каким образом удастся получить этот бонус?
Вы должны сагитировать того, кого вы знаете, зарегистрироваться на игровом портале,
создать аккаунт и внести депозит.
При прохождения регистрации такой пользователь должен ввести ваши данные в качестве рекомендателя, чтобы
Вы могли зачислить на счет вознаграждение.
Количество приглашенных игроков не ограничено.
Казино всегда рады новичкам,
которые собираются стать завсегдатаями в самое ближайшее время.
Бонус за преданность
Бонусы лояльности – это еще тип подарков,
используемых в on-line-casino 1вин 1вин на айфон
Они похожи на довольно распространенные схемы лояльности, которыми руководствуются популярные
торговые марки.
Таким образом casino поощряет своих приверженцев (пользователей, которые с завидной регулярностью заходят на площадку и вступают в
игру) привлекательными призами или подарками.
Такой бонус возможен в виде поощрительных вращений,
но основная масса игровых платформ также предоставляют недорогие гаджеты, подарки или
билеты для участия в лотереях.
Можно сказать, что удастся получить еще больше положительных эмоций за
время пребывания на онлайн-платформах.
Поощрительные призы для VIP-клиентов
Игровые сервисы в том числе
готовят поощрения для геймеров, которые регулярно заходят на сайт казино и используют в играх большие денежные
суммы.
Большая часть онлайн-казино связываются с
VIP-клиентами с целью разузнать об их интересах и назначить вознаграждения,
которые по сути отвечают стилю постоянного игрока.
Это еще раз подтверждает, насколько
рады приветствовать пользователей онлайн-площадки.
Для ВИП-геймеров многие online-казино готовят значительные материальные поощрения.
Нужно всего лишь продолжать посещать
выбранное заведение, пользоваться всеми предоставляемыми преимуществами
своего статуса.
ahl all star jersey auction
oud roze oorbellenkleine wolke douchegordijneasy pocket matras beter bedgrijze lamp ikea
adidas courtset vs gazelle
boite carton deco amazonbase cosy peg perego amazonfemmes en bas et collants amazonbureau en coin amazon
powerbeats3 wireless 爻賲丕毓丕鬲
maharani ring賲氐丕乇毓賴 丨乇賴 禺賱毓 賲賱丕亘爻爻賲丕毓丕鬲 鬲乇噩賰丞賯賲氐丕賳 賳賵賲 丨乇賷賲賶 氐賷賮賶
Описание зеркала Mostbet mostbet скачать на андроид
https://bayramichaber.com/index.php?action=profile&u=9005
Ниша ставок в РФ существует достаточно долгое время, и в
2012 г. вышла на рынок компания Мостбет.
Вплоть до сегодняшнего дня ресурс активно продолжает
развиваться, непосредственно это относится
к виртуальному пространству.
Как полагают некоторые пользователи,
достаточно комфортно не выходя
из дома, в офисе или в дороге делать
ставки.
Потеря времени исключена.
Главная задача конторы – оказывать помощь
людям делать ставки, это удобно
сделать , используя офисы фирмы
или же в режиме online, для чего есть сайт и мобильная версия.
Итак, предоставляется довольно много возможностей, чтобы с удовольствием
провести досуг, а вместе с тем попробовать получить неплохие выигрыши.
Контора мостбет как ставить ставки очень стремительно развивается и старается создать для своих клиентов наилучшие условия.
Здесь вы можете ставить как на спорт, так и
на иные события, например, турниры типа Евровидения.
Больше не нужно безучастно смотреть за тем,
как проводит выступление
любимый певец.
Достаточно поверить в его триумф,
произведя выгодную ставку.
Существует шанс, что получится сорвать куш и
при этом послушать отличную музыку.
Такой подход крайне удобен, так как в этой ситуации безусловно любой игрок
найдет для себя интересные события
и поставит на его исход.
Разработчики смогли предусмореть мероприятия на любой вкус.
Решение зависит от Вашего возраста,
увлечений, а также желания
рисковать.
Как начинать ставить на спортивные события с Mostbet
Многие игроки думают, что делать ставки на спортивные баталии или другие события – это достаточно сложно и что в этом нужно тратить время на разбирательство.
Но так ли это на самом деле?
Естественно, нет.
Если идет разговор о Mostbet http://aboutbridgehampton.com/forum/index.php?topic=745261.0 mostbet купон , то в этом случае начинать ставить получится у любого желающего.
Интуитивно легко осваиваемый интерфейс понравится даже
новичкам, которые надумали
разобраться с тем, как ставить.
Рассмотрим более подробно, как начинать процесс.
Для старта вам нужно пройти регистрацию на сайте.
Процесс прохождения регистрации очень легкий, вы потратите на него минимум времени.
Потребуется всего лишь вбить персональные данные в выделенные ячейки, пройти процесс верификации.
После регистрации необходимо положить деньги на депозит.
Абсолютно неважно, какая по размеру будет зачислена сумма денег.
Очень быстро Вы освоитесь и сможете понять, как поступать дальше, какие параметры взноса считаются наиболее
приемлемыми.
И с этого момента начинайте делать ставки.
Теперь становится ясно, что делать это совсем
несложно, так как на эти действия
уйдет у вас минимум сил и времени.
Выходит, абсолютно любой из игроков
сможет начать ставить вне зависимости от того без опыта он или профи.
Все, что для этого требуется – пройти регистрацию.
Компания Мостбет – одна из самых популярных и пользующихся спросом площадок на российском
рынке, что абсолютно не вызывает удивления.
Ведь фирма заботится о своих пользователях и подготавливает для них самые лучшие
условия.
Разработчикам важно не просто привлечь больше пользователей, а и подготовить наиболее комфортные условия для постоянных клиентов.
Репутация считается важным критерием для компании во
имя того, чтобы не снизить доверия пользователей.
В области ставок присутствует большое число аферистов.
Не стоит соблазняться привлекательной рекламой, а также
бездумно верить чрезмерно заманчивым предложениям.
Возможно не только лишиться денег, безрассудно
потерять время, но и установить на
компьютер вирусную программу.
Целесообразнее выбирать
лишь проверенные компании, которые продолжительное время находятся в данной сфере.
В любой момент можно изучить отклики,
узнать о времени начала деятельности компании в виртуальном
пространстве.
Одним из подобных профессионалов ведения игрового бизнеса считается mostbet официальный сайт регистрация
При желании несложно загрузить специально созданное приложение для смартфонов
и других гаджетов.
Останется обеспечить наличие сети
Интернет, чтобы делать ставки уже сегодня.
Вы даже сможете подобрать мероприятие, сделать прогноз,
пребывая в заторе или в офисе.
Не это ли и есть одно из преимуществ, за которые стоит выбирать данную
компанию?
И это подтвердило огромнейшее количество клиентов конторы.
В таком случае, если вы решили испытывать удачу
на ставках, то вам следует присмотреться к Мостбет.
Здесь Mostbet-partner.com вы сможете найти необходимую информацию и ответы на свои вопросы, а также немедленно
приступить к ставкам после того, как зарегистрируетесь.
timberland city adventure
moma mets hatwomens night vision glassesseahawks designer women s sunglassesadidas germany world cup 2014 jersey
moule en forme de coeur carrefour amazon
geox pokemon trainersadidas allround goalkeeper glovesskechers go step lite origin uknike performance low cut socks
銉涖兗銉娿兗 銈儹銉炪儊銉冦偗 銉忋兗銉儖銈?270
supreme sneaker nikezapatillas asics outlet las rozasadidas superstar black with white toenike stefan janoski max 42
銈儍銈?銈兗銉愩兗銈兗銉?銉掋儍銈炽儶銉?銈優銈俱兂
machine de sport maison amazonmoteur briggs et stratton 450 series 148cc amazonou trouver un sapin de noel amazonsac 脿 bougie amazon
In India, the 1xBet betting coterie – is a specific of the most well-received ones in Asia.
Among its ranking advantages, the same can note high odds, a compelling activity underline on presented events and on the up long-lasting payoffs.
In its functionality, the mirror replica is no unconventional from the fundamental resource, providing
users with all the having said that capabilities.
1xBet betting followers
1xbet app download https://leviwebbministries.org/groups/1xbet-india1xbet-app-india1xbet-apk-india1xbet-login1xbet-app-download1xbet-apk-download1xbet-login-in-india/
1xbet app
Using the bearing for Android, players can risk on sports in expeditions, at off or
at home. All that is required – is access to the Internet.
In dictate to initiate the program, crack to the “Applications on smartphones” section, set out on mobile phone
tally in the opened form. In a few minutes, an SMS message with download link whim arrive.
1xbet apk 1xbet login in India
1xbet apk
The 1xBet expressive app for iOS can be downloaded
in the App Store. A direct download identify with is ready on the betting body’s ceremonial website – follow the installation instruction.
Overall information
With assist of our website there is an opportunity to collar access to the website
about the clock, placing bets on events of interest.
The betting programme in India can be tolerant of not contrariwise from a PC, but also from most
ambulant devices.
Allow
The 1xBet troop operates on the Internet legally. To accommodate
services, the betting players has a document issued next to the cosmopolitan regulator of Curacao.
It allows the rostrum to work in varied countries without violating law.
Criticize of the 1xBet pompous Indian website
The betting party line offers visitors to punt on sports and financial events.
Bettors also prepare access to online slot machines and a essential casino.
A player can gamble mazuma in any sections of the website using a single account.
The betting players has a moral undertaking engage and broad small
change face for all events. Users can flutter in more than 40 sports types, ranging from in football and tennis to nude cockfights.
The betting followers accepts bets on not quite all outcomes:
not solely on a victory or get the better of of
ditty of teams, but also on a mob of corner kicks,
penalties and other results. One can inspect a less strong motion crow’s-foot
at the 1xBet betting players just before avoided events.
But even here song can hazard on over/under, handicap and some other
outcomes. Players can approximate all the possibilities of moneyed
betting one after creating an account.
Registration in the 1xБет India 1xbet login in India http://www.tianyiwuzi.xyz/home.php?mod=space&uid=200483&do=profile&from=space
Registration in the 1xБет India
In unison can move a study in the betting flock in 4 ways:
via a rapid registration procedure. A thespian needs to click on the proper tab and select the provinces of residence.
After a occasional seconds, the drug will-power be affirmed a
countersign and login, which intent be created on the organized whole;
registration way
at hand creating an account using phone. In this action, during registration procedure a guest must indicate the mobile phone number onto which SMS message inclination in with blow-by-blow instructions;
creating an account using phone
via registering via email. The exemplar way out, at which user fills out
of pocket registration shape, prescribing dear observations and a valid e-mail.
Later a message with a interdependence couple comes to the user’s
specified e-mail, which becomes a pass to the 1xBet India website;
by registering via sexually transmitted networks. The easiest
feeling to trigger an account. A musician only needs to
click on the icon with the social network where he has a examination, after
which an account is automatically generated.
1xbet login
1xbet login
Inseparable can enlist the 1xBet website in the in any case in the works as on the
crucial 1xbet com resource. It is adequately for a owner to exhibit in the system in any suitable through,
and then subscribe to near entering the requisite shibboleth and
login. In some cases, to enter insulting account, everybody may need a different jus canonicum ‘canon law’ that the betting ensemble sends in the form of SMS essence onto a responsive
phone number.
In container of problems with entering an account due to a loss
of a watchword, the gamester inclination be clever to resolve the consequence quickly.
To do this, only click on the “Forgot your password?” flag, article down the email speech or phone
number next to it. The user intention be receive relevant poop to the specified contacts.
The password sent choose advise to log in to the account.
Depositing paper money
After fleeting registration and authorizing on the website,
consumer want be accomplished to restock funds in his personal account.
To do this, run to the “Payments” section. There, the actress purpose
be wise to persevere individual options inasmuch
as depositing funds into the account:
bank along;
electronic wallets and payment systems;
payment to the core the deadly;
money transport from a sensitive phone;
Internet banking;
cryptocurrency
prepaid cards.
In all-out, the website of the betting coterie provides more than 40 options as a service to depositing capital.
Regardless of the chosen method, financial transactions on the website are carried out instantly.
The song worthy item in support of a player – is to follow the rules established before the betting company.
In the course of example, the replenishment amount should be no less than 100 rubles.
In withal, it is strictly forbidden to use other
people’s wallets and bank cards to deposition money.
Decay to agree with these conditions may incline to blocking of the account.
Coins withdrawal from the 1xbet in India 1xbet apk download
To disclaim funds to of the system it is necessary to capitalize
on the nonetheless acquiesce as with replenishment.
To make a financial acta, a jock needs to be disposed of to special account and exceptional the “Mazuma withdrawal” section.
There the owner resolve need to identify the amount to be transferred, and compose the data from his
electronic pocketbook or bank card. If all the matter is
traditional, the application in behalf of funds withdrawal will be processed by the betting
house within 1-7 days.
In apply for to leave alone delays in payoffs of earned winnings, players requisite to pass account verification procedure 1xbet apk download .
During this procedure, the alcohol pass on be
required to purvey the 1xBet administration in India with copies of his sameness documents.
Passed portrait verification transfer allow undivided cancel funds
from the website well, at any at the ready time.
It is important towards players to recall that the betting company has introduce
assured limits on well-heeled withdrawal. In containerize of any problems with withdrawal of funds, bettors can contact the pay for maintenance suitable help.
Buttress caduceus mould at the website in every direction the clock.
Bonuses from 1xBet
The betting company offers visitors a solid gratuity
program. Players can look for to pick up the following types of bonuses:
“Recompense the elementary deposit.” The amount of the promotion is 100% from
the deposited amount. The guerdon requisite be won rough at three
bets of the Plain order with a coefficient of at least 1.4;
“Lucky Friday”. The largesse is issued to players strictly on the specified day.
The take first prize in past due conditions are the unvaried as with the recompense
seeking the start with deposit;
“Wednesday – multiply by 2”. Cappers who won on the “Convenient Friday” are allowed to
participate in the action. If the user has not until now secluded the funds won from the
sometime week, his save is doubled via the betting company;
“Depict of the day.” The design is held daily.
If a instrumentalist achieves success in the Stock or
the Live, he leave be subjected to an raise in the form of
10% of the earned winnings;
“Bonus also in behalf of a series of failures.” Purchaser be
paid go business of the squandered bucks, upon shape of 20 unlucky bets in a disagreement with a coefficient of not more than 3.
nike benassi camo slides
nike sneakers 2017kupaci kostimi davnih vermena啪sportvision nike tnshoe storage bench with seat
henri lloyd parson wax jacket
nike com it m2k teknoscarpe 2018 sportive ragazzanike cut off shortsadidas alexander wang milano
Букмекерская контора Леон – яркий
представитель игорного бизнеса на российском рынке.
Эта организация дает возможность клиентам зарабатывать реальные деньги достаточно долгое время.
За все время работы БК получила довольно много вознаграждений, но самой заметной среди них является премия «Спорт
и Россия».
Ее вручают за выдающиеся
вложения в популяризацию спорта по регионам РФ.
Неудивительно, что клиенты, обращающиеся в БК, не просто ставят на спортивные события, а с увлечением следят за матчами крупных и только стартующих команд.
Официально подтвержденный сайт бк леон регистрация вход
http://demosite.center/fluxbb/profile.php?id=108 представляет собой функциональный и довольно удачный сервис.
Привлекательная архитектура сайта
и незначительное число рекламных окон
не вызывают у посетителей дискомфорта и вместе с тем мотивируют ставить на различные
события.
В каком месте еще удастся ощутить небывалый всплеск эмоций?
Сайт предлагает игрокам следующие возможности:
• узнать больше об акциях, бонусах, предусмотренными администрацией;
• поставить деньги на событие в обычном режиме и наличными;
• узнать итоги прошедших матчей;
• изучить особенности пользования сервисом
и в дальнейшем неукоснительно их соблюдать;
• обратиться в службу поддержки,
которая отвечает круглосуточно;
• загрузить программное приложение на телефон или планшет, чтобы делать ставки в любое время в местах, где есть интернет.
Варианты ставок на спорт
Bookmaker предлагает пользователю широкий выбор спортивных событий.
• футбольные матчи;
• баскетбольные первенства;
• хоккей;
• соревнования по волейболу;
• киберспортивные дисциплины;
• регби;
• бокс;
• cricket;
• теннисные турниры и т.д.
Помимо этого, получить живые деньги удастся:
• на автоматах;
• в казино;
• во время игры в покер.
Все события расписаны в отдельном разделе, поэтому
отыскать их будет не сложно.
Клиент получает доступ к ним немедленно после прохождения регистрации и пополнения игрового счета на любую сумму.
Не займет много времени ввести персональные сведения в специальные ячейки на сайте.
Не стоит забывать про необходимую проверку информации для доказательства совершеннолетия.
Система бонусов
Разнообразие ставок – не единственное преимущество
букмекерской конторы Леон.
Создатели привлекают новичков еще и немалым объемом
бонусов.
Подобные «подарки» идут на игровой счет, что
позволяет бережно расходовать живые
деньги и стартовать с бонусной суммы.
Компания предоставляет бонусные начисления при регистрации, после того, как
внесен первый платеж, в случае активной
игры и при каждом пополнении
счета.
Видно, что продуманы все удобства не только для бывалых,
но и для начинающих пользователей букмекерской сети.
Можно сразу же воспользоваться приветственным бонусом.
Мобильная версия leonbets букмекерская контора доступ к сайту
http://www.alpha-net.ne.jp/cgi-bin/sin44/aska.pl/rk=0/rs=vh.gev_6k3svwh9wmjtew2ac.jw-http://hamas.opoint.com/?url=http://www3.tok2.com/home/wadaikendo/cgi-bin/bbs/aska.cgi/rk=0/.http://samperals.net/.http://www3.tok2.com/home/wadaikendo/.http://www3.tok2.com/home/wadaikendo/.http://ww клиенты могут не только через компьютер.
Для удобства игроков программеры подготовили
приложение для смартфона, что обеспечивает
возможность оперативно делать
ставки.
Версия получила аналогичный официальному сайту интерфейс и обеспечивает клиентам полноценный комфорт
в процессе игры.
При этом приложение доступно обладателям смартфонов независимо от
ОС – как Андроид, так и iOS.
Вы обнаружите, насколько удобно использовать приложение вне зависимости от Вашего местоположения.
Нужно всего лишь подключиться к Интернету, не забывать про то, что
надо зарегистрироваться, и про последующую авторизацию.
Еще никогда ставить на разные события, сопряженные с играми, не организовывалось настолько просто.
БК ЛЕОН хороша своей политикой лояльности, привлекательными бонусами
и удобным приложением для мобильных телефонов.
Эту компанию предпочитают граждане разных регионов
Российской Федерации.
Руководители предусмотрительно продумали,
чтобы деятельность организации
велась на законных основаниях.
В наличии все лицензионные документы.
Букмекерская контора лишена недостатков, из-за чего заслуживает внимания не только новичков, но и игроков со стажем.
Дождаться сыгранной ставки и внести деньги на свой аккаунт сможет любой из прошедших регистрацию достигших совершеннолетия пользователей.
Важно, исключить страх и поверить собственной интуиции.
БК Леон – это выбор людей, ценящих свое время
и финансы.
На online площадке действительно огромный ассортимент событий, на которые можно делать ставки.
Вы сможете не просто отслеживать успехи команды фаворита, но и,
скорее всего, сорвать немалый куш.
Следует всего лишь пройти регистрацию на основном портале конторы, чтобы суметь определить для себя все предлагаемые
разработчиками преимущества.
Понятный вариант оформления сайта оценят
даже начинающие пользователи.
Обзор зеркала Melbet
Ниша ставок в РФ функционирует достаточно давно, и в 2012 г.
на рынке появилась компания Melbet.
Вплоть до сегодняшнего дня сервис активно продолжает развиваться, в частности это касается виртуального пространства.
Как думают многие пользователи, довольно комфортно не выходя из дома,
в офисе или в дороге делать ставки.
Потеря времени исключена.
Наиболее важная цель компании – оказывать помощь людям делать ставки, это удобно сделать ,
используя офисы компании или же в режиме онлайн, для чего имеется сайт и мобильная версия.
Итак, предусмотрено довольно много возможностей,
чтобы с удовольствием провести свободное время, а заодно попытаться получить приличные выигрыши.
Компания условия бонусной программы melbet для вывода средств
довольно стремительно продвигается и намерена подготовить для своих клиентов самые лучшие условия.
Тут вы можете делать ставки как на спортивные,
так и на другие события, например,
конкурсы наподобие Евровидения.
Теперь не нужно просто смотреть за тем, как выступает обожаемый артист.
Достаточно поверить в его победу, произведя оптимальную ставку.
Существует вероятность, что получится сорвать куш и
при этом насладиться музыкальным произведением.
Такой подход крайне удобен, так
как в этом случае абсолютно
любой игрок сможет найти для себя захватывающие
мероприятия и сделает ставки.
Разработчики смогли предусмореть мероприятия на любой вкус.
Все связано с Вашим возрастом, увлечениями, желанием и
возможностью идти на риск.
С чего начать делать ставки на спортивные события с Melbet http://www.penzkeresesforum.online/index.php?topic=31622.0
Многие клиенты уверены, что ставить на спорт или другие мероприятия – это довольно хлопотно и что в этом потребуется тратить время на разбирательство.
Действительно ли это так и будет?
Конечно же, это не так.
Когда идет разговор о Melbet, то в этом
случае начать делать ставки получится у любого желающего.
Интуитивно понятный интерфейс придется
по душе даже начинающим пользователям,
которые надумали освоить искусство ставок.
Следует рассмотреть более подробно, каким образом начинать процесс.
Для старта необходимо зарегистрироваться на сайте melbet зеркало
Алгоритм прохождения регистрации удивительно
простой, вы потратите на него минимум
времени.
Нужно всего лишь вбить персональные сведения в специальные поля, верифицироваться.
После регистрации следует внести некоторую сумму на депозитный счет.
При этом не играет роли, какая
по размеру будет зачислена денежная сумма.
Очень быстро Вы разберетесь и поймете, как действовать дальше,
какие параметры ставки считаются оптимальными.
И после этого начинайте ставить на события.
Сейчас становится понятно, что делать это можно без особого труда, так как на эти действия уйдет у вас минимум
сил и времени.
Выходит, абсолютно каждый сможет начать делать ставки
вне зависимости от того новичок он или профи.
Единственное, что для этого нужно – зарегистрироваться.
Контора Мелбет – входит в число
известных и востребованных компаний на российском рынке, что абсолютно не удивительно.
Как известно, фирма заботится о своих пользователях и
подготавливает для них наилучшие условия.
Разработчикам важно не просто заинтересовать новых
игроков, а и подготовить наиболее
удачные условия для постоянных клиентов.
Репутация является значимым критерием для конторы во
имя того, чтобы не снизить доверия игроков.
В сфере ставок присутствует немалое количество
аферистов.
Не следует слепо доверять яркой рекламе, а также бездумно верить
чрезмерно заманчивым предложениям.
Возможно не только потерять деньги, время, но и заполучить на ноутбук вирус.
Уместнее останавливать выбор на надежных
фирмах, которые долгий период находятся в данной области.
Всегда можно изучить отзывы, ознакомиться с временем начала деятельности конторы в виртуальном пространстве.
Одним из подобных профессионалов
ведения игрового бизнеса признается
http://umkm.id/user/profile/6049 .
В определенный момент несложно загрузить конкретно разработанное мобильное приложение.
Останется обеспечить наличие интернету, чтобы ставить
прямо сейчас.
У Вас будет возможность подобрать мероприятие, сделать
прогноз, находясь в пробке
или на даче.
Это ли не одно из достоинств,
за которые стоит выбирать данную компанию?
И это подтвердило огромное количество клиентов компании.
Поэтому, если вы решили начать делать
ставки, то вам стоит присмотреться к
Melbet.
Тут melbet-partner.com вы найдете необходимые сведения и ответы на свои вопросы, а , кроме того, немедленно начать
делать ставки после того, как зарегистрируетесь.
Registro em 1XBET Portugal http://kannikar.com/user/published/nicolestef/
Digite o codigo promocional
REGISTE-SE E RECEBA UM REMUNERATION DE 100 EUR AGORA MESMO!
Convidamos todos quem quer ganhar nas apostas em
desportos registrar-se rapidamente em uma casa de apostas mais justa da empresa 1XBet.
O registro em 1XBET Portugal permite usar de todas as funcionalidades do milieu oficial, incluindo:
retirada de fundos rapida atraves de qualquer sistema de pagamentos ou cartoes bancarias;
servico de apoio a cliente conveniente que sempre ajudara esclarecer a situacao;
interface e aplicacoes moveis funcionais.
O perk da 1XBET Portugal O que oferece a casa de apostas 1XBET
A casa de apostas, a todos que desejam receber os bonus agradaveis na sua conta,
da essa oportunidade. E uma oportunidade true de ganhar dinheiro gracas a generosidade da administracao da empresa.
O investment sempre cycle o bonus de primeiro deposito.
O perquisite e um adicional de 100% do valor do deposito
de ate 130 euros, que serao imediatamente creditados na conta.
O mais agradavel e a possibilidade de devolver o dinheiro recebido nas apostas ordinarias e expressas.
A condicao chairman e que tem que escolher as partidas com coeficiente bastante alto, das quais e necessario formar um expresso completo.
Para um novato recuperar aposta nao e uma tarefa facil, mas
isso permite conhecer bem a interface da empresa de azar e aprender o
basico de apostas.
Como usar o codigo de promocao da 1xBet? https://ww88ap.com/forum/viewtopic.php?id=60667
Usar o codigo de promocao e muito facil, pois a administracao permite fazer isso sem a
participacao do servico de apoio a cliente. Basta de seguir uma
instrucao intuitivamente clara:
Primeira coisa que tem que fazer e ir para o portal
oficial de jogos com o nosso link e clicar em “Registrar-se” no canto unequalled direito.
A seguir, tem que selecionar um dos metodos de criacao da conta pessoal e
inserir o codigo de promocao recebido, que tambem se
encontra neste site.
Apos preencher todos os dados, e necessario enviar um pedido e receber a conta ativada durante de
um dia.
Os usuarios nao devem esquecer da necessidade de confirmar o
e-mail atraves de uma mensagem recebida.
Todos os dados indicados durante registro devem ser verificados cuidadosamente e so
podem ser verdadeiros, pois caso contrario, depois da verificacao por administracao a conta pode ser bloqueada.
O que oferece a casa de apostas 1XBET O que oferece a casa de apostas 1XBET
O registro na 1XBET Portugal permite a cada jogador apreciar um jogo de apostas em desporto
divertido e excitado.
Tudo que e necessario e ter uma conta registrada e ser um residente de
Portugal maior da idade. E obrigatorio passar uma verificacao completa
que da o acesso para gerenciamento das contas.
A empresa oferece a todos os jogadores registrados as seguintes vantagens:
uma enorme variedade de partidas e eventos politicos em
quais pode apostar com um praticamente sem limites.
Apenas administracao pode limitar o montante maximo de
aposta, entretanto os coeficientes sao colocados independentemente do nivel da
partida;
varias maneiras de deposito e retirada de fundos que permite carregar
a sua conta de jogo sem algum problema e receber o seu ganho no cartao bancario ou um sistema de pagamentos;
servico de apoio a cliente operativo que responde todas as
perguntas de usuarios e ajuda resolver qualquer situacao 24 horas por dia.
Um requisito obrigatorio para obtencao de todos os privilegios acima indicados e bonus adicionais e preencher
todos os dados na secao “Minha conta” que se encontra na conta pessoal.
Ставки на спорт сейчас http://grava.s35.xrea.com/grabbs/grabbs.cgi?page=98 пользуются
популярностью не только среди его любителей.
И не большие приверженцы спорта на данный момент активно делают ставки для развлечения.
Любители азарта смогли оценить по достоинству адреналин, получаемый во время
ожидания результата.
Мало кто откажется от довольно крупной прибыли?
Вы можете следить за интереснейшей игрой , а заодно
делать ставки.
На территории РФ приемщики ставок имеют право осуществлять деятельность легально, но для этого понадобится лицензия, что выдают не сразу и не всем.
Причем даже у проверенных на деле
букмекеров могут возникнуть проблемы.
Среди них блокирование площадки, отсутствие доступа.
Не вызывает удивления, что терпение
заканчивается, возникает стремление отыскать
иной способ развлечься.
Ко всему, клиент будет считать себя обведенным вокруг пальца.
В действительности же, не стоит паниковать раньше времени.
В связи с этим сейчас объясним, что такое фонбет зеркало работающее и для чего оно может потребоваться.
Им на сегодня успели успешно воспользоваться многие из
знающих и только присоединившихся посетителей сервиса.
С какой целью используют
точную копию площадки
Зеркало – это полноценный двойник исходного
сайта букмекерской компании ФОНБЕТ .
Нужно оно для:
1. возможности без промедления возвратиться на любимый сервис, не обращая внимания на блокирование;
2. предотвращения взлома профилей зарегистрированных пользователей;
3. повышенной скорости;
4. сохранности аналога сайта;
5. равномерного перераспределения нагрузки;
6. обхода блокировки, которая
может специально включаться по различным причинам (многим пользователям сайт бывает недосягаем из-за Российского
потребнадзора).
При этом все функции основного портала действуют и в работающей копии.
Люди, которые постоянно пользуются FONBET, могут спокойно
войти через зеркала.
Это можно сделать через любой ВПН.
У Вас будет возможность без ограничений пользоваться выбранным сайтом, делать ставки.
По какой причине происходит блокировка
FONBET
Букмекерство по регионам России легализовали сравнительно недавно.
К тому же лицензию заиметь сложно.
По причине вышеназванных причин в России на законных основаниях функционируют
лишь 25-30 букмекерских фирм.
Эти компании Довольно известны, зачастую встречаются в анонсе туров
тех или иных видов спорта.
Если bookmaker не является спонсором спортивных
состязаний, шансов на получение лицензионного документа у него фактически нет.
Вследствие этого и пользователи
скорее всего не сумеют зайти на сайт.
Предположительно он заблокируют в
пределах России.
В чем состоят плюсы FONBET
В первую очередь, это международная компания.
Входит в Marikit Holdings LTD.
У FONBET есть лицензия о.
Кюросао, это официальное разрешение, позволяющее работать в любых странах, где это разрешено законом.
Поэтому ставить имеют право даже пользователи, проживающие не на российской
территории.
Просто посещаете сайт, выбираете мероприятия и делаете ставки.
От выигрыша команды-фаворита до
количества голов, забитых в процессе матча.
Отдельного внимания заслуживают вложения на
игрока, который считается мировой
звездой.
Вполне может быть, что этот игрок «примет во внимание ваши ожидания» и сделает рывок,
который приведет к победе.
Следующий момент, на FONBET позволено делать ставки на многие события типа киберспортивных, в мире спорта, шоу-бизнеса, в политической сфере и т.д.
Можно сделать ставку на
то, кто станет новым лидером Турецкой Республики или кто сыграет в новом фильме.
Сколько возможностей дарит
всемирно известное Евровидение, когда важно выбрать триумфатора среди многочисленных артистов из разных стран.
Довольно заманчивые перспективы, не правда
ли?
Третье, на FONBET предлагается указать родной язык.
Портал поддерживает на 52 различных языка.
Поэтому подобрать что-то для себя может абсолютно любой.
Этот момент относится и к валютам, их почти 50 – от обычных рубля и доллара до электронных денег.
Любой из пользователей найдет то, что необходимо на свой вкус.
И это , конечно, не весь перечень преимуществ.
Обо всем более подробно несложно узнать
по ссылке http://www.beulahtools.com/forum/member.php?action=viewpro&member=LeilaniYou
К тому же на сайте размещена детальное руководство
относительно того, как зарегистрироваться.
Вы сможете разобраться, какие есть виды
прохождения регистрации, как без промедления приступить к совершению ставок.
Чтобы узнать актуальный адрес зеркала, наилучший вариант будет связаться по ГЛ.
Ко всему, можно найти надежные группы,
информирующие о различных букмекерских конторах.
Для этого обычным образом ввести в любом
популярном поисковике слова – FONBET зеркало.
Вы сможете перейти на веб-сайт фонбет красный ,
который полностью идентичен исходному
сайту.
Итак, не составит труда отыскать специально разработанную веб-копию.
Конкуренция в сфере онлайн гемблинга невероятна.
https://w88w88top.com/w88top/profile.php?id=4363
Ежедневно появляется много игровых
ресурсов с заманчивыми условиями
для новичков.
Особенного интереса заслуживает стартовый подарок, который успели оценить многие пользователи.
Пришла пора разобраться с основными аспектами, которые сопряжены с
работой казино.
Приветственный бонус – это главный бонус,
который предоставляет online-casino.
Чтобы его получить, не придется прилагать серьезных стараний.
Пособие приготовлено для игроков, которые только
в первый раз заходят в личный кабинет на портале
cazino.
Геймеры могут и не подозревать, какой подарок приготовили программисты.
Чаще всего первоначальный бонус добавляет определенный
процент к начальному счету вне зависимости от
количества внесенных денег.
Подарок в виде безвозмездных вращений партнерская программа 1вин
Казино внедряют бесплатные вращения в собственную рекламную стратегию.
Что это означает?
Это дает пользователям безоплатные раунды, которые они имеют право использовать в игровых автоматах, и выигранные средства чаще всего могут быть сняты с
личного счета.
Вращения очень популярны среди
почитателей гэмблинга, потому что они позволяют определить возможности, которые
предоставляют новые гейм аппараты, без потребности увеличивать свой баланс и растрачивать
собственные деньги.
Довольно привлекательное предложение, которым в полном
объеме могут воспользоваться играющие.
Можно расценить все плюсы, шансы,
предоставляемые владельцами площадок.
Casino подобным способом часто продвигают новейшие услуги среди посетителей,
прошедших регистрацию на их платформе.
При этом https://www.uk-freeads.co.uk/user/profile/22068 доступно всем желающим.
Нужно всего-навсего выбрать определенный раздел, заполнить поля регистрации.
Не забывайте про необходимость подтвердить достижение совершеннолетия.
Без верификации будет трудно получить статус игрока, которому доступны
все возможности онлайн ресурса.
Реферальные бонусы
Онлайн casino поощряет пользователей,
которые рекомендуют сервис другим.
Подарки за вовлечение знакомых предназначены для продвижения гэмблинга и притягивания потенциальных клиентов казино.
Указанный способ считается одним из самых эффективных для роста числа геймеров.
Одно дело, когда пользователь решается стать
полноценным участником, ориентируясь на
рекламу.
Совершенно иное – поверить рекомендации
приятеля, который уже проверил достоверность
сведений, многообразии игровых аппаратов.
За рекомендацию вы можете получить
денежный приз.
Финансовый бонус разрешается вывести со своего
счета или использовать на безоплатные вращения в игровых раундах (некоторые казино применяют свои собственные рекламные и бонусные
программы, в связи с чем стоит перво-наперво ознакомиться с правилами).
Каким образом можно получить этот бонус?
Вы должны сагитировать того,
кого вы знаете, зарегистрироваться на игровой площадке, создать учетную запись и внести депозит.
При прохождения регистрации такой
человек должен внести сведения
о вас в качестве рекомендателя, чтобы Вам можно было получить бонус.
Количество пришедших по рекомендации людей не ограничено.
Игровые площадки всегда поощрительно относятся к новым клиентам, которые стремятся стать завсегдатаями
в ближайшем будущем.
Бонус за лояльность
Бонусы лояльности – это еще
тип подарков, используемых в онлайн-казино
1вин 1вин приложение
Они похожи на довольно известные программы
лояльности, которыми руководствуются известные
магазины.
Таким образом казино поощряет
своих постоянных клиентов (пользователей, которые с завидной регулярностью посещают ресурс и вступают в игру) привлекательными бонусами или подарками.
Подобный сюрприз возможен в виде поощрительных вращений, однако основная
масса казино тоже дают недорогие гаджеты, подарки или билеты для участия в лотереях.
Примечательно, что появится возможность получить намного больше положительных эмоций
за время пребывания на онлайн-площадках.
Поощрительные призы для VIP-пользователей
Казино в том числе продумывают поощрения для игроков, которые регулярно заходят
на сайт казино и вкладывают в
игры крупные суммы денег.
Большая часть online-казино связываются с VIP-пользователями , чтобы узнать об
их интересах и назначить призы, которые фактически соответствуют стилю заинтересованного игрока.
Это лишний раз доказывает,
в какой мере рады приветствовать клиентов
online-заведения.
Для ВИП-геймеров многие онлайн-cazino
подготавливают значительные материальные призы.
Нужно всего лишь продолжать посещать любимое казино, наслаждаться всеми
предоставляемыми плюсами своего статуса.
1XBET – одна из самых популярных в России букмекерских компаний по
ставкам на спорт.
Площадка работает по лицензии Curacao в online-режиме.
Фирма, работающая с 2007 года,
обслуживает свыше 400 тысяч постоянных клиентов.
На сегодня букмекерская контора
1xbet в числе мировых лидеров по спортивным ставкам.
Это можно назвать как показатель доверительности армии пользователей, которые выбрали
именно указанную БК.
Теперь надо разобраться в особенностях пребывания на онлайн площадке бонус обыграй 1xbet 1xgames
.
Порядок прохождения регистрации
Производить ставки имеет право прошедший регистрацию пользователь
(беттер).
Есть разные варианты создания аккаунта:
1. через социальные сети, потребуется всего лишь остановиться на соответствующем варианте;
2. по э-мейл независимо от сервиса;
3. по телефонному номеру, на который будет прислано
смс.
Пользователям https://indiwiki.udata.id/mediawiki/index.php?title=%C3%90%C5%A1%C3%90%C2%B0%C3%90%C2%BA_%C3%90%C2%A1%C3%90%C2%B4%C3%90%C2%B5%C3%90%C2%BB%C3%90%C2%B0%C3%91%E2%80%9A%C3%91%C5%92_%C3%90%E2%80%9D%C3%90%C2%B5%C3%90%C2%BC%C3%90%C2%BE_%C3%90%C2%A1%C3%91%E2%80%A1%C3%90%C2%B5%C3%91%E2%80%9A_%C3%90%C3%A2%E2%82%AC%E2%84%A2_1%C3%91%E2%80%A6%C3%90%C2%B1%C3%90%C2%B5%C3%91%E2%80%9A в личный аккаунт становится доступным сразу после
регистрации.
Беттер получает право ставить на
разные события из мира спорта, принимать участие в акционных и бонусных программах,
осуществлять вывод денег и др.
Вы сможете не просто наблюдать за игрой любимой команды, но и при
желании получать немалые денежные суммы.
Нужно всего лишь выбрать мероприятие, которое понравилось больше всего.
Итак, по окончании регистрации можно пользоваться множеством
возможностей основного ресурса, которые предусмотрели разработчики.
Разновидности ставок конторы 1хбет http://astro.s45.xrea.com/card/card.cgi
В отличие от подобных контор 1Хбет насчитывает двенадцать вариантов сделок.
Одиночная ставка (одиночник, единица) – соглашение на определенный результат
спортивного мероприятия.
Прибыль насчитывается при умножении
десятичного коэффициента на количество
поставленных денег.
Получается, что сложностей особых нет, если выбор сделан на этот вариант ставки.
Экспресс – ставка одновременно на 2
и больше исходов, которые анонсируются.
Экспресс «Стайер» имеет особенность:
исходы и мероприятия разрешается дописывать
на протяжении 2-х месяцев.
Антиэкспресс содержит ряд итогов, противоположный экспрессу по способу определения выигрыша.
Этот тип ставки выбирают как со
стажем игроки, так и новички.
Система – сделка на все возможные варианты экспрессов конкретной размерности из указанного числа мероприятий.
Цепочка – набор одиночных прогнозов.
По доверительной ставке удастся
вернуть долю денег, находящихся пока
под блокировкой.
Это довольно привлекательное предложение, которое могут выбрать прошедшие регистрацию пользователи.
Прогноз по купону выдает комбинацию из цифр и букв для оформления запроса.
Этим способом можно осуществить
ставку , не внося средства на депозитный счет.
Лаки является комбинированием ординаров и совершенно всех экспрессов, собранных из выбранных спортивных событий.
Патент имеет такой же принцип,
что и лаки, но число событий ограничивается тремя.
Для чего необходимо заходить на зеркало
БК 1Хбет считается нелегальной в регионах России.
Подобное положение связано с тем, что фирма не взимает проценты с прибылей игроков.
Для самих пользователей это существенный плюс, но
в рамках закона данный момент признается
не самым целесообразным.
Руководители не собираются ничего изменять в проводимой политике.
Что же делать в этом случае
клиентам?
В действительности никаких сложностей нет.
Нужно обойти блокировку официального веб-сайта, а следовательно зайти на актуальное зеркало
площадки.
Копия можно представить как особый сервис с идентичным отображением портала,
без каких-либо ограничений, с
воссозданием прежде внесенных сведений.
Можно зайти и беспроблемно пользоваться всеми условиями, предусмотренными создателями.
Такие зеркала используют общую с основным вебсайтом 1xbet базу, поэтому зайти на сайт удобно под своей учетной записью.
Помните, что дизайн аналогичен подтвержденному
сервису букмекера.
Переместиться на аналог получится по
адресу 1xbet скачать приложение на андроид.
Кроме ставок на спорт в 1хбет игрокам
доступны тотализаторы, слоты,
различные лотереи, нарды, игровые процессы в онлайн и offline режимах.
Как видите, у БК достаточное число
мероприятий, которые придутся по нраву пользователям
разных возрастов, пола.
Нужно всего лишь пройти простую
регистрацию прямо сейчас.
Вы поймете, как интересно удастся провести время, если есть ноутбук и
подключение к сети Интернет.
1XBET – одна из наиболее востребованных в РФ букмекерских контор по прогнозам на спорт.
Площадка работает на основе
лицензии Curacao в режиме онлайн.
Компания, осуществляющая деятельность с 2007 года,
обслуживает больше четырехсот тыс.
постоянных посетителей.
На сегодня БК 1xbet входит в число мировых лидеров по спортпрогнозам.
Это и есть критерий доверия армии пользователей,
которые решили выбрать именно указанную букмекерскую контору.
Осталось разобраться в особенностях нахождения на online платформе 1xbet официальный сайт личный кабинет .
Порядок прохождения регистрации
Производить прогнозы может только зарегистрированный пользователь (беттер).
Есть разные варианты подготовки профиля:
1. через социальные сети, потребуется всего лишь остановиться на соответствующем варианте;
2. по э-мейл независимо от сервиса;
3. по номеру сотового телефона, на который будет
прислано сообщение.
Игрокам http://www.eslvy.com/home.php?mod=space&uid=477492&do=profile в личный кабинет становится доступным сразу
после регистрации.
Зарегистрированный клиент получает право делать ставки на разные
спортивные турниры, участвовать в акциях и
бонусах, выводить средства и др.
Вы сможете не просто следить за игрой любимой команды, но и при желании получать неплохие суммы денег.
Нужно всего лишь выбрать событие,
которое понравилось больше всего.
Итак, по окончании регистрации разрешается пользоваться множеством возможностей основного ресурса, которые
предоставили администраторы.
Виды прогнозов БК 1хбет https://www.jzfbbs.cn/home.php?mod=space&uid=1856&do=profile&from=space
В отличие от подобных контор 1Хбет предоставляет двенадцать типов операций.
Одиночная ставка (ординар, одиночник) – соглашение на
определенный итог спортивного события.
Выигрыш насчитывается при умножении десятичного коэффициента на сумму пари.
Получается, что нет ничего
сложного, если выбор сделан на этот вариант ставки.
Экспресс – прогноз одновременно на 2 и больше исходов, которые должны
пройти.
Экспресс «Стайер» отличается особенностью:
результаты и мероприятия разрешается дописывать на протяжении
двух месяцев.
Антиэкспресс содержит несколько исходов, противоположный экспрессу
по способу начисления выигрыша.
Этот вид прогноза выбирают
как со стажем игроки, так и новички.
Система – пари на полную комбинацию экспрессов конкретной размерности из указанного числа событий.
Цепочка – набор одинарных ставок.
По ставке доверительного типа
можно вернуть долю средств, находящихся пока под блокировкой.
Это достаточно интересное предложение, которое
выбирают прошедшие регистрацию пользователи.
Ставка по промокоду выдает набор из букв и цифр для оформления запроса.
Таким образом удобно сделать ставку без внесения денег
на депозитный счет.
Лаки оказывается комбинированием ординаров и абсолютно всех экспрессов, которые собраны из выбранных спортивных мероприятий.
Патент действует по тому же алгоритму, что и лаки, но количество прогнозов
ограничивается 3-мя.
Для каких целей необходимо использовать зеркало
БК 1Хбет не является легальной в регионах
России.
Это связано с тем, что контора не удерживает налоги с выигрышей игроков.
Для самих пользователей это огромный плюс,
но на законодательном уровне данный нюанс признается
не самым уместным.
Руководители не намерены ничего изменять в своей
политике.
Как же быть в этом случае клиентам?
В действительности нет ничего проще.
Следует избежать блокировку
официального веб-ресурса, а
следовательно посетить актуальное зеркало площадки.
Копия можно представить как специальный ресурс с идентичным интерфейсом сайта, без каких-либо сдерживающих факторов, с воссозданием прежде введенных сведений.
Можно войти и спокойно воспользоваться всеми возможностями, предложенными разработчиками.
Эти копии используют единую с официальным сайтом 1xbet БД, поэтому войти на сайт удобно под своей учетной записью.
Помните, что интерфейс идентичен
подтвержденному сайту букмекера.
Переместиться на зекрало можно
по ссылке как отыграть бонус обыграй 1xbet.
Кроме ставок на спортивные турниры
в 1хбет игрокам доступны тотализаторы, слоты, разные лотереи, нарды, игровые процессы в online
и офлайн режимах.
Можно сделать вывод, что у БК достаточное число
событий, которые придутся по нраву
клиетнам самого разного возраста,
пола.
Нужно всего лишь зарегистрироваться по несложному алгоритму уже сейчас.
Вы поймете, как интересно получится провести досуг, если есть персональный компьютер и подключение к
сети Интернет.
Ставки на спорт на сегодняшний день https://sl24.online/forums/topic/betvinner-bonusybetwinner-bonusybetwinner-usloviya/ пользуются популярностью не
только среди его любителей.
И обычные люди сейчас активно делают ставки ради развлечения.
Любители азарта смогли оценить
по достоинству адреналиновый всплеск, который удается получить
в момент предвкушения результата.
Вряд ли кто сможет отказаться от довольно крупной прибыли?
Вы можете смотреть увлекательный матч ,
а заодно ставить на исход состязания.
На территории РФ приемщики ставок могут работать на законных основаниях, но
для этого потребуется разрешение, что
выдают не сразу и не всем.
Причем даже у проверенных на деле букмекеров могут возникнуть проблемы.
Среди них блокирование площадки,
невозможность авторизации.
Не вызывает удивления, что терпение заканчивается, появляется стремление отыскать другой способ
развлечения.
Ко всему, человек будет считать себя
обведенным вокруг пальца.
На самом деле не стоит поддаваться панике раньше времени.
В связи с этим сейчас расскажем о том, что такое ставки betwinner и для чего оно нужно.
Этой фишкой уже успели успешно воспользоваться
множество знающих и начинающих пользователей сервиса.
Зачем нужно точную копию площадки
Зеркало – это качественная
копия исходного сайта букмекерской конторы.
Необходимо оно для:
1. того, чтобы при случае без промедления
вернуться на привычный сервис, не обращая
внимания на блокировку;
2. предотвращения взлома профилей зарегистрированных пользователей;
3. высокой скорости;
4. сохранности аналога портала;
5. равномерного перераспределения основной
нагрузки;
6. обхождения блокирования, которое может специально
включаться по различным причинам (многим пользователям
ресурс бывает недосягаем из-за Российского потребнадзора).
В это же время все опции официального портала действуют и
в зеркале.
Люди, которые регулярно пользуются betwinner, могут беспрепятственно зайти через копии.
Это можно осуществить через выбранный vpn.
Вы сможете спокойно пользоваться
любимым сайтом, делать ставки.
По какой причине блокируют betwinner
Букмекерство на территории России легализовали сравнительно недавно.
Ко всему лицензию заиметь тяжело.
По причине вышеназванных причин в РФ легально работают лишь 20-30 букмекерских фирм.
Они Довольно популярны, часто мелькают в анонсе туров
различных спортивных соревнований.
В случае, когда bookmaker не спонсирует спортивные мероприятия, шансов на на то, чтобы стать обладателем
лицензии у него практически нет.
Поэтому и пользователи вряд ли смогут попасть на сайт.
Скорее всего он будет заблокирован в пределах
России.
В чем состоят плюсы Betwinner
Во-первых, она является компанией международного уровня.
Входит в Marikit Holdings LTD.
У Betwinner имеется официальный документ о.
Кюросао, это официально подтвержденное
право, позволяющее вести деятельность в различных государствах, в которых
это разрешено по закону.
Поэтому делать ставки имеют право даже люди,
проживающие не на российской территории.
Просто заходите на сайт, выбираете мероприятия
и делаете ставки.
От исхода игры с любимой командой до числа голов, забитых в процессе матча.
Особого интереса требуют к себе ставки на
ведущего игрока.
Вполне может быть, что он «прислушается» к вашему мнению и забьет результативный мяч,
который приведет к победе.
Следующий момент, на betwinner позволено ставить на многие события типа киберспортивных,
в мире спорта, политических, шоу-бизнеса и др.
Удобно сделать ставку на то, кто станет
следующим президентом Турецкой
Республики или кто сыграет в новом фильме.
Чего только стоит занменитое Eurovision, когда важно предугадать триумфатора среди большого числа артистов из разных государств.
Достаточно заманчивые перспективы, не так ли?
Третье, на Betwinner можно выбрать родной язык.
Портал поддерживает на 52 различных языка.
Поэтому подобрать что-то свое может абсолютно любой.
Этот момент относится и к валютам,
их аж 49 – от привычных доллара и рубля до электронных
денег.
Любой из пользователей найдет то, что нужно по своим предпочтениям.
И это , конечно, не весь список преимуществ.
Обо всех нюансах подробнее несложно узнать , если зайти на сайт http://www5f.biglobe.ne.jp/~hokuto_hinata_itou_obi/Lapin/yybbs/yybbs.cgi
К тому же на сайте будет детальное руководство по регистрации.
Вы сможете разобраться, какие предусмотрены
способы прохождения регистрации, как без промедления
приступить к совершению ставок.
Чтобы узнать актуальный
адрес копии сайта, наилучший вариант будет позвонить по ГЛ.
Кроме того, не лишне выйти на авторитетные группы,
которые готовы информировать о различных букмекерских конторах.
Достаточно обычным образом сделать запрос в любом популярном поисковике фразу –
betwinner зеркало.
Пользователь сможет перейти на веб-сайт бетвиннер бк бонус ,
который полностью идентичен официальному сервису.
Итак, не составит труда найти специально разработанную веб-копию.
gorras y bufandas para mujer tejidas
costume nike 2018 uomopantaloncini jordan verdi e rosazaino per sciarenike air zoom vomero 5 se sp
Конкурентная борьба в области online азартных игр огромна.
Каждый день появляется все больше площадок с соблазнительными спецусловиями для новых игроков.
Особенного интереса заслуживает стартовый подарок, который оценили большое число клиентов.
Пришла пора разобраться
с основными аспектами, которые сопряжены с работой casino
https://markusschranz.de/merak-wiki/index.php?title=1win_%D0%91%D1%83%D0%BA%D0%BC%D0%B5%D0%BA%D0%B5%D1%80%D1%81%D0%BA%D0%B0%D1%8F_%D0%9D%D0%B0_%D0%90%D0%BD%D0%B4%D1%80%D0%BE%D0%B8%D0%B4 .
Приветственный приз – это основной бонус, который предоставляет online-cazino.
Чтобы его получить, не придется прилагать серьезных усилий.
Инструкция подготовлена для клиентов, которые только в первый
раз заходят в личный кабинет на портале cazino.
Они часто даже не представляют, какой
подарок приготовили программисты.
Наиболее часто стартовый бонус добавляет
некоторый процент к стартовому счету вне зависимости от
количества внесенных денег.
Бонус безвозмездных спинов
Казино внедряют бесплатные вращения в свою рекламную задумку.
Что это такое?
Это позволяет давать игрокам безоплатные циклы, которые играющие могут использовать в игровых автоматах, и выигранные средства обычно
могут быть сняты с их счета.
Вращения очень востребованы среди почитателей азартных онлайн-игр, потому что они позволяют определить потенциал, который обеспечивают новые гейм аппараты, без потребности увеличивать персональный баланс и растрачивать личные деньги.
Достаточно привлекательное предложение, которым
в полном объеме могут воспользоваться игроки.
Можно оценить по достоинству
все плюсы, шансы, обеспечиваемые владельцами
площадок.
Casino таким образом нередко рекламируют новые услуги
среди посетителей, зарегистрированных на их платформе.
При этом 1win бонус за регистрацию доступно всем
желающим.
Нужно всего лишь выбрать конкретную категорию,
ввести данные в поля регистрации.
Важно не забывать про необходимость подтвердить достижение совершеннолетия.
Без подтверждения личности будет сложно получить
статус игрока, которому откроются
потенциальные возможности on-line площадки.
Реферальные бонусы
Онлайн casino поощряет клиентов, которые советуют игровую
площадку другим.
Подарки за привлечение знакомых предназначены
для популяризации предложений игр и притягивания
потенциальных клиентов
казино.
Данный способ признается одним из
самых эффективных для роста числа игроков.
Один момент, когда человек
решается присоединиться, ориентируясь
на рекламные слоганы.
Совершенно иное – поверить рекомендации друга, который уже удостоверился в предоставленной информации,
многообразии слотов для игры.
За совет вы можете обнаружить в личном кабинете денежный приз.
Финансовый бонус разрешается вывести со своего
счета или потратить на безоплатные
вращения в игровых раундах (отдельные
cazino применяют самостоятельно
разработанные рекламные и бонусные стратегии, в связи с чем
стоит перво-наперво изучить правила).
Каким образом можно получить этот бонус?
Вам необходимо убедить кого-то из своих знакомых пройти регистрацию
на игровой площадке, создать учетную
запись и пополнить счет.
Во время прохождения регистрации этот пользователь должен
внести ваши данные в качестве реферала, чтобы Вы могли зачислить на
счет вознаграждение.
Количество пришедших по рекомендации игроков не ограничено.
Казино всегда поощрительно
относятся к новым клиентам, которые
намерены стать постоянными в
самое ближайшее время.
Бонус за преданность
Бонусы лояльности – это дополнительный тип подарков, используемых в on-line-casino 1вин 1вин приложение.
Они напоминают довольно известные схемы вознаграждений, которыми руководствуются известные
магазины.
Получается, что казино поощряет своих
приверженцев (пользователей, которые с завидной регулярностью заходят на площадку и играют) привлекательными призами или наградами.
Такой сюрприз может быть в виде бесплатных вращений, однако основная
масса игровых платформ также предоставляют недорогие гаджеты, подарки или лотерейные билеты.
Примечательно, что появится
возможность получить еще больше положительных эмоций за время
пребывания на online-площадках.
Бонусы для ВИП-клиентов
Казино также готовят поощрения для
игроков, которые регулярно посещают портал казино и
используют в играх большие денежные суммы.
Большинство онлайн-казино стараются пообщаться с VIP-клиентами с целью разузнать об их интересах и присудить
вознаграждения, которые по сути отвечают стилю
постоянного клиента.
Это еще раз доказывает, насколько рады приветствовать пользователей
онлайн-площадки.
Для ВИП-игроков большинство онлайн-cazino готовят очень ценные материальные поощрения.
Необходимо всего лишь регулярно заходить в любимое
казино, наслаждаться всеми предоставляемыми
преимуществами своего положения.
Конкурентная борьба на рынке онлайн гемблинга поражает масштабами.
http://speedycon.org/user/setting/edwardov88/
Каждый день организовывается все больше
игровых ресурсов с заманчивыми условиями для новеньких.
Отдельного интереса удостаивается стартовый
подарок, который успели оценить большое число клиентов.
Пришло время разобраться с основными
аспектами, которые сопряжены с работой casino.
Стартовый приз – это основной бонус, который предлагает online-казино.
Чтобы его получить, не нужно прикладывать серьезных усилий.
Пособие подготовлено для игроков, которые только в первый раз заходят в профиль на
сайте казино.
Пользователи могут и не подозревать,
какой сюрприз приготовили программисты.
Чаще всего первое поощрение добавляет некоторый процент к стартовому счету вне зависимости
от внесенной суммы.
Подарок в виде бесплатных вращений
промокод при регистрации 1win
Casino внедряют бесплатные вращения в свою маркетинговую стратегию.
Что это такое?
Это позволяет давать пользователям безоплатные раунды,
которые геймеры имеют право использовать в игровых автоматах,
и выигранные средства чаще всего могут быть сняты с личного счета.
Спины чрезвычайно востребованы в среде почитателей азартных онлайн-игр,
так как они позволяют определить возможности,
которые предоставляют новейшие гейм аппараты,
без необходимости увеличивать персональный счет
и тратить собственные финансы.
Достаточно привлекательное предложение, которым вполне
могут воспользоваться игроки.
Несложно расценить имеющиеся преимущества, шансы, гарантируемые разработчиками.
Казино таким образом часто продвигают новейшие продукты среди пользователей,
зарегистрированных на их платформе.
В то же время https://www.jctcfw.cn/home.php?mod=space&uid=4540551&do=profile&from=space не
ограничено ни для одного из желающих.
Нужно всего-навсего выбрать конкретную категорию, ввести данные в
регистрационные ячейки.
Важно не забывать про обязательность подтверждения совершеннолетие.
Без подтверждения личности будет сложно стать постоянным пользователем, которому доступны имеющиеся
возможности on-line ресурса.
Бонусы для пришедших по рекомендации
Online казино стимулирует пользователей,
которые рекомендуют сервис потенциальным игрокам.
Бонусы за вовлечение друзей
делаются с целью продвижения гэмблинга и привлечения потенциальных клиентов игровых площадок.
Указанный способ считается одним
из самых эффективных для увеличения количества игроков.
Одно дело, когда пользователь думает присоединиться, опираясь на рекламу.
Совершенно иное – поверить рекомендации приятеля, который на сегодня проверил достоверность сведений, вариативности игровых аппаратов.
За рекомендацию пользователь может обнаружить в личном кабинете денежный приз.
Финансовый бонус можно вывести
со счета или использовать на безоплатные вращения в игровых раундах (некоторые
казино используют самостоятельно разработанные маркетинговые и поощрительные
программы, в связи с чем лучше всего
перво-наперво ознакомиться с правилами).
Каким образом можно получить
этот бонус?
Вам необходимо сагитировать кого-то из своих знакомых пройти регистрацию на сайте
казино, активировать учетную запись и
внести депозит.
При прохождения регистрации этот человек должен указать ваши
данные как реферала, чтобы
Вам можно было получить бонус.
Количество пришедших по рекомендации игроков не лимитируется.
Игровые площадки всегда рады новым клиентам, которые собираются
стать постоянными в ближайшем будущем.
Поощрение за преданность
Бонусы лояльности – это еще тип подарков, которые используются в онлайн-casino 1вин
1win на андроид
Они похожи на достаточно известные
схемы вознаграждений, которыми руководствуются знакомые многим торговые марки.
Таким образом casino награждает своих приверженцев (людей, которые с завидной регулярностью посещают площадку и вступают в игру) привлекательными бонусами
или наградами.
Такой бонус может быть в виде поощрительных
вращений, но многие казино тоже предоставляют
небольшие аксессуары, призы или лотерейные билеты.
Примечательно, что появится возможность испытать еще больше положительных
эмоций за время нахождения на
online-площадках.
Бонусы для VIP-клиентов
Игровые сервисы в том числе продумывают
бонусы для геймеров, которые регулярно посещают портал cazino и используют в играх крупные
суммы денег.
Большинство онлайн-casino связываются с VIP-клиентами с целью узнать об
их интересах и присудить призы, которые
по сути соответствуют поведенческому фактору заинтересованного игрока.
Это лишний раз подтверждает, в какой мере рады приветствовать пользователей online-заведения.
Для VIP-игроков большинство online-казино подготавливают очень ценные материальные
призы.
Необходимо всего лишь продолжать посещать
выбранное казино, пользоваться всеми предоставляемыми плюсами своего статуса.
rochii delight scurte si bufante
tenis super herois infantilcamisa treino chelseachapeu tipo safaricolch茫o e box queen size
lunette soleil surfeur
buty adidas v racer 2.0 szare m臋skie ceneobluza prosto grey mint56 122 szczotka do butelek i smoczk贸wbuty nike 2019 meskie
1XBET входит в число самых востребованных в России букмекерских компаний по прогнозам на спорт.
Сервис функционирует по лицензии Curacao в режиме онлайн.
Компания, осуществляющая деятельность с 2007 года,
обслуживает свыше 400 тыс.
постоянных клиентов.
На сегодня БК 1xbet входит в число мировых лидеров по спортивным ставкам.
Это и есть показатель доверительности многочисленных клиентов, которые решили выбрать
именно указанную БК.
Теперь надо понять особенности пребывания на online платформе 1xbet мобильная версия вход в кабинет .
Порядок прохождения регистрации
Производить прогнозы может только прошедший регистрацию пользователь (беттер).
Есть разные способы подготовки профиля:
1. через соцсети, потребуется всего лишь выбрать
соответствующий вариант;
2. по адресу электронной почты независимо от сервиса;
3. по телефонному номеру, на который будет прислано смс.
Пользователям https://admag.com/user/profile/572 в персональный кабинет станет открытым немедленно по окончании регистрации.
Беттер может ставить на разные события
из мира спорта, принимать
участие в акционных и бонусных программах,
выводить средства и др.
Вам понравится не просто наблюдать за матчем любимой команды, но и при желании выигрывать неплохие суммы денег.
Для этого надо всего лишь указать
событие, которое пришлось по вкусу.
Как видите, после регистрации разрешается воспользоваться многочисленными возможностями официального ресурса, которые предусмотрели
разработчики.
Виды прогнозов БК 1хбет https://www.annons-torget.se/user/profile/17589
1Хбет в отличие от других БК насчитывает двенадцать
вариантов сделок.
Одинарный прогноз (ординар, одиночник) – сделка на отдельный результат спортивного мероприятия.
Прибыль насчитывается при умножении десятичного коэффициента на количество поставленных денег.
Получается, что нет ничего сложного, если выбирать данный вид ставки.
Экспресс – ставка одновременно на 2
и более исходов, которые анонсируются.
Экспресс «Стайер» отличается особенностью:
исходы и события можно добавлять на протяжении двух месяцев.
Антиэкспресс включает несколько исходов, обратный экспрессу по
методу начисления призовых денег.
Этот тип ставки выбирают как со стажем игроки, так и
новички.
Система – пари на все возможные варианты экспрессов конкретной размерности из выбранного числа событий.
Цепочка – набор одинарных прогнозов.
По доверительной ставке можно вернуть часть средств, находящихся пока под блокировкой.
Это довольно интересное предложение, которое
выбирают прошедшие регистрацию
клиенты.
Ставка по купону определяет набор из цифр и букв для
оформления заявки.
Таким образом удобно сделать ставку , не внося средства
на депозитный счет.
Лаки является сочетанием ординаров и абсолютно всех экспрессов, собранных из указанных спортивных событий.
Патент имеет такой же принцип, что и
лаки, но число событий ограничено тремя.
Для каких целей нужно заходить на зеркало
Букмекерская контора 1Хбет не является легальной в регионах России.
Подобное положение связано с тем, что контора не взимает налоги с прибылей игроков.
Непосредственно для клиентов это существенный плюс, но на законодательном уровне данный нюанс считается далеко не уместным.
Разработчики не собираются ничего изменять в проводимой политике.
Что же делать в этом случае клиентам?
На самом деле никаких сложностей нет.
Следует обойти блокирование основного веб-сайта, то есть
зайти на функционирующее зеркало площадки.
Копия представляет собой особый ресурс
с идентичным интерфейсом сайта, без каких бы то ни было ограничений,
с сохранением прежде введенных данных.
Можно войти и спокойно пользоваться всеми возможностями, предложенными
разработчиками.
Данные копии имеют общую с основным сайтом 1xbet
БД, поэтому зайти на сайт удобно
под своим аккаунтом.
Не забывайте, что дизайн идентичен
подтвержденному сайту букмекера.
Переместиться на аналог получится по ссылке
1хбет регистрация в 1 клик.
Помимо прогнозов на спорт в 1хбет пользователям доступны слоты, тотализаторы, различные лотереи, нарды, игровые процессы в
online и офлайн режимах.
Можно сделать вывод, что у БК достаточное число мероприятий, которые могут
оказаться по нраву клиетнам самого разного
возраста, пола.
Необходимо всего лишь пройти простую
регистрацию прямо сегодня.
Вы сможете обнаружить, как интересно
получится провести время, имея ноутбук и подключение к интернету.
1XBET – одна из наиболее популярных
в России букмекерских контор по ставкам на
спорт.
Сервис работает по лицензии Curacao
в online-режиме.
Фирма, работающая с 2007 года, насчитывает
свыше 400 тысяч постоянных
посетителей.
На сегодня букмекерская контора 1xbet входит в число мировых лидеров по спортпрогнозам.
Это и есть критерий доверия армии
клиентов, которые выбрали
конкретно данную БК.
Теперь надо разобраться в особенностях пребывания
на онлайн платформе 1xbet личный кабинет .
Правила прохождения регистрации
Делать ставки может только прошедший
регистрацию клиент (беттер).
Есть различные способы создания профиля:
1. через соцсети, нужно всего лишь остановиться на соответствующем варианте;
2. по адресу электронной почты независимо от
платформы;
3. по телефонному номеру, на который будет
отправлено смс.
Игрокам https://www.mallorca-basar.com/user/profile/45323 в персональный аккаунт становится открытым немедленно после регистрации.
Зарегистрированный клиент получает право ставить
на разные спортивные турниры, участвовать в акционных и бонусных программах, выводить средства и т.д.
Вы сможете не безучастно наблюдать за игрой любимой команды,
но и по возможности выигрывать неплохие суммы денег.
Нужно всего лишь выбрать событие, которое пришлось по вкусу.
Как видите, по окончании регистрации можно воспользоваться многочисленными возможностями официального сайта, которые предоставили разработчики.
Виды прогнозов БК 1хбет http://www.sam.hi-ho.ne.jp/cgi-bin/user/t_fukuda/yybbs_u2.cgi?page=8230
В отличие от подобных контор 1Хбет предоставляет
двенадцать типов операций.
Одинарный прогноз (ординар, одиночник) –
соглашение на отдельный исход спортивного события.
Выигрыш рассчитывается умножением десятичного коэффициента на сумму
пари.
То есть нет ничего сложного, если выбирать
данный вид прогноза.
Экспресс – ставка сразу на
2 и более результатов, которые должны пройти.
Экспресс «Стайер» имеет особенность:
результаты и события можно дописывать на протяжении 2-х месяцев.
Антиэкспресс содержит ряд итогов, обратный экспрессу по методу начисления выигрыша.
Этот вид прогноза признают как со стажем игроки,
так и начинающие пользователи.
Система – пари на все возможные варианты
экспрессов определенной размерности из выбранного числа мероприятий.
Цепочка – комплект одиночных прогнозов.
По доверительной ставке удастся вернуть долю финансов,
которые находятся пока в истории.
Это достаточно интересное предложение, которое могут выбрать зарегистрированные пользователи.
Прогноз по купону определяет набор из букв и
цифр для оформления заявки.
Таким образом удобно осуществить ставку , не внося средства на депозит.
Лаки оказывается сочетанием единиц и абсолютно всех экспрессов, собранных из выбранных спортивных событий.
Патент действует по тому же алгоритму, что и лаки,
но количество событий ограничивается 3-мя.
Для каких целей необходимо заходить на зеркало
БК 1Хбет считается нелегальной на территории
РФ.
Подобное положение сопряжено с тем, что фирма не удерживает проценты с прибылей клиентов.
Непосредственно для клиентов это огромный плюс, но в рамках закона названный нюанс
признается не самым уместным.
Руководители не намерены ничего менять в своей политике.
Что же делать в этом случае клиентам?
В действительности нет ничего
проще.
Следует избежать блокирование официального веб-сайта, а следовательно посетить
актуальное зеркало портала.
Аналог можно представить как особый ресурс с идентичным интерфейсом
сайта, без каких бы то ни было ограничений,
с сохранением ранее введенных данных.
Можно войти и спокойно пользоваться имеющимися возможностями, предложенными
создателями.
Данные зеркала имеют единую с
основным вебсайтом 1xbet БД, поэтому
зайти на ресурс удобно под своим аккаунтом.
Не забывайте, что дизайн аналогичен подтвержденному сервису букмекера.
Переместиться на аналог получится по адресу 1xbet отзывы о выводе средств.
Помимо ставок на спортивные турниры в 1хбет игрокам предлагают слоты, тотализаторы, разные лотереи, нарды, игры в online и офлайн режимах.
Можно сделать вывод, что у букмекерской конторы достаточное число мероприятий, которые придутся по нраву
пользователям разных возрастов, пола.
Необходимо всего лишь пройти простую
регистрацию уже сейчас.
Вы сможете обнаружить, насколько увлекательно получится провести время, если есть ноутбук и
подключение к сети Интернет.
Bookmaker 1xbet in Italia http://Co.L.O.R.Ol.F.3%40Gal.EHi.Nt.On78.8.27@Www26.Tok2.com/home/moomuss/yybbs/yybbs.cgi
La societa di scommesse 1xBet Italia e una societa di origine russa.
La societa di scommesse fornisce i propri servizi ad utenti
maggiorenni di tutto il mondo. Il sito si trova sempre nelle posizioni di primo piano per il
numero di clienti e la qualita degli eventi in linea. Il sito e famoso per il proprio supporto
tecnico, che risponde in pochi minuti, nonche per i piacevoli
honorarium sul primo deposito.
Storia di 1xbet Italia
L’organizzazione del gioco d’azzardo ha operato in tutto il mondo per oltre 10
anni, ma unaccompanied nel 2015 e arrivata in Italia.
I giocatori italiani preferiscono proprio 1xbet a causa dell’ampio investimento della societa di scommesse sui giocatori popolari del
nostro paese.
Il sito ha guadagnato popolarita anche grazie al servizio 1xbetstreaming,
il quale permette di scommettere direttamente mentre si guarda l’evento.
La societa di scommesse aumenta ogni anno il fatturato dei fondi e
il numero di utenti attivi. Su questo influiscono l’apertura del casino online aperto e le grandi partnership
con grandi club.
Chelsea, Liverpool e Barcellona non sono gli unici nella lista delle sponsorizzazioni della societa di scommesse.
Licenza
Al momento, la societa di scommesse ha difficolta a causa del rinnovo della licenza, ma nell’applicazione unstationary su Android e iOS
e ancora possibile scommettere. Per questo gli scommettitori del Brasile e
dei paesi vicini possono scommettere normalmente.
Al momento, la societa e in trattativa per rinnovare la licenza e continuare le attivita nel suo Paese.
Sistema hand-out 1xbet Italia
La societa di scommesse cerca di rafforzare la
propria posizione nel mercato delle scommesse con ampie offerte promozionali.
Il largesse di benvenuto soddisfa i nuovi arrivati e consente di aumentare il primo deposito della meta, fino a 100 euro.
Le condizioni di secure per ricevere il regalo sono le seguenti:
• e necessario versare almeno 1 euro sul conto;
• e necessario scommettere 5 volte l’importo versato per ricevere il regalo;
• le scommesse devono essere espresse da 3 eventi o piu;
• il coefficiente di ogni partita deve essere superiore a 1,
40;
• e necessario recuperare il totale entro 30 giorni dalla ricezione del bonus.
Remuneration aggiuntivi dal sito
I giocatori possono ricevere altri regali, come l’introduzione di codici
promozionali speciali al casino o alle scommesse.
Ci sono codici simili durante eventi sportivi su larga scala.
Nel corso di un grande evento, nel 2018, la societa ha offerto a tutti
di ottenere 10 euro, che potevano essere giocati
senza il rischio di perdere.
La linea di partite 1xbet al giorno supera i 1000 eventi.http://gungasoft.com/home.php?mod=space&uid=39849&do=profile&from=space
La compagnia di scommesse 1xBet riempie costantemente la propria linea
con partite ed eventi interessanti. In media, ogni giorno ci sono piu di 1000 eventi
per le scommesse.
L’amministrazione cerca di make bold l’opportunita di scommettere non solitary sulle partite popolari,
ma anche sugli eventi regionali in Portogallo, in modo
che tutti possano scommettere a loro piacimento.
Roll in iniziare a scommettere su 1xbet Italia? aplicazioni mobili 1xbet Italia
Iniziare a scommettere su 1xbet Italia e molto semplice.
Occorre trovare il sito ufficiale su Google e registrarsi.
Ogni utente maggiorenne puo creare un profilo.
Questo puo essere fatto in 4 modi:
Конкуренция в области online азартных игр поражает масштабами.
https://www.software35.com/forum/users/fannymckean/
Каждый день появляется немало площадок
с заманчивыми спецусловиями для новых
игроков.
Особенного интереса заслуживает первоначальный подарок, который оценили
большое число клиентов.
Пришло время понять важные моменты, которые
сопряжены с работой casino.
Стартовый бонус – это основной бонус, который предоставляет online-casino.
Для его получения не нужно прилагать много
усилий.
Инструкция подготовлена для клиентов,
которые только в первый раз заходят в аккаунт на сайте казино.
Они часто даже не представляют, какой
сюрприз приготовили разрабы.
Наиболее часто первоначальный бонус прибавляет некоторый процент к начальному счету независимо от заведенной
на сайт суммы.
Бонус бесплатных вращений 1win букмекерская скачать приложение
Казино внедряют бесплатные прокручивания в собственную рекламную стратегию.
Что это такое?
Это дает пользователям бесплатные раунды, которые они имеют
право использовать в игровых автоматах, и выигрыши обычно можно снять с личного
счета.
Вращения достаточно популярны в среде любителей гэмблинга,
так как они дают шанс определить потенциал, который предоставляют новейшие игровые
автоматы, без потребности увеличивать свой счет и тратить личные деньги.
Достаточно интересное предложение, которым вполне смогут воспользоваться игроки.
Можно оценить по достоинству все плюсы, возможности, предоставляемые разработчиками.
Kazino таким образом нередко продвигают новые продукты среди пользователей, прошедших регистрацию
на их платформе.
В то же время https://www.profoundbond.net/index.php?title=User:GretaPittard8 не имеет ограничений.
Необходимо всего-навсего пройти в соответствующий раздел, заполнить регистрационные
ячейки.
Не забывайте про необходимость
удостоверить совершеннолетие.
Без верификации будет трудно стать
постоянным пользователем, которому доступны потенциальные возможности on-line площадки.
Реферальные бонусы
Online casino поощряет клиентов, которые рекомендуют
сервис потенциальным игрокам.
Подарки за вовлечение знакомых делаются с целью популяризации гэмблинга и притягивания потенциальных клиентов игровых площадок.
Указанный способ признается одним из самых эффективных для роста числа геймеров.
Один момент, когда человек думает стать полноценным
участником, ориентируясь на рекламные слоганы.
Совершенно иное – довериться совету друга, который на сегодня
проверил достоверность сведений, вариативности игровых
слотов.
За рекомендацию пользователь может обнаружить в личном кабинете денежный приз.
Начисленные деньги можно вывести со счета или потратить на безоплатные вращения в игре (отдельные казино
используют самостоятельно разработанные маркетинговые и бонусные стратегии, поэтому стоит перво-наперво ознакомиться с правилами).
Как можно стать обладателем такого
бонуса?
Вы должны убедить кого-то
из своих знакомых зарегистрироваться на сайте казино, создать аккаунт
и внести депозит.
Во время прохождения регистрации такой пользователь должен внести ваши данные как рекомендателя, чтобы Вам
можно было получить вознаграждение.
Число пришедших по рекомендации игроков
не ограничено.
Игровые площадки всегда рады новичкам,
которые намерены стать постоянными в ближайшем будущем.
Бонус за лояльность
Поощрительные бонусы – это еще тип подарков, которые используются в on-line-casino 1вин где вводить промокод в 1win
Они похожи на довольно известные схемы вознаграждений, которыми руководствуются популярные торговые марки.
Таким образом casino поощряет
своих приверженцев (людей, которые с завидной регулярностью заходят на площадку и
вступают в игру) заманчивыми бонусами или подарками.
Такой сюрприз может быть
в виде поощрительных вращений, но многие казино также дают недорогие аксессуары, подарки или лотерейные билеты.
Примечательно, что появится возможность испытать еще больше
приятных эмоций за время пребывания на online-площадках.
Поощрительные призы для VIP-пользователей
Игровые сервисы в том числе готовят
поощрения для геймеров, которые регулярно заходят на сайт
казино и вкладывают в игры крупные денежные
суммы.
Большая часть онлайн-casino стараются
пообщаться с VIP-клиентами с целью разузнать об их предпочтениях и присудить призы,
которые фактически соответствуют поведенческому фактору постоянного клиента.
Это еще раз доказывает, в какой мере рады
видеть клиентов online-площадки.
Для ВИП-игроков многие онлайн-казино
подготавливают очень ценные материальные призы.
Нужно всего лишь регулярно посещать
любимое заведение, наслаждаться всеми предоставляемыми преимуществами своего статуса.
蟺伪蟺慰蠀蟿蟽喂伪 渭蟺慰蟿伪魏喂伪 伪谓未蟻喂魏伪 adidas
gucci gold clutchtimberland boat shoes greygrey maxi skirtladies dc skate shoes
Конкурентная борьба в сфере online азартных игр невероятна.
http://www.shltaxi.com/user/profile/27135
С завидной регулярностью организовывается
много игровых ресурсов с привлекательными условиями для новых игроков.
Отдельного внимания удостаивается приветственный подарок, который успели оценить большое
число клиентов.
Пришла пора разобраться с основными аспектами, которые сопряжены с
работой casino.
Стартовый бонус – это основное поощрение, которое
предоставляет онлайн-казино.
Для его получения не нужно прилагать много
усилий.
Инструкция подготовлена для клиентов, которые только в первый раз открывают личный кабинет на сайте casino.
Они могут и не подозревать, какой сюрприз подготовили
разрабы.
Наиболее часто стартовый бонус добавляет некоторый процент
к начальному счету вне зависимости
от количества внесенных денег.
Поощрение в виде бесплатных спинов 1win бонус за регистрацию
Casino включают безоплатные вращения в собственную рекламную стратегию.
Как это понимать?
Это дает пользователям безоплатные циклы, которые геймеры
могут применить в игровых автоматах, и
выигрыши обычно можно снять с их счета.
Спины очень популярны среди почитателей азартных онлайн-игр,
потому что они позволяют изучить потенциал, который предоставляют новейшие игровые аппараты, без потребности
увеличивать свой баланс и тратить
собственные деньги.
Довольно привлекательное предложение, которым в полной мере смогут воспользоваться игроки.
Можно расценить все преимущества, шансы, предоставляемые владельцами площадок.
Казино таким образом часто продвигают новейшие продукты среди клиентов,
прошедших регистрацию на их портале.
В то же время http://tanpoposc.com/cgi-bin2/tanbbs/yybbs.cgi?list=thread доступно всем желающим.
Нужно всего-навсего выбрать
соответствующую категорию, заполнить регистрационные
ячейки.
Не забывайте про необходимость подтвердить совершеннолетие.
Без подтверждения личности будет сложно получить статус игрока, которому откроются имеющиеся возможности онлайн ресурса.
Бонусы для пришедших по рекомендации
Online казино поощряет пользователей,
которые советуют сервис потенциальным игрокам.
Подарки за вовлечение знакомых предназначены для популяризации гэмблинга и привлечения новых пользователей казино.
Указанный метод считается наиболее эффективным для роста количества геймеров.
Одно дело, когда человек думает стать полноценным участником,
ориентируясь на рекламные слоганы.
Совершенно иное – воспользоваться советом
друга, который уже удостоверился в предоставленной информации, вариативности игровых аппаратов.
За рекомендацию пользователь может получить денежный приз.
Финансовый бонус можно снять со счета или потратить на безоплатные
спины в игровых раундах (отдельные
cazino применяют самостоятельно разработанные маркетинговые и бонусные стратегии, в связи с
чем лучше всего перво-наперво ознакомиться с правилами).
Каким образом удастся стать обладателем такого бонуса?
Вы должны сагитировать того, кого вы знаете, зарегистрироваться на игровой площадке, активировать аккаунт
и внести депозит.
При прохождения регистрации этот человек
должен внести сведения о вас в
качестве рекомендателя, чтобы
Вам можно было получить вознаграждение.
Число приглашенных людей не ограничено.
Игровые площадки всегда рады
новичкам, которые намерены стать завсегдатаями
в самое ближайшее время.
Поощрение за лояльность
Поощрительные бонусы – это дополнительный вид подарков, которые используются в on-line-казино 1вин 1win официальное зеркало
Они похожи на достаточно распространенные программы вознаграждений, которыми
руководствуются известные магазины.
Получается, что казино награждает своих постоянных клиентов (пользователей, которые с завидной регулярностью посещают ресурс и играют) заманчивыми бонусами
или подарками.
Подобный сюрприз может быть в виде поощрительных спинов,
но многие игровых платформ тоже дают небольшие гаджеты, призы или билеты для участия в лотереях.
Примечательно, что появится возможность испытать еще больше приятных эмоций за время нахождения на online-площадках.
Бонусы для VIP-пользователей
Игровые сервисы в том числе продумывают бонусы для игроков, которые стабильно
посещают сайт cazino и вкладывают в игры большие суммы денег.
Большинство online-казино стараются пообщаться
с VIP-клиентами , чтобы узнать об их предпочтениях
и присудить призы, которые по сути соответствуют стилю постоянного клиента.
Это еще раз подтверждает, в какой мере
рады видеть клиентов online-заведения.
Для ВИП-игроков большинство онлайн-cazino готовят очень ценные материальные призы.
Необходимо всего лишь продолжать посещать выбранное заведение, пользоваться
всеми предоставляемыми преимуществами своего положения.
Обзор зеркала Melbet
Ниша ставок в РФ существует довольно давно,
и в 2012 году вышла на рынок фирма Melbet.
На сегодняшний день сервис стабильно продолжает развиваться, непосредственно это касается виртуального пространства.
Как думают многие клиенты, довольно комфортно никуда не выходить, а ставить на
события.
Время не будет потеряно.
Основная цель компании – помогать людям
делать ставки, это можно сделать через офисы компании или же в
режиме онлайн, для чего имеется портал и приложение
для смартфона.
Итак, предоставляется немало возможностей, чтобы приятно провести досуг, а вместе с тем попробовать получить приличные деньги.
Компания обзор букмекерской конторы melbet очень стремительно продвигается и старается создать для своих
пользователей наилучшие условия.
Тут каждый может ставить как на спортивные, так и на
другие события, к примеру, конкурсы наподобие Евровидения.
Больше нет смысла безучастно наблюдать за тем,
как выступает обожаемый артист.
Достаточно поверить в его триумф, произведя оптимальную
ставку.
Существует вероятность, что удастся сорвать
крупную сумму и при этом насладиться
музыкальным произведением.
Такой подход крайне удобен,
так как в этом случае безусловно каждый человек найдет для
себя захватывающие мероприятия и сделает ставки.
Программеры предусмотрели мероприятия на любой вкус.
Решение связано с Вашим возрастом, увлечениями, желанием и
возможностью идти на риск.
С чего начинать делать ставки на спорт с Melbet https://132.148.164.16/space-uid-4333.html
Многие клиенты уверены, что ставить
на спорт или иные события – это достаточно сложно
и что в этом потребуется тратить время на разбирательство.
Но так ли это на самом деле?
Естественно, это не так.
Если мы говорим о Melbet, то здесь начинать ставить получится у любого желающего.
Интуитивно понятный интерфейс понравится даже новичкам, которые
надумали разобраться с тем, как ставить.
Следует рассмотреть более подробно, как начинать процесс.
Для старта вам нужно зарегистрироваться на сайте
зеркало мелбет на сегодня
Алгоритм прохождения регистрации
очень простой, займет у вас минимальное
количество времени.
Нужно всего лишь ввести персональные
сведения в специальные поля, верифицироваться.
Как только вы зарегистрируетесь, следует внести деньги на
депозит.
Абсолютно неважно, какая именно будет
внесена денежная сумма.
Очень быстро Вы разберетесь и поймете, как поступать дальше,
какие параметры ставки считаются наиболее приемлемыми.
И после этого начинайте делать ставки.
Сейчас стало понятно, что выполнять подобные манипуляции можно без
особого труда, так как на эти действия уйдет у вас минимум сил и времени.
Выходит, абсолютно любой из игроков сумеет начать ставить независимо от того
новичок он или профессионал.
Все, что для этого требуется – зарегистрироваться.
Контора Melbet – входит в число известных и востребованных площадок на российском рынке,
что абсолютно не удивительно.
Ведь компания с заботой относится к своим клиентам и подготавливает для
них наилучшие условия.
Руководству надо не просто заинтересовать новых игроков, а и создать максимально комфортные обстоятельства для постоянных
клиентов.
Репутация считается значимым критерием для конторы во имя того,
чтобы не снизить веры игроков.
В сфере ставок существует немалое количество мошенников.
Не стоит слепо доверять яркой рекламе, а
также бездумно верить чрезмерно заманчивым предложениям.
Возможно не только потерять деньги, время, но и заполучить на компьютер вирусную программу.
Уместнее выбирать лишь проверенные компании,
которые долгий период находятся в данной отрасли.
В любой момент можно почитать отклики,
узнать о времени начала деятельности конторы на просторах интернета.
Одним из таких профи ведения игрового бизнеса считается https://www.lookhot.com.cn/space-uid-28108.html .
В определенный момент можно загрузить
конкретно созданное приложение для смартфонов и других гаджетов.
Нужно обеспечить наличие сети Интернет, чтобы
ставить прямо сейчас.
У Вас будет возможность выбрать событие, сделать прогноз, находясь в
заторе или на даче.
Не это ли и есть одно из достоинств, за которые следует останавливать выбор на этой букмекерской конторе?
Именно это подтвердило огромнейшее число пользователей
компании.
Вот почему, если вы решили испытывать удачу на ставках, то вам следует обратить внимание на Melbet.
Тут melbet-partner.com вы сможете найти необходимую информацию и решения своих вопросов,
а , кроме того, немедленно начать делать ставки после регистрации.
Bookmaker 1xbet in Italia https://gameshanhdong.com/forum/profile.php?id=15589
La societa di scommesse 1xBet Italia e una societa di origine russa.
La societa di scommesse fornisce i propri servizi ad utenti maggiorenni di tutto il mondo.
Il sito si trova sempre nelle posizioni di primo piano per il numero di clienti e la qualita degli eventi in linea.
Il sito e famoso per il proprio supporto tecnico, che risponde in pochi minuti, nonche per i piacevoli gratuity sul primo deposito.
Storia di 1xbet Italia
L’organizzazione del gioco d’azzardo ha operato in tutto il mondo per oltre 10 anni, ma alone nel 2015 e arrivata in Italia.
I giocatori italiani preferiscono proprio 1xbet a causa dell’ampio investimento della societa di scommesse sui giocatori
popolari del nostro paese.
Il sito ha guadagnato popolarita anche grazie al servizio 1xbetstreaming, il quale permette di scommettere
direttamente mentre si guarda l’evento.
La societa di scommesse aumenta ogni anno il fatturato dei fondi e il numero di utenti attivi.
Su questo influiscono l’apertura del casino online aperto e le grandi partnership con grandi club.
Chelsea, Liverpool e Barcellona non sono gli unici nella lista delle
sponsorizzazioni della societa di scommesse.
Licenza
Al momento, la societa di scommesse ha difficolta a causa del rinnovo della licenza, ma nell’applicazione
ambulatory su Android e iOS e ancora possibile scommettere.
Per questo gli scommettitori del Brasile e dei paesi vicini possono
scommettere normalmente. Al momento, la societa e
in trattativa per rinnovare la licenza e continuare le attivita nel suo Paese.
Sistema reward 1xbet Italia
La societa di scommesse cerca di rafforzare la propria posizione nel mercato
delle scommesse con ampie offerte promozionali. Il extra
di benvenuto soddisfa i nuovi arrivati e consente di aumentare il primo deposito della
meta, fino a 100 euro. Le condizioni di base per ricevere il regalo sono le
seguenti:
• e necessario versare almeno 1 euro sul conto;
• e necessario scommettere 5 volte l’importo versato per ricevere il regalo;
• le scommesse devono essere espresse da 3 eventi o piu;
• il coefficiente di ogni partita deve essere superiore a 1,40;
• e necessario recuperare il totale entro 30 giorni
dalla ricezione del bonus.
Gratuity aggiuntivi dal sito
I giocatori possono ricevere altri regali, move l’introduzione di codici promozionali speciali al casino o
alle scommesse.
Ci sono codici simili durante eventi sportivi su larga scala.
Nel corso di un grande evento, nel 2018, la societa ha offerto a tutti di ottenere 10 euro,
che potevano essere giocati senza il rischio di perdere.
La linea di partite 1xbet al giorno supera i 1000 eventi.https://forum.exis-work.ru/profile.php?id=63154
La compagnia di scommesse 1xBet riempie costantemente la propria linea con partite ed
eventi interessanti. In media, ogni giorno ci sono piu di 1000 eventi per le scommesse.
L’amministrazione cerca di defy l’opportunita di scommettere non unaccompanied sulle
partite popolari, ma anche sugli eventi regionali in Portogallo,
in modo che tutti possano scommettere a loro piacimento.
Settle iniziare a scommettere su 1xbet Italia? Casinò 1xbet
Iniziare a scommettere su 1xbet Italia e molto semplice.
Occorre trovare il sito ufficiale su Google e registrarsi.
Ogni utente maggiorenne puo creare un profilo. Questo puo
essere fatto in 4 modi:
Букмекерская компания Леон – заметный представитель
игорного бизнеса на отечественном рынке.
Она позволяет людям зарабатывать живую копейку не
первый год.
За все время деятельности БК смогла заслужить немало призов, однако самой значимой среди них считается премия «Спорт и Россия».
Ее вручают за особый вклад в
развитие спорта по регионам РФ.
Не вызывает удивления то, что клиенты, обращающиеся
в букмекерскую контору, не только делают ставки, а с увлечением следят за играми известных и только стартующих команд.
Официально подтвержденный сайт официальный сайт leon bk
https://forum.ipxe.org/member.php?action=profile&uid=608598 представляет собой функциональный и
довольно удачный сервис.
Привлекательная архитектура вебсайта
и незначительное число рекламных окон не
раздражают пользователей и вместе с тем стимулируют ставить на различные события.
Где еще удастся испытать небывалый взрыв эмоций?
Сайт предоставляет играющим возможность:
• ознакомиться с бонусной политикой, акциями, которые
предусмотрены администрацией;
• сделать ставку на игру в привычным способом и Live;
• посмотреть результаты прошедших событий;
• прочитать особенности пользования сервисом и в дальнейшем неукоснительно им
следовать;
• обратиться в службу поддержки, которая работает 24/7;
• скачать приложение на смартфон, чтобы делать ставки в удобное
время в зонах, где ловит сеть.
Варианты ставок на спортивные события
Bookmaker готов предложить клиенту широкий ассортимент
спортивных событий.
• футбол;
• баскетбол;
• хоккей;
• волейбол;
• киберспортивные дисциплины;
• регби;
• боксерские поединки;
• cricket;
• теннисные турниры и др.
Кроме этого, получить живые деньги удастся:
• на автоматах;
• в casino;
• во время игры в покер.
Все мероприятия представлены на отдельной странице, поэтому найти их не
составит труда.
Клиент будет иметь доступ к ним немедленно
после прохождения оформления учетной записи
и внесения на счет любой суммы денег.
Это недолго вбить персональные данные в отведенные ячейки на портале.
Важно не забывать про обязательную проверку информации для
доказательства достижения совершеннолетнего возраста.
Система бонусов
Разнообразие ставок – не последнее достоинство букмекерской конторы Леон.
Администраторы привлекают новичков еще и немалым количеством поощрений.
Такие сюрпризы идут на игровой счет,
что позволяет экономить живые деньги и
стартовать с поощрительной суммы.
Контора предоставляет бонусные
начисления при регистрации,
после того, как внесен первый платеж,
при стабильной активности игрока и после каждого
внесения денег на счет.
Как видите, созданы все удобства не
только для опытных, но и
для стартующих клиентов букмекерской сети.
Получится немедленно воспользоваться приветственным бонусом.
Особенности мобильного приложения леон контора регистрация
http://mddsgjkh886.com/comment/html/?22441.html клиенты могут не только посредством компьютера.
Для удобства игроков программеры предусмотрели
мобильную версию, что позволяет быстро ставить.
Версия получила идентичный основному
порталу дизайн и гарантирует клиентам
полноценный комфорт во время выполнения ставок.
При этом приложение доступно владельцам смартфонов
независимо от ОС – как Андроид, так и iOS.
Вы обнаружите, насколько легко использовать приложение
независимо от Вашего местоположения.
Нужно всего лишь подключиться к сети интернет,
не забывать про регистрацию и про последующую
авторизацию.
Еще никогда сделать ставки
на разные события, связанные с матчами,
не было настолько просто.
Букмекерская контора ЛЕОН отличается своей программой лояльности,
привлекательными призами и
удобным мобильным приложением.
Ее выбирают для себя жители различных областей РФ.
Разработчики предусмотрели, чтобы работа конторы велась на законных основаниях.
В наличии необходимые разрешения.
Букмекерская контора не имеет недочетов, в
связи с чем пользуется спросом
не только новичков, но и опытных
игроков.
Дождаться сыгравшей ставки и пополнить
личный счет сможет каждый из зарегистрированных
совершеннолетних пользователей.
Главное, исключить страх и поверить собственной интуиции.
Букмекерская контора Леон – это предпочтение людей, которые ценят свое время и финансы.
На онлайн платформе реально огромный ассортимент
событий, на которые предлагается сделать ставки.
Вы сможете не только отслеживать успехи любимой
команды, но и, козможно,
получить большой выигрыш.
Следует всего лишь зарегистрироваться на
официальном сайте конторы, чтобы суметь
оценить все предлагаемые разработчиками преимущества.
Понятный вариант оформления сайта удовлетворит даже начинающих игроков.
Excellent beat ! I wish to apprentice while you amend your web site, how
could i subscribe for a blog website? The account helped me a acceptable deal.
I had been a little bit acquainted of this your broadcast offered bright clear idea
1XBET – одна из наиболее популярных в РФ букмекерских контор по
прогнозам на спортивные события.
Сервис работает на основе лицензии Кюрасао в режиме онлайн.
Компания, работающая с 2007 г.,
насчитывает больше четырехсот тысяч постоянных посетителей.
На сегодня букмекерская контора 1xbet в числе мировых лидеров по спортпрогнозам.
Это можно назвать как критерий доверия армии клиентов, которые выбрали именно данную БК.
Осталось понять особенности пребывания на online площадке как воспользоваться бонусом обыграй 1хбет .
Правила прохождения регистрации
Производить прогнозы имеет право зарегистрированный клиент (беттер).
Известны разные способы создания профиля:
1. через социальные сети, потребуется всего лишь
остановиться на соответствующем варианте;
2. по адресу электронной почты вне зависимости от
сервиса;
3. по телефонному номеру, на который будет отправлено смс.
Пользователям http://cgi.www5b.biglobe.ne.jp/~leen/cgi-bin/bbs/yybbs.cgi/%20resu в личный кабинет
становится доступным сразу по окончании регистрации.
Зарегистрированный клиент может ставить на выбранные спортивные турниры, принимать участие в акционных
и бонусных программах, осуществлять
вывод денег и др.
Вам понравится не безучастно наблюдать за матчем выбранного состава игроков, но и
при желании получать неплохие денежные суммы.
Для этого надо всего лишь выбрать событие, которое пришлось по вкусу.
Как видите, после регистрации можно пользоваться многочисленными возможностями основного ресурса, которые предусмотрели разработчики.
Разновидности ставок БК 1хбет http://fumi.s22.xrea.com/cgi-bin/aska/aska.cgi/contact.php
1Хбет в отличие от других БК предоставляет двенадцать типов сделок.
Одиночная ставка (одиночник, единица) – сделка на определенный исход спортивного
события.
Выигрыш насчитывается при
умножении коэффициента в десятичном
формате на количество поставленных денег.
То есть сложностей особых нет,
если выбирать этот вариант прогноза.
Экспресс – прогноз одновременно на 2
и больше исходов, которые анонсируются.
Экспресс «Стайер» отличается особенностью:
результаты и мероприятия разрешается добавлять в течение двух месяцев.
Антиэкспресс содержит ряд исходов,
противоположный экспрессу по способу определения выигрыша.
Этот вид ставки признают как опытные игроки,
так и начинающие пользователи.
Система – пари на все возможные варианты экспрессов конкретной размерности из выбранного числа событий.
Цепочка – комплект одинарных ставок.
По ставке доверительного типа можно вернуть часть денег, находящихся пока под блокировкой.
Это довольно интересное предложение, которое выбирают зарегистрированные пользователи.
Ставка по промокоду выдает комбинацию из букв
и цифр для оформления заявки.
Этим способом удобно осуществить ставку без внесения
денег на депозитный счет.
Лаки оказывается комбинированием единиц и совершенно всех экспрессов,
собранных из указанных спортивных мероприятий.
Патент действует по тому же алгоритму,
что и лаки, но число прогнозов ограничивается 3-мя.
Для каких целей необходимо заходить
на зеркало
Букмекерская контора 1Хбет считается нелегальной в
регионах России.
Подобное положение сопряжено
с тем, что контора не взимает проценты с выигрышей
клиентов.
Для самих пользователей это огромный плюс, но
на законодательном уровне названный момент
считается далеко не целесообразным.
Разработчики не собираются что-либо менять в
своей политике.
Как же быть в такой ситуации пользователям?
В действительности никаких сложностей
нет.
Следует избежать блокировку основного веб-сайта, то есть зайти на актуальное
зеркало портала.
Зеркало представляет собой специальный сервис
с идентичным отображением портала, без каких-либо ограничений, с воссозданием ранее внесенных данных.
Разрешается войти и спокойно воспользоваться имеющимися
возможностями, предложенными создателями.
Такие копии используют общую с официальным вебсайтом 1xbet БД, поэтому войти
на сайт удобно под своей учетной записью.
Не забывайте, что интерфейс аналогичен официальному сайту букмекера.
Переместиться на аналог получится по адресу 1xbet демо счет как открыть.
Кроме прогнозов на спорт в 1хбет пользователям предлагают тотализаторы, слоты, различные лотереи,
нарды, игровые процессы в онлайн и офлайн режимах.
Как видите, у БК оптимальное число событий, которые могут оказаться по вкусу клиетнам самого разного возраста, пола.
Необходимо всего лишь зарегистрироваться по несложному алгоритму уже сейчас.
Вы поймете, насколько увлекательно удастся провести время, если есть ноутбук и подключение к интернету.
cerchietti fai da te
sandler tan bootvans wedge sneakers pricekyrie irving shoe commercialuk shoe size to us mens clothing
1XBET входит в число наиболее востребованных в России букмекерских контор по ставкам на спортивные события.
Сервис работает по лицензии Curacao в online-режиме.
Компания, работающая с 2007 г., обслуживает свыше 400 тыс.
постоянных посетителей.
На сегодня букмекерская контора 1xbet
в числе мировых лидеров
по спортпрогнозам.
Это и есть критерий доверительности
многочисленных клиентов, которые решили выбрать
именно данную букмекерскую контору.
Теперь надо разобраться в особенностях нахождения на online площадке 1хбет зеркало рабочее .
Порядок прохождения регистрации
Делать ставки может только зарегистрированный клиент (беттер).
Известны различные варианты создания аккаунта:
1. через соцсети, потребуется всего лишь остановиться на соответствующем варианте;
2. по адресу электронной почты независимо от
платформы;
3. по телефонному номеру, на который будет отправлено сообщение.
Пользователям http://www.kochi-yeg.ne.jp/cgi/bbs/teisei/index.html в персональный аккаунт станет
открытым немедленно по окончании регистрации.
Беттер получает право делать ставки на
выбранные события из мира спорта,
участвовать в акциях и бонусах,
осуществлять вывод денег и др.
Вам понравится не безучастно наблюдать за матчем
выбранного состава игроков, но и по возможности получать немалые денежные суммы.
Нужно всего лишь указать событие,
которое понравилось больше всего.
Итак, по окончании регистрации разрешается воспользоваться множеством возможностей официального сайта,
которые предоставили администраторы.
Разновидности ставок БК 1хбет https://www.rentcom.info/user/profile/44585
1Хбет в отличие от других БК предоставляет 12 вариантов операций.
Одиночная ставка (одиночник, единица)
– соглашение на отдельный исход спортивного мероприятия.
Выигрыш рассчитывается при умножении десятичного коэффициента на сумму
пари.
Получается, что нет ничего сложного, если выбирать данный вариант ставки.
Экспресс – ставка одновременно на 2 и более исходов, которые анонсируются.
Экспресс «Стайер» имеет особенность:
результаты и мероприятия разрешается добавлять в течение 2-х месяцев.
Антиэкспресс содержит несколько исходов, обратный экспрессу по методу начисления выигрыша.
Такой вид прогноза признают как опытные игроки, так и новички.
Система – сделка на все возможные варианты экспрессов
конкретной размерности из выбранного
числа мероприятий.
Цепочка – набор одиночных прогнозов.
По ставке доверительного типа
можно получить часть финансов, находящихся пока
под блокировкой.
Это достаточно привлекательное предложение, которое выбирают зарегистрированные пользователи.
Ставка по промокоду определяет комбинацию из букв и цифр для оформления заявки.
Таким образом можно осуществить
ставку без внесения денег на депозит.
Лаки оказывается сочетанием ординаров и совершенно всех экспрессов, которые собраны
из указанных спортивных мероприятий.
Патент действует по тому же алгоритму, что и лаки,
но число событий ограничено тремя.
Для каких целей необходимо использовать зеркало
БК 1Хбет не является легальной в регионах России.
Подобное положение связано с тем, что фирма не
удерживает налоги с выигрышей клиентов.
Для самих пользователей это огромный
плюс, но на законодательном уровне данный момент считается далеко не целесообразным.
Руководители не собираются ничего менять
в своей политике.
Как же быть в этом случае
клиентам?
В действительности нет ничего проще.
Нужно обойти блокировку основного веб-ресурса, а следовательно
посетить функционирующее зеркало портала.
Копия можно представить как специальный сервис с точным интерфейсом сайта, без каких бы то ни было ограничений, с
сохранением ранее введенных сведений.
Разрешается войти и беспроблемно пользоваться
имеющимися возможностями, предусмотренными разработчиками.
Данные копии имеют общую с официальным вебсайтом 1xbet базу, поэтому зайти на ресурс можно под своим аккаунтом.
Помните, что дизайн аналогичен подтвержденному
сервису букмекера.
Перейти на аналог получится по адресу 1xbet приложение android.
Кроме ставок на спортивные турниры в 1хбет игрокам доступны
тотализаторы, слоты, разные лотереи, нарды, игровые процессы в
online и offline режимах.
Можно сделать вывод, что у букмекерской конторы оптимальное количество событий, которые придутся
по вкусу клиетнам разных возрастов, пола.
Нужно всего лишь зарегистрироваться
по несложному алгоритму прямо сейчас.
Вы сможете обнаружить, как интересно получится провести досуг, если есть персональный компьютер и доступ к интернету.
Обзор зеркала Mostbet мостбет зеркало на прямо сейчас
http://agrawaldugdhalaya.com/?option=com_k2&view=itemlist&task=user&id=302387
Ниша ставок в РФ функционирует довольно давно, и в 2012 году
на рынке появилась фирма Mostbet.
На сегодняшний день ресурс активно развивается, в частности это относится к виртуальному пространству.
Как полагают некоторые клиенты, довольно комфортно не выходя из
дома, в офисе или в дороге делать ставки.
Время не будет потеряно.
Основная цель конторы – оказывать помощь людям делать
ставки, это можно сделать , используя офисы компании или же в режиме online, для этого имеется портал и мобильная
версия.
Итак, предоставляется немало возможностей, чтобы приятно провести свободное время, а заодно
попробовать получить неплохие
выигрыши.
Компания мостбет войти в личный кабинет очень стремительно
продвигается и старается подготовить для
своих клиентов самые лучшие
возможности.
Здесь вы можете делать ставки как
на спорт, так и на другие мероприятия, например, конкурсы типа Eurovision.
Теперь не нужно просто наблюдать за тем, как проводит выступление
любимый артист.
Стоит всего лишь поверить в его победу, сделав выгодную
ставку.
Есть шанс, что получится заполучить крупную сумму и при
этом послушать отличную музыку.
Такой подход крайне удобен, так как в этой ситуации абсолютно
любой игрок найдет для себя интересные события и сделает ставки.
Разработчики предусмотрели мероприятия на любой
вкус.
Решение зависит от Вашего возраста, увлечений, а
также желания рисковать.
Как начинать делать ставки
на спорт с Mostbet
Многие игроки уверены, что делать ставки на
спортивные баталии или другие
мероприятия – это достаточно хлопотно и что в
этом нужно тратить время на разбирательство.
Но так ли это на самом
деле?
Конечно же, это не так.
Если мы говорим о Мостбет http://www.mediline.ba/?option=com_k2&view=itemlist&task=user&id=1156193 мостбет вход войти моя страница ,
то здесь начинать ставить сможет каждый.
На уровне интуиции легко
осваиваемый интерфейс понравится
даже новичкам, которые только решили разобраться с тем, как ставить.
Рассмотрим подробнее, каким образом начинать процесс.
Для старта вам нужно пройти регистрацию на сайте.
Процесс прохождения регистрации
очень легкий, займет у вас минимум времени.
Потребуется всего лишь вбить личные сведения в выделенные ячейки,
пройти процесс верификации.
Как только вы зарегистрируетесь, необходимо
положить деньги на депозит.
При этом не играет роли, какая именно будет зачислена денежная сумма.
Очень быстро Вы освоитесь и сможете
понять, как действовать дальше,
какие размеры взноса считаются наиболее приемлемыми.
И с этого момента вы можете начать делать ставки.
Сейчас стало ясно, что делать это совсем несложно, потому
что этот процесс займет у вас минимальное количество сил
и времени.
Таким образом, абсолютно каждый сумеет начать делать ставки вне зависимости от того без опыта он
или профессионал.
Все, что для этого нужно – пройти регистрацию.
Контора Mostbet – одна из самых известных и востребованных площадок на рынке России, что
абсолютно не удивительно.
Ведь компания заботится о своих пользователях
и предлагает для них самые лучшие
условия.
Разработчикам важно не
просто привлечь больше пользователей, но и создать
наиболее удачные условия для постоянных клиентов.
Репутация является важным критерием для компании
во имя того, чтобы не снизить доверия игроков.
В сфере ставок присутствует немалое количество мошенников.
Не следует слепо доверять яркой рекламе,
а также бездумно верить чрезмерно заманчивым предложениям.
Возможно не только потерять деньги,
время, но и установить на компьютер вирусную программу.
Целесообразнее выбирать лишь проверенные компании, которые долгий период пребывают в игровой области.
В любой момент можно почитать отклики, ознакомиться с временем появления конторы на
просторах интернета.
Одним из подобных профи ведения игрового бизнеса считается mostbet войти
При желании можно загрузить специально
разработанное приложение для смартфонов и других гаджетов.
Останется обеспечить наличие сети Интернет, чтобы делать
ставки прямо сейчас.
У Вас будет возможность выбрать мероприятие,
спрогнозировать результат, пребывая в пробке или в
офисе.
Не это ли и есть одно из достоинств, за которые стоит останавливать выбор
на этой букмекерской конторе?
Именно это подтверждает огромнейшее количество
игроков конторы.
Вот почему, если вы решили испытывать удачу на ставках, то вам
стоит присмотреться к Мостбет.
Здесь Mostbet-partner.com вы сможете найти важную информацию
и ответы на свои вопросы, а , кроме того, сразу начать делать ставки после регистрации.
Обзор Melbet зеркала
Рынок ставок в России функционирует
довольно давно, и в 2012 г. вышла на рынок фирма Melbet.
На сегодняшний день сервис активно развивается, в частности это касается виртуального
пространства.
Как полагают некоторые клиенты, довольно удобно никуда
не выходить, а ставить на события.
Время не будет потеряно.
Наиболее важная задача компании – помогать игрокам ставить, это
удобно выполнить , используя офисы
компании или же в режиме онлайн, для чего есть портал и приложение
для смартфона.
Итак, предоставляется довольно много возможностей, чтобы с удовольствием
провести досуг, а вместе с тем попробовать заработать неплохие выигрыши.
Компания melbet мобильная версия сайта довольно активно продвигается и намерена создать для своих клиентов самые лучшие условия.
Тут вы можете ставить как на спорт, так и на иные мероприятия, например, турниры типа Eurovision.
Больше не нужно безучастно наблюдать за тем, как выступает любимый артист.
Стоит всего лишь поверить в его победу, сделав выгодную ставку.
Есть вероятность, что удастся заполучить крупную сумму и при этом насладиться
музыкальным произведением.
Это очень удобно, так как
в этой ситуации абсолютно любой игрок найдет
для себя интересные мероприятия
и поставит на его исход.
Разработчики смогли предусмореть мероприятия на любой вкус.
Все зависит от того, сколько Вам лет, чем вы увлекаетесь и способны ли рисковать.
Как начать ставить на спортивные события с Мелбет http://p857.cn/home.php?mod=space&uid=10062&do=profile
Многие игроки думают, что ставить на
спорт или иные мероприятия – это достаточно сложно и что в этом нужно долго разбираться.
Но так ли это на самом деле?
Конечно же, это не так.
Когда мы говорим о Мелбет, то здесь начинать ставить
получится у любого желающего.
Интуитивно легко осваиваемый интерфейс придется по душе даже новичкам, которые надумали
разобраться с тем, как ставить.
Рассмотрим более подробно, как начать
это делать.
Для начала вам нужно зарегистрироваться
на сайте промокоды melbet на фрибут
Алгоритм прохождения регистрации удивительно простой, займет у вас минимум времени.
Нужно всего лишь ввести личные сведения в выделенные ячейки, пройти процесс верификации.
После регистрации надо будет внести деньги на
депозит.
Абсолютно неважно, какая именно
будет зачислена сумма денег.
Очень быстро Вы разберетесь и сможете понять, каким образом поступать
дальше, какие параметры взноса считаются оптимальными.
И после этого вы можете начать делать ставки.
Теперь становится ясно, что выполнять подобные манипуляции можно без особого труда,
потому что на эти действия уйдет у
вас минимум времени и сил.
Таким образом, абсолютно каждый сумеет начать ставить вне зависимости от того новичок он или профи.
Все, что для этого требуется –
зарегистрироваться.
Контора Melbet – одна из самых популярных
и пользующихся спросом площадок на российском рынке, что совсем не удивительно.
Ведь компания с заботой относится к своим клиентам и подготавливает
для них самые лучшие условия.
Разработчикам надо не просто
заинтересовать новых игроков, но и создать наиболее комфортные обстоятельства для
завсегдатаев.
Репутация является важным
критерием для конторы во имя того, чтобы не снизить доверия пользователей.
В сфере ставок существует большое количество
аферистов.
Не следует соблазняться привлекательной рекламой, а также бездумно верить чрезмерно заманчивым предложениям.
Возможно не только лишиться денег, безрассудно потерять время, но
и установить на компьютер вирусную программу.
Целесообразнее останавливать выбор на надежных фирмах, которые долгий период пребывают в данной сфере.
Всегда можно изучить отзывы, узнать о времени
начала деятельности конторы на просторах интернета.
Одним из подобных профи ведения игрового бизнеса
считается http://www.33sn.net/home.php?mod=space&uid=229020&do=profile&from=space .
В определенный момент можно загрузить специально разработанное приложение для смартфонов и других гаджетов.
Нужно подсоединиться к сети Интернет, чтобы ставить прямо сейчас.
Вы даже сможете выбрать мероприятие, спрогнозировать результат,
пребывая в заторе или на даче.
Это ли не одно из преимуществ, за которые стоит
останавливать выбор на этой букмекерской конторе?
Именно это подтверждает огромнейшее количество клиентов конторы.
В таком случае, если вы решили начать делать
ставки, то вам следует обратить внимание на Melbet.
Тут melbet-partner.com вы найдете важную информацию и ответы на свои вопросы, а , кроме
того, немедленно приступить к
ставкам после регистрации.
Букмекерская контора Леон –
яркий участник отрасли азартных игр на отечественном рынке.
Она дает возможность людям зарабатывать реальные деньги достаточно долгое время.
За годы работы БК смогла заслужить немало вознаграждений, однако самой заметной
среди них является премия «Спорт и Россия».
Ее дают за выдающиеся вложения в популяризацию спортивных игр
на территории РФ.
Неудивительно, что клиенты, обращающиеся в БК, не просто делают ставки,
а активно следят за играми
известных и небольших команд.
Официально подтвержденный портал
леон промокод при регистрации
http://www.maoyouhe.com/home.php?mod=space&uid=1401454&do=profile позиционируется как функциональный
и довольно удачный ресурс.
Привлекательная архитектура вебсайта и незначительное
число рекламных окон доставляют пользователям удовольствие и вместе с тем мотивируют ставить
на различные события.
Где еще получится ощутить небывалый взрыв эмоций?
Сервис предлагает играющим следующие возможности:
• ознакомиться с бонусной политикой, акциями, предусмотренными администрацией;
• поставить деньги на событие в привычным способом
и наличными;
• узнать итоги завершившихся матчей;
• прочитать правила и впоследствии неукоснительно им следовать;
• обратиться в службу техподдержки, которая отвечает круглосуточно;
• загрузить программное приложение
на телефон или планшет, чтобы
ставить независимо от времени суток в местах, где ловит сеть.
Варианты ставок на спортивные события
Букмекер предлагает клиенту широкий
ассортимент спортивных событий.
• футбол;
• баскетбол;
• хоккей;
• соревнования по волейболу;
• киберспортивные дисциплины;
• регби;
• бокс;
• cricket;
• теннис и др.
Помимо этого, получить живые деньги удастся:
• на автоматах;
• в казино;
• во время игры в покер.
Все события расписаны на отдельной странице,
это значит, что отыскать их будет
не сложно.
Клиент будет иметь доступ к ним
немедленно по окончании
оформления учетной записи
и внесения на счет любой суммы
денег.
Это недолго ввести личные сведения в
специальные поля на сайте.
Не стоит забывать про обязательную проверку информации для доказательства совершеннолетия.
Бонусная система
Богатый выбор ставок – не последнее достоинство БК Леон.
Администраторы привлекают новых игроков еще
и немалым количеством бонусов.
Подобные «подарки» уходят на игровой счет, что позволяет экономить реальные финансы и начинать делать ставки с бонусной суммы.
Компания дарит бонусы после прохождения регистрации, при внесении первого депозита, при стабильной активности игрока и при каждом пополнении
счета.
Как видите, созданы все условия
не только для опытных, но и для начинающих пользователей букмекерской сети.
Получится немедленно ввести в дело приветственный презент.
Мобильная версия бонус код бк леон
https://www.dushiol.com/home.php?mod=space&uid=20721&do=profile клиенты могут
не только через компьютер.
Для комфорта играющих разработчики предусмотрели мобильную версию, что
позволяет оперативно ставить.
Версия получила идентичный основному порталу интерфейс и обеспечивает пользователям максимум
удобств во время выполнения ставок.
При этом приложение доступно обладателям смартфонов на любой ОС – как Андроид, так и iOS.
Вы убедитесь, насколько удобно
использовать приложение независимо от Вашего местоположения.
Нужно всего лишь подключиться к Интернету, не забывать про регистрацию и про необходимость авторизоваться.
Еще никогда сделать ставки на различные события, сопряженные с матчами, не было настолько легко.
Букмекерская контора ЛЕОН отличается своей политикой поощрений, привлекательными призами и удобным мобильным приложением.
Эту компанию предпочитают граждане разных областей РФ.
Разработчики предусмотрительно
продумали, чтобы деятельность организации велась
на законных основаниях.
Для этого имеются все лицензии.
Букмекерская компания лишена недостатков, из-за чего пользуется спросом не только новичков, но и
игроков со стажем.
Провести время в ожидании сыгранной
ставки и внести деньги на личный аккаунт получает возможность любой из зарегистрированных достигших совершеннолетия клиентов.
Важно, бояться и довериться внутреннему голосу.
Букмекерская контора Леон – это выбор пользователей, ценящих свое время
и финансы.
На онлайн платформе действительно огромный
выбор мероприятий, на которые можно делать
ставки.
Вам удастся не только следить за успехами команды фаворита, но и, козможно, получить большой куш.
Следует всего лишь пройти регистрацию на основном сайте конторы, чтобы суметь оценить все представленные основателями преимущества.
Адекватный для понимания интерфейс удовлетворит даже начинающих игроков.
In India, the 1xBet betting comrades – is a specific of the
most common ones in Asia. Among its ranking
advantages, one can note enormous odds, a sympathetic action procedure on presented events and
honest established payoffs. In its functionality, the reflection likeness is no different from the
main resource, providing users with all the same capabilities.
1xBet betting gathering
1xbet app download https://osderby.com/wiki/User:HeribertoChampli
1xbet app
Using the pertinence in place of Android, players can bet on sports in travel, at work or at home.
All that is required – is access to the Internet. In order to
initiate the program, go to the “Applications on smartphones” part, write mobile
phone tally in the opened form. In a hardly minutes, an SMS idea with
download link will arrive.
1xbet apk 1xbet app download
1xbet apk
The 1xBet portable app as a replacement for iOS can be downloaded in the App Store.
A rule download link is present on the betting body’s solemn website
– follow the station instruction.
Normal word
With help of our website there is an occasion to collar access to the website about the clock, placing bets on events of interest.
The betting platform in India can be tolerant of not exclusively from a PC, but also from most non-stationary devices.
License
The 1xBet troop operates on the Internet legally. To provide
services, the betting players has a permit issued by
the global regulator of Curacao. It allows the party line
to coax in divers countries without violating law.
Inspection of the 1xBet official Indian website
The betting stand offers visitors to punt on sports and
monetary events. Bettors also be experiencing access to online slot machines and a practical casino.
A player can wager bread in any sections of the website using a individual account.
The betting company has a satisfactory undertaking extraction and bird filthy
lucre face on all events. Users can flutter in more
than 40 sports types, ranging from lay football and tennis to crazy
cockfights.
The betting company accepts bets on almost all outcomes: not only on a superiority or
undoing of ditty of teams, but also on a tot up
of corner kicks, penalties and other results. One can inspect a
less strong action crow’s-foot at the 1xBet betting company
merely ahead unsought after events. But equal here one
can stake on over/under, barrier and some other outcomes. Players can evaluate all
the possibilities of moneyed betting only after creating an account.
Registration in the 1xБет India 1xbet login http://satguide.org/index.php?title=1xbet_India_1xbet_App_India_1xbet_Apk_India_1xbet_Login_1xbet_App_Download_1xbet_Apk_Download_1xbet_Login_In_India
Registration in the 1xБет India
In unison can move a draw in the betting company in 4 ways:
via a quick registration procedure. A player needs to click on the proper tag and
distinguish the provinces of residence. After a scattering seconds, the buyer drive be given a watchword and
login, which leave be created on the system;
registration way
by creating an account using phone. In this action,
during registration methodology a visitor necessity direct attention to the nimble phone slues
onto which SMS address intent in with circumstantial instructions;
creating an account using phone
about registering via email. The exemplar option, at which operator fills escape registration form, prescribing dear observations and a valid
e-mail. Later a message with a interdependence couple comes to the consumer’s
specified e-mail, which becomes a pass to the 1xBet India website;
close registering via venereal networks. The easiest crumble to motivate an account.
A sportswoman however needs to click on the icon with the popular network
where he has a examination, after which an account is automatically generated.
1xbet login
1xbet login
Individual can enlist the 1xBet website in the selfsame way as on the major 1xbet com
resource. It is sufficient for a consumer to exhibit in the system
in any at one’s fingertips way, and then subscribe to
near entering the requisite shibboleth and login. In some cases, to penetrate insulting account, anybody may sine qua non a dear jus divinum ‘divine law’ that the betting proprietorship sends in the pose of SMS dispatch
onto a mobile phone number.
In situation of problems with entering an account anticipated
to a shrinkage of a password, the contender inclination be skilled to resolve the end quickly.
To do this, only click on the “Forgot your password?” handle, editorial down the email hail
or phone mass next to it. The narcotic addict drive be obtain relative
facts to the specified contacts. The countersign sent will servants to log in to the account.
Depositing paper money
After fleeting registration and authorizing on the website, consumer drive be masterly to replace funds in his personal account.
To do this, run to the “Payments” section. There, the participant desire be wise to persevere numerous options
in place of depositing funds into the account:
bank transfer;
electronic wallets and payment systems;
payment toe the vdu = ‘visual display unit’;
spondulicks transmit from a mobile phone;
Internet banking;
cryptocurrency
prepaid cards.
In all-out, the website of the betting company provides more than 40 options as a
service to depositing capital. Regardless of the chosen method,
economic transactions on the website are carried out instantly.
The song leading factor over the extent of a musician – is to conclude the rules established by the
betting company. For pattern, the replenishment amount should be no less than 100
rubles. In withal, it is strictly forbidden to abuse other people’s wallets and bank cards to deposit money.
Loser to yield with these conditions may lead to blocking of the account.
Spinach withdrawal from the 1xbet in India 1xbet app India
To leave funds out of the set-up it is imperative to use the same acquiesce as with replenishment.
To frame a economic transaction, a musician needs to be disposed of to offensive account and supreme the “Banknotes withdrawal” section.
There the buyer wishes need to mention the amount to be transferred,
and transcribe the figures from his electronic wallet or bank card.
If all the data is reprove, the application for funds withdrawal determination be processed
on the betting assembly within 1-7 days.
In order to escape delays in payoffs of earned
winnings, players necessity to pass account verification procedure 1xbet login .
During this moving, the owner pass on be required to lend
the 1xBet application in India with copies of his agreement documents.
Passed biographical verification wishes allow one withdraw funds from the website
far, at any within easy reach time.
It is distinguished on players to remember that the betting company has set assured limits
on in clover withdrawal. In containerize of any problems with withdrawal of funds,
bettors can connection the in maintenance in regard to help.
Stand by alpenstock mould at the website about the
clock.
Bonuses from 1xBet
The betting assemblage offers visitors a solid compensation program.
Players can expect to receive the following types of bonuses:
“In behalf of the from the word go deposit.” The amount of the encouragement
is 100% from the deposited amount. The gain must be won go at three bets of the Speak order with a
coefficient of at least 1.4;
“Favoured Friday”. The tip is issued to players strictly on the specified day.
The take first prize in bankroll b reverse conditions are the
same as with the make something representing the first put;
“Wednesday – multiply near 2”. Cappers who won on the “Lucky Friday” are allowed to participate in the action. If the purchaser
has not in the future withdrawn the funds won from the sometime week, his deposit is
doubled past the betting company;
“Depict of the day.” The over b draft is held daily.
If a player achieves big name in the Stock or the Complete, he leave bear an raise in the appearance of 10%
of the earned winnings;
“Bonus quest of a series of failures.” Drug profit without hope take a hand
in of the irrecoverable money, upon shape of 20 unsuccessful bets in a series with a coefficient of not
more than 3.
1XBET входит в число самых востребованных в России букмекерских компаний по прогнозам на спортивные события.
Сервис работает на основе лицензии Curacao в online-режиме.
Компания, осуществляющая деятельность с 2007 года,
насчитывает свыше 400 тыс. постоянных клиентов.
На сегодняшний день букмекерская контора 1xbet входит в число
мировых лидеров по спортивным ставкам.
Это и есть критерий доверительности армии пользователей, которые выбрали именно указанную БК.
Теперь надо понять особенности
пребывания на online площадке 1хбет зеркало рабочее .
Порядок прохождения регистрации
Делать прогнозы может только прошедший регистрацию пользователь (беттер).
Есть различные способы подготовки аккаунта:
1. через соцсети, потребуется всего лишь выбрать
соответствующий вариант;
2. по адресу электронной почты
вне зависимости от сервиса;
3. по номеру сотового телефона, на который
придет смс.
Пользователям https://rockfishlax.com/library/index.php/User:JacquettaZ13 в личный кабинет станет открытым сразу
по окончании регистрации.
Беттер может ставить на выбранные события из мира спорта,
принимать участие в акциях и бонусах, выводить средства и др.
Вам понравится не просто наблюдать за матчем выбранного состава игроков, но и при желании
получать немалые денежные суммы.
Для этого надо всего лишь указать
мероприятие, которое пришлось по вкусу.
Итак, после регистрации разрешается пользоваться множеством возможностей официального
ресурса, которые предусмотрели
разработчики.
Разновидности прогнозов БК 1хбет http://182.191.119.233/ActivityFeed/MyProfile/tabid/60/userId/104676/Default.aspx
В отличие от подобных контор 1Хбет насчитывает двенадцать типов сделок.
Одиночная ставка (одиночник,
единица) – соглашение на отдельный результат спортивного
события.
Прибыль насчитывается умножением коэффициента в десятичном формате на количество поставленных денег.
То есть нет ничего сложного, если выбирать этот вариант прогноза.
Экспресс – прогноз одновременно
на 2 и более результатов, которые должны пройти.
Экспресс «Стайер» отличается особенностью:
результаты и события разрешается дописывать
на протяжении двух месяцев.
Антиэкспресс включает несколько итогов, противоположный экспрессу по способу определения призовых денег.
Этот тип ставки выбирают как опытные игроки, так и новички.
Система – пари на все возможные варианты экспрессов конкретной размерности из указанного числа мероприятий.
Цепочка – комплект одиночных
ставок.
По ставке доверительного типа можно вернуть часть денег,
находящихся пока под блокировкой.
Это достаточно привлекательное предложение, которое
могут выбрать прошедшие регистрацию клиенты.
Прогноз по купону выдает комбинацию из букв и цифр для оформления заявки.
Таким образом можно осуществить ставку без внесения денег на
депозит.
Лаки оказывается сочетанием ординаров и совершенно
всех экспрессов, собранных из выбранных спортивных
событий.
Патент имеет такой же принцип,
что и лаки, но количество событий ограничивается тремя.
Для каких целей нужно использовать зеркало
БК 1Хбет не является легальной в регионах России.
Это связано с тем, что фирма не взимает проценты с прибылей игроков.
Для самих пользователей это
огромный плюс, но на законодательном уровне данный нюанс
признается не самым целесообразным.
Разработчики не собираются что-либо изменять в проводимой
политике.
Как же быть в такой ситуации пользователям?
На самом деле нет ничего проще.
Нужно обойти блокировку официального веб-сайта,
то есть зайти на функционирующее зеркало площадки.
Копия можно представить как особый сервис с идентичным
интерфейсом сайта, без каких-либо сдерживающих
факторов, с сохранением ранее введенных данных.
Можно войти и беспроблемно воспользоваться
имеющимися возможностями, предложенными создателями.
Эти копии имеют единую с официальным вебсайтом 1xbet
базу, поэтому зайти на сайт можно под своей учетной
записью.
Помните, что дизайн аналогичен
подтвержденному сервису букмекера.
Переместиться на зекрало получится по ссылке букмекерская контора 1xbet.
Кроме прогнозов на спорт в 1хбет
игрокам доступны тотализаторы,
слоты, разные лотереи, нарды,
игры в онлайн и офлайн режимах.
Как видите, у букмекерской конторы достаточное количество мероприятий,
которые придутся по нраву пользователям самого разного возраста,
пола.
Необходимо всего лишь зарегистрироваться по несложному алгоритму уже сейчас.
Вы сможете обнаружить, насколько увлекательно удастся
провести время, имея ноутбук
и доступ к сети Интернет.
Обзор зеркала Mostbet мостбет зеркало войти
https://www.freeads-edinburgh.co.uk/user/profile/10340
Рынок ставок в России существует довольно давно, и
в 2012 г. вышла на рынок компания Мостбет.
На сегодняшний день ресурс стабильно продолжает развиваться, непосредственно это относится к виртуальному пространству.
Как полагают многие клиенты,
довольно удобно не выходя из дома, в офисе или в
дороге делать ставки.
Потеря времени исключена.
Главная цель компании – оказывать помощь игрокам делать ставки, это удобно выполнить , используя офисы фирмы или же в режиме online,
для чего есть портал и приложение для смартфона.
Итак, предоставляется довольно много возможностей, чтобы приятно
провести досуг, а вместе с тем попытаться получить неплохие выигрыши.
Контора mostbet скачать приложение на андроид очень активно продвигается и старается создать для своих
клиентов наилучшие возможности.
Тут каждый может делать ставки как
на спортивные, так и на другие события,
к примеру, турниры наподобие Eurovision.
Больше нет смысла безучастно смотреть за тем,
как проводит выступление любимый исполнитель.
Достаточно начать верить
в его триумф, произведя выгодную ставку.
Есть вероятность, что получится сорвать куш , а заодно насладиться музыкальным произведением.
Такой подход крайне удобен, так как в этой
ситуации абсолютно любой человек
найдет для себя захватывающие события и
поставит на его исход.
Программеры смогли предусмореть
мероприятия на любой вкус.
Все зависит от Вашего возраста, увлечений,
а также желания рисковать.
С чего начинать делать ставки на спорт с
Мостбет
Многие игроки думают, что делать ставки на спортивные баталии или другие
события – это довольно хлопотно и что в этом нужно тратить время на разбирательство.
Действительно ли это так и будет?
Естественно, это не так.
Когда идет разговор о Мостбет
http://cgi.www5b.biglobe.ne.jp/~leen/cgi-bin/bbs/yybbs.cgi/yybbs.cgi? mostbet официальный сайт вход регистрация моя страница , то в этом случае начать делать ставки получится у любого желающего.
На уровне интуиции понятный интерфейс понравится даже начинающим пользователям,
которые только решили освоить искусство ставок.
Следует рассмотреть подробнее, каким образом начинать процесс.
Для начала необходимо зарегистрироваться на портале.
Алгоритм прохождения регистрации очень легкий,
вы потратите на него минимум времени.
Потребуется всего лишь вбить личные данные
в выделенные ячейки, верифицироваться.
Как только вы зарегистрируетесь, надо будет
положить деньги на депозитный счет.
При этом не играет роли, какая по размеру будет внесена денежная сумма.
Совсем скоро Вы разберетесь и сможете понять,
каким образом действовать дальше, какие размеры взноса являются наиболее приемлемыми.
И после этого вы можете начать делать ставки.
Теперь стало понятно, что делать это
совсем несложно, так как этот процесс займет у
вас минимум сил и времени.
Выходит, абсолютно каждый сможет начать ставить независимо от
того без опыта он или профессионал.
Все, что для этого требуется – зарегистрироваться.
Контора Мостбет – входит в число популярных и востребованных
площадок на рынке России, что совсем не вызывает удивления.
Ведь контора заботится о своих пользователях и предлагает для
них наилучшие условия.
Руководству важно не просто привлечь больше пользователей, а и создать максимально удачные условия для постоянных клиентов.
Имидж считается значимым показателем
для конторы во имя того, чтобы не снизить веры
игроков.
В сфере ставок присутствует большое количество аферистов.
Не следует слепо доверять яркой рекламе,
а также идти на поводу у слишком выгодных условий.
Возможно не только лишиться денег, безрассудно потерять время, но
и установить на компьютер вирусную
программу.
Целесообразнее выбирать лишь проверенные компании, которые долгий период пребывают
в игровой сфере.
Всегда можно почитать отзывы, ознакомиться с
временем появления компании в виртуальном пространстве.
Среди подобных профессионалов ведения игрового бизнеса
признается mostbet бонусы при регистрации
При желании несложно скачать специально созданное
приложение для смартфонов и других гаджетов.
Останется получить доступ к сети Интернет, чтобы ставить с
сегодняшнего дня.
Вы даже сможете выбрать мероприятие,
спрогнозировать результат, находясь в заторе или в офисе.
Это ли не одно из преимуществ, за которые стоит выбирать данную компанию?
Именно это подтверждает огромное число пользователей конторы.
Поэтому, если вы решили начать делать
ставки, то вам следует обратить внимание на Мостбет.
Здесь Mostbet-partner.com вы найдете важную информацию и решения своих вопросов, а также
сразу приступить к ставкам после регистрации.
1XBET входит в число самых востребованных в России букмекерских контор по ставкам на спортивные события.
Площадка работает на основе лицензии
Кюрасао в online-режиме.
Фирма, осуществляющая деятельность с
2007 г., насчитывает свыше 400 тысяч постоянных посетителей.
На сегодняшний день букмекерская контора 1xbet входит в число
мировых лидеров по спортивным ставкам.
Это и есть критерий доверия армии пользователей, которые выбрали именно указанную букмекерскую контору.
Осталось понять особенности пребывания на онлайн площадке бонус обыграй 1xbet условия акции понедельник .
Правила прохождения регистрации
Производить ставки имеет право
зарегистрированный клиент (беттер).
Есть разные варианты создания профиля:
1. через соцсети, нужно всего лишь
остановиться на соответствующем варианте;
2. по э-мейл независимо от платформы;
3. по телефонному номеру, на который придет
смс.
Пользователям http://ssshape.com/home.php?mod=space&uid=91673&do=profile&from=space в личный аккаунт станет доступным немедленно после
регистрации.
Беттер получает право делать ставки на выбранные
события из мира спорта, принимать участие в акционных и бонусных программах, выводить
средства и др.
Вам понравится не просто следить за матчем выбранного состава игроков, но и по возможности выигрывать немалые суммы денег.
Нужно всего лишь выбрать событие, которое понравилось
больше всего.
Как видите, по окончании регистрации разрешается пользоваться множеством возможностей основного сайта,
которые предусмотрели разработчики.
Разновидности прогнозов БК 1хбет https://projectredwiki.com/wiki/User:GrazynaBertie14
1Хбет в отличие от других БК насчитывает 12 вариантов сделок.
Одинарный прогноз (ординар, одиночник) – соглашение
на определенный результат
спортивного события.
Выигрыш насчитывается при умножении десятичного коэффициента на количество поставленных денег.
Получается, что нет ничего сложного, если выбирать данный вариант прогноза.
Экспресс – прогноз одновременно на два и более результатов,
которые анонсируются.
Экспресс «Стайер» имеет особенность:
исходы и события разрешается дописывать на протяжении двух месяцев.
Антиэкспресс содержит несколько
исходов, противоположный экспрессу по методу
определения выигрыша.
Такой тип ставки выбирают
как со стажем игроки, так и начинающие пользователи.
Система – пари на полную комбинацию экспрессов определенной размерности из выбранного количества
мероприятий.
Цепочка – набор одиночных прогнозов.
По доверительной ставке можно вернуть долю денег, которые находятся пока под блокировкой.
Это довольно привлекательное предложение, которое выбирают
прошедшие регистрацию пользователи.
Ставка по промокоду определяет комбинацию из цифр и букв для подготовки запроса.
Этим способом можно сделать ставку , не внося средства на депозит.
Лаки является сочетанием ординаров и абсолютно всех экспрессов, которые собраны из указанных спортивных мероприятий.
Патент имеет такой же принцип,
что и лаки, но количество событий ограничивается 3-мя.
Для каких целей необходимо использовать зеркало
Букмекерская контора 1Хбет не
является легальной на территории РФ.
Подобное положение сопряжено с тем, что фирма не
взимает проценты с прибылей игроков.
Непосредственно для клиентов это огромный плюс,
но в рамках закона данный нюанс признается не самым уместным.
Разработчики не собираются ничего менять в своей
политике.
Как же быть в этом случае клиентам?
На самом деле нет ничего проще.
Следует избежать блокирование официального веб-сайта, то есть посетить функционирующее зеркало портала.
Зеркало представляет собой особый ресурс с точным интерфейсом сайта, без каких бы то ни было ограничений, с
воссозданием ранее введенных сведений.
Разрешается зайти и беспроблемно воспользоваться всеми условиями, предусмотренными разработчиками.
Данные зеркала используют общую с основным сайтом 1xbet БД, поэтому войти на сайт удобно под своим аккаунтом.
Помните, что интерфейс идентичен подтвержденному сервису
букмекера.
Переместиться на аналог можно по
ссылке аккаунт с балансом 1xbet.
Помимо прогнозов на спорт в 1хбет игрокам предлагают тотализаторы,
слоты, различные лотереи, нарды, игры в online и offline режимах.
Как видите, у БК достаточное число мероприятий, которые могут оказаться по вкусу пользователям самого разного возраста,
пола.
Необходимо всего лишь пройти простую регистрацию прямо сегодня.
Вы сможете обнаружить, насколько увлекательно получится провести время, если
есть персональный компьютер и подключение к сети Интернет.
Обзор зеркала Melbet
Рынок ставок в России функционирует довольно долгое время, и в 2012 г.
вышла на рынок компания Мелбет.
На сегодняшний день сервис стабильно
продолжает развиваться, непосредственно это
относится к виртуальному пространству.
Как думают некоторые клиенты, довольно комфортно не
выходя из дома, в офисе или в дороге ставить на события.
Потеря времени исключена.
Наиболее важная задача компании – оказывать помощь людям ставить, это удобно выполнить , используя офисы фирмы или же
в режиме онлайн, для этого есть
сайт и приложение для смартфона.
Как видите,, предоставляется немало способов, чтобы с удовольствием провести свободное время, а заодно попытаться заработать приличные деньги.
Компания мелбет проблемы с выводом очень активно
продвигается и старается создать
для своих пользователей самые
лучшие возможности.
Тут вы можете делать ставки
как на спортивные, так и на другие мероприятия, к примеру, конкурсы наподобие Eurovision.
Больше не нужно безучастно наблюдать за тем, как выступает обожаемый исполнитель.
Достаточно начать верить в его победу, сделав оптимальную ставку.
Существует вероятность, что
получится сорвать куш и при этом насладиться
музыкальным произведением.
Это очень удобно, так как в этом случае безусловно любой игрок сможет найти для себя захватывающие события и поставит на его исход.
Разработчики предусмотрели мероприятия на все
предпочтения.
Все связано с Вашим возрастом, увлечениями, желанием и возможностью идти на риск.
С чего начать ставить на спортивные события с Melbet http://earthjp.net/youtube/?list=thread
Некоторые клиенты уверены, что делать ставки
на спорт или иные события – это достаточно хлопотно
и что в этом потребуется тратить время на разбирательство.
Но так ли это на самом деле?
Конечно же, нет.
Если идет разговор о Мелбет, то в этом случае начинать ставить сможет каждый.
Интуитивно понятный интерфейс придется по
душе даже новичкам, которые надумали разобраться с тем,
как ставить.
Следует рассмотреть более подробно, как начать это делать.
Для старта вам нужно зарегистрироваться на сайте melbet букмекерская приложение
Алгоритм прохождения регистрации удивительно простой, займет у вас минимальное количество времени.
Нужно всего лишь ввести личные данные в специальные
ячейки, пройти процесс
верификации.
Как только вы зарегистрируетесь,
необходимо внести некоторую сумму на
депозит.
Абсолютно не играет роли, какая
по размеру будет внесена сумма денег.
Совсем скоро Вы разберетесь и сможете понять, как действовать дальше, какие параметры взноса считаются наиболее приемлемыми.
И после этого начинайте ставить
на события.
Теперь становится понятно, что
делать это совершенно не сложно, так как этот процесс займет
у вас минимум времени и сил.
Выходит, абсолютно каждый сможет начать делать
ставки независимо от того без опыта он или профи.
Единственное, что для этого нужно – пройти
регистрацию.
Контора Мелбет – одна из самых известных и востребованных площадок на рынке России,
что абсолютно не удивительно.
Как известно, фирма заботится о своих пользователях и подготавливает для них самые лучшие условия.
Разработчикам важно не просто привлечь новых игроков, но
и создать наиболее комфортные условия для завсегдатаев.
Репутация считается значимым показателем для конторы во имя того, чтобы не снизить доверия пользователей.
В области ставок присутствует немалое количество мошенников.
Не следует соблазняться привлекательной рекламой, а также идти на поводу у слишком выгодных
условий.
Можно не только лишиться денег, безрассудно
потерять время, но и установить на компьютер вирус.
Целесообразнее выбирать лишь проверенные компании, которые продолжительное время находятся в данной сфере.
В любой момент можно почитать отклики, ознакомиться
с временем появления конторы на просторах
интернета.
Одним из подобных профессионалов своего дела считается http://85.187.138.11/index.php?action=profile;u=152610 .
В определенный момент несложно скачать
специально разработанное мобильное приложение.
Останется получить доступ
к сети Интернет, чтобы ставить прямо сейчас.
Вы даже сможете выбрать мероприятие, сделать прогноз, находясь в пробке или за городом.
Это ли не одно из преимуществ, за которые стоит выбирать данную компанию?
Именно это подтверждает огромное количество игроков компании.
Поэтому, если вы хотите испытывать удачу на
ставках, то вам следует присмотреться
к Мелбет.
Здесь melbet-partner.com вы найдете необходимую информацию
и решения своих вопросов, а также сразу начать делать ставки после регистрации.
眉bungsaufgaben deutsch 2 klasse amazon
veste manteau homme nike zalandonike m2k feknoecharpe froufrou mode d emploipub nike vapormax flyknit
Описание зеркала Mostbet mostbet регистрация
http://www.reinventingorganizationswiki.com/fr/index.php?title=Utilisateur:EvanSousa55
Рынок ставок в России существует
довольно долгое время, и в 2012 году на рынке появилась компания Мостбет.
На сегодняшний день сервис активно развивается, в
частности это касается виртуального пространства.
Как думают некоторые пользователи, достаточно удобно никуда не выходить, а ставить на события.
Никаких потерь времени.
Основная цель конторы – оказывать помощь игрокам ставить, это
удобно сделать через офисы фирмы или же в режиме online, для этого есть портал и приложение для смартфона.
Как видите,, предусмотрено немало
возможностей, чтобы приятно провести досуг, а вместе
с тем попробовать заработать
неплохие суммы.
Компания мостбет войти в личный кабинет довольно активно продвигается и
старается создать для своих клиентов наилучшие возможности.
Здесь каждый может делать ставки как на спорт, так и на другие события, например,
конкурсы типа Eurovision.
Больше не нужно просто наблюдать за тем,
как выступает обожаемый артист.
Достаточно поверить в его победу,
произведя выгодную ставку.
Существует вероятность, что удастся
заполучить крупную сумму и
при этом послушать отличную музыку.
Это очень удобно, так как в этой ситуации
абсолютно каждый игрок найдет для себя захватывающие мероприятия
и поставит на его исход.
Программеры смогли предусмореть события на все
предпочтения.
Все связано с Вашим возрастом, увлечениями, желанием
и возможностью идти на риск.
Как начать ставить на спорт с Мостбет
Некоторые клиенты думают, что ставить на спорт или иные события – это довольно сложно и что в алгоритме потребуется тратить время на разбирательство.
Но так ли это на самом деле?
Естественно, это не так.
Когда идет разговор о Мостбет http://mysterywiki.com/index.php/User:AimeeTroiano859 mostbet как делать ставки ,
то в этом случае начать делать ставки сможет каждый.
На уровне интуиции понятный
интерфейс понравится даже новичкам,
которые только решили освоить искусство ставок.
Рассмотрим подробнее, каким образом начать это делать.
Для начала необходимо пройти регистрацию на портале.
Алгоритм прохождения регистрации удивительно простой, займет у вас минимум времени.
Нужно всего лишь вбить персональные сведения в
выделенные ячейки, верифицироваться.
После регистрации надо будет положить деньги
на депозитный счет.
Абсолютно неважно, какая по размеру будет внесена сумма денег.
Очень быстро Вы освоитесь и сможете понять, как
действовать дальше, какие параметры ставки считаются
оптимальными.
И с этого момента начинайте делать ставки.
Теперь стало ясно, что выполнять подобные
манипуляции можно без особого труда, так как на эти действия уйдет у вас минимум сил и времени.
Таким образом, абсолютно каждый сможет начать ставить независимо от
того новичок он или профессионал.
Все, что для этого требуется – пройти регистрацию.
Контора Mostbet – одна из самых известных и
востребованных компаний на российском
рынке, что абсолютно не
удивительно.
Ведь контора заботится о своих пользователях
и предлагает для них самые лучшие условия.
Разработчикам надо не просто привлечь больше пользователей,
но и подготовить наиболее комфортные условия
для постоянных клиентов.
Имидж считается важным критерием
для конторы во имя того, чтобы не снизить веры игроков.
В области ставок существует
немалое число мошенников.
Не следует слепо доверять яркой
рекламе, а также бездумно верить чрезмерно заманчивым предложениям.
Можно не только лишиться денег, безрассудно потерять время, но и установить на ноутбук вирус.
Целесообразнее останавливать выбор на надежных фирмах, которые длительное время пребывают в данной области.
В любой момент можно изучить отзывы, узнать о времени появления компании в
виртуальном пространстве.
Одним из подобных профи ведения игрового бизнеса признается букмекерская mostbet
При желании можно загрузить конкретно созданное приложение для смартфонов и других гаджетов.
Останется обеспечить наличие сети Интернет,
чтобы ставить уже сегодня.
Вы даже сможете подобрать событие, сделать прогноз,
находясь в пробке или за городом.
Не это ли и есть одно из преимуществ, за
которые следует останавливать выбор на этой букмекерской конторе?
И это подтверждает огромное количество игроков компании.
В таком случае, если вы решили испытывать удачу
на ставках, то вам следует обратить
внимание на Mostbet.
Здесь Mostbet-partner.com вы найдете важную информацию и ответы на свои вопросы,
а , кроме того, немедленно начать делать ставки после того, как зарегистрируетесь.
Обзор зеркала Mostbet мостбет вход войти
http://www.hangzhour.com/home.php?mod=space&uid=132735&do=profile&from=space
Ниша ставок в РФ функционирует довольно долгое время, и в 2012 году вышла на рынок компания Мостбет.
На сегодняшний день сервис активно
продолжает развиваться, непосредственно это касается виртуального
пространства.
Как полагают некоторые клиенты, достаточно комфортно
никуда не выходить, а ставить на события.
Потеря времени исключена.
Наиболее важная задача конторы – оказывать помощь игрокам делать ставки, это можно сделать через офисы фирмы или же в режиме онлайн, для этого имеется сайт и приложение для смартфона.
Итак, предоставляется немало возможностей, чтобы
с удовольствием провести свободное
время, а заодно попытаться заработать
приличные суммы.
Контора mostbet зеркало рабочее очень стремительно развивается и
намерена подготовить для
своих пользователей самые лучшие возможности.
Тут вы можете ставить как на спорт, так и на иные мероприятия, например, турниры наподобие Eurovision.
Больше нет смысла безучастно наблюдать за тем, как выступает любимый певец.
Достаточно начать верить
в его победу, произведя оптимальную ставку.
Существует вероятность, что получится заполучить куш и при
этом насладиться музыкальным произведением.
Это очень удобно, так как в этом случае безусловно каждый игрок найдет для себя захватывающие
события и сделает ставки.
Разработчики предусмотрели мероприятия
на любой вкус.
Решение связано с Вашим возрастом, увлечениями, желанием и
возможностью идти на риск.
Как начинать ставить на спортивные события с Mostbet
Многие игроки думают, что ставить на спортивные баталии или другие мероприятия – это достаточно сложно и что в алгоритме потребуется
тратить время на разбирательство.
Но так ли это на самом деле?
Естественно, это не так.
Когда мы говорим о Мостбет https://wiki.hookedmagazin.de/wiki/Benutzer:RoxannaStolp0 mostbet официальный сайт вход регистрация моя страница , то
в этом случае начать делать ставки сможет каждый.
Интуитивно понятный интерфейс понравится даже начинающим пользователям, которые только решили разобраться с тем, как ставить.
Рассмотрим более подробно, как начинать
процесс.
Для начала вам нужно пройти регистрацию
на сайте.
Процесс прохождения регистрации удивительно легкий, займет у вас минимальное количество времени.
Нужно всего лишь ввести личные данные в выделенные поля, верифицироваться.
После регистрации надо будет
положить деньги на депозит.
При этом не играет роли, какая по
размеру будет зачислена денежная сумма.
Совсем скоро Вы разберетесь и сможете понять, каким образом поступать дальше, какие
размеры взноса считаются оптимальными.
И после этого вы можете начать делать ставки.
Теперь становится ясно, что выполнять подобные манипуляции совсем несложно, потому
что на эти действия уйдет
у вас минимальное количество времени и сил.
Выходит, абсолютно любой из
игроков сможет начать делать ставки независимо от того новичок он или
профи.
Все, что для этого требуется –
пройти регистрацию.
Контора Mostbet – входит в число популярных и пользующихся спросом компаний на российском рынке, что совсем не
удивительно.
Ведь контора с заботой относится к своим клиентам и подготавливает для них наилучшие условия.
Разработчикам важно не просто привлечь больше пользователей, но и создать наиболее удачные обстоятельства для постоянных клиентов.
Репутация считается важным показателем для компании во имя того, чтобы не
потерять доверия игроков.
В сфере ставок присутствует
большое количество мошенников.
Не стоит соблазняться привлекательной рекламой, а также бездумно верить чрезмерно заманчивым предложениям.
Возможно не только лишиться денег, безрассудно потерять время, но и заполучить на ноутбук вирусную
программу.
Целесообразнее останавливать выбор на надежных фирмах,
которые долгий период находятся в игровой сфере.
Всегда можно почитать отзывы, ознакомиться с временем
начала деятельности компании
в виртуальном пространстве.
Одним из подобных профи своего дела считается мостбет как ставить ставки
При желании можно загрузить конкретно созданное мобильное приложение.
Нужно обеспечить наличие интернету, чтобы ставить
уже сегодня.
У Вас будет возможность выбрать событие, сделать прогноз, находясь в пробке или на даче.
Не это ли и есть одно из преимуществ, за которые следует останавливать выбор на этой
букмекерской конторе?
И это подтвердило огромное число игроков конторы.
Вот почему, если вы решили испытывать удачу на ставках, то вам стоит присмотреться к Mostbet.
Здесь Mostbet-partner.com вы найдете важную информацию и решения
своих вопросов, а также немедленно
приступить к ставкам после регистрации.
Конкуренция в сфере online азартных игр невероятна.
http://mamasonice.com/home.php?mod=space&uid=761119&do=profile
С завидной регулярностью появляется
немало площадок с заманчивыми спецусловиями для новых игроков.
Особенного внимания заслуживает приветственный подарок,
который смогли оценить большое число клиентов.
Настала пора разобраться с основными аспектами, которые сопряжены с работой casino.
Стартовый бонус – это основной бонус, который предлагает онлайн-казино.
Для его получения не придется прилагать
много стараний.
Пособие подготовлено для клиентов, которые только в
первый раз заходят в личный кабинет на сайте
casino.
Геймеры могут и не подозревать,
какой подарок подготовили программисты.
Наиболее часто первое поощрение прибавляет определенный процент к стартовому счету независимо от внесенной суммы.
Поощрение в виде безвозмездных вращений 1win минимальная ставка
Казино включают безоплатные прокручивания в собственную маркетинговую стратегию.
Как это понимать?
Это дает пользователям бесплатные циклы, которые геймеры имеют право использовать в игровых автоматах, и
выигранные средства чаще всего можно снять с их счета.
Спины достаточно популярны в среде любителей гэмблинга, так как они дают
шанс определить потенциал, который предоставляют новые гейм аппараты,
с исключением потребности пополнять свой
баланс и тратить собственные деньги.
Достаточно привлекательное предложение, которым вполне
смогут воспользоваться игроки.
Несложно оценить по достоинству все плюсы, возможности, обеспечиваемые разработчиками.
Kazino подобным способом зачастую продвигают новейшие
услуги среди клиентов, зарегистрированных на их портале.
При этом http://51.68.175.152/smf/index.php?action=profile;u=676 доступно для всех любителей игры.
Необходимо всего лишь пройти в
определенный раздел, ввести данные в
регистрационные ячейки.
Не забывайте про необходимость
подтвердить достижение совершеннолетия.
Без подтверждения личности будет трудно
стать постоянным пользователем,
которому откроются потенциальные возможности on-line площадки.
Реферальные бонусы
Online casino стимулирует пользователей, которые советуют
игровую площадку потенциальным игрокам.
Бонусы за вовлечение знакомых предназначены для
продвижения гэмблинга и привлечения новых пользователей игровых площадок.
Данный метод считается наиболее эффективным для роста количества игроков.
Одно дело, когда посетитель думает стать полноценным участником, опираясь на рекламу.
Совершенно иное – довериться совету друга,
который уже убедился в правдивости данных, многообразии слотов для игры.
За совет вы можете получить некоторую сумму денег.
Финансовый бонус можно
снять со своего счета или использовать на безоплатные вращения в
игровых раундах (некоторые cazino используют свои собственные рекламные и поощрительные программы,
поэтому лучше всего сначала ознакомиться
с правилами).
Как можно получить этот бонус?
Вы должны убедить кого-то из своих знакомых зарегистрироваться на
сайте казино, активировать учетную запись и внести депозит.
При прохождения регистрации этот пользователь должен внести сведения о вас
как рекомендателя, чтобы Вам можно было зачислить на счет бонус.
Количество пришедших по
рекомендации людей не лимитируется.
Казино всегда рады новым клиентам, которые стремятся стать постоянными в
ближайшем будущем.
Бонус за лояльность
Бонусы лояльности – это еще вид подарков, которые используются
в on-line-casino 1вин 1win официальное зеркало
Они похожи на достаточно известные
схемы вознаграждений, которыми руководствуются
популярные магазины.
Получается, что casino поощряет своих постоянных клиентов (людей, которые с
завидной регулярностью заходят на ресурс и вступают в игру) заманчивыми бонусами или подарками.
Такой бонус возможен в форме бесплатных вращений, однако многие игровых платформ тоже предоставляют
недорогие аксессуары, призы
или лотерейные билеты.
Можно сказать, что появится возможность
получить намного больше приятных эмоций в течение пребывания на online-платформах.
Поощрительные призы для
ВИП-игроков
Казино также готовят бонусы для игроков, которые
стабильно заходят на портал cazino
и вкладывают в игры большие денежные суммы.
Большая часть онлайн-казино стараются пообщаться с ВИП-клиентами с целью узнать об их интересах и назначить призы, которые фактически соответствуют стилю заинтересованного клиента.
Это лишний раз подтверждает, насколько рады приветствовать пользователей online-площадки.
Для ВИП-игроков большинство online-казино готовят очень ценные материальные призы.
Необходимо всего лишь продолжать заходить в
выбранное заведение, наслаждаться всеми предоставляемыми плюсами своего положения.
In India, the 1xBet betting company – is one of the
most well-received ones in Asia. Among its main advantages, equal can note
enormous odds, a sympathetic vigour underline on presented events and on the up long-lasting payoffs.
In its functionality, the depict likeness is no unique
from the main resource, providing users with all the even so capabilities.
1xBet betting followers
1xbet app download http://www.zhuming.cc/home.php?mod=space&uid=125940&do=profile&from=space
1xbet app
Using the pertinence for the sake Android, players can risk on sports
in touring, at post or at home. All that is required – is
access to the Internet. In order to initiate the
program, leave to the “Applications for smartphones” division, set out on non-stationary phone number in the opened form.
In a few minutes, an SMS idea with download link require arrive.
1xbet apk 1xbet app download
1xbet apk
The 1xBet expressive app for iOS can be downloaded in the App Store.
A escort download element is available on the betting body’s
official website – look into b pursue the installation instruction.
General information
With avoid of our website there is an opening
to contemplate c get access to the website far the clock,
placing bets on events of interest. The betting platform in India can be hardened not contrariwise from
a PC, but also from most ambulant devices.
Entitle
The 1xBet troop operates on the Internet legally. To present services,
the betting friends has a permit issued next to the
international regulator of Curacao. It allows the platform to coax in varied countries
without violating law.
Review of the 1xBet official Indian website
The betting party line offers visitors to punt on sports
and financial events. Bettors also entertain access to online slot machines and a
virtual casino. A player can wager bills in any sections of the website using a individual account.
The betting company has a good vitality limit
and bird money oblique for all events. Users can flutter
in more than 40 sports types, ranging from in football and tennis to
exotic cockfights.
The betting companionship accepts bets on not quite all outcomes: not only on a crushing or defeat of inseparable of
teams, but also on a mob of corner kicks, penalties and other results.
One can observe a less unshakeable vitality activity at the 1xBet betting players merely in advance avoided events.
But sedate here an individual can hazard on over/under, check and some other outcomes.
Players can quantify all the possibilities of greenbacks betting only after creating an account.
Registration in the 1xБет India 1xbet app India https://bonq99.com/forum/profile.php?id=4825
Registration in the 1xБет India
Unified can move a draw in the betting company in 4 ways:
via a hurried registration procedure. A thespian needs to
click on the appropriate tab and select the territory of
residence. After a scattering seconds, the buyer will be affirmed a shibboleth and
login, which leave be created next to the system;
registration way
by creating an account using phone. In this box, during registration strategy a visitor
requisite direct attention to the alert phone slues onto which SMS
communiqu‚ inclination appear with ornate instructions;
creating an account using phone
via registering via email. The standard choice, at which owner fills visible registration form, prescribing dear materials and a valid e-mail.
Later a missive with a association comes to the consumer’s specified
e-mail, which becomes a pass to the 1xBet India website;
by registering via sexually transmitted networks.
The easiest crumble to set going an account. A player however needs to click on the icon with the communal
network where he has a examination, after which an account is automatically generated.
1xbet login
1xbet login
Individual can enlist the 1xBet website in the same way as
on the major 1xbet com resource. It is adequately in the interest a user to exhibit
in the procedure in any serviceable way,
and then authorize near entering the necessary password and login.
In some cases, to sign personal account, everybody may sine qua non a dear jus canonicum
‘canon law’ that the betting visitors sends in the form of SMS dispatch onto
a transportable phone number.
In case of problems with entering an account anticipated to a shrinkage of a countersign, the punter drive be competent to solve the consequence quickly.
To do this, just click on the “Forgot your password?” flag, article down the
email speak or phone handful next to it. The user drive be come by allied facts to the specified contacts.
The shibboleth sent will arrogate to log in to the account.
Depositing paper money
After partiality registration and authorizing on the website, user drive be able to provide full of funds in his personal account.
To do this, seek the company of to the “Payments” section. There,
the player will be wise to persevere numerous options in place of depositing funds
into the account:
bank over;
electronic wallets and payment systems;
payment to the core the terminal;
specie transfer from a motorized phone;
Internet banking;
cryptocurrency
prepaid cards.
In whole, the website of the betting coterie provides more than 40 options
conducive to depositing capital. Regardless of the chosen method, monetary transactions on the website are carried out
instantly. The entire important factor in support of a sportsman – is to conclude the rules established past the betting company.
For lesson, the replenishment amount should be no less than 100 rubles.
In totalling, it is strictly forbidden to utilize other people’s wallets and bank cards
to put money. Miscarriage to comply with these conditions may
lead to blocking of the account.
Spinach withdrawal from the 1xbet in India 1xbet app India
To leave funds in of the way it is compelling to interest the nevertheless way as with replenishment.
To create a fiscal deal, a musician needs to count to personal account and supreme the “Money withdrawal” section. There the owner will dire to indicate the
amount to be transferred, and write the data from his
electronic billfold or bank card. If all the data is unimpeachable, the devotion for
funds withdrawal will be processed by the betting assembly within 1-7 days.
In harmony to refrain from delays in payoffs of earned winnings, players necessity to pass account verification procedure 1xbet app India .
During this gate, the user will be required to state
look after the 1xBet administration in India with copies of
his identity documents. Passed profile verification want allow one withdraw funds from the website far,
at any convenient time.
It is notable on players to recall that the betting party has set assured limits
on well-heeled withdrawal. In case of any problems with withdrawal of funds, bettors can in the in maintenance suitable help.
Fund standard mould at the website throughout
the clock.
Bonuses from 1xBet
The betting assemblage offers visitors a sound compensation program.
Players can expect to profit the following types
of bonuses:
“An eye to the first deposit.” The amount of
the encouragement is 100% from the deposited amount. The prize essential be
won bet on a support at three bets of the Speak variety with a coefficient of at least 1.4;
“Favoured Friday”. The tip is issued to players strictly on the
specified day. The take first prize in past due
conditions are the same as with the make something representing the anything else put;
“Wednesday – multiply by way of 2”. Cappers who won on the “Charmed Friday” are allowed to participate
in the action. If the user has not hitherto distant the funds won from the sometime week,
his down payment is doubled via the betting convention;
“Express of the day.” The choose is held daily. If a player achieves big name in the Line or the Complete, he leave
be subjected to an raise in the envisage of 10% of the earned winnings;
“Perk also in behalf of a series of failures.” Drug profit go take
a hand in of the gone by the board shin-plasters, upon up of
20 hapless bets in a falling-out with a coefficient of not more than 3.
rains regnjakke herre gr氓
delonghi kaffeemaschine magnifica sdamen stiefeletten gore texwalbusch 2 hemden f眉r einen preisadidas umh盲ngetasche camo black
1XBET входит в число наиболее востребованных в РФ букмекерских контор по прогнозам на спорт.
Площадка функционирует по лицензии Curacao в режиме онлайн.
Фирма, работающая с 2007 года,
насчитывает свыше четырехсот тыс.
постоянных посетителей.
На сегодня БК 1xbet входит в число
мировых лидеров по спортпрогнозам.
Это можно назвать как показатель доверия многочисленных клиентов, которые выбрали именно указанную БК.
Осталось разобраться в особенностях
пребывания на online платформе 1xbet личный кабинет .
Правила прохождения регистрации
Производить прогнозы имеет право прошедший регистрацию клиент (беттер).
Известны разные варианты подготовки аккаунта:
1. через соцсети, нужно всего лишь остановиться на
соответствующем варианте;
2. по э-мейл независимо от сервиса;
3. по номеру сотового телефона,
на который придет смс.
Пользователям http://www.1pdeals.co.uk/forum/profile.php?id=76439 в личный аккаунт станет открытым немедленно после
регистрации.
Зарегистрированный клиент может
ставить на разные спортивные турниры,
принимать участие в акционных и бонусных программах,
осуществлять вывод денег и др.
Вы сможете не безучастно следить за игрой любимой команды, но и при желании получать неплохие
денежные суммы.
Для этого надо всего лишь выбрать мероприятие, которое пришлось по вкусу.
Итак, по окончании регистрации
можно пользоваться множеством возможностей основного сайта, которые предусмотрели разработчики.
Разновидности прогнозов БК 1хбет
http://www2s.biglobe.ne.jp/~t-naoki/cgi-bin/fantasy.cgi
1Хбет в отличие от других БК предоставляет двенадцать вариантов операций.
Одинарный прогноз (ординар, одиночник) – соглашение на определенный исход спортивного события.
Выигрыш насчитывается умножением коэффициента в десятичном формате на сумму
пари.
То есть сложностей особых нет, если выбор сделан
на этот вариант ставки.
Экспресс – ставка сразу на 2 и более
результатов, которые должны пройти.
Экспресс «Стайер» имеет особенность: результаты и мероприятия разрешается
добавлять на протяжении двух месяцев.
Антиэкспресс содержит несколько итогов, противоположный экспрессу
по способу определения выигрыша.
Этот вид прогноза признают как
опытные игроки, так и начинающие пользователи.
Система – пари на все возможные варианты экспрессов определенной размерности из указанного
числа событий.
Цепочка – комплект одинарных прогнозов.
По доверительной ставке можно получить часть средств, которые находятся
пока в истории.
Это достаточно интересное предложение,
которое могут выбрать зарегистрированные клиенты.
Ставка по промокоду выдает комбинацию из букв и цифр для подготовки запроса.
Таким образом удобно осуществить ставку , не
внося средства на депозит.
Лаки является комбинированием единиц и абсолютно всех экспрессов,
которые собраны из указанных спортивных событий.
Патент действует по тому же алгоритму, что и лаки, но количество событий ограничено тремя.
Для чего нужно использовать
зеркало
Букмекерская контора 1Хбет не является легальной в регионах России.
Это сопряжено с тем, что контора не взимает налоги
с прибылей клиентов.
Для самих пользователей это существенный плюс, но на законодательном уровне данный момент считается далеко не целесообразным.
Руководители не собираются ничего менять в проводимой политике.
Как же быть в этом случае пользователям?
На самом деле никаких сложностей нет.
Следует избежать блокировку основного веб-сайта, то есть посетить актуальное
зеркало площадки.
Аналог можно представить как
специальный сервис с идентичным интерфейсом сайта, без каких-либо ограничений, с
сохранением прежде внесенных данных.
Разрешается зайти и беспроблемно
воспользоваться всеми условиями, предложенными создателями.
Такие зеркала имеют общую с официальным сайтом 1xbet
базу, поэтому зайти на ресурс можно под своим аккаунтом.
Помните, что интерфейс аналогичен подтвержденному сайту
букмекера.
Переместиться на зекрало можно по
ссылке 1xbet первое пополнение.
Кроме ставок на спортивные турниры в 1хбет пользователям предлагают тотализаторы,
слоты, разные лотереи, нарды, игровые процессы в online и офлайн режимах.
Можно сделать вывод, что у букмекерской конторы оптимальное число мероприятий, которые
могут оказаться по вкусу клиетнам разных возрастов,
пола.
Необходимо всего лишь пройти простую регистрацию прямо сегодня.
Вы сможете обнаружить, насколько увлекательно
удастся провести досуг, имея ноутбук и доступ
к сети Интернет.
self lacing nike mag buy
robe desigual 2017accessoires 1920 boucles d oreillesnike free x metcon 2 whitela performance organisationnelle de la marque adidas
OLIMP https://ultrapedia.org/wiki/index.php/User:IvaBenson72 – одна
из самых популярных в России букмекерских компаний по ставкам на спортивные события.
Площадка функционирует на основе лицензии Curacao в online-режиме.
Фирма, осуществляющая деятельность с 2007 г., обслуживает свыше четырехсот тысяч постоянных клиентов.
На сегодняшний день букмекерская контора
OLIMP входит в число флагманов по спортпрогнозам.
Это можно назвать как критерий доверительности армии пользователей, которые решили выбрать конкретно данную БК.
Осталось понять особенности нахождения на онлайн платформе.
Правила прохождения регистрации
Делать ставки имеет право зарегистрированный пользователь (беттер).
Есть различные варианты создания аккаунта:
1. через социальные сети, потребуется всего лишь остановиться на соответствующем варианте;
2. по адресу электронной почты независимо от
сервиса;
3. по номеру сотового телефона,
на который будет прислано смс.
Игрокам бк олимп отзывы
в личный кабинет становится открытым немедленно по окончании регистрации.
Беттер получает право ставить на разные события из мира спорта,
участвовать в акционных и бонусных программах,
осуществлять вывод денег и т.д.
Вам понравится не безучастно следить
за игрой любимой команды, но и при желании выигрывать немалые суммы денег.
Для этого надо всего лишь выбрать мероприятие, которое понравилось больше всего.
Как видите, по окончании регистрации разрешается воспользоваться
многочисленными возможностями
официального ресурса, которые предоставили администраторы.
Разновидности прогнозов конторы Олимп
В отличие от подобных контор Олимп предоставляет 12 вариантов сделок.
Одинарный прогноз (ординар, одиночник) – сделка на определенный итог
спортивного события.
Прибыль рассчитывается умножением десятичного коэффициента на сумму пари.
Получается, что сложностей особых нет, если выбор
сделан на этот вид прогноза.
Экспресс – ставка сразу на два и более исходов, которые анонсируются.
Экспресс «Стайер» имеет особенность: результаты и
события можно дописывать на протяжении 2-х месяцев.
Антиэкспресс содержит ряд
итогов, обратный экспрессу по методу определения выигрыша.
Такой тип прогноза выбирают как со стажем игроки, так и начинающие пользователи.
Система – пари на все возможные варианты экспрессов конкретной размерности из указанного числа мероприятий.
Цепочка – набор одиночных ставок.
По ставке доверительного типа удастся получить долю денег,
которые находятся пока в истории.
Это довольно интересное предложение, которое могут выбрать прошедшие
регистрацию пользователи.
Прогноз по купону определяет комбинацию из
букв и цифр для подготовки запроса.
Этим способом можно осуществить ставку без внесения денег на депозитный счет.
Лаки является комбинированием ординаров и совершенно всех экспрессов, собранных из
выбранных спортивных мероприятий.
Патент действует по тому же алгоритму, что и лаки, но количество событий ограничено тремя.
Для каких целей необходимо использовать зеркало бк олимп официальный
БК Олимп считается нелегальной на территории РФ.
Подобное положение связано
с тем, что компания не удерживает проценты с выигрышей клиентов.
Непосредственно для клиентов это существенный плюс, но на законодательном уровне названный нюанс считается не самым уместным.
Руководители не собираются что-либо менять
в проводимой политике.
Что же делать в этом случае пользователям?
На самом деле нет ничего проще.
Следует избежать блокирование основного веб-сайта, а следовательно посетить актуальное зеркало портала.
Копия можно представить как особый сервис с идентичным отображением сайта, без каких бы то ни
было ограничений, с сохранением ранее внесенных
данных.
Разрешается войти и беспроблемно воспользоваться
всеми возможностями, предложенными создателями.
Данные копии имеют общую с основным сайтом OLIMP базу, поэтому зайти на ресурс можно под своей учетной записью.
Помните, что интерфейс идентичен подтвержденному сервису букмекера.
Переместиться на зекрало получится по адресу http://yuletd.net/comment/html/?4724.html
Помимо прогнозов на спортивные турниры в Олимп игрокам предлагают слоты, тотализаторы, разные лотереи, нарды, игровые процессы в онлайн и офлайн режимах.
Как видите, у БК оптимальное количество событий, которые могут оказаться по вкусу клиетнам разных возрастов, пола.
Нужно всего лишь зарегистрироваться по
несложному алгоритму уже сейчас.
Вы сможете обнаружить, насколько увлекательно удастся провести время,
имея ноутбук и подключение к интернету.
Ставки на спорт сейчас http://thhwz.com/home.php?mod=space&uid=101785&do=profile&from=space пользуются популярностью не только среди болельщиков.
И обычные люди сейчас регулярно пытаются успешно спрогнозировать ради удовольствия.
Они смогли оценить по достоинству адреналиновый всплеск, который удается получить во время предвкушения итогов.
Вряд ли кто откажется от довольно
выгодного выигрыша?
Вам удастся смотреть увлекательный матч , а
заодно делать ставки.
В регионах РФ приемщики ставок могут осуществлять деятельность легально, но для этого понадобится разрешение, что предоставляют не быстро и не
каждому.
Причем даже у честных букмекеров довольно часто возникают
проблемы.
Это может быть блокировка сайта, невозможность авторизации.
Не вызывает удивления, что терпение заканчивается, возникает стремление отыскать иной способ развлечения.
Да и человек посчитает себя обманутым.
В действительности же, нет смысла поддаваться панике
раньше времени.
Поэтому сейчас объясним, что собой
представляет скачать бетвиннер на андроид официальный и зачем оно нужно.
Этой фишкой на сегодня успели успешно воспользоваться множество знающих и начинающих посетителей
ресурса.
Зачем нужно точную копию площадки
Зеркало – это полноценная копия исходного портала букмекерской конторы.
Необходимо оно для:
1. того, чтобы при случае оперативно вернуться на
любимый ресурс, забыв про блокирование;
2. предотвращения взлома профилей зарегистрированных посетителей;
3. высокой скорости;
4. сохранения аналога портала;
5. распределения запросов;
6. обхода блокирования, которое может устанавливаться в силу
разных причин (некоторым клиентам ресурс может быть недоступен из-за Российского потребнадзора).
При этом в полном объеме опции официального сайта действуют и в зеркале.
Люди, которые постоянно пользуются betwinner,
имеют возможность беспрепятственно
зайти через зеркала.
Это удастся сделать через любой ВПН.
У Вас будет возможность спокойно пользоваться выбранным ресурсом, делать ставки.
По какой причине происходит блокировка betwinner
Букмекерство по регионам Российской Федерации
имеет легальный статус сравнительно
недавно.
Ко всему лицензионное разрешение
получить тяжело.
Из-за этих двух причин в РФ на законных основаниях функционируют примерно 25-30 букмекерских фирм.
Эти компании достаточно известны, часто встречаются в рекламе туров тех или
иных видов спорта.
В случае, когда букмекер не спонсирует спортивные мероприятия, шансов на получение лицензии у него практически нет.
Поэтому и пользователи скорее всего не смогут зайти на сайт.
Предположительно портал будет заблокирован на территории
Российской Федерации.
Какие состоят плюсы Betwinner
Во-первых, это международная компания.
Входит в Marikit Holdings LTD.
У Betwinner есть официальный документ о.
Кюросао, это официально подтвержденное право, позволяющее работать в любых государствах, в которых это
разрешено по закону.
Поэтому делать ставки могут даже люди,
проживающие не на российской территории.
Просто заходите на площадку, выбираете мероприятия и делаете ставки.
От выигрыша команды-фаворита до количества голов, забитых в процессе игры.
Особого интереса требуют к себе ставки
на игрока, который считается мировой звездой.
Не исключено, что он «примет во
внимание ваши ожидания» и сделает рывок, ведущий к
победе.
Следующий момент, на betwinner можно делать ставки на многие события типа спортивных,
киберспортивных, шоу-бизнеса, в политической сфере и т.д.
Можно поставить на то, кто станет следующим
лидером Турецкой Республики или кто будет сниматься в анонсированном фильме.
Сколько возможностей дарит занменитое Евровидение, когда появляется шанс выбрать победителя в когорте
большого числа артистов из многих государств.
Довольно привлекательные
перспективы, не правда ли?
В-третьих, на Betwinner можно выбрать наиболее подходящий язык.
Портал рассчитан на пятьдесят два различных языка.
В связи с этим найти что-то для себя может абсолютно любой.
Это же относится и к валютам,
их почти 50 – от привычных рубля
и доллара до электронных денег.
Любой из пользователей найдет то, что нужно на свой вкус.
И это , конечно, не весь перечень достоинств.
Обо всем более подробно несложно
узнать по ссылке http://qiandao.abcgame.cc/home.php?mod=space&uid=53560&do=profile&from=space
К тому же на сайте будет подробная инструкция по регистрации.
Вы сможете разобраться, какие есть
виды прохождения регистрации, как без промедления
начать делать ставки.
Если необходимо узнать действующий адрес зеркала, лучше всего связаться по ГЛ.
Ко всему, можно выйти на авторитетные
сообщества, информирующие о различных
букмекерских агентствах.
Для этого обычным образом сделать запрос в наиболее
привычной поисковой системе слова – betwinner зеркало.
Пользователь сможет оказаться на веб-ресурсе как ставить ставки на betwinner , который на 100% отвечает официальному
сервису.
Итак, нет ничего проще, чем отыскать для конкретных целей разработанное зеркало.
Конкуренция на рынке online гемблинга
огромна. https://www.mercadaocantu.com.br/user/profile/375498
Каждый день организовывается
все больше игровых ресурсов с соблазнительными спецусловиями
для новеньких.
Отдельного интереса заслуживает первоначальный бонус,
который смогли оценить многие пользователи.
Настала пора понять важные моменты, которые связаны с работой казино.
Приветственный приз – это главный бонус, который предоставляет online-казино.
Чтобы его получить, не нужно прилагать много усилий.
Пособие подготовлено для клиентов, которые
только впервые заходят в профиль на портале cazino.
Геймеры могут и не подозревать, какой сюрприз приготовили программисты.
Наиболее часто первое поощрение прибавляет
некоторый процент к начальному счету вне
зависимости от внесенной суммы.
Поощрение в виде безвозмездных спинов 1win приложение на айфон
Казино включают бесплатные прокручивания в свою маркетинговую стратегию.
Как это понимать?
Это позволяет давать игрокам безоплатные циклы, которые играющие имеют право применить в игровых автоматах, и выигранные
средства обычно можно снять с их счета.
Вращения очень востребованы в
среде любителей гэмблинга, так как они позволяют определить потенциал, который предоставляют новые гейм аппараты, без потребности пополнять персональный
баланс и тратить личные
деньги.
Достаточно интересное предложение,
которым в полном объеме смогут
воспользоваться геймеры.
Несложно оценить по достоинству имеющиеся преимущества,
возможности, обеспечиваемые разработчиками.
Kazino таким образом часто рекламируют новейшие услуги среди посетителей,
прошедших регистрацию на их портале.
В то же время http://www.leningradskaya.org/d/user/profile/46235 не
имеет ограничений.
Необходимо всего-навсего
выбрать соответствующую
категорию, заполнить регистрационные ячейки.
Не забывайте про обязательность подтверждения достижение совершеннолетия.
Без подтверждения личности будет сложно стать постоянным пользователем, которому
доступны все возможности онлайн
площадки.
Бонусы для пришедших по
рекомендации
Online casino стимулирует пользователей, которые советуют сервис
другим.
Подарки за вовлечение друзей делаются с целью продвижения
предложений игр и притягивания новых пользователей
казино.
Данный способ считается наиболее эффективным для роста количества геймеров.
Один момент, когда посетитель решается стать полноценным участником, ориентируясь на рекламные слоганы.
Совершенно иное – поверить рекомендации друга, который на сегодня удостоверился в предоставленной
информации, вариативности слотов для
игры.
За совет пользователь может
обнаружить в личном кабинете некоторую сумму денег.
Начисленные деньги можно вывести
со своего счета или использовать
на безоплатные вращения в игровых раундах
(отдельные казино применяют свои собственные рекламные
и поощрительные программы,
в связи с чем лучше всего перво-наперво изучить правила).
Как можно стать обладателем такого бонуса?
Вам необходимо убедить кого-то из своих знакомых
пройти регистрацию на игровой
площадке, создать аккаунт
и внести депозит.
Во время прохождения регистрации этот человек должен указать сведения
о вас как реферала, чтобы Вам можно
было зачислить на счет вознаграждение.
Количество пришедших по рекомендации игроков
не ограничено.
Игровые площадки всегда рады новичкам, которые намерены стать
завсегдатаями в самое ближайшее время.
Поощрение за лояльность
Поощрительные бонусы – это еще вид подарков, которые
используются в on-line-casino 1вин промокод при регистрации 1win
Они напоминают довольно известные схемы лояльности, которыми руководствуются знакомые многим торговые марки.
Таким образом casino награждает своих приверженцев (людей, которые с завидной регулярностью заходят на ресурс и вступают в игру) привлекательными призами или наградами.
Такой бонус возможен в виде поощрительных
спинов, но многие игровых платформ также предоставляют небольшие аксессуары, призы или билеты для участия в лотереях.
Можно сказать, что удастся получить
намного больше приятных впечатлений
в течение пребывания на online-площадках.
Бонусы для ВИП-пользователей
Игровые сервисы также продумывают бонусы для игроков, которые регулярно посещают сайт казино
и используют в играх крупные денежные суммы.
Большинство online-casino связываются с VIP-клиентами , чтобы
узнать об их предпочтениях
и назначить призы, которые по сути соответствуют стилю постоянного клиента.
Это лишний раз доказывает, в какой мере
рады видеть клиентов онлайн-заведения.
Для ВИП-игроков многие онлайн-казино подготавливают очень ценные материальные призы.
Необходимо всего лишь регулярно заходить в выбранное заведение,
наслаждаться всеми предоставляемыми преимуществами
своего статуса.
suresiyle kullan?labiliyor. 1xbet mobil versiyon
• Kredi Kart?
Visa kartlar?n?z ile 10 TL, Master Card ile 15
TL alt limitle part yapabilirsiniz. Master Playing-card sahibiyseniz 5 TL uzeri tutarlar?
cekebilirsiniz.
• WebMoney
WebMoney yontemini kullan?yorsan?z 3 TL alt limitle keep, 5 TL ve uzeri tutarlarla
da cekim talebi verebilirsiniz.
• EcoPayz
Slightest 3 TL ile yat?r?m, maksimum 5 TL ile cekim yapabilirsiniz.
• AstroPay
3 TL ve uzeri tutarlar? yat?rabiliyorken 5 TL ve uzerindeki tutarlar
icinde cekim talebi verebilirsiniz.
• Paykasa
Kulland?g?n?z odeme yontemi Paykasa ise 3 TL alt limitin uzerindeki
tum tutarlar? an?nda yat?rabilirsiniz. Cekim talebi icin minimal islem tutar?
5 TL’dir.
• PayKwik
Yaln?zca stash away islemleri icin 3 TL alt limitle kullan?labilmektedir.
1xbet Reward ve Promosyonlar? https://wikicorp.org/index.php?title=User:RheaRosser487
Her yeni bahis cut off gibi Turkler icinde bonuslar en onemli k?s?md?r.
1xbet bahis sitesi de bunu en iyi sekilde sunmaktad?r.
• Hos Geldin Bonusu
Uyeliginizi act?ktan hemen sonra yapacag?n?z
ilk lay islemine sunulan bonustur. En fazla 300 TL’ye kadar yararlanabileceginiz bu promosyondan %100 oran?nda yararlanabilirsiniz.
• PromoCode Bonusu
• Telex Bonusu
• Y?ld?z Jackpot Promosyonu
• Bahis Kuponlar? Savas? Turnuvas?
• 1xRace Bonusu
• Dogum Gunu Bonusu
1xbet Musteri Hizmetleri
1xbet canl? destek hizmeti sunuyor ancak bunun haricinde de cok ilginc bir dan?smanl?k hizmeti veriyor.
Her bahis sitesinde gordugumuz mesaj yoluyla ulas?m, correspondence yordam?yla adresinden iletisim mumkun. Bunlar?n haricinde ise
yurt ici servis numaras?yla musterilerine telefon destegi sunuyor.
1xbet Guvenilir Mi?
Bahis oynatma lisans?n? Curacao uzerinden alm?s olan 1xbet Limited sirketi Turkiye’nin koklu platformlar?
aras?nda bulunuyor. Lisans?n?n haricinde de GoDaddy taraf?ndan saglanm?s olan SSL sertifikas?n?n aktif oldugunu gorebiliyoruz.
1xbet Genel Degerlendirme 1xbet Bahis
1xbet guncel giris adresi ise 1x-turkey.com olarak guncellendi.
Bahis dunyas?nda ayr?cal?kl? bir bahis yelpazesini bir araya getiren sirketin gerek
bonuslar?yla, gerek an?nda odeme yontemleriyle gerekse guvenilirligiyle
dikkat cekmeye devam ettigini soyleyebiliriz.
In India, the 1xBet betting coterie – is entire of the most well-received ones in Asia.
Among its ranking advantages, one can note acute odds, a good ways line on presented events and legitimate long-lasting
payoffs. In its functionality, the looking-glass duplication is no unique from
the biggest resource, providing users with all the even so
capabilities.
1xBet betting followers
1xbet app download http://rnspl.com/component/k2/itemlist/user/7319
1xbet app
Using the pertinence for Android, players can risk on sports in travel, at work or at home.
All that is required – is access to the Internet. In clean to initiate the program, crack to the “Applications for smartphones” section, write
non-stationary phone tally in the opened form. In a few minutes, an SMS idea with
download vinculum whim arrive.
1xbet apk 1xbet apk India
1xbet apk
The 1xBet mobile app as a replacement for iOS can be downloaded in the App Store.
A rule download link is available on the betting pty’s solemn website – mirror the station instruction.
General communication
With expropriate of our website there is an occasion to
contemplate c get access to the website far the clock,
placing bets on events of interest. The betting programme in India can be used not one from
a PC, but also from most ambulant devices.
Entitle
The 1xBet troop operates on the Internet legally. To provide services,
the betting friends has a permit issued next to the global regulator
of Curacao. It allows the rostrum to coax in varied countries without violating
law.
Inspection of the 1xBet official Indian website
The betting stand offers visitors to hazard on sports and financial events.
Bettors also prepare access to online opening machines and a essential casino.
A athlete can bet bread in any sections of the website using a
single account. The betting followers has a good action limit and broad money oblique on all events.
Users can play in more than 40 sports types,
ranging from lay football and tennis to imported cockfights.
The betting coterie accepts bets on not quite all outcomes: not only
on a superiority or get the better of of inseparable of teams, but also
on a number of corner kicks, penalties and other results.
Complete can memorialize a less unshakeable action strip at
the 1xBet betting circle only before avoided events.
But regular here song can bet on over/under, handicap and some other outcomes.
Players can quantify all the possibilities of moneyed betting only
after creating an account.
Registration in the 1xБет India 1xbet india https://www.metin2xmely.ro/forum/viewtopic.php?t=23005
Registration in the 1xБет India
In unison can turn on a graph in the betting flock in 4 ways:
via a rapid registration procedure. A thespian needs to click on the happy tab and select the mountains of residence.
After a scattering seconds, the drug will-power be
given a password and login, which will be created by the organized whole;
registration procedure
next to creating an account using phone. In this specimen, during registration strategy a company sine qua non direct attention to the alert phone number
onto which SMS message intent in with circumstantial instructions;
creating an account using phone
by registering via email. The exemplar choice, at which owner fills out of pocket registration form,
prescribing dear observations and a valid e-mail. Later a missive
with a fasten together comes to the user’s specified e-mail,
which becomes a pass to the 1xBet India website;
past registering via venereal networks. The easiest feeling to activate an account.
A sportswoman single needs to click on the icon with the communal network where
he has a chart, after which an account is automatically
generated.
1xbet login
1xbet login
Individual can pierce the 1xBet website in the
same in the works as on the major 1xbet com resource. It is enough in search a user to up in the system
in any suitable way, and then okay away entering the life-and-death shibboleth and
login. In some cases, to enter in the flesh account, a particular may
prerequisite a dear jus divinum ‘divine law’ that the betting proprietorship sends in the
pose of SMS dispatch onto a transportable phone
number.
In container of problems with entering an account due to a loss of a
watchword, the gamester inclination be able to solve the consequence quickly.
To do this, only click on the “Forgot your password?” ticket,
writing down the email hail or phone mass next to it. The owner intention be receive relevant facts to the specified contacts.
The watchword sent choose help to log in to the account.
Depositing paper money
After fleeting registration and authorizing on the website, user last will and
testament be accomplished to replace funds in his intimate account.
To do this, fit to the “Payments” section. There, the participant will dig various options in place of depositing funds into the account:
bank along;
electronic wallets and payment systems;
payment through the mortal;
greenbacks over from a animated phone;
Internet banking;
cryptocurrency
prepaid cards.
In unalloyed, the website of the betting associates provides more than 40 options instead of depositing capital.
Regardless of the chosen method, financial transactions on the website are carried missing instantly.
The entire important trend benefit of a player – is to serve the rules established past the betting company.
In the course of instance, the replenishment amount should be no less than 100 rubles.
In appendix, it is strictly forbidden to abuse other people’s wallets and bank cards to deposition money.
Miscarriage to agree with these conditions may be to blocking of the account.
Money withdrawal from the 1xbet in India 1xbet india
To withdraw funds in of the way it is necessary to utter
the unmodified acquiesce as with replenishment. To make a pecuniary annals, a
musician needs to elapse to live account and supreme the “Money withdrawal” section. There the owner leave need
to identify the amount to be transferred, and inscribe the text
from his electronic wallet or bank card. If all
the data is traditional, the effort in behalf of funds withdrawal wish
be processed on the betting company within 1-7 days.
In harmony to leave alone delays in payoffs of earned winnings, players desideratum to pass account verification procedure 1xbet app download
. During this procedure, the alcohol will be required to lend the 1xBet application in India with copies of his identity documents.
Passed portrait verification will admit one cancel
funds from the website easily, at any accessible time.
It is distinguished towards players to reminisce over that the betting party has
set assured limits on well-heeled withdrawal.
In happening of any problems with withdrawal of funds, bettors can contact the be supportive of accommodation in regard to help.
Support alpenstock mould at the website in every direction the clock.
Bonuses from 1xBet
The betting business offers visitors a solid bonus program.
Players can presume to pick up the following types of bonuses:
“An eye to the elementary deposit.” The amount of the promotion is 100% from the deposited
amount. The purse requisite be won rough at three bets of the Express type with a coefficient of at least 1.4;
“Favoured Friday”. The gratuity is issued to players strictly on the specified day.
The get bankroll b reverse conditions are the same as with the award after the leading lay down;
“Wednesday – multiply by way of 2”. Cappers who won on the “Favoured Friday” are allowed to participate in the action. If the consumer has not until now detached the funds won from the recent week,
his put is doubled by the betting partnership;
“Demonstrate of the day.” The choose is held daily.
If a sportsman achieves achievement in the Tailback or the
Abide, he will endure an extend in the appearance of 10% of the
earned winnings;
“Perk also in behalf of a series of failures.” Purchaser profit without hope part of the
irrecoverable money, upon shape of 20 hapless bets
in a row with a coefficient of not more than 3.
Конкурентная борьба в сфере online
гемблинга огромна.
Ежедневно появляется немало площадок с соблазнительными
условиями для новых игроков.
Особенного внимания заслуживает
стартовый подарок, который оценили многие пользователи.
Пришла пора разобраться с основными аспектами, которые
связаны с функционированием casino http://meadowsweethall.org/1%D0%B2%D0%B8%D0%BD_%D0%91%D0%BA .
Стартовый приз – это главный бонус, который предоставляет онлайн-казино.
Чтобы его получить, не придется прилагать много усилий.
Инструкция подготовлена для
игроков, которые только впервые открывают аккаунт на
сайте казино.
Пользователи могут и не подозревать, какой подарок подготовили разрабы.
Наиболее часто первоначальный
бонус прибавляет определенный процент к стартовому счету независимо от
заведенной на сайт суммы.
Поощрение в виде бесплатных спинов
Casino внедряют безоплатные прокручивания в свою рекламную стратегию.
Что это означает?
Такой подход дает игрокам бесплатные циклы, которые играющие могут использовать в игровых
автоматах, и выигранные средства чаще всего
можно снять с их счета.
Вращения достаточно популярны в среде любителей азартных онлайн-игр,
потому что они позволяют определить возможности, которые обеспечивают новые игровые
аппараты, с исключением потребности
увеличивать свой счет и растрачивать личные финансы.
Довольно интересное предложение, которым
вполне смогут воспользоваться
игроки.
Можно оценить по достоинству все плюсы, шансы,
обеспечиваемые разработчиками.
Казино подобным способом нередко продвигают новые продукты среди посетителей, прошедших регистрацию на их портале.
В то же время 1вин бонус не ограничено ни для одного из желающих.
Необходимо всего-навсего пройти в соответствующий раздел,
ввести данные в регистрационные
ячейки.
Не забывайте про необходимость подтвердить совершеннолетие.
Без верификации будет трудно получить статус игрока, которому
доступны имеющиеся возможности on-line
площадки.
Реферальные бонусы
Online казино стимулирует пользователей, которые советуют сервис потенциальным игрокам.
Бонусы за вовлечение знакомых делаются
с целью популяризации гэмблинга и притягивания новых пользователей казино.
Указанный метод считается наиболее эффективным
для роста числа игроков.
Одно дело, когда посетитель решается стать
полноценным участником, опираясь на рекламу.
Совершенно другое – поверить рекомендации друга, который
уже удостоверился в предоставленной информации, вариативности игровых слотов.
За совет вы можете обнаружить в личном кабинете некоторую сумму денег.
Начисленные деньги разрешается вывести со своего
счета или использовать на безоплатные спины в игре (отдельные cazino используют самостоятельно разработанные маркетинговые и поощрительные стратегии, в
связи с чем лучше всего
перво-наперво изучить правила).
Каким образом можно стать обладателем такого бонуса?
Вам необходимо убедить кого-то
из своих знакомых зарегистрироваться на игровой площадке, активировать аккаунт и пополнить счет.
Во время прохождения регистрации этот человек должен указать сведения о вас
как рекомендателя, чтобы Вам можно было получить
вознаграждение.
Количество пришедших по рекомендации игроков не лимитируется.
Игровые площадки всегда рады новичкам, которые стремятся стать завсегдатаями в самое
ближайшее время.
Поощрение за лояльность
Бонусы лояльности – это еще вид бонусов, используемых в on-line-casino 1вин 1win ставки приложение.
Они напоминают достаточно известные программы вознаграждений, которыми управляют популярные торговые марки.
Получается, что casino поощряет своих приверженцев (пользователей,
которые регулярно посещают площадку и вступают
в игру) привлекательными бонусами
или подарками.
Такой сюрприз может быть в форме поощрительных
вращений, однако основная масса игровых платформ тоже предоставляют небольшие
гаджеты, подарки или билеты для участия в лотереях.
Можно сказать, что появится возможность
получить намного больше
положительных впечатлений за время нахождения на online-площадках.
Бонусы для VIP-игроков
Казино также продумывают поощрения для игроков, которые
регулярно посещают портал cazino и вкладывают в игры большие
денежные суммы.
Большая часть онлайн-казино связываются с VIP-пользователями с целью разузнать об
их предпочтениях и присудить призы, которые по сути соответствуют поведенческому фактору заинтересованного игрока.
Это еще раз подтверждает, в какой мере рады видеть клиентов online-площадки.
Для ВИП-игроков большинство online-казино готовят очень ценные
материальные поощрения.
Необходимо всего лишь регулярно заходить
в выбранное казино, наслаждаться всеми предоставляемыми
преимуществами своего статуса.
suresiyle kullan?labiliyor. Bonuslar 1xbet Türkiye
• Kredi Kart?
Visa kartlar?n?z ile 10 TL, Chief Christmas card ile 15 TL alt limitle set yapabilirsiniz.
Master Birthday card sahibiyseniz 5 TL uzeri tutarlar?
cekebilirsiniz.
• WebMoney
WebMoney yontemini kullan?yorsan?z 3 TL alt limitle lodge, 5
TL ve uzeri tutarlarla da cekim talebi verebilirsiniz.
• EcoPayz
Least 3 TL ile yat?r?m, maksimum 5 TL ile cekim
yapabilirsiniz.
• AstroPay
3 TL ve uzeri tutarlar? yat?rabiliyorken 5 TL ve uzerindeki tutarlar icinde cekim
talebi verebilirsiniz.
• Paykasa
Kulland?g?n?z odeme yontemi Paykasa ise 3 TL alt limitin uzerindeki tum tutarlar?
an?nda yat?rabilirsiniz. Cekim talebi icin lowest islem tutar?
5 TL’dir.
• PayKwik
Yaln?zca deposit islemleri icin 3 TL alt limitle kullan?labilmektedir.
1xbet Honorarium ve Promosyonlar? http://cgi2.bekkoame.ne.jp/cgi-bin/user/u31943/chitose/bbs2/aska.cgi/p;id=158999.html%20
Her yeni bahis sever gibi Turkler icinde bonuslar en onemli k?s?md?r.
1xbet bahis sitesi de bunu en iyi sekilde sunmaktad?r.
• Hos Geldin Bonusu
Uyeliginizi act?ktan hemen sonra yapacag?n?z ilk deposit islemine sunulan bonustur.
En fazla 300 TL’ye kadar yararlanabileceginiz bu promosyondan %100 oran?nda yararlanabilirsiniz.
• PromoCode Bonusu
• Telex Bonusu
• Y?ld?z Jackpot Promosyonu
• Bahis Kuponlar? Savas? Turnuvas?
• 1xRace Bonusu
• Dogum Gunu Bonusu
1xbet Musteri Hizmetleri
1xbet canl? destek hizmeti sunuyor ancak bunun haricinde de cok ilginc bir dan?smanl?k hizmeti veriyor.
Her bahis sitesinde gordugumuz mesaj yoluyla ulas?m, despatch yordam?yla adresinden iletisim mumkun. Bunlar?n haricinde ise yurt ici servis numaras?yla musterilerine telefon destegi sunuyor.
1xbet Guvenilir Mi?
Bahis oynatma lisans?n? Curacao uzerinden alm?s
olan 1xbet Limited sirketi Turkiye’nin koklu platformlar?
aras?nda bulunuyor. Lisans?n?n haricinde de GoDaddy taraf?ndan saglanm?s olan SSL
sertifikas?n?n aktif oldugunu gorebiliyoruz.
1xbet Genel Degerlendirme Android için 1xbet’i indirin
1xbet guncel giris adresi ise 1x-turkey.com olarak guncellendi.
Bahis dunyas?nda ayr?cal?kl? bir bahis yelpazesini bir araya getiren sirketin gerek bonuslar?yla, gerek an?nda odeme yontemleriyle gerekse guvenilirligiyle dikkat cekmeye devam
ettigini soyleyebiliriz.
Обзор Melbet зеркала
Рынок ставок в России функционирует довольно долгое
время, и в 2012 году вышла на рынок фирма Мелбет.
На сегодняшний день ресурс активно продолжает развиваться, в частности это касается виртуального
пространства.
Как полагают многие пользователи, довольно удобно не выходя из дома, в офисе или в дороге ставить на события.
Время не будет потеряно.
Главная задача конторы – оказывать помощь игрокам ставить,
это можно выполнить , используя офисы
фирмы или же в режиме онлайн, для чего имеется портал и приложение для
смартфона.
Итак, предоставляется довольно много возможностей, чтобы приятно
провести досуг, а заодно попробовать получить неплохие выигрыши.
Компания бк мелбет отзывы довольно стремительно развивается и старается создать для своих пользователей самые лучшие
условия.
Здесь каждый может ставить как на спорт, так и на иные мероприятия,
к примеру, турниры типа Eurovision.
Теперь не нужно просто смотреть за тем, как
проводит выступление любимый
исполнитель.
Достаточно начать верить в его
триумф, сделав выгодную ставку.
Существует шанс, что удастся сорвать куш
и при этом послушать отличную музыку.
Такой подход крайне удобен, так как в этой ситуации безусловно каждый человек найдет для
себя захватывающие события
и сделает ставки.
Программеры предусмотрели события на все
предпочтения.
Решение связано с Вашим возрастом, увлечениями, желанием и возможностью идти
на риск.
С чего начинать ставить на спорт с Melbet http://www.wiki-peps.fr/mediawiki/index.php/Utilisateur:Tawanna9807
Некоторые клиенты думают, что ставить на
спортивные баталии или иные мероприятия – это довольно хлопотно и
что в этом потребуется тратить время на разбирательство.
Действительно ли это так и будет?
Естественно, нет.
Если идет разговор о Мелбет, то здесь
начать делать ставки получится у любого желающего.
На уровне интуиции легко осваиваемый интерфейс придется по душе
даже начинающим пользователям, которые надумали освоить искусство ставок.
Следует рассмотреть подробнее, каким образом начать
это делать.
Для начала вам нужно пройти регистрацию на портале установить мелбет приложение
Алгоритм прохождения регистрации удивительно легкий, вы потратите на
него минимум времени.
Потребуется всего лишь вбить личные сведения
в выделенные ячейки, пройти процесс верификации.
После регистрации необходимо положить
некоторую сумму на депозитный счет.
При этом не играет роли, какая именно будет зачислена сумма денег.
Совсем скоро Вы освоитесь и сможете понять,
каким образом действовать дальше,
какие параметры ставки считаются оптимальными.
И с этого момента начинайте ставить на события.
Сейчас стало понятно, что
делать это можно без особого труда, так как на эти действия уйдет у
вас минимум времени и сил.
Выходит, абсолютно любой из игроков сумеет начать делать
ставки вне зависимости от того без опыта он или профи.
Все, что для этого нужно – пройти регистрацию.
Компания Melbet – входит в число популярных и пользующихся спросом площадок на рынке России, что совсем не вызывает удивления.
Как известно, контора с
заботой относится к своим клиентам и предлагает для них самые лучшие
условия.
Разработчикам важно не просто заинтересовать новых игроков, но и создать наиболее комфортные обстоятельства для завсегдатаев.
Репутация считается значимым показателем
для конторы во имя того, чтобы не потерять доверия пользователей.
В области ставок существует немалое число мошенников.
Не следует слепо доверять яркой рекламе,
а также бездумно верить чрезмерно заманчивым предложениям.
Можно не только потерять деньги, время,
но и заполучить на компьютер вирусную программу.
Целесообразнее останавливать выбор
на надежных фирмах, которые
долгий период пребывают в
игровой области.
Всегда можно изучить отклики, узнать о
времени появления конторы на просторах интернета.
Среди подобных профессионалов своего дела считается http://www.manchestermassage.net/forum/index.php?topic=3057.0 .
При желании можно загрузить специально
созданное приложение для смартфонов и других гаджетов.
Останется подсоединиться к сети
Интернет, чтобы ставить уже сегодня.
Вы даже сможете выбрать мероприятие, спрогнозировать результат, находясь в пробке или в офисе.
Это ли не одно из преимуществ, за которые стоит останавливать выбор на этой букмекерской конторе?
Именно это подтвердило огромное количество клиентов компании.
Поэтому, если вы хотите испытывать удачу на ставках, то вам стоит присмотреться
к Мелбет.
Здесь melbet-partner.com вы сможете найти
необходимые сведения и решения своих вопросов,
а , кроме того, немедленно начать делать ставки после регистрации.
銈儶銈儶銈?銈搞儯銈ゃ儹
adidas spezial sort stadiumtr忙ningsbukser herre hummelorigine and hjelm and site dknike mercurial vapor 13 elite fg orange sort limited edition
Registro em 1XBET Portugal http://datalab.dscloud.me/xe/index.php?mid=board_freetalk&document_srl=52232
Digite o codigo promocional
REGISTE-SE E RECEBA UM BONUS DE 100 EUR AGORA MESMO!
Convidamos todos quem quer ganhar nas apostas em desportos registrar-se rapidamente em uma casa de apostas mais justa da
empresa 1XBet.
O registro em 1XBET Portugal permite usar de
todas as funcionalidades do place oficial, incluindo:
retirada de fundos rapida atraves de qualquer sistema de
pagamentos ou cartoes bancarias;
servico de apoio a cliente conveniente que sempre ajudara esclarecer a situacao;
interface e aplicacoes moveis funcionais.
O hand-out da 1XBET Portugal download da 1xbet para android
A casa de apostas, a todos que desejam receber os honorarium agradaveis na sua
conta, da essa oportunidade. E uma oportunidade genuine
de ganhar dinheiro gracas a generosidade da administracao da empresa.
O pre-eminent sempre era o perquisite de primeiro deposito.
O honorarium e um adicional de 100% do valor do deposito de
ate 130 euros, que serao imediatamente creditados na conta.
O mais agradavel e a possibilidade de devolver o dinheiro recebido nas apostas ordinarias e
expressas.
A condicao principal e que tem que escolher as partidas com coeficiente bastante alto, das quais e necessario formar um expresso completo.
Para um novato recuperar aposta nao e uma tarefa facil, mas isso permite conhecer bem a interface
da empresa de azar e aprender o basico de apostas.
Como usar o codigo de promocao da 1xBet? http://piksel72.venez.fr/mediawiki-1.34.2/index.php?title=Utilisateur:ValentinMuller
Usar o codigo de promocao e muito facil, pois a administracao permite fazer isso sem a participacao do
servico de apoio a cliente. Basta de seguir uma instrucao intuitivamente clara:
Primeira coisa que tem que fazer e ir para o portal oficial de
jogos com o nosso relationship e clicar em “Registrar-se” no canto select direito.
A seguir, tem que selecionar um dos metodos de criacao da conta pessoal e inserir o codigo
de promocao recebido, que tambem se encontra neste site.
Apos preencher todos os dados, e necessario enviar um pedido e receber a conta
ativada durante de um dia.
Os usuarios nao devem esquecer da necessidade de confirmar o e-mail atraves de uma mensagem recebida.
Todos os dados indicados durante registro devem ser verificados cuidadosamente e so podem ser verdadeiros, pois caso contrario, depois da
verificacao por administracao a conta pode ser
bloqueada.
O que oferece a casa de apostas 1XBET Faezr o download da 1xbet para iphone
O registro na 1XBET Portugal permite a cada jogador apreciar um jogo de apostas
em desporto divertido e excitado.
Tudo que e necessario e ter uma conta registrada e ser
um residente de Portugal maior da idade. E obrigatorio passar uma verificacao completa que da
o acesso para gerenciamento das contas.
A empresa oferece a todos os jogadores registrados as seguintes vantagens:
uma enorme variedade de partidas e eventos politicos em quais pode apostar com um
praticamente sem limites.
Apenas administracao pode limitar o montante maximo de aposta,
entretanto os coeficientes sao colocados independentemente do
nivel da partida;
varias maneiras de deposito e retirada de fundos que
permite carregar a sua conta de jogo sem algum problema e receber o
seu ganho no cartao bancario ou um sistema de pagamentos;
servico de apoio a cliente operativo que responde todas as
perguntas de usuarios e ajuda resolver qualquer situacao 24 horas por dia.
Um requisito obrigatorio para obtencao de todos os privilegios acima indicados e gratuity adicionais e preencher todos os dados na secao “Minha conta” que se encontra na
conta pessoal.
Обзор Melbet зеркала
Рынок ставок в РФ существует довольно давно, и в 2012 году вышла на рынок фирма Melbet.
Вплоть до сегодняшнего дня сервис
стабильно развивается, в частности это относится к виртуальному пространству.
Как полагают некоторые клиенты, достаточно удобно не выходя
из дома, в офисе или в дороге ставить на
события.
Никаких потерь времени.
Наиболее важная цель компании –
помогать людям делать ставки, это удобно сделать через
офисы фирмы или же в режиме online, для этого имеется портал и мобильная версия.
Итак, предоставляется довольно много
возможностей, чтобы приятно провести свободное время, а вместе с тем попробовать заработать неплохие деньги.
Компания отказ в выводе средств melbet довольно стремительно развивается и старается подготовить для своих пользователей
наилучшие условия.
Здесь вы можете делать
ставки как на спорт, так и на другие мероприятия, к
примеру, конкурсы типа Eurovision.
Теперь не нужно просто наблюдать за тем,
как проводит выступление любимый исполнитель.
Стоит всего лишь начать верить в его победу, сделав выгодную ставку.
Существует вероятность, что удастся заполучить крупную
сумму , а заодно послушать отличную музыку.
Это очень удобно, так как в этом случае безусловно любой человек
найдет для себя интересные мероприятия и
поставит на его исход.
Программеры предусмотрели
события на любой вкус.
Все связано с Вашим возрастом, увлечениями, желанием
и возможностью идти на риск.
С чего начать ставить на спортивные события
с Мелбет http://www.anapapansion.ru/modules.php?name=Your_Account&op=userinfo&username=ConcettaLe
Многие игроки думают, что делать ставки на спорт или другие
события – это достаточно хлопотно и что в этом нужно долго разбираться.
Действительно ли это так
и будет?
Естественно, это не так.
Когда идет разговор о Melbet, то здесь начинать ставить
получится у любого желающего.
На уровне интуиции понятный интерфейс понравится даже начинающим
пользователям, которые только решили разобраться с тем, как ставить.
Рассмотрим подробнее, как начинать процесс.
Для старта необходимо пройти
регистрацию на портале скачать melbet на андроид
Процесс прохождения регистрации удивительно легкий, займет у вас минимум времени.
Нужно всего лишь ввести персональные данные в выделенные поля,
пройти процесс верификации.
После регистрации надо будет положить некоторую сумму на депозитный счет.
Абсолютно не играет роли, какая по размеру будет зачислена денежная сумма.
Очень быстро Вы разберетесь
и поймете, как поступать дальше,
какие параметры взноса являются оптимальными.
И после этого вы можете начать
делать ставки.
Сейчас стало ясно, что выполнять подобные манипуляции совершенно не сложно,
потому что этот процесс займет у вас
минимум времени и сил.
Таким образом, абсолютно любой из игроков сумеет начать ставить вне зависимости от того
новичок он или профи.
Единственное, что для этого нужно – зарегистрироваться.
Контора Мелбет – входит в число
известных и пользующихся спросом компаний
на российском рынке, что абсолютно не вызывает удивления.
Как известно, фирма с заботой относится к
своим клиентам и подготавливает для них наилучшие условия.
Разработчикам важно не просто привлечь больше пользователей, а и
создать наиболее комфортные условия для постоянных клиентов.
Имидж считается значимым критерием
для конторы во имя того, чтобы не снизить веры игроков.
В сфере ставок присутствует большое количество
аферистов.
Не стоит соблазняться привлекательной рекламой,
а также бездумно верить чрезмерно
заманчивым предложениям.
Можно не только лишиться денег, безрассудно потерять время, но и установить на ноутбук вирусную программу.
Целесообразнее останавливать выбор на надежных фирмах, которые длительное
время находятся в данной области.
Всегда можно почитать отзывы, узнать о времени начала деятельности компании в виртуальном пространстве.
Одним из таких профессионалов
своего дела признается http://kaceyisms.com/melbet-%d0%b1%d1%83%d0%ba%d0%bc%d0%b5%d0%ba%d0%b5%d1%80%d1%81%d0%ba%d0%b0%d1%8f-%d0%ba%d0%be%d0%bd%d1%82%d0%be%d1%80%d0%b0%d0%bc%d0%b5%d0%bb%d0%b1%d0%b5%d1%82-%d0%b1%d1%83%d0%ba%d0%bc%d0%b5%d0%ba .
В определенный момент несложно скачать специально разработанное мобильное приложение.
Останется подсоединиться
к сети Интернет, чтобы ставить уже сегодня.
У Вас будет возможность подобрать мероприятие,
спрогнозировать результат, пребывая в заторе или в офисе.
Не это ли и есть одно из преимуществ,
за которые стоит останавливать выбор
на этой букмекерской конторе?
И это подтверждает огромное число игроков конторы.
Поэтому, если вы решили испытывать удачу на ставках, то вам стоит присмотреться к Melbet.
Тут melbet-partner.com вы найдете необходимые сведения и ответы на свои вопросы, а , кроме того, немедленно начать делать ставки после регистрации.
Описание Mostbet зеркала mostbet зеркало
http://scoutserv.com/home.php?mod=space&uid=27984&do=profile&from=space
Ниша ставок в России функционирует достаточно давно, и в 2012 году на рынке появилась фирма
Мостбет.
Вплоть до сегодняшнего дня сервис стабильно развивается, в частности это
относится к виртуальному пространству.
Как полагают многие пользователи, довольно комфортно
не выходя из дома, в офисе или в дороге делать ставки.
Потеря времени исключена.
Главная задача конторы – оказывать помощь людям ставить, это удобно сделать ,
используя офисы фирмы или же в режиме онлайн, для этого имеется сайт и мобильная версия.
Как видите,, предоставляется немало возможностей, чтобы с удовольствием провести досуг,
а вместе с тем попытаться получить приличные деньги.
Контора мостбет войти в личный кабинет
очень активно продвигается и намерена создать для своих пользователей наилучшие возможности.
Здесь каждый может делать ставки как на спорт, так и на другие события,
к примеру, турниры наподобие Eurovision.
Теперь нет смысла просто смотреть за
тем, как проводит выступление обожаемый артист.
Стоит всего лишь поверить в его триумф, произведя оптимальную ставку.
Существует шанс, что удастся сорвать куш , а заодно насладиться музыкальным произведением.
Такой подход крайне удобен, так как в этой ситуации безусловно
каждый игрок сможет найти для себя захватывающие мероприятия и сделает
ставки.
Разработчики смогли предусмореть события на любой вкус.
Решение зависит от того, сколько Вам лет, чем вы увлекаетесь и способны ли рисковать.
С чего начинать ставить на спортивные события с
Mostbet
Многие клиенты уверены, что делать ставки на спорт или
иные мероприятия – это довольно сложно и что
в этом потребуется долго разбираться.
Действительно ли это так и будет?
Конечно же, это не так.
Когда идет разговор о Mostbet
http://kj.nodong.org/elec_03/3263997 mostbet промокод на ставку , то в этом
случае начинать ставить получится у любого желающего.
На уровне интуиции легко осваиваемый интерфейс понравится даже новичкам, которые надумали освоить искусство ставок.
Рассмотрим подробнее, каким образом начинать процесс.
Для начала необходимо пройти регистрацию на сайте.
Процесс прохождения регистрации очень легкий, вы потратите на него минимальное количество времени.
Нужно всего лишь ввести персональные сведения в
специальные поля, верифицироваться.
Как только вы зарегистрируетесь, следует внести деньги на депозитный счет.
Абсолютно не играет роли,
какая именно будет внесена денежная
сумма.
Совсем скоро Вы освоитесь и сможете понять, каким образом поступать дальше, какие размеры взноса являются наиболее приемлемыми.
И с этого момента вы можете начать делать ставки.
Теперь становится понятно, что выполнять подобные манипуляции совершенно не сложно, так
как на эти действия уйдет у вас минимальное количество сил и времени.
Выходит, абсолютно каждый сумеет начать
делать ставки вне зависимости
от того без опыта он или профи.
Все, что для этого требуется
– зарегистрироваться.
Контора Мостбет – одна из самых популярных и востребованных площадок на рынке России, что совсем не удивительно.
Ведь контора заботится о своих пользователях и подготавливает для них наилучшие условия.
Руководству важно не просто привлечь новых
игроков, а и создать максимально удачные обстоятельства для постоянных клиентов.
Имидж считается важным критерием для компании во имя того, чтобы не потерять
веры пользователей.
В сфере ставок существует немалое
количество аферистов.
Не стоит слепо доверять яркой рекламе, а также
идти на поводу у слишком выгодных условий.
Возможно не только потерять деньги,
время, но и установить на компьютер вирус.
Уместнее выбирать лишь проверенные компании, которые долгий период находятся в игровой отрасли.
Всегда можно почитать отклики, ознакомиться с временем появления конторы на
просторах интернета.
Среди подобных профи ведения игрового бизнеса считается мостбет вход войти моя страница
При желании несложно загрузить специально разработанное приложение для смартфонов и других гаджетов.
Нужно обеспечить наличие сети Интернет,
чтобы ставить уже сегодня.
Вы даже сможете подобрать событие, сделать прогноз, пребывая в заторе или
на даче.
Не это ли и есть одно из достоинств, за которые следует останавливать выбор
на этой букмекерской конторе?
Именно это подтверждает огромное число клиентов компании.
В таком случае, если вы
решили испытывать удачу на ставках, то вам стоит обратить внимание на Мостбет.
Тут Mostbet-partner.com вы сможете найти
необходимую информацию и
ответы на свои вопросы, а также немедленно начать делать ставки после того, как
зарегистрируетесь.
Конкурентная борьба в сфере online гемблинга невероятна.
https://physioexrx.com/index.php/User:SusanHardesty
С завидной регулярностью появляется
много площадок с заманчивыми условиями для новеньких.
Отдельного интереса заслуживает
приветственный подарок, который оценили большое число
клиентов.
Пришла пора разобраться с основными аспектами, которые сопряжены с функционированием
казино.
Стартовый приз – это основное поощрение, которое предлагает online-казино.
Для его получения не нужно прилагать много стараний.
Пособие подготовлено для клиентов,
которые только впервые открывают аккаунт на сайте cazino.
Пользователи могут и не подозревать,
какой сюрприз приготовили программисты.
Наиболее часто первоначальный бонус добавляет определенный процент к первому пополнению счета независимо от количества
внесенных денег.
Подарок в виде бесплатных вращений 1win букмекерская скачать приложение
Казино включают бесплатные прокручивания в свою рекламную стратегию.
Что это означает?
Это дает игрокам безоплатные раунды,
которые играющие могут использовать в игровых автоматах, и выигрыши
чаще всего можно снять с их
счета.
Вращения достаточно популярны в среде почитателей азартных онлайн-игр, потому что они позволяют определить потенциал, который обеспечивают новейшие гейм аппараты,
без потребности пополнять свой счет и
тратить личные финансы.
Достаточно интересное предложение, которым вполне
могут воспользоваться геймеры.
Можно расценить имеющиеся преимущества,
шансы, предоставляемые владельцами площадок.
Casino таким образом зачастую рекламируют новые услуги среди посетителей, зарегистрированных на их сайте.
При этом http://siliconvalleytalk.xyz/blogs/viewstory/2253 доступно всем желающим.
Необходимо всего лишь пройти в определенный раздел, заполнить поля регистрации.
Важно не забывать про необходимость удостоверить совершеннолетие.
Без верификации будет сложно
получить статус игрока, которому откроются потенциальные возможности онлайн ресурса.
Бонусы для пришедших по рекомендации
Онлайн casino поощряет клиентов, которые советуют игровую площадку другим.
Бонусы за вовлечение знакомых
делаются с целью продвижения предложений
игр и притягивания новых пользователей казино.
Указанный способ считается одним из самых эффективных для роста числа геймеров.
Одно дело, когда пользователь решается присоединиться, опираясь на рекламу.
Совершенно иное – воспользоваться советом
приятеля, который уже убедился в правдивости данных,
многообразии игровых аппаратов.
За совет вы можете получить некоторую сумму денег.
Начисленные деньги можно снять
со своего счета или потратить на
безоплатные вращения в игровых раундах (некоторые казино применяют
самостоятельно разработанные маркетинговые и поощрительные стратегии,
в связи с чем стоит перво-наперво ознакомиться
с правилами).
Каким образом удастся стать обладателем такого бонуса?
Вы должны сагитировать кого-то из
своих знакомых пройти регистрацию на сайте казино, активировать учетную запись и пополнить счет.
При прохождения регистрации этот человек
должен указать ваши данные как
рекомендателя, чтобы Вам можно было получить бонус.
Количество пришедших по рекомендации игроков не лимитируется.
Игровые площадки всегда рады новым клиентам, которые стремятся стать завсегдатаями в самое
ближайшее время.
Бонус за лояльность
Поощрительные бонусы – это дополнительный вид бонусов, используемых в on-line-казино 1вин 1win официальный сайт зеркало
Они похожи на достаточно известные схемы вознаграждений, которыми руководствуются знакомые многим магазины.
Таким образом casino награждает своих приверженцев (пользователей, которые с завидной регулярностью заходят на ресурс и вступают в игру)
привлекательными бонусами или подарками.
Подобный бонус может быть в виде бесплатных спинов, но основная
масса игровых платформ также предоставляют недорогие гаджеты, призы или лотерейные
билеты.
Можно сказать, что удастся испытать намного больше положительных впечатлений в течение пребывания на онлайн-площадках.
Поощрительные призы для ВИП-клиентов
Игровые сервисы также готовят поощрения для игроков,
которые регулярно посещают портал казино и используют
в играх крупные денежные суммы.
Большинство online-казино связываются с ВИП-пользователями , чтобы разузнать об их интересах
и присудить призы, которые фактически соответствуют стилю постоянного игрока.
Это лишний раз доказывает, насколько
рады приветствовать пользователей online-площадки.
Для ВИП-геймеров большинство онлайн-cazino готовят очень ценные материальные поощрения.
Нужно всего лишь регулярно заходить в
любимое казино, наслаждаться
всеми предоставляемыми преимуществами своего
статуса.
Конкурентная борьба на рынке онлайн гемблинга огромна.
https://edosk.ru/user/profile/2249
Ежедневно появляется немало игровых ресурсов с соблазнительными спецусловиями для новых игроков.
Отдельного интереса удостаивается приветственный бонус,
который смогли оценить многие пользователи.
Пришла пора понять важные моменты, которые связаны с работой casino.
Приветственный приз – это основное поощрение, которое предлагает
online-casino.
Для его получения не придется прилагать серьезных усилий.
Инструкция подготовлена для клиентов,
которые только впервые заходят в
профиль на сайте казино.
Геймеры часто даже не представляют, какой подарок
подготовили программисты.
Наиболее часто первое поощрение добавляет определенный процент к начальному счету независимо от внесенной суммы.
Поощрение в виде безвозмездных спинов 1win приложение андроид
Казино внедряют бесплатные вращения в
собственную рекламную стратегию.
Как это понимать?
Это позволяет давать игрокам бесплатные циклы, которые геймеры имеют
право использовать в игровых автоматах, и выигранные средства обычно
можно снять с личного счета.
Спины чрезвычайно востребованы среди любителей азартных онлайн-игр, так как они дают шанс определить возможности, которые предоставляют новые гейм аппараты, с исключением необходимости увеличивать персональный счет и растрачивать собственные финансы.
Довольно интересное предложение, которым в полном объеме смогут воспользоваться играющие.
Можно оценить по достоинству
имеющиеся плюсы, возможности, обеспечиваемые разработчиками.
Казино таким образом зачастую рекламируют новые
услуги среди пользователей, зарегистрированных на их
платформе.
В то же время http://www.newtea97.com/home.php?mod=space&uid=39185&do=profile&from=space доступно для
всех любителей игры.
Нужно всего лишь выбрать определенный раздел, ввести данные в поля
регистрации.
Не забывайте про обязательность подтверждения совершеннолетие.
Без подтверждения личности будет сложно стать постоянным пользователем, которому доступны имеющиеся возможности on-line
площадки.
Реферальные бонусы
Онлайн casino поощряет пользователей, которые рекомендуют игровую площадку потенциальным
игрокам.
Бонусы за вовлечение знакомых предназначены для популяризации предложений игр и притягивания
потенциальных клиентов игровых площадок.
Указанный способ признается одним из самых эффективных для роста
числа геймеров.
Один момент, когда человек решается присоединиться,
опираясь на рекламу.
Совершенно иное – поверить рекомендации друга, который на сегодня убедился в правдивости данных, вариативности игровых аппаратов.
За совет вы можете обнаружить в личном кабинете некоторую сумму денег.
Финансовый бонус можно снять
со счета или потратить на бесплатные
спины в игровых раундах
(некоторые казино используют самостоятельно разработанные рекламные и поощрительные программы, поэтому стоит сначала ознакомиться с правилами).
Как можно стать обладателем такого
бонуса?
Вы должны убедить кого-то из своих знакомых пройти регистрацию на игровой площадке, создать учетную
запись и пополнить счет.
При прохождения регистрации
этот человек должен ввести ваши данные
как реферала, чтобы Вам можно было получить вознаграждение.
Количество пришедших по рекомендации людей не лимитируется.
Казино всегда поощрительно относятся к новым
клиентам, которые собираются стать завсегдатаями в ближайшем будущем.
Бонус за преданность
Поощрительные бонусы – это еще вид подарков,
используемых в on-line-казино
1вин 1win зеркало рабочее на сегодня
Они напоминают достаточно распространенные схемы вознаграждений, которыми управляют известные магазины.
Таким образом casino награждает
своих постоянных клиентов (пользователей, которые
с завидной регулярностью заходят на ресурс и играют) привлекательными призами или наградами.
Такой сюрприз возможен в форме бесплатных
спинов, однако многие казино тоже предоставляют небольшие аксессуары, подарки или лотерейные
билеты.
Примечательно, что появится возможность испытать еще больше приятных эмоций за время нахождения на онлайн-платформах.
Бонусы для ВИП-клиентов
Казино в том числе готовят бонусы для игроков, которые регулярно
посещают портал казино и
вкладывают в игры крупные суммы денег.
Большая часть online-casino связываются с VIP-пользователями ,
чтобы разузнать об их интересах и присудить призы,
которые фактически отвечают
стилю заинтересованного игрока.
Это еще раз подтверждает, насколько рады
видеть клиентов онлайн-площадки.
Для ВИП-геймеров большинство online-cazino готовят
значительные материальные поощрения.
Необходимо всего лишь регулярно посещать любимое казино, наслаждаться всеми предоставляемыми преимуществами своего положения.
1XBET входит в число наиболее популярных в России букмекерских контор
по ставкам на спорт.
Площадка работает по лицензии Curacao в online-режиме.
Фирма, осуществляющая деятельность с 2007 г., насчитывает больше четырехсот тысяч постоянных клиентов.
На сегодня БК 1xbet входит в число флагманов
по спортивным ставкам.
Это можно назвать как показатель доверительности многочисленных пользователей, которые выбрали конкретно указанную БК.
Осталось понять особенности нахождения на онлайн сервисе 1xbet зеркало сейчас .
Порядок прохождения регистрации
Производить прогнозы имеет право
зарегистрированный пользователь (беттер).
Есть различные варианты подготовки аккаунта:
1. через соцсети, нужно всего лишь остановиться на соответствующем варианте;
2. по адресу электронной почты
независимо от сервиса;
3. по номеру сотового телефона,
на который будет прислано смс.
Пользователям https://tewiki.iiit.ac.in/index.php/%E0%B0%B5%E0%B0%BE%E0%B0%A1%E0%B1%81%E0%B0%95%E0%B0%B0%E0%B0%BF:JerrodOsman в личный аккаунт становится открытым сразу по окончании регистрации.
Беттер может ставить на разные события из мира спорта, участвовать
в акциях и бонусах, осуществлять вывод денег и др.
Вам понравится не безучастно наблюдать за матчем любимой команды, но и по возможности получать неплохие суммы денег.
Нужно всего лишь выбрать мероприятие, которое
пришлось по вкусу.
Как видите, после регистрации можно пользоваться многочисленными возможностями официального сайта, которые предоставили администраторы.
Виды прогнозов БК 1хбет https://www.ssyyy.cn/space-uid-4328.html
В отличие от подобных контор 1Хбет насчитывает 12 вариантов операций.
Одинарный прогноз (ординар, одиночник) – соглашение
на отдельный исход спортивного события.
Прибыль рассчитывается при умножении десятичного коэффициента на сумму пари.
Получается, что сложностей особых
нет, если выбор сделан на
этот вид прогноза.
Экспресс – ставка сразу на 2 и более результатов, которые анонсируются.
Экспресс «Стайер» отличается особенностью: исходы
и мероприятия разрешается добавлять в течение двух месяцев.
Антиэкспресс включает ряд итогов,
противоположный экспрессу по
методу определения выигрыша.
Этот вид прогноза выбирают как опытные игроки, так и новички.
Система – пари на полную комбинацию экспрессов определенной
размерности из выбранного числа мероприятий.
Цепочка – набор одиночных
ставок.
По доверительной ставке можно вернуть
долю финансов, которые находятся пока в истории.
Это довольно интересное предложение, которое могут выбрать зарегистрированные клиенты.
Ставка по купону определяет набор из цифр и
букв для подготовки запроса.
Таким образом можно осуществить ставку без
внесения денег на депозитный счет.
Лаки оказывается сочетанием ординаров и абсолютно всех экспрессов, собранных из указанных
спортивных событий.
Патент действует по тому же алгоритму,
что и лаки, но количество прогнозов ограничивается
тремя.
Для каких целей необходимо использовать зеркало
Букмекерская контора 1Хбет
не является легальной на территории РФ.
Подобное положение связано с тем,
что компания не удерживает проценты
с прибылей клиентов.
Для самих пользователей это существенный
плюс, но на законодательном уровне данный нюанс считается не самым целесообразным.
Разработчики не собираются ничего изменять в проводимой политике.
Как же быть в такой ситуации клиентам?
В действительности никаких сложностей нет.
Нужно избежать блокирование официального веб-ресурса,
а следовательно посетить актуальное зеркало портала.
Зеркало можно представить как особый сервис с точным отображением портала, без каких-либо сдерживающих факторов, с воссозданием прежде внесенных сведений.
Разрешается зайти и беспроблемно
пользоваться всеми условиями, предусмотренными создателями.
Такие зеркала используют общую с основным сайтом 1xbet
базу, поэтому войти на ресурс удобно под своей учетной записью.
Не забывайте, что дизайн идентичен подтвержденному
сайту букмекера.
Перейти на аналог можно по адресу
как вывести бонус с 1хбет.
Кроме ставок на спорт в 1хбет игрокам предлагают слоты, тотализаторы, разные лотереи, нарды, игровые процессы в online и
offline режимах.
Как видите, у букмекерской конторы оптимальное количество событий, которые могут оказаться по нраву пользователям самого разного возраста, пола.
Необходимо всего лишь пройти простую регистрацию уже сейчас.
Вы поймете, насколько увлекательно
удастся провести время, если есть персональный компьютер и подключение к интернету.
In India, the 1xBet betting comrades – is entire of the most
well-received ones in Asia. Aggregate its ranking advantages, equal can note acute odds, a
sympathetic ways procedure on presented events and legitimate stable payoffs.
In its functionality, the depict duplication is no unique from the biggest resource, providing users with all the yet capabilities.
1xBet betting gathering
1xbet app download http://www.sam.hi-ho.ne.jp/cgi-bin/user/t_fukuda/yybbs_u2.cgi?page=8230
1xbet app
Using the bearing as a replacement for Android, players can flutter on sports in tours, at off or at home.
All that is required – is access to the Internet. In sequence to institute the program, crack to the
“Applications on smartphones” portion, enter non-stationary phone
thousand in the opened form. In a insufficient minutes, an SMS missive with download link desire arrive.
1xbet apk 1xbet app India
1xbet apk
The 1xBet portable app since iOS can be downloaded
in the App Store. A direct download element is present on the betting body’s proper website
– mirror the station instruction.
Normal communication
With expropriate of our website there is an time to contemplate c get access to the
website about the clock, placing bets on events of interest.
The betting dais in India can be used not one from a PC, but also from most mobile devices.
Entitle
The 1xBet troop operates on the Internet legally.
To present services, the betting friends has a
permit issued by the cosmopolitan regulator of Curacao. It allows the
policy to exertion in many countries without violating law.
Review of the 1xBet valid Indian website
The betting platform offers visitors to venture on sports and monetary events.
Bettors also entertain access to online slit machines and a essential
casino. A athlete can gamble bread in any sections of the website using
a distinct account. The betting players has a satisfactory manner line
and bird small change line for all events. Users can bet in more than 40 sports types, ranging from hot football and tennis to imported cockfights.
The betting coterie accepts bets on approximately all
outcomes: not only on a victory or undoing of inseparable of teams, but also on a copy
of corner kicks, penalties and other results. Entire can inspect a less hard vitality crow’s-foot at the 1xBet betting retinue merely
ahead unsought after events. But even here song can bet on over/under, check and
some other outcomes. Players can quantify all the possibilities of moneyed betting no
greater than after creating an account.
Registration in the 1xБет India 1xbet apk download https://www.isaan.live/User:AlizaXpd13026491
Registration in the 1xБет India
Inseparable can activate a profile in the betting company in 4 ways:
via a hurried registration procedure. A entertainer needs to click
on the appropriate tab and single out the provinces of residence.
After a not many seconds, the drug discretion be confirmed a shibboleth and login, which
wish be created next to the method;
registration advance
by creating an account using phone. In this case, during registration methodology a
visitant must bespeak the alert phone slues onto which SMS point inclination appear with ornate instructions;
creating an account using phone
by registering via email. The exemplar choice, at which operator fills out of pocket registration contour, prescribing
dear observations and a valid e-mail. Later a communiqu‚ with a interdependence couple comes to the consumer’s specified e-mail, which becomes a pass to the 1xBet India website;
beside registering via venereal networks. The easiest way
to trigger an account. A sportswoman single needs to click on the
icon with the group network where he has a profile, after which an account is automatically generated.
1xbet login
1xbet login
Individual can put down the 1xBet website in the even so crumble as on the main 1xbet com resource.
It is adequately in the interest a consumer to exhibit in the procedure
in any convenient way, and then subscribe to near entering the essential watchword and login. In some cases, to penetrate intimate account, everybody may need
a particular code that the betting company sends
in the form of SMS essence onto a transportable phone number.
In case of problems with entering an account due to a forfeiture of a
countersign, the player will be able to into the issue quickly.
To do this, objective click on the “Forgot your password?” tab, writing down the email hail or phone handful next to it.
The owner drive be receive relevant poop to the specified contacts.
The password sent choose advise to log in to the account.
Depositing money
After partiality registration and authorizing on the website, user drive be adept
to provide full of funds in his individual account. To do this, fit to the “Payments” section. There,
the actress commitment see individual options on the side of depositing funds into the account:
bank delivery;
electronic wallets and payment systems;
payment toe the vdu = ‘visual display unit’;
spondulicks transfer from a animated phone;
Internet banking;
cryptocurrency
prepaid cards.
In all-out, the website of the betting coterie provides more than 40 options for depositing capital.
Regardless of the chosen method, economic transactions on the website are
carried completely instantly. The a particular important factor over the
extent of a player – is to conclude the rules established by the betting company.
In the course of instance, the replenishment amount should be no less than 100
rubles. In withal, it is strictly forbidden to abuse other people’s wallets and bank cards to part money.
Decay to agree with these conditions may lead to blocking
of the account.
Spinach withdrawal from the 1xbet in India 1xbet apk India
To take back funds to of the way it is necessary to use the same mode as with replenishment.
To create a financial acta, a jock needs to elapse to live account and
supreme the “Lolly withdrawal” section. There the buyer will exigency to
mention the amount to be transferred, and compose the text from his
electronic billfold or bank card. If all the data is correct, the devotion for funds withdrawal wish be
processed on the betting circle within 1-7 days.
In system to refrain from delays in payoffs of
earned winnings, players necessity to pass account
verification procedure 1xbet apk download .
During this originate in, the owner choice be required to state look after the 1xBet administration in India with copies of his identity documents.
Passed also nett verification transfer permit one cancel funds from the website far, at any convenient time.
It is well-connected for players to commemorate that the betting company has
introduce certain limits on well-heeled withdrawal.
In event of any problems with withdrawal of funds, bettors can in the
support advice for help. Support caduceus function at the website in every
direction the clock.
Bonuses from 1xBet
The betting assemblage offers visitors a solid bonus program.
Players can foresee to pick up the following types of bonuses:
“For the from the word go deposit.” The amount of the animation is 100% from the
deposited amount. The guerdon must be won go at three bets of the Speak order with a coefficient of
at least 1.4;
“Favoured Friday”. The largesse is issued to players strictly
on the specified day. The win past due conditions are the unvaried as
with the reward after the start with put;
“Wednesday – multiply by way of 2”. Cappers who won on the “Convenient Friday” are allowed
to participate in the action. If the purchaser has not until now withdrawn the funds won from the recent week,
his deposit is doubled by the betting company;
“Express of the day.” The over b draft is held daily.
If a player achieves achievement in the Dance or the Abide, he will receive an developing in the form of 10% of the earned winnings;
“Honorarium quest of a series of failures.” Purchaser profit go part of the gone by the board
change, upon up of 20 hapless bets in a series with a coefficient of not
more than 3.
Букмекерская контора Леон – заметный участник игорного бизнеса на отечественном рынке.
Эта организация позволяет клиентам
зарабатывать живую копейку не первый год.
За годы деятельности БК смогла заслужить немало
призов, однако наиболее заметной среди них
считается награда «Спорт и Россия».
Ее дают за особый вклад в популяризацию спорта
по регионам Российской Федерации.
Не вызывает удивления то,
что люди, обращающиеся в букмекерскую контору, не только ставят на спортивные события, а с увлечением следят за играми
известных и небольших команд.
Официальный портал приложение леон
http://www.dzzksd.com/home.php?mod=space&uid=76399&do=profile&from=space позиционируется как функциональный и
довольно удачный сервис.
Приятный интерфейс сайта и незначительное
количество рекламных окон не вызывают у
посетителей дискомфорта и вместе с тем стимулируют ставить на различные события.
Где еще получится испытать небывалый всплеск
адреналина?
Сервис предоставляет игрокам следующие возможности:
• ознакомиться с бонусной политикой, акциями, которые
предусмотрены администрацией;
• сделать ставку на игру в обычном режиме и
Live;
• посмотреть результаты завершившихся матчей;
• изучить правила и в дальнейшем строго
им следовать;
• связаться со службой техподдержки, которая работает круглосуточно;
• скачать приложение на
телефон или планшет, чтобы ставить в удобное время в местах,
где есть интернет.
Варианты ставок на спортивные события
Bookmaker предлагает клиенту широкий ассортимент спортивных событий.
• футбол;
• баскетбол;
• хоккей;
• волейбол;
• киберспортивные дисциплины;
• регби;
• боксерские поединки;
• cricket;
• теннис и т.д.
Кроме этого, получить реальные рубли получится:
• на автоматах;
• в casino;
• во время игры в покер.
Все мероприятия расписаны в отдельном разделе, поэтому найти их будет не сложно.
Пользователь получает возможность изучить
их немедленно после прохождения регистрации и пополнения игрового счета на любую сумму.
Это недолго ввести личные сведения в специальные ячейки на портале.
Важно не забывать про необходимую верификацию для подтверждения совершеннолетия.
Система бонусов
Разнообразие вложений – не последнее преимущество БК Леон.
Администраторы привлекают новых игроков еще и внушительным количеством бонусов.
Такие «подарки» идут на личный счет, тем
самым позволяя бережно расходовать реальные
финансы и стартовать с бонусных средств.
Компания дарит бонусные начисления после
прохождения регистрации, при внесении первого
депозита, в случае активной игры и
после каждого внесения денег на счет.
Как видите, продуманы все удобства не только для бывалых, но и для стартующих клиентов букмекерской сети.
Получится немедленно воспользоваться приветственным бонусом.
Особенности мобильного приложения леон бонусы
https://foro.programarg.com/member.php?action=profile&uid=142 клиенты могут не
только посредством компьютера.
Для комфорта играющих программеры предусмотрели
приложение для смартфона, что
позволяет быстро делать ставки.
Приложение имеет аналогичный официальному сайту интерфейс и гарантирует клиентам полноценный комфорт во
время игры.
При этом приложение доступно обладателям телефонов на любой ОС – как Андроид, так и iOS.
Вы обнаружите, насколько легко пользоваться приложением вне зависимости от того,
где Вы находитесь.
Достаточно всего лишь получить доступ к сети
интернет, помнить про регистрацию
и про последующую авторизацию.
Еще никогда ставить на различные аспекты, связанные с играми, не было так
легко.
БК ЛЕОН отличается своей программой
поощрений, выгодными призами
и понятным приложением для мобильных телефонов.
Эту компанию выбирают для себя граждане различных регионов Российской Федерации.
Разработчики предусмотрели,
чтобы деятельность конторы велась легально.
В наличии необходимые разрешения.
Букмекерская контора
не имеет недостатков, в связи с чем заслуживает внимания не
только новичков, но и игроков со стажем.
Дождаться сыгранной ставки и внести деньги
на личный счет сможет любой из прошедших регистрацию совершеннолетних пользователей.
Главное, бояться и поверить своему чутью.
Букмекерская контора Леон – это
выбор людей, ценящих личное время и деньги.
На online платформе действительно огромный выбор мероприятий, на которые предлагается сделать ставки.
Вы сможете не просто отслеживать успехи
любимой команды, но и, скорее всего, сорвать
немалый выигрыш.
Следует всего лишь зарегистрироваться на основном портале БК, чтобы суметь определить для себя
все предлагаемые разработчиками преимущества.
Понятный интерфейс удовлетворит даже начинающих игроков.
veste adidas satin bleu 1990
shoe dubbin or polish dr martensopel corsa c anh盲ngerkupplungdr reinhard salomonnorth face the borealis rucksack
nike cortez se metal
nike free rn flyknit 2018 wceinture homme le tanneurair jordan future premium on feetnike air jordan premium
Обзор Mostbet зеркала бк mostbet
https://m.liancaiweb.com/forum.php?mod=viewthread&tid=32299
Ниша ставок в России функционирует достаточно
давно, и в 2012 г. вышла на рынок фирма Mostbet.
На сегодняшний день ресурс активно развивается, в частности это касается
виртуального пространства.
Как полагают многие пользователи, довольно удобно не выходя из дома, в офисе или
в дороге ставить на события.
Потеря времени исключена.
Наиболее важная задача компании – помогать людям делать ставки, это
удобно выполнить , используя офисы компании или же в режиме
online, для чего есть портал и мобильная версия.
Как видите,, предоставляется довольно много способов, чтобы приятно провести свободное время,
а вместе с тем попытаться заработать приличные выигрыши.
Компания mostbet ставки довольно стремительно развивается и намерена подготовить для
своих клиентов самые лучшие возможности.
Тут каждый может ставить как на спорт, так и на
другие события, например, конкурсы типа Eurovision.
Больше не нужно просто наблюдать за тем, как проводит выступление любимый певец.
Стоит всего лишь начать верить в
его триумф, сделав выгодную ставку.
Есть шанс, что получится сорвать крупную сумму , а
заодно насладиться музыкальным произведением.
Такой подход крайне удобен,
так как в этой ситуации безусловно каждый человек сможет найти для себя интересные мероприятия и поставит на его исход.
Программеры предусмотрели события на все предпочтения.
Решение зависит от того, сколько
Вам лет, чем вы увлекаетесь и способны ли рисковать.
Как начать ставить на спорт с Mostbet
Многие игроки думают, что ставить
на спорт или иные события – это достаточно хлопотно и что в этом нужно долго разбираться.
Но так ли это на самом деле?
Естественно, нет.
Когда мы говорим о Мостбет http://dictaf.net/fitness/MOSTBET-STAVKI-mostbet-STAVKI-MOSTBET-STAVKI-NA–2/ mostbet скачать на телефон андроид , то
в этом случае начинать ставить сможет каждый.
Интуитивно понятный интерфейс
понравится даже начинающим
пользователям, которые надумали освоить искусство ставок.
Следует рассмотреть более
подробно, как начинать процесс.
Для старта вам нужно пройти регистрацию
на сайте.
Процесс прохождения регистрации удивительно легкий, займет у вас минимум времени.
Потребуется всего лишь вбить личные данные в специальные поля, пройти процесс верификации.
Как только вы зарегистрируетесь, надо будет
положить некоторую сумму на депозитный
счет.
Абсолютно неважно, какая именно будет зачислена сумма денег.
Совсем скоро Вы освоитесь и сможете понять, как поступать дальше, какие параметры взноса считаются оптимальными.
И с этого момента начинайте ставить на события.
Теперь стало ясно, что выполнять подобные манипуляции совсем несложно, потому что
этот процесс займет у вас минимум времени и
сил.
Таким образом, абсолютно любой
из игроков сумеет начать делать ставки вне зависимости от того
новичок он или профи.
Единственное, что для этого требуется – пройти регистрацию.
Контора Mostbet – одна из самых известных и востребованных площадок на рынке России,
что абсолютно не удивительно.
Ведь компания заботится о своих пользователях и подготавливает для них самые лучшие условия.
Разработчикам надо не просто заинтересовать больше пользователей,
а и создать максимально комфортные условия для постоянных клиентов.
Репутация является важным критерием для компании во имя
того, чтобы не потерять
доверия игроков.
В сфере ставок присутствует большое количество мошенников.
Не стоит слепо доверять яркой рекламе, а также идти на поводу у слишком выгодных условий.
Можно не только потерять деньги,
время, но и установить на компьютер вирус.
Уместнее останавливать выбор на надежных фирмах, которые
длительное время находятся в игровой отрасли.
Всегда можно почитать отзывы, узнать
о времени начала деятельности конторы в виртуальном пространстве.
Среди подобных профи своего дела
считается мостбет бонус при регистрации без депозита
В определенный момент несложно загрузить конкретно разработанное мобильное приложение.
Останется подсоединиться к сети Интернет, чтобы делать ставки уже сегодня.
У Вас будет возможность выбрать
событие, спрогнозировать результат,
находясь в пробке или за городом.
Это ли не одно из преимуществ, за которые следует останавливать
выбор на этой букмекерской конторе?
И это подтвердило огромное число клиентов конторы.
Вот почему, если вы хотите
испытывать удачу на ставках,
то вам стоит присмотреться к Mostbet.
Здесь Mostbet-partner.com вы сможете найти необходимые
сведения и ответы на свои вопросы,
а также немедленно начать делать ставки
после того, как зарегистрируетесь.
Bookmaker 1xbet in Italia http://xn--9rqw9pzsay9a679c.xn--kbto70f.com/forum.php?mod=viewthread&tid=24119
La societa di scommesse 1xBet Italia e una societa di origine russa.
La societa di scommesse fornisce i propri servizi ad utenti maggiorenni
di tutto il mondo. Il sito si trova sempre nelle posizioni di primo
piano per il numero di clienti e la qualita degli
eventi in linea. Il sito e famoso per il proprio supporto tecnico, che risponde in pochi minuti, nonche per i piacevoli perquisite sul primo deposito.
Storia di 1xbet Italia
L’organizzazione del gioco d’azzardo ha operato in tutto
il mondo per oltre 10 anni, ma solo nel 2015 e arrivata in Italia.
I giocatori italiani preferiscono proprio 1xbet a causa
dell’ampio investimento della societa di scommesse sui giocatori popolari del nostro paese.
Il sito ha guadagnato popolarita anche grazie al servizio 1xbetstreaming,
il quale permette di scommettere direttamente mentre si guarda l’evento.
La societa di scommesse aumenta ogni anno il
fatturato dei fondi e il numero di utenti attivi. Su questo influiscono
l’apertura del casino online aperto e le grandi
partnership con grandi club.
Chelsea, Liverpool e Barcellona non sono gli unici nella lista delle sponsorizzazioni della societa
di scommesse.
Licenza
Al momento, la societa di scommesse ha difficolta a causa del rinnovo della licenza,
ma nell’applicazione mobile su Android e iOS e ancora possibile scommettere.
Per questo gli scommettitori del Brasile e dei paesi vicini possono scommettere normalmente.
Al momento, la societa e in trattativa per rinnovare la licenza e continuare le attivita nel suo Paese.
Sistema remuneration 1xbet Italia
La societa di scommesse cerca di rafforzare la propria posizione nel mercato delle scommesse con ampie offerte
promozionali. Il extra di benvenuto soddisfa i nuovi arrivati e consente di aumentare il primo deposito della meta,
fino a 100 euro. Le condizioni di basis per ricevere il regalo sono le
seguenti:
• e necessario versare almeno 1 euro sul conto;
• e necessario scommettere 5 volte l’importo versato per ricevere
il regalo;
• le scommesse devono essere espresse da 3 eventi o piu;
• il coefficiente di ogni partita deve essere superiore a 1,40;
• e necessario recuperare il totale entro 30 giorni dalla ricezione del bonus.
Bonus aggiuntivi dal sito
I giocatori possono ricevere altri regali, wake up l’introduzione
di codici promozionali speciali al casino o alle scommesse.
Ci sono codici simili durante eventi sportivi su larga scala.
Nel corso di un grande evento, nel 2018, la societa ha offerto a tutti di ottenere
10 euro, che potevano essere giocati senza il rischio di perdere.
La linea di partite 1xbet al giorno supera
i 1000 eventi.https://www.teamsfusat.wiki/User:ScottyGxg54
La compagnia di scommesse 1xBet riempie costantemente la propria linea con partite ed eventi interessanti.
In media, ogni giorno ci sono piu di 1000 eventi per le
scommesse.
L’amministrazione cerca di provoke l’opportunita di scommettere non solitary sulle partite popolari,
ma anche sugli eventi regionali in Portogallo, in modo che tutti possano scommettere a
loro piacimento.
Settle iniziare a scommettere su 1xbet Italia?
Casinò 1xbet
Iniziare a scommettere su 1xbet Italia e molto semplice.
Occorre trovare il sito ufficiale su Google e registrarsi.
Ogni utente maggiorenne puo creare un profilo. Questo puo
essere fatto in 4 modi:
low cut tops no bra
leather and fur jacket womensbirkenstock lace up bootsvivienne westwood mens shirtslipsy vip
Registro em 1XBET Portugal https://ww88ap.com/forum/viewtopic.php?id=60667
Digite o codigo promocional
REGISTE-SE E RECEBA UM BONUS DE 100 EUR AGORA MESMO!
Convidamos todos quem quer ganhar nas apostas em desportos
registrar-se rapidamente em uma casa de apostas mais justa
da empresa 1XBet.
O registro em 1XBET Portugal permite usar de todas as
funcionalidades do position oficial, incluindo:
retirada de fundos rapida atraves de qualquer sistema de pagamentos ou cartoes bancarias;
servico de apoio a cliente conveniente que sempre ajudara esclarecer a
situacao;
interface e aplicacoes moveis funcionais.
O tip da 1XBET Portugal download da 1xbet para android
A casa de apostas, a todos que desejam receber os honorarium agradaveis
na sua conta, da essa oportunidade. E uma oportunidade actual de ganhar dinheiro gracas a generosidade da administracao da empresa.
O owner sempre cycle o remuneration de primeiro deposito.
O bonus e um adicional de 100% do valor do deposito
de ate 130 euros, que serao imediatamente creditados na conta.
O mais agradavel e a possibilidade de devolver o dinheiro recebido nas apostas
ordinarias e expressas.
A condicao principal e que tem que escolher as partidas com coeficiente bastante alto, das quais e necessario formar um expresso completo.
Para um novato recuperar aposta nao e uma tarefa facil, mas isso permite conhecer bem a interface da
empresa de azar e aprender o basico de apostas.
Como usar o codigo de promocao da 1xBet? https://screenplay.press/index.php?topic=83.0
Usar o codigo de promocao e muito facil, pois a administracao permite fazer isso sem a participacao
do servico de apoio a cliente. Basta de seguir uma instrucao intuitivamente clara:
Primeira coisa que tem que fazer e ir para o portal oficial de jogos
com o nosso link e clicar em “Registrar-se” no canto superior direito.
A seguir, tem que selecionar um dos metodos de criacao da conta pessoal e inserir o
codigo de promocao recebido, que tambem se encontra neste site.
Apos preencher todos os dados, e necessario enviar um pedido e receber a conta ativada durante de um dia.
Os usuarios nao devem esquecer da necessidade de
confirmar o e-mail atraves de uma mensagem recebida.
Todos os dados indicados durante registro devem ser
verificados cuidadosamente e so podem ser verdadeiros, pois caso
contrario, depois da verificacao por administracao a conta pode ser bloqueada.
O que oferece a casa de apostas 1XBET Registro em 1XBET Portugal
O registro na 1XBET Portugal permite a cada jogador apreciar um jogo de apostas em desporto divertido e excitado.
Tudo que e necessario e ter uma conta registrada e ser um residente de Portugal maior da idade.
E obrigatorio passar uma verificacao completa
que da o acesso para gerenciamento das contas.
A empresa oferece a todos os jogadores registrados as seguintes vantagens:
uma enorme variedade de partidas e eventos politicos em quais pode apostar com
um praticamente sem limites.
Apenas administracao pode limitar o montante maximo de aposta, entretanto os coeficientes sao colocados independentemente do nivel da partida;
varias maneiras de deposito e retirada de fundos que permite carregar a sua conta de jogo sem algum problema e receber o seu ganho no cartao bancario ou um sistema de pagamentos;
servico de apoio a cliente operativo que responde todas
as perguntas de usuarios e ajuda resolver qualquer situacao 24
horas por dia.
Um requisito obrigatorio para obtencao de todos os privilegios acima indicados e bonus adicionais
e preencher todos os dados na secao “Minha conta” que se encontra na conta pessoal.
suresiyle kullan?labiliyor. 1xbet mobil versiyon
• Kredi Kart?
Visa kartlar?n?z ile 10 TL, Main Card ile 15 TL alt limitle sediment yapabilirsiniz.
King-fish Card sahibiyseniz 5 TL uzeri tutarlar? cekebilirsiniz.
• WebMoney
WebMoney yontemini kullan?yorsan?z 3 TL alt limitle keep, 5 TL ve uzeri tutarlarla
da cekim talebi verebilirsiniz.
• EcoPayz
Least 3 TL ile yat?r?m, maksimum 5 TL ile cekim yapabilirsiniz.
• AstroPay
3 TL ve uzeri tutarlar? yat?rabiliyorken 5 TL ve uzerindeki tutarlar
icinde cekim talebi verebilirsiniz.
• Paykasa
Kulland?g?n?z odeme yontemi Paykasa ise 3 TL alt limitin uzerindeki
tum tutarlar? an?nda yat?rabilirsiniz. Cekim talebi icin lowest islem tutar?
5 TL’dir.
• PayKwik
Yaln?zca stash away islemleri icin 3 TL alt limitle kullan?labilmektedir.
1xbet Honorarium ve Promosyonlar? https://wikilights.org/index.php?title=User:KristianOuthwait
Her yeni bahis slice gibi Turkler icinde bonuslar en onemli k?s?md?r.
1xbet bahis sitesi de bunu en iyi sekilde sunmaktad?r.
• Hos Geldin Bonusu
Uyeliginizi act?ktan hemen sonra yapacag?n?z ilk lees islemine sunulan bonustur.
En fazla 300 TL’ye kadar yararlanabileceginiz bu promosyondan %100
oran?nda yararlanabilirsiniz.
• PromoCode Bonusu
• Trade mark mailgram Bonusu
• Y?ld?z Jackpot Promosyonu
• Bahis Kuponlar? Savas? Turnuvas?
• 1xRace Bonusu
• Dogum Gunu Bonusu
1xbet Musteri Hizmetleri
1xbet canl? destek hizmeti sunuyor ancak bunun haricinde de
cok ilginc bir dan?smanl?k hizmeti veriyor.
Her bahis sitesinde gordugumuz mesaj yoluyla ulas?m, correspondence yordam?yla adresinden iletisim
mumkun. Bunlar?n haricinde ise yurt ici servis numaras?yla musterilerine telefon destegi
sunuyor.
1xbet Guvenilir Mi?
Bahis oynatma lisans?n? Curacao uzerinden alm?s olan 1xbet Meagre sirketi Turkiye’nin koklu platformlar?
aras?nda bulunuyor. Lisans?n?n haricinde de GoDaddy taraf?ndan saglanm?s olan SSL sertifikas?n?n aktif oldugunu gorebiliyoruz.
1xbet Genel Degerlendirme 1xbet mobil versiyon
1xbet guncel giris adresi ise 1x-turkey.com olarak guncellendi.
Bahis dunyas?nda ayr?cal?kl? bir bahis yelpazesini bir araya getiren sirketin gerek bonuslar?yla, gerek an?nda
odeme yontemleriyle gerekse guvenilirligiyle dikkat cekmeye devam ettigini soyleyebiliriz.
OLIMP https://www.freeads-southampton.co.uk/user/profile/8641 входит в число наиболее популярных в России букмекерских компаний по ставкам на
спортивные события.
Площадка функционирует по лицензии Curacao в режиме онлайн.
Компания, работающая с 2007
г., насчитывает больше 400 тысяч постоянных клиентов.
На сегодняшний день БК OLIMP входит в число
флагманов по спортивным ставкам.
Это и есть показатель
доверительности армии пользователей,
которые выбрали конкретно данную БК.
Осталось понять особенности нахождения на онлайн платформе.
Правила прохождения регистрации
Производить прогнозы может только прошедший регистрацию клиент (беттер).
Есть разные способы создания
профиля:
1. через соцсети, потребуется всего лишь
остановиться на соответствующем варианте;
2. по э-мейл вне зависимости
от сервиса;
3. по телефонному номеру, на
который будет отправлено смс.
Игрокам бк олимп зеркало сайта работающее в личный кабинет
станет открытым немедленно после регистрации.
Зарегистрированный клиент получает право делать
ставки на выбранные события из мира спорта, принимать участие в акционных
и бонусных программах, выводить средства и др.
Вы сможете не просто следить за матчем выбранного состава
игроков, но и при желании получать
неплохие денежные суммы.
Для этого надо всего лишь указать мероприятие,
которое понравилось больше всего.
Как видите, после регистрации разрешается воспользоваться многочисленными возможностями основного ресурса,
которые предусмотрели администраторы.
Виды прогнозов конторы Олимп
Олимп в отличие от других БК
насчитывает двенадцать типов операций.
Одинарный прогноз (одиночник, единица) – сделка на определенный результат спортивного мероприятия.
Прибыль насчитывается умножением коэффициента в десятичном формате на сумму пари.
То есть нет ничего сложного,
если выбор сделан на этот вид ставки.
Экспресс – прогноз одновременно на 2 и больше
результатов, которые должны пройти.
Экспресс «Стайер» имеет особенность:
результаты и мероприятия можно добавлять
в течение двух месяцев.
Антиэкспресс содержит ряд исходов, обратный экспрессу
по методу начисления выигрыша.
Этот вид ставки выбирают как со стажем игроки, так и
новички.
Система – сделка на полную комбинацию
экспрессов конкретной размерности из указанного
числа событий.
Цепочка – комплект одинарных ставок.
По доверительной ставке удастся получить
часть средств, которые находятся пока в истории.
Это довольно привлекательное предложение, которое могут выбрать зарегистрированные пользователи.
Ставка по промокоду определяет комбинацию из цифр
и букв для подготовки заявки.
Этим способом можно сделать ставку без внесения денег на депозитный счет.
Лаки является комбинированием ординаров и совершенно всех экспрессов,
которые собраны из выбранных спортивных мероприятий.
Патент имеет такой же принцип, что и лаки, но количество прогнозов ограничивается 3-мя.
Для чего нужно заходить на зеркало бк олимп бонус при регистрации
Букмекерская контора Олимп
считается нелегальной на территории РФ.
Подобное положение связано с тем,
что компания не удерживает налоги с выигрышей клиентов.
Непосредственно для клиентов это существенный плюс,
но на законодательном уровне данный нюанс считается не
самым уместным.
Разработчики не намерены ничего менять в своей
политике.
Как же быть в такой ситуации пользователям?
На самом деле никаких сложностей нет.
Следует избежать блокировку основного веб-ресурса, а следовательно зайти на функционирующее зеркало портала.
Зеркало представляет собой специальный сервис с точным интерфейсом
портала, без каких бы то ни было ограничений,
с воссозданием ранее введенных сведений.
Можно войти и спокойно пользоваться всеми условиями,
предусмотренными разработчиками.
Такие копии имеют единую с официальным сайтом OLIMP базу,
поэтому войти на ресурс удобно
под своим аккаунтом.
Помните, что дизайн аналогичен подтвержденному
сайту букмекера.
Переместиться на аналог можно по
ссылке http://118.24.181.53/home.php?mod=space&uid=552548&do=profile&from=space
Кроме прогнозов на спортивные турниры в Олимп пользователям предлагают тотализаторы, слоты, разные лотереи, нарды,
игровые процессы в онлайн и офлайн режимах.
Как видите, у БК оптимальное
число событий, которые могут оказаться по
вкусу пользователям разных возрастов,
пола.
Необходимо всего лишь пройти простую регистрацию прямо сейчас.
Вы сможете обнаружить, насколько увлекательно
удастся провести досуг, имея персональный компьютер и доступ
к интернету.
Обзор Melbet зеркала
Рынок ставок в РФ существует довольно долгое время, и в 2012 г.
на рынке появилась компания Melbet.
Вплоть до сегодняшнего дня ресурс активно развивается,
непосредственно это касается виртуального пространства.
Как думают некоторые клиенты, достаточно комфортно не выходя из дома,
в офисе или в дороге ставить на события.
Потеря времени исключена.
Основная задача компании – помогать
игрокам ставить, это можно выполнить через офисы фирмы или же в режиме online, для чего есть портал и мобильная
версия.
Как видите,, предоставляется
довольно много способов, чтобы приятно
провести досуг, а заодно попробовать заработать неплохие
деньги.
Компания melbet скрин баланса довольно стремительно продвигается и намерена
подготовить для своих пользователей самые лучшие условия.
Здесь каждый может ставить как на спортивные, так и на другие мероприятия,
например, турниры типа Евровидения.
Больше не нужно безучастно смотреть за тем, как
проводит выступление любимый исполнитель.
Стоит всего лишь поверить в его победу,
сделав оптимальную ставку.
Существует вероятность, что удастся заполучить куш и при
этом насладиться музыкальным произведением.
Это очень удобно, так как в этом
случае безусловно любой игрок найдет для себя интересные
мероприятия и поставит на его исход.
Программеры предусмотрели мероприятия на любой вкус.
Все зависит от Вашего возраста,
увлечений, а также желания рисковать.
С чего начинать делать
ставки на спорт с Melbet https://wiki.avora15.org/index.php/Utilisateur:MeaganTorrance9
Некоторые игроки думают, что делать ставки на спортивные баталии или иные
мероприятия – это довольно хлопотно и что в алгоритме нужно тратить время на разбирательство.
Действительно ли это так
и будет?
Естественно, нет.
Когда мы говорим о Мелбет, то в этом случае начать делать ставки сможет каждый.
На уровне интуиции понятный интерфейс придется по душе даже новичкам, которые только
решили освоить искусство ставок.
Рассмотрим подробнее, как начинать процесс.
Для старта вам нужно зарегистрироваться на сайте мелбет баланс
Процесс прохождения регистрации удивительно легкий, займет у
вас минимальное количество времени.
Потребуется всего лишь ввести персональные данные в специальные ячейки, верифицироваться.
Как только вы зарегистрируетесь, необходимо внести некоторую сумму на депозитный счет.
Абсолютно не играет роли, какая по размеру
будет зачислена сумма денег.
Совсем скоро Вы освоитесь и поймете,
каким образом поступать дальше, какие размеры взноса являются
наиболее приемлемыми.
И с этого момента вы можете начать делать ставки.
Теперь становится понятно, что делать это совершенно не сложно, потому что на эти действия уйдет у вас минимум сил и времени.
Таким образом, абсолютно каждый сможет начать ставить независимо от того новичок он или профи.
Все, что для этого нужно – пройти регистрацию.
Контора Melbet – входит в число популярных и пользующихся
спросом компаний на российском рынке, что совсем не вызывает удивления.
Как известно, контора с заботой относится к своим клиентам и
предлагает для них самые лучшие условия.
Руководству надо не просто заинтересовать новых игроков, а и подготовить
максимально удачные условия для завсегдатаев.
Репутация является важным показателем для
конторы во имя того, чтобы не снизить доверия
игроков.
В сфере ставок существует большое количество мошенников.
Не следует слепо доверять
яркой рекламе, а также идти на поводу у слишком выгодных условий.
Возможно не только лишиться денег, безрассудно потерять
время, но и заполучить на компьютер вирусную программу.
Целесообразнее выбирать лишь проверенные компании, которые продолжительное время находятся в
данной области.
В любой момент можно изучить отзывы, ознакомиться с временем появления компании в виртуальном пространстве.
Среди подобных профи ведения игрового
бизнеса считается https://helpus.ai/forum/index.php?action=profile;u=56487 .
При желании можно загрузить специально разработанное мобильное приложение.
Останется подсоединиться к интернету, чтобы делать ставки уже сегодня.
Вы даже сможете выбрать событие, сделать прогноз, находясь
в пробке или за городом.
Не это ли и есть одно из достоинств, за которые следует выбирать данную компанию?
И это подтвердило огромное число клиентов компании.
Вот почему, если вы решили испытывать удачу на ставках, то вам стоит
присмотреться к Мелбет.
Тут melbet-partner.com вы найдете необходимую информацию и
ответы на свои вопросы, а , кроме того, сразу начать делать ставки после того, как
зарегистрируетесь.
u path run shoes adidas
膷izme za ki拧uwhere to learn mop potsc a 30 popusta namuske i zenske jakne i kapute suboticanike jordan white
Букмекерская контора Леон –
заметный представитель отрасли азартных
игр на российском рынке.
Эта организация дает возможность людям зарабатывать реальные деньги не первый год.
За годы работы БК получила довольно много вознаграждений,
но наиболее заметной среди них является премия «Спорт и Россия».
Ее дают за выдающиеся вложения в развитие спортивных игр на территории
РФ.
Неудивительно, что клиенты, которые
обращаются в букмекерскую контору,
не просто делают ставки, а с увлечением следят за играми известных
и небольших команд.
Официально подтвержденный
портал бк леон на андроид
http://gamesieunhan.net/forum/profile.php?id=27303 представляет
собой стабильно функционирующий
и довольно удачный ресурс.
Привлекательная архитектура сайта и незначительное число окошек под рекламу не вызывают у посетителей дискомфорта и при этом мотивируют
на новые ставки.
В каком месте еще удастся испытать невероятный взрыв
эмоций?
Сайт предоставляет игрокам возможность:
• узнать больше об акциях, бонусах, предусмотренными администрацией;
• поставить деньги на игру в обычном режиме
и Live;
• посмотреть итоги прошедших событий;
• изучить особенности пользования сервисом и впоследствии неукоснительно им следовать;
• обратиться в службу техподдержки, которая работает круглосуточно;
• загрузить программное приложение на телефон или планшет, чтобы ставить в удобное время в зонах,
где есть сеть.
Ставки на спорт
Букмекер предлагает клиенту богатый выбор
спортивных событий.
• футбольные матчи;
• баскетбольные первенства;
• хоккей;
• соревнования по волейболу;
• киберспортивные дисциплины;
• rugby;
• боксерские поединки;
• крикет;
• теннис и т.д.
Кроме этого, получить реальные деньги получится:
• на слотах;
• в casino;
• в покере.
Предстоящие мероприятия представлены в отдельном разделе, это значит, что отыскать их не составит труда.
Клиент будет иметь возможность изучить их сразу по окончании регистрации и пополнения игрового счета на любую сумму.
Это недолго ввести персональные данные в отведенные ячейки на портале.
Не стоит забывать про обязательную верификацию
для доказательства совершеннолетия.
Бонусная система
Богатый выбор ставок – не последнее достоинство БК Леон.
Администраторы способствуют заходу новичков еще и внушительным количеством бонусов.
Подобные сюрпризы идут на личный счет,
тем самым позволяя бережно
расходовать живые деньги и начинать делать ставки с бонусной суммы.
Контора предоставляет бонусы при регистрации, при внесении
первого депозита, при стабильной активности игрока и после каждого внесения денег на счет.
Видно, что продуманы все удобства
не только для бывалых, но и для
стартующих пользователей букмекерской системы.
Получится немедленно воспользоваться приветственным бонусом.
Мобильная версия букмекерское приложение леон
https://www.fbnewspost.com/index.php?action=profile;u=17550 пользователи
имеют право не только посредством компьютера.
Для комфорта игроков разработчики предусмотрели
мобильную версию, что позволяет быстро делать
ставки.
Приложение имеет идентичный официальному сайту интерфейс и обеспечивает клиентам
максимум удобств во время игры.
При этом приложение доступно обладателям
смартфонов на любой ОС – как Android, так и иос.
Вы убедитесь, как удобно использовать приложение вне зависимости от Вашего местоположения.
Достаточно всего лишь подключиться к сети интернет, помнить про регистрацию
и про последующую авторизацию.
Еще никогда сделать ставки на различные
события, сопряженные с играми, не было
так просто.
Букмекерская контора ЛЕОН отличается своей программой поощрений, привлекательными призами и
удобным мобильным приложением.
Эту компанию предпочитают граждане разных регионов Российской Федерации.
Руководители предусмотрели, чтобы деятельность конторы велась на законных основаниях.
В наличии все лицензионные документы.
Букмекерская компания не имеет недостатков, в связи с чем заслуживает внимания не только новеньких,
но и игроков со стажем.
Провести время в ожидании сыгранной ставки и внести деньги на свой счет
сможет любой из прошедших регистрацию совершеннолетних
клиентов.
Важно, исключить страх и поверить собственной интуиции.
Букмекерская контора Леон – это предпочтение людей, ценящих личное время и деньги.
На онлайн платформе действительно большой ассортимент событий, на которые можно ставить.
Вам удастся не просто отслеживать успехи любимой команды, но и, скорее всего, получить немалый выигрыш.
Следует всего лишь пройти регистрацию на
официальном портале конторы, чтобы суметь оценить все предлагаемые основателями преимущества.
Понятный интерфейс оценят даже начинающие пользователи.
l谩bnyom kulcstart贸
銉撱兗銈点兂 閫氳博 銉儑銈c兗銈?/a>銉忋兗銉堝瀷 銉愩儍銈?銉栥儵銉炽儔绲愬 寮?鏈嶈 鍜岃銉戙兂銈广儓銈掑饱銇勩仧濂崇銇曘伨銇ㄣ儧銉嗐儷銇ex 瓒呮鍏冦偛銈ゃ儬 銉嶃儣銉嗐儱銉笺儗
Обзор зеркала Melbet
Рынок ставок в РФ существует достаточно давно, и в 2012 г.
вышла на рынок компания Мелбет.
На сегодняшний день сервис активно продолжает развиваться, в частности это относится к виртуальному пространству.
Как полагают многие пользователи, довольно удобно никуда не
выходить, а ставить на события.
Потеря времени исключена.
Основная цель конторы – оказывать помощь людям ставить, это
удобно сделать , используя офисы фирмы или же в режиме онлайн, для чего имеется портал и мобильная версия.
Итак, предоставляется довольно много
способов, чтобы с удовольствием провести
досуг, а вместе с тем попытаться получить приличные суммы.
Компания скачать melbet на андроид бесплатно довольно активно продвигается и старается подготовить для своих
клиентов самые лучшие возможности.
Тут каждый может делать ставки как на спортивные,
так и на иные события, например, конкурсы наподобие
Евровидения.
Больше не нужно просто смотреть за тем, как выступает обожаемый певец.
Достаточно начать верить в
его триумф, произведя оптимальную ставку.
Существует вероятность, что удастся
заполучить крупную сумму и при этом насладиться музыкальным
произведением.
Это очень удобно, так как в этом случае безусловно каждый человек найдет для себя захватывающие мероприятия и сделает ставки.
Программеры предусмотрели события на все предпочтения.
Все зависит от того, сколько Вам лет,
чем вы увлекаетесь и способны ли рисковать.
С чего начинать делать ставки на спорт с Melbet https://screenplay.press/index.php?topic=85.0
Многие игроки думают, что ставить на спортивные баталии или другие мероприятия – это довольно
сложно и что в этом нужно
тратить время на разбирательство.
Но так ли это на самом деле?
Конечно же, нет.
Когда мы говорим о Melbet, то здесь начать
делать ставки сможет каждый.
На уровне интуиции понятный интерфейс придется по душе даже новичкам,
которые только решили освоить искусство ставок.
Следует рассмотреть подробнее, как начать это делать.
Для начала необходимо пройти регистрацию на портале промокод мелбет фрибет
Алгоритм прохождения регистрации очень
легкий, вы потратите на него минимум времени.
Потребуется всего лишь ввести личные сведения в выделенные ячейки, верифицироваться.
Как только вы зарегистрируетесь, следует положить деньги на
депозитный счет.
При этом не играет роли, какая именно будет зачислена
сумма денег.
Очень быстро Вы освоитесь и
поймете, как действовать дальше,
какие параметры ставки являются оптимальными.
И после этого начинайте делать ставки.
Теперь становится понятно, что выполнять подобные манипуляции можно без особого труда, потому что на
эти действия уйдет у вас минимальное количество сил и времени.
Выходит, абсолютно любой из игроков сможет начать делать ставки независимо от того без
опыта он или профи.
Единственное, что для этого нужно –
зарегистрироваться.
Контора Melbet – одна из самых популярных и востребованных компаний на рынке России, что совсем не удивительно.
Ведь компания заботится о своих пользователях и предлагает для них наилучшие условия.
Разработчикам важно не просто заинтересовать новых игроков,
но и создать максимально удачные условия для завсегдатаев.
Репутация является значимым показателем для
компании во имя того, чтобы не снизить доверия пользователей.
В области ставок существует большое число мошенников.
Не стоит соблазняться привлекательной рекламой, а также идти на поводу у слишком выгодных
условий.
Возможно не только потерять деньги, время, но и установить на ноутбук
вирус.
Уместнее останавливать выбор на надежных фирмах,
которые длительное время пребывают в данной отрасли.
В любой момент можно почитать отклики, узнать о времени
появления компании в виртуальном пространстве.
Одним из подобных профи ведения игрового бизнеса считается https://iranrgt.com/index.php/topic,93318.0.html .
При желании несложно скачать
конкретно разработанное приложение для смартфонов и других гаджетов.
Останется подсоединиться к сети Интернет, чтобы ставить прямо сейчас.
У Вас будет возможность выбрать мероприятие, сделать прогноз, находясь в заторе или
на даче.
Не это ли и есть одно из преимуществ, за которые стоит останавливать
выбор на этой букмекерской конторе?
И это подтвердило огромнейшее количество клиентов компании.
Поэтому, если вы решили начать делать ставки,
то вам следует присмотреться к Melbet.
Тут melbet-partner.com вы сможете найти необходимую информацию
и ответы на свои вопросы, а также немедленно приступить к ставкам после регистрации.
suresiyle kullan?labiliyor. Android için 1xbet’i indirin
• Kredi Kart?
Visa kartlar?n?z ile 10 TL, Manager Calling-card
ile 15 TL alt limitle deposit yapabilirsiniz. Principal Playing-card sahibiyseniz 5 TL uzeri tutarlar?
cekebilirsiniz.
• WebMoney
WebMoney yontemini kullan?yorsan?z 3 TL alt limitle lodge, 5 TL ve
uzeri tutarlarla da cekim talebi verebilirsiniz.
• EcoPayz
Least 3 TL ile yat?r?m, maksimum 5 TL ile cekim yapabilirsiniz.
• AstroPay
3 TL ve uzeri tutarlar? yat?rabiliyorken 5 TL ve uzerindeki tutarlar icinde cekim talebi verebilirsiniz.
• Paykasa
Kulland?g?n?z odeme yontemi Paykasa ise 3 TL alt limitin uzerindeki tum tutarlar?
an?nda yat?rabilirsiniz. Cekim talebi icin lowest
islem tutar? 5 TL’dir.
• PayKwik
Yaln?zca leave islemleri icin 3 TL alt limitle kullan?labilmektedir.
1xbet Reward ve Promosyonlar? https://physioexrx.com/index.php/T%C3%BCrkiye_de_1xbet_Bahis_%C5%9Firketi_1xbet_Uygulama_1xbet_Mobil_Versiyon_Android_I%C3%A7in_1xbet_i_Indirin_1xbet_Bahis_Bonuslar_1xbet_T%C3%BCrkiye
Her yeni bahis stop gibi Turkler icinde bonuslar en onemli k?s?md?r.
1xbet bahis sitesi de bunu en iyi sekilde sunmaktad?r.
• Hos Geldin Bonusu
Uyeliginizi act?ktan hemen sonra yapacag?n?z ilk deposit islemine
sunulan bonustur. En fazla 300 TL’ye kadar yararlanabileceginiz bu
promosyondan %100 oran?nda yararlanabilirsiniz.
• PromoCode Bonusu
• Trade mark mailgram Bonusu
• Y?ld?z Jackpot Promosyonu
• Bahis Kuponlar? Savas? Turnuvas?
• 1xRace Bonusu
• Dogum Gunu Bonusu
1xbet Musteri Hizmetleri
1xbet canl? destek hizmeti sunuyor ancak bunun haricinde de cok ilginc bir dan?smanl?k hizmeti
veriyor. Her bahis sitesinde gordugumuz mesaj yoluyla ulas?m, post yordam?yla
adresinden iletisim mumkun. Bunlar?n haricinde ise yurt ici
servis numaras?yla musterilerine telefon destegi sunuyor.
1xbet Guvenilir Mi?
Bahis oynatma lisans?n? Curacao uzerinden alm?s olan 1xbet
Meagre sirketi Turkiye’nin koklu platformlar? aras?nda bulunuyor.
Lisans?n?n haricinde de GoDaddy taraf?ndan saglanm?s olan SSL sertifikas?n?n aktif oldugunu gorebiliyoruz.
1xbet Genel Degerlendirme Bonuslar 1xbet Türkiye
1xbet guncel giris adresi ise 1x-turkey.com olarak
guncellendi. Bahis dunyas?nda ayr?cal?kl? bir bahis yelpazesini bir araya getiren sirketin gerek bonuslar?yla, gerek an?nda
odeme yontemleriyle gerekse guvenilirligiyle dikkat cekmeye devam ettigini
soyleyebiliriz.
1XBET входит в число самых популярных в России букмекерских контор
по ставкам на спортивные события.
Площадка функционирует на основе лицензии Curacao в
online-режиме.
Фирма, осуществляющая деятельность с 2007
г., обслуживает больше 400 тысяч постоянных посетителей.
На сегодняшний день букмекерская
контора 1xbet в числе мировых лидеров
по спортпрогнозам.
Это можно назвать как показатель доверительности армии
клиентов, которые выбрали именно указанную БК.
Теперь надо разобраться в особенностях нахождения на online сервисе как вывести бонус обыграй 1xbet .
Порядок прохождения регистрации
Делать ставки имеет право зарегистрированный пользователь (беттер).
Есть различные варианты подготовки аккаунта:
1. через соцсети, нужно всего лишь остановиться на соответствующем варианте;
2. по адресу электронной почты независимо от сервиса;
3. по телефонному номеру, на который придет смс.
Пользователям http://employmentodisha.com/index.php?page=user&action=pub_profile&id=11236 в личный кабинет станет открытым немедленно после регистрации.
Зарегистрированный клиент получает право ставить на разные спортивные турниры,
участвовать в акционных и бонусных программах, выводить средства и т.д.
Вы сможете не безучастно наблюдать за матчем любимой команды, но и по возможности получать неплохие суммы денег.
Для этого надо всего лишь выбрать событие,
которое пришлось по вкусу.
Как видите, после регистрации можно воспользоваться многочисленными возможностями основного сайта, которые предусмотрели
администраторы.
Виды прогнозов БК 1хбет http://energomontag.com/user/profile/720212
1Хбет в отличие от других БК насчитывает 12 вариантов сделок.
Одиночная ставка (ординар, одиночник) –
соглашение на определенный исход спортивного события.
Прибыль насчитывается умножением десятичного коэффициента на количество поставленных денег.
То есть сложностей особых нет, если выбор сделан на этот вид прогноза.
Экспресс – прогноз одновременно на
два и больше результатов, которые должны пройти.
Экспресс «Стайер» отличается особенностью: результаты и события можно дописывать на
протяжении 2-х месяцев.
Антиэкспресс включает несколько итогов, обратный экспрессу по способу определения
выигрыша.
Такой вид ставки выбирают как опытные игроки,
так и новички.
Система – пари на полную комбинацию экспрессов определенной
размерности из выбранного числа событий.
Цепочка – набор одиночных прогнозов.
По ставке доверительного типа удастся получить долю средств, находящихся пока в истории.
Это довольно интересное предложение, которое могут выбрать прошедшие регистрацию пользователи.
Прогноз по промокоду выдает комбинацию из цифр и букв
для оформления заявки.
Этим способом удобно сделать ставку без внесения денег
на депозит.
Лаки является сочетанием единиц и абсолютно всех экспрессов,
которые собраны из указанных
спортивных событий.
Патент имеет такой же принцип, что и лаки,
но количество прогнозов
ограничено 3-мя.
Для чего нужно использовать зеркало
Букмекерская контора 1Хбет считается нелегальной на территории РФ.
Подобное положение сопряжено с тем,
что фирма не взимает проценты с прибылей игроков.
Непосредственно для клиентов это существенный плюс, но в рамках закона названный момент признается
далеко не уместным.
Разработчики не намерены ничего менять в проводимой политике.
Как же быть в такой ситуации
пользователям?
В действительности никаких сложностей
нет.
Следует обойти блокирование
основного веб-сайта, а следовательно зайти на функционирующее зеркало площадки.
Аналог представляет собой специальный сервис с идентичным интерфейсом портала, без
каких-либо ограничений, с сохранением ранее внесенных данных.
Можно войти и беспроблемно пользоваться имеющимися возможностями,
предложенными разработчиками.
Данные зеркала имеют общую с официальным
сайтом 1xbet БД, поэтому войти на сайт
удобно под своей учетной записью.
Помните, что дизайн аналогичен подтвержденному сервису букмекера.
Перейти на аналог можно по ссылке 1xbet мобильная версия на сегодня.
Кроме ставок на спорт в 1хбет игрокам предлагают слоты, тотализаторы, разные лотереи, нарды, игры
в онлайн и офлайн режимах.
Можно сделать вывод, что у букмекерской конторы оптимальное число
событий, которые придутся по нраву клиетнам самого разного возраста, пола.
Необходимо всего лишь зарегистрироваться по несложному алгоритму прямо сейчас.
Вы сможете обнаружить, насколько увлекательно удастся провести досуг, если есть персональный компьютер и
доступ к сети Интернет.
Registro em 1XBET Portugal https://wiki.eg-team.de/index.php?title=Registro_Em_1XBET_Portugal_O_Que_Oferece_A_Casa_De_Apostas_1XBET_download_Da_1xbet_Para_Android_Faezr_O_Download_Da_1xbet_Para_Iphone
Digite o codigo promocional
REGISTE-SE E RECEBA UM BONUS DE 100 EUR AGORA MESMO!
Convidamos todos quem quer ganhar nas apostas em desportos registrar-se rapidamente em uma casa de apostas mais justa da empresa 1XBet.
O registro em 1XBET Portugal permite usar de todas as funcionalidades do milieu oficial, incluindo:
retirada de fundos rapida atraves de qualquer sistema de
pagamentos ou cartoes bancarias;
servico de apoio a cliente conveniente que sempre ajudara esclarecer a
situacao;
interface e aplicacoes moveis funcionais.
O tip da 1XBET Portugal Faezr o download da 1xbet para iphone
A casa de apostas, a todos que desejam receber os compensation agradaveis na
sua conta, da essa oportunidade. E uma oportunidade
genuine de ganhar dinheiro gracas a generosidade da administracao da
empresa.
O investment sempre cycle o perk de primeiro deposito.
O perquisite e um adicional de 100% do valor do deposito de ate 130 euros, que serao imediatamente creditados na
conta.
O mais agradavel e a possibilidade de devolver o dinheiro recebido nas apostas ordinarias e expressas.
A condicao chairman e que tem que escolher as partidas com coeficiente bastante alto, das quais e necessario formar
um expresso completo.
Para um novato recuperar aposta nao e uma tarefa facil, mas isso permite conhecer bem a interface da empresa de azar
e aprender o basico de apostas.
Como usar o codigo de promocao da 1xBet? http://enlcy.com/home.php?mod=space&uid=61490&do=profile
Usar o codigo de promocao e muito facil, pois a
administracao permite fazer isso sem a participacao do servico de apoio a
cliente. Basta de seguir uma instrucao intuitivamente clara:
Primeira coisa que tem que fazer e ir para o portal oficial de jogos com o
nosso relationship e clicar em “Registrar-se” no canto select direito.
A seguir, tem que selecionar um dos metodos de criacao da conta pessoal e inserir o codigo de promocao recebido, que tambem se
encontra neste site.
Apos preencher todos os dados, e necessario enviar um pedido e receber
a conta ativada durante de um dia.
Os usuarios nao devem esquecer da necessidade de confirmar o e-mail atraves de uma mensagem recebida.
Todos os dados indicados durante registro devem ser
verificados cuidadosamente e so podem ser verdadeiros, pois caso contrario, depois da
verificacao por administracao a conta pode ser bloqueada.
O que oferece a casa de apostas 1XBET O que oferece a casa de apostas 1XBET
O registro na 1XBET Portugal permite a cada jogador apreciar
um jogo de apostas em desporto divertido e excitado.
Tudo que e necessario e ter uma conta registrada e ser um residente
de Portugal maior da idade. E obrigatorio passar uma verificacao completa que da o acesso para
gerenciamento das contas.
A empresa oferece a todos os jogadores registrados as seguintes vantagens:
uma enorme variedade de partidas e eventos politicos em quais pode apostar
com um praticamente sem limites.
Apenas administracao pode limitar o montante maximo de aposta, entretanto
os coeficientes sao colocados independentemente
do nivel da partida;
varias maneiras de deposito e retirada de fundos que permite
carregar a sua conta de jogo sem algum problema e receber o seu ganho no cartao bancario ou um sistema de pagamentos;
servico de apoio a cliente operativo que responde todas as perguntas de usuarios e ajuda resolver qualquer situacao 24 horas por dia.
Um requisito obrigatorio para obtencao de todos os privilegios acima indicados e bonus adicionais e preencher
todos os dados na secao “Minha conta” que se encontra na
conta pessoal.
suresiyle kullan?labiliyor. Türkiye’de 1xbet bahis şirketi
• Kredi Kart?
Visa kartlar?n?z ile 10 TL, Manager Christmas card ile 15 TL
alt limitle set yapabilirsiniz. Master Business card sahibiyseniz 5 TL uzeri tutarlar?
cekebilirsiniz.
• WebMoney
WebMoney yontemini kullan?yorsan?z 3 TL alt limitle consign, 5 TL ve
uzeri tutarlarla da cekim talebi verebilirsiniz.
• EcoPayz
Minimum 3 TL ile yat?r?m, maksimum 5 TL ile cekim yapabilirsiniz.
• AstroPay
3 TL ve uzeri tutarlar? yat?rabiliyorken 5 TL ve uzerindeki
tutarlar icinde cekim talebi verebilirsiniz.
• Paykasa
Kulland?g?n?z odeme yontemi Paykasa ise 3 TL alt limitin uzerindeki
tum tutarlar? an?nda yat?rabilirsiniz. Cekim talebi icin minimum islem
tutar? 5 TL’dir.
• PayKwik
Yaln?zca leave islemleri icin 3 TL alt limitle kullan?labilmektedir.
1xbet Honorarium ve Promosyonlar? http://supportwakefield.com/index.php/T%C3%BCrkiye_de_1xbet_Bahis_%C5%9Firketi_1xbet_Uygulama_1xbet_Mobil_Versiyon_Android_I%C3%A7in_1xbet_i_Indirin_1xbet_Bahis_Bonuslar_1xbet_T%C3%BCrkiye
Her yeni bahis cut off gibi Turkler icinde bonuslar
en onemli k?s?md?r. 1xbet bahis sitesi de bunu en iyi sekilde sunmaktad?r.
• Hos Geldin Bonusu
Uyeliginizi act?ktan hemen sonra yapacag?n?z ilk lay islemine sunulan bonustur.
En fazla 300 TL’ye kadar yararlanabileceginiz bu promosyondan %100
oran?nda yararlanabilirsiniz.
• PromoCode Bonusu
• In france bleu Bonusu
• Y?ld?z Jackpot Promosyonu
• Bahis Kuponlar? Savas? Turnuvas?
• 1xRace Bonusu
• Dogum Gunu Bonusu
1xbet Musteri Hizmetleri
1xbet canl? destek hizmeti sunuyor ancak bunun haricinde de cok ilginc bir dan?smanl?k hizmeti veriyor.
Her bahis sitesinde gordugumuz mesaj yoluyla ulas?m, mail yordam?yla
adresinden iletisim mumkun. Bunlar?n haricinde ise yurt ici servis
numaras?yla musterilerine telefon destegi sunuyor.
1xbet Guvenilir Mi?
Bahis oynatma lisans?n? Curacao uzerinden alm?s olan 1xbet Little
sirketi Turkiye’nin koklu platformlar? aras?nda
bulunuyor. Lisans?n?n haricinde de GoDaddy taraf?ndan saglanm?s olan SSL sertifikas?n?n aktif oldugunu gorebiliyoruz.
1xbet Genel Degerlendirme 1xbet mobil versiyon
1xbet guncel giris adresi ise 1x-turkey.com olarak guncellendi.
Bahis dunyas?nda ayr?cal?kl? bir bahis yelpazesini bir araya getiren sirketin gerek bonuslar?yla, gerek an?nda odeme yontemleriyle gerekse guvenilirligiyle dikkat cekmeye devam
ettigini soyleyebiliriz.
Описание зеркала Melbet
Рынок ставок в РФ функционирует
достаточно долгое время, и в 2012 г.
вышла на рынок компания Melbet.
На сегодняшний день сервис стабильно продолжает
развиваться, непосредственно это касается виртуального пространства.
Как полагают некоторые клиенты, достаточно комфортно никуда
не выходить, а делать ставки.
Никаких потерь времени.
Наиболее важная задача компании –
помогать людям ставить, это можно сделать через
офисы компании или же в режиме
онлайн, для чего имеется сайт и приложение для смартфона.
Итак, предусмотрено немало способов, чтобы приятно провести досуг, а заодно попытаться получить приличные деньги.
Контора как зайти на сайт зеркало мелбет
довольно активно продвигается и намерена создать для своих клиентов наилучшие возможности.
Здесь каждый может делать ставки как на спортивные, так и на
другие события, к примеру, турниры наподобие Eurovision.
Больше не нужно безучастно наблюдать за тем,
как выступает обожаемый исполнитель.
Стоит всего лишь поверить в его
победу, сделав выгодную ставку.
Существует шанс, что удастся сорвать
куш и при этом послушать
отличную музыку.
Это очень удобно, так как в этой ситуации безусловно любой игрок найдет для себя интересные мероприятия и поставит
на его исход.
Программеры смогли предусмореть мероприятия на все предпочтения.
Все связано с Вашим возрастом, увлечениями,
желанием и возможностью идти на риск.
Как начинать ставить на спорт с Мелбет https://xn—-7sbbecd2ene8ac.xn--p1ai/user/profile/99605
Некоторые игроки уверены, что ставить
на спортивные баталии или другие
события – это достаточно сложно и что в
этом потребуется тратить время на
разбирательство.
Но так ли это на самом деле?
Естественно, нет.
Если идет разговор о Мелбет, то здесь начать делать ставки
получится у любого желающего.
Интуитивно легко осваиваемый интерфейс понравится даже
начинающим пользователям, которые только решили разобраться с тем, как ставить.
Следует рассмотреть подробнее, как начать
это делать.
Для старта необходимо пройти регистрацию на портале melbet букмекерская контора
Алгоритм прохождения регистрации очень простой,
займет у вас минимум времени.
Нужно всего лишь вбить персональные данные в специальные ячейки, пройти процесс верификации.
После регистрации надо будет положить некоторую
сумму на депозитный счет.
При этом не играет роли, какая именно
будет внесена сумма денег.
Очень быстро Вы разберетесь и сможете понять, как поступать дальше,
какие размеры взноса являются
оптимальными.
И после этого вы можете начать делать
ставки.
Сейчас становится понятно,
что выполнять подобные манипуляции можно без особого труда, потому
что этот процесс займет у вас минимум сил и времени.
Таким образом, абсолютно каждый
сумеет начать ставить независимо от того без опыта он или профессионал.
Единственное, что для этого требуется – пройти регистрацию.
Контора Melbet – одна из самых популярных
и востребованных компаний на российском рынке, что
абсолютно не удивительно.
Ведь контора заботится о своих пользователях и предлагает для них наилучшие условия.
Разработчикам надо не просто привлечь новых игроков, но
и подготовить наиболее комфортные обстоятельства для завсегдатаев.
Имидж является значимым показателем для компании во имя того, чтобы
не потерять веры игроков.
В сфере ставок присутствует немалое число мошенников.
Не следует слепо доверять яркой рекламе, а также идти на поводу
у слишком выгодных условий.
Можно не только потерять деньги, время,
но и заполучить на ноутбук вирус.
Уместнее выбирать лишь проверенные компании,
которые длительное время находятся в игровой отрасли.
Всегда можно почитать отклики, ознакомиться с временем начала деятельности компании в виртуальном
пространстве.
Одним из таких профессионалов ведения игрового бизнеса признается http://fitnesstypes.com/story.php?title=melbet-BUKMEKERSKAYA-KONTORA-MELBET-BUKMEKERSKAYA- .
При желании несложно скачать специально разработанное
мобильное приложение.
Нужно получить доступ к интернету,
чтобы делать ставки с сегодняшнего дня.
Вы даже сможете подобрать событие,
сделать прогноз, пребывая в пробке или в офисе.
Это ли не одно из преимуществ, за которые следует останавливать выбор
на этой букмекерской конторе?
И это подтверждает огромное число пользователей конторы.
Вот почему, если вы хотите начать делать ставки, то вам стоит обратить внимание
на Melbet.
Здесь melbet-partner.com вы сможете найти необходимую информацию и
ответы на свои вопросы, а , кроме того, немедленно начать делать ставки после того, как зарегистрируетесь.
1XBET – одна из наиболее востребованных в России букмекерских контор по прогнозам на
спорт.
Сервис функционирует на основе лицензии Кюрасао в online-режиме.
Компания, осуществляющая деятельность с 2007 года, обслуживает свыше
400 тыс. постоянных посетителей.
На сегодня букмекерская контора 1xbet
входит в число мировых лидеров по спортпрогнозам.
Это и есть критерий доверительности многочисленных пользователей, которые
решили выбрать именно указанную БК.
Осталось разобраться в особенностях пребывания на online площадке
1xbet ставки на спорт .
Правила прохождения регистрации
Делать прогнозы может только зарегистрированный клиент (беттер).
Есть различные варианты создания аккаунта:
1. через соцсети, нужно всего лишь выбрать соответствующий вариант;
2. по адресу электронной
почты независимо от сервиса;
3. по телефонному номеру, на
который будет прислано смс.
Игрокам http://fault.ybeamdulltnderwearertwe.S.e@projectag.net/cgi/tawabbs/yybbs.cgi?room=room1 в личный аккаунт становится открытым немедленно по окончании регистрации.
Беттер получает право делать ставки на разные
события из мира спорта, принимать участие в акционных и бонусных программах, осуществлять вывод денег и др.
Вам понравится не просто следить за игрой
выбранного состава игроков, но
и при желании выигрывать неплохие суммы денег.
Нужно всего лишь указать мероприятие, которое пришлось
по вкусу.
Как видите, по окончании регистрации
можно пользоваться многочисленными возможностями официального сайта, которые
предоставили администраторы.
Разновидности прогнозов БК 1хбет https://ww88ap.com/forum/profile.php?id=6080
В отличие от подобных контор 1Хбет
насчитывает двенадцать типов сделок.
Одиночная ставка (одиночник,
единица) – соглашение на определенный результат спортивного мероприятия.
Выигрыш насчитывается умножением коэффициента в десятичном формате на количество поставленных
денег.
Получается, что сложностей особых нет, если выбирать
этот вид ставки.
Экспресс – прогноз сразу на два и более исходов, которые анонсируются.
Экспресс «Стайер» отличается особенностью: исходы и мероприятия
можно дописывать на протяжении двух месяцев.
Антиэкспресс включает ряд итогов, обратный экспрессу
по способу начисления выигрыша.
Такой тип ставки признают как опытные игроки, так и новички.
Система – пари на все возможные варианты
экспрессов конкретной размерности из указанного
количества событий.
Цепочка – набор одинарных прогнозов.
По ставке доверительного типа удастся получить долю средств,
находящихся пока под блокировкой.
Это достаточно привлекательное
предложение, которое выбирают зарегистрированные клиенты.
Ставка по промокоду определяет комбинацию из букв и
цифр для подготовки запроса.
Таким образом можно сделать ставку
, не внося средства на депозит.
Лаки является сочетанием единиц и абсолютно всех экспрессов, собранных из указанных спортивных
мероприятий.
Патент имеет такой же принцип,
что и лаки, но число событий ограничено тремя.
Для каких целей необходимо заходить на зеркало
Букмекерская контора 1Хбет считается
нелегальной в регионах России.
Подобное положение связано с
тем, что компания не взимает проценты с прибылей клиентов.
Непосредственно для клиентов это существенный
плюс, но в рамках закона данный нюанс признается
не самым целесообразным.
Руководители не намерены ничего изменять в проводимой политике.
Что же делать в этом случае пользователям?
На самом деле нет ничего проще.
Следует избежать блокировку основного веб-ресурса, то есть зайти на
функционирующее зеркало портала.
Копия представляет собой особый ресурс с идентичным отображением сайта, без
каких бы то ни было сдерживающих факторов,
с сохранением ранее внесенных данных.
Разрешается войти и беспроблемно воспользоваться всеми возможностями,
предложенными создателями.
Такие копии используют единую с официальным вебсайтом
1xbet базу, поэтому войти на сайт удобно под своим аккаунтом.
Помните, что интерфейс идентичен подтвержденному сервису
букмекера.
Перейти на зекрало можно по адресу ставки 1xbet зеркало.
Кроме прогнозов на спортивные турниры в 1хбет игрокам доступны слоты,
тотализаторы, различные лотереи, нарды,
игровые процессы в онлайн и offline
режимах.
Можно сделать вывод, что у БК оптимальное число
мероприятий, которые придутся по
вкусу пользователям разных возрастов, пола.
Необходимо всего лишь зарегистрироваться по несложному алгоритму
уже сейчас.
Вы сможете обнаружить, как интересно получится провести досуг,
имея ноутбук и доступ к сети Интернет.
Описание Melbet зеркала
Рынок ставок в РФ функционирует довольно
давно, и в 2012 году вышла на рынок компания Melbet.
Вплоть до сегодняшнего дня сервис стабильно
продолжает развиваться, в частности
это относится к виртуальному пространству.
Как думают некоторые пользователи, достаточно удобно не
выходя из дома, в офисе или в дороге делать ставки.
Потеря времени исключена.
Главная задача конторы – оказывать помощь игрокам
ставить, это удобно выполнить , используя
офисы фирмы или же в режиме online, для
этого есть портал и приложение для смартфона.
Как видите,, предусмотрено довольно много возможностей, чтобы
с удовольствием провести свободное время,
а вместе с тем попробовать
получить приличные выигрыши.
Контора melbet вывод денег довольно активно продвигается и старается
подготовить для своих пользователей самые лучшие возможности.
Тут каждый может ставить
как на спорт, так и на иные события, к примеру, турниры наподобие Евровидения.
Теперь не нужно просто смотреть за тем, как проводит выступление обожаемый артист.
Достаточно начать верить в его триумф,
произведя выгодную ставку.
Есть вероятность, что получится сорвать крупную сумму ,
а заодно послушать отличную музыку.
Такой подход крайне удобен, так как в этом случае абсолютно любой человек сможет найти для себя захватывающие события и поставит на его исход.
Программеры смогли предусмореть
мероприятия на любой вкус.
Все зависит от того, сколько Вам лет, чем
вы увлекаетесь и способны ли рисковать.
Как начать ставить на спорт
с Мелбет https://medinsult.ru/forum/index.php?action=profile;u=36131
Многие клиенты уверены, что делать ставки
на спортивные баталии или другие мероприятия – это достаточно сложно и что в этом нужно тратить время на разбирательство.
Действительно ли это так и будет?
Естественно, нет.
Когда мы говорим о Мелбет, то в
этом случае начинать ставить сможет каждый.
На уровне интуиции легко осваиваемый интерфейс придется по вкусу даже
новичкам, которые надумали освоить искусство ставок.
Следует рассмотреть подробнее, как
начинать процесс.
Для начала вам нужно зарегистрироваться на
сайте скачать melbet на андроид
Алгоритм прохождения регистрации удивительно простой,
вы потратите на него минимум времени.
Потребуется всего лишь вбить личные
сведения в выделенные поля, верифицироваться.
Как только вы зарегистрируетесь, необходимо внести деньги на депозитный счет.
Абсолютно не играет роли, какая
по размеру будет зачислена сумма денег.
Совсем скоро Вы разберетесь и сможете понять, как действовать дальше,
какие параметры взноса считаются наиболее
приемлемыми.
И после этого вы можете начать ставить на события.
Сейчас стало понятно, что выполнять подобные манипуляции можно без особого труда, потому что этот
процесс займет у вас минимальное количество времени и сил.
Таким образом, абсолютно каждый сможет начать ставить
вне зависимости от того новичок он или профи.
Единственное, что для этого нужно – пройти
регистрацию.
Контора Мелбет – входит в число известных и пользующихся спросом площадок на российском рынке, что совсем не вызывает удивления.
Как известно, фирма заботится
о своих пользователях и подготавливает для них самые лучшие условия.
Руководству надо не просто привлечь больше
пользователей, но и создать максимально удачные условия для постоянных клиентов.
Репутация считается важным критерием для компании во имя того, чтобы не потерять веры игроков.
В области ставок присутствует немалое число аферистов.
Не стоит соблазняться привлекательной рекламой, а также бездумно
верить чрезмерно заманчивым предложениям.
Можно не только потерять деньги,
время, но и установить на компьютер
вирус.
Уместнее выбирать лишь проверенные компании, которые долгий период находятся в данной сфере.
В любой момент можно почитать отзывы, ознакомиться
с временем появления компании на просторах интернета.
Одним из подобных профи своего дела считается http://www.hisen.hmti.ac.by/mediawiki/index.php/User:RoryGoldberg .
В определенный момент несложно
скачать специально созданное
мобильное приложение.
Останется подсоединиться к интернету, чтобы
ставить прямо сейчас.
Вы даже сможете выбрать событие, сделать
прогноз, находясь в заторе или в офисе.
Не это ли и есть одно из достоинств, за которые следует останавливать выбор на этой букмекерской конторе?
Именно это подтвердило огромное количество клиентов конторы.
Вот почему, если вы хотите испытывать удачу на
ставках, то вам следует обратить внимание
на Melbet.
Тут melbet-partner.com вы найдете необходимые
сведения и решения своих вопросов, а , кроме того, немедленно приступить
к ставкам после того, как зарегистрируетесь.
OLIMP http://47.110.4.243/home.php?mod=space&uid=4399&do=profile&from=space входит
в число самых популярных в России букмекерских контор по
прогнозам на спортивные события.
Сервис функционирует по лицензии Кюрасао
в online-режиме.
Компания, работающая с 2007 года,
обслуживает свыше четырехсот тыс.
постоянных посетителей.
На сегодняшний день букмекерская контора OLIMP в числе мировых лидеров по спортивным ставкам.
Это и есть показатель доверительности
многочисленных пользователей, которые выбрали именно
данную БК.
Осталось понять особенности нахождения
на онлайн платформе.
Правила прохождения регистрации
Делать ставки может только
зарегистрированный пользователь
(беттер).
Есть различные способы подготовки профиля:
1. через социальные сети, нужно всего лишь выбрать соответствующий вариант;
2. по э-мейл независимо от платформы;
3. по телефонному номеру, на который будет отправлено смс.
Игрокам промокод бк олимп 2020 в персональный аккаунт станет доступным
немедленно по окончании регистрации.
Зарегистрированный клиент может
ставить на разные спортивные турниры, участвовать в акционных и бонусных
программах, осуществлять вывод денег и др.
Вам понравится не просто наблюдать за игрой любимой команды, но и по возможности получать немалые суммы денег.
Для этого надо всего лишь указать событие, которое пришлось по вкусу.
Как видите, после регистрации можно
пользоваться множеством
возможностей официального ресурса, которые предоставили разработчики.
Виды прогнозов БК Олимп
Олимп в отличие от других БК насчитывает двенадцать типов операций.
Одинарный прогноз (одиночник, единица) – соглашение на определенный результат спортивного события.
Выигрыш насчитывается умножением
коэффициента в десятичном формате на сумму пари.
То есть сложностей особых нет, если выбирать
этот вид прогноза.
Экспресс – прогноз сразу на 2 и больше результатов, которые должны пройти.
Экспресс «Стайер» имеет особенность: результаты и мероприятия можно добавлять в течение двух месяцев.
Антиэкспресс включает ряд итогов, противоположный экспрессу
по способу определения выигрыша.
Этот вид ставки выбирают как
со стажем игроки, так и новички.
Система – пари на полную комбинацию экспрессов конкретной размерности из выбранного числа
событий.
Цепочка – комплект одиночных прогнозов.
По ставке доверительного типа можно вернуть часть финансов, находящихся пока в истории.
Это достаточно интересное предложение, которое выбирают прошедшие регистрацию клиенты.
Прогноз по промокоду определяет комбинацию из
цифр и букв для оформления заявки.
Таким образом можно осуществить ставку , не
внося средства на депозит.
Лаки является сочетанием единиц и совершенно всех экспрессов, собранных из выбранных спортивных событий.
Патент имеет такой же принцип, что и
лаки, но количество событий ограничивается тремя.
Для чего нужно заходить на зеркало бк олимп кз
БК Олимп не является легальной в регионах России.
Это связано с тем, что контора не удерживает проценты с выигрышей клиентов.
Непосредственно для клиентов это существенный плюс, но в рамках закона
данный момент считается
не самым целесообразным.
Руководители не намерены ничего менять в проводимой политике.
Что же делать в этом случае клиентам?
На самом деле никаких сложностей нет.
Нужно избежать блокировку основного веб-сайта, то есть посетить актуальное
зеркало площадки.
Зеркало представляет собой специальный ресурс с идентичным интерфейсом сайта, без каких бы то ни было сдерживающих факторов, с сохранением ранее введенных данных.
Можно зайти и беспроблемно воспользоваться всеми возможностями, предложенными разработчиками.
Такие зеркала используют общую с официальным вебсайтом OLIMP БД,
поэтому зайти на сайт удобно под своей учетной записью.
Помните, что интерфейс идентичен подтвержденному
сайту букмекера.
Перейти на зекрало получится по ссылке http://dreamsknights.peacefully.jp/yybbs/yybbs.cgi
Кроме ставок на спортивные турниры в Олимп
игрокам предлагают тотализаторы,
слоты, разные лотереи, нарды,
игровые процессы в online и offline режимах.
Как видите, у БК достаточное число мероприятий, которые придутся по вкусу пользователям разных возрастов, пола.
Нужно всего лишь зарегистрироваться по несложному алгоритму прямо сегодня.
Вы сможете обнаружить, как интересно получится провести время, если есть ноутбук и доступ к интернету.
Everyone loves what you guys arе usually uup too.
Thiѕ type оf clever woгk and coverage! Kеep uⲣ the
great workѕ guyys I’ve aadded yoᥙ guys tօ our
blogroll.
Mʏ web ⲣage – mexican porn
magbificent ρoints altogether, ʏou simply received a
emblem neᴡ reader. Ꮤhat may yοu recommend about yoᥙr pot that yⲟu maԀe some days
ago? Any positive?
Мү site; pokimane porn
銉戙兂 銉曘儷銉笺儓 鐎埜
賲賱丕亘爻 丕胤賮丕賱 亘賳丕鬲 賱賱毓賷丿 2010丕爻丕賵乇 亘賵賱丕乇 a300賳馗丕乇丕鬲 賲丕乇賰 賰乇賵爻丨賯賷亘丞 鬲丿乇賷亘賷 毓賳 丕賱丕賱賯丕亍 賵丕賱禺胤丕亘賴
Магазины Apple в Ростове-на-Дону с низкими ценами airpods ростов
Цена – основной мера выбора чтобы большинства потребителей.
Помощь с официальными дилерами американского производителя
– залог минимального ценника.
В то же эра стоит смекать, что разные дилеры могут устанавливать приманка собственные наценки, следовательно
имеет значение сравнить цена интересующей модели вмиг в нескольких торговых точках.
Одинокий из онлайн магазинов,
какой предлагает ассортимент продукции Apple
по хорошим ценам
Подозрительно низких цен всегда
же лучше избегать. Под видом дешевого iPhone недобросовестные поставщики могут продать
вам подделку из Китая. Для месте оригинального телефона
может оказаться бывший в
эксплуатации смартфон, либо
техника, которую вернули сообразно гарантии,
либо смартфон с неисправностями, либо потрепанный витринный
экземпляр.
Магазины с официальной гарантией в Ростове-на-Дону http://www5f.biglobe.ne.jp/~ueda/yybbs/yybbs.cgi?list=thread
Сообразно понятным причинам рекомендуется выбирать всего те магазины, которые поставляют сертифицированную продукцию,
технику Apple с соответствующими гарантиями
оригинальности, в заводской упаковке.
Подтвердить высокое цвет лабаз повинен документами, а не один для словах.
Как принцип, любой правительственный дилер непременно предложит гарантию
для частный товар, займется гарантийным и пост-гарантийным
обслуживанием iPhone, iPad, Apple Keep one’s eyes peeled и других
девайсов Apple. Когда у магазина есть особенный сервисный фокус,
ровно тогда, это весомое преимущество.
Магазины с комфортным обслуживанием
Низкие цены и залог оригинальности – это, несомненно,
хорошо, но далече не все, сколько может предложить лабаз техники Apple в Ростове-на-Дону.
К дополнительным услугам,
которые делают толстый лабаз лучшим в
своем сегменте, позволительно отнести полноценную консультационную поддержку потребителя, включая помощь в активации, настройке устройства, переносе данных с одного iPhone
для другой, услуга в регистрации учетных записей и
беспричинно далее. Наличие собственной служжбы
оперативной доставки заказов по городу
тоже довольно лишним поводом выбрать именно сей магазин.
Также разительно неплохо, ежели
лавка предлагает беспредельный запас аксессуаров чтобы смартфонов.
Таким образом, вы можете собрать толстый
ассортимент для комфортного использования всякий модели iPhone
в одном месте, и уже вследствие
несколько минут потом оплаты начать использовать именно тем девайсом, какой подходит
вам во всех отношениях. Подробную информацию о расширенном каталоге аксессуаров чтобы iPhone в Ростове-на-Дону
вы можете получить по ссылке
– iphone в ростове
Combination of resistances|electric current|class12th|physics
by Nayan jha negarapoker dominoqq login http://www.cutieqs.com/link?url=https://foro.unionfansub.com%2Fmember.php%3Faction%3Dprofile%26uid%3D145678/ | negarapoker situs dominoqq terpercaya
windbreaker bmw z3
stan smith la redouteveste en jean pull and bearbrave soul bomber 脿 carreaux avec col en sherparobe pull jaune fluo
2019.11.17: 容错,高可用和灾备 标题里面的三个术语,很容易混淆,专业人员有时也会用错 https://www.1390.com.tw/?d=www.thann.com.tw/sitemap/page-9
Bookmaker 1xbet in Italia https://old.netherwiki.org/view/User:SammyC3300
La societa di scommesse 1xBet Italia e una societa di
origine russa. La societa di scommesse fornisce i propri
servizi ad utenti maggiorenni di tutto il mondo.
Il sito si trova sempre nelle posizioni di primo piano per il numero di clienti e la qualita degli eventi in linea.
Il sito e famoso per il proprio supporto tecnico, che risponde in pochi minuti, nonche per i piacevoli gratuity sul primo deposito.
Storia di 1xbet Italia
L’organizzazione del gioco d’azzardo ha operato in tutto il mondo per oltre 10 anni, ma alone nel 2015
e arrivata in Italia. I giocatori italiani preferiscono proprio 1xbet a causa dell’ampio investimento della societa di scommesse sui giocatori popolari del
nostro paese.
Il sito ha guadagnato popolarita anche grazie al servizio 1xbetstreaming, il quale permette di scommettere direttamente mentre
si guarda l’evento.
La societa di scommesse aumenta ogni anno il fatturato dei fondi e il numero di utenti attivi.
Su questo influiscono l’apertura del casino online aperto e le grandi partnership con grandi club.
Chelsea, Liverpool e Barcellona non sono gli unici nella lista delle sponsorizzazioni della
societa di scommesse.
Licenza
Al momento, la societa di scommesse ha difficolta a causa del rinnovo della licenza, ma nell’applicazione expressive su Android e iOS e ancora
possibile scommettere. Per questo gli scommettitori del Brasile e dei paesi vicini
possono scommettere normalmente. Al momento, la societa e in trattativa per rinnovare la
licenza e continuare le attivita nel suo Paese.
Sistema hand-out 1xbet Italia
La societa di scommesse cerca di rafforzare la propria posizione
nel mercato delle scommesse con ampie offerte promozionali.
Il extra di benvenuto soddisfa i nuovi arrivati e consente di aumentare il primo deposito della
meta, fino a 100 euro. Le condizioni di base per ricevere il regalo sono le seguenti:
• e necessario versare almeno 1 euro sul conto;
• e necessario scommettere 5 volte l’importo versato per ricevere il regalo;
• le scommesse devono essere espresse da 3 eventi o piu;
• il coefficiente di ogni partita deve essere superiore a 1,
40;
• e necessario recuperare il totale entro 30 giorni dalla
ricezione del bonus.
Remuneration aggiuntivi dal sito
I giocatori possono ricevere altri regali, come l’introduzione
di codici promozionali speciali al casino o alle scommesse.
Ci sono codici simili durante eventi sportivi su
larga scala. Nel corso di un grande evento,
nel 2018, la societa ha offerto a tutti di ottenere 10 euro,
che potevano essere giocati senza il rischio di perdere.
La linea di partite 1xbet al giorno supera i 1000 eventi.http://f.r.a.g.Ra.nc.E.rnmn@www18.tok2.com/home/Reckless/cgi-bin/fan/fantasy.cgi/contact.php
La compagnia di scommesse 1xBet riempie costantemente la propria linea con partite ed eventi interessanti.
In media, ogni giorno ci sono piu di 1000 eventi
per le scommesse.
L’amministrazione cerca di make bold l’opportunita di scommettere non unaccompanied sulle
partite popolari, ma anche sugli eventi regionali in Portogallo, in modo
che tutti possano scommettere a loro piacimento.
Come iniziare a scommettere su 1xbet Italia? Storia di 1xbet Italia
Iniziare a scommettere su 1xbet Italia e molto semplice.
Occorre trovare il sito ufficiale su Google e
registrarsi. Ogni utente maggiorenne puo creare un profilo.
Questo puo essere fatto in 4 modi:
suresiyle kullan?labiliyor. Türkiye’de 1xbet bahis şirketi
• Kredi Kart?
Visa kartlar?n?z ile 10 TL, Main Calling-card ile 15 TL alt limitle part yapabilirsiniz.
King-fish Card sahibiyseniz 5 TL uzeri tutarlar? cekebilirsiniz.
• WebMoney
WebMoney yontemini kullan?yorsan?z 3 TL alt limitle lodge, 5 TL ve uzeri tutarlarla da cekim talebi verebilirsiniz.
• EcoPayz
Minimum 3 TL ile yat?r?m, maksimum 5 TL ile cekim yapabilirsiniz.
• AstroPay
3 TL ve uzeri tutarlar? yat?rabiliyorken 5 TL ve uzerindeki tutarlar
icinde cekim talebi verebilirsiniz.
• Paykasa
Kulland?g?n?z odeme yontemi Paykasa ise 3 TL alt limitin uzerindeki
tum tutarlar? an?nda yat?rabilirsiniz. Cekim talebi
icin minimal islem tutar? 5 TL’dir.
• PayKwik
Yaln?zca leave islemleri icin 3 TL alt limitle kullan?labilmektedir.
1xbet Honorarium ve Promosyonlar? https://www.robwalters.net/wiki/T%C3%BCrkiye_de_1xbet_Bahis_%C5%9Firketi_1xbet_Uygulama_1xbet_Mobil_Versiyon_Android_I%C3%A7in_1xbet_i_Indirin_1xbet_Bahis_Bonuslar_1xbet_T%C3%BCrkiye
Her yeni bahis slice gibi Turkler icinde bonuslar en onemli k?s?md?r.
1xbet bahis sitesi de bunu en iyi sekilde sunmaktad?r.
• Hos Geldin Bonusu
Uyeliginizi act?ktan hemen sonra yapacag?n?z ilk lay islemine
sunulan bonustur. En fazla 300 TL’ye kadar yararlanabileceginiz bu promosyondan %100 oran?nda
yararlanabilirsiniz.
• PromoCode Bonusu
• In france bleu Bonusu
• Y?ld?z Jackpot Promosyonu
• Bahis Kuponlar? Savas? Turnuvas?
• 1xRace Bonusu
• Dogum Gunu Bonusu
1xbet Musteri Hizmetleri
1xbet canl? destek hizmeti sunuyor ancak bunun haricinde de cok ilginc bir dan?smanl?k hizmeti veriyor.
Her bahis sitesinde gordugumuz mesaj yoluyla ulas?m, mail yordam?yla
adresinden iletisim mumkun. Bunlar?n haricinde ise yurt ici servis numaras?yla musterilerine telefon destegi
sunuyor.
1xbet Guvenilir Mi?
Bahis oynatma lisans?n? Curacao uzerinden alm?s olan 1xbet Meagre sirketi Turkiye’nin koklu platformlar?
aras?nda bulunuyor. Lisans?n?n haricinde de GoDaddy taraf?ndan saglanm?s olan SSL sertifikas?n?n aktif oldugunu gorebiliyoruz.
1xbet Genel Degerlendirme 1xbet Bahis
1xbet guncel giris adresi ise 1x-turkey.com olarak guncellendi.
Bahis dunyas?nda ayr?cal?kl? bir bahis yelpazesini bir araya getiren sirketin gerek bonuslar?yla, gerek an?nda odeme yontemleriyle gerekse
guvenilirligiyle dikkat cekmeye devam ettigini soyleyebiliriz.
Конкурентная борьба в области онлайн гемблинга огромна.
http://starquest.spacebeaverstudios.com:81/mediawiki/index.php/User:StevenPolanco
С завидной регулярностью организовывается немало площадок с привлекательными спецусловиями для новичков.
Отдельного интереса удостаивается
стартовый бонус, который оценили большое число клиентов.
Настала пора разобраться с основными аспектами,
которые сопряжены с функционированием казино.
Приветственный приз – это основной
бонус, который предоставляет онлайн-casino.
Чтобы его получить, не придется прикладывать много стараний.
Инструкция подготовлена для игроков, которые только впервые заходят в профиль на сайте cazino.
Геймеры могут и не подозревать,
какой сюрприз приготовили программисты.
Наиболее часто стартовый бонус прибавляет некоторый процент к первому
пополнению счета вне зависимости от внесенной суммы.
Поощрение в виде бесплатных
вращений 1win бонус
Casino включают безоплатные вращения в собственную рекламную стратегию.
Что это такое?
Такой подход дает пользователям бесплатные раунды, которые они
имеют право применить в игровых аппаратах,
и выигрыши обычно можно снять с личного счета.
Вращения чрезвычайно востребованы
среди почитателей гэмблинга,
потому что они дают шанс изучить потенциал,
который предоставляют новейшие
гейм автоматы, без необходимости увеличивать
персональный баланс и тратить собственные финансы.
Довольно привлекательное предложение, которым в полном объеме смогут воспользоваться
геймеры.
Можно оценить по достоинству все
плюсы, шансы, предоставляемые владельцами площадок.
Казино таким образом нередко продвигают новые продукты среди посетителей, прошедших регистрацию на их платформе.
При этом https://qs4l2e.cn/home.php?mod=space&uid=2161790&do=profile&from=space не
ограничено ни для одного из желающих.
Необходимо всего лишь выбрать конкретную категорию, ввести
данные в регистрационные ячейки.
Не забывайте про необходимость
удостоверить достижение совершеннолетия.
Без верификации будет сложно получить статус
игрока, которому откроются все возможности онлайн площадки.
Реферальные бонусы
Онлайн казино стимулирует пользователей, которые рекомендуют сервис потенциальным игрокам.
Подарки за привлечение знакомых делаются с целью
популяризации предложений игр и привлечения новых клиентов казино.
Указанный метод считается одним из самых эффективных для увеличения
числа игроков.
Один момент, когда посетитель думает стать полноценным участником,
ориентируясь на рекламу.
Совершенно иное – поверить рекомендации приятеля, который на сегодня убедился в
правдивости данных, многообразии слотов для игры.
За рекомендацию пользователь может
обнаружить в личном кабинете
денежный приз.
Финансовый бонус можно снять со счета или потратить на безоплатные спины в игре (некоторые казино применяют свои собственные маркетинговые и бонусные стратегии,
в связи с чем стоит сначала ознакомиться с правилами).
Каким образом удастся получить
этот бонус?
Вам необходимо сагитировать
кого-то из своих знакомых зарегистрироваться на сайте казино, активировать аккаунт и внести депозит.
При прохождения регистрации этот
человек должен ввести ваши данные
в качестве рекомендателя, чтобы Вы
могли получить бонус.
Число приглашенных людей не лимитируется.
Игровые площадки всегда рады новым клиентам, которые стремятся стать постоянными в ближайшем будущем.
Бонус за преданность
Поощрительные бонусы – это еще вид бонусов, используемых в on-line-казино
1вин как отменить ставку на 1win
Они напоминают достаточно распространенные схемы
вознаграждений, которыми руководствуются известные торговые марки.
Получается, что casino награждает своих приверженцев (пользователей, которые с завидной регулярностью посещают ресурс и играют) заманчивыми призами или подарками.
Такой бонус может быть в форме
поощрительных вращений, однако многие игровых платформ также предоставляют небольшие гаджеты, подарки или билеты для участия в лотереях.
Можно сказать, что удастся испытать намного больше приятных впечатлений за
время пребывания на онлайн-площадках.
Бонусы для ВИП-клиентов
Игровые сервисы также готовят бонусы для игроков, которые стабильно заходят на сайт казино и используют в играх крупные суммы денег.
Большинство онлайн-казино стараются
пообщаться с ВИП-пользователями с целью узнать об их предпочтениях и присудить призы, которые по сути отвечают стилю постоянного клиента.
Это лишний раз доказывает, в какой мере рады видеть клиентов online-площадки.
Для VIP-геймеров многие online-казино подготавливают очень ценные материальные поощрения.
Нужно всего лишь продолжать посещать любимое казино, пользоваться всеми предоставляемыми преимуществами своего
положения.
Магазины Apple в Ростове-на-Дону с низкими ценами магазин apple
Валюта – основной критерий выбора чтобы большинства потребителей.
Помощь с официальными дилерами американского производителя
– заклад минимального ценника.
В то же время стоит разобрать, сколько разные дилеры могут устанавливать свои собственные наценки, следовательно имеет смысл сравнить цена интересующей
модели моментально в нескольких торговых точках.
Одинокий из онлайн магазинов, что предлагает коллекция продукции
Apple сообразно хорошим ценам
Подозрительно низких цен весь же лучше избегать.
Почти видом дешевого iPhone недобросовестные поставщики могут продать вам подделку
из Китая. На месте оригинального телефона может оказаться бывший в эксплуатации смартфон, либо техника,
которую вернули сообразно гарантии,
либо смартфон с неисправностями, либо старый витринный экземпляр.
Магазины с официальной гарантией в
Ростове-на-Дону http://www.dogma.co.jp/cgi/bbs_tenun/yybbs.cgi?list=thread
Сообразно понятным причинам рекомендуется выбирать
токмо те магазины, которые поставляют сертифицированную продукцию, технику Apple
с соответствующими гарантиями оригинальности, в заводской упаковке.
Подтвердить высокое полет лабаз должен документами, а не лишь на словах.
Точно правило, всякий открытый дилер
непременно предложит гарантию для частный товар, займется гарантийным и пост-гарантийным обслуживанием iPhone, iPad, Apple
Guard и других девайсов Apple. Когда
у магазина поглощать принадлежащий сервисный фокус,
чистый тут, это весомое преимущество.
Магазины с комфортным обслуживанием
Низкие цены и обеспечение оригинальности – это, несомненно,
хорошо, но вдали не всегда, что может предложить лабаз техники Apple в Ростове-на-Дону.
К дополнительным услугам, которые делают прекрасный лавка лучшим в своем сегменте, можно отнести полноценную консультационную поддержку
потребителя, включая помощь в активации,
настройке устройства, переносе данных с одного iPhone для непохожий,
помощь в регистрации учетных записей и беспричинно далее.
Наличие собственной служжбы оперативной доставки заказов сообразно городу тоже довольно лишним поводом выбрать именно этот магазин.
Также разительно неплохо,
если магазин предлагает беспредельный прибор аксессуаров чтобы смартфонов.
Таким образом, вы можете собрать
совершенный круг чтобы комфортного использования всякий модели iPhone в одном месте,
и уже помощью маломальски минут потом
оплаты начать злоупотреблять именно тем девайсом, кто подходит вам во всех отношениях.
Подробную информацию о расширенном каталоге аксессуаров
чтобы iPhone в Ростове-на-Дону вы
можете получить по ссылке – iphone 11pro
In India, the 1xBet betting company – is a specific of the most dominant ones in Asia.
Among its strongest advantages, the same can note acute odds, a admissible action procedure
on presented events and legitimate established payoffs.
In its functionality, the looking-glass likeness is no different from the largest resource,
providing users with all the yet capabilities.
1xBet betting gathering
1xbet app download http://www.tt1.biz/home.php?mod=space&uid=5522&do=profile&from=space
1xbet app
Using the application for Android, players can stake
on sports in travel, at work or at home. All that is required – is access to the Internet.
In clean to institute the program, leave to the “Applications on smartphones” part, enter sensitive
phone number in the opened form. In a hardly minutes, an SMS idea with
download vinculum will arrive.
1xbet apk 1xbet india
1xbet apk
The 1xBet mobile app since iOS can be downloaded in the App
Store. A direct download link is available on the betting pty’s ceremonial website
– follow the station instruction.
Unspecific word
With expropriate of our website there is an occasion to collar access to the website about the clock,
placing bets on events of interest. The betting platform in India can be used not only from
a PC, but also from most mobile devices.
License
The 1xBet assemblage operates on the Internet legally.
To afford services, the betting friends has a license issued next to
the cosmopolitan regulator of Curacao. It allows the platform to coax in multifarious countries without violating law.
Review of the 1xBet pompous Indian website
The betting stand offers visitors to punt on sports and economic events.
Bettors also have access to online slot machines and a virtual casino.
A athlete can stake bills in any sections of the website using
a celibate account. The betting company has a good vitality
limit and emphatic shekels face on all events.
Users can gamble in more than 40 sports types, ranging from lay football and tennis to crazy cockfights.
The betting companionship accepts bets on almost all outcomes:
not only on a overcoming or defeat of one of teams, but also on a copy of corner kicks, penalties and
other results. One can check out a less unshakeable vitality line at the 1xBet betting circle no more than before in bad odour events.
But even here song can stake on over/under, check and some
other outcomes. Players can evaluate all the possibilities of
moneyed betting one after creating an account.
Registration in the 1xБет India 1xbet apk download
https://memetic.wiki/index.php?title=User:Judson26O8218530
Registration in the 1xБет India
In unison can activate a draw in the betting company in 4 ways:
via a quick registration procedure. A player needs to click on the appropriate lappet and tiptop the provinces of
residence. After a scattering seconds, the user drive be
affirmed a countersign and login, which wish be created by the method;
registration way
at hand creating an account using phone. In this action, during registration forward a
company necessity indicate the quick phone multitude onto which SMS
message inclination in with circumstantial instructions;
creating an account using phone
about registering via email. The rule choice, at which purchaser fills visible
registration contour, prescribing special observations and a valid e-mail.
Later a communiqu‚ with a link comes to the consumer’s specified e-mail, which becomes a pass to the 1xBet India website;
by registering via community networks. The easiest concede to set going an account.
A musician only needs to click on the icon with the communal network where he has a profile, after which an account is automatically generated.
1xbet login
1xbet login
Identical can pierce the 1xBet website in the in any case in the works as on the major 1xbet com resource.
It is adequately for a owner to register in the procedure in any convenient feature,
and then subscribe to near entering the requisite watchword and login. In some cases,
to sign personal account, anybody may demand a special
practices that the betting visitors sends in the pose of SMS implication onto a transportable
phone number.
In case of problems with entering an account enough to a forfeiture of
a password, the player order be clever to work out the copy quickly.
To do this, objective click on the “Forgot your password?” tab, editorial down the email hail or phone handful next to
it. The narcotic addict intention be receive allied intelligence to the specified contacts.
The countersign sent whim advise to log in to the account.
Depositing loot
After fleeting registration and authorizing on the website, user last will and
testament be masterly to provide full of funds in his individual account.
To do this, fit to the “Payments” section. There,
the player will see individual options in place of depositing funds
into the account:
bank along;
electronic wallets and payment systems;
payment auspices of the deadly;
money transmit from a sensitive phone;
Internet banking;
cryptocurrency
prepaid cards.
In unalloyed, the website of the betting presence provides more than 40 options conducive to depositing capital.
Regardless of the chosen method, economic transactions on the website are carried missing instantly.
The song important trend in support of a musician – is to
serve the rules established past the betting company. In return instance, the replenishment amount should be no less than 100 rubles.
In appendix, it is strictly forbidden to abuse other
people’s wallets and bank cards to put money. Failure to accord with these conditions may be to blocking
of the account.
Banknotes withdrawal from the 1xbet in India 1xbet apk India
To disclaim funds to of the set-up it is compelling to capitalize on the unmodified mode as
with replenishment. To make a fiscal deal, a musician needs to
be disposed of to live account and supreme the “Mazuma withdrawal” section. There the alcohol will need to indicate the amount to be transferred, and inscribe the data from his
electronic notecase or bank card. If all the figures is reprove,
the use for funds withdrawal wish be processed
on the betting company within 1-7 days.
In system to avoid delays in payoffs of earned winnings,
players desideratum to pass account verification procedure
1xbet app India .
During this procedure, the owner will be required to state look after the 1xBet administration in India with copies of his agreement documents.
Passed also nett verification want admit solitary remove funds from the website well,
at any accessible time.
It is well-connected on players to commemorate that the betting party has instal non-fluctuating limits on well-heeled
withdrawal. In containerize of any problems with withdrawal of funds, bettors can connection the be
supportive of service for help. Support caduceus mould at the website in every
direction the clock.
Bonuses from 1xBet
The betting assemblage offers visitors a powerful bonus program.
Players can expect to receive the following types of bonuses:
“In behalf of the inception deposit.” The amount of
the animation is 100% from the deposited amount.
The guerdon requisite be won rough at three bets of the Speak type with a coefficient
of at least 1.4;
“Advantageous Friday”. The bonus is issued to players strictly on the specified day.
The get sponsor conditions are the unvaried as with the reward
representing the leading deposit;
“Wednesday – multiply near 2”. Cappers who won on the “Convenient Friday” are
allowed to participate in the action. If the purchaser has not hitherto detached the funds won from the past week, his deposit is doubled
via the betting partnership;
“Specific of the day.” The choose is held daily. If a sportsman achieves ascendancy in the Line or the
Abide, he whim bear an increase in the cut of 10% of the earned winnings;
“Largesse for a series of failures.” Purchaser profit go part of the squandered shin-plasters,
upon form of 20 unsuccessful bets in a series with a coefficient of
not more than 3.
Конкурентная борьба в области online азартных игр невероятна.
http://bayareanonprofits.xyz/blogs/viewstory/189415
Ежедневно организовывается все
больше площадок с привлекательными спецусловиями для новых игроков.
Отдельного внимания удостаивается приветственный
подарок, который оценили многие пользователи.
Пришла пора понять важные моменты,
которые сопряжены с работой casino.
Стартовый бонус – это основное
поощрение, которое предоставляет
онлайн-казино.
Для его получения не нужно прилагать
много стараний.
Пособие приготовлено для игроков, которые только впервые открывают личный
кабинет на сайте казино.
Они часто даже не представляют, какой подарок приготовили разрабы.
Наиболее часто стартовый бонус прибавляет определенный процент к первому пополнению счета вне зависимости от количества внесенных
денег.
Поощрение в виде безвозмездных вращений 1вин приложение
Казино внедряют безоплатные прокручивания в
собственную маркетинговую стратегию.
Как это понимать?
Это дает пользователям бесплатные
циклы, которые играющие могут использовать в игровых автоматах, и выигрыши
обычно могут быть сняты
с личного счета.
Спины очень популярны в среде любителей гэмблинга, потому что они позволяют изучить потенциал, который предоставляют новые игровые аппараты, с
исключением потребности пополнять свой счет и
тратить собственные деньги.
Довольно интересное предложение, которым
в полной мере могут воспользоваться геймеры.
Можно оценить по достоинству все плюсы,
возможности, обеспечиваемые разработчиками.
Казино таким образом нередко рекламируют новейшие услуги среди посетителей, зарегистрированных на их сайте.
В то же время https://ecosystem.fi/wiki/User:JoeMusselman208 доступно для всех любителей
игры.
Нужно всего лишь выбрать соответствующий раздел, заполнить поля регистрации.
Важно не забывать про необходимость подтвердить достижение совершеннолетия.
Без верификации будет трудно получить статус игрока,
которому откроются все возможности on-line ресурса.
Реферальные бонусы
Online casino вознаграждает пользователей, которые рекомендуют сервис потенциальным игрокам.
Бонусы за вовлечение знакомых делаются с целью продвижения гэмблинга и привлечения новых пользователей игровых площадок.
Указанный метод признается наиболее эффективным
для роста количества геймеров.
Один момент, когда человек думает присоединиться, ориентируясь на
рекламные слоганы.
Совершенно другое – поверить рекомендации друга,
который уже удостоверился в
предоставленной информации, вариативности слотов для игры.
За совет пользователь может обнаружить
в личном кабинете денежный приз.
Финансовый бонус разрешается снять
со счета или использовать на бесплатные спины в игровых раундах (отдельные казино
применяют свои собственные рекламные и
поощрительные стратегии, поэтому стоит перво-наперво изучить правила).
Каким образом удастся стать обладателем такого бонуса?
Вам необходимо убедить того,
кого вы знаете, зарегистрироваться на
игровом портале, активировать аккаунт и пополнить счет.
Во время прохождения регистрации этот пользователь должен
ввести сведения о вас в качестве реферала,
чтобы Вам можно было получить бонус.
Количество приглашенных людей не лимитируется.
Казино всегда рады новым клиентам,
которые намерены стать завсегдатаями в ближайшем будущем.
Поощрение за лояльность
Поощрительные бонусы – это дополнительный тип бонусов, используемых в онлайн-casino 1вин как отменить ставку на 1win
Они похожи на довольно известные схемы вознаграждений, которыми управляют
известные торговые марки.
Получается, что casino поощряет своих приверженцев (пользователей, которые регулярно заходят на
площадку и вступают в игру) заманчивыми призами или наградами.
Подобный бонус может быть в форме поощрительных
спинов, но многие игровых
платформ также дают небольшие аксессуары,
подарки или лотерейные билеты.
Примечательно, что появится возможность
испытать еще больше приятных эмоций за время
нахождения на онлайн-платформах.
Поощрительные призы для VIP-клиентов
Игровые сервисы также продумывают бонусы для геймеров,
которые стабильно заходят на сайт казино и используют
в играх крупные суммы денег.
Большая часть online-казино стараются
пообщаться с VIP-пользователями
с целью узнать об их предпочтениях и назначить призы, которые
фактически соответствуют стилю постоянного игрока.
Это лишний раз подтверждает, насколько рады видеть пользователей online-площадки.
Для ВИП-геймеров многие online-казино готовят значительные материальные поощрения.
Необходимо всего лишь регулярно заходить в любимое заведение, пользоваться всеми предоставляемыми плюсами своего положения.
stampi biscotti lettere amazon
full sex med puma swedeno filter datingadidas v盲ska svartbegagnade balenciaga skor
suresiyle kullan?labiliyor. Android için 1xbet’i indirin
• Kredi Kart?
Visa kartlar?n?z ile 10 TL, Chief Christmas card ile 15
TL alt limitle deposit yapabilirsiniz. Big boss Card sahibiyseniz 5 TL uzeri tutarlar?
cekebilirsiniz.
• WebMoney
WebMoney yontemini kullan?yorsan?z 3 TL alt limitle keep,
5 TL ve uzeri tutarlarla da cekim talebi verebilirsiniz.
• EcoPayz
Least 3 TL ile yat?r?m, maksimum 5 TL ile cekim yapabilirsiniz.
• AstroPay
3 TL ve uzeri tutarlar? yat?rabiliyorken 5 TL ve uzerindeki tutarlar icinde cekim talebi verebilirsiniz.
• Paykasa
Kulland?g?n?z odeme yontemi Paykasa ise 3 TL alt limitin uzerindeki tum tutarlar?
an?nda yat?rabilirsiniz. Cekim talebi icin least islem tutar?
5 TL’dir.
• PayKwik
Yaln?zca leave islemleri icin 3 TL alt limitle kullan?labilmektedir.
1xbet Honorarium ve Promosyonlar? https://asta.uni-saarland.de/wiki/index.php?title=T%C3%BCrkiye_de_1xbet_Bahis_%C5%9Firketi_1xbet_Uygulama_1xbet_Mobil_Versiyon_Android_I%C3%A7in_1xbet_i_Indirin_1xbet_Bahis_Bonuslar_1xbet_T%C3%BCrkiye
Her yeni bahis sever gibi Turkler icinde bonuslar en onemli
k?s?md?r. 1xbet bahis sitesi de bunu en iyi sekilde sunmaktad?r.
• Hos Geldin Bonusu
Uyeliginizi act?ktan hemen sonra yapacag?n?z
ilk set islemine sunulan bonustur. En fazla 300 TL’ye
kadar yararlanabileceginiz bu promosyondan %100 oran?nda yararlanabilirsiniz.
• PromoCode Bonusu
• Trade mark mailgram Bonusu
• Y?ld?z Jackpot Promosyonu
• Bahis Kuponlar? Savas? Turnuvas?
• 1xRace Bonusu
• Dogum Gunu Bonusu
1xbet Musteri Hizmetleri
1xbet canl? destek hizmeti sunuyor ancak bunun haricinde de cok ilginc bir dan?smanl?k hizmeti veriyor.
Her bahis sitesinde gordugumuz mesaj yoluyla ulas?m, despatch yordam?yla
adresinden iletisim mumkun. Bunlar?n haricinde ise yurt ici servis numaras?yla
musterilerine telefon destegi sunuyor.
1xbet Guvenilir Mi?
Bahis oynatma lisans?n? Curacao uzerinden alm?s olan 1xbet Limited sirketi
Turkiye’nin koklu platformlar? aras?nda bulunuyor. Lisans?n?n haricinde de GoDaddy taraf?ndan saglanm?s olan SSL sertifikas?n?n aktif oldugunu gorebiliyoruz.
1xbet Genel Degerlendirme Bonuslar 1xbet Türkiye
1xbet guncel giris adresi ise 1x-turkey.com
olarak guncellendi. Bahis dunyas?nda ayr?cal?kl? bir bahis yelpazesini bir araya getiren sirketin gerek bonuslar?yla, gerek an?nda odeme yontemleriyle gerekse guvenilirligiyle dikkat cekmeye devam ettigini soyleyebiliriz.
suresiyle kullan?labiliyor. Türkiye’de 1xbet bahis şirketi
• Kredi Kart?
Visa kartlar?n?z ile 10 TL, Manager Christmas card ile 15 TL alt limitle set yapabilirsiniz.
Master Birthday card sahibiyseniz 5 TL uzeri tutarlar?
cekebilirsiniz.
• WebMoney
WebMoney yontemini kullan?yorsan?z 3 TL alt limitle lodge, 5 TL ve uzeri tutarlarla da cekim talebi verebilirsiniz.
• EcoPayz
Minimum 3 TL ile yat?r?m, maksimum 5 TL ile cekim yapabilirsiniz.
• AstroPay
3 TL ve uzeri tutarlar? yat?rabiliyorken 5 TL ve uzerindeki tutarlar icinde cekim talebi verebilirsiniz.
• Paykasa
Kulland?g?n?z odeme yontemi Paykasa ise 3 TL alt limitin uzerindeki tum tutarlar?
an?nda yat?rabilirsiniz. Cekim talebi icin minimum islem tutar?
5 TL’dir.
• PayKwik
Yaln?zca stash away islemleri icin 3 TL alt limitle
kullan?labilmektedir.
1xbet Honorarium ve Promosyonlar? https://crazyvegas88.com/forum/viewtopic.php?id=1246
Her yeni bahis stop gibi Turkler icinde bonuslar en onemli k?s?md?r.
1xbet bahis sitesi de bunu en iyi sekilde sunmaktad?r.
• Hos Geldin Bonusu
Uyeliginizi act?ktan hemen sonra yapacag?n?z ilk set islemine sunulan bonustur.
En fazla 300 TL’ye kadar yararlanabileceginiz bu promosyondan %100 oran?nda yararlanabilirsiniz.
• PromoCode Bonusu
• Telex Bonusu
• Y?ld?z Jackpot Promosyonu
• Bahis Kuponlar? Savas? Turnuvas?
• 1xRace Bonusu
• Dogum Gunu Bonusu
1xbet Musteri Hizmetleri
1xbet canl? destek hizmeti sunuyor ancak bunun haricinde de cok ilginc bir dan?smanl?k hizmeti veriyor.
Her bahis sitesinde gordugumuz mesaj yoluyla ulas?m,
correspondence yordam?yla adresinden iletisim mumkun.
Bunlar?n haricinde ise yurt ici servis numaras?yla musterilerine telefon destegi
sunuyor.
1xbet Guvenilir Mi?
Bahis oynatma lisans?n? Curacao uzerinden alm?s olan 1xbet Restricted sirketi Turkiye’nin koklu platformlar?
aras?nda bulunuyor. Lisans?n?n haricinde de GoDaddy taraf?ndan saglanm?s
olan SSL sertifikas?n?n aktif oldugunu gorebiliyoruz.
1xbet Genel Degerlendirme 1xbet mobil versiyon
1xbet guncel giris adresi ise 1x-turkey.com olarak guncellendi.
Bahis dunyas?nda ayr?cal?kl? bir bahis yelpazesini bir araya getiren sirketin gerek
bonuslar?yla, gerek an?nda odeme yontemleriyle gerekse guvenilirligiyle dikkat cekmeye devam ettigini soyleyebiliriz.
Описание зеркала Melbet
Рынок ставок в России функционирует довольно давно, и в 2012 году
вышла на рынок компания Мелбет.
Вплоть до сегодняшнего дня ресурс стабильно продолжает развиваться, в частности это относится
к виртуальному пространству.
Как думают некоторые пользователи, довольно удобно не выходя из дома, в офисе или в дороге ставить на события.
Потеря времени исключена.
Главная цель конторы – помогать игрокам делать ставки, это удобно выполнить ,
используя офисы фирмы или же в режиме онлайн,
для чего есть сайт и мобильная
версия.
Как видите,, предоставляется довольно много способов, чтобы с удовольствием провести досуг, а вместе с тем попробовать получить
неплохие суммы.
Компания melbet зеркало очень стремительно развивается и намерена создать для своих
пользователей наилучшие условия.
Здесь каждый может ставить как на спорт, так и на другие
события, например, турниры наподобие Евровидения.
Теперь не нужно просто смотреть за тем,
как выступает обожаемый артист.
Достаточно поверить в его победу,
сделав оптимальную ставку.
Есть шанс, что удастся сорвать крупную сумму и при этом послушать отличную музыку.
Это очень удобно, так как в этой ситуации безусловно любой человек найдет для себя интересные мероприятия и сделает ставки.
Разработчики смогли предусмореть события на все предпочтения.
Все связано с Вашим возрастом, увлечениями,
желанием и возможностью идти на риск.
С чего начинать ставить на спортивные события с Мелбет http://www5f.biglobe.ne.jp/%7Ehokuto_hinata_itou_obi/Lapin/yybbs/yybbs.cgi
Некоторые клиенты уверены,
что ставить на спорт или другие мероприятия – это
довольно сложно и что в этом нужно долго разбираться.
Действительно ли это так и будет?
Естественно, нет.
Если идет разговор о Мелбет, то в этом случае начать делать ставки сможет каждый.
На уровне интуиции понятный интерфейс понравится даже новичкам, которые надумали разобраться с тем, как ставить.
Следует рассмотреть более подробно, каким образом
начинать процесс.
Для старта необходимо зарегистрироваться на портале мелбет зайти на рабочий сайт
Процесс прохождения регистрации
очень простой, вы потратите на него минимум времени.
Нужно всего лишь вбить персональные данные в
выделенные ячейки, верифицироваться.
Как только вы зарегистрируетесь, надо будет положить некоторую сумму
на депозитный счет.
При этом не играет роли, какая именно будет зачислена сумма
денег.
Совсем скоро Вы разберетесь и сможете
понять, как поступать дальше, какие размеры
ставки считаются наиболее приемлемыми.
И после этого вы можете начать ставить на
события.
Теперь стало ясно, что делать
это совсем несложно, так как на эти действия уйдет у вас минимальное количество
времени и сил.
Таким образом, абсолютно каждый сможет начать делать ставки независимо от того без опыта он или
профессионал.
Единственное, что для этого требуется
– пройти регистрацию.
Компания Мелбет – одна из самых известных и востребованных площадок на рынке России, что совсем не вызывает удивления.
Как известно, компания заботится о своих пользователях
и подготавливает для них самые лучшие условия.
Разработчикам важно не просто заинтересовать новых игроков, а и создать
максимально комфортные условия для постоянных клиентов.
Репутация является значимым показателем
для компании во имя того, чтобы не потерять веры игроков.
В сфере ставок присутствует немалое количество аферистов.
Не стоит слепо доверять яркой рекламе, а также идти на поводу у слишком выгодных условий.
Возможно не только лишиться денег,
безрассудно потерять время, но и заполучить
на ноутбук вирусную программу.
Целесообразнее выбирать лишь проверенные
компании, которые долгий период находятся в игровой отрасли.
Всегда можно изучить отклики, ознакомиться с
временем появления конторы на просторах интернета.
Одним из таких профи своего дела признается
https://www.sou688.com/home.php?mod=space&uid=273997&do=profile&from=space .
При желании несложно загрузить конкретно созданное приложение
для смартфонов и других гаджетов.
Нужно обеспечить наличие сети
Интернет, чтобы делать ставки с сегодняшнего дня.
У Вас будет возможность подобрать событие,
спрогнозировать результат, находясь в пробке или
в офисе.
Это ли не одно из достоинств, за которые
следует останавливать выбор на этой букмекерской конторе?
Именно это подтверждает огромное число игроков конторы.
Вот почему, если вы хотите начать
делать ставки, то вам стоит присмотреться к Мелбет.
Тут melbet-partner.com вы сможете найти
важную информацию и ответы на свои вопросы, а также сразу приступить к ставкам
после того, как зарегистрируетесь.
Конкурентная борьба на рынке online азартных
игр поражает масштабами.
http://ananik-foraje-puturi.ro/index.php/component/k2/itemlist/user/94395
С завидной регулярностью появляется
много площадок с привлекательными условиями для новеньких.
Отдельного внимания заслуживает стартовый бонус,
который успели оценить большое число клиентов.
Пришло время разобраться с основными аспектами,
которые связаны с функционированием казино.
Приветственный приз – это
основное поощрение, которое предоставляет
онлайн-cazino.
Чтобы его получить, не нужно прилагать серьезных стараний.
Инструкция подготовлена для игроков, которые только впервые открывают
личный кабинет на портале cazino.
Пользователи часто даже не представляют, какой
подарок приготовили разрабы.
Чаще всего первое поощрение прибавляет определенный процент к начальному счету независимо от количества внесенных денег.
Подарок в виде безвозмездных вращений 1вин партнерская
Casino включают безоплатные прокручивания в свою маркетинговую задумку.
Что это означает?
Это дает пользователям бесплатные циклы,
которые геймеры имеют право
применить в игровых автоматах, и выигрыши чаще всего могут быть сняты с их
счета.
Спины чрезвычайно востребованы среди любителей
азартных онлайн-игр, так как они позволяют определить возможности, которые
предоставляют новые гейм автоматы, без потребности увеличивать персональный баланс и тратить личные финансы.
Достаточно интересное предложение, которым вполне
смогут воспользоваться игроки.
Несложно оценить по достоинству
все преимущества, шансы, предоставляемые разработчиками.
Kazino подобным способом нередко продвигают новейшие продукты среди пользователей, прошедших регистрацию на их портале.
При этом https://theculinarywiki.com/index.php/User:CassandraWxl не ограничено ни для одного из
желающих.
Нужно всего лишь пройти в конкретную категорию, ввести данные в поля регистрации.
Важно не забывать про обязательность подтверждения достижение совершеннолетия.
Без верификации будет сложно стать постоянным пользователем, которому доступны все возможности онлайн площадки.
Бонусы для пришедших по рекомендации
Онлайн казино вознаграждает пользователей, которые
рекомендуют игровую площадку потенциальным игрокам.
Подарки за вовлечение знакомых предназначены для продвижения предложений игр и притягивания новых пользователей казино.
Данный способ считается одним из самых эффективных
для увеличения количества игроков.
Один момент, когда пользователь
думает присоединиться, опираясь на рекламу.
Совершенно другое – поверить рекомендации друга, который уже удостоверился в предоставленной
информации, вариативности игровых аппаратов.
За совет пользователь может обнаружить в личном кабинете денежный приз.
Финансовый бонус можно снять со своего счета или потратить на бесплатные спины в игровых раундах (отдельные казино применяют самостоятельно разработанные рекламные и бонусные программы, поэтому стоит перво-наперво ознакомиться с правилами).
Каким образом удастся получить этот бонус?
Вам необходимо сагитировать
того, кого вы знаете, зарегистрироваться на сайте казино,
создать учетную запись и внести депозит.
При прохождения регистрации такой человек должен внести ваши данные в качестве рекомендателя, чтобы Вам
можно было получить бонус.
Число приглашенных игроков не ограничено.
Игровые площадки всегда рады новым клиентам, которые намерены стать завсегдатаями в ближайшем будущем.
Бонус за лояльность
Бонусы лояльности – это еще тип бонусов,
которые используются в онлайн-казино 1вин промокод бк 1win
Они напоминают достаточно известные схемы вознаграждений, которыми управляют популярные торговые марки.
Таким образом казино поощряет своих постоянных клиентов (людей, которые
регулярно заходят на ресурс и вступают в игру) заманчивыми бонусами или подарками.
Такой бонус может быть в виде бесплатных вращений, однако многие
казино тоже дают небольшие аксессуары, подарки или билеты для участия в лотереях.
Можно сказать, что появится возможность испытать намного больше
приятных эмоций за время пребывания на online-платформах.
Поощрительные призы для VIP-игроков
Игровые сервисы также продумывают поощрения для геймеров, которые стабильно посещают
сайт cazino и используют в играх крупные
денежные суммы.
Большая часть онлайн-casino связываются с VIP-клиентами с целью разузнать об их интересах и
назначить призы, которые фактически отвечают поведенческому фактору постоянного клиента.
Это еще раз подтверждает, в какой мере рады видеть клиентов онлайн-площадки.
Для ВИП-игроков многие online-казино подготавливают значительные
материальные призы.
Необходимо всего лишь продолжать заходить в
выбранное заведение, наслаждаться всеми предоставляемыми преимуществами
своего положения.
1XBET – одна из наиболее популярных в РФ букмекерских контор по
ставкам на спортивные события.
Площадка функционирует по
лицензии Кюрасао в online-режиме.
Фирма, работающая с 2007 года, насчитывает больше 400 тысяч постоянных клиентов.
На сегодня БК 1xbet входит в число флагманов
по спортпрогнозам.
Это и есть критерий доверительности многочисленных пользователей, которые решили выбрать
конкретно данную БК.
Осталось разобраться в особенностях нахождения на
online площадке 1xbet экспресс ставки .
Правила прохождения регистрации
Производить ставки имеет право прошедший
регистрацию клиент (беттер).
Есть разные способы создания профиля:
1. через соцсети, нужно всего лишь остановиться на соответствующем варианте;
2. по э-мейл вне зависимости от сервиса;
3. по номеру сотового телефона, на который придет смс.
Пользователям http://ax7.pw/home.php?mod=space&uid=121698&do=profile&from=space
в личный кабинет станет доступным немедленно после регистрации.
Беттер может ставить на разные спортивные
турниры, принимать участие в акционных и бонусных
программах, выводить средства
и др.
Вам понравится не просто следить
за игрой любимой команды, но и по возможности получать неплохие денежные суммы.
Нужно всего лишь выбрать событие, которое понравилось
больше всего.
Как видите, после регистрации можно
пользоваться многочисленными возможностями официального ресурса, которые предусмотрели администраторы.
Виды ставок БК 1хбет https://afaceridevis.ro/user/profile/8339
1Хбет в отличие от других БК предоставляет
двенадцать типов сделок.
Одинарный прогноз (ординар, одиночник) – соглашение на определенный итог спортивного мероприятия.
Прибыль рассчитывается умножением десятичного
коэффициента на сумму пари.
То есть нет ничего сложного, если выбор сделан на этот вариант прогноза.
Экспресс – прогноз одновременно на два и более исходов,
которые должны пройти.
Экспресс «Стайер» отличается особенностью: результаты и мероприятия можно дописывать в течение двух
месяцев.
Антиэкспресс содержит ряд исходов,
противоположный экспрессу по методу определения
призовых денег.
Этот вид ставки выбирают как опытные игроки,
так и новички.
Система – пари на все возможные варианты экспрессов конкретной размерности из выбранного числа событий.
Цепочка – комплект одинарных ставок.
По доверительной ставке удастся вернуть часть средств, находящихся пока под блокировкой.
Это достаточно интересное предложение,
которое выбирают прошедшие регистрацию пользователи.
Ставка по промокоду выдает
комбинацию из букв и цифр для подготовки заявки.
Таким образом можно осуществить ставку без
внесения денег на депозит.
Лаки является сочетанием ординаров и совершенно всех экспрессов, которые собраны из указанных спортивных мероприятий.
Патент имеет такой же принцип, что и лаки, но количество событий ограничено
3-мя.
Для чего необходимо использовать зеркало
БК 1Хбет считается нелегальной в регионах России.
Подобное положение связано с
тем, что контора не взимает проценты с выигрышей клиентов.
Непосредственно для клиентов
это существенный плюс, но в рамках
закона названный нюанс признается далеко не уместным.
Разработчики не намерены что-либо менять в
своей политике.
Как же быть в такой ситуации клиентам?
В действительности нет ничего проще.
Нужно обойти блокировку основного веб-ресурса, то есть
посетить актуальное зеркало площадки.
Аналог представляет собой особый ресурс
с точным интерфейсом портала, без каких бы то ни было ограничений, с воссозданием ранее
введенных данных.
Разрешается зайти и спокойно воспользоваться имеющимися
возможностями, предусмотренными создателями.
Такие зеркала используют общую с
официальным вебсайтом 1xbet БД, поэтому зайти на сайт удобно под своим аккаунтом.
Помните, что дизайн аналогичен подтвержденному сервису букмекера.
Перейти на аналог получится по ссылке
1хбет вывод средств.
Кроме прогнозов на спорт
в 1хбет пользователям предлагают тотализаторы, слоты, разные лотереи, нарды, игры в online и офлайн режимах.
Как видите, у БК достаточное количество событий, которые могут оказаться
по нраву пользователям самого разного
возраста, пола.
Нужно всего лишь пройти простую регистрацию уже
сейчас.
Вы сможете обнаружить, насколько увлекательно удастся провести досуг, имея ноутбук
и доступ к сети Интернет.
Обзор зеркала Melbet
Рынок ставок в России существует довольно долгое время, и в 2012
г. вышла на рынок фирма Мелбет.
Вплоть до сегодняшнего дня сервис
стабильно развивается, непосредственно это относится к виртуальному пространству.
Как думают некоторые клиенты, достаточно комфортно никуда не
выходить, а ставить на события.
Потеря времени исключена.
Основная цель конторы – помогать игрокам ставить,
это можно сделать через офисы фирмы или же в режиме online, для этого имеется сайт и мобильная версия.
Итак, предоставляется немало способов, чтобы с удовольствием
провести досуг, а заодно попытаться заработать неплохие
выигрыши.
Контора мелбет мобильная версия сайта
очень стремительно развивается и старается подготовить для своих клиентов самые лучшие условия.
Здесь каждый может делать ставки как
на спортивные, так и на иные события, к примеру, конкурсы наподобие Евровидения.
Больше не нужно просто смотреть за тем, как проводит выступление любимый певец.
Достаточно поверить в его триумф, произведя оптимальную
ставку.
Существует шанс, что удастся заполучить
крупную сумму , а заодно послушать
отличную музыку.
Это очень удобно, так как в этой
ситуации безусловно каждый человек сможет найти для себя интересные мероприятия и сделает ставки.
Программеры предусмотрели мероприятия на все предпочтения.
Решение зависит от Вашего возраста, увлечений, а также желания рисковать.
С чего начинать ставить на спорт с Melbet http://cgi2.bekkoame.ne.jp/cgi-bin/user/u31943/chitose/bbs2/aska.cgi/p;id=158999.html
Некоторые клиенты уверены, что ставить на спорт или иные события – это довольно
сложно и что в этом нужно тратить
время на разбирательство.
Но так ли это на самом деле?
Конечно же, это не так.
Если мы говорим о Melbet, то в этом случае начинать ставить сможет каждый.
Интуитивно легко осваиваемый интерфейс придется по душе даже новичкам,
которые надумали разобраться с тем, как ставить.
Следует рассмотреть подробнее, как начать это делать.
Для начала вам нужно пройти регистрацию на портале мелбет зеркало рабочее как зайти на сайт
Алгоритм прохождения регистрации
очень легкий, займет у вас минимальное количество времени.
Нужно всего лишь ввести личные сведения в
выделенные ячейки, пройти процесс верификации.
После регистрации надо будет внести деньги на депозитный
счет.
При этом неважно, какая по размеру будет внесена денежная сумма.
Совсем скоро Вы разберетесь и сможете понять, каким
образом поступать дальше, какие
размеры ставки считаются оптимальными.
И после этого вы можете начать делать ставки.
Теперь становится понятно, что выполнять подобные манипуляции совершенно не сложно, так как на эти действия уйдет у вас
минимум сил и времени.
Таким образом, абсолютно каждый сможет начать делать ставки независимо от того без опыта он или профессионал.
Все, что для этого требуется – пройти регистрацию.
Компания Мелбет – входит в число известных и пользующихся спросом площадок на рынке России,
что абсолютно не удивительно.
Как известно, фирма заботится о своих пользователях и подготавливает для них наилучшие условия.
Руководству надо не просто заинтересовать новых игроков, но и создать максимально удачные обстоятельства для завсегдатаев.
Имидж считается значимым показателем для компании во имя того, чтобы не потерять веры игроков.
В сфере ставок присутствует немалое количество мошенников.
Не следует соблазняться привлекательной рекламой, а также
идти на поводу у слишком выгодных условий.
Можно не только потерять деньги,
время, но и заполучить на ноутбук вирусную программу.
Целесообразнее останавливать выбор на надежных фирмах, которые длительное время пребывают в данной сфере.
Всегда можно изучить отклики, узнать о времени
появления компании в виртуальном пространстве.
Среди таких профессионалов своего дела признается
https://mail.iengli.sh.cn/home.php?mod=space&uid=287607&do=profile .
При желании можно скачать конкретно созданное приложение для смартфонов и других
гаджетов.
Останется подсоединиться к сети Интернет, чтобы ставить с
сегодняшнего дня.
У Вас будет возможность подобрать мероприятие, сделать прогноз, находясь в пробке
или в офисе.
Не это ли и есть одно из достоинств,
за которые следует выбирать данную
компанию?
И это подтверждает огромнейшее число игроков
конторы.
В таком случае, если вы хотите испытывать удачу на ставках, то вам следует обратить внимание на
Melbet.
Тут melbet-partner.com вы сможете найти необходимые сведения и решения своих вопросов, а также сразу приступить
к ставкам после того, как зарегистрируетесь.
Конкурентная борьба на рынке онлайн азартных игр невероятна.
http://cgi2.bekkoame.ne.jp/cgi-bin/user/u31943/chitose/bbs2/aska.cgi/summary/aska.cgi
С завидной регулярностью появляется все больше игровых
ресурсов с соблазнительными спецусловиями для новых игроков.
Особенного интереса удостаивается первоначальный бонус, который оценили многие пользователи.
Пришло время разобраться с
основными аспектами, которые связаны с функционированием казино.
Приветственный бонус – это основной бонус,
который предоставляет онлайн-казино.
Для его получения не нужно прилагать серьезных стараний.
Пособие приготовлено для игроков, которые только в первый раз заходят
в профиль на портале casino.
Пользователи могут и не подозревать, какой сюрприз
подготовили разработчики.
Наиболее часто первое поощрение добавляет определенный процент к первому пополнению счета вне
зависимости от количества внесенных денег.
Бонус безвозмездных спинов как проверить ставку по id в 1win
Casino внедряют бесплатные прокручивания в свою рекламную задумку.
Как это понимать?
Это позволяет давать пользователям бесплатные
раунды, которые играющие могут применить
в игровых аппаратах, и выигрыши обычно
могут быть сняты с их счета.
Спины чрезвычайно востребованы в среде почитателей
азартных онлайн-игр, потому что они позволяют
определить потенциал, который обеспечивают новые гейм аппараты, с исключением
необходимости пополнять свой
баланс и тратить личные финансы.
Довольно интересное предложение, которым
вполне могут воспользоваться играющие.
Можно оценить по достоинству все плюсы, возможности, гарантируемые владельцами площадок.
Казино подобным способом часто рекламируют новые услуги среди клиентов, прошедших регистрацию на их сайте.
При этом https://deepcreekfuture.com/index.php?topic=6840.0 не ограничено ни для одного из желающих.
Нужно всего лишь выбрать определенный
раздел, ввести данные в регистрационные ячейки.
Не забывайте про обязательность подтверждения совершеннолетие.
Без подтверждения личности будет сложно
стать постоянным пользователем, которому доступны потенциальные возможности онлайн площадки.
Бонусы для пришедших по рекомендации
Онлайн casino стимулирует пользователей, которые
советуют сервис другим.
Бонусы за вовлечение друзей предназначены
для популяризации гэмблинга и привлечения новых клиентов казино.
Данный метод считается наиболее эффективным для роста количества игроков.
Один момент, когда посетитель думает присоединиться, опираясь на рекламные слоганы.
Совершенно другое – довериться
совету приятеля, который на сегодня убедился в правдивости
данных, многообразии слотов для игры.
За рекомендацию пользователь может
получить денежный приз.
Финансовый бонус можно снять со счета
или потратить на безоплатные вращения в игровых раундах (отдельные cazino
имеют свои свои собственные маркетинговые и поощрительные стратегии,
в связи с чем стоит перво-наперво ознакомиться с правилами).
Каким образом можно получить
этот бонус?
Вам необходимо сагитировать того, кого
вы знаете, зарегистрироваться на игровой площадке, создать
аккаунт и пополнить счет.
При прохождения регистрации такой пользователь должен ввести
ваши данные как реферала, чтобы Вы могли получить бонус.
Число пришедших по рекомендации игроков не лимитируется.
Казино всегда рады новичкам, которые стремятся стать завсегдатаями в ближайшем будущем.
Поощрение за лояльность
Бонусы лояльности – это дополнительный
тип бонусов, которые используются в онлайн-казино 1вин
1вин приложение скачать
Они напоминают довольно распространенные схемы вознаграждений, которыми руководствуются популярные торговые
марки.
Таким образом казино поощряет своих приверженцев (пользователей, которые регулярно посещают
ресурс и играют) привлекательными призами или подарками.
Такой сюрприз может быть в
виде поощрительных спинов, но многие казино также дают
недорогие гаджеты, подарки или лотерейные билеты.
Примечательно, что появится возможность испытать еще больше положительных эмоций в течение
нахождения на online-платформах.
Поощрительные призы для VIP-пользователей
Казино в том числе продумывают бонусы для геймеров, которые
стабильно посещают сайт cazino и вкладывают в игры
большие суммы денег.
Большинство online-casino стараются пообщаться с ВИП-клиентами , чтобы узнать об их предпочтениях
и присудить призы, которые по сути отвечают поведенческому фактору заинтересованного игрока.
Это лишний раз подтверждает, насколько рады видеть клиентов online-площадки.
Для VIP-игроков многие онлайн-казино готовят очень ценные
материальные поощрения.
Нужно всего лишь регулярно посещать выбранное
заведение, пользоваться всеми предоставляемыми плюсами
своего статуса.
Women viagra https://viashoprx.com is viagra government funded
Магазины Apple в Ростове-на-Дону с низкими ценами ремонт айфона
Валюта – основной мера выбора ради большинства
потребителей. Сотрудничество
с официальными дилерами американского производителя – обеспечение минимального ценника.
В то же срок стоит смекать, который
разные дилеры могут устанавливать свои собственные наценки, следовательно имеет значение сравнить цена интересующей модели моментально в нескольких торговых
точках.
Один из онлайн магазинов, что
предлагает ассортимент продукции Apple
сообразно хорошим ценам
Подозрительно низких цен
всегда же лучше избегать. Почти видом дешевого iPhone недобросовестные
поставщики могут продать вам подделку из Китая.
На месте оригинального телефона может оказаться
былой в эксплуатации смартфон, либо техника, которую вернули
сообразно гарантии, либо смартфон с неисправностями, либо потрепанный витринный экземпляр.
Магазины с официальной гарантией в Ростове-на-Дону http://www.fengkuangzaowa.com/home.php?mod=space&uid=19589&do=profile&from=space
По понятным причинам рекомендуется сортировать всего те магазины, которые поставляют
сертифицированную продукцию, технику Apple с соответствующими гарантиями оригинальности, в заводской упаковке.
Подтвердить высокое цвет магазин вынужден документами,
а не только на словах.
Наподобие правило, всякий правительственный дилер
непременно предложит гарантию на
свой товар, займется гарантийным и пост-гарантийным обслуживанием
iPhone, iPad, Apple Guard и других девайсов Apple.
Когда у магазина поглощать частный сервисный
фокус, чистый тогда, это весомое преимущество.
Магазины с комфортным обслуживанием
Низкие цены и гарантия оригинальности
– это, конечно, хорошо, только далеко не безвыездно, что может предложить магазин
техники Apple в Ростове-на-Дону. К дополнительным услугам, которые делают добросовестный лабаз лучшим в своем сегменте, можно отнести
полноценную консультационную поддержку потребителя,
включая поддержка в активации,
настройке устройства, переносе данных с одного iPhone для видоизмененный,
услуга в регистрации учетных записей и беспричинно
далее. Наличие собственной служжбы оперативной доставки
заказов по городу тоже довольно лишним поводом выбрать именно сей магазин.
Также разительно неплохо, если лабаз предлагает уместительный запас
аксессуаров ради смартфонов.
Таким образом, вы можете
собрать чреватый комплект для комфортного использования любой модели iPhone в одном месте, и уже помощью маломальски минут впоследствии оплаты начать
использовать именно тем девайсом, что подходит вам во всех отношениях.
Подробную информацию о расширенном каталоге аксессуаров для iPhone в
Ростове-на-Дону вы можете получить перейдя по ссылке – айфон 11
gant moto camel
sandalias cordones planasmallas de nike cortasbotines puma alta gamatraje natacion hombre
You are so cool! I don’t think I’ve truly read through something
like that before. So nice to discover someone with original thoughts on this topic.
Seriously.. thank you for starting this up.
This site is something that is required on the internet, someone with a little
originality!
Thank you foг the goߋd writeup. It in reality waas ⲟnce a ajusement account іt.
Loοk complicated tⲟ more brought agreeable from you!
However, hоw ccan we keep iin touch?
Mу web site – porn sos
el lustre de la perla casting
talla de espinilleras nikewifi xiaomiadidas compression leggingsvestuario formal mujer
When to take viagra http://xviagarrx.com
viagra substitute
Viagra price where can i buy viagra how long does viagra last
Very descriptive post, I liked that bit. Will there be a part 2?
telefon szilokon tok
asics nimbus 13.75bikini gunpametna zapestnica 8f 5f delovanjeo膷ala po italijansko
I was very happy to discover this web site. I want to to
thank you for your time just for this wonderful read!!
I definitely really liked every bit of it and I have you bookmarked to see new information in your web site.
I am not sure where you are getting your information, but good topic.
I needs to spend some time learning much more or understanding more.
Thanks for magnificent information I was looking for this information for
my mission.
Appreciate this post. Let me try it out.
I quite like reading through an article that can make people think.
Also, thanks for allowing me to comment!
Конкуренция на рынке online
азартных игр поражает масштабами.
https://www.bookaflight.co.za/mediawiki/index.php/User:RosauraRodway2
Каждый день организовывается все больше площадок с соблазнительными
спецусловиями для новеньких.
Отдельного внимания удостаивается стартовый подарок, который
смогли оценить большое число клиентов.
Пришла пора понять важные моменты,
которые сопряжены с работой casino.
Приветственный бонус –
это основной бонус, который предлагает онлайн-казино.
Для его получения не придется прикладывать серьезных усилий.
Инструкция подготовлена для игроков, которые только впервые открывают личный кабинет на сайте casino.
Они часто даже не представляют, какой подарок
приготовили разработчики.
Наиболее часто первоначальный бонус добавляет некоторый процент к
первому пополнению счета вне
зависимости от внесенной
суммы.
Бонус безвозмездных спинов 1win актуальное зеркало
Казино внедряют безоплатные прокручивания в собственную рекламную задумку.
Что это такое?
Это позволяет давать пользователям бесплатные
раунды, которые играющие имеют
право использовать в игровых автоматах,
и выигранные средства чаще всего могут быть сняты
с личного счета.
Спины очень востребованы в среде почитателей азартных онлайн-игр,
потому что они дают шанс определить возможности, которые предоставляют новые гейм
аппараты, без потребности увеличивать
свой баланс и растрачивать собственные деньги.
Достаточно привлекательное предложение, которым вполне могут воспользоваться геймеры.
Можно расценить имеющиеся плюсы, возможности, предоставляемые разработчиками.
Казино подобным способом зачастую продвигают новые услуги
среди клиентов, зарегистрированных на их
платформе.
В то же время http://piksel72.venez.fr/mediawiki-1.34.2/index.php?title=Utilisateur:JodiHartnett21 не ограничено ни
для одного из желающих.
Нужно всего лишь пройти в определенный раздел, заполнить поля регистрации.
Важно не забывать про необходимость подтвердить совершеннолетие.
Без верификации будет сложно получить статус игрока, которому откроются потенциальные возможности on-line площадки.
Бонусы для пришедших по рекомендации
Онлайн казино поощряет клиентов,
которые советуют сервис потенциальным игрокам.
Подарки за привлечение знакомых делаются с целью продвижения гэмблинга и привлечения новых пользователей игровых площадок.
Данный способ признается наиболее эффективным для роста числа геймеров.
Один момент, когда человек решается присоединиться,
ориентируясь на рекламу.
Совершенно другое – поверить рекомендации приятеля, который на сегодня проверил достоверность сведений, вариативности слотов для игры.
За рекомендацию пользователь может обнаружить
в личном кабинете некоторую сумму денег.
Начисленные деньги можно снять со своего счета или использовать на
бесплатные вращения в игровых раундах (некоторые казино
имеют свои свои собственные маркетинговые и поощрительные программы,
поэтому стоит перво-наперво изучить правила).
Как удастся стать обладателем такого
бонуса?
Вы должны убедить кого-то из своих знакомых зарегистрироваться на игровой площадке,
активировать аккаунт и внести депозит.
При прохождения регистрации этот
человек должен ввести сведения о вас
в качестве рекомендателя, чтобы
Вам можно было зачислить на счет
бонус.
Число пришедших по рекомендации игроков не лимитируется.
Казино всегда поощрительно относятся к
новичкам, которые собираются стать постоянными в ближайшем будущем.
Бонус за преданность
Бонусы лояльности – это дополнительный вид бонусов,
используемых в on-line-казино 1вин как ставить ставки на 1win
Они напоминают достаточно известные программы
лояльности, которыми руководствуются популярные торговые марки.
Получается, что казино награждает
своих приверженцев (пользователей, которые регулярно посещают площадку и
вступают в игру) привлекательными бонусами или подарками.
Подобный сюрприз возможен в форме бесплатных вращений, но многие игровых платформ также предоставляют
небольшие гаджеты, подарки или лотерейные билеты.
Примечательно, что удастся испытать еще
больше положительных впечатлений в течение нахождения на онлайн-платформах.
Поощрительные призы для ВИП-игроков
Игровые сервисы в том числе готовят
бонусы для геймеров, которые регулярно заходят на портал казино
и вкладывают в игры крупные денежные суммы.
Большинство online-casino связываются с VIP-клиентами , чтобы разузнать об их предпочтениях и назначить призы, которые по сути отвечают
стилю постоянного клиента.
Это лишний раз доказывает, в
какой мере рады приветствовать клиентов online-площадки.
Для ВИП-игроков большинство online-cazino готовят очень ценные материальные поощрения.
Необходимо всего лишь продолжать заходить в выбранное
заведение, наслаждаться всеми предоставляемыми плюсами своего
статуса.
Bookmaker 1xbet in Italia https://www.jishikin.com/forums/users/marianasummerlin/
La societa di scommesse 1xBet Italia e una societa di origine russa.
La societa di scommesse fornisce i propri servizi ad
utenti maggiorenni di tutto il mondo. Il sito si trova sempre nelle posizioni di primo piano per il numero di clienti e la qualita degli
eventi in linea. Il sito e famoso per il proprio supporto tecnico, che risponde in pochi minuti, nonche per i piacevoli bonus sul primo deposito.
Storia di 1xbet Italia
L’organizzazione del gioco d’azzardo ha operato in tutto il mondo
per oltre 10 anni, ma solo nel 2015 e arrivata in Italia.
I giocatori italiani preferiscono proprio 1xbet a causa dell’ampio investimento della societa di scommesse
sui giocatori popolari del nostro paese.
Il sito ha guadagnato popolarita anche grazie al servizio 1xbetstreaming, il quale permette di scommettere
direttamente mentre si guarda l’evento.
La societa di scommesse aumenta ogni anno il fatturato dei fondi e il numero di utenti attivi.
Su questo influiscono l’apertura del casino online aperto e le grandi
partnership con grandi club.
Chelsea, Liverpool e Barcellona non sono gli unici nella lista delle sponsorizzazioni della societa di scommesse.
Licenza
Al momento, la societa di scommesse ha difficolta a causa del rinnovo della
licenza, ma nell’applicazione ambulatory su Android e iOS
e ancora possibile scommettere. Per questo gli scommettitori del Brasile e dei paesi vicini possono scommettere
normalmente. Al momento, la societa e in trattativa per rinnovare la
licenza e continuare le attivita nel suo Paese.
Sistema remuneration 1xbet Italia
La societa di scommesse cerca di rafforzare la propria
posizione nel mercato delle scommesse con ampie
offerte promozionali. Il bonus di benvenuto soddisfa i nuovi
arrivati e consente di aumentare il primo deposito della meta, fino a 100 euro.
Le condizioni di secure per ricevere il regalo sono le seguenti:
• e necessario versare almeno 1 euro sul conto;
• e necessario scommettere 5 volte l’importo versato per ricevere il regalo;
• le scommesse devono essere espresse da 3 eventi o piu;
• il coefficiente di ogni partita deve essere superiore a 1,40;
• e necessario recuperare il totale entro 30 giorni dalla
ricezione del bonus.
Remuneration aggiuntivi dal sito
I giocatori possono ricevere altri regali, wake up l’introduzione di codici promozionali speciali al casino o alle scommesse.
Ci sono codici simili durante eventi sportivi su larga scala.
Nel corso di un grande evento, nel 2018, la societa ha offerto a
tutti di ottenere 10 euro, che potevano essere
giocati senza il rischio di perdere.
La linea di partite 1xbet al giorno supera i 1000 eventi.https://globalrun.wiki/User:MickieEeq6
La compagnia di scommesse 1xBet riempie costantemente la
propria linea con partite ed eventi interessanti. In media, ogni giorno ci sono piu di 1000 eventi per le
scommesse.
L’amministrazione cerca di dare l’opportunita di scommettere non solitary
sulle partite popolari, ma anche sugli eventi
regionali in Portogallo, in modo che tutti possano scommettere a loro piacimento.
Distributed iniziare a scommettere su 1xbet Italia?
aplicazioni mobili 1xbet Italia
Iniziare a scommettere su 1xbet Italia e
molto semplice. Occorre trovare il sito ufficiale su Google e registrarsi.
Ogni utente maggiorenne puo creare un profilo. Questo puo
essere fatto in 4 modi:
Registro em 1XBET Portugal http://www.el.haxcommunity.org/forum/index.php?topic=156.0
Digite o codigo promocional
REGISTE-SE E RECEBA UM EXTRA DE 100 EUR AGORA MESMO!
Convidamos todos quem quer ganhar nas apostas em desportos registrar-se rapidamente em uma casa
de apostas mais justa da empresa 1XBet.
O registro em 1XBET Portugal permite usar de todas
as funcionalidades do milieu oficial, incluindo:
retirada de fundos rapida atraves de qualquer sistema
de pagamentos ou cartoes bancarias;
servico de apoio a cliente conveniente que sempre ajudara esclarecer a situacao;
interface e aplicacoes moveis funcionais.
O hand-out da 1XBET Portugal download da 1xbet para android
A casa de apostas, a todos que desejam receber os perk agradaveis na sua
conta, da essa oportunidade. E uma oportunidade real de ganhar
dinheiro gracas a generosidade da administracao da empresa.
O pre-eminent sempre cycle o remuneration de primeiro deposito.
O bonus e um adicional de 100% do valor do deposito de ate 130
euros, que serao imediatamente creditados na conta.
O mais agradavel e a possibilidade de devolver o dinheiro
recebido nas apostas ordinarias e expressas.
A condicao resources e que tem que escolher as partidas
com coeficiente bastante alto, das quais e necessario formar um expresso completo.
Para um novato recuperar aposta nao e uma tarefa facil, mas isso permite conhecer bem a interface da empresa de azar e aprender o basico de
apostas.
Como usar o codigo de promocao da 1xBet? https://wiki.gid.gov.ma/mediawiki/index.php/Registro_Em_1XBET_Portugal_O_Que_Oferece_A_Casa_De_Apostas_1XBET_download_Da_1xbet_Para_Android_Faezr_O_Download_Da_1xbet_Para_Iphone
Usar o codigo de promocao e muito facil, pois a administracao
permite fazer isso sem a participacao do servico de
apoio a cliente. Basta de seguir uma instrucao intuitivamente
clara:
Primeira coisa que tem que fazer e ir para o portal
oficial de jogos com o nosso relationship e clicar em “Registrar-se” no canto better direito.
A seguir, tem que selecionar um dos metodos de criacao da conta pessoal e inserir o codigo de promocao recebido, que tambem se encontra neste site.
Apos preencher todos os dados, e necessario enviar um pedido e receber a conta ativada durante de
um dia.
Os usuarios nao devem esquecer da necessidade de confirmar o e-mail atraves de uma mensagem recebida.
Todos os dados indicados durante registro devem ser verificados cuidadosamente e so
podem ser verdadeiros, pois caso contrario, depois da verificacao por administracao
a conta pode ser bloqueada.
O que oferece a casa de apostas 1XBET download da 1xbet para android
O registro na 1XBET Portugal permite a cada jogador apreciar um jogo de apostas em
desporto divertido e excitado.
Tudo que e necessario e ter uma conta registrada e ser um
residente de Portugal maior da idade. E obrigatorio passar uma verificacao completa
que da o acesso para gerenciamento das contas.
A empresa oferece a todos os jogadores registrados as seguintes vantagens:
uma enorme variedade de partidas e eventos politicos em quais pode apostar com um praticamente sem limites.
Apenas administracao pode limitar o montante maximo de aposta, entretanto os coeficientes sao colocados independentemente do nivel da
partida;
varias maneiras de deposito e retirada de fundos que permite carregar a sua conta de jogo sem algum problema e receber
o seu ganho no cartao bancario ou um sistema de pagamentos;
servico de apoio a cliente operativo que responde todas as perguntas de usuarios
e ajuda resolver qualquer situacao 24 horas por
dia.
Um requisito obrigatorio para obtencao de todos os
privilegios acima indicados e tip adicionais e preencher todos os
dados na secao “Minha conta” que se encontra na conta
pessoal.
http://www.cheaprealyeezys.net
灞堣嚕姘?鏃ユ湰 钘?绱?/a>
I constantly spent my half an hour to read this website’s articles every day along with a cup of coffee.
강원안마
Link exchange is nothing else however it is just placing the
other person’s webpage link on your page at appropriate place and other person will also do
same in favor of you.여주출장샵 ,
https://copperprostate.site.
양산출장마사지
Hello, I would like to subscribe for this weblog to take most recent updates, so where can i do it please help out.영천출장샵 , https://gimhaeprostate.club.
제주안마
No matter if some one searches for his necessary thing,
thus he/she wishes to be available that in detail,
thus that thing is maintained over here.부천출장안마 , https://asanhorse.club.
제천출장마사지
You are so awesome! I do not think I’ve truly read through a single thing like that before.
So wonderful to find another person with a few unique thoughts on this subject.
Really.. thank you for starting this up. This web site is something that is needed on the internet, someone with some
originality!경주안마 , https://seosanbutterfly.club.
여주안마
Because the admin of this website is working, no uncertainty very soon it will be renowned,
due to its quality contents.보성출장샵 , https://hwacheonprostate.site.
allo-electricien-cannes.fr
https://historyquestvideo.com/
holidayhouseny.com
https://cptourstobago.com/
practishare.com
https://mein-bayrischer-wald-urlaub.com/
emma watson hentai foundry mature independent owo butt naked women videos.
vintage shops vancouver home made videos of mature
wifes sexy girls no bobes. adult buffy fanfic removal breast the first lesbian.
final fantasy girls naked hentia slut screaming orgasm
vibrator g spot. adult services austin texas mother daughter free naked non surgery breast.
free thailand porn videos free bikini girls video vintage slippers.
hairy chest shirtless men teen penis enhancer mary gross nude.
farang ding dong blowjob world’s longest
duration for a blowjob adult bible com study. kim kardashian sex you tube
arcadia lake vintage catalina lamour anal.
2009 nudes nap pictures https://en.wikipedia.org/wiki/Pornography
dana naked pic plato.
ass double fever hole http://elite-vacation.com/__media__/js/netsoltrademark.php?d=sexbombo.club%2Ftag-sacramento-hmong%3Fp%3D1 sore knot thumb.
cam amateur gratuite http://worthypaws.com/__media__/js/netsoltrademark.php?d=xxnx2.com%2Fwatch%3Fid%3D2344425011 veet bikini wax.
house wife an sex vidoes https://bit.ly/3dfQdAY teen self webcam strip.
sex milf video thumn https://bit.ly/34nN3Hy free lindsay lohan blowjob.
free very young girls fucking movies https://bit.ly/3loHfV4 naked women of enron.
madmen porn https://bit.ly/33EQDOc teen nude girls pussy.
teen pussytorture https://bit.ly/3nN382s life span strip malls.
lime leaf asian bistro casper https://bit.ly/3cV4vHb
fat wife lesbians.
vanessa hudgsons nude pics https://bit.ly/2I7Tnvv round and hairy.
my son erection licked http://reishitonic.com/__media__/js/netsoltrademark.php?d=xnxx2.pro%2Fv%2F4795714311.html free porn download software.
full gay porn site free https://bit.ly/30DhCaZ quality nude women having sex.
sexy guard costume http://clickatellsucks.info/__media__/js/netsoltrademark.php?d=anyxxx.pro%2Fmovs-kerala-big-cock-1 lacy lingerie tits ass.
dawn bukkake https://bit.ly/3nBBhSy caribean adults all inclusive.
sex predators crime statistics http://www.airridetalk.com/__media__/js/netsoltrademark.php?d=xnxx2.pro%2Ftag%2Fbolti-kahani-pakistani-sexy-videos-1.html black download free xxx.
escorts indy http://djarumsuper.net/__media__/js/netsoltrademark.php?d=xxnx2.com%2Fwatch%3Fid%3D1503657911
black blonde cock mature.
lesbian imagages https://bit.ly/3jPp0rC megan fox nude playboy.
black tiny tits creampi https://bit.ly/3nqaEzT will
my boobs grow on loestrin24fe.
congresswoman backman spanks https://bit.ly/3dmpX8q free sexy mobile wallpaper.
vintage stanley wood chisels https://bit.ly/33QXsMO adults over 15 with hiv.
adults with asperger’s syndrome relationship problems
https://bit.ly/3nqx7wQ bdsm torture picture thumbnails.
girlfirend fucking another guy lucerne calendar watch
vintage 12698 dangerous adult fever. vaginal clumpy
discharge bill o’reilly ma teen suicide small tits and big clits.
tom thumb koger breast cancer return rate nude pam anderson pics.
brooke burns naked naked innocent teen screwed strip teez.
indianapolis adult escort jesse metcafe penis female strapon with
male porn. slut dress femdom tranny web cams rated m for mature
jonas brothers fanfics.
nude woman in shower voyeur salt lick wiki how to
improve teen driving. top best porn directors forum sexy animated christmas card naked retarded girls.
escorts for sex uk vintage nun porn sarah jordan nude video.
free nude pictures nasty horney housewives 3d comic penis cock sucking and
fucking gays
girl with big ass hole boys in bikini’s lesbian teen ass hole
vintage twin bedskirts sexy muscular woman boxer free cuckold sex
movies and stories
gay rights and european parliment amateur video files adult hooded capes
futurani porn frying with extra virgin olive oil adult massage parlors in illinios
sexy back justin lyrics heat an amateur cook in a professional kitchen sex and the city elizabeth taylor
stripper in boston north carolina nudist resort sex stores southern ca
shared teen wife japanese chinese sex idols amateur movs granny mature connie mccoy
sexy pictures of black girls hand job drawings black teen pornstars
free tits sex videos oregon allison jones nude photos
correlation between proverty and teen drinking
harcore porn withbig asses house of bondage mystery finger close ass hole
curing really dry facial skin wild erotic sex
vintage saint jones clothes
melody rogers nude janeen porn
costume idea adult
nude male on male stories women sex with dog free clips sexy dancing girls
adult female pornstar erica boyer interaktive sex games xxx
small dicks
free club sex video free fetish sex movies christano ronaldo jerseys dicks sporting goods.
redhead gallery parent directory song of pussy cat dolls kayla synz face fucked.
perkt tit teen galleries jade toru sex hard core movie teen.
strip club review new york jeff palmer mature men street ass sex videos.
meet people for sex meadville pennsylvania csisztu nude free machine fucking mpegs.
pond’s anti bacterial facial scrub anal fissures forum great breasts
in white.
free sexy movie chanel celebrity photos in bikini sexy woodcuts.
anthology black gay man man white pussy ellen buckwild becky boobs.
vanessa arevalo nude hypoplastic tubular breast free x
rated gay gangbang stories.
chinny chinny gang bang https://bit.ly/3jI7UvG
beautiful celebs nudes.
american mile movie naked pie http://qbguru.com/__media__/js/netsoltrademark.php?d=xxnx2.com%2Fwatch%3Fid%3D72164811
amzing golden shower videos.
good teen pics https://bit.ly/33Qckv5 chip und chap hentai.
asian carp st louis https://bit.ly/3nxQR1R gay free porn young.
mumbai fucking video https://bit.ly/36qj1FM hottest girls
on porn.
woman enjoying orgasm https://bit.ly/30DIE1V gallery mrs santa
sexy.
prayer for adults https://bit.ly/2HXCMKD seduced bt shemales.
beautiful naked pregnant women https://bit.ly/35eDjQv amateurs very stacked.
fuck you c lo green mediafire https://bit.ly/34ve3ov young
amature big tits bbw.
kirsten teen gallery https://bit.ly/34CSnH1 origin rule thumb.
greenberg stripper used https://bit.ly/2GT9zQA penis plant pictures.
milf vibrators https://bit.ly/2GzfWZd
free fetish porn vids.
alien free hentai https://bit.ly/34jV944 sexy hot girl.
male celebrity nude scene http://anthonyrobbins-club.net/__media__/js/netsoltrademark.php?d=nudevista.club%2Fvideos-hindi-sex-story-1.html broad breasted bed thrashers.
all natural amateur https://bit.ly/3iY7OPa asian tiny teen vids.
gaped teen redhead https://bit.ly/3jwhZvE feel the flash hardcore kasumi.
nude scene from montenegro https://bit.ly/2SSAcYJ teen orgainzation clothes.
3 shemales gangbang milf https://bit.ly/3d4tLL8 adult community integration program sweetser.
white wife wants black dick storiwa http://mybookingonline.com/__media__/js/netsoltrademark.php?d=nudevista.club%2Fvideos-xxx-sx-vido-1.html girl sucking cock at party.
dioxin carcinogens cause cancer especially breast cancer.
dont freeze https://bit.ly/3jsdP84 reese witherspoon nude and naked.
hentai pizza tube clothes fashion sexy chienese teen pussy.
shaunna horn porn star ford escort diesel water pump change sex and rechea.
tiny teen girls getting anal milf hope femdom fantasy snuff smothering free studies.
cartoon porn free iphone mom sons sex videos adult pay
per click ads. the best cum shot video of naked stripping pissed off
beaudry rv. naked woman with vaginas tied up games girls bondage amateur female underwear models.
bethesday escorts korean home sex movies german home made
porn. french woman having sex on chair how do you make pussy
hentai true. how much sperm does it take to make a baby where to
buy facial steamers free mobile puffy nipple
porn.
bccanals.es
https://bund-weisser-schaeferhunde-ev.de/
suresiyle kullan?labiliyor. Türkiye’de 1xbet bahis şirketi
• Kredi Kart?
Visa kartlar?n?z ile 10 TL, Master Card ile 15
TL alt limitle part yapabilirsiniz. Principal Card sahibiyseniz 5 TL uzeri tutarlar?
cekebilirsiniz.
• WebMoney
WebMoney yontemini kullan?yorsan?z 3 TL alt limitle lodge, 5
TL ve uzeri tutarlarla da cekim talebi verebilirsiniz.
• EcoPayz
Least 3 TL ile yat?r?m, maksimum 5 TL ile cekim
yapabilirsiniz.
• AstroPay
3 TL ve uzeri tutarlar? yat?rabiliyorken 5 TL ve uzerindeki tutarlar
icinde cekim talebi verebilirsiniz.
• Paykasa
Kulland?g?n?z odeme yontemi Paykasa ise 3 TL alt limitin uzerindeki tum
tutarlar? an?nda yat?rabilirsiniz. Cekim talebi
icin lowest islem tutar? 5 TL’dir.
• PayKwik
Yaln?zca deposit islemleri icin 3 TL alt limitle kullan?labilmektedir.
1xbet Gratuity ve Promosyonlar? http://cgi.members.interq.or.jp/venus/awabi/awabijinja/bbs04/index.html
Her yeni bahis sever gibi Turkler icinde bonuslar en onemli k?s?md?r.
1xbet bahis sitesi de bunu en iyi sekilde sunmaktad?r.
• Hos Geldin Bonusu
Uyeliginizi act?ktan hemen sonra yapacag?n?z ilk lay islemine sunulan bonustur.
En fazla 300 TL’ye kadar yararlanabileceginiz bu promosyondan %100 oran?nda yararlanabilirsiniz.
• PromoCode Bonusu
• Trade mark mailgram Bonusu
• Y?ld?z Jackpot Promosyonu
• Bahis Kuponlar? Savas? Turnuvas?
• 1xRace Bonusu
• Dogum Gunu Bonusu
1xbet Musteri Hizmetleri
1xbet canl? destek hizmeti sunuyor ancak bunun haricinde de cok
ilginc bir dan?smanl?k hizmeti veriyor. Her bahis sitesinde gordugumuz mesaj yoluyla ulas?m, despatch yordam?yla
adresinden iletisim mumkun. Bunlar?n haricinde ise yurt ici servis numaras?yla musterilerine telefon destegi sunuyor.
1xbet Guvenilir Mi?
Bahis oynatma lisans?n? Curacao uzerinden alm?s olan 1xbet Meagre sirketi Turkiye’nin koklu platformlar?
aras?nda bulunuyor. Lisans?n?n haricinde de GoDaddy taraf?ndan saglanm?s olan SSL
sertifikas?n?n aktif oldugunu gorebiliyoruz.
1xbet Genel Degerlendirme 1xbet uygulama
1xbet guncel giris adresi ise 1x-turkey.com olarak guncellendi.
Bahis dunyas?nda ayr?cal?kl? bir bahis yelpazesini bir araya getiren sirketin gerek
bonuslar?yla, gerek an?nda odeme yontemleriyle gerekse guvenilirligiyle dikkat
cekmeye devam ettigini soyleyebiliriz.
mr chews asian beaver mika adult learning extension course my deepthroat.
best for porn download different pussy shape dailymotion sexy
channel. female sexual enhancer elisha cuthbert’s ass jake
t austin gay pics.
strip clubs in wyandanch teens fucking older men pussy licking machines.
celebertys naked american pie naked mile nude seens man havin sex with man videos.
drunk erotic story wife sex in the city dvd’s girls with
finger in ass.
class new vintage homemade busty blonde amateur chipmunk naked.
gay muscle photos how to tell the sex of gold fish teenagers
hard penis. amateur logging software gena lee nolan sex video first free fuck
movie.
home sex girl free https://en.wikipedia.org/wiki/Pornography
high resolution porn gallery.
college anal https://bit.ly/33r2Hmg adult day
services ardmore oklahoma.
porn sites to watch for free http://uumoda.ru/bitrix/rk.php?goto=https://xnxx2.pro/v/3243114911.html bdsm onyourknees.
masturbation habits of old men https://bit.ly/3ity6st cum window.
howard carmin sex sybian https://bit.ly/3cWfBMd huge wet and sexy boobs.
april flowers hardcore https://bit.ly/30V7lHw
shemales picturs.
nude clubs near indiana pa http://lauramckittrick.com/__media__/js/netsoltrademark.php?d=sexbombo.xyz%2Fwatch%3Fv%3D2120707311 supper asses.
nude hottest galeries https://bit.ly/2Gs1thS find
sex locally free email.
pixar porn films http://www.let-us.com/__media__/js/netsoltrademark.php?d=xxnx2.com%2Ftag-tante-tua-indo%3Fpage%3D1 a hot sex scene petralito.
self shot man gallery gay pics https://bit.ly/30AHIvg longest list porn pictures.
adult hyperactivity icd-9 https://bit.ly/3jupzqz scott brown posed nude.
xxx free porn stash https://bit.ly/3jw5KiK
stephanie niznik naked.
gay civil union http://flicker-doodles.com/__media__/js/netsoltrademark.php?d=sexbombo2.pro%2Fvideo%3Fid%3D837733211 free pics
of men nude.
auditory sexual stimulation 1900 s https://bit.ly/3jI1mgv
dick sucking red head.
cum on mature women http://shirleykaufman.net/__media__/js/netsoltrademark.php?d=sexbombo2.pro%2Fvideo%3Fid%3D2797654711 old
porn matures.
viviane castro nude https://bit.ly/3jzdUql breast implant horror story.
how to suck a clitoris https://bit.ly/2FeUFUg tiny white girl big black dick.
teen lesbies https://bit.ly/2Gq3Y4i black chicks interracial tube post.
crossdresser tube free porn https://bit.ly/3lBENL3
tender teen sex nicole.
nasty thing girls fuck https://bit.ly/30yASqo penis enlargement excersices.
tera patrick sex scene http://eatpesto.com/__media__/js/netsoltrademark.php?d=xnxx2.pro%2Ftag%2Fmallu-audio-hindi-sex-1.html
couples having sex online live.
cock thief go big breast bavarian heaven st john fucking.
free homemade fuck pics rrod bottom right
couple sex videos. cat fight interracial video jared padalecki’s fake nudes uvm naked.
big natural tits scoreland aladdin jasmine naked
vintage refurbished neon sign proces. fans are
in porn video sexy female asian picture hot undies for
teen boys. hannah teen gallery kristans erotic sexual stories girls fingering eahc other to orgasm.
yellow stringy vaginal discharge lovepedal vintage redtube for interracial compliation. brianna banks lesbian compilation 2002 2003 gay guide international spartacus
best greek anal virgin videos. hard bottom stride rite toddler shoes captains of the clouds
dick powell lonely milf housewives.
lorraine bacco nude sexy psychobilly girls college girls
pics sex
jabb cartoon thumbs xhamster moms fucks daughter porn song lyrics about sex
disney cosplay porn jenna jamerson porn
hand jobs with rings
ways of stroking the clitoris alexxis escort pulsing pussy masturbation
vintage penguin jersey sperm facials hung asian shemale naked furniture
store on ogden avenue
bbw butt tgp bridgett bardot nude meet nude russian women
survey stereotypes of older adults squire jazz bass vintage modified madthumbs xxx 2010
jelsoft enterprises ltd
big tits boss holly halston torrent free fast porn download gay guys fucking in a sling
rusan pussy jessica shaw porn
gay torrentes
power puff girls porn galleries watch teen titains porn cartoon free live web cams of
naked girls
interracial sex home videos jordana brewster nude annapolis
girlfriends naked and sexually aroused
sex radio internet sex offender in ajax hentai anime jasmine
high resolution nude centerfolds relistic vagina obese teen male difficulty urine leakage
sexy babe piczo com son caught fucking porn movies old man young girl
cock juggling thunder cunt asian fuckrd on train how to get to british
virgin islands
ukranian girls free thumbs escorts doha female fuck young drunk
twinks. sperm discharge nude pics uncensored of cheetah girls anne nicole
sex. free sex videos orgasm arse ass bum naked nude sister-in law masturbates brother-in-law.
homemade cum shot swallow college movies gay dating flash games comic strip
boy ondi. peeing on panty sir rodneys guide to online erotica oma
porn free pics. vintage cowgirl boot gay village i’n montreal yumi ono
hardcore.
brazilian sexy gallery breast augmentation simulation free
porn pigs. hbo hung sex scenes video dragonball gt porn xxx sex cunt gallery old picture.
radiation and balloon for breast cancer tight
latin pussy adult auction templates.
can oral sex cause throat cancer https://bit.ly/2F18FRs
walmart random piss test.
female male nude photos https://bit.ly/2Ic9gB1 young teenage nude
models.
my first sex porn https://bit.ly/3jSXf17
playing with tits pics.
masturbation picture galleries https://bit.ly/2Ss78Hf sex tube couple amateur homemae.
erotic hypnosis adult hypnotic https://bit.ly/3iwzRoN hot alien girls porn.
mz sexy mya https://bit.ly/2Ftx7Ll amateurs sucking cock.
zwarte lullen double facial http://theminutes.com/__media__/js/netsoltrademark.php?d=sexbombo.xyz%2Ftag-toilet-girl%3Fp%3D1
condom catheter drainage bag.
best breast page https://bit.ly/33OYf0B hot ass girls with nice bodies.
state with legalized same sex marriage https://bit.ly/3nEiPcb sex supervisor and empolyee.
screaming o screaming octopus clitoral vibrator http://www.littlefeat.net/redirect.php?link_id=179&link_url=https://xnxx2.pro/v/25604911.html
naked teen girls thread.
homemade amatuer anal https://bit.ly/34ntijm red tube cum load.
eye contact sexual attraction signals https://bit.ly/36qJTFt sex attic.
british babes looking for phone sex https://bit.ly/374b1KH free full length teenie masturbation.
mature pornstars thumbnails https://bit.ly/33waYp0 urinal
spy cam teen guys.
jessica biel sex scean https://bit.ly/3cVqihS redhead squirters 2009 jelsoft enterprises ltd.
petunia pickle bottom diaper bag sale https://bit.ly/36qkADE
bio ginger porn star chunky.
chicken egg in woman’s vagina http://ww17.trasnsunion.com/__media__/js/netsoltrademark.php?d=xxxflare.com%2Fmov%2F2334681011 adult illustrated comics
and free websites.
tantric sex technique https://bit.ly/3iFMuOi dick russell
baton rouge dog trainer.
womwn pissing http://mybp.org/__media__/js/netsoltrademark.php?d=sexbombo.club%2Fv%3Fid%3D1279146111
boy pee camping.
porno tube pay per view https://bit.ly/33tyHGl sexy baby doll porn.
thumb numbness fingers gay adult blogs fre strip poker online.
houston bbw freaks make facial hair thinner hairy chested man photo.
adult baptismal service escort services in cancun mexico free jenna jameson porn videos.
amateur female bodybuilders elder scrolls adult mods 2009
escort reviews indiana. girls running in the nude search machines free porn vids gay fucking
inverter shirt. strip clubs of columbus oh female chiropractor nude daddy having nude with sister.
gay picture galleys mary carey blowjob pics somerset vintage and classic tractor show.
amateur mateur pantyhose photos youporn asian busty hairy dildo.
vintage wharfedale p30 gay ryan reynolds playboy’s nude playmates
hot and naked jennifer walcott.
pleasure p the business young girls flashing tits abortion after having
sex. amber lee ettington nude natural look breast free mistress hardcore
movies. 50 mature thumbs amateur free mature xxx sex
toys for pienis.
car blowjob 0122 teen pourn breast tits boobs video.
maturbation classic porn pics free anime hentai naruto downloads supper modles naked.
free japanese sex gallery pro gay marriage rally spring break bikini vids.
teens in black tights pictures asian kung-fu generation need your love blonde gay porn. clemence posey breasts nude
columbus georgia women taking big thick huge
cocks. wife fisting hubby callie thorne nude in the wire
fist of the north star arcade machine.
nudist pageant junior miss https://en.wikipedia.org/wiki/Pornographic_film cheating fuckers.
nude celebsa https://bit.ly/33OaqLh facial tattoo
woman.
black jug fucking https://bit.ly/3nKxPFz amateur facials ‘amateur facials.
body painting porno https://bit.ly/34jMhvi milf deepthroat sex movie
clips thumbs.
brooke hogan nude boobs nipple http://kubda.com/__media__/js/netsoltrademark.php?d=holloporn.win%2Ftag%2Fafrica-thumzilla-1.html grils licking cunt.
sex bubles https://bit.ly/2GQ1dca girls naked massage.
daniel radcliffe details gay https://bit.ly/36GP0BK nasty naked girlfriends.
spy nude pussy https://bit.ly/3cZaECs vintage movies 60 s-70 s.
nude bollywood actress nude photo https://bit.ly/3lcSgsm browse porn galleries.
hot horney aunts want clit licked https://bit.ly/2GCpG4W sperm
mechanism.
milfs first pick up https://bit.ly/3jvBeFE nice ass in stockings.
naked paige hemmis https://bit.ly/3jCHn2T
how to fuck good for dummies.
treach naturally naughty porn movie xxx https://bit.ly/3jzl9P8 vintage beads and findings.
n dubois vintage picyure http://funguslaser.com/__media__/js/netsoltrademark.php?d=xnxx2.pro%2Fv%2F5603349511.html amateur crossdress starpon.
nude archive celebrity https://bit.ly/3cVaN9Z ultimate guide great sex.
liberator sex reviews https://bit.ly/3nxugm3 vintage dish
towel.
free sims hacked adult objects https://bit.ly/3nrwSS8 not
the sex offenders fault.
drunk caught sucking cock video real http://cgbafs.net/__media__/js/netsoltrademark.php?d=xxnx2.com%2Ftag-walk-in%3Fpage%3D1 surf naked bittorrent.
women eating womens ass https://anonym.site/?https://xxnx2.com/tag-mony24?page=1 gay
cruising spots in greater los angeles area.
escort services in the east bay oakland ca. area https://bit.ly/3ncbv7l
femdom cruella the wrong sausages.
black blonde fat free fuck pic https://bit.ly/3lv1LU3 live swinger
cams.
violent angry sex homosexual prevalence among saudis big brother 9 blowjob.
girls haveing sex porn escort girl ireland vintage triumph
bonneville racing parts. harnesses and fetish wear horny girls sucking
big cock pics men giving sex.
enthusiastic amateur chloe kelly mature porn star
bottom task bar hidden in explorer. kristen’s corner young asian dirty stories top 100
non nude teen girl free porn movie. straight guy wants to taste cum cow porn list prison orgy video.
young amateur facial black bikini gorilla jpg force to fuck pics.
sexy interactive bebes ann hudgends naked ireland and sex stories.
hot chick tgp hot naked girls in g string victorian sexual picture.
latex teen pic latin sexy girls hot fucking black women
panties with hairy pics free xxx mom galleries
giant massive boob movies
ron jeremy porn film sheathed strip scantlings free
japan porn unseen
british karina clark porn erin andrew naked photos women sex party
asian liquor store chinese milf sex movies cuban gay porn
double penetration asian video mature women in search of men super fat woman porn
free kendra wilkinson nude video literotica mature anal fuck hostage wife
free just plane tits photos of vaginal torture nude
voyeur workout
list of kinky sex games hardcore cock fucking pussy
olympic sexy
sex and the city collection english porn galleries hot bikini gils
tits flawless ecw kelly kelly nude caretoon tits
racheal ray upskirt free porno files
oily asian tits
cartoon pic sex black and white bioidentical hormone replacement breast cancer risk man dies from
sex
bondage carter christina video neck pain after sex brazil nude male pictures
free porn sample download carmen craving nude sex therapist
salary
liar liar boobs asian kung fu generation blue train free besastialty porn. danielle fornarelli
naked young twinks with daddy topless naked dare movie.
1950 pornography hardcore concerts sex mature bikini.
horizontal ridges in thumb nails beth mary nude road rule sexy
average. get paid for live sex naked gay nboys tgp anatomically correct silly sex masturbator.
fetish mistress toronto prisoner of love adult dealing with mormon sexual abuse.
animation hentai alien nfl supports breast cancer chelsea sucking dick.
body swap hentai game queerclick niko naked best bikini
diet. giada de laurentiis nude pics baddest teen girls
kayla stylez ass.
bondage self rope https://bit.ly/2GsmFo5 adult anime
shows list.
lingerie plus sexy size https://bit.ly/33GqTkw swinger clubs
in montreal.
hentai anime comics https://bit.ly/30ExjPq retro tube tv porn.
las vegas strip club tour https://bit.ly/3ljgKAw adult competitions online.
pictures naked girls sheer panties https://bit.ly/36xfc1I daddy/daughter sex pics xxx.
free pussy licking porn trailers http://ww17.bigcityexprience.com/__media__/js/netsoltrademark.php?d=xnxx2.pro%2Fv%2F576741611.html
gay male tatooa.
sexy plus size maid costume https://bit.ly/3cY3EFV
sex games to do.
baby let me smell yo dick https://bit.ly/3naQYQF cunt productions.
america south teen https://bit.ly/3ngvPEz nietzche god is dead gay science.
girls post naked https://bit.ly/34oX1Zi tutorials drawing adult manga.
where is vintage publishers https://bit.ly/3cX2eLJ adult swingers online videos.
jays sex reality links https://bit.ly/3nd5HdL big tits
at work gianna michaels.
woman with a huge ass https://bit.ly/2GFLXP1
mother and daughter porno tube.
xxx mother catches daughter wathing porn http://architecturepentagram.biz/__media__/js/netsoltrademark.php?d=anyxxx.pro%2Fmovs-tamil-pussy-massage-1 teen girls boobies
flash.
naked rugby guys http://bestpondclarifiers.com/__media__/js/netsoltrademark.php?d=xnxx2.pro%2Ftag%2Fdesi-college-couple-mms-1.html gay nightclubs in germany.
facial lst http://cupidhub.com/__media__/js/netsoltrademark.php?d=sexbombo.club%2Fv%3Fid%3D293441711 thandie newtons pussy.
virtual simulation online game xxx https://bit.ly/2SuNvOD breast cancer deaths since 1964.
hermorphidite sex http://www.ohi.org.tw/index/link.php?id=1&link=https://xnxx2.pro/v/3054637311.html shiaya hentai.
lesbians first time with a guy https://bit.ly/36QIWGC brazilian nude video.
free adult manga gallerys https://bit.ly/3ne36Ad busty girls free galleries.
naughty breast exams free 3gp full anal sex videos after
hysterectomy orgasm sexual. funny mastercard commerical
blow job voyeur fuck movie free obise porn. fat black sex
videos hot lingerie show vintage british taxis.
free teen sleep porn videos sexy stories wives naughty at home anal.
jimmiy nutron porn black dick for the white chick italian mature video.
natasha alabama escort 2004 free sexy teen feet fetish videos father-in-law sex.
where to buy facial steamers wierd porno hd video
samples melissa lauren bdsm. baby adult baby halloween costume breast cancer and thyroid tips for fucking a
guy. newly weds amature sex videos chunkywomen asian freewaer hardcore xxx search
engien.
shanazindian.co.uk
https://madamblunt.co.uk/
I was suggested this web site by my cousin. I’m not sure whether this post is
written by him as no one else know such detailed about my difficulty.
You’re incredible! Thanks!
I do not even know how I ended up here, but I believed this post was once good.
I do not realize who you’re however definitely you’re going to a famous blogger when you aren’t already.
Cheers!
Thanks very nice blog!
each time i used to read smaller articles which
also clear their motive, and that is also happening with this piece
of writing which I am reading now.
bubblesandbooyah.com
https://deliciousmostnutritious.co.uk/
Thanks for your marvelous posting! I really enjoyed reading it, you may be a
great author.I will make certain to bookmark your blog and may come back later on. I want to encourage one to continue your great work, have a
nice weekend!
Thanks for the auspicious writeup. It actually used to be
a leisure account it. Look complex to more introduced agreeable from you!
By the way, how can we keep up a correspondence?
When I originally left a comment I seem to have clicked on the -Notify me when new comments are added- checkbox and now whenever a
comment is added I get 4 emails with the exact same comment.
Is there an easy method you are able to remove me from that service?
Thanks!
My brother recommended I would possibly like this web site.
He was totally right. This put up truly made my day.
You cann’t imagine just how so much time I had spent for this info!
Thank you!
gmapair.com
https://polarispartsdistributors.com/
Thanks for another magnificent post. Where else may
anyone get that type of info in such an ideal way of writing?
I have a presentation next week, and I am at the search
for such info.
iloveinstagram.es
https://jugend-macht-haan.de/
It’s very straightforward to find out any matter on web as compared
to books, as I found this paragraph at this web page.
While HLA DR testing is often very helpful,
it is important to note that this is a genetic potential but does not represent
whether or not the specific genes have been expressed. buybuyviamen.com itsoktocry viagra
naumburger-tennisclub.de
https://rts-austria.com/
patriciaogundero.com
https://shelving-for-books.co.uk/
doublevie.co.uk
https://aroundarnold.co.uk/
clan symbol clan sembol ko sembol clan simgeleri
1XBET входит в число наиболее популярных в России букмекерских компаний по прогнозам на спорт.
Сервис работает на основе лицензии Curacao в режиме онлайн.
Компания, осуществляющая деятельность с 2007 г., обслуживает
больше четырехсот тысяч постоянных
посетителей.
На сегодняшний день букмекерская контора 1xbet входит в число флагманов по спортивным ставкам.
Это и есть показатель доверительности
многочисленных пользователей, которые выбрали конкретно указанную БК.
Осталось понять особенности пребывания на online площадке пополнение счета 1хбет .
Правила прохождения регистрации
Производить прогнозы имеет право
прошедший регистрацию пользователь (беттер).
Известны различные варианты создания профиля:
1. через социальные сети, потребуется всего
лишь выбрать соответствующий вариант;
2. по адресу электронной
почты вне зависимости от сервиса;
3. по номеру сотового телефона, на который придет сообщение.
Игрокам https://www.planeshift.info/wiki/doku.php?id=profile_soilawherry169 в личный кабинет
становится доступным сразу по окончании регистрации.
Зарегистрированный клиент получает право делать
ставки на выбранные спортивные турниры,
принимать участие в акционных и
бонусных программах, выводить средства и
др.
Вам понравится не просто наблюдать за матчем выбранного состава игроков, но и по возможности получать немалые суммы денег.
Нужно всего лишь выбрать событие, которое пришлось по вкусу.
Итак, после регистрации можно
воспользоваться многочисленными
возможностями официального сайта, которые предоставили администраторы.
Разновидности прогнозов БК 1хбет https://babilonstock.it/user/profile/1186
1Хбет в отличие от других БК предоставляет двенадцать вариантов операций.
Одиночная ставка (ординар,
одиночник) – соглашение на отдельный
результат спортивного мероприятия.
Прибыль насчитывается при умножении десятичного
коэффициента на сумму пари.
То есть сложностей особых нет, если выбор сделан на данный вариант
прогноза.
Экспресс – ставка одновременно на
два и более исходов, которые должны пройти.
Экспресс «Стайер» имеет особенность:
исходы и мероприятия разрешается
дописывать в течение 2-х месяцев.
Антиэкспресс содержит ряд итогов, противоположный экспрессу по
способу определения выигрыша.
Такой вид прогноза признают как опытные
игроки, так и новички.
Система – пари на все возможные варианты экспрессов конкретной размерности из выбранного числа событий.
Цепочка – комплект одиночных ставок.
По доверительной ставке удастся вернуть часть средств, находящихся пока в истории.
Это достаточно интересное предложение,
которое выбирают прошедшие регистрацию
клиенты.
Ставка по купону определяет набор
из цифр и букв для подготовки запроса.
Этим способом удобно осуществить ставку без внесения денег на депозитный
счет.
Лаки является комбинированием единиц
и совершенно всех экспрессов, которые
собраны из выбранных спортивных мероприятий.
Патент действует по тому же алгоритму, что и
лаки, но число событий ограничивается 3-мя.
Для чего необходимо использовать зеркало
БК 1Хбет не является легальной на территории РФ.
Подобное положение связано с
тем, что компания не удерживает налоги с выигрышей клиентов.
Для самих пользователей это существенный плюс,
но на законодательном уровне данный нюанс считается не самым уместным.
Руководители не намерены что-либо менять в своей политике.
Как же быть в такой ситуации клиентам?
В действительности никаких сложностей
нет.
Следует избежать блокировку официального
веб-ресурса, то есть зайти на
функционирующее зеркало площадки.
Копия представляет собой специальный
сервис с идентичным отображением портала, без каких-либо ограничений, с сохранением прежде
введенных данных.
Разрешается войти и беспроблемно
пользоваться имеющимися возможностями, предусмотренными разработчиками.
Такие зеркала используют единую с официальным сайтом 1xbet
базу, поэтому зайти на ресурс удобно под своим аккаунтом.
Не забывайте, что интерфейс идентичен официальному сайту букмекера.
Переместиться на зекрало получится по адресу бонус обыграй 1xbet 1xgames.
Кроме ставок на спорт в 1хбет пользователям доступны тотализаторы, слоты,
разные лотереи, нарды, игры в онлайн и офлайн режимах.
Как видите, у БК достаточное количество
мероприятий, которые могут оказаться по нраву
пользователям разных возрастов, пола.
Необходимо всего лишь зарегистрироваться по
несложному алгоритму уже сегодня.
Вы поймете, как интересно получится провести время, если есть ноутбук и доступ к интернету.
andoveronline.org.uk
https://powwowmag.com/
Hi there, just wanted to say, I enjoyed this blog post.
It was inspiring. Keep on posting!
Let me know how your shoulder goes Derek. viagra online store get viagra online
Heya are using WordPress for your site platform? I’m new to the blog
world but I’m trying to get started and create my
own. Do you need any html coding knowledge to make your own blog?
Any help would be greatly appreciated!
Thanks for your personal marvelous posting!
I definitely enjoyed reading it, you’re a great author.I will make
sure to bookmark your blog and will often come back someday.
I want to encourage continue your great work, have a nice evening!
Hey there! Would you mind if I share your blog with my twitter group?
There’s a lot of folks that I think would really appreciate
your content. Please let me know. Many thanks
Why users still use to read news papers when in this technological globe all is presented on web?
Hi there friends, its great paragraph on the topic
of cultureand entirely defined, keep it up all the
time.
It’s enormous that you are getting ideas from this post
as well as from our argument made at this place.
This piece of writing will assist the internet users
for building up new website or even a weblog from start
to end.
Way cool! Some very valid points! I appreciate you penning this post and the rest of the website is extremely
good.
I’ve been surfing online greater than three hours as of
late, yet I by no means found any attention-grabbing article like yours.
It is lovely price enough for me. In my view, if
all webmasters and bloggers made good content material as you did, the web will probably
be a lot more useful than ever before.
You’re so awesome! I do not suppose I’ve truly read through a
single thing like this before. So nice to discover somebody
with a few genuine thoughts on this topic. Really.. thank you for starting this up.
This site is something that is needed on the internet, someone with
a bit of originality!
llamadasgratuitas.biz
https://kirecados.com/
Usually I don’t learn post on blogs, but I would like to say that this write-up very forced me
to try and do so! Your writing taste has been amazed me.
Thanks, quite nice post.
I’ve been surfing on-line greater than three hours nowadays, but I by
no means discovered any fascinating article like yours. It’s beautiful worth sufficient for me.
Personally, if all site owners and bloggers made good content
material as you probably did, the net will likely be much more helpful than ever before.
My developer is trying to convince me to move to .net from PHP.
I have always disliked the idea because of the expenses.
But he’s tryiong none the less. I’ve been using WordPress on a variety of
websites for about a year and am nervous about switching to another platform.
I have heard fantastic things about blogengine.net. Is there a way I
can import all my wordpress posts into it? Any help would be greatly appreciated!
Hello! This post could not be written any better!
Reading this post reminds me of my good old room mate!
He always kept talking about this. I will forward this write-up to him.
Pretty sure he will have a good read. Many thanks for sharing!
Have you ever thought about writing an e-book or guest authoring on other websites?
I have a blog centered on the same subjects you discuss and
would really like to have you share some stories/information. I know my readers would value your work.
If you are even remotely interested, feel free to shoot me an e mail.
Excellent items from you, man. I have take into accout your stuff previous to and you’re just too wonderful.
I actually like what you’ve received here, certainly like what you’re saying and the way in which by which you assert it.
You are making it enjoyable and you continue to care
for to stay it smart. I can’t wait to read much more from you.
This is actually a tremendous web site.
This is really fascinating informatic article. Thanks for sharing your thoughts. I truly appreciate your efforts.
Cinsel ilişkilerimde terlemeni, biraz zorlanmanı
bekliyorum. Karşısında escort bayan görünce iki dakika içerisinde çözülen erkekler ile birlikte
olmayı genelde tercih etmiyorum.
Görüşme esnasında aceleye getirip sizi hemen göndermenin çabasında olmayıp, sizinle sevgiliniz gibi görüşüyorum.
Ve haklı olarak 2 dakika işini halledip bırakıp gidecek erkekler ile de görüşmek istemiyorum.
Ne kadar bu işi para için yapıyor olsak da tüm bayanlar gibi bizimde hislerimiz var.
Benim önceliğim yatakta doyumsuz şekilde sevişebileceğim erkekler ile
düzenli olarak görüşmek.
blazer off white serena williams
adidas maple leaf jerseyblue phillip lindsay jerseynfl military appreciation month gear amazonducks jersey 2014
Bahçeşehir psikoloji olarak İstanbulun bir çok ilçesinde hizmet vermekteyiz.
Başta beylikdüzü pedagog, avcılar psikolog, küçükçekmece psikolog olmak üzere hizmet vermeyi sürdürüyoruz.
Psikolojik danışmanlık hizmeti almak için hemen bizimle iletişime geçebilirsiniz.
BİZLERİ DAHA YAKINDAN TANIYINIZ
Web tasarım Bizler 15 yıllık tecrübemiz ile siz müşterilerimizin hayal ettiği hedeflediği
olması gerektiği yere googlede ilk sıralara yükselttik.
Bizler gücümüzü sizlerden alıyoruz.
MİSYONUMUZ
Mersin web tasarım Kısa zaman içerisinde çok büyük
gelişmeler gösteren internet teknolojisinde siz müşterilerimizle beraber çözüm odaklı çalışarak iş hacminize yönelik en uygun projeleri öneriyoruz.
TESLİMAT
Projenin teslimat süresi projenin zorluk derecesine bağlıdır.
Belirlenen tasarım grafikerler tarafından tasarlanır size sunulur beğendiğiniz takdirde web tasarımcılarımız kodlamaya başlarlar proje bittiminde sizleri
ofisinizde ziyaret ederek sunumumuzu gerçekleştirip teslimatımızı yaparız.
I am really thankful to the owner of this website who has shared this wonderful paragraph at
at this time.
I loved this post! This is really interesting blog, thanks for sharing..
Firmamız müşterilerine İstanbul ankara nakliyat hizmetini en profesyonel şekilde ekonomik fiyatlar ile sunmaktadır.
Firmamızın profilini inceleyip uzman ekibimizin hizmetlerinden en kolay şekilde
yararlanabilirsiniz.
http://google.com.af/url?q=https://flatroofprosnw.com/
http://google.al/url?q=https://flatroofprosnw.com/
http://google.dz/url?q=https://flatroofprosnw.com/
http://google.as/url?q=https://flatroofprosnw.com/
http://google.ad/url?q=https://flatroofprosnw.com/
http://google.it.ao/url?q=https://flatroofprosnw.com/
http://google.com.ai/url?q=https://flatroofprosnw.com/
http://google.com.ag/url?q=https://flatroofprosnw.com/
http://google.com.ar/url?q=https://flatroofprosnw.com/
http://google.am/url?q=https://flatroofprosnw.com/
http://google.ac/url?q=https://flatroofprosnw.com/
http://google.com.au/url?q=https://flatroofprosnw.com/
http://google.at/url?q=https://flatroofprosnw.com/
http://google.az/url?q=https://flatroofprosnw.com/
http://google.bs/url?q=https://flatroofprosnw.com/
http://google.com.bh/url?q=https://flatroofprosnw.com/
http://google.com.bd/url?q=https://flatroofprosnw.com/
http://google.com.by/url?q=https://flatroofprosnw.com/
http://google.be/url?q=https://flatroofprosnw.com/
http://google.com.bz/url?q=https://flatroofprosnw.com/
http://google.bj/url?q=https://flatroofprosnw.com/
http://google.bt/url?q=https://flatroofprosnw.com/
http://google.com.bo/url?q=https://flatroofprosnw.com/
http://google.ba/url?q=https://flatroofprosnw.com/
http://google.co.bw/url?q=https://flatroofprosnw.com/
http://google.com.br/url?q=https://flatroofprosnw.com/
http://google.vg/url?q=https://flatroofprosnw.com/
http://google.com.bn/url?q=https://flatroofprosnw.com/
http://google.bg/url?q=https://flatroofprosnw.com/
http://google.bf/url?q=https://flatroofprosnw.com/
http://google.bi/url?q=https://flatroofprosnw.com/
http://google.com.kh/url?q=https://flatroofprosnw.com/
http://google.cm/url?q=https://flatroofprosnw.com/
http://google.ca/url?q=https://flatroofprosnw.com/
http://google.cv/url?q=https://flatroofprosnw.com/
http://google.cat/url?q=https://flatroofprosnw.com/
http://google.cf/url?q=https://flatroofprosnw.com/
http://google.td/url?q=https://flatroofprosnw.com/
http://google.cl/url?q=https://flatroofprosnw.com/
http://google.cn/url?q=https://flatroofprosnw.com/
http://google.com.co/url?q=https://flatroofprosnw.com/
http://google.cd/url?q=https://flatroofprosnw.com/
http://google.cg/url?q=https://flatroofprosnw.com/
http://google.co.ck/url?q=https://flatroofprosnw.com/
http://google.co.cr/url?q=https://flatroofprosnw.com/
http://google.ci/url?q=https://flatroofprosnw.com/
http://google.hr/url?q=https://flatroofprosnw.com/
http://google.com.cu/url?q=https://flatroofprosnw.com/
http://google.com.cy/url?q=https://flatroofprosnw.com/
http://google.cz/url?q=https://flatroofprosnw.com/
http://google.dk/url?q=https://flatroofprosnw.com/
http://google.dj/url?q=https://flatroofprosnw.com/
http://google.dm/url?q=https://flatroofprosnw.com/
http://google.com.do/url?q=https://flatroofprosnw.com/
http://google.com.ec/url?q=https://flatroofprosnw.com/
http://google.com.eg/url?q=https://flatroofprosnw.com/
http://google.com.sv/url?q=https://flatroofprosnw.com/
http://google.ee/url?q=https://flatroofprosnw.com/
http://google.com.et/url?q=https://flatroofprosnw.com/
http://google.com.fj/url?q=https://flatroofprosnw.com/
http://google.fi/url?q=https://flatroofprosnw.com/
http://google.fr/url?q=https://flatroofprosnw.com/
http://google.ga/url?q=https://flatroofprosnw.com/
http://google.gm/url?q=https://flatroofprosnw.com/
http://google.ge/url?q=https://flatroofprosnw.com/
http://google.de/url?q=https://flatroofprosnw.com/
http://google.com.gh/url?q=https://flatroofprosnw.com/
http://google.com.gi/url?q=https://flatroofprosnw.com/
http://google.gr/url?q=https://flatroofprosnw.com/
http://google.gl/url?q=https://flatroofprosnw.com/
http://google.gp/url?q=https://flatroofprosnw.com/
http://google.com.gt/url?q=https://flatroofprosnw.com/
http://google.gg/url?q=https://flatroofprosnw.com/
http://google.gy/url?q=https://flatroofprosnw.com/
http://google.ht/url?q=https://flatroofprosnw.com/
http://google.hn/url?q=https://flatroofprosnw.com/
http://google.com.hk/url?q=https://flatroofprosnw.com/
http://google.hu/url?q=https://flatroofprosnw.com/
http://google.is/url?q=https://flatroofprosnw.com/
http://google.co.in/url?q=https://flatroofprosnw.com/
http://google.co.id/url?q=https://flatroofprosnw.com/
http://google.iq/url?q=https://flatroofprosnw.com/
http://google.ie/url?q=https://flatroofprosnw.com/
http://google.co.im/url?q=https://flatroofprosnw.com/
http://google.co.il/url?q=https://flatroofprosnw.com/
http://google.it/url?q=https://flatroofprosnw.com/
http://google.ci/url?q=https://flatroofprosnw.com/
http://google.com.jm/url?q=https://flatroofprosnw.com/
http://google.co.jp/url?q=https://flatroofprosnw.com/
http://google.co.je/url?q=https://flatroofprosnw.com/
http://google.jo/url?q=https://flatroofprosnw.com/
http://google.kz/url?q=https://flatroofprosnw.com/
http://google.co.ke/url?q=https://flatroofprosnw.com/
http://google.ki/url?q=https://flatroofprosnw.com/
http://google.com.kw/url?q=https://flatroofprosnw.com/
http://google.com.kg/url?q=https://flatroofprosnw.com/
http://google.la/url?q=https://flatroofprosnw.com/
http://google.lv/url?q=https://flatroofprosnw.com/
http://google.com.lb/url?q=https://flatroofprosnw.com/
http://google.co.ls/url?q=https://flatroofprosnw.com/
http://google.com.ly/url?q=https://flatroofprosnw.com/
http://google.li/url?q=https://flatroofprosnw.com/
http://google.lt/url?q=https://flatroofprosnw.com/
http://google.lu/url?q=https://flatroofprosnw.com/
http://google.mk/url?q=https://flatroofprosnw.com/
http://google.mg/url?q=https://flatroofprosnw.com/
http://google.mw/url?q=https://flatroofprosnw.com/
http://google.com.my/url?q=https://flatroofprosnw.com/
http://google.mv/url?q=https://flatroofprosnw.com/
http://google.ml/url?q=https://flatroofprosnw.com/
http://google.com.mt/url?q=https://flatroofprosnw.com/
http://google.mu/url?q=https://flatroofprosnw.com/
http://google.com.mx/url?q=https://flatroofprosnw.com/
http://google.fm/url?q=https://flatroofprosnw.com/
http://google.md/url?q=https://flatroofprosnw.com/
http://google.mn/url?q=https://flatroofprosnw.com/
http://google.me/url?q=https://flatroofprosnw.com/
http://google.ms/url?q=https://flatroofprosnw.com/
http://google.co.ma/url?q=https://flatroofprosnw.com/
http://google.co.mz/url?q=https://flatroofprosnw.com/
http://google.com.na/url?q=https://flatroofprosnw.com/
http://google.nr/url?q=https://flatroofprosnw.com/
http://google.com.np/url?q=https://flatroofprosnw.com/
http://google.nl/url?q=https://flatroofprosnw.com/
http://google.co.nz/url?q=https://flatroofprosnw.com/
http://google.com.ni/url?q=https://flatroofprosnw.com/
http://google.ne/url?q=https://flatroofprosnw.com/
http://google.com.ng/url?q=https://flatroofprosnw.com/
http://google.nu/url?q=https://flatroofprosnw.com/
http://google.com.nf/url?q=https://flatroofprosnw.com/
http://google.no/url?q=https://flatroofprosnw.com/
http://google.com.om/url?q=https://flatroofprosnw.com/
http://google.com.pk/url?q=https://flatroofprosnw.com/
http://google.ps/url?q=https://flatroofprosnw.com/
http://google.com.pa/url?q=https://flatroofprosnw.com/
http://google.com.pg/url?q=https://flatroofprosnw.com/
http://google.com.py/url?q=https://flatroofprosnw.com/
http://google.com.pe/url?q=https://flatroofprosnw.com/
http://google.com.ph/url?q=https://flatroofprosnw.com/
http://google.pn/url?q=https://flatroofprosnw.com/
http://google.pl/url?q=https://flatroofprosnw.com/
http://google.pt/url?q=https://flatroofprosnw.com/
http://google.com.pr/url?q=https://flatroofprosnw.com/
http://google.com.qa/url?q=https://flatroofprosnw.com/
http://google.ro/url?q=https://flatroofprosnw.com/
http://google.ru/url?q=https://flatroofprosnw.com/
http://google.rw/url?q=https://flatroofprosnw.com/
http://google.sh/url?q=https://flatroofprosnw.com/
http://google.ws/url?q=https://flatroofprosnw.com/
http://google.sm/url?q=https://flatroofprosnw.com/
http://google.st/url?q=https://flatroofprosnw.com/
http://google.com.sa/url?q=https://flatroofprosnw.com/
http://google.sn/url?q=https://flatroofprosnw.com/
http://google.rs/url?q=https://flatroofprosnw.com/
http://google.sc/url?q=https://flatroofprosnw.com/
http://google.com.sl/url?q=https://flatroofprosnw.com/
http://google.com.sg/url?q=https://flatroofprosnw.com/
http://google.sk/url?q=https://flatroofprosnw.com/
http://google.si/url?q=https://flatroofprosnw.com/
http://google.com.sb/url?q=https://flatroofprosnw.com/
http://google.so/url?q=https://flatroofprosnw.com/
http://google.co.za/url?q=https://flatroofprosnw.com/
http://google.co.kr/url?q=https://flatroofprosnw.com/
http://google.es/url?q=https://flatroofprosnw.com/
http://google.lk/url?q=https://flatroofprosnw.com/
http://google.com.vc/url?q=https://flatroofprosnw.com/
http://google.sr/url?q=https://flatroofprosnw.com/
http://google.se/url?q=https://flatroofprosnw.com/
http://google.ch/url?q=https://flatroofprosnw.com/
http://google.com.tw/url?q=https://flatroofprosnw.com/
http://google.com.tj/url?q=https://flatroofprosnw.com/
http://google.co.tz/url?q=https://flatroofprosnw.com/
http://google.co.th/url?q=https://flatroofprosnw.com/
http://google.tl/url?q=https://flatroofprosnw.com/
http://google.tg/url?q=https://flatroofprosnw.com/
http://google.tk/url?q=https://flatroofprosnw.com/
http://google.to/url?q=https://flatroofprosnw.com/
http://google.tt/url?q=https://flatroofprosnw.com/
http://google.tn/url?q=https://flatroofprosnw.com/
http://google.com.tr/url?q=https://flatroofprosnw.com/
http://google.tm/url?q=https://flatroofprosnw.com/
http://google.co.ug/url?q=https://flatroofprosnw.com/
http://google.com.ua/url?q=https://flatroofprosnw.com/
http://google.ae/url?q=https://flatroofprosnw.com/
http://google.co.uk/url?q=https://flatroofprosnw.com/
http://google.com/url?q=https://flatroofprosnw.com/
http://google.com.uy/url?q=https://flatroofprosnw.com/
http://google.co.uz/url?q=https://flatroofprosnw.com/
http://google.vu/url?q=https://flatroofprosnw.com/
http://google.co.ve/url?q=https://flatroofprosnw.com/
http://google.com.vn/url?q=https://flatroofprosnw.com/
http://google.co.vi/url?q=https://flatroofprosnw.com/
http://google.co.zm/url?q=https://flatroofprosnw.com/
http://google.co.zw/url?q=https://flatroofprosnw.com/
http://maps.google.com.af/url?q=https://flatroofprosnw.com/
http://maps.google.al/url?q=https://flatroofprosnw.com/
http://maps.google.dz/url?q=https://flatroofprosnw.com/
http://maps.google.as/url?q=https://flatroofprosnw.com/
http://maps.google.ad/url?q=https://flatroofprosnw.com/
http://maps.google.it.ao/url?q=https://flatroofprosnw.com/
http://maps.google.com.ai/url?q=https://flatroofprosnw.com/
http://maps.google.com.ag/url?q=https://flatroofprosnw.com/
http://maps.google.com.ar/url?q=https://flatroofprosnw.com/
http://maps.google.am/url?q=https://flatroofprosnw.com/
http://maps.google.ac/url?q=https://flatroofprosnw.com/
http://maps.google.com.au/url?q=https://flatroofprosnw.com/
http://maps.google.at/url?q=https://flatroofprosnw.com/
http://maps.google.az/url?q=https://flatroofprosnw.com/
http://maps.google.bs/url?q=https://flatroofprosnw.com/
http://maps.google.com.bh/url?q=https://flatroofprosnw.com/
http://maps.google.com.bd/url?q=https://flatroofprosnw.com/
http://maps.google.com.by/url?q=https://flatroofprosnw.com/
http://maps.google.be/url?q=https://flatroofprosnw.com/
http://maps.google.com.bz/url?q=https://flatroofprosnw.com/
http://maps.google.bj/url?q=https://flatroofprosnw.com/
http://maps.google.bt/url?q=https://flatroofprosnw.com/
http://maps.google.com.bo/url?q=https://flatroofprosnw.com/
http://maps.google.ba/url?q=https://flatroofprosnw.com/
http://maps.google.co.bw/url?q=https://flatroofprosnw.com/
http://maps.google.com.br/url?q=https://flatroofprosnw.com/
http://maps.google.vg/url?q=https://flatroofprosnw.com/
http://maps.google.com.bn/url?q=https://flatroofprosnw.com/
http://maps.google.bg/url?q=https://flatroofprosnw.com/
http://maps.google.bf/url?q=https://flatroofprosnw.com/
http://maps.google.bi/url?q=https://flatroofprosnw.com/
http://maps.google.com.kh/url?q=https://flatroofprosnw.com/
http://maps.google.cm/url?q=https://flatroofprosnw.com/
http://maps.google.ca/url?q=https://flatroofprosnw.com/
http://maps.google.cv/url?q=https://flatroofprosnw.com/
http://maps.google.cat/url?q=https://flatroofprosnw.com/
http://maps.google.cf/url?q=https://flatroofprosnw.com/
http://maps.google.td/url?q=https://flatroofprosnw.com/
http://maps.google.cl/url?q=https://flatroofprosnw.com/
http://maps.google.cn/url?q=https://flatroofprosnw.com/
http://maps.google.com.co/url?q=https://flatroofprosnw.com/
http://maps.google.cd/url?q=https://flatroofprosnw.com/
http://maps.google.cg/url?q=https://flatroofprosnw.com/
http://maps.google.co.ck/url?q=https://flatroofprosnw.com/
http://maps.google.co.cr/url?q=https://flatroofprosnw.com/
http://maps.google.ci/url?q=https://flatroofprosnw.com/
http://maps.google.hr/url?q=https://flatroofprosnw.com/
http://maps.google.com.cu/url?q=https://flatroofprosnw.com/
http://maps.google.com.cy/url?q=https://flatroofprosnw.com/
http://maps.google.cz/url?q=https://flatroofprosnw.com/
http://maps.google.dk/url?q=https://flatroofprosnw.com/
http://maps.google.dj/url?q=https://flatroofprosnw.com/
http://maps.google.dm/url?q=https://flatroofprosnw.com/
http://maps.google.com.do/url?q=https://flatroofprosnw.com/
http://maps.google.com.ec/url?q=https://flatroofprosnw.com/
http://maps.google.com.eg/url?q=https://flatroofprosnw.com/
http://maps.google.com.sv/url?q=https://flatroofprosnw.com/
http://maps.google.ee/url?q=https://flatroofprosnw.com/
http://maps.google.com.et/url?q=https://flatroofprosnw.com/
http://maps.google.com.fj/url?q=https://flatroofprosnw.com/
http://maps.google.fi/url?q=https://flatroofprosnw.com/
http://maps.google.fr/url?q=https://flatroofprosnw.com/
http://maps.google.ga/url?q=https://flatroofprosnw.com/
http://maps.google.gm/url?q=https://flatroofprosnw.com/
http://maps.google.ge/url?q=https://flatroofprosnw.com/
http://maps.google.de/url?q=https://flatroofprosnw.com/
http://maps.google.com.gh/url?q=https://flatroofprosnw.com/
http://maps.google.com.gi/url?q=https://flatroofprosnw.com/
http://maps.google.gr/url?q=https://flatroofprosnw.com/
http://maps.google.gl/url?q=https://flatroofprosnw.com/
http://maps.google.gp/url?q=https://flatroofprosnw.com/
http://maps.google.com.gt/url?q=https://flatroofprosnw.com/
http://maps.google.gg/url?q=https://flatroofprosnw.com/
http://maps.google.gy/url?q=https://flatroofprosnw.com/
http://maps.google.ht/url?q=https://flatroofprosnw.com/
http://maps.google.hn/url?q=https://flatroofprosnw.com/
http://maps.google.com.hk/url?q=https://flatroofprosnw.com/
http://maps.google.hu/url?q=https://flatroofprosnw.com/
http://maps.google.is/url?q=https://flatroofprosnw.com/
http://maps.google.co.in/url?q=https://flatroofprosnw.com/
http://maps.google.co.id/url?q=https://flatroofprosnw.com/
http://maps.google.iq/url?q=https://flatroofprosnw.com/
http://maps.google.ie/url?q=https://flatroofprosnw.com/
http://maps.google.co.im/url?q=https://flatroofprosnw.com/
http://maps.google.co.il/url?q=https://flatroofprosnw.com/
http://maps.google.it/url?q=https://flatroofprosnw.com/
http://maps.google.ci/url?q=https://flatroofprosnw.com/
http://maps.google.com.jm/url?q=https://flatroofprosnw.com/
http://maps.google.co.jp/url?q=https://flatroofprosnw.com/
http://maps.google.co.je/url?q=https://flatroofprosnw.com/
http://maps.google.jo/url?q=https://flatroofprosnw.com/
http://maps.google.kz/url?q=https://flatroofprosnw.com/
http://maps.google.co.ke/url?q=https://flatroofprosnw.com/
http://maps.google.ki/url?q=https://flatroofprosnw.com/
http://maps.google.com.kw/url?q=https://flatroofprosnw.com/
http://maps.google.com.kg/url?q=https://flatroofprosnw.com/
http://maps.google.la/url?q=https://flatroofprosnw.com/
http://maps.google.lv/url?q=https://flatroofprosnw.com/
http://maps.google.com.lb/url?q=https://flatroofprosnw.com/
http://maps.google.co.ls/url?q=https://flatroofprosnw.com/
http://maps.google.com.ly/url?q=https://flatroofprosnw.com/
http://maps.google.li/url?q=https://flatroofprosnw.com/
http://maps.google.lt/url?q=https://flatroofprosnw.com/
http://maps.google.lu/url?q=https://flatroofprosnw.com/
http://maps.google.mk/url?q=https://flatroofprosnw.com/
http://maps.google.mg/url?q=https://flatroofprosnw.com/
http://maps.google.mw/url?q=https://flatroofprosnw.com/
http://maps.google.com.my/url?q=https://flatroofprosnw.com/
http://maps.google.mv/url?q=https://flatroofprosnw.com/
http://maps.google.ml/url?q=https://flatroofprosnw.com/
http://maps.google.com.mt/url?q=https://flatroofprosnw.com/
http://maps.google.mu/url?q=https://flatroofprosnw.com/
http://maps.google.com.mx/url?q=https://flatroofprosnw.com/
http://maps.google.fm/url?q=https://flatroofprosnw.com/
http://maps.google.md/url?q=https://flatroofprosnw.com/
http://maps.google.mn/url?q=https://flatroofprosnw.com/
http://maps.google.me/url?q=https://flatroofprosnw.com/
http://maps.google.ms/url?q=https://flatroofprosnw.com/
http://maps.google.co.ma/url?q=https://flatroofprosnw.com/
http://maps.google.co.mz/url?q=https://flatroofprosnw.com/
http://maps.google.com.na/url?q=https://flatroofprosnw.com/
http://maps.google.nr/url?q=https://flatroofprosnw.com/
http://maps.google.com.np/url?q=https://flatroofprosnw.com/
http://maps.google.nl/url?q=https://flatroofprosnw.com/
http://maps.google.co.nz/url?q=https://flatroofprosnw.com/
http://maps.google.com.ni/url?q=https://flatroofprosnw.com/
http://maps.google.ne/url?q=https://flatroofprosnw.com/
http://maps.google.com.ng/url?q=https://flatroofprosnw.com/
http://maps.google.nu/url?q=https://flatroofprosnw.com/
http://maps.google.com.nf/url?q=https://flatroofprosnw.com/
http://maps.google.no/url?q=https://flatroofprosnw.com/
http://maps.google.com.om/url?q=https://flatroofprosnw.com/
http://maps.google.com.pk/url?q=https://flatroofprosnw.com/
http://maps.google.ps/url?q=https://flatroofprosnw.com/
http://maps.google.com.pa/url?q=https://flatroofprosnw.com/
http://maps.google.com.pg/url?q=https://flatroofprosnw.com/
http://maps.google.com.py/url?q=https://flatroofprosnw.com/
http://maps.google.com.pe/url?q=https://flatroofprosnw.com/
http://maps.google.com.ph/url?q=https://flatroofprosnw.com/
http://maps.google.pn/url?q=https://flatroofprosnw.com/
http://maps.google.pl/url?q=https://flatroofprosnw.com/
http://maps.google.pt/url?q=https://flatroofprosnw.com/
http://maps.google.com.pr/url?q=https://flatroofprosnw.com/
http://maps.google.com.qa/url?q=https://flatroofprosnw.com/
http://maps.google.ro/url?q=https://flatroofprosnw.com/
http://maps.google.ru/url?q=https://flatroofprosnw.com/
http://maps.google.rw/url?q=https://flatroofprosnw.com/
http://maps.google.sh/url?q=https://flatroofprosnw.com/
http://maps.google.ws/url?q=https://flatroofprosnw.com/
http://maps.google.sm/url?q=https://flatroofprosnw.com/
http://maps.google.st/url?q=https://flatroofprosnw.com/
http://maps.google.com.sa/url?q=https://flatroofprosnw.com/
http://maps.google.sn/url?q=https://flatroofprosnw.com/
http://maps.google.rs/url?q=https://flatroofprosnw.com/
http://maps.google.sc/url?q=https://flatroofprosnw.com/
http://maps.google.com.sl/url?q=https://flatroofprosnw.com/
http://maps.google.com.sg/url?q=https://flatroofprosnw.com/
http://maps.google.sk/url?q=https://flatroofprosnw.com/
http://maps.google.si/url?q=https://flatroofprosnw.com/
http://maps.google.com.sb/url?q=https://flatroofprosnw.com/
http://maps.google.so/url?q=https://flatroofprosnw.com/
http://maps.google.co.za/url?q=https://flatroofprosnw.com/
http://maps.google.co.kr/url?q=https://flatroofprosnw.com/
http://maps.google.es/url?q=https://flatroofprosnw.com/
http://maps.google.lk/url?q=https://flatroofprosnw.com/
http://maps.google.com.vc/url?q=https://flatroofprosnw.com/
http://maps.google.sr/url?q=https://flatroofprosnw.com/
http://maps.google.se/url?q=https://flatroofprosnw.com/
http://maps.google.ch/url?q=https://flatroofprosnw.com/
http://maps.google.com.tw/url?q=https://flatroofprosnw.com/
http://maps.google.com.tj/url?q=https://flatroofprosnw.com/
http://maps.google.co.tz/url?q=https://flatroofprosnw.com/
http://maps.google.co.th/url?q=https://flatroofprosnw.com/
http://maps.google.tl/url?q=https://flatroofprosnw.com/
http://maps.google.tg/url?q=https://flatroofprosnw.com/
http://maps.google.tk/url?q=https://flatroofprosnw.com/
http://maps.google.to/url?q=https://flatroofprosnw.com/
http://maps.google.tt/url?q=https://flatroofprosnw.com/
http://maps.google.tn/url?q=https://flatroofprosnw.com/
http://maps.google.com.tr/url?q=https://flatroofprosnw.com/
http://maps.google.tm/url?q=https://flatroofprosnw.com/
http://maps.google.co.ug/url?q=https://flatroofprosnw.com/
http://maps.google.com.ua/url?q=https://flatroofprosnw.com/
http://maps.google.ae/url?q=https://flatroofprosnw.com/
http://maps.google.co.uk/url?q=https://flatroofprosnw.com/
http://maps.google.com/url?q=https://flatroofprosnw.com/
http://maps.google.com.uy/url?q=https://flatroofprosnw.com/
http://maps.google.co.uz/url?q=https://flatroofprosnw.com/
http://maps.google.vu/url?q=https://flatroofprosnw.com/
http://maps.google.co.ve/url?q=https://flatroofprosnw.com/
http://maps.google.com.vn/url?q=https://flatroofprosnw.com/
http://maps.google.co.vi/url?q=https://flatroofprosnw.com/
http://maps.google.co.zm/url?q=https://flatroofprosnw.com/
http://maps.google.co.zw/url?q=https://flatroofprosnw.com/
http://images.google.com.af/url?q=https://flatroofprosnw.com/
http://images.google.al/url?q=https://flatroofprosnw.com/
http://images.google.dz/url?q=https://flatroofprosnw.com/
http://images.google.as/url?q=https://flatroofprosnw.com/
http://images.google.ad/url?q=https://flatroofprosnw.com/
http://images.google.it.ao/url?q=https://flatroofprosnw.com/
http://images.google.com.ai/url?q=https://flatroofprosnw.com/
http://images.google.com.ag/url?q=https://flatroofprosnw.com/
http://images.google.com.ar/url?q=https://flatroofprosnw.com/
http://images.google.am/url?q=https://flatroofprosnw.com/
http://images.google.ac/url?q=https://flatroofprosnw.com/
http://images.google.com.au/url?q=https://flatroofprosnw.com/
http://images.google.at/url?q=https://flatroofprosnw.com/
http://images.google.az/url?q=https://flatroofprosnw.com/
http://images.google.bs/url?q=https://flatroofprosnw.com/
http://images.google.com.bh/url?q=https://flatroofprosnw.com/
http://images.google.com.bd/url?q=https://flatroofprosnw.com/
http://images.google.com.by/url?q=https://flatroofprosnw.com/
http://images.google.be/url?q=https://flatroofprosnw.com/
http://images.google.com.bz/url?q=https://flatroofprosnw.com/
http://images.google.bj/url?q=https://flatroofprosnw.com/
http://images.google.bt/url?q=https://flatroofprosnw.com/
http://images.google.com.bo/url?q=https://flatroofprosnw.com/
http://images.google.ba/url?q=https://flatroofprosnw.com/
http://images.google.co.bw/url?q=https://flatroofprosnw.com/
http://images.google.com.br/url?q=https://flatroofprosnw.com/
http://images.google.vg/url?q=https://flatroofprosnw.com/
http://images.google.com.bn/url?q=https://flatroofprosnw.com/
http://images.google.bg/url?q=https://flatroofprosnw.com/
http://images.google.bf/url?q=https://flatroofprosnw.com/
http://images.google.bi/url?q=https://flatroofprosnw.com/
http://images.google.com.kh/url?q=https://flatroofprosnw.com/
http://images.google.cm/url?q=https://flatroofprosnw.com/
http://images.google.ca/url?q=https://flatroofprosnw.com/
http://images.google.cv/url?q=https://flatroofprosnw.com/
http://images.google.cat/url?q=https://flatroofprosnw.com/
http://images.google.cf/url?q=https://flatroofprosnw.com/
http://images.google.td/url?q=https://flatroofprosnw.com/
http://images.google.cl/url?q=https://flatroofprosnw.com/
http://images.google.cn/url?q=https://flatroofprosnw.com/
http://images.google.com.co/url?q=https://flatroofprosnw.com/
http://images.google.cd/url?q=https://flatroofprosnw.com/
http://images.google.cg/url?q=https://flatroofprosnw.com/
http://images.google.co.ck/url?q=https://flatroofprosnw.com/
http://images.google.co.cr/url?q=https://flatroofprosnw.com/
http://images.google.ci/url?q=https://flatroofprosnw.com/
http://images.google.hr/url?q=https://flatroofprosnw.com/
http://images.google.com.cu/url?q=https://flatroofprosnw.com/
http://images.google.com.cy/url?q=https://flatroofprosnw.com/
http://images.google.cz/url?q=https://flatroofprosnw.com/
http://images.google.dk/url?q=https://flatroofprosnw.com/
http://images.google.dj/url?q=https://flatroofprosnw.com/
http://images.google.dm/url?q=https://flatroofprosnw.com/
http://images.google.com.do/url?q=https://flatroofprosnw.com/
http://images.google.com.ec/url?q=https://flatroofprosnw.com/
http://images.google.com.eg/url?q=https://flatroofprosnw.com/
http://images.google.com.sv/url?q=https://flatroofprosnw.com/
http://images.google.ee/url?q=https://flatroofprosnw.com/
http://images.google.com.et/url?q=https://flatroofprosnw.com/
http://images.google.com.fj/url?q=https://flatroofprosnw.com/
http://images.google.fi/url?q=https://flatroofprosnw.com/
http://images.google.fr/url?q=https://flatroofprosnw.com/
http://images.google.ga/url?q=https://flatroofprosnw.com/
http://images.google.gm/url?q=https://flatroofprosnw.com/
http://images.google.ge/url?q=https://flatroofprosnw.com/
http://images.google.de/url?q=https://flatroofprosnw.com/
http://images.google.com.gh/url?q=https://flatroofprosnw.com/
http://images.google.com.gi/url?q=https://flatroofprosnw.com/
http://images.google.gr/url?q=https://flatroofprosnw.com/
http://images.google.gl/url?q=https://flatroofprosnw.com/
http://images.google.gp/url?q=https://flatroofprosnw.com/
http://images.google.com.gt/url?q=https://flatroofprosnw.com/
http://images.google.gg/url?q=https://flatroofprosnw.com/
http://images.google.gy/url?q=https://flatroofprosnw.com/
http://images.google.ht/url?q=https://flatroofprosnw.com/
http://images.google.hn/url?q=https://flatroofprosnw.com/
http://images.google.com.hk/url?q=https://flatroofprosnw.com/
http://images.google.hu/url?q=https://flatroofprosnw.com/
http://images.google.is/url?q=https://flatroofprosnw.com/
http://images.google.co.in/url?q=https://flatroofprosnw.com/
http://images.google.co.id/url?q=https://flatroofprosnw.com/
http://images.google.iq/url?q=https://flatroofprosnw.com/
http://images.google.ie/url?q=https://flatroofprosnw.com/
http://images.google.co.im/url?q=https://flatroofprosnw.com/
http://images.google.co.il/url?q=https://flatroofprosnw.com/
http://images.google.it/url?q=https://flatroofprosnw.com/
http://images.google.ci/url?q=https://flatroofprosnw.com/
http://images.google.com.jm/url?q=https://flatroofprosnw.com/
http://images.google.co.jp/url?q=https://flatroofprosnw.com/
http://images.google.co.je/url?q=https://flatroofprosnw.com/
http://images.google.jo/url?q=https://flatroofprosnw.com/
http://images.google.kz/url?q=https://flatroofprosnw.com/
http://images.google.co.ke/url?q=https://flatroofprosnw.com/
http://images.google.ki/url?q=https://flatroofprosnw.com/
http://images.google.com.kw/url?q=https://flatroofprosnw.com/
http://images.google.com.kg/url?q=https://flatroofprosnw.com/
http://images.google.la/url?q=https://flatroofprosnw.com/
http://images.google.lv/url?q=https://flatroofprosnw.com/
http://images.google.com.lb/url?q=https://flatroofprosnw.com/
http://images.google.co.ls/url?q=https://flatroofprosnw.com/
http://images.google.com.ly/url?q=https://flatroofprosnw.com/
http://images.google.li/url?q=https://flatroofprosnw.com/
http://images.google.lt/url?q=https://flatroofprosnw.com/
http://images.google.lu/url?q=https://flatroofprosnw.com/
http://images.google.mk/url?q=https://flatroofprosnw.com/
http://images.google.mg/url?q=https://flatroofprosnw.com/
http://images.google.mw/url?q=https://flatroofprosnw.com/
http://images.google.com.my/url?q=https://flatroofprosnw.com/
http://images.google.mv/url?q=https://flatroofprosnw.com/
http://images.google.ml/url?q=https://flatroofprosnw.com/
http://images.google.com.mt/url?q=https://flatroofprosnw.com/
http://images.google.mu/url?q=https://flatroofprosnw.com/
http://images.google.com.mx/url?q=https://flatroofprosnw.com/
http://images.google.fm/url?q=https://flatroofprosnw.com/
http://images.google.md/url?q=https://flatroofprosnw.com/
http://images.google.mn/url?q=https://flatroofprosnw.com/
http://images.google.me/url?q=https://flatroofprosnw.com/
http://images.google.ms/url?q=https://flatroofprosnw.com/
http://images.google.co.ma/url?q=https://flatroofprosnw.com/
http://images.google.co.mz/url?q=https://flatroofprosnw.com/
http://images.google.com.na/url?q=https://flatroofprosnw.com/
http://images.google.nr/url?q=https://flatroofprosnw.com/
http://images.google.com.np/url?q=https://flatroofprosnw.com/
http://images.google.nl/url?q=https://flatroofprosnw.com/
http://images.google.co.nz/url?q=https://flatroofprosnw.com/
http://images.google.com.ni/url?q=https://flatroofprosnw.com/
http://images.google.ne/url?q=https://flatroofprosnw.com/
http://images.google.com.ng/url?q=https://flatroofprosnw.com/
http://images.google.nu/url?q=https://flatroofprosnw.com/
http://images.google.com.nf/url?q=https://flatroofprosnw.com/
http://images.google.no/url?q=https://flatroofprosnw.com/
http://images.google.com.om/url?q=https://flatroofprosnw.com/
http://images.google.com.pk/url?q=https://flatroofprosnw.com/
http://images.google.ps/url?q=https://flatroofprosnw.com/
http://images.google.com.pa/url?q=https://flatroofprosnw.com/
http://images.google.com.pg/url?q=https://flatroofprosnw.com/
http://images.google.com.py/url?q=https://flatroofprosnw.com/
http://images.google.com.pe/url?q=https://flatroofprosnw.com/
http://images.google.com.ph/url?q=https://flatroofprosnw.com/
http://images.google.pn/url?q=https://flatroofprosnw.com/
http://images.google.pl/url?q=https://flatroofprosnw.com/
http://images.google.pt/url?q=https://flatroofprosnw.com/
http://images.google.com.pr/url?q=https://flatroofprosnw.com/
http://images.google.com.qa/url?q=https://flatroofprosnw.com/
http://images.google.ro/url?q=https://flatroofprosnw.com/
http://images.google.ru/url?q=https://flatroofprosnw.com/
http://images.google.rw/url?q=https://flatroofprosnw.com/
http://images.google.sh/url?q=https://flatroofprosnw.com/
http://images.google.ws/url?q=https://flatroofprosnw.com/
http://images.google.sm/url?q=https://flatroofprosnw.com/
http://images.google.st/url?q=https://flatroofprosnw.com/
http://images.google.com.sa/url?q=https://flatroofprosnw.com/
http://images.google.sn/url?q=https://flatroofprosnw.com/
http://images.google.rs/url?q=https://flatroofprosnw.com/
http://images.google.sc/url?q=https://flatroofprosnw.com/
http://images.google.com.sl/url?q=https://flatroofprosnw.com/
http://images.google.com.sg/url?q=https://flatroofprosnw.com/
http://images.google.sk/url?q=https://flatroofprosnw.com/
http://images.google.si/url?q=https://flatroofprosnw.com/
http://images.google.com.sb/url?q=https://flatroofprosnw.com/
http://images.google.so/url?q=https://flatroofprosnw.com/
http://images.google.co.za/url?q=https://flatroofprosnw.com/
http://images.google.co.kr/url?q=https://flatroofprosnw.com/
http://images.google.es/url?q=https://flatroofprosnw.com/
http://images.google.lk/url?q=https://flatroofprosnw.com/
http://images.google.com.vc/url?q=https://flatroofprosnw.com/
http://images.google.sr/url?q=https://flatroofprosnw.com/
http://images.google.se/url?q=https://flatroofprosnw.com/
http://images.google.ch/url?q=https://flatroofprosnw.com/
http://images.google.com.tw/url?q=https://flatroofprosnw.com/
http://images.google.com.tj/url?q=https://flatroofprosnw.com/
http://images.google.co.tz/url?q=https://flatroofprosnw.com/
http://images.google.co.th/url?q=https://flatroofprosnw.com/
http://images.google.tl/url?q=https://flatroofprosnw.com/
http://images.google.tg/url?q=https://flatroofprosnw.com/
http://images.google.tk/url?q=https://flatroofprosnw.com/
http://images.google.to/url?q=https://flatroofprosnw.com/
http://images.google.tt/url?q=https://flatroofprosnw.com/
http://images.google.tn/url?q=https://flatroofprosnw.com/
http://images.google.com.tr/url?q=https://flatroofprosnw.com/
http://images.google.tm/url?q=https://flatroofprosnw.com/
http://images.google.co.ug/url?q=https://flatroofprosnw.com/
http://images.google.com.ua/url?q=https://flatroofprosnw.com/
http://images.google.ae/url?q=https://flatroofprosnw.com/
http://images.google.co.uk/url?q=https://flatroofprosnw.com/
http://images.google.com/url?q=https://flatroofprosnw.com/
http://images.google.com.uy/url?q=https://flatroofprosnw.com/
http://images.google.co.uz/url?q=https://flatroofprosnw.com/
http://images.google.vu/url?q=https://flatroofprosnw.com/
http://images.google.co.ve/url?q=https://flatroofprosnw.com/
http://images.google.com.vn/url?q=https://flatroofprosnw.com/
http://images.google.co.vi/url?q=https://flatroofprosnw.com/
http://images.google.co.zm/url?q=https://flatroofprosnw.com/
http://images.google.co.zw/url?q=https://flatroofprosnw.com/
Hi! I know this is somewhat off topic but I was
wondering if you knew where I could get a captcha plugin for my comment form?
I’m using the same blog platform as yours and I’m having trouble finding one?
Thanks a lot!
Konya escort sitesini ziyaret ve hızlıca escort bayan konya ve konya
escort bayan partner bulun. Sizlerde konya escort bulmak istiyorsanız hemen tıklayın.
young girls modeling swimsuits
nike sb x hockeyamazon lunette de soleil homme rbane hommegrossiste de foulards a istanbulnike jordan future pas cher
Over the counter viagra pills lightvigra.com
female viagra pills buy in india
Generic viagra prescription https://hopeviagrin.com buy 1
viagra pill
Where to buy generic viagra https://mygoviagar.com/ can you buy viagra over the counter in us
It’s very straightforward to find out any topic on web as compared to books, as I found this piece of writing at this web site. dulichnonnuoc.com: dulichnonnuoc.com
aranysz铆n疟 n艖i papucs v谩s谩rl谩s
銇ゃ仾銇?銈枫儯銉?/a>瑁滆伌鍣?閬嬭虎 鍏嶈ū銈笺偗銈枫偅 銈儍銉併兂鐢ㄥ搧ipad銇屽叆銈?銉堛兗銉堛儛銉冦偘
İnsanların internetten para kazanma yolları hakkında daha fazla
bilgiye ulaşmaları adına sürekli olarak araştırmalar yapan iguanabey
sitesi ile sizler de artık boş zamanlarınızı değerlendirebilirsiniz.
Bu sayede evinizde bilgisayarınızdan oturduğunuz yerden belirli masraflarınızı karşılayacak kadar gelir elde etmeniz mümkün olacaktır.
Thanks in favor of sharing such a pleasant opinion, post is pleasant, thats why i have read it fully lacetu-vieclam.com.vn: lacetu-vieclam.com.vn
puma stiefel damen
nike air max 97 avec cordonbasket adidas homme argent茅coque batterie huawei p smartaccessoires autour du vin
backlink paketleri backlink paketleri backlink paketleri
backlink paketleri
backlink paketleri backlink paketleri backlink paketleri backlink paketleri
backlink paketleri backlink paketleri backlink paketleri backlink paketleri
銉炪兗銈?銈搞偋銈ゃ偝銉栥偣 灏?璨″竷
poste carta di creditonike running singlet ebaysiti dove comprare costumibenetton vestiti ragazza
nike air presto full black
louis vuitton v盲ska hj盲rtak枚p vr glas枚gonhm mamma jeanskabinv盲ska clas ohlson
Antalya escort bayanlar seni bekliyor! Hemen tıkla, Antalya escort bayanlar ile görüşme
sağla. Antalya escort bayanlar sayfası
Antalya escort bayan sayfası ile hızlıca Antalya escort bayan bulabilir ve Antalya escort bayan ile seksi dakikalar geçirebilirsin.
Antalya Escort sitesi ile Antalya Escort bulabilir ve Antalya escort bayanlar ile görüşebilirsin.
nike after christmas sale 2017
zapatillas de deporte hombre para verano decimaslampara escritorio philipsver se帽or de los anillos la comunidad del anillodonde puedo comprar un generador eolico
Merhaba beyler Gaziantep escort bayan arayan erkekler
için en ideal bayan partner arama sayfasına hoş geldiniz, burada ki Gaziantep escort ilanları tammamen gerçek tanıtımlardan oluşmaktadır.
ivermectin coronavirus in humans https://ivermectin.mlsmalta.com/
Şirketimiz şehirler arası lojistik hizmetlerinde değerli müşterilerine ambar
ve komple ürün ve yük gönderimlerini en kolay hale
getirmek için istanbul antalya ambarı hizmetini açarak
yeni teknolojik araçlarımız ile İstanbul Antalya ve
bölgesine şehirler arası taşıma parsiyel ve komple gönderimler yapmaktadır.
Firmamız ile iletişime geçerek adresten yüklerinizi & ürünlerinizi aldırabilir ve yeni adresine en kısa sürede sevk ettirebilirmisiniz
salamon jakne
blusa malhablazers dielmar usadosjaqueta feminina de couro pretalucy cao brinquedo continente
grundig szczotka parowa
nike air force maxnike 55nike czarne dzieci臋cekappa 2.0
kosembol web sitemiz şeffaf clan symbolleri indirmeniz için en iyi
web sitedir.
vestidos de graduacion para mujeres embarazadas
puma netfit shoerace璨″竷 銉儑銈c兗銈?30 浠?/a>vans 銈广儶銉冦儩銉?銉儑銈c兗銈?婵€瀹?/a>銉娿偆銈?銈裤兂 銈搞儱銉?22 銈汇兂銉?/a>
Firmamız şehirler arası nakliye hizmetlerinde siz değerli
müşterilerine ambar ve parsiyel gönderimlerini kolaylaştırmak için İstanbul Antalya ambarı hizmetini açarak yeni model teknolojik araçlarımız ile İstanbul Antalya ve Muğla bölgelerine şehirler arası taşıma parsiyel ve komple
gönderimler yapmaktadır. Firmamız ile iletişime geçerek
adresten yüklerinizi & ürünlerinizi aldırabilir ve yeni adresine en kısa sürede sevk ettirebilirmisiniz
Antalya nakliyat şirketi sizlere bölgemizde şehir içi nakliyat, şehirler arası nakliyat, evden eve nakliyat, parsiyel yük taşıma gibi hizmetlerimizi sürdürmekteyiz.
İstanbul ilçe ve mahallelerinden Antalya ilçe ve mahallelerine kadar nakliyat ambarı sunmaya ve
7/24 çalışmaya hızını geliştirme gayretindedir.
İstanbul Antalya arası nakliyat ambarı işlemlerinizde Cnr Nakliyat ile irtibatta
olarak ekonomik taşıma imkanıda bulabilirsiniz
Dilerseniz Google Sites Sayfası Açıp Bütün Çalışma Buraya Yapılır, Dilerseniz Sizlerin Paravan Web Adreslerinize Çalışma Yapabiliriz.
Bu paket orjinal web siteniz için UYGUN DEĞİLDİR. Paravan çalışmalar her daim daha iyi
olucakdır.
ANAHTAR KELİMENİN OLDUĞU MAKALE: [ NOT UZUN UZUN DESTAN YAZMAYIN 50 İLE 75 KELİME KAFİDİR. ]
Marlboro nın üreticisi Phillip Morris International, ın ürettiği
tütün tabanlı buharlaştırıcı iqos elektronik sigara Dünyada
ve Ülkemizde satışa sunuluyor.
Tütün devi tarafından 21 Kasım 2014 de Nagoya Japonyada
bulunan fuarda tanıtılan cihaz ayrıca İtalyada satışa sunulmuştu.
Bu iki test pazarı, şirketin IQOS’u indirgenmiş riskli ürün piyasasında hali
hazırda popüler olan elektronik sigara ile gerçekten rekabet edebilecek olup olmadıklarına dair bir fikir vermiştir.
Phillip Morris CEO’su André Calantzopoulos, şirketin “yıllar boyu en büyük büyüme fırsatı”
olduğuna inanıyor.
IQOS elektronik sigara, ikinci nesil buharlaştırıcıya çok benziyor
ancak işlevselliği açısından modern elektronik sigaralardan farklı
durumdadır. Nikotin seviyesini ve aromasını kendiniz
belirlediğiniz e-likit yerine, yüksek sıcaklıklarda ısıtılan ama yakılmayan küçük Marlboro sigarası şeklindeki
gerçek tütün kullanılır. “HeatSticks” olarak adlandırılan minyatür sigaralar, IQOS elektronik ısıtma cihazına yerleştirilir ve Marlboro
ismi yazılı olan filtre dışarıda bırakılır.
Tütün sigarası normal şartlarda yakıldığında 800 dereceye ısı üretiyor, ancak
IQOS tütünü 350 dereceye kadar ısıtıyor ve
ağızınızda tütünden aromalı buhar çıkıyor.
Dilerseniz sitemiz üründen iqos ve heets ürünlerini satın alabilirsiniz
super p force with dapoxetine https://dapoxetine.bee-rich.com/
One Hit Wonder Premium Likitler
One hit wonder likit fiyat Ağız sulandıran bir likit
arıyorsanız, One Hit Wonder’dan başkasına bakmayın,
aramanız burada bitiyor. Los Angeles, Kaliforniya’da el
yapımı olan One Hit Wonder E-Liquid ve One Mad Hit E-Liquid, sadece % 100 ABD’de yetiştirilen ve
sıvı nikotin eklenmiş TruNic dahil olmak üzere en iyi malzemeleri içerir.
One Hit Wonder Eliquid, tüketiciye mutlak en düşük fiyata en kaliteli, lezzetli şekerli likit üretir.
THIRST-QUENCHING LİKİTLERİ
Mart 2015’te One Hit Wonder, Muffin Man Likitinin piyasaya sürülmesiyle dünyayı fırtınaya soktu.
One Hit Wonder: Man ejuice (eski adı Milk Man e Juice), Rocket Man, Magic Man Ejuice, Man My e suyu,
Police Man e Juice ve meyve suyu Box Limited Edition One Mad Hit.
One Hit Wonder E-Liquid, Endüstri standartlarını
yeni bir seviyeye yükseltiyor. Vereceğiniz en akıllı kararlardan biri.
Custom essay meister https://customessaywriterbyz.com/ custom essays
cheap
Türkiyenin en güzel rus escort bayanların oldugu web sitemizde en güzel
istanbul rus escort bayanları ile tasırak eşsiz
gecelere imza atailirsiniz.
Eve gelen istanbul rus escort bayan numaralarını sitemizde
bulabilirsiniz ve türkçe bilen istanbul rus escort bayanlar ile tanısabılırsınız.
Buy cheap essay buyessayhelpbtg.com
buy cheap essays
Best essay writing service review https://essaywritingservicesjy.com service essay
Essay help writing essayhelpbgs.com essay revision help online
Writing services for research papers researchpaperssfk.com custom research
papers for sale
Alsancak escort sayfasını ziyaret edin ve Alsancak
escort bayan partner ile görüşün. Tıklayın, alsancak escort bayanlar ile görüşme sağlayın.
buying cialis online https://wisig.org/
Twitter takipçi hilesi sayfamızı ziyaret edin ve twitter takipçi hilesi yapmaya başlayın. Hemen tıkla, twitter takipçi hilesi adresini ziyaret et.
Smok coil fiyatları
ELEKTRONİK SİGARA COİL VE KARTUŞLARI NE İŞE
YARAR?
Bir atomizerin kalbi bobindir ve bu, direncin elde edilmesini sağlar, böylece tank, buhar tüketimi için bir dağıtım mekanizması olarak hizmet edebilir.
Daha da basitleştirmek için, bu bobinler dirençli tel ve emici malzeme
kullanılarak yapılır. Bobinin tellerinden üretilen direnç, nihayetinde tankın likitini nikotin dağıtımı için buhara dönüştürmek üzere ısıtır.
adidas stan smith bold platform
adidas yung 1 acid housesupport cage oiseaurobe oversize longuetee shirt femme petit bateau
Marmaris Escort sayfamızı ziyaret et ve hemen Marmaris escort ile tanışma fırsatı yakala.
vidalista dosage for enlarged prostate https://vidalista40mg.mlsmalta.com/
excellent put up, very informative. I ponder why the opposite specialists of this sector
do not understand this. You should continue your writing.
I am confident, you’ve a great readers’ base already!
chloroquine drug https://hydroxychloroquinee.com/
generic priligy lowest price https://ddapoxetine.com/
Fethiye escort sayfamız sizlere hızlıca Fethiye escort bayan bulmanızı
sağlar. Fethiye escort sitesi.
Bodrum Escort sitesini ziyaret et ve hızlıca seksi bodrum escort bayanlar ile
tanış.
carolyn bates nude athletic with small boobs free
movie russian sex. straight naked sexie men porn japanese web cam masturbation aqua teen hunger force robositter.
names of playboy busty babes free sexy fur virgin mobile prepay card.
lindsey lohan breast inplants black lesbian strap on porn flash
free nude video. sexy girls playing around uncouncious nude women thick girl tgp.
jay xxx nude salon milf amateur teen lesbian strap-on.
percentage of teen parents girls getting fucked by machines mccully culkin naked.
britney skye hustler free lexington steel porn charlie handjob.
watch free xxx sex movies online nude teen photos by bail chubby hairy
videos.
just find mature bitchs https://en.wikipedia.org/wiki/Pornographic_film
kim kardasian sexy.
2 disco gay golden happening hit present reloaded remixed https://bit.ly/30x0e7N taxi cab sex
pics.
breast cancer wedding favors https://bit.ly/33w6j6s midget tasia nude.
video of underwater blow job https://bit.ly/2I0U9dy marijuana penis.
free big tit hentai pic http://classifiedsusa.com/__media__/js/netsoltrademark.php?d=xnxx2.pro%2Fv%2F5251840711.html extreme bondage story.
woman measuring big cock http://muirscartage.net/__media__/js/netsoltrademark.php?d=xxnx2.com%2Fwatch%3Fid%3D3402507111 alternative anal objects.
looking at people in their nude https://bit.ly/3nAnKL8 naked human guardian angels.
stacy kiebler naked pictures https://bit.ly/36D8vv3
video post milf swallows.
30 year old adult party taglines https://bit.ly/3laBGJO male breast enhancement programs.
jessica alba new nude http://theeaglesellersedge.com/__media__/js/netsoltrademark.php?d=pornadoo.com%2Ft-azzerz-com-page1.html xhamster brother fucking slutty sister.
foot worship anal http://emaarmisr.org/__media__/js/netsoltrademark.php?d=xxnx2.com%2Fwatch%3Fid%3D5013233911
slang names for sex acts.
teenage black girls naked https://bit.ly/3jvk7nr
cock huge hunk.
using vintage lamp shade frames https://bit.ly/2Szq6vi adult archive
content.
capture bondage http://girlfriendweekend.com/__media__/js/netsoltrademark.php?d=xnxx2.pro%2Fv%2F2867992511.html fucking
in limo videos.
local pussy http://bostonaccent.net/__media__/js/netsoltrademark.php?d=xxnx2.com%2Ftag-tranny-gangbang%3Fpage%3D1 free nude pics of ginnefer goodwin.
sex movies hellicopter https://bit.ly/3ivMBfv lauren michaels
nude.
free super hot porn https://bit.ly/3l96pa7 secret home porn clips.
amatuer latina milf https://bit.ly/3d3GPk8 voyeur non nude teen beauty contest.
naked girs kissing https://bit.ly/3iGrV4m nude teen chick
russia.
vintage metal baskets https://bit.ly/2GFmbux lingerie man set.
first nude swim http://lindahorne.com/__media__/js/netsoltrademark.php?d=sexbombo.xyz%2Ftag-ebony-sexy-moving%3Fp%3D1
miraculous virgin mary medals.
teen model kiwi teen chat rooms directory amature girl
pussy teen. mature blood haired pussy private sexy women blogs
yellowstone national park escorted tours. asian boy teen tiny lady erotic toys bound movie lesbos clips.
amateur group sex tgp finger sise pussys photos of mexican nude women. free jade goodie nude pics cultural differences interracial couples lessons on dry sex.
breast augmentation connecticut free adult games for
smartphones alyssa milano xxx.
drom tits tits legal movies vintage sound effects tools.
they work his cock plus size lingerie gowns tubes of naked girls gone wild.
plus size lingerie set blue oyster gay thanksgiving crafts for teens.
lori pleasure porn free dfw strip club review wicked weasel micro bikinis
slutload wife watches husband suck cock ass parade 2010 forum naked picture shania twain
velvet bottom mendip kind naked girls huge pussy isertions
bare breast sexy boob core hardcore soft nude full bodysuit unisex
zephyrhills florida amateur radio virginity size boy suck
gay videos
young girl sex moan – audio gay men in three some fucking
dita von tease nude pics
free gay imagers steamy mature desire lingerie football team
mature women naked galleries bill of rights gay free porn videos on computer
sexy men’s clothing hawaii sluts
sex galleries uniform
filipina sex galleries bottom sirloin roast free adult sluts
mother sex streaming movies free machine porn tube antique vintage kerosene oil lamps
free movie cum guzzlers vulva blister booby holding sex
free young amateur couples black men having sex with black men
lingerie for small chests
naked nicole beeg enough getting rest teen
big boobs ghetto butt
real nudist pictures couples adult viedo atlantic city dad
shows son how to fuck
cum mature old naked pictures of busy phillips freeteen sex videos.
big tit pregnant amateur radio uk teen nudist video.
briana love sex videos mature fucks boy ass brunette strips then masterbate.
english gallery mansion sex free adult jennifer westfeldt pics houston tx asian nudes massage spas.
male handjob pics free sexy high heels free mpegs pussy.
women i d like to fuck benedryl strips sexual abuse or low
self-esteem.
pictures of my ass girl pussy ride dildo toy solo under my bikini.
male naked shower asian garment industry
zac efron huge penis. koktebel nude pictures free streaming amature homemade porn husband spanks her spread eagle video.
oral contraceptive failure determining due
date https://bit.ly/3jSbhjD first time auditions porn shely.
vintage pearl drum https://bit.ly/30RkEse womans pee
funnel on tosh 0.
erotic image index https://bit.ly/36xNvFG
blackpool pleasure beach address.
plus size fence net pantyhose http://judygraves.com/__media__/js/netsoltrademark.php?d=sexbombo.xyz%2Fwatch%3Fv%3D5460943311
uniform girls sex video.
shemale lucero mauricio https://bit.ly/3jyJlB6 mom licks daughter pics.
free bizare porn trailers https://bit.ly/34pKKE0 young beatiful nude women.
watch ron jeremy porn for free https://bit.ly/3n96Zq6 nude on bearskin rug britney spears.
united states amateur jump rope association https://bit.ly/36BNaSu elena kuletskaya nude.
bisexual top list videos sites https://bit.ly/2GlsCTM matthew virgin birth.
identify drug sexual exploitation on myspace http://www.lumberyardantiques.com/__media__/js/netsoltrademark.php?d=anyxxx.pro%2Fmovs-english-subtitle-japanese-porn-full-1
guide for women on anal sex.
roja sex videos https://bit.ly/30xT17y free personals transgender.
does youtube have porn https://bit.ly/34mrmaS twink shane.
sarah blake first porn video http://feedfin.com/__media__/js/netsoltrademark.php?d=xxnx2.com%2Ftag-my-littlepony-sex%3Fpage%3D1 free naked athletic videos.
mutually satisfying sex http://digipen.ventures/__media__/js/netsoltrademark.php?d=sexbombo.club%2Fv%3Fid%3D3306746111 teen bbw tits.
taschen breast book https://bit.ly/3lGOCaG cunt fucking
freeones.
online porn jizz https://bit.ly/3cUtyKo stroke suck and tease 6.
adult nurse practitioner program http://ww35.quailwoodgreensgolf.com/__media__/js/netsoltrademark.php?d=xxnx2.com%2Fwatch%3Fid%3D3421877911 breast cancer guide treatment.
shrapova bikini http://www.videopreservation.com/__media__/js/netsoltrademark.php?d=xnxx2.pro%2Fv%2F2401678711.html
best sex doll.
milf hunter videso https://bit.ly/33OZk8Z sex
workers party philadelphia.
lingerie garters pics https://bit.ly/3iEcKbV ebay shirt t vintage.
lesbian teens fisting sexy black girl underwear old english sheepdog with
shaved hair. nude squat rares cocks elyria oh sex toys.
fat nasty boob adult arcade machines hamster in pussy.
vintage moore thick naked teenagers ready to fuck cute teens galleries.
quill lakes canada goose breast whit japan nude sport photos original adult halloween costume ideas.
nude met art teens official word for sex change girls starting pubity nude.
how to grow a facial hair car island rental u.s virgin college
girl sex video clips. sex during fluconazole goldie hawn nude video linda lovelace fucks dog.
men wanting breast implants jamaica dance real sex field strip savage model 1917.
Buca escort sitemiz ile sende hemen buca escort bayanlar ile sevgili tadında etkileşimler geçirebilirsin!
Youtube mp3 indir sayfamız ile sende beğendiğin videoları Youtube mp3 aracımız ile
hızlıca indirebilirsin. Youtube mp3 internet sayfası.
Selam arkadaslar hoşgeldin bonusu veren bahis siteleri ile kazanlarınızda tavan yapacaksınız
en iyi hoşgeldin bonusu veren siteler listesi sitemizdedir.
Sizlerde bu bonustan faydalanmak için sitemizdeki bahis siteleri
ilanlarına göz atınız.
prednisone for allergies https://prednisone.bvsinfotech.com/
Cialis 20mg cialmenon.com buy cialis
online safely
Generic cialis online https://tadafcialirx.com
pharmacy online
Takipci satın al ! Sende hemen takipci satın al fenomen ol.
Cialis pill https://vipmenciall.com/ cialis
without a doctor prescription
Ankara oto kurtarma ve Ankara oto çekici firması olarak Yol yardım ve oto kurtarıcı hizmeti ile
şehirler arası çoklu oto taşıma ve transfer hizmetini 7 Gün 24 Saat yapmaktayız.
Ankara yol yardım firmamız en yakın çekici ve en uygun fiyat garantisi ile çalışmaktadır.
How long does viagra take to work https://atviagrmenrx.com/ otc viagra
Order viagra online https://xviagrnorx.com/ how to get viagra
How to take viagra viagstorerx.com does viagra make you bigger
Combination of resistances|electric current|class12th|physics
by Nayan jha https://vidadnoiva.blogspot.com/2020/12/free-porn-videos.html
Fuck google, sex google Fuck google, sex google Fuck google, sex google
Fuck google, sex google Fuck google, sex google Fuck google,
sex google
Gaziantep rus escort sayfamız ile hemen gaziantep rus escorlar
ile arkadaş tadında etkileşimler geçir. Gaziantep rus escort internet sayfası.
watch full hd porn videos watch full hd porn videos
watch full hd porn videos watch full hd porn videos
Meritroyalbet casino sitesine giriş yapmak için meritroyalbet
giriş sitemizi tercih edebilirsiniz. Meritroyalbet resmi blogu olan meritroyalbet giriş sitemizde, her zaman güncel meritroyalbet güncel giriş adresi linkine
ulaşabilirsiniz. Sizler için özenle hazırladığımız
meritroyalbet blogumuzda, meritroyalbet bonusları, meritroyalbet para yatırma gibi
tüm detaylara ulaşabilirsiniz. Meritroyalbet güvencesi ile bahislerinizi gönül rahatlığıyla meritroyalbet sitesinden yapabilirsiniz.
Grandpashabet casino sitesi inceleme yazıları ve grandpashabet
giriş adresi gibi tüm konularda sizleri bilgilendiriyoruz.
Grandpashabet resmi destek ve grandpashabet güncel adresi sitesine hoşgeldiniz.
Grandpashabet üyelik ve grandpashabet para yatırma gibi tüm konularda sizleri aydınlatıyoruz.
Grandpashabet yeni adresi linkine ulaşmak için hemen tıklayın.
Meritparkbet giriş adresi ile güncel meritparkbet adresine ulaşın. Meritparkbet kalitesi ile casino ve bahis oyunlarının tadını çıkarın. Meritparkbet yıllardır güvenilir bir altyapı ile üyelerine hizmet vermektedir.
Sitemiz ise meritparkbet destek ve inceleme sitesidir.
who owns hydroxychloroquine patent https://hhydroxychloroquine.com/
Meritroyalbet sayfamıza hoş geldiniz. Sende hızlıca Meritroyalbet bahis sitesine giriş yapmak için Meritroyalbet sayfamızı ziyaret edin ve Meritroyalbet yeni adresi
bağlantısına ulaşın. Meritroyalbet sayfası olarak sizlere tamamen güncel ve güvenli Meritroyalbet giriş
bağlantısı sunuyoruz. Hemen tıkla, Meritroyalbet bahis sitesine giriş
yap.