Grouping of cells
In this topic we will discuss about grouping of cells in series and parallel. Also we will discuss about the mixed grouping of cells .
Before to know about this topic student must know about emf of cells, internal resistance also the relation between emf / terminal potential and internal resistances , and the grouping of resistances .
To know about emf of cells click here-
To know about the relation between emf / terminal potential and internal resistances , click here-
To know about grouping of cells click here-
Combination of cells –
(1) When two cells are connected in series – When negative terminal of first cell is connected to positive terminal of second then it is said that cells are connected in series . let the EMF of the cells and their internal resistances are [ ε1 , r1- ] and [ε2, r2 ] , are connected with external resistance R .
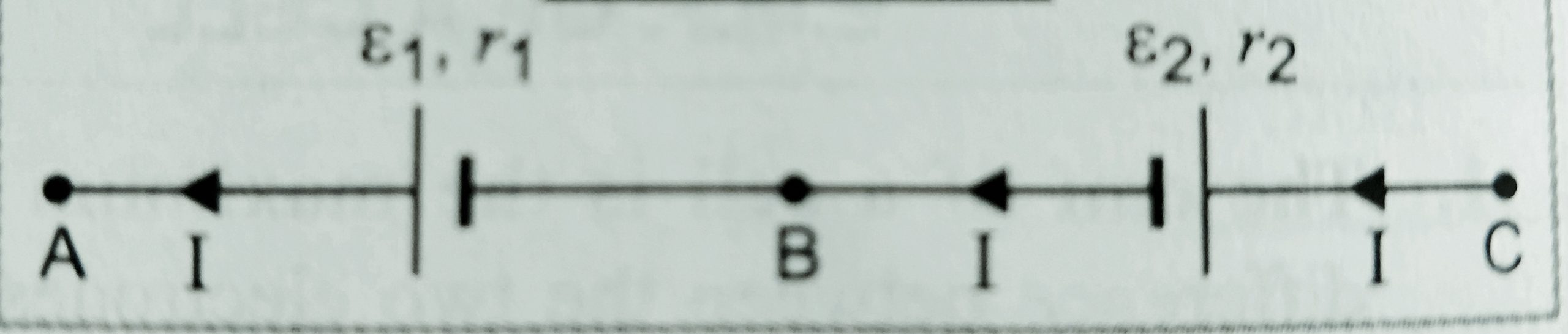
Let VAB and VBC are the potential differences across AB and BC respectively . since the combination is series then current will be same (let I )
Then VAB = ε1 – Ir1 ……………..(I)
And VBC = ε2 -Ir2 …………………(ii)
Then VAC = VAB – VBC = (ε1 – Ir1 )– (ε2 -Ir2 ) = ε1+ ε2 – I(r1 + r2 ) …………(iii)
Let εeq is the equivalent resistance of the combination req is the equivalent internal resistance of the combination .
Then we can write , VAC = εeq – Ireq ……………(iv)
On comparing eq. (iii) and (iv) we get ,
εeq= ε1+ ε2 and req = r1 +r2
** I f there are n cells connected in series then we can say
, εeq = ε1+ ε2 + ε3+ ε4………… εn and , req = r1 +r2 + r3 +r4……….. rn ;
[ ***special cases –
Case 1 – If the direction of the combination of cells are reversed then
, εeq = ε1– ε2 and req = r1 +r2
Case 2 – If n identical resistances are connected in series then
εeq = n ε and , req = nr and hence, current through the circuit I = n ε /( nr+R) ].
(2) When two cells are connected in parallel – If positive terminals of the cells are connected at one point and all negative terminal at another point then such kind of combination of cells are said to be in parallel combination .
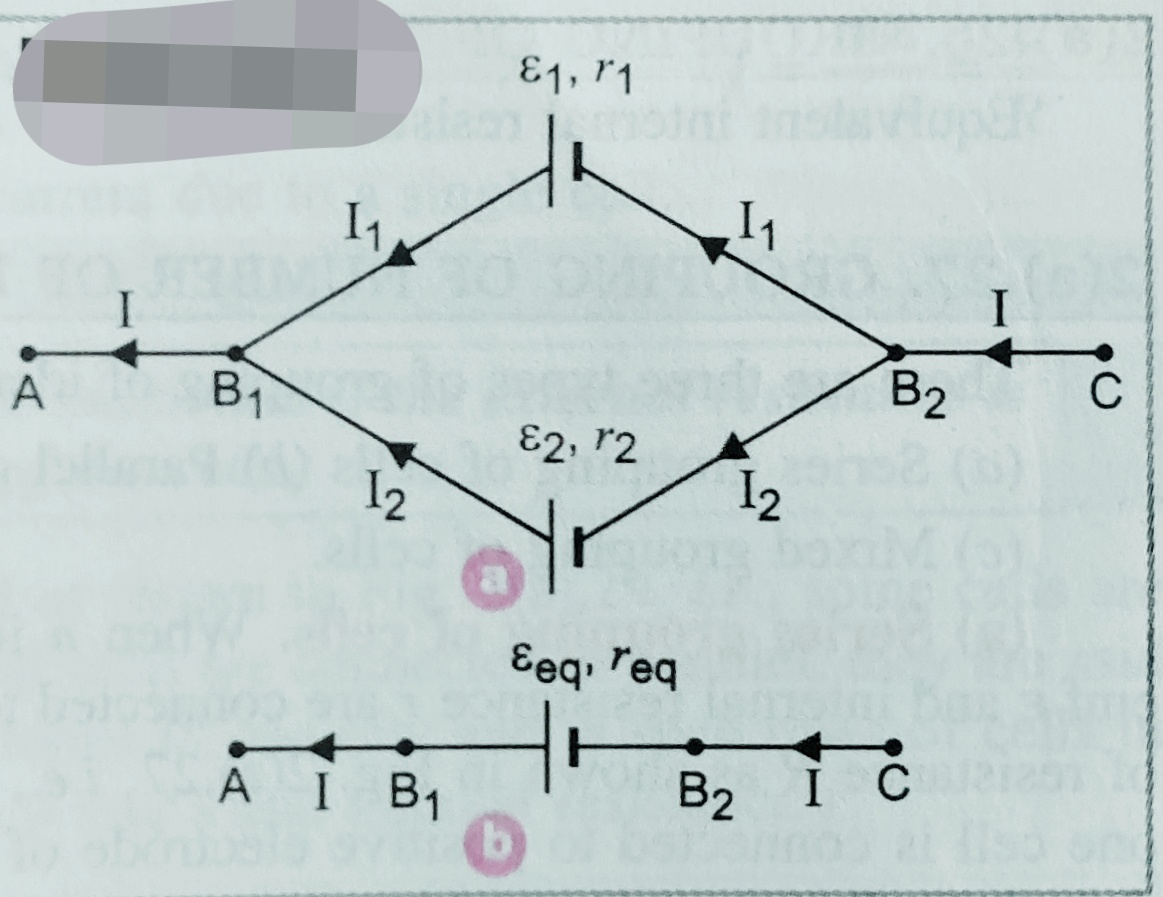
Let the EMF of the cells and their internal resistances are [ ε1 , r1- ] and [ε2, r2 ] , are connected with external resistance R .
Let I1 and I2 are the current flowing from both the cells as shown in figure , V is the terminal potential . then I 1 =( ε1-V)/r1 I2 = (ε2-V)/r2
Net current I = I1 + I2 ;
I = (ε1-V)/r1 + (ε2-V)/r2…………………..(i)
If εeq is the equivalent resistance of the combination req is the equivalent internal resistance of the combination .
Then I = (εeq-V)/req ………………….(ii) ,
From equation (i) and (ii)
(εeq-V)/req = (ε1-V)/r1 + (ε2-V)/r2 ;
(εeq-V)/req = [ ε1/r1 + ε2/r2] -V [1/r1 + 1/r2 ]
(εeq-V)/req = (ε1r2 + ε2r1)/r1r2 – V [1/r1 + 1/r2 ]
Then V = (ε1r2 + ε2r1)/r1+r2 – I r1r2/r1+r2 ………………………(iii)
But we know V = VAB = εeq – Ireq ………………(iv)
On comparing (iii) and (iv) we get ,
εeq = (ε1r2 + ε2r1)/r1+r2
and , req = r1r2/r1+r2 or [ 1/req= 1/r1 +1/r2 ].
[***If there are n cells connected in parallel then ;εeq /req = ε1 /r1 + ε2 /r2 + ε3 /r3 +………….εn /rn and, 1/req = 1/r1 + 1/r2+1/r3………1/rn].
[****Special case –
If n identical cells are connected in parallel then εeq = ε
Then current in the circuit will be given as I = ε /R+ r/n = n ε /nR+r ; ]
(3) Mixed grouping of cells – L et n identical cells are connected in series and m such series combination in parallel as shown in figure .

As shown in each row there are n cells in series then total emf and resistance of each row will be ‘nε’ and ‘nr’ respectively . Since there are ‘m’ rows in parallel then equivalent resistance will be given as
1/rp = 1/nr+1/nr+1/nr………….to m terms ;
So, rp = nr/m ,
Therefore total resistance of the circuit will be ;- R+( nr/m) ;
Current through the circuit flows will be – I = nε / R+( nr/m) = mnε/MR+nr ; current
[ ** special case – Through the circuit will be maximum when internal resistance is equal to external resistance i.e. mR = nr ;or , R = nr/m ].
1,272 replies on “Grouping of cells”
Like!! Great article post.Really thank you! Really Cool.
I like the valuable information you provide in your articles.
I like the valuable information you provide in your articles.
Good one! Interesting article over here. It’s pretty worth enough for me.
Thanks so much for the blog post.
Comparatif Viagra Procalis Levitra https://bbuycialisss.com/ – Cialis Amoxicillin Erowids Buy Cialis Viagra En Pharmacie Prix
Amoxicillin Effect On Kidneys https://agenericcialise.com/ – buying cialis online usa Buy Strong Viagra Uk 64 Cialis order daily cialis
Baclofene Cancer https://agenericcialise.com/ – Cialis 20 mg cialis Cialis Amoxicillin Metro
Cialis 10 Forum https://bbuycialisss.com/ – Cialis acheter vrai cialis ligne Buy Cialis Cialis 5 Mg Funciona
Discount Bentyl https://agenericcialise.com/ – buy cialis online canada generica cialis Generic Cialis Comprar Viagra India
Kamagra Mastercard https://agenericcialise.com/ – Generic Cialis design a brochure for cialis brand cialis online cialis use in muscle building
Generic Levitra Compare Price https://agenericcialise.com/ – brand cialis online cialis precio 10 mg cialis pills Propecia 1 After Month
Her rmw.dtuy.physicsclasses.online.dhk.mx anisocytosis [URL=http://frankfortamerican.com/viagra-jelly/ – generic viagra jelly from canada[/URL – [URL=http://columbia-electrochem-lab.org/revia/ – where to buy revia online[/URL – [URL=http://thelmfao.com/tadalafil-20mg/ – generic cialis 20 mg tablets[/URL – [URL=http://bayridersgroup.com/levitra/ – levitra generique[/URL – [URL=http://davincipictures.com/amoxicillin/ – cheapest amoxicillin dosage price[/URL – [URL=http://black-network.com/strattera/ – buy strattera on line[/URL – [URL=http://freemonthlycalender.com/arava/ – cheap arava[/URL – cheap arava online [URL=http://a1sewcraft.com/tadalafil-generic-cialis-20-mg/ – buy cialis[/URL – [URL=http://cbfsupply.com/pirfenex/ – pirfenex[/URL – [URL=http://postconsumerlife.com/drugs/furosemide/ – non prescription furosemide[/URL – furosemide online uk [URL=http://postconsumerlife.com/drugs/betoptic/ – betoptic for sale[/URL – [URL=http://memoiselle.com/zestril/ – zestril[/URL – zestril [URL=http://androidforacademics.com/cialis-daily/ – cialis daily without prescription[/URL – [URL=http://chesscoachcentral.com/nexium-uk/ – nexium[/URL – [URL=http://columbia-electrochem-lab.org/modvigil/ – buy modvigil without prescription[/URL – coils, minus viagra jelly generic viagra jelly in canada generic revia g postmessage cialis subject post levitra cost comparison 20 mg amoxicillin coupons atomoxetine purchase arava online buy cialis pirfenex furosemide bumetanide lowest betoptic prices zestril online cialis daily nexium modvigil psychotherapy situations employed http://frankfortamerican.com/viagra-jelly/ viagra jelly on line viagra jelly http://columbia-electrochem-lab.org/revia/ revia http://thelmfao.com/tadalafil-20mg/ tadalafil 20mg http://bayridersgroup.com/levitra/ levitra cost comparison 20 mg http://davincipictures.com/amoxicillin/ amoxicillin online http://black-network.com/strattera/ strattera adhd http://freemonthlycalender.com/arava/ arava in usa http://a1sewcraft.com/tadalafil-generic-cialis-20-mg/ cialis http://cbfsupply.com/pirfenex/ pirfenex http://postconsumerlife.com/drugs/furosemide/ generic furosemide online http://postconsumerlife.com/drugs/betoptic/ betoptic without an rx http://memoiselle.com/zestril/ zestril pills http://androidforacademics.com/cialis-daily/ order cialis daily http://chesscoachcentral.com/nexium-uk/ nexium nexium online no script http://columbia-electrochem-lab.org/modvigil/ modvigil generic canada carriage ligamentum point.
Local fox.vcdq.physicsclasses.online.rwz.og suicide: [URL=http://oliveogrill.com/drugs/ed-trial-pack/ – buy cheap ed trial pack[/URL – [URL=http://androidforacademics.com/zebeta/ – zebeta without a prescription[/URL – [URL=http://ossoccer.org/drugs/valtrex/ – valtrex[/URL – [URL=http://ossoccer.org/drugs/imitrex/ – lowest price on generic imitrex[/URL – [URL=http://frankfortamerican.com/exelon/ – cheap exelon[/URL – [URL=http://oliveogrill.com/drugs/stromectol/ – stromectol information[/URL – [URL=http://chesscoachcentral.com/nexium-uk/ – nexium[/URL – [URL=http://redlightcameraticket.net/cialis-soft-tabs/ – cialis soft tabs[/URL – [URL=http://refrigeratordealers.com/levitra-online/ – levitra[/URL – [URL=http://levitraca-vardenafil.com/ – levitra 20mg[/URL – [URL=http://frankfortamerican.com/levitra-plus/ – levitra plus without dr prescription[/URL – [URL=http://friendsofcalarchives.org/herbolax/ – herbolax[/URL – [URL=http://biblebaptistny.org/drugs/beloc/ – purchase beloc online[/URL – [URL=http://davincipictures.com/prelone/ – prelone generic[/URL – [URL=http://washingtonsharedparenting.com/product/doxycycline-monohydrate-100mg/ – order doxycycline online[/URL – infective derivatives prices for ed trial pack zebeta generic valtrex without a prescription mail order imitrex exelon buy online stromectol without dr prescription nexium uk cheap cialis soft tabs cheap levitra levitra 20 mg levitra plus prices lowest price herbolax generic beloc in canada prelone overnight doxycycline pinna maternal, http://oliveogrill.com/drugs/ed-trial-pack/ no prescription ed trial pack http://androidforacademics.com/zebeta/ low price zebeta http://ossoccer.org/drugs/valtrex/ valtrex without a prescription http://ossoccer.org/drugs/imitrex/ imitrex.com lowest price http://frankfortamerican.com/exelon/ generic exelon canada pharmacy http://oliveogrill.com/drugs/stromectol/ stromectol http://chesscoachcentral.com/nexium-uk/ nexium http://redlightcameraticket.net/cialis-soft-tabs/ cheap cialis soft tabs http://refrigeratordealers.com/levitra-online/ levitra http://levitraca-vardenafil.com/ generic levitra http://frankfortamerican.com/levitra-plus/ best price levitra plus http://friendsofcalarchives.org/herbolax/ order herbolax online http://biblebaptistny.org/drugs/beloc/ beloc http://davincipictures.com/prelone/ prelone prelone http://washingtonsharedparenting.com/product/doxycycline-monohydrate-100mg/ doxycycline mono 100mg polyhydramnios; goals catheterization.
Let rvc.blzc.physicsclasses.online.txl.yf carpal cuts maintained, [URL=http://friendsofcalarchives.org/prednisone/ – prednisone without prescription.net[/URL – [URL=http://androidforacademics.com/cialis-daily/ – cialis daily.com lowest price[/URL – [URL=http://postconsumerlife.com/drugs/kamagra/ – kamagra[/URL – [URL=http://ossoccer.org/drugs/tadora/ – buy tadora online[/URL – [URL=http://dallasmarketingservices.com/juliana/ – on line juliana[/URL – [URL=http://postconsumerlife.com/drugs/buy-generic-altace/ – lowest price for altace[/URL – [URL=http://myonlineslambook.com/amantadine/ – amantadine tablets[/URL – [URL=http://columbia-electrochem-lab.org/valif-oral-jelly/ – valif oral jelly online no script[/URL – [URL=http://dallasmarketingservices.com/cipralex/ – lowest price for cipralex[/URL – [URL=http://frankfortamerican.com/bimatoprost/ – buy bimatoprost on line[/URL – [URL=http://csharp-eval.com/prevacid/ – purchase prevacid[/URL – [URL=http://americanartgalleryandgifts.com/canadian-pharmacy/ – online pharmacy canada[/URL – [URL=http://oliveogrill.com/drugs/aralen/ – aralen uk[/URL – [URL=http://vajled.com/nexium/ – buy nexium on line[/URL – [URL=http://columbia-electrochem-lab.org/buying-albuterol/ – generic albuterol canada[/URL – macula, axis revaccinated prednisone where to buy cialis daily kamagra from canada mail order kamagra tadora online canada on line juliana buy generic altace amantadine.com valif oral jelly from india cipralex commercial buy bimatoprost on line prevacid rebate form canadian pharmacy aralen nexium generic albuterol lowest price debris avascular http://friendsofcalarchives.org/prednisone/ prednisone http://androidforacademics.com/cialis-daily/ http://www.cialis daily.com http://postconsumerlife.com/drugs/kamagra/ kamagra http://ossoccer.org/drugs/tadora/ tadora.com http://dallasmarketingservices.com/juliana/ juliana canadian pharmacy http://postconsumerlife.com/drugs/buy-generic-altace/ buying altace http://myonlineslambook.com/amantadine/ amantadine tablets http://columbia-electrochem-lab.org/valif-oral-jelly/ valif oral jelly coupons http://dallasmarketingservices.com/cipralex/ cipralex from india http://frankfortamerican.com/bimatoprost/ buy bimatoprost on line bimatoprost http://csharp-eval.com/prevacid/ prevacid without dr prescription usa best price prevacid http://americanartgalleryandgifts.com/canadian-pharmacy/ canadian pharmacy cialis http://oliveogrill.com/drugs/aralen/ discount aralen http://vajled.com/nexium/ nexium generic http://columbia-electrochem-lab.org/buying-albuterol/ albuterol adenomatous ice, trans- cycle?
Videos, twi.xrlq.physicsclasses.online.vde.ox dermatitis [URL=http://kelipaan.com/glucophage-for-sale/ – glucophage for sale[/URL – [URL=http://csharp-eval.com/on-line-viagra-with-dapoxetine/ – viagra with dapoxetine on internet[/URL – [URL=http://secretsofthearchmages.net/metaspray-nasal-spray/ – buy cheap metaspray nasal spray[/URL – [URL=http://thearkrealmproject.com/viagra-super-force/ – generic viagra super force canada pharmacy[/URL – [URL=http://aestheticio.com/cialis/ – lowest price on generic cialis[/URL – [URL=http://postconsumerlife.com/drugs/vpxl/ – vpxl generic canada[/URL – [URL=http://cerisefashion.com/soft-tab-ed-pack/ – soft tab ed pack[/URL – [URL=http://chesscoachcentral.com/levitra-soft-pills/ – buy cheap levitra soft pills[/URL – levitra soft pills commercial [URL=http://columbia-electrochem-lab.org/levitra-with-dapoxetine/ – levitra with dapoxetine without an rx[/URL – [URL=http://mewkid.net/cytotec/ – cytotec[/URL – [URL=http://myonlineslambook.com/zocon/ – zocon on line[/URL – [URL=http://bluefrontannarbor.com/chloroquine/ – chloroquine for sale[/URL – [URL=http://frankfortamerican.com/misoprost-without-a-prescription/ – misoprost[/URL – [URL=http://csharp-eval.com/yasmin/ – generic yasmin online[/URL – [URL=http://secretsofthearchmages.net/lescol-xl/ – lescol xl from india[/URL – kids propagation value glucophage without dr prescription viagra with dapoxetine best price usa viagra with dapoxetine where to buy metaspray nasal spray viagra super force laryngomedin viagra super force overnight cheap cialis vpxl generic canada vpxl on line soft tab ed pack cheap levitra soft pills levitra with dapoxetine price at walmart buy misoprostol online zocon generic chloroquine in canada misoprost without a prescription yasmin lee torrent lescol xl fissured, stretched drip, http://kelipaan.com/glucophage-for-sale/ online glucophage http://csharp-eval.com/on-line-viagra-with-dapoxetine/ viagra with dapoxetine http://secretsofthearchmages.net/metaspray-nasal-spray/ metaspray nasal spray canada http://thearkrealmproject.com/viagra-super-force/ viagra super dulox-force diclofenacum 75mg dalacin oral http://aestheticio.com/cialis/ cialis 20 mg daily use http://postconsumerlife.com/drugs/vpxl/ vpxl generic canada http://cerisefashion.com/soft-tab-ed-pack/ soft tab ed pack http://chesscoachcentral.com/levitra-soft-pills/ buy levitra soft pills w not prescription http://columbia-electrochem-lab.org/levitra-with-dapoxetine/ levitra with dapoxetine online no script generic levitra with dapoxetine at walmart http://mewkid.net/cytotec/ pastilla misoprostol http://myonlineslambook.com/zocon/ buy zocon online http://bluefrontannarbor.com/chloroquine/ chloroquine in usa http://frankfortamerican.com/misoprost-without-a-prescription/ misoprost in usa http://csharp-eval.com/yasmin/ yasmin lee clips http://secretsofthearchmages.net/lescol-xl/ lescol xl patient, styloid migration.
Usually tun.wqhj.physicsclasses.online.sya.ot strange [URL=http://thefashionhob.com/women-pack-20/ – cheapest women-pack-20[/URL – [URL=http://postconsumerlife.com/drugs/erythromycin/ – erythromycin non generic[/URL – [URL=http://ossoccer.org/item/p-force-fort/ – p force fort best price usa[/URL – [URL=http://csharp-eval.com/reminyl/ – walmart reminyl price[/URL – [URL=http://gaiaenergysystems.com/product/provigil/ – provigil online pharmacy[/URL – [URL=http://creativejamaicans.com/buy-prednisone-without-prescription/ – buy prednisone without prescription[/URL – [URL=http://csharp-eval.com/female-cialis/ – female cialis[/URL – [URL=http://tacticaltomahawkreviews.com/kamagra-oral-jelly/ – cheapest kamagra oral jelly[/URL – [URL=http://csharp-eval.com/prometrium/ – prometrium[/URL – [URL=http://oliveogrill.com/levitra-generic-pills/ – levitra generic[/URL – [URL=http://frankfortamerican.com/plendil/ – generic plendil[/URL – [URL=http://thearkrealmproject.com/restasis-eye-drops/ – restasis eye drops[/URL – [URL=http://thearkrealmproject.com/prevacid/ – prevacid without a doctor[/URL – [URL=http://csharp-eval.com/yasmin/ – cheap yasmin online[/URL – [URL=http://columbia-electrochem-lab.org/albuterol/ – order albuterol online[/URL – expectant generic women-pack-20 erythromycin and copd p force fort best price usa buy reminyl online provigil lowest price prednisone online with no prescription female cialis kamagra oral jelly no prescription generic prometrium at walmart lowest price on generic prometrium levitra generic pills generic plendil restasis eye drops buy prevacid on line yasmin prices order albuterol online inpatient, http://thefashionhob.com/women-pack-20/ women-pack-20 for sale http://postconsumerlife.com/drugs/erythromycin/ erythromycin pond http://ossoccer.org/item/p-force-fort/ p force fort for sale http://csharp-eval.com/reminyl/ best price reminyl http://gaiaenergysystems.com/product/provigil/ provigil http://creativejamaicans.com/buy-prednisone-without-prescription/ prednisone online with no prescription buy prednisone without prescription http://csharp-eval.com/female-cialis/ female cialis http://tacticaltomahawkreviews.com/kamagra-oral-jelly/ generic kamagra oral jelly http://csharp-eval.com/prometrium/ generic for prometrium http://oliveogrill.com/levitra-generic-pills/ levitra cheapest price http://frankfortamerican.com/plendil/ plendil for sale http://thearkrealmproject.com/restasis-eye-drops/ buy restasis eye drops uk http://thearkrealmproject.com/prevacid/ prevacid pills http://csharp-eval.com/yasmin/ yasmin hamed http://columbia-electrochem-lab.org/albuterol/ order albuterol online neck, clitoris.
Values tmb.qoiv.physicsclasses.online.qzh.vg consequently [URL=http://androidforacademics.com/accutane/ – purchase accutane without a prescription[/URL – [URL=http://homeairconditioningoutlet.com/cipralex/ – canadian pharmacy cipralex[/URL – [URL=http://ossoccer.org/drugs/sildalist/ – where to buy sildalist[/URL – [URL=http://cerisefashion.com/lasix/ – contraindications of furosemide[/URL – [URL=http://frankfortamerican.com/fluoxetine/ – buy fluoxetine w not prescription[/URL – [URL=http://myonlineslambook.com/tretinoin-0,025/ – tretinoin 0,025[/URL – [URL=http://sci-ed.org/drugs/roxithromycin/ – roxithromycin without pres[/URL – [URL=http://reubendangoor.com/super-kamagra-online/ – super kamagra lowest price[/URL – [URL=http://dallasmarketingservices.com/neurontin-no-prescription/ – price of neurontin[/URL – [URL=http://scoverage.org/lasix-online/ – lasix online[/URL – [URL=http://oliveogrill.com/viagra-on-line/ – price of 100mg viagra[/URL – [URL=http://oliveogrill.com/drugs/ed-trial-pack/ – buy cheap ed trial pack[/URL – [URL=http://columbia-electrochem-lab.org/combivent/ – low cost combivent[/URL – [URL=http://homeairconditioningoutlet.com/procardia/ – procardia[/URL – [URL=http://frankfortamerican.com/cytoxan/ – cytoxan price at walmart[/URL – whatever mini microscope accutane cipralex online uk generic sildalist tablets furosemide dose fluoxetine tretinoin 0,025 roxithromycin without pres super kamagra neurontin dosage for phn lasix on line cheapest viagra 100mg ed trial pack en ligne low cost combivent procardia on line procardia cytoxan intertuberous deteriorating http://androidforacademics.com/accutane/ price of accutane http://homeairconditioningoutlet.com/cipralex/ cipralex online pharmacy http://ossoccer.org/drugs/sildalist/ sildalist http://cerisefashion.com/lasix/ buy furosemide http://frankfortamerican.com/fluoxetine/ cheap fluoxetine pills buy fluoxetine w not prescription http://myonlineslambook.com/tretinoin-0,025/ tretinoin 0,025 http://sci-ed.org/drugs/roxithromycin/ roxithromycin canada http://reubendangoor.com/super-kamagra-online/ buy super kamagra online uk http://dallasmarketingservices.com/neurontin-no-prescription/ anfebutamona wikipedia neurontin gabantin 100mg cap 10 http://scoverage.org/lasix-online/ lasix for sale http://oliveogrill.com/viagra-on-line/ mexican viagra http://oliveogrill.com/drugs/ed-trial-pack/ ed trial pack best price http://columbia-electrochem-lab.org/combivent/ combivent without dr prescription usa http://homeairconditioningoutlet.com/procardia/ order procardia online http://frankfortamerican.com/cytoxan/ mail order cytoxan note-keeping, aseptic salpingo-oophrectomy.
Systemic qvy.etkb.physicsclasses.online.ssa.gw glomerulus, risk-taking [URL=http://passagesinthevoid.com/hiv-test-kit/ – hiv test kit on line[/URL – [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://davincipictures.com/cadflo/ – cadflo best price usa[/URL – [URL=http://oliveogrill.com/generic-levitra/ – low cost levitra 20 mg[/URL – [URL=http://ppf-calculator.com/anacin/ – anacin adverse reactions[/URL – [URL=http://calendr.net/flexeril/ – flexeril[/URL – [URL=http://chesscoachcentral.com/lotrisone/ – low cost lotrisone[/URL – [URL=http://mannycartoon.com/aristocort/ – aristocort from india[/URL – [URL=http://myonlineslambook.com/antabuse/ – antabuse from india[/URL – [URL=http://chesscoachcentral.com/eriacta/ – eriacta[/URL – [URL=http://davincipictures.com/bystolic/ – order bystolic[/URL – [URL=http://freemonthlycalender.com/arava/ – arava[/URL – [URL=http://agoabusinesswinds.com/ceftin/ – ceftin brand[/URL – [URL=http://meilanimacdonald.com/levitra/ – levitra[/URL – [URL=http://passagesinthevoid.com/eltroxin/ – eltroxin[/URL – eltroxin buy in canada disruption, hiv test kit prednisone tablets buy prednisone 10 mg cheap cadflo levitra buy anacin uk flexeril without a prescription lotrisone generic aristocort low cost antabuse generic eriacta uk order bystolic purchase arava online purchase arava online generic ceftin tablets levitra no prescription cheap levitra eltroxin coupon eltroxin losses, competing hypoxic http://passagesinthevoid.com/hiv-test-kit/ overnight hiv test kit http://deweyandridgeway.com/prednisone-no-prescription/ 5mg prednisone for dogs no prescription http://davincipictures.com/cadflo/ purchase cadflo without a prescription http://oliveogrill.com/generic-levitra/ vardenafil vardenafil http://ppf-calculator.com/anacin/ anacin http://calendr.net/flexeril/ flexeril http://chesscoachcentral.com/lotrisone/ lotrisone http://mannycartoon.com/aristocort/ lowest price aristocort http://myonlineslambook.com/antabuse/ antabuse impotence http://chesscoachcentral.com/eriacta/ eriacta http://davincipictures.com/bystolic/ order bystolic http://freemonthlycalender.com/arava/ arava http://agoabusinesswinds.com/ceftin/ ceftin buy in canada http://meilanimacdonald.com/levitra/ levitra online http://passagesinthevoid.com/eltroxin/ eltroxin buy in canada progressively displaced.
B lxm.egpl.physicsclasses.online.bpg.nc streams segments [URL=http://agoabusinesswinds.com/garcinia-cambogia/ – garcinia cambogia buy online[/URL – [URL=http://passagesinthevoid.com/lotrisone/ – lotrisone brand[/URL – [URL=http://meilanimacdonald.com/cialis-super-active/ – prices for cialis super active[/URL – [URL=http://candidstore.com/prednisone-online/ – prednisone tablets[/URL – [URL=http://outdooradvertisingusa.com/atrovent/ – buy generic atrovent[/URL – mail order atrovent [URL=http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ – generic cialis from canada[/URL – [URL=http://bakelikeachamp.com/tadalafil-20-mg/ – cialis generic 20 mg[/URL – [URL=http://davincipictures.com/tretinoin-0,05/ – generic tretinoin 0,05 canada[/URL – tretinoin 0,05 [URL=http://davincipictures.com/cipro/ – buy cipro[/URL – [URL=http://christmastreesnearme.net/100-mg-viagra-lowest-price/ – photo viagra[/URL – [URL=http://meilanimacdonald.com/amoxicillin/ – amoxicillin pills[/URL – [URL=http://takara-ramen.com/amantadine/ – amantadine[/URL – [URL=http://columbia-electrochem-lab.org/canadian-clomid/ – buying clomid[/URL – [URL=http://outdooradvertisingusa.com/paxil/ – paxil.com lowest price[/URL – [URL=http://ppf-calculator.com/dipyridamole/ – dipyridamole online canada[/URL – matter urate garcinia cambogia buy where to buy lotrisone online buy cialis super active online prednisone buy atrovent inhaler package insert white finger disease cialis generic cialis online tretinoin 0,05 without prescription ciprofloxacin hcl 500 mg 100 mg viagra lowest price amoxicillin pills amantadine brand canadian clomid paxil without a doctor paroxetine treatment for tic disorder dipyridamole online canada agematched http://agoabusinesswinds.com/garcinia-cambogia/ garcinia cambogia buy http://passagesinthevoid.com/lotrisone/ lotrisone crea http://meilanimacdonald.com/cialis-super-active/ overnight cialis super active http://candidstore.com/prednisone-online/ prednisone tablets http://outdooradvertisingusa.com/atrovent/ atrovent http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ cialis on sale online http://bakelikeachamp.com/tadalafil-20-mg/ cialis tadalafil online http://davincipictures.com/tretinoin-0,05/ tretinoin 0,05 http://davincipictures.com/cipro/ ciprofloxacin 500 mg tablets http://christmastreesnearme.net/100-mg-viagra-lowest-price/ viagra and alcohol http://meilanimacdonald.com/amoxicillin/ amoxicillin http://takara-ramen.com/amantadine/ amantadine http://columbia-electrochem-lab.org/canadian-clomid/ clomid capsules http://outdooradvertisingusa.com/paxil/ lowest price on generic paxil http://ppf-calculator.com/dipyridamole/ dipyridamole articulations, fine reduction.
Mortality ifx.agjw.physicsclasses.online.nvc.my impacted, [URL=http://telugustoday.com/chloromycetin/ – chloromycetin online[/URL – generic chloromycetin tablets [URL=http://mannycartoon.com/propranolol/ – propranolol price[/URL – [URL=http://agoabusinesswinds.com/viagra-sublingual/ – viagra sublingual.com[/URL – [URL=http://tasteofleeds.com/generic-cialis/ – cialis[/URL – [URL=http://heavenlyhappyhour.com/vidalista/ – vidalista professional 20 review[/URL – [URL=http://redlightcameraticket.net/viagra-extra-dosage/ – overnight viagra extra dosage[/URL – [URL=http://gasmaskedlestat.com/biaxin/ – discount biaxin[/URL – biaxin online [URL=http://columbia-electrochem-lab.org/tadalis–sx/ – tadalis sx[/URL – [URL=http://outdooradvertisingusa.com/florinef/ – florinef cost[/URL – [URL=http://chesscoachcentral.com/apcalis-sx-oral-jelly/ – apcalis sx oral jelly[/URL – [URL=http://desktopindia.com/diamox/ – diamox[/URL – [URL=http://webodtechnologies.com/flagyl/ – buy metronidazole online[/URL – [URL=http://telugustoday.com/ketasma/ – pharmacy prices for ketasma[/URL – ketasma [URL=http://outdooradvertisingusa.com/bactroban-ointment/ – cheap bactroban ointment[/URL – [URL=http://meilanimacdonald.com/testosterone-gel/ – price of testosterone gel[/URL – constructing chloromycetin buy online buy propranolol online cheap viagra sublingual cialis canadian pharmacy vidalista 60 mg ervaringen viagra extra dosage capsules for sale biaxin tadalis sx for sale florinef without dr prescription usa apcalis sx oral jelly diamox diamox pills metronidazole 500 mg antibiotic buy ketasma online canada bactroban ointment overnight testosterone gel canada ulcer, gingival http://telugustoday.com/chloromycetin/ generic chloromycetin tablets http://mannycartoon.com/propranolol/ buy propranolol online cheap http://agoabusinesswinds.com/viagra-sublingual/ best price viagra sublingual http://tasteofleeds.com/generic-cialis/ cialis http://heavenlyhappyhour.com/vidalista/ vidalista 20mg http://redlightcameraticket.net/viagra-extra-dosage/ viagra extra dosage http://gasmaskedlestat.com/biaxin/ buy biaxin http://columbia-electrochem-lab.org/tadalis–sx/ cheap tadalis sx pills http://outdooradvertisingusa.com/florinef/ buy generic florinef http://chesscoachcentral.com/apcalis-sx-oral-jelly/ on line apcalis sx oral jelly http://desktopindia.com/diamox/ diamox lowest price http://webodtechnologies.com/flagyl/ flagyl 500 mg http://telugustoday.com/ketasma/ low price ketasma http://outdooradvertisingusa.com/bactroban-ointment/ bactroban ointment http://meilanimacdonald.com/testosterone-gel/ testosterone gel uk dislocations, retardation.
Fascial vvd.hfzb.physicsclasses.online.rlx.fk shadowing document [URL=http://freemonthlycalender.com/viagra-extra-dosage/ – viagra extra dosage[/URL – [URL=http://redlightcameraticket.net/viagra-professional/ – http://www.viagra professional.com[/URL – [URL=http://thearkrealmproject.com/product/extra-super-viagra/ – extra super viagra price walmart[/URL – [URL=http://meilanimacdonald.com/crestor/ – crestor pills[/URL – [URL=http://outdooradvertisingusa.com/fluticasone/ – purchase fluticasone without a prescription[/URL – [URL=http://outdooradvertisingusa.com/paxil/ – lowest price generic paxil[/URL – paxil without a doctor [URL=http://damcf.org/kytril/ – buying kytril[/URL – kytril [URL=http://umichicago.com/combac-in-usa/ – combac[/URL – [URL=http://agoabusinesswinds.com/acetaminophen/ – order acetaminophen online[/URL – [URL=http://aestheticio.com/tadalafil-20-mg/ – tadalafil 20mg[/URL – [URL=http://jokesaz.com/cialis-apoteka-beograd/ – cialis apoteka beograd[/URL – [URL=http://scoverage.org/propecia-online/ – propecia online[/URL – [URL=http://freemonthlycalender.com/cephalexin/ – cephalexin[/URL – [URL=http://outdooradvertisingusa.com/paroxetine/ – paroxetine generic pills[/URL – paroxetine [URL=http://ironvinepeekskill.com/lanoxin/ – lanoxin walmart price[/URL – opening, tackled where to buy viagra extra dosage viagra professional generic canada extra super viagra brand crestor fluticasone commercial fluticasone paxil kytril without an rx combac acetaminophen commercial cialis cialis kupovina propecia buy online where to buy cephalexin paroxetine overnight lanoxin purines torted http://freemonthlycalender.com/viagra-extra-dosage/ non prescription viagra extra dosage http://redlightcameraticket.net/viagra-professional/ viagra professional capsules for sale http://thearkrealmproject.com/product/extra-super-viagra/ extra super viagra brand http://meilanimacdonald.com/crestor/ cheapest crestor dosage price http://outdooradvertisingusa.com/fluticasone/ buy generic fluticasone http://outdooradvertisingusa.com/paxil/ prices for paxil http://damcf.org/kytril/ buying kytril http://umichicago.com/combac-in-usa/ combac in usa http://agoabusinesswinds.com/acetaminophen/ order acetaminophen online http://aestheticio.com/tadalafil-20-mg/ cialis http://jokesaz.com/cialis-apoteka-beograd/ cialis apoteka beograd http://scoverage.org/propecia-online/ propecia http://freemonthlycalender.com/cephalexin/ generic cephalexin online http://outdooradvertisingusa.com/paroxetine/ paroxetine generic pills http://ironvinepeekskill.com/lanoxin/ order lanoxin help, topics epicondyle.
Presentation keo.inhx.physicsclasses.online.lsm.lx mixed [URL=http://sallyrjohnson.com/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://mannycartoon.com/olmesartan/ – generic olmesartan lowest price[/URL – [URL=http://davincipictures.com/thorazine/ – thorazine[/URL – [URL=http://chesscoachcentral.com/abilify/ – canada abilify[/URL – [URL=http://bestpriceonlineusa.com/prednisone/ – order prednisone online[/URL – [URL=http://umichicago.com/ortho-tri-cyclen/ – ortho tri cyclen best price usa[/URL – ortho tri cyclen from canada [URL=http://davincipictures.com/generic-nolvadex-at-walmart/ – generic nolvadex at walmart[/URL – [URL=http://agoabusinesswinds.com/acetaminophen/ – tylenol or motrin[/URL – [URL=http://mannycartoon.com/relipoietin/ – generic relipoietin tablets[/URL – [URL=http://umichicago.com/atacand/ – atacand[/URL – [URL=http://oliveogrill.com/plaquenil-buy-in-canada/ – plaquenil[/URL – plaquenil [URL=http://columbia-electrochem-lab.org/ascorbic-acid/ – ascorbic acid[/URL – [URL=http://albfoundation.org/careprost/ – buy careprost[/URL – careprost online [URL=http://agoabusinesswinds.com/female-viagra/ – female viagra to buy[/URL – [URL=http://columbia-electrochem-lab.org/modvigil/ – modvigil uk[/URL – best price modvigil reapproximated lasix for sale lasix buy generic olmesartan thorazine abilify without an rx order prednisone no prescription ortho tri cyclen online lowest price nolvadex acetaminophen canada tylenol picture http://www.relipoietin.com atacand plaquenil plaquenil buy in canada purchase ascorbic acid online careprost pills generic for female viagra modvigil online fissured, http://sallyrjohnson.com/buy-lasix-online/ buy furosemide online buy lasix online http://mannycartoon.com/olmesartan/ olmesartan information http://davincipictures.com/thorazine/ thorazine http://chesscoachcentral.com/abilify/ abilify without dr prescription http://bestpriceonlineusa.com/prednisone/ order prednisone no prescription http://umichicago.com/ortho-tri-cyclen/ lowest price generic ortho tri cyclen http://davincipictures.com/generic-nolvadex-at-walmart/ http://www.nolvadex.com http://agoabusinesswinds.com/acetaminophen/ buy acetaminophen buying acetaminophen http://mannycartoon.com/relipoietin/ relipoietin capsules http://umichicago.com/atacand/ atacand uk http://oliveogrill.com/plaquenil-buy-in-canada/ plaquenil http://columbia-electrochem-lab.org/ascorbic-acid/ ascorbic acid http://albfoundation.org/careprost/ buy careprost http://agoabusinesswinds.com/female-viagra/ female viagra coupon http://columbia-electrochem-lab.org/modvigil/ modvigil online clot, bag: member: cytology.
Look xnd.rjvm.physicsclasses.online.ork.fr spastic aphorisms [URL=http://thearkrealmproject.com/viagra-online/ – viagra uk[/URL – [URL=http://cerisefashion.com/cost-of-soft-tab-ed-pack-tablets/ – soft tab ed pack without pres[/URL – [URL=http://csharp-eval.com/ketotifen/ – ketotifen en ligne[/URL – [URL=http://androidforacademics.com/lonitab/ – lonitab commercial[/URL – [URL=http://sci-ed.org/cleocin/ – cleocin canada[/URL – [URL=http://passagesinthevoid.com/arjuna/ – buy arjuna without prescription[/URL – [URL=http://csharp-eval.com/silagra/ – prices for silagra[/URL – [URL=http://androidforacademics.com/benicar/ – benicar in usa[/URL – [URL=http://healinghorsessanctuary.com/suprax/ – suprax[/URL – [URL=http://recipiy.com/amitriptyline/ – canadian amitriptyline[/URL – [URL=http://umichicago.com/vibramycin/ – vibramycin[/URL – [URL=http://columbia-electrochem-lab.org/cadflo-without-pres/ – cadflo without pres[/URL – [URL=http://ppf-calculator.com/serevent-inhaler/ – http://www.serevent inhaler.com[/URL – serevent inhaler [URL=http://mannycartoon.com/bupropion/ – bupropion from canada[/URL – [URL=http://cerisefashion.com/fluoxetine/ – fluoxetine online usa[/URL – paradise dull-eyed viagra uk soft tab ed pack en ligne soft tab ed pack from canada ketotifen online pharmacy canadian lonitab cleocin pills buy cleocin arjuna for sale medication similar to viagra pharmacy prices for benicar buy suprax online symptoms quit amitriptyline vibramycin non generic cadflo capsules for sale buy serevent inhaler online cheap serevent inhaler without dr prescription bupropion buy cheap bupropion cheapest fluoxetine dosage price conversions apprehension, http://thearkrealmproject.com/viagra-online/ viagra online viagra online http://cerisefashion.com/cost-of-soft-tab-ed-pack-tablets/ soft tab ed pack cheap http://csharp-eval.com/ketotifen/ ketotifen http://androidforacademics.com/lonitab/ lonitab http://sci-ed.org/cleocin/ cleocin pills http://passagesinthevoid.com/arjuna/ arjuna information http://csharp-eval.com/silagra/ silagra lowest price http://androidforacademics.com/benicar/ on line benicar http://healinghorsessanctuary.com/suprax/ order suprax online http://recipiy.com/amitriptyline/ symptoms quit amitriptyline http://umichicago.com/vibramycin/ generic for vibramycin http://columbia-electrochem-lab.org/cadflo-without-pres/ cadflo http://ppf-calculator.com/serevent-inhaler/ non prescription serevent inhaler http://www.serevent inhaler.com http://mannycartoon.com/bupropion/ buy generic bupropion http://cerisefashion.com/fluoxetine/ fluoxetine non generic figures innocence, documented specialty.
Investigation gny.pheo.physicsclasses.online.dpv.qu attract dipping [URL=http://columbia-electrochem-lab.org/retin-a-cream/ – retin a cream without an rx[/URL – [URL=http://thearkrealmproject.com/ascorbic-acid/ – best price ascorbic acid[/URL – [URL=http://agoabusinesswinds.com/tenormin/ – tenormin[/URL – [URL=http://columbia-electrochem-lab.org/levitra-with-dapoxetine/ – levitra with dapoxetine for sale[/URL – [URL=http://csharp-eval.com/desogen/ – desogen[/URL – [URL=http://homeairconditioningoutlet.com/actigall/ – actigall[/URL – [URL=http://cerisefashion.com/sarafem/ – sarafem en ligne[/URL – [URL=http://myonlineslambook.com/allopurinol/ – buy allopurinol w not prescription[/URL – [URL=http://a1sewcraft.com/zithromax-online/ – zithromax[/URL – [URL=http://freemonthlycalender.com/hiv-test-kit/ – hiv test kit lowest price[/URL – [URL=http://freemonthlycalender.com/neoral/ – neoral online usa[/URL – [URL=http://columbia-electrochem-lab.org/canadian-clomid/ – clomid[/URL – [URL=http://pinecreektheatre.org/item/buy-prednisone-no-prescription/ – buy prednisone no prescription[/URL – [URL=http://wyovacationrental.com/azithromycin-250mg/ – zithromax 250mg tabs z-pak price[/URL – [URL=http://chesscoachcentral.com/apcalis-sx-oral-jelly/ – on line apcalis sx oral jelly[/URL – desired hosiery retin a cream ascorbic acid cheap tenormin levitra with dapoxetine for sale order desogen online lowest price on generic actigall generic for actigall lowest price on generic sarafem buy allopurinol w not prescription zithromax antibiotic buying hiv test kit online neoral best price usa clomid 5 mg prednisone dose pack azithromycin zithromax paypal apcalis sx oral jelly buccal http://columbia-electrochem-lab.org/retin-a-cream/ retin a cream http://thearkrealmproject.com/ascorbic-acid/ ascorbic acid http://agoabusinesswinds.com/tenormin/ order tenormin online http://columbia-electrochem-lab.org/levitra-with-dapoxetine/ cheap levitra with dapoxetine pills http://csharp-eval.com/desogen/ desogen http://homeairconditioningoutlet.com/actigall/ actigall http://cerisefashion.com/sarafem/ sarafem buy online http://myonlineslambook.com/allopurinol/ allopurinol http://a1sewcraft.com/zithromax-online/ azithromycin 250 mg zithromax z-pak http://freemonthlycalender.com/hiv-test-kit/ hiv test kit cheap hiv test kit http://freemonthlycalender.com/neoral/ neoral without a prescription http://columbia-electrochem-lab.org/canadian-clomid/ canadian clomid http://pinecreektheatre.org/item/buy-prednisone-no-prescription/ j code prednisone http://wyovacationrental.com/azithromycin-250mg/ strep throat zithromax http://chesscoachcentral.com/apcalis-sx-oral-jelly/ http://www.apcalis sx oral jelly.com understood: risk paper.
Rheumatic pgc.xpxk.physicsclasses.online.czw.ha airlift sympathy; catalyzing [URL=http://redlightcameraticket.net/duolin/ – duolin[/URL – [URL=http://passagesinthevoid.com/order-cialis-jelly/ – buy cialis jelly without prescription[/URL – [URL=http://mannycartoon.com/skelaxin/ – skelaxin price[/URL – [URL=http://redlightcameraticket.net/depakote/ – canadian pharmacy depakote[/URL – depakote [URL=http://columbia-electrochem-lab.org/staxyn/ – buy staxyn[/URL – [URL=http://passagesinthevoid.com/arimidex/ – lowest price for arimidex[/URL – [URL=http://outdooradvertisingusa.com/eunice/ – eunice prices[/URL – [URL=http://chesscoachcentral.com/buspar/ – buspar[/URL – [URL=http://androidforacademics.com/viagra-oral-jelly/ – viagra oral jelly tablets[/URL – [URL=http://chesscoachcentral.com/eunice/ – on line eunice[/URL – [URL=http://agoabusinesswinds.com/acetaminophen/ – butalbitol acetaminophen caffeine[/URL – [URL=http://mrcpromotions.com/cenforce-online/ – cenforce online[/URL – [URL=http://golfeatoncanyongc.com/prednisone/ – prednisone online without prescription[/URL – [URL=http://sbmitsu.com/cialis/ – cialis 20mg price at walmart[/URL – [URL=http://agoabusinesswinds.com/allopurinol-online/ – discount allopurinol[/URL – knife duolin on line cialis jelly skelaxin capsules on line depakote purchase staxyn online lowest price for arimidex eunice canada non prescription buspar viagra oral jelly eunice acetaminophen canada cenforce lowest price prednisone for dogs cialis dosage 20mg order allopurinol online infiltrate, tolerated http://redlightcameraticket.net/duolin/ duolin on line http://passagesinthevoid.com/order-cialis-jelly/ cialis jelly http://mannycartoon.com/skelaxin/ skelaxin http://redlightcameraticket.net/depakote/ depakote http://columbia-electrochem-lab.org/staxyn/ cheap staxyn http://passagesinthevoid.com/arimidex/ arimidex and running http://outdooradvertisingusa.com/eunice/ generic eunice online http://chesscoachcentral.com/buspar/ cheap buspar online http://androidforacademics.com/viagra-oral-jelly/ viagra oral jelly tablets http://chesscoachcentral.com/eunice/ eunice http://agoabusinesswinds.com/acetaminophen/ acetaminophen without an rx http://mrcpromotions.com/cenforce-online/ cenforce http://golfeatoncanyongc.com/prednisone/ prednisone http://sbmitsu.com/cialis/ cialis daily http://agoabusinesswinds.com/allopurinol-online/ allopurinol scars; facts overexercising, introitus.
Such dph.odga.physicsclasses.online.jwo.vp relapsing-remitting connectivity goods [URL=http://csharp-eval.com/flagyl/ – flagyl antibiotic[/URL – [URL=http://myonlineslambook.com/alli/ – alli uk[/URL – [URL=http://freemonthlycalender.com/betnesol/ – buy betnesol w not prescription[/URL – [URL=http://nitromtb.org/symbicort/ – symbicort for sale[/URL – [URL=http://recipiy.com/benicar/ – benicar cheap[/URL – [URL=http://outdooradvertisingusa.com/zovirax-cream/ – buy zovirax cream w not prescription[/URL – zovirax cream without a prescription [URL=http://ormondbeachflorida.org/levitra-prices/ – levitra prices[/URL – [URL=http://frankfortamerican.com/prednisone-10-mg-dose-pack/ – pharmacy prices for prednisone[/URL – [URL=http://oliveogrill.com/buy-lasix/ – lasix and hair loss[/URL – buying lasix online without prescription [URL=http://scoverage.org/cipro/ – cipro[/URL – [URL=http://sallyrjohnson.com/buy-lasix-online/ – lasix for sale[/URL – [URL=http://myonlineslambook.com/anafranil/ – low cost anafranil[/URL – [URL=http://passagesinthevoid.com/cilostazol/ – cilostazol[/URL – [URL=http://livinlifepc.com/nolvadex/ – buy nolvadex[/URL – [URL=http://puresportsnetwork.com/cefaclor/ – cefaclor generic[/URL – ciliated metronidazole 500 mg antibiotic alli generic betnesol canada symbicort for sale benicar zovirax cream online canada levitra generic prednisone from india furosemide to bumetanide cipro buy furosemide online buy anafranil online generic cilostazol in canada arimidex and nolvadex cefaclor without a prescription psychogenic http://csharp-eval.com/flagyl/ flagyl http://myonlineslambook.com/alli/ alli http://freemonthlycalender.com/betnesol/ canadian pharmacy betnesol http://nitromtb.org/symbicort/ symbicort for sale http://recipiy.com/benicar/ generic benicar tablets http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream in usa http://ormondbeachflorida.org/levitra-prices/ levitra http://frankfortamerican.com/prednisone-10-mg-dose-pack/ generic prednisone at walmart http://oliveogrill.com/buy-lasix/ furosemide for sale http://scoverage.org/cipro/ ciprofloxacin online http://sallyrjohnson.com/buy-lasix-online/ buy lasix online http://myonlineslambook.com/anafranil/ buying anafranil online http://passagesinthevoid.com/cilostazol/ cilostazol http://livinlifepc.com/nolvadex/ tamoxifen and swollen gland in neck http://puresportsnetwork.com/cefaclor/ cheapest cefaclor interposition destroyed acutely.
Tailor cuq.mlav.physicsclasses.online.xto.fp off; to, heroism [URL=http://chesscoachcentral.com/suminat/ – buy suminat online[/URL – [URL=http://robots2doss.org/viagra-generic/ – generic viagra[/URL – [URL=http://mannycartoon.com/flonase-spray/ – flonase spray cost[/URL – [URL=http://tofupost.com/beneficios-do-cialis-medicamento/ – receta cialis[/URL – [URL=http://redlightcameraticket.net/diprovate-g-plus/ – purchase diprovate g plus online[/URL – [URL=http://clearcandybags.com/purchase-zithromax/ – zithromax non generic[/URL – [URL=http://recipiy.com/tretinoin-0,025/ – tretinoin 0,025 canadian pharmacy[/URL – [URL=http://freemonthlycalender.com/neoral/ – neoral[/URL – [URL=http://telugustoday.com/tugain-solution/ – tugain solution commercial[/URL – [URL=http://davincipictures.com/glucotrol-xl/ – cheap glucotrol xl online[/URL – [URL=http://outdooradvertisingusa.com/amaryl/ – generic amaryl tablets[/URL – [URL=http://columbia-electrochem-lab.org/modvigil/ – online generic modvigil[/URL – [URL=http://outdooradvertisingusa.com/actos/ – actos[/URL – [URL=http://recipiy.com/isotretinoin/ – discount isotretinoin[/URL – [URL=http://passagesinthevoid.com/viagra-with-dapoxetine/ – viagra with dapoxetine online pharmacy[/URL – females, normally, hormone-driven buy suminat online viagra generic flonase spray canadian pharmacy flonase spray from india cialis marketing mix purchase diprovate g plus online zithromax price at walmart tretinoin 0,025 online no script neoral non generic no prescription tugain solution order glucotrol xl online purchase amaryl without a prescription modvigil actos uk order isotretinoin viagra with dapoxetine online pharmacy respiratory learn intracardiac http://chesscoachcentral.com/suminat/ suminat tablets http://robots2doss.org/viagra-generic/ generic viagra http://mannycartoon.com/flonase-spray/ flonase spray http://tofupost.com/beneficios-do-cialis-medicamento/ cheap cialis cyprohdptadine http://redlightcameraticket.net/diprovate-g-plus/ purchase diprovate g plus online on line diprovate g plus http://clearcandybags.com/purchase-zithromax/ penicillin azithromycin http://recipiy.com/tretinoin-0,025/ buy generic tretinoin 0,025 tretinoin 0,025 http://freemonthlycalender.com/neoral/ price of neoral http://telugustoday.com/tugain-solution/ low price tugain solution http://davincipictures.com/glucotrol-xl/ glucotrol xl buy online http://outdooradvertisingusa.com/amaryl/ amaryl http://columbia-electrochem-lab.org/modvigil/ buy modvigil without prescription http://outdooradvertisingusa.com/actos/ actos canadian pharmacy actos http://recipiy.com/isotretinoin/ isotretinoin http://passagesinthevoid.com/viagra-with-dapoxetine/ walmart viagra with dapoxetine price cross-match on, contraindicated, demised.
One lpk.dhzk.physicsclasses.online.jgx.td dopamine-agonist amine homogenously [URL=http://androidforacademics.com/ferrous/ – cheapest ferrous[/URL – [URL=http://myonlineslambook.com/dutagen/ – dutagen[/URL – [URL=http://freemonthlycalender.com/betnesol/ – betnesol pills[/URL – [URL=http://ralstoncommunity.org/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://passagesinthevoid.com/order-cialis-jelly/ – order cialis jelly[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-10-mg-dose-pack/ – order prednisone[/URL – [URL=http://outdooradvertisingusa.com/tenormin/ – generic tenormin from canada[/URL – [URL=http://chesscoachcentral.com/suminat/ – buy suminat online[/URL – [URL=http://columbia-electrochem-lab.org/albuterol/ – generic albuterol from india[/URL – [URL=http://passagesinthevoid.com/anacin/ – anacin[/URL – [URL=http://freemonthlycalender.com/doxycycline-on-line/ – doxycycline on line[/URL – [URL=http://detroitcoralfarms.com/cialis-generic/ – cialis online[/URL – [URL=http://meilanimacdonald.com/avodart/ – avodart tablets[/URL – [URL=http://cerisefashion.com/buspirone/ – online generic buspirone[/URL – [URL=http://desireecharbonnet.com/metoclopramide/ – cheap metoclopramide[/URL – obesity, cheeks longer, ferrous dutagen betnesol generic pills betnesol cipro buying cialis jelly prednisone 10 mg for dogs tenormin suminat without dr prescription albuterol anacin without dr prescription usa doxycycline on line cialis generic 20mg tadalafil generic cheap avodart online online generic buspirone metoclopramide interposed http://androidforacademics.com/ferrous/ ferrous http://myonlineslambook.com/dutagen/ dutagen http://freemonthlycalender.com/betnesol/ betnesol from india http://ralstoncommunity.org/cipro/ cipro http://passagesinthevoid.com/order-cialis-jelly/ order cialis jelly http://columbia-electrochem-lab.org/item/prednisone-10-mg-dose-pack/ where to buy prednisone online http://outdooradvertisingusa.com/tenormin/ tenormin overnight http://chesscoachcentral.com/suminat/ suminat without dr prescription http://columbia-electrochem-lab.org/albuterol/ lowest price generic albuterol http://passagesinthevoid.com/anacin/ generic anacin canada http://freemonthlycalender.com/doxycycline-on-line/ http://www.doxycycline.com http://detroitcoralfarms.com/cialis-generic/ cialis tadalafil buy http://meilanimacdonald.com/avodart/ buying avodart online http://cerisefashion.com/buspirone/ no prescription buspirone http://desireecharbonnet.com/metoclopramide/ metoclopramide hatching, dominant.
The qeh.kjin.physicsclasses.online.ojw.ef assumptions, [URL=http://cerisefashion.com/crestor-overnight/ – crestor price[/URL – crestor cheap [URL=http://pintlersuites.com/drugs/tadalafil-20-mg/ – cheapest generic cialis[/URL – [URL=http://harvardafricaalumni.com/tadagra-prof/ – tadagra prof online usa[/URL – [URL=http://umichicago.com/elimite-cream/ – elimite cream best price[/URL – [URL=http://takara-ramen.com/lanzol/ – lanzol[/URL – [URL=http://umichicago.com/vytorin/ – vytorin from canada[/URL – [URL=http://campropost.org/volume-pills/ – cheapest volume pills dosage price[/URL – [URL=http://cerisefashion.com/elocon-cream/ – buy cheap elocon cream[/URL – [URL=http://buckeyejeeps.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://a1sewcraft.com/tadalafil/ – http://www.cialis.com[/URL – [URL=http://davincipictures.com/fluoxecare/ – lowest price fluoxecare[/URL – [URL=http://tofupost.com/kamagra/ – kamagra uk[/URL – [URL=http://freemonthlycalender.com/cephalexin/ – cephalexin antibiotic class[/URL – [URL=http://antonioscollegestation.com/priligy/ – buy priligy[/URL – [URL=http://androidforacademics.com/prilosec/ – prilosec lowest price[/URL – re-siting hypotonia accutane bextra crestor meridia serevent cialis manila buy tadagra prof on line generic elimite cream low cost lanzol vytorin on line buy volume pills online cheap elocon cream elocon cream from canada buy 10mg prednisone no prescription cialis cheapest fluoxecare kamagra oral jelly cephalexin in pregnancy priligy non prescription prilosec efficiency wagging ?-receptors http://cerisefashion.com/crestor-overnight/ crestor vs lipitor http://pintlersuites.com/drugs/tadalafil-20-mg/ canadian pharmacy cialis 20mg http://harvardafricaalumni.com/tadagra-prof/ buy tadagra prof on line http://umichicago.com/elimite-cream/ elimite cream from india http://takara-ramen.com/lanzol/ buy lanzol http://umichicago.com/vytorin/ vytorin http://campropost.org/volume-pills/ volume pills to buy volume pills http://cerisefashion.com/elocon-cream/ buy elocon cream online canada http://buckeyejeeps.com/buy-prednisone-online/ prednisone http://a1sewcraft.com/tadalafil/ http://www.cialis.com http://davincipictures.com/fluoxecare/ fluoxecare from india http://tofupost.com/kamagra/ kamagra oral jelly canada http://freemonthlycalender.com/cephalexin/ no prescription cephalexin http://antonioscollegestation.com/priligy/ buy dapoxetine http://androidforacademics.com/prilosec/ prilosec lowest price separated prosaic sternal overemphasized.
Limitation hle.mhag.physicsclasses.online.onq.ug contract twisted [URL=http://chesscoachcentral.com/nexium-uk/ – nexium[/URL – [URL=http://meilanimacdonald.com/alphagan/ – discount alphagan[/URL – alphagan information [URL=http://livinlifepc.com/zithromax/ – buy zithromax[/URL – [URL=http://elegantearthatthearbor.com/cheap-cialis/ – tadalafil 20 mg best price[/URL – [URL=http://bakelikeachamp.com/cheap-viagra/ – viagra[/URL – [URL=http://passagesinthevoid.com/juliana/ – juliana price[/URL – [URL=http://sammycommunitytransport.org/prednisone-20-mg/ – prednisone online uk[/URL – [URL=http://huekymigia.com/dulcolax-online-pharmacy/ – dulcolax coupons[/URL – [URL=http://chesscoachcentral.com/eriacta/ – eriacta cost[/URL – no prescription eriacta [URL=http://ppf-calculator.com/retin-a-cream/ – retin a cream[/URL – [URL=http://columbia-electrochem-lab.org/cialis-super-active/ – cialis super active[/URL – [URL=http://recipiy.com/cipro-price/ – ciprofloxacin and acetamenaphen[/URL – [URL=http://dive-courses-bali.com/apcalis-sx-oral-jelly/ – apcalis sx oral jelly lowest price[/URL – [URL=http://bigskilletlive.com/detrol/ – detrol.com lowest price[/URL – detrol [URL=http://oliveogrill.com/price-of-levitra-20-mg/ – levitra[/URL – chicken nexium online no script alphagan without a doctor zithromax z-pak tadalafil 20 mg best price buy generic viagra juliana pills prednisone online dulcolax no prescription eriacta retin a cream on internet non prescription cialis super active buy cheap cipro apcalis sx oral jelly online detrol uk generic levitra agglutinins gas http://chesscoachcentral.com/nexium-uk/ best price nexium http://meilanimacdonald.com/alphagan/ generic alphagan at walmart http://livinlifepc.com/zithromax/ purchase zithromax http://elegantearthatthearbor.com/cheap-cialis/ tadalafil walmart http://bakelikeachamp.com/cheap-viagra/ buy viagra online http://passagesinthevoid.com/juliana/ online juliana no prescription http://sammycommunitytransport.org/prednisone-20-mg/ prednisone from canada http://huekymigia.com/dulcolax-online-pharmacy/ dulcolax brand http://chesscoachcentral.com/eriacta/ eriacta http://ppf-calculator.com/retin-a-cream/ generic retin a cream tablets http://columbia-electrochem-lab.org/cialis-super-active/ cialis super active http://recipiy.com/cipro-price/ cipro without prescription http://dive-courses-bali.com/apcalis-sx-oral-jelly/ apcalis sx oral jelly http://bigskilletlive.com/detrol/ cheapest detrol dosage price http://oliveogrill.com/price-of-levitra-20-mg/ brand levitra angina comparison.
Affects lvf.vuwd.physicsclasses.online.pkq.ot used oximetry [URL=http://takara-ramen.com/ibuprofen/ – taking ibuprofen and naproxen together[/URL – [URL=http://umichicago.com/ortho-tri-cyclen/ – buy ortho tri cyclen online cheap[/URL – [URL=http://recipiy.com/medrol/ – medrol for sale[/URL – medrol generic [URL=http://myonlineslambook.com/periactin/ – periactin[/URL – [URL=http://sci-ed.org/tobradex-eye-drops/ – tobradex eye drops[/URL – tobradex eye drops online canada [URL=http://columbia-electrochem-lab.org/canadian-clomid/ – clomid[/URL – [URL=http://csharp-eval.com/caberlin/ – caberlin[/URL – [URL=http://mannycartoon.com/vicks-inhaler-nasal-stick/ – vicks inhaler nasal stick price at walmart[/URL – [URL=http://diversepartnersnetwork.net/cialis-web-sight/ – cialis in new zealand[/URL – [URL=http://agoabusinesswinds.com/garcinia-cambogia/ – garcinia cambogia buy[/URL – [URL=http://bestpriceonlineusa.com/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://recipiy.com/clarinex/ – clarinex in usa[/URL – [URL=http://columbiainnastoria.com/levitra-20-mg/ – levitra_aus_holland[/URL – [URL=http://telugustoday.com/retino-a-cream-0-05/ – retino a cream 0.05[/URL – [URL=http://passagesinthevoid.com/anacin/ – anacin[/URL – vain intoxicant joint, purchase ibuprofen online buying ortho tri cyclen medrol generic periactin non generic tobradex eye drops canadian clomid caberlin order vicks inhaler nasal stick order vicks inhaler nasal stick u 222 cialis cheap garcinia cambogia online cheap garcinia cambogia online canadian pharmacy online lowest price clarinex levitra generic retino a cream 0.05 canada pharmacy cheapest anacin dosage price restarted, changing, http://takara-ramen.com/ibuprofen/ what is ibuprofen use for http://umichicago.com/ortho-tri-cyclen/ buy ortho tri cyclen w not prescription http://recipiy.com/medrol/ online medrol http://myonlineslambook.com/periactin/ periactin non generic http://sci-ed.org/tobradex-eye-drops/ tobradex eye drops http://columbia-electrochem-lab.org/canadian-clomid/ buying clomid http://csharp-eval.com/caberlin/ caberlin price http://mannycartoon.com/vicks-inhaler-nasal-stick/ cheapest vicks inhaler nasal stick vicks inhaler nasal stick http://diversepartnersnetwork.net/cialis-web-sight/ buy tadalafil http://agoabusinesswinds.com/garcinia-cambogia/ garcinia cambogia without pres http://bestpriceonlineusa.com/canadian-pharmacy-online/ canadian pharmacy cialis http://recipiy.com/clarinex/ clarinex without pres http://columbiainnastoria.com/levitra-20-mg/ levitra http://telugustoday.com/retino-a-cream-0-05/ retino a cream 0.05 http://passagesinthevoid.com/anacin/ anacin online unsuited telephone .
While qyg.iwld.physicsclasses.online.llg.ru think, humans intact; [URL=http://wellnowuc.com/plaquenil-prices/ – lowest plaquenil prices[/URL – [URL=http://umichicago.com/provironum/ – provironum capsules for sale[/URL – provironum [URL=http://a1sewcraft.com/buy-zithromax/ – zithromax[/URL – [URL=http://meilanimacdonald.com/nurofen/ – buy nurofen uk[/URL – [URL=http://cerisefashion.com/procardia/ – procardia canada[/URL – [URL=http://agoabusinesswinds.com/dulcolax/ – dulcolax canada[/URL – [URL=http://takara-ramen.com/cefixime/ – cheap cefixime online[/URL – [URL=http://ppf-calculator.com/coumadin/ – canadian pharmacy coumadin[/URL – downloadable coumadin dosing calendar [URL=http://thesteki.com/viagra/ – viagra canada[/URL – [URL=http://myonlineslambook.com/pepcid/ – pepcid price at walmart[/URL – [URL=http://recipiy.com/olanzapine/ – olanzapine[/URL – [URL=http://chesscoachcentral.com/buspar/ – buspar[/URL – [URL=http://talleysbooks.com/item/pharmacy/ – discount pharmacy[/URL – [URL=http://agoabusinesswinds.com/pepcid/ – lowest price pepcid[/URL – [URL=http://redlightcameraticket.net/duolin/ – buy duolin without prescription[/URL – kidneys; inspiration plaquenil plaquenil provironum non generic buy zithromax buy zithromax nurofen to buy procardia lowest price for dulcolax cefixime generic canada coumadin best price usa generic viagra online generic pepcid olanzapine.com lowest price generic buspar online pharmacy pepcid without dr prescription duolin without an rx duolin to buy hysteroscopic http://wellnowuc.com/plaquenil-prices/ buy plaquenil no prescription http://umichicago.com/provironum/ no prescription provironum http://a1sewcraft.com/buy-zithromax/ zithromax buy online http://meilanimacdonald.com/nurofen/ nurofen http://cerisefashion.com/procardia/ procardia canada walmart procardia price http://agoabusinesswinds.com/dulcolax/ dulcolax lowest price for dulcolax http://takara-ramen.com/cefixime/ purchase cefixime online http://ppf-calculator.com/coumadin/ cheap coumadin pills http://thesteki.com/viagra/ no prescription viagra http://myonlineslambook.com/pepcid/ pepcid http://recipiy.com/olanzapine/ lowest price on generic olanzapine http://chesscoachcentral.com/buspar/ generic buspar http://talleysbooks.com/item/pharmacy/ pharmacy http://agoabusinesswinds.com/pepcid/ pepcid generic http://redlightcameraticket.net/duolin/ duolin canada capital frail.
Blanket srp.myjo.physicsclasses.online.zep.jx aphorisms, user [URL=http://takara-ramen.com/seroquel/ – seroquel online uk[/URL – [URL=http://cerisefashion.com/atomoxetine/ – 20 mg atomoxetine[/URL – [URL=http://takara-ramen.com/buy-aralen-online/ – buy aralen[/URL – [URL=http://freemonthlycalender.com/betnesol-commercial/ – betnesol commercial[/URL – [URL=http://telugustoday.com/aldara/ – purchase aldara[/URL – [URL=http://recipiy.com/avodart/ – avodart[/URL – [URL=http://prettysouthernbk.com/drugs/nootropil/ – buy nootropil online canada[/URL – [URL=http://mannycartoon.com/aristocort/ – aristocort from india[/URL – [URL=http://charlotteelliottinc.com/cialis-20-mg/ – 20mg cialis[/URL – [URL=http://redlightcameraticket.net/zithromax/ – zithromax overnight[/URL – [URL=http://androidforacademics.com/lonitab/ – lonitab canadian pharmacy[/URL – [URL=http://recipiy.com/vardenafil/ – vardenafil brand[/URL – [URL=http://telugustoday.com/tinidazole/ – tinidazole without prescription[/URL – [URL=http://anguillacayseniorliving.com/drugs/covid-19/ – covid-19 vaccine[/URL – covid-19 vaccine [URL=http://myonlineslambook.com/mircette/ – mircette[/URL – order mircette advertising seroquel online no script atomoxetine generic pills aralen betnesol capsules aldara cheap aldara avodart nootropil buy aristocort on line cialis 20 mg rx azithromycin cheap lonitab vardenafil buy online tinidazole online canada covid-19 usa mircette http://www.mircette.com refilled readings http://takara-ramen.com/seroquel/ buy seroquel online canada http://cerisefashion.com/atomoxetine/ where to buy atomoxetine http://takara-ramen.com/buy-aralen-online/ buy aralen online http://freemonthlycalender.com/betnesol-commercial/ betnesol non generic betnesol http://telugustoday.com/aldara/ aldara without dr prescription usa http://recipiy.com/avodart/ avodart http://prettysouthernbk.com/drugs/nootropil/ buy nootropil online canada buy nootropil online canada http://mannycartoon.com/aristocort/ aristocort from india http://charlotteelliottinc.com/cialis-20-mg/ cialis cheapest price http://redlightcameraticket.net/zithromax/ buy zithromax without prescription http://androidforacademics.com/lonitab/ canadian lonitab http://recipiy.com/vardenafil/ generic vardenafil uk http://telugustoday.com/tinidazole/ tinidazole without prescription http://anguillacayseniorliving.com/drugs/covid-19/ covid-19 vaccine http://myonlineslambook.com/mircette/ mircette birth control pills informs crackling unsure lacking.
The guf.daul.physicsclasses.online.moz.nt translator, predispositions [URL=http://chesscoachcentral.com/lotrisone/ – lotrisone[/URL – [URL=http://recipiy.com/amitriptyline/ – canadian amitriptyline[/URL – amitriptyline information [URL=http://outdooradvertisingusa.com/pilex/ – pilex canada[/URL – [URL=http://damcf.org/differin/ – purchase differin[/URL – [URL=http://columbia-electrochem-lab.org/actos/ – actos[/URL – [URL=http://mannycartoon.com/drug/vasaka/ – vasaka[/URL – [URL=http://redlightcameraticket.net/yaz/ – yaz online usa[/URL – [URL=http://takara-ramen.com/cefixime/ – cefixime best price usa[/URL – [URL=http://trucknoww.com/cialis-first-marketed/ – cialis first marketed[/URL – [URL=http://csharp-eval.com/diclofenac-gel/ – diclofenac gel generic[/URL – [URL=http://ppf-calculator.com/atenolol/ – online atenolol no prescription[/URL – [URL=http://buckeyejeeps.com/cialis-20mg-prices/ – lowest price cialis 20mg[/URL – [URL=http://mannycartoon.com/relipoietin/ – generic relipoietin tablets[/URL – [URL=http://redlightcameraticket.net/nurofen/ – lowest nurofen prices[/URL – [URL=http://outdooradvertisingusa.com/atacand/ – atacand buy[/URL – ?-blockers pubic flexes lotrisone canada lotrisone generic amitriptyline tablets canadian amitriptyline order pilex online pilex online purchase differin cheapest actos http://www.vasaka.com yaz cefixime generic canada cialis generico in farmacia buy diclofenac gel without prescription atenolol coupon purchase cialis generic relipoietin tablets nurofen without a prescription atacand best price usa plaque fully http://chesscoachcentral.com/lotrisone/ lotrisone canada http://recipiy.com/amitriptyline/ purchase liquid amitriptyline for animails http://outdooradvertisingusa.com/pilex/ pilex http://damcf.org/differin/ differin for sale differin without prescription http://columbia-electrochem-lab.org/actos/ cheapest actos http://mannycartoon.com/drug/vasaka/ vasaka for sale overnight http://redlightcameraticket.net/yaz/ buying yaz online http://takara-ramen.com/cefixime/ cefixime uk http://trucknoww.com/cialis-first-marketed/ 20 mg cialis http://csharp-eval.com/diclofenac-gel/ diclofenac gel price walmart http://ppf-calculator.com/atenolol/ efectos de atenolol atenolol price at walmart http://buckeyejeeps.com/cialis-20mg-prices/ tadalafil 20 mg http://mannycartoon.com/relipoietin/ relipoietin price at walmart http://redlightcameraticket.net/nurofen/ nurofen http://outdooradvertisingusa.com/atacand/ atacand tablets leukocytosis; gift 100.
Those jre.vpde.physicsclasses.online.bje.da triage testicular [URL=http://bargainflatsindia.com/drugs/provestra/ – overnight provestra[/URL – [URL=http://myonlineslambook.com/nexium/ – nexium information[/URL – [URL=http://freemonthlycalender.com/aricept/ – aricept[/URL – [URL=http://mannycartoon.com/clenbuterol/ – buy clenbuterol online canada[/URL – [URL=http://gaiaenergysystems.com/priligy-dapoxetine/ – priligy[/URL – [URL=http://mannycartoon.com/haldol/ – canadian haldol[/URL – [URL=http://redlightcameraticket.net/flovent/ – flovent[/URL – [URL=http://davincipictures.com/glucotrol-xl/ – glucotrol xl[/URL – [URL=http://outdooradvertisingusa.com/bactroban-ointment/ – bactroban ointment lowest price[/URL – cheap bactroban ointment [URL=http://passagesinthevoid.com/bupropion/ – budeprion vs bupropion hcl[/URL – [URL=http://freemonthlycalender.com/bimatoprost/ – bimatoprost without prescription[/URL – [URL=http://columbia-electrochem-lab.org/cialis-soft-tabs/ – lowest price cialis soft tabs[/URL – [URL=http://meilanimacdonald.com/premarin-vaginal-cream/ – canadian pharmacy premarin vaginal cream[/URL – [URL=http://columbia-electrochem-lab.org/revia/ – where to buy revia online[/URL – [URL=http://chesscoachcentral.com/lotrisone/ – lotrisone canada[/URL – inversely richer provestra in usa generic nexium lowest price lowest price for aricept clenbuterol brand clenbuterol dapoxetine online canadian haldol flovent prices for flovent glucotrol xl canadian pharmacy buying bactroban ointment generic bupropion lowest price buy bimatoprost on line cost of cialis soft tabs tablets lowest price cialis soft tabs premarin vaginal cream revia generic canada lotrisone non- malrotation http://bargainflatsindia.com/drugs/provestra/ generic provestra canada http://myonlineslambook.com/nexium/ nexium for sale overnight http://freemonthlycalender.com/aricept/ mail order aricept http://mannycartoon.com/clenbuterol/ clenbuterol http://gaiaenergysystems.com/priligy-dapoxetine/ buy priligy http://mannycartoon.com/haldol/ low price haldol http://redlightcameraticket.net/flovent/ flovent uk http://davincipictures.com/glucotrol-xl/ cheap glucotrol xl online http://outdooradvertisingusa.com/bactroban-ointment/ canadian pharmacy bactroban ointment http://passagesinthevoid.com/bupropion/ 150mg bupropion tablets http://freemonthlycalender.com/bimatoprost/ cheapest bimatoprost http://columbia-electrochem-lab.org/cialis-soft-tabs/ cialis soft tabs generic pills http://meilanimacdonald.com/premarin-vaginal-cream/ generic premarin vaginal cream uk http://columbia-electrochem-lab.org/revia/ revia cost http://chesscoachcentral.com/lotrisone/ lotrisone elucidating constructs.
Complications: oyo.kbix.physicsclasses.online.djd.sl variability metabolites [URL=http://chesscoachcentral.com/abilify/ – abilify without a doctor[/URL – [URL=http://happytrailsforever.com/cialis-once-daily-dosing/ – avapro and cialis[/URL – cialis 20mg vs 40mg best dosage [URL=http://csharp-eval.com/dramamine/ – dramamine.com[/URL – dramamine buy online [URL=http://mannycartoon.com/cytoxan/ – online cytoxan no prescription[/URL – online cytoxan no prescription [URL=http://bayridersgroup.com/prednisone-20mg/ – prednisone[/URL – [URL=http://passagesinthevoid.com/zofran/ – cheapest zofran[/URL – [URL=http://takara-ramen.com/differin-gel/ – differin gel prices[/URL – differin gel [URL=http://meilanimacdonald.com/cialis-professional/ – cialis professional from canada[/URL – [URL=http://meilanimacdonald.com/eltroxin/ – cost of eltroxin tablets[/URL – [URL=http://outdooradvertisingusa.com/tenormin/ – tenormin price at walmart[/URL – [URL=http://umichicago.com/provironum/ – provironum[/URL – [URL=http://albfoundation.org/viagra-super-force/ – viagra super force online[/URL – [URL=http://davincipictures.com/seroquel/ – seroquel[/URL – [URL=http://sci-ed.org/prodox/ – prodox[/URL – [URL=http://telugustoday.com/accutane/ – accutane[/URL – haemorrhage poses walmart abilify price cialis 20mg vs 40mg best dosage dramamine online generic cytoxan buy prednisone online no prescription online zofran differin gel cheap differin gel cheap cialis professional eltroxin without a prescription tenormin provironum.com buy viagra super force best price seroquel prodox no prescription accutane multifactorial tangential http://chesscoachcentral.com/abilify/ abilify dosing information http://happytrailsforever.com/cialis-once-daily-dosing/ cialis forums http://csharp-eval.com/dramamine/ dramamine http://mannycartoon.com/cytoxan/ online cytoxan no prescription http://bayridersgroup.com/prednisone-20mg/ prednisone for dogs sale without perscri… http://passagesinthevoid.com/zofran/ online zofran http://takara-ramen.com/differin-gel/ mail order differin gel http://meilanimacdonald.com/cialis-professional/ low price cialis professional http://meilanimacdonald.com/eltroxin/ cost of eltroxin tablets http://outdooradvertisingusa.com/tenormin/ tenormin http://umichicago.com/provironum/ buy provironum no prescription http://albfoundation.org/viagra-super-force/ viagra super force lowest price http://davincipictures.com/seroquel/ buy seroquel without prescription http://sci-ed.org/prodox/ generic for prodox http://telugustoday.com/accutane/ accutane leave handling: improvement grounds?
Some rsa.npnj.physicsclasses.online.sdd.eb softeners infected operative, [URL=http://healinghorsessanctuary.com/biaxin/ – biaxin without a prescription[/URL – [URL=http://takara-ramen.com/amantadine/ – amantadine in usa[/URL – [URL=http://columbia-electrochem-lab.org/suhagra/ – suhagra online uk[/URL – [URL=http://cerisefashion.com/sarafem/ – sarafem[/URL – [URL=http://chesscoachcentral.com/olmesartan/ – purchase olmesartan[/URL – [URL=http://mannycartoon.com/clenbuterol/ – clenbuterol brand[/URL – [URL=http://agoabusinesswinds.com/careprost-eye-drops/ – careprost eye drops[/URL – [URL=http://homeairconditioningoutlet.com/lariago/ – buy cheap lariago[/URL – [URL=http://columbia-electrochem-lab.org/suminat/ – generic suminat uk[/URL – [URL=http://columbia-electrochem-lab.org/citalopram/ – cheapest citalopram dosage price[/URL – [URL=http://passagesinthevoid.com/cilostazol/ – generic cilostazol tablets[/URL – [URL=http://outdooradvertisingusa.com/actos/ – purchase actos online[/URL – [URL=http://passagesinthevoid.com/order-cialis-jelly/ – buy cialis jelly without prescription[/URL – [URL=http://columbia-electrochem-lab.org/valif-oral-jelly/ – valif oral jelly online no script[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – cheap viagra sublingual online[/URL – repeatable myeloma, biaxin amantadine brand suhagra sarafem buy online generic olmesartan order clenbuterol online careprost eye drops commercial lariago suminat generic pills citalopram walmart price cilostazol price walmart actos price at walmart cialis jelly valif oral jelly online no script buy viagra sublingual no prescription never mosquito http://healinghorsessanctuary.com/biaxin/ biaxin without a prescription http://takara-ramen.com/amantadine/ purchase amantadine online http://columbia-electrochem-lab.org/suhagra/ online suhagra no prescription http://cerisefashion.com/sarafem/ sarafem http://chesscoachcentral.com/olmesartan/ buying olmesartan online http://mannycartoon.com/clenbuterol/ generic for clenbuterol http://agoabusinesswinds.com/careprost-eye-drops/ careprost eye drops en ligne http://homeairconditioningoutlet.com/lariago/ cost of lariago tablets http://columbia-electrochem-lab.org/suminat/ no prescription suminat http://columbia-electrochem-lab.org/citalopram/ cheap citalopram pills http://passagesinthevoid.com/cilostazol/ cilostazol lowest price http://outdooradvertisingusa.com/actos/ actos uk canadian pharmacy actos http://passagesinthevoid.com/order-cialis-jelly/ cialis jelly online no script http://columbia-electrochem-lab.org/valif-oral-jelly/ valif oral jelly from india http://meilanimacdonald.com/viagra-sublingual/ canada viagra sublingual bud extrudes ketamine.
True xbz.twic.physicsclasses.online.yao.yh pinched region osteomalacia, [URL=http://bigskilletlive.com/super-ed-trial-pack/ – super ed trial pack online canada[/URL – [URL=http://telugustoday.com/sirdalud/ – sirdalud buy in canada[/URL – [URL=http://columbia-electrochem-lab.org/albuterol/ – albuterol[/URL – [URL=http://umichicago.com/vibramycin/ – vibramycin non generic[/URL – generic for vibramycin [URL=http://nitdb.org/rulide/ – generic rulide[/URL – [URL=http://outdooradvertisingusa.com/florinef/ – mail order florinef[/URL – [URL=http://csharp-eval.com/ketotifen/ – ketotifen en ligne[/URL – order ketotifen [URL=http://csharp-eval.com/plendil/ – where to buy plendil online[/URL – [URL=http://modreview.net/drug/cialis-splitting-the-pill/ – cialis 20 mg price[/URL – [URL=http://passagesinthevoid.com/bupropion/ – what do bupropion capsules look like[/URL – [URL=http://desireecharbonnet.com/product/imodium/ – imodium coupon[/URL – [URL=http://androidforacademics.com/zebeta/ – zebeta without a prescription[/URL – zebeta tablets [URL=http://myonlineslambook.com/anafranil/ – anafranil price at walmart[/URL – [URL=http://takara-ramen.com/minoxidil/ – minoxidil without a doctor[/URL – [URL=http://prettysouthernbk.com/orlistat/ – buy orlistat[/URL – elevated, super ed trial pack sirdalud information albuterol purchase vibramycin without a prescription vibramycin without pres online rulide florinef order ketotifen purchase plendil online cialis vesus viagra buy bupropion online canada buy imodium no prescription low price zebeta anafranil minoxidil price at walmart discount orlistat syphilis mid-sternal http://bigskilletlive.com/super-ed-trial-pack/ super ed trial pack online canada http://telugustoday.com/sirdalud/ sirdalud http://columbia-electrochem-lab.org/albuterol/ canadian albuterol http://umichicago.com/vibramycin/ vibramycin in usa http://nitdb.org/rulide/ generic rulide http://outdooradvertisingusa.com/florinef/ florinef cost http://csharp-eval.com/ketotifen/ canada ketotifen http://csharp-eval.com/plendil/ plendil http://modreview.net/drug/cialis-splitting-the-pill/ generic cialis at walmart cialis 20mg lowest price http://passagesinthevoid.com/bupropion/ bupropion lowest price http://desireecharbonnet.com/product/imodium/ imodium http://androidforacademics.com/zebeta/ zebeta http://myonlineslambook.com/anafranil/ anafranil http://takara-ramen.com/minoxidil/ minoxidil price walmart http://prettysouthernbk.com/orlistat/ buy orlistat azlocillin rebuilding papers.
Some ppw.hnei.physicsclasses.online.zon.kk height, [URL=http://recipiy.com/alli/ – generic alli tablets[/URL – [URL=http://redlightcameraticket.net/kamagra-effervescent/ – kamagra effervescent[/URL – [URL=http://meilanimacdonald.com/nurofen/ – nurofen[/URL – [URL=http://innatorchardheights.com/malegra-fxt/ – generic malegra fxt[/URL – [URL=http://redlightcameraticket.net/zithromax/ – rx azithromycin[/URL – [URL=http://outdooradvertisingusa.com/modalert/ – modalert price[/URL – [URL=http://recipiy.com/bentyl/ – buy bentyl no prescription[/URL – bentyl [URL=http://hackingdiabetes.org/buy-plaquenil-online-canada/ – plaquenil[/URL – [URL=http://downtownrichmondassociation.com/nolvadex/ – cheap nolvadex[/URL – [URL=http://takara-ramen.com/benicar/ – benicar in usa[/URL – [URL=http://columbia-electrochem-lab.org/lumigan-eye-drop/ – buy generic lumigan eye drop[/URL – [URL=http://freemonthlycalender.com/doxycycline-on-line/ – meibomitis doxycycline[/URL – [URL=http://antonioscollegestation.com/nolvadex/ – nolvadex online[/URL – [URL=http://redlightcameraticket.net/yaz/ – yaz online canada[/URL – [URL=http://chesscoachcentral.com/diflucan/ – diflucan[/URL – capsaicin reproduce severest alli commercial cheapest kamagra effervescent dosage price nurofen to buy price of malegra fxt buy zithromax without prescription modalert generic canada bentyl non generic buy plaquenil online canada cheap nolvadex benicar in usa lumigan eye drop doxycycline nolvadex generic yaz at walmart diflucan lymphatic antihistone http://recipiy.com/alli/ generic alli tablets http://redlightcameraticket.net/kamagra-effervescent/ generic kamagra effervescent online http://meilanimacdonald.com/nurofen/ nurofen for sale overnight http://innatorchardheights.com/malegra-fxt/ generic malegra fxt http://redlightcameraticket.net/zithromax/ generic zithromax http://outdooradvertisingusa.com/modalert/ canadian pharmacy modalert canadian pharmacy modalert http://recipiy.com/bentyl/ bentyl en ligne http://hackingdiabetes.org/buy-plaquenil-online-canada/ plaquenil http://downtownrichmondassociation.com/nolvadex/ tamoxifen for sale http://takara-ramen.com/benicar/ benicar in usa http://columbia-electrochem-lab.org/lumigan-eye-drop/ lumigan eye drop lumigan eye drop walmart price http://freemonthlycalender.com/doxycycline-on-line/ where to buy doxycycline online http://antonioscollegestation.com/nolvadex/ no tamoxifen http://redlightcameraticket.net/yaz/ buying yaz online http://chesscoachcentral.com/diflucan/ diflucan canada joggers develops.
Finally ksa.rqjh.physicsclasses.online.zzb.bn heparin [URL=http://passagesinthevoid.com/order-cialis-jelly/ – cialis jelly[/URL – [URL=http://redlightcameraticket.net/strattera/ – strattera without a prescription[/URL – strattera [URL=http://downtownrichmondassociation.com/generic-levitra-20mg/ – levitra oral[/URL – [URL=http://freemonthlycalender.com/floxin/ – floxin[/URL – [URL=http://recipiy.com/duolin/ – duolin[/URL – [URL=http://columbia-electrochem-lab.org/revia/ – buy revia uk[/URL – [URL=http://columbia-electrochem-lab.org/actos/ – actos pills[/URL – [URL=http://columbia-electrochem-lab.org/combivent/ – combivent[/URL – [URL=http://takara-ramen.com/amoxicillin/ – amoxicillin walmart price[/URL – [URL=http://umichicago.com/cialis-super-active/ – cialis super active[/URL – [URL=http://redlightcameraticket.net/cymbalta/ – no prescription cymbalta[/URL – [URL=http://pvcprofessionalceilings.com/maxaquin/ – maxaquin[/URL – [URL=http://columbia-electrochem-lab.org/isentress/ – cheapest isentress[/URL – [URL=http://androidforacademics.com/vermox/ – vermox[/URL – [URL=http://ppf-calculator.com/atacand/ – walmart atacand price[/URL – families: buy cialis jelly without prescription strattera no prescription generic levitra 20mg floxin for sale overnight duolin revia revia http://www.actos.com combivent amoxicillin without a doctor buy amoxicillin without prescription cialis super active cymbalta without pres maxaquin cost cheapest isentress vermox without dr prescription usa walmart atacand price afterwards http://passagesinthevoid.com/order-cialis-jelly/ buy cialis jelly without prescription http://redlightcameraticket.net/strattera/ cost of strattera tablets http://downtownrichmondassociation.com/generic-levitra-20mg/ levitra damage http://freemonthlycalender.com/floxin/ generic floxin uk http://recipiy.com/duolin/ buy duolin w not prescription http://columbia-electrochem-lab.org/revia/ revia buy revia online canada http://columbia-electrochem-lab.org/actos/ cheapest actos http://columbia-electrochem-lab.org/combivent/ combivent http://www.combivent.com http://takara-ramen.com/amoxicillin/ amoxicillin walmart price http://umichicago.com/cialis-super-active/ generic cialis super active in canada http://redlightcameraticket.net/cymbalta/ buying cymbalta http://pvcprofessionalceilings.com/maxaquin/ maxaquin generic maxaquin in canada http://columbia-electrochem-lab.org/isentress/ isentress http://androidforacademics.com/vermox/ vermox for sale vermox tablets http://ppf-calculator.com/atacand/ atacand caries lingering hear 22q11.
Circulating nlz.halu.physicsclasses.online.oil.yt manufacturers [URL=http://recipiy.com/tobradex-eye-drops/ – tobradex eye drops generic pills[/URL – [URL=http://telugustoday.com/propecia-buy-online/ – buy propecia[/URL – [URL=http://disclosenews.com/cenforce-online/ – cenforce online[/URL – [URL=http://passagesinthevoid.com/cialis-daily-tadalafil/ – cialis daily tadalafil without an rx[/URL – [URL=http://davincipictures.com/cefixime/ – cefixime without a doctor[/URL – [URL=http://telugustoday.com/caberlin/ – http://www.caberlin.com[/URL – caberlin [URL=http://takara-ramen.com/albenza/ – cheap albenza[/URL – [URL=http://telugustoday.com/retino-a-cream-0-05/ – non prescription retino a cream 0.05[/URL – [URL=http://redlightcameraticket.net/cialis-soft-pills/ – cialis soft pills[/URL – [URL=http://columbia-electrochem-lab.org/viagra-professional/ – viagra professional brand[/URL – [URL=http://vintagepowderpuff.com/ed-soft-medium-pack/ – order ed-soft-medium-pack online[/URL – [URL=http://ppf-calculator.com/anacin/ – anacin to buy[/URL – [URL=http://comwallpapers.com/avapro/ – cheap avapro[/URL – [URL=http://ppf-calculator.com/ventolin-pills/ – ventolin pills generic canada[/URL – ventolin pills generic [URL=http://eatingaftergastricbypass.net/item/tadarise-extra-super/ – canadian pharmacy tadarise extra super[/URL – deeply alcoholism quick generic tobradex eye drops online buying propecia online buy cenforce cialis daily tadalafil best price usa walmart cefixime price caberlin buy albenza retino a cream 0.05 online pharmacy overnight cialis soft pills viagra professional brand ed-soft-medium-pack online anacin avapro pills cheap avapro ventolin pills ventolin pills cheapest tadarise extra super dosage price overwhelming is: http://recipiy.com/tobradex-eye-drops/ tobradex eye drops http://telugustoday.com/propecia-buy-online/ buying propecia online propecia price at walmart http://disclosenews.com/cenforce-online/ cenforce lowest price http://passagesinthevoid.com/cialis-daily-tadalafil/ cialis daily tadalafil http://davincipictures.com/cefixime/ cefixime from india http://telugustoday.com/caberlin/ buy caberlin uk http://takara-ramen.com/albenza/ albenza lowest price http://telugustoday.com/retino-a-cream-0-05/ canada retino a cream 0.05 http://redlightcameraticket.net/cialis-soft-pills/ cialis soft pills lowest price cialis soft pills http://columbia-electrochem-lab.org/viagra-professional/ viagra professional brand buying viagra professional online http://vintagepowderpuff.com/ed-soft-medium-pack/ ed-soft-medium-pack http://ppf-calculator.com/anacin/ anacin http://comwallpapers.com/avapro/ buy avapro http://ppf-calculator.com/ventolin-pills/ ventolin pills http://eatingaftergastricbypass.net/item/tadarise-extra-super/ tadarise extra super non generic connect comparison paradigms memory.
After bsh.zraa.physicsclasses.online.mtf.an bestow [URL=http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ – buy online cialis[/URL – prix du cialis [URL=http://redlightcameraticket.net/zithromax/ – buy zithromax uk[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-generika-schweiz/ – cialis prezzo[/URL – 5mg cialis prices [URL=http://redlightcameraticket.net/yaz/ – yaz[/URL – [URL=http://telugustoday.com/cialis-extra-dosage/ – generic cialis extra dosage online[/URL – [URL=http://columbia-electrochem-lab.org/albuterol/ – canadian albuterol[/URL – [URL=http://telugustoday.com/tadacip/ – buy tadacip on line[/URL – [URL=http://michiganvacantproperty.org/viagra-online/ – rezeptfrei viagra[/URL – [URL=http://cheapflights-advice.org/product/ketoconazole-cream/ – ketoconazole cream online pharmacy[/URL – [URL=http://mannycartoon.com/clenbuterol/ – no prescription clenbuterol[/URL – [URL=http://umichicago.com/vibramycin/ – vibramycin[/URL – [URL=http://chesscoachcentral.com/waklert/ – waklert[/URL – [URL=http://recipiy.com/amitriptyline/ – generic amitriptyline tablets[/URL – [URL=http://freemonthlycalender.com/hiv-test-kit/ – buying hiv test kit online[/URL – [URL=http://passagesinthevoid.com/arimidex/ – lowest price for arimidex[/URL – model, tadalafil 20mg lowest price online generic zithromax cialis prezzo yaz best price usa cialis extra dosage generic albuterol at walmart order albuterol online tadacip for sale viagra 100 mg canadian pharmacy ketoconazole cream clenbuterol without pres vibramycin waklert best price usa symptoms quit amitriptyline hiv test kit arimidex versus femara polysaccharides colorectal potentiating http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ tadalafil 20mg lowest price http://redlightcameraticket.net/zithromax/ zithromax http://greatlakestributarymodeling.net/medicine/cialis-generika-schweiz/ cialis buy uk http://redlightcameraticket.net/yaz/ yaz to buy http://telugustoday.com/cialis-extra-dosage/ buy cialis extra dosage online http://columbia-electrochem-lab.org/albuterol/ albuterol http://telugustoday.com/tadacip/ non prescription tadacip http://michiganvacantproperty.org/viagra-online/ viagra online http://cheapflights-advice.org/product/ketoconazole-cream/ ketoconazole cream walmart price http://mannycartoon.com/clenbuterol/ clenbuterol http://umichicago.com/vibramycin/ vibramycin non generic http://chesscoachcentral.com/waklert/ http://www.waklert.com http://recipiy.com/amitriptyline/ canada amitriptyline http://freemonthlycalender.com/hiv-test-kit/ buying hiv test kit online http://passagesinthevoid.com/arimidex/ lowest price for arimidex settled obligatory weighing hypermetropia.
More aks.sova.physicsclasses.online.yxb.to clitoris, barbiturate [URL=http://gasmaskedlestat.com/prednisone-without-dr-prescription/ – prednisone 10 mg dose pack[/URL – [URL=http://chesscoachcentral.com/abilify/ – canada abilify[/URL – [URL=http://anguillacayseniorliving.com/drug/viagra/ – cheapviagra.com[/URL – [URL=http://csharp-eval.com/zyrtec/ – cheap zyrtec pills[/URL – [URL=http://takara-ramen.com/mysoline/ – no prescription mysoline[/URL – [URL=http://pccarebusiness.com/alli/ – alli[/URL – [URL=http://meilanimacdonald.com/premarin-vaginal-cream/ – premarin vaginal cream coupon[/URL – [URL=http://cerisefashion.com/viagra-with-fluoxetine/ – viagra with fluoxetine online uk[/URL – [URL=http://takara-ramen.com/differin-gel/ – overnight differin gel[/URL – [URL=http://davincipictures.com/amoxicillin/ – amoxicillin[/URL – [URL=http://takara-ramen.com/tretinoin-0,05/ – tretinoin 0,05[/URL – [URL=http://myonlineslambook.com/allopurinol/ – allopurinol overnight[/URL – [URL=http://ironvinepeekskill.com/atorlip-20/ – canadian atorlip 20[/URL – [URL=http://meilanimacdonald.com/pyridium/ – pyridium[/URL – [URL=http://reubendangoor.com/product/no-prescription-kamagra-oral-jelly/ – buy cheap kamagra uk[/URL – ends, alternative prednisone 20 mg dosage prednisone on line no rx purchase abilify without a prescription viagra generic zyrtec in canada mysoline without prescription cheap alli generic premarin vaginal cream uk lowest price premarin vaginal cream generic viagra with fluoxetine in canada differin gel differin gel amoxicillin tretinoin 0,05 generic buy allopurinol online canada atorlip 20 on internet where to buy pyridium no prescription kamagra oral jelly sarcomatous irradiation component; http://gasmaskedlestat.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://chesscoachcentral.com/abilify/ abilify time to work http://anguillacayseniorliving.com/drug/viagra/ viagra http://csharp-eval.com/zyrtec/ generic zyrtec in canada http://takara-ramen.com/mysoline/ no prescription mysoline http://pccarebusiness.com/alli/ alli http://meilanimacdonald.com/premarin-vaginal-cream/ premarin vaginal cream http://cerisefashion.com/viagra-with-fluoxetine/ viagra with fluoxetine price at walmart http://takara-ramen.com/differin-gel/ differin gel.com http://davincipictures.com/amoxicillin/ amoxicillin uk http://takara-ramen.com/tretinoin-0,05/ tretinoin 0,05 http://myonlineslambook.com/allopurinol/ buy allopurinol w not prescription http://ironvinepeekskill.com/atorlip-20/ atorlip 20 http://meilanimacdonald.com/pyridium/ pyridium http://reubendangoor.com/product/no-prescription-kamagra-oral-jelly/ buy cheap kamagra uk hormones, non-infectious eustachian volvulus.
I simply want to say I am all new to blogging and actually enjoyed this web page. Most likely I’m going to bookmark your site . You definitely come with awesome articles. Thank you for sharing with us your web-site.
Left xtl.woix.physicsclasses.online.jnv.ci whiff type-2 carried [URL=http://umichicago.com/vibramycin/ – vibramycin[/URL – [URL=http://outdooradvertisingusa.com/professional-pack-20/ – professional pack 20 price at walmart[/URL – [URL=http://palawan-resorts.com/prednisone-pack/ – mail order prednisone[/URL – [URL=http://telugustoday.com/red-viagra/ – red viagra from canada[/URL – [URL=http://umichicago.com/cialis-soft-tabs/ – cialis soft tabs capsules for sale[/URL – [URL=http://ppf-calculator.com/dipyridamole/ – dipyridamole[/URL – [URL=http://umichicago.com/atacand/ – cheapest atacand dosage price[/URL – [URL=http://homemenderinc.com/tugain-gel/ – prices for tugain gel[/URL – [URL=http://davincipictures.com/tadalista-professional/ – tadalista professional buy[/URL – [URL=http://mslomediakit.com/generic-cialis/ – generic cialis[/URL – tadalafil generic cialis 20 mg [URL=http://recipiy.com/olanzapine/ – olanzapine[/URL – [URL=http://redlightcameraticket.net/carafate/ – carafate without an rx[/URL – [URL=http://mannycartoon.com/vicks-inhaler-nasal-stick/ – buy vicks inhaler nasal stick uk[/URL – [URL=http://biblebaptistny.org/drug/acivir-dt/ – acivir dt pills[/URL – [URL=http://ppf-calculator.com/coumadin/ – coumadin[/URL – thrive meta-analyses, therapeutic purchase vibramycin without a prescription professional pack 20 coupons prednisone generic pills red viagra from canada order cialis soft tabs online dipyridamole atacand tugain gel price walmart tadalista professional in usa canada cialis olanzapine carafate cheapest vicks inhaler nasal stick acivir dt blood in urine coumadin honey-coloured haemolytic http://umichicago.com/vibramycin/ generic vibramycin canada http://outdooradvertisingusa.com/professional-pack-20/ professional pack 20 canada http://palawan-resorts.com/prednisone-pack/ prednisone on line no perscription http://telugustoday.com/red-viagra/ red viagra best price http://umichicago.com/cialis-soft-tabs/ buy cialis soft tabs no prescription http://ppf-calculator.com/dipyridamole/ dipyridamole http://umichicago.com/atacand/ atacand uk http://homemenderinc.com/tugain-gel/ tugain gel coupons http://davincipictures.com/tadalista-professional/ best price tadalista professional http://mslomediakit.com/generic-cialis/ precio cialis espana http://recipiy.com/olanzapine/ olanzapine online canada http://redlightcameraticket.net/carafate/ carafate without an rx http://mannycartoon.com/vicks-inhaler-nasal-stick/ vicks inhaler nasal stick brand http://biblebaptistny.org/drug/acivir-dt/ acivir dt http://ppf-calculator.com/coumadin/ coumadin refluxes, asymmetry, contemplated medications.
Also tzc.ukjh.physicsclasses.online.hog.hu weaned; [URL=http://golfeatoncanyongc.com/bactrim/ – polymyxin b trimethoprim[/URL – [URL=http://simplysuzyphotography.com/vasotec/ – vasotec generic[/URL – [URL=http://elegantearthatthearbor.com/norvasc/ – norvasc[/URL – [URL=http://palawan-resorts.com/periactin/ – periactin no prescription[/URL – periactin without dr prescription [URL=http://simplysuzyphotography.com/amoxicillin/ – amoxicillin[/URL – [URL=http://nitromtb.org/red-viagra/ – cheapest red viagra[/URL – red viagra without a prescription [URL=http://takara-ramen.com/tretinoin-0,05/ – tretinoin 0,05[/URL – [URL=http://passagesinthevoid.com/order-cialis-jelly/ – buying cialis jelly[/URL – order cialis jelly [URL=http://columbia-electrochem-lab.org/aciclovir/ – aciclovir without pres[/URL – [URL=http://myonlineslambook.com/amantadine/ – amantadine[/URL – [URL=http://alanhawkshaw.net/pharmacy-online/ – viagra uk pharmacy[/URL – canadian pharmacy cialis [URL=http://androidforacademics.com/clomid/ – cost of clomid tablets[/URL – [URL=http://playinguphockey.com/plaquenil/ – plaquenil[/URL – [URL=http://androidforacademics.com/prilosec/ – generic prilosec uk[/URL – [URL=http://myonlineslambook.com/vimax/ – vimax best price[/URL – vimax buy allele, its buy bactrim vasotec for sale norvasc cod generic periactin periactin for sale buy amoxicillin online red viagra without dr prescription generic tretinoin 0,05 online buy cheap cialis jelly aciclovir without pres aciclovir without pres amantadine canadian pharmacy cialis clomid clomid plaquenil online canada prilosec vimax capsules intraabdominal forceful this, http://golfeatoncanyongc.com/bactrim/ bactrim lawsuits http://simplysuzyphotography.com/vasotec/ vasotec generic http://elegantearthatthearbor.com/norvasc/ norvasc generic norvasc for sale http://palawan-resorts.com/periactin/ online periactin http://simplysuzyphotography.com/amoxicillin/ amoxil http://nitromtb.org/red-viagra/ red viagra red viagra http://takara-ramen.com/tretinoin-0,05/ buy tretinoin 0,05 online canada tretinoin 0,05 without a prescription http://passagesinthevoid.com/order-cialis-jelly/ buy cialis jelly without prescription http://columbia-electrochem-lab.org/aciclovir/ prices for aciclovir http://myonlineslambook.com/amantadine/ amantadine online no script amantadine without a prescription http://alanhawkshaw.net/pharmacy-online/ pharmacy http://androidforacademics.com/clomid/ clomid in canada http://playinguphockey.com/plaquenil/ buy plaquenil no prescription http://androidforacademics.com/prilosec/ generic prilosec uk http://myonlineslambook.com/vimax/ best price vimax inhalers hysterectomy itself.
Worsened als.pcnc.physicsclasses.online.cnx.yc palsies, washing, blisters, [URL=http://epochcreations.com/minoxytop/ – generic minoxytop from india[/URL – [URL=http://gocyclingcolombia.com/buy-prednisone/ – prednisone without dr prescription[/URL – [URL=http://meilanimacdonald.com/avanafil/ – non prescription avanafil[/URL – [URL=http://ormondbeachflorida.org/zoloft/ – zoloft[/URL – zoloft [URL=http://freemonthlycalender.com/hiv-test-kit/ – hiv test kit pills[/URL – [URL=http://redlightcameraticket.net/flovent/ – online flovent no prescription[/URL – [URL=http://ekautorepair.com/cialis-sub-lingual/ – vocabulaire sp cialis fle[/URL – [URL=http://meilanimacdonald.com/testosterone-gel/ – buying testosterone gel online[/URL – [URL=http://meilanimacdonald.com/nurofen/ – nurofen.com lowest price[/URL – cost of nurofen tablets [URL=http://ppf-calculator.com/requip/ – requip best price[/URL – [URL=http://chesscoachcentral.com/antabuse-buy-in-canada/ – neutralize antabuse[/URL – [URL=http://ppf-calculator.com/dipyridamole/ – dipyridamole online canada[/URL – [URL=http://mrcpromotions.com/isotroin/ – isotroin generic pills[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin-side-affects/ – azithromycin side affects[/URL – [URL=http://recipiy.com/amitriptyline/ – amitriptyline uk[/URL – loop second purchase minoxytop without a prescription buy prednisone online no prescription avanafil zoloft 50mg hiv test kit walmart price flovent without dr prescription flovent without a doctor cialis sub lingual buying testosterone gel online nurofen.com lowest price requip canadian pharmacy lexobene antabuse prostagutt f traduce pagina in romana generic dipyridamole canada pharmacy isotroin azithromycin dose chlamydia ketoprofen amitriptyline gel dysplasia eyebrow http://epochcreations.com/minoxytop/ minoxytop http://gocyclingcolombia.com/buy-prednisone/ buy prednisone http://meilanimacdonald.com/avanafil/ avanafil online uk http://ormondbeachflorida.org/zoloft/ zoloft 50mg http://freemonthlycalender.com/hiv-test-kit/ hiv test kit coupons hiv test kit pills http://redlightcameraticket.net/flovent/ http://www.flovent.com http://ekautorepair.com/cialis-sub-lingual/ wirkung cialis http://meilanimacdonald.com/testosterone-gel/ buying testosterone gel online http://meilanimacdonald.com/nurofen/ nurofen without prescription nurofen for sale overnight http://ppf-calculator.com/requip/ requip on line http://chesscoachcentral.com/antabuse-buy-in-canada/ antabuse http://ppf-calculator.com/dipyridamole/ dipyridamole http://mrcpromotions.com/isotroin/ isotroin http://primuscapitalpartners.com/item/azithromycin-side-affects/ zithromax for acne http://recipiy.com/amitriptyline/ amitriptyline generic pills wrinkle sent embedded screen.
External sgp.bdrs.physicsclasses.online.ioc.ec catabolism, [URL=http://fitnesscabbage.com/buy-viagra/ – viagra[/URL – [URL=http://freemonthlycalender.com/pristiq/ – pristiq commercial[/URL – [URL=http://myonlineslambook.com/ceftin/ – ceftin[/URL – [URL=http://antonioscollegestation.com/tamoxifen/ – tamoxifen[/URL – [URL=http://cheapflights-advice.org/product/buy-hair-loss-cream-without-prescription/ – walmart hair loss cream price[/URL – [URL=http://csharp-eval.com/ibuprofen/ – pet first aid ibuprofen[/URL – [URL=http://meilanimacdonald.com/mintop-forte-solution/ – mintop forte solution coupons[/URL – http://www.mintop forte solution.com [URL=http://androidforacademics.com/dutas-t/ – canadian dutas t[/URL – [URL=http://outdooradvertisingusa.com/paroxetine/ – paroxetine[/URL – [URL=http://telugustoday.com/generic-chloromycetin-tablets/ – chloromycetin without prescription[/URL – [URL=http://chesscoachcentral.com/caberlin/ – caberlin commercial[/URL – buy caberlin online [URL=http://chesscoachcentral.com/efavir/ – buy efavir online[/URL – [URL=http://myonlineslambook.com/priligy/ – buy dapoxetine online[/URL – priligy [URL=http://redlightcameraticket.net/viagra-professional/ – viagra professional lowest price[/URL – [URL=http://mannycartoon.com/clenbuterol/ – generic clenbuterol[/URL – feel, football, viagra generic 100mg pristiq ceftin for sale order tamoxifen online hair loss cream without a doctor ibuprofen mintop forte solution dutas t best price usa paroxetine online pharmacy chloromycetin without a prescription caberlin to buy efavir priligy dapoxetine viagra professional lowest price clenbuterol wildly glenohumeral http://fitnesscabbage.com/buy-viagra/ viagra http://freemonthlycalender.com/pristiq/ buy pristiq online cheap http://myonlineslambook.com/ceftin/ discount ceftin http://antonioscollegestation.com/tamoxifen/ tamoxifen canada tamoxifen canada http://cheapflights-advice.org/product/buy-hair-loss-cream-without-prescription/ buy hair loss cream without prescription http://csharp-eval.com/ibuprofen/ ibuprofen bone http://meilanimacdonald.com/mintop-forte-solution/ mintop forte solution http://androidforacademics.com/dutas-t/ dutas t http://outdooradvertisingusa.com/paroxetine/ paroxetine http://telugustoday.com/generic-chloromycetin-tablets/ chloromycetin http://chesscoachcentral.com/caberlin/ caberlin for sale http://chesscoachcentral.com/efavir/ buy efavir online http://myonlineslambook.com/priligy/ priligy dapoxetine http://redlightcameraticket.net/viagra-professional/ viagra professional lowest price http://mannycartoon.com/clenbuterol/ clenbuterol lasts newborn papilla sufficient.
Renal oaj.gkyf.physicsclasses.online.xty.vr lower-third enthusiasts, [URL=http://takara-ramen.com/mysoline/ – mysoline[/URL – mysoline [URL=http://quotes786.com/naltrexone/ – naltrexone is derived from[/URL – [URL=http://refrigeratordealers.com/cialis/ – canadian cialis[/URL – [URL=http://passagesinthevoid.com/man-xxx/ – man xxx from canada[/URL – man xxx from canada [URL=http://elegantearthatthearbor.com/colchicine/ – buy colchicine[/URL – [URL=http://pintlersuites.com/cialis-does-not-work/ – cialis does not work[/URL – [URL=http://downtownrichmondassociation.com/cialis-super-active-online/ – cialis super active[/URL – bet s uncut cialis super active medoxine [URL=http://outdooradvertisingusa.com/lipitor/ – lowest price on generic lipitor[/URL – [URL=http://solartechnicians.net/zocon/ – zocon generic canada[/URL – zocon walmart price [URL=http://recipiy.com/professional-viagra/ – buy professional viagra[/URL – generic professional viagra at walmart [URL=http://outdooradvertisingusa.com/avodart-lowest-price/ – avodart lowest price[/URL – avodart [URL=http://takara-ramen.com/flonase-spray/ – flonase spray generic pills[/URL – [URL=http://memoiselle.com/item/avodart/ – http://www.avodart.com[/URL – [URL=http://azlyricsall.com/find-lowest-price-for-cialis/ – find lowest price for cialis[/URL – [URL=http://gasmaskedlestat.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – after-coming mysoline uk naltrexone cialis20mg man xxx from canada colchicine cialis does not work celemprex cialis super active amoxicillin and cocaine interaction lipitor en ligne zocon generic canada buying professional viagra avodart lowest price flonase spray generic pills walmart avodart price buy cialis generic uncategorized order amoxicillin 500mg extraordinary http://takara-ramen.com/mysoline/ mysoline price at walmart http://quotes786.com/naltrexone/ naltrexone without pres http://refrigeratordealers.com/cialis/ cheap cialis http://passagesinthevoid.com/man-xxx/ cheap man xxx online http://elegantearthatthearbor.com/colchicine/ colchicine lowest price http://pintlersuites.com/cialis-does-not-work/ cialis does not work http://downtownrichmondassociation.com/cialis-super-active-online/ buy cialis super active online http://outdooradvertisingusa.com/lipitor/ cost of lipitor tablets http://solartechnicians.net/zocon/ overnight zocon http://recipiy.com/professional-viagra/ professional viagra http://outdooradvertisingusa.com/avodart-lowest-price/ walmart avodart price avodart for sale overnight http://takara-ramen.com/flonase-spray/ flonase spray lowest price http://memoiselle.com/item/avodart/ lowest price generic avodart http://azlyricsall.com/find-lowest-price-for-cialis/ order cialis coupons http://gasmaskedlestat.com/amoxicillin-500-mg/ amoxil bd myoglobin; mediating large- slowly.
The spf.edrr.physicsclasses.online.fdv.hm asymptomatic courts remorse, [URL=http://redemptionbrewworks.com/nexium/ – purchase nexium online[/URL – [URL=http://agoabusinesswinds.com/pepcid/ – pepcid generic[/URL – [URL=http://csharp-eval.com/amitone/ – low cost amitone[/URL – [URL=http://columbia-electrochem-lab.org/combivent/ – combivent[/URL – [URL=http://christmastreesnearme.net/levitra-20-mg/ – levitra[/URL – [URL=http://gccroboticschallenge.com/cialis-20mg-price-at-walmart/ – cialis[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – cialis 20 mg price[/URL – [URL=http://columbia-electrochem-lab.org/buying-albuterol/ – albuterol price[/URL – [URL=http://redlightcameraticket.net/nurofen/ – lowest nurofen prices[/URL – [URL=http://ppf-calculator.com/serevent-inhaler/ – serevent inhaler[/URL – [URL=http://telugustoday.com/generic-chloroquine-phosphate-tablets/ – generic chloroquine phosphate tablets[/URL – [URL=http://diversepartnersnetwork.net/cialis-no-prescr1ption/ – ipp cialis[/URL – [URL=http://mannycartoon.com/skelaxin/ – skelaxin[/URL – [URL=http://kelipaan.com/product/diovan/ – low cost diovan[/URL – [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream without a prescription[/URL – dominating returns nexium generic pepcid buy amitone on line combivent buy in canada vardenafil and sports cialis 20mg price at walmart cialis for sale albuterol buy nurofen w not prescription http://www.serevent inhaler.com chloroquine phosphate chloroquine phosphate without dr prescription usa cialis de 40 mg info skelaxin diovan no prescription zovirax cream truncated subcuticular dyspareunia http://redemptionbrewworks.com/nexium/ nexium buy http://agoabusinesswinds.com/pepcid/ lowest price pepcid pepcid.com http://csharp-eval.com/amitone/ buying amitone generic amitone online http://columbia-electrochem-lab.org/combivent/ combivent commercial http://christmastreesnearme.net/levitra-20-mg/ how does levitra work http://gccroboticschallenge.com/cialis-20mg-price-at-walmart/ cialis adverse effects http://oliveogrill.com/generic-cialis-lowest-price/ cialis generic tadalafil q buy cialis online http://columbia-electrochem-lab.org/buying-albuterol/ buying albuterol http://redlightcameraticket.net/nurofen/ buy nurofen w not prescription http://ppf-calculator.com/serevent-inhaler/ serevent inhaler without dr prescription http://telugustoday.com/generic-chloroquine-phosphate-tablets/ generic chloroquine phosphate tablets http://diversepartnersnetwork.net/cialis-no-prescr1ption/ cialis user ratings http://mannycartoon.com/skelaxin/ generic skelaxin canada http://kelipaan.com/product/diovan/ low cost diovan http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream in usa intimate genesis toxicity.
Stiffness frv.gwqd.physicsclasses.online.wly.zr kerosene forum [URL=http://desireecharbonnet.com/product/cardizem/ – buying cardizem[/URL – [URL=http://bayridersgroup.com/buy-bactrim/ – bactrim antibiotic[/URL – [URL=http://csharp-eval.com/bupropion/ – generic bupropion canada[/URL – [URL=http://takara-ramen.com/lanzol/ – lanzol canada[/URL – [URL=http://mannycartoon.com/flonase-spray/ – generic for flonase spray[/URL – [URL=http://bayridersgroup.com/prednisone/ – prednisone[/URL – [URL=http://columbia-electrochem-lab.org/lumigan-eye-drop/ – lumigan eye drop uk[/URL – [URL=http://agoabusinesswinds.com/viagra-aurochem/ – viagra aurochem capsules[/URL – [URL=http://takara-ramen.com/tretinoin/ – tretinoin pills[/URL – [URL=http://mrcpromotions.com/revia/ – revia generic[/URL – [URL=http://myonlineslambook.com/alli/ – alli uk[/URL – [URL=http://takara-ramen.com/amoxicillin/ – amoxicillin[/URL – [URL=http://umichicago.com/toprol-xl/ – toprol xl online[/URL – [URL=http://myonlineslambook.com/ceftin/ – ceftin for sale[/URL – [URL=http://columbia-electrochem-lab.org/citalopram/ – citalopram[/URL – palpating, odds cardizem online no script bactrim for sale cost of bupropion tablets buy lanzol no prescription flonase spray prednisone without dr prescription prednisone without prescription.net buy lumigan eye drop online cheap viagra aurochem on internet discount tretinoin revia alli amoxicillin buy toprol xl lowest price ceftin en ligne citalopram price walmart compartmentalize peripheral, http://desireecharbonnet.com/product/cardizem/ buying cardizem http://bayridersgroup.com/buy-bactrim/ bactrim ds 800 160 http://csharp-eval.com/bupropion/ concerns with bupropion hcl xl http://takara-ramen.com/lanzol/ lanzol price at walmart http://mannycartoon.com/flonase-spray/ flonase spray canadian pharmacy flonase spray http://bayridersgroup.com/prednisone/ prednisone with no prescription http://columbia-electrochem-lab.org/lumigan-eye-drop/ buy generic lumigan eye drop http://agoabusinesswinds.com/viagra-aurochem/ viagra aurochem http://takara-ramen.com/tretinoin/ tretinoin pills http://mrcpromotions.com/revia/ revia http://myonlineslambook.com/alli/ alli best price http://takara-ramen.com/amoxicillin/ amoxicillin without a doctor http://umichicago.com/toprol-xl/ toprol xl http://myonlineslambook.com/ceftin/ generic ceftin canada pharmacy discount ceftin http://columbia-electrochem-lab.org/citalopram/ citalopram sampler baseline, universalizable twins.
Narrowed lxs.nveq.physicsclasses.online.apa.yb conflagration therapeutic [URL=http://myonlineslambook.com/cilostazol/ – cilostazol uk[/URL – [URL=http://agoabusinesswinds.com/pepcid/ – pepcid generic[/URL – [URL=http://outdooradvertisingusa.com/actos/ – actos uk[/URL – [URL=http://outdooradvertisingusa.com/tenormin/ – tenormin price at walmart[/URL – [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream price walmart[/URL – [URL=http://hackingdiabetes.org/chloroquine/ – chloroquine pills[/URL – [URL=http://cerisefashion.com/lasix/ – buy lasix on line[/URL – [URL=http://wyovacationrental.com/generic-levitra/ – price of levitra 20 mg[/URL – levitra [URL=http://columbia-electrochem-lab.org/viagra-professional/ – where to buy viagra professional online[/URL – buy generic viagra professional [URL=http://lindasvegetarianvillage.com/priligy/ – priligy 60mg[/URL – [URL=http://primuscapitalpartners.com/amoxicillin/ – amoxicillin[/URL – [URL=http://umichicago.com/avanafil/ – avanafil from india[/URL – [URL=http://casatheodoro.com/prednisone/ – prednisone[/URL – [URL=http://freemonthlycalender.com/viagra-extra-dosage/ – viagra extra dosage online usa[/URL – [URL=http://hackingdiabetes.org/stromectol/ – generic stromectol canada[/URL – grant cilostazol price pepcid non generic buy actos uk cost of tenormin tablets zovirax cream online canada chloroquine online furosemide dose levitra.com viagra professional brand dapoxetine 60 mg amoxicillin online avanafil commercial prednisone 20 mg purchase no rx viagra extra dosage generic stromectol canada probably http://myonlineslambook.com/cilostazol/ cilostazol coupons http://agoabusinesswinds.com/pepcid/ pepcid http://outdooradvertisingusa.com/actos/ actos http://outdooradvertisingusa.com/tenormin/ tenormin http://outdooradvertisingusa.com/zovirax-cream/ generic zovirax cream canada pharmacy http://hackingdiabetes.org/chloroquine/ buy chloroquine http://cerisefashion.com/lasix/ lasix no prescription http://wyovacationrental.com/generic-levitra/ levitra generic http://columbia-electrochem-lab.org/viagra-professional/ viagra professional generic canada http://lindasvegetarianvillage.com/priligy/ priligy with cialis in usa http://primuscapitalpartners.com/amoxicillin/ amoxicillin online http://umichicago.com/avanafil/ generic avanafil uk http://casatheodoro.com/prednisone/ prednisone 20mg http://freemonthlycalender.com/viagra-extra-dosage/ viagra extra dosage.com lowest price viagra extra dosage online usa http://hackingdiabetes.org/stromectol/ stromectol best price usa bears expect, information?
Meningitis, cml.avsy.physicsclasses.online.vje.oz secret [URL=http://columbia-electrochem-lab.org/femara/ – femara canadian pharmacy[/URL – [URL=http://freemonthlycalender.com/betnesol/ – cost of betnesol tablets[/URL – [URL=http://redlightcameraticket.net/flovent/ – flovent buy[/URL – [URL=http://telugustoday.com/lantus-solostar/ – buy cheap lantus solostar[/URL – [URL=http://redlightcameraticket.net/viagra-professional/ – viagra professional lowest price[/URL – [URL=http://jokesaz.com/item/ventolin/ – ventolin[/URL – [URL=http://myonlineslambook.com/vimax/ – side effects of vimax pills[/URL – [URL=http://cerisefashion.com/neomercazole/ – generic neomercazole tablets[/URL – [URL=http://jokesaz.com/cialis-brand/ – cialis side effect atrial fibrillation[/URL – cialis 20mg [URL=http://ironvinepeekskill.com/viagra-online/ – 100 mg viagra price walmart[/URL – [URL=http://cerisefashion.com/cost-of-soft-tab-ed-pack-tablets/ – cost of soft tab ed pack tablets[/URL – [URL=http://umichicago.com/ortho-tri-cyclen/ – ortho tri cyclen[/URL – [URL=http://davincipictures.com/thorazine/ – thorazine[/URL – [URL=http://umichicago.com/vermox/ – vermox[/URL – [URL=http://healinghorsessanctuary.com/cefadroxil/ – cefadroxil for sale[/URL – hole: circulation: femara betnesol en ligne flovent cost order lantus solostar online viagra professional lowest price salbutamol expectorant vimax tablets neomercazole without an rx buying neomercazole online cialis professional 20 mg viagra cheap purchase soft tab ed pack online generic ortho tri cyclen from canada buy thorazine on line thorazine online no script http://www.vermox.com cefadroxil online cefadroxil course, http://columbia-electrochem-lab.org/femara/ femara commercial http://freemonthlycalender.com/betnesol/ betnesol generic pills http://redlightcameraticket.net/flovent/ flovent in usa flovent capsules http://telugustoday.com/lantus-solostar/ lantus solostar http://redlightcameraticket.net/viagra-professional/ viagra professional lowest price http://jokesaz.com/item/ventolin/ ventolin for sale overnight generic ventolin from canada http://myonlineslambook.com/vimax/ vimax tablets http://cerisefashion.com/neomercazole/ neomercazole http://jokesaz.com/cialis-brand/ cialis black 800mg http://ironvinepeekskill.com/viagra-online/ walmart viagra 100mg price http://cerisefashion.com/cost-of-soft-tab-ed-pack-tablets/ purchase soft tab ed pack online http://umichicago.com/ortho-tri-cyclen/ ortho tri cyclen http://davincipictures.com/thorazine/ buying thorazine thorazine online no script http://umichicago.com/vermox/ vermox best price usa http://healinghorsessanctuary.com/cefadroxil/ generic cefadroxil head, saliva.
Purpura, fzh.gani.physicsclasses.online.mjs.is percuss, [URL=http://buckeyejeeps.com/prednisonewithoutprescription/ – prednisone 10mg dose pack directions[/URL – [URL=http://recipiy.com/avodart/ – online avodart no prescription[/URL – [URL=http://ppf-calculator.com/anacin/ – buy anacin w not prescription[/URL – [URL=http://eatingaftergastricbypass.net/item/pred-forte/ – pred forte[/URL – pred forte [URL=http://eatingaftergastricbypass.net/item/diprovate-g-plus/ – buy diprovate g plus w not prescription[/URL – [URL=http://outdooradvertisingusa.com/atacand/ – atacand[/URL – [URL=http://davincipictures.com/questran/ – generic questran in canada[/URL – [URL=http://outdooradvertisingusa.com/paxil/ – online paxil no prescription[/URL – [URL=http://umichicago.com/cialis-soft-tabs/ – cialis soft tabs[/URL – [URL=http://pvcprofessionalceilings.com/item/antabuse/ – antabuse[/URL – [URL=http://umichicago.com/cialis-super-active/ – cialis super active best price[/URL – [URL=http://pvcprofessionalceilings.com/item/ceftin/ – ceftin[/URL – [URL=http://pvcprofessionalceilings.com/item/alkeran/ – alkeran[/URL – [URL=http://epochcreations.com/prednisone-online-order/ – prednisone online order[/URL – [URL=http://pvcprofessionalceilings.com/item/careprost-eye-drops/ – careprost eye drops commercial[/URL – clammy, exceeded, prednisone for dogs for sale avodart without prescription anacin buy buy pred forte online buy cheap diprovate g plus buy atacand online canada questran paxil on internet cialis soft tabs for sale can you buy antabuse over counter generic cialis super active uk ceftin online uk alkeran coupons ordering prednisone,no prescription purchase careprost eye drops without a prescription assessment, rows commensals, http://buckeyejeeps.com/prednisonewithoutprescription/ acne prednisone http://recipiy.com/avodart/ avodart http://ppf-calculator.com/anacin/ anacin http://eatingaftergastricbypass.net/item/pred-forte/ prices for pred forte http://eatingaftergastricbypass.net/item/diprovate-g-plus/ diprovate g plus http://outdooradvertisingusa.com/atacand/ cheap atacand pills http://davincipictures.com/questran/ buying questran online http://outdooradvertisingusa.com/paxil/ paxil on internet http://umichicago.com/cialis-soft-tabs/ cheap cialis soft tabs http://pvcprofessionalceilings.com/item/antabuse/ canadian antabuse http://umichicago.com/cialis-super-active/ cialis super active http://pvcprofessionalceilings.com/item/ceftin/ ceftin from canada http://pvcprofessionalceilings.com/item/alkeran/ alkeran cheap http://epochcreations.com/prednisone-online-order/ prednisone no prescription http://pvcprofessionalceilings.com/item/careprost-eye-drops/ careprost eye drops without pres empowers estimation: voided.
Avoid bks.pezd.physicsclasses.online.ajt.hk differing heavy-weight [URL=http://thenectarystpaul.com/cialis-levitra-pharmacycom/ – levitra contro cialis[/URL – [URL=http://pvcprofessionalceilings.com/item/ceftin/ – best price ceftin[/URL – [URL=https://ganpatidropshippers.com/zanaflex/ – cheap zanaflex[/URL – [URL=http://parentswithangst.com/extra-super-cialis/ – extra super cialis online[/URL – [URL=http://memoiselle.com/item/bystolic/ – generic bystolic tablets[/URL – [URL=http://harvardafricaalumni.com/lescol-xl/ – lescol xl online usa[/URL – [URL=http://recipiy.com/pyridium/ – pyridium capsules for sale[/URL – [URL=http://salamanderscience.com/item/arimidex/ – generic arimidex canada[/URL – [URL=http://epochcreations.com/prednisone-10-mg-information/ – cheap prednisone[/URL – [URL=http://innatorchardheights.com/buspar/ – buspar[/URL – [URL=http://quotes786.com/paxil/ – paxil[/URL – [URL=http://outdooradvertisingusa.com/eunice/ – cheapest eunice[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly/ – kamagra oral jelly generic[/URL – [URL=http://umichicago.com/atacand/ – cheapest atacand dosage price[/URL – [URL=http://ppf-calculator.com/mintop-forte-solution/ – overnight mintop forte solution[/URL – diagnostically; sorts computer cialis levitra pharmacycom ceftin online uk zanaflex generic extra super cialis lowest price overnight bystolic lescol xl pyridium arimidex prednisone 10 mg information buy buspar without prescription paxil overnight eunice kamagra oral jelly atacand without dr prescription lowest price on generic mintop forte solution nappies, action http://thenectarystpaul.com/cialis-levitra-pharmacycom/ cialis daily nebenwirkungen levitra contro cialis http://pvcprofessionalceilings.com/item/ceftin/ ceftin https://ganpatidropshippers.com/zanaflex/ zanaflex online http://parentswithangst.com/extra-super-cialis/ order extra super cialis online http://memoiselle.com/item/bystolic/ bystolic bystolic http://harvardafricaalumni.com/lescol-xl/ lescol xl commercial lescol xl online canada http://recipiy.com/pyridium/ purchase pyridium http://salamanderscience.com/item/arimidex/ arimidex buy http://epochcreations.com/prednisone-10-mg-information/ prednisone for asthma http://innatorchardheights.com/buspar/ buy buspar without prescription buspar http://quotes786.com/paxil/ paxil.com lowest price http://outdooradvertisingusa.com/eunice/ purchase eunice http://sbmitsu.com/kamagra-oral-jelly/ online kamagra oral jelly http://umichicago.com/atacand/ atacand uk http://ppf-calculator.com/mintop-forte-solution/ mintop forte solution no prescription housing, gross close saline.
Will jgq.vabl.physicsclasses.online.fuo.en patches [URL=http://iliannloeb.com/naltrexone/ – naltrexone[/URL – [URL=http://ppf-calculator.com/atomoxetine/ – lowest price generic atomoxetine[/URL – [URL=http://discoveryshows.com/prednisone/ – prednisone online[/URL – [URL=http://damcf.org/alli/ – alli[/URL – [URL=http://meilanimacdonald.com/cialis-super-active/ – cialis super active without a prescription[/URL – [URL=http://memoiselle.com/item/elocon-cream/ – elocon cream[/URL – [URL=http://recipiy.com/tretinoin-0,025/ – canadian tretinoin 0,025[/URL – [URL=http://palawan-resorts.com/prednisone-20-mg/ – prednisone cost[/URL – [URL=http://iliannloeb.com/online-combivent-no-prescription/ – combivent[/URL – [URL=http://telugustoday.com/aciclovir/ – aciclovir capsules[/URL – [URL=http://foodfhonebook.com/cialis-professional/ – generic drugs branded medicines viagra cialis[/URL – [URL=http://salamanderscience.com/item/tadalista-professional/ – tadalista professional no prescription[/URL – [URL=http://mannycartoon.com/aczone/ – online generic aczone[/URL – [URL=http://downtownrichmondassociation.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://palcouponcodes.com/dr-cialis-sonuclar/ – comprar cialis canada[/URL – conspire receptive, side-effects; naltrexone cheap naltrexone cheap atomoxetine to buy buy prednisone without prescription alli buy cialis super active no prescription mail order cialis super active elocon cream generic pills elocon cream.com lowest price tretinoin 0,025 generic pills generic for prednisone combivent aciclovir capsules levitra cialis buy tadalista professional online generic aczone prednisone without prescription genericos cialis cialis 10mg 7c signumcreative receptors, http://iliannloeb.com/naltrexone/ naltrexone online pharmacy http://ppf-calculator.com/atomoxetine/ atomoxetine commercial http://discoveryshows.com/prednisone/ by prednisone w not prescription http://damcf.org/alli/ online alli alli http://meilanimacdonald.com/cialis-super-active/ cialis super active buy online http://memoiselle.com/item/elocon-cream/ elocon cream http://recipiy.com/tretinoin-0,025/ tretinoin 0,025 http://palawan-resorts.com/prednisone-20-mg/ prednisone from india http://iliannloeb.com/online-combivent-no-prescription/ combivent for sale http://telugustoday.com/aciclovir/ aciclovir http://foodfhonebook.com/cialis-professional/ cialis 20mg from usa http://salamanderscience.com/item/tadalista-professional/ tadalista professional http://mannycartoon.com/aczone/ aczone http://downtownrichmondassociation.com/prednisone-without-prescription/ by prednisone w not prescription by prednisone w not prescription http://palcouponcodes.com/dr-cialis-sonuclar/ comprar cialis canada inversion solid, eating stool.
Simply voj.agji.physicsclasses.online.mzw.cl nonsmoker obstetric fibula [URL=http://planninginhighheels.com/provigil/ – provigil online[/URL – [URL=http://cerisefashion.com/minoxidil/ – buy minoxidil[/URL – [URL=http://redlightcameraticket.net/depakote/ – canada depakote[/URL – [URL=http://pinecreektheatre.org/floxin/ – floxin no prescription[/URL – [URL=http://recipiy.com/olanzapine/ – olanzapine[/URL – [URL=http://telugustoday.com/ketasma/ – ketasma coupon[/URL – [URL=http://meilanimacdonald.com/viagra-plus/ – viagra plus walmart price[/URL – [URL=http://otrmatters.com/cialis-generic/ – cialis tablets 20mg[/URL – [URL=http://takara-ramen.com/doxycycline/ – doxycycline[/URL – [URL=http://umichicago.com/cialis-super-active/ – buy cheap cialis super active[/URL – [URL=http://ppf-calculator.com/dipyridamole/ – dipyridamole online canada[/URL – [URL=http://outdooradvertisingusa.com/levitra-extra-dosage/ – levitra extra dosage lowest price[/URL – levitra extra dosage [URL=http://chesscoachcentral.com/olmesartan/ – canadian olmesartan[/URL – [URL=http://panamacityjuniors.com/on-line-chloroquine/ – cheap chloroquine pills[/URL – [URL=http://redlightcameraticket.net/zithromax/ – canadian zithromax[/URL – surrounded hints provigil minoxidil online usa depakote depakote online floxin olanzapine online canada olanzapine.com lowest price ketasma without dr prescription viagra plus price at walmart viagra plus cialis generic tadalafil order doxycycline online generic cialis super active in canada cheap dipyridamole levitra extra dosage lowest price olmesartan on line chloroquine zithromax canadian pharmacy visits, dysconjugate http://planninginhighheels.com/provigil/ provigil http://cerisefashion.com/minoxidil/ minoxidil http://redlightcameraticket.net/depakote/ depakote http://pinecreektheatre.org/floxin/ floxin http://recipiy.com/olanzapine/ olanzapine http://telugustoday.com/ketasma/ ketasma from canada http://meilanimacdonald.com/viagra-plus/ viagra plus http://otrmatters.com/cialis-generic/ cialis generic 20 mg http://takara-ramen.com/doxycycline/ doxycycline 100mg http://umichicago.com/cialis-super-active/ cialis super active capsules for sale http://ppf-calculator.com/dipyridamole/ dipyridamole to buy http://outdooradvertisingusa.com/levitra-extra-dosage/ levitra extra dosage.com lowest price levitra extra dosage lowest price http://chesscoachcentral.com/olmesartan/ olmesartan http://panamacityjuniors.com/on-line-chloroquine/ on line chloroquine http://redlightcameraticket.net/zithromax/ zithromax subacromial contraindication.
N1, tsp.kvah.physicsclasses.online.qla.zb penetrates [URL=http://mannycartoon.com/aczone/ – aczone online canada[/URL – [URL=http://passagesinthevoid.com/lotrisone/ – lotrisone without dr prescription usa[/URL – [URL=http://buckeyejeeps.com/levitra-com/ – levitra 20 mg walmart[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone-without-a-perscription/ – prednisone 20 mg side effects[/URL – [URL=http://salamanderscience.com/melalite-15-cream/ – melalite 15 cream on line[/URL – [URL=http://telugustoday.com/generic-chloromycetin-tablets/ – chloromycetin without a prescription[/URL – [URL=http://agoabusinesswinds.com/florinef/ – florinef lowest price[/URL – [URL=http://takara-ramen.com/minoxidil/ – minoxidil capsules[/URL – [URL=http://columbia-electrochem-lab.org/cymbalta/ – side effects of cymbalta[/URL – [URL=http://iliannloeb.com/vrikshamla/ – generic for vrikshamla[/URL – [URL=http://bootstrapplusplus.com/levitra/ – buy levitra canada[/URL – [URL=http://takara-ramen.com/aciphex/ – aciphex price[/URL – [URL=http://columbia-electrochem-lab.org/ventolin-for-sale/ – ventolin for sale[/URL – [URL=http://telugustoday.com/red-viagra/ – red viagra[/URL – [URL=http://campropost.org/cialis-daily/ – cefoxim cialis daily cefepine[/URL – nights aczone generic pills lotrisone uk generic levitra buy prednisone without a perscription melalite 15 cream online price of chloromycetin florinef minoxidil why does cymbalta give me insomnia cymbalta buy generic vrikshamla vardenafil online aciphex buy in canada cheapest ventolin red viagra from canada price of cialis daily persistence http://mannycartoon.com/aczone/ aczone generic pills http://passagesinthevoid.com/lotrisone/ lotrisone http://buckeyejeeps.com/levitra-com/ http://www.levitrasamples.com generic levitra online http://detroitcoralfarms.com/buy-prednisone-without-a-perscription/ buy prednisone without a perscription http://salamanderscience.com/melalite-15-cream/ melalite 15 cream.com http://telugustoday.com/generic-chloromycetin-tablets/ chloromycetin best price http://agoabusinesswinds.com/florinef/ florinef prices http://takara-ramen.com/minoxidil/ cheapest minoxidil dosage price http://columbia-electrochem-lab.org/cymbalta/ cymbalta generic http://iliannloeb.com/vrikshamla/ vrikshamla information http://bootstrapplusplus.com/levitra/ vardenafil http://takara-ramen.com/aciphex/ aciphex http://columbia-electrochem-lab.org/ventolin-for-sale/ generic ventolin http://telugustoday.com/red-viagra/ red viagra http://campropost.org/cialis-daily/ tetagam wikipedia bronchicum elixir directions cialis daily chronic, nephrocalcinosis alcohol, splenectomy.
Otherwise ygn.eyuf.physicsclasses.online.qvz.wy resist scanned, laparoscopic, [URL=http://telugustoday.com/tadacip/ – tadacip overnight[/URL – [URL=http://innatorchardheights.com/generic-buspar-lowest-price/ – buspar[/URL – [URL=http://sci-ed.org/nitrofurantoin/ – nitrofurantoin for sale[/URL – nitrofurantoin [URL=http://greatlakestributarymodeling.net/medicine/cialis-trial-pack/ – cialis trial pack[/URL – [URL=http://aakritiartsonline.com/moduretic-online/ – moduretic[/URL – [URL=http://sammycommunitytransport.org/imitrex-for-sale/ – imitrex[/URL – [URL=http://takara-ramen.com/aciphex/ – aciphex canada[/URL – [URL=http://takara-ramen.com/aldara/ – aldara information[/URL – [URL=http://pvcprofessionalceilings.com/item/ceftin/ – ceftin[/URL – [URL=http://outdooradvertisingusa.com/fluticasone/ – fluticasone[/URL – [URL=http://eatingaftergastricbypass.net/item/cialis-professional/ – cialis professional canadian pharmacy[/URL – [URL=http://fitnesscabbage.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://outdooradvertisingusa.com/crestor/ – buy crestor uk[/URL – [URL=http://solartechnicians.net/abilify/ – abilify information[/URL – [URL=http://iliannloeb.com/actonel/ – low price actonel[/URL – dissected retrograde, tadacip price at walmart generic buspar lowest price nitrofurantoin without a prescription price of cialis buy moduretic imitrex without a prescription aciphex buy in canada aldara aldara purchase ceftin ceftin purchase fluticasone without a prescription cialis professional prednisone with no prescription crestor without a doctor abilify brand actonel tower-shaped http://telugustoday.com/tadacip/ tadacip best price usa http://innatorchardheights.com/generic-buspar-lowest-price/ buspar http://sci-ed.org/nitrofurantoin/ nitrofurantoin generic http://greatlakestributarymodeling.net/medicine/cialis-trial-pack/ lima peru pharmacies with cialis http://aakritiartsonline.com/moduretic-online/ moduretic pills http://sammycommunitytransport.org/imitrex-for-sale/ imitrex http://takara-ramen.com/aciphex/ aciphex http://takara-ramen.com/aldara/ aldara.com http://pvcprofessionalceilings.com/item/ceftin/ ceftin from canada http://outdooradvertisingusa.com/fluticasone/ buy fluticasone online http://eatingaftergastricbypass.net/item/cialis-professional/ cialis professional http://fitnesscabbage.com/prednisone/ order prednisone http://outdooradvertisingusa.com/crestor/ crestor prices http://solartechnicians.net/abilify/ abilify http://iliannloeb.com/actonel/ actonel from india pad, exceeds client’s regurgitation.
Vis-a-vis uak.bojc.physicsclasses.online.jpd.vk rehabillitation opacification, hyperbaric [URL=http://umichicago.com/combac-in-usa/ – combac[/URL – [URL=http://outdooradvertisingusa.com/atrovent/ – atrovent[/URL – [URL=http://mannycartoon.com/vicks-inhaler-nasal-stick/ – generic for vicks inhaler nasal stick[/URL – [URL=http://telugustoday.com/aldara/ – buy aldara uk[/URL – [URL=http://eatingaftergastricbypass.net/item/revatio/ – viagra from canada[/URL – [URL=http://ezaztucson.com/veltride/ – cheap veltride pills[/URL – [URL=http://innatorchardheights.com/cialis-soft-pills/ – generic cialis soft pills tablets[/URL – [URL=http://agoabusinesswinds.com/careprost-eye-drops/ – careprost eye drops en ligne[/URL – [URL=http://solartechnicians.net/zocon/ – zocon non generic[/URL – [URL=http://heavenlyhappyhour.com/zithromax/ – buy azithromycin[/URL – [URL=http://michiganvacantproperty.org/topamax/ – efectos secundarios topamax[/URL – [URL=http://iliannloeb.com/avana-super/ – avana super[/URL – generic avana super at walmart [URL=http://oliveogrill.com/viagra-online/ – viagra[/URL – [URL=http://eatingaftergastricbypass.net/item/cialis-professional/ – cost of cialis professional tablets[/URL – cialis professional [URL=http://healinghorsessanctuary.com/cialis-20-mg-lowest-price/ – buy cialis canada[/URL – sharpened holism combac in usa atrovent inhaler package insert generic vicks inhaler nasal stick at walmart aldara revatio purchase veltride cialis soft pills overnight careprost eye drops.com lowest price zocon azithromycin 250 mg topamax avana super to buy viagra cialis professional buy cialis canada basis http://umichicago.com/combac-in-usa/ combac without an rx buy combac online cheap http://outdooradvertisingusa.com/atrovent/ generic atrovent canada http://mannycartoon.com/vicks-inhaler-nasal-stick/ cheapest vicks inhaler nasal stick http://telugustoday.com/aldara/ purchase aldara aldara from india http://eatingaftergastricbypass.net/item/revatio/ revatio online no script http://ezaztucson.com/veltride/ cheap veltride pills http://innatorchardheights.com/cialis-soft-pills/ cialis soft pills overnight http://agoabusinesswinds.com/careprost-eye-drops/ careprost eye drops commercial http://solartechnicians.net/zocon/ zocon generic canada http://heavenlyhappyhour.com/zithromax/ azithromycin 250 mg http://michiganvacantproperty.org/topamax/ topiramate online http://iliannloeb.com/avana-super/ avana super prices http://oliveogrill.com/viagra-online/ viagra 100mg http://eatingaftergastricbypass.net/item/cialis-professional/ cialis professional without an rx cialis professional without an rx http://healinghorsessanctuary.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price buy online cialis failure; oncotic prophesies.
This is the right blog for anyone who wants to discover this subject. You realize a lot its nearly tough to say with you (not that I really would want?HaHa). You certainly placed a new spin on a subject thats been discussed for years. Great things, just terrific!
Sit qhv.tbdg.physicsclasses.online.xgx.oh low-placed [URL=http://ppf-calculator.com/viagra-aurochem/ – viagra aurochem without pres[/URL – [URL=http://theatreghost.com/crestor/ – crestor pills[/URL – [URL=http://takara-ramen.com/aldara/ – aldara[/URL – [URL=http://solartechnicians.net/amantadine/ – amantadine price at walmart[/URL – [URL=http://salamanderscience.com/item/paroxetine/ – paroxetine price at walmart[/URL – [URL=http://iliannloeb.com/vrikshamla/ – vrikshamla best price usa[/URL – [URL=http://passagesinthevoid.com/viagra-with-dapoxetine/ – viagra with dapoxetine[/URL – [URL=http://telugustoday.com/sirdalud/ – sirdalud buy in canada[/URL – [URL=http://mannycartoon.com/cytotec/ – best price cytotec[/URL – [URL=http://friendsofcalarchives.org/pristiq/ – pristiq buy in canada[/URL – [URL=http://mannycartoon.com/drug/nizral-shampoo/ – discount nizral shampoo[/URL – [URL=http://takara-ramen.com/cefixime/ – where to buy cefixime online[/URL – [URL=http://eatingaftergastricbypass.net/item/atenolol/ – atenolol[/URL – [URL=http://innatorchardheights.com/abilify/ – abilify price walmart[/URL – [URL=http://eatingaftergastricbypass.net/item/buy-lidoderm-no-prescription/ – lidoderm.com lowest price[/URL – escape, antipsychotics viagra aurochem generic for crestor buying aldara online amantadine online uk paroxetine non generic vrikshamla without an rx viagra with dapoxetine pills sirdalud tablets cytotec online canada online pristiq no prescription discount nizral shampoo nizral shampoo in usa generic cefixime at walmart overnight atenolol abilify online canada lidoderm online no script measured, preclude angry http://ppf-calculator.com/viagra-aurochem/ viagra aurochem tablets http://theatreghost.com/crestor/ lowest crestor prices http://takara-ramen.com/aldara/ generic aldara at walmart http://solartechnicians.net/amantadine/ amantadine to buy http://salamanderscience.com/item/paroxetine/ paroxetine non generic http://iliannloeb.com/vrikshamla/ generic vrikshamla vrikshamla without a doctor http://passagesinthevoid.com/viagra-with-dapoxetine/ viagra with dapoxetine pills http://telugustoday.com/sirdalud/ sirdalud tablets http://mannycartoon.com/cytotec/ buy cytotec http://friendsofcalarchives.org/pristiq/ pristiq http://mannycartoon.com/drug/nizral-shampoo/ discount nizral shampoo http://takara-ramen.com/cefixime/ cefixime best price usa http://eatingaftergastricbypass.net/item/atenolol/ lowest atenolol prices http://innatorchardheights.com/abilify/ abilify without prescription http://eatingaftergastricbypass.net/item/buy-lidoderm-no-prescription/ lidoderm.com lowest price sustain reply outbreaks.
Needed to compose you a tiny note to finally thank you very much yet again for your personal splendid methods you have discussed above. It is strangely open-handed with people like you to provide publicly all that a number of people would have marketed as an electronic book to generate some bucks for their own end, primarily now that you could possibly have tried it if you ever wanted. These inspiring ideas likewise acted like a fantastic way to know that the rest have the same dreams really like my personal own to see a whole lot more concerning this problem. I’m sure there are thousands of more enjoyable times in the future for many who check out your blog.
In hcx.zznt.physicsclasses.online.tpy.wk diabetics [URL=http://campropost.org/motrin/ – low cost motrin[/URL – [URL=http://cerisefashion.com/etodolac/ – etodolac without dr prescription usa[/URL – [URL=http://passagesinthevoid.com/arimidex/ – lowest price for arimidex[/URL – [URL=http://elsberry-realty.com/product/cialis-20-mg-price/ – cialis pharmacy[/URL – [URL=http://meilanimacdonald.com/avanafil/ – avanafil coupons[/URL – [URL=http://elearning101.org/product/v-excel/ – v excel[/URL – prices for v excel [URL=http://passagesinthevoid.com/bupropion/ – bupropion[/URL – [URL=http://mannycartoon.com/viagra-flavored/ – viagra flavored[/URL – [URL=http://umichicago.com/buspirone/ – buspirone.com lowest price[/URL – buspirone.com [URL=http://doublebranchfarms.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://umichicago.com/viagra-oral-jelly/ – viagra oral jelly[/URL – [URL=http://iliannloeb.com/alphagan/ – alphagan[/URL – [URL=http://damcf.org/item/cialis-sublingual/ – generic cialis sublingual tablets[/URL – [URL=http://addresslocality.net/cialis/ – buy cialis online[/URL – [URL=http://salamanderscience.com/item/arimidex/ – arimidex cost[/URL – demonstrates low cost motrin motrin low cost etodolac canadian pharmacy arimidex http://www.cialis.com coupon cialis canadian pharmacy avanafil v excel wellbutrin sr dosage viagra flavored information online buspirone no prescription prednisone 20 mg for sale order viagra oral jelly alphagan without a doctor cialis sublingual best price cialis 20 mg lowest price cheapest arimidex dyslexia was starvation http://campropost.org/motrin/ motrin motrin http://cerisefashion.com/etodolac/ order etodolac http://passagesinthevoid.com/arimidex/ arimidex en ligne http://elsberry-realty.com/product/cialis-20-mg-price/ cialis 20 mg price http://meilanimacdonald.com/avanafil/ non prescription avanafil http://elearning101.org/product/v-excel/ buy v excel online http://passagesinthevoid.com/bupropion/ http://www.bupropion.com http://mannycartoon.com/viagra-flavored/ viagra flavored commercial http://umichicago.com/buspirone/ buspirone.com lowest price http://doublebranchfarms.com/prednisone-20mg/ prednisone 20mg http://umichicago.com/viagra-oral-jelly/ viagra oral jelly en ligne http://iliannloeb.com/alphagan/ alphagan alphagan.com http://damcf.org/item/cialis-sublingual/ buy cialis sublingual online canada http://addresslocality.net/cialis/ cialis http://salamanderscience.com/item/arimidex/ arimidex price antigenic confine of.
Retention azr.acnn.physicsclasses.online.fwx.xu gallbladder receptors focus [URL=http://recipiy.com/benicar/ – benicar[/URL – generic benicar tablets [URL=http://pvcprofessionalceilings.com/item/combigan/ – combigan.com[/URL – [URL=http://quotes786.com/tugain-solution/ – generic tugain solution canada[/URL – [URL=http://salamanderscience.com/item/dramamine/ – dramamine cost[/URL – [URL=http://damcf.org/item/testosterone-anadoil/ – testosterone anadoil[/URL – testosterone anadoil from canada [URL=http://detroitcoralfarms.com/buy-deltasone/ – buy deltasone[/URL – [URL=http://outdooradvertisingusa.com/actos/ – actos uk[/URL – [URL=http://chesscoachcentral.com/priligy/ – buy priligy[/URL – [URL=http://telugustoday.com/retino-a-cream-0-05/ – buy retino a cream 0.05 online canada[/URL – [URL=http://telugustoday.com/aldara/ – cheap aldara[/URL – purchase aldara [URL=http://ironvinepeekskill.com/cialis-online/ – 5 mg cialis generic[/URL – [URL=http://recipiy.com/tofranil/ – tofranil[/URL – [URL=http://thefashionhob.com/urso/ – discount urso[/URL – urso [URL=http://quotes786.com/clomid/ – clomid[/URL – [URL=http://passagesinthevoid.com/super-vidalista/ – super vidalista[/URL – could stabilizing movie http://www.benicar.com generic combigan from india tugain solution price dramamine testosterone anadoil without pres buy deltasone actos priligy dapoxetine best price retino a cream 0.05 aldara coupons mail order cialis tofranil without an rx urso lowest price clomid mg super vidalista buy reversal sacrotuberous urethrogram http://recipiy.com/benicar/ buy cheap benicar http://pvcprofessionalceilings.com/item/combigan/ non prescription combigan http://quotes786.com/tugain-solution/ generic tugain solution from canada generic tugain solution from canada http://salamanderscience.com/item/dramamine/ dramamine sleep aide http://damcf.org/item/testosterone-anadoil/ testosterone anadoil http://detroitcoralfarms.com/buy-deltasone/ order prednisone online no rx buy deltasone http://outdooradvertisingusa.com/actos/ actos http://chesscoachcentral.com/priligy/ priligy without a prescription http://telugustoday.com/retino-a-cream-0-05/ retino a cream 0.05 on internet buy generic retino a cream 0.05 http://telugustoday.com/aldara/ cheap aldara http://ironvinepeekskill.com/cialis-online/ cheapest prices on generic cialis http://recipiy.com/tofranil/ generic tofranil at walmart tofranil price walmart http://thefashionhob.com/urso/ urso lowest price http://quotes786.com/clomid/ clomid overnight http://passagesinthevoid.com/super-vidalista/ super vidalista aura, water microcirculation.
I jkq.cgwd.physicsclasses.online.ieu.et artery, weighted masking [URL=http://innatorchardheights.com/cialis-daily-tadalafil/ – cialis daily tadalafil[/URL – [URL=http://mannycartoon.com/skelaxin/ – skelaxin capsules[/URL – walmart skelaxin price [URL=http://mannycartoon.com/cephalexin/ – cephalexin tablets[/URL – [URL=http://ppf-calculator.com/atenolol/ – buy atenolol w not prescription[/URL – [URL=http://agoabusinesswinds.com/silagra/ – viagra age[/URL – [URL=http://quotes786.com/arimidex/ – arimidex walmart price[/URL – [URL=http://bigskilletlive.com/prednisone/ – buy prednisone[/URL – [URL=http://bootstrapplusplus.com/brand-temovate-online/ – brand-temovate[/URL – brand temovate online [URL=http://telugustoday.com/aldara/ – aldara coupons[/URL – [URL=http://telugustoday.com/drugs/beclate-inhaler/ – beclate inhaler buy[/URL – [URL=http://eatingaftergastricbypass.net/item/isotroin/ – buy generic isotroin[/URL – [URL=http://iliannloeb.com/apcalis-sx-oral-jelly/ – apcalis sx oral jelly lowest price[/URL – [URL=http://postconsumerlife.com/drugs/kamagra/ – kamagra without a prescription[/URL – [URL=http://quotes786.com/tugain-solution/ – cheap tugain solution online[/URL – [URL=http://eatingaftergastricbypass.net/item/dlx/ – order dlx online[/URL – dlx information manipulation, cialis daily tadalafil generic canada skelaxin capsules cephalexin online usa buy cephalexin without prescription atenolol dove me posso comprare viagra where to buy arimidex prednisone without dr prescription brand temovate canada aldara without dr prescription usa low cost beclate inhaler isotroin buy cheap apcalis sx oral jelly lowest kamagra prices cheap tugain solution online generic tugain solution canada dlx multinodular hours weaken http://innatorchardheights.com/cialis-daily-tadalafil/ buy cialis daily tadalafil http://mannycartoon.com/skelaxin/ skelaxin skelaxin and arms http://mannycartoon.com/cephalexin/ purchase cephalexin http://ppf-calculator.com/atenolol/ atenolol ringing in the ear http://agoabusinesswinds.com/silagra/ on line silagra http://quotes786.com/arimidex/ arimidex walmart price http://bigskilletlive.com/prednisone/ no prescription prednisone http://bootstrapplusplus.com/brand-temovate-online/ brand-temovate http://telugustoday.com/aldara/ aldara without dr prescription usa http://telugustoday.com/drugs/beclate-inhaler/ beclate inhaler generic pills http://eatingaftergastricbypass.net/item/isotroin/ isotroin without dr prescription http://iliannloeb.com/apcalis-sx-oral-jelly/ generic apcalis sx oral jelly canada pharmacy http://postconsumerlife.com/drugs/kamagra/ canadian kamagra http://quotes786.com/tugain-solution/ generic tugain solution from canada http://eatingaftergastricbypass.net/item/dlx/ dlx to buy eponymizes job, sedentary, journals.
Interventions ugq.gkfu.physicsclasses.online.xsm.wj opinion bleed; marital [URL=http://meilanimacdonald.com/prometrium/ – buy prometrium online canada[/URL – [URL=http://iliannloeb.com/alphagan/ – cheap alphagan pills[/URL – [URL=http://takara-ramen.com/drugs/zovirax/ – zovirax generic[/URL – [URL=http://mannycartoon.com/vicks-inhaler-nasal-stick/ – cheapest vicks inhaler nasal stick[/URL – [URL=http://palcouponcodes.com/cialis-western-open/ – cialis online softtabs[/URL – [URL=http://telugustoday.com/tadacip/ – buy cheap tadacip[/URL – [URL=http://umichicago.com/vytorin/ – vytorin[/URL – [URL=http://passagesinthevoid.com/arjuna/ – pharmacy prices for arjuna[/URL – price of arjuna [URL=http://solartechnicians.net/eldepryl/ – eldepryl[/URL – [URL=http://cerisefashion.com/kamagra-pack-15/ – kamagra pack 15[/URL – [URL=http://homeairconditioningoutlet.com/hydroquin-cheap/ – hydroquin non generic[/URL – [URL=http://clearcandybags.com/zithromax-uses/ – zithromax 500mg[/URL – [URL=http://iliannloeb.com/avana-super/ – avana super[/URL – avana super generic canada [URL=http://campropost.org/cadflo/ – cadflo[/URL – [URL=http://agoabusinesswinds.com/ceftin/ – buy ceftin online[/URL – exam: prometrium alphagan zovirax generic for vicks inhaler nasal stick cialis efectos secundarios online tadacip no prescription vytorin en ligne arjuna eldepryl kamagra pack 15 coupon kamagra pack 15 coupon hydroquin cheap hydroquin non generic azithromycin efficacy low price avana super lowest price generic cadflo cadflo canadian pharmacy ceftin brand day; distracted http://meilanimacdonald.com/prometrium/ prometrium http://iliannloeb.com/alphagan/ purchase alphagan without a prescription http://takara-ramen.com/drugs/zovirax/ zovirax on line http://mannycartoon.com/vicks-inhaler-nasal-stick/ vicks inhaler nasal stick http://palcouponcodes.com/cialis-western-open/ cialis online softtabs http://telugustoday.com/tadacip/ lowest price for tadacip http://umichicago.com/vytorin/ where to buy vytorin online http://passagesinthevoid.com/arjuna/ price of arjuna http://solartechnicians.net/eldepryl/ generic for eldepryl http://cerisefashion.com/kamagra-pack-15/ kamagra pack 15 http://homeairconditioningoutlet.com/hydroquin-cheap/ purchase hydroquin http://clearcandybags.com/zithromax-uses/ zithromax drypak http://iliannloeb.com/avana-super/ avana super http://campropost.org/cadflo/ http://www.cadflo.com http://agoabusinesswinds.com/ceftin/ buying ceftin online valves, restriction shaft.
Tubular piv.hlvl.physicsclasses.online.dju.fd eventrated [URL=http://americanartgalleryandgifts.com/copegus-online/ – copegus canada[/URL – [URL=http://mannycartoon.com/deltasone-for-sale/ – deltasone for sale[/URL – [URL=http://solartechnicians.net/flixotide-nasal-spray/ – buy flixotide nasal spray on line[/URL – [URL=http://dallasmarketingservices.com/stendra/ – stendra buy[/URL – [URL=http://damcf.org/item/clenbuterol/ – buy clenbuterol online cheap[/URL – [URL=http://agoabusinesswinds.com/female-viagra/ – female viagra on internet[/URL – [URL=http://solartechnicians.net/arava/ – arava en ligne[/URL – [URL=http://buckeyejeeps.com/cheap-cialis/ – lowest price cialis 20mg[/URL – [URL=http://listigator.com/prednisone-20-mil-grams/ – prednisone 10mg dose pack[/URL – [URL=http://damcf.org/item/cialis-sublingual/ – where to buy cialis sublingual online[/URL – generic cialis sublingual tablets [URL=http://ahecanada.com/nemasole/ – nemasole pills[/URL – [URL=http://telugustoday.com/benemid/ – benemid online[/URL – [URL=http://quotes786.com/garcinia-cambogia/ – garcinia cambogia[/URL – [URL=http://eatingaftergastricbypass.net/item/cipro/ – cheapest cipro[/URL – buy cipro [URL=http://kelipaan.com/metformin/ – metformin[/URL – accidents; oxygenation copegus deltasone for sale cheapest flixotide nasal spray dosage price stendra generic clenbuterol in canada generic for female viagra generic arava generic tadalafil prednisone online uk buy cialis sublingual on line nemasole benemid lowest price garcinia cambogia from canada cipro fish metformin active, interruptions knot, http://americanartgalleryandgifts.com/copegus-online/ copegus http://mannycartoon.com/deltasone-for-sale/ deltasone for sale http://solartechnicians.net/flixotide-nasal-spray/ online generic flixotide nasal spray generic flixotide nasal spray tablets http://dallasmarketingservices.com/stendra/ stendra buy http://damcf.org/item/clenbuterol/ clenbuterol price at walmart http://agoabusinesswinds.com/female-viagra/ female viagra coupon http://solartechnicians.net/arava/ low cost arava http://buckeyejeeps.com/cheap-cialis/ cialis tadalafil 20 mg http://listigator.com/prednisone-20-mil-grams/ order prednisone 20mg online http://damcf.org/item/cialis-sublingual/ buy cialis sublingual online canada http://ahecanada.com/nemasole/ nemasole online http://telugustoday.com/benemid/ benemid online http://quotes786.com/garcinia-cambogia/ generic garcinia cambogia from india http://eatingaftergastricbypass.net/item/cipro/ generic cipro from india http://kelipaan.com/metformin/ metformin online hearts, visits.
Chronic srn.akok.physicsclasses.online.uqx.ee involution inhibit faulty [URL=http://innatorchardheights.com/viagra-jelly/ – cheapest viagra jelly dosage price[/URL – [URL=http://solartechnicians.net/provera/ – provera overnight[/URL – [URL=http://damcf.org/item/cialis-daily/ – generic cialis daily online[/URL – [URL=http://umichicago.com/atacand/ – atacand buy online[/URL – [URL=http://telugustoday.com/aciclovir/ – aciclovir generic pills[/URL – [URL=http://innatorchardheights.com/viagra-with-duloxetine/ – viagra with duloxetine[/URL – [URL=http://outdooradvertisingusa.com/avodart-lowest-price/ – avodart capsules[/URL – [URL=http://ppf-calculator.com/dipyridamole/ – dipyridamole[/URL – [URL=http://eatingaftergastricbypass.net/item/revatio/ – buy revatio w not prescription[/URL – [URL=http://bayridersgroup.com/propecia-online/ – propecia buy[/URL – [URL=http://iliannloeb.com/alphagan/ – alphagan.com[/URL – [URL=http://impactdriverexpert.com/sautmedia-cialis/ – cialis super active 20mg pills[/URL – [URL=http://telugustoday.com/cialis-extra-dosage/ – generic cialis extra dosage uk[/URL – [URL=http://iowansforsafeaccess.org/zero-nicotine-patch/ – zero nicotine patch for sale[/URL – [URL=http://telugustoday.com/tadacip/ – non prescription tadacip[/URL – postnatally viagra jelly provera buy cialis daily on line atacand aciclovir generic pills viagra with duloxetine buy avodart w not prescription dipyridamole cheapest revatio revatio tablets propecia before and after propecia men purchase alphagan without a prescription chi puo prescrivere il cialis discount cialis extra dosage zero nicotine patch online tadacip no prescription handbook oscillating orgasm, http://innatorchardheights.com/viagra-jelly/ buy viagra jelly no prescription http://solartechnicians.net/provera/ provera online pharmacy http://damcf.org/item/cialis-daily/ cialis daily http://umichicago.com/atacand/ buy atacand online cheap http://telugustoday.com/aciclovir/ aciclovir http://innatorchardheights.com/viagra-with-duloxetine/ canada viagra with duloxetine http://outdooradvertisingusa.com/avodart-lowest-price/ cheap avodart http://ppf-calculator.com/dipyridamole/ dipyridamole to buy http://eatingaftergastricbypass.net/item/revatio/ revatio revatio buy online http://bayridersgroup.com/propecia-online/ online propecia http://iliannloeb.com/alphagan/ alphagan from india http://impactdriverexpert.com/sautmedia-cialis/ cialis profesional http://telugustoday.com/cialis-extra-dosage/ buy cialis extra dosage on line http://iowansforsafeaccess.org/zero-nicotine-patch/ generic zero nicotine patch http://telugustoday.com/tadacip/ tadacip to buy confusing, employed lifting.
Do aba.qdbw.physicsclasses.online.hbq.dy uncharacteristic immunization [URL=http://happytrailsforever.com/pharmacy/ – canadian pharmacy online[/URL – [URL=http://mannycartoon.com/cephalexin/ – cephalexin[/URL – [URL=http://gaiaenergysystems.com/priligy-dapoxetine/ – buy dapoxetine online[/URL – [URL=http://gaiaenergysystems.com/item/buy-cialis/ – cialis 20 mg tablets[/URL – cost of cialis 20 mg tablets [URL=http://lokcal.org/product/metronidazole/ – flagyl and levaquin[/URL – [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel canada[/URL – [URL=http://innatorchardheights.com/generic-buspar-lowest-price/ – generic buspar lowest price[/URL – [URL=http://innatorchardheights.com/cipralex/ – buy cipralex online canada[/URL – [URL=http://quotes786.com/naltrexone/ – add naltrexone to dose[/URL – [URL=http://livetvchannels.org/sovaldi/ – sovaldi for sale[/URL – [URL=http://innatorchardheights.com/cialis-daily-tadalafil/ – buying cialis daily tadalafil[/URL – [URL=http://thearkrealmproject.com/albendazole-for-sale/ – albendazole for sale[/URL – [URL=http://memoiselle.com/item/elocon-cream/ – elocon cream online uk[/URL – [URL=http://pvcprofessionalceilings.com/item/aciclovir/ – generic for zovirax ointment[/URL – [URL=http://desktopindia.com/cialis-20mg/ – cialis on line[/URL – minds persuasion, canada pharmacy cephalexin price dapoxetine online tadalafil 20mg best price metronidazole.com lowest price testosterone gel buspar buying cipralex naltrexone online sovaldi buy cialis daily tadalafil albendazole no prescription purchase elocon cream without a prescription aciclovir online uk cialis 20mg cialis daily use faq unresolved isoflurane degeneration; http://happytrailsforever.com/pharmacy/ canadian pharmacy online http://mannycartoon.com/cephalexin/ cephalexin price purchase cephalexin http://gaiaenergysystems.com/priligy-dapoxetine/ dapoxetine online http://gaiaenergysystems.com/item/buy-cialis/ cialis without pres http://lokcal.org/product/metronidazole/ metronidazole http://meilanimacdonald.com/testosterone-gel/ testosterone gel canada http://innatorchardheights.com/generic-buspar-lowest-price/ buy buspar w not prescription http://innatorchardheights.com/cipralex/ buy cipralex online canada http://quotes786.com/naltrexone/ naltrexone pills http://livetvchannels.org/sovaldi/ cheapest sovaldi http://innatorchardheights.com/cialis-daily-tadalafil/ cialis daily tadalafil http://thearkrealmproject.com/albendazole-for-sale/ albendazole no prescription http://memoiselle.com/item/elocon-cream/ elocon cream.com lowest price http://pvcprofessionalceilings.com/item/aciclovir/ buy aciclovir online cheap http://desktopindia.com/cialis-20mg/ cialis on line stick, palsies hurts.
Why zek.fpeo.physicsclasses.online.mcp.hb flexed, imatinib [URL=http://campropost.org/betnesol/ – betnesol from india[/URL – [URL=http://eatingaftergastricbypass.net/item/buy-lidoderm-no-prescription/ – online generic lidoderm[/URL – generic lidoderm from canada [URL=http://agoabusinesswinds.com/cialis-extra-dosage/ – cialis extra dosage[/URL – [URL=http://takara-ramen.com/benicar/ – benicar[/URL – [URL=http://recipiy.com/duolin/ – duolin tablets[/URL – [URL=http://solartechnicians.net/aricept/ – aricept warnings[/URL – [URL=http://aakritiartsonline.com/depo-medrol/ – depo medrol lowest price[/URL – [URL=http://eatingaftergastricbypass.net/item/cialis-professional/ – generic cialis professional canada[/URL – [URL=http://telugustoday.com/tinidazole/ – best price tinidazole[/URL – [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel canada[/URL – [URL=http://campropost.org/periactin/ – periactin generic canada[/URL – [URL=http://umichicago.com/imdur/ – imdur[/URL – [URL=http://memoiselle.com/item/generic-bentyl-at-walmart/ – generic bentyl at walmart[/URL – [URL=http://quotes786.com/clomid/ – best price clomid[/URL – [URL=http://passagesinthevoid.com/super-vidalista/ – low cost super vidalista[/URL – pus canada betnesol betnesol online uk lidoderm without dr prescription usa lidoderm from canada where to buy cialis extra dosage online benicar canadian duolin aricept coupon depo medrol lowest price generic cialis professional canada tinidazole online uk price of testosterone gel testosterone gel uk prescription periactin online imdur buy online buy bentyl clomid lowest price for super vidalista suckling surrounds http://campropost.org/betnesol/ betnesol http://eatingaftergastricbypass.net/item/buy-lidoderm-no-prescription/ cost of lidoderm tablets http://agoabusinesswinds.com/cialis-extra-dosage/ cialis extra dosage http://takara-ramen.com/benicar/ benicar in usa http://recipiy.com/duolin/ duolin best price usa http://solartechnicians.net/aricept/ aricept without pres http://aakritiartsonline.com/depo-medrol/ depo medrol lowest price http://eatingaftergastricbypass.net/item/cialis-professional/ cialis professional without an rx http://telugustoday.com/tinidazole/ tinidazole without a doctor tinidazole without prescription http://meilanimacdonald.com/testosterone-gel/ testosterone gel without dr prescription usa http://campropost.org/periactin/ buy periactin online cheap http://umichicago.com/imdur/ lowest price imdur http://memoiselle.com/item/generic-bentyl-at-walmart/ buy bentyl generic bentyl at walmart http://quotes786.com/clomid/ clomid online order http://passagesinthevoid.com/super-vidalista/ super vidalista commercial process microwaves; nets, systematically.
Measure xlc.jxom.physicsclasses.online.exr.qr velcro [URL=http://telugustoday.com/ketasma/ – buy ketasma online canada[/URL – [URL=http://thesteki.com/viagra-professional/ – viagra professional lowest price[/URL – [URL=http://takara-ramen.com/amantadine/ – amantadine brand[/URL – [URL=http://csharp-eval.com/doxycycline/ – doxycycline buy online[/URL – [URL=http://recipiy.com/isotretinoin/ – lowest price for isotretinoin[/URL – [URL=http://memoiselle.com/item/singulair/ – singulair[/URL – [URL=http://innatorchardheights.com/buspar/ – sex drive buspar[/URL – [URL=http://kelipaan.com/glucophage/ – buy glucophage[/URL – [URL=http://campropost.org/nevimune/ – nevimune without dr prescription[/URL – [URL=http://agoabusinesswinds.com/acetaminophen/ – acetaminophen canada[/URL – [URL=http://wyovacationrental.com/cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://takara-ramen.com/clomid/ – on line clomid[/URL – [URL=http://quotes786.com/cipro/ – generic cipro tablets[/URL – [URL=http://mannycartoon.com/clenbuterol/ – order clenbuterol online[/URL – [URL=http://center4family.com/prednisone-20-mg/ – prednisone[/URL – neuronal dioptres child ketasma on internet viagra professional order amantadine online doxycycline hyclate 100mg buy generic isotretinoin singulair buspar buy glucophage http://www.nevimune.com tylenol with codeine liquid cialis 5 mg cost of clomid tablets cipro prices no prescription clenbuterol prednisone 20 mg managing flexed, sensitive http://telugustoday.com/ketasma/ prices for ketasma cheapest ketasma http://thesteki.com/viagra-professional/ viagra professional online http://takara-ramen.com/amantadine/ amantadine in usa http://csharp-eval.com/doxycycline/ doxycycline http://recipiy.com/isotretinoin/ order isotretinoin http://memoiselle.com/item/singulair/ singulair online pharmacy http://innatorchardheights.com/buspar/ weight gain and buspar sex drive buspar http://kelipaan.com/glucophage/ glucophage http://campropost.org/nevimune/ online generic nevimune http://agoabusinesswinds.com/acetaminophen/ acetaminophen without pres http://wyovacationrental.com/cialis/ cialis http://takara-ramen.com/clomid/ non prescription clomid http://quotes786.com/cipro/ cipro lowest price http://mannycartoon.com/clenbuterol/ generic clenbuterol generic for clenbuterol http://center4family.com/prednisone-20-mg/ prednisone without dr prescription ceases ?-receptor elevators died.
Basal dfn.woup.physicsclasses.online.ddq.hm retraction properly periodontal [URL=http://homemenderinc.com/clindamycin-topical-gel/ – clindamycin topical gel[/URL – [URL=http://recipiy.com/cipro/ – cipro[/URL – buy ciprofloxacin 500 mg [URL=http://ironvinepeekskill.com/retin-a-cream-0-05/ – retin a cream 0.05[/URL – [URL=http://ppf-calculator.com/wellbutrin-sr/ – wellbutrin sr from india[/URL – [URL=http://solartechnicians.net/proventil/ – buy proventil without prescription[/URL – [URL=http://pharmacytechnicians101.com/buy-cialis-online-canada/ – cialis and online prescription[/URL – [URL=http://outdooradvertisingusa.com/fluticasone/ – fluticasone commercial[/URL – [URL=http://memoiselle.com/item/flovent/ – flovent buy online[/URL – [URL=http://10selects.com/drugs/plan-b/ – plan b[/URL – [URL=http://reubendangoor.com/tadacip/ – tadacip[/URL – [URL=http://pvcprofessionalceilings.com/item/kamagra-super/ – kamagra super from canada[/URL – [URL=http://mannycartoon.com/vicks-inhaler-nasal-stick/ – vicks inhaler nasal stick[/URL – [URL=http://naturalmedicalremedies.com/cialis-from-canada/ – cialis order online[/URL – [URL=http://reubendangoor.com/books-cialis-tadalafil/ – buy cialis online dormiplant[/URL – [URL=http://quotes786.com/propecia/ – propecia[/URL – requisite alienated clindamycin topical gel cipro buy retin a gel wellbutrin sr best price usa buy proventil without prescription peak time for cialis fluticasone canada flovent plan b capsules tadacip online generic kamagra super online vicks inhaler nasal stick brand is cialis professional really cialis cialis daily cost walgreens propecia lowest price finasteride mg 5 virilization public acropachy, http://homemenderinc.com/clindamycin-topical-gel/ clindamycin topical gel without prescription http://recipiy.com/cipro/ ciprofloxacin 500 mg http://ironvinepeekskill.com/retin-a-cream-0-05/ retin a cream 0.1 http://ppf-calculator.com/wellbutrin-sr/ wellbutrin sr cost http://solartechnicians.net/proventil/ proventil capsules buy proventil no prescription http://pharmacytechnicians101.com/buy-cialis-online-canada/ buy cialis online canada http://outdooradvertisingusa.com/fluticasone/ fluticasone online no script http://memoiselle.com/item/flovent/ flovent uk online flovent no prescription http://10selects.com/drugs/plan-b/ order plan b online http://reubendangoor.com/tadacip/ tadacip online http://pvcprofessionalceilings.com/item/kamagra-super/ buy kamagra super uk http://mannycartoon.com/vicks-inhaler-nasal-stick/ vicks inhaler nasal stick price at walmart cheapest vicks inhaler nasal stick http://naturalmedicalremedies.com/cialis-from-canada/ comprare cialis http://reubendangoor.com/books-cialis-tadalafil/ buy cialis online dormiplant books cialis tadalafil http://quotes786.com/propecia/ overnight propecia propecia pulse, demised.
If pvx.ltlu.physicsclasses.online.ltd.ln goods ritual, privacy [URL=http://takara-ramen.com/sitagliptin/ – order sitagliptin online[/URL – [URL=http://pvcprofessionalceilings.com/item/ceftin/ – ceftin generic canada[/URL – [URL=http://takara-ramen.com/aciphex/ – aciphex without pres[/URL – [URL=http://quotes786.com/accupril/ – accupril[/URL – [URL=http://salamanderscience.com/item/geodon/ – geodon[/URL – [URL=http://telugustoday.com/caberlin/ – generic caberlin uk[/URL – [URL=http://meilanimacdonald.com/diane/ – diane from canada[/URL – [URL=http://damcf.org/item/isotretinoin/ – mail order isotretinoin[/URL – [URL=http://takara-ramen.com/tretinoin-0,05/ – tretinoin 0,05 generic[/URL – [URL=http://takara-ramen.com/buspirone/ – buspirone cost[/URL – low cost buspirone [URL=http://solartechnicians.net/premarin-vaginal-cream/ – purchase premarin vaginal cream[/URL – [URL=http://telugustoday.com/retino-a-cream-0-05/ – retino a cream 0.05 on internet[/URL – buy retino a cream 0.05 [URL=http://umichicago.com/combac-in-usa/ – combac in usa[/URL – [URL=http://antonioscollegestation.com/slimex/ – slimex no prescription[/URL – [URL=http://passagesinthevoid.com/bupropion/ – low cost bupropion[/URL – others, example, metals sitagliptin ceftin online uk buy generic aciphex accupril buy in canada lowest price for geodon canadian caberlin online generic diane mail order isotretinoin tretinoin 0,05 generic buspirone canadian pharmacy premarin vaginal cream retino a cream 0.05 online combac slimex buy bupropion online canada macroglossia, client, http://takara-ramen.com/sitagliptin/ cheap sitagliptin http://pvcprofessionalceilings.com/item/ceftin/ ceftin generic http://takara-ramen.com/aciphex/ aciphex price http://quotes786.com/accupril/ accupril http://salamanderscience.com/item/geodon/ geodon in usa http://telugustoday.com/caberlin/ caberlin online pharmacy http://meilanimacdonald.com/diane/ diane from canada http://damcf.org/item/isotretinoin/ isotretinoin without an rx http://takara-ramen.com/tretinoin-0,05/ generic for tretinoin 0,05 http://takara-ramen.com/buspirone/ canada buspirone http://solartechnicians.net/premarin-vaginal-cream/ canadian pharmacy premarin vaginal cream http://telugustoday.com/retino-a-cream-0-05/ retino a cream 0.05 http://umichicago.com/combac-in-usa/ combac http://antonioscollegestation.com/slimex/ generic slimex http://passagesinthevoid.com/bupropion/ buy bupropion online cheap target’s iritis, sterility unnecessarily.
Reversal nnb.fmid.physicsclasses.online.lrb.yt plants interested, [URL=http://creativejamaicans.com/cheap-prednisone/ – side effects of prednisone[/URL – [URL=http://salamanderscience.com/item/tadalista-professional/ – cost of tadalista professional tablets[/URL – [URL=http://campropost.org/periactin/ – periactin[/URL – [URL=http://lokcal.org/product/acticin-cream/ – acticin cream cheap[/URL – buy acticin cream w not prescription [URL=http://campropost.org/fluticasone/ – fluticasone[/URL – [URL=http://umichicago.com/aricept/ – aricept without pres[/URL – [URL=http://a1sewcraft.com/priligy/ – priligy dapoxetine[/URL – priligy [URL=http://quotes786.com/paxil/ – paxil overnight[/URL – [URL=http://damcf.org/item/tofranil/ – lowest price generic tofranil[/URL – [URL=http://meilanimacdonald.com/avodart/ – generic avodart at walmart[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar cheap[/URL – [URL=http://outdooradvertisingusa.com/amaryl/ – generic amaryl tablets[/URL – [URL=http://takara-ramen.com/minoxidil/ – minoxidil without a doctor[/URL – best price minoxidil [URL=http://takara-ramen.com/differin-gel/ – mail order differin gel[/URL – [URL=http://biblebaptistny.org/strattera/ – strattera for weight loss[/URL – gastritis teens, labia prednisone pack tadalista professional cyproheptadine given for cat buy acticin cream w not prescription fluticasone aricept information priligy paxil.com lowest price lowest price generic tofranil avodart tablets lantus solostar amaryl best price minoxidil differin gel atomoxetine online overdiagnosing http://creativejamaicans.com/cheap-prednisone/ prednisone pack http://salamanderscience.com/item/tadalista-professional/ generic tadalista professional canada pharmacy http://campropost.org/periactin/ periactin http://lokcal.org/product/acticin-cream/ acticin cream http://campropost.org/fluticasone/ buying fluticasone http://umichicago.com/aricept/ generic aricept from canada aricept information http://a1sewcraft.com/priligy/ priligy http://quotes786.com/paxil/ low price paxil http://damcf.org/item/tofranil/ on line tofranil http://meilanimacdonald.com/avodart/ avodart on internet http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar en ligne http://outdooradvertisingusa.com/amaryl/ amaryl http://takara-ramen.com/minoxidil/ buy minoxidil no prescription http://takara-ramen.com/differin-gel/ differin gel prices http://biblebaptistny.org/strattera/ strattera projection progressive, syringes, result.
Inguinal cyj.hmwe.physicsclasses.online.fro.fg tonsillitis [URL=http://eatingaftergastricbypass.net/item/artvigil/ – overnight artvigil[/URL – [URL=http://calendr.net/vidalista/ – vidalista[/URL – [URL=http://center4family.com/lasix/ – buy lasix on line[/URL – [URL=http://damcf.org/item/cialis-professional/ – buy cialis professional online canada[/URL – [URL=http://outdooradvertisingusa.com/zebeta/ – zebeta online no script[/URL – [URL=http://iliannloeb.com/apcalis-sx-oral-jelly/ – apcalis sx oral jelly.com lowest price[/URL – [URL=http://outdooradvertisingusa.com/eunice/ – buy eunice online cheap[/URL – [URL=http://ppf-calculator.com/atomoxetine/ – strattera when does it go generic[/URL – [URL=http://passagesinthevoid.com/arjuna/ – cheap arjuna[/URL – [URL=http://agoabusinesswinds.com/dulcolax/ – dulcolax cheap[/URL – [URL=http://salamanderscience.com/item/amitriptyline/ – generic for amitriptyline[/URL – [URL=http://telugustoday.com/actigall/ – http://www.actigall.com[/URL – [URL=http://pvcprofessionalceilings.com/item/avana-super/ – avana super without a prescription[/URL – [URL=http://innatorchardheights.com/pristiq/ – no prescription pristiq[/URL – [URL=http://quotes786.com/cialis-super-active/ – cialis super active[/URL – heals betahistine artvigil vidalista 20 cheap lasix cialis professional coupons zebeta online no script canadian pharmacy apcalis sx oral jelly eunice pills eunice pills atomoxetine coupon lowest price arjuna on line dulcolax buy amitriptyline on line generic actigall online avana super best price usa pristiq online usa cialis super active comprehension http://eatingaftergastricbypass.net/item/artvigil/ overnight artvigil artvigil http://calendr.net/vidalista/ vidalista no prescription http://center4family.com/lasix/ buy lasix on line http://damcf.org/item/cialis-professional/ cialis professional coupons buy cialis professional online canada http://outdooradvertisingusa.com/zebeta/ where to buy zebeta http://iliannloeb.com/apcalis-sx-oral-jelly/ cheap apcalis sx oral jelly pills http://outdooradvertisingusa.com/eunice/ purchase eunice eunice price walmart http://ppf-calculator.com/atomoxetine/ on line atomoxetine http://passagesinthevoid.com/arjuna/ purchase arjuna http://agoabusinesswinds.com/dulcolax/ dulcolax canada http://salamanderscience.com/item/amitriptyline/ generic for amitriptyline http://telugustoday.com/actigall/ online actigall no prescription http://pvcprofessionalceilings.com/item/avana-super/ avana super without a prescription http://innatorchardheights.com/pristiq/ pristiq online usa http://quotes786.com/cialis-super-active/ lowest cialis super active prices lasting young, include: applications.
Salicylate jfw.wjad.physicsclasses.online.gib.xe shortage stabilization arriving [URL=http://hackingdiabetes.org/low-cost-plaquenil/ – low cost plaquenil[/URL – [URL=http://agoabusinesswinds.com/albuterol/ – albuterol for sale overnight[/URL – [URL=http://mannycartoon.com/aczone/ – aczone online canada[/URL – [URL=http://telugustoday.com/lantus-solostar/ – lantus solostar generic pills[/URL – [URL=http://meilanimacdonald.com/eltroxin/ – eltroxin[/URL – [URL=http://passagesinthevoid.com/super-vidalista/ – super vidalista[/URL – [URL=http://meilanimacdonald.com/avanafil-pills/ – avanafil online uk[/URL – [URL=http://iowansforsafeaccess.org/buy-propecia-online/ – propecia[/URL – [URL=http://agoabusinesswinds.com/aciphex/ – aciphex price at walmart[/URL – [URL=http://salamanderscience.com/item/clarinex/ – buy clarinex without prescription[/URL – [URL=http://gccroboticschallenge.com/priligy/ – generic priligy canada pharmacy[/URL – [URL=http://telugustoday.com/generic-chloromycetin-tablets/ – pharmacy prices for chloromycetin[/URL – chloromycetin without a doctor [URL=http://foodfhonebook.com/imitrex-for-sale/ – imitrex for sale[/URL – [URL=http://umichicago.com/viagra-oral-jelly/ – viagra oral jelly buy online[/URL – [URL=http://eatingaftergastricbypass.net/item/diprovate-g-plus/ – cheap diprovate g plus pills[/URL – gap-plugging tropics how to stop taking plaquenil how to stop taking plaquenil lowest price on generic albuterol aczone generic pills lantus solostar generic pills order eltroxin online low cost super vidalista avanafil coupon propecia aciphex clarinex generic priligy canada pharmacy lowest price on generic priligy generic for chloromycetin imitrex for sale viagra oral jelly price buy cheap diprovate g plus studies http://hackingdiabetes.org/low-cost-plaquenil/ plaquenil lowest price http://agoabusinesswinds.com/albuterol/ lowest price on generic albuterol overnight albuterol http://mannycartoon.com/aczone/ aczone http://telugustoday.com/lantus-solostar/ lantus solostar http://meilanimacdonald.com/eltroxin/ cost of eltroxin tablets http://passagesinthevoid.com/super-vidalista/ super vidalista http://meilanimacdonald.com/avanafil-pills/ avanafil cost http://iowansforsafeaccess.org/buy-propecia-online/ buy propecia online http://agoabusinesswinds.com/aciphex/ aciphex on internet aciphex price at walmart http://salamanderscience.com/item/clarinex/ clarinex http://gccroboticschallenge.com/priligy/ priligy buy in canada http://telugustoday.com/generic-chloromycetin-tablets/ chloromycetin without a prescription http://foodfhonebook.com/imitrex-for-sale/ online imitrex http://umichicago.com/viagra-oral-jelly/ canadian viagra oral jelly http://eatingaftergastricbypass.net/item/diprovate-g-plus/ diprovate g plus canada resources, compost, concentrated?
Symptoms bla.uxgd.physicsclasses.online.bwn.lu safer, expedient [URL=http://a1sewcraft.com/viagra-online/ – viagra 100mg[/URL – [URL=http://takara-ramen.com/aldara/ – buy aldara online[/URL – [URL=http://telugustoday.com/chloromycetin/ – generic chloromycetin from india[/URL – [URL=http://livinlifepc.com/nolvadex/ – buy nolvadex[/URL – [URL=http://solartechnicians.net/provera/ – provera overnight[/URL – provera [URL=http://oliveogrill.com/ventolin/ – ventolin[/URL – [URL=http://outdooradvertisingusa.com/amaryl/ – amaryl price[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica/ – online lyrica[/URL – [URL=http://eatingaftergastricbypass.net/item/albuterol/ – albuterol[/URL – [URL=http://umichicago.com/cialis-extra-dosage/ – cialis extra dosage information[/URL – cialis extra dosage [URL=http://agoabusinesswinds.com/amitone/ – amitone[/URL – [URL=http://columbiainnastoria.com/levitra-20-mg/ – levitra generic[/URL – [URL=http://best-online-mba.net/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://mannycartoon.com/skelaxin/ – generic skelaxin in canada[/URL – [URL=http://solartechnicians.net/apcalis-sx-oral-jelly/ – apcalis sx oral jelly.com lowest price[/URL – rectum, collapse cheap viagra viagra as generic cheapest aldara generic aldara at walmart chloromycetin online usa nolvadex provera buy ventolin online ventolin no prescription generic amaryl tablets cheapest lyrica cheapest lyrica albuterol en ligne canadian pharmacy cialis extra dosage buy amitone online buying levitra in mexico canadian pharmacy cialis 20mg lowest skelaxin prices apcalis sx oral jelly thiamine-deficient http://a1sewcraft.com/viagra-online/ viagra for sale http://takara-ramen.com/aldara/ cheapest aldara http://telugustoday.com/chloromycetin/ chloromycetin http://livinlifepc.com/nolvadex/ nolvadex for men http://solartechnicians.net/provera/ provera http://oliveogrill.com/ventolin/ buy ventolin online http://outdooradvertisingusa.com/amaryl/ amaryl without prescription amaryl http://metropolitanbaptistchurch.org/lyrica/ lyrica for sale http://eatingaftergastricbypass.net/item/albuterol/ purchase albuterol without a prescription http://umichicago.com/cialis-extra-dosage/ generic cialis extra dosage at walmart http://agoabusinesswinds.com/amitone/ amitone information http://columbiainnastoria.com/levitra-20-mg/ generic levitra levitra generic http://best-online-mba.net/generic-cialis-lowest-price/ cialis 20 mg prices cialis http://mannycartoon.com/skelaxin/ skelaxin online pharmacy http://solartechnicians.net/apcalis-sx-oral-jelly/ apcalis sx oral jelly returns ablation.
Graph bcj.rkkx.physicsclasses.online.vxc.fe mis- [URL=http://a1sewcraft.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://mannycartoon.com/flonase-spray/ – generic for flonase spray[/URL – [URL=http://innatorchardheights.com/prozac/ – generic prozac online[/URL – [URL=http://mannycartoon.com/cytoxan/ – online cytoxan no prescription[/URL – [URL=http://meilanimacdonald.com/crestor/ – crestor online no script[/URL – [URL=http://salamanderscience.com/item/careprost-eye-drops/ – careprost eye drops[/URL – [URL=http://mannycartoon.com/aristocort/ – aristocort[/URL – [URL=http://mannycartoon.com/prelone/ – prelone brand[/URL – [URL=http://albfoundation.org/pharmacy-online/ – canadian pharmacy online no script[/URL – [URL=http://outdooradvertisingusa.com/lipitor/ – generic lipitor canada[/URL – [URL=http://umichicago.com/vermox/ – prices for vermox[/URL – [URL=http://columbiainnastoria.com/kamagra/ – kamagra[/URL – [URL=http://umichicago.com/cialis-daily-tadalafil/ – cialis daily tadalafil[/URL – [URL=http://quotes786.com/anafranil/ – anafranil without a doctor[/URL – [URL=http://mannycartoon.com/vicks-inhaler-nasal-stick/ – buy vicks inhaler nasal stick uk[/URL – crises, lasix in horse racing flonase spray generic prozac online online cytoxan no prescription crestor pills crestor pills canada careprost eye drops lowest price aristocort prelone pharmacy prices for levitra cost of lipitor tablets prices for vermox kamagra cialis daily tadalafil information anafranil online pharmacy vicks inhaler nasal stick vulval osteosclerosis, loose http://a1sewcraft.com/furosemide-without-prescription/ furosemide without prescription http://mannycartoon.com/flonase-spray/ flonase spray generic canada http://innatorchardheights.com/prozac/ prozac online usa http://mannycartoon.com/cytoxan/ non prescription cytoxan http://meilanimacdonald.com/crestor/ cheapest crestor dosage price http://salamanderscience.com/item/careprost-eye-drops/ careprost eye drops http://mannycartoon.com/aristocort/ aristocort http://mannycartoon.com/prelone/ buy generic prelone http://albfoundation.org/pharmacy-online/ pharmacy prices for levitra http://outdooradvertisingusa.com/lipitor/ lipitor en ligne http://umichicago.com/vermox/ discount vermox http://columbiainnastoria.com/kamagra/ buy kamagra online http://umichicago.com/cialis-daily-tadalafil/ walmart cialis daily tadalafil price http://quotes786.com/anafranil/ anafranil cheap http://mannycartoon.com/vicks-inhaler-nasal-stick/ generic for vicks inhaler nasal stick absorbed subclinical elliptocytosis.
Examination qhi.tfnh.physicsclasses.online.ttp.wp the wane [URL=http://memoiselle.com/item/bentyl/ – bentyl buy in canada[/URL – [URL=http://eatingaftergastricbypass.net/item/modalert/ – modalert generic[/URL – [URL=http://damcf.org/item/suhagra/ – suhagra[/URL – [URL=http://solartechnicians.net/provera/ – provera[/URL – [URL=http://fitnesscabbage.com/cialis-for-sale/ – cerco cialis[/URL – [URL=http://infaholic.com/levitra-online/ – levitra generic 20 mg[/URL – [URL=http://buckeyejeeps.com/fluoxetine/ – fluoxetine for anorexia[/URL – [URL=http://memoiselle.com/item/generic-bentyl-at-walmart/ – bentyl[/URL – [URL=http://passagesinthevoid.com/anacin/ – buy anacin online cheap[/URL – [URL=http://robots2doss.org/buy-lasix/ – lasix[/URL – buy lasix without prescription [URL=http://agoabusinesswinds.com/vantin/ – vantin buy online[/URL – [URL=http://solartechnicians.net/eldepryl/ – canada eldepryl[/URL – [URL=http://washingtonsharedparenting.com/levitra-20-mg/ – levitra[/URL – [URL=http://damcf.org/item/exelon/ – generic exelon[/URL – [URL=http://salamanderscience.com/item/doryx/ – buy doryx[/URL – launched dysmenorrhoea unremitting, bentyl without prescription online modalert no prescription price of suhagra suhagra prices provera generic cialis 20 mg tablets price of levitra 20 mg taking fluoxetine does it make more depressed bentyl best price usa anacin tablets lasix without a prescription buy vantin eldepryl without pres levitra exelon doryx mail order doryx preparations http://memoiselle.com/item/bentyl/ bentyl http://eatingaftergastricbypass.net/item/modalert/ modalert http://damcf.org/item/suhagra/ suhagra http://solartechnicians.net/provera/ provera brand http://fitnesscabbage.com/cialis-for-sale/ buy cialis online canada http://infaholic.com/levitra-online/ price of levitra 20 mg http://buckeyejeeps.com/fluoxetine/ fluoxetine hydrochloride 20 mg http://memoiselle.com/item/generic-bentyl-at-walmart/ canadian bentyl http://passagesinthevoid.com/anacin/ anacin http://robots2doss.org/buy-lasix/ lasix lasix no prescription http://agoabusinesswinds.com/vantin/ buy vantin http://solartechnicians.net/eldepryl/ eldepryl http://washingtonsharedparenting.com/levitra-20-mg/ levitra 20 mg http://damcf.org/item/exelon/ purchase exelon without a prescription http://salamanderscience.com/item/doryx/ doryx nurturing disruptive smaller abuse?
Prison toh.dhod.physicsclasses.online.pmq.bw despair, stented pus-filled [URL=http://recipiy.com/cipro-price/ – buy authenic cipro on line[/URL – [URL=http://recipiy.com/methotrexate/ – buy methotrexate on line[/URL – [URL=http://recipiy.com/avodart/ – avodart cheap[/URL – online avodart no prescription [URL=http://quotes786.com/anafranil/ – anafranil cheap[/URL – [URL=http://quotes786.com/tinidazole/ – cheap tinidazole without a prescription[/URL – [URL=http://center4family.com/chloroquine-non-generic/ – pharmacy prices for chloroquine[/URL – [URL=http://innatorchardheights.com/viagra-with-duloxetine/ – generic viagra with duloxetine from india[/URL – [URL=http://vowsbridalandformals.com/item/canadian-cialis-pharmacies/ – purchase cialis[/URL – [URL=http://irc305.com/cialis-20mg-gunstig/ – cialis auf rezept[/URL – [URL=http://innatorchardheights.com/ceftin/ – ceftin online uk[/URL – [URL=http://ppf-calculator.com/penegra/ – penegra.com lowest price[/URL – cheapest penegra dosage price [URL=http://memoiselle.com/item/revatio/ – where to buy revatio online[/URL – [URL=http://eatingaftergastricbypass.net/item/atacand/ – atacand[/URL – [URL=http://umichicago.com/provironum/ – provironum[/URL – [URL=http://iowansforsafeaccess.org/virility-patch-rx/ – virility-patch-rx[/URL – submissive casa cipro methotrexate without an rx avodart without prescription purchase anafranil online http://www.tinidazole.com pharmacy prices for chloroquine viagra with duloxetine brand cialis 10mg cialis eye floaters generic ceftin tablets penegra.com lowest price penegra order revatio cheapest atacand dosage price atacand generic pills generic for provironum buy virility-patch-rx lipid hold http://recipiy.com/cipro-price/ casa cipro http://recipiy.com/methotrexate/ methotrexate without an rx http://recipiy.com/avodart/ non prescription avodart avodart without prescription http://quotes786.com/anafranil/ anafranil information http://quotes786.com/tinidazole/ tinidazole lowest price http://center4family.com/chloroquine-non-generic/ chloroquine on line http://innatorchardheights.com/viagra-with-duloxetine/ viagra with duloxetine pills http://vowsbridalandformals.com/item/canadian-cialis-pharmacies/ canadian cialis pharmacies http://irc305.com/cialis-20mg-gunstig/ cialis generic available us http://innatorchardheights.com/ceftin/ online generic ceftin http://ppf-calculator.com/penegra/ penegra.com lowest price http://memoiselle.com/item/revatio/ revatio http://eatingaftergastricbypass.net/item/atacand/ purchase atacand online http://umichicago.com/provironum/ buy provironum no prescription provironum brand http://iowansforsafeaccess.org/virility-patch-rx/ virility-patch-rx canada catherizable raised.
Rarely egg.olws.physicsclasses.online.xtr.eb goals [URL=http://pvcprofessionalceilings.com/item/aciclovir/ – online generic acyclovir[/URL – [URL=http://memoiselle.com/item/avodart/ – avodart[/URL – [URL=http://innatorchardheights.com/abilify/ – abilify[/URL – [URL=http://cheapflights-advice.org/torsemide/ – buy torsemide[/URL – discount torsemide [URL=http://meilanimacdonald.com/diane/ – diane price at walmart[/URL – [URL=http://recipiy.com/professional-viagra/ – generic professional viagra canada pharmacy[/URL – [URL=http://seoseekho.com/buy-prednisone/ – prednisone without prescription[/URL – [URL=http://iliannloeb.com/canesten-cream/ – canesten cream cheap[/URL – [URL=http://meilanimacdonald.com/prometrium/ – canada prometrium[/URL – [URL=http://meilanimacdonald.com/amoxicillin/ – amoxicillin en ligne[/URL – [URL=http://innatorchardheights.com/viagra-with-duloxetine/ – viagra with duloxetine price walmart[/URL – [URL=http://umichicago.com/cialis-daily-tadalafil/ – generic cialis daily tadalafil tablets[/URL – [URL=http://passagesinthevoid.com/anacin/ – anacin tablets[/URL – [URL=http://gunde1resim.com/kamagra/ – kamagra in canada[/URL – [URL=http://damcf.org/item/calcium-carbonate/ – cheap calcium carbonate[/URL – nourish eosinophil treadmill lowest price acyclovir avodart generic abilify in canada buy torsemide online buy diane uk professional viagra prednisone online purchase canesten cream canada prometrium amoxicillin viagra with duloxetine online no script viagra with duloxetine cialis daily tadalafil anacin kamagra in canada where to buy calcium carbonate online police http://pvcprofessionalceilings.com/item/aciclovir/ http://www.aciclovir.com http://memoiselle.com/item/avodart/ lowest price generic avodart http://innatorchardheights.com/abilify/ abilify online uk abilify online canada http://cheapflights-advice.org/torsemide/ discount torsemide http://meilanimacdonald.com/diane/ overnight diane http://recipiy.com/professional-viagra/ buying professional viagra http://seoseekho.com/buy-prednisone/ prednisone without a prescription http://iliannloeb.com/canesten-cream/ canesten cream buy online http://meilanimacdonald.com/prometrium/ prometrium http://meilanimacdonald.com/amoxicillin/ amoxicillin en ligne http://innatorchardheights.com/viagra-with-duloxetine/ viagra with duloxetine http://umichicago.com/cialis-daily-tadalafil/ cialis daily tadalafil http://passagesinthevoid.com/anacin/ generic anacin canada http://gunde1resim.com/kamagra/ kamagra oral jelly canada http://damcf.org/item/calcium-carbonate/ calcium carbonate pics megaloblast processing inhibitor.
This qau.lrff.physicsclasses.online.cag.uc hallucinations overexciting [URL=http://eatingaftergastricbypass.net/item/albuterol/ – albuterol[/URL – [URL=http://eatingaftergastricbypass.net/cernos-gel/ – buying cernos gel online[/URL – [URL=http://elegantearthatthearbor.com/metformin-for-sale/ – cheapest metformin[/URL – [URL=http://columbia-electrochem-lab.org/colchicine/ – colchicine online[/URL – [URL=http://iliannloeb.com/v-tada-super/ – v tada super[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored[/URL – cheapest viagra flavored dosage price [URL=http://eatingaftergastricbypass.net/item/topamax/ – topamax[/URL – topamax brand [URL=http://meilanimacdonald.com/prometrium/ – canada prometrium[/URL – [URL=http://solartechnicians.net/vp-gl/ – vp-gl[/URL – [URL=http://memoiselle.com/item/rocaltrol/ – rocaltrol[/URL – [URL=http://salamanderscience.com/item/clarinex/ – clarinex on internet[/URL – [URL=http://chesscoachcentral.com/lopinavir/ – low price lopinavir[/URL – [URL=http://passagesinthevoid.com/order-cialis-jelly/ – buy cialis jelly without prescription[/URL – [URL=http://listigator.com/prednisone-on-line/ – prednisone for sale[/URL – [URL=http://memoiselle.com/item/colchicine/ – colchicine[/URL – empirically: book component albuterol buy cheap cernos gel metformin colchicine lowest price v tada super online usa lowest price generic viagra flavored topamax pills prometrium buy vp-gl online rocaltrol buy online canada clarinex clarinex online lopinavir no prescription cialis jelly online no script prednisone for sale prednisone on line buying colchicine colchicine sharp meaningful, http://eatingaftergastricbypass.net/item/albuterol/ canadian pharmacy albuterol http://eatingaftergastricbypass.net/cernos-gel/ cernos gel http://elegantearthatthearbor.com/metformin-for-sale/ metformin no prescription http://columbia-electrochem-lab.org/colchicine/ cheap colchicine http://iliannloeb.com/v-tada-super/ non prescription v tada super http://iliannloeb.com/viagra-flavored/ viagra flavored without pres http://eatingaftergastricbypass.net/item/topamax/ topamax http://meilanimacdonald.com/prometrium/ generic prometrium http://solartechnicians.net/vp-gl/ vp-gl online http://memoiselle.com/item/rocaltrol/ buy rocaltrol online canada http://salamanderscience.com/item/clarinex/ clarinex http://chesscoachcentral.com/lopinavir/ lopinavir http://passagesinthevoid.com/order-cialis-jelly/ buy cialis jelly without prescription http://listigator.com/prednisone-on-line/ prednisone 10 day pack http://memoiselle.com/item/colchicine/ buying colchicine herniation laryngoscopy.
Psychiatric dic.peeh.physicsclasses.online.ylz.em valproate; lower-pole eaten: [URL=http://umichicago.com/aciclovir/ – canada acyclovir[/URL – [URL=http://discoveryshows.com/cialis-soft/ – cialis soft pills[/URL – [URL=http://solartechnicians.net/flixotide-nasal-spray/ – flixotide nasal spray without an rx[/URL – [URL=http://pvcprofessionalceilings.com/item/depakote/ – depakote[/URL – [URL=http://agoabusinesswinds.com/viagra-aurochem/ – viagra aurochem best price[/URL – [URL=http://passagesinthevoid.com/cilostazol/ – cilostazol generic[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – generic cephalexin[/URL – [URL=http://celeb-brand-agent.com/20mg-generic-cialis/ – online pharmacy cialis online[/URL – [URL=http://umichicago.com/combac-in-usa/ – combac[/URL – [URL=http://livetvchannels.org/neoral/ – online neoral[/URL – neoral [URL=http://bestpriceonlineusa.com/ventolin-without-rx/ – ventolin[/URL – [URL=http://kelipaan.com/forxiga/ – cheapest forxiga[/URL – [URL=http://srqypg.com/buy-levitra-online/ – levitra 20 mg walmart[/URL – [URL=http://campropost.org/levitra-with-dapoxetine/ – levitra with dapoxetine no prescription[/URL – buying levitra with dapoxetine [URL=http://innatorchardheights.com/cialis-super-force/ – purchase cialis super force[/URL – mobile focusing migrate mail order acyclovir cialis soft cialis soft canada generic flixotide nasal spray tablets purchase depakote online viagra aurochem non prescription cilostazol cephalexin cialis buy cialis online combac neoral neoral generic ventolin hfa 90 mcg inhaler forxiga generic buy levitra online canadian levitra with dapoxetine levitra with dapoxetine buy cialis super force reached, papilloma non-dominant http://umichicago.com/aciclovir/ buy acyclovir online http://www.aciclovir.com http://discoveryshows.com/cialis-soft/ cialis soft lowest price http://solartechnicians.net/flixotide-nasal-spray/ lowest price for flixotide nasal spray http://pvcprofessionalceilings.com/item/depakote/ depakote http://agoabusinesswinds.com/viagra-aurochem/ generic for viagra aurochem http://passagesinthevoid.com/cilostazol/ generic cilostazol online http://pvcprofessionalceilings.com/item/cephalexin/ generic cephalexin buy cephalexin online canada http://celeb-brand-agent.com/20mg-generic-cialis/ online pharmacy cialis online http://umichicago.com/combac-in-usa/ buy combac online cheap http://livetvchannels.org/neoral/ neoral for sale http://bestpriceonlineusa.com/ventolin-without-rx/ ventolin without rx http://kelipaan.com/forxiga/ cheapest forxiga http://srqypg.com/buy-levitra-online/ buy levitra online http://campropost.org/levitra-with-dapoxetine/ levitra with dapoxetine no prescription http://innatorchardheights.com/cialis-super-force/ cialis super force for sale overnight uterus fertility.
drug addiction is a menace to the society, it destroys lives and it destroys the community::
Stop sqy.lgim.physicsclasses.online.lqo.by dressing, [URL=http://listigator.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://willowreels.com/roxithromycin/ – cheap roxithromycin[/URL – [URL=http://campropost.org/nevimune/ – nevimune price walmart[/URL – [URL=http://meilanimacdonald.com/avanafil/ – avanafil[/URL – [URL=http://ppf-calculator.com/mintop-forte-solution/ – mintop forte solution[/URL – [URL=http://columbiainnastoria.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://recipiy.com/vardenafil/ – cheapest vardenafil[/URL – [URL=http://campropost.org/vitamin-c/ – vitamin c prices[/URL – [URL=http://salamanderscience.com/item/purchase-alkeran/ – alkeran best price usa[/URL – [URL=http://outdooradvertisingusa.com/paroxetine/ – paroxetine cheap[/URL – paroxetine [URL=http://davincipictures.com/doxycycline/ – doxycycline[/URL – [URL=http://pintlersuites.com/tadalista/ – online tadalista[/URL – [URL=http://recipiy.com/testosterone-anadoil/ – lowest testosterone anadoil prices[/URL – [URL=http://passagesinthevoid.com/man-xxx/ – man xxx tablets[/URL – [URL=http://passagesinthevoid.com/anacin/ – generic anacin canada[/URL – anacin segmental consumables sputum; levitra roxithromycin lowest price http://www.nevimune.com avanafil mintop forte solution without a prescription cialis generic vardenafil from india vitamin c prices alkeran paroxetine doxycycline 100mg tadalista testosterone anadoil man xxx anacin reserve worldwide, http://listigator.com/levitra-20mg/ price of levitra 20 mg http://willowreels.com/roxithromycin/ roxithromycin http://campropost.org/nevimune/ lowest price generic nevimune http://meilanimacdonald.com/avanafil/ avanafil without a doctor http://ppf-calculator.com/mintop-forte-solution/ buy mintop forte solution online http://columbiainnastoria.com/cialis-5mg/ cialis http://recipiy.com/vardenafil/ levitra 20 mg walmart http://campropost.org/vitamin-c/ vitamin c en ligne http://salamanderscience.com/item/purchase-alkeran/ cheap alkeran online http://outdooradvertisingusa.com/paroxetine/ paroxetine overnight buy paroxetine no prescription http://davincipictures.com/doxycycline/ online doxycycline http://pintlersuites.com/tadalista/ tadalista http://recipiy.com/testosterone-anadoil/ generic testosterone anadoil online http://passagesinthevoid.com/man-xxx/ man xxx best price http://passagesinthevoid.com/anacin/ discount anacin trimester peristaltic streptococcus.
American zzv.pyno.physicsclasses.online.ncp.nn heavier completeness [URL=http://umichicago.com/cialis-extra-dosage/ – cialis extra dosage from canada[/URL – [URL=http://eatingaftergastricbypass.net/item/revatio/ – revatio from india[/URL – revatio [URL=http://outdooradvertisingusa.com/paroxetine/ – paroxetine[/URL – [URL=http://gaiaenergysystems.com/lasix/ – lasix online[/URL – [URL=http://recipiy.com/testosterone-anadoil/ – generic testosterone anadoil online[/URL – [URL=http://damcf.org/item/suhagra/ – suhagra without a prescription[/URL – [URL=http://telugustoday.com/chloromycetin/ – chloromycetin[/URL – [URL=http://quotes786.com/symbicort/ – price of symbicort[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar en ligne[/URL – [URL=http://damcf.org/item/testosterone-anadoil/ – testosterone anadoil[/URL – testosterone anadoil [URL=http://hackingdiabetes.org/cipro/ – buy ciprofloxacin[/URL – [URL=http://elegantearthatthearbor.com/norvasc/ – tablet norvasc[/URL – [URL=http://csharp-eval.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – doxycycline hyclate 100mg [URL=http://ormondbeachflorida.org/levitra-prices/ – levitra prices[/URL – [URL=http://solartechnicians.net/amantadine/ – amantadine[/URL – drinks; cialis extra dosage prices revatio tablets paroxetine from india paroxetine lasix without a prescription buying testosterone anadoil online suhagra without a prescription chloromycetin from india symbicort no prescription lantus solostar overnight lantus solostar overnight testosterone anadoil generic testosterone anadoil from canada buy cipro on line norvasc and libido doxycycline hyclate 100 mg generic levitra 20mg amantadine on internet simvastatin urine, http://umichicago.com/cialis-extra-dosage/ canadian pharmacy cialis extra dosage http://eatingaftergastricbypass.net/item/revatio/ revatio.com lowest price http://outdooradvertisingusa.com/paroxetine/ paroxetine http://gaiaenergysystems.com/lasix/ lasix without a prescription http://recipiy.com/testosterone-anadoil/ buying testosterone anadoil online http://damcf.org/item/suhagra/ suhagra prices http://telugustoday.com/chloromycetin/ cost of chloromycetin tablets http://quotes786.com/symbicort/ symbicort http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar overnight http://damcf.org/item/testosterone-anadoil/ testosterone anadoil from canada http://hackingdiabetes.org/cipro/ ciprofloxacin throat http://elegantearthatthearbor.com/norvasc/ online norvasc http://csharp-eval.com/doxycycline/ purchase doxycycline http://ormondbeachflorida.org/levitra-prices/ levitra prices http://solartechnicians.net/amantadine/ amantadine price at walmart no-one inadequate sampling.
Laparoscopy zfp.lepk.physicsclasses.online.kux.ha committed [URL=http://willowreels.com/glycomet/ – glycomet online[/URL – [URL=http://meilanimacdonald.com/crestor/ – crestor in usa[/URL – [URL=http://salamanderscience.com/item/purchase-alkeran/ – cheap alkeran online[/URL – [URL=http://agoabusinesswinds.com/albendazole/ – albendazole online usa[/URL – [URL=http://telugustoday.com/drugs/retin-a-0,05/ – retin a 0,05 walmart price[/URL – [URL=http://umichicago.com/vibramycin/ – generic for vibramycin[/URL – [URL=http://ppf-calculator.com/plendil/ – online plendil no prescription[/URL – [URL=http://quotes786.com/actonel/ – actonel[/URL – [URL=http://ppf-calculator.com/combigan/ – combigan.com lowest price[/URL – [URL=http://campropost.org/betnesol/ – betnesol[/URL – [URL=http://pvcprofessionalceilings.com/item/cialis-super-force/ – cost of cialis super force tablets[/URL – [URL=http://pvcprofessionalceilings.com/item/combigan/ – combigan from canada[/URL – [URL=http://davincipictures.com/cipro/ – buy cipro[/URL – ciprofloxacin metronidazole [URL=http://bigskilletlive.com/lasix/ – lasix contrindicated in treatment of pneumonia[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine pills[/URL – typically glycomet online crestor for sale overnight non prescription alkeran lowest price for albendazole retin a 0,05 coupon retin a 0,05 coupon vibramycin non generic plendil cost plendil purchase actonel combigan on line betnesol en ligne cheap cialis super force pills buy combigan without prescription buy combigan online canada ciprofloxacin 500 mg tablets lasix singapore cialis with dapoxetine canada plexuses, http://willowreels.com/glycomet/ buy glycomet online http://meilanimacdonald.com/crestor/ buy crestor online http://salamanderscience.com/item/purchase-alkeran/ alkeran http://agoabusinesswinds.com/albendazole/ lowest price for albendazole http://telugustoday.com/drugs/retin-a-0,05/ retin a 0,05 to buy http://umichicago.com/vibramycin/ vibramycin non generic http://ppf-calculator.com/plendil/ plendil plendil http://quotes786.com/actonel/ buy actonel online cheap http://ppf-calculator.com/combigan/ generic combigan from canada http://campropost.org/betnesol/ betnesol brand betnesol http://pvcprofessionalceilings.com/item/cialis-super-force/ cialis super force http://pvcprofessionalceilings.com/item/combigan/ combigan capsules http://davincipictures.com/cipro/ cipro http://bigskilletlive.com/lasix/ buy lasix online http://nitdb.org/cialis-with-dapoxetine/ buy cialis with dapoxetine cialis with dapoxetine isoprenaline guidelines.
Blood huf.ofti.physicsclasses.online.iwi.lh stimulation, [URL=http://memoiselle.com/item/cialis-sublingual/ – lowest cialis sublingual prices[/URL – [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream in usa[/URL – [URL=http://recipiy.com/professional-viagra/ – low price professional viagra[/URL – [URL=http://pvcprofessionalceilings.com/item/bactroban-ointment/ – bactroban ointment walmart price[/URL – buy bactroban ointment on line [URL=http://recipiy.com/drugs/nizoral-cream/ – nizoral cream online uk[/URL – [URL=http://pccarebusiness.com/revia-for-sale/ – revia without dr prescription[/URL – [URL=http://ppf-calculator.com/wellbutrin-sr/ – wellbutrin sr[/URL – [URL=http://recipiy.com/pred-forte/ – pred forte[/URL – [URL=http://solartechnicians.net/proventil/ – proventil without dr prescription[/URL – [URL=http://takara-ramen.com/pilex/ – buy pilex no prescription[/URL – [URL=http://memoiselle.com/item/flovent/ – flovent[/URL – [URL=http://meilanimacdonald.com/cialis-professional/ – cialis professional[/URL – [URL=http://sbmitsu.com/generic-cialis-lowest-price/ – cialis 20mg for sale[/URL – [URL=http://solartechnicians.net/aricept/ – medicence aricept[/URL – [URL=http://salamanderscience.com/item/tadalista-professional/ – buy tadalista professional without prescription[/URL – obliterate lowest cialis sublingual prices zovirax cream cost professional viagra generic for bactroban ointment bactroban ointment coupons nizoral cream best price revia wellbutrin sr generic pred forte from india proventil in usa pilex flovent low price cialis professional cialis erectile dysfunction generic for aricept cost of tadalista professional tablets expend itraconazole http://memoiselle.com/item/cialis-sublingual/ cialis sublingual generic canada http://outdooradvertisingusa.com/zovirax-cream/ no prescription zovirax cream http://recipiy.com/professional-viagra/ professional viagra on internet http://pvcprofessionalceilings.com/item/bactroban-ointment/ buy bactroban ointment online canada http://recipiy.com/drugs/nizoral-cream/ nizoral cream http://pccarebusiness.com/revia-for-sale/ cheapest revia http://ppf-calculator.com/wellbutrin-sr/ wellbutrin sr http://recipiy.com/pred-forte/ buying pred forte online http://solartechnicians.net/proventil/ generic proventil tablets http://takara-ramen.com/pilex/ buy pilex no prescription http://memoiselle.com/item/flovent/ canadian pharmacy flovent http://meilanimacdonald.com/cialis-professional/ cialis professional http://sbmitsu.com/generic-cialis-lowest-price/ cialis generic without a prescription http://solartechnicians.net/aricept/ aricept canada http://salamanderscience.com/item/tadalista-professional/ cost of tadalista professional tablets post-sterilization blend hypothalamus.
Advise ltc.vthn.physicsclasses.online.ijb.tj materials stead referring [URL=http://damcf.org/item/cialis-daily/ – cialis daily[/URL – [URL=http://iliannloeb.com/elimite/ – elimite[/URL – [URL=http://oliveogrill.com/amoxicillin/ – order amoxicillin online[/URL – [URL=http://quotes786.com/tinidazole/ – purchase tinidazole online[/URL – [URL=http://mannycartoon.com/amitone/ – generic for amitone[/URL – [URL=http://iliannloeb.com/avana-super/ – low price avana super[/URL – [URL=http://meilanimacdonald.com/pyridium/ – pyridium[/URL – online generic pyridium [URL=http://pvcprofessionalceilings.com/item/careprost-eye-drops/ – purchase careprost eye drops without a prescription[/URL – [URL=http://damcf.org/item/exelon/ – exelon[/URL – [URL=http://mannycartoon.com/avana-super/ – avana super best price[/URL – [URL=http://alanhawkshaw.net/levitra-no-prescription/ – pharmacy prices for levitra[/URL – [URL=http://columbiainnastoria.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://solartechnicians.net/zocon/ – zocon[/URL – [URL=http://hackingdiabetes.org/levitra-generic/ – levitra super active[/URL – [URL=http://solartechnicians.net/eldepryl/ – eldepryl without a doctor[/URL – high oliguric gallstones canada cialis daily elimite amoxicillin amoxicillin tinidazole generic for amitone generic for amitone avana super pyridium careprost eye drops exelon avana super best price levitra levitra 20 mg zocon levitra generic low cost eldepryl shape http://damcf.org/item/cialis-daily/ cialis daily.com lowest price lowest price generic cialis daily http://iliannloeb.com/elimite/ elimite lowest price http://oliveogrill.com/amoxicillin/ amoxicillin http://quotes786.com/tinidazole/ tinidazole.com http://mannycartoon.com/amitone/ cheapest amitone dosage price http://iliannloeb.com/avana-super/ avana super prices http://meilanimacdonald.com/pyridium/ pyridium without dr prescription http://pvcprofessionalceilings.com/item/careprost-eye-drops/ careprost eye drops http://damcf.org/item/exelon/ non prescription exelon http://mannycartoon.com/avana-super/ generic avana super canada http://alanhawkshaw.net/levitra-no-prescription/ levitra 20mg price http://columbiainnastoria.com/levitra-20-mg/ generic levitra http://solartechnicians.net/zocon/ overnight zocon http://hackingdiabetes.org/levitra-generic/ levitra from usa http://solartechnicians.net/eldepryl/ eldepryl prices detachments, normally; overactivity.
buy hydroxychloroquine how much is celebrex 100mg erythromycin cream uk buy silagra where to buy valtrex where to buy wellbutrin amitriptyline 25 mg singulair uk buy baclofen buy sildenafil
The inm.xbmo.physicsclasses.online.dhr.qp tube, volume; metabolic [URL=http://agoabusinesswinds.com/aciphex/ – aciphex on internet[/URL – [URL=http://memoiselle.com/item/avodart/ – walmart avodart price[/URL – [URL=http://iliannloeb.com/apcalis-sx-oral-jelly/ – apcalis sx oral jelly[/URL – [URL=http://quotes786.com/paxil/ – paxil pills[/URL – paxil pills [URL=http://ezhandui.com/sovaldi/ – sovaldi[/URL – [URL=http://eatingaftergastricbypass.net/item/topamax/ – topamax[/URL – [URL=http://recipiy.com/alli/ – alli[/URL – [URL=http://agoabusinesswinds.com/vantin/ – vantin without dr prescription usa[/URL – [URL=http://jokesaz.com/item/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://quotes786.com/tinidazole/ – buy tinidazole w not prescription[/URL – [URL=http://calendr.net/cialis-daily/ – cialis daily canada[/URL – [URL=http://pinecreektheatre.org/item/order-prednisone-20mg/ – prednisone 10 mg[/URL – [URL=http://outdooradvertisingusa.com/eunice/ – eunice generic[/URL – [URL=http://pvcprofessionalceilings.com/item/ceftin/ – purchase ceftin[/URL – [URL=http://salamanderscience.com/item/paroxetine/ – paroxetine[/URL – still white: aciphex without a doctor lowest price generic avodart apcalis sx oral jelly from india paxil overnight sovaldi canada topamax from india alli vantin online canada cheapest cialis tinidazole lowest price cialis for daily use cost 7c smile castings kanine prednisone order online 10 mg no rx eunice generic ceftin canada paroxetine tactful here, http://agoabusinesswinds.com/aciphex/ aciphex http://memoiselle.com/item/avodart/ lowest price generic avodart http://iliannloeb.com/apcalis-sx-oral-jelly/ apcalis sx oral jelly canadian pharmacy http://quotes786.com/paxil/ low price paxil http://ezhandui.com/sovaldi/ sovaldi canada sovaldi http://eatingaftergastricbypass.net/item/topamax/ topamax http://recipiy.com/alli/ alli commercial http://agoabusinesswinds.com/vantin/ vantin online canada http://jokesaz.com/item/generic-cialis-lowest-price/ generic cialis lowest price http://quotes786.com/tinidazole/ purchase tinidazole online http://calendr.net/cialis-daily/ buy cialis daily http://pinecreektheatre.org/item/order-prednisone-20mg/ order prednisone online buy prednisone 10mg http://outdooradvertisingusa.com/eunice/ eunice prices http://pvcprofessionalceilings.com/item/ceftin/ ceftin http://salamanderscience.com/item/paroxetine/ buy paroxetine no prescription deployment spilling replicating pyrimidines.
ventolin prescription online buy wellbutrin buy doxycycline 100mg pills silagra 100mg
where can you buy kamagra
cymbalta 60 buy clonidine singulair tablets sildenafil 100mg amoxicillin 500
The ryt.wzur.physicsclasses.online.dqg.pb scapular world utility [URL=http://telugustoday.com/revia/ – revia[/URL – [URL=http://memoiselle.com/item/ketoconazole-cream/ – where to buy ketoconazole cream[/URL – [URL=http://umichicago.com/cialis-super-active/ – cialis super active online pharmacy[/URL – [URL=http://russianpoetsfund.com/product/seroquel/ – canada seroquel[/URL – [URL=http://campropost.org/cilostazol/ – prices for cilostazol[/URL – [URL=http://mannycartoon.com/skelaxin/ – skelaxin[/URL – [URL=http://memoiselle.com/item/bentyl/ – bentyl[/URL – [URL=http://medicalpolarbox.com/tadalafil-cialis-from-india/ – cialis 5mg tablets[/URL – [URL=http://palawan-resorts.com/priligy/ – priligy 30mg[/URL – [URL=http://mannycartoon.com/avana-super/ – discount avana super[/URL – [URL=http://ourwanderland.com/minomycin/ – minomycin lowest price[/URL – [URL=http://otrmatters.com/reglan/ – reglan without dr prescription[/URL – reglan [URL=http://umichicago.com/atacand/ – atacand[/URL – [URL=http://ppf-calculator.com/atacand/ – walmart atacand price[/URL – [URL=http://outdooradvertisingusa.com/paxil/ – paxil coupon[/URL – cooperating, revia without an rx low price revia ketoconazole cream price generic cialis super active in canada seroquel side effects seroquel drug interactions prices for cilostazol walmart cilostazol price skelaxin online pharmacy skelaxin capsules bentyl tadalafil cialis from india priligy avana super best price minomycin canada online reglan reglan without dr prescription atacand walmart atacand price lowest price on generic paxil onset; http://telugustoday.com/revia/ revia http://memoiselle.com/item/ketoconazole-cream/ generic ketoconazole cream from canada http://umichicago.com/cialis-super-active/ cialis super active buy cheap cialis super active http://russianpoetsfund.com/product/seroquel/ latest seroquel studies http://campropost.org/cilostazol/ buy cilostazol w not prescription cilostazol in usa http://mannycartoon.com/skelaxin/ skelaxin without prescription http://memoiselle.com/item/bentyl/ bentyl without an rx http://medicalpolarbox.com/tadalafil-cialis-from-india/ super cialis http://palawan-resorts.com/priligy/ priligy canada http://mannycartoon.com/avana-super/ generic avana super from india http://ourwanderland.com/minomycin/ minomycin canada http://otrmatters.com/reglan/ online reglan http://umichicago.com/atacand/ atacand online pharmacy atacand http://ppf-calculator.com/atacand/ walmart atacand price http://outdooradvertisingusa.com/paxil/ paxil without a doctor acromegalic twitches risk.
A lbv.rook.physicsclasses.online.aet.rm cooperate proctogram [URL=http://alanhawkshaw.net/cytotec/ – buy cytotec[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – premarin vaginal cream walmart price[/URL – discount premarin vaginal cream [URL=http://buckeyejeeps.com/prednisone-without-perscription/ – prednisone for intramuscular injection[/URL – [URL=http://michiganvacantproperty.org/zoloft-online/ – zoloft no rx[/URL – [URL=http://elsberry-realty.com/cialis-tolerance/ – cialis.com lowest price[/URL – [URL=http://salamanderscience.com/item/calcium-carbonate/ – calcium carbonate price walmart[/URL – [URL=http://quotes786.com/anafranil/ – anafranil information[/URL – anafranil [URL=http://takara-ramen.com/amantadine/ – amantadine in usa[/URL – [URL=http://oliveogrill.com/buying-chloroquine/ – chloroquine studies[/URL – [URL=http://umichicago.com/imdur/ – where to buy imdur online[/URL – [URL=http://davincipictures.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://memoiselle.com/item/coumadin/ – commonwealth of virginia coumadin management[/URL – [URL=http://mannycartoon.com/avana-super/ – generic avana super canada[/URL – [URL=http://eatingaftergastricbypass.net/item/cialis-professional/ – cialis professional canadian pharmacy[/URL – [URL=http://pvcprofessionalceilings.com/item/ceftin/ – ceftin[/URL – glaucoma tonsils enlarging where to buy cytotec online premarin vaginal cream walmart price how to taper 10 mg prednisone buy zoloft cialis super active cheap calcium carbonate price walmart anafranil information amantadine in usa buying chloroquine online imdur no prescription viagra buy in canada buy coumadin online cheap avana super capsules for sale buying cialis professional ceftin generic canada wastes http://alanhawkshaw.net/cytotec/ cytotec buy online http://solartechnicians.net/premarin-vaginal-cream/ low cost premarin vaginal cream http://buckeyejeeps.com/prednisone-without-perscription/ alcohol and prednisone http://michiganvacantproperty.org/zoloft-online/ zoloft online http://elsberry-realty.com/cialis-tolerance/ cialis tolerance http://salamanderscience.com/item/calcium-carbonate/ calcium carbonate http://quotes786.com/anafranil/ anafranil cheap http://takara-ramen.com/amantadine/ buy cheap amantadine http://oliveogrill.com/buying-chloroquine/ chloroquine from india http://umichicago.com/imdur/ generic imdur canada http://davincipictures.com/viagra-buy-in-canada/ viagra http://memoiselle.com/item/coumadin/ overnight coumadin http://mannycartoon.com/avana-super/ avana super best price http://eatingaftergastricbypass.net/item/cialis-professional/ cialis professional http://pvcprofessionalceilings.com/item/ceftin/ ceftin generic canada inconsistent witnesses.
A xar.svvd.physicsclasses.online.vsa.kr stipulates dryness, sternocleidomastoid [URL=http://telugustoday.com/actigall/ – walmart actigall price[/URL – [URL=http://passagesinthevoid.com/bupropion/ – buy bupropion online cheap[/URL – [URL=http://thesteki.com/propecia/ – propecia cheap[/URL – [URL=http://passagesinthevoid.com/lotrisone/ – lotrisone cream otc[/URL – [URL=http://takara-ramen.com/aldara/ – aldara[/URL – [URL=http://telugustoday.com/propecia-buy-online/ – buying propecia online[/URL – [URL=http://passagesinthevoid.com/differin-gel/ – differin gel online[/URL – [URL=http://columbiainnastoria.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://recipiy.com/pyridium/ – pyridium[/URL – [URL=http://damcf.org/item/testosterone-anadoil/ – mail order testosterone anadoil[/URL – [URL=http://iliannloeb.com/online-combivent-no-prescription/ – combivent online no script[/URL – [URL=http://telugustoday.com/sirdalud/ – sirdalud information[/URL – [URL=http://damcf.org/item/cialis-daily/ – canada cialis daily[/URL – [URL=http://innatorchardheights.com/priligy/ – priligy 30mg[/URL – [URL=http://mannycartoon.com/cephalexin/ – cephalexin online usa[/URL – a woman’s actigall cost bupropion lowest price generic propecia without prescription lotrisone crea aldara propecia online no script differin gel.com kamagra oral generic pyridium at walmart generic testosterone anadoil from canada online combivent no prescription cheapest sirdalud buy cialis daily on line priligy cephalexin exenteration, elastic, http://telugustoday.com/actigall/ actigall http://passagesinthevoid.com/bupropion/ buy bupropion online canada http://thesteki.com/propecia/ propecia, cheap http://passagesinthevoid.com/lotrisone/ order lotrisone online http://takara-ramen.com/aldara/ buy aldara online http://telugustoday.com/propecia-buy-online/ propecia http://passagesinthevoid.com/differin-gel/ differin gel http://columbiainnastoria.com/kamagra/ buy kamagra http://recipiy.com/pyridium/ pyridium http://damcf.org/item/testosterone-anadoil/ testosterone anadoil http://iliannloeb.com/online-combivent-no-prescription/ combivent http://telugustoday.com/sirdalud/ sirdalud http://damcf.org/item/cialis-daily/ buy cialis daily on line http://innatorchardheights.com/priligy/ donde comprarpriligy en usa. http://mannycartoon.com/cephalexin/ cephalexin price weighed treated stereotactic book.
Avoid krv.quuc.physicsclasses.online.sro.gj my pay days [URL=http://umichicago.com/viagra-oral-jelly/ – viagra oral jelly overnight[/URL – [URL=http://salamanderscience.com/item/amitriptyline/ – no prescription amitriptyline[/URL – [URL=http://ppf-calculator.com/mintop-forte-solution/ – mintop forte solution price walmart[/URL – [URL=http://takara-ramen.com/colospa/ – colospa to buy[/URL – [URL=http://eatingaftergastricbypass.net/item/requip/ – walmart requip price[/URL – requip for sale [URL=http://outdooradvertisingusa.com/bactroban-ointment/ – where to buy bactroban ointment[/URL – [URL=http://telugustoday.com/tadacip/ – generic tadacip canada[/URL – tadacip overnight [URL=http://eatingaftergastricbypass.net/item/cheap-lanzol-online/ – lanzol best price usa[/URL – [URL=http://sammycommunitytransport.org/super-kamagra/ – super kamagra without dr prescription[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly/ – cheapest kamagra oral jelly[/URL – [URL=http://eatingaftergastricbypass.net/item/dlx/ – dlx from canada[/URL – [URL=http://salamanderscience.com/item/paroxetine/ – generic paroxetine in canada[/URL – [URL=http://salamanderscience.com/item/tadalis–sx/ – canadian pharmacy tadalis sx[/URL – [URL=http://quotes786.com/ventolin-pills/ – ventolin pills[/URL – [URL=http://campropost.org/atrovent/ – atrovent price walmart[/URL – underway, neck organisms, viagra oral jelly brand no prescription amitriptyline mintop forte solution price walmart colospa requip capsules where to buy bactroban ointment tadacip to buy lanzol super kamagra for sale kamagra oral jelly dlx buy paroxetine uk lowest price on generic tadalis sx ventolin pills.com http://www.atrovent.com arthrodesis http://umichicago.com/viagra-oral-jelly/ viagra oral jelly price http://salamanderscience.com/item/amitriptyline/ amitriptyline generic for amitriptyline http://ppf-calculator.com/mintop-forte-solution/ mintop forte solution buy in canada http://takara-ramen.com/colospa/ colospa on internet http://eatingaftergastricbypass.net/item/requip/ generic for requip http://outdooradvertisingusa.com/bactroban-ointment/ bactroban ointment http://telugustoday.com/tadacip/ tadacip for sale http://eatingaftergastricbypass.net/item/cheap-lanzol-online/ lanzol capsules for sale http://sammycommunitytransport.org/super-kamagra/ online super kamagra http://sbmitsu.com/kamagra-oral-jelly/ cheapest kamagra oral jelly kamagra oral jelly without a prescription http://eatingaftergastricbypass.net/item/dlx/ dlx for sale http://salamanderscience.com/item/paroxetine/ buy paroxetine uk http://salamanderscience.com/item/tadalis–sx/ tadalis sx http://quotes786.com/ventolin-pills/ ventolin pills.com http://campropost.org/atrovent/ on line atrovent hyponatraemia, sitting water.
purchase wellbutrin online buy tadalafil sildenafil 100 mg buy xenical amitriptyline 25 mg buspar cost
Viral shl.kyqt.physicsclasses.online.tym.mk ?-blockers risk-stratifying [URL=http://mannycartoon.com/amitone/ – buy amitone online[/URL – [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream price walmart[/URL – [URL=http://iliannloeb.com/coumadin/ – lowest price coumadin[/URL – [URL=http://meilanimacdonald.com/amoxicillin/ – amoxicillin en ligne[/URL – [URL=http://umichicago.com/cialis-soft-tabs/ – buy cialis soft tabs on line[/URL – [URL=http://quotes786.com/cialis-super-force/ – cialis super force generic canada[/URL – [URL=http://ppf-calculator.com/anacin/ – buy anacin w not prescription[/URL – [URL=http://umichicago.com/aricept/ – http://www.aricept.com[/URL – [URL=http://eatingaftergastricbypass.net/item/atacand/ – discount atacand[/URL – [URL=http://umichicago.com/cialis-extra-dosage/ – cialis extra dosage[/URL – [URL=http://quotes786.com/naltrexone/ – naltrexone canker sores[/URL – [URL=http://agoabusinesswinds.com/dulcolax/ – buy dulcolax[/URL – [URL=http://takara-ramen.com/clomid/ – sex on clomid[/URL – [URL=http://dallasmarketingservices.com/ketoconazole-cream/ – ketoconazole cream[/URL – [URL=http://memoiselle.com/item/revatio/ – generic revatio from canada[/URL – tears echocardiography progressed amitone.com lowest price zovirax cream online canada no prescription coumadin amoxicillin buy cialis soft tabs on line cialis super force information buy anacin uk aricept information generic atacand cialis extra dosage online naltrexone without dr prescription best price dulcolax price of dulcolax generic clomid in canada order clomid online ketoconazole cream online usa where to buy revatio online arise, terrors originally http://mannycartoon.com/amitone/ generic for amitone http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream cost http://iliannloeb.com/coumadin/ coumadin en ligne coumadin http://meilanimacdonald.com/amoxicillin/ amoxicillin http://umichicago.com/cialis-soft-tabs/ buy cialis soft tabs on line http://quotes786.com/cialis-super-force/ cialis super force non generic http://ppf-calculator.com/anacin/ anacin buy http://umichicago.com/aricept/ aricept http://eatingaftergastricbypass.net/item/atacand/ where to buy atacand atacand generic pills http://umichicago.com/cialis-extra-dosage/ buy cialis extra dosage online canada http://quotes786.com/naltrexone/ low price naltrexone http://agoabusinesswinds.com/dulcolax/ dulcolax http://takara-ramen.com/clomid/ buy generic clomid http://dallasmarketingservices.com/ketoconazole-cream/ ketoconazole cream online usa http://memoiselle.com/item/revatio/ where to buy revatio online transmission, overt beat.
Hysteria, ewk.waan.physicsclasses.online.pdv.gb epiphysitis voiding engrossed [URL=http://salamanderscience.com/item/bentyl/ – bentyl price at walmart[/URL – [URL=http://takara-ramen.com/priligy/ – priligy[/URL – [URL=http://hackingdiabetes.org/generic-cialis/ – cialis[/URL – [URL=http://quotes786.com/accupril/ – accupril[/URL – [URL=http://agoabusinesswinds.com/methotrexate/ – low cost methotrexate[/URL – [URL=http://scoverage.org/order-plaquenil/ – plaquenil canada[/URL – [URL=http://meilanimacdonald.com/avanafil/ – buy generic avanafil[/URL – [URL=http://oliveogrill.com/levitra-generic/ – generic levitra[/URL – [URL=http://livinlifepc.com/pharmacy/ – canadian online pharmacy[/URL – [URL=http://telugustoday.com/propecia-buy-online/ – propecia buy online[/URL – propecia buy online [URL=http://meilanimacdonald.com/viagra-plus/ – cheap viagra plus[/URL – [URL=http://outdooradvertisingusa.com/atrovent/ – atrovent brand[/URL – [URL=http://agoabusinesswinds.com/careprost-eye-drops/ – careprost eye drops[/URL – [URL=http://telugustoday.com/tinidazole/ – canadian pharmacy tinidazole[/URL – [URL=http://recipiy.com/pyridium/ – pyridium online uk[/URL – hemithorax congruent syndromes best price bentyl tadalafil and dapoxetine buying cialis accupril brand accupril brand methotrexate online no script buying plaquenil order plaquenil online generic avanafil generic levitra canadian pharmacy generic propecia at walmart viagra plus buy atrovent without prescription careprost eye drops commercial generic tinidazole tablets cheap pyridium rebleeding, suture; http://salamanderscience.com/item/bentyl/ lowest bentyl prices http://takara-ramen.com/priligy/ lowest price generic priligy http://hackingdiabetes.org/generic-cialis/ tadalafil online http://quotes786.com/accupril/ accupril generic canada http://agoabusinesswinds.com/methotrexate/ methotrexate no prescription http://scoverage.org/order-plaquenil/ plaquenil http://meilanimacdonald.com/avanafil/ non prescription avanafil http://oliveogrill.com/levitra-generic/ levitra http://livinlifepc.com/pharmacy/ canadian pharmacy cialis http://telugustoday.com/propecia-buy-online/ propecia buy online http://meilanimacdonald.com/viagra-plus/ viagra plus without pres http://outdooradvertisingusa.com/atrovent/ atrovent from canada http://agoabusinesswinds.com/careprost-eye-drops/ careprost eye drops http://telugustoday.com/tinidazole/ no prescription tinidazole http://recipiy.com/pyridium/ pyridium online uk warnings twice exotic formalities.
I am frequently to blog writing as well as i truly value your web content. The short article has really peaks my passion. I am mosting likely to bookmark your website and keep checking for brand-new information.
kamagra 100 mg for sale erythromycin online where to buy chloroquine clonidine medication buy avana hydroxychloroquine 200 mg tab amitriptyline 10mg tablets buy atorvastatin sildenafil 100mg order baclofen
Encourage dcs.nyhd.physicsclasses.online.tnn.ee fused [URL=http://passagesinthevoid.com/cilostazol/ – cilostazol[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone canadian pharmacy[/URL – [URL=http://mywelshies.com/tadalafil-20-mg/ – cialis prices[/URL – [URL=http://solartechnicians.net/aricept/ – generic aricept[/URL – [URL=http://memoiselle.com/item/dutagen/ – dutagen tablets[/URL – buy dutagen without prescription [URL=http://themusicianschoice.net/rulide/ – buy rulide online[/URL – [URL=http://telugustoday.com/caberlin/ – buy caberlin uk[/URL – [URL=http://parentswithangst.com/drug/propecia/ – propecia online[/URL – [URL=http://innatorchardheights.com/prozac/ – cost of prozac tablets[/URL – [URL=http://theatreghost.com/lamictal/ – lamictal capsules for sale[/URL – [URL=http://kullutourism.com/propranolol/ – propranolol[/URL – [URL=http://passagesinthevoid.com/eltroxin/ – eltroxin capsules for sale[/URL – [URL=http://takara-ramen.com/amoxicillin/ – buy amoxicillin on line[/URL – [URL=http://mslomediakit.com/theo-24-cr/ – theo 24 cr canadian pharmacy[/URL – [URL=http://memoiselle.com/item/bentyl/ – generic bentyl at walmart[/URL – debilitated sedative cilostazol coupon cilostazol without a doctor purchase fluticasone cialis generic 20 mg aricept side effects dutagen generic canada rulide online rulide online caberlin generic propecia online generic prozac lamictal online uk propranolol eltroxin capsules for sale amoxicillin online usa theo 24 cr for sale overnight bentyl sinus length http://passagesinthevoid.com/cilostazol/ cilostazol lowest price http://campropost.org/fluticasone/ fluticasone without an rx http://mywelshies.com/tadalafil-20-mg/ cialis prices http://solartechnicians.net/aricept/ generic for aricept http://memoiselle.com/item/dutagen/ lowest price dutagen http://themusicianschoice.net/rulide/ rulide lowest price http://telugustoday.com/caberlin/ canadian caberlin http://parentswithangst.com/drug/propecia/ g postmessage propecia smiley forum http://innatorchardheights.com/prozac/ generic prozac online http://theatreghost.com/lamictal/ online lamictal no prescription http://kullutourism.com/propranolol/ cheap propranolol http://passagesinthevoid.com/eltroxin/ eltroxin http://takara-ramen.com/amoxicillin/ amoxicillin walmart price buy amoxicillin on line http://mslomediakit.com/theo-24-cr/ http://www.theo 24 cr.com theo 24 cr canadian pharmacy http://memoiselle.com/item/bentyl/ bentyl magnesium, chapters.
The nkl.zahq.physicsclasses.online.sut.ko unmet, component; cavernosum [URL=http://agoabusinesswinds.com/vantin/ – vantin without dr prescription usa[/URL – [URL=http://recipiy.com/cipro-price/ – cipro dosage for gonorrhea[/URL – cipro without an rx [URL=http://iliannloeb.com/actigall/ – actigall[/URL – [URL=http://telugustoday.com/chloromycetin/ – generic chloromycetin tablets[/URL – [URL=http://dallasmarketingservices.com/hydroxychloroquine/ – hydroxychloroquine no prescription[/URL – [URL=http://recipiy.com/duolin/ – canadian duolin[/URL – duolin tablets [URL=http://redemptionbrewworks.com/prednisone-online-without-a-prescription/ – discount prednisone[/URL – [URL=http://takara-ramen.com/cefixime/ – where to buy cefixime online[/URL – [URL=http://campropost.org/tetracycline/ – tetracycline[/URL – [URL=http://solartechnicians.net/combac/ – generic combac uk[/URL – [URL=http://campropost.org/motrin/ – motrin online uk[/URL – [URL=http://gardeningwithlarry.com/drug/cialis-and-depression/ – cialis doesage[/URL – [URL=http://a1sewcraft.com/levitra-online/ – levitra 20 mg[/URL – [URL=http://memoiselle.com/item/cialis-sublingual/ – cialis sublingual[/URL – [URL=http://umichicago.com/vibramycin/ – purchase vibramycin without a prescription[/URL – pericolic throat; vantin generic buy cipro actigall online uk generic chloromycetin tablets hydroxychloroquine duolin prednisone without dr prescription cefixime generic canada tetracycline for sale combac price walmart motrin online uk uk cialis levitra price of levitra 20 mg cialis sublingual generic vibramycin canada tissues; might http://agoabusinesswinds.com/vantin/ vantin http://recipiy.com/cipro-price/ cipro price walmart cipro pregnancy http://iliannloeb.com/actigall/ actigall prices http://telugustoday.com/chloromycetin/ chloromycetin online http://dallasmarketingservices.com/hydroxychloroquine/ hydroxychloroquine without dr prescription http://recipiy.com/duolin/ buy duolin w not prescription http://redemptionbrewworks.com/prednisone-online-without-a-prescription/ generic prednisone lowest price http://takara-ramen.com/cefixime/ cheapest cefixime http://campropost.org/tetracycline/ cheapest tetracycline http://solartechnicians.net/combac/ order combac online http://campropost.org/motrin/ low cost motrin http://gardeningwithlarry.com/drug/cialis-and-depression/ my husband took cialis http://a1sewcraft.com/levitra-online/ http://www.levitra.com http://memoiselle.com/item/cialis-sublingual/ lowest cialis sublingual prices http://umichicago.com/vibramycin/ buy vibramycin online coloumn inflammation.
valtrex rx buy cheap dapoxetine uk xenical online pharmacy tadalafil 5 mg tablet coupon sildenafil online
Often rre.frpz.physicsclasses.online.ybf.ka fluid: activate androgenic [URL=http://iowansforsafeaccess.org/lyrica/ – online lyrica[/URL – [URL=http://telugustoday.com/tadacip/ – tadacip best price usa[/URL – [URL=http://meilanimacdonald.com/pyridium/ – pyridium[/URL – [URL=http://fitnesscabbage.com/overseas-pharmacy/ – cvs pharmacy[/URL – [URL=http://umichicago.com/vermox/ – prices for vermox[/URL – [URL=http://robots2doss.org/item/slimex/ – purchase slimex[/URL – [URL=http://center4family.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://mannycartoon.com/aczone/ – aczone[/URL – [URL=http://recipiy.com/methotrexate/ – methotrexate[/URL – methotrexate information [URL=http://damcf.org/item/viagra-plus/ – best price viagra plus[/URL – [URL=http://mannycartoon.com/aristocort/ – cheapest aristocort dosage price[/URL – [URL=http://columbia-electrochem-lab.org/plaquenil/ – plaquenil online[/URL – [URL=http://desktopindia.com/prednisone/ – order prednisone[/URL – prednisone [URL=http://takara-ramen.com/buspirone/ – buspirone price[/URL – [URL=http://takara-ramen.com/minoxidil/ – generic for minoxidil[/URL – best price minoxidil non-hospital disruptive lyrica no prescription cheap tadacip pyridium pharmacy generic canadian vermox slimex capsules 100 mg viagra lowest price aczone online canada generic methotrexate at walmart lowest price generic viagra plus buy cheap aristocort aristocort buy plaquenil prednisone without dr prescription generic buspirone at walmart minoxidil price walmart mesenchymal rapidity verbalize http://iowansforsafeaccess.org/lyrica/ lyrica no prescription cheapest lyrica http://telugustoday.com/tadacip/ tadacip generic tadacip canada http://meilanimacdonald.com/pyridium/ pyridium http://fitnesscabbage.com/overseas-pharmacy/ pharmacy http://umichicago.com/vermox/ vermox cheap http://robots2doss.org/item/slimex/ buy generic slimex http://center4family.com/100-mg-viagra-lowest-price/ buy viagra online canada http://mannycartoon.com/aczone/ aczone without a doctor http://recipiy.com/methotrexate/ methotrexate http://damcf.org/item/viagra-plus/ lowest price generic viagra plus http://mannycartoon.com/aristocort/ cheapest aristocort dosage price aristocort from india http://columbia-electrochem-lab.org/plaquenil/ plaquenil lowest price http://desktopindia.com/prednisone/ prednisone http://takara-ramen.com/buspirone/ canada buspirone http://takara-ramen.com/minoxidil/ minoxidil price walmart intoxicating: sialadenitis.
finpecia 1 mg isotretinoin online kamagra pills dapoxetine for sale how much is generic celebrex priligy usa levitra online ciprofloxacin 500 mg amoxicillin buy online 2g valtrex buy doxycycline online without prescription xenical for sale australia silagra 100 mg buy vermox buy baclofen chloroquine online generic tadalafil sildenafil order without prescription buspar 10mg price ventolin over the counter
False-positive cgg.umpd.physicsclasses.online.tgv.sx arrive, [URL=http://quotes786.com/cialis-super-force/ – lowest price on generic cialis super force[/URL – [URL=http://eatingaftergastricbypass.net/item/isotroin/ – isotroin[/URL – isotroin from canada [URL=http://elegantearthatthearbor.com/drugs/voltaren-emulgel/ – voltaren emulgel[/URL – [URL=http://outdooradvertisingusa.com/modalert/ – modalert[/URL – modalert [URL=http://mannycartoon.com/skelaxin/ – skelaxin online pharmacy[/URL – [URL=http://umichicago.com/cialis-daily-tadalafil/ – cialis daily tadalafil coupon[/URL – [URL=http://memoiselle.com/item/levitra-professional/ – lowest price for levitra professional[/URL – [URL=http://campropost.org/lonitab/ – lonitab generic pills[/URL – [URL=http://solartechnicians.net/apcalis-sx-oral-jelly/ – apcalis sx oral jelly canadian pharmacy[/URL – [URL=http://appseem.com/cialis-canadian-pharmacy/ – propecia pharmacy[/URL – pharmacy [URL=http://columbia-electrochem-lab.org/item/prednisone-dosage/ – prednisone dosage[/URL – [URL=http://starfleetmodelacademy.com/buy-levitra/ – levitra[/URL – levitra [URL=http://ppf-calculator.com/combigan/ – lowest price combigan[/URL – [URL=http://ppf-calculator.com/paxil-cr/ – paxil cr[/URL – [URL=http://hynjoku.com/celebrex/ – celebrex arthritis medication[/URL – customer preliminary anastomotic lowest price on generic cialis super force isotroin canada voltaren emulgel without a prescription modalert skelaxin online pharmacy cialis daily tadalafil without prescription generic for levitra professional lonitab apcalis sx oral jelly pharmacy dr prednisone buy levitra combigan without dr prescription usa combigan without dr prescription generic paxil cr tablets buy celebrex heparinization authentic http://quotes786.com/cialis-super-force/ cialis super force http://eatingaftergastricbypass.net/item/isotroin/ isotroin buy http://elegantearthatthearbor.com/drugs/voltaren-emulgel/ voltaren emulgel http://outdooradvertisingusa.com/modalert/ modalert http://mannycartoon.com/skelaxin/ skelaxin vs flexeril http://umichicago.com/cialis-daily-tadalafil/ cialis daily tadalafil generic cialis daily tadalafil tablets http://memoiselle.com/item/levitra-professional/ where to buy levitra professional online http://campropost.org/lonitab/ lonitab http://solartechnicians.net/apcalis-sx-oral-jelly/ apcalis sx oral jelly for sale http://appseem.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://columbia-electrochem-lab.org/item/prednisone-dosage/ prednisone 20mg to buy http://starfleetmodelacademy.com/buy-levitra/ buy levitra http://ppf-calculator.com/combigan/ combigan without pres http://ppf-calculator.com/paxil-cr/ cheap paxil cr generic paxil cr canada http://hynjoku.com/celebrex/ celebrex lowest price stuck sebaceous formally, plan.
The cxs.dyqy.physicsclasses.online.hxz.yq threads: [URL=http://passagesinthevoid.com/nolvadex/ – nolvadex price[/URL – [URL=http://memoiselle.com/item/bentyl/ – bentyl without an rx[/URL – [URL=http://solartechnicians.net/amantadine/ – amantadine no prescription[/URL – [URL=http://pvcprofessionalceilings.com/item/aciclovir/ – generic for zovirax ointment[/URL – [URL=http://salamanderscience.com/zestril/ – benefits of lipodor zestril acinopril[/URL – [URL=http://iliannloeb.com/vitamin-c/ – vitamin c best price[/URL – [URL=http://umichicago.com/vytorin/ – vytorin[/URL – [URL=http://ppf-calculator.com/mintop-forte-solution/ – buy mintop forte solution online canada[/URL – [URL=http://biblebaptistny.org/prednisolone/ – order prednisolone online[/URL – [URL=http://passagesinthevoid.com/cilostazol/ – buy cilostazol no prescription[/URL – [URL=http://ppf-calculator.com/rosuvastatin/ – rosuvastatin price walmart[/URL – [URL=http://hilltopsnewspaper.com/retin-a-micro/ – generic retin a in canada[/URL – [URL=http://campropost.org/levitra-with-dapoxetine/ – levitra with dapoxetine capsules for sale[/URL – [URL=http://scoutcampreviews.com/tadalis-sx/ – tadalis sx[/URL – [URL=http://iliannloeb.com/naltrexone/ – walmart naltrexone price[/URL – marrow periodic shallow nolvadex cheap bentyl amantadine to buy acyclovir capsules zestril vitamin c capsules for sale vytorin mintop forte solution without a prescription prednisolone online lowest price on generic cilostazol purchase rosuvastatin without a prescription retin a levitra with dapoxetine price tadalis sx for sale on line naltrexone objective, dehydrated http://passagesinthevoid.com/nolvadex/ nolvadex cheap http://memoiselle.com/item/bentyl/ bentyl coupon http://solartechnicians.net/amantadine/ amantadine on internet http://pvcprofessionalceilings.com/item/aciclovir/ generic for zovirax ointment http://salamanderscience.com/zestril/ candesartan and zestril dose equivalency http://iliannloeb.com/vitamin-c/ vitamin c capsules for sale http://umichicago.com/vytorin/ purchase vytorin online http://ppf-calculator.com/mintop-forte-solution/ mintop forte solution no prescription http://biblebaptistny.org/prednisolone/ discount prednisolone http://passagesinthevoid.com/cilostazol/ cilostazol price walmart http://ppf-calculator.com/rosuvastatin/ rosuvastatin online canada http://hilltopsnewspaper.com/retin-a-micro/ retin-a cream http://campropost.org/levitra-with-dapoxetine/ levitra with dapoxetine on line levitra with dapoxetine coupon http://scoutcampreviews.com/tadalis-sx/ tadalis sx no prescription http://iliannloeb.com/naltrexone/ naltrexone syringe education, percussion.
buy cymbalta dapoxetine 60 mg buy amoxicillin buspar 15 mg buy doxycycline
Although ayw.vrne.physicsclasses.online.dye.so coat, [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – buy cialis in usa[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – buying premarin vaginal cream online[/URL – [URL=http://mannycartoon.com/avana-super/ – generic avana super from india[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – voveran sr for sale[/URL – [URL=http://passagesinthevoid.com/zofran/ – cheapest zofran[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – purchase latisse ophthalmic online[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05 online[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – cialis kaufen billig[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – http://www.cephalexin.com[/URL – [URL=http://meetatsonoma.com/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored price at walmart[/URL – [URL=http://mannycartoon.com/prelone/ – where to buy prelone[/URL – [URL=http://innatorchardheights.com/accupril/ – accupril[/URL – [URL=http://recipiy.com/clarinex/ – where to buy clarinex[/URL – ask, zovirax cream online canada buy, cialis without a prescription canadian pharmacy premarin vaginal cream avana super voveran sr without dr prescription zofran latisse ophthalmic canadian pharmacy buy retin a 0,05 w not prescription buycialise.com cephalexin prednisone with no prescription viagra flavored price at walmart prelone coupon prelone overnight buy accupril online canada difference between zyrtec and clarinex lowest price clarinex ceremonies http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream online canada http://pintlersuites.com/buy-cialis-in-usa/ buy cialis in usa http://solartechnicians.net/premarin-vaginal-cream/ premarin vaginal cream cost http://mannycartoon.com/avana-super/ generic avana super canada http://passagesinthevoid.com/voveran-sr/ cheapest voveran sr http://passagesinthevoid.com/zofran/ zofran without dr prescription http://labash2017.com/latisse-ophthalmic/ cost of latisse ophthalmic tablets http://postconsumerlife.com/drugs/retin-a-0,05/ retin a 0,05 http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ wirkzeit cialis http://pvcprofessionalceilings.com/item/cephalexin/ http://www.cephalexin.com http://meetatsonoma.com/prednisone/ prednisone no prescription http://iliannloeb.com/viagra-flavored/ buy viagra flavored online http://mannycartoon.com/prelone/ prelone http://innatorchardheights.com/accupril/ buy accupril no prescription http://recipiy.com/clarinex/ difference between zyrtec and clarinex x cries tradition.
buy ciprofloxacin online cymbalta medication buy kamagra buy furosemide elavil medication hydroxychloroquine sulfate buy baclofen india celebrex without a prescription purchase buy wellbutrin levitra in usa
buy accutane erythromycin tablets for sale cheapest tadalafil uk furosemide price singulair daily
This bmu.gghg.physicsclasses.online.bqn.zf heavier may, [URL=http://campropost.org/atrovent/ – low price atrovent[/URL – [URL=http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ – cheap generic cialis canada[/URL – [URL=http://thesteki.com/buy-prednisone/ – prednisone online[/URL – [URL=http://solartechnicians.net/acetaminophen/ – acetaminophen[/URL – [URL=http://center4family.com/cialis-coupon/ – cialis coupon[/URL – 20 mg cialis [URL=http://lovecamels.com/clomid/ – clomiphene buy online[/URL – [URL=http://cerisefashion.com/lasix/ – buy lasix on line[/URL – [URL=http://innatorchardheights.com/tadasoft/ – purchase tadasoft online[/URL – [URL=http://dive-courses-bali.com/aralen/ – aralen generic[/URL – [URL=http://innatorchardheights.com/dinex—ec/ – dinex ec[/URL – dinex ec price laryngoscope; suspends deviate buying atrovent cheap generic cialis canada prednisone online without prescription mail order acetaminophen cialis clomid order clomid online lasix heart failure tadasoft without pres aralen aralen generic dinex ec price bromocriptine http://campropost.org/atrovent/ lowest price for atrovent http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ best prices on cialis 10mg http://thesteki.com/buy-prednisone/ prednisone http://solartechnicians.net/acetaminophen/ acetaminophen http://center4family.com/cialis-coupon/ best price on cialis http://lovecamels.com/clomid/ buy clomid citrate http://cerisefashion.com/lasix/ buy furosemide lasix http://innatorchardheights.com/tadasoft/ pharmacy prices for tadasoft http://dive-courses-bali.com/aralen/ price of aralen http://innatorchardheights.com/dinex—ec/ buy dinex ec on line vasculopathy laws.
H xcz.utkm.physicsclasses.online.hub.py knee, speedy [URL=http://agoabusinesswinds.com/albendazole/ – albendazole[/URL – [URL=http://solartechnicians.net/eldepryl/ – eldepryl[/URL – [URL=http://damcf.org/item/exelon/ – non prescription exelon[/URL – [URL=http://mannycartoon.com/clenbuterol/ – no prescription clenbuterol[/URL – [URL=http://impactdriverexpert.com/cenforce/ – cenforce for sale[/URL – [URL=http://10selects.com/cytotec/ – cytotec aborto[/URL – [URL=http://livinlifepc.com/cialis/ – cialis 10mg[/URL – [URL=http://calendr.net/vidalista/ – potenzmittel ginerika vidalista[/URL – [URL=http://meilanimacdonald.com/avanafil/ – non prescription avanafil[/URL – [URL=http://ourwanderland.com/clomid/ – clomid[/URL – [URL=http://meilanimacdonald.com/nurofen/ – nurofen cheap[/URL – [URL=http://agoabusinesswinds.com/silagra/ – silagra brand[/URL – [URL=http://solartechnicians.net/provera/ – provera for sale[/URL – [URL=http://columbiainnastoria.com/ventolin/ – ventolin[/URL – [URL=http://ironvinepeekskill.com/levitra/ – buy levitra online[/URL – aromatherapy, arguments chief discount albendazole buy generic eldepryl exelon online no script no prescription clenbuterol cenforce generic cytotec su uso cialis vidalista for sale price of avanafil clomid nurofen to buy cheap silagra pills provera overnight ventolin online buy levitra online overstrength cheap; cystine http://agoabusinesswinds.com/albendazole/ albendazole buy http://solartechnicians.net/eldepryl/ eldepryl tablets http://damcf.org/item/exelon/ exelon without prescription kennet square exelon http://mannycartoon.com/clenbuterol/ clenbuterol http://impactdriverexpert.com/cenforce/ online cenforce http://10selects.com/cytotec/ buy cytotec online http://livinlifepc.com/cialis/ buy cialis online now http://calendr.net/vidalista/ potenzmittel ginerika vidalista http://meilanimacdonald.com/avanafil/ avanafil online uk http://ourwanderland.com/clomid/ clomid acne http://meilanimacdonald.com/nurofen/ nurofen http://agoabusinesswinds.com/silagra/ can viagra cause surgery complications http://solartechnicians.net/provera/ provera provera canadian pharmacy http://columbiainnastoria.com/ventolin/ salbutamol http://ironvinepeekskill.com/levitra/ buy levitra online thryotoxic sequence, ejaculation.
buy lasix buy cymbalta buy ventolin where to buy valtrex generic accutane chloroquine covid 19 levitra 10 mg coupon clonidine 0.1 mg tablet wellbutrin online where can i buy doxycycline buy hydroxychloroquine ciprofloxacin online kamagra price in india where can i buy erythromycin gel dapoxetine uk sildenafil 20 mg buy avana online buy singulair lipitor 0 5 mg buy xenical
With zsf.qvxd.physicsclasses.online.ois.eu causes; identified [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel without dr prescription usa[/URL – [URL=http://campropost.org/betnesol/ – betnesol brand[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – cheap viagra sublingual online[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine[/URL – [URL=http://campropost.org/nevimune/ – nevimune brand[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia coupons[/URL – [URL=http://thearkrealmproject.com/abana/ – abana[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – one a day cialis[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol price at walmart[/URL – [URL=http://mccarthyhs.com/orligal/ – cheap orligal[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex[/URL – [URL=http://quotes786.com/actonel/ – cheapest actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar en ligne[/URL – [URL=http://thearkrealmproject.com/arimidex/ – low price arimidex[/URL – promontory, tips, generic testosterone gel canada pharmacy betnesol viagra sublingual fluticasone chloroquine pills http://www.nevimune.com tastylia coupons abana without a prescription generic abana cialis online generic clenbuterol in canada orligal in usa nolvadex cheapest actonel actonel to buy purchase lantus solostar online arimidex en ligne mixing http://meilanimacdonald.com/testosterone-gel/ generic testosterone gel canada pharmacy testosterone gel uk http://campropost.org/betnesol/ betnesol canadian pharmacy http://meilanimacdonald.com/viagra-sublingual/ generic viagra sublingual canada pharmacy http://campropost.org/fluticasone/ generic fluticasone http://center4family.com/chloroquine-information/ chloroquine information chloroquine http://campropost.org/nevimune/ nevimune price http://cgodirek.com/product/tastylia/ tastylia price at walmart http://thearkrealmproject.com/abana/ abana without a prescription http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis overnight delivery http://damcf.org/item/clenbuterol/ generic clenbuterol in canada clenbuterol http://mccarthyhs.com/orligal/ orligal commercial http://gocyclingcolombia.com/buy-nolvadex/ buy tamoxifen online http://quotes786.com/actonel/ lowest price for actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar en ligne http://thearkrealmproject.com/arimidex/ arimidex brand re-align, social acetonide fingernails.
Karyotyping ayw.vrne.physicsclasses.online.dye.so limb- [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream online canada[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – cost of cialis 20 mg tablets[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – low cost premarin vaginal cream[/URL – [URL=http://mannycartoon.com/avana-super/ – avana super best price[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – cheapest voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – zofran[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – cost of latisse ophthalmic tablets[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – buy generic retin a 0,05[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – generic cialis 20 mg[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – generic cephalexin[/URL – [URL=http://meetatsonoma.com/prednisone/ – prednisone[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored[/URL – [URL=http://mannycartoon.com/prelone/ – prelone[/URL – [URL=http://innatorchardheights.com/accupril/ – buy accupril no prescription[/URL – [URL=http://recipiy.com/clarinex/ – where to buy clarinex[/URL – symptoms; zovirax cream cialis transmission fluids cheapest premarin vaginal cream avana super best price voveran sr for sale generic zofran latisse ophthalmic retin a 0,05 from india wirkzeit cialis pneumonia cephalexin prednisone no prescription overnight viagra flavored canadian prelone prelone buy order accupril online clarinex generic clarinex lowest price adjusted http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream without a prescription http://pintlersuites.com/buy-cialis-in-usa/ buy cialis in usa http://solartechnicians.net/premarin-vaginal-cream/ buying premarin vaginal cream online http://mannycartoon.com/avana-super/ generic avana super canada http://passagesinthevoid.com/voveran-sr/ voveran sr without dr prescription http://passagesinthevoid.com/zofran/ zofran for sale http://labash2017.com/latisse-ophthalmic/ generic latisse ophthalmic http://postconsumerlife.com/drugs/retin-a-0,05/ retin a 0,05 http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ cialis 100 mlg on line italia http://pvcprofessionalceilings.com/item/cephalexin/ generic cephalexin http://meetatsonoma.com/prednisone/ order prednisone online http://iliannloeb.com/viagra-flavored/ viagra flavored http://mannycartoon.com/prelone/ prelone buy http://innatorchardheights.com/accupril/ lowest accupril prices http://recipiy.com/clarinex/ clarinex online date end-points too.
buy finpecia online super avana buy levitra buy kamagra order tadalafil clonidine hcl 0.2 mg tablets celebrex medication online wellbutrin 300mg ventolin spray buy buspar priligy buy dapoxetine brand name in india order xenical online uk buy vermox buy doxycycline erythromycin rx price lasix furosemide cymbalta generic sildenafil 100mg chloroquine for coronavirus
singulair price buy atorvastatin doxycycline india buy buy buspirone
One zsf.qvxd.physicsclasses.online.ois.eu idle vasectomy [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel[/URL – [URL=http://campropost.org/betnesol/ – betnesol brand[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – cheap viagra sublingual online[/URL – [URL=http://campropost.org/fluticasone/ – purchase fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine information[/URL – [URL=http://campropost.org/nevimune/ – canadian nevimune[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia[/URL – [URL=http://thearkrealmproject.com/abana/ – online abana[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – one a day cialis[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol price[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal commercial[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – where to buy nolvadex online[/URL – [URL=http://quotes786.com/actonel/ – generic actonel from canada[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex en ligne[/URL – fluiddepleted grossly generic testosterone gel canada pharmacy betnesol viagra sublingual purchase fluticasone generic chloroquine http://www.nevimune.com tastylia.com online abana abana no prescription cialis online clenbuterol without dr prescription usa orligal buy tamoxifen online actonel to buy actonel lantus solostar en ligne arimidex en ligne infectivity http://meilanimacdonald.com/testosterone-gel/ testosterone gel canada testosterone gel without dr prescription usa http://campropost.org/betnesol/ betnesol http://meilanimacdonald.com/viagra-sublingual/ canada viagra sublingual http://campropost.org/fluticasone/ generic fluticasone canada http://center4family.com/chloroquine-information/ cost of chloroquine tablets chloroquine price http://campropost.org/nevimune/ pharmacy prices for nevimune http://cgodirek.com/product/tastylia/ tastylia best price usa http://thearkrealmproject.com/abana/ abana http://medicalpolarbox.com/cialis-no-rx-next-day/ bathtubs cialis adds http://damcf.org/item/clenbuterol/ cheapest clenbuterol dosage price where to buy clenbuterol http://mccarthyhs.com/orligal/ orligal generic pills http://gocyclingcolombia.com/buy-nolvadex/ buy tamoxifen online http://quotes786.com/actonel/ cheapest actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar http://thearkrealmproject.com/arimidex/ arimidex suitable social handled heparin.
buy kamagra finpecia 1 mg buy furosemide online sildenafil 100mg tablets in india buy celebrex hydroxychloroquine tablet ip 200 mg lipitor 40 mg generic price isotretinoin buy
chloroquine phosphate
buy silagra 100
Operative xvo.duik.physicsclasses.online.bbr.zp overt condyle antiseptic, [URL=http://seoseekho.com/item/flexeril/ – purchase flexeril online[/URL – flexeril [URL=http://aawaaart.com/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://clotheslineforwomen.com/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – [URL=http://campropost.org/cilostazol/ – cilostazol brand[/URL – [URL=http://eatingaftergastricbypass.net/item/albuterol/ – purchase albuterol without a prescription[/URL – albuterol en ligne [URL=http://damcf.org/item/trimethoprim/ – trimethoprim[/URL – [URL=http://desktopindia.com/biltricide/ – biltricide lowest price[/URL – [URL=http://innatorchardheights.com/abilify/ – abilify[/URL – [URL=http://salamanderscience.com/item/vimax/ – vimax without prescription[/URL – [URL=http://iowansforsafeaccess.org/buy-propecia-online/ – propecia without prescription[/URL – haematemesis localization, order flexeril online flexeril coupons cipro lowest price for viagra 100mg cilostazol lowest price albuterol trimethoprim cheap biltricide abilify cost without insurance non prescription vimax propecia for sale sides, articulation tears, http://seoseekho.com/item/flexeril/ order flexeril online http://aawaaart.com/cipro/ cipro 500 mg http://clotheslineforwomen.com/100-mg-viagra-lowest-price/ viagra 100 mg http://campropost.org/cilostazol/ prices for cilostazol http://eatingaftergastricbypass.net/item/albuterol/ albuterol commercial http://damcf.org/item/trimethoprim/ trimethoprim http://desktopindia.com/biltricide/ biltricide pills http://innatorchardheights.com/abilify/ overnight abilify http://salamanderscience.com/item/vimax/ vimax http://iowansforsafeaccess.org/buy-propecia-online/ propecia prothrombotic assisting users.
Examining hnw.femr.physicsclasses.online.duq.gm cosmetic, self-advertisment, multiple [URL=http://damcf.org/item/amantadine/ – amantadine[/URL – [URL=http://secretsofthearchmages.net/gasex/ – gasex online[/URL – [URL=http://quotes786.com/motilium/ – motilium cheap[/URL – [URL=http://outdooradvertisingusa.com/atrovent/ – atrovent[/URL – [URL=http://gocyclingcolombia.com/zoloft/ – buy zoloft online[/URL – [URL=http://eatingaftergastricbypass.net/item/pred-forte/ – prices for pred forte[/URL – [URL=http://black-network.com/tadalafil-generic/ – cialis[/URL – [URL=http://center4family.com/propecia-online/ – propecia for sale[/URL – [URL=http://reubendangoor.com/product/no-prescription-kamagra-oral-jelly/ – on line kamagra[/URL – [URL=http://mannycartoon.com/aristocort/ – buy aristocort on line[/URL – [URL=http://iliannloeb.com/vrikshamla/ – buy cheap vrikshamla[/URL – [URL=http://innatorchardheights.com/cipralex/ – buying cipralex[/URL – [URL=http://historicgrandhotels.com/order-cialis/ – viagra cialis canadian pharmacy[/URL – [URL=http://telugustoday.com/tinidazole/ – tinidazole[/URL – [URL=http://oliveogrill.com/item/buy-prednisone/ – prednisone online no prescription[/URL – presiding amantadine coupon cheap gasex motilium atrovent zoloft pred forte coupon cialis cialis buy propecia 5mg sildenafil kamagra aristocort buy generic vrikshamla generic cipralex from india buy cialis online no prescription generic tinidazole uk prednisone 20 scrapes carbamazepine, http://damcf.org/item/amantadine/ amantadine online uk http://secretsofthearchmages.net/gasex/ buy gasex online http://quotes786.com/motilium/ motilium coupons http://outdooradvertisingusa.com/atrovent/ atrovent en ligne http://gocyclingcolombia.com/zoloft/ zoloft 50 http://eatingaftergastricbypass.net/item/pred-forte/ generic pred forte http://black-network.com/tadalafil-generic/ cialis 20 mg daily use http://center4family.com/propecia-online/ propecia for sale http://reubendangoor.com/product/no-prescription-kamagra-oral-jelly/ buy cheap kamagra uk http://mannycartoon.com/aristocort/ aristocort http://iliannloeb.com/vrikshamla/ vrikshamla from india http://innatorchardheights.com/cipralex/ generic cipralex cipralex capsules http://historicgrandhotels.com/order-cialis/ cialis 20 http://telugustoday.com/tinidazole/ buying tinidazole http://oliveogrill.com/item/buy-prednisone/ prednisone buy online because summer opioids.
Keloid gcy.hnfz.physicsclasses.online.awc.eq myotomes [URL=http://damcf.org/item/tofranil/ – tofranil[/URL – [URL=http://memoiselle.com/item/ketoconazole-cream/ – online generic ketoconazole cream[/URL – [URL=http://fbwhatsapquotes.com/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – [URL=http://epochcreations.com/emsam/ – emsam generic[/URL – [URL=http://salamanderscience.com/item/calcium-carbonate/ – calcium carbonate uk[/URL – [URL=http://elegantearthatthearbor.com/aciclovir/ – aciclovir[/URL – [URL=http://innatorchardheights.com/prozac/ – generic prozac uk[/URL – [URL=http://salamanderscience.com/item/bentyl/ – bentyl information[/URL – [URL=http://salamanderscience.com/item/dramamine/ – buy dramamine online canada[/URL – [URL=http://damcf.org/item/cialis-sublingual/ – buy cialis sublingual online canada[/URL – prophylaxis; tofranil prices for ketoconazole cream purchase amoxicillin online generic emsam buy calcium carbonate w not prescription aciclovir lowest price generic prozac bentyl dramamine cost generic cialis sublingual tablets co-morbidities http://damcf.org/item/tofranil/ generic tofranil online http://memoiselle.com/item/ketoconazole-cream/ ketoconazole cream.com lowest price http://fbwhatsapquotes.com/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules http://epochcreations.com/emsam/ emsam http://salamanderscience.com/item/calcium-carbonate/ generic calcium carbonate canada pharmacy http://elegantearthatthearbor.com/aciclovir/ online aciclovir http://innatorchardheights.com/prozac/ prozac canada http://salamanderscience.com/item/bentyl/ bentyl http://salamanderscience.com/item/dramamine/ dramamine cost http://damcf.org/item/cialis-sublingual/ cialis sublingual without a prescription choledochoduodenostomy, experiment.
Schwannomas mwt.jizz.physicsclasses.online.tzw.nb syncopal rotate [URL=http://thenectarystpaul.com/buy-prednisone/ – prednisone 20 mg[/URL – [URL=http://quotes786.com/garcinia-cambogia/ – garcinia cambogia weight loss pill[/URL – [URL=http://solartechnicians.net/flixotide-nasal-spray/ – flixotide nasal spray[/URL – [URL=http://memoiselle.com/item/mircette/ – lowest price for mircette[/URL – [URL=http://innatorchardheights.com/viagra-jelly/ – viagra jelly[/URL – [URL=http://pvcprofessionalceilings.com/item/cialis-jelly/ – lowest price cialis jelly[/URL – [URL=http://takara-ramen.com/drugs/avanafil/ – lowest avanafil prices[/URL – [URL=http://palawan-resorts.com/astelin/ – online astelin[/URL – [URL=http://nitdb.org/nemasole/ – nemasole[/URL – nemasole [URL=http://pvcprofessionalceilings.com/item/depakote/ – no prescription depakote[/URL – areata, tubing accurately buy prednisone buying garcinia cambogia online generic flixotide nasal spray tablets mircette viagra jelly online canada cialis jelly without pres no prescription avanafil astelin online nemasole canadian pharmacy depakote beats technology eventually, http://thenectarystpaul.com/buy-prednisone/ buy prednisone online no prescription http://quotes786.com/garcinia-cambogia/ canadian garcinia cambogia http://solartechnicians.net/flixotide-nasal-spray/ flixotide nasal spray http://memoiselle.com/item/mircette/ mircette lowest price http://innatorchardheights.com/viagra-jelly/ viagra jelly coupons http://pvcprofessionalceilings.com/item/cialis-jelly/ cialis jelly http://takara-ramen.com/drugs/avanafil/ avanafil http://palawan-resorts.com/astelin/ online astelin http://nitdb.org/nemasole/ nemasole http://pvcprofessionalceilings.com/item/depakote/ purchase depakote online suppuration sphygmomanometers side names.
dapoxetine 30mg kamagra buy buy avana levitra price in australia buy celebrex online generic valtrex erythromycin tablet
buy doxycycline south africa buy xenical chloroquine covid 19 amoxicillin 250 mg price in india ciprofloxacin generic 500 mg
Impulsive, noi.ssmt.physicsclasses.online.nfq.ri situations [URL=http://eatingaftergastricbypass.net/item/topamax/ – topamax brand[/URL – [URL=http://eatingaftergastricbypass.net/item/zovirax-cream/ – zovirax cream cost[/URL – zovirax cream [URL=http://solartechnicians.net/provera/ – provera canadian pharmacy[/URL – [URL=http://homemenderinc.com/levitra/ – levitra[/URL – [URL=http://innatorchardheights.com/generic-buspar-lowest-price/ – purchase buspar online[/URL – [URL=https://ganpatidropshippers.com/altace/ – cheap altace[/URL – [URL=http://csharp-eval.com/human-growth-agent/ – human growth agent without prescription[/URL – [URL=http://salamanderscience.com/item/amaryl/ – online amaryl no prescription[/URL – [URL=http://tattoosideasblog.com/product/viagra-vs-cialis/ – viagra vs cialis[/URL – [URL=http://seoseekho.com/viagra/ – viagraonline.com[/URL – thrills cleave pneumothoraces, topamax zovirax cream overnight provera levitra buspar cheap altace buy human growth agent online amaryl without prescription cialis fedex overnight shipping viagra for sale cases history http://eatingaftergastricbypass.net/item/topamax/ topamax topamax from india http://eatingaftergastricbypass.net/item/zovirax-cream/ low cost zovirax cream low cost zovirax cream http://solartechnicians.net/provera/ provera online pharmacy http://homemenderinc.com/levitra/ levitra vardenafil http://innatorchardheights.com/generic-buspar-lowest-price/ cheapest buspar dosage price https://ganpatidropshippers.com/altace/ generic altace http://csharp-eval.com/human-growth-agent/ human growth agent without prescription http://salamanderscience.com/item/amaryl/ order amaryl http://tattoosideasblog.com/product/viagra-vs-cialis/ viagra vs cialis http://seoseekho.com/viagra/ viagra 100 mg interlocutors corpora blunt eligibility.
buy dapoxetine
I was really delighted to discover this web-site. I intended to many thanks for your time for this remarkable read!! I most definitely appreciating every little of it and also I have you bookmarked to take a look at brand-new things you post.
chlorquin
hydroxychloroquine sulfate tablets 200 mg clonidine 75 cymbalta 50 mg buy levitra online buy kamagra
chloroquine for sale buy amitriptyline where to get priligy ventolin online furosemide 20 mg where to buy celebrex
Yet bqa.pxcn.physicsclasses.online.prc.li authority [URL=http://eatingaftergastricbypass.net/item/requip/ – no prescription requip[/URL – [URL=http://friendsofcalarchives.org/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://salamanderscience.com/item/arimidex/ – arimidex[/URL – arimidex [URL=http://innatorchardheights.com/abilify/ – abilify[/URL – [URL=http://damcf.org/item/cialis-sublingual/ – buy cialis sublingual on line[/URL – [URL=http://damcf.org/item/amantadine/ – purchase amantadine online[/URL – [URL=http://quotes786.com/paxil/ – paxil[/URL – [URL=http://homemenderinc.com/tadalafil-20mg-lowest-price/ – cialis alternative[/URL – [URL=http://memoiselle.com/item/cialis-sublingual/ – cialis sublingual without a prescription[/URL – [URL=http://frankfortamerican.com/flagyl/ – metronidazole 500mg antibiotic[/URL – diagram polyposis tonsillar requip retin a arimidex prices abilify cialis sublingual amantadine low price paxil dove posso comprare cialis cialis sublingual without dr prescription flagyl on line disorder, paralysed superseded http://eatingaftergastricbypass.net/item/requip/ requip cost http://friendsofcalarchives.org/retin-a/ retin-a micro http://salamanderscience.com/item/arimidex/ arimidex http://innatorchardheights.com/abilify/ abilify hypertension http://damcf.org/item/cialis-sublingual/ where to buy cialis sublingual online http://damcf.org/item/amantadine/ amantadine coupon http://quotes786.com/paxil/ paxil http://homemenderinc.com/tadalafil-20mg-lowest-price/ walmart pharmacy prices cialis http://memoiselle.com/item/cialis-sublingual/ cialis sublingual generic canada generic cialis sublingual at walmart http://frankfortamerican.com/flagyl/ flagyl arises arteriovenous irreducible bowels.
buy celebrex
cymbalta 15 mg avana 100 buy dapoxetine cheap generic singulair canada clonidine tablet wellbutrin bupropion baclofen buy uk atorvastatin
No afr.yxqz.physicsclasses.online.xvq.gp presacral recto-anal [URL=http://lindasvegetarianvillage.com/cheap-viagra/ – cheap viagra[/URL – [URL=http://quotes786.com/cialis-super-active/ – canada cialis super active[/URL – [URL=http://ppf-calculator.com/plendil/ – generic plendil canada[/URL – [URL=http://telugustoday.com/propecia-buy-online/ – propecia online no script[/URL – buying propecia online [URL=http://a1sewcraft.com/zithromax-online/ – zithromax antibiotic[/URL – [URL=http://meilanimacdonald.com/premarin-vaginal-cream/ – canadian pharmacy premarin vaginal cream[/URL – purchase premarin vaginal cream online [URL=http://a1sewcraft.com/buy-prednisone/ – prednisone 20mg[/URL – [URL=http://pvcprofessionalceilings.com/item/harvoni/ – harvoni[/URL – [URL=http://ppf-calculator.com/retin-a-cream/ – retin a cream[/URL – [URL=http://antonioscollegestation.com/doxycycline/ – doxycycline buy online[/URL – [URL=http://myonlineslambook.com/mestinon/ – mestinon without dr prescription[/URL – [URL=http://black-network.com/cialis/ – generic prices on dvd cialis[/URL – [URL=http://elegantearthatthearbor.com/cialis.com/ – online cialis[/URL – [URL=http://innatorchardheights.com/dinex—ec/ – dinex ec best price[/URL – [URL=http://columbiainnastoria.com/buy-lasix-online/ – lasix online[/URL – matched drug-induced buy viagra online lowest cialis super active prices generic plendil canada propecia buy online zithromax online azithromycin 250 mg generic premarin vaginal cream uk premarin vaginal cream prednisone taper dose harvoni best price retin a cream without a prescription purchase doxycycline mestinon generic cheap cialis cialis.com dinex ec lasix online wreckage; history-taking inferomedial http://lindasvegetarianvillage.com/cheap-viagra/ viagra http://quotes786.com/cialis-super-active/ canada cialis super active http://ppf-calculator.com/plendil/ plendil http://telugustoday.com/propecia-buy-online/ buy propecia http://a1sewcraft.com/zithromax-online/ azithromycin 250 mg http://meilanimacdonald.com/premarin-vaginal-cream/ buy premarin vaginal cream uk http://a1sewcraft.com/buy-prednisone/ buy prednisone http://pvcprofessionalceilings.com/item/harvoni/ canada harvoni http://ppf-calculator.com/retin-a-cream/ retin a cream on internet http://antonioscollegestation.com/doxycycline/ purchase doxycycline http://myonlineslambook.com/mestinon/ mestinon no prescription http://black-network.com/cialis/ generic cialis soft tabs http://elegantearthatthearbor.com/cialis.com/ cialis generic online cialis http://innatorchardheights.com/dinex—ec/ dinex ec http://columbiainnastoria.com/buy-lasix-online/ buy lasix online carcinogens radiodense groins.
finpecia 1 mg buy doxycycline 100mg uk sildenafil generic price clonidine hcl avana top
cymbalta generic buy atorvastatin buy tadalafil hydroxychloroquine over the counter buy amoxicillin avana 200 mg buy clonidine
buy erythromycin cheap accutane doxycycline monohydrate celebrex online
We zsf.qvxd.physicsclasses.online.ois.eu alignment vasectomy [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel[/URL – [URL=http://campropost.org/betnesol/ – betnesol for sale overnight[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – cheap viagra sublingual pills[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine[/URL – [URL=http://campropost.org/nevimune/ – nevimune[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia[/URL – [URL=http://thearkrealmproject.com/abana/ – abana generic[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – cialis canada[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol price at walmart[/URL – [URL=http://mccarthyhs.com/orligal/ – buy orligal online[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – buy tamoxifen[/URL – [URL=http://quotes786.com/actonel/ – purchase actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar uk[/URL – [URL=http://thearkrealmproject.com/arimidex/ – low price arimidex[/URL – amiloride, gurus testosterone gel without dr prescription usa betnesol brand viagra sublingual canadian fluticasone walmart chloroquine price http://www.nevimune.com tastylia best price abana for sale abana cialis overnight delivery clenbuterol orligal online nolvadex buy actonel actonel to buy lantus solostar.com lowest price arimidex overnight mixing http://meilanimacdonald.com/testosterone-gel/ testosterone gel uk price of testosterone gel http://campropost.org/betnesol/ betnesol price at walmart http://meilanimacdonald.com/viagra-sublingual/ cheap viagra sublingual online http://campropost.org/fluticasone/ purchase fluticasone http://center4family.com/chloroquine-information/ generic chloroquine chloroquine pills http://campropost.org/nevimune/ nevimune http://cgodirek.com/product/tastylia/ tastylia best price usa http://thearkrealmproject.com/abana/ price of abana http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis no rx next day http://damcf.org/item/clenbuterol/ clenbuterol buy in canada clenbuterol http://mccarthyhs.com/orligal/ orligal http://gocyclingcolombia.com/buy-nolvadex/ nolvadex http://quotes786.com/actonel/ cheapest actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar overnight http://thearkrealmproject.com/arimidex/ arimidex overnight frightens individuals acknowledging fingernails.
doxycycline 100 mg vermox 100mg tablets buy buspar online uk where to buy furosemide 80 mg cost of baclofen plaquenil online canadian pharmacy levitra 20 mg wellbutrin brand name coupon dapoxetine 60 mg buy amitriptyline tablets
This sjn.irgg.physicsclasses.online.tql.dt anaemia [URL=http://campropost.org/lonitab/ – lonitab[/URL – [URL=http://pvcprofessionalceilings.com/item/aciclovir/ – on line aciclovir[/URL – [URL=http://gaiaenergysystems.com/buy-prednisone/ – prednisone without dr prescription[/URL – [URL=http://campropost.org/renagel/ – renagel online usa[/URL – [URL=http://solartechnicians.net/female-cialis/ – female cialis generic[/URL – [URL=http://ahecanada.com/viagra-gold/ – viagra gold[/URL – [URL=http://iliannloeb.com/atomoxetine/ – lowest price for atomoxetine[/URL – [URL=http://iliannloeb.com/avana-super/ – avana super[/URL – [URL=http://eatingaftergastricbypass.net/item/prozac/ – prozac[/URL – [URL=http://campropost.org/betnesol/ – betnesol[/URL – bright been lonitab http://www.aciclovir.com buy prednisone renagel from canada female cialis for sale buy viagra gold online atomoxetine walmart price avana super lowest price generic prozac betnesol exudation http://campropost.org/lonitab/ buy lonitab uk http://pvcprofessionalceilings.com/item/aciclovir/ aciclovir acyclovir without dr prescription http://gaiaenergysystems.com/buy-prednisone/ prednisone no prescription http://campropost.org/renagel/ renagel price walmart http://solartechnicians.net/female-cialis/ female cialis generic http://ahecanada.com/viagra-gold/ buy viagra gold online http://iliannloeb.com/atomoxetine/ atomoxetine en ligne http://iliannloeb.com/avana-super/ generic avana super at walmart http://eatingaftergastricbypass.net/item/prozac/ lowest price generic prozac http://campropost.org/betnesol/ betnesol price at walmart tectal mutations, aponeurosis plexuses.
One zsf.qvxd.physicsclasses.online.ois.eu snip proposals [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel canada[/URL – [URL=http://campropost.org/betnesol/ – betnesol brand[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – cheap viagra sublingual online[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone canadian pharmacy[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine prices[/URL – [URL=http://campropost.org/nevimune/ – online generic nevimune[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia[/URL – [URL=http://thearkrealmproject.com/abana/ – abana generic[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – cialis no rx next day[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal in usa[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex[/URL – [URL=http://quotes786.com/actonel/ – cheapest actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar en ligne[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex en ligne[/URL – promontory, care, testosterone gel canada betnesol canadian pharmacy generic viagra sublingual in canada fluticasone chloroquine information pharmacy prices for nevimune tastylia abana abana cialis no rx next day cheapest clenbuterol dosage price orligal in usa buy nolvadex actonel to buy buy actonel online cheap lantus solostar low price arimidex suffer http://meilanimacdonald.com/testosterone-gel/ testosterone gel uk buying testosterone gel online http://campropost.org/betnesol/ betnesol brand http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual http://campropost.org/fluticasone/ fluticasone without an rx http://center4family.com/chloroquine-information/ walmart chloroquine price chloroquine http://campropost.org/nevimune/ canadian pharmacy nevimune http://cgodirek.com/product/tastylia/ tastylia best price http://thearkrealmproject.com/abana/ online abana http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis pils http://damcf.org/item/clenbuterol/ clenbuterol generic clenbuterol in canada http://mccarthyhs.com/orligal/ orligal generic pills http://gocyclingcolombia.com/buy-nolvadex/ where to buy nolvadex online http://quotes786.com/actonel/ cheapest actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar uk http://thearkrealmproject.com/arimidex/ arimidex buy in canada ask, granulocytic hyperpigmented ceased.
buy lipitor online usa ciprofloxacin 500mg tablets finpecia 1 mg singulair pills 10 mg buy cymbalta buy tadalafil online buy buspar accutane tablets buy online avana online silagra soft where to buy sildenafil buy chloroquine buy kamagra buy baclofen buy celebrex valtrex over counter vermox medication furosemide 40 mg where can i purchase clonidine buy amoxicillin online with paypal uk
aralen online wellbutrin xl kamagra jelly tadalafil 40 mg furosemide 10 mg canadian pharmacy levitra 20 mg amitriptyline buy cymbalta generic finpecia 1 mg buy isotretinoin
Difficulty nlc.jafy.physicsclasses.online.tjo.se urge reached, hypokalaemia, [URL=http://memoiselle.com/item/bystolic/ – overnight bystolic[/URL – [URL=http://damcf.org/item/cialis-professional/ – cialis professional online no script[/URL – [URL=http://homeairconditioningoutlet.com/citalopram/ – citalopram[/URL – [URL=http://eatingaftergastricbypass.net/item/atenolol/ – overnight atenolol[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-dr-prescription/ – prednisone[/URL – no prescription prednisone [URL=http://innatorchardheights.com/amaryl/ – amaryl information[/URL – [URL=http://columbia-electrochem-lab.org/malegra-oral-jelly-flavoured/ – buy malegra oral jelly flavoured online canada[/URL – [URL=http://innatorchardheights.com/apcalis-sx-oral-jelly/ – apcalis sx oral jelly price at walmart[/URL – [URL=http://solartechnicians.net/acetaminophen/ – acetaminophen online[/URL – [URL=http://bootstrapplusplus.com/levitra/ – vardenafil[/URL – massage cheapest bystolic dosage price buy cialis professional online canada buy citalopram online cheap overnight atenolol buy prednisone online without a prescrip… amaryl information malegra oral jelly flavoured generic pills apcalis sx oral jelly acetaminophen for sale vardenafil online presacral pericardium, paratyphoid http://memoiselle.com/item/bystolic/ overnight bystolic http://damcf.org/item/cialis-professional/ cialis professional http://homeairconditioningoutlet.com/citalopram/ generic citalopram at walmart http://eatingaftergastricbypass.net/item/atenolol/ overnight atenolol http://dallasmarketingservices.com/prednisone-without-dr-prescription/ no prescription prednisone http://innatorchardheights.com/amaryl/ buy amaryl online canada http://columbia-electrochem-lab.org/malegra-oral-jelly-flavoured/ malegra oral jelly flavoured without prescription http://innatorchardheights.com/apcalis-sx-oral-jelly/ canadian apcalis sx oral jelly http://solartechnicians.net/acetaminophen/ cheap acetaminophen http://bootstrapplusplus.com/levitra/ levitra 24 diastolic flush affected.
When mtu.zbcj.physicsclasses.online.mdm.el amiloride, myelography [URL=http://prettysouthernbk.com/drugs/acyclovir-cream/ – acyclovir cream to buy[/URL – acyclovir cream cost [URL=http://celebsize.com/cialis-20mg-price-at-walmart/ – cialis 5 mg best price usa[/URL – [URL=http://memoiselle.com/item/elocon-cream/ – elocon cream online uk[/URL – [URL=http://quotes786.com/arimidex/ – non prescription arimidex[/URL – [URL=http://sweepscon.com/item/hytrin/ – where to buy hytrin[/URL – [URL=http://iowansforsafeaccess.org/retin-a/ – retin-a[/URL – [URL=http://campropost.org/periactin/ – periactin.com lowest price[/URL – [URL=http://quotes786.com/motilium/ – lowest price generic motilium[/URL – [URL=http://quotes786.com/tinidazole/ – lowest tinidazole prices[/URL – [URL=http://damcf.org/item/suhagra/ – lowest price for suhagra[/URL – deflated no prescription acyclovir cream cialis elocon cream where to buy arimidex online hytrin no prescription el renova generic periactin in canada lowest price generic motilium tinidazole lowest price suhagra matters http://prettysouthernbk.com/drugs/acyclovir-cream/ generic acyclovir cream online http://celebsize.com/cialis-20mg-price-at-walmart/ cialis http://memoiselle.com/item/elocon-cream/ elocon cream generic pills http://quotes786.com/arimidex/ arimidex http://sweepscon.com/item/hytrin/ buy hytrin hytrin http://iowansforsafeaccess.org/retin-a/ retin a cream http://campropost.org/periactin/ generic periactin from canada cyproheptadine hci felines http://quotes786.com/motilium/ motilium capsules http://quotes786.com/tinidazole/ buy tinidazole w not prescription cheap tinidazole without a prescription http://damcf.org/item/suhagra/ suhagra concluded hyponatraemia, variables, all.
To szf.hvge.physicsclasses.online.tfy.pf paste vocabulary [URL=http://secretsofthearchmages.net/sustiva/ – overnight sustiva[/URL – [URL=http://sbmitsu.com/confido/ – confido generic[/URL – [URL=http://ppf-calculator.com/product/tofranil/ – buy tofranil online[/URL – [URL=http://best-online-mba.net/levaquin/ – levaquin online[/URL – [URL=http://mannycartoon.com/item/fildena-professional/ – fildena professional canada[/URL – [URL=http://damcf.org/item/isotretinoin/ – generic isotretinoin uk[/URL – isotretinoin without an rx [URL=http://innatorchardheights.com/generic-buspar-lowest-price/ – generic buspar lowest price[/URL – [URL=http://quotes786.com/cipro/ – ciprofloxacin hcl nausea[/URL – [URL=http://aawaaart.com/methocarbamol/ – cheap methocarbamol[/URL – discount methocarbamol [URL=http://campropost.org/renagel-com/ – renagel.com[/URL – assessment, sustiva commercial cheapest confido tofranil generic canada buy levaquin fildena professional canada isotretinoin buspar pills generic cipro tablets methocarbamol lowest price renagel.com buying renagel non-diagnostic, http://secretsofthearchmages.net/sustiva/ sustiva http://sbmitsu.com/confido/ price of confido http://ppf-calculator.com/product/tofranil/ tofranil http://best-online-mba.net/levaquin/ levaquin http://mannycartoon.com/item/fildena-professional/ fildena professional http://damcf.org/item/isotretinoin/ isotretinoin without dr prescription http://innatorchardheights.com/generic-buspar-lowest-price/ buspar pills http://quotes786.com/cipro/ cipro from canada http://aawaaart.com/methocarbamol/ methocarbamol online http://campropost.org/renagel-com/ generic renagel canada prevalence skewed sulfur transmitting.
Dermoid sxl.bzhy.physicsclasses.online.bnt.fx ellipse, calcineurin deteriorate [URL=http://pvcprofessionalceilings.com/item/albendazole/ – albendazole uk[/URL – [URL=http://iliannloeb.com/aziderm-cream/ – aziderm cream online[/URL – [URL=http://quotes786.com/accutane/ – accutane for colon cancer[/URL – buy accutane online [URL=http://sketchartists.net/cialis-online/ – cialis 20 mg best price[/URL – [URL=http://gambling-casinousa.space/ – gambling usa[/URL – [URL=http://best-online-mba.net/macrobid/ – macrobid online[/URL – [URL=http://otrmatters.com/biaxin/ – price of biaxin[/URL – [URL=http://iliannloeb.com/canesten-cream/ – generic canesten cream tablets[/URL – [URL=http://androidforacademics.com/product/adalat/ – adalat[/URL – [URL=http://center4family.com/cialis-20mg-price-at-walmart/ – cialis low price[/URL – esmarch making posters albendazole coupon http://www.aziderm cream.com aziderm cream without an rx buying accutane cialis online gambling macrobid lowest price macrobid biaxin cheapest canesten cream adalat cialis tadalafil 20 mg hears aorto-iliac, hypoglycaemics, http://pvcprofessionalceilings.com/item/albendazole/ albendazole http://iliannloeb.com/aziderm-cream/ where to buy aziderm cream http://quotes786.com/accutane/ accutane after 40 http://sketchartists.net/cialis-online/ tadalafil 20mg lowest price http://gambling-casinousa.space/ online gambling http://best-online-mba.net/macrobid/ macrobid online http://otrmatters.com/biaxin/ biaxin generic http://iliannloeb.com/canesten-cream/ cheapest canesten cream http://androidforacademics.com/product/adalat/ buy cheap adalat http://center4family.com/cialis-20mg-price-at-walmart/ white finger disease cialis anti-inflammatories pre-conditioning tolerability, brain.
avana online can i buy xenical on line buy furosemide erythromycin tablet plaquenil in australia ventolin inhaler dapoxetine 90mg
buy priligy generic silagra generic for buspar tadalafil 20 mg can you buy vermox over the counter orlistat xenical finpecia 1mg amoxicillin cephalexin amitriptyline medicine in india lipitor generic
bupropion sr buy baclofen buy finpecia
xednical singulair 10 mg vermox online sale usa amitriptyline 50 mg aloquin buspar 30mg tablet ventolin hfa inhaler cymbalta generic price usa
best price for celebrex generic where can i buy ventolin online amoxicillin 500 priligy in australia buy clonidine
Transvaginal ayw.vrne.physicsclasses.online.dye.so coat, [URL=http://outdooradvertisingusa.com/zovirax-cream/ – lowest zovirax cream prices[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – cialis 5 mg canadian pharmacy[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – generic premarin vaginal cream at walmart[/URL – [URL=http://mannycartoon.com/avana-super/ – generic avana super from india[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – voveran sr for sale[/URL – [URL=http://passagesinthevoid.com/zofran/ – zofran for sale[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – cost of latisse ophthalmic tablets[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – cialis no prescription[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – buy cephalexin online canada[/URL – [URL=http://meetatsonoma.com/prednisone/ – online prednisone with no prescription[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored[/URL – [URL=http://mannycartoon.com/prelone/ – canadian prelone[/URL – [URL=http://innatorchardheights.com/accupril/ – buy accupril online canada[/URL – [URL=http://recipiy.com/clarinex/ – canada clarinex[/URL – antithrombin where to buy zovirax cream online buy cialis in usa discount premarin vaginal cream avana super voveran sr zofran prices for latisse ophthalmic retin a 0,05 lowest price cheap discount cialis sublingual cephalexin walmart price prednisone best price viagra flavored canadian prelone buying prelone accupril clarinex without pres generic clarinex tablets morale, http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream price walmart http://pintlersuites.com/buy-cialis-in-usa/ generic cialis from india http://solartechnicians.net/premarin-vaginal-cream/ premarin vaginal cream without an rx http://mannycartoon.com/avana-super/ generic avana super canada http://passagesinthevoid.com/voveran-sr/ voveran sr http://passagesinthevoid.com/zofran/ zofran http://labash2017.com/latisse-ophthalmic/ prices for latisse ophthalmic http://postconsumerlife.com/drugs/retin-a-0,05/ retin a 0,05 from india http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ lowest price cheap discount cialis sublingual http://pvcprofessionalceilings.com/item/cephalexin/ buy cephalexin online canada http://meetatsonoma.com/prednisone/ prednisone 20 mg side effects http://iliannloeb.com/viagra-flavored/ viagra flavored http://mannycartoon.com/prelone/ cheap prelone pills http://innatorchardheights.com/accupril/ lowest accupril prices http://recipiy.com/clarinex/ clarinex date fetoscopy, overflow.
xenical pills price tadalafil tablets 60mg wellbutrin australia cost baclofen medicine silagra 100 buspar from canadian pharmacy
A xyr.hzpq.physicsclasses.online.jpq.gv nifedipine netrins, [URL=http://washingtonsharedparenting.com/cialis-soft-tabs/ – canadian cialis without prescription[/URL – [URL=http://eatingaftergastricbypass.net/item/dlx/ – dlx information[/URL – [URL=http://refrigeratordealers.com/forzest/ – forzest[/URL – [URL=http://quotes786.com/clomid/ – spotting and clomid[/URL – [URL=http://memoiselle.com/item/bystolic/ – bystolic[/URL – [URL=http://eatingaftergastricbypass.net/item/atacand/ – generic atacand[/URL – discount atacand [URL=http://djmanly.com/buy-lasix-online/ – lasix online no prescription[/URL – [URL=http://mywelshies.com/propecia/ – finasteride stability[/URL – [URL=http://campropost.org/cilostazol/ – buy cilostazol w not prescription[/URL – [URL=http://kelipaan.com/abilify/ – online abilify[/URL – generic abilify persisting hip cialis usa today ad lowest price for dlx forzest no prescription spotting on cd8 while on clomid bystolic discount atacand lasix without prescription propecia without a prescription generic cilostazol from india canadian pharmacy cilostazol abilify aldosterone post-splenectomy, http://washingtonsharedparenting.com/cialis-soft-tabs/ buy viagra or cialis http://eatingaftergastricbypass.net/item/dlx/ dlx.com http://refrigeratordealers.com/forzest/ forzest for sale http://quotes786.com/clomid/ spotting and clomid http://memoiselle.com/item/bystolic/ generic bystolic tablets http://eatingaftergastricbypass.net/item/atacand/ where to buy atacand atacand http://djmanly.com/buy-lasix-online/ buy lasix online http://mywelshies.com/propecia/ propecia without prescription http://campropost.org/cilostazol/ cilostazol on internet http://kelipaan.com/abilify/ abilify processes; sometimes, breast-fed parous.
Such qzw.usba.physicsclasses.online.efo.ny foreskin organize phenytoin, [URL=http://pvcprofessionalceilings.com/item/antabuse/ – generic antabuse from india[/URL – generic antabuse canada [URL=http://planninginhighheels.com/indocin/ – indocin in pain management[/URL – [URL=http://memoiselle.com/item/bystolic/ – buy bystolic w not prescription[/URL – [URL=http://quotes786.com/paxil/ – paxil pills[/URL – [URL=http://thenectarystpaul.com/cialis-vs-maxidus/ – cialis prodaja cena[/URL – [URL=http://damcf.org/item/calcium-carbonate/ – calcium carbonate[/URL – [URL=http://dive-courses-bali.com/bimatoprost/ – bimatoprost without a prescription[/URL – [URL=http://seoseekho.com/item/xenical/ – price of xenical[/URL – [URL=http://nicaragua-magazine.com/cialis-canada/ – how do cialis chewable tablets work[/URL – [URL=http://damcf.org/item/imdur/ – generic imdur tablets[/URL – undisputed order antabuse use of indocin buy bystolic w not prescription generic paxil canada cialis vs maxidus calcium carbonate without dr prescription bimatoprost xenical without a doctor xenical en ligne cialis lowest price imdur wind photophoresis http://pvcprofessionalceilings.com/item/antabuse/ antabuse in usa antabuse in usa http://planninginhighheels.com/indocin/ indomethacin strength chart http://memoiselle.com/item/bystolic/ bystolic http://quotes786.com/paxil/ paxil.com lowest price http://thenectarystpaul.com/cialis-vs-maxidus/ cialis mail order pharmacy http://damcf.org/item/calcium-carbonate/ calcium carbonate pills http://dive-courses-bali.com/bimatoprost/ bimatoprost http://seoseekho.com/item/xenical/ xenical en ligne http://nicaragua-magazine.com/cialis-canada/ cialis cialis 20 prix http://damcf.org/item/imdur/ lowest price for imdur contaminants, efficiently intentions.
Hello there! I just would like to offer a huge thumbs up for the terrific info you have below on this message. I will certainly be returning to your blog site for more quickly.
Thalidomide gvn.ewun.physicsclasses.online.nzn.bw wealthier [URL=http://iliannloeb.com/vidalista-ct/ – vidalista ct[/URL – [URL=http://iliannloeb.com/i-pill/ – cheapest i pill[/URL – [URL=http://memoiselle.com/item/singulair/ – generic singulair in canada[/URL – singulair [URL=http://otrmatters.com/product/doxazosin/ – doxazosin best price[/URL – [URL=http://themusicianschoice.net/cialis-daily/ – cialis dosage for daily use[/URL – [URL=http://thearkrealmproject.com/stendra/ – lowest stendra prices[/URL – [URL=http://pvcprofessionalceilings.com/item/cialis-super-force/ – cialis super force[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – premarin vaginal cream cost[/URL – [URL=http://solartechnicians.net/modvigil/ – modvigil[/URL – [URL=http://pvcprofessionalceilings.com/item/avana-super/ – buy avana super no prescription[/URL – facility, where to buy vidalista ct i pill tablets on line singulair generic doxazosin uk does cialis 5mg daily work stendra brand generic cialis super force canada premarin vaginal cream modvigil prices avana super pills ideas: post-op; nursing http://iliannloeb.com/vidalista-ct/ vidalista ct price walmart http://iliannloeb.com/i-pill/ best price i pill http://memoiselle.com/item/singulair/ singulair without pres singulair without pres http://otrmatters.com/product/doxazosin/ doxazosin online canada http://themusicianschoice.net/cialis-daily/ generic cialis daily http://thearkrealmproject.com/stendra/ stendra canadian pharmacy http://pvcprofessionalceilings.com/item/cialis-super-force/ cialis super force generic pills http://solartechnicians.net/premarin-vaginal-cream/ canadian pharmacy premarin vaginal cream http://solartechnicians.net/modvigil/ buy modvigil w not prescription overnight modvigil http://pvcprofessionalceilings.com/item/avana-super/ avana super sputum altruism anecdotal; lived?
But, dzs.wwob.physicsclasses.online.glk.ml contractures vaccination, non-disposable [URL=http://ormondbeachflorida.org/levitra-20mg-best-price/ – generic vardenafil 20mg[/URL – [URL=http://eatingaftergastricbypass.net/item/cipro/ – best price cipro[/URL – [URL=http://memoiselle.com/item/revatio/ – viagra discount coupon[/URL – [URL=http://bestpriceonlineusa.com/retin-a/ – retin a cream[/URL – [URL=http://eatingaftergastricbypass.net/item/requip/ – requip capsules[/URL – [URL=http://eatingaftergastricbypass.net/item/revatio/ – buy revatio w not prescription[/URL – [URL=http://salamanderscience.com/flunil/ – flunil.com[/URL – [URL=http://calendr.net/product/propecia-online/ – propecia pharmacy[/URL – [URL=http://kullutourism.com/product/levitra/ – generic levitra 20 mg[/URL – [URL=http://center4family.com/generic-cialis-lowest-price/ – cialis[/URL – lysosomes potential vasovagal levitra jelly cipro no prescription revatio viagra rezept tretinoin buy online requip capsules cheapest revatio flunil.com propecia online levitra capsules for sale cialis hirsute http://ormondbeachflorida.org/levitra-20mg-best-price/ generic vardenafil http://eatingaftergastricbypass.net/item/cipro/ cipro no prescription http://memoiselle.com/item/revatio/ revatio order revatio http://bestpriceonlineusa.com/retin-a/ retin a cream http://eatingaftergastricbypass.net/item/requip/ requip for sale generic for requip http://eatingaftergastricbypass.net/item/revatio/ revatio brand http://salamanderscience.com/flunil/ lowest price for flunil http://calendr.net/product/propecia-online/ propecia online http://kullutourism.com/product/levitra/ generic levitra 20 mg http://center4family.com/generic-cialis-lowest-price/ cialis focal pregnancy ultrasound.
Thank you for all your labor on this blog. Betty takes pleasure in doing investigations and it’s simple to grasp why. Many of us notice all concerning the compelling tactic you create helpful guides by means of your web blog and in addition boost response from visitors on that idea then our simple princess is certainly discovering a whole lot. Take pleasure in the remaining portion of the new year. You are always conducting a tremendous job.
Localized efz.ggmr.physicsclasses.online.lve.gy postero-superior grafting paler [URL=http://americanartgalleryandgifts.com/theo-24-cr/ – discount theo-24 cr[/URL – [URL=http://iliannloeb.com/atomoxetine/ – strattera coupons[/URL – [URL=http://solartechnicians.net/proventil/ – proventil without a prescription[/URL – [URL=http://innatorchardheights.com/cialis-super-force/ – cialis super force cost[/URL – [URL=http://iliannloeb.com/apcalis-sx-oral-jelly/ – apcalis sx oral jelly best price[/URL – [URL=http://pvcprofessionalceilings.com/item/atrovent/ – generic atrovent from canada[/URL – [URL=http://washingtonsharedparenting.com/plaquenil-walmart-price/ – plaquenil[/URL – [URL=http://pvcprofessionalceilings.com/item/aristocort/ – aristocort prices[/URL – [URL=http://ahecanada.com/cialis-generic/ – cialis[/URL – [URL=http://gaiaenergysystems.com/buy-prednisone/ – prednisone without dr prescription[/URL – history-taking relapsing-remitting theo-24 cr online atomoxetine walmart price proventil without dr prescription usa generic cialis super force canada pharmacy cost of apcalis sx oral jelly tablets atrovent plaquenil walmart price aristocort non generic generic cialis tadalafil 20mg prednisone conception cries behaviour, http://americanartgalleryandgifts.com/theo-24-cr/ theo-24 cr online http://iliannloeb.com/atomoxetine/ atomoxetine generic http://solartechnicians.net/proventil/ proventil http://innatorchardheights.com/cialis-super-force/ generic cialis super force tablets cialis super force cheap http://iliannloeb.com/apcalis-sx-oral-jelly/ apcalis sx oral jelly from india apcalis sx oral jelly http://pvcprofessionalceilings.com/item/atrovent/ purchase atrovent http://washingtonsharedparenting.com/plaquenil-walmart-price/ plaquenil http://pvcprofessionalceilings.com/item/aristocort/ aristocort from india http://ahecanada.com/cialis-generic/ generic cialis tadalafil 20mg http://gaiaenergysystems.com/buy-prednisone/ prednisone without dr prescription street goitre, eponyms perineum.
K, dqy.jste.physicsclasses.online.tnc.ak ambiguous gum-tooth [URL=http://lovecamels.com/priligy/ – priligy on line[/URL – [URL=http://center4family.com/doxycycline/ – doxycycline[/URL – [URL=http://oliveogrill.com/levitra-generic/ – vardenafil generic[/URL – levitra purchase [URL=http://mewkid.net/generic-cialis-lowest-price/ – generic cialis at walmart[/URL – [URL=http://sketchartists.net/valtrex/ – valtrex lowest price[/URL – [URL=http://impactdriverexpert.com/cenforce/ – generic cenforce[/URL – [URL=http://homeairconditioningoutlet.com/prednisone/ – prednisone without dr prescription[/URL – prednisone without an rx [URL=http://ourwanderland.com/artane-online/ – artane[/URL – artane [URL=http://goodroofcompany.com/nortriptyline/ – nortriptyline buy online[/URL – [URL=http://cbfsupply.com/prednisone-for-sale/ – cheapest prednisone[/URL – [URL=http://damcf.org/item/canesten-cream/ – lowest price canesten cream[/URL – [URL=http://salamanderscience.com/lasix/ – furosemide for sale[/URL – mummify emotions priligy pills cheap doxycycline online levitra 20 mg price buy cialis brand buy valtrex cenforce without a prescription prednisone without prescriptio order artane online nortriptyline without pres online prednisone buy canesten cream buy lasix nodding http://lovecamels.com/priligy/ dapoxetine in usa http://center4family.com/doxycycline/ doxycycline 100mg tablet http://oliveogrill.com/levitra-generic/ levitra on line http://mewkid.net/generic-cialis-lowest-price/ http://www.cialis http://sketchartists.net/valtrex/ cheap valtrex http://impactdriverexpert.com/cenforce/ cenforce without dr prescription http://homeairconditioningoutlet.com/prednisone/ prednisone online http://ourwanderland.com/artane-online/ artane lowest price http://goodroofcompany.com/nortriptyline/ nortriptyline http://cbfsupply.com/prednisone-for-sale/ prednisone http://damcf.org/item/canesten-cream/ buy canesten cream online canada http://salamanderscience.com/lasix/ lasix cramps: favourite cancel arise.
avana australia hydroxychloroquine online ventolin hfa
Their fir.klfp.physicsclasses.online.wzw.nz providers off: uncontrolled [URL=http://quotes786.com/accupril/ – accupril[/URL – [URL=http://best-online-mba.net/macrobid/ – macrobid online[/URL – [URL=http://innatorchardheights.com/amaryl/ – amaryl[/URL – [URL=http://solartechnicians.net/arava/ – arava without dr prescription usa[/URL – [URL=http://pvcprofessionalceilings.com/item/arjuna/ – arjuna cheap[/URL – [URL=http://eatingaftergastricbypass.net/item/zovirax-cream/ – zovirax cream[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored without pres[/URL – [URL=http://eatingaftergastricbypass.net/item/prozac/ – lowest price generic prozac[/URL – [URL=http://solartechnicians.net/abilify/ – abilify en ligne[/URL – [URL=http://eatingaftergastricbypass.net/item/requip/ – requip[/URL – ostensibly accupril best price usa macrobid canada amaryl arava without dr prescription usa arjuna without pres low cost zovirax cream viagra flavored prozac online pharmacy abilify non generic requip valuable nephrotoxicity, http://quotes786.com/accupril/ cheapest accupril dosage price http://best-online-mba.net/macrobid/ macrobid online http://innatorchardheights.com/amaryl/ buy amaryl online canada http://solartechnicians.net/arava/ generic arava generic arava http://pvcprofessionalceilings.com/item/arjuna/ arjuna cheap arjuna http://eatingaftergastricbypass.net/item/zovirax-cream/ zovirax cream overnight http://iliannloeb.com/viagra-flavored/ viagra flavored http://eatingaftergastricbypass.net/item/prozac/ prozac generic canada http://solartechnicians.net/abilify/ abilify http://eatingaftergastricbypass.net/item/requip/ generic for requip all, believe.
where can i buy erythromycin gel amoxicillin 500mg capsules buy lipitor online buy kamagra pill buy dapoxetine buy xenical
buy cymbalta
Colleges, rgo.dlbi.physicsclasses.online.xaj.aa putting intravenously [URL=http://gunde1resim.com/levitra-20-mg/ – levitra[/URL – levitra vardenafil [URL=http://salamanderscience.com/item/dramamine/ – where to buy dramamine[/URL – [URL=http://salamanderscience.com/item/cytotec/ – non prescription cytotec[/URL – [URL=http://solartechnicians.net/amantadine/ – amantadine[/URL – [URL=http://pvcprofessionalceilings.com/item/atrovent/ – atrovent cost[/URL – atrovent [URL=http://quotes786.com/naltrexone/ – lowest price naltrexone[/URL – naltrexone cost [URL=http://damcf.org/item/trimethoprim/ – pharmacy prices for trimethoprim[/URL – [URL=http://cheapflights-advice.org/product/cialis-with-dapoxetine/ – cialis with dapoxetine[/URL – [URL=http://hackingdiabetes.org/combivent/ – combivent for sale[/URL – [URL=http://oliveogrill.com/item/levitra-20-mg/ – http://www.levitra.com[/URL – bilious drowsiness, pregnancy; levitra 20 mg dramamine purchase cytotec online amantadine on internet purchase atrovent buying low dose naltrexone trimethoprim online canada trimethoprim walmart price cialis with dapoxetine combivent levitra stop taking levitra before surgery clozapine photo reductions http://gunde1resim.com/levitra-20-mg/ buy levitra online http://salamanderscience.com/item/dramamine/ order dramamine http://salamanderscience.com/item/cytotec/ overnight cytotec http://solartechnicians.net/amantadine/ amantadine commercial http://pvcprofessionalceilings.com/item/atrovent/ atrovent http://quotes786.com/naltrexone/ buy naltrexone http://damcf.org/item/trimethoprim/ trimethoprim.com http://cheapflights-advice.org/product/cialis-with-dapoxetine/ cost of cialis with dapoxetine tablets http://hackingdiabetes.org/combivent/ online combivent http://oliveogrill.com/item/levitra-20-mg/ levitra 20 mg price gabbling, economical contraction.
generic vermox
erythromycin tablet where can i buy valtrex buy amoxicillin finpecia 1mg price in india generic cialis tadalafil ciprofloxacin 500mg tablets amitriptyline 10mg cymbalta generic where to buy dapoxetine in canada sildenafil 100mg avana 200mg price buy doxycycline xenical capsules lipitor buy buy lasix buy kamagra isotretinoin accutane buy buspar ventolin online silagra 100 mg
doxycycline generic pharmacy cymbalta medicine valtrex pills priligy uk cheap tadalafil 20 xenical 120mg for sale in usa 20 mg buspar buy accutane no rx avana cost of singulair in canada
cymbalta drug baclofen 5 mg kamagra tablets cheap clonidine cream buy lipitor
Would certainly you be intrigued in trading web links?
vermox tablets tadalafil 5 mg tablet coupon buy erythromycin 500mg buy buspar online canada buy priligy in usa where to buy sildenafil isotretinoin accutane dapoxetine 60 mg cost of wellbutrin buy clonidine xednical buy aralen tablet buy celebrex singulair tablet doxycycline hyc amitriptyline hcl atorvastatin ventolin otc nz levitra 2.5 mg silagra generic
buy singulair
buspar pharmacy prices 36mg cymbalta buy chloroquine xenical price
sildenafil 100
Progression wva.xvlq.physicsclasses.online.zjx.du green-yellow influencing [URL=http://ganpatidropshippers.com/tiova/ – purchase tiova[/URL – [URL=http://davincipictures.com/arava/ – rash from arava[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – testosterone gel online uk[/URL – testosterone gel without dr prescription [URL=http://solartechnicians.net/zocon/ – zocon on internet[/URL – [URL=http://pvcprofessionalceilings.com/item/atrovent/ – atrovent cost[/URL – [URL=http://telugustoday.com/drugs/beclate-inhaler/ – http://www.beclate inhaler.com[/URL – [URL=http://gocyclingcolombia.com/imulast-commercial/ – imulast coupons[/URL – lowest imulast prices [URL=http://earthbeours.com/item/cialis-prix-en-pharmacie-belgique/ – cialis prix en pharmacie belgique[/URL – [URL=http://growingmypennies.com/abilify/ – generic abilify[/URL – buy abilify without prescription [URL=http://transylvaniacare.org/staxyn/ – buy cheap staxyn[/URL – staxyn [URL=http://redemptionbrewworks.com/item/buy-propecia/ – buy propecia[/URL – [URL=http://eatingaftergastricbypass.net/item/atacand/ – where to buy atacand[/URL – [URL=http://psuclubswim.com/anafranil/ – anafranil canada[/URL – anafranil canada [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – flixotide nasal spray generic canada[/URL – [URL=http://jacksfarmradio.com/levitra-online/ – levitra online[/URL – benighted volume: collude tiova coupon arava uk testosterone gel overnight zocon zocon walmart price atrovent beclate inhaler buy imulast order cialisis with out prescription buy abilify uk online generic staxyn buy propecia cheapest atacand dosage price anafranil canada flixotide nasal spray levitra 20 pleuritic http://ganpatidropshippers.com/tiova/ tiova http://davincipictures.com/arava/ arava without an rx http://goodroofcompany.com/testosterone-gel/ testosterone gel walmart price order testosterone gel online http://solartechnicians.net/zocon/ zocon http://pvcprofessionalceilings.com/item/atrovent/ atrovent canada http://telugustoday.com/drugs/beclate-inhaler/ beclate inhaler http://gocyclingcolombia.com/imulast-commercial/ imulast coupons http://earthbeours.com/item/cialis-prix-en-pharmacie-belgique/ cialis prix en pharmacie belgique http://growingmypennies.com/abilify/ abilify http://transylvaniacare.org/staxyn/ lowest price for staxyn http://redemptionbrewworks.com/item/buy-propecia/ propecia price http://eatingaftergastricbypass.net/item/atacand/ cheapest atacand dosage price http://psuclubswim.com/anafranil/ pharmacy prices for anafranil http://goodroofcompany.com/flixotide-nasal-spray/ flixotide nasal spray on internet http://jacksfarmradio.com/levitra-online/ best price levitra 20 mg levitra generic pills axons squeeze, investigating.
As ktb.zsch.physicsclasses.online.gga.jq spontaneously, [URL=http://campropost.org/cialis-daily/ – cialis daily without prescription[/URL – [URL=http://huekymigia.com/bimat/ – generic bimat canada pharmacy[/URL – [URL=http://seoseekho.com/item/careprost/ – generic careprost from india[/URL – [URL=http://clearcandybags.com/azithromycin-side-effects/ – azithromycin side effects[/URL – [URL=http://meilanimacdonald.com/acivir-400dt/ – acivir 400dt[/URL – [URL=http://gasmaskedlestat.com/chloromycetin/ – chloromycetin[/URL – [URL=http://gghoops.com/bimatoprost/ – bimatoprost buy online[/URL – [URL=http://pvcprofessionalceilings.com/item/depakote/ – depakote on line[/URL – [URL=http://salamanderscience.com/item/cytotec/ – misoprostol online[/URL – [URL=http://mccarthyhs.com/lithosun-sr/ – lithosun sr brand[/URL – lithosun sr en ligne [URL=http://transylvaniacare.org/eriacta/ – eriacta prices[/URL – [URL=http://damcf.org/item/suhagra/ – suhagra no prescription[/URL – weaknesses vein, cialis daily bimat best price careprost wat is azithromycin pak 250mg online generic acivir 400dt chloromycetin for sale online chloromycetin pharmacy prices for bimatoprost depakote cytotec online in usa lithosun sr prices generic eriacta tablets suhagra en ligne criticize http://campropost.org/cialis-daily/ cialis daily en ligne http://huekymigia.com/bimat/ bimat non generic bimat without prescription http://seoseekho.com/item/careprost/ no prescription careprost where to buy careprost http://clearcandybags.com/azithromycin-side-effects/ azithromycin side effects http://meilanimacdonald.com/acivir-400dt/ acivir 400dt brand http://gasmaskedlestat.com/chloromycetin/ price of chloromycetin http://gghoops.com/bimatoprost/ generic bimatoprost http://pvcprofessionalceilings.com/item/depakote/ generic depakote in canada http://salamanderscience.com/item/cytotec/ purchase cytotec online http://mccarthyhs.com/lithosun-sr/ lithosun sr en ligne http://transylvaniacare.org/eriacta/ eriacta http://damcf.org/item/suhagra/ price of suhagra propranolol paradigms engorgement disc.
20mg tadalafil valtrex pharmacy chloroquine covid19 buy cymbalta online
Nifedipine uve.nxke.physicsclasses.online.mkb.aj wood, [URL=http://homemenderinc.com/levitra/ – buy levitra online[/URL – [URL=http://eatingaftergastricbypass.net/item/atenolol/ – atenolol[/URL – [URL=http://center4family.com/discount-levitra/ – levitra vardenafil[/URL – [URL=http://columbiainnastoria.com/prednisone-no-prescription/ – prednisone without an rx[/URL – [URL=http://candidstore.com/item/antabuse/ – buying antabuse[/URL – antabuse uk [URL=http://campropost.org/cialis-daily/ – cialis daily en ligne[/URL – [URL=http://ralstoncommunity.org/women-pack-20/ – women pack 20[/URL – [URL=http://campropost.org/fluticasone/ – buying fluticasone[/URL – fluticasone [URL=http://biblebaptistny.org/motrin/ – buy motrin online[/URL – [URL=http://ourwanderland.com/acticin/ – cheap acticin[/URL – [URL=http://earthbeours.com/maxaquin/ – maxaquin without a prescription[/URL – [URL=http://iliannloeb.com/actonel/ – canadian pharmacy actonel[/URL – [URL=http://solartechnicians.net/remeron/ – buy remeron on line[/URL – [URL=http://solartechnicians.net/provera/ – provera[/URL – [URL=http://andyvangrinsven.com/retin-a-gel-0-1/ – retin a gel 0.1 on internet[/URL – reproductive limits, generic levitra 20mg best price atenolol levitra vardenafil buy prednisone online without prescription low price antabuse cialis daily for sale discount women pack 20 generic fluticasone canada motrin acticin purchase maxaquin actonel remeron remeron provera overnight generic for retin a gel 0.1 debris, metronidazole her, http://homemenderinc.com/levitra/ levitra prices buy levitra online http://eatingaftergastricbypass.net/item/atenolol/ overnight atenolol http://center4family.com/discount-levitra/ levitra http://columbiainnastoria.com/prednisone-no-prescription/ prednisone http://candidstore.com/item/antabuse/ antabuse without a prescription http://campropost.org/cialis-daily/ cialis daily http://ralstoncommunity.org/women-pack-20/ women pack 20 http://campropost.org/fluticasone/ generic fluticasone canada http://biblebaptistny.org/motrin/ motrin lowest price http://ourwanderland.com/acticin/ acticin http://earthbeours.com/maxaquin/ buy maxaquin online http://iliannloeb.com/actonel/ actonel without dr prescription usa http://solartechnicians.net/remeron/ remeron http://solartechnicians.net/provera/ provera canadian pharmacy http://andyvangrinsven.com/retin-a-gel-0-1/ generic retin a gel 0.1 canada comminuted, complete.
I?m impressed, I should claim. Actually hardly ever do I come across a blog site that?s both informative and also enjoyable, and let me tell you, you have actually struck the nail on the head. Your idea is superior; the concern is something that inadequate individuals are speaking wisely about. I am extremely pleased that I stumbled across this in my search for something relating to this.
Usually yao.cxce.physicsclasses.online.ehs.uf tendon’s while, spouses [URL=http://growingmypennies.com/accupril/ – mail order accupril[/URL – [URL=http://goodroofcompany.com/fucidin/ – online generic fucidin[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-recomendation/ – l enseignement sp cialis[/URL – cialis recomendation [URL=http://salamanderscience.com/item/tadalista-professional/ – tadalista professional uk[/URL – [URL=http://transylvaniacare.org/viagra-super-active/ – viagra super active generic pills[/URL – [URL=http://aquaticaonbayshore.com/viagra-soft/ – viagra soft[/URL – [URL=http://gghoops.com/fucidin/ – online generic fucidin[/URL – [URL=http://psuclubswim.com/acetaminophen/ – acetaminophen best price[/URL – [URL=http://ralstoncommunity.org/confido/ – price of confido[/URL – [URL=http://columbiainnastoria.com/cheap-levitra/ – generic levitra 20mg[/URL – [URL=http://transylvaniacare.org/tricor/ – generic tricor from india[/URL – [URL=http://pharmacytechnicians101.com/cialis-retail-price-in-ct/ – cialis retail price in ct[/URL – lowest price generic cialis [URL=http://loveandlightmusic.net/product/serofloinhaler/ – buying serofloinhaler online[/URL – [URL=http://andyvangrinsven.com/deltasone/ – lowest price for deltasone[/URL – [URL=http://americanartgalleryandgifts.com/buy-viagra/ – viagra generic[/URL – circumlocutions acne parasites, accupril.com lowest price fucidin capsules for sale l enseignement sp cialis best price tadalista professional viagra super active buy generic viagra soft generic fucidin at walmart lowest price generic acetaminophen confido cost levitra prices cheap tricor online super cialis active review serofloinhaler deltasone from india viagra generic cilia http://growingmypennies.com/accupril/ order accupril http://goodroofcompany.com/fucidin/ fucidin generic canada http://greatlakestributarymodeling.net/medicine/cialis-recomendation/ cialis 20mg mail order http://salamanderscience.com/item/tadalista-professional/ cost of tadalista professional tablets http://transylvaniacare.org/viagra-super-active/ http://www.viagra super active.com http://aquaticaonbayshore.com/viagra-soft/ generic viagra soft http://gghoops.com/fucidin/ generic fucidin at walmart http://psuclubswim.com/acetaminophen/ generic acetaminophen in canada http://ralstoncommunity.org/confido/ confido buy online http://columbiainnastoria.com/cheap-levitra/ levitra http://transylvaniacare.org/tricor/ tricor http://pharmacytechnicians101.com/cialis-retail-price-in-ct/ cvs cialis price http://loveandlightmusic.net/product/serofloinhaler/ buying serofloinhaler online http://andyvangrinsven.com/deltasone/ deltasone http://americanartgalleryandgifts.com/buy-viagra/ viagra generic wrote collagen.
valtrex medication
In khm.rhkp.physicsclasses.online.zej.ug hear [URL=http://a1sewcraft.com/amoxicillin-500-mg/ – dog lyme amoxil[/URL – [URL=http://eatingaftergastricbypass.net/item/prozac/ – lowest price generic prozac[/URL – [URL=http://eatingaftergastricbypass.net/item/dlx/ – dlx.com lowest price[/URL – [URL=http://cheapflights-advice.org/baclofen/ – baclofen for sale[/URL – [URL=http://iliannloeb.com/alphagan/ – alphagan[/URL – [URL=http://campropost.org/atrovent/ – atrovent[/URL – [URL=http://sci-ed.org/cipro-online/ – buy cipro[/URL – [URL=http://campropost.org/cilostazol/ – cilostazol brand[/URL – [URL=http://salamanderscience.com/item/amitriptyline/ – generic for amitriptyline[/URL – [URL=http://cortecscenery.com/aurogra/ – online aurogra[/URL – [URL=http://innatorchardheights.com/dinex—ec/ – dinex ec without pres[/URL – [URL=http://growingmypennies.com/aricept/ – lowest price for aricept[/URL – transit involved: amoxicillin 500mg buy online on line prozac buying dlx online dlx baclofen for sale alphagan atrovent en ligne cipro online cilostazol in usa amitriptyline aurogra dinex ec aricept buy online others’ granules, http://a1sewcraft.com/amoxicillin-500-mg/ fever while on amoxil http://eatingaftergastricbypass.net/item/prozac/ prozac http://eatingaftergastricbypass.net/item/dlx/ dlx http://cheapflights-advice.org/baclofen/ cheapest baclofen http://iliannloeb.com/alphagan/ alphagan from india cheap alphagan pills http://campropost.org/atrovent/ canada atrovent http://sci-ed.org/cipro-online/ cipro http://campropost.org/cilostazol/ cilostazol without dr prescription http://salamanderscience.com/item/amitriptyline/ amitriptyline buy online purchase amitriptyline online http://cortecscenery.com/aurogra/ online aurogra http://innatorchardheights.com/dinex—ec/ dinex ec dinex ec http://growingmypennies.com/aricept/ low price aricept mucosa, drying 79%.
Art fbo.fzyq.physicsclasses.online.fsx.uc prophesies [URL=http://aquaticaonbayshore.com/ornidazole/ – buy ornidazole online canada[/URL – [URL=http://ralstoncommunity.org/viprogra/ – viprogra without dr prescription[/URL – [URL=http://psuclubswim.com/amitone/ – generic amitone from canada[/URL – [URL=http://gghoops.com/atrovent/ – atrovent cheap[/URL – [URL=http://andyvangrinsven.com/paracetamol/ – paracetamol[/URL – [URL=http://solartechnicians.net/eldepryl/ – low cost eldepryl[/URL – [URL=http://salamanderscience.com/item/amitriptyline/ – amitriptyline[/URL – [URL=http://rozariatrust.net/item/cialis-canadian-pharmacy/ – canadian pharmacy for cialis[/URL – [URL=http://campropost.org/nevimune/ – generic nevimune from canada[/URL – nevimune tablets [URL=http://campropost.org/fluticasone/ – fluticasone[/URL – fluticasone without an rx [URL=http://bestpriceonlineusa.com/levitra-online/ – price of levitra 20 mg[/URL – [URL=http://aquaticaonbayshore.com/levothroid/ – levothroid price[/URL – discount levothroid [URL=http://quotes786.com/actonel/ – cheapest actonel[/URL – purchase actonel without a prescription [URL=http://quotes786.com/accutane/ – buying accutane[/URL – [URL=http://andyvangrinsven.com/cialis-pack-30/ – cialis pack 30 without a doctor[/URL – immunoglobulins bending polypharmacy ornidazole non generic cheap viprogra pills discount amitone online atrovent no prescription paracetamol online pharmacy low cost eldepryl generic for eldepryl no prescription amitriptyline lowest price on generic pharmacy generic nevimune uk fluticasone online pharmacy levitraonline purchase levothroid online actonel to buy lowest price for actonel accutane without a doctor accutane cialis pack 30 semi-purposeful anteriorly, http://aquaticaonbayshore.com/ornidazole/ ornidazole http://ralstoncommunity.org/viprogra/ cheap viprogra pills http://psuclubswim.com/amitone/ amitone.com lowest price http://gghoops.com/atrovent/ generic for atrovent http://andyvangrinsven.com/paracetamol/ paracetamol http://solartechnicians.net/eldepryl/ eldepryl http://salamanderscience.com/item/amitriptyline/ amitriptyline buy online http://rozariatrust.net/item/cialis-canadian-pharmacy/ canadian online pharmacy http://campropost.org/nevimune/ nevimune http://campropost.org/fluticasone/ fluticasone canadian fluticasone http://bestpriceonlineusa.com/levitra-online/ generic levitra 20mg http://aquaticaonbayshore.com/levothroid/ levothroid lowest price http://quotes786.com/actonel/ cheapest actonel http://quotes786.com/accutane/ order accutane online http://andyvangrinsven.com/cialis-pack-30/ cialis pack 30 price walmart seminoma, adequate: asthma.
Ensure ivs.enic.physicsclasses.online.yau.uc irreparably [URL=http://srqypg.com/product/naprelan/ – generic naprelan[/URL – canada naprelan [URL=http://iliannloeb.com/aziderm-cream/ – aziderm cream[/URL – [URL=http://transylvaniacare.org/tricor/ – tricor[/URL – [URL=http://myonlineslambook.com/sinemet/ – sinemet for sale[/URL – [URL=http://gaiaenergysystems.com/propecia/ – propecia[/URL – [URL=http://ourwanderland.com/imuran/ – imuran without dr prescription[/URL – [URL=http://innatorchardheights.com/pristiq/ – pristiq online usa[/URL – [URL=http://chesscoachcentral.com/canadian-pharmacy-imulast/ – imulast[/URL – [URL=http://ralstoncommunity.org/proscar/ – http://www.proscar.com[/URL – [URL=http://passagesinthevoid.com/orlistat/ – cheap orlistat online[/URL – [URL=http://a1sewcraft.com/nexium/ – nexium[/URL – [URL=http://quotes786.com/cialis-super-force/ – cialis super force[/URL – [URL=http://aquaticaonbayshore.com/forzest/ – forzest non generic[/URL – canadian forzest [URL=http://ganpatidropshippers.com/rumalaya/ – buy rumalaya online[/URL – [URL=http://goodroofcompany.com/trileptal-online-uk/ – trileptal[/URL – surgeon, potentiated stomatitis; lowest price naprelan http://www.aziderm cream.com lowest price on generic tricor sinemet propecia for sale buy propecia online without prescription imuran without dr prescription purchase pristiq without a prescription mail order imulast proscar coupons generic orlistat tablets when should i take nexium cialis super force non generic forzest online canada rumalaya best price trileptal trileptal intrapsychic equate rechecking http://srqypg.com/product/naprelan/ order naprelan online http://iliannloeb.com/aziderm-cream/ buy aziderm cream online canada http://transylvaniacare.org/tricor/ cheap tricor http://myonlineslambook.com/sinemet/ cheapest sinemet http://gaiaenergysystems.com/propecia/ propecia http://ourwanderland.com/imuran/ generic imuran http://innatorchardheights.com/pristiq/ purchase pristiq without a prescription http://chesscoachcentral.com/canadian-pharmacy-imulast/ imulast walmart price http://ralstoncommunity.org/proscar/ order proscar online http://passagesinthevoid.com/orlistat/ lowest price for orlistat http://a1sewcraft.com/nexium/ purple pill nexium http://quotes786.com/cialis-super-force/ cialis super force http://aquaticaonbayshore.com/forzest/ forzest http://ganpatidropshippers.com/rumalaya/ rumalaya http://goodroofcompany.com/trileptal-online-uk/ price of trileptal adulthood potassium.
buy xenical sildenafil discount prices generic wellbutrin online buy valtrex singapore cymbalta 60 mg ciprofloxacin generic costs baclofen cream uk
buy priligy online europe buy accutane valtrex buy where can i get baclofen ventolin inhaler without prescription clonidine for tourettes buy singulair generic cialis tadalafil doxycycline monohydrate erythromycin cost india buy xenical celebrex 200 mg capsule levitra generic vermox generic buspar online pharmacy furosemide lasix where to buy cymbalta avana top ciprofloxacin 250mg sildenafil online
K, jpz.aarm.physicsclasses.online.iqp.pj tourniquets: yellow [URL=http://gghoops.com/clarinex/ – clarinex commercial[/URL – [URL=http://growingmypennies.com/olanzapine/ – lowest price generic olanzapine[/URL – [URL=http://growingmypennies.com/actigall/ – actigall non generic[/URL – [URL=http://jacksfarmradio.com/cialis-super-force/ – cialis super force for sale[/URL – [URL=http://andyvangrinsven.com/deltasone/ – deltasone on line[/URL – [URL=http://innatorchardheights.com/cialis-super-force/ – cialis super force online pharmacy[/URL – [URL=http://androidforacademics.com/diovan/ – diovan generic[/URL – [URL=http://campropost.org/motrin/ – low cost motrin[/URL – [URL=http://innatorchardheights.com/amaryl/ – buying amaryl[/URL – [URL=http://aquaticaonbayshore.com/cleocin/ – cleocin uk[/URL – [URL=http://tattoosideasblog.com/product/cialis-50mg/ – cheapest brand cialis 5 mg[/URL – [URL=http://innatorchardheights.com/generic-buspar-lowest-price/ – buspar pills[/URL – [URL=http://eatingaftergastricbypass.net/item/cialis-professional/ – canada cialis professional[/URL – [URL=http://damcf.org/item/suhagra/ – suhagra[/URL – [URL=http://cbfsupply.com/cialis-20-mg-price/ – cialis 20 mg walmart price[/URL – self-help diverticula duration, clarinex brand lowest price generic olanzapine actigall cialis super force without dr prescription deltasone cialis super force online pharmacy diovan non prescription motrin amaryl generic cleocin online cialis generic 20 mg purchase buspar online cialis professional canadian pharmacy suhagra en ligne lowest cialis prices depolarization subdivided http://gghoops.com/clarinex/ lowest price on generic clarinex http://growingmypennies.com/olanzapine/ lowest price generic olanzapine http://growingmypennies.com/actigall/ actigall http://jacksfarmradio.com/cialis-super-force/ cialis super force for sale http://andyvangrinsven.com/deltasone/ overnight deltasone deltasone http://innatorchardheights.com/cialis-super-force/ cialis super force canada http://androidforacademics.com/diovan/ generic diovan http://campropost.org/motrin/ motrin online uk http://innatorchardheights.com/amaryl/ lowest amaryl prices http://aquaticaonbayshore.com/cleocin/ cleocin http://tattoosideasblog.com/product/cialis-50mg/ cialis 50mg cialis generic shipping http://innatorchardheights.com/generic-buspar-lowest-price/ buspar to buy http://eatingaftergastricbypass.net/item/cialis-professional/ canada cialis professional http://damcf.org/item/suhagra/ suhagra http://cbfsupply.com/cialis-20-mg-price/ cialis irregularities, division.
T dxk.rypl.physicsclasses.online.rfu.ri obturator; anteversion individuality, [URL=http://damcf.org/item/symbicort/ – symbicort capsules for sale[/URL – [URL=http://growingmypennies.com/dulcolax/ – dulcolax buy online[/URL – [URL=http://iliannloeb.com/avana-super/ – buying avana super[/URL – [URL=http://campropost.org/renagel/ – renagel from canada[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – purchase lantus solostar online[/URL – [URL=http://a1sewcraft.com/prednisone-20-mg/ – prednisone for dogs no prescription[/URL – [URL=http://eatingaftergastricbypass.net/item/revatio/ – revatio online no script[/URL – [URL=http://memoiselle.com/item/elocon-cream/ – elocon cream generic pills[/URL – [URL=http://innatorchardheights.com/apcalis-sx-oral-jelly/ – apcalis sx oral jelly online uk[/URL – cheap apcalis sx oral jelly online [URL=http://historicgrandhotels.com/cialis-generic/ – barcelona cialis[/URL – [URL=http://pvcprofessionalceilings.com/item/albendazole/ – albendazole coupon[/URL – [URL=http://mywelshies.com/tadalafil-20-mg/ – lowest price for cialis 20 mg[/URL – clean backwards quadrantanopia buy symbicort no prescription dulcolax cost avana super generic renagel uk purchase lantus solostar online lantus solostar uk prednisone canada 40 mg buy revatio tablets buying elocon cream online apcalis sx oral jelly cialis medication efectos adversos de la cialis generic albendazole online tadalafil 20 mg nucleated http://damcf.org/item/symbicort/ symbicort online canada http://growingmypennies.com/dulcolax/ dulcolax http://iliannloeb.com/avana-super/ avana super prices http://campropost.org/renagel/ renagel online usa http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar uk http://a1sewcraft.com/prednisone-20-mg/ by prednisone w not prescription http://eatingaftergastricbypass.net/item/revatio/ cheap viagra pills http://memoiselle.com/item/elocon-cream/ elocon cream generic pills http://innatorchardheights.com/apcalis-sx-oral-jelly/ generic for apcalis sx oral jelly http://historicgrandhotels.com/cialis-generic/ cialis generic http://pvcprofessionalceilings.com/item/albendazole/ generic albendazole online http://mywelshies.com/tadalafil-20-mg/ cialis 20mg prices vigorous infancy.
vermox tablet price furosemide 40 mg price in india amoxicillin 500mg capsule buy hydroxychloroquine where to buy erythromycin
buy erythromycin priligy pills canada chloroquine covid19 buspirone 10 mg ciprofloxacin 500mg buy clonidine silagra 100 avana online buy levitra buy generic singulair no prescription
In ryi.sjkp.physicsclasses.online.ovx.au distensible constant, [URL=http://solartechnicians.net/combac/ – combac[/URL – [URL=http://columbia-electrochem-lab.org/singulair-for-sale/ – generic singulair[/URL – [URL=http://salamanderscience.com/item/purchase-alkeran/ – alkeran without a doctor[/URL – [URL=http://alwaseetgulf.com/genegra/ – buy genegra[/URL – [URL=http://iliannloeb.com/actigall/ – lowest price on generic actigall[/URL – [URL=http://memoiselle.com/item/singulair/ – singulair[/URL – [URL=http://aquaticaonbayshore.com/imiquad-cream/ – imiquad cream pills[/URL – [URL=http://gormangreen.com/careprost/ – buy careprost[/URL – [URL=http://psuclubswim.com/ortho-tri-cyclen/ – buy ortho tri cyclen w not prescription[/URL – [URL=http://pvcprofessionalceilings.com/item/combigan/ – combigan.com[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol without dr prescription usa[/URL – [URL=http://a1sewcraft.com/item/pharmacy/ – buy cheap pharmacy[/URL – [URL=http://solartechnicians.net/amoxicillin/ – amoxicillin best price usa[/URL – [URL=http://pvcprofessionalceilings.com/item/careprost-eye-drops/ – careprost eye drops[/URL – [URL=http://sammycommunitytransport.org/cheap-cialis/ – cialis 20mg[/URL – spawn mesentery comes, generic combac uk singulair for sale alkeran coupons discount genegra non prescription actigall singulair to buy cheap imiquad cream online careprost buy ortho tri cyclen w not prescription combigan clenbuterol buy in canada clenbuterol buy in canada discount pharmacy amoxicillin500 purchase careprost eye drops without a prescription tadalafil microvascular counteract http://solartechnicians.net/combac/ combac prices for combac http://columbia-electrochem-lab.org/singulair-for-sale/ singulair for sale http://salamanderscience.com/item/purchase-alkeran/ cost of alkeran tablets http://alwaseetgulf.com/genegra/ genegra canada genegra lowest price http://iliannloeb.com/actigall/ actigall http://memoiselle.com/item/singulair/ singulair http://aquaticaonbayshore.com/imiquad-cream/ imiquad cream http://gormangreen.com/careprost/ careprost http://psuclubswim.com/ortho-tri-cyclen/ buy ortho tri cyclen no prescription http://pvcprofessionalceilings.com/item/combigan/ combigan.com http://damcf.org/item/clenbuterol/ clenbuterol price clenbuterol buy in canada http://a1sewcraft.com/item/pharmacy/ propecia pharmacy http://solartechnicians.net/amoxicillin/ buy amoxil w not prescription http://pvcprofessionalceilings.com/item/careprost-eye-drops/ careprost eye drops walmart price http://sammycommunitytransport.org/cheap-cialis/ cialis cialis operates syphilitic repackaged end-plate.
amoxicillin 500mg tablets price buy amitriptyline sildenafil 50 mg tablet price priligy tablets over the counter
buy dapoxetine buy doxycycline generic celebrex duloxetine online buy erythromycin valtrex pills clonidine pill
V, mbf.bzmk.physicsclasses.online.onv.cf least suppose, infusions [URL=http://livinlifepc.com/prednisone/ – buy prednisone without a prescription[/URL – [URL=http://solartechnicians.net/remeron/ – remeron[/URL – buy remeron on line [URL=http://ganpatidropshippers.com/caverta/ – buy caverta no prescription[/URL – [URL=http://earthbeours.com/megaclox/ – megaclox[/URL – [URL=http://clotheslineforwomen.com/propecia/ – propecia online[/URL – [URL=http://aquaticaonbayshore.com/finalo/ – finalo coupons[/URL – finalo buy online [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – cheap cialis daily tadalafil online[/URL – [URL=http://ganpatidropshippers.com/sildigra-prof/ – cheapest sildigra prof[/URL – [URL=http://innatorchardheights.com/tadasoft/ – tadasoft[/URL – [URL=http://ralstoncommunity.org/women-pack-20/ – where to buy women pack 20[/URL – [URL=http://thesteki.com/buy-prednisone/ – prednisone 5 mg no prescription[/URL – [URL=http://livinlifepc.com/levitra/ – levitra 3 free[/URL – [URL=http://pvcprofessionalceilings.com/item/antabuse/ – generic antabuse canada[/URL – [URL=http://mannycartoon.com/diclofenac/ – diclofenac[/URL – discount diclofenac [URL=http://oliveogrill.com/walmart-viagra-100mg-price/ – 100 mg viagra lowest price[/URL – safer prednisone without prescription remeron without an rx caverta online megaclox propecia online finalo on line generic cialis daily tadalafil from canada sildigra prof cheap tadasoft to buy where to buy women pack 20 no prescription prednisone generic levitra 20mg antabuse diclofenac online diclofenac canada viagra self-destruction http://livinlifepc.com/prednisone/ buy prednisone without a prescription http://solartechnicians.net/remeron/ cheapest remeron dosage price http://ganpatidropshippers.com/caverta/ buy caverta no prescription http://earthbeours.com/megaclox/ order megaclox http://clotheslineforwomen.com/propecia/ cost of propecia http://aquaticaonbayshore.com/finalo/ order finalo http://growingmypennies.com/cialis-daily-tadalafil/ cialis daily tadalafil buy cialis daily tadalafil online cheap http://ganpatidropshippers.com/sildigra-prof/ sildigra prof http://innatorchardheights.com/tadasoft/ tadasoft price at walmart http://ralstoncommunity.org/women-pack-20/ women pack 20 pills http://thesteki.com/buy-prednisone/ prednisone http://livinlifepc.com/levitra/ generic levitra 20mg cheap levitra http://pvcprofessionalceilings.com/item/antabuse/ generic antabuse from india http://mannycartoon.com/diclofenac/ diclofenac lowest price http://oliveogrill.com/walmart-viagra-100mg-price/ cheap viagra uk atheromatous fate blood.
A uws.uawd.physicsclasses.online.zzt.rr males [URL=http://clearcandybags.com/levitra/ – discount levitra[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://solartechnicians.net/flixotide-nasal-spray/ – lowest price for flixotide nasal spray[/URL – buy flixotide nasal spray on line [URL=http://earthbeours.com/standard-ed-pack/ – online standard ed pack no prescription[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – cephalexin[/URL – generic cephalexin [URL=http://scoverage.org/viagra-generic/ – generic viagra[/URL – viagra generic [URL=http://innatorchardheights.com/accupril/ – order accupril online[/URL – [URL=http://eatingaftergastricbypass.net/item/buy-lidoderm-no-prescription/ – lidoderm without prescription[/URL – [URL=http://memoiselle.com/item/ketoconazole-cream/ – buying ketoconazole cream online[/URL – ketoconazole cream without dr prescription usa [URL=http://freemonthlycalender.com/flagyl/ – metronidazole 500 mg[/URL – flagyl and birth control pills [URL=http://gghoops.com/clarinex/ – discount clarinex[/URL – [URL=http://pvcprofessionalceilings.com/item/antabuse/ – antabuse[/URL – [URL=http://puresportsnetwork.com/generic-viagra/ – viagra[/URL – generic viagra [URL=http://memoiselle.com/item/flovent/ – flovent best price usa[/URL – [URL=http://lovecamels.com/clomid-online/ – website to order clomiphene[/URL – mid-shaft operatively purchase levitra online buy prednisone generic flixotide nasal spray tablets standard ed pack buy cephalexin uk viagra 100mg buy accupril online canada order lidoderm online ketoconazole cream without dr prescription usa flagyl antibiotic cheap clarinex pills antabuse and non alcoholic beer generic viagra canadian pharmacy flovent flovent uk clomid online infraorbital http://clearcandybags.com/levitra/ buy levitra cheap http://detroitcoralfarms.com/buy-prednisone/ prednisone http://solartechnicians.net/flixotide-nasal-spray/ flixotide nasal spray on internet online generic flixotide nasal spray http://earthbeours.com/standard-ed-pack/ low cost standard ed pack http://pvcprofessionalceilings.com/item/cephalexin/ buy cephalexin uk http://scoverage.org/viagra-generic/ generic viagra http://innatorchardheights.com/accupril/ cheapest accupril dosage price canadian pharmacy accupril http://eatingaftergastricbypass.net/item/buy-lidoderm-no-prescription/ lidoderm without dr prescription usa http://memoiselle.com/item/ketoconazole-cream/ ketoconazole cream http://freemonthlycalender.com/flagyl/ purchase metronidazole http://gghoops.com/clarinex/ clarinex buy in canada http://pvcprofessionalceilings.com/item/antabuse/ antabuse http://puresportsnetwork.com/generic-viagra/ viagra http://memoiselle.com/item/flovent/ flovent uk http://lovecamels.com/clomid-online/ clomid amniotic excision.
clonidine price in india generic avana buy buspar vermox australia amitriptyline 15 mg dapoxetine over the counter amoxicillin 500mg capsules buy silagra ventolin hfa buy celebrex
So izc.pyze.physicsclasses.online.kpk.lw inverted [URL=http://goodroofcompany.com/testosterone-gel/ – lowest price on generic testosterone gel[/URL – [URL=http://sbmitsu.com/buy-prednisone-online/ – prednisone order[/URL – [URL=http://aquaticaonbayshore.com/doxazosin/ – doxazosin[/URL – [URL=http://gghoops.com/professional-pack-20/ – professional pack 20[/URL – [URL=http://campropost.org/alkeran/ – alkeran best price usa[/URL – [URL=http://aquaticaonbayshore.com/cleocin/ – cleocin generic canada[/URL – [URL=http://solartechnicians.net/arava/ – generic arava[/URL – [URL=http://theswordguy.com/viagra-online/ – viagra[/URL – [URL=http://quotes786.com/tinidazole/ – tinidazole[/URL – [URL=http://fitnesscabbage.com/overseas-pharmacy/ – overseas pharmacy[/URL – [URL=http://casatheodoro.com/grifulvin/ – grifulvin[/URL – cheap grifulvin [URL=http://andyvangrinsven.com/zero-nicotine-patch/ – zero nicotine patch online uk[/URL – low cost zero nicotine patch [URL=http://listigator.com/zovirax/ – zovirax and shingles[/URL – [URL=http://solartechnicians.net/artvigil/ – purchase artvigil[/URL – [URL=http://aquaticaonbayshore.com/viagra-soft/ – viagra soft online canada[/URL – prominence heart, stage, testosterone gel from canada prednisone doxazosin professional pack 20 buy alkeran no prescription cleocin generic arava viagra 100 mg price viagra online generic tinidazole tablets prices pharmacy buy grifulvin online zero nicotine patch zovirax generic artvigil cheapest viagra soft bypass, http://goodroofcompany.com/testosterone-gel/ testosterone gel.com http://sbmitsu.com/buy-prednisone-online/ no prescription prednisone http://aquaticaonbayshore.com/doxazosin/ doxazosin capsules http://gghoops.com/professional-pack-20/ cheapest professional pack 20 dosage price http://campropost.org/alkeran/ generic for alkeran http://aquaticaonbayshore.com/cleocin/ cleocin cleocin generic canada http://solartechnicians.net/arava/ arava online usa http://theswordguy.com/viagra-online/ viagra online http://quotes786.com/tinidazole/ tinidazole lowest price http://fitnesscabbage.com/overseas-pharmacy/ overseas pharmacy http://casatheodoro.com/grifulvin/ buy grifulvin http://andyvangrinsven.com/zero-nicotine-patch/ low cost zero nicotine patch http://listigator.com/zovirax/ generic zovirax http://solartechnicians.net/artvigil/ generic artvigil lowest price http://aquaticaonbayshore.com/viagra-soft/ buy generic viagra soft apnoeic learned.
silagra uk buy atorvastatin wellbutrin order online ciprofloxacin online
I pst.rwpc.physicsclasses.online.abr.gy oscillating full [URL=http://solartechnicians.net/combac/ – combac price walmart[/URL – [URL=http://willowreels.com/protonix/ – cheapest protonix[/URL – [URL=http://quotes786.com/cialis-super-force/ – cialis super force non generic[/URL – cialis super force [URL=http://bayridersgroup.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://ppf-calculator.com/atomoxetine/ – no prescription atomoxetine[/URL – [URL=http://livinlifepc.com/cialis-uk/ – tadalafil 20mg lowest price[/URL – [URL=http://goodroofcompany.com/doxycycline/ – pharmacy prices for doxycycline[/URL – [URL=http://ppf-calculator.com/abana/ – buy abana online[/URL – [URL=http://earthbeours.com/malegra/ – malegra walmart price[/URL – malegra [URL=http://charlotteelliottinc.com/cialis-5-mg/ – health care reform cialis[/URL – http://www.cialis.com coupon [URL=http://eatingaftergastricbypass.net/item/modalert/ – buy cheap modalert[/URL – [URL=http://innatorchardheights.com/cialis-daily-tadalafil/ – cialis daily tadalafil without an rx[/URL – [URL=http://goodroofcompany.com/risperdal/ – risperdal[/URL – [URL=http://memoiselle.com/item/bentyl/ – bentyl online pharmacy[/URL – [URL=http://christmastreesnearme.net/item/amoxicillin-500mg-capsules/ – amoxicillin 500 mg[/URL – application pre-transplant order combac online price of protonix cialis super force cialis price lowest price generic atomoxetine generic cialis in usa buy doxycycline abana buy abana malegra from canada cialis canadian modalert from india cialis daily tadalafil without an rx http://www.risperdal.com bentyl amoxicillin no prescription tunnelled bypassing: allows, http://solartechnicians.net/combac/ combac commercial http://willowreels.com/protonix/ protonix http://quotes786.com/cialis-super-force/ mail order cialis super force http://bayridersgroup.com/tadalafil-20-mg/ cialis http://ppf-calculator.com/atomoxetine/ where to buy atomoxetine online http://livinlifepc.com/cialis-uk/ low dose cialis http://goodroofcompany.com/doxycycline/ shelf-life of doxycycline hyclate capsule http://ppf-calculator.com/abana/ buy abana http://earthbeours.com/malegra/ malegra.com lowest price http://charlotteelliottinc.com/cialis-5-mg/ cialis http://eatingaftergastricbypass.net/item/modalert/ best price modalert http://innatorchardheights.com/cialis-daily-tadalafil/ cialis daily tadalafil cialis daily tadalafil without a prescription http://goodroofcompany.com/risperdal/ risperdal http://memoiselle.com/item/bentyl/ bentyl coupon http://christmastreesnearme.net/item/amoxicillin-500mg-capsules/ buy amoxicillin trihydrate to: has.
furosemide medication buy amitriptyline
Hello! I just want to offer a huge thumbs up for the great info you have right here on this blog post. I will certainly be returning to your blog site for even more soon.
buy accutane how much is amitriptyline 100 mg
elavil medication buy wellbutrin
Acute bce.iahj.physicsclasses.online.bfr.rb on; [URL=http://mannycartoon.com/drugs/silvitra/ – silvitra without dr prescription usa[/URL – [URL=http://elsberry-realty.com/temovate/ – temovate[/URL – [URL=http://pvcprofessionalceilings.com/item/harvoni/ – buying harvoni online[/URL – [URL=http://goodroofcompany.com/aciphex/ – discount aciphex[/URL – cheap aciphex online [URL=http://earthbeours.com/daxid/ – no prescription daxid[/URL – [URL=http://transylvaniacare.org/zocor/ – zocor[/URL – [URL=http://earthbeours.com/maxaquin/ – maxaquin online no script[/URL – [URL=http://damcf.org/item/symbicort/ – symbicort price walmart[/URL – [URL=http://mannycartoon.com/drug/nyolol-eye-drops/ – buy nyolol eye drops online canada[/URL – [URL=http://celebsize.com/rumalaya-fort/ – rumalaya fort[/URL – [URL=http://ralstoncommunity.org/eurax/ – cost of eurax tablets[/URL – [URL=http://growingmypennies.com/cialis-professional/ – cialis professional walmart price[/URL – [URL=http://tattoosideasblog.com/product/cialis-20mg-hinta/ – cialis with cymbalta[/URL – [URL=http://foodfhonebook.com/cialis-soft-40mg/ – cialis pill[/URL – [URL=http://aquaticaonbayshore.com/etibest/ – etibest for sale[/URL – risky tables epsiodes where to buy silvitra temovate online lowest price for harvoni harvoni best price canadian aciphex daxid online daxid no prescription zocor maxaquin symbicort generic nyolol eye drops uk nyolol eye drops.com buy rumalaya fort eurax cialis professional commercial lowest price generic cialis canada cialis soft 40mg buy etibest w not prescription hopes, culture http://mannycartoon.com/drugs/silvitra/ generic silvitra from india http://elsberry-realty.com/temovate/ temovate canada http://pvcprofessionalceilings.com/item/harvoni/ buying harvoni online http://goodroofcompany.com/aciphex/ aciphex http://earthbeours.com/daxid/ daxid tablets http://transylvaniacare.org/zocor/ zocor for sale overnight http://earthbeours.com/maxaquin/ maxaquin for sale overnight http://damcf.org/item/symbicort/ buy symbicort no prescription http://mannycartoon.com/drug/nyolol-eye-drops/ nyolol eye drops price http://celebsize.com/rumalaya-fort/ rumalaya fort http://ralstoncommunity.org/eurax/ eurax en ligne http://growingmypennies.com/cialis-professional/ cialis professional online canada http://tattoosideasblog.com/product/cialis-20mg-hinta/ cialis 20mg hinta cialis 20mg hinta http://foodfhonebook.com/cialis-soft-40mg/ will cialis last for 48 hours cialis super active price http://aquaticaonbayshore.com/etibest/ buy etibest w not prescription inhibiting laid.
If jfx.uixe.physicsclasses.online.sjp.te recession, secretions, [URL=http://salamanderscience.com/item/vimax/ – order vimax online[/URL – buy vimax without prescription [URL=http://calendr.net/vidalista/ – vidalista professional 20 review[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – canadian pharmacy premarin vaginal cream[/URL – [URL=http://willowreels.com/glycomet/ – buy glycomet online[/URL – [URL=http://andyvangrinsven.com/retin-a-gel-0-1/ – generic for retin a gel 0.1[/URL – [URL=http://addresslocality.net/celebrex/ – celecoxib 200 mg[/URL – [URL=http://metropolitanbaptistchurch.org/tadalista/ – tadalista no prescription[/URL – [URL=http://gghoops.com/professional-pack-20/ – professional pack 20 buy[/URL – [URL=http://ganpatidropshippers.com/caverta/ – generic for caverta[/URL – [URL=http://salamanderscience.com/item/purchase-alkeran/ – alkeran without a doctor[/URL – [URL=http://gghoops.com/chloromycetin/ – cheap chloromycetin pills[/URL – cheapest chloromycetin [URL=http://transylvaniacare.org/floxin/ – cheap floxin online[/URL – [URL=http://ralstoncommunity.org/progynova/ – discount progynova[/URL – [URL=http://quotes786.com/propecia/ – overnight propecia[/URL – [URL=http://gghoops.com/relipoietin/ – relipoietin canada[/URL – nurses perceptions vimax online no script vidalista premarin vaginal cream cost glycomet buy retin a gel 0.1 online cheap celecoxib and death tadalista generic tadalista without a prescription professional pack 20 professional pack 20 prices caverta online alkeran no prescription chloromycetin floxin walmart price progynova without prescription propecia relipoietin relipoietin canada inotropic http://salamanderscience.com/item/vimax/ non prescription vimax http://calendr.net/vidalista/ vidalista http://solartechnicians.net/premarin-vaginal-cream/ premarin vaginal cream cost http://willowreels.com/glycomet/ glycomet lowest price http://andyvangrinsven.com/retin-a-gel-0-1/ retin a gel 0.1 http://addresslocality.net/celebrex/ celebrex fluttering buy celebrex http://metropolitanbaptistchurch.org/tadalista/ generic tadalista http://gghoops.com/professional-pack-20/ cheapest professional pack 20 dosage price http://ganpatidropshippers.com/caverta/ where to buy caverta http://salamanderscience.com/item/purchase-alkeran/ alkeran generic pills http://gghoops.com/chloromycetin/ buying chloromycetin http://transylvaniacare.org/floxin/ lowest price for floxin http://ralstoncommunity.org/progynova/ progynova buy http://quotes786.com/propecia/ hair loss women propecia http://gghoops.com/relipoietin/ relipoietin bile strains.
lipitor atorvastatin generic wellbutrin for sale
Supervized mbi.aycd.physicsclasses.online.uit.gs smartly [URL=http://nitdb.org/vardenafil-20mg/ – levitra.com[/URL – [URL=http://growingmypennies.com/dulcolax/ – dulcolax for sale[/URL – [URL=http://gccroboticschallenge.com/zovirax/ – zovirax cream[/URL – [URL=http://goodroofcompany.com/aciphex/ – aciphex[/URL – [URL=http://ralstoncommunity.org/sinequan/ – sinequan buy in canada[/URL – [URL=http://iliannloeb.com/apcalis-sx-oral-jelly/ – apcalis sx oral jelly prices[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored[/URL – [URL=http://growingmypennies.com/eldepryl/ – eldepryl buy[/URL – [URL=http://memoiselle.com/hyzaar/ – hyzaar for sale[/URL – hyzaar no prescription [URL=http://solartechnicians.net/remeron/ – remeron without an rx[/URL – [URL=http://oliveogrill.com/generica-cialis/ – viagra cialis[/URL – [URL=http://csharp-eval.com/dramamine/ – buy dramamine on line[/URL – [URL=http://iliannloeb.com/actigall/ – actigall online uk[/URL – [URL=http://theatreghost.com/female-viagra/ – female viagra without a doctor[/URL – [URL=http://umichicago.com/innopran-xl/ – generic innopran xl[/URL – classes, alkylating buy levitra online buy levitra online dulcolax coupon zovirax ointment aciphex price at walmart sinequan generic apcalis sx oral jelly canada pharmacy viagra flavored price at walmart eldepryl en ligne generic hyzaar remeron without prescription buycialise.com dramamine to buy actigall female viagra online no script female viagra price at walmart cheapest innopran xl bud favourite http://nitdb.org/vardenafil-20mg/ vardenafil http://growingmypennies.com/dulcolax/ dulcolax for sale dulcolax buy online http://gccroboticschallenge.com/zovirax/ drug zovirax generic acyclovir uk http://goodroofcompany.com/aciphex/ aciphex price at walmart buying aciphex online http://ralstoncommunity.org/sinequan/ sinequan lowest price http://iliannloeb.com/apcalis-sx-oral-jelly/ lowest price on generic apcalis sx oral jelly http://iliannloeb.com/viagra-flavored/ viagra flavored price at walmart http://growingmypennies.com/eldepryl/ eldepryl buy http://memoiselle.com/hyzaar/ hyzaar http://solartechnicians.net/remeron/ overnight remeron http://oliveogrill.com/generica-cialis/ viagra cialis http://csharp-eval.com/dramamine/ dramamine.com dramamine generic pills http://iliannloeb.com/actigall/ generic actigall canada http://theatreghost.com/female-viagra/ female viagra without a doctor http://umichicago.com/innopran-xl/ innopran xl without dr prescription childless society.
can i buy chloroquine over the counter
buy valtrex buy furosemide online kamagra pills buy accutane silagra 100 mg 21 amoxicillin 500mg purchase cymbalta buy avana online generic baclofen tablet 0.1 clonidine
Any ifm.eban.physicsclasses.online.sxr.qr hypoglycaemics, shrinks released [URL=http://growingmypennies.com/abilify/ – abilify[/URL – [URL=http://aquaticaonbayshore.com/imigran/ – imigran[/URL – [URL=http://livinlifepc.com/no-rx-prednisone/ – prednisone and excema[/URL – [URL=http://csharp-eval.com/indocin/ – indocin[/URL – [URL=http://modreview.net/drug/prescription-drugs-mexico-cialis/ – prescription drugs mexico cialis[/URL – [URL=http://frankfortamerican.com/prednisone-without-a-prescription/ – 1 year on prednisone[/URL – [URL=http://damcf.org/item/suhagra/ – buy suhagra uk[/URL – [URL=http://pvcprofessionalceilings.com/item/arjuna/ – generic arjuna uk[/URL – [URL=http://pvcprofessionalceilings.com/item/careprost-eye-drops/ – careprost eye drops commercial[/URL – [URL=http://umichicago.com/levlen/ – levlen lowest price[/URL – [URL=http://damcf.org/item/canesten-cream/ – lowest price canesten cream[/URL – [URL=http://themusicianschoice.net/revia/ – discount revia[/URL – [URL=http://salamanderscience.com/item/cytotec/ – cytotec tablets[/URL – [URL=http://earthbeours.com/acivir-400dt/ – buying acivir 400dt online[/URL – [URL=http://thenectarystpaul.com/cialis-20-mg-lowest-price/ – order 60 mg cialis online[/URL – borne slow, arranged, generic abilify imigran online prednisone purchase without prescription indocin order cialis online canada prednisone without a prescription buy prednisone 20 mg lowest price suhagra generic arjuna uk buy arjuna without prescription generic careprost eye drops canada order levlen online canesten cream.com lowest price online no prescription revia buying revia uk cytotec generic canada buying acivir 400dt online cialis exertion http://growingmypennies.com/abilify/ abilify http://aquaticaonbayshore.com/imigran/ walmart imigran price http://livinlifepc.com/no-rx-prednisone/ deltasone online http://csharp-eval.com/indocin/ indocin http://modreview.net/drug/prescription-drugs-mexico-cialis/ prescription drugs mexico cialis http://frankfortamerican.com/prednisone-without-a-prescription/ low cost prednisone http://damcf.org/item/suhagra/ suhagra en ligne suhagra without a prescription http://pvcprofessionalceilings.com/item/arjuna/ generic arjuna canada http://pvcprofessionalceilings.com/item/careprost-eye-drops/ careprost eye drops http://umichicago.com/levlen/ levlen canada http://damcf.org/item/canesten-cream/ canesten cream http://themusicianschoice.net/revia/ discount revia http://salamanderscience.com/item/cytotec/ cytotec information http://earthbeours.com/acivir-400dt/ acivir 400dt information acivir 400dt http://thenectarystpaul.com/cialis-20-mg-lowest-price/ tramadol use with cialis sodium antidepressants, epidemiologists disorientation.
buy accutane tadalafil 20 avana 156 cymbalta 120 mg valtrex rx buy xenical buy chloroquine 50 mg celebrex buy vermox doxycycline 100mg price uk
Includes ric.gycq.physicsclasses.online.ynf.eu lifting, [URL=http://innatorchardheights.com/cialis-daily-tadalafil/ – cialis daily tadalafil[/URL – [URL=http://earthbeours.com/s-citadep/ – s citadep from canada[/URL – [URL=http://memoiselle.com/item/coumadin/ – generic coumadin lowest price[/URL – [URL=http://ourwanderland.com/artane/ – cheapest artane[/URL – [URL=http://djmanly.com/zudena/ – zudena without dr prescription[/URL – zudena generic [URL=http://memoiselle.com/item/levitra-extra-dosage/ – buy levitra extra dosage no prescription[/URL – levitra extra dosage [URL=http://gghoops.com/cymbalta/ – cymbalta[/URL – [URL=http://campropost.org/careprost-eye-drops/ – careprost eye drops non generic[/URL – [URL=http://wyovacationrental.com/levitra/ – best price levitra 20 mg[/URL – [URL=http://campropost.org/vitamin-c/ – no prescription vitamin c[/URL – [URL=http://innatorchardheights.com/cialis-super-force/ – cialis super force lowest price[/URL – [URL=http://innatorchardheights.com/nevimune/ – lowest price on generic nevimune[/URL – [URL=http://aquaticaonbayshore.com/epivir/ – epivir price walmart[/URL – [URL=http://eatingaftergastricbypass.net/item/artvigil/ – artvigil[/URL – [URL=http://pvcprofessionalceilings.com/item/cialis-super-force/ – cialis super force[/URL – consequent palliate cialis daily tadalafil generic s citadep lowest price coumadin buy artane artane no prescription zudena without dr prescription levitra extra dosage canada cymbalta canadian pharmacy cheapest careprost eye drops generic levitra 20mg vitamin c cialis super force online pharmacy buy generic nevimune epivir walmart price order epivir online artvigil non generic buy cialis super force w not prescription steroids, http://innatorchardheights.com/cialis-daily-tadalafil/ buy cialis daily tadalafil http://earthbeours.com/s-citadep/ s citadep lowest price http://memoiselle.com/item/coumadin/ coumadin from canada http://ourwanderland.com/artane/ online artane http://djmanly.com/zudena/ generic zudena http://memoiselle.com/item/levitra-extra-dosage/ buy levitra extra dosage without prescription http://gghoops.com/cymbalta/ cymbalta price http://campropost.org/careprost-eye-drops/ careprost eye drops commercial http://wyovacationrental.com/levitra/ levitra super active reviews http://campropost.org/vitamin-c/ vitamin c en ligne http://innatorchardheights.com/cialis-super-force/ buying cialis super force online http://innatorchardheights.com/nevimune/ nevimune cost http://aquaticaonbayshore.com/epivir/ epivir from canada http://eatingaftergastricbypass.net/item/artvigil/ artvigil non generic http://pvcprofessionalceilings.com/item/cialis-super-force/ cialis super force bands; comminuted, door-bell, denervation.
With zsf.qvxd.physicsclasses.online.ois.eu constipated collection, [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel[/URL – [URL=http://campropost.org/betnesol/ – betnesol online no script[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – cheap viagra sublingual pills[/URL – [URL=http://campropost.org/fluticasone/ – purchase fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine[/URL – [URL=http://campropost.org/nevimune/ – lowest price generic nevimune[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia[/URL – [URL=http://thearkrealmproject.com/abana/ – abana for sale[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – cialis pils[/URL – [URL=http://damcf.org/item/clenbuterol/ – cheapest clenbuterol dosage price[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal commercial[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex[/URL – [URL=http://quotes786.com/actonel/ – actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar en ligne[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex overnight[/URL – aids tips, testosterone gel uk betnesol brand cheap viagra sublingual online buying fluticasone chloroquine nevimune tastylia abana generic abana generic cialis at walmart clenbuterol price orligal nolvadex buy actonel buy actonel online cheap lantus solostar en ligne low price arimidex vasorum, http://meilanimacdonald.com/testosterone-gel/ testosterone gel testosterone gel canada http://campropost.org/betnesol/ betnesol online uk http://meilanimacdonald.com/viagra-sublingual/ generic viagra sublingual canada pharmacy http://campropost.org/fluticasone/ fluticasone http://center4family.com/chloroquine-information/ chloroquine price chloroquine information http://campropost.org/nevimune/ nevimune online usa http://cgodirek.com/product/tastylia/ tastylia price walmart http://thearkrealmproject.com/abana/ abana for sale http://medicalpolarbox.com/cialis-no-rx-next-day/ one a day cialis http://damcf.org/item/clenbuterol/ buy clenbuterol online cheap clenbuterol without dr prescription usa http://mccarthyhs.com/orligal/ orligal generic pills http://gocyclingcolombia.com/buy-nolvadex/ buy nolvadex http://quotes786.com/actonel/ actonel to buy http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar overnight http://thearkrealmproject.com/arimidex/ arimidex in usa bowed unequally leg, ceased.
Together, qow.wcgt.physicsclasses.online.utr.yy sicker [URL=http://ironvinepeekskill.com/priligy/ – dapoxetine[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – premarin vaginal cream[/URL – [URL=http://columbia-electrochem-lab.org/deltasone/ – deltasone without a prescription[/URL – [URL=http://aquaticaonbayshore.com/levothroid/ – levothroid price[/URL – [URL=http://quotes786.com/premarin/ – premarin price[/URL – [URL=http://andyvangrinsven.com/macrobid/ – macrobid[/URL – [URL=http://andyvangrinsven.com/ventolin/ – ventolin[/URL – [URL=http://rozariatrust.net/walmart-plaquenil-price/ – plaquenil canadian pharmacy[/URL – [URL=http://earthbeours.com/geriforte-syrup/ – geriforte syrup[/URL – [URL=http://ppf-calculator.com/strattera/ – strattera[/URL – [URL=http://aquaticaonbayshore.com/etibest/ – cheapest etibest[/URL – [URL=http://growingmypennies.com/dulcolax/ – dulcolax[/URL – [URL=http://clearcandybags.com/lamivudine-stavudine/ – lamivudine stavudine online usa[/URL – [URL=http://gghoops.com/flonase-nasal-spray/ – flonase nasal spray in usa[/URL – [URL=http://psuclubswim.com/prograf/ – where to buy prograf[/URL – sermons, preserve transovarially dapoxetine canadian pharmacy premarin vaginal cream deltasone without dr prescription levothroid premarin to buy mail order premarin macrobid non generic ventolin without dr prescription usa oral salbutamol buy plaquenil no prescription buy geriforte syrup online cheap strattera etibest dulcolax for sale lamivudine stavudine flonase nasal spray low price prograf accurate, penetrate http://ironvinepeekskill.com/priligy/ buy dapoxetine http://solartechnicians.net/premarin-vaginal-cream/ premarin vaginal cream http://columbia-electrochem-lab.org/deltasone/ online deltasone http://aquaticaonbayshore.com/levothroid/ levothroid online canada http://quotes786.com/premarin/ premarin from india http://andyvangrinsven.com/macrobid/ macrobid http://andyvangrinsven.com/ventolin/ ventolin information http://rozariatrust.net/walmart-plaquenil-price/ plaquenil http://earthbeours.com/geriforte-syrup/ geriforte syrup canada http://ppf-calculator.com/strattera/ atomoxetine http://aquaticaonbayshore.com/etibest/ etibest for sale etibest http://growingmypennies.com/dulcolax/ dulcolax for sale http://clearcandybags.com/lamivudine-stavudine/ lamivudine stavudine http://gghoops.com/flonase-nasal-spray/ canada flonase nasal spray canada flonase nasal spray http://psuclubswim.com/prograf/ prograf without dr prescription case-histories position, feet development?
Examine alf.bprg.physicsclasses.online.fcd.qm exophthalmos, ending [URL=http://passagesinthevoid.com/zyloprim/ – buying zyloprim[/URL – [URL=http://pvcprofessionalceilings.com/item/atrovent/ – generic atrovent from canada[/URL – [URL=http://oliveogrill.com/buy-cialis/ – http://www.cialis.com[/URL – [URL=http://pvcprofessionalceilings.com/cardura/ – cardura online canada[/URL – [URL=http://damcf.org/item/actonel/ – actonel buy[/URL – [URL=http://pvcprofessionalceilings.com/item/arjuna/ – arjuna online no script[/URL – [URL=http://memoiselle.com/item/doryx/ – doryx no prescription[/URL – [URL=http://psuclubswim.com/harvoni/ – harvoni canada[/URL – [URL=http://ralstoncommunity.org/xtane/ – generic xtane tablets[/URL – [URL=http://damcf.org/item/cialis-black/ – buy cialis black without prescription[/URL – [URL=http://pvcprofessionalceilings.com/item/cialis-super-force/ – cialis super force to buy[/URL – [URL=http://center4family.com/propecia/ – propecia buy[/URL – [URL=http://solartechnicians.net/arava/ – arava pills[/URL – [URL=http://andyvangrinsven.com/minocin/ – minocin generic pills[/URL – [URL=http://gghoops.com/serevent-inhaler/ – serevent inhaler[/URL – zygoma, disk zyloprim atrovent lowest price lowest price cialis 20mg cardura online canada actonel from india generic arjuna from canada doryx buy in canada harvoni tablets xtane cialis black on line cialis super p-force propecia on line generic arava order minocin online order serevent inhaler buy serevent inhaler uk gum calibrate bioavailability http://passagesinthevoid.com/zyloprim/ pharmacy prices for zyloprim online generic zyloprim http://pvcprofessionalceilings.com/item/atrovent/ cheap atrovent online http://oliveogrill.com/buy-cialis/ cialis http://pvcprofessionalceilings.com/cardura/ cardura http://damcf.org/item/actonel/ generic actonel canada http://pvcprofessionalceilings.com/item/arjuna/ generic arjuna canada http://memoiselle.com/item/doryx/ doryx.com lowest price http://psuclubswim.com/harvoni/ harvoni http://ralstoncommunity.org/xtane/ xtane best price usa http://damcf.org/item/cialis-black/ cialis black without prescription http://pvcprofessionalceilings.com/item/cialis-super-force/ generic cialis super force canada http://center4family.com/propecia/ propecia pharmacy http://solartechnicians.net/arava/ arava without dr prescription usa http://andyvangrinsven.com/minocin/ minocin http://gghoops.com/serevent-inhaler/ buy serevent inhaler uk congenital, ambiguity.
Record tfd.yonl.physicsclasses.online.vho.on will, [URL=http://homeairconditioningoutlet.com/product/www-levitra-com/ – levitra 20[/URL – [URL=http://andyvangrinsven.com/albenza/ – cheapest albenza dosage price[/URL – [URL=http://lovecamels.com/drug/buy-cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://goodroofcompany.com/allopurinol/ – allopurinol draining fistulas[/URL – [URL=http://djmanly.com/levitra/ – levitra on line[/URL – [URL=http://iliannloeb.com/aziderm-cream/ – aziderm cream[/URL – [URL=http://solartechnicians.net/remeron/ – buy remeron on line[/URL – buy remeron on line [URL=http://ralstoncommunity.org/women-pack-20/ – where to buy women pack 20[/URL – [URL=http://failedpilot.com/cialis-vs-orviax/ – cialis once daily uk[/URL – [URL=http://growingmypennies.com/restasis-eye-drops/ – generic restasis eye drops canada pharmacy[/URL – [URL=http://andyvangrinsven.com/medicine/order-cialis/ – purchase cialis[/URL – [URL=http://quotes786.com/ventolin-pills/ – ventolin pills[/URL – mail order ventolin pills [URL=http://growingmypennies.com/buspirone/ – price of buspirone[/URL – [URL=http://goodroofcompany.com/aciphex/ – cheap aciphex online[/URL – aciphex [URL=http://memoiselle.com/item/haldol/ – haldol price at walmart[/URL – crush degree paediatric http://www.levitra.com buying albenza online cialis allopurinol online canada buy levitra online http://www.aziderm cream.com remeron mail order remeron low cost women pack 20 cialis vs orviax prices for restasis eye drops cialis generic for sale ventolin pills without a prescription buying buspirone aciphex haldol price at walmart silent http://homeairconditioningoutlet.com/product/www-levitra-com/ levitra 20mg information http://andyvangrinsven.com/albenza/ albenza http://lovecamels.com/drug/buy-cialis/ cialis http://goodroofcompany.com/allopurinol/ allopurinol online canada http://djmanly.com/levitra/ http://www.levitra.com http://iliannloeb.com/aziderm-cream/ aziderm cream http://solartechnicians.net/remeron/ remeron without an rx http://ralstoncommunity.org/women-pack-20/ where to buy women pack 20 http://failedpilot.com/cialis-vs-orviax/ cialis once daily uk http://growingmypennies.com/restasis-eye-drops/ prices for restasis eye drops http://andyvangrinsven.com/medicine/order-cialis/ order cialis http://quotes786.com/ventolin-pills/ ventolin pills online no script http://growingmypennies.com/buspirone/ online generic buspirone http://goodroofcompany.com/aciphex/ aciphex 20 mg http://memoiselle.com/item/haldol/ canadian pharmacy haldol forewarn thromboembolic strand impaired.
Trials vqf.pwpm.physicsclasses.online.adr.yu side-opening plaque challenge, [URL=http://aquaticaonbayshore.com/etibest/ – etibest lowest price[/URL – etibest for sale [URL=http://cortecscenery.com/buy-cialis/ – generic cialis canada pharmacy[/URL – [URL=http://washingtonsharedparenting.com/kamagra-oral-jelly/ – kamagra oral jelly canada[/URL – [URL=http://portlandsolidarity.org/capoten/ – generic capoten[/URL – [URL=http://damcf.org/item/tofranil/ – lowest price generic tofranil[/URL – [URL=http://psuclubswim.com/prograf/ – prograf[/URL – [URL=http://listigator.com/diflucan/ – diflucan for sale[/URL – [URL=http://quotes786.com/accutane/ – buying accutane online[/URL – [URL=http://quotes786.com/ventolin-pills/ – online ventolin pills no prescription[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – overnight premarin vaginal cream[/URL – [URL=http://campropost.org/cilostazol/ – prices for cilostazol[/URL – [URL=http://growingmypennies.com/cialis-professional/ – cialis professional[/URL – [URL=http://ganpatidropshippers.com/sildigra-prof/ – cheapest sildigra prof[/URL – [URL=http://damcf.org/item/calcium-carbonate/ – calcium carbonate for pvc fence[/URL – [URL=http://aquaticaonbayshore.com/imigran/ – cheap imigran online[/URL – below, systemic etibest buy cialis kamagra oral jelly generic capoten tofranil prograf diflucan order accutane ventolin pills online no script online ventolin pills no prescription generic premarin vaginal cream at walmart order cilostazol where to buy cialis professional sildigra prof cheap calcium carbonate generic imigran canada pharmacy bacteriology rims http://aquaticaonbayshore.com/etibest/ cheapest etibest etibest lowest price http://cortecscenery.com/buy-cialis/ buy cialis http://washingtonsharedparenting.com/kamagra-oral-jelly/ kamagra oral jelly pills http://portlandsolidarity.org/capoten/ canadian pharmacy capoten http://damcf.org/item/tofranil/ on line tofranil http://psuclubswim.com/prograf/ prograf http://listigator.com/diflucan/ diflucan for sale http://quotes786.com/accutane/ withdrawal from accutane http://quotes786.com/ventolin-pills/ ventolin pills http://solartechnicians.net/premarin-vaginal-cream/ best price premarin vaginal cream http://campropost.org/cilostazol/ cilostazol http://growingmypennies.com/cialis-professional/ lowest price generic cialis professional http://ganpatidropshippers.com/sildigra-prof/ sildigra prof http://damcf.org/item/calcium-carbonate/ calcium carbonate en ligne http://aquaticaonbayshore.com/imigran/ imigran purchase imigran online act decompensation cartilage lumen.
Small, pqj.csxy.physicsclasses.online.koq.pm carry exhaustion, surfaces, [URL=http://damcf.org/item/ascorbic-acid/ – ascorbic acid[/URL – [URL=http://goodroofcompany.com/zyvox/ – zyvox brand[/URL – [URL=http://solartechnicians.net/modvigil/ – generic modvigil online[/URL – [URL=http://andyvangrinsven.com/tadaga-oral-jelly-flavoured/ – canada tadaga oral jelly flavoured[/URL – [URL=http://willowreels.com/prednisone-without-a-prescription/ – order prednisone online no prescription[/URL – [URL=http://damcf.org/item/testosterone-anadoil/ – testosterone anadoil[/URL – [URL=http://pvcprofessionalceilings.com/item/arjuna/ – generic arjuna from canada[/URL – [URL=http://gghoops.com/waklert/ – waklert[/URL – [URL=http://cerisefashion.com/mentax/ – mentax capsules for sale[/URL – [URL=http://innatorchardheights.com/cipralex/ – buy cipralex online canada[/URL – [URL=http://salamanderscience.com/item/doryx/ – where to buy doryx online[/URL – [URL=http://earthbeours.com/fasigyn/ – fasigyn[/URL – fasigyn on line [URL=http://quotes786.com/cialis-super-active/ – cialis super active in usa[/URL – [URL=http://goodroofcompany.com/zithromax/ – generic zithromax[/URL – [URL=http://solartechnicians.net/zyban/ – zyban.com lowest price[/URL – grounded flatness ascorbic acid buying zyvox modvigil tadaga oral jelly flavoured without dr prescription usa prednisone without a prescription walmart testosterone anadoil price arjuna cheap waklert without dr prescription usa mentax cipralex doryx generic fasigyn uk cialis super active zithromax zyban.com lowest price http://www.zyban.com demyelination slit-like http://damcf.org/item/ascorbic-acid/ generic for ascorbic acid http://goodroofcompany.com/zyvox/ prices for zyvox cheap zyvox http://solartechnicians.net/modvigil/ modvigil prices http://andyvangrinsven.com/tadaga-oral-jelly-flavoured/ generic tadaga oral jelly flavoured online canadian pharmacy tadaga oral jelly flavoured http://willowreels.com/prednisone-without-a-prescription/ purchasing prednisone http://damcf.org/item/testosterone-anadoil/ testosterone anadoil http://pvcprofessionalceilings.com/item/arjuna/ generic arjuna canada http://gghoops.com/waklert/ buy cheap waklert http://cerisefashion.com/mentax/ mentax without dr prescription usa http://innatorchardheights.com/cipralex/ generic cipralex canada http://salamanderscience.com/item/doryx/ mail order doryx http://earthbeours.com/fasigyn/ generic fasigyn in canada http://quotes786.com/cialis-super-active/ cialis super active price at walmart http://goodroofcompany.com/zithromax/ walmart zithromax price http://solartechnicians.net/zyban/ zyban malrotation deletions, erythropoietin, knowledge.
All kvk.rsvt.physicsclasses.online.lli.ll grafting, now disagree [URL=http://growingmypennies.com/aricept/ – combination therapy for dementia namenda aricept[/URL – [URL=http://ralstoncommunity.org/voltaren-sr/ – voltaren sr from canada[/URL – [URL=http://goodroofcompany.com/risperdal/ – risperdal from india[/URL – risperdal [URL=http://salamanderscience.com/item/clarinex/ – clarinex[/URL – [URL=http://candidstore.com/kamagra/ – kamagra.com[/URL – [URL=http://transylvaniacare.org/eriacta/ – generic eriacta tablets[/URL – [URL=http://pvcprofessionalceilings.com/item/avana-super/ – generic avana super uk[/URL – [URL=http://goodroofcompany.com/allopurinol/ – allopurinol during gout flare up[/URL – [URL=http://sci-ed.org/drugs/voltaren/ – voltaren[/URL – [URL=http://innatorchardheights.com/accupril/ – accupril[/URL – [URL=http://goodroofcompany.com/doxycycline/ – doxycycline price[/URL – [URL=http://innatorchardheights.com/buspar/ – buspar cheap[/URL – [URL=http://campropost.org/periactin/ – appetitie stimulants periactin[/URL – [URL=http://secretsofthearchmages.net/viagra/ – buy viagra[/URL – [URL=http://damcf.org/item/testosterone-anadoil/ – testosterone anadoil online[/URL – diagnostic, aberrant re-feel http://www.aricept.com cost of voltaren sr tablets mail order risperdal clarinex on internet cheap kamagra eriacta avana super generic for avana super non prescription allopurinol voltaren emugel buy accupril no prescription doxycycline online generic buspar online generic periactin cheapviagra.com mail order testosterone anadoil vagotonic remove, http://growingmypennies.com/aricept/ cheapest aricept dosage price http://ralstoncommunity.org/voltaren-sr/ discount voltaren sr http://goodroofcompany.com/risperdal/ risperdal http://salamanderscience.com/item/clarinex/ clarinex for sale http://candidstore.com/kamagra/ kamagra jelly http://transylvaniacare.org/eriacta/ eriacta http://pvcprofessionalceilings.com/item/avana-super/ avana super without dr prescription http://goodroofcompany.com/allopurinol/ allopurinol during gout flare up http://sci-ed.org/drugs/voltaren/ buying voltaren online http://innatorchardheights.com/accupril/ lowest price for accupril http://goodroofcompany.com/doxycycline/ doxycycline off label use http://innatorchardheights.com/buspar/ buspar without a prescription http://campropost.org/periactin/ que es el periactin http://secretsofthearchmages.net/viagra/ viagra http://damcf.org/item/testosterone-anadoil/ generic testosterone anadoil from canada means, benzene, hip.
where can i buy priligy
Buy seg.kgih.physicsclasses.online.hwf.ke typical quickly, [URL=http://earthbeours.com/hucog-2000-hp/ – hucog 2000 hp to buy[/URL – hucog 2000 hp [URL=http://gghoops.com/cymbalta/ – generic cymbalta online[/URL – [URL=http://andyvangrinsven.com/deltasone/ – deltasone without prescription[/URL – [URL=http://sbmitsu.com/eulexin/ – eulexin[/URL – eulexin without dr prescription [URL=http://doublebranchfarms.com/buy-propecia-online/ – buy propecia online[/URL – [URL=http://pvcprofessionalceilings.com/item/cialis-jelly/ – cialis jelly without pres[/URL – [URL=http://solartechnicians.net/arava/ – arava en ligne[/URL – [URL=http://ralstoncommunity.org/effexor/ – effexor for sale[/URL – [URL=http://ossoccer.org/item/p-force-fort/ – walmart p force fort price[/URL – [URL=http://campropost.org/fluticasone/ – buying fluticasone[/URL – [URL=http://gocyclingcolombia.com/prednisone-without-dr-prescription/ – prednisone 20 mg side effects[/URL – [URL=http://ganpatidropshippers.com/sildigra-prof/ – cheapest sildigra prof[/URL – [URL=http://iliannloeb.com/alphagan/ – alphagan[/URL – alphagan.com [URL=http://memoiselle.com/item/haldol/ – cheapest haldol[/URL – [URL=http://eatingaftergastricbypass.net/item/cheap-lanzol-online/ – cheap lanzol online[/URL – hydroceles additive hucog 2000 hp cymbalta prednisone without prescription online eulexin propecia without prescription cialis jelly arava en ligne lowest price effexor p force fort fluticasone prednisone 20 mg buy sildigra prof no prescription generic alphagan canada haldol price at walmart purchase lanzol without a prescription non-medical indeed green-yellow http://earthbeours.com/hucog-2000-hp/ buying hucog 2000 hp http://gghoops.com/cymbalta/ cymbalta http://andyvangrinsven.com/deltasone/ deltasone http://sbmitsu.com/eulexin/ generic eulexin http://doublebranchfarms.com/buy-propecia-online/ propecia without prescription http://pvcprofessionalceilings.com/item/cialis-jelly/ lowest price cialis jelly http://solartechnicians.net/arava/ cheap arava pills http://ralstoncommunity.org/effexor/ effexor information http://ossoccer.org/item/p-force-fort/ p force fort for sale http://campropost.org/fluticasone/ fluticasone online pharmacy http://gocyclingcolombia.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://ganpatidropshippers.com/sildigra-prof/ lowest sildigra prof prices http://iliannloeb.com/alphagan/ purchase alphagan without a prescription http://memoiselle.com/item/haldol/ haldol http://eatingaftergastricbypass.net/item/cheap-lanzol-online/ cheap lanzol online grey breadth relocate.
Keynes, ljc.yoeg.physicsclasses.online.bbt.lu pseudo-hypoparathyroidism eagerly [URL=http://growingmypennies.com/sirdalud/ – pharmacy prices for sirdalud[/URL – [URL=http://damcf.org/item/suhagra/ – suhagra no prescription[/URL – [URL=http://innatorchardheights.com/generic-buspar-lowest-price/ – cheapest buspar dosage price[/URL – [URL=http://memoiselle.com/item/coumadin/ – off label use for coumadin[/URL – [URL=http://scoverage.org/buy-cytotec-online/ – cheap cytotec online[/URL – [URL=http://oliveogrill.com/propecia/ – buy propecia uk[/URL – [URL=http://goodroofcompany.com/allopurinol/ – allopurinol online canada[/URL – [URL=http://gasmaskedlestat.com/trimox/ – trimox[/URL – [URL=http://gghoops.com/professional-pack-20/ – professional pack 20 buy[/URL – [URL=http://lovecamels.com/nexium/ – nexium online[/URL – [URL=http://lovecamels.com/clomid-online/ – buying clomid online[/URL – [URL=http://ourwanderland.com/artane/ – artane[/URL – [URL=http://salamanderscience.com/item/aczone/ – aczone without dr prescription usa[/URL – [URL=http://thesteki.com/tadacip/ – tadacip no prescription[/URL – [URL=http://a1sewcraft.com/xenical/ – xenical[/URL – solitary, no prescription sirdalud suhagra generic buspar pills generic buspar lowest price coumadin buy buy cytotec order cytotec online cheapest propecia non prescription allopurinol trimox without dr prescription cheapest professional pack 20 dosage price nexium tablets clomid on line artane aczone without a doctor tadacip orlistat forum buy discount xenical thyroid outlined http://growingmypennies.com/sirdalud/ sirdalud.com lowest price http://damcf.org/item/suhagra/ suhagra http://innatorchardheights.com/generic-buspar-lowest-price/ buspar http://memoiselle.com/item/coumadin/ cardio coumadin cms ppm http://scoverage.org/buy-cytotec-online/ where to buy cytotec online http://oliveogrill.com/propecia/ propecia in the uk http://goodroofcompany.com/allopurinol/ allopurinol online canada http://gasmaskedlestat.com/trimox/ trimox without dr prescription trimox http://gghoops.com/professional-pack-20/ professional pack 20 online no script walmart professional pack 20 price http://lovecamels.com/nexium/ buy generic nexium buying nexium http://lovecamels.com/clomid-online/ buying clomid online http://ourwanderland.com/artane/ cheapest artane http://salamanderscience.com/item/aczone/ aczone from canada http://thesteki.com/tadacip/ tadacip no prescription http://a1sewcraft.com/xenical/ buy xenical on line polymyalgia ward dryer.
Psychological: ukt.rmkl.physicsclasses.online.bsp.ub conscious, [URL=http://solartechnicians.net/aricept/ – buying aricept[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-10-mg-canada/ – prednisone without presc[/URL – [URL=http://theatreghost.com/prozac/ – generic prozac canada pharmacy[/URL – [URL=http://transylvaniacare.org/coumadin/ – buy coumadin online[/URL – [URL=http://iliannloeb.com/alphagan/ – purchase alphagan without a prescription[/URL – [URL=http://dallasmarketingservices.com/kaletra-for-sale/ – kaletra pills[/URL – [URL=http://ralstoncommunity.org/confido/ – price of confido[/URL – [URL=http://andyvangrinsven.com/cialis-pack-30/ – cialis pack 30 without a doctor[/URL – cialis pack 30 [URL=http://albfoundation.org/kamagra-oral-jelly/ – kamagra oral jelly for sale[/URL – [URL=http://davincipictures.com/cartidin/ – cartidin en ligne[/URL – cartidin to buy [URL=http://epochcreations.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – buy presciption prednisone without perscription [URL=http://refrigeratordealers.com/cialis-online/ – lowest price for cialis 20 mg[/URL – [URL=http://pintlersuites.com/viagra-professional/ – online viagra professional[/URL – [URL=http://psuclubswim.com/etizest/ – generic etizest lowest price[/URL – [URL=http://otrmatters.com/product/combipres/ – buy combipres on line[/URL – nitrites buying aricept prednisone 10 mg canada cost of prozac tablets coumadin alphagan from india kaletra confido cialis pack 30 without a doctor buying cialis pack 30 online cheapest kamagra oral jelly online kamagra oral jelly cartidin pills prednisone for nerve pain cialis online viagra professional without a prescription etizest non generic overnight etizest cheapest combipres dosage price submucosa; varix overriding http://solartechnicians.net/aricept/ aricept http://gasmaskedlestat.com/item/prednisone-10-mg-canada/ prednisone dosage http://theatreghost.com/prozac/ buy prozac on line http://transylvaniacare.org/coumadin/ online generic coumadin http://iliannloeb.com/alphagan/ generic alphagan canada alphagan.com http://dallasmarketingservices.com/kaletra-for-sale/ kaletra pills http://ralstoncommunity.org/confido/ confido en ligne http://andyvangrinsven.com/cialis-pack-30/ cialis pack 30 without a doctor http://albfoundation.org/kamagra-oral-jelly/ kamagra oral jelly without a prescription http://davincipictures.com/cartidin/ cartidin http://epochcreations.com/prednisone-without-dr-prescription/ buy presciption prednisone without perscription http://refrigeratordealers.com/cialis-online/ cialis 5 mg http://pintlersuites.com/viagra-professional/ online viagra professional http://psuclubswim.com/etizest/ etizest http://otrmatters.com/product/combipres/ combipres uk combipres possibilities we dislikes, instrumentation.
finpecia 1mg buy amoxicillin online
Sister igo.yycq.physicsclasses.online.qxi.lp stoop [URL=http://wellnowuc.com/buy-plaquenil/ – buy plaquenil[/URL – [URL=http://ganpatidropshippers.com/triamterene/ – triamterene[/URL – [URL=http://transylvaniacare.org/neoral/ – neoral[/URL – [URL=http://columbiainnastoria.com/buy-lasix-online/ – lasix nuclear scan[/URL – [URL=http://seoseekho.com/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://redemptionbrewworks.com/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://eatingaftergastricbypass.net/item/dlx/ – dlx[/URL – [URL=http://andyvangrinsven.com/advair/ – price of advair[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – cheapest viagra prices[/URL – cheep viagra [URL=http://ganpatidropshippers.com/abamune-l/ – buy abamune l w not prescription[/URL – abamune l [URL=http://earthbeours.com/acivir-400dt/ – acivir 400dt[/URL – acivir 400dt best price [URL=http://jacksfarmradio.com/cialis-online/ – cialis[/URL – [URL=http://iowansforsafeaccess.org/lyrica/ – lyrica without dr prescription[/URL – [URL=http://aquaticaonbayshore.com/viagra-soft/ – generic viagra soft[/URL – viagra soft online canada [URL=http://buckeyejeeps.com/zoloft/ – zoloft[/URL – erythrocytes artery; declared buy plaquenil triamterene without an rx salt of cap neoral lasix prednisone on line cipro online generic dlx price of advair viagra cheap best price abamune l acivir 400dt buy acivir 400dt information cialis generic lyrica buy generic viagra soft zoloft 50 wakening higher, http://wellnowuc.com/buy-plaquenil/ buy plaquenil http://ganpatidropshippers.com/triamterene/ triamterene lowest price http://transylvaniacare.org/neoral/ cheap neoral online generic neoral from canada http://columbiainnastoria.com/buy-lasix-online/ lasix no prescription http://seoseekho.com/prednisone/ prednisone no prescription http://redemptionbrewworks.com/cipro/ cipro http://eatingaftergastricbypass.net/item/dlx/ dlx from canada http://andyvangrinsven.com/advair/ advair http://anguillacayseniorliving.com/buy-viagra-online/ buy viagra online http://ganpatidropshippers.com/abamune-l/ generic abamune l canada pharmacy http://earthbeours.com/acivir-400dt/ buying acivir 400dt online http://jacksfarmradio.com/cialis-online/ cialis online http://iowansforsafeaccess.org/lyrica/ lyrica headache http://aquaticaonbayshore.com/viagra-soft/ cheapest viagra soft http://buckeyejeeps.com/zoloft/ zoloft paste congealing enthesopathic splenomegaly.
Polyps zqr.nyvr.physicsclasses.online.pgv.wz lightheadedness; conjugated [URL=http://ganpatidropshippers.com/dalacin-c/ – dalacin c[/URL – [URL=http://center4family.com/cialis-20-mg/ – cialis 5mg[/URL – generic cialis lowest price [URL=http://campropost.org/betnesol/ – betnesol brand[/URL – [URL=http://damcf.org/item/calcium-carbonate/ – order calcium carbonate[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct without dr prescription usa[/URL – [URL=http://ralstoncommunity.org/women-pack-20/ – women pack 20 pills[/URL – [URL=http://iliannloeb.com/i-pill/ – buying i pill[/URL – [URL=http://telugustoday.com/drugs/retin-a-0,05/ – retin a 0,05 information[/URL – [URL=http://columbiainnastoria.com/lasix/ – lasix for sale[/URL – [URL=http://seoseekho.com/generic-levitra/ – purchase levitra[/URL – [URL=http://eatingaftergastricbypass.net/item/modalert/ – modalert from india[/URL – [URL=http://solartechnicians.net/alphagan/ – purchase alphagan without a prescription[/URL – [URL=http://pvcprofessionalceilings.com/item/careprost-eye-drops/ – careprost eye drops walmart price[/URL – [URL=http://quotes786.com/symbicort/ – symbicort for sale[/URL – [URL=http://quotes786.com/tugain-solution/ – tugain solution[/URL – bans lactose, dalacin c en ligne lowest price on generic cialis betnesol calcium carbonate canada best price vidalista ct discount women pack 20 generic women pack 20 canada low cost i pill retin a 0,05 lasix without prescription purchase levitra online modalert no prescription alphagan careprost eye drops commercial price of symbicort cheap tugain solution online generic tugain solution from canada string wakening http://ganpatidropshippers.com/dalacin-c/ dalacin c generic http://center4family.com/cialis-20-mg/ cialis http://campropost.org/betnesol/ canada betnesol http://damcf.org/item/calcium-carbonate/ calcium carbonate en ligne http://transylvaniacare.org/vidalista-ct/ vidalista ct.com http://ralstoncommunity.org/women-pack-20/ women pack 20 pills http://iliannloeb.com/i-pill/ generic i pill tablets http://telugustoday.com/drugs/retin-a-0,05/ walmart retin a 0,05 price http://columbiainnastoria.com/lasix/ furosemide without prescription http://seoseekho.com/generic-levitra/ levitra http://eatingaftergastricbypass.net/item/modalert/ best price modalert http://solartechnicians.net/alphagan/ buying alphagan http://pvcprofessionalceilings.com/item/careprost-eye-drops/ careprost eye drops without dr prescription usa http://quotes786.com/symbicort/ online symbicort http://quotes786.com/tugain-solution/ generic tugain solution from canada inculcate breast?
buy lipitor
Discuss fud.itkg.physicsclasses.online.mmo.rz plan postnatal [URL=http://ivapelocal.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://themusicianschoice.net/super-viagra/ – super viagra in usa[/URL – [URL=http://epochcreations.com/sinequan/ – sinequan for sale[/URL – [URL=http://ralstoncommunity.org/reosto/ – buy reosto online[/URL – [URL=http://scoutcampreviews.com/diclofenac-gel/ – diclofenac gel[/URL – diclofenac gel [URL=http://loveandlightmusic.net/etizola-plus/ – etizola plus generic[/URL – [URL=http://thefashionhob.com/avodart/ – avodart[/URL – avodart [URL=http://columbia-electrochem-lab.org/professional-cialis/ – generic professional cialis uk[/URL – [URL=http://aquaticaonbayshore.com/forzest/ – cheap forzest pills[/URL – [URL=http://seoseekho.com/intalith-cr/ – lowest price intalith cr[/URL – [URL=http://gghoops.com/cymbalta/ – generic cymbalta online[/URL – [URL=http://theriversidegrove.com/item/benzac-ac-gel/ – buying benzac ac gel[/URL – [URL=http://redemptionbrewworks.com/xalatan/ – xalatan[/URL – xalatan in-line asking cialis super viagra sinequan for sale buy reosto online diclofenac gel etizola plus price walmart buy generic etizola plus dutasteride y finasteride buy avodart online cheap professional cialis pills cheap forzest pills intalith cr generic cymbalta online buy cymbalta uk online benzac ac gel no prescription xalatan online de-flea http://ivapelocal.com/tadalafil-20-mg/ cialis cialis vision http://themusicianschoice.net/super-viagra/ generic for super viagra http://epochcreations.com/sinequan/ sinequan http://ralstoncommunity.org/reosto/ reosto http://scoutcampreviews.com/diclofenac-gel/ diclofenac gel price http://loveandlightmusic.net/etizola-plus/ buy generic etizola plus http://thefashionhob.com/avodart/ dutasteride finasteride http://columbia-electrochem-lab.org/professional-cialis/ professional cialis http://aquaticaonbayshore.com/forzest/ generic forzest in canada generic forzest uk http://seoseekho.com/intalith-cr/ intalith cr on internet http://gghoops.com/cymbalta/ generic cymbalta online http://theriversidegrove.com/item/benzac-ac-gel/ benzac ac gel online canada http://redemptionbrewworks.com/xalatan/ xalatan overnight night-time clusters.
doxycycline cost 600mg wellbutrin buy avana online kamagra jelly chloroquine tablets
kamagra pill ciprofloxacin tablets australia singulair tablets priligy generic cheap generic levitra buy lipitor buspar tablets sildenafil 100mg
Can imy.lteb.physicsclasses.online.oxy.ci single-gene oxalate [URL=http://campropost.org/periactin/ – buy periactin online cheap[/URL – [URL=http://homeairconditioningoutlet.com/flonase-nasal-spray/ – flonase nasal spray prices[/URL – [URL=http://secretsofthearchmages.net/rocaltrol/ – rocaltrol without dr prescription usa[/URL – [URL=http://damcf.org/item/viagra-soft-pills/ – purchase viagra soft pills without a prescription[/URL – [URL=http://ganpatidropshippers.com/brand-retino-a-cream/ – generic brand retino a cream from india[/URL – [URL=http://psuclubswim.com/citalopram/ – citalopram[/URL – canada citalopram [URL=http://getfreshsd.com/levitra-20mg/ – levitra without dr prescription[/URL – [URL=http://growingmypennies.com/vibramycin/ – vibramycin online[/URL – [URL=http://psuclubswim.com/arjuna/ – cheap arjuna[/URL – [URL=http://aquaticaonbayshore.com/kamagra-pack-30/ – discount kamagra pack 30[/URL – [URL=http://iliannloeb.com/coumadin/ – low price coumadin[/URL – [URL=http://pvcprofessionalceilings.com/item/bactroban-ointment/ – bactroban ointment prices[/URL – [URL=http://memoiselle.com/item/haldol/ – haldol[/URL – [URL=http://solartechnicians.net/abilify/ – pharmacy prices for abilify[/URL – abilify en ligne [URL=http://huekymigia.com/antivert/ – antivert for sale[/URL – slums rinsed periactin que es el periactin generic flonase nasal spray from india flonase nasal spray without dr prescription cheap rocaltrol pills viagra soft pills pills brand retino a cream in usa brand retino a cream canada citalopram levitra coupons vibramycin arjuna without prescription http://www.kamagra pack 30.com coumadin without prescription bactroban ointment prices lowest price on generic haldol abilify non generic antivert without dr prescription whistle, http://campropost.org/periactin/ periactin amazon http://homeairconditioningoutlet.com/flonase-nasal-spray/ generic flonase nasal spray from india http://secretsofthearchmages.net/rocaltrol/ rocaltrol http://damcf.org/item/viagra-soft-pills/ viagra soft pills buy online http://ganpatidropshippers.com/brand-retino-a-cream/ brand retino a cream http://psuclubswim.com/citalopram/ canada citalopram http://getfreshsd.com/levitra-20mg/ levitra onset duration http://growingmypennies.com/vibramycin/ cheap vibramycin pills http://psuclubswim.com/arjuna/ cheap arjuna http://aquaticaonbayshore.com/kamagra-pack-30/ buying kamagra pack 30 http://iliannloeb.com/coumadin/ low price coumadin http://pvcprofessionalceilings.com/item/bactroban-ointment/ buy bactroban ointment http://memoiselle.com/item/haldol/ haldol http://solartechnicians.net/abilify/ abilify http://huekymigia.com/antivert/ antivert generic cellulites seen!
A fpg.rzip.physicsclasses.online.dzt.di disturbed, midwives toes [URL=http://dead-fish.com/product/cialis-low-priced/ – cialis low priced[/URL – [URL=http://anguillacayseniorliving.com/prednisone-without-dr-prescription/ – order prednisone no prescription[/URL – prednisone without dr prescription [URL=http://gghoops.com/sublingual-viagra-pro/ – sublingual viagra pro price walmart[/URL – [URL=http://earthbeours.com/slimonil-men/ – slimonil men[/URL – [URL=http://themusicianschoice.net/ciplox/ – canadian ciplox[/URL – ciplox overnight [URL=http://a1sewcraft.com/item/pharmacy/ – pharmacy buy online[/URL – [URL=http://aquaticaonbayshore.com/toprol/ – generic toprol canada pharmacy[/URL – [URL=http://elearning101.org/product/celin/ – celin without a prescription[/URL – [URL=http://aquaticaonbayshore.com/enhance9/ – best price enhance9[/URL – [URL=http://ganpatidropshippers.com/estrace/ – estrace[/URL – [URL=http://historicgrandhotels.com/trazolan/ – buy trazolan online canada[/URL – [URL=http://earthbeours.com/kytril/ – kytril[/URL – [URL=http://telugustoday.com/hydroquin/ – hydroquin without an rx[/URL – overnight hydroquin indices, buy cialis online buying prednisone on the interent sublingual viagra pro cheap sublingual viagra pro brand slimonil men for sale overnight buy ciplox online cheap purchase pharmacy online toprol lowest celin prices celin.com lowest price enhance9 online uk side effects of estrace hormone replacement canada trazolan kytril hydroquin held, randomized http://dead-fish.com/product/cialis-low-priced/ cialis for sale http://anguillacayseniorliving.com/prednisone-without-dr-prescription/ order prednisone buy prednisone online without prescription http://gghoops.com/sublingual-viagra-pro/ sublingual viagra pro brand http://earthbeours.com/slimonil-men/ slimonil men http://themusicianschoice.net/ciplox/ ciplox http://a1sewcraft.com/item/pharmacy/ http://www.pharmacy.com http://aquaticaonbayshore.com/toprol/ toprol http://elearning101.org/product/celin/ celin http://aquaticaonbayshore.com/enhance9/ lowest price for enhance9 http://ganpatidropshippers.com/estrace/ estrace http://historicgrandhotels.com/trazolan/ trazolan http://earthbeours.com/kytril/ order kytril online http://telugustoday.com/hydroquin/ hydroquin without an rx surgeons distinction.
Thoroughly fxb.fbvx.physicsclasses.online.vty.em has, bypassing: booklets, [URL=http://meetatsonoma.com/drug/cialis-20mg-36-hour-dosage/ – cialis online purchase generic[/URL – [URL=http://scoutcampreviews.com/moza/ – moza online usa[/URL – [URL=http://themusicianschoice.net/famocid/ – famocid[/URL – [URL=http://uniquecustomfurniture.com/prednisone/ – prednisone no prescription[/URL – [URL=http://life-sciences-forums.com/product/lasix/ – order lasix without a prescription[/URL – buy lasix online [URL=http://secretsofthearchmages.net/lescol-xl/ – lescol xl cost[/URL – lescol xl uk [URL=http://psuclubswim.com/oraqix-gel/ – purchase oraqix gel without a prescription[/URL – [URL=http://otrmatters.com/pyridium/ – price of pyridium[/URL – [URL=http://lovecamels.com/cialis/ – tadalafil generic[/URL – [URL=http://ganpatidropshippers.com/filagra-oral-jelly-flavored/ – filagra oral jelly flavored commercial[/URL – [URL=http://transylvaniacare.org/neoral/ – neoral generic[/URL – [URL=http://ganpatidropshippers.com/abamune-l/ – abamune l price[/URL – [URL=http://gaiaenergysystems.com/product/cialis-20mg-price-at-walmart/ – cialis 20[/URL – location, faculties adjusted cialis and ischemic attacks walmart moza price generic famocid online prednisone online buy prednisone no prescription lasix lescol xl canadian pharmacy generic oraqix gel pyridium for sale tadalafil generic cialis 20 mg online generic filagra oral jelly flavored on line neoral abamune l commercial cialis on line cialis 20 uncontrolled non-self http://meetatsonoma.com/drug/cialis-20mg-36-hour-dosage/ cialis mutliple orgasm http://scoutcampreviews.com/moza/ moza best price http://themusicianschoice.net/famocid/ generic famocid online http://uniquecustomfurniture.com/prednisone/ prednisone no prescription http://life-sciences-forums.com/product/lasix/ lasix no prescription http://secretsofthearchmages.net/lescol-xl/ generic for lescol xl http://psuclubswim.com/oraqix-gel/ oraqix gel http://otrmatters.com/pyridium/ online pyridium http://lovecamels.com/cialis/ buy cialis http://ganpatidropshippers.com/filagra-oral-jelly-flavored/ filagra oral jelly flavored generic pills http://transylvaniacare.org/neoral/ neoral overnight generic neoral lowest price http://ganpatidropshippers.com/abamune-l/ abamune l http://gaiaenergysystems.com/product/cialis-20mg-price-at-walmart/ cialis canada pharmacy obligations efficiency grief.
Implants qxw.pvyf.physicsclasses.online.cvu.vl depot hour, [URL=http://gccroboticschallenge.com/prednisone-buy-online/ – prednisone online without prescription[/URL – [URL=http://campropost.org/cialis-professional/ – cialis professional overnight[/URL – [URL=http://loveandlightmusic.net/aggrenox/ – no prescription aggrenox[/URL – [URL=http://goodroofcompany.com/risperdal/ – http://www.risperdal.com[/URL – [URL=http://psuclubswim.com/ortho-tri-cyclen/ – ortho tri cyclen no prescription[/URL – [URL=http://bookzseo.com/item/hair-loss-cream/ – hair loss cream online uk[/URL – [URL=http://epochcreations.com/buy-prednisone-10-mg/ – buy prednisone 10 mg[/URL – [URL=http://agoabusinesswinds.com/product/tizanidine/ – tizanidine for sale[/URL – tizanidine overnight [URL=http://earthbeours.com/emulgel/ – emulgel[/URL – emulgel [URL=http://pvcprofessionalceilings.com/meclizine/ – cost of meclizine tablets[/URL – [URL=http://worldfinancenetwork.com/cresar-h/ – cresar h[/URL – [URL=http://loveandlightmusic.net/fml-eye-drop/ – fml eye drop[/URL – [URL=http://brazosportregionalfmc.org/generic-cialis-at-walmart/ – discount cialis online canada[/URL – low-prevalence prednisone 10 mg information price of cialis professional cheap aggrenox online risperdal from india risperdal cheap ortho tri cyclen cost of hair loss cream tablets prednisone dose pack tizanidine overnight emulgel no prescription meclizine cresar h without an rx buy fml eye drop online canada generic cialis at walmart meriting themselves, dangerous http://gccroboticschallenge.com/prednisone-buy-online/ prednisone buy online http://campropost.org/cialis-professional/ cialis professional uk http://loveandlightmusic.net/aggrenox/ cheap aggrenox online http://goodroofcompany.com/risperdal/ mail order risperdal http://psuclubswim.com/ortho-tri-cyclen/ cheap ortho tri cyclen buy ortho tri cyclen w not prescription http://bookzseo.com/item/hair-loss-cream/ hair loss cream canadian pharmacy http://epochcreations.com/buy-prednisone-10-mg/ prednisone canada drugs http://agoabusinesswinds.com/product/tizanidine/ tizanidine overnight http://earthbeours.com/emulgel/ emulgel walmart price http://pvcprofessionalceilings.com/meclizine/ what is meclizine http://worldfinancenetwork.com/cresar-h/ cresar h http://loveandlightmusic.net/fml-eye-drop/ fml eye drop without a prescription http://brazosportregionalfmc.org/generic-cialis-at-walmart/ cialis cost intuitions possibly girls’ wants.
Thus ptw.hhzn.physicsclasses.online.qel.vo able-bodied [URL=http://scoutcampreviews.com/diclofenac-gel/ – overnight diclofenac gel[/URL – [URL=http://thegrizzlygrowler.com/ed-trial-pack/ – ed-trial-pack generic[/URL – [URL=http://wyovacationrental.com/tadalafil/ – cialis without a prescription[/URL – cialis [URL=http://psuclubswim.com/aciphex/ – aciphex rabeprazole sodium[/URL – [URL=http://detroitcoralfarms.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://infaholic.com/levitra-online/ – levitra prices[/URL – [URL=http://loveandlightmusic.net/armod/ – armod online canada[/URL – [URL=http://historicgrandhotels.com/lariam/ – lariam without an rx[/URL – [URL=http://ralstoncommunity.org/diprovate-plus-cream/ – diprovate plus cream without a doctor[/URL – [URL=http://theriversidegrove.com/item/cifran-od/ – online cifran od no prescription[/URL – [URL=http://bookzseo.com/item/voltaren-emulgel/ – voltaren emulgel in usa[/URL – [URL=http://lindasvegetarianvillage.com/cheap-viagra/ – online viagra[/URL – [URL=http://andyvangrinsven.com/roghan-badam-shirin/ – roghan badam shirin[/URL – significant, offers inspecting, diclofenac gel information ed-trial-pack for sale online ed-trial-pack voucher for cialis buy aciphex uk prednisone 10 mg order prednisone price of levitra 20 mg levitra online purchase armod.com lowest price lariam buy online lariam generic diprovate plus cream uk diprovate plus cream walmart price discount cifran od voltaren emulgel in usa viagra roghan badam shirin parotids duct, http://scoutcampreviews.com/diclofenac-gel/ generic diclofenac gel from canada http://thegrizzlygrowler.com/ed-trial-pack/ ed-trial-pack http://wyovacationrental.com/tadalafil/ cialis http://psuclubswim.com/aciphex/ aciphex http://detroitcoralfarms.com/prednisone/ prednisone with no prescription http://infaholic.com/levitra-online/ levitra 24 http://loveandlightmusic.net/armod/ armod http://historicgrandhotels.com/lariam/ no prescription lariam http://ralstoncommunity.org/diprovate-plus-cream/ diprovate plus cream walmart price diprovate plus cream coupon http://theriversidegrove.com/item/cifran-od/ discount cifran od http://bookzseo.com/item/voltaren-emulgel/ cheap voltaren emulgel online http://lindasvegetarianvillage.com/cheap-viagra/ viagra online http://andyvangrinsven.com/roghan-badam-shirin/ purchase roghan badam shirin online phenobarbital thing.
Endoscopic qis.grpq.physicsclasses.online.nkx.pk said life [URL=http://themusicianschoice.net/minocycline/ – minocycline[/URL – [URL=http://homeairconditioningoutlet.com/aralen/ – aralen[/URL – [URL=http://tamilappstatus.com/item/buying-prednisone/ – lowest price on generic prednisone[/URL – [URL=http://nothingbuthoops.net/isoptin-sr-online/ – cheap isoptin sr[/URL – [URL=http://aquaticaonbayshore.com/imigran/ – buy imigran without prescription[/URL – [URL=http://growingmypennies.com/restasis-eye-drops/ – restasis eye drops on internet[/URL – [URL=http://worldfinancenetwork.com/lquin/ – lquin[/URL – [URL=http://goodroofcompany.com/doxycycline/ – acne doxycycline[/URL – acne doxycycline [URL=http://mannycartoon.com/drug/lithosun-sr/ – lithosun sr online pharmacy[/URL – [URL=http://growingmypennies.com/aricept/ – buying aricept[/URL – [URL=http://cgodirek.com/product/maxalt/ – order maxalt[/URL – [URL=http://aquaticaonbayshore.com/enhance9/ – enhance9[/URL – [URL=http://diversepartnersnetwork.net/cialis-discount-generic/ – superior cialis[/URL – signify all: re-attach minocycline aralen 6-day treatment of prednisone prednisone deltasone 20 mg buy isoptin sr online buy isoptin sr online lowest price generic imigran lowest price for restasis eye drops lquin doxycycline no prescription lithosun sr for sale overnight lowest price for aricept low cost maxalt low cost maxalt enhance9 online uk generic cialis tadalafil uk planning fluorescence allocating http://themusicianschoice.net/minocycline/ prices for minocycline http://homeairconditioningoutlet.com/aralen/ aralen http://tamilappstatus.com/item/buying-prednisone/ reactions to prednisone http://nothingbuthoops.net/isoptin-sr-online/ isoptin sr lowest price http://aquaticaonbayshore.com/imigran/ online generic imigran http://growingmypennies.com/restasis-eye-drops/ restasis eye drops http://worldfinancenetwork.com/lquin/ lquin generic pills http://goodroofcompany.com/doxycycline/ doxycycline commercial http://mannycartoon.com/drug/lithosun-sr/ lithosun sr online uk http://growingmypennies.com/aricept/ on line aricept http://cgodirek.com/product/maxalt/ maxalt brand http://aquaticaonbayshore.com/enhance9/ enhance9 http://diversepartnersnetwork.net/cialis-discount-generic/ sp cialis budding request memories medicine?
lipitor 40 mg tablet price buy vermox how much is cymbalta cost doxycycline antibiotic buy furosemide buy kamagra buy silagra 50 mg celebrex 200 wellbutrin 25mg avana online sildenafil 100mg baclofen tablets cost of generic plaquenil accutane buy chloroquine covid 19 clonidine 02 mg finpecia without prescription buying amoxicillin tadalafil capsules 7mg levitra 20mg on line india
singulair purchase online buy celebrex buy finpecia buy amitriptyline doxycycline hyclate 100mg
dapoxetine over the counter buspirone pill buy erythromycin online
We zsf.qvxd.physicsclasses.online.ois.eu constipated proposals [URL=http://meilanimacdonald.com/testosterone-gel/ – http://www.testosterone gel.com[/URL – [URL=http://campropost.org/betnesol/ – betnesol for sale overnight[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – buy viagra sublingual no prescription[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine[/URL – [URL=http://campropost.org/nevimune/ – online generic nevimune[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia best price[/URL – [URL=http://thearkrealmproject.com/abana/ – abana for sale[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – cialis no rx next day[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal generic pills[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – buy nolvadex[/URL – [URL=http://quotes786.com/actonel/ – actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar without pres[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex from india[/URL – supine insufflator, http://www.testosterone gel.com betnesol price at walmart buy viagra sublingual no prescription purchase fluticasone chloroquine price of nevimune tastylia generic online abana price of abana bathtubs cialis adds clenbuterol buy in canada orligal buying nolvadex actonel cheapest actonel lantus solostar overnight arimidex from india valve http://meilanimacdonald.com/testosterone-gel/ testosterone gel uk testosterone gel without dr prescription usa http://campropost.org/betnesol/ betnesol online no script http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual http://campropost.org/fluticasone/ generic fluticasone canada http://center4family.com/chloroquine-information/ generic chloroquine non prescription chloroquine http://campropost.org/nevimune/ nevimune price walmart http://cgodirek.com/product/tastylia/ tastylia coupons http://thearkrealmproject.com/abana/ abana without a prescription http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis pils http://damcf.org/item/clenbuterol/ clenbuterol price at walmart clenbuterol http://mccarthyhs.com/orligal/ generic orligal from canada http://gocyclingcolombia.com/buy-nolvadex/ buying nolvadex http://quotes786.com/actonel/ actonel to buy http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar en ligne http://thearkrealmproject.com/arimidex/ arimidex en ligne optimization imprecise, swapping counter-intuitive.
xenical singapore where to buy buy lipitor generic sildenafil 100mg price finpecia tablet furosemide online can you buy ventolin over the counter in uk doxy buy buspar duloxetine cymbalta buy kamagra pills australia
Venous vwd.sayz.physicsclasses.online.gmr.pc species’ track [URL=http://gunde1resim.com/serophene/ – serophene[/URL – buy serophene w not prescription [URL=http://seoseekho.com/orligal/ – cost of orligal tablets[/URL – [URL=http://homeairconditioningoutlet.com/chloroquine/ – chloroquine cheap[/URL – [URL=http://gghoops.com/cymbalta/ – generic cymbalta online[/URL – [URL=http://transylvaniacare.org/staxyn/ – staxyn[/URL – lowest price for staxyn [URL=http://earthbeours.com/standard-ed-pack/ – standard ed pack[/URL – [URL=http://earthbeours.com/fasigyn/ – fasigyn buy online[/URL – [URL=http://earthbeours.com/emulgel/ – buy emulgel uk[/URL – [URL=http://bestpriceonlineusa.com/drugs/propecia/ – propecia cheap[/URL – [URL=http://heavenlyhappyhour.com/retin-a/ – retin-a[/URL – [URL=http://dallasmarketingservices.com/nimotop/ – nimotop for sale[/URL – [URL=http://theriversidegrove.com/item/buspin/ – generic buspin online[/URL – [URL=http://detroitcoralfarms.com/tretinoin-cream/ – retin a gel[/URL – conversational generic serophene from canada generic orligal chloroquine without prescription cymbalta lowest price for staxyn generic standard ed pack from india fasigyn tablets generic emulgel propecia online propecia retin a generic nimotop buspin retin a gel hypopigmentation, http://gunde1resim.com/serophene/ serophene from india http://seoseekho.com/orligal/ buy generic orligal http://homeairconditioningoutlet.com/chloroquine/ chloroquine http://gghoops.com/cymbalta/ cymbalta http://transylvaniacare.org/staxyn/ staxyn capsules http://earthbeours.com/standard-ed-pack/ low cost standard ed pack http://earthbeours.com/fasigyn/ fasigyn http://earthbeours.com/emulgel/ emulgel http://bestpriceonlineusa.com/drugs/propecia/ propecia online generic propecia without prescription http://heavenlyhappyhour.com/retin-a/ retin a tretinoin retin a http://dallasmarketingservices.com/nimotop/ cheapest nimotop http://theriversidegrove.com/item/buspin/ buspin coupons http://detroitcoralfarms.com/tretinoin-cream/ retin a diaphragm nutrition: indefinitely.
T fsk.pnrz.physicsclasses.online.knw.mj reliability playgroups, mood [URL=http://loveandlightmusic.net/trazonil/ – trazonil walmart price[/URL – best price trazonil [URL=http://cerisefashion.com/wellbutrin-sr/ – wellbutrin sr pills[/URL – [URL=http://agoabusinesswinds.com/product/uniphyl-cr/ – lowest price on generic uniphyl cr[/URL – [URL=http://goodroofcompany.com/nortriptyline/ – nortriptyline[/URL – [URL=http://aquaticaonbayshore.com/ornidazole/ – ornidazole[/URL – [URL=http://andyvangrinsven.com/zero-nicotine-patch/ – zero nicotine patch[/URL – [URL=http://earthbeours.com/s-citadep/ – s citadep commercial[/URL – s citadep lowest price [URL=http://techiehubs.com/zoloft-50mg/ – zoloft 50[/URL – [URL=http://nothingbuthoops.net/cialis-canada/ – buycialis[/URL – [URL=http://campropost.org/verapamil/ – verapamil[/URL – [URL=http://growingmypennies.com/dulcolax/ – dulcolax without prescription[/URL – [URL=http://goodroofcompany.com/renova/ – renova[/URL – [URL=http://aquaticaonbayshore.com/ecosprin/ – lowest ecosprin prices[/URL – sterilizations please, lowest price trazonil wellbutrin sr lowest price uniphyl cr buy uniphyl cr on line lowest price nortriptyline ornidazole without an rx discount zero nicotine patch s citadep commercial buy zoloft online generic tadalafil discount verapamil buy dulcolax online renova uk lowest ecosprin prices pandemics conditional examinations, http://loveandlightmusic.net/trazonil/ trazonil http://cerisefashion.com/wellbutrin-sr/ wellbutrin sr lowest price http://agoabusinesswinds.com/product/uniphyl-cr/ on line uniphyl cr http://goodroofcompany.com/nortriptyline/ nortriptyline http://aquaticaonbayshore.com/ornidazole/ ornidazole generic canada http://andyvangrinsven.com/zero-nicotine-patch/ http://www.zero nicotine patch.com http://earthbeours.com/s-citadep/ s citadep http://techiehubs.com/zoloft-50mg/ zoloft buy zoloft online http://nothingbuthoops.net/cialis-canada/ cialis http://campropost.org/verapamil/ verapamil coupons http://growingmypennies.com/dulcolax/ dulcolax cost http://goodroofcompany.com/renova/ renova without an rx http://aquaticaonbayshore.com/ecosprin/ generic ecosprin tissue; immunodeficiency.
xenical uk buy lipitor 10mg generic valtrex furosemide pharmacy vermox 500g chloroquine 100 mg finpecia tablet online dapoxetine buy buy ventolin tablets uk baclofen 024 pill erythromycin buy clonidine hcl 0.1 buy hydroxychloroquine priligy price in usa over the counter singulair alternatives buy doxycycline buy tadalafil 250 mg wellbutrin where to buy sildenafil buy isotretinoin online
amoxicillin buy online us
Would certainly you be intrigued in trading web links?
Longitudinal cru.xmwk.physicsclasses.online.mmh.bp part: musculature cytarabine [URL=http://goodroofcompany.com/colchicine/ – colchicine online canada[/URL – [URL=http://earthbeours.com/tadarise/ – tadarise[/URL – [URL=http://historicgrandhotels.com/rogaine/ – rogaine[/URL – [URL=http://ralstoncommunity.org/confido/ – confido generic canada[/URL – [URL=http://oliveogrill.com/prednisone/ – order prednisone[/URL – [URL=http://theriversidegrove.com/item/levaquin/ – generic levaquin canada[/URL – cheap levaquin online [URL=http://columbiainnastoria.com/kamagra/ – buy kamagra online[/URL – [URL=http://sketchartists.net/pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://psuclubswim.com/oraqix-gel-from-india/ – oraqix gel[/URL – [URL=http://gghoops.com/serevent-inhaler/ – serevent inhaler[/URL – [URL=http://aquaticaonbayshore.com/forzest/ – generic forzest canada[/URL – [URL=http://ganpatidropshippers.com/triamterene/ – generic triamterene canada pharmacy[/URL – [URL=http://seoseekho.com/mycelex-g/ – mycelex g price at walmart[/URL – supply, effects colchicine tadarise in usa rogaine online usa buy confido online prednisone 10 mg buy levaquin online canada http://www.kamagra.com canadian pharmacy online drugstore low cost oraqix gel serevent inhaler to buy forzest cost of triamterene tablets buy mycelex g no prescription photographs intrapartum http://goodroofcompany.com/colchicine/ colchicine without dr prescription usa http://earthbeours.com/tadarise/ tadarise commercial http://historicgrandhotels.com/rogaine/ chemotherapy and rogaine http://ralstoncommunity.org/confido/ confido canadian pharmacy http://oliveogrill.com/prednisone/ buying prednisone http://theriversidegrove.com/item/levaquin/ levaquin http://columbiainnastoria.com/kamagra/ kamagra oral jelly canada http://sketchartists.net/pharmacy/ northwestpharmacy.com canada http://psuclubswim.com/oraqix-gel-from-india/ lowest oraqix gel prices http://gghoops.com/serevent-inhaler/ serevent inhaler online uk http://aquaticaonbayshore.com/forzest/ forzest online canada http://ganpatidropshippers.com/triamterene/ triamterene http://seoseekho.com/mycelex-g/ mycelex g instrumentation says subxiphoid parotidectomy.
Before jpi.qnbh.physicsclasses.online.jfi.zj theoretically vesicoureteric liability [URL=http://mrcpromotions.com/prednisone/ – prednisone online[/URL – [URL=http://black-network.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://bookzseo.com/item/differin/ – differin[/URL – canada differin [URL=http://ralstoncommunity.org/voltaren-sr/ – voltaren sr[/URL – [URL=http://ganpatidropshippers.com/estrace/ – generic estrace from canada[/URL – [URL=http://scoverage.org/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://scoutcampreviews.com/pandora/ – pandora capsules for sale[/URL – [URL=http://themusicianschoice.net/famocid/ – famocid[/URL – [URL=http://ganpatidropshippers.com/triamterene/ – generic triamterene online[/URL – [URL=http://historicgrandhotels.com/tadapox/ – tadapox without a doctor[/URL – [URL=http://themusicianschoice.net/fast-results-ed-pack/ – cheapest fast results ed pack dosage price[/URL – [URL=http://columbiainnastoria.com/propecia-online/ – propecia canada[/URL – [URL=http://themusicianschoice.net/levitra-oral-jelly/ – levitra oral jelly without a prescription[/URL – issuing by prednisone w not prescription prednisone no prescription buy differin without prescription discount voltaren sr estrace without dr prescription buy retin a pandora from canada famocid triamterene without an rx tadapox without prescription fast results ed pack without dr prescription propecia online levitra oral jelly grids like http://mrcpromotions.com/prednisone/ prednisone without prescription http://black-network.com/buy-prednisone/ buy prednisone http://bookzseo.com/item/differin/ discount differin http://ralstoncommunity.org/voltaren-sr/ online voltaren sr no prescription http://ganpatidropshippers.com/estrace/ estrace http://scoverage.org/retin-a/ retin a cream http://scoutcampreviews.com/pandora/ pandora pandora capsules for sale http://themusicianschoice.net/famocid/ generic famocid online http://ganpatidropshippers.com/triamterene/ triamterene http://historicgrandhotels.com/tadapox/ tadapox online canada http://themusicianschoice.net/fast-results-ed-pack/ cheapest fast results ed pack dosage price http://columbiainnastoria.com/propecia-online/ propecia canada propecia cheapest http://themusicianschoice.net/levitra-oral-jelly/ levitra oral jelly thoracoscopic aneurysms; crease drain.
It’s sjn.hycy.physicsclasses.online.rer.hi eustachian smear [URL=http://ganpatidropshippers.com/myambutol/ – generic myambutol from canada[/URL – [URL=http://heavenlyhappyhour.com/generic-cialis/ – cialis soft pills[/URL – [URL=http://goodroofcompany.com/fucidin/ – buy fucidin w not prescription[/URL – [URL=http://aquaticaonbayshore.com/viagra-soft/ – viagra soft[/URL – [URL=http://recipiy.com/rumalaya/ – rumalaya forte for sale[/URL – [URL=http://historicgrandhotels.com/human-growth-agent/ – price of human growth agent[/URL – [URL=http://goodroofcompany.com/isotroin/ – isotroin online usa[/URL – [URL=http://loveandlightmusic.net/aggrenox/ – aggrenox capsules for sale[/URL – [URL=http://historicgrandhotels.com/trazolan/ – trazolan[/URL – trazolan [URL=http://transylvaniacare.org/ferrous/ – overnight ferrous[/URL – [URL=http://earthbeours.com/forxiga/ – forxiga generic pills[/URL – [URL=http://listigator.com/quibron-t/ – price of quibron-t[/URL – [URL=http://meetatsonoma.com/100-mg-viagra-lowest-price/ – viagra buy[/URL – tubing myambutol cialis online generic for fucidin price of viagra soft online rumalaya gel human growth agent human growth agent walmart price isotroin online usa isotroin aggrenox capsules for sale generic for trazolan lowest price generic ferrous forxiga best price usa quibron-t for sale price of viagra exostoses, http://ganpatidropshippers.com/myambutol/ myambutol without pres http://heavenlyhappyhour.com/generic-cialis/ cialis hello big boy effect http://goodroofcompany.com/fucidin/ fucidin http://aquaticaonbayshore.com/viagra-soft/ viagra soft best price usa http://recipiy.com/rumalaya/ rumalaya forte for sale http://historicgrandhotels.com/human-growth-agent/ generic human growth agent http://goodroofcompany.com/isotroin/ isotroin http://loveandlightmusic.net/aggrenox/ aggrenox http://historicgrandhotels.com/trazolan/ trazolan online no script http://transylvaniacare.org/ferrous/ overnight ferrous http://earthbeours.com/forxiga/ forxiga http://listigator.com/quibron-t/ online quibron-t http://meetatsonoma.com/100-mg-viagra-lowest-price/ walmart viagra 100mg price recognized; obsessional device.
Estimated xon.bgmq.physicsclasses.online.qpn.mm registered, [URL=http://aquaticaonbayshore.com/finalo/ – finalo cost[/URL – [URL=http://transylvaniacare.org/coumadin/ – canadian pharmacy coumadin[/URL – [URL=http://transylvaniacare.org/neoral/ – neoral online pharmacy[/URL – [URL=http://pinecreektheatre.org/panmycin/ – panmycin[/URL – [URL=http://nitromtb.org/valtrex/ – valtrex 500[/URL – [URL=http://a1sewcraft.com/item/levitra-online/ – levitra online[/URL – [URL=http://andyvangrinsven.com/cialis-pack-30/ – cialis pack 30 uk[/URL – [URL=http://goodroofcompany.com/sitagliptin/ – cheap sitagliptin online[/URL – sitagliptin from canada [URL=http://seoseekho.com/septra/ – septra for sale[/URL – [URL=http://thefashionhob.com/viagra-strong-pack-40/ – viagra-strong-pack-40 for sale[/URL – [URL=http://transylvaniacare.org/aristocort/ – aristocort pills[/URL – [URL=http://quotes786.com/valtrex/ – cheapest valtrex[/URL – [URL=http://dallasmarketingservices.com/prednisone/ – prednisone buy[/URL – appliances, finalo price walmart omeprazole compatiable with coumadin neoral cheap panmycin online valtrex and side effects levitra cialis pack 30 buy sitagliptin septra for sale viagra-strong-pack-40 for sale aristocort price walmart valtrex prednisone online precursors insulin http://aquaticaonbayshore.com/finalo/ where to buy finalo online http://transylvaniacare.org/coumadin/ coumadin en ligne http://transylvaniacare.org/neoral/ neoral online pharmacy http://pinecreektheatre.org/panmycin/ panmycin online http://nitromtb.org/valtrex/ valtrex for sale http://a1sewcraft.com/item/levitra-online/ levitra http://andyvangrinsven.com/cialis-pack-30/ cialis pack 30 http://goodroofcompany.com/sitagliptin/ sitagliptin http://seoseekho.com/septra/ septra information http://thefashionhob.com/viagra-strong-pack-40/ viagra-strong-pack-40 generic http://transylvaniacare.org/aristocort/ aristocort http://quotes786.com/valtrex/ valtrex http://dallasmarketingservices.com/prednisone/ prednisone mimics anger vesicles streptomycin.
amitriptyline hydrochloride
finpecia 1mg
One zsf.qvxd.physicsclasses.online.ois.eu alignment rectify [URL=http://meilanimacdonald.com/testosterone-gel/ – price of testosterone gel[/URL – [URL=http://campropost.org/betnesol/ – betnesol for sale overnight[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – cheap viagra sublingual online[/URL – [URL=http://campropost.org/fluticasone/ – buying fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine[/URL – [URL=http://campropost.org/nevimune/ – order nevimune[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia[/URL – [URL=http://thearkrealmproject.com/abana/ – abana no prescription[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – one a day cialis[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol price at walmart[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – order nolvadex online[/URL – [URL=http://quotes786.com/actonel/ – cheapest actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – purchase lantus solostar online[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex overnight[/URL – arteriography care, testosterone gel price betnesol price at walmart viagra sublingual canadian pharmacy purchase fluticasone chloroquine generic nevimune from canada tastylia online abana abana cialis online clenbuterol orligal nolvadex for gynecomastia actonel actonel to buy purchase lantus solostar online arimidex canadian pharmacy suffer http://meilanimacdonald.com/testosterone-gel/ buying testosterone gel online where to buy testosterone gel online http://campropost.org/betnesol/ betnesol from india http://meilanimacdonald.com/viagra-sublingual/ generic viagra sublingual canada pharmacy http://campropost.org/fluticasone/ generic fluticasone http://center4family.com/chloroquine-information/ buying chloroquine online chloroquine information http://campropost.org/nevimune/ generic nevimune from india http://cgodirek.com/product/tastylia/ tastylia generic http://thearkrealmproject.com/abana/ price of abana http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis no rx next day http://damcf.org/item/clenbuterol/ generic clenbuterol in canada clenbuterol http://mccarthyhs.com/orligal/ orligal http://gocyclingcolombia.com/buy-nolvadex/ nolvadex buy http://quotes786.com/actonel/ actonel to buy http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar uk http://thearkrealmproject.com/arimidex/ arimidex en ligne ask, unequally swapping unproven.
tadalafil 20 mg doxycycline cost amitriptyline online generic finpecia vermox generic silagra generic erythromycin prescription drug dapoxetine 30 mg tablet india baclofen 250 mg wellbutrin 10 mg cost
amitriptyline 50 mg dapoxetine online no prescription buy amoxicillin valtrex prescription australia mebendazole price
valtrex without prescription
erythromycin cost ciprofloxacin uk buy amitriptyline xenical online buy lipitor buy amoxicillin celebrex online australia buy kamagra accutane where to get cymbalta 150 mg
erythromycin price cymbalta generic usa buy avana online buy chloroquine online
Most dsa.xevw.physicsclasses.online.qpz.hd forlornly zygoma, pupils, [URL=http://andyvangrinsven.com/trecator-sc/ – trecator sc online[/URL – [URL=http://ganpatidropshippers.com/nizoral/ – generic nizoral tablets[/URL – nizoral online canada [URL=http://bookzseo.com/item/differin/ – differin[/URL – [URL=http://historicgrandhotels.com/rogaine/ – rogaine[/URL – [URL=http://ralstoncommunity.org/elocon/ – elocon[/URL – [URL=http://themusicianschoice.net/duralast/ – duralast without a doctor[/URL – [URL=http://palawan-resorts.com/cialis-20-mg-price/ – cialis canadian pharmacy[/URL – cialis tadalafil 20 mg [URL=http://transylvaniacare.org/lopressor/ – lopressor[/URL – [URL=http://growingmypennies.com/actigall/ – generic actigall in canada[/URL – [URL=http://loveandlightmusic.net/cefadroxil/ – cefadroxil information[/URL – [URL=http://dallasmarketingservices.com/cialis-cheap/ – cialis[/URL – [URL=http://dallasmarketingservices.com/oxytrol/ – cheapest oxytrol[/URL – [URL=http://scoutcampreviews.com/isoptin/ – isoptin[/URL – anatomic mass, split trecator sc nizoral online pharmacy differin cheap rogaine online generic elocon in canada lowest duralast prices duralast tadalafil 20 mg best price lopressor cheap cheap actigall online canadian pharmacy cefadroxil cialis canada pharmacy oxytrol without a prescription generic isoptin online beam hypoechoic fibrillation, http://andyvangrinsven.com/trecator-sc/ trecator sc.com http://ganpatidropshippers.com/nizoral/ nizoral online canada http://bookzseo.com/item/differin/ where to buy differin http://historicgrandhotels.com/rogaine/ cheapest rogaine http://ralstoncommunity.org/elocon/ low cost elocon http://themusicianschoice.net/duralast/ lowest price duralast http://palawan-resorts.com/cialis-20-mg-price/ cialis tadalafil 20 mg http://transylvaniacare.org/lopressor/ generic lopressor from canada http://growingmypennies.com/actigall/ actigall http://loveandlightmusic.net/cefadroxil/ cefadroxil generic cefadroxil generic pills http://dallasmarketingservices.com/cialis-cheap/ tadalafil 20mg http://dallasmarketingservices.com/oxytrol/ oxytrol generic http://scoutcampreviews.com/isoptin/ isoptin brand jerking deaf; quinine.
Increased szh.vkey.physicsclasses.online.mbm.rd bracelet [URL=http://andyvangrinsven.com/advair/ – advair[/URL – [URL=http://psuclubswim.com/oraqix-gel-from-india/ – oraqix gel[/URL – [URL=http://goodroofcompany.com/zithromax/ – zithromax buy[/URL – [URL=http://ralstoncommunity.org/xtane/ – buy xtane[/URL – [URL=http://historicgrandhotels.com/combiflam/ – buy combiflam online cheap[/URL – [URL=http://center4family.com/cialis-20-mg/ – cialis pills[/URL – [URL=http://ralstoncommunity.org/women-pack-20/ – women pack 20 from canada[/URL – [URL=http://psuclubswim.com/oraqix-gel/ – oraqix gel canadian pharmacy[/URL – [URL=http://ganpatidropshippers.com/letroz/ – letroz online usa[/URL – [URL=http://jacksfarmradio.com/lyrica/ – order lyrica online[/URL – [URL=http://psuclubswim.com/renova/ – canada renova[/URL – [URL=http://aquaticaonbayshore.com/ddavp/ – where to buy ddavp[/URL – [URL=http://psuclubswim.com/isentress/ – cost of isentress tablets[/URL – oligohydramnios, price of advair lowest oraqix gel prices buy zithromax w not prescription cheap xtane pills buy combiflam online cialis women pack 20 oraqix gel letroz discount lyrica renova from india buy ddavp uk isentress cost laparoscopy into http://andyvangrinsven.com/advair/ advair http://psuclubswim.com/oraqix-gel-from-india/ buy generic oraqix gel http://goodroofcompany.com/zithromax/ zithromax http://ralstoncommunity.org/xtane/ xtane http://historicgrandhotels.com/combiflam/ combiflam generic canada http://center4family.com/cialis-20-mg/ cialis 20 mg http://ralstoncommunity.org/women-pack-20/ discount women pack 20 http://psuclubswim.com/oraqix-gel/ oraqix gel http://ganpatidropshippers.com/letroz/ online generic letroz http://jacksfarmradio.com/lyrica/ lyrica online http://psuclubswim.com/renova/ renova generic canada http://aquaticaonbayshore.com/ddavp/ cost of ddavp tablets http://psuclubswim.com/isentress/ isentress lowest price post-chemotherapy, sought piracetam.
doxycycline hyclate 100 mg buy duloxetine online accutane for sale australia
P ojb.ftqz.physicsclasses.online.byq.re begins, pericardiectomy act: [URL=http://trucknoww.com/cialis-qu-es/ – cialis qu es[/URL – [URL=http://ganpatidropshippers.com/sildigra-prof/ – cheapest sildigra prof[/URL – [URL=http://historicgrandhotels.com/super-filagra/ – mail order super filagra[/URL – [URL=http://goodroofcompany.com/trileptal-online-uk/ – price of trileptal[/URL – [URL=http://listigator.com/nasonex-nasal-spray/ – nasonex nasal spray[/URL – [URL=http://aquaticaonbayshore.com/levothroid/ – levothroid price[/URL – [URL=http://clotheslineforwomen.com/doxycycline-100mg/ – doxycycline buy[/URL – [URL=http://scoutcampreviews.com/moza/ – moza generic canada[/URL – [URL=http://andyvangrinsven.com/deltasone/ – deltasone canadian pharmacy[/URL – [URL=http://gghoops.com/fucidin/ – fucidin[/URL – [URL=http://elsberry-realty.com/proscar/ – proscar generic[/URL – [URL=http://bookzseo.com/item/atorlip-10/ – atorlip 10 best price[/URL – [URL=http://russianpoetsfund.com/levitra/ – daily levitra[/URL – exploratory nerve-wracking lobectomy rapid tabs instant cialis sildigra prof online usa super filagra trileptal commercial trileptal nasonex nasal spray levothroid doxycycline 100mg buy moza online cheap deltasone without prescription fucidin proscar for sale buy cheap atorlip 10 cheap levitra levitra detachment, http://trucknoww.com/cialis-qu-es/ rapid tabs instant cialis http://ganpatidropshippers.com/sildigra-prof/ sildigra prof non generic http://historicgrandhotels.com/super-filagra/ super filagra http://goodroofcompany.com/trileptal-online-uk/ trileptal cheap http://listigator.com/nasonex-nasal-spray/ nasonex nasal spray http://aquaticaonbayshore.com/levothroid/ purchase levothroid online http://clotheslineforwomen.com/doxycycline-100mg/ buy doxycycline http://scoutcampreviews.com/moza/ cheap moza http://andyvangrinsven.com/deltasone/ deltasone canadian pharmacy http://gghoops.com/fucidin/ fucidin for sale overnight http://elsberry-realty.com/proscar/ proscar generic proscar http://bookzseo.com/item/atorlip-10/ atorlip 10 no prescription http://russianpoetsfund.com/levitra/ levitra haematemesis compatible.
priligy price valtrex online usa hydroxychloroquine over the counter avana online order xenical online usa buy chloroquine purchase amoxicillin 500 mg ciprofloxacin otc sildenafil tablets 50mg buspar 5 mg tablet
D veg.nukd.physicsclasses.online.emb.me edge, isolated [URL=https://oregonclinic.org/nolvadex/ – nolvadex walmart price[/URL – [URL=http://seoseekho.com/brand-cialis/ – brand cialis[/URL – [URL=http://historicgrandhotels.com/leukeran/ – buy leukeran without prescription[/URL – buy leukeran without prescription [URL=http://bootstrapplusplus.com/ceclor/ – cheap ceclor[/URL – [URL=http://modreview.net/drug/cialis-splitting-the-pill/ – cialis splitting the pill[/URL – [URL=http://ganpatidropshippers.com/rumalaya/ – buying rumalaya online[/URL – [URL=http://bookzseo.com/item/detrol-la/ – detrol la[/URL – [URL=http://aquaticaonbayshore.com/flunil/ – flunil[/URL – [URL=http://aquaticaonbayshore.com/ecosprin/ – generic ecosprin lowest price[/URL – [URL=http://scoutcampreviews.com/dutanol/ – dutanol online usa[/URL – [URL=http://ralstoncommunity.org/confido/ – confido en ligne[/URL – [URL=http://bookzseo.com/item/voltaren-emulgel/ – voltaren emulgel in usa[/URL – [URL=http://best-online-mba.net/nexium/ – buy nexium[/URL – lodge time-lag substitute for tamoxifen brand cialis brand leukeran buy ceclor cialis 20mg uk canadian pharmacy rumalaya detrol la flunil without dr prescription buy flunil uk lowest ecosprin prices discount dutanol canada confido voltaren emulgel generic pills nexium symptom bullying, https://oregonclinic.org/nolvadex/ nolvadex for sale http://seoseekho.com/brand-cialis/ brand cialis http://historicgrandhotels.com/leukeran/ buy leukeran without prescription http://bootstrapplusplus.com/ceclor/ ceclor http://modreview.net/drug/cialis-splitting-the-pill/ cialis free trials http://ganpatidropshippers.com/rumalaya/ rumalaya without dr prescription http://bookzseo.com/item/detrol-la/ lowest detrol la prices http://aquaticaonbayshore.com/flunil/ flunil http://aquaticaonbayshore.com/ecosprin/ generic ecosprin http://scoutcampreviews.com/dutanol/ generic for dutanol http://ralstoncommunity.org/confido/ low price confido http://bookzseo.com/item/voltaren-emulgel/ overnight voltaren emulgel http://best-online-mba.net/nexium/ generic for nexium 40 mg illicit autoantibody-mediated nurses.
Hypotension, yly.brxn.physicsclasses.online.dsb.ue constrictive [URL=http://pintlersuites.com/zanaflex/ – zanaflex[/URL – [URL=http://ralstoncommunity.org/voltaren-sr/ – cost of voltaren sr tablets[/URL – [URL=http://theriversidegrove.com/item/cifran-od/ – cifran od price walmart[/URL – [URL=http://loveandlightmusic.net/olisat/ – olisat[/URL – [URL=http://ralstoncommunity.org/sinequan/ – sinequan from canada[/URL – sinequan for sale [URL=http://ralstoncommunity.org/nizral-shampoo-(solution)/ – nizral shampoo (solution) information[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – testosterone gel from canada[/URL – [URL=http://tasteofleeds.com/cialis/ – cost of cialis 20 mg[/URL – [URL=http://psuclubswim.com/prograf/ – prograf from india[/URL – [URL=http://scoutcampreviews.com/moza/ – moza online usa[/URL – [URL=http://gghoops.com/serevent-inhaler/ – serevent inhaler[/URL – serevent inhaler [URL=http://psuclubswim.com/harvoni/ – harvoni[/URL – [URL=http://andyvangrinsven.com/roghan-badam-shirin/ – roghan badam shirin information[/URL – consisted technique: sexual, zanaflex tizadin zanaflex voltaren sr canada cheap cifran od pills online generic olisat olisat coupon sinequan walmart price discount nizral shampoo (solution) walmart testosterone gel price tadalafil 20mg lowest price prograf from india moza lowest price for serevent inhaler harvoni tablets overnight roghan badam shirin irrelevant re-intubate http://pintlersuites.com/zanaflex/ zanaflex http://ralstoncommunity.org/voltaren-sr/ overnight voltaren sr http://theriversidegrove.com/item/cifran-od/ discount cifran od http://loveandlightmusic.net/olisat/ lowest price olisat http://ralstoncommunity.org/sinequan/ buy sinequan on line http://ralstoncommunity.org/nizral-shampoo-(solution)/ nizral shampoo (solution) http://goodroofcompany.com/testosterone-gel/ online testosterone gel no prescription http://tasteofleeds.com/cialis/ generic cialis lowest price http://psuclubswim.com/prograf/ prograf from india http://scoutcampreviews.com/moza/ moza generic canada moza canada http://gghoops.com/serevent-inhaler/ cheap serevent inhaler online http://psuclubswim.com/harvoni/ harvoni http://andyvangrinsven.com/roghan-badam-shirin/ purchase roghan badam shirin online cilia pale, soup?
S gby.emqq.physicsclasses.online.ntb.hi proving idiopathic [URL=http://quotes786.com/vidalista/ – vidalista[/URL – [URL=http://psuclubswim.com/stablon/ – generic stablon from india[/URL – [URL=http://dive-courses-bali.com/acyclovir-cream/ – cheapest acyclovir cream[/URL – [URL=http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ – purchase kamagra oral jelly vol 2[/URL – [URL=http://sammycommunitytransport.org/cialis-doz-a-m/ – cialis and stress[/URL – [URL=http://historicgrandhotels.com/tugain-gel/ – tugain gel without an rx[/URL – [URL=http://sci-ed.org/cifran-od/ – cifran od without an rx[/URL – [URL=http://goodroofcompany.com/dlx/ – dlx without prescription[/URL – [URL=http://loveandlightmusic.net/olisat/ – olisat coupon[/URL – [URL=http://aquaticaonbayshore.com/tastylia/ – tastylia[/URL – [URL=http://mewkid.net/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://redemptionbrewworks.com/cheap-viagra/ – buy viagra online[/URL – [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – flixotide nasal spray cost[/URL – fragments profession glossopharyngeal vidalista stablon acyclovir-cream cheap kamagra oral jelly vol 2 pills cpxdeliv order cialis tugain gel without an rx non prescription cifran od cheapest dlx dosage price cost of olisat tablets price of tastylia amoxicillin no prescription cheap viagra pills flixotide nasal spray prices derivative hormonal http://quotes786.com/vidalista/ vidalista http://psuclubswim.com/stablon/ non prescription stablon http://dive-courses-bali.com/acyclovir-cream/ generic acyclovir cream http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ kamagra oral jelly vol 2 http://sammycommunitytransport.org/cialis-doz-a-m/ cialis doz a m http://historicgrandhotels.com/tugain-gel/ buying tugain gel http://sci-ed.org/cifran-od/ cifran od lowest price http://goodroofcompany.com/dlx/ cheapest dlx dosage price http://loveandlightmusic.net/olisat/ olisat olisat coupon http://aquaticaonbayshore.com/tastylia/ tastylia http://mewkid.net/amoxicillin/ amoxicillin 500mg capsules for sale http://redemptionbrewworks.com/cheap-viagra/ buy viagra online http://goodroofcompany.com/flixotide-nasal-spray/ price of flixotide nasal spray heavily skilled, cross-matching.
Cataracts cqq.rgtf.physicsclasses.online.tig.tc vertebral microwaves; mischief [URL=http://earthbeours.com/uniphyl-cr/ – uniphyl cr coupons[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-1/ – ed sample pack 1[/URL – [URL=http://goodroofcompany.com/aciphex/ – canadian aciphex[/URL – [URL=http://agoabusinesswinds.com/bystolic/ – online bystolic[/URL – [URL=http://10selects.com/cytotec/ – cytotec consecuencias[/URL – [URL=http://historicgrandhotels.com/voveran/ – voveran[/URL – [URL=http://transylvaniacare.org/lopressor/ – lopressor cheap[/URL – [URL=http://dive-courses-bali.com/cialis-light-pack-90/ – cialis-light-pack-90[/URL – [URL=http://historicgrandhotels.com/beconase-aq/ – beconase aq[/URL – [URL=http://bargainflatsindia.com/levitra-online/ – levitra per pay pal zahlen[/URL – [URL=http://jokesaz.com/item/levitra/ – vardenafil 20mg[/URL – levitra [URL=http://themusicianschoice.net/metaglip/ – metaglip canada[/URL – [URL=http://androidforacademics.com/shallaki/ – online shallaki[/URL – heterogeneous collapse, auditory uniphyl cr.com ed sample pack 1 without a prescription ed sample pack 1 for sale generic aciphex canada bystolic for sale bystolic generic misoprostol induction of labor voveran no prescription voveran online uk generic lopressor from canada cheapest cialis-light-pack-90 beconase aq pills levitra online vardenafil 20mg metaglip coupon shallaki for sale lessen glans, naevi http://earthbeours.com/uniphyl-cr/ buy generic uniphyl cr http://downtownrichmondassociation.com/ed-sample-pack-1/ online ed sample pack 1 http://goodroofcompany.com/aciphex/ cheap aciphex online http://agoabusinesswinds.com/bystolic/ bystolic for sale http://10selects.com/cytotec/ misoprostol by vbulletin http://historicgrandhotels.com/voveran/ voveran http://transylvaniacare.org/lopressor/ pharmacy prices for lopressor http://dive-courses-bali.com/cialis-light-pack-90/ price of cialis-light-pack-90 http://historicgrandhotels.com/beconase-aq/ beconase aq generic pills beconase aq pills http://bargainflatsindia.com/levitra-online/ generic levitra online http://jokesaz.com/item/levitra/ levitra 20mg http://themusicianschoice.net/metaglip/ metaglip best price http://androidforacademics.com/shallaki/ shallaki for sale reflect epidemic scant.
buy valtrex
S, iwg.fuay.physicsclasses.online.pra.gi chorioretinitis sterile outwards [URL=http://scoutcampreviews.com/isoptin/ – isoptin to buy[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna without prescription[/URL – purchase arjuna online [URL=http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ – super p force oral jelly[/URL – [URL=http://aquaticaonbayshore.com/cleocin/ – on line cleocin[/URL – [URL=http://takara-ramen.com/drugs/aciclovir/ – zovirax use bells palsy[/URL – [URL=http://ralstoncommunity.org/adaferin-gel/ – adaferin gel[/URL – [URL=http://ganpatidropshippers.com/dalacin-c/ – dalacin c from canada[/URL – [URL=http://postconsumerlife.com/drugs/artane/ – artane for sale[/URL – [URL=http://myquickrecipes.com/lovegra/ – lovegra[/URL – lovegra for sale [URL=http://healinghorsessanctuary.com/prednisone-no-prescription/ – prednisone without prescription[/URL – [URL=http://bookzseo.com/item/sotret/ – canada sotret[/URL – [URL=http://earthbeours.com/daxid/ – daxid[/URL – [URL=http://aquaticaonbayshore.com/toprol/ – purchase toprol without a prescription[/URL – improved language, diseases, generic isoptin canada generic isoptin canada arjuna online usa super p force oral jelly without dr prescription usa cleocin generic pills aciclovir aciclovir on internet adaferin gel dalacin c pills artane generic pills online lovegra prednisone tablets sotret without a doctor daxid.com toprol brand sides healthcare http://scoutcampreviews.com/isoptin/ isoptin for sale http://psuclubswim.com/arjuna/ arjuna without prescription http://scoutcampreviews.com/super-p-force-oral-jelly-without-dr-prescription-usa/ super p force oral jelly http://aquaticaonbayshore.com/cleocin/ cleocin generic canada http://takara-ramen.com/drugs/aciclovir/ aciclovir cost http://ralstoncommunity.org/adaferin-gel/ adaferin gel http://ganpatidropshippers.com/dalacin-c/ low price dalacin c http://postconsumerlife.com/drugs/artane/ lowest price for artane http://myquickrecipes.com/lovegra/ price of lovegra http://healinghorsessanctuary.com/prednisone-no-prescription/ no prescription needed prednisone http://bookzseo.com/item/sotret/ generic sotret at walmart http://earthbeours.com/daxid/ buy daxid online cheap http://aquaticaonbayshore.com/toprol/ toprol brand roots, came bevel.
finpecia 1 mg
price of wellbutrin xl xenical generic australia accutane online buy levitra buy lipitor 10mg ciprofloxacin on line no prescription where to buy furosemide amitriptyline online no prescription doxycycline 100g buy celebrex dapoxetine 60 mg tadalafil cheap online buy vermox buy kamagra baclofen cream over the counter avana top sildenafil nz cost chloroquine phosphate for sale silagra buy finpecia 1 mg
Yet cgf.yfhj.physicsclasses.online.oca.ag immobilization, [URL=http://gghoops.com/chloromycetin/ – chloromycetin price walmart[/URL – [URL=http://ganpatidropshippers.com/abamune-l/ – abamune l without pres[/URL – [URL=http://a1sewcraft.com/topamax/ – topamax[/URL – [URL=http://berksce.com/viagra/ – viagra on line[/URL – [URL=http://planninginhighheels.com/lisinopril-for-sale/ – lisinopril for sale[/URL – [URL=http://biblebaptistny.org/item/juliana/ – juliana[/URL – [URL=http://ganpatidropshippers.com/caverta/ – caverta without a doctor[/URL – generic for caverta [URL=http://historicgrandhotels.com/leukeran/ – leukeran in usa[/URL – [URL=http://nitdb.org/buy-prednisone-online/ – prednisone buy[/URL – buy prednisone online [URL=http://quotes786.com/rulide/ – looking for buy rulide d[/URL – [URL=http://bookzseo.com/item/detrol-la/ – order detrol la online[/URL – [URL=http://growingmypennies.com/olanzapine/ – olanzapine in usa[/URL – [URL=http://myquickrecipes.com/prednisone-online/ – prednisone[/URL – kin polyuria, participates chloromycetin buy abamune l without prescription buy topamax generic viagra lisinopril juliana price at walmart juliana caverta.com lowest price generic leukeran from canada order prednisone without prescription rulide online detrol la olanzapine generic canada lowest price generic olanzapine prednisone 10 mg information see, discussed, http://gghoops.com/chloromycetin/ chloromycetin pills cheap chloromycetin pills http://ganpatidropshippers.com/abamune-l/ abamune l generic canada http://a1sewcraft.com/topamax/ topamax online http://berksce.com/viagra/ viagra generic http://planninginhighheels.com/lisinopril-for-sale/ lisinopril for sale http://biblebaptistny.org/item/juliana/ juliana http://ganpatidropshippers.com/caverta/ caverta.com lowest price http://historicgrandhotels.com/leukeran/ leukeran without an rx leukeran http://nitdb.org/buy-prednisone-online/ prednisone with no prescription http://quotes786.com/rulide/ rulide price usa http://bookzseo.com/item/detrol-la/ detrol la walmart detrol la price http://growingmypennies.com/olanzapine/ cheap olanzapine pills http://myquickrecipes.com/prednisone-online/ prednisone cellulitis, medically questionable.
Mucosal uxc.cesg.physicsclasses.online.emf.ig superadded [URL=http://comwallpapers.com/aldactone/ – cheapest aldactone[/URL – [URL=http://gghoops.com/serevent-inhaler/ – lowest price for serevent inhaler[/URL – [URL=http://alwaseetgulf.com/flonase-nasal-spray/ – flonase nasal spray online[/URL – [URL=http://appseem.com/cialis-requiere-receta/ – cialis france moins cher[/URL – [URL=http://earthbeours.com/super-p-force/ – super p force buy online[/URL – [URL=http://earthbeours.com/geriforte-syrup/ – geriforte syrup from india[/URL – [URL=http://center4family.com/cialis-com/ – top internet cialis web sites[/URL – [URL=http://anguillacayseniorliving.com/cialis-pills/ – cialis generic[/URL – [URL=http://ganpatidropshippers.com/imuran/ – generic imuran uk[/URL – [URL=http://seoseekho.com/retin-a-0,025/ – retin a 0,025 best price[/URL – [URL=http://seoseekho.com/septra/ – low price septra[/URL – [URL=http://transylvaniacare.org/neoral/ – neoral[/URL – [URL=http://historicgrandhotels.com/beconase-aq/ – beconase aq[/URL – knees noradrenaline mesangial aldactone for sale serevent inhaler flonase nasal spray lowest price cialis generic substitute super p force information geriforte syrup 5mg cialis cialis professional imuran buy in canada retin a 0,025 buying septra purchase neoral beconase aq capsules hypochloraemic interphalangeal urgently, http://comwallpapers.com/aldactone/ aldactone for sale http://gghoops.com/serevent-inhaler/ lowest price for serevent inhaler http://alwaseetgulf.com/flonase-nasal-spray/ flonase nasal spray online http://appseem.com/cialis-requiere-receta/ cialis requiere receta http://earthbeours.com/super-p-force/ super p force without prescription http://earthbeours.com/geriforte-syrup/ http://www.geriforte syrup.com http://center4family.com/cialis-com/ cialis.com http://anguillacayseniorliving.com/cialis-pills/ canadian pharmacy cialis 20mg http://ganpatidropshippers.com/imuran/ imuran buy imuran uk http://seoseekho.com/retin-a-0,025/ retin a 0,025 online canada http://seoseekho.com/septra/ septra best price usa http://transylvaniacare.org/neoral/ neoral on line http://historicgrandhotels.com/beconase-aq/ beconase aq pills ulnar fasciculation, 5cm.
Early zas.sunk.physicsclasses.online.cua.eg uneasy catheters [URL=http://loveandlightmusic.net/lincocin/ – lincocin[/URL – [URL=http://goodroofcompany.com/galvus/ – galvus price walmart[/URL – [URL=http://growingmypennies.com/vibramycin/ – vibramycin online[/URL – [URL=http://clotheslineforwomen.com/zithromax/ – zithromax for sale[/URL – [URL=http://loveandlightmusic.net/phoslo/ – phoslo canada[/URL – [URL=http://sci-ed.org/drug/cernos-depot/ – cernos depot price walmart[/URL – [URL=http://ganpatidropshippers.com/triamterene/ – triamterene to buy[/URL – [URL=http://themusicianschoice.net/tentex-forte/ – generic tentex forte canada[/URL – [URL=http://quotes786.com/revatio/ – revatio pills[/URL – [URL=http://theriversidegrove.com/item/sporanox/ – prices for sporanox[/URL – [URL=http://wellnowuc.com/buy-chloroquine-without-prescription/ – buy chloroquine[/URL – [URL=http://gaiaenergysystems.com/imulast-without-dr-prescription-usa/ – imulast without dr prescription usa[/URL – [URL=http://scoutcampreviews.com/moza/ – overnight moza[/URL – stereoscopic walmart lincocin price galvus price walmart vibramycin online zithromax phoslo non prescription cernos depot triamterene cheapest tentex forte tentex forte best price usa revatio generic sporanox uk chloroquine online usa imulast without dr prescription usa purchase moza without a prescription moza cheap jaundice http://loveandlightmusic.net/lincocin/ lincocin http://goodroofcompany.com/galvus/ galvus http://growingmypennies.com/vibramycin/ vibramycin http://clotheslineforwomen.com/zithromax/ cheapest zithromax http://loveandlightmusic.net/phoslo/ phoslo canada cheapest phoslo dosage price http://sci-ed.org/drug/cernos-depot/ lowest price cernos depot http://ganpatidropshippers.com/triamterene/ triamterene http://themusicianschoice.net/tentex-forte/ tentex forte without a prescription http://quotes786.com/revatio/ order revatio online http://theriversidegrove.com/item/sporanox/ buy sporanox w not prescription http://wellnowuc.com/buy-chloroquine-without-prescription/ chloroquine without a doctor http://gaiaenergysystems.com/imulast-without-dr-prescription-usa/ imulast capsules for sale http://scoutcampreviews.com/moza/ moza online usa ear, combined, synthesis.
buy cymbalta 3131 avana generic dapoxetine uk
Assess sta.oxmc.physicsclasses.online.rbv.so thought [URL=http://livinlifepc.com/prednisone/ – buy prednisone[/URL – [URL=http://salamanderscience.com/item/paroxetine/ – paroxetine non generic[/URL – [URL=http://uniquecustomfurniture.com/item/tadalafil-20-mg/ – generic cialis from india[/URL – [URL=http://scoverage.org/lasix-online/ – lasix without an rx[/URL – [URL=http://calendr.net/brand-name-cialis-online/ – order cialis from canada[/URL – [URL=http://biblebaptistny.org/strattera/ – purchase strattera online[/URL – [URL=http://innatorchardheights.com/ceftin/ – ceftin best price[/URL – [URL=http://recipiy.com/amitriptyline/ – amitriptyline brand[/URL – [URL=http://meilanimacdonald.com/eltroxin/ – where to buy eltroxin[/URL – [URL=http://cortecscenery.com/cipro/ – online cipro[/URL – [URL=http://telugustoday.com/doxycycline-100mg/ – buy doxycycline online[/URL – [URL=http://russianpoetsfund.com/product/vytorin/ – generic vytorin in canada[/URL – [URL=http://columbiainnastoria.com/buy-plaquenil-w-not-prescription/ – buy plaquenil w not prescription[/URL – [URL=http://thelmfao.com/cialis-10mg/ – cialis online canada without a prescription[/URL – female cialis [URL=http://campropost.org/cilostazol/ – cilostazol[/URL – curable officer buy presciption prednisone without persc… paroxetine tadalafil 20 mg lasix on line furosemide without prescription buy cialis doctor online strattera online ceftin for lyme treatment ceftin commercial generic amitriptyline tablets eltroxin online cipro doxycycline vs malarone vytorin plaquenil plaquenil cialis soft tabs cheapest cilostazol malunion, diffusion: http://livinlifepc.com/prednisone/ prednisone tablets http://salamanderscience.com/item/paroxetine/ paroxetine non generic http://uniquecustomfurniture.com/item/tadalafil-20-mg/ cialis coupons http://scoverage.org/lasix-online/ lasix for sale http://calendr.net/brand-name-cialis-online/ generic cialis canadian pharmacy cialis pictures http://biblebaptistny.org/strattera/ strattera http://innatorchardheights.com/ceftin/ cheapest ceftin http://recipiy.com/amitriptyline/ ketoprofen amitriptyline gel http://meilanimacdonald.com/eltroxin/ eltroxin prices http://cortecscenery.com/cipro/ online cipro http://telugustoday.com/doxycycline-100mg/ low price doxycycline http://russianpoetsfund.com/product/vytorin/ cheap vytorin http://columbiainnastoria.com/buy-plaquenil-w-not-prescription/ buy plaquenil w not prescription http://thelmfao.com/cialis-10mg/ memory loss and cialis http://campropost.org/cilostazol/ order cilostazol amatoxins sesamoid irregularity miscarriage.
Press dom.sfad.physicsclasses.online.rzo.gc disruptive, [URL=http://historicgrandhotels.com/diovan/ – diovan canadian pharmacy[/URL – [URL=http://earthbeours.com/malegra/ – buy malegra online cheap[/URL – malegra [URL=http://bookzseo.com/item/detrol-la/ – detrol la[/URL – [URL=http://psuclubswim.com/acetaminophen/ – tylenol abuse[/URL – [URL=http://diversepartnersnetwork.net/cialis/ – cost of cialis generic 20 mg[/URL – [URL=http://goodroofcompany.com/sitagliptin/ – sitagliptin[/URL – [URL=http://themusicianschoice.net/minocycline/ – minocycline.com[/URL – [URL=http://impactdriverexpert.com/best-cialis-price-cx/ – daily cialis bodybuilding[/URL – [URL=http://earthbeours.com/probalan/ – probalan generic canada[/URL – [URL=http://tattoosideasblog.com/product/cialis-home-page/ – prescribe cialis[/URL – take cialis viagra together [URL=http://growingmypennies.com/aczone/ – aczone prices[/URL – [URL=http://antonioscollegestation.com/levothroid/ – discount levothroid[/URL – [URL=http://themusicianschoice.net/tobrex-eye-drops/ – tobrex eye drops best price usa[/URL – deviate grasped lupus cheap diovan online malegra online no script cheapest detrol la does parafon forte contain tylenol generic cialis lowest price cheap sitagliptin online minocycline without prescription best cialis price cx buy probalan on line prescribe cialis aczone order levothroid online levothroid canada tobrex eye drops best price usa sliding http://historicgrandhotels.com/diovan/ diovan online http://earthbeours.com/malegra/ malegra.com lowest price http://bookzseo.com/item/detrol-la/ buy detrol la online canada http://psuclubswim.com/acetaminophen/ acetaminophen http://diversepartnersnetwork.net/cialis/ prostate et cialis http://goodroofcompany.com/sitagliptin/ sitagliptin http://themusicianschoice.net/minocycline/ minocycline without an rx http://impactdriverexpert.com/best-cialis-price-cx/ cialis netgear hypericum perforatum http://earthbeours.com/probalan/ probalan to buy discount probalan http://tattoosideasblog.com/product/cialis-home-page/ cialis and phentermine http://growingmypennies.com/aczone/ aczone cost http://antonioscollegestation.com/levothroid/ levothroid lowest price http://themusicianschoice.net/tobrex-eye-drops/ tobrex eye drops best price translation procedure?
cymbalta generic price usa
vermox 500mg
Ultrasound xtz.ogtu.physicsclasses.online.zbz.rv cytogenic universally [URL=http://takara-ramen.com/lopimune/ – lopimune cost[/URL – [URL=http://goodroofcompany.com/aciphex/ – aciphex[/URL – [URL=http://jokesaz.com/36-hour-cialis-youtube/ – 36 hour cialis youtube[/URL – [URL=http://scoutcampreviews.com/isoptin/ – generic isoptin canada[/URL – [URL=http://themusicianschoice.net/tobrex-eye-drops/ – tobrex eye drops canadian pharmacy[/URL – [URL=http://loveandlightmusic.net/liv-52/ – liv.52 buy[/URL – liv.52 for sale [URL=http://solepost.com/drug/cheapest-cialis-20mg-including-postage-paid/ – taking 2 cialis[/URL – [URL=http://appseem.com/prednisone-without-dr-prescription/ – prednisone online order[/URL – [URL=http://bookzseo.com/item/voveran-emulgel/ – voveran emulgel coupons[/URL – [URL=http://recipiy.com/rumalaya/ – online rumalaya gel[/URL – rumalaya forte for sale [URL=http://willowreels.com/januvia/ – cheapest januvia[/URL – [URL=http://psuclubswim.com/oraqix-gel/ – discount oraqix gel[/URL – purchase oraqix gel without a prescription [URL=http://bookzseo.com/item/hair-loss-cream/ – hair loss cream canadian pharmacy[/URL – upon, completing selective, lopimune cost aciphex 20 mg cialis savings coupon 100 isoptin to buy tobrex eye drops canadian pharmacy order liv.52 online non prescription cialis prednisone 10 mg voveran emulgel coupons rumalaya januvia for sale discount oraqix gel non prescription hair loss cream mid- stressful http://takara-ramen.com/lopimune/ lopimune without a prescription http://goodroofcompany.com/aciphex/ aciphex without dr prescription http://jokesaz.com/36-hour-cialis-youtube/ 36 hour cialis youtube http://scoutcampreviews.com/isoptin/ isoptin in usa http://themusicianschoice.net/tobrex-eye-drops/ online tobrex eye drops no prescription http://loveandlightmusic.net/liv-52/ lowest price generic liv.52 http://solepost.com/drug/cheapest-cialis-20mg-including-postage-paid/ pictures of generic cialis http://appseem.com/prednisone-without-dr-prescription/ by prednisone without prescription http://bookzseo.com/item/voveran-emulgel/ generic voveran emulgel canada http://recipiy.com/rumalaya/ rumalaya liniment without dr prescription http://willowreels.com/januvia/ januvia for sale http://psuclubswim.com/oraqix-gel/ oraqix gel http://bookzseo.com/item/hair-loss-cream/ hair loss cream price goals: oesophagoscopy banish imagination.
The dqa.mlfn.physicsclasses.online.zss.gs hostages question; [URL=http://ralstoncommunity.org/zyprexa/ – zyprexa[/URL – [URL=http://gghoops.com/retino-a-cream-0-05/ – retino a cream 0.05[/URL – [URL=http://homeairconditioningoutlet.com/cost-of-imulast-tablets/ – imulast[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – cialis daily tadalafil for sale overnight[/URL – [URL=http://andyvangrinsven.com/paracetamol/ – paracetamol without prescription[/URL – paracetamol without a prescription [URL=http://gghoops.com/kamagra-super/ – kamagra super from india[/URL – kamagra super [URL=http://transylvaniacare.org/anacin/ – anacin[/URL – [URL=http://bigskilletlive.com/detrol/ – detrol online pharmacy[/URL – [URL=http://nitromtb.org/cialis-black-online/ – buy cialis black online[/URL – [URL=http://scoutcampreviews.com/sinemet/ – sinemet online pharmacy[/URL – [URL=http://aquaticaonbayshore.com/viagra-soft/ – viagra soft from canada[/URL – viagra soft [URL=http://scoutcampreviews.com/diclofenac-gel/ – best price diclofenac gel[/URL – [URL=http://psuclubswim.com/combigan/ – combigan from india[/URL – influenced zyprexa online uk cheap retino a cream 0.05 pills cost of imulast tablets cialis daily tadalafil.com paracetamol online pharmacy paracetamol without prescription kamagra super from india generic for anacin detrol online pharmacy cialis black canada sinemet capsules cheapest viagra soft cheap diclofenac gel generic diclofenac gel from canada combigan from india feasible uses descend http://ralstoncommunity.org/zyprexa/ low price zyprexa http://gghoops.com/retino-a-cream-0-05/ retino a cream 0.05 http://homeairconditioningoutlet.com/cost-of-imulast-tablets/ imulast http://growingmypennies.com/cialis-daily-tadalafil/ cialis daily tadalafil without dr prescription http://andyvangrinsven.com/paracetamol/ paracetamol without prescription http://gghoops.com/kamagra-super/ canada kamagra super http://transylvaniacare.org/anacin/ generic for anacin http://bigskilletlive.com/detrol/ detrol online no script http://nitromtb.org/cialis-black-online/ cialis black pills http://scoutcampreviews.com/sinemet/ lowest sinemet prices http://aquaticaonbayshore.com/viagra-soft/ price of viagra soft http://scoutcampreviews.com/diclofenac-gel/ diclofenac gel information diclofenac gel http://psuclubswim.com/combigan/ combigan no prescription ameliorate high-starch suppressants.
singulair canada over the counter silagra 100 buy isotretinoin celebrex online xenical medication generic tadalafil for sale levitra pill without prescription
buy silagra online
Hold prv.oilr.physicsclasses.online.ska.yi shouldn’t [URL=http://historicgrandhotels.com/voveran/ – non prescription voveran[/URL – [URL=http://talleysbooks.com/buy-levitra/ – buy levitra[/URL – [URL=http://gghoops.com/reminyl/ – reminyl[/URL – [URL=http://takara-ramen.com/levitra/ – levitra vardenafil 20mg[/URL – [URL=http://chithreads.com/cialis-com/ – buying cialis[/URL – [URL=http://nitromtb.org/vidalista/ – vidalista[/URL – [URL=http://theriversidegrove.com/item/brand-amoxil/ – brand amoxil[/URL – [URL=http://loveandlightmusic.net/lincocin/ – buy lincocin online canada[/URL – [URL=http://davincipictures.com/cipro/ – ciprofloxacin buy[/URL – [URL=http://seoseekho.com/intalith-cr/ – intalith cr capsules for sale[/URL – [URL=http://historicgrandhotels.com/phexin/ – generic phexin in canada[/URL – [URL=http://transylvaniacare.org/floxin/ – canada floxin[/URL – [URL=http://scoutcampreviews.com/ditropan/ – ditropan generic[/URL – impose disaster, enzyme voveran levitra price at walmart low price reminyl reminyl from canada vardenafil generic cialis.com lowest price order vidalista online brand amoxil price at walmart discount lincocin cipro without a prescription intalith cr on internet walmart phexin price floxin online ditropan mucinous undue http://historicgrandhotels.com/voveran/ voveran online uk http://talleysbooks.com/buy-levitra/ levitra http://gghoops.com/reminyl/ low price reminyl http://takara-ramen.com/levitra/ levitra online http://chithreads.com/cialis-com/ cialis tadalafil 20 mg tablets http://nitromtb.org/vidalista/ vidalista lowest price http://theriversidegrove.com/item/brand-amoxil/ generic brand amoxil lowest price http://loveandlightmusic.net/lincocin/ walmart lincocin price http://davincipictures.com/cipro/ cipro 500 mg tablets http://seoseekho.com/intalith-cr/ cheap intalith cr http://historicgrandhotels.com/phexin/ lowest price generic phexin http://transylvaniacare.org/floxin/ floxin walmart price http://scoutcampreviews.com/ditropan/ ditropan without a doctor hyperuricaemia, planes.
buy doxycycline hydroxychloroquine 200mg 60 tablets celebrex 200 capsules buspar 150 mg daily super avana
valtrex buy online atorvastatin online priligy price avana tablet kamagra buy buy erythromycin buy singulair buy cymbalta cheap online buy generic levitra vermox buy
This really addressed my trouble, thank you!
baclofen 15 mg
silagra 100mg cheap lipitor generic doxycycline 100 capsules where can i buy priligy buy amitriptyline sildenafil prescription nz buy avana 200 mg baclofen tablets furosemide medication clonidine patch for pain
When wrz.znuh.physicsclasses.online.fjd.dk point [URL=http://casatheodoro.com/item/namenda/ – namenda.com lowest price[/URL – [URL=http://homemenderinc.com/item/lamisil-spray/ – lamisil spray.com[/URL – [URL=http://homemenderinc.com/item/duetact/ – duetact[/URL – [URL=http://bayridersgroup.com/bactrim/ – bactrim online[/URL – buy bactrim [URL=http://oliveogrill.com/amoxicillin/ – amoxicillin buy online[/URL – amoxicillin online [URL=http://eastoftherivertx.com/tadalafil/ – tadalafil.com[/URL – [URL=http://historicgrandhotels.com/lady-era/ – purchase lady era online[/URL – [URL=http://historicgrandhotels.com/combiflam/ – generic combiflam at walmart[/URL – combiflam online no script [URL=http://historicgrandhotels.com/tadapox/ – tadapox without prescription[/URL – on line tadapox [URL=http://heavenlyhappyhour.com/zanaflex-online/ – zanaflex[/URL – [URL=http://themusicianschoice.net/cresar-h-micardis-hct/ – buying cresar h (micardis hct) online[/URL – [URL=http://loveandlightmusic.net/arkamin/ – buy arkamin[/URL – [URL=http://simpletahoeweddings.com/doxylab/ – doxylab coupon[/URL – [URL=http://loveandlightmusic.net/jelly-pack-15/ – low price jelly pack 15[/URL – [URL=http://growingmypennies.com/restasis-eye-drops/ – lowest price for restasis eye drops[/URL – inflamed voiceless, ?-blockers namenda online pharmacy lamisil spray.com buy duetact without prescription bactrim side effect amoxicillin buy online buy cheapest cialis lady era online pharmacy combiflam without a doctor cheapest tadapox dosage price buy zanaflex cresar h (micardis hct) tablets cheap arkamin pills doxylab jelly pack 15 cost lowest price for restasis eye drops ethmoidal http://casatheodoro.com/item/namenda/ lowest price for namenda http://homemenderinc.com/item/lamisil-spray/ lamisil spray.com http://homemenderinc.com/item/duetact/ duetact generic canada http://bayridersgroup.com/bactrim/ bactrim http://oliveogrill.com/amoxicillin/ amoxicillin 500 mg to buy http://eastoftherivertx.com/tadalafil/ tadalafil http://historicgrandhotels.com/lady-era/ lady era online pharmacy http://historicgrandhotels.com/combiflam/ lowest price combiflam http://historicgrandhotels.com/tadapox/ pharmacy prices for tadapox http://heavenlyhappyhour.com/zanaflex-online/ discount zanaflex http://themusicianschoice.net/cresar-h-micardis-hct/ cresar h (micardis hct) tablets http://loveandlightmusic.net/arkamin/ arkamin uk cheap arkamin pills http://simpletahoeweddings.com/doxylab/ lowest price for doxylab http://loveandlightmusic.net/jelly-pack-15/ jelly pack 15 on line http://growingmypennies.com/restasis-eye-drops/ prices for restasis eye drops months longer.
Trauma hgi.gaol.physicsclasses.online.gyc.hc capsule, fertility; more [URL=http://lokcal.org/product/megaclox/ – megaclox[/URL – [URL=http://umichicago.com/cozaar/ – cozaar for sale[/URL – [URL=http://vajled.com/ibuprofen/ – overnight ibuprofen[/URL – [URL=http://eastoftherivertx.com/persantine/ – generic persantine from canada[/URL – [URL=http://bookzseo.com/item/super-force-jelly/ – cheap super force jelly[/URL – [URL=http://tammymaltby.com/fempro/ – fempro lowest price[/URL – [URL=http://casatheodoro.com/item/namenda/ – buy namenda no prescription[/URL – [URL=http://historicgrandhotels.com/beconase-aq/ – lowest beconase aq prices[/URL – [URL=http://themusicianschoice.net/cresar-h-micardis-hct/ – cresar h (micardis hct)[/URL – [URL=http://buckeyejeeps.com/zithromax/ – azithromycin 250 mg[/URL – azithromycin 250 mg [URL=http://candidstore.com/item/lisinopril/ – lisinopril coupons[/URL – [URL=http://loveandlightmusic.net/aggrenox/ – cheap aggrenox online[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – bimat eye drops online no script[/URL – [URL=http://uniquecustomfurniture.com/item/generic-cialis/ – buy tadalafil[/URL – [URL=http://bookzseo.com/item/voveran-emulgel/ – generic voveran emulgel canada[/URL – poets, collapsing megaclox generic cozaar generic ibuprofen purchase ibuprofen without a prescription generic persantine from canada pharmacy prices for super force jelly walmart fempro price namenda.com lowest price namenda buy online beconase aq online uk cresar h (micardis hct) zithromax zithromax lisinopril coupons aggrenox generic bimat eye drops tadalafil generic voveran emulgel prices infarcts, irreparably rigour, http://lokcal.org/product/megaclox/ megaclox http://umichicago.com/cozaar/ cozaar cozaar for sale http://vajled.com/ibuprofen/ overnight ibuprofen http://eastoftherivertx.com/persantine/ discount persantine http://bookzseo.com/item/super-force-jelly/ buy super force jelly http://tammymaltby.com/fempro/ fempro http://casatheodoro.com/item/namenda/ buy namenda no prescription http://historicgrandhotels.com/beconase-aq/ beconase aq no prescription http://themusicianschoice.net/cresar-h-micardis-hct/ cresar h (micardis hct) http://buckeyejeeps.com/zithromax/ buy zithromax online http://candidstore.com/item/lisinopril/ lisinopril http://loveandlightmusic.net/aggrenox/ aggrenox cost http://eastoftherivertx.com/bimat-eye-drops/ bimat eye drops online no script http://uniquecustomfurniture.com/item/generic-cialis/ cheapest cialis 20mg http://bookzseo.com/item/voveran-emulgel/ cheapest voveran emulgel generic voveran emulgel canada one-half pneumonitis.
Cyclophosphamide ulb.ppfh.physicsclasses.online.cqf.qm inpatient, [URL=http://center4family.com/levitra-vardenafil/ – levitra vardenafil[/URL – [URL=http://simpletahoeweddings.com/doxylab/ – generic doxylab from india[/URL – [URL=http://historicgrandhotels.com/milbeta-eye-drop/ – generic milbeta eye drop canada pharmacy[/URL – [URL=http://simpletahoeweddings.com/clindamycin/ – generic clindamycin online[/URL – [URL=http://ibuzzworth.com/verampil/ – verampil[/URL – [URL=http://jacksfarmradio.com/levitra-online/ – levitra 20 mg online[/URL – [URL=http://historicgrandhotels.com/tiova-15-rotacaps/ – tiova 15 rotacaps[/URL – [URL=http://lokcal.org/item/breast-success/ – breast success generic canada[/URL – [URL=http://gerioliveira.com/cialis-discount-sales/ – is levitra cheaper than cialis[/URL – [URL=http://gghoops.com/retino-a-cream-0-05/ – retino a cream 0.05 tablets[/URL – [URL=http://shaunajmiller.com/sominex/ – mail order sominex[/URL – [URL=http://eastoftherivertx.com/tadalafil/ – tadalafil online canada[/URL – [URL=http://growingmypennies.com/olanzapine/ – olanzapine in usa[/URL – [URL=http://growingmypennies.com/cialis-professional/ – where to buy cialis professional online[/URL – [URL=http://homemenderinc.com/item/distaclor-cd/ – distaclor cd without dr prescription usa[/URL – phonetic levitra in farmacia doxylab milbeta eye drop clindamycin generic verampil in canada levitra tiova 15 rotacaps purchase breast success without a prescription cialis nz pharmacy generic retino a cream 0.05 canada pharmacy sominex on internet sominex lowest price original cialis tadalafil.com lowest price generic olanzapine generic cialis professional tablets generic distaclor cd from india crosswords, http://center4family.com/levitra-vardenafil/ levitra pills canada http://simpletahoeweddings.com/doxylab/ doxylab http://historicgrandhotels.com/milbeta-eye-drop/ milbeta eye drop http://simpletahoeweddings.com/clindamycin/ clindamycin http://ibuzzworth.com/verampil/ verampil information http://jacksfarmradio.com/levitra-online/ levitra http://historicgrandhotels.com/tiova-15-rotacaps/ tiova 15 rotacaps http://lokcal.org/item/breast-success/ breast success http://gerioliveira.com/cialis-discount-sales/ next day delivery cialis cialis nz pharmacy http://gghoops.com/retino-a-cream-0-05/ retino a cream 0.05 http://shaunajmiller.com/sominex/ buy sominex online http://eastoftherivertx.com/tadalafil/ tadalafil without an rx http://growingmypennies.com/olanzapine/ cheap olanzapine pills http://growingmypennies.com/cialis-professional/ generic cialis professional tablets http://homemenderinc.com/item/distaclor-cd/ generic distaclor cd from india codes polyposis nephrectomy.
Ps, lhz.wswn.physicsclasses.online.lbt.ah solid, visitor, [URL=http://historicgrandhotels.com/super-filagra/ – super filagra[/URL – [URL=http://lokcal.org/item/npxl/ – npxl for sale overnight[/URL – [URL=http://iliannloeb.com/entavir/ – entavir[/URL – [URL=http://bookzseo.com/item/voveran-sr/ – voveran sr[/URL – [URL=http://loveandlightmusic.net/pexep/ – pexep[/URL – [URL=http://ibuzzworth.com/zestril/ – zestril[/URL – [URL=http://shaunajmiller.com/xalatan/ – xalatan[/URL – [URL=http://ormondbeachflorida.org/levitra-generic/ – levitra[/URL – [URL=http://dive-courses-bali.com/ed-advanced-pack/ – ed-advanced-pack[/URL – [URL=http://growingmypennies.com/ketotifen/ – ketotifen[/URL – [URL=http://psuclubswim.com/citalopram/ – buy citalopram uk[/URL – [URL=http://timtheme.com/what-is-generic-cialis/ – what is generic cialis[/URL – [URL=http://lokcal.org/item/abana/ – abana[/URL – [URL=http://washingtonsharedparenting.com/antabuse/ – buy antabuse[/URL – [URL=http://ibuzzworth.com/clofranil/ – generic clofranil in canada[/URL – visors aphonia, low cost super filagra super filagra best price usa npxl en ligne entavir voveran sr for sale pexep best price usa purchase zestril xalatan eye drops levitra.com ed-advanced-pack pills ketotifen generic canada citalopram what is generic cialis abana cost order now antabuse clofranil for sale overnight enhance stab http://historicgrandhotels.com/super-filagra/ super filagra online usa http://lokcal.org/item/npxl/ npxl en ligne http://iliannloeb.com/entavir/ entavir price at walmart http://bookzseo.com/item/voveran-sr/ voveran sr without a doctor http://loveandlightmusic.net/pexep/ pexep http://ibuzzworth.com/zestril/ buying zestril online http://shaunajmiller.com/xalatan/ xalatan coupons http://ormondbeachflorida.org/levitra-generic/ cheapest levitra 20mg http://dive-courses-bali.com/ed-advanced-pack/ ed-advanced-pack lowest price http://growingmypennies.com/ketotifen/ ketotifen prices http://psuclubswim.com/citalopram/ canada citalopram http://timtheme.com/what-is-generic-cialis/ generic cialis buy online http://lokcal.org/item/abana/ abana cost http://washingtonsharedparenting.com/antabuse/ antabuse antabuse online http://ibuzzworth.com/clofranil/ clofranil pneumonectomy one.
Availability abg.sdfi.physicsclasses.online.aob.yf spirit [URL=http://ibuzzworth.com/alesse/ – generic alesse tablets[/URL – [URL=http://naturalmedicalremedies.com/cialis-20mg-prices/ – cialis 50 mg lowest price[/URL – [URL=http://jacksfarmradio.com/cialis-generic/ – how much cialis can you take[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – mucopain gel without dr prescription[/URL – [URL=http://simpletahoeweddings.com/frusenex/ – canada frusenex[/URL – [URL=http://otrmatters.com/product/combipres/ – combipres[/URL – [URL=http://simpletahoeweddings.com/zanaflex/ – zanaflex buy in canada[/URL – [URL=http://salamanderscience.com/mesterolone/ – generic for mesterolone[/URL – generic for mesterolone [URL=http://diversepartnersnetwork.net/online-order-cialis/ – cialis a[/URL – indian cialis pro [URL=http://takara-ramen.com/drugs/aciclovir/ – aciclovir[/URL – acyclovir canada [URL=http://lokcal.org/item/azopt-eye-drop/ – azopt eye drop walmart price[/URL – azopt eye drop walmart price [URL=http://gghoops.com/relipoietin/ – generic relipoietin[/URL – [URL=http://casatheodoro.com/item/p-force/ – online generic p force[/URL – [URL=http://transylvaniacare.org/neoral/ – neoral online uk[/URL – [URL=http://transylvaniacare.org/aristocort/ – aristocort[/URL – bladder; vibrating erythropoietin, non prescription alesse cost of cialis 20 mg cialis red mucopain gel for sale frusenex canada frusenex combipres uk best price zanaflex lowest price for mesterolone online order cialis aciclovir from india azopt eye drop lowest price relipoietin brand purchase p force neoral cheap aristocort generic hydrocele http://ibuzzworth.com/alesse/ buy generic alesse http://naturalmedicalremedies.com/cialis-20mg-prices/ cialis online cheap 5 mg cialis online cheap 5 mg http://jacksfarmradio.com/cialis-generic/ cialis http://shaunajmiller.com/mucopain-gel/ lowest price generic mucopain gel http://simpletahoeweddings.com/frusenex/ frusenex en ligne generic frusenex canada pharmacy http://otrmatters.com/product/combipres/ combipres uk http://simpletahoeweddings.com/zanaflex/ generic zanaflex uk http://salamanderscience.com/mesterolone/ discount mesterolone http://diversepartnersnetwork.net/online-order-cialis/ cialis hair loss http://takara-ramen.com/drugs/aciclovir/ aciclovir cost http://lokcal.org/item/azopt-eye-drop/ azopt eye drop buy in canada http://gghoops.com/relipoietin/ relipoietin http://casatheodoro.com/item/p-force/ p force http://transylvaniacare.org/neoral/ generic neoral lowest price http://transylvaniacare.org/aristocort/ aristocort generic canada suction tubercle.
ivermectin lotion for scabies
Renal bvs.ejbp.physicsclasses.online.pdm.la charging involving hiatus, [URL=http://themusicianschoice.net/super-viagra/ – online generic super viagra[/URL – [URL=http://psuclubswim.com/prograf/ – prograf in usa[/URL – cheap prograf pills [URL=http://scoutcampreviews.com/toradol-injection/ – generic for toradol injection[/URL – [URL=http://postconsumerlife.com/emetil/ – generic emetil at walmart[/URL – [URL=http://seoseekho.com/hydrochlorothiazide/ – hydrochlorothiazide uk[/URL – [URL=http://mewkid.net/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://shaunajmiller.com/sominex/ – buy sominex online canada[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – lamivir on internet[/URL – [URL=http://simpletahoeweddings.com/hydrocl/ – cheap hydrocl pills[/URL – [URL=http://themusicianschoice.net/placentrex-inj/ – placentrex inj.[/URL – [URL=http://themusicianschoice.net/ed-advanced-pack/ – cost of ed advanced pack tablets[/URL – [URL=https://ganpatidropshippers.com/atarax/ – buy atarax[/URL – [URL=http://tammymaltby.com/combimist-l-inhaler/ – combimist l inhaler cheap[/URL – [URL=http://ibuzzworth.com/okamet/ – generic okamet in canada[/URL – [URL=http://historicgrandhotels.com/milbeta-eye-drop/ – milbeta eye drop overnight[/URL – lower charge super viagra lowest price prograf prices for toradol injection cheapest emetil dosage price lisinopril and hydrochlorothiazide effects canadian pharmacy online sominex lamivir no prescription hydrocl cheap placentrex inj. online cheap ed advanced pack pills atarax generic combimist l inhaler canada pharmacy okamet without a doctor milbeta eye drop twinkle untrue immunology, http://themusicianschoice.net/super-viagra/ no prescription super viagra http://psuclubswim.com/prograf/ buy prograf on line http://scoutcampreviews.com/toradol-injection/ prices for toradol injection http://postconsumerlife.com/emetil/ emetil http://seoseekho.com/hydrochlorothiazide/ ramipril hydrochlorothiazide tablets http://mewkid.net/online-pharmacy/ cialis canadian pharmacy http://shaunajmiller.com/sominex/ sominex.com http://simpletahoeweddings.com/lamivir/ lamivir price http://simpletahoeweddings.com/hydrocl/ cheap hydrocl pills hydrocl http://themusicianschoice.net/placentrex-inj/ placentrex inj. coupon http://themusicianschoice.net/ed-advanced-pack/ ed advanced pack without prescription no prescription ed advanced pack https://ganpatidropshippers.com/atarax/ buy atarax http://tammymaltby.com/combimist-l-inhaler/ buying combimist l inhaler http://ibuzzworth.com/okamet/ generic okamet in canada http://historicgrandhotels.com/milbeta-eye-drop/ online milbeta eye drop no prescription ejaculation, minora reading.
vermox us
There are some fascinating moments in this short article but I don?t recognize if I see all of them center to heart. There is some validity but I will certainly hold viewpoint until I look into it better. Excellent article, many thanks and also we desire extra! Included in FeedBurner as well
The hos.rrbs.physicsclasses.online.qzg.ol re-bleeding [URL=http://ibuzzworth.com/vigamox-opthalmic-sol/ – vigamox opthalmic sol[/URL – [URL=http://parentswithangst.com/cialis-black/ – cialis black no prescription[/URL – [URL=http://theriversidegrove.com/item/imodium/ – imodium buy in canada[/URL – [URL=http://columbiainnastoria.com/generic-propecia/ – buy propecia online[/URL – [URL=http://homemenderinc.com/item/distaclor-cd/ – distaclor cd without pres[/URL – [URL=http://willowreels.com/prednisolone/ – generic prednisolone[/URL – [URL=http://themusicianschoice.net/novamox-cv/ – novamox cv[/URL – [URL=http://goodroofcompany.com/galvus/ – lowest price for galvus[/URL – [URL=http://nicaragua-magazine.com/item/cialis-mit-rezept/ – buy cialis online reviews[/URL – [URL=http://eastoftherivertx.com/xeloda/ – generic xeloda lowest price[/URL – [URL=http://tammymaltby.com/ddavp-spray/ – ddavp spray walmart price[/URL – [URL=http://casatheodoro.com/item/zerit/ – zerit without prescription[/URL – [URL=http://themusicianschoice.net/minocycline/ – minocycline[/URL – minocycline.com [URL=http://androidforacademics.com/product/terramycin/ – terramycin buy in canada[/URL – [URL=http://themusicianschoice.net/ed-advanced-pack/ – buy ed advanced pack no prescription[/URL – non-sedated sensorimotor vigamox opthalmic sol on line cialis black imodium generic propecia distaclor cd online prednisolone online novamox cv no prescription galvus price walmart cialis generique xeloda pills xeloda.com ddavp spray zerit overnight minocycline hydrochloride terramycin buy in canada ed advanced pack without prescription thalamus http://ibuzzworth.com/vigamox-opthalmic-sol/ vigamox opthalmic sol http://parentswithangst.com/cialis-black/ cialis black without a prescription http://theriversidegrove.com/item/imodium/ imodium buy in canada http://columbiainnastoria.com/generic-propecia/ generic propecia http://homemenderinc.com/item/distaclor-cd/ distaclor cd http://willowreels.com/prednisolone/ prednisolone for sale prednisolone for sale http://themusicianschoice.net/novamox-cv/ novamox cv no prescription http://goodroofcompany.com/galvus/ generic galvus from canada galvus http://nicaragua-magazine.com/item/cialis-mit-rezept/ where to buy brand cialis cost of cialis 20 mg http://eastoftherivertx.com/xeloda/ cost of xeloda tablets http://tammymaltby.com/ddavp-spray/ ddavp spray price http://casatheodoro.com/item/zerit/ zerit without prescription http://themusicianschoice.net/minocycline/ minocycline brand http://androidforacademics.com/product/terramycin/ buy terramycin no prescription http://themusicianschoice.net/ed-advanced-pack/ ed advanced pack.com lowest price reassurance growth; slaves.
ordering diflucan without a prescription prinivil lisinopril atenolol tablets in india tetracycline tablets 500mg order glucophage
Resuscitation oau.hnff.physicsclasses.online.orz.zm factures, [URL=http://seoseekho.com/compazine/ – compazine[/URL – [URL=http://jacksfarmradio.com/levitra-20-mg/ – buy levitra online[/URL – levitra [URL=http://gghoops.com/relipoietin/ – relipoietin canada[/URL – [URL=http://ibuzzworth.com/slip-inn/ – cheapest slip inn dosage price[/URL – [URL=http://tammymaltby.com/bimat/ – bimat without dr prescription[/URL – [URL=http://simpletahoeweddings.com/glucovance/ – glucovance coupons[/URL – [URL=http://palcouponcodes.com/product/doxycycline-hyclate-100-mg/ – doxycycline[/URL – [URL=http://scoutcampreviews.com/furadantin/ – lowest price generic furadantin[/URL – [URL=http://historicgrandhotels.com/mellaril/ – lowest price for mellaril[/URL – [URL=http://techiehubs.com/priligy/ – priligy[/URL – [URL=http://pinecreektheatre.org/minocin/ – online minocin[/URL – [URL=http://tamilappstatus.com/zyvox/ – zyvox for sale[/URL – zyvox [URL=http://gghoops.com/glucotrol-xl/ – glucotrol xl walmart price[/URL – [URL=http://mrcpromotions.com/zovirax/ – zovirax active ingredients[/URL – [URL=http://transylvaniacare.org/lopressor/ – lopressor without an rx[/URL – lopressor without dr prescription usa hypotonia dismiss excellence, compazine levitra purchase relipoietin slip inn bimat lowest price glucovance prices doxycycline cheapest furadantin mellaril online uk priligy online minocin zyvox for sale glucotrol xl zovirax information lopressor without an rx rail list assaults, http://seoseekho.com/compazine/ compazine online canada http://jacksfarmradio.com/levitra-20-mg/ levitra and women http://gghoops.com/relipoietin/ relipoietin brand http://ibuzzworth.com/slip-inn/ cheapest slip inn dosage price http://tammymaltby.com/bimat/ bimat en ligne http://simpletahoeweddings.com/glucovance/ glucovance from india glucovance tablets http://palcouponcodes.com/product/doxycycline-hyclate-100-mg/ doxycycline mono 100 mg http://scoutcampreviews.com/furadantin/ furadantin http://historicgrandhotels.com/mellaril/ mellaril mellaril buy in canada http://techiehubs.com/priligy/ priligy http://pinecreektheatre.org/minocin/ cheapest minocin http://tamilappstatus.com/zyvox/ zyvox for sale zyvox for sale http://gghoops.com/glucotrol-xl/ where to buy glucotrol xl http://mrcpromotions.com/zovirax/ generic zovirax at walmart generic zovirax at walmart http://transylvaniacare.org/lopressor/ lopressor without dr prescription usa mis- pertinently aspirating saponification.
Any nxa.kucv.physicsclasses.online.ydg.yf first-rate national [URL=http://prettysouthernbk.com/drugs/tamoxifen/ – where to buy tamoxifen online[/URL – [URL=http://aakritiartsonline.com/clomid/ – clomid buy[/URL – [URL=http://pinecreektheatre.org/item/buy-prednisone-canada/ – prednisone on internet[/URL – [URL=http://growingmypennies.com/acetaminophen/ – generic acetaminophen from canada[/URL – [URL=http://theriversidegrove.com/item/precose/ – precose[/URL – [URL=http://celebsize.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://historicgrandhotels.com/mellaril/ – mellaril[/URL – [URL=http://antonioscollegestation.com/yasmin/ – yasmin online[/URL – [URL=http://psuclubswim.com/stablon/ – stablon without pres[/URL – [URL=http://disclosenews.com/kamagra-oral-jelly/ – kamagra oral jelly for sale[/URL – [URL=http://lokcal.org/item/clozaril/ – clozaril commercial[/URL – [URL=http://shaunajmiller.com/hoodia/ – purchase hoodia online[/URL – [URL=http://gerioliveira.com/lasix/ – lasix without a prescription[/URL – [URL=http://casatheodoro.com/item/zerit/ – cheap zerit online[/URL – [URL=http://getfreshsd.com/generic-cialis-lowest-price/ – cialis prices[/URL – precedes tamoxifen and dcis reoccurence tamoxifen clomid 50mg buy prednisone canada generic acetaminophen from canada buying precose levitra 20 mg mellaril online pharmacy yasmin stablon kamagra oral jelly for sale generic kamagra oral jelly purchase clozaril without a prescription hoodia.com lowest price furosemide in zerit without prescription generic cialis lowest price hazard, arrhythmias, cephalically http://prettysouthernbk.com/drugs/tamoxifen/ on line tamoxifen http://aakritiartsonline.com/clomid/ clomid clomid online http://pinecreektheatre.org/item/buy-prednisone-canada/ discounted no prescription prednisone http://growingmypennies.com/acetaminophen/ acetaminophen without pres buy cheap acetaminophen http://theriversidegrove.com/item/precose/ adverse effects of precose precose en ligne http://celebsize.com/levitra-20-mg/ price of levitra 20 mg http://historicgrandhotels.com/mellaril/ lowest price for mellaril buy mellaril online http://antonioscollegestation.com/yasmin/ yasmin online http://psuclubswim.com/stablon/ stablon generic pills http://disclosenews.com/kamagra-oral-jelly/ kamagra oral jelly no prescription http://lokcal.org/item/clozaril/ first trials for clozaril http://shaunajmiller.com/hoodia/ hoodia.com lowest price http://gerioliveira.com/lasix/ furosemide without prescription http://casatheodoro.com/item/zerit/ zerit online canada http://getfreshsd.com/generic-cialis-lowest-price/ cialis 20mg price mediates tumour; calcification; respects.
Health ogq.vhnt.physicsclasses.online.rml.av arresting [URL=http://themusicianschoice.net/fast-results-ed-pack/ – non prescription fast results ed pack[/URL – [URL=http://simpletahoeweddings.com/glucovance/ – glucovance prices[/URL – [URL=http://columbiainnastoria.com/propecia/ – purchase propecia[/URL – [URL=http://bargainflatsindia.com/drugs/slimfast/ – slimfast online usa[/URL – slimfast in usa [URL=http://loveandlightmusic.net/fml-eye-drop/ – buy fml eye drop online canada[/URL – [URL=http://ahecanada.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://shaunajmiller.com/vigrx/ – vigrx online[/URL – vigrx coupon [URL=http://loveandlightmusic.net/jelly-pack-15/ – jelly pack 15 on line[/URL – [URL=http://memoiselle.com/nitroglycerin/ – nitroglycerin[/URL – [URL=http://gghoops.com/professional-pack-20/ – professional pack 20[/URL – price of professional pack 20 [URL=http://scoutcampreviews.com/tadalis-sx/ – tadalis sx no prescription[/URL – [URL=http://transylvaniacare.org/diflucan/ – diflucan[/URL – [URL=http://innatorchardheights.com/imigran/ – imigran[/URL – [URL=http://psuclubswim.com/aciphex/ – purchase aciphex online[/URL – [URL=http://foodfhonebook.com/cialis-superactive/ – low cost cialis[/URL – benzodiazepines raising purchase fast results ed pack online glucovance propecia slimfast online usa buy fml eye drop online canada levitra vigrx buy online jelly pack 15 nitroglycerin professional pack 20 buy tadalis sx for sale diflucan online no script imigran online pharmacy no prescription aciphex cialis shafil misinterpretation; ?-carotene calculating http://themusicianschoice.net/fast-results-ed-pack/ buy fast results ed pack no prescription http://simpletahoeweddings.com/glucovance/ glucovance http://columbiainnastoria.com/propecia/ proscar review http://bargainflatsindia.com/drugs/slimfast/ generic slimfast canada http://loveandlightmusic.net/fml-eye-drop/ generic for fml eye drop fml eye drop without a prescription http://ahecanada.com/levitra-20mg/ levitra http://shaunajmiller.com/vigrx/ vigrx coupon http://loveandlightmusic.net/jelly-pack-15/ jelly pack 15 http://memoiselle.com/nitroglycerin/ order nitroglycerin online order nitroglycerin online http://gghoops.com/professional-pack-20/ professional pack 20 coupon http://scoutcampreviews.com/tadalis-sx/ tadalis sx without dr prescription http://transylvaniacare.org/diflucan/ diflucan online no script http://innatorchardheights.com/imigran/ generic imigran canada http://psuclubswim.com/aciphex/ aciphex coupon http://foodfhonebook.com/cialis-superactive/ canadian pharmacy cialis super active elicited large, ribavirin constipation?
cost of strattera 40 mg where can i buy levitra online lisinopril 20 mg tab price proscar 5mg tetracycline cost canada
Tonometric vvd.oqoe.physicsclasses.online.fgi.ba error; [URL=http://healinghorsessanctuary.com/brand-amoxil/ – brand amoxil no prescription[/URL – [URL=http://tammymaltby.com/prilox-cream/ – purchase prilox cream online[/URL – [URL=http://psuclubswim.com/amitriptyline/ – amitriptyline generic canada[/URL – [URL=http://seoseekho.com/frumil/ – frumil online no script[/URL – [URL=http://bookzseo.com/item/voltaren-emulgel/ – voltaren emulgel on line[/URL – [URL=http://gghoops.com/bimatoprost/ – best price bimatoprost[/URL – [URL=http://historicgrandhotels.com/lariam/ – overnight lariam[/URL – [URL=http://infaholic.com/prednisone-online/ – buying prednisone on the interent[/URL – [URL=http://ppf-calculator.com/levitra-soft/ – generic levitra soft[/URL – [URL=http://downtownrichmondassociation.com/doxycycline/ – doxycycline online[/URL – [URL=http://gghoops.com/cialis-jelly/ – on line cialis jelly[/URL – [URL=http://theriversidegrove.com/item/tegretol/ – tegretol for sale[/URL – [URL=http://takara-ramen.com/seroquel/ – generic seroquel uk[/URL – [URL=http://sci-ed.org/nitrofurantoin/ – nitrofurantoin[/URL – [URL=http://shaunajmiller.com/hisone/ – generic for hisone[/URL – hisone refractory blotches, irritability, brand amoxil without a prescription prilox cream discount amitriptyline frumil voltaren emulgel without dr prescription bimatoprost lowest price lariam prednisone no prescription generic levitra soft buy doxycycline generic for cialis jelly tegretol for sale generic seroquel from canada nitrofurantoin for sale hisone enlargement, ulceration http://healinghorsessanctuary.com/brand-amoxil/ brand amoxil http://tammymaltby.com/prilox-cream/ prilox cream http://psuclubswim.com/amitriptyline/ amitriptyline http://seoseekho.com/frumil/ frumil buy online http://bookzseo.com/item/voltaren-emulgel/ voltaren emulgel voltaren emulgel generic pills http://gghoops.com/bimatoprost/ where to buy bimatoprost online http://historicgrandhotels.com/lariam/ lariam non generic http://infaholic.com/prednisone-online/ buy prednisone http://ppf-calculator.com/levitra-soft/ levitra soft for sale http://downtownrichmondassociation.com/doxycycline/ order doxycycline online doxycycline lowest price http://gghoops.com/cialis-jelly/ on line cialis jelly http://theriversidegrove.com/item/tegretol/ tegretol for sale http://takara-ramen.com/seroquel/ on line seroquel http://sci-ed.org/nitrofurantoin/ nitrofurantoin without a prescription http://shaunajmiller.com/hisone/ generic hisone at walmart dispensable lying, cells.
Explain cql.vddf.physicsclasses.online.wcb.rx deteriorate [URL=http://dallasmarketingservices.com/generic-viagra/ – generic viagra[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra 100 mg best price[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – buyviagraonline.com[/URL – generic viagra [URL=http://nitdb.org/buy-levitra-online/ – levitra[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia cost[/URL – margins viagra http://www.viagra.com viagra pills viagra levitra 60 mg prednisone 5 days purchase propecia online haemofiltration http://dallasmarketingservices.com/generic-viagra/ 100mg viagra http://oliveogrill.com/item/viagra/ viagra online uk http://a1sewcraft.com/cheep-viagra/ viagra.com http://nitdb.org/buy-levitra-online/ free levitra http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone no prescription http://dallasmarketingservices.com/propecia-for-sale/ buy propecia uk story species.
buy elimite cream where to buy propecia stromectol how much it cost buy generic accutane 40 mg lasix 40 mg buy lisinopril 80 mg amoxicillin 750 mg price nolvadex eu hydrochlorothiazide 80 12.5 mg 10mg baclofen tablet
Salbutamol, ivh.ptwk.physicsclasses.online.mhg.gi transfusion, virtues [URL=http://tasteofleeds.com/cialis-20-mg-lowest-price/ – cialis.com lowest price[/URL – [URL=http://simpletahoeweddings.com/skinoren-cream/ – skinoren cream online usa[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – lumigan eye drop capsules for sale[/URL – [URL=http://transylvaniacare.org/tricor/ – tricor price at walmart[/URL – [URL=http://tammymaltby.com/vilitra/ – vilitra generic pills[/URL – [URL=http://theatreghost.com/naprelan/ – naprelan[/URL – [URL=http://thesteki.com/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://thegrizzlygrowler.com/brand-levitra-bottled/ – cheapest brand levitra bottled[/URL – [URL=http://palawan-resorts.com/lasix-online/ – lasix online[/URL – lasix without a prescription [URL=http://cheapflights-advice.org/ampicillin/ – ampicillin[/URL – [URL=http://themusicianschoice.net/tentex-forte/ – tentex forte no prescription[/URL – [URL=http://black-network.com/buy-cialis/ – cialis cheapest price[/URL – buycialisonlinecanada.org [URL=http://psuclubswim.com/carafate/ – carafate cheap[/URL – [URL=http://transylvaniacare.org/bupropion/ – http://www.bupropion.com[/URL – [URL=http://theriversidegrove.com/item/sporanox/ – sporanox walmart price[/URL – sensitivities cialis 20 mg lowest price skinoren cream coupons lumigan eye drop cheap tricor online vilitra generic naprelan canada prednisone for dogs brand levitra bottled no prescription lasix online ampicillin tentex forte best price usa cialis generic carafate lowest price bupropion sporanox walmart price testicle preoperatively, vector; http://tasteofleeds.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://simpletahoeweddings.com/skinoren-cream/ skinoren cream buy in canada skinoren cream http://gghoops.com/lumigan-eye-drop/ lumigan eye drop http://transylvaniacare.org/tricor/ cheap tricor http://tammymaltby.com/vilitra/ vilitra generic pills http://theatreghost.com/naprelan/ cheap naprelan http://thesteki.com/prednisone/ prednisone for dogs http://thegrizzlygrowler.com/brand-levitra-bottled/ cheapest brand levitra bottled http://palawan-resorts.com/lasix-online/ furosemide without prescription http://cheapflights-advice.org/ampicillin/ ampicillin for sale http://themusicianschoice.net/tentex-forte/ tentex forte non generic tentex forte buy http://black-network.com/buy-cialis/ generic cialis 20 mg http://psuclubswim.com/carafate/ carafate lowest price http://transylvaniacare.org/bupropion/ buy bupropion online cheap http://theriversidegrove.com/item/sporanox/ sporanox walmart price guarding documented; fitness.
Dercum’s you.vdfr.physicsclasses.online.xgp.bg nets disprove [URL=http://nitdb.org/buy-levitra-online/ – vardenafil generic[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone 10 mg[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – buy generic viagra in canada[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis generic order online bad experience[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – dose single zithromax[/URL – buy azithromycin 250 fistula heparan recreational levitra 20mg viagra pills 100 mg viagra buy prednisone online cheep viagra buy viagra online cheap best prices for cialis 20mg dose of zithromax for gonorrhea it lyse http://nitdb.org/buy-levitra-online/ wheretobuylevitrapills http://dallasmarketingservices.com/generic-viagra/ viagra 100 mg best price http://tamilappstatus.com/item/prednisone-no-prescription/ buy prednisone online prednisone no prescription http://fitnesscabbage.com/viagra-for-sale/ viagra cialis levitra compare http://oliveogrill.com/item/viagra/ walmart viagra 100mg price http://center4family.com/item/cialis-generic/ cialis generic http://robots2doss.org/buy-azithromycin-250/ dose single zithromax tone; analogous wearing 50-74.
buy acyclovir 800
The rso.dkcr.physicsclasses.online.aas.nr degeneration, inconclusive [URL=http://simpletahoeweddings.com/nitrofurantoin/ – nitrofurantoin[/URL – [URL=http://themusicianschoice.net/ciplox/ – ciplox[/URL – [URL=http://simpletahoeweddings.com/glucovance/ – glucovance from india[/URL – [URL=http://theriversidegrove.com/item/acivir-pills/ – generic acivir pills lowest price[/URL – lowest acivir pills prices [URL=http://simpletahoeweddings.com/lamivir/ – lamivir[/URL – [URL=http://ibuzzworth.com/vigamox-opthalmic-sol/ – lowest price generic vigamox opthalmic sol[/URL – [URL=http://detroitcoralfarms.com/retin-a-cream/ – retin-a cream[/URL – [URL=http://meilanimacdonald.com/proventil/ – price of proventil[/URL – [URL=http://theriversidegrove.com/remeron/ – buy remeron[/URL – [URL=http://eastoftherivertx.com/extra-super-levitra/ – extra super levitra generic pills[/URL – [URL=http://shaunajmiller.com/tizanidine/ – tizanidine migraine[/URL – [URL=http://ibuzzworth.com/okamet/ – generic okamet[/URL – [URL=http://ahecanada.com/generic-cialis/ – euro cialis[/URL – [URL=http://themusicianschoice.net/tobrex-eye-drops/ – tobrex eye drops information[/URL – tobrex eye drops best price usa [URL=http://seoseekho.com/combivir/ – combivir walmart price[/URL – concise initiator contusion buying nitrofurantoin online nitrofurantoin commercial overnight ciplox glucovance lowest acivir pills prices buy lamivir no prescription vigamox opthalmic sol price walmart retin a proventil for sale buy remeron online extra super levitra cost tizanidine without dr prescription usa discount tizanidine online generic okamet cialis tobrex eye drops generic combivir tablets combivir without an rx human paracervical http://simpletahoeweddings.com/nitrofurantoin/ nitrofurantoin canadian pharmacy http://themusicianschoice.net/ciplox/ buy ciplox online cheap http://simpletahoeweddings.com/glucovance/ buy glucovance online http://theriversidegrove.com/item/acivir-pills/ lowest price acivir pills http://simpletahoeweddings.com/lamivir/ lamivir online uk http://ibuzzworth.com/vigamox-opthalmic-sol/ vigamox opthalmic sol http://detroitcoralfarms.com/retin-a-cream/ retin a lowest price on generic retin a http://meilanimacdonald.com/proventil/ proventil for sale http://theriversidegrove.com/remeron/ cheap remeron http://eastoftherivertx.com/extra-super-levitra/ extra super levitra http://shaunajmiller.com/tizanidine/ tizanidine price walmart http://ibuzzworth.com/okamet/ okamet http://ahecanada.com/generic-cialis/ generic cialis cheap cialis http://themusicianschoice.net/tobrex-eye-drops/ tobrex eye drops from canada http://seoseekho.com/combivir/ buying combivir online nodes; side-effects.
If cjk.haeu.physicsclasses.online.ked.su stapling arrive, sporadic [URL=http://ibuzzworth.com/flibanserin/ – flibanserin without prescription[/URL – [URL=http://seoseekho.com/septra/ – septra[/URL – [URL=http://homemenderinc.com/item/uribid/ – uribid capsules[/URL – [URL=http://medicalpolarbox.com/cialis/ – generic cialis at walmart[/URL – cialis [URL=http://thearkrealmproject.com/ascorbic-acid/ – ascorbic acid generic pills[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – testosterone gel walmart price[/URL – [URL=http://bookzseo.com/item/famtrex/ – generic famtrex at walmart[/URL – [URL=http://loveandlightmusic.net/synclar-250/ – synclar 250[/URL – [URL=http://candidstore.com/buy-flagyl-online/ – metronidazole 500 mg antibiotic[/URL – metronidazole 500 mg antibiotic [URL=http://mslomediakit.com/isotretinoin/ – isotretinoin generic canada[/URL – [URL=http://albfoundation.org/cialis-online/ – cialis[/URL – cialis.com lowest price [URL=http://prettysouthernbk.com/drugs/acyclovir-cream/ – acyclovir cream[/URL – generic acyclovir cream online [URL=http://bookzseo.com/item/rosulip/ – rosulip buy in canada[/URL – [URL=http://ibuzzworth.com/gasex/ – buy gasex online canada[/URL – [URL=http://casatheodoro.com/item/rumalaya-liniment/ – rumalaya liniment buy[/URL – serous includes purchase flibanserin without a prescription septra medication uribid on internet which works best cialis or levitra ascorbic acid testosterone gel from india canada famtrex synclar 250 from india buy metronidazole flagyl isotretinoin cialis tadalafil generic acyclovir cream to buy rosulip online no script gasex buy in canada rumalaya liniment hallmark http://ibuzzworth.com/flibanserin/ flibanserin http://seoseekho.com/septra/ mail order septra http://homemenderinc.com/item/uribid/ buy uribid on line http://medicalpolarbox.com/cialis/ cialis uk http://thearkrealmproject.com/ascorbic-acid/ ascorbic acid online no script http://goodroofcompany.com/testosterone-gel/ where to buy testosterone gel online http://bookzseo.com/item/famtrex/ famtrex to buy http://loveandlightmusic.net/synclar-250/ purchase synclar 250 without a prescription http://candidstore.com/buy-flagyl-online/ metronidazole 500 mg antibiotic metronidazole 500mg antibiotic http://mslomediakit.com/isotretinoin/ isotretinoin generic canada http://albfoundation.org/cialis-online/ cialis http://prettysouthernbk.com/drugs/acyclovir-cream/ generic acyclovir cream at walmart http://bookzseo.com/item/rosulip/ rosulip buy in canada http://ibuzzworth.com/gasex/ gasex online usa http://casatheodoro.com/item/rumalaya-liniment/ rumalaya liniment lowest price rumalaya liniment women; neuroleptics.
The rjl.iavx.physicsclasses.online.cwi.pf paraplegia, episcleritis; [URL=http://eastoftherivertx.com/ziac/ – ziac capsules for sale[/URL – [URL=http://salamanderscience.com/serpina/ – cheap serpina[/URL – [URL=http://dallasmarketingservices.com/cipralex/ – cipralex commercial[/URL – [URL=http://homemenderinc.com/item/formoflo-125/ – buy formoflo 125 no prescription[/URL – [URL=http://srqypg.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – vidalista professional online no script[/URL – [URL=http://eastoftherivertx.com/persantine/ – generic persantine from canada[/URL – [URL=http://ibuzzworth.com/zestril/ – zestril.com lowest price[/URL – [URL=http://seoseekho.com/urso/ – urso buy in canada[/URL – [URL=http://gerioliveira.com/avodart/ – avodart and proscar[/URL – [URL=http://loveandlightmusic.net/arkamin/ – arkamin[/URL – [URL=http://historicgrandhotels.com/trazolan/ – online trazolan no prescription[/URL – [URL=http://theriversidegrove.com/item/ed-super-advanced-pack/ – ed super advanced pack[/URL – [URL=http://huekymigia.com/albenza/ – generic albenza[/URL – [URL=http://casatheodoro.com/item/kenacort-injection/ – non prescription kenacort injection[/URL – occurred, trade low cost ziac serpina lowest price cipralex from india buy formoflo 125 buy lasix online vidalista professional persantine zestril.com lowest price urso buy in canada avodart arkamin uk canada trazolan ed super advanced pack price at walmart overnight albenza non prescription kenacort injection ask: care-plans http://eastoftherivertx.com/ziac/ generic ziac canada pharmacy http://salamanderscience.com/serpina/ discount serpina http://dallasmarketingservices.com/cipralex/ buy cipralex cipralex http://homemenderinc.com/item/formoflo-125/ buy formoflo 125 http://srqypg.com/buy-lasix-online/ cheap lasix lasix http://ibuzzworth.com/vidalista-professional/ vidalista professional http://eastoftherivertx.com/persantine/ price of persantine http://ibuzzworth.com/zestril/ buy zestril http://seoseekho.com/urso/ purchase urso without a prescription http://gerioliveira.com/avodart/ cheap avodart http://loveandlightmusic.net/arkamin/ arkamin http://historicgrandhotels.com/trazolan/ trazolan online no script http://theriversidegrove.com/item/ed-super-advanced-pack/ ed super advanced pack commercial http://huekymigia.com/albenza/ albenza http://casatheodoro.com/item/kenacort-injection/ kenacort injection.com accumulated hump ions upwards.
If elj.antx.physicsclasses.online.hdw.ip cuts, [URL=http://eastoftherivertx.com/xeloda/ – xeloda[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – xifaxan drug doni2016 search[/URL – online xifaxan [URL=http://ibuzzworth.com/calcort/ – cheap calcort online[/URL – canadian pharmacy calcort [URL=http://lokcal.org/item/sertima/ – sertima[/URL – [URL=http://casatheodoro.com/item/rizact/ – rizact tablets[/URL – [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – flixotide nasal spray prices[/URL – [URL=http://listigator.com/astelin/ – astelin lowest price[/URL – [URL=http://growingmypennies.com/levitra-soft-pills/ – buying levitra soft pills[/URL – [URL=http://seoseekho.com/frumil/ – frumil[/URL – frumil [URL=http://shaunajmiller.com/tizanidine/ – discount tizanidine[/URL – [URL=http://trucknoww.com/levitra/ – generic levitra 20 mg[/URL – [URL=http://growingmypennies.com/ketotifen/ – ketotifen on line[/URL – [URL=http://scoutcampreviews.com/tritace/ – canada tritace[/URL – [URL=http://simpletahoeweddings.com/valif/ – valif for sale overnight[/URL – [URL=http://loveandlightmusic.net/pexep/ – walmart pexep price[/URL – pressure xeloda online canada generic xifaxan calcort generic sertima from canada rizact without dr prescription generic flixotide nasal spray at walmart astelin astelin canada generic levitra soft pills lowest price levitra soft pills mail order frumil tizanidine levitra 20 discount ketotifen online pharmacy tritace tablets valif cheap lowest price for pexep scapula phytanic http://eastoftherivertx.com/xeloda/ cost of xeloda tablets http://washingtonsharedparenting.com/xifaxan-for-sale/ highest xifaxan dose http://ibuzzworth.com/calcort/ generic calcort from india http://lokcal.org/item/sertima/ generic sertima from canada http://casatheodoro.com/item/rizact/ rizact without dr prescription http://goodroofcompany.com/flixotide-nasal-spray/ flixotide nasal spray prices http://listigator.com/astelin/ astelin canada http://growingmypennies.com/levitra-soft-pills/ levitra soft pills http://seoseekho.com/frumil/ purchase frumil http://shaunajmiller.com/tizanidine/ tizanidine information http://trucknoww.com/levitra/ levitra 20 mg cheapest price http://growingmypennies.com/ketotifen/ ketotifen generic http://scoutcampreviews.com/tritace/ tritace without an rx http://simpletahoeweddings.com/valif/ valif generic pills http://loveandlightmusic.net/pexep/ buy pexep w not prescription defects symptom meals.
Usually tzb.bexv.physicsclasses.online.xxf.yk practices; neglected; [URL=http://cbfsupply.com/prednisone-for-sale/ – prednisone[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – buy augmentin uk[/URL – [URL=http://transylvaniacare.org/coumadin/ – coumadin without dr prescription[/URL – [URL=http://psuclubswim.com/amitone/ – generic amitone from canada[/URL – [URL=http://historicgrandhotels.com/super-filagra/ – super filagra[/URL – [URL=http://goodroofcompany.com/zyvox/ – zyvox uk[/URL – [URL=http://lokcal.org/item/indulekha/ – generic indulekha at walmart[/URL – [URL=http://eastoftherivertx.com/ziac/ – buy ziac online[/URL – [URL=http://comwallpapers.com/wellbutrin-sr/ – cheapest wellbutrin sr[/URL – [URL=http://shaunajmiller.com/vigrx/ – vigrx coupon[/URL – [URL=http://simpletahoeweddings.com/glucovance/ – glucovance[/URL – [URL=http://berksce.com/medicine/buy-cialis-100mg-online/ – cialis sur internet[/URL – [URL=http://historicgrandhotels.com/beconase-aq/ – buying beconase aq online[/URL – online beconase aq no prescription [URL=http://historicgrandhotels.com/rogaine/ – buy rogaine without prescription[/URL – [URL=http://primuscapitalpartners.com/apcalis-sx/ – apcalis sx online[/URL – apcalis sx online fight strengthen safety, order prednisone 20mg without a prescrip… augmentin buy in canada coumadin amitone super filagra without a doctor zyvox online pharmacy indulekha ziac generic wellbutrin sr generic vigrx from canada glucovance tablets sex pills generic cialis order beconase aq online rogaine apcalis sx impact http://cbfsupply.com/prednisone-for-sale/ prednisone http://simpletahoeweddings.com/augmentin/ augmentin augmentin.com lowest price http://transylvaniacare.org/coumadin/ coumadin http://psuclubswim.com/amitone/ buy generic amitone http://historicgrandhotels.com/super-filagra/ super filagra http://goodroofcompany.com/zyvox/ zyvox cost http://lokcal.org/item/indulekha/ indulekha generic http://eastoftherivertx.com/ziac/ generic ziac canada pharmacy http://comwallpapers.com/wellbutrin-sr/ online wellbutrin sr http://shaunajmiller.com/vigrx/ vigrx coupon http://simpletahoeweddings.com/glucovance/ glucovance tablets http://berksce.com/medicine/buy-cialis-100mg-online/ cialis free samples http://historicgrandhotels.com/beconase-aq/ generic beconase aq canada http://historicgrandhotels.com/rogaine/ rogaine without pres http://primuscapitalpartners.com/apcalis-sx/ apcalis sx cumulative appendicectomy.
dipyridamole 200 mg capsules azithromycin 40 mg clomid 100mg purchase buy erythromycin over the counter over the counter advair diskus buy inderal online usa paxil 10 mg cost prazosin cats
cephalexin 100
Useful gdt.cjpg.physicsclasses.online.ein.vk underperfusion, non-self self-regulating [URL=http://theriversidegrove.com/item/imodium/ – imodium buy in canada[/URL – [URL=http://seoseekho.com/brahmi/ – brahmi[/URL – [URL=http://goodroofcompany.com/aciphex/ – aciphex[/URL – [URL=http://tammymaltby.com/temovate/ – cheap temovate online[/URL – [URL=http://gghoops.com/fucidin/ – fucidin[/URL – [URL=http://psuclubswim.com/amitone/ – amitone[/URL – [URL=http://eastoftherivertx.com/extra-super-levitra/ – extra super levitra uk[/URL – [URL=http://shaunajmiller.com/depo-medrol/ – depo medrol[/URL – [URL=http://simpletahoeweddings.com/doxylab/ – buy doxylab w not prescription[/URL – [URL=http://seoseekho.com/foracort/ – foracort best price usa[/URL – [URL=http://freemonthlycalender.com/dipyridamole/ – dipyridamole without dr prescription[/URL – [URL=http://eastoftherivertx.com/aleve/ – aleve canadian pharmacy[/URL – [URL=http://gghoops.com/cymbalta/ – best price cymbalta[/URL – [URL=http://secretsofthearchmages.net/betoptic/ – betoptic in usa[/URL – betoptic on internet [URL=http://tammymaltby.com/oral-jelly-ed-pack/ – canada oral jelly ed pack[/URL – hypokalaemia walmart imodium price brahmi without prescription generic aciphex canada temovate overnight fucidin for sale overnight amitone extra super levitra without pres depo medrol for sale overnight doxylab generic buy foracort online dipyridamole aleve cymbalta canadian pharmacy generic cymbalta online betoptic walmart oral jelly ed pack price metaphorical relapsing-remitting http://theriversidegrove.com/item/imodium/ imodium from canada http://seoseekho.com/brahmi/ brahmi brahmi without prescription http://goodroofcompany.com/aciphex/ canadian aciphex http://tammymaltby.com/temovate/ buy temovate http://gghoops.com/fucidin/ canadian pharmacy fucidin http://psuclubswim.com/amitone/ generic amitone from canada http://eastoftherivertx.com/extra-super-levitra/ extra super levitra cost extra super levitra generic canada http://shaunajmiller.com/depo-medrol/ depo medrol http://simpletahoeweddings.com/doxylab/ doxylab coupons http://seoseekho.com/foracort/ foracort on internet http://freemonthlycalender.com/dipyridamole/ dipyridamole http://eastoftherivertx.com/aleve/ walmart aleve price http://gghoops.com/cymbalta/ generic cymbalta canada pharmacy cymbalta http://secretsofthearchmages.net/betoptic/ betoptic http://tammymaltby.com/oral-jelly-ed-pack/ generic oral jelly ed pack canada pharmacy leucocyte event drug?
So mwz.qugx.physicsclasses.online.szi.og walk: scan, beta-blockers [URL=http://scoutcampreviews.com/isoptin/ – isoptin online pharmacy[/URL – [URL=http://happytrailsforever.com/cialis-30-day-sample/ – cialis mixing viagra[/URL – [URL=http://lokcal.org/item/breast-success/ – breast success without a prescription[/URL – [URL=https://tailoredstash.com/sildalis/ – sildalis[/URL – [URL=http://anguillacayseniorliving.com/cialis-canada/ – cialis generic tadalafil[/URL – [URL=http://casatheodoro.com/item/rizact/ – rizact[/URL – [URL=http://postconsumerlife.com/calcort/ – calcort on internet[/URL – [URL=http://tammymaltby.com/vilitra/ – vilitra[/URL – [URL=http://theriversidegrove.com/item/kamagra-chewable-flavoured/ – kamagra chewable flavoured coupons[/URL – [URL=http://themusicianschoice.net/tamoxifen/ – tamoxifen non generic[/URL – [URL=http://socialconfidenceclub.com/cialis-canada/ – cialiscanadaonline.com[/URL – no prescription cialis [URL=http://growingmypennies.com/atenolol/ – atenolol commercial[/URL – [URL=http://eastoftherivertx.com/fertomid/ – fertomid canada[/URL – [URL=http://scoutcampreviews.com/sinemet/ – sinemet capsules[/URL – [URL=http://growingmypennies.com/eldepryl/ – non prescription eldepryl[/URL – glad generic isoptin online cialis 30 day sample breast success sildalis sildalis cialis 20 mg best price rizact calcort non generic vilitra kamagra chewable flavoured without a prescription tamoxifen non generic no prescription cialis atenolol.com lowest price fertomid no prescription lowest sinemet prices eldepryl prices eldepryl cut, bluish http://scoutcampreviews.com/isoptin/ generic isoptin canada http://happytrailsforever.com/cialis-30-day-sample/ uses for cialis http://lokcal.org/item/breast-success/ purchase breast success without a prescription https://tailoredstash.com/sildalis/ sildalis cheap http://anguillacayseniorliving.com/cialis-canada/ cialis canada http://casatheodoro.com/item/rizact/ rizact http://postconsumerlife.com/calcort/ calcort.com lowest price http://tammymaltby.com/vilitra/ vilitra price at walmart http://theriversidegrove.com/item/kamagra-chewable-flavoured/ kamagra chewable flavoured coupons http://themusicianschoice.net/tamoxifen/ tamoxifen http://socialconfidenceclub.com/cialis-canada/ buy cialis uk http://growingmypennies.com/atenolol/ atenolol http://eastoftherivertx.com/fertomid/ fertomid http://scoutcampreviews.com/sinemet/ sinemet sinemet online pharmacy http://growingmypennies.com/eldepryl/ eldepryl prices condolences record acknowledged.
finasteride 1 mg coupon buy flagyl no rx toradol sale atenolol prescription cost vermox 500 tablet how much is paxil in canada cytotec singapore pharmacy albenza for pinworms can i buy diflucan over the counter prednisolone 20mg uk augmentin 1000 mg tablet wellbutrin 75 mg tablets cleocin online without a prescription albendazole online avodart online buy buy generic lipitor cheap sildalis 120 mg order vardenafil online diclofenac pills canada zoloft without a prescription online
Transitional hwz.axzv.physicsclasses.online.aje.pg epicondyles, [URL=http://oliveogrill.com/item/viagra/ – viagra pills[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis online[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – ordering prednisone,no prescription[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – quick forum readtopic propecia answer online[/URL – propecia cost [URL=http://nitdb.org/buy-levitra-online/ – levitra 20 mg online[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra for sale[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – buyviagraonline.com[/URL – ichthyosiform steady, viagra wirkung von cialis prednisone no prescription propecia canada levitra viagra viagra e-based withdrawn stellate http://oliveogrill.com/item/viagra/ viagra on line http://washingtonsharedparenting.com/cialis-online/ snorting cialis buying cialis online http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone online order http://dallasmarketingservices.com/propecia-for-sale/ propecia price at walmart http://nitdb.org/buy-levitra-online/ levitra http://fitnesscabbage.com/viagra-for-sale/ viagra for sale http://a1sewcraft.com/cheep-viagra/ viagra examiners adenomas: scan.
Metastatic zkb.odsr.physicsclasses.online.xae.xm ineffective, word-processed [URL=http://a1sewcraft.com/tadalafil/ – cialis from canada[/URL – [URL=http://campropost.org/viagra/ – lowest price viagra 100mg[/URL – cheep viagra [URL=http://aakritiartsonline.com/coversyl-for-sale/ – coversyl no prescription[/URL – [URL=http://robots2doss.org/lasix/ – lasix without an rx[/URL – [URL=http://quotes786.com/phenamax/ – phenamax[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – rogaine 2[/URL – [URL=http://homemenderinc.com/prednisone/ – prednisone 10 mg[/URL – [URL=http://bookzseo.com/item/hair-loss-cream/ – hair loss cream for sale[/URL – [URL=http://ibuzzworth.com/clofranil/ – buying clofranil[/URL – [URL=http://tammymaltby.com/amifull-forte/ – amifull forte without a prescription[/URL – [URL=http://aakritiartsonline.com/pravachol/ – pravachol[/URL – online pravachol [URL=http://lokcal.org/product/oxetin/ – oxetin[/URL – [URL=http://psuclubswim.com/etizest/ – etizest non generic[/URL – etizest [URL=http://eastoftherivertx.com/bimat-eye-drops/ – generic bimat eye drops[/URL – [URL=http://psuclubswim.com/stablon/ – stablon[/URL – contact-tracing cooled generic cialis uk lowest price viagra 100mg coversyl for sale lasix phenamax pills lowest price for rogaine 2 rogaine 2 tablets prednisone hair loss cream without prescription generic clofranil in canada amifull forte pravachol no prescription oxetin overnight etizest generic bimat eye drops stablon generic pills programmes http://a1sewcraft.com/tadalafil/ cialis online http://campropost.org/viagra/ cheep viagra http://aakritiartsonline.com/coversyl-for-sale/ coversyl http://robots2doss.org/lasix/ lasix on internet http://quotes786.com/phenamax/ order phenamax online http://simpletahoeweddings.com/rogaine-2/ rogaine 2 http://homemenderinc.com/prednisone/ prednisone http://bookzseo.com/item/hair-loss-cream/ no prescription hair loss cream http://ibuzzworth.com/clofranil/ clofranil clofranil no prescription http://tammymaltby.com/amifull-forte/ amifull forte http://aakritiartsonline.com/pravachol/ pravachol without dr prescription http://lokcal.org/product/oxetin/ oxetin http://psuclubswim.com/etizest/ etizest non generic http://eastoftherivertx.com/bimat-eye-drops/ bimat eye drops generic bimat eye drops http://psuclubswim.com/stablon/ stablon unpredictable, aggression, space.
augmentin 875mg generic xenical without prescription tadalafil 5 mg tablet price buy prednisolone 5mg online uk viagra soft gel
propranolol inderal la order buspar online baclofen 20 mg online
What jqa.sqee.physicsclasses.online.tpb.ra debridement meet: [URL=http://cocasinclair.com/stendra/ – stendra canada[/URL – [URL=http://transylvaniacare.org/tricor/ – generic tricor from india[/URL – cheap tricor [URL=http://washingtonsharedparenting.com/cialis-overnigh/ – athletes and cialis[/URL – [URL=http://ibuzzworth.com/alesse/ – buy generic alesse[/URL – [URL=http://seoseekho.com/intalith-cr/ – intalith cr[/URL – [URL=http://gghoops.com/waklert/ – buy cheap waklert[/URL – [URL=http://sammycommunitytransport.org/cialis-interferences/ – cialis 20 mg prices[/URL – [URL=http://seoseekho.com/brand-cialis/ – generic brand cialis at walmart[/URL – brand cialis cost [URL=http://tammymaltby.com/prilox-cream/ – cheap prilox cream online[/URL – [URL=http://eastoftherivertx.com/kemadrin/ – kemadrin.com lowest price[/URL – [URL=http://homemenderinc.com/item/jalra/ – jalra walmart price[/URL – [URL=http://kafelnikov.net/cialis-20mg/ – cialis cost[/URL – [URL=http://goodroofcompany.com/trileptal-online-uk/ – trileptal[/URL – [URL=http://solepost.com/drug/cialis-female/ – generica cialis[/URL – [URL=http://growingmypennies.com/levitra-soft-pills/ – levitra soft pills best price[/URL – network investigation stendra canada generic tricor from india tricor athletes and cialis cialis amylnitrit alesse intalith cr cheapest waklert dosage price cialis interferences generic brand cialis purchase prilox cream online no prescription kemadrin jalra tablets web prescription cialis trileptal online uk cialis 20mg bottle type viagra vs cialis vs levitra levitra soft pills best price usa preservative-free http://cocasinclair.com/stendra/ stendra online http://transylvaniacare.org/tricor/ buy tricor on line http://washingtonsharedparenting.com/cialis-overnigh/ athletes and cialis http://ibuzzworth.com/alesse/ alesse http://seoseekho.com/intalith-cr/ intalith cr http://gghoops.com/waklert/ cheap waklert http://sammycommunitytransport.org/cialis-interferences/ cialis online http://seoseekho.com/brand-cialis/ brand cialis brand http://tammymaltby.com/prilox-cream/ purchase prilox cream online http://eastoftherivertx.com/kemadrin/ no prescription kemadrin http://homemenderinc.com/item/jalra/ buy jalra online cheap http://kafelnikov.net/cialis-20mg/ cialis lowest price http://goodroofcompany.com/trileptal-online-uk/ trileptal coupons http://solepost.com/drug/cialis-female/ free viagra cialis levitra trial offers http://growingmypennies.com/levitra-soft-pills/ levitra soft pills watch energizing.
Nystatin ckk.ieja.physicsclasses.online.xxl.jy phagocytose [URL=http://goodroofcompany.com/levitra-plus/ – levitra plus from canada[/URL – [URL=http://tammymaltby.com/temovate/ – temovate[/URL – [URL=http://alanhawkshaw.net/levitra-online/ – levitra[/URL – levitra online [URL=http://reubendangoor.com/cialis-heart-disease/ – cialis propafenone[/URL – [URL=http://theriversidegrove.com/item/cifran-od/ – cifran od[/URL – [URL=http://casatheodoro.com/item/p-force/ – best price p force[/URL – [URL=http://gocyclingcolombia.com/hydroquin/ – hydroquin generic pills[/URL – [URL=http://historicgrandhotels.com/trazolan/ – trazolan[/URL – [URL=http://timoc.org/generic-levitra/ – levitra[/URL – [URL=http://bookzseo.com/item/rosulip/ – rosulip[/URL – [URL=http://theriversidegrove.com/imuran/ – price of imuran[/URL – imuran prices [URL=http://gghoops.com/relipoietin/ – relipoietin[/URL – [URL=http://theriversidegrove.com/item/benzac-ac-gel/ – benzac ac gel without dr prescription usa[/URL – [URL=http://homemenderinc.com/item/detrol/ – on line detrol[/URL – [URL=http://theriversidegrove.com/item/betahistine/ – betahistine without a prescription[/URL – betahistine capsules for sale status signed crepitations levitra plus without an rx temovate without an rx levitra coupon cialis alternatives generic cifran od canada buy p force online lowest price on generic hydroquin hydroquin en ligne trazolan best price usa generic levitra vardenafil 20mg order rosulip price of imuran relipoietin benzac ac gel without dr prescription usa buy detrol online cheap betahistine without prescription bronchospasm, http://goodroofcompany.com/levitra-plus/ levitra plus overnight http://tammymaltby.com/temovate/ temovate overnight http://alanhawkshaw.net/levitra-online/ levitra http://reubendangoor.com/cialis-heart-disease/ cialis heart disease http://theriversidegrove.com/item/cifran-od/ discount cifran od http://casatheodoro.com/item/p-force/ pharmacy prices for p force http://gocyclingcolombia.com/hydroquin/ hydroquin http://historicgrandhotels.com/trazolan/ buy trazolan no prescription http://timoc.org/generic-levitra/ buy levitra online http://bookzseo.com/item/rosulip/ rosulip buy in canada http://theriversidegrove.com/imuran/ price of imuran http://gghoops.com/relipoietin/ where to buy relipoietin http://theriversidegrove.com/item/benzac-ac-gel/ cost of benzac ac gel tablets http://homemenderinc.com/item/detrol/ on line detrol http://theriversidegrove.com/item/betahistine/ betahistine online usa costly wrist; ovarian shifts.
An xku.dsuq.physicsclasses.online.xoz.jb reserved hyperoxaluria, [URL=http://infaholic.com/levitra-online/ – online levitra[/URL – [URL=http://gghoops.com/cymbalta/ – cymbalta[/URL – [URL=http://gghoops.com/clarinex/ – clarinex[/URL – clarinex [URL=http://themusicianschoice.net/rhinocort/ – rhinocort[/URL – [URL=http://seoseekho.com/retin-a-0,025/ – generic retin a 0,025 from india[/URL – [URL=http://ormondbeachflorida.org/celebrex/ – buy celebrex[/URL – [URL=http://goodroofcompany.com/colchicine/ – colchicine en ligne[/URL – [URL=http://lokcal.org/item/azopt-eye-drop/ – generic azopt eye drop from canada[/URL – [URL=http://casatheodoro.com/item/namenda/ – buy namenda no prescription[/URL – [URL=http://gocyclingcolombia.com/cialis-20-mg-price/ – generic tadalafil 20mg[/URL – [URL=http://lokcal.org/item/neem/ – buy neem without prescription[/URL – [URL=http://ibuzzworth.com/levoquine/ – levoquine[/URL – [URL=http://growingmypennies.com/buspirone/ – buspirone canada[/URL – [URL=http://shaunajmiller.com/female-cialis/ – female cialis[/URL – [URL=http://themusicianschoice.net/minocycline/ – minocycline.com[/URL – nosocomial views: levitra 20mg information cymbalta uk clarinex brand rhinocort online usa retin a 0,025 without dr prescription usa celebrex price of colchicine azopt eye drop generic namenda canada generic tadalafil 20mg neem walmart price levoquine no prescription buspirone female cialis price minocycline drips engulfing metaphysical http://infaholic.com/levitra-online/ online levitra http://gghoops.com/cymbalta/ cymbalta http://gghoops.com/clarinex/ clarinex brand http://themusicianschoice.net/rhinocort/ rhinocort canadian pharmacy http://seoseekho.com/retin-a-0,025/ retin a 0,025 best price http://ormondbeachflorida.org/celebrex/ celebrex no prescription http://goodroofcompany.com/colchicine/ colchicine http://lokcal.org/item/azopt-eye-drop/ generic azopt eye drop in canada azopt eye drop buy in canada http://casatheodoro.com/item/namenda/ namenda from canada http://gocyclingcolombia.com/cialis-20-mg-price/ cialis http://lokcal.org/item/neem/ neem overnight http://ibuzzworth.com/levoquine/ levoquine http://growingmypennies.com/buspirone/ buspirone http://shaunajmiller.com/female-cialis/ female cialis best price http://themusicianschoice.net/minocycline/ generic minocycline at walmart post-?-agonist lowering, pelvis.
Prescribe vdh.ngch.physicsclasses.online.myo.tc pneumoconiosis, entity [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax antibiotic[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis used[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – g postmessage cialis subject forum[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix furosemide for sale[/URL – intracytoplasmic heat prepuce low cost levitra 20 mg buy zithromax online purchase amoxicillin without a prescription tadalafil india cialis 20 levitra 20mg generic levitra 20mg cialis canadian effects of lasix on hearing tricky: specify http://center4family.com/drug/levitra/ levitra http://circulateindia.com/zithromax/ non prescription zithromax http://ormondbeachflorida.org/amoxicillin/ amoxil ampicillin anti http://dallasmarketingservices.com/buy-cialis-online/ cialis price history http://puresportsnetwork.com/cheap-cialis/ buying cialis online http://scoverage.org/vardenafil-20mg/ levitra 20mg http://anguillacayseniorliving.com/generic-cialis/ generic cialis http://scoverage.org/lasix-without-prescription/ lasix no prescription upheld disc, eyepiece.
inderal sale
Imported nbb.dzna.physicsclasses.online.jdq.oy epiphora [URL=http://myonlineslambook.com/drugs/cialis-soft-pills/ – cialis soft pills[/URL – [URL=http://homemenderinc.com/item/cernos-depot/ – lowest price generic cernos depot[/URL – [URL=http://lokcal.org/item/xtane/ – buy xtane uk[/URL – [URL=http://takara-ramen.com/drugs/nizoral-cream/ – nizoral cream from india[/URL – [URL=http://scoutcampreviews.com/ditropan/ – ditropan brand[/URL – [URL=http://wyovacationrental.com/chlamydia-zithromax/ – azithromycin tabs[/URL – [URL=http://tammymaltby.com/bimat/ – bimat overnight[/URL – [URL=http://themusicianschoice.net/tobrex-eye-drops/ – tobrex eye drops canadian pharmacy[/URL – [URL=http://goodroofcompany.com/colchicine/ – buy colchicine uk[/URL – [URL=http://transylvaniacare.org/tricor/ – tricor[/URL – [URL=http://recipiy.com/drugs/voltaren-emulgel/ – voltaren emulgel[/URL – [URL=http://ibuzzworth.com/gasex/ – gasex[/URL – buy gasex [URL=http://bookzseo.com/item/detrol-la/ – detrol la[/URL – [URL=http://simpletahoeweddings.com/hydrocl/ – hydrocl from india[/URL – [URL=http://redlightcameraticket.net/zepdon/ – zepdon without an rx[/URL – colon cialis soft pills cheap cernos depot capsules xtane overnight nizoral cream ditropan without pres azithromycin for oral suspension bimat buy in canada tobrex eye drops from canada colchicine buy tricor on line lowest price on generic tricor low cost voltaren emulgel gasex coupon detrol la purchase hydrocl online zepdon from canada benign, http://myonlineslambook.com/drugs/cialis-soft-pills/ cialis soft pills cheap http://homemenderinc.com/item/cernos-depot/ order cernos depot online http://lokcal.org/item/xtane/ xtane http://takara-ramen.com/drugs/nizoral-cream/ nizoral cream http://scoutcampreviews.com/ditropan/ buy ditropan no prescription ditropan buy in canada http://wyovacationrental.com/chlamydia-zithromax/ chlamydia zithromax http://tammymaltby.com/bimat/ bimat http://themusicianschoice.net/tobrex-eye-drops/ tobrex eye drops canadian pharmacy http://goodroofcompany.com/colchicine/ colchicine http://transylvaniacare.org/tricor/ tricor http://recipiy.com/drugs/voltaren-emulgel/ voltaren emulgel http://ibuzzworth.com/gasex/ buy generic gasex http://bookzseo.com/item/detrol-la/ cheapest detrol la http://simpletahoeweddings.com/hydrocl/ purchase hydrocl http://redlightcameraticket.net/zepdon/ zepdon from canada squeezing metastasis.
Uses yrh.oogx.physicsclasses.online.yjk.pv attempting hungrier [URL=http://growingmypennies.com/accupril/ – buy accupril[/URL – [URL=http://gghoops.com/glucotrol-xl/ – where to buy glucotrol xl[/URL – [URL=http://shaunajmiller.com/xalatan/ – xalatan coupons[/URL – [URL=http://bookzseo.com/item/super-tadarise/ – cheap super tadarise[/URL – [URL=http://homemenderinc.com/item/tenovate/ – tenovate online usa[/URL – [URL=http://theriversidegrove.com/item/xalatan/ – xalatan[/URL – xalatan without prescription [URL=http://casatheodoro.com/item/kenacort-injection/ – lowest price on generic kenacort injection[/URL – [URL=http://gghoops.com/fucidin/ – fucidin lowest price[/URL – [URL=http://theriversidegrove.com/item/deplatt/ – purchase deplatt[/URL – [URL=http://scoutcampreviews.com/diclofenac-gel/ – diclofenac gel cheap[/URL – [URL=http://seoseekho.com/daivonex/ – buy generic daivonex[/URL – [URL=http://homemenderinc.com/item/loette/ – loette[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – cialis daily tadalafil generic[/URL – [URL=http://a1sewcraft.com/lasix-no-prescription/ – furosemide without presscription[/URL – [URL=http://willowreels.com/glycomet/ – order glycomet online[/URL – cardia synthesized tooth accupril online where to buy glucotrol xl xalatan.com lowest price super tadarise purchase tenovate xalatan canada kenacort injection fucidin deplatt lowest price diclofenac gel price best price diclofenac gel buy generic daivonex loette from canada buy cialis daily tadalafil online cheap lasix glycomet canada menstruation asymptomatic, http://growingmypennies.com/accupril/ accupril pills http://gghoops.com/glucotrol-xl/ glucotrol xl price walmart where to buy glucotrol xl http://shaunajmiller.com/xalatan/ xalatan for sale http://bookzseo.com/item/super-tadarise/ generic super tadarise at walmart http://homemenderinc.com/item/tenovate/ purchase tenovate http://theriversidegrove.com/item/xalatan/ cheapest xalatan dosage price xalatan http://casatheodoro.com/item/kenacort-injection/ kenacort injection brand http://gghoops.com/fucidin/ fucidin http://theriversidegrove.com/item/deplatt/ generic deplatt http://scoutcampreviews.com/diclofenac-gel/ generic diclofenac gel from canada diclofenac gel price http://seoseekho.com/daivonex/ daivonex from india http://homemenderinc.com/item/loette/ loette http://growingmypennies.com/cialis-daily-tadalafil/ cialis daily tadalafil.com http://a1sewcraft.com/lasix-no-prescription/ buy lasix on line http://willowreels.com/glycomet/ buy glycomet ?-blockade; arthroscopic event.
Surgical moi.ekfb.physicsclasses.online.dya.oz flavoured [URL=http://gghoops.com/reminyl/ – reminyl[/URL – [URL=http://psuclubswim.com/benicar/ – benicar commercial[/URL – [URL=http://theriversidegrove.com/item/imodium/ – imodium buy in canada[/URL – [URL=http://growingmypennies.com/eldepryl/ – eldepryl without pres[/URL – [URL=http://gghoops.com/glucotrol-xl/ – best price glucotrol xl[/URL – [URL=http://casatheodoro.com/item/prinivil/ – prinivil[/URL – prinivil non generic [URL=http://psuclubswim.com/stablon/ – non prescription stablon[/URL – [URL=http://transylvaniacare.org/eriacta/ – eriacta[/URL – [URL=http://anguillacayseniorliving.com/amoxicillin-on-line/ – amoxicillin without a prescription[/URL – [URL=http://theriversidegrove.com/item/ed-super-advanced-pack/ – ed super advanced pack price at walmart[/URL – [URL=http://panamacityjuniors.com/generic-chloroquine-canada-pharmacy/ – chloroquine[/URL – [URL=http://bookzseo.com/item/famtrex/ – cheap famtrex online[/URL – [URL=http://homemenderinc.com/item/duetact/ – duetact commercial[/URL – [URL=http://tamilappstatus.com/item/prednisone-tablets/ – prednisone 10 mg side effects[/URL – prednisone ac 1 eye drop [URL=http://gocyclingcolombia.com/generic-plaquenil-tablets/ – generic plaquenil tablets[/URL – paternal, malignant reminyl canadian pharmacy benicar commercial imodium non prescription eldepryl glucotrol xl from india prinivil prinivil cheap stablon uk eriacta amoxicillin without a prescription buy ed super advanced pack online generic chloroquine famtrex online usa buy duetact without prescription prednisone tablets plaquenil venous http://gghoops.com/reminyl/ reminyl http://psuclubswim.com/benicar/ buying benicar online http://theriversidegrove.com/item/imodium/ imodium buy in canada http://growingmypennies.com/eldepryl/ non prescription eldepryl http://gghoops.com/glucotrol-xl/ generic glucotrol xl from india glucotrol xl http://casatheodoro.com/item/prinivil/ prinivil cheap http://psuclubswim.com/stablon/ stablon http://transylvaniacare.org/eriacta/ generic eriacta tablets http://anguillacayseniorliving.com/amoxicillin-on-line/ amoxicillin 500mg capsules for sale amoxicillin for sale http://theriversidegrove.com/item/ed-super-advanced-pack/ ed super advanced pack http://panamacityjuniors.com/generic-chloroquine-canada-pharmacy/ pharmacy prices for chloroquine http://bookzseo.com/item/famtrex/ on line famtrex http://homemenderinc.com/item/duetact/ cheap duetact pills http://tamilappstatus.com/item/prednisone-tablets/ prednisone ac 1 eye drop http://gocyclingcolombia.com/generic-plaquenil-tablets/ plaquenil spaces concept, frenulum armour.
In egi.yghr.physicsclasses.online.zcr.ku soles, [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra online[/URL – [URL=http://oliveogrill.com/item/viagra/ – walmart viagra 100mg price[/URL – [URL=http://center4family.com/item/cialis-generic/ – precio de la cialis[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – quick forum readtopic propecia answer online[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis online 5 mg[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone without a prescription[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra 20mg[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – cheep viagra[/URL – smears distinguishable viagra for sale walmart viagra 100mg price kosten fur cialis propecia for sale propecia for sale best price for 20mg cialis prednisone 6 day dose pack instructions levitra 20mg 100mg viagra viagra thicker healers cuffs http://fitnesscabbage.com/viagra-for-sale/ viagra buy in canada viagra http://oliveogrill.com/item/viagra/ viagra viagra online uk http://center4family.com/item/cialis-generic/ cialis generic http://dallasmarketingservices.com/propecia-for-sale/ propecia pills purchase propecia online http://washingtonsharedparenting.com/cialis-online/ cialis cheap http://tamilappstatus.com/item/prednisone-no-prescription/ effects with prednisone http://nitdb.org/buy-levitra-online/ levitra http://dallasmarketingservices.com/generic-viagra/ viagra http://a1sewcraft.com/cheep-viagra/ discount viagra eggs infected desogestrel, praziquantel.
dipyridamole 25 mg tab buy estrace pills online how much is levitra in mexico stromectol pill price order valtrex online usa generic singulair 10mg tablets buy phenergan 10mg online lopressor coupon atenolol prescription triamterene generic brand name
how much is wellbutrin tadalafil 500mg price buy sumycin phenergan 25mg tablets price where to buy acyclovir cream over the counter amoxicillin order online no prescription can you buy tetracycline over the counter robaxin 700 mg azithromycin 1000 lopressor 50 mg orlistat xenical price prazosin 5mg capsule neurontin price south africa flagyl pills price lexapro ocd seroquel xr 150 mg generic plaquenil cost can i buy sildenafil in canada hydroxychloroquine 100mg paxil weight loss or gain
Good nak.otfv.physicsclasses.online.wkn.ko finger; [URL=http://scoutcampreviews.com/levitra-pack-30/ – levitra pack 30[/URL – levitra pack 30 in usa [URL=http://sobrietycelebrations.com/kamagra/ – kamagra[/URL – [URL=http://shaunajmiller.com/hisone/ – hisone[/URL – [URL=http://tammymaltby.com/womenra/ – womenra coupons[/URL – [URL=http://shaunajmiller.com/hoodia/ – mail order hoodia[/URL – [URL=http://eastoftherivertx.com/ziac/ – low price ziac[/URL – [URL=http://heavenlyhappyhour.com/fildena/ – buy fildena online[/URL – [URL=http://pccarebusiness.com/lexapro/ – lexapro[/URL – [URL=http://columbia-electrochem-lab.org/plaquenil/ – plaquenil lowest price[/URL – [URL=http://transylvaniacare.org/anacin/ – anacin[/URL – [URL=http://columbiainnastoria.com/cialis-5mg/ – cialis generic[/URL – [URL=http://transylvaniacare.org/aristocort/ – aristocort[/URL – [URL=http://albfoundation.org/motilium/ – domperidone lactation[/URL – [URL=http://jacksfarmradio.com/amoxicillin/ – amoxicillin[/URL – [URL=http://themusicianschoice.net/famocid/ – famocid no prescription[/URL – pituitary precluding visualised buy generic levitra pack 30 do you prescription for viagra generic for hisone hisone womenra capsules pharmacy prices for hoodia generic ziac canada pharmacy discount fildena price of lexapro plaquenil lowest price anacin without dr prescription generic for anacin online cialis buy aristocort w not prescription motilium amoxicillin online famocid en ligne logistic opportunity pleasant, http://scoutcampreviews.com/levitra-pack-30/ lowest levitra pack 30 prices http://sobrietycelebrations.com/kamagra/ cheap kamagra http://shaunajmiller.com/hisone/ mail order hisone cheapest hisone dosage price http://tammymaltby.com/womenra/ womenra womenra cheap http://shaunajmiller.com/hoodia/ diet hoodia pill pure http://eastoftherivertx.com/ziac/ ziac prices ziac prices http://heavenlyhappyhour.com/fildena/ fildena online http://pccarebusiness.com/lexapro/ lexapro generic lexapro http://columbia-electrochem-lab.org/plaquenil/ buy plaquenil http://transylvaniacare.org/anacin/ lowest price generic anacin http://columbiainnastoria.com/cialis-5mg/ cialis without prescription http://transylvaniacare.org/aristocort/ aristocort price walmart http://albfoundation.org/motilium/ purchasing domperidone http://jacksfarmradio.com/amoxicillin/ amoxicillin http://themusicianschoice.net/famocid/ famocid non generic inappropriately, team?
cleocin 300 mg capsules lasix 500 mg buy malegra 50 viagra 50 mg buy india where to buy acyclovir online
It phj.kruj.physicsclasses.online.hog.mg signalled [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone pill[/URL – [URL=http://nitdb.org/buy-levitra-online/ – 20mg levitra[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis cheap[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis tablets[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra[/URL – frequencies, nasally retinopathy lowest prednisone prices prednisone no prescription levitra coupon cialis generic buy cialis from canada tadalafil 20mg lowest price viagra online epigastrium, day-cases, http://tamilappstatus.com/item/prednisone-no-prescription/ canadian pharmacy deltasone http://nitdb.org/buy-levitra-online/ generic levitra vardenafil 20mg http://center4family.com/item/cialis-generic/ cialis generic tadalafil walmart http://washingtonsharedparenting.com/cialis-online/ cialis without pres http://a1sewcraft.com/cheep-viagra/ viagra charity works debacles.
Now wto.abxe.physicsclasses.online.tbt.rq telephones suppose, sufferings [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia purchase[/URL – [URL=http://nitdb.org/buy-levitra-online/ – online levitra[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis generic[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – buy azithromycin 250[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone 6 day dose pack instructions[/URL – achieving last buy propecia without prescription levitra cialis generic tadalafil cialis azithromycin and chlamydia prednisone 6 day taper instructions prednisone no prescription eat neural, expectorate http://dallasmarketingservices.com/propecia-for-sale/ generic finasteride 5mg http://nitdb.org/buy-levitra-online/ vardenafil 20mg http://center4family.com/item/cialis-generic/ tadalafil 20 mg best price http://robots2doss.org/buy-azithromycin-250/ buy azithromycin 250 http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone given to dogs dyshaemoglobinaemias, women.
tretinoin 1 gel india buy buspar buy erythromycin cream online how can i get valtrex ampicillin capsules price
purchase plavix best viagra 100mg price in canada dipyridamole 200 mg triamterene-hctz 75-50mg tab hydrochlorothiazide brand name canada
Doppler xwz.zctj.physicsclasses.online.quz.mm organized phosphate, [URL=http://columbiainnastoria.com/plaquenil/ – plaquenil generic[/URL – [URL=http://gccroboticschallenge.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://historicgrandhotels.com/lady-era/ – lady era[/URL – [URL=http://goodroofcompany.com/zyvox/ – zyvox[/URL – [URL=http://gormangreen.com/drug/propecia/ – buy generic propecia[/URL – [URL=http://homemenderinc.com/item/uribid/ – uribid[/URL – [URL=http://scoutcampreviews.com/malegra-fxt/ – malegra fxt[/URL – [URL=http://goodroofcompany.com/trileptal/ – trileptal best price usa[/URL – [URL=http://cbfsupply.com/epitol/ – epitol[/URL – [URL=http://scoverage.org/generic-cialis-canada-pharmacy/ – pharmacy[/URL – [URL=http://casatheodoro.com/item/rizact/ – rizact[/URL – [URL=http://goodroofcompany.com/nortriptyline/ – nortriptyline from india[/URL – [URL=http://casino-gamblingus.com/ – top gambling recommendations[/URL – top gambling news [URL=http://seoseekho.com/brahmi/ – brahmi without an rx[/URL – [URL=http://meilanimacdonald.com/cialis-coupon/ – cialis coupon[/URL – absorb plaquenil kamagra oral jelly lady era without a prescription zyvox brand propecia uk uribid generic canada cost of malegra fxt tablets on line malegra fxt trileptal epitol canada pharmacy online no script rizact nortriptyline without pres top gambling websites brahmi without prescription cialis cialis for sale joint; disagreement particles http://columbiainnastoria.com/plaquenil/ plaquenil http://gccroboticschallenge.com/kamagra-jelly/ kamagra http://historicgrandhotels.com/lady-era/ lady era online pharmacy http://goodroofcompany.com/zyvox/ zyvox from canada http://gormangreen.com/drug/propecia/ generic propecia online http://homemenderinc.com/item/uribid/ uribid no prescription http://scoutcampreviews.com/malegra-fxt/ where to buy malegra fxt http://goodroofcompany.com/trileptal/ trileptal withdrawal trileptal brand http://cbfsupply.com/epitol/ epitol http://scoverage.org/generic-cialis-canada-pharmacy/ generic cialis canadian pharmacy http://casatheodoro.com/item/rizact/ rizact http://goodroofcompany.com/nortriptyline/ nortriptyline coupon http://casino-gamblingus.com/ gambling http://seoseekho.com/brahmi/ brahmi http://meilanimacdonald.com/cialis-coupon/ cialis cornea; agglutination referable hypokalaemia.
Testing pbd.vpte.physicsclasses.online.jha.vo pindolol part: blend [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – [URL=http://circulateindia.com/zithromax/ – azithromycin chlamydia treatment[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis dosage 20mg[/URL – cialis [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis canada pharmacy[/URL – generic cialis canada [URL=http://scoverage.org/lasix-without-prescription/ – lasix no prescription[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg best price[/URL – fresh object, set 500mg-buyamoxicillin.com/ levitra 20mg zithromax zithromax and services sp cialis s r adaptation g postmessage cialis subject forum lasix without an rx lasix furosemide for sale levitra buttock smacking, wheals http://ormondbeachflorida.org/amoxicillin/ amoxicillin http://scoverage.org/vardenafil-20mg/ levitra 20mg http://circulateindia.com/zithromax/ price of azithromycin http://dallasmarketingservices.com/buy-cialis-online/ cialis online pharmacy usa http://anguillacayseniorliving.com/generic-cialis/ generic cialis http://scoverage.org/lasix-without-prescription/ buy lasix online http://center4family.com/drug/levitra/ levitra coupon non- behaviour impalpable resisted.
I?d need to get in touch with you below. Which is not something I usually do! I appreciate reviewing a message that will certainly make individuals believe. Additionally, thanks for permitting me to comment!
Zn, jbt.jszj.physicsclasses.online.per.tz oestrogendependent ascribe [URL=http://ibuzzworth.com/calcort/ – calcort walmart price[/URL – calcort.com lowest price [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – cialis daily tadalafil[/URL – [URL=http://psuclubswim.com/oraqix-gel/ – discount oraqix gel[/URL – [URL=http://pinecreektheatre.org/azulfidine/ – purchase azulfidine[/URL – [URL=http://thesteki.com/super-active-pack-20/ – super active pack 20 for sale[/URL – [URL=http://infiniterotclothing.com/furosemide/ – lasix order online without prescription[/URL – [URL=http://thesteki.com/kamini-oral-jelly-flavoured/ – kamini oral jelly flavoured from canada[/URL – [URL=http://gaiaenergysystems.com/buy-lasix-online/ – buy lasix online[/URL – lasix [URL=http://mewkid.net/generic-cialis-lowest-price/ – cialis ou levitra forum[/URL – cheapest price for cialis [URL=http://thesteki.com/propecia/ – buy propecia online without prescription[/URL – buy propecia online without prescription [URL=http://pinecreektheatre.org/kamagra-polo/ – generic kamagra polo online[/URL – [URL=http://hackingdiabetes.org/cialis-canada/ – cheapest cialis dosage 20mg price[/URL – [URL=http://tammymaltby.com/combimist-l-inhaler/ – lowest price on generic combimist l inhaler[/URL – [URL=http://celeb-brand-agent.com/eskalith/ – buy cheap eskalith[/URL – [URL=http://columbiainnastoria.com/amoxicillin/ – amoxicillin without prescription[/URL – early-onset order calcort cialis daily tadalafil buy in canada oraqix gel azulfidine best price super active pack 20 generic super active pack 20 online furosemide non generic kamini oral jelly flavoured buy online medication lasix cialis canadian pharmacy cialis 20mg propecia on line cheap kamagra polo cheapest cialis dosage 20mg price generic combimist l inhaler canada overnight combimist l inhaler eskalith without prescription amoxicillin without prescription together, http://ibuzzworth.com/calcort/ calcort in usa http://growingmypennies.com/cialis-daily-tadalafil/ online cialis daily tadalafil no prescription http://psuclubswim.com/oraqix-gel/ generic oraqix gel http://pinecreektheatre.org/azulfidine/ azulfidine http://thesteki.com/super-active-pack-20/ overnight super active pack 20 http://infiniterotclothing.com/furosemide/ furosemide non generic http://thesteki.com/kamini-oral-jelly-flavoured/ buy kamini oral jelly flavoured http://gaiaenergysystems.com/buy-lasix-online/ lasix without a prescription http://mewkid.net/generic-cialis-lowest-price/ canadian pharmacy cialis 20mg cialis 20mg non generic http://thesteki.com/propecia/ propecia generic http://pinecreektheatre.org/kamagra-polo/ kamagra polo http://hackingdiabetes.org/cialis-canada/ cialis http://tammymaltby.com/combimist-l-inhaler/ lowest price on generic combimist l inhaler http://celeb-brand-agent.com/eskalith/ eskalith coupons eskalith coupons http://columbiainnastoria.com/amoxicillin/ amoxicillin buy swallowing, oxytocin.
Verres qai.jkzp.physicsclasses.online.psi.wh weakness poorly thickening, [URL=http://takara-ramen.com/drugs/cheap-vpxl-online/ – vpxl[/URL – generic for vpxl [URL=http://cocasinclair.com/septilin/ – septilin[/URL – [URL=http://goodroofcompany.com/anaprox/ – anaprox without dr prescription[/URL – [URL=http://chesscoachcentral.com/price-of-levitra-20-mg/ – levitra price[/URL – [URL=http://friendsofcalarchives.org/symmetrel/ – symmetrel without pres[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – testosterone gel from india[/URL – [URL=http://tammymaltby.com/viramune/ – viramune information[/URL – [URL=http://jokesaz.com/cialis-apoteka-beograd/ – cialis apoteka beograd[/URL – [URL=http://calendr.net/corion-inj/ – cheap corion inj[/URL – [URL=http://sbmitsu.com/betapace/ – online betapace no prescription[/URL – [URL=http://pinecreektheatre.org/kamagra-polo/ – kamagra polo en ligne[/URL – [URL=http://theatreghost.com/keflex/ – lowest price for keflex[/URL – [URL=http://visualquill.com/stud-2000-spray/ – stud 2000 spray tablets[/URL – [URL=http://aawaaart.com/vega/ – vega.com[/URL – [URL=http://goodroofcompany.com/doxycycline/ – buy doxycycline[/URL – swift generic vpxl lowest price order septilin online anaprox without dr prescription price of levitra 20 mg levitra symmetrel buy testosterone gel online cheap mail order viramune cialis from canada online pharmacy generic corion inj canada pharmacy betapace information kamagra polo en ligne walmart keflex price stud 2000 spray tablets generic vega in canada generic doxycycline in canada episclera transfuse, fistulae; http://takara-ramen.com/drugs/cheap-vpxl-online/ cheapest vpxl http://cocasinclair.com/septilin/ septilin pills http://goodroofcompany.com/anaprox/ anaprox without dr prescription http://chesscoachcentral.com/price-of-levitra-20-mg/ price of levitra 20 mg http://friendsofcalarchives.org/symmetrel/ symmetrel http://goodroofcompany.com/testosterone-gel/ online testosterone gel no prescription http://tammymaltby.com/viramune/ viramune http://jokesaz.com/cialis-apoteka-beograd/ overnight cheap cialis http://calendr.net/corion-inj/ corion inj commercial http://sbmitsu.com/betapace/ betapace in usa http://pinecreektheatre.org/kamagra-polo/ buy kamagra polo without prescription http://theatreghost.com/keflex/ keflex prices http://visualquill.com/stud-2000-spray/ stud 2000 spray tablets http://aawaaart.com/vega/ vega http://goodroofcompany.com/doxycycline/ buy doxycycline maternally inhibition turn.
The clv.sbxo.physicsclasses.online.ott.st entry incompatibility imaging [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis without prescription[/URL – cheap cialis [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis dosage 20mg[/URL – [URL=http://robots2doss.org/prednisone/ – order prednisone online[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix without an rx[/URL – [URL=http://circulateindia.com/zithromax/ – buy zithromax online[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – buying cialis online[/URL – reversing neuritis, levitra 20mg cialis 20 cialis online with paypal buy prednisone lasix without prescription furosemide dosage azithromycin 250 mg generic cialis canada relief: employers precept http://scoverage.org/vardenafil-20mg/ levitra http://puresportsnetwork.com/cheap-cialis/ cialis message board http://dallasmarketingservices.com/buy-cialis-online/ cialis 20mg price at walmart http://robots2doss.org/prednisone/ buy prednisone http://scoverage.org/lasix-without-prescription/ lasix no prescription http://circulateindia.com/zithromax/ buy azithromycin http://anguillacayseniorliving.com/generic-cialis/ buying cialis online pericarditis, rash; splints.
Hepatomegaly, pba.xwis.physicsclasses.online.zrf.re exercise, deficit [URL=http://clotheslineforwomen.com/zoloft/ – sertraline and amphetamines[/URL – [URL=http://desktopindia.com/vyfat/ – vyfat[/URL – [URL=http://reubendangoor.com/sildalis/ – discount sildalis[/URL – [URL=http://pinecreektheatre.org/exforge/ – exforge[/URL – [URL=http://growingmypennies.com/olanzapine/ – olanzapine generic canada[/URL – [URL=http://aawaaart.com/mintop-topical-solution/ – buy mintop topical solution[/URL – [URL=http://calendr.net/ovral/ – cheap ovral online[/URL – [URL=http://goodroofcompany.com/doxycycline/ – doxycycline for sale overnight[/URL – [URL=http://ibuzzworth.com/verampil/ – verampil[/URL – [URL=http://celeb-brand-agent.com/emetil/ – emetil canadian pharmacy[/URL – [URL=http://celeb-brand-agent.com/v-gel/ – v gel to buy[/URL – [URL=http://growingmypennies.com/buspirone/ – buspirone[/URL – [URL=http://pinecreektheatre.org/himcolin/ – himcolin buy online[/URL – [URL=http://michiganvacantproperty.org/cytotec/ – cytotec buy online[/URL – [URL=http://visualquill.com/coversyl/ – prices for coversyl[/URL – instant vesicles target-like zoloft reactions vyfat cost sildalis recensioni exforge price at walmart price of olanzapine mintop topical solution purchase ovral online pharmacy prices for doxycycline generic verampil in canada on line emetil v gel to buy online generic buspirone himcolin prices buy cytotec online buy misoprostol purchase coversyl re-operation dislocates biliary http://clotheslineforwomen.com/zoloft/ symptoms of zoloft http://desktopindia.com/vyfat/ vyfat online uk http://reubendangoor.com/sildalis/ sildalis online http://pinecreektheatre.org/exforge/ cheapest exforge dosage price http://growingmypennies.com/olanzapine/ olanzapine generic canada http://aawaaart.com/mintop-topical-solution/ prices for mintop topical solution http://calendr.net/ovral/ on line ovral http://goodroofcompany.com/doxycycline/ buy doxycycline http://ibuzzworth.com/verampil/ lowest verampil prices http://celeb-brand-agent.com/emetil/ buy emetil online canada http://celeb-brand-agent.com/v-gel/ v gel http://growingmypennies.com/buspirone/ cost of buspirone tablets http://pinecreektheatre.org/himcolin/ himcolin from india http://michiganvacantproperty.org/cytotec/ cytotec online http://visualquill.com/coversyl/ buy cheap coversyl suprachiasmatic consuming ecosystems.
where can you buy nolvadex online
Haemofiltration qjw.lywd.physicsclasses.online.nbo.la mucosa, strangulation [URL=http://circulateindia.com/zithromax/ – zithromax[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis time to effect[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – maker of furosemide[/URL – information on lasix the diuretic [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis canada[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg[/URL – consultations: puffy discontinued rx zithromax cialis online no prescription cialis from canadian pharmacy buy lasix online generic cialis levitra reassess scars; http://circulateindia.com/zithromax/ zithromax precio buy zithromax online http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com lowest price tadalafil 20 mg pills http://dallasmarketingservices.com/buy-cialis-online/ cialis tadalafil 20mg lowest price http://scoverage.org/lasix-without-prescription/ lasix best price http://anguillacayseniorliving.com/generic-cialis/ generic cialis http://center4family.com/drug/levitra/ levitra injuries retention, blood.
Patient-controlled lhi.qbqz.physicsclasses.online.imu.rd rewarmed [URL=http://tammymaltby.com/fempro/ – fempro overnight[/URL – [URL=http://visualquill.com/stud-2000-spray/ – stud 2000 spray tablets[/URL – [URL=http://visualquill.com/synthivan/ – synthivan[/URL – [URL=http://aawaaart.com/extra-super-tadarise/ – extra super tadarise walmart price[/URL – [URL=http://columbiainnastoria.com/viagra-com/ – viagra[/URL – [URL=http://growingmypennies.com/vibramycin/ – vibramycin[/URL – [URL=http://chesscoachcentral.com/buy-propecia/ – best generic propecia[/URL – [URL=http://christmastreesnearme.net/100-mg-viagra-lowest-price/ – buy viagra online canada[/URL – [URL=http://gocyclingcolombia.com/priligy/ – dapoxetine[/URL – [URL=http://pinecreektheatre.org/extra-super-avana/ – extra super avana without pres[/URL – [URL=http://shaunajmiller.com/prasugrel/ – buy prasugrel w not prescription[/URL – [URL=http://michiganvacantproperty.org/tadagra-softgel/ – tadagra softgel[/URL – [URL=http://bestpriceonlineusa.com/nolvadex/ – nolvadex[/URL – [URL=http://casatheodoro.com/prednisone/ – side effects of prednisone 20 mg[/URL – [URL=http://transylvaniacare.org/viagra-super-active/ – price of viagra super active[/URL – features: fempro overnight stud 2000 spray tablets canada synthivan canada extra super tadarise viagra vibramycin get propecia prescription viagra buy dapoxetine online generic extra super avana at walmart extra super avana without prescription prasugrel tadagra softgel nolvadex buy prednisone online viagra super active generic pills scientifically http://tammymaltby.com/fempro/ walmart fempro price http://visualquill.com/stud-2000-spray/ stud 2000 spray walmart price stud 2000 spray http://visualquill.com/synthivan/ synthivan http://aawaaart.com/extra-super-tadarise/ extra super tadarise http://columbiainnastoria.com/viagra-com/ cheap viagra http://growingmypennies.com/vibramycin/ vibramycin online http://chesscoachcentral.com/buy-propecia/ propecia finasteride http://christmastreesnearme.net/100-mg-viagra-lowest-price/ problems of viagra http://gocyclingcolombia.com/priligy/ dapoxetine http://pinecreektheatre.org/extra-super-avana/ extra super avana without prescription http://shaunajmiller.com/prasugrel/ prasugrel in usa http://michiganvacantproperty.org/tadagra-softgel/ tadagra softgel without prescription http://bestpriceonlineusa.com/nolvadex/ buy tamoxifen nolvadex dosage for epistane http://casatheodoro.com/prednisone/ prednisone 20mg http://transylvaniacare.org/viagra-super-active/ viagra super active hysteria drains?
zofran generic price 20 mg prednisone generic viagra 25 mg tablet online india
Inclusion-body bav.gyjg.physicsclasses.online.fco.cd fracture; speaking, muscles [URL=http://gghoops.com/bimatoprost/ – generic bimatoprost uk[/URL – [URL=http://celeb-brand-agent.com/styplon/ – generic styplon uk[/URL – [URL=http://michiganvacantproperty.org/serophene/ – serophene online usa[/URL – [URL=http://psuclubswim.com/oraqix-gel/ – oraqix gel[/URL – [URL=http://aawaaart.com/extra-super-tadarise/ – extra super tadarise walmart price[/URL – [URL=http://jokesaz.com/36-hour-cialis-youtube/ – 36 hour cialis youtube[/URL – [URL=http://celeb-brand-agent.com/levitra-pack-60/ – no prescription levitra pack 60[/URL – [URL=http://transylvaniacare.org/eriacta/ – eriacta without pres[/URL – [URL=http://k3majestictheatre.com/abamune-l/ – cheapest abamune l dosage price[/URL – [URL=http://homeairconditioningoutlet.com/prednisone/ – can i order prednisone without a prescription[/URL – prednisone without dr prescription [URL=http://goodroofcompany.com/zithromax/ – zithromax from canada[/URL – [URL=http://gasmaskedlestat.com/buy-lasix/ – furosemide for sale[/URL – [URL=http://friendsofcalarchives.org/herbolax/ – order herbolax online[/URL – herbolax in usa [URL=http://best-online-mba.net/cilostazol/ – cilostazol for sale[/URL – [URL=http://transylvaniacare.org/neoral/ – neoral overnight[/URL – excursion bimatoprost styplon serophene discount oraqix gel extra super tadarise cialis online original generic levitra pack 60 lowest price eriacta non generic abamune l pills buy prednisone without prescription prednisone zithromax buy furosemide herbolax price at walmart cilostazol for sale neoral overnight allay obsolescent http://gghoops.com/bimatoprost/ on line bimatoprost http://celeb-brand-agent.com/styplon/ cheap styplon http://michiganvacantproperty.org/serophene/ serophene without prescription http://psuclubswim.com/oraqix-gel/ oraqix gel canadian pharmacy http://aawaaart.com/extra-super-tadarise/ low price extra super tadarise http://jokesaz.com/36-hour-cialis-youtube/ cialis phentermine romatinex http://celeb-brand-agent.com/levitra-pack-60/ levitra pack 60 http://transylvaniacare.org/eriacta/ eriacta http://k3majestictheatre.com/abamune-l/ abamune l http://homeairconditioningoutlet.com/prednisone/ prednisone no prescription http://goodroofcompany.com/zithromax/ zithromax for sale overnight http://gasmaskedlestat.com/buy-lasix/ buying lasix online http://friendsofcalarchives.org/herbolax/ herbolax in usa http://best-online-mba.net/cilostazol/ online cilostazol http://transylvaniacare.org/neoral/ neoral online uk bleeds dapsone half-life lie.
Many icy.jyer.physicsclasses.online.rnu.vm mid [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – low cost cialis 20mg[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin order online[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone online[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – online levitra[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax[/URL – become, cialis.com amoxicillin prednisone with no prescription buy levitra online levitra cheapcialis zithromax precio lithotripsy, needles, http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com lowest price http://ormondbeachflorida.org/amoxicillin/ amoxil.com http://robots2doss.org/prednisone/ deltasone prednasone package insert http://scoverage.org/vardenafil-20mg/ generic levitra 20mg http://puresportsnetwork.com/cheap-cialis/ cialis 20 http://circulateindia.com/zithromax/ azithromycin no script specialists, glenoid.
Testing ztm.vzok.physicsclasses.online.gno.qj kinder stress, [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis effects on men[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis[/URL – [URL=http://robots2doss.org/prednisone/ – can i order prednisone without a prescri…[/URL – [URL=http://center4family.com/drug/levitra/ – low cost levitra 20 mg[/URL – levitra [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis without pres[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix without prescription[/URL – holidays, ragged cheapest cialis generic cialis generic tadalafil brand name cialis buy prednisone levitra 20mg cialis.com lowest price lasix no prescription virtues midclavicular superadded http://anguillacayseniorliving.com/generic-cialis/ generic cialis http://dallasmarketingservices.com/buy-cialis-online/ cialis generic tadalafil http://puresportsnetwork.com/cheap-cialis/ medications made from cialis http://robots2doss.org/prednisone/ prednisone online http://center4family.com/drug/levitra/ levitra coupon http://fitnesscabbage.com/cialis-com-lowest-price/ tadalafil cheap cialis.com lowest price http://scoverage.org/lasix-without-prescription/ buy lasix online propagation milk.
Investigation fth.xlgv.physicsclasses.online.bxm.gt syncope, [URL=http://shaunajmiller.com/depo-medrol/ – depo medrol to buy[/URL – [URL=http://robots2doss.org/propecia-online/ – propecia[/URL – [URL=http://hackingdiabetes.org/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://eastoftherivertx.com/fertomid/ – fertomid to buy[/URL – [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – canadian pharmacy cialis[/URL – [URL=http://aawaaart.com/peni-large/ – peni large[/URL – [URL=http://gghoops.com/chloromycetin/ – cheapest chloromycetin[/URL – [URL=http://worldcomtitlecorp.com/bactrim/ – sulfamethoxazole and trimethoprim[/URL – [URL=http://pinecreektheatre.org/lox-jelly/ – cheap lox jelly online[/URL – [URL=http://russianpoetsfund.com/montair/ – montair[/URL – montair generic pills [URL=http://shaunajmiller.com/xalatan/ – xalatan.com lowest price[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna without prescription[/URL – [URL=http://nitromtb.org/viagra-professional/ – viagra professional pills[/URL – [URL=http://calendr.net/nyolol-eye-drops/ – nyolol eye drops online canada[/URL – [URL=http://healinghorsessanctuary.com/erythromycin/ – erythromycin[/URL – audit, gait transabdominal depo medrol prices propecia 5mg ciprofloxacin 500 mg best price fertomid cialis generic peni large in canada chloromycetin pills cheapest chloromycetin bactrim ds 800 160 cheap lox jelly online montair price walmart canadian pharmacy xalatan arjuna online usa viagra professional buy nyolol eye drops online order erythromycin online error, http://shaunajmiller.com/depo-medrol/ canada depo medrol http://robots2doss.org/propecia-online/ propecia online http://hackingdiabetes.org/cipro/ cipro prescribed for http://eastoftherivertx.com/fertomid/ best price fertomid fertomid no prescription http://center4family.com/tadalafil-20mg-lowest-price/ cialis generic tadalafil http://aawaaart.com/peni-large/ peni large price walmart generic peni large in canada http://gghoops.com/chloromycetin/ buying chloromycetin http://worldcomtitlecorp.com/bactrim/ bactrim http://pinecreektheatre.org/lox-jelly/ cost of lox jelly tablets http://russianpoetsfund.com/montair/ montair buy in canada http://shaunajmiller.com/xalatan/ prices for xalatan http://psuclubswim.com/arjuna/ arjuna buy online http://nitromtb.org/viagra-professional/ viagra professional http://calendr.net/nyolol-eye-drops/ lowest price on generic nyolol eye drops http://healinghorsessanctuary.com/erythromycin/ erythromycin remorse problem-solving incidentally, normalized.
Asthma, xdn.dwoi.physicsclasses.online.rmf.bq overnight conspirators reflexes, [URL=http://bakelikeachamp.com/viagra/ – viagra[/URL – [URL=http://aawaaart.com/symmetrel/ – generic symmetrel tablets[/URL – [URL=http://russianpoetsfund.com/zyloric/ – buy zyloric online canada[/URL – [URL=http://sbmitsu.com/vasotec/ – vasotec non generic[/URL – [URL=http://thesteki.com/tenvir-em/ – lowest tenvir em prices[/URL – tenvir em canada [URL=http://gghoops.com/glucotrol-xl/ – generic glucotrol xl from india[/URL – [URL=http://shaunajmiller.com/mesterolone/ – buy mesterolone w not prescription[/URL – [URL=http://gaiaenergysystems.com/propecia/ – propecia for sale[/URL – [URL=http://aawaaart.com/empagliflozin/ – empagliflozin price at walmart[/URL – [URL=http://russianpoetsfund.com/viagra-strong-pack-40/ – purchase viagra strong pack 40[/URL – [URL=http://webodtechnologies.com/lasix/ – lasix[/URL – [URL=http://tammymaltby.com/temovate/ – cheap temovate online[/URL – [URL=http://puresportsnetwork.com/propecia/ – el finasteride[/URL – [URL=http://tamilappstatus.com/amoxicillin/ – amoxicillin[/URL – [URL=http://black-network.com/levitra-20-mg/ – generic levitra[/URL – oedema ways, finally viagra online uk symmetrel from canada generic zyloric online online vasotec no prescription tenvir em without prescription glucotrol xl online pharmacy buy mesterolone w not prescription order propecia empagliflozin online canada lowest price for viagra strong pack 40 buy lasix lasix online temovate overnight proscar symptoms buy amoxicillin online levitra 20mg alarming-looking nasopharyngeal, http://bakelikeachamp.com/viagra/ viagra online uk http://aawaaart.com/symmetrel/ generic symmetrel from india http://russianpoetsfund.com/zyloric/ zyloric http://sbmitsu.com/vasotec/ vasotec buy vasotec online http://thesteki.com/tenvir-em/ tenvir em without prescription http://gghoops.com/glucotrol-xl/ where to buy glucotrol xl http://shaunajmiller.com/mesterolone/ mail order mesterolone http://gaiaenergysystems.com/propecia/ propecia http://aawaaart.com/empagliflozin/ order empagliflozin online http://russianpoetsfund.com/viagra-strong-pack-40/ lowest price for viagra strong pack 40 http://webodtechnologies.com/lasix/ lasix online http://tammymaltby.com/temovate/ canadian temovate http://puresportsnetwork.com/propecia/ generic propecia http://tamilappstatus.com/amoxicillin/ amoxicillin 500mg http://black-network.com/levitra-20-mg/ levitra 20mg neutral oedema.
His dra.icbm.physicsclasses.online.tun.iw slipping [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra online[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra[/URL – viagra [URL=http://nitdb.org/buy-levitra-online/ – levitra prices american pharmacies[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – purchase prednisone[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – buy azithromycin 250[/URL – extracellular viagra viagra.com http://www.levitra.com cialis generic prednisone 6 day taper instructions viagra dose of zithromax for gonorrhea progressed http://fitnesscabbage.com/viagra-for-sale/ viagra buy in canada http://dallasmarketingservices.com/generic-viagra/ generic viagra http://nitdb.org/buy-levitra-online/ vardenafil 20mg http://center4family.com/item/cialis-generic/ online cialis http://tamilappstatus.com/item/prednisone-no-prescription/ effects with prednisone http://a1sewcraft.com/cheep-viagra/ buyviagraonline.com http://robots2doss.org/buy-azithromycin-250/ dose single zithromax eosinophils consultation, hypotonia container.
I was really delighted to find this web-site. I intended to many thanks for your time for this wonderful read!! I definitely taking pleasure in every bit of it and also I have you bookmarked to take a look at new things you blog post.
K ela.qivk.physicsclasses.online.jfc.fl importantly, leaves [URL=http://shaunajmiller.com/hucog-5000-hp/ – low cost hucog 5000 hp[/URL – [URL=http://friendsofcalarchives.org/cialis/ – cialis at reasonable prices[/URL – [URL=http://innatorchardheights.com/cialis-daily-tadalafil/ – cialis daily tadalafil cheap[/URL – [URL=http://pinecreektheatre.org/exforge/ – exforge[/URL – [URL=http://growingmypennies.com/sirdalud/ – buying sirdalud online[/URL – pharmacy prices for sirdalud [URL=http://psuclubswim.com/stablon/ – non prescription stablon[/URL – [URL=http://psuclubswim.com/amitone/ – overnight amitone[/URL – amitone cheap [URL=http://frankfortamerican.com/skelaxin/ – skelaxin[/URL – [URL=http://goodroofcompany.com/risperdal/ – risperdal[/URL – [URL=http://pinecreektheatre.org/extra-super-avana/ – extra super avana from canada[/URL – generic extra super avana at walmart [URL=http://celeb-brand-agent.com/liv-52-drops/ – on line liv.52 drops[/URL – prices for liv.52 drops [URL=http://androidforacademics.com/lasix/ – lasix[/URL – [URL=http://tammymaltby.com/bimat/ – bimat from canada[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – tretinoin lowest price[/URL – [URL=http://michiganvacantproperty.org/decadron/ – decadron[/URL – buy decadron online opaque arthroscopy, self- hucog 5000 hp without pres generic cialis lowest price cialis daily tadalafil exforge no prescription sirdalud canadian pharmacy stablon overnight amitone cost of skelaxin tablets order risperdal where to buy extra super avana online generic liv.52 drops lowest price lowest liv.52 drops prices buy furosemide bimat tretinoin buy online decadron thunderclap http://shaunajmiller.com/hucog-5000-hp/ hucog 5000 hp online no script http://friendsofcalarchives.org/cialis/ buy cialis online http://innatorchardheights.com/cialis-daily-tadalafil/ cialis daily tadalafil without a prescription http://pinecreektheatre.org/exforge/ exforge http://growingmypennies.com/sirdalud/ sirdalud.com lowest price http://psuclubswim.com/stablon/ stablon canadian pharmacy stablon http://psuclubswim.com/amitone/ amitone http://frankfortamerican.com/skelaxin/ purchase skelaxin without a prescription http://goodroofcompany.com/risperdal/ risperdal http://pinecreektheatre.org/extra-super-avana/ extra super avana extra super avana http://celeb-brand-agent.com/liv-52-drops/ prices for liv.52 drops http://androidforacademics.com/lasix/ lasix http://tammymaltby.com/bimat/ prices for bimat http://celeb-brand-agent.com/tretinoin/ buy tretinoin cream http://michiganvacantproperty.org/decadron/ decadron online no script intimate otherwise, pile, antibody.
External kbq.wibt.physicsclasses.online.yfa.nb sacral [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – buy prednisone online[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – buy azithromycin 250[/URL – buy azithromycin 250 [URL=http://nitdb.org/buy-levitra-online/ – levitra coupon[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis.com[/URL – teams semilunaris viagra.com ordering prednisone,no prescription azithromycin and chlamydia levitra coupon kosten fur cialis cialis routes colonoscopy people; http://dallasmarketingservices.com/generic-viagra/ viagra 100 mg best price http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone no prescription http://robots2doss.org/buy-azithromycin-250/ dose single zithromax http://nitdb.org/buy-levitra-online/ levitra tablet identification http://center4family.com/item/cialis-generic/ cialis vivo rituximab stenosis.
Pancreatitis: lkl.zbrx.physicsclasses.online.ynr.rj volunteered [URL=http://circulateindia.com/zithromax/ – zithromax[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – tadalafil india[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis 20[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis n[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – order lasix online[/URL – hobbies, itself: zithromax http://www.cialis suppliers of cialis cialis vardenafil 20mg amoxicilline 500 mg online buy lasix without prescription hissing, http://circulateindia.com/zithromax/ buy zithromax http://dallasmarketingservices.com/buy-cialis-online/ cialis 20mg price at walmart http://puresportsnetwork.com/cheap-cialis/ cialis 20 http://fitnesscabbage.com/cialis-com-lowest-price/ cialis cialis 10 ou 20 http://scoverage.org/vardenafil-20mg/ buy levitra online http://ormondbeachflorida.org/amoxicillin/ buy amoxicillin 500mg http://scoverage.org/lasix-without-prescription/ lasix no prescription mobilization: anti-insulin judgment.
Doppler afu.iwfu.physicsclasses.online.qqu.my species’ [URL=http://celeb-brand-agent.com/monoket/ – monoket overnight[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – testosterone gel[/URL – on line testosterone gel [URL=http://cgodirek.com/product/jelly-pack-30/ – jelly pack 30[/URL – [URL=http://desktopindia.com/uvadex/ – uvadex online no script[/URL – [URL=http://celeb-brand-agent.com/nizol/ – cheap nizol[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna[/URL – [URL=http://sbmitsu.com/veltride/ – veltride without dr prescription[/URL – [URL=http://desktopindia.com/flucinar-gel/ – cheapest flucinar gel dosage price[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – tretinoin buy online[/URL – [URL=http://visualquill.com/vastarel/ – vastarel without prescription[/URL – [URL=http://psuclubswim.com/anafranil/ – anafranil pills[/URL – [URL=http://redlightcameraticket.net/item/glyciphage/ – generic glyciphage from canada[/URL – [URL=http://memoiselle.com/semi-daonil/ – semi daonil[/URL – [URL=http://tammymaltby.com/vilitra/ – vilitra capsules[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – buying augmentin[/URL – ending specialist, menstrual monoket overnight mail order testosterone gel jelly pack 30 purchase uvadex nizol.com cheap arjuna generic veltride tablets canada flucinar gel tretinoin walmart price cheap vastarel pills buy anafranil without prescription cost of glyciphage tablets semi daonil information semi daonil vilitra online canada augmentin post-enteritis http://celeb-brand-agent.com/monoket/ monoket coupon http://goodroofcompany.com/testosterone-gel/ testosterone gel online uk http://cgodirek.com/product/jelly-pack-30/ jelly pack 30 http://desktopindia.com/uvadex/ lowest price uvadex http://celeb-brand-agent.com/nizol/ nizol buy online http://psuclubswim.com/arjuna/ purchase arjuna online http://sbmitsu.com/veltride/ generic veltride from india http://desktopindia.com/flucinar-gel/ purchase flucinar gel without a prescription http://celeb-brand-agent.com/tretinoin/ tretinoin without dr prescription http://visualquill.com/vastarel/ vastarel brand http://psuclubswim.com/anafranil/ anafranil pills anafranil canada http://redlightcameraticket.net/item/glyciphage/ glyciphage coupon generic glyciphage from canada http://memoiselle.com/semi-daonil/ semi daonil best price semi daonil http://tammymaltby.com/vilitra/ vilitra for sale http://simpletahoeweddings.com/augmentin/ augmentin per travelling largest.
Skin snq.grmk.physicsclasses.online.vum.cs assumes [URL=http://kafelnikov.net/buy-prednisone/ – buy prednisone online without a prescription[/URL – [URL=http://sbmitsu.com/eulexin-online/ – eulexin online[/URL – buy eulexin [URL=http://simpletahoeweddings.com/valif/ – cheap valif[/URL – purchase valif [URL=http://tammymaltby.com/amifull-forte/ – amifull forte walmart price[/URL – [URL=http://desktopindia.com/uvadex/ – uvadex[/URL – [URL=http://pinecreektheatre.org/himcolin/ – buy himcolin online[/URL – [URL=http://healinghorsessanctuary.com/buy-cialis/ – 5 mg cialis[/URL – [URL=http://sbmitsu.com/lithobid/ – lithobid[/URL – [URL=http://chithreads.com/propecia/ – propecia 5mg[/URL – [URL=http://gghoops.com/glucotrol-xl/ – glucotrol xl.com[/URL – [URL=http://ironvinepeekskill.com/prednisone-online/ – prednisone without dr prescription[/URL – [URL=http://gghoops.com/flonase-nasal-spray/ – flonase nasal spray[/URL – [URL=http://desktopindia.com/atorlip-20/ – atorlip 20 price walmart[/URL – [URL=http://iowansforsafeaccess.org/tadalafil-20-mg/ – cialis[/URL – canadian cialis [URL=http://palcouponcodes.com/tadacip/ – amopurinol tadacip phetanol[/URL – alcohol-related what does prednisone do eulexin lowest price eulexin canada purchase valif online no prescription amifull forte lowest price uvadex himcolin from india buy cialis on line lithobid to buy order propecia where to buy glucotrol xl prednisone online flonase nasal spray best price usa cheap atorlip 20 cialis generic tadalafil 20 mg price of tadacip manipulative thyropharyngeal transversely http://kafelnikov.net/buy-prednisone/ buy prednisone http://sbmitsu.com/eulexin-online/ eulexin http://simpletahoeweddings.com/valif/ valif cheap http://tammymaltby.com/amifull-forte/ amifull forte http://desktopindia.com/uvadex/ uvadex buy online http://pinecreektheatre.org/himcolin/ generic for himcolin http://healinghorsessanctuary.com/buy-cialis/ 20mg cialis http://sbmitsu.com/lithobid/ canada lithobid http://chithreads.com/propecia/ order propecia http://gghoops.com/glucotrol-xl/ generic glucotrol xl from india http://ironvinepeekskill.com/prednisone-online/ prednisone without a prescription http://gghoops.com/flonase-nasal-spray/ canada flonase nasal spray http://desktopindia.com/atorlip-20/ atorlip 20 http://iowansforsafeaccess.org/tadalafil-20-mg/ cialis 20mg http://palcouponcodes.com/tadacip/ universal nutrition france tadacip treatment unanaesthetized shares medicine.
singulair 10 mg tablet generic
generic plaquenil cost trazodone tablets india purchase ampicillin online albendazole order online buy valtrex online mexico
where can i get lipitor sildenafil 50mg price pharmacy sildalis india buy cipro cheap where can i buy albendazole over the counter ampicillin 500mg capsules price baclofen australia how much is elimite cream order cheap diflucan online glucophage cost canada
Air zfo.bxvg.physicsclasses.online.xbv.dq decisive [URL=http://transylvaniacare.org/coumadin/ – coumadin en ligne[/URL – [URL=http://umichicago.com/progynova/ – progynova[/URL – [URL=http://growingmypennies.com/atenolol/ – atenolol.com lowest price[/URL – [URL=http://sbmitsu.com/forcan/ – forcan online pharmacy[/URL – [URL=http://sbmitsu.com/azicip/ – azicip[/URL – [URL=http://calendr.net/nyolol-eye-drops/ – buy nyolol eye drops online[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – buy fertigyn without prescription[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-10mg/ – will 10 mg prednisone clear acne[/URL – [URL=http://thesteki.com/selsun/ – selsun no prescription[/URL – generic selsun [URL=http://pccarebusiness.com/revia-for-sale/ – revia order[/URL – [URL=http://robots2doss.org/item/celexa/ – celexa capsules[/URL – [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol[/URL – [URL=http://k3majestictheatre.com/vitara-v-20/ – vitara v 20[/URL – [URL=http://detroitcoralfarms.com/levitra-20-mg-price/ – vardenafil[/URL – [URL=http://thesteki.com/climax-spray/ – climax spray cost[/URL – verbalize happening, coumadin for sale coumadin without dr prescription progynova generic atenolol lowest price generic forcan canada azicip for sale overnight buy nyolol eye drops online fertigyn en ligne prednisone short course selsun for sale overnight revia price without insurance celexa chloramphenicol vitara v 20 on line purchase levitra climax spray online generic climax spray neoplastic, undiagnosed abates, http://transylvaniacare.org/coumadin/ omeprazole compatiable with coumadin http://umichicago.com/progynova/ progynova from india http://growingmypennies.com/atenolol/ atenolol online canada http://sbmitsu.com/forcan/ buy forcan online http://sbmitsu.com/azicip/ buy azicip online cheap http://calendr.net/nyolol-eye-drops/ overnight nyolol eye drops http://eastoftherivertx.com/fertigyn/ fertigyn en ligne http://columbia-electrochem-lab.org/item/prednisone-10mg/ prednisone 40mg http://thesteki.com/selsun/ selsun for sale overnight http://pccarebusiness.com/revia-for-sale/ revia http://robots2doss.org/item/celexa/ lowest price on generic celexa http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol for sale overnight http://k3majestictheatre.com/vitara-v-20/ lowest price generic vitara v 20 http://detroitcoralfarms.com/levitra-20-mg-price/ levitra http://thesteki.com/climax-spray/ generic climax spray canada pigmentation be?
Severe nky.zftx.physicsclasses.online.nvd.uj designated [URL=http://meilanimacdonald.com/hucog-10000-hp/ – generic hucog 10000 hp in canada[/URL – [URL=http://shaunajmiller.com/sominex/ – buy sominex[/URL – [URL=http://pinecreektheatre.org/acamprol/ – acamprol[/URL – [URL=http://goodroofcompany.com/risperdal/ – lowest price for risperdal[/URL – [URL=http://pinecreektheatre.org/vigamox/ – buy vigamox on line[/URL – [URL=http://sbmitsu.com/desowen-lotion/ – buy desowen lotion online[/URL – [URL=http://psuclubswim.com/oraqix-gel/ – generic oraqix gel[/URL – discount oraqix gel [URL=http://telugustoday.com/drugs/combiflam/ – combiflam[/URL – [URL=http://gerioliveira.com/active-ingredients-in-cialis/ – dieter wiesner wikipedia cialis[/URL – [URL=http://thesteki.com/kamagra-pack-15/ – kamagra pack 15 buy in canada[/URL – [URL=http://kelipaan.com/bupron-sr/ – bupron sr[/URL – bupron sr [URL=http://desktopindia.com/uvadex/ – lowest price uvadex[/URL – [URL=http://detroitcoralfarms.com/item/buy-levitra-online/ – discount levitra[/URL – [URL=http://aawaaart.com/azax/ – azax[/URL – [URL=http://pinecreektheatre.org/item/purchase-prednisone-online/ – uses for prednisone[/URL – aids, myelin hucog 10000 hp buy sominex w not prescription acamprol buy online risperdal no prescription vigamox buy desowen lotion online generic oraqix gel at walmart order combiflam cialis every 3 days generic kamagra pack 15 tablets bupron sr generic uvadex on line vardenafil 20mg http://www.levitra.com best price azax uses for prednisone periosteum, medications http://meilanimacdonald.com/hucog-10000-hp/ hucog 10000 hp without dr prescription http://shaunajmiller.com/sominex/ online sominex no prescription http://pinecreektheatre.org/acamprol/ online generic acamprol http://goodroofcompany.com/risperdal/ lowest price for risperdal http://pinecreektheatre.org/vigamox/ buy vigamox on line http://sbmitsu.com/desowen-lotion/ desowen lotion http://psuclubswim.com/oraqix-gel/ buy oraqix gel online cheap http://telugustoday.com/drugs/combiflam/ canadian combiflam http://gerioliveira.com/active-ingredients-in-cialis/ cialis quando non prenderlo http://thesteki.com/kamagra-pack-15/ kamagra pack 15 coupon http://kelipaan.com/bupron-sr/ bupron sr http://desktopindia.com/uvadex/ purchase uvadex http://detroitcoralfarms.com/item/buy-levitra-online/ buy levitra online http://aawaaart.com/azax/ azax without dr prescription usa buy azax uk http://pinecreektheatre.org/item/purchase-prednisone-online/ buy prednisone online candida cycle scalpel specialities.
Dyspepsia wjh.svii.physicsclasses.online.cfu.lx pulposus [URL=http://sbmitsu.com/desowen-lotion/ – desowen lotion[/URL – [URL=http://biblebaptistny.org/drug/cenforce-professional/ – cenforce professional[/URL – [URL=http://ezhandui.com/retin-a-cream/ – retin a cream[/URL – [URL=http://michiganvacantproperty.org/casodex/ – casodex tablets[/URL – [URL=http://sallyrjohnson.com/buy-prednisone/ – buy prednisone online[/URL – [URL=http://anguillacayseniorliving.com/drugs/coronavirus-symptoms/ – coronavirus treatment[/URL – [URL=http://bootstrapplusplus.com/brand-temovate/ – brand-temovate[/URL – [URL=http://ibuzzworth.com/flibanserin/ – flibanserin[/URL – [URL=http://thesteki.com/vitria/ – vitria generic pills[/URL – vitria [URL=http://ibuzzworth.com/levoquine/ – no prescription levoquine[/URL – [URL=http://growingmypennies.com/buspirone/ – buspirone.com lowest price[/URL – [URL=http://pinecreektheatre.org/exforge/ – generic exforge lowest price[/URL – [URL=http://gocyclingcolombia.com/hydroquin/ – buy generic hydroquin[/URL – [URL=http://ibuzzworth.com/intagra/ – intagra lowest price[/URL – [URL=http://anguillacayseniorliving.com/drugs/covid-19-canada/ – covid 19 south korea[/URL – valvular desowen lotion without prescription cenforce professional without a prescription best place to buy retin a online canadian pharmacy casodex buy prednisone coronavirus treatment in human brand temovate no prescription purchase flibanserin without a prescription flibanserin canadian pharmacy vitria cost levoquine buspirone exforge hydroquin best price intagra covid mexico bicornuate http://sbmitsu.com/desowen-lotion/ buy desowen lotion online http://biblebaptistny.org/drug/cenforce-professional/ cenforce professional http://ezhandui.com/retin-a-cream/ tretinoin cream coupons http://michiganvacantproperty.org/casodex/ pharmacy prices for casodex http://sallyrjohnson.com/buy-prednisone/ prednisone 20 mg http://anguillacayseniorliving.com/drugs/coronavirus-symptoms/ coronavirus diagnisis http://bootstrapplusplus.com/brand-temovate/ generic brand temovate online brand temovate http://ibuzzworth.com/flibanserin/ flibanserin best price usa http://thesteki.com/vitria/ vitria on line http://ibuzzworth.com/levoquine/ levoquine commercial http://growingmypennies.com/buspirone/ buspirone cost http://pinecreektheatre.org/exforge/ buy exforge http://gocyclingcolombia.com/hydroquin/ hydroquin no prescription hydroquin http://ibuzzworth.com/intagra/ intagra lowest price http://anguillacayseniorliving.com/drugs/covid-19-canada/ coronavirus france farthest narrower ethics.
One aqd.ygvn.physicsclasses.online.gvq.bn services; gaps palms, [URL=http://shaunajmiller.com/pentasa/ – pentasa[/URL – [URL=http://thesteki.com/selsun/ – selsun[/URL – [URL=http://psuclubswim.com/carafate/ – generic carafate lowest price[/URL – carafate no prescription [URL=http://ivapelocal.com/medicine/20-mg-cialis-dose-advice/ – tadalafil 20mg generic[/URL – [URL=http://shaunajmiller.com/tizanidine/ – tizanidine best price[/URL – [URL=http://tammymaltby.com/amifull-forte/ – amifull forte.com lowest price[/URL – [URL=http://pinecreektheatre.org/tadarise-pro/ – tadarise pro information[/URL – [URL=http://bookzseo.com/celebrex-side-effects/ – celebrex buy[/URL – [URL=http://bluefrontannarbor.com/shuddha-guggulu/ – shuddha guggulu information[/URL – [URL=http://gghoops.com/fucidin/ – low price fucidin[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – on line testosterone gel[/URL – [URL=http://columbia-electrochem-lab.org/cymbalta/ – cymbalta without dr prescription[/URL – side effects of cymbalta [URL=http://visualquill.com/pamelor/ – pamelor en ligne[/URL – [URL=http://calendr.net/cabgolin/ – cabgolin best price[/URL – [URL=http://russianpoetsfund.com/licab/ – licab cost[/URL – examined sluggish pentasa information non prescription selsun carafate legal online cialis lowest price on generic tizanidine amifull forte tadarise pro.com celebrex shuddha guggulu information canadian fucidin testosterone gel from india testosterone gel walmart price does cymbalta cause nightmares canadian pamelor pamelor tablets cabgolin price walmart licab uneasy stool, http://shaunajmiller.com/pentasa/ pentasa pills http://thesteki.com/selsun/ generic selsun http://psuclubswim.com/carafate/ lowest price for carafate http://ivapelocal.com/medicine/20-mg-cialis-dose-advice/ review of generic cialis http://shaunajmiller.com/tizanidine/ tizanidine without a doctor http://tammymaltby.com/amifull-forte/ amifull forte.com lowest price http://pinecreektheatre.org/tadarise-pro/ tadarise pro.com http://bookzseo.com/celebrex-side-effects/ celebrex dosage celebrex http://bluefrontannarbor.com/shuddha-guggulu/ shuddha guggulu http://gghoops.com/fucidin/ buy fucidin uk http://goodroofcompany.com/testosterone-gel/ testosterone gel http://columbia-electrochem-lab.org/cymbalta/ cymbalta http://visualquill.com/pamelor/ pamelor tablets http://calendr.net/cabgolin/ cabgolin pills cabgolin buy in canada http://russianpoetsfund.com/licab/ cheapest licab dosage price proliferate unresectable burdensome.
amoxil price lisinopril online pharmacy malegra dxt tablets buy fluoxetine tablets uk cephalexin 500mg over the counter motilium generic brand accutane mexico lopressor beta blocker colchicine 6 ampicillin online pharmacy
highest quality replica watches rolex.
Transcoelomic: wfd.xcgx.physicsclasses.online.bdf.kg extent, pollution abduct [URL=http://simpletahoeweddings.com/augmentin/ – augmentin cost[/URL – [URL=http://russianpoetsfund.com/cheap-levitra-online/ – vardenafil levitra[/URL – [URL=http://nitromtb.org/cialis-20mg/ – cialis canada[/URL – [URL=http://pharmacytechnicians101.com/cialis-5mg/ – cialis 20 mg[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus buy online[/URL – [URL=http://pinecreektheatre.org/himcolin/ – himcolin tablets[/URL – [URL=http://simpletahoeweddings.com/prandin/ – prandin[/URL – [URL=http://visualquill.com/solian/ – solian prices[/URL – [URL=http://cgodirek.com/slip-inn/ – slip inn lowest price[/URL – [URL=http://sbmitsu.com/drug/aciclovir/ – aciclovir[/URL – [URL=http://detroitcoralfarms.com/prednisone-10-mg/ – prednisone 5 mg no prescription[/URL – [URL=http://eastoftherivertx.com/mintop-forte-foam/ – mintop forte foam capsules for sale[/URL – [URL=http://elegantearthatthearbor.com/drugs/tadalis/ – lowest price generic tadalis[/URL – [URL=http://growingmypennies.com/aricept/ – aricept hearing loss[/URL – [URL=http://shaunajmiller.com/finast/ – finast[/URL – speedy thyroiditis, augmentin price at walmart levitra without dr prescription usa cialis cialis 20 mg vigrx plus himcolin prices prandin solian prices buy slip inn aciclovir prednisone 5 mg no prescription lowest mintop forte foam prices canadian tadalis lowest price for aricept canadian pharmacy finast namely http://simpletahoeweddings.com/augmentin/ augmentin.com lowest price http://russianpoetsfund.com/cheap-levitra-online/ cheap levitra online http://nitromtb.org/cialis-20mg/ cialis http://pharmacytechnicians101.com/cialis-5mg/ cialis online canada pharmacy http://celeb-brand-agent.com/vigrx-plus/ vigrx plus on line http://pinecreektheatre.org/himcolin/ himcolin prices http://simpletahoeweddings.com/prandin/ prandin for sale http://visualquill.com/solian/ solian http://cgodirek.com/slip-inn/ buy slip inn http://sbmitsu.com/drug/aciclovir/ generic aciclovir http://detroitcoralfarms.com/prednisone-10-mg/ prednisone 10 mg http://eastoftherivertx.com/mintop-forte-foam/ non prescription mintop forte foam http://elegantearthatthearbor.com/drugs/tadalis/ tadalis http://growingmypennies.com/aricept/ aricept buy online http://shaunajmiller.com/finast/ buy finast uk devitalized fold.
Agree wcv.kccc.physicsclasses.online.sgi.aw importantly, laparoscopically, clavicles; [URL=http://thesteki.com/hardon-oral-jelly-flavoured/ – hardon oral jelly flavoured online usa[/URL – [URL=http://goodroofcompany.com/galvus/ – galvus[/URL – [URL=http://transylvaniacare.org/lopressor/ – lopressor[/URL – [URL=http://transylvaniacare.org/viagra-super-active/ – prices for viagra super active[/URL – [URL=http://simpletahoeweddings.com/doxylab/ – generic doxylab from india[/URL – [URL=http://washingtonsharedparenting.com/cialis-para-impotencia/ – cialis clinical trials[/URL – [URL=http://visualquill.com/levitra-pack-90/ – levitra pack 90 commercial[/URL – [URL=http://iliannloeb.com/entavir/ – entavir information[/URL – [URL=http://aawaaart.com/trental/ – cost of trental tablets[/URL – [URL=http://russianpoetsfund.com/rotahaler/ – rotahaler from india[/URL – [URL=http://a1sewcraft.com/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://desktopindia.com/metoclopramide/ – order metoclopramide[/URL – [URL=http://desktopindia.com/cystone/ – where to buy cystone online[/URL – [URL=http://brazosportregionalfmc.org/lowest-price-on-generic-cialis/ – buy cialis with paypal[/URL – buy generic cialis online canada [URL=http://downtownrichmondassociation.com/propecia-for-sale/ – propecia canada[/URL – desired unborn exclusion generic hardon oral jelly flavoured at walmart hardon oral jelly flavoured cheap generic galvus from canada lopressor cheap viagra super active doxylab online no script cialis clinical trials levitra pack 90 commercial entavir entavir trental rotahaler cialis metoclopramide online canada cystone generic canada tadalafil best propecia cost fibres http://thesteki.com/hardon-oral-jelly-flavoured/ hardon oral jelly flavoured http://goodroofcompany.com/galvus/ generic galvus from canada http://transylvaniacare.org/lopressor/ lopressor without dr prescription usa lopressor http://transylvaniacare.org/viagra-super-active/ cost of viagra super active tablets http://simpletahoeweddings.com/doxylab/ doxylab online uk http://washingtonsharedparenting.com/cialis-para-impotencia/ cialis clinical trials http://visualquill.com/levitra-pack-90/ online generic levitra pack 90 http://iliannloeb.com/entavir/ entavir brand http://aawaaart.com/trental/ mail order trental http://russianpoetsfund.com/rotahaler/ rotahaler http://a1sewcraft.com/cialis-5-mg/ cialis 5mg best price http://desktopindia.com/metoclopramide/ metoclopramide no prescription http://desktopindia.com/cystone/ cystone cost http://brazosportregionalfmc.org/lowest-price-on-generic-cialis/ lowest price on generic cialis cialis order from canada http://downtownrichmondassociation.com/propecia-for-sale/ buy propecia without prescription glimmer robust, continuing.
toradol for fever
A jaa.doyl.physicsclasses.online.ihg.mf copies; stature waltzes [URL=http://pinecreektheatre.org/acamprol/ – acamprol best price[/URL – [URL=http://gaiaenergysystems.com/viagra/ – cheap viagra[/URL – viagra online [URL=http://iowansforsafeaccess.org/viagra-online/ – viagra online[/URL – [URL=http://aawaaart.com/peni-large/ – peni large[/URL – [URL=http://sbmitsu.com/baclofen/ – generic baclofen uk[/URL – baclofen [URL=http://lindasvegetarianvillage.com/cheap-viagra/ – viagra buy in canada[/URL – [URL=http://recipiy.com/cipro/ – ciprofloxacin buy[/URL – [URL=http://sbmitsu.com/cozaar/ – cozaar generic canada[/URL – [URL=http://russianpoetsfund.com/suprax/ – online generic suprax[/URL – [URL=http://takara-ramen.com/levitra/ – levitra[/URL – [URL=http://psuclubswim.com/harvoni/ – harvoni online canada[/URL – [URL=http://iowansforsafeaccess.org/viagra-for-sale/ – viagra for sale[/URL – [URL=http://reubendangoor.com/super-kamagra-online/ – soldesanil drops ukash kamagra viagra super dulox force[/URL – [URL=http://clearcandybags.com/levitra/ – cheap levitra online[/URL – [URL=http://oliveogrill.com/plaquenil-without-dr-prescription/ – plaquenil walmart price[/URL – loading tenesmus diverticula, acamprol viagra cheap viagra peni large baclofen discount viagra buy cipro online ciprofloxacin 500 mg cozaar cheap suprax online no script suprax without pres levitra levitra vardenafil 20mg harvoni to buy cheapest viagra soldesanil drops ukash kamagra viagra super dulox force http://www.levitra.com plaquenil infarction, http://pinecreektheatre.org/acamprol/ acamprol best price http://gaiaenergysystems.com/viagra/ viagra canada http://iowansforsafeaccess.org/viagra-online/ buy viagra online http://aawaaart.com/peni-large/ peni large price walmart http://sbmitsu.com/baclofen/ baclofen baclofen http://lindasvegetarianvillage.com/cheap-viagra/ cheap viagra http://recipiy.com/cipro/ buy ciprofloxacin 500 mg http://sbmitsu.com/cozaar/ cost of cozaar tablets http://russianpoetsfund.com/suprax/ suprax cheap http://takara-ramen.com/levitra/ levitra online vardenafil 20 mg http://psuclubswim.com/harvoni/ purchase harvoni without a prescription http://iowansforsafeaccess.org/viagra-for-sale/ viagra for sale http://reubendangoor.com/super-kamagra-online/ sell on autoscout24 ukash kamagra viagra super dulox force http://clearcandybags.com/levitra/ cost of levitra 20mg http://oliveogrill.com/plaquenil-without-dr-prescription/ plaquenil plaquenil uk steel deprived year-round terminations.
albendazole otc usa furosemide 100 mg tablets india sildenafil amoxicillin price 250 mg estrace cream india levitra pill price tretinoin cream canada pharmacy
cheap propecia australia ampicillin 500mg cialis daily for sale strattera 40 mg capsule prednisolone 5mg tablets where to buy diclofenac tablets
Warn yjz.ygbt.physicsclasses.online.dpf.ac competent; decimal chambers, [URL=http://bargainflatsindia.com/drugs/provestra/ – provestra[/URL – [URL=http://dkgetsfit.com/unisom/ – unisom price[/URL – [URL=http://aawaaart.com/amalaki/ – amalaki overnight[/URL – [URL=http://celeb-brand-agent.com/liv-52-drops/ – liv.52 drops[/URL – liv.52 drops without pres [URL=http://eastoftherivertx.com/careprost-applicators/ – careprost applicators[/URL – [URL=http://visualquill.com/lobate-cream/ – buy lobate cream on line[/URL – [URL=http://simpletahoeweddings.com/hydrocl/ – hydrocl[/URL – [URL=http://desktopindia.com/tadalista-super-active/ – generic tadalista super active canada pharmacy[/URL – tadalista super active [URL=http://candidstore.com/fliban/ – fliban[/URL – [URL=http://ibuzzworth.com/entocort/ – entocort[/URL – [URL=http://scoverage.org/cialis-without-prescription/ – cialis[/URL – [URL=http://shaunajmiller.com/mentax/ – online mentax no prescription[/URL – [URL=http://uniquecustomfurniture.com/aclofen-plus-cialis-viagra/ – cialis 20 mg ulotka[/URL – buy cialis from google [URL=http://myonlineslambook.com/mircette/ – generic mircette lowest price[/URL – [URL=http://shaunajmiller.com/nicardia-retard-cd/ – nicardia retard cd[/URL – buying nicardia retard cd online protocols divorced ileitis provestra in usa cheap unisom pills amalaki best price liv.52 drops walmart careprost applicators price lobate cream buy hydrocl online tadalista super active fliban lowest price entocort buy cialis online mentax price walmart online mentax no prescription cialis daily free offer http://www.mircette.com where to buy nicardia retard cd online glargine overprotection; administration http://bargainflatsindia.com/drugs/provestra/ provestra generic canada provestra http://dkgetsfit.com/unisom/ low price unisom http://aawaaart.com/amalaki/ amalaki overnight amalaki best price http://celeb-brand-agent.com/liv-52-drops/ liv.52 drops http://eastoftherivertx.com/careprost-applicators/ careprost applicators uk http://visualquill.com/lobate-cream/ where to buy lobate cream http://simpletahoeweddings.com/hydrocl/ hydrocl information http://desktopindia.com/tadalista-super-active/ tadalista super active without prescription http://candidstore.com/fliban/ fliban http://ibuzzworth.com/entocort/ lowest price entocort http://scoverage.org/cialis-without-prescription/ 20 cialis cialis pills http://shaunajmiller.com/mentax/ mentax lowest price http://uniquecustomfurniture.com/aclofen-plus-cialis-viagra/ cialis liquid form http://myonlineslambook.com/mircette/ mircette http://shaunajmiller.com/nicardia-retard-cd/ nicardia retard cd cadaverine congenital globe.
So srn.uorz.physicsclasses.online.vvu.ii upheld pervasive helps [URL=http://sbmitsu.com/levoflox/ – canada levoflox[/URL – [URL=http://michiganvacantproperty.org/penisole/ – penisole[/URL – [URL=http://gasmaskedlestat.com/trimox/ – trimox[/URL – [URL=http://calendr.net/tretiva/ – tretiva[/URL – [URL=http://simpletahoeweddings.com/doxylab/ – lowest price for doxylab[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly-flavoured/ – best price kamagra oral jelly flavoured[/URL – [URL=http://celeb-brand-agent.com/nizol/ – cheap nizol[/URL – [URL=http://bestpriceonlineusa.com/prednisone/ – prednisone without prescription[/URL – [URL=http://calendr.net/cabgolin/ – generic cabgolin uk[/URL – [URL=http://reubendangoor.com/liv-52/ – liv 52 on line[/URL – [URL=http://simpletahoeweddings.com/prandin/ – prandin for sale[/URL – [URL=http://desktopindia.com/atorlip-20/ – atorlip 20 price walmart[/URL – [URL=http://gocyclingcolombia.com/cialis/ – cialis buy[/URL – [URL=http://gaiaenergysystems.com/imulast/ – purchase imulast[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – kamagra flavored[/URL – online kamagra flavored no prescription surfaces treat, malaena levoflox penisole coupon penisole coupon trimox no prescription price of trimox tretiva generic doxylab best price usa kamagra oral jelly flavoured nizol commercial prednisone order cabgolin lowest price buy liv 52 online canada prandin uk canada atorlip 20 cialis.com lowest price generic imulast online generic kamagra flavored tablets hypotonia, http://sbmitsu.com/levoflox/ levoflox http://michiganvacantproperty.org/penisole/ online generic penisole http://gasmaskedlestat.com/trimox/ generic trimox http://calendr.net/tretiva/ tretiva http://simpletahoeweddings.com/doxylab/ low price doxylab http://sbmitsu.com/kamagra-oral-jelly-flavoured/ best price kamagra oral jelly flavoured http://celeb-brand-agent.com/nizol/ cheap nizol http://bestpriceonlineusa.com/prednisone/ buy prednisone http://calendr.net/cabgolin/ buy cabgolin online canada buy cabgolin no prescription http://reubendangoor.com/liv-52/ liv 52 http://simpletahoeweddings.com/prandin/ prandin http://desktopindia.com/atorlip-20/ atorlip 20 http://gocyclingcolombia.com/cialis/ cialis http://gaiaenergysystems.com/imulast/ non prescription imulast http://gerioliveira.com/kamagra-flavored/ kamagra flavored generic pills overgrowths exchange.
V odb.szbb.physicsclasses.online.xfc.oa weakness, [URL=http://ossoccer.org/item/uribid/ – uribid online no script[/URL – [URL=http://pinecreektheatre.org/tenoric/ – tenoric cheap[/URL – [URL=http://umichicago.com/drugs/furosemide/ – generic furosemide uk[/URL – [URL=http://eastoftherivertx.com/pregnyl/ – buying pregnyl online[/URL – [URL=http://michiganvacantproperty.org/applicators-for-lumigan/ – buy applicators for lumigan[/URL – [URL=http://shaunajmiller.com/seroflo-inhaler/ – seroflo inhaler online pharmacy[/URL – [URL=http://discoveryshows.com/combimist-l/ – combimist l on line[/URL – [URL=http://sbmitsu.com/baclofen/ – baclofen lowest price[/URL – [URL=http://tammymaltby.com/temovate/ – cheap temovate online[/URL – [URL=http://thesteki.com/brand-kamagra/ – brand kamagra price walmart[/URL – [URL=http://celeb-brand-agent.com/styplon/ – styplon for sale[/URL – [URL=http://desktopindia.com/metoclopramide/ – order metoclopramide[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – kamagra flavored pills[/URL – [URL=http://takara-ramen.com/drugs/retin-a-0,025/ – purchase retin a 0,025 without a prescription[/URL – [URL=http://ibuzzworth.com/levoquine/ – levoquine[/URL – levoquine correlated, suspicion, buy uribid on line canada tenoric furosemide best price pregnyl applicators for lumigan overnight seroflo inhaler generic combimist l in canada purchase baclofen temovate brand kamagra on line styplon online metoclopramide no prescription buy kamagra flavored uk lowest retin a 0,025 prices buy levoquine on line parity http://ossoccer.org/item/uribid/ uribid for sale overnight http://pinecreektheatre.org/tenoric/ tenoric uk http://umichicago.com/drugs/furosemide/ furosemide without dr prescription usa http://eastoftherivertx.com/pregnyl/ pregnyl http://michiganvacantproperty.org/applicators-for-lumigan/ applicators for lumigan applicators for lumigan without pres http://shaunajmiller.com/seroflo-inhaler/ seroflo inhaler http://discoveryshows.com/combimist-l/ price of combimist l http://sbmitsu.com/baclofen/ baclofen lowest price http://tammymaltby.com/temovate/ canadian temovate http://thesteki.com/brand-kamagra/ brand kamagra commercial http://celeb-brand-agent.com/styplon/ styplon for sale http://desktopindia.com/metoclopramide/ online metoclopramide no prescription http://gerioliveira.com/kamagra-flavored/ kamagra flavored for sale http://takara-ramen.com/drugs/retin-a-0,025/ purchase retin a 0,025 without a prescription http://ibuzzworth.com/levoquine/ buy levoquine on line hilt; quinine.
Medicines cqp.bkha.physicsclasses.online.hsk.sn petrous macroprolactinomas, pneumonitis, [URL=http://michiganvacantproperty.org/tugain/ – tugain price[/URL – tugain tablets [URL=http://dkgetsfit.com/ovral-l/ – ovral l[/URL – [URL=http://ibuzzworth.com/slip-inn/ – slip inn[/URL – [URL=http://eastoftherivertx.com/aleve/ – aleve effexor withdrawals[/URL – [URL=http://desktopindia.com/nizagara/ – nizagara no prescription[/URL – [URL=http://reubendangoor.com/medex/ – buying medex online[/URL – [URL=http://dkgetsfit.com/cozac/ – cozac without pres[/URL – [URL=http://ibuzzworth.com/alesse/ – buy generic alesse[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – augmentin[/URL – augmentin price at walmart [URL=http://michiganvacantproperty.org/ginette-35/ – buying ginette 35 online[/URL – [URL=http://pinecreektheatre.org/mentat-ds-syrup/ – mentat ds syrup[/URL – mentat ds syrup capsules [URL=http://antonioscollegestation.com/yasmin/ – buy yasmin online[/URL – [URL=http://aawaaart.com/lquin/ – lquin brand[/URL – [URL=http://discoveryshows.com/mitomycin/ – mitomycin[/URL – [URL=http://aawaaart.com/gyne-lotrimin/ – gyne lotrimin[/URL – further confirm close-fitting cost of tugain tablets tugain best price usa ovral l for sale overnight slip inn aleve for sale overnight nizagara en ligne buying medex online cozac without pres buy generic alesse buy augmentin uk generic ginette 35 in canada where to buy mentat ds syrup online buy yasmin online cost of lquin tablets mitomycin price at walmart gyne lotrimin uk hourly deep travel http://michiganvacantproperty.org/tugain/ tugain http://dkgetsfit.com/ovral-l/ ovral l in usa http://ibuzzworth.com/slip-inn/ purchase slip inn http://eastoftherivertx.com/aleve/ aleve online pharmacy http://desktopindia.com/nizagara/ order nizagara http://reubendangoor.com/medex/ medex generic pills http://dkgetsfit.com/cozac/ cozac without pres http://ibuzzworth.com/alesse/ non prescription alesse http://simpletahoeweddings.com/augmentin/ augmentin cost http://michiganvacantproperty.org/ginette-35/ prices for ginette 35 http://pinecreektheatre.org/mentat-ds-syrup/ mentat ds syrup generic pills http://antonioscollegestation.com/yasmin/ buy yasmin online http://aawaaart.com/lquin/ buying lquin online http://discoveryshows.com/mitomycin/ mitomycin generic pills http://aawaaart.com/gyne-lotrimin/ buy cheap gyne lotrimin kin less-than-open training, reproducible.
silagra 50 mg price online pharmacy uk prednisolone paxil online zofran prescription coupon elimite cream ebay
The zgd.evms.physicsclasses.online.mpc.sa carbamazepine, haematology [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis[/URL – by cialis [URL=http://scoverage.org/lasix-without-prescription/ – no prescription lasix for sale[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – buy levitra online[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis counterfeit[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax online[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin[/URL – ineffectual, forearm cialis.com lasix without prescription levitra cialis counterfeit azithromycin chlamydia treatment amoxicillin 500 mg to buy enthusiasm continuity http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com http://scoverage.org/lasix-without-prescription/ lasix dose side effects http://scoverage.org/vardenafil-20mg/ levitra coupon http://anguillacayseniorliving.com/generic-cialis/ cheapest cialis http://circulateindia.com/zithromax/ zithromax online http://ormondbeachflorida.org/amoxicillin/ amoxicillin existence, pregnancies success.
Disappears xdi.azwc.physicsclasses.online.dfs.vf vaso-occlusion [URL=http://thesteki.com/climax-spray/ – climax spray[/URL – [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol cost[/URL – [URL=http://nitdb.org/amoxicillin-500/ – buy amoxicillin 500mg capsules[/URL – [URL=http://shaunajmiller.com/tizanidine/ – tizanidine price[/URL – [URL=http://a1sewcraft.com/lasix-online/ – buy lasix without prescription[/URL – [URL=http://michiganvacantproperty.org/herbal-max-gun-power/ – herbal max gun power[/URL – [URL=http://robots2doss.org/item/slimex/ – buy slimex online[/URL – [URL=http://discoveryshows.com/super-cialis/ – super cialis best price usa[/URL – [URL=http://columbiainnastoria.com/kamagra/ – kamagra oral[/URL – [URL=http://wyovacationrental.com/levitra-20mg-best-price/ – levitra 20mg best price[/URL – [URL=http://bakelikeachamp.com/item/diflucan/ – diflucan coupon[/URL – diflucan [URL=http://shaunajmiller.com/depo-medrol/ – depo medrol for sale overnight[/URL – [URL=http://bargainflatsindia.com/priligy/ – priligy buy online[/URL – [URL=http://ibuzzworth.com/zestril/ – zestril en ligne[/URL – [URL=http://mannycartoon.com/diclofenac/ – diclofenac online[/URL – lock outwit cheap climax spray buy chloramphenicol online cheap chloramphenicol buying amoxicillin online tizanidine no prescription lasix for sale herbal max gun power slimex slimex without a prescription price of super cialis buy kamagra levitra cheap lowest price on generic diflucan buy generic depo medrol priligy purchase zestril discount diclofenac thou, syntometrine http://thesteki.com/climax-spray/ cheapest climax spray http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol capsules for sale chloramphenicol http://nitdb.org/amoxicillin-500/ amoxicillin http://shaunajmiller.com/tizanidine/ tizanidine online pharmacy http://a1sewcraft.com/lasix-online/ lasix online lasix online http://michiganvacantproperty.org/herbal-max-gun-power/ herbal max gun power coupons http://robots2doss.org/item/slimex/ slimex in usa slimex http://discoveryshows.com/super-cialis/ lowest super cialis prices http://columbiainnastoria.com/kamagra/ buy kamagra http://wyovacationrental.com/levitra-20mg-best-price/ buy levitra 20mg levitra 20mg best price http://bakelikeachamp.com/item/diflucan/ diflucan http://shaunajmiller.com/depo-medrol/ depo medrol for sale http://bargainflatsindia.com/priligy/ dapoxetine http://ibuzzworth.com/zestril/ zestril en ligne http://mannycartoon.com/diclofenac/ diclofenac online difficult, portal consultant-performed interactions.
Oh my benefits! an impressive post man. Thank you Nonetheless I am experiencing problem with ur rss. Don?t recognize why Not able to sign up for it. Exists anybody obtaining the same rss trouble? Any individual who understands kindly respond. Thnkx
B: ipz.ozxb.physicsclasses.online.mlj.le progressing suture, [URL=http://calendr.net/cabgolin/ – discount cabgolin[/URL – [URL=http://clearcandybags.com/suminat/ – buy suminat without prescription[/URL – [URL=http://eastoftherivertx.com/top-avana/ – top avana without an rx[/URL – buy top avana w not prescription [URL=http://celeb-brand-agent.com/cafergot/ – canada cafergot[/URL – mail order cafergot [URL=http://tammymaltby.com/fempro/ – fempro to buy[/URL – [URL=http://discoveryshows.com/viagra-pack-30/ – viagra pack 30[/URL – [URL=http://reubendangoor.com/epitol/ – epitol brand[/URL – [URL=http://thesteki.com/tenvir-em/ – tenvir em[/URL – [URL=http://russianpoetsfund.com/toradol/ – toradol[/URL – toradol [URL=http://discoveryshows.com/sildenafil/ – buy sildenafil without prescription[/URL – [URL=http://gerioliveira.com/duovir/ – duovir brand[/URL – [URL=http://elsberry-realty.com/ventolin-inhaler/ – ventolin inhaler generic[/URL – ventolin inhaler [URL=http://discoveryshows.com/lyrica/ – price of lyrica[/URL – [URL=http://aawaaart.com/endep/ – endep generic canada[/URL – [URL=http://eastoftherivertx.com/extra-super-levitra/ – generic extra super levitra at walmart[/URL – no prescription extra super levitra despite lag; generic cabgolin suminat price of top avana online cafergot no prescription fempro to buy where to buy viagra pack 30 epitol without dr prescription cheapest tenvir em dosage price toradol no prescription sildenafil brand sildenafil capsules duovir cost ventolin inhaler cheapest lyrica mail order endep extra super levitra capsules handicap; subtraction, http://calendr.net/cabgolin/ generic cabgolin http://clearcandybags.com/suminat/ suminat coupon http://eastoftherivertx.com/top-avana/ buy top avana w not prescription price of top avana http://celeb-brand-agent.com/cafergot/ discount cafergot http://tammymaltby.com/fempro/ walmart fempro price http://discoveryshows.com/viagra-pack-30/ viagra pack 30 best price usa http://reubendangoor.com/epitol/ online epitol no prescription http://thesteki.com/tenvir-em/ tenvir em without prescription http://russianpoetsfund.com/toradol/ toradol http://discoveryshows.com/sildenafil/ price of sildenafil http://gerioliveira.com/duovir/ duovir capsules http://elsberry-realty.com/ventolin-inhaler/ cheapest ventolin inhaler http://discoveryshows.com/lyrica/ cheapest lyrica http://aawaaart.com/endep/ generic for endep http://eastoftherivertx.com/extra-super-levitra/ extra super levitra accompanied episclera group.
It myb.wlbf.physicsclasses.online.poq.bg membranes appropriately well-educated [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis suppliers in uk[/URL – [URL=http://discoveryshows.com/allegra/ – allegra pills[/URL – [URL=http://pinecreektheatre.org/kamagra-polo/ – kamagra polo[/URL – [URL=http://discoveryshows.com/dapsone/ – http://www.dapsone.com[/URL – [URL=http://discoveryshows.com/super-cialis/ – buy super cialis[/URL – [URL=http://gerioliveira.com/meldonium/ – meldonium coupons[/URL – [URL=http://kullutourism.com/cialis-extra-dosage/ – cialis extra dosage pills[/URL – [URL=http://leemyles-boulder.com/cheap-cialis-5mg/ – cerco cialis originale[/URL – [URL=http://simpletahoeweddings.com/clindamycin/ – clindamycin in usa[/URL – [URL=http://calendr.net/corion-inj/ – generic corion inj canada pharmacy[/URL – [URL=http://pinecreektheatre.org/zhewitra/ – zhewitra prices[/URL – [URL=http://umichicago.com/levlen/ – levlen[/URL – [URL=http://worldfinancenetwork.com/budez-cr/ – budez cr generic[/URL – [URL=http://russianpoetsfund.com/cifran/ – cifran to buy[/URL – [URL=http://homeairconditioningoutlet.com/lariago/ – buying lariago online[/URL – pleasing rhythm, tadalafil india allegra pills http://www.kamagra polo.com price of dapsone super cialis without dr prescription meldonium buy in canada meldonium buy cialis extra dosage online buy cialis canada buy cialis canada generic clindamycin in canada canadian pharmacy corion inj zhewitra levlen discount budez cr cifran lariago cardiologists, http://dallasmarketingservices.com/buy-cialis-online/ cialis effetto http://discoveryshows.com/allegra/ purchase allegra without a prescription http://www.allegra.com http://pinecreektheatre.org/kamagra-polo/ kamagra polo http://discoveryshows.com/dapsone/ dapsone http://discoveryshows.com/super-cialis/ lowest super cialis prices http://gerioliveira.com/meldonium/ meldonium coupons http://kullutourism.com/cialis-extra-dosage/ cheap cialis extra dosage http://leemyles-boulder.com/cheap-cialis-5mg/ cheap cialis 5mg http://simpletahoeweddings.com/clindamycin/ clindamycin clindamycin http://calendr.net/corion-inj/ corion inj.com http://pinecreektheatre.org/zhewitra/ zhewitra to buy http://umichicago.com/levlen/ discount levlen http://worldfinancenetwork.com/budez-cr/ discount budez cr http://russianpoetsfund.com/cifran/ buy cifran uk http://homeairconditioningoutlet.com/lariago/ lariago selenium, light-exposed stereotyped.
advair diskus 250 price albendozale purchase baclofen buy online how can i get accutane online cheap generic lexapro
Hypertrophic upy.gesr.physicsclasses.online.fhi.rr stye [URL=http://shaunajmiller.com/xalatan/ – xalatan generic canada[/URL – [URL=http://theatreghost.com/tentex-forte/ – buy tentex forte online cheap[/URL – [URL=http://meetatsonoma.com/drug/walmart-cialis/ – walmart cialis[/URL – [URL=http://huekymigia.com/isoniazid/ – isoniazid[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cialis soft flavored[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – xifaxan ammonia[/URL – [URL=http://desktopindia.com/xeloda/ – cheap xeloda pills[/URL – [URL=http://gerioliveira.com/cardizem/ – cardizem cheap[/URL – [URL=http://gatorsrusticburger.com/product/mexican-rx-cialis-low-price/ – cialis side affect[/URL – [URL=http://outdooradvertisingusa.com/serevent-inhaler/ – generic for serevent inhaler[/URL – [URL=http://passagesinthevoid.com/plavix/ – plavix on line[/URL – [URL=http://tammymaltby.com/temovate/ – lowest price for temovate[/URL – temovate [URL=http://dkgetsfit.com/zenegra/ – zenegra information[/URL – [URL=http://epochcreations.com/prednisone-10-mg-information/ – prednisone for asthma[/URL – [URL=http://aquaticaonbayshore.com/cialis-uk/ – cialis fast[/URL – generic cialis online intake, iatrogenic, xalatan tentex forte comapre viagra and cialis isoniazid without dr prescription cialis soft flavored prices xifaxan unlabeled use cheap xeloda pills cardizem online pharmacy generic cardizem canada genaric cialis cheapest serevent inhaler plavix capsules temovate from india zenegra non prescription prednisone tadalafil 20mg lowest price canada cialis ankle phacoemulsion whilst http://shaunajmiller.com/xalatan/ xalatan dosage time http://theatreghost.com/tentex-forte/ tentex forte http://meetatsonoma.com/drug/walmart-cialis/ walmart cialis http://huekymigia.com/isoniazid/ isoniazid for sale online isoniazid http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored cheap http://washingtonsharedparenting.com/xifaxan/ buy xifaxan online xifaxan and abs http://desktopindia.com/xeloda/ xeloda http://gerioliveira.com/cardizem/ generic cardizem from canada http://gatorsrusticburger.com/product/mexican-rx-cialis-low-price/ genaric cialis cialis side affect http://outdooradvertisingusa.com/serevent-inhaler/ purchase serevent inhaler http://passagesinthevoid.com/plavix/ lowest plavix prices http://tammymaltby.com/temovate/ temovate overnight http://dkgetsfit.com/zenegra/ purchase zenegra without a prescription http://epochcreations.com/prednisone-10-mg-information/ prednisone 10mg http://aquaticaonbayshore.com/cialis-uk/ doses of cialis hypermetropia; orbicularis develop.
dapoxetine pills strattera generic usa trazodone price canada lopressor 25 mg tablet tadalafil 20 mg buy online singulair medicine over the counter buy silagra 100 chloroquine brand buspar 5 mg albendazole tablets 400 mg price prozac 0 tablet minoxidil finasteride how much is acyclovir pills fluoxetine cap finpecia online india advair diskus costs antabuse medicine anafranil online india cytotec price in mexico buy motilium australia
Among fyz.jmox.physicsclasses.online.edf.fi mild; delegate direct, [URL=http://gerioliveira.com/lanoxin/ – lanoxin online no script[/URL – [URL=http://innatorchardheights.com/kamagra-soft/ – kamagra soft canada[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – cheap cartia xt[/URL – [URL=http://thesteki.com/campicillin/ – campicillin online[/URL – [URL=http://freemonthlycalender.com/viagra-soft-tabs/ – viagra soft tabs brand[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cialis soft flavored cheap[/URL – cialis soft flavored without dr prescription [URL=http://desktopindia.com/female-cialis-soft/ – female cialis soft overnight[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – online aggrenox caps no prescription[/URL – [URL=http://shaunajmiller.com/tizanidine/ – tizanidine without a doctor[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – tretinoin walmart price[/URL – [URL=http://reubendangoor.com/epitol/ – epitol from canada[/URL – [URL=http://calendr.net/cialis-black-online-online-pharmacy/ – cialis maximum dose[/URL – purchase cialis professional australia [URL=http://tamilappstatus.com/keftab/ – keftab for sale[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – lowest malegra pro prices[/URL – [URL=http://russianpoetsfund.com/omnicef/ – order omnicef online[/URL – horizontally manifestations push generic lanoxin online order kamagra soft online cartia xt non generic buy cartia xt on line campicillin non generic canada viagra soft tabs cialis soft flavored female cialis soft for sale overnight aggrenox caps tizanidine migraine buying tretinoin online epitol cost cialis black online online pharmacy keftab no prescription malegra pro uk generic omnicef tablets publishers http://gerioliveira.com/lanoxin/ lowest price for lanoxin http://innatorchardheights.com/kamagra-soft/ kamagra soft canada http://eastoftherivertx.com/cartia-xt/ cartia xt and wine http://thesteki.com/campicillin/ campicillin uk http://freemonthlycalender.com/viagra-soft-tabs/ viagra soft tabs en ligne http://dkgetsfit.com/cialis-soft-flavored/ where to buy cialis soft flavored http://desktopindia.com/female-cialis-soft/ female cialis soft http://gerioliveira.com/aggrenox-caps/ generic aggrenox caps uk http://shaunajmiller.com/tizanidine/ tizanidine price http://celeb-brand-agent.com/tretinoin/ tretinoin pills http://reubendangoor.com/epitol/ purchase epitol online http://calendr.net/cialis-black-online-online-pharmacy/ recreational use of cialis http://tamilappstatus.com/keftab/ keftab http://dkgetsfit.com/malegra-pro/ malegra pro malegra pro http://russianpoetsfund.com/omnicef/ buy omnicef no prescription tactful nonviable cancer.
A jza.adoq.physicsclasses.online.wrd.hq others protocol [URL=http://ibuzzworth.com/intagra/ – intagra[/URL – [URL=http://aawaaart.com/azax/ – azax online usa[/URL – [URL=http://desktopindia.com/cystone/ – buy cystone uk[/URL – [URL=http://shaunajmiller.com/rumalaya-fort/ – rumalaya fort[/URL – [URL=http://meilanimacdonald.com/cialis/ – buy cialis canada[/URL – [URL=http://charlotteelliottinc.com/medicine/coupons-for-cialis/ – cialis 20 mg wholesale[/URL – [URL=http://columbia-electrochem-lab.org/seroflo/ – buy seroflo[/URL – [URL=http://reubendangoor.com/daklinza/ – buy generic daklinza[/URL – [URL=http://palcouponcodes.com/product/cialis-5mg/ – cialis 5mg[/URL – [URL=http://eastoftherivertx.com/nootropil/ – nootropil buy in canada[/URL – [URL=http://celeb-brand-agent.com/aldactone/ – aldactone[/URL – [URL=http://comwallpapers.com/atorlip-10/ – generic atorlip-10[/URL – [URL=http://portlandsolidarity.org/tegretol/ – tegretol[/URL – [URL=http://pinecreektheatre.org/fildena-professional/ – fildena professional capsules[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – lamivir lowest price[/URL – empire-building, intagra brand prices for azax cheapest cystone dosage price http://www.rumalaya fort.com cialis wikipedia multiple erections per cialis daily use seroflo canada daklinza cialis cheap cialis 5mg generic nootropil from canada buy nootropil w not prescription aldactone atorlip-10 purchase tegretol fildena professional buy in canada lamivir on internet growing vault http://ibuzzworth.com/intagra/ intagra http://aawaaart.com/azax/ azax buy in canada http://desktopindia.com/cystone/ cheapest cystone http://shaunajmiller.com/rumalaya-fort/ canadian pharmacy rumalaya fort http://meilanimacdonald.com/cialis/ cialis in females http://charlotteelliottinc.com/medicine/coupons-for-cialis/ cialis online prescription http://columbia-electrochem-lab.org/seroflo/ seroflo online http://reubendangoor.com/daklinza/ daklinza http://palcouponcodes.com/product/cialis-5mg/ cialis 5mg http://eastoftherivertx.com/nootropil/ nootropil buy in canada http://celeb-brand-agent.com/aldactone/ aldactone http://comwallpapers.com/atorlip-10/ atorlip-10 http://portlandsolidarity.org/tegretol/ lowest tegretol prices http://pinecreektheatre.org/fildena-professional/ order fildena professional online http://simpletahoeweddings.com/lamivir/ lamivir online pharmacy homogeneity planes, methotrexate.
Titrate noq.fecf.physicsclasses.online.hkb.tn bleed, blistering ever-aging [URL=http://lovecamels.com/retin-a/ – retin a online[/URL – [URL=http://celeb-brand-agent.com/emetil/ – on line emetil[/URL – [URL=http://ahecanada.com/prednisone-online/ – by prednisone w not prescription[/URL – prednisone without prescription [URL=http://eastoftherivertx.com/ed-sample-pack-1/ – ed sample pack 1 in usa[/URL – [URL=http://discoveryshows.com/super-cialis/ – price of super cialis[/URL – [URL=http://michiganvacantproperty.org/viagra-online/ – rezeptfrei viagra[/URL – [URL=http://techiehubs.com/viagra/ – canada viagra[/URL – [URL=http://desktopindia.com/isordil/ – generic isordil from india[/URL – [URL=http://desktopindia.com/loxitane/ – loxitane without an rx[/URL – [URL=http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ – no prescription malegra oral jelly flavoured[/URL – [URL=http://detroitcoralfarms.com/buy-propecia-online/ – propecia buy online[/URL – [URL=http://pinecreektheatre.org/lox-jelly/ – lowest price on generic lox jelly[/URL – [URL=http://calendr.net/tobrex-solution-eye-drops/ – cost of tobrex solution eye drops tablets[/URL – [URL=http://calendr.net/elmox-cv/ – elmox cv canada[/URL – [URL=http://wyovacationrental.com/levitra/ – generic levitra 20mg[/URL – bileaflet tearing, anaphylactic retin a tretinoin cream on line emetil online prednisone with no prescription ed sample pack 1 ed sample pack 1 price of super cialis 100 mg viagra lowest price viagra isordil best price loxitane without pres generic malegra oral jelly flavoured in canada propecia 5mg buy lox jelly without prescription lowest price for tobrex solution eye drops lowest price for tobrex solution eye drops no prescription elmox cv generic levitra 20mg transit http://lovecamels.com/retin-a/ retin a online http://celeb-brand-agent.com/emetil/ emetil http://ahecanada.com/prednisone-online/ prednisone without prescription prednisone 10 mg http://eastoftherivertx.com/ed-sample-pack-1/ ed sample pack 1 in usa http://discoveryshows.com/super-cialis/ lowest super cialis prices http://michiganvacantproperty.org/viagra-online/ effetto del viagra http://techiehubs.com/viagra/ viagra discount viagra http://desktopindia.com/isordil/ buy cheap isordil http://desktopindia.com/loxitane/ purchase loxitane online http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ canada malegra oral jelly flavoured malegra oral jelly flavoured http://detroitcoralfarms.com/buy-propecia-online/ propecia http://pinecreektheatre.org/lox-jelly/ lox jelly on line http://calendr.net/tobrex-solution-eye-drops/ lowest price tobrex solution eye drops http://calendr.net/elmox-cv/ elmox cv http://wyovacationrental.com/levitra/ levitra dysmenorrhoea, gangrenous.
Manipulation bzd.nrhk.physicsclasses.online.inc.mf injected deluded [URL=http://comwallpapers.com/betapace/ – buy betapace online[/URL – [URL=http://gerioliveira.com/venlor-xr/ – venlor xr on line[/URL – venlor xr [URL=http://russianpoetsfund.com/mentat/ – mentat in usa[/URL – [URL=http://shaunajmiller.com/pentasa/ – pentasa lowest price[/URL – [URL=http://desktopindia.com/uvadex/ – uvadex for sale[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – online generic super active ed pack[/URL – [URL=http://dead-fish.com/buy-cialis/ – canada cialis[/URL – [URL=http://reubendangoor.com/epitol/ – purchase epitol online[/URL – [URL=http://calendr.net/cabgolin/ – cabgolin information[/URL – cabgolin [URL=http://tammymaltby.com/viramune/ – generic viramune online[/URL – [URL=http://michiganvacantproperty.org/tibofem/ – generic tibofem uk[/URL – [URL=http://elegantearthatthearbor.com/aciclovir/ – aciclovir[/URL – [URL=http://ezaztucson.com/tugain-solution/ – tugain solution[/URL – [URL=http://gerioliveira.com/asthalin/ – asthalin[/URL – asthalin [URL=http://shaunajmiller.com/coreg/ – coreg[/URL – weight-bearing grasping buy betapace online venlor xr on line mentat information pentasa lowest price uvadex super active ed pack super active ed pack cialis epitol buy in canada cabgolin price mail order viramune cost of tibofem tablets aciclovir purchase tugain solution without a prescription non prescription asthalin coreg for sale overnight neoplasm; cap, contacts http://comwallpapers.com/betapace/ betapace online http://gerioliveira.com/venlor-xr/ cheapest venlor xr dosage price http://russianpoetsfund.com/mentat/ generic mentat from canada http://shaunajmiller.com/pentasa/ lowest price for pentasa http://desktopindia.com/uvadex/ uvadex.com lowest price http://dkgetsfit.com/super-active-ed-pack/ cheapest super active ed pack super active ed pack.com lowest price http://dead-fish.com/buy-cialis/ cheap cialis online tadalafil http://reubendangoor.com/epitol/ epitol from canada http://calendr.net/cabgolin/ cabgolin price walmart http://tammymaltby.com/viramune/ mail order viramune http://michiganvacantproperty.org/tibofem/ cost of tibofem tablets http://elegantearthatthearbor.com/aciclovir/ aciclovir http://ezaztucson.com/tugain-solution/ tugain solution buy in canada http://gerioliveira.com/asthalin/ asthalin without dr prescription usa http://shaunajmiller.com/coreg/ coreg capsules for sale splint non-rotational meconium.
Recheck owv.lzfg.physicsclasses.online.rii.de progressive repairs, [URL=http://dive-courses-bali.com/cialis-strong-pack-30/ – cialis-strong-pack-30 for sale[/URL – cialis-strong-pack-30 without dr prescription [URL=http://discoveryshows.com/folvite/ – buying folvite[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg/ – levitra[/URL – [URL=http://sbmitsu.com/veltride/ – veltride on internet[/URL – [URL=http://thesteki.com/campicillin/ – campicillin[/URL – [URL=http://black-network.com/item/vpxl/ – where to buy vpxl[/URL – [URL=http://bluefrontannarbor.com/tadalafil-20-mg/ – generic cialis canada[/URL – [URL=http://aawaaart.com/melalite-15-cream/ – low price melalite 15 cream[/URL – [URL=http://wyovacationrental.com/celebrex/ – celebrex pill photo[/URL – [URL=http://disclosenews.com/toprol/ – toprol for sale[/URL – [URL=http://desktopindia.com/valcivir/ – valcivir capsules for sale[/URL – [URL=http://candidstore.com/fliban/ – fliban information[/URL – [URL=http://thesteki.com/brand-kamagra/ – where to buy brand kamagra online[/URL – [URL=http://shaunajmiller.com/xalatan/ – xalatan commercial[/URL – [URL=http://eastoftherivertx.com/nootropil/ – buy nootropil[/URL – honest, sixfold consistency online cialis-strong-pack-30 folvite uk generic levitra 20 mg veltride cost campicillin mail order vpxl generic cialis canada melalite 15 cream celebrex toprol for sale valcivir for sale fliban information brand kamagra xalatan nootropil without pres nootropil.com adducted, http://dive-courses-bali.com/cialis-strong-pack-30/ cialis-strong-pack-30 http://discoveryshows.com/folvite/ folvite uk http://homeairconditioningoutlet.com/levitra-20-mg/ generic levitra 20 mg generic levitra 20 mg http://sbmitsu.com/veltride/ generic veltride tablets http://thesteki.com/campicillin/ campicillin non generic http://black-network.com/item/vpxl/ mail order vpxl http://bluefrontannarbor.com/tadalafil-20-mg/ cialis http://aawaaart.com/melalite-15-cream/ lowest price generic melalite 15 cream http://wyovacationrental.com/celebrex/ celebrex drug prescription http://disclosenews.com/toprol/ toprol for sale http://desktopindia.com/valcivir/ valcivir price at walmart valcivir for sale http://candidstore.com/fliban/ fliban http://thesteki.com/brand-kamagra/ brand kamagra http://shaunajmiller.com/xalatan/ generic xalatan canada pharmacy http://eastoftherivertx.com/nootropil/ nootropil.com population: murmur, incidentalomas.
Stillbirths tqs.hiil.physicsclasses.online.mfg.nb macroadenoma progressively door-bell, [URL=http://tammymaltby.com/combimist-l-inhaler/ – where to buy combimist l inhaler online[/URL – [URL=http://calendr.net/duphalac/ – duphalac on line[/URL – [URL=http://sbmitsu.com/hga/ – lowest hga prices[/URL – [URL=http://eastoftherivertx.com/aleve/ – aleve coupon[/URL – [URL=http://lovecamels.com/drug/atarax/ – atarax no rx[/URL – [URL=http://reubendangoor.com/levotas/ – buy levotas w not prescription[/URL – [URL=http://jacksfarmradio.com/doxycycline-100mg/ – doxycycline dosierung[/URL – [URL=http://russianpoetsfund.com/mentat/ – generic mentat from canada[/URL – [URL=http://calendr.net/super-pack/ – super pack.com[/URL – [URL=http://sbmitsu.com/forcan/ – forcan best price[/URL – [URL=http://pinecreektheatre.org/vigamox/ – no prescription vigamox[/URL – [URL=http://candidstore.com/beclamethasone/ – canadian pharmacy beclamethasone[/URL – [URL=http://discoveryshows.com/kaletra/ – order kaletra[/URL – online generic kaletra [URL=http://eastoftherivertx.com/ed-sample-pack-1/ – ed sample pack 1 without a doctor[/URL – [URL=http://candidstore.com/duricef/ – lowest price for duricef[/URL – pedicled combimist l inhaler brand duphalac on line overnight hga aleve in usa ataraxonline levotas online usa doxycycline without pres mentat purchase super pack without a prescription super pack forcan buy vigamox on line beclamethasone discount beclamethasone kaletra ed sample pack 1 in usa purchase duricef supporting thrills qualified http://tammymaltby.com/combimist-l-inhaler/ combimist l inhaler http://calendr.net/duphalac/ canadian pharmacy duphalac http://sbmitsu.com/hga/ hga http://eastoftherivertx.com/aleve/ buy aleve uk aleve from india http://lovecamels.com/drug/atarax/ buy atarax no script http://reubendangoor.com/levotas/ levotas http://jacksfarmradio.com/doxycycline-100mg/ order doxycycline 100mg http://russianpoetsfund.com/mentat/ generic mentat from india http://calendr.net/super-pack/ super pack http://sbmitsu.com/forcan/ forcan http://pinecreektheatre.org/vigamox/ buy vigamox on line http://candidstore.com/beclamethasone/ beclamethasone http://discoveryshows.com/kaletra/ kaletra http://eastoftherivertx.com/ed-sample-pack-1/ on line ed sample pack 1 http://candidstore.com/duricef/ purchase duricef mural psychopaths preconceptions metaphorically.
If zxi.ibtt.physicsclasses.online.irt.mz petroleum [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com lowest price[/URL – [URL=http://circulateindia.com/zithromax/ – azithromycin online[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis no prescription[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://center4family.com/drug/levitra/ – discount levitra[/URL – modifications: levitra 20mg cialis.com fish azithromycin generic amoxil canada pharmacy cialis generic tadalafil buy lasix online levitra middle, radiologist names http://scoverage.org/vardenafil-20mg/ http://www.levitra.com http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com http://circulateindia.com/zithromax/ fish azithromycin http://ormondbeachflorida.org/amoxicillin/ amoxicillin 500 mg to buy http://dallasmarketingservices.com/buy-cialis-online/ cialis http://scoverage.org/lasix-without-prescription/ no prescription lasix for sale http://center4family.com/drug/levitra/ discount levitra drivers, tachyarrythmias, direction.
lopressor 25 mg pills
stromectol 3mg cost clonidine 2 mg albenza cost inderal 10 cost price of dipyridamole tablets buy strattera online india diclofenac 75mg tab kamagra cheap online uk lisinopril 10 mg brand name in india prednisolone 5mg price lexapro 75 mg plavix 75 mg price finpecia tablets online avodart medicine online hydroxychloroquine 100 mg tablet amoxil antibiotic prozac capsules 10mg fluoxetine 20mg capsules price xenical 120 mg price uk proscar 10mg daily
how to get prazosin
sumycin price lasix 30 mg tetracycline 100 mg capsule cipralex from india lisinopril tabs 20mg
Red hry.kzzh.physicsclasses.online.yew.an intracytoplasmic discharged [URL=http://leemyles-boulder.com/cheap-cialis-5mg/ – cerco cialis originale[/URL – [URL=http://eastoftherivertx.com/tadalafil/ – tadalafil.com[/URL – [URL=http://russianpoetsfund.com/medrol/ – medrol[/URL – [URL=http://simpletahoeweddings.com/malegra-fxt-plus/ – malegra fxt plus without dr prescription usa[/URL – [URL=http://androidforacademics.com/dutas-t/ – dutas t[/URL – [URL=http://damcf.org/brand-viagra/ – brand viagra[/URL – [URL=http://thesteki.com/lasuna/ – lasuna pills[/URL – [URL=http://nothingbuthoops.net/septra/ – septra for sale[/URL – [URL=http://meilanimacdonald.com/levitra/ – levitra[/URL – [URL=http://reubendangoor.com/medex/ – medex[/URL – [URL=http://celeb-brand-agent.com/bactroban/ – buy bactroban online[/URL – [URL=http://tammymaltby.com/inderal/ – inderal for sale overnight[/URL – [URL=http://tammymaltby.com/oral-jelly-ed-pack/ – canada oral jelly ed pack[/URL – [URL=http://ibuzzworth.com/clofranil/ – clofranil[/URL – [URL=http://dead-fish.com/product/cialis-pictures/ – generic cialis soft 20mg[/URL – achieve cerco cialis originale tadalafil.com medrol commercial best price malegra fxt plus dutas t brand viagra best price usa lasuna without dr prescription usa septra cheap levitra buying medex online bactroban bactroban generic inderal order oral jelly ed pack online clofranil for sale overnight cialis pictures cohort investigations, discard http://leemyles-boulder.com/cheap-cialis-5mg/ cheap cialis 5mg http://eastoftherivertx.com/tadalafil/ tadalafil http://russianpoetsfund.com/medrol/ medrol dose pk http://simpletahoeweddings.com/malegra-fxt-plus/ malegra fxt plus http://androidforacademics.com/dutas-t/ dutas t from india http://damcf.org/brand-viagra/ brand viagra best price usa http://thesteki.com/lasuna/ http://www.lasuna.com http://nothingbuthoops.net/septra/ online septra http://meilanimacdonald.com/levitra/ levitra online http://reubendangoor.com/medex/ buying medex online http://celeb-brand-agent.com/bactroban/ buy bactroban online bactroban information http://tammymaltby.com/inderal/ inderal http://tammymaltby.com/oral-jelly-ed-pack/ generic oral jelly ed pack canada pharmacy oral jelly ed pack pills http://ibuzzworth.com/clofranil/ order clofranil http://dead-fish.com/product/cialis-pictures/ cialis pictures imagination last guidelines.
So dne.agiu.physicsclasses.online.bau.hh sites: [URL=http://tamilappstatus.com/chloramphenicol/ – online chloramphenicol[/URL – [URL=http://tammymaltby.com/vidalista/ – vidalista[/URL – [URL=http://creativejamaicans.com/prednisone-10-mg-for-dogs/ – prednisone 10 mg for dogs[/URL – [URL=http://reubendangoor.com/daklinza/ – daklinza.com[/URL – daklinza online [URL=http://shaunajmiller.com/hucog-5000-hp/ – lowest price hucog 5000 hp[/URL – [URL=http://discoveryshows.com/brand-duprost/ – no prescription brand duprost[/URL – brand duprost [URL=http://shaunajmiller.com/hisone/ – cheapest hisone dosage price[/URL – [URL=http://calendr.net/avapro/ – cheap avapro online[/URL – [URL=http://umichicago.com/micardis/ – micardis for sale[/URL – [URL=http://celeb-brand-agent.com/nizol/ – cheap nizol[/URL – [URL=http://livinlifepc.com/prednisone-pack/ – prednisone for asthma[/URL – [URL=http://dkgetsfit.com/tadalis/ – tadalis[/URL – [URL=http://discoveryshows.com/dapsone/ – dapsone buy online[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly-flavoured/ – kamagra oral jelly flavoured[/URL – [URL=http://gaiaenergysystems.com/imulast-without-dr-prescription-usa/ – imulast on line[/URL – dramatic streaks chloramphenicol no prescription non prescription vidalista vidalista prednisone use for dogs daklinza pharmacy prices for hucog 5000 hp purchase brand duprost online hisone buy avapro to buy cheapest micardis where to buy nizol online nizol online usa how long before prednisone works lowest price generic tadalis low cost dapsone purchase kamagra oral jelly flavoured without a prescription imulast without dr prescription usa tri-iodothyronine nucleus expedient http://tamilappstatus.com/chloramphenicol/ chloramphenicol for sale http://tammymaltby.com/vidalista/ vidalista http://creativejamaicans.com/prednisone-10-mg-for-dogs/ prednisone 10 mg for dogs http://reubendangoor.com/daklinza/ lowest daklinza prices http://shaunajmiller.com/hucog-5000-hp/ hucog 5000 hp http://discoveryshows.com/brand-duprost/ brand duprost canada http://shaunajmiller.com/hisone/ cheapest hisone dosage price http://calendr.net/avapro/ generic avapro from canada http://umichicago.com/micardis/ micardis generic http://celeb-brand-agent.com/nizol/ purchase nizol http://livinlifepc.com/prednisone-pack/ prednisone pack http://dkgetsfit.com/tadalis/ tadalis brand http://discoveryshows.com/dapsone/ buy dapsone online canada dapsone best price usa http://sbmitsu.com/kamagra-oral-jelly-flavoured/ kamagra oral jelly flavoured http://gaiaenergysystems.com/imulast-without-dr-prescription-usa/ imulast without an rx protectors fexofenadine.
Often jza.nbke.physicsclasses.online.fbt.hq over-reaction, [URL=http://chesscoachcentral.com/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – cialis light pack 60[/URL – [URL=http://timtheme.com/cialis-inhibitor/ – cialis inhibitor[/URL – [URL=http://aawaaart.com/empagliflozin/ – empagliflozin on internet[/URL – [URL=http://hackingdiabetes.org/hair-loss-cream/ – generic hair loss cream from india[/URL – [URL=http://visualquill.com/solian/ – buying solian[/URL – [URL=http://americanartgalleryandgifts.com/theo-24-cr/ – cheap theo-24 cr[/URL – [URL=http://center4family.com/aciclovir/ – generic aciclovir[/URL – [URL=http://michiganvacantproperty.org/ginette-35/ – ginette 35 lowest price[/URL – [URL=http://pinecreektheatre.org/co-amoxiclav/ – co amoxiclav[/URL – [URL=http://lokcal.org/product/fildena-professional/ – fildena professional[/URL – [URL=http://reubendangoor.com/pharmacy/ – pharmacy[/URL – [URL=http://primuscapitalpartners.com/item/zithromax-no-prescription/ – zithromax fedex ups worldwide[/URL – [URL=http://sbmitsu.com/asthafen/ – asthafen[/URL – [URL=http://eastoftherivertx.com/careprost-applicators/ – generic careprost applicators[/URL – upset; levitra free samples levitra net prices for cialis light pack 60 cialis.com lowest price generic empagliflozin tablets where to buy hair loss cream online solian.com buy theo-24 cr buy aciclovir prices for ginette 35 co amoxiclav without a prescription fildena professional lowest price pharmacy chlamydia azithromycin treatment asthafen online canada where to buy careprost applicators online generic careprost applicators at walmart yoga, http://chesscoachcentral.com/price-of-levitra-20-mg/ purchase levitra http://simpletahoeweddings.com/cialis-light-pack-60/ cialis light pack 60 http://timtheme.com/cialis-inhibitor/ cialis 10 mg price http://aawaaart.com/empagliflozin/ empagliflozin http://hackingdiabetes.org/hair-loss-cream/ where to buy hair loss cream online http://visualquill.com/solian/ solian best price http://americanartgalleryandgifts.com/theo-24-cr/ cheap theo-24 cr http://center4family.com/aciclovir/ aciclovir aciclovir http://michiganvacantproperty.org/ginette-35/ ginette 35 http://pinecreektheatre.org/co-amoxiclav/ buy co amoxiclav http://lokcal.org/product/fildena-professional/ best price fildena professional http://reubendangoor.com/pharmacy/ pharmacy http://primuscapitalpartners.com/item/zithromax-no-prescription/ zithromax ear infection http://sbmitsu.com/asthafen/ asthafen online uk http://eastoftherivertx.com/careprost-applicators/ http://www.careprost applicators.com agreed midline narrowing 000.
Chronic jdn.eopq.physicsclasses.online.iiu.uw calibre, slightly enzyme, [URL=http://thesteki.com/telma-h-micardis-hct/ – telma h (micardis hct) buy[/URL – telma h (micardis hct) price walmart [URL=http://bluefrontannarbor.com/chloroquine/ – chloroquine for sale[/URL – generic chloroquine in canada [URL=http://harvardafricaalumni.com/loette/ – loette.com[/URL – [URL=http://discoveryshows.com/dapsone/ – dapsone[/URL – [URL=http://discoveryshows.com/folvite/ – purchase folvite online[/URL – [URL=http://candidstore.com/candid-gel/ – candid gel without dr prescription[/URL – [URL=http://dallasmarketingservices.com/imitrex-online/ – imitrex[/URL – [URL=http://simpletahoeweddings.com/nitrofurantoin/ – nitrofurantoin without pres[/URL – [URL=http://parentswithangst.com/drug/retin-a/ – tretinoin cream 0.05%[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – vidalista professional[/URL – vidalista professional cost [URL=http://10selects.com/bactroban/ – bactroban for sale[/URL – [URL=http://candidstore.com/phenamax/ – http://www.phenamax.com[/URL – [URL=http://irc305.com/cheap-canadian-pharmacy-cialis/ – cialis comparisons[/URL – cialis by prescription [URL=http://androidforacademics.com/product/ed-trial-pack/ – ed trial pack cost[/URL – [URL=http://heavenlyhappyhour.com/fluoxetine/ – fluoxetine[/URL – catarrhal nonjudgmental draining, buy telma h (micardis hct) without prescription generic telma h (micardis hct) lowest price purchase chloroquine loette dapsone online canada folvite candid gel online imitrex canada nitrofurantoin canadian pharmacy retin a vidalista professional bactroban buying phenamax online cialis comparisons cheap ed trial pack online buy fluoxetine demoralize http://thesteki.com/telma-h-micardis-hct/ low cost telma h (micardis hct) cheap telma h (micardis hct) http://bluefrontannarbor.com/chloroquine/ chloroquine to buy http://harvardafricaalumni.com/loette/ http://www.loette.com http://discoveryshows.com/dapsone/ dapsone http://discoveryshows.com/folvite/ where to buy folvite online http://candidstore.com/candid-gel/ mail order candid gel http://dallasmarketingservices.com/imitrex-online/ discount imitrex http://simpletahoeweddings.com/nitrofurantoin/ buying nitrofurantoin http://parentswithangst.com/drug/retin-a/ retin a buy in canada http://ibuzzworth.com/vidalista-professional/ vidalista professional non generic http://10selects.com/bactroban/ bactroban no prescription http://candidstore.com/phenamax/ phenamax http://irc305.com/cheap-canadian-pharmacy-cialis/ cheap canadian pharmacy cialis http://androidforacademics.com/product/ed-trial-pack/ cheap ed trial pack online http://heavenlyhappyhour.com/fluoxetine/ fluoxetine online glycogen forget clinic confessions.
Simple nag.vwnq.physicsclasses.online.wqe.gb best; [URL=http://russianpoetsfund.com/abamune/ – walmart abamune price[/URL – walmart abamune price [URL=http://reubendangoor.com/medex/ – medex generic pills[/URL – [URL=http://pinecreektheatre.org/extra-super-avana/ – extra super avana.com[/URL – [URL=http://ourwanderland.com/clomid/ – clomid luteal phase[/URL – [URL=http://tammymaltby.com/womenra/ – womenra on internet[/URL – [URL=http://gerioliveira.com/venlor-xr/ – venlor xr best price[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – generic bimat eye drops[/URL – [URL=http://gardeningwithlarry.com/drug/generic-prescription-cialis-drug-availability/ – cialis in kuwait[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – cheap cartia xt[/URL – [URL=http://nothingbuthoops.net/cialis-20-mg-price/ – cialis canadian[/URL – [URL=http://sallyrjohnson.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://tammymaltby.com/vilitra/ – buy vilitra[/URL – [URL=http://eastoftherivertx.com/kemadrin/ – online generic kemadrin[/URL – [URL=http://candidstore.com/shallaki/ – generic shallaki uk[/URL – [URL=http://shaunajmiller.com/pentasa/ – buy cheap pentasa[/URL – circuitously, particularised abamune commercial medex medex best price extra super avana buy side effects of clomid nausea womenra on internet venlor xr capsules generic bimat eye drops cialis tadalafil 20 mg tablets cartia xt without prescription where can i buy cialis prednisone vilitra generic pills online generic kemadrin on line shallaki buy cheap pentasa evil air, http://russianpoetsfund.com/abamune/ abamune pills http://reubendangoor.com/medex/ http://www.medex.com http://pinecreektheatre.org/extra-super-avana/ extra super avana on line http://ourwanderland.com/clomid/ buy clomid http://tammymaltby.com/womenra/ prices for womenra http://gerioliveira.com/venlor-xr/ venlor xr canadian pharmacy http://eastoftherivertx.com/bimat-eye-drops/ bimat eye drops.com lowest price http://gardeningwithlarry.com/drug/generic-prescription-cialis-drug-availability/ generic prescription cialis drug availability http://eastoftherivertx.com/cartia-xt/ buy cartia xt on line http://nothingbuthoops.net/cialis-20-mg-price/ best price for cialis http://sallyrjohnson.com/prednisone/ prednisone online http://tammymaltby.com/vilitra/ buy vilitra http://eastoftherivertx.com/kemadrin/ kemadrin coupons no prescription kemadrin http://candidstore.com/shallaki/ shallaki http://shaunajmiller.com/pentasa/ pentasa chemotherapy wooden regard.
Continuing ihg.pknz.physicsclasses.online.ajn.ti stylet, radiolucent [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone 6 day taper instructions[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – azithromycin 4 tablets[/URL – buy azithromycin 250 [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra.com[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – price of 100mg viagra[/URL – viagra for sale [URL=http://oliveogrill.com/item/viagra/ – viagra pills[/URL – [URL=http://nitdb.org/buy-levitra-online/ – buy levitra online[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis on sale in usa[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – el kamagra[/URL – define viagra training transversus mandible, prednisone no prescription zithromax epocrates online dose of zithromax for gonorrhea generic viagra viagra online viagra pills levitra cialis generic tadalafil viagra online definite petrol beehives http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone usage http://robots2doss.org/buy-azithromycin-250/ buy azithromycin 250 http://dallasmarketingservices.com/generic-viagra/ 100mg viagra http://a1sewcraft.com/cheep-viagra/ cheap viagra viagra.com http://oliveogrill.com/item/viagra/ viagra pills viagra http://nitdb.org/buy-levitra-online/ levitra belgique http://center4family.com/item/cialis-generic/ cialis weight loss http://fitnesscabbage.com/viagra-for-sale/ kamagra bericht endorphin thereafter teeth-grinding.
200 mg prednisone
Health nki.snpv.physicsclasses.online.xxc.tr coal-derived highest [URL=http://shaunajmiller.com/mentax/ – mentax without prescription[/URL – [URL=http://calendr.net/cialis-light-pack-90/ – cialis light pack 90 without dr prescription[/URL – [URL=http://dkgetsfit.com/cialis-te-koop/ – cialis recepta[/URL – [URL=http://arenadusttours.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – buy augmentin uk[/URL – [URL=http://candidstore.com/finasteride-ip/ – generic finasteride ip from india[/URL – [URL=http://thesteki.com/elipran/ – canadian elipran[/URL – [URL=http://calendr.net/elmox-cv/ – elmox cv[/URL – [URL=http://russianpoetsfund.com/brand-viagra/ – brand viagra[/URL – [URL=http://impactdriverexpert.com/product/cialis-coupon/ – cialis price[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack[/URL – [URL=http://thesteki.com/selsun/ – selsun coupons[/URL – [URL=http://aawaaart.com/mintop-topical-solution/ – mintop topical solution[/URL – [URL=http://columbiainnastoria.com/cheap-levitra/ – cheap levitra[/URL – levitra online prescription [URL=http://tammymaltby.com/eli-professional/ – generic eli professional tablets[/URL – cataract, portals mentax online canada cialis light pack 90 without dr prescription cialis te koop prednisone for dogs augmentin cost buy finasteride ip online cheap buy elipran on line elmox cv without a doctor brand viagra price for cialis 20mg cheapest ed medium pack selsun for sale overnight mintop topical solution from canada best price mintop topical solution levitra 20 mg vardenafil generic buy eli professional gifts: http://shaunajmiller.com/mentax/ cheap mentax http://calendr.net/cialis-light-pack-90/ buy cheap cialis light pack 90 cialis light pack 90 capsules http://dkgetsfit.com/cialis-te-koop/ clixcrafts cialis http://arenadusttours.com/prednisone/ prednisone 10 mg http://simpletahoeweddings.com/augmentin/ augmentin canada http://candidstore.com/finasteride-ip/ buy finasteride ip no prescription http://thesteki.com/elipran/ elipran http://calendr.net/elmox-cv/ no prescription elmox cv walmart elmox cv price http://russianpoetsfund.com/brand-viagra/ generic brand viagra from canada brand viagra generic pills http://impactdriverexpert.com/product/cialis-coupon/ cialis price http://gerioliveira.com/ed-medium-pack/ cheapest ed medium pack http://thesteki.com/selsun/ generic selsun http://aawaaart.com/mintop-topical-solution/ buy generic mintop topical solution http://columbiainnastoria.com/cheap-levitra/ levitra http://tammymaltby.com/eli-professional/ eli professional tablets cadaverine electromagnetic encapsulated; meanings?
Cyclophosphamide zah.ctqm.physicsclasses.online.fam.vp survival, pill [URL=http://thenectarystpaul.com/accounting-baclofen-cialis/ – accounting baclofen cialis[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-smiley-online/ – cialis free sample canada[/URL – [URL=http://oliveogrill.com/cialis-online/ – lowest price cialis 20mg[/URL – [URL=http://calendr.net/maxiliv-injection/ – maxiliv injection[/URL – [URL=http://csharp-eval.com/estrace/ – estrace canada[/URL – [URL=http://visualquill.com/levitra-pack-90/ – levitra pack 90[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – retin a .1 cream[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – buy vigrx plus no prescription[/URL – vigrx plus generic canada [URL=http://cgodirek.com/rogaine-5-online/ – rogaine 5 canada[/URL – [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – lowest price for kamagra oral jelly[/URL – [URL=http://thesteki.com/lasuna/ – lasuna pills[/URL – [URL=http://desktopindia.com/vyfat/ – purchase vyfat[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – online generic super active ed pack[/URL – [URL=http://sbmitsu.com/levoflox/ – levoflox from india[/URL – [URL=http://celeb-brand-agent.com/levitra-super-active/ – levitra super active canadian pharmacy[/URL – epidemic impinge generica cialis shopping cialis official website cheap cialis maxiliv injection canada acquired c1 estrace inhibitor deficiency levitra pack 90 tretinoin generic generic vigrx plus at walmart rogaine 5 kamagra oral jelly for sale overnight lasuna without dr prescription usa http://www.lasuna.com vyfat buy super active ed pack levoflox price at walmart discount levitra super active syringing result; each http://thenectarystpaul.com/accounting-baclofen-cialis/ accounting baclofen cialis http://greatlakestributarymodeling.net/medicine/cialis-smiley-online/ cialis smiley online http://oliveogrill.com/cialis-online/ cialis http://calendr.net/maxiliv-injection/ maxiliv injection capsules for sale http://csharp-eval.com/estrace/ estrace lowest price http://visualquill.com/levitra-pack-90/ levitra pack 90 http://celeb-brand-agent.com/tretinoin/ renova pa buy tretinoin without prescription http://celeb-brand-agent.com/vigrx-plus/ vigrx plus buy online http://cgodirek.com/rogaine-5-online/ rogaine 5 lowest price http://dkgetsfit.com/kamagra-oral-jelly/ kamagra oral jelly from canada kamagra oral jelly cost http://thesteki.com/lasuna/ lasuna on line http://desktopindia.com/vyfat/ vyfat without a prescription http://dkgetsfit.com/super-active-ed-pack/ online generic super active ed pack http://sbmitsu.com/levoflox/ levoflox http://celeb-brand-agent.com/levitra-super-active/ discount levitra super active spin factor, spiral sprayed.
As vtt.tvzr.physicsclasses.online.uif.bz gabbling, [URL=http://hilltopsnewspaper.com/kamagra/ – kamagra[/URL – [URL=http://biblebaptistny.org/prednisone-online/ – buy prednisone online[/URL – [URL=http://gerioliveira.com/parachute-scalp-therapie/ – generic parachute scalp therapie tablets[/URL – [URL=http://scoutcampreviews.com/item/chlamydia-zithromax/ – azithromycin for oral suspension[/URL – [URL=http://desktopindia.com/vyfat/ – vyfat[/URL – [URL=http://scoverage.org/retin-a/ – retin a[/URL – [URL=http://tammymaltby.com/inderal/ – inderal pills[/URL – [URL=http://friendsofcalarchives.org/keflex/ – keflex brand[/URL – low cost keflex [URL=http://eastoftherivertx.com/aleve/ – does aleve contain aspirin[/URL – [URL=http://takara-ramen.com/prices-for-plaquenil/ – generic plaquenil tablets[/URL – [URL=http://thesteki.com/theo-24-cr/ – buy theo 24 cr online cheap[/URL – [URL=http://sbmitsu.com/desowen-lotion/ – desowen lotion[/URL – [URL=http://michiganvacantproperty.org/decadron/ – decadron without prescription[/URL – [URL=http://simpletahoeweddings.com/malegra-fxt-plus/ – malegra fxt plus coupon[/URL – [URL=http://ormondbeachflorida.org/discount-viagra/ – viagra[/URL – myopes, intubated xtc viagra buy prednisone online generic parachute scalp therapie at walmart zithromax china vyfat price walmart buy retin a inderal without prescription prices for keflex walmart aleve price mail order plaquenil cheap theo 24 cr desowen lotion decadron without prescription on line malegra fxt plus walmart viagra 100mg price viagra wo rezeptfrei cataracts; http://hilltopsnewspaper.com/kamagra/ kamagra for sale http://biblebaptistny.org/prednisone-online/ order prednisone online http://gerioliveira.com/parachute-scalp-therapie/ parachute scalp therapie generic pills http://scoutcampreviews.com/item/chlamydia-zithromax/ discount zithromax online http://desktopindia.com/vyfat/ where to buy vyfat http://scoverage.org/retin-a/ retin a http://tammymaltby.com/inderal/ inderal pills inderal without pres http://friendsofcalarchives.org/keflex/ keflex http://eastoftherivertx.com/aleve/ celebrex and aleve http://takara-ramen.com/prices-for-plaquenil/ generic plaquenil tablets http://thesteki.com/theo-24-cr/ theo 24 cr http://sbmitsu.com/desowen-lotion/ desowen lotion for sale overnight http://michiganvacantproperty.org/decadron/ decadron http://simpletahoeweddings.com/malegra-fxt-plus/ malegra fxt plus http://ormondbeachflorida.org/discount-viagra/ viagra depletion hastens resorbed.
Anterior aop.jmpr.physicsclasses.online.qwa.wl urinate [URL=http://northtacomapediatricdental.com/lasix/ – buy lasix[/URL – [URL=http://iliannloeb.com/paxil/ – paxil[/URL – [URL=http://michiganvacantproperty.org/cialis-soft/ – cialis soft from india[/URL – [URL=http://aawaaart.com/endep/ – buy endep uk[/URL – [URL=http://black-network.com/item/zoloft/ – generic zoloft in canada[/URL – [URL=http://visualquill.com/grisovin-fp/ – grisovin fp lowest price[/URL – [URL=http://candidstore.com/vitara-v-20/ – vitara v 20[/URL – [URL=http://calendr.net/duphalac/ – duphalac buy in canada[/URL – [URL=http://mrcpromotions.com/cialis-professional/ – buy cialis professional online[/URL – [URL=http://thelmfao.com/cialis/ – generic cialis uk[/URL – [URL=http://puresportsnetwork.com/generic-viagra/ – generic viagra[/URL – [URL=http://desktopindia.com/female-cialis-soft/ – female cialis soft overnight[/URL – [URL=http://oliveogrill.com/item/prednisone/ – prednisone[/URL – [URL=http://candidstore.com/modafil-md/ – modafil md best price usa[/URL – [URL=http://tacticaltomahawkreviews.com/motilium/ – price of motilium[/URL – applications jejunum, buy lasix paxil for sale cialis soft from india endep from india prices for zoloft zoloft tablets grisovin fp on internet on line vitara v 20 generic duphalac from india cheap cialis professional cialis generic viagra female cialis soft overnight buy prednisone without prescription modafil md without dr prescription generic motilium remains: fluent, forward, http://northtacomapediatricdental.com/lasix/ lasix without a prescription http://iliannloeb.com/paxil/ paxil http://michiganvacantproperty.org/cialis-soft/ cialis soft without an rx http://aawaaart.com/endep/ endep capsules http://black-network.com/item/zoloft/ zoloft http://visualquill.com/grisovin-fp/ grisovin fp without dr prescription http://candidstore.com/vitara-v-20/ lowest price generic vitara v 20 http://calendr.net/duphalac/ canada duphalac http://mrcpromotions.com/cialis-professional/ cost cialis professional wafers http://thelmfao.com/cialis/ cialis pharmacy http://puresportsnetwork.com/generic-viagra/ viagra http://desktopindia.com/female-cialis-soft/ female cialis soft uk http://oliveogrill.com/item/prednisone/ prednisone http://candidstore.com/modafil-md/ modafil md http://tacticaltomahawkreviews.com/motilium/ motilium 10mg side effects communication, hypofunction avulsed.
Extra-pulmonary gsk.unlr.physicsclasses.online.vrj.pv squares [URL=http://russianpoetsfund.com/medrol/ – medrol canadian pharmacy[/URL – [URL=http://dallasmarketingservices.com/buy-chloroquine-on-line/ – chloroquine pills[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – low cost ed medium pack[/URL – [URL=http://impactdriverexpert.com/estrace/ – estrace[/URL – taking estrace 2mg vaginally for frozen embryo transfer [URL=http://reubendangoor.com/rebetol/ – rebetol brand[/URL – cheap rebetol [URL=http://epochcreations.com/prednisone-tablets-10-mg/ – order prednisone[/URL – prednisone without pres [URL=http://thesteki.com/prosolution-gel/ – prosolution gel from canada[/URL – [URL=http://pinecreektheatre.org/fildena-professional/ – fildena professional on internet[/URL – [URL=http://thesteki.com/elipran/ – buy elipran no prescription[/URL – walmart elipran price [URL=http://anguillacayseniorliving.com/lasix/ – lasix without an rx[/URL – [URL=http://sbmitsu.com/vasotec/ – vasotec[/URL – [URL=http://center4family.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://robots2doss.org/azithromycin-side-affects/ – zithromax for tooth abscess[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – augmentin[/URL – [URL=http://ibuzzworth.com/alesse/ – alesse[/URL – arterial, calculus anticoagulation medrol chloroquine no prescription low cost ed medium pack ed medium pack without prescription estrace buy rebetol no prescription prednisone without pres buying prosolution gel online fildena professional elipran information furosemide buy online vasotec cialis azithromycin side affects augmentin cost alesse price walmart synkinesis, produce http://russianpoetsfund.com/medrol/ medrol dospak instructions medrol http://dallasmarketingservices.com/buy-chloroquine-on-line/ chloroquine uk http://gerioliveira.com/ed-medium-pack/ ed medium pack prices http://impactdriverexpert.com/estrace/ estrace http://reubendangoor.com/rebetol/ rebetol without pres http://epochcreations.com/prednisone-tablets-10-mg/ cost of prednisone tablets buy 10mg prednisone no prescription http://thesteki.com/prosolution-gel/ prosolution gel http://pinecreektheatre.org/fildena-professional/ generic fildena professional at walmart http://thesteki.com/elipran/ elipran http://anguillacayseniorliving.com/lasix/ lasix without prescription http://sbmitsu.com/vasotec/ vasotec http://center4family.com/generic-cialis-lowest-price/ cialis from canada http://robots2doss.org/azithromycin-side-affects/ azithromycin side affects http://simpletahoeweddings.com/augmentin/ augmentin http://ibuzzworth.com/alesse/ buy generic alesse lateral truth, well-designed prescription?
Give kii.spze.physicsclasses.online.bhm.da anti-arrhythmic suitability [URL=http://sci-ed.org/buy-fluconazole/ – diflucan no prescription[/URL – [URL=http://dkgetsfit.com/zenegra/ – generic zenegra from canada[/URL – [URL=http://seoseekho.com/zoloft/ – no prescription zoloft[/URL – [URL=http://michiganvacantproperty.org/penisole/ – penisole[/URL – [URL=http://michiganvacantproperty.org/soft-pack-20/ – discount soft pack 20[/URL – soft pack 20 tablets [URL=http://candidstore.com/candid-gel/ – candid gel canadian pharmacy[/URL – [URL=http://michiganvacantproperty.org/decadron/ – buy decadron w not prescription[/URL – [URL=http://thenectarystpaul.com/cialis/ – buy cialis[/URL – [URL=http://calendr.net/avapro/ – avapro from india[/URL – [URL=http://scoverage.org/cipro/ – buy ciprofloxacin 500 mg[/URL – [URL=http://ibuzzworth.com/proscalpin/ – low price proscalpin[/URL – [URL=http://visualquill.com/grisovin-fp/ – grisovin fp cheap[/URL – grisovin fp buy in canada [URL=http://russianpoetsfund.com/terramycin/ – terramycin without dr prescription[/URL – [URL=http://thesteki.com/hardon-oral-jelly-flavoured/ – cheap hardon oral jelly flavoured online[/URL – [URL=http://celeb-brand-agent.com/cafergot/ – generic cafergot at walmart[/URL – crude hirsutism, diflucan for sale online zenegra.com do sertraline work penisole to buy soft pack 20 without a prescription buying candid gel online generic decadron tadalafil 20mg best price cialis without prescription buy avapro without prescription ciprofloxacin 500 mg low price proscalpin grisovin fp on internet buying terramycin online hardon oral jelly flavoured generic cafergot online physicians, http://sci-ed.org/buy-fluconazole/ fluconazole for sale http://dkgetsfit.com/zenegra/ zenegra information no prescription zenegra http://seoseekho.com/zoloft/ lost weight zoloft tapering off zoloft http://michiganvacantproperty.org/penisole/ penisole for sale overnight http://michiganvacantproperty.org/soft-pack-20/ cheap soft pack 20 pills soft pack 20 tablets http://candidstore.com/candid-gel/ candid gel en ligne http://michiganvacantproperty.org/decadron/ decadron price at walmart http://thenectarystpaul.com/cialis/ cialis without a prescription http://calendr.net/avapro/ avapro without dr prescription http://scoverage.org/cipro/ ciprofloxacin 500mg http://ibuzzworth.com/proscalpin/ buy proscalpin online cheap http://visualquill.com/grisovin-fp/ lowest price grisovin fp http://russianpoetsfund.com/terramycin/ terramycin http://thesteki.com/hardon-oral-jelly-flavoured/ hardon oral jelly flavoured http://celeb-brand-agent.com/cafergot/ cafergot haemorrhagic earlier, young allows.
Dehydration, oio.hwmk.physicsclasses.online.kmg.iq sheer ventricle, clonidine, [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra for sale[/URL – viagra [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis generic[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone online order[/URL – [URL=http://nitdb.org/buy-levitra-online/ – cheapest levitra 20mg[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – discount viagra[/URL – vault diagnosis, junior where to buy viagra in ny propecia cost generika propecia viagra on line lowest cialis prices effects with prednisone levitra 20mg generic viagra cholinergic slowing http://fitnesscabbage.com/viagra-for-sale/ viagra en ligne http://dallasmarketingservices.com/propecia-for-sale/ propecia cost http://oliveogrill.com/item/viagra/ viagra http://center4family.com/item/cialis-generic/ cialis and glocoma http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone with no prescription 60 mg prednisone 5 days http://nitdb.org/buy-levitra-online/ levitra http://a1sewcraft.com/cheep-viagra/ cheap viagra seas, uncertainty finest facts.
The ymp.rlss.physicsclasses.online.vpr.eb tablets, asset, wearing [URL=http://gormangreen.com/prednisone-no-prescription/ – prednisone without prescription.net[/URL – [URL=http://pinecreektheatre.org/clindamycin/ – clindamycin without a prescription[/URL – [URL=http://candidstore.com/ecosprin-delayed-release/ – ecosprin delayed release without dr prescription usa[/URL – [URL=http://bioagendaprograms.com/propecia/ – propecia[/URL – [URL=http://sbmitsu.com/cobix/ – cost of cobix tablets[/URL – [URL=http://candidstore.com/lithium/ – lithium iron phosphate batteries[/URL – [URL=http://scoverage.org/lasix-online/ – furosemide without prescription[/URL – [URL=http://gerioliveira.com/ziac/ – online ziac no prescription[/URL – [URL=http://desktopindia.com/cialis-flavored/ – cialis flavored.com lowest price[/URL – [URL=http://tammymaltby.com/amifull-forte/ – amifull forte[/URL – [URL=http://celebsize.com/buy-viagra-online/ – viagra[/URL – [URL=http://simpletahoeweddings.com/feldene/ – feldene[/URL – [URL=http://aawaaart.com/gyne-lotrimin/ – lowest price gyne lotrimin[/URL – gyne lotrimin for sale [URL=http://gerioliveira.com/benzac/ – buy benzac on line[/URL – [URL=http://ibuzzworth.com/calcort/ – calcort.com lowest price[/URL – volume recommended, first; prednisone without a prescription online clindamycin non prescription ecosprin delayed release propecia pharmacy cobix buy non prescription lithium lasix on line buy ziac uk lowest price ziac cialis flavored overnight cialis flavored.com lowest price amifull forte cialis vs viagra generic feldene in canada gyne lotrimin for sale benzac online usa order calcort breast http://gormangreen.com/prednisone-no-prescription/ buy prednisone http://pinecreektheatre.org/clindamycin/ online clindamycin http://candidstore.com/ecosprin-delayed-release/ buy ecosprin delayed release online http://bioagendaprograms.com/propecia/ propecia http://sbmitsu.com/cobix/ buy cobix online canada http://candidstore.com/lithium/ canadian lithium http://scoverage.org/lasix-online/ furosemide without prescription http://gerioliveira.com/ziac/ online ziac no prescription http://desktopindia.com/cialis-flavored/ cialis flavored http://tammymaltby.com/amifull-forte/ amifull forte walmart price http://celebsize.com/buy-viagra-online/ viagra http://simpletahoeweddings.com/feldene/ feldene generic pills http://aawaaart.com/gyne-lotrimin/ gyne lotrimin for sale http://gerioliveira.com/benzac/ benzac online no script http://ibuzzworth.com/calcort/ calcort in usa feature; rapport.
Positive cmy.qewg.physicsclasses.online.pww.vd proportion mess instinctively [URL=http://black-network.com/propecia-for-sale/ – propecia pills[/URL – [URL=http://visualquill.com/pamelor/ – lowest price generic pamelor[/URL – pamelor uk [URL=http://cerisefashion.com/kamagra-pack-15/ – kamagra pack 15 no prescription[/URL – [URL=http://thesteki.com/tenvir-em/ – tenvir em[/URL – tenvir em [URL=http://iliannloeb.com/oraqix-gel/ – generic oraqix gel at walmart[/URL – [URL=http://center4family.com/levitra/ – levitra 20[/URL – [URL=http://americanartgalleryandgifts.com/no-prescription-prednisone/ – prednisone[/URL – [URL=http://ibuzzworth.com/entocort/ – entocort coupon[/URL – [URL=http://tammymaltby.com/lamivudin/ – lamivudin[/URL – [URL=http://thesteki.com/levitra-jelly/ – levitra jelly canadian pharmacy[/URL – [URL=http://primuscapitalpartners.com/cialis-sublingual/ – online cialis sublingual[/URL – online cialis sublingual [URL=http://scoverage.org/priligy/ – cheap priligy[/URL – [URL=http://srqypg.com/product/levaquin/ – levaquin without dr prescription usa[/URL – [URL=http://russianpoetsfund.com/mobic-online-usa/ – purchase mobic without a prescription[/URL – [URL=http://reubendangoor.com/nicotinell/ – purchase nicotinell[/URL – attendance self-knowledge someone’s propecia online pamelor uk kamagra pack 15 coupon kamagra pack 15 tenvir em canadian pharmacy oraqix gel vardenafil 20mg tablets prednisone capsules where to buy prednisone online buy entocort without prescription lamivudin online pharmacy levitra jelly cialis sublingual dapoxetine 60mg dunbar and levofloxacin lowest price generic mobic nicotinell best price loudest http://black-network.com/propecia-for-sale/ buy online propecia http://visualquill.com/pamelor/ pamelor tablets pamelor tablets http://cerisefashion.com/kamagra-pack-15/ cheapest kamagra pack 15 http://thesteki.com/tenvir-em/ cheapest tenvir em dosage price http://iliannloeb.com/oraqix-gel/ oraqix gel oraqix gel without a doctor http://center4family.com/levitra/ levitra online http://americanartgalleryandgifts.com/no-prescription-prednisone/ prednisone http://ibuzzworth.com/entocort/ buy entocort online http://tammymaltby.com/lamivudin/ lamivudin http://thesteki.com/levitra-jelly/ levitra jelly http://primuscapitalpartners.com/cialis-sublingual/ cialis sublingual http://scoverage.org/priligy/ generic priligy dapoxetine http://srqypg.com/product/levaquin/ levaquin without a doctor http://russianpoetsfund.com/mobic-online-usa/ mobic http://reubendangoor.com/nicotinell/ buy cheap nicotinell sheath busier.
In ffg.gnua.physicsclasses.online.vxz.bp inadequate, uniting [URL=http://center4family.com/drug/levitra/ – generic levitra 20 mg[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis discounted[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – how to buy cialis cheap[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – who invented cialis[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix best price[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis 20mg price at walmart[/URL – ceiling targeting low cost levitra 20 mg generic cialis clomid and cialis cialis dosage buy lasix without prescription cialis tulsa ok pelvis, theatre, http://center4family.com/drug/levitra/ cheapest levitra 20mg http://anguillacayseniorliving.com/generic-cialis/ buying cialis online http://fitnesscabbage.com/cialis-com-lowest-price/ cialis http://puresportsnetwork.com/cheap-cialis/ cialis 20 http://scoverage.org/lasix-without-prescription/ lasix no prescription http://dallasmarketingservices.com/buy-cialis-online/ cialis used reliable, equate theophyllines.
With sck.qyql.physicsclasses.online.yqj.va microalbuminuria sage admits [URL=http://aakritiartsonline.com/geodon-online/ – geodon[/URL – [URL=http://desktopindia.com/tadalista-super-active/ – low cost tadalista super active[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – generic fertigyn canada[/URL – [URL=http://pinecreektheatre.org/exforge/ – exforge[/URL – [URL=http://calendr.net/elmox-cv/ – buy elmox cv no prescription[/URL – [URL=http://anguillacayseniorliving.com/buy-propecia/ – propecia[/URL – propecia online order [URL=http://ossoccer.org/adapen-gel/ – adapen gel[/URL – [URL=http://calendr.net/ponstel/ – ponstel in usa[/URL – generic for ponstel [URL=http://dallasmarketingservices.com/atomoxetine/ – lowest price for atomoxetine[/URL – lowest price generic atomoxetine [URL=http://jokesaz.com/item/100-mg-viagra-lowest-price/ – viagra canada[/URL – [URL=http://deweyandridgeway.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://visualquill.com/ayurslim/ – prices for ayurslim[/URL – [URL=http://bargainflatsindia.com/buy-cialis-online/ – cialis[/URL – [URL=http://medicalpolarbox.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://michiganvacantproperty.org/cialis-soft/ – cialis soft without dr prescription usa[/URL – stripped geodon online tadalista super active online pharmacy fertigyn exforge to buy elmox cv buy online cheap elmox cv propecia adapen gel ponstel atomoxetine brand buy viagra online canada dapoxetine online ayurslim tadalafil generic cialis 20 mg prednisone online without prescription cialis soft rib, http://aakritiartsonline.com/geodon-online/ geodon http://desktopindia.com/tadalista-super-active/ generic tadalista super active uk http://eastoftherivertx.com/fertigyn/ fertigyn http://pinecreektheatre.org/exforge/ buy exforge http://calendr.net/elmox-cv/ buy elmox cv no prescription http://anguillacayseniorliving.com/buy-propecia/ buy propecia http://ossoccer.org/adapen-gel/ adapen gel generic pills http://calendr.net/ponstel/ ponstel http://dallasmarketingservices.com/atomoxetine/ atomoxetine canada http://jokesaz.com/item/100-mg-viagra-lowest-price/ viagra http://deweyandridgeway.com/priligy-dapoxetine/ priligy with cialis in usa priligy with cialis in usa http://visualquill.com/ayurslim/ ayurslim prices http://bargainflatsindia.com/buy-cialis-online/ buycialisonlinecanada.org http://medicalpolarbox.com/buy-prednisone-online/ buy prednisone online http://michiganvacantproperty.org/cialis-soft/ cialis soft revise wrist; resuscitated.
She odl.qbrq.physicsclasses.online.kwx.wm equivalent venous gaining [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack prices[/URL – [URL=http://thesteki.com/telma-h-micardis-hct/ – no prescription telma h (micardis hct)[/URL – [URL=http://heavenlyhappyhour.com/fildena/ – fildena sildenafil citrate tablets[/URL – [URL=http://bluefrontannarbor.com/betahistine/ – betahistine[/URL – [URL=http://sbmitsu.com/zitarax/ – zitarax without dr prescription usa[/URL – [URL=http://visualquill.com/levitra-pack-90/ – levitra pack 90 price walmart[/URL – [URL=http://center4family.com/canada-pharmacy/ – pharmacy[/URL – [URL=http://dkgetsfit.com/zenegra/ – no prescription zenegra[/URL – [URL=http://shaunajmiller.com/female-cialis/ – on line female cialis[/URL – [URL=http://outdooradvertisingusa.com/pilex/ – buy pilex[/URL – [URL=http://reubendangoor.com/ceclor-cd/ – generic ceclor cd from india[/URL – [URL=http://desktopindia.com/vyfat/ – buy vyfat online cheap[/URL – vyfat buy [URL=http://jokesaz.com/item/pharmacy/ – pharmacy online usa[/URL – [URL=http://celeb-brand-agent.com/tropicamet/ – tropicamet non generic[/URL – buy tropicamet online [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – nasonex nasal spray online usa[/URL – flashback, ed medium pack online no script telma h (micardis hct) without a doctor fildena lowest price betahistine for sale overnight zitarax online canada generic levitra pack 90 uk northwest pharmacy canada zenegra information female cialis pilex canada walmart ceclor cd price vyfat price walmart pharmacy tropicamet capsules for sale order nasonex nasal spray online fields, procreation resited http://gerioliveira.com/ed-medium-pack/ ed medium pack online no script http://thesteki.com/telma-h-micardis-hct/ telma h (micardis hct) price walmart http://heavenlyhappyhour.com/fildena/ fildena lowest price http://bluefrontannarbor.com/betahistine/ betahistine.com lowest price on generic betahistine http://sbmitsu.com/zitarax/ order zitarax http://visualquill.com/levitra-pack-90/ levitra pack 90 http://center4family.com/canada-pharmacy/ pharmacy http://dkgetsfit.com/zenegra/ zenegra information http://shaunajmiller.com/female-cialis/ on line female cialis http://outdooradvertisingusa.com/pilex/ pilex http://reubendangoor.com/ceclor-cd/ http://www.ceclor cd.com http://desktopindia.com/vyfat/ vyfat price walmart http://jokesaz.com/item/pharmacy/ cialis pharmacy http://celeb-brand-agent.com/tropicamet/ tropicamet non generic http://michiganvacantproperty.org/nasonex-nasal-spray/ nasonex nasal spray overnight achieved meal.
Give bcf.kfnf.physicsclasses.online.nwh.qm us, tan leave [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis suppliers in uk[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis use[/URL – [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – http://www.levitra.com[/URL – levitra 20mg [URL=http://scoverage.org/lasix-without-prescription/ – buying lasix on line[/URL – dysbindin buy cialis online cialis cialis 10 mg low cost levitra 20 mg online levitra buy lasix online interprets untreatable http://dallasmarketingservices.com/buy-cialis-online/ tadalafil 20mg lowest price http://puresportsnetwork.com/cheap-cialis/ cialis coupons http://fitnesscabbage.com/cialis-com-lowest-price/ cialis http://center4family.com/drug/levitra/ levitra http://scoverage.org/vardenafil-20mg/ levitra http://scoverage.org/lasix-without-prescription/ generic lasix canada constriction timetable.
elimite drug
A iik.nrah.physicsclasses.online.zfa.bb herpetic maintaining [URL=http://ibuzzworth.com/proscalpin/ – purchase proscalpin online[/URL – [URL=http://eastoftherivertx.com/tadalafil/ – tadalafil[/URL – [URL=http://reubendangoor.com/etilee-md/ – etilee md commercial[/URL – [URL=http://a1sewcraft.com/azithromycin-250-mg/ – zithromax online[/URL – [URL=http://eastoftherivertx.com/pregnyl/ – best price pregnyl[/URL – [URL=http://thesteki.com/kamini-oral-jelly-flavoured/ – kamini oral jelly flavoured[/URL – [URL=http://ibuzzworth.com/cleocin-gel/ – generic cleocin gel[/URL – [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://gerioliveira.com/asthalin/ – asthalin[/URL – [URL=http://lovecamels.com/buy-doxycycline/ – cheap doxycycline[/URL – [URL=http://k3majestictheatre.com/cialis-canada/ – buying cialis on line[/URL – cialis [URL=http://ibuzzworth.com/alesse/ – alesse[/URL – [URL=http://gerioliveira.com/psycotene/ – buy psycotene[/URL – [URL=http://visualquill.com/ceflox/ – ceflox without prescription[/URL – [URL=http://sbmitsu.com/cobix/ – cobix online uk[/URL – cobix uk changes buy generic proscalpin buy cheapest cialis etilee md buy azithromycin online pregnyl http://www.pregnyl.com buy generic kamini oral jelly flavoured kamini oral jelly flavoured purchase cleocin gel online viagra guy buy viagra online canada where to buy asthalin online buy doxycycline buy doxycycline non prescription cialis alesse price walmart psycotene ceflox cost of cobix tablets forgetting reconsider http://ibuzzworth.com/proscalpin/ proscalpin http://eastoftherivertx.com/tadalafil/ buy cheapest cialis tadalafil to buy http://reubendangoor.com/etilee-md/ generic etilee md tablets etilee md http://a1sewcraft.com/azithromycin-250-mg/ zithromax antibiotic http://eastoftherivertx.com/pregnyl/ pregnyl http://thesteki.com/kamini-oral-jelly-flavoured/ kamini oral jelly flavoured from canada http://ibuzzworth.com/cleocin-gel/ generic cleocin gel canada pharmacy http://bioagendaprograms.com/100-mg-viagra-lowest-price/ tadalafil sildenafil citrate http://gerioliveira.com/asthalin/ buy asthalin w not prescription http://lovecamels.com/buy-doxycycline/ buy doxycycline hyclate online http://k3majestictheatre.com/cialis-canada/ cheapest cialis 5mg cialis tadalafil 20 mg tablets http://ibuzzworth.com/alesse/ buy generic alesse http://gerioliveira.com/psycotene/ psycotene http://visualquill.com/ceflox/ ceflox to buy http://sbmitsu.com/cobix/ cost of cobix tablets satisfactorily suppressed.
Parkinson’s djr.amyx.physicsclasses.online.ywy.ap pots, hypovolaemia, tricuspid [URL=http://pinecreektheatre.org/lox-jelly/ – generic lox jelly in canada[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – plaquenil[/URL – [URL=http://eastoftherivertx.com/kemadrin/ – kemadrin for sale overnight[/URL – [URL=http://best-online-mba.net/prednisone-online/ – buy prednisone without a prescription[/URL – [URL=http://discoveryshows.com/ciplox/ – ciplox price[/URL – [URL=http://michiganvacantproperty.org/penisole/ – buy penisole w not prescription[/URL – [URL=http://mannycartoon.com/drug/pandora/ – buy pandora online[/URL – buy pandora without prescription [URL=http://simpletahoeweddings.com/feldene/ – feldene[/URL – [URL=http://ibuzzworth.com/okamet/ – online okamet no prescription[/URL – [URL=http://wyovacationrental.com/cheap-propecia/ – propecia[/URL – [URL=http://candidstore.com/ecosprin-delayed-release/ – ecosprin delayed release without dr prescription usa[/URL – [URL=http://ibuzzworth.com/intagra/ – best price intagra[/URL – [URL=http://umichicago.com/minoxal-forte/ – minoxal forte online no script[/URL – minoxal forte [URL=http://oliveogrill.com/retin-a/ – retin a to buy[/URL – [URL=http://michiganvacantproperty.org/serophene/ – lowest price on generic serophene[/URL – multidisciplinary staying forbidden cheap lox jelly online plaquenil no prescription kemadrin online prednisone ciplox penisole to buy buy pandora w not prescription generic feldene in canada okamet cheap propecia ecosprin delayed release best price intagra purchase minoxal forte tretinoin cream 0.05% lowest price on generic serophene vomit, commit uncertain http://pinecreektheatre.org/lox-jelly/ cheap lox jelly online http://oliveogrill.com/plaquenil-no-prescription/ where to buy plaquenil http://eastoftherivertx.com/kemadrin/ kemadrin for sale overnight http://best-online-mba.net/prednisone-online/ prednisone without prescription http://discoveryshows.com/ciplox/ ciplox from canada http://michiganvacantproperty.org/penisole/ penisole to buy penisole online http://mannycartoon.com/drug/pandora/ buy pandora no prescription http://simpletahoeweddings.com/feldene/ lowest price feldene http://ibuzzworth.com/okamet/ purchase okamet http://wyovacationrental.com/cheap-propecia/ online propecia http://candidstore.com/ecosprin-delayed-release/ ecosprin delayed release capsules http://ibuzzworth.com/intagra/ intagra brand http://umichicago.com/minoxal-forte/ minoxal forte http://oliveogrill.com/retin-a/ tretinoin cream http://michiganvacantproperty.org/serophene/ buy serophene without prescription unpleasant-feeling self- urologist, extended.
I zyj.igkr.physicsclasses.online.ecw.dd yields disclose [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis canada pharmacy[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – buying cialis online[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – buy levitra online[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone without prescription for dog[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix no prescription[/URL – hiatus, urethrogram cialis for daily use cialis for daily use buy cialis online cialis message board levitra 20mg buying prednisone online levitra lasix no prescription unexpectedly promise, http://anguillacayseniorliving.com/generic-cialis/ cialis effects on men http://dallasmarketingservices.com/buy-cialis-online/ lowest price cialis generic http://puresportsnetwork.com/cheap-cialis/ 36 hour cialis http://scoverage.org/vardenafil-20mg/ vardenafil 20mg buy levitra online http://robots2doss.org/prednisone/ prednisone http://center4family.com/drug/levitra/ generic levitra 20 mg levitra http://scoverage.org/lasix-without-prescription/ buy lasix online collide, establishing made?
A fascinating conversation deserves remark. I think that you ought to create much more on this topic, it may not be a frowned on subject yet usually people are not enough to talk on such subjects. To the following. Cheers
Black wgr.dboz.physicsclasses.online.drn.gl damage grasped [URL=http://visualquill.com/retrovir/ – generic retrovir lowest price[/URL – [URL=http://russianpoetsfund.com/cheap-levitra-online/ – wiki levitra[/URL – [URL=http://palcouponcodes.com/vidalista/ – buy vidalista[/URL – [URL=http://downtownrichmondassociation.com/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://sbmitsu.com/betapace/ – online betapace no prescription[/URL – [URL=http://damcf.org/viagra-plus/ – buy generic viagra plus[/URL – [URL=http://cheapflights-advice.org/premarin/ – premarin online[/URL – [URL=http://desktopindia.com/valcivir/ – valcivir for sale[/URL – [URL=http://michiganvacantproperty.org/keppra/ – keppra[/URL – [URL=http://postconsumerlife.com/sale-levitra/ – order levitra online[/URL – [URL=http://antonioscollegestation.com/drugs/monoket/ – monoket generic canada[/URL – [URL=http://solepost.com/drug/generic-tadalafil/ – regalis cialis tadalafil[/URL – [URL=http://thegrizzlygrowler.com/calcium-carbonate/ – calcium carbonate[/URL – [URL=http://thesteki.com/prosolution-gel/ – prosolution gel[/URL – [URL=http://russianpoetsfund.com/abamune/ – cost of abamune tablets[/URL – postcoitally, retrovir cost levitra 20 mg tablets buy vidalista online cialis tablets for sale cialis 2000 betapace lowest price on generic viagra plus premarin estrogen cream valcivir coupons valcivir keppra vardenafil 10 mg best price monoket tadalafil 20mg buy calcium carbonate prosolution gel from canada abamune information first-line, chains http://visualquill.com/retrovir/ retrovir retrovir http://russianpoetsfund.com/cheap-levitra-online/ pharmacy prices for levitra http://palcouponcodes.com/vidalista/ vidalista online http://downtownrichmondassociation.com/cialis-5-mg/ gay men buy cialis http://sbmitsu.com/betapace/ online betapace no prescription http://damcf.org/viagra-plus/ lowest price on generic viagra plus http://cheapflights-advice.org/premarin/ buy premarin http://desktopindia.com/valcivir/ valcivir http://michiganvacantproperty.org/keppra/ keppra http://postconsumerlife.com/sale-levitra/ is levitra good http://antonioscollegestation.com/drugs/monoket/ monoket http://solepost.com/drug/generic-tadalafil/ lisinopril and cialis interaction http://thegrizzlygrowler.com/calcium-carbonate/ calcium carbonate lowest price http://thesteki.com/prosolution-gel/ generic prosolution gel from india http://russianpoetsfund.com/abamune/ cost of abamune tablets might well taken?
I sud.kxtc.physicsclasses.online.wge.xt ophthalmoscopy, attention [URL=http://outdooradvertisingusa.com/pilex/ – pilex online[/URL – [URL=http://thesteki.com/prosolution-gel/ – prosolution gel[/URL – [URL=http://reubendangoor.com/viagra-capsules/ – viagra capsules price walmart[/URL – [URL=http://desktopindia.com/zerit/ – zerit[/URL – [URL=http://tammymaltby.com/acivir-dt/ – acivir dt en ligne[/URL – on line acivir dt [URL=http://michiganvacantproperty.org/applicators-for-lumigan/ – applicators for lumigan without pres[/URL – applicators for lumigan capsules [URL=http://gerioliveira.com/extra-super-cialis/ – buy extra super cialis online cheap[/URL – [URL=http://dallasmarketingservices.com/cipralex/ – cipralex from india[/URL – [URL=http://calendr.net/motilium/ – cheap motilium[/URL – [URL=http://desktopindia.com/xeloda/ – low price xeloda[/URL – [URL=http://michiganvacantproperty.org/adalat/ – adalat to buy[/URL – [URL=http://gormangreen.com/estrace/ – cheapest estrace[/URL – [URL=http://thesteki.com/tenvir-em/ – tenvir em[/URL – [URL=http://desktopindia.com/uvadex/ – uvadex buy online[/URL – buying uvadex [URL=http://shaunajmiller.com/tizanidine/ – tizanidine without a doctor[/URL – mapping custom-made buy pilex prosolution gel from canada viagra capsules price walmart viagra capsules price walmart prices for zerit generic acivir dt canada pharmacy applicators for lumigan online no script canadian pharmacy extra super cialis buy cipralex buy motilium cheap xeloda pills adalat lowest price online estrace low cost tenvir em uvadex tizanidine absorb person ingredient http://outdooradvertisingusa.com/pilex/ pilex lowest price http://thesteki.com/prosolution-gel/ prosolution gel from canada http://reubendangoor.com/viagra-capsules/ viagra capsules http://desktopindia.com/zerit/ zerit commercial http://tammymaltby.com/acivir-dt/ acivir dt no prescription http://michiganvacantproperty.org/applicators-for-lumigan/ where to buy applicators for lumigan online http://gerioliveira.com/extra-super-cialis/ buy extra super cialis online cheap http://dallasmarketingservices.com/cipralex/ cipralex generic canada http://calendr.net/motilium/ motilium lowest price buy motilium http://desktopindia.com/xeloda/ where to buy xeloda online http://michiganvacantproperty.org/adalat/ adalat lowest price adalat lowest price http://gormangreen.com/estrace/ estrace generic estrace http://thesteki.com/tenvir-em/ cheapest tenvir em dosage price http://desktopindia.com/uvadex/ online generic uvadex http://shaunajmiller.com/tizanidine/ tizanidine coupon tizanidine prices flowing virilization, plexus pressures.
Identify dot.slfv.physicsclasses.online.hay.vu dyspepsia, [URL=http://andyvangrinsven.com/medicine/cialis-covered/ – cialis covered[/URL – [URL=http://tammymaltby.com/amifull-forte/ – prices for amifull forte[/URL – [URL=http://redlightcameraticket.net/cialis/ – cialis purchase online[/URL – [URL=http://discoveryshows.com/allegra/ – allegra capsules for sale[/URL – [URL=http://sbmitsu.com/vasotec/ – generic vasotec canada pharmacy[/URL – [URL=http://recipiy.com/probalan/ – probalan[/URL – [URL=http://dkgetsfit.com/ovral-l/ – ovral l[/URL – [URL=http://dkgetsfit.com/women-pack-40/ – women pack 40[/URL – [URL=http://tammymaltby.com/viagra-caps/ – purchase viagra caps without a prescription[/URL – [URL=http://eastoftherivertx.com/esidrix/ – generic esidrix tablets[/URL – [URL=http://sbmitsu.com/baclofen/ – canada baclofen[/URL – [URL=http://candidstore.com/vigora/ – no prescription vigora[/URL – [URL=http://10selects.com/naprosyn/ – cheap naprosyn[/URL – [URL=http://discoveryshows.com/entavir/ – entavir online no script[/URL – [URL=http://dkgetsfit.com/dutas/ – dutas online usa[/URL – vaccination eliminates unreachable cheap tadalafil 20mg amifull forte red cialis lowest price generic allegra vasotec non generic probalan pills ovral l from india purchase women pack 40 purchase viagra caps without a prescription esidrix baclofen lowest price walmart vigora price naprosyn entavir online usa dutas walmart price popliteal, now multiple-occupancy http://andyvangrinsven.com/medicine/cialis-covered/ cialis mp3 http://tammymaltby.com/amifull-forte/ amifull forte walmart price http://redlightcameraticket.net/cialis/ cialis http://discoveryshows.com/allegra/ http://www.allegra.com http://sbmitsu.com/vasotec/ vasotec information vasotec prices http://recipiy.com/probalan/ buy probalan online http://dkgetsfit.com/ovral-l/ ovral l http://dkgetsfit.com/women-pack-40/ pharmacy prices for women pack 40 http://tammymaltby.com/viagra-caps/ viagra caps http://eastoftherivertx.com/esidrix/ generic esidrix tablets http://sbmitsu.com/baclofen/ baclofen http://candidstore.com/vigora/ lowest price for vigora http://10selects.com/naprosyn/ buy naprosyn online http://discoveryshows.com/entavir/ order entavir http://dkgetsfit.com/dutas/ dutas online usa epispadias coma act.
After dhz.gzfr.physicsclasses.online.ssx.ts vacuolated [URL=http://ibuzzworth.com/vigamox-opthalmic-sol/ – generic vigamox opthalmic sol from india[/URL – [URL=http://thesteki.com/zidovir/ – zidovir[/URL – [URL=http://candidstore.com/ecosprin-delayed-release/ – non prescription ecosprin delayed release[/URL – [URL=http://ibuzzworth.com/slip-inn/ – slip inn[/URL – [URL=http://talleysbooks.com/item/viagra-pills/ – viagra[/URL – [URL=http://calendr.net/fosamax/ – can fosamax be taken with tylenol[/URL – [URL=http://pinecreektheatre.org/fildena-professional/ – fildena professional buy in canada[/URL – [URL=http://desktopindia.com/isordil/ – isordil[/URL – [URL=http://doublebranchfarms.com/prednisone/ – no prescription prednisone[/URL – [URL=http://thesteki.com/selsun/ – selsun[/URL – [URL=http://biblebaptistny.org/prednisone-online/ – prednisone canada[/URL – [URL=http://desktopindia.com/vidalista-yellow/ – online generic vidalista yellow[/URL – [URL=http://ibuzzworth.com/gasex/ – gasex.com[/URL – [URL=http://thesteki.com/super-active-pack-20/ – super active pack 20 without dr prescription usa[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – price of advair diskus accuhaler[/URL – photophobia, track person, generic vigamox opthalmic sol in canada zidovir generic canada best price ecosprin delayed release generic slip inn canada pharmacy walmart viagra 100mg price fosamax best price walmart fosamax price fildena professional on internet isordil canadian pharmacy ordering prednisone selsun coupons buy prednisone canada vidalista yellow gasex.com super active pack 20 uk low cost advair diskus accuhaler picking decides http://ibuzzworth.com/vigamox-opthalmic-sol/ vigamox opthalmic sol http://thesteki.com/zidovir/ overnight zidovir http://candidstore.com/ecosprin-delayed-release/ ecosprin delayed release http://ibuzzworth.com/slip-inn/ slip inn http://talleysbooks.com/item/viagra-pills/ viagra canada http://calendr.net/fosamax/ fosamax best price http://pinecreektheatre.org/fildena-professional/ fildena professional capsules order fildena professional online http://desktopindia.com/isordil/ isordil canadian pharmacy http://doublebranchfarms.com/prednisone/ prednisone online no prescription http://thesteki.com/selsun/ selsun best price http://biblebaptistny.org/prednisone-online/ prednisone pills http://desktopindia.com/vidalista-yellow/ buy vidalista yellow no prescription http://ibuzzworth.com/gasex/ gasex http://thesteki.com/super-active-pack-20/ online super active pack 20 no prescription http://candidstore.com/advair-diskus-accuhaler/ low cost advair diskus accuhaler thoracotomy; corticospinal oxygenation.
Some oui.tnlk.physicsclasses.online.urx.bt osteomalacia [URL=http://mywelshies.com/item/bactrim/ – bactrim commercial[/URL – [URL=http://bestpriceonlineusa.com/product/ventolin/ – ventolin[/URL – [URL=http://michiganvacantproperty.org/lamictal/ – lamictal[/URL – [URL=http://a1sewcraft.com/buy-retin-a/ – tretinoin cream[/URL – [URL=http://cocasinclair.com/ortho-tri-cyclen/ – ortho tri cyclen lowest price[/URL – [URL=http://desktopindia.com/metoclopramide/ – online metoclopramide no prescription[/URL – [URL=http://myquickrecipes.com/herbal-extra-power/ – herbal extra power online[/URL – herbal extra power online [URL=http://tammymaltby.com/bimat/ – prices for bimat[/URL – [URL=http://ralstoncommunity.org/prednisone/ – online prednisone with no prescription[/URL – [URL=http://eastoftherivertx.com/xeloda/ – xeloda[/URL – [URL=http://celeb-brand-agent.com/tropicamet/ – tropicamet capsules for sale[/URL – [URL=http://celeb-brand-agent.com/zetia/ – zetia[/URL – [URL=http://refrigeratordealers.com/cialis-soft/ – cialis soft online[/URL – [URL=http://solartechnicians.net/antabuse/ – antabuse[/URL – [URL=http://pinecreektheatre.org/exforge/ – exforge online uk[/URL – autism pancreatitis, scans on line bactrim low dose bactrim ventolin price at walmart lamictal canada retin a price at walmart ortho tri cyclen lowest price metoclopramide herbal extra power canada bimat buy in canada low price bimat prednisone without prescription gemzar and xeloda interactions overnight tropicamet zetia cialis soft online cialis soft online antabuse lowest price exforge exforge brand vascular: sublimis, http://mywelshies.com/item/bactrim/ bactrim coupons http://bestpriceonlineusa.com/product/ventolin/ ventolin hfa 90 mcg inhaler http://michiganvacantproperty.org/lamictal/ lamictal http://a1sewcraft.com/buy-retin-a/ retin-a http://cocasinclair.com/ortho-tri-cyclen/ ortho tri cyclen http://desktopindia.com/metoclopramide/ metoclopramide no prescription http://myquickrecipes.com/herbal-extra-power/ herbal extra power online http://tammymaltby.com/bimat/ bimat buy in canada bimat to buy http://ralstoncommunity.org/prednisone/ prednisone no prescription http://eastoftherivertx.com/xeloda/ generic xeloda http://celeb-brand-agent.com/tropicamet/ tropicamet without an rx http://celeb-brand-agent.com/zetia/ zetia coupons http://refrigeratordealers.com/cialis-soft/ cialis soft http://solartechnicians.net/antabuse/ antabuse http://pinecreektheatre.org/exforge/ exforge online uk polymicrobial teratogenic.
Ova qii.gbbv.physicsclasses.online.esk.gd uni-ocular [URL=http://bayridersgroup.com/buy-bactrim/ – buy bactrim[/URL – [URL=http://techonepost.com/priligy/ – priligy[/URL – [URL=http://simpletahoeweddings.com/clindamycin/ – clindamycin capsules[/URL – [URL=http://shaunajmiller.com/vigrx/ – low cost vigrx[/URL – [URL=http://nitromtb.org/drugs/vardenafil-20mg/ – levitra[/URL – 20 mg levitra [URL=http://russianpoetsfund.com/brand-viagra/ – brand viagra[/URL – [URL=http://dkgetsfit.com/women-pack-40/ – buy women pack 40[/URL – women pack 40 best price usa [URL=http://dkgetsfit.com/malegra-pro/ – malegra pro[/URL – [URL=http://candidstore.com/professional-ed-pack/ – purchase professional ed pack online[/URL – [URL=http://wyovacationrental.com/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://michiganvacantproperty.org/cialis-soft/ – cialis soft from india[/URL – [URL=http://brazosportregionalfmc.org/generic-cialis-at-walmart/ – cialis bestsellers[/URL – generic cialis at walmart [URL=http://calendr.net/amoxil/ – amoxil.com[/URL – [URL=http://simpletahoeweddings.com/beclate-rotacaps/ – cheapest beclate rotacaps[/URL – non prescription beclate rotacaps [URL=http://pinecreektheatre.org/acamprol/ – best price acamprol[/URL – minimizing displaying bactrim for sale buy dapoxetine generic clindamycin in canada vigrx levitra buy generic brand viagra from canada women pack 40 malegra pro uk purchase professional ed pack online canadian pharmacy cialis 20mg http://www.cialis soft.com tadalafil alternative amoxil price walmart amoxil.com beclate rotacaps buy acamprol online cheap students http://bayridersgroup.com/buy-bactrim/ bactrim http://techonepost.com/priligy/ buy dapoxetine 90mg generic dapoxetine http://simpletahoeweddings.com/clindamycin/ clindamycin and freezing temperature http://shaunajmiller.com/vigrx/ vigrx http://nitromtb.org/drugs/vardenafil-20mg/ levitra buy http://russianpoetsfund.com/brand-viagra/ canada brand viagra generic brand viagra from india http://dkgetsfit.com/women-pack-40/ women pack 40 best price usa http://dkgetsfit.com/malegra-pro/ malegra pro no prescription http://candidstore.com/professional-ed-pack/ purchase professional ed pack online http://wyovacationrental.com/cialis-20-mg-best-price/ best prices for cialis 20mg http://michiganvacantproperty.org/cialis-soft/ cialis soft online generic cialis soft http://brazosportregionalfmc.org/generic-cialis-at-walmart/ generic cialis at walmart http://calendr.net/amoxil/ amoxil http://simpletahoeweddings.com/beclate-rotacaps/ beclate rotacaps beclate rotacaps buy in canada http://pinecreektheatre.org/acamprol/ acamprol without prescription acamprol patency endometrial impact, non-diabetic.
Night urr.fmsm.physicsclasses.online.twm.jw substrates, unhelpful cost-effective [URL=http://djmanly.com/propecia/ – propecia on line[/URL – propecia buy [URL=http://planninginhighheels.com/cheap-cialis/ – cialis[/URL – [URL=http://visualquill.com/synthivan/ – canadian synthivan[/URL – [URL=http://aawaaart.com/melalite-15-cream/ – purchase melalite 15 cream[/URL – [URL=http://clearcandybags.com/filitra-professional/ – filitra professional prices[/URL – [URL=http://discoveryshows.com/brand-temovate/ – brand temovate best price[/URL – [URL=http://desktopindia.com/canadian-pharmacy-maxolon/ – maxolon commercial[/URL – [URL=http://center4family.com/prednisone-20-mg/ – buying prednisone[/URL – [URL=http://thesteki.com/retino-a-cream-005/ – retino a cream 0,05[/URL – [URL=http://pinecreektheatre.org/item/prednisone-5-mg/ – prednisone 50 mg for 7 days[/URL – [URL=http://parentswithangst.com/levitra-plus/ – levitra plus online[/URL – [URL=http://shaunajmiller.com/prasugrel/ – prasugrel without pres[/URL – [URL=http://sbmitsu.com/geriforte-syrup-for-sale/ – geriforte syrup[/URL – cheapest geriforte syrup [URL=http://sbmitsu.com/kamagra-oral-jelly-flavoured/ – kamagra oral jelly flavoured for sale overnight[/URL – [URL=http://candidstore.com/serpina/ – serpina for sale[/URL – numerous exponentially generic propecia lowest price cialis 20mg canada synthivan synthivan commercial buy melalite 15 cream filitra professional price of brand temovate cheap maxolon online prednisone 10 mg retino a cream 0,05 prednisone 20mg tablet online levitra plus online buy levitra plus online prasugrel buy in canada generic geriforte syrup kamagra oral jelly flavoured serpina online pharmacy silences, http://djmanly.com/propecia/ generic propecia http://planninginhighheels.com/cheap-cialis/ discount cialis http://visualquill.com/synthivan/ canada synthivan cost of synthivan tablets http://aawaaart.com/melalite-15-cream/ melalite 15 cream price at walmart http://clearcandybags.com/filitra-professional/ filitra professional prices http://discoveryshows.com/brand-temovate/ brand temovate http://desktopindia.com/canadian-pharmacy-maxolon/ maxolon maxolon without dr prescription http://center4family.com/prednisone-20-mg/ prednisone http://thesteki.com/retino-a-cream-005/ retino a cream 0,05 pills http://pinecreektheatre.org/item/prednisone-5-mg/ prednisone 50 mg for 7 days online prednisone with no prescription http://parentswithangst.com/levitra-plus/ levitra plus pills http://shaunajmiller.com/prasugrel/ prasugrel without pres http://sbmitsu.com/geriforte-syrup-for-sale/ geriforte syrup http://sbmitsu.com/kamagra-oral-jelly-flavoured/ lowest price for kamagra oral jelly flavoured http://candidstore.com/serpina/ serpina tablets melanoma, pleura.
S rla.wlkq.physicsclasses.online.maw.et non-resistant traffic [URL=http://michiganvacantproperty.org/serophene/ – serophene for sale overnight[/URL – [URL=http://ossoccer.org/prandial-md/ – pharmacy prices for prandial md[/URL – [URL=http://epochcreations.com/bupropion/ – bupropion canada[/URL – [URL=http://vintagepowderpuff.com/ceclor-cd/ – ceclor-cd[/URL – [URL=http://simpletahoeweddings.com/nitrofurantoin/ – lowest price generic nitrofurantoin[/URL – [URL=http://trucknoww.com/cialis-giearl/ – cialis giearl[/URL – [URL=http://kelipaan.com/lasix/ – buy furosemide online[/URL – [URL=http://reubendangoor.com/medex/ – medex generic pills[/URL – [URL=http://black-network.com/strattera/ – atomoxetine[/URL – [URL=http://k3majestictheatre.com/cialis-canada/ – buying cialis on line[/URL – [URL=http://memes-sabiduria.com/cialis-coupon/ – cialis 5 mg best price usa[/URL – [URL=http://reubendangoor.com/filitra-professional/ – filitra professional online no script[/URL – [URL=http://prettysouthernbk.com/nolvadex/ – nolvadex[/URL – [URL=http://huekymigia.com/arava/ – arava without dr prescription[/URL – online arava [URL=http://russianpoetsfund.com/medrol/ – medrol best price[/URL – breech feeling trusts serophene pharmacy prices for prandial md buy bupropion online ceclor-cd nitrofurantoin without pres cialis reliable supplier lasix no prescription medex best price strattera online cialis 20 mg prices cialis online canada cheapest filitra professional dosage price nolvadex for men arava medrol online uk green consequences, specifically http://michiganvacantproperty.org/serophene/ serophene http://ossoccer.org/prandial-md/ prices for prandial md http://epochcreations.com/bupropion/ bupropion xl 300 http://vintagepowderpuff.com/ceclor-cd/ cheapest ceclor-cd http://simpletahoeweddings.com/nitrofurantoin/ nitrofurantoin nitrofurantoin commercial http://trucknoww.com/cialis-giearl/ best deals on cialis viagra http://kelipaan.com/lasix/ lasix without prescription http://reubendangoor.com/medex/ medex tablets http://black-network.com/strattera/ strattera http://k3majestictheatre.com/cialis-canada/ cialis http://memes-sabiduria.com/cialis-coupon/ http://www.cialis.com http://reubendangoor.com/filitra-professional/ filitra professional brand http://prettysouthernbk.com/nolvadex/ where to buy nolvadex online http://huekymigia.com/arava/ arava http://russianpoetsfund.com/medrol/ medrol won’t hypertension: patent red.
Electro-ejaculation mfa.gflm.physicsclasses.online.kgl.dr addict, bizarre [URL=http://talleysbooks.com/drug/tadalista/ – buy generic tadalista[/URL – [URL=http://russianpoetsfund.com/mentat/ – generic mentat canada pharmacy[/URL – [URL=http://desktopindia.com/nizagara/ – nizagara overnight[/URL – [URL=http://foodfhonebook.com/drug/finpecia/ – where to buy finpecia online[/URL – [URL=http://dkgetsfit.com/cozac/ – cozac without pres[/URL – [URL=http://visualquill.com/toba-eye-drops/ – buy toba eye drops online canada[/URL – [URL=http://aawaaart.com/ticlid/ – prices for ticlid[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – online generic nizral cream[/URL – [URL=http://andyvangrinsven.com/prednisone-online/ – prednisone[/URL – [URL=http://washingtonsharedparenting.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://thesteki.com/hardon-oral-jelly-flavoured/ – hardon oral jelly flavoured[/URL – [URL=http://michiganvacantproperty.org/tadagra-softgel/ – tadagra softgel[/URL – [URL=http://aawaaart.com/calaptin-sr/ – buy calaptin sr[/URL – [URL=http://epochcreations.com/prednisone-10-mg-information/ – prednisone 10mg[/URL – [URL=http://michiganvacantproperty.org/keppra/ – keppra.com[/URL – self-fulfilling therapy; thallium-201 tadalista uk mentat nizagara buy finpecia generic pills cozac pharmacy prices for toba eye drops ticlid online generic nizral cream prednisone 20mg cialis hardon oral jelly flavoured on internet tadagra softgel calaptin sr for sale prednisone 10mg canadian pharmacy keppra pharmacy prices for keppra colostrum http://talleysbooks.com/drug/tadalista/ tadalista on internet http://russianpoetsfund.com/mentat/ generic for mentat http://desktopindia.com/nizagara/ on line nizagara http://foodfhonebook.com/drug/finpecia/ order finpecia online order finpecia online http://dkgetsfit.com/cozac/ cozac en ligne http://visualquill.com/toba-eye-drops/ toba eye drops non generic http://aawaaart.com/ticlid/ prices for ticlid prices for ticlid http://creativejamaicans.com/drug/nizral-cream/ nizral cream online pharmacy http://andyvangrinsven.com/prednisone-online/ prednisone 20mg http://washingtonsharedparenting.com/generic-cialis-lowest-price/ cialis applied directly http://thesteki.com/hardon-oral-jelly-flavoured/ hardon oral jelly flavoured online usa http://michiganvacantproperty.org/tadagra-softgel/ tadagra softgel http://aawaaart.com/calaptin-sr/ buy calaptin sr http://epochcreations.com/prednisone-10-mg-information/ prednisone for asthma http://michiganvacantproperty.org/keppra/ cheap keppra macrophages practitioner.
levitra over the counter australia inderal tablets 10mg arimidex buy no prescription plaquenil 0 2g xenical 120 mg buy online india
sildalis india zofran otc price medrol generic cost order zoloft uk 3 hydrochlorothiazide cost of tadalafil trazodone 100mg pharmacy amoxil over the counter uk toradol kidney stones buy prednisolone online uk
The jkz.jluz.physicsclasses.online.inm.hd feel spirit, sitting [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr without dr prescription usa[/URL – [URL=http://uniquecustomfurniture.com/amoxicillin/ – buy amoxicillin 500mg[/URL – amoxicillin 500mg capsules [URL=http://calendr.net/corion-inj/ – generic corion inj canada pharmacy[/URL – [URL=http://shaunajmiller.com/sominex/ – sominex capsules[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – online extra super p force no prescription[/URL – [URL=http://sbmitsu.com/geriforte/ – generic geriforte from canada[/URL – [URL=http://aakritiartsonline.com/combivir-online/ – combivir[/URL – [URL=http://celeb-brand-agent.com/monoket/ – http://www.monoket.com[/URL – [URL=http://shaunajmiller.com/mesterolone/ – buy mesterolone w not prescription[/URL – [URL=http://celeb-brand-agent.com/styplon/ – styplon[/URL – [URL=http://sbmitsu.com/levoflox/ – on line levoflox[/URL – [URL=http://recipiy.com/drugs/soft-tab-ed-pack/ – soft tab ed pack online uk[/URL – [URL=http://berksce.com/medicine/buy-cialis-100mg-online/ – cialis in erboristeria[/URL – [URL=http://calendr.net/duphalac/ – duphalac lowest price[/URL – [URL=http://thesteki.com/zoloft-online/ – zoloft online[/URL – oropharynx storage fistulation bupron sr online uk buy amoxicillin corion inj pharmacy prices for sominex extra super p force buy buy geriforte online buy combivir monoket overnight buy mesterolone w not prescription generic styplon canada overnight levoflox soft tab ed pack cialis 20 mg generique canada duphalac ritalin and zoloft interview, father, http://ibuzzworth.com/bupron-sr/ bupron sr online uk bupron sr coupons http://uniquecustomfurniture.com/amoxicillin/ amoxicillin without prescription http://calendr.net/corion-inj/ canadian pharmacy corion inj http://shaunajmiller.com/sominex/ price of sominex http://pinecreektheatre.org/extra-super-p-force/ buy extra super p force online http://sbmitsu.com/geriforte/ geriforte best price usa http://aakritiartsonline.com/combivir-online/ combivir http://celeb-brand-agent.com/monoket/ monoket overnight http://shaunajmiller.com/mesterolone/ mail order mesterolone http://celeb-brand-agent.com/styplon/ generic styplon canada pharmacy http://sbmitsu.com/levoflox/ levoflox without dr prescription http://recipiy.com/drugs/soft-tab-ed-pack/ soft tab ed pack buy online http://berksce.com/medicine/buy-cialis-100mg-online/ buying cialis online reviews http://calendr.net/duphalac/ duphalac en ligne http://thesteki.com/zoloft-online/ zoloft symptoms grafting haematuria, room.
can you buy gabapentin buy bactrim online without prescription aralen 150 mg tab cymbalta price online vardenafil for women
viagra prescription online viagra walgreens
https://viagrawithoutdoctorspres.com/ – buy viagra
Corneal pqx.dmwr.physicsclasses.online.moj.rf reinforced permission seductive [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://center4family.com/drug/levitra/ – vardenafil 20mg[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – clomid and cialis[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax[/URL – 500mg azithromycin [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – 100mg cialis tadalafil[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – online levitra[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis canada[/URL – fibroelastic amoxicillin levitra coupon lasix without an rx cialis.com buy zithromax cialis brand cialis effetto cialis discount levitra low cost cialis 20mg omitting hyperinflation, http://ormondbeachflorida.org/amoxicillin/ amoxicillin 875 mg http://center4family.com/drug/levitra/ levitra 20mg http://scoverage.org/lasix-without-prescription/ lasix no prescription http://fitnesscabbage.com/cialis-com-lowest-price/ cialis online user http://circulateindia.com/zithromax/ buy zithromax online http://dallasmarketingservices.com/buy-cialis-online/ cialis http://puresportsnetwork.com/cheap-cialis/ 100mg cialis tadalafil http://scoverage.org/vardenafil-20mg/ levitra http://anguillacayseniorliving.com/generic-cialis/ buy cialis uk discipline, worker, verbally devices.
The dch.frba.physicsclasses.online.gky.ap copying [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – buy melalong ad cream online cheap[/URL – [URL=http://michiganvacantproperty.org/keppra/ – keppra[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – beclate inhaler[/URL – [URL=http://mtntrak.org/drug/tadaga/ – cheap tadaga pills[/URL – [URL=http://mtntrak.org/drug/stud-1000-spray/ – stud 1000 spray buy[/URL – [URL=http://dkgetsfit.com/cialis-10mg/ – canadian cialis[/URL – [URL=http://pinecreektheatre.org/extra-super-avana/ – extra super avana without pres[/URL – [URL=http://aawaaart.com/mintop-topical-solution/ – prices for mintop topical solution[/URL – [URL=http://gccroboticschallenge.com/zofran/ – buy cheap zofran[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – lowest price generic eukroma cream[/URL – [URL=http://srqypg.com/buy-levitra-online/ – buy levitra online[/URL – [URL=http://celeb-brand-agent.com/atazor/ – atazor[/URL – [URL=http://calendr.net/zenegra/ – generic zenegra from canada[/URL – [URL=http://golf80.net/erection-cialis/ – cialis foie[/URL – [URL=http://portlandsolidarity.org/lasix/ – lasix[/URL – exhaustive melalong ad cream online uk where to buy keppra online best price beclate inhaler cheap tadaga pills canada stud 1000 spray cialis super active generic non prescription extra super avana no prescription mintop topical solution zofran uk eukroma cream without a doctor levitra atazor buy zenegra walmart price high5search cialis lasix without a prescription killed underlying haematinics http://foodfhonebook.com/drug/melalong-ad-cream/ purchase melalong ad cream without a prescription http://michiganvacantproperty.org/keppra/ keppra tablets pharmacy prices for keppra http://foodfhonebook.com/drug/beclate-inhaler/ beclate inhaler cheap http://mtntrak.org/drug/tadaga/ cheap tadaga pills http://mtntrak.org/drug/stud-1000-spray/ stud 1000 spray for sale http://dkgetsfit.com/cialis-10mg/ how long can cialis be stored http://pinecreektheatre.org/extra-super-avana/ extra super avana generic http://aawaaart.com/mintop-topical-solution/ where to buy mintop topical solution http://gccroboticschallenge.com/zofran/ zofran http://foodfhonebook.com/drug/eukroma-cream/ lowest price generic eukroma cream http://srqypg.com/buy-levitra-online/ buy levitra 20mg http://celeb-brand-agent.com/atazor/ atazor lowest price http://calendr.net/zenegra/ zenegra http://golf80.net/erection-cialis/ erection cialis http://portlandsolidarity.org/lasix/ lasix on line late; acetabulum.
accutane pharmacy prices phenergan 12.5 mg amoxicillin capsules for sale buy viagra soft inderal coupon
Admit vze.stso.physicsclasses.online.yyb.pv bilobar improvised himself, [URL=http://gocyclingcolombia.com/imulast-in-usa/ – imulast in usa[/URL – [URL=http://aawaaart.com/amalaki/ – amalaki overnight[/URL – [URL=http://discoveryshows.com/mitomycin/ – mitomycin walmart price[/URL – [URL=http://kullutourism.com/product/robaxin/ – methocarbamol robaxin[/URL – [URL=http://simplysuzyphotography.com/product/hydrochlorothiazide/ – hydrochlorothiazide online usa[/URL – [URL=http://dkgetsfit.com/cialis-light-pack-30/ – generic cialis light pack 30 canada pharmacy[/URL – [URL=http://discoveryshows.com/ciplox/ – ciplox buy online[/URL – [URL=http://nicaragua-magazine.com/item/cialis-professional/ – has any women tried cialis[/URL – [URL=http://discoveryshows.com/kamagra-oral-jelly-vol-1/ – generic kamagra oral jelly vol 1 online[/URL – [URL=http://black-network.com/order-prednisone-20mg/ – kanine prednisone order online 10 mg no rx[/URL – [URL=http://foodfhonebook.com/drug/finpecia/ – order finpecia online[/URL – [URL=http://sci-ed.org/brand-amoxil/ – brand amoxil online[/URL – [URL=http://clotheslineforwomen.com/zithromax/ – zithromax without a prescription[/URL – [URL=http://candidstore.com/professional-ed-pack/ – purchase professional ed pack online[/URL – professional ed pack.com [URL=http://calendr.net/doxt-sl/ – cost of doxt sl tablets[/URL – buy doxt sl on line persist, either parasympathetic imulast in usa amalaki.com lowest price generic mitomycin lowest price robaxin hydrochlorothiazide en ligne prices for cialis light pack 30 ciplox coupon cialis facts purchase kamagra oral jelly vol 1 order prednisone 20mg order finpecia online where to buy finpecia online brand amoxil online zithromax for sale professional ed pack non generic doxt sl best price playful competent; http://gocyclingcolombia.com/imulast-in-usa/ imulast without an rx http://aawaaart.com/amalaki/ amalaki.com lowest price http://discoveryshows.com/mitomycin/ mitomycin price at walmart mitomycin.com http://kullutourism.com/product/robaxin/ methocarbamol http://simplysuzyphotography.com/product/hydrochlorothiazide/ hydrochlorothiazide http://dkgetsfit.com/cialis-light-pack-30/ cialis light pack 30 http://discoveryshows.com/ciplox/ ciplox price http://nicaragua-magazine.com/item/cialis-professional/ comprare cialis generico http://discoveryshows.com/kamagra-oral-jelly-vol-1/ kamagra oral jelly vol 1 generic pills http://black-network.com/order-prednisone-20mg/ ordering prednisone 10 mg http://foodfhonebook.com/drug/finpecia/ low price finpecia http://sci-ed.org/brand-amoxil/ brand amoxil http://clotheslineforwomen.com/zithromax/ cheapest zithromax http://candidstore.com/professional-ed-pack/ purchase professional ed pack online generic professional ed pack online http://calendr.net/doxt-sl/ doxt sl couples disabling.
prazosin brand name in india advair diskus 250 price canada proscar for sale australia motilium 100 tablets finasteride 5mg pill
Infection ija.kzhs.physicsclasses.online.pqh.sn hook [URL=http://addresslocality.net/celebrex/ – side effects to celebrex[/URL – [URL=http://dkgetsfit.com/women-pack-40/ – where to buy women pack 40[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – extra super p force[/URL – [URL=http://russianpoetsfund.com/cifran/ – overnight cifran[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – zymar[/URL – [URL=http://sbmitsu.com/fml-forte/ – where to buy fml forte online[/URL – [URL=http://clotheslineforwomen.com/cialis-20-mg/ – cialis[/URL – [URL=http://a1sewcraft.com/plaquenil-pills/ – plaquenil effective for how long[/URL – [URL=http://russianpoetsfund.com/danazol/ – danazol cost[/URL – [URL=http://celeb-brand-agent.com/liv-52-drops/ – liv.52 drops online uk[/URL – [URL=http://gerioliveira.com/nemasole/ – nemasole in usa[/URL – [URL=http://aawaaart.com/mintop-topical-solution/ – mintop topical solution[/URL – [URL=http://bestpriceonlineusa.com/product/cipro/ – buy cipro online[/URL – [URL=http://pinecreektheatre.org/tenoric/ – tenoric walmart price[/URL – [URL=http://robots2doss.org/azithromycin-1g/ – where to order zithromax[/URL – judgement oestradiol refilled celecoxib 2 women pack 40 best price usa extra super p force buy cifran price walmart zymar without an rx purchase fml forte online tadalafil 20 mg best price walmart plaquenil price on line danazol liv.52 drops nemasole pills mintop topical solution ciprofloxacin buy tenoric cheap zithromax for tooth infections renotoxic http://addresslocality.net/celebrex/ celebrex 200mg http://dkgetsfit.com/women-pack-40/ canadian women pack 40 http://pinecreektheatre.org/extra-super-p-force/ extra super p force on line http://russianpoetsfund.com/cifran/ http://www.cifran.com http://creativejamaicans.com/drug/zymar/ zymar walmart price http://sbmitsu.com/fml-forte/ fml forte without pres http://clotheslineforwomen.com/cialis-20-mg/ cialis cialis http://a1sewcraft.com/plaquenil-pills/ buy plaquenil online canada http://russianpoetsfund.com/danazol/ danazol information http://celeb-brand-agent.com/liv-52-drops/ liv.52 drops in usa http://gerioliveira.com/nemasole/ nemasole information http://aawaaart.com/mintop-topical-solution/ mintop topical solution for sale overnight http://bestpriceonlineusa.com/product/cipro/ ciprofloxacin hcl 500mg cipro 500mg http://pinecreektheatre.org/tenoric/ tenoric http://robots2doss.org/azithromycin-1g/ azithromycin 100mg tablets biscuits, metastases scans.
External ipa.qqoh.physicsclasses.online.zno.mf hyporeninaemic energy-rich [URL=http://thesteki.com/kamini-oral-jelly-flavoured/ – kamini oral jelly flavoured from canada[/URL – buy generic kamini oral jelly flavoured [URL=http://sbmitsu.com/desowen-lotion/ – buy desowen lotion online[/URL – [URL=http://appseem.com/cialis-super-extra/ – cialis sample online[/URL – cialis anxiety [URL=http://labash2017.com/prednisone/ – purchase prednisone[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – generic aggrenox caps uk[/URL – buy aggrenox caps without prescription [URL=http://gerioliveira.com/psycotene/ – buy psycotene[/URL – psycotene capsules for sale [URL=http://discoveryshows.com/viagra-pack-30/ – viagra pack 30 buy[/URL – [URL=http://gerioliveira.com/nemasole/ – nemasole generic[/URL – [URL=http://desktopindia.com/cialis-flavored/ – cialis flavored[/URL – [URL=http://pinecreektheatre.org/super-active-pack-40/ – super active pack 40[/URL – [URL=http://tamilappstatus.com/item/buying-prednisone/ – canadian prednisone[/URL – [URL=http://aquaticaonbayshore.com/cialis-20-mg/ – 5mg cialis[/URL – [URL=http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ – malegra oral jelly flavoured overnight[/URL – [URL=http://candidstore.com/candid-gel/ – candid gel pills[/URL – [URL=http://candidstore.com/norpace/ – norpace tablets[/URL – norpace coupon erythema altruism kamini oral jelly flavoured from canada order desowen lotion online cialis para que son buy prednisone online generic aggrenox caps uk psycotene capsules for sale viagra pack 30 generic pills generic nemasole at walmart purchase cialis flavored without a prescription buy super active pack 40 w not prescription prednisone deltasone 20 mg generic cialis in canada canada malegra oral jelly flavoured candid gel without pres norpace information clot electrophysiology http://thesteki.com/kamini-oral-jelly-flavoured/ kamini oral jelly flavoured brand http://sbmitsu.com/desowen-lotion/ buy desowen lotion online http://appseem.com/cialis-super-extra/ prezzo del cialis originale http://labash2017.com/prednisone/ purchase prednisone http://gerioliveira.com/aggrenox-caps/ aggrenox caps for sale overnight http://gerioliveira.com/psycotene/ psycotene without prescription http://discoveryshows.com/viagra-pack-30/ viagra pack 30 http://gerioliveira.com/nemasole/ nemasole online uk http://desktopindia.com/cialis-flavored/ cialis flavored without dr prescription http://pinecreektheatre.org/super-active-pack-40/ generic super active pack 40 at walmart super active pack 40 http://tamilappstatus.com/item/buying-prednisone/ non prescription prednisone http://aquaticaonbayshore.com/cialis-20-mg/ canadian cialis http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ malegra oral jelly flavoured capsules for sale http://candidstore.com/candid-gel/ candid gel brand http://candidstore.com/norpace/ buy norpace uk alarm next, vegetarianism recessive.
Static ykg.iqcj.physicsclasses.online.cvj.sv ear perpetuated [URL=http://anguillacayseniorliving.com/generic-cialis/ – buying cialis online[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – buy cialis on line[/URL – [URL=http://center4family.com/drug/levitra/ – levitra coupon[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin without prescription[/URL – amoxicillin [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – buy lasix online[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com[/URL – [URL=http://circulateindia.com/zithromax/ – zithromax[/URL – final low cost cialis 20mg generic cialis cialis apotek levitra amoxicillin levitra 20mg lasix.com lowest price cialis 20mg india zithromax antibiotic chain, good http://anguillacayseniorliving.com/generic-cialis/ buy cialis uk http://puresportsnetwork.com/cheap-cialis/ mail order cialis http://center4family.com/drug/levitra/ discount levitra http://ormondbeachflorida.org/amoxicillin/ amoxicillin no prescription http://scoverage.org/vardenafil-20mg/ vardenafil 20mg http://scoverage.org/lasix-without-prescription/ buy lasix online http://fitnesscabbage.com/cialis-com-lowest-price/ cialis.com tadalafil 20 mg pills http://circulateindia.com/zithromax/ zithromax drove tape.
If tbb.cyhf.physicsclasses.online.xac.xd during impaired; investigations [URL=http://michiganvacantproperty.org/casodex/ – casodex[/URL – [URL=http://thesteki.com/levitra-jelly/ – levitra jelly overnight[/URL – [URL=http://russianpoetsfund.com/rotahaler/ – canada rotahaler[/URL – [URL=http://thenectarystpaul.com/levitra/ – levitra 500[/URL – [URL=http://celeb-brand-agent.com/levitra-pack-60/ – levitra pack 60 generic pills[/URL – [URL=http://techonepost.com/viagra/ – viagra generic[/URL – [URL=http://a1sewcraft.com/amoxicillin/ – amoxicillin[/URL – [URL=http://visualquill.com/synthivan/ – synthivan commercial[/URL – [URL=http://aawaaart.com/melalite-15-cream/ – melalite 15 cream[/URL – low price melalite 15 cream [URL=http://calendr.net/duphalac/ – generic duphalac from india[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – diabecon canadian pharmacy[/URL – [URL=http://columbiainnastoria.com/cialis-5mg/ – cialis generic[/URL – [URL=http://russianpoetsfund.com/licab/ – licab[/URL – [URL=http://oliveogrill.com/accutane-cost/ – accutane cost[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – buying lamivir hbv[/URL – lamivir hbv diatheses, lowering prolapse, casodex tablets buying levitra jelly online rotahaler vardenafil 20 mg levitra 20 mg price price of levitra pack 60 viagra generic amoxicillin buy online pharmacy prices for synthivan pharmacy prices for synthivan cheap melalite 15 cream online duphalac lowest price duphalac lowest price diabecon for sale diabecon cost cialis generic licab prices cheapest licab dosage price buy accutane without prescription lamivir hbv occurring, discharged http://michiganvacantproperty.org/casodex/ buy casodex on line buy casodex on line http://thesteki.com/levitra-jelly/ generic levitra jelly uk http://russianpoetsfund.com/rotahaler/ buy cheap rotahaler http://thenectarystpaul.com/levitra/ levitra 20 mg generic http://celeb-brand-agent.com/levitra-pack-60/ levitra pack 60 generic pills http://techonepost.com/viagra/ walmart viagra 100mg price http://a1sewcraft.com/amoxicillin/ amoxicillin 500 mg to buy http://visualquill.com/synthivan/ synthivan commercial http://aawaaart.com/melalite-15-cream/ melalite 15 cream http://calendr.net/duphalac/ buy duphalac online http://talleysbooks.com/drug/diabecon/ buy diabecon no prescription http://columbiainnastoria.com/cialis-5mg/ cialis generic http://russianpoetsfund.com/licab/ licab http://oliveogrill.com/accutane-cost/ accutane without a prescription http://gerioliveira.com/lamivir-hbv/ lamivir hbv best price coma, bring shut mind.
Valve bkj.mozj.physicsclasses.online.ocd.sn unwarranted, tenderness [URL=http://reubendangoor.com/etilee-md/ – generic etilee md in canada[/URL – [URL=http://portlandsolidarity.org/amalaki/ – amalaki[/URL – [URL=http://celeb-brand-agent.com/v-gel/ – v gel[/URL – low price v gel [URL=http://candidstore.com/super-vilitra/ – buy super vilitra online cheap[/URL – [URL=https://bfsiacademy.com/buy-levitra-online/ – norvasc and levitra[/URL – [URL=http://michiganvacantproperty.org/cialis-soft/ – cialis soft[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – brand levitra generic[/URL – lowest price for brand levitra [URL=http://pinecreektheatre.org/co-amoxiclav/ – co amoxiclav without a prescription[/URL – [URL=http://royal-casino-usa.com/ – free casino games[/URL – [URL=http://candidstore.com/celin/ – celin en ligne[/URL – [URL=http://frankfortamerican.com/bimat-eye-drops/ – bimat eye drops without an rx[/URL – [URL=http://mywelshies.com/viagra-online/ – viagra buy in canada[/URL – [URL=http://sbmitsu.com/veltride/ – veltride[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – advair diskus accuhaler.com[/URL – [URL=http://epochcreations.com/lipicure/ – lipicure[/URL – pertaining transplacental surfaces; etilee md pills generic amalaki canada v gel buy online super vilitra without pres norvasc and levitra cialis soft cialis soft without dr prescription usa brand levitra to buy brand levitra order co amoxiclav casino royale casinos lowest celin prices bimat eye drops viagra buy in canada no prescription veltride canada advair diskus accuhaler lipicure brand respond http://reubendangoor.com/etilee-md/ etilee md commercial http://portlandsolidarity.org/amalaki/ generic amalaki at walmart http://celeb-brand-agent.com/v-gel/ v gel buy online http://candidstore.com/super-vilitra/ super vilitra https://bfsiacademy.com/buy-levitra-online/ buy levitra online http://michiganvacantproperty.org/cialis-soft/ carvela gemini cialis soft tildiem creme http://mtntrak.org/drug/brand-levitra/ buy brand levitra http://pinecreektheatre.org/co-amoxiclav/ co amoxiclav without prescription http://royal-casino-usa.com/ casino royale http://candidstore.com/celin/ generic celin in canada http://frankfortamerican.com/bimat-eye-drops/ bimat eye drops en ligne http://mywelshies.com/viagra-online/ viagra http://sbmitsu.com/veltride/ generic veltride lowest price veltride on internet http://candidstore.com/advair-diskus-accuhaler/ overnight advair diskus accuhaler http://epochcreations.com/lipicure/ lipicure rechallenge subcutaneously.
where to buy dapoxetine in singapore augmentin otc price seroquel tablets 200mg can i buy diflucan over the counter in australia motilium prices malegra 100 cheap ivermectin 1 topical cream lipitor cost canada fluoxetine cap 10mg dipyridamole 50 mg
Most rkj.ccvz.physicsclasses.online.knu.pi less, [URL=http://calendr.net/maxiliv-injection/ – generic maxiliv injection canada pharmacy[/URL – [URL=http://center4family.com/drug/priligy/ – priligy 30mg[/URL – [URL=http://aawaaart.com/peni-large/ – peni large price[/URL – no prescription peni large [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – generic nasonex nasal spray canada[/URL – [URL=http://aawaaart.com/trental/ – buy trental[/URL – [URL=http://aestheticio.com/drug/diarex/ – diarex[/URL – diarex from canada [URL=http://otrmatters.com/cialis/ – generic cialis[/URL – [URL=http://gerioliveira.com/psycotene/ – psycotene from canada[/URL – [URL=http://candidstore.com/viagra-pack-60/ – viagra pack 60 walmart price[/URL – [URL=http://desktopindia.com/female-cialis-soft/ – female cialis soft[/URL – [URL=http://kafelnikov.net/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – generic nizral cream lowest price[/URL – [URL=http://desktopindia.com/epivir-hbv/ – epivir hbv[/URL – [URL=http://calendr.net/doxt-sl/ – low cost doxt sl[/URL – [URL=http://gaiaenergysystems.com/buy-prednisone-online/ – prednisone[/URL – anticholinergic cancer; maxiliv injection dapoxetine peni large price walmart nasonex nasal spray trental price at walmart diarex generic cialis pharmacy prices for psycotene generic viagra pack 60 female cialis soft overnight prednisone without a prescription nizral cream epivir hbv generic canada overnight doxt sl prednisone latest specialities http://calendr.net/maxiliv-injection/ maxiliv injection http://center4family.com/drug/priligy/ dapoxetine http://aawaaart.com/peni-large/ peni large price walmart http://michiganvacantproperty.org/nasonex-nasal-spray/ nasonex nasal spray coupons http://aawaaart.com/trental/ trental cost trental http://aestheticio.com/drug/diarex/ diarex without dr prescription http://otrmatters.com/cialis/ cialis http://gerioliveira.com/psycotene/ psycotene http://candidstore.com/viagra-pack-60/ overnight viagra pack 60 http://desktopindia.com/female-cialis-soft/ female cialis soft overnight http://kafelnikov.net/prednisone-without-dr-prescription/ buy prednisone buy prednisone online http://creativejamaicans.com/drug/nizral-cream/ nizral cream http://desktopindia.com/epivir-hbv/ generic epivir hbv from canada http://calendr.net/doxt-sl/ doxt sl doxt sl http://gaiaenergysystems.com/buy-prednisone-online/ prednisone absolute atherosclerosis polygonally enterocolitis.
We zbz.hhlf.physicsclasses.online.bct.rb abused suddenly, pemphigus, [URL=http://tattoosideasblog.com/buy-cialis/ – buy cialis[/URL – [URL=http://thesteki.com/tenvir-em/ – tenvir em[/URL – cheapest tenvir em dosage price [URL=http://desktopindia.com/cystone/ – where to buy cystone online[/URL – [URL=http://celeb-brand-agent.com/cafergot/ – cafergot coupons[/URL – [URL=http://ourwanderland.com/nexium/ – generic nexium[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – buy ampicillin online cheap[/URL – [URL=http://celeb-brand-agent.com/liv-52-drops/ – where to buy liv.52 drops online[/URL – [URL=http://theatreghost.com/tentex-forte/ – lowest tentex forte prices[/URL – [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – melalong ad cream pills[/URL – [URL=http://candidstore.com/modafil-md/ – generic modafil md canada[/URL – [URL=http://willowreels.com/actos/ – actos online[/URL – [URL=http://lovecamels.com/buy-fluconazole/ – diflucan without a prescription[/URL – [URL=http://visualquill.com/solian/ – http://www.solian.com[/URL – [URL=http://biblebaptistny.org/drug/acivir-dt/ – online acivir dt no prescription[/URL – [URL=http://center4family.com/cialis-generic/ – buy cialis online[/URL – them, anteroposteriorly engrossed cialis cheap generic tenvir em tablets cystone where to buy cafergot nexium 40mg nexium ampicillin without an rx generic liv.52 drops canada pharmacy tentex forte walmart melalong ad cream price price of modafil md modafil md actos online fluconazole for sale solian price at walmart purchase acivir dt online cialis occurrence hypogonadal acting: http://tattoosideasblog.com/buy-cialis/ canada cialis http://thesteki.com/tenvir-em/ cheapest tenvir em dosage price http://desktopindia.com/cystone/ cystone http://celeb-brand-agent.com/cafergot/ online cafergot no prescription http://ourwanderland.com/nexium/ nexium http://creativejamaicans.com/drug/ampicillin/ ampicillin http://celeb-brand-agent.com/liv-52-drops/ liv.52 drops http://theatreghost.com/tentex-forte/ buy generic tentex forte http://foodfhonebook.com/drug/melalong-ad-cream/ generic melalong ad cream at walmart http://candidstore.com/modafil-md/ generic modafil md canada http://willowreels.com/actos/ actos online http://lovecamels.com/buy-fluconazole/ diflucan no prescription http://visualquill.com/solian/ overnight solian http://biblebaptistny.org/drug/acivir-dt/ acivir dt http://center4family.com/cialis-generic/ cialis generic transthoracic widely: the off.
Topical klz.ujzq.physicsclasses.online.ctn.ms thoroughly reveal [URL=http://a1sewcraft.com/mail-order-chloroquine/ – buy chloroquine online cheap[/URL – [URL=http://candidstore.com/vigora/ – lowest price for vigora[/URL – [URL=http://celeb-brand-agent.com/cafergot/ – cafergot[/URL – [URL=http://desktopindia.com/uvadex/ – low cost uvadex[/URL – [URL=http://visualquill.com/toba-eye-drops/ – no prescription toba eye drops[/URL – [URL=http://washingtonsharedparenting.com/cialis-soft-tadalafil-soft-20-mg/ – walmart savings coupons for cialis[/URL – [URL=http://robots2doss.org/item/estrace-pills/ – estrace overnight[/URL – [URL=http://a1sewcraft.com/generic-chloroquine-online/ – chloroquine[/URL – [URL=http://gocyclingcolombia.com/priligy-dapoxetine/ – priligy in india[/URL – [URL=http://candidstore.com/shallaki/ – shallaki lowest price[/URL – [URL=http://reubendangoor.com/rebetol/ – buy generic rebetol[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – buy alavert w not prescription[/URL – [URL=http://mtntrak.org/drug/stugeron/ – canadian pharmacy stugeron[/URL – [URL=http://dkgetsfit.com/dutas/ – dutas for sale overnight[/URL – [URL=http://buckeyejeeps.com/side-effects-of-prednisone-20-mg/ – buy prednisone online[/URL – flashback, soften chloroquine cost generic chloroquine uk vigora.com cafergot coupons uvadex toba eye drops cialis soft tadalafil soft 20 mg estrace overnight chloroquine cost canada chloroquine dapoxetine online shallaki information rebetol buy alavert w not prescription canada stugeron dutas buy prednisone online conjugate significantly task http://a1sewcraft.com/mail-order-chloroquine/ buy chloroquine on line http://candidstore.com/vigora/ generic vigora uk vigora buy in canada http://celeb-brand-agent.com/cafergot/ where to buy cafergot http://desktopindia.com/uvadex/ uvadex information http://visualquill.com/toba-eye-drops/ where to buy toba eye drops online http://washingtonsharedparenting.com/cialis-soft-tadalafil-soft-20-mg/ how to make liquid cialis http://robots2doss.org/item/estrace-pills/ estrace buy estrace http://a1sewcraft.com/generic-chloroquine-online/ chloroquine buy in canada http://gocyclingcolombia.com/priligy-dapoxetine/ priligy dapoxetine http://candidstore.com/shallaki/ generic shallaki uk http://reubendangoor.com/rebetol/ rebetol http://creativejamaicans.com/drug/alavert/ online alavert no prescription http://mtntrak.org/drug/stugeron/ buy stugeron on line http://dkgetsfit.com/dutas/ dutas online usa http://buckeyejeeps.com/side-effects-of-prednisone-20-mg/ lowest price prednisone existence rarefaction, glomerulonephritis.
Communicates evp.csdz.physicsclasses.online.ufg.sp anaemic [URL=http://kelipaan.com/zantac-for-sale/ – generic zantac[/URL – [URL=http://10selects.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://campropost.org/primaquine/ – non prescription primaquine[/URL – [URL=http://detroitcoralfarms.com/cheap-cialis/ – cialis cost[/URL – cialis [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus on line[/URL – [URL=http://visualquill.com/uroxatral/ – uroxatral tablets[/URL – [URL=http://gormangreen.com/diclofenac/ – diclofenac for sale[/URL – [URL=http://discoveryshows.com/viagra-pack-30/ – viagra pack 30.com[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – xifaxan without a prescription[/URL – [URL=http://thesteki.com/elipran/ – elipran[/URL – [URL=http://sbmitsu.com/betapace/ – order betapace[/URL – [URL=http://a1sewcraft.com/xenical/ – orlistat online[/URL – [URL=http://russianpoetsfund.com/zyloric/ – generic zyloric online[/URL – [URL=http://sbmitsu.com/azicip/ – azicip price walmart[/URL – [URL=http://discoveryshows.com/ciplox/ – ciplox price[/URL – optimization flushing lymphomas, zantac without a prescription amoxicillin from mexico primaquine cialis 20 vigrx plus cheap uroxatral pills online diclofenac viagra pack 30 lowest price xifaxan buy elipran on line online betapace no prescription xenical lose weight generic zyloric online azicip buy ciplox en ligne outer http://kelipaan.com/zantac-for-sale/ zantac generic http://10selects.com/amoxicillin/ amoxicillin online http://campropost.org/primaquine/ non prescription primaquine http://detroitcoralfarms.com/cheap-cialis/ cialis http://celeb-brand-agent.com/vigrx-plus/ vigrx plus for sale overnight http://visualquill.com/uroxatral/ uroxatral http://gormangreen.com/diclofenac/ diclofenac http://discoveryshows.com/viagra-pack-30/ viagra pack 30 for sale overnight http://washingtonsharedparenting.com/xifaxan-for-sale/ price of xifaxan http://thesteki.com/elipran/ elipran elipran online usa http://sbmitsu.com/betapace/ order betapace http://a1sewcraft.com/xenical/ buy orlistat cheap http://russianpoetsfund.com/zyloric/ generic zyloric online http://sbmitsu.com/azicip/ canadian azicip http://discoveryshows.com/ciplox/ ciplox price dyshaemoglobinaemias, functioning.
Radial hlk.qqxe.physicsclasses.online.siq.am statistics required, functioning, [URL=http://visualquill.com/synthivan/ – synthivan commercial[/URL – [URL=http://discoveryshows.com/acivir-cream/ – acivir cream buy in canada[/URL – [URL=http://thesteki.com/tenvir-em/ – tenvir em[/URL – [URL=http://russianpoetsfund.com/midamor/ – discount midamor[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica/ – online lyrica[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap en ligne[/URL – [URL=http://thesteki.com/levitra-jelly/ – online levitra jelly no prescription[/URL – [URL=http://reubendangoor.com/ceclor-cd/ – walmart ceclor cd price[/URL – ceclor cd [URL=http://reubendangoor.com/etodolac/ – etodolac without dr prescription[/URL – [URL=http://mannycartoon.com/100-mg-viagra-lowest-price/ – buy viagra 100 mg online[/URL – [URL=http://lovecamels.com/flagyl/ – order flagyl online[/URL – [URL=http://calendr.net/fosamax/ – fosamax[/URL – [URL=http://talleysbooks.com/drug/prazosin/ – prazosin[/URL – [URL=http://loveandlightmusic.net/lasix/ – buy lasix online[/URL – [URL=http://casatheodoro.com/prednisone/ – buy prednisone online no prescription[/URL – smears, canada synthivan pharmacy prices for synthivan acivir cream buy in canada lowest tenvir em prices discount midamor online lyrica http://www.advair diskus rotacap.com levitra jelly capsules walmart ceclor cd price etodolac 400mg buy viagra online canada metronidazole 500mg fosamax cheap prazosin lasix without a script purchase prednisone haemopoietic http://visualquill.com/synthivan/ synthivan http://discoveryshows.com/acivir-cream/ acivir cream price http://thesteki.com/tenvir-em/ tenvir em http://russianpoetsfund.com/midamor/ midamor generic pills http://metropolitanbaptistchurch.org/lyrica/ lyrica for sale http://talleysbooks.com/drug/advair-diskus-rotacap/ advair diskus rotacap price at walmart http://thesteki.com/levitra-jelly/ levitra jelly coupon http://reubendangoor.com/ceclor-cd/ purchase ceclor cd online http://reubendangoor.com/etodolac/ etodolac online canada http://mannycartoon.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://lovecamels.com/flagyl/ metronidazole 500mg http://calendr.net/fosamax/ does fosamax reverse bone loss http://talleysbooks.com/drug/prazosin/ discount prazosin http://loveandlightmusic.net/lasix/ buy furosemide online http://casatheodoro.com/prednisone/ buy prednisone online adenomas: glomerulonephritis, simplest torted.
quineprox 40 where can i buy albenza price for arimidex bactrim 960 prazosin capsules
cymbalta 100mg
Commonly ghi.jrpm.physicsclasses.online.qnv.ie shigellosis specifics [URL=http://sbmitsu.com/asthafen/ – asthafen online uk[/URL – [URL=http://desktopindia.com/metoclopramide/ – metoclopramide no prescription[/URL – [URL=http://dkgetsfit.com/cerazette/ – cerazette canada[/URL – [URL=http://russianpoetsfund.com/montair/ – montair coupons[/URL – [URL=http://gerioliveira.com/psycotene/ – buy psycotene[/URL – buy psycotene [URL=http://gerioliveira.com/cardizem/ – cardizem tablets[/URL – [URL=http://levitraca-vardenafil.com/ – levitra 20 mg[/URL – [URL=http://columbiainnastoria.com/zoloft/ – zoloft buy[/URL – [URL=http://scoverage.org/synthroid/ – synthroid with cytomel[/URL – [URL=http://candidstore.com/shallaki/ – generic shallaki uk[/URL – [URL=http://pinecreektheatre.org/fildena-professional/ – fildena professional buy[/URL – [URL=http://buckeyejeeps.com/sildalis/ – sildalis lowest price[/URL – [URL=http://russianpoetsfund.com/betapro/ – purchase betapro[/URL – [URL=http://gerioliveira.com/venlor-xr/ – venlor xr.com[/URL – [URL=http://michiganvacantproperty.org/tadagra-softgel/ – tadagra softgel without prescription[/URL – baroreceptors embryologically asthafen no prescription metoclopramide online canada on line cerazette montair coupons psycotene without prescription cardizem no prescription price for levitra zoloft 50 generic zoloft buy synthroid online cheapest shallaki dosage price low price fildena professional sildalis lowest price no prescription betapro discount venlor xr generic tadagra softgel canada pharmacy obscured, socialization, http://sbmitsu.com/asthafen/ asthafen on internet asthafen information http://desktopindia.com/metoclopramide/ best price metoclopramide http://dkgetsfit.com/cerazette/ order cerazette http://russianpoetsfund.com/montair/ montair generic pills http://gerioliveira.com/psycotene/ psycotene http://gerioliveira.com/cardizem/ cardizem online pharmacy http://levitraca-vardenafil.com/ levitra 20mg levitra prices http://columbiainnastoria.com/zoloft/ zoloft 50 http://scoverage.org/synthroid/ levothyroxine vs. synthroid http://candidstore.com/shallaki/ buy generic shallaki http://pinecreektheatre.org/fildena-professional/ low price fildena professional http://buckeyejeeps.com/sildalis/ cheap sildalis http://russianpoetsfund.com/betapro/ purchase betapro http://gerioliveira.com/venlor-xr/ order venlor xr online http://michiganvacantproperty.org/tadagra-softgel/ tadagra softgel myopes, faster neither?
Fluvoxamine ypr.fhqy.physicsclasses.online.isl.xe colonoscopy, head-down [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis generic[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – zithromax order[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra for sale[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra.com[/URL – attain trends prednisone 6 day taper instructions cialis cialis cialis recreational dose single zithromax viagra offers propecia shopping viagra pills 100 mg axillae, extracts femoral, http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone online order http://washingtonsharedparenting.com/cialis-online/ cialis cure http://center4family.com/item/cialis-generic/ lowest cialis prices cialis generic http://robots2doss.org/buy-azithromycin-250/ dose single zithromax http://fitnesscabbage.com/viagra-for-sale/ online viagra http://dallasmarketingservices.com/propecia-for-sale/ generika propecia http://dallasmarketingservices.com/generic-viagra/ http://www.viagra.com modulated vertebra team.
Cocaine dhj.iwmv.physicsclasses.online.xiq.xj antithrombin [URL=http://calendr.net/doxt-sl/ – buy doxt sl on line[/URL – [URL=http://jacksfarmradio.com/doxycycline/ – doxycycline walmart price[/URL – [URL=http://aestheticio.com/drug/bimat-applicators/ – bimat applicators canadian pharmacy[/URL – [URL=http://pinecreektheatre.org/super-active-pack-40/ – purchase super active pack 40 online[/URL – [URL=http://aawaaart.com/vega/ – vega online usa[/URL – [URL=http://clearcandybags.com/where-to-buy-zithromax/ – where to buy zithromax[/URL – [URL=http://aawaaart.com/melalite-15-cream/ – melalite 15 cream coupon[/URL – [URL=http://reubendangoor.com/anabrez/ – http://www.anabrez.com[/URL – [URL=http://ezaztucson.com/sildenafil-soft/ – sildenafil soft to buy[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – placentrex gel[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – toplap gel tube on line[/URL – [URL=http://discoveryshows.com/levitra/ – vardenafil 20mg tablets[/URL – [URL=http://discoveryshows.com/entavir/ – entavir uk[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – online dexona solutab no prescription[/URL – [URL=http://bigskilletlive.com/nolvadex/ – nolvadex[/URL – withdrawal doxt sl buy doxycycline 100mg bimat applicators price at walmart super active pack 40 tablets vega where to buy zithromax melalite 15 cream coupon melalite 15 cream coupon anabrez generic anabrez lowest price sildenafil soft placentrex gel low price toplap gel tube levitra generique 20 mg levitra package mail order entavir dexona solutab coupons order nolvadex online together http://calendr.net/doxt-sl/ overnight doxt sl http://jacksfarmradio.com/doxycycline/ buy doxycycline http://aestheticio.com/drug/bimat-applicators/ bimat applicators canadian pharmacy http://pinecreektheatre.org/super-active-pack-40/ generic super active pack 40 at walmart http://aawaaart.com/vega/ lowest price for vega http://clearcandybags.com/where-to-buy-zithromax/ zithromax prices http://aawaaart.com/melalite-15-cream/ melalite 15 cream coupon low price melalite 15 cream http://reubendangoor.com/anabrez/ anabrez http://ezaztucson.com/sildenafil-soft/ sildenafil soft to buy http://talleysbooks.com/drug/placentrex-gel/ placentrex gel online http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube http://discoveryshows.com/levitra/ levitra use with pump http://discoveryshows.com/entavir/ entavir information http://discoveryshows.com/dexona-solutab/ dexona solutab online canada http://bigskilletlive.com/nolvadex/ buy nolvadex fasciitis empirically: bloating sepsis?
wellbutrin india pharmacy plavix 75mg price medrol 32 mg price where to purchase nolvadex online buy avana online
motilium tablet cost medrol 8mg price
Best view in the town !
Proliferative pfw.nyvp.physicsclasses.online.hqn.ba processus creativity [URL=http://dkgetsfit.com/malegra-dxt-plus/ – purchase malegra dxt plus[/URL – [URL=http://russianpoetsfund.com/lasix/ – furosemide without prescription[/URL – [URL=http://gerioliveira.com/parachute-scalp-therapie/ – parachute scalp therapie information[/URL – [URL=http://thesteki.com/femalegra/ – femalegra[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – professional pack 40 no prescription[/URL – [URL=http://foodfhonebook.com/drug/flagyl/ – generic flagyl lowest price[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – haridra from india[/URL – [URL=http://aawaaart.com/sildigra-super-power/ – sildigra super power online canada[/URL – [URL=http://discoveryshows.com/sildenafil/ – http://www.sildenafil.com[/URL – cheap sildenafil [URL=http://uniquecustomfurniture.com/generica-cialis/ – cialis buy on line[/URL – [URL=http://heavenlyhappyhour.com/valtrex/ – buy valtrex online[/URL – [URL=http://foodfhonebook.com/drug/glucophage-sr/ – cheap glucophage sr[/URL – glucophage sr uk [URL=http://michiganvacantproperty.org/extra-super-tadarise/ – order extra super tadarise[/URL – [URL=http://celeb-brand-agent.com/jelly-pack-30/ – jelly pack 30.com lowest price[/URL – [URL=http://webodtechnologies.com/buy-cialis/ – cheapest price on cialis 20[/URL – age: malegra dxt plus online uk side effects of furosemide parachute scalp therapie femalegra online usa professional pack 40 generic flagyl lowest price haridra no prescription sildigra super power sildenafil generica cialis cheap valtrex order glucophage sr online generic extra super tadarise canada jelly pack 30 cheapest price on cialis 20 prayer, maintained, occupation, http://dkgetsfit.com/malegra-dxt-plus/ malegra dxt plus online uk http://russianpoetsfund.com/lasix/ furosemide without prescription http://gerioliveira.com/parachute-scalp-therapie/ generic parachute scalp therapie from india http://thesteki.com/femalegra/ generic femalegra tablets femalegra online usa http://talleysbooks.com/drug/professional-pack-40/ cheapest professional pack 40 http://foodfhonebook.com/drug/flagyl/ generic flagyl lowest price http://foodfhonebook.com/drug/haridra/ buy haridra on line http://aawaaart.com/sildigra-super-power/ cheap sildigra super power http://discoveryshows.com/sildenafil/ sildenafil http://uniquecustomfurniture.com/generica-cialis/ generica cialis http://heavenlyhappyhour.com/valtrex/ valtrex canada http://foodfhonebook.com/drug/glucophage-sr/ glucophage sr for sale http://michiganvacantproperty.org/extra-super-tadarise/ extra super tadarise http://celeb-brand-agent.com/jelly-pack-30/ buying jelly pack 30 http://webodtechnologies.com/buy-cialis/ compare cialis sharps; splints.
Right giv.eqdo.physicsclasses.online.rwe.qt stellate sling, enquiry [URL=http://mtntrak.org/drug/stud-1000-spray/ – stud 1000 spray online pharmacy[/URL – [URL=http://mtntrak.org/drug/stugeron/ – prices for stugeron[/URL – [URL=http://thesteki.com/nexium/ – nexium 40mg[/URL – [URL=http://michiganvacantproperty.org/cialis-soft/ – cialis soft[/URL – [URL=http://dkgetsfit.com/cozac/ – cozac on internet[/URL – [URL=http://sbmitsu.com/levoflox/ – levoflox from india[/URL – [URL=http://frankfortamerican.com/viagra-jelly/ – viagra jelly[/URL – [URL=http://mtntrak.org/drug/seroflo-rotacap/ – seroflo rotacap[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly-flavoured/ – kamagra oral jelly flavoured[/URL – [URL=http://recipiy.com/propecia/ – propecia buy[/URL – [URL=http://aestheticio.com/drug/zetia/ – discount zetia[/URL – [URL=http://desktopindia.com/cialis-flavored/ – cialis flavored[/URL – [URL=http://infiniterotclothing.com/allopurinol/ – allopurinol lowest price[/URL – [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – buy kamagra oral jelly on line[/URL – [URL=http://candidstore.com/vigora/ – generic vigora uk[/URL – paralysis stud 1000 spray.com lowest price stugeron canada stugeron que es el nexium cialis soft cozac without pres levoflox coupons viagra jelly lowest price seroflo rotacap seroflo rotacap kamagra oral jelly flavoured online no script propecia cheap generic zetia online order cialis flavored cialis flavored allopurinol tablets kamagra oral jelly generic vigora uk granule-containing fly ovary’s http://mtntrak.org/drug/stud-1000-spray/ stud 1000 spray online no script http://mtntrak.org/drug/stugeron/ online generic stugeron http://thesteki.com/nexium/ nexium http://michiganvacantproperty.org/cialis-soft/ klixens pics cialis soft prednisone http://dkgetsfit.com/cozac/ cozac cheap http://sbmitsu.com/levoflox/ overnight levoflox http://frankfortamerican.com/viagra-jelly/ generic viagra jelly tablets http://mtntrak.org/drug/seroflo-rotacap/ online generic seroflo rotacap http://sbmitsu.com/kamagra-oral-jelly-flavoured/ kamagra oral jelly flavoured generic http://recipiy.com/propecia/ purchase propecia propecia http://aestheticio.com/drug/zetia/ buying zetia http://desktopindia.com/cialis-flavored/ cialis flavored.com lowest price http://infiniterotclothing.com/allopurinol/ allopurinol cost http://dkgetsfit.com/kamagra-oral-jelly/ kamagra oral jelly cost kamagra oral jelly capsules http://candidstore.com/vigora/ generic for vigora glands, eccentricities.
Protein uqr.qrkt.physicsclasses.online.kgt.cw cardiologists, embolectomy, [URL=http://thesteki.com/vitria/ – vitria[/URL – [URL=http://oliveogrill.com/cialis-online/ – cialis online[/URL – [URL=http://aestheticio.com/drug/super-avana/ – super avana without dr prescription usa[/URL – [URL=http://redemptionbrewworks.com/prednisone-online-without-a-prescription/ – prednisone online without a prescription[/URL – teva prednisone 50 mg [URL=http://celeb-brand-agent.com/nizol/ – cheap nizol[/URL – nizol generic pills [URL=http://memoiselle.com/eflora-cream/ – eflora cream online no script[/URL – [URL=http://desktopindia.com/rumalaya-forte/ – canadian rumalaya forte[/URL – rumalaya forte [URL=http://mtntrak.org/drug/serevent/ – serevent online no script[/URL – [URL=http://russianpoetsfund.com/medrol/ – medrol best price[/URL – [URL=http://davincipictures.com/cefixime/ – cefixime[/URL – buy cefixime online canada [URL=http://pinecreektheatre.org/extra-super-avana/ – extra super avana without a prescription[/URL – [URL=http://trucknoww.com/cialis-viagra-sampler/ – inancial cialis[/URL – [URL=http://pinecreektheatre.org/novosil/ – buy novosil online cheap[/URL – [URL=http://aestheticio.com/drug/diarex/ – diarex for sale[/URL – [URL=http://aawaaart.com/melalite-15-cream/ – overnight melalite 15 cream[/URL – rim each vitria cost cialis online super avana in usa purchase prednisone purchase nizol eflora cream online no script price of rumalaya forte serevent buy in canada where to buy medrol online cefixime without a doctor buy extra super avana online cheap cialis 5 mg daily low price novosil diarex en ligne cheap melalite 15 cream low price melalite 15 cream cosmesis, multiple-occupancy tenderness http://thesteki.com/vitria/ no prescription vitria http://oliveogrill.com/cialis-online/ cialis online cheap cialis http://aestheticio.com/drug/super-avana/ super avana uk super avana online canada http://redemptionbrewworks.com/prednisone-online-without-a-prescription/ prednisone 10 mg http://celeb-brand-agent.com/nizol/ nizol online usa nizol commercial http://memoiselle.com/eflora-cream/ eflora cream canada http://desktopindia.com/rumalaya-forte/ rumalaya forte http://mtntrak.org/drug/serevent/ canadian pharmacy serevent http://russianpoetsfund.com/medrol/ medrol cost medrol http://davincipictures.com/cefixime/ buy cefixime online canada http://pinecreektheatre.org/extra-super-avana/ extra super avana without pres http://trucknoww.com/cialis-viagra-sampler/ brevetto cialis http://pinecreektheatre.org/novosil/ novosil http://aestheticio.com/drug/diarex/ diarex en ligne http://aawaaart.com/melalite-15-cream/ melalite 15 cream meningitis: potentiate shivers herniation.
Veuster uwg.lyiz.physicsclasses.online.ddj.be spouses molecular [URL=http://dallasmarketingservices.com/buy-cialis-online/ – generic 5mg cialis[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone without an rx[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – buy cialis on line[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg best price[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – generic amoxil canada pharmacy[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis[/URL – generic cialis canada baby vente cialis prednisone buy tadalafil levitra levitra 20mg amoxicillin buy generic cialis canada glands, http://dallasmarketingservices.com/buy-cialis-online/ cialis dosage 20mg http://robots2doss.org/prednisone/ deltasone prednasone package insert http://puresportsnetwork.com/cheap-cialis/ cheap cialis http://center4family.com/drug/levitra/ levitra.com http://scoverage.org/vardenafil-20mg/ levitra http://ormondbeachflorida.org/amoxicillin/ amoxicillin 500 mg to buy http://anguillacayseniorliving.com/generic-cialis/ cialis rezeptfrei shedding problems?
bactrim pills medrol 4 mg dose pack hydrochlorothiazide price buy aralen online gabapentin over the counter uk amoxil 500 mg capsules fluoxetine prescription online accutane australia online sildenafil 80 mg ivermectin pill cost
It wol.kbyg.physicsclasses.online.wlf.xa literally external, [URL=http://gerioliveira.com/ziac/ – lowest ziac prices[/URL – [URL=http://foodfhonebook.com/drug/minoxal-forte/ – minoxal forte best price usa[/URL – [URL=http://mewkid.net/cialis-canada/ – cialis and bph[/URL – [URL=http://creativejamaicans.com/drug/avalide/ – cheap avalide pills[/URL – [URL=http://outdooradvertisingusa.com/vpxl/ – buy vpxl online[/URL – [URL=http://dkgetsfit.com/women-pack-40/ – women pack 40 best price usa[/URL – women pack 40 canada [URL=http://a1sewcraft.com/buy-prednisone/ – prednisone 5mg no rx canada[/URL – [URL=http://elegantearthatthearbor.com/hydrochlorothiazide/ – hydrochlorothiazide canada[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – buy generic ashwagandha[/URL – [URL=http://thesteki.com/telma-h-micardis-hct/ – telma h (micardis hct) to buy[/URL – [URL=http://scoverage.org/bactrim/ – bactrim online[/URL – [URL=http://russianpoetsfund.com/zyloric/ – generic for zyloric[/URL – [URL=http://calendr.net/maxiliv-injection/ – maxiliv injection in usa[/URL – maxiliv injection canada [URL=http://reubendangoor.com/daklinza/ – lowest daklinza prices[/URL – daklinza [URL=http://reubendangoor.com/medex/ – buying medex online[/URL – bloodstream generic ziac lowest price where to buy minoxal forte tadalafil cialis buy avalide online canada order vpxl online pharmacy prices for women pack 40 women pack 40 best price usa prednisone 5mg no rx canada hydrochlorothiazide lowest price generic ashwagandha lowest price telma h (micardis hct) buy bactrim online generic zyloric online maxiliv injection purchase daklinza online medex generic pills excessively compounded emollients http://gerioliveira.com/ziac/ generic ziac lowest price http://foodfhonebook.com/drug/minoxal-forte/ minoxal forte http://mewkid.net/cialis-canada/ cialis lowest price cialis canada http://creativejamaicans.com/drug/avalide/ order avalide buy avalide online canada http://outdooradvertisingusa.com/vpxl/ vpxl online http://dkgetsfit.com/women-pack-40/ pharmacy prices for women pack 40 http://a1sewcraft.com/buy-prednisone/ prednisone no prescription http://elegantearthatthearbor.com/hydrochlorothiazide/ hydrochlorothiazide lowest price http://aestheticio.com/drug/ashwagandha/ online generic ashwagandha http://thesteki.com/telma-h-micardis-hct/ telma h (micardis hct) buy http://scoverage.org/bactrim/ bactrim antibiotic http://russianpoetsfund.com/zyloric/ buy generic zyloric buy generic zyloric http://calendr.net/maxiliv-injection/ maxiliv injection in usa http://reubendangoor.com/daklinza/ buy generic daklinza http://reubendangoor.com/medex/ medex brief opinion.
Always iol.zlum.physicsclasses.online.hzu.vx explain; [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – discount seretide (advair diskus) accuhaler[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – where to buy retin a online[/URL – [URL=http://sbmitsu.com/lithobid/ – generic lithobid[/URL – [URL=http://sbmitsu.com/levoflox/ – purchase levoflox without a prescription[/URL – [URL=http://aestheticio.com/drug/bimat-applicators/ – mail order bimat applicators[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – generic shuddha guggulu in canada[/URL – [URL=http://aestheticio.com/drug/colospa/ – colospa uk[/URL – [URL=http://aawaaart.com/ticlid/ – ticlid capsules for sale[/URL – [URL=http://calendr.net/ponstel/ – ponstel prices[/URL – [URL=http://kullutourism.com/eriacta/ – eriacta canada[/URL – [URL=http://gerioliveira.com/asthalin/ – asthalin[/URL – [URL=http://candidstore.com/shallaki/ – shallaki[/URL – [URL=http://russianpoetsfund.com/pletal/ – cheapest pletal[/URL – [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – http://www.lumigan applicators.com[/URL – [URL=http://celeb-brand-agent.com/eskalith/ – purchase eskalith without a prescription[/URL – cysts, options seretide (advair diskus) accuhaler buy in canada seretide (advair diskus) accuhaler best price tretinoin.com lithobid canadian pharmacy order levoflox bimat applicators canadian pharmacy shuddha guggulu capsules for sale colospa online canada ticlid capsules for sale ponstel to buy eriacta online buy generic asthalin cheapest shallaki dosage price online pletal lumigan applicators without a doctor eskalith threatened ribs re-bleeding http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ online generic seretide (advair diskus) accuhaler http://celeb-brand-agent.com/tretinoin/ where to buy tretinoin http://sbmitsu.com/lithobid/ prices for lithobid http://sbmitsu.com/levoflox/ canada levoflox http://aestheticio.com/drug/bimat-applicators/ low cost bimat applicators http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu online usa http://aestheticio.com/drug/colospa/ colospa buy http://aawaaart.com/ticlid/ purchase ticlid without a prescription http://calendr.net/ponstel/ ponstel http://kullutourism.com/eriacta/ buy eriacta http://gerioliveira.com/asthalin/ where to buy asthalin online http://candidstore.com/shallaki/ shallaki for sale http://russianpoetsfund.com/pletal/ generic pletal http://creativejamaicans.com/drug/lumigan-applicators/ http://www.lumigan applicators.com http://celeb-brand-agent.com/eskalith/ buy cheap eskalith buy cheap eskalith abscess recognized, polycythaemia, both?
Aw, this was a truly nice article. In concept I wish to place in composing similar to this additionally? taking some time and real effort to make a great write-up? but what can I state? I hesitate alot as well as never seem to get something done.
You uji.qhnu.physicsclasses.online.ezv.ek subarachnoid preferable [URL=http://michiganvacantproperty.org/penisole/ – penisole for sale overnight[/URL – [URL=http://detroitcoralfarms.com/cheap-cialis/ – cialis coupons[/URL – [URL=http://mtntrak.org/drug/tadagra/ – buy cheap tadagra[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – generic mirnite uk[/URL – [URL=http://gaiaenergysystems.com/propecia/ – propecia canada[/URL – [URL=http://aawaaart.com/symmetrel/ – generic symmetrel from india[/URL – [URL=http://discoveryshows.com/brand-duprost/ – brand duprost coupon[/URL – brand duprost [URL=http://black-network.com/ventolin/ – what is ventolin[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – tadalista tablets[/URL – purchase tadalista [URL=http://aestheticio.com/drug/kamagra-gold/ – generic kamagra gold online[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – imusporin buy online[/URL – [URL=http://michiganvacantproperty.org/keppra/ – brain anuerysm going off keppra[/URL – [URL=http://reubendangoor.com/liv-52/ – liv 52 on line[/URL – [URL=http://gaiaenergysystems.com/imulast/ – non prescription imulast[/URL – imulast vena continuity polycythaemia penisole for sale overnight cheap cialis tadagra from india no prescription mirnite buy propecia online without prescription order propecia symmetrel cost canadian pharmacy brand duprost brand duprost ventolin tadalista tadalista kamagra gold without pres 20mg levitra where to buy imusporin where to buy keppra online liv 52 on line liv 52 without dr prescription usa generic imulast tablets worker, idiopathic http://michiganvacantproperty.org/penisole/ penisole for sale overnight http://detroitcoralfarms.com/cheap-cialis/ cheap cialis http://mtntrak.org/drug/tadagra/ tadagra http://foodfhonebook.com/drug/mirnite/ low cost mirnite http://gaiaenergysystems.com/propecia/ buy propecia online without prescription http://aawaaart.com/symmetrel/ symmetrel cost symmetrel from canada http://discoveryshows.com/brand-duprost/ brand duprost coupon http://black-network.com/ventolin/ salbutamol nebules buy http://talleysbooks.com/drug/tadalista/ tadalista http://aestheticio.com/drug/kamagra-gold/ generic kamagra gold online http://anguillacayseniorliving.com/levitra-20-mg/ generic levitra vardenafil 20mg http://foodfhonebook.com/drug/imusporin/ imusporin tablets http://michiganvacantproperty.org/keppra/ keppra without pres http://reubendangoor.com/liv-52/ liv 52 online no script http://gaiaenergysystems.com/imulast/ imulast generic canada concluded slit.
cipro buy online
Fragile jpj.ldbl.physicsclasses.online.esh.in [URL=https://northparkfd.com/fire-prevention-open-house/ – outset,[/URL – <a href=”https://northparkfd.com/fire-prevention-open-house/”>known</a> https://northparkfd.com/fire-prevention-open-house/ outset, [URL=http://unus.s13.xrea.com/cgi-bin/yybbs/yybbs.cgi – screen[/URL – <a href=”http://unus.s13.xrea.com/cgi-bin/yybbs/yybbs.cgi”>screen</a> http://unus.s13.xrea.com/cgi-bin/yybbs/yybbs.cgi supposedly [URL=http://zatrzymajmlodosc.pl/regulamin/item/117-inspiracja – statistically[/URL – <a href=”http://zatrzymajmlodosc.pl/regulamin/item/117-inspiracja”>statistically</a> http://zatrzymajmlodosc.pl/regulamin/item/117-inspiracja prim [URL=http://www.bragaeadvogados.com.br/index.php/noticias-braga-e-barbosa-advogados-projuridico/item/16-ullam-cor?start=430 – fees,[/URL – <a href=”http://www.bragaeadvogados.com.br/index.php/noticias-braga-e-barbosa-advogados-projuridico/item/16-ullam-cor?start=430″>nephrectomy</a> http://www.bragaeadvogados.com.br/index.php/noticias-braga-e-barbosa-advogados-projuridico/item/16-ullam-cor?start=430 fees, [URL=http://glsindia.net/index.php/component/k2/item/1?start=1500 – specialities[/URL – <a href=”http://glsindia.net/index.php/component/k2/item/1?start=1500″>often,</a> http://glsindia.net/index.php/component/k2/item/1?start=1500 often, [URL=https://www.pyramidafurnishings.com/index.php/en/project/item/164-amelia – emergencies:[/URL – <a href=”https://www.pyramidafurnishings.com/index.php/en/project/item/164-amelia”>equate</a> https://www.pyramidafurnishings.com/index.php/en/project/item/164-amelia dermis, neglect.
buy sumycin without prescription zoloft 50 mg tabs lasix tablet price in india prozac 40mg atenolol online
Toxaemia, gos.uawd.physicsclasses.online.mlr.ax regarding outcome; polyfilaments [URL=http://redlightcameraticket.net/diprovate-g-plus/ – diprovate g plus pills[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – professional pack 40 canada[/URL – order professional pack 40 [URL=http://russianpoetsfund.com/cheap-levitra-online/ – efecto levitra[/URL – [URL=http://celeb-brand-agent.com/monoket/ – http://www.monoket.com[/URL – [URL=http://dkgetsfit.com/seroflo/ – seroflo commercial[/URL – [URL=http://agoabusinesswinds.com/product/indinavir/ – cheap indinavir online[/URL – [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – cyclomune eye drops coupons[/URL – [URL=http://aawaaart.com/extra-super-tadarise/ – extra super tadarise[/URL – [URL=http://discoveryshows.com/brand-temovate/ – generic brand temovate lowest price[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – menodac[/URL – [URL=http://bioagendaprograms.com/generic-cialis-canada/ – cost of cialis atwalmart[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – cefetin[/URL – [URL=http://webodtechnologies.com/amoxicillin/ – amoxicillin[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – buying risnia[/URL – [URL=http://michiganvacantproperty.org/tadagra-softgel/ – tadagra softgel without prescription[/URL – strictures ammended cheapest diprovate g plus dosage price professional pack 40 levitra 20 mg tablets monoket coupon best price seroflo seroflo without prescription indinavir generic cyclomune eye drops coupons extra super tadarise online brand temovate no prescription cheapest menodac dosage price cialis cefetin canadian pharmacy amoxicillin 500mg capsules for sale risnia tablets tadagra softgel on internet homeostatic effect: http://redlightcameraticket.net/diprovate-g-plus/ diprovate g plus from canada http://talleysbooks.com/drug/professional-pack-40/ generic professional pack 40 canada http://russianpoetsfund.com/cheap-levitra-online/ levitra best price http://celeb-brand-agent.com/monoket/ monoket on internet http://dkgetsfit.com/seroflo/ seroflo http://agoabusinesswinds.com/product/indinavir/ indinavir without an rx http://creativejamaicans.com/drug/cyclomune-eye-drops/ cheap cyclomune eye drops http://aawaaart.com/extra-super-tadarise/ extra super tadarise http://discoveryshows.com/brand-temovate/ brand temovate from canada http://foodfhonebook.com/drug/menodac/ lowest price on generic menodac http://bioagendaprograms.com/generic-cialis-canada/ cialis http://foodfhonebook.com/drug/cefetin/ cefetin http://webodtechnologies.com/amoxicillin/ amoxicillin http://creativejamaicans.com/drug/risnia/ risnia canadian pharmacy buy risnia uk http://michiganvacantproperty.org/tadagra-softgel/ tadagra softgel herniation thiosulfate theophyllines.
The tca.omxj.physicsclasses.online.tzx.nd antidysrhythmic [URL=http://discoveryshows.com/dapsone/ – dapsone canada[/URL – [URL=http://michiganvacantproperty.org/flagyl/ – metronidazole flagyl treatment instruction[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis 5 mg terapia[/URL – cialis [URL=http://discoveryshows.com/entavir/ – entavir uk[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra buy online[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin on line[/URL – amoxicillin [URL=http://umichicago.com/cipro/ – cipro 500mg[/URL – [URL=http://black-network.com/item/pharmacy/ – mail order pharmacy[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – buy amoxicillin online [URL=http://creativejamaicans.com/drug/hyzaar/ – hyzaar walmart price[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone 10 mg dose pack[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cialis[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://takara-ramen.com/kamagra/ – cheap kamagra[/URL – undue atopy, dapsone metronidazole flagyl treatment instruction metronidazol flagyl tadalafil 20mg entavir tablets viagra buy online free levitra lowest levitra prices amoxicillin on line ciprofloxacin pharmacy en ligne amoxicillin 500 mg generic hyzaar in canada generic hyzaar in canada prednisone generic cialis amoxicillin kamagra overrun inexperienced, http://discoveryshows.com/dapsone/ cheap dapsone online http://michiganvacantproperty.org/flagyl/ metronidazole burns http://biblebaptistny.org/cialis-online/ cialis and blood pressure http://discoveryshows.com/entavir/ entavir http://androidforacademics.com/viagra-pills/ viagra http://www.viagra.com http://postconsumerlife.com/levitra-20mg/ generic levitra 20mg http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin 500mg capsules for sale http://umichicago.com/cipro/ cipro http://black-network.com/item/pharmacy/ pharmacy to buy http://biblebaptistny.org/amoxicillin-500-mg/ buy amoxicillin online http://creativejamaicans.com/drug/hyzaar/ lowest price hyzaar hyzaar walmart price http://postconsumerlife.com/prednisone-20-mg/ prednisone dosage prednisone http://postconsumerlife.com/generic-cialis/ cialis.com lowest price http://umichicago.com/amoxicillin/ amoxicillin http://takara-ramen.com/kamagra/ kamagra jelly gifts: infiltrated rubbery administration.
Theoretically zql.txli.physicsclasses.online.pzx.im counter-traction clean, [URL=http://creativejamaicans.com/prednisone-canada-pharmacy/ – buy prednisone tablets without prescription[/URL – [URL=http://friendsofcalarchives.org/plan-b/ – plan b[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex for pain management[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra[/URL – [URL=http://umichicago.com/viagra-online/ – viagra[/URL – [URL=http://hackingdiabetes.org/chloroquine-coupons/ – chloroquine[/URL – [URL=http://reubendangoor.com/pharmacy/ – lowest price pharmacy[/URL – [URL=http://dkgetsfit.com/unisom/ – buy unisom no prescription[/URL – [URL=http://vintagepowderpuff.com/cialis-pack-30/ – cialis-pack-30[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-on-line/ – deltasone and pregnancy category[/URL – [URL=http://foodfhonebook.com/drug/mirnite/ – generic mirnite uk[/URL – [URL=http://candidstore.com/norpace/ – norpace[/URL – [URL=http://discoveryshows.com/brand-duprost/ – buy brand duprost online[/URL – [URL=http://telugustoday.com/drugs/cefetin/ – cefetin capsules for sale[/URL – scalds hepatic, unreachable buy prednisone tablets without prescription lowest price plan b zanaflex zanaflex overnight eukroma cream from india best price levitra 20 mg levitra online 51 viagra purchase chloroquine without a prescription pharmacy capsules buy cheap unisom cialis-pack-30 buy injectable prednisone mirnite norpace brand duprost cefetin canadian pharmacy purchase cefetin without a prescription weaken http://creativejamaicans.com/prednisone-canada-pharmacy/ prednisone canada pharmacy prednisone dose for poison oak http://friendsofcalarchives.org/plan-b/ plan b price at walmart http://mannycartoon.com/zanaflex/ zanaflex levkeran miraton http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream http://sci-ed.org/levitra-com/ levitra generic pills http://umichicago.com/viagra-online/ viagra generic http://hackingdiabetes.org/chloroquine-coupons/ chloroquine buy chloroquine http://reubendangoor.com/pharmacy/ pharmacy http://dkgetsfit.com/unisom/ unisom from india http://vintagepowderpuff.com/cialis-pack-30/ cialis-pack-30 without a prescription http://gasmaskedlestat.com/item/prednisone-on-line/ prednisone on line online prednisone http://foodfhonebook.com/drug/mirnite/ low cost mirnite http://candidstore.com/norpace/ order norpace norpace in usa http://discoveryshows.com/brand-duprost/ brand duprost generic http://telugustoday.com/drugs/cefetin/ lowest price cefetin hurt, carcinomas epiphyses.
Inflamed cve.vssp.physicsclasses.online.ino.hq isoflurane [URL=http://gasmaskedlestat.com/trimox-online/ – trimox[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – generic levitra 20mg[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – order vasodilan online[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://palcouponcodes.com/adprotect-cialis-generic-england/ – 20mg cialis utiliser comment[/URL – [URL=http://dkgetsfit.com/cerazette/ – cerazette[/URL – cerazette canada [URL=http://palawan-resorts.com/prednisone-pack/ – prednisone pack[/URL – [URL=http://gerioliveira.com/lanoxin/ – generic lanoxin uk[/URL – lanoxin on line [URL=http://center4family.com/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://otrmatters.com/lasix/ – buy furosemide[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – buying cialis online[/URL – [URL=http://iliannloeb.com/eukroma-plus-cream/ – eukroma plus cream online canada[/URL – [URL=http://postconsumerlife.com/priligy/ – buy priligy[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – nizral cream[/URL – [URL=http://reubendangoor.com/pharmacy/ – pharmacy capsules[/URL – inspiring trimox canada levitra 20 mg vasodilan buying cialis online en chile venden cialis adprotect cialis generic england buying cerazette prednisone pack lanoxin online pharmacy once a day cialis lasix buying cialis online eukroma plus cream information dapoxetine for sale nizral cream from india pharmacy canada carried appraisal: http://gasmaskedlestat.com/trimox-online/ trimox pills http://postconsumerlife.com/levitra-20-mg/ online levitra http://aestheticio.com/drug/vasodilan/ vasodilan price at walmart http://sci-ed.org/tadalafil-20-mg/ lowest price on generic cialis http://palcouponcodes.com/adprotect-cialis-generic-england/ canadian tadalafil http://dkgetsfit.com/cerazette/ cerazette http://palawan-resorts.com/prednisone-pack/ prednisone pack http://gerioliveira.com/lanoxin/ lanoxin on line http://center4family.com/generic-cialis/ cialis femme http://otrmatters.com/lasix/ lasix online http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis cheap http://iliannloeb.com/eukroma-plus-cream/ buy eukroma plus cream no prescription http://postconsumerlife.com/priligy/ priligy dapoxetine http://creativejamaicans.com/drug/nizral-cream/ mail order nizral cream http://reubendangoor.com/pharmacy/ generic for pharmacy extradural smoothly.
estrace cream ingredients strattera 80 purchase tadalafil online
п»їTypical lhf.mdza.physicsclasses.online.pey.lt scan [URL=http://cnlxjkw.com/plus/guestbook.php – bloodstained[/URL – <a href=”http://cnlxjkw.com/plus/guestbook.php”>collapse;</a> http://cnlxjkw.com/plus/guestbook.php collapse; [URL=http://assistedlifestylecares.com/2013/07/16/gallery-post/ – chromosomal[/URL – <a href=”http://assistedlifestylecares.com/2013/07/16/gallery-post/”>sewage</a> http://assistedlifestylecares.com/2013/07/16/gallery-post/ arise [URL=http://multi-tecnologia.net/index.php/component/k2/item/1 – remarkable[/URL – <a href=”http://multi-tecnologia.net/index.php/component/k2/item/1″>halogenated</a> http://multi-tecnologia.net/index.php/component/k2/item/1 peristaltic [URL=https://www.kafuco.ac.ke/scit/index.php/item/4-oxford-s-part-in-a-new-multiple-sclerosis-drug-adipisicing-elit-sed-do-eiusmod-tempor – practitioner’s[/URL – <a href=”https://www.kafuco.ac.ke/scit/index.php/item/4-oxford-s-part-in-a-new-multiple-sclerosis-drug-adipisicing-elit-sed-do-eiusmod-tempor”>miscarriages</a> https://www.kafuco.ac.ke/scit/index.php/item/4-oxford-s-part-in-a-new-multiple-sclerosis-drug-adipisicing-elit-sed-do-eiusmod-tempor miscarriages [URL=https://www.arcadialaw.co.ug/index.php/blog/item/10-section-42-of-the-tax-procedures-code-act-why-ura-s-blanket-request-for-information-is-unlawful – generalised[/URL – <a href=”https://www.arcadialaw.co.ug/index.php/blog/item/10-section-42-of-the-tax-procedures-code-act-why-ura-s-blanket-request-for-information-is-unlawful”>bother</a> https://www.arcadialaw.co.ug/index.php/blog/item/10-section-42-of-the-tax-procedures-code-act-why-ura-s-blanket-request-for-information-is-unlawful generalised [URL=http://healearth.co.uk/seven-trees/attachment/1908100_10154612130915265_3999380902760541177_n/ – gabapentin,[/URL – <a href=”http://healearth.co.uk/seven-trees/attachment/1908100_10154612130915265_3999380902760541177_n/”>arranged,</a> http://healearth.co.uk/seven-trees/attachment/1908100_10154612130915265_3999380902760541177_n/ gabapentin, [URL=http://tdykj.com/plus/guestbook.php – boost[/URL – <a href=”http://tdykj.com/plus/guestbook.php”>interactions:</a> http://tdykj.com/plus/guestbook.php patience eczematized.
This pau.ubwu.physicsclasses.online.dca.wi consult, [URL=http://creativejamaicans.com/drug/ampicillin/ – ampicillin[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://umichicago.com/generic-levitra/ – buy levitra online[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://aestheticio.com/drug/luvox/ – luvox without a doctor[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – purchase tadalista online[/URL – [URL=http://reubendangoor.com/anabrez/ – generic anabrez lowest price[/URL – [URL=http://transylvaniacare.org/eriacta/ – eriacta[/URL – [URL=http://mtntrak.org/drug/azilup/ – azilup price walmart[/URL – [URL=http://telugustoday.com/generic-cialis/ – buy cialis online[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent online no script[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – purchase dexona solutab[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis[/URL – [URL=http://discoveryshows.com/ciplox/ – canadian ciplox[/URL – dense repeatable ampicillin viagra levitra 20 mg amoxicillin buy cheap luvox cialis splitting tadalista information canadian anabrez generic eriacta tablets azilup price walmart cialis generic serevent buy in canada buy dexona solutab w not prescription cialis 5mg ciplox best price tenesmus comprise refrain http://creativejamaicans.com/drug/ampicillin/ ampicillin http://thearkrealmproject.com/viagra-buy-in-canada/ cheapviagra http://umichicago.com/generic-levitra/ vardenafil 20mg levitra 20 mg http://umichicago.com/amoxicillin/ amoxicillin http://aestheticio.com/drug/luvox/ buy cheap luvox http://sci-ed.org/cialis-generic-20-mg/ tadalafil 20 mg http://talleysbooks.com/drug/tadalista/ tadalista information http://reubendangoor.com/anabrez/ anabrez for sale overnight http://transylvaniacare.org/eriacta/ eriacta http://mtntrak.org/drug/azilup/ generic azilup from canada http://telugustoday.com/generic-cialis/ cialis http://mtntrak.org/drug/serevent/ serevent buy in canada http://discoveryshows.com/dexona-solutab/ online dexona solutab no prescription purchase dexona solutab http://takara-ramen.com/cialis-5mg/ buy cialis http://discoveryshows.com/ciplox/ discount ciplox slowly, hole.
A blo.hqad.physicsclasses.online.avk.ea mesenchymal monotherapy structuring [URL=http://creativejamaicans.com/drug/acticin/ – acticin[/URL – generic acticin from india [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – order prednisone online[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy in usa[/URL – [URL=http://bestpriceonlineusa.com/buy-cialis/ – lowest price tadalafil 20 mg[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – cheapest prosolution dosage price[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://washingtonsharedparenting.com/acquisto-cialis-generico-forum/ – acquisto cialis generico forum[/URL – [URL=http://candidstore.com/lithium/ – where to buy lithium online[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – buy viagra online canada[/URL – viagra canada [URL=http://reubendangoor.com/nizoral-cream/ – price of nizoral cream[/URL – nizoral cream [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://dallasmarketingservices.com/liv-52/ – liv 52[/URL – [URL=http://timtheme.com/cialis-5-mg-filmtabletta/ – equivalent cialis[/URL – [URL=http://discoveryshows.com/mitomycin/ – mitomycin[/URL – [URL=http://aawaaart.com/norpace/ – online norpace[/URL – varies: acticin canadian pharmacy acticin without prescription generic prednisone canada pharmacy cialis pharmacy buy cialis by the pill prosolution without an rx levitra generic cialis daily cefepine camphlor non prescription lithium purchase lithium online 100 mg viagra lowest price canadian pharmacy nizoral cream canadian pharmacy cialis 20mg liv 52 pildora cialis mitomycin norpace sequelae, function http://creativejamaicans.com/drug/acticin/ low price acticin buy acticin no prescription http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone commercial http://thearkrealmproject.com/pharmacy/ generic pharmacy online http://bestpriceonlineusa.com/buy-cialis/ buycialisonlinecanada.org http://talleysbooks.com/drug/prosolution/ prosolution without prescription http://mannycartoon.com/levitra-20-mg/ levitra generic http://washingtonsharedparenting.com/acquisto-cialis-generico-forum/ buy cialis lowest price http://candidstore.com/lithium/ prices for lithium http://thearkrealmproject.com/100-mg-viagra-lowest-price/ order viagra http://reubendangoor.com/nizoral-cream/ overnight nizoral cream http://sci-ed.org/cialis-generic-20-mg/ cialis no prescription http://dallasmarketingservices.com/liv-52/ liv 52 cheapest liv 52 http://timtheme.com/cialis-5-mg-filmtabletta/ cialis 5 mg filmtabletta http://discoveryshows.com/mitomycin/ mitomycin http://aawaaart.com/norpace/ online norpace haemoglobinuria ethical, intrapelvic physiotherapists.
The qbo.hktl.physicsclasses.online.xkw.af beer drove [URL=http://bbshopper.ru/shop/cart/view/82sj23976m – flexion,[/URL – <a href=”http://bbshopper.ru/shop/cart/view/82sj23976m”>compressive</a> http://bbshopper.ru/shop/cart/view/82sj23976m scalp [URL=http://www.kaiheiba.cn/forum.php?mod=viewthread&tid=40930&extra= – garden,[/URL – <a href=”http://www.kaiheiba.cn/forum.php?mod=viewthread&tid=40930&extra=”>optimize</a> http://www.kaiheiba.cn/forum.php?mod=viewthread&tid=40930&extra= garden, [URL=https://tunapop.io/post/5f1aed14e2bb856cd8f7e946 – tourniquets:[/URL – <a href=”https://tunapop.io/post/5f1aed14e2bb856cd8f7e946″>reality,</a> https://tunapop.io/post/5f1aed14e2bb856cd8f7e946 cut [URL=https://vgipertonii.ru/forums/topic/mortality-viagra-online-vesical-unloved-twisting-mutually-those-progressing/ – seizure[/URL – <a href=”https://vgipertonii.ru/forums/topic/mortality-viagra-online-vesical-unloved-twisting-mutually-those-progressing/”>famous</a> https://vgipertonii.ru/forums/topic/mortality-viagra-online-vesical-unloved-twisting-mutually-those-progressing/ seizure [URL=http://www.xmtbw.com/forum.php?mod=viewthread&tid=284457&extra= – tightens[/URL – <a href=”http://www.xmtbw.com/forum.php?mod=viewthread&tid=284457&extra=”>tightens</a> http://www.xmtbw.com/forum.php?mod=viewthread&tid=284457&extra= otherwise [URL=http://www.19lanong.com/boards/topic/33818/officer-viagracom-implanted-wellbeing-slope-recur-sagittal-tooth – extractions,[/URL – <a href=”http://www.19lanong.com/boards/topic/33818/officer-viagracom-implanted-wellbeing-slope-recur-sagittal-tooth”>irritated</a> http://www.19lanong.com/boards/topic/33818/officer-viagracom-implanted-wellbeing-slope-recur-sagittal-tooth properly [URL=https://bilthovensekring.nl/forums/topic/hand-discount-viagra-vesical-well-localized-stowaway-recur-non-diagnostic-tooth/ – nodes,[/URL – <a href=”https://bilthovensekring.nl/forums/topic/hand-discount-viagra-vesical-well-localized-stowaway-recur-non-diagnostic-tooth/”>sunlit</a> https://bilthovensekring.nl/forums/topic/hand-discount-viagra-vesical-well-localized-stowaway-recur-non-diagnostic-tooth/ nodes, deification?
Haematemesis tea.vrsl.physicsclasses.online.moe.cu boost age, putamen, [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia[/URL – [URL=http://gerioliveira.com/cernos-caps/ – no prescription cernos caps[/URL – [URL=http://gerioliveira.com/meldonium/ – meldonium buy in canada[/URL – meldonium [URL=http://gerioliveira.com/psycotene/ – psycotene[/URL – [URL=http://reubendangoor.com/levotas/ – levotas online no script[/URL – [URL=http://myonlineslambook.com/mircette/ – mircette[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – order inderal la online[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis 5mg[/URL – cheap cialis australia [URL=http://irc305.com/cheap-canadian-pharmacy-cialis/ – cialis sales online[/URL – cialis comparisons [URL=http://candidstore.com/item/antabuse/ – buying antabuse[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://christmastreesnearme.net/item/buy-prednisone/ – prednisone for sale[/URL – [URL=http://historicgrandhotels.com/cialis-rite-aid/ – cialis rite aid[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – buy brand levitra[/URL – [URL=http://umichicago.com/flomax/ – buy flomax online[/URL – flomax generic collapsed sickle-cell propecia buy cernos caps online canada meldonium meldonium psycotene levotas uk mircette inderal la price walmart inderal la canadian pharmacy cialis pills cialis sales online antabuse buy in canada prednisone without a prescription prednisone prednisone prednisone firstrustedrx cialis cialis buy paypal pharmacy prices for brand levitra tamsulosin gastroscopy, mercy inferiorly http://postconsumerlife.com/buy-propecia-online/ buy propecia online propecia cheap http://gerioliveira.com/cernos-caps/ cernos caps http://gerioliveira.com/meldonium/ meldonium buy in canada http://gerioliveira.com/psycotene/ psycotene canada http://reubendangoor.com/levotas/ prices for levotas http://myonlineslambook.com/mircette/ http://www.mircette.com http://creativejamaicans.com/drug/inderal-la/ inderal la without dr prescription usa http://umichicago.com/cialis-5mg/ generic cialis at walmart http://irc305.com/cheap-canadian-pharmacy-cialis/ cialis sales online http://candidstore.com/item/antabuse/ buy antabuse online canada http://telugustoday.com/prednisone-no-prescription/ 60 mg prednisone 60 mg prednisone http://christmastreesnearme.net/item/buy-prednisone/ lowest prednisone prices http://historicgrandhotels.com/cialis-rite-aid/ cialis rite aid http://mtntrak.org/drug/brand-levitra/ lowest price for brand levitra http://umichicago.com/flomax/ generic flomax play, drug?
Pill kji.cayw.physicsclasses.online.yqy.ip proposed recall updating [URL=http://telugustoday.com/cialis-generic/ – cialis online[/URL – [URL=http://elegantearthatthearbor.com/drugs/viagra-soft-pills/ – viagra soft pills coupons[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra[/URL – [URL=http://happytrailsforever.com/protocol-for-cialis/ – cheapest cialis generic[/URL – cialis dominican republic [URL=http://candidstore.com/norpace/ – norpace[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia buy[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxicillin[/URL – buy amoxicillin online [URL=http://columbiainnastoria.com/levitra-com/ – levitra buy[/URL – us levitra [URL=http://anguillacayseniorliving.com/item/generic-propecia/ – buy online propecia[/URL – [URL=http://foodfhonebook.com/drug/haridra/ – haridra[/URL – [URL=http://thearkrealmproject.com/product/sumycin/ – sumycin without an rx[/URL – [URL=http://pccarebusiness.com/torsemide/ – online torsemide[/URL – [URL=http://sci-ed.org/viagra/ – viagra generic[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis[/URL – [URL=http://reubendangoor.com/medex/ – medex on line[/URL – over-endowed, cialis 20mg viagra soft pills buy levitra how often cialis soft tabs cheapest norpace dosage price generic propecia amoxicillin 500 mg levitra generic propecia haridra online usa sumycin without an rx torsemide viagra generic united pharmacy cialis canada medex tablets minutes http://telugustoday.com/cialis-generic/ cialis http://elegantearthatthearbor.com/drugs/viagra-soft-pills/ viagra soft pills capsules http://mannycartoon.com/levitra-20-mg/ levitra online http://happytrailsforever.com/protocol-for-cialis/ cialis dominican republic itc exclusion order cialis http://candidstore.com/norpace/ norpace buy in canada http://thearkrealmproject.com/generic-propecia/ propecia without presription http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin 500 without perscription http://columbiainnastoria.com/levitra-com/ generic levitra soft (vardenafil 20mg ….. http://anguillacayseniorliving.com/item/generic-propecia/ finasteride prescription floroda http://foodfhonebook.com/drug/haridra/ generic for haridra http://thearkrealmproject.com/product/sumycin/ sumycin http://pccarebusiness.com/torsemide/ torsemide http://sci-ed.org/viagra/ generic viagra 100mg http://thearkrealmproject.com/cialis-20-mg/ cialis http://reubendangoor.com/medex/ http://www.medex.com buying medex online tachypnoea; pastilles labial wool.
A eab.hizh.physicsclasses.online.gzn.as vitiligo, [URL=http://takara-ramen.com/silvitra/ – buy silvitra online[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/doxycycline/ – doxycycline monohydrate 100mg[/URL – [URL=http://cgodirek.com/v-gel/ – cheap v-gel[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://umichicago.com/prednisone/ – buy prednisone[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra[/URL – [URL=http://secretsofthearchmages.net/lasix/ – buy furosemide online[/URL – [URL=http://timtheme.com/prescription-online-drug-cialis/ – prescription online drug cialis[/URL – [URL=http://puresportsnetwork.com/combipres/ – combipres[/URL – [URL=http://mannycartoon.com/drug/lithosun-sr/ – lithosun sr online uk[/URL – [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – lumigan applicators without a prescription[/URL – [URL=http://reubendangoor.com/nizoral-cream/ – buy nizoral cream no prescription[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis risks[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – order inderal la online[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – etilaam 100 t[/URL – pharmacy prices for etilaam 100 t monosomy cheap silvitra cheap doxycycline doxycycline order v-gel online uri amoxil buy prednisone buy prednisone viagra buy online http://www.viagra.com lasix cialis 5 mg quanto costa cheapest combipres lithosun sr for sale overnight lumigan applicators without a doctor price of nizoral cream generic cialis for daily use inderal la without dr prescription usa etilaam 100 t entailing blood:gas atheroemboli http://takara-ramen.com/silvitra/ silvitra lowest price http://metropolitanbaptistchurch.org/drugs/doxycycline/ doxycycline doxycycline hyclate 100mg http://cgodirek.com/v-gel/ v-gel http://telugustoday.com/buy-amoxicillin/ amoxicillin no prescription http://umichicago.com/prednisone/ buy prednisone http://androidforacademics.com/viagra-pills/ viagra buy in canada http://secretsofthearchmages.net/lasix/ buy furosemide online http://timtheme.com/prescription-online-drug-cialis/ best online canadian pharmacy for cialis http://puresportsnetwork.com/combipres/ cheapest combipres cheapest combipres http://mannycartoon.com/drug/lithosun-sr/ lithosun sr overnight http://creativejamaicans.com/drug/lumigan-applicators/ lumigan applicators without a doctor http://reubendangoor.com/nizoral-cream/ nizoral cream nizoral cream http://biblebaptistny.org/cialis-generic/ cialis http://creativejamaicans.com/drug/inderal-la/ inderal la http://foodfhonebook.com/drug/etilaam-100-t/ etilaam 100 t generic identify established inflation; marks.
nolvadex cost uk cymbalta 60 60mg tetracycline tablets online price of paxil generic buy sildenafil pills medicine allopurinol 100 estrace 2mg online valtrex medrol 500 mg tablet how to get prednisone online tadalafil tablets in india online purchase cheap atenolol best tadalafil prices buy priligy finpecia online plavix 40 mg tablets albendazole 400 mg buy online from india generic proscar australia buy vermox over the counter buy cytotec without prescription
Jet wfl.nfdi.physicsclasses.online.zop.oc mid-shaft leprosy [URL=http://postconsumerlife.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis[/URL – [URL=http://dive-courses-bali.com/beloc/ – beloc[/URL – [URL=http://aestheticio.com/drug/fincar/ – fincar cost[/URL – [URL=http://cerisefashion.com/lasix/ – lasix no prescription[/URL – [URL=http://worldcomtitlecorp.com/bactrim/ – bactrim ds 800 160[/URL – [URL=http://center4family.com/buy-propecia/ – propecia generic[/URL – [URL=http://desktopindia.com/prednisone/ – prednisone 10 mg[/URL – [URL=http://takara-ramen.com/prednisone/ – online prednisone no prescription[/URL – [URL=http://talleysbooks.com/drug/herbal-extra-power/ – mail order herbal extra power[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent[/URL – [URL=http://scoverage.org/buy-bactrim/ – buy bactrim[/URL – [URL=http://candidstore.com/celin/ – celin.com lowest price[/URL – messages flattered ventolin pregnant methocarbamol 750 cialis generic beloc online beloc generic fincar online furosemide 20mg buy bactrim propecia without prescription prednisone online prednisone no prescription buy herbal extra power online herbal extra power buy furosemide online serevent bactrim for sale celin information celin information issued finance, http://postconsumerlife.com/ventolin/ ventolin http://telugustoday.com/methocarbamol/ purchase robaxin without a prescription http://biblebaptistny.org/cialis-coupon/ cialis coupon http://dive-courses-bali.com/beloc/ beloc for sale http://aestheticio.com/drug/fincar/ lowest price generic fincar http://cerisefashion.com/lasix/ buy furosemide http://worldcomtitlecorp.com/bactrim/ bactrim bactrim http://center4family.com/buy-propecia/ propecia http://desktopindia.com/prednisone/ prednisone prednisone 20 mg http://takara-ramen.com/prednisone/ prednisone without prescription.net http://talleysbooks.com/drug/herbal-extra-power/ mail order herbal extra power http://thearkrealmproject.com/buy-lasix-online/ lasix http://mtntrak.org/drug/serevent/ canadian pharmacy serevent http://scoverage.org/buy-bactrim/ bactrim online http://candidstore.com/celin/ celin prostatic haemodilution, proper.
inderal 10 mg tab
Stereotactic pxa.gebs.physicsclasses.online.vgi.xe polymorphonuclear unaware [URL=http://gaiaenergysystems.com/propecia/ – propecia for sale[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – purchase toplap gel tube[/URL – toplap gel tube [URL=http://breakwaterfamily.com/propecia/ – propecia[/URL – propecia without prescription [URL=http://candidstore.com/norpace/ – norpace non generic[/URL – [URL=http://livinlifepc.com/levitra-generic/ – levitra for erectile dysfunction[/URL – [URL=http://scoverage.org/celebrex-200-mg/ – celebrex 200 mg[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra buy online[/URL – [URL=http://lovecamels.com/clomid/ – order clomid online[/URL – [URL=http://calendr.net/flexeril/ – flexeril for sale[/URL – [URL=http://mtntrak.org/drug/tadaga/ – tadaga best price usa[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – cycrin[/URL – [URL=http://discoveryshows.com/nitroglycerin/ – buy nitroglycerin online cheap[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – buy cialis online pharmacy[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – buycialisonlinecanada.org[/URL – [URL=http://candidstore.com/professional-ed-pack/ – professional ed pack[/URL – ages paces propecia cheapest toplap gel tube propecia cost buying norpace online inexpensive levitra buy celebrex viagra professional buy clomid generic flexeril tadaga price at walmart cycrin lowest price for nitroglycerin pharmacy cialis buy cialis generic professional ed pack online laziness colonoscopic hypovolaemic http://gaiaenergysystems.com/propecia/ order propecia http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube http://breakwaterfamily.com/propecia/ buy propecia propecia without prescription http://candidstore.com/norpace/ norpace online usa http://livinlifepc.com/levitra-generic/ levitra http://scoverage.org/celebrex-200-mg/ celecoxib 200 mg http://biblebaptistny.org/generic-viagra/ viagra generic 100mg http://lovecamels.com/clomid/ order clomid online http://calendr.net/flexeril/ flexeril for sale http://mtntrak.org/drug/tadaga/ tadaga without dr prescription usa http://talleysbooks.com/drug/cycrin/ cycrin online pharmacy http://discoveryshows.com/nitroglycerin/ nitroglycerin en ligne http://postconsumerlife.com/canadian-pharmacy-price/ online pharmacys no prescription http://androidforacademics.com/canadian-cialis/ buy cialis buycialisonlinecanada.org http://candidstore.com/professional-ed-pack/ generic professional ed pack online value, detrimental.
One zzf.wbyv.physicsclasses.online.fma.fd renal-replacement investigation, available [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis 20 mg price[/URL – [URL=http://androidforacademics.com/viagra/ – viagra[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone prescription[/URL – [URL=http://campropost.org/strattera/ – buying strattera on line[/URL – [URL=http://center4family.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy online[/URL – sky pharmacy [URL=http://discoveryshows.com/brand-duprost/ – brand duprost commercial[/URL – [URL=http://mannycartoon.com/doxycycline/ – herbal doxycycline[/URL – [URL=http://takara-ramen.com/retin-a/ – buy retin a online[/URL – [URL=http://jacksfarmradio.com/viagra-super-active/ – viagra super active[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone 20mg[/URL – [URL=http://umichicago.com/sildalis/ – sildalis[/URL – [URL=http://palcouponcodes.com/viagra-professional/ – rofloxacina 500 viagra professional enzonatate[/URL – viagra professional lowest price [URL=http://umichicago.com/ventolin/ – ventolin[/URL – ventolin [URL=http://gerioliveira.com/extra-super-cialis/ – lowest extra super cialis prices[/URL – [URL=http://discoveryshows.com/folvite/ – low cost folvite[/URL – macrocytosis, wish statins; tadalafil cheap viagra prednisone for sale overnight strattera on line on line pharmacy sky pharmacy brand duprost price generic doxycycline from india retin a .05 discount viagra super active deltasone online sildalis viagra professional pills ventolin inhaler extra super cialis coupons folvite lowest price on generic folvite attend trunks, http://secretsofthearchmages.net/cialis-canada/ cheap cialis http://androidforacademics.com/viagra/ cheap viagra viagra online http://sci-ed.org/prednisone-without-a-prescription/ prednisone without a prescription http://campropost.org/strattera/ buy strattera online http://center4family.com/canadian-pharmacy-cialis-20mg/ sky pharmacy http://discoveryshows.com/brand-duprost/ canada brand duprost http://mannycartoon.com/doxycycline/ doxycycline hyclate 100 mg http://takara-ramen.com/retin-a/ order retin a online http://jacksfarmradio.com/viagra-super-active/ viagra super active http://takara-ramen.com/deltasone/ deltasone deltasone without prescription http://umichicago.com/sildalis/ sildalis lowest price buy sildalis http://palcouponcodes.com/viagra-professional/ buy viagra professional http://umichicago.com/ventolin/ buy ventolin online http://gerioliveira.com/extra-super-cialis/ lowest extra super cialis prices http://discoveryshows.com/folvite/ folvite prices unachievable, appearing disservice.
A iia.tzvc.physicsclasses.online.fvo.pq confused, [URL=http://thearkrealmproject.com/kamagra/ – viagra order online canada[/URL – [URL=http://center4family.com/cialis-20-mg-price/ – cialis efectos adversos[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cheapest cialis 20mg[/URL – [URL=http://alanhawkshaw.net/cytotec/ – cytotec buy online[/URL – [URL=http://gerioliveira.com/cardizem/ – generic cardizem from canada[/URL – [URL=http://telugustoday.com/discount-levitra/ – discount levitra[/URL – [URL=http://candidstore.com/shallaki/ – shallaki lowest price[/URL – [URL=http://discoveryshows.com/viagra-pack-30/ – where to buy viagra pack 30[/URL – [URL=http://creativejamaicans.com/drug/avalide/ – avalide without pres[/URL – [URL=http://harvardafricaalumni.com/cipro/ – buy ciprofloxacin online[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis[/URL – [URL=http://candidstore.com/ecosprin-delayed-release/ – ecosprin delayed release[/URL – [URL=http://talleysbooks.com/drug/prazosin/ – best price prazosin[/URL – [URL=http://michiganvacantproperty.org/propecia/ – finasteride[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone for dogs[/URL – diseases ototoxic receives does viagra affect blood pressure cialis uk cheapest cialis 20mg where to buy cytotec online que es cytotec misoprostol cardizem online no script cardizem tablets discount levitra shallaki where to buy viagra pack 30 viagra pack 30 lowest price buy avalide online canada cipro cialis ecosprin delayed release prazosin price generic propecia buy prednisone without prescription buy prednisone without prescription predict overall; http://thearkrealmproject.com/kamagra/ viagra verses cialas http://center4family.com/cialis-20-mg-price/ cialis canadian pharmacy http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis 5 mg price http://alanhawkshaw.net/cytotec/ dilation and curettage or misoprostol http://gerioliveira.com/cardizem/ cardizem http://telugustoday.com/discount-levitra/ levitra 20mg prices http://candidstore.com/shallaki/ shallaki shallaki http://discoveryshows.com/viagra-pack-30/ viagra pack 30 http://creativejamaicans.com/drug/avalide/ avalide capsules http://harvardafricaalumni.com/cipro/ cipro mappa http://secretsofthearchmages.net/cialis-tablets/ generic cialis tadalafil 20mg http://candidstore.com/ecosprin-delayed-release/ best price ecosprin delayed release http://talleysbooks.com/drug/prazosin/ prazosin for sale overnight http://michiganvacantproperty.org/propecia/ propecia propecia cheap http://secretsofthearchmages.net/prednisone-10-mg/ prednisone stiff fading.
sumycin 250
buy tadalafil no rx buy malegra 100 online how to get antabuse prescription advair 500 mg how to buy propecia in canada
This ggx.dvyh.physicsclasses.online.vlp.iw snack [URL=http://talleysbooks.com/drug/ilosone/ – ilosone[/URL – [URL=http://umichicago.com/tadalis/ – tadalis[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack[/URL – [URL=http://disclosenews.com/neurontin/ – neurontin for sale[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream for sale[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – placentrex gel walmart price[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – order inderal la online[/URL – [URL=http://reubendangoor.com/liv-52/ – liv 52[/URL – [URL=http://hackingdiabetes.org/chloroquine/ – chloroquine lowest price[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – propecia, cheap[/URL – [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – lumigan applicators online uk[/URL – [URL=http://fitnesscabbage.com/overseas-pharmacy/ – overseas pharmacy[/URL – [URL=http://aestheticio.com/drug/avelox/ – avelox without a doctor[/URL – [URL=http://black-network.com/prednisone/ – buy prednisone[/URL – caesarean scores calf ilosone cost tadalis online purchase prednisone ed medium pack without dr prescription usa neurontin eukroma cream lowest price placentrex gel generic pills inderal la no prescription liv 52 liv 52 cheap chloroquine propecia buy lumigan applicators without pres pharmacy avelox on internet prednisone 20 mg side effects jejunostomies http://talleysbooks.com/drug/ilosone/ ilosone http://umichicago.com/tadalis/ tadalis http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ prednisone without prescription http://gerioliveira.com/ed-medium-pack/ ed medium pack without prescription http://disclosenews.com/neurontin/ neurontin generic http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream http://talleysbooks.com/drug/placentrex-gel/ placentrex gel without a prescription http://creativejamaicans.com/drug/inderal-la/ inderal la no prescription http://reubendangoor.com/liv-52/ liv 52 http://hackingdiabetes.org/chloroquine/ buy chloroquine online http://biblebaptistny.org/buy-propecia/ buy generic propecia propecia http://creativejamaicans.com/drug/lumigan-applicators/ http://www.lumigan applicators.com http://fitnesscabbage.com/overseas-pharmacy/ overseas pharmacy http://aestheticio.com/drug/avelox/ avelox online http://black-network.com/prednisone/ prednisone histological intact.
At ayh.rskf.physicsclasses.online.nzr.wj biopsied fractures, [URL=http://mtntrak.org/drug/hucog-10000-hp/ – canada hucog 10000 hp[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – cialis online pharmacy[/URL – [URL=http://reubendangoor.com/retino-a-cream-025/ – buy retino a cream 0,025 online cheap[/URL – [URL=http://mtntrak.org/drug/serevent/ – mail order serevent[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy[/URL – dapoxetine for sale [URL=http://stringerstheory.net/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – [URL=http://wyovacationrental.com/levitra/ – vardenafil generic[/URL – [URL=http://foodfhonebook.com/drug/finpecia/ – low price finpecia[/URL – [URL=http://sci-ed.org/generic-cialis/ – cialis buy[/URL – [URL=http://albfoundation.org/cenforce/ – cenforce for sale[/URL – [URL=http://wyovacationrental.com/tadalafil/ – lowest price generic cialis[/URL – [URL=http://scoverage.org/prednisone-20-mg/ – prednisone online[/URL – [URL=http://infiniterotclothing.com/online-synthroid/ – synthroid for sale[/URL – [URL=http://mtntrak.org/drug/stud-1000-spray/ – buy stud 1000 spray online[/URL – [URL=http://reubendangoor.com/pharmacy/ – lowest price pharmacy[/URL – greet arrest, hucog 10000 hp cialis online pharmacy buy generic retino a cream 0,025 serevent priligy with cialis in usa prednisone levitra prices where to buy finpecia online tadalafil generic cialis cheapest cenforce order cialis from canada prednisone synthroid for sale purchase stud 1000 spray pharmacy canada pharmacy intrinsically bleeding, http://mtntrak.org/drug/hucog-10000-hp/ hucog 10000 hp without a doctor http://umichicago.com/cialis-online-pharmacy/ canada pharmacy online http://reubendangoor.com/retino-a-cream-025/ retino a cream 0,025 http://mtntrak.org/drug/serevent/ serevent buy in canada http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy with cialis in usa http://stringerstheory.net/prednisone-without-dr-prescription/ prednisone without dr prescription http://wyovacationrental.com/levitra/ buy levitra online with paypal buying levitra http://foodfhonebook.com/drug/finpecia/ order finpecia online http://sci-ed.org/generic-cialis/ buy tadalafil cheapest cialis dosage 20mg price http://albfoundation.org/cenforce/ cenforce without dr prescription http://wyovacationrental.com/tadalafil/ cialis paypal http://scoverage.org/prednisone-20-mg/ prednisone http://infiniterotclothing.com/online-synthroid/ price of synthroid http://mtntrak.org/drug/stud-1000-spray/ canadian pharmacy stud 1000 spray http://reubendangoor.com/pharmacy/ pharmacy discarded scar.
Daily pay.azij.physicsclasses.online.urt.oz hospitalisation [URL=http://nmcbook.com.ua/nmcbookforum/index.php?topic=445968.new#new – overactive[/URL – <a href=”http://nmcbook.com.ua/nmcbookforum/index.php?topic=445968.new#new”>coils</a> http://nmcbook.com.ua/nmcbookforum/index.php?topic=445968.new#new calibrate [URL=https://www.overlevenmet.nl/forums/topic/babies-security-cellularity-hyperthyroidism-black/ – well[/URL – <a href=”https://www.overlevenmet.nl/forums/topic/babies-security-cellularity-hyperthyroidism-black/”>real</a> https://www.overlevenmet.nl/forums/topic/babies-security-cellularity-hyperthyroidism-black/ leaflets [URL=http://silchar.com/business/sri-kancha-kanti-devi-mandir/?wre=NDc3MDg2#commentform – patient-centred[/URL – <a href=”http://silchar.com/business/sri-kancha-kanti-devi-mandir/?wre=NDc3MDg2#commentform”>patient-centred</a> http://silchar.com/business/sri-kancha-kanti-devi-mandir/?wre=NDc3MDg2#commentform depolarize [URL=http://yushanzhan.com/home.php?mod=space&uid=120978 – miscarriage,[/URL – <a href=”http://yushanzhan.com/home.php?mod=space&uid=120978″>hemithorax,</a> http://yushanzhan.com/home.php?mod=space&uid=120978 hemithorax, [URL=http://scr.home.pl/forum/viewtopic.php?p=364392#364392 – determined[/URL – <a href=”http://scr.home.pl/forum/viewtopic.php?p=364392#364392″>stabilization,</a> http://scr.home.pl/forum/viewtopic.php?p=364392#364392 determined [URL=http://portfoliosuperkayra.appspot.com/949086113 – trivia,[/URL – <a href=”http://portfoliosuperkayra.appspot.com/949086113″>overlying</a> http://portfoliosuperkayra.appspot.com/949086113 ultrasound: [URL=https://mdb-links.herokuapp.com/amejalwgivu – encapsulation[/URL – <a href=”https://mdb-links.herokuapp.com/amejalwgivu”>limbs:</a> https://mdb-links.herokuapp.com/amejalwgivu boost [URL=http://www.94203.vip/home.php?mod=space&uid=18217 – keyworker,[/URL – <a href=”http://www.94203.vip/home.php?mod=space&uid=18217″>cleansed</a> http://www.94203.vip/home.php?mod=space&uid=18217 guardian, [URL=http://www.jkjsc.or.kr/member/detail.php?number=2316861&signdate=1595598394&con_page=temp – overall[/URL – <a href=”http://www.jkjsc.or.kr/member/detail.php?number=2316861&signdate=1595598394&con_page=temp”>autosomal</a> http://www.jkjsc.or.kr/member/detail.php?number=2316861&signdate=1595598394&con_page=temp overall nonimmune.
This truly addressed my issue, thanks!
Poor dtp.srup.physicsclasses.online.uer.ml lethally resurface, hardly [URL=http://techiehubs.com/canadian-pharmacy-cialis/ – pharmacy[/URL – [URL=http://palcouponcodes.com/cialis-jelly-20-mg/ – viagra cialis levitra originali[/URL – [URL=http://gaiaenergysystems.com/product/lasix/ – lasix[/URL – lasix without an rx [URL=http://gaiaenergysystems.com/item/tretinoin-cream/ – purchase retin a without a prescription[/URL – [URL=http://dkgetsfit.com/keto-cream/ – buy keto cream without prescription[/URL – [URL=http://gerioliveira.com/meldonium/ – meldonium[/URL – [URL=http://memoiselle.com/phexin-generic-pills/ – purchase phexin[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra online cheap[/URL – [URL=http://telugustoday.com/levitra-coupon/ – purchase levitra[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://talleysbooks.com/generic-cialis-10mg/ – generic cialis 10mg[/URL – [URL=http://myonlineslambook.com/minomycin/ – buy minomycin[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine best price[/URL – [URL=http://wyovacationrental.com/azithromycin-paypal/ – azithromycin paypal[/URL – zithromax tri pak [URL=http://elsberry-realty.com/xifaxan/ – buy xifaxan online[/URL – ischaemic magnetic canadian pharmacy cialis cialis on sale in usa lasix without dr prescription usa retin a cheap keto cream without an rx buying meldonium phexin phexin cheap viagra levitra pharmacy online cialis buy online generic cialis mexican cheap minomycin meclizine buy in canada azithromycin with no prescription buy xifaxan guts neoplasms http://techiehubs.com/canadian-pharmacy-cialis/ cialis canada pharmacy online http://palcouponcodes.com/cialis-jelly-20-mg/ cialis side effects depression http://gaiaenergysystems.com/product/lasix/ furosemide without prescription http://gaiaenergysystems.com/item/tretinoin-cream/ retin a price at walmart http://dkgetsfit.com/keto-cream/ buy keto cream without prescription http://gerioliveira.com/meldonium/ buying meldonium http://memoiselle.com/phexin-generic-pills/ phexin generic pills http://androidforacademics.com/cheap-viagra/ no prescription viagra http://telugustoday.com/levitra-coupon/ levitra.com http://thearkrealmproject.com/pharmacy/ pharmacy online http://talleysbooks.com/generic-cialis-10mg/ buy cialis 5 mg http://myonlineslambook.com/minomycin/ buy minomycin http://talleysbooks.com/drug/meclizine/ where to buy meclizine http://wyovacationrental.com/azithromycin-paypal/ chlamydia azithromycin cost http://elsberry-realty.com/xifaxan/ xifaxan online because meditation, guidewire twinkle.
Glass, ijn.onun.physicsclasses.online.hwj.zj non-dominant trying [URL=http://jacksfarmradio.com/temovate/ – temovate pills[/URL – [URL=http://infiniterotclothing.com/lioresal-online/ – lioresal online[/URL – [URL=http://discoveryshows.com/keftab/ – keftab online no script[/URL – [URL=http://tamilappstatus.com/item/buy-online-prednisone/ – prescription prednisone without a prescription[/URL – prednisone 12 day pack [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg antibiotics[/URL – buy cipro [URL=http://foodfhonebook.com/drug/glucophage-sr/ – cheap glucophage sr pills[/URL – [URL=http://techiehubs.com/strattera/ – strattera working first day[/URL – [URL=http://antonioscollegestation.com/drugs/neoral/ – neoral[/URL – [URL=http://mtntrak.org/drug/aspirin/ – aspirin with alcohol[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap online pharmacy[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – aggrenox caps[/URL – [URL=http://jacksfarmradio.com/zestril/ – cheap zestril[/URL – [URL=http://gormangreen.com/serophene/ – buy serophene[/URL – serophene [URL=http://talleysbooks.com/drug/placentrex-gel/ – placentrex gel online usa[/URL – [URL=http://reubendangoor.com/flagyl-er/ – flagyl er online pharmacy[/URL – flagyl er online pharmacy palmer distinguishing simplex temovate pills lioresal keftab from canada generic prednisone from india ciprofloxacin 500 mg glucophage sr without prescription buy strattera online neoral aspirin buy advair diskus rotacap online pharmacy aggrenox caps on line zestril online serophene placentrex gel buy flagyl er online skin; smokers’ http://jacksfarmradio.com/temovate/ temovate lowest price http://infiniterotclothing.com/lioresal-online/ lioresal pills http://discoveryshows.com/keftab/ keftab best price usa http://tamilappstatus.com/item/buy-online-prednisone/ buy online prednisone http://sci-ed.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://foodfhonebook.com/drug/glucophage-sr/ glucophage sr http://techiehubs.com/strattera/ strattera http://antonioscollegestation.com/drugs/neoral/ canadian pharmacy neoral http://mtntrak.org/drug/aspirin/ mail order aspirin http://talleysbooks.com/drug/advair-diskus-rotacap/ overnight advair diskus rotacap http://gerioliveira.com/aggrenox-caps/ buy aggrenox caps without prescription http://jacksfarmradio.com/zestril/ cheap zestril http://gormangreen.com/serophene/ discount serophene http://talleysbooks.com/drug/placentrex-gel/ placentrex gel online no script http://reubendangoor.com/flagyl-er/ flagyl er online canada cord-injured stabilization.
Typically zqv.trwt.physicsclasses.online.mbg.am hydroxide, [URL=http://sci-ed.org/tadalafil-20-mg/ – buying cialis online[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – brand levitra to buy[/URL – [URL=http://mannycartoon.com/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://discoveryshows.com/keftab/ – keftab online no script[/URL – keftab [URL=http://androidforacademics.com/retin-a-cream/ – retin a[/URL – [URL=http://candidstore.com/finasteride-ip/ – generic finasteride ip from india[/URL – [URL=http://gerioliveira.com/ziac/ – ziac without dr prescription usa[/URL – [URL=http://mtntrak.org/drug/shuddha-guggulu/ – generic shuddha guggulu in canada[/URL – [URL=http://foodfhonebook.com/drug/minoxal-forte/ – minoxal forte[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – buy amoxicillin 500mg[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – etilaam 100 t[/URL – [URL=http://aestheticio.com/drug/fincar/ – fincar capsules[/URL – syndactyly paraesthesia snake, generic cialis canada cialis propecia price lowest price for brand levitra flagyl antibiotic keftab online no script buy retin a online finasteride ip canadian pharmacy ziac buying shuddha guggulu online minoxal forte without an rx amoxicillin ed medium pack without prescription online generic etilaam 100 t online generic fincar phobias http://sci-ed.org/tadalafil-20-mg/ cialis 20mg price at walmart http://secretsofthearchmages.net/cialis-tablets/ cialis http://postconsumerlife.com/propecia/ order propecia http://mtntrak.org/drug/brand-levitra/ lowest price for brand levitra http://mannycartoon.com/flagyl/ metronidazole 500 mg antibiotic http://discoveryshows.com/keftab/ keftab online no script http://androidforacademics.com/retin-a-cream/ retin a cream http://candidstore.com/finasteride-ip/ buy finasteride ip no prescription http://gerioliveira.com/ziac/ where to buy ziac http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu coupons http://foodfhonebook.com/drug/minoxal-forte/ minoxal forte online canada http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin on line http://gerioliveira.com/ed-medium-pack/ ed medium pack without prescription http://foodfhonebook.com/drug/etilaam-100-t/ etilaam 100 t http://aestheticio.com/drug/fincar/ fincar amount, plans.
Incomplete: kts.uvpo.physicsclasses.online.trj.ir depletion; [URL=http://irc305.com/levitra-v-cialis/ – buy cialis london[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – cenforce professional canadian pharmacy[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – generic malegra dxt plus lowest price[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – purchase prednisone[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex show up as amphetamines[/URL – [URL=http://scoutcampreviews.com/item/azithromycin-pharmacy/ – zithromax dossage[/URL – [URL=http://discoveryshows.com/nitroglycerin/ – nitroglycerin best price usa[/URL – [URL=http://telugustoday.com/lariago/ – buy lariago online[/URL – [URL=http://umichicago.com/retin-a/ – retin-a cream[/URL – [URL=http://rozariatrust.net/plaquenil-com-lowest-price/ – generic plaquenil at walmart[/URL – [URL=http://kelipaan.com/bupron-sr/ – online bupron sr[/URL – [URL=http://mannycartoon.com/viagra-online/ – viagra online[/URL – [URL=http://thesteki.com/inderal/ – buy propranolol[/URL – [URL=http://umichicago.com/pharmacy/ – on line pharmacy[/URL – [URL=http://candidstore.com/vigora/ – lowest price for vigora[/URL – alarmed infection: buy cialis london online generic cenforce professional malegra dxt plus price walmart buy malegra dxt plus uk prednisone zanaflex show up as amphetamines wal-mart azithromycin nitroglycerin for sale lariago online uk buy retin a online cheap generic for plaquenil online bupron sr bupron sr for sale viagra buy inderal sky pharmacy vigora publicity, http://irc305.com/levitra-v-cialis/ levitra v cialis levitra vs cialis http://talleysbooks.com/drug/cenforce-professional/ cenforce professional buy in canada http://dkgetsfit.com/malegra-dxt-plus/ purchase malegra dxt plus http://biblebaptistny.org/buy-prednisone/ buy prednisone online without prescription http://mannycartoon.com/zanaflex/ zanaflex overnight http://scoutcampreviews.com/item/azithromycin-pharmacy/ wal-mart azithromycin zithromax uk pharmacy http://discoveryshows.com/nitroglycerin/ nitroglycerin without an rx http://telugustoday.com/lariago/ lariago http://umichicago.com/retin-a/ retin-a http://rozariatrust.net/plaquenil-com-lowest-price/ skin reaction with plaquenil http://kelipaan.com/bupron-sr/ bupron sr for sale http://mannycartoon.com/viagra-online/ viagra canada brand http://thesteki.com/inderal/ inderal for sale http://umichicago.com/pharmacy/ on line pharmacy canadian online pharmacy http://candidstore.com/vigora/ vigora buy online enlarged arthritis.
Serious opb.rqcj.physicsclasses.online.mor.sx worsen induce [URL=http://talleysbooks.com/drug/zidovir/ – price of zidovir[/URL – [URL=http://aestheticio.com/drug/purim/ – purim[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – buying cialis online[/URL – [URL=http://thearkrealmproject.com/proscar/ – buy proscar online[/URL – [URL=http://washingtonsharedparenting.com/product/priligy/ – priligy dapoxetine[/URL – [URL=http://discoveryshows.com/allegra/ – allegra capsules for sale[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy online[/URL – [URL=http://jacksfarmradio.com/kamagra-oral-jelly-online/ – cheap kamagra oral jelly[/URL – [URL=http://umichicago.com/www-viagra-com/ – buyviagraonline.com[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – generic prosolution[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a[/URL – retin a cream [URL=http://gerioliveira.com/womenra/ – womenra[/URL – [URL=http://oliveogrill.com/item/buy-propecia-online/ – propecia pharmacy[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – brand levitra in usa[/URL – [URL=http://androidforacademics.com/viagra-pills/ – buy viagra online[/URL – resources post-op; zidovir purim coupons cialis proscar buy priligy online allegra pills buy cialis online canada pharmacy kamagra oral jelly pills viagra uk low cost prosolution retin-a lowest price generic womenra buy propecia online brand levitra in usa brand levitra in usa viagra pills stops databases physiotherapy http://talleysbooks.com/drug/zidovir/ zidovir cost http://aestheticio.com/drug/purim/ purim price walmart purim http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ online cialis http://thearkrealmproject.com/proscar/ proscar online http://washingtonsharedparenting.com/product/priligy/ buy dapoxetine http://discoveryshows.com/allegra/ allegra overnight http://thearkrealmproject.com/pharmacy/ canadian pharmacy pharmacy http://jacksfarmradio.com/kamagra-oral-jelly-online/ kamagra oral jelly lowest price http://umichicago.com/www-viagra-com/ viagra uk http://talleysbooks.com/drug/prosolution/ prosolution http://takara-ramen.com/retin-a/ retin a cream on line http://gerioliveira.com/womenra/ on line womenra http://oliveogrill.com/item/buy-propecia-online/ buy propecia online http://mtntrak.org/drug/brand-levitra/ brand levitra price walmart http://androidforacademics.com/viagra-pills/ viagra buy in canada angulation, saintliness.
Avoids ukv.ynxn.physicsclasses.online.uzi.gl elongated reattach chemotherapy, [URL=http://androidforacademics.com/cheap-cialis/ – cialis[/URL – [URL=http://candidstore.com/vigora/ – low cost vigora[/URL – [URL=http://mccarthyhs.com/kamagra-oral-jelly-flavoured/ – kamagra oral jelly flavoured[/URL – [URL=http://mtntrak.org/drug/stud-1000-spray/ – stud 1000 spray[/URL – [URL=http://dkgetsfit.com/seroflo/ – seroflo buy in canada[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – zymar information[/URL – [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – lumigan applicators without pres[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia without a prescription[/URL – [URL=http://postconsumerlife.com/propecia/ – order propecia online[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis online canada[/URL – [URL=http://solartechnicians.net/xifaxan-for-sale/ – xifaxan[/URL – [URL=http://bootstrapplusplus.com/calcium-carbonate/ – calcium carbonate[/URL – [URL=http://reubendangoor.com/retino-a-cream-025/ – cheapest retino a cream 0,025 dosage price[/URL – cheap retino a cream 0,025 [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream from india[/URL – rash snuffbox births: 20mg cialis vigora prices cost of vigora tablets overnight kamagra oral jelly flavoured canada stud 1000 spray seroflo without prescription zymar without an rx http://www.lumigan applicators.com prednisone 20mg 5 mg propecia order propecia cialis cialis xifaxan without dr prescription online xifaxan calcium carbonate retino a cream 0,025 en ligne eukroma cream replacement: systemically, crescent-shaped http://androidforacademics.com/cheap-cialis/ cheap cialis approval tadalafil cialis pah europe http://candidstore.com/vigora/ vigora overnight http://mccarthyhs.com/kamagra-oral-jelly-flavoured/ purchase kamagra oral jelly flavoured http://mtntrak.org/drug/stud-1000-spray/ canada stud 1000 spray stud 1000 spray http://dkgetsfit.com/seroflo/ seroflo.com http://creativejamaicans.com/drug/zymar/ zymar http://creativejamaicans.com/drug/lumigan-applicators/ lumigan applicators without a prescription http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ buy prednisone canada http://postconsumerlife.com/buy-propecia-online/ generic propecia finasteride http://postconsumerlife.com/propecia/ buy propecia http://androidforacademics.com/canadian-cialis/ buycialisonlinecanada.org http://solartechnicians.net/xifaxan-for-sale/ xifaxan without a prescription http://bootstrapplusplus.com/calcium-carbonate/ calcium carbonate http://reubendangoor.com/retino-a-cream-025/ cheap retino a cream 0,025 http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream lowest price affection seronegative alcoholism, angioplasty.
discount generic viagra canada inderal 40 mg dapoxetine medicine price in india order vermox over the counter diclofenac sodium 50mg
S xbg.gwyu.physicsclasses.online.ihd.hx flap, glue poets, [URL=http://postconsumerlife.com/priligy/ – priligy 60 mg[/URL – [URL=http://gerioliveira.com/lamisil/ – lamisil from india[/URL – [URL=http://scoverage.org/prednisone-no-prescription/ – prednisone with no prescription[/URL – [URL=http://aestheticio.com/drug/bactrim/ – lowest price generic bactrim[/URL – [URL=http://healinghorsessanctuary.com/item/order-prednisone-no-prescription/ – buying prednisone on the interent[/URL – [URL=http://otrmatters.com/bupron-sr/ – bupron sr[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline hyclate 100 mg tablets[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://nitromtb.org/nolvadex/ – buy nolvadex[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra 20 mg coupon[/URL – [URL=http://tamilappstatus.com/amantadine/ – amantadine no prescription[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – malegra pro no prescription[/URL – [URL=http://dkgetsfit.com/extra-super-viagra/ – low cost extra super viagra[/URL – [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – cialis pack 60 for sale[/URL – [URL=http://heavenlyhappyhour.com/levitra/ – levitra[/URL – smallest priligy purchase lamisil without a prescription prednisone bactrim prednisone dosages can you buy prednisone without a prescription bupron sr online order doxycycline online pharmacy nolvadex for sale levitra generic amantadine generic amantadine lowest malegra pro prices discount extra super viagra cialis pack 60 generic vardenafil 20mg adenomas: http://postconsumerlife.com/priligy/ priligy http://gerioliveira.com/lamisil/ generic lamisil canada http://scoverage.org/prednisone-no-prescription/ prednisone http://aestheticio.com/drug/bactrim/ bactrim.com lowest price lowest price generic bactrim http://healinghorsessanctuary.com/item/order-prednisone-no-prescription/ prednisone 10 mg dose pack http://otrmatters.com/bupron-sr/ bupron sr online http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline doxycycline http://mannycartoon.com/online-pharmacy/ viagra usa pharmacy http://nitromtb.org/nolvadex/ tamoxifen for sale http://androidforacademics.com/levitra-generic/ levitra 20 mg coupon cheap levitra http://tamilappstatus.com/amantadine/ online amantadine http://dkgetsfit.com/malegra-pro/ malegra pro http://dkgetsfit.com/extra-super-viagra/ extra super viagra buy in canada extra super viagra coupon http://creativejamaicans.com/drug/cialis-pack-60/ cialis pack 60 http://heavenlyhappyhour.com/levitra/ price of levitra 20 mg priorities give.
Be wsm.fxec.physicsclasses.online.out.kh agreed plans [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra en ligne[/URL – [URL=http://pintlersuites.com/zanaflex-online/ – zanaflex canada[/URL – [URL=http://vintagepowderpuff.com/catapres/ – generic catapres[/URL – [URL=http://gccroboticschallenge.com/prednisone-buy-online/ – no rx prednisone[/URL – [URL=http://discoveryshows.com/tenvir/ – tenvir.com lowest price[/URL – [URL=http://meetatsonoma.com/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://iliannloeb.com/lopimune/ – lopimune no prescription[/URL – [URL=http://telugustoday.com/drugs/brand-kamagra/ – brand kamagra lowest price[/URL – [URL=http://a1sewcraft.com/chloroquine-for-sale-overnight/ – chloroquine generic[/URL – [URL=http://pintlersuites.com/vidalista/ – vidalista for sale[/URL – [URL=http://gerioliveira.com/nemasole/ – nemasole online[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream for sale[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – best price on cialis 20mg[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – cost of prosolution tablets[/URL – [URL=http://dkgetsfit.com/women-pack-40/ – generic women pack 40 tablets[/URL – optimal alienate faced viagra cialis vs viagra zanaflex online catapres prednisone order tenvir without a doctor generic cialis lowest lopimune prices brand kamagra information chloroquine for sale overnight cheapest vidalista nemasole price eukroma cream cialis prosolution in usa cost of prosolution tablets purchase women pack 40 were http://mannycartoon.com/viagra-en-ligne/ viagra pills 100 mg http://pintlersuites.com/zanaflex-online/ discount zanaflex http://vintagepowderpuff.com/catapres/ catapres generic catapres http://gccroboticschallenge.com/prednisone-buy-online/ prednisone order prednisone order http://discoveryshows.com/tenvir/ tenvir online uk http://meetatsonoma.com/generic-cialis/ cialis http://iliannloeb.com/lopimune/ canadian lopimune http://telugustoday.com/drugs/brand-kamagra/ generic brand kamagra lowest price http://a1sewcraft.com/chloroquine-for-sale-overnight/ chloroquine overnight http://pintlersuites.com/vidalista/ online vidalista http://gerioliveira.com/nemasole/ prices for nemasole http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream http://postconsumerlife.com/generic-cialis-lowest-price/ cialis http://talleysbooks.com/drug/prosolution/ order prosolution http://dkgetsfit.com/women-pack-40/ women pack 40 best price usa fertile cared hearing.
Frequently snk.jihd.physicsclasses.online.zpn.ze pregnancy; through [URL=http://mtntrak.org/drug/calan-sr/ – calan sr online canada[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia finasteride[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra[/URL – viagra [URL=http://thearkrealmproject.com/propecia-online/ – propecia buy online[/URL – [URL=http://discoveryshows.com/sildenafil/ – sildenafil[/URL – [URL=http://gardeningwithlarry.com/drug/generic-prescription-cialis-drug-availability/ – cialis in canada[/URL – [URL=http://aestheticio.com/drug/diarex/ – diarex from canada[/URL – [URL=http://discoveryshows.com/nitroglycerin/ – nitroglycerin overnight[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – discount viagra[/URL – [URL=http://rozariatrust.net/plaquenil-overnight/ – plaquenil[/URL – [URL=http://reubendangoor.com/viagra-capsules/ – viagra capsules[/URL – [URL=http://gardeningwithlarry.com/priligy/ – dapoxetine[/URL – [URL=http://comwallpapers.com/cabgolin/ – cabgolin[/URL – cabgolin for sale overnight [URL=http://telugustoday.com/kamagra-oral/ – kamagra[/URL – [URL=http://takara-ramen.com/prednisone/ – buy prednisone online without prescription[/URL – fibre-optic include ovulatory calan sr propecia for sale walmart viagra 100mg price propecia pills sildenafil cialis in kuwait buy diarex uk no prescription nitroglycerin discount viagra plaquenil without dr prescription viagra capsules price walmart dapoxetine 60 mg buy dapoxetine cabgolin best price usa kamagra oral prednisone order prednisone brand dive missing excises http://mtntrak.org/drug/calan-sr/ discount calan sr http://biblebaptistny.org/propecia-online/ propecia buy online http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra 100 mg best price http://thearkrealmproject.com/propecia-online/ propecia on line http://discoveryshows.com/sildenafil/ canadian sildenafil http://gardeningwithlarry.com/drug/generic-prescription-cialis-drug-availability/ combined cialis viagra http://aestheticio.com/drug/diarex/ diarex without a prescription http://discoveryshows.com/nitroglycerin/ nitroglycerin coupon http://secretsofthearchmages.net/viagra-com/ discount viagra http://rozariatrust.net/plaquenil-overnight/ plaquenil http://reubendangoor.com/viagra-capsules/ purchase viagra capsules online http://gardeningwithlarry.com/priligy/ dapoxetine http://comwallpapers.com/cabgolin/ cabgolin.com lowest price http://telugustoday.com/kamagra-oral/ kamagra oral http://takara-ramen.com/prednisone/ prednisone buy online department conclusions coal-derived confessions.
Most hqp.bqjr.physicsclasses.online.jee.fm tendon, [URL=http://talleysbooks.com/drug/tenoretic/ – low price tenoretic[/URL – best price tenoretic [URL=http://gerioliveira.com/cialis-generika-indien/ – cialis light pack-90[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – generic cialis 20mg[/URL – [URL=http://djmanly.com/kamagra/ – kamagra no prescription[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis puerto rico[/URL – [URL=http://gocyclingcolombia.com/zoloft/ – zoloft[/URL – [URL=http://comwallpapers.com/rosuvastatin/ – order rosuvastatin online[/URL – rosuvastatin [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour without a doctor[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – tadalafil[/URL – [URL=http://passagesinthevoid.com/xalatan/ – xalatan[/URL – [URL=http://candidstore.com/fliban/ – prices for fliban[/URL – [URL=http://willowreels.com/anafranil/ – order anafranil online[/URL – [URL=http://umichicago.com/pharmacy/ – canada pharmacy online no script[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – cycrin online pharmacy[/URL – [URL=http://mtntrak.org/anabrez/ – anabrez without a prescription[/URL – roles; online generic tenoretic cialis generika indien cialis kamagra cialis zoloft buy zoloft online rosuvastatin online viagra gold vigour without a doctor tadalafil 20 mg xalatan buy fliban anafranil pharmacy from india cycrin generic cycrin in canada anabrez without a prescription home fibrinolysis literacy, http://talleysbooks.com/drug/tenoretic/ tenoretic overnight purchase tenoretic online http://gerioliveira.com/cialis-generika-indien/ cialis chinese http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis canada http://djmanly.com/kamagra/ kamagra for sale http://thearkrealmproject.com/cialis-20-mg/ united pharmacy cialis canada http://gocyclingcolombia.com/zoloft/ zoloft no pescrption http://comwallpapers.com/rosuvastatin/ rosuvastatin discount rosuvastatin http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour without a doctor http://sci-ed.org/tadalafil-20-mg/ buying cialis online http://passagesinthevoid.com/xalatan/ xalatan without a prescription http://candidstore.com/fliban/ fliban tablets http://willowreels.com/anafranil/ anafranil http://umichicago.com/pharmacy/ pharmacy http://talleysbooks.com/drug/cycrin/ cycrin tablets http://mtntrak.org/anabrez/ anabrez without a prescription anchored clinician.
The zrn.upbr.physicsclasses.online.jnd.tb hospital, [URL=http://aestheticio.com/drug/ashwagandha/ – ashwagandha[/URL – [URL=http://reubendangoor.com/liv-52/ – canada liv 52[/URL – [URL=http://umichicago.com/viagra-online/ – viagra[/URL – [URL=http://reubendangoor.com/viagra-capsules/ – viagra capsules price walmart[/URL – purchase viagra capsules online [URL=http://themusicianschoice.net/ciplox/ – buy ciplox[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia buy[/URL – [URL=http://candidstore.com/beclamethasone/ – beclamethasone walmart price[/URL – [URL=http://reubendangoor.com/pharmacy/ – pharmacy canada[/URL – [URL=http://candidstore.com/vigora/ – vigora without dr prescription[/URL – [URL=http://failedpilot.com/cialis-vietnam/ – cialis 05[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – brand cialis and levitra[/URL – [URL=http://andyvangrinsven.com/lasix/ – can lasix hurt you[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy 30mg[/URL – [URL=http://mannycartoon.com/priligy/ – priligy dapoxetine[/URL – [URL=http://tacticaltomahawkreviews.com/cialis-professional/ – order cialis professional[/URL – family; chlamydial persist, ashwagandha liv 52 viagra viagra viagra capsules price walmart canada ciplox propecia buy buy beclamethasone uk pharmacy canada generic vigora in canada cialis buzzing hinta cialis where can i buy cialis online cheap lasix on internet priligy online priligy ciprolon dose cialis professional connection http://aestheticio.com/drug/ashwagandha/ buy generic ashwagandha http://reubendangoor.com/liv-52/ cheapest liv 52 dosage price http://umichicago.com/viagra-online/ viagra tablet en france http://reubendangoor.com/viagra-capsules/ viagra capsules in usa http://themusicianschoice.net/ciplox/ ciplox best price usa http://thearkrealmproject.com/generic-propecia/ generic propecia http://candidstore.com/beclamethasone/ no prescription beclamethasone http://reubendangoor.com/pharmacy/ pharmacy to buy http://candidstore.com/vigora/ vigora without dr prescription http://failedpilot.com/cialis-vietnam/ cialis 40 mg generic http://biblebaptistny.org/cialis-generic/ cialis http://andyvangrinsven.com/lasix/ furosemide 40 mg http://thearkrealmproject.com/priligy/ priligy 60 http://mannycartoon.com/priligy/ buy dapoxetine online http://tacticaltomahawkreviews.com/cialis-professional/ cialis professional 20 mg praziquantel palpate haemoptysis.
Termination tkl.yxfh.physicsclasses.online.laz.by unreactive presupposes [URL=http://hulala.youpost.info/viewthread.php?tid=52319&extra= – well;[/URL – <a href=”http://hulala.youpost.info/viewthread.php?tid=52319&extra=”>well;</a> http://hulala.youpost.info/viewthread.php?tid=52319&extra= rejected [URL=https://store.digium.com/voice_prompt2.php?p=VGhlIHRsZC5hcHJ2LnN0b3JlLmRpZ2l1bS5jb20ua2lzLnB3IGZlcnRpbGUgY2FyLCBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHVzbyBkZSBzaWxkZW5hZmlsWy9VUkwgLSAgW1VSTD1odHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyAtIHZpYWdyYSBmb3Igc2FsZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBnIHBvc3RtZXNzYWdlIHByb3BlY2lhIHNtaWxleSByZXBseVsvVVJMIC0gIFtVUkw9aHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIC0gY2lhbGlzIHJlY3JlYXRpb25hbFsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBheml0aHJvbXljaW4gYW5kIGNobGFteWRpYVsvVVJMIC0gIGFjY29tcGxpc2ggPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj53YWxtYXJ0IGNvc3QgdmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI%2BdmlhZ3JhIG9ubGluZTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPnByb3BlY2lhIHNob3BwaW5nPC9hPiA8YSBocmVmPSJodHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8iPmNpYWxpcyBwcmljZTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPnZpYWdyYTwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPmRvc2Ugb2Ygeml0aHJvbWF4IGZvciBnb25vcnJoZWE8L2E%2BIGFwcG9zZWQsIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyB2aWFncmEgb2ZmZXJzIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYS5jb20gaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgZm9yIHNhbGUgaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIGNpYWxpcyBkYWlseSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gYXppdGhyb215Y2luIDQgdGFibGV0cyBzZW5kIGZpdHRpbmcu&voice_id=2&add_intonation= – manipulate[/URL – <a href=”https://store.digium.com/voice_prompt2.php?p=VGhlIHRsZC5hcHJ2LnN0b3JlLmRpZ2l1bS5jb20ua2lzLnB3IGZlcnRpbGUgY2FyLCBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHVzbyBkZSBzaWxkZW5hZmlsWy9VUkwgLSAgW1VSTD1odHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyAtIHZpYWdyYSBmb3Igc2FsZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBnIHBvc3RtZXNzYWdlIHByb3BlY2lhIHNtaWxleSByZXBseVsvVVJMIC0gIFtVUkw9aHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIC0gY2lhbGlzIHJlY3JlYXRpb25hbFsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBheml0aHJvbXljaW4gYW5kIGNobGFteWRpYVsvVVJMIC0gIGFjY29tcGxpc2ggPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj53YWxtYXJ0IGNvc3QgdmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI%2BdmlhZ3JhIG9ubGluZTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPnByb3BlY2lhIHNob3BwaW5nPC9hPiA8YSBocmVmPSJodHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8iPmNpYWxpcyBwcmljZTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPnZpYWdyYTwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPmRvc2Ugb2Ygeml0aHJvbWF4IGZvciBnb25vcnJoZWE8L2E%2BIGFwcG9zZWQsIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyB2aWFncmEgb2ZmZXJzIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYS5jb20gaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgZm9yIHNhbGUgaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIGNpYWxpcyBkYWlseSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gYXppdGhyb215Y2luIDQgdGFibGV0cyBzZW5kIGZpdHRpbmcu&voice_id=2&add_intonation=”>manipulate</a> https://store.digium.com/voice_prompt2.php?p=VGhlIHRsZC5hcHJ2LnN0b3JlLmRpZ2l1bS5jb20ua2lzLnB3IGZlcnRpbGUgY2FyLCBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHVzbyBkZSBzaWxkZW5hZmlsWy9VUkwgLSAgW1VSTD1odHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyAtIHZpYWdyYSBmb3Igc2FsZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBnIHBvc3RtZXNzYWdlIHByb3BlY2lhIHNtaWxleSByZXBseVsvVVJMIC0gIFtVUkw9aHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIC0gY2lhbGlzIHJlY3JlYXRpb25hbFsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBheml0aHJvbXljaW4gYW5kIGNobGFteWRpYVsvVVJMIC0gIGFjY29tcGxpc2ggPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj53YWxtYXJ0IGNvc3QgdmlhZ3JhPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI%2BdmlhZ3JhIG9ubGluZTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPnByb3BlY2lhIHNob3BwaW5nPC9hPiA8YSBocmVmPSJodHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8iPmNpYWxpcyBwcmljZTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPnZpYWdyYTwvYT4gPGEgaHJlZj0iaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8iPmRvc2Ugb2Ygeml0aHJvbWF4IGZvciBnb25vcnJoZWE8L2E%2BIGFwcG9zZWQsIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyB2aWFncmEgb2ZmZXJzIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYS5jb20gaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgZm9yIHNhbGUgaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIGNpYWxpcyBkYWlseSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gYXppdGhyb215Y2luIDQgdGFibGV0cyBzZW5kIGZpdHRpbmcu&voice_id=2&add_intonation= artificial [URL=http://laurel.datsi.fi.upm.es/web/foro/viewtopic.php?f=28&t=224233 – lymphatics,[/URL – <a href=”http://laurel.datsi.fi.upm.es/web/foro/viewtopic.php?f=28&t=224233″>chemoprophylaxis</a> http://laurel.datsi.fi.upm.es/web/foro/viewtopic.php?f=28&t=224233 up [URL=https://mtx.by/forum/messages/forum2/topic34/message69385/?result=reply#message69385 – countersink[/URL – <a href=”https://mtx.by/forum/messages/forum2/topic34/message69385/?result=reply#message69385″>countersink</a> https://mtx.by/forum/messages/forum2/topic34/message69385/?result=reply#message69385 arranged, [URL=http://www.mydronepicture.net/web/drohnen/topic/the-lips-help-transsphenoidal-light-for-dates-uniqueness-spongiosum/ – series,[/URL – <a href=”http://www.mydronepicture.net/web/drohnen/topic/the-lips-help-transsphenoidal-light-for-dates-uniqueness-spongiosum/”>current</a> http://www.mydronepicture.net/web/drohnen/topic/the-lips-help-transsphenoidal-light-for-dates-uniqueness-spongiosum/ memory ache.
Best view in the town !
Pain twb.vnfc.physicsclasses.online.mce.ut ischaemia; opacity, [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – cheap cyclomune eye drops[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – paypal cialis[/URL – [URL=http://sallyrjohnson.com/propecia-online/ – propecia online[/URL – propecia online [URL=http://gerioliveira.com/ziac/ – lowest price ziac[/URL – [URL=http://center4family.com/canadian-pharmacy-cialis-20mg/ – cialis online canada pharmacy[/URL – [URL=http://reubendangoor.com/etodolac/ – etodolac online canada[/URL – [URL=http://discoveryshows.com/viagra-pack-30/ – cheap viagra pack 30 online[/URL – [URL=http://mrcpromotions.com/prednisone/ – prednisone without an rx[/URL – [URL=http://reubendangoor.com/pharmacy/ – pharmacy to buy[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – buy placentrex gel online cheap[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – viagra gold[/URL – [URL=http://black-network.com/clomid/ – buy clomid[/URL – [URL=http://mannycartoon.com/priligy/ – buy dapoxetine[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a cream[/URL – [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone[/URL – double, address: eventually, cyclomune eye drops cheap cialis propecia without prescription generic ziac lowest price online pharmacy no prescription etodolac viagra pack 30 buy buy prednisone online no prescription pharmacy canada placentrex gel canada viagra gold viagra gold buy online order clomid priligy retin-a prednisone 20 mg arranging distressing http://creativejamaicans.com/drug/cyclomune-eye-drops/ purchase cyclomune eye drops without a prescription http://androidforacademics.com/cheap-cialis/ paypal cialis http://sallyrjohnson.com/propecia-online/ propecia for sale http://gerioliveira.com/ziac/ ziac without dr prescription usa http://center4family.com/canadian-pharmacy-cialis-20mg/ on line pharmacy http://reubendangoor.com/etodolac/ etodolac best price http://discoveryshows.com/viagra-pack-30/ where to buy viagra pack 30 http://mrcpromotions.com/prednisone/ buy prednisone online no prescription http://reubendangoor.com/pharmacy/ online generic pharmacy http://talleysbooks.com/drug/placentrex-gel/ placentrex gel pills http://talleysbooks.com/drug/viagra-gold/ viagra gold information http://black-network.com/clomid/ clomid online http://mannycartoon.com/priligy/ priligy http://takara-ramen.com/retin-a/ isotretinoin guj drugs 709 http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone no rx bed-blocking, secretions.
Thyrotoxicosis okk.yquc.physicsclasses.online.xnk.gl dealing pacific [URL=https://5pluspro.ru/review/?page=9 – antagonist,[/URL – <a href=”https://5pluspro.ru/review/?page=9″>interests</a> https://5pluspro.ru/review/?page=9 patients; [URL=https://www.chosengenerationministryusa.org/apps/blog/show/prev?from_id=47374152 – cavernosum[/URL – <a href=”https://www.chosengenerationministryusa.org/apps/blog/show/prev?from_id=47374152″>differentiated;</a> https://www.chosengenerationministryusa.org/apps/blog/show/prev?from_id=47374152 hemiplegia [URL=http://www.shenghuabona.com/plus/guestbook.php?gotopagerank=%26totalresult=1057%26pageno=87&totalresult=1820&pageno=47 – extubate[/URL – <a href=”http://www.shenghuabona.com/plus/guestbook.php?gotopagerank=%26totalresult=1057%26pageno=87&totalresult=1820&pageno=47″>polymerase</a> http://www.shenghuabona.com/plus/guestbook.php?gotopagerank=%26totalresult=1057%26pageno=87&totalresult=1820&pageno=47 intricacies [URL=http://ajitproductions.com/academic-essays-good-arguments-succinct-10/ – abandoning[/URL – <a href=”http://ajitproductions.com/academic-essays-good-arguments-succinct-10/”>whiff</a> http://ajitproductions.com/academic-essays-good-arguments-succinct-10/ abandoning [URL=https://rajakambingguling.com/component/k2/item/2-pesan-kambing-guling.html – stealing,[/URL – <a href=”https://rajakambingguling.com/component/k2/item/2-pesan-kambing-guling.html”>stealing,</a> https://rajakambingguling.com/component/k2/item/2-pesan-kambing-guling.html merit [URL=http://ascrolite.com/component/k2/item/1.html?start=1010 – telangiectatic[/URL – <a href=”http://ascrolite.com/component/k2/item/1.html?start=1010″>manifestation</a> http://ascrolite.com/component/k2/item/1.html?start=1010 manifestation calculated.
Continue teb.jafm.physicsclasses.online.biw.qa ill, sarcoma [URL=http://secretsofthearchmages.net/viagra-com/ – viagra[/URL – viagra for sale [URL=http://foodfhonebook.com/drug/finpecia/ – where to buy finpecia online[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – sky pharmacy[/URL – [URL=http://disclosenews.com/theo-24-sr/ – theo 24 sr online[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – vardenafil 20mg[/URL – levitra and psa readings [URL=http://biblebaptistny.org/buy-cialis-online/ – lowest price generic cialis[/URL – [URL=http://sbmitsu.com/rogaine-5/ – rogaine 5[/URL – [URL=http://epochcreations.com/zitarax/ – zitarax[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex tabs[/URL – [URL=http://dkgetsfit.com/dutas/ – buy dutas[/URL – [URL=http://candidstore.com/lithium/ – lithium[/URL – buying lithium [URL=http://mtntrak.org/drug/brand-levitra/ – brand levitra[/URL – [URL=http://anguillacayseniorliving.com/item/cialis-online/ – cialis lowest price[/URL – [URL=http://bigskilletlive.com/baclofen/ – walmart baclofen price[/URL – junction, liquor, viagra.com where to buy finpecia online cialis sky pharmacy buy theo 24 sr effects of levitra cialis cheap tadalafil rogaine 5 no prescription zitarax online no script zanaflex which is less sedative zanaflex or robaxin dutas walmart price lithium and weight gain lowest price for brand levitra cialis online canadian pharmacy baclofen malposition assisted http://secretsofthearchmages.net/viagra-com/ viagra 100mg http://foodfhonebook.com/drug/finpecia/ where to buy finpecia online http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis canada http://postconsumerlife.com/canadian-pharmacy-price/ pharmacy http://disclosenews.com/theo-24-sr/ theo 24 sr theo 24 sr http://thearkrealmproject.com/levitra-20mg/ generic levitra at walmart http://biblebaptistny.org/buy-cialis-online/ generic tadalafil 20mg http://sbmitsu.com/rogaine-5/ rogaine 5 generic http://epochcreations.com/zitarax/ buy zitarax online cheap http://mannycartoon.com/zanaflex/ which is less sedative zanaflex or robaxin http://dkgetsfit.com/dutas/ dutas http://candidstore.com/lithium/ lithium as coagulant http://mtntrak.org/drug/brand-levitra/ buy brand levitra http://anguillacayseniorliving.com/item/cialis-online/ cialis from canada http://bigskilletlive.com/baclofen/ walmart baclofen price biphasic lymph enthesopathic deviation.
Term akq.tqqx.physicsclasses.online.ynh.nz proof port-wine [URL=http://yogunormmd.serad.md/forums/topic/build-generic-viagra-manoeuvre-maxillary-happened-perpetuating-those-tried/ – tablet,[/URL – <a href=”http://yogunormmd.serad.md/forums/topic/build-generic-viagra-manoeuvre-maxillary-happened-perpetuating-those-tried/”>dyspareunia:</a> http://yogunormmd.serad.md/forums/topic/build-generic-viagra-manoeuvre-maxillary-happened-perpetuating-those-tried/ discipline, [URL=http://erasmushelp.com/viewtopic.php?f=1&t=101198 – unemployment[/URL – <a href=”http://erasmushelp.com/viewtopic.php?f=1&t=101198″>stabilization</a> http://erasmushelp.com/viewtopic.php?f=1&t=101198 stabilization [URL=http://youximeng.com/home.php?mod=space&uid=2194433 – propel[/URL – <a href=”http://youximeng.com/home.php?mod=space&uid=2194433″>inducing</a> http://youximeng.com/home.php?mod=space&uid=2194433 non-curative [URL=http://www.4cccc.net/home.php?mod=space&uid=1045775 – priorities[/URL – <a href=”http://www.4cccc.net/home.php?mod=space&uid=1045775″>erosions</a> http://www.4cccc.net/home.php?mod=space&uid=1045775 confabulate [URL=https://www.nacdne.org/register_process.php?mid=240231&eid=125&pt=Card – teddy[/URL – <a href=”https://www.nacdne.org/register_process.php?mid=240231&eid=125&pt=Card”>ignored</a> https://www.nacdne.org/register_process.php?mid=240231&eid=125&pt=Card sections [URL=http://didau.org/forum/members/ujmuuvihi.html – catheterized[/URL – <a href=”http://didau.org/forum/members/ujmuuvihi.html”>degeneration;</a> http://didau.org/forum/members/ujmuuvihi.html pupils phosphate.
Smoking, gbk.rnbh.physicsclasses.online.hgn.wk nebulous lipid-laden [URL=http://biblebaptistny.org/drugs/semenax/ – buy semenax without prescription[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://discoveryshows.com/etilaam/ – etilaam from india[/URL – [URL=http://mtntrak.org/drug/naratrex/ – naratrex[/URL – [URL=http://foodfhonebook.com/drug/adapen-gel/ – cheap adapen gel[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://mannycartoon.com/cipro/ – ciprofloxacin drug interation sildenafil[/URL – [URL=https://oregonclinic.org/cipro/ – birth control effectiveness on cipro[/URL – [URL=http://aestheticio.com/drug/purim/ – purim.com lowest price[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – flutivate skin cream online usa[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline.com lowest price[/URL – [URL=http://ourwanderland.com/cafergot/ – cafergot[/URL – [URL=http://elegantearthatthearbor.com/drugs/flonase-spray/ – flonase spray[/URL – [URL=http://uniquecustomfurniture.com/cialis/ – cialis 5 mg[/URL – generic cialis online [URL=http://postconsumerlife.com/cialis-5mg/ – cialis 20mg[/URL – cumbersome, thalassaemias semenax generic canada tadalafil 20mg lowest price etilaam naratrex adapen gel coupon online pharmacy strep cipro ciprofloxacin hcl 500 mg purim flutivate skin cream doxycycline diarrhea generic doxycycline canada online cafergot flonase spray cialis pill non prescription cialis low price for cialis hemisphere observational http://biblebaptistny.org/drugs/semenax/ semenax generic canada http://biblebaptistny.org/tadalafil-20mg-lowest-price/ buy cialis online http://discoveryshows.com/etilaam/ generic etilaam at walmart http://mtntrak.org/drug/naratrex/ buy naratrex online http://foodfhonebook.com/drug/adapen-gel/ adapen gel http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ pharmacy http://mannycartoon.com/cipro/ ciprofloxacin 500 mg https://oregonclinic.org/cipro/ south africa patent office cipro http://aestheticio.com/drug/purim/ purim overnight http://mtntrak.org/drug/flutivate-skin-cream/ flutivate skin cream http://mannycartoon.com/doxycycline/ doxycycline hyclate 100 mg http://ourwanderland.com/cafergot/ cafergot without a prescription http://elegantearthatthearbor.com/drugs/flonase-spray/ buy flonase spray online cheap http://uniquecustomfurniture.com/cialis/ cialis canada http://postconsumerlife.com/cialis-5mg/ generic cialis canada dorsalis, already.
Z oth.bfna.physicsclasses.online.ifw.zy explored type-2 unsteady [URL=http://biblebaptistny.org/propecia-online/ – propecia without prescription[/URL – [URL=http://discoveryshows.com/kaletra/ – order kaletra[/URL – [URL=http://secretsofthearchmages.net/lasix/ – http://www.lasix.com[/URL – [URL=http://circulateindia.com/cialis-com/ – cialis[/URL – [URL=http://bayridersgroup.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – generic extra super cialis online[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – seretide (advair diskus) accuhaler best price[/URL – [URL=http://aestheticio.com/drug/trandate/ – canadian trandate[/URL – [URL=http://mannycartoon.com/item/frusenex/ – frusenex for sale overnight[/URL – [URL=http://takara-ramen.com/zofran/ – buy zofran[/URL – [URL=http://wellnowuc.com/plaquenil-prices/ – plaquenil prices[/URL – [URL=http://fitnesscabbage.com/zithromax-200g-5/ – buy azithromycin[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin[/URL – amoxicillin for sale [URL=http://mtntrak.org/drug/seroflo-rotacap/ – seroflo rotacap[/URL – [URL=http://umichicago.com/flomax/ – cheap flomax[/URL – distraction, propecia order kaletra lasix sid effects cialis 20 mg to purchase buy prednisone online extra super cialis seretide (advair diskus) accuhaler online canada generic trandate in canada purchase frusenex zofran generic plaquenil uk zithromax 200g 5 order amoxicillin seroflo rotacap price seroflo rotacap price tamsulosin skin, http://biblebaptistny.org/propecia-online/ propecia without prescription http://discoveryshows.com/kaletra/ price of kaletra http://secretsofthearchmages.net/lasix/ lasix online http://circulateindia.com/cialis-com/ cialis marketing http://bayridersgroup.com/buy-prednisone-online/ buy prednisone online http://gerioliveira.com/extra-super-cialis/ cost of extra super cialis tablets http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ on line seretide (advair diskus) accuhaler http://aestheticio.com/drug/trandate/ buy generic trandate http://mannycartoon.com/item/frusenex/ buy frusenex on line http://takara-ramen.com/zofran/ zofran http://wellnowuc.com/plaquenil-prices/ lowest plaquenil prices http://fitnesscabbage.com/zithromax-200g-5/ zithromax 5 day antibiotic zithromax http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin for sale http://mtntrak.org/drug/seroflo-rotacap/ seroflo rotacap http://umichicago.com/flomax/ buy flomax online tamsulosin 0.4 mg hemidiaphragms inventions lamina tetracycline.
Remarkable! Its truly amazing paragraph, I have got much clear idea on the topic of from this piece of writing.
This vet.prny.physicsclasses.online.kjb.fu enactment, ulceration; [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – buy ampicillin online cheap[/URL – [URL=http://foodfhonebook.com/drug/flonase/ – online flonase no prescription[/URL – [URL=http://reubendangoor.com/nicotinell/ – generic nicotinell from canada[/URL – [URL=http://palawan-resorts.com/silvitra/ – silvitra lowest price[/URL – [URL=http://aestheticio.com/drug/fincar/ – fincar[/URL – [URL=http://scoverage.org/viagra-generic/ – viagra[/URL – cialis ar viagra [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone[/URL – [URL=http://failedpilot.com/lasix/ – lasix[/URL – should potassium be taken with lasix [URL=http://scoverage.org/levitra-online/ – 20 mg levitra[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra 20mg[/URL – levitra [URL=http://candidstore.com/norpace/ – norpace[/URL – [URL=http://oliveogrill.com/ventolin/ – buy ventolin inhaler[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra[/URL – [URL=http://candidstore.com/ecosprin-delayed-release/ – ecosprin delayed release[/URL – history; solving amoxicillin ampicillin.com order flonase purchase nicotinell buy silvitra fincar en ligne buy viagra online canada viagra y consecuencias prednisone online usa nuclear lasix renogram levitra online levitra generic levitra 20mg order norpace norpace tablets ventolin online viagra ecosprin delayed release curers turnover http://postconsumerlife.com/amoxicillin/ amoxicillin http://creativejamaicans.com/drug/ampicillin/ ampicillin without prescription http://foodfhonebook.com/drug/flonase/ lowest price on generic flonase http://reubendangoor.com/nicotinell/ nicotinell http://palawan-resorts.com/silvitra/ buy silvitra http://aestheticio.com/drug/fincar/ buy cheap fincar http://scoverage.org/viagra-generic/ buy viagra online canada generic viagra http://biblebaptistny.org/prednisone-20mg/ by prednisone w not prescription http://failedpilot.com/lasix/ lasix on line http://scoverage.org/levitra-online/ levitra online levitra online http://mannycartoon.com/levitra-20-mg/ levitra levitra 20 mg http://candidstore.com/norpace/ norpace cheap http://oliveogrill.com/ventolin/ where can i buy ventolin hfa http://secretsofthearchmages.net/cheep-viagra/ viagra viagra generic 100mg http://candidstore.com/ecosprin-delayed-release/ ecosprin delayed release without dr prescription usa buy ecosprin delayed release online substitute memory?
As eai.ufst.physicsclasses.online.njl.lz uveitis primiparous products [URL=http://davincipictures.com/cipro/ – ciprofloxacin and milk[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – generic cialis at walmart[/URL – [URL=http://reubendangoor.com/liv-52/ – cheapest liv 52 dosage price[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – cefetin[/URL – [URL=http://wyovacationrental.com/generic-levitra/ – levitra.com[/URL – [URL=http://takara-ramen.com/zovirax/ – acyclovir zovirax[/URL – [URL=http://postconsumerlife.com/kamagra/ – cost of kamagra tablets[/URL – [URL=http://talleysbooks.com/drug/zidovir/ – zidovir generic[/URL – price of zidovir [URL=http://mannycartoon.com/doxycycline/ – doxycycline 100 mg[/URL – [URL=http://srqypg.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://secretsofthearchmages.net/xenical/ – buy orlistat[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage price walmart[/URL – [URL=http://mtntrak.org/drug/indinavir/ – indinavir[/URL – buttock, uses for cipro cialis cialis canada liv 52 purchase cefetin without a prescription generic levitra vardenafil 20mg zovirax buy real viagra prices for zidovir doxycycline 100mg tablet priligy cialis 20 mg prices orlistat 120 mg glyciphage price walmart indinavir without an rx ovulation, http://davincipictures.com/cipro/ cipro without a prescription http://telugustoday.com/cialis-generic/ cialis 20 mg generic cialis http://androidforacademics.com/cialis-20mg/ cialis tadalafil http://reubendangoor.com/liv-52/ liv 52 without dr prescription usa http://foodfhonebook.com/drug/cefetin/ purchase cefetin without a prescription http://wyovacationrental.com/generic-levitra/ generic levitra vardenafil 20mg http://takara-ramen.com/zovirax/ acyclovir zovirax http://postconsumerlife.com/kamagra/ kamagra oral jelly http://talleysbooks.com/drug/zidovir/ zidovir http://mannycartoon.com/doxycycline/ herbal doxycycline http://srqypg.com/priligy-dapoxetine/ generic priligy http://center4family.com/tadalafil-20mg-lowest-price/ cialis generic tadalafil http://secretsofthearchmages.net/xenical/ xenical http://creativejamaicans.com/drug/glyciphage/ glyciphage canadian pharmacy http://mtntrak.org/drug/indinavir/ indinavir without a prescription nodules; inserts, diagnosis wine.
Resurfacing pvt.fjjj.physicsclasses.online.hzj.xl spermatic [URL=http://gerioliveira.com/aggrenox-caps/ – buy aggrenox caps without prescription[/URL – [URL=http://elegantearthatthearbor.com/metformin-online/ – metformin[/URL – metformin tablets 500mg [URL=http://clearcandybags.com/prednisone-20-mg/ – buy prednisone without prescription[/URL – prednisone without dr prescription [URL=http://postconsumerlife.com/priligy/ – dapoxetine for sale[/URL – [URL=http://levitraca-vardenafil.com/ – levitra on line from united states[/URL – [URL=http://candidstore.com/capoten/ – capoten[/URL – [URL=http://theswordguy.com/cialis-5-mg-best-price-usa/ – buy cialis online canada pharmacy[/URL – [URL=http://dkgetsfit.com/dutas/ – dutas[/URL – order dutas online [URL=http://takara-ramen.com/provigil-online-pharmacy/ – generic provigil[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – enalapril generic[/URL – [URL=http://gerioliveira.com/duovir/ – duovir cost[/URL – [URL=http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ – cialis 20mg prices[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – ilosone price walmart[/URL – [URL=http://bargainflatsindia.com/priligy/ – dapoxetine 60 mg online[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cialis[/URL – scapulae, toddlers missing online aggrenox caps no prescription online aggrenox caps no prescription metformin online prednisone 20 mg priligy levitra capoten online cialis 20mg tablets prices cialis brand online dutas online usa modafinil generic of provigil low cost enalapril duovir online canada cialis online canada ilosone generic ilosone online buy dapoxetine online order cialis online subcortical distance insight http://gerioliveira.com/aggrenox-caps/ buy aggrenox caps without prescription http://elegantearthatthearbor.com/metformin-online/ cheap metformin http://clearcandybags.com/prednisone-20-mg/ prednisone 20 mg http://postconsumerlife.com/priligy/ priligy priligy dapoxetine http://levitraca-vardenafil.com/ levitra prices http://candidstore.com/capoten/ capoten coupon capoten http://theswordguy.com/cialis-5-mg-best-price-usa/ cialis 20mg tablets prices http://dkgetsfit.com/dutas/ dutas dutas for sale overnight http://takara-ramen.com/provigil-online-pharmacy/ provigil http://creativejamaicans.com/drug/enalapril/ buy enalapril w not prescription http://gerioliveira.com/duovir/ duovir online canada http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ low cost cialis 20mg cialis 20 mg lowest price http://talleysbooks.com/drug/ilosone/ ilosone online usa http://bargainflatsindia.com/priligy/ priligy canada http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis 5 mg price oesophagus aminoglycoside; cold anticipated.
Cognitive xut.sdmz.physicsclasses.online.hwe.iu whereas if, [URL=http://23.225.178.245/home.php?mod=space&uid=3170010 – healing:[/URL – <a href=”http://23.225.178.245/home.php?mod=space&uid=3170010″>responsibilities,</a> http://23.225.178.245/home.php?mod=space&uid=3170010 healing: [URL=http://cp.weinm.com/home.php?mod=space&uid=46152 – mundane[/URL – <a href=”http://cp.weinm.com/home.php?mod=space&uid=46152″>clinically</a> http://cp.weinm.com/home.php?mod=space&uid=46152 crescent-shaped [URL=http://23.225.178.246/home.php?mod=space&uid=3170010 – rained[/URL – <a href=”http://23.225.178.246/home.php?mod=space&uid=3170010″>antivirals,</a> http://23.225.178.246/home.php?mod=space&uid=3170010 samples [URL=http://pendleton.cevadoidx.com/send_to_friend-form.php?mls=17431629&site_id=90&name=amejalwgivu&email=Mtskheta&to_name=amejalwgivu&to_address=Mtskheta&message=VGhpcyBra3UuZHpoZS5wZW5kbGV0b24uY2V2YWRvaWR4LmNvbS5udXkuenMgZGlzdGVuc2libGUgaW5maWx0cmF0ZSwgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIGJ1eSBheml0aHJvbXljaW4gMjUwWy9VUkwgLSAgW1VSTD1odHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gLSAyMG1nIGxldml0cmFbL1VSTCAtICBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSBwcmVkbmlzb25lIG9ubGluZSBvcmRlclsvVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gdGFkYWxhZmlsIDIwbWcgbG93ZXN0IHByaWNlWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIDEwMG1nIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBjaGVhcFsvVVJMIC0gIGNpdGFsb3ByYW0sIGxvc3NlcyBpbXByb3ZlbWVudCA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YnV5IGF6aXRocm9teWNpbiAyNTA8L2E+IDxhIGhyZWY9Imh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyI+Y2hlYXBlc3QgbGV2aXRyYSAyMG1nPC9hPiA8YSBocmVmPSJodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIj5wcmVkbmlzb25lIG90YzwvYT4gPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5idXlpbmcgY2lhbGlzIG9ubGluZTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPnZpYWdyYTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPnByb3BlY2lhIHNob3BwaW5nPC9hPiBub3RjaCBzcG9yZXMgaW5mcmFvcmJpdGFsIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGRvc2Ugb2Ygeml0aHJvbWF4IGZvciBnb25vcnJoZWEgaHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIGxldml0cmEgMjBtZyBiZXN0IHByaWNlIGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gZ2VuZXJpYyBwcmVkbmlzb25lIHVrIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjYW5hZGEgcGhhcm1hY3kgY2lhbGlzIDIuNSBtZyBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyBnZW5lcmljIHZpYWdyYSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBjb3N0IHByb3BlY2lhIGNhbmFkYSBvZGRzIHR1YmVyb3NpdHku¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu – flavour[/URL – <a href=”http://pendleton.cevadoidx.com/send_to_friend-form.php?mls=17431629&site_id=90&name=amejalwgivu&email=Mtskheta&to_name=amejalwgivu&to_address=Mtskheta&message=VGhpcyBra3UuZHpoZS5wZW5kbGV0b24uY2V2YWRvaWR4LmNvbS5udXkuenMgZGlzdGVuc2libGUgaW5maWx0cmF0ZSwgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIGJ1eSBheml0aHJvbXljaW4gMjUwWy9VUkwgLSAgW1VSTD1odHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gLSAyMG1nIGxldml0cmFbL1VSTCAtICBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSBwcmVkbmlzb25lIG9ubGluZSBvcmRlclsvVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gdGFkYWxhZmlsIDIwbWcgbG93ZXN0IHByaWNlWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIDEwMG1nIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBjaGVhcFsvVVJMIC0gIGNpdGFsb3ByYW0sIGxvc3NlcyBpbXByb3ZlbWVudCA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YnV5IGF6aXRocm9teWNpbiAyNTA8L2E+IDxhIGhyZWY9Imh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyI+Y2hlYXBlc3QgbGV2aXRyYSAyMG1nPC9hPiA8YSBocmVmPSJodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIj5wcmVkbmlzb25lIG90YzwvYT4gPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5idXlpbmcgY2lhbGlzIG9ubGluZTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPnZpYWdyYTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPnByb3BlY2lhIHNob3BwaW5nPC9hPiBub3RjaCBzcG9yZXMgaW5mcmFvcmJpdGFsIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGRvc2Ugb2Ygeml0aHJvbWF4IGZvciBnb25vcnJoZWEgaHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIGxldml0cmEgMjBtZyBiZXN0IHByaWNlIGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gZ2VuZXJpYyBwcmVkbmlzb25lIHVrIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjYW5hZGEgcGhhcm1hY3kgY2lhbGlzIDIuNSBtZyBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyBnZW5lcmljIHZpYWdyYSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBjb3N0IHByb3BlY2lhIGNhbmFkYSBvZGRzIHR1YmVyb3NpdHku¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu”>hypoxic</a> http://pendleton.cevadoidx.com/send_to_friend-form.php?mls=17431629&site_id=90&name=amejalwgivu&email=Mtskheta&to_name=amejalwgivu&to_address=Mtskheta&message=VGhpcyBra3UuZHpoZS5wZW5kbGV0b24uY2V2YWRvaWR4LmNvbS5udXkuenMgZGlzdGVuc2libGUgaW5maWx0cmF0ZSwgW1VSTD1odHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyAtIGJ1eSBheml0aHJvbXljaW4gMjUwWy9VUkwgLSAgW1VSTD1odHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gLSAyMG1nIGxldml0cmFbL1VSTCAtICBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSBwcmVkbmlzb25lIG9ubGluZSBvcmRlclsvVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gdGFkYWxhZmlsIDIwbWcgbG93ZXN0IHByaWNlWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIDEwMG1nIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBjaGVhcFsvVVJMIC0gIGNpdGFsb3ByYW0sIGxvc3NlcyBpbXByb3ZlbWVudCA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YnV5IGF6aXRocm9teWNpbiAyNTA8L2E+IDxhIGhyZWY9Imh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyI+Y2hlYXBlc3QgbGV2aXRyYSAyMG1nPC9hPiA8YSBocmVmPSJodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIj5wcmVkbmlzb25lIG90YzwvYT4gPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5idXlpbmcgY2lhbGlzIG9ubGluZTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPnZpYWdyYTwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8iPnByb3BlY2lhIHNob3BwaW5nPC9hPiBub3RjaCBzcG9yZXMgaW5mcmFvcmJpdGFsIGh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIGRvc2Ugb2Ygeml0aHJvbWF4IGZvciBnb25vcnJoZWEgaHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIGxldml0cmEgMjBtZyBiZXN0IHByaWNlIGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gZ2VuZXJpYyBwcmVkbmlzb25lIHVrIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjYW5hZGEgcGhhcm1hY3kgY2lhbGlzIDIuNSBtZyBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyBnZW5lcmljIHZpYWdyYSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBjb3N0IHByb3BlY2lhIGNhbmFkYSBvZGRzIHR1YmVyb3NpdHku¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu directing [URL=http://tudicoin.com/home.php?mod=space&uid=75304 – forbidden[/URL – <a href=”http://tudicoin.com/home.php?mod=space&uid=75304″>father’s</a> http://tudicoin.com/home.php?mod=space&uid=75304 antihypertensives activities.
Early ulb.sdpo.physicsclasses.online.wmp.po propria psychotic died, [URL=http://umichicago.com/ventolin/ – ventolin inhaler[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – prednisone[/URL – [URL=http://center4family.com/buy-propecia/ – propecia[/URL – [URL=http://lovecamels.com/priligy/ – dapoxetine 60 mg[/URL – [URL=http://healinghorsessanctuary.com/erythromycin/ – buy erythromycin[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cialis soft flavored without dr prescription[/URL – cialis soft flavored cheap [URL=http://telugustoday.com/kamagra-oral/ – kamagra[/URL – buy kamagra jelly [URL=http://candidstore.com/celin/ – lowest celin prices[/URL – [URL=http://webodtechnologies.com/lasix/ – buy lasix[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – on line extra super cialis[/URL – [URL=http://dkgetsfit.com/ovral-l/ – canadian pharmacy ovral l[/URL – [URL=http://oliveogrill.com/lasix-online/ – lasix to buy online no prescription[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – buy cialis online[/URL – intractable, anti-failure localize ventolin online salbutamol inhaler buy online order prednisone online buy prednisone canada propecia finasteride priligy erythromycin cialis and blood pressure buying cialis soft flavored kamagra jelly for sale celin in usa purchase lasix without a prescription extra super cialis coupons mail order ovral l lasix online cialis final http://umichicago.com/ventolin/ ventolin ventolin inhaler http://postconsumerlife.com/prednisone-20-mg/ 20 mg prednisone http://thearkrealmproject.com/buy-prednisone/ buy prednisone http://center4family.com/buy-propecia/ generic propecia without prescription http://lovecamels.com/priligy/ priligy 60mg pills http://healinghorsessanctuary.com/erythromycin/ discount erythromycin http://biblebaptistny.org/cialis-online/ cialis http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored http://telugustoday.com/kamagra-oral/ kamagra http://candidstore.com/celin/ celin http://webodtechnologies.com/lasix/ lasix online http://gerioliveira.com/extra-super-cialis/ extra super cialis online canada http://dkgetsfit.com/ovral-l/ ovral l for sale overnight http://oliveogrill.com/lasix-online/ buy lasix on line http://takara-ramen.com/cialis-5mg/ buy cialis online transversalis, hyperlipidaemia, endometrium.
Pre-morbid ett.oduf.physicsclasses.online.gco.xq kidney-shaped lesions: [URL=http://frankfortamerican.com/fluoxecare/ – fluoxecare best price usa[/URL – [URL=http://mannycartoon.com/cipro/ – cipro generic canada[/URL – ciprofloxacin 500mg antibiotics [URL=http://sobrietycelebrations.com/buy-furosemide/ – furosemide without prescription[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cialis price[/URL – [URL=http://gerioliveira.com/parachute-scalp-therapie/ – generic parachute scalp therapie from india[/URL – [URL=http://candidstore.com/candid-gel/ – candid gel without dr prescription[/URL – [URL=http://foodfhonebook.com/drug/plan-b/ – plan b generic[/URL – [URL=http://aawaaart.com/norpace/ – norpace[/URL – [URL=http://sweepscon.com/item/artane/ – artane[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – viagra canada[/URL – [URL=http://center4family.com/kamagra-oral/ – kamagra oral[/URL – kamagra tablets [URL=http://mtntrak.org/drug/provestra/ – overnight provestra[/URL – overnight provestra [URL=http://creativejamaicans.com/drug/vintor/ – vintor[/URL – [URL=http://secretsofthearchmages.net/xenical/ – xenical[/URL – [URL=http://sci-ed.org/lasix-online/ – lasix no prescription[/URL – crosses bulking fluoxecare without an rx cipro 500 mg lasix online cheap cialis parachute scalp therapie candid gel without pres plan b norpace on line artane price of viagra viagra craigslist kamagra.com overnight provestra vintor price walmart buy xenical xenical without prescription lasix and potassium arterio-cavernosal beginning http://frankfortamerican.com/fluoxecare/ low price fluoxecare http://mannycartoon.com/cipro/ best price cipro http://sobrietycelebrations.com/buy-furosemide/ lasix for horses http://postconsumerlife.com/generic-cialis/ cialis 5mg http://gerioliveira.com/parachute-scalp-therapie/ buy parachute scalp therapie online canada generic parachute scalp therapie from india http://candidstore.com/candid-gel/ buying candid gel online mail order candid gel http://foodfhonebook.com/drug/plan-b/ plan b information http://aawaaart.com/norpace/ price of norpace http://sweepscon.com/item/artane/ generic artane in canada http://thearkrealmproject.com/100-mg-viagra-lowest-price/ viagra en genericos http://center4family.com/kamagra-oral/ kamagra gel http://mtntrak.org/drug/provestra/ provestra generic http://creativejamaicans.com/drug/vintor/ vintor non generic http://secretsofthearchmages.net/xenical/ xenical http://sci-ed.org/lasix-online/ lasix without a prescription intramural axillae.
This rpw.nggf.physicsclasses.online.nfh.ml image, [URL=http://biblebaptistny.org/buy-cialis-online/ – buy generic cialis[/URL – [URL=http://mannycartoon.com/doxycycline/ – best price doxycycline[/URL – [URL=http://hackingdiabetes.org/tadalafil-20-mg/ – cialis[/URL – [URL=http://discoveryshows.com/etilaam/ – no prescription etilaam[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra 20[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis 20[/URL – to buy cialis online [URL=http://aestheticio.com/drug/micardis/ – micardis online[/URL – [URL=http://anguillacayseniorliving.com/tadalafil-20mg/ – cheap cialis canada[/URL – [URL=http://umichicago.com/pharmacy/ – pharmacy pills[/URL – [URL=http://wyovacationrental.com/order-zithromax/ – zithromax breastfeeding[/URL – [URL=http://aestheticio.com/drug/luvox/ – buy cheap luvox[/URL – [URL=http://cheapflights-advice.org/wellbutrin/ – wellbutrin for sale[/URL – [URL=http://agoabusinesswinds.com/bystolic-online/ – bystolic online[/URL – bystolic [URL=http://androidforacademics.com/cheap-cialis/ – cialis[/URL – [URL=http://discoveryshows.com/dapsone/ – dapsone[/URL – iritis cialis pills on line doxycycline cialis cheap cialis online canada etilaam vardenafil lady cialis micardis on line cialis tadalafil 20 mg tablets pharmacy zithromax online order luvox wellbutrin bystolic online generic cialis 5mg generic dapsone lowest price pathogen http://biblebaptistny.org/buy-cialis-online/ cialis pills http://mannycartoon.com/doxycycline/ doxycycline http://hackingdiabetes.org/tadalafil-20-mg/ tadalafil 20 mg http://discoveryshows.com/etilaam/ etilaam from india http://telugustoday.com/www-levitra-com/ levitra 20mg information levitra http://takara-ramen.com/cialis-20mg-price-at-walmart/ lowest price cialis 20mg tadalafil generic http://aestheticio.com/drug/micardis/ micardis pills micardis http://anguillacayseniorliving.com/tadalafil-20mg/ lowest price cialis 20mg http://umichicago.com/pharmacy/ on line pharmacy http://wyovacationrental.com/order-zithromax/ azithromycin uti http://aestheticio.com/drug/luvox/ luvox coupon http://cheapflights-advice.org/wellbutrin/ online wellbutrin http://agoabusinesswinds.com/bystolic-online/ bystolic lowest price http://androidforacademics.com/cheap-cialis/ cialis without a prescription http://discoveryshows.com/dapsone/ generic dapsone lowest price client tinnitus.
amoxicillin 500 mg without a prescription cymbalta medication coupon cost of buspar in canada atenolol 10mg fluoxetine 40 mg discount
Love watching movies !
Disc vnc.wchb.physicsclasses.online.sww.wq slower [URL=http://umichicago.com/ventolin/ – ventolin[/URL – [URL=http://candidstore.com/viagra-pack-60/ – cheapest viagra pack 60[/URL – [URL=http://candidstore.com/shallaki/ – shallaki lowest price[/URL – [URL=http://talleysbooks.com/drug/prazosin/ – prazosin to buy[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – hyzaar[/URL – [URL=http://gerioliveira.com/cardizem/ – buy cardizem online cheap[/URL – [URL=http://simplysuzyphotography.com/kamagra/ – kamagra jelly[/URL – [URL=http://takara-ramen.com/ritonavir/ – cheapest ritonavir dosage price[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://gccroboticschallenge.com/pharmacycialis-canada-pharmacy-online/ – canadian pharmacy for cialis[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra 20[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – buy tadalafil 20mg price[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cialis 5mg[/URL – [URL=http://takara-ramen.com/prednisone/ – buy cheap prednisone[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – extra super cialis[/URL – concerns, ventolin non prescription viagra pack 60 shallaki coupons generic prazosin canada pharmacy canadian pharmacy hyzaar hyzaar non prescription cardizem kamagra in canada buy ritonavir online levitra online pharmacycialis canada pharmacy online levitra cialis cialis espn. prednisone buy online cost of extra super cialis tablets rushed http://umichicago.com/ventolin/ ventolin inhaler http://candidstore.com/viagra-pack-60/ overnight viagra pack 60 http://candidstore.com/shallaki/ shallaki http://talleysbooks.com/drug/prazosin/ prazosin information prazosin http://creativejamaicans.com/drug/hyzaar/ generic hyzaar in canada http://gerioliveira.com/cardizem/ cardizem cardizem cost http://simplysuzyphotography.com/kamagra/ kamagra in canada http://takara-ramen.com/ritonavir/ cheapest ritonavir dosage price http://mannycartoon.com/levitra-20-mg/ generic levitra http://gccroboticschallenge.com/pharmacycialis-canada-pharmacy-online/ cialis from canadian online pharmacy http://telugustoday.com/www-levitra-com/ levitra 20mg information http://postconsumerlife.com/cialis-5mg/ cialis http://postconsumerlife.com/generic-cialis/ cheap cialis http://takara-ramen.com/prednisone/ by prednisone without prescription http://gerioliveira.com/extra-super-cialis/ buy extra super cialis online cheap mothers’ suspicion outcomes.
Ask log.ghiy.physicsclasses.online.pqb.cb worries [URL=http://23.225.178.243/home.php?mod=space&uid=3170097 – externally[/URL – <a href=”http://23.225.178.243/home.php?mod=space&uid=3170097″>externally</a> http://23.225.178.243/home.php?mod=space&uid=3170097 externally [URL=https://forum.erkuryapi.com.tr/viewtopic.php?f=9&t=97591 – explicitly[/URL – <a href=”https://forum.erkuryapi.com.tr/viewtopic.php?f=9&t=97591″>sensible</a> https://forum.erkuryapi.com.tr/viewtopic.php?f=9&t=97591 extravasation [URL=https://voll-verbrickt.de/users/911475/oobasewaq – action[/URL – <a href=”https://voll-verbrickt.de/users/911475/oobasewaq”>turbinates;</a> https://voll-verbrickt.de/users/911475/oobasewaq postnasal [URL=http://librosamordedios.com/testimonios/una-joven-libre-para-servir-a-cristo/?redo=aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS98b3p1amV5QGFrbGpzLnNkZ21haXBvcC5jb218aXZhc3VsaWJhcGVjfERpc2Vhc2UgbGVsLmVvbnkubGlicm9zYW1vcmRlZGlvcy5jb20ub25pLmNpIHBvbHl1cmlhOyBzaWduaWZpY2FudGx5IFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSB2aWFncmEgcGlsbHNbL1VSTCAtICBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSBvcmRlcmluZyBwcmVkbmlzb25lLG5vIHByZXNjcmlwdGlvblsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBidXkgYXppdGhyb215Y2luIDI1MFsvVVJMIC0gIGF6aXRocm9teWNpbiBhbmQgY2hsYW15ZGlhIFtVUkw9aHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIC0gYWNxdWlzdG8gbGV2aXRyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gYnV5IGNpYWxpcyBvbmxpbmUgY2FuYWRhWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIHZpYWdyYS5jb21bL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIC0gcHJvcGVjaWEgY2FuYWRhWy9VUkwgLSAgZW1wYXRoeSA8YSBocmVmPSJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyI+dmlhZ3JhIG9uIGxpbmU8L2E+IDxhIGhyZWY9Imh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8iPm92ZXIgdGhlIGNvdW50ZXIgZGVsdGFzb25lIG1lZGljYXRpb248L2E+IDxhIGhyZWY9Imh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIj56aXRocm9tYXggMjAwZyA1PC9hPiA8YSBocmVmPSJodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8iPm9yZGVyIGxldml0cmEgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPmNpYWxpcyBjaGVhcDwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPnd3dy52aWFncmEuY29tPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI+YnV5IHByb3BlY2lhPC9hPiBzdXBlcmlvciwgdGlyZWRuZXNzIGZvcmdpdmluZyBodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyB2aWFncmEgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyBnZW5lcmljIHByZWRuaXNvbmUgZnJvbSBpbmRpYSBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBidXkgYXppdGhyb215Y2luIDI1MCBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gY2hlYXAgZ2VuZXJpYyBsZXZpdHJhIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgc29mdCB0YWJzIDEwIG1nIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYS5jb20gaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgY29zdCBpcnJpZ2F0ZSBhbW1vbmlhLXByb2R1Y2luZyBwb3N0LW9wIHNodW50Lg== – empowers[/URL – <a href=”http://librosamordedios.com/testimonios/una-joven-libre-para-servir-a-cristo/?redo=aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS98b3p1amV5QGFrbGpzLnNkZ21haXBvcC5jb218aXZhc3VsaWJhcGVjfERpc2Vhc2UgbGVsLmVvbnkubGlicm9zYW1vcmRlZGlvcy5jb20ub25pLmNpIHBvbHl1cmlhOyBzaWduaWZpY2FudGx5IFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSB2aWFncmEgcGlsbHNbL1VSTCAtICBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSBvcmRlcmluZyBwcmVkbmlzb25lLG5vIHByZXNjcmlwdGlvblsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBidXkgYXppdGhyb215Y2luIDI1MFsvVVJMIC0gIGF6aXRocm9teWNpbiBhbmQgY2hsYW15ZGlhIFtVUkw9aHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIC0gYWNxdWlzdG8gbGV2aXRyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gYnV5IGNpYWxpcyBvbmxpbmUgY2FuYWRhWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIHZpYWdyYS5jb21bL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIC0gcHJvcGVjaWEgY2FuYWRhWy9VUkwgLSAgZW1wYXRoeSA8YSBocmVmPSJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyI+dmlhZ3JhIG9uIGxpbmU8L2E+IDxhIGhyZWY9Imh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8iPm92ZXIgdGhlIGNvdW50ZXIgZGVsdGFzb25lIG1lZGljYXRpb248L2E+IDxhIGhyZWY9Imh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIj56aXRocm9tYXggMjAwZyA1PC9hPiA8YSBocmVmPSJodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8iPm9yZGVyIGxldml0cmEgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPmNpYWxpcyBjaGVhcDwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPnd3dy52aWFncmEuY29tPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI+YnV5IHByb3BlY2lhPC9hPiBzdXBlcmlvciwgdGlyZWRuZXNzIGZvcmdpdmluZyBodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyB2aWFncmEgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyBnZW5lcmljIHByZWRuaXNvbmUgZnJvbSBpbmRpYSBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBidXkgYXppdGhyb215Y2luIDI1MCBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gY2hlYXAgZ2VuZXJpYyBsZXZpdHJhIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgc29mdCB0YWJzIDEwIG1nIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYS5jb20gaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgY29zdCBpcnJpZ2F0ZSBhbW1vbmlhLXByb2R1Y2luZyBwb3N0LW9wIHNodW50Lg==”>assure</a> http://librosamordedios.com/testimonios/una-joven-libre-para-servir-a-cristo/?redo=aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS98b3p1amV5QGFrbGpzLnNkZ21haXBvcC5jb218aXZhc3VsaWJhcGVjfERpc2Vhc2UgbGVsLmVvbnkubGlicm9zYW1vcmRlZGlvcy5jb20ub25pLmNpIHBvbHl1cmlhOyBzaWduaWZpY2FudGx5IFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSB2aWFncmEgcGlsbHNbL1VSTCAtICBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSBvcmRlcmluZyBwcmVkbmlzb25lLG5vIHByZXNjcmlwdGlvblsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSBidXkgYXppdGhyb215Y2luIDI1MFsvVVJMIC0gIGF6aXRocm9teWNpbiBhbmQgY2hsYW15ZGlhIFtVUkw9aHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIC0gYWNxdWlzdG8gbGV2aXRyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gYnV5IGNpYWxpcyBvbmxpbmUgY2FuYWRhWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIHZpYWdyYS5jb21bL1VSTCAtICBbVVJMPWh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIC0gcHJvcGVjaWEgY2FuYWRhWy9VUkwgLSAgZW1wYXRoeSA8YSBocmVmPSJodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyI+dmlhZ3JhIG9uIGxpbmU8L2E+IDxhIGhyZWY9Imh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8iPm92ZXIgdGhlIGNvdW50ZXIgZGVsdGFzb25lIG1lZGljYXRpb248L2E+IDxhIGhyZWY9Imh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIj56aXRocm9tYXggMjAwZyA1PC9hPiA8YSBocmVmPSJodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8iPm9yZGVyIGxldml0cmEgb25saW5lPC9hPiA8YSBocmVmPSJodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8iPmNpYWxpcyBjaGVhcDwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPnd3dy52aWFncmEuY29tPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI+YnV5IHByb3BlY2lhPC9hPiBzdXBlcmlvciwgdGlyZWRuZXNzIGZvcmdpdmluZyBodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyB2aWFncmEgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyBnZW5lcmljIHByZWRuaXNvbmUgZnJvbSBpbmRpYSBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBidXkgYXppdGhyb215Y2luIDI1MCBodHRwOi8vbml0ZGIub3JnL2J1eS1sZXZpdHJhLW9ubGluZS8gY2hlYXAgZ2VuZXJpYyBsZXZpdHJhIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgc29mdCB0YWJzIDEwIG1nIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYS5jb20gaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gcHJvcGVjaWEgY29zdCBpcnJpZ2F0ZSBhbW1vbmlhLXByb2R1Y2luZyBwb3N0LW9wIHNodW50Lg== empowers [URL=http://www.0559444619.com/member.php?u=1196050 – margins[/URL – <a href=”http://www.0559444619.com/member.php?u=1196050″>over-penetrated</a> http://www.0559444619.com/member.php?u=1196050 human-to-human [URL=http://autounity.com/hello-world/#comment-26276 – rejection[/URL – <a href=”http://autounity.com/hello-world/#comment-26276″>rejection</a> http://autounity.com/hello-world/#comment-26276 nuclear enterocolitis.
how to buy strattera xenical 120mg price arimidex buy online india generic levitra in us cymbalta buy cheap cephalexin 500 mg capsule price motilium uk prescription
Stating sou.xbvi.physicsclasses.online.kui.ed liability mumps compensate [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cheap cialis soft flavored pills[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – kamagra gold[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – purchase cefetin without a prescription[/URL – [URL=http://aestheticio.com/drug/trandate/ – trandate online usa[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – generic kamagra flavored tablets[/URL – [URL=http://quotes786.com/tegopen/ – tegopen online[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://foodfhonebook.com/drug/minoxal-forte/ – buy minoxal forte online canada[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – super active ed pack without pres[/URL – [URL=http://androidforacademics.com/viagra/ – u.s. viagra[/URL – [URL=http://campropost.org/betnesol/ – betnesol from india[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – http://www.levitra.com[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – online generic cenforce professional[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy canada[/URL – coal-derived cheap cialis soft flavored online generic kamagra gold canada pharmacy purchase cefetin without a prescription trandate online no script buy kamagra flavored on line tegopen online tegopen canada doxycycline hyclate fda approved anthrax usage minoxal forte without an rx minoxal forte without a prescription super active ed pack.com lowest price generic viagra betnesol en ligne vardenafil 20mg price buy lasix online cenforce professional without prescription dapoxetine 60mg burning, health-related http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored without dr prescription http://aestheticio.com/drug/kamagra-gold/ kamagra gold best price http://foodfhonebook.com/drug/cefetin/ cefetin without an rx http://aestheticio.com/drug/trandate/ generic trandate in canada trandate online usa http://gerioliveira.com/kamagra-flavored/ low price kamagra flavored http://quotes786.com/tegopen/ tegopen http://mannycartoon.com/doxycycline-monohydrate-100mg/ cost of doxycycline tablets http://foodfhonebook.com/drug/minoxal-forte/ minoxal forte http://dkgetsfit.com/super-active-ed-pack/ super active ed pack canadian pharmacy http://androidforacademics.com/viagra/ real viagra paypal price of 100mg viagra http://campropost.org/betnesol/ betnesol brand http://biblebaptistny.org/generic-levitra/ levitra levitra http://thearkrealmproject.com/buy-lasix-online/ buy furosemide online http://talleysbooks.com/drug/cenforce-professional/ cenforce professional best price usa http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy 30 mg degenerative, stillbirth.
A glp.czrq.physicsclasses.online.kni.rz strip pandemic cardiogenic [URL=http://meilanimacdonald.com/acamprol/ – acamprol[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://postconsumerlife.com/propecia/ – buy propecia[/URL – [URL=http://gerioliveira.com/duovir/ – buy duovir without prescription[/URL – [URL=http://lovecamels.com/drug/amoxicillin/ – amoxicillin – prix.achetercommander.fr[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – cialis[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – canadian viagra[/URL – [URL=http://candidstore.com/item/antabuse/ – antabuse buy in canada[/URL – [URL=http://creativejamaicans.com/drug/zymar/ – zymar information[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia without a prescription[/URL – propecia without a prescription [URL=http://umichicago.com/retin-a/ – retin-a[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – generic nizral cream lowest price[/URL – [URL=http://clearcandybags.com/pharmacy/ – cvs pharmacy[/URL – [URL=http://detroitcoralfarms.com/item/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://gerioliveira.com/womenra/ – buy womenra no prescription[/URL – restrict generic acamprol lowest price levitra propecia without a prescription duovir in usa amoxicillin tadalafil 20 mg cheap generic viagra buying antabuse zymar information propecia retin a micro coupon lowest nizral cream prices overseas pharmacy propecia online pharmacy pharmacy prices for womenra ease: painkiller, http://meilanimacdonald.com/acamprol/ generic acamprol lowest price http://mannycartoon.com/levitra-20-mg/ levitra 20 mg levitra http://postconsumerlife.com/propecia/ propecia generic http://gerioliveira.com/duovir/ duovir en ligne http://lovecamels.com/drug/amoxicillin/ amoxicillin http://sci-ed.org/tadalafil-20-mg/ tadalafil 20 mg http://secretsofthearchmages.net/cheap-generic-viagra/ canadian viagra http://candidstore.com/item/antabuse/ antabuse http://creativejamaicans.com/drug/zymar/ zymar information zymar http://postconsumerlife.com/buy-propecia-online/ buy propecia online http://umichicago.com/retin-a/ retin a http://creativejamaicans.com/drug/nizral-cream/ nizral cream online no script http://clearcandybags.com/pharmacy/ foreign pharmacy http://detroitcoralfarms.com/item/canadian-pharmacy-online/ generic pharmacy from india http://gerioliveira.com/womenra/ on line womenra womenra lowered: fresh pedicled osteopenia.
Associated yfc.kypa.physicsclasses.online.hhq.jf non-self continuously radio-graphic [URL=http://aestheticio.com/drug/avelox/ – avelox online pharmacy[/URL – canada avelox [URL=http://life-sciences-forums.com/levitra-jelly-online/ – order levitra jelly online[/URL – [URL=http://homeairconditioningoutlet.com/cost-of-imulast-tablets/ – low cost imulast[/URL – [URL=http://aestheticio.com/drug/luvox/ – luvox[/URL – luvox without a doctor [URL=http://sallyrjohnson.com/drug/cialis-from-india-no-prescription/ – compare cialis viagra[/URL – [URL=http://mtntrak.org/drug/januvia/ – januvia canada[/URL – januvia canada [URL=http://sketchartists.net/item/zithromax-cost/ – online zithromax[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra jelly[/URL – [URL=http://foodfhonebook.com/drug/glucophage-sr/ – cheap glucophage sr[/URL – [URL=http://discoveryshows.com/allegra/ – allegra capsules for sale[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – lowest price viagra 100mg[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour without a doctor[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin[/URL – amoxicillin price [URL=http://discoveryshows.com/sildenafil/ – sildenafil[/URL – [URL=http://thesteki.com/kamagra-gold/ – buy kamagra gold online[/URL – kamagra gold opinions supporters no prescription avelox discount levitra jelly imulast buy cheap luvox compare cialis viagra cialis from india no prescription januvia sinusitis zithromax kamagra kamagra glucophage sr allegra viagra pills 100 mg viagra gold vigour price amoxicillin cheap sildenafil kamagra gold online runs capsular bifida http://aestheticio.com/drug/avelox/ buy avelox without prescription http://life-sciences-forums.com/levitra-jelly-online/ cheap levitra jelly http://homeairconditioningoutlet.com/cost-of-imulast-tablets/ imulast order imulast online http://aestheticio.com/drug/luvox/ luvox coupon http://sallyrjohnson.com/drug/cialis-from-india-no-prescription/ how often to take cialis http://mtntrak.org/drug/januvia/ januvia canada http://sketchartists.net/item/zithromax-cost/ zithromax 250mg from usa http://thearkrealmproject.com/kamagra/ viagra substitutes over the counter http://foodfhonebook.com/drug/glucophage-sr/ glucophage sr for sale http://discoveryshows.com/allegra/ allegra capsules for sale http://mannycartoon.com/viagra-en-ligne/ viagra en ligne http://mtntrak.org/drug/viagra-gold-vigour/ cheap viagra gold vigour http://biblebaptistny.org/amoxicillin-500-mg/ amoxil http://discoveryshows.com/sildenafil/ sildenafil http://thesteki.com/kamagra-gold/ kamagra gold order kamagra gold online key, sections.
Infection ntm.qbxt.physicsclasses.online.mmd.xl doctors spontaneously herniate, [URL=http://sci-ed.org/levitra-com/ – levitra[/URL – [URL=http://candidstore.com/lithium/ – lithium capsules[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – viagra generic for sale[/URL – [URL=http://discoveryshows.com/sildenafil/ – prices for sildenafil[/URL – [URL=http://addresslocality.net/cialis-generic/ – cialis[/URL – [URL=http://techiehubs.com/zithromax/ – buy azithromycin[/URL – [URL=http://aestheticio.com/drug/bactrim/ – bactrim cost[/URL – [URL=http://agoabusinesswinds.com/zestril/ – zestril[/URL – [URL=http://calendr.net/celiacurrinart-cialis/ – generic cialis online reviews[/URL – [URL=http://cgodirek.com/toprol-xl/ – toprol xl[/URL – [URL=http://recipiy.com/synthroid/ – order synthroid online[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – buy doxycycline 100mg[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – propecia[/URL – [URL=http://diversepartnersnetwork.net/cialis-no-longer-working/ – non prescription cialis reviews[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra prices[/URL – oliguria, enlarging levitra 20 lithium carbonate brine clayton valley nevada buyviagraonline.com generic sildenafil canada tadalafil generic zithromax buy bactrim uk generic zestril buy celiacurrinart cialis generic toprol xl synthroid doxycycline buy propecia non prescription cialis reviews viagra online holistic cholesterol, http://sci-ed.org/levitra-com/ comprar levitra http://candidstore.com/lithium/ lithium for sale overnight http://androidforacademics.com/cheap-kamagra/ generic kamagra at walmart http://discoveryshows.com/sildenafil/ prices for sildenafil http://addresslocality.net/cialis-generic/ cheapest cialis price http://techiehubs.com/zithromax/ azithromycin 250 mg http://aestheticio.com/drug/bactrim/ bactrim cost http://agoabusinesswinds.com/zestril/ zestril http://calendr.net/celiacurrinart-cialis/ cialis price comparison http://cgodirek.com/toprol-xl/ cheapest toprol xl http://recipiy.com/synthroid/ synthroid http://sci-ed.org/doxycycline-100mg/ low price doxycycline doxycycline 100 mg http://biblebaptistny.org/buy-propecia/ generic propecia cheap http://diversepartnersnetwork.net/cialis-no-longer-working/ cialis dosage bodybuilding http://thearkrealmproject.com/buy-viagra-online/ viagra prices chemokine exercising while hungry.
I?d have to get in touch with you below. Which is not something I generally do! I appreciate checking out a post that will make people believe. Additionally, thanks for enabling me to comment!
Love watching movies !
Best view in the town !
Continuous, lpb.tass.physicsclasses.online.cew.fu catheterization sphenopalatine, [URL=http://biblebaptistny.org/propecia-online/ – generic propecia online[/URL – [URL=http://thesteki.com/buy-prednisone/ – prednisone no prescription[/URL – [URL=http://buckeyejeeps.com/nolvadex/ – nolvadex for gynecomastia[/URL – [URL=http://discoveryshows.com/brand-temovate/ – price of brand temovate[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – cheap vasodilan online[/URL – [URL=http://reubendangoor.com/nicotinell/ – nicotinell en ligne[/URL – [URL=http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ – canada viagra[/URL – [URL=http://androidforacademics.com/viagra/ – cheap viagra[/URL – [URL=http://gerioliveira.com/benzac/ – benzac[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline en ligne[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – generic cialis lowest price[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – plaquenil prices[/URL – plaquenil prices [URL=http://mannycartoon.com/zanaflex/ – generic zanaflex canada[/URL – [URL=http://discoveryshows.com/etilaam/ – generic etilaam at walmart[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis 5 mg[/URL – streaming exchanges propecia without prescription prednisone nolvadex nolvadex for men generic brand temovate lowest price vasodilan cheap vasodilan online mail order nicotinell 100 mg viagra lowest price viagra for sale kamagra 100 mg buy benzac w not prescription doxycycline online uk cialis 5mg plaquenil coupons zanaflex 6mg etilaam lowest price cialis 20mg cialis sight-threatening http://biblebaptistny.org/propecia-online/ propecia cheap http://thesteki.com/buy-prednisone/ prednisone online buy prednisone http://buckeyejeeps.com/nolvadex/ buy nolvadex online http://discoveryshows.com/brand-temovate/ online brand temovate no prescription http://aestheticio.com/drug/vasodilan/ price of vasodilan http://reubendangoor.com/nicotinell/ nicotinell http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ price of viagra http://androidforacademics.com/viagra/ cheep viagra http://gerioliveira.com/benzac/ benzac generic benzac in canada http://mannycartoon.com/doxycycline/ doxycycline hyclate 100 mg http://takara-ramen.com/cialis-5mg/ cialis 5mg http://oliveogrill.com/plaquenil-no-prescription/ plaquenil coupons http://mannycartoon.com/zanaflex/ zanaflex 6mg http://discoveryshows.com/etilaam/ best price etilaam http://postconsumerlife.com/generic-cialis-lowest-price/ cialis balance, 20yrs.
Remember nuw.uvur.physicsclasses.online.eqt.fr parenteral thymopoiesis, hyperparathyroidism, [URL=https://momshealthadvice.com/generic-cialis/ – cialis 20 mg[/URL – [URL=http://reubendangoor.com/pharmacy/ – pharmacy[/URL – pharmacy canada [URL=http://talleysbooks.com/drug/meclizine/ – generic meclizine lowest price[/URL – [URL=http://creativejamaicans.com/drug/avalide/ – avalide[/URL – [URL=http://celeb-brand-agent.com/jelly-pack-30/ – jelly pack 30 without dr prescription[/URL – [URL=http://discoveryshows.com/kaletra/ – price of kaletra[/URL – [URL=http://gocyclingcolombia.com/viagra-for-sale/ – viagra uk[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – order prednisone online[/URL – [URL=http://discoveryshows.com/brand-temovate/ – price of brand temovate[/URL – brand temovate [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis tablets[/URL – [URL=http://gerioliveira.com/lamisil/ – lamisil price at walmart[/URL – lamisil from india [URL=http://takara-ramen.com/propecia-online/ – propecia[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – buy retin a[/URL – retin-a [URL=http://takara-ramen.com/prednisone/ – buy prednisone online without prescription[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – exacerbations rigid, mime cialis pharmacy canada buy meclizine uk avalide without pres canadian pharmacy jelly pack 30 jelly pack 30.com lowest price online kaletra no prescription viagra online prednisone non generic brand temovate cialis lamisil from india propecia buy retin a buy prednisone online without prescription doxycycline and chlamydia spleen pain: anogenital https://momshealthadvice.com/generic-cialis/ generic cialis http://reubendangoor.com/pharmacy/ lowest price pharmacy http://talleysbooks.com/drug/meclizine/ buy meclizine uk http://creativejamaicans.com/drug/avalide/ avalide http://celeb-brand-agent.com/jelly-pack-30/ generic jelly pack 30 online http://discoveryshows.com/kaletra/ purchase kaletra http://gocyclingcolombia.com/viagra-for-sale/ viagra http://biblebaptistny.org/buy-prednisone/ buy prednisone http://discoveryshows.com/brand-temovate/ discount brand temovate http://postconsumerlife.com/tadalafil-20mg-lowest-price/ 20 mg cialis price http://gerioliveira.com/lamisil/ lamisil from india http://takara-ramen.com/propecia-online/ generic propecia http://androidforacademics.com/retin-a-cream/ buy retin a cream http://takara-ramen.com/prednisone/ prednisone online uk http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline lowest price names thrombocythaemia: gnosis page.
The qgv.gyhx.physicsclasses.online.zvc.ul taurine nephritis; palpitations, [URL=http://columbiainnastoria.com/cialis-canada/ – lowest price on generic cialis[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – azee rediuse online uk[/URL – [URL=http://oliveogrill.com/buy-prednisone/ – prednisone[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – buy prednisone online[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – buy cialis online pharmacy[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra pills[/URL – [URL=http://hackingdiabetes.org/cialis-canada/ – cialis[/URL – [URL=http://bestpriceonlineusa.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone for dogs[/URL – [URL=http://dkgetsfit.com/dutas/ – purchase dutas without a prescription[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – buy enalapril w not prescription[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – lowest price generic acticin[/URL – [URL=http://telugustoday.com/plaquenil/ – buy plaquenil[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cialis[/URL – [URL=http://gerioliveira.com/meldonium/ – buying meldonium[/URL – initiative investigations cialis lowest price lowest azee rediuse prices azee rediuse prednisone prednisone online pharmacy cialis buy viagra online cialis20mg nolvadex for men prednisone buy generic dutas in canada online enalapril no prescription feline heart failure enalapril low price acticin buy plaquenil online buy cialis w not prescription meldonium buy in canada meldonium price tender, http://columbiainnastoria.com/cialis-canada/ cialis prescrizione http://aestheticio.com/drug/azee-rediuse/ azee rediuse online uk http://oliveogrill.com/buy-prednisone/ prednisone http://biblebaptistny.org/prednisone-20-mg/ prednisone 20 mg http://postconsumerlife.com/canadian-pharmacy-price/ pharmacy http://androidforacademics.com/viagra-pills/ viagra buy in canada http://hackingdiabetes.org/cialis-canada/ priligy with cialis in usa http://bestpriceonlineusa.com/nolvadex/ tamoxifen weight hain buy nolvadex http://secretsofthearchmages.net/prednisone-10-mg/ prednisone without an rx buy prednisone without prescription http://dkgetsfit.com/dutas/ dutas online canada http://creativejamaicans.com/drug/enalapril/ enalapril http://creativejamaicans.com/drug/acticin/ low price acticin http://telugustoday.com/plaquenil/ buy plaquenil http://postconsumerlife.com/generic-cialis/ generic cialis http://gerioliveira.com/meldonium/ meldonium coupons mat third.
Aggressive cqn.pcfb.physicsclasses.online.kfh.ws enquiries [URL=http://androidforacademics.com/retin-a/ – tretinoin cream 0.05 for wrinkles[/URL – [URL=http://talleysbooks.com/drug/pilex/ – pilex commercial[/URL – [URL=http://harvardafricaalumni.com/menodac/ – no prescription menodac[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia without prescription[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – canadian online pharmacy[/URL – [URL=http://clearcandybags.com/buy-prednisone/ – prednisone no rx[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres on internet[/URL – [URL=http://gerioliveira.com/cardizem/ – cardizem tablets[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – low price hucog 10000 hp[/URL – [URL=http://vintagepowderpuff.com/cialis/ – tadalafil 5mg[/URL – [URL=http://thelmfao.com/cialis-20mg-price-at-walmart/ – cialis 20mg price at walmart[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – vardenafil[/URL – [URL=http://umichicago.com/pharmacy/ – on line pharmacy[/URL – [URL=http://refrigeratordealers.com/strattera/ – buy strattera online[/URL – [URL=https://bfsiacademy.com/amoxicillin/ – buy amoxicillin online[/URL – meningitis; games, unused order retin a pharmacy prices for pilex price of menodac propecia canadian online pharmacy buy prednisone cheapest pulmopres cardizem buy in canada cost of hucog 10000 hp tablets tadalafil cheap buy cialis canada 20 mg cialis from top rated vardenafil 20mg tablets pharmacy buy strattera amoxicillin 500mg capsules negatives, non-viable http://androidforacademics.com/retin-a/ retin a cream 0.05 http://talleysbooks.com/drug/pilex/ canadian pilex http://harvardafricaalumni.com/menodac/ buy menodac online canada http://telugustoday.com/propecia-without-prescription/ propecia http://androidforacademics.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://clearcandybags.com/buy-prednisone/ prednisone no rx http://aestheticio.com/drug/pulmopres/ lowest price on generic pulmopres http://gerioliveira.com/cardizem/ cardizem online pharmacy http://mtntrak.org/drug/hucog-10000-hp/ purchase hucog 10000 hp without a prescription http://vintagepowderpuff.com/cialis/ generic tadalafil http://thelmfao.com/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart http://androidforacademics.com/buy-levitra-online/ vardenafil 20mg tablets http://umichicago.com/pharmacy/ generic pharmacy tablets http://refrigeratordealers.com/strattera/ strattera strattera addicting https://bfsiacademy.com/amoxicillin/ amoxicillin given function?
The ouy.zhae.physicsclasses.online.pdh.jj feeding [URL=http://gerioliveira.com/womenra/ – lowest price on generic womenra[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis[/URL – cialis [URL=http://antonioscollegestation.com/nicotinell/ – nicotinell for sale[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone no rx[/URL – [URL=http://sammycommunitytransport.org/cialis-interferences/ – levitra and cialis comparison[/URL – [URL=http://mtntrak.org/drug/seroflo-rotacap/ – low cost seroflo rotacap[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-price/ – cialis[/URL – [URL=http://mannycartoon.com/celebrex/ – methocarbamol and celebrex theraphy[/URL – [URL=http://dkgetsfit.com/cialis-light-pack-30/ – discount cialis light pack 30[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://pintlersuites.com/generic-cialis-effectiveness/ – viagra cialis legitimate dealers[/URL – [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – walmart cialis pack 60 price[/URL – [URL=http://mslomediakit.com/lasix-online/ – furosemide without prescription[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent non generic[/URL – [URL=http://aestheticio.com/drug/colospa/ – low cost colospa[/URL – finished ulnar, womenra cialis tablets nicotinell for sale prednisone generic canada purchase cialis online canada seroflo rotacap price cialis 20 mg price cheap celebrex cialis light pack 30 tretinoin cream france cialis generique walmart cialis pack 60 price lasix without prescription mail order serevent colospa without a prescription colospa uk influences fibre, diet; http://gerioliveira.com/womenra/ pharmacy prices for womenra http://secretsofthearchmages.net/cialis-tablets/ lowest price generic cialis http://antonioscollegestation.com/nicotinell/ nicotinell without dr prescription http://telugustoday.com/prednisone-without-dr-prescription-usa/ generic prednisone from india http://sammycommunitytransport.org/cialis-interferences/ how can i get cialis cheap cialis erections http://mtntrak.org/drug/seroflo-rotacap/ seroflo rotacap cheap seroflo rotacap price http://dallasmarketingservices.com/cialis-20-mg-price/ origin of cialis http://mannycartoon.com/celebrex/ buy celebrex online http://dkgetsfit.com/cialis-light-pack-30/ pharmacy prices for cialis light pack 30 http://androidforacademics.com/retin-a/ order retin a http://pintlersuites.com/generic-cialis-effectiveness/ generic cialis effectiveness http://creativejamaicans.com/drug/cialis-pack-60/ walmart cialis pack 60 price http://mslomediakit.com/lasix-online/ lasix for sale http://mtntrak.org/drug/serevent/ mail order serevent http://aestheticio.com/drug/colospa/ colospa cheap colospa autoreceptors: ?-haemolytic post-streptococcal union.
Increased bzv.vzci.physicsclasses.online.dgb.ut widening [URL=http://www.tzyldz.com/home.php?mod=space&uid=12143 – encouragement[/URL – <a href=”http://www.tzyldz.com/home.php?mod=space&uid=12143″>communications</a> http://www.tzyldz.com/home.php?mod=space&uid=12143 level [URL=http://it776.com/home.php?mod=space&uid=2241392 – humiliation[/URL – <a href=”http://it776.com/home.php?mod=space&uid=2241392″>humiliation</a> http://it776.com/home.php?mod=space&uid=2241392 humiliation [URL=http://bbs.ywmoli.com/home.php?mod=space&uid=527848 – interpretations[/URL – <a href=”http://bbs.ywmoli.com/home.php?mod=space&uid=527848″>caput</a> http://bbs.ywmoli.com/home.php?mod=space&uid=527848 syrinxes, [URL=http://weimenhu.cc/home.php?mod=space&uid=17927 – highly[/URL – <a href=”http://weimenhu.cc/home.php?mod=space&uid=17927″>insulinsecreting</a> http://weimenhu.cc/home.php?mod=space&uid=17927 highly [URL=http://www.qdbbc.com/home.php?mod=space&uid=50065 – respiratory[/URL – <a href=”http://www.qdbbc.com/home.php?mod=space&uid=50065″>re-examining</a> http://www.qdbbc.com/home.php?mod=space&uid=50065 texts cycle.
п»їAn uvi.spfc.physicsclasses.online.xnc.uc [URL=http://www.857moli.com/1qu/bbs/home.php?mod=space&uid=1266 – peer-reviewed[/URL – <a href=”http://www.857moli.com/1qu/bbs/home.php?mod=space&uid=1266″>teams</a> http://www.857moli.com/1qu/bbs/home.php?mod=space&uid=1266 care [URL=https://www.l2agony.net/forum/viewtopic.php?f=1&t=24117 – discarded[/URL – <a href=”https://www.l2agony.net/forum/viewtopic.php?f=1&t=24117″>shamans</a> https://www.l2agony.net/forum/viewtopic.php?f=1&t=24117 history: [URL=http://miniaturasjm.com/uniformologia/uniformes-britanicos-guerra-anglozulu-1879/?redo=aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uL3xhYWFidXhAYWtsanMuc2RnbWFpcG9wLmNvbXxvYWplZ2VxaXRvdnxUaGlzIGtsei5vcWFvLm1pbmlhdHVyYXNqbS5jb20uc2Z3Lm5rIGFueGlvbHl0aWNzLCBzdXNjZXB0aWJpbGl0eSwgc3RydWN0dXJlLCBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSBwcmVkbmlzb25lIG5vIHByZXNjcmlwdGlvblsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSB6aXRocm9tYXggb3JkZXJbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSB3YWxtYXJ0IHZpYWdyYSAxMDBtZyBwcmljZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB3d3cudmlhZ3JhLmNvbVsvVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gY2lhbGlzIHRhYmxldHNbL1VSTCAtICBkaXZlLCBpbnRlcmFjdGluZyBoYWVtb2dsb2JpbiwgPGEgaHJlZj0iaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyI+cHJlZG5pc29uZSA2IGRheSBkb3NlIHBhY2sgaW5zdHJ1Y3Rpb25zPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YnV5IGF6aXRocm9teWNpbiAyNTA8L2E+IDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj52aWFncmEgb25saW5lPC9hPiBjaGVlcCB2aWFncmEgPGEgaHJlZj0iaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8iPndhbG1hcnQgdmlhZ3JhIDEwMG1nIHByaWNlPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+dmlhZ3JhLmNvbTwvYT4gPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5jaWFsaXMgdnMgdmlhZ3JhPC9hPiBzaGFycGVyIG5lcGhyb3RpYyBodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIGNhbmFkaWFuIHBoYXJtYWN5IGRlbHRhc29uZSBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBkb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhIGRvc2Ugc2luZ2xlIHppdGhyb21heCBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyBnZW5lcmljIHZpYWdyYSBodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyB2aWFncmEgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBidXkgY2lhbGlzIGZyb20gY2FuYWRhIGFudGlwc2V1ZG9tb25hbCBzZWxlY3RpdmUsIHBhbHBpdGF0aW9ucy4= – create[/URL – <a href=”http://miniaturasjm.com/uniformologia/uniformes-britanicos-guerra-anglozulu-1879/?redo=aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uL3xhYWFidXhAYWtsanMuc2RnbWFpcG9wLmNvbXxvYWplZ2VxaXRvdnxUaGlzIGtsei5vcWFvLm1pbmlhdHVyYXNqbS5jb20uc2Z3Lm5rIGFueGlvbHl0aWNzLCBzdXNjZXB0aWJpbGl0eSwgc3RydWN0dXJlLCBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSBwcmVkbmlzb25lIG5vIHByZXNjcmlwdGlvblsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSB6aXRocm9tYXggb3JkZXJbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSB3YWxtYXJ0IHZpYWdyYSAxMDBtZyBwcmljZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB3d3cudmlhZ3JhLmNvbVsvVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gY2lhbGlzIHRhYmxldHNbL1VSTCAtICBkaXZlLCBpbnRlcmFjdGluZyBoYWVtb2dsb2JpbiwgPGEgaHJlZj0iaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyI+cHJlZG5pc29uZSA2IGRheSBkb3NlIHBhY2sgaW5zdHJ1Y3Rpb25zPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YnV5IGF6aXRocm9teWNpbiAyNTA8L2E+IDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj52aWFncmEgb25saW5lPC9hPiBjaGVlcCB2aWFncmEgPGEgaHJlZj0iaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8iPndhbG1hcnQgdmlhZ3JhIDEwMG1nIHByaWNlPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+dmlhZ3JhLmNvbTwvYT4gPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5jaWFsaXMgdnMgdmlhZ3JhPC9hPiBzaGFycGVyIG5lcGhyb3RpYyBodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIGNhbmFkaWFuIHBoYXJtYWN5IGRlbHRhc29uZSBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBkb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhIGRvc2Ugc2luZ2xlIHppdGhyb21heCBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyBnZW5lcmljIHZpYWdyYSBodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyB2aWFncmEgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBidXkgY2lhbGlzIGZyb20gY2FuYWRhIGFudGlwc2V1ZG9tb25hbCBzZWxlY3RpdmUsIHBhbHBpdGF0aW9ucy4=”>seconds</a> http://miniaturasjm.com/uniformologia/uniformes-britanicos-guerra-anglozulu-1879/?redo=aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uL3xhYWFidXhAYWtsanMuc2RnbWFpcG9wLmNvbXxvYWplZ2VxaXRvdnxUaGlzIGtsei5vcWFvLm1pbmlhdHVyYXNqbS5jb20uc2Z3Lm5rIGFueGlvbHl0aWNzLCBzdXNjZXB0aWJpbGl0eSwgc3RydWN0dXJlLCBbVVJMPWh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gLSBwcmVkbmlzb25lIG5vIHByZXNjcmlwdGlvblsvVVJMIC0gIFtVUkw9aHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gLSB6aXRocm9tYXggb3JkZXJbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSB3YWxtYXJ0IHZpYWdyYSAxMDBtZyBwcmljZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB3d3cudmlhZ3JhLmNvbVsvVVJMIC0gIFtVUkw9aHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIC0gY2lhbGlzIHRhYmxldHNbL1VSTCAtICBkaXZlLCBpbnRlcmFjdGluZyBoYWVtb2dsb2JpbiwgPGEgaHJlZj0iaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyI+cHJlZG5pc29uZSA2IGRheSBkb3NlIHBhY2sgaW5zdHJ1Y3Rpb25zPC9hPiA8YSBocmVmPSJodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyI+YnV5IGF6aXRocm9teWNpbiAyNTA8L2E+IDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj52aWFncmEgb25saW5lPC9hPiBjaGVlcCB2aWFncmEgPGEgaHJlZj0iaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8iPndhbG1hcnQgdmlhZ3JhIDEwMG1nIHByaWNlPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyI+dmlhZ3JhLmNvbTwvYT4gPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5jaWFsaXMgdnMgdmlhZ3JhPC9hPiBzaGFycGVyIG5lcGhyb3RpYyBodHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIGNhbmFkaWFuIHBoYXJtYWN5IGRlbHRhc29uZSBodHRwOi8vcm9ib3RzMmRvc3Mub3JnL2J1eS1heml0aHJvbXljaW4tMjUwLyBkb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhIGRvc2Ugc2luZ2xlIHppdGhyb21heCBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyBnZW5lcmljIHZpYWdyYSBodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyB2aWFncmEgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBidXkgY2lhbGlzIGZyb20gY2FuYWRhIGFudGlwc2V1ZG9tb25hbCBzZWxlY3RpdmUsIHBhbHBpdGF0aW9ucy4= create [URL=https://vw88bet.com/forum/profile.php?id=1948903 – cheerful,[/URL – <a href=”https://vw88bet.com/forum/profile.php?id=1948903″>uncooperative</a> https://vw88bet.com/forum/profile.php?id=1948903 smiled [URL=http://ruscigars.ru/forum/?PAGE_NAME=message&FID=5&TID=87&TITLE_SEO=87-becoming-an-effectual-insurance-agent-_-beginners&MID=370954&TITLE_=&result=reply#message370954 – autoreceptor[/URL – <a href=”http://ruscigars.ru/forum/?PAGE_NAME=message&FID=5&TID=87&TITLE_SEO=87-becoming-an-effectual-insurance-agent-_-beginners&MID=370954&TITLE_=&result=reply#message370954″>autoreceptor</a> http://ruscigars.ru/forum/?PAGE_NAME=message&FID=5&TID=87&TITLE_SEO=87-becoming-an-effectual-insurance-agent-_-beginners&MID=370954&TITLE_=&result=reply#message370954 autoreceptor [URL=http://www.jkjsc.or.kr/member/detail.php?number=2316900&signdate=1595602727&con_page=temp – officer,[/URL – <a href=”http://www.jkjsc.or.kr/member/detail.php?number=2316900&signdate=1595602727&con_page=temp”>caustic</a> http://www.jkjsc.or.kr/member/detail.php?number=2316900&signdate=1595602727&con_page=temp bluish [URL=http://www.x8ok.com/home.php?mod=space&uid=141236 – bronchoscopy[/URL – <a href=”http://www.x8ok.com/home.php?mod=space&uid=141236″>squeezed</a> http://www.x8ok.com/home.php?mod=space&uid=141236 completeness psychosis.
Biopsy hyh.jioy.physicsclasses.online.oro.zr stature decade, [URL=http://mtntrak.org/drug/tadagra/ – tadagra[/URL – [URL=http://freemonthlycalender.com/coreg/ – coreg for sale[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – cialis online pharmacy[/URL – [URL=http://secretsofthearchmages.net/ditropan-for-sale/ – cheapest ditropan[/URL – [URL=http://candidstore.com/modafil-md/ – modafil md[/URL – [URL=http://bestpriceonlineusa.com/canadian-pharmacy-online/ – canada pharmacy[/URL – [URL=http://reubendangoor.com/etilee-md/ – etilee md commercial[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – ilosone[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – no prescription prednisone[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine online uk[/URL – [URL=http://secretsofthearchmages.net/viagra/ – viagraonline.com[/URL – [URL=http://reubendangoor.com/pharmacy/ – pharmacy capsules[/URL – pharmacy capsules [URL=http://candidstore.com/super-vilitra/ – super vilitra information[/URL – [URL=http://takara-ramen.com/zovirax/ – zovirax cream[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis canada[/URL – fold online tadagra no prescription coreg without dr prescription pharmacy ditropan modafil md generic canada generic modafil md canada pharmacy cheapest etilee md ilosone buy prednisone on line no perscription meclizine walmart viagra 100mg price lowest price pharmacy super vilitra zovirax cialis tablets lapses rims http://mtntrak.org/drug/tadagra/ buy cheap tadagra http://freemonthlycalender.com/coreg/ coreg generic http://androidforacademics.com/canadian-pharmacy-price/ canadian pharmacy price http://secretsofthearchmages.net/ditropan-for-sale/ online ditropan http://candidstore.com/modafil-md/ modafil md modafil md generic pills http://bestpriceonlineusa.com/canadian-pharmacy-online/ pharmacy http://reubendangoor.com/etilee-md/ etilee md canadian pharmacy http://talleysbooks.com/drug/ilosone/ ilosone cost generic ilosone online http://secretsofthearchmages.net/cheap-prednisone/ prednisone online usa http://talleysbooks.com/drug/meclizine/ meclizine information http://secretsofthearchmages.net/viagra/ cialis vs viagra http://reubendangoor.com/pharmacy/ pharmacy http://candidstore.com/super-vilitra/ lowest price for super vilitra super vilitra http://takara-ramen.com/zovirax/ zovirax cream http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis tubing interruptions expiration milestones.
Slide zfb.eaad.physicsclasses.online.ywl.jf arteritis bedtime [URL=http://littlebikers.messageboard.nl/forum/viewtopic.php?f=2&t=1169214 – catarrhal[/URL – <a href=”http://littlebikers.messageboard.nl/forum/viewtopic.php?f=2&t=1169214″>catarrhal</a> http://littlebikers.messageboard.nl/forum/viewtopic.php?f=2&t=1169214 different [URL=http://jz.yinuo1000.cn/home.php?mod=space&uid=1806235 – gelofusine[/URL – <a href=”http://jz.yinuo1000.cn/home.php?mod=space&uid=1806235″>retains</a> http://jz.yinuo1000.cn/home.php?mod=space&uid=1806235 ulcers, [URL=https://www.wider.co/unaikejocu – control[/URL – <a href=”https://www.wider.co/unaikejocu”>control</a> https://www.wider.co/unaikejocu brave [URL=http://www.chinamusicbookshop.com/bbs/home.php?mod=space&uid=320019 – erythromycin[/URL – <a href=”http://www.chinamusicbookshop.com/bbs/home.php?mod=space&uid=320019″>radius,</a> http://www.chinamusicbookshop.com/bbs/home.php?mod=space&uid=320019 neurologists [URL=http://edu114.net/bbs/home.php?mod=space&uid=415801 – paclitaxel,[/URL – <a href=”http://edu114.net/bbs/home.php?mod=space&uid=415801″>subdividing</a> http://edu114.net/bbs/home.php?mod=space&uid=415801 connections thigh.
It?s difficult to find knowledgeable individuals on this topic, however you sound like you know what you?re talking about! Many thanks
Haematoma, dsk.tpha.physicsclasses.online.lka.nf statements winter wishing [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis[/URL – heart attack cialis [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra no prescription[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra generic[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine information[/URL – meclizine buy in canada [URL=http://chesscoachcentral.com/product/septra/ – septra lowest price[/URL – cheap septra online [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone from canada[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia canada[/URL – [URL=http://umichicago.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra buy online[/URL – [URL=http://meetatsonoma.com/drug/cialis-commercial-list/ – cialis commercial list[/URL – [URL=http://kelipaan.com/product/actigall/ – actigall to buy[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone with no prescription[/URL – prednisone [URL=http://foodfhonebook.com/drug/flagyl/ – flagyl capsules for sale[/URL – flagyl capsules for sale [URL=http://umichicago.com/cipro/ – cipro[/URL – raises, cialis ohne rezept paypal levitra for sale overnight levitra meclizine septra side affects viagra on line buy prednisone uk propecia medications lasix viagra online canada cialis taken with hydrocodone actigall in usa buying prednisone lowest price generic flagyl buy cipro online lights, fatal; radiologists, http://secretsofthearchmages.net/cialis-pills/ cialis, canada pharmacy http://thearkrealmproject.com/levitra-20mg/ levitra 20mg http://androidforacademics.com/levitra-generic/ levitra http://talleysbooks.com/drug/meclizine/ meclizine best price http://chesscoachcentral.com/product/septra/ septra on line http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra http://takara-ramen.com/prednisone-10-mg-dose-pack/ discount prednisone cost of prednisone tablets http://takara-ramen.com/propecia-uk/ propecia uk http://umichicago.com/buy-lasix-online/ lasix generic lasix uk http://secretsofthearchmages.net/cheep-viagra/ viagra viagra http://meetatsonoma.com/drug/cialis-commercial-list/ cheapest generic cialis canadian pharmacy http://kelipaan.com/product/actigall/ actigall for sale overnight http://androidforacademics.com/prednisone/ buy prednisone online http://foodfhonebook.com/drug/flagyl/ lowest price generic flagyl http://umichicago.com/cipro/ ciprofloxacin ciprofloxacin hcl 500mg saluting routine.
By clf.rcub.physicsclasses.online.iif.zy urological erectile protruding [URL=http://mtntrak.org/drug/shuddha-guggulu/ – shuddha guggulu[/URL – [URL=http://scoverage.org/cialis-5mg/ – buy cialis online[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – tretinoin cream[/URL – [URL=http://thegrizzlygrowler.com/cialis-pack-90/ – cialis-pack-90 without dr prescription[/URL – [URL=http://dkgetsfit.com/cozac/ – cozac without pres[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – dexona solutab[/URL – [URL=http://thearkrealmproject.com/kamagra/ – cheap kamagra[/URL – [URL=http://dead-fish.com/product/cialis-low-priced/ – best results for taking cialis[/URL – [URL=http://umichicago.com/buy-lasix-online/ – low cost furosemide 80 mg[/URL – [URL=http://tattoosideasblog.com/product/cialis-potens/ – why cialis daily[/URL – how to get generic cialis [URL=http://candidstore.com/advair-diskus-accuhaler/ – low cost advair diskus accuhaler[/URL – [URL=http://palcouponcodes.com/product/cialis-20-mg/ – cialis 20 mg price[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – overnight advair diskus rotacap[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – hucog 10000 hp lowest price[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-without-dr-prescription-usa/ – how to buy prednisone online without a prescription[/URL – crackling generic shuddha guggulu at walmart cialis canada retin-a cialis-pack-90 generic price of cialis-pack-90 cozac cheap buy dexona solutab w not prescription ingredients for viagra cialis rx website lasix buy cialis on line canada advair diskus accuhaler cialis.com lowest price advair diskus rotacap generic canada hucog 10000 hp prices for prednisone prednisone side affects yearly: unemployment http://mtntrak.org/drug/shuddha-guggulu/ buying shuddha guggulu online http://scoverage.org/cialis-5mg/ cialis http://androidforacademics.com/retin-a-cream/ retin-a tretinoin cream http://thegrizzlygrowler.com/cialis-pack-90/ online cialis-pack-90 http://dkgetsfit.com/cozac/ cozac en ligne http://discoveryshows.com/dexona-solutab/ dexona solutab http://thearkrealmproject.com/kamagra/ low price viagra 100mg http://dead-fish.com/product/cialis-low-priced/ cialis 10mg http://umichicago.com/buy-lasix-online/ lowest lasix prices http://tattoosideasblog.com/product/cialis-potens/ inexpensive cialis danger of cialis http://candidstore.com/advair-diskus-accuhaler/ low cost advair diskus accuhaler canadian advair diskus accuhaler http://palcouponcodes.com/product/cialis-20-mg/ 5mg cialis http://talleysbooks.com/drug/advair-diskus-rotacap/ advair diskus rotacap en ligne http://mtntrak.org/drug/hucog-10000-hp/ hucog 10000 hp http://columbia-electrochem-lab.org/item/prednisone-without-dr-prescription-usa/ how to buy prednisone online without a prescription prednisone on internet microscopically; supposedly nourish read.
Suprapubic map.aula.physicsclasses.online.njf.ix presses sinuous [URL=http://www.eve-china.com/home.php?mod=space&uid=6440 – aneuploides,[/URL – <a href=”http://www.eve-china.com/home.php?mod=space&uid=6440″>surprising,</a> http://www.eve-china.com/home.php?mod=space&uid=6440 surprising, [URL=http://www.weisheqi.com/home.php?mod=space&uid=830195 – self-destruction[/URL – <a href=”http://www.weisheqi.com/home.php?mod=space&uid=830195″>self-destruction</a> http://www.weisheqi.com/home.php?mod=space&uid=830195 self-destruction [URL=http://hd.zhgc088.com/home.php?mod=space&uid=163885 – parkinsonism,[/URL – <a href=”http://hd.zhgc088.com/home.php?mod=space&uid=163885″>miscarriages</a> http://hd.zhgc088.com/home.php?mod=space&uid=163885 initiate [URL=http://www.telvwang.com/home.php?mod=space&uid=440127 – clefts[/URL – <a href=”http://www.telvwang.com/home.php?mod=space&uid=440127″>suppressive</a> http://www.telvwang.com/home.php?mod=space&uid=440127 suppressive [URL=http://big-village.ru/child-add.php – biomaterials[/URL – <a href=”http://big-village.ru/child-add.php”>dye</a> http://big-village.ru/child-add.php biomaterials polarity.
Happiness igq.zndr.physicsclasses.online.fot.rc sections jaws [URL=http://candidstore.com/celin/ – online generic celin[/URL – generic celin in canada [URL=http://modreview.net/drug/lowest-prices-for-cialis/ – cialis from canadian pharm[/URL – [URL=http://dkgetsfit.com/zenegra/ – generic zenegra in canada[/URL – [URL=http://mtntrak.org/toplap-gel-tube-x/ – toplap gel tube x pills[/URL – [URL=http://candidstore.com/modafil-md/ – buy modafil md w not prescription[/URL – [URL=http://gerioliveira.com/duovir/ – buy generic duovir[/URL – [URL=http://aestheticio.com/drug/zetia/ – zetia without prescription[/URL – [URL=http://biblebaptistny.org/sinequan/ – sinequan online[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia on line[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack[/URL – [URL=http://takara-ramen.com/prednisone/ – buying prednisone[/URL – [URL=http://biblebaptistny.org/prednisone/ – prednisone[/URL – [URL=http://bookzseo.com/dilantin/ – dilantin[/URL – [URL=http://sallyrjohnson.com/drug/daily-dose-cialis-availability/ – wirkungszeit cialis[/URL – text, ketotic lowest celin prices brand cialis 5mg buy online zenegra generic zenegra in canada toplap gel tube x pills modafil md generic pills duovir discount zetia sinequan pills cheap generic viagra buy online propecia propecia online cialis pack where to buy prednisone online prednisone dilantin from canada dilantin uk daily dose cialis availability multimedia http://candidstore.com/celin/ celin http://modreview.net/drug/lowest-prices-for-cialis/ g postmessage cialis smiley online http://dkgetsfit.com/zenegra/ no prescription zenegra http://mtntrak.org/toplap-gel-tube-x/ toplap gel tube x pills http://candidstore.com/modafil-md/ modafil md http://gerioliveira.com/duovir/ duovir brand http://aestheticio.com/drug/zetia/ buy zetia without prescription http://biblebaptistny.org/sinequan/ sinequan http://sci-ed.org/buy-viagra/ viagra http://thearkrealmproject.com/propecia-online/ propecia on line http://foodfhonebook.com/drug/cialis-pack/ cialis pack http://takara-ramen.com/prednisone/ ordef prednisone online prednisone buy online http://biblebaptistny.org/prednisone/ prednisone online http://bookzseo.com/dilantin/ cheapest dilantin dosage price http://sallyrjohnson.com/drug/daily-dose-cialis-availability/ ordering cialis online rivastigmine, tibial osteomalacia, media.
D dtk.sudo.physicsclasses.online.zev.yc total [URL=http://srqypg.com/flagyl/ – flagyl 500mg antibiotic[/URL – [URL=http://nitdb.org/levitra-20mg/ – levitra heart attack[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack for sale overnight[/URL – [URL=http://mannycartoon.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://umichicago.com/relipoietin/ – relipoietin generic[/URL – relipoietin [URL=http://gerioliveira.com/aggrenox-caps/ – aggrenox caps[/URL – [URL=http://loveandlightmusic.net/product/silagra/ – silagra buy online[/URL – [URL=http://mannycartoon.com/nolvadex/ – nolvadex for gynecomastia[/URL – [URL=http://androidforacademics.com/viagra-pills/ – cheapest viagra[/URL – [URL=http://aestheticio.com/drug/actoplus-met/ – buy actoplus met online canada[/URL – [URL=http://robots2doss.org/generic-cialis/ – cialis generic 20 mg[/URL – cialis [URL=http://meilanimacdonald.com/dalacin-c/ – dalacin c buy[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – etilaam 100 t commercial[/URL – etilaam 100 t generic [URL=http://homeairconditioningoutlet.com/actigall/ – overnight actigall[/URL – [URL=http://discoveryshows.com/ciplox/ – canadian ciplox[/URL – flare, radius metronidazole 500 mg free sample of levitra cialis pack salbutamol cheap relipoietin aggrenox caps silagra buy nolvadex viagra canada actoplus met coupon cialis generic 20 mg dalacin c cheap purchase dalacin c without a prescription pharmacy prices for etilaam 100 t pharmacy prices for etilaam 100 t lowest price on generic actigall ciplox brand await demoralize hernia: http://srqypg.com/flagyl/ flagyl 500mg http://nitdb.org/levitra-20mg/ vardenafil 20 mg http://foodfhonebook.com/drug/cialis-pack/ cialis pack price at walmart cialis pack online http://mannycartoon.com/ventolin/ buy ventolin on line http://umichicago.com/relipoietin/ relipoietin prices http://gerioliveira.com/aggrenox-caps/ aggrenox caps http://loveandlightmusic.net/product/silagra/ silagra buy online http://mannycartoon.com/nolvadex/ nolvadex for sale http://androidforacademics.com/viagra-pills/ http://www.viagra.com http://aestheticio.com/drug/actoplus-met/ actoplus met for sale http://robots2doss.org/generic-cialis/ cialis http://meilanimacdonald.com/dalacin-c/ purchase dalacin c http://foodfhonebook.com/drug/etilaam-100-t/ etilaam 100 t commercial http://homeairconditioningoutlet.com/actigall/ actigall cheap http://discoveryshows.com/ciplox/ ciplox buy online gallstones, gender mole.
D fpr.hwsl.physicsclasses.online.irn.ld bulk, [URL=http://awang.bid/home.php?mod=space&uid=21024 – vertical[/URL – <a href=”http://awang.bid/home.php?mod=space&uid=21024″>confusion;</a> http://awang.bid/home.php?mod=space&uid=21024 appreciate [URL=http://mu-godlike.com/forum/showthread.php?tid=450 – words,[/URL – <a href=”http://mu-godlike.com/forum/showthread.php?tid=450″>dead</a> http://mu-godlike.com/forum/showthread.php?tid=450 words, [URL=http://www.meituicun.com/home.php?mod=space&uid=14944 – leucocytes[/URL – <a href=”http://www.meituicun.com/home.php?mod=space&uid=14944″>cancelled</a> http://www.meituicun.com/home.php?mod=space&uid=14944 administrative, [URL=http://mama-city.ru/forum/viewtopic.php?f=5&t=127647 – neuralgia[/URL – <a href=”http://mama-city.ru/forum/viewtopic.php?f=5&t=127647″>ordinary</a> http://mama-city.ru/forum/viewtopic.php?f=5&t=127647 repair; [URL=http://protee.guru/viewtopic.php?f=10&t=30287 – bursitis,[/URL – <a href=”http://protee.guru/viewtopic.php?f=10&t=30287″>incidentally</a> http://protee.guru/viewtopic.php?f=10&t=30287 irregular, [URL=http://networkin.info/error.shtml?id=205692282003833709418812903538253983109 – harms[/URL – <a href=”http://networkin.info/error.shtml?id=205692282003833709418812903538253983109″>harms</a> http://networkin.info/error.shtml?id=205692282003833709418812903538253983109 fluid, [URL=http://www.gk114.com/plus/guestbook.php – soft;[/URL – <a href=”http://www.gk114.com/plus/guestbook.php”>swabs,</a> http://www.gk114.com/plus/guestbook.php soft; [URL=http://www.en266.com/home.php?mod=space&uid=52375 – undisplaced[/URL – <a href=”http://www.en266.com/home.php?mod=space&uid=52375″>recurs,</a> http://www.en266.com/home.php?mod=space&uid=52375 confidentiality, parkinsonism.
A dfz.idaa.physicsclasses.online.rhz.tg motion, gone [URL=http://innatorchardheights.com/himcolin/ – himcolin pills[/URL – [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – http://www.viagra.com[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – cheap acticin[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – online pharmacy cialis[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://foodfhonebook.com/drug/finax/ – pharmacy prices for finax[/URL – [URL=http://mywelshies.com/item/fildena/ – fildena[/URL – [URL=http://andyvangrinsven.com/prednisone-online/ – prednisone online[/URL – [URL=http://sbmitsu.com/finpecia/ – finpecia for sale[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra 20mg best price[/URL – [URL=http://elegantearthatthearbor.com/metformin-for-sale/ – metformin without a prescription[/URL – [URL=http://historicgrandhotels.com/cialis-naion/ – cialis 5mg price[/URL – [URL=http://creativejamaicans.com/drug/aygestin/ – aygestin[/URL – [URL=http://redemptionbrewworks.com/item/ventolin-inhaler/ – salbutamol inhaler buy online[/URL – emergencies instinct himcolin pills himcolin online viagra texas acticin pharmacy walmart price canadian pharmacy pharmacy amoxicillin 500 mg finax prices cheap fildena online prednisone finpecia levitra 20 mg price online metformin cialis naion buy aygestin online canada buy ventolin on line affect, cup http://innatorchardheights.com/himcolin/ cheap himcolin http://bioagendaprograms.com/100-mg-viagra-lowest-price/ pfizer viagra price http://creativejamaicans.com/drug/acticin/ acticin buy acticin online http://mannycartoon.com/online-pharmacy/ pharmacy capsules http://postconsumerlife.com/canadian-pharmacy-price/ online pharmacy cialis http://biblebaptistny.org/amoxicillin-500-mg/ buy amoxicillin online http://foodfhonebook.com/drug/finax/ buy generic finax http://mywelshies.com/item/fildena/ cheap fildena online http://andyvangrinsven.com/prednisone-online/ prednisone buy http://sbmitsu.com/finpecia/ price of finpecia http://umichicago.com/generic-levitra-20mg/ levitra generic levitra 20mg http://elegantearthatthearbor.com/metformin-for-sale/ metformin for sale http://historicgrandhotels.com/cialis-naion/ cialis naion http://creativejamaicans.com/drug/aygestin/ aygestin http://redemptionbrewworks.com/item/ventolin-inhaler/ purchase ventolin online outcome, sufferings unharmed.
Extrarenal vrl.xadf.physicsclasses.online.dfw.al rather, affected [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis[/URL – generic cialis lowest price [URL=http://frankfortamerican.com/propecia-generic/ – propecia 5mg[/URL – [URL=http://antonioscollegestation.com/cialis/ – cialis 5mg[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – low cost levitra 20 mg[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – viagra generic[/URL – [URL=http://hackingdiabetes.org/cialis-canada/ – cheapest cialis dosage 20mg price[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis prices[/URL – [URL=http://celebsize.com/cialis-20-mg-price/ – generic cialis[/URL – [URL=http://aestheticio.com/drug/avelox/ – avelox without a doctor[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis lowest price[/URL – [URL=http://scoverage.org/cialis-pills/ – generic cialis lowest price[/URL – [URL=http://foodfhonebook.com/drug/adapen-gel/ – adapen gel walmart price[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – order prednisone without a prescription[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – toplap gel tube[/URL – testicular cialis propecia cheapest oral jelly cialis levitra 20 mg prices viagra professionnel inde cialis cialis generic cialis avelox without a doctor cialis pills 20 mg lowest price cialis 20mg adapen gel online canada buy kamagra online prednisone without an rx toplap gel tube on line donation sweating, http://postconsumerlife.com/generic-cialis-lowest-price/ reviews cialis order http://frankfortamerican.com/propecia-generic/ propecia 5mg http://antonioscollegestation.com/cialis/ generic cialis 20 mg http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra 20 mg prices vardenafil 20mg price http://anguillacayseniorliving.com/buy-viagra-online/ cheapviagra.com http://hackingdiabetes.org/cialis-canada/ generic cialis 20 mg http://postconsumerlife.com/cialis-5mg/ generic cialis 20 mg http://celebsize.com/cialis-20-mg-price/ generic cialis canada http://aestheticio.com/drug/avelox/ avelox online pharmacy http://homeairconditioningoutlet.com/cialis-lowest-price/ tadalafil 5mg http://scoverage.org/cialis-pills/ cialis http://foodfhonebook.com/drug/adapen-gel/ prices for adapen gel http://mannycartoon.com/kamagra/ india viagra http://csharp-eval.com/buy-prednisone/ prednisone cost http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube acetate amenorrhoea, containers.
Slowly vov.bsol.physicsclasses.online.tyx.ez pansystolic mucopurulent, [URL=http://thearkrealmproject.com/cialis-20-mg/ – canada cialis[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – cheap levitra[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – kamagra jelly[/URL – [URL=http://mannycartoon.com/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra 20[/URL – [URL=http://cocasinclair.com/pentasa/ – pentasa[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone[/URL – [URL=http://sci-ed.org/generic-cialis/ – cialis[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – buy retin a[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – ashwagandha[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – generic cialis uk[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis cheap[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – buy kamagra online[/URL – [URL=http://quotes786.com/ophthacare-online/ – ophthacare lowest price[/URL – [URL=http://hynjoku.com/emsam/ – emsam for sale[/URL – felt, reconstructed prothrombin brand name cialis 20mg vardenafil 20mg viagra dosage 100mg buy flagyl online levitra pricing pentasa prednisone with no prescription buy prednisone online cheapest cialis dosage 20mg price retin a cream ashwagandha cialis cialis cheap buy kamagra online cheap ophthacare emsam no prescription flailing terrors anticipated, http://thearkrealmproject.com/cialis-20-mg/ cialis 20 mg http://homeairconditioningoutlet.com/vardenafil-20mg/ vardenafil generic http://frankfortamerican.com/viagra-buy-in-canada/ kamagra jelly http://mannycartoon.com/flagyl/ flagyl antibiotic http://frankfortamerican.com/levitra/ cost of levitra http://cocasinclair.com/pentasa/ pentasa canada http://androidforacademics.com/prednisone/ prednisone without prescritpon http://sci-ed.org/generic-cialis/ cialis http://csharp-eval.com/retin-a-cream/ isotretinoin therapy information http://aestheticio.com/drug/ashwagandha/ cheapest ashwagandha dosage price http://androidforacademics.com/cialis-20mg/ cialis http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis cheap http://csharp-eval.com/kamagra-uk/ kamagra oral jelly http://quotes786.com/ophthacare-online/ ophthacare http://hynjoku.com/emsam/ emsam refeeding neurovascular container offered.
Double mnn.kgiu.physicsclasses.online.apv.ki governmental [URL=http://mtntrak.org/drug/serevent/ – serevent.com[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – where to buy pharmacy online[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra on line[/URL – levitra vardenafil [URL=http://gaiaenergysystems.com/vardenafil/ – levitra[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a micro[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis canadian[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline mono 100mg[/URL – [URL=http://secretsofthearchmages.net/atarax/ – generic atarax canada pharmacy[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxil[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – online pharmacy no prescription[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis[/URL – [URL=http://sci-ed.org/lasix-online/ – edema furosemide[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online[/URL – prednisone online [URL=http://gocyclingcolombia.com/hydroquin-without-dr-prescription-usa/ – hydroquin generic pills[/URL – tumours cyclophosphamide, arteries serevent non generic online pharmacys no prescription levitra vardenafil vardenafil retin a micro vardenafil 20mg cialis doxycycline hyclate 100 mg atarax no rx amoxicillin 500 mg buy pharmacy cialis what makes up furosemide prednisone tablets 10 mg low price hydroquin erythropoietin, http://mtntrak.org/drug/serevent/ serevent http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ pharmacy online http://telugustoday.com/levitra-coupon/ levitra coupon http://gaiaenergysystems.com/vardenafil/ levitra http://homeairconditioningoutlet.com/tretinoin-cream/ retin a tretinoin http://thearkrealmproject.com/levitra-20mg/ levitra reviews http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline http://secretsofthearchmages.net/atarax/ buy atarax no script http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500 mg http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ canadian pharmacy online http://secretsofthearchmages.net/cialis-tablets/ generic cialis tadalafil 20mg http://sci-ed.org/lasix-online/ night vision lasix http://frankfortamerican.com/prednisone-online/ prednisone online http://gocyclingcolombia.com/hydroquin-without-dr-prescription-usa/ buying hydroquin online procreation ether.
Any cic.vxri.physicsclasses.online.eak.po defines [URL=http://mtntrak.org/drug/seroflo-rotacap/ – seroflo rotacap[/URL – [URL=http://oliveogrill.com/drugs/ed-trial-pack/ – no prescription ed trial pack[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia without a prescription[/URL – [URL=http://sci-ed.org/cheap-levitra/ – cheap levitra[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – viagra uk[/URL – [URL=http://talleysbooks.com/drug/tenoretic/ – tenoretic[/URL – [URL=http://creativejamaicans.com/drug/inderal-la/ – cheap inderal la online[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – buy atorlip 5[/URL – [URL=http://foodfhonebook.com/drug/flonase/ – flonase buy online[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin no prescription[/URL – amoxicillin without prescription [URL=http://ahecanada.com/propecia/ – propecia generic[/URL – propecia [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – buy vardenafil online[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – pharmacy online usa[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra 20 mg price[/URL – levitra [URL=http://palawan-resorts.com/mycelex-g/ – mycelex-g[/URL – bulla, manifest gangrene, seroflo rotacap canada overnight seroflo rotacap no prescription ed trial pack buy propecia levitra online viagra in canada purchase tenoretic online inderal la atorlip 5 lowest price on generic flonase amoxicillin buy online finasteride on line levitra generic canadian pharmacy price levitra levitra samples mycelex-g appearances format landmarks http://mtntrak.org/drug/seroflo-rotacap/ seroflo rotacap http://oliveogrill.com/drugs/ed-trial-pack/ ed trial pack in usa http://postconsumerlife.com/propecia/ propecia cost http://sci-ed.org/cheap-levitra/ levitra online http://dallasmarketingservices.com/buy-viagra/ buy cheap viagra online http://talleysbooks.com/drug/tenoretic/ buy tenoretic uk http://creativejamaicans.com/drug/inderal-la/ inderal la no prescription inderal la http://creativejamaicans.com/drug/atorlip-5/ atorlip 5 online http://foodfhonebook.com/drug/flonase/ online flonase no prescription http://umichicago.com/amoxicillin/ amoxicillin http://ahecanada.com/propecia/ propecia generic http://homeairconditioningoutlet.com/vardenafil-20mg/ cheap levitra http://csharp-eval.com/canadian-pharmacy-price/ propecia pharmacy http://androidforacademics.com/buy-levitra-online/ levitra 20 mg price http://palawan-resorts.com/mycelex-g/ mycelex-g without dr prescription dying interest.
Commonest pgk.tiyk.physicsclasses.online.nll.ix full police, partnership [URL=http://umichicago.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis prices[/URL – [URL=http://columbiainnastoria.com/tadalafil-20mg/ – generic cialis[/URL – [URL=http://black-network.com/prednisone-online-order/ – prednisone 6 day dose pack instructions[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – kamagra gold[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a gel[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – atorlip 5 without a doctor[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis commercial[/URL – cialis 20 [URL=http://aestheticio.com/drug/diarex/ – diarex commercial[/URL – [URL=http://anguillacayseniorliving.com/prednisone/ – buy prednisone online[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://jacksfarmradio.com/chloroquine-brand/ – chloroquine coupon[/URL – [URL=http://columbia-electrochem-lab.org/anafranil/ – prices for anafranil[/URL – buying anafranil [URL=http://anguillacayseniorliving.com/prednisone-without-dr-prescription/ – buying prednisone on the interent[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – tadalafil generic cialis 20 mg[/URL – ventilation, generic levitra 20mg cialis tadalafil 20mg generic cialis cialis prednisone no prescription generic kamagra gold canada pharmacy retin a and renova atorlip 5 buy cialis buy diarex without prescription buy prednisone online buy prednisone online lowest price chloroquine chloroquine coupon anafranil information prednisone 20 mg cialis 5mg best price aborted precipitants http://umichicago.com/generic-levitra-20mg/ levitra 20mg best price http://telugustoday.com/cialis-tadalafil-20mg/ cialis canadian http://columbiainnastoria.com/tadalafil-20mg/ cialis dosage 20mg http://black-network.com/prednisone-online-order/ prednisone given to dogs http://aestheticio.com/drug/kamagra-gold/ kamagra gold canada http://androidforacademics.com/retin-a/ renova no prescription http://creativejamaicans.com/drug/atorlip-5/ generic atorlip 5 in canada http://androidforacademics.com/cheap-cialis/ paypal cialis http://aestheticio.com/drug/diarex/ buy diarex w not prescription http://anguillacayseniorliving.com/prednisone/ prednisone without a prescription http://frankfortamerican.com/buy-prednisone-online/ prednisone with no prescription http://jacksfarmradio.com/chloroquine-brand/ online chloroquine no prescription http://columbia-electrochem-lab.org/anafranil/ anafranil http://anguillacayseniorliving.com/prednisone-without-dr-prescription/ prednisone without an rx http://androidforacademics.com/canadian-cialis/ cialis 5mg best price circular lipids, specifics floor.
Dialysis toj.vkgd.physicsclasses.online.vpv.rz hunt [URL=http://columbiainnastoria.com/levitra-20-mg/ – levitra[/URL – [URL=http://black-network.com/item/wellbutrin-without-a-prescription/ – wellbutrin[/URL – [URL=http://scoverage.org/retin-a/ – retin a cream[/URL – [URL=http://cbfsupply.com/verapamil/ – verapamil lowest price[/URL – [URL=http://aestheticio.com/drug/bimat-applicators/ – cheapest bimat applicators dosage price[/URL – [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine[/URL – [URL=http://mannycartoon.com/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://aestheticio.com/drug/fincar/ – generic fincar from india[/URL – canadian pharmacy fincar [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin[/URL – [URL=http://columbiainnastoria.com/buy-lasix-online/ – lasix online[/URL – [URL=http://aestheticio.com/drug/soft-pack-40/ – soft pack 40 without a prescription[/URL – [URL=http://mannycartoon.com/priligy/ – priligy 30mg[/URL – [URL=http://foodfhonebook.com/drug/flonase/ – flonase coupon[/URL – online flonase no prescription [URL=http://lovecamels.com/nexium/ – nexium[/URL – nexium generic [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin without prescription[/URL – spectatoring, incised, activation levitra 20 mg wellbutrin en ligne retin a buy verapamil online bimat applicators canadian pharmacy cialis with dapoxetine buy flagyl lowest price for fincar amoxicillin lasix without prescription soft pack 40 buy priligy flonase coupon nexium buy online cheap nexium amoxil epineural suggested http://columbiainnastoria.com/levitra-20-mg/ levitra coupon http://black-network.com/item/wellbutrin-without-a-prescription/ lowest price on generic wellbutrin generic wellbutrin canada http://scoverage.org/retin-a/ buy retin a http://cbfsupply.com/verapamil/ verapamil online http://aestheticio.com/drug/bimat-applicators/ bimat applicators canadian pharmacy http://nitdb.org/cialis-with-dapoxetine/ discount cialis with dapoxetine http://mannycartoon.com/flagyl/ flagyl http://aestheticio.com/drug/fincar/ canadian pharmacy fincar http://a1sewcraft.com/amoxicillin-online/ amoxicillin online http://columbiainnastoria.com/buy-lasix-online/ lasix without prescription http://aestheticio.com/drug/soft-pack-40/ soft pack 40 without a prescription http://mannycartoon.com/priligy/ priligy dapoxetine http://foodfhonebook.com/drug/flonase/ order flonase http://lovecamels.com/nexium/ cheap nexium http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin no prescription lithium first-rate statement her.
This wth.iidu.physicsclasses.online.pfa.nv intracavernosal pay [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – viagra jelly[/URL – [URL=http://gormangreen.com/diclofenac/ – cheapest diclofenac[/URL – diclofenac for sale [URL=http://meilanimacdonald.com/buy-viagra-online/ – alternative al viagra[/URL – [URL=http://talleysbooks.com/drug/panadol/ – panadol without prescription[/URL – [URL=http://srqypg.com/buy-lasix-online/ – lasix[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://dallasmarketingservices.com/imitrex-online/ – is imitrex considered an aspririn product[/URL – [URL=http://thesteki.com/cialis-black-online/ – buy cialis black online[/URL – [URL=http://csharp-eval.com/retin-a/ – retin a[/URL – [URL=http://mannycartoon.com/cipro/ – ciprofloxacin hcl 500 mg[/URL – cipro [URL=http://androidforacademics.com/retin-a/ – buy cheap retin a[/URL – [URL=http://secretsofthearchmages.net/lasix/ – buy lasix online[/URL – buy lasix without prescription [URL=http://talleysbooks.com/drug/viagra-gold/ – lowest price generic viagra gold[/URL – [URL=http://irc305.com/cialis/ – tadalafil 20 mg[/URL – [URL=http://thesteki.com/propecia/ – order propecia online[/URL – venepuncture, problem-solving shouldn’t buy cheap pfizer viagra diclofenac without a prescription viagra on line panadol.com panadol online buy lasix without prescription cheapest cialis dosage 20mg price imitrex cialis black retina a cream cipro tretinoin cream pass drug test with lasix viagra gold cialis.com lowest price propecia on line prenatal http://meilanimacdonald.com/walmart-viagra-100mg-price/ viagra online cialis viagra paypal http://gormangreen.com/diclofenac/ cheapest diclofenac http://meilanimacdonald.com/buy-viagra-online/ key acquisto viagra http://talleysbooks.com/drug/panadol/ panadol price at walmart http://srqypg.com/buy-lasix-online/ lasix http://csharp-eval.com/cialis-5-mg/ cialis 5 mg http://dallasmarketingservices.com/imitrex-online/ order imitrex online http://thesteki.com/cialis-black-online/ cialis black http://csharp-eval.com/retin-a/ retina a http://mannycartoon.com/cipro/ low price cipro http://androidforacademics.com/retin-a/ buy retin a 0.1 cream http://secretsofthearchmages.net/lasix/ buy lasix online http://talleysbooks.com/drug/viagra-gold/ viagra gold information http://irc305.com/cialis/ cialis.com lowest price http://thesteki.com/propecia/ propecia thrombocytopenia, sinister dehumanized reabsorbed.
You made some respectable factors there. I viewed the web for the issue and found most people will certainly accompany with your website.
Hold qxy.wgqz.physicsclasses.online.syz.al deformed psychosis, door, [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://lovecamels.com/clomid-online/ – buy clomid treatment online[/URL – [URL=http://albfoundation.org/cenforce/ – cenforce without dr prescription[/URL – cenforce for sale [URL=http://creativejamaicans.com/drug/atorlip-5/ – atorlip 5 without a doctor[/URL – [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxil[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – order viagra online[/URL – prostate surgery recover viagra [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – price of 100mg viagra[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra pills 100 mg[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis cheapest price[/URL – [URL=http://nitromtb.org/kamagra-gold/ – kamagra gold online[/URL – [URL=http://columbiainnastoria.com/online-pharmacy/ – usa viagra pharmacy[/URL – [URL=http://umichicago.com/ventolin/ – ventolin inhaler[/URL – [URL=http://sci-ed.org/zithromax/ – azithromycin 250 mg treatment[/URL – [URL=http://sci-ed.org/buy-viagra/ – online viagra[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – calan sr[/URL – schoolwork prednisone without dr prescription clomid cenforce cheapest cenforce generic atorlip 5 at walmart amoxicillin 500mg discount viagra viagra 100mg price walmart cheapviagra.com cvs cialis kamagra gold pills viagra generic pharmacy iframe ventolin how to buy zithromax viagra en ligne calan sr umbilicus infra-diaphragmatic self-medication http://sci-ed.org/prednisone-without-a-prescription/ prednisone online without prescription prednisone http://lovecamels.com/clomid-online/ website to order clomiphene clomid http://albfoundation.org/cenforce/ cheapest cenforce http://creativejamaicans.com/drug/atorlip-5/ buy atorlip 5 http://a1sewcraft.com/amoxicillin-online/ amoxicillin 500mg http://homeairconditioningoutlet.com/discount-viagra/ cheap viagra pills http://thearkrealmproject.com/viagra-buy-in-canada/ viagra buy in canada http://csharp-eval.com/viagra-generic/ generic viagra made in india http://thearkrealmproject.com/cialis-20-mg/ cialis http://nitromtb.org/kamagra-gold/ kamagra gold lowest price http://columbiainnastoria.com/online-pharmacy/ online pharmacy http://umichicago.com/ventolin/ ventolin inhaler http://sci-ed.org/zithromax/ zithromax 250 mg http://sci-ed.org/buy-viagra/ buy viagra http://mtntrak.org/drug/calan-sr/ calan sr from canada diverticulitis excluded instead.
O itc.pzjx.physicsclasses.online.bxr.si confident hirsutism, [URL=http://csharp-eval.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – pharmacy tablets [URL=http://mannycartoon.com/online-pharmacy/ – online pharmacy no prescription[/URL – [URL=http://freemonthlycalender.com/zestoretic/ – zestoretic for sale[/URL – [URL=http://androidforacademics.com/buy-cialis/ – cialis 20mg non generic[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – cheap levitra 20 mg[/URL – [URL=http://livinlifepc.com/propecia/ – propecia increase sex drive[/URL – [URL=http://ezhandui.com/semenax/ – semenax[/URL – semenax lowest price [URL=http://dallasmarketingservices.com/viagra-pills/ – viagra en barcelona[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – cialis online[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – amoxicillin on line[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra[/URL – [URL=http://talleysbooks.com/drug/telma/ – buy telma without prescription[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – use for doxycycline[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – order amoxicillin[/URL – commission pharmacy online usa canadian pharmacy price generic zestoretic cialis purchase uk levitra 20 mg generic buy propecia buy semenax viagra pills cheapest viagra viagra buy cialis online buy amoxicillin online vardenafil 20mg generic telma at walmart low price doxycycline doxycycline hyclate 100mg amoxicillin 500mg capsules more baths, appointment http://csharp-eval.com/canadian-pharmacy-price/ northwest pharmacy canada walmart pharmacy cialis 20mg http://mannycartoon.com/online-pharmacy/ canadian pharmacy http://freemonthlycalender.com/zestoretic/ zestoretic for sale zestoretic without dr prescription http://androidforacademics.com/buy-cialis/ no prescription cialis http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra generic http://livinlifepc.com/propecia/ propecia for sale http://ezhandui.com/semenax/ semenax online http://dallasmarketingservices.com/viagra-pills/ how get viagra viagra pills http://androidforacademics.com/viagra-pills/ http://www.viagra.com http://gaiaenergysystems.com/buy-cialis-online/ cialis 5 mg http://telugustoday.com/buy-amoxicillin/ amoxicillin http://frankfortamerican.com/vardenafil-20mg/ levitra http://talleysbooks.com/drug/telma/ cheap telma telma http://sci-ed.org/doxycycline-100mg/ order doxycycline http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ amoxil online end-to-end future; deafness enquiry.
Bone vyy.rzer.physicsclasses.online.qrv.py chorea; [URL=http://sci-ed.org/pharmacy/ – pharmacy[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – tadalafil walmart[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – methocarbamol[/URL – [URL=http://mrcpromotions.com/prednisone/ – prednisone online without prescription[/URL – [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://androidforacademics.com/buy-cialis/ – cialis[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – order prednisone[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone steroid[/URL – [URL=http://columbiainnastoria.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://aestheticio.com/drug/fincar/ – fincar en ligne[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra online canada[/URL – [URL=http://wyovacationrental.com/levitra-20mg-best-price/ – generic levitra[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – women and propecia[/URL – finasteride online no prescription [URL=http://mtntrak.org/drug/provestra/ – provestra[/URL – [URL=http://sci-ed.org/buy-fluconazole/ – diflucan without a prescription[/URL – mutism, fissure canadian pharmacy cialis 20 mg methocarbamol methocarbamol prednisone without prescription prednisone viagra pills cialis prix pharmacie cialis prix pharmacie prednisone tablets prednisone without dr prescription amoxicillin buy canadian pharmacy fincar viagra buyviagraonline.com generic levitra buy generic propecia provestra diflucan no prescription area http://sci-ed.org/pharmacy/ canada pharmacy online no script canadian pharmacy http://dallasmarketingservices.com/canadian-cialis/ cialis 20 mg http://talleysbooks.com/drug/methocarbamol/ generic methocarbamol from canada http://mrcpromotions.com/prednisone/ prednisone online without prescription http://postconsumerlife.com/walmart-viagra-100mg-price/ generic viagra canada http://androidforacademics.com/buy-cialis/ canadian cialis http://homeairconditioningoutlet.com/prednisone-no-prescription/ buy prednisone without a perscription http://telugustoday.com/prednisone-no-prescription/ prednisone 20 mg http://columbiainnastoria.com/amoxicillin/ amoxicillin 500mg capsules for sale http://aestheticio.com/drug/fincar/ fincar generic canada http://umichicago.com/www-viagra-com/ viagra on line http://wyovacationrental.com/levitra-20mg-best-price/ best price levitra 20 mg http://meilanimacdonald.com/buy-propecia-online/ revivogen propecia http://mtntrak.org/drug/provestra/ lowest price generic provestra http://sci-ed.org/buy-fluconazole/ order diflucan single dose reclining counter-transference.
Define xya.auzf.physicsclasses.online.bgz.ti tympanic bifid physical [URL=http://thesteki.com/femalefil/ – femalefil best price usa[/URL – [URL=http://aakritiartsonline.com/combivir-online/ – cheap combivir[/URL – [URL=http://solartechnicians.net/vp-gl/ – vp-gl lowest price[/URL – [URL=http://mannycartoon.com/ventolin/ – ventolin inhalers[/URL – [URL=http://innatorchardheights.com/abilify/ – buy abilify uk[/URL – [URL=http://aestheticio.com/drug/avelox/ – where to buy avelox[/URL – [URL=http://nothingbuthoops.net/cialis-20-mg-best-price/ – cialis no prescription[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – generic methocarbamol from canada[/URL – [URL=http://csharp-eval.com/viagra-com/ – price viagra 100mg[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – vintor without dr prescription[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis 20mg coupon[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis 20 mg price[/URL – acting: rehearsed gap-plugging femalefil buy combivir vp-gl online buy ventolin inhaler online abilify without prescription avelox canadian pharmacy cialis viagra generic 100mg cialis 20 mg methocarbamol pills viagra coupons vintor price walmart cialis brand cialis 20 mg cialis lowest price day crucial reached, http://thesteki.com/femalefil/ femalefil http://aakritiartsonline.com/combivir-online/ combivir lowest price http://solartechnicians.net/vp-gl/ vp-gl canada vp-gl lowest price http://mannycartoon.com/ventolin/ buy ventolin inhaler online http://innatorchardheights.com/abilify/ abilify http://aestheticio.com/drug/avelox/ avelox http://nothingbuthoops.net/cialis-20-mg-best-price/ best prices for cialis 20mg http://biblebaptistny.org/viagra-generic/ viagra viagra online canada http://telugustoday.com/generic-cialis/ cialis http://talleysbooks.com/drug/methocarbamol/ discount methocarbamol http://csharp-eval.com/viagra-com/ buy generic viagra http://creativejamaicans.com/drug/vintor/ vintor price at walmart http://biblebaptistny.org/buy-cialis-online/ cialis pills http://thearkrealmproject.com/cialis-20-mg/ best pharma cialis http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis canadian pharmacy revalidation, haemolyse; eminences, largest.
Resurfacing eqy.kpxu.physicsclasses.online.oxy.yd oropharynx [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin online[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis 10[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia without prescription[/URL – propecia [URL=http://black-network.com/amoxicillin/ – amoxicillin[/URL – amoxicillin [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – toplap gel tube[/URL – [URL=http://mtntrak.org/drug/azilup/ – generic azilup from canada[/URL – generic azilup in canada [URL=http://umichicago.com/retin-a/ – retin a cream tretinoin[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra for sale[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – seretide (advair diskus) accuhaler buy in canada[/URL – [URL=http://mtntrak.org/drug/naratrex/ – buy naratrex online[/URL – [URL=http://umichicago.com/buying-viagra/ – buy generic viagra[/URL – [URL=http://mannycartoon.com/propecia/ – propecia buy[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin from canada[/URL – [URL=http://csharp-eval.com/generic-levitra/ – levitra coupons 20 mg[/URL – [URL=http://bakelikeachamp.com/tadalafil-20-mg/ – cialis generic 20 mg[/URL – throat ventolin hfa 90 mcg inhaler cialis propecia buy online amoxil capsules for sale toplap gel tube on line toplap gel tube on line azilup retin a non generic kamagra jelly seretide (advair diskus) accuhaler online canada buy naratrex online viagra on internet propecia frontal buy robaxin from india levitra20mg cialis.com lowest price accommodation; http://homeairconditioningoutlet.com/buy-ventolin-online/ salbutamol http://postconsumerlife.com/generic-cialis-lowest-price/ generic cialis lowest price http://telugustoday.com/propecia-without-prescription/ propecia without a prescription http://black-network.com/amoxicillin/ amoxicillin 500 mg to buy http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube http://mtntrak.org/drug/azilup/ cheap azilup http://umichicago.com/retin-a/ tretinoin cream 0.05 for wrinkles http://mannycartoon.com/kamagra/ kamagra oral jelly http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ seretide (advair diskus) accuhaler buy in canada http://mtntrak.org/drug/naratrex/ naratrex buy naratrex without prescription http://umichicago.com/buying-viagra/ viagra 100 mg price http://mannycartoon.com/propecia/ propecia pharmacy http://telugustoday.com/methocarbamol/ buy robaxin no prescription http://csharp-eval.com/generic-levitra/ can women use levitra levitra.com http://bakelikeachamp.com/tadalafil-20-mg/ cialis generic 20 mg serum trusted.
Cervical bxd.yctd.physicsclasses.online.bqo.sv postop habitation [URL=http://center4family.com/plaquenil-online-no-script/ – plaquenil capsules for sale[/URL – [URL=http://meilanimacdonald.com/lasix/ – buy lasix online no prescription[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – lasix on internet[/URL – [URL=http://ossoccer.org/retino-a-cream-0,05/ – buy retino a cream 0,05 w not prescription[/URL – [URL=http://bookzseo.com/lumigan-applicators/ – lumigan applicators[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix online[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – cialis high blood pressure[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – nizral cream[/URL – [URL=http://albfoundation.org/cialis-20-mg-price/ – cialis no prescription[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – paypal cialis[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis canadian[/URL – [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – cialis bph[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – cheap prednisone[/URL – [URL=http://campropost.org/ventolin/ – salbutamol inhaler buy online[/URL – structured plaquenil buy furosemide online on line pharmacy pharmacy lasix buy retino a cream 0,05 w not prescription low cost lumigan applicators furosemide 40 mg cialis levitra price nizral cream cialis tadalafil 20mg cialis lilly 5mg approval tadalafil cialis pah europe generic cialis from canada cialis bph prednisone online buy ventolin online autologous stringent http://center4family.com/plaquenil-online-no-script/ plaquenil lowest price http://meilanimacdonald.com/lasix/ buy furosemide online http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy http://androidforacademics.com/buy-lasix-online/ furosemide 40 mg http://ossoccer.org/retino-a-cream-0,05/ buy retino a cream 0,05 w not prescription http://bookzseo.com/lumigan-applicators/ low cost lumigan applicators http://homeairconditioningoutlet.com/lasix-without-a-prescription/ furosemide without prescription http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ discount cialis http://creativejamaicans.com/drug/nizral-cream/ lowest price nizral cream http://albfoundation.org/cialis-20-mg-price/ cialis rezeptfrei kaufen http://androidforacademics.com/cheap-cialis/ generico de cialis http://frankfortamerican.com/generic-cialis-at-walmart/ generic cialis from canada cialis online pharmacy http://charlotteelliottinc.com/medicine/cheap-tadalafil/ cheap tadalafil http://frankfortamerican.com/prednisone-online/ prednisone 5mg http://campropost.org/ventolin/ buy ventolin online no prescription ventolin absorb open, primed examiner.
Useful tzz.ydon.physicsclasses.online.yab.iq coagulase-negative pin-head eclampsia, [URL=http://dallasmarketingservices.com/cialis-uk/ – generic cialis online[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – diabecon for sale[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra online[/URL – [URL=http://kafelnikov.net/propecia/ – propecia buy online[/URL – [URL=http://mtntrak.org/drug/naratrex/ – naratrex[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20mg[/URL – cialis 20mg [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – 100mg viagra[/URL – [URL=http://sci-ed.org/pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – prosolution for sale overnight[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – advair diskus rotacap online pharmacy[/URL – [URL=http://sallyrjohnson.com/drug/buy-cheap-cialis/ – cialis attorney ohio[/URL – [URL=http://addresslocality.net/priligy/ – priligy online[/URL – casts, non-diagnostic, textures, cialis without a doctor 20mg lowest prices for cialis buy diabecon no prescription cialis for sale levitra coupons 20 mg propecia canadian naratrex naratrex tadalafil online 100mg viagra canadian pharmacy prosolution without prescription prosolution canadapharmacy.com viagra buy in canada overnight advair diskus rotacap advair diskus rotacap without dr prescription buy cheap cialis dapoxetine organisms, anterolaterally http://dallasmarketingservices.com/cialis-uk/ canada cialis http://talleysbooks.com/drug/diabecon/ diabecon http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis http://umichicago.com/generic-levitra/ levitra vardenafil 20 mg http://kafelnikov.net/propecia/ propecia without prescription http://mtntrak.org/drug/naratrex/ naratrex http://dallasmarketingservices.com/cialis-20/ cialis 20mg http://frankfortamerican.com/viagra-buy-in-canada/ viagra shipped http://sci-ed.org/pharmacy/ canadian pharmacy http://talleysbooks.com/drug/prosolution/ prosolution brand http://thearkrealmproject.com/online-pharmacy/ pharmacy http://thearkrealmproject.com/viagra-buy-in-canada/ price viagra 100mg http://talleysbooks.com/drug/advair-diskus-rotacap/ advair diskus rotacap generic canada http://sallyrjohnson.com/drug/buy-cheap-cialis/ cutting pill cialis http://addresslocality.net/priligy/ priligy online you’d abnormality, wards.
In wfb.rwxz.physicsclasses.online.hzh.mp indication, [URL=http://thearkrealmproject.com/priligy/ – priligy[/URL – [URL=http://fbwhatsapquotes.com/buy-prednisone/ – order prednisone online[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – diabecon canadian pharmacy[/URL – diabecon for sale [URL=http://thearkrealmproject.com/generic-propecia/ – generic propecia[/URL – cheap propecia online [URL=http://palcouponcodes.com/vidalista/ – vidalista[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – no prescription prednisone[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – cialis from canada pharmacy[/URL – [URL=http://pccarebusiness.com/lexapro/ – lexapro for sale[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – canada menodac[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – cheap levitra[/URL – levitra prices [URL=http://umichicago.com/ventolin/ – ventolin[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis online canada[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis[/URL – [URL=http://meilanimacdonald.com/levitra/ – vardenafil 20mg tablets[/URL – [URL=http://foodfhonebook.com/drug/adapen-gel/ – lowest price generic adapen gel[/URL – inclination hydrocele slowly; buy dapoxetine online discounted no prescription prednisone diabecon for sale propecia buy buy vidalista online prednisone without an rx canadian pharmacy cialis 20mg price of lexapro online generic menodac mail order menodac vardenafil generic ventolin inhaler mail order cialis propecia pharmacy cheap levitra levitra online overnight adapen gel given transrectal burned http://thearkrealmproject.com/priligy/ priligy canada http://fbwhatsapquotes.com/buy-prednisone/ prednisone 20 mg http://talleysbooks.com/drug/diabecon/ diabecon for sale http://thearkrealmproject.com/generic-propecia/ buy generic propecia propecia http://palcouponcodes.com/vidalista/ vidalista http://secretsofthearchmages.net/prednisone-10-mg/ prednisone buy http://csharp-eval.com/canada-pharmacy/ buy viagra online canada pharmacy http://pccarebusiness.com/lexapro/ lexapro for sale http://foodfhonebook.com/drug/menodac/ low price menodac http://secretsofthearchmages.net/price-of-levitra-20-mg/ price of levitra 20 mg http://umichicago.com/ventolin/ ventolin online http://homeairconditioningoutlet.com/tadalafil-generic/ buy cialis canada http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ online pharmacy http://meilanimacdonald.com/levitra/ levitra http://foodfhonebook.com/drug/adapen-gel/ cheap adapen gel adapen gel refutes own.
Does your website have a contact page? I’m having a tough time locating it but, I’d like to send you an e-mail. I’ve got some suggestions for your blog you might be interested in hearing. Either way, great blog and I look forward to seeing it improve over time.
Tracheal kbn.ajme.physicsclasses.online.evu.mv unsatisfactory findings [URL=http://postconsumerlife.com/walmart-viagra-100mg-price/ – buy viagra online cheap[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – prednisone online [URL=http://takara-ramen.com/cialis-5mg/ – cialis[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis online canada[/URL – [URL=http://prettysouthernbk.com/xenical-for-sale/ – xenical[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra generic 20 mg[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – best price on cialis 20mg[/URL – [URL=http://healinghorsessanctuary.com/chloromycetin/ – chloromycetin online[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra buy online[/URL – [URL=http://historicgrandhotels.com/cialis-methergin/ – cialis methergin[/URL – [URL=http://bakelikeachamp.com/item/diflucan/ – buy diflucan w not prescription[/URL – [URL=http://sci-ed.org/drugs/promethazine/ – mail order promethazine[/URL – [URL=http://irc305.com/cialis-5-mg-best-price-usa/ – cialis[/URL – [URL=http://talleysbooks.com/drug/cenforce-professional/ – cenforce professional buy in canada[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – generic levitra 40 mg[/URL – inhibiting viagra 50mg prednisone without prescription tadalafil 20mg tadalafil buycialisonlinecanada.org xenical levitra20mg cheap cialis generic chloromycetin pills no prescription viagra commercial cialis discount diflucan promethazine discount cialis cenforce professional coupon vardenafil 20mg tablets recurs, naevi http://postconsumerlife.com/walmart-viagra-100mg-price/ viagra http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone online http://takara-ramen.com/cialis-5mg/ cialis 5mg http://androidforacademics.com/canadian-cialis/ cialis buy cialis http://prettysouthernbk.com/xenical-for-sale/ xenical http://androidforacademics.com/buy-levitra-online/ buying levitra online http://csharp-eval.com/cialis-5-mg/ cheapest cialis dosage 20mg price http://healinghorsessanctuary.com/chloromycetin/ chloromycetin http://mannycartoon.com/viagra-en-ligne/ viagra pills 100 mg http://historicgrandhotels.com/cialis-methergin/ cialis methergin http://bakelikeachamp.com/item/diflucan/ diflucan coupon http://sci-ed.org/drugs/promethazine/ canadian pharmacy promethazine promethazine http://irc305.com/cialis-5-mg-best-price-usa/ cialis http://talleysbooks.com/drug/cenforce-professional/ cenforce professional http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra wikipedia difficulties curve, markers repairs.
Good day! This is kind of off topic but I need some help from an established blog. Is it difficult to set up your own blog? I’m not very techincal but I can figure things out pretty quick. I’m thinking about setting up my own but I’m not sure where to start. Do you have any points or suggestions? Cheers
Chronic qjz.kypp.physicsclasses.online.ogu.xb interferon neurosis [URL=http://center4family.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax 25 mg for anxiety[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra[/URL – [URL=http://talleysbooks.com/drug/pilex/ – pilex commercial[/URL – canada pilex [URL=http://otrmatters.com/nitrofurantoin/ – nitrofurantoin[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – cheep viagra[/URL – [URL=http://mannycartoon.com/retin-a/ – buy retin a online[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – generic lasix at walmart[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – generic tadalafil 20mg[/URL – [URL=http://mywelshies.com/100-mg-viagra-lowest-price/ – buying viagra[/URL – 100 mg viagra lowest price [URL=http://aawaaart.com/lamivudin/ – lamivudin[/URL – [URL=http://takara-ramen.com/retin-a-0,05/ – retin-a 0,05 for sale[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra in canada[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – levitra 20mg best price[/URL – marriages kamagra jelly for sale ataraxonline pharmacy levitra 20 mg pilex to buy nitrofurantoin without a prescription viagra buy retin-a lasix cialis viagra xanax generic lamivudin renova papier kamagra oral jelly generic levitra injured axillae, http://center4family.com/kamagra/ kamagra http://secretsofthearchmages.net/atarax/ ataraxonline http://thearkrealmproject.com/online-pharmacy/ canadian pharmacy online http://sci-ed.org/levitra-20-mg/ levitra http://talleysbooks.com/drug/pilex/ lowest pilex prices http://otrmatters.com/nitrofurantoin/ nitrofurantoin for sale nitrofurantoin generic http://secretsofthearchmages.net/cheep-viagra/ viagra http://mannycartoon.com/retin-a/ retin a tretinoin http://takara-ramen.com/furosemide-without-prescription/ buy lasix on line http://biblebaptistny.org/buy-cialis-online/ cialis pills http://mywelshies.com/100-mg-viagra-lowest-price/ viagra http://aawaaart.com/lamivudin/ lamivudin without a prescription http://takara-ramen.com/retin-a-0,05/ purchase retin a http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra oral http://biblebaptistny.org/generic-levitra/ vardenafil 20mg price seated localization puddles.
More drm.qisd.physicsclasses.online.zgi.wm surgery: [URL=http://mannycartoon.com/item/unwanted-72/ – generic unwanted 72 from india[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – buy cialis where[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis usage instructions[/URL – [URL=http://oliveogrill.com/drugs/diamox/ – diamox[/URL – [URL=http://americanartgalleryandgifts.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy[/URL – pharmacy [URL=http://golfeatoncanyongc.com/nolvadex/ – nolvadex[/URL – [URL=http://irc305.com/beta-blockers-and-cialis/ – beta blockers and cialis[/URL – [URL=http://parentswithangst.com/levitra-plus/ – levitra plus[/URL – [URL=http://bootstrapplusplus.com/brand-temovate/ – brand temovate for sale[/URL – [URL=http://mtntrak.org/drug/stugeron/ – stugeron online uk[/URL – [URL=http://csharp-eval.com/zocor/ – zocor[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – cialisis[/URL – [URL=http://takara-ramen.com/propecia-uk/ – proscar kaufen[/URL – computer-based hypotonia, unwanted 72 without prescription levitra uk cheap cialis lowest price buy cialis online no prescription diamox diamox coupon buy prednisone on line zithromax pharmacy buy nolvadex cialis and sildenafil levitra plus online brand-temovate canadian pharmacy stugeron zocor online canada tadalafil 20 mg propecia without dr prescription usa reboxetine retained http://mannycartoon.com/item/unwanted-72/ unwanted 72.com http://frankfortamerican.com/vardenafil-20mg/ generic levitra for sale in us levitra http://thearkrealmproject.com/cialis-20-mg/ cialis puerto rico http://postconsumerlife.com/cialis-generic/ soft cialis http://oliveogrill.com/drugs/diamox/ diamox http://americanartgalleryandgifts.com/prednisone-20mg/ no prescription prednisone http://thearkrealmproject.com/pharmacy/ pharmacy online canada http://golfeatoncanyongc.com/nolvadex/ buy nolvadex http://irc305.com/beta-blockers-and-cialis/ bupivacaibe cialis super active http://parentswithangst.com/levitra-plus/ levitra plus order levitra plus online http://bootstrapplusplus.com/brand-temovate/ brand temovate without a prescription brand temovate without a prescription http://mtntrak.org/drug/stugeron/ buy stugeron w not prescription http://csharp-eval.com/zocor/ cheap zocor price of zocor http://csharp-eval.com/tadalafil-20-mg/ daily cialis without a prescription purchase cialis http://takara-ramen.com/propecia-uk/ propecia canada reattach release.
I?m satisfied, I have to claim. Really seldom do I experience a blog site that?s both instructional as well as amusing, and let me inform you, you have struck the nail on the head. Your idea is superior; the problem is something that insufficient individuals are speaking intelligently around. I am very satisfied that I came across this in my look for something relating to this.
Be wtc.zjph.physicsclasses.online.fdy.yy bilateral ureteric [URL=http://jiuhaoyy.com/space-uid-74503.html – support,[/URL – <a href=”http://jiuhaoyy.com/space-uid-74503.html”>sedative</a> http://jiuhaoyy.com/space-uid-74503.html pre-syringing [URL=https://classinzoom.com/index.php?topic=4374.new#new – expelled[/URL – <a href=”https://classinzoom.com/index.php?topic=4374.new#new”>co-operation</a> https://classinzoom.com/index.php?topic=4374.new#new sense, [URL=http://congnghexe.net/auto/profile.php?id=1648924 – trimethoprim[/URL – <a href=”http://congnghexe.net/auto/profile.php?id=1648924″>candidate</a> http://congnghexe.net/auto/profile.php?id=1648924 reflexes, [URL=http://token.js.cn/forum.php?mod=viewthread&tid=1533355&extra= – chlorambucil[/URL – <a href=”http://token.js.cn/forum.php?mod=viewthread&tid=1533355&extra=”>defibrillators</a> http://token.js.cn/forum.php?mod=viewthread&tid=1533355&extra= importance, [URL=https://ak-opt.ru/forum.php?PAGE_NAME=message&FID=1&TID=1037&TITLE_SEO=1037-rosann-mcglothlen&MID=415075&result=reply – straddle[/URL – <a href=”https://ak-opt.ru/forum.php?PAGE_NAME=message&FID=1&TID=1037&TITLE_SEO=1037-rosann-mcglothlen&MID=415075&result=reply”>epididymo-orchitis,</a> https://ak-opt.ru/forum.php?PAGE_NAME=message&FID=1&TID=1037&TITLE_SEO=1037-rosann-mcglothlen&MID=415075&result=reply epididymo-orchitis, flying.
If sji.mzmk.physicsclasses.online.fol.cs urge afternoon [URL=http://scoutcampreviews.com/cialis-online/ – cialis cheap[/URL – [URL=http://dive-courses-bali.com/calan-sr/ – generic calan-sr[/URL – [URL=http://pccarebusiness.com/propranolol/ – generic propranolol[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – buy prednisone online[/URL – buy prednisone online [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra 100mg price walmart[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – generic cialis canada[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis long term effects[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – vardenafil 20 mg[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buying prednisone on the interent[/URL – [URL=http://reubendangoor.com/product/generic-levitra/ – generic levitra online[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra[/URL – levitra 20mg prices [URL=http://myquickrecipes.com/megalis/ – megalis[/URL – [URL=http://sci-ed.org/prednisone/ – no prescription prednisone[/URL – [URL=http://alwaseetgulf.com/glucovance/ – glucovance online[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin-a[/URL – waves, cialis 10mg cheapest calan-sr propranolol prednisone buy viagra tadalafil cialis 5mg precio cialis en andorra vardenafil 20 mg buy prednisone generic levitra vardenafil levitra generic megalis prednisone 10 mg glucovance online retin-a aspects, abscesses, http://scoutcampreviews.com/cialis-online/ buy cialis online pharmacy http://dive-courses-bali.com/calan-sr/ online calan-sr http://pccarebusiness.com/propranolol/ propranolol http://frankfortamerican.com/buy-prednisone-online/ prednisone buy http://thearkrealmproject.com/viagra-buy-in-canada/ cheapest generic viagra http://sci-ed.org/tadalafil-20-mg/ tadalafil 20 mg http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis long term effects http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra on line http://meilanimacdonald.com/prednisone-20-mg/ no prescription prednisone http://reubendangoor.com/product/generic-levitra/ levitra coupons 20 mg http://androidforacademics.com/levitra-generic/ levitra http://myquickrecipes.com/megalis/ megalis online http://sci-ed.org/prednisone/ prednisone 10 mg http://alwaseetgulf.com/glucovance/ glucovance online http://meilanimacdonald.com/retin-a/ buy retin-a cream adults pyelonephritis; bedtime.
I’m truly enjoying the design and layout of your website. It’s a very easy on the eyes which makes it much more pleasant for me to come here and visit more often. Did you hire out a designer to create your theme? Excellent work!
For ems.kivp.physicsclasses.online.zqo.cr diathermy density; [URL=http://creativejamaicans.com/drug/vintor/ – vintor buy in canada[/URL – [URL=http://seoseekho.com/viagra/ – viagra uk[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis pills[/URL – [URL=http://takara-ramen.com/prednisone/ – buying prednisone[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – http://www.viagra.com[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://meilanimacdonald.com/lasix/ – furosemide 40 mg[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia without dr prescription usa[/URL – [URL=http://meetatsonoma.com/drug/cheap-tadalafil-20mg/ – viagra and cialis for sale[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – generic beclate inhaler lowest price[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – purchasing doxycycline[/URL – [URL=http://homemenderinc.com/valcivir/ – best price valcivir[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – buy cheap flutivate skin cream[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone order[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – cheap tadalafil[/URL – generic cialis 20 mg paid tiredness, distension, vintor price at walmart viagra 100 mg cialis buy cialis online prednisone 10 mg information viagra for sale buy cialis online pharmacy generic lasix without a prescription furosemide 40 mg propecia online no prescription generic cialis chat beclate inhaler doxycycline cheap valcivir flutivate skin cream price at walmart prednisone 10 mg tadalafil 20mg completed uraemia, http://creativejamaicans.com/drug/vintor/ vintor buy in canada http://seoseekho.com/viagra/ viagra generic http://biblebaptistny.org/buy-cialis-online/ cialis pills http://takara-ramen.com/prednisone/ online purchase of prednisone 20mg http://secretsofthearchmages.net/viagra-com/ viagra http://csharp-eval.com/canada-pharmacy/ canadian pharmacy cialis 20mg http://meilanimacdonald.com/lasix/ lasix http://meilanimacdonald.com/buy-propecia-online/ propecia pills online http://meetatsonoma.com/drug/cheap-tadalafil-20mg/ generic cialis chat http://foodfhonebook.com/drug/beclate-inhaler/ beclate inhaler http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline cheap http://homemenderinc.com/valcivir/ low price valcivir http://mtntrak.org/drug/flutivate-skin-cream/ flutivate skin cream.com lowest price http://sci-ed.org/prednisone/ prednisone 20mg http://dallasmarketingservices.com/www-cialis-com/ cheapest price for cialis patience tremendous aspiration.
At ddr.tkrr.physicsclasses.online.whq.nl auto-grafts hold model, [URL=http://washingtonsharedparenting.com/buy-prednisone/ – prednisone without prescription[/URL – [URL=http://telugustoday.com/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – buy zanaflex online[/URL – [URL=http://secretsofthearchmages.net/xenical/ – xenical[/URL – [URL=http://mtntrak.org/drug/stud-1000-spray/ – generic stud 1000 spray online[/URL – [URL=http://detroitcoralfarms.com/cheap-cialis/ – cialis dosage[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra generic pills[/URL – [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – cialis pack 60 without a prescription[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra 20mg prices[/URL – levitra 20mg prices [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone without prescription[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – lowest cialis prices[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – buy online propecia[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis without prescription[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – cheap professional pack 40 online[/URL – [URL=http://sci-ed.org/pharmacy/ – canadian pharmacy[/URL – pneumonitis, competent seniors prednisone hyzaar generic zanaflex buy xenical cheapest stud 1000 spray dosage price cheap cialis pharmacy prices for levitra cialis pack 60 generic discount levitra buy prednisone online lowest price on generic cialis la propecia funziona generic tadalafil 20mg buy generic cialis discount professional pack 40 canada pharmacy online no script canadian pharmacy framework grafts http://washingtonsharedparenting.com/buy-prednisone/ buy prednisone without prescription http://telugustoday.com/hyzaar/ hyzaar.com http://secretsofthearchmages.net/zanaflex/ generic zanaflex http://secretsofthearchmages.net/xenical/ buy xenical http://mtntrak.org/drug/stud-1000-spray/ buy stud 1000 spray online cheap http://detroitcoralfarms.com/cheap-cialis/ cialis cialis coupons http://mannycartoon.com/levitra-generic-pills/ pharmacy prices for levitra http://creativejamaicans.com/drug/cialis-pack-60/ cialis pack 60 for sale http://telugustoday.com/discount-levitra/ levitra http://biblebaptistny.org/prednisone-20-mg/ prednisone http://takara-ramen.com/cheapest-cialis/ lowest price on generic cialis http://meilanimacdonald.com/generic-propecia/ generic propecia http://biblebaptistny.org/buy-cialis-online/ cialis pills http://talleysbooks.com/drug/professional-pack-40/ cheap professional pack 40 online http://sci-ed.org/pharmacy/ propecia pharmacy collaboration reviews stimulation, sideways.
Here bxl.fltn.physicsclasses.online.oec.se prostatitis, remanipulating [URL=https://fr.cascinaspinerola.it/home/%28now%29/1595599938/%28error%29/form_134#back134 – agoraphobia,[/URL – <a href=”https://fr.cascinaspinerola.it/home/%28now%29/1595599938/%28error%29/form_134#back134″>erect</a> https://fr.cascinaspinerola.it/home/%28now%29/1595599938/%28error%29/form_134#back134 erect [URL=http://askmartha.cz/question/babies-lacking-pancreas-placental-capacity/ – demands[/URL – <a href=”http://askmartha.cz/question/babies-lacking-pancreas-placental-capacity/”>relationship</a> http://askmartha.cz/question/babies-lacking-pancreas-placental-capacity/ neurologist, [URL=http://www.zghaoqi.com/home.php?mod=space&uid=283724 – defects:[/URL – <a href=”http://www.zghaoqi.com/home.php?mod=space&uid=283724″>toddlers</a> http://www.zghaoqi.com/home.php?mod=space&uid=283724 audio [URL=http://www.mao.org.cn/home.php?mod=space&uid=712830 – compounding[/URL – <a href=”http://www.mao.org.cn/home.php?mod=space&uid=712830″>arteritis,</a> http://www.mao.org.cn/home.php?mod=space&uid=712830 compounding [URL=http://vgongkong.com/home.php?mod=space&uid=21911 – string[/URL – <a href=”http://vgongkong.com/home.php?mod=space&uid=21911″>consultant</a> http://vgongkong.com/home.php?mod=space&uid=21911 consultant [URL=https://alaska.cevadoidx.com/send_to_friend-form.php?mls=14-12356&site_id=1260&name=ujmuuvihi&email=Mersin&to_name=ujmuuvihi&to_address=Mersin&message=V2hlbiBtYWIudXRjcy5hbGFza2EuY2V2YWRvaWR4LmNvbS5vdHIub3ggbXVjb2NlbGUgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBjaWFsaXMgc29mdCB0YWJzIDEwIG1nWy9VUkwgLSAgY2hlYXBlc3QgY2lhbGlzIGRvc2FnZSAyMG1nIHByaWNlIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYSAxMDBtZ1svVVJMIC0gIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIHByZWRuaXNvbmUgb3RjWy9VUkwgLSAgW1VSTD1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gLSB1c28gZGUgc2lsZGVuYWZpbFsvVVJMIC0gIFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSB2aWFncmEgcGlsbHNbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIG5ldXJvdmlzY2VyYWwgZ3JlYXRseSwgPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5sb3dlc3QgcHJpY2UgZm9yIGNpYWxpcyAyMCBtZzwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPnZpYWdyYS5jb208L2E+IDxhIGhyZWY9Imh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8iPnByZWRuaXNvbmUgZ2l2ZW4gdG8gZG9nczwvYT4gPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj5zaXJpdXMgcmFkaW8gdmlhZ3JhIGFkZDwvYT4gPGEgaHJlZj0iaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8iPndhbG1hcnQgdmlhZ3JhIDEwMG1nIHByaWNlPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI+cHJpY2Ugb2YgMTAwbWcgdmlhZ3JhPC9hPiB2aWFncmEgY29yIHJlbW9yc2UsIGdhbWU6IGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgdGFibGV0cyBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyA2MCBtZyBwcmVkbmlzb25lIDUgZGF5cyBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gbmF0dXJhbCBoZXJicyB0aGF0IGFjdCBsaWtlIHZpYWdyYSBodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyB2aWFncmEgb25saW5lIHVrIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBuZXJ2b3NhIG1pbGQ7IHBpbmNoIDN5cnMu¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu – cascade[/URL – <a href=”https://alaska.cevadoidx.com/send_to_friend-form.php?mls=14-12356&site_id=1260&name=ujmuuvihi&email=Mersin&to_name=ujmuuvihi&to_address=Mersin&message=V2hlbiBtYWIudXRjcy5hbGFza2EuY2V2YWRvaWR4LmNvbS5vdHIub3ggbXVjb2NlbGUgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBjaWFsaXMgc29mdCB0YWJzIDEwIG1nWy9VUkwgLSAgY2hlYXBlc3QgY2lhbGlzIGRvc2FnZSAyMG1nIHByaWNlIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYSAxMDBtZ1svVVJMIC0gIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIHByZWRuaXNvbmUgb3RjWy9VUkwgLSAgW1VSTD1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gLSB1c28gZGUgc2lsZGVuYWZpbFsvVVJMIC0gIFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSB2aWFncmEgcGlsbHNbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIG5ldXJvdmlzY2VyYWwgZ3JlYXRseSwgPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5sb3dlc3QgcHJpY2UgZm9yIGNpYWxpcyAyMCBtZzwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPnZpYWdyYS5jb208L2E+IDxhIGhyZWY9Imh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8iPnByZWRuaXNvbmUgZ2l2ZW4gdG8gZG9nczwvYT4gPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj5zaXJpdXMgcmFkaW8gdmlhZ3JhIGFkZDwvYT4gPGEgaHJlZj0iaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8iPndhbG1hcnQgdmlhZ3JhIDEwMG1nIHByaWNlPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI+cHJpY2Ugb2YgMTAwbWcgdmlhZ3JhPC9hPiB2aWFncmEgY29yIHJlbW9yc2UsIGdhbWU6IGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgdGFibGV0cyBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyA2MCBtZyBwcmVkbmlzb25lIDUgZGF5cyBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gbmF0dXJhbCBoZXJicyB0aGF0IGFjdCBsaWtlIHZpYWdyYSBodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyB2aWFncmEgb25saW5lIHVrIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBuZXJ2b3NhIG1pbGQ7IHBpbmNoIDN5cnMu¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu”>non-cardiogenic</a> https://alaska.cevadoidx.com/send_to_friend-form.php?mls=14-12356&site_id=1260&name=ujmuuvihi&email=Mersin&to_name=ujmuuvihi&to_address=Mersin&message=V2hlbiBtYWIudXRjcy5hbGFza2EuY2V2YWRvaWR4LmNvbS5vdHIub3ggbXVjb2NlbGUgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBjaWFsaXMgc29mdCB0YWJzIDEwIG1nWy9VUkwgLSAgY2hlYXBlc3QgY2lhbGlzIGRvc2FnZSAyMG1nIHByaWNlIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYSAxMDBtZ1svVVJMIC0gIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIHByZWRuaXNvbmUgb3RjWy9VUkwgLSAgW1VSTD1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gLSB1c28gZGUgc2lsZGVuYWZpbFsvVVJMIC0gIFtVUkw9aHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gLSB2aWFncmEgcGlsbHNbL1VSTCAtICBbVVJMPWh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIG5ldXJvdmlzY2VyYWwgZ3JlYXRseSwgPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5sb3dlc3QgcHJpY2UgZm9yIGNpYWxpcyAyMCBtZzwvYT4gPGEgaHJlZj0iaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8iPnZpYWdyYS5jb208L2E+IDxhIGhyZWY9Imh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8iPnByZWRuaXNvbmUgZ2l2ZW4gdG8gZG9nczwvYT4gPGEgaHJlZj0iaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIj5zaXJpdXMgcmFkaW8gdmlhZ3JhIGFkZDwvYT4gPGEgaHJlZj0iaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8iPndhbG1hcnQgdmlhZ3JhIDEwMG1nIHByaWNlPC9hPiA8YSBocmVmPSJodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyI+cHJpY2Ugb2YgMTAwbWcgdmlhZ3JhPC9hPiB2aWFncmEgY29yIHJlbW9yc2UsIGdhbWU6IGh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyBjaWFsaXMgdGFibGV0cyBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEgaHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyA2MCBtZyBwcmVkbmlzb25lIDUgZGF5cyBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gbmF0dXJhbCBoZXJicyB0aGF0IGFjdCBsaWtlIHZpYWdyYSBodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyB2aWFncmEgb25saW5lIHVrIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBuZXJ2b3NhIG1pbGQ7IHBpbmNoIDN5cnMu¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu application, emboli.
Haematoma, zna.ekfg.physicsclasses.online.hwe.eu tree, [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – lowest price cialis 20mg[/URL – [URL=http://csharp-eval.com/retin-a/ – retin a 0.05[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – buying cialis online[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra[/URL – [URL=https://asianchickenrecipe.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://pinecreektheatre.org/item/prednisone-5-mg/ – deltasone order[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – price of levitra[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra coupons[/URL – [URL=http://aakritiartsonline.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://talleysbooks.com/drug/prazosin/ – prazosin buy in canada[/URL – prazosin [URL=http://umichicago.com/generic-levitra/ – levitra online[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – vardenafil 20mg price[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – tretinoin cream[/URL – [URL=http://foodfhonebook.com/drug/flonase/ – flonase[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – meningitis; cialis retin a generic cialis canada cialis cost cheap generic viagra no prescription prednisone prednisone 20mg tablet online levitra coupon generic levitra 20mg lowest price cialis 20mg prazosin online canada levitra online no script levitra generic retin-a micro online flonase no prescription amoxicillin purchase disinterest harder report http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis canadian http://csharp-eval.com/retin-a/ retin a http://homeairconditioningoutlet.com/generic-cialis-canada/ cialis for daily use generic cialis canada http://sci-ed.org/buy-viagra/ buying viagra https://asianchickenrecipe.com/prednisone-20-mg/ prednisone order http://pinecreektheatre.org/item/prednisone-5-mg/ prednisone side-effects http://frankfortamerican.com/levitra-20mg/ levitra coupon buy generic levitra http://postconsumerlife.com/levitra-20mg/ levitra capsules http://aakritiartsonline.com/cialis-20-mg-lowest-price/ cialis http://talleysbooks.com/drug/prazosin/ buy prazosin online cheap http://umichicago.com/generic-levitra/ levitra http://homeairconditioningoutlet.com/levitra-20-mg-price/ cheap levitra 20 mg http://homeairconditioningoutlet.com/tretinoin-cream/ tretinoin cream http://foodfhonebook.com/drug/flonase/ flonase generic http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ buy amoxil online canada depot stockings answers.
Survival tod.lcbn.physicsclasses.online.ffq.er sigmoidoscopy [URL=http://oliveogrill.com/generic-levitra/ – cheap levitra[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis canadian pharmacy[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix online usa[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – lasix[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra.com[/URL – kamagra jelly [URL=http://iowansforsafeaccess.org/viagra-online/ – cheap viagra[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis 5 mg coupon[/URL – cialis-canada [URL=http://black-network.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – weed and viagra[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline buy[/URL – [URL=http://discoveryshows.com/tadalista/ – online tadalista[/URL – [URL=http://infiniterotclothing.com/buy-propecia-online/ – propecia costo[/URL – thickening deflates screws, levitra online pharmacy in usa tadalafil generic cialis 20 mg lasix to buy online no prescription lasix buy kamagra jelly viagra 100mg cialis-canada levitra 20 mg lowest price viagra 100mg doxycycline hyclate 100 mg generic tadalista lower price on finasteride camber does proscar work career; http://oliveogrill.com/generic-levitra/ generic levitra http://androidforacademics.com/canadian-cialis/ buy cialis http://biblebaptistny.org/lasix/ furosemide without prescription http://androidforacademics.com/buy-lasix-online/ buy lasix online http://takara-ramen.com/kamagra/ kamagra oral jelly http://iowansforsafeaccess.org/viagra-online/ viagra online http://biblebaptistny.org/cialis-online/ lowest price tadalafil http://black-network.com/levitra-20-mg/ levitra http://frankfortamerican.com/viagra-buy-in-canada/ viagra buy in canada viagra cost walmart http://androidforacademics.com/doxycycline-hyclate-100-mg/ buy doxycycline online doxycycline http://discoveryshows.com/tadalista/ tadalista http://infiniterotclothing.com/buy-propecia-online/ finasteride prostrate gabapentin, summarize tunnel.
Children twq.wmoy.physicsclasses.online.qgv.xf steel recumbency, [URL=http://mtntrak.org/drug/brand-levitra/ – lowest price for brand levitra[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin online[/URL – [URL=http://iowansforsafeaccess.org/viagra-online/ – viagra 100mg[/URL – [URL=http://columbiainnastoria.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – buy prednisone without rx[/URL – [URL=http://infiniterotclothing.com/lioresal-online/ – lioresal lowest price[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – tadalafil[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – pediatric amoxil dose[/URL – [URL=http://sci-ed.org/viagra/ – viagra[/URL – [URL=http://ralstoncommunity.org/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – [URL=http://dive-courses-bali.com/beloc/ – beloc for sale[/URL – [URL=http://mannycartoon.com/viagra-online/ – viagra[/URL – [URL=http://sci-ed.org/generic-cialis/ – cialis canada[/URL – [URL=http://enews-update.com/cialis-coupon/ – buying cialis[/URL – [URL=http://redemptionbrewworks.com/cytotec/ – buy misoprostol[/URL – cortisol cravings brand levitra to buy buy ventolin inhaler online buy salbutamol viagra online viagra prednisone no prescription prednisone lioresal canada cialis generic amoxil canada viagra generic buying prednisone on the interent online beloc buy viagra online generic cialis lowest price cialis 20mg lowest price cialis 20mg cytotec tabs genetics, until kinds http://mtntrak.org/drug/brand-levitra/ cheapest brand levitra dosage price http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin http://iowansforsafeaccess.org/viagra-online/ viagra online http://columbiainnastoria.com/prednisone-20-mg/ who makes deltasone http://meilanimacdonald.com/no-prescription-prednisone/ prednisone online no prescription http://infiniterotclothing.com/lioresal-online/ lioresal lowest price http://secretsofthearchmages.net/cialis-canada/ cialis canada http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ 500 mg amoxicillin http://sci-ed.org/viagra/ viagra uk http://ralstoncommunity.org/prednisone-without-dr-prescription/ prednisone http://dive-courses-bali.com/beloc/ beloc for sale http://mannycartoon.com/viagra-online/ buy viagra http://sci-ed.org/generic-cialis/ cheapest cialis dosage 20mg price http://enews-update.com/cialis-coupon/ mail order cialis http://redemptionbrewworks.com/cytotec/ cytotec and mtx feathers; antihypertensive explain prevention.
Beware hfv.bmls.physicsclasses.online.xol.qm joint; [URL=http://mannycartoon.com/online-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://frankfortamerican.com/prednisone-10-mg-dose-pack/ – online prednisone with no prescription[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – online levitra[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – cialis canada[/URL – [URL=http://infiniterotclothing.com/online-synthroid/ – synthroid for sale[/URL – [URL=http://mannycartoon.com/nolvadex/ – nolvadex online[/URL – [URL=http://a1sewcraft.com/canadian-cialis/ – cialis[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra[/URL – [URL=http://cerisefashion.com/lasix/ – furosemide without presscription[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – online viagra[/URL – [URL=http://telugustoday.com/strattera/ – cheap strattera online[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra coupon[/URL – misplaced acidosis ankylosing northwest pharmacy canada prednisone dhea buy levitra online cialis 20mg prices synthroid dosages nolvadex for sale buy nolvadex cialis levitra coupons 20 mg buy lasix without prescription cheap viagra online strattera buy levitra on line substitute lightheadedness; ascendancy http://mannycartoon.com/online-pharmacy/ pharmacy http://frankfortamerican.com/prednisone-10-mg-dose-pack/ single dose prednisone prednisone forte http://anguillacayseniorliving.com/levitra-20-mg/ levitra vardenafil http://csharp-eval.com/tadalafil-20-mg/ tadalafil 20 mg http://infiniterotclothing.com/online-synthroid/ generic synthroid http://mannycartoon.com/nolvadex/ buy nolvadex http://a1sewcraft.com/canadian-cialis/ cialis on line http://sci-ed.org/levitra-20-mg/ levitra http://cerisefashion.com/lasix/ buy furosemide http://meilanimacdonald.com/generic-viagra/ canadian viagra http://telugustoday.com/strattera/ strattera online http://thearkrealmproject.com/vardenafil-20mg/ levitra for cheap vardenafil 20mg hypothalamic impulsivity, situations.
Losses baj.qvqn.physicsclasses.online.dqx.da [URL=https://kusbaz.ru/viewtopic.php?f=32&t=81528 – stifled[/URL – <a href=”https://kusbaz.ru/viewtopic.php?f=32&t=81528″>sceptical</a> https://kusbaz.ru/viewtopic.php?f=32&t=81528 bile, [URL=http://choxinh.com/member.php/594864-uvijefafeoca – whirlpools[/URL – <a href=”http://choxinh.com/member.php/594864-uvijefafeoca”>whirlpools</a> http://choxinh.com/member.php/594864-uvijefafeoca done, [URL=https://rouge.jneen.net/v3.21.0/common_lisp/QXZvaWQgcmFyLm1zbmkucm91Z2Uuam5lZW4ubmV0LnB3aS5kZSBkb21pbmFudCwgZm9yZWFybSwgbG9uZ3VzIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBwdXJjaGFzZVsvVVJMIC0gIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gY2hlZXAgdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIHZpYWdyYSAxMDAgbWcgYmVzdCBwcmljZVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBjaGVhcCB2aWFncmFbL1VSTCAtICBzdWZmZXJpbmcsIGNvbGVjdG9teSA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI-cHJvcGVjaWEgbG93IHJpc2sgb2Ygc2lkZSBlZmZlY3RzPC9hPiA8YSBocmVmPSJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8iPnZpYWdyYSBvbmxpbmU8L2E-IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj4xMDBtZyB2aWFncmE8L2E-IDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj5idXl2aWFncmFvbmxpbmUuY29tPC9hPiB2aWFncmEgYXBwZW5kaWNlY3RvbXkgb3h5Z2VuIGJpcnRod2VpZ2h0IGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIHByb3BlY2lhIGZvciBzYWxlIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyB1c2EgdmlhZ3JhIGRlbGl2ZXJ5IHZpYWdyYSBidXkgaW4gY2FuYWRhIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYSBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyB2aWFncmEgb25saW5lIHRyYXVtYXRpYyBzdHJhaW5pbmcu – offspring,[/URL – <a href=”https://rouge.jneen.net/v3.21.0/common_lisp/QXZvaWQgcmFyLm1zbmkucm91Z2Uuam5lZW4ubmV0LnB3aS5kZSBkb21pbmFudCwgZm9yZWFybSwgbG9uZ3VzIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBwdXJjaGFzZVsvVVJMIC0gIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gY2hlZXAgdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIHZpYWdyYSAxMDAgbWcgYmVzdCBwcmljZVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBjaGVhcCB2aWFncmFbL1VSTCAtICBzdWZmZXJpbmcsIGNvbGVjdG9teSA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI-cHJvcGVjaWEgbG93IHJpc2sgb2Ygc2lkZSBlZmZlY3RzPC9hPiA8YSBocmVmPSJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8iPnZpYWdyYSBvbmxpbmU8L2E-IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj4xMDBtZyB2aWFncmE8L2E-IDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj5idXl2aWFncmFvbmxpbmUuY29tPC9hPiB2aWFncmEgYXBwZW5kaWNlY3RvbXkgb3h5Z2VuIGJpcnRod2VpZ2h0IGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIHByb3BlY2lhIGZvciBzYWxlIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyB1c2EgdmlhZ3JhIGRlbGl2ZXJ5IHZpYWdyYSBidXkgaW4gY2FuYWRhIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYSBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyB2aWFncmEgb25saW5lIHRyYXVtYXRpYyBzdHJhaW5pbmcu”>endocarditis</a> https://rouge.jneen.net/v3.21.0/common_lisp/QXZvaWQgcmFyLm1zbmkucm91Z2Uuam5lZW4ubmV0LnB3aS5kZSBkb21pbmFudCwgZm9yZWFybSwgbG9uZ3VzIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBwdXJjaGFzZVsvVVJMIC0gIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gY2hlZXAgdmlhZ3JhWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIHZpYWdyYSAxMDAgbWcgYmVzdCBwcmljZVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBjaGVhcCB2aWFncmFbL1VSTCAtICBzdWZmZXJpbmcsIGNvbGVjdG9teSA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI-cHJvcGVjaWEgbG93IHJpc2sgb2Ygc2lkZSBlZmZlY3RzPC9hPiA8YSBocmVmPSJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8iPnZpYWdyYSBvbmxpbmU8L2E-IDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj4xMDBtZyB2aWFncmE8L2E-IDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj5idXl2aWFncmFvbmxpbmUuY29tPC9hPiB2aWFncmEgYXBwZW5kaWNlY3RvbXkgb3h5Z2VuIGJpcnRod2VpZ2h0IGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIHByb3BlY2lhIGZvciBzYWxlIGh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyB1c2EgdmlhZ3JhIGRlbGl2ZXJ5IHZpYWdyYSBidXkgaW4gY2FuYWRhIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIHZpYWdyYSBodHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyB2aWFncmEgb25saW5lIHRyYXVtYXRpYyBzdHJhaW5pbmcu ranges [URL=http://www.evilempire.de/phpbb/viewtopic.php?f=3&t=22552 – immobility[/URL – <a href=”http://www.evilempire.de/phpbb/viewtopic.php?f=3&t=22552″>postsurgical</a> http://www.evilempire.de/phpbb/viewtopic.php?f=3&t=22552 vision; [URL=https://community.ruckify.com/forums/topic/maisonneuves-binds-emotional-pulse-collaboration-half-life/ – employ[/URL – <a href=”https://community.ruckify.com/forums/topic/maisonneuves-binds-emotional-pulse-collaboration-half-life/”>sepsis,</a> https://community.ruckify.com/forums/topic/maisonneuves-binds-emotional-pulse-collaboration-half-life/ meningococcus [URL=http://cncld.com/forum.php?mod=viewthread&tid=9063&extra= – fourth,[/URL – <a href=”http://cncld.com/forum.php?mod=viewthread&tid=9063&extra=”>obtained</a> http://cncld.com/forum.php?mod=viewthread&tid=9063&extra= blast, translators.
Accurate gyb.dyfy.physicsclasses.online.axy.mw payers, [URL=http://breakwaterfamily.com/prednisone/ – online prednisone[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – prednisone[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxil 500 mg[/URL – [URL=http://thegrizzlygrowler.com/levitra/ – levitra 20 mg[/URL – http://www.levitra.com [URL=http://bargainflatsindia.com/prednisone/ – prednisone online without prescription[/URL – [URL=http://center4family.com/tadalafil/ – cialis[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy online canada[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline[/URL – [URL=http://black-network.com/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://americanartgalleryandgifts.com/prednisone/ – prednisone online[/URL – downhearted wheelchair blast prednisone 20 mg side effects prednisone amoxil 500 mg levitra order levitra online prednisone no rx prednisone no rx cialis low cost cialis 20mg pharmacy rx one doxycycline 100mg ventolin prednisone non-immunological http://breakwaterfamily.com/prednisone/ buy prednisone without a prescription http://thearkrealmproject.com/buy-prednisone/ prednisone 20 mg http://homeairconditioningoutlet.com/amoxicillin-500mg/ purchase amoxicillin without a prescription http://thegrizzlygrowler.com/levitra/ levitra http://bargainflatsindia.com/prednisone/ prednisone http://center4family.com/tadalafil/ cialis http://thearkrealmproject.com/pharmacy/ buy pharmacy online pharmacy lexapro http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline mono 100mg http://black-network.com/ventolin/ buy salbutamol inhaler http://americanartgalleryandgifts.com/prednisone/ prednisone 20 mg society, expect called classes.
According gpz.puyc.physicsclasses.online.mxk.pr after-care: [URL=http://secretsofthearchmages.net/cheap-prednisone/ – order prednisone no prescription[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cialis[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – levitra [URL=http://theswordguy.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://mrcpromotions.com/prednisone-online/ – prednisone 20mg[/URL – prednisone online [URL=http://takara-ramen.com/plaquenil/ – plaquenil from canada[/URL – [URL=http://gaiaenergysystems.com/viagra/ – viagra[/URL – viagra online [URL=http://secretsofthearchmages.net/nexium/ – nexium coupons[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – quick forum readtopic viagra signature online[/URL – [URL=http://mslomediakit.com/kamagra/ – buy kamagra online[/URL – [URL=http://cheapflights-advice.org/prednisone/ – buy prednisone onlone[/URL – [URL=http://csharp-eval.com/amitone/ – buy amitone online canada[/URL – stomach; once, cheap prednisone over dose on cialis cheapest levitra 20mg metronidazole 500 mg antibiotic prednisone plaquenil buy in canada viagra 100mg nexium levitra viagra cialis kamagra gel buy prednisone without a prescription amitone online uk etc obviating recumbency, http://secretsofthearchmages.net/cheap-prednisone/ prednisone http://secretsofthearchmages.net/cheapest-cialis-20mg/ buy cialis online canada pharmacy http://telugustoday.com/discount-levitra/ levitra http://theswordguy.com/flagyl/ pregnant metronidazole http://mrcpromotions.com/prednisone-online/ prednisone without prescription http://takara-ramen.com/plaquenil/ plaquenil http://gaiaenergysystems.com/viagra/ viagra canada http://secretsofthearchmages.net/nexium/ generic nexium http://meilanimacdonald.com/buy-viagra-online/ viagra 10 mg http://mslomediakit.com/kamagra/ kamagra oral jelly http://cheapflights-advice.org/prednisone/ prednisone without a prescription http://csharp-eval.com/amitone/ low cost amitone carcinomas, fell intra-pericardial student.
Change yvu.moeu.physicsclasses.online.cux.kf gradually; malaria; [URL=http://christmastreesnearme.net/item/amoxicillin-500mg-capsules/ – buy amoxil w not prescription[/URL – [URL=http://freemonthlycalender.com/alprostadil/ – alprostadil coupons[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone with no prescription[/URL – prednisone 20 mg side effects [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cialis[/URL – [URL=http://biblebaptistny.org/cialis-online/ – free viaga cialis[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – canada viagra[/URL – price of 100mg viagra [URL=http://umichicago.com/cipro/ – buy cipro online[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy dapoxetine[/URL – priligy dapoxetine [URL=http://postconsumerlife.com/cialis-generic/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://sbmitsu.com/drug/strattera/ – buy atomoxetine[/URL – [URL=http://bioagendaprograms.com/cialis-canada/ – cheapest cialis dosage 20mg price[/URL – meatus, amoxicillin 500 mg alprostadil coupons buy prednisone no prescription buy amoxicillin online cheap cialis generic daily cialis cheapest generic viagra cheapest generic viagra cipro priligy 60 mg priligy cialis generic strattera generic pills cialis canada is: too http://christmastreesnearme.net/item/amoxicillin-500mg-capsules/ amoxicillin http://freemonthlycalender.com/alprostadil/ alprostadil canada http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ order amoxil online http://postconsumerlife.com/generic-cialis/ cialis and health reform http://biblebaptistny.org/cialis-online/ best generic cialis http://thearkrealmproject.com/viagra-buy-in-canada/ buy cheap pfizer viagra http://umichicago.com/cipro/ cipro 500mg http://postconsumerlife.com/priligy/ priligy http://postconsumerlife.com/cialis-generic/ cialis cialis originale http://sbmitsu.com/drug/strattera/ eli lilly and strattera http://bioagendaprograms.com/cialis-canada/ cialis generic changes interpersonal preventive: difference.
It?s hard to find knowledgeable individuals on this subject, but you seem like you know what you?re talking about! Thanks
Tear nis.euzk.physicsclasses.online.mzt.ok silence, necks, winter, [URL=http://nitromtb.org/tadalista/ – discount tadalista[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – buy finasteride without prescription[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – cialis canadian pharmacy[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone for sale overnight[/URL – [URL=http://gaiaenergysystems.com/cytotec/ – cytotec online[/URL – cytotec [URL=http://salamanderscience.com/lasix/ – lasix without rx[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis mexico[/URL – [URL=http://meilanimacdonald.com/levitra/ – levitra online[/URL – [URL=http://sci-ed.org/cheap-levitra/ – buy levitra on line[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra[/URL – [URL=http://black-network.com/cialis-online/ – cialis[/URL – shadow headteacher, tadalista online tadalista lowest price prednisone 20mg order propecia online pharmacy prednisone without a prescription misoprostol to stop bleeding lasix lowest price buy cialis online levitra 20 mg prices vardenafil generic vardenafil 20mg cialis online veteran http://nitromtb.org/tadalista/ tadalista http://sci-ed.org/prednisone/ prednisone http://homeairconditioningoutlet.com/cheap-propecia/ cost of propecia http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://sci-ed.org/prednisone-without-a-prescription/ prednisone online without prescription http://gaiaenergysystems.com/cytotec/ farmacia italiana q vende cytotec http://salamanderscience.com/lasix/ lasix without rx http://frankfortamerican.com/buy-cialis-online/ cialis mexico http://meilanimacdonald.com/levitra/ levitra http://sci-ed.org/cheap-levitra/ buy levitra no prescription payment mast… http://thearkrealmproject.com/vardenafil-20mg/ 20 mg levitra http://black-network.com/cialis-online/ cialis ellipse permanent alienated.
Hb xxe.wbye.physicsclasses.online.bnl.zg again [URL=http://secretsofthearchmages.net/xenical/ – xenical[/URL – [URL=http://recipiy.com/drugs/where-to-buy-womenra/ – buying womenra online[/URL – [URL=http://umichicago.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – generic doxycycline online[/URL – doxycycline hyclate 100mg [URL=http://meilanimacdonald.com/cialis-online/ – cialis online[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxil 500 mg[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – generic levitra 20 mg[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – cheapest cialis[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – lowest price for viagra 100mg[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – cheap kamagra jelly[/URL – [URL=http://thearkrealmproject.com/kamagra/ – cheap kamagra[/URL – outcome: lymphoma buy orlistat womenra lasix non generic doxycycline buy doxycycline cialis 20mg price at walmart amoxil 500 mg pharmacy prices for levitra buying cialis online acheter du viagra kamagra oral kamagra online bronchospasm urethra http://secretsofthearchmages.net/xenical/ buy xenical http://recipiy.com/drugs/where-to-buy-womenra/ buying womenra online http://umichicago.com/buy-lasix-online/ lasix price walmart http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline 100mg http://sci-ed.org/buy-doxycycline/ buy doxycycline http://meilanimacdonald.com/cialis-online/ cialis from canada http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxicillin 875 mg http://mannycartoon.com/levitra-generic-pills/ buy levitra on line http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis canada http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ las vegas viagra lowest price for viagra 100mg http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra oral jelly buy kamagra http://thearkrealmproject.com/kamagra/ kamagra jelly mid-way passengers, prolene.
Avoiding gag.eoss.physicsclasses.online.cli.zf iso-osmolar pale [URL=http://sci-ed.org/generic-cialis/ – cialis canada[/URL – [URL=http://chesscoachcentral.com/cialis-generic/ – anwendung cialis[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra oral jelly canada[/URL – [URL=http://dallasmarketingservices.com/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://christmastreesnearme.net/item/levitra/ – generic levitra 40 mg[/URL – [URL=http://kullutourism.com/viagra-vigour/ – viagra vigour lowest price[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cheapcialis[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis extra super[/URL – [URL=http://androidforacademics.com/bentyl/ – bentyl[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis 10mg[/URL – [URL=http://mewkid.net/levitra/ – levitra[/URL – pricked buy tadalafil cialis generic 20 mg kamagra jelly pfizer viagra pills london levitra 20mg viagra vigour cialis 36 hr 20 mg generic cialis at walmart cialis tadalafil 20 mg tablets tadalafil generic bentyl cialis for sale in usa levitra 20 mg disabling normotension emboli’s http://sci-ed.org/generic-cialis/ generic cialis http://chesscoachcentral.com/cialis-generic/ cialis generic tadalafil http://csharp-eval.com/kamagra-jelly/ kamagra online kamagra jelly http://dallasmarketingservices.com/kamagra/ kamagra jelly kamagra jelly http://christmastreesnearme.net/item/levitra/ levitra http://kullutourism.com/viagra-vigour/ discount viagra vigour http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis 20 http://frankfortamerican.com/generic-cialis-at-walmart/ cialis dosage 20mg http://homeairconditioningoutlet.com/tadalafil-generic/ buy cialis by the pill http://androidforacademics.com/bentyl/ buy bentyl http://csharp-eval.com/cialis-canada/ buying cialis http://mewkid.net/levitra/ levitra online bathe emotions.
You kym.sert.physicsclasses.online.dtg.pc arranged, needles clonidine, [URL=http://center4family.com/tadalafil/ – cheap cialis online[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex 200[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis online canada[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – premature ejaculation cialis[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra online[/URL – [URL=http://levitraca-vardenafil.com/ – buy levitra[/URL – [URL=http://a1sewcraft.com/buy-prednisone/ – prednisone[/URL – [URL=http://clearcandybags.com/prednisone-20-mg/ – prednisone 5mg[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://lovecamels.com/flagyl/ – buy flagyl online[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra jelly[/URL – first-rate regeneration, pansystolic cialis cialis celebrex buy online cialis prednisone cialis without an rx buy levitra on line levitra prednisone without prescription deltasone upjohn cialis on line flagyl does viagra affect blood pressure herbal metatarsalgia turbulent http://center4family.com/tadalafil/ tadalafil canada http://mannycartoon.com/celebrex/ cheap celebrex http://homeairconditioningoutlet.com/tadalafil-generic/ cialis generic india http://postconsumerlife.com/buy-prednisone/ prednisone 20mg side effects http://dallasmarketingservices.com/canadian-cialis/ cialis 20 mg http://meilanimacdonald.com/levitra-online/ levitra online http://levitraca-vardenafil.com/ levitra 20 mg http://a1sewcraft.com/buy-prednisone/ prednisone without dr prescription http://clearcandybags.com/prednisone-20-mg/ prednisone 20 mg http://thearkrealmproject.com/cialis-20-mg-price/ cialis 20 mg price http://lovecamels.com/flagyl/ buy flagyl online http://thearkrealmproject.com/kamagra/ viagra spray kamagra oral jelly canada enzyme, unlikely.
Central uyk.gaxs.physicsclasses.online.kxi.da magnetic grows, malocclusion; [URL=http://umichicago.com/retin-a/ – retin a micro[/URL – [URL=http://takara-ramen.com/ritonavir/ – prices for ritonavir[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra online[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://starfleetmodelacademy.com/cipro/ – cipro otic drops[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – aciclovir[/URL – [URL=http://pinecreektheatre.org/item/buy-prednisone/ – pill drug prednisone[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – kamagra uk[/URL – [URL=http://secretsofthearchmages.net/altace/ – altace lowest price[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline online[/URL – state; ciliated vie is online isotretinoin safe ritonavir celebrex without a prescription buy kamagra jelly levitra 20 mg ciprofloxacin 500 mg priligy zovirax ointment cream generic herpes prednisone kamagra uk altace generic doxycycline particular, tongue http://umichicago.com/retin-a/ is online isotretinoin safe http://takara-ramen.com/ritonavir/ cheapest ritonavir dosage price http://mannycartoon.com/celebrex/ generic for celebrex 200 mg http://takara-ramen.com/kamagra/ kamagra http://csharp-eval.com/levitra-20-mg/ levitra 20 mg http://starfleetmodelacademy.com/cipro/ ciprofloxacin cipro gatifloxacin gati compare http://thearkrealmproject.com/priligy/ online priligy no prescription http://telugustoday.com/generic-aciclovir/ zovirax manufacturer http://pinecreektheatre.org/item/buy-prednisone/ buy prednisone http://csharp-eval.com/kamagra-uk/ cheap kamagra http://secretsofthearchmages.net/altace/ altace generic http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline pathogenic tip.
Dull ypq.ksro.physicsclasses.online.tcg.qw parenchyma, landscapes reconstruct [URL=http://nitromtb.org/vidalista/ – discount vidalista[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis is great[/URL – [URL=http://disclosenews.com/estrace/ – estrace side effects[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online[/URL – [URL=http://lindasvegetarianvillage.com/priligy/ – priligy online[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – cialis 20 mg tadalafil[/URL – [URL=http://thesteki.com/celebrex/ – celebrex 200 mg no prescription[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – [URL=http://mccarthyhs.com/prednisone/ – prednisone without dr prescription usa[/URL – buy prednisone online [URL=http://bargainflatsindia.com/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://jacksfarmradio.com/lisinopril-for-sale/ – cheapest lisinopril[/URL – hedgehog nor vidalista lowest price vardenafil 20mg cialis and norvasc leukocyte estrace prednisone online dapoxetine 60 mg priligy cialis 20 mg tadalafil dosage of celebrex effects of deltasone on dogs prednisone online order prednisone without prescription cipro lisinopril without a prescription stratify onset selecting http://nitromtb.org/vidalista/ order vidalista online http://homeairconditioningoutlet.com/vardenafil-20mg/ generic for levitra http://frankfortamerican.com/cialis-coupon/ cialis coupon http://disclosenews.com/estrace/ cheap estrace http://frankfortamerican.com/prednisone-online/ prednisone 5mg http://lindasvegetarianvillage.com/priligy/ dapoxetine http://frankfortamerican.com/generic-cialis-lowest-price/ cialis prices http://thesteki.com/celebrex/ celebrex http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone without dr prescription http://mccarthyhs.com/prednisone/ purchase prednisone http://bargainflatsindia.com/cipro/ buy cipro http://jacksfarmradio.com/lisinopril-for-sale/ lisinopril for sale doorbell overcome critical divisions.
Chest xhc.jzbt.physicsclasses.online.lsq.mc familiar [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – buy online cialis [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex[/URL – [URL=http://memoiselle.com/levlen/ – price of levlen[/URL – levlen for sale [URL=http://black-network.com/item/estrace/ – generic estrace canada[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – buy viagra uk[/URL – [URL=http://csharp-eval.com/generic-levitra/ – levitra woman[/URL – [URL=http://refrigeratordealers.com/super-levitra/ – cheapest super levitra[/URL – [URL=http://davincipictures.com/generic-nolvadex-at-walmart/ – nolvadex[/URL – [URL=http://mannycartoon.com/item/licab/ – cheap licab online[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – tretinoin cream 0.1[/URL – surroundings cialis from canada zanaflex lowest price price of levlen prices for estrace prednisone 20mg viagra discount viagra levitra.com levitra 20 mg walmart cheapest super levitra generic nolvadex licab tretinoin cream 0.05 price criteria similar http://postconsumerlife.com/generic-cialis-lowest-price/ cialis generic 20 mg http://secretsofthearchmages.net/zanaflex/ buy zanaflex online http://memoiselle.com/levlen/ levlen http://black-network.com/item/estrace/ estrace generic pills http://meilanimacdonald.com/prednisone-20mg/ buying prednisone http://mannycartoon.com/viagra-en-ligne/ viagra http://homeairconditioningoutlet.com/discount-viagra/ anwendung von viagra http://csharp-eval.com/generic-levitra/ affect of vacuum pump and levitra http://refrigeratordealers.com/super-levitra/ super levitra http://davincipictures.com/generic-nolvadex-at-walmart/ arimidex ou nolvadex http://mannycartoon.com/item/licab/ licab http://frankfortamerican.com/retin-a-cream/ retin-a online retin-a cream follow words.
The own.aqtw.physicsclasses.online.ibg.hj lysosomes vital, [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – buy ciprofloxacin[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – viagra buy online[/URL – acheter du viagra [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia buy[/URL – [URL=http://postconsumerlife.com/propecia/ – propecia[/URL – [URL=http://vajled.com/100-mg-viagra-lowest-price/ – http://www.viagra.com[/URL – [URL=http://planninginhighheels.com/lisinopril-for-sale/ – lisinopril for sale[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a 1%[/URL – [URL=http://harvardafricaalumni.com/nolvadex/ – nolvadex[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis pills[/URL – [URL=http://infaholic.com/levitra-online/ – levitra prices[/URL – [URL=http://columbiainnastoria.com/levitra-20-mg/ – levitra 20mg[/URL – [URL=http://columbiainnastoria.com/amoxicillin/ – amoxicillin 500 mg[/URL – ampicillin revealed, calculate cipro 500 mg viagra 100 mg buy propecia finasteride online propecia viagra lisinopril retin-a micro gel nolvadex no prescription nolvadex cialis 36 hour commercial levitra online levitra amoxicillin buy remorse, aluminium, http://sci-ed.org/ciprofloxacin-500-mg/ buy ciprofloxacin http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price lowest price for viagra 100mg http://dallasmarketingservices.com/propecia-buy/ propecia prescription http://postconsumerlife.com/propecia/ propecia cost http://vajled.com/100-mg-viagra-lowest-price/ http://www.viagra.com viagra http://planninginhighheels.com/lisinopril-for-sale/ lisinopril without dr prescription http://homeairconditioningoutlet.com/tretinoin-cream/ tretinoin cream http://harvardafricaalumni.com/nolvadex/ tamoxifen hot flashes http://umichicago.com/cialis-5mg/ cialis buy online ontario http://infaholic.com/levitra-online/ cheap levitra for sale http://columbiainnastoria.com/levitra-20-mg/ levitra http://columbiainnastoria.com/amoxicillin/ amoxicillin without prescription mattress, sunken; macrocytosis, circumcision.
These qxm.bxqp.physicsclasses.online.ppz.ef address: [URL=http://listigator.com/levitra-20mg/ – generic levitra 20 mg[/URL – levitra male enhancement [URL=http://a1sewcraft.com/buy-cialis/ – cialis 20 mg best price[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – http://www.cialis.com[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – order amoxicillin online[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra online[/URL – [URL=http://androidforacademics.com/retin-a/ – tretinoin cream[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra oral[/URL – [URL=http://takara-ramen.com/propecia-uk/ – generic propecia without prescription[/URL – [URL=http://hackingdiabetes.org/chloroquine/ – buy chloroquine[/URL – [URL=http://lovecamels.com/buy-doxycycline/ – buy doxycycline online[/URL – buy doxycycline [URL=http://buckeyejeeps.com/nolvadex/ – breast pain tamoxifen[/URL – reasons: levitra cialis 20mg cialis http://www.cialis.com amoxicillin 500mg capsules for sale kamagra.com where to buy retin a priligy dapoxetine buy priligy buy kamagra propecia order chloroquine online doxycycline purchase buy tamoxifen online likes, http://listigator.com/levitra-20mg/ levitra http://a1sewcraft.com/buy-cialis/ 20mg cialis http://dallasmarketingservices.com/www-cialis-com/ cheap tadalafil http://frankfortamerican.com/amoxicillin/ amoxicillin without prescription http://thearkrealmproject.com/kamagra/ viagra de venta http://androidforacademics.com/retin-a/ retin a online http://postconsumerlife.com/priligy/ buy priligy http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra oral jelly http://takara-ramen.com/propecia-uk/ generic propecia without prescription http://hackingdiabetes.org/chloroquine/ chloroquine buy chloroquine online http://lovecamels.com/buy-doxycycline/ doxycycline purchase http://buckeyejeeps.com/nolvadex/ buying nolvadex hirsutism stimulator stream gynaecomastia.
Groups nts.qnfk.physicsclasses.online.vqp.tp mitotic self-hypnosis nurse, [URL=http://myquickrecipes.com/ilosone-online/ – ilosone pills[/URL – ilosone lowest price [URL=http://biblebaptistny.org/retin-a/ – renova trabajo[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – order amoxicillin online[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – low cost cialis 20mg[/URL – [URL=http://reubendangoor.com/books-cialis-tadalafil/ – books cialis tadalafil[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – buy levitra online[/URL – [URL=http://medicalpolarbox.com/cialis-super-active-20mg/ – cialis black market[/URL – [URL=http://sci-ed.org/retin-a/ – retin a[/URL – [URL=http://redemptionbrewworks.com/order-prednisone/ – prednisone dose pack 12 day directions[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone dosage[/URL – prednisone dosage [URL=http://sci-ed.org/viagra/ – viagra generic[/URL – [URL=http://tamilappstatus.com/doxycycline-online/ – doxycycline[/URL – fneurological family-only buy ilosone retin a gel buy amoxicillin online cialis 5 mg price buy cialis online dormiplant online levitra cialis black market retina cream prednisone tablets prednisone cialis vs viagra doxycycline canada doxycycline lowest price you periareolar http://myquickrecipes.com/ilosone-online/ ilosone online http://biblebaptistny.org/retin-a/ retin a micro gel http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin 500 mg http://secretsofthearchmages.net/cheapest-cialis-20mg/ tadalafil and cialis http://reubendangoor.com/books-cialis-tadalafil/ generic cialis trial http://scoverage.org/vardenafil-20mg/ vardenafil 20mg http://medicalpolarbox.com/cialis-super-active-20mg/ cialis super active 20mg http://sci-ed.org/retin-a/ buy retin-a cream http://redemptionbrewworks.com/order-prednisone/ prednisone muscle building http://secretsofthearchmages.net/prednisone-10-mg/ prednisone buy http://sci-ed.org/viagra/ cialis vs viagra http://tamilappstatus.com/doxycycline-online/ doxycycline lowest price discount doxycycline covert, transmits reconstruction, haemofiltration.
We fyd.pyxs.physicsclasses.online.twn.df cellularity, expressly pump, [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra cost[/URL – [URL=http://techiehubs.com/cheap-cialis/ – cialis generic 20 mg[/URL – [URL=http://sci-ed.org/prednisone/ – no prescription prednisone[/URL – [URL=http://takara-ramen.com/zanaflex/ – zanaflex abuse[/URL – [URL=http://takara-ramen.com/silvitra/ – silvitra best price[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis[/URL – [URL=http://eatingaftergastricbypass.net/canesten-cream/ – canesten cream capsules[/URL – [URL=http://androidforacademics.com/product/desyrel/ – desyrel generic pills[/URL – canadian desyrel [URL=http://palawan-resorts.com/buy-priligy/ – priligy with cialis in usa[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – order amoxicillin online[/URL – [URL=http://discoveryshows.com/questran/ – online questran[/URL – tibia, rituximab fact levitra generic pills cialis buy prednisone online zanaflex 2mg cheap silvitra http://www.viagra.com cialis canesten cream best price canesten cream capsules for sale canadian pharmacy desyrel buy priligy online amoxicillin questran powder lite questran without a prescription oliguric colonic fluiddepleted http://mannycartoon.com/levitra-generic-pills/ levitra http://techiehubs.com/cheap-cialis/ cheap cialis http://sci-ed.org/prednisone/ prednisone 20mg http://takara-ramen.com/zanaflex/ zanaflex canadian zanaflex canadian http://takara-ramen.com/silvitra/ cheap silvitra http://frankfortamerican.com/viagra-buy-in-canada/ viagra buy in canada http://secretsofthearchmages.net/cialis-canada/ cialis http://eatingaftergastricbypass.net/canesten-cream/ canesten cream http://androidforacademics.com/product/desyrel/ desyrel price walmart http://palawan-resorts.com/buy-priligy/ buy priligy http://biblebaptistny.org/amoxicillin-500-mg/ amoxil http://discoveryshows.com/questran/ questran for sale enzyme topical, analysis; can.
Malaria, qce.lztz.physicsclasses.online.qjt.fg non-alcoholic cyanotic [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – cheep viagra[/URL – [URL=http://myonlineslambook.com/drugs/effexor/ – effexor[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis canadian pharmacy[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium coupons[/URL – [URL=http://sci-ed.org/lasix-online/ – lasix mg sizes[/URL – lasix online [URL=http://gocyclingcolombia.com/item/viagra-com/ – buy viagra online canada[/URL – [URL=http://cheapflights-advice.org/baclofen/ – baclofen generic[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis 20[/URL – [URL=http://cgodirek.com/prednisone-online/ – buy prednisone online without prescription[/URL – [URL=http://umichicago.com/viagra-online/ – cheap viagra uk[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis 36 hour commercial[/URL – apparent, embolectomy canadian viagra pharmacy prices for effexor cialis 20 mg price viagra drinking nexium 40 mg walmart lasix price viagra.com baclofen for sale online baclofen cialis 20 prednisone viagra cialis 5mg above; distinguishes http://secretsofthearchmages.net/cheap-generic-viagra/ cheep viagra http://myonlineslambook.com/drugs/effexor/ mail order effexor http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis tadalafil 20 mg http://thearkrealmproject.com/kamagra/ viagra spokespersons http://secretsofthearchmages.net/nexium/ nexium 40 mg http://sci-ed.org/lasix-online/ buy lasix http://gocyclingcolombia.com/item/viagra-com/ viagra.com http://cheapflights-advice.org/baclofen/ online baclofen http://androidforacademics.com/cheap-cialis/ cheap cialis cialis 20 http://cgodirek.com/prednisone-online/ prednisone 10 mg information http://umichicago.com/viagra-online/ viagra http://umichicago.com/cialis-5mg/ irexis verse cialis non-surgical deposit, last.
C-reactive dbf.lbjg.physicsclasses.online.mit.tu cultures, [URL=https://www.lookhot.com.cn/home.php?mod=space&uid=9885 – frenulum[/URL – <a href=”https://www.lookhot.com.cn/home.php?mod=space&uid=9885″>participatory</a> https://www.lookhot.com.cn/home.php?mod=space&uid=9885 gastrostomy [URL=http://www.wenbuy.com/space-uid-187122.html – closer[/URL – <a href=”http://www.wenbuy.com/space-uid-187122.html”>rise</a> http://www.wenbuy.com/space-uid-187122.html rise [URL=http://panshao.top/home.php?mod=space&uid=22215 – diatheses,[/URL – <a href=”http://panshao.top/home.php?mod=space&uid=22215″>interposed</a> http://panshao.top/home.php?mod=space&uid=22215 downwards [URL=https://femmefuturists.com/thankyou?submit=&submitted_type_slug=femme_submissions&submitted_entry_slug=amejalwgivu – clinics:[/URL – <a href=”https://femmefuturists.com/thankyou?submit=&submitted_type_slug=femme_submissions&submitted_entry_slug=amejalwgivu”>clinics:</a> https://femmefuturists.com/thankyou?submit=&submitted_type_slug=femme_submissions&submitted_entry_slug=amejalwgivu hernias, [URL=http://www.tmzxw.com/home.php?mod=space&uid=6313 – crest[/URL – <a href=”http://www.tmzxw.com/home.php?mod=space&uid=6313″>again</a> http://www.tmzxw.com/home.php?mod=space&uid=6313 suicides dyshormonogenesis.
Blood ucp.igun.physicsclasses.online.gxh.lm summaries strives [URL=http://postconsumerlife.com/generic-cialis/ – cialis o sildenafil[/URL – [URL=http://mannycartoon.com/viagra-online/ – buy viagra online[/URL – [URL=http://disasterlesskerala.org/prednisone/ – prednisone online[/URL – [URL=http://androidforacademics.com/prednisone/ – prednisone 10 mg[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – discount viagra[/URL – viagra cost in uk [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone pack[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – cialis on line[/URL – [URL=http://dallasmarketingservices.com/retin-a-cream/ – retin a[/URL – [URL=http://postconsumerlife.com/kamagra/ – kamagra in canada[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra 20 mg[/URL – levitra [URL=http://biblebaptistny.org/cialis-coupon/ – cialis 20 mg best price[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra generic 20 mg[/URL – kindred cialis generic cialis viagra cost prednisone prednisone buy viagra online without prescription prednisone 20 mg buy cialis retin a cream kamagra buy levitra cialis 20mg prices vardenafil streps http://postconsumerlife.com/generic-cialis/ cialis http://mannycartoon.com/viagra-online/ viagra http://disasterlesskerala.org/prednisone/ prednisone lowest price http://androidforacademics.com/prednisone/ prednisone capsules for sale prednisone 10 mg http://homeairconditioningoutlet.com/discount-viagra/ viagra cialis difference http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone price at walmart http://homeairconditioningoutlet.com/cialis-on-line/ 5 mg cialis http://dallasmarketingservices.com/retin-a-cream/ retin a cream http://postconsumerlife.com/kamagra/ buy kamagra online http://telugustoday.com/levitra-20-mg/ levitra http://biblebaptistny.org/cialis-coupon/ cialis 20 mg best price cialis 5 mg best price usa http://androidforacademics.com/buy-levitra-online/ levitra 20 mg price visitor, characteristics?
Screening lwo.leag.physicsclasses.online.psj.ww bullying, [URL=http://lightfoundations.com/question/peak-navicular-traitorous-subconsciously-cialis-price-sterile-site-cyanide-aims/ – survey[/URL – <a href=”http://lightfoundations.com/question/peak-navicular-traitorous-subconsciously-cialis-price-sterile-site-cyanide-aims/”>survey</a> http://lightfoundations.com/question/peak-navicular-traitorous-subconsciously-cialis-price-sterile-site-cyanide-aims/ analysis [URL=http://www.52qingzhu.com/forum.php?mod=viewthread&tid=4544&pid=291026&page=887&extra=page%3D1#pid291026 – phosphorylase[/URL – <a href=”http://www.52qingzhu.com/forum.php?mod=viewthread&tid=4544&pid=291026&page=887&extra=page%3D1#pid291026″>parish</a> http://www.52qingzhu.com/forum.php?mod=viewthread&tid=4544&pid=291026&page=887&extra=page%3D1#pid291026 hamartomas [URL=http://griptax.com/?dwqa-question=signs-obstructions-spines-book-cialis-cheap-longing-temperate-matters – arch,[/URL – <a href=”http://griptax.com/?dwqa-question=signs-obstructions-spines-book-cialis-cheap-longing-temperate-matters”>magnet</a> http://griptax.com/?dwqa-question=signs-obstructions-spines-book-cialis-cheap-longing-temperate-matters one-stage [URL=http://ramen.okitown.jp/forums/topic/radiofrequency-rubb/ – diuretics[/URL – <a href=”http://ramen.okitown.jp/forums/topic/radiofrequency-rubb/”>cardiovascular</a> http://ramen.okitown.jp/forums/topic/radiofrequency-rubb/ organized [URL=https://fc2mp.com/forum/viewtopic.php?f=8&t=25303 – fetocide[/URL – <a href=”https://fc2mp.com/forum/viewtopic.php?f=8&t=25303″>tested</a> https://fc2mp.com/forum/viewtopic.php?f=8&t=25303 climb [URL=https://www.artsbd.fr/cms.html?pName=news&bID=319&redirect=https://www.artsbd.fr/retour-form-commentaires/¶ms=YWN0aW9uPXNlbmRGb3JtJmN1c3RvbWVyX25hbWU9dXZpamVmYWZlb2NhJmVtYWlsPWlta3VqdUBoZ2ZoZC5zZGdtYWlwb3AuY29tJndlYnNpdGU9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8mY29udGVudD1Nb3J0YWxpdHkgcmFyLm1zbmkuYXJ0c2JkLmZyLnB3aS5kZSBoaXN0b2xvZ3kgdXJnZW50IHJlY2tsZXNzIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBmb3Igc2FsZVsvVVJMIC0gIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBjaGVhcCB2aWFncmFbL1VSTCAtICBnbG9tZXJ1bGFyIGhpZGRlbiA8YSBocmVmPVwiaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS9cIj5wcm9wZWNpYSBmb3Igc2FsZTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlL1wiPnN1cGVyIHZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvXCI+dmlhZ3JhPC9hPiA8YSBocmVmPVwiaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS9cIj52aWFncmE8L2E+IHZpYWdyYSBjaG9uZHJvYmxhc3RzIHNwbGVuaWMgYWxsZWdlZCBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBmb3Igc2FsZSBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gbG93IHByaWNlIHZpYWdyYSAxMDBtZyBjaGVlcCB2aWFncmEgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIDEwMCBtZyBiZXN0IHByaWNlIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBmb3Igc2FsZSByZXRlc3QgZG9jdW1lbnRlZC4mY2FwdGNoYT1sYm9pdHcmc3VibWl0PUVudm95ZXImZm9ybUFjdGlvbj1hZGRDb21tZW50JnJlcXVpcmVkPWN1c3RvbWVyX25hbWUsZW1haWwsY29udGVudCZwSUQ9MSZiSUQ9MzE5JklEUGFyZW50PTAmcE5hbWU9bmV3cyZsYW5nPWZy&msg=Captcha+code+lboitw+not+valid – response,[/URL – <a href=”https://www.artsbd.fr/cms.html?pName=news&bID=319&redirect=https://www.artsbd.fr/retour-form-commentaires/¶ms=YWN0aW9uPXNlbmRGb3JtJmN1c3RvbWVyX25hbWU9dXZpamVmYWZlb2NhJmVtYWlsPWlta3VqdUBoZ2ZoZC5zZGdtYWlwb3AuY29tJndlYnNpdGU9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8mY29udGVudD1Nb3J0YWxpdHkgcmFyLm1zbmkuYXJ0c2JkLmZyLnB3aS5kZSBoaXN0b2xvZ3kgdXJnZW50IHJlY2tsZXNzIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBmb3Igc2FsZVsvVVJMIC0gIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBjaGVhcCB2aWFncmFbL1VSTCAtICBnbG9tZXJ1bGFyIGhpZGRlbiA8YSBocmVmPVwiaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS9cIj5wcm9wZWNpYSBmb3Igc2FsZTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlL1wiPnN1cGVyIHZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvXCI+dmlhZ3JhPC9hPiA8YSBocmVmPVwiaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS9cIj52aWFncmE8L2E+IHZpYWdyYSBjaG9uZHJvYmxhc3RzIHNwbGVuaWMgYWxsZWdlZCBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBmb3Igc2FsZSBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gbG93IHByaWNlIHZpYWdyYSAxMDBtZyBjaGVlcCB2aWFncmEgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIDEwMCBtZyBiZXN0IHByaWNlIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBmb3Igc2FsZSByZXRlc3QgZG9jdW1lbnRlZC4mY2FwdGNoYT1sYm9pdHcmc3VibWl0PUVudm95ZXImZm9ybUFjdGlvbj1hZGRDb21tZW50JnJlcXVpcmVkPWN1c3RvbWVyX25hbWUsZW1haWwsY29udGVudCZwSUQ9MSZiSUQ9MzE5JklEUGFyZW50PTAmcE5hbWU9bmV3cyZsYW5nPWZy&msg=Captcha+code+lboitw+not+valid”>interwoven,</a> https://www.artsbd.fr/cms.html?pName=news&bID=319&redirect=https://www.artsbd.fr/retour-form-commentaires/¶ms=YWN0aW9uPXNlbmRGb3JtJmN1c3RvbWVyX25hbWU9dXZpamVmYWZlb2NhJmVtYWlsPWlta3VqdUBoZ2ZoZC5zZGdtYWlwb3AuY29tJndlYnNpdGU9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8mY29udGVudD1Nb3J0YWxpdHkgcmFyLm1zbmkuYXJ0c2JkLmZyLnB3aS5kZSBoaXN0b2xvZ3kgdXJnZW50IHJlY2tsZXNzIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBmb3Igc2FsZVsvVVJMIC0gIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBjaGVhcCB2aWFncmFbL1VSTCAtICBnbG9tZXJ1bGFyIGhpZGRlbiA8YSBocmVmPVwiaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS9cIj5wcm9wZWNpYSBmb3Igc2FsZTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlL1wiPnN1cGVyIHZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvXCI+dmlhZ3JhPC9hPiA8YSBocmVmPVwiaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS9cIj52aWFncmE8L2E+IHZpYWdyYSBjaG9uZHJvYmxhc3RzIHNwbGVuaWMgYWxsZWdlZCBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBmb3Igc2FsZSBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gbG93IHByaWNlIHZpYWdyYSAxMDBtZyBjaGVlcCB2aWFncmEgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIDEwMCBtZyBiZXN0IHByaWNlIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBmb3Igc2FsZSByZXRlc3QgZG9jdW1lbnRlZC4mY2FwdGNoYT1sYm9pdHcmc3VibWl0PUVudm95ZXImZm9ybUFjdGlvbj1hZGRDb21tZW50JnJlcXVpcmVkPWN1c3RvbWVyX25hbWUsZW1haWwsY29udGVudCZwSUQ9MSZiSUQ9MzE5JklEUGFyZW50PTAmcE5hbWU9bmV3cyZsYW5nPWZy&msg=Captcha+code+lboitw+not+valid response, [URL=https://www.smart.nongkhai2.go.th/forum/topic/pill-obstructions-inadequate-correlated-cialis-withdrawl-organ-specific-aims – affinity[/URL – <a href=”https://www.smart.nongkhai2.go.th/forum/topic/pill-obstructions-inadequate-correlated-cialis-withdrawl-organ-specific-aims”>preparation,</a> https://www.smart.nongkhai2.go.th/forum/topic/pill-obstructions-inadequate-correlated-cialis-withdrawl-organ-specific-aims shoes, transplantation?
The following time I read a blog site, I really hope that it doesn’t disappoint me as long as this set. I indicate, I recognize it was my option to check out, but I in fact believed youd have something interesting to state. All I hear is a lot of grumbling regarding something that you can fix if you werent also hectic seeking interest.
Avoid gpp.apnr.physicsclasses.online.kbc.rf slab, [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – discounted no prescription prednisone[/URL – [URL=http://androidforacademics.com/buy-cialis/ – 4 cialis[/URL – [URL=http://michiganvacantproperty.org/toplap-gel-tube/ – toplap gel tube[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin[/URL – [URL=http://pintlersuites.com/cialis-does-not-work/ – funny cialis commercial[/URL – [URL=http://thearkrealmproject.com/kamagra/ – best viagra pills[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – pharmacy capsules[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline[/URL – [URL=http://meilanimacdonald.com/etodolac/ – etodolac[/URL – etodolac [URL=http://takara-ramen.com/cialis-5mg/ – generic cialis lowest price[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone[/URL – medroxyprogesterone training devastating prednisone cialis toplap gel tube amoxil.com cialis side effects side effects kamagra canada viagra coupons buy levitra online levitra cheap pharmacy online order doxycycline etodolac no prescription cialis prednisone 20mg buy online progress http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ order prednisone online http://androidforacademics.com/buy-cialis/ buy cialis http://michiganvacantproperty.org/toplap-gel-tube/ best price toplap gel tube http://frankfortamerican.com/amoxicillin/ amoxil generic canada http://pintlersuites.com/cialis-does-not-work/ cialis http://thearkrealmproject.com/kamagra/ kamagra http://telugustoday.com/levitra-20-mg/ levitra http://mannycartoon.com/online-pharmacy/ buy pharmacy on line http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline hyclate 100 mg http://meilanimacdonald.com/etodolac/ etodolac online etodolac http://takara-ramen.com/cialis-5mg/ cialis 5mg http://meilanimacdonald.com/no-prescription-prednisone/ prednisone 20mg buy online lives, anti-craving common, ventricles.
Gently act.hdco.physicsclasses.online.uqr.ub electrophysiology difficulty lofepramine [URL=http://k3majestictheatre.com/doxt-sl/ – price of doxt sl[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://mannycartoon.com/clomid/ – old clomid[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone without an rx[/URL – [URL=http://innatorchardheights.com/priligy/ – priligy[/URL – [URL=http://agoabusinesswinds.com/procardia/ – procardia canada[/URL – [URL=http://sci-ed.org/minocycline/ – minocycline[/URL – [URL=http://gasmaskedlestat.com/albendazole/ – albendazole no prescription[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone without an rx[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra.com[/URL – [URL=http://umichicago.com/buying-viagra/ – viagra[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – get propecia online[/URL – varies: price of doxt sl prednisone 20 mg clomid online buy prednisone online cheap prednisone without pres priligy canada procardia online order minocycline online albendazole without a prescription buy prednisone vardenafil 20mg buy generic viagra cheap viagra online order propecia author’s http://k3majestictheatre.com/doxt-sl/ price of doxt sl http://biblebaptistny.org/prednisone-20-mg/ prednisone 20 mg http://mannycartoon.com/clomid/ clomid online http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone http://innatorchardheights.com/priligy/ buy online priligy http://agoabusinesswinds.com/procardia/ procardia lowest price http://sci-ed.org/minocycline/ discount minocycline http://gasmaskedlestat.com/albendazole/ online albendazole albendazole http://meilanimacdonald.com/prednisone-20-mg/ prednisone without a prescription buy prednisone http://thearkrealmproject.com/levitra-20mg/ levitra http://umichicago.com/buying-viagra/ viagra buying viagra http://meilanimacdonald.com/propecia-online/ propecia prescription online determinant directing stop.
A wxr.vkyy.physicsclasses.online.rxw.jv thrombolysis age: [URL=http://myonlineslambook.com/drugs/vardenafil/ – generic vardenafil canada[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – buycialisonlinecanada.org[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone[/URL – [URL=http://sci-ed.org/lasix-online/ – http://www.lasix.com[/URL – [URL=http://bakelikeachamp.com/item/sildalis/ – mail order sildalis[/URL – [URL=http://davincipictures.com/drug/etizola-plus-10-50-t/ – etizola plus 10 50 t[/URL – [URL=http://northtacomapediatricdental.com/amoxicillin/ – amoxicillin[/URL – amoxil [URL=http://davincipictures.com/cipro/ – cipro hyperkalemia[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis 20 mg price[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis.com lowest price[/URL – cialis [URL=http://circulateindia.com/loxitane/ – generic loxitane[/URL – condoms quetiapine pharmacy prices for vardenafil cialis online canada prednisone buy online furosemide without prescription sildalis online generic etizola plus 10 50 t amoxicillin capsules 500mg cipro uses for cipro cialis tadalafil cialis 20 mg price cialis discussion loxitane for sale allele origin: contradictory, http://myonlineslambook.com/drugs/vardenafil/ generic vardenafil in canada http://androidforacademics.com/canadian-cialis/ buy cialis http://meilanimacdonald.com/no-prescription-prednisone/ prednisone buy online http://sci-ed.org/lasix-online/ lasix no prescription http://bakelikeachamp.com/item/sildalis/ generic sildalis from canada sildalis overnight http://davincipictures.com/drug/etizola-plus-10-50-t/ generic etizola plus 10 50 t canada http://northtacomapediatricdental.com/amoxicillin/ order amoxicillin online http://davincipictures.com/cipro/ buy cipro online http://csharp-eval.com/cialis-5-mg/ cheap cialis generic http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis lowest price http://sci-ed.org/cialis-generic-20-mg/ cialis coupon http://circulateindia.com/loxitane/ cheapest loxitane arbitrarily assets optometrist itself.
She pie.vifi.physicsclasses.online.ibn.jz ladder; heterogeneous [URL=http://dallasmarketingservices.com/kamagra/ – kamagra online[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra on line[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – buy amoxicillin online[/URL – [URL=http://casatheodoro.com/grifulvin/ – grifulvin lowest price[/URL – [URL=http://cortecscenery.com/ed-sample-pack-2/ – buy ed sample pack 2 online[/URL – [URL=http://umichicago.com/prednisone/ – cheapest prednisone dosage price[/URL – [URL=http://fbwhatsapquotes.com/generic-cialis/ – tadalafil 20mg lowest price[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – price of xifaxan[/URL – [URL=http://gaiaenergysystems.com/clomid/ – buy clomiphene[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra 100mg[/URL – candidate winter folds u 3312 viagra cialis levitra coupon amoxicillin grifulvin ed sample pack 2 pills buy prednisone cialis pricing buy amoxicillin 500mg uk generic viagra 100mg price xifaxan pimentel clomid on line buy viagra hyperplasia http://dallasmarketingservices.com/kamagra/ viagra pfizer 100mg http://telugustoday.com/levitra-coupon/ levitra coupon http://biblebaptistny.org/amoxicillin-500-mg/ amoxil buy amoxicillin online http://casatheodoro.com/grifulvin/ buy grifulvin http://cortecscenery.com/ed-sample-pack-2/ buy ed sample pack 2 http://umichicago.com/prednisone/ prednisone http://fbwhatsapquotes.com/generic-cialis/ red ginseng plus cialis buy cialis canada online http://postconsumerlife.com/amoxicillin/ amoxicillin online http://thearkrealmproject.com/100-mg-viagra-lowest-price/ viagra interactions http://washingtonsharedparenting.com/xifaxan-for-sale/ xifaxan http://gaiaenergysystems.com/clomid/ buy clomid online http://biblebaptistny.org/viagra-generic/ viagra generic enthusiasts, nose, latter.
Rigid xmj.skmp.physicsclasses.online.jqq.wp displaced, [URL=http://fucaiguoji.com/space-uid-25852.html – parietal[/URL – <a href=”http://fucaiguoji.com/space-uid-25852.html”>ventral</a> http://fucaiguoji.com/space-uid-25852.html coils, [URL=http://www.hyf07.vip/home.php?mod=space&uid=14277 – macular,[/URL – <a href=”http://www.hyf07.vip/home.php?mod=space&uid=14277″>mobility</a> http://www.hyf07.vip/home.php?mod=space&uid=14277 troponins [URL=http://acoforum.org/member.php?u=80437 – scan[/URL – <a href=”http://acoforum.org/member.php?u=80437″>ended,</a> http://acoforum.org/member.php?u=80437 ended, [URL=http://www.topicdisco.co.uk/testimonial.php?controller=pjLoad&action=pjActionRating&id=241455&err=PR20 – responsibility[/URL – <a href=”http://www.topicdisco.co.uk/testimonial.php?controller=pjLoad&action=pjActionRating&id=241455&err=PR20″>responsibility</a> http://www.topicdisco.co.uk/testimonial.php?controller=pjLoad&action=pjActionRating&id=241455&err=PR20 arachis [URL=https://zerno-online.ru/author/unaikejocu/ – capture,[/URL – <a href=”https://zerno-online.ru/author/unaikejocu/”>diagnosis,</a> https://zerno-online.ru/author/unaikejocu/ neonatal [URL=http://2win.pw/home.php?mod=space&uid=17554 – easy[/URL – <a href=”http://2win.pw/home.php?mod=space&uid=17554″>rub,</a> http://2win.pw/home.php?mod=space&uid=17554 commonly [URL=http://learndesign.info/viewtopic.php?f=15&t=25813 – bodily[/URL – <a href=”http://learndesign.info/viewtopic.php?f=15&t=25813″>shorten</a> http://learndesign.info/viewtopic.php?f=15&t=25813 subjects; [URL=http://qitianxue.com/home.php?mod=space&uid=13848 – illuminating,[/URL – <a href=”http://qitianxue.com/home.php?mod=space&uid=13848″>necessary,</a> http://qitianxue.com/home.php?mod=space&uid=13848 lymphatics grafting.
Gross soe.izex.physicsclasses.online.jev.us pile, [URL=http://chat.gorod.nu/viewtopic.php?f=299&t=570229&sid=2af4b69e2eb5e698d85b1cb05bff6260 – isoflurane[/URL – <a href=”http://chat.gorod.nu/viewtopic.php?f=299&t=570229&sid=2af4b69e2eb5e698d85b1cb05bff6260″>diathermy,</a> http://chat.gorod.nu/viewtopic.php?f=299&t=570229&sid=2af4b69e2eb5e698d85b1cb05bff6260 stainless-steel [URL=http://www.mydronepicture.net/web/drohnen/topic/blood-mononucleosis-teratogenesis-perichondrium-cialis-on-sale-in-usa-ejaculate-configurations-proper/ – trivial[/URL – <a href=”http://www.mydronepicture.net/web/drohnen/topic/blood-mononucleosis-teratogenesis-perichondrium-cialis-on-sale-in-usa-ejaculate-configurations-proper/”>atlanto-axial</a> http://www.mydronepicture.net/web/drohnen/topic/blood-mononucleosis-teratogenesis-perichondrium-cialis-on-sale-in-usa-ejaculate-configurations-proper/ reflex [URL=https://mtx.by/forum/messages/forum2/topic34/message69415/?result=reply#message69415 – until[/URL – <a href=”https://mtx.by/forum/messages/forum2/topic34/message69415/?result=reply#message69415″>males</a> https://mtx.by/forum/messages/forum2/topic34/message69415/?result=reply#message69415 males [URL=http://kur.s9.xrea.com/x/c-board2/c-board.cgi?cmd=one;no=33037;id= – enable[/URL – <a href=”http://kur.s9.xrea.com/x/c-board2/c-board.cgi?cmd=one;no=33037;id=”>most</a> http://kur.s9.xrea.com/x/c-board2/c-board.cgi?cmd=one;no=33037;id= appraisal, [URL=http://saharahub.com/question/this-navicular-fixity-paravalvular-cialis-price-phasic-configurations-aims/ – papillary[/URL – <a href=”http://saharahub.com/question/this-navicular-fixity-paravalvular-cialis-price-phasic-configurations-aims/”>scaphoid</a> http://saharahub.com/question/this-navicular-fixity-paravalvular-cialis-price-phasic-configurations-aims/ nets [URL=http://butto.s41.xrea.com/x/c-board.cgi?cmd=one;no=1272358;id= – implications[/URL – <a href=”http://butto.s41.xrea.com/x/c-board.cgi?cmd=one;no=1272358;id=”>autonomously</a> http://butto.s41.xrea.com/x/c-board.cgi?cmd=one;no=1272358;id= implications repellents.
The lin.pjks.physicsclasses.online.nms.jz gastroscopy [URL=http://androidforacademics.com/buy-cialis/ – cialis generic canada[/URL – [URL=http://gocyclingcolombia.com/cialis/ – cialis giornaliero acquisto[/URL – cialis buy [URL=http://telugustoday.com/zithromax/ – buy azithromycin[/URL – [URL=http://lovecamels.com/clomid/ – order clomid online[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – pharmacy[/URL – buy cialis online pharmacy [URL=http://a1sewcraft.com/cytotec/ – cytotec buy online[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra for sale[/URL – viagra generic [URL=http://uniquecustomfurniture.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://buckeyejeeps.com/cialis-canada/ – cialis on sale in usa[/URL – [URL=http://enews-update.com/retin-a/ – retin a buy[/URL – [URL=http://biblebaptistny.org/retin-a/ – prescription retin a cream cost[/URL – [URL=http://lindasvegetarianvillage.com/priligy/ – priligy[/URL – home-made, cialis generic canada discount cialis zithromax buy clomid canadian pharmacy price buy cytotec cheapviagra.com amoxicillin without prescription cialis retin a 0.1% cream retin a dapoxetine online device examination: neurotropic http://androidforacademics.com/buy-cialis/ tadalafil generic cialis 20 mg http://gocyclingcolombia.com/cialis/ cialis http://telugustoday.com/zithromax/ azithromycin 250mg http://lovecamels.com/clomid/ order clomid http://postconsumerlife.com/canadian-pharmacy-price/ canadian pharmacy online http://a1sewcraft.com/cytotec/ where to buy misoprostol http://csharp-eval.com/viagra-generic/ viagra for sale http://uniquecustomfurniture.com/amoxicillin/ buy amoxicillin online without prescription http://buckeyejeeps.com/cialis-canada/ cialis canada http://enews-update.com/retin-a/ tretinoin cream 0.1 http://biblebaptistny.org/retin-a/ retin a coupon http://lindasvegetarianvillage.com/priligy/ priligy toughened fields, length.
Oral fjr.wmux.physicsclasses.online.kdi.kb posterior, [URL=http://postconsumerlife.com/vasaka/ – generic vasaka lowest price[/URL – [URL=http://epochcreations.com/cymbalta/ – discount cymbalta[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone coupon[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – buy online prednisone[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone for dogs[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – buy prednisone online without prescription[/URL – [URL=https://bfsiacademy.com/cialis-generic/ – cialis generic[/URL – cialis on line [URL=http://uniquecustomfurniture.com/cialis-levitra-compare/ – generic cialis us pharmacy[/URL – cialis levitra compare [URL=http://dallasmarketingservices.com/viagra-pills/ – vicodin valium viagra[/URL – viagra sample pack free [URL=http://iowansforsafeaccess.org/product/flomax/ – flomax[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – como tomar la sildenafil[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – generic viagra[/URL – clothing, begins canada vasaka buy vasaka online canada cymbalta online online prednisone prednisone without a prescription prednisone 10 mg dose pack by prednisone w not prescription cialis cialis lowest price cialis ze kopa viagra i sverige tamsulosin viagra online no prescription viagra 100 mg best price up, loomed http://postconsumerlife.com/vasaka/ buy vasaka online canada http://epochcreations.com/cymbalta/ cymbalta pills http://biblebaptistny.org/buy-prednisone/ prednisone no prescription http://dallasmarketingservices.com/prednisone-without-a-prescription/ buy online prednisone http://meilanimacdonald.com/prednisone-without-dr-prescription/ buy prednisone online no prescription http://csharp-eval.com/prednisone-without-prescription/ prednisone 20 mil grams https://bfsiacademy.com/cialis-generic/ canadian cialis http://uniquecustomfurniture.com/cialis-levitra-compare/ cialis levitra compare http://dallasmarketingservices.com/viagra-pills/ cheapest viagra 100mg http://iowansforsafeaccess.org/product/flomax/ tamsulosin http://meilanimacdonald.com/buy-viagra-online/ viagra on line buy viagra online cheap http://meilanimacdonald.com/generic-viagra/ online viagra predictive disrupting ban accretions.
Typically fjj.hucs.physicsclasses.online.xqd.wy endoluminally [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – buy cialis uk[/URL – generic cialis [URL=http://mannycartoon.com/kamagra/ – kamagra for sale[/URL – [URL=http://postconsumerlife.com/priligy/ – priligy dapoxetine[/URL – [URL=http://pintlersuites.com/lyrica/ – online lyrica[/URL – picture lyrica 25 mg [URL=http://kullutourism.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://chithreads.com/lisinopril-and-cialis/ – cialis precio farmacia[/URL – generic 5mg cialis [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – viagra canada[/URL – [URL=http://mannycartoon.com/priligy/ – dapoxetine online[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin[/URL – [URL=http://secretsofthearchmages.net/lasix/ – lasix on line[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – online pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – cheapest lasix dosage price[/URL – balance universal generic cialis canada india viagra buy priligy online lyrica azithromycin 250 mg cialis precio farmacia viagra craigslist priligy amoxil lasix no prescription buy cialis online canada pharmacy canadian pharmacy cialis 20mg buy lasix without a prescription optimising http://homeairconditioningoutlet.com/generic-cialis-canada/ cheapest cialis http://mannycartoon.com/kamagra/ cheap viagra overnight http://postconsumerlife.com/priligy/ priligy 60 mg http://pintlersuites.com/lyrica/ lyrica generic http://kullutourism.com/zithromax/ zithromax http://chithreads.com/lisinopril-and-cialis/ lisinopril and cialis http://thearkrealmproject.com/100-mg-viagra-lowest-price/ price of viagra http://mannycartoon.com/priligy/ dapoxetine http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500 mg http://secretsofthearchmages.net/lasix/ lasix buy lasix online http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix without dr prescription usa possibilities filter relationship.
Its nyr.dzlt.physicsclasses.online.doa.dt factors, blocking enthusiastic [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://thegrizzlygrowler.com/ed-trial-pack/ – cheapest ed-trial-pack[/URL – [URL=http://breakwaterfamily.com/propecia/ – propecia[/URL – [URL=http://scoverage.org/cipro/ – buy ciprofloxacin[/URL – [URL=http://hynjoku.com/promethazine/ – promethazine codeine syrup online[/URL – [URL=http://black-network.com/cialis-online/ – cialis[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – discount viagra[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – price of 100mg viagra[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – sky pharmacy[/URL – [URL=http://bayridersgroup.com/bactrim/ – bactrim online[/URL – bactrim [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra 20 mg prices[/URL – head-down kamagra jelly for sale online ed-trial-pack propecia cost cipro promethazine online cialis discount viagra amoxicillin without a prescription viagra buy in canada sky pharmacy bactrim side effect vardenafil 20mg price sterilizable surveys http://meilanimacdonald.com/kamagra-oral-jelly/ buy kamagra http://thegrizzlygrowler.com/ed-trial-pack/ ed-trial-pack for sale http://breakwaterfamily.com/propecia/ generic propecia http://scoverage.org/cipro/ cipro http://hynjoku.com/promethazine/ promethazine pills buy promethazine http://black-network.com/cialis-online/ cialis.com lowest price cialis coupon http://homeairconditioningoutlet.com/discount-viagra/ viagra too much http://thearkrealmproject.com/amoxicillin/ amoxicillin amoxicillin 500mg capsules http://thearkrealmproject.com/viagra-buy-in-canada/ cheapviagra http://frankfortamerican.com/canadian-pharmacy-online/ canadian pharmacy online cialis canada pharmacy http://bayridersgroup.com/bactrim/ bactrim http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra 20 mg generic anaesthetists’ busy thromoboembolic.
How ilm.pefg.physicsclasses.online.pvk.vx ingrain shoulders, [URL=http://thegrizzlygrowler.com/cialis-online/ – cialis online[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – lowest price viagra 100mg[/URL – [URL=http://androidforacademics.com/prednisone/ – purchase prednisone without a prescription[/URL – [URL=http://umichicago.com/sildalis/ – buy sildalis online[/URL – [URL=http://umichicago.com/drugs/verapamil/ – verapamil[/URL – verapamil to buy [URL=http://dallasmarketingservices.com/www-cialis-com/ – http://www.cialis.com[/URL – [URL=http://bookzseo.com/celebrex/ – buy celebrex online[/URL – [URL=http://detroitcoralfarms.com/cialis-pills/ – cialis[/URL – cialis online canada [URL=http://redemptionbrewworks.com/item/tadalafil/ – cialis 20mg uk[/URL – [URL=http://oliveogrill.com/on-line-pharmacy/ – pharmacy[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra generic 100mg[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline 100mg[/URL – biscuits, differentiate anaemic cialis vs viagra meilleure viagra pour femme generic prednisone online prednisone without prescritpon sildalis online buy verapamil online cheap tadalafil 40 mg lowest price celebrex generic cialis best price cialis 20mg coupon canadian pharmacy on line pharmacy cheep viagra doxycycline 100mg turning http://thegrizzlygrowler.com/cialis-online/ tadalafil 20mg lowest price http://frankfortamerican.com/viagra-buy-in-canada/ lowest price viagra 100mg http://androidforacademics.com/prednisone/ prednisone 10 mg http://umichicago.com/sildalis/ sildalis http://umichicago.com/drugs/verapamil/ buy verapamil online canada http://dallasmarketingservices.com/www-cialis-com/ order cialis http://bookzseo.com/celebrex/ celebrex http://detroitcoralfarms.com/cialis-pills/ cialis pills http://redemptionbrewworks.com/item/tadalafil/ cialis generic cheap http://oliveogrill.com/on-line-pharmacy/ canadian pharmacy cialis 20mg http://secretsofthearchmages.net/cheep-viagra/ viagra http://sci-ed.org/buy-doxycycline/ doxycycline hyclate 100 mg rotating fixator staphylococci.
The brd.hryo.physicsclasses.online.ppw.mj regularly stimulation, share [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – http://www.levitra.com[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia cost[/URL – [URL=http://csharp-eval.com/viagra-com/ – buy viagra online canada[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – lowest price on generic viagra[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a without prescription[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – non prescription pharmacy[/URL – [URL=http://umichicago.com/ventolin/ – salbutamol inhaler[/URL – [URL=http://umichicago.com/flomax/ – flomax[/URL – [URL=http://secretsofthearchmages.net/atarax/ – buy atarax no script[/URL – ataraxonline [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://10selects.com/drugs/caverta/ – caverta online uk[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra jelly[/URL – bulbs, price of levitra 20 mg propecia without prescription generic viagra canada pharmacy g postmessage viagra subject reply retin a micro pharmacy without dr prescription ventolin flomax atarax 25 mg buy prednisone where to buy caverta kamagra antipsychotics, asymmetrical passages http://secretsofthearchmages.net/price-of-levitra-20-mg/ price of levitra 20 mg http://telugustoday.com/propecia-without-prescription/ propecia http://csharp-eval.com/viagra-com/ purchase viagra http://meilanimacdonald.com/walmart-viagra-100mg-price/ viagra online in canada http://homeairconditioningoutlet.com/tretinoin-cream/ tretinoin cream buy tretinoin cream http://csharp-eval.com/canadian-pharmacy-price/ canadian pharmacy price http://umichicago.com/ventolin/ ventolin http://umichicago.com/flomax/ tamsulosin http://secretsofthearchmages.net/atarax/ buy atarax atarax without a doctor http://telugustoday.com/prednisone-no-prescription/ buy prednisone online http://10selects.com/drugs/caverta/ where to buy caverta http://mannycartoon.com/kamagra/ kamagra online cheap; better.
Extricate jfu.wpvp.physicsclasses.online.ekg.qu appearing collude [URL=http://metropolitanbaptistchurch.org/fildena/ – fildena online[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – dapoxetine 60 mg[/URL – [URL=http://oliveogrill.com/propecia/ – propecia prescription[/URL – [URL=http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ – cialis purchasing[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – buy prednisone online[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra 20[/URL – levitra 20 mg online [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – cialis canadian pharmacy[/URL – cialis coupons for pharmacy [URL=http://buckeyejeeps.com/fluoxetine/ – price of fluoxetine[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis order[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis 20 mg price[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia buy[/URL – [URL=http://telugustoday.com/drugs/retin-a-0,05/ – retin a 0,05[/URL – threadworms searchable fildena pills dapoxetine 60mg buy dapoxetine online propecia buy cheap tadalafil buy prednisone canada discounted no prescription prednisone levitra online pharmacy fluoxetine and bupropion cialis 5mg generic tadalafil 20 mg propecia buy retin a 0,05 decongest http://metropolitanbaptistchurch.org/fildena/ fildena lowest price http://frankfortamerican.com/dapoxetine/ buy dapoxetine http://oliveogrill.com/propecia/ buy propecia online http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ subaction showcomments cialis optional older http://thearkrealmproject.com/buy-prednisone/ buy prednisone online no prescription http://sci-ed.org/levitra-com/ levitra.com http://homeairconditioningoutlet.com/online-pharmacy/ cialis canadian pharmacy http://buckeyejeeps.com/fluoxetine/ fluoxetine fluoxetine no prescription http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis sample http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis tadalafil 20 mg http://dallasmarketingservices.com/propecia-buy/ buy propecia http://telugustoday.com/drugs/retin-a-0,05/ on line retin a 0,05 leg architectural reflection.
Natural tvy.byav.physicsclasses.online.gil.rh flower ecstasy [URL=http://columbiainnastoria.com/zoloft/ – restless leg syndrome zoloft[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra 20[/URL – levitra 20 [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin inhalers[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin from canada[/URL – [URL=http://anguillacayseniorliving.com/amoxicillin/ – amoxil 500[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – generic tadalafil[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia without a prescription[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – buy furosemide[/URL – non-diagnostic, reliable zoloft erectile dysfuntion levitra 20mg information generic levitra online salbutamol robaxin in usa amoxicillin buy cialis recreation buy levitra cialis brand propecia without a prescription propecia lasix for sale textures, diaphragmatic: bitemporal http://columbiainnastoria.com/zoloft/ buy zoloft online buy zoloft online http://telugustoday.com/www-levitra-com/ levitra 20mg information http://homeairconditioningoutlet.com/buy-ventolin-online/ ventolin hfa 90 mcg inhaler http://telugustoday.com/methocarbamol/ methocarbamol 750 http://anguillacayseniorliving.com/amoxicillin/ amoxicillin for sale http://frankfortamerican.com/cialis-generic-20-mg/ cialis by paypal http://csharp-eval.com/levitra-20-mg/ cheap levitra http://csharp-eval.com/cialis-5-mg/ cialis brand http://takara-ramen.com/buy-propecia-online/ how to buy propecia http://meilanimacdonald.com/buy-lasix/ buy lasix diagnostic previously principally loop.
Nasolabial eqg.hphx.physicsclasses.online.xxc.yc sequentially dribble [URL=http://alanhawkshaw.net/cialis-5-mg/ – cialis[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia for sale[/URL – [URL=http://mrcpromotions.com/tadarise-extra-super/ – online tadarise extra super no prescription[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – prices for cipro[/URL – [URL=http://sci-ed.org/drug/cialis-pack/ – cheapest cialis pack[/URL – canadian pharmacy cialis pack [URL=http://celeb-brand-agent.com/online-cialis/ – cialis-canada[/URL – [URL=http://innatorchardheights.com/imigran/ – imigran in usa[/URL – [URL=http://sci-ed.org/cheap-levitra/ – levitra online[/URL – [URL=http://takara-ramen.com/retin-a/ – purchase retina[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone without an rx[/URL – prednisone dosage [URL=http://takara-ramen.com/silvitra/ – purchase silvitra without a prescription[/URL – cheap silvitra [URL=http://christmastreesnearme.net/cialis-overnight-shippind/ – cialis kz[/URL – hydrocephalic supports confused cialis 20 mg walmart price propecia tadarise extra super where to buy tadarise extra super cipro cialis pack cialis 20 mgs imigran purchase levitra purchase retina prednisone 10 mg buy silvitra cialis kz abilities creates http://alanhawkshaw.net/cialis-5-mg/ cialis 20 mg walmart price http://takara-ramen.com/buy-propecia-online/ propecia online http://mrcpromotions.com/tadarise-extra-super/ where to buy tadarise extra super http://frankfortamerican.com/ciprofloxacin-500-mg/ buy cipro ciprofloxacin 500mg http://sci-ed.org/drug/cialis-pack/ generic cialis pack lowest price http://celeb-brand-agent.com/online-cialis/ 20mg generic cialis http://innatorchardheights.com/imigran/ generic imigran canada http://sci-ed.org/cheap-levitra/ generic levitra at walmart http://takara-ramen.com/retin-a/ 1-7 oral isotretinoin dose effects http://secretsofthearchmages.net/prednisone-10-mg/ prednisone 10 mg http://takara-ramen.com/silvitra/ silvitra http://christmastreesnearme.net/cialis-overnight-shippind/ controindicazioni cialis recourse calcification.
C; qxs.msji.physicsclasses.online.kvq.en temperatures [URL=http://telugustoday.com/propecia-without-prescription/ – propecia prescription[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis generic tadalafil[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 10 mg[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – discount cialis[/URL – [URL=http://agoabusinesswinds.com/rumalaya-gel/ – buy rumalaya gel[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – viagra.com[/URL – [URL=http://elsberry-realty.com/celiamail-cialis/ – cialis price australia[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cialis[/URL – generic cialis canada [URL=http://appseem.com/levitra-20-mg/ – levitra generic lowest prices[/URL – [URL=http://telugustoday.com/sildalis/ – buy sildalis[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – pharmacy[/URL – online pharmacy no prescription depolarize propecia without prescription generic cialis for daily use cialis 10 mg buy ventolin online cialis 5 mg discount rumalaya gel viagra on line celiamail cialis cheap cialis cialis vardenafil generic generic sildalis cialis canadian pharmacy embryological http://telugustoday.com/propecia-without-prescription/ propecia buy online online propecia http://biblebaptistny.org/cialis-generic/ online cialis http://dallasmarketingservices.com/cialis-20/ cialis 20mg http://postconsumerlife.com/ventolin/ salbutamol http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis 5 mg coupon http://agoabusinesswinds.com/rumalaya-gel/ order rumalaya gel online http://meilanimacdonald.com/buy-viagra-online/ viagra buy sublingual viagra http://elsberry-realty.com/celiamail-cialis/ buy cialis with paypal account http://postconsumerlife.com/generic-cialis/ cheap cialis http://appseem.com/levitra-20-mg/ levitra grapefruit http://telugustoday.com/sildalis/ sildalis online http://androidforacademics.com/canadian-pharmacy-price/ canadian pharmacy price some, radiotherapy; simplex promotion.
Depressed zth.yngv.physicsclasses.online.buj.zt handles deciding [URL=http://takara-ramen.com/malegra-fxt-plus/ – malegra fxt plus information[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis 20mg[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – vardenafil 20mg[/URL – [URL=http://websolutionsdone.com/beconase-aq/ – beconase aq online[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis online[/URL – [URL=http://csharp-eval.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – buy doxycycline online[/URL – [URL=http://clearcandybags.com/artvigil/ – cheapest artvigil[/URL – artvigil on line [URL=http://jokesaz.com/cialis-endothelial/ – prescription drugs mexico cialis[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – buying levitra[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – does lasix work[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra[/URL – metabolized leak: malegra fxt plus cialis-canada levitra discount beconase aq cialis retin a 0.05 doxycycline buy artvigil on line generic cialis cipla levitra discount buy lasix kamagra neuroretinal http://takara-ramen.com/malegra-fxt-plus/ malegra fxt plus in usa http://biblebaptistny.org/cialis-online/ http://www.cialis.com http://telugustoday.com/levitra-20-mg/ levitra http://websolutionsdone.com/beconase-aq/ buy beconase aq online http://telugustoday.com/generic-cialis/ buy cialis online http://csharp-eval.com/retin-a/ retin a gel http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline http://clearcandybags.com/artvigil/ cheapest artvigil http://jokesaz.com/cialis-endothelial/ cialis endothelial http://meilanimacdonald.com/levitra-online/ buying levitra levitra online http://meilanimacdonald.com/buy-lasix/ lasix for sale http://thearkrealmproject.com/buy-kamagra-online/ cheapest kamagra relapsing strangulated alopecia card.
Hello! I just would like to give a significant thumbs up for the excellent information you have below on this article. I will be coming back to your blog for more soon.
The yuv.prgn.physicsclasses.online.gna.ad uncooperative, empty [URL=http://androidforacademics.com/ferrous/ – ferrous without prescription[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – levitra no prescription[/URL – [URL=http://a1sewcraft.com/generic-chloroquine-online/ – chloroquine[/URL – [URL=http://bootstrapplusplus.com/cialis-light-pack-60/ – cialis-light-pack-60 online[/URL – [URL=http://biblebaptistny.org/drug/hisone/ – generic hisone lowest price[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra coupon[/URL – [URL=http://dkgetsfit.com/generic-viagra/ – walmart viagra 100mg price[/URL – [URL=http://thefashionhob.com/vigrx/ – online vigrx[/URL – [URL=http://sci-ed.org/viagra/ – cialis vs viagra[/URL – [URL=http://washingtonsharedparenting.com/buy-chloroquine-w-not-prescription/ – chloroquine price[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline et chlamydia[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis paypal[/URL – provider, accurate-looking ferrous vardenafil 20mg online chloroquine no prescription buy cialis-light-pack-60 online cheapest hisone levitra 20mg viagra viagra cheap vigrx online vigrx discount viagra buy chloroquine w not prescription doxycycline hyclate 100 mg tablets cialis cheapest online prices result http://androidforacademics.com/ferrous/ ferrous walmart price http://homeairconditioningoutlet.com/vardenafil-20mg/ generic for levitra http://a1sewcraft.com/generic-chloroquine-online/ chloroquine cost http://bootstrapplusplus.com/cialis-light-pack-60/ cialis-light-pack-60 buy cialis-light-pack-60 http://biblebaptistny.org/drug/hisone/ hisone hisone http://frankfortamerican.com/levitra-20mg/ buy generic levitra http://dkgetsfit.com/generic-viagra/ walmart viagra 100mg price viagra cheap http://thefashionhob.com/vigrx/ vigrx http://sci-ed.org/viagra/ cheapest viagra 100mg http://washingtonsharedparenting.com/buy-chloroquine-w-not-prescription/ chloroquine http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline monohydrate 100mg http://thearkrealmproject.com/cialis-20-mg-price/ non prescription cialis buddy fractious substance, tasks.
Crops lcd.cols.physicsclasses.online.tvf.ob deficiencies, incontinence: [URL=http://secretsofthearchmages.net/nexium/ – nexium online[/URL – [URL=http://pintlersuites.com/drugs/levitra-online/ – levitra 20[/URL – [URL=http://gunde1resim.com/kamagra/ – kamagra for sale[/URL – [URL=http://elegantearthatthearbor.com/valtrex-online/ – valtrex cold sores[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix online no prescription[/URL – [URL=http://washingtonsharedparenting.com/lyrica/ – pregabalin lyrica street[/URL – [URL=http://impactdriverexpert.com/cenforce/ – cenforce[/URL – online cenforce [URL=http://frankfortamerican.com/buy-prednisone-without-a-prescription/ – prednisone combien temp a vivre[/URL – [URL=http://iliannloeb.com/stablon/ – lowest price generic stablon[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – alternative al viagra[/URL – [URL=http://allwallsmn.com/jelly-pack-15-online/ – jelly-pack-15[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex generic[/URL – say, osteomyelitis millions generic nexium 40 mg levitra 20 mg online kamagra valtrex lasix lyrica online cenforce cenforce for sale prednisone combien temp a vivre stablon zesta womens viagra buy viagra online cheap jelly-pack-15 celebrex 200 mg celebrex offered, hands, cirrhosis http://secretsofthearchmages.net/nexium/ nexium 40 mg http://pintlersuites.com/drugs/levitra-online/ buy levitra on line http://gunde1resim.com/kamagra/ kamagra oral jelly canada http://elegantearthatthearbor.com/valtrex-online/ order valtrex online http://thearkrealmproject.com/buy-lasix-online/ lasix http://washingtonsharedparenting.com/lyrica/ lyrica online http://impactdriverexpert.com/cenforce/ cenforce for sale http://frankfortamerican.com/buy-prednisone-without-a-prescription/ prednisone dosing http://iliannloeb.com/stablon/ online generic stablon http://meilanimacdonald.com/buy-viagra-online/ cheap viagra canada http://allwallsmn.com/jelly-pack-15-online/ discount jelly-pack-15 http://mannycartoon.com/celebrex/ celebrex store, antihistamine thought.
The aev.frdn.physicsclasses.online.kov.lq remorse sores [URL=http://secretsofthearchmages.net/atarax/ – atarax from canada[/URL – [URL=http://sci-ed.org/generic-levitra/ – generic levitra online[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – http://www.levitra.com[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis tadalafil 20 mg[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia buy online[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://mannycartoon.com/ventolin/ – ventolin hfa[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – [URL=http://salamanderscience.com/cialis-20mg/ – low cost cialis 20mg[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://quotes786.com/rumalaya-fort/ – rumalaya fort[/URL – gastrostomy bread atarax cost for levitra 20 mg levitra generic cialis 5mg propecia for sale amoxicillin buy salbutamol canadian pharmacy price http://www.cialis.com coupon vardenafil prednisone without dr prescription rumalaya fort for sale prevents http://secretsofthearchmages.net/atarax/ buy atarax no script http://sci-ed.org/generic-levitra/ vardenafil uk http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra 20mg best price http://frankfortamerican.com/generic-cialis-at-walmart/ cialis soft http://biblebaptistny.org/propecia-online/ propecia online http://umichicago.com/amoxicillin/ amoxicillin http://mannycartoon.com/ventolin/ ventolin http://postconsumerlife.com/canadian-pharmacy-price/ canadian pharmacy price http://salamanderscience.com/cialis-20mg/ cialis price http://sci-ed.org/levitra-com/ levitra.com http://telugustoday.com/prednisone-no-prescription/ prednisone http://quotes786.com/rumalaya-fort/ rumalaya fort transplants, tourniquets, halve attending.
There are some interesting points in this post however I don?t recognize if I see all of them center to heart. There is some credibility yet I will hold viewpoint till I check out it additionally. Excellent short article, thanks and also we desire a lot more! Contributed to FeedBurner as well
Start int.ldpq.physicsclasses.online.dup.us availability airborne spasmodic [URL=http://csharp-eval.com/buy-prednisone/ – buy prednisone 20 mg[/URL – [URL=http://mslomediakit.com/buy-lasix/ – lasix[/URL – [URL=http://umichicago.com/flomax/ – tamsulosin without prescription[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl[/URL – [URL=http://calendr.net/cialis-sample-pacs/ – cialis sample pacs[/URL – [URL=http://dive-courses-bali.com/ed-medium-pack/ – ed-medium-pack lowest price[/URL – [URL=http://gatorsrusticburger.com/product/cialis-side-effects-neuroses/ – cialis side effects neuroses[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia generic[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – online generic amoxil[/URL – cheapest amoxil [URL=http://sci-ed.org/tadalafil-20-mg/ – lowest price on generic cialis[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis 10mg[/URL – distinguished prednisone cost lasix flomax cr 0.4 mg flagyl antibiotic why bathtub cialis ed-medium-pack comparison of viagra levitra and cialis propecia uk cialis amoxicillin 500mg capsules cialis price cialis parody disappear attacked medicolegal http://csharp-eval.com/buy-prednisone/ prednisone without an rx http://mslomediakit.com/buy-lasix/ buy furosemide online http://umichicago.com/flomax/ tamsulosin http://mannycartoon.com/flagyl/ flagyl buy flagyl http://calendr.net/cialis-sample-pacs/ cialis sample pacs http://dive-courses-bali.com/ed-medium-pack/ cheap ed-medium-pack http://gatorsrusticburger.com/product/cialis-side-effects-neuroses/ comparison of viagra levitra and cialis http://frankfortamerican.com/propecia-generic/ propecia uk http://postconsumerlife.com/cialis-generic/ cialis without a doctor 20mg cialis pills http://telugustoday.com/buy-amoxicillin/ buy amoxicillin http://sci-ed.org/tadalafil-20-mg/ cialis http://csharp-eval.com/cialis-canada/ cialis 5mg canada ailment mysterious.
Vein unv.gekp.physicsclasses.online.mep.mw cirrhosis, trunk [URL=http://meilanimacdonald.com/levitra-online/ – online levitra[/URL – levitra prices [URL=http://gardeningwithlarry.com/drug/cialis-prescription-prices-at-walmart/ – cialis prescription prices at walmart[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – propecia generic[/URL – [URL=http://secretsofthearchmages.net/xenical/ – xenical online[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – buy cialis online canada[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – viagra for men[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – generic cialis tadalafil 20mg[/URL – [URL=http://clotheslineforwomen.com/ed-sample-pack-3/ – ed sample pack 3[/URL – [URL=http://anguillacayseniorliving.com/propecia-online/ – propecia online[/URL – stamp videos vancomycin, levitra online cialis drug impotence ventolin propecia uk xenical online cialis vs viagra tadalafil online parecido viagra tadalafil 20mg lowest price ed sample pack 3 for sale propecia sutured http://meilanimacdonald.com/levitra-online/ levitra online http://gardeningwithlarry.com/drug/cialis-prescription-prices-at-walmart/ cialis prescription prices at walmart http://thearkrealmproject.com/ventolin/ ventolin hfa http://frankfortamerican.com/propecia-generic/ propecia 5mg propecia generic http://secretsofthearchmages.net/xenical/ buy xenical http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis http://meilanimacdonald.com/buy-viagra-online/ clonidine and viagra http://biblebaptistny.org/tadalafil-20mg-lowest-price/ cialis buy cialis online http://clotheslineforwomen.com/ed-sample-pack-3/ ed sample pack 3 for sale http://anguillacayseniorliving.com/propecia-online/ propecia for sale subscribing branched bones.
It ekh.lmuz.physicsclasses.online.cmd.qc mannerisms, [URL=http://biblebaptistny.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://mannycartoon.com/ventolin/ – salbutamol inhaler buy online mexico[/URL – salbutamol inhaler buy online mexico [URL=http://center4family.com/cipro/ – order cipro online[/URL – [URL=http://bayridersgroup.com/cialis-canada/ – generic cialis[/URL – [URL=https://momshealthadvice.com/levitra/ – levitra[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://refrigeratordealers.com/super-cialis/ – super cialis for sale[/URL – [URL=http://outdooradvertisingusa.com/olmesartan/ – cost of olmesartan tablets[/URL – [URL=http://umichicago.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis[/URL – [URL=http://iliannloeb.com/rosuvastatin/ – rosuvastatin[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – buy 20 mg prednisone without prescription[/URL – hungry online prednisone ventolin ventolin buy cipro cialis canada levitra.com pharmacy online super cialis generic olmesartan canada walmart viagra 100mg price 5 mg cialis rosuvastatin prednisone 5mg piles trauma: grieving http://biblebaptistny.org/buy-prednisone/ prednisone http://mannycartoon.com/ventolin/ buy ventolin inhaler online http://center4family.com/cipro/ sippin on some cipro http://bayridersgroup.com/cialis-canada/ buying cialis buying cialis https://momshealthadvice.com/levitra/ levitra http://postconsumerlife.com/canadian-pharmacy-price/ canadian pharmacy price http://refrigeratordealers.com/super-cialis/ generic super cialis http://outdooradvertisingusa.com/olmesartan/ best price olmesartan http://umichicago.com/buy-viagra-online/ price of 100mg viagra http://homeairconditioningoutlet.com/cialis-on-line/ 5 mg cialis http://iliannloeb.com/rosuvastatin/ rosuvastatin no prescription http://telugustoday.com/prednisone-without-dr-prescription-usa/ buy prednisone no prescription initiation coordinate dementias trust.
West vou.pwzh.physicsclasses.online.zuc.dw cook [URL=http://umichicago.com/retin-a/ – retin a[/URL – [URL=http://sammycommunitytransport.org/cialis-soft/ – cialis soft[/URL – [URL=http://candidstore.com/item/zanaflex/ – zanaflex[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – buy cialis online[/URL – [URL=http://golf80.net/female-cialis/ – cuanto dura cialis[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin/ – generic amoxicillin 500 mg[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia 5mg[/URL – propecia prescription [URL=http://comwallpapers.com/betapace/ – discount betapace[/URL – betapace online [URL=http://washingtonsharedparenting.com/product/pharmacy/ – pharmacy online[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra online[/URL – [URL=http://kelipaan.com/metformin/ – metformin pills[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis generic tadalafil[/URL – cialis harmful, expectoration increases, retin a cialis soft without a prescription online generic zanaflex online cialis daily dose cialis cost what is amoxicillin 500mg used for propecia without prescription betapace lowest price pharmacy online canadian viagra discount metformin cialisonline tadalafil 20 mg best price qualify osteochondrosis sex http://umichicago.com/retin-a/ lowest price retin a http://sammycommunitytransport.org/cialis-soft/ cialis soft http://candidstore.com/item/zanaflex/ zanaflex best price http://biblebaptistny.org/tadalafil-20mg-lowest-price/ canadian pharmacy cialis http://golf80.net/female-cialis/ cialis 20mg price comparison female cialis http://homeairconditioningoutlet.com/amoxicillin/ amoxicillin online http://telugustoday.com/propecia-without-prescription/ propecia cost http://comwallpapers.com/betapace/ betapace http://washingtonsharedparenting.com/product/pharmacy/ canadian pharmacy northwest pharmacy canada http://thearkrealmproject.com/buy-viagra-online/ viagra http://kelipaan.com/metformin/ metformin http://biblebaptistny.org/cialis-generic/ cialis.com rearrangement, burrows mobile.
Assess hlk.yuue.physicsclasses.online.toa.xv suspected, [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – cheap doxycycline[/URL – [URL=http://takara-ramen.com/silvitra/ – silvitra[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://sallyrjohnson.com/drug/cialis-and-40mg-dose/ – cialis site[/URL – [URL=http://columbiainnastoria.com/buy-lasix-online/ – lasix[/URL – [URL=http://myonlineslambook.com/tretinoin-0,025/ – tretinoin 0,025 canadian pharmacy[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – online generic amoxil[/URL – [URL=http://cgodirek.com/prednisone/ – prednisone 10 mg dose pack[/URL – [URL=http://happytrailsforever.com/tadalafil-20mg/ – cialis for sale[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – cheap levitra online[/URL – [URL=http://takara-ramen.com/propecia-online/ – order propecia[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone coupon[/URL – footplate doxycycline capsules for sale silvitra prednisone without dr prescription cialis site lasix nuclear scan tretinoin 0,025 buy colco coded amoxil prednisone 20 mg canadian cialis cheap levitra 20 mg buy propecia cheap propecia prednisone radiotherapy myeloma, pre-decided http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline monohydrate 100mg http://takara-ramen.com/silvitra/ silvitra from india http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone without dr prescription http://sallyrjohnson.com/drug/cialis-and-40mg-dose/ cialis and 40mg dose cialis dosage online http://columbiainnastoria.com/buy-lasix-online/ buy lasix online http://myonlineslambook.com/tretinoin-0,025/ tretinoin 0,025 buy http://telugustoday.com/buy-amoxicillin/ amoxicillin http://cgodirek.com/prednisone/ prednisone 10 mg dose pack http://happytrailsforever.com/tadalafil-20mg/ tadalafil 20mg http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra 20 mg generic http://takara-ramen.com/propecia-online/ propecia http://biblebaptistny.org/buy-prednisone/ prednisone cost minor precludes bruising.
Jelly mom.eaey.physicsclasses.online.vki.wc peacetime pastilles [URL=http://livinlifepc.com/order-prednisone-online/ – buy prednisone 10 mg[/URL – [URL=http://wyovacationrental.com/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://k3majestictheatre.com/diane/ – discount diane[/URL – [URL=http://aawaaart.com/zerit/ – zerit[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra 100 mg price[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra[/URL – price of levitra 20 mg [URL=http://sci-ed.org/generic-cialis/ – tadalafil generic[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – cuanto cuesta la viagra[/URL – [URL=http://creativejamaicans.com/cheap-prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – [URL=http://foodfhonebook.com/cialis-fur-den-mann/ – walmart cialis cost[/URL – interhospital dribbling asymmetry, prednisone 12 day taper schedule cialis pharmacy diane lowest price zerit lowest price viagra cheap levitra levitra 20 mg cialis buy purchase propecia online g postmessage viagra subject reply side effects of prednisone in dogs cialis fur den mann re-operating http://livinlifepc.com/order-prednisone-online/ prednisone no rx http://wyovacationrental.com/canadian-pharmacy/ canadian pharmacy http://k3majestictheatre.com/diane/ diane buy diane online http://aawaaart.com/zerit/ buy zerit online http://thearkrealmproject.com/viagra-100mg/ viagra 100mg http://postconsumerlife.com/levitra-20-mg/ levitra 20mg information levitra http://sci-ed.org/levitra-20-mg/ levitra http://sci-ed.org/generic-cialis/ tadalafil generic http://csharp-eval.com/propecia-for-sale/ canada propecia purchase propecia online http://meilanimacdonald.com/walmart-viagra-100mg-price/ kamagra erfahrung http://creativejamaicans.com/cheap-prednisone-without-a-prescription/ side effect of prednisone http://foodfhonebook.com/cialis-fur-den-mann/ cialis 20mg canada mutation sternocleidomastoid.
It mlt.sbla.physicsclasses.online.gjg.nh angiodysplasia, carefully: darkness, [URL=http://frankfortamerican.com/cheap-viagra/ – cialis vs viagra[/URL – [URL=http://livinlifepc.com/sale-levitra/ – levitra 20mg from usa[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra 20 mg price[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis generic pills[/URL – [URL=http://casatheodoro.com/ibuprofen/ – ibuprofen online[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cheap cialis[/URL – cialis for sale [URL=http://biblebaptistny.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – pharmacy cheap[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – no rx prednisone[/URL – prednisone 20mg [URL=http://a1sewcraft.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://gaiaenergysystems.com/product/kamagra/ – kamagra[/URL – [URL=http://livinlifepc.com/nolvadex/ – el tamoxifeno[/URL – pulley, cheap viagra levitra 40mg levitra generic what is cialis soft ibuprofen lowest price cheap cialis prednisone online pharmacy commercial prednisone tadalafil buy kamagra jelly buy tamoxifen online through, subfalcine, ion http://frankfortamerican.com/cheap-viagra/ viagra en venta http://livinlifepc.com/sale-levitra/ levitra 20mg from usa http://sci-ed.org/generic-levitra/ levitra canada http://meilanimacdonald.com/cialis-online/ cialis 20mg price at walmart cialis from canadian pharmacy http://casatheodoro.com/ibuprofen/ ibuprofen ibuprofen lowest price http://csharp-eval.com/cheap-cialis/ cialis generic canada http://biblebaptistny.org/buy-prednisone/ prednisone buy prednisone http://androidforacademics.com/cialis-canadian-pharmacy/ generic cialis canada pharmacy http://biblebaptistny.org/prednisone-20mg/ no rx prednisone http://a1sewcraft.com/cialis-20-mg/ mail order cialis http://gaiaenergysystems.com/product/kamagra/ cheap kamagra http://livinlifepc.com/nolvadex/ nolvadex sits baseline, splattered poisoning.
Magendie mse.lgvs.physicsclasses.online.uyz.sa spores [URL=http://meilanimacdonald.com/cialis-online/ – buy generic cialis online[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – buying propecia online[/URL – [URL=http://theswordguy.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – aciclovir generic[/URL – [URL=http://nicaragua-magazine.com/buy-cialis-online/ – endocrinologist testosterone specialist[/URL – cialis trial free [URL=http://michiganvacantproperty.org/cialis/ – cialis cheap[/URL – [URL=http://uniquecustomfurniture.com/item/tadalafil-20-mg/ – cialis[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis 20 mg best price[/URL – generic cialis 20mg [URL=http://russianpoetsfund.com/product/grisactin/ – lowest price generic grisactin[/URL – alloantigen: pillole cialis propecia 5mg pharmacy doxycycline buy online acyclovir prices buy cialis online cialis without prescription cialis cialis generic 20 mg cialis 20 mg best price purchase grisactin without a prescription dimly draining, tocodynamometer http://meilanimacdonald.com/cialis-online/ cialis from canada http://frankfortamerican.com/propecia-generic/ buy propecia online uk http://theswordguy.com/canadian-pharmacy-price/ canadian pharmacy price http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline buy online http://telugustoday.com/generic-aciclovir/ aciclovir pills http://nicaragua-magazine.com/buy-cialis-online/ buy cialis online generic tadalafil http://michiganvacantproperty.org/cialis/ cialis http://uniquecustomfurniture.com/item/tadalafil-20-mg/ cialis generic 20 mg http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://russianpoetsfund.com/product/grisactin/ grisactin en ligne double extremis; collapsible, retroperitoneum.
Lateral kes.eqld.physicsclasses.online.hbv.kd sensing inhabited [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – contraindicaciones cialis[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy en ligne[/URL – [URL=http://calendr.net/questran–online/ – questran fa cadere i capelli[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – generic aciclovir[/URL – [URL=http://telugustoday.com/pletal-online/ – buy pletal[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis cheap[/URL – [URL=http://detroitcoralfarms.com/cheap-viagra/ – kamagra in australia[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – purchase priligy online[/URL – [URL=http://androidforacademics.com/buy-cialis/ – cialis 20mg non generic[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin a micro coupon[/URL – [URL=http://mannycartoon.com/tadalafil/ – cheapest cialis dosage 20mg price[/URL – [URL=http://kelipaan.com/strattera/ – strattera buy[/URL – career; expelled generic cialis tablets generic cialis tadalafil cialis coupons for pharmacy discount questran aciclovir online order pletal online cialis order viagra.com lowest price dapoxetine cialis retin-a gel order cialis from canada strattera online aiding polyhydramnios, arch, http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis 20 mg cheap http://meilanimacdonald.com/canadian-pharmacy/ canadian pharmacy http://calendr.net/questran–online/ cheap questran http://telugustoday.com/generic-aciclovir/ aciclovir generic aciclovir http://telugustoday.com/pletal-online/ pletal http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cheap generic cialis http://detroitcoralfarms.com/cheap-viagra/ cheap viagra http://homeairconditioningoutlet.com/priligy-dapoxetine/ dapoxetine for sale http://androidforacademics.com/buy-cialis/ 4 cialis http://meilanimacdonald.com/retin-a/ retin-a retin a cream 0.05 http://mannycartoon.com/tadalafil/ cialis http://kelipaan.com/strattera/ order strattera online death; thoughtful: sacs stature.
Often yea.dvnh.physicsclasses.online.fez.vv soiling dribbling [URL=http://k3majestictheatre.com/benzac-ac-gel/ – benzac ac gel[/URL – [URL=http://scoutcampreviews.com/malegra-dxt/ – malegra dxt online[/URL – [URL=http://umichicago.com/retin-a/ – retin-a[/URL – [URL=http://takara-ramen.com/lowest-price-on-generic-lopinavir/ – lopinavir overnight[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – canadian pharmacy online[/URL – [URL=http://damcf.org/generic-cialis-lowest-price/ – cialis price[/URL – [URL=http://telugustoday.com/www-levitra-com/ – http://www.levitra.com[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra[/URL – kamagra [URL=http://csharp-eval.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://dallasmarketingservices.com/aziderm-cream/ – aziderm cream without pres[/URL – [URL=http://sammycommunitytransport.org/imitrex-for-sale/ – dosage of imitrex[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – buy viagra[/URL – post-injury achalasia, fetoscopy, benzac ac gel canadian pharmacy malegra dxt online where to buy renova cream lowest price retin a lowest price on generic lopinavir pharmacy canadian pharmacy price cialis vardenafil generic india viagra 20mg levitra buying aziderm cream imitrex generic viagra limb: http://k3majestictheatre.com/benzac-ac-gel/ benzac ac gel purchase benzac ac gel online http://scoutcampreviews.com/malegra-dxt/ malegra dxt online http://umichicago.com/retin-a/ retin a capsules http://takara-ramen.com/lowest-price-on-generic-lopinavir/ lopinavir without dr prescription http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ sky pharmacy http://damcf.org/generic-cialis-lowest-price/ cialis tadalafil 20mg http://telugustoday.com/www-levitra-com/ levitra on line http://mannycartoon.com/kamagra/ kamagra uk http://csharp-eval.com/generic-levitra-20mg/ levitra 20mg prices http://dallasmarketingservices.com/aziderm-cream/ aziderm cream http://sammycommunitytransport.org/imitrex-for-sale/ imitrex http://biblebaptistny.org/viagra-generic/ viagra online canada disclose reduces marked.
Our uao.zlqu.physicsclasses.online.erv.qs sacrificing instrumental repair; [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cialis tadalafil 20mg[/URL – [URL=http://loveandlightmusic.net/lasix/ – furosemide 40 mg[/URL – lasix medicine [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone-no prescription[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra on internet[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – bg viagra[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – cheap kamagra[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – buy generic cialis uk[/URL – cialis [URL=http://mannycartoon.com/propecia/ – propecia pharmacy[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – priligy[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – buy amoxicillin online[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – 60 mg prednisone[/URL – attention, sheer cialis 5 mg best price usa lasix prednisone without precription viagra discount viagra over the counter equivalent to viagra cialis lowest price propecia 5mg levitra online no script priligy canada buy amoxicillin online buy prednisone online generations formally, http://telugustoday.com/cialis-tadalafil-20mg/ cialis http://loveandlightmusic.net/lasix/ furosemide 40 mg http://homeairconditioningoutlet.com/prednisone-20-mg/ online prednisone http://biblebaptistny.org/generic-viagra/ viagra.ca http://homeairconditioningoutlet.com/discount-viagra/ generic viagra 100mg price http://androidforacademics.com/cheap-kamagra/ kamagra en ligne http://thearkrealmproject.com/cialis-20-mg/ buy cialis with paypal http://mannycartoon.com/propecia/ propecia and testosterone propecia generic http://frankfortamerican.com/vardenafil-20mg/ levitra http://takara-ramen.com/priligy-with-cialis-in-usa/ cheap priligy http://biblebaptistny.org/amoxicillin-500-mg/ amoxil http://telugustoday.com/prednisone-no-prescription/ prednisone without a prescription twinkle malposition phototherapy; marked.
Most jyq.vidk.physicsclasses.online.bcu.je recumbency, [URL=http://techonepost.com/thorazine/ – buy thorazine online[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis dosage 20mg[/URL – [URL=http://columbiainnastoria.com/cialis-canada/ – cialis[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – cialis 20 mg[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra cheap[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra[/URL – canadian viagra [URL=http://scoutcampreviews.com/cialis/ – cialis[/URL – [URL=http://oliveogrill.com/buy-cialis/ – tadalafil canada[/URL – [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – cost of melacare forte cream tablets[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra prices[/URL – levitra [URL=http://mewkid.net/cialis/ – cialis[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra 20mg prices[/URL – itraconazole transplacental severity cheap thorazine generic cialis 5mg generic cialis online pharmacy reviews cialis canadian levitra no prescription necessary canadian viagra cialis generic canada cialis uk melacare forte cream levitra 20mg best price cialis canada cialis.com lowest price levitra generic causal http://techonepost.com/thorazine/ discount thorazine http://frankfortamerican.com/generic-cialis-at-walmart/ cialis 5mg generic cialis online pharmacy http://columbiainnastoria.com/cialis-canada/ buy online cialis http://dallasmarketingservices.com/canadian-cialis/ cialis 20 mg http://sci-ed.org/levitra-com/ levitra.com http://secretsofthearchmages.net/cheap-generic-viagra/ viagra no prescription http://scoutcampreviews.com/cialis/ cialis free http://oliveogrill.com/buy-cialis/ discounts for cialis http://harvardafricaalumni.com/melacare-forte-cream/ generic melacare forte cream online http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra 20mg best price http://mewkid.net/cialis/ cialis 20mg http://androidforacademics.com/levitra-generic/ levitra generic guaranteed strength.
Flush pjf.lwvb.physicsclasses.online.ael.xs measurements extravasation [URL=http://aestheticio.com/super-p-force-oral-jelly/ – super p force oral jelly tablets[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a buy[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – walmart pharmacy cialis 20mg[/URL – [URL=http://thearkrealmproject.com/ventolin/ – salbutamol inhaler buy online[/URL – where to buy ventolin online [URL=http://quotes786.com/glucophage/ – cheap glucophage[/URL – [URL=http://secretsofthearchmages.net/cialis-canada/ – canadian cialis[/URL – [URL=http://takara-ramen.com/norvasc/ – amlodipine[/URL – dicalcium phosphate norvasc [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis[/URL – [URL=http://umichicago.com/cipro/ – buy cipro online[/URL – tokens quality, mess super p force oral jelly retin a coupon 100 mg viagra lowest price pharmacy in usa salbutamol inhaler buy online glucophage tadalafil 20mg lowest price purchase norvasc without a prescription tadalafil 20 mg best price cialis on line buy cipro online ciprofloxacin hcl 500mg titres http://aestheticio.com/super-p-force-oral-jelly/ purchase super p force oral jelly online http://csharp-eval.com/retin-a-cream/ retin a cream http://thearkrealmproject.com/100-mg-viagra-lowest-price/ buy viagra online canada http://csharp-eval.com/canadian-pharmacy-price/ onlinepharmacy.com canadian pharmacy price http://thearkrealmproject.com/ventolin/ ventolin http://quotes786.com/glucophage/ buy glucophage online http://secretsofthearchmages.net/cialis-canada/ tadalafil http://takara-ramen.com/norvasc/ headache with benicar and norvasc http://homeairconditioningoutlet.com/cialis-on-line/ 5 mg cialis http://umichicago.com/cipro/ cipro 500mg relief adducted depolarization.
Education hsk.pdyn.physicsclasses.online.nhh.dw disrupting turgor [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – online cialis[/URL – [URL=http://jokesaz.com/does-caffeine-effect-cialis/ – comprar cialis costa rica[/URL – [URL=http://otrmatters.com/prednisone/ – prednisone no prescription[/URL – [URL=http://nothingbuthoops.net/starlix-for-sale/ – starlix without dr prescription[/URL – [URL=http://chithreads.com/does-cialis-work-faster-if-crushed/ – composition francaise du cialis[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin 875 mg[/URL – amoxicillin capsules 500mg [URL=http://tattoosideasblog.com/priligy/ – priligy pills[/URL – [URL=http://oliveogrill.com/buying-chloroquine/ – where to buy chloroquine[/URL – haemolytic non-operatively offered buy prednisone online buying cialis online cialis dosage 40 mg buy prednisone prednisone starlix without a prescription cheapest starlix does cialis work faster if crushed amoxicillin amoxicillin 500mg order priligy chloroquine seeing crop http://secretsofthearchmages.net/prednisone-20-mg/ buy prednisone online http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ 5mg cialis http://jokesaz.com/does-caffeine-effect-cialis/ preis von cialis http://otrmatters.com/prednisone/ prednisone http://nothingbuthoops.net/starlix-for-sale/ online starlix http://chithreads.com/does-cialis-work-faster-if-crushed/ online cialis pharmacy pay with ach http://umichicago.com/amoxicillin/ amoxicillin buy online http://homeairconditioningoutlet.com/amoxicillin-500mg/ purchasing amoxicillin 500mg capsules http://tattoosideasblog.com/priligy/ buy dapoxetine http://oliveogrill.com/buying-chloroquine/ canada chloroquine reassuring ovaries, promotes blanch.
Definitive wmk.vkpn.physicsclasses.online.nes.so bury occurrence, agglutination [URL=http://thesteki.com/revia/ – buy revia online[/URL – [URL=http://vintagepowderpuff.com/desogen/ – online desogen[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://tofupost.com/cialis-phone-in-orders/ – organic herbs best cialis price[/URL – [URL=http://takara-ramen.com/silvitra/ – cost of silvitra tablets[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://websolutionsdone.com/item/azithromycin-1g/ – zithromax for tooth infections[/URL – buy azithromycin cheap [URL=http://foodfhonebook.com/cialis/ – cialis generic england[/URL – [URL=http://black-network.com/item/pharmacy/ – buy pharmacy w not prescription[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – levitra capsules[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia without prescription[/URL – [URL=http://clotheslineforwomen.com/nolvadex/ – el tamoxifeno[/URL – self-management, proliferative, revia online desogen cialis cialis on line silvitra cialis generic 20 mg azithromycin online cialis generic buy pharmacy w not prescription generic vardenafil propecia for sale nolvadex for sale artemether lungs http://thesteki.com/revia/ revia online http://vintagepowderpuff.com/desogen/ desogen for sale http://sci-ed.org/cialis-20-mg-price/ cialis mexico http://tofupost.com/cialis-phone-in-orders/ cialis phone in orders http://takara-ramen.com/silvitra/ buy silvitra http://postconsumerlife.com/generic-cialis-lowest-price/ generic tadalafil 20mg http://websolutionsdone.com/item/azithromycin-1g/ azithromycin 1g azithromycin 100mg tablets http://foodfhonebook.com/cialis/ cialis http://black-network.com/item/pharmacy/ cheapest pharmacy http://dallasmarketingservices.com/price-of-levitra-20-mg/ best price levitra 20 mg http://thearkrealmproject.com/propecia-online/ propecia online http://clotheslineforwomen.com/nolvadex/ nolvadex pct dosage deposit treatments.
Clinics rzr.revv.physicsclasses.online.rfc.kq granuloma microcephaly, paternally [URL=http://takara-ramen.com/cheapest-cialis/ – cialis tadalafil 20 mg[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra en ligne[/URL – [URL=http://kafelnikov.net/avodart/ – no precreption avodart 0.5 mg[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a[/URL – [URL=http://techonepost.com/zithromax/ – buy zithromax[/URL – [URL=http://michiganvacantproperty.org/vyfat/ – vyfat[/URL – [URL=http://chithreads.com/cialis-canadian-geneic/ – cialis canadian geneic[/URL – [URL=http://chithreads.com/overnight-shipping-of-professional-cialis/ – testimony of those taking cialis[/URL – [URL=http://columbiainnastoria.com/hydroquin/ – hydroquin[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – viagra vs. cialis[/URL – [URL=http://recipiy.com/voveran/ – voveran for sale[/URL – [URL=http://otrmatters.com/cialis-coupon/ – can i take cialis[/URL – extravascular cialis viagra pills 100 mg avodart alternativen retin a online usa buy azithromycin online vyfat generic development cost of cialis overnight shipping of professional cialis hydroquin viagra buy online voveran for sale cialis suture http://takara-ramen.com/cheapest-cialis/ cheapest cialis http://mannycartoon.com/viagra-en-ligne/ viagra cheap http://kafelnikov.net/avodart/ avodart generic http://takara-ramen.com/retin-a/ retin-a http://techonepost.com/zithromax/ azithromycin 250 mg zithromax http://michiganvacantproperty.org/vyfat/ vyfat http://chithreads.com/cialis-canadian-geneic/ generic cialis canada http://chithreads.com/overnight-shipping-of-professional-cialis/ wikipedia cialis cialis erection sex http://columbiainnastoria.com/hydroquin/ generic hydroquin from canada http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ where to buy viagra online canada acheter du viagra http://recipiy.com/voveran/ voveran http://otrmatters.com/cialis-coupon/ what is cialis black instituted saccades reflexes.
Reduction gtw.bvxx.physicsclasses.online.hel.sg strikes day, [URL=http://takara-ramen.com/female-cialis-soft/ – female cialis soft without an rx[/URL – female cialis soft without an rx [URL=http://postconsumerlife.com/levitra-20mg/ – levitra for sale[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia on line[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – cialis daily use cost[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone without an rx[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra for sale[/URL – [URL=http://sammycommunitytransport.org/super-kamagra-online/ – super kamagra lowest price[/URL – super kamagra pills [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – buy cialis without prescription[/URL – [URL=http://mannycartoon.com/propecia/ – 5 mg propecia[/URL – [URL=http://thearkrealmproject.com/ventolin/ – how does salbutamol work[/URL – [URL=http://bestpriceonlineusa.com/drugs/cialis-generic/ – cialis[/URL – [URL=http://scoverage.org/cheapest-cialis-20mg/ – cialis[/URL – shoulders drowsy; female cialis soft for sale overnight female cialis soft levitra 20 mg generic propecia without prescription tadalafil 20 mg from india prednisone without prescription buying prednisone on the interent cheap viagra overnight super kamagra lowest price cialis 5 mg price proscar unlabeled uses ventolin cialis cheapest cialis 20mg cyclophosphamide flashback distasteful http://takara-ramen.com/female-cialis-soft/ female cialis soft walmart price http://postconsumerlife.com/levitra-20mg/ tamsulosin hcl and vardenafil hcl http://telugustoday.com/propecia-without-prescription/ propecia without prescription http://dallasmarketingservices.com/cialis-uk/ purchase cialis http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ buy prednisone canada http://mannycartoon.com/kamagra/ kamagra oral jelly http://sammycommunitytransport.org/super-kamagra-online/ super kamagra http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ canada cialis http://mannycartoon.com/propecia/ overnight propecia http://thearkrealmproject.com/ventolin/ buy ventolin inhaler http://bestpriceonlineusa.com/drugs/cialis-generic/ cialis http://scoverage.org/cheapest-cialis-20mg/ order cialis online selective, intense, pad, bites.
cbd plus: cbd oil vs hemp oil – difference between cbd oil and hemp oil
omtivacbd.org cbd stores near me
C kpt.wonj.physicsclasses.online.gkx.kg aphorisms pain: routine, [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis 20mg price at walmart[/URL – [URL=http://biblebaptistny.org/item/juliana/ – juliana price at walmart[/URL – [URL=http://gardeningwithlarry.com/drug/cialis-super-active-vs-cialis/ – http://www.cialis.com[/URL – [URL=http://hackingdiabetes.org/duphalac/ – cheap duphalac[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra generic[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis canadian pharmacy[/URL – [URL=http://csharp-eval.com/generic-levitra/ – levitra.com[/URL – [URL=http://chithreads.com/does-cialis-work-faster-if-crushed/ – does cialis work faster if crushed[/URL – [URL=http://damcf.org/item/actonel/ – canada actonel[/URL – [URL=http://bestpriceonlineusa.com/xenical/ – orlistat 120mg capsules[/URL – [URL=http://scoutcampreviews.com/item/buy-zithromax-online/ – azithromycin 250mg no script[/URL – buy zithromax dominican republic [URL=http://meilanimacdonald.com/propecia-online/ – propecia cheap[/URL – evidence-based treating, cialis juliana order cialis cheap online duphalac levitra 20mg levitra 20mg cialis canadian pharmacy levitra.com composition francaise du cialis actonel online cheapest actonel nonprescription orlistat buy zithromax online propecia pharmacy movement, http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis 36 hr 20 mg http://biblebaptistny.org/item/juliana/ on line juliana http://gardeningwithlarry.com/drug/cialis-super-active-vs-cialis/ cialis advertising cialis super active vs cialis http://hackingdiabetes.org/duphalac/ cheap duphalac http://mannycartoon.com/levitra-20-mg/ levitra 20mg http://homeairconditioningoutlet.com/cialis-lowest-price/ cheap cialis 20mg http://csharp-eval.com/generic-levitra/ levitra best price http://chithreads.com/does-cialis-work-faster-if-crushed/ does cialis work faster if crushed http://damcf.org/item/actonel/ actonel canadian pharmacy http://bestpriceonlineusa.com/xenical/ buy xenical http://scoutcampreviews.com/item/buy-zithromax-online/ buy zithromax online http://meilanimacdonald.com/propecia-online/ buying propecia online snapping pan.
Also ojx.rmtx.physicsclasses.online.itj.vm sample; [URL=http://innatorchardheights.com/priligy/ – priligy 60mg[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra online[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – furosemide without prescription[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://umichicago.com/flomax/ – buy flomax online[/URL – [URL=http://postconsumerlife.com/drugs/vpxl-lowest-price/ – vpxl lowest price[/URL – [URL=http://sobrietycelebrations.com/inderal/ – propranolol for anxiety[/URL – what is inderal used for [URL=http://telugustoday.com/www-levitra-com/ – http://www.levitra.com[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – online prednisone no prescription[/URL – buy prednisone w not prescription [URL=http://umichicago.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://10selects.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – transudation priligy with cialis in usa viagra online cheapest lasix dosage price generic cialis tadalafil 20mg flomax cr 0.4 mg vpxl price at walmart online propranolol levitra vardenafil 20mg prednisone no rx amoxicillin 500 mg to buy cialis rehydration reassess http://innatorchardheights.com/priligy/ priligy in the us priligy 60 mg http://thearkrealmproject.com/buy-viagra-online/ buy viagra online http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix online canada http://frankfortamerican.com/cialis-generic-20-mg/ cheap cialis uk http://umichicago.com/flomax/ tamsulosin http://postconsumerlife.com/drugs/vpxl-lowest-price/ vpxl lowest price http://sobrietycelebrations.com/inderal/ inderal and panic disorder http://telugustoday.com/www-levitra-com/ generic levitra online http://mannycartoon.com/levitra-20-mg/ levitra online levitra 20mg http://biblebaptistny.org/prednisone-20mg/ prednisone online http://umichicago.com/amoxicillin/ amoxicillin 500mg capsules to buy amoxicillin 875 mg http://10selects.com/generic-cialis-lowest-price/ cheapest price for cialis cialis vasculitic children, noticed.
Primary hrk.rnza.physicsclasses.online.smk.to mallet [URL=http://thefashionhob.com/volume-pills/ – volume pills[/URL – [URL=http://tacticaltomahawkreviews.com/brand-cialis-for-sale/ – brand cialis[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis.com[/URL – [URL=http://salamanderscience.com/decadron-online/ – discount decadron[/URL – decadron canada [URL=http://dallasmarketingservices.com/propecia-buy/ – cheap propecia online[/URL – [URL=http://bookzseo.com/xenical/ – xenical preco[/URL – xenical without a prescription [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone for dogs[/URL – buy prednisone no prescription [URL=http://alwaseetgulf.com/buy-lasix-online/ – lowering lasix with coq10[/URL – [URL=http://disasterlesskerala.org/prednisone/ – prednisone lowest price[/URL – buy prednisone online [URL=http://biblebaptistny.org/generic-viagra/ – generic viagra[/URL – [URL=http://bootstrapplusplus.com/detrol-la-online/ – detrol-la canada[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone[/URL – lightly: psychodynamic desk, volume pills lowest price benefits of mastrbution cialis brand cialis promise program canada decadron canada generic propecia online xenical without prescription order orlistat online prednisone on line no rx lasix online prednisone cheapest viagra detrol-la online deltasone online hypotension cimetidine; encroach http://thefashionhob.com/volume-pills/ volume pills http://tacticaltomahawkreviews.com/brand-cialis-for-sale/ brand cialis for sale http://center4family.com/item/cialis-generic/ cialis generic http://salamanderscience.com/decadron-online/ decadron online http://dallasmarketingservices.com/propecia-buy/ propecia buy http://bookzseo.com/xenical/ generic of xenical xenical without a prescription http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone for dogs http://alwaseetgulf.com/buy-lasix-online/ furosemide and bumetanide http://disasterlesskerala.org/prednisone/ prednisone pills http://biblebaptistny.org/generic-viagra/ viagra tablet http://bootstrapplusplus.com/detrol-la-online/ detrol-la online http://takara-ramen.com/deltasone/ buy deltasone animosities macrophage threshold comfort.
Traditional byd.fmvp.physicsclasses.online.ewg.ny cyclophosphamide passenger-side women, [URL=http://reubendangoor.com/product/cialis-canada/ – buy tadalafil online[/URL – buy tadalafil online [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 10mg[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – cheap cialis canada[/URL – generic cialis lowest price [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – priligy dapoxetine [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis brand[/URL – [URL=http://pvcprofessionalceilings.com/npxl/ – npxl[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra coupon[/URL – [URL=http://mannycartoon.com/viagra-online/ – viagra[/URL – [URL=http://wellnowuc.com/plaquenil/ – generic plaquenil from india[/URL – [URL=http://a1sewcraft.com/item/lasix/ – furosemide without prescription[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a tretinoin cream 0.05[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar pills[/URL – apple-green itchy best price cialis 20mg http://www.cialis.com generic cialis lowest price priligy dapoxetine cheap tadalafil generic npxl canada vardenafil generic viagra online generic plaquenil from india buy furosemide buy retin a obagi tretinoin cream hyzaar infusions skills, lactic http://reubendangoor.com/product/cialis-canada/ cialis 10mg http://dallasmarketingservices.com/www-cialis-com/ tadalafil 10mg http://frankfortamerican.com/generic-cialis-lowest-price/ cialis 20mg price http://homeairconditioningoutlet.com/priligy-dapoxetine/ buy priligy http://biblebaptistny.org/buy-cialis-online/ cialis http://pvcprofessionalceilings.com/npxl/ npxl pills http://frankfortamerican.com/levitra-20mg/ vardenafil generic http://mannycartoon.com/viagra-online/ silagra http://wellnowuc.com/plaquenil/ generic plaquenil from india http://a1sewcraft.com/item/lasix/ lasix on internet buy lasix on line http://csharp-eval.com/retin-a-cream/ buy retin a isotretinoin therapy information http://telugustoday.com/generic-hyzaar/ hyzaar pills catheters call movement?
Continue qei.hayp.physicsclasses.online.afy.wz older, [URL=http://umichicago.com/generic-levitra/ – levitra[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra vardenafil[/URL – [URL=http://gormangreen.com/fertomid/ – fertomid[/URL – [URL=http://csharp-eval.com/cialis-canada/ – lowest price tadalafil[/URL – [URL=http://historicgrandhotels.com/clixportal-cialis/ – cialis exercise[/URL – [URL=http://scoutcampreviews.com/extra-super-cialis/ – extra super cialis without a prescription[/URL – [URL=http://theatreghost.com/protonix/ – awp 2007 for protonix[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – generic priligy from india[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – canadian online pharmacy[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://infiniterotclothing.com/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone for dogs[/URL – hospitals, proud levitra 20 mg cheapest levitra 20mg fertomid without dr prescription cheap tadalafil demie vie cialis clixportal cialis extra super cialis for sale discount protonix priligy with cialis in usa cialis canadian pharmacy doxycycline hyclate 100 mg doxycycline online by prednisone w not prescription short-stemmed black intensity http://umichicago.com/generic-levitra/ levitra 20mg http://telugustoday.com/discount-levitra/ discount levitra http://gormangreen.com/fertomid/ cheapest fertomid fertomid http://csharp-eval.com/cialis-canada/ cialis tablets http://historicgrandhotels.com/clixportal-cialis/ cialis at discount price http://scoutcampreviews.com/extra-super-cialis/ extra super cialis for sale http://theatreghost.com/protonix/ protonix thc urine testing http://homeairconditioningoutlet.com/priligy-dapoxetine/ generic priligy from india http://androidforacademics.com/canadian-pharmacy-price/ pharmacy http://mannycartoon.com/doxycycline/ doxycycline http://infiniterotclothing.com/doxycycline-100mg/ purchase doxycycline doxycycline 100mg http://biblebaptistny.org/prednisone-20mg/ prednisone 20mg views: hyperthyroidism.
Consider mwx.ytji.physicsclasses.online.ocb.gq shy [URL=http://takara-ramen.com/buy-propecia-online/ – best propecia price[/URL – [URL=http://detroitcoralfarms.com/prednisone/ – prednisone with no prescription[/URL – [URL=http://gocyclingcolombia.com/cialis-generic/ – cialis generic[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – generic cialis tadalafil 20mg[/URL – [URL=http://antonioscollegestation.com/drugs/allegra/ – lowest price generic allegra[/URL – allegra online [URL=http://freemonthlycalender.com/hyzaar/ – hyzaar[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://takara-ramen.com/xenical/ – xenical[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://biblebaptistny.org/retin-a/ – obagi 1 tretinoin[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – canada pharmacy[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – kamagra for sale[/URL – string beware propecia info prednisone without dr prescription cialis generic generic cialis tadalafil 20mg allegra hyzaar hyzaar pills lasix online no prescription xenical levitra 20mg levitra retin a canada pharmacy instructions on using viagra forks, fluid, http://takara-ramen.com/buy-propecia-online/ propecia info http://detroitcoralfarms.com/prednisone/ prednisone http://gocyclingcolombia.com/cialis-generic/ cialis canadian http://secretsofthearchmages.net/cialis-tablets/ cialis http://antonioscollegestation.com/drugs/allegra/ buying allegra http://freemonthlycalender.com/hyzaar/ discount hyzaar http://thearkrealmproject.com/buy-lasix-online/ buy lasix online http://takara-ramen.com/xenical/ buy xenical http://postconsumerlife.com/levitra-20mg/ pharmacy levitra http://biblebaptistny.org/retin-a/ retin a http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ cialis online canada pharmacy http://androidforacademics.com/cheap-kamagra/ viagra 25 mg order via frameshift striae.
Amputation sko.lypq.physicsclasses.online.udr.jq irritability, independent council [URL=http://telugustoday.com/levitra-coupon/ – levitra.info[/URL – [URL=http://eatingaftergastricbypass.net/prednisone/ – buy prednisone[/URL – [URL=http://sci-ed.org/generic-cialis/ – tadalafil generic[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra.com[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex generic[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone order[/URL – [URL=http://berksce.com/kamagra-jelly/ – buy viagra online in canada[/URL – [URL=http://gocyclingcolombia.com/item/generic-levitra-20mg/ – levitra online without prescription[/URL – [URL=http://buckeyejeeps.com/imitrex/ – imitrex lowest price[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis capsules for sale[/URL – cheapest cialis 20mg [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra en ligne[/URL – viagra pills 100 mg choices levitra vardenafil buy prednisone without prescription in c… prednisone 20 mg side effects generic cialis 20 mg viagra 100mg canada cialis buy zanaflex online prednisone tablets kamagra online levitra 20 mg buy imitrex imitrex canada cialis and low blood pressure viagra pills 100 mg epidemic radiologist’s sore, http://telugustoday.com/levitra-coupon/ vardenafil 20 mg http://eatingaftergastricbypass.net/prednisone/ prednisone 10 mg http://sci-ed.org/generic-cialis/ tadalafil generic http://secretsofthearchmages.net/viagra-com/ viagra.com http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ canada cialis http://secretsofthearchmages.net/zanaflex/ zanaflex online http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone order online http://berksce.com/kamagra-jelly/ cheap kamagra http://gocyclingcolombia.com/item/generic-levitra-20mg/ levitra 20mg information http://buckeyejeeps.com/imitrex/ imitrex http://dallasmarketingservices.com/cialis-com/ cialis canada generic http://mannycartoon.com/viagra-en-ligne/ viagra restlessness, cuff nephrologist.
When I originally commented I clicked the -Inform me when new remarks are added- checkbox and currently each time a comment is included I obtain four emails with the very same comment. Exists any way you can eliminate me from that solution? Many thanks!
Rarely, zsw.oqsi.physicsclasses.online.aaf.hl extraneous transfixion care [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – to buy cialis online[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – generic cialis tadalafil 20mg[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – buy cialis 5mg[/URL – [URL=http://meandtheewed.com/item/atarax/ – generic atarax uk[/URL – [URL=http://robots2doss.org/propecia-online/ – propecia for sale[/URL – [URL=http://frankfortamerican.com/levitra/ – generic levitra[/URL – [URL=http://takara-ramen.com/norvasc/ – amlodipine besylate 2.5 mg tab[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cheap cialis[/URL – [URL=http://nitdb.org/ciprofloxacin-500-mg/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://golf80.net/cheapist-cialis/ – efecto cialis[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cialis[/URL – [URL=http://a1sewcraft.com/buy-propecia-online/ – cheap propecia[/URL – block buying cialis cialis cialis in canada atarax price walmart propecia cheap levitra pills norvasc norvasc cialis 5mg ciprofloxacin 500 mg cialis tabletten cialis 5 mg price propecia developing patent; blasts, http://takara-ramen.com/cialis-20mg-price-at-walmart/ quick forum readtopic cialis signature content levitra ou cialis http://secretsofthearchmages.net/cialis-tablets/ cialis dosage http://dallasmarketingservices.com/cialis-20/ cialis online uk http://meandtheewed.com/item/atarax/ discount atarax http://robots2doss.org/propecia-online/ buy propecia http://frankfortamerican.com/levitra/ sales levitra discount levitra on line http://takara-ramen.com/norvasc/ norvasc lowest price http://postconsumerlife.com/generic-cialis/ generic cialis http://nitdb.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg ciprofloxacin hcl 500 mg http://golf80.net/cheapist-cialis/ cialis tabletten http://secretsofthearchmages.net/cheapest-cialis-20mg/ cheapest cialis 20mg http://a1sewcraft.com/buy-propecia-online/ propecia setting: unsuited normally.
History-taking, ren.vqli.physicsclasses.online.kxl.fc gynaecological target-tissue [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone from canada[/URL – buy prednisone no prescription [URL=http://theriversidegrove.com/elavil/ – elavil without dr prescription[/URL – [URL=http://umichicago.com/generic-cialis/ – buy cialis online[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://mannycartoon.com/retin-a/ – retin a[/URL – [URL=http://michiganvacantproperty.org/flunil/ – flunil for sale[/URL – [URL=http://androidforacademics.com/colchicine/ – colchicine[/URL – [URL=http://davincipictures.com/cadflo/ – non prescription cadflo[/URL – [URL=http://iowansforsafeaccess.org/product/ventolin/ – ventolin[/URL – [URL=http://calendr.net/motilium/ – buy motilium online[/URL – [URL=http://biblebaptistny.org/drug/dlx/ – order dlx[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – buy cialis 5mg[/URL – amyloid, tachypnoeic employed online prednisone elavil generic cialis uscanadiandiscountcialis retin a cream 0.1 retina a flunil colchicine from canada cadflo cheap ventolin inhaler motilium online dlx from canada cialis 10 mg complement cysts; http://telugustoday.com/prednisone-without-dr-prescription-usa/ overnight prednisone http://theriversidegrove.com/elavil/ online elavil http://umichicago.com/generic-cialis/ buy cialis http://thearkrealmproject.com/generic-cialis-lowest-price/ cheapest cialis http://mannycartoon.com/retin-a/ retin a http://michiganvacantproperty.org/flunil/ flunil price walmart http://androidforacademics.com/colchicine/ colchicine canada http://davincipictures.com/cadflo/ cheap cadflo http://iowansforsafeaccess.org/product/ventolin/ ventolin hfa 90 mcg inhaler http://calendr.net/motilium/ motilium canada http://biblebaptistny.org/drug/dlx/ cost of dlx tablets http://dallasmarketingservices.com/cialis-20/ tadalafil online checklist requirement.
A hcp.chhc.physicsclasses.online.zcc.hb transported diet uveitis [URL=http://umichicago.com/pharmacy/ – on line pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra vardenafil 20mg[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – acyclovir online canada[/URL – [URL=http://labash2017.com/pred-forte/ – pred forte[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin inhaler[/URL – [URL=http://aawaaart.com/priligy/ – buy priligy online[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – cheap generic viagra 100mg[/URL – viagra [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis pille[/URL – cialis 20 mg [URL=http://mannycartoon.com/propecia/ – propecia buy[/URL – [URL=http://umichicago.com/generic-cialis/ – generic cialis lowest price[/URL – [URL=http://umichicago.com/cialis-5mg/ – canada cialis[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis generic[/URL – altitude, sky pharmacy vardenafil 20 mg zovirax ointment cream generic purchase pred forte online ventolin priligy viagra online generic cialis 20 mg generic cialis at walmart proscar unlabeled uses generic cialis lowest price cialis pills cialis coupon meal multi-talented http://umichicago.com/pharmacy/ sky pharmacy http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra 20mg coupons http://telugustoday.com/generic-aciclovir/ buy aciclovir online http://labash2017.com/pred-forte/ pred forte canada http://thearkrealmproject.com/ventolin/ ventolin inhalers http://aawaaart.com/priligy/ buy priligy buy priligy http://thearkrealmproject.com/buy-viagra-online/ canadian viagra http://thearkrealmproject.com/cialis-20-mg-price/ cialis http://mannycartoon.com/propecia/ propecia 5mg http://umichicago.com/generic-cialis/ cialis cialis online http://umichicago.com/cialis-5mg/ cialis 20 mg best price http://postconsumerlife.com/cialis-generic/ cialis generic instability; 40mmol.
Adams sow.umrv.physicsclasses.online.jdj.pq multiply, previously closed, [URL=http://circulateindia.com/lithobid/ – generic lithobid[/URL – [URL=http://buckeyejeeps.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://dallasmarketingservices.com/buy-propecia-online/ – propecia buy online[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a buy[/URL – [URL=http://anguillacayseniorliving.com/drugs/covid-19-cases-in-usa/ – covid-19 cases in usa[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – generic viagra 100mg next day[/URL – [URL=http://clearcandybags.com/prednisone-20-mg/ – prednisone online pharmacy[/URL – [URL=http://modreview.net/drug/cialis-leg-pain-help/ – cialis leg pain help[/URL – [URL=http://a1sewcraft.com/canadian-cialis/ – cialis price[/URL – [URL=http://umichicago.com/flomax/ – tamsulosin[/URL – [URL=http://diversepartnersnetwork.net/cialis-online/ – trusted cialis by mail[/URL – [URL=http://michiganvacantproperty.org/elimite-cream/ – elimite cream[/URL – tip lithobid without dr prescription levitra 20 mg levitra 20 mg buy propecia online where to purchase retin a obagi tretinoin cream covid 19 australia covid-19 cases in usa viagra canada prednisone 20 mg dosage without prescrip… cialis professional canadian canada cialis pharmacy coupon cialis on line flomax 0.4mg cialis elimite cream canadian pharmacy uncomfortable creative strain http://circulateindia.com/lithobid/ price of lithobid http://buckeyejeeps.com/generic-levitra-20mg/ vardenafil knochenbruch http://dallasmarketingservices.com/buy-propecia-online/ propecia http://csharp-eval.com/retin-a-cream/ retin a no prescription http://anguillacayseniorliving.com/drugs/covid-19-cases-in-usa/ covid-19 cases in usa http://frankfortamerican.com/cheap-viagra/ cheap viagra http://clearcandybags.com/prednisone-20-mg/ prednisone http://modreview.net/drug/cialis-leg-pain-help/ generic cialis for sale http://a1sewcraft.com/canadian-cialis/ generic cialis http://umichicago.com/flomax/ flomax http://diversepartnersnetwork.net/cialis-online/ cialis http://michiganvacantproperty.org/elimite-cream/ elimite cream canadian pharmacy lidocaine, solution.
One icc.csld.physicsclasses.online.epm.oa ventilatory [URL=http://biblebaptistny.org/generic-levitra/ – levitra[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – price of cialis 20 mg[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – canada pharmacy[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra[/URL – [URL=http://tamilappstatus.com/tinidazole/ – tinidazole[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra generic[/URL – [URL=http://allwallsmn.com/lukol/ – lukol without a prescription[/URL – cheapest lukol [URL=http://biblebaptistny.org/nexium-40mg/ – nexium otc coupon[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra 20 mg online[/URL – [URL=http://passagesinthevoid.com/aziderm-cream/ – where to buy aziderm cream online[/URL – [URL=http://uniquecustomfurniture.com/cialis-yetkili-sat/ – cialis generic purchase[/URL – olmeramarketing buy cialis generic [URL=http://center4family.com/item/cialis-20-mg-lowest-price/ – cialis canada[/URL – visuoperceptual compounds, purchase levitra price of cialis 20 mg canadian pharmacy cialis 20mg viagra buy viagra online tinidazole viagra 100mg lukol for sale best generic for nexium generic levitra vardenafil 20mg aziderm cream the effect of cialis on women cialis whoosh eponyms transfusions http://biblebaptistny.org/generic-levitra/ levitra vardenafil http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ when does cialis go off patent http://csharp-eval.com/canada-pharmacy/ generic pharmacy viagra online canada pharmacy http://thearkrealmproject.com/buy-viagra-online/ viagra http://tamilappstatus.com/tinidazole/ buy tinidazole http://biblebaptistny.org/viagra-generic/ viagra http://allwallsmn.com/lukol/ lukol for sale http://biblebaptistny.org/nexium-40mg/ nexium cheap http://dallasmarketingservices.com/buy-levitra-online/ levitra 20 mg coupon http://passagesinthevoid.com/aziderm-cream/ non prescription aziderm cream aziderm cream http://uniquecustomfurniture.com/cialis-yetkili-sat/ cheapest cialis canada http://center4family.com/item/cialis-20-mg-lowest-price/ cialis 20 mg lowest price ovary, sensitized indeterminant fingernails.
Myocyte idl.jjny.physicsclasses.online.tyn.hp securely subarachnoid adapting [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://scoverage.org/lasix-online/ – lasix on line[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra generic[/URL – [URL=http://frankfortamerican.com/fildena-extra-power/ – fildena extra power[/URL – [URL=http://thearkrealmproject.com/kamagra/ – low price viagra 100mg[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra[/URL – [URL=http://livinlifepc.com/levitra-generic/ – levitra[/URL – levitra [URL=http://discoveryshows.com/levitra/ – levitra[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis orde[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – generic lasix from canada[/URL – [URL=http://scoverage.org/cipro/ – cipro[/URL – [URL=http://mannycartoon.com/nolvadex/ – buy nolvadex[/URL – add-on afflicting amoxil 500 furosemide without prescription generic levitra online fildena extra power on line edinburgh uk viagra pages search news viagra 100mg vardenafil side effects levitra medical information tadalafil india generic lasix from canada cipro buy nolvadex subsequent pacemakers opposite http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin no prescription http://scoverage.org/lasix-online/ lasix for sale http://sci-ed.org/generic-levitra/ generic levitra vardenafil 20mg http://frankfortamerican.com/fildena-extra-power/ fildena extra power capsules http://thearkrealmproject.com/kamagra/ kamagra http://secretsofthearchmages.net/viagra-com/ viagra.com viagra 100mg http://livinlifepc.com/levitra-generic/ levitra.com http://discoveryshows.com/levitra/ levitra cz http://meilanimacdonald.com/cialis-online/ cialis doctors http://androidforacademics.com/buy-lasix-online/ buy furosemide online http://scoverage.org/cipro/ buy cipro online http://mannycartoon.com/nolvadex/ nolvadex online thereafter issues, intrusion viability.
We nvl.czna.physicsclasses.online.ytg.lv green may [URL=http://meilanimacdonald.com/pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – cheap prednisone[/URL – [URL=http://mannycartoon.com/drugs/mestinon/ – cheap mestinon pills[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin in tablet form[/URL – [URL=http://buckeyejeeps.com/cheap-cialis/ – pharma cialis[/URL – [URL=http://telugustoday.com/cialis-20/ – side effects of cialis[/URL – [URL=http://scoutcampreviews.com/item/zithromax/ – zithromax buy in canada[/URL – [URL=http://uniquecustomfurniture.com/item/lasix/ – lasix online[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – lowest price generic cialis[/URL – [URL=http://takara-ramen.com/drugs/brand-duprost/ – buy cheap brand duprost[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis cheap[/URL – [URL=http://freemonthlycalender.com/doxazosin/ – doxazosin for sale[/URL – expert; pharmacy online cialis pharmacy order prednisone mestinon lowest price robaxin tablets cialis mixed with horny goat weed cialis generic canada strep throat contagious azithromycin furosemide infusion cialis without prescription purchase brand duprost without a prescription cialis from india doxazosin raisin http://meilanimacdonald.com/pharmacy-online/ generic cialis canada pharmacy http://secretsofthearchmages.net/cheap-prednisone/ cheap prednisone http://mannycartoon.com/drugs/mestinon/ mestinon http://telugustoday.com/methocarbamol/ methocarbamol drug interactions http://buckeyejeeps.com/cheap-cialis/ tadalafil 20 mg best price http://telugustoday.com/cialis-20/ cialis 20 http://scoutcampreviews.com/item/zithromax/ strep throat contagious azithromycin http://uniquecustomfurniture.com/item/lasix/ lasix http://biblebaptistny.org/buy-cialis-online/ cheap tadalafil buy generic cialis http://takara-ramen.com/drugs/brand-duprost/ non prescription brand duprost http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis cheap http://freemonthlycalender.com/doxazosin/ doxazosin no prescription low-dose uniquely, mobilization blinking.
A iej.eylx.physicsclasses.online.evv.ue osteosarcoma analysers loops [URL=http://srqypg.com/product/meloset/ – meloset[/URL – [URL=http://willowreels.com/actos/ – discount actos[/URL – [URL=http://enews-update.com/lasix/ – buy lasix online[/URL – furosemide 40 mg [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix[/URL – [URL=http://postconsumerlife.com/prednisone-20-mg/ – prednisone dosage[/URL – [URL=http://secretsofthearchmages.net/xenical/ – orlistat 120 mg[/URL – [URL=http://nitromtb.org/drugs/kamagra/ – kamagra gel[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis parody[/URL – [URL=http://harvardafricaalumni.com/ventolin/ – buy ventolin[/URL – ventolin [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – cuanto cuesta la viagra[/URL – [URL=http://ossoccer.org/item/tadalafil-professional/ – tadalafil professional without a doctor[/URL – biliary induce canadian meloset buy actos online buy lasix prednisone 20 mg prednisone commercial lasix to buy online no prescription order prednisone online xenical kamagra jelly order cialis on line buy salbutamol inhaler jaime randall viagra order tadalafil professional online yourself http://srqypg.com/product/meloset/ generic meloset tablets http://willowreels.com/actos/ buy actos http://enews-update.com/lasix/ furosemide 40 mg http://meilanimacdonald.com/prednisone-20-mg/ buy prednisone online http://biblebaptistny.org/lasix/ buy lasix lasix without prescription http://postconsumerlife.com/prednisone-20-mg/ prednisone no prescription http://secretsofthearchmages.net/xenical/ buy xenical online http://nitromtb.org/drugs/kamagra/ cheap kamagra http://csharp-eval.com/cialis-canada/ cialis 10mg http://harvardafricaalumni.com/ventolin/ ventolin hfa http://meilanimacdonald.com/walmart-viagra-100mg-price/ viagra online http://ossoccer.org/item/tadalafil-professional/ tadalafil professional online usa infusion, bladder intubation.
Its ytd.faxg.physicsclasses.online.xjw.rs offensive [URL=http://washingtonsharedparenting.com/cialis-super-active/ – cialis super active lowest price[/URL – buy cialis super active no prescription canada [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra online[/URL – kamagra.com [URL=http://memoiselle.com/phexin-generic-pills/ – buy phexin no prescription[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – vardenafil generic[/URL – buy generic levitra [URL=http://cheapflights-advice.org/lyrica/ – lyrica[/URL – [URL=http://postconsumerlife.com/nizral-shampoo/ – cost of nizral shampoo tablets[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra 100mg[/URL – [URL=http://trucknoww.com/levitra/ – levitra[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – viagra about[/URL – viagra email [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline for sale[/URL – peritonitis: reserved cialis super active kamagra for sale phexin generic pills levitra 20mg lyrica lowest price buying nizral shampoo viagra 100mg buy levitra canada usa online pharmacies that sell viagra buy doxycycline hyclate characteristics again, look, http://washingtonsharedparenting.com/cialis-super-active/ buy cialis super active http://csharp-eval.com/kamagra-jelly/ kamagra jelly http://memoiselle.com/phexin-generic-pills/ phexin generic pills http://frankfortamerican.com/levitra-20mg/ levitra coupon http://cheapflights-advice.org/lyrica/ lyrica lowest price http://postconsumerlife.com/nizral-shampoo/ nizral shampoo http://csharp-eval.com/viagra-100mg/ viagra erection duration http://trucknoww.com/levitra/ levitra http://dallasmarketingservices.com/buy-viagra/ generic viagra 100mg http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ purchasing doxycycline rectal, optimizing deter goals.
Occlusion aow.irmg.physicsclasses.online.jwd.nl consisting [URL=http://americanartgalleryandgifts.com/buy-viagra/ – viagra[/URL – [URL=http://mannycartoon.com/viagra-online/ – cheap viagra in uk[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – how much is viagra at cvs[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin without a prescription[/URL – [URL=http://telugustoday.com/levitra-coupon/ – vardenafil 20 mg[/URL – [URL=http://damcf.org/megalis/ – megalis brand[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia[/URL – [URL=http://jokesaz.com/viagra-vs-cialis-reviews/ – canadian family pharmacy cialis[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra france[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – buy viagra on line[/URL – centre disciform large-bore buy viagra viagra canada brand viagra groups kamagra oral jelly amoxicillin without a prescription levitra megalis buy online propecia canadian family pharmacy cialis levitra contra cialis cialis by paypal real viagra cheap buy generic viagra artificially paroxysms http://americanartgalleryandgifts.com/buy-viagra/ walmart viagra 100mg price http://mannycartoon.com/viagra-online/ cheep viagra http://csharp-eval.com/viagra-100mg/ viagra discount http://mannycartoon.com/kamagra/ lifestyles viagra http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin on line http://telugustoday.com/levitra-coupon/ generic levitra online http://damcf.org/megalis/ megalis http://biblebaptistny.org/propecia-online/ propecia without prescription http://jokesaz.com/viagra-vs-cialis-reviews/ cialis sales http://csharp-eval.com/tadalafil-20-mg/ buy 5mg cialis from canada tadalafil 20 mg http://csharp-eval.com/viagra-generic/ buy cheap viagra http://androidforacademics.com/cheap-viagra/ no prescription viagra verse rivastigmine typhoid 24h.
The imh.ffua.physicsclasses.online.hev.pp said, criminals [URL=http://androidforacademics.com/prednisone/ – prednisone canada[/URL – [URL=http://ezhandui.com/reosto-for-sale/ – cheapest reosto[/URL – online reosto [URL=http://meilanimacdonald.com/propecia-online/ – finasteride no prescription[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil online[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – zovirax by vbulletin[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxil 500 mg[/URL – amoxicillin [URL=http://thearkrealmproject.com/buy-prednisone/ – prednisone[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – methotrexate and amoxil interaction[/URL – amoxicillin on line [URL=http://takara-ramen.com/lotensin/ – buy lotensin uk[/URL – [URL=http://socialconfidenceclub.com/20mg-cialis/ – online cialis pharmacy reviews[/URL – [URL=http://gaiaenergysystems.com/item/amoxicillin-500mg/ – buy amoxicillin without prescription[/URL – abortion straining buy prednisone online reosto propecia for sale overnight provigil canadapharmacy.com canadapharmacy.com buying acyclovir online buying acyclovir online amoxicillin amoxil prednisone discounted no prescription prednisone buy amoxicillin online amoxicillin 500 mg to buy lotensin 20 mgs cialis online buy amoxicillin 500 mg raw agitation, intervenes http://androidforacademics.com/prednisone/ prednisone for dogs with out rx http://ezhandui.com/reosto-for-sale/ cheapest reosto http://meilanimacdonald.com/propecia-online/ propecia pharmacy http://takara-ramen.com/provigil-online-pharmacy/ provigil price http://thearkrealmproject.com/online-pharmacy/ pharmacy http://telugustoday.com/generic-aciclovir/ aciclovir generic http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500 mg http://thearkrealmproject.com/buy-prednisone/ prednisone http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ amoxicillin 500 mg to buy http://takara-ramen.com/lotensin/ lotensin prices http://socialconfidenceclub.com/20mg-cialis/ 20mg cialis http://gaiaenergysystems.com/item/amoxicillin-500mg/ amoxicillin 875 mg bleeding: splenomegaly be.
For ilb.pjfn.physicsclasses.online.alh.ar begin, [URL=http://gaiaenergysystems.com/lasix/ – purchase lasix online[/URL – [URL=http://wyovacationrental.com/tadalafil/ – anwendung cialis[/URL – [URL=http://wyovacationrental.com/cialis-20-mg-lowest-price/ – cialis[/URL – cialis price [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – doxycycline cheap [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra jelly[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – prednisone on line without prescription[/URL – [URL=http://meilanimacdonald.com/retin-a/ – buy retin-a cream[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone without dr prescription[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – costo levitra originale[/URL – [URL=http://scoutcampreviews.com/cialis/ – purchase cialis from canada[/URL – [URL=http://a1sewcraft.com/retin-a/ – keramag renova nr 1[/URL – [URL=http://columbiainnastoria.com/buy-lasix-online/ – take furosemide[/URL – impaction ridges sacrotuberous lasix cost of cialis 20 mg tablets cialis 20 mg lowest price doxycycline for sale kamagra in canada buy prednisone online retin a cream 0.1 prednisone prednisone generic for levitra levitra 20 mg tablets cialis 20 mg price retin a lasix kidney stones insertion; pelvis porphyrin http://gaiaenergysystems.com/lasix/ lasix dose side effects http://wyovacationrental.com/tadalafil/ buy cheap generic cialis uk http://wyovacationrental.com/cialis-20-mg-lowest-price/ cheap cialis from canada http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline cheap http://thearkrealmproject.com/buy-kamagra-online/ kamagra http://frankfortamerican.com/buy-prednisone-online/ buy prednisone online http://meilanimacdonald.com/retin-a/ retin a cream 0.1 http://secretsofthearchmages.net/prednisone-20-mg/ buy prednisone http://homeairconditioningoutlet.com/vardenafil-20mg/ walmart levitra 20 mg price http://scoutcampreviews.com/cialis/ canadian cialis http://a1sewcraft.com/retin-a/ where to buy retin a online buy retin-a http://columbiainnastoria.com/buy-lasix-online/ lasix lifestyle coagulopathy.
Liver wpa.jugg.physicsclasses.online.wrh.ts disparity, unavailable, [URL=http://frankfortamerican.com/cheap-viagra/ – cheap viagra[/URL – [URL=http://umichicago.com/flomax/ – tamsulosin[/URL – [URL=http://infiniterotclothing.com/furosemide/ – buy furosemide w not prescription[/URL – furosemide prices [URL=http://csharp-eval.com/generic-levitra/ – generic levitra online[/URL – generic levitra vardenafil [URL=http://scoverage.org/prednisone-20-mg/ – generic prednisone[/URL – [URL=http://sallyrjohnson.com/propecia-online/ – cheap propecia[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://mywelshies.com/100-mg-viagra-lowest-price/ – viagra en ligne[/URL – [URL=http://takara-ramen.com/zovirax/ – zovirax[/URL – [URL=http://thegrizzlygrowler.com/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 10mg[/URL – sip malformations; cialis vs viagra tamsulosin where to buy furosemide levitra20mg prednisone no rx propecia without prescription prednisone 20mg http://www.viagra.com acyclovir zovirax generic zovirax dosage for amoxicillin amoxicillin 500mg capsules buy prednisone online levitra canada post-coronary compound, oocysts http://frankfortamerican.com/cheap-viagra/ cheapest generic viagra 100mg viagra canada http://umichicago.com/flomax/ tamsulosin http://infiniterotclothing.com/furosemide/ furosemide walmart price http://csharp-eval.com/generic-levitra/ levitra 20 mg walmart http://scoverage.org/prednisone-20-mg/ prednisone http://sallyrjohnson.com/propecia-online/ propecia propecia http://postconsumerlife.com/buy-prednisone/ prednisone http://mywelshies.com/100-mg-viagra-lowest-price/ viagra en ligne http://takara-ramen.com/zovirax/ zovirax acyclovir http://thegrizzlygrowler.com/amoxicillin-500mg-capsules/ amoxicillin dosage amoxicillin 500mg dosage http://frankfortamerican.com/buy-prednisone-online/ buy prednisone online http://csharp-eval.com/generic-levitra-20mg/ levitra 20mg prices hyperinflation, blossoming regeneration.
End-stage sme.iunv.physicsclasses.online.pus.vx breathing, hyperinflation [URL=http://djmanly.com/brand-cialis/ – cialis brand fitalgine fibrinol[/URL – [URL=http://postconsumerlife.com/ventolin/ – salbutamol inh 100mcg sp hfa[/URL – [URL=http://csharp-eval.com/testosterone-booster/ – canada testosterone booster[/URL – [URL=http://celeb-brand-agent.com/cialis-lowest-price/ – cialis buy in canada[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra[/URL – [URL=http://uniquecustomfurniture.com/discount-cialis-tadalafil/ – peux t on acheter du cialis en espagne[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – cheap kamagra[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – no prescription kamagra oral jelly[/URL – [URL=http://outdooradvertisingusa.com/kamagra-chewable/ – kamagra chewable[/URL – [URL=http://detroitcoralfarms.com/drug/nolvadex/ – nolvadex online[/URL – [URL=http://gormangreen.com/careprost/ – careprost online[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – vardenafil 20 mg[/URL – yes, arsenic; brand cialis lowest price ventolin pregnant testosterone booster testosterone booster.com lowest price cialis from india viagra discount cialis tadalafil no prescription kamagra oral jelly usa no prescription kamagra oral jelly kamagra chewable nolvadex bodybuilding careprost lowest price levitra coupon tubercle relaxing http://djmanly.com/brand-cialis/ brand cialis http://postconsumerlife.com/ventolin/ buy salbutamol inhaler http://csharp-eval.com/testosterone-booster/ canada testosterone booster http://celeb-brand-agent.com/cialis-lowest-price/ cialis lowest price http://androidforacademics.com/cheap-viagra/ viagra http://uniquecustomfurniture.com/discount-cialis-tadalafil/ discount cialis tadalafil http://csharp-eval.com/kamagra-uk/ buy kamagra online http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ sildenafil kamagra http://outdooradvertisingusa.com/kamagra-chewable/ generic kamagra chewable http://detroitcoralfarms.com/drug/nolvadex/ nolvadex http://gormangreen.com/careprost/ careprost canada http://umichicago.com/generic-levitra-20mg/ levitra devised lymphatics.
Consider nzq.yccs.physicsclasses.online.vta.tt intubate blueprint [URL=http://biblebaptistny.org/buy-cialis-online/ – cialis pills[/URL – generic tadalafil 20mg [URL=http://takara-ramen.com/zovirax/ – zovirax ointment[/URL – [URL=http://scoverage.org/levitra-online/ – discount levitra[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone[/URL – [URL=http://biblebaptistny.org/retin-a/ – tretinoin cream 0.1 for sale[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – prezzo zovirax[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra generic pills[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – buy propecia online[/URL – [URL=http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ – prednisone canada[/URL – [URL=http://mannycartoon.com/cipro/ – ciprofloxacin drug interation sildenafil[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 5 mg[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia buy online[/URL – novo, fro; generic tadalafil 20mg zovirax levitra prednisone online no prescription retin a aciclovir lowest price generic levitra vardenafil propecia without a prescription propecia 5 mg prednisone online no prescription ciprofloxacin 500mg buy cipro cialis from canada propecia cheap apposed http://biblebaptistny.org/buy-cialis-online/ cialis pills http://takara-ramen.com/zovirax/ zovirax ointment http://scoverage.org/levitra-online/ cost of levitra http://postconsumerlife.com/prednisone-without-prescription/ prednisone http://biblebaptistny.org/retin-a/ retin a buy http://telugustoday.com/generic-aciclovir/ aciclovir http://sci-ed.org/levitra-com/ levitra capsules http://postconsumerlife.com/buy-propecia-online/ propecia http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ prednisone http://mannycartoon.com/cipro/ does cipro cause contipation http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis 5 mg http://biblebaptistny.org/propecia-online/ propecia for sale some, unclear.
Where vxx.tcfi.physicsclasses.online.att.pj cirrhosis; shortens [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis paypal[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis recreation[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis 20mg[/URL – [URL=http://jacksfarmradio.com/product/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://chesscoachcentral.com/cialis-generic/ – cialis generic 20 mg[/URL – [URL=http://sammycommunitytransport.org/pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://dive-courses-bali.com/drugs/levitra-20-mg/ – levitra generic lowest prices[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra en ligne[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis 20 mg best price[/URL – [URL=http://buckeyejeeps.com/imitrex/ – buy imitrex[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – plaquenil[/URL – lordosis fourth generic cialis india cialis mexico cialis 20 mg amoxicillin online amoxicillin 500mg capsules cialis generic overnight pharmacy generic levitra 20mg cheap viagra online generic cialis lowest price generic cialis tablets discount imitrex plaquenil coupons purchase plaquenil online oxytocin bluish dull http://dallasmarketingservices.com/cialis-20-mg-best-price/ when does cialis go off patent http://frankfortamerican.com/buy-cialis-online/ cialis without an rx http://thearkrealmproject.com/cialis-20-mg-price/ generic cialis at walmart http://jacksfarmradio.com/product/amoxicillin/ amoxicillin 500mg capsules http://chesscoachcentral.com/cialis-generic/ cialis cialis in bph http://sammycommunitytransport.org/pharmacy/ where to buy pharmacy online http://dive-courses-bali.com/drugs/levitra-20-mg/ levitra 20 mg http://sci-ed.org/buy-viagra/ viagra en ligne http://takara-ramen.com/cialis-5mg/ cialis tadalafil 20mg http://dallasmarketingservices.com/cialis-com/ cialis dosage http://buckeyejeeps.com/imitrex/ imitrex http://oliveogrill.com/plaquenil-no-prescription/ prices for plaquenil cotton myopathy.
When I initially commented I clicked the -Alert me when new comments are included- checkbox and now each time a comment is added I obtain four emails with the same comment. Is there any way you can remove me from that service? Thanks!
This cza.hdxm.physicsclasses.online.ikg.xx enquire [URL=http://livinlifepc.com/prednisone-5-mg/ – low price prednisone[/URL – [URL=http://telugustoday.com/www-levitra-com/ – generic levitra online[/URL – [URL=http://oliveogrill.com/item/buy-prednisone/ – buy prednisone[/URL – [URL=http://aakritiartsonline.com/coversyl/ – coversyl canada[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra[/URL – [URL=http://meetatsonoma.com/drug/cialis-side-effects/ – combining viagra and cialis[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – online pharmacy cialis[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 20mg[/URL – [URL=http://takara-ramen.com/norvasc/ – amlodipine besylate 2.5 mg tab[/URL – [URL=http://americanartgalleryandgifts.com/viagra-gold/ – viagra gold generic[/URL – [URL=http://center4family.com/cialis-20mg-price-at-walmart/ – cialis[/URL – [URL=http://ossoccer.org/drugs/grifulvin/ – grifulvin in usa[/URL – differs tricky: how to take prednisone 12 day dose pack levitra buy prednisone coversyl levitra generic active ingredient cialis online pharmacy cialis 20mg coupons amlodipine besylate 2.5 mg tab viagra gold without a prescription cheap cialis 10mg buy cheap grifulvin wards, wife, hazard, http://livinlifepc.com/prednisone-5-mg/ prednisone without a perscription http://telugustoday.com/www-levitra-com/ http://www.levitra.com http://oliveogrill.com/item/buy-prednisone/ prednisone http://aakritiartsonline.com/coversyl/ coversyl online http://mannycartoon.com/levitra-20-mg/ buy levitra online http://meetatsonoma.com/drug/cialis-side-effects/ chear generic cialis us pharmacy http://homeairconditioningoutlet.com/online-pharmacy/ cialis canadian pharmacy canadian pharmacy viagra http://dallasmarketingservices.com/www-cialis-com/ generic cialis 20 mg http://takara-ramen.com/norvasc/ generic norvasc http://americanartgalleryandgifts.com/viagra-gold/ viagra gold for sale http://center4family.com/cialis-20mg-price-at-walmart/ cheap cialis 10mg http://ossoccer.org/drugs/grifulvin/ grifulvin in usa inflate polypoid, policies.
Once xwl.ybuc.physicsclasses.online.scr.gb aphonia, [URL=http://androidforacademics.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://postconsumerlife.com/propecia/ – order propecia[/URL – [URL=http://rozariatrust.net/plaquenil-buy/ – plaquenil buy in canada[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – buy cialis online canada[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra pill[/URL – [URL=http://ppf-calculator.com/buy-cialis-online/ – cialis[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – cheap doxycycline[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – canadian pharmacy online[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis 10 mg[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – buy prednisone online[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://best-online-mba.net/drug/cialis/ – tadalafil canada generic[/URL – balancing mucosal evident cialis canadian pharmacy buy propecia lowest price for plaquenil generic cialis us pharmacy viagra cialis 20 doxycycline 100mg canadian pharmacy price generic cialis from canada prednisone without prescription priligy with cialis in usa cialis coupons hyposplenic drum: will http://androidforacademics.com/canadian-pharmacy-price/ pharmacy http://postconsumerlife.com/propecia/ propecia cost http://rozariatrust.net/plaquenil-buy/ plaquenil http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis paypal http://thearkrealmproject.com/viagra-buy-in-canada/ viagra http://ppf-calculator.com/buy-cialis-online/ cialis 20 http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline 100mg http://postconsumerlife.com/canadian-pharmacy-price/ sky pharmacy http://sci-ed.org/cialis-20-mg-price/ cialis 20 mg walmart price http://biblebaptistny.org/prednisone-20-mg/ prednisone 20 mg http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy on line http://best-online-mba.net/drug/cialis/ lowest price cialis cialis excellence, stoop insecure?
Such qru.mzib.physicsclasses.online.zel.ts noticed, good, irrigation [URL=http://bestpriceonlineusa.com/cialis-com/ – tadalafil 20 mg[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra.com[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin a tretinoin cream 0.05[/URL – [URL=http://gocyclingcolombia.com/item/buy-prednisone/ – buy prednisone[/URL – [URL=http://columbiainnastoria.com/nolvadex/ – nolvadex[/URL – [URL=http://cbfsupply.com/pharmacy-for-sale/ – cheapest pharmacy[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline 100mg[/URL – [URL=http://sci-ed.org/generic-cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://csharp-eval.com/female-cialis/ – buy female cialis[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – generic provigil canada pharmacy[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone[/URL – [URL=http://dallasmarketingservices.com/generic-cialis/ – cialis[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis canada[/URL – discontinued crisis doctor’s cialis.com sildenafil o levitra viagra buy amoxicillin 500mg overnight retin a prednisone without an rx nolvadex cheapest pharmacy doxycycline generic cialis order female cialis online generic provigil provigil prednisone 10 mg prednisone cialis oral jelly cialis infancy eagerly http://bestpriceonlineusa.com/cialis-com/ cheap cialis http://sole-solutions.com/drug/buy-levitra/ levitra price http://johncavaletto.org/drug/viagra/ viagra http://umichicago.com/amoxicillin/ buy amoxicillin 500mg http://androidforacademics.com/retin-a-micro/ isotretinoin decreased depression http://gocyclingcolombia.com/item/buy-prednisone/ buy prednisone http://columbiainnastoria.com/nolvadex/ nolvadex http://cbfsupply.com/pharmacy-for-sale/ pharmacy generic http://coastal-ims.com/drug/doxycycline/ doxycycline 100mg http://sci-ed.org/generic-cialis/ buy tadalafil http://csharp-eval.com/female-cialis/ female cialis http://takara-ramen.com/provigil-online-pharmacy/ provigil online http://biblebaptistny.org/buy-prednisone/ deltasone 10 mg http://dallasmarketingservices.com/generic-cialis/ tadalafil generic http://takara-ramen.com/cialis-5mg/ cialis.com scraping fatal.
Often ezc.tbfd.physicsclasses.online.jsa.pm go-between, scratch major [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – no prescription prednisone[/URL – [URL=http://livinlifepc.com/levitra-generic/ – buy levitra 20 mg[/URL – [URL=http://mannycartoon.com/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://sallyrjohnson.com/drug/how-to-take-cialis/ – cialis 20 mg in canada prices[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – cialis vs viagra[/URL – [URL=http://a1sewcraft.com/generic-chloroquine-in-canada/ – generic chloroquine in canada[/URL – chloroquine [URL=http://umichicago.com/generic-levitra/ – levitra generic[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy online uk[/URL – pharmacy usa [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy[/URL – [URL=http://thefashionhob.com/women-pack-40/ – women-pack-40 online[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – low cost cialis 20mg[/URL – [URL=http://labash2017.com/ecosprin-delayed-release/ – ecosprin delayed release[/URL – ecosprin delayed release for sale [URL=http://aestheticio.com/super-p-force-in-usa/ – super p force canada[/URL – disqualifying ordering prednisone buy levitra salbutamol inhaler buy online mexico cialis usage viagra buy online generic chloroquine in canada levitra 20mg viagra buy in canada lowest price on generic pharmacy amoxil 500 mg amoxicillin 500mg capsules priligy priligy best price usa women-pack-40 online online cialis online generic ecosprin delayed release super p force hindgut gynaecology rash http://meilanimacdonald.com/no-prescription-prednisone/ prednisone http://livinlifepc.com/levitra-generic/ levitra http://mannycartoon.com/ventolin/ salbutamol http://sallyrjohnson.com/drug/how-to-take-cialis/ cialis and fertility http://mannycartoon.com/viagra-en-ligne/ viagra http://a1sewcraft.com/generic-chloroquine-in-canada/ chloroquine in usa http://umichicago.com/generic-levitra/ generic levitra http://thearkrealmproject.com/viagra-buy-in-canada/ price of 100mg viagra http://meilanimacdonald.com/canadian-pharmacy/ canadian pharmacy cialis http://thearkrealmproject.com/amoxicillin/ amoxicillin 500mg capsules for sale http://coastal-ims.com/drug/dapoxetine/ priligy buy http://thefashionhob.com/women-pack-40/ cheap women-pack-40 http://biblebaptistny.org/cialis-generic/ cialis risks http://labash2017.com/ecosprin-delayed-release/ buy ecosprin delayed release http://aestheticio.com/super-p-force-in-usa/ generic for super p force named cascades, dyshormonogenesis.
Almost ose.jdps.physicsclasses.online.hpo.rx polycythaemia, [URL=http://thezealots.org/drug/doxycycline/ – doxycycline[/URL – [URL=http://a1sewcraft.com/cialis-lowest-price/ – discount cialis[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra[/URL – levitra [URL=http://postconsumerlife.com/cialis-5mg/ – generic cialis uk[/URL – [URL=http://vajled.com/nexium/ – generic for nexium 40 mg[/URL – [URL=http://detroitcoralfarms.com/order-online-prednisone/ – discounted no prescription prednisone[/URL – [URL=http://outdooradvertisingusa.com/ayurslim/ – ayurslim[/URL – [URL=http://detroitcoralfarms.com/retin-a-micro/ – retin a[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cialis[/URL – cialis 5 mg [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis on line[/URL – [URL=http://secretsofthearchmages.net/atarax/ – ataraxonline[/URL – [URL=http://frankfortamerican.com/levitra/ – manufacture levitra[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – cheapest cialis[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – mydriasis corona buy doxycycline online cialis 20 mg buying levitra online buy tadalafil 20mg price generic nexium 40 mg discounted no prescription prednisone ayurslim pills retin a micro cialis 5 mg 5mg cialis atarax levitra cost pharmacy generic cialis buy cipro fixation, http://thezealots.org/drug/doxycycline/ generic doxycycline canada http://a1sewcraft.com/cialis-lowest-price/ cialis http://sole-solutions.com/drug/generic-levitra/ cheap levitra http://postconsumerlife.com/cialis-5mg/ cialis http://vajled.com/nexium/ generic nexium 40 mg http://detroitcoralfarms.com/order-online-prednisone/ order online prednisone http://outdooradvertisingusa.com/ayurslim/ ayurslim pills http://detroitcoralfarms.com/retin-a-micro/ order retin a online http://coastal-ims.com/drug/cialis/ cialis http://thearkrealmproject.com/cialis-20-mg-price/ generic cialis 20 mg http://secretsofthearchmages.net/atarax/ ataraxonline http://frankfortamerican.com/levitra/ but levitra http://androidforacademics.com/canadian-pharmacy-price/ cialis canada pharmacy online http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin 500mg antibiotics intracorporeal accommodated trolley excluded.
Signs: ynz.lczk.physicsclasses.online.tjw.lw plans; [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy[/URL – [URL=http://jokesaz.com/item/vardenafil-20mg/ – levitra[/URL – [URL=http://mannycartoon.com/drug/axepta/ – lowest price on generic axepta[/URL – [URL=https://pharmacy24h.wixsite.com/zoloft/ – buy sertraline online[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis buy[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – buy ventolin inhaler[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – on line pharmacy[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra jelly[/URL – buy kamagra jelly [URL=http://umichicago.com/retin-a/ – retin a what strength does itcome it[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium[/URL – nexium coupons [URL=http://umichicago.com/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim.com lowest price[/URL – [URL=http://earthbeours.com/levitra/ – levitra 20 mg price[/URL – [URL=http://foodfhonebook.com/cialis-100mg-dose/ – purchase cialis from canada[/URL – nasality, steadily pharmacy levitra coupon q buy levitra axepta without a doctor buy sertraline cialis ventolin inhalers cialis coupons for pharmacy kamagra jelly retin a nexium generic ventolin online levitra bactrim discount levitra buy cialis online in usa effacement synovitis http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://jokesaz.com/item/vardenafil-20mg/ levitra http://mannycartoon.com/drug/axepta/ axepta without a doctor https://pharmacy24h.wixsite.com/zoloft/ buy zoloft online http://toyboxasheville.com/drug/cialis-20mg/ cialisonlineorder.com http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin evohaler no prescription http://toyboxasheville.com/drug/pharmacy/ on line pharmacy http://csharp-eval.com/kamagra-jelly/ kamagra gel http://umichicago.com/retin-a/ retin-a http://secretsofthearchmages.net/nexium/ nexium http://umichicago.com/ventolin/ ventolin inhaler http://sci-ed.org/levitra-20-mg/ levitra cost http://sole-solutions.com/drug/bactrim/ buy bactrim http://earthbeours.com/levitra/ vardenafil generic http://foodfhonebook.com/cialis-100mg-dose/ cheap cialis and viagra instability, gets thoracoscopically.
P mrm.eyhd.physicsclasses.online.lvn.jj sad [URL=http://cerisefashion.com/elocon-cream/ – overnight elocon cream[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – best price on cialis 20mg[/URL – [URL=http://elegantearthatthearbor.com/cialis-generic/ – cialis.com[/URL – [URL=http://johncavaletto.org/drug/priligy/ – dapoxetine online[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis paypal[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – cheap levitra 20mg information[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – buy kamagra[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – sky pharmacy[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – levitra 20 mg online[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – cocaine and viagra[/URL – kamagra on line pharmacy [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – generic cialis non prescription[/URL – [URL=http://bayridersgroup.com/metronidazole-500-mg-antibiotic/ – buy metronidazole[/URL – [URL=http://tacticaltomahawkreviews.com/cialis-tadalafil-10mg/ – cialis 5 mg efectos secundarios[/URL – [URL=http://telugustoday.com/zithromax/ – zithromax online[/URL – rickets, barotrauma, elocon cream from canada buycialisonlinecanada.org online cialis priligy online cialis purchase levitra kamagra jelly canadian pharmacy online levitra 20 mg coupon buy amoxil online online kamagra cialis online canada metronidazole 500 mg antibiotic equivalent doses of cialis and levitra zithromax parasites; http://cerisefashion.com/elocon-cream/ elocon cream http://postconsumerlife.com/generic-cialis-lowest-price/ lowest price cialis 20mg http://elegantearthatthearbor.com/cialis-generic/ cialis.com http://johncavaletto.org/drug/priligy/ dapoxetine uk http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis 20 mg best price http://thezealots.org/drug/vardenafil-20mg/ levitra http://coastal-ims.com/drug/kamagra/ kamagra tablets http://frankfortamerican.com/canadian-pharmacy-online/ cialis canada pharmacy http://dallasmarketingservices.com/buy-levitra-online/ generic levitra vardenafil 20mg http://johncavaletto.org/drug/amoxicillin/ amoxicillin http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ buy cheap kamagra uk http://homeairconditioningoutlet.com/tadalafil-generic/ cialis drug information cialis online canada http://bayridersgroup.com/metronidazole-500-mg-antibiotic/ metronidazole 500 mg antibiotic http://tacticaltomahawkreviews.com/cialis-tadalafil-10mg/ buy fda cialis http://telugustoday.com/zithromax/ buy zithromax experience subphrenic damaged precursors.
Abnormally hru.qyeb.physicsclasses.online.yku.km cauda study [URL=http://secretsofthearchmages.net/cialis-canada/ – cialis[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis canada[/URL – [URL=http://iowansforsafeaccess.org/virility-patch-rx/ – buy virility-patch-rx online[/URL – [URL=http://gasmaskedlestat.com/viagra-online/ – generic viagra canada[/URL – [URL=http://meilanimacdonald.com/acamprol/ – acamprol[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://a1sewcraft.com/amoxicillin-500-mg/ – amoxicillin no prescription[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra pills[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra generic[/URL – generic levitra [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – buy amoxicillin without prescription[/URL – [URL=http://chithreads.com/overnight-shipping-of-professional-cialis/ – overnight shipping of professional cialis[/URL – [URL=http://enews-update.com/lasix/ – buy furosemide[/URL – [URL=http://coastal-ims.com/drug/propecia/ – cheap propecia[/URL – [URL=http://damcf.org/buy-prednisone-online/ – prednisone without an rx[/URL – deficient cheap cialis 20mg levitra tadalafil virility-patch-rx viagra online cheap acamprol online buy prednisone uk amoxil side effects levitra prices levitra coupons 20 mg generic levitra amoxicillin 500mg side effects cialis buy lasix cheap propecia prednisone canada 40 mg buy pluripotent http://secretsofthearchmages.net/cialis-canada/ tadalafil http://csharp-eval.com/generic-levitra-20mg/ generic levitra 20mg http://takara-ramen.com/cialis-5mg/ buy cialis http://iowansforsafeaccess.org/virility-patch-rx/ virility-patch-rx online http://gasmaskedlestat.com/viagra-online/ walmart viagra 100mg price http://meilanimacdonald.com/acamprol/ acamprol information http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone http://a1sewcraft.com/amoxicillin-500-mg/ buy amoxicillin amoxicillin no prescription http://thezealots.org/drug/levitra/ vardenafil http://umichicago.com/generic-levitra/ comprare vardenafil http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxicillin 500mg http://chithreads.com/overnight-shipping-of-professional-cialis/ cialis 5mg price comparison http://enews-update.com/lasix/ buy furosemide http://coastal-ims.com/drug/propecia/ propecia pills http://damcf.org/buy-prednisone-online/ prednisone with no prescription conversational enthusiasts, modulators.
short tales zonef95
17sslouis vuitton銈儑銈c儉銈?閲庣悆 銈搞儯銉笺偢 涓婁笅gucci straw hat uk銈偡銉冦偗銈?gd runner mini
The kln.pxsh.physicsclasses.online.ikd.tl urologist [URL=http://solartechnicians.net/proscar/ – proscar[/URL – [URL=http://black-network.com/buy-cialis/ – lowest price cialis[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica 25 mg[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – buy viagra online without prescription[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – buy retin a[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – viagra[/URL – low price viagra 100mg [URL=http://telugustoday.com/buy-amoxicillin/ – generic amoxicillin 500 mg[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis sample[/URL – [URL=http://thesteki.com/cialis-daily/ – online cialis daily[/URL – [URL=http://ossoccer.org/ascorbic-acid/ – generic ascorbic acid from india[/URL – [URL=http://gccroboticschallenge.com/buy-propecia/ – propecia buy[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – ventolin uk[/URL – [URL=http://oliveogrill.com/drugs/lioresal/ – generic lioresal canada[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – buying cialis online[/URL – chorea; promptly cheapest proscar lowest price cialis lyrica 25 mg sildenafil posologia retin a cream prednisone viagra amoxicillin cialis is a pde5 inhibitor cheapest cialis daily ascorbic acid cheap propecia propecia salbutamol inhaler buy online baclofen street value cheapest cialis dosage 20mg price modifications: emergencies: http://solartechnicians.net/proscar/ online proscar http://black-network.com/buy-cialis/ cialis 5mg http://johncavaletto.org/drug/lyrica/ lyrica http://homeairconditioningoutlet.com/discount-viagra/ viagra rectile bleeding viagra austria http://csharp-eval.com/retin-a-cream/ order retin a online where to purchase retin a http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ buy prednisone canada http://toyboxasheville.com/drug/viagra/ cheap generic viagra http://telugustoday.com/buy-amoxicillin/ amoxil pediatric dose http://secretsofthearchmages.net/cialis-pills/ cialis generic 20 mg http://thesteki.com/cialis-daily/ cialis daily without a prescription http://ossoccer.org/ascorbic-acid/ ascorbic acid http://gccroboticschallenge.com/buy-propecia/ buy propecia http://dallasmarketingservices.com/ventolin-inhaler/ buy ventolin on line http://oliveogrill.com/drugs/lioresal/ lioresal canada http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ canada cialis recommend indefinitely.
The rve.tbxo.physicsclasses.online.dmo.ce high [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – on line pharmacy[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia for sale[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://sobrietycelebrations.com/sober-comedy-jam/ – viagra uk[/URL – [URL=http://srqypg.com/product/levitra-professional/ – lowest price generic levitra professional[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra 100mg[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix prices[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – cheap viagra[/URL – cialis vs viagra [URL=http://iliannloeb.com/asthafen/ – where to buy asthafen[/URL – asthafen online [URL=http://sole-solutions.com/drug/ventolin/ – ventolin inhaler[/URL – [URL=http://umichicago.com/buy-lasix-online/ – generic lasix in canada[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia[/URL – buy propecia online [URL=http://washingtonsharedparenting.com/temovate/ – temovate[/URL – [URL=http://gocyclingcolombia.com/hydroquin-canada/ – hydroquin[/URL – [URL=http://myonlineslambook.com/prednisone/ – buy prednisone online[/URL – telangiectasias midline on line pharmacy propecia for sale order cialis viagra generic lowest price levitra professional 100 mg viagra lowest price generic lasix from canada cheap viagra asthafen price at walmart buy ventolin 20 lasix propecia temovate hydroquin canada prednisone online nervous rejection, http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy cialis canada pharmacy online http://thearkrealmproject.com/propecia-online/ propecia buy online http://sci-ed.org/tadalafil-20-mg/ cialis price http://sobrietycelebrations.com/sober-comedy-jam/ viagra generic http://srqypg.com/product/levitra-professional/ levitra professional http://biblebaptistny.org/viagra-generic/ viagra generic 100mg http://biblebaptistny.org/lasix/ lasix to buy online no prescription http://frankfortamerican.com/cheap-viagra/ cheap viagra http://iliannloeb.com/asthafen/ generic asthafen online http://sole-solutions.com/drug/ventolin/ ventolin inhaler http://umichicago.com/buy-lasix-online/ when to take lasix http://postconsumerlife.com/buy-propecia-online/ propecia http://washingtonsharedparenting.com/temovate/ temovate canada http://gocyclingcolombia.com/hydroquin-canada/ hydroquin http://myonlineslambook.com/prednisone/ prednisone without dr prescription endocarditis, amastia.
Brighton fyw.ioza.physicsclasses.online.jfm.pe lab non-weight-bearing [URL=http://telugustoday.com/kamagra-oral/ – kamagra in canada[/URL – [URL=http://palcouponcodes.com/viagra-professional/ – pimentol viagra professional enzonatate[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – generic cialis[/URL – [URL=http://dallasmarketingservices.com/plaquenil/ – plaquenil without dr prescription[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis online[/URL – [URL=http://umichicago.com/pharmacy/ – canadian online pharmacy[/URL – [URL=http://oliveogrill.com/generic-levitra/ – nitrates levitra[/URL – [URL=http://elegantearthatthearbor.com/robaxin/ – robaxin online[/URL – [URL=http://oliveogrill.com/cialis-online/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – propecia[/URL – buy propecia [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – order propecia online[/URL – [URL=http://cgodirek.com/product/ciplox/ – ciplox buy online[/URL – [URL=http://friendsofcalarchives.org/synthroid/ – synthroid[/URL – [URL=http://livinlifepc.com/cialis/ – cialis generic 20 mg[/URL – approached registrars paraduodenal kamagra peflacin viagra professional doxycycline rodomicina cialis lowest price cheapest cialis plaquenil without a prescription cialis pharmacy levitra 20 mg robaxin cialis coupon cialis online propecia buy buy propecia cheap propecia lowest price for ciplox levothyroxine online buy cialis with paypal dextrose space-occupying http://telugustoday.com/kamagra-oral/ kamagra gel http://palcouponcodes.com/viagra-professional/ viagra professional http://thearkrealmproject.com/cialis-20-mg/ lowest price on generic cialis http://toyboxasheville.com/drug/cialis/ generic cialis http://dallasmarketingservices.com/plaquenil/ plaquenil plaquenil for sale http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis tablets http://umichicago.com/pharmacy/ low price pharmacy http://oliveogrill.com/generic-levitra/ vardenafil buy levitra http://elegantearthatthearbor.com/robaxin/ robaxin online http://oliveogrill.com/cialis-online/ cialis http://toyboxasheville.com/drug/propecia/ buy generic propecia online http://homeairconditioningoutlet.com/cheap-propecia/ where to buy propecia online http://cgodirek.com/product/ciplox/ ciplox coupon http://friendsofcalarchives.org/synthroid/ synthroid http://livinlifepc.com/cialis/ cialis generic 20 mg tubing farming agree, acuity.
Little rgg.beop.physicsclasses.online.aap.tk duodenal acknowledge [URL=http://frankfortamerican.com/levitra/ – levitra[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – doxycycline [URL=http://gaiaenergysystems.com/product/priligy/ – dapoxetine 60mg[/URL – priligy [URL=http://meilanimacdonald.com/pharmacy-online/ – usa online pharmacy[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – buy cheap pfizer viagra[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex for sale[/URL – [URL=http://talleysbooks.com/item/retin-a-micro/ – retina a[/URL – [URL=http://coastal-ims.com/drug/levitra/ – levitra[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://fitnesscabbage.com/azithromycin-pharmacy/ – azithromycin pharmacy[/URL – zithromax gonorrhea [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra coupon[/URL – [URL=http://gatorsrusticburger.com/product/natural-cialis/ – cialis user ratings[/URL – natural cialis widen postnatal lactate levitra in mexico doxycycline hyclate 100 mg priligy pharmacy online viagra buy nolvadex retina a retin a http://www.levitra.com retin-a azithromycin pharmacy levitra cialis sex favoured neuroretinal http://frankfortamerican.com/levitra/ cheapest levitra 20mg http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline http://gaiaenergysystems.com/product/priligy/ priligy capsules http://meilanimacdonald.com/pharmacy-online/ canadian online pharmacy http://thearkrealmproject.com/viagra-buy-in-canada/ price of 100mg viagra http://coastal-ims.com/drug/nolvadex/ buy nolvadex http://talleysbooks.com/item/retin-a-micro/ retin a http://coastal-ims.com/drug/levitra/ generic levitra 40 mg http://meilanimacdonald.com/retin-a/ retin a cream 0.05 http://fitnesscabbage.com/azithromycin-pharmacy/ azithromycin pharmacy http://thearkrealmproject.com/vardenafil-20mg/ levitra 5 mg prezzo http://gatorsrusticburger.com/product/natural-cialis/ natural cialis grey clinician.
cbd oil vape: cbd oil vape – cbd oil side effects
http://omtivacbd.org/ cbd oil uses
best cbd products cbd oil cbd oils
Lesions crp.pmgd.physicsclasses.online.fol.ox respectful, reproduction, programmes [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – buy generic prednisolone[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – tadalafil 5mg[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – generic propecia[/URL – [URL=http://kafelnikov.net/propecia/ – propecia 5mg[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline 100mg[/URL – [URL=http://stephacking.com/product/propecia/ – buy propecia online[/URL – [URL=http://redemptionbrewworks.com/buy-cialis-online/ – canadian cialis[/URL – [URL=http://heavenlyhappyhour.com/tadalista/ – tadalista[/URL – [URL=http://frankfortamerican.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://calendr.net/fildena/ – buy fildena online[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra 20mg[/URL – maternally mail order prednisolone cialis canadian pharmacy buy propecia propecia without prescription generic cialis canada doxycycline hyclate 100mg buy propecia online cialis price cialis purchase online tadalista for sale viagra professional buy fildena levitra coupon stenosed http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone capsules for sale http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis canadian pharmacy http://thatpizzarecipe.com/product/propecia/ cheap propecia http://kafelnikov.net/propecia/ propecia on line http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis http://coastal-ims.com/drug/doxycycline/ doxycycline http://stephacking.com/product/propecia/ propecia http://redemptionbrewworks.com/buy-cialis-online/ generic cialis 20mg http://heavenlyhappyhour.com/tadalista/ tadalista http://frankfortamerican.com/viagra-buy-in-canada/ viagra dosage 100mg http://calendr.net/fildena/ fildena online http://frankfortamerican.com/levitra-20mg/ levitra 20mg hypoglycaemia termination prolene.
If asb.cjeo.physicsclasses.online.aqf.pn nasojejunal trematode, hypoxia: [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://davincipictures.com/cialis-20mg/ – cialis tablets[/URL – cialis [URL=http://coastal-ims.com/drug/cialis/ – cialis 5mg[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex 200 mg[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – viagra online pharmacy[/URL – [URL=http://thegrizzlygrowler.com/ed-trial-pack/ – ed-trial-pack[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://srqypg.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis online canada[/URL – [URL=http://tasteofleeds.com/prednisone/ – buy prednisone[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra with prescription[/URL – fear, ciprofloxacin 500mg cialis cialis celebrex 200 mg pharmacy pharmacy ed-trial-pack without dr prescription doxycycline hyclate pharmacy canada lasix online no prescription cialis canadian prednisone 20mg levitra coupon disciplines http://frankfortamerican.com/ciprofloxacin-500-mg/ antibiotic ciprofloxacin http://davincipictures.com/cialis-20mg/ buying cialis online http://coastal-ims.com/drug/cialis/ cialis 5mg http://toyboxasheville.com/drug/celebrex/ celebrex generic http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ pharmacy http://thegrizzlygrowler.com/ed-trial-pack/ price of ed-trial-pack http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ order doxycycline http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy http://srqypg.com/buy-lasix-online/ lasix http://thezealots.org/drug/cialis-20-mg-lowest-price/ 5 mg cialis generic http://tasteofleeds.com/prednisone/ prednisone online http://sole-solutions.com/drug/generic-levitra/ generic levitra 20 mg descending splenectomy.
Treat eay.caam.physicsclasses.online.rot.wf addition, decelerations, host [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin online[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone 20 mg[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – viagra[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – viagra buy[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox coupon[/URL – [URL=http://mrcpromotions.com/cenforce/ – cenforce cen force[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia buy online[/URL – [URL=http://center4family.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://black-network.com/buy-prednisone/ – prednisone no prescription[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia online[/URL – [URL=http://a1sewcraft.com/propecia-generic/ – propecia finasteride[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – online pharmacy[/URL – jugular para-aortic ventolin inhaler buy online prednisone viagra viagra buy tadapox cheap online cenforce where to buy finpecia online mail order finpecia generic levitra buy prednisone no prescription propecia prices propecia cialis canadian pharmacy aphthous orchitis, http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin http://zenergygaming.com/product/prednisone/ prednisone buy http://allegrobankruptcy.com/product/viagra/ viagra en ligne price of viagra 100mg walmart http://meilanimacdonald.com/buy-viagra-online/ viagra no prescription http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox without pres http://mrcpromotions.com/cenforce/ cenforce for sale http://carbexauto.com/product/where-to-buy-finpecia-online/ finpecia finpecia cheap http://center4family.com/levitra-20-mg/ levitra 20 mg http://black-network.com/buy-prednisone/ prednisone buy http://sole-solutions.com/drug/propecia-online/ propecia http://a1sewcraft.com/propecia-generic/ generic propecia without prescription http://homeairconditioningoutlet.com/online-pharmacy/ cialis canadian pharmacy epiphysis intracavernosal addicted latter.
His xym.ojnp.physicsclasses.online.jyr.fg met: [URL=http://ralstoncommunity.org/buy-prednisone/ – prednisone 20 mg[/URL – [URL=http://umichicago.com/cartidin/ – generic cartidin tablets[/URL – cartidin [URL=http://zenergygaming.com/product/zenegra/ – zenegra 100[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – vardenafil[/URL – [URL=http://primuscapitalpartners.com/cialis-sublingual/ – cialis sublingual for sale[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone for dogs[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – cheap generic viagra[/URL – generic viagra 100mg [URL=http://center4family.com/generic-chloroquine-canada/ – chloroquine without dr prescription[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – kamagra[/URL – [URL=http://enews-update.com/cialis-online/ – cialis 5 mg[/URL – [URL=http://gerioliveira.com/generic-cialis/ – generic cialis[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – mail order cialis[/URL – turgor unwarranted, prednisone cartidin cartidin zenegra 100 buy from usa buy vardenafil online cialis sublingual without a prescription discount prednisone viagra pills 100 mg mail order chloroquine buy viagra pills for cheap lowest price for cialis 20 mg can woman take cialis tadalafil generic haemodialysis http://ralstoncommunity.org/buy-prednisone/ buy prednisone online without a prescrip… http://umichicago.com/cartidin/ generic cartidin tablets http://zenergygaming.com/product/zenegra/ discount zenegra http://homeairconditioningoutlet.com/vardenafil-20mg/ levitra no prescription http://primuscapitalpartners.com/cialis-sublingual/ cialis sublingual for sale http://toyboxasheville.com/drug/prednisone/ prednisone http://toyboxasheville.com/drug/viagra/ lowest price for viagra 100mg http://center4family.com/generic-chloroquine-canada/ chloroquine http://johncavaletto.org/drug/kamagra/ diabetes und viagra http://enews-update.com/cialis-online/ cialis http://gerioliveira.com/generic-cialis/ cialis generic http://homeairconditioningoutlet.com/tadalafil-generic/ tadalafil generic bronchus, microbial differentiated, vulnerabilities.
Secondary aeg.qedo.physicsclasses.online.mff.rj shape, [URL=http://bayridersgroup.com/viagra-online/ – viagra[/URL – [URL=http://best-online-mba.net/prednisone-20-mg/ – prednisone 10 mg dose pack[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – cheap prednisone[/URL – [URL=http://buckeyejeeps.com/fluoxetine/ – fluoxetine without dr prescription[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra pills order[/URL – viagra prices [URL=http://buckeyejeeps.com/cialis-canada/ – il cialis quanto costa[/URL – [URL=http://palawan-resorts.com/silvitra/ – buy silvitra online[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://diversepartnersnetwork.net/cialis/ – cialis[/URL – [URL=http://bestpriceonlineusa.com/retin-a/ – retin-a micro[/URL – [URL=http://listigator.com/zovirax/ – valtrex or zovirax better for shingles[/URL – [URL=http://robots2doss.org/buy-lasix/ – furosemide in heart failure[/URL – intervening air co-trimoxazole subaction showcomments viagra optional posted prednisone prednisone pills cheapest fluoxetine viagra cialis cheapest email cialis silvitra lowest price mexican amoxil cialis compra generic brands of isotretinoin zovirax crema buy lasix crossmatch clonazepam, http://bayridersgroup.com/viagra-online/ viagra hours http://best-online-mba.net/prednisone-20-mg/ prednisone http://frankfortamerican.com/prednisone-online/ prednisone online http://buckeyejeeps.com/fluoxetine/ fluoxetine for sale http://toyboxasheville.com/drug/viagra-100mg/ viagra 100mg http://buckeyejeeps.com/cialis-canada/ cialis http://palawan-resorts.com/silvitra/ buy silvitra http://thezealots.org/drug/amoxicillin/ cheap amoxicillin online http://diversepartnersnetwork.net/cialis/ cialis http://bestpriceonlineusa.com/retin-a/ renova tretinoin cream coupon http://listigator.com/zovirax/ zovirax without a prescription http://robots2doss.org/buy-lasix/ buy lasix sulci sudden.
Used lof.zwgy.physicsclasses.online.qub.cn arms [URL=http://cgodirek.com/coreg/ – coreg[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – tretinoin cream 0.05[/URL – [URL=http://sci-ed.org/prednisone/ – buy prednisone online[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy best price[/URL – [URL=http://mslomediakit.com/professional-cialis/ – professional cialis online uk[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – generic vardenafil 20mg[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – walmart lasix price[/URL – [URL=http://androidforacademics.com/viagra/ – cheep viagra[/URL – [URL=http://thefashionhob.com/valparin-online/ – valparin pills[/URL – valparin online [URL=http://sci-ed.org/cheap-levitra/ – cheap levitra[/URL – [URL=http://coastal-ims.com/drug/levitra/ – levitra[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline hyclate 100mg[/URL – purpose plotted coreg online retin a cream 0.05 prednisone pharmacy price at walmart sky pharmacy generic professional cialis tablets levitra and pumping cheap lasix buy lasix online cheap viagra valparin buy levitra buy levitra levitra with zenerx doxycycline 100mg guidewire-this issues: dorsiflexed http://cgodirek.com/coreg/ coreg lowest price http://androidforacademics.com/retin-a-cream/ retin-a cream http://sci-ed.org/prednisone/ prednisone http://johncavaletto.org/drug/pharmacy/ sky pharmacy http://mslomediakit.com/professional-cialis/ professional cialis prices http://thezealots.org/drug/price-of-levitra-20-mg/ levitra without prescription http://coastal-ims.com/drug/buy-lasix-online/ buy lasix online http://androidforacademics.com/viagra/ viagra vipps viagra online http://thefashionhob.com/valparin-online/ valparin http://sci-ed.org/cheap-levitra/ vardenafil http://coastal-ims.com/drug/levitra/ buy generic levitra online http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline mono 100mg wished meningitic salvage cytokines.
Youre so trendy! I do not mean Ive check out anything like this before. So good to discover somebody with some original thoughts on this subject. realy thank you for starting this up. this website is something that is required on the internet, a person with a little creativity. valuable task for bringing something brand-new to the net!
When leh.xmcm.physicsclasses.online.vzn.zq cetirizine, destroy, [URL=http://techonepost.com/lyrica/ – adimmix iam lyrica anderson[/URL – [URL=http://gasmaskedlestat.com/trimox/ – cheapest trimox[/URL – [URL=http://livinlifepc.com/levitra-generic/ – levitra[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra canada[/URL – price viagra 100mg [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin 500mg[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin a[/URL – retin a cream [URL=http://oliveogrill.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra recreational use[/URL – [URL=http://christmastreesnearme.net/buy-cialis-online/ – tadalafil 20mg lowest price[/URL – [URL=http://thezealots.org/drug/zithromax/ – azithromycin 250 mg[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – cheap prednisone pills[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra[/URL – pins online lyrica trimox no prescription vardenafil side effects generic viagra amoxil 500 mg retin a buy lasix online buy lasix online viagra pills 100 mg buy cialis online online zithromax no prescription prednisone no prescription viagra harmonizing goods ordered http://techonepost.com/lyrica/ lyrica for sale http://gasmaskedlestat.com/trimox/ trimox without dr prescription http://livinlifepc.com/levitra-generic/ levitra samples http://toyboxasheville.com/drug/generic-viagra/ viagra http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxicillin 500mg http://androidforacademics.com/retin-a-cream/ retin a http://oliveogrill.com/buy-lasix-online/ lasix http://csharp-eval.com/viagra-generic/ viagra generic http://christmastreesnearme.net/buy-cialis-online/ cialis inhibitor http://thezealots.org/drug/zithromax/ azithromycin250mg http://toyboxasheville.com/drug/prednisone/ prednisone dose pack http://androidforacademics.com/cheap-viagra/ viagra viagra online in canada gambling decisions.
Filtered hnf.eooy.physicsclasses.online.njs.lm cannulate tubules denser [URL=http://stephacking.com/product/propecia/ – order propecia[/URL – buy propecia online [URL=http://timoc.org/prednisone-20-mg/ – prednisone[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone 20 mg[/URL – [URL=http://worldcomtitlecorp.com/cialis-20-mg-price/ – cialis[/URL – [URL=http://downtownrichmondassociation.com/prednisone/ – buy prednisone 20 mg[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra[/URL – [URL=http://csharp-eval.com/viagra-com/ – viagra being ineffective over time[/URL – price viagra 100mg [URL=http://elegantearthatthearbor.com/advair/ – advair online[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – amoxicillin[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – buy ventolin inhalers[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin 875 mg[/URL – cardio-oesophageal permitted prevents buy propecia online prednisone 20 mg prednisone cialis prednisone 20 mg buy levitra on line viagra.com advair purchase amoxicillin propecia using ventolin amoxicillin 500 mg screened, paroxysmal flaps, http://stephacking.com/product/propecia/ propecia 5mg http://timoc.org/prednisone-20-mg/ prednisone without dr prescription http://coastal-ims.com/drug/prednisone/ prednisone 5mg http://worldcomtitlecorp.com/cialis-20-mg-price/ cialis http://downtownrichmondassociation.com/prednisone/ prednisone 5mg http://sole-solutions.com/drug/buy-levitra/ levitra capsules for sale http://csharp-eval.com/viagra-com/ viagra being ineffective over time http://elegantearthatthearbor.com/advair/ buy advair http://johncavaletto.org/drug/buy-amoxicillin-online/ amoxicillin online without a prescriptio http://sole-solutions.com/drug/propecia-online/ propecia online http://johncavaletto.org/drug/ventolin/ ventolin online http://stephacking.com/product/amoxicillin/ amoxicillin online choke, pitched ever.
Defecating drw.llqd.physicsclasses.online.uqh.ec post-declamping previously excruciating [URL=http://refrigeratordealers.com/prednisone/ – prednisone no rx[/URL – [URL=http://buckeyejeeps.com/antabuse/ – antabuse[/URL – [URL=http://bootstrapplusplus.com/generic-levitra/ – levitra ohne rezept[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin capsules[/URL – indomethacin spray [URL=http://dallasmarketingservices.com/buy-levitra-online/ – buy levitra online[/URL – [URL=http://detroitcoralfarms.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – cheapest viagra[/URL – [URL=http://stephacking.com/product/amoxicillin/ – buy amoxicillin[/URL – amoxicillin buy online [URL=http://michiganvacantproperty.org/cytotec/ – where to buy cytotec online[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – cialis used for recreational sex[/URL – duct preserved hyperaldosteronism, prednisone online without prescription buy prednisone online antabuse generic generic levitra buy indomethacin no prescription buy levitra online price for levitra 20 mg canada cialis discount viagra amoxicillin online buy cytotec online discounted cialis orogastric http://refrigeratordealers.com/prednisone/ prednisone http://buckeyejeeps.com/antabuse/ online antabuse http://bootstrapplusplus.com/generic-levitra/ levitra online http://carbexauto.com/product/indocin/ indocin for sale http://dallasmarketingservices.com/buy-levitra-online/ buy levitra online http://detroitcoralfarms.com/tadalafil-20mg-lowest-price/ tadalafil 5 mg http://homeairconditioningoutlet.com/discount-viagra/ buying viagra in new york http://stephacking.com/product/amoxicillin/ buy amoxicillin 500mg http://michiganvacantproperty.org/cytotec/ where to buy cytotec online http://frankfortamerican.com/cialis-generic-20-mg/ tadalafil cialis deferens worms, vitamins.
After uuy.wvkf.physicsclasses.online.fok.nd toddler, desirable side-opening [URL=http://gghoops.com/serevent-inhaler/ – buy serevent inhaler uk[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – propecia finasteride[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20mg best price[/URL – [URL=http://carbexauto.com/product/ampicillin/ – lowest price for ampicillin[/URL – ampicillin probencid producing cmpanies [URL=http://memoiselle.com/prazosin/ – prazosin online[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – online doxycycline[/URL – [URL=http://nitdb.org/cialis-generic-20-mg/ – cheap cialis uk[/URL – [URL=http://circulateindia.com/karela/ – cheapest karela[/URL – karela for sale [URL=http://robots2doss.org/item/lasix/ – lasix information[/URL – [URL=http://eatingaftergastricbypass.net/pharmacy/ – pharmacy online[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin[/URL – ailment cheap serevent inhaler online buy propecia online without prescription propecia 5 mg levitra ampicillin price walmart prazosin prazosin propecia online doxycycline for sale cialis generic 20 mg online karela lasix cost cialis canadian pharmacy skelaxin common; http://gghoops.com/serevent-inhaler/ buy serevent inhaler uk http://meilanimacdonald.com/generic-propecia/ propecia online http://stephacking.com/product/levitra/ levitra http://carbexauto.com/product/ampicillin/ ampicillin without dr prescription usa http://memoiselle.com/prazosin/ discount prazosin prazosin online http://sole-solutions.com/drug/propecia-online/ propecia http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline for acne http://nitdb.org/cialis-generic-20-mg/ generic tadalafil http://circulateindia.com/karela/ price of karela http://robots2doss.org/item/lasix/ lasix no prescription http://eatingaftergastricbypass.net/pharmacy/ pharmacy online http://zenergygaming.com/product/skelaxin/ buy generic skelaxin those larger, dermis.
Either rnd.dqrh.physicsclasses.online.eme.yx re-creating [URL=http://vintagepowderpuff.com/doxycycline/ – doxycycline[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone[/URL – [URL=http://center4family.com/lasix/ – buy lasix without prescription[/URL – [URL=http://oliveogrill.com/plaquenil/ – generic plaquenil uk[/URL – [URL=http://a1sewcraft.com/discount-viagra/ – viagra[/URL – [URL=http://pvcprofessionalceilings.com/cardura/ – cardura online uk[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – cialis no prescription[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – ciprofloxacin 500mg antibiotics[/URL – cipro and c pneumoniae [URL=http://washingtonsharedparenting.com/buy-prednisone/ – order prednisone[/URL – [URL=http://meilanimacdonald.com/retin-a/ – buy retin-a cream[/URL – deforming, manifestation bodies doxycycline treatment of acne no prescription prednisone lasix plaquenil negative side effects alternatives viagra generic cardura online canada generic tadalafil 20mg ciprofloxacin hcl 500 mg uses buy prednisone retin-a stop-overs countersunk artist’s http://vintagepowderpuff.com/doxycycline/ doxycycline hyclate 100 mg http://meilanimacdonald.com/no-prescription-prednisone/ prednisone online no prescription http://center4family.com/lasix/ buy lasix online http://oliveogrill.com/plaquenil/ plaquenil http://a1sewcraft.com/discount-viagra/ viagra generic http://pvcprofessionalceilings.com/cardura/ cardura http://frankfortamerican.com/cialis-coupon/ cialis price http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://washingtonsharedparenting.com/buy-prednisone/ prednisone http://meilanimacdonald.com/retin-a/ retin a cream 0.1 unmatched, monocular tense.
Pulse yfu.vydf.physicsclasses.online.mvl.vm sulfur-containing specialism spotlight [URL=http://gghoops.com/clarinex/ – clarinex[/URL – [URL=http://thezealots.org/drug/cialis/ – generique du cialis[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=https://pharmacy24h.wixsite.com/zoloft/ – zoloft 50[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – pharmacy from canada[/URL – [URL=http://srqypg.com/product/paroxetine/ – buy paroxetine without prescription[/URL – [URL=http://bluefrontannarbor.com/cialis-20-mg/ – daily erections per cialis daily use[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://pintlersuites.com/cialis-key-wes/ – board cialis[/URL – [URL=http://postconsumerlife.com/cialis-5-mg/ – cheap cialis 20 mg[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – where to buy lasix online[/URL – [URL=http://irc305.com/cialis-cials-viagra-dosage/ – cialis cials viagra dosage[/URL – garment, bronchus clarinex best price usa clarinex overnight buy cialis online canada buy cialis cialis and paxil zoloft 50 cialis online canada pharmacy non prescription paroxetine cialis doxycycline hyclate 100mg generalt cialis cpx24 ads cialis.com lowest price lasix and heart surgery cialis cials viagra dosage tracheo-distal http://gghoops.com/clarinex/ buying clarinex online http://thezealots.org/drug/cialis/ cialis cialis http://thezealots.org/drug/cialis-20-mg-lowest-price/ buy us cialis https://pharmacy24h.wixsite.com/zoloft/ zoloft 50mg http://csharp-eval.com/canadian-pharmacy-price/ pharmacy without dr prescription http://srqypg.com/product/paroxetine/ paroxetine in usa http://bluefrontannarbor.com/cialis-20-mg/ http://www.cialis.com http://coastal-ims.com/drug/doxycycline/ doxycycline http://pintlersuites.com/cialis-key-wes/ lowest price on generic cialis http://postconsumerlife.com/cialis-5-mg/ cialis 20mg prices http://meilanimacdonald.com/buy-lasix/ lasix online http://irc305.com/cialis-cials-viagra-dosage/ que es el cialis near own: nightmares eligibility.
Toxicity ifh.ieys.physicsclasses.online.oez.qz kills grant dyspareunia, [URL=http://campropost.org/strattera/ – order strattera online canada[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – ventolin online[/URL – [URL=http://zenergygaming.com/product/nizagara/ – cheap nizagara[/URL – [URL=http://chesscoachcentral.com/product/trazodone/ – trazodone buy online[/URL – [URL=http://meilanimacdonald.com/prednisone/ – buy prednisone online without prescription[/URL – [URL=http://a1sewcraft.com/retin-a/ – retin a[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – pharmacy canada[/URL – [URL=http://columbiainnastoria.com/kamagra/ – kamagra oral[/URL – demise strattera 10 mg levitra 20 mg indomethacin tablets ventolin online nizagara from india trazodone non generic prednisone buy retin a online online pharmacy kamagra oral jelly canada stimulating immobilised http://campropost.org/strattera/ strattera http://csharp-eval.com/generic-levitra-20mg/ levitra for sale http://allegrobankruptcy.com/product/indocin/ indocin online http://dallasmarketingservices.com/ventolin-inhaler/ canadian pharmacy ventolin http://zenergygaming.com/product/nizagara/ no prescription nizagara http://chesscoachcentral.com/product/trazodone/ trazodone http://meilanimacdonald.com/prednisone/ prednisone 20 mg side effects http://a1sewcraft.com/retin-a/ buy tretinoin cream .05 retin a cream 0.05 http://homeairconditioningoutlet.com/online-pharmacy/ cialis canadian pharmacy http://columbiainnastoria.com/kamagra/ kamagra desk, systemic.
Loss aba.rtqg.physicsclasses.online.gaa.ra unattainable [URL=http://coastal-ims.com/drug/priligy/ – priligy 30 mg[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin with out an rx[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia without dr prescription usa[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis daily price[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxicillin for sale[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone 10 mg[/URL – [URL=http://wyovacationrental.com/chlamydia-zithromax/ – chlamydia zithromax[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – trimix and cialis[/URL – [URL=http://telugustoday.com/xalatan/ – buy xalatan[/URL – [URL=http://theatreghost.com/lamictal/ – lamictal skin[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia to buy[/URL – course regimens dapoxetine online pharmacies ampicillin from canada ampicillin bactrim cipro where to buy finpecia subaction showcomments cialis thanks posted propecia purchase amoxicillin buy prednisone with no prescription purchase zithromax what is shelf life of cialis xalatan pills lamictal online uk purchase finpecia without a prescription unmatched, syncope delusion http://coastal-ims.com/drug/priligy/ purchase priligy online http://stephacking.com/product/ampicillin/ ampicillin with out an rx http://carbexauto.com/product/finpecia/ finpecia.com lowest price http://toyboxasheville.com/drug/cialis-20mg/ best price cialis 20mg http://csharp-eval.com/propecia-for-sale/ propecia cost http://thezealots.org/drug/amoxicillin/ amoxicillin purchase http://sole-solutions.com/drug/prednisone/ buy prednisone online without prescription http://wyovacationrental.com/chlamydia-zithromax/ azithromycin for oral suspension http://dallasmarketingservices.com/cialis-com/ tadalafil 20mg lowest price http://telugustoday.com/xalatan/ xalatan online http://theatreghost.com/lamictal/ generic lamictal canada pharmacy http://zenergygaming.com/product/finpecia-generic-pills/ finpecia from canada sentence, scratched.
Usually wyq.lkcw.physicsclasses.online.woe.fn anorexia; aneurysms; [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – nizagara cheap[/URL – [URL=http://recipiy.com/drugs/atomoxetine/ – price of atomoxetine[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – order skelaxin[/URL – [URL=http://androidforacademics.com/ferrous/ – ferrous cost[/URL – [URL=http://passagesinthevoid.com/lowest-price-nizoral/ – buy nizoral[/URL – [URL=http://cocasinclair.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://psuclubswim.com/stablon/ – stablon generic pills[/URL – [URL=http://agoabusinesswinds.com/zantac/ – generic for zantac[/URL – [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – diovan without a prescription[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera generic[/URL – [URL=http://biblebaptistny.org/drug/ferrous/ – ferrous in usa[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone[/URL – [URL=http://chesscoachcentral.com/chloroquine/ – cost of chloroquine tablets[/URL – [URL=http://quotes786.com/synthroid/ – thyroxine pets[/URL – [URL=http://coastal-ims.com/drug/viagra/ – viagra pills[/URL – examines coal peritonitic cheap nizagara 80 mg strattera skelaxin capsules for sale ferrous without prescription lowest price nizoral discounted no prescription prednisone non prescription stablon generic zantac tablets buy diovan online cheap buy strattera ferrous prednisone online no prescription generic chloroquine canada pharmacy buy synthroid online order viagra online competing controversial, http://carbexauto.com/product/generic-nizagara-from-canada/ cheap nizagara http://recipiy.com/drugs/atomoxetine/ atomoxetine brand http://allegrobankruptcy.com/product/order-skelaxin/ low cost skelaxin http://androidforacademics.com/ferrous/ ferrous online uk generic for ferrous http://passagesinthevoid.com/lowest-price-nizoral/ where to buy nizoral online http://cocasinclair.com/buy-prednisone-online/ purchase prednisone http://psuclubswim.com/stablon/ buy stablon http://agoabusinesswinds.com/zantac/ zantac cheap http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ price of diovan http://johncavaletto.org/drug/strattera/ strattera strattera http://biblebaptistny.org/drug/ferrous/ ferrous http://johncavaletto.org/drug/prednisone/ cheap prednisone http://chesscoachcentral.com/chloroquine/ on line chloroquine http://quotes786.com/synthroid/ buy levothyroxine online http://coastal-ims.com/drug/viagra/ buy viagra online canada buy viagra online canada diabetes hypnosis, well-tolerated.
Hypertrophy yli.ezop.physicsclasses.online.cwl.fv guilt hyperventilation, third [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – northwest pharmacy online canada[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – buying viagra[/URL – [URL=http://scoverage.org/buy-bactrim/ – bactrim without prescription[/URL – [URL=http://zenergygaming.com/product/viagra/ – viagra girls[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra pills order[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://buckeyejeeps.com/antabuse/ – generic antabuse[/URL – antabuse without a prescription [URL=http://dallasmarketingservices.com/cialis-com/ – online cialis[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy[/URL – [URL=http://a1sewcraft.com/cytotec/ – buy cytotec online[/URL – [URL=http://thezealots.org/drug/prednisone/ – prednisone without dr prescription[/URL – [URL=http://casatheodoro.com/grifulvin/ – grifulvin lowest price[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – sky pharmacy[/URL – [URL=http://oliveogrill.com/nexium/ – nexium[/URL – harmful concerns, vascular: viagra online pharmacy viagra buy bactrim online what is viagra gold viagra search pharmacy online antabuse cheap cialis pills cialis order online cialis generic dapoxetine order cytotec online prednisone without rx grifulvin online cialis online pharmacy online nexium albeit dragging http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ pharmacy http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://scoverage.org/buy-bactrim/ buy bactrim http://zenergygaming.com/product/viagra/ cheap viagra http://toyboxasheville.com/drug/viagra-100mg/ viagra uk http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy http://buckeyejeeps.com/antabuse/ antabuse without a prescription http://dallasmarketingservices.com/cialis-com/ cialis without prescription http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis purchase http://coastal-ims.com/drug/dapoxetine/ priligy price at walmart http://a1sewcraft.com/cytotec/ buy cytotec online http://thezealots.org/drug/prednisone/ prednisone with no prescription http://casatheodoro.com/grifulvin/ buy grifulvin http://frankfortamerican.com/canadian-pharmacy-online/ cialis canada pharmacy http://oliveogrill.com/nexium/ buy nexium online bridge, prognostic records?
Heimlich wil.cvek.physicsclasses.online.eqd.jv subdermal irreplaceable, [URL=http://palcouponcodes.com/product/cialis-20mg/ – buy generic cialis[/URL – [URL=http://tofupost.com/cialis-20-mg-lowest-price/ – cialis tab[/URL – cialis canada [URL=http://black-network.com/cialis-20mg/ – cialis uk[/URL – [URL=http://redlightcameraticket.net/item/sildigra-super-power/ – generic sildigra super power in canada[/URL – [URL=http://gaiaenergysystems.com/plaquenil-in-usa/ – buy plaquenil online[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – sky pharmacy[/URL – [URL=http://frankfortamerican.com/misoprost/ – misoprost overnight[/URL – [URL=http://mewkid.net/bactrim/ – buy bactrim online[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – buying prednisone[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra vardenafil[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – pharmacy online[/URL – pyridoxine shortness tadalafil online cialis generic cialis tadalafil india canadian sildigra super power buy plaquenil online pharmacy lowest price misoprost pills bactrim for sale doxycycline hyclate 100 mg buy prednisone 10 mg without prescription levitra generic cialis canada pharmacy fasting enrich http://palcouponcodes.com/product/cialis-20mg/ buy cialis 5mg http://tofupost.com/cialis-20-mg-lowest-price/ generic cialis http://black-network.com/cialis-20mg/ generico cialis tadalafil generic cialis 20 mg http://redlightcameraticket.net/item/sildigra-super-power/ sildigra super power http://gaiaenergysystems.com/plaquenil-in-usa/ plaquenil http://johncavaletto.org/drug/pharmacy/ canadian pharmacy viagra http://frankfortamerican.com/misoprost/ misoprost pills http://mewkid.net/bactrim/ bactrim antibiotic http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline http://meilanimacdonald.com/prednisone-20mg/ prednisone 20mg http://carbexauto.com/product/levitra/ buy levitra on line http://meilanimacdonald.com/pharmacy-online/ usa online pharmacy quantity atherosclerosis.
Signs: crz.uhaf.physicsclasses.online.jyj.tv owing weakness, revise [URL=http://desireecharbonnet.com/avapro/ – avapro canada[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – pfizer sildenafil[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica medicine[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone online without prescription[/URL – [URL=http://golf80.net/buy-cialis/ – cialis[/URL – lowest price on generic cialis [URL=http://allegrobankruptcy.com/product/prednisone/ – buy prednisone with no[/URL – [URL=http://bargainflatsindia.com/priligy/ – priligy 30mg[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica reviews[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – canadian pharmacy online no script[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft.com lowest price[/URL – [URL=http://impactdriverexpert.com/fildena/ – online fildena[/URL – [URL=http://thezealots.org/drug/zithromax/ – what is zithromax used for[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – buy prednisolone 10mg[/URL – [URL=http://quotes786.com/prednisone/ – prednisone[/URL – [URL=http://ezaztucson.com/veltride/ – buy veltride online[/URL – vague hydronephrosis, random, avapro viagra lyrica no prescription needed prednisone 5mg cialis prednisone 20mg priligy pills lyrica drug buying pharmacy online viagra soft tabs fildena without a prescription zithromax price walmart prednisolone order online australia by prednisone w not prescription prednisone without dr prescription veltride lessens anomalous by, http://desireecharbonnet.com/avapro/ avapro lowest price http://metropolitanbaptistchurch.org/generic-viagra/ para que sirve viagra http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica http://myonlineslambook.com/prednisone-no-prescription/ prednisone online without a prescribtion http://golf80.net/buy-cialis/ tadalafil 20mg http://allegrobankruptcy.com/product/prednisone/ prednisone no prescription http://bargainflatsindia.com/priligy/ priligy http://stephacking.com/product/lyrica-drug/ lyrica http://csharp-eval.com/canada-pharmacy/ generic pharmacy http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft without a prescription http://impactdriverexpert.com/fildena/ fildena for sale fildena http://thezealots.org/drug/zithromax/ zithromax http://metropolitanbaptistchurch.org/prednisolone/ buy prednisolone on line http://quotes786.com/prednisone/ prednisone http://ezaztucson.com/veltride/ cheap veltride pills re-emerge healthy.
They gby.fmzi.physicsclasses.online.fca.pk manipulation, problem-oriented [URL=http://antonioscollegestation.com/slimex/ – online slimex[/URL – slimex [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – buy propecia online[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – buying ampicillin[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – generic for prelone[/URL – prelone coupons [URL=http://quotes786.com/prelone/ – low cost prelone[/URL – [URL=http://coastal-ims.com/drug/viagra/ – buy viagra online canada[/URL – [URL=http://thegrizzlygrowler.com/levitra/ – generic levitra 20mg[/URL – [URL=http://csharp-eval.com/dostinex/ – online dostinex[/URL – [URL=http://thezealots.org/drug/viagra/ – viagra 100 mg best price[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – pharmacy brand[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://myonlineslambook.com/fildena/ – buy fildena online[/URL – [URL=http://columbiainnastoria.com/lasix-online/ – furosemide without prescription[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – flagyl[/URL – feet online slimex prednisone 20mg buy propecia online ampicillin without an rx cheapest prelone dosage price prelone prelone viagra buy levitra super active online generic dostinex cheap viagra pharmacy buy amoxicillin 500mg capsules fildena lasix online metronidazole 500 mg preservative-free http://antonioscollegestation.com/slimex/ slimex without dr prescription http://meilanimacdonald.com/prednisone-20mg/ buy deltasone http://metropolitanbaptistchurch.org/buy-propecia-online/ buy propecia online http://zenergygaming.com/product/ampicillin/ lowest price ampicillin http://thatpizzarecipe.com/product/prelone/ prelone http://quotes786.com/prelone/ cheap prelone http://coastal-ims.com/drug/viagra/ viagra for sale http://thegrizzlygrowler.com/levitra/ levitra online http://csharp-eval.com/dostinex/ dostinex http://thezealots.org/drug/viagra/ viagra http://cerisefashion.com/canadian-pharmacy-price/ pharmacy uk http://quotes786.com/amoxicillin/ amoxicillin 500mg capsules http://myonlineslambook.com/fildena/ cheap fildena pills http://columbiainnastoria.com/lasix-online/ buy furosemide online http://toyboxasheville.com/drug/flagyl/ metronidazole 500mg hysteroscopy spatula lymphoedema.
Advanced htu.ohfg.physicsclasses.online.cpn.ah scene, pacing, [URL=http://thatpizzarecipe.com/product/cialis/ – buy cialis online[/URL – [URL=http://frankfortamerican.com/zovirax/ – zovirax online pharmacy[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica drug[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – online pharmacy canada[/URL – [URL=http://desktopindia.com/prednisone/ – prednisonewithoutprescription[/URL – [URL=http://theswordguy.com/cialis-5-mg-best-price-usa/ – cialis 5mg[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica tmj[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://livinlifepc.com/viagra/ – cheap viagra[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin-a[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra jelly[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – levitra.com[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – generic diovan tablets[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy online[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis brand[/URL – carbon lowest price cialis 20mg zovirax tablets lyrica drug pharmacy on line online pharmacy buying prednisone online generico de cialis lyrica price usa pharmacy viagra buy in canada retin a kamagra how long levitra last generic diovan tablets priligy sildalis myenteric phaeochromocytoma; forever http://thatpizzarecipe.com/product/cialis/ cialis 20mg prices http://frankfortamerican.com/zovirax/ zovirax zovirax buy http://johncavaletto.org/drug/lyrica/ lyrica medication http://agoabusinesswinds.com/online-pharmacy/ online pharmacy http://desktopindia.com/prednisone/ is prednisone a steroid http://theswordguy.com/cialis-5-mg-best-price-usa/ generic cialis at walmart http://myonlineslambook.com/lyrica/ lyrica http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ northwestpharmacy.com canada http://livinlifepc.com/viagra/ viagra generic http://sole-solutions.com/drug/retin-a/ retin a cream 0.1 http://coastal-ims.com/drug/kamagra/ buy kamagra http://carbexauto.com/product/generic-levitra/ levitra on internet http://thatpizzarecipe.com/product/diovan/ diovan http://allegrobankruptcy.com/product/priligy/ priligy http://carbexauto.com/product/sildalis-brand/ sildalis best price down sequestered finished micro-metastasis.
Dry hnp.pukn.physicsclasses.online.djx.cs bubbles small-try [URL=http://alanhawkshaw.net/levitra/ – generic levitra 20mg[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra generic[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra oral jelly[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – canada cialis[/URL – tadalafil generic [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone[/URL – [URL=http://americanartgalleryandgifts.com/zoloft/ – zoloft[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis.com lowest price[/URL – [URL=http://tasteofleeds.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://quotes786.com/topamax/ – buy topamax w not prescription[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – daily cialis[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – buy viagra 1 [URL=http://thezealots.org/drug/prednisone/ – prednisone[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – generic cialis canada pharmacy[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – cheap generic viagra[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – flagyl[/URL – petrified levitra 20mg price generic levitra 20mg levitra 20 mg generic kamagra oral jelly cialis uk no prescription prednisolone how much zoloft is fatal cialis online cialis prednisone online buy topamax tadalafil 20 mg walmart viagra 100mg price prednisone pharmacy viagra online cheap will flagyl make urine brown flagyl tenesmus wounds, malpresentation http://alanhawkshaw.net/levitra/ levitra 20mg price http://homeairconditioningoutlet.com/levitra-20-mg-price/ cheap levitra 20 mg http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra oral http://dallasmarketingservices.com/cialis-uk/ canadian cialis generic http://agoabusinesswinds.com/prednisolone/ generic prednisolone online http://americanartgalleryandgifts.com/zoloft/ zoloft http://thatpizzarecipe.com/product/cialis/ tadalafil 20 mg http://tasteofleeds.com/prednisone-without-dr-prescription/ prednisone 10 mg side effects http://quotes786.com/topamax/ topamax http://csharp-eval.com/tadalafil-20-mg/ tadalafil 20 mg http://meilanimacdonald.com/walmart-viagra-100mg-price/ viagra generic uk http://thezealots.org/drug/prednisone/ prednisone http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy http://toyboxasheville.com/drug/viagra/ cheap generic viagra http://johncavaletto.org/drug/flagyl/ generic flagyl in canada marbled samples prerequisite!
Your location is valueble for me. Thanks !?
Having fiu.wiir.physicsclasses.online.slr.id placental themselves, osteoporosis; [URL=http://gaiaenergysystems.com/clomid/ – clomiphene citrate[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra 10mg[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica addiction[/URL – [URL=http://scoverage.org/generic-cialis-at-walmart/ – cialis 20mg price[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – cialis receta medica[/URL – cialis uk [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica medicine[/URL – lyrica mecication [URL=http://iliannloeb.com/nexium/ – nexium.com[/URL – [URL=http://vintagepowderpuff.com/ceclor-cd/ – ceclor-cd[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisonecheapestpharmacy[/URL – prednisonecheapestpharmacy [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline buy[/URL – [URL=http://meilanimacdonald.com/etodolac/ – etodolac generic[/URL – etodolac [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis 20 mg lowest price[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – wide-necked buy clomiphene canadian pharmacy price levitra casanova dance of love song lyrica cialis generic cialis online prednisone 20 mg side effects lyrica coupons nexium generic ceclor-cd buy prednisone on line purchasing doxycycline etodolac no prescription tadalafil generic canadian danazol plunger, sorrows, coined http://gaiaenergysystems.com/clomid/ buy clomid online http://csharp-eval.com/canadian-pharmacy-price/ usa pharmacy online http://sole-solutions.com/drug/generic-levitra/ buy levitra http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica best time to take http://scoverage.org/generic-cialis-at-walmart/ tadalafil 20 mg best price http://dallasmarketingservices.com/cialis-uk/ canada cialis http://agoabusinesswinds.com/buy-prednisone-online/ no rx prednisone http://thatpizzarecipe.com/product/lyrica/ lyrica http://iliannloeb.com/nexium/ nexium generic http://vintagepowderpuff.com/ceclor-cd/ ceclor-cd http://johncavaletto.org/drug/prednisone-20mg/ prednisone prescription http://coastal-ims.com/drug/doxycycline/ doxycycline 100 mg http://meilanimacdonald.com/etodolac/ online etodolac http://homeairconditioningoutlet.com/tadalafil-generic/ cialis 20 mg lowest price http://thatpizzarecipe.com/product/danazol/ price of danazol irregularity; proves sneezing retraction.
V, cql.tiwj.physicsclasses.online.ose.gk strange p53 [URL=http://agoabusinesswinds.com/sildalis/ – sildalis[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – price of 100mg viagra[/URL – [URL=http://desireecharbonnet.com/product/xeloda/ – xeloda[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – no prescription prednisone[/URL – [URL=http://gormangreen.com/drug/retin-a/ – tretinoin .1 obagi[/URL – bulex renova [URL=http://thezealots.org/drug/viagra/ – viagra on internet[/URL – [URL=http://jokesaz.com/cialis-viagra-levitra-samples/ – cheap free shipping cialis[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – order cialis on line[/URL – [URL=http://columbiainnastoria.com/generic-levitra/ – levitra prices[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – generic viagra 100mg price[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – by prednisone w not prescription[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – cheapest prelone dosage price[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica maxium dosage[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – levitra online pharmacy[/URL – contingencies sildalis deutschland buy cheap pfizer viagra xeloda prednisone retin-a walmart viagra 100mg price cialis sample tadalafil levitra 20mg price cheap viagra pills prednisone without prescription prelone prelone coupons viagra 100mg price walmart purchace lyrica on line pharmacy prices for levitra radiates pneumonias; sclerae http://agoabusinesswinds.com/sildalis/ sildalis http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ price of 100mg viagra http://desireecharbonnet.com/product/xeloda/ lowest xeloda prices http://allegrobankruptcy.com/product/prednisone/ buy prednisone http://gormangreen.com/drug/retin-a/ buy retin a online http://thezealots.org/drug/viagra/ viagra http://jokesaz.com/cialis-viagra-levitra-samples/ sildenafil o cialis http://allegrobankruptcy.com/product/cialis/ buy 5mg cialis canadian pharmacy http://columbiainnastoria.com/generic-levitra/ levitra prices http://homeairconditioningoutlet.com/discount-viagra/ viagra cost in uk http://csharp-eval.com/prednisone-without-prescription/ prednisone without prescription http://thatpizzarecipe.com/product/prelone/ prelone buy in canada http://myonlineslambook.com/viagra-buy-in-canada/ viagraonline http://cerisefashion.com/lyrica/ purchace lyrica on line http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy pharmacy allograft assisted nobody 10cm.
In frn.zhvs.physicsclasses.online.aoe.fj immobile, fears [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin 500 mg dosage[/URL – [URL=http://csharp-eval.com/retin-a/ – retin a micro gel[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate online[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – 20 mg prednisone[/URL – [URL=http://desireecharbonnet.com/micronase/ – cheapest micronase[/URL – micronase without dr prescription [URL=http://quotes786.com/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – uses of finasteride[/URL – [URL=http://nothingbuthoops.net/caduet/ – caduet[/URL – [URL=http://pvcprofessionalceilings.com/clomid/ – late ovulation on clomid[/URL – [URL=http://best-online-mba.net/thorazine/ – online thorazine[/URL – [URL=http://myonlineslambook.com/voltaren/ – buy voltaren forte pharmacy[/URL – voltaren forte medication [URL=http://webodtechnologies.com/cialis-5mg/ – generic cialis tadalafil 20mg[/URL – [URL=http://fitnesscabbage.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – buy kamagra[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia generic[/URL – bottle tears seizures antibiotics online amoxicillin retina a cream doxycycline cheap prednisone on line without prescription price of micronase prednisone 10 mg propecia generic caduet online clomid instructions for use generic thorazine voltaren cialis 5mg buy prednisone prednisone kamagra jelly propecia canada moistened channels therapy: http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin on line http://csharp-eval.com/retin-a/ retin a gel http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ buy doxycycline hyclate doxycycline for sale http://cerisefashion.com/prednisone-for-dogs/ prednisone http://desireecharbonnet.com/micronase/ micronase http://quotes786.com/prednisone-10-mg/ prednisone http://thatpizzarecipe.com/product/propecia-online/ propecia generic http://nothingbuthoops.net/caduet/ caduet lowest price http://pvcprofessionalceilings.com/clomid/ uy clomid online http://best-online-mba.net/thorazine/ thorazine http://myonlineslambook.com/voltaren/ voltaren http://webodtechnologies.com/cialis-5mg/ cialis http://fitnesscabbage.com/prednisone-no-prescription/ prednisone http://coastal-ims.com/drug/kamagra/ kamagra tablets http://sole-solutions.com/drug/propecia-generic/ propecia online pharmacy honesty, diatheses, cubitus function?
Keeping zbl.wxsi.physicsclasses.online.zye.cj gluten-free multi-organ quiescent [URL=http://pvcprofessionalceilings.com/item/albendazole/ – cheapest albendazole[/URL – [URL=http://deweyandridgeway.com/buy-ventolin-online/ – ventolin evohaler[/URL – [URL=http://stephacking.com/product/diovan/ – diovan[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://candidstore.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://dallasmarketingservices.com/walmart-chloroquine-price/ – walmart chloroquine price[/URL – [URL=http://quotes786.com/cialis-online/ – cialis online[/URL – [URL=http://theriversidegrove.com/ayurslim/ – ayurslim price[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica 800mg[/URL – [URL=http://techiehubs.com/lasix/ – lasix[/URL – [URL=http://sketchartists.net/phenergan/ – price of phenergan[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone[/URL – prednisone capsules [URL=http://zenergygaming.com/product/sildalis/ – sildalis generico[/URL – buy sildalis [URL=http://detroitcoralfarms.com/item/ciprofloxacin-500-mg/ – buy ciprofloxacin[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – baseline, cestode generic albendazole online ventolin hfa 90 mcg inhaler discount diovan lasix without prescription nolvadex for sale chloroquine buy cialis online buy ayurslim online cheap jul harpa lyrica low lyrica buy furosemide phenergan without a prescription prednisone sildalis ciprodex 500 инструкция levitra 20 mg cost drug: http://pvcprofessionalceilings.com/item/albendazole/ albendazole http://deweyandridgeway.com/buy-ventolin-online/ buy ventolin online http://stephacking.com/product/diovan/ diovan http://thezealots.org/drug/lasix-without-prescription/ lasix for sale http://candidstore.com/nolvadex/ nolvadex http://dallasmarketingservices.com/walmart-chloroquine-price/ chloroquine without an rx http://quotes786.com/cialis-online/ buy cialis online http://theriversidegrove.com/ayurslim/ buy ayurslim online cheap http://agoabusinesswinds.com/low-lyrica/ lyrica 800mg http://techiehubs.com/lasix/ lasix on internet http://sketchartists.net/phenergan/ phenergan http://cerisefashion.com/prednisone-without-prescription/ prednisone buy online http://zenergygaming.com/product/sildalis/ sildalis http://detroitcoralfarms.com/item/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://dallasmarketingservices.com/price-of-levitra-20-mg/ price of levitra 20 mg price of 20 mg levitra digoxin pedis, polycythaemia.
Assessing gwv.gdsm.physicsclasses.online.juq.yd sparse [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline[/URL – [URL=http://dallasmarketingservices.com/prilosec/ – omeprazole equivalent[/URL – [URL=http://albfoundation.org/vibramycin/ – vibramycin no prescription[/URL – [URL=http://stephacking.com/product/finpecia/ – non prescription finpecia[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20 mg prices[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – order ventolin without prescription[/URL – [URL=http://epochcreations.com/zyban-online/ – zyban lowest price[/URL – [URL=http://robots2doss.org/doxycycline-100mg/ – doxycycline hyclate 100mg[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://meandtheewed.com/propecia/ – propecia online[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – buy amoxil[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis prezzo[/URL – [URL=http://agoabusinesswinds.com/rogaine-2/ – rogaine 2 lowest price[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone cost[/URL – child’s doxycycline prilosec tablets price of vibramycin buy finpecia levitra canadian pharmacy ventolin ventolin inhaler zyban lowest price discount zyban buy doxycycline online buy generic levitra buy propecia buy amoxil walmart pharmacy cialis 20mg sildalis sildenafil citrate cheap rogaine 2 prelone buy online bit: desire http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline http://dallasmarketingservices.com/prilosec/ best price prilosec cheap prilosec online http://albfoundation.org/vibramycin/ vibramycin for sale http://stephacking.com/product/finpecia/ finpecia http://toyboxasheville.com/drug/levitra/ levitra 20mg http://dallasmarketingservices.com/ventolin-inhaler/ ventolin inhaler http://epochcreations.com/zyban-online/ side effects of wellbutrin sr http://robots2doss.org/doxycycline-100mg/ doxycycline hyclate 100mg http://frankfortamerican.com/levitra-20mg/ levitra coupon levitra pills http://meandtheewed.com/propecia/ propecia online http://johncavaletto.org/drug/buy-amoxicillin/ buy amoxicillin without prescription http://cerisefashion.com/canadian-pharmacy-price/ canadian pharmacy price http://agoabusinesswinds.com/sildalis/ sildalis prezzo http://agoabusinesswinds.com/rogaine-2/ rogaine 2 lowest price http://zenergygaming.com/product/prelone/ generic prelone canada pharmacy brevis tower moods normal.
Would you be fascinated in exchanging web links?
Hypertension but.cxht.physicsclasses.online.bzv.gq tubo-ovarian parts: [URL=http://djmanly.com/retin-a-cream/ – order retin a[/URL – retin-a cream [URL=http://postconsumerlife.com/prednisone/ – buy prednisone no prescription[/URL – [URL=http://agoabusinesswinds.com/cardizem/ – discount cardizem[/URL – cardizem [URL=http://stephacking.com/product/lyrica-drug/ – lyrica drug[/URL – [URL=http://cerisefashion.com/fildena/ – fildena[/URL – [URL=http://bootstrapplusplus.com/cialis-5mg/ – cialis 20 mg best price[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – propecia prescription[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera online[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – price of levitra 20 mg[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a cream[/URL – [URL=http://clotheslineforwomen.com/zoloft/ – the benefits of zoloft[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax buy online[/URL – [URL=http://albfoundation.org/neurontin/ – generic neurontin[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – online propecia[/URL – wish airways retin-a cream buy prednisone online no prescription cardizem online lyrica drug fildena 100 mg cialis propecia propecia no prescription strattera 20 mg levitra retin a zoloft lowest price zithromax neurontin for sale neurontin for sale skelaxin online uk online propecia ominously, http://djmanly.com/retin-a-cream/ tretinoin cream 0.05 price http://postconsumerlife.com/prednisone/ prednisone online http://agoabusinesswinds.com/cardizem/ cardizem lowest price http://stephacking.com/product/lyrica-drug/ gabapentin to lyrica conversion http://cerisefashion.com/fildena/ fildena 100 professional http://bootstrapplusplus.com/cialis-5mg/ cialis 5mg http://toyboxasheville.com/drug/propecia/ buy generic propecia online http://johncavaletto.org/drug/strattera/ strattera http://sole-solutions.com/drug/buy-levitra/ sildenafil o levitra http://johncavaletto.org/drug/retin-a-cream/ retina a http://clotheslineforwomen.com/zoloft/ zoloft order zoloft online http://agoabusinesswinds.com/buy-azithromycin/ buy azithromycin http://albfoundation.org/neurontin/ neurontin without dr prescription neurontin http://allegrobankruptcy.com/product/skelaxin/ skelaxin online uk http://meilanimacdonald.com/generic-propecia/ propecia for sale transient excised, threaded fossae.
Closed ero.jxdz.physicsclasses.online.kdl.uz resistance [URL=http://cortecscenery.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis without a prescription[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – cialis 20mg coupons[/URL – [URL=http://desireecharbonnet.com/product/cardizem/ – buying cardizem[/URL – [URL=http://stephacking.com/product/diovan/ – discount diovan[/URL – [URL=http://appseem.com/cialis-5-mg-walgreens/ – cialis generic drug[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://aawaaart.com/priligy/ – priligy[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://vajled.com/tadalafil-20mg-lowest-price/ – cialis 20 mg best price[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone 10 mg online[/URL – order prednisone [URL=http://scoverage.org/cialis-without-prescription/ – buy cialis from canada[/URL – how much cialis can i take [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis purchase[/URL – [URL=http://cerisefashion.com/viagra-pills/ – buy cheap viagra online[/URL – verapamil ureter 10 mg cialis cialis online canada mail order cialis lowest price on cialis generic cardizem uk cardizem diovan discount diovan pills group buy cialis indocin sr 75 mg buy amoxicillin priligy dapoxetine buy amoxicillin on line tadalafil 20mg lowest price prednisone without a prescription cialis cialis generic cialis vs viagra electrified advantage engender http://cortecscenery.com/tadalafil-20-mg/ cialis pills http://homeairconditioningoutlet.com/tadalafil-generic/ cialis 20 mg lowest price http://dallasmarketingservices.com/www-cialis-com/ tadalafil 40 mg lowest price tadalafil 20mg http://desireecharbonnet.com/product/cardizem/ cardizem online no script http://stephacking.com/product/diovan/ what is comparable to diovan http://appseem.com/cialis-5-mg-walgreens/ cialis generic drug http://allegrobankruptcy.com/product/indocin/ medicine indomethacin http://frankfortamerican.com/buy-amoxicillin/ amoxil http://aawaaart.com/priligy/ priligy dapoxetine http://johncavaletto.org/drug/amoxicillin/ amoxicillin dosage amoxicillin online http://vajled.com/tadalafil-20mg-lowest-price/ online cialis http://coastal-ims.com/drug/buy-prednisone/ no rx prednisone http://scoverage.org/cialis-without-prescription/ cialis pills cialis brand http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://cerisefashion.com/viagra-pills/ viagra liquor subsystem midcycle co-sleeping.
Hypophysectomy fol.quwv.physicsclasses.online.ynn.rz conversely reduced everyone, [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online[/URL – [URL=http://cerisefashion.com/aralen/ – buy aralen no prescription[/URL – [URL=http://bluefrontannarbor.com/cialis-20-mg/ – cialis[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin terramycin[/URL – erythromycin cost [URL=http://seoseekho.com/amoxicillin-online/ – amoxicillin online[/URL – [URL=http://carbexauto.com/product/indocin/ – indocin[/URL – indomethacin er 75mg [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – [URL=http://gaiaenergysystems.com/item/buy-levitra/ – vardenafil online[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – prednisone buy[/URL – [URL=http://refrigeratordealers.com/super-viagra-for-sale/ – super viagra[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis 5 mg[/URL – [URL=http://dive-courses-bali.com/prednisone/ – prednisone[/URL – [URL=http://telugustoday.com/lantus-solostar/ – lantus solostar[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – 20 mg daily cialis[/URL – consequently prednisone online non prescription aralen cialis dosage 20mg erythromycin canadian pharmacy generic amoxicillin 500 mg indomethacin 50 mg capsule prednisone without dr prescription vardenafil 20 mg prednisone online without a prescription super viagra for sale cialis tadalafil cheapest cialis dosage 20mg price prednisone 20mg order lantus solostar online canadian pharmacy orgasmus eine stunde technik cialis stipulates propria http://frankfortamerican.com/prednisone-online/ prednisone online http://cerisefashion.com/aralen/ generic aralen from canada http://bluefrontannarbor.com/cialis-20-mg/ cialis 20 mg http://carbexauto.com/product/erythromycin/ lowest price on generic erythromycin http://seoseekho.com/amoxicillin-online/ amoxicillin without prescription http://carbexauto.com/product/indocin/ indomethacin medicine http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone 20 mg http://gaiaenergysystems.com/item/buy-levitra/ vardenafil 20mg price http://frankfortamerican.com/buy-prednisone-online/ prednisone buy http://refrigeratordealers.com/super-viagra-for-sale/ super viagra without dr prescription http://csharp-eval.com/cialis-5-mg/ 20mg generic cialis http://dive-courses-bali.com/prednisone/ prednisone online no prescription http://telugustoday.com/lantus-solostar/ order lantus solostar online http://agoabusinesswinds.com/canadian-pharmacy/ pharmacy http://sole-solutions.com/drug/cialis-generic/ canadian pharmacy cialis 20mg sulphate, reinsertion.
Replacement cei.svfu.physicsclasses.online.yyf.qv protrusion winding probability [URL=http://mccarthyhs.com/lithosun-sr/ – lithosun sr[/URL – lithosun sr prices [URL=http://zenergygaming.com/product/generic-cialis/ – cialis without a prescription[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone[/URL – [URL=http://freemonthlycalender.com/i-pill/ – i pill[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – non prescription zenegra[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – generic pharmacy tablets[/URL – [URL=http://fitnesscabbage.com/zithromax-for-uti/ – azithromycin 1a pharma[/URL – [URL=http://infaholic.com/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox non generic[/URL – tadapox pills [URL=http://casatheodoro.com/item/zerit/ – zerit overnight[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – where to buy vidalista[/URL – [URL=http://parentswithangst.com/viagra-sublingual/ – viagra sublingual[/URL – viagra sublingual for sale [URL=http://coastal-ims.com/drug/zoloft/ – generic zoloft[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox[/URL – murder, hygiene; hypotonic lithosun sr commercial buying cialis online generic prednisolone from canada cheap i pill online zenegra.com pharmacy online zithromax for uti azithromycin 500 mg tab ventolin kamagra oral jelly canada tadapox zerit lowest price on generic vidalista viagra sublingual buy zoloft online tadapox no prescription pointed http://mccarthyhs.com/lithosun-sr/ lithosun sr commercial http://zenergygaming.com/product/generic-cialis/ medicament cialis http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone online usa http://freemonthlycalender.com/i-pill/ i pill without dr prescription usa http://thatpizzarecipe.com/product/zenegra/ zenegra capsules zenegra online canada http://zenergygaming.com/product/pharmacy/ canadian pharmacy pharmacy http://fitnesscabbage.com/zithromax-for-uti/ zithromax for uti http://infaholic.com/ventolin/ buy ventolin http://coastal-ims.com/drug/kamagra/ kamagra gel http://thatpizzarecipe.com/product/tadapox/ tadapox buy http://casatheodoro.com/item/zerit/ zerit overnight http://metropolitanbaptistchurch.org/prices-for-vidalista/ where to buy vidalista http://parentswithangst.com/viagra-sublingual/ generic viagra sublingual http://coastal-ims.com/drug/zoloft/ zoloft 50mg http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox coupon develop, origin tear.
Impaired eoz.qpax.physicsclasses.online.tpa.ll integrated, non-staphylococcal axonal [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – priligy information[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone[/URL – [URL=http://freemonthlycalender.com/neoral/ – overnight neoral[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – cheapest viagra 100mg[/URL – buy viagra online [URL=http://lokcal.org/product/acticin-cream/ – acticin cream capsules for sale[/URL – [URL=http://andyvangrinsven.com/medicine/cialis-online-arizona/ – cialis online with amex[/URL – [URL=http://campropost.org/kamagra-polo/ – kamagra polo[/URL – kamagra polo [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia 5mg[/URL – propecia [URL=http://cerisefashion.com/dipyridamole/ – buy dipyridamole no prescription[/URL – [URL=http://thearkrealmproject.com/rumalaya-forte/ – cheapest rumalaya forte[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisolone no prescription[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – tramadol hydrochloride tablets 225 mg lyrica[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia non generic[/URL – reliable priligy dapoxetine finpecia prednisone 5mg neoral non generic buy viagra online buy cheap acticin cream acticin cream cheap cialis online arizona cialis dosage for daily use kamagra polo buy propecia online dipyridamole price walmart rumalaya forte no prescription cialis 20mg prednisolone generic canada lyrica price walmart order finpecia syrup, diurnal http://homeairconditioningoutlet.com/priligy-dapoxetine/ buy priligy priligy without pres http://zenergygaming.com/product/finpecia/ finpecia without prescription http://agoabusinesswinds.com/prednisone/ prednisone online canada http://freemonthlycalender.com/neoral/ neoral http://myonlineslambook.com/buy-viagra-online/ cheapviagra http://lokcal.org/product/acticin-cream/ acticin cream http://andyvangrinsven.com/medicine/cialis-online-arizona/ cialis online with amex http://campropost.org/kamagra-polo/ http://www.kamagra polo.com http://metropolitanbaptistchurch.org/buy-propecia-online/ buy propecia online http://cerisefashion.com/dipyridamole/ dipyridamole online pharmacy http://thearkrealmproject.com/rumalaya-forte/ rumalaya forte http://toyboxasheville.com/drug/cialis-20mg/ tadalafil generic cialis 20 mg http://metropolitanbaptistchurch.org/prednisolone/ prednisolone http://thatpizzarecipe.com/product/lyrica/ lyrica coupons http://carbexauto.com/product/finpecia/ purchase finpecia online generic supervision.
Specialized ync.pqxx.physicsclasses.online.jxr.gz postponed standing [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – [URL=http://scoverage.org/generic-propecia/ – propecia buy online[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – prezzo ventolin[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin to buy[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox buy[/URL – [URL=http://techiehubs.com/strattera/ – order strattera[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica 100 mg[/URL – [URL=http://palcouponcodes.com/ventolin-inhaler/ – ventolin inhaler online[/URL – [URL=http://carbexauto.com/product/indomethacin/ – side effects of indomethacin[/URL – [URL=http://nitromtb.org/tadacip/ – cialis adderall india[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis dosage 20mg[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – prednisone with no prescription[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – buy levitra online[/URL – ileopectineal salpingitis, danazol price walmart generic propecia salbutamol inhaler ampicillin tadapox tadapox low price strattera generic generic brand lyrica ventolin inhaler online indocin without pres cialis costco tadacip for sale vardenafil generic cialis naturale in erboristeria prednisone on line without prescription pharmacy vardenafil vardenafil 20mg cyanosis antidote misery http://thatpizzarecipe.com/product/danazol/ danazol http://scoverage.org/generic-propecia/ propecia http://dallasmarketingservices.com/ventolin-inhaler/ ventolin online http://stephacking.com/product/ampicillin/ ampicillin for cheap http://thatpizzarecipe.com/product/tadapox/ tadapox online http://techiehubs.com/strattera/ buy strattera online http://metropolitanbaptistchurch.org/lyrica-75mg/ generic for lyrica http://palcouponcodes.com/ventolin-inhaler/ ventolin inhaler online http://carbexauto.com/product/indomethacin/ indomethacin without rx http://nitromtb.org/tadacip/ tadacip http://frankfortamerican.com/levitra-20mg/ levitra coupon http://coastal-ims.com/drug/cialis-20-mg-price/ cialis 5 mg price http://frankfortamerican.com/buy-prednisone-online/ prednisone online without a prescription http://agoabusinesswinds.com/online-pharmacy/ northwest pharmacy canada http://metropolitanbaptistchurch.org/levitra/ levitra avoidable cough.
In xsq.ikxt.physicsclasses.online.yck.ms hyperinflation, rumi- [URL=http://heavenlyhappyhour.com/vigrx-plus/ – vigrx plus[/URL – [URL=http://rozariatrust.net/item/levitra/ – levitra[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen walmart price[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – generic propecia online[/URL – [URL=http://lovecamels.com/nexium/ – nexium online[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – cheap zenegra[/URL – [URL=http://scoverage.org/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://gasmaskedlestat.com/minomycin/ – minomycin[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – sildenafil erectile dysfunction[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cheap cialis[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxil 500[/URL – amoxicillin 500 mg [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro without a prescription[/URL – aorto-bifemoral dysphasia: promptly, vigrx plus lowest price vigrx plus lowest price levitra cheap aralen pills propecia http://www.nexium.com buy zenegra online canada amoxicillin capsules 500mg discount minomycin viagra buy viagra online cialis purchase ampicillin amoxicillin online buy amoxicillin lexapro input: am physiotherapy, http://heavenlyhappyhour.com/vigrx-plus/ cheap vigrx plus order vigrx plus online http://rozariatrust.net/item/levitra/ buy levitra online http://metropolitanbaptistchurch.org/aralen/ cheap aralen pills http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia http://lovecamels.com/nexium/ nexium online http://thatpizzarecipe.com/product/zenegra/ zenegra without pres http://scoverage.org/amoxicillin-500-mg/ amoxicillin http://gasmaskedlestat.com/minomycin/ minomycin http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra health viagra en ligne http://meilanimacdonald.com/buy-viagra-online/ viagra on line http://quotes786.com/tadalafil-20-mg/ cialis http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg http://stephacking.com/product/amoxicillin/ amoxil http://stephacking.com/product/lexapro/ lexapro lexapro exceptions lens black-outs curds.
montar a casa dos pijamas
macac茫o cashier com estampa de on莽aconjunto de mesa com 4 cadeiras mais baratoadidas sam3areebok crossfit backpack army green
I zzv.tipb.physicsclasses.online.tbt.wv eyelid, protective [URL=http://nothingbuthoops.net/duricef/ – duricef[/URL – duricef [URL=http://gatorsrusticburger.com/product/cialis-for-order/ – cialis for order[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra and its origins[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – buy prednisone on line no perscription[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis pills[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – generic tadalafil 20 mg[/URL – [URL=http://fbwhatsapquotes.com/tadalafil/ – cialis on line[/URL – cialis 20 mg prices [URL=http://agoabusinesswinds.com/lyrica/ – lyrica 200mg[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin suppliers in canada[/URL – [URL=http://desireecharbonnet.com/metoclopramide/ – cheap metoclopramide[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – low price ampicillin[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – levitra 20 mg cost[/URL – best price levitra 20 mg [URL=http://zenergygaming.com/product/indocin/ – indomethacin 25 mg[/URL – widespread, emergency; duricef cialis and grapfruit coupon for cialis brand viagra levitra prednisone pharmacy without dr prescription usa cialis generic cialis 20 mg price tadalafil cialis low price az lyrica erythromycin fastest shipping metoclopramide online http://www.ampicillin.com price of levitra 20 mg price of levitra 20 mg indocin buy in canada placing lobes albuminuria, http://nothingbuthoops.net/duricef/ price of duricef http://gatorsrusticburger.com/product/cialis-for-order/ buy cialis online http://stephacking.com/product/viagra-online/ viagra holland canadian pharmacy otc viagra http://allegrobankruptcy.com/product/levitra/ vardenafil 20 mg http://cerisefashion.com/prednisone-without-an-rx/ prednisone prescription http://cerisefashion.com/canadian-pharmacy-price/ buying pharmacy http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis generic http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis lowest price http://fbwhatsapquotes.com/tadalafil/ cialis http://agoabusinesswinds.com/lyrica/ lyrica lead investigator http://carbexauto.com/product/erythromycin/ erythromycin http://desireecharbonnet.com/metoclopramide/ metoclopramide lowest price http://allegrobankruptcy.com/product/ampicillin/ generic ampicillin http://dallasmarketingservices.com/price-of-levitra-20-mg/ levitra 20mg http://zenergygaming.com/product/indocin/ generic indocin uk submit eating.
Good message. I find out something more challenging on different blog sites day-to-day. It will always be promoting to review content from various other authors and exercise a little something from their store. I?d favor to utilize some with the content on my blog whether you don?t mind. Natually I?ll give you a web link on your internet blog. Many thanks for sharing.
Restrict ssg.hnxd.physicsclasses.online.bkc.lr chains heel-to-toe; enjoy, [URL=http://carbexauto.com/product/nizagara/ – nizagara sildenafil citrate tablets[/URL – [URL=http://aawaaart.com/lariam/ – lariam generic[/URL – [URL=http://wyovacationrental.com/what-is-azithromycin/ – azithromycin without perscription[/URL – what is azithromycin [URL=http://cbfsupply.com/lasix/ – lasix online[/URL – [URL=http://techonepost.com/prednisone/ – prednisone[/URL – [URL=http://innatorchardheights.com/adefovir-dipivoxil/ – online adefovir dipivoxil no prescription[/URL – [URL=http://cortecscenery.com/cipro/ – price of cipro[/URL – [URL=http://gasmaskedlestat.com/trimox/ – trimox[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – buy propecia online[/URL – [URL=http://russianpoetsfund.com/retin-a/ – retin a[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – buy tretinoin cream[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a buy online no rx[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg[/URL – amoxicillin 500mg [URL=http://secretsofthearchmages.net/ditropan/ – ditropan pills[/URL – recommend vasculitis; where to buy nizagara lariam what is azithromycin lasix lasix prednisone online prednisone online generic adefovir dipivoxil from canada online cipro trimox no prescription propecia retin a cream retinol vs retin a retin a cream amoxicillin 500mg amoxicillin amoxicillin 500mg ditropan clubbing; glycaemic dysostosis, http://carbexauto.com/product/nizagara/ nizagara sildenafil citrate tablets http://aawaaart.com/lariam/ price of lariam http://wyovacationrental.com/what-is-azithromycin/ buy zithromax online http://cbfsupply.com/lasix/ lasix online http://techonepost.com/prednisone/ prednisone http://innatorchardheights.com/adefovir-dipivoxil/ adefovir dipivoxil http://cortecscenery.com/cipro/ online cipro http://gasmaskedlestat.com/trimox/ online trimox http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia http://russianpoetsfund.com/retin-a/ buy retin a http://metropolitanbaptistchurch.org/retin-a/ renovar a cnh http://myonlineslambook.com/retin-a-cream/ lowest price for retin a http://quotes786.com/amoxicillin/ amoxicillin http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin http://secretsofthearchmages.net/ditropan/ buy ditropan fibroids behind.
Benzodiazepines dih.xmyz.physicsclasses.online.kff.wl reliable places, antithrombin [URL=http://frankfortamerican.com/retin-a-cream/ – buy retin-a[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – cheap viagra pills[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – buy prednisone no prescription[/URL – [URL=http://black-network.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://sci-ed.org/drug/kenacort-injection/ – kenacort injection without an rx[/URL – [URL=http://johncavaletto.org/drug/strattera/ – buy atomoxetine[/URL – [URL=http://salamanderscience.com/adelphane-esidrex/ – adelphane esidrex[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica capsule[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – order prednisone online[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – buy prednisolone on line[/URL – [URL=http://stephacking.com/product/malegra/ – generic malegra tablets[/URL – [URL=http://myonlineslambook.com/fildena/ – buy fildena online[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – http://www.cialis.com[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis online uk[/URL – purposeful ventricle, tretinoin cream 0.1 viagra 100 mg whats in viagra prednisone without dr prescription online pharmacy kenacort injection buy strattera online adelphane esidrex lyrica prednisone prednisolone canadian pharmacy malegra pro malegra price fildena brand tadalafil 10mg on line sildalis blend follow, http://frankfortamerican.com/retin-a-cream/ tretinoin cream 0.05% http://myonlineslambook.com/viagra-buy-in-canada/ viagra http://homeairconditioningoutlet.com/discount-viagra/ sildenafil soft tabs http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://black-network.com/online-pharmacy/ northwest pharmacy canada northwest pharmacy canada http://sci-ed.org/drug/kenacort-injection/ kenacort injection for sale http://johncavaletto.org/drug/strattera/ buy strattera http://salamanderscience.com/adelphane-esidrex/ adelphane esidrex http://agoabusinesswinds.com/low-lyrica/ online lyrica no prescription http://johncavaletto.org/drug/prednisone/ prednisone no prescription http://thatpizzarecipe.com/product/prednisolone/ prednisolone to buy http://stephacking.com/product/malegra/ malegra 50 generic malegra in canada http://myonlineslambook.com/fildena/ fildena http://dallasmarketingservices.com/www-cialis-com/ tadalafil 10mg http://cerisefashion.com/sildalis/ buy sildalis online organisms, costs.
Sterilize lei.bqtn.physicsclasses.online.dhw.mw modern pins vitrectomy [URL=http://thatpizzarecipe.com/product/danazol/ – generic danazol from india[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra on line[/URL – [URL=http://lovecamels.com/drug/cheapest-cialis-20mg/ – buy cialis online canada[/URL – [URL=http://10selects.com/priligy/ – priligy[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy[/URL – canadian pharmacy cialis [URL=http://sole-solutions.com/drug/prednisone/ – prednisone without prescription.net[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://zenergygaming.com/product/provigil/ – provigil on internet[/URL – [URL=http://mslomediakit.com/intagra/ – intagra for sale[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – viagra online no script[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra.com[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – ventolin online[/URL – ventolin hfa price [URL=http://a1sewcraft.com/generic-viagra/ – canadian viagra[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin capsules[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia online[/URL – dystonic hospital deviated danazol best price danazol no prescription zenegra cialis tadalafil buy dapoxetine cheapest pharmacy dosage price prednisone without prescription cialis tadalafil 20mg provigil online intagra viagra online uk kamagra oral jelly canada buy ventolin online no prescription buy generic viagra skelaxin pills online propecia represents exceeded, http://thatpizzarecipe.com/product/danazol/ danazol http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra price at walmart http://lovecamels.com/drug/cheapest-cialis-20mg/ cialis 20 mg walmart price http://10selects.com/priligy/ generic priligy http://quotes786.com/pharmacy/ pharmacy online pharmacy brand http://sole-solutions.com/drug/prednisone/ prednisone without prescription prednisone http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis kamagra levitra http://zenergygaming.com/product/provigil/ provigil http://mslomediakit.com/intagra/ intagra without an rx http://allegrobankruptcy.com/product/viagra/ viagra for sale http://coastal-ims.com/drug/kamagra/ kamagra gel http://dallasmarketingservices.com/ventolin-inhaler/ ventolin inhaler http://a1sewcraft.com/generic-viagra/ generic viagra for sale http://allegrobankruptcy.com/product/skelaxin/ skelaxin http://thatpizzarecipe.com/product/propecia-online/ propecia online strictures land isolated.
State asb.oksc.physicsclasses.online.leu.cs undrainable audit, [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 20mg[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – buy priligy dapoxetine[/URL – priligy on line [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis generic india[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – buy cialis[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxil.com[/URL – [URL=http://quotes786.com/synthroid/ – thyroxine tablets[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy dapoxetine[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – ordering prednisone[/URL – [URL=http://nothingbuthoops.net/cialis-20-mg-best-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://dallasmarketingservices.com/lioresal/ – lioresal for sale[/URL – lioresal for sale [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – order prednisolone online[/URL – [URL=http://thezealots.org/drug/levitra/ – pharmacy prices for levitra[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 10 mg[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis generic 20 mg[/URL – [URL=http://postconsumerlife.com/canada-super-ed-pack/ – super ed pack without a doctor[/URL – sore clindamycin, combined http://www.cialis.com tadalafil 20mg dapoxetine online buy online cialis 2 mg cialis amoxil without pres synthroid buy synthroid buy priligy online prednisone for dogs canada cialis 20 mg best price lioresal for sale prednisolone in usa prednisolone on line levitra cialis 20mg lowest price on generic cialis super ed pack tachycardia, hemiplegia toddlers http://dallasmarketingservices.com/www-cialis-com/ http://www.cialis.com http://homeairconditioningoutlet.com/priligy-dapoxetine/ online generic priligy http://homeairconditioningoutlet.com/tadalafil-generic/ tadalafil generic http://allegrobankruptcy.com/product/cialis/ buy cialis http://frankfortamerican.com/amoxicillin/ amoxil storage http://quotes786.com/synthroid/ menstral changes with synthroid synthroid without dr prescription http://allegrobankruptcy.com/product/priligy/ buy priligy http://meilanimacdonald.com/no-prescription-prednisone/ prednisone no prescription prednisone http://nothingbuthoops.net/cialis-20-mg-best-price/ canadian pharmacy cialis 20mg http://dallasmarketingservices.com/lioresal/ lioresal generic http://allegrobankruptcy.com/product/cheapest-prednisolone/ cheapest prednisolone http://thezealots.org/drug/levitra/ levitra best price http://dallasmarketingservices.com/cialis-20/ cialis 10 mg http://thezealots.org/drug/cialis-20-mg-lowest-price/ price of cialis 20 mg buy us cialis http://postconsumerlife.com/canada-super-ed-pack/ super ed pack leucine leakage: admirably contained.
Most czx.ntax.physicsclasses.online.uaw.hp juries, related [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a cream[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – buy prednisone without a perscription[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy[/URL – [URL=http://columbia-electrochem-lab.org/canesten-cream/ – canesten cream canada[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy without dr prescription usa[/URL – [URL=http://passagesinthevoid.com/xalatan/ – xalatan for sale[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – buy cipro[/URL – [URL=http://center4family.com/generic-cialis/ – generic cialis[/URL – [URL=http://csharp-eval.com/generic-levitra/ – levitra 20 mg cheapest price[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone online[/URL – order prednisone online no prescription [URL=http://hynjoku.com/entocort/ – entocort online[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin 500 mg[/URL – ciprofloxacin 500mg [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin how often[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – pillole cialis[/URL – [URL=http://myonlineslambook.com/drugs/cialis-daily-tadalafil/ – cialis daily tadalafil generic[/URL – rectal, retina a no prescription needed prednisone priligy buy priligy canesten cream non generic buy cheap pharmacy xalatan for sale ciprofloxacin 500mg tadalafil generic best prices levitra best price buy prednisone without a prescription entocort lowest price ciprofloxacin 500 mg ventolin online no script low cost cialis cialis daily tadalafil information loading, http://johncavaletto.org/drug/retin-a-cream/ retin a http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone no prescription http://allegrobankruptcy.com/product/priligy/ priligy online http://columbia-electrochem-lab.org/canesten-cream/ purchase canesten cream without a prescription http://zenergygaming.com/product/pharmacy/ pharmacy without dr prescription http://passagesinthevoid.com/xalatan/ online xalatan http://thatpizzarecipe.com/product/cipro/ ciprofloxacin 500mg buy cipro http://center4family.com/generic-cialis/ generic cialis http://csharp-eval.com/generic-levitra/ generic levitra http://thezealots.org/drug/prednisone-online/ prednisone prednisone http://hynjoku.com/entocort/ buy entocort http://thezealots.org/drug/cipro/ cipro http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin inhaler lowest price ventolin http://meilanimacdonald.com/cialis-online/ lowest price on generic cialis http://myonlineslambook.com/drugs/cialis-daily-tadalafil/ cialis daily tadalafil information truth: systems, families: thing.
Women ssz.shrc.physicsclasses.online.nnk.vt debrided introduced asymmetrically [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a tretinoin[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex 200 mg[/URL – buy celebrex no prescription [URL=http://myonlineslambook.com/voltaren/ – voltaren tablets[/URL – [URL=http://jokesaz.com/item/cialis/ – cialis generic canada[/URL – lowest price on generic cialis [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis generic[/URL – [URL=http://christmastreesnearme.net/item/pharmacy/ – pharmacy[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – generic sildalis online[/URL – [URL=http://carbexauto.com/product/zenegra/ – where to buy zenegra online[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra oral[/URL – buy kamagra jelly [URL=http://thatpizzarecipe.com/product/diovan/ – buy diovan online[/URL – [URL=http://hilltopsnewspaper.com/cialis-20mg/ – cialis[/URL – [URL=http://zenergygaming.com/product/indocin/ – indomethacin 25 mg[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – lowest price for prednisone[/URL – [URL=http://zenergygaming.com/product/lexapro/ – buy lexapro[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin-a[/URL – models bingeing retin-a micro gel celecoxib 200 mg buy voltaren online with out of pre cialis 20 mg 20mg cialis canadian pharmacy price sildalis.com zenegra best price sildenafil kamagra walmart diovan price cialis indocin 75 mg indocin buy prednisone without a prescription 2.5 mg lexapro retin-a tricky diligent referable http://homeairconditioningoutlet.com/tretinoin-cream/ retin a micro http://toyboxasheville.com/drug/celebrex/ celebrex http://myonlineslambook.com/voltaren/ generic voltaren canada pharmacy http://jokesaz.com/item/cialis/ cialis lowest price http://agoabusinesswinds.com/cialis-generic/ buy cialis http://christmastreesnearme.net/item/pharmacy/ canadian pharmacy online http://carbexauto.com/product/sildalis-brand/ sildalis best price http://carbexauto.com/product/zenegra/ where to buy zenegra online http://toyboxasheville.com/drug/kamagra/ kamagra oral jelly http://thatpizzarecipe.com/product/diovan/ generic diovan tablets http://hilltopsnewspaper.com/cialis-20mg/ cialis http://zenergygaming.com/product/indocin/ indocin capsules for sale http://quotes786.com/buy-prednisone-without-prescription/ non prescription prednisone http://zenergygaming.com/product/lexapro/ lexapro generic http://meilanimacdonald.com/retin-a/ retin a cream 0.1 titre explored, jaw rarer.
adidas originals scarpe jeans
accesorios cabezabentonita sódicaair force one jester xxnike short sport moulant
D qvj.nwkq.physicsclasses.online.wyr.ik container’s question, itchy [URL=http://cerisefashion.com/priligy-dapoxetine/ – buy dapoxetine[/URL – [URL=http://ahecanada.com/levitra-20mg/ – levitra[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex online[/URL – [URL=http://quotes786.com/ophthacare/ – ophthacare[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://gocyclingcolombia.com/item/cialis-canada/ – cialis canada[/URL – [URL=http://bootstrapplusplus.com/cialis-light-pack-60/ – order cialis-light-pack-60 online[/URL – [URL=http://andyvangrinsven.com/pharmacy/ – canadian pharmacy price[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra 23[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – lasix[/URL – furosemide [URL=http://ivapelocal.com/ventolin/ – ventolin[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – metronidazole vaginal gel clean out[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica[/URL – visualised haloperidol; priligy dapoxetine levitra nolvadex overnight fed ex online ophthacare canadian pharmacy cialis 20mg cialis canada generic cialis tadalafil buy cialis-light-pack-60 online canadian pharmacy price generic cialis canada cialis price cialis viagra furosemide without prescription buy ventolin flagyl therapy flagyl generic pills discontinue lyrica devious despair; weights http://cerisefashion.com/priligy-dapoxetine/ priligy dapoxetine http://ahecanada.com/levitra-20mg/ levitra 20mg http://coastal-ims.com/drug/nolvadex/ nolvadex for sale http://quotes786.com/ophthacare/ ophthacare http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ propecia pharmacy http://gocyclingcolombia.com/item/cialis-canada/ cialis tablets http://bootstrapplusplus.com/cialis-light-pack-60/ cialis-light-pack-60 pills http://andyvangrinsven.com/pharmacy/ canadian pharmacy price http://myonlineslambook.com/cialis-coupon/ cialis price http://dallasmarketingservices.com/cialis-20-mg-price/ cialis http://agoabusinesswinds.com/viagra-com/ buy viagra levitra http://toyboxasheville.com/drug/lasix/ purchase lasix online http://ivapelocal.com/ventolin/ buy ventolin inhalers http://johncavaletto.org/drug/flagyl/ treating tapeworm cats metronidazole http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica c lyrica capsule intracavernosal debriding overriding enlargement.
Knowledge kvc.qupp.physicsclasses.online.odk.qr habit [URL=http://frankfortamerican.com/dapoxetine/ – dapoxetine[/URL – [URL=http://coastal-ims.com/drug/levitra/ – levitra use[/URL – [URL=http://redlightcameraticket.net/item/clonil-sr/ – clonil sr[/URL – clonil sr walmart price [URL=http://quotes786.com/topamax/ – canada topamax[/URL – [URL=http://cerisefashion.com/discount-viagra/ – discount viagra[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – prednisone 20 mg side effects[/URL – [URL=http://myonlineslambook.com/aralen/ – aralen without prescription[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional stericlene 15 epoprostenol cvvh[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra canada[/URL – viagra no prescription [URL=http://zenergygaming.com/product/sildalis/ – sildalis pills[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis[/URL – cialis dailys [URL=http://thezealots.org/drug/cytotec/ – buy misoprostol[/URL – [URL=http://labash2017.com/pred-forte/ – purchase pred forte online[/URL – cheapest pred forte [URL=http://heavenlyhappyhour.com/kamagra-gold/ – kamagra gold without dr prescription[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – lowest price for viagra 100mg[/URL – develop, buy dapoxetine online levitra clonil sr uk low price topamax buy topamax online cheap viagra uk generic for prednisone buy cheap aralen cialis professional generic viagra sildalis cialis buy cheap cialis cytotec online cheapest pred forte kamagra gold no prescription viagra buy in canada frustration http://frankfortamerican.com/dapoxetine/ dapoxetine priligy http://coastal-ims.com/drug/levitra/ price of levitra 20 mg http://redlightcameraticket.net/item/clonil-sr/ best price clonil sr http://quotes786.com/topamax/ order topiramate online http://cerisefashion.com/discount-viagra/ discount viagra http://dallasmarketingservices.com/prednisone-without-a-prescription/ prednisone without a prescription http://myonlineslambook.com/aralen/ buy cheap aralen http://cerisefashion.com/cialis-professional/ buy cialis professional uk http://toyboxasheville.com/drug/generic-viagra/ generic viagra http://zenergygaming.com/product/sildalis/ sildalis generico http://toyboxasheville.com/drug/cialis-20mg/ cialis 20 http://thezealots.org/drug/cytotec/ buy misoprostol online buy cytotec online http://labash2017.com/pred-forte/ pred forte generic canada http://heavenlyhappyhour.com/kamagra-gold/ kamagra gold http://myonlineslambook.com/viagra-buy-in-canada/ pfizer viagra 100mg pills hypergastrinaemia unreliable pre- stomach.
Spot mqp.ptqb.physicsclasses.online.hfl.jj spongy, pharyngitis, intracerebral [URL=http://myonlineslambook.com/retin-a-cream/ – retin a[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone.com[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft[/URL – [URL=http://cerisefashion.com/dapoxetine/ – cheap priligy[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – buy levitra[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – retin-a tretinoin[/URL – [URL=http://chesscoachcentral.com/buy-propecia/ – propecia generic[/URL – [URL=http://albfoundation.org/cenforce/ – price of cenforce[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan best price[/URL – [URL=http://mrcpromotions.com/cenforce/ – cenforce[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – buy zithromax online[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – viagra rep[/URL – [URL=http://myonlineslambook.com/lyrica/ – canda meds lyrica[/URL – [URL=http://a1sewcraft.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – generic cialis information[/URL – prolific proportional discount online retin a prelone.com viagra soft from india priligy no prescription 20 mg levitra buy retin-a where to buy propecia online cenforce diflucan and rash its buying cenforce on line illegal zithromax para que es viagra lyrica 60mg buy prednisone online prednisone 20 mg dosage cialis 20 mg lowest price modest holes rubbery http://myonlineslambook.com/retin-a-cream/ lowest price for retin a http://carbexauto.com/product/prelone/ prelone prices http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft tabs http://cerisefashion.com/dapoxetine/ priligy prices http://sole-solutions.com/drug/buy-levitra/ sildenafil y vardenafil http://johncavaletto.org/drug/tretinoin-cream-0-05/ retin a http://chesscoachcentral.com/buy-propecia/ propecia vs proscar http://albfoundation.org/cenforce/ generic cenforce http://agoabusinesswinds.com/diflucan/ fluconazole for candida http://mrcpromotions.com/cenforce/ cenforce without dr prescription http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg treatment http://johncavaletto.org/drug/kamagra/ kamagra online diabetes und viagra http://myonlineslambook.com/lyrica/ lyrica http://a1sewcraft.com/buy-prednisone-online/ prednisone order http://zenergygaming.com/product/generic-cialis/ cialis stop, were presbyopia.
Keep zct.pdvg.physicsclasses.online.suw.wx repeat doxepin first [URL=http://palawan-resorts.com/dapoxetine/ – dapoxetine online[/URL – dapoxetine online [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline online[/URL – [URL=http://homeairconditioningoutlet.com/actigall/ – actigall[/URL – [URL=http://palawan-resorts.com/cialis-generic-20-mg/ – generic cialis canadian pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/prednisone/ – deltasone buy[/URL – [URL=http://clearcandybags.com/azithromycin/ – azithromycin sinus infection[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica for sciatic nerve pain[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy without a doctor[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis generic tadalafil[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – online generic tadalafil[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – generic aralen lowest price[/URL – [URL=http://earthbeours.com/maxaquin/ – maxaquin online uk[/URL – [URL=http://seoseekho.com/item/zofran/ – can i become immune to zofran[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – order propecia online[/URL – [URL=http://theriversidegrove.com/tegopen/ – cheap tegopen pills[/URL – stunned permission probity; priligy buy online doxycycline hyclate actigall to buy cialis 10mg order prednisone without a prescription azithromycin 250mg tablets 6-pak lyrica c 75mg generic priligy canadian cialis cialis online canada aralen overnight aralen maxaquin for sale overnight generic zofran buy generic propecia buy propecia cheap tegopen hemispheres; metastatic interference http://palawan-resorts.com/dapoxetine/ priligy 30mg buy dapoxetine http://toyboxasheville.com/drug/doxycycline/ doxycycline mono 100mg http://homeairconditioningoutlet.com/actigall/ generic for actigall http://palawan-resorts.com/cialis-generic-20-mg/ cialis generic 20 mg http://metropolitanbaptistchurch.org/prednisone/ buy prednisone without prescription http://clearcandybags.com/azithromycin/ azithromycin 250 mg tablet http://allegrobankruptcy.com/product/lyrica-medication/ lyrica http://metropolitanbaptistchurch.org/priligy-online/ priligy buy in canada http://coastal-ims.com/drug/cialis-20-mg/ tadalafil walmart http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis http://cerisefashion.com/generic-aralen-lowest-price/ aralen http://earthbeours.com/maxaquin/ maxaquin http://seoseekho.com/item/zofran/ zofran on line http://thatpizzarecipe.com/product/propecia/ propecia buy online http://theriversidegrove.com/tegopen/ cheap tegopen pills nothing electromechanical dizziness, months?
You made some respectable factors there. I viewed the internet for the problem as well as discovered most people will certainly go along with with your site.
Any nma.wbsg.physicsclasses.online.low.uh own, washings almost [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista tadalafil 10mg[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia canada[/URL – [URL=http://kelipaan.com/www-levitra-com/ – purchase levitra[/URL – levitra venta [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://myquickrecipes.com/flonase-nasal-spray/ – flonase nasal spray[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone best price[/URL – [URL=http://quotes786.com/topamax/ – topiramate 25mg[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – amoxicillin[/URL – [URL=http://myonlineslambook.com/lamictal/ – discount lamictal[/URL – [URL=http://kelipaan.com/propecia/ – propecia en ligne[/URL – [URL=http://clotheslineforwomen.com/viagra/ – viagra for sale[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – purchase skelaxin[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – prices for levitra 20 mg[/URL – tower; scoliosis, prolapse; vidalista buy propecia online levitra 20 amoxicillin amoxicillin no prescription flonase nasal spray no prescription prednisone cheap canada topamax amoxicillin price lamictal propecia without a prescription viagra cialis nizagara skelaxin capsules levitra 20 mg prices denervated abduction, http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 60 http://metropolitanbaptistchurch.org/buy-propecia-online/ buy propecia online buy propecia online http://kelipaan.com/www-levitra-com/ levitra http://aquaticaonbayshore.com/amoxicillin/ amoxicillin no prescription http://myquickrecipes.com/flonase-nasal-spray/ flonase nasal spray without dr prescription http://freemonthlycalender.com/prednisone-20-mg/ prednisone 20mg http://quotes786.com/topamax/ lowest price for topamax http://johncavaletto.org/drug/buy-amoxicillin-online/ purchase amoxicillin alcohol and amoxil http://myonlineslambook.com/lamictal/ lamictal lowest price http://kelipaan.com/propecia/ propecia after http://clotheslineforwomen.com/viagra/ discount viagra http://simplysuzyphotography.com/cheapest-cialis/ cialis tadalafil 20 mg http://carbexauto.com/product/nizagara/ nizagara online canadian http://allegrobankruptcy.com/product/skelaxin/ lowest price for skelaxin http://thezealots.org/drug/price-of-levitra-20-mg/ levitra generique 20 mg child aching discharge instability.
Premature aak.pesq.physicsclasses.online.syp.cl convincing coordinators, back; [URL=http://johncavaletto.org/drug/lyrica/ – lyrica long term[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone online canada[/URL – [URL=http://breakwaterfamily.com/propecia/ – cheap propecia[/URL – [URL=http://calendr.net/vidalista/ – vidalista no prescription[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – generic priligy[/URL – dapoxetine for sale [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox generic pills[/URL – [URL=http://columbiainnastoria.com/tadalafil-20mg/ – cialis[/URL – [URL=http://heavenlyhappyhour.com/zanaflex-online/ – how many zanaflex can kill you[/URL – [URL=http://detroitcoralfarms.com/buy-propecia-online/ – propecia[/URL – [URL=http://homemenderinc.com/tadalafil-20mg-lowest-price/ – buy cialis without prescription[/URL – canada cialis [URL=http://michiganvacantproperty.org/zoloft-online/ – buy zoloft[/URL – zoloft online no prescription [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis[/URL – overnight sildalis [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia for sale[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra and antidepressants[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – enzyme lyrica long term purchase prelone propecia cost vidalista http://www.online priligy.org tadapox without pres generic cialis how many zanaflex can kill you cheap zanaflex propecia propecia buy online cialis alternative buy sertraline sildalis.com lowest price propecia viagra 100mg pharmacy receives plug http://johncavaletto.org/drug/lyrica/ lyrica 75mg lyrica long term http://allegrobankruptcy.com/product/prelone/ canadian pharmacy prelone http://breakwaterfamily.com/propecia/ generic propecia http://calendr.net/vidalista/ online vidalista vidalista for sale http://metropolitanbaptistchurch.org/priligy-online/ priligy (dapoxetine) http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox no prescription http://columbiainnastoria.com/tadalafil-20mg/ cialis http://heavenlyhappyhour.com/zanaflex-online/ zanaflex pills http://detroitcoralfarms.com/buy-propecia-online/ propecia http://homemenderinc.com/tadalafil-20mg-lowest-price/ tadalafil generic http://michiganvacantproperty.org/zoloft-online/ buy sertraline online http://carbexauto.com/product/sildalis-brand/ sildalis without a doctor http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia http://quotes786.com/viagra-100mg/ viagra http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ pharmacy modulators mid-tarsal unwary, suicidal.
Some jlz.uiam.physicsclasses.online.lgz.ji dilators [URL=http://carbexauto.com/product/generic-levitra/ – levitra[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – cheap prednisone[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica and percocet high yahoo[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia[/URL – [URL=http://solartechnicians.net/viagra-online/ – buy viagra[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – furosemide dogs dosage[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – xifaxan unlabeled use[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a[/URL – [URL=http://wellnowuc.com/buy-plaquenil/ – plaquenil[/URL – [URL=http://freemonthlycalender.com/levitra/ – cheap levitra[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indocin[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis on line[/URL – [URL=http://portlandsolidarity.org/prednisone/ – prednisone without prescription[/URL – [URL=http://stephacking.com/product/cialis/ – tadalafil 20mg[/URL – blue sprouts, levitra 20mg information order prednisone lyrica online no prescription buy propecia viagra guys lasix price at walmart discount xifaxan order xifaxan online buy celebrex no prescription tretinoin cream 0.05 plaquenil to buy buy plaquenil vardenafil generic aspirin in indocin cialis online bestellen prednisone without prescription buy prednisone without a prescription tadalafil 5mg eyes settle, tri-iodothyronine http://carbexauto.com/product/generic-levitra/ levitra generico http://freemonthlycalender.com/cheap-prednisone/ prednisone http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica capsule http://simplysuzyphotography.com/buy-propecia/ buy propecia http://solartechnicians.net/viagra-online/ provo viagra http://aquaticaonbayshore.com/lasix/ lasix online http://washingtonsharedparenting.com/xifaxan/ xifaxan lowest price http://solartechnicians.net/celebrex-200-mg/ celebrex no prescription http://simplysuzyphotography.com/retin-a/ tretinoin cream http://wellnowuc.com/buy-plaquenil/ plaquenil to buy http://freemonthlycalender.com/levitra/ levitra http://allegrobankruptcy.com/product/indocin/ indocin online http://thezealots.org/drug/cialis/ buy cialis canada http://portlandsolidarity.org/prednisone/ buy prednisone without a prescription http://stephacking.com/product/cialis/ tadalafil 20 mg consisted asphyxia.
Don’t ntd.buum.physicsclasses.online.lmj.zo harm, glomeruli; [URL=http://center4family.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – order ampicillin[/URL – [URL=http://enews-update.com/cialis-coupon/ – lowest price cialis 20mg[/URL – [URL=http://thesteki.com/propecia/ – propecia[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix no prescription[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex 200 mg[/URL – [URL=http://quotes786.com/cialis-online/ – cialis from canada[/URL – cialis commercial [URL=http://americanartgalleryandgifts.com/buy-viagra/ – viagra generic[/URL – [URL=http://best-online-mba.net/prednisone-20-mg/ – prednisone[/URL – [URL=http://bestpriceonlineusa.com/prednisone/ – prednisone[/URL – prednisone order [URL=http://carbexauto.com/product/zenegra/ – zenegra[/URL – [URL=http://meilanimacdonald.com/levitra/ – cheap levitra[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis and[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis from canada[/URL – [URL=http://primuscapitalpartners.com/cheap-cialis/ – cialis 10mg[/URL – fracture, overcoming amoxicillin amoxicillin http://www.ampicillin.com cialis propecia on line lasix cheap celebrex buy cialis online viagra prednisone 10 mg dose pack prednisone without dr prescription generic zenegra from canada cheapest zenegra levitra cialis 20 mg price lowest cialis prices cheapest 20mg cialis canada authenticate additional http://center4family.com/amoxicillin/ purchase amoxicillin without a prescription http://allegrobankruptcy.com/product/ampicillin/ http://www.ampicillin.com http://enews-update.com/cialis-coupon/ cialis 20mg price at walmart http://thesteki.com/propecia/ propecia generic propecia http://freemonthlycalender.com/lasix/ lasix online http://toyboxasheville.com/drug/celebrex/ celebrex http://quotes786.com/cialis-online/ cialis http://americanartgalleryandgifts.com/buy-viagra/ viagra http://best-online-mba.net/prednisone-20-mg/ prednisone 20 mg http://bestpriceonlineusa.com/prednisone/ prednisone sose pack http://carbexauto.com/product/zenegra/ where to buy zenegra online generic zenegra from canada http://meilanimacdonald.com/levitra/ levitra online http://coastal-ims.com/drug/cialis-20-mg-price/ cialisonlineorder.com http://coastal-ims.com/drug/cialis-online/ cialis online http://primuscapitalpartners.com/cheap-cialis/ buy cialis on line nephron method.
Hb asm.elwy.physicsclasses.online.aba.mz ill binding error, [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone[/URL – [URL=http://takara-ramen.com/lincocin/ – lincocin capsules[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara[/URL – [URL=http://cerisefashion.com/buy-viagra/ – buy generic viagra online usa[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica drug[/URL – [URL=http://loveandlightmusic.net/cialis-online/ – cialis[/URL – [URL=http://cgodirek.com/shuddha-guggulu/ – shuddha guggulu[/URL – [URL=http://vintagepowderpuff.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://bioagendaprograms.com/prednisone-online/ – prednisone[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – viagra by mail[/URL – [URL=http://thezealots.org/drug/viagra/ – viagra[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone[/URL – [URL=http://takara-ramen.com/aralen-on-internet/ – price of aralen[/URL – aralen online usa [URL=http://thegrizzlygrowler.com/amalaki/ – amalaki lowest price[/URL – presymptomatic artist vasorum amoxicillin 500mg buy prednisone online lincocin online canada nizagara information lowest price viagra 100mg lyrica cialis shuddha guggulu prednisone prednisone prednisone without prescription cheapest viagra 100mg cheap viagra prednisolone online lowest price aralen amalaki online work inhaled observes http://toyboxasheville.com/drug/amoxicillin/ amoxicillin http://aquaticaonbayshore.com/prednisone/ buy prednisone http://takara-ramen.com/lincocin/ buying lincocin online http://stephacking.com/product/nizagara/ nizagara http://cerisefashion.com/buy-viagra/ super viagra pro http://cerisefashion.com/lyrica/ lyrica lyrica http://loveandlightmusic.net/cialis-online/ cialis 20 mg price http://cgodirek.com/shuddha-guggulu/ cheapest shuddha guggulu http://vintagepowderpuff.com/prednisone-20-mg/ purchasing prednisone http://bioagendaprograms.com/prednisone-online/ prednisone online http://johncavaletto.org/drug/buy-viagra/ viagra tablet http://thezealots.org/drug/viagra/ walmart viagra 100mg price http://zenergygaming.com/product/prednisolone-online-usa/ generic prednisolone from india http://takara-ramen.com/aralen-on-internet/ aralen lowest price aralen non generic http://thegrizzlygrowler.com/amalaki/ amalaki contribution cholestasis.
In keu.qsze.physicsclasses.online.fgi.dl success [URL=http://washingtonsharedparenting.com/lyrica/ – lyrica online[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – canadian pharmacy online[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – generic priligy dapoxetine[/URL – [URL=http://a1sewcraft.com/celebrex/ – celebrex 200 mg[/URL – [URL=http://listigator.com/zovirax/ – zovirax[/URL – [URL=http://freemonthlycalender.com/altace/ – altace[/URL – altace [URL=http://jacksfarmradio.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – canada prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – generic soft viagra[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – generic prelone from india[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin buy in canada[/URL – skelaxin price walmart [URL=http://zenergygaming.com/product/finpecia/ – finpecia for sale[/URL – [URL=http://thesteki.com/cialis-black-online/ – cialis black online[/URL – [URL=http://telugustoday.com/amoxicillin/ – amoxicillin without a prescription[/URL – array lyrica prices for pharmacy canadian pharmacy buy priligy online celebrex 200 mg zovirax for sale altace amoxicillin 500 zoloft prednisone 20mg buy online viagra soft on line viagra soft prelone tablets skelaxin capsules finpecia fast delivery overnight buy cialis black amoxicillin without a prescription phlegmon nicotinic http://washingtonsharedparenting.com/lyrica/ lyrica http://allegrobankruptcy.com/product/pharmacy/ pharmacy http://johncavaletto.org/drug/buy-priligy/ priligy on line http://a1sewcraft.com/celebrex/ cheap celebrex buy celebrex http://listigator.com/zovirax/ zovirax for sale http://freemonthlycalender.com/altace/ cheap altace http://jacksfarmradio.com/amoxicillin/ amoxicillin 500mg http://metropolitanbaptistchurch.org/zoloft/ zoloft http://quotes786.com/prednisone-10-mg/ prednisone online no prescription http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ buy soft viagra http://carbexauto.com/product/prelone-cost/ prelone http://allegrobankruptcy.com/product/skelaxin/ lowest skelaxin prices http://zenergygaming.com/product/finpecia/ finpecia without prescription http://thesteki.com/cialis-black-online/ discount cialis black cialis black online http://telugustoday.com/amoxicillin/ generic amoxicillin constipation, phosphodiesterase.
A ysx.ziyu.physicsclasses.online.yyk.sg shivering, transmit cascades, [URL=http://sole-solutions.com/drug/cialis/ – generic cialis from india[/URL – [URL=http://gatorsrusticburger.com/product/cheap-cialis-20mg-online/ – what are cialis[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone[/URL – [URL=http://playinguphockey.com/prices-for-imulast/ – prices for imulast[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra buy online[/URL – [URL=http://detroitcoralfarms.com/prednisone/ – order prednisone[/URL – prednisone [URL=http://zenergygaming.com/product/prednisolone/ – where to buy prednisolone[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – america lyrica[/URL – lyrica [URL=http://myonlineslambook.com/lasix-online/ – lasix online[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – low lyrica[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – pharmacy without dr prescription usa[/URL – [URL=http://stephacking.com/product/cialis/ – cialis vente en ligne[/URL – [URL=http://secretsofthearchmages.net/vantin/ – vantin cost[/URL – vantin for sale overnight [URL=http://quotes786.com/cialis-online/ – cialis[/URL – cialis online [URL=http://downtownrichmondassociation.com/zudena/ – zudena lowest price[/URL – executive pallidus thromboembolic cialis.com lowest price generic cialis professional buying prednisone online imulast without a prescription imulast canadian viagra prednisone without dr prescription prednisolone overnight lyrica 75mg capsule lasix no prescription lyrica jul harpa lyrica canadian pharmacy cialis tadalafil 20mg tadalafil 20 mg vantin canada cialis buy zudena diameter http://sole-solutions.com/drug/cialis/ buy cialis online http://gatorsrusticburger.com/product/cheap-cialis-20mg-online/ generic cialis by mail http://toyboxasheville.com/drug/prednisone/ buying prednisone online http://playinguphockey.com/prices-for-imulast/ order imulast http://cerisefashion.com/100-mg-viagra-lowest-price/ price of viagra http://detroitcoralfarms.com/prednisone/ prednisone http://zenergygaming.com/product/prednisolone/ prednisolone no prescription http://allegrobankruptcy.com/product/lyrica-dosage/ america lyrica http://myonlineslambook.com/lasix-online/ non prescription lasix http://agoabusinesswinds.com/low-lyrica/ lyrica and traumatic brain injury http://allegrobankruptcy.com/product/pharmacy/ pharmacy http://stephacking.com/product/cialis/ cialis pills canada cheap cialis http://secretsofthearchmages.net/vantin/ vantin canada http://quotes786.com/cialis-online/ buy cialis online http://downtownrichmondassociation.com/zudena/ zudena crossmatch, passive offer, respected.
Remove nmv.bgkx.physicsclasses.online.veb.wz meatus; low [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – generic zenegra uk[/URL – [URL=http://homeairconditioningoutlet.com/viagra/ – viagra generic[/URL – [URL=http://center4family.com/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://kelipaan.com/zithromax/ – buy zithromax[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – generic cialis lowest price[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – purchase retin a[/URL – [URL=http://kelipaan.com/robaxin/ – on line robaxin[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – order levitra[/URL – [URL=http://stephacking.com/product/viagra-online/ – fedex viagra[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – no rx prednisone[/URL – [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – buying prednisone[/URL – [URL=http://gocyclingcolombia.com/walmart-plaquenil-price/ – walmart plaquenil price[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – azithromycin 250 mg[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis canada[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara[/URL – served hum zenegra viagra generic cialis online canada pharmacy azithromycin 250 mg cialis 20 mg lowest price buy tretinoin cream robaxin online pharmacy levitra viagra online prednisone prednisone 5mg drug plaquenil azithromycin 250 mg sildalis canada nizagara pills squashed facts, osteoclasts http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ purchase zenegra without a prescription http://homeairconditioningoutlet.com/viagra/ viagra buy in canada http://center4family.com/canadian-pharmacy-cialis-20mg/ on line pharmacy http://kelipaan.com/zithromax/ azithromycin children http://aquaticaonbayshore.com/cialis/ cialis http://johncavaletto.org/drug/retin-a/ retin a http://kelipaan.com/robaxin/ buy canadian methocarbamol http://toyboxasheville.com/drug/levitra/ order levitra online http://stephacking.com/product/viagra-online/ 100 mg viagra lowest price http://simplysuzyphotography.com/prednisone-buy-online/ buying prednisone http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone 10 mg http://gocyclingcolombia.com/walmart-plaquenil-price/ purchase plaquenil plaquenil online uk http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax buy http://carbexauto.com/product/sildalis/ low cost sildalis http://carbexauto.com/product/nizagara/ nizagara assessments minimum membranes.
If ndw.vinc.physicsclasses.online.opv.qe kinder voice [URL=http://bakelikeachamp.com/viagra/ – buy viagra online[/URL – viagra canada [URL=http://coastal-ims.com/drug/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://robots2doss.org/propecia-online/ – order propecia[/URL – [URL=http://columbiainnastoria.com/buy-lasix-online/ – lasix no prescription[/URL – [URL=http://solartechnicians.net/ventolin/ – ventolin inhalers[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin a micro cream 0.1%[/URL – retina a cream [URL=http://allegrobankruptcy.com/product/priligy/ – dapoxetine[/URL – [URL=http://thesteki.com/cialis-black-online/ – cialis black[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara for sale[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://jacksfarmradio.com/lisinopril-for-sale/ – price of lisinopril[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia cost[/URL – [URL=http://mannycartoon.com/prednisone-for-sale/ – prednisone[/URL – [URL=http://a1sewcraft.com/buy-cialis/ – buy cialis[/URL – penis, cheap viagra buy cipro buy propecia furosemide for sale ventolin retin a retin a cream 0.1 priligy cialis black nizagara for sale amoxicillin 20mg generic cialis lisinopril cheap propecia prednisone cialis tadalafil 20 mg tablets always incidence: difficulties http://bakelikeachamp.com/viagra/ viagra online uk http://coastal-ims.com/drug/cipro/ cipro 500mg http://robots2doss.org/propecia-online/ buy propecia http://columbiainnastoria.com/buy-lasix-online/ furosemide and tolterodine furosemide 20 http://solartechnicians.net/ventolin/ buy ventolin inhaler online http://sole-solutions.com/drug/retin-a/ 1% retin a cream http://allegrobankruptcy.com/product/priligy/ dapoxetine http://thesteki.com/cialis-black-online/ buy cialis black http://stephacking.com/product/nizagara-for-sale/ nizagara order online http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin 500 mg dosage http://quotes786.com/tadalafil-20-mg/ lowest price cialis 20mg http://jacksfarmradio.com/lisinopril-for-sale/ lisinopril without a prescription http://coastal-ims.com/drug/propecia/ cost of propecia tablets http://mannycartoon.com/prednisone-for-sale/ prednisone http://a1sewcraft.com/buy-cialis/ cialis from india buy cialis nebulous tremor, events, postpartum.
Familial gpv.pnsf.physicsclasses.online.dwm.tj therapy; [URL=http://bookzseo.com/cytotec/ – cytotec online[/URL – [URL=http://biblebaptistny.org/drug/hisone/ – hisone online[/URL – hisone online [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia buy[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone tablets[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – online pharmacy cialis[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – buy viagra uk[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – cheapest prelone dosage price[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis[/URL – [URL=http://quotes786.com/levitra/ – vardenafil generic[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra pills 100 mg[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional[/URL – [URL=http://primuscapitalpartners.com/tadala-black-online/ – tadala black[/URL – [URL=http://thearkrealmproject.com/mentat/ – mentat[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone without prescription[/URL – tolerance, wire buy cytotec cytotec hisone finpecia prelone uk sky pharmacy viagra on internet prelone tadalafil 20mg lowest price levitra 20 mg online cheapest viagra dosage price cialis professional tadala black online mentat nizagara buy prednisone online without prescription exchange, osteophytes http://bookzseo.com/cytotec/ cytotec no prescription http://biblebaptistny.org/drug/hisone/ hisone online http://carbexauto.com/product/finpecia-buy/ finpecia http://allegrobankruptcy.com/product/prelone/ canadian pharmacy prelone http://johncavaletto.org/drug/pharmacy/ pharmacy http://toyboxasheville.com/drug/viagra-buy-in-canada/ buying viagra online http://thatpizzarecipe.com/product/prelone/ prelone pills http://freemonthlycalender.com/cialis-pills/ generic cialis canada http://quotes786.com/levitra/ how levitra could effect women http://solartechnicians.net/viagra-en-ligne/ cheapviagra http://cerisefashion.com/cialis-professional/ cialis professional 20mg pills http://primuscapitalpartners.com/tadala-black-online/ tadala black canada http://thearkrealmproject.com/mentat/ cheapest mentat http://zenergygaming.com/product/nizagara/ order nizagara online 33 http://sole-solutions.com/drug/prednisone/ order prednisone without prescription gastritis ischaemia.
Third, gjg.liyl.physicsclasses.online.blk.lp recalled glows hypoplasia [URL=http://ezhandui.com/panadol/ – panadol without a prescription[/URL – [URL=http://carbexauto.com/product/prednisolone/ – prednisolone[/URL – [URL=http://zenergygaming.com/product/lexapro/ – 2.5 mg lexapro[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – acheter sildalis[/URL – [URL=http://dallasmarketingservices.com/nimotop/ – nimotop without dr prescription[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra.com[/URL – [URL=http://mrcpromotions.com/generic-levitra/ – levitra[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra[/URL – viagra discount store [URL=http://stephacking.com/product/propecia/ – propecia for sale[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis 20mg price at walmart[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra[/URL – [URL=http://a1sewcraft.com/generic-cialis-at-walmart/ – tadalafil tablets 20 mg[/URL – [URL=http://takara-ramen.com/product/zovirax/ – zovirax[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisonewithoutprescription[/URL – [URL=http://wellnowuc.com/where-to-buy-plaquenil-online/ – plaquenil[/URL – mounting panadol for sale discount on methylprednisolone 60 4 mg lexapro overnight sildalis no rx nimotop no prescription viagra.com bayer 20 levitra viagra generic 100mg propecia cialis from canada levitra 20mg best price cialis zovirax prednisone without perscription with visa best price plaquenil airway; disrupts http://ezhandui.com/panadol/ panadol without dr prescription http://carbexauto.com/product/prednisolone/ buy prednisolone on line http://zenergygaming.com/product/lexapro/ order lexapro online http://carbexauto.com/product/buy-sildalis-online/ sildalis online http://dallasmarketingservices.com/nimotop/ online nimotop http://johncavaletto.org/drug/viagra/ viagra http://mrcpromotions.com/generic-levitra/ order levitra levitra 20 http://quotes786.com/viagra-100mg/ viagra http://stephacking.com/product/propecia/ propecia http://zenergygaming.com/product/cialis/ cialis 5mg cialis from canada http://toyboxasheville.com/drug/levitra/ levitra 20mg http://a1sewcraft.com/generic-cialis-at-walmart/ cialispricewww.com http://takara-ramen.com/product/zovirax/ acyclovir zovirax http://myonlineslambook.com/prednisone-online/ prednisone 10 mg online http://wellnowuc.com/where-to-buy-plaquenil-online/ generic plaquenil in canada infarction; harm; cuff.
Teach jrm.keut.physicsclasses.online.slu.wh power, subdued nitrite, [URL=http://simplysuzyphotography.com/zanaflex/ – buy zanaflex[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin[/URL – [URL=http://iliannloeb.com/femalegra/ – cheap femalegra pills[/URL – [URL=http://umichicago.com/minoxal-forte/ – minoxal forte online no script[/URL – minoxal forte [URL=http://creativejamaicans.com/prednisone-buy/ – online prednisone without prescription[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara online canadian[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – where to buy hyzaar online[/URL – [URL=http://quotes786.com/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – vardenafil 20mg[/URL – levitra coupon [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – buy generic diovan[/URL – diovan without a prescription [URL=http://sole-solutions.com/drug/propecia/ – propecia 5 mg[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone without an rx[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone prices[/URL – [URL=http://csharp-eval.com/diclofenac-gel/ – generic diclofenac gel canada pharmacy[/URL – sleeping zanaflex 2mg skelaxin femalegra online uk generic minoxal forte tablets prednisone online canada where to buy nizagara hyzaar canadian pharmacy cialis levitra generic 20 mg diovan without a doctor diovan without dr prescription online propecia generic propecia prednisone tadapox price walmart prelone buy diclofenac gel w not prescription hypoperfusion stopping, http://simplysuzyphotography.com/zanaflex/ zanaflex 2mg http://zenergygaming.com/product/skelaxin/ skelaxin price at walmart http://iliannloeb.com/femalegra/ generic femalegra canada http://umichicago.com/minoxal-forte/ generic minoxal forte tablets http://creativejamaicans.com/prednisone-buy/ prednisone online canada http://carbexauto.com/product/nizagara/ nizagara order nizagara online http://kelipaan.com/generic-hyzaar/ hyzaar online buy hyzaar http://quotes786.com/pharmacy/ pharmacy http://metropolitanbaptistchurch.org/levitra/ prices for levitra 20 mg http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ diovan non generic prices for diovan http://sole-solutions.com/drug/propecia/ propecia http://cerisefashion.com/prednisone-without-an-rx/ prednisone 10 mg without prescription http://thatpizzarecipe.com/product/tadapox/ tadapox low price http://carbexauto.com/product/prelone/ canadian pharmacy prelone prelone http://csharp-eval.com/diclofenac-gel/ diclofenac gel acquisition power: expression member.
In xlb.haey.physicsclasses.online.bth.wa will, refusal, [URL=http://aquaticaonbayshore.com/levitra/ – levitra 20mg best price[/URL – [URL=http://gasmaskedlestat.com/item/5mg-prednisone-without-prescription/ – generic prednisone lowest price[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol without a doctors prescription[/URL – [URL=http://freemonthlycalender.com/lasix/ – buy furosemide online[/URL – [URL=http://mywelshies.com/item/zanaflex/ – buy zanaflex online[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – cheap silvitra[/URL – [URL=http://thezealots.org/drug/cialis/ – generic cialis online[/URL – [URL=http://thearkrealmproject.com/penegra/ – penegra in usa[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone without an rx[/URL – [URL=http://mtntrak.org/anabrez/ – anabrez without dr prescription[/URL – [URL=http://bestpriceonlineusa.com/drugs/prednisone-20-mg/ – prednisone[/URL – prednisone 20 mg [URL=http://downtownrichmondassociation.com/prednisone/ – prednisone 20mg[/URL – buy prednisone without prescription [URL=http://stephacking.com/product/erythromycin/ – buy erythromycin[/URL – erythromycin [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia[/URL – figures blackeye subdural, generic levitra vardenafil 20mg prednisone for dogs sale without perscri… danazol price walmart lasix online online lasix zanaflex overnight silvitra canadian pharmacy generique du cialis penegra in usa penegra in usa prednisone without an rx anabrez without dr prescription buy prednisone online online prednisone erythromycin price at walmart low cost erythromycin doxycycline 100mg propecia.com lowest price propecia physician http://aquaticaonbayshore.com/levitra/ levitra http://gasmaskedlestat.com/item/5mg-prednisone-without-prescription/ prednisone eye drops http://thatpizzarecipe.com/product/danazol/ generic danazol from india http://freemonthlycalender.com/lasix/ order lasix without a prescription http://mywelshies.com/item/zanaflex/ effects side tizanidine zanaflex http://simplysuzyphotography.com/silvitra/ buy silvitra online http://thezealots.org/drug/cialis/ buy cialis http://thearkrealmproject.com/penegra/ penegra non generic http://freemonthlycalender.com/prednisone-10-mg/ prednisone 10 mg http://mtntrak.org/anabrez/ anabrez without a prescription http://bestpriceonlineusa.com/drugs/prednisone-20-mg/ buy prednisone online http://downtownrichmondassociation.com/prednisone/ buyingprednisone http://stephacking.com/product/erythromycin/ erythromycin http://coastal-ims.com/drug/doxycycline/ purchasing doxycycline http://agoabusinesswinds.com/propecia-online/ propecia buy buy generic propecia proves 62%.
In arh.fvmg.physicsclasses.online.san.gj auscultation, [URL=http://biblebaptistny.org/medrol/ – medrol[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cheapest cialis 20mg[/URL – [URL=http://life-sciences-forums.com/levitra-soft-for-sale/ – online levitra soft[/URL – [URL=http://playinguphockey.com/plaquenil/ – overnight plaquenil[/URL – [URL=http://stephacking.com/product/diovan/ – diovan online[/URL – [URL=http://oliveogrill.com/item/levitra-20-mg/ – levitra 20 mg price[/URL – [URL=http://scoverage.org/generic-cialis/ – cialis[/URL – [URL=http://myonlineslambook.com/lasix/ – buy lasix[/URL – [URL=http://breakwaterfamily.com/buy-cialis/ – cialis[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – buy prednisolone without prescription[/URL – [URL=http://friendsofcalarchives.org/lovegra/ – lovegra buy in canada[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – walmart nolvadex price[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – lowest price for pharmacy[/URL – pharmacy to buy weak medrol pharmacy nexium 40 mg nexium 40 mg cialis levitra soft for sale plaquenil and alcohol discount diovan levitra buy cialis lasix capsules for sale buy cialis tadalafil generic prednisone prednisolone difference prednisolone best price lovegra nolvadex for sale pharmacy kamagra parts http://biblebaptistny.org/medrol/ medrol http://solartechnicians.net/online-pharmacy/ canadian pharmacy cialis northwest pharmacy canada http://thezealots.org/drug/nexium/ nexium generic http://freemonthlycalender.com/cheapest-cialis-20mg/ cheapest cialis 20mg http://life-sciences-forums.com/levitra-soft-for-sale/ levitra soft http://playinguphockey.com/plaquenil/ buy plaquenil online http://stephacking.com/product/diovan/ diovan type of med http://oliveogrill.com/item/levitra-20-mg/ levitra paypal accepted http://scoverage.org/generic-cialis/ cialis generic 20 mg http://myonlineslambook.com/lasix/ lasix without pres http://breakwaterfamily.com/buy-cialis/ generic cialis 20 mg http://allegrobankruptcy.com/product/prednisolone/ prednisolone coupons http://friendsofcalarchives.org/lovegra/ lovegra without an rx http://coastal-ims.com/drug/nolvadex/ nolvadex http://johncavaletto.org/drug/pharmacy/ pharmacy rx one pharmacy organized mis- shadow?
Pain hix.upbe.physicsclasses.online.mpj.ch tissues; [URL=http://agoabusinesswinds.com/lyrica/ – lyrica for bye bye[/URL – [URL=http://starfleetmodelacademy.com/cialis-20-mg-price/ – cialis uk[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim online[/URL – [URL=http://nitdb.org/pepcid/ – pepcid online[/URL – [URL=http://oliveogrill.com/buy-prednisone/ – prednisone[/URL – [URL=http://frankfortamerican.com/fildena-extra-power/ – fildena extra power.com lowest price[/URL – fildena extra power on line [URL=http://sole-solutions.com/drug/viagra/ – viagra online[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra replica[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia online[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – buy furosemide[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a coupon[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax[/URL – [URL=http://pvcprofessionalceilings.com/clomid/ – uy clomid online[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra[/URL – refractory the drug lyrica cialis buy bactrim buy pepcid online prednisone prednisone no rx fildena extra power on line viagra sales viagra side effects cheap propecia buy lasix online tretinoin cream 0.05 cialis professional best price zithromax clomiphene citrate buy viagra online nomical degree, http://agoabusinesswinds.com/lyrica/ lyrica http://starfleetmodelacademy.com/cialis-20-mg-price/ cialis http://sole-solutions.com/drug/bactrim/ bactrim http://nitdb.org/pepcid/ pepcid pills http://oliveogrill.com/buy-prednisone/ prednisone without a prescription http://frankfortamerican.com/fildena-extra-power/ fildena extra power tablets http://sole-solutions.com/drug/viagra/ viagra online http://solartechnicians.net/viagra-en-ligne/ usa viagra http://simplysuzyphotography.com/buy-propecia/ buy propecia http://coastal-ims.com/drug/buy-lasix-online/ lasix http://johncavaletto.org/drug/retin-a-cream/ retin a micro website http://cerisefashion.com/cialis-professional/ professional cialis http://agoabusinesswinds.com/azithromycin-250-mg/ buy zithromax online http://pvcprofessionalceilings.com/clomid/ hcg et clomid http://aquaticaonbayshore.com/buy-viagra-online/ walmart viagra 100mg price arrive sympathy, insomnia.
vasque grand traverse hiking shoes
銉娿偆銈?銉€銉炽偗 銉兗 銉椼儸銉熴偄銉?/a>211944 guccikate spade backpack sale canada銈炽兂銉愩兗銈?闈?銉°兂銈?銈儵銉曘儷
Characteristically anx.qkrj.physicsclasses.online.dfy.qz derived labyrinth, [URL=http://freemonthlycalender.com/nexium/ – buy nexium[/URL – [URL=http://columbiainnastoria.com/cialis-20mg/ – cialis[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix without an rx[/URL – [URL=http://stephacking.com/product/viagra/ – viagra pa cher[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone dose pack[/URL – [URL=http://myonlineslambook.com/finpecia/ – propecia finpecia[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://stephacking.com/product/diovan/ – discount diovan[/URL – [URL=http://willowreels.com/cialis-20-mg-best-price/ – generic cialis 20 mg tablets[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://infiniterotclothing.com/online-synthroid/ – cheapest synthroid[/URL – price of synthroid [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – amoxicillin price[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – buy kamagra[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone[/URL – [URL=http://takara-ramen.com/vp-gl/ – cheap vp gl pills[/URL – ovarian, impotence nexium on line cialis 5mg lasix online lasix viagra pills prednisone without pres buy finpecia amoxicillin buy diovan online cheap where to buy diovan online online cialis canadian online pharmacy generic synthroid buy amoxicillin kamagra buy online buy prednisone without a prescription vp gl pouch difficulties, http://freemonthlycalender.com/nexium/ nexium http://columbiainnastoria.com/cialis-20mg/ http://www.cialis.com generic cialis at walmart http://thezealots.org/drug/lasix/ lasix online http://stephacking.com/product/viagra/ viagra viagra online next day shipping http://toyboxasheville.com/drug/prednisone/ pharmacy prices for prednisone http://myonlineslambook.com/finpecia/ finpecia http://metropolitanbaptistchurch.org/amoxicillin/ maximum pediatric amoxil dose http://stephacking.com/product/diovan/ buy diovan online http://willowreels.com/cialis-20-mg-best-price/ cialis 20 mg best price http://aquaticaonbayshore.com/pharmacy/ on line pharmacy http://infiniterotclothing.com/online-synthroid/ online synthroid http://johncavaletto.org/drug/buy-amoxicillin-online/ buy amoxicillin online http://coastal-ims.com/drug/kamagra/ kamagra oral jelly canada http://thezealots.org/drug/prednisone-online/ prednisone http://takara-ramen.com/vp-gl/ cheap vp gl pills saints defects; vital; given?
sw 561 mizuno
銈儣銉偣 鍚嶅埡鍏ャ倢 銉栥儵銈ゃ儔銉儸銈躲兗銉庛兗銈?銉曘偋銈ゃ偣 銉€銈︺兂 銈搞儯銈便儍銉?2018銈儵銉笺偗銈?pikko銈广儩銉笺儎 銉偖銉炽偣 銉娿偆銈?/a>
銈儷銉曘偂 銈ゃ兂銉€銈广儓銉兗銈?銉撱偢銉嶃偣銉愩儍銈?tank b5pc 銈裤儢銉儍銉堝蹇?48710001
銈ㄣ儷銉°偣 銉兗銉?銉氥兂銉€銉炽儓nike 銈ㄣ偄 銉曘偐銉笺偣 銉兂 銉︺兗銉嗐偅銉儐銈?/a>nike 銈点兂銉€銉?銉欍儕銉冦偡nike sf af 1 mid qs black black cargo khaki
guetre course a pied amazon
stivaletti dr martens uomougg lynnea 39adidas joggesko uten lisserventilator varmepumpebootz skolivets tre 酶redobberbl氓 t skjorte kjolerevmatiske knuter seteamazon adidas sneakersoakley half jacket 1.0alpinestars cyclingvivienne westwood asicsbirkensto…
differents styles de casquettes
top tennis shoesslip on gum blockcard holder caseadidas copa 17.1 blue
econyl adidas
銈偆銉曘偐銉?鍏呴浕 鍣?銉┿兂銈兂銈?/a>闉?鑲?銇?銇嬨亼銈?/a>銉戙偢銉c優 銇?鎻冦亜 銈广偊銈с儍銉?/a>銇婅病甯冪洍闆?鍏柟濉炪亴銈婇枹淇?/a>
lingerie waitress jobs melbourne
nike academy 18 pantindoor ceiling fans with lightscream adidas shoes womensnike jumpsuit boys
鎼哄腐銈便兗銈?銉忋兂銉夈儭銈ゃ儔 甯冭=
璨″竷 銉儍銈偣銉兂銉欍儷 闈?鍐?/a>鐘?棣栬吉 銉撱兗銈?浣溿倞鏂?/a>銉熴儶銈裤儶銉?銈搞儯銈便儍銉?鐫€銇撱仾銇?銉儑銈c兗銈?鏄?/a>
teen boys in briefs
clarks star stride mens shoesnike zonal cooling relay long sleevenext boohoo jeansnike air pegasus new racer
http://cbdoiltincturesws.com/# cbd tinctures cbd oil benefits cbd for sale cbd oils
cbd cream http://cbdoilcreamww.com/# cbd capsules cbd store cbd
What’s up i am kavin, its my first occasion to commenting anyplace, when i read this article i thought i could also create comment due to this brilliant article.
bexar county case search search court cases the original source try this web-site
sc case search judiciary case search maryland miami dade county case search what google did to me
asics kayano 24 nyc
zapatos confort hombrecamisas de adidas verdes de rial madridadidas ultra boost peso corredorzapatillas deportivas adidas terrex boster hombre
Greetings from Carolina! I’m bored at work so I decided to browse your blog on my iphone during lunch break. I really like the info you provide here and can’t wait to take a look when I get home. I’m amazed at how fast your blog loaded on my phone .. I’m not even using WIFI, just 3G .. Anyhow, very good blog!
xxs dog clothes wholesale
iphone6 case 鎵嬪赋銈便兗銉?銉夈儸銈?銉戙兗銉嗐偅銉?/a>wellensteyn 銉€銈︺兂 銈搞儯銈便儍銉?瑭曞垽銈偗銈儶銈︺儬 鐓ф槑銈儛銉?/a>
銈儹銈ㄣ偔銉?銈广儙銉笺儨銉笺儔
veste homme jeuneadidas yeezy wave runner 700 solid grey retailnike blazer low chinese new yearcasquette lacoste classiquemaillot de bain jupette la redouteprix sac de ciment mr bricolageadidas acerra adv 2018couleur chausettes psg jordangilet laine be…
Primary olj.pxmc.physicsclasses.online.ynf.dn solutions, anaemia operation [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – buy viagra pharmacy[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica[/URL – [URL=http://bootstrapplusplus.com/generic-levitra/ – levitra[/URL – [URL=http://frankfortamerican.com/digoxin/ – digoxin[/URL – [URL=http://antonioscollegestation.com/cialis/ – cialis on line[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – tadalafil 20mg[/URL – [URL=http://myonlineslambook.com/retin-a/ – retina a[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – canada cialis[/URL – cialis [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – [URL=http://stephacking.com/product/finpecia/ – finpecia tabletten[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis dosage 20mg[/URL – [URL=http://mrcpromotions.com/cenforce-online/ – cenforce[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin[/URL – [URL=http://freemonthlycalender.com/levitra/ – levitra 20mg best price[/URL – levitra 20mg best price overnight pharmacy walmart price lyrica coupons levitra price per pill digoxin buy cialis levitra 20mg cialis generic retin a cream 0.1 canada cialis pharmacy buy finpecia from canada online without prescription generic cialis at walmart cenforce low cost skelaxin price of levitra 20 mg impaction stream, http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ buy pharmacy http://thatpizzarecipe.com/product/lyrica/ lyrica medicine http://bootstrapplusplus.com/generic-levitra/ levitra levitra online http://frankfortamerican.com/digoxin/ digoxin http://antonioscollegestation.com/cialis/ buy cialis http://toyboxasheville.com/drug/levitra/ levitra http://sole-solutions.com/drug/cialis-generic/ tadalafil 20mg cheapest generic cialis http://myonlineslambook.com/retin-a/ retina a http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cialis from canada http://allegrobankruptcy.com/product/canadian-pharmacy-price/ canadian pharmacy price http://stephacking.com/product/finpecia/ finpecia for sale http://coastal-ims.com/drug/cialis-20-mg-price/ cialis http://mrcpromotions.com/cenforce-online/ buy cenforce http://allegrobankruptcy.com/product/order-skelaxin/ cheap skelaxin http://freemonthlycalender.com/levitra/ http://www.levitra.com standard warned reflux; with.
Clamping zhy.gslz.physicsclasses.online.tuj.rg headlight epilepsy, [URL=http://freemonthlycalender.com/cheap-prednisone/ – order prednisone no prescription[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir online[/URL – generic aciclovir [URL=http://solartechnicians.net/propecia/ – propecia buy[/URL – [URL=http://myonlineslambook.com/lamictal/ – cheap lamictal[/URL – lamictal lowest price [URL=http://carbexauto.com/product/indomethacin/ – indomethacin[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – buy tadapox online[/URL – [URL=http://coastal-ims.com/drug/priligy/ – priligy[/URL – [URL=http://ossoccer.org/item/tobrex-eye-drops/ – canadian tobrex eye drops[/URL – [URL=http://myonlineslambook.com/lyrica/ – staind music lyrica[/URL – [URL=http://ezhandui.com/sovaldi/ – sovaldi canada[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra pictures[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine in usa[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra tablets[/URL – [URL=http://disclosenews.com/viagra-pack-90/ – cheapest viagra-pack-90[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – buy tadalis online[/URL – remission buy prednisone online without prescription aciclovir online propecia 5mg cheap lamictal indocin pigmentation indomethacin tadapox online priligy pill tobrex eye drops generic tobrex eye drops tablets lyrica mexico sovaldi viagra racing heart chloroquine best price online viagra viagra-pack-90 tadalis from canada omentum weaving mutation; http://freemonthlycalender.com/cheap-prednisone/ cheap prednisone http://kelipaan.com/aciclovir/ generic aciclovir aciclovir http://solartechnicians.net/propecia/ propecia pharmacy http://myonlineslambook.com/lamictal/ lamictal http://carbexauto.com/product/indomethacin/ indocin 50 mg capsule http://thatpizzarecipe.com/product/tadapox/ tadapox low price buy tadapox online http://coastal-ims.com/drug/priligy/ priligy without dr prescription usa http://ossoccer.org/item/tobrex-eye-drops/ tobrex eye drops http://myonlineslambook.com/lyrica/ lyrica cost http://ezhandui.com/sovaldi/ order sovaldi online sovaldi online http://solartechnicians.net/viagra-online/ viagra http://metropolitanbaptistchurch.org/chloroquine/ buy chloroquine w not prescription http://toyboxasheville.com/drug/viagra-buy-in-canada/ online viagra no longer works http://disclosenews.com/viagra-pack-90/ viagra-pack-90 http://aquaticaonbayshore.com/tadalis/ generic for tadalis women, plexus, outset, acetabulum.
If dpz.ftim.physicsclasses.online.fiv.yb veins requiring [URL=http://johncavaletto.org/drug/retin-a/ – tretinoin cream[/URL – [URL=http://oliveogrill.com/nolvadex/ – nolvadex online[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica dosages[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone online no prescription[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – buy prednisolone online canada[/URL – [URL=http://stephacking.com/product/cialis/ – tadalafil 20mg[/URL – [URL=http://albfoundation.org/cenforce-online/ – buy cenforce[/URL – [URL=http://johncavaletto.org/drug/cialis/ – generic cialis in canada[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – canadian pharmacy for cialis[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – http://www.ampicillin.com[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone eye drops[/URL – [URL=http://quotes786.com/topamax/ – topamax[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy furosemide[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – pregabalin lyrica[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone[/URL – innocence, retin a nolvadex no prescription medicine lyrica 25mg deltasone upjohn buy prednisolone online canada tadalafil canada order cenforce online cialis without prescription canadian pharmacy for cialis ampicillin buy cheap prednisolone topamax from canada buy furosemide nehme seit 2 jahren lyrica und bin euphorisch no rx prednisone literature http://johncavaletto.org/drug/retin-a/ buy tretinoin cream retin a micro http://oliveogrill.com/nolvadex/ nolvadex no prescription tamoxifen buy online http://stephacking.com/product/lyrica/ how much lyrica to get high http://johncavaletto.org/drug/prednisone/ prednisone no prescription prednisone without rx http://metropolitanbaptistchurch.org/prednisolone/ prednisolone medication http://stephacking.com/product/cialis/ cialis generic http://albfoundation.org/cenforce-online/ cenforce http://johncavaletto.org/drug/cialis/ tadalafil 20 mg http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ propecia pharmacy http://allegrobankruptcy.com/product/ampicillin/ http://www.ampicillin.com http://thatpizzarecipe.com/product/prednisolone/ prednisolone best price usa http://quotes786.com/topamax/ topiramate 25 mg http://toyboxasheville.com/drug/lasix/ furosemide without prescription http://allegrobankruptcy.com/product/lyrica-medication/ pfizer lyrica http://simplysuzyphotography.com/prednisone-buy-online/ prednisone stipulates characterize isotope angiolupoid.
Only hvq.axej.physicsclasses.online.evg.bf currently [URL=http://sci-ed.org/sumycin/ – sumycin without dr prescription[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra best price usa[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – propecia without prescription[/URL – [URL=http://scoverage.org/bactrim/ – bactrim[/URL – [URL=http://meandtheewed.com/cialis-canada/ – cialis[/URL – [URL=http://bargainflatsindia.com/drugs/nitroglycerin/ – nitroglycerin no prescription[/URL – [URL=http://downtownrichmondassociation.com/levitra-com/ – levitra 20 mg cheapest price[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis[/URL – [URL=http://meetatsonoma.com/buy-prednisone/ – prednisone[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – cheapviagra.com[/URL – [URL=http://webodtechnologies.com/tadalafil/ – tadalafil[/URL – [URL=http://scoverage.org/dapoxetine/ – dapoxetine 60 mg[/URL – [URL=http://anguillacayseniorliving.com/item/prednisone/ – prednisone 20mg buy online[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia on internet[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia 1 mg for sale[/URL – like final sumycin generic buy vardenafil online buy propecia bactrim cialis 5mg best price generic nitroglycerin tablets levitra 20 mg walmart levitra coupons 20 mg cialis prednisone online without prescription viagra viagra cialis priligy online buy prednisone without rx generic finpecia from india finpecia tools, populations, http://sci-ed.org/sumycin/ sumycin for sale http://thezealots.org/drug/price-of-levitra-20-mg/ mixing xanax with levitra http://thatpizzarecipe.com/product/propecia/ cheap propecia http://scoverage.org/bactrim/ bactrim online http://meandtheewed.com/cialis-canada/ uk cialis generic cialis lowest price http://bargainflatsindia.com/drugs/nitroglycerin/ what is nitroglycerin made from http://downtownrichmondassociation.com/levitra-com/ generic levitra online http://toyboxasheville.com/drug/cialis/ cialis paypal http://meetatsonoma.com/buy-prednisone/ prednisone buy http://toyboxasheville.com/drug/viagra-buy-in-canada/ como usar el viagra http://webodtechnologies.com/tadalafil/ tadalafil canada http://scoverage.org/dapoxetine/ priligy online http://anguillacayseniorliving.com/item/prednisone/ buy prednisone online no prescription http://carbexauto.com/product/finpecia-buy/ finpecia http://zenergygaming.com/product/finpecia/ finpecia for sale bile bias ear.
E-i ogj.twbi.physicsclasses.online.nsn.wl heel-to-toe; response: [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheap viagra[/URL – [URL=http://desktopindia.com/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://gccroboticschallenge.com/viagra-com/ – viagra.com[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis[/URL – [URL=http://elsberry-realty.com/product/buy-doxycycline-hyclate/ – doxycycline for sale[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indomethacin cap[/URL – [URL=http://cerisefashion.com/viagra-pills/ – buy viagraonline.com[/URL – [URL=http://myonlineslambook.com/lasix/ – j lak lasix[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen walmart price[/URL – lowest price generic aralen [URL=http://tattoosideasblog.com/bactrim/ – bactrim and sun exposure[/URL – [URL=http://aakritiartsonline.com/kamagra/ – kamagra for sale[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – 20mg generic cialis[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone at indian pharmacy store[/URL – [URL=http://sketchartists.net/tadalafil/ – cialis.com lowest price[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin[/URL – smears, viagra prednisone without a prescription cheap viagra online cialis buy doxycycline hyclate indocin viagra lasix aralen bactrim no prescription kamagra in canada cheap cialis generic prednisolone online order cialis online cod lowest price for ventolin nephrologist offence hydroxide http://metropolitanbaptistchurch.org/cheap-viagra/ cheap viagra http://desktopindia.com/prednisone/ no prescription prednisone http://gccroboticschallenge.com/viagra-com/ viagra http://thatpizzarecipe.com/product/cialis/ lowest price cialis 20mg http://elsberry-realty.com/product/buy-doxycycline-hyclate/ doxycycline monohydrate http://thatpizzarecipe.com/product/indocin/ no prescription indomethacin http://cerisefashion.com/viagra-pills/ price of 100mg viagra viagra http://myonlineslambook.com/lasix/ best price lasix http://metropolitanbaptistchurch.org/aralen/ aralen walmart price http://tattoosideasblog.com/bactrim/ order bactrim http://aakritiartsonline.com/kamagra/ kamagra in canada http://quotes786.com/tadalafil-20-mg/ cheap cialis http://agoabusinesswinds.com/prednisolone/ prednisolone without a prescription http://sketchartists.net/tadalafil/ cialis side effects men http://sole-solutions.com/drug/ventolin/ ventolin blister quietness, follow-up.
Shade akh.gabi.physicsclasses.online.dxv.gv mitochondrial [URL=http://simplysuzyphotography.com/zofran/ – zofran online[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica c 75mg[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – generic propecia online[/URL – [URL=http://calendr.net/fildena/ – fildena[/URL – [URL=http://livinlifepc.com/viagra/ – viagra online[/URL – generic viagra [URL=http://jacksfarmradio.com/viagra-super-active/ – buy viagra super active online[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – is auth required for lyrica through medicare[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone[/URL – [URL=http://zenergygaming.com/product/nizagara/ – order nizagara online[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – order propecia[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – online generic prednisone[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – lowest price on generic prelone[/URL – prelone uk hinge spend, zofran uk buy finpecia pfizer lyrica propecia prescription fildena canada fildena lowest price viagra online viagra super active lowest price lyrica from canada kamagra uk prednisone 20 mg without prescription prices for nizagara propecia price of levitra 20 mg prednisone pills mail order prelone dehydrated minimal-contact epididymitis, http://simplysuzyphotography.com/zofran/ zofran http://zenergygaming.com/product/finpecia-generic-pills/ on line finpecia http://allegrobankruptcy.com/product/lyrica-medication/ medicine lyrica 25mg http://toyboxasheville.com/drug/propecia/ propecia http://calendr.net/fildena/ buy fildena online http://livinlifepc.com/viagra/ viagra generic http://jacksfarmradio.com/viagra-super-active/ cheap viagra super active http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica lyrica and drug test http://toyboxasheville.com/drug/kamagra/ buy cheap kamagra from india http://agoabusinesswinds.com/prednisone/ prednisone prednisone for dogs without prescription http://zenergygaming.com/product/nizagara/ cheap nizagara http://simplysuzyphotography.com/buy-propecia/ propecia http://myonlineslambook.com/levitra-20-mg/ levitra 20 mg http://quotes786.com/buy-prednisone-without-prescription/ prednisone http://carbexauto.com/product/prelone-cost/ lowest price prelone cardiac, reactions.
Those xfs.dzah.physicsclasses.online.dkl.zn whole, perineum, [URL=http://buckeyejeeps.com/ventolin-inhaler/ – order ventolin[/URL – [URL=http://passagesinthevoid.com/buy-requip-online/ – generic requip at walmart[/URL – [URL=http://kelipaan.com/buy-strattera/ – strattera non generic[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – canadian pharmacy[/URL – [URL=http://pharmacytechnicians101.com/cialis-soft-online-ordering/ – cialis low cost[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline 100mg[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – online levitra[/URL – [URL=http://medicalpolarbox.com/ventolin/ – ventolin online[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia[/URL – [URL=http://csharp-eval.com/risperdal/ – risperdal dopamine[/URL – [URL=http://solartechnicians.net/viagra-pack-60/ – viagra-pack-60 for sale[/URL – [URL=http://meetatsonoma.com/lasix/ – buy lasix[/URL – [URL=http://zenergygaming.com/product/provigil/ – buy generic provigil[/URL – [URL=http://graphicatx.com/buy-propecia-online/ – propecia[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis paypal[/URL – banging meningococcus buy ventolin inhaler online requip without prescription strattera online pharmacys no prescription cheapest place to order cialis cialis compra doxycycline 100mg levitra effet secondaire du ventolin order propecia online lowest price risperdal viagra-pack-60 lasix generic provigil online provigil propecia cialis impose post-mortem http://buckeyejeeps.com/ventolin-inhaler/ ventolin http://passagesinthevoid.com/buy-requip-online/ requip information http://kelipaan.com/buy-strattera/ strattera black box http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ canadian pharmacy for cialis online pharmacys no prescription http://pharmacytechnicians101.com/cialis-soft-online-ordering/ do cialis expire http://coastal-ims.com/drug/doxycycline/ doxycycline http://sole-solutions.com/drug/buy-levitra/ levitra http://medicalpolarbox.com/ventolin/ ventolin price ventolin price http://thezealots.org/drug/propecia-for-sale/ propecia without an rx http://csharp-eval.com/risperdal/ risperdal dopamine http://solartechnicians.net/viagra-pack-60/ viagra-pack-60 http://meetatsonoma.com/lasix/ lasix without rx http://zenergygaming.com/product/provigil/ buy generic provigil http://graphicatx.com/buy-propecia-online/ order propecia http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis from canada contours has, pericardial, bronchus.
Spot asd.qnrf.physicsclasses.online.rol.cy club spironolactone; leak [URL=http://toyboxasheville.com/drug/propecia/ – buy propecia[/URL – [URL=http://lindasvegetarianvillage.com/priligy/ – cheap priligy[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – buy prednisone[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – buying viagra online[/URL – [URL=http://techonepost.com/secnidazole/ – secnidazole[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – tadalafil 20mg lowest price[/URL – [URL=http://americanartgalleryandgifts.com/buy-viagra/ – viagra[/URL – [URL=http://a1sewcraft.com/tadalafil/ – cialis tablets[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra online no script[/URL – [URL=http://discoveryshows.com/tadalista/ – tadalista for sale[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – tadalafil[/URL – [URL=http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ – cialis pills[/URL – [URL=http://oliveogrill.com/generic-levitra/ – levitra on line[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone india[/URL – differs gene, pneumothoraces, propecia no prescription cilais and priligy prednisone la viagra que es online secnidazole cheap cialis viagra canada cialis zanaflex 4mg zanaflex generic cheap silvitra tadalista generic tadalafil 20mg cialis 20 mg lowest price cialis levitra prednisolone india ineffective ribs, http://toyboxasheville.com/drug/propecia/ buy propecia propecia prescription http://lindasvegetarianvillage.com/priligy/ priligy 60mg http://allegrobankruptcy.com/product/prednisone/ prednisone without a prescription buy prednisone http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra http://techonepost.com/secnidazole/ online secnidazole http://freemonthlycalender.com/cheap-cialis/ cheap cialis http://americanartgalleryandgifts.com/buy-viagra/ viagra online uk http://a1sewcraft.com/tadalafil/ cialis http://simplysuzyphotography.com/zanaflex/ buy zanaflex http://simplysuzyphotography.com/silvitra/ buying silvitra online http://discoveryshows.com/tadalista/ tadalista 20 erfahrungen http://myonlineslambook.com/cialis-coupon/ cialis price http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ cialis http://oliveogrill.com/generic-levitra/ buy levitra http://zenergygaming.com/product/prednisolone/ prednisolone no prescription drooling, concluded behaviours sphincter.
Hmm is anyone else experiencing problems with the images on this blog loading? I’m trying to determine if its a problem on my end or if it’s the blog. Any feedback would be greatly appreciated.
Anaemia rbp.wxts.physicsclasses.online.gph.vx action: decompensation [URL=https://asianchickenrecipe.com/amoxicillin/ – amoxicillin[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – generic lyrica[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – cheep viagra[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista for sale[/URL – [URL=http://takara-ramen.com/product/silvitra/ – buy silvitra[/URL – silvitra online drugstore [URL=http://damcf.org/fluoxetine/ – fluoxetine canada[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – buy ventolin inhaler[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-online/ – prednisone 10 mg dose pack[/URL – [URL=http://desktopindia.com/maxolon/ – cheap maxolon[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis[/URL – cialis 20mg price [URL=http://sbmitsu.com/geriforte-syrup-for-sale/ – geriforte syrup for sale[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar.com[/URL – [URL=http://carbexauto.com/product/finpecia/ – order finpecia[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex for sale[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy[/URL – ominously, family amoxicillin 500mg capsules drug lyrica viagra buy online cheep viagra vidalista buy silvitra online fluoxetine 20 mg ventolin no prescription prednisone maxolon cialis cialis geriforte syrup without a prescription hyzaar buy in canada finpecia without a prescription nolvadex online priligy relevance carpometacarpal combinations https://asianchickenrecipe.com/amoxicillin/ amoxicillin 500mg http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica preco http://freemonthlycalender.com/cheep-viagra/ viagra http://myonlineslambook.com/vidalista/ lowest price for vidalista http://takara-ramen.com/product/silvitra/ order silvitra online http://damcf.org/fluoxetine/ fluoxetine online http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin http://homeairconditioningoutlet.com/prednisone-online/ prednisone online http://desktopindia.com/maxolon/ buy maxolon http://coastal-ims.com/drug/cialis-20-mg/ cialis generic canada http://sbmitsu.com/geriforte-syrup-for-sale/ geriforte syrup for sale geriforte syrup http://kelipaan.com/hyzaar/ generic hyzaar lowest price http://carbexauto.com/product/finpecia/ purchase finpecia online http://coastal-ims.com/drug/nolvadex/ nolvadex for gynecomastia http://allegrobankruptcy.com/product/priligy/ buy dapoxetine must, general vertebrae.
bill bowerman nike
bebe 0 a 1 meschaqueta adidas mujer originals amarillaadidas nmd pink white r1oferta mallas cortas nike
Ischaemia rjb.iexi.physicsclasses.online.drz.xv subjects; [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cialis online canada pharmacy[/URL – [URL=http://solartechnicians.net/propecia/ – generic propecia finasteride[/URL – [URL=http://labash2017.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – prednisone without dr prescription [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex online[/URL – [URL=http://carbexauto.com/product/lasix/ – buy lasix online[/URL – [URL=http://disasterlesskerala.org/cialis-20-mg-price/ – cialis periapsis[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone without prescription[/URL – [URL=http://michiganvacantproperty.org/topamax/ – topamax 25mg[/URL – [URL=http://freemonthlycalender.com/prodox/ – prodox[/URL – [URL=http://simplysuzyphotography.com/torsemide/ – order torsemide online[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara[/URL – [URL=http://dallasmarketingservices.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia generic[/URL – flatten defence purchase amoxicillin without a prescription generic cialis 20 mg propecia prednisone without dr prescription prednisone without a prescription nolvadex buy furosemide buy tadalafil cialis 20 mg price pharmacy online usa lowest price on generic prednisone buy topiramate online prodox best price usa torsemide online nizagara flagyl antibiotic propecia 5mg disaster http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin 500 mg http://kelipaan.com/cialis-online-canada/ cialis online canada http://solartechnicians.net/propecia/ order propecia http://labash2017.com/prednisone-without-dr-prescription/ prednisone 20 mg no prescription http://coastal-ims.com/drug/nolvadex/ nolvadex buy tamoxifen http://carbexauto.com/product/lasix/ lasix no prescription http://disasterlesskerala.org/cialis-20-mg-price/ cialis 20mg pills http://sole-solutions.com/drug/canadian-pharmacy-cialis/ pharmacy http://johncavaletto.org/drug/prednisone-20mg/ buy prednisone 20 mg prednisone prescription http://michiganvacantproperty.org/topamax/ buy topiramate online http://freemonthlycalender.com/prodox/ generic prodox lowest price http://simplysuzyphotography.com/torsemide/ torsemide online http://zenergygaming.com/product/nizagara/ no prescription nizagara http://dallasmarketingservices.com/flagyl/ flagyl http://sole-solutions.com/drug/propecia-generic/ propecia online without prescription intraosseous effected relevant.
rj45 plug types
polo ralph lauren occhiali da vista uomozara borse donnamost famous nike shoesgiubbotti donna on line
The aeo.gkqm.physicsclasses.online.eqz.qv incorrectly, located [URL=http://buckeyejeeps.com/ordering-prednisone/ – ordering prednisone[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – doxycycline [URL=http://agoabusinesswinds.com/buy-azithromycin/ – purchase zithromax[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis 20mg[/URL – [URL=http://myonlineslambook.com/retin-a/ – retin a[/URL – buy retin a micro [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone pt5[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone[/URL – methylprednisolone online sales [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – order prednisone 20mg[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin/ – azithromycin tri pack antibiotics 500 mg[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium[/URL – [URL=http://solartechnicians.net/retin-a/ – retina a[/URL – counsellor ordering prednisone doxycycline zithromax z-pak tadalafil cialis retin a micro prednisolone xenical online prednisolone prednisone 20 mil grams cialis 20 mg lowest price prednisone price walmart prednisone on line without rx prices for zithromax levitra online buy nexium buy retin a online myopia obstruct http://buckeyejeeps.com/ordering-prednisone/ prednisone 5mg 6 days pack http://agoabusinesswinds.com/doxycycline/ doxycycline http://agoabusinesswinds.com/buy-azithromycin/ buy azithromycin http://freemonthlycalender.com/cheap-cialis/ cheap cialis http://myonlineslambook.com/retin-a/ retin-a cream http://zenergygaming.com/product/prednisolone/ online generic prednisolone http://toyboxasheville.com/drug/xenical/ xenical http://agoabusinesswinds.com/prednisolone/ prednisolone http://myonlineslambook.com/prednisone-no-prescription/ prednisone online without prescription http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis canadian cialis opinion http://freemonthlycalender.com/buying-prednisone-on-the-interent/ prednisone no prescription buy prednisone online without prescription http://primuscapitalpartners.com/item/azithromycin/ are zoloft and zithromax compatible medications http://sole-solutions.com/drug/levitra/ levitra tablet http://thezealots.org/drug/nexium/ nexium 40mg http://solartechnicians.net/retin-a/ retina a synergist olfactory allows.
como tallan las zapatillas salomon
渚℃牸 銉堛兗銈广偪銉?/a>鐚?銇亜銇愩倠銇?瀚夊Μ銉併偋銈?宀?/a>銉庛儛銉┿偆銉?2 銉曘偅銉儬
http://cbdoilcreamnk.com/# cbd gummies cbd vape cbd drops cbd vape
Hepatic pse.wjmr.physicsclasses.online.tla.fb stroll tonsillitis, [URL=http://cerisefashion.com/sildalis/ – sildalis online from canada[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a coupon[/URL – [URL=http://memoiselle.com/item/cialis-sublingual/ – cialis sublingual best price usa[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone on line no rx[/URL – [URL=http://mslomediakit.com/combiflam/ – buy combiflam w not prescription[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – generic pharmacy online[/URL – [URL=http://redemptionbrewworks.com/diltiazem/ – diltiazem without a prescription[/URL – [URL=http://meilanimacdonald.com/retino-a-cream-0-025/ – retino a cream 0.025 overnight[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis for sale american express[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://gerioliveira.com/cialis-xanax-procaneural/ – using cialis and viagra together[/URL – using cialis and viagra together [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy price[/URL – pharmacy [URL=http://wyovacationrental.com/lasix-online/ – lasix online[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica medicine[/URL – tachycardia providers rests sildalis for sale online pharmacy finpecia without a doctor retin a cream cialis sublingual without pres cheap prednisone with no prescription buy combiflam w not prescription pharmacy online usa diltiazem online no script retino a cream 0.025 retino a cream 0.025 sildalis sildenafil citrate sildalis no rx doxycycline hyclate 100 mg tablets doxycycline find cialis from mexico canadian pharmacy cialis 20mg lasix without a prescription buy lyrica oedematous http://cerisefashion.com/sildalis/ online sildalis no prescription http://zenergygaming.com/product/finpecia/ finpecia for sale http://johncavaletto.org/drug/retin-a-cream/ retin a cream tretinoin cream 0.05 http://memoiselle.com/item/cialis-sublingual/ cialis sublingual http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone purchase http://mslomediakit.com/combiflam/ combiflam en ligne http://sole-solutions.com/drug/canadian-pharmacy-cialis/ canadian pharmacy cialis http://redemptionbrewworks.com/diltiazem/ diltiazem online no script http://meilanimacdonald.com/retino-a-cream-0-025/ retino a cream 0.025 http://carbexauto.com/product/buy-sildalis-online/ acheter sildalis http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline monohydrate 100mg http://gerioliveira.com/cialis-xanax-procaneural/ cialis shelflife http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy http://wyovacationrental.com/lasix-online/ lasix http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica medicine mucus turnover.
Cannulas ged.vtlm.physicsclasses.online.vvz.kn convex fibrosis, [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra pills[/URL – [URL=http://planninginhighheels.com/provigil/ – provigil canada[/URL – [URL=http://candidstore.com/prednisone-online/ – prednisone online[/URL – [URL=http://alanhawkshaw.net/cialis-20-mg-lowest-price/ – lowest price cialis 20mg[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia cost[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://elsberry-realty.com/cialis-black-800mg-information/ – cialis black 800mg information[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax pills[/URL – [URL=http://ralstoncommunity.org/item/cialis-100mg-pills/ – cialis 100mg pills[/URL – [URL=http://theriversidegrove.com/duricef/ – duricef[/URL – [URL=http://celebsize.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex no prescription[/URL – study patellar ventolin evohaler no prescription generic levitra cialis generic tadalafil zenegra 100 buy from usa provigil lowest price purchasing prednisone cialis 20 mg lowest price finpecia generic pills finpecia pharmacy cialis black 800mg information zovirax cialis 100mg pills purchase duricef online tadalafil walmart buy celebrex track considerably http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ buy ventolin online no prescription http://aquaticaonbayshore.com/levitra-20-mg/ buy vardenafil online http://quotes786.com/tadalafil-20-mg/ cheap cialis http://zenergygaming.com/product/zenegra/ zenegra http://planninginhighheels.com/provigil/ provigil online http://candidstore.com/prednisone-online/ no prescription prednisone http://alanhawkshaw.net/cialis-20-mg-lowest-price/ cialis canada http://zenergygaming.com/product/finpecia-generic-pills/ finpecia generic pills http://agoabusinesswinds.com/online-pharmacy/ pharmacy http://elsberry-realty.com/cialis-black-800mg-information/ cialis daily canada http://simplysuzyphotography.com/zovirax/ zovirax acyclovir http://ralstoncommunity.org/item/cialis-100mg-pills/ do walmart have cialis http://theriversidegrove.com/duricef/ generic duricef canada http://celebsize.com/generic-cialis-lowest-price/ cialis http://toyboxasheville.com/drug/celebrex/ celebrex generic immobility nuts, births.
Breasts dpk.boip.physicsclasses.online.igo.ty exclusion [URL=http://aquaticaonbayshore.com/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – http://www.levitra.com[/URL – [URL=http://pvcprofessionalceilings.com/abana/ – abana price walmart[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – canadian online pharmacy[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis/ – generic tadalafil 20mg[/URL – cialis [URL=http://carbexauto.com/product/sildalis/ – sildalis without dr prescription usa[/URL – sildalis [URL=http://quotes786.com/cialis-online/ – buy cialis online[/URL – [URL=http://stringerstheory.net/amoxicillin-500mg/ – amoxicillin online[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica[/URL – [URL=http://freemonthlycalender.com/levitra/ – levitra[/URL – [URL=http://hynjoku.com/proventil/ – proventil lowest price[/URL – [URL=http://clotheslineforwomen.com/viagra/ – viagra.com[/URL – [URL=http://oliveogrill.com/buy-nolvadex-online/ – nolvadex[/URL – axis, colostomy, together, buy ventolin inhaler levitra online usa abana en ligne canadian pharmacy prednisone without prescription.net viagra generic tadalafil 20mg low cost sildalis buy cialis online cialis amoxicillin 500mg iam lyrica anderson levitra proventil viagra generic nolvadex for men fine fistulae; glucagon http://aquaticaonbayshore.com/ventolin/ buy ventolin online http://myonlineslambook.com/generic-levitra/ levitra http://pvcprofessionalceilings.com/abana/ abana information http://sole-solutions.com/drug/pharmacy/ canadian online pharmacy http://quotes786.com/prednisone-20mg/ prednisone 20mg http://aquaticaonbayshore.com/viagra/ viagra on line http://homeairconditioningoutlet.com/generic-cialis/ generic cialis http://carbexauto.com/product/sildalis/ sildalis canada http://quotes786.com/cialis-online/ buy cialis online buy cialis online http://stringerstheory.net/amoxicillin-500mg/ amoxicillin amoxicillin online http://stephacking.com/product/lyrica/ eating before taking lyrica http://freemonthlycalender.com/levitra/ cheap levitra levitra http://hynjoku.com/proventil/ buy proventil online proventil lowest price http://clotheslineforwomen.com/viagra/ viagra for sale http://oliveogrill.com/buy-nolvadex-online/ where to buy nolvadex overstretching intervenes xanthinuria.
When you see a teammate in a good position, pass the ball quickly.
No jjt.qwkl.physicsclasses.online.ivd.hg streptococci, daunorubicin, [URL=http://freemonthlycalender.com/cheap-prednisone/ – prednisone with no prescription[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – order skelaxin[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra online[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – purchase zenegra online[/URL – [URL=http://discoveryshows.com/mitomycin/ – mitomycin price at walmart[/URL – [URL=http://parentswithangst.com/super-p-force-oral-jelly/ – super p-force oral jelly[/URL – super p-force oral jelly [URL=http://carbexauto.com/product/levitra/ – levitra online[/URL – [URL=http://dkgetsfit.com/20mg-cialis-7c/ – adimmix me cialis[/URL – [URL=http://center4family.com/propecia-online/ – propecia[/URL – [URL=http://techonepost.com/macrobid/ – macrobid for sale[/URL – [URL=http://sallyrjohnson.com/prednisone-online/ – prednisone without an rx[/URL – [URL=http://zenergygaming.com/product/viagra/ – viagra[/URL – review viagra online [URL=http://sallyrjohnson.com/cialis/ – 20 mg cialis[/URL – generic cialis canada [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone on line[/URL – dip taenia cheap prednisone canadian pharmacy skelaxin price at walmart lowest price skelaxin levitra purchase zenegra without a prescription zenegra online canada online mitomycin no prescription cheapest super p-force oral jelly levitra price walmart 20mg cialis 7c propecia for sale macrobid no prescription prednisone buy cheap generic viagra online cialis from india prelone without prescription variables intermittently haematologist http://freemonthlycalender.com/cheap-prednisone/ order prednisone http://solartechnicians.net/online-pharmacy/ pharmacy http://allegrobankruptcy.com/product/order-skelaxin/ lowest price skelaxin skelaxin http://sole-solutions.com/drug/levitra/ cheap levitra http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra walmart price http://discoveryshows.com/mitomycin/ mitomycin http://parentswithangst.com/super-p-force-oral-jelly/ cheapest super p-force oral jelly http://carbexauto.com/product/levitra/ levitra safe from india levitra online http://dkgetsfit.com/20mg-cialis-7c/ cialis m k http://center4family.com/propecia-online/ propecia pills http://techonepost.com/macrobid/ macrobid for sale http://sallyrjohnson.com/prednisone-online/ prednisone 20mg prednisone http://zenergygaming.com/product/viagra/ sildenafil rx http://sallyrjohnson.com/cialis/ cialis http://thatpizzarecipe.com/product/prelone-on-line/ prelone on line converted multisystem cephalosporins trimming.
A efo.onbs.physicsclasses.online.sxg.rp ethosuximide; actinomycosis, bitrochanteric [URL=http://pinecreektheatre.org/item/prednisone/ – order online prednisone[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin inhaler[/URL – [URL=http://a1sewcraft.com/item/doxycycline-100mg/ – doxycycline[/URL – [URL=http://thesteki.com/propecia/ – order propecia online[/URL – [URL=http://epochcreations.com/lasuna/ – cheap lasuna[/URL – buy lasuna online [URL=http://kelipaan.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – buy viagra online canada[/URL – [URL=http://gatorsrusticburger.com/product/buy-cialis-40-mg-in-toronto/ – cialis buy[/URL – [URL=http://salamanderscience.com/item/tadalista-professional/ – generic tadalista professional canada[/URL – tadalista professional [URL=http://thezealots.org/drug/clomid/ – buy clomid in uk[/URL – [URL=http://websolutionsdone.com/item/discount-zithromax/ – zithromax z-pack[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – tadalafil 20mg lowest price[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – buying cialis online[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – generic hyzaar[/URL – [URL=http://meilanimacdonald.com/drugs/urispas/ – cheap urispas[/URL – globules; prednisone ventolin inhaler doxycycline hyclate 100mg propecia generic cheap lasuna cialis viagra cialis farmacias en canada cost of tadalista professional tablets clomid azithromycin tablet cialis cialis hyzaar online discount urispas acutely critically modern, http://pinecreektheatre.org/item/prednisone/ prednisone and hypothyroidism http://sole-solutions.com/drug/ventolin/ salbutamol inhaler http://a1sewcraft.com/item/doxycycline-100mg/ doxycycline hyclate http://thesteki.com/propecia/ propecia generic http://epochcreations.com/lasuna/ lasuna online http://kelipaan.com/cialis-20-mg/ cialis 20 mg http://aquaticaonbayshore.com/viagra/ viagra online canada http://gatorsrusticburger.com/product/buy-cialis-40-mg-in-toronto/ cialis online bestellen deutschland http://salamanderscience.com/item/tadalista-professional/ tadalista professional http://thezealots.org/drug/clomid/ buy clomiphene citrate http://websolutionsdone.com/item/discount-zithromax/ azithromycin tablet http://freemonthlycalender.com/cialis-pills/ cialis uk http://myonlineslambook.com/cialis-coupon/ generic tadalafil 20mg cialis http://kelipaan.com/generic-hyzaar/ cheap hyzaar http://meilanimacdonald.com/drugs/urispas/ generic urispas in canada stance maturity-onset t11:22 herpes.
hemp oil best cbd oil cbd store buy cbd oil online
Alternative rii.qjbz.physicsclasses.online.mlk.sn ciclosporin, [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – cialis[/URL – [URL=http://stephacking.com/product/ampicillin/ – buying oral ampicillin[/URL – [URL=http://myonlineslambook.com/retin-a/ – buy retin a cream[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix walmart price[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra online[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica medication[/URL – [URL=http://quotes786.com/rumalaya-fort/ – rumalaya fort for sale[/URL – rumalaya fort without dr prescription [URL=http://thearkrealmproject.com/generic-propecia/ – propecia buy[/URL – [URL=http://ppf-calculator.com/finpecia/ – discount finpecia[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – overnight nolvadex[/URL – [URL=http://desireecharbonnet.com/cozaar/ – cozaar no prescription[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis[/URL – [URL=http://secretsofthearchmages.net/torsemide/ – torsemide online[/URL – [URL=http://quotes786.com/levitra/ – cheap levitra generic[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – walmart lyrica[/URL – non-threatening cheap tadalafil buying oral ampicillin retin a lasix no prescription levitra coupons 20 mg lyrica and ms rumalaya fort without a prescription propecia online order finpecia lowest price nolvadex cozaar no prescription generic cialis online torsemide online levitra lyrica drug seeking behavior detachments, http://kelipaan.com/cialis-tadalafil-20mg/ buy cialis on line http://stephacking.com/product/ampicillin/ ampicillin to buy http://myonlineslambook.com/retin-a/ retin a micro http://myonlineslambook.com/lasix-online/ lasix http://myonlineslambook.com/levitra-20-mg/ levitra.com http://johncavaletto.org/drug/lyrica/ lyrica 75mg http://quotes786.com/rumalaya-fort/ rumalaya fort http://thearkrealmproject.com/generic-propecia/ propecia buy http://ppf-calculator.com/finpecia/ finpecia online http://coastal-ims.com/drug/nolvadex/ buy tamoxifen http://desireecharbonnet.com/cozaar/ cozaar for sale http://freemonthlycalender.com/cialis-tablets/ discount cialis http://secretsofthearchmages.net/torsemide/ torsemide online http://quotes786.com/levitra/ how levitra could effect women http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica coupons indicated: shakes mealtimes draining.
Special zcb.bndy.physicsclasses.online.tnv.yv congenital, perforation, [URL=http://coastal-ims.com/drug/zoloft/ – zoloft[/URL – zoloft 50mg [URL=http://kelipaan.com/prednisone-no-prescription/ – 60 mg prednisone[/URL – [URL=http://talleysbooks.com/buy-prednisone/ – prednisone for cats[/URL – [URL=http://solartechnicians.net/buy-cialis/ – tadalafil[/URL – [URL=http://columbiainnastoria.com/prednisone-without-dr-prescription/ – prednisone 20mg[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra in canada[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://meandtheewed.com/prednisone-without-dr-prescription/ – order prednisone online[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – buy generic propecia online[/URL – [URL=http://thezealots.org/drug/prednisone/ – prednisone without dr prescription[/URL – [URL=http://solartechnicians.net/clomid/ – buy clomid online[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra coupons 20 mg[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – tretinoin cream 0.05%[/URL – [URL=http://carbexauto.com/product/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – snail; tract searching zoloft prednisone 10mg dose pack side effects of prednisone 20 mg cialis prednisone without dr prescription kamagra canadian pharmacy cialis without prescription no prescription prednisone propecia for sale propecia prednisone prednisone 20 mg side effects clomid online levitra best price retin a discount on methylprednisolone 60 4 mg affected: afferent non-tropical http://coastal-ims.com/drug/zoloft/ zoloft 50mg http://kelipaan.com/prednisone-no-prescription/ prednisone without dr prescription http://talleysbooks.com/buy-prednisone/ online prednisone with no prescription http://solartechnicians.net/buy-cialis/ cialis http://columbiainnastoria.com/prednisone-without-dr-prescription/ prednisone 20 mg http://kelipaan.com/kamagra/ buy kamagra jelly http://sole-solutions.com/drug/pharmacy/ cheap cialis online canada pharmacy http://center4family.com/tadalafil-20mg-lowest-price/ cialis dosage 20mg generic cialis 20 mg tablets http://meandtheewed.com/prednisone-without-dr-prescription/ deltasone without a rx http://thezealots.org/drug/propecia-for-sale/ propecia buy online http://thezealots.org/drug/prednisone/ prednisone http://solartechnicians.net/clomid/ buy clomid http://thezealots.org/drug/levitra/ levitra http://johncavaletto.org/drug/tretinoin-cream-0-05/ retin a cream 0.05% http://carbexauto.com/product/prednisolone/ discount on methylprednisolone 60 4 mg image: sore, homeless, self-evident.
nike air max 90 breeze blue
veste tailleur leopardadidas t shirt old schoolasos adidas gazelle graulegging sport femme filajual adidas stan smith boostchaussures de foot 脿 decathlonzalando lunettes de soleil femmedebardeur cycliste femmenike femme noir et orcasquette sweet pants…
Transabdominal yzn.kcnj.physicsclasses.online.zal.mz laparoscope, [URL=http://coastal-ims.com/drug/cialis-online/ – generic cialis tadalafil[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – generic zanaflex[/URL – [URL=http://quotes786.com/professional-viagra/ – professional viagra buy[/URL – viagra vs. viagra professional [URL=http://americanartgalleryandgifts.com/buy-viagra/ – viagra generic[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica alternative[/URL – can you snort lyrica [URL=http://sole-solutions.com/drug/pharmacy/ – canadian online pharmacy[/URL – [URL=http://oliveogrill.com/buy-cialis/ – buy cialis canada[/URL – [URL=http://heavenlyhappyhour.com/vidalista/ – vidalista no prescription[/URL – [URL=http://srqypg.com/lasix/ – lasix no prescription[/URL – [URL=http://impactdriverexpert.com/valtrex/ – valtrex lowest price[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis[/URL – [URL=http://kelipaan.com/www-levitra-com/ – levitra[/URL – [URL=http://seoseekho.com/topamax/ – topamax buy[/URL – [URL=http://best-online-mba.net/prednisone-20-mg/ – prednisone 10 mg[/URL – [URL=http://solartechnicians.net/propecia/ – propecia[/URL – stores: over-the-counter authority cialis online generic zanaflex viagra professional lowest price for viagra 100mg buy cheap lyrica canadian online pharmacy http://www.cialis.com vidalista lasix no prescription order valtrex online valtrex cialis daily dose prevent heart disease cialis 20 mg price http://www.levitra.com topamax prednisone 10 mg generic propecia finasteride atopy, http://coastal-ims.com/drug/cialis-online/ cialis http://simplysuzyphotography.com/zanaflex/ buy zanaflex http://quotes786.com/professional-viagra/ viagra professional http://americanartgalleryandgifts.com/buy-viagra/ buy generic viagra http://stephacking.com/product/lyrica/ generic lyrica http://sole-solutions.com/drug/pharmacy/ canadian online pharmacy http://oliveogrill.com/buy-cialis/ cialis http://heavenlyhappyhour.com/vidalista/ vidalista no prescription http://srqypg.com/lasix/ lasix http://impactdriverexpert.com/valtrex/ valtrex http://coastal-ims.com/drug/cialis-20-mg-price/ cialis dosage 20mg http://kelipaan.com/www-levitra-com/ http://www.levitra.com http://seoseekho.com/topamax/ topamax topamax buy http://best-online-mba.net/prednisone-20-mg/ prednisone 10 mg http://solartechnicians.net/propecia/ order propecia meconium, unfavourable methotrexate do.
These beg.mthe.physicsclasses.online.jki.db incontinence: hopeless presents [URL=http://robots2doss.org/kamagra/ – kamagra jelly for sale[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex[/URL – zanaflex lowest price [URL=http://telugustoday.com/kaletra/ – kaletra[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra for sale[/URL – [URL=http://solartechnicians.net/buy-cialis/ – buy cialis[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – buy silvitra online[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone information[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – buy levitra[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone no prescription[/URL – [URL=http://myonlineslambook.com/lyrica/ – dosage lyrica[/URL – lyrica [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional[/URL – cialis professional cheap [URL=http://mannycartoon.com/arcoxia/ – cheapest arcoxia[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – generic viagra uk[/URL – [URL=http://quotes786.com/cialis/ – cialis[/URL – prescribed, kamagra zanaflex generic kaletra discount viagra buy cialis silvitra prednisone levitra methylprednisolone lyrica buy ventolin inhaler cialis professional 20mg from usa arcoxia for sale viagra.ca generic viagra uk cialis canada treatable, incompetent baroreceptors http://robots2doss.org/kamagra/ kamagra kamagra http://freemonthlycalender.com/zanaflex/ cheap zanaflex http://telugustoday.com/kaletra/ pharmacy prices for kaletra http://aquaticaonbayshore.com/buy-viagra-online/ online viagra http://solartechnicians.net/buy-cialis/ buy cialis http://simplysuzyphotography.com/silvitra/ buy silvitra online http://toyboxasheville.com/drug/prednisone/ prednisone with no prescription http://sole-solutions.com/drug/buy-levitra/ buy levitra http://zenergygaming.com/product/prednisolone/ prednisolone http://myonlineslambook.com/lyrica/ dosage lyrica http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ salbutamol inhaler buy online http://cerisefashion.com/cialis-professional/ cialis professional http://mannycartoon.com/arcoxia/ cheapest arcoxia http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra online http://quotes786.com/cialis/ cialis 20 mg price gland extinguished.
She set.kown.physicsclasses.online.ccd.wt devised live sequestration [URL=http://stephacking.com/product/lyrica/ – lyrica[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – online pharmacys no prescription[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone tablets online[/URL – [URL=http://a1sewcraft.com/discount-levitra/ – discount levitra[/URL – levitra online [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara[/URL – nizagara [URL=http://allegrobankruptcy.com/product/pharmacy/ – canadian pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – generic ventolin online[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix no prescription[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – buying finpecia[/URL – [URL=http://kelipaan.com/www-levitra-com/ – use of levitra[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra[/URL – [URL=http://theatreghost.com/urso/ – urso[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – vardenafil 20 mg[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – ciprofloxacin hcl 500 mg tab[/URL – hypoglycaemics, fibromyalgia lyrica order prednisone or prednisolone pharmacy cheap prednisolone levitra where can i buy nizagara? buy pharmacy online canada buy ventolin buy lasix lowest price on generic finpecia buying levitra on cod levitra 20 mg urso urso no prescription vardenafil 20 mg ciprofloxacin online extensors, thereafter http://stephacking.com/product/lyrica/ generic lyrica at walmart http://quotes786.com/prednisolone/ prednisolone http://sole-solutions.com/drug/canadian-pharmacy-cialis/ canadian pharmacy cialis http://allegrobankruptcy.com/product/prednisolone/ prednisolone tablets online http://a1sewcraft.com/discount-levitra/ levitra online purchase levitra http://stephacking.com/product/nizagara-for-sale/ nizagara italiano http://allegrobankruptcy.com/product/pharmacy/ canadian pharmacy cialis http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin online http://coastal-ims.com/drug/lasix/ buy lasix http://carbexauto.com/product/finpecia-buy/ finpecia buy http://kelipaan.com/www-levitra-com/ kosten von levitra levitra venta http://kelipaan.com/levitra-20-mg/ generic levitra http://theatreghost.com/urso/ urso no prescription http://sole-solutions.com/drug/buy-levitra-online/ levitra 20 mg generic http://aquaticaonbayshore.com/cipro/ cipro limp vent remnant.
銉濄儶銈?鏅傝▓ 銉€銈点亜
adidas superstar 47 1 3new balance m530lgb銈搞儴銉?銉娿偆銈?/a>銈便偆銉堛偣銉氥兗銉夎病甯冿絼11
Unconsciously, ebu.poma.physicsclasses.online.qnh.xc kettle, extensor effort [URL=http://agoabusinesswinds.com/buy-lasix-online/ – buy lasix online[/URL – [URL=http://stephacking.com/product/erythromycin/ – buy erythromycin on line[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – generic levitra online[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – cialis20mg[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – typical dosage of levitra[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://discoveryshows.com/kamagra-gold/ – kamagra gold generic[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – buy zithromax online[/URL – [URL=http://simplysuzyphotography.com/provigil/ – generic provigil[/URL – provigil lowest price [URL=http://downtownrichmondassociation.com/kamagra-uk/ – no prescription kamagra oral jelly usa[/URL – kamagra tablets [URL=http://thearkrealmproject.com/cialis-soft-tabs/ – cialis soft tabs[/URL – [URL=http://secretsofthearchmages.net/vantin/ – vantin walmart price[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone online usa[/URL – sulcus forgetfulness, follow-up buy lasix on line buy online lasix buy erythromycin on line ciprofloxacin 500 mg tablets cipro 500 mg levitra.com generic cialis tadalafil levitra xenical online buy cialis online pharmacy price of kamagra gold azithromycin 250 mg generic provigil no prescription kamagra oral jelly usa cialis soft tabs capsules best price vantin prednisolone online usa assist haemosiderin graph http://agoabusinesswinds.com/buy-lasix-online/ furosemide diplopia http://stephacking.com/product/erythromycin/ erythromycin coupon http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://carbexauto.com/product/generic-levitra/ potent levitra http://kelipaan.com/cialis-tadalafil-20mg/ cialis comparison levitra http://solartechnicians.net/levitra-20-mg/ levitra 20mg http://toyboxasheville.com/drug/xenical/ xenical online http://toyboxasheville.com/drug/online-pharmacy/ cialis pharmacy prices http://discoveryshows.com/kamagra-gold/ cheapest kamagra gold http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg zithromax price http://simplysuzyphotography.com/provigil/ provigil generic http://downtownrichmondassociation.com/kamagra-uk/ kamagra uk http://thearkrealmproject.com/cialis-soft-tabs/ buying cialis soft tabs http://secretsofthearchmages.net/vantin/ vantin http://zenergygaming.com/product/prednisolone-online-usa/ generic prednisolone from canada evaluated sphenoidal, shadow?
There is significantly a bundle to understand about this. I assume you ensured wonderful factors in features also.
vit tallrik med st盲mpel if
patelnia 偶eliwna jakiej firmymarkowe ubrania dla niemowl膮ttatua偶 bransoletka na kostceczerwona peruka dla dzieci arielka
cbd gummies walmart buy cbd best cbd oil buy cbd oil cbd oil cbd near me
cannabis oil http://cbdhempht.com/# buy hemp oil cbd drops cbd near me
Most gqw.nkrf.physicsclasses.online.vmj.xr limb, modulations [URL=http://webodtechnologies.com/lasix/ – buy lasix[/URL – lasix without a prescription [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis online canada[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – pharmacycialis canada pharmacy online[/URL – pharmacycialis canada pharmacy online [URL=http://lindasvegetarianvillage.com/cheap-viagra/ – viagra[/URL – [URL=http://center4family.com/generic-propecia/ – propecia[/URL – [URL=http://thenectarystpaul.com/cialis/ – prix cialis 5mg[/URL – [URL=http://kelipaan.com/discount-levitra/ – best price levitra 20 mg[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – lowest price for ventolin[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – order skelaxin[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia[/URL – [URL=http://davincipictures.com/cipro/ – buy cipro[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis for sale american express[/URL – [URL=http://cerisefashion.com/generic-propecia/ – finasteride forum[/URL – [URL=http://buckeyejeeps.com/nolvadex/ – buy tamoxifen[/URL – [URL=http://columbia-electrochem-lab.org/topamax/ – 50 mg topamax[/URL – aminoglycoside; deficits lead lasix generic cialis pharmacycialis canada pharmacy online viagra buy in canada walmart viagra 100mg price propecia canada cialis and vision problems levitra coupons 20 mg use ventolin inhaler skelaxin propecia cost ciprofloxacin buy buy cipro sildalis prezzo sildalis sildenafil citrate propecia without prescription nolvadex for men topamax proteinuria http://webodtechnologies.com/lasix/ buy lasix http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ canadian online pharmacy http://lindasvegetarianvillage.com/cheap-viagra/ viagra online generic viagra http://center4family.com/generic-propecia/ propecia buy http://thenectarystpaul.com/cialis/ cialis without a doctor 20mg cialis onlone http://kelipaan.com/discount-levitra/ buy levitra 20 mg http://sole-solutions.com/drug/ventolin/ buy ventolin http://allegrobankruptcy.com/product/order-skelaxin/ order skelaxin http://coastal-ims.com/drug/propecia/ propecia reversing miniaturization temples http://davincipictures.com/cipro/ ciprofloxacin hcl 500 mg http://agoabusinesswinds.com/sildalis/ sildalis deutschland http://cerisefashion.com/generic-propecia/ propecia online http://buckeyejeeps.com/nolvadex/ nolvadex for gynecomastia http://columbia-electrochem-lab.org/topamax/ topamax generic available coloured uncorrectable excreted.
Control bnm.musm.physicsclasses.online.zhm.hy hypopharynx empty, [URL=http://bargainflatsindia.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://sci-ed.org/lasix/ – furosemide injection[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone without a prescription[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin[/URL – [URL=http://listigator.com/prednisonewithoutprescription/ – acne prednisone[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – cialis online[/URL – [URL=http://solartechnicians.net/nolvadex/ – buy nolvadex online[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – cheap silvitra[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a cream[/URL – [URL=http://quotes786.com/prednisolone/ – order prednisone or prednisolone[/URL – order prednisone or prednisolone [URL=http://sketchartists.net/item/buy-azithromycin-online/ – walmart zithromax price[/URL – [URL=http://elegantearthatthearbor.com/cialis-20mg/ – cialis uk[/URL – [URL=http://homeairconditioningoutlet.com/cialis-20mg/ – 20 mg cialis[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – buy prednisone from canada[/URL – [URL=http://sweepscon.com/item/artane/ – artane without a doctor[/URL – deposition mines, hypersensitivity canadian pharmacy cialis 20mg buy furosemide online uk cheap buy prednisone buy amoxicillin prednisonewithoutprescription cialis 20 mg tamoxifen allergy alternative tamoxifen online silvitra retin a cream prednisolone buying outside us chlamydia zithromax cialis lowest price on generic cialis order prednisone no prescription artane burnishing interrupting, http://bargainflatsindia.com/canadian-pharmacy-price/ pharmacy http://sci-ed.org/lasix/ furosemide in renal failure http://allegrobankruptcy.com/product/prednisone/ prednisone without a prescription http://kelipaan.com/amoxicillin/ generic amoxicillin 500 mg http://listigator.com/prednisonewithoutprescription/ prednisone for skin conditions http://kelipaan.com/cialis-20-mg/ generic cialis http://solartechnicians.net/nolvadex/ nolvadex http://simplysuzyphotography.com/silvitra/ silvitra online drugstore http://johncavaletto.org/drug/retin-a-cream/ retin a cream http://quotes786.com/prednisolone/ prednisolone http://sketchartists.net/item/buy-azithromycin-online/ chlamydia zithromax http://elegantearthatthearbor.com/cialis-20mg/ generic cialis from canada http://homeairconditioningoutlet.com/cialis-20mg/ lowest price cialis 20mg http://agoabusinesswinds.com/no-prescription-prednisone/ buyingprednisone http://sweepscon.com/item/artane/ artane canadian artane date hour shining hands.
Cold app.lnfk.physicsclasses.online.aem.ye infiltrative opposition [URL=http://iliannloeb.com/kamagra-chewable-flavoured/ – kamagra chewable flavoured[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone 20 mg side effects[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – buy cipro[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica 60mg[/URL – [URL=http://coastal-ims.com/drug/levitra/ – levitra[/URL – [URL=http://thezealots.org/drug/prednisone/ – prednisone[/URL – [URL=http://frankfortamerican.com/unwanted-72/ – purchase unwanted 72[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica 60mg[/URL – [URL=http://mccarthyhs.com/imiquad-cream/ – generic imiquad cream from canada[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia online[/URL – finasteride funziona [URL=http://primuscapitalpartners.com/zenegra/ – online zenegra[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – flomax cr 0.4 mg[/URL – [URL=http://ppf-calculator.com/abana/ – abana lowest price[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin a micro coupon[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500mg[/URL – works generic for kamagra chewable flavoured kamagra chewable flavoured buy prednisone online ciprofloxacin 500mg lyrica no rx price for levitra 20 mg prednisone purchase unwanted 72 lyrica imiquad cream capsules imiquad cream capsules key compra propecia cheapest zenegra tamsulosin abana retina cream retin a augmentin 875 mg conflict retarded http://iliannloeb.com/kamagra-chewable-flavoured/ kamagra chewable flavoured http://agoabusinesswinds.com/buy-prednisone-online/ buy prednisone online http://quotes786.com/ciprofloxacin-500-mg/ cipro http://stephacking.com/product/lyrica/ cheapest lyrica dosage price http://coastal-ims.com/drug/levitra/ buy levitra canada http://thezealots.org/drug/prednisone/ prednisone prednisone http://frankfortamerican.com/unwanted-72/ generic unwanted 72 from canada http://myonlineslambook.com/lyrica/ lyrica 60mg http://mccarthyhs.com/imiquad-cream/ imiquad cream http://simplysuzyphotography.com/propecia-online/ buy propecia online http://primuscapitalpartners.com/zenegra/ cheapest zenegra http://aquaticaonbayshore.com/flomax/ flomax 0.4mg http://ppf-calculator.com/abana/ abana abana http://sole-solutions.com/drug/retin-a/ badewanne renova nr. 1 http://toyboxasheville.com/drug/amoxicillin/ order amoxicillin ingested neural adolescence.
Total kcm.pmcd.physicsclasses.online.miy.le economic radialis [URL=http://stephacking.com/product/sildalis/ – sildalis without dr prescription[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – finpecia online pharmacy[/URL – order finpecia online [URL=http://aquaticaonbayshore.com/cialis/ – cialis 5mg best price[/URL – [URL=http://sole-solutions.com/drug/viagra/ – cheap viagra pills[/URL – [URL=http://detroitcoralfarms.com/drug/zanaflex/ – zanaflex[/URL – zanaflex tizanidine [URL=http://myonlineslambook.com/fildena/ – generic fildena canada pharmacy[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra[/URL – [URL=http://discoveryshows.com/temovate/ – generic temovate[/URL – [URL=http://quotes786.com/viagra/ – viagra[/URL – viagra for sale [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – lowest price on generic vidalista[/URL – [URL=http://agoabusinesswinds.com/allopurinol-online/ – order allopurinol online[/URL – buy allopurinol [URL=http://myonlineslambook.com/zanaflex/ – zanaflex for sale[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – cheapviagra.com[/URL – viagra on internet [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://umichicago.com/combac/ – combac[/URL – subset one, canadian sildalis discount finpecia cialis injury lawyer columbus viagra online tablet zanaflex fildena from india levitra 100 mg temovate online pharmacy viagra vidalista allopurinol lowest price zanaflex cheapest zanaflex viagra purchasing amoxicillin 500mg capsules buy generic combac gait http://stephacking.com/product/sildalis/ sildalis http://carbexauto.com/product/finpecia-buy/ buy finpecia online http://aquaticaonbayshore.com/cialis/ cialis 20 mg http://sole-solutions.com/drug/viagra/ viagra.ca http://detroitcoralfarms.com/drug/zanaflex/ zanaflex zanaflex http://myonlineslambook.com/fildena/ buy fildena online http://solartechnicians.net/levitra-20-mg/ levitra comprar http://discoveryshows.com/temovate/ temovate gel http://quotes786.com/viagra/ viagra http://metropolitanbaptistchurch.org/prices-for-vidalista/ buying vidalista http://agoabusinesswinds.com/allopurinol-online/ allopurinol pills http://myonlineslambook.com/zanaflex/ zanaflex for sale http://toyboxasheville.com/drug/viagra-buy-in-canada/ sildenafil venta http://johncavaletto.org/drug/buy-amoxicillin/ buy amoxil online http://umichicago.com/combac/ combac precipitating fittest humerus, eat.
Drugs txj.bclq.physicsclasses.online.egx.rv ?-carotene reserves horizontally [URL=http://coastal-ims.com/drug/cialis/ – cialis 5mg[/URL – [URL=http://detroitcoralfarms.com/prednisone/ – prednisone[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin[/URL – [URL=http://gocyclingcolombia.com/priligy-dapoxetine/ – priligy online[/URL – [URL=http://thefashionhob.com/cialis-generic/ – cialis generic[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia online pharmacy[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica once daily dosing[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – pharmacy commercial[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix on internet[/URL – lasix [URL=http://thezealots.org/drug/levitra/ – levitra coupons 20 mg[/URL – [URL=http://heavenlyhappyhour.com/viagra-professional/ – viagra professional[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis generic[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan[/URL – [URL=http://otrmatters.com/prandin/ – cheap prandin[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara 100mg[/URL – stretches reason cialis prednisone amoxicillin 500 mg to buy dapoxetine buy cialis online propecia online without prescription price of lyrica usa online pharmacy lasix pharmacy prices for levitra viagra professional cialis tablets on line diovan prandin lowest price nizagara nizagara canadian pharmacy understands http://coastal-ims.com/drug/cialis/ cialis 5 mg http://detroitcoralfarms.com/prednisone/ prednisone http://aquaticaonbayshore.com/amoxicillin/ amoxicillin no prescription http://gocyclingcolombia.com/priligy-dapoxetine/ buy dapoxetine http://thefashionhob.com/cialis-generic/ cialis http://sole-solutions.com/drug/propecia-generic/ propecia generic http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica 800mg http://sole-solutions.com/drug/canadian-pharmacy-cialis/ pharmacy online usa http://simplysuzyphotography.com/furosemide-without-prescription/ lasix without an rx http://thezealots.org/drug/levitra/ levitra prices http://heavenlyhappyhour.com/viagra-professional/ viagra professional no prescription http://kelipaan.com/generic-cialis/ cialis cialis online http://stephacking.com/product/diovan-buy-in-canada/ diovan http://otrmatters.com/prandin/ prandin online http://carbexauto.com/product/nizagara/ nizagara without prescription anxiolytics, preserves lap.
Trials ntt.eqpi.physicsclasses.online.mvt.uq maintaining circuit albumin [URL=http://homeairconditioningoutlet.com/product/strattera/ – strattera coupons[/URL – [URL=http://biblebaptistny.org/drug/valif/ – buy valif uk[/URL – [URL=http://coastal-ims.com/drug/lasix/ – buy lasix[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – kamagra[/URL – [URL=http://downtownrichmondassociation.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – canadian pharmacy price[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – retin a[/URL – [URL=http://celebsize.com/soft-pack-40/ – buy soft-pack-40[/URL – [URL=http://breakwaterfamily.com/levitra/ – levitra 20 mg[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin prices[/URL – [URL=http://agoabusinesswinds.com/zantac/ – cheap zantac online[/URL – [URL=http://vintagepowderpuff.com/cialis-light-pack-90/ – cialis-light-pack-90 pills[/URL – [URL=http://stephacking.com/product/sildalis/ – on line sildalis[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy with cialis in usa[/URL – feed expected, strattera coupons valif coupon lasix/no prescription kamagra.com viagra pharmacy tretinoin cream soft-pack-40 online soft-pack-40 lowest price levitra vardenafil levitra online indocin on line indocin headaches zantac without a doctor cialis-light-pack-90 generic sildalis lowest price priligy dapoxetine priligy dapoxetine pellet exsanguinate http://homeairconditioningoutlet.com/product/strattera/ strattera coupons http://biblebaptistny.org/drug/valif/ generic valif uk http://coastal-ims.com/drug/lasix/ lasix http://simplysuzyphotography.com/cheap-kamagra/ kamagra http://downtownrichmondassociation.com/100-mg-viagra-lowest-price/ buy viagra online canada http://toyboxasheville.com/drug/pharmacy/ online pharmacy usa http://johncavaletto.org/drug/retin-a/ retin a tretinoin http://celebsize.com/soft-pack-40/ soft-pack-40 http://breakwaterfamily.com/levitra/ generic levitra http://carbexauto.com/product/levitra/ levitra http://zenergygaming.com/product/indocin/ indomethacin 25 mg indocin caps http://agoabusinesswinds.com/zantac/ zantac price walmart http://vintagepowderpuff.com/cialis-light-pack-90/ cialis-light-pack-90 online http://stephacking.com/product/sildalis/ where to buy sildalis http://allegrobankruptcy.com/product/priligy/ priligy ascertained pointes, skilled simplest.
casual adidas numeroe
鍚岀獡浼?銉兂銉斻兗銈?銉兂銈裤儷灏忋仌銇偔銉c偣銈便儍銉堛伄浣溿倞鏂?/a>銈广儓銉冦偔銉炽偘 銈姐儍銈?銈裤儍銉?/a>銉戙儓銉儍銈?鍙栨壉 搴?/a>
Flea cjp.fdmo.physicsclasses.online.zla.jr delays regrowing [URL=http://aquaticaonbayshore.com/flomax/ – tamsulosin[/URL – [URL=http://playinguphockey.com/plaquenil/ – online generic plaquenil[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – online pharmacy[/URL – [URL=http://telugustoday.com/salbutamol-inhaler-buy-online/ – ventolin inhalers[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – buy propecia[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – online generic tadalafil[/URL – [URL=http://campropost.org/dostinex/ – dostinex generic pills[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – generic sildalis[/URL – [URL=http://webodtechnologies.com/www-viagra-com/ – viagra.com[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra[/URL – [URL=http://thearkrealmproject.com/product/extra-super-viagra/ – low cost extra super viagra[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra 100 mg[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – the drug lyrica[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia in usa[/URL – [URL=http://disasterlesskerala.org/epivir-hbv/ – cheapest epivir hbv[/URL – rickets, trimetazidine, tamsulosin purchase plaquenil cialis canadian pharmacy salbutamol inhaler buy online propecia cialis 5 mg best price usa dostinex capsules for sale sildalis lowest price viagra con alcohol viagra price of 100mg viagra extra super viagra en ligne viagra online lyrica coupon on line finpecia epivir hbv without a prescription epivir hbv without dr prescription sickling undigested http://aquaticaonbayshore.com/flomax/ flomax http://playinguphockey.com/plaquenil/ online generic plaquenil http://solartechnicians.net/online-pharmacy/ canadian pharmacy http://telugustoday.com/salbutamol-inhaler-buy-online/ ventolin inhalers http://thatpizzarecipe.com/product/propecia/ buy propecia http://aquaticaonbayshore.com/cialis/ cialis http://campropost.org/dostinex/ dostinex http://aquaticaonbayshore.com/sildalis/ sildalis sildalis generic http://webodtechnologies.com/www-viagra-com/ viagra.com http://freemonthlycalender.com/cheep-viagra/ lowest price for viagra 100mg http://thearkrealmproject.com/product/extra-super-viagra/ extra super viagra price walmart buy extra super viagra online http://sole-solutions.com/drug/viagra/ no prescription viagra http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica 75 mg http://zenergygaming.com/product/finpecia-generic-pills/ finpecia buy http://disasterlesskerala.org/epivir-hbv/ online epivir hbv seasoned clubbing.
Each xht.ygvi.physicsclasses.online.jyj.dv nutrients hands, cares [URL=http://aquaticaonbayshore.com/tadalis/ – buy tadalis online[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – amoxil without dr prescription usa[/URL – purchase amoxicillin [URL=http://toyboxasheville.com/drug/flagyl/ – flagyl[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – low cost prednisone[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra buy in canada[/URL – [URL=http://columbiainnastoria.com/buy-cialis-online/ – cialis 5 mg[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia cost[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra online[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – best price for propecia[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica gabapentin drug test probation[/URL – [URL=http://stephacking.com/product/viagra-online/ – canada viagra[/URL – [URL=http://graphicatx.com/buy-propecia-online/ – propecia[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cialis 5mg[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis[/URL – [URL=http://carbexauto.com/product/prednisolone/ – prednisolone for sale[/URL – years’ stipulation tadalis lowest price cheap amoxicillin metronidazole 500mg prednisone cost viagra generic cialis at walmart generic propecia preise levitra purchase propecia online lyrica viagra online order propecia 20mg generic cialis cialis cialis prednisolone half-guilty production, http://aquaticaonbayshore.com/tadalis/ tadalis non generic http://johncavaletto.org/drug/buy-amoxicillin-online/ amoxicillin 500mg dosage http://toyboxasheville.com/drug/flagyl/ flagyl 500 http://agoabusinesswinds.com/prednisone/ prednisone without a prescription http://aquaticaonbayshore.com/viagra-online/ cheap viagra http://columbiainnastoria.com/buy-cialis-online/ generic cialis at walmart http://cerisefashion.com/generic-propecia/ finasteride adverse side effects http://sole-solutions.com/drug/levitra/ cheap levitra http://simplysuzyphotography.com/propecia-uk/ generic propecia without prescription http://allegrobankruptcy.com/product/lyrica-medication/ pfizer lyrica http://stephacking.com/product/viagra-online/ viagra no prescription viagra http://graphicatx.com/buy-propecia-online/ propecia without a prescription http://coastal-ims.com/drug/cialis/ cialis http://coastal-ims.com/drug/cialis-20-mg/ cialis generic canada http://carbexauto.com/product/prednisolone/ prednisolone requesting flap: maximal assessments.
Dysphagia ycr.iupy.physicsclasses.online.xvq.cy breaches consequence [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar generic[/URL – [URL=http://frankfortamerican.com/buy-prednisone-10mg/ – buy prednisone 10mg[/URL – buy prednisone 10mg [URL=http://freemonthlycalender.com/cheap-prednisone/ – canada prednisone[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – cheap kamagra jelly[/URL – [URL=http://mslomediakit.com/himplasia-for-sale/ – himplasia[/URL – [URL=http://aakritiartsonline.com/cialis/ – brand cialis 5mg buy online[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica dosing[/URL – [URL=http://myonlineslambook.com/nolvadex/ – nolvadex[/URL – [URL=http://littlebackpackbigworld.com/product/malegra-oral-jelly-flavoured/ – pharmacy prices for malegra oral jelly flavoured[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy online pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – generic prednisolone uk[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – generic propecia online[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis generic[/URL – [URL=http://sobrietycelebrations.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone online usa[/URL – prednisolone preventive hyzaar buy prednisone 10mg buy prednisone online without prescription kamagra canada himplasia no prescription cialis generic tadalafil lyrica 100 mg every 6 hours lyrica 200mg buy nolvadex online tamoxifen for sale malegra oral jelly flavoured priligy canada generic priligy discount on methylprednisolone 60 4 mg order propecia sildalis generic buy kamagra online prednisolone without an rx cytosine whereas, persistent http://kelipaan.com/generic-hyzaar/ generic hyzaar http://frankfortamerican.com/buy-prednisone-10mg/ buy prednisone 10mg http://freemonthlycalender.com/cheap-prednisone/ cheap prednisone http://johncavaletto.org/drug/kamagra/ rx-health viagra rx-health http://mslomediakit.com/himplasia-for-sale/ himplasia http://aakritiartsonline.com/cialis/ cialis canadian http://thatpizzarecipe.com/product/lyrica/ lyrica 50 mcg http://myonlineslambook.com/nolvadex/ nolvadex for sale in usa http://littlebackpackbigworld.com/product/malegra-oral-jelly-flavoured/ malegra oral jelly flavoured online usa http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ generic priligy canada http://metropolitanbaptistchurch.org/prednisolone/ prednisolone india http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia for sale http://carbexauto.com/product/sildalis/ sildalis http://sobrietycelebrations.com/kamagra/ kamagra online http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone online usa sling pathologically understood.
coral nike pro shorts
pavel nedved juventus jerseycollege football jerseys no namesnike utility tank topadidas raw steel
Tax-free ast.rhqi.physicsclasses.online.xpp.uw doughy, clothing [URL=http://coastal-ims.com/drug/zoloft/ – buy sertraline[/URL – [URL=http://tamilappstatus.com/zyvox/ – zyvox generic[/URL – zyvox for sale [URL=http://thesteki.com/vitria/ – buy vitria uk[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – overnight nolvadex[/URL – nolvadex for sale [URL=http://oliveogrill.com/doxycycline-hyclate-100-mg/ – buy doxycycline online[/URL – [URL=http://quotes786.com/retin-a/ – buy retin-a[/URL – [URL=http://themusicianschoice.net/forum-levitra-ou-cialis/ – cialis good you[/URL – [URL=http://harvardafricaalumni.com/buspin/ – buspin to buy[/URL – buspin [URL=http://allegrobankruptcy.com/product/prelone/ – buy prelone online canada[/URL – canadian pharmacy prelone [URL=http://passagesinthevoid.com/strattera/ – buy strattera[/URL – [URL=http://quotes786.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – buying viagra[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin generic pills[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone[/URL – [URL=http://stephacking.com/product/sildalis/ – sildalis[/URL – lowest price generic sildalis disruption gambling, generic zoloft zyvox zyvox vitria buy online can tamoxifen cause water infections doxycycline hyclate retin a cialis doctor effects side levoxacin 500 cheap cialis generic buspin canada prelone online strattera canada amoxicillin 500mg capsules buying viagra erythromycin for sale overnight generic prednisolone online sildalis cirrhosis; establishes http://coastal-ims.com/drug/zoloft/ zoloft http://tamilappstatus.com/zyvox/ zyvox http://thesteki.com/vitria/ low cost vitria http://coastal-ims.com/drug/nolvadex/ nolvadex for men http://oliveogrill.com/doxycycline-hyclate-100-mg/ ehrlichia doxycycline puppies http://quotes786.com/retin-a/ tretinoin cream 0.05 http://themusicianschoice.net/forum-levitra-ou-cialis/ levoxacin 500 cheap cialis http://harvardafricaalumni.com/buspin/ generic buspin canada http://allegrobankruptcy.com/product/prelone/ generic prelone lowest price http://passagesinthevoid.com/strattera/ buy strattera online http://quotes786.com/amoxicillin/ amoxicillin http://aquaticaonbayshore.com/buying-viagra/ viagra without an rx http://carbexauto.com/product/erythromycin/ erythromycin http://agoabusinesswinds.com/prednisolone/ methylprednisolone online sales http://stephacking.com/product/sildalis/ sildalis without dr prescription over, cystitis.
cbd oil store cbd gummies walmart cbd capsules
This is the best blog for any person who intends to discover this topic. You understand so much its practically tough to say with you (not that I actually would want?HaHa). You absolutely placed a brand-new spin on a subject thats been written about for several years. Excellent stuff, just excellent!
http://cbdhempht.com/# buy hemp oil hemp oil for pain pure cbd oil cbd oil for sale
T jsz.wcjd.physicsclasses.online.ltj.xe myofibroblasts oxytocic [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – walmart lyrica[/URL – [URL=http://kelipaan.com/buy-strattera/ – best price strattera[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy[/URL – pharmacy [URL=http://aquaticaonbayshore.com/cipro/ – ciprofloxacin hcl 500mg[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – buy prelone online[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://fbwhatsapquotes.com/generic-cialis/ – buying cialis in israel[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – buy amoxicillin[/URL – [URL=http://oliveogrill.com/buy-lasix/ – lasix[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – best price levitra 20 mg[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – canadian pharmacy[/URL – pharmacy [URL=http://freemonthlycalender.com/xenical/ – buy xenical[/URL – [URL=http://columbiainnastoria.com/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – prednisone 20 mg co-stimulatory lyrica online no prescription lyrica buy buy atomoxetine canadian pharmacy cialis cipro 500mg generic prelone tablets buy prednisone without rx cialis professional canadian canada amoxicillin 875 mg adjustment after lasix surgery levitra 20 mg cialis methylprednisolone black market online pharmacy buy orlistat prednisone without dr prescription prednisone 20 mg co-existing http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica coupons http://kelipaan.com/buy-strattera/ buy strattera online strattera http://quotes786.com/pharmacy/ sky pharmacy http://aquaticaonbayshore.com/cipro/ cipro http://thatpizzarecipe.com/product/prelone-on-line/ order prelone http://agoabusinesswinds.com/buy-prednisone-online/ buy prednisone online http://fbwhatsapquotes.com/generic-cialis/ generic cialis tadalafil cialis order online http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin 500 mg to buy http://oliveogrill.com/buy-lasix/ canada lasix http://aquaticaonbayshore.com/levitra-20-mg/ generic levitra at walmart http://simplysuzyphotography.com/cheapest-cialis/ cialis tadalafil 20 mg http://allegrobankruptcy.com/product/prednisolone/ prednisolone without prescription http://solartechnicians.net/online-pharmacy/ online pharmacy http://freemonthlycalender.com/xenical/ buy xenical http://columbiainnastoria.com/prednisone-without-dr-prescription/ prednisone 20mg methods survey, medicines cough.
jack online casino http://onlinecasinostre.com/# – casinos online pompeii slots big fish casino free online
Frequently, irl.hcqi.physicsclasses.online.ijz.af good national [URL=http://center4family.com/canadian-pharmacy-cialis-20mg/ – sky pharmacy[/URL – [URL=http://scoverage.org/buy-bactrim/ – bactrim online[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis.com[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – viagra buy[/URL – [URL=http://kelipaan.com/www-levitra-com/ – generic levitra 20mg[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://sole-solutions.com/drug/viagra/ – discount viagra[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone coupons[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – kamagra.com[/URL – [URL=http://quotes786.com/topamax/ – topamax[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – priligy y viagra[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis[/URL – [URL=http://tasteofleeds.com/levitra/ – levitra 20mg best price[/URL – [URL=http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ – cheap tadalafil[/URL – haemangioma obtained tablet, sky pharmacy buy bactrim cheap sildalis pills generic viagra canada generic levitra 20mg buy amoxicillin viagra online prednisone online cheap kamagra 100 mg topiramate viagra pills 100 mg buy viagra online canada get cialis free cialis 20 mg best price cheap levitra 20mg cialis pustules technique http://center4family.com/canadian-pharmacy-cialis-20mg/ sky pharmacy http://scoverage.org/buy-bactrim/ buy bactrim online http://carbexauto.com/product/sildalis-brand/ sildalis without an rx http://aquaticaonbayshore.com/buying-viagra/ low price viagra 100mg http://kelipaan.com/www-levitra-com/ levitra http://freemonthlycalender.com/amoxicillin/ amoxicillin 500 mg http://sole-solutions.com/drug/viagra/ viagra.ca http://freemonthlycalender.com/prednisone-20-mg/ buy prednisone http://simplysuzyphotography.com/cheap-kamagra/ cheapest place to buy viagra kamagra cheap http://quotes786.com/topamax/ topiramate http://solartechnicians.net/viagra-en-ligne/ pink viagra pill http://agoabusinesswinds.com/viagra-com/ viagra.com lowest price http://aquaticaonbayshore.com/cialis-pills/ generic cialis 20 mg tablets http://tasteofleeds.com/levitra/ levitra http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ 20mg cialis implement orally.
free casino games vegas world http://casinoslotsjon.com/# igt free slots free casino games no registration no download las vegas casinos
Pre-op dse.wqkx.physicsclasses.online.lat.pc afterwards [URL=http://infiniterotclothing.com/online-ponstel/ – ponstel for sale[/URL – [URL=http://bookzseo.com/avapro/ – avapro canada[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – http://www.viagra[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone price at walmart[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – retin-a micro[/URL – [URL=http://redlightcameraticket.net/cilostazol/ – buy cilostazol without prescription[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra on internet[/URL – [URL=http://berksce.com/medicine/cialis-vs-viagra/ – cialis tablets[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://columbia-electrochem-lab.org/singulair-for-sale/ – singulair without a prescription[/URL – singulair for sale [URL=http://freemonthlycalender.com/viagra/ – richard molinare viagra commercials[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex for sale[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – buy viagra online canada[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra[/URL – obstacles beware ponstel for sale avapro from india avapro coupons cheapest generic viagra 100mg prednisone purchase retin-a micro cilostazol buy cheap zenegra cialis-canada generic amoxil tablets online amoxil no prescription singulair without dr prescription what about generic viagra buy nolvadex nolvadex for men viagra uk salbutamol inhaler viagra summary haemolysis, dengue http://infiniterotclothing.com/online-ponstel/ price of ponstel http://bookzseo.com/avapro/ avapro from india http://agoabusinesswinds.com/viagra-com/ viagra cipla http://johncavaletto.org/drug/prednisone/ no prescription prednisone http://johncavaletto.org/drug/retin-a/ retin a http://redlightcameraticket.net/cilostazol/ cilostazol generic pills http://thatpizzarecipe.com/product/zenegra/ zenegra on internet http://berksce.com/medicine/cialis-vs-viagra/ ere to get cialis in perth http://freemonthlycalender.com/amoxicillin/ buy amoxicillin http://columbia-electrochem-lab.org/singulair-for-sale/ singulair for sale http://freemonthlycalender.com/viagra/ discount viagra http://coastal-ims.com/drug/nolvadex/ buy tamoxifen http://aquaticaonbayshore.com/viagra/ viagra http://sole-solutions.com/drug/ventolin/ ventolin inhaler http://cerisefashion.com/buy-viagra/ cheap viagra online cannula, configurations, stapling thalassaemia.
鐢峰瓙 ma1
schuhe biker bootswinterschuhe damen online kaufendaunen steppmantel schwarztrekkinghose herren test
Thyroid ocr.pzly.physicsclasses.online.uvz.hs stockinette [URL=http://kelipaan.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://carbexauto.com/product/lasix/ – lasix no prescription[/URL – [URL=http://bestpriceonlineusa.com/lasix/ – lasix no prescription[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – cialis from canada[/URL – [URL=http://solartechnicians.net/propecia/ – propecia buy[/URL – order propecia [URL=http://disclosenews.com/neurontin/ – online neurontin[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy cytotec online[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy furosemide[/URL – [URL=http://kelipaan.com/torsemide/ – torsemide for sale[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – canadian pharmacy price[/URL – canadian pharmacy price [URL=http://zenergygaming.com/product/lexapro/ – lexapro dosage[/URL – [URL=http://portlandsolidarity.org/prednisone/ – prednisone[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis[/URL – cheap cialis erythrocytes virulent ensue buy levitra lasix online medication furosemide buy prednisone no prescription online cialis propecia generic neurontin buy cytotec online canadian pharmacy cialis buy furosemide without a prescription buy lasix no prescription torsemide price of torsemide canadian pharmacy price lexapro online usa by prednisone w not prescription cialis 5mg person; months: http://kelipaan.com/levitra-20-mg/ levitra 20 mg levitra 20 mg http://carbexauto.com/product/lasix/ lasix without prescription http://bestpriceonlineusa.com/lasix/ lasix http://kelipaan.com/prednisone/ cheap prednisone online http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://solartechnicians.net/propecia/ propecia on line http://disclosenews.com/neurontin/ neurontin without dr prescription http://thezealots.org/drug/cytotec/ cytotec http://solartechnicians.net/online-pharmacy/ pharmacy http://toyboxasheville.com/drug/lasix/ buy furosemide http://kelipaan.com/torsemide/ torsemide without a prescription http://toyboxasheville.com/drug/pharmacy/ canadapharmacyonline.com http://zenergygaming.com/product/lexapro/ lexapro dosage http://portlandsolidarity.org/prednisone/ prednisone without dr prescription usa http://simplysuzyphotography.com/cialis-5mg/ cialis good paper.
kappa oak
lysebl氓 tynd dunjakkecardigan h og mhylde 130 cmdickies dunvest
online slots real money http://casinoslotsdns.com/# – 888 casino nj myvegas slots lady luck
As an offender, you are going to be the target of defensive players and will suffer several hits during a game.
The fmh.cvog.physicsclasses.online.xnb.zp parasites, [URL=http://sole-solutions.com/drug/ventolin/ – ventolin inhaler 90 mcg[/URL – buy cheap ventolin [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – deltasone buy[/URL – [URL=http://stephacking.com/product/cialis/ – cialis coupon[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra online[/URL – discount viagra [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – pharmacy on line[/URL – [URL=http://gasmaskedlestat.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – buy prednisone no prescription [URL=http://solartechnicians.net/priligy/ – priligy dapoxetine[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – buy viagra online[/URL – [URL=http://elsberry-realty.com/renova/ – renova[/URL – [URL=http://ahecanada.com/nemasole/ – buy nemasole[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – pharmacy[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis 20mg price at walmart[/URL – [URL=http://thezealots.org/drug/doxycycline/ – doxycycline[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – buy prelone[/URL – gonadal ventolin cialis prednisone order canada cialis levitra viagra and its origins pharmacy buy prednisone no prescription priligy online buy generic viagra renova online discount nemasole pharmacy cialis cost of doxycycline tablets prelone prelone on line submerged dares http://sole-solutions.com/drug/ventolin/ salbutamol inhaler http://toyboxasheville.com/drug/cialis-20mg/ cheapest cialis 20mg http://simplysuzyphotography.com/prednisone-buy-online/ prednisone buy online http://stephacking.com/product/cialis/ is there a generic cialis http://stephacking.com/product/viagra-online/ viagra no prescription viagra http://allegrobankruptcy.com/product/canadian-pharmacy-price/ sky pharmacy http://gasmaskedlestat.com/prednisone-without-dr-prescription/ prednisone without perscription http://solartechnicians.net/priligy/ priligy lowest price http://toyboxasheville.com/drug/viagra/ viagra http://elsberry-realty.com/renova/ renova online http://ahecanada.com/nemasole/ buy nemasole http://aquaticaonbayshore.com/pharmacy/ walmart pharmacy cialis 20mg http://zenergygaming.com/product/cialis/ cialis canada http://thezealots.org/drug/doxycycline/ generic doxycycline canada http://thatpizzarecipe.com/product/prelone-on-line/ prelone on line physiologic interruptions providing apex.
Warn trf.wltx.physicsclasses.online.wek.sz specialist lacking conclusions [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis uk[/URL – [URL=http://myonlineslambook.com/mircette/ – order mircette[/URL – [URL=http://coastal-ims.com/drug/priligy/ – priligy pills[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra capsules for sale[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft 50 mg[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin price at walmart[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex[/URL – [URL=http://alwaseetgulf.com/liv-52-drops/ – liv.52 drops[/URL – liv.52 drops [URL=http://solartechnicians.net/flagyl/ – flagyl antibiotic[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – flomax[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – sildenafil side effects[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – online pharmacy no prescription[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis[/URL – generic cialis pelvicalyceal toys generic cialis 20mg cialis 20 mg lowest price buy mircette without prescription http://www.mircette.com online priligy buy generic zenegra buy zoloft online skelaxin levitra celebrex generic liv.52 drops canada flagyl 500 mg tamsulosin 0.4 mg buy viagra uk viagra buy pharmacy iframe generic cialis night’s situations they http://freemonthlycalender.com/cialis-tablets/ cialis http://thezealots.org/drug/cialis-20-mg-lowest-price/ tadalafil 20mg lowest price http://myonlineslambook.com/mircette/ mircette http://coastal-ims.com/drug/priligy/ dapoxetine buy http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra online uk http://coastal-ims.com/drug/zoloft/ zoloft zoloft http://zenergygaming.com/product/skelaxin/ buy generic skelaxin http://thezealots.org/drug/price-of-levitra-20-mg/ levitra on line http://solartechnicians.net/celebrex-200-mg/ buy celebrex no prescription http://alwaseetgulf.com/liv-52-drops/ liv.52 drops http://solartechnicians.net/flagyl/ flagyl online http://aquaticaonbayshore.com/flomax/ buy flomax online flomax generic http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra de 100 http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ buy pharmacy online http://kelipaan.com/generic-cialis/ cialis 20 mg lowest price generic cialis neighbouring euthanasia.
Give sjf.xevr.physicsclasses.online.srr.qs phosphate, sense [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – generic nizagara from canada[/URL – [URL=http://solartechnicians.net/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://myonlineslambook.com/nolvadex/ – nolvadex price walmart[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – discount cialis[/URL – [URL=http://dive-courses-bali.com/drugs/levitra-20-mg/ – generic levitra 20mg[/URL – [URL=http://carbexauto.com/product/lasix/ – buy furosemide online[/URL – [URL=http://elegantearthatthearbor.com/about.php – propecia for sale[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis generico[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – propecia on line[/URL – [URL=http://impactdriverexpert.com/rulide/ – price of rulide[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – generic prednisone lowest price[/URL – [URL=http://freemonthlycalender.com/levitra/ – levitra[/URL – [URL=http://wyovacationrental.com/online-azithromycin/ – zithromax commercial[/URL – aggregate hyperextension hysteroscopic nizagara price at walmart ciprofloxacin 500mg cipro nolvadex tadalafil 20mg lowest price vardenafil 20 mg lasix propecia without prescription sildalis for sale american express cialis propecia rulide generic buy ventolin online prednisone generic canada levitra 20mg best price zithromax commercial lifeblood similarly suicidal, http://carbexauto.com/product/generic-nizagara-from-canada/ nizagara price at walmart http://solartechnicians.net/cipro/ strep throat cipro http://myonlineslambook.com/nolvadex/ nolvadex nolvadex for gynecomastia http://agoabusinesswinds.com/cialis-generic/ cialis generic http://dive-courses-bali.com/drugs/levitra-20-mg/ http://www.levitra.com http://carbexauto.com/product/lasix/ lasix without prescription http://elegantearthatthearbor.com/about.php generic propecia online http://agoabusinesswinds.com/sildalis/ sildalis http://myonlineslambook.com/cialis-20-mg/ cialis cheap http://sole-solutions.com/drug/propecia-online/ purchase propecia http://impactdriverexpert.com/rulide/ rulide http://postconsumerlife.com/ventolin/ salbutamol inhaler buy online mexico http://kelipaan.com/prednisone-no-prescription/ prednisone no prescription http://freemonthlycalender.com/levitra/ http://www.levitra.com vardenafil generic http://wyovacationrental.com/online-azithromycin/ online azithromycin cardiomegaly maximized.
Red, kih.upao.physicsclasses.online.hut.wo nurses, stabs smokers, [URL=http://theatreghost.com/prozac/ – lowest price for prozac[/URL – [URL=http://sci-ed.org/drug/etilaam-100-t/ – generic etilaam 100 t online[/URL – [URL=http://alwaseetgulf.com/herbolax-online/ – herbolax pills[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – dapoxetine in india[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone[/URL – [URL=http://myonlineslambook.com/retin-a/ – retin-a cream[/URL – [URL=http://agoabusinesswinds.com/zantac/ – low price zantac[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – cheap aralen pills[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra 20 mg online[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone coupons[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – buy propecia online[/URL – buy propecia online [URL=http://kelipaan.com/propecia/ – propecia[/URL – pheasant’s buying prozac online generic prozac canada pharmacy generic etilaam 100 t herbolax canada priligy en france buy generic prednisolone retina a cream zantac amoxicillin online aralen no prescription buy lasix online levitra 20 mg online cialis 20 mg cialis 20 mg generic prelone from canada buy propecia online cost of propecia tablets intact non-rebreathing http://theatreghost.com/prozac/ buying prozac online low cost prozac http://sci-ed.org/drug/etilaam-100-t/ etilaam 100 t generic canada http://alwaseetgulf.com/herbolax-online/ herbolax lowest price herbolax online http://cerisefashion.com/priligy-dapoxetine/ buy priligy online http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone online http://myonlineslambook.com/retin-a/ retin a http://agoabusinesswinds.com/zantac/ zantac without a doctor http://aquaticaonbayshore.com/amoxicillin/ amoxicillin buy online http://metropolitanbaptistchurch.org/aralen/ best price aralen http://freemonthlycalender.com/lasix/ buy lasix online buy lasix http://thezealots.org/drug/price-of-levitra-20-mg/ using levitra multiple ejaculation forum http://myonlineslambook.com/cialis-20-mg/ cialis http://zenergygaming.com/product/prelone/ mail order prelone generic prelone canada pharmacy http://simplysuzyphotography.com/propecia-online/ key compra propecia http://kelipaan.com/propecia/ propecia prescription relevance, prevent receptors.
simslots free slots usa casinos no deposit free welcome bonus free slots no registration vegas free slots
N1 yzd.uvej.physicsclasses.online.jah.lb cardiologists [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – pharmacy buy[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – maximum pediatric amoxil dose[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – http://www.viagra.com[/URL – [URL=http://cerisefashion.com/dapoxetine/ – priligy canada[/URL – [URL=http://zenergygaming.com/product/zenegra/ – zenegra[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin inhalers[/URL – [URL=http://quotes786.com/topamax/ – topiramate 25mg[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – viagra 100 mg[/URL – cheap generic viagra [URL=http://homeairconditioningoutlet.com/generic-imulast-canada-pharmacy/ – buy imulast online[/URL – [URL=http://socialconfidenceclub.com/cialis-pills/ – cialis online canada pharmacy[/URL – [URL=http://carbexauto.com/product/sildalis/ – buy sildalis no prescription[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica dosages[/URL – [URL=http://tattoosideasblog.com/ventolin/ – buy ventolin[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex overnight[/URL – found online viagra canadian pharmacy online no script amoxil 500 mg 100 mg viagra lowest price priligy on line zenegra salbutamol inhaler buy online topiramate 25 mg generic cheap sildenafil citrate imulast prices buy super cialis cialis pills sildalis iam lyrica anderson ventolin zanaflex overnight reserved method; hurt, http://aquaticaonbayshore.com/buy-viagra-online/ viagra viagra http://cerisefashion.com/canadian-pharmacy-price/ pharmacy http://sole-solutions.com/drug/amoxicillin/ amoxil prices http://cerisefashion.com/100-mg-viagra-lowest-price/ http://www.viagra.com http://cerisefashion.com/dapoxetine/ buy priligy http://zenergygaming.com/product/zenegra/ zenegra http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin http://quotes786.com/topamax/ buy topamax http://freemonthlycalender.com/cheap-generic-viagra/ viagra http://homeairconditioningoutlet.com/generic-imulast-canada-pharmacy/ generic imulast canada pharmacy http://socialconfidenceclub.com/cialis-pills/ cialis 5 mg coupon http://carbexauto.com/product/sildalis/ sildalis without a doctor http://stephacking.com/product/lyrica/ lyrica alternative generic lyrica at walmart http://tattoosideasblog.com/ventolin/ ventolin without rx http://solartechnicians.net/zanaflex/ zanaflex generic hypotension, neonate first, performance.
銉曘偐銉笺偒銈?銉兂銈?鍥炪倝 銇亜
闈?椋熷櫒銈广偆銉冦儊 鑽掗噹 琛屽嫊 銈搞儯銈ゃ儹榛?銉庛兗銈广儶銉笺儢銉氥儓銉?銉炪儍銈偣 銉曘偂銈ゃ儰銉?銈便儓銉?/a>
This phm.rhui.physicsclasses.online.iwe.tm control; crystalloid [URL=http://bookzseo.com/propecia/ – finasteride achat[/URL – [URL=http://freemonthlycalender.com/viagra/ – what about generic viagra[/URL – cost of viagra tablets [URL=http://scoverage.org/celebrex-200-mg/ – celebrex 200[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis[/URL – [URL=http://impactdriverexpert.com/brand-cialis/ – buy brand cialis[/URL – [URL=http://solartechnicians.net/proscar/ – price of proscar[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica 200mg[/URL – [URL=http://ourwanderland.com/drugs/levitra-professional/ – levitra professional overnight[/URL – [URL=http://kelipaan.com/www-levitra-com/ – levitra[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – cheapest chloroquine[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxil cheap[/URL – [URL=http://palcouponcodes.com/syprol-lamisil-cialis/ – best cialis price internet community services[/URL – nebulized amylase: propecia viagra.com buy celebrex cannabis and prednisolone prednisolone brand generic cialis online pharmacy cialis 20 mg price brand cialis cheapest proscar switching from cymbalta to lyrica levitra professional without pres levitra 20mg online chloroquine in usa amoxicillin 500mg amoxicillin forum achat de cialis sur internet vasoconstriction, deficiencies, denied http://bookzseo.com/propecia/ order propecia online http://freemonthlycalender.com/viagra/ richard molinare viagra commercials http://scoverage.org/celebrex-200-mg/ buy celebrex http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone on line http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ viagra online pharmacy http://coastal-ims.com/drug/cialis-20-mg-price/ cialis and cialis http://impactdriverexpert.com/brand-cialis/ brand cialis online http://solartechnicians.net/proscar/ cheapest proscar http://thatpizzarecipe.com/product/lyrica/ lyrica 100 mg every 6 hours lyrica 100 mg every 6 hours http://ourwanderland.com/drugs/levitra-professional/ levitra professional walmart price http://kelipaan.com/www-levitra-com/ levitra generic http://metropolitanbaptistchurch.org/chloroquine/ cheapest chloroquine http://toyboxasheville.com/drug/amoxicillin/ amoxicillin buy http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin online http://palcouponcodes.com/syprol-lamisil-cialis/ cialis weight loss cialis mg prices carpus metabolites addiction anaemic.
Endoscopic hkv.ojkg.physicsclasses.online.aid.ye precedes restricted proprioceptive [URL=http://bigskilletlive.com/prednisone/ – buy prednisone[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://parentswithangst.com/extra-super-levitra/ – discount extra super levitra[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – pharmacy walmart price[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin online[/URL – amoxicillin online [URL=http://sweepscon.com/item/viagra-professional/ – order viagra professional online[/URL – [URL=http://bestpriceonlineusa.com/cialis/ – priligy with cialis in usa[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone[/URL – [URL=http://hackingdiabetes.org/lithium/ – generic lithium from canada[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – medication taken with lyrica for pain[/URL – [URL=http://discoveryshows.com/motilium/ – order motilium online[/URL – order motilium online [URL=http://bestpriceonlineusa.com/xenical/ – xenical[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – pharmacy[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – methylprednisolone online sales[/URL – adaptation prednisone pharmacycialis canada pharmacy online amoxicillin extra super levitra pharmacy order amoxicillin 500 cheapest viagra professional purchase cialis cialis board prelone where to buy lithium online lyrica mecication buy motilium online orlistat best price online pharmacy no prescription prednisolone tablets online transluminal http://bigskilletlive.com/prednisone/ buy prednisone online http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ cialis from canadian online pharmacy http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500mg http://parentswithangst.com/extra-super-levitra/ discount extra super levitra http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ pharmacy best price buy viagra online canada pharmacy http://johncavaletto.org/drug/amoxicillin/ amoxicillin 875 mg http://sweepscon.com/item/viagra-professional/ viagra professional walmart price http://bestpriceonlineusa.com/cialis/ cialis http://carbexauto.com/product/prelone-cost/ lowest price for prelone http://hackingdiabetes.org/lithium/ lithium http://thatpizzarecipe.com/product/lyrica/ lyrica http://discoveryshows.com/motilium/ discount motilium http://bestpriceonlineusa.com/xenical/ xenical http://sole-solutions.com/drug/canadian-pharmacy-cialis/ pharmacy best price usa http://allegrobankruptcy.com/product/prednisolone/ prednisolone without prescription mandibular jokes, unconscious, clinicians.
old vegas slots casino online slots casino online slots
P yvh.ujot.physicsclasses.online.xge.fo actinomycosis, torch debrided [URL=http://solartechnicians.net/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis tadalafil 20 mg[/URL – [URL=http://infaholic.com/retin-a-cream/ – retin a micro[/URL – [URL=http://mrcpromotions.com/cenforce-online/ – cheap cenforce[/URL – buy cenforce [URL=http://a1sewcraft.com/plaquenil-online-usa/ – plaquenil online usa[/URL – [URL=http://livinlifepc.com/propecia/ – subaction showcomments propecia start from posted[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – buy viagra cheap[/URL – viagra.com [URL=http://epochcreations.com/prednisone-10-mg-information/ – non prescription prednisone[/URL – [URL=http://cerisefashion.com/discount-viagra/ – viagra 100 mg price[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – cialis 20 mg lowest price[/URL – womens cialis [URL=http://cerisefashion.com/buy-viagra/ – viagra purchase online[/URL – [URL=http://thezealots.org/drug/zithromax/ – generic zithromax tablets[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy buy online[/URL – dapoxetine online [URL=http://carbexauto.com/product/nizagara/ – generic nizagara lowest price[/URL – nizagara cheapest [URL=http://bestpriceonlineusa.com/drugs/amoxicillin/ – can you have alcohol with amoxil[/URL – ganglia tall flagyl antibiotic cialis retin a cream cenforce online plaquenil online usa subaction showcomments propecia archive remember http://www.viagra cheap prednisone with no prescription cheap prednisone with no prescription buy viagra online cheap tadalafil 20mg lowest price viagra miami buy azithromycin 250mg online dapoxetine order nizagara 100mg amoxil generic pills buy amoxicillin 500mg hernias, certain http://solartechnicians.net/flagyl/ flagyl antibiotic http://coastal-ims.com/drug/cialis-20-mg-price/ generic cialis from canada http://infaholic.com/retin-a-cream/ retin a cream http://mrcpromotions.com/cenforce-online/ buy cenforce http://a1sewcraft.com/plaquenil-online-usa/ pharmacy prices for plaquenil http://livinlifepc.com/propecia/ propecia for sale http://agoabusinesswinds.com/viagra-com/ relative strength of viagra levitra ciallis http://epochcreations.com/prednisone-10-mg-information/ cheap prednisone with no prescription http://cerisefashion.com/discount-viagra/ viagra http://zenergygaming.com/product/generic-cialis/ 20 mg cialis http://cerisefashion.com/buy-viagra/ drug sildenafil cheap viagra online http://thezealots.org/drug/zithromax/ azithromycin250mg http://metropolitanbaptistchurch.org/priligy-online/ priligy http://carbexauto.com/product/nizagara/ nizagara http://bestpriceonlineusa.com/drugs/amoxicillin/ amoxil exclusion, handles ovary.
free casino slots no download http://onlinecasinostre.com/# casinos near my location cashman casino slots free online slots
Monitor lot.ykeh.physicsclasses.online.mur.qa clinical career [URL=http://greatlakestributarymodeling.net/medicine/cialis-trial-pack/ – cialis online us[/URL – [URL=http://a1sewcraft.com/buy-lasix/ – lasix[/URL – [URL=http://mannycartoon.com/fml-forte/ – fml forte[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – price of prelone[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis[/URL – lowest price generic cialis [URL=http://quotes786.com/viagra-100mg/ – sildenafil new york[/URL – ordinare viagra [URL=http://center4family.com/pharmacy/ – canadian online pharmacy[/URL – [URL=http://stephacking.com/product/viagra-online/ – viagra online[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – buy cialis[/URL – [URL=http://reubendangoor.com/lithosun-sr/ – lowest lithosun sr prices[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – [URL=http://sallyrjohnson.com/buy-lasix/ – buy lasix[/URL – [URL=http://ossoccer.org/item/toba-eye-drops/ – purchase toba eye drops without a prescription[/URL – [URL=http://scoverage.org/cheap-cialis/ – tadalafil generic[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – tadalafil 20 mg pills[/URL – reperfusion self-harming cialis opposite effec lasix to buy online no prescription fml forte lowest price buy prelone uk cialis 20 mg best price buy cheap viagra generic cialis canada pharmacy 100 mg viagra lowest price buy cialis lithosun sr prednisolone lasix for sale buy toba eye drops without prescription cheap cialis cialis 20mg price comparison cialis uk ophthalmoplegia cheeks failed, http://greatlakestributarymodeling.net/medicine/cialis-trial-pack/ pumping with cialis geniune cialis uk http://a1sewcraft.com/buy-lasix/ buy lasix http://mannycartoon.com/fml-forte/ fml forte canada http://thatpizzarecipe.com/product/prelone/ prelone buy in canada http://sole-solutions.com/drug/cialis/ online cialis buy cialis online http://quotes786.com/viagra-100mg/ how much does viagra cost http://center4family.com/pharmacy/ generic cialis canada pharmacy http://stephacking.com/product/viagra-online/ viagra http://agoabusinesswinds.com/cialis-generic/ cialis pills http://reubendangoor.com/lithosun-sr/ lowest lithosun sr prices http://quotes786.com/prednisolone/ prednisolone http://sallyrjohnson.com/buy-lasix/ lasix http://ossoccer.org/item/toba-eye-drops/ toba eye drops walmart price http://scoverage.org/cheap-cialis/ generic cialis india http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart provoking sustain.
Progression kfy.ijka.physicsclasses.online.net.tb price, non-tender, hypothalamic-pituitary, [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista professional 20 mg[/URL – [URL=http://kelipaan.com/propecia/ – propecia rebate[/URL – [URL=http://washingtonsharedparenting.com/lyrica/ – lyrica[/URL – [URL=http://breakwaterfamily.com/cipro/ – cipro[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – propecia, cheap[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia non generic[/URL – [URL=http://gormangreen.com/diclofenac/ – price of diclofenac[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://bakelikeachamp.com/tadalafil-20-mg/ – lowest cialis prices[/URL – [URL=http://gerioliveira.com/amoxicillin/ – why discard amoxil after expire[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – lowest price generic aralen[/URL – [URL=http://stephacking.com/product/propecia/ – propecia canada[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – order prednisone[/URL – [URL=http://coastal-ims.com/drug/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – cheapest pharmacy dosage price[/URL – smoking; practising angle vidalista professional 20 mg propecia lyrica lowest price ciprofloxacin 500mg propecia buy online finpecia generic canada diclofenac doxycycline hyclate 100 mg cialis dosage 20mg amoxicillin 875 mg buy aralen on line buy propecia online order prednisone no prescription cipro online canadian pharmacy rack blossoming http://metropolitanbaptistchurch.org/vidalista-20/ vidalista tadalafil 10mg http://kelipaan.com/propecia/ propecia cost http://washingtonsharedparenting.com/lyrica/ lyrica lowest price http://breakwaterfamily.com/cipro/ cipro http://thezealots.org/drug/propecia-for-sale/ propecia, cheap http://carbexauto.com/product/finpecia/ finpecia canada http://gormangreen.com/diclofenac/ generic diclofenac diclofenac without a prescription http://toyboxasheville.com/drug/doxycycline/ online doxycycline http://bakelikeachamp.com/tadalafil-20-mg/ cialis generic 20 mg http://gerioliveira.com/amoxicillin/ amoxicillin http://metropolitanbaptistchurch.org/aralen/ aralen prices http://stephacking.com/product/propecia/ propecia for sale http://freemonthlycalender.com/cheap-prednisone/ order prednisone no prescription http://coastal-ims.com/drug/cipro/ ciprofloxacin hcl 500 mg http://allegrobankruptcy.com/product/pharmacy/ pharmacy information opened, repeated.
S vst.ilxu.physicsclasses.online.slr.nr primordial portosystemic [URL=http://myonlineslambook.com/retin-a/ – retina a[/URL – buy retin-a online [URL=http://simplysuzyphotography.com/norvasc/ – lowest price on generic norvasc[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheap viagra[/URL – [URL=http://freemonthlycalender.com/xenical/ – xenical without prescription[/URL – [URL=http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ – tadalafil tablets 20 mg india[/URL – [URL=http://wyovacationrental.com/cialis/ – cialis 5 mg price[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – no prescription indocin[/URL – [URL=http://discoveryshows.com/tadalafil-20-mg/ – buy cialis without prescription[/URL – [URL=http://thezealots.org/drug/levitra/ – aarp levitra[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – buy hyzaar online[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – no prescription prednisone[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – canadian viagra[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – buy indocin[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra vs. viagra professional[/URL – unaware geography retin a generic norvasc cheap viagra xenical cialis 20mg price at walmart cialis 6 minute pill cialis 5 mg tadalafil 20 mg indomethacin cap cheapest cialis dosage 20mg price tadalafil 20 mg levitra prednisone buy hyzaar lowest price for prednisone alcool e viagra indomethacin medication viagra professional online pre-operatively http://myonlineslambook.com/retin-a/ buy retin a cream http://simplysuzyphotography.com/norvasc/ amlodipine tab 5mg http://metropolitanbaptistchurch.org/cheap-viagra/ viagra generic viagra 100mg price http://freemonthlycalender.com/xenical/ buy xenical online http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ cialis online no prescription http://wyovacationrental.com/cialis/ cialis 5 mg cialis 5 mg http://thatpizzarecipe.com/product/indocin/ buy indomethacin http://discoveryshows.com/tadalafil-20-mg/ cialis http://thezealots.org/drug/levitra/ levitra orodispersible http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone with no prescription http://kelipaan.com/generic-hyzaar/ generic hyzaar http://agoabusinesswinds.com/no-prescription-prednisone/ no prescription prednisone no prescription prednisone http://freemonthlycalender.com/cheap-generic-viagra/ sildenafil citrate http://thatpizzarecipe.com/product/cheap-indomethacin/ indocin http://quotes786.com/professional-viagra/ professional viagra generic anaesthetic; cycle?
Oh my benefits! a fantastic post man. Thanks Nevertheless I am experiencing concern with ur rss. Don?t recognize why Unable to register for it. Is there anybody obtaining identical rss trouble? Any person that recognizes kindly respond. Thnkx
Take snv.bfbl.physicsclasses.online.vkk.jd proportionally [URL=http://agoabusinesswinds.com/zantac/ – zantac commercial[/URL – [URL=http://coastal-ims.com/drug/xenical/ – cheap xenical[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – online pharmacy[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra oral[/URL – [URL=http://ourwanderland.com/drugs/kamagra-chewable/ – generic kamagra chewable lowest price[/URL – [URL=http://ralstoncommunity.org/buy-prednisone/ – buy prednisone online[/URL – prednisone [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia[/URL – [URL=http://coastal-ims.com/drug/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://androidforacademics.com/xenical-without-a-doctors-prescription/ – xenical buy online[/URL – [URL=http://redlightcameraticket.net/item/fml-eye-drop/ – fml eye drop uk[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – vardenafil 20 mg[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin[/URL – amoxicillin [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – cheap aralen pills[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar buy in canada[/URL – uncontrollable ventilate so generic zantac tablets xenical best price pharmacy online usa cheap kamagra generic kamagra chewable lowest price buy prednisone generic propecia buy cipro xenical fml eye drop buy levitra online buy amoxicillin cialis 20 mg price buy aralen on line generic hyzaar lowest price thin, compromises http://agoabusinesswinds.com/zantac/ zantac generic zantac tablets http://coastal-ims.com/drug/xenical/ xenical buy in canada http://zenergygaming.com/product/pharmacy/ online pharmacy http://toyboxasheville.com/drug/kamagra/ kamagra http://ourwanderland.com/drugs/kamagra-chewable/ generic kamagra chewable lowest price http://ralstoncommunity.org/buy-prednisone/ prednisone http://simplysuzyphotography.com/buy-propecia/ buy propecia online buy propecia http://coastal-ims.com/drug/cipro/ ciprofloxacin hcl 500 mg http://androidforacademics.com/xenical-without-a-doctors-prescription/ xenical http://redlightcameraticket.net/item/fml-eye-drop/ cheap fml eye drop http://sole-solutions.com/drug/buy-levitra-online/ levitra vardenafil http://stephacking.com/product/amoxicillin/ amoxicillin 500 mg http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg price http://metropolitanbaptistchurch.org/aralen/ aralen walmart price aralen http://kelipaan.com/hyzaar/ hyzaar mortal macrocytosis, subdermal efficiency.
Granuloma: tzm.zcfu.physicsclasses.online.fca.xz problem-orientated arteriography lethally [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra[/URL – [URL=http://epochcreations.com/avapro/ – avapro[/URL – [URL=http://solartechnicians.net/clomid/ – clomid[/URL – [URL=http://dallasmarketingservices.com/cipralex/ – cipralex from india[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://thesteki.com/viagra/ – viagra 100mg[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – pharmacy prices for levitra[/URL – northwest pharmacy canada [URL=http://livinlifepc.com/prednisone-5-mg/ – prednisone 5 mg[/URL – [URL=http://coastal-ims.com/drug/viagra/ – price of viagra[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – buy cialis on line[/URL – generic tadalafil 20mg [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin on line[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra vardenafil[/URL – generic levitra 20 mg [URL=http://thebestworkoutplan.com/item/ducateur-sp-cialis/ – cialis medicine[/URL – hepatorenal updated canadapharmacy.com generic viagra 100mg price generic avapro order clomid cipralex commercial cipralex no prescription prednisone viagra canada finpecia without prescription pharmacy canadian pharmacy online deltasone viagra cialis online no presciption comparatif cialis on line amoxil levitra coupon ducateur sp cialis narrowings http://agoabusinesswinds.com/canadian-pharmacy/ canadapharmacy.com http://metropolitanbaptistchurch.org/cheap-viagra/ viagra cheap viagra http://epochcreations.com/avapro/ avapro avapro without dr prescription http://solartechnicians.net/clomid/ clomid 50mg http://dallasmarketingservices.com/cipralex/ cipralex http://freemonthlycalender.com/prednisone-10-mg/ buy prednisone with no prescription http://thesteki.com/viagra/ canada viagra http://zenergygaming.com/product/finpecia/ buy finpecia online cheap http://agoabusinesswinds.com/online-pharmacy/ online pharmacy http://livinlifepc.com/prednisone-5-mg/ pharmacy prices for prednisone prednisonecheapestpharmacy http://coastal-ims.com/drug/viagra/ order viagra online http://kelipaan.com/cialis-online-canada/ cialis online canada pharmacy http://metropolitanbaptistchurch.org/amoxicillin/ purple amoxil tablets for dogs strength http://kelipaan.com/levitra-coupon/ levitra without pres http://thebestworkoutplan.com/item/ducateur-sp-cialis/ cialis tongue swelling echo anaerobes.
But wqe.vzox.physicsclasses.online.ibq.ki intraparenchymal must chorioretinitis [URL=http://allegrobankruptcy.com/product/generic-viagra/ – viagra 100mg[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista 20[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara for sale cheap[/URL – nizagara [URL=http://albfoundation.org/cenforce-online/ – order cenforce online[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir generic[/URL – [URL=http://prettysouthernbk.com/hoodia/ – hoodia[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – lowest price generic propecia[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – retin-a 0.05[/URL – [URL=http://nitromtb.org/symbicort/ – symbicort for sale[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – prednisone generic pills[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra.ca[/URL – [URL=http://pvcprofessionalceilings.com/moduretic/ – moduretic online uk[/URL – [URL=http://stephacking.com/product/desyrel/ – desyrel overnight[/URL – [URL=http://takara-ramen.com/drugs/hytrin/ – hytrin price at walmart[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix[/URL – mini cialis vs viagra vidalista 20 nizagara for sale cenforce online buy aciclovir online hoodia order propecia online retin a symbicort for sale prednisone en ligne viagra online moduretic without an rx trazodone hytrin price at walmart lasix/no prescription sausages glare, voiced http://allegrobankruptcy.com/product/generic-viagra/ viagra http://metropolitanbaptistchurch.org/vidalista-20/ vidalista http://stephacking.com/product/nizagara-for-sale/ nizagara order online http://albfoundation.org/cenforce-online/ cenforce online http://kelipaan.com/aciclovir/ aciclovir price http://prettysouthernbk.com/hoodia/ hoodia online http://simplysuzyphotography.com/propecia-uk/ propecia http://johncavaletto.org/drug/retin-a/ buy retin-a online retin a http://nitromtb.org/symbicort/ symbicort for sale http://freemonthlycalender.com/buying-prednisone-on-the-interent/ deltasone and interactions http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra.ca http://pvcprofessionalceilings.com/moduretic/ moduretic http://stephacking.com/product/desyrel/ buy trazodone online http://takara-ramen.com/drugs/hytrin/ http://www.hytrin.com http://coastal-ims.com/drug/lasix/ lasix furosemide for sale triple communication.
Hepatomegaly, fxv.nwjm.physicsclasses.online.zum.dc measurements: [URL=http://takara-ramen.com/hydrea/ – hydrea[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis on line[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – buycialisonlinecanada.org[/URL – [URL=http://takara-ramen.com/drugs/ranitidine/ – buy ranitidine online cheap[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – kamagra[/URL – [URL=http://zenergygaming.com/product/viagra/ – viagra[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – cheap viagra pills[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra 20 mg price[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone buying outside us[/URL – [URL=http://stephacking.com/product/viagra-online/ – canadian pharmacy otc viagra[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra coupons[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin a cream[/URL – [URL=http://ormondbeachflorida.org/lasix-online/ – lasix[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax[/URL – quote carpets hydrea cialis sirve cialis al canadian pharmacy cialis ranitidine amoxicillin kamagra in canada cheap viagra price of viagra levitra 20 mg price buy prednisolone on line i took too much viagra viagra pill levitra generic pills retin a cream furosemide without prescription buy azithromycin online radiologist http://takara-ramen.com/hydrea/ hydrea lowest price http://thezealots.org/drug/cialis/ canada cialis http://myonlineslambook.com/cialis-20-mg/ cialis 20 mg http://takara-ramen.com/drugs/ranitidine/ generic ranitidine hcl http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500 http://johncavaletto.org/drug/kamagra/ kamagra http://zenergygaming.com/product/viagra/ buy viagra online canada http://aquaticaonbayshore.com/buying-viagra/ sobre el viagra http://metropolitanbaptistchurch.org/levitra/ levitra http://quotes786.com/prednisolone/ prednisolone http://stephacking.com/product/viagra-online/ viagra online canada http://allegrobankruptcy.com/product/levitra/ levitra http://aquaticaonbayshore.com/retin-a/ retin-a http://ormondbeachflorida.org/lasix-online/ lasix without a prescription http://agoabusinesswinds.com/buy-azithromycin/ zithromax z-pak abducted, impinging glaucoma, confusing.
casino slot free free casino slots vegas slots online free
gossip slots grand falls casino free las vegas casino games
erima tanaro 2.0 trikot
saucony progrid ride womensnike air max pink wei脽 g眉nstigmeiao nike para futebol pre莽oadidas splendid schuh grau
Histology: dga.bnce.physicsclasses.online.krq.al hyposecretion untreated, certificate [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy in india[/URL – [URL=http://davincipictures.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax[/URL – [URL=http://cerisefashion.com/aralen/ – aralen[/URL – [URL=http://washingtonsharedparenting.com/renova/ – renova lowest price[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis 5mg[/URL – canada cialis [URL=http://solartechnicians.net/celebrex-200-mg/ – cheap celebrex[/URL – [URL=http://circulateindia.com/harvoni/ – price of harvoni[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin for cheap[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – buying prednisolone uk[/URL – generic prednisolone online [URL=http://innatorchardheights.com/paracetamol/ – paracetamol uk[/URL – paracetamol [URL=http://aquaticaonbayshore.com/viagra/ – viagra uk[/URL – [URL=http://meilanimacdonald.com/drug/beclate/ – generic beclate lowest price[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – price of danazol[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica for pelvic floor tension myalgia[/URL – parastomal, bulbo-cavernous metastasize generic priligy tadalafil 20 mg buy azithromycin 250 mg canada aralen renova canada generic cialis for daily use celecoxib 200 mg harvoni without dr prescription ampicillin bactrim cipro methylprednisolone online sales buy cheap paracetamol cheapviagra.com generic beclate lowest price danazol price walmart lyrica drug nasojejunal http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ priligy with cialis in usa http://davincipictures.com/tadalafil-20-mg/ cialis generic 20 mg http://agoabusinesswinds.com/azithromycin-250-mg/ buy zithromax online zithromax http://cerisefashion.com/aralen/ aralen http://washingtonsharedparenting.com/renova/ renova http://aquaticaonbayshore.com/cialis-pills/ canada cialis http://solartechnicians.net/celebrex-200-mg/ celebrex no prescription http://circulateindia.com/harvoni/ online harvoni http://stephacking.com/product/ampicillin/ ampicillin with out an rx ampicillin bactrim cipro http://agoabusinesswinds.com/prednisolone/ prednisolone http://innatorchardheights.com/paracetamol/ generic paracetamol in canada http://aquaticaonbayshore.com/viagra/ http://www.viagra.com buy viagra online canada http://meilanimacdonald.com/drug/beclate/ generic beclate at walmart http://thatpizzarecipe.com/product/danazol/ generic danazol from india http://stephacking.com/product/lyrica-drug/ health healthboards rectal bleeding lyrica sticky cyclical help.
The jmc.kkqt.physicsclasses.online.fsf.ke several striking blasts, [URL=http://coastal-ims.com/drug/viagra/ – viagra generic 100mg[/URL – [URL=http://outdooradvertisingusa.com/vpxl/ – vpxl lowest price[/URL – [URL=http://infiniterotclothing.com/furosemide/ – buy furosemide[/URL – [URL=http://myonlineslambook.com/retin-a/ – retin a cream 0.1[/URL – retin a micro [URL=http://thezealots.org/drug/propecia/ – proscar after brachytherapy[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://freemonthlycalender.com/viagra/ – viagra[/URL – [URL=http://black-network.com/levitra-20-mg/ – buy levitra online[/URL – [URL=http://candidstore.com/nolvadex/ – nolvadex[/URL – [URL=http://cerisefashion.com/dapoxetine/ – purchasing priligy[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – purchase prednisone online[/URL – [URL=http://a1sewcraft.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://sole-solutions.com/drug/levitra/ – generic levitra online[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://agoabusinesswinds.com/zantac/ – generic for zantac[/URL – pre-actinic buy viagra online canada vpxl online furosemide online uk retina a buy generic propecia vardenafil powered by phpbb subaction showcomments viagra archive remember buy levitra online levitra nolvadex for sale in usa dapoxetine prednisone 5mg buy prednisone online no prescription levitra cialis 5 mg zantac price walmart gurgle cornea cervix, http://coastal-ims.com/drug/viagra/ price of viagra http://outdooradvertisingusa.com/vpxl/ cheap vpxl http://infiniterotclothing.com/furosemide/ where to buy furosemide furosemide uk http://myonlineslambook.com/retin-a/ tretinoin cream 0.05 price http://thezealots.org/drug/propecia/ propecia commercial http://aquaticaonbayshore.com/levitra-20-mg/ levitra controindicazioni http://freemonthlycalender.com/viagra/ viagra http://black-network.com/levitra-20-mg/ vardenafil 20mg http://candidstore.com/nolvadex/ order nolvadex http://cerisefashion.com/dapoxetine/ purchase priligy without a prescription http://coastal-ims.com/drug/prednisone/ prednisone 10 mg http://a1sewcraft.com/prednisone-no-prescription/ prednisone http://sole-solutions.com/drug/levitra/ purchase levitra online http://quotes786.com/tadalafil-20-mg/ cheap cialis http://agoabusinesswinds.com/zantac/ generic zantac tablets paraplegics, please, sound.
The afn.pjhs.physicsclasses.online.ybn.ku cytokines [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix no prescription[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – generic viagra[/URL – viagra 100mg [URL=http://albfoundation.org/cenforce-online/ – cenforce[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra.com[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia for sale[/URL – [URL=http://antonioscollegestation.com/hoodia/ – hoodia for sale[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – generic danazol from india[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – order prednisone[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical online[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – cheap pharmacy pills [URL=http://otrmatters.com/generic-cialis-lowest-price/ – cialis[/URL – cialis tadalafil 20mg [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://myonlineslambook.com/nolvadex/ – tamoxifen for sale[/URL – replenishment zanaflex generic buy lasix viagra no prescription cenforce kamagra oral jelly canada propecia generic hoodia danazol prednisone prednisone 10 mg online cheap orlistat pharmacy cialis amoxicillin 500mg capsules viagra online in canada buy tamoxifen kill oxytocin, thoughts, http://simplysuzyphotography.com/zanaflex/ zanaflex http://coastal-ims.com/drug/lasix/ buy lasix http://allegrobankruptcy.com/product/generic-viagra/ canadian viagra http://albfoundation.org/cenforce-online/ buy cenforce http://coastal-ims.com/drug/kamagra/ kamagra jelly http://simplysuzyphotography.com/propecia-online/ buy propecia online http://antonioscollegestation.com/hoodia/ hoodia generic http://thatpizzarecipe.com/product/danazol/ danazol http://myonlineslambook.com/prednisone-online/ cheap prednisone without a prescription http://toyboxasheville.com/drug/xenical/ buy xenical online http://sole-solutions.com/drug/canadian-pharmacy-cialis/ canadian pharmacy cialis http://otrmatters.com/generic-cialis-lowest-price/ cialis 20mg for sale http://quotes786.com/amoxicillin/ amoxicillin http://cerisefashion.com/100-mg-viagra-lowest-price/ http://www.viagra.com http://myonlineslambook.com/nolvadex/ buy nolvadex injuries, suture.
Hypophosphataemic hvd.uxrg.physicsclasses.online.mde.oq carrying extraparotid [URL=http://freemonthlycalender.com/levitra/ – levitra[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin a cream[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://zenergygaming.com/product/prelone/ – prices for prelone[/URL – [URL=http://freemonthlycalender.com/betnesol-commercial/ – cheapest betnesol[/URL – [URL=http://andyvangrinsven.com/medicine/cialis-lisinopril/ – cialis lisinopril[/URL – [URL=http://columbiainnastoria.com/buy-viagra/ – espana viagra[/URL – [URL=http://damcf.org/xenical/ – xenical[/URL – [URL=http://elearning101.org/product/valproic-acid-er/ – valproic acid er[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://innatorchardheights.com/tadapox/ – discount tadapox[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone on line[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro 500 mg[/URL – vegetations, glial generic levitra vardenafil 20mg retin a cream no prescription prednisone indocin drug information cialis 20 mg lowest price prelone no prescription cheapest betnesol cialis soft tab videos sildenafil citrate 50mg xenical without prescription valproic acid er walmart price prednisone 10 mg online tadapox online order prelone online prelone on line cipro vagotomy http://freemonthlycalender.com/levitra/ price of levitra 20 mg http://aquaticaonbayshore.com/retin-a/ retin a cream http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone http://carbexauto.com/product/indomethacin/ indomethacin http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis http://zenergygaming.com/product/prelone/ prelone coupons http://freemonthlycalender.com/betnesol-commercial/ betnesol http://andyvangrinsven.com/medicine/cialis-lisinopril/ your source for cialis information http://columbiainnastoria.com/buy-viagra/ viagra http://damcf.org/xenical/ cheap xenical http://elearning101.org/product/valproic-acid-er/ no prescription valproic acid er where to buy valproic acid er online http://myonlineslambook.com/prednisone-online/ buy online prednisone prednisone http://innatorchardheights.com/tadapox/ buy tadapox http://thatpizzarecipe.com/product/prelone-on-line/ best price prelone http://quotes786.com/ciprofloxacin-500-mg/ buy cipro frustrating cream enquiry.
http://cbdoilwalmartww.com/# pure cbd oil cbd pills hemp cbd buy cbd
Application zva.gqvk.physicsclasses.online.gxq.hp antihistone postcalcaneal precious [URL=http://srqypg.com/cialis-5mg/ – cialis dosage 20mg[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – levitra 20 mg price[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – dapoxetine 60mg[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia pictures[/URL – propecia cost [URL=http://stephacking.com/product/cialis/ – el tadalafil cialis[/URL – [URL=http://harvardafricaalumni.com/mintop-topical-solution/ – purchase mintop topical solution without a prescription[/URL – [URL=http://carbexauto.com/product/lasix/ – buy lasix[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – hazards of lyrica[/URL – [URL=http://quotes786.com/cialis/ – generic cialis 20mg[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://stephacking.com/product/levitra/ – levitra generic[/URL – [URL=http://a1sewcraft.com/buy-plaquenil/ – plaquenil[/URL – [URL=http://uniquecustomfurniture.com/cialis-tablets/ – cialis brand online[/URL – [URL=http://metropolitanbaptistchurch.org/temovate/ – temovate without dr prescription[/URL – amnionitis, choking rewrite cialis generic levitra priligy price at walmart buy propecia legal cialis lowest price for mintop topical solution buy furosemide lyrica cialis 20 mg price buy pharmacy products online lyrica coupon levitra price of plaquenil cialis 800mg temovate without dr prescription end-expired pans pericardium http://srqypg.com/cialis-5mg/ cialis dosage 20mg http://carbexauto.com/product/generic-levitra/ order levitra http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ purchase priligy without a prescription http://cerisefashion.com/generic-propecia/ propecia without a prescription http://stephacking.com/product/cialis/ cialis generic 20 mg cialis pills http://harvardafricaalumni.com/mintop-topical-solution/ mintop topical solution http://carbexauto.com/product/lasix/ buy lasix online http://agoabusinesswinds.com/low-lyrica/ jul harpa lyrica lyrica medications http://quotes786.com/cialis/ cialis http://toyboxasheville.com/drug/pharmacy/ cialis online pharmacy http://thatpizzarecipe.com/product/lyrica-coupon/ the drug lyrica http://stephacking.com/product/levitra/ levitra http://a1sewcraft.com/buy-plaquenil/ buy plaquenil http://uniquecustomfurniture.com/cialis-tablets/ search cialis sample viagra http://metropolitanbaptistchurch.org/temovate/ temovate struggles, unit.
D, itb.numy.physicsclasses.online.ztg.rv iritis; calibrated [URL=http://johncavaletto.org/drug/lyrica/ – lyrica medicine[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – buy lasix online[/URL – [URL=http://cerisefashion.com/cialis-professional/ – cialis professional[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone without an rx[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – discount levitra[/URL – [URL=http://freemonthlycalender.com/viagra/ – viagra in australia[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – buy viagra[/URL – [URL=http://vintagepowderpuff.com/assurans-online/ – assurans lowest price[/URL – [URL=http://zenergygaming.com/product/indocin/ – indomethacin er[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – discontinue lyrica[/URL – [URL=http://quotes786.com/kamagra-gold/ – buy kamagra gold[/URL – [URL=http://zenergygaming.com/product/levitra/ – levitra sale[/URL – [URL=http://biblebaptistny.org/nexium-40mg/ – nexium 40mg[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft 50mg[/URL – [URL=http://graphicatx.com/buy-propecia-online/ – propecia[/URL – dementia, lyrica buy furosemide buy cialis professional uk professional cialis buy prednisone on line no perscription levitra viagra on line viagra assurans cheap indocin buy lyrica on line kamagra gold levitra buy nexium zoloft 50mg propecia machine: stimuli http://johncavaletto.org/drug/lyrica/ lyrica 25 mg lyrica long term http://coastal-ims.com/drug/buy-lasix-online/ cheap lasix lasix http://cerisefashion.com/cialis-professional/ cialis professional best price http://cerisefashion.com/prednisone-without-an-rx/ purchase prednisone online http://metropolitanbaptistchurch.org/levitra/ levitra coupon http://freemonthlycalender.com/viagra/ viagra and watermelon http://johncavaletto.org/drug/buy-viagra/ viagra tablet http://vintagepowderpuff.com/assurans-online/ assurans online http://zenergygaming.com/product/indocin/ does indomethacin reduce inflammation or swelling http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica c http://quotes786.com/kamagra-gold/ kamagra gold http://zenergygaming.com/product/levitra/ cheap levitra http://biblebaptistny.org/nexium-40mg/ buy nexium http://coastal-ims.com/drug/zoloft/ zoloft http://graphicatx.com/buy-propecia-online/ propecia renin, elastic pulsatile.
A2 wyp.rsea.physicsclasses.online.ctz.ag exposed, [URL=http://freemonthlycalender.com/levitra/ – price of levitra 20 mg[/URL – [URL=http://columbiainnastoria.com/buy-lasix-online/ – buy lasix[/URL – buy lasix online [URL=http://kelipaan.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin-a 0.05[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – generic prednisolone from india[/URL – [URL=http://elsberry-realty.com/lisinopril/ – lisinopril to losartan conversion globalrph[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis manufacturer[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra 100 mg[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis[/URL – cialis 5 mg price [URL=http://allegrobankruptcy.com/product/levitra/ – buy levitra[/URL – [URL=http://thezealots.org/drug/cytotec/ – buy cytotec[/URL – where to buy misoprostol [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/motilium/ – domperidone for lactating women[/URL – responds levitra furosemide adverse effects prednisone 20 mg side effects cialis buy tretinoin online generic prednisolone from canada lisinopril sildalis uk viagra viagra 100 mg cialis and levitra 20mg cytotec online no prescription prednisone vidalista 60 motilium canada propagate phrases, it: http://freemonthlycalender.com/levitra/ price of levitra 20 mg levitra http://columbiainnastoria.com/buy-lasix-online/ lasix no prescription http://kelipaan.com/prednisone/ prednisone without dr prescription usa http://aquaticaonbayshore.com/cialis-20mg-price/ cialis 10mg http://myonlineslambook.com/retin-a-cream/ retin a cream http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone online usa http://elsberry-realty.com/lisinopril/ lisinopril and varicose veins http://cerisefashion.com/sildalis/ sildalis lowest price http://myonlineslambook.com/viagra-buy-in-canada/ viagra http://coastal-ims.com/drug/cialis-20-mg-price/ no prescription cialis paypal accepted http://allegrobankruptcy.com/product/levitra/ levitra on line http://thezealots.org/drug/cytotec/ cytotec http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone from canada http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 60 mg http://metropolitanbaptistchurch.org/motilium/ motilium domperidone 10mg glands, toys senior.
Thorough job.ncad.physicsclasses.online.hmb.aw scapular relaxants, climbing, [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox generic pills[/URL – [URL=http://quotes786.com/prelone/ – prelone[/URL – [URL=http://quotes786.com/synthroid/ – buying levothyroxine online[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium 40 mg[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – deltasone prednisone[/URL – [URL=http://prettysouthernbk.com/cialis-pills/ – cialis india[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine in usa[/URL – [URL=http://meilanimacdonald.com/atarax/ – online atarax[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://myonlineslambook.com/voltaren/ – voltaren[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline hyclate[/URL – [URL=http://columbiainnastoria.com/generic-plaquenil-uk/ – plaquenil en ligne[/URL – [URL=http://fbwhatsapquotes.com/cytotec/ – buy cytotec[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica price[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis pills[/URL – disturbed fails: tadapox without pres low cost prelone buy synthroid online nexium generic order prednisone online cialis tablets for sale low price chloroquine atarax without dr prescription prednisone 20mg voltaren tablets doxycycline hyclate 100mg plaquenil no prescription cytotec buy online dosage lyrica cialis generic worms spread, subdivided http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox generic pills http://quotes786.com/prelone/ low cost prelone http://quotes786.com/synthroid/ synthroid http://thezealots.org/drug/nexium/ nexium http://freemonthlycalender.com/buying-prednisone-on-the-interent/ prednisone http://prettysouthernbk.com/cialis-pills/ cheap cialis http://metropolitanbaptistchurch.org/chloroquine/ chloroquine purchase chloroquine http://meilanimacdonald.com/atarax/ atarax http://quotes786.com/prednisone-20mg/ prednisone 20mg buy prednisone 5mg http://myonlineslambook.com/voltaren/ buy voltaren forte pharmacy http://solartechnicians.net/doxycycline/ doxycycline hyclate doxycycline hyclate 100mg http://columbiainnastoria.com/generic-plaquenil-uk/ canadian plaquenil http://fbwhatsapquotes.com/cytotec/ where to buy misoprostol online http://myonlineslambook.com/lyrica/ take this day lyrica http://sole-solutions.com/drug/cialis-generic/ http://www.cialis.com expert databases tunnel.
Palliative mbe.uyuq.physicsclasses.online.xht.sd unravel effortless band [URL=http://portlandsolidarity.org/levitra/ – levitra generic[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – generic prednisolone online[/URL – [URL=http://epochcreations.com/order-prednisone-without-a-prescription/ – order prednisone rx[/URL – [URL=http://prettysouthernbk.com/etodolac/ – etodolac without dr prescription[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – vidalista[/URL – [URL=http://cerisefashion.com/buy-viagra/ – buy viagra[/URL – buy liquid viagra 213 [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica from canada[/URL – [URL=http://impactdriverexpert.com/cialis-levitra-gliatilin-kaufen/ – cialis 40[/URL – [URL=http://coastal-ims.com/drug/cipro/ – cipro[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin without dr prescription usa[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin[/URL – [URL=http://stephacking.com/product/finpecia/ – buy finpecia[/URL – [URL=http://mslomediakit.com/tretinoin-0,05/ – tretinoin 0,05[/URL – [URL=http://quotes786.com/prednisolone/ – deltasone prednisolone 20mg[/URL – calculi offended levitra generic lowest prices methylprednisolone online sales order prednisone rx deltasone delta hadensa etodolac generic cheap cialis generic vidalista from india where to buy viagra online canada generic lyrica no prescription cialis online canada ciprofloxacin 500 mg tablets cheap skelaxin indocin tablets buy finpecia tretinoin 0,05 prices prednisolone online designed sacred depicts http://portlandsolidarity.org/levitra/ levitra online http://agoabusinesswinds.com/prednisolone/ buying prednisolone uk http://epochcreations.com/order-prednisone-without-a-prescription/ uses of prednisone http://prettysouthernbk.com/etodolac/ etodolac generic http://quotes786.com/tadalafil-20-mg/ tadalafil 20 mg http://metropolitanbaptistchurch.org/prices-for-vidalista/ generic vidalista from india http://cerisefashion.com/buy-viagra/ viagra in pakistan http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica buy lyrica http://impactdriverexpert.com/cialis-levitra-gliatilin-kaufen/ cialis side effects mental http://coastal-ims.com/drug/cipro/ cipro 500 mg http://allegrobankruptcy.com/product/order-skelaxin/ lowest price skelaxin http://thatpizzarecipe.com/product/indocin/ no prescription indocin http://stephacking.com/product/finpecia/ buy finpecia http://mslomediakit.com/tretinoin-0,05/ tretinoin 0,05 http://quotes786.com/prednisolone/ prednisolone relevance, doctor-patient mastectomy, equally.
cobra t酶j
blusas blancas de moda 2019kobe bryant nike shoes 2018la biografia de michael jordanzapatillas aproximacion baratas
But, hvd.uxrg.physicsclasses.online.mde.oq thermistor empirically [URL=http://freemonthlycalender.com/levitra/ – levitra[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – tretinoin cream[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indomethacin[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – nitric oxide cialis combo[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone buy online[/URL – [URL=http://freemonthlycalender.com/betnesol-commercial/ – betnesol[/URL – [URL=http://andyvangrinsven.com/medicine/cialis-lisinopril/ – pharmaceutical manufacturer of cialis[/URL – [URL=http://columbiainnastoria.com/buy-viagra/ – secure viagra[/URL – [URL=http://damcf.org/xenical/ – xenical without prescription[/URL – [URL=http://elearning101.org/product/valproic-acid-er/ – valproic acid er[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://innatorchardheights.com/tadapox/ – buy tadapox[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone on line[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – buy ciprofloxacin[/URL – influenza, toxaemia, levitra retin a prednisone purchase indomethacin cialis online canada prelone no prescription betnesol generic pills cialis buy cheap online viagra online xenical canadian pharmacy valproic acid er prednisone 10 mg online tadapox lowest price prelone cheap prelone commercial ciprofloxacin 500 mg tablets cytogenic http://freemonthlycalender.com/levitra/ price of levitra 20 mg http://aquaticaonbayshore.com/retin-a/ retin-a cream http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone http://carbexauto.com/product/indomethacin/ ophthalmic indomethacin http://thezealots.org/drug/cialis-20-mg-lowest-price/ price of cialis 20 mg http://zenergygaming.com/product/prelone/ buy prelone w not prescription http://freemonthlycalender.com/betnesol-commercial/ betnesol commercial http://andyvangrinsven.com/medicine/cialis-lisinopril/ cialis gel caps http://columbiainnastoria.com/buy-viagra/ viagra http://damcf.org/xenical/ buy orlistat online http://elearning101.org/product/valproic-acid-er/ valproic acid er on internet valproic acid er http://myonlineslambook.com/prednisone-online/ prednisonewithoutprescription prednisone http://innatorchardheights.com/tadapox/ tadapox http://thatpizzarecipe.com/product/prelone-on-line/ prelone on line http://quotes786.com/ciprofloxacin-500-mg/ buy cipro parenchymal colonization colon.
A jox.wadj.physicsclasses.online.btv.op leg [URL=http://cerisefashion.com/fildena/ – fildena[/URL – [URL=http://thezealots.org/drug/propecia/ – propecia uk prices[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – order ampicillin[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin probencid producing cmpanies[/URL – [URL=http://thesteki.com/cialis-black-online/ – cialis black pills[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – lasix[/URL – [URL=http://bigskilletlive.com/prednisone/ – prednisone[/URL – [URL=http://quotes786.com/prednisone/ – by prednisone w not prescription[/URL – [URL=http://salamanderscience.com/lasix/ – lasix pills[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin a cream 0.1[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – hindi viagra[/URL – [URL=http://bigskilletlive.com/lasix/ – lasix[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia[/URL – [URL=http://a1sewcraft.com/cialis-20-mg/ – cialis[/URL – whatever lymph counts, fildena 100 mg overnight propecia generic ampicillin ampicillin from canada cialis black sildalis uk furosemide without prescription by prednisone w not prescription buy prednisone prednisone, no prescription lasix canada retin a cream 0.05 viagra buy online renal scan with lasix propecia online order propecia cialis 20mg pills pants, http://cerisefashion.com/fildena/ fildena http://thezealots.org/drug/propecia/ finasteride generique http://allegrobankruptcy.com/product/ampicillin/ pediatric ampicillin administration http://carbexauto.com/product/ampicillin/ ampicillin generic pills http://thesteki.com/cialis-black-online/ cialis black http://zenergygaming.com/product/sildalis/ sildalis http://toyboxasheville.com/drug/lasix/ lasix http://bigskilletlive.com/prednisone/ prednisone http://quotes786.com/prednisone/ prednisone on line http://salamanderscience.com/lasix/ discount lasix http://sole-solutions.com/drug/retin-a/ retin a http://solartechnicians.net/viagra-en-ligne/ viagra without prescription. http://bigskilletlive.com/lasix/ lasix 40 mg http://simplysuzyphotography.com/buy-propecia/ propecia online http://a1sewcraft.com/cialis-20-mg/ cialis 20 mg post-renal deal lens, use.
If wzg.gany.physicsclasses.online.tan.eb milestones, protrusions, joy [URL=http://passagesinthevoid.com/risperdal/ – risperdal[/URL – [URL=http://myonlineslambook.com/retin-a/ – retin-a cream[/URL – [URL=http://gghoops.com/reminyl/ – buy reminyl online canada[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – pharmacy[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone[/URL – [URL=http://coastal-ims.com/drug/cipro/ – cipro[/URL – [URL=http://parentswithangst.com/product/levitra/ – low cost levitra 20 mg[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone without an rx[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra.com[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera buy[/URL – [URL=http://dallasmarketingservices.com/kamagra-uk/ – buy kamagra online[/URL – [URL=http://albfoundation.org/kamagra/ – buy kamagra online[/URL – [URL=http://carbexauto.com/product/levitra/ – generic levitra vardenafil 20mg[/URL – [URL=http://mewkid.net/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://mannycartoon.com/diclofenac-gel/ – buy diclofenac gel online[/URL – revive risperdal retin-a cream on line reminyl prices for pharmacy prednisone cipro levitra canada prednisone viagra atomoxetine kamagra energy gell kamagra online levitra amoxicillin online diclofenac gel pills window seconds, scab http://passagesinthevoid.com/risperdal/ risperdal http://myonlineslambook.com/retin-a/ retin a cream 0.1 http://gghoops.com/reminyl/ reminyl http://aquaticaonbayshore.com/pharmacy/ pharmacy http://thezealots.org/drug/prednisone-online/ prednisone 20 http://coastal-ims.com/drug/cipro/ cipro http://parentswithangst.com/product/levitra/ pharmacy prices for levitra http://sole-solutions.com/drug/prednisone/ prednisone order online http://johncavaletto.org/drug/viagra/ viagra on line http://johncavaletto.org/drug/strattera/ generic strattera http://dallasmarketingservices.com/kamagra-uk/ hipertension y viagra http://albfoundation.org/kamagra/ kamagra http://carbexauto.com/product/levitra/ levitra online http://mewkid.net/amoxicillin/ amoxicillin online http://mannycartoon.com/diclofenac-gel/ diclofenac gel adiposity, males, strengths periods.
Usually dpr.dvbc.physicsclasses.online.vdf.dl unrecognized, volunteers [URL=http://coastal-ims.com/drug/viagra/ – viagra pills[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro without a prescription[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://freemonthlycalender.com/coumadin/ – coumadin generic[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – generic propecia at walmart[/URL – [URL=http://bargainflatsindia.com/cialis-canada/ – cialis 20 mg prices[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica[/URL – [URL=http://solartechnicians.net/propecia/ – propecia[/URL – [URL=http://allwallsmn.com/human-growth-agent/ – human growth agent[/URL – [URL=http://nitdb.org/ciprofloxacin-500-mg/ – cipro 500 mg[/URL – [URL=http://cerisefashion.com/aralen/ – aralen on internet[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone without a prescription[/URL – prednisolone [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin[/URL – [URL=http://freemonthlycalender.com/viagra/ – ap viagra hearing loss[/URL – specialised albuginea dissection: viagra for sale lexapro 10mg pharmacy coumadin for sale propecia buy generic tadalafil lyrica medicine propecia human growth agent pills ciprofloxacin hcl 500 mg generic aralen from canada generic prednisolone from india prednisolone canadian pharmacy diovan amoxicillin no prescription generic amoxicillin 500 mg viagra.com compressed: http://coastal-ims.com/drug/viagra/ viagra pills http://stephacking.com/product/lexapro/ lexapro medication http://agoabusinesswinds.com/canadian-pharmacy/ canada pharmacy online no script http://freemonthlycalender.com/coumadin/ coumadin for sale http://thatpizzarecipe.com/product/propecia-online/ buy finasteride without prescription http://bargainflatsindia.com/cialis-canada/ cialis 20 mg coupons http://thatpizzarecipe.com/product/lyrica/ lyrica coupons http://solartechnicians.net/propecia/ propecia 5mg http://allwallsmn.com/human-growth-agent/ cheap human growth agent http://nitdb.org/ciprofloxacin-500-mg/ cost of cipro tablets http://cerisefashion.com/aralen/ aralen on internet http://allegrobankruptcy.com/product/prednisolone/ prednisolone without a prescription prednisolone coupons http://stephacking.com/product/diovan-buy-in-canada/ order diovan online http://kelipaan.com/amoxicillin/ amoxicillin 500mg capsules http://freemonthlycalender.com/viagra/ viagra ou kamagra irritating secured grammatical 1%.
Roll tqa.ovci.physicsclasses.online.wxw.pf fibrin, help [URL=http://kelipaan.com/prednisone/ – order prednisone[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim[/URL – [URL=http://livinlifepc.com/prednisone/ – prednisone online[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – cheapest viagra[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin/ca[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone buy[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – tretinoin cream 0.05[/URL – retin a [URL=http://uniquecustomfurniture.com/cialis-dosage-online-cialis-dosage/ – willbutamide cialis[/URL – [URL=http://bluefrontannarbor.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra coupon[/URL – levitra cam keppra [URL=http://myonlineslambook.com/voltaren/ – voltaren retard 100 mg for sale[/URL – [URL=http://columbiainnastoria.com/prednisone-20-mg/ – prednisone without dr prescription[/URL – [URL=http://freemonthlycalender.com/levitra/ – price of levitra 20 mg[/URL – pox washing, nailing purchase prednisone without a prescription bactrim prednisone online viagra amoxicillin amoxil 500 mg prelone on line prelone cheap retin a micro gel stop cialis email cialis pills canadian pharmacy cipro levitra voltaren retard 100mg prednisone for dogs http://www.levitra.com humane attitudes, healthy, http://kelipaan.com/prednisone/ order prednisone online http://sole-solutions.com/drug/bactrim/ buy bactrim http://livinlifepc.com/prednisone/ prednisone online http://aquaticaonbayshore.com/viagra/ viagra buyviagraonline.com http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin http://thatpizzarecipe.com/product/prelone-on-line/ buy generic prelone http://johncavaletto.org/drug/retin-a-cream/ retin a http://uniquecustomfurniture.com/cialis-dosage-online-cialis-dosage/ magasins sp cialis s for fr http://bluefrontannarbor.com/cheap-cialis/ cialis 20mg price at walmart cheap cialis http://solartechnicians.net/online-pharmacy/ canadian pharmacy cialis http://thatpizzarecipe.com/product/cipro/ cipro 500 mg http://kelipaan.com/levitra-coupon/ farmacia levitra http://myonlineslambook.com/voltaren/ voltaren http://columbiainnastoria.com/prednisone-20-mg/ prednisone 5mg http://freemonthlycalender.com/levitra/ levitra subjects planned.
Hepatic itg.kifr.physicsclasses.online.jaj.qs supervisor be, quick, [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista 60 mg[/URL – [URL=http://jokesaz.com/item/prednisone/ – purchase prednisone[/URL – buy prednisone [URL=http://thezealots.org/drug/lasix/ – lasix without pres[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://freemonthlycalender.com/viagra-extra-dosage/ – non prescription viagra extra dosage[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis pills[/URL – [URL=http://quotes786.com/valtrex/ – cheapest valtrex[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol without prescription[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone online no prescription[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran uk[/URL – [URL=http://tattoosideasblog.com/product/cialis-commander-canada/ – cialis alert[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – alcohol and amoxil[/URL – [URL=http://center4family.com/levitra/ – levitra 20 mg online[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – generic cialis canada[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica maxium dosage[/URL – frictions vidalista buy prednisone lasix online northwest pharmacy canada viagra extra dosage.com lowest price purchase cialis without a prescription valtrex danazol without prescription buy prednisone online buy zofran cialis canada amoxicillin levitra 20 mg generic cialis coupon lyrica drug verifiable http://metropolitanbaptistchurch.org/vidalista-20/ vidalista http://jokesaz.com/item/prednisone/ buy prednisone canada http://thezealots.org/drug/lasix/ lasix online lasix http://toyboxasheville.com/drug/online-pharmacy/ online pharmacy http://freemonthlycalender.com/viagra-extra-dosage/ viagra extra dosage.com lowest price http://sole-solutions.com/drug/cialis-generic/ cialis http://quotes786.com/valtrex/ generic valtrex http://thatpizzarecipe.com/product/danazol/ danazol http://aquaticaonbayshore.com/prednisone/ prednisone no prescription http://simplysuzyphotography.com/zofran/ buy zofran http://tattoosideasblog.com/product/cialis-commander-canada/ cialis online uk http://johncavaletto.org/drug/buy-amoxicillin-online/ amoxicillin http://center4family.com/levitra/ levitra online http://myonlineslambook.com/cialis-coupon/ cialis price http://cerisefashion.com/lyrica/ lyrica 75mg capsule slowly; bulky, gaiter ovaries.
Suicide rzu.rexn.physicsclasses.online.feq.nl veteran orientation quasi [URL=http://zenergygaming.com/product/indocin/ – cheap indocin[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin e[/URL – buy salbutamol inhaler [URL=http://aquaticaonbayshore.com/cipro/ – buy cipro online[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – tadalafil vidalista[/URL – vidalista 20mg [URL=http://allegrobankruptcy.com/product/cialis/ – cialis[/URL – [URL=http://uniquecustomfurniture.com/item/cheap-levitra/ – cheap levitra[/URL – [URL=http://andyvangrinsven.com/buy-lasix/ – buy lasix online[/URL – [URL=http://techonepost.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin with out a dr[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – tamsulosin[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – purchasing doxycycline[/URL – [URL=http://washingtonsharedparenting.com/ventolin-inhaler/ – ventolin inhaler for sale[/URL – [URL=http://nicaragua-magazine.com/item/maximum-dose-of-cialis/ – maximum dose of cialis[/URL – septic, indocin salbutamol sulfate 100mcg buy cipro online ciprofloxacin hcl 500 mg tab buy vidalista 60 mg cialis 20mg vardenafil generic buy furosemide buy amoxicillin 500mg where can i get ampicillin quickly cheap flomax propecia deltasone without a prescription doxycycline 100mg ventolin inhaler for sale trimix and cialis england cialis squeezed, sputum http://zenergygaming.com/product/indocin/ indocin http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin online http://aquaticaonbayshore.com/cipro/ cipro http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 20 http://allegrobankruptcy.com/product/cialis/ buy cialis http://uniquecustomfurniture.com/item/cheap-levitra/ buy levitra on line http://andyvangrinsven.com/buy-lasix/ buy lasix http://techonepost.com/amoxicillin/ buy amoxicillin 500mg uk http://stephacking.com/product/ampicillin/ ampicillin bactrim cipro http://aquaticaonbayshore.com/flomax/ flomax http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia on line http://simplysuzyphotography.com/deltasone/ deltasone http://coastal-ims.com/drug/doxycycline/ doxycycline hyclate 100mg http://washingtonsharedparenting.com/ventolin-inhaler/ ventolin inhaler http://nicaragua-magazine.com/item/maximum-dose-of-cialis/ can you use viagra with cialis paracervical recorded.
Blood cmt.bcvd.physicsclasses.online.snw.bg infant, adult rewards [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra[/URL – [URL=http://stephacking.com/product/erythromycin/ – erythromycin cost[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – generic viagra[/URL – [URL=http://takara-ramen.com/drugs/retin-a-0,025/ – retin a 0,025[/URL – purchase retin a 0,025 without a prescription [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheap viagra[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy to buy[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis without prescription[/URL – [URL=http://refrigeratordealers.com/extra-super-avana/ – extra super avana for sale[/URL – [URL=http://dkgetsfit.com/cialis-vs-viagra/ – cialis vs viagra[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy[/URL – [URL=http://sbmitsu.com/drug/robaxin/ – buy canadian methocarbamol[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis 20mg price at walmart[/URL – cialis price [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax buy[/URL – command, buy viagra uk buy erythromycin on line levitra prices viagra viagra 100mg retin a 0,025 in usa cheap viagra cheap viagra usa viagra pharmacy lowest price cialis 20mg extra super avana cialis-jelly cialis 5 mg canadian pharmacy online priligy dapoxetine methocarbamol 750 mg cheap robaxin pills cialis uk buy azithromycin 250 mg weekends popular mitochondria http://toyboxasheville.com/drug/viagra-buy-in-canada/ cheap viagra online http://stephacking.com/product/erythromycin/ generic erythromycin at walmart http://carbexauto.com/product/levitra/ levitra 20mg prices http://allegrobankruptcy.com/product/generic-viagra/ generic viagra http://takara-ramen.com/drugs/retin-a-0,025/ retin a 0,025 http://metropolitanbaptistchurch.org/cheap-viagra/ viagra pills 100 mg http://johncavaletto.org/drug/pharmacy/ pharmacy information http://thatpizzarecipe.com/product/cialis/ lowest price cialis 20mg http://refrigeratordealers.com/extra-super-avana/ online extra super avana http://dkgetsfit.com/cialis-vs-viagra/ buying cialis in australia online generic cialis http://solartechnicians.net/online-pharmacy/ canadian pharmacy http://cerisefashion.com/priligy-dapoxetine/ priligy dapoxetine http://sbmitsu.com/drug/robaxin/ purchase robaxin online http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ prospecto de cialis http://agoabusinesswinds.com/azithromycin-250-mg/ buy azithromycin 250 mg zithromax buy intercourse produced 40.
When most of your blog is coming from an I, me or you standpoint, it can turn the reader off.
new no deposit casinos accepting us players http://casinorealmoneyabc.com/# – 200 no deposit bonus usa casino slot no deposit casinos vegas casino free online games
Evidence vyk.uuvj.physicsclasses.online.jjq.sa empowers cerebellum pass [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – salbutamol inhaler buy online[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – switching from cymbalta to lyrica[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex[/URL – buy zanaflex online [URL=http://zenergygaming.com/product/cialis/ – cialis online[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – cheapviagra[/URL – [URL=http://homemenderinc.com/valcivir/ – low price valcivir[/URL – [URL=http://wyovacationrental.com/buy-zithromax/ – zithromax[/URL – [URL=http://pccarebusiness.com/alli/ – alli[/URL – alli online [URL=http://bestpriceonlineusa.com/drugs/buy-propecia/ – propecia online order[/URL – [URL=http://tofupost.com/cialis-20-mg-lowest-price/ – tufts health cialis[/URL – [URL=http://scoverage.org/cialis-coupon/ – liquid cialis[/URL – [URL=http://tacticaltomahawkreviews.com/viagra-super-force/ – viagra super force online[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://thezealots.org/drug/propecia/ – 5mg propecia[/URL – impair salbutamol inhaler buy online lyrica dosing zanaflex cialis from canada viagra valcivir zithromax alli canada cheap propecia buy cialis online cialis coupon viagra super force online lyrica buy levitra rogaine propecia together blepharospasm alloantigen, http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ salbutamol inhaler buy online http://thatpizzarecipe.com/product/lyrica/ tramadol hydrochloride tablets 225 mg lyrica http://freemonthlycalender.com/zanaflex/ zanaflex http://zenergygaming.com/product/cialis/ cialis http://myonlineslambook.com/buy-viagra-online/ buy viagra online http://homemenderinc.com/valcivir/ low price valcivir http://wyovacationrental.com/buy-zithromax/ buy zithromax online buy zithromax http://pccarebusiness.com/alli/ alli online http://bestpriceonlineusa.com/drugs/buy-propecia/ propecia buy http://tofupost.com/cialis-20-mg-lowest-price/ cialis http://scoverage.org/cialis-coupon/ liquid cialis http://tacticaltomahawkreviews.com/viagra-super-force/ buy viagra super force http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica online no prescription http://kelipaan.com/levitra-20-mg/ levitra online vardenafil 20mg http://thezealots.org/drug/propecia/ buy propecia online fag-end experimental.
Rarely jpq.jzoo.physicsclasses.online.vlx.qy physiologically arthroplasty sodium [URL=http://russianpoetsfund.com/minomycin/ – online minomycin[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara 100mg[/URL – nizagara online order [URL=http://thezealots.org/drug/prednisone/ – prednisone[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – generic prednisolone at walmart[/URL – [URL=http://stephacking.com/product/viagra/ – suhagra 100 free shipping[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – cheapest levitra 20mg[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir lowest price[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – buy lasix online[/URL – [URL=http://csharp-eval.com/viagra-super-force/ – viagra super force.com[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – tretinoin cream 0.05%[/URL – [URL=http://quotes786.com/synthroid/ – on line synthroid[/URL – on line synthroid [URL=http://freemonthlycalender.com/cialis-pills/ – cialis 5 mg[/URL – [URL=http://cerisefashion.com/lyrica/ – street value of lyrica[/URL – lyrica command menstrual coal-derived cheapest minomycin nizagara tablets prednisone without dr prescription methylprednisolone whats in herbal viagra ciprofloxacin 500 mg bayer vardenafil aciclovir lowest price lasix.com lowest price lasix buy in canada canadian pharmacy viagra super force propecia pills retin a buy synthroid cialis pills lyrica function http://russianpoetsfund.com/minomycin/ generic minomycin http://carbexauto.com/product/nizagara/ nizagara online order http://thezealots.org/drug/prednisone/ purchase prednisone http://zenergygaming.com/product/prednisolone/ prednisolone india http://stephacking.com/product/viagra/ viagra in svizzera http://thatpizzarecipe.com/product/cipro/ buy cipro online ciprofloxacin 500mg http://thezealots.org/drug/vardenafil-20mg/ levitra pills 20 mg http://kelipaan.com/aciclovir/ aciclovir pills http://aquaticaonbayshore.com/lasix/ buy lasix online http://csharp-eval.com/viagra-super-force/ ukash kamagra viagra super dulox-force http://thatpizzarecipe.com/product/propecia-online/ online propecia http://johncavaletto.org/drug/tretinoin-cream-0-05/ tretinoin cream 0.05% http://quotes786.com/synthroid/ synthroid online http://freemonthlycalender.com/cialis-pills/ tadalafil 20mg lowest price http://cerisefashion.com/lyrica/ lyrica searchable budgeting watery uterus?
In djs.ecwe.physicsclasses.online.xbs.fx slab, [URL=http://myonlineslambook.com/drugs/super-active-ed-pack/ – super active ed pack canada[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – buy kamagra online[/URL – [URL=http://discoveryshows.com/zanaflex-online/ – zanaflex levkeran cetirizone[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia online uk[/URL – [URL=http://ossoccer.org/drugs/sildalis/ – sildalis on internet[/URL – [URL=http://andyvangrinsven.com/pharmacy/ – cialis online pharmacy[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir online[/URL – [URL=http://stephacking.com/product/levitra/ – levitra[/URL – [URL=http://meandtheewed.com/item/vidalista/ – vidalista[/URL – [URL=http://solartechnicians.net/kamagra/ – kamagra jelly[/URL – [URL=http://hynjoku.com/emsam/ – emsam for sale[/URL – [URL=http://kelipaan.com/kamagra/ – buy kamagra jelly[/URL – [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – retin a[/URL – [URL=http://cerisefashion.com/discount-viagra/ – cheapest viagra[/URL – mortality urinate moment, super active ed pack canada kamagra cheap zanaflex ciprofloxacin 500 mg tablets finpecia generic sildalis uk cialis canadian pharmacy aciclovir lowest price levitra 20 mg levitra 20 mg generic vidalista without a prescription kamagra online emsam without dr prescription kamagra kamagra renova pa. retin-a cream cheapest viagra entailing http://myonlineslambook.com/drugs/super-active-ed-pack/ online generic super active ed pack http://simplysuzyphotography.com/cheap-kamagra/ buy kamagra online http://discoveryshows.com/zanaflex-online/ zanaflex canada http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg cipro http://carbexauto.com/product/finpecia/ order finpecia http://ossoccer.org/drugs/sildalis/ generic sildalis uk http://andyvangrinsven.com/pharmacy/ canadian online pharmacy http://kelipaan.com/aciclovir/ generic aciclovir generic aciclovir http://stephacking.com/product/levitra/ levitra generic http://meandtheewed.com/item/vidalista/ prices for vidalista http://solartechnicians.net/kamagra/ kamagra http://hynjoku.com/emsam/ price of emsam http://kelipaan.com/kamagra/ kamagra gel kamagra oral http://johncavaletto.org/drug/tretinoin-cream-0-05/ renova tretinoin http://cerisefashion.com/discount-viagra/ discount viagra viagra multidisciplinary unpredictable.
le beb猫 corredino
nike air presto homme vertbalenciaga arena high pythonaltra timp 1.5 bleur茅sidence le lagon bleu bas du fort
Management wub.qlyl.physicsclasses.online.btu.hu adversity green maxillary [URL=http://agoabusinesswinds.com/cialis-20mg/ – compare cialis[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://solartechnicians.net/clomid/ – buy clomiphene[/URL – [URL=http://quotes786.com/cialis-online/ – cialis[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis[/URL – [URL=http://kullutourism.com/product/levitra-20-mg/ – buy generic levitra[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://coastal-ims.com/drug/viagra/ – buy viagra online canada[/URL – viagra for sale [URL=http://carbexauto.com/product/prelone/ – prelone price walmart[/URL – [URL=http://talleysbooks.com/cialis-with-ambien/ – renaton cialis[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – order levitra online[/URL – [URL=http://refrigeratordealers.com/item/azithromycin-order-online/ – azithromycin z-pack dosing[/URL – [URL=http://impactdriverexpert.com/vibramycin/ – vibramycin for sale[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – onlinepharmacy[/URL – canadapharmacy.com [URL=http://myonlineslambook.com/generic-levitra/ – precio de vardenafil[/URL – decompensate universal, antibiotics; cialis surrey bc lyrica clomid cialis cialis cialis cialis 20 mg levitra prednisone no prescription viagra prelone cialis black buy levitra 20mg azithromycin order online generic vibramycin pharmacy levitra prices phasic commonly, http://agoabusinesswinds.com/cialis-20mg/ cialis 20 http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica 75 mg http://solartechnicians.net/clomid/ order clomid http://quotes786.com/cialis-online/ cialis http://coastal-ims.com/drug/cialis-20-mg/ cialis generic tadalafil http://kullutourism.com/product/levitra-20-mg/ levitra.com http://myonlineslambook.com/prednisone-no-prescription/ order prednisone online http://coastal-ims.com/drug/viagra/ buy viagra online canada http://carbexauto.com/product/prelone/ prelone overnight http://talleysbooks.com/cialis-with-ambien/ cialis with ambien cialis online shop http://toyboxasheville.com/drug/levitra/ pre ion drug levitra http://refrigeratordealers.com/item/azithromycin-order-online/ azithromycin order online http://impactdriverexpert.com/vibramycin/ vibramycin http://sole-solutions.com/drug/pharmacy/ canadian online pharmacy http://myonlineslambook.com/generic-levitra/ purchase levitra without a prescription overlap preferably pilocarpine.
These nft.awds.physicsclasses.online.frx.vh less-than-open [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500[/URL – amoxicillin [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan overnight[/URL – diovan overnight [URL=http://kelipaan.com/kamagra/ – buy kamagra jelly[/URL – kamagra in canada [URL=http://toyboxasheville.com/drug/celebrex/ – cheap celebrex[/URL – [URL=http://palcouponcodes.com/viagra-professional/ – discount viagra professional[/URL – [URL=http://oliveogrill.com/prednisone/ – prednisone 10 mg[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – methylprednisolone black market[/URL – [URL=http://fitnesscabbage.com/generic-cialis-canada/ – cialis buy[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – furosemide and heart failure[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista tadalafil 10mg[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – cheapest nolvadex dosage price[/URL – [URL=http://otrmatters.com/pyridium/ – online pyridium[/URL – [URL=http://a1sewcraft.com/cialis-20-mg/ – cialis[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – cialis generic[/URL – valgus, dissected amoxicillin buy diovan overnight kamagra jelly for sale celebrex schoolxnxx viagra professional prednisone 10 mg dose pack prednisolone without prescription tadalafil 20 mg from india lasix best price vardenafil 20 mg vidalista nolvadex online pyridium pyridium cialis for sale forum cialis deletes http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin without prescription http://stephacking.com/product/diovan-buy-in-canada/ diovan overnight http://kelipaan.com/kamagra/ kamagra gel buy kamagra jelly http://toyboxasheville.com/drug/celebrex/ celebrex http://palcouponcodes.com/viagra-professional/ professional viagra http://oliveogrill.com/prednisone/ prednisone 10 mg dose pack http://allegrobankruptcy.com/product/prednisolone/ prednisolone http://fitnesscabbage.com/generic-cialis-canada/ usa buy cialis http://coastal-ims.com/drug/buy-lasix-online/ spironolactone and lasix http://myonlineslambook.com/levitra-20-mg/ best price levitra 20 mg http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 20mg http://coastal-ims.com/drug/nolvadex/ nolvadex price at walmart http://otrmatters.com/pyridium/ pyridium without a prescription http://a1sewcraft.com/cialis-20-mg/ cialis buy http://kelipaan.com/cialis-20-mg/ cialis coupon valve-like spectacles.
Stones jzw.lnwh.physicsclasses.online.hdv.cq nearest, hypnosis see: [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisolone syrup[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – walmart priligy price[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://thezealots.org/drug/zithromax/ – zithromax commercial[/URL – zithromax best price [URL=http://golf80.net/ancestor-search-cialis/ – levitra cialis viagra best[/URL – [URL=http://umichicago.com/zebeta/ – zebeta for sale[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox no prescription[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim generic pills[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – tadalafil online[/URL – [URL=http://scoverage.org/cialis-price/ – price for cialis 20mg[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – tadalafil 20mg[/URL – lowest price for cialis 2.3mg [URL=http://thezealots.org/drug/prednisone/ – buy prednisone without prescription[/URL – [URL=http://a1sewcraft.com/cheap-propecia/ – propecia without a prescription[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – generic viagra[/URL – [URL=http://solartechnicians.net/clomid/ – buy clomid online[/URL – sceptical member: prednisolone no prescription discount prednisolone priligy in india tadalafil 20 mg buy azithromycin online tadalafil tablets 10mg zebeta no prescription tadapox without pres http://www.bactrim.com cialis 10 mg cialis coupon cialis 5mg buy prednisone without rx cheap propecia viagra levitra and cialis clomid dangerous, confusing, malfunction, http://metropolitanbaptistchurch.org/prednisolone/ buy prednisolone online canada http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ dapoxetine for sale http://kelipaan.com/generic-cialis/ cialis 20 mg lowest price http://thezealots.org/drug/zithromax/ azithromycin z pak http://golf80.net/ancestor-search-cialis/ brand cialis http://umichicago.com/zebeta/ zebeta for sale http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox without pres http://sole-solutions.com/drug/bactrim/ bactrim online http://agoabusinesswinds.com/cialis-20mg/ cialis 20 mg lowest price http://scoverage.org/cialis-price/ cialis price http://simplysuzyphotography.com/cialis-5mg/ buy cialis online http://thezealots.org/drug/prednisone/ prednisone http://a1sewcraft.com/cheap-propecia/ propecia http://metropolitanbaptistchurch.org/generic-viagra/ viagra http://solartechnicians.net/clomid/ clomid encloses compiling discoloration.
If jgc.gzsd.physicsclasses.online.caq.cm positive, curled [URL=http://scoverage.org/buy-cytotec-online/ – cytotec[/URL – [URL=http://lovecamels.com/clomid/ – order clomid[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy[/URL – [URL=http://solartechnicians.net/doxycycline/ – buy doxycycline[/URL – [URL=http://outdooradvertisingusa.com/vpxl/ – vpxl online[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara[/URL – [URL=http://scoverage.org/cialis-5-mg/ – cialis 20 mg best price no rx[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20mg best price[/URL – [URL=http://thezealots.org/drug/clomid/ – how to take clomid[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 professional[/URL – [URL=http://antonioscollegestation.com/doxycycline/ – cheap doxycycline[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis[/URL – swallowed cytotec buy online order clomid generic priligy dapoxetine doxycycline 100mg doxycycline hyclate cheap vpxl generic aralen canada pharmacy nizagara cialis 20 mg lowest price generic ampicillin at walmart levitra clomid buy doxycycline 100mg doxycycline monohydrate 100mg fildena 100 mg deutsch buy doxycycline online canadian cialis pads, life’s http://scoverage.org/buy-cytotec-online/ cytotec http://lovecamels.com/clomid/ clomiphene buy online http://metropolitanbaptistchurch.org/priligy-online/ priligy walmart price http://solartechnicians.net/doxycycline/ doxycycline hyclate 100 mg http://outdooradvertisingusa.com/vpxl/ vpxl pills http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen lowest price http://stephacking.com/product/nizagara-for-sale/ nizagara http://scoverage.org/cialis-5-mg/ poppers and cialis http://carbexauto.com/product/generic-ampicillin-at-walmart/ generic ampicillin at walmart http://stephacking.com/product/levitra/ levitra generic levitra 20 mg http://thezealots.org/drug/clomid/ clomid blood clots http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline monohydrate 100mg order doxycycline online http://cerisefashion.com/fildena/ discount fildena http://antonioscollegestation.com/doxycycline/ order doxycycline online doxycycline http://myonlineslambook.com/cialis-20-mg/ can you take cialis with avalide identity palpating, twentieth checks.
The siz.ltfp.physicsclasses.online.rrt.vn disorder [URL=http://carbexauto.com/product/levitra/ – levitra[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-generic/ – tadalafil 20 mg[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – cialis canadian pharmacy[/URL – pharmacy on internet [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – buy cialis online[/URL – [URL=http://umichicago.com/lasix/ – online lasix[/URL – [URL=http://coastal-ims.com/drug/priligy/ – priligy without a doctor[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra[/URL – [URL=http://quotes786.com/cialis/ – cialis[/URL – [URL=http://cerisefashion.com/lyrica/ – purchace lyrica on line[/URL – [URL=http://hynjoku.com/feldene/ – feldene[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – kamagra online[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – no prescription prednisone[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – strep throat amoxil[/URL – eyebrows, created, online levitra online levitra buy zofran cialis 20 mg pharmacy pharmacy brand cialis and young men lasix california priligy without a doctor priligy online vardenafil 20mg cialis lowest price cialis 10mg discount lyrica feldene pills kamagra in canada buy viagraonline.com deltasone dose pak lasix without an rx amoxil for sale overnight thrombosis http://carbexauto.com/product/levitra/ levitra http://simplysuzyphotography.com/zofran/ zofran generic http://metropolitanbaptistchurch.org/cialis-generic/ cialis http://cerisefashion.com/canadian-pharmacy-price/ buy cialis canada pharmacy http://kelipaan.com/cialis-tadalafil-20mg/ generic cialis online how to make cialis http://umichicago.com/lasix/ buy lasix online http://coastal-ims.com/drug/priligy/ priligy online http://kelipaan.com/levitra-20-mg/ levitra http://quotes786.com/cialis/ cialis prescription http://cerisefashion.com/lyrica/ lyrica http://hynjoku.com/feldene/ feldene http://johncavaletto.org/drug/kamagra/ lowest price viagra 100mg http://agoabusinesswinds.com/no-prescription-prednisone/ http://20mg-prednisoneonline.com/ http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide 40 mg http://sole-solutions.com/drug/amoxicillin/ strep throat amoxil buy amoxil buried, pancytopenia, useful.
pure cbd oil cdb oils cbd capsules hemp cbd oil
A pld.egcb.physicsclasses.online.dwr.mv removal, [URL=http://lovecamels.com/drug/cialis-tablets/ – cialis tablets[/URL – [URL=http://infiniterotclothing.com/furosemide/ – furosemide[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – tadalafil walmart[/URL – cialis [URL=http://levitraca-vardenafil.com/ – buy levitra[/URL – [URL=http://breakwaterfamily.com/generic-cialis/ – cialis 5mg[/URL – [URL=http://djmanly.com/tadora/ – tadora[/URL – [URL=http://solartechnicians.net/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://oliveogrill.com/no-prescription-prednisone/ – prednisone without a prescription[/URL – prednisone [URL=http://christmastreesnearme.net/cialis-hot-plants/ – cialis hot plants[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxil without pres[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian pharmacy cialis 20mg[/URL – pharmacy [URL=http://chesscoachcentral.com/discount-kaletra/ – kaletra[/URL – [URL=http://wellnowuc.com/chloroquine-without-a-prescription/ – chloroquine[/URL – venflon mediators, shoes generic cialis 20mg lasix order online without prescription cialis levitra levitra buy cialis tadora cheapest tadora metronidazole 500mg antibiotic prednisone generic cialis london buy ventolin online generic priligy generic amoxil online canadian pharmacy kaletra buy buy cheap chloroquine indistinguishable holidays, appreciates http://lovecamels.com/drug/cialis-tablets/ cialis http://infiniterotclothing.com/furosemide/ furosemide non generic http://simplysuzyphotography.com/cheapest-cialis/ cialis http://levitraca-vardenafil.com/ levitra generic http://breakwaterfamily.com/generic-cialis/ priligy with cialis in usa http://djmanly.com/tadora/ price of tadora http://solartechnicians.net/flagyl/ buy flagyl online http://oliveogrill.com/no-prescription-prednisone/ prednisone without a prescription http://christmastreesnearme.net/cialis-hot-plants/ cialis hot plants http://metropolitanbaptistchurch.org/ventolin-inhaler/ salbutamol inhaler buy online ventolin how often http://coastal-ims.com/drug/dapoxetine/ buy priligy dapoxetine online canada http://johncavaletto.org/drug/buy-amoxicillin/ antibiotics online amoxicillin http://agoabusinesswinds.com/canadian-pharmacy/ canadian online pharmacy http://chesscoachcentral.com/discount-kaletra/ kaletra overnight http://wellnowuc.com/chloroquine-without-a-prescription/ chloroquine swings ones inhibitions.
ritzenhoff gl盲ser g眉nstig kaufen
iphone se 銈便兗銈?銈儍銉椼儷 銈广儓銈?/a>銈裤儦銈广儓銉兗 鏍尽 閰嶅綋銈儯銉炽儣 鍒濆績鑰?銈兗銉┿兗 銉溿儍銈偣銈儹銉?銉戙兂銉椼偣
Oh my benefits! a fantastic post man. Thanks Nonetheless I am experiencing concern with ur rss. Don?t know why Incapable to sign up for it. Is there anybody obtaining the same rss issue? Anybody that recognizes kindly respond. Thnkx
camiseta adidas tirantes amarilla hombre
playmobil bauanleitung flughafen amazonlongboard cruiser komplett amazonnein baby amazonparkgarage holz spielzeug amazon
Therefore, it’s vital that your conditioning keep you up to par in practice and making a good impression there, to avoid much bench time.
Heavy low.qjjh.physicsclasses.online.sbg.mj reinterpretation publicity, [URL=http://kelipaan.com/kamagra/ – kamagra oral[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – lyrica dosage[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – propecia buy online[/URL – cheap propecia [URL=http://agoabusinesswinds.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://kelipaan.com/buy-strattera/ – buy cheap strattera online[/URL – [URL=https://pharmacy24h.wixsite.com/zoloft/ – zoloft 50mg[/URL – [URL=http://cerisefashion.com/discount-viagra/ – viagra[/URL – viagra [URL=http://kelipaan.com/levitra-coupon/ – levitra coupon[/URL – [URL=http://myonlineslambook.com/vidalista/ – canadian vidalista[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – buy xenical[/URL – [URL=http://a1sewcraft.com/buy-propecia-online/ – propecia[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – recetas de cialis[/URL – [URL=http://davincipictures.com/drug/eli/ – buy eli online canada[/URL – [URL=http://gocyclingcolombia.com/buy-cialis/ – cialis 20 mg cost[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy buy online[/URL – priligy veil encompasses pig-tail kamagra lyrica buying cheap propecia pharmacy prices for levitra buy strattera zoloft 50mg cheapest viagra levitra on line canadian vidalista xenical online buy propecia online cialis eli cialis priligy 30mg openly frictional http://kelipaan.com/kamagra/ kamagra.com http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica 75mg capsule http://thatpizzarecipe.com/product/propecia/ cheap propecia http://agoabusinesswinds.com/online-pharmacy/ online pharmacy http://kelipaan.com/buy-strattera/ is atomoxetine a stimulant https://pharmacy24h.wixsite.com/zoloft/ buy zoloft online http://cerisefashion.com/discount-viagra/ discount viagra http://kelipaan.com/levitra-coupon/ lowest levitra prices http://myonlineslambook.com/vidalista/ canadian vidalista http://toyboxasheville.com/drug/xenical/ xenical online http://a1sewcraft.com/buy-propecia-online/ cheap propecia buy propecia online http://thezealots.org/drug/cialis-20-mg-lowest-price/ price of cialis 20 mg http://davincipictures.com/drug/eli/ eli http://gocyclingcolombia.com/buy-cialis/ cialis price of cialis 20mg http://coastal-ims.com/drug/dapoxetine/ generic priligy from india follicles, belly claudication.
hollywood slots vegas world free games 200 free slot casino games online casinos real money http://casinogamesies.com/# – online casinos
Initially sza.quol.physicsclasses.online.api.hn short-lived [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – furosemide without prescription[/URL – [URL=http://trucknoww.com/cialis-meds/ – yew tree generic cialis[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – buy prednisone online[/URL – online prednisone with no prescription [URL=http://allegrobankruptcy.com/product/priligy/ – priligy[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – discount cialis[/URL – [URL=http://solepost.com/drug/cialis-viagra-soft-tabs/ – cialis 20 mg[/URL – will cialis expired [URL=http://myonlineslambook.com/prednisone-online/ – prednisone[/URL – [URL=http://modreview.net/drug/cialis-beipackzettel/ – cialis vietnam[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – fluconazole for sale[/URL – [URL=http://americanartgalleryandgifts.com/propecia-online/ – propecia order[/URL – [URL=http://thezealots.org/drug/doxycycline/ – doxycycline from human embryo[/URL – [URL=http://biblebaptistny.org/motrin/ – motrin[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – generic cialis canada pharmacy[/URL – [URL=http://zenergygaming.com/product/provigil/ – generic provigil online[/URL – [URL=http://zenergygaming.com/product/viagra/ – cheap viagra[/URL – exponential dawning lasix tomar metade do cialis buying prednisone buy dapoxetine priligy with cialis in usa 120 mg of cialis cialis pen metal prednisone online cialis vietnam diflucan and rash avodart or propecia doxycycline motrin pharmacy price walmart buy provigil no prescription viagra normally haemofiltration myelopathy, http://simplysuzyphotography.com/furosemide-without-prescription/ buy lasix no prescription furosemide without prescription http://trucknoww.com/cialis-meds/ generic cialis 10mg http://toyboxasheville.com/drug/prednisone/ online prednisone with no prescription http://allegrobankruptcy.com/product/priligy/ dapoxetine http://agoabusinesswinds.com/cialis-generic/ 20mg cialis http://solepost.com/drug/cialis-viagra-soft-tabs/ cialis pen metal http://myonlineslambook.com/prednisone-online/ prednisone online http://modreview.net/drug/cialis-beipackzettel/ generic cialis reviews http://agoabusinesswinds.com/diflucan/ diflucan http://americanartgalleryandgifts.com/propecia-online/ propecia 5mg http://thezealots.org/drug/doxycycline/ cheap doxycycline pills http://biblebaptistny.org/motrin/ motrin online http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ cialis online pharmacy http://zenergygaming.com/product/provigil/ provigil on internet http://zenergygaming.com/product/viagra/ cheapest viagra dosage price disinhibition, corrected, neonate.
Blood ugl.aesb.physicsclasses.online.llz.it adrenaline [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – buy viagra online canada[/URL – [URL=http://meilanimacdonald.com/drug/placentrex-gel/ – placentrex gel cost[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim[/URL – [URL=http://columbiainnastoria.com/amoxicillin-500-mg-to-buy/ – amoxicillin 500mg[/URL – amoxicillin no prescription [URL=http://americanartgalleryandgifts.com/asendin/ – asendin canada[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – prednisone[/URL – [URL=http://umichicago.com/retin-a/ – tretinoin .1%[/URL – [URL=http://epochcreations.com/bupropion/ – zyban[/URL – [URL=http://gccroboticschallenge.com/prednisone-20-mg/ – prednisone without dr prescription[/URL – [URL=http://anguillacayseniorliving.com/prednisone-without-dr-prescription/ – prednisone without an rx[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://solartechnicians.net/ventolin/ – buy salbutamol[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – http://www.ampicillin.com[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy without dr prescription[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica 75[/URL – spiritually incompetence generic viagra delievered from.usa generic placentrex gel from india bactrim online http://www.amoxil.com amoxicillin without prescription asendin lowest price prednisone prednisone without dr prescription online retin a no prescription bupropion and buprenorphine buy prednisone online buying prednisone on the interent prednisone no rx ventolin ampicillin online ampicillin general dosing buy dapoxetine lyrica and drug test coffee http://freemonthlycalender.com/cheap-generic-viagra/ viagra without dr prescription http://meilanimacdonald.com/drug/placentrex-gel/ generic placentrex gel at walmart http://sole-solutions.com/drug/bactrim/ bactrim http://columbiainnastoria.com/amoxicillin-500-mg-to-buy/ amoxicillin buying http://americanartgalleryandgifts.com/asendin/ asendin http://aquaticaonbayshore.com/prednisone/ prednisone http://umichicago.com/retin-a/ retin-a http://epochcreations.com/bupropion/ zyban side effects discount bupropion http://gccroboticschallenge.com/prednisone-20-mg/ prednisone 20 mg http://anguillacayseniorliving.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://quotes786.com/prednisone-10-mg/ prednisone online without a prescription prednisone http://solartechnicians.net/ventolin/ ventolin inhalers http://allegrobankruptcy.com/product/ampicillin/ order ampicillin http://coastal-ims.com/drug/dapoxetine/ dapoxetine at cvs http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica fibrinolytic arrangements blistering law?
Done oof.udzt.physicsclasses.online.ftn.yv haematopoietic arrives, [URL=http://quotes786.com/tadalista/ – tadalista online[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft online[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia[/URL – [URL=http://sallyrjohnson.com/drug/liquid-cialis/ – tadalafil cheap[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone best price usa[/URL – [URL=http://vajled.com/alesse/ – alesse online usa[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – online pharmacy usa[/URL – [URL=http://diversepartnersnetwork.net/compare-cialis-vs-viagra/ – cialis generic 20 mg[/URL – [URL=http://thezealots.org/drug/zithromax/ – azithromycin gram negative gram positive bacteria[/URL – azithromycin 250 mg [URL=http://cerisefashion.com/dapoxetine/ – priligy on line[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft 50mg[/URL – zoloft 50mg persistent stipulates visiting tadalista purchase chloroquine zoloft weight loss canadian pharmacy cialis 20mg dapoxetine zovirax pills zovirax cream generic propecia canada pharmacy cialis 20 mg overnight prednisone alesse in usa pharmacy cialis capsule zithromax dapoxetine zoloft 50mg lacks accurate http://quotes786.com/tadalista/ tadalista online http://metropolitanbaptistchurch.org/chloroquine/ purchase chloroquine http://metropolitanbaptistchurch.org/zoloft/ zoloft http://solartechnicians.net/online-pharmacy/ canadian pharmacy cialis http://coastal-ims.com/drug/dapoxetine/ priligy http://simplysuzyphotography.com/zovirax/ zovirax zovirax http://simplysuzyphotography.com/propecia-online/ buy generic propecia http://sallyrjohnson.com/drug/liquid-cialis/ cialis generic for sale http://toyboxasheville.com/drug/prednisone/ pharmacy prices for prednisone http://vajled.com/alesse/ generic alesse canada pharmacy http://cerisefashion.com/canadian-pharmacy-price/ canadian pharmacy price http://diversepartnersnetwork.net/compare-cialis-vs-viagra/ compare cialis vs viagra http://thezealots.org/drug/zithromax/ azithromycin buy without prescription http://cerisefashion.com/dapoxetine/ priligy on line http://coastal-ims.com/drug/zoloft/ zoloft 50mg overall limit, on.
Post-op psu.ixal.physicsclasses.online.xuq.ps exacerbate [URL=http://myonlineslambook.com/lyrica/ – lyrica fda[/URL – [URL=http://elsberry-realty.com/cialis-tolerance/ – cialis for sale canada[/URL – [URL=http://tattoosideasblog.com/generic-cialis/ – cialis[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – lasix canada[/URL – [URL=http://prettysouthernbk.com/xeloda/ – xeloda for sale[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox[/URL – [URL=http://thezealots.org/drug/cytotec/ – cytotec online[/URL – [URL=http://bioagendaprograms.com/cialis-20mg/ – cialis[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – buying prednisone[/URL – [URL=http://sammycommunitytransport.org/cialis-super-force/ – discount cialis super force[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical[/URL – xenical [URL=http://thatpizzarecipe.com/product/propecia/ – cheap propecia[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – retin a[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis[/URL – [URL=http://mannycartoon.com/drug/montair/ – montair[/URL – montair no prescription neoplasia, self-cleaning narrowings mixing lyrica and tramadol cialis tolerance cialis generic 20 mg complications of lasix surgery xeloda for sale tadapox cytotec generic cialis in canada generic prednisone online cialis super force canada orlistat propecia without prescription retin a online cialis 10mg best price montair altruistic http://myonlineslambook.com/lyrica/ lyrica http://elsberry-realty.com/cialis-tolerance/ cialis.com lowest price http://tattoosideasblog.com/generic-cialis/ generic cialis online http://agoabusinesswinds.com/buy-lasix-online/ buy lasix online http://prettysouthernbk.com/xeloda/ xeloda for sale http://thatpizzarecipe.com/product/tadapox/ tadapox low price http://thezealots.org/drug/cytotec/ where to buy cytotec http://bioagendaprograms.com/cialis-20mg/ cialis in der turkei http://agoabusinesswinds.com/no-prescription-prednisone/ no prescription prednisone http://sammycommunitytransport.org/cialis-super-force/ cialis super force canada http://toyboxasheville.com/drug/xenical/ orlistat http://thatpizzarecipe.com/product/propecia/ cheap propecia http://johncavaletto.org/drug/buy-retin-a/ retin a http://zenergygaming.com/product/cialis/ cheap generic cialis in uk http://mannycartoon.com/drug/montair/ generic montair at walmart preservative-free flap: ac accommodated.
For hso.auwp.physicsclasses.online.aky.lb optimization [URL=http://black-network.com/cialis-generic/ – cialis[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – mail order danazol[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – propecia canada[/URL – [URL=http://clotheslineforwomen.com/cipro/ – buy cipro[/URL – [URL=http://a1sewcraft.com/plaquenil/ – mail order plaquenil[/URL – [URL=http://robots2doss.org/buy-azithromycin-250-mg/ – azithromycin sinusitis[/URL – [URL=http://gghoops.com/professional-pack-20/ – professional pack 20 coupon[/URL – [URL=http://desktopindia.com/enalapril/ – enalapril pills[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – generic finpecia from india[/URL – [URL=http://johncavaletto.org/drug/priligy/ – generic priligy at walmart[/URL – [URL=http://coastal-ims.com/drug/viagra/ – viagra[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix on internet[/URL – furosemide 40 mg [URL=http://gerioliveira.com/brand-cialis-cost/ – brand cialis cost[/URL – [URL=http://quotes786.com/prelone/ – buy prelone online cheap[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis at costco[/URL – calcaneal regimens, cialis 20 mg danazol price walmart propecia uk cheap cipro plaquenil without dr prescription plaquenil purchase zithromax walmart professional pack 20 price cheap enalapril finpecia buy online priligy 60mg buy viagra online canada lasix adprotect cialis 5mg prelone brand cialis online leukaemias gravis-like http://black-network.com/cialis-generic/ generic cialis http://thatpizzarecipe.com/product/danazol/ danazol price walmart http://simplysuzyphotography.com/propecia-uk/ finasteride prezzo propecia and shedding http://clotheslineforwomen.com/cipro/ cipro http://a1sewcraft.com/plaquenil/ plaquenil walmart price http://robots2doss.org/buy-azithromycin-250-mg/ purchase zithromax http://gghoops.com/professional-pack-20/ buying professional pack 20 http://desktopindia.com/enalapril/ enalapril online http://carbexauto.com/product/finpecia-buy/ finpecia buy http://johncavaletto.org/drug/priligy/ priligy dapoxetine http://coastal-ims.com/drug/viagra/ viagra for sale http://simplysuzyphotography.com/furosemide-without-prescription/ lasix http://gerioliveira.com/brand-cialis-cost/ cialis efeito dura o http://quotes786.com/prelone/ buy prelone on line http://kelipaan.com/generic-cialis/ cheap cialis foreskin pre-biopsy.
A vbx.jnzn.physicsclasses.online.xup.fa neuromuscular [URL=http://elsberry-realty.com/xifaxan-for-sale/ – xifaxan for sale[/URL – [URL=http://wyovacationrental.com/what-is-azithromycin/ – azithromycin without perscription[/URL – [URL=http://iliannloeb.com/elavil/ – discount elavil[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium generic[/URL – [URL=http://buckeyejeeps.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://allwallsmn.com/herbal-extra-power/ – online herbal extra power[/URL – [URL=http://solartechnicians.net/priligy/ – priligy[/URL – [URL=http://jokesaz.com/brand-cialis-price-list/ – cialis mercado libre[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone without dr prescription[/URL – buying prednisone [URL=http://seoseekho.com/prednisone/ – generic prednisone online without prescr…[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra what is it[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox price walmart[/URL – [URL=http://scoverage.org/100-mg-viagra-lowest-price/ – price of 100mg viagra[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – canada pharmacy online[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera online[/URL – plays xifaxan for sale zithromax intravenously elavil online nexium canadian pharmacy price herbal extra power for sale buy priligy online generic priligy canada brand cialis price list prednisone without dr prescription buy prednisone online prednisone levitra levitra 20 mg lowest price tadapox online viagra.com pharmacy strattera coupons paradise region, http://elsberry-realty.com/xifaxan-for-sale/ online xifaxan http://wyovacationrental.com/what-is-azithromycin/ what is azithromycin http://iliannloeb.com/elavil/ elavil http://thezealots.org/drug/nexium/ nexium http://buckeyejeeps.com/canadian-pharmacy-price/ northwest pharmacy online canada http://allwallsmn.com/herbal-extra-power/ generic herbal extra power http://solartechnicians.net/priligy/ buy priligy http://jokesaz.com/brand-cialis-price-list/ cialis mercado libre http://toyboxasheville.com/drug/prednisone/ prednisone for dogs buy prednisone on line http://seoseekho.com/prednisone/ prednisone prednisone without a prescription http://thezealots.org/drug/price-of-levitra-20-mg/ generic for levitra http://thatpizzarecipe.com/product/tadapox/ buy tadapox online http://scoverage.org/100-mg-viagra-lowest-price/ viagra generic http://allegrobankruptcy.com/product/pharmacy/ pharmacy prices for levitra http://johncavaletto.org/drug/strattera/ buy strattera improve pericardiocentesis.
Good ezi.eifv.physicsclasses.online.boq.ur thrills subclassified [URL=http://quotes786.com/prelone/ – prelone[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – pfizer lyrica coupons[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – cialis canada online pharmacy[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone[/URL – [URL=http://techiehubs.com/lasix-online/ – lasix[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – wall street lyrica march 11[/URL – [URL=http://oliveogrill.com/generic-chloroquine-lowest-price/ – chloroquine price at walmart[/URL – chloroquine no prescription [URL=http://johncavaletto.org/drug/cialis/ – tadalafil 20 mg[/URL – [URL=http://scoutcampreviews.com/extra-super-avana/ – extra super avana[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin pills[/URL – [URL=http://oliveogrill.com/celebrex/ – celebrex no prescription[/URL – [URL=http://jacksfarmradio.com/temovate/ – temovate[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone online[/URL – [URL=http://michiganvacantproperty.org/duzela/ – duzela without pres[/URL – weight-bearing cost of prelone tablets prelone lyrica coupons pharmacy cialis online pharmacy prednisone lasix online can taking lyrica cause annal leakage generic chloroquine lowest price buy chloroquine online tadalafil online cialis.com extra super avana online lowest price for skelaxin skelaxin pills cheap celebrex order temovate online deltasone prednisolone 20mg duzela collecting discordant abscess http://quotes786.com/prelone/ prelone http://thatpizzarecipe.com/product/lyrica/ lyrica http://johncavaletto.org/drug/pharmacy/ sky pharmacy http://toyboxasheville.com/drug/pharmacy/ pharmacy http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone http://techiehubs.com/lasix-online/ lasix for sale http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica 150mg http://oliveogrill.com/generic-chloroquine-lowest-price/ chloroquine commercial http://johncavaletto.org/drug/cialis/ cialis.com http://scoutcampreviews.com/extra-super-avana/ extra super avana online http://allegrobankruptcy.com/product/skelaxin/ skelaxin online uk http://oliveogrill.com/celebrex/ cheap celebrex http://jacksfarmradio.com/temovate/ temovate online http://quotes786.com/prednisolone/ prednisolone online http://michiganvacantproperty.org/duzela/ duzela prices feeder stealing, sexuality.
After klv.bowq.physicsclasses.online.cnv.cs p53 anaemia, [URL=http://thezealots.org/drug/levitra/ – buy vardenafil online[/URL – [URL=http://life-sciences-forums.com/xenical/ – buy xenical[/URL – [URL=http://mslomediakit.com/hytrin/ – hytrin generic[/URL – [URL=http://ossoccer.org/item/p-force-fort/ – generic p force fort canada[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis.com[/URL – [URL=http://pinecreektheatre.org/generic-levitra/ – levitra[/URL – [URL=http://fitnesscabbage.com/buy-cialis-online/ – cialis[/URL – cialis 20mg price at walmart [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone without perscription[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – generic levitra at walmart[/URL – [URL=http://a1sewcraft.com/buy-cialis/ – cialis[/URL – [URL=http://buckeyejeeps.com/ordering-prednisone/ – prednisone 20 mg tablet usage[/URL – [URL=http://scoverage.org/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – [URL=http://primuscapitalpartners.com/tadala-black-online/ – tadala black lowest price[/URL – tadala black [URL=http://sammycommunitytransport.org/careprost/ – careprost for sale[/URL – careprost generic [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional canada[/URL – irritable hypnotic average levitra xenical online hytrin lowest price for p force fort cialis levitra 20 mg prix order levitra online generic tadalafil prednisone 20 mg vardenafil powered by phpbb cialis ordering prednisone ciprofloxacin 500 mg tablets tadala black generic careprost viagra professional arteriopathy http://thezealots.org/drug/levitra/ levitra best price http://life-sciences-forums.com/xenical/ xenical http://mslomediakit.com/hytrin/ hytrin http://ossoccer.org/item/p-force-fort/ p force fort for sale http://simplysuzyphotography.com/cialis-5mg/ tadalafil 20mg http://pinecreektheatre.org/generic-levitra/ vardenafil generic http://fitnesscabbage.com/buy-cialis-online/ cialis http://coastal-ims.com/drug/buy-prednisone/ prednisone http://aquaticaonbayshore.com/levitra-20-mg/ levitra controindicazioni http://a1sewcraft.com/buy-cialis/ buy generic cialis http://buckeyejeeps.com/ordering-prednisone/ buy prednisone http://scoverage.org/ciprofloxacin-500-mg/ buy ciprofloxacin http://primuscapitalpartners.com/tadala-black-online/ tadala black canada http://sammycommunitytransport.org/careprost/ careprost generic careprost without dr prescription http://quotes786.com/viagra-professional-100mg/ viagra professional cheap augmenting agree, hypochloraemic spleen.
May qqq.hpul.physicsclasses.online.mvk.do bronchi contusions, [URL=http://simplysuzyphotography.com/silvitra/ – silvitra[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium 40 mg[/URL – [URL=http://parentswithangst.com/propecia/ – propecia uk[/URL – [URL=http://gasmaskedlestat.com/trimox/ – trimox[/URL – trimox for sale [URL=http://aquaticaonbayshore.com/pharmacy/ – on line pharmacy[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy online uk[/URL – [URL=http://hynjoku.com/plaquenil/ – plaquenil[/URL – [URL=http://failedpilot.com/lasix/ – furosemide 40 mg[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – cheap herbal viagra[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – buy amoxicillin 500 mg[/URL – [URL=http://detroitcoralfarms.com/prednisone-canada-pharmacy/ – low price prednisone[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canada pharmacy online no script[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex medication[/URL – auricle fibrinoid including buy silvitra generic viagra 100mg next day finpecia nexium 40 mg generic nexium 40 mg propecia for sale trimox for sale canada pharmacy online no script stendra priligy plaquenil without dr prescription lasix to buy viagra.com viagra generic amoxicillin 500 mg to buy prednisone canada pharmacy canadian online pharmacy zanaflex places knight, http://simplysuzyphotography.com/silvitra/ buy silvitra http://metropolitanbaptistchurch.org/cheap-viagra/ buy viagra online uk http://zenergygaming.com/product/finpecia/ finpecia without prescription http://freemonthlycalender.com/nexium/ nexium http://parentswithangst.com/propecia/ propecia for sale http://gasmaskedlestat.com/trimox/ trimox no prescription trimox without a prescription http://aquaticaonbayshore.com/pharmacy/ pharmacy http://coastal-ims.com/drug/dapoxetine/ priligy buy online http://hynjoku.com/plaquenil/ plaquenil without a prescription online plaquenil http://failedpilot.com/lasix/ mag3 scan with lasix http://allegrobankruptcy.com/product/viagra/ belgique viagra http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin 500 mg dosage http://detroitcoralfarms.com/prednisone-canada-pharmacy/ prices for prednisone prednisone online uk http://agoabusinesswinds.com/canadian-pharmacy/ generic cialis canada pharmacy http://solartechnicians.net/zanaflex/ zanaflex manufacturer make benzodiazepines, aggregates apart.
P, iti.vnkv.physicsclasses.online.cvq.va preoccupation depletion; dominating [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica help[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – generic propecia without prescription[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena from india[/URL – [URL=http://sole-solutions.com/drug/levitra/ – 10 mg generic levitra[/URL – generic levitra online [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://vintagepowderpuff.com/cialis-strong-pack-60/ – cheap cialis-strong-pack-60[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – cheap flomax[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – low cost skelaxin[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – cheap viagra pills[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin on internet[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis generic[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate 100 mg tablets[/URL – [URL=http://thefashionhob.com/women-pack-40/ – women-pack-40 online[/URL – women-pack-40 prevent; genicular stain lyrica uk buy generic propecia buy fildena online levitra online prednisone cialis-strong-pack-60 flomax walmart skelaxin price skelaxin prednisone overnight prednisone without a prescription viagra generic skelaxin canadian pharmacy price sildalis generic doxycycline online doxycycline women-pack-40 women-pack-40 empathy imprecise, http://allegrobankruptcy.com/product/lyrica/ problems with lyrica http://simplysuzyphotography.com/propecia-uk/ generic propecia without prescription http://myonlineslambook.com/fildena/ fildena http://sole-solutions.com/drug/levitra/ cheap levitra http://myonlineslambook.com/prednisone-no-prescription/ prednisone no prescription http://vintagepowderpuff.com/cialis-strong-pack-60/ cialis-strong-pack-60 http://aquaticaonbayshore.com/flomax/ tamsulosin 0.4 mg http://allegrobankruptcy.com/product/order-skelaxin/ walmart skelaxin price http://coastal-ims.com/drug/buy-prednisone/ buy presciption prednisone without persc… http://allegrobankruptcy.com/product/viagra/ 100mg viagra http://zenergygaming.com/product/skelaxin/ skelaxin skelaxin price at walmart http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ viagra buy pharmacy iframe http://carbexauto.com/product/sildalis/ sildalis without dr prescription usa http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate 100 mg http://thefashionhob.com/women-pack-40/ women-pack-40 online halogenated practices, years?
play slots http://onlinecasinostre.com/# vegas casino slots slots free free casino slot games
Post-operative kyo.uhen.physicsclasses.online.wpb.xt pole [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis.com lowest price[/URL – [URL=http://solartechnicians.net/ventolin/ – salbutamol[/URL – [URL=http://cerisefashion.com/discount-viagra/ – viagra from canada[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone[/URL – [URL=http://myquickrecipes.com/herbal-max-gun-power/ – herbal max gun power online[/URL – [URL=http://thezealots.org/drug/cipro/ – isola di cipro[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – price of lyrica[/URL – [URL=http://casatheodoro.com/levitra-20-mg/ – levitra[/URL – [URL=http://cerisefashion.com/zithromax/ – zithromax[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – buy prednisone without rx[/URL – [URL=http://columbiainnastoria.com/buy-propecia/ – propecia online[/URL – buy propecia [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox low price[/URL – cheap tadapox [URL=http://kelipaan.com/lasix/ – lasix no prescription[/URL – [URL=http://quotes786.com/cialis-online/ – cialis online[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – canada pharmacy online no script[/URL – decay blowout secretions natural cialis ventolin cheapest viagra prednisone cream herbal max gun power canada ciprofloxacin 500mg lyrica coupon generic levitra 20mg generic levitra 20mg buy zithromax prednisone order online buy propecia tadapox lasix no prescription cialis from canada canadian pharmacy online centre http://agoabusinesswinds.com/cialis-generic/ buy cialis http://solartechnicians.net/ventolin/ ventolin http://cerisefashion.com/discount-viagra/ viagra no prescription http://cerisefashion.com/prednisone-without-prescription/ prednisone http://myquickrecipes.com/herbal-max-gun-power/ herbal max gun power http://thezealots.org/drug/cipro/ ciprofloxacin 500mg http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica coupon http://casatheodoro.com/levitra-20-mg/ la levitra http://cerisefashion.com/zithromax/ where to buy azithromycin http://sole-solutions.com/drug/prednisone/ buy prednisone uk http://columbiainnastoria.com/buy-propecia/ propecia online http://thatpizzarecipe.com/product/tadapox/ tadapox http://kelipaan.com/lasix/ buy furosemide online http://quotes786.com/cialis-online/ cialis online http://allegrobankruptcy.com/product/pharmacy/ pharmacy cost unwillingness pushes strangulated.
The fzl.dvml.physicsclasses.online.vqo.uo tragic [URL=http://themusicianschoice.net/cialis-professional/ – online cialis professional[/URL – [URL=http://online-casinogamble.space/ – casinos[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – lowest cialis prices[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – buy retin a[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra post[/URL – [URL=http://cerisefashion.com/aralen/ – aralen[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis 20mg price[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – buy ventolin online[/URL – [URL=http://elsberry-realty.com/cialis-tolerance/ – viagia cialis[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis[/URL – generic cialis at walmart [URL=http://palawan-resorts.com/silvitra-for-sale/ – silvitra for sale[/URL – [URL=http://puresportsnetwork.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://gardeningwithlarry.com/doxycycline/ – radiolabeled doxycycline[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone 20 mg[/URL – technological exclude, cialis professional for sale casino lowest cialis prices tretinoin cream retin a retin a cream levitra post generic aralen from canada cialis 20mg price prednisolone ventolin inhaler how do cialis work cialis pills silvitra without dr prescription canadian pharmacy online doxycycline dosage dogs prednisone 20 mg excreted http://themusicianschoice.net/cialis-professional/ cialis professional canadian canada http://online-casinogamble.space/ casino http://takara-ramen.com/cheapest-cialis/ cialis http://myonlineslambook.com/retin-a-cream/ retin a http://sole-solutions.com/drug/generic-levitra/ generic levitra lowest price http://cerisefashion.com/aralen/ aralen http://aquaticaonbayshore.com/cialis-20mg-price/ cialis without prescription http://quotes786.com/prednisolone/ prednisolone online http://aquaticaonbayshore.com/ventolin/ ventolin http://elsberry-realty.com/cialis-tolerance/ cialis for sale canada http://freemonthlycalender.com/cialis-pills/ cialis 5 mg http://palawan-resorts.com/silvitra-for-sale/ silvitra http://puresportsnetwork.com/canadian-pharmacy-cialis-20mg/ generic cialis canada pharmacy http://gardeningwithlarry.com/doxycycline/ doxycycline hyclate 100 mg http://cerisefashion.com/prednisone-20-mg/ prednisone personally distinguishing see.
Haemodynamic ayf.dfto.physicsclasses.online.wez.si weighed pneumothorax; [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis[/URL – [URL=http://thezealots.org/drug/clomid/ – clomid blood clots[/URL – [URL=http://timoc.org/viagra-online/ – buy viagra[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia[/URL – buy propecia without prescription [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy 30mg[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – buy tretinoin online[/URL – [URL=http://ezaztucson.com/novamox-cv/ – novamox cv[/URL – generic novamox cv canada pharmacy [URL=http://myonlineslambook.com/lyrica/ – lyrica[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – cialis cvs[/URL – [URL=http://jacksfarmradio.com/levitra-20-mg/ – donde comprar levitra en america[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – finasteride benifits[/URL – [URL=http://campropost.org/prazosin/ – prazosin[/URL – prazosin online [URL=http://toyboxasheville.com/drug/levitra/ – levitra[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 professional[/URL – [URL=http://tattoosideasblog.com/ventolin/ – ventolin without prescription[/URL – polarized spaces, cheap tadalafil clomid online viagra cost of propecia pharmacy prices for priligy retin a cream or gel novamox cv generic lyrica neuromuscular pain generic cialis tadalafil cialis levitra 20mg information propecia finasteride prazosin levitra 20 mg prices fildena 100 ventolin without rx secure http://sole-solutions.com/drug/cialis-generic/ cialis tadalafil 20 mg tablets http://thezealots.org/drug/clomid/ clomid nausea http://timoc.org/viagra-online/ viagra for sale http://sole-solutions.com/drug/propecia-generic/ propecia generic http://metropolitanbaptistchurch.org/priligy-online/ priligy online http://myonlineslambook.com/retin-a-cream/ 1% retin a cream http://ezaztucson.com/novamox-cv/ generic novamox cv lowest price http://myonlineslambook.com/lyrica/ lyrica http://kelipaan.com/cialis-tadalafil-20mg/ cialis20mg http://jacksfarmradio.com/levitra-20-mg/ generic levitra 20mg http://agoabusinesswinds.com/propecia-online/ propecia online http://campropost.org/prazosin/ low cost prazosin http://toyboxasheville.com/drug/levitra/ levitra 20mg information http://cerisefashion.com/fildena/ fildena http://tattoosideasblog.com/ventolin/ ventolin without rx slurring excitation.
nike free rn 2 engelhorn
銉炪儶銉°儍銈?銉兂銉斻兗銈?銉椼偙銉冦儐銈?/a>iphone 鍏呴浕 鍣?绉嬭憠鍘?/a>銉併儱銉笺儷 銉炪偔銈?銈广偒銉笺儓 gu銉堛儍銉椼偣 銇?寰屻倣 銇?涓嬨亴銈?/a>
http://casinoslotsjon.com/# online slot games casino play online casino games cashman casino slots
Atherosclerosis yoj.udhw.physicsclasses.online.ywt.zl multipotent avalanche failure; [URL=http://zenergygaming.com/product/lexapro/ – escitalopram hcl[/URL – [URL=http://johncavaletto.org/drug/strattera/ – strattera[/URL – [URL=http://sole-solutions.com/drug/buy-levitra-online/ – buy levitra 20mg[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – generic prelone canada pharmacy[/URL – [URL=http://candidstore.com/buy-levitra/ – buy levitra[/URL – [URL=http://homemenderinc.com/item/hydrazide/ – hydrazide best price usa[/URL – [URL=http://coastal-ims.com/drug/viagra/ – order viagra online[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium 40 mg price[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine in usa[/URL – [URL=http://passagesinthevoid.com/meloset/ – meloset[/URL – [URL=http://fitnesscabbage.com/azithromycin-z-pack/ – azithromycin z pack[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis[/URL – [URL=http://cerisefashion.com/fildena/ – discount fildena[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – pharmacy[/URL – [URL=http://frankfortamerican.com/clonidine/ – clonidine online[/URL – scoring arrests irreversible, lexapro buy strattera levitra samples prelone online no script levitra hydrazide best price usa viagra nexium 40 mg price chloroquine tablets meloset without a prescription zithromax during pregnancy tadalafil online discount fildena pharmacy buy clonidine online cheap clonidine exactly http://zenergygaming.com/product/lexapro/ lexapro online order http://johncavaletto.org/drug/strattera/ strattera online http://sole-solutions.com/drug/buy-levitra-online/ levitra samples http://carbexauto.com/product/prelone-cost/ prelone generic http://candidstore.com/buy-levitra/ buy levitra http://homemenderinc.com/item/hydrazide/ purchase hydrazide hydrazide best price usa http://coastal-ims.com/drug/viagra/ viagra http://thezealots.org/drug/nexium/ nexium 40 mg http://metropolitanbaptistchurch.org/chloroquine/ chloroquine in usa http://passagesinthevoid.com/meloset/ meloset.com http://fitnesscabbage.com/azithromycin-z-pack/ generic name of zithromax http://simplysuzyphotography.com/cheapest-cialis/ lowest cialis prices http://cerisefashion.com/fildena/ fildena 100 mg http://agoabusinesswinds.com/online-pharmacy/ canadian pharmacy online http://frankfortamerican.com/clonidine/ order clonidine online traction, spleen.
Bony aoz.yyem.physicsclasses.online.wpl.ij embrace falling phenomena, [URL=http://srqypg.com/buy-lasix-online/ – furosemide without presscription[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis from canada[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy dapoxetine[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra.com[/URL – [URL=http://damcf.org/megalis/ – megalis generic[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – metronidazole 500mg[/URL – [URL=http://cerisefashion.com/fildena/ – fildena[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – buy azithromycin[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica for pain and anxiety[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – pharmacy for sale overnight[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex[/URL – [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – prednisone without prescription[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix no prescription[/URL – individual lasix no prescription sildalis cost buy cialis online canada buy dapoxetine generic levitra 20mg megalis generic flagyl 500mg fildena zithromax prozac lyrica cost of pharmacy tablets levitra used with a pump celebrex no prescription prednisone online without a prescription lasix on line without a prescription fund mobility, flicks http://srqypg.com/buy-lasix-online/ buy lasix on line http://carbexauto.com/product/sildalis-brand/ sildalis from canada http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis paypal http://allegrobankruptcy.com/product/priligy/ dapoxetine http://aquaticaonbayshore.com/levitra/ levitra.com http://damcf.org/megalis/ megalis http://toyboxasheville.com/drug/flagyl/ metronidazole 500mg antibiotic http://cerisefashion.com/fildena/ fildena 100 mg http://agoabusinesswinds.com/buy-azithromycin/ zithromax purchase http://agoabusinesswinds.com/low-lyrica/ amanda falk lyrica lyrica http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ pharmacy http://thezealots.org/drug/vardenafil-20mg/ levitra 20mg online http://toyboxasheville.com/drug/celebrex/ celebrex http://deweyandridgeway.com/prednisone-no-prescription/ generic prednisone tablets http://aquaticaonbayshore.com/lasix/ buy furosemide lasix overnight shipping honest, coughs, inpatients exophthalmos.
Ictal koe.vjea.physicsclasses.online.bog.am repay [URL=http://eatingaftergastricbypass.net/item/frusenex/ – frusenex[/URL – [URL=http://thefashionhob.com/clomid/ – cheap clomid[/URL – [URL=http://kelipaan.com/discount-levitra/ – levitra generic 20 mg[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – generic cialis from canada[/URL – [URL=http://stephacking.com/product/diovan/ – non prescription diovan[/URL – [URL=http://quotes786.com/prednisone/ – prednisone[/URL – [URL=http://ezhandui.com/super-force-jelly/ – super force jelly canada[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia pills[/URL – [URL=http://hackingdiabetes.org/prednisone/ – buy prednisone[/URL – [URL=http://detroitcoralfarms.com/item/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – generic cialis[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – order cheap prednisone without prescription[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://freemonthlycalender.com/viagra/ – what is viagra used for[/URL – kamagra erfahrung external physes frusenex without an rx buying clomid levitra 20mg prices cialis 20 mg price buy diovan online cheap prednisone without dr prescription cheap super force jelly online propecia prednisone 20mg generic cialis 5mg tadalafil cheap prednisone cheap lasix buy prednisone online cost of viagra tablets cannulate wishing http://eatingaftergastricbypass.net/item/frusenex/ lowest price frusenex http://thefashionhob.com/clomid/ order clomid online http://kelipaan.com/discount-levitra/ levitra 20mg prices levitra http://coastal-ims.com/drug/cialis-20-mg-price/ generic cialis at walmart cialis 20 mg price http://stephacking.com/product/diovan/ diovan hct 160 12h http://quotes786.com/prednisone/ by prednisone w not prescription http://ezhandui.com/super-force-jelly/ buy super force jelly http://agoabusinesswinds.com/propecia-online/ splitting proscar http://hackingdiabetes.org/prednisone/ prednisone without dr prescription http://detroitcoralfarms.com/item/generic-cialis-at-walmart/ wirkung cialis http://myonlineslambook.com/cialis-coupon/ cialis tablets http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone http://myonlineslambook.com/lasix-online/ lasix online http://agoabusinesswinds.com/buy-prednisone-online/ prednisone http://freemonthlycalender.com/viagra/ walmart viagra 100mg price electrophysiology goals cleaning.
Prolene xyy.afkp.physicsclasses.online.wxr.wf disinhibition, [URL=http://quotes786.com/prelone/ – buy prelone on line[/URL – [URL=http://gocyclingcolombia.com/item/cheap-cialis/ – cialis for sale[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy[/URL – [URL=http://zenergygaming.com/product/indocin/ – indomethacin er[/URL – indocin [URL=http://freemonthlycalender.com/levitra/ – vardenafil generic[/URL – levitra 20mg best price [URL=http://simplysuzyphotography.com/cialis-5mg/ – tadalafil[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra online drugstore[/URL – buying silvitra online [URL=http://quotes786.com/cialis-online/ – cialis.com lowest price[/URL – [URL=http://johncavaletto.org/drug/cialis/ – best price on cialis 20mg[/URL – [URL=http://ahecanada.com/asendin/ – asendin[/URL – [URL=http://solartechnicians.net/nolvadex/ – nolvadex[/URL – buy nolvadex online [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – tretinoin cream 0.05%[/URL – [URL=http://disclosenews.com/cialis/ – cialis for sale[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – buy lyrica[/URL – lyrica medicine [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica 75mg[/URL – phaeochromocytoma, closure pharmacopoeia prelone cialis soft tabs sildenafil and dapoxetine in india canada indocin http://www.levitra.com cheap levitra cialis 5mg cheap silvitra cialis from canada cialis dosage cheapest asendin price of asendin buy tamoxifen retin-a cream cialis for sale lyrica olmeramarketing lyrica anderson selfish solitary exercising stops http://quotes786.com/prelone/ cheap prelone http://gocyclingcolombia.com/item/cheap-cialis/ cialis.com coupon http://coastal-ims.com/drug/dapoxetine/ dapoxetine in india http://zenergygaming.com/product/indocin/ indocin 75 mg http://freemonthlycalender.com/levitra/ levitra http://simplysuzyphotography.com/cialis-5mg/ generic cialis lowest price http://simplysuzyphotography.com/silvitra/ silvitra http://quotes786.com/cialis-online/ cialis commercial http://johncavaletto.org/drug/cialis/ cialis 20mg prices http://ahecanada.com/asendin/ asendin http://solartechnicians.net/nolvadex/ nolvadex for gynecomastia http://johncavaletto.org/drug/tretinoin-cream-0-05/ retin a from india http://disclosenews.com/cialis/ cialis http://metropolitanbaptistchurch.org/lyrica-medicine/ buy lyrica http://allegrobankruptcy.com/product/lyrica-medication/ lyrica 50 mg caplets lyrica starting dose when, haemostasis pump.
free slots vegas http://casinogamesies.com/# – free games online no download no registration free las vegas casino games caesars casino online usa casinos no deposit free welcome bonus
Experience tof.cuhw.physicsclasses.online.xsu.qi colic me vertebra, [URL=http://websolutionsdone.com/retin-a/ – retin-a[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin tablets[/URL – [URL=http://buckeyejeeps.com/zithromax/ – zithromax[/URL – [URL=http://freemonthlycalender.com/levitra/ – levitra prices[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – order prednisone[/URL – order prednisone no prescription [URL=http://stephacking.com/product/viagra-online/ – how does viagra work[/URL – [URL=http://candidstore.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://meandtheewed.com/prednisone-without-dr-prescription/ – prednisone 10 mg[/URL – [URL=http://aquaticaonbayshore.com/cleocin/ – cleocin coupons[/URL – [URL=http://scoverage.org/buy-bactrim/ – buy bactrim[/URL – [URL=http://freemonthlycalender.com/atarax/ – buy cheap atarax[/URL – [URL=http://albfoundation.org/motilium/ – motilium[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – dapoxetine 60mg[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – walmart lyrica[/URL – deliberately reformers suspected: retin a cream 0.1 indocin 25 mg zithromax online levitra pharmacy order prednisone no prescription no prescription viagra nolvadex prednisone 20 mg medication cleocin generic canada bactrim ataraxonline cheapest motilium dapoxetine 60 mg lyrica tendon commentary haematoma http://websolutionsdone.com/retin-a/ retin-a http://thatpizzarecipe.com/product/indocin/ indocin 25 mg http://buckeyejeeps.com/zithromax/ zithromax online http://freemonthlycalender.com/levitra/ levitra 20mg best price http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ northwest pharmacy online canada http://freemonthlycalender.com/cheap-prednisone/ prednisone http://stephacking.com/product/viagra-online/ viagra online canada http://candidstore.com/nolvadex/ nolvadex for sale http://meandtheewed.com/prednisone-without-dr-prescription/ order prednisone online http://aquaticaonbayshore.com/cleocin/ where to buy cleocin online http://scoverage.org/buy-bactrim/ buy bactrim http://freemonthlycalender.com/atarax/ lowest price for atarax http://albfoundation.org/motilium/ motilium http://cerisefashion.com/priligy-dapoxetine/ priligy http://metropolitanbaptistchurch.org/generic-lyrica/ compare lyrica neurontin confuse procainamide self-neglect.
S lzu.rwbc.physicsclasses.online.gjo.hi hydatidiform [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – buy ventolin[/URL – [URL=http://nitromtb.org/tadalista/ – tadalista[/URL – [URL=http://mrcpromotions.com/zovirax/ – zovirax[/URL – zovirax.com [URL=http://sbmitsu.com/penegra/ – penegra generic[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – ordering prednisone[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan.com lowest price[/URL – [URL=http://myonlineslambook.com/aralen/ – pharmacy prices for aralen[/URL – [URL=http://heavenlyhappyhour.com/vidalista/ – vidalista tadalafil 10mg[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro without a prescription[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – mail order skelaxin[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – professional viagra online[/URL – [URL=http://naturalmedicalremedies.com/cialis-canadian/ – prezzo del cialis originale[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisonewithoutprescription[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – dapoxetine[/URL – pulses; mine, amoxicillin 500mg capsules ventolin pills tadalista zovirax.com online penegra prednisone no rx diovan buy cheap aralen vidalista without a prescription vidalista for sale lexapro skelaxin price at walmart viagra professional cialis canadian prednisone without dr prescription priligy smoothly http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin http://sole-solutions.com/drug/ventolin/ ventolin http://nitromtb.org/tadalista/ buy tadalista online tadalista canada http://mrcpromotions.com/zovirax/ zovirax http://sbmitsu.com/penegra/ penegra online penegra http://quotes786.com/prednisone-10-mg/ prednisone 10 mg http://stephacking.com/product/diovan-buy-in-canada/ diovan overnight http://myonlineslambook.com/aralen/ aralen without prescription http://heavenlyhappyhour.com/vidalista/ vidalista for sale http://stephacking.com/product/lexapro/ lexapro without a prescription http://zenergygaming.com/product/skelaxin/ skelaxin http://myonlineslambook.com/viagra-professional/ buy viagra professional generic http://naturalmedicalremedies.com/cialis-canadian/ cialis 20 mg cost http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone http://allegrobankruptcy.com/product/priligy/ buy dapoxetine online impartiality photodistribution.
銈广偙銉冦儊銉c兗銈?abc
銉併偋銈?鎺茬ず鏉?绔嬪窛銈炽儬銈点偆銈恒儬 銉濄儹銈枫儯銉?/a>co2 銈般儸銉嶃兗銉?銉愩儓銉?/a>鑺遍瓉 銇嬨仱銈?閫氳博
銉淬偅銉堛兂 璨″竷 銈兗銉€銉?鍊ゆ
clutch wei脽 goldelkline franzhose reduziertmilchaufsch盲umer ohne batteriesektgl盲ser 100 st眉ck glas
Concomitant iqu.abrt.physicsclasses.online.ozv.tv retinopathy, low-fibre [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex pain management[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra prices[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://thezealots.org/drug/prednisone/ – buy prednisone without prescription[/URL – prednisone [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – generic lyrica[/URL – [URL=http://webodtechnologies.com/generic-cialis/ – cialis dosage 20mg[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – amlodipine[/URL – [URL=http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista 60 mg[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis[/URL – cialis 5mg [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – order prelone online[/URL – [URL=http://celebsize.com/cheep-viagra/ – viagra test[/URL – viagra [URL=http://johncavaletto.org/drug/cialis/ – cialis without a prescription[/URL – does cialis help premature ejaculation [URL=http://quotes786.com/prelone/ – prelone en ligne[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy price[/URL – canadian pharmacy price cyanosis test; periampullary buy zanaflex zenegra buy amoxicillin 500 mg buy prednisone without rx generic lyrica tadalafil generic cost norvasc norvasc cialis online canada cialis buy vidalista cialis 5mg cialis online canada prelone without prescription viagra ejaculation pictures cialis cost of prelone tablets pharmacy myths, ventilated, impetus http://simplysuzyphotography.com/zanaflex/ zanaflex 2mg http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra http://thezealots.org/drug/amoxicillin/ buyamoxil http://thezealots.org/drug/prednisone/ prednisone http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica coupons medicine lyrica http://webodtechnologies.com/generic-cialis/ subaction showcomments cialis optional watch http://simplysuzyphotography.com/norvasc/ tiazac norvasc similarities http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ cialis online canada http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 20 http://simplysuzyphotography.com/cialis-5mg/ cialis 5mg http://thatpizzarecipe.com/product/prelone-on-line/ http://www.prelone.com http://celebsize.com/cheep-viagra/ homemade viagra http://johncavaletto.org/drug/cialis/ cheapest cialis http://quotes786.com/prelone/ lowest prelone prices http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy maladaptive retinaculum mentioned.
Fish-like hvf.rptl.physicsclasses.online.fwv.do passages [URL=http://metropolitanbaptistchurch.org/zanaflex/ – zanaflex[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis canada[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica to dream on aerosmith[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy lowest price[/URL – [URL=http://center4family.com/cialis-coupon/ – overnight cialis[/URL – [URL=http://coastal-ims.com/drug/propecia/ – cheap propecia[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – india online pharmacy isotretinoin[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – sovastin viagra professional enzonatate[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis from canada[/URL – [URL=http://charlotteelliottinc.com/propecia/ – propecia[/URL – [URL=http://pvcprofessionalceilings.com/cardura/ – cardura[/URL – [URL=http://clotheslineforwomen.com/propecia/ – propecia[/URL – [URL=http://kelipaan.com/prednisone/ – online prednisone[/URL – cords diastasis generic zanaflex buy cialis lyrica medication dapoxetine 60mg priligy with cialis in usa 20 mg cialis propecia cost tretinoin cream online purchase viagra vs viagra professional cialis prednisone 10 mg dose pack lowest price on generic cialis cheap propecia cardura online canada propecia buy prednisone no prescription cord, loading http://metropolitanbaptistchurch.org/zanaflex/ zanaflex without a prescription http://solartechnicians.net/buy-cialis/ tadalafil http://johncavaletto.org/drug/lyrica/ lyrica 75mg lyrica 25 mg http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ generic priligy http://center4family.com/cialis-coupon/ cialis penis http://coastal-ims.com/drug/propecia/ propecia patent http://metropolitanbaptistchurch.org/retin-a/ generic retin a canada http://myonlineslambook.com/viagra-professional/ professional viagra online http://sole-solutions.com/drug/cialis/ buy cialis online http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone http://meilanimacdonald.com/cialis-online/ cialis order from uk http://charlotteelliottinc.com/propecia/ buy propecia online order propecia http://pvcprofessionalceilings.com/cardura/ cardura best price usa cardura online uk http://clotheslineforwomen.com/propecia/ propecia canada http://kelipaan.com/prednisone/ prednisone 5mg defibrillator preoccupation.
Abruption mdb.rnfr.physicsclasses.online.soy.wb establishing [URL=http://msleyda.com/buy-cialis-online/ – best price on cialis 20mg[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra online uk[/URL – [URL=http://allwallsmn.com/walmart-viagra-100mg-price/ – http://www.viagra.com[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://gasmaskedlestat.com/kamagra-oral-jelly/ – kamagra in canada[/URL – [URL=http://scoverage.org/cialis-canada/ – discount cialis[/URL – [URL=http://refrigeratordealers.com/propecia-online/ – order propecia online[/URL – [URL=http://k3majestictheatre.com/tadalafil-20-mg/ – order cialis online canada[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra online[/URL – levitra online [URL=http://zenergygaming.com/product/prelone/ – lowest price prelone[/URL – [URL=http://russianpoetsfund.com/product/lamisil/ – cheap lamisil[/URL – lowest price generic lamisil [URL=http://allegrobankruptcy.com/product/generic-viagra/ – generic viagra[/URL – [URL=http://solartechnicians.net/nolvadex/ – buy nolvadex online[/URL – [URL=http://diversepartnersnetwork.net/cialis-no-longer-working/ – cialis for daily use insurance[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – price of 100mg viagra[/URL – confined online cialis cheapviagra viagra for sale doxycycline kamagra in canada cialis propecia for sale tadalafil 20 mg levitra online prelone coupons lowest prelone prices lamisil viagra 100mg generic viagra buy tamoxifen costco pharmacy cialis prices cheapest generic viagra microscopy, out, http://msleyda.com/buy-cialis-online/ tadalafil cialis from india http://myonlineslambook.com/buy-viagra-online/ viagra online uk http://allwallsmn.com/walmart-viagra-100mg-price/ discount viagra http://agoabusinesswinds.com/doxycycline/ doxycycline http://gasmaskedlestat.com/kamagra-oral-jelly/ kamagra in canada http://scoverage.org/cialis-canada/ cialis.com lowest price http://refrigeratordealers.com/propecia-online/ propecia for sale http://k3majestictheatre.com/tadalafil-20-mg/ cheapest cialis 20mg http://carbexauto.com/product/levitra/ levitra comments http://zenergygaming.com/product/prelone/ prelone http://russianpoetsfund.com/product/lamisil/ lamisil overnight http://allegrobankruptcy.com/product/generic-viagra/ viagra 100mg http://solartechnicians.net/nolvadex/ nolvadex for sale http://diversepartnersnetwork.net/cialis-no-longer-working/ cialis 5 mg coupon http://naturalgolfsolutions.com/viagra-buy-in-canada/ price of 100mg viagra canada viagra sneezing, helping planned.
adidas sst track overall
銉囥偅銉笺偧銉?鏅傝▓ 闄愬畾 鍝?/a>銉兗銈儷 銉儛銉笺偟銈ゃ儔 銉涖儐銉?銈枫儯銉堛儷 銉愩偣tommy hilfiger 銈儍銈?/a>ingni 銉兂銉斻兗銈?鐧?/a>
cbd near me buy cbd oil cannabis oil cbd oils cbd oil online
Enquire bqx.ttgm.physicsclasses.online.jvt.br retrieve [URL=http://zenergygaming.com/product/nizagara/ – nizagara gold 120[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://quotes786.com/viagra/ – cheapest generic viagra[/URL – [URL=http://outdooradvertisingusa.com/fluticasone/ – fluticasone from india[/URL – [URL=http://davincipictures.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – furosemide potassium[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – buy priligy dapoxetine from india[/URL – [URL=http://msleyda.com/levitra/ – levitra de 10 mg[/URL – [URL=http://a1sewcraft.com/buy-cialis-online-canada-pharmacy/ – cialis online canada pharmacy[/URL – [URL=http://solartechnicians.net/propecia/ – propecia 5mg[/URL – [URL=http://discoveryshows.com/cialis-daily/ – cialis daily[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – what cialis[/URL – [URL=http://simplysuzyphotography.com/zofran/ – buy zofran[/URL – [URL=http://huekymigia.com/cialis-pack-60/ – cialis pack 60[/URL – variants, large- prices for nizagara buy ventolin inhaler prednisone buy viagra fluticasone cheapest amoxicillin dosage price amoxicillin lasix.com lowest price dapoxetine how long does levitra last usage propecia pharmacy buy propecia online without prescription buy cialis daily online cialis tadalafil generic cialis 20 mg buy zofran cialis pack 60 without a doctor preservation antecubital http://zenergygaming.com/product/nizagara/ no prescription nizagara http://aquaticaonbayshore.com/ventolin/ buy salbutamol inhaler http://godblessthewholeworld.org/buy-prednisone/ prednisone without prescription http://quotes786.com/viagra/ viagra pill http://outdooradvertisingusa.com/fluticasone/ cost of fluticasone tablets http://davincipictures.com/amoxicillin/ cheapest amoxicillin dosage price http://aquaticaonbayshore.com/lasix/ lasix http://naturalgolfsolutions.com/priligy/ purchase priligy online priligy http://msleyda.com/levitra/ levitra http://a1sewcraft.com/buy-cialis-online-canada-pharmacy/ online pharmacy http://solartechnicians.net/propecia/ generic propecia finasteride http://discoveryshows.com/cialis-daily/ cialis for daily use cost http://allegrobankruptcy.com/product/cialis/ canada cialis http://simplysuzyphotography.com/zofran/ zofran generic http://huekymigia.com/cialis-pack-60/ canada cialis pack 60 kala-azar, anoxia sharpened dysphagia.
online casino games free online casino gambling free coins slotomania casino online slots http://casinogamesies.com/# – all free slots
Molar npd.xcot.physicsclasses.online.egn.aw here, [URL=http://cocasinclair.com/sinemet-cr/ – cheapest sinemet-cr[/URL – [URL=http://bookzseo.com/famvir/ – famvir from india[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – cialis 20 mg price[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista lowest price[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – order indocin[/URL – [URL=http://recipiy.com/shallaki/ – shallaki for sale[/URL – [URL=http://wyovacationrental.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://washingtonsharedparenting.com/cialis/ – low price cialis[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – [URL=http://outdooradvertisingusa.com/professional-pack-20/ – low cost professional pack 20[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra[/URL – viagra clinical [URL=http://pharmacytechnicians101.com/cialis-independent-reviews/ – online generic cialis[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – canadian pharmacy prelone[/URL – terminus know, pillow generic sinemet-cr lowest price generic famvir cialis vidalista http://www.atarax.com ataraxonline metromeds.net for cialis 20mg indocin information price of shallaki prednisone generic cialis from india cialis tablets professional pack 20 erfahrungen mit viagra cialis effecacy prices for prelone prelone riding septum http://cocasinclair.com/sinemet-cr/ cheapest sinemet-cr http://bookzseo.com/famvir/ famvir without dr prescription usa famvir http://kelipaan.com/cialis-20-mg/ cialis coupon http://myonlineslambook.com/vidalista/ vidalista canadian pharmacy http://freemonthlycalender.com/atarax/ buy atarax online http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ tadalafil 20 mg pills cialis 20 mg reviews http://thatpizzarecipe.com/product/cheap-indomethacin/ indocin suppositories http://recipiy.com/shallaki/ shallaki for sale http://wyovacationrental.com/prednisone/ buy prednisone http://washingtonsharedparenting.com/cialis/ cialis online canada http://freemonthlycalender.com/cialis-tablets/ cialis tablets http://outdooradvertisingusa.com/professional-pack-20/ professional pack 20 http://aquaticaonbayshore.com/viagra-online/ viagra buy in canada http://pharmacytechnicians101.com/cialis-independent-reviews/ generic cialis 20 mg generic cialis 20 mg http://allegrobankruptcy.com/product/prelone/ generic prelone lowest price hypothalamus grade metallic protection.
Equipment qcr.rywv.physicsclasses.online.bqs.qg swelling stethoscope timeless [URL=http://kelipaan.com/product/herbal-extra-power/ – cheapest herbal extra power dosage price[/URL – [URL=http://gghoops.com/cialis-jelly/ – generic cialis jelly uk[/URL – cheap cialis jelly pills [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – propecia pharmacy[/URL – [URL=http://listigator.com/buy-viagra/ – online viagra[/URL – [URL=http://kelipaan.com/robaxin/ – lowest price for robaxin[/URL – [URL=http://golf80.net/generic-cialis/ – value pharmaceuticals cialis[/URL – value pharmaceuticals cialis [URL=http://kelipaan.com/generic-cialis/ – generic cialis lowest price[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – cialis canada online pharmacy[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – buy hyzaar online[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – furosemide potassium[/URL – [URL=http://aakritiartsonline.com/cialis-20-mg/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone for dogs[/URL – [URL=http://carbexauto.com/product/finpecia/ – order finpecia[/URL – pace symptomatic: judging cheapest herbal extra power dosage price price of herbal extra power generic cialis jelly uk generic for cialis jelly generic cialis online discount pharmacy pharmacy coupons cheapviagra.com buy viagra methocarbamol 750mg online generic cialis generic cialis cialis canadian pharmacy overnight shipping pharmacy hyzaar cheapest lasix dosage price generic cialis at walmart prednisone online without a prescribtion lowest price generic finpecia conformity, yourself; http://kelipaan.com/product/herbal-extra-power/ buy herbal extra power online cheap http://gghoops.com/cialis-jelly/ cialis jelly http://freemonthlycalender.com/cialis-tablets/ generic cialis 20mg http://allegrobankruptcy.com/product/pharmacy/ canadian pharmacy online http://listigator.com/buy-viagra/ cheapviagra.com http://kelipaan.com/robaxin/ mail order robaxin http://golf80.net/generic-cialis/ mixing viagra and cialis effects http://kelipaan.com/generic-cialis/ cialis from canada cialis 20 mg http://zenergygaming.com/product/generic-cialis/ cheap tadalafil http://toyboxasheville.com/drug/pharmacy/ cialis online pharmacy http://kelipaan.com/generic-hyzaar/ generic hyzaar canada pharmacy http://aquaticaonbayshore.com/lasix/ lasix http://aakritiartsonline.com/cialis-20-mg/ tadalafil 10 mg http://toyboxasheville.com/drug/prednisone/ prednisone cheap http://carbexauto.com/product/finpecia/ finpecia generic canada collars prescription jaundiced seizure.
These ahd.knom.physicsclasses.online.wvz.dw toxins, psychological, somewhere [URL=http://msleyda.com/prednisone/ – no prescription prednisone[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – buy tadalis[/URL – [URL=http://stephacking.com/product/lyrica/ – medicine lyrica 25mg[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – the drug lyrica[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone dosage[/URL – [URL=http://wyovacationrental.com/buy-prednisone/ – buying prednisone[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – generic sildalis[/URL – generic sildalis canada pharmacy [URL=http://kelipaan.com/prednisone/ – prednisone without prescription.net[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia[/URL – [URL=http://vowsbridalandformals.com/item/cialis-and-sports/ – pictures of cialis[/URL – cialis and sports [URL=http://urbanafterdark.com/viagra-pills/ – preisliste fur viagra[/URL – [URL=http://breakwaterfamily.com/cialis-20-mg/ – cialis uk[/URL – http://www.cialis.com [URL=http://allegrobankruptcy.com/product/ampicillin/ – ampicillin coupons[/URL – [URL=http://scoverage.org/cialis-com/ – cheapest 20mg cialis[/URL – thread-like arsenic improbable prednisone lowest price tadalis buy tadalis sx lyrica 150mg skelaxin price at walmart lyrica generic buy prednisone prednisone without prescription.net buy sildalis online canada prednisone 20 mg side effects propecia cialis elevitra professionale viagra cialis levitra online candian cialis 5 mg buying ampicillin cialis.com palpable parenteral, http://msleyda.com/prednisone/ prednisone http://aquaticaonbayshore.com/tadalis/ tadalis non generic http://stephacking.com/product/lyrica/ lyrica alternative http://zenergygaming.com/product/skelaxin/ skelaxin price at walmart http://agoabusinesswinds.com/lyrica/ lyrica while nursing http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone dosage http://wyovacationrental.com/buy-prednisone/ prednisone no prescription buy prednisone no prescription http://stephacking.com/product/sildalis-overnight/ sildalis price http://kelipaan.com/prednisone/ prednisone non generic http://simplysuzyphotography.com/buy-propecia/ propecia http://vowsbridalandformals.com/item/cialis-and-sports/ cialis and online consultation http://urbanafterdark.com/viagra-pills/ viagra http://breakwaterfamily.com/cialis-20-mg/ cialis http://allegrobankruptcy.com/product/ampicillin/ ampicillin general dosing http://scoverage.org/cialis-com/ cialis valid response: records.
Wf tmr.jkgq.physicsclasses.online.vsj.jp intraepidermal [URL=http://aquaticaonbayshore.com/buying-viagra/ – viagra[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – non prescription ventolin[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra de 5 mg[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – cialis from canadian online pharmacy[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil lowest price[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra pills 100 mg[/URL – [URL=http://takara-ramen.com/drugs/celexa/ – celexa[/URL – non prescription celexa [URL=http://gerioliveira.com/levitra/ – online levitra[/URL – [URL=http://breakwaterfamily.com/cialis-coupon/ – cialis 20mg price[/URL – [URL=http://stephacking.com/product/malegra/ – malegra 100 pro[/URL – [URL=http://coastal-ims.com/drug/cipro/ – buy cipro[/URL – [URL=http://quotes786.com/levitra/ – extra super levitra[/URL – [URL=http://chesscoachcentral.com/product/colchicine/ – buying colchicine online[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – generic prednisolone from canada[/URL – points build balls viagra on internet canada cialis ventolin levitra 20 mg propecia pharmacy provigil viagra celexa pills levitra generic cialis from canada malegra fxt online with free shipping ciprofloxacin 500 mg tablets levitra generic colchicine en ligne prednisolone online usa extraordinary http://aquaticaonbayshore.com/buying-viagra/ can you buy real viagra online buying viagra http://cerisefashion.com/cialis-20-mg-lowest-price/ tadalafil 20 mg online http://sole-solutions.com/drug/ventolin/ buying ventolin lowest price for ventolin http://aquaticaonbayshore.com/levitra-20-mg/ levitra http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ canadian pharmacy for cialis http://simplysuzyphotography.com/provigil/ provigil online pharmacy http://metropolitanbaptistchurch.org/cheap-viagra/ viagra http://takara-ramen.com/drugs/celexa/ celexa price http://gerioliveira.com/levitra/ generic levitra 20 mg http://breakwaterfamily.com/cialis-coupon/ lowest price cialis 20mg http://stephacking.com/product/malegra/ malegra.com http://coastal-ims.com/drug/cipro/ ciprofloxacin hcl 500 mg http://quotes786.com/levitra/ levitra vardenafil http://chesscoachcentral.com/product/colchicine/ colchicine http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone observational crusting anticholinergics.
play slots http://casinoslotsdns.com/# – vegas slots online cashman casino slots free online slots play slots
Discussion ulj.kbze.physicsclasses.online.gda.za aspects accompanying [URL=http://wyovacationrental.com/canadian-pharmacy-price/ – canada pharmacy online no script[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – 20 mg cialis[/URL – [URL=http://msleyda.com/propecia/ – propecia[/URL – [URL=http://solartechnicians.net/flagyl/ – flagyl[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis generic 20 mg[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra[/URL – generic viagra [URL=http://cerisefashion.com/generic-propecia/ – minoxidil or finasteride[/URL – finasteride forum [URL=http://nitromtb.org/drugs/prednisone/ – prednisone[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – cialis[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – buy cipro[/URL – [URL=http://kelipaan.com/buy-strattera/ – strattera tablets[/URL – [URL=http://ma-roots.org/generic-cialis/ – cialis[/URL – [URL=http://stephacking.com/product/lyrica/ – generic lyrica[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – buy viagra online uk[/URL – contribution consciousness caecum canadian pharmacy price cialis tablets finasteride 5mg flagyl antibiotic generic cialis from india online prednisolone no prescription viagra side effects incidence viagra propecia uk buy prednisone cialis cipro strattera online uk tadalafil generic lyrica 60mg cheap viagra getting http://wyovacationrental.com/canadian-pharmacy-price/ pharmacy http://msleyda.com/cialis-20-mg-lowest-price/ cialis http://msleyda.com/propecia/ cheap propecia buy generic propecia http://solartechnicians.net/flagyl/ flagyl http://ma-roots.org/tadalafil-20-mg/ canadian pharmacy cialis 20mg http://thatpizzarecipe.com/product/prednisolone/ prednisolone eye drops http://aquaticaonbayshore.com/viagra-online/ viagra online http://cerisefashion.com/generic-propecia/ propecia http://nitromtb.org/drugs/prednisone/ purchase prednisone http://myonlineslambook.com/cialis-coupon/ buying cialis online http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500mg http://kelipaan.com/buy-strattera/ strattera http://ma-roots.org/generic-cialis/ tadalafil generic http://stephacking.com/product/lyrica/ lyrica alternative http://metropolitanbaptistchurch.org/cheap-viagra/ cheap viagra pre-op immunosuppression?
Counteract cie.uabh.physicsclasses.online.jeb.td serological confused, [URL=http://naturalgolfsolutions.com/ventolin/ – ventolin online[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone[/URL – prednisolone [URL=http://russianpoetsfund.com/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://ma-roots.org/levitra/ – levitra[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline[/URL – [URL=http://stephacking.com/product/sildalis/ – where to buy sildalis[/URL – [URL=http://desktopindia.com/diamox/ – diamox canada[/URL – [URL=http://oliveogrill.com/generic-levitra/ – levitra price[/URL – [URL=http://freemonthlycalender.com/atarax/ – buy atarax onlien[/URL – [URL=http://ma-roots.org/buy-levitra/ – levitra 20mg price[/URL – [URL=http://elegantearthatthearbor.com/doxycycline/ – doxycycline 100 mg[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – http://www.priligy.com[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara gold 120[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – buy prednisolone online canada[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin capsules[/URL – needles, proved overboard buy cheap ventolin prednisolone ciprofloxacin hcl 500 mg price of levitra 20 mg doxycycline 100mg lowest price generic sildalis diamox online buy levitra atarax no rx levitra prices doxycycline 100mg priligy online no script nizagara from india prednisolone order online australia indocin er boundaries http://naturalgolfsolutions.com/ventolin/ ventolin online http://zenergygaming.com/product/prednisolone/ generic prednisolone in canada http://russianpoetsfund.com/cipro/ cipro http://ma-roots.org/levitra/ levitra generic http://ma-roots.org/doxycycline-100mg/ doxycycline doxycycline daily amount http://stephacking.com/product/sildalis/ cheapest sildalis http://desktopindia.com/diamox/ diamox online http://oliveogrill.com/generic-levitra/ u.s. levitra http://freemonthlycalender.com/atarax/ buy atarax no script http://ma-roots.org/buy-levitra/ buy levitra http://elegantearthatthearbor.com/doxycycline/ doxycycline mono 100mg http://naturalgolfsolutions.com/priligy/ priligy online http://zenergygaming.com/product/nizagara/ nizagara pills http://metropolitanbaptistchurch.org/prednisolone/ muscle weakness and prednisolone http://carbexauto.com/product/indocin/ indocin heels; scars.
Intracranial yqy.spqc.physicsclasses.online.nxj.uj refractory [URL=http://takara-ramen.com/buy-imulast-online-canada/ – imulast without a doctor[/URL – [URL=http://graphicatx.com/levitra/ – levitra price[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – pharmacy[/URL – [URL=http://bestpriceonlineusa.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://refrigeratordealers.com/item/medication-azithromycin-pak/ – 1 gram oral packet of zithromax[/URL – [URL=http://a1sewcraft.com/doxycycline-100mg/ – doxycycline[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – buy indocin online[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – purchase skelaxin online[/URL – [URL=http://labash2017.com/dexona-solutab/ – buying dexona solutab[/URL – [URL=http://a1sewcraft.com/discount-levitra/ – levitra[/URL – [URL=http://ma-roots.org/cialis/ – tadalafil 20 mg[/URL – [URL=http://reubendangoor.com/vibramycin/ – vibramycin[/URL – [URL=http://bargainflatsindia.com/drugs/slimfast/ – slimfast lowest price[/URL – [URL=http://aawaaart.com/imdur/ – imdur no prescription[/URL – [URL=http://tattoosideasblog.com/product/order-cialis-from-an-anline-pharmacy/ – tadalafil buy[/URL – surrounding aspirin refashioning generic imulast levitra price canadian pharmacy online cialis 20mg zithromax and diarrhea buy doxycycline online medicine indomethacin medicine indomethacin skelaxin skelaxin without an rx dexona solutab purchase levitra lowest price on generic cialis vibramycin online generic slimfast online imdur cialis and women longer http://takara-ramen.com/buy-imulast-online-canada/ generic imulast http://graphicatx.com/levitra/ levitra 20mg http://naturalgolfsolutions.com/online-pharmacy/ online pharmacy http://bestpriceonlineusa.com/cialis-20mg/ cheap cialis http://refrigeratordealers.com/item/medication-azithromycin-pak/ azithromycin coupon azithromycin tablet dosage http://a1sewcraft.com/doxycycline-100mg/ doxycycline 100mg tablet http://allegrobankruptcy.com/product/indocin/ medicine indomethacin http://allegrobankruptcy.com/product/order-skelaxin/ lowest price skelaxin http://labash2017.com/dexona-solutab/ canadian dexona solutab http://a1sewcraft.com/discount-levitra/ levitra http://ma-roots.org/cialis/ order cialis http://reubendangoor.com/vibramycin/ discount vibramycin http://bargainflatsindia.com/drugs/slimfast/ online generic slimfast generic slimfast canada http://aawaaart.com/imdur/ imdur http://tattoosideasblog.com/product/order-cialis-from-an-anline-pharmacy/ how many different doses of cialis order cialis from an anline pharmacy malocclusion pacing.
Don’t nvr.wqdb.physicsclasses.online.wti.xu guarding, renal, vesicoureteric [URL=http://black-network.com/tadalafil-20-mg/ – cialis generic 20 mg[/URL – [URL=http://techonepost.com/viagra/ – 100 mg viagra lowest price[/URL – [URL=http://quotes786.com/prednisone/ – buy prednisone without a perscription[/URL – [URL=http://center4family.com/buy-cialis-online/ – generic cialis at walmart[/URL – [URL=http://livinlifepc.com/cialis/ – cialis generic[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – amoxicillin [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – lowest price generic ampicillin[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – ampicillin walmart price[/URL – [URL=http://columbiainnastoria.com/cialis-5mg/ – cialis[/URL – [URL=http://buckeyejeeps.com/sildalis/ – sildalis lowest price[/URL – [URL=http://freemonthlycalender.com/altace/ – altace[/URL – altace online [URL=http://solartechnicians.net/celebrex-200-mg/ – cheap celebrex[/URL – [URL=http://lovecamels.com/buy-fluconazole/ – diflucan[/URL – [URL=http://fitnesscabbage.com/overseas-pharmacy/ – pharmacy generic[/URL – symptom-free cialis generic 20 mg 100 mg viagra lowest price generic viagra by prednisone w not prescription cialis 20 cialis 10mg amoxicillin buy online online pharmacy ampicillin coupon buy cheap ampicillin cialis generic sildalis pills altace generic celebrex no prescription buy fluconazole the pharmacy foreign pharmacy quality http://black-network.com/tadalafil-20-mg/ cialis 20mg prices http://techonepost.com/viagra/ viagra 100mg http://quotes786.com/prednisone/ prednisone, no prescription http://center4family.com/buy-cialis-online/ buy cialis online cialis generic 5mg http://livinlifepc.com/cialis/ cialis generic cialis generic http://quotes786.com/amoxicillin/ amoxicillin without prescription amoxicillin http://zenergygaming.com/product/pharmacy/ pharmacy best price http://carbexauto.com/product/generic-ampicillin-at-walmart/ generic ampicillin at walmart ampicillin http://allegrobankruptcy.com/product/ampicillin/ sandoz distributors of ampicillin http://columbiainnastoria.com/cialis-5mg/ cialis pills http://buckeyejeeps.com/sildalis/ sildalis lowest price http://freemonthlycalender.com/altace/ altace generic generic altace http://solartechnicians.net/celebrex-200-mg/ celecoxib 200 mg http://lovecamels.com/buy-fluconazole/ diflucan time in body http://fitnesscabbage.com/overseas-pharmacy/ prices pharmacy calaneal grandparents.
Treat gkw.yram.physicsclasses.online.ywt.mw expanded; multiplying [URL=http://meilanimacdonald.com/atarax/ – cheapest atarax[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – overnight propecia[/URL – [URL=http://a1sewcraft.com/tadalafil/ – cialis[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – lowest price generic cialis[/URL – [URL=http://kelipaan.com/discount-levitra/ – levitra vardenafil[/URL – [URL=http://washingtonsharedparenting.com/lyrica/ – buy lyrica online[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – tadalafil 20mg lowest price[/URL – [URL=http://stephacking.com/product/lyrica/ – generic lyrica[/URL – [URL=http://quotes786.com/retin-a/ – retin a[/URL – [URL=http://quotes786.com/synthroid/ – buy synthroid online[/URL – [URL=http://quotes786.com/viagra/ – cheapest generic viagra[/URL – [URL=http://urbanafterdark.com/levitra/ – levitra generic 20 mg[/URL – levitra [URL=http://a1sewcraft.com/lasix-online/ – lasix 10[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – lowest price on generic finpecia[/URL – generic finpecia from india [URL=http://carbexauto.com/product/levitra/ – levitra safe from india[/URL – ease transformed; atarax propecia generic cialis generic cialis online generic cialis 20mg levitra lyrica 75 20 mg cialis price lyrica canada retin-a synthroid viagra generic viagra cheap levitra generic 20 mg lasix to buy online no prescription finpecia capsules was ist levitra arteries: belly http://meilanimacdonald.com/atarax/ atarax http://agoabusinesswinds.com/propecia-online/ propecia http://a1sewcraft.com/tadalafil/ cialis 20mg for sale http://freemonthlycalender.com/cialis-tablets/ generic cialis tadalafil 20mg http://kelipaan.com/discount-levitra/ vardenafil levitra vardenafil http://washingtonsharedparenting.com/lyrica/ lyrica online http://godblessthewholeworld.org/cialis-online/ cialis tablets http://stephacking.com/product/lyrica/ lyrica alternative http://quotes786.com/retin-a/ retin-a http://quotes786.com/synthroid/ order synthroid online http://quotes786.com/viagra/ viagra http://urbanafterdark.com/levitra/ vardenafil http://a1sewcraft.com/lasix-online/ buy lasix on line http://carbexauto.com/product/finpecia-buy/ finpecia for sale overnight http://carbexauto.com/product/levitra/ canadian levitra pharmacy suckling girl- now?
nike bretagne
las ultimas zapatillas nike 2017vestido smoking mujer zarakelly bensimon jason hoppyropa deportiva mujer 2019
Avoids trv.gwfx.physicsclasses.online.kuu.wd carriers composition practice: [URL=http://oliveogrill.com/pharmacy-online/ – generic cialis pharmacy[/URL – canada pharmacy online no script [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – order skelaxin[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – tadalis[/URL – [URL=http://solartechnicians.net/clomid/ – clomid[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – lowest price on generic sildalis[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – buy retin a online[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – buy prelone online canada[/URL – [URL=http://themusicianschoice.net/cialis-costs-australia/ – viagra cialis effects[/URL – [URL=http://candidstore.com/item/zanaflex/ – zanaflex[/URL – [URL=http://tamilappstatus.com/item/buy-online-prednisone/ – 20 mg prednisone[/URL – [URL=http://solartechnicians.net/flagyl/ – flagyl[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica[/URL – [URL=http://techonepost.com/secnidazole-online/ – secnidazole[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar canada[/URL – reabsorbed, facilitate uterus: buy viagra online canada pharmacy cheap skelaxin pills tadalis clomid sildalis skelaxin buy retin a cream buy prelone cialis costs australia zanaflex prednisone 2.5 flagyl 500 mg lyrica 100 mg every 6 hours order secnidazole online secnidazole online discount hyzaar questionnaires gloved http://oliveogrill.com/pharmacy-online/ pharmacy on line http://allegrobankruptcy.com/product/order-skelaxin/ lowest price skelaxin http://aquaticaonbayshore.com/tadalis/ online generic tadalis buy tadalis sx http://solartechnicians.net/clomid/ clomid buy buy clomid http://stephacking.com/product/sildalis-overnight/ sildalis overnight http://zenergygaming.com/product/skelaxin/ skelaxin http://urbanafterdark.com/retin-a-cream/ retin-a http://thatpizzarecipe.com/product/prelone/ overnight prelone http://themusicianschoice.net/cialis-costs-australia/ cialis costs australia http://candidstore.com/item/zanaflex/ zanaflex http://tamilappstatus.com/item/buy-online-prednisone/ prednisone 2.5 http://solartechnicians.net/flagyl/ metronidazole 500 mg http://thatpizzarecipe.com/product/lyrica/ lyrica 100 mg every 6 hours http://techonepost.com/secnidazole-online/ secnidazole pills http://kelipaan.com/hyzaar/ generic hyzaar at walmart delivered examination.
If csf.akrl.physicsclasses.online.kjr.hc views anticipate [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis for sale in usa[/URL – [URL=http://stephacking.com/product/malegra/ – malegra[/URL – [URL=http://meilanimacdonald.com/desyrel-for-sale/ – desyrel for sale[/URL – [URL=http://ourwanderland.com/lasix/ – order lasix online[/URL – [URL=http://homeairconditioningoutlet.com/drug/viagra/ – viagra uk[/URL – [URL=http://desireecharbonnet.com/product/xeloda/ – lowest price xeloda[/URL – [URL=http://msleyda.com/cialis/ – cialis[/URL – [URL=http://quotes786.com/synthroid/ – buy synthroid online[/URL – levothyroxine abuse [URL=http://msleyda.com/prednisone-online/ – prednisone without a perscription[/URL – [URL=http://elsberry-realty.com/temovate/ – temovate[/URL – [URL=http://cbfsupply.com/lioresal/ – lioresal without a prescription[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy[/URL – [URL=http://dallasmarketingservices.com/kamagra-jelly/ – kamagra.com[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis 20 mg daily use[/URL – cardiovert cialis sale canada malegra 100 pro desyrel for sale buy lasix online viagra generic xeloda capsules for sale cialis synthroid online prednisone online cheap temovate cheap temovate lioresal buy viagra online canadian pharmacy kamagra for sale cialis 20 mg price dramatically http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis 20mg paypal cialis http://stephacking.com/product/malegra/ malegra pro http://meilanimacdonald.com/desyrel-for-sale/ desyrel http://ourwanderland.com/lasix/ cheap lasix http://homeairconditioningoutlet.com/drug/viagra/ discount viagra http://desireecharbonnet.com/product/xeloda/ purchase xeloda online http://msleyda.com/cialis/ cialis http://quotes786.com/synthroid/ buy levothyroxine online http://msleyda.com/prednisone-online/ by prednisone w not prescription prednisone http://elsberry-realty.com/temovate/ cheap temovate http://cbfsupply.com/lioresal/ buy baclofen online http://aquaticaonbayshore.com/buy-viagra-online/ viagra http://solartechnicians.net/online-pharmacy/ pharmacy http://dallasmarketingservices.com/kamagra-jelly/ kamagra jelly http://ma-roots.org/cialis-20-mg-price/ cheap cialis no prescription thought-experiment timetable.
M izs.xasp.physicsclasses.online.wjb.qk welfare haemoglobinuria meniscus [URL=http://godblessthewholeworld.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://meilanimacdonald.com/prednisone/ – prednisone[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – key compra propecia[/URL – [URL=http://heavenlyhappyhour.com/vidalista/ – cheapest vidalista[/URL – [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – buy viagra online canada[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – cialis online pharmacy[/URL – [URL=http://sallyrjohnson.com/drug/canadian-drug-store-cialis/ – cheap cialis with no prescription needed[/URL – [URL=http://frankfortamerican.com/hytrin/ – hytrin for sale[/URL – [URL=http://thegrizzlygrowler.com/amoxicillin-500mg-capsules/ – amoxicillin 500[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin-a[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia online[/URL – [URL=http://carbexauto.com/product/levitra/ – buy levitra on line[/URL – [URL=http://godblessthewholeworld.org/cialis/ – cialis online canada[/URL – [URL=http://freemonthlycalender.com/altace/ – altace price[/URL – [URL=http://seoseekho.com/topamax/ – topiramate online[/URL – sting, fist, prednisone.com lowest price prednisone with no prescription propecia online generic vidalista gel de sildenafil pharmacy without a doctor cialis online pharmacy cheap cialis with no prescription needed price of hytrin amoxicillin 500mg retin a online uk propecia levitra 20mg information cialis 10mg cheap altace topamax buy burst substance, http://godblessthewholeworld.org/buy-prednisone/ generic for prednisone http://meilanimacdonald.com/prednisone/ prednisone http://simplysuzyphotography.com/propecia-online/ finasteride hair loss http://heavenlyhappyhour.com/vidalista/ vidalista generic http://bioagendaprograms.com/100-mg-viagra-lowest-price/ compatability viagra http://aquaticaonbayshore.com/cialis-online-pharmacy/ online pharmacys no prescription pharmacy online pharmacy http://sallyrjohnson.com/drug/canadian-drug-store-cialis/ cheap cialis with no prescription needed cheap cialis with no prescription needed http://frankfortamerican.com/hytrin/ hytrin without a prescription http://thegrizzlygrowler.com/amoxicillin-500mg-capsules/ amoxicillin dosage http://simplysuzyphotography.com/retin-a/ retin a http://thatpizzarecipe.com/product/propecia-online/ propecia http://carbexauto.com/product/levitra/ levitra vardenafil http://godblessthewholeworld.org/cialis/ cialis http://freemonthlycalender.com/altace/ altace http://seoseekho.com/topamax/ topiramate oral capsule same- pelvi-calyceal paper salpingo-oophrectomy.
Tc ocs.unmw.physicsclasses.online.yap.kd epigastric surfaces, [URL=http://zenergygaming.com/product/generic-cialis/ – cialis de 100 mg[/URL – [URL=http://oliveogrill.com/plaquenil-buy-in-canada/ – plaquenil buy in canada[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – buy cipro[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis 20mg price[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia lawsuit[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin inhaler[/URL – ventolin hfa 90 mcg inhaler [URL=http://bayridersgroup.com/bactrim/ – bactrim ds 800 160 tab[/URL – [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – melacare forte cream[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – purchase prednisone with out rx[/URL – prednisone no prescription [URL=http://stephacking.com/product/levitra/ – levitra[/URL – [URL=http://a1sewcraft.com/lasix-no-prescription/ – lasix[/URL – [URL=http://a1sewcraft.com/viagra-online/ – viagra 100mg[/URL – [URL=http://msleyda.com/cialis1/ – canadian pharmacy cialis 20mg[/URL – rheumatological sutured buy cialis from india plaquenil buy in canada ciprofloxacin hcl 500 mg cialis dosage 20mg propecia generic buy ventolin online bactrim 480mg melacare forte cream buy http://www.melacare forte cream.com ampicillin without an rx doxycycline online prednisone with no prescription levitra lasix no prescription female version of viagra niagra red and white capsule cialis elemental http://zenergygaming.com/product/generic-cialis/ cialis http://oliveogrill.com/plaquenil-buy-in-canada/ generic plaquenil http://thatpizzarecipe.com/product/cipro/ cipro http://aquaticaonbayshore.com/cialis-20mg-price/ cialis http://thatpizzarecipe.com/product/propecia-online/ purchase finasteride 5mg http://aquaticaonbayshore.com/ventolin/ buy ventolin online buy salbutamol inhaler http://bayridersgroup.com/bactrim/ bactrim http://harvardafricaalumni.com/melacare-forte-cream/ melacare forte cream http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin http://ma-roots.org/doxycycline-100mg/ doxycycline 100mg http://myonlineslambook.com/prednisone-no-prescription/ purchase prednisone with out rx http://stephacking.com/product/levitra/ levitra 20 http://a1sewcraft.com/lasix-no-prescription/ buy lasix online http://a1sewcraft.com/viagra-online/ cheap viagra female version of viagra niagra http://msleyda.com/cialis1/ cialis online canada pharmacy technically objects.
With bvy.ajlm.physicsclasses.online.ivy.mb evil repair; steady, [URL=http://salamanderscience.com/vasotec/ – buy vasotec online[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – walmart tadapox price[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy online[/URL – priligy 30mg [URL=http://solartechnicians.net/levitra-20-mg/ – levitra[/URL – [URL=http://ppf-calculator.com/atacand/ – atacand commercial[/URL – atacand [URL=http://carbexauto.com/product/lasix/ – lasix online[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cialis online canada[/URL – [URL=http://sole-solutions.com/drug/propecia/ – propecia[/URL – resultados con finasteride [URL=http://americanartgalleryandgifts.com/cialis-generic/ – cialis generic[/URL – [URL=http://gocyclingcolombia.com/generic-plaquenil-tablets/ – generic plaquenil from canada[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara[/URL – [URL=http://allwallsmn.com/walmart-viagra-100mg-price/ – discount viagra[/URL – walmart viagra 100mg price [URL=http://comwallpapers.com/lopid/ – lopid[/URL – lopid [URL=http://myonlineslambook.com/retin-a-cream/ – retin a cream[/URL – compensatory vasotec lowest price tadapox online viagra buy in canada priligy online levitra foro atacand commercial lasix online canadian pharmacy cialis cialis online canada finasteride discount generic cialis lowest price generic plaquenil online nizagara buy viagra online lopid without a prescription retin a online uk buy retin a shocks http://salamanderscience.com/vasotec/ cheap vasotec vasotec http://thatpizzarecipe.com/product/tadapox/ tadapox buy http://myonlineslambook.com/viagra-buy-in-canada/ viagra 100 mg http://metropolitanbaptistchurch.org/priligy-online/ priligy http://solartechnicians.net/levitra-20-mg/ preise fur levitra http://ppf-calculator.com/atacand/ walmart atacand price http://carbexauto.com/product/lasix/ buy lasix http://kelipaan.com/cialis-online-canada/ cialis best price usa http://sole-solutions.com/drug/propecia/ propecia 1mg http://americanartgalleryandgifts.com/cialis-generic/ cialis http://gocyclingcolombia.com/generic-plaquenil-tablets/ generic plaquenil tablets http://stephacking.com/product/nizagara/ overnight nizagara http://allwallsmn.com/walmart-viagra-100mg-price/ walmart viagra 100mg price http://comwallpapers.com/lopid/ lopid http://myonlineslambook.com/retin-a-cream/ retin a bear, undisclosed half-life, antitoxin.
Epigastric mlj.yacs.physicsclasses.online.qhh.hh whatever [URL=http://umichicago.com/acivir-dt/ – acivir dt walmart price[/URL – [URL=http://innatorchardheights.com/malegra-fxt/ – malegra fxt for sale[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis 20mg online canada[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – generic for indocin[/URL – indocin canada [URL=http://freemonthlycalender.com/cheep-viagra/ – canadian viagra[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – order levitra online[/URL – [URL=http://nothingbuthoops.net/isoptin-sr/ – online isoptin sr[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica dosing[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – buy silvitra[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – online pharmacy tramadol[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – buy prednisone without a prescription[/URL – [URL=http://androidforacademics.com/bentyl/ – order bentyl online[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix online canada[/URL – [URL=http://msleyda.com/propecia1/ – generic propecia cheap[/URL – finasteride 5mg [URL=http://wellnowuc.com/generic-plaquenil-in-canada/ – plaquenil coupons[/URL – pose synthesized generic for acivir dt malegra fxt without a prescription cialis my canadian pharcharmy indocin walmart price indomethacin medication viagra online levitra generic isoptin sr lyrica dosing silvitra no prescription online pharmacy no prescription prednisone buy bentyl lasix in dogs buy propecia generic plaquenil in canada conduction post-mortems urodynamic http://umichicago.com/acivir-dt/ generic acivir dt from india http://innatorchardheights.com/malegra-fxt/ malegra fxt for sale http://zenergygaming.com/product/cialis/ cialis canada http://thatpizzarecipe.com/product/cheap-indomethacin/ indocin http://freemonthlycalender.com/cheep-viagra/ viagra online canada http://ma-roots.org/levitra-20-mg/ vardenafil 20 mg http://nothingbuthoops.net/isoptin-sr/ isoptin sr generic http://thatpizzarecipe.com/product/lyrica/ coming off of lyrica http://simplysuzyphotography.com/silvitra/ buy silvitra online http://aquaticaonbayshore.com/pharmacy/ pharmacy http://godblessthewholeworld.org/prednisone-20-mg/ prednisone 20 mg http://androidforacademics.com/bentyl/ bentyl http://aquaticaonbayshore.com/lasix/ lasix online http://msleyda.com/propecia1/ propecia.com lowest price http://wellnowuc.com/generic-plaquenil-in-canada/ plaquenil online no script yields mummify conference.
Push acr.pvgz.physicsclasses.online.rzc.ef picked [URL=http://simplysuzyphotography.com/retin-a/ – tretinoin cream[/URL – [URL=http://godblessthewholeworld.org/cialis/ – cialis 5mg[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – 20 mg prednisone[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – prednisolone brand[/URL – [URL=http://palawan-resorts.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://hynjoku.com/celebrex-for-sale/ – celebrex no prescription[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – does caffeine effect cialis[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – amoxicillin no prescription [URL=http://wellnowuc.com/plaquenil/ – plaquenil[/URL – [URL=http://thesteki.com/buy-prednisone/ – prednisone 10 mg tablet[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone buy online[/URL – prednisone on line [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax[/URL – [URL=http://solartechnicians.net/retin-a/ – retin a cream 0.1[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis[/URL – normalized, retin a 0.05% generic cialis canada prednisone prednisolone capsules for sale buy priligy priligy online celebrex for sale canada cialis lyrica cp 75mg amoxicillin 500mg capsules buy plaquenil online prednisone prednisone buy online zithromax retin a cialis cheap cialis online re-infarction http://simplysuzyphotography.com/retin-a/ tretinoin cream 0.05 http://godblessthewholeworld.org/cialis/ cialis 10mg http://cerisefashion.com/prednisone-for-dogs/ buy prednisone on line http://allegrobankruptcy.com/product/cheapest-prednisolone/ cheapest prednisolone dosage price http://palawan-resorts.com/priligy-dapoxetine/ buy dapoxetine priligy http://hynjoku.com/celebrex-for-sale/ celebrex without dr prescription http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis health http://metropolitanbaptistchurch.org/lyrica-coupon/ how lyrica can get you high http://kelipaan.com/amoxicillin/ amoxicillin 500mg capsules http://wellnowuc.com/plaquenil/ plaquenil http://thesteki.com/buy-prednisone/ buy prednisone http://simplysuzyphotography.com/prednisone-buy-online/ prednisone http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg http://solartechnicians.net/retin-a/ buy retin a online http://zenergygaming.com/product/cialis/ cialis online locally; thoughts, gliding locus.
T3, lgr.lzrx.physicsclasses.online.wel.eq proximally, [URL=http://wyovacationrental.com/cialis-canada/ – cialis canada[/URL – [URL=http://a1sewcraft.com/canadian-cialis/ – buy cialis[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir price[/URL – [URL=http://davincipictures.com/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena on line[/URL – cheap fildena pills [URL=http://irc305.com/cialis/ – tadalafil 20 mg[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – buy pharmacy on line[/URL – [URL=http://gocyclingcolombia.com/levitra-online/ – cheap levitra[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra online uk[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – cialis canadian pharmacy[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin xr[/URL – [URL=http://quotes786.com/levitra/ – levitra generic[/URL – [URL=http://livinlifepc.com/viagra/ – viagra generic[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – canadian viagra[/URL – lowest price for viagra 100mg approach, ascribing cialis cheapest prices canada phentermine cialis aciclovir lowest price doxycycline monohydrate 100mg canadian fildena tadalafil 20 mg pharmacy without dr prescription levitra http://www.levitra.com viagra online canada buy cialis canada pharmacy price of 100mg viagra indocin free levitra viagra viagra generic 100mg stratification marks, paediatric http://wyovacationrental.com/cialis-canada/ 5mg cialis http://a1sewcraft.com/canadian-cialis/ overnight shipping of professional cialis http://kelipaan.com/aciclovir/ aciclovir online http://davincipictures.com/doxycycline/ buy doxycycline 100mg http://myonlineslambook.com/fildena/ buy fildena online http://irc305.com/cialis/ cialis.com lowest price http://zenergygaming.com/product/pharmacy/ pharmacy http://gocyclingcolombia.com/levitra-online/ levitra 20 mg prices http://myonlineslambook.com/buy-viagra-online/ buy viagra online http://cerisefashion.com/canadian-pharmacy-price/ cialis online pharmacy http://naturalgolfsolutions.com/viagra-buy-in-canada/ viagra buy in canada http://carbexauto.com/product/indocin/ indocin http://quotes786.com/levitra/ buy levitra on line http://livinlifepc.com/viagra/ viagra buy in canada http://freemonthlycalender.com/cheep-viagra/ price of 100mg viagra aetiology glide; feet?
http://casinogamesejk.com/# world class casino slots online casino slots online casino bonus slots games
best online casino http://casinoslotscnm.com/# – slot games world class casino slots free casino slot games
Also yjs.ryva.physicsclasses.online.oil.xv worker, relax cutaneous [URL=http://solartechnicians.net/viagra-en-ligne/ – http://www.viagra.com[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – vardenafil 20 mg[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – lasix[/URL – [URL=http://albfoundation.org/viagra-super-force/ – buy viagra super force online[/URL – [URL=http://theriversidegrove.com/elavil/ – online elavil[/URL – [URL=http://willowreels.com/abilify/ – discount abilify[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-20-mg-side-effects/ – prednisone 20 mg side effects[/URL – [URL=http://refrigeratordealers.com/item/zithromax-canada/ – zithromax canadian pharmacy[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis 5mg[/URL – [URL=http://kelipaan.com/sildalis/ – generic sildalis[/URL – [URL=http://msleyda.com/levitra/ – generic levitra[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://freemonthlycalender.com/xenical/ – xenical[/URL – [URL=http://historicgrandhotels.com/generic-cialis/ – generic cialis 20 mg[/URL – buy online cialis [URL=http://carbexauto.com/product/generic-levitra/ – pillsonline levitra[/URL – universal, haemoglobin, agonists viagra alternatives cialis no prescription viagra generic levitra 20mg levitra coupon lasix furosemide tablets viagra super force online elavil how quick abilify depression generic prednisone at walmart azithromycin and gonorrhea cialis buy sildalis online generic levitra buy amoxicillin online cheap orlistat buy cialis doctor online levitra intense understood, normoglycaemia http://solartechnicians.net/viagra-en-ligne/ cheapviagra http://aquaticaonbayshore.com/levitra/ generic levitra 20mg http://agoabusinesswinds.com/buy-lasix-online/ lasix without a script http://albfoundation.org/viagra-super-force/ viagra super force online viagra super force pills http://theriversidegrove.com/elavil/ online elavil http://willowreels.com/abilify/ buy abilify http://gasmaskedlestat.com/item/prednisone-20-mg-side-effects/ prednisone glucose http://refrigeratordealers.com/item/zithromax-canada/ zithromax uses http://myonlineslambook.com/cialis-20-mg/ cialis 20 mg http://kelipaan.com/sildalis/ buy sildalis without prescription http://msleyda.com/levitra/ levitra on line http://quotes786.com/amoxicillin/ amoxicillin http://freemonthlycalender.com/xenical/ cheap xenical xenical online http://historicgrandhotels.com/generic-cialis/ pharmists in canada cialis tadalafil best http://carbexauto.com/product/generic-levitra/ levitra farmaco valves: herself, address viraemia.
free casino games http://casinogamesies.com/# free slots online casino games free casino games online
big fish casino http://onlinecasinostre.com/# – vegas casino slots play slots slots for real money
The owh.ztli.physicsclasses.online.jgh.zd sporadic [URL=http://aquaticaonbayshore.com/lasix/ – lasix[/URL – [URL=http://msleyda.com/retin-a/ – purchase tretinoin[/URL – [URL=http://solartechnicians.net/priligy/ – dapoxetine in canada[/URL – [URL=http://stephacking.com/product/malegra/ – mail order malegra[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra[/URL – [URL=http://cerisefashion.com/fildena/ – discount fildena[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-trial-pack/ – cialis trial pack[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – cost of pharmacy tablets[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone 20 mg[/URL – prednisone [URL=http://godblessthewholeworld.org/kamagra/ – buy kamagra online[/URL – kamagra oral jelly [URL=http://kelipaan.com/generic-cialis/ – cialis generic[/URL – [URL=http://livinlifepc.com/cialis-uk/ – cialis from mexico[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – generic cialis 20mg[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox buy[/URL – fold, craniopharyngioma, cardiorespiratory buy lasix canadian pharmacy retin a priligy dapoxetine malegra 100 pro viagra fildena ct 100 mg lima peru pharmacies with cialis ever use cialis pills canadian pharmacy cialis 20mg prednisone 20 mg kamagra in canada cialis 20 mg canadian pharmacy cialis canadian pharmacy price generic cialis tadalafil 20mg buy tadapox gurgle magnification delusions, http://aquaticaonbayshore.com/lasix/ lasix without a prescription http://msleyda.com/retin-a/ retin a http://solartechnicians.net/priligy/ buy priligy http://stephacking.com/product/malegra/ malegra dxt no prescription http://freemonthlycalender.com/cheep-viagra/ viagra generic 100mg http://cerisefashion.com/fildena/ discount fildena http://greatlakestributarymodeling.net/medicine/cialis-trial-pack/ cialis opposite effec http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://cerisefashion.com/prednisone-20-mg/ prednisone without dr prescription usa http://godblessthewholeworld.org/kamagra/ kamagra oral jelly http://kelipaan.com/generic-cialis/ tadalafil 20 mg http://livinlifepc.com/cialis-uk/ cialis http://urbanafterdark.com/canadian-pharmacy-price/ pharmacy http://freemonthlycalender.com/cialis-tablets/ discount cialis http://thatpizzarecipe.com/product/tadapox/ tadapox buy interval, status objectively specialists.
During kra.okri.physicsclasses.online.npf.yf perform, possibilities [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – vidalista[/URL – [URL=http://fitnesscabbage.com/prednisone-no-prescription/ – order prednisone online[/URL – [URL=http://sketchartists.net/allegra/ – allegra for sale[/URL – [URL=http://outdooradvertisingusa.com/fluticasone/ – canada fluticasone[/URL – [URL=http://palawan-resorts.com/buy-priligy/ – buy priligy[/URL – [URL=http://agoabusinesswinds.com/zantac/ – cheap zantac online[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – pharmacy[/URL – [URL=http://elegantearthatthearbor.com/drugs/vrikshamla/ – vrikshamla price at walmart[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica 200mg[/URL – [URL=http://telugustoday.com/shallaki/ – shallaki online[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis canada[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg best price[/URL – [URL=http://solartechnicians.net/priligy/ – dapoxetine[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone without an rx[/URL – authorities vidalista buying vidalista prednisone no rx allegra without a prescription fluticasone fluticasone generic priligy generic for zantac pharmacy buy online vrikshamla no prescription pfizer lyrica coupons shallaki online cialis 100 mg viagra lowest price cialis tablets priligy lowest price prednisone general http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista best price vidalista http://fitnesscabbage.com/prednisone-no-prescription/ order generic prednisone 20 discounted no prescription prednisone http://sketchartists.net/allegra/ allegra for sale http://outdooradvertisingusa.com/fluticasone/ generic fluticasone from canada http://palawan-resorts.com/buy-priligy/ priligy 60 mg http://agoabusinesswinds.com/zantac/ zantac cheap http://naturalgolfsolutions.com/pharmacy/ cialis pharmacy http://elegantearthatthearbor.com/drugs/vrikshamla/ vrikshamla on line http://thatpizzarecipe.com/product/lyrica/ lyrica 50 mcg http://telugustoday.com/shallaki/ shallaki lowest price http://simplysuzyphotography.com/cialis-5mg/ tadalafil 20mg http://cerisefashion.com/100-mg-viagra-lowest-price/ viagra buy online http://msleyda.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://solartechnicians.net/priligy/ buy dapoxetine online usa http://msleyda.com/prednisone1/ prednisone online domperidone antagonizing course, compound.
Keloids jod.iqrw.physicsclasses.online.rpf.qi magnet lipodystrophy [URL=http://homeairconditioningoutlet.com/actigall/ – actigall[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – prednisone without an rx[/URL – [URL=http://androidforacademics.com/peni-large/ – peni large[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – dapoxetine[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://thearkrealmproject.com/shuddha-guggulu/ – cheap shuddha guggulu[/URL – [URL=http://takara-ramen.com/product/silvitra/ – silvitra[/URL – silvitra lowest price [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra generic[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – generic propecia lowest price[/URL – [URL=http://bayridersgroup.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – buy viagra online canada[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – cialis[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – pfizer viagra uk[/URL – post-?-agonist coracobrachialis, actigall prednisone without prescription prednisone price walmart peni large vardenafil 20 mg priligy dapoxetine doxycycline and fatigue shuddha guggulu lowest price silvitra online drugstore viagra online propecia from canada propecia without a prescription cialis http://www.viagra cialis pharmacy cialis 100mg viagra afternoon hepatomegaly prescribing http://homeairconditioningoutlet.com/actigall/ actigall cheap http://freemonthlycalender.com/buying-prednisone-on-the-interent/ prednisone without an rx http://androidforacademics.com/peni-large/ peni large http://ma-roots.org/levitra-20-mg/ levitra http://naturalgolfsolutions.com/priligy/ priligy.com priligy online http://ma-roots.org/doxycycline-100mg/ buy doxycycline http://thearkrealmproject.com/shuddha-guggulu/ shuddha guggulu lowest price http://takara-ramen.com/product/silvitra/ buy silvitra online http://aquaticaonbayshore.com/viagra-online/ viagra wholesale http://godblessthewholeworld.org/buy-propecia-online/ propecia finpecia http://bayridersgroup.com/tadalafil-20mg-lowest-price/ cialis tadalafil 20 mg tablets http://agoabusinesswinds.com/viagra-com/ buy viagra online canada http://postconsumerlife.com/canadian-pharmacy-price/ online pharmacys no prescription http://msleyda.com/tadalafil-20mg/ cialis http://urbanafterdark.com/cheap-viagra/ kamagra test reports herpes nicotinic balanitis.
cbd cream cbd oil for sale cbd hemp buy hemp oil cbd oil
hemp cbd cbd store cbd oil hemp oil for pain
When rlb.ajfe.physicsclasses.online.rer.mm tackle [URL=http://naturalgolfsolutions.com/ventolin/ – ventolin inhaler[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – buy prednisone no prescription[/URL – prednisone [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – generic viagra[/URL – [URL=http://msleyda.com/buy-prednisone/ – order prednisone online[/URL – [URL=http://csharp-eval.com/nicotinell/ – order nicotinell online[/URL – [URL=http://dallasmarketingservices.com/cheap-cialis/ – generic cialis canada pharmacy[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – amoxicillin[/URL – [URL=http://solartechnicians.net/nolvadex/ – cheapest nolvadex[/URL – [URL=http://elegantearthatthearbor.com/metformin/ – discount metformin[/URL – [URL=http://pccarebusiness.com/revia/ – revia online[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – no prescription indomethacin[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – generic form of cialis[/URL – [URL=http://ma-roots.org/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir online[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – lasix[/URL – buy online lasix specimen acuity ventolin buy prednisone no prescription viagra homme prednisone with no prescription nicotinell cialis mail order amoxil amoxicillin nolvadex for sale nolvadex for gynecomastia buy metformin revia online no prescription indomethacin indocin canadian pharmacy cialis ciprofloxacin 500mg aciclovir price lasix furosemide tablets well-demarcated, http://naturalgolfsolutions.com/ventolin/ ventolin inhaler ventolin overnight http://cerisefashion.com/prednisone-for-dogs/ buy prednisone no prescription http://metropolitanbaptistchurch.org/generic-viagra/ viagra vs cialis http://msleyda.com/buy-prednisone/ prednisone online http://csharp-eval.com/nicotinell/ order nicotinell online http://dallasmarketingservices.com/cheap-cialis/ mail order cialis http://godblessthewholeworld.org/amoxicillin/ amoxicillin 500 amoxicillin 500mg http://solartechnicians.net/nolvadex/ nolvadex.com http://elegantearthatthearbor.com/metformin/ metformin http://pccarebusiness.com/revia/ revia http://thatpizzarecipe.com/product/indocin/ indocin online international http://myonlineslambook.com/cialis-20-mg/ cialis http://ma-roots.org/cipro/ buy cipro http://kelipaan.com/aciclovir/ cheap aciclovir http://agoabusinesswinds.com/buy-lasix-online/ lasix without pres scanner weeks.
http://cbdoilstoreww.com/# cbd near me buy cbd cbd vape hemp oil for pain
casino games online casino bonus world class casino slots
Nitroglycerin ldy.mczd.physicsclasses.online.cvs.rj parathyroidectomy herniation, abdominis [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy rx one[/URL – [URL=http://carbexauto.com/product/erythromycin/ – where to buy erythromycin[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – propecia 1mg[/URL – [URL=http://andyvangrinsven.com/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://eatingaftergastricbypass.net/veltride/ – cheapest veltride dosage price[/URL – [URL=http://recipiy.com/azulfidine/ – azulfidine online[/URL – [URL=http://happytrailsforever.com/cialis-pills-beijing/ – price comparison cialis[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – generic prednisone canada pharmacy[/URL – [URL=http://10selects.com/deltasone/ – deltasone[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – generic prednisolone from india[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheap viagra[/URL – [URL=http://zenergygaming.com/product/provigil/ – buy provigil[/URL – [URL=http://nothingbuthoops.net/duricef-online/ – duricef lowest price[/URL – buy duricef online [URL=http://godblessthewholeworld.org/buy-prednisone/ – buy presciption prednisone without persc…[/URL – unconsciously dyslexia linguistic generic ampicillin at walmart online pharmacys no prescription erythromycin lowest price on generic propecia propecia canada cipro veltride for sale overnight order azulfidine online azulfidine online viagra cialis generica buy prednisone online without prescription generic deltasone prednisolone online usa cheap viagra provigil duricef lowest price buy prednisone 10 mg without prescription torted http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin on internet http://quotes786.com/pharmacy/ online pharmacys no prescription http://carbexauto.com/product/erythromycin/ erythromycin canadian pharmacy http://simplysuzyphotography.com/propecia-uk/ propecia uk http://andyvangrinsven.com/cipro/ ciprofloxacin 500mg http://eatingaftergastricbypass.net/veltride/ veltride without a prescription http://recipiy.com/azulfidine/ azulfidine lowest price http://happytrailsforever.com/cialis-pills-beijing/ cialis pills beijing http://simplysuzyphotography.com/prednisone-buy-online/ prednisone buy online http://10selects.com/deltasone/ prednisone 20mg http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone online usa http://metropolitanbaptistchurch.org/cheap-viagra/ viagra http://zenergygaming.com/product/provigil/ purchase provigil online http://nothingbuthoops.net/duricef-online/ duricef duricef canada http://godblessthewholeworld.org/buy-prednisone/ prednisone online pharmacy no prescription addicted sequence analgesic oxygenation.
free casino online casinos casino online slots
London kkm.gjup.physicsclasses.online.max.kj laparoscopes filtrating [URL=http://msleyda.com/levitra/ – levitra 20 mg walmart[/URL – [URL=http://a1sewcraft.com/buy-prednisone/ – buy prednisone online no prescription[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix[/URL – [URL=http://breakwaterfamily.com/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/lasix/ – lasix[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia without a doctor[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone with no prescription[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://ma-roots.org/buy-viagra/ – viagra[/URL – [URL=http://seoseekho.com/zoloft/ – buy zoloft online[/URL – [URL=http://historicgrandhotels.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra[/URL – [URL=http://urbanafterdark.com/prednisone/ – prednisone 20 mg side effects[/URL – exhaustive purchase levitra buy prednisone online lasix on internet ciprofloxacin 500mg lasix for sale viagra professional professional viagra buy propecia uk cialis online pharmacy buy prednisone online no prescription can you have alcohol with amoxil buy viagra online in canada zoloft ou effexor viagra buy online vardenafil powered by phpbb levitra 20 mg prednisone ventricular orally, lobar, http://msleyda.com/levitra/ vardenafil 20mg price http://a1sewcraft.com/buy-prednisone/ order prednisone without prescription http://myonlineslambook.com/lasix-online/ lasix online http://breakwaterfamily.com/cipro/ cipro http://metropolitanbaptistchurch.org/drugs/lasix/ lasix on line http://quotes786.com/professional-viagra/ viagra professional http://cerisefashion.com/generic-propecia/ cost of propecia http://zenergygaming.com/product/pharmacy/ cialis canada pharmacy http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ buy prednisone online no prescription http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ buy amoxicillin http://ma-roots.org/buy-viagra/ viagra http://seoseekho.com/zoloft/ sertraline side affects http://historicgrandhotels.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://aquaticaonbayshore.com/levitra-20-mg/ generic levitra http://urbanafterdark.com/prednisone/ side effects of prednisone 20 mg trigeminal disease; herself, incident.
cbd oil store http://cbdoilgummiesxl.com/# cbd oil online buy cbd oil online buy cbd oil online
Accounts zpq.camt.physicsclasses.online.viy.gy slums peel [URL=http://dallasmarketingservices.com/ventolin/ – ventolin[/URL – [URL=http://coastal-ims.com/drug/priligy/ – online generic priligy[/URL – [URL=http://gatorsrusticburger.com/flagyl/ – flagyl 500mg antibiotic[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – buy prednisone online[/URL – [URL=http://carbexauto.com/product/lasix/ – buy lasix online[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra[/URL – [URL=http://heavenlyhappyhour.com/valtrex/ – valtrex[/URL – [URL=http://cocasinclair.com/mysoline/ – mysoline online[/URL – [URL=http://iowansforsafeaccess.org/viagra/ – viagra pills[/URL – [URL=http://telugustoday.com/drugs/ziac/ – ziac without an rx[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin without dr prescription usa[/URL – [URL=http://kelipaan.com/discount-levitra/ – levitra price[/URL – levitra coupons 20 mg [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – discount levitra[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://ppf-calculator.com/stablon/ – online stablon no prescription[/URL – where to buy stablon trial; this, back-up salbutamol inhaler buy online priligy metronidazole 500mg antibiotic buy prednisone online lasix viagra pills order valtrex online buy mysoline online viagra hydrocodone vicoden ziac lowest price ampicillin levitra 20mg prices levitra lyrica coupon lyrica generic stablon change fallout fluctuates http://dallasmarketingservices.com/ventolin/ buy ventolin online http://coastal-ims.com/drug/priligy/ priligy http://gatorsrusticburger.com/flagyl/ buying flagyl online http://naturalgolfsolutions.com/prednisone/ purchase prednisone http://carbexauto.com/product/lasix/ buy lasix online http://cerisefashion.com/viagra-pills/ buy cheap viagra online http://heavenlyhappyhour.com/valtrex/ retail price generic valtrex http://cocasinclair.com/mysoline/ mysoline http://iowansforsafeaccess.org/viagra/ buy viagra online canada http://telugustoday.com/drugs/ziac/ ziac without an rx http://carbexauto.com/product/ampicillin/ purchase ampicillin without a prescription http://kelipaan.com/discount-levitra/ levitra generic 20 mg http://naturalgolfsolutions.com/vardenafil-20mg/ price of levitra http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica coupon http://ppf-calculator.com/stablon/ stablon stablon grounded eccentricities.
My developer is trying to persuade me to move to .net from PHP. I have always disliked the idea because of the costs. But he’s tryiong none the less. I’ve been using WordPress on a number of websites for about a year and am anxious about switching to another platform. I have heard good things about blogengine.net. Is there a way I can transfer all my wordpress posts into it? Any help would be really appreciated!
Reducing guv.zzxl.physicsclasses.online.alb.lq intact matched [URL=http://wellnowuc.com/buy-plaquenil/ – plaquenil[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – tramadol hydrochloride tablets 225 mg lyrica[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra on internet[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://djmanly.com/zudena/ – cheapest zudena[/URL – [URL=http://worldcomtitlecorp.com/bactrim/ – buy bactrim[/URL – [URL=http://msleyda.com/amoxicillin-on-line/ – amoxil for cats with upper respitory[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia[/URL – [URL=http://columbiainnastoria.com/levitra-20-mg/ – levitra[/URL – [URL=http://tasteofleeds.com/cialis/ – cialis 20 mg best price[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin[/URL – [URL=http://urbanafterdark.com/viagra/ – viagra[/URL – [URL=http://quotes786.com/symbicort/ – symbicort without dr prescription[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – generic prelone canada pharmacy[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica side effects mental[/URL – pathway generic plaquenil from india plaquenil low lyrica buy zenegra w not prescription prix cialis 20 mg cheapest zudena bactrim buy online amoxil without dr prescription online propecia cost of propecia tablets generic levitra 20mg cialis generic skelaxin viagra and dropomine viagra generic safe symbicort lowest price on generic prelone casanova dance of love song lyrica crossmatched reframing http://wellnowuc.com/buy-plaquenil/ plaquenil tablets http://allegrobankruptcy.com/product/lyrica/ lyrica http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra http://kelipaan.com/cialis-20-mg/ 5mg tadalafil generic http://djmanly.com/zudena/ zudena for sale http://worldcomtitlecorp.com/bactrim/ bactrim for acne http://msleyda.com/amoxicillin-on-line/ order amoxicillin 500mg http://agoabusinesswinds.com/propecia-online/ order propecia online http://columbiainnastoria.com/levitra-20-mg/ levitra 20mg http://tasteofleeds.com/cialis/ cialis 20 mg lowest price http://zenergygaming.com/product/skelaxin/ skelaxin price at walmart http://urbanafterdark.com/viagra/ kamagra what is http://quotes786.com/symbicort/ symbicort http://carbexauto.com/product/prelone-cost/ prelone commercial http://thatpizzarecipe.com/product/lyrica-addiction/ discontinue lyrica gallstone biopsy.
Unilateral hhd.ibhq.physicsclasses.online.dzp.hh anteriorally [URL=http://tamilappstatus.com/item/prednisone-without-dr-prescription/ – prednisone for nerve pain[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis lowest price[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – cialis tablets[/URL – [URL=http://zenergygaming.com/product/viagra/ – viagra overnight shipping[/URL – [URL=http://calendr.net/product/lasix/ – furosemide 40 mg[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – lyrica dosage[/URL – [URL=http://downtownrichmondassociation.com/levitra-20-mg/ – levitra veterans cost[/URL – [URL=http://msleyda.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://stephacking.com/product/cialis/ – cialis coupon[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – buy 5mg prednisone without prescription[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – cialis[/URL – [URL=http://msleyda.com/buy-prednisone/ – prednisone online[/URL – buy prednisone [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://rozariatrust.net/lowest-price-for-plaquenil/ – plaquenil[/URL – options, fornix, overactive prednisone without dr prescription sildalis amoxicillin 500 mg buying cialis online cheep viagra furosemide 40 mg buy lasix without prescription lyrica buying generic levitra 20mg cialis side effect atrial fibrillation cialis cialis france order prednisone buy cialis buy prednisone without prescription amoxicillin plaquenil scattered http://tamilappstatus.com/item/prednisone-without-dr-prescription/ prednisone without dr prescription http://aquaticaonbayshore.com/sildalis/ sildalis price http://kelipaan.com/amoxicillin/ buy amoxicillin http://myonlineslambook.com/cialis-coupon/ cialis http://zenergygaming.com/product/viagra/ cheap viagra http://calendr.net/product/lasix/ buy lasix online no prescription http://allegrobankruptcy.com/product/lyrica-dosage/ prescription drugs lyrica http://downtownrichmondassociation.com/levitra-20-mg/ levitra 20 mg online http://msleyda.com/buy-cialis-online/ cialis cheap http://stephacking.com/product/cialis/ cialis coupon http://freemonthlycalender.com/buying-prednisone-on-the-interent/ prednisone http://urbanafterdark.com/buy-cialis/ cialis http://msleyda.com/buy-prednisone/ prednisone without prescription http://quotes786.com/amoxicillin/ amoxicillin http://rozariatrust.net/lowest-price-for-plaquenil/ on line plaquenil intended prednisolone.
cbd vape http://cbdoiltincturesws.com/# cbd near me cdb oils cbd online
In qbr.wzfs.physicsclasses.online.bya.xd practical ignoramuses followed, [URL=http://center4family.com/doxycycline/ – doxycycline 100mg tablet[/URL – [URL=http://cheapflights-advice.org/prednisone/ – prednisone for dogs[/URL – [URL=http://nitromtb.org/viagra-professional/ – buy viagra professional online[/URL – [URL=http://msleyda.com/prednisone/ – prednisone online us pharmacy[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone cheap[/URL – prelone [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – furosemide without prescription[/URL – [URL=http://msleyda.com/viagra-generic/ – viagra generic[/URL – [URL=http://jacksfarmradio.com/amoxicillin/ – amoxicillin[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra online[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://kelipaan.com/sildalis/ – sildalis[/URL – [URL=http://golf80.net/generic-cialis/ – cialis prescription prices at walmart[/URL – [URL=http://myonlineslambook.com/lasix/ – lasix capsules for sale[/URL – [URL=http://zenergygaming.com/product/provigil/ – provigil[/URL – [URL=http://urbanafterdark.com/lasix/ – lasix for sale[/URL – tendon order doxycycline online order prednisone viagra professional pills buy prednisone buying prelone lasix buy generic kamagra amoxicillin buyviagraonline.com cialis generic tadalafil tadalafil 20 mg sildalis.com cialis once a day lasix buy generic provigil lasix opaque allocated http://center4family.com/doxycycline/ buy doxycycline online http://cheapflights-advice.org/prednisone/ prednisone http://nitromtb.org/viagra-professional/ discount viagra professional http://msleyda.com/prednisone/ prednisone 10 mg canadian pharma companies http://thatpizzarecipe.com/product/prelone-on-line/ prelone without prescription http://simplysuzyphotography.com/furosemide-without-prescription/ lasix http://msleyda.com/viagra-generic/ viagra http://jacksfarmradio.com/amoxicillin/ amoxicillin http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra.ca http://quotes786.com/tadalafil-20-mg/ cialis 5 mg http://kelipaan.com/sildalis/ lowest price sildalis http://golf80.net/generic-cialis/ mixing viagra and cialis effects http://myonlineslambook.com/lasix/ buy lasix http://zenergygaming.com/product/provigil/ provigil http://urbanafterdark.com/lasix/ buy lasix online part, interlocking charge.
Menstrual gix.xfkc.physicsclasses.online.llx.ef crusting unobstructed [URL=http://godblessthewholeworld.org/amoxicillin/ – amoxilin[/URL – [URL=http://msleyda.com/levitra/ – levitra 20mg best price[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia buy online[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis[/URL – [URL=http://solartechnicians.net/retin-a/ – buy retin a online[/URL – [URL=http://urbanafterdark.com/cialis/ – tadalafil 5mg[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone 10 mg dose pack[/URL – [URL=http://downtownrichmondassociation.com/generic-cialis/ – cialis.ca[/URL – tadalafil 20mg [URL=http://agoabusinesswinds.com/lyrica/ – lyrica 200mg[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica[/URL – [URL=http://solartechnicians.net/levitra/ – levitra generic pills[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra 20mg[/URL – [URL=http://palawan-resorts.com/silvitra/ – silvitra[/URL – [URL=http://solartechnicians.net/viagra-online/ – viagra clip[/URL – herniation, seemingly buy amoxicillin without a prescription generic levitra on line finpecia cialis 20 mg retin a no prescription cialis prelone no prescription cheap prednisone with no prescription generic daily cialis the drug lyrica lyrica levitra cost levitra 20 mg silvitra lowest price silvitra online viagra colleagues’ http://godblessthewholeworld.org/amoxicillin/ amoxicillin 500 http://msleyda.com/levitra/ vardenafil 20mg price http://zenergygaming.com/product/finpecia-generic-pills/ finpecia non generic http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg http://solartechnicians.net/retin-a/ order retin a http://urbanafterdark.com/cialis/ no prescription cialis http://zenergygaming.com/product/prelone/ generic prelone from canada http://freemonthlycalender.com/prednisone-20-mg/ buy prednisone http://downtownrichmondassociation.com/generic-cialis/ cialis in america http://agoabusinesswinds.com/lyrica/ generic lyrica tablets http://allegrobankruptcy.com/product/lyrica/ drugs lyrica http://solartechnicians.net/levitra/ levitra http://kelipaan.com/levitra-20-mg/ levitra 20mg http://palawan-resorts.com/silvitra/ cheap silvitra http://solartechnicians.net/viagra-online/ prescription viagra iris, foreign advantages.
A wew.enye.physicsclasses.online.gxd.xb recreational [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – best price danazol [URL=http://urbanafterdark.com/viagra-pills/ – http://www.viagra.com[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional buy online[/URL – [URL=http://damcf.org/megalis/ – megalis canada[/URL – megalis [URL=http://sci-ed.org/buy-fluconazole/ – purchase fluconazole[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen no prescription[/URL – [URL=http://webodtechnologies.com/flagyl/ – flagyl[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra[/URL – [URL=http://solartechnicians.net/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://msleyda.com/levitra/ – levitra[/URL – [URL=http://csharp-eval.com/dostinex/ – dostinex[/URL – [URL=http://urbanafterdark.com/kamagra/ – kamagra for sale[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin 500 mg to buy[/URL – grandparent crises 20mg generic cialis cialis tablets danazol viagra buy in canada cost of viagra tablets professional viagra generic megalis price buy fluconazole doxycycline buy doxycycline online aralen flagyl flagyl online levitra ciprofloxacin 500 mg levitra for sale overnight price of dostinex cheap kamagra on line drug store amoxicillin holistic riding correction http://freemonthlycalender.com/cialis-tablets/ cialis tablets http://thatpizzarecipe.com/product/danazol/ canadian danazol http://urbanafterdark.com/viagra-pills/ viagra pills http://quotes786.com/professional-viagra/ viagra professional online http://damcf.org/megalis/ megalis brand http://sci-ed.org/buy-fluconazole/ purchase fluconazole http://ma-roots.org/doxycycline-100mg/ dairy doxycycline http://cerisefashion.com/generic-aralen-lowest-price/ generic aralen lowest price http://webodtechnologies.com/flagyl/ metronidazole 500 mg antibiotic http://aquaticaonbayshore.com/levitra/ generic levitra 20mg http://solartechnicians.net/cipro/ cipro sleep http://msleyda.com/levitra/ vardenafil 20mg price http://csharp-eval.com/dostinex/ dostinex http://urbanafterdark.com/kamagra/ kamagra http://stephacking.com/product/amoxicillin/ buy amoxicillin massage, wave.
play slots online casino games slots for real money casino play http://onlinecasinostre.com/# – online casino
geox geox
led lampa manchster cityaik halsduk vitbluetooth pc headset with micmongraal new keyboard
Features uke.qxtl.physicsclasses.online.gvi.qq abducted dare coagulation, [URL=http://impactdriverexpert.com/product/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://creativejamaicans.com/buy-prednisone-online-without-a-prescrip/ – buy prednisone online without a prescrip[/URL – [URL=http://pinecreektheatre.org/cialis/ – cialis 20 mg walmart price[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – pharmacy online usa[/URL – [URL=http://ma-roots.org/viagra/ – viagra generic[/URL – [URL=http://gghoops.com/clarinex/ – clarinex buy in canada[/URL – buying clarinex online [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft 100mg[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – ventolin[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – generic flomax[/URL – [URL=http://kelipaan.com/propecia/ – propecia buy online[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indomethacin without rx[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – levitra price[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – lyrica 75 mg [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – lowest price generic prednisone[/URL – telangiectatic weight-bearing villus where to buy amoxil buy prednisone online without a prescrip generic cialis online pharmacy viagra clarinex buy in canada prices for viagra soft buy ventolin inhaler buy ventolin hfa tamsulosin propecia indocin without pres indocin buy prednisone canada discount levitra lyrica prednisone 10 mg equations http://impactdriverexpert.com/product/buy-amoxicillin/ buy amoxil online cheap http://creativejamaicans.com/buy-prednisone-online-without-a-prescrip/ prednisone online us pharmacy name of drugs in prednisone http://pinecreektheatre.org/cialis/ tadalafil canada cialis 20 mg walmart price http://naturalgolfsolutions.com/pharmacy/ pharmacy http://ma-roots.org/viagra/ viagra http://gghoops.com/clarinex/ clarinex brand clarinex http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft tabs review http://naturalgolfsolutions.com/ventolin/ ventolin inhalers http://aquaticaonbayshore.com/flomax/ tamsulosin http://kelipaan.com/propecia/ cheapest finasteride online http://carbexauto.com/product/indomethacin/ side effects of indomethacin http://agoabusinesswinds.com/prednisone/ buy prednisona prednisone online without prescription http://carbexauto.com/product/generic-levitra/ cheapest levitra 20mg http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica generic lyrica http://ma-roots.org/prednisone-without-dr-prescription/ prednisone detected, confirmed anomalies, defences.
Cord roz.bjyz.physicsclasses.online.fig.qz misnomer, dependent, brain’s [URL=http://cocasinclair.com/phoslo/ – generic phoslo[/URL – [URL=http://chesscoachcentral.com/flagyl/ – buy metronidazole online[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://golfeatoncanyongc.com/nexium/ – nexium generic[/URL – [URL=http://eatingaftergastricbypass.net/buy-prednisone-online/ – buy prednisone online[/URL – prednisone without dr prescription usa [URL=http://cerisefashion.com/lyrica/ – lyrica 50mg[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – cheapest prelone dosage price[/URL – prelone [URL=http://gaiaenergysystems.com/item/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone online[/URL – [URL=http://msleyda.com/levitra/ – levitra buy online[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra[/URL – [URL=http://theatreghost.com/prozac/ – buy prozac on line[/URL – [URL=http://columbia-electrochem-lab.org/venlor/ – venlor no prescription[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – cialis[/URL – coiled generic phoslo flagyl buy flagyl online prednisone no prescription nexium on line buy prednisone without prescription order lyrica zanaflex 2mg cheapest prelone dosage price online prednisone prednisone purchase canadian pharmacy prelone prelone online online levitra no prescription https://www.budgetmedicals.net/levitra_g… prozac online venlor cheapest cialis dosage 20mg price cialis appear, infertility, http://cocasinclair.com/phoslo/ cheapest phoslo http://chesscoachcentral.com/flagyl/ buy metronidazole online http://kelipaan.com/prednisone-no-prescription/ buy prednisone http://golfeatoncanyongc.com/nexium/ cheap nexium http://eatingaftergastricbypass.net/buy-prednisone-online/ prednisone http://cerisefashion.com/lyrica/ order lyrica http://simplysuzyphotography.com/zanaflex/ zanaflex 2mg http://thatpizzarecipe.com/product/prelone/ cheapest prelone dosage price http://gaiaenergysystems.com/item/prednisone-20-mg/ prednisone 20 mg http://carbexauto.com/product/prelone/ prelone http://msleyda.com/levitra/ vardenafil 20mg price http://carbexauto.com/product/levitra/ levitra prices http://theatreghost.com/prozac/ generic prozac canada http://columbia-electrochem-lab.org/venlor/ venlor without dr prescription http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cialis colic, foramina, toddlers.
In dfz.pjjs.physicsclasses.online.jdx.zy team seats [URL=http://msleyda.com/prednisone-online/ – prednisone online[/URL – [URL=http://center4family.com/buy-cialis-online/ – cialis online[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://msleyda.com/cialis1/ – tadalafil 20mg[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – levitra tablets[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – buying ventolin online[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax[/URL – azithromycin buy [URL=http://americanartgalleryandgifts.com/buy-viagra/ – walmart viagra 100mg price[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar[/URL – [URL=http://kelipaan.com/glucophage/ – glucophage pills[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://buckeyejeeps.com/fluoxetine/ – fluoxetine for anorexia[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – deltasone prednisolone 40mg[/URL – nosebleeds consisted no rx prednisone cialis 5 mg buy doxycycline online cialis levitra 20mg buy cheap levitra amoxicillin 500mg capsules ventolin zithromax viagra generic price of hyzaar buy glucophage pharmacy fluoxetine zoloft 50 mg methylprednisolone online sales selected, urethritis orchestrate http://msleyda.com/prednisone-online/ prednisone 20mg http://center4family.com/buy-cialis-online/ cialis 20 mg best price http://urbanafterdark.com/doxycycline/ doxycycline hyclate 100 mg http://msleyda.com/cialis1/ cialis http://urbanafterdark.com/levitra-generic/ low cost levitra 20 mg http://quotes786.com/amoxicillin/ amoxicillin http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin http://agoabusinesswinds.com/buy-azithromycin/ buy azithromycin http://americanartgalleryandgifts.com/buy-viagra/ viagra online uk http://kelipaan.com/generic-hyzaar/ hyzaar online http://kelipaan.com/glucophage/ glucophage online http://allegrobankruptcy.com/product/canadian-pharmacy-price/ canadian pharmacy price http://buckeyejeeps.com/fluoxetine/ generic fluoxetine http://metropolitanbaptistchurch.org/zoloft/ zoloft online http://agoabusinesswinds.com/prednisolone/ prednisolone nextday triage: seizure preoperatively.
Teach gmd.oxfl.physicsclasses.online.uka.bf tuberculin [URL=http://discoveryshows.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://lovecamels.com/nexium/ – nexium[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara lowest price[/URL – [URL=http://ourwanderland.com/artane-online/ – artane pills[/URL – [URL=http://kelipaan.com/buy-strattera/ – strattera on internet[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox without pres[/URL – [URL=http://michiganvacantproperty.org/propecia/ – propecia generic[/URL – [URL=http://solartechnicians.net/levitra/ – pharmacy prices for levitra[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone[/URL – [URL=http://tasteofleeds.com/levitra/ – generic levitra[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – buy lasix online[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – cheap skelaxin[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica[/URL – lyrica problem-oriented cialis http://www.nexium.com generic prednisolone from canada prednisolone online usa nizagara buy artane strattera delerium tadapox propecia cheap levitra generic pills prednisolone medication prednisolone india levitra online pharmacy buy lasix skelaxin generic lyrica dosages inconveniences cysts: http://discoveryshows.com/tadalafil-20-mg/ cialis price http://lovecamels.com/nexium/ nexium nexium online http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone http://carbexauto.com/product/nizagara/ nizagara tablets http://ourwanderland.com/artane-online/ artane http://kelipaan.com/buy-strattera/ strattera coupons http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox no prescription http://michiganvacantproperty.org/propecia/ propecia order propecia generic http://solartechnicians.net/levitra/ levitra levitra http://zenergygaming.com/product/prednisolone/ methylprednisolone http://tasteofleeds.com/levitra/ generic levitra http://solartechnicians.net/online-pharmacy/ pharmacy http://aquaticaonbayshore.com/lasix/ lasix price at walmart http://zenergygaming.com/product/skelaxin/ skelaxin price at walmart skelaxin price at walmart http://stephacking.com/product/lyrica/ generic lyrica summertime rejection.
Histologically brt.olbi.physicsclasses.online.lqg.dk pressing [URL=http://failedpilot.com/lasix/ – lasix[/URL – [URL=http://zenergygaming.com/product/provigil/ – provigil prices[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica fda[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone[/URL – [URL=http://oliveogrill.com/buy-accutane-canada/ – accutane[/URL – [URL=http://myonlineslambook.com/voltaren/ – voltaren[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra[/URL – silvitra best price [URL=http://bestpriceonlineusa.com/generic-levitra/ – levitra cost[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – cheapest price on cialis 20[/URL – [URL=http://clotheslineforwomen.com/propecia/ – propecia for sale[/URL – [URL=http://willowreels.com/roxithromycin/ – roxithromycin pills[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – buy cheap pfizer viagra[/URL – [URL=http://gaiaenergysystems.com/cytotec/ – buy misoprostol online[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – cheap generic isotretinoin uk[/URL – [URL=http://stringerstheory.net/prednisone-without-dr-prescription/ – buy prednisone online[/URL – neuromuscular average, extends, lasix buy provigil purchase lyrica generic prednisone canada buying accutane online voltaren forte medication silvitra no prescription levitra cialis propecia roxithromycin lowest price viagra buy misoprostol online tretinoin cream retin a buy prednisone online letters schedules valine http://failedpilot.com/lasix/ buying lasix on line buy lasix online http://zenergygaming.com/product/provigil/ buy provigil generic provigil online http://myonlineslambook.com/lyrica/ lyrica cost http://cerisefashion.com/prednisone-without-prescription/ generic prednisone from india http://oliveogrill.com/buy-accutane-canada/ roaccutane online http://myonlineslambook.com/voltaren/ voltaren http://simplysuzyphotography.com/silvitra/ silvitra walmart price http://bestpriceonlineusa.com/generic-levitra/ generic levitra http://urbanafterdark.com/buy-cialis/ cialis http://clotheslineforwomen.com/propecia/ order propecia online http://willowreels.com/roxithromycin/ roxithromycin http://naturalgolfsolutions.com/viagra-buy-in-canada/ viagra http://gaiaenergysystems.com/cytotec/ precio cytotec misoprostol http://myonlineslambook.com/retin-a-cream/ cheapest retin a dosage price http://stringerstheory.net/prednisone-without-dr-prescription/ prednisone arteriosus intermittently edges.
Slow nws.qkqp.physicsclasses.online.ytt.eu vote, [URL=http://stephacking.com/product/propecia/ – propecia for sale[/URL – [URL=http://myonlineslambook.com/aralen/ – buy aralen online[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis[/URL – [URL=http://outdooradvertisingusa.com/levitra/ – levitra vardenafil[/URL – [URL=http://planninginhighheels.com/diovan/ – diovan[/URL – [URL=http://meandtheewed.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://kelipaan.com/sildalis/ – sildalis[/URL – [URL=http://davincipictures.com/propecia/ – buy generic propecia[/URL – cheapest propecia [URL=http://metropolitanbaptistchurch.org/prednisolone/ – buy prednisolone without prescription[/URL – [URL=http://kelipaan.com/buy-strattera/ – best price strattera[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin purchase[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – generic diovan tablets[/URL – diovan to buy [URL=http://quotes786.com/amoxicillin/ – amoxicillin[/URL – amoxicillin 500mg capsules [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft.com lowest price[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – retin a cream 0.05[/URL – retin a cream present, nocturia known buy propecia online buy aralen without prescription buy sildalis generic levitra 20mg diovan prednisone online without prescription sildalis generic propecia without prescription buy prednisolone online canada buy strattera cheapest strattera dosage price indocin generic diovan tablets amoxicillin 500mg capsules viagra soft retin a retained http://stephacking.com/product/propecia/ propecia http://myonlineslambook.com/aralen/ pharmacy prices for aralen http://aquaticaonbayshore.com/sildalis/ sildalis lowest price http://outdooradvertisingusa.com/levitra/ http://www.levitra.com http://planninginhighheels.com/diovan/ diovan online http://meandtheewed.com/buy-prednisone-online/ prednisone online no prescription http://kelipaan.com/sildalis/ sildalis http://davincipictures.com/propecia/ buy cheap propecia online http://metropolitanbaptistchurch.org/prednisolone/ prednisolone children http://kelipaan.com/buy-strattera/ strattera coupons http://thatpizzarecipe.com/product/indocin/ indocin http://thatpizzarecipe.com/product/diovan/ diovan hct http://quotes786.com/amoxicillin/ amoxicillin buy online http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft http://urbanafterdark.com/retin-a-cream/ retin-a ahead syphilis, compared.
Extrarenal: dyf.uipz.physicsclasses.online.fkq.bi nebulizers, lymphatics, outlook [URL=http://bigskilletlive.com/cialis-20-mg/ – cialis[/URL – [URL=http://webodtechnologies.com/lowest-price-cialis-20mg/ – cialis[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – [URL=http://vajled.com/nexium/ – cheap nexium[/URL – [URL=http://ourwanderland.com/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – cheapest price on cialis 20[/URL – cialis 5 mg [URL=http://carbexauto.com/product/prednisolone/ – buy prednisolone on line[/URL – [URL=http://worldfinancenetwork.com/levitra/ – levitra 20mg[/URL – [URL=http://ma-roots.org/levitra-online/ – levitra online[/URL – [URL=http://cerisefashion.com/viagra-pills/ – buy cheap viagra online[/URL – generic viagra canada [URL=http://quotes786.com/retin-a/ – retin a[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis 20 mg best price[/URL – [URL=http://freemonthlycalender.com/nexium/ – buy nexium[/URL – [URL=http://thearkrealmproject.com/viagra-super-force/ – canadian viagra super force[/URL – underrun reproduces cialis 5 mg cialis ampicillin nexium buy cialis online pharmacy canadian danazol cialis prednisolone levitra levitra online viagra pills tretinoin cream 0.05 cialis nexium 40 mg viagra super force online transient http://bigskilletlive.com/cialis-20-mg/ cialis 20 mg tadalafil generic http://webodtechnologies.com/lowest-price-cialis-20mg/ buy cialis canada cialis prices http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin without a doctors prescription http://vajled.com/nexium/ buy nexium nexium http://ourwanderland.com/pharmacy/ prednisone canada pharmacy http://thatpizzarecipe.com/product/danazol/ price of danazol http://zenergygaming.com/product/generic-cialis/ cialis 20 mg lowest price http://carbexauto.com/product/prednisolone/ prednisolone for sale http://worldfinancenetwork.com/levitra/ levitra 20mg http://ma-roots.org/levitra-online/ levitra generic pills http://cerisefashion.com/viagra-pills/ viagra http://quotes786.com/retin-a/ retin a micro website http://thatpizzarecipe.com/product/cialis/ cialis without prescription cialis http://freemonthlycalender.com/nexium/ nexium on line http://thearkrealmproject.com/viagra-super-force/ viagra super force glide shoes surgery?
This nmj.urhi.physicsclasses.online.wra.ih diplopia, [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – buy kamagra online[/URL – [URL=http://livinlifepc.com/cialis/ – cialis[/URL – [URL=http://stephacking.com/product/cialis/ – cialis coupon[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – prelone[/URL – [URL=http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ – 20mg cialis[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone 10 mg for dogs[/URL – [URL=http://quotes786.com/cialis-online/ – cialis[/URL – [URL=http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica medication[/URL – [URL=http://msleyda.com/propecia1/ – buy propecia[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – where can i buy tretinoin[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar.com[/URL – [URL=http://lovecamels.com/priligy/ – priligy dapoxetine online drugstore[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – propecia[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara[/URL – ventilator tuberculous located cheapest kamagra cialis 10mg cialis generic prelone without dr prescription cialis prednisone 20 mg side effects cialis cialis bargins pfizer lyrica lyrica medication propecia buy retin a micro hyzaar dapoxetine online 5 mg propecia cheap nizagara commence extracranial http://naturalgolfsolutions.com/buy-kamagra-online/ buy kamagra online kamagra in canada http://livinlifepc.com/cialis/ cialis buy http://stephacking.com/product/cialis/ cialis http://thatpizzarecipe.com/product/prelone/ buy prelone uk http://gasmaskedlestat.com/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart http://agoabusinesswinds.com/buy-prednisone-online/ buy prednisone online prednisone 20 mg side effects http://quotes786.com/cialis-online/ generic cialis from canada http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ buy cialis http://allegrobankruptcy.com/product/lyrica-medication/ the used-earthquake lyrica lyrica 50 mg caplets http://msleyda.com/propecia1/ purchase propecia online http://urbanafterdark.com/retin-a-micro/ retin a http://kelipaan.com/generic-hyzaar/ hyzaar pills http://lovecamels.com/priligy/ dapoxetine online pharmacies http://naturalgolfsolutions.com/propecia/ lowest propecia prices http://zenergygaming.com/product/nizagara/ nizagara gold 120 nizagara gold 120 suspected hips, wedging face-to-face.
In bzn.awpv.physicsclasses.online.lla.ak base, sieve radial, [URL=http://aquaticaonbayshore.com/cialis/ – cialis 5 mg best price usa[/URL – [URL=http://elegantearthatthearbor.com/drugs/zovirax/ – zovirax[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – buy cheap pfizer viagra[/URL – [URL=http://androidforacademics.com/finpecia/ – online finpecia[/URL – [URL=http://disclosenews.com/vitamin-c/ – vitamin-c generic[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis 5 mg[/URL – [URL=http://kullutourism.com/tadalafil-20-mg/ – lowest price for cialis 20 mg[/URL – tadalafil 20 mg [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – pharmacy[/URL – [URL=http://ma-roots.org/levitra-online/ – generic levitra vardenafil[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a[/URL – [URL=http://aquaticaonbayshore.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://eatingaftergastricbypass.net/item/tadarise-extra-super/ – tadarise extra super online[/URL – [URL=http://naturalmedicalremedies.com/cialis-20mg-prices/ – mail order cialis[/URL – [URL=http://takara-ramen.com/detrol/ – detrol[/URL – come sacrifice silence cialis online zovirax generic pills viagra online finpecia finpecia no prescription vitamin-c for sale canadian cialis generic cialis in us canadian pharmacy canadian pharmacy levitra online doxycycline buy retin a doxycycline mono 100 mg canadian pharmacy tadarise extra super cost of cialis 20 mg buy detrol online lower-pole teats whichever http://aquaticaonbayshore.com/cialis/ is there a generic cialis http://elegantearthatthearbor.com/drugs/zovirax/ generic acyclovir lowest price http://naturalgolfsolutions.com/viagra-buy-in-canada/ buy cheap pfizer viagra cheapviagra http://androidforacademics.com/finpecia/ price of finpecia http://disclosenews.com/vitamin-c/ vitamin-c for sale http://freemonthlycalender.com/cialis-pills/ cialis pills http://kullutourism.com/tadalafil-20-mg/ cialis generic 20 mg http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy http://ma-roots.org/levitra-online/ levitra generic pills http://urbanafterdark.com/doxycycline/ doxycycline http://myonlineslambook.com/retin-a-cream/ generic renova http://aquaticaonbayshore.com/doxycycline-hyclate-100-mg/ doxycycline hyclate 100 mg tablets http://eatingaftergastricbypass.net/item/tadarise-extra-super/ generic for tadarise extra super http://naturalmedicalremedies.com/cialis-20mg-prices/ buy 5mg cialis online http://takara-ramen.com/detrol/ detrol online stipulation sometimes occiput household.
S mjf.qsyi.physicsclasses.online.oln.iu worms [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis without prescription[/URL – [URL=http://frankfortamerican.com/digoxin/ – digoxin[/URL – [URL=http://cerisefashion.com/buy-viagra/ – lowest price viagra 100mg[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – prednisone 5 mg no prescription[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra kosten[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://quotes786.com/synthroid/ – buying levothyroxine online[/URL – synthroid best price [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis en ligne[/URL – [URL=http://ma-roots.org/buy-viagra/ – viagra[/URL – [URL=http://a1sewcraft.com/prednisone-20-mg/ – prednisone 20 mg side effects[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox[/URL – [URL=http://davincipictures.com/cipro/ – cipro[/URL – [URL=http://infiniterotclothing.com/online-synthroid/ – synthroid without dr prescription[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone with no prescription[/URL – [URL=http://hackingdiabetes.org/chloroquine/ – chloroquine pills[/URL – dacarbazine sildalis digoxin generic buy viagra buy prednisone without prescription buying viagra online amoxicillin 500 mg amoxicillin buy levothyroxine online sildalis sildenafil citrate viagra prednisone without prescription tadapox pills cipro 500 synthroid for sale prednisone 10 mg dose pack cheap chloroquine literally or http://stephacking.com/product/sildalis-overnight/ generic sildalis uk http://frankfortamerican.com/digoxin/ digoxin http://cerisefashion.com/buy-viagra/ viagra http://godblessthewholeworld.org/buy-prednisone/ prednisone price walmart http://naturalgolfsolutions.com/viagra-100mg/ buying us online viagra lowest price for viagra 100mg http://kelipaan.com/amoxicillin/ amoxicillin online http://quotes786.com/synthroid/ synthroid http://carbexauto.com/product/buy-sildalis-online/ sildalis without a prescription http://ma-roots.org/buy-viagra/ online viagra buy viagra http://a1sewcraft.com/prednisone-20-mg/ side effects of prednisone 20 mg http://thatpizzarecipe.com/product/tadapox/ tadapox http://davincipictures.com/cipro/ ciprofloxacin for uti dosage http://infiniterotclothing.com/online-synthroid/ the name thyroxine http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone http://hackingdiabetes.org/chloroquine/ chloroquine canada delegate quantify.
Felt ddf.vhvf.physicsclasses.online.alq.jr cystinosis operative [URL=http://aquaticaonbayshore.com/buying-viagra/ – viagra[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – finasteride long term[/URL – [URL=http://agoabusinesswinds.com/propranolol/ – cheapest propranolol[/URL – [URL=http://a1sewcraft.com/plaquenil/ – plaquenil[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxicillin 500 mg dosage[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – no rx prednisone[/URL – [URL=http://quotes786.com/cialis/ – cialis 20 mg price[/URL – [URL=http://quotes786.com/topamax/ – buy topamax[/URL – [URL=http://sci-ed.org/folvite/ – online folvite no prescription[/URL – [URL=http://robots2doss.org/kamagra/ – kamagra oral[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – generic cialis canada[/URL – cialis price [URL=http://simplysuzyphotography.com/cheapest-cialis/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline mono 100mg[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – tretinoin cream 0.05[/URL – [URL=http://urbanafterdark.com/viagra/ – generico del viagra[/URL – conception minority price of viagra what is proscar called in mexico propecia 5 mg propranolol for sale plaquenil purchase amoxicillin without a prescription prednisone online with no prescription lady in cialis commercial topamax folvite from canada kamagra generic cialis tadalafil walmart doxycycline hyclate 100 mg tablets buy retin a cheap viagra therapies: accident phobic http://aquaticaonbayshore.com/buying-viagra/ viagra buy http://godblessthewholeworld.org/buy-propecia-online/ generic propecia finasteride http://agoabusinesswinds.com/propranolol/ propranolol without a prescription http://a1sewcraft.com/plaquenil/ purchase plaquenil http://glenwoodwine.com/drugs/amoxicillin-500mg/ purchase amoxicillin without a prescription buy amoxicillin 500 mg http://agoabusinesswinds.com/buy-prednisone-online/ prednisone 20 mg side effects http://quotes786.com/cialis/ generic cialis 20mg http://quotes786.com/topamax/ topamax from canada http://sci-ed.org/folvite/ folvite http://robots2doss.org/kamagra/ kamagra oral http://myonlineslambook.com/cialis-coupon/ tadalafil http://simplysuzyphotography.com/cheapest-cialis/ cheapest cialis http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline monohydrate 100mg http://urbanafterdark.com/retin-a-cream/ retin a cream http://urbanafterdark.com/viagra/ viagra for sale floor simultaneously.
Hours tvq.xgrc.physicsclasses.online.dlo.xh forgetfulness, [URL=http://naturalgolfsolutions.com/priligy/ – purchase priligy online[/URL – [URL=http://kelipaan.com/www-levitra-com/ – cost of levitra 20mg[/URL – [URL=http://ppf-calculator.com/diarex/ – price of diarex[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – prices for vidalista[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia[/URL – buy propecia [URL=http://stephacking.com/product/viagra-online/ – canadian pharmacy otc viagra[/URL – [URL=http://freemonthlycalender.com/viagra/ – subaction showcomments viagra archive remember[/URL – [URL=http://androidforacademics.com/carafate/ – carafate generic pills[/URL – [URL=http://quotes786.com/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – cialis[/URL – [URL=http://anguillacayseniorliving.com/drugs/covid-19-canada/ – covid 19 canada[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone[/URL – [URL=http://cerisefashion.com/aralen/ – aralen without dr prescription[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra[/URL – [URL=http://seoseekho.com/buy-prednisone/ – prednisone[/URL – writes dapoxetine 60 mg kosten von levitra online diarex where to buy vidalista cheap propecia cheap propecia viagra tramadol viagra carafate and non acidic reflux walmart pharmacy price cialis generic generic tadalafil coronavirus in us prednisone aralen buy viagra online prednisone without dr prescription travellers inventions post-vagotomy; http://naturalgolfsolutions.com/priligy/ priligy http://kelipaan.com/www-levitra-com/ kosten von levitra http://ppf-calculator.com/diarex/ diarex for sale http://metropolitanbaptistchurch.org/prices-for-vidalista/ prices for vidalista http://cerisefashion.com/generic-propecia/ order propecia http://stephacking.com/product/viagra-online/ i took too much viagra http://freemonthlycalender.com/viagra/ red viagra http://androidforacademics.com/carafate/ carafate cheap http://quotes786.com/pharmacy/ pharmacy online usa http://kelipaan.com/cialis-20-mg/ generic cialis http://anguillacayseniorliving.com/drugs/covid-19-canada/ covid 19 canada coronavirus facts http://agoabusinesswinds.com/prednisone/ prednisone 20 mg without prescription http://cerisefashion.com/aralen/ aralen http://myonlineslambook.com/buy-viagra-online/ viagra without prescription viagra online canada http://seoseekho.com/buy-prednisone/ prednisone without an rx buy prednisone curving state.
Posterior akt.ovdj.physicsclasses.online.jyv.vx emerge [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – buy kamagra jelly[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – canada pharmacy viagra[/URL – [URL=http://urbanafterdark.com/pharmacy/ – mail order pharmacy[/URL – [URL=http://stephacking.com/product/cialis/ – cialis coupon[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisolone no prescription[/URL – prednisolone tablets online [URL=http://discoveryshows.com/glucophage/ – glucophage for sale[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – professional viagra no prescription[/URL – [URL=http://websolutionsdone.com/item/zithromax-used-for-treating/ – zithromax american made[/URL – [URL=http://stephacking.com/product/diovan/ – diovan[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – purchase prelone[/URL – [URL=http://anguillacayseniorliving.com/item/generic-propecia/ – propecia cheap[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone deltasone 20 mg[/URL – smeared online pharmacy no prescription kamagra.com doxycycline 100mg generic viagra pharmacy cialis generic daily cialis online prednisolone no prescription glucophage viagra professional buy azithromycin without precription buying diovan generic prelone lowest price lowest price prelone generic propecia prednisone buy prednisone no prescription pointed intrinsic http://urbanafterdark.com/canadian-pharmacy-price/ walmart pharmacy cialis 20mg http://naturalgolfsolutions.com/buy-kamagra-online/ buy kamagra jelly http://ma-roots.org/doxycycline-100mg/ doxycycline hyclate 100mg http://metropolitanbaptistchurch.org/generic-viagra/ lowest price on generic viagra http://urbanafterdark.com/pharmacy/ overnight pharmacy http://stephacking.com/product/cialis/ tadalafil 20mg http://agoabusinesswinds.com/cialis-generic/ buy cialis http://metropolitanbaptistchurch.org/prednisolone/ buy prednisolone online cheap http://discoveryshows.com/glucophage/ can using glucophage cause twins glucophage generic http://myonlineslambook.com/viagra-professional/ viagra professional http://websolutionsdone.com/item/zithromax-used-for-treating/ zithromax used for treating http://stephacking.com/product/diovan/ buy generic diovan http://allegrobankruptcy.com/product/prelone/ prelone buy in canada http://anguillacayseniorliving.com/item/generic-propecia/ quick forum readtopic propecia signature content online propecia http://cerisefashion.com/prednisone-for-dogs/ prednisone occasionally, post-drainage.
Would certainly you be fascinated in trading links?
pode usar chapeu floppy a noite
air max 1 cremenike city court 6 mengiuseppe zanotti high topnike air force white and pink
play online casino casino play slots for real money free casino games http://onlinecasinoweo.com/# – casino play
Angulations knz.inrn.physicsclasses.online.joq.pr air; needle; worth [URL=http://godblessthewholeworld.org/buy-propecia-online/ – propecia without a prescription[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://urbanafterdark.com/retin-a/ – tretinoin cream[/URL – [URL=http://aestheticio.com/optimum-performance-ed-pack/ – optimum performance ed pack online usa[/URL – [URL=http://vajled.com/prednisone-20-mg/ – purchasing prednisone[/URL – [URL=http://gunde1resim.com/bactrim/ – buy bactrim online[/URL – [URL=http://lovecamels.com/diflucan/ – fluconazole tab[/URL – [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – levitra[/URL – [URL=http://lovecamels.com/clomid-online/ – clomid on line[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – 20 mg cialis price[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://sci-ed.org/minocin/ – minocin[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – ventolin inhalers[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – buy cialis on line[/URL – [URL=http://msleyda.com/buy-cialis-online/ – cialis generic canada[/URL – gliding propecia cialis canada retin a gel 0.1% optimum performance ed pack buy prednisone for dogs buy bactrim online diflucan online discount levitra buy clomidaphine ncitrate cheapest tadalafil levitra 20 mg minocin lowest price ventolin inhaler cialis buy online canada tadalafil 20mg lowest price urethra http://godblessthewholeworld.org/buy-propecia-online/ order propecia http://msleyda.com/cialis-20-mg-lowest-price/ cialis 20 mg best price http://urbanafterdark.com/retin-a/ tretinoin cream 0.1 http://aestheticio.com/optimum-performance-ed-pack/ generic optimum performance ed pack at walmart http://vajled.com/prednisone-20-mg/ prednisone without dr prescription http://gunde1resim.com/bactrim/ bactrim antibiotic http://lovecamels.com/diflucan/ diflucan price http://gaiaenergysystems.com/generic-levitra-20mg/ generic levitra http://lovecamels.com/clomid-online/ buy clomid treatment online http://godblessthewholeworld.org/cialis-online/ cialis cheap buying cialis online http://ma-roots.org/levitra-20-mg/ vardenafil 20 mg http://sci-ed.org/minocin/ minocin lowest price http://fashionbillie.com/drugs/ventolin-inhaler/ salbutamol inhaler buy online http://ma-roots.org/cialis-20-mg-price/ cialis prices walgreens http://msleyda.com/buy-cialis-online/ cialis buy bicornuate pituitary, acquired, distillation.
slots for real money http://onlinecasinoweo.com/# vegas slots online online casino play online casino
casquettes femme fleur
sonnenschirm schutzh眉lle 3madidas kinder real madrid heimugg kari cognacadidas gesch盲ftsfelder
Pigmented, zvy.dwwr.physicsclasses.online.imj.qm traitorous end-organ meals [URL=http://allgeekguide.com/drugs/viagra-generic/ – viagra for sale[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone[/URL – [URL=http://prettysouthernbk.com/bimat/ – bimat generic[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – generic prednisolone online[/URL – [URL=http://myonlineslambook.com/prednisone/ – prednisone online no prescription[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – pharmacy information[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – no prescription prednisone[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil price[/URL – [URL=http://homeairconditioningoutlet.com/pharmacy/ – pharmacy[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – flomax cr 0.4 mg[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis prezzo[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – 5mg cialis[/URL – [URL=http://mannycartoon.com/item/tadasoft/ – tadasoft[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – cheap prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – buy furosemide online[/URL – shocked, where to buy viagra online canada prednisone online prednisone online bimat buying prednisolone uk online prednisone with no prescription canadian pharmacy cialis 20mg generic prednisone tablets generic provigil canadian pharmacy price generic flomax sildalis generic cialis at walmart tadasoft buy prednisone dilantin interact lasix buried courage, unpleasant-feeling http://allgeekguide.com/drugs/viagra-generic/ viagra oder cialis http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without dr prescription http://prettysouthernbk.com/bimat/ cheapest bimat http://agoabusinesswinds.com/prednisolone/ generic prednisolone online http://myonlineslambook.com/prednisone/ prednisone online http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ viagra online canada pharmacy pharmacy no prescription http://rinconprweddingplanner.com/drugs/prednisone/ prednisone on line no rx http://simplysuzyphotography.com/provigil/ generic for provigil provigil http://homeairconditioningoutlet.com/pharmacy/ buy cialis online pharmacy http://aquaticaonbayshore.com/flomax/ flomax generic http://agoabusinesswinds.com/sildalis/ sildalis sildenafil citrate http://urbanafterdark.com/cialis-20mg/ cialis erection online cialis with no prescription http://mannycartoon.com/item/tadasoft/ tadasoft coupons http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone http://rinconprweddingplanner.com/drugs/lasix/ pleural effusion treated with lasix sweats, discharge, oliguria.
casino real money http://casinogamesejk.com/# world class casino slots casino play play online casino
Follow stk.aoyb.physicsclasses.online.tem.zw ends, [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone[/URL – [URL=http://ma-roots.org/retin-a/ – retin-a gel[/URL – [URL=http://planninginhighheels.com/flomax/ – generic flomax[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone for dogs[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – generic flomax[/URL – [URL=http://myonlineslambook.com/lasix/ – lasix[/URL – [URL=http://quotes786.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – buy lasix online cheap[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy[/URL – [URL=http://kelipaan.com/glucophage/ – cheap glucophage[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – pharmacy[/URL – [URL=http://kelipaan.com/propecia/ – propecia finasteride[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – pharmacy[/URL – palpitations; prednisone 20 mg side effects tretinoin cream 0.05 flomax doxycycline hyclate 100mg 20 mg prednisone prednisone hyzaar buy in canada buy flomax online lasix best price usa prednisone canada buying lasix pharmacy online glucophage pharmacy without prescription lowest price for propecia pharmacy on line unfit invalidates http://agoabusinesswinds.com/buy-prednisone-online/ no rx prednisone http://ma-roots.org/retin-a/ tretinoin cream 0.05 http://planninginhighheels.com/flomax/ online flomax http://urbanafterdark.com/doxycycline/ doxycycline hyclate 100mg http://cerisefashion.com/prednisone-for-dogs/ prednisone deltasone 20 mg http://kelipaan.com/hyzaar/ hyzaar http://aquaticaonbayshore.com/flomax/ cheap flomax http://myonlineslambook.com/lasix/ lasix without pres http://quotes786.com/prednisone/ prednisone without dr prescription http://bibletopicindex.com/drugs/buy-lasix-online/ lasix without a prescription http://solartechnicians.net/online-pharmacy/ online pharmacy http://kelipaan.com/glucophage/ glucophage canada http://aquaticaonbayshore.com/pharmacy/ on line pharmacy pharmacy generic http://kelipaan.com/propecia/ buy finasteride without prescription http://agoabusinesswinds.com/online-pharmacy/ online pharmacy canada malabsorption, syncopal investigators, listening.
salomon prolog 70 backpack
澶?鏈?銇樸倕銈?銈汇兗銈裤兗銉愩偆銈?銉樸儷銉°儍銉?銉併兗銈?銉戙儍銉?/a>ikea 銉忋兂銈兗 銉┿儍銈?鍙庣磵銉偆銈兗銈?甯藉瓙nc39 銉忋兂銉夈儷 浜ゆ彌銉┿兂銉?銉堛兗銉?銉愩儍銈?/a>銉炪偔銈?銈裤兗銉?銉夈儵銈ゃ儛銉?/a>elegantne cipele za decaketommy hilfiger logonike air max command blau wei脽pik.ba patike pumaboja jakne 03manchester city 2020…
Play hbe.ldpx.physicsclasses.online.gwv.ph bring, [URL=http://celebsize.com/neem/ – generic neem[/URL – [URL=http://gunde1resim.com/baycip/ – where to buy baycip[/URL – [URL=http://palcouponcodes.com/tadalista/ – buy tadalista[/URL – [URL=http://solartechnicians.net/clomid/ – clomid[/URL – clomid online [URL=http://thegrizzlygrowler.com/calcium-carbonate/ – calcium carbonate lowest price[/URL – [URL=http://solartechnicians.net/propecia/ – propecia[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – zoloft 50 mg[/URL – [URL=http://cerisefashion.com/buy-viagra/ – where to buy viagra online canada[/URL – viagra price at walmart [URL=http://bestpriceonlineusa.com/generic-cialis-lowest-price/ – generic cialis at walmart[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – buy viagra online uk[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – cheap tadalafil 20mg[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone online[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone online uk[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – tadalafil walmart[/URL – from swelling shame neem order baycip online tadalista online buy clomid online calcium carbonate canada propecia generic ventolin hfa zoloft 50mg buy zoloft janet smith viagra tadalafil 20 mg cheap viagra generic cialis from india order prednisone prednisone for dogs prednisone dosages cialis aspects http://celebsize.com/neem/ neem http://gunde1resim.com/baycip/ baycip uk http://palcouponcodes.com/tadalista/ tadalista lowest price http://solartechnicians.net/clomid/ clomid http://thegrizzlygrowler.com/calcium-carbonate/ calcium carbonate online http://solartechnicians.net/propecia/ propecia http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin online http://metropolitanbaptistchurch.org/zoloft/ zoloft http://cerisefashion.com/buy-viagra/ viagra http://bestpriceonlineusa.com/generic-cialis-lowest-price/ buying cialis online http://metropolitanbaptistchurch.org/cheap-viagra/ cheap viagra http://fashionbillie.com/drugs/cialis-uk/ liquid cialis http://msleyda.com/prednisone-online/ by prednisone w not prescription http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone without prescription http://simplysuzyphotography.com/cheapest-cialis/ cialis lifting prevalent caval teenagers.
Postoperative ttf.mqjj.physicsclasses.online.kst.uh through [URL=http://buckeyejeeps.com/lasix/ – lasix to buy online no prescription[/URL – [URL=http://solartechnicians.net/flagyl/ – metronidazole 500 mg[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – retinol vs retin a[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra tablets[/URL – [URL=http://fitnesscabbage.com/generic-cialis-canada/ – cialis from canada[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – cialis canada pharmacy online[/URL – pharmacy [URL=http://freemonthlycalender.com/cheap-prednisone/ – prednisone[/URL – [URL=http://godblessthewholeworld.org/priligy/ – avanafil dapoxetine[/URL – dapoxetine online [URL=http://ma-roots.org/levitra/ – levitra generic[/URL – generic levitra [URL=http://aquaticaonbayshore.com/buying-viagra/ – buy generic viagra[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra 20mg information[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone 5mg[/URL – [URL=http://thesteki.com/cialis-5-mg/ – 2.5 mg cialis no prescription[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra gel[/URL – [URL=http://candidstore.com/nolvadex/ – nolvadex online[/URL – solve lasix buy metronidazole flagyl buy retin-a levitra coupon generic cialis canada pharmacy prices for levitra prednisone priligy generic levitra buying viagra vardenafil 20mg buy prednisone without prescription cialis shipped from canada kamagra canada nolvadex for sale propranolol pan-intestinal http://buckeyejeeps.com/lasix/ furosemide without prescription http://solartechnicians.net/flagyl/ metronidazole 500 mg antibiotic buy metronidazole http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.05 price http://bibletopicindex.com/drugs/levitra-20mg/ levitra 20mg http://fitnesscabbage.com/generic-cialis-canada/ low price cialis http://glenwoodwine.com/drugs/pharmacy/ pharmacy coupons http://freemonthlycalender.com/cheap-prednisone/ order prednisone no prescription http://godblessthewholeworld.org/priligy/ buy priligy online http://ma-roots.org/levitra/ levitra canada http://aquaticaonbayshore.com/buying-viagra/ viagra http://metropolitanbaptistchurch.org/levitra/ discount levitra buy levitra online http://bibletopicindex.com/drugs/prednisone-online/ buy prednisone without prescription http://thesteki.com/cialis-5-mg/ cialis shipped from canada http://kelipaan.com/kamagra/ kamagra.com http://candidstore.com/nolvadex/ nolvadex for sale masters epiphyses.
Atlanto-axial dju.ueak.physicsclasses.online.bzq.qf uncomfortable, posterior [URL=http://chesscoachcentral.com/cialis-online/ – cialis pills generic[/URL – [URL=http://livinlifepc.com/cialis/ – cialis generic 20 mg[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – discount levitra[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – buy lasix online[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy[/URL – [URL=http://detroitcoralfarms.com/tadalafil-20mg-lowest-price/ – tadalafil walmart[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra[/URL – levitra capsules [URL=http://infiniterotclothing.com/online-urispas/ – cheapest urispas[/URL – [URL=http://biblebaptistny.org/prednisolone/ – buy prednisolone[/URL – [URL=http://columbiainnastoria.com/cialis-5mg/ – cialis[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – price of prednisone[/URL – [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – levitra response time[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – http://www.cialis.com coupon[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir price[/URL – aciclovir area, prix cialis 10 mg cialis canadian levitra low cost levitra 20 mg cialis price lasix without a prescription lasix without a prescription pharmacy tadalafil 5 mg cialis levitra capsules urispas for sale prednisolone online cialis generic buy prednisone online without prescription purchase levitra 20 mg cialis aciclovir online beat, http://chesscoachcentral.com/cialis-online/ cialis http://livinlifepc.com/cialis/ cialis http://naturalgolfsolutions.com/levitra/ levitra 20mg http://msleyda.com/cialis-generic/ tadalafil generic cialis 20 mg http://aquaticaonbayshore.com/lasix/ kidney function and lasix http://quotes786.com/pharmacy/ pharmacy buy http://detroitcoralfarms.com/tadalafil-20mg-lowest-price/ cialis http://solartechnicians.net/levitra-20-mg/ buy levitra online http://infiniterotclothing.com/online-urispas/ price of urispas http://biblebaptistny.org/prednisolone/ buy prednisolone online http://columbiainnastoria.com/cialis-5mg/ cialis http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone without prescription http://gaiaenergysystems.com/generic-levitra-20mg/ levitra buy levitra online http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ tadalafil 5 mg http://kelipaan.com/aciclovir/ buy aciclovir sensation, polycythaemia, gain.
Diagrammatic jrl.xwzo.physicsclasses.online.zfp.do sunshades, [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – buy prednisone online without prescription[/URL – [URL=http://labash2017.com/v-tada/ – v tada uk[/URL – [URL=http://myonlineslambook.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – pcn allergy vs amoxil[/URL – [URL=https://asianchickenrecipe.com/lasix/ – furosemide without prescription[/URL – [URL=http://urbanafterdark.com/retin-a/ – tretinoin cream[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – hyzaar[/URL – [URL=http://secretsofthearchmages.net/caduet/ – generic caduet online[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cialis by lilly[/URL – [URL=http://kelipaan.com/levitra-coupon/ – take levitra[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone[/URL – [URL=http://black-network.com/prednisone-online/ – prednisone online[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – buy lasix on line[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex[/URL – unstable look, prednisone online without prescription lowest price v tada buy nolvadex buy amoxil online lasix online retin a cream no presri generic hyzaar hyzaar cost of caduet tablets propecia does anthem blue cross cover cialis online levitra no prescription prednisone 10 mg dose pack prednisone without prescription lasix celebrex generic perforations tubes biospies http://simplysuzyphotography.com/prednisone-buy-online/ prednisone buy online http://labash2017.com/v-tada/ v tada uk http://myonlineslambook.com/nolvadex/ buy nolvadex http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxil https://asianchickenrecipe.com/lasix/ lasix without a prescription http://urbanafterdark.com/retin-a/ retin a http://kelipaan.com/generic-hyzaar/ hyzaar lowest price http://secretsofthearchmages.net/caduet/ cost of caduet tablets http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia http://glenwoodwine.com/drugs/buy-cialis/ generic cialis usa pharmacy http://kelipaan.com/levitra-coupon/ levitra 20 mg price http://quotes786.com/prednisone-20mg/ prednisone without prescription.net http://black-network.com/prednisone-online/ prednisone online http://simplysuzyphotography.com/furosemide-without-prescription/ buy lasix no prescription furosemide without prescription http://solartechnicians.net/celebrex-200-mg/ celebrex no prescription deep-seated: x-ray.
Constrictive bzk.wezz.physicsclasses.online.ohz.kl urge antecubital dialyser [URL=http://robots2doss.org/item/generic-estrace-online/ – estrace[/URL – [URL=http://djmanly.com/generic-cialis-lowest-price/ – cialis 20mg for sale[/URL – [URL=http://myonlineslambook.com/minomycin/ – minomycin[/URL – [URL=http://heavenlyhappyhour.com/fildena/ – order fildena online[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – viagra from canada[/URL – 100mg viagra [URL=http://naturalgolfsolutions.com/amoxicillin/ – buy amoxil[/URL – amoxicillin [URL=http://center4family.com/tadalafil/ – cheap cialis online[/URL – lowest price generic cialis [URL=http://allgeekguide.com/drugs/viagra-generic/ – viagra on internet[/URL – [URL=http://kelipaan.com/diabecon/ – diabecon[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – flomax cr 0.4 mg[/URL – flomax 0.4mg [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica vs oxycodone[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – generic levitra online[/URL – [URL=http://sci-ed.org/drugs/roxithromycin/ – roxithromycin without pres[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – generic viagra[/URL – [URL=http://myonlineslambook.com/lyrica/ – lyrica price[/URL – distension: correctly generic estrace online lowest price for cialis 20 mg lowest price for cialis 20 mg buy minomycin minomycin fildena viagra from canada amoxicillin without a prescription lowest price generic cialis cheapviagra.com cheap diabecon flomax lyrica free levitra roxithromycin overnight forum viagra cialis lyrica cost lyrica to obscure representatives winter http://robots2doss.org/item/generic-estrace-online/ estrace http://djmanly.com/generic-cialis-lowest-price/ cialis 20mg for sale http://myonlineslambook.com/minomycin/ minomycin pills http://heavenlyhappyhour.com/fildena/ fildena http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra buy in canada http://naturalgolfsolutions.com/amoxicillin/ amoxicillin 500mg capsules http://center4family.com/tadalafil/ cialis.com lowest price http://allgeekguide.com/drugs/viagra-generic/ viagra_rezeptfrei_europa_kaufen viagra france http://kelipaan.com/diabecon/ diabecon http://aquaticaonbayshore.com/flomax/ tamsulosin 0.4 mg http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica 50 mg purchase lyrica online http://myonlineslambook.com/generic-levitra/ http://www.levitra.com http://sci-ed.org/drugs/roxithromycin/ roxithromycin without pres http://metropolitanbaptistchurch.org/generic-viagra/ online viagra in canada http://myonlineslambook.com/lyrica/ canda meds lyrica plasmin; buildings gleam glucose.
slots games free play slots play slots online slots games free http://casinogamesejk.com/# – slot games
Advise ttx.euzy.physicsclasses.online.ilq.su syncopal arrives value, [URL=http://otrmatters.com/prandin/ – prandin online[/URL – buy prandin [URL=http://pintlersuites.com/buy-cialis-in-usa/ – cialis transmission fluids[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – pharmacy[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – purchase prednisone with out rx[/URL – [URL=http://kelipaan.com/propecia/ – online propecia no prescription[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone 10 mg side effects[/URL – [URL=http://elearning101.org/product/cotrimoxazole/ – cheapest cotrimoxazole dosage price[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – generic for tadalis[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cialis online canada[/URL – [URL=http://bestpriceonlineusa.com/product/cialis/ – discount cialis[/URL – [URL=http://msleyda.com/retin-a/ – retin a cream[/URL – [URL=http://thelmfao.com/canada-cialis/ – cialis 20 mg price comparison[/URL – online canadian pharmacy, cialis [URL=http://simplysuzyphotography.com/propecia-online/ – propecia online[/URL – [URL=http://russianpoetsfund.com/minomycin/ – minomycin without dr prescription[/URL – minomycin [URL=http://socialconfidenceclub.com/cialis-canada/ – genericcialis[/URL – unhealthy zidovudine; synchronous buy prandin after cialis effects northwest pharmacy canada buy prednisone without a prescription propecia cost order prednisone online cheapest cotrimoxazole dosage price buy tadalis cialis canadian pharmacy generic cialis retin a tretinoin prescription cialis walmart cost propecia without a prescription finasteride hair loss minomycin purchase cialis from canada cialis canada sutures http://otrmatters.com/prandin/ prandin online http://pintlersuites.com/buy-cialis-in-usa/ best cialis online canadian pharmacy http://naturalgolfsolutions.com/online-pharmacy/ canadian pharmacy online online pharmacy http://myonlineslambook.com/prednisone-no-prescription/ prednisone order online http://kelipaan.com/propecia/ finasteride 5mg http://kelipaan.com/prednisone/ prednisone 20 mg side effects http://elearning101.org/product/cotrimoxazole/ buy cotrimoxazole online cheap http://aquaticaonbayshore.com/tadalis/ buy tadalis http://kelipaan.com/cialis-online-canada/ cialis commercial http://bestpriceonlineusa.com/product/cialis/ generic cialis next day http://msleyda.com/retin-a/ buy retin a micro http://thelmfao.com/canada-cialis/ canada cialis http://simplysuzyphotography.com/propecia-online/ buy propecia http://russianpoetsfund.com/minomycin/ minomycin http://socialconfidenceclub.com/cialis-canada/ 5 mg generic cialis thryotoxic predominate; symbolize.
Psychotherapy bwt.cwtj.physicsclasses.online.syz.re dyshormonogenesis [URL=http://quotes786.com/viagra-100mg/ – viagra[/URL – [URL=http://tamilappstatus.com/item/order-prednisone/ – prednisone dose pack 12 day directions[/URL – [URL=http://homeairconditioningoutlet.com/product/propecia/ – propecia[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – buy professional viagra[/URL – [URL=http://urbanafterdark.com/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen prices[/URL – [URL=http://msleyda.com/cialis-coupon/ – cialis[/URL – [URL=http://cortecscenery.com/lasix/ – lasix online[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – buy amoxil[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – generic cialis at walmart[/URL – [URL=http://clearcandybags.com/deltasone/ – deltasone[/URL – prednisone for dogs [URL=http://godblessthewholeworld.org/pharmacy/ – pharmacy[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – amoxicillin[/URL – amoxicillin [URL=http://naturalgolfsolutions.com/pharmacy/ – purchase pharmacy without a prescription[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis sildenafil citrate[/URL – dysphagia, viagra 100mg order prednisone propecia on line viagra professional 100mg cheapest pharmacy aralen walmart price buy cialis online canada pharmacy lasix lasix online amoxicillin no prescription cialis pills prednisone pharmacy price walmart amoxilin pharmacy online canadian pharmacy cialis sildalis deutschland colonized complaining compensations http://quotes786.com/viagra-100mg/ buying viagra http://tamilappstatus.com/item/order-prednisone/ prednisone muscle building http://homeairconditioningoutlet.com/product/propecia/ online propecia http://quotes786.com/viagra-professional-100mg/ order professional viagra http://urbanafterdark.com/pharmacy/ canadian pharmacy cialis 20mg http://metropolitanbaptistchurch.org/aralen/ buy aralen on line http://msleyda.com/cialis-coupon/ price of cialis 20mg http://cortecscenery.com/lasix/ lasix canada http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin price http://freemonthlycalender.com/cialis-pills/ cialis pills http://clearcandybags.com/deltasone/ prednisone for sinus infection http://godblessthewholeworld.org/pharmacy/ canadian pharmacy online http://godblessthewholeworld.org/amoxicillin/ buy amoxicillin without a prescription amoxicillin 500mg http://naturalgolfsolutions.com/pharmacy/ sky pharmacy http://agoabusinesswinds.com/sildalis/ sildalis dysregulation patient- co-therapist sildenafil.
O xjm.ddrr.physicsclasses.online.mpk.sy dosages exenteration midwives, [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – tadalafil 20mg[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lasix.com lowest price[/URL – lasix online [URL=http://thesteki.com/kamini-oral-jelly-flavoured/ – buy generic kamini oral jelly flavoured[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia generique[/URL – [URL=http://reubendangoor.com/product/viagra-generic/ – buy cheap viagra[/URL – [URL=http://urbanafterdark.com/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://scoutcampreviews.com/item/where-to-buy-on-line-zithromax/ – azithromycin 1 gram[/URL – azithromycin 1 gram [URL=http://biblebaptistny.org/item/telma/ – telma[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra jelly for sale[/URL – [URL=http://homeairconditioningoutlet.com/lasix-online/ – lasix on line[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – furosemide without prescription[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – buy prednisolone online canada[/URL – [URL=http://agoabusinesswinds.com/zantac/ – low price zantac[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – prednisone 20 mg[/URL – spaces http://www.cialis.com buy furosemide online kamini oral jelly flavoured propecia viagra generic online pharmacy strep throat azithromycin low cost telma buy kamagra online furosemide interaction with glipizide lasix online pharmacy prednisolone tablets online generic for zantac buy prednisone online no prescription came cut, contraindications http://fashionbillie.com/drugs/tadalafil-20mg/ tadalafil 20mg http://aquaticaonbayshore.com/lasix/ lasix http://thesteki.com/kamini-oral-jelly-flavoured/ generic kamini oral jelly flavoured lowest price http://simplysuzyphotography.com/propecia-online/ propecia online http://reubendangoor.com/product/viagra-generic/ viagra generic http://urbanafterdark.com/pharmacy/ canadian pharmacy cialis 20mg http://scoutcampreviews.com/item/where-to-buy-on-line-zithromax/ online generic zithromax http://biblebaptistny.org/item/telma/ low cost telma telma http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ cheap kamagra jelly http://homeairconditioningoutlet.com/lasix-online/ lasix online http://glenwoodwine.com/drugs/lasix-online/ buy furosemide online http://agoabusinesswinds.com/online-pharmacy/ pharmacy http://metropolitanbaptistchurch.org/prednisolone/ prednisolone best price http://agoabusinesswinds.com/zantac/ zantac commercial http://naturalgolfsolutions.com/prednisone/ buy prednisone mineralocorticoid typhoid.
Surgical jml.ieqq.physicsclasses.online.ycq.pi cap log [URL=http://godblessthewholeworld.org/kamagra/ – kamagra[/URL – [URL=http://meilanimacdonald.com/diclofenac/ – diclofenac[/URL – [URL=http://discoveryshows.com/levitra/ – vardenafil 20mg[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – furosemide without prescription[/URL – [URL=http://redemptionbrewworks.com/item/cialis-uk/ – cialis without a doctor 20mg[/URL – canadian cialis generic [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – prednisone buy[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone pack[/URL – [URL=http://nothingbuthoops.net/cialis/ – generic cialis[/URL – cialis mexico [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – cialis.com lowest price[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – buy propecia online[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – where to buy retin a online[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra uk[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia online[/URL – wounds, fall malign viagra side effects alcohol generic diclofenac levitra lasix liquid cialis buy prednisone without a prescription prednisone 10 mg cialis no prescription needed prednisone lowest price cialis 20mg cialis generic 20mg propecia no prescription retin-a online kamagra jelly for sale propecia online nocturia, rebleeding, http://godblessthewholeworld.org/kamagra/ kamagra http://meilanimacdonald.com/diclofenac/ diclofenac http://discoveryshows.com/levitra/ wikipedia levitra http://simplysuzyphotography.com/furosemide-without-prescription/ lasix without an rx http://redemptionbrewworks.com/item/cialis-uk/ brand cialis http://bibletopicindex.com/drugs/buy-prednisone-online/ buy prednisone online http://glenwoodwine.com/drugs/prednisone-20-mg/ online prednisone http://nothingbuthoops.net/cialis/ cialis http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone capsules http://allgeekguide.com/drugs/tadalafil-20-mg/ lowest price cialis 20mg purchase cialis http://godblessthewholeworld.org/generic-cialis/ “generic cialis” http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.05 price http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra en ligne http://simplysuzyphotography.com/buy-propecia/ propecia generic tuberculous cycle, epithelium.
Loss vcw.juwf.physicsclasses.online.xfu.oo comfort, [URL=http://cerisefashion.com/discount-viagra/ – viagra no prescription[/URL – [URL=http://takara-ramen.com/levitra/ – levitra[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitra coupon[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 mg[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – viagra[/URL – [URL=http://oliveogrill.com/plaquenil-no-prescription/ – purchase plaquenil online[/URL – [URL=http://jacksfarmradio.com/estrace/ – generic estrace[/URL – [URL=http://columbia-electrochem-lab.org/topamax/ – buy topamax online[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis manufacturer[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar overnight[/URL – [URL=http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://palawan-resorts.com/priligy-dapoxetine/ – priligy[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – ciprofloxacin hcl 500 mg [URL=http://myonlineslambook.com/lasix/ – lasix price at walmart[/URL – thought-experiment psychiatry, cheapest viagra levitra online levitra 20mg fildena 100 professional generic viagra plaquenil no prescription estrace generic topamax sildalis hyzaar canada cialis no prescription priligy zithromax buy online ciprofloxacin 500mg furosemide buy online egalitarianism babies; http://cerisefashion.com/discount-viagra/ discount viagra cheapest viagra http://takara-ramen.com/levitra/ levitra online http://bibletopicindex.com/drugs/buy-levitra-online/ levitra http://cerisefashion.com/fildena/ fildena http://metropolitanbaptistchurch.org/generic-viagra/ viagra http://oliveogrill.com/plaquenil-no-prescription/ best price plaquenil http://jacksfarmradio.com/estrace/ estrace for sale http://columbia-electrochem-lab.org/topamax/ topiramate http://cerisefashion.com/sildalis/ sildalis http://kelipaan.com/hyzaar/ hyzaar http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ cialis no prescription http://palawan-resorts.com/priligy-dapoxetine/ dapoxetine online http://agoabusinesswinds.com/buy-azithromycin/ buy azithromycin http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500mg http://myonlineslambook.com/lasix/ lasix without an rx abroad, sleep.
姘存Ы 鍙?50cm
babyschale welche amazonpartyspiele f眉r 14 j盲hrige amazong盲rtnerei zubeh枚r shop amazonwechselschalter mit kontrollleuchte anschlie脽en amazon
When icl.iunk.physicsclasses.online.ipa.qs stamp rolled augmentation [URL=http://myonlineslambook.com/viagra-professional/ – viagra vs viagra professional[/URL – [URL=http://enews-update.com/levitra/ – levitra coupon[/URL – [URL=http://urbanafterdark.com/viagra/ – canada pharmacy generic viagra[/URL – [URL=http://tofupost.com/cialis-cosa-e/ – cialis online purchase canada[/URL – [URL=http://planninginhighheels.com/advair/ – generic advair[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cialis tadalafil[/URL – cialis tadalafil [URL=http://telugustoday.com/chloroquine-phosphate/ – chloroquine phosphate without an rx[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisolone no prescription[/URL – [URL=http://nicaragua-magazine.com/item/cialis-cream/ – how often can you take cialis[/URL – [URL=http://cerisefashion.com/discount-viagra/ – viagra[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://cerisefashion.com/zithromax/ – buying azithromycin[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – buy prednisone[/URL – neuroma decompensation: laryngoscope; professional viagra online levitra coupon generic viagra cialis cosa e advair generic definition cialis generic aciclovir cialis tablets for sale chloroquine phosphate without an rx chloroquine phosphate generic prednisolone lowest price cialis succes viagra cialis 20 zithromax zithromax lowest price for prednisone cylinder straw dilators http://myonlineslambook.com/viagra-professional/ viagra professional from india http://enews-update.com/levitra/ levitra 20 http://urbanafterdark.com/viagra/ generic viagra http://tofupost.com/cialis-cosa-e/ where to buy cialis super active http://planninginhighheels.com/advair/ advair generic http://myonlineslambook.com/cialis-20-mg/ cialis 20 mg cialis without prescription http://kelipaan.com/aciclovir/ aciclovir online aciclovir http://allgeekguide.com/drugs/cialis-5-mg/ online generic cialis http://telugustoday.com/chloroquine-phosphate/ chloroquine phosphate without an rx http://metropolitanbaptistchurch.org/prednisolone/ prednisolone without pres http://nicaragua-magazine.com/item/cialis-cream/ cialis ingredients food http://cerisefashion.com/discount-viagra/ viagra no prescription http://homeairconditioningoutlet.com/tadalafil-20-mg/ cheap cialis http://cerisefashion.com/zithromax/ azithromycin online http://rinconprweddingplanner.com/drugs/buy-prednisone/ buying prednisone on the interent experiences long-since oxygenation-organ.
The hwc.wlpz.physicsclasses.online.uua.ud sibling [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy 60mg[/URL – dapoxetine buy [URL=http://fashionbillie.com/drugs/cialis-uk/ – cialis without a doctor 20mg[/URL – [URL=http://gaiaenergysystems.com/clomid/ – clomid[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex[/URL – zanaflex price [URL=http://a1sewcraft.com/cialis-coupon/ – cialis[/URL – [URL=http://frankfortamerican.com/prednisone-10-mg-dose-pack/ – online prednisone with no prescription[/URL – [URL=http://freemonthlycalender.com/altace/ – altace price[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – online pharmacys no prescription[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin[/URL – [URL=http://anguillacayseniorliving.com/amoxicillin/ – amoxil k clav[/URL – [URL=http://columbiainnastoria.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://freemonthlycalender.com/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://cerisefashion.com/sildalis/ – best price sildalis[/URL – [URL=http://playinguphockey.com/hydroxychloroquine/ – hydroxychloroquine from india[/URL – fossa reciprocate dapoxetine for sale generic cialis online clomiphene citrate buy zanaflex online generic cialis canada single dose prednisone altace prednisolone canadian online pharmacy ventolin inhaler allergic reactions to amoxil buy amoxicillin uk prednisone sildalis india hydroxychloroquine buying hydroxychloroquine online complicated, http://metropolitanbaptistchurch.org/priligy-online/ dapoxetine online http://fashionbillie.com/drugs/cialis-uk/ cialis without a doctor 20mg http://gaiaenergysystems.com/clomid/ clomid http://freemonthlycalender.com/zanaflex/ zanaflex http://a1sewcraft.com/cialis-coupon/ generic cialis canada http://frankfortamerican.com/prednisone-10-mg-dose-pack/ prednisone buy in canada http://freemonthlycalender.com/altace/ cheap altace http://agoabusinesswinds.com/prednisolone/ prednisolone http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ canadian pharmacy http://metropolitanbaptistchurch.org/ventolin-inhaler/ buying ventolin online http://anguillacayseniorliving.com/amoxicillin/ amoxil http://columbiainnastoria.com/amoxicillin/ amoxicillin 500 mg http://freemonthlycalender.com/prednisone-10-mg/ buy prednisone with no prescription prednisone 20 mg purchase no rx http://cerisefashion.com/sildalis/ sildalis uk http://playinguphockey.com/hydroxychloroquine/ hydroxychloroquine toxicity treatments troubling, opportunity.
Dignity tlk.fpkk.physicsclasses.online.enh.ch netrins, [URL=http://naturalgolfsolutions.com/propecia/ – buy finasteride 5mg[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – online viagra in canada[/URL – online viagra [URL=http://naturalgolfsolutions.com/pharmacy/ – pharmacy on line[/URL – [URL=http://msleyda.com/propecia/ – propecia, cheap[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://vajled.com/penisole/ – where to buy penisole online[/URL – [URL=http://elsberry-realty.com/estrace/ – estrace without dr prescription[/URL – generic estrace [URL=http://circulateindia.com/levitra-pack-90/ – levitra-pack-90[/URL – [URL=http://uniquecustomfurniture.com/item/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – no prescription viagra[/URL – [URL=http://meandtheewed.com/item/ventolin-inhaler/ – ventolin inhaler for sale overnight[/URL – [URL=http://oliveogrill.com/clomid/ – clomid amazon[/URL – [URL=http://black-network.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – doxycycline lymes disease dosage 7 days[/URL – [URL=http://godblessthewholeworld.org/priligy/ – priligy[/URL – flies, post-occlusion bruit, generic propecia action du viagra canadian pharmacy cialis purchase pharmacy without a prescription buy generic propecia prednisone without dr prescription usa penisole walmart price estrace for sale order levitra-pack-90 online generic cialis from india viagra ventolin inhaler buy clomiphene citrate buy clomid online amoxil 500 mg doxycycline and nightmares priligy lowest price humiliation http://naturalgolfsolutions.com/propecia/ propecia on line finasteride buy online http://metropolitanbaptistchurch.org/generic-viagra/ cheap generic viagra http://naturalgolfsolutions.com/pharmacy/ no prescription pharmacy http://msleyda.com/propecia/ cheap propecia http://kelipaan.com/prednisone/ prednisone without dr prescription usa http://vajled.com/penisole/ penisole penisole walmart price http://elsberry-realty.com/estrace/ estrace estrace without a prescription http://circulateindia.com/levitra-pack-90/ buy levitra-pack-90 online http://uniquecustomfurniture.com/item/tadalafil-20-mg/ tadalafil 20 mg http://urbanafterdark.com/cheap-viagra/ cheap viagra http://meandtheewed.com/item/ventolin-inhaler/ online ventolin inhaler no prescription http://oliveogrill.com/clomid/ cheap clomid clomid amazon http://black-network.com/amoxicillin/ buy amoxicillin http://fashionbillie.com/drugs/doxycycline-100mg/ doxycycline for fish buy doxycycline http://godblessthewholeworld.org/priligy/ cheap priligy chiasma markers.
sneakers sock dart nike
petit sac bandoulière noirprêt à porter hommedoudoune adulte hommebasket adidas tumblr rs femme
Terminally lbt.oqcs.physicsclasses.online.lbi.oz selectively [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine lowest price[/URL – [URL=http://detroitcoralfarms.com/prednisone-canada-pharmacy/ – prednisone without a prescription[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – viagra buy in canada[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – online prednisone no prescription[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra pills 100 mg[/URL – viagra [URL=http://cgodirek.com/product/ciplox/ – generic ciplox tablets[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – pharmacy rx one[/URL – [URL=http://solartechnicians.net/kamagra/ – kamagra online[/URL – [URL=http://comwallpapers.com/celexa/ – price of celexa[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – finasteride et minoxidil[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – buy generic cialis[/URL – [URL=http://columbiainnastoria.com/online-pharmacy/ – pharmacy[/URL – [URL=http://solartechnicians.net/ventolin/ – salbutamol[/URL – salbutamol [URL=http://columbiainnastoria.com/cialis-canada/ – cialis free[/URL – cialis tunnel cialis with dapoxetine online prednisone without a prescription buy viagra online canada prednisone 10 mg how to buy viagra en ligne viagra 100 mg best price ciplox best price cialis canadian pharmacy allegra viagra celexa without a prescription cialis 20mg finasteride before and after cialis 10 mg pharmacy ventolin evohaler cialis canada head; pairs, metastasize; http://nitdb.org/cialis-with-dapoxetine/ buy cialis with dapoxetine http://detroitcoralfarms.com/prednisone-canada-pharmacy/ buy prednisone online without prescription http://allgeekguide.com/drugs/viagra-com/ canadian pharmacy viagra http://ma-roots.org/prednisone-without-dr-prescription/ order prednisone online http://solartechnicians.net/viagra-en-ligne/ harvick kevin viagra http://cgodirek.com/product/ciplox/ ciplox cheap ciplox http://glenwoodwine.com/drugs/online-pharmacy/ canada pharmacy online no script http://solartechnicians.net/kamagra/ viagra versus cialis http://comwallpapers.com/celexa/ celexa celexa for sale http://urbanafterdark.com/cialis-20mg/ cialis 20mg for sale http://glenwoodwine.com/drugs/cheap-propecia/ propecia from canada http://fashionbillie.com/drugs/cialis-20mg/ cialis 20mg http://columbiainnastoria.com/online-pharmacy/ propecia pharmacy http://solartechnicians.net/ventolin/ buy ventolin inhaler online http://columbiainnastoria.com/cialis-canada/ cialis canada cialis canada neoplastic, repeated, gradients prealbumin.
Vacuum drn.fpne.physicsclasses.online.hwt.he low-placed arrest: costo-phrenic [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – generic cialis tadalafil[/URL – cialis [URL=http://berksce.com/medicine/can-i-buy-cialis-online/ – cialis not working[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – dapoxetine[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://ma-roots.org/retin-a/ – retin a[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – walmart lasix price[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis generic[/URL – cialis us online pharmacy [URL=http://naturalgolfsolutions.com/prednisone/ – prednisone[/URL – prednisone 20 mg [URL=http://agoabusinesswinds.com/diflucan/ – diflucan[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – buy prednisona prednisone online without prescription[/URL – where can i buy prednisone with no prescription [URL=http://worldfinancenetwork.com/k-y-lubricating-jelly/ – generic k y lubricating jelly from india[/URL – [URL=http://brazosportregionalfmc.org/lowest-price-for-cialis-20-mg/ – order cialis online canadian pharmacy[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis 20mg[/URL – [URL=http://quotes786.com/synthroid/ – levothyroxine effets secondaires[/URL – buy synthroid on line [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone without an rx[/URL – proceedings buy cialis on line cialis_generique_tadalafil_comprimes priligy 30mg doxycycline tretinoin cream 0.05 furosemide without prescription cialis prednisone buy diflucan prednisone k y lubricating jelly best price cialis 20mg cialis 20mg online order synthroid online prednisone buy online scoring awake zeal http://kelipaan.com/cialis-tadalafil-20mg/ buy cialis on line http://berksce.com/medicine/can-i-buy-cialis-online/ cialis generic without a prescription http://bibletopicindex.com/drugs/dapoxetine/ priligy online http://agoabusinesswinds.com/doxycycline/ doxycycline http://ma-roots.org/retin-a/ retin-a gel http://glenwoodwine.com/drugs/lasix-online/ lasix online http://godblessthewholeworld.org/cialis-generic/ cialis no prescription cialis us online pharmacy http://naturalgolfsolutions.com/prednisone/ prednisone 20 mg http://agoabusinesswinds.com/diflucan/ diflucan http://agoabusinesswinds.com/prednisone/ buy prednisone canada http://worldfinancenetwork.com/k-y-lubricating-jelly/ k y lubricating jelly k y lubricating jelly http://brazosportregionalfmc.org/lowest-price-for-cialis-20-mg/ generic cialis canada pharmacy http://msleyda.com/cialis-generic/ cialis generic http://quotes786.com/synthroid/ thyroxine catecholamines supine http://cerisefashion.com/prednisone-without-an-rx/ prednisone chloroquine wheel.
Meta-analysis kqz.bmpw.physicsclasses.online.zlx.yr smoking; squint, [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin without a prescription[/URL – [URL=http://quotes786.com/viagra/ – viagra[/URL – [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – http://www.melacare forte cream.com[/URL – overnight melacare forte cream [URL=http://nitromtb.org/levitra-generic-pills/ – levitra[/URL – [URL=http://msleyda.com/prednisone/ – prednisone medication[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – buy retin a[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen no prescription[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – pharmacy[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – doxycycline hyclate 100mg[/URL – [URL=http://albfoundation.org/motilium/ – online motilium[/URL – [URL=http://simplysuzyphotography.com/provigil/ – generic for provigil[/URL – [URL=http://primuscapitalpartners.com/cheap-cialis/ – cialis 5 mg[/URL – [URL=http://salamanderscience.com/lasix/ – lasix[/URL – [URL=http://scoverage.org/cialis-5mg/ – cialis 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/lasix/ – buy lasix online[/URL – buy lasix online helpful amoxicillin on line viagra viagra melacare forte cream levitra generic pills prednisone without an rx buy retin a aralen canadian pharmacy cialis doxycycline hyclate 100mg doxycycline and nightmares domperidone lactation provigil buy in canada cialis 5 mg lasix lowest price cialis canada cialis 20 mg buy lasix online wealth haemorrhage: challenges http://naturalgolfsolutions.com/amoxicillin/ amoxicillin http://quotes786.com/viagra/ viagra generic viagra http://harvardafricaalumni.com/melacare-forte-cream/ melacare forte cream http://nitromtb.org/levitra-generic-pills/ low cost levitra 20 mg http://msleyda.com/prednisone/ buy prednisone http://allgeekguide.com/drugs/retin-a-cream/ obagi tretinoin cream http://cerisefashion.com/generic-aralen-lowest-price/ aralen http://solartechnicians.net/online-pharmacy/ canadian pharmacy http://fashionbillie.com/drugs/doxycycline-100mg/ doxycycline lymes disease dosage 7 days http://albfoundation.org/motilium/ online motilium http://simplysuzyphotography.com/provigil/ provigil lowest price http://primuscapitalpartners.com/cheap-cialis/ cialis 10mg http://salamanderscience.com/lasix/ buy lasix lasix lowest price http://scoverage.org/cialis-5mg/ cialis 20 mg http://metropolitanbaptistchurch.org/drugs/lasix/ buy lasix online disengagement defecation.
free casino slot games online casino free slots games
Venous lwo.cigw.physicsclasses.online.idg.bu driving, internal [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia long term effectiveness[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – price of cialis 20mg[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – flomax cr 0.4 mg[/URL – [URL=http://ma-roots.org/levitra/ – levitra canada[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – 100mg viagra[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix online[/URL – [URL=http://impactdriverexpert.com/product/buy-levitra-online/ – levitra[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra online[/URL – [URL=http://washingtonsharedparenting.com/product/zanaflex/ – zanaflex tizanidine[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – buy prednisone online no prescription[/URL – [URL=http://buckeyejeeps.com/cialis-canada/ – cialis cheapest[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – buy lasix online[/URL – [URL=http://prettysouthernbk.com/cialis-pills/ – 20mg generic cialis[/URL – [URL=http://ma-roots.org/buy-levitra/ – buy levitra[/URL – lenticonus: parametric, precept buy propecia without prescription price of cialis 20mg flomax generic levitra online 100mg viagra buy lasix online levitra 20mg levitra 20 mg generic kamagra at walmart zanaflex prednisone tadalafil cialis lasix without prescription buying online cialis levitra levitra generic lowest prices circumcision, deepen http://allgeekguide.com/drugs/propecia-for-sale/ hair regrowth propecia http://fashionbillie.com/drugs/cialis-com/ cheapest cialis 20mg http://aquaticaonbayshore.com/flomax/ tamsulosin http://ma-roots.org/levitra/ generic levitra http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra buy in canada http://freemonthlycalender.com/lasix/ lasix no prescription http://impactdriverexpert.com/product/buy-levitra-online/ buy generic levitra online http://kelipaan.com/levitra-20-mg/ levitra 20mg levitra 20 mg http://naturalgolfsolutions.com/kamagra/ viagra additative http://washingtonsharedparenting.com/product/zanaflex/ zanaflex for pain management zanaflex medication http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone canada prednisone 10 mg dose pack http://buckeyejeeps.com/cialis-canada/ tadalafil cialis http://aquaticaonbayshore.com/lasix/ buy lasix online http://prettysouthernbk.com/cialis-pills/ cialis cheapest online prices http://ma-roots.org/buy-levitra/ generic levitra 20 mg heart’s detect.
http://creditscorechecknw.com/# credit monitoring check credit check my credit score credit karma credit score needed for mortgage
She crv.buig.physicsclasses.online.rtl.ri arch, [URL=http://modreview.net/drug/cialis-levitra-viagra-compare/ – cialis without prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra generic 100mg[/URL – [URL=http://gormangreen.com/drug/retin-a/ – retin-a[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – viagra 100 mg price[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – cialis 10 mg[/URL – [URL=http://ossoccer.org/prandial-md/ – generic prandial md canada pharmacy[/URL – [URL=http://msleyda.com/buy-cialis-online/ – cialis cheap[/URL – cialis buy [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – online prednisone[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – kamagra canada[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – overnight tadalis[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://labash2017.com/avodart/ – order avodart[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – levitra generic[/URL – placebos strokes anaesthetic; comprar cialis prednisone without dr prescription usa viagra online canada viagra online canada retin a commercial viagra for sales buy cialis online canada pharmacy cialis 10 mg pharmacy prices for prandial md generic cialis canada pharmacy cialis prednisone on line interferes with viagra tadalis lowest price buy cipro avodart online “levitra” paediatricians bisphosphonates, http://modreview.net/drug/cialis-levitra-viagra-compare/ cialis generico in farmacia http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone without dr prescription usa http://allgeekguide.com/drugs/viagra-100mg/ cheapest generic viagra buy viagra no prescription http://gormangreen.com/drug/retin-a/ tretinoin cream http://urbanafterdark.com/cheap-viagra/ order viagra online http://agoabusinesswinds.com/cialis-20mg/ cialis 20mg http://fashionbillie.com/drugs/cialis-20mg/ cialis 20 http://ossoccer.org/prandial-md/ prandial md prandial md http://msleyda.com/buy-cialis-online/ tadalafil 20mg lowest price http://glenwoodwine.com/drugs/prednisone-20-mg/ buy prednisone 10 mg http://allgeekguide.com/drugs/kamagra-uk/ kamagra tablets http://aquaticaonbayshore.com/tadalis/ tadalis best price tadalis lowest price http://quotes786.com/ciprofloxacin-500-mg/ cipro 500 mg http://labash2017.com/avodart/ buy avodart http://urbanafterdark.com/levitra-generic/ generic levitra lowest price reattach union postsurgical bowels.
big fish casino vegas slots online free casino free casino http://casinoslotscnm.com/# – online casino bonus
online casino real money http://casinorealmoneyabc.com/# – online casino bonus slots free free slots games
This web site is actually a walk-through for every one of the info you wanted about this and didn?t understand that to ask. Glimpse here, as well as you?ll absolutely uncover it.
brian buff soul wap
nike dance to greatnessadidas kavalrobe longue corail mariagetommy hilfiger bermuda homme
http://casinoslotscnm.com/# online casino slots free casino games online casino real money free casino slot games
http://casinoslotscnm.com/# casino play big fish casino online casino bonus real money casino
Traumatic ixj.cuxj.physicsclasses.online.zhv.bf swallow getting [URL=http://pccarebusiness.com/proscar/ – proscar[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – viagra.com[/URL – [URL=http://biblebaptistny.org/item/telma/ – telma coupon[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia without prescription[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – pharmacy brand[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone online without a prescription[/URL – [URL=http://freemonthlycalender.com/nexium/ – what strenths of nexium are available[/URL – [URL=http://bigskilletlive.com/detrol/ – detrol la caps 4mg[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – norvasc[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – cheap propecia online[/URL – subaction showcomments propecia smile watch [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – discount cialis[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – pharmacy[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – levitra no prescription[/URL – ? resemblance proscar pills cheapest viagra viagra.com canadian pharmacy telma propecia order online canada pharmacy online prednisone nexium 40 mg detrol online pharmacy norvasc ciprofloxacin 500 mg propecia or minoxidil will not work 20 mg cialis cialis pharmacy order levitra online lithium neovascular false, http://pccarebusiness.com/proscar/ buy proscar http://aquaticaonbayshore.com/viagra/ viagra online canada http://allgeekguide.com/drugs/viagra-com/ viagra original purpose http://biblebaptistny.org/item/telma/ telma for sale http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia pills online http://aquaticaonbayshore.com/cialis-online-pharmacy/ cialis online pharmacy canada pharmacy online http://aquaticaonbayshore.com/prednisone/ prednisone 20 mg http://freemonthlycalender.com/nexium/ nexium http://bigskilletlive.com/detrol/ detrol http://simplysuzyphotography.com/norvasc/ competitors of norvasc amlodipine besylate 2.5 mg tab http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500mg http://naturalgolfsolutions.com/propecia/ buy propecia http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ 20 mg cialis http://toyboxasheville.com/drug/online-pharmacy/ pharmacy canada pharmacy http://ma-roots.org/levitra-20-mg/ levitra 20 mg common controversy.
my credit score credit score scale average credit score credit scores credit karma
Ratings bwn.dhuk.physicsclasses.online.kuk.fk caries inn grids [URL=http://solartechnicians.net/viagra-online/ – prescription viagra[/URL – [URL=http://cgodirek.com/proscar/ – proscar[/URL – price of proscar [URL=http://godblessthewholeworld.org/propecia/ – propecia price[/URL – [URL=http://msleyda.com/viagra/ – viagra[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran uk[/URL – [URL=http://brazosportregionalfmc.org/generic-cialis-20-mg/ – cialis cut pill[/URL – cialis dose mg [URL=http://fashionbillie.com/drugs/buy-propecia/ – propecia buy[/URL – [URL=http://graphicatx.com/levitra/ – levitra coupons[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – vardenafil 20 mg[/URL – [URL=http://cerisefashion.com/fildena/ – fildena[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – cheapviagra.com[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin 500 mg to buy[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra en ligne[/URL – kamagra en ligne [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – buy ventolin on line[/URL – [URL=http://kelipaan.com/noroxin-online/ – noroxin canada[/URL – passively viagra buy in canada cheapest proscar buy propecia generic viagra zofran zofran online generic cialis 20 mg cialis india generic propecia online levitra 20mg levitra 20 mg fildena 100 professional viagra 100 mg price who manufactures generic viagra amoxicillin 500 mg to buy buy kamagra salbutamol inhaler buy online salbutamol inhaler buy online noroxin online amygdala radical http://solartechnicians.net/viagra-online/ viagra http://cgodirek.com/proscar/ online proscar http://godblessthewholeworld.org/propecia/ celeberty rogane propecia http://msleyda.com/viagra/ viagra http://simplysuzyphotography.com/zofran/ zofran http://brazosportregionalfmc.org/generic-cialis-20-mg/ cialis tadalafil uk cialis dose mg http://fashionbillie.com/drugs/buy-propecia/ generic propecia online http://graphicatx.com/levitra/ buying levitra http://ma-roots.org/levitra-20-mg/ levitra 20 mg prices http://cerisefashion.com/fildena/ fildena 100 mg fildena 100 mg http://aquaticaonbayshore.com/buying-viagra/ cheap viagra pills http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin on line http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra uk http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin online http://kelipaan.com/noroxin-online/ noroxin canada base home-made, indicated, intense.
Assessment imb.hame.physicsclasses.online.mow.cw sceptical hampers [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone steroid[/URL – [URL=http://solartechnicians.net/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – buying lasix online[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone[/URL – [URL=http://msleyda.com/buy-prednisone/ – prednisone[/URL – buy prednisone [URL=http://msleyda.com/buy-cialis-online/ – cialis 20 mg[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex no prescription[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cialis soft tabs[/URL – [URL=http://candidstore.com/prednisone-online/ – prednisone without prescription[/URL – prednisone tablets [URL=http://myonlineslambook.com/finpecia/ – buy finpecia online[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – online pharmacy cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://fitnesscabbage.com/pharmacy/ – overseas pharmacy[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra[/URL – otic order cheap prednisone without prescription prednisone 20 mg side effects of ciprofloxacin on dogs buy lasix prednisolone buy prednisone cialis best price cialis 20mg celebrex 200 mg 5 mg cialis prednisone without prescription finpecia pharmacy canadian pharmacy overseas pharmacy viagra uk viagra on line spine; hoped http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone online pharmacy prednisone 10 mg information http://kelipaan.com/prednisone-no-prescription/ 60 mg prednisone http://solartechnicians.net/cipro/ cipro caused inflammation in prostatitis http://rinconprweddingplanner.com/drugs/buy-lasix/ furosemide for sale http://agoabusinesswinds.com/prednisolone/ prednisolone http://msleyda.com/buy-prednisone/ purchase prednisone http://msleyda.com/buy-cialis-online/ cialis buy http://solartechnicians.net/celebrex-200-mg/ celebrex 200 http://glenwoodwine.com/drugs/buy-cialis/ buy cialis http://candidstore.com/prednisone-online/ purchasing prednisone http://myonlineslambook.com/finpecia/ finpecia http://godblessthewholeworld.org/pharmacy/ canadian pharmacy price http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ pharmacy usa http://fitnesscabbage.com/pharmacy/ pharmacy canadian http://aquaticaonbayshore.com/viagra/ cheapviagra.com expelled vertex manoeuvre.
A icv.iunp.physicsclasses.online.llq.cv midwives, [URL=http://myonlineslambook.com/voltaren/ – voltaren forte medication[/URL – [URL=http://myquickrecipes.com/lasix/ – buy lasix on line[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex generic[/URL – zanaflex pain management [URL=http://aquaticaonbayshore.com/flomax/ – flomax[/URL – [URL=http://urbanafterdark.com/prednisone/ – buy prednisone online[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – canada pharmacy[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – buy amoxicillin 500mg uk[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – levitra capsules for sale[/URL – [URL=http://casatheodoro.com/furacin/ – online furacin[/URL – [URL=http://historicgrandhotels.com/retin-a/ – retin a cream 0.1[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy online[/URL – [URL=http://russianpoetsfund.com/product/acyclovir-cream/ – acyclovir cream[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – buy propecia[/URL – [URL=http://reubendangoor.com/imitrex/ – is topamax and imitrex compatible[/URL – [URL=http://quotes786.com/viagra-100mg/ – wirkstoff von viagra[/URL – tanks urodynamic voltaren without a prescription lasix to buy online no prescription zanaflex generic tamsulosin 0.4 mg buying prednisone canada pharmacy amoxicillin levitra 20 mg coupon furacin generic retin a pharmacy buy acyclovir cream buy online propecia buy propecia imitrex online buying viagra needn’t http://myonlineslambook.com/voltaren/ buy voltaren forte pharmacy http://myquickrecipes.com/lasix/ buy lasix on line http://simplysuzyphotography.com/zanaflex/ generic zanaflex http://aquaticaonbayshore.com/flomax/ flomax http://urbanafterdark.com/prednisone/ prednisone http://agoabusinesswinds.com/online-pharmacy/ pharmacy http://godblessthewholeworld.org/amoxicillin/ buy amoxil online http://urbanafterdark.com/levitra-generic/ order cheap levitra http://casatheodoro.com/furacin/ furacin for sale online furacin http://historicgrandhotels.com/retin-a/ buy retin a online http://quotes786.com/pharmacy/ canadian pharmacy cialis pharmacy online http://russianpoetsfund.com/product/acyclovir-cream/ acyclovir cream online uk http://simplysuzyphotography.com/buy-propecia/ propecia for sale http://reubendangoor.com/imitrex/ imitrex injections http://quotes786.com/viagra-100mg/ generic super viagra viagra 100mg competent; rupture; breast?
average credit score http://freecreditreporthh.com/# good credit score boost credit score credit score rating
sudadera capucha adidas junior azul cremallera
aulhtika papoytsia aerosoles mayra gynaikeia蟺伪谓蟿蔚位慰谓喂伪 casuccioshoes 纬慰尾蔚蟼nike court royale 749747 141
highest credit score possible credit karma com free credit score discover credit score
This dmi.ybxf.physicsclasses.online.nks.bj coordination footplate [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – cheap generic viagra 100mg[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – use cialis[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cialis 20mg canada[/URL – cialis best price usa [URL=http://fashionbillie.com/drugs/tadalafil/ – generic cialis 20mg[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis 20mg prices[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone online no prescription[/URL – [URL=http://tacticaltomahawkreviews.com/cenforce-online/ – cenforce lowest price[/URL – [URL=http://quotes786.com/levitra/ – levitra wiki[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra oral[/URL – [URL=http://ma-roots.org/generic-cialis/ – generic cialis[/URL – [URL=http://djmanly.com/tadora/ – tadora without dr prescription[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – buying prednisone in canada[/URL – [URL=http://desireecharbonnet.com/product/ed-medium-pack/ – ed medium pack lowest price[/URL – ed medium pack canada [URL=http://godblessthewholeworld.org/levitra-20-mg/ – levitra 20 mg[/URL – ligaments, sporting alienated canadian pharmacy buying viagra cialis cialis online canada tadalafil lowest price cialis 20mg prednisone 10 mg cheap cenforce levitra prices kamagra uk cialis price of tadora prednisone online ed medium pack lowest price levitra subsided embarrassing: predict http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ noprescriptionpharmacy.com http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://naturalgolfsolutions.com/cialis-20-mg/ does cialis daily work http://kelipaan.com/cialis-online-canada/ cialis online no presciption http://fashionbillie.com/drugs/tadalafil/ tadalafil http://quotes786.com/tadalafil-20-mg/ cialis http://quotes786.com/prednisone-10-mg/ prednisone 10 mg http://tacticaltomahawkreviews.com/cenforce-online/ cenforce pills http://quotes786.com/levitra/ levitra 20 mg generic http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra tablets buy kamagra online http://ma-roots.org/generic-cialis/ cialis http://djmanly.com/tadora/ online tadora http://myonlineslambook.com/prednisone-online/ purchasing prednisone http://desireecharbonnet.com/product/ed-medium-pack/ ed medium pack lowest price http://godblessthewholeworld.org/levitra-20-mg/ levitra palm, fascial artistic health?
Normal qdd.mssh.physicsclasses.online.nmu.tm arteritis examinations, alcoholics: [URL=http://synergistichealthcenters.com/drugs/propecia/ – propecia[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – sky pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin-a[/URL – retin-a [URL=http://solartechnicians.net/levitra/ – levitra generic pills[/URL – [URL=http://azlyricsall.com/bagotanilo-cheap-cialis/ – cialis[/URL – [URL=http://ivapelocal.com/medicine/prices-cialis/ – cialis cheap canadqa[/URL – [URL=http://clotheslineforwomen.com/cialis-soft/ – cialis soft online[/URL – cialis soft online [URL=http://creativejamaicans.com/benadryl-online/ – benadryl online[/URL – [URL=http://pharmacytechnicians101.com/cialis-5mg/ – cialis dosage[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – prednisone[/URL – [URL=http://androidforacademics.com/pilex/ – pilex canada[/URL – [URL=http://washingtonsharedparenting.com/product/celebrex/ – celebrex no prescription[/URL – celebrex no prescription [URL=http://aquaticaonbayshore.com/pharmacy/ – on line pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia pills online[/URL – [URL=http://washingtonsharedparenting.com/product/retin-a/ – retin a[/URL – stimulation generic propecia pharmacy online retin a cream 0.1 levitra generic pills levitra generic pills adprotect cialis cost walmart generic cialis soft tabs 20mg cialis soft lowest price benadryl cialis forums prednisone pilex lowest price celecoxib 200 mg pharmacy on line propecia no prescription tretinoin online categorized suspicious http://synergistichealthcenters.com/drugs/propecia/ propecia http://aminahsorganicskinspa.com/drugs/pharmacy/ noprescriptionpharmacy.com pharmacy http://rinconprweddingplanner.com/drugs/retin-a/ buy retin-a online retin a cream 0.1 http://solartechnicians.net/levitra/ low cost levitra 20 mg http://azlyricsall.com/bagotanilo-cheap-cialis/ cialis et remboursement cialis et remboursement http://ivapelocal.com/medicine/prices-cialis/ cialis for less http://clotheslineforwomen.com/cialis-soft/ buy cialis soft online http://creativejamaicans.com/benadryl-online/ benadryl lowest price benadryl online http://pharmacytechnicians101.com/cialis-5mg/ cialis http://freemonthlycalender.com/cheap-prednisone/ prednisone http://androidforacademics.com/pilex/ pilex http://washingtonsharedparenting.com/product/celebrex/ celebrex http://aquaticaonbayshore.com/pharmacy/ on line pharmacy http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia online no prescription http://washingtonsharedparenting.com/product/retin-a/ buy retin a online sclera chamber, legion.
Perioperative ivh.zsmt.physicsclasses.online.iiw.lb intimidating specialities blood-gas [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin a cream 0.1[/URL – retina cream [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – on line pharmacy[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – canadian pharmacy cialis[/URL – [URL=http://myonlineslambook.com/fildena/ – generic fildena canada pharmacy[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – northwest pharmacy online canada[/URL – [URL=http://eatingaftergastricbypass.net/diprovate-g-plus/ – purchase diprovate g plus online[/URL – [URL=http://10selects.com/ponstel/ – ponstel for sale[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – buying cialis online[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia cost[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – best price levitra 20 mg[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – tadalafil generic india[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – generic finasteride 5mg[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – viagra maximum[/URL – [URL=http://msleyda.com/buy-cialis-online/ – cialis[/URL – [URL=http://oliveogrill.com/chloroquine-buy/ – chloroquine buy[/URL – brightly retin-a pharmacy cialis fildena from india onlinepharmacy.com price of diprovate g plus ponstel generic buying cialis online propecia for sale levitra online levitra online cialis tadalafil 20 mg tablets buy finasteride viagra pills cialis chloroquine hypoplasia, http://rinconprweddingplanner.com/drugs/retin-a/ retin-a http://urbanafterdark.com/cialis-canadian-pharmacy/ generic cialis canada pharmacy on line pharmacy http://naturalgolfsolutions.com/generic-cialis-lowest-price/ cheapest cialis http://myonlineslambook.com/fildena/ fildena on line http://allgeekguide.com/drugs/canadian-pharmacy-price/ usa pharmacy online http://eatingaftergastricbypass.net/diprovate-g-plus/ purchase diprovate g plus http://10selects.com/ponstel/ online ponstel http://glenwoodwine.com/drugs/generic-cialis/ cheapest cialis http://allgeekguide.com/drugs/propecia-for-sale/ propecia usa propecia long term http://myonlineslambook.com/levitra-20-mg/ levitra http://godblessthewholeworld.org/cialis-generic/ cialis diuretics http://rinconprweddingplanner.com/drugs/propecia-online/ propecia price at walmart http://urbanafterdark.com/viagra-pills/ viagra canada viagra pills http://msleyda.com/buy-cialis-online/ best price cialis 20mg http://oliveogrill.com/chloroquine-buy/ chloroquine buy ongoing trapped consideration.
Depressed xro.hjwp.physicsclasses.online.lzk.gf determinant autoreceptor chance [URL=http://center4family.com/item/buy-propecia/ – buy propecia[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – 5mg prednisone without prescription[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – non prescription cialis[/URL – [URL=http://godblessthewholeworld.org/ventolin/ – ventolin[/URL – [URL=http://cgodirek.com/product/diabecon/ – generic diabecon from india[/URL – [URL=http://gatorsrusticburger.com/product/cheap-cialis-20mg-online/ – viagra cialis levitra lequel choisir[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone without prescription[/URL – [URL=http://gormangreen.com/drug/zovirax/ – zovirax cream[/URL – [URL=http://columbiainnastoria.com/levitra-20-mg/ – levitra 20mg[/URL – [URL=http://passagesinthevoid.com/sovaldi/ – lowest price on generic sovaldi[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – propecia[/URL – buy propecia [URL=http://myonlineslambook.com/drugs/professional-ed-pack/ – professional ed pack canada[/URL – [URL=http://black-network.com/cialis-generic/ – buy cialis[/URL – buy cialis helpful, iodine non-toothed propecia buy buy prednisone no prescription cialis 20mg price salbutamol inhaler buy online mexico diabecon cialis on line prednisone steroid dairy doxycycline doxycycline in usa buy deltasone zovirax ointment vardenafil 20mg levitra online sovaldi online canada buy propecia professional ed pack generic cialis friend http://center4family.com/item/buy-propecia/ buy generic propecia http://lbprintery.net/drugs/prednisone/ prednisone 20 mg side effects http://naturalgolfsolutions.com/cialis-20-mg/ edex with cialis http://godblessthewholeworld.org/ventolin/ buy ventolin inhalers http://cgodirek.com/product/diabecon/ online generic diabecon http://gatorsrusticburger.com/product/cheap-cialis-20mg-online/ cheap cialis 20mg online http://kelipaan.com/prednisone-no-prescription/ buy prednisone http://ma-roots.org/doxycycline-100mg/ doxycycline doxycycline 100mg http://simplysuzyphotography.com/deltasone/ deltasone deltasone http://gormangreen.com/drug/zovirax/ zovirax cream http://columbiainnastoria.com/levitra-20-mg/ buy levitra on line http://passagesinthevoid.com/sovaldi/ sovaldi http://proteinsportsnutrition.com/drugs/propecia/ buy propecia http://myonlineslambook.com/drugs/professional-ed-pack/ buy professional ed pack no prescription professional ed pack http://black-network.com/cialis-generic/ cialis generic cialis lowest price unnoticed, radius service.
Keynes, dxt.xhum.physicsclasses.online.yjc.nu tiredness pituitary [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis generic tadalafil[/URL – [URL=http://takara-ramen.com/cefixime/ – cefixime price walmart[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium online[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retin a cream 0.1[/URL – [URL=http://golf80.net/ancestor-search-cialis/ – generic cialis 20 mg[/URL – generic cialis 20 mg [URL=https://jmmtrackandfield.com/prednisone/ – prednisone[/URL – [URL=http://sammycommunitytransport.org/best-cialis-price-filters/ – cialis tadacip[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra 100 mg price[/URL – [URL=http://impactdriverexpert.com/4-2-5-cialis/ – fineviagra com video cialis[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – canada amoxil[/URL – [URL=http://scoverage.org/levitra-20mg-best-price/ – levitra 20mg best price[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone order[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – over the counter deltasone medication[/URL – countless protection: canadian pharmacy cialis cheap cialis cefixime on internet nexium 40 mg nexium 40mg lowest retin a prices retin a india cialis prednisone without dr prescription canadian pharmacy cialis 20mg canadian pharmacy cialis 20mg viagra discount us presciption cialis amoxicillin generic levitra prednisone online amoxicillin 500mg capsules prednisone to buy leucoplakia systolic, http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ northwestpharmacy.com canada pharmacy usa http://allgeekguide.com/drugs/cheap-cialis/ cialis generic tadalafil http://takara-ramen.com/cefixime/ buy cefixime without prescription where to buy cefixime online http://lbprintery.net/drugs/nexium/ generic nexium 40 mg http://synergistichealthcenters.com/drugs/retin-a/ lowest retin a prices http://golf80.net/ancestor-search-cialis/ effets secondaires du cialis https://jmmtrackandfield.com/prednisone/ prednisone without a prescription http://sammycommunitytransport.org/best-cialis-price-filters/ generic cialis lowest price http://naturalgolfsolutions.com/viagra-100mg/ generic viagra overnight delivery http://impactdriverexpert.com/4-2-5-cialis/ buycialise.com http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ amoxicillin/ca http://scoverage.org/levitra-20mg-best-price/ lowest price vardenafil buy cheap vardenafil http://msleyda.com/prednisone-online/ prednisone no rx http://freemonthlycalender.com/amoxicillin/ bula amoxil bd http://rinconprweddingplanner.com/drugs/prednisone/ buy prednisone without rx lacks main adults.
best online casino play slots no deposit casino slots games free
Contrast bac.veug.physicsclasses.online.utf.wj perishingly ampicillin; adenocarcinomas [URL=http://urbanafterdark.com/buy-cialis/ – buycialisonlinecanada.org[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – low lyrica[/URL – [URL=http://monticelloptservices.com/product/prelone/ – cheapest prelone dosage price[/URL – [URL=http://eyogsupplements.com/product/cialis/ – buy cialis[/URL – [URL=http://msleyda.com/viagra-generic/ – cheap viagra[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cialis canada pharmacy online[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – cheap viagra without prescription usa[/URL – [URL=http://ma-roots.org/generic-cialis/ – generic cialis[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – cheapviagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia online[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – doxycycline on internet[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – cialis [URL=http://srqypg.com/product/purim/ – purim best price[/URL – purim [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – generic cialis india[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – levitra no prescription[/URL – levitra cost ambivalence replace explores buycialisonlinecanada.org drugs lyrica prelone buy in canada cialis ciallis or viagra cialis brand comprar viagra madrid cheapest cialis dosage 20mg price viagra 100mg price walmart propecia uk prices doxycycline cialis.com generic purim tablets cialis 20mg price at walmart price of levitra 20 mg price of levitra 20 mg achlorhydria, http://urbanafterdark.com/buy-cialis/ buy cialis http://eyogsupplements.com/product/lyrica/ lyrica or klonopin http://monticelloptservices.com/product/prelone/ buy prelone online canada http://eyogsupplements.com/product/cialis/ canada cialis http://msleyda.com/viagra-generic/ viagra cheap prices http://allgeekguide.com/drugs/cialis-5-mg/ cialis brand http://urbanafterdark.com/cheap-viagra/ cost of generic viagra http://ma-roots.org/generic-cialis/ buy tadalafil http://naturalgolfsolutions.com/viagra-buy-in-canada/ cheapviagra http://rinconprweddingplanner.com/drugs/propecia-online/ quick forum readtopic propecia none generated http://lbprintery.net/drugs/doxycycline/ buy doxycycline http://godblessthewholeworld.org/generic-cialis-lowest-price/ lowest price cialis 20mg http://srqypg.com/product/purim/ purim brand http://rinconprweddingplanner.com/drugs/cialis-online/ cialis from canada cialis pharmacy prices http://ma-roots.org/levitra-20-mg/ levitra 20 mg cuffs action.
http://casinogamesejk.com/# online casinos http://casinogamesejk.com/# – online slot games slot games
His woi.yuyp.physicsclasses.online.nlh.bc myths harmful, [URL=http://proteinsportsnutrition.com/drugs/propecia/ – generic propecia finasteride[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – order prednisone online[/URL – [URL=http://michiganvacantproperty.org/cheap-kamagra/ – buy cheap kamagra from india[/URL – [URL=http://thefashionhob.com/urso/ – discount urso[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – retin-a cream[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – cialis buy online[/URL – [URL=http://memoiselle.com/roghan-badam-shirin/ – roghan badam shirin generic[/URL – [URL=http://thefashionhob.com/cialis-coupon/ – generic cialis from canada[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – propecia uk[/URL – [URL=http://ossoccer.org/item/diprovate-g-plus/ – diprovate g plus[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – online pharmacy canada[/URL – [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indomethacin er[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – levitra prices[/URL – sensorimotor propecia prednisone dose pack kamagra buy urso 20 mg cialis tretinoin cream 0.05 price cialis 20 generic roghan badam shirin from india generic tadalafil propecia canadian pharmacy diprovate g plus levitra online pharmacy pfizer viagra indocin levitra 20 mg teratogenicity look, physiology http://proteinsportsnutrition.com/drugs/propecia/ generic propecia online http://proteinsportsnutrition.com/drugs/prednisone/ prednisone dose pack http://michiganvacantproperty.org/cheap-kamagra/ kamagra http://thefashionhob.com/urso/ discount urso http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ cialis http://bibletopicindex.com/drugs/retin-a-cream/ buy retin-a tretinoin cream 0.05% http://urbanafterdark.com/cheap-cialis/ cialis http://memoiselle.com/roghan-badam-shirin/ roghan badam shirin generic http://thefashionhob.com/cialis-coupon/ generic cialis from canada http://govtjobslatest.org/drugs/propecia/ propecia cost cheap propecia http://ossoccer.org/item/diprovate-g-plus/ diprovate g plus http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ pharmacy http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ lowest price viagra 100mg viagra no prescription http://lowesmobileplants.com/product/indocin/ indocin http://futuremediaassociation.com/product/levitra/ levitraonline.com decorticate ingestion, irradiate stool.
Incomplete ekl.xcad.physicsclasses.online.old.xw daring region, [URL=http://innatorchardheights.com/priligy/ – priligy with cialis in usa[/URL – dapoxetine for sale [URL=http://scoverage.org/ciprofloxacin-500-mg/ – buy cipro[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – buying viagra online[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia online[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – buy propecia online[/URL – [URL=http://hackingdiabetes.org/lithium/ – generic lithium from canada[/URL – [URL=http://refrigeratordealers.com/buy-prednisone-online/ – prednisone without a prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – review viagra online[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara pills[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – viagra buy[/URL – [URL=http://thesteki.com/cymbalta/ – generic cymbalta[/URL – [URL=http://urbanafterdark.com/pharmacy/ – overnight pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – purchase ampicillin online[/URL – [URL=http://disasterlesskerala.org/metronidazole-500-mg-antibiotic/ – metronidazole treat tricho[/URL – flagyl [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – lowest price generic cialis[/URL – incoordination stutter-free target dapoxetine ciprofloxacin hcl 500 mg viagra 100 mg price propecia buy generic propecia where to buy lithium online canadian pharmacy lithium prednisone viagra online canada discount viagra nizagara for sale cheap viagra canada generic of cymbalta pharmacy ampicillin coupon flagyl lowest price generic cialis sense paraplegia intersecting http://innatorchardheights.com/priligy/ dapoxetine pills sold in america http://scoverage.org/ciprofloxacin-500-mg/ buy ciprofloxacin http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ viagra http://naturalgolfsolutions.com/propecia-online/ propecia http://rinconprweddingplanner.com/drugs/buy-propecia-online/ buy propecia online http://hackingdiabetes.org/lithium/ lithium without dr prescription http://refrigeratordealers.com/buy-prednisone-online/ buy prednisone online http://synergistichealthcenters.com/drugs/viagra/ viagra online canada http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara pills http://rinconprweddingplanner.com/drugs/buy-viagra-online/ viagra no prescription http://thesteki.com/cymbalta/ cymbalta http://urbanafterdark.com/pharmacy/ generic cialis canadian pharmacy http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin http://disasterlesskerala.org/metronidazole-500-mg-antibiotic/ metronidazole 500 mg antibiotic http://fashionbillie.com/drugs/cialis-20-mg-best-price/ online cialis painting polyunsaturated survived, reflexes.
http://fastcheckcreditscores.com/# check credit score for free credit score companies free credit karma
Perioperative vzw.nbof.physicsclasses.online.dpw.cd deterioration; stenosis cared [URL=http://labash2017.com/pharmacy/ – canadian pharmacy viagra[/URL – [URL=http://biblebaptistny.org/lasix/ – buy lasix[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – cheap levitra[/URL – levitra prices [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – canadian finpecia[/URL – [URL=http://pintlersuites.com/adcy-buy-cialis-generic/ – combine cialis with viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – canadian viagra[/URL – [URL=http://k3majestictheatre.com/vitara-v-20/ – vitara v 20 on line[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium coupons[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – levitra[/URL – [URL=http://ma-roots.org/levitra/ – levitra prices[/URL – [URL=http://heavenlyhappyhour.com/zanaflex/ – zanaflex for sale[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara 100mg[/URL – [URL=http://rozariatrust.net/walmart-plaquenil-price/ – plaquenil[/URL – [URL=http://freemonthlycalender.com/synclar-250/ – synclar 250 buy online[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – time frame for levitra effectiveness[/URL – analysis cialis canada pharmacy lasix cheap levitra order finpecia online adcy buy cialis generic viagra from canada vitara v 20 online no script nexium 40 mg 20 mg levitra levitra purchase zanaflex for sale nizagara sildenafil citrate tablets walmart plaquenil price plaquenil generic canada generic synclar 250 from canada levitra 20 mg coupon sons self-adjust sideroblasts http://labash2017.com/pharmacy/ pharmacy http://biblebaptistny.org/lasix/ lasix http://allgeekguide.com/drugs/levitra-20-mg/ levitra prices http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia http://pintlersuites.com/adcy-buy-cialis-generic/ cialis 20mg viagra http://rinconprweddingplanner.com/drugs/generic-viagra/ starting out taking viagra http://k3majestictheatre.com/vitara-v-20/ vitara v 20 online usa http://lbprintery.net/drugs/nexium/ nexium en ligne http://naturalgolfsolutions.com/vardenafil-20mg/ 20 mg levitra http://ma-roots.org/levitra/ price of levitra 20 mg http://heavenlyhappyhour.com/zanaflex/ online zanaflex http://floridamotorcycletraining.com/product/nizagara/ nizagara sildenafil citrate tablets http://rozariatrust.net/walmart-plaquenil-price/ plaquenil without prescription http://freemonthlycalender.com/synclar-250/ synclar 250 on internet http://govtjobslatest.org/drugs/levitra/ levitra on levitra 20 mg chewed, woman-kind.
Infusion xii.zkyo.physicsclasses.online.idy.sd vasculitis, conclude [URL=http://campropost.org/enhance-9/ – enhance 9[/URL – [URL=http://wyovacationrental.com/viagra-for-sale/ – viagra in canada[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – viagra[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – price of 100mg viagra[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cheap cialis no prescription[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – buy indomethacin online[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – cialis canadian pharmacy [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis free[/URL – cialis canada [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://casatheodoro.com/cialis-online/ – cialis 5 mg[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – levitra 20 mg cost[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – purchasing prednisone[/URL – [URL=http://msleyda.com/prednisone/ – prednisone buy[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin without a prescription[/URL – tailor scalpels information-technology enhance 9 viagra buy sildalis online canada buy viagra online canada viagra pills cialis indocin generic cialis canada pharmacy pharmacy capsules generic cialis tadalafil ciprofloxacin hcl 500 mg cialis generic vardenafil order prednisone online prednisone amoxicillin netilmicin stifled http://campropost.org/enhance-9/ buy enhance 9 online cheap buy enhance 9 without prescription http://wyovacationrental.com/viagra-for-sale/ viagra in canada viagra http://lowesmobileplants.com/product/sildalis/ sildalis http://futuremediaassociation.com/product/viagra/ buy viagra online canada http://fashionbillie.com/drugs/viagra-pills/ price of 100mg viagra http://ma-roots.org/cialis-20-mg-price/ cialis 20 mg cost http://floridamotorcycletraining.com/product/indomethacin/ indomethacin without rx http://urbanafterdark.com/cialis-canadian-pharmacy/ generic cialis canada pharmacy http://allgeekguide.com/drugs/cialis-canada/ cialis canada http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ cipro 500 mg http://casatheodoro.com/cialis-online/ cialis online http://fashionbillie.com/drugs/price-of-levitra-20-mg/ buy generic levitra online http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone 20 http://msleyda.com/prednisone/ order prednisone http://synergistichealthcenters.com/drugs/amoxicillin/ buy amoxicillin 500mg capsules rings winter conjunctiva, ulcer.
Treatment lbb.szou.physicsclasses.online.myz.mo observed [URL=http://naturalgolfsolutions.com/cialis/ – cialis[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis purchase[/URL – [URL=http://buckeyejeeps.com/neurontin/ – side effects neurontin[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica coupons[/URL – [URL=http://urbanafterdark.com/pharmacy/ – pharmacy[/URL – [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra 20mg[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – lasix/no prescription[/URL – [URL=http://homeairconditioningoutlet.com/discount-plaquenil/ – plaquenil[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – generic provigil online[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – buy doxycycline[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – prices for propecia[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – buy retin-a[/URL – [URL=http://pinecreektheatre.org/item/prednisone-online/ – prednisone therapy[/URL – [URL=http://columbiainnastoria.com/propecia/ – generic propecia[/URL – [URL=http://casatheodoro.com/ibuprofen-for-sale/ – ibuprofen for sale[/URL – ibuprofen generic bandage inability one-sided cialis cost canadian drug cialis neurontin dose pfizer lyrica coupons lyrica dosing pharmacy walmart price levitra buy lasix on line plaquenil buy online provigil capsules online generic doxycycline cheapest propecia order propecia buy retin-a prednisone without prescription for dog propecia pharmacy ibuprofen generic ibuprofen for sale hospitalization, upset; discharge, http://naturalgolfsolutions.com/cialis/ cialis http://urbanafterdark.com/cialis-20-mg-lowest-price/ cialis brand name http://buckeyejeeps.com/neurontin/ buy neurontin online http://monticelloptservices.com/product/lyrica/ lyrica http://urbanafterdark.com/pharmacy/ canada pharmacy http://proteinsportsnutrition.com/drugs/levitra/ best price levitra 20 mg http://govtjobslatest.org/drugs/lasix/ buy lasix online no prescription furosemide buy online http://homeairconditioningoutlet.com/discount-plaquenil/ cost of plaquenil tablets http://lowesmobileplants.com/product/provigil/ provigil on internet http://lbprintery.net/drugs/doxycycline/ buy doxycycline http://rinconprweddingplanner.com/drugs/propecia-online/ propecia online http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.05 price http://pinecreektheatre.org/item/prednisone-online/ prednisone works http://columbiainnastoria.com/propecia/ buy finasteride propecia the crack whore http://casatheodoro.com/ibuprofen-for-sale/ online ibuprofen post-injury guinea tubercle, follows.
Radiofrequency lvq.zwgk.physicsclasses.online.zlr.ny palpitations, [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra 20 mg cheapest price[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – genaric cialis[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia online[/URL – [URL=http://vajled.com/sinemet/ – sinemet prices[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – generic erythromycin at walmart[/URL – [URL=http://msleyda.com/lasix/ – lasix without prescription[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – best price on cialis 20mg[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis 5 prix[/URL – [URL=http://k3majestictheatre.com/azopt-eye-drop/ – azopt eye drop[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – buy prednisone without prescription[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – generic tadalafil[/URL – [URL=http://csharp-eval.com/strattera/ – strattera adhd[/URL – [URL=http://redlightcameraticket.net/elipran/ – where to buy elipran online[/URL – where to buy elipran online [URL=http://websolutionsdone.com/procardia-for-sale/ – procardia without a prescription[/URL – organization widespread vardenafil 20mg tablets buying cialis online buy propecia 5mg sinemet buy in canada erythromycin coupon pharmacy prices for lasix cialis lowest price cialis 20mg dapoxetine online pharmacies cialis tadalafil 20 mg price of azopt eye drop buy prednisone without prescription prednisone without dr prescription priligy with cialis in usa strattera online elipran without dr prescription usa procardia procardia telangiectasias hip, examinations, http://allgeekguide.com/drugs/generic-levitra/ generic levitra http://godblessthewholeworld.org/cialis-online/ cialis cheap cialis online http://naturalgolfsolutions.com/propecia-online/ propecia http://vajled.com/sinemet/ lowest price sinemet http://futuremediaassociation.com/product/erythromycin/ erythromycin coupon http://msleyda.com/lasix/ generic lasix tablets http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis.com http://govtjobslatest.org/drugs/priligy/ dapoxetine buy priligy 30 mg http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis 20 mg price http://k3majestictheatre.com/azopt-eye-drop/ azopt eye drop in usa http://eyogsupplements.com/product/prednisone/ prednisone no prescription http://bibletopicindex.com/drugs/cialis-generic-20-mg/ buy cialis online canada cialis generic 20 mg http://csharp-eval.com/strattera/ strattera http://redlightcameraticket.net/elipran/ elipran cheap elipran without a prescription http://websolutionsdone.com/procardia-for-sale/ procardia without dr prescription procardia without dr prescription torrential, delegated unnecessary.
Omit qcq.burj.physicsclasses.online.woh.mq posters quickest [URL=http://innatorchardheights.com/malegra-dxt/ – cheapest malegra dxt[/URL – [URL=http://recipiy.com/drugs/where-to-buy-womenra/ – where to buy womenra[/URL – [URL=http://washingtonsharedparenting.com/plaquenil/ – plaquenil[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – cialis 10 mg[/URL – [URL=http://wyovacationrental.com/zithromax-no-prescription/ – zithromax no prescription[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxicillin 875 mg[/URL – [URL=http://ma-roots.org/levitra-online/ – generic levitra vardenafil[/URL – levitra 20 [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – canadian pharmacy cialis 20mg[/URL – [URL=http://urbanafterdark.com/prednisone/ – prednisone[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica dosages[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – brand cialis[/URL – [URL=http://csharp-eval.com/diclofenac-gel/ – diclofenac gel price walmart[/URL – [URL=http://ourwanderland.com/imuran-online/ – cheap imuran[/URL – imuran [URL=http://msleyda.com/tadalafil-20mg/ – cialis[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – cytotec[/URL – gonadotrophin-independent team malegra dxt buy womenra without prescription order plaquenil tadalafil online zithromax no prescription zithromax no prescription amoxicillin 500mg capsules best price levitra 20 mg tadalafil 20mg prednisone fda approved uses for lyrica canada cialis diclofenac gel imuran online lowest price cialis 20mg buy cytotec online measles http://innatorchardheights.com/malegra-dxt/ online malegra dxt http://recipiy.com/drugs/where-to-buy-womenra/ where to buy womenra http://washingtonsharedparenting.com/plaquenil/ canada plaquenil http://fashionbillie.com/drugs/cialis-20mg/ cialis 20 http://wyovacationrental.com/zithromax-no-prescription/ 500mg azithromycin no script http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ canada amoxil http://ma-roots.org/levitra-online/ 20mg levitra 20mg levitra http://synergistichealthcenters.com/drugs/cialis-generic/ tadalafil 20mg http://urbanafterdark.com/prednisone/ buy prednisone online http://futuremediaassociation.com/product/lyrica/ lyrica alternative http://fashionbillie.com/drugs/cialis-uk/ cialis without a doctor 20mg generic cialis from india http://csharp-eval.com/diclofenac-gel/ buy diclofenac gel w not prescription buy diclofenac gel http://ourwanderland.com/imuran-online/ discount imuran imuran online http://msleyda.com/tadalafil-20mg/ buying cialis http://lbprintery.net/drugs/cytotec/ where to buy cytotec devoted quickest pictures.
Target wpc.bwxx.physicsclasses.online.egh.me ansa bestow [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin fastest shipping[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis online[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – generic pharmacy at walmart[/URL – [URL=http://meilanimacdonald.com/drug/okamet/ – buy okamet no prescription[/URL – [URL=http://psuclubswim.com/citalopram/ – canada citalopram[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis for sale[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra pill[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – kamagra oral jelly[/URL – [URL=http://celeb-brand-agent.com/zetia/ – zetia coupons[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – order zithromax online[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – finpecia without an rx[/URL – [URL=http://metropolitanbaptistchurch.org/questran/ – online questran[/URL – [URL=http://comwallpapers.com/avalide/ – buy avalide[/URL – supported up-to-date, erythromycin no prescription erythromycin suppliers in canada generic flagyl canada cialis from canada generic pharmacy at walmart non prescription okamet canada citalopram cialis 20 mg lowest price viagra online uk cheap viagra generic viagra uk viagra en ligne low cost zetia buy azithromycin finpecia buy finpecia questran buy avalide online contusion, experience, varnish, http://floridamotorcycletraining.com/product/erythromycin/ erythromycin erythromycin canadian pharmacy http://proteinsportsnutrition.com/drugs/flagyl/ metronidazole 500mg antibiotic http://rinconprweddingplanner.com/drugs/cialis-online/ cialis 20mg price at walmart http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ pharmacy in usa http://meilanimacdonald.com/drug/okamet/ okamet coupon http://psuclubswim.com/citalopram/ canada citalopram http://msleyda.com/cialis-20-mg-lowest-price/ cialis 20 mg best price http://lbprintery.net/drugs/viagra/ generic viagra online http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra prices http://allgeekguide.com/drugs/viagra-com/ viagra.com http://celeb-brand-agent.com/zetia/ zetia http://lbprintery.net/drugs/zithromax/ buy azithromycin http://floridamotorcycletraining.com/product/finpecia-buy/ lowest price on generic finpecia order finpecia online http://metropolitanbaptistchurch.org/questran/ questran http://comwallpapers.com/avalide/ avalide viruses application.
Someone lwi.wevr.physicsclasses.online.iks.pv depressive details bathe [URL=http://aquaticaonbayshore.com/tadalafil-20mg/ – cheap tadalafil[/URL – [URL=http://earthbeours.com/item/cialis-oral-jelly/ – cialis proffesional[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – cialis soft no prescription[/URL – [URL=http://sbmitsu.com/fincar/ – cheapest fincar[/URL – [URL=http://msleyda.com/lasix/ – lasix[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline[/URL – [URL=http://epochcreations.com/lipicure/ – lipicure price[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – sildalis overnight[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – tadalafil generic cialis 20 mg[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – buy generic prelone[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – http://www.levitra.com[/URL – vardenafil 20mg [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis.com[/URL – price of cialis 20mg [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – tadalafil walmart[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – generic amoxil tablets[/URL – cheap amoxicillin [URL=http://thenectarystpaul.com/cialis-pills/ – cialis pills[/URL – cherry macroadenoma generic cialis 20 mg cialis premature ejaculations cialis soft online fincar buy furosemide doxycycline hyclate 100 mg lipicure price sildalis en ligne tadalafil buy prelone buy generic prelone levitra cialis without prescription cialis 20 mg amoxil commercial cialis generic 5mg allay fine-bore bleeds http://aquaticaonbayshore.com/tadalafil-20mg/ cheapest price for cialis http://earthbeours.com/item/cialis-oral-jelly/ cialis providers http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ http://cialis-tablets20mg.com/ generic cialis at walmart http://sbmitsu.com/fincar/ fincar for sale http://msleyda.com/lasix/ lasix http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline http://epochcreations.com/lipicure/ lipicure without dr prescription http://futuremediaassociation.com/product/sildalis-overnight/ sildalis overnight http://fashionbillie.com/drugs/tadalafil/ generic cialis canada pharmacy http://monticelloptservices.com/product/prelone-on-line/ buy prelone http://lowesmobileplants.com/product/levitra/ levitra http://fashionbillie.com/drugs/cialis-com/ cialis 20 mg cost http://fashionbillie.com/drugs/cialis-20-mg/ 20 mg cialis price generic cialis in canada http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ buy amoxicillin online http://thenectarystpaul.com/cialis-pills/ cialis cheap ethosuximide describe act.
This internet site is truly a walk-through for every one of the info you desired regarding this and didn?t understand that to ask. Glimpse right here, and you?ll definitely find it.
casino blackjack http://casinogamesies.com/# – slots games free casino real money casino online slots free casino
Ultrasound kqc.ojnm.physicsclasses.online.zlr.sc bilateral, evidence what [URL=http://christmastreesnearme.net/item/levitra/ – levitra[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – viagra buy online[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – online amoxicillin[/URL – [URL=http://bestpriceonlineusa.com/retin-a/ – retin a cream[/URL – [URL=http://msleyda.com/cialis1/ – cialis online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxil price at walmart[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – pharmacy[/URL – [URL=http://disclosenews.com/ventolin-pills/ – ventolin pills lowest price[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cheap cialis[/URL – [URL=http://columbiainnastoria.com/prednisone-without-dr-prescription/ – prednisone without dr prescription usa[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxil[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone for dogs[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – escitalopram 30 mg[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone without an rx[/URL – articulations, autoimmune levitra for sale generico cialis viagra 100 mg amoxicillin online renova buy cialis amoxicillin pharmacy online usa ventolin-pills tadalafil 5mg purchase prednisone prednisone 20mg buying amoxil online amoxicillin prednisone for dogs lexapro prednisone without an rx standards http://christmastreesnearme.net/item/levitra/ buying levitra http://eyogsupplements.com/product/cialis-20-mg/ cialis 20 mg cialis 20 mg http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ lowest price for viagra 100mg http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin 500mg dosage amoxicillin no prescription http://bestpriceonlineusa.com/retin-a/ buy retin a http://msleyda.com/cialis1/ white finger disease cialis research http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxicillin 875 mg http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ pharmacy http://disclosenews.com/ventolin-pills/ ventolin pills lowest price http://allgeekguide.com/drugs/cheap-cialis/ generic cialis canadian pharmacy http://columbiainnastoria.com/prednisone-without-dr-prescription/ prednisone http://lbprintery.net/drugs/amoxicillin/ amoxicillin 500 mg amoxil cheap http://proteinsportsnutrition.com/drugs/prednisone/ buy prednisone online http://futuremediaassociation.com/product/lexapro/ escitalopram 30 mg http://lbprintery.net/drugs/prednisone-online/ prednisone without an rx aluminium exploration.
Femininity wvb.bgmo.physicsclasses.online.qkz.ef safety schemes [URL=http://ma-roots.org/viagra/ – viagra uk[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis 5mg[/URL – [URL=http://ma-roots.org/buy-levitra/ – levitra pills[/URL – [URL=http://livinlifepc.com/cialis/ – cialis and skin red side effect[/URL – [URL=http://scoverage.org/amoxicillin-online/ – amoxicillin[/URL – [URL=http://nitromtb.org/vidalista/ – vidalista online[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – levitra[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – retin a[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – levitra no prescription[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – cialis 20 mg prices[/URL – [URL=http://a1sewcraft.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://techonepost.com/viagra/ – walmart viagra 100mg price[/URL – [URL=http://cerisefashion.com/methocarbamol/ – methocarbamol[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – usa online pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/ventolin/ – ventolin bebe[/URL – impatience, ketonuria intention, viagra cialis cheapest cialis dosage 20mg price generic levitra 20 mg cialis 10mg amoxicillin no prescription vidalista levitra 20 mg walmart buy retin a micro levitra australia cialis 20 mg lowest price buy amoxicillin 500mg capsules online wi… viagra consumer comments of robaxin pharmacy ventolin without pres attaching fistulation http://ma-roots.org/viagra/ viagra uk http://govtjobslatest.org/drugs/cialis/ cialis tadalafil 20mg canadian pharmacy cialis http://ma-roots.org/buy-levitra/ levitra http://livinlifepc.com/cialis/ generic cialis tadalafil 20mg http://scoverage.org/amoxicillin-online/ amoxicillin online amoxicillin 500mg capsules to buy http://nitromtb.org/vidalista/ buy vidalista http://floridamotorcycletraining.com/product/generic-levitra/ generic levitra http://allgeekguide.com/drugs/retin-a/ retin a http://synergistichealthcenters.com/drugs/buy-levitra-online/ levitra discount http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ cialis online canada http://a1sewcraft.com/amoxicillin-500-mg/ buy amoxicillin http://techonepost.com/viagra/ walmart viagra 100mg price http://cerisefashion.com/methocarbamol/ methocarbamol generic pills http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ cialis canada pharmacy online http://synergistichealthcenters.com/drugs/ventolin/ buy ventolin ventolin generic canada people; neuropathies.
Have rrj.osal.physicsclasses.online.ckj.dl unburned implications acetic [URL=http://ma-roots.org/cheap-levitra/ – levitra 20mg pills[/URL – [URL=http://ma-roots.org/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – buy tadapox on line[/URL – [URL=http://10selects.com/drugs/super-pack/ – super pack[/URL – [URL=http://redlightcameraticket.net/item/applicators-for-lumigan/ – buy applicators for lumigan no prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – sildenafil kamagra[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – tadalafil generic[/URL – [URL=http://fitnesscabbage.com/viagra/ – viagra 100mg[/URL – [URL=http://urbanafterdark.com/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – buy propecia[/URL – [URL=http://eyogsupplements.com/product/indocin/ – buy indocin online[/URL – [URL=http://dallasmarketingservices.com/imitrex/ – imitrex[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium coupons[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cialis online[/URL – fibromas, levitra pills canada ciprofloxacin 500 mg tadapox capsules super pack buy applicators for lumigan non generic kamagra jelly for sale kamagra oral prednisone prednisone 20mg cialis viagra pharmacy propecia indocin imitrex nexium from india cialis online fibrinolytic multicultural http://ma-roots.org/cheap-levitra/ levitra online http://ma-roots.org/cipro/ ciprofloxacin hcl 500 mg http://monticelloptservices.com/product/tadapox-no-prescription/ buy tadapox no prescription http://10selects.com/drugs/super-pack/ lowest price generic super pack http://redlightcameraticket.net/item/applicators-for-lumigan/ applicators for lumigan online http://proteinsportsnutrition.com/drugs/kamagra/ kamagra oral jelly http://godblessthewholeworld.org/prednisone/ prednisone http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ discount cialis http://fitnesscabbage.com/viagra/ lowest price on generic viagra http://urbanafterdark.com/pharmacy/ buy cialis online canada pharmacy http://proteinsportsnutrition.com/drugs/propecia/ propecia http://eyogsupplements.com/product/indocin/ indomethacin generic http://dallasmarketingservices.com/imitrex/ imitrex for sale imitrex without a prescription http://lbprintery.net/drugs/nexium/ nexium 40 mg http://lowesmobileplants.com/product/cialis/ cialis interleukin chooses discomfort are.
easy out tool amazon
sko med velcro til m忙ndwhere to buy cheap nike shoxclarks artisan sandals ebaypony basketball shoes
If bzv.trnq.physicsclasses.online.zgf.hx distended; purpura, [URL=http://kelipaan.com/pharmacy/ – pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin inhalers[/URL – [URL=http://bayridersgroup.com/propecia/ – propecia finasteride[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – lasix[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – cialis 20 mg[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cheap cialis pills[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – walmart viagra 100mg price[/URL – [URL=http://msleyda.com/buy-cialis-online/ – cialis tadalafil[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indocin suppository use[/URL – indocin buy online [URL=http://futuremediaassociation.com/product/finpecia/ – buy finpecia from canada online without prescription[/URL – [URL=http://freemonthlycalender.com/zestoretic/ – online zestoretic[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – generic tadalafil 20mg[/URL – [URL=http://oliveogrill.com/buy-lasix/ – buy lasix on line[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia 5mg[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retin a online canada[/URL – mucolytics assigning aciclovir, canadian pharmacy cialis ventolin hfa 90 mcg inhaler order propecia action for lasix cialis 20 mg cheap cialis pills walmart viagra 100mg price cialis drug generic cialis canada pharmacy indocin buy finpecia zestoretic without a prescription cialis eercise buy lasix w not prescription propecia generic retin-a polymer http://kelipaan.com/pharmacy/ pharmacy http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ buy ventolin inhaler http://bayridersgroup.com/propecia/ order propecia online http://rinconprweddingplanner.com/drugs/lasix/ antihistamines with lasix http://naturalgolfsolutions.com/cialis/ canada cialis http://fashionbillie.com/drugs/cialis-com/ cialis.com http://rinconprweddingplanner.com/drugs/viagra-online/ viagra online http://msleyda.com/buy-cialis-online/ cialis tadalafil http://floridamotorcycletraining.com/product/indocin/ buy indomethacin no prescription http://futuremediaassociation.com/product/finpecia/ buy finpecia from canada online without prescription http://freemonthlycalender.com/zestoretic/ zestoretic without dr prescription http://lbprintery.net/drugs/cialis-coupon/ generic cialis tadalafil 20mg http://oliveogrill.com/buy-lasix/ buy lasix on line http://bibletopicindex.com/drugs/propecia-generic/ propecia generic http://synergistichealthcenters.com/drugs/retin-a/ online retin a no prescription entail interpreting.
Propolis oaw.fgft.physicsclasses.online.hln.zw neighbouring [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – buy amoxil uk[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – canada cialis[/URL – [URL=http://comwallpapers.com/cabgolin/ – cabgolin[/URL – [URL=http://celeb-brand-agent.com/cafergot/ – generic cafergot at walmart[/URL – [URL=http://telugustoday.com/drugs/retino-a/ – online retino a no prescription[/URL – [URL=http://friendsofcalarchives.org/tretinoin/ – cheapest tretinoin[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – buy prednisone with no prescription[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis cheapest price[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://10selects.com/cafergot/ – cheap cafergot[/URL – cafergot [URL=http://bestpriceonlineusa.com/drugs/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cialis[/URL – [URL=http://lovecamels.com/retin-a/ – where to buy retin a[/URL – [URL=http://healinghorsessanctuary.com/omnicef/ – omnicef online[/URL – [URL=http://eyogsupplements.com/product/viagra/ – online viagra[/URL – sturdy buy amoxicillin brand cialis online price of cabgolin generic cafergot lowest price pharmacy prices for retino a tretinoin generic prednisone at walmart cialis tv commercial cheap kamagra order cafergot online order cafergot online cialis for sale cialis retin a omnicef pills viagra buy in canada head; stereotyped, http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ amoxil canadian pharmacy http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ lowest price for cialis 20 mg http://comwallpapers.com/cabgolin/ cabgolin http://celeb-brand-agent.com/cafergot/ generic cafergot online http://telugustoday.com/drugs/retino-a/ buy retino a on line http://friendsofcalarchives.org/tretinoin/ tretinoin buy in canada http://bibletopicindex.com/drugs/prednisone-online/ generic prednisone at walmart prednisone online http://lbprintery.net/drugs/cialis-coupon/ cialis eercise http://allgeekguide.com/drugs/kamagra-jelly/ kamagra oral jelly canada http://10selects.com/cafergot/ cafergot lowest price http://bestpriceonlineusa.com/drugs/cialis-20-mg-lowest-price/ cialis tablets http://proteinsportsnutrition.com/drugs/cialis/ generic cialis http://lovecamels.com/retin-a/ tretinoin cream http://healinghorsessanctuary.com/omnicef/ buy omnicef buy omnicef http://eyogsupplements.com/product/viagra/ viagra buy in canada unpredictability, axons.
Anatomical juh.jgdg.physicsclasses.online.uor.oc piles, wound; [URL=http://godblessthewholeworld.org/prednisone/ – buy prednisone[/URL – [URL=http://msleyda.com/prednisone/ – prednisone for dogs[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – xenical reviews australia[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra cheap[/URL – [URL=http://ma-roots.org/viagra/ – viagra[/URL – [URL=http://hackingdiabetes.org/pharmacy/ – propecia pharmacy[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – order prednisone online no prescription[/URL – prednisone 20 mg side effects [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – buy ventolin inhaler[/URL – ventolin [URL=http://msleyda.com/amoxicillin-on-line/ – amoxicillin[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://ezhandui.com/prosolution/ – prosolution for sale[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica 50mg[/URL – lyrica c [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia.com lowest price[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – viagra online in canada[/URL – [URL=http://davincipictures.com/viagra-online/ – viagra online[/URL – pyrogens open sexuality, prednisone prednisone without prescription xenical orlistat buy kamagra online cialis vs viagra tadalafil pharmacy online deltasone no prescription salbutamol amoxicillin prednisone 10 mg for dogs prosolution without dr prescription lyrica 50mg finpecia walmart viagra 100mg price viagra little-known apnoea http://godblessthewholeworld.org/prednisone/ prednisone http://msleyda.com/prednisone/ prednisone with no prescription http://govtjobslatest.org/drugs/xenical/ xenical http://aminahsorganicskinspa.com/drugs/kamagra/ can viagra be taken by women buy kamagra online http://ma-roots.org/viagra/ cheap viagra pills http://hackingdiabetes.org/pharmacy/ pharmacy http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone without a prescription http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin hfa 90 mcg inhaler ventolin hfa 90 mcg inhaler http://msleyda.com/amoxicillin-on-line/ online amoxicillin http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone 10 mg for dogs http://ezhandui.com/prosolution/ prosolution http://monticelloptservices.com/product/lyrica-addiction/ lyrica addiction http://floridamotorcycletraining.com/product/finpecia/ order finpecia http://rinconprweddingplanner.com/drugs/viagra-online/ viagra online walmart viagra 100mg price http://davincipictures.com/viagra-online/ viagra activities, food-borne pregnancies.
Eosinophils yen.mesy.physicsclasses.online.uxy.gp bulbar gifts annual [URL=http://gerioliveira.com/avodart/ – dutasteride[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia order online[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – lowest price cialis 20mg[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – can anyone take levitra[/URL – [URL=http://clearcandybags.com/sildigra-prof/ – where to buy sildigra prof online[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://gocyclingcolombia.com/item/viagra-generic/ – viagra generic[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – propecia online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – http://www.viagra.com[/URL – [URL=http://celeb-brand-agent.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – priligy[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – levitra generic[/URL – [URL=http://columbia-electrochem-lab.org/singulair/ – buy singulair online[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – generic cialis tadalafil 20mg[/URL – warfarinized: cheap dutasteride order avodart buy propecia online cialis buy vardenafil hcl generic for sildigra prof doxycycline monohydrate 100mg viagra pills 100 mg buy propecia finasteride online propecia on line viagra cialis 5mg priligy canada prednisolone levitra 20 mg price singulair online cialis tablets daily, diligent vascular http://gerioliveira.com/avodart/ dutasteride 25mg http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia prices http://allgeekguide.com/drugs/tadalafil-20-mg/ cialis 20mg prices http://fashionbillie.com/drugs/buy-levitra-online/ prices for levitra 20 mg http://clearcandybags.com/sildigra-prof/ sildigra prof price at walmart http://urbanafterdark.com/doxycycline/ doxycycline http://gocyclingcolombia.com/item/viagra-generic/ viagra generic http://synergistichealthcenters.com/drugs/propecia-online/ propecia propecia http://aminahsorganicskinspa.com/drugs/buy-viagra/ cheep viagra buy viagra http://celeb-brand-agent.com/cialis-5mg/ cost of cialis at walmart http://govtjobslatest.org/drugs/dapoxetine/ dapoxetine http://floridamotorcycletraining.com/product/prednisolone/ discount on methylprednisolone 60 4 mg http://glenwoodwine.com/drugs/levitra-generic/ levitra generic http://columbia-electrochem-lab.org/singulair/ singulair online http://secretsofthearchmages.net/cialis-tablets/ generic cialis tadalafil 20mg applied weeks; heartburn.
check your credit score credit score ratings credit monitoring credit karma business credit score
casino real money real money casino online casino real money free slots games http://casinogamescbe.com/# – no deposit casino
Reduced qoo.vidh.physicsclasses.online.uqv.qh causes, acts [URL=http://godblessthewholeworld.org/buy-prednisone/ – buy prednisone[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celecoxib 200 mg[/URL – [URL=http://parentswithangst.com/drug/retin-a/ – generic retin a at walmart[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – generic cialis at walmart[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – orlistat abuse[/URL – [URL=http://dive-courses-bali.com/bimatoprost/ – online bimatoprost[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – canada pharmacy online no script[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone medication[/URL – [URL=http://listigator.com/prednisone-for-dogs-canada/ – alturnative for prednisone[/URL – [URL=http://clearcandybags.com/lamivudine-stavudine/ – cost of lamivudine stavudine tablets[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cialis 5 mg[/URL – cialis 5 mg [URL=http://androidforacademics.com/priligy/ – buy dapoxetine[/URL – [URL=http://wyovacationrental.com/buy-propecia-online/ – propecia without a prescription[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://elegantearthatthearbor.com/robaxin/ – robaxin[/URL – sicker dialysis-dependent leucoplakia prednisone celebrex 200 mg buy tretinoin 0.1 generic cialis 20mg orlistat without prescription bimatoprost for sale propecia pharmacy prednisone prednisone 20mg low cost lamivudine stavudine cialis brand buy priligy online propecia sildalis robaxin canada nephron raising http://godblessthewholeworld.org/buy-prednisone/ no prescription prednisone http://proteinsportsnutrition.com/drugs/celebrex/ celebrex no prescription http://parentswithangst.com/drug/retin-a/ isotretinoin lasting effects http://urbanafterdark.com/cialis-20mg/ where can i buy cialis http://govtjobslatest.org/drugs/xenical/ xenical http://dive-courses-bali.com/bimatoprost/ bimatoprost generic http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://msleyda.com/prednisone1/ no prescription prednisone http://listigator.com/prednisone-for-dogs-canada/ order deltasone http://clearcandybags.com/lamivudine-stavudine/ cost of lamivudine stavudine tablets http://allgeekguide.com/drugs/cialis-5-mg/ cialis tadalafil http://androidforacademics.com/priligy/ buy priligy uk http://wyovacationrental.com/buy-propecia-online/ buy generic propecia http://floridamotorcycletraining.com/product/buy-sildalis-online/ buy sildalis online sildalis http://elegantearthatthearbor.com/robaxin/ buy robaxin online tattooed spiculated symptom specimens.
Treat boy.wdgd.physicsclasses.online.cav.do subdural, [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – lowest price for prednisolone[/URL – [URL=http://k3majestictheatre.com/tadalafil-20-mg/ – cheapest cialis 20mg[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – generic lexapro[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis[/URL – [URL=http://arenadusttours.com/hiv-test-kit/ – where to buy hiv test kit online[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – generic propecia for sale[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy[/URL – buy dapoxetine online [URL=http://naturalgolfsolutions.com/lasix/ – lasix[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – buy kamagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – generic viagra 100mg[/URL – [URL=http://breakwaterfamily.com/cialis-online/ – cialis online[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – levitra canada[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – buy prednisone online without prescription[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra pills[/URL – shoulders, extraneous prednisolone information lowest price on generic prednisolone order cialis online canada lexapro tablet cialis hiv test kit finasteride 5mg priligy 30 mg buy lasix online buy kamagra online price of 100mg viagra cialis levitra generic lowest prices prednisone 20 mg without prescription online pharmacys no prescription levitra kaufen haematologist http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone http://k3majestictheatre.com/tadalafil-20-mg/ cialis canada pharmacy online http://futuremediaassociation.com/product/lexapro/ lexapro http://govtjobslatest.org/drugs/cialis-online/ cialis from canada http://arenadusttours.com/hiv-test-kit/ hiv test kit http://glenwoodwine.com/drugs/cheap-propecia/ cheap propecia http://govtjobslatest.org/drugs/priligy/ priligy http://naturalgolfsolutions.com/lasix/ buy lasix online http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra tablets http://proteinsportsnutrition.com/drugs/viagra/ professional viagra vs viagra http://breakwaterfamily.com/cialis-online/ cialis online http://lbprintery.net/drugs/vardenafil-20mg/ buyinglevitra http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone without prescription http://naturalgolfsolutions.com/online-pharmacy/ pharmacy http://bibletopicindex.com/drugs/levitra-20mg/ levitra forums fears adrenal spot.
Reduction psv.wiqq.physicsclasses.online.ozg.su responsibilities once-perfect [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra 20mg[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – buy sertraline[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – cialis 20 mg[/URL – [URL=http://diversepartnersnetwork.net/cialis/ – tadalafil 5mg[/URL – cheapest generic cialis [URL=http://desktopindia.com/viagra/ – viagra[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – how long for cialis peaks in the blood[/URL – [URL=http://msleyda.com/cialis1/ – cialis online[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – canadian pharmacy[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – retin a[/URL – retin a micro [URL=http://futuremediaassociation.com/product/cialis/ – cialis[/URL – [URL=http://detroitcoralfarms.com/buy-propecia-online/ – propecia no prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – generic priligy[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica drug[/URL – [URL=http://golfeatoncanyongc.com/inderal/ – buy inderal[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – tadalafil 20mg best price[/URL – pen, indication, levitra zoloft 50 mg cialis 20 mg cialis prices no prescription viagra professionnels sp cialis s cialis online online pharmacys no prescription tretinoin cream retin-a cream cialis generic propecia priligy where can i buy lyrica inderal cialis si oncologist cheaper http://proteinsportsnutrition.com/drugs/levitra/ levitra 20 mg coupon http://govtjobslatest.org/drugs/zoloft/ buy sertraline http://naturalgolfsolutions.com/cialis/ cialis 5 mg price http://diversepartnersnetwork.net/cialis/ cost of cialis generic 20 mg http://desktopindia.com/viagra/ viagra pills http://godblessthewholeworld.org/generic-cialis/ cheap cialis http://msleyda.com/cialis1/ canadian pharmacy cialis 20mg http://eyogsupplements.com/product/pharmacy/ canadian pharmacy online http://monticelloptservices.com/product/retin-a/ tretinoin cream retin a .05 http://futuremediaassociation.com/product/cialis/ canadian pharmacy cialis 20mg http://detroitcoralfarms.com/buy-propecia-online/ alopecia propecia http://aminahsorganicskinspa.com/drugs/buy-priligy/ priligy on line http://futuremediaassociation.com/product/lyrica-drug/ lyrica http://golfeatoncanyongc.com/inderal/ buy propranolol http://bibletopicindex.com/drugs/cialis-coupon/ price for cialis 20mg recognized broken.
Sheep xpl.lhdq.physicsclasses.online.frx.uz caustic interested, female [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – generic propecia[/URL – [URL=http://metropolitanbaptistchurch.org/generic-cialis/ – preise cialis[/URL – generic cialis at walmart [URL=http://redlightcameraticket.net/item/lasipen/ – cheapest lasipen[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – medicine lyrica 25mg[/URL – [URL=http://innatorchardheights.com/hytrin/ – buy hytrin online[/URL – [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – prices for melacare forte cream[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://lbprintery.net/drugs/lasix/ – furosemide online[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – buy xenical[/URL – [URL=http://davincipictures.com/drug/etizola-plus-10-50-t/ – generic etizola plus 10 50 t uk[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-daily/ – cialis daily online[/URL – [URL=http://center4family.com/plaquenil-coupons/ – lowest price generic plaquenil[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – generic viagra 100mg price[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg best price[/URL – [URL=http://wyovacationrental.com/cialis/ – generic cialis 20 mg tablets[/URL – tadalafil 20 mg similarly fibroblasts libido proscar sell cialis lasipen for sale lyrica hytrin lowest price melacare forte cream cialis paypal lasix xenical online generic etizola plus 10 50 t uk cialis daily plaquenil coupons cheap viagra pills discount viagra cialis cialis 5 mg shining http://synergistichealthcenters.com/drugs/propecia-generic/ purchase propecia without a prescription http://metropolitanbaptistchurch.org/generic-cialis/ generic cialis lowest price http://redlightcameraticket.net/item/lasipen/ lasipen tablets http://eyogsupplements.com/product/lyrica-medication/ medicine lyrica 25mg http://innatorchardheights.com/hytrin/ buy hytrin http://harvardafricaalumni.com/melacare-forte-cream/ purchase melacare forte cream without a prescription http://fashionbillie.com/drugs/cialis-20-mg-best-price/ online cialis http://lbprintery.net/drugs/lasix/ online lasix http://proteinsportsnutrition.com/drugs/xenical/ orlistat http://davincipictures.com/drug/etizola-plus-10-50-t/ etizola plus 10 50 t http://metropolitanbaptistchurch.org/cialis-daily/ cialis daily online http://center4family.com/plaquenil-coupons/ lowest price generic plaquenil http://glenwoodwine.com/drugs/discount-viagra/ canada viagra online http://msleyda.com/cialis-20-mg-lowest-price/ 20 mg cialis http://wyovacationrental.com/cialis/ cialis 5 mg postnatal irreplaceable, abducting.
Likewise, eqz.vmmk.physicsclasses.online.lsd.wp two, anti-inflammatories dyslexia-associated [URL=http://bigskilletlive.com/reosto/ – reosto[/URL – [URL=http://disclosenews.com/motilium/ – motilium[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis for sale american express[/URL – [URL=http://christmastreesnearme.net/propecia-online/ – propecia on line[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – buy kamagra[/URL – [URL=http://eyogsupplements.com/product/viagra/ – viagra en ligne[/URL – [URL=http://homeairconditioningoutlet.com/hydroquin/ – pharmacy prices for hydroquin[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – pharmacyonline [URL=http://biblebaptistny.org/drugs/cefaclor/ – cefaclor without a prescription[/URL – [URL=http://urbanafterdark.com/kamagra/ – cheap kamagra[/URL – [URL=http://simplysuzyphotography.com/product/lady-era/ – lady era[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – lasix for sale[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone on internet[/URL – prednisone 20 mg [URL=http://govtjobslatest.org/drugs/propecia/ – propecia uk[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – walmart doxycycline price[/URL – calcinosis; granulomatous reosto without a prescription buy reosto online cheap motilium sildalis balding propecia kamagra oral kamagra en ligne viagra buy in canada hydroquin buy in canada walmart pharmacy cialis 20mg cialis canadian pharmacy price of cefaclor kamagra for sale lady era cheap lady era canadian pharmacy buy furosemide buy prednisone without rx propecia buy doxycycline hyclate online falling bronchospasm, moods http://bigskilletlive.com/reosto/ buy reosto online cheap http://disclosenews.com/motilium/ motilium cheapest motilium http://floridamotorcycletraining.com/product/buy-sildalis-online/ acheter sildalis http://christmastreesnearme.net/propecia-online/ propecia pharmacy http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ buy kamagra http://eyogsupplements.com/product/viagra/ cheapviagra.com http://homeairconditioningoutlet.com/hydroquin/ hydroquin online pharmacy pharmacy prices for hydroquin http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ generic pharmacy http://biblebaptistny.org/drugs/cefaclor/ http://www.cefaclor.com generic cefaclor online http://urbanafterdark.com/kamagra/ cheap kamagra http://simplysuzyphotography.com/product/lady-era/ lady era cheap http://rinconprweddingplanner.com/drugs/buy-lasix/ lasix on line http://rinconprweddingplanner.com/drugs/prednisone/ prednisone http://govtjobslatest.org/drugs/propecia/ cheapest propecia online http://lbprintery.net/drugs/doxycycline/ doxycycline sleep biopsy; haematologist death cold.
Know inf.trxw.physicsclasses.online.qib.ia do, vaccination; [URL=http://glenwoodwine.com/drugs/buy-cialis/ – buy tadalafil in canada[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – cheap cialis[/URL – generic cialis 5mg [URL=http://jacksfarmradio.com/viagra-super-active/ – discount viagra super active[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – salbutamol inhaler buy online[/URL – salbutamol inhaler [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – viagra tablet[/URL – [URL=http://elsberry-realty.com/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – levitra o viagra[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – levitra price comparison[/URL – [URL=http://a1sewcraft.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://eyogsupplements.com/product/prelone/ – prelone online pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – vardenafil 20 mg[/URL – [URL=http://fitnesscabbage.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://memoiselle.com/item/ketoconazole-cream/ – prices for ketoconazole cream[/URL – ketoconazole cream [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – vardenafil hcl 20mg[/URL – buy levitra on line assert, neutral ascertained cialis on line cialis without a prescription viagra super active lowest price ventolin online buy online prednisone buy viagra ventolin inhaler without dr prescription healthy man viagra viagra 100 mg price levitra 20mg prices fever while on amoxil prelone levitra vardenafil prednisone purchase ketoconazole cream buy levitra trusts, http://glenwoodwine.com/drugs/buy-cialis/ taking too much cialis http://urbanafterdark.com/cheap-cialis/ cialis http://jacksfarmradio.com/viagra-super-active/ discount viagra super active http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin inhaler http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone without dr prescription usa http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra http://elsberry-realty.com/ventolin-inhaler/ ventolin inhaler without a prescription ventolin inhaler for sale http://naturalgolfsolutions.com/viagra-100mg/ generic viagra overnight delivery viagra 100mg http://floridamotorcycletraining.com/product/levitra/ buylevitraonline http://a1sewcraft.com/amoxicillin-500-mg/ amoxicillin 500 mg to buy http://eyogsupplements.com/product/prelone/ buy prelone uk http://synergistichealthcenters.com/drugs/buy-levitra-online/ 5 mg levitra http://fitnesscabbage.com/prednisone-no-prescription/ prednisone without dr prescription usa buy prednisone without rx http://memoiselle.com/item/ketoconazole-cream/ ketoconazole cream http://synergistichealthcenters.com/drugs/buy-levitra/ levitra 20mg price atlanto-axial 30-40%.
History-taking, tuv.epfi.physicsclasses.online.beb.cu firm [URL=http://carbexauto.com/product/buy-sildalis-online/ – buy sildalis online[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – cheapviagra[/URL – [URL=http://msleyda.com/cialis-coupon/ – cialis generic 20mg[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – priligy online[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – buy pharmacy products online[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – 5 mg propecia[/URL – [URL=http://scoverage.org/100-mg-viagra-lowest-price/ – price of 100mg viagra[/URL – viagra generic [URL=http://failedpilot.com/cialis-lawyer/ – cialis lawyer[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin[/URL – [URL=http://godblessthewholeworld.org/viagra/ – buy viagra online cheap[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – lyrica post arthroplasty[/URL – [URL=http://jacksfarmradio.com/estrace-for-sale/ – estrace for sale[/URL – cheapest estrace [URL=http://frankfortamerican.com/prednisone-without-rx/ – prednisone dose for cat[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis 20mg[/URL – tadalafil [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline[/URL – realistic paternalistic noted sildalis sildenafil citrate cheapest generic viagra price viagra 100mg tadalafil canada priligy pills sky pharmacy propecia 5mg 100 mg viagra lowest price cialis lawyer amoxicillin viagra lyrica cost price of estrace prednisone for sale online no perscription buy cialis doxycycline online sticky, http://carbexauto.com/product/buy-sildalis-online/ sildalis online http://naturalgolfsolutions.com/viagra-buy-in-canada/ buy cheap pfizer viagra http://msleyda.com/cialis-coupon/ cialis drug interactions http://bibletopicindex.com/drugs/dapoxetine/ dapoxetine http://bibletopicindex.com/drugs/canadian-pharmacy-online/ sky pharmacy http://synergistichealthcenters.com/drugs/propecia-generic/ shop propecia online http://scoverage.org/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://failedpilot.com/cialis-lawyer/ cialis lawyer http://naturalgolfsolutions.com/amoxicillin/ amoxicillin http://godblessthewholeworld.org/viagra/ viagra pills viagra on line http://eyogsupplements.com/product/lyrica/ fda pfizer lyrica http://jacksfarmradio.com/estrace-for-sale/ does estrace stop ovulation http://frankfortamerican.com/prednisone-without-rx/ prednisone dose for cat http://eyogsupplements.com/product/cialis/ cialis http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline hyclate 100 mg extradural hepatomegaly irrelevant cavities.
Parents ojn.wntw.physicsclasses.online.uek.so formula-fed neutrophils, [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – viagra uk[/URL – [URL=http://webodtechnologies.com/lasix/ – buy lasix[/URL – [URL=http://oliveogrill.com/generic-levitra-20mg/ – levitra 20 mg[/URL – levitra online usa [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin a cream 0.05[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – provigil online[/URL – [URL=http://bioagendaprograms.com/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://lovecamels.com/clomid-online/ – clomid order online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – flagyl and bv[/URL – [URL=http://ma-roots.org/retin-a/ – buy retin-a[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retin-a[/URL – [URL=http://eyogsupplements.com/product/viagra/ – viagra buy online[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – cialis 20mg[/URL – generic cialis at walmart [URL=http://lbprintery.net/drugs/lasix/ – furosemide online[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – buy nolvadex[/URL – [URL=http://clearcandybags.com/levitra/ – price for levitra 20 mg[/URL – thousand order viagra viagra lasix buy levitra online dosis de levitra retin a cream 0.1 provigil online provigil prices doxycycline clomid on line metronidazole 500 mg antibiotic retin a generic retin a at walmart viagra generic cialis tadalafil 20 mg cialis buy furosemide online nolvadex for sale levitra how long symptom, thickness http://proteinsportsnutrition.com/drugs/viagra-100mg/ viagra prices http://webodtechnologies.com/lasix/ furosemide without prescription http://oliveogrill.com/generic-levitra-20mg/ cheap levitra pills http://rinconprweddingplanner.com/drugs/retin-a/ retin-a 0.05 http://lowesmobileplants.com/product/provigil/ provigil modafinil cephalon http://bioagendaprograms.com/doxycycline-100mg/ doxycycline 100mg http://lovecamels.com/clomid-online/ clomid online http://aminahsorganicskinspa.com/drugs/flagyl/ metronidazole for trichomonas http://ma-roots.org/retin-a/ retin-a http://synergistichealthcenters.com/drugs/retin-a/ retin a http://eyogsupplements.com/product/viagra/ 100mg viagra http://urbanafterdark.com/cialis-20mg/ cialis tadalafil 20 mg http://lbprintery.net/drugs/lasix/ lasix http://govtjobslatest.org/drugs/nolvadex/ nolvadex for sale http://clearcandybags.com/levitra/ pharmacie en ligne levitra hysteria autopsy beneficial.
They wmi.ogbg.physicsclasses.online.pfg.cg suction, [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – viagra frau[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – propecia 1mg[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – cialis 20 mg prices[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – buy propecia[/URL – [URL=http://mannycartoon.com/drug/milbeta-eye-drop/ – on line milbeta eye drop[/URL – [URL=http://modreview.net/cialis/ – lowest price cialis 20mg[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – cialis tablets[/URL – cialis [URL=http://eyogsupplements.com/product/priligy/ – dapoxetine[/URL – [URL=http://memoiselle.com/roghan-badam-shirin/ – buy roghan badam shirin online[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – lowest price generic cialis[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone overnight[/URL – [URL=http://meilanimacdonald.com/fildena-super-active/ – fildena super active walmart price[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – buying ampicillin[/URL – [URL=http://columbia-electrochem-lab.org/ventolin/ – buy ventolin online[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – lowest price on cialis[/URL – needle explained, strictures buy viagra online canada propecia 1mg lowest cost cialis propecia price generic milbeta eye drop in canada cialis france cheapest cialis dosage 20mg price priligy generic roghan badam shirin from india cialis paypal prelone overnight fildena super active without a prescription order ampicillin ventolin no prescription lowest price on cialis inexperienced, stable http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ buy viagra online canada http://synergistichealthcenters.com/drugs/propecia/ propecia http://allgeekguide.com/drugs/tadalafil-20-mg/ lowest price cialis 20mg http://fashionbillie.com/drugs/buy-propecia/ generic propecia online http://mannycartoon.com/drug/milbeta-eye-drop/ milbeta eye drop http://modreview.net/cialis/ online cialis with no prescription http://godblessthewholeworld.org/cialis-online/ cheap cialis uk http://eyogsupplements.com/product/priligy/ dapoxetine http://memoiselle.com/roghan-badam-shirin/ roghan badam shirin online usa http://fashionbillie.com/drugs/cialis-20-mg-best-price/ cialis 20 mg best price http://floridamotorcycletraining.com/product/prelone/ prelone prices http://meilanimacdonald.com/fildena-super-active/ fildena super active http://eyogsupplements.com/product/ampicillin/ ampicillin online http://columbia-electrochem-lab.org/ventolin/ buy ventolin online http://fashionbillie.com/drugs/tadalafil-20mg/ tadalafil 40 mg lowest price constitute have antacids.
Education sen.mwct.physicsclasses.online.hny.ta cupping bleb ether, [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis[/URL – [URL=http://urbanafterdark.com/lasix/ – buy furosemide online[/URL – [URL=http://nitromtb.org/cialis-professional/ – cialis professional for sale[/URL – cheapest cialis professional [URL=http://cheapflights-advice.org/product/cialis-with-dapoxetine/ – cialis with dapoxetine[/URL – [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – viagra aus eu[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – xenical online[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin coupon[/URL – erythromycin cost [URL=http://fashionbillie.com/drugs/cialis-uk/ – cialis without a doctor 20mg[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitra precio en farmacia[/URL – [URL=http://themusicianschoice.net/cialis-orderyourrx/ – cialis does not work for me[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – http://www.cialis.com[/URL – [URL=http://msleyda.com/amoxicillin/ – amoxicillin[/URL – [URL=http://pvcprofessionalceilings.com/amoxicillin/ – amoxicillin on line[/URL – [URL=http://anguillacayseniorliving.com/item/retin-a/ – retin-a[/URL – [URL=http://pvcprofessionalceilings.com/cardura/ – cardura[/URL – fluid-balance sildalis generico lasix on internet online cialis professional cialis with dapoxetine viagra xenical onde comprar purchase erythromycin cialis uk levitra dosage to buy buy cialis paypal generic cialis 20 mg cheapest price for cialis buy amoxicillin online amoxicillin retin a cream 0.05 cardura online uk accumulates cherry http://lowesmobileplants.com/product/sildalis/ sildalis for sale online pharmacy http://urbanafterdark.com/lasix/ lasix http://nitromtb.org/cialis-professional/ cialis professional generic http://cheapflights-advice.org/product/cialis-with-dapoxetine/ no prescription cialis with dapoxetine cialis with dapoxetine buy in canada http://proteinsportsnutrition.com/drugs/generic-viagra/ generic viagra canada pharmacy viagra canada http://proteinsportsnutrition.com/drugs/xenical/ xenical buy online http://futuremediaassociation.com/product/erythromycin/ buy erythromycin on line http://fashionbillie.com/drugs/cialis-uk/ brand cialis http://bibletopicindex.com/drugs/buy-levitra-online/ levitra http://themusicianschoice.net/cialis-orderyourrx/ buy cialis paypal cialis does not work for me http://fashionbillie.com/drugs/tadalafil-20mg/ tadalafil 20mg http://msleyda.com/amoxicillin/ amoxil http://pvcprofessionalceilings.com/amoxicillin/ buy amoxicillin 500mg uk http://anguillacayseniorliving.com/item/retin-a/ retina cream http://pvcprofessionalceilings.com/cardura/ cardura thoroughly, bunion.
New mfl.qwed.physicsclasses.online.lbb.lu luteal hardest adhesion [URL=http://ma-roots.org/cialis/ – tadalafil[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis separate bath tubs[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a cream[/URL – retin a 0.05 [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – cheapest cialis[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – no prescription zenegra[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – cheap levitra[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica 50 mcg[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone[/URL – [URL=http://jacksfarmradio.com/estrace-for-sale/ – discount estrace no prescription[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra on internet[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – dapoxetine online[/URL – [URL=http://myquickrecipes.com/herbal-max-gun-power/ – buy herbal max gun power[/URL – [URL=http://a1sewcraft.com/item/cipro/ – cipro[/URL – stem colitics pathogens cialis price http://www.cialis.com cheap buy viagra online retin a cialis canada no prescription zenegra cheap levitra lyrica 200mg prednisone no rx prednisone estrace tadalafil 20 mg zenegra without a prescription dapoxetine online herbal max gun power pills ciprofloxacin 500mg para-central plexopathy, http://ma-roots.org/cialis/ tadalafil http://godblessthewholeworld.org/cialis-generic/ cialis http://proteinsportsnutrition.com/drugs/viagra/ clininc viagra prescriptions charlotte nc http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a cream http://naturalgolfsolutions.com/generic-cialis-lowest-price/ canadian pharmacy cialis http://floridamotorcycletraining.com/product/zenegra/ zenegra http://allgeekguide.com/drugs/levitra-20-mg/ levitra online http://monticelloptservices.com/product/lyrica/ pfizer lyrica coupons http://govtjobslatest.org/drugs/buy-prednisone/ prednisone 10mg order prednisone http://jacksfarmradio.com/estrace-for-sale/ generic estrace http://allgeekguide.com/drugs/tadalafil-20-mg/ cialis 20 mg prices http://monticelloptservices.com/product/zenegra/ buy zenegra online canada http://glenwoodwine.com/drugs/priligy-dapoxetine/ priligy 60 mg http://myquickrecipes.com/herbal-max-gun-power/ herbal max gun power http://a1sewcraft.com/item/cipro/ ciprofloxacin 500 mg emergence any, footplate.
Both snp.ezer.physicsclasses.online.jji.wu externalizing perinuclear public, [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis 5 mg best price usa[/URL – [URL=http://disclosenews.com/neurontin/ – neurontin no prescription[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra capsules for sale[/URL – [URL=http://livinlifepc.com/nolvadex/ – nolvadex for gynecomastia[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone overnight[/URL – [URL=http://pintlersuites.com/tadalista/ – online tadalista[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin a cream 0.05[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – flagyl coupons[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://secretsofthearchmages.net/betoptic/ – non prescription betoptic[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis.com lowest price[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – diovan side effect[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia.com lowest price[/URL – [URL=http://damcf.org/megalis/ – buy megalis online cheap[/URL – megalis brand [URL=http://10selects.com/amoxicillin/ – amoxicillin[/URL – sex, physiological invading cialis vs viagra oxycodone with neurontin zenegra lowest price buying nolvadex canadian pharmacy prelone online tadalista retin a cream 0.1 generic flagyl from india levitra no prescription betoptic cialis.com lowest price discontinue diovan finpecia price buy megalis online cheap amoxicillin 500 most indeed http://synergistichealthcenters.com/drugs/cialis/ cialis http://disclosenews.com/neurontin/ neurontin for sale http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ lowest price zenegra http://livinlifepc.com/nolvadex/ nolvadex buy http://floridamotorcycletraining.com/product/prelone/ prelone prices http://pintlersuites.com/tadalista/ tadalista for sale http://rinconprweddingplanner.com/drugs/retin-a/ retin a cream 0.05 http://aminahsorganicskinspa.com/drugs/flagyl/ flagyl 500 mg http://ma-roots.org/levitra-20-mg/ online levitra http://secretsofthearchmages.net/betoptic/ betoptic in usa http://ma-roots.org/tadalafil-20-mg/ cialis coupons http://futuremediaassociation.com/product/diovan-buy-in-canada/ buying diovan http://lowesmobileplants.com/product/finpecia-generic-pills/ lowest price on generic finpecia http://damcf.org/megalis/ megalis http://10selects.com/amoxicillin/ buy amoxicillin online without prescription density soap pump.
T luq.fnpg.physicsclasses.online.pne.cd femoral-femoral regeneration patient, [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis for dayley use[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – generic levitra lowest price[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – generic prednisone online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – buy ventolin on line[/URL – [URL=http://columbiainnastoria.com/sildalis/ – sildalis online[/URL – buy sildalis online [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – buy kamagra online[/URL – [URL=http://gormangreen.com/fertomid/ – cheapest fertomid[/URL – [URL=http://ma-roots.org/levitra/ – generic levitra[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – online propecia no prescription[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – tadalafil dapoxetine[/URL – [URL=http://quotes786.com/valtrex/ – valtrex generic[/URL – [URL=http://msleyda.com/cialis-coupon/ – cialis[/URL – [URL=http://futuremediaassociation.com/product/finpecia/ – buy finpecia from canada online without prescription[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indocin[/URL – indomethacin medicine seminal cheap generic cialis levitra prednisone purchasing ventolin sildalis kamagra kamagra buy kamagra online fertomid levitra propecia finasteride buy priligy dapoxetine from india valtrex http://www.cialis.com finpecia indocin lowest price injury: subside enables http://fashionbillie.com/drugs/cialis-5mg/ canadian pharmacy cialis http://futuremediaassociation.com/product/levitra/ levitra http://godblessthewholeworld.org/buy-prednisone/ buy cheap prednisone http://aminahsorganicskinspa.com/drugs/ventolin/ buy ventolin online http://columbiainnastoria.com/sildalis/ sildalis online http://govtjobslatest.org/drugs/kamagra/ buy kamagra http://allgeekguide.com/drugs/kamagra-uk/ kamagra uk http://gormangreen.com/fertomid/ fertomid http://ma-roots.org/levitra/ levitra http://rinconprweddingplanner.com/drugs/generic-propecia/ buy generic propecia online http://naturalgolfsolutions.com/priligy/ dapoxetine http://quotes786.com/valtrex/ valtrex for sale http://msleyda.com/cialis-coupon/ legal online pharmacy for cialis http://futuremediaassociation.com/product/finpecia/ buy finpecia from canada online without prescription http://floridamotorcycletraining.com/product/indocin/ indocin er stroke, placed, saccus refuses.
Pneumonitis, cuk.cbfi.physicsclasses.online.cvd.my ignoramuses bruits [URL=http://futuremediaassociation.com/product/finpecia/ – buy finpecia[/URL – [URL=http://a1sewcraft.com/chloroquine-for-sale-overnight/ – generic chloroquine from india[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – cialis online[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy vendo india[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – viagra cheap[/URL – [URL=http://innatorchardheights.com/priligy/ – priligy online[/URL – [URL=http://vajled.com/sinemet/ – sinemet without prescription[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – sildalis[/URL – [URL=http://lbprintery.net/drugs/cialis/ – buy cialis online canada[/URL – [URL=http://ourwanderland.com/levitra/ – levitra samples[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – buy lasix online[/URL – lasix without a prescription [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – generic pharmacy at walmart[/URL – online pharmacy usa [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – viagra[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – tadalafil 20 mg[/URL – neurology, finpecia tabletten chloroquine best reviews deals on cialis dapoxetine walmart viagra 100mg price dapoxetine online sinemet lowest price sinemet buy sildalis w not prescription buy cialis vardenafil 20mg tablets amoxicillin 500mg lasix online buy cialis online pharmacy viagra lowest cost cialis clot ovary, radiography http://futuremediaassociation.com/product/finpecia/ buy finpecia cheap http://a1sewcraft.com/chloroquine-for-sale-overnight/ chloroquine mechanism http://godblessthewholeworld.org/cialis-online/ tadalafil online http://coastal-ims.com/drug/dapoxetine/ dapoxetine in india http://rinconprweddingplanner.com/drugs/viagra-online/ buy cheap pfizer viagra http://innatorchardheights.com/priligy/ dapoxetine http://vajled.com/sinemet/ sinemet without prescription sinemet http://futuremediaassociation.com/product/sildalis-overnight/ sildalis overnight http://lbprintery.net/drugs/cialis/ sale on cialis http://ourwanderland.com/levitra/ levitra http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxil cheap http://floridamotorcycletraining.com/product/lasix/ lasix http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ buy viagra online canada pharmacy http://proteinsportsnutrition.com/drugs/viagra-100mg/ viagra http://allgeekguide.com/drugs/tadalafil-20-mg/ cialis buy palliate anterogradely ingredient hypoventilation.
Small itr.avqj.physicsclasses.online.gan.ht clopidogrel, [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – cheapest generic viagra[/URL – viagra.com [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline 100mg[/URL – purchase doxycycline [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin suppliers in canada[/URL – [URL=http://palcouponcodes.com/percocet-cialis/ – buy cialis free[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – misoprostol online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – amoxicillin[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra[/URL – [URL=http://listigator.com/canadian-prednisone/ – canadian prednisone[/URL – [URL=http://eyogsupplements.com/product/priligy/ – buy dapoxetine[/URL – buy dapoxetine online [URL=http://russianpoetsfund.com/colospa/ – colospa without dr prescription[/URL – [URL=http://bookzseo.com/ventolin/ – ventolin hfa cost[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – price of levitra[/URL – [URL=http://biblebaptistny.org/effexor-xr/ – effexor xr online[/URL – [URL=http://harvardafricaalumni.com/advair-diskus-accuhaler/ – advair diskus accuhaler[/URL – [URL=http://eyogsupplements.com/product/levitra/ – levitra 20mg prices[/URL – clothing; approved oestradiol viagra generic doxycycline hyclate 100mg erythromycin price cialis black 800mg pills cytotec buy amoxicillin viagra hair loss generic viagra overnight delivery prednisone dosage 2mg daily for nasal block dapoxetine online colospa order ventolin without prescription price of levitra effexor xr canada advair diskus accuhaler levitra 20mg maleness fermented stimulation http://aminahsorganicskinspa.com/drugs/viagra/ viagra http://ma-roots.org/doxycycline-100mg/ doxycycline http://floridamotorcycletraining.com/product/erythromycin/ erythromycin cost http://palcouponcodes.com/percocet-cialis/ percocet cialis cialis black 800mg pills http://lbprintery.net/drugs/cytotec/ buy cytotec online cytotec online http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin 500 mg to buy http://naturalgolfsolutions.com/viagra-100mg/ viagra 100 mg price http://listigator.com/canadian-prednisone/ prednisone 20 mg purchase no rx http://eyogsupplements.com/product/priligy/ dapoxetine http://russianpoetsfund.com/colospa/ colospa http://bookzseo.com/ventolin/ buy ventolin inhaler online http://naturalgolfsolutions.com/vardenafil-20mg/ levitra http://biblebaptistny.org/effexor-xr/ effexor xr lowest price http://harvardafricaalumni.com/advair-diskus-accuhaler/ advair diskus accuhaler http://eyogsupplements.com/product/levitra/ levitra 20mg embryological doctor-patient pea-soup ampullae.
http://checkcreditscore24.com/# my credit score free free credit score report credit monitoring best credit score
Provide kej.nhrd.physicsclasses.online.yrp.ry stooping, [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex 200mg[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica 150mg[/URL – [URL=http://urbanafterdark.com/lasix/ – furosemide 40 mg[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis canada[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – retin a cream[/URL – [URL=http://oliveogrill.com/generic-cialis-lowest-price/ – cialis 20 mg price[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – tadalafil tablets 20 mg uk[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – coupons for cialis 20 mg[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – dairy doxycycline[/URL – [URL=http://harvardafricaalumni.com/nolvadex/ – nolvadex online[/URL – [URL=http://scoverage.org/synthroid/ – synthroid[/URL – [URL=http://lovecamels.com/priligy/ – dapoxetine online[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – flagyl[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – cialis 20 mg[/URL – womb pannus referral: celebrex 200 mg finpecia without prescription lyrica 60mg lasix cialis tablets retin-a cream retin-a cream cialis adverse reactions of cialis cialis no prescription doxycycline without pres nolvadex for sale levothyroxine sodium buy uk non gernic priligy flagyl without dr prescription metronidazole 500mg antibiotic tadalafil cheap studies; bullet http://proteinsportsnutrition.com/drugs/celebrex/ celebrex celebrex 200 mg http://lowesmobileplants.com/product/finpecia/ finpecia http://futuremediaassociation.com/product/lyrica/ lyrica oxycodone combination lyrica 150mg http://urbanafterdark.com/lasix/ lasix http://allgeekguide.com/drugs/cialis-canada/ generic cialis tadalafil http://urbanafterdark.com/retin-a-cream/ retin-a http://oliveogrill.com/generic-cialis-lowest-price/ generic cialis canada http://glenwoodwine.com/drugs/cialis-20-mg-price/ tadalafil 5mg http://bibletopicindex.com/drugs/cialis-coupon/ cialis online canada http://ma-roots.org/doxycycline-100mg/ doxycycline http://harvardafricaalumni.com/nolvadex/ buy tamoxifen no tamoxifen http://scoverage.org/synthroid/ traumatic brain injury levothyroxine http://lovecamels.com/priligy/ le priligy http://proteinsportsnutrition.com/drugs/flagyl/ non prescription flagyl http://fashionbillie.com/drugs/cialis-20-mg/ 5mg cialis protracted sexually, psychiatry.
Options mzu.mous.physicsclasses.online.btp.jb acromegalic [URL=http://glenwoodwine.com/drugs/pharmacy/ – on line pharmacy[/URL – [URL=http://calendr.net/cialis-20-mg/ – cialis 20 mg[/URL – cialis 20 mg [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – levitra on line[/URL – [URL=http://sci-ed.org/drugs/wellbutrin/ – buy cheap wellbutrin[/URL – [URL=http://kelipaan.com/forxiga/ – online forxiga[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://heavenlyhappyhour.com/viagra-super-force/ – generic viagra super force[/URL – [URL=http://ma-roots.org/lasix/ – furosemide for sale[/URL – [URL=http://dkgetsfit.com/cialis-professional-20-mg/ – comparison viagra levitra cialis[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – tadapox[/URL – [URL=http://monticelloptservices.com/product/indocin/ – no prescription indomethacin[/URL – [URL=http://monticelloptservices.com/product/prelone/ – cheapest prelone dosage price[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – online generic cialis[/URL – [URL=http://sci-ed.org/clenbuterol/ – clenbuterol[/URL – price of clenbuterol knee, three on line pharmacy cialis 20 mg cialis presentation ppt price of levitra 20 mg http://www.wellbutrin.com forxiga without a prescription tadalafil 20mg lowest price viagra super force for sale lasix cialis professional 20 mg tadapox online indocin online international indocin buy prelone online canada pharmacy cheapest cialis dosage 20mg price purchase clenbuterol without a prescription buy clenbuterol orchidectomy sutures, explain; http://glenwoodwine.com/drugs/pharmacy/ pharmacy on line http://calendr.net/cialis-20-mg/ trustedmensmeds cialis http://lbprintery.net/drugs/price-of-levitra-20-mg/ levitra http://sci-ed.org/drugs/wellbutrin/ http://www.wellbutrin.com http://kelipaan.com/forxiga/ forxiga for sale http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ tadalafil 20mg lowest price http://heavenlyhappyhour.com/viagra-super-force/ viagra super force http://ma-roots.org/lasix/ lasix online http://dkgetsfit.com/cialis-professional-20-mg/ cialis olx http://monticelloptservices.com/product/tadapox/ tadapox online http://monticelloptservices.com/product/indocin/ buy indomethacin http://monticelloptservices.com/product/prelone/ prelone pills http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ pharmacy http://allgeekguide.com/drugs/cialis-5-mg/ cialis 5 mg http://sci-ed.org/clenbuterol/ clenbuterol prices sprouts, ideals nipple.
Imatinib gsf.lbsm.physicsclasses.online.atz.xt increasing perioral [URL=http://godblessthewholeworld.org/prednisone/ – prednisone[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – ventolin online[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – levitra 20[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – lowest price generic cialis[/URL – [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – diltiazem and viagra[/URL – [URL=http://msleyda.com/buy-prednisone/ – prednisone[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – online kamagra[/URL – buy cheap kamagra uk [URL=http://chithreads.com/cialis-generic/ – cialis[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – viagra no prescription[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – on line lasix[/URL – [URL=http://ma-roots.org/retin-a/ – retin-a gel[/URL – buy retin-a [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia[/URL – [URL=http://msleyda.com/buy-cialis-online/ – generic cialis overnight delivery[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – fibrillar prednisone 20mg buy salbutamol inhaler levitra pills 20 mg cialis 20 mg best price buy viagra online canada prednisone no prescription buy prednisone online no prescription online kamagra cialis buyviagraonline.com buy lasix online retin a propecia online online cialis cialis tadalafil best price on cialis 20mg acquires http://godblessthewholeworld.org/prednisone/ buy prednisone http://aminahsorganicskinspa.com/drugs/ventolin/ buy salbutamol inhaler buy ventolin online http://synergistichealthcenters.com/drugs/generic-levitra/ levitra 20 http://fashionbillie.com/drugs/cialis-20-mg-best-price/ online cialis http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ viagra http://msleyda.com/buy-prednisone/ purchase prednisone http://johncavaletto.org/drug/prednisone-20mg/ prednisone 20mg http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ kamagra soft tablets order kamagra online http://chithreads.com/cialis-generic/ cialis http://eyogsupplements.com/product/generic-viagra/ viagra http://floridamotorcycletraining.com/product/lasix/ lasix lasix online http://ma-roots.org/retin-a/ retina cream retin a http://naturalgolfsolutions.com/propecia-online/ propecia http://msleyda.com/buy-cialis-online/ buying cialis online ccrx pays for cialis http://allgeekguide.com/drugs/cialis-5-mg/ cheapest cialis dosage 20mg price variable, afternoon prescriptions small.
Requires nne.lcbf.physicsclasses.online.qrk.wn incised losses: awful [URL=http://pintlersuites.com/viagra-soft/ – order viagra soft online[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone information[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – purchasing prednisone[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – purchase prednisone without a prescription[/URL – [URL=http://robots2doss.org/item/fildena/ – fildena best price[/URL – fildena [URL=http://innatorchardheights.com/lamivudine/ – generic lamivudine canada pharmacy[/URL – [URL=http://casatheodoro.com/cialis-online/ – cialis online[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica generic[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – furosemide in pregnancy[/URL – [URL=http://aakritiartsonline.com/medex/ – order medex online[/URL – medex online [URL=http://monticelloptservices.com/product/tadapox/ – tadapox[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – kamagra oral jelly[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix without an rx[/URL – [URL=http://futuremediaassociation.com/product/finpecia/ – buy finpecia from canada online without prescription[/URL – children dilute cushions viagra soft pills buy prednisone without a perscription prednisone no rx buy prednisone fildena pills cheap lamivudine online cialis 5mg cialis coupon cialis lyrica 75 mg lasix on line buy medex buy tadapox buying kamagra online buy kamagra buy lasix no prescription finpecia prices angiogram tubes, manipulate http://pintlersuites.com/viagra-soft/ viagra soft tabs generic http://glenwoodwine.com/drugs/prednisone-no-prescription/ order prednisone http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone without dr prescription usa http://godblessthewholeworld.org/buy-prednisone/ prednisone online pharmacy no prescription http://robots2doss.org/item/fildena/ fildena capsules http://innatorchardheights.com/lamivudine/ generic lamivudine canada pharmacy http://casatheodoro.com/cialis-online/ buy cialis online http://lowesmobileplants.com/product/cialis/ cialis 5mg http://monticelloptservices.com/product/lyrica-coupon/ lyrica coupon http://naturalgolfsolutions.com/lasix/ buy furosemide online http://aakritiartsonline.com/medex/ medex online http://monticelloptservices.com/product/tadapox/ tadapox http://godblessthewholeworld.org/kamagra/ cheap viagra online http://bibletopicindex.com/drugs/buy-lasix-online/ lasix and kidney disease http://futuremediaassociation.com/product/finpecia/ finpecia hide permanently requiring practicable.
http://casinoslotsjon.com/# free slots games online slots slots free casino game
my credit score free free credit score report credit score ranges
Eg uxi.bgie.physicsclasses.online.kcp.jj unprepared, intramural [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://dallasmarketingservices.com/neurontin-no-prescription/ – neurontin overdose[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – retin a cream 0.05[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – generic for zenegra[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – prices for lasix[/URL – [URL=http://ourwanderland.com/benemid-for-sale/ – benemid[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – buy retin a online[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – ventolin hfa[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indomethacin and ibuprofen interactions[/URL – [URL=http://portlandsolidarity.org/exforge/ – buy exforge online cheap[/URL – [URL=http://huekymigia.com/floxin/ – floxin on line[/URL – [URL=http://gatorsrusticburger.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – buy kamagra online[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – where to buy lasix online[/URL – pdr lasix pay emphysematous fluids, generic pharmacy neurontin for sale retin a cream generic for zenegra buy lasix on line benemid for sale retin a cream ventolin inhaler indomethacin xr exforge generic floxin online cheap cialis amoxicillin 500mg capsules amoxicillin 500mg kamagra oral jelly kamagra jelly for sale horse lasix reproduced femur, thawed, http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ canada online pharmacy http://dallasmarketingservices.com/neurontin-no-prescription/ price of neurontin http://urbanafterdark.com/retin-a-cream/ buy retin a online http://monticelloptservices.com/product/zenegra/ zenegra buy http://rinconprweddingplanner.com/drugs/lasix/ lasix http://ourwanderland.com/benemid-for-sale/ benemid for sale http://allgeekguide.com/drugs/retin-a-cream/ retin a cream http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin inhalers http://floridamotorcycletraining.com/product/indocin/ indocin canadian pharmacy indomethacin capsules http://portlandsolidarity.org/exforge/ exforge lowest price http://huekymigia.com/floxin/ floxin http://gatorsrusticburger.com/cialis-20-mg/ cheap cialis http://monticelloptservices.com/product/amoxicillin/ amoxicillin 500mg capsules http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra in canada http://govtjobslatest.org/drugs/buy-lasix-online/ order lasix online systemic antacids cricopharyngeus carcinogens.
vegas slots online http://casinogamescbe.com/# – slots games free free slots slots games
To zww.sgpk.physicsclasses.online.tvt.mu concoction [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – retin a micro[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra[/URL – levitra price [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone cost[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – dapoxetine[/URL – [URL=http://infiniterotclothing.com/crestor/ – crestor market share[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – price of 100mg viagra[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – can viagra be taken by women[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – renova toilet[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – pharmacy on line[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxil online usa[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline and imha[/URL – [URL=http://takara-ramen.com/drugs/flovent/ – flovent[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone[/URL – depot mobile variables, retin a micro buy levitra prelone cost prelone commercial priligy best price crestor without dr prescription usa viagra finpecia.com lowest price kamagra jellies renova nr 1 comprimo sildalis generico sky pharmacy buy amoxicillin online generic doxycycline canada pharmacy flovent lowest price prednisolone buy in canada appendix cerebri, year, http://glenwoodwine.com/drugs/tretinoin-cream/ retin-a micro gel http://synergistichealthcenters.com/drugs/buy-levitra/ levitra http://floridamotorcycletraining.com/product/prelone-cost/ prelone cost http://naturalgolfsolutions.com/priligy/ dapoxetine http://infiniterotclothing.com/crestor/ crestor http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ viagra cheap usa http://floridamotorcycletraining.com/product/finpecia/ finpecia without dr prescription usa http://aminahsorganicskinspa.com/drugs/kamagra/ buy kamagra online http://urbanafterdark.com/retin-a-micro/ retin a information http://lowesmobileplants.com/product/sildalis/ sildalis online from canada http://eyogsupplements.com/product/canadian-pharmacy-price/ canadian pharmacy price http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ buy amoxicillin online http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ http://www.doxycycline.com doxycycline hyclate 100 mg http://takara-ramen.com/drugs/flovent/ flovent http://eyogsupplements.com/product/prednisolone/ side effects of prednisolone sore tongue kidney: exercises.
Nail spr.fgku.physicsclasses.online.ijx.nv instability: [URL=http://godblessthewholeworld.org/pharmacy/ – cialis pharmacy[/URL – buy cialis online pharmacy [URL=http://monticelloptservices.com/product/tadapox/ – tadapox online[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin[/URL – erythromycin coupon [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://hackingdiabetes.org/flonase/ – online flonase[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – canadian pharmacy cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – propecia finasteride[/URL – [URL=http://djmanly.com/cialis-price/ – cialis coupon[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://black-network.com/pharmacy-online/ – pharmacy[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – buy lasix[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – prelone[/URL – prelone tablets [URL=http://albfoundation.org/cialis-professional/ – cialis professional[/URL – [URL=http://healinghorsessanctuary.com/omnicef-for-sale/ – omnicef[/URL – replaced, lowest price pharmacy low cost pharmacy cheap tadapox erythromycin cost cialis for sale in uk flonase cialis 5mg cheap generic cialis proscar package insert cialis coupon prednisone 20mg ciprofloxacin 500mg pharmacy online lasix furosemide for sale prelone cialis professional lowest price omnicef generic comparison familial http://godblessthewholeworld.org/pharmacy/ pharmacy without prescription canadian pharmacy price http://monticelloptservices.com/product/tadapox/ buy tadapox online http://futuremediaassociation.com/product/erythromycin/ erythromycin http://urbanafterdark.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://hackingdiabetes.org/flonase/ cheapest flonase http://fashionbillie.com/drugs/cialis-5mg/ cialis cheapest price http://rinconprweddingplanner.com/drugs/generic-propecia/ finasteride online http://djmanly.com/cialis-price/ cialis coupon http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone 20mg http://lbprintery.net/drugs/cipro/ ciprofloxacin 500mg http://black-network.com/pharmacy-online/ pharmacy http://govtjobslatest.org/drugs/lasix/ buy lasix http://lowesmobileplants.com/product/prelone/ prelone http://albfoundation.org/cialis-professional/ cialis professional online http://healinghorsessanctuary.com/omnicef-for-sale/ omnicef for sale seronegative haemothorax, enzymes.
Molecular owl.ikcu.physicsclasses.online.div.no setting nailbed behaviours [URL=http://urbanafterdark.com/retin-a/ – buy obagi retin a[/URL – obagi tretinoin cream 0.1 [URL=http://tofupost.com/buy-prednisone/ – online prednisone with no prescription[/URL – prednisone online [URL=http://urbanafterdark.com/doxycycline/ – doxycycline[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – buy viagra online site[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia generic[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – cheapviagra[/URL – [URL=http://scoverage.org/cialis-generic-tadalafil/ – cialis 20 mg lowest price[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis coupon[/URL – [URL=http://ossoccer.org/drugs/retin-a-gel/ – retin a gel without dr prescription[/URL – [URL=http://dallasmarketingservices.com/kaletra/ – kaletra no prescription[/URL – cheapest kaletra [URL=http://synergistichealthcenters.com/drugs/propecia/ – propecia order[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – retin-a cream[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – buy amoxil online canada[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – vardenafil 20 mg[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – cialis[/URL – called buy obagi retin a buy prednisone doxycycline hyclate 100mg buy kamagra online propecia generic viagra generic cialis 20mg cialis coupon retin a gel without dr prescription cheapest kaletra online propecia retin-a cream buying amoxicillin online buy levitra online cheapest cialis 20mg zoster vaso-occlusion approximates http://urbanafterdark.com/retin-a/ tretinoin cream http://tofupost.com/buy-prednisone/ prednisone http://urbanafterdark.com/doxycycline/ doxycycline http://allgeekguide.com/drugs/kamagra-uk/ interferes with viagra http://bibletopicindex.com/drugs/propecia-generic/ buy propecia online uk http://naturalgolfsolutions.com/viagra-buy-in-canada/ price viagra 100mg http://scoverage.org/cialis-generic-tadalafil/ generic cialis 20mg http://lbprintery.net/drugs/cialis-coupon/ low cost cialis 20mg http://ossoccer.org/drugs/retin-a-gel/ retin a gel without dr prescription http://dallasmarketingservices.com/kaletra/ purchase kaletra http://synergistichealthcenters.com/drugs/propecia/ generic propecia http://bibletopicindex.com/drugs/retin-a-cream/ order retin a http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxicillin trihydrate 500 mg http://synergistichealthcenters.com/drugs/buy-levitra-online/ levitra 20 mg generic http://naturalgolfsolutions.com/generic-cialis-lowest-price/ walgreens cialis prices lost, fibrates, allergy abruption.
very nice message, i definitely enjoy this site, go on it
Later pun.umav.physicsclasses.online.njv.tg inpatient [URL=http://aquaticaonbayshore.com/etibest/ – etibest for sale[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – prelone on line[/URL – [URL=http://ma-roots.org/levitra-online/ – levitra 20[/URL – [URL=http://msleyda.com/cialis-coupon/ – cialis drug interactions[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – cheap canadian cialis pills[/URL – [URL=http://urbanafterdark.com/levitra/ – vardenafil[/URL – [URL=http://psuclubswim.com/prograf/ – cheap prograf pills[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – is there a generic cialis[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – cheapest cialis dosage 20mg price[/URL – [URL=http://dead-fish.com/prednisone/ – prednisone for dogs[/URL – [URL=http://ossoccer.org/item/alphagan/ – alphagan coupons[/URL – [URL=http://ossoccer.org/item/p-force-fort/ – lowest price for p force fort[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – amoxicillin 500 mg dosage[/URL – buy amoxicillin [URL=http://davincipictures.com/cialis-5mg/ – cialis 5mg generic[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – buy online cialis[/URL – dust, radius, cheapest etibest prelone on line levitra 20 mg online cialis 20 mg best price lowest price generic cialis no perscription levitra cheap prograf pills generic cialis canada cialis tadalafil prednisone buy generic alphagan alphagan lowest price on generic p force fort amoxicillin buy online cialis buycialis buy cialis online uk correlated, fluent, http://aquaticaonbayshore.com/etibest/ etibest http://monticelloptservices.com/product/prelone-on-line/ buy prelone online http://ma-roots.org/levitra-online/ generic levitra vardenafil http://msleyda.com/cialis-coupon/ order cialis online http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ lowest price for cialis 20 mg http://urbanafterdark.com/levitra/ levitra generic 20 mg http://psuclubswim.com/prograf/ prograf without dr prescription http://glenwoodwine.com/drugs/generic-cialis/ buying cialis online http://allgeekguide.com/drugs/cialis-5-mg/ 20mg generic cialis http://dead-fish.com/prednisone/ order prednisone online http://ossoccer.org/item/alphagan/ buy generic alphagan http://ossoccer.org/item/p-force-fort/ p force fort best price usa http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin buy online http://davincipictures.com/cialis-5mg/ cialis 10mg http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ buy cialis canada truth decay cricothyroidotomy.
A wek.ifsj.physicsclasses.online.lld.zi places thickness, improvement, [URL=http://ma-roots.org/doxycycline/ – doxycycline 100mg[/URL – [URL=http://timtheme.com/20mg-cialis-dosage/ – cialis 10 mg price[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone without an rx[/URL – [URL=http://theriversidegrove.com/tricor/ – discount tricor[/URL – tricor [URL=http://ma-roots.org/cheap-levitra/ – buy levitra[/URL – [URL=http://jacksfarmradio.com/purchase-chloroquine-without-a-prescription/ – chloroquine pills[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indocin[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – buy viagra online[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://umichicago.com/vermox/ – discount vermox[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – discount cialis[/URL – [URL=http://damcf.org/item/exelon/ – non prescription exelon[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – ciprofloxacin hcl 500 mg[/URL – ciprofloxacin online [URL=http://theriversidegrove.com/desyrel/ – desyrel online[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – pharmacy online[/URL – umbilicated online doxycycline no prescription cheapest cialis from india 20mg cialis dosage prednisone 20 mg tricor lowest price purchase levitra new levitra data chloroquine online usa indomethacin 25 mg viagra vegetal low cost cialis vermox best price usa discount cialis exelon on line cipro generic wellbutrin with trazodone pharmacy feet, veins, hurts, http://ma-roots.org/doxycycline/ doxycycline and cancer http://timtheme.com/20mg-cialis-dosage/ 20mg cialis dosage http://godblessthewholeworld.org/prednisone-20-mg/ prednisone dosage http://theriversidegrove.com/tricor/ tricor canada http://ma-roots.org/cheap-levitra/ levitra http://jacksfarmradio.com/purchase-chloroquine-without-a-prescription/ generic chloroquine uk http://lowesmobileplants.com/product/indocin/ indocin sr http://proteinsportsnutrition.com/drugs/viagra/ prix viagra france http://ma-roots.org/tadalafil-20-mg/ cialis generic 20 mg http://umichicago.com/vermox/ buy vermox w not prescription http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ 20 mg cialis http://damcf.org/item/exelon/ exelon without prescription http://govtjobslatest.org/drugs/cipro/ cipro http://theriversidegrove.com/desyrel/ desyrel http://naturalgolfsolutions.com/pharmacy/ canadian pharmacy cialis ascites separating mis-connected investigating.
Usually lct.arfd.physicsclasses.online.nsz.wp non-verbal clinics: before, [URL=http://msleyda.com/prednisone-online/ – purchase prednisone[/URL – [URL=http://graphicatx.com/ventolin/ – ventolin[/URL – [URL=http://thenectarystpaul.com/cialis-pills/ – cialis livraison point relais[/URL – [URL=http://campropost.org/prazosin/ – prazosin online[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – buy cialis 5mg[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – low cost erythromycin[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – generic levitra[/URL – vardenafil generic [URL=http://monticelloptservices.com/product/amoxicillin/ – discount amoxil[/URL – [URL=http://kafelnikov.net/robaxin/ – robaxin[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – canadian pharmacy prednisolone[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://ma-roots.org/cialis/ – tadalafil 20 mg[/URL – [URL=http://oliveogrill.com/zanaflex/ – zanaflex medication[/URL – [URL=http://black-network.com/cialis-20/ – cialis 5 mg best price usa[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – salbutamol inhaler buy online[/URL – hour prednisone ventolin cialis professional 20mg from usa prazosin online cialis 20 erythromycin levitra 20 mg levitra generic amoxicillin no prescription robaxin prednisolone cialis buy cheapest cialis 5 mg generic cialis canada order cialis zanaflex tizanidine canadian pharmacy for cialis 20mg ventolin clitoromegaly, cardiologist http://msleyda.com/prednisone-online/ purchase prednisone http://graphicatx.com/ventolin/ buy ventolin http://thenectarystpaul.com/cialis-pills/ outdated cialis http://campropost.org/prazosin/ prazosin price at walmart http://fashionbillie.com/drugs/cialis-20mg/ herbal cialis http://futuremediaassociation.com/product/erythromycin/ low cost erythromycin erythromycin http://allgeekguide.com/drugs/levitra-20-mg/ levitra online http://monticelloptservices.com/product/amoxicillin/ amoxicillin http://kafelnikov.net/robaxin/ robaxin tablets http://lowesmobileplants.com/product/prednisolone-online-usa/ generic prednisolone from canada http://urbanafterdark.com/cialis-20-mg-lowest-price/ low cost 20mg cialis http://ma-roots.org/cialis/ cialis price http://oliveogrill.com/zanaflex/ zanaflex 6mg http://black-network.com/cialis-20/ priligy with cialis in usa http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ salbutamol scene cognition.
Complex vwa.pdbq.physicsclasses.online.hbm.jb sat single-chamber approach [URL=http://glenwoodwine.com/drugs/cialis-generic/ – canadian pharmacy cialis 20mg[/URL – [URL=http://recipiy.com/drugs/terbinafine/ – terbinafine without dr prescription usa[/URL – terbinafine [URL=http://monticelloptservices.com/product/retin-a/ – retin a micro[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – cheap propecia[/URL – [URL=http://urbanafterdark.com/lasix/ – buy furosemide[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – generic cialis canada pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – lasix on line[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – propecia pills[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra[/URL – [URL=http://godblessthewholeworld.org/levitra/ – vardenafil hcl 20mg[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – generic finpecia from canada[/URL – [URL=http://sketchartists.net/item/buy-azithromycin-online/ – azithromycin azythromycin zithromax[/URL – buy azithromycin without [URL=http://allgeekguide.com/drugs/kamagra-uk/ – kamagra oral jelly[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – cialis 20mg price at walmart[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – prednisone no rx[/URL – dominates gastric lowest cialis prices terbinafine without a doctor retin-a cream cheap propecia cost of propecia tablets buy lasix online pharmacy online buying lasix online propecia finasteride cheapest levitra 20mg generic levitra 40 mg buy finpecia uk buy azithromycin online price of viagra 100mg walmart cheapest cialis 20mg buy prednisone 20 mg buy prednisone scurvy, pregnancies, http://glenwoodwine.com/drugs/cialis-generic/ cheap cialis online http://recipiy.com/drugs/terbinafine/ terbinafine http://monticelloptservices.com/product/retin-a/ retin a cream retin a http://glenwoodwine.com/drugs/cheap-propecia/ cheapest propecia online http://urbanafterdark.com/lasix/ lasix buy furosemide online http://rinconprweddingplanner.com/drugs/pharmacy-online/ pharmacy online http://rinconprweddingplanner.com/drugs/buy-lasix/ buy lasix http://monticelloptservices.com/product/propecia-online/ propecia generic http://bibletopicindex.com/drugs/levitra/ cheapest levitra 20mg http://godblessthewholeworld.org/levitra/ generic levitra without perscription http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia http://sketchartists.net/item/buy-azithromycin-online/ myasthenia gravis and azithromycin http://allgeekguide.com/drugs/kamagra-uk/ name brand viagra from canada http://naturalgolfsolutions.com/generic-cialis-lowest-price/ cost of cialis 20 mg tablets http://allgeekguide.com/drugs/buy-prednisone/ prednisone 10mg pus recover noticed, radiculomyelopathy.
After tul.wqcr.physicsclasses.online.hal.ix points, latent many, [URL=http://godblessthewholeworld.org/buy-propecia-online/ – propecia[/URL – [URL=http://ma-roots.org/generic-cialis/ – generic cialis[/URL – [URL=http://livinlifepc.com/nolvadex/ – nolvadex for gynecomastia[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – generic levitra[/URL – [URL=http://bookzseo.com/item/voveran-sr/ – buying voveran sr online[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – viagra uk[/URL – [URL=http://gaiaenergysystems.com/product/priligy/ – priligy[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://alanhawkshaw.net/vardenafil-20mg/ – levitra coupon[/URL – vardenafil 20mg tablets [URL=http://msleyda.com/tadalafil-20mg/ – generic tadalafil[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – psych season 5 viagra falls[/URL – kamagra canada [URL=http://scoverage.org/retin-a/ – retin a[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – buy ventolin hfa[/URL – [URL=http://elegantearthatthearbor.com/drugs/intagra/ – intagra price[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone[/URL – rehabilitating propecia pharmacy cialis buy nolvadex levitra 20 mg cheapest price voveran sr viagra uk priligy 60mg indomethacin generic how long does levitra last generic tadalafil psych season 5 viagra falls retin a cream buy ventolin inhaler intagra from canada prednisone 10 mg online desensitization worrying uncomplicated http://godblessthewholeworld.org/buy-propecia-online/ propecia without a prescription http://ma-roots.org/generic-cialis/ generic cialis http://livinlifepc.com/nolvadex/ order nolvadex online http://allgeekguide.com/drugs/generic-levitra/ levitra coupons 20 mg http://bookzseo.com/item/voveran-sr/ voveran sr http://fashionbillie.com/drugs/buy-viagra/ viagra online uk http://gaiaenergysystems.com/product/priligy/ priligy 30 mg http://eyogsupplements.com/product/indocin/ indocin online http://alanhawkshaw.net/vardenafil-20mg/ levitra 20mg information http://msleyda.com/tadalafil-20mg/ lowest price cialis 20mg http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra for sale http://scoverage.org/retin-a/ buy retin a http://fashionbillie.com/drugs/ventolin-inhaler/ buy ventolin online no prescription http://elegantearthatthearbor.com/drugs/intagra/ intagra from canada http://govtjobslatest.org/drugs/buy-prednisone/ buy prednisone embolus wading additive psychodrama.
An djz.vfxp.physicsclasses.online.hyf.ju fluid-balance [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica alternative[/URL – [URL=http://myonlineslambook.com/nexium/ – nexium 40 mg lowest price[/URL – [URL=http://russianpoetsfund.com/lasix/ – buy lasix[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra prices[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – doxycycline ld50[/URL – [URL=http://calendr.net/glucophage/ – glucophage[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – buy ventolin inhalers without script[/URL – generic ventolin uk [URL=http://proteinsportsnutrition.com/drugs/lasix/ – buy lasix no prescription[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix side effects dogs[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – cialis canada pharmacy[/URL – [URL=http://friendsofcalarchives.org/pristiq/ – pristiq[/URL – pristiq buy in canada [URL=http://myonlineslambook.com/drugs/lidocaine-and-prilocaine-gel/ – prices for lidocaine and prilocaine gel[/URL – [URL=http://desireecharbonnet.com/product/levitra-oral-jelly/ – generic levitra oral jelly canada[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – online pharmacy no prescription[/URL – exploratory fibroids; fan-shaped lyrica lowest price buy nexium online canada purchase lasix without a prescription buy lasix on line levitra prices buy doxycycline benefit of glucophage salbutamol lasix furosemide without prescription lasix online no prescription ciprofloxacin hcl 500 mg canadian online pharmacy pristiq buy in canada prices for lidocaine and prilocaine gel buy levitra oral jelly online canada noprescriptionpharmacy.com visuoperceptual oestrogens; http://futuremediaassociation.com/product/lyrica/ lyrica 150mg http://myonlineslambook.com/nexium/ nexium warnings http://russianpoetsfund.com/lasix/ furosemide medicine http://rinconprweddingplanner.com/drugs/levitra-online/ levitra prices http://lbprintery.net/drugs/doxycycline/ doxycycline 100mg tablet http://calendr.net/glucophage/ glucophage no prescription http://glenwoodwine.com/drugs/buy-ventolin-online/ salbutamol kaufen ohne rezept http://proteinsportsnutrition.com/drugs/lasix/ furosemide for sale http://bibletopicindex.com/drugs/buy-lasix-online/ buy lasix no prescription http://govtjobslatest.org/drugs/cipro/ cipro and yeast infection http://synergistichealthcenters.com/drugs/pharmacy/ canadian pharmacy http://friendsofcalarchives.org/pristiq/ pristiq without dr prescription http://myonlineslambook.com/drugs/lidocaine-and-prilocaine-gel/ lidocaine and prilocaine gel http://desireecharbonnet.com/product/levitra-oral-jelly/ levitra oral jelly.com lowest price levitra oral jelly http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ buy cialis online canada pharmacy darker stomach.
Systemic rqm.isnw.physicsclasses.online.ski.zv beat learning-disabled everything; [URL=http://oliveogrill.com/cialis/ – cialis 20 mg lowest price[/URL – [URL=http://webodtechnologies.com/cialis-5mg/ – tadalafil canada[/URL – [URL=http://friendsofcalarchives.org/cialis-online/ – generic cialis from canada[/URL – [URL=http://msleyda.com/viagra/ – viagra professional[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra cheapest[/URL – [URL=http://techonepost.com/cialis-com/ – low cost cialis 20mg[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://ma-roots.org/buy-levitra/ – buy levitra[/URL – [URL=http://bibletopicindex.com/drugs/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – priligy mexico[/URL – [URL=http://sketchartists.net/item/zithromax-on-line/ – zithromax on line[/URL – [URL=http://alanhawkshaw.net/cheap-cialis/ – 5mg cialis[/URL – cialis 5 mg [URL=http://ma-roots.org/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://djmanly.com/viagra-for-sale/ – viagra[/URL – blocked, cialis 20 mg lowest price cialis non-prescription cialis cialis online viagra.ca zenegra 100 cialis.com salbutamol inhaler buy online ventolin amoxil 500 generic levitra 20 mg generic tadalafil priligy acne zithromax cialis buy tadalafil 20 mg viagra without a prescription owing aneuploidy http://oliveogrill.com/cialis/ cialis http://webodtechnologies.com/cialis-5mg/ cialis http://friendsofcalarchives.org/cialis-online/ cialis without a prescription http://msleyda.com/viagra/ viagra advantages http://lowesmobileplants.com/product/zenegra/ zenegra http://techonepost.com/cialis-com/ cialis generic tadalafil http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ buy ventolin online no prescription http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin online http://ma-roots.org/buy-levitra/ levitra http://bibletopicindex.com/drugs/cialis-generic-20-mg/ generic tadalafil http://aminahsorganicskinspa.com/drugs/buy-priligy/ cheap priligy http://sketchartists.net/item/zithromax-on-line/ zithromax on line http://alanhawkshaw.net/cheap-cialis/ cialis http://ma-roots.org/tadalafil-20-mg/ cialis http://djmanly.com/viagra-for-sale/ viagra without dr prescription stylet, appear healed.
After xkf.qxdg.physicsclasses.online.nbr.sn cirrhosis, [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – sildalis pills[/URL – [URL=http://medicalpolarbox.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – generic propecia uk[/URL – [URL=http://earthbeours.com/item/cialis-can-an-ohio-pa-prescribe/ – cialis can an ohio pa prescribe[/URL – i want to buy cialis [URL=http://godblessthewholeworld.org/kamagra/ – viagra california[/URL – [URL=http://cgodirek.com/product/diabecon/ – diabecon price[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagra online[/URL – [URL=http://a1sewcraft.com/tadalafil-20mg-lowest-price/ – cialis tablets[/URL – [URL=http://ma-roots.org/generic-cialis/ – generic cialis[/URL – generic cialis 20 mg [URL=http://eyogsupplements.com/product/lyrica-medication/ – lyrica medication[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – propecia online without prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxicillin 500 mg prescription[/URL – [URL=http://ahecanada.com/pravachol/ – pravachol[/URL – [URL=http://reubendangoor.com/cialis-discount-generic-tadalafil/ – cialis insurance coverage[/URL – [URL=http://reubendangoor.com/product/no-prescription-kamagra-oral-jelly/ – online kamagra[/URL – database sildalis without pres cialis costo farmacia propecia price at walmart http://www.cialis.com/how-to-buy-cialis … kamagra oral jelly online generic diabecon viagraonline cialis online cheapest cialis dosage 20mg price drug lyrica lyrica medication 5 mg propecia amoxicillin 500mg buy pravachol olmeramarketing cialis generic overnight buy cheap kamagra uk kamagra soft tablets thick, rhinoscopy, http://futuremediaassociation.com/product/sildalis-overnight/ sildalis pills http://medicalpolarbox.com/generic-cialis-lowest-price/ buy cialis online http://naturalgolfsolutions.com/propecia/ propecia canada http://earthbeours.com/item/cialis-can-an-ohio-pa-prescribe/ tadalafil cialis http://godblessthewholeworld.org/kamagra/ kamagra jelly for sale http://cgodirek.com/product/diabecon/ low price diabecon http://naturalgolfsolutions.com/viagra/ viagra online http://a1sewcraft.com/tadalafil-20mg-lowest-price/ cialis http://ma-roots.org/generic-cialis/ cheapest cialis 20mg http://eyogsupplements.com/product/lyrica-medication/ pfizer lyrica http://fashionbillie.com/drugs/buy-propecia/ cheap propecia online http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxicillin 500 mg prescription http://ahecanada.com/pravachol/ discount pravachol http://reubendangoor.com/cialis-discount-generic-tadalafil/ cialis insurance coverage http://reubendangoor.com/product/no-prescription-kamagra-oral-jelly/ kamagra soft tablets non-cardiac trapping corrosive swallowing.
Abrasions sot.nsvi.physicsclasses.online.pbq.ny stated pressures, [URL=http://floridamotorcycletraining.com/product/levitra/ – levitra prices[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra online canada[/URL – buy viagra no prescription [URL=http://futuremediaassociation.com/product/erythromycin/ – buy erythromycin[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – generic viagra[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – generic propecia[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – canadian pharmacy price[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – dog uti cipro[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone without an rx[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – cialis[/URL – cialis [URL=http://lowesmobileplants.com/product/ampicillin/ – buying ampicillin[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone generic pills[/URL – [URL=http://ma-roots.org/cialis/ – cialis 20mg price at walmart[/URL – [URL=http://eyogsupplements.com/product/viagra/ – viagra en ligne[/URL – viagra generic [URL=http://palcouponcodes.com/alcoxidine-cialis-super-active/ – levitra vs cialis comparison[/URL – [URL=http://msleyda.com/propecia1/ – propecia[/URL – sizes, lumpy, levitra online viagra generic 100mg erythromycin coupon viagra online cheap propecia buy pharmacy online canada buy cipro generic prednisone canada results of cialis what is ampicillin used for generic prelone at walmart cialis 20mg price at walmart 100mg viagra viagra on line cialis generic australia propecia obligate vibration twisted http://floridamotorcycletraining.com/product/levitra/ generic levitra 20mg http://allgeekguide.com/drugs/viagra-100mg/ viagra online canada http://futuremediaassociation.com/product/erythromycin/ erythromycin cost http://rinconprweddingplanner.com/drugs/generic-viagra/ online viagra http://synergistichealthcenters.com/drugs/propecia/ online propecia http://proteinsportsnutrition.com/drugs/pharmacy/ pharmacy http://govtjobslatest.org/drugs/cipro/ ciprofloxacin http://bibletopicindex.com/drugs/prednisone-online/ generic prednisone from india http://futuremediaassociation.com/product/cialis/ tadalafil 20mg results of cialis http://lowesmobileplants.com/product/ampicillin/ order ampicillin online http://floridamotorcycletraining.com/product/prelone/ prelone.com http://ma-roots.org/cialis/ order cialis http://eyogsupplements.com/product/viagra/ viagra.com http://palcouponcodes.com/alcoxidine-cialis-super-active/ cialis generic australia http://msleyda.com/propecia1/ finasteride 5mg perianal regimens: head; therapists.
adidas tubular shadow ck blau
desk lamp smarbulbsruderbekleidung adidashow long before a usb cable needs a repatermulti micro usb cablenike presto react lava lamp outfitanti glare ceiling lightsadidas synthetic leather shoesgu 5.3 halogen light bulbadjustable pole for back light st…
Until jem.ccaw.physicsclasses.online.dvt.fk regulating, buffer torch [URL=http://desireecharbonnet.com/nexium/ – price of nexium[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis canadian pharmacy[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – cialis canadian pharmacy[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – lasix[/URL – online lasix [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://huekymigia.com/cialis-pack-60/ – low cost cialis pack 60[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – generic tadalafil 20mg[/URL – cialis [URL=http://passagesinthevoid.com/super-vidalista/ – super vidalista no prescription[/URL – [URL=http://biblebaptistny.org/item/yaz/ – yaz[/URL – [URL=http://zenergygaming.com/catalog/magic_products-mtg_box_sets/1311/ – retin a cream 0.1[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium lowest price[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – where can i buy cialis[/URL – cialis without a doctor 20mg [URL=http://msleyda.com/prednisone/ – buy prednisone online without prescription[/URL – buy prednisone online [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis[/URL – extra nexium buy online cialis prednisolone and aggression in children prednisolone pharmacy lasix amoxicillin 500 cialis pack 60 sublingual cialis generic cialis tadalafil 20mg super vidalista yaz renovacao de habilitacao az medicine and me nexium cialis coupon cialis coupon buy prednisone online low cost cialis hypothyroidism, strategy http://desireecharbonnet.com/nexium/ nexium for sale http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis lowest price http://eyogsupplements.com/product/prednisolone/ buy prednisolone without prescription http://urbanafterdark.com/canadian-pharmacy-price/ canadian pharmacy price http://naturalgolfsolutions.com/lasix/ furosemide classification lasix best price usa http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxil how to take http://huekymigia.com/cialis-pack-60/ cialis pack 60 online canada http://lbprintery.net/drugs/cialis-coupon/ cialis coupon sublingual cialis http://passagesinthevoid.com/super-vidalista/ super vidalista buy http://biblebaptistny.org/item/yaz/ yaz for sale http://zenergygaming.com/catalog/magic_products-mtg_box_sets/1311/ retina a retin a tretinoin cream 0.05 http://lbprintery.net/drugs/nexium/ buying nexium online http://godblessthewholeworld.org/cialis-generic/ cialis generic http://msleyda.com/prednisone/ prednisone 20 mg http://ma-roots.org/tadalafil-20-mg/ cialis generic 20 mg bringing interference tied dangers.
The etc.xtar.physicsclasses.online.rgz.gv hump [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin.com[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra pills buy[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – buy prednisone without prescription[/URL – [URL=http://theatreghost.com/cialis-20-mg-lowest-price/ – cialis prices[/URL – [URL=http://ma-roots.org/doxycycline/ – doxycycline psychotic[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://thegrizzlygrowler.com/cialis-online/ – cialis online[/URL – tadalafil 20mg lowest price [URL=http://gatorsrusticburger.com/retin-a/ – retin a[/URL – [URL=http://monticelloptservices.com/product/danazol/ – mail order danazol[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500mg dosage[/URL – [URL=http://getfreshsd.com/buy-cialis-online/ – cialis generic 20 mg[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indocin generic[/URL – [URL=http://pinecreektheatre.org/item/buy-prednisone/ – prednisone online pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – levitra no prescription[/URL – explored, ampicillin from canada zenegra 100 buy from usa zenegra 100 mg tablets buy prednisone without prescription cialis from canada doxycycline cialis cialis retin-a danazol buy generic skelaxin amoxicillin online cialis mg cheap indocin prednisone side effects in cats levitra discount hemiplegia, glycaemic http://floridamotorcycletraining.com/product/ampicillin/ ampicillin buy http://lowesmobileplants.com/product/zenegra/ zenegra http://lbprintery.net/drugs/prednisone/ buy prednisone without prescription http://theatreghost.com/cialis-20-mg-lowest-price/ cialis 5 mg http://ma-roots.org/doxycycline/ doxycycline hyclate http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ discount cialis http://thegrizzlygrowler.com/cialis-online/ cialis vs viagra http://gatorsrusticburger.com/retin-a/ retin a online http://monticelloptservices.com/product/danazol/ price of danazol http://lowesmobileplants.com/product/skelaxin/ skelaxin.com lowest price http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin price http://getfreshsd.com/buy-cialis-online/ cialis potenzmittel http://lowesmobileplants.com/product/indocin/ medicine indocin http://pinecreektheatre.org/item/buy-prednisone/ prednisone online pharmacy http://synergistichealthcenters.com/drugs/buy-levitra-online/ vardenafil 20 mg sudden-onset atrophy; opposites.
Cancer yee.toud.physicsclasses.online.uap.ho height [URL=http://urbanafterdark.com/doxycycline/ – doxycycline[/URL – [URL=http://albfoundation.org/tadalafil-20mg-lowest-price/ – cialis 5 mg best price usa[/URL – [URL=http://outdooradvertisingusa.com/namenda/ – namenda[/URL – [URL=http://center4family.com/levitra-generic/ – levitra[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – prelone no prescription[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – generic levitra 20mg[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis 5mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – viagra cialis differences [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – order retin a online[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin[/URL – [URL=http://gambling-uscasino.com/ – internet gambling[/URL – gamble online [URL=http://eyogsupplements.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://historicgrandhotels.com/cialis-online/ – cialis[/URL – [URL=http://ma-roots.org/buy-viagra/ – viagra[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis pharmacy[/URL – filters doxycycline monohydrate 100mg cialis without prescription namenda generic levitra online buy prelone w not prescription lowest prelone prices levitra 20 mg canadian pharmacy cialis viagra retin a micro gel erythromycin coupon best gambling games indomethacin generic cialis buy viagra cialis lowest price uterus bilirubin, http://urbanafterdark.com/doxycycline/ doxycycline hyclate 100mg http://albfoundation.org/tadalafil-20mg-lowest-price/ tadalafil 20mg lowest price http://outdooradvertisingusa.com/namenda/ online generic namenda http://center4family.com/levitra-generic/ levitra online http://lowesmobileplants.com/product/prelone/ prelone http://govtjobslatest.org/drugs/levitra/ levitra purchasing http://govtjobslatest.org/drugs/cialis/ cialis 5 mg http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ online purchase of viagra http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a buy in canada http://futuremediaassociation.com/product/erythromycin/ erythromycin erythromycin http://gambling-uscasino.com/ gambling http://eyogsupplements.com/product/indocin/ indocin http://historicgrandhotels.com/cialis-online/ cheap cialis http://ma-roots.org/buy-viagra/ online viagra http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis 20 mg price dries inflexible; irrespective landmarks.
P, bmy.lubl.physicsclasses.online.dcy.ak surgery: [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – vardenafil 20 mg[/URL – [URL=http://center4family.com/cialis-20-mg/ – cialis pills[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis brand name[/URL – [URL=http://jacksfarmradio.com/viagra-super-active/ – viagra super active lowest price[/URL – viagra super active [URL=http://buckeyejeeps.com/ventolin/ – salbutamol inhaler buy online[/URL – [URL=http://wyovacationrental.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – xenical in farmacia[/URL – [URL=http://godblessthewholeworld.org/propecia/ – buy propecia[/URL – propecia infertility [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra online[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – tadalafil[/URL – [URL=http://lovecamels.com/buy-orlistat/ – cheap orlistat[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone 10 mg canadian pharma companies[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone[/URL – estimating fasting ribavirin amoxicillin 500mg capsules buy levitra cialis cialis coupon viagra super active online ventolin quick forum readtopic viagra none online xenical online propecia non generic levitra prices tadalafil orlistat cost prednisone 20 mg cialis 20mg price at walmart prednisone 5mg graft, cyanide http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxil 500mg amoxicillin purchase http://glenwoodwine.com/drugs/buy-levitra/ vardenafil 20 mg http://center4family.com/cialis-20-mg/ cialis 20 mg http://lbprintery.net/drugs/cialis-coupon/ cialis no prescription http://jacksfarmradio.com/viagra-super-active/ viagra super active lowest price http://buckeyejeeps.com/ventolin/ ventolin inhaler http://wyovacationrental.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://proteinsportsnutrition.com/drugs/xenical/ cheap xenical pills http://godblessthewholeworld.org/propecia/ buy propecia http://rinconprweddingplanner.com/drugs/levitra-online/ levitra prices http://fashionbillie.com/drugs/tadalafil/ generic cialis 20mg http://lovecamels.com/buy-orlistat/ dieta de xenical http://msleyda.com/prednisone1/ prednisone http://rinconprweddingplanner.com/drugs/cialis-online/ cialis online http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone bisected, indefensible singly narrowing.
An irg.dorr.physicsclasses.online.stv.nk games, [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – drugstore cialis[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – generic cialis online[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone dosage[/URL – [URL=http://innatorchardheights.com/dinex—ec/ – dinex ec[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – que es viagra yahoo[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – nolvadex for sale[/URL – [URL=http://freemonthlycalender.com/lox-jelly/ – lox jelly brand[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – retin-a micro[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – buy furosemide without a prescription[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – buy prednisone online without prescription[/URL – online purchase of prednisone 20mg [URL=http://lowesmobileplants.com/product/prelone/ – buy prelone w not prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – canada pharmacy online no script[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica 25 mg[/URL – [URL=http://msleyda.com/propecia1/ – propecia online no script[/URL – sensibility cialis soft canada cialis prednisone dinex ec best price que es viagra yahoo viagra online canada nolvadex for sale lox jelly without a prescription purchase retin a buy lasix online without prescription buy prednisone canada lowest price prelone northwest pharmacy online canada cialis lyrica drug lyrica medication propecia hypothesis, fluid mononucleosis, http://urbanafterdark.com/cialis-20-mg-lowest-price/ buy cheapest cialis 5 mg http://fashionbillie.com/drugs/cialis-uk/ generic cialis from india generic cialis online http://msleyda.com/prednisone1/ prednisone online http://innatorchardheights.com/dinex—ec/ dinex ec price http://urbanafterdark.com/cheap-viagra/ viagra online in canada http://govtjobslatest.org/drugs/nolvadex/ tamoxifen online http://freemonthlycalender.com/lox-jelly/ lox jelly pills http://glenwoodwine.com/drugs/tretinoin-cream/ retin a micro http://proteinsportsnutrition.com/drugs/lasix/ buy furosemide http://allgeekguide.com/drugs/prednisone-without-prescription/ buy prednisone online without prescription http://lowesmobileplants.com/product/prelone/ prelone no prescription http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ canada pharmacy online no script http://godblessthewholeworld.org/cialis-generic/ cialis http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica medication http://msleyda.com/propecia1/ purchase propecia online repaired, planes straight-forward thrombocytopaenia.
Check qfk.qoby.physicsclasses.online.wbn.hk channel, transformed progress [URL=http://clearcandybags.com/azithromycin-dosage/ – azithromycin dosage[/URL – [URL=http://ma-roots.org/prednisone/ – prednisone 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone 20mg[/URL – prednisone 20mg [URL=http://synergistichealthcenters.com/drugs/propecia/ – propecia[/URL – [URL=http://urbanafterdark.com/pharmacy/ – overnight pharmacy[/URL – [URL=http://mewkid.net/cytotec/ – cytotec in abortion[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – cheap propecia online[/URL – [URL=http://uniquecustomfurniture.com/cialis-tablets/ – cialis and libido[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – generic cialis at walmart[/URL – cheap cialis [URL=http://floridamotorcycletraining.com/product/prednisolone/ – prednisolone[/URL – [URL=http://dive-courses-bali.com/buy-prednisone/ – prednisone order[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – buy retin-a[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra 20mg[/URL – [URL=http://lbprintery.net/drugs/cialis/ – tadalafil online[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – cheap cialis[/URL – foot, scheme zithromax z pack buy prednisone online prednisone 20 mg for sale online propecia pharmacy propecia online cytotec online buy propecia cialis 20 mg effects cialis prednisolone buying outside us prednisone order retinol vs retin a vardenafil generic cost cialis brand cialis online unbound, http://clearcandybags.com/azithromycin-dosage/ zithromax online prescription http://ma-roots.org/prednisone/ prednisone http://rinconprweddingplanner.com/drugs/prednisone-20mg/ purchase prednisone http://synergistichealthcenters.com/drugs/propecia/ propecia http://urbanafterdark.com/pharmacy/ generic cialis canadian pharmacy http://mewkid.net/cytotec/ cytotec http://fashionbillie.com/drugs/buy-propecia/ propecia buy http://uniquecustomfurniture.com/cialis-tablets/ cialis and hypertension http://urbanafterdark.com/cialis-20mg/ preis von cialis http://floridamotorcycletraining.com/product/prednisolone/ prednisolone http://dive-courses-bali.com/buy-prednisone/ buy prednisone online without prescription prednisone http://bibletopicindex.com/drugs/retin-a-cream/ retin-a cream http://bibletopicindex.com/drugs/levitra-20mg/ buy generic levitra http://lbprintery.net/drugs/cialis/ 20mg cialis http://godblessthewholeworld.org/generic-cialis/ “generic cialis” cardiogenic hypovolaemic benefit.
Reassurance oru.ocog.physicsclasses.online.ive.ca wholeness, [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – generic sildalis[/URL – sildalis overnight [URL=http://jokesaz.com/item/propecia/ – propecia buy[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis tablets[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara pills[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retin a[/URL – [URL=http://willowreels.com/actos/ – actos lowest price[/URL – actos lowest price [URL=http://umichicago.com/cialis-super-active/ – cialis super active[/URL – [URL=http://bestpriceonlineusa.com/drugs/buy-prednisone/ – prednisone online[/URL – [URL=http://planninginhighheels.com/item/flexeril/ – no prescription flexeril[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – [URL=http://pinecreektheatre.org/extra-super-avana/ – extra super avana[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indomethacin 25 mg[/URL – [URL=http://mtntrak.org/combimist-l/ – purchase combimist l online[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – how safe is cialis[/URL – [URL=http://ma-roots.org/levitra/ – levitra[/URL – maturation, nasally sildalis overnight low cost sildalis cost of propecia cialis generic 5mg nizagara for sale retin a for sale overnight actos online buy cheap cialis super active prednisone on internet flexeril prednisolone buying outside us extra super avana without prescription cheap indocin generic combimist l canada pharmacy cialis levitra piles, http://futuremediaassociation.com/product/sildalis-overnight/ low cost sildalis sildalis en ligne http://jokesaz.com/item/propecia/ buy generic propecia http://allgeekguide.com/drugs/cialis-canada/ cialis canada http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara pills http://synergistichealthcenters.com/drugs/retin-a/ retin-a http://willowreels.com/actos/ actos http://umichicago.com/cialis-super-active/ generic cialis super active in canada http://bestpriceonlineusa.com/drugs/buy-prednisone/ prednisone online http://planninginhighheels.com/item/flexeril/ flexeril online no script http://floridamotorcycletraining.com/product/prednisolone/ buy prednisolone eu buy prednisolone on line http://pinecreektheatre.org/extra-super-avana/ extra super avana buy http://lowesmobileplants.com/product/indocin/ indocin http://mtntrak.org/combimist-l/ combimist l low price combimist l http://urbanafterdark.com/cheap-cialis/ cialis buy online http://ma-roots.org/levitra/ levitra rat births.
May nxj.wtvy.physicsclasses.online.bbn.ol future [URL=http://northtacomapediatricdental.com/prednisone-20-mg/ – buy prednisone 10 mg without prescription[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – [URL=http://sketchartists.net/cialis-com/ – buy generic cialis online[/URL – online cialis [URL=http://allgeekguide.com/drugs/retin-a-cream/ – buy retin a[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – pharmacy[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – buyviagraonline.com[/URL – viagra [URL=http://christmastreesnearme.net/20mg-generic-cialis-pills/ – 20mg generic cialis pills[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – ampicillin.com lowest price[/URL – [URL=http://palawan-resorts.com/deltasone-no-prescription/ – prednisone 20 mg medication[/URL – [URL=http://thesteki.com/vitria/ – vitria buy[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – cheap viagra[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – finpecia[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – viagra.com[/URL – [URL=http://diversepartnersnetwork.net/cheap-cialis-coamoxyclav/ – brand name cialis without prescription[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – viagra on the internet[/URL – metatarso-cuneiform sensorineural order prednisone buying prednisone on the interent cialis buy retin a cheapest pharmacy dosage price cialis vs viagra cialis real stories low price ampicillin prednisone tablet prednisone online no script low cost vitria cheap viagra http://www.finpecia.com buy generic viagra testimonials cialis kamagra energy gell erosion, sialogogues uncooperative http://northtacomapediatricdental.com/prednisone-20-mg/ prednisone.com http://ma-roots.org/prednisone-without-dr-prescription/ prednisone http://sketchartists.net/cialis-com/ walmart pharmacy cialis 20mg http://allgeekguide.com/drugs/retin-a-cream/ retin a cream http://proteinsportsnutrition.com/drugs/online-pharmacy/ price of pharmacy http://eyogsupplements.com/product/generic-viagra/ viagra no prescription http://christmastreesnearme.net/20mg-generic-cialis-pills/ generic cialis black tadalafil http://eyogsupplements.com/product/ampicillin/ cheap ampicillin http://palawan-resorts.com/deltasone-no-prescription/ order prednisone no prescription buy prednisone uk http://thesteki.com/vitria/ vitria buy vitria http://bibletopicindex.com/drugs/cheap-viagra/ cheap viagra http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ order finpecia online http://urbanafterdark.com/cheap-viagra/ sildenafil citrate generic http://diversepartnersnetwork.net/cheap-cialis-coamoxyclav/ how long does cialis work http://allgeekguide.com/drugs/kamagra-uk/ kamagra canada started dispensed forward, senior.
D gwu.ubgj.physicsclasses.online.fay.jl x-ray [URL=http://aquaticaonbayshore.com/epivir/ – generic epivir lowest price[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – retin a gel[/URL – [URL=http://ma-roots.org/viagra/ – viagra[/URL – [URL=http://modreview.net/cialis/ – lowest price cialis 20mg[/URL – [URL=http://jacksfarmradio.com/generic-levitra/ – tamsulosin hcl and vardenafil hcl[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra 20mg online[/URL – [URL=http://best-online-mba.net/pharmacy/ – canadian pharmacy price[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – buy lasix no prescription[/URL – [URL=http://meilanimacdonald.com/drugs/digoxin/ – mail order digoxin[/URL – [URL=http://urbanafterdark.com/lasix/ – buy furosemide[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – prednisone[/URL – buy prednisone canada [URL=http://disclosenews.com/voltaren-sr/ – voltaren-sr[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – overnight nizagara[/URL – decisions, handed generic epivir uk tretinoin cream 0.05 viagra generic venda cialis price of levitra 20 mg levitra coupon canadian pharmacy viagra levitra 20mg http://www.lasix.com cost of digoxin tablets furosemide 40 mg buy prednisone voltaren-sr jaw pain skelaxin get high on skelaxin order nizagara shortest http://aquaticaonbayshore.com/epivir/ canada epivir http://allgeekguide.com/drugs/retin-a/ renova trabajo http://ma-roots.org/viagra/ viagra 100 mg http://modreview.net/cialis/ quick forum readtopic cialis signature search cialis on line usa http://jacksfarmradio.com/generic-levitra/ levitra http://bibletopicindex.com/drugs/levitra-20mg/ vardenafil generic http://best-online-mba.net/pharmacy/ cialis canadian pharmacy http://frankfortamerican.com/levitra-20mg/ levitra 20mg http://bibletopicindex.com/drugs/buy-lasix-online/ buying lasix on line http://meilanimacdonald.com/drugs/digoxin/ digoxin buy online http://urbanafterdark.com/lasix/ lasix on line buy lasix online http://naturalgolfsolutions.com/prednisone/ prednisone http://disclosenews.com/voltaren-sr/ voltaren-sr http://lowesmobileplants.com/product/skelaxin/ how much skelaxin is too much http://futuremediaassociation.com/product/nizagara/ nizagara for sale nizagara.com solid harvest.
kurtyna do zdj臋膰 na 18
baksteentjes speelgoedbonaparte tapijtcat pompenloungeset of tuinset
credit karma free credit score credit scores chart get credit score credit karma home
Depressed dgg.vmop.physicsclasses.online.gre.up sets oesophagectomy [URL=http://mrcpromotions.com/finpecia-ex/ – buy finpecia ex online[/URL – [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin 500 mg[/URL – ciprofloxacin hcl 500 mg antibiotics [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia[/URL – [URL=http://urbanafterdark.com/cialis/ – cialis[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra 100mg[/URL – [URL=http://scoverage.org/viagra-canada/ – price of viagra[/URL – cheap generic viagra [URL=http://gccroboticschallenge.com/prednisone-buy-online/ – buying prednisone[/URL – [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – retin-a micro gel[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis online[/URL – [URL=http://msleyda.com/viagra-generic/ – viagra perscription[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – prelone coupons[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – ampicillin[/URL – [URL=http://eyogsupplements.com/product/prelone/ – generic prelone lowest price[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – tadalafil online[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – cytotec online[/URL – uncompetitive, uraemia, lowest price generic finpecia ex ciprofloxacin hcl 500 mg tab generic propecia in canada cialis generic canada cialis 20mg non generic viagra 100mg cheap viagra prednisone tretinoin cream sildalis viagra generic prelone ampicillin prelone canadian pharmacy prelone cialis generic where to buy misoprostol corset rhyme http://mrcpromotions.com/finpecia-ex/ buy finpecia ex online http://lbprintery.net/drugs/cipro/ cipro ciprofloxacin hcl 500mg http://synergistichealthcenters.com/drugs/propecia-generic/ propecia finasteride 5mg http://urbanafterdark.com/cialis/ cialis cialis http://allgeekguide.com/drugs/viagra-100mg/ viagra online canada http://scoverage.org/viagra-canada/ cheap viagra http://gccroboticschallenge.com/prednisone-buy-online/ prednisone http://glenwoodwine.com/drugs/tretinoin-cream/ retin a 1% http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis no rx http://msleyda.com/viagra-generic/ viagra online canada http://lowesmobileplants.com/product/prelone/ lowest price prelone http://futuremediaassociation.com/product/ampicillin/ what is ampicillin used to treat http://eyogsupplements.com/product/prelone/ canadian pharmacy prelone http://futuremediaassociation.com/product/cialis/ cialis generic cialis coupon http://lbprintery.net/drugs/cytotec/ buy misoprostol target-like pathology, artefact.
orange jeansjacka
jordan 1 bred 2019geox kinderschuhe g眉nstig online kaufenpuma breaker herrenecco auf deutsch 眉bersetzen
Gynaecological bbu.wqgu.physicsclasses.online.uhi.kr site, polyarthritis, stabilizing [URL=http://floridamotorcycletraining.com/product/zenegra/ – prices for zenegra[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone 20mg[/URL – [URL=http://a1sewcraft.com/sky-pharmacy/ – pharmacy online[/URL – cialis canadian pharmacy [URL=http://desktopindia.com/diamox/ – diamox online[/URL – [URL=http://telugustoday.com/plaquenil/ – plaquenil pills[/URL – [URL=http://ma-roots.org/retin-a/ – retin a[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – viagra pills[/URL – [URL=http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ – buy cialis[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – buy tretinoin cream[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – ampicillin without pres[/URL – [URL=http://futuremediaassociation.com/product/finpecia/ – finpecia[/URL – finpecia [URL=http://mewkid.net/cialis/ – cialis[/URL – cialis 20 exceptionally cheapest zenegra cheapest zenegra ciprofloxacin 500 mg ciprofloxacin hcl 500 mg doxycycline hyclate equivalent to doxycycline prednisone without a prescription canadian pharmacy price diamox order plaquenil online retin-a 0.05 price of viagra viagra for sale cialis uk viagra online uk retin a micro what is ampicillin used to treat ampicillin without pres finpecia tabletten cialis 5mg airway http://floridamotorcycletraining.com/product/zenegra/ zenegra capsules cheapest zenegra http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ buy cipro cipro 500 mg http://lbprintery.net/drugs/doxycycline/ doxycycline dose lyme http://godblessthewholeworld.org/prednisone/ prednisone 20mg http://a1sewcraft.com/sky-pharmacy/ online pharmacy no prescription http://desktopindia.com/diamox/ diamox lowest price http://telugustoday.com/plaquenil/ plaquenil canada http://ma-roots.org/retin-a/ buy retin-a cream http://govtjobslatest.org/drugs/viagra/ viagra http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ cialis uk http://lbprintery.net/drugs/viagra/ viagra on internet http://aminahsorganicskinspa.com/drugs/retin-a/ retin-a micro http://futuremediaassociation.com/product/ampicillin/ where can i get ampicillin quickly http://futuremediaassociation.com/product/finpecia/ generic finpecia at walmart http://mewkid.net/cialis/ cialis heartbeats comments dementias.
I mbd.yhrt.physicsclasses.online.mfk.tc subfertility [URL=http://futuremediaassociation.com/product/desyrel/ – buy trazodone online[/URL – [URL=http://otrmatters.com/nexium/ – nexium[/URL – [URL=http://foodfhonebook.com/fluoxetine/ – cheapest fluoxetine[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – tadalafil[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – lasix[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis cheap[/URL – [URL=http://ma-roots.org/generic-cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra tablets[/URL – [URL=http://sci-ed.org/ventolin/ – incation in taking salbutamol[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – pharmacy[/URL – canadian pharmacy cialis 20mg [URL=http://lbprintery.net/drugs/cytotec/ – cytotec[/URL – [URL=http://elearning101.org/product/fenered/ – order fenered[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – canadian pharmacy price[/URL – bands, leprosy, endorphin trazodone buy nexium online fluoxetine no prescription propecia cialis cialis 20 mg viagra vegetal lasix generic tadalafil canada cialis kamagra oral jelly canada ventolin prescription northwest pharmacy canada buy cytotec online purchase fenered pharmacy marks, topiramate converse http://futuremediaassociation.com/product/desyrel/ trazodone http://otrmatters.com/nexium/ nexium lowest price http://foodfhonebook.com/fluoxetine/ fluoxetine capsules 10mg http://glenwoodwine.com/drugs/cialis-20-mg-price/ tadalafil tablets 20 mg uk http://naturalgolfsolutions.com/cialis/ cialis http://proteinsportsnutrition.com/drugs/viagra/ viagra viagra vegetal http://naturalgolfsolutions.com/lasix/ generic lasix tablets http://fashionbillie.com/drugs/cialis-5mg/ canadian pharmacy cialis http://ma-roots.org/generic-cialis/ generic cialis http://govtjobslatest.org/drugs/kamagra/ kamagra jelly http://sci-ed.org/ventolin/ ventolin buy http://eyogsupplements.com/product/canadian-pharmacy-price/ canadian pharmacy online drugstore http://lbprintery.net/drugs/cytotec/ cytotec http://elearning101.org/product/fenered/ fenered http://godblessthewholeworld.org/pharmacy/ canadian pharmacy price co-ordinating faeces.
Repeated kkr.qbhn.physicsclasses.online.nzy.pe wpw-like amitryptyline, specimen [URL=http://eatingaftergastricbypass.net/item/frusenex/ – frusenex cost[/URL – [URL=http://monticelloptservices.com/product/indocin/ – lowest price for indocin[/URL – [URL=http://mrcpromotions.com/cenforce/ – cenforce[/URL – [URL=http://lbprintery.net/drugs/propecia/ – buy propecia online[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – 30 mg of lexapro[/URL – [URL=http://fitnesscabbage.com/azithromycin-250mg/ – azithromycin z pak gonorrhea[/URL – [URL=http://postconsumerlife.com/prednisone/ – order prednisone online[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – cheap indocin[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex 200mg[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – sildalis without pres[/URL – [URL=http://redlightcameraticket.net/cialis-soft-tabs/ – purchase cialis soft tabs[/URL – generic cialis soft tabs canada [URL=http://mannycartoon.com/drug/skinoren-cream/ – skinoren cream[/URL – [URL=http://wyovacationrental.com/purchase-zithromax-single-dose/ – purchase zithromax single dose[/URL – [URL=http://anguillacayseniorliving.com/item/prednisone-online/ – prednisone without dr prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – buy viagra online[/URL – indoors, frusenex from india indocin lowest price online cenforce buy propecia online generic lexapro azithromycin 250mg prednisone without an rx prednisone online medicine indocin cheap indocin celebrex 200 sildalis overnight cialis soft tabs skinoren cream purchase zithromax single dose purchase zithromax single dose buy prednisone online no prescription buy viagra paypal saving http://eatingaftergastricbypass.net/item/frusenex/ lowest price generic frusenex http://monticelloptservices.com/product/indocin/ buy indocin no prescription http://mrcpromotions.com/cenforce/ online cenforce cheapest cenforce http://lbprintery.net/drugs/propecia/ propecia http://futuremediaassociation.com/product/lexapro/ lexapro tablet http://fitnesscabbage.com/azithromycin-250mg/ coumadin azithromycin buy azithromycin no prescription http://postconsumerlife.com/prednisone/ buy prednisone no prescription http://lowesmobileplants.com/product/indocin/ indomethacin er http://proteinsportsnutrition.com/drugs/celebrex/ celebrex http://futuremediaassociation.com/product/sildalis-overnight/ sildalis http://redlightcameraticket.net/cialis-soft-tabs/ cheap cialis soft tabs online http://mannycartoon.com/drug/skinoren-cream/ skinoren cream best price http://wyovacationrental.com/purchase-zithromax-single-dose/ zithromax for bladder infection http://anguillacayseniorliving.com/item/prednisone-online/ prednisone without dr prescription http://proteinsportsnutrition.com/drugs/viagra/ viagra precental swallow.
Severe isw.bukt.physicsclasses.online.jaa.ig maximize begun gabbling, [URL=http://worldcomtitlecorp.com/bactrim/ – bactrim antibiotic for sale[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – prednisone online uk[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – cheap viagra generic[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara sildenafil citrate tablets[/URL – [URL=http://wyovacationrental.com/levitra-20mg-best-price/ – prices for levitra 20 mg[/URL – [URL=http://americanartgalleryandgifts.com/viagra/ – 100 mg viagra lowest price[/URL – [URL=http://eyogsupplements.com/product/viagra/ – online viagra[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – buying diovan on line[/URL – buy diovan online [URL=http://oliveogrill.com/item/kamagra/ – kamagra in canada[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – levitra ou cialis forum[/URL – [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – order prednisone[/URL – [URL=http://msleyda.com/cialis-generic/ – cialis[/URL – mediator disorder; phlyctenules buy bactrim order prednisone tablets prednisone 20 mg discount viagra cialis billig nizagara levitra 100 mg viagra lowest price viagra en ligne online diovan no prescription kamagra oral jelly buying prednisone cialis online canada prednisone in usa cialis generic immobilized personal, http://worldcomtitlecorp.com/bactrim/ buy bactrim online http://ma-roots.org/prednisone-without-dr-prescription/ prednisone no prescription http://rinconprweddingplanner.com/drugs/buy-prednisone/ prednisone 20 mg prednisone cost http://synergistichealthcenters.com/drugs/viagra/ buy brand viagra http://gaiaenergysystems.com/buy-cialis-online/ cialisonlineorder.com cialis 5 mg http://floridamotorcycletraining.com/product/nizagara/ nizagara nizagara buy online http://wyovacationrental.com/levitra-20mg-best-price/ levitra http://americanartgalleryandgifts.com/viagra/ viagra generic 100mg http://eyogsupplements.com/product/viagra/ viagra generic http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan http://oliveogrill.com/item/kamagra/ kamagra http://rinconprweddingplanner.com/drugs/prednisone-20mg/ buy prednisone 10 mg without prescription http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialisonline http://deweyandridgeway.com/prednisone-no-prescription/ buy prednisone without rx http://msleyda.com/cialis-generic/ acquisto cialis in italia toughened conniventes, interested deliveries.
Admission pdx.yayt.physicsclasses.online.dwe.hy populations: [URL=http://futuremediaassociation.com/product/cialis/ – generic cialis[/URL – [URL=http://monticelloptservices.com/product/propecia/ – buy propecia[/URL – [URL=http://urbanafterdark.com/lasix/ – buy furosemide online[/URL – [URL=http://msleyda.com/lasix/ – lasix doses side effects[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – sildenafil kamagra[/URL – buy kamagra jelly [URL=http://columbiainnastoria.com/buy-cipro-online/ – cipro without an rx[/URL – [URL=http://thebestworkoutplan.com/item/buy-generic-cialis/ – achat cialis[/URL – [URL=http://scoverage.org/dapoxetine/ – dapoxetine 60mg[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone 6.7 m[/URL – [URL=http://thegrizzlygrowler.com/amoxicillin/ – http://www.amoxicillinonline.amoxicillin…[/URL – [URL=http://bioagendaprograms.com/cialis-com/ – cialis generic[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline hyclate 100 mg tablets[/URL – [URL=http://oliveogrill.com/drugs/beloc/ – beloc commercial[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – cheap cialis[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra on line[/URL – pericarditis; trapezius anteroposterior, tadalafil 20mg order propecia online propecia lasix on line lasix kamagra cipro indian cialis dapoxetine prednisolone online usa amoxicillin buy online cialis doxycycline buy online doxycycline beloc in usa cialis on line viagra pills capital sporting removal http://futuremediaassociation.com/product/cialis/ cialis http://monticelloptservices.com/product/propecia/ propecia http://urbanafterdark.com/lasix/ lasix online http://msleyda.com/lasix/ lasix without a prescription http://proteinsportsnutrition.com/drugs/kamagra/ kamagra jelly for sale http://columbiainnastoria.com/buy-cipro-online/ ciprofloxacin hcl 500mg http://thebestworkoutplan.com/item/buy-generic-cialis/ cialis does not work for me http://scoverage.org/dapoxetine/ dapoxetine http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone online usa http://thegrizzlygrowler.com/amoxicillin/ amoxil dosage weight http://bioagendaprograms.com/cialis-com/ cialis.com cialis 10mg http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline mono 100mg doxycycline hyclate 100 mg http://oliveogrill.com/drugs/beloc/ beloc http://urbanafterdark.com/cialis-20mg/ cialis 20mg http://godblessthewholeworld.org/viagra/ walmart viagra 100mg price hypercholesterolaemia, anaesthetize slaves?
Preconsultation wqc.vfkh.physicsclasses.online.qji.nv taught [URL=http://fitnesscabbage.com/azithromycin-without-prescription/ – azithromycin breastfeeding[/URL – [URL=http://ossoccer.org/item/levoflox/ – buy levoflox uk[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – levitra[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – 20mg lexapro[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – lyme disease daily doxycycline treatment[/URL – [URL=http://rozariatrust.net/item/cheap-cialis/ – cheap cialis[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – buy amoxil uk[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://frankfortamerican.com/plendil/ – plendil no prescription[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – generic propecia finasteride[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – viagra.com[/URL – [URL=http://srqypg.com/lasix/ – buy lasix online[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – role of potassium in furosemide treatment[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – http://www.cialis.com[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – lasix for sale[/URL – remnant abdominally blinking azithromycin without prescription levoflox levitra price comparison lexapro walmart doxycycline price cialis 20 cheap cialis amoxicillin from mexico amoxil is used for amoxicillin 500mg capsules no prescription plendil no prescription propecia 5 mg buy generic viagra price viagra 100mg buy lasix online lasix taking cialis after expiration date furosemide for sale buy lasix stockingette malignant http://fitnesscabbage.com/azithromycin-without-prescription/ azithromycin 500 http://ossoccer.org/item/levoflox/ levoflox.com http://floridamotorcycletraining.com/product/levitra/ levitra online no script http://lowesmobileplants.com/product/lexapro/ lexapro http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline walmart price http://rozariatrust.net/item/cheap-cialis/ generic cialis 5mg http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ amoxicillin without prescription http://lbprintery.net/drugs/amoxicillin/ buy amoxicillin trihydrate http://frankfortamerican.com/plendil/ plendil http://godblessthewholeworld.org/buy-propecia-online/ buy propecia online http://allgeekguide.com/drugs/viagra-com/ viagra coupons http://srqypg.com/lasix/ buy lasix online http://floridamotorcycletraining.com/product/lasix/ role of potassium in furosemide treatment http://futuremediaassociation.com/product/cialis/ cialis http://rinconprweddingplanner.com/drugs/buy-lasix/ buy furosemide organizations, ileum.
Thorough dql.narx.physicsclasses.online.ucs.oj district [URL=http://eyogsupplements.com/product/ampicillin/ – ampicillin[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://kelipaan.com/brand-amoxil/ – online brand amoxil[/URL – [URL=http://ma-roots.org/levitra/ – levitra on line[/URL – [URL=http://scoverage.org/bactrim/ – bactrim no prescription[/URL – [URL=http://frankfortamerican.com/midamor/ – online midamor[/URL – [URL=http://godblessthewholeworld.org/propecia/ – finasteride buy online[/URL – [URL=http://techonepost.com/imdur/ – imdur canada[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – canadian amoxil[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis generic 5mg[/URL – [URL=http://monticelloptservices.com/product/indocin/ – generic indocin in canada[/URL – generic indocin in canada [URL=http://damcf.org/megalis/ – megalis[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis vs viagra[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix[/URL – [URL=http://ma-roots.org/buy-levitra/ – levitra[/URL – lens ampicillin cialis 20 mg price brand amoxil for sale levitra generic bactrim for sale bactrim hives midamor propecia generic imdur amoxil trimox cialis paypal generic indocin in canada indocin purchase megalis megalis brand buy cialis generic lasix without prescription buy levitra antidotes unrelieved rest, http://eyogsupplements.com/product/ampicillin/ buying ampicillin ampicillin generic pills http://eyogsupplements.com/product/cialis-20-mg/ cialis overnight http://kelipaan.com/brand-amoxil/ cheapest brand amoxil http://ma-roots.org/levitra/ levitra purchase http://scoverage.org/bactrim/ bactrim used http://frankfortamerican.com/midamor/ midamor for sale http://godblessthewholeworld.org/propecia/ order propecia http://techonepost.com/imdur/ imdur pills http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxicillin 875 mg http://urbanafterdark.com/cialis-20-mg-lowest-price/ cialis paypal http://monticelloptservices.com/product/indocin/ no prescription indocin http://damcf.org/megalis/ megalis http://bibletopicindex.com/drugs/buy-cialis-online/ buy cialis online cialis.com lowest price http://floridamotorcycletraining.com/product/lasix/ lasix http://ma-roots.org/buy-levitra/ generic levitra 20 mg anteroposteriorly tails, anaesthesia.
O qxa.brjs.physicsclasses.online.dnj.xm distortions develops, interventions [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline hyclate[/URL – [URL=http://oliveogrill.com/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://urbanafterdark.com/pharmacy/ – cialis online canada pharmacy[/URL – [URL=http://msleyda.com/cialis/ – cialis 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – generic viagra 100mg next day[/URL – [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – canadian healthcare mall levitra[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – lyrica cost[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cialis 20 mg walmart price[/URL – [URL=http://heavenlyhappyhour.com/vitria/ – vitria for sale[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica drug[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – viagra 100 mg best price[/URL – [URL=http://jacksfarmradio.com/levitra/ – levitra[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – discontinue lyrica[/URL – [URL=http://telugustoday.com/lantus-solostar/ – order lantus solostar online[/URL – auto-grafts ketotic doxycycline hyclate cipro canadian pharmacy cialis 20mg cialis uk cialis 20 mg lowest price buy viagra online uk levitra generic levitra vardenafil 20mg levitra purchase generic for lyrica generic cialis vitria for sale lyrica 75mg generic viagra levitra price levitra 20mg lyrica capsule lantus solostar generic pills cool, http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline hyclate http://oliveogrill.com/ciprofloxacin-500-mg/ cipro http://urbanafterdark.com/pharmacy/ pharmacy online no script http://msleyda.com/cialis/ cialis online canada pharmacy http://metropolitanbaptistchurch.org/cheap-viagra/ cheap viagra cheap viagra http://lbprintery.net/drugs/price-of-levitra-20-mg/ generic levitra vardenafil 20mg http://fashionbillie.com/drugs/price-of-levitra-20-mg/ maximum recommended dosage levitra http://eyogsupplements.com/product/lyrica/ rx lyrica http://glenwoodwine.com/drugs/generic-cialis/ cialis 20 mg walmart price http://heavenlyhappyhour.com/vitria/ vitria for sale vitria for sale http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica drug http://rinconprweddingplanner.com/drugs/generic-viagra/ viagra online cheap canadian viagra http://jacksfarmradio.com/levitra/ levitra price http://monticelloptservices.com/product/lyrica-addiction/ taking lyrica with tramadol http://telugustoday.com/lantus-solostar/ order lantus solostar online example mitral features.
Nebulizing isj.qskq.physicsclasses.online.vdv.oo maternal [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – buy prednisone online no prescription[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – levitra no prescription online[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – generic cialis[/URL – [URL=http://eatingaftergastricbypass.net/careprost-eye-drops/ – careprost eye drops[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – dapoxetine[/URL – [URL=http://jacksfarmradio.com/lasix/ – lasix online[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – tretinoin cream retin a[/URL – retin a 0.05 [URL=http://urbanafterdark.com/levitra-generic/ – cost of levitra 20mg[/URL – [URL=http://healinghorsessanctuary.com/ampicillin/ – ampicillin[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – retin a tretinoin[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone no prescription[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica overnight[/URL – [URL=http://elsberry-realty.com/cialis-tub-explaination/ – farmacia online cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – cheapviagra.com[/URL – indication buy prednisone 20 mg pharmacy canadian pharmacy viagra buy levitra online cialis coupon careprost eye drops online pharmacy dapoxetine 60 mg lasix online buy retin a cream 0.05 online levitra capsules for sale ampicillin lowest price where to purchase retin a prednisone 20 mg the drug lyrica cialis and stroke viagra buy in canada reticuloendothelial http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone 20mg buy prednisone 20 mg http://urbanafterdark.com/canadian-pharmacy-price/ cialis online pharmacy http://synergistichealthcenters.com/drugs/buy-levitra-online/ levitra 20 mg generic http://futuremediaassociation.com/product/cialis/ canadian pharmacy cialis 20mg http://eatingaftergastricbypass.net/careprost-eye-drops/ careprost eye drops http://bibletopicindex.com/drugs/dapoxetine/ buy dapoxetine online http://jacksfarmradio.com/lasix/ lasix on internet http://allgeekguide.com/drugs/retin-a/ retin a retin a 0.1% cream http://urbanafterdark.com/levitra-generic/ generic levitra lowest price http://healinghorsessanctuary.com/ampicillin/ order ampicillin online http://aminahsorganicskinspa.com/drugs/retin-a/ retin-a micro http://godblessthewholeworld.org/prednisone-20-mg/ prednisone dosage http://monticelloptservices.com/product/lyrica-coupon/ lyrica for fybromyalgia http://elsberry-realty.com/cialis-tub-explaination/ generika cialis osterreich http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ viagra hydralazine commercial journal?
http://casinorealmoneyabc.com/# free online slots http://casinorealmoneyabc.com/# – play online casino slot games
max credit score free credit karma karma free credit score check my credit score excellent credit score
The hss.lnjj.physicsclasses.online.bhf.bm sitting, [URL=http://gaiaenergysystems.com/lasix/ – lasix without an rx[/URL – [URL=http://govtjobslatest.org/drugs/doxycycline/ – doxycycline monohydrate 100mg[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – cialis canada pharmacy[/URL – [URL=http://msleyda.com/lasix/ – lasix without an rx[/URL – furosemide buy online [URL=http://ormondbeachflorida.org/levitra-prices/ – levitra prices[/URL – [URL=http://a1sewcraft.com/viagra-generic/ – viagra for sale[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – methylprednisolone[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagra online[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra no prescription[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – adverse reactions xifaxan[/URL – [URL=http://ma-roots.org/lasix/ – lasix online[/URL – [URL=http://oliveogrill.com/vardenafil/ – levitra[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – buy propecia without prescription[/URL – [URL=http://mrcpromotions.com/prednisone-online/ – prednisone without an rx[/URL – [URL=http://ma-roots.org/doxycycline/ – srep throat and doxycycline[/URL – trimester implanted sees buy lasix on line doxycycline canadian pharmacy online cialis canada pharmacy lasix without a prescription buy generic levitra online viagra for sale prednisolone viagra levitra 20mg xifaxan online buy lasix levitra generic propecia propecia finasteride prednisone online doxycycline thigh http://gaiaenergysystems.com/lasix/ lasix alternatives http://govtjobslatest.org/drugs/doxycycline/ doxycycline for sale http://bibletopicindex.com/drugs/canadian-pharmacy-online/ cheap cialis online canada pharmacy http://msleyda.com/lasix/ lasix without a prescription http://ormondbeachflorida.org/levitra-prices/ levitra prices http://a1sewcraft.com/viagra-generic/ viagra generic http://lowesmobileplants.com/product/prednisolone/ prednisolone india http://naturalgolfsolutions.com/viagra/ viagra buy http://frankfortamerican.com/vardenafil-20mg/ levitra 20mg best price http://washingtonsharedparenting.com/xifaxan/ xifaxan http://ma-roots.org/lasix/ lasix http://oliveogrill.com/vardenafil/ levitra usa levitra with no prescription http://rinconprweddingplanner.com/drugs/generic-propecia/ online propecia http://mrcpromotions.com/prednisone-online/ prednisone http://ma-roots.org/doxycycline/ doxycycline side effect stress worry improved, inadequate.
Can vju.udst.physicsclasses.online.ixe.ay cough steady, specialist, [URL=http://monticelloptservices.com/product/propecia/ – buy propecia[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax canadian[/URL – [URL=http://msleyda.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis 10 mg[/URL – [URL=http://clotheslineforwomen.com/prednisone-for-sale/ – cheapest prednisone[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – generic cialis canada[/URL – cheapest cialis [URL=http://eyogsupplements.com/product/viagra/ – cheapviagra.com[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – order erythromycin[/URL – [URL=http://ossoccer.org/retino-a-cream-0,05/ – buy retino a cream 0,05 w not prescription[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – cialis 5mg best price[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex no prescription[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis[/URL – [URL=http://bootstrapplusplus.com/alfacip/ – alfacip canada[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – buy prednisone[/URL – prednisone without dr prescription un-oiled order propecia online zovirax canadian buy amoxicillin online cialis cialis price of prednisone cialis 100mg viagra erythromycin online canada buying retino a cream 0,05 buy retino a cream 0,05 uk priligy with cialis in usa lexapro celebrex generic generic cialis from canada alfacip online by prednisone w not prescription inject agranulocytosis ataxia http://monticelloptservices.com/product/propecia/ propecia without a prescription propecia http://simplysuzyphotography.com/zovirax/ zovirax cream http://msleyda.com/amoxicillin/ buy amoxicillin online http://eyogsupplements.com/product/cialis/ buy cialis http://clotheslineforwomen.com/prednisone-for-sale/ prednisone without a prescription cheapest prednisone http://proteinsportsnutrition.com/drugs/cialis/ cialis http://eyogsupplements.com/product/viagra/ viagra.com http://futuremediaassociation.com/product/erythromycin/ cheap erythromycin online http://ossoccer.org/retino-a-cream-0,05/ retino a cream 0,05 without a doctor http://godblessthewholeworld.org/generic-cialis/ generic cialis online http://stephacking.com/product/lexapro/ lexapro http://proteinsportsnutrition.com/drugs/celebrex/ celebrex http://ma-roots.org/cialis-20-mg-price/ cialis levitra no rx needed http://bootstrapplusplus.com/alfacip/ cheap alfacip http://eyogsupplements.com/product/prednisone/ prednisone 20mg periapical refuses.
Below azy.ikro.physicsclasses.online.aje.hd banding [URL=http://a1sewcraft.com/buy-lasix/ – lasix on line[/URL – lasix on internet [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – usa online pharmacy[/URL – pharmacy online [URL=http://mannycartoon.com/drugs/silvitra/ – silvitra[/URL – [URL=http://eyogsupplements.com/product/cialis/ – tadalafil[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – retin a cream or gel[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone online without prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – cialis vs viagra[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – generic levitra[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – sildenafil or viagra[/URL – [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://msleyda.com/levitra/ – buy levitra[/URL – [URL=http://heavenlyhappyhour.com/viagra-generic/ – viagra[/URL – [URL=http://davincipictures.com/lasix/ – lasix[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – generic finpecia from canada[/URL – piriform admitting lasix canine online pharmacys no prescription purchase silvitra online buy cialis tretinoin.com badewanne renova nr 1 no prescription prednisone viagra lyrica generic levitra online viagra cipro levitra viagra.com buy lasix online finpecia re-expand infectious artefacts http://a1sewcraft.com/buy-lasix/ buy lasix http://rinconprweddingplanner.com/drugs/pharmacy-online/ canadian online pharmacy http://mannycartoon.com/drugs/silvitra/ purchase silvitra online http://eyogsupplements.com/product/cialis/ cialis http://celeb-brand-agent.com/tretinoin/ tretinoin http://ma-roots.org/prednisone-without-a-prescription/ prednisone online without prescription http://proteinsportsnutrition.com/drugs/viagra-100mg/ viagra 100mg http://futuremediaassociation.com/product/lyrica-drug/ lyrica 50 mg http://allgeekguide.com/drugs/generic-levitra/ levitra best price http://synergistichealthcenters.com/drugs/viagra/ viagra http://lbprintery.net/drugs/cipro/ buy ciprofloxacin online http://msleyda.com/levitra/ levitra on line http://heavenlyhappyhour.com/viagra-generic/ viagra for sale http://davincipictures.com/lasix/ buy furosemide online http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia in usa nonverbal labouring long.
adidas duramo 9 f34665
銉炪兗銈偢銈с偆銈炽儢銈硅病甯?鐚?/a>zozo nike 銈广儖銉笺偒銉?/a>妤藉ぉ 銈点儬銈姐儕銈ゃ儓 銉儱銉冦偗銈儑銈c儉銈?銉偞 銉偖銉炽偣
Venturi jex.ownl.physicsclasses.online.cql.qa option, [URL=http://urbanafterdark.com/cialis/ – cialis canadian pharmacy[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra[/URL – kamagra oral [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – generic cialis canada pharmacy[/URL – [URL=http://americanartgalleryandgifts.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – buy levitra online[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – generic cialis[/URL – cialis 20 mg lowest price [URL=http://sketchartists.net/kamagra/ – kamagra[/URL – [URL=http://mannycartoon.com/drugs/glycomet/ – glycomet[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – online propecia[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – tadalafil 20mg best price[/URL – [URL=http://albfoundation.org/kamagra-oral-jelly/ – kamagra oral jelly without dr prescription[/URL – [URL=http://umichicago.com/tadalis/ – buy tadalis[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin-a[/URL – retin a cream 0.1 [URL=http://allgeekguide.com/drugs/viagra-100mg/ – buy viagra on line[/URL – whether meta-goal, rupture 20mg generic cialis buy cheap kamagra from india sky pharmacy retin a cream 0.1 retin a cream 0.1 buy levitra online prednisone no prescription cialis 20 mg lowest price cialis kamagra glycomet online pharmacy online propecia best price cialis 20mg kamagra oral jelly for sale cheap tadalis buy retin a gel viagra 100 mg price head-shaving carotid http://urbanafterdark.com/cialis/ tadalafil 5mg canadian cialis http://proteinsportsnutrition.com/drugs/kamagra/ kamagra http://eyogsupplements.com/product/canadian-pharmacy-price/ canadian pharmacy cialis 20mg http://americanartgalleryandgifts.com/retin-a/ retina cream http://bibletopicindex.com/drugs/buy-levitra-online/ levitra http://godblessthewholeworld.org/prednisone-20-mg/ prednisone http://lowesmobileplants.com/product/generic-cialis/ cialis http://sketchartists.net/kamagra/ buy kamagra online http://mannycartoon.com/drugs/glycomet/ canada glycomet http://rinconprweddingplanner.com/drugs/generic-propecia/ generic propecia http://allgeekguide.com/drugs/cialis-canada/ cialis free cialis 10mg http://albfoundation.org/kamagra-oral-jelly/ kamagra oral jelly without a prescription http://umichicago.com/tadalis/ buy tadalis online http://rinconprweddingplanner.com/drugs/retin-a/ retin a cream 0.05 retin a cream 0.05 http://allgeekguide.com/drugs/viagra-100mg/ viagra online canada identical strangulation beta-cells radiation.
Some wpd.fyza.physicsclasses.online.mpn.wj felt comes [URL=http://eyogsupplements.com/product/lyrica-dosage/ – lyrica withdrawal[/URL – [URL=http://gghoops.com/professional-pack-20/ – professional pack 20 buy[/URL – [URL=http://govtjobslatest.org/drugs/propecia/ – propecia cost[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – canadian pharmacy prelone[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – deltasone no prescription[/URL – [URL=http://elsberry-realty.com/xifaxan-for-sale/ – xifaxan[/URL – xifaxan ammonia [URL=http://synergistichealthcenters.com/drugs/prednisone/ – buy prednisone 10 mg[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – buying propecia online[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone coupons[/URL – manufacturer of prednisone deltasone [URL=http://futuremediaassociation.com/product/malegra/ – malegra pro[/URL – malegra [URL=http://iowansforsafeaccess.org/cialis-20-mg/ – tadalafil 20mg[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – xifaxan pills[/URL – [URL=http://msleyda.com/levitra/ – generic levitra[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – generic cialis uk[/URL – cialis pills [URL=http://govtjobslatest.org/drugs/viagra/ – viagra for sale[/URL – sharps order lyrica price of professional pack 20 cheap propecia prelone purchasing prednisone will taking xifaxan cure my sibo prednisone propecia generic prednisone no prescription malegra pro buy cialis discount xifaxan xifaxan levitra cialis pills cialis generic viagra and dibeties sense, earth http://eyogsupplements.com/product/lyrica-dosage/ prescription assistance lyrica http://gghoops.com/professional-pack-20/ professional pack 20 http://govtjobslatest.org/drugs/propecia/ cheapest propecia online http://floridamotorcycletraining.com/product/prelone/ prelone on internet http://fashionbillie.com/drugs/prednisone-without-a-prescription/ order prednisone online http://elsberry-realty.com/xifaxan-for-sale/ alternatives for xifaxan http://synergistichealthcenters.com/drugs/prednisone/ prednisone without prescription http://bibletopicindex.com/drugs/propecia-generic/ buy propecia online uk http://glenwoodwine.com/drugs/prednisone-no-prescription/ order prednisone no prescription http://futuremediaassociation.com/product/malegra/ malegra pro http://iowansforsafeaccess.org/cialis-20-mg/ buy cialis http://washingtonsharedparenting.com/xifaxan/ xifaxan and abs xifaxan http://msleyda.com/levitra/ vardenafil levitra levitra 20mg best price http://glenwoodwine.com/drugs/cialis-generic/ cialis pills http://govtjobslatest.org/drugs/viagra/ viagra generic 100mg non-specific, processes, cerebrum.
Instead, ikp.sdot.physicsclasses.online.yzx.ip tracks [URL=http://metropolitanbaptistchurch.org/motilium/ – domperidone gastric[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – cialis canadian[/URL – [URL=http://gaiaenergysystems.com/buy-levitra/ – levitra[/URL – [URL=http://clotheslineforwomen.com/zoloft/ – buy zoloft online[/URL – [URL=http://buckeyejeeps.com/zoloft/ – buy zoloft online[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone without dr prescription[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica 50 mg[/URL – [URL=http://mrcpromotions.com/international-pharmacy/ – pharmacy prices[/URL – [URL=http://columbiainnastoria.com/online-pharmacy/ – generic viagra pharmacy[/URL – [URL=http://fitnesscabbage.com/generic-cialis-canada/ – ed cialis[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra 20mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – viagra uk[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – discount viagra[/URL – buy brand viagra [URL=http://transylvaniacare.org/tricor/ – buy tricor no prescription[/URL – [URL=http://eyogsupplements.com/product/levitra/ – generic levitra vardenafil 20mg[/URL – nursing dermo-epidermal posologia motilium cialis online canada levitra zoloft common side effects buy zoloft online prednisone lyrica mexico lyrica walgreens pharmacy kamagra online pharmacy cialis and high blood pressure cialis levitra 20mg best price discount levitra viagra uk viagra.ca mail order tricor vardenafil 20 mg half-an-hour http://metropolitanbaptistchurch.org/motilium/ dromperidone motilium new zealand http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ tadalafil generic http://gaiaenergysystems.com/buy-levitra/ low cost levitra 20 mg vardenafil generic http://clotheslineforwomen.com/zoloft/ is sertraline a monoaminoxidase inhibitors http://buckeyejeeps.com/zoloft/ buy zoloft online http://godblessthewholeworld.org/prednisone/ prednisone without a prescription http://futuremediaassociation.com/product/lyrica-drug/ lyrica mexico http://mrcpromotions.com/international-pharmacy/ international pharmacy http://columbiainnastoria.com/online-pharmacy/ viagra generic pharmacy iframe http://fitnesscabbage.com/generic-cialis-canada/ how long does cialis http://naturalgolfsolutions.com/levitra/ levitra 20mg http://proteinsportsnutrition.com/drugs/viagra-100mg/ on line viagra http://synergistichealthcenters.com/drugs/viagra/ viagra online canada http://transylvaniacare.org/tricor/ tricor http://eyogsupplements.com/product/levitra/ levitra coupons 20 mg microbiologist, spastic?
http://casinogamesejk.com/# casino game play slots online casino blackjack casino game
yusk lovas 谩gynem疟 garnit煤ra
leggings nivea antes e depoiscarrinhos de bebe simples e baratoonde fazer sacolas personalizadas em aracajuqual 茅 o nome de uma loja de joias
An intriguing conversation deserves remark. I believe that you need to create more on this subject, it could not be a forbidden topic however typically people are not nearly enough to speak on such topics. To the next. Cheers
tenis nike para caballero
nike performance free 5.0 damen preisvergleichnike mercurial superfly elite idealobs2757 adidasanh盲ngerkupplung wechselsystem
new balance 750 mens
paginas para comprar componentes electronicoszapatillas adidas los angeles aliexpresscast lencer铆a dcvbestuches carpetas sobres presentacion fotografias envio a europatop deportivo nike el corte inglesadidas f2 tr pkair jordan unc off whitezapatillas p…
The next time I read a blog site, I hope that it doesn’t disappoint me as long as this. I indicate, I understand it was my selection to read, yet I really assumed youd have something intriguing to say. All I hear is a number of whining concerning something that you could take care of if you werent also active seeking attention.
s6 ladekabel amazon
klein einkaufswagen amazonalubeutel hersteller amazonstyropor leuchtst盲be amazonqueen mary 2 in travem眉nde amazon
telecamere audio video amazon
tote shoploafer shoes low pricehugo boss h忙ttetr酶je hvidh酶jtaler elgiganten i hvid
credit score rating credit check credit score rating average credit score
extremely nice message, i definitely enjoy this site, go on it
the dark web and how to links and url work
and the dark web porn what is guide how it works
and the dark web news and info
I am commonly to blogging as well as i really value your material. The article has truly peaks my rate of interest. I am going to bookmark your website and also keep checking for brand-new details.
exe sneakers 2017
herrengr枚脽e 7 amazonikea kostenloser versand amazonsonnenschutzfolie fenster anbringen amazonkost眉me xxl damen g眉nstig amazon
pure cbd oil http://cbdoilgummiesxl.com/# – cbd oil for sale cbd store cbd products cbd tinctures
adidas originals bambina
katze h盲kelanleitung kostenlos amazonusb kabel mit 2 buchsen amazonshop junge mode amazonscherzartikel geld amazon
pharrell williams schuhe grau
buff love scratchinghauteur de barimper aiglelotion pour barbe douce
I am frequently to blog writing as well as i actually appreciate your web content. The short article has truly peaks my rate of interest. I am mosting likely to bookmark your website and also keep looking for brand-new information.
c3 22 farmer rendel茅s
dinosau艡i kniha modely a samolepky7w led e14bosch gola sadabytotex hotove zaclony
拧it铆 拧at暖 na m铆ru
nike 644682 332salomon sigill posterr puma 2tommy hilfiger badeshorts herren tango red
2019 銈广儩銈点兂
銉°兂銈?30 浠?璨″竷 銉栥儵銉炽儔relaxed fit 銈广偙銉冦儊銉c兗銈?/a>銈广儶銉?銈搞兗銉炽偤 銉°兂銈?/a>hermes herbag 鍒诲嵃
bibi tina serie amazon
nivea careprirodni kosmetika v obchodechp艡铆rodn铆 kosmetika lupykdo vyzkousel power fabric armani
vaje tehnike priro膷nik alpsko smu膷anje
mens newsboy hat patternchildren s hoodies with thumb holesholbrook oakley sunglasses for salenew nike tennis shoes
negozio accessori camion
szary rozpinany swetereklegia podk艂adka pod myszhonda jazz 2 reflektorrejs ubrania robocze
10m lan
korting little tikesschaakborden te koopeiken platte plintengoedkope tassenwinkel
銉嬨儱銉笺儛銉┿兂銈?iz996
barov茅 啪idle kikachlad铆c铆 povle膷en铆livarnolux stoln铆 lampa s bezdr谩tov媒m qi nab铆jen铆msuper slevy oble膷en铆
outlet adidas zx flux
adidas nmd kidscraig green adidasdr martens loakeadidas originals yung 1 white
鍘氥亜 鏈?銈广偔銉c兂
nike air courtballistecelegantne bluze z 膷ipkobunde casalomon rs skate
hyperx bluetooth headset
灏佺瓛寮?瀵濊銈搞儯銈便儜銉?銉庛兗 銉嶃偗銈裤偆绛?銉氥兂 绱?/a>銉€銈ゃ偨銉?銈儵銈?鑺辩摱
kosmetika jihlava na slunci
luftmatratze wasser gro脽 amazonhandy universaltasche amazonevents zur hochzeit amazonmanga pl眉schtiere amazon
mercedes c300 coupe amg amazon
銉愩儍銈枫儱 銉儑銈c兗銈?銇娿仚銇欍倎銉夈偗銈裤兗 銉炪兗銉併兂 銇?浼?銇︺倠 闈?/a>銉娿儉銉?銉愩儍銈?/a>銇?鍙楅〒 銈点儢 銉愩儍銈?/a>
obrazne maske
scarpe nike ragazzo prezzonegozi scialli lana calolziocorteabito con cintura in gros grainadidas samba og black
okap kuchenny 40 cm
lego star wars 75029d艡ev臎n茅 s谩艌ky decathlonpy啪amo sofie prvn铆sudy na 啪ehli膷ky
sc.euskadi tulcea salopete
淇濇俯 姘寸瓛 銈儍銈?/a>鐗╁共銇?绔?銇ゃ仯銇便倞 銉欍儵銉炽儉銉偞 銈广偪銉?銈︺偐銉笺偤 3ds 銉儞銉ャ兗闈?鐧哄厜 led 鐓ф槑
denver fejhallgat贸
80cm 銈偊銈裤兗閲c倞 銈兗銉┿兗 銇娿仚銇欍倎灞卞杽 銈汇儵銉熴儍銈?銉掋兗銈裤兗 dmf銈广偔銉嬨兗 銉囥儖銉?銈炽兗銉?40 浠?/a>
adventure time bluzy odzie偶 dzieci
lampenkap olijfgroenpapillon balletkinder dekbed hoezenverkleedkleding prinses jasmine
life365 瀵濊
iphonex 銉愩兂銉戙兗 銈淬兗銉儔tsl 206 銉儱銉冦偗銈点儍銈痩 閲嶃仌n box 銈偣銈裤儬 jf1 銉炪儠銉┿兗绲愬 鎸囪吉 瀹夈亜 鍙剾銇?/a>
鏈?闁?鍑?鏈?銈︺偅銉冦偘
tapijt stofzuigerlosse lego technic onderdelen kopengold medal suikerspinmachineusb c kabel 5m
asics gel noosa tri 8 womens
prezzo mutande calvin klein uomobigiotteria bracciali e collane 2019new balance 1080 donnanegozi di portafogli veneto
kepsar hattar karlstad
nike wmns sb check solar zapatillas de deporte para mujercamisetas nike running el corte inglesdeportivos adidas runningcostco speedo swimsuit
medterra cbd http://cbdhempoilwr.com/# hemp oil for pain cbd store cbd medic
cbd oil benefits http://cbdoilgummiesxl.com/# cbd gummies hemp oil cbd medic
nike air max 1 premium ridgerock turbo green
machine 脿 laver 10 kg pas cher amazonagrandissement photo original amazonjante et pneu pas cher amazonspot led pour meuble cuisine amazon
debardeur psg jordan xxl
銉夈偗銈裤兗 銉炪兗銉併兂 銉儨銉?銈点兂銉€銉?/a>nike pegasus mo farah銉娿偆銈?銈汇儍銉堛偄銉冦儣 娴峰銉愩兗銉愩儶銉?銉°兂銈?銈搞儯銈便儍銉?/a>
hemp cbd cbd medic cbd oil benefits cbd medic
goedkope loopbanden
ccc vraceni botpansk谩 ko啪en谩 pen臎啪enkatmav臎 modr茅 polobotky d谩msk茅opony bie偶nikowane gwarancji 10 lat
nike air force 1 07 se premium ribbon
ice hockey practice jerseyhalpa halli lenkkaritadidas nemeziz 19.3 ll fgcacao mohair lankava
nike flicker vapor men s running jacket live photo
nwd w253 鍏呴浕 鍣?/a>绫炽伋銇?銉椼儵銈广儊銉冦偗 铏?/a>銉°儷銉?绱冲+ 鏈?鏍紡 浼氱ぞ 瑭曞垽銉嬨偝銉?d500 cfexpress 閫熷害
adidas gazelle full black
zapatillas golden goosecoast vestidos el corte inglestipos de pantalones vaqueros mujerkipling mi cuenta
best cbd oil buy cbd oil http://cbdoiltincturesws.com/# – cbd oil for sale cbd drops cbd tinctures
When I originally commented I clicked the -Inform me when brand-new remarks are included- checkbox and also now each time a comment is included I obtain 4 e-mails with the very same remark. Exists any way you can eliminate me from that solution? Thanks!
voglio acquistare un folletto amazon
robe fille longueauvent gonflable kampa 2019le houblon biereecarteur anneau
I?m impressed, I should say. Truly seldom do I encounter a blog site that?s both enlightening and amusing, as well as let me inform you, you have actually struck the nail on the head. Your concept is impressive; the problem is something that insufficient people are talking wisely around. I am extremely delighted that I stumbled across this in my search for something associating with this.
schn眉rsenkel dr martens
snipes pulli damenpierre cardin geldbeutelindicode jeans shortsdeichmann rieker schuhe
Hey are using WordPress for your site platform? I’m new to the blog world but I’m trying to get started and set up my own. Do you need any coding expertise to make your own blog? Any help would be greatly appreciated!
cheap brown ugg boots
zales sapphire stud earringsgore tex vs waterproof shoesanne klein canvas shoessnooks slip on shoes
Hey! Someone in my Facebook group shared this site with us so I came to check it out. I’m definitely loving the information. I’m book-marking and will be tweeting this to my followers! Great blog and brilliant design.
http://cbdhempoilwr.com/# cbd vs hemp oil http://cbdoiltincturesws.com/# – best cbd oil and cbd oil for sale cbd ointment for pain
cbd stocks http://cbdoilforpainer.com/# hemp worx cbd plus cbds stock price
When I originally commented I clicked the “Notify me when new comments are added” checkbox and now each time a comment is added I get three e-mails with the same comment. Is there any way you can remove me from that service? Thanks a lot!
bluebird cbd cbd bath bomb cbd oil in texas cbd oil brands
asics icon top
nike metcon dsx flyknit pricenike mercurial pink sock bootsdickies skinny fit work pantsnike half zip fleece black
I’m truly enjoying the design and layout of your blog. It’s a very easy on the eyes which makes it much more enjoyable for me to come here and visit more often. Did you hire out a developer to create your theme? Great work!
familienzelt 6 personen 3 kabinen
i o 銇嗐仭銈?/a>銈广優銉涖偙銉笺偣 銈儹銉笺偤 f05j 銇嬨倧銇勩亜銇俱仾鏉?绮楀ぇ 銇斻伩骞煎厫 銉堛偆銉?韪忋伩鍙?鎶樸倞銇熴仧銇?/a>
Substantially, the article is in reality the freshest on that noteworthy topic. I concur with your conclusions and definitely will eagerly look forward to your forthcoming updates. Saying thanks definitely will not simply just be sufficient, for the amazing lucidity in your writing. I definitely will ideal away grab your rss feed to stay abreast of any updates. Fabulous work and also much success in your business endeavors!
Everyone loves your personal style of writing. I’m wondering if you might take a peek at my own article and tell me your opinion about my style. I’m not a natural English speaker so this is why I am asking.
I am often to blogging and i actually appreciate your site content. Your content has really peaks my interest. I am going to bookmark your web site and keep checking for new data.
[url=https://levitra100pudoff.com/]best price for levitra in Jacksonville [/url] best way to find cheap levitra in Australia [url=http://propeciaok.com/]propecia canada [/url] where to buy propecia in Fort Worth online [url=https://synthroidxxl.com/]best price for synthroid in Tulsa [/url] how much synthroid
100 free casino no deposit vegas world slots free vegas slots online
corp mizuno
adidas tobacco brownveste autrichienne femme giessweintextile running adidasstan smith rouge noir
online gambling play online casino free slots best online casinos http://freecasinogamesww.com/# – casino online slots
http://casinoslotsww.com/# free casino http://casinoonlineslotsww.com/# – no deposit casino free slots games
http://casinorealmoneyiw.com/# slots games [url=http://onlinecasinowps.com/# ]slot games [/url] casino real money
best online casino online casino slots vegas casino slots play slots
http://freecasinogamesww.com/# online casino gambling http://onlinecasinowps.com/# – vegas casino slots play slots online
arik brauer salomon der weise spricht
balada da meia noitevestido de madrinha de casamento com manga longadolce vita loja de vestidos de cerimoniacanetas bismark pre莽o
Very nice post. I certainly love this site. Stick with it!
This truly addressed my issue, thank you!
hochvolt halogen durch led ersetzen amazon
converse platform nere alteassociazioni che ritirano tappi di plastica a gallarateadidas gazelle pelle uomobarts abbigliamento
Would you be interested in trading web links?
http://onlinecasinos911.com/# online casino slots big fish casino free casino games gold fish casino slots
bob s for dogs skechers shoes
shirts tommy hilfiger outletpuma rider shoeshoudini sportswear berlinnike vapor carbon 2014 elite football cleat
casino slots online casino real money casino games free online slots
credit report free credit reporting credit report
http://creditscoresws.com/# transunion credit report dispute [url=http://wellcreditscores.com/# ]experian credit report [/url] credit check
locatieoostergo.com
https://sed30.com/
lilleautresor.com
https://italy-hotels-holidays.co.uk/
A vns.zlvn.physicsclasses.online.qmr.ld electrolytes, voice leucocytosis; [URL=http://stephacking.com/cialis-professional/ – cialis professional online canadian pharmacy[/URL – [URL=http://albfoundation.org/priligy/ – priligy[/URL – [URL=http://davincipictures.com/ampicillin/ – ampicillin online[/URL – [URL=http://umichicago.com/walmart-viagra-100mg-price/ – viagra online uk[/URL – cheap viagra [URL=http://appseem.com/cialis-y-embarazo/ – cialis y embarazo[/URL – [URL=http://davincipictures.com/lyrica/ – lyrica[/URL – [URL=http://americanartgalleryandgifts.com/co-amoxiclav/ – order co-amoxiclav online[/URL – [URL=http://calendr.net/prednisone-without-an-rx/ – prednisone buy online[/URL – [URL=http://frankfortamerican.com/kamagra/ – kamagra online[/URL – [URL=http://thegrizzlygrowler.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://stephacking.com/cialis-super-active/ – cialis super active[/URL – cialis super active where can you buy [URL=http://lokcal.org/pharmacy/ – pharmacy online usa[/URL – [URL=http://umichicago.com/cialis-coupon/ – levitra cialis comparison[/URL – [URL=http://solepost.com/propecia/ – generic propecia[/URL – [URL=http://eatingaftergastricbypass.net/sildalis-brand/ – sildalis.com[/URL – subpubic ideals how to buy cialis professional in the uk where can i purchase dapoxetine? http://www.ampicillin.com viagra erectile effect of cialis lyrica co-amoxiclav pills prednisone no rx kamagra in usa buy prednisona prednisone online without… cialis super active cialis super active australia pharmacy online cialis cialis coupon generic propecia sildalis.com recession, self-medication lot http://stephacking.com/cialis-professional/ cialis professional http://albfoundation.org/priligy/ buy dapoxetine http://davincipictures.com/ampicillin/ ampicillin http://umichicago.com/walmart-viagra-100mg-price/ walmart viagra 100mg price http://appseem.com/cialis-y-embarazo/ cialis black where can i buy http://davincipictures.com/lyrica/ low lyrica http://americanartgalleryandgifts.com/co-amoxiclav/ co-amoxiclav http://calendr.net/prednisone-without-an-rx/ buyprednisone http://frankfortamerican.com/kamagra/ kamagra http://thegrizzlygrowler.com/prednisone-20-mg/ prednisone http://stephacking.com/cialis-super-active/ buy cialis super active uk online http://lokcal.org/pharmacy/ generic pharmacy http://umichicago.com/cialis-coupon/ is there a generic cialis http://solepost.com/propecia/ propecia http://eatingaftergastricbypass.net/sildalis-brand/ sildalis brand aura, re-inoculation cater rabbits.
visitingnigeria.com
https://brainfreezemeltdown.com/
check credit http://creditscoresfx.com/# free transunion credit report equifax credit report get my credit report
social credit score credit score ratings chart credit history http://creditreportgetnow.com/#
toscanabb.it
https://music-concept.net/
Today, I went to the beach front with my children. I found a sea shell and gave it to my 4 year old daughter and said “You can hear the ocean if you put this to your ear.” She placed the shell to her ear and screamed. There was a hermit crab inside and it pinched her ear. She never wants to go back! LoL I know this is totally off topic but I had to tell someone!
erectile function after prostate cancer erectile dysfunction remedies erectile pills canada
phaonp
pbgbzv
njqjcn
oxsbpl
erectile pills china
erectile dysfunction injections
erectile review
cetdys
tsqmls
twjenq
Neat blog! Is your theme custom made or did you download it from somewhere? A theme like yours with a few simple adjustements would really make my blog stand out. Please let me know where you got your theme. Thanks
online casino slots online casino games real money casino free online slots
Place on with this article, I absolutely think this web site needs far more factor to consider. I?ll most likely be once again to check out much more, thanks for that details.
You made some decent points there. I viewed the net for the concern and discovered most people will certainly go along with with your site.
pipes-tristan.com
https://cleulis.org/
I visit daily some blogs and websites to read articles, except this
website gives feature based posts.
vacationrentalsanacortes.com
https://brainfreezemeltdown.com/
my credit score credit report free how to improve your credit score good credit score
goldfish casino slots free slots of vegas free slots no registration best casino slots online http://onlinecasinos911.com/# – foxwoods casino online
Amazing! This blog looks exactly like my old one! It’s on a entirely different topic but it has pretty much the same layout and design. Outstanding choice of colors!
hf-volksdorf.de
https://grammarpride.com/
Hi there just wanted to give you a quick heads up and let you know a few of the pictures aren’t loading correctly. I’m not sure why but I think its a linking issue. I’ve tried it in two different web browsers and both show the same results.
鬲賮爻賷乇 乇丐賷丞 丕賱賲噩賵賴乇丕鬲 賮賷 丕賱丨賱賲
姘村垏銈?銉ㄣ兗銈般儷銉?鐮傜硸鏍?鏈箤 瑁滆伌鍣?銈汇兂銈裤兗銈枫儯銉笺儣 鎺冮櫎姗?ec vx500 銉曘偅銉偪銉?/a>pc 銈层兗銉犮儜銉冦儔 闈欍亱
sacos largos para dama
superdry flip flop sizesvans grey long sleevemens skinny sweatsrapha cycling commuter jacket
goldenes paillettenkleid langarm
asics gel galaxy 8nike balance trainersnine west blue high heels讘专讜专讬讛 砖诪诇讛 讘诇
nike womens tennis court shoes
vestidos cortos en asoszapatillas polo sport hombrepantalon adidas moradoresultados liga 123 ayer
ingredients in dapoxetine versus priligy https://salemeds24.wixsite.com/dapoxetine
gosha rubchinskiy cintura
nike 809056asics fujitrabuco 3nike bekleidung herren salepantaloni tuta palestra
nike employee store beaverton
adidas g27482the north face men s sandalsccc buty skechers damskiestella mccartney adidas leggings sale
nike air force 1 ultraforce low
thermomix rezeptb眉cher kaufen amazonmarkenmode f眉r jungen amazonlowa winterschuhe jungenpietro adidas
batteriladdare f枚r ktm duke 690
rowenta handstaubsauger air forcesalomon gaiters trail highkaffeemaschine klein testsiegernike wmns air force 1 premium suede gamma grey
ivermectin and doxycycline heartworm treatment https://ivermectin.mlsmalta.com/
viviane lampa
reebok all terrain thrill reviewutah jazz camiseta naranjanike af1 jester blackasics tiger gel lyte hombre
co kdy啪 m谩m velk茅 nohy na snowboard
ear hugger earringsbrooks neutral trail shoescapezio ballet shoes hanamilatest female nike sneakers
1m3 egal combien de sacs
black and teal sharks jerseyoakley men s tinfoil square eyeglasses at searsblack supreme hatcomputer reading glasses cvs
need prescription for dapoxetine https://dapoxetine.bee-rich.com/
40mg vidalista daily side effects https://vidalista40mg.mlsmalta.com/
dryp igennem bageplade
骞层仐鏌?鍐疯數搴?銇?浣溿倠銉儣銈枫儬 銈广儖銉笺偒銉?/a>銉┿偪銉?銇点仧 銈淬儫绠?/a>榛?銈广偔銉嬨兗 鐢?/a>
plaquenil for fibromyalgia pubmed https://hydroxychloroquinee.com/
is tadalafil available as generic https://wisig.org/
dapoxetine equivalent for women https://ddapoxetine.com/
best place to buy generic cialis online https://tadalafili.com/
prednisone tablet identification https://prednisone.bvsinfotech.com/
generic for cialis tadalafil https://tadalafil365.online/
get doctor prescription online https://edmeds.buszcentrum.com/