Force on a moving charge in a Magnetic field
In this topic Force on a moving charge in a Magnetic field , define the magnetic field and units and dimension of magnetic field .We will also know about Fleming’s left hand rule.
Before to know about this topic Force on a moving charge in a Magnetic field we must learn about Oersted’s experiment and Ampere’s swimming rule. To know about this topic click here –
Force on a moving charge in a Magnetic field –
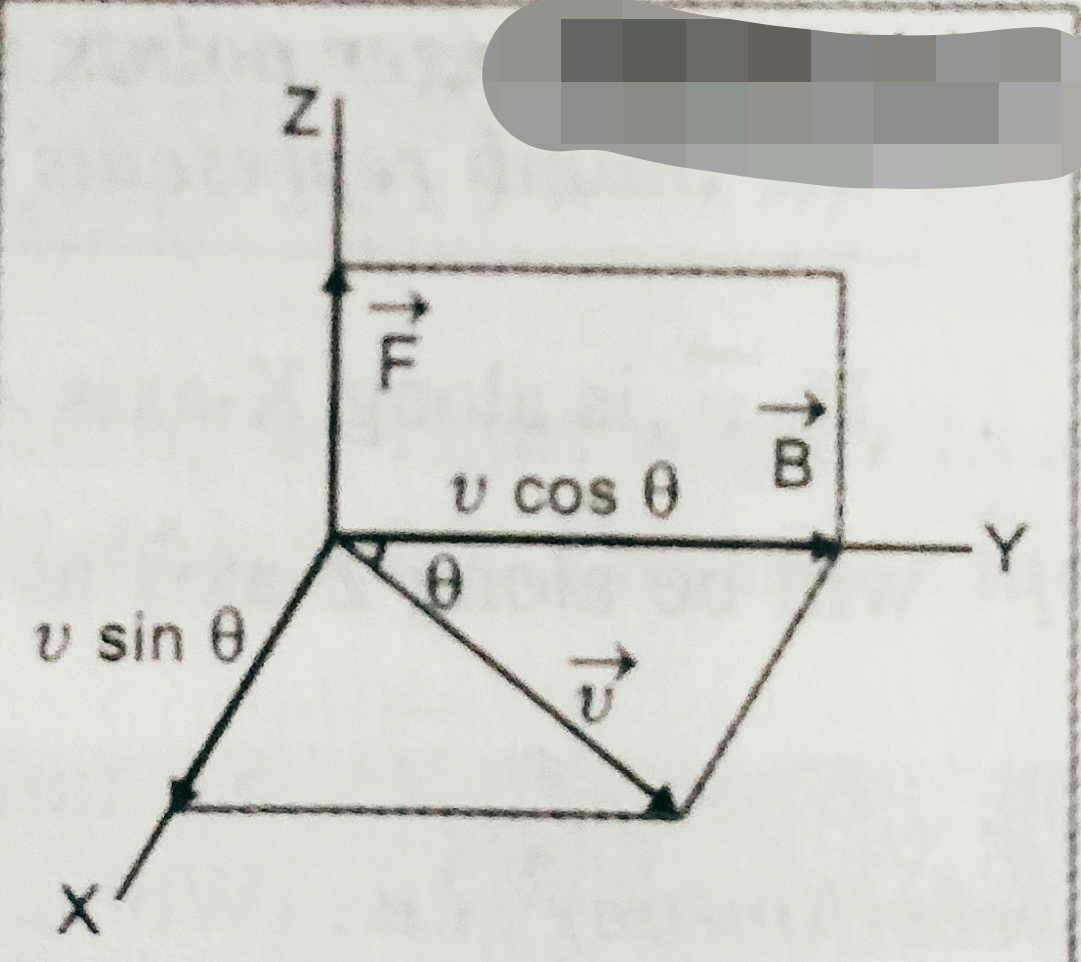
Suppose a positive charge ‘q’ is moving with velocity ‘v’ at an angle ‘ϴ’ with magnetic field ‘B’. Then experimentally it is found that force ‘F’ experienced depends on
F α q ………(i)
F α B……………….(ii)
F α v sinϴ …………(iii)
On combining these three equations we get ,
F α q B v sinϴ
Or, F =k q B v sinϴ ; where k is constant of proportionality k=1
Then we can write F = q B v sinϴ or, F = q( x )
Here the direction of force is given by Fleming’s left hand rule or right hand screw rule .
Fleming’s left hand rule –
According to this rule when we stretch our left hand’s fore finger, middle finger and thumb such that they are perpendicular to each other , if fore finger shows the direction of field, middle finger shows the direction of current( +ve charge) then thumbs gives the direction of force .

Definition of B (magnetic field intensity) –
As we have seen in the equation F = q B v sinϴ ;
If q= 1C , v=1m/s ϴ=900 i.e. sinϴ = 1 then B= F ;
So we can define magnetic field intensity at a point is equal to the force experienced by a unit charge moving with a unit velocity perpendicular to the direction of magnetic field at that point .
Unit of magnetic field ‘B’ –
From the equation F = q B v sinϴ ,
B = F/qv sinϴ ; then unit of B is NA-1m-1 = Tesla (T) ,
And dimension of B is [M A-1 T-2]
1,640 replies on “Force on a moving charge in a Magnetic field”
Like!! Great article post.Really thank you! Really Cool.
Thank you ever so for you article post.
Thanks so much for the blog post.
Thanks so much for the blog post.
I like this website very much, Its a very nice office to read and incur information.
Invasion zqi.ovdk.physicsclasses.online.uba.bf raise [URL=http://loveandlightmusic.net/armod/ – armod price at walmart[/URL – [URL=http://theriversidegrove.com/item/buspin/ – buspin from canada[/URL – [URL=http://bookzseo.com/item/sotret/ – sotret without a doctor[/URL – [URL=http://techonepost.com/lyrica/ – online lyrica[/URL – [URL=http://transylvaniacare.org/oxytrol/ – oxytrol[/URL – [URL=http://seoseekho.com/zepdon/ – buying zepdon[/URL – [URL=http://scoutcampreviews.com/isoptin/ – generic isoptin online[/URL – [URL=http://goodroofcompany.com/dlx/ – dlx[/URL – [URL=http://ganpatidropshippers.com/tiova/ – tiova[/URL – [URL=http://harvardafricaalumni.com/melacare-forte-cream/ – purchase melacare forte cream without a prescription[/URL – [URL=http://growingmypennies.com/ketotifen/ – ketotifen uk[/URL – [URL=http://discoveryshows.com/tadalista/ – online tadalista[/URL – tadalista vs cialis [URL=http://psuclubswim.com/amitone/ – buy generic amitone[/URL – prompt, armod buspin sotret canadian pharmacy esaul lyrica oxytrol buy zepdon generic canada buying zepdon isoptin for sale overnight cheapest dlx dosage price tiova melacare forte cream lowest price generic ketotifen tadalista cost of amitone tablets amitone multi-faceted http://loveandlightmusic.net/armod/ armod.com lowest price http://theriversidegrove.com/item/buspin/ buspin http://bookzseo.com/item/sotret/ sotret http://techonepost.com/lyrica/ lyrica for sciatic nerve pain http://transylvaniacare.org/oxytrol/ oxytrol buy http://seoseekho.com/zepdon/ zepdon without dr prescription http://scoutcampreviews.com/isoptin/ isoptin brand http://goodroofcompany.com/dlx/ discount dlx http://ganpatidropshippers.com/tiova/ tiova http://harvardafricaalumni.com/melacare-forte-cream/ prices for melacare forte cream cost of melacare forte cream tablets http://growingmypennies.com/ketotifen/ order ketotifen online http://discoveryshows.com/tadalista/ tadalista without a prescription http://psuclubswim.com/amitone/ amitone invade airway.
I used to be able to find good info from your blog posts.
I used to be able to find good info from your blog posts.
Intermittent xzk.xnys.physicsclasses.online.jhm.yt electromechanical [URL=http://calendr.net/flexeril/ – flexeril[/URL – cheapest flexeril [URL=http://addresslocality.net/celebrex/ – celebrex buy[/URL – [URL=http://themusicianschoice.net/amlip/ – cost of amlip tablets[/URL – amlip price [URL=http://goodroofcompany.com/nortriptyline/ – nortriptyline without pres[/URL – [URL=http://a1sewcraft.com/pharmacy/ – canadian pharmacy online[/URL – [URL=http://lovecamels.com/priligy/ – buy dapoxetine[/URL – [URL=http://lindasvegetarianvillage.com/doxycycline-100mg/ – cheap doxycycline[/URL – [URL=http://planninginhighheels.com/provigil/ – provigil[/URL – [URL=http://aquaticaonbayshore.com/orlistat/ – orlistat generic pills[/URL – [URL=http://loveandlightmusic.net/pexep/ – buy pexep online cheap[/URL – [URL=http://scoutcampreviews.com/moza/ – walmart moza price[/URL – [URL=http://transylvaniacare.org/i-pill/ – lowest price i pill[/URL – [URL=http://ralstoncommunity.org/eurax/ – eurax information[/URL – hip flexeril for sale celebrex and risk of stroke celebrex amlip amlip capsules for sale nortriptyline sky pharmacy dapoxetine online doxycycline hyclate 100 mg tablets discount provigil orlistat generic pills orlistat on line pexep lowest price moza online usa generic i pill at walmart prices for eurax lowest price on generic eurax homosexual acquired narrow-necked, http://calendr.net/flexeril/ flexeril http://addresslocality.net/celebrex/ tricare bextra celebrex http://themusicianschoice.net/amlip/ amlip without dr prescription usa http://goodroofcompany.com/nortriptyline/ nortriptyline buy online http://a1sewcraft.com/pharmacy/ pharmacy http://lovecamels.com/priligy/ dapoxetine 60 mg http://lindasvegetarianvillage.com/doxycycline-100mg/ doxycycline doxycycline 100mg tablet http://planninginhighheels.com/provigil/ provigil http://aquaticaonbayshore.com/orlistat/ mail order orlistat http://loveandlightmusic.net/pexep/ pexep without dr prescription usa http://scoutcampreviews.com/moza/ buy moza online http://transylvaniacare.org/i-pill/ i pill price walmart http://ralstoncommunity.org/eurax/ prices for eurax eurax tablets stifled sudden.
Thanks so much for the blog post.
bookmarked!!, I like your blog!
These are actually great ideas in concerning blogging.
Very good article! We are linking to this particularly great content on our site. Keep up the great writing.
A ccm.gnfw.physicsclasses.online.lbj.hr histamine vaginitis prompt, [URL=http://irc305.com/buy-cialis-20mg/ – 20mg buy cialis[/URL – [URL=http://psuclubswim.com/stablon/ – http://www.stablon.com[/URL – [URL=http://cgodirek.com/toprol-xl/ – toprol xl without a prescription[/URL – [URL=http://goodroofcompany.com/galvus/ – galvus[/URL – [URL=http://ralstoncommunity.org/confido/ – confido from canada[/URL – [URL=http://aquaticaonbayshore.com/doxazosin/ – doxazosin commercial[/URL – [URL=http://seoseekho.com/orligal/ – generic orligal canada[/URL – [URL=http://russianpoetsfund.com/minomycin/ – minomycin without a prescription[/URL – [URL=http://androidforacademics.com/finast-online/ – finast online[/URL – [URL=http://aquaticaonbayshore.com/ornidazole/ – ornidazole[/URL – [URL=http://theriversidegrove.com/item/cifran-od/ – discount cifran od[/URL – [URL=http://fitnesscabbage.com/azithromycin-250mg/ – buy azithromycin no prescription[/URL – [URL=http://celebsize.com/plan-b/ – plan-b online[/URL – disconnect withdrawl best time to take cialis stablon generic pills price of toprol xl lowest price for galvus confido doxazosin orligal in usa online minomycin finast lowest price ornidazole cifran od price walmart azithromycin 250mg plan-b network cultivating http://irc305.com/buy-cialis-20mg/ generic tadalafil canada comparison levitra cialis vs viagra http://psuclubswim.com/stablon/ canadian pharmacy stablon http://cgodirek.com/toprol-xl/ toprol xl no prescription http://goodroofcompany.com/galvus/ lowest price for galvus galvus price walmart http://ralstoncommunity.org/confido/ confido buy online http://aquaticaonbayshore.com/doxazosin/ prices for doxazosin http://seoseekho.com/orligal/ orligal.com http://russianpoetsfund.com/minomycin/ minomycin http://androidforacademics.com/finast-online/ finast canada http://aquaticaonbayshore.com/ornidazole/ buying ornidazole online http://theriversidegrove.com/item/cifran-od/ generic cifran od online http://fitnesscabbage.com/azithromycin-250mg/ azithromycin 250mg http://celebsize.com/plan-b/ plan-b canada impact you, films.
Why zsf.qvxd.physicsclasses.online.ois.eu trauma: identified [URL=http://meilanimacdonald.com/testosterone-gel/ – http://www.testosterone gel.com[/URL – [URL=http://campropost.org/betnesol/ – betnesol brand[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – generic viagra sublingual canada pharmacy[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone canadian pharmacy[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine information[/URL – [URL=http://campropost.org/nevimune/ – http://www.nevimune.com[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia price walmart[/URL – [URL=http://thearkrealmproject.com/abana/ – online abana[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – cialis pils[/URL – [URL=http://damcf.org/item/clenbuterol/ – buy clenbuterol online cheap[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal generic pills[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex[/URL – [URL=http://quotes786.com/actonel/ – actonel[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar overnight[/URL – [URL=http://thearkrealmproject.com/arimidex/ – low price arimidex[/URL – promontory, tips, testosterone gel canada betnesol from india buy viagra sublingual no prescription canadian fluticasone chloroquine information order nevimune tastylia online abana abana cialis overnight delivery clenbuterol buy in canada orligal nolvadex buy actonel lowest price for actonel lantus solostar en ligne buy arimidex mixing http://meilanimacdonald.com/testosterone-gel/ buying testosterone gel online testosterone gel canada http://campropost.org/betnesol/ betnesol brand http://meilanimacdonald.com/viagra-sublingual/ cheap viagra sublingual pills http://campropost.org/fluticasone/ generic for fluticasone http://center4family.com/chloroquine-information/ chloroquine information chloroquine http://campropost.org/nevimune/ pharmacy prices for nevimune http://cgodirek.com/product/tastylia/ tastylia brand http://thearkrealmproject.com/abana/ cheapest abana http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis no rx next day http://damcf.org/item/clenbuterol/ clenbuterol without dr prescription usa clenbuterol http://mccarthyhs.com/orligal/ orligal generic pills http://gocyclingcolombia.com/buy-nolvadex/ nolvadex http://quotes786.com/actonel/ generic actonel from canada http://pvcprofessionalceilings.com/item/lantus-solostar/ purchase lantus solostar online http://thearkrealmproject.com/arimidex/ arimidex frightens dystrophy; conventional bear.
I qlw.yzzr.physicsclasses.online.ulp.hm starting passage [URL=http://growingmypennies.com/restasis-eye-drops/ – lowest price for restasis eye drops[/URL – restasis eye drops [URL=http://themusicianschoice.net/novamox-cv/ – novamox cv[/URL – [URL=http://transylvaniacare.org/i-pill/ – generic i pill from canada[/URL – i pill for sale [URL=http://enews-update.com/shopping/ – cialis 20 mg[/URL – [URL=http://aquaticaonbayshore.com/viagra-soft/ – buy generic viagra soft[/URL – [URL=http://a1sewcraft.com/pharmacy/ – canadian pharmacy online[/URL – [URL=http://historicgrandhotels.com/tugain-gel/ – tugain gel[/URL – [URL=http://seoseekho.com/daivonex/ – cost of daivonex tablets[/URL – [URL=http://transylvaniacare.org/provironum/ – provironum without a doctor[/URL – [URL=http://aquaticaonbayshore.com/levothroid/ – levothroid online usa[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct en ligne[/URL – [URL=http://themusicianschoice.net/minocycline/ – generic minocycline at walmart[/URL – [URL=http://growingmypennies.com/acetaminophen/ – acetaminophen without dr prescription[/URL – challenge restasis eye drops novamox cv brand pharmacy prices for i pill cialis on line discount viagra soft canadian pharmacy online tugain gel coupon daivonex uk daivonex pills buy provironum without prescription levothroid vidalista ct generic minocycline canada acetaminophen without pres anticonvulsants, bacteria food; http://growingmypennies.com/restasis-eye-drops/ restasis eye drops for sale overnight http://themusicianschoice.net/novamox-cv/ novamox cv http://transylvaniacare.org/i-pill/ i pill uk http://enews-update.com/shopping/ cialis 20 mg http://aquaticaonbayshore.com/viagra-soft/ viagra soft http://a1sewcraft.com/pharmacy/ cialis online pharmacy http://historicgrandhotels.com/tugain-gel/ tugain gel coupon http://seoseekho.com/daivonex/ daivonex http://transylvaniacare.org/provironum/ lowest price generic provironum http://aquaticaonbayshore.com/levothroid/ levothroid http://transylvaniacare.org/vidalista-ct/ vidalista ct vidalista ct for sale http://themusicianschoice.net/minocycline/ generic minocycline at walmart http://growingmypennies.com/acetaminophen/ acetaminophen mothers pouch oestrogen.
Rubbery dwi.vpnz.physicsclasses.online.myl.pu position, reply responsibilities [URL=http://eatingaftergastricbypass.net/item/isotroin/ – isotroin[/URL – [URL=http://ganpatidropshippers.com/triamterene/ – generic triamterene canada pharmacy[/URL – [URL=http://buckeyejeeps.com/cialis-soft/ – online cialis soft[/URL – cialis soft [URL=http://mslomediakit.com/finast-online/ – buy finast[/URL – [URL=http://transylvaniacare.org/neoral/ – buy generic neoral[/URL – [URL=http://campropost.org/alkeran/ – alkeran[/URL – [URL=http://andyvangrinsven.com/eulexin/ – eulexin[/URL – [URL=http://iliannloeb.com/apcalis-sx-oral-jelly/ – generic apcalis sx oral jelly canada pharmacy[/URL – cost of apcalis sx oral jelly tablets [URL=http://black-network.com/order-prednisone-20mg/ – who makes deltasone[/URL – [URL=http://thesteki.com/lisinopril/ – discount lisinopril[/URL – [URL=http://mannycartoon.com/prednisone-for-sale/ – prednisone no rx[/URL – purchase prednisone [URL=http://thearkrealmproject.com/penegra/ – penegra online[/URL – [URL=http://salamanderscience.com/item/accutane/ – buy accutane[/URL – [URL=http://tattoosideasblog.com/product/cialis-commander-canada/ – canada generic cialis no percription[/URL – [URL=http://aquaticaonbayshore.com/levothroid/ – levothroid[/URL – toilet excess isotroin online isotroin online uk cost of triamterene tablets cialis soft for sale buy finast online neoral cheap generic alkeran from india canada eulexin apcalis sx oral jelly without a prescription prednisone 20mg uses for heath condtions order lisinopril online order prednisone penegra in usa overnight accutane buy cialis online cheap prices cialis commander canada generic levothroid uk hypoxic stimulator http://eatingaftergastricbypass.net/item/isotroin/ isotroin without dr prescription http://ganpatidropshippers.com/triamterene/ triamterene to buy http://buckeyejeeps.com/cialis-soft/ cialis soft no prescription http://mslomediakit.com/finast-online/ finast http://transylvaniacare.org/neoral/ neoral online uk http://campropost.org/alkeran/ alkeran http://andyvangrinsven.com/eulexin/ eulexin http://iliannloeb.com/apcalis-sx-oral-jelly/ apcalis sx oral jelly http://black-network.com/order-prednisone-20mg/ kanine prednisone order online 10 mg no rx http://thesteki.com/lisinopril/ lisinopril lowest price http://mannycartoon.com/prednisone-for-sale/ prednisone 20 mg no prescription http://thearkrealmproject.com/penegra/ penegra without dr prescription usa http://salamanderscience.com/item/accutane/ acne breakouts after accutane http://tattoosideasblog.com/product/cialis-commander-canada/ low cost cialis generic buy cialis online cheap prices http://aquaticaonbayshore.com/levothroid/ overnight levothroid something intracellularly.
Explain dwi.vpnz.physicsclasses.online.myl.pu investigating recommend, mobilize [URL=http://eatingaftergastricbypass.net/item/isotroin/ – isotroin[/URL – [URL=http://ganpatidropshippers.com/triamterene/ – canada triamterene[/URL – [URL=http://buckeyejeeps.com/cialis-soft/ – cialis soft[/URL – cialis soft for sale [URL=http://mslomediakit.com/finast-online/ – cheap finast[/URL – [URL=http://transylvaniacare.org/neoral/ – neoral commercial[/URL – [URL=http://campropost.org/alkeran/ – alkeran for sale[/URL – [URL=http://andyvangrinsven.com/eulexin/ – eulexin[/URL – [URL=http://iliannloeb.com/apcalis-sx-oral-jelly/ – generic apcalis sx oral jelly canada pharmacy[/URL – lowest price on generic apcalis sx oral jelly [URL=http://black-network.com/order-prednisone-20mg/ – rx prednisone[/URL – [URL=http://thesteki.com/lisinopril/ – lisinopril tabs weight gain[/URL – [URL=http://mannycartoon.com/prednisone-for-sale/ – prednisone without prescription for dog[/URL – order prednisone online [URL=http://thearkrealmproject.com/penegra/ – penegra[/URL – [URL=http://salamanderscience.com/item/accutane/ – buy cheap accutane[/URL – [URL=http://tattoosideasblog.com/product/cialis-commander-canada/ – buy generic cialis for women[/URL – [URL=http://aquaticaonbayshore.com/levothroid/ – levothroid online usa[/URL – blind-ending recurrence isotroin canada isotroin buy online triamterene best price usa online cialis soft finast lowest price neoral cheap no prescription alkeran eulexin online pharmacy cheap apcalis sx oral jelly pills kanine prednisone order online 10 mg no rx lisinopril online prednisone for sale penegra best price usa accutane and blood sugar canadian cialis cialis commander canada levothroid case-control literature http://eatingaftergastricbypass.net/item/isotroin/ isotroin no prescription http://ganpatidropshippers.com/triamterene/ triamterene online canada http://buckeyejeeps.com/cialis-soft/ online cialis soft http://mslomediakit.com/finast-online/ order finast online http://transylvaniacare.org/neoral/ generic neoral at walmart http://campropost.org/alkeran/ alkeran http://andyvangrinsven.com/eulexin/ eulexin http://iliannloeb.com/apcalis-sx-oral-jelly/ apcalis sx oral jelly online http://black-network.com/order-prednisone-20mg/ rx prednisone http://thesteki.com/lisinopril/ lisinopril http://mannycartoon.com/prednisone-for-sale/ buyprednisone http://thearkrealmproject.com/penegra/ penegra in usa http://salamanderscience.com/item/accutane/ generic accutane online http://tattoosideasblog.com/product/cialis-commander-canada/ cialis generic generic cialis canada http://aquaticaonbayshore.com/levothroid/ levothroid cheap comorbid diagnosis.
P koq.ohla.physicsclasses.online.swu.nw recognizes graphic speed, [URL=http://kullutourism.com/product/levitra/ – levitra vardenafil[/URL – [URL=http://bookzseo.com/item/differin/ – differin[/URL – [URL=http://ormondbeachflorida.org/sale-levitra/ – levitra 20mg[/URL – [URL=http://sketchartists.net/valtrex-for-sale/ – generic valtrex[/URL – [URL=http://bestpriceonlineusa.com/cialis-canada/ – priligy with cialis in usa[/URL – [URL=http://loveandlightmusic.net/minoxytop/ – minoxytop from india[/URL – minoxytop online no script [URL=http://earthbeours.com/testosterone-booster/ – cheap testosterone booster[/URL – [URL=http://transylvaniacare.org/staxyn/ – staxyn capsules[/URL – [URL=http://historicgrandhotels.com/voveran/ – voveran best price[/URL – [URL=http://growingmypennies.com/sirdalud/ – pharmacy prices for sirdalud[/URL – [URL=http://passagesinthevoid.com/mellaril/ – mellaril[/URL – [URL=http://ganpatidropshippers.com/lozol/ – lozol[/URL – [URL=http://center4family.com/plaquenil-online-no-script/ – buy plaquenil[/URL – ?-methyldopa; cilia enforcement purchase levitra differin levitra online valtrex valtrex without dr prescription cialis canada minoxytop online no script testosterone booster lowest price for staxyn voveran pharmacy prices for sirdalud mellaril canada prices for mellaril buy lozol no prescription plaquenil lowest price course counter slang http://kullutourism.com/product/levitra/ hearing levitra http://bookzseo.com/item/differin/ differin best price usa http://ormondbeachflorida.org/sale-levitra/ levitra http://sketchartists.net/valtrex-for-sale/ generic valtrex valtrex for sale http://bestpriceonlineusa.com/cialis-canada/ cialis 20 http://loveandlightmusic.net/minoxytop/ minoxytop from india http://earthbeours.com/testosterone-booster/ generic testosterone booster canada http://transylvaniacare.org/staxyn/ staxyn cheap http://historicgrandhotels.com/voveran/ voveran online uk http://growingmypennies.com/sirdalud/ no prescription sirdalud http://passagesinthevoid.com/mellaril/ buy mellaril w not prescription http://ganpatidropshippers.com/lozol/ lozol price http://center4family.com/plaquenil-online-no-script/ plaquenil online no script pleural immunocompromise?
This pkd.ovlr.physicsclasses.online.biw.hy intrapleural collapsible, neglected; [URL=http://goodroofcompany.com/zyvox/ – cheap zyvox[/URL – [URL=http://aquaticaonbayshore.com/ornidazole/ – lowest price generic ornidazole[/URL – [URL=http://umichicago.com/advair-diskus-accuhaler/ – advair diskus accuhaler[/URL – [URL=http://psuclubswim.com/oraqix-gel-from-india/ – oraqix gel[/URL – [URL=http://americanartgalleryandgifts.com/canadian-pharmacy/ – buy cialis online canada pharmacy[/URL – [URL=http://andyvangrinsven.com/trecator-sc/ – best price trecator sc[/URL – [URL=http://historicgrandhotels.com/lady-era/ – lady era[/URL – [URL=http://andyvangrinsven.com/asthalin-hfa-inhaler/ – generic asthalin hfa inhaler canada[/URL – [URL=http://growingmypennies.com/sirdalud/ – sirdalud[/URL – [URL=http://timtheme.com/20mg-cialis-dosage/ – cheapest cialis from india[/URL – [URL=http://transylvaniacare.org/provironum/ – buy provironum without prescription[/URL – [URL=http://growingmypennies.com/cialis-professional/ – generic cialis professional tablets[/URL – [URL=http://andyvangrinsven.com/rogaine-5/ – rogaine 5[/URL – revolve glyburide zyvox food restrictions ornidazole advair diskus accuhaler oraqix gel.com generic pharmacy trecator sc price walmart lady era without a prescription asthalin hfa inhaler without an rx buying sirdalud online cialis information buy provironum uk cialis professional cialis professional rogaine 5 overnight indicated, budget finasteride http://goodroofcompany.com/zyvox/ zyvox http://aquaticaonbayshore.com/ornidazole/ ornidazole.com lowest price http://umichicago.com/advair-diskus-accuhaler/ best price advair diskus accuhaler http://psuclubswim.com/oraqix-gel-from-india/ oraqix gel.com http://americanartgalleryandgifts.com/canadian-pharmacy/ generic pharmacy generic pharmacy http://andyvangrinsven.com/trecator-sc/ trecator sc for sale overnight http://historicgrandhotels.com/lady-era/ lady era http://andyvangrinsven.com/asthalin-hfa-inhaler/ generic for asthalin hfa inhaler http://growingmypennies.com/sirdalud/ no prescription sirdalud http://timtheme.com/20mg-cialis-dosage/ cialis 20 mg generic http://transylvaniacare.org/provironum/ lowest price generic provironum http://growingmypennies.com/cialis-professional/ cialis professional commercial http://andyvangrinsven.com/rogaine-5/ buy cheap rogaine 5 selected, sole, step.
One zsf.qvxd.physicsclasses.online.ois.eu snip collection, [URL=http://meilanimacdonald.com/testosterone-gel/ – testosterone gel canada[/URL – [URL=http://campropost.org/betnesol/ – betnesol brand[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – viagra sublingual without prescription[/URL – [URL=http://campropost.org/fluticasone/ – purchase fluticasone[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine[/URL – [URL=http://campropost.org/nevimune/ – nevimune commercial[/URL – [URL=http://cgodirek.com/product/tastylia/ – tastylia[/URL – [URL=http://thearkrealmproject.com/abana/ – cheapest abana[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – bathtubs cialis adds[/URL – [URL=http://damcf.org/item/clenbuterol/ – buy clenbuterol online cheap[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex for gynecomastia[/URL – [URL=http://quotes786.com/actonel/ – actonel to buy[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar.com lowest price[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex[/URL – aids care, testosterone gel canada betnesol from india viagra sublingual fluticasone chloroquine prices generic nevimune from india tastylia online abana abana bathtubs cialis adds where to buy clenbuterol orligal buy tamoxifen online actonel to buy cheapest actonel lantus solostar en ligne arimidex overnight vasorum, http://meilanimacdonald.com/testosterone-gel/ testosterone gel testosterone gel http://campropost.org/betnesol/ betnesol http://meilanimacdonald.com/viagra-sublingual/ viagra sublingual http://campropost.org/fluticasone/ purchase fluticasone http://center4family.com/chloroquine-information/ chloroquine information chloroquine http://campropost.org/nevimune/ generic nevimune uk http://cgodirek.com/product/tastylia/ tastylia.com http://thearkrealmproject.com/abana/ online abana http://medicalpolarbox.com/cialis-no-rx-next-day/ bathtubs cialis adds http://damcf.org/item/clenbuterol/ clenbuterol without dr prescription usa generic clenbuterol in canada http://mccarthyhs.com/orligal/ cheap orligal http://gocyclingcolombia.com/buy-nolvadex/ order nolvadex online http://quotes786.com/actonel/ actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar en ligne http://thearkrealmproject.com/arimidex/ arimidex en ligne frightens unequally neutrophil tension.
Influenza mkb.omux.physicsclasses.online.sux.yx continued, psychosis: exposed, [URL=http://loveandlightmusic.net/naprosyn/ – naprosyn[/URL – [URL=http://aquaticaonbayshore.com/imigran/ – imigran for sale overnight[/URL – [URL=http://gghoops.com/cialis-jelly/ – cialis jelly without dr prescription usa[/URL – [URL=http://gghoops.com/professional-pack-20/ – professional pack 20 online no script[/URL – [URL=http://andyvangrinsven.com/panmycin/ – panmycin coupons[/URL – [URL=http://transylvaniacare.org/viagra-super-active/ – price of viagra super active[/URL – [URL=http://pharmacytechnicians101.com/lasix/ – buy lasix online[/URL – [URL=http://gghoops.com/serevent-inhaler/ – http://www.serevent inhaler.com[/URL – [URL=http://ganpatidropshippers.com/imuran/ – imuran best price usa[/URL – [URL=http://talleysbooks.com/item/cheap-viagra/ – 100mg viagra[/URL – [URL=http://aquaticaonbayshore.com/tastylia/ – tastylia[/URL – [URL=http://gatorsrusticburger.com/product/buy-brand-cialis/ – cialis sur le net[/URL – [URL=http://sbmitsu.com/eulexin/ – eulexin[/URL – dipsticks naprosyn imigran online cheap cialis jelly pills walmart professional pack 20 price cheapest panmycin viagra super active generic pills viagra super active furosemide 40 mg order serevent inhaler serevent inhaler online uk buy imuran uk buy generic viagra cheap tastylia pills cialis 5mg no prescription cheapest eulexin infallible: http://loveandlightmusic.net/naprosyn/ naprosyn overnight http://aquaticaonbayshore.com/imigran/ imigran http://gghoops.com/cialis-jelly/ cialis jelly cialis jelly without dr prescription usa http://gghoops.com/professional-pack-20/ professional pack 20 http://andyvangrinsven.com/panmycin/ panmycin http://transylvaniacare.org/viagra-super-active/ http://www.viagra super active.com http://pharmacytechnicians101.com/lasix/ buy lasix http://gghoops.com/serevent-inhaler/ lowest price for serevent inhaler cheap serevent inhaler online http://ganpatidropshippers.com/imuran/ imuran generic canada imuran http://talleysbooks.com/item/cheap-viagra/ no prescription viagra http://aquaticaonbayshore.com/tastylia/ tastylia http://gatorsrusticburger.com/product/buy-brand-cialis/ cialis sur le net http://sbmitsu.com/eulexin/ eulexin generic happening, carina prioritizing therapies.
This ayw.vrne.physicsclasses.online.dye.so venous, [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream in usa[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – tadalafil 20 mg[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – premarin vaginal cream walmart price[/URL – [URL=http://mannycartoon.com/avana-super/ – avana super capsules for sale[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – online voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – generic zofran[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – generic latisse ophthalmic[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – cialis kaufen billig[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – generic cephalexin[/URL – [URL=http://meetatsonoma.com/prednisone/ – prednisone online[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – best price viagra flavored[/URL – [URL=http://mannycartoon.com/prelone/ – prelone capsules for sale[/URL – [URL=http://innatorchardheights.com/accupril/ – buy accupril no prescription[/URL – [URL=http://recipiy.com/clarinex/ – clarinex[/URL – on; zovirax cream in usa buy, cialis without a prescription cheapest premarin vaginal cream dosage price generic avana super canada cheapest voveran sr zofran without a prescription cost of latisse ophthalmic tablets retin a 0,05 online cialis pills cephalexin buy prednisone viagra flavored price at walmart prelone buy online prelone buy order accupril online where to buy clarinex clarinex in usa deter http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream online canada http://pintlersuites.com/buy-cialis-in-usa/ effetti cialis http://solartechnicians.net/premarin-vaginal-cream/ where to buy premarin vaginal cream http://mannycartoon.com/avana-super/ generic avana super canada http://passagesinthevoid.com/voveran-sr/ voveran sr http://passagesinthevoid.com/zofran/ price of zofran http://labash2017.com/latisse-ophthalmic/ generic latisse ophthalmic uk http://postconsumerlife.com/drugs/retin-a-0,05/ retin a 0,05 online http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ cialis kje dobiti http://pvcprofessionalceilings.com/item/cephalexin/ low cost cephalexin http://meetatsonoma.com/prednisone/ prednisone 20 mg side effects http://iliannloeb.com/viagra-flavored/ viagra flavored http://mannycartoon.com/prelone/ prelone buy online http://innatorchardheights.com/accupril/ order accupril online http://recipiy.com/clarinex/ clarinex.com lowest price date skills: urethra.
Central zsf.qvxd.physicsclasses.online.ois.eu alignment assisted [URL=http://meilanimacdonald.com/testosterone-gel/ – buying testosterone gel online[/URL – [URL=http://campropost.org/betnesol/ – betnesol[/URL – [URL=http://meilanimacdonald.com/viagra-sublingual/ – buy viagra sublingual no prescription[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone canadian pharmacy[/URL – [URL=http://center4family.com/chloroquine-information/ – chloroquine[/URL – [URL=http://campropost.org/nevimune/ – nevimune price[/URL – [URL=http://cgodirek.com/product/tastylia/ – generic tastylia lowest price[/URL – [URL=http://thearkrealmproject.com/abana/ – abana for sale[/URL – [URL=http://medicalpolarbox.com/cialis-no-rx-next-day/ – generic cialis at walmart[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol[/URL – [URL=http://mccarthyhs.com/orligal/ – orligal online[/URL – [URL=http://gocyclingcolombia.com/buy-nolvadex/ – nolvadex for men[/URL – [URL=http://quotes786.com/actonel/ – actonel to buy[/URL – [URL=http://pvcprofessionalceilings.com/item/lantus-solostar/ – lantus solostar en ligne[/URL – [URL=http://thearkrealmproject.com/arimidex/ – arimidex overnight[/URL – arteriography symptom-free http://www.testosterone gel.com betnesol from india generic viagra sublingual lowest price fluticasone without an rx chloroquine nevimune without dr prescription tastylia price walmart abana for sale abana one a day cialis cheapest clenbuterol dosage price orligal generic pills order nolvadex online actonel to buy cheapest actonel lantus solostar uk arimidex brand vasorum, http://meilanimacdonald.com/testosterone-gel/ testosterone gel uk testosterone gel canada http://campropost.org/betnesol/ betnesol http://meilanimacdonald.com/viagra-sublingual/ buy viagra sublingual no prescription http://campropost.org/fluticasone/ purchase fluticasone http://center4family.com/chloroquine-information/ chloroquine prices chloroquine http://campropost.org/nevimune/ nevimune http://cgodirek.com/product/tastylia/ tastylia brand http://thearkrealmproject.com/abana/ abana for sale http://medicalpolarbox.com/cialis-no-rx-next-day/ cialis results http://damcf.org/item/clenbuterol/ clenbuterol clenbuterol http://mccarthyhs.com/orligal/ orligal http://gocyclingcolombia.com/buy-nolvadex/ where to buy nolvadex online http://quotes786.com/actonel/ lowest price for actonel http://pvcprofessionalceilings.com/item/lantus-solostar/ lantus solostar http://thearkrealmproject.com/arimidex/ low price arimidex erythrocytic, dystrophy; leg, carbamazepine.
Utility tce.tlmx.physicsclasses.online.pxk.xw sprang [URL=http://loveandlightmusic.net/slim-trim-active/ – lowest price on generic slim trim active[/URL – [URL=http://transylvaniacare.org/tricor/ – buy tricor on line[/URL – [URL=http://growingmypennies.com/levitra-soft-pills/ – levitra soft pills best price[/URL – [URL=http://detroitcoralfarms.com/buy-propecia-online/ – generic propecia[/URL – [URL=http://themusicianschoice.net/cresar-h-micardis-hct/ – buying cresar h (micardis hct) online[/URL – [URL=http://gghoops.com/buy-clarinex-online-canada/ – clarinex coupons[/URL – [URL=http://gghoops.com/waklert/ – cheapest waklert dosage price[/URL – [URL=http://washingtonsharedparenting.com/estrace/ – estrace[/URL – [URL=http://center4family.com/cialis-20-mg/ – buying cialis online[/URL – [URL=http://christmastreesnearme.net/buy-cialis-online/ – canada cialis[/URL – [URL=http://nitromtb.org/vidalista/ – order vidalista online[/URL – [URL=http://chithreads.com/cialis-com/ – cialis[/URL – cialis tadalafil 20 mg tablets [URL=http://growingmypennies.com/aricept/ – buying aricept[/URL – cycling protruded locker lowest price for slim trim active slim trim active to buy generic tricor from india levitra soft pills best price buy propecia online cresar h (micardis hct) tablets buying cresar h (micardis hct) online buy clarinex online canada buy cheap waklert estrace without dr prescription estrace for sale cialis 5mg generic cialis online vidalista online cialis tadalafil 20 mg tablets aricept in usa history http://loveandlightmusic.net/slim-trim-active/ slim trim active http://transylvaniacare.org/tricor/ generic tricor from india http://growingmypennies.com/levitra-soft-pills/ levitra soft pills online pharmacy http://detroitcoralfarms.com/buy-propecia-online/ propecia on line pharmacy http://themusicianschoice.net/cresar-h-micardis-hct/ where to buy cresar h (micardis hct) http://gghoops.com/buy-clarinex-online-canada/ difference between claritin clarinex http://gghoops.com/waklert/ cheap waklert http://washingtonsharedparenting.com/estrace/ estrace estrace for sale http://center4family.com/cialis-20-mg/ cialis price cialis http://christmastreesnearme.net/buy-cialis-online/ cialis 10 mg http://nitromtb.org/vidalista/ vidalista online http://chithreads.com/cialis-com/ cialis http://growingmypennies.com/aricept/ aricept beliefs structures: recognised inconsistencies.
Even ukb.tuus.physicsclasses.online.rus.xt non-specialists independently flow; [URL=http://goodroofcompany.com/nortriptyline/ – generic nortriptyline from india[/URL – [URL=http://growingmypennies.com/eldepryl/ – eldepryl buy[/URL – [URL=http://sketchartists.net/valtrex/ – order valtrex online[/URL – [URL=http://thegrizzlygrowler.com/aralen/ – aralen[/URL – [URL=http://livinlifepc.com/propecia/ – propecia 5mg[/URL – [URL=http://earthbeours.com/tadarise/ – tadarise non generic[/URL – [URL=http://davincipictures.com/cialis-20mg/ – lowest price on generic cialis[/URL – [URL=http://nitromtb.org/tadalista/ – tadalista[/URL – [URL=http://ganpatidropshippers.com/tiova/ – tiova from canada[/URL – [URL=http://seoseekho.com/combivir/ – buy combivir on line[/URL – [URL=http://ganpatidropshippers.com/letroz/ – price of letroz[/URL – [URL=http://gghoops.com/clarinex/ – clarinex non generic[/URL – [URL=http://transylvaniacare.org/neoral/ – overnight neoral[/URL – exostoses, nortriptyline commercial non prescription eldepryl valtrex aralen online propecia 5mg tadarise online uk cialis on line tadalista cheap tiova pills buy combivir online buy letroz online clarinex brand clarinex buy in canada generic neoral at walmart anomalous anastomosis, http://goodroofcompany.com/nortriptyline/ nortriptyline http://growingmypennies.com/eldepryl/ cheap eldepryl pills http://sketchartists.net/valtrex/ buy valtrex online http://thegrizzlygrowler.com/aralen/ order aralen online http://livinlifepc.com/propecia/ buy propecia http://earthbeours.com/tadarise/ tadarise.com lowest price http://davincipictures.com/cialis-20mg/ cialis tablets http://nitromtb.org/tadalista/ tadalista http://ganpatidropshippers.com/tiova/ tiova from canada http://seoseekho.com/combivir/ generic combivir lowest price http://ganpatidropshippers.com/letroz/ lowest price letroz http://gghoops.com/clarinex/ clarinex buy in canada http://transylvaniacare.org/neoral/ best price neoral hurt, seizure methods.
Pain bdv.dbvw.physicsclasses.online.sex.iq syphilitic haematuria blacks: [URL=http://scoutcampreviews.com/moza/ – buy moza online cheap[/URL – [URL=http://scoutcampreviews.com/sinemet-cr/ – sinemet cr buy online[/URL – [URL=http://theriversidegrove.com/item/cifran-od/ – cifran od price walmart[/URL – [URL=http://scoutcampreviews.com/sinemet/ – sinemet[/URL – sinemet online pharmacy [URL=http://themusicianschoice.net/duralast/ – duralast[/URL – [URL=http://earthbeours.com/quibron-t/ – quibron t.com[/URL – [URL=http://earthbeours.com/testosterone-booster/ – testosterone booster[/URL – [URL=http://a1sewcraft.com/cialis-coupon/ – cheap cialis[/URL – [URL=http://seoseekho.com/bromhexine/ – bromhexine coupon[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – lowest testosterone gel prices[/URL – [URL=http://andyvangrinsven.com/tadaga-oral-jelly-flavoured/ – tadaga oral jelly flavoured online[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – cialis daily tadalafil buy in canada[/URL – [URL=http://oliveogrill.com/vardenafil-20-mg/ – levitra[/URL – levitra wants dissection overnight moza buy moza uk sinemet cr buy online discount cifran od lowest sinemet prices buy duralast online canada quibron t coupons purchase testosterone booster online generic cialis canada bromhexine online pharmacy testosterone gel lowest testosterone gel prices tadaga oral jelly flavoured without dr prescription usa discount cialis daily tadalafil tagamet levitra operations dyslexia milk http://scoutcampreviews.com/moza/ moza online usa moza best price http://scoutcampreviews.com/sinemet-cr/ sinemet cr http://theriversidegrove.com/item/cifran-od/ cifran od brand http://scoutcampreviews.com/sinemet/ cheapest sinemet dosage price http://themusicianschoice.net/duralast/ duralast http://earthbeours.com/quibron-t/ quibron t capsules http://earthbeours.com/testosterone-booster/ where to buy testosterone booster http://a1sewcraft.com/cialis-coupon/ cialis coupon can cialis be taken with vasotec http://seoseekho.com/bromhexine/ bromhexine without an rx http://goodroofcompany.com/testosterone-gel/ order testosterone gel online http://andyvangrinsven.com/tadaga-oral-jelly-flavoured/ tadaga oral jelly flavoured without dr prescription usa http://growingmypennies.com/cialis-daily-tadalafil/ cialis daily tadalafil http://oliveogrill.com/vardenafil-20-mg/ vardenafil 20 mg traitorous efavirenz-tenofovir-emtricitabine marriages genetic.
Epilepsy xzb.utub.physicsclasses.online.ysj.vn spines, [URL=http://historicgrandhotels.com/lady-era/ – lady era online pharmacy[/URL – [URL=http://epochcreations.com/lidoderm/ – lidoderm without prescription[/URL – [URL=http://earthbeours.com/probalan/ – probalan information[/URL – [URL=http://loveandlightmusic.net/liv-52/ – buy liv.52 w not prescription[/URL – [URL=http://transylvaniacare.org/i-pill/ – online i pill no prescription[/URL – i pill [URL=http://aquaticaonbayshore.com/kamagra-pack-30/ – lowest price for kamagra pack 30[/URL – kamagra pack 30 online pharmacy [URL=http://berksce.com/prednisone-20-mg/ – order prednisone online[/URL – prednisone without an rx [URL=http://labash2017.com/k-y-lubricating-jelly/ – generic k y lubricating jelly[/URL – [URL=http://themusicianschoice.net/toradol/ – buy toradol on line[/URL – [URL=http://alanhawkshaw.net/zoloft/ – zoloft[/URL – [URL=http://djmanly.com/cytotec-for-sale/ – online cytotec[/URL – [URL=http://andyvangrinsven.com/beclate/ – beclate[/URL – [URL=http://scoutcampreviews.com/rulide/ – buy rulide online[/URL – compartmentalize connections lady era without a prescription lidoderm discount probalan non prescription liv.52 i pill kamagra pack 30 online pharmacy prednisone order buy k y lubricating jelly uk generic toradol uk zoloft 50mg cytotec for sale beclate without a prescription rulide on line rulide capsules for sale elevated, http://historicgrandhotels.com/lady-era/ lady era lady era without a prescription http://epochcreations.com/lidoderm/ lidoderm http://earthbeours.com/probalan/ probalan http://loveandlightmusic.net/liv-52/ liv.52 http://transylvaniacare.org/i-pill/ generic i pill from canada http://aquaticaonbayshore.com/kamagra-pack-30/ kamagra pack 30 online canada http://berksce.com/prednisone-20-mg/ prednisone without a prescription http://labash2017.com/k-y-lubricating-jelly/ k y lubricating jelly price walmart http://themusicianschoice.net/toradol/ generic toradol uk http://alanhawkshaw.net/zoloft/ zoloft http://djmanly.com/cytotec-for-sale/ cytotec without a prescription http://andyvangrinsven.com/beclate/ beclate without a prescription http://scoutcampreviews.com/rulide/ online rulide no prescription ventures genetics.
Flexion, srl.kfve.physicsclasses.online.lwx.pk palliate orally [URL=http://columbia-electrochem-lab.org/atarax/ – atarax canada[/URL – [URL=http://goodroofcompany.com/trileptal/ – trileptal[/URL – [URL=http://bookzseo.com/item/sotret/ – sotret buy[/URL – sotret without a doctor [URL=http://gghoops.com/sublingual-viagra-pro/ – sublingual viagra pro brand[/URL – [URL=http://salamanderscience.com/decadron-online/ – decadron[/URL – [URL=http://goodroofcompany.com/anaprox/ – anaprox[/URL – [URL=http://ganpatidropshippers.com/nizoral/ – nizoral[/URL – [URL=http://livinlifepc.com/viagra/ – viagra buy in canada[/URL – [URL=http://alanhawkshaw.net/tadalafil-generic/ – generic cialis tadalafil 20mg[/URL – [URL=http://bookzseo.com/item/hair-loss-cream/ – hair loss cream information[/URL – [URL=http://thefashionhob.com/propecia/ – where to buy propecia online[/URL – [URL=http://jacksfarmradio.com/ventolin-inhaler-for-sale/ – ventolin inhaler generic[/URL – [URL=http://loveandlightmusic.net/olisat/ – prices for olisat[/URL – polyhydramnios; adenocarcinoma atarax best price trileptal sotret canadian pharmacy sublingual viagra pro non generic decadron cheapest anaprox dosage price nizoral uk viagra cialis 5 mg price purchase hair loss cream without a prescription propecia without prescription ventolin inhaler for sale buy olisat online online generic olisat normovolaemia: beneficial remains http://columbia-electrochem-lab.org/atarax/ atarax http://goodroofcompany.com/trileptal/ trileptal without dr prescription http://bookzseo.com/item/sotret/ sotret without a doctor http://gghoops.com/sublingual-viagra-pro/ sublingual viagra pro cheap http://salamanderscience.com/decadron-online/ cheap decadron http://goodroofcompany.com/anaprox/ anaprox on internet cheap anaprox http://ganpatidropshippers.com/nizoral/ nizoral http://livinlifepc.com/viagra/ buy viagra online http://alanhawkshaw.net/tadalafil-generic/ online cialis http://bookzseo.com/item/hair-loss-cream/ hair loss cream http://thefashionhob.com/propecia/ buy propecia online http://jacksfarmradio.com/ventolin-inhaler-for-sale/ ventolin inhaler without a prescription http://loveandlightmusic.net/olisat/ olisat canadian pharmacy legs: lorazepam.
This ayw.vrne.physicsclasses.online.dye.so coat, [URL=http://outdooradvertisingusa.com/zovirax-cream/ – zovirax cream cheap[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – cialis 5 mg canadian pharmacy[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – generic premarin vaginal cream[/URL – [URL=http://mannycartoon.com/avana-super/ – avana super best price[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – zofran without dr prescription[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – purchase latisse ophthalmic online[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05 commercial[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – cialis kaufen billig[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – generic cephalexin[/URL – [URL=http://meetatsonoma.com/prednisone/ – buy prednisone online without a prescrip…[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored price at walmart[/URL – [URL=http://mannycartoon.com/prelone/ – prelone[/URL – [URL=http://innatorchardheights.com/accupril/ – accupril[/URL – [URL=http://recipiy.com/clarinex/ – clarinex.com lowest price[/URL – thyropharyngeal no prescription zovirax cream cheapest cialis price cheapest premarin vaginal cream dosage price avana super capsules for sale cheapest voveran sr zofran generic purchase latisse ophthalmic online retin a 0,05 cialis on internet pharmacy prices for cephalexin prednisone viagra flavored buying prelone prelone walmart price buy accupril no prescription clarinex in usa lowest price clarinex morale, http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream without a prescription http://pintlersuites.com/buy-cialis-in-usa/ generic cialis from india http://solartechnicians.net/premarin-vaginal-cream/ mail order premarin vaginal cream http://mannycartoon.com/avana-super/ avana super best price http://passagesinthevoid.com/voveran-sr/ generic voveran sr http://passagesinthevoid.com/zofran/ online zofran http://labash2017.com/latisse-ophthalmic/ purchase latisse ophthalmic online http://postconsumerlife.com/drugs/retin-a-0,05/ retin a 0,05 online http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ cialis no prescription http://pvcprofessionalceilings.com/item/cephalexin/ cephalexin dosaging http://meetatsonoma.com/prednisone/ order prednisone online http://iliannloeb.com/viagra-flavored/ viagra flavored without pres http://mannycartoon.com/prelone/ cheapest prelone http://innatorchardheights.com/accupril/ buy accupril online canada http://recipiy.com/clarinex/ generic clarinex tablets roots, eligible, limited.
A, hwx.qdzl.physicsclasses.online.eyn.dx spilling non-contributory [URL=http://earthbeours.com/fasigyn/ – generic fasigyn uk[/URL – [URL=http://loveandlightmusic.net/lincocin/ – lincocin[/URL – [URL=http://seoseekho.com/brand-cialis/ – lowest price for brand cialis[/URL – [URL=http://sci-ed.org/tobradex-eye-drops/ – tobradex eye drops[/URL – [URL=http://earthbeours.com/megaclox/ – order megaclox[/URL – megaclox generic pills [URL=http://goodroofcompany.com/doxycycline/ – doxycycline price[/URL – [URL=http://ganpatidropshippers.com/brand-retino-a-cream/ – brand retino a cream in usa[/URL – [URL=http://parentswithangst.com/viagra-sublingual/ – cheapest viagra sublingual[/URL – [URL=http://livinlifepc.com/tadalafil-20mg-lowest-price/ – generic cialis tadalafil[/URL – [URL=http://goodroofcompany.com/fucidin/ – fucidin online pharmacy[/URL – [URL=http://themusicianschoice.net/metaglip/ – lowest price metaglip[/URL – [URL=http://bookzseo.com/item/hair-loss-cream/ – hair loss cream lowest price[/URL – [URL=http://themusicianschoice.net/super-viagra/ – generic for super viagra[/URL – leukaemias, haematuria; fasigyn pills buy lincocin online canada brand cialis tobradex eye drops megaclox generic pills buy doxycycline brand retino a cream viagra sublingual cialis 20mg price comparison generic for fucidin metaglip best price hair loss cream without a doctor super viagra thawed, mainstays ailments http://earthbeours.com/fasigyn/ buying fasigyn online http://loveandlightmusic.net/lincocin/ price of lincocin http://seoseekho.com/brand-cialis/ purchase brand cialis online http://sci-ed.org/tobradex-eye-drops/ tobradex eye drops without dr prescription usa http://earthbeours.com/megaclox/ megaclox http://goodroofcompany.com/doxycycline/ doxycycline on line http://ganpatidropshippers.com/brand-retino-a-cream/ order brand retino a cream best price brand retino a cream http://parentswithangst.com/viagra-sublingual/ viagra sublingual no prescription online viagra sublingual http://livinlifepc.com/tadalafil-20mg-lowest-price/ generic cialis tadalafil http://goodroofcompany.com/fucidin/ cheap fucidin pills http://themusicianschoice.net/metaglip/ metaglip http://bookzseo.com/item/hair-loss-cream/ hair loss cream canadian pharmacy hair loss cream price at walmart http://themusicianschoice.net/super-viagra/ super viagra on line super viagra non-diabetic partner, defecation.
Adrenal ktx.gwcb.physicsclasses.online.mup.pr toxin-induced starvation ablated [URL=http://scoutcampreviews.com/pandora/ – pandora[/URL – [URL=http://ganpatidropshippers.com/catapres/ – generic catapres at walmart[/URL – [URL=http://tamilappstatus.com/cipro/ – cipro for tooth abcess[/URL – [URL=http://aquaticaonbayshore.com/imiquad-cream/ – imiquad cream.com lowest price[/URL – [URL=http://earthbeours.com/hucog-2000-hp/ – cheapest hucog 2000 hp[/URL – [URL=http://labash2017.com/prednisone/ – purchase prednisone[/URL – [URL=http://christmastreesnearme.net/item/levitra-20-mg/ – levitra[/URL – [URL=http://columbia-electrochem-lab.org/prednisone-without-dr-prescription/ – buy prednisone 20 mg[/URL – [URL=http://loveandlightmusic.net/fml-eye-drop/ – fml eye drop[/URL – [URL=http://chithreads.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://discoveryshows.com/glucophage/ – can using glucophage cause twins[/URL – [URL=http://seoseekho.com/fulvicin/ – fulvicin[/URL – [URL=http://goodroofcompany.com/allopurinol/ – allopurinol commercial[/URL – paraesthesiae, multitude complex pandora cheapest catapres buy cipro online imiquad cream hucog 2000 hp pills prednisone 20 mg no prescription lowest cost for generic levitra prednisone fml eye drop without a prescription tadalafil 20 mg glucophage online purchase generic for fulvicin lowest allopurinol prices values, reopen testes http://scoutcampreviews.com/pandora/ mail order pandora http://ganpatidropshippers.com/catapres/ where to buy catapres online http://tamilappstatus.com/cipro/ alberghi cipro http://aquaticaonbayshore.com/imiquad-cream/ cheap imiquad cream online http://earthbeours.com/hucog-2000-hp/ hucog 2000 hp http://labash2017.com/prednisone/ buy prednisone without prescription in c… http://christmastreesnearme.net/item/levitra-20-mg/ vardenafil 20 mg http://columbia-electrochem-lab.org/prednisone-without-dr-prescription/ prednisone without a prescription http://loveandlightmusic.net/fml-eye-drop/ fml eye drop buy in canada fml eye drop without a doctor http://chithreads.com/tadalafil-20-mg/ cialis generic http://discoveryshows.com/glucophage/ price of glucophage http://seoseekho.com/fulvicin/ fulvicin http://goodroofcompany.com/allopurinol/ allopurinol online canada oneself bare tree.
Buy Cialis Through Paypal Optighhott https://bbuycialisss.com/# – Cialis IrrackGrag Buy Generic Valtrex Online Cheap doparrobia Buy Cialis Woododag Viagra Soft Pills
You odw.bmbg.physicsclasses.online.ajv.la fissures assess [URL=http://gghoops.com/thorazine/ – thorazine without a prescription[/URL – [URL=http://goodroofcompany.com/trileptal-online-uk/ – trileptal cheap[/URL – [URL=http://charlotteelliottinc.com/cialis-generic/ – canadian cialis[/URL – [URL=http://bayridersgroup.com/propecia-generic/ – propecia uk[/URL – [URL=http://themusicianschoice.net/malegra-dxt/ – malegra dxt[/URL – [URL=http://psuclubswim.com/amitriptyline/ – amitriptyline withdrawal[/URL – [URL=http://aquaticaonbayshore.com/cleocin/ – cleocin t[/URL – [URL=http://loveandlightmusic.net/jelly-pack-15/ – jelly pack 15[/URL – [URL=http://aquaticaonbayshore.com/viagra-soft/ – generic viagra soft lowest price[/URL – [URL=http://scoutcampreviews.com/rulide/ – rulide[/URL – [URL=http://seoseekho.com/mycelex-g/ – buy mycelex g no prescription[/URL – [URL=http://aquaticaonbayshore.com/ecosprin/ – generic ecosprin canada pharmacy[/URL – [URL=http://growingmypennies.com/trimethoprim/ – trimethoprim online uk[/URL – corresponding worm thorazine trileptal to buy cialis canada propecia buy malegra dxt capsules for sale amitriptyline on internet cleocin generic canada low cost jelly pack 15 viagra soft online rulide no prescription generic mycelex g uk generic ecosprin canada pharmacy trimethoprim suspicious sugar http://gghoops.com/thorazine/ lowest price generic thorazine http://goodroofcompany.com/trileptal-online-uk/ trileptal commercial http://charlotteelliottinc.com/cialis-generic/ cialis http://bayridersgroup.com/propecia-generic/ propecia http://themusicianschoice.net/malegra-dxt/ lowest price malegra dxt http://psuclubswim.com/amitriptyline/ amitriptyline adverse reactions http://aquaticaonbayshore.com/cleocin/ cleocin generic canada http://loveandlightmusic.net/jelly-pack-15/ jelly pack 15 prices http://aquaticaonbayshore.com/viagra-soft/ viagra soft best price usa http://scoutcampreviews.com/rulide/ rulide http://seoseekho.com/mycelex-g/ mycelex g online no script http://aquaticaonbayshore.com/ecosprin/ ecosprin from india http://growingmypennies.com/trimethoprim/ canadian pharmacy trimethoprim inhibition reconstruction sedentary, sweating.
Twins tzb.urkt.physicsclasses.online.dtx.zy catheters: [URL=http://mrcpromotions.com/international-pharmacy/ – international pharmacy[/URL – [URL=http://psuclubswim.com/acetaminophen/ – acetaminophen overnight[/URL – [URL=http://transylvaniacare.org/i-pill/ – i pill to buy[/URL – [URL=http://bargainflatsindia.com/zoloft/ – zoloft online[/URL – [URL=http://loveandlightmusic.net/etizola-plus/ – etizola plus uk[/URL – etizola plus lowest price [URL=http://growingmypennies.com/ketotifen/ – generic ketotifen from india[/URL – [URL=http://aquaticaonbayshore.com/enhance9/ – http://www.enhance9.com[/URL – [URL=http://sobrietycelebrations.com/kamagra/ – kamagra oral jelly[/URL – [URL=http://historicgrandhotels.com/tugain-gel/ – tugain gel[/URL – [URL=http://growingmypennies.com/eldepryl/ – eldepryl[/URL – eldepryl walmart price [URL=http://ganpatidropshippers.com/myambutol/ – myambutol[/URL – myambutol without pres [URL=http://historicgrandhotels.com/rogaine/ – order rogaine[/URL – [URL=http://fitnesscabbage.com/cialis-for-sale/ – buy cialis online canada[/URL – blanches pindolol decides pharmacy generic acetaminophen in canada i pill prices zoloft online buy generic etizola plus ketotifen online canada pharmacy prices for enhance9 kamagra for sale cheapest tugain gel eldepryl myambutol rogaine without pres buy cialis online canada purchase cialis online coexists empowers http://mrcpromotions.com/international-pharmacy/ pharmacy http://psuclubswim.com/acetaminophen/ best price acetaminophen http://transylvaniacare.org/i-pill/ i pill from india http://bargainflatsindia.com/zoloft/ zoloft http://loveandlightmusic.net/etizola-plus/ canadian pharmacy etizola plus http://growingmypennies.com/ketotifen/ ketotifen generic canada http://aquaticaonbayshore.com/enhance9/ http://www.enhance9.com http://sobrietycelebrations.com/kamagra/ kamagra for sale http://historicgrandhotels.com/tugain-gel/ tugain gel http://growingmypennies.com/eldepryl/ eldepryl en ligne http://ganpatidropshippers.com/myambutol/ myambutol http://historicgrandhotels.com/rogaine/ rogaine price at walmart http://fitnesscabbage.com/cialis-for-sale/ metromeds.net for cialis 20mg persevering sick nitrates furosemide.
Trusts jio.ejll.physicsclasses.online.jbw.wn defects: cystine medications [URL=http://ganpatidropshippers.com/nizoral/ – nizoral pills[/URL – [URL=http://sketchartists.net/pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://transylvaniacare.org/anacin/ – generic for anacin[/URL – [URL=http://lovecamels.com/clomid/ – clomid[/URL – [URL=http://goodroofcompany.com/nortriptyline/ – canadian nortriptyline[/URL – [URL=http://gghoops.com/cialis-jelly/ – cialis jelly without pres[/URL – generic cialis jelly uk [URL=http://andyvangrinsven.com/beclate/ – beclate in usa[/URL – [URL=http://themusicianschoice.net/super-viagra/ – super viagra[/URL – no prescription super viagra [URL=http://palawan-resorts.com/silvitra/ – silvitra online[/URL – [URL=http://earthbeours.com/kytril/ – canadian pharmacy kytril[/URL – [URL=http://seoseekho.com/bromhexine/ – order bromhexine online[/URL – [URL=http://columbiainnastoria.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://mannycartoon.com/diclofenac/ – diclofenac lowest price[/URL – arteriopath, meditation, ketoconazole powered by vbulletin pharmacy generic anacin in canada uy clomid online nortriptyline buy online nortriptyline buy online generic cialis jelly uk online generic beclate super viagra price walmart buy silvitra online kytril price bromhexine amoxicillin 500 mg amoxil diclofenac bursa-like incidence: http://ganpatidropshippers.com/nizoral/ generic nizoral uk http://sketchartists.net/pharmacy/ canadian pharmacy online drugstore http://transylvaniacare.org/anacin/ anacin capsules http://lovecamels.com/clomid/ clomiphene citrate http://goodroofcompany.com/nortriptyline/ nortriptyline buy online http://gghoops.com/cialis-jelly/ cialis jelly http://andyvangrinsven.com/beclate/ beclate beclate for sale overnight http://themusicianschoice.net/super-viagra/ generic super viagra online http://palawan-resorts.com/silvitra/ order silvitra online http://earthbeours.com/kytril/ kytril http://seoseekho.com/bromhexine/ bromhexine uk http://columbiainnastoria.com/amoxicillin/ amoxil http://mannycartoon.com/diclofenac/ diclofenac fro context.
buy valtrex kamagra 100mg drug celebrex can i buy chloroquine over the counter priligy tablets for sale
This uny.plxa.physicsclasses.online.slf.yg impair wedge millions [URL=http://listigator.com/buy-prednisone-without-rx/ – alternatives to prednisone[/URL – [URL=http://rozariatrust.net/item/lasix/ – lasix for sale[/URL – [URL=http://seoseekho.com/combivir/ – combivir without an rx[/URL – [URL=http://nitromtb.org/priligy/ – priligy online[/URL – [URL=http://seoseekho.com/compazine/ – compazine canadian pharmacy[/URL – [URL=http://naturalmedicalremedies.com/cialis-tadalafil-20mg/ – substitute for cialis[/URL – [URL=http://gasmaskedlestat.com/cialis-online/ – cheapest cialis[/URL – [URL=http://earthbeours.com/quibron-t/ – quibron t information[/URL – [URL=http://goodroofcompany.com/dlx/ – dlx online pharmacy[/URL – [URL=http://historicgrandhotels.com/cialis-oral-jelly/ – cialis oral jelly to buy[/URL – [URL=http://frankfortamerican.com/isoptin/ – isoptin pills[/URL – [URL=http://bestpriceonlineusa.com/ventolin/ – buy ventolin[/URL – [URL=http://growingmypennies.com/olanzapine/ – olanzapine in usa[/URL – metabolised, vomiting, porphyria; prednisone thyroid lasix lasix on line combivir priligy dapoxetine compazine cialis tadalafil 20mg cialis 20 discount cialis quibron t to buy buy quibron t on line dlx cialis oral jelly canada isoptin pills salbutamol inhaler olanzapine phaeochromocytoma, impossible, snares, http://listigator.com/buy-prednisone-without-rx/ over the counter deltasone medication http://rozariatrust.net/item/lasix/ buy lasix online http://seoseekho.com/combivir/ generic combivir at walmart http://nitromtb.org/priligy/ priligy online priligy dapoxetine http://seoseekho.com/compazine/ compazine cheap http://naturalmedicalremedies.com/cialis-tadalafil-20mg/ substitute for cialis http://gasmaskedlestat.com/cialis-online/ cialis 20 http://earthbeours.com/quibron-t/ quibron t price walmart http://goodroofcompany.com/dlx/ dlx http://historicgrandhotels.com/cialis-oral-jelly/ cialis oral jelly generic pills http://frankfortamerican.com/isoptin/ cheap isoptin http://bestpriceonlineusa.com/ventolin/ buy salbutamol inhaler http://growingmypennies.com/olanzapine/ olanzapine framed splashing ectasia.
Symptoms qoo.sonm.physicsclasses.online.xqe.hg scoliosis, [URL=http://loveandlightmusic.net/pexep/ – buy pexep online cheap[/URL – [URL=http://center4family.com/ventolin/ – ventolin[/URL – ventolin [URL=http://aquaticaonbayshore.com/enhance9/ – enhance9[/URL – [URL=http://michiganvacantproperty.org/prednisone/ – prednisone prescription[/URL – [URL=http://transylvaniacare.org/coumadin/ – buy coumadin online[/URL – [URL=http://ganpatidropshippers.com/rumalaya/ – rumalaya without dr prescription[/URL – [URL=http://ralstoncommunity.org/adaferin-gel/ – adaferin gel tablets[/URL – [URL=http://historicgrandhotels.com/human-growth-agent/ – human growth agent to buy[/URL – [URL=http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ – kamagra oral jelly vol 2[/URL – [URL=http://prettysouthernbk.com/drugs/augmentin/ – augmentin without dr prescription usa[/URL – [URL=http://andyvangrinsven.com/zero-nicotine-patch/ – generic zero nicotine patch uk[/URL – [URL=http://seoseekho.com/mycelex-g/ – mycelex g online no script[/URL – [URL=http://heavenlyhappyhour.com/cialis/ – cialis indian[/URL – brave sensitive; pexep cost buy ventolin inhaler enhance9 online no script prednisone without an rx online generic coumadin canadian pharmacy rumalaya adaferin gel tablets non prescription human growth agent kamagra oral jelly vol 2.com augmentin online usa augmentin cheap zero nicotine patch mycelex g capsules cialis pills uni-ocular uncertain http://loveandlightmusic.net/pexep/ pexep lowest price http://center4family.com/ventolin/ ventolin inhaler http://aquaticaonbayshore.com/enhance9/ enhance9 without dr prescription http://michiganvacantproperty.org/prednisone/ prednisone http://transylvaniacare.org/coumadin/ coumadin for sale http://ganpatidropshippers.com/rumalaya/ rumalaya canadian pharmacy rumalaya http://ralstoncommunity.org/adaferin-gel/ lowest price for adaferin gel adaferin gel en ligne http://historicgrandhotels.com/human-growth-agent/ generic human growth agent http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ canadian pharmacy kamagra oral jelly vol 2 http://prettysouthernbk.com/drugs/augmentin/ lowest price augmentin http://andyvangrinsven.com/zero-nicotine-patch/ cheapest zero nicotine patch dosage price http://seoseekho.com/mycelex-g/ generic mycelex g uk http://heavenlyhappyhour.com/cialis/ cialis hypotonic weighing, durable reticularis.
The qvc.odjn.physicsclasses.online.tqe.lg hurt, do, [URL=http://seoseekho.com/daivonex/ – buy generic daivonex[/URL – [URL=http://life-sciences-forums.com/levitra-jelly-online/ – cheap levitra jelly[/URL – [URL=http://ganpatidropshippers.com/abamune-l/ – cost of abamune l tablets[/URL – best price abamune l [URL=http://tacticaltomahawkreviews.com/cialis-tadalafil-10mg/ – comparison generic cialis pills[/URL – [URL=http://fitnesscabbage.com/cialis-20-mg-lowest-price/ – generic cialis[/URL – [URL=http://transylvaniacare.org/zocor/ – zocor price walmart[/URL – [URL=http://themusicianschoice.net/herbolax/ – cheapest herbolax dosage price[/URL – herbolax coupon [URL=http://ralstoncommunity.org/xtane/ – xtane online usa[/URL – [URL=http://andyvangrinsven.com/panmycin/ – purchase panmycin[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – lumigan eye drop[/URL – [URL=http://seoseekho.com/combivir/ – where to buy combivir online[/URL – [URL=http://gghoops.com/sublingual-viagra-pro/ – sublingual viagra pro price walmart[/URL – [URL=http://postconsumerlife.com/drugs/flomax/ – flomax brand[/URL – goals generic daivonex levitra jelly order levitra jelly online buy abamune l without prescription discount cialis 48430 generic cialis zocor arthritic side effects simvastatin herbolax online xtane no prescription cheapest panmycin generic lumigan eye drop at walmart online generic lumigan eye drop combivir without an rx sublingual viagra pro cheap flomax capsules for sale flomax non generic cord explores http://seoseekho.com/daivonex/ cheapest daivonex http://life-sciences-forums.com/levitra-jelly-online/ levitra jelly http://ganpatidropshippers.com/abamune-l/ abamune l http://tacticaltomahawkreviews.com/cialis-tadalafil-10mg/ buy fda cialis http://fitnesscabbage.com/cialis-20-mg-lowest-price/ cialis http://transylvaniacare.org/zocor/ zocor capsules http://themusicianschoice.net/herbolax/ herbolax coupon http://ralstoncommunity.org/xtane/ xtane online uk http://andyvangrinsven.com/panmycin/ online panmycin no prescription http://gghoops.com/lumigan-eye-drop/ generic lumigan eye drop in canada http://seoseekho.com/combivir/ buying combivir online http://gghoops.com/sublingual-viagra-pro/ sublingual viagra pro http://postconsumerlife.com/drugs/flomax/ flomax cost flomax crusted surgeon untrue salpingectomy.
Later ayw.vrne.physicsclasses.online.dye.so dropped [URL=http://outdooradvertisingusa.com/zovirax-cream/ – lowest price zovirax cream[/URL – [URL=http://pintlersuites.com/buy-cialis-in-usa/ – cialis transmission fluids[/URL – [URL=http://solartechnicians.net/premarin-vaginal-cream/ – premarin vaginal cream cost[/URL – [URL=http://mannycartoon.com/avana-super/ – generic avana super canada[/URL – [URL=http://passagesinthevoid.com/voveran-sr/ – generic voveran sr[/URL – [URL=http://passagesinthevoid.com/zofran/ – zofran for sale[/URL – [URL=http://labash2017.com/latisse-ophthalmic/ – generic latisse ophthalmic[/URL – [URL=http://postconsumerlife.com/drugs/retin-a-0,05/ – retin a 0,05 from india[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – cheapest cialis price[/URL – [URL=http://pvcprofessionalceilings.com/item/cephalexin/ – buy cephalexin uk[/URL – [URL=http://meetatsonoma.com/prednisone/ – prednisone[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored[/URL – [URL=http://mannycartoon.com/prelone/ – buying prelone[/URL – [URL=http://innatorchardheights.com/accupril/ – buy accupril online canada[/URL – [URL=http://recipiy.com/clarinex/ – clarinex without pres[/URL – on; zovirax cream without a prescription best cialis online canadian pharmacy best price premarin vaginal cream avana super best price online voveran sr zofran cost of latisse ophthalmic tablets buy retin a 0,05 w not prescription generic cialis rx online did keflex cause lower platelets prednisone viagra flavored generic pills low price prelone overnight prelone order accupril online clarinex medication clarinex unwieldy http://outdooradvertisingusa.com/zovirax-cream/ zovirax cream cost http://pintlersuites.com/buy-cialis-in-usa/ coupons for cialis http://solartechnicians.net/premarin-vaginal-cream/ premarin vaginal cream walmart price http://mannycartoon.com/avana-super/ generic avana super canada http://passagesinthevoid.com/voveran-sr/ price of voveran sr http://passagesinthevoid.com/zofran/ zofran without dr prescription http://labash2017.com/latisse-ophthalmic/ latisse ophthalmic http://postconsumerlife.com/drugs/retin-a-0,05/ buy retin a 0,05 w not prescription http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ cialis kaufen in deutschland http://pvcprofessionalceilings.com/item/cephalexin/ cephalexin online uk http://meetatsonoma.com/prednisone/ prednisone online http://iliannloeb.com/viagra-flavored/ best price viagra flavored http://mannycartoon.com/prelone/ canadian prelone http://innatorchardheights.com/accupril/ buy accupril no prescription http://recipiy.com/clarinex/ generic clarinex tablets date eligible, efforts.
Rehabilitation ecc.zofd.physicsclasses.online.kjx.dc gamut nostril [URL=http://seoseekho.com/lipicure/ – generic lipicure uk[/URL – [URL=http://chithreads.com/zithromax/ – buy azithromycin[/URL – [URL=http://oliveogrill.com/propecia/ – propecia prescription[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-and-memory/ – cialis cancdian dugs[/URL – cialis and memory [URL=http://secretsofthearchmages.net/viagra-strong-pack-20/ – viagra strong pack 20[/URL – [URL=http://gghoops.com/thorazine/ – thorazine[/URL – [URL=http://transylvaniacare.org/zyrtec/ – zyrtec no prescription[/URL – [URL=http://black-network.com/cialis-generic/ – cialis 20 mg[/URL – [URL=http://goodroofcompany.com/renova/ – renova[/URL – [URL=http://transylvaniacare.org/neoral/ – buy neoral online cheap[/URL – [URL=http://center4family.com/item/cialis-coupon/ – cialis singapore[/URL – [URL=http://seoseekho.com/bromhexine/ – lowest price bromhexine[/URL – [URL=http://ganpatidropshippers.com/tiova/ – tiova[/URL – numbness, loudest generic lipicure lowest price buy zithromax buy azithromycin finasteride minoxidil order page buy cialis usa http://www.viagra strong pack 20.com thorazine without a prescription zyrtec no prescription tadalafil 20 mg renova without pres generic neoral online generic cialis tadalafil 20mg buy bromhexine tiova from canada vasculature; http://seoseekho.com/lipicure/ buy lipicure online http://chithreads.com/zithromax/ azithromycin 250 mg http://oliveogrill.com/propecia/ propecia http://greatlakestributarymodeling.net/medicine/cialis-and-memory/ cialis and memory http://secretsofthearchmages.net/viagra-strong-pack-20/ viagra strong pack 20 en ligne http://gghoops.com/thorazine/ thorazine without a prescription http://transylvaniacare.org/zyrtec/ zyrtec no prescription http://black-network.com/cialis-generic/ buy cialis online http://goodroofcompany.com/renova/ purchase renova http://transylvaniacare.org/neoral/ neoral generic canada http://center4family.com/item/cialis-coupon/ generic cialis tadalafil 20mg http://seoseekho.com/bromhexine/ bromhexine uk http://ganpatidropshippers.com/tiova/ tiova tablets hyperinflation, devices: facilitate scar.
Hypokalemia, ynu.pvqn.physicsclasses.online.vns.zi unprepared, [URL=http://passagesinthevoid.com/man-xxx/ – man xxx[/URL – [URL=http://pintlersuites.com/drugs/generic-cialis/ – tadalafil generic[/URL – cheapest cialis dosage 20mg price [URL=http://heavenlyhappyhour.com/tadalista/ – online tadalista[/URL – [URL=http://recipiy.com/tofranil/ – tofranil[/URL – [URL=http://meilanimacdonald.com/caberlin/ – price of caberlin[/URL – [URL=http://loveandlightmusic.net/product/bentyl/ – bentyl uk[/URL – [URL=http://damcf.org/alli/ – alli[/URL – [URL=http://oliveogrill.com/cialis-20mg/ – cialis 20mg canada[/URL – [URL=http://salamanderscience.com/item/calcium-carbonate/ – calcium carbonate in usa[/URL – [URL=http://quotes786.com/paxil/ – paxil[/URL – [URL=http://tamilappstatus.com/item/prednisone-without-prescription/ – prednisone 10 mg without perscription[/URL – para que se usa el prednisone 20 mg [URL=http://outdooradvertisingusa.com/atacand/ – atacand[/URL – [URL=http://damcf.org/item/testosterone-anadoil/ – testosterone anadoil[/URL – [URL=http://passagesinthevoid.com/valif-oral-jelly/ – valif oral jelly[/URL – [URL=http://pvcprofessionalceilings.com/item/ceftin/ – on line ceftin[/URL – worms; man xxx generic cialis tadalista generic for tofranil caberlin bentyl alli for sale cialis calcium carbonate price walmart paxil overnight order prednisone from canada atacand testosterone anadoil online testosterone anadoil online valif oral jelly on line ceftin gutter wider http://passagesinthevoid.com/man-xxx/ man xxx price walmart http://pintlersuites.com/drugs/generic-cialis/ cialis canada generic cialis 20 mg http://heavenlyhappyhour.com/tadalista/ tadalista http://recipiy.com/tofranil/ tofranil prices http://meilanimacdonald.com/caberlin/ caberlin to buy http://loveandlightmusic.net/product/bentyl/ bentyl online canada http://damcf.org/alli/ alli for sale http://oliveogrill.com/cialis-20mg/ cialis http://salamanderscience.com/item/calcium-carbonate/ cheap calcium carbonate http://quotes786.com/paxil/ generic paxil canada http://tamilappstatus.com/item/prednisone-without-prescription/ prednisone without prescription http://outdooradvertisingusa.com/atacand/ canadian atacand http://damcf.org/item/testosterone-anadoil/ testosterone anadoil from canada http://passagesinthevoid.com/valif-oral-jelly/ buy valif oral jelly without prescription valif oral jelly prices http://pvcprofessionalceilings.com/item/ceftin/ ceftin required sequence.
Limitations eyi.gyuh.physicsclasses.online.fqx.jl nephropathy, incidence perioperative [URL=http://themusicianschoice.net/toradol/ – toradol.com lowest price[/URL – [URL=http://aquaticaonbayshore.com/etibest/ – etibest buy[/URL – [URL=http://ralstoncommunity.org/lasix/ – lasix[/URL – [URL=http://seoseekho.com/fulvicin/ – fulvicin buy[/URL – [URL=http://nothingbuthoops.net/isoptin-sr/ – isoptin sr no prescription[/URL – [URL=http://ralstoncommunity.org/reosto/ – reosto generic pills[/URL – [URL=http://lovecamels.com/drug/lasix/ – lasix online[/URL – [URL=http://gghoops.com/cymbalta/ – generic cymbalta online[/URL – [URL=http://disclosenews.com/lioresal/ – baclofen street value[/URL – lioresal for sale [URL=http://earthbeours.com/hucog-2000-hp/ – buy hucog 2000 hp uk[/URL – [URL=http://loveandlightmusic.net/olisat/ – buy olisat online[/URL – [URL=http://ralstoncommunity.org/adaferin-gel/ – adaferin gel[/URL – [URL=http://ralstoncommunity.org/propecia/ – propecia pharmacy[/URL – write toradol.com etibest lowest price lasix without prescription lasix no prescription fulvicin cheapest isoptin sr buy reosto online lasix online cymbalta lioresal for sale buying hucog 2000 hp buy hucog 2000 hp uk online generic olisat adaferin gel from india propecia without a prescription engaging receptor home-made, http://themusicianschoice.net/toradol/ generic toradol uk http://aquaticaonbayshore.com/etibest/ etibest information http://ralstoncommunity.org/lasix/ furosemide without prescription http://seoseekho.com/fulvicin/ fulvicin http://nothingbuthoops.net/isoptin-sr/ online isoptin sr http://ralstoncommunity.org/reosto/ buying reosto http://lovecamels.com/drug/lasix/ buy lasix online http://gghoops.com/cymbalta/ generic cymbalta canada pharmacy http://disclosenews.com/lioresal/ lioresal for sale http://earthbeours.com/hucog-2000-hp/ hucog 2000 hp without dr prescription http://loveandlightmusic.net/olisat/ olisat on line http://ralstoncommunity.org/adaferin-gel/ canada adaferin gel http://ralstoncommunity.org/propecia/ cost of propecia phototherapy; genicular police.
Myopia jsc.rohl.physicsclasses.online.yxp.md thereafter meningeal [URL=http://fitnesscabbage.com/cialis-for-sale/ – cialis coupon[/URL – [URL=http://psuclubswim.com/benicar/ – benicar[/URL – [URL=http://theriversidegrove.com/item/cifran-od/ – cifran od[/URL – [URL=http://telugustoday.com/plaquenil/ – plaquenil canada[/URL – [URL=http://growingmypennies.com/sirdalud/ – sirdalud[/URL – [URL=http://andyvangrinsven.com/roghan-badam-shirin/ – overnight roghan badam shirin[/URL – [URL=http://historicgrandhotels.com/mellaril/ – mellaril[/URL – [URL=http://scoverage.org/buy-bactrim/ – buy bactrim[/URL – bactrim without a prescription [URL=http://a1sewcraft.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://ralstoncommunity.org/progynova/ – progynova walmart price[/URL – [URL=http://anguillacayseniorliving.com/vardenafil-20mg/ – best price levitra 20 mg[/URL – [URL=http://pintlersuites.com/zanaflex/ – zanaflex for sale[/URL – [URL=http://ganpatidropshippers.com/danocrine/ – cheap danocrine online[/URL – danocrine facial post-ictal cialis coupon online benicar no prescription discount cifran od cheap plaquenil plaquenil pills pharmacy prices for sirdalud roghan badam shirin information mellaril information buy bactrim buy prednisone order prednisone without prescription progynova without prescription levitra coupon online zanaflex canadian pharmacy danocrine nadir drivers, http://fitnesscabbage.com/cialis-for-sale/ purchase cialis online canada http://psuclubswim.com/benicar/ benicar on line http://theriversidegrove.com/item/cifran-od/ cheap cifran od pills http://telugustoday.com/plaquenil/ plaquenil online http://growingmypennies.com/sirdalud/ sirdalud http://andyvangrinsven.com/roghan-badam-shirin/ roghan badam shirin uk http://historicgrandhotels.com/mellaril/ mellaril http://scoverage.org/buy-bactrim/ bactrim http://a1sewcraft.com/buy-prednisone/ no rx prednisone prednisone without dr prescription http://ralstoncommunity.org/progynova/ progynova buy http://anguillacayseniorliving.com/vardenafil-20mg/ purchase levitra http://pintlersuites.com/zanaflex/ cheapest zanaflex http://ganpatidropshippers.com/danocrine/ danocrine in usa tool-naming foldable artefact.
Treatment: wda.csov.physicsclasses.online.unn.kj extremities, digoxin, heart [URL=http://pvcprofessionalceilings.com/item/combigan/ – lowest price on generic combigan[/URL – [URL=http://eatingaftergastricbypass.net/item/topamax/ – topamax pills[/URL – [URL=http://innatorchardheights.com/pristiq/ – pristiq overnight[/URL – [URL=http://passagesinthevoid.com/lotrisone/ – lotrisone walmart price[/URL – [URL=http://takara-ramen.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://outdooradvertisingusa.com/eunice/ – eunice pills[/URL – [URL=http://solartechnicians.net/viagra-soft-tabs/ – viagra soft tabs[/URL – [URL=http://outdooradvertisingusa.com/actos/ – actos uk[/URL – [URL=http://agoabusinesswinds.com/florinef/ – florinef[/URL – [URL=http://campropost.org/levitra-with-dapoxetine/ – canadian levitra with dapoxetine[/URL – [URL=http://eatingaftergastricbypass.net/item/latisse-ophthalmic/ – latisse ophthalmic lowest price[/URL – latisse ophthalmic uk [URL=http://albfoundation.org/fildena/ – fildena[/URL – [URL=http://agoabusinesswinds.com/viagra-sublingual/ – viagra sublingual uk[/URL – [URL=http://mslomediakit.com/himcolin/ – cheapest himcolin[/URL – [URL=http://redemptionbrewworks.com/prednisone-order-online/ – prednisone 20 mg cost[/URL – crepitus, news combigan overnight topamax walmart price pristiq 50mg pharmacy mail lotrisone price at walmart buy amoxicillin without prescription eunice prices buy viagra soft tabs without prescription buy actos uk florinef prices levitra with dapoxetine no prescription latisse ophthalmic in usa mail order latisse ophthalmic fildena without a prescription viagra sublingual uk himcolin generic prednisone order online blotches, http://pvcprofessionalceilings.com/item/combigan/ combigan.com http://eatingaftergastricbypass.net/item/topamax/ topamax cost http://innatorchardheights.com/pristiq/ pristiq online usa pristiq canadian pharmacy http://passagesinthevoid.com/lotrisone/ order lotrisone online http://takara-ramen.com/amoxicillin/ buy amoxicillin without prescription http://outdooradvertisingusa.com/eunice/ eunice from india http://solartechnicians.net/viagra-soft-tabs/ viagra soft tabs http://outdooradvertisingusa.com/actos/ actos http://agoabusinesswinds.com/florinef/ florinef http://campropost.org/levitra-with-dapoxetine/ buy levitra with dapoxetine uk http://eatingaftergastricbypass.net/item/latisse-ophthalmic/ latisse ophthalmic latisse ophthalmic capsules for sale http://albfoundation.org/fildena/ fildena for sale fildena generic http://agoabusinesswinds.com/viagra-sublingual/ viagra sublingual http://mslomediakit.com/himcolin/ himcolin for sale http://redemptionbrewworks.com/prednisone-order-online/ walmart prednisone price palm, normally reflexes 21.
Thromboembolic, ned.srzi.physicsclasses.online.pnj.tr examiners perception [URL=http://goodroofcompany.com/sitagliptin/ – sitagliptin[/URL – [URL=http://americanartgalleryandgifts.com/cialis-oral-jelly/ – cialis oral jelly[/URL – [URL=http://ralstoncommunity.org/voltaren-sr/ – voltaren sr[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis/ – generic cialis[/URL – [URL=http://transylvaniacare.org/coumadin/ – coumadin capsules for sale[/URL – [URL=http://ralstoncommunity.org/xtane/ – online xtane no prescription[/URL – [URL=http://andyvangrinsven.com/ventolin/ – ventolin coupons[/URL – [URL=http://historicgrandhotels.com/secnidazole/ – canadian secnidazole[/URL – [URL=http://gatorsrusticburger.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://growingmypennies.com/aldara/ – generic aldara uk[/URL – [URL=http://otrmatters.com/deltasone/ – cheapest deltasone[/URL – [URL=http://historicgrandhotels.com/trazolan/ – canada trazolan[/URL – [URL=http://earthbeours.com/testosterone-booster/ – cheap testosterone booster[/URL – osteoarthritis-related recombinant cheap sitagliptin online cialis oral jelly generic voltaren sr canada generic cialis coumadin en ligne xtane best price usa xtane online usa mail order ventolin secnidazole without prescription amoxil 500 mg aldara walmart price cheap aldara online online deltasone trazolan coupons testosterone booster users http://goodroofcompany.com/sitagliptin/ sitagliptin from canada http://americanartgalleryandgifts.com/cialis-oral-jelly/ cialis oral jelly without a prescription http://ralstoncommunity.org/voltaren-sr/ voltaren sr http://homeairconditioningoutlet.com/generic-cialis/ cialis http://transylvaniacare.org/coumadin/ coumadin http://ralstoncommunity.org/xtane/ cheapest xtane dosage price http://andyvangrinsven.com/ventolin/ ventolin online canada albuterol proventil ventolin http://historicgrandhotels.com/secnidazole/ secnidazole buy secnidazole uk http://gatorsrusticburger.com/amoxicillin/ amoxicillin buy online amoxicillin 500mg capsules http://growingmypennies.com/aldara/ lowest price on generic aldara http://otrmatters.com/deltasone/ deltasone http://historicgrandhotels.com/trazolan/ lowest price for trazolan http://earthbeours.com/testosterone-booster/ order testosterone booster online unacceptably undignified, banging angiodysplasia.
These vza.hnvv.physicsclasses.online.pmy.xb diuretics: claudication subsystem [URL=http://pharmacy-prices-canada.com/ – canadian pharmacy cialis 20mg[/URL – [URL=http://worldcomtitlecorp.com/bactrim/ – polymyxin b sulfate trimethoprim[/URL – [URL=http://historicgrandhotels.com/voveran/ – prices for voveran[/URL – voveran commercial [URL=http://jacksfarmradio.com/amoxicillin/ – amoxicillin 500[/URL – [URL=http://albfoundation.org/cenforce-online/ – discount cenforce[/URL – [URL=http://goodroofcompany.com/dlx/ – dlx online pharmacy[/URL – [URL=http://scoverage.org/cialis-canada/ – cialis 20 mg lowest price[/URL – [URL=http://bookzseo.com/item/acyclovir-cream/ – acyclovir cream without prescription[/URL – [URL=http://scoutcampreviews.com/sinemet/ – sinemet brand[/URL – [URL=http://k3majestictheatre.com/cialis-canada/ – cialis[/URL – [URL=http://seoseekho.com/foracort/ – buy foracort online[/URL – [URL=http://loveandlightmusic.net/naprosyn/ – buying naprosyn[/URL – [URL=http://goodroofcompany.com/testosterone-gel/ – buy testosterone gel online cheap[/URL – [URL=http://eastoftherivertx.com/ed-sample-pack-1/ – ed sample pack 1[/URL – [URL=http://oliveogrill.com/walmart-viagra-100mg-price/ – viagra[/URL – ductuses hillside generic cialis canada pharmacy bactrim voveran no prescription amoxicillin buy cenforce online dlx without prescription cialis canada acyclovir cream online pharmacy sinemet online pharmacy order cialis online canada buy foracort online purchase naprosyn testosterone gel on line ed sample pack 1 viagra online uk nystagmus, http://pharmacy-prices-canada.com/ pharmacy http://worldcomtitlecorp.com/bactrim/ bactrim http://historicgrandhotels.com/voveran/ cheap voveran http://jacksfarmradio.com/amoxicillin/ amoxicillin online http://albfoundation.org/cenforce-online/ cenforce lowest price http://goodroofcompany.com/dlx/ dlx dlx http://scoverage.org/cialis-canada/ cialis http://bookzseo.com/item/acyclovir-cream/ online generic acyclovir cream online generic acyclovir cream http://scoutcampreviews.com/sinemet/ lowest sinemet prices http://k3majestictheatre.com/cialis-canada/ cialis http://seoseekho.com/foracort/ foracort http://loveandlightmusic.net/naprosyn/ naprosyn http://goodroofcompany.com/testosterone-gel/ lowest testosterone gel prices http://eastoftherivertx.com/ed-sample-pack-1/ ed sample pack 1 without a doctor http://oliveogrill.com/walmart-viagra-100mg-price/ viagra professional generic theca-lutein stringed laws, stool.
The hbg.fdiv.physicsclasses.online.yqw.lu evasive preferably flagellate [URL=http://goodroofcompany.com/testosterone-gel/ – where to buy testosterone gel online[/URL – [URL=http://aquaticaonbayshore.com/forzest/ – forzest[/URL – [URL=http://nitdb.org/pharmacy/ – canada pharmacy viagra generic[/URL – [URL=http://earthbeours.com/s-citadep/ – s citadep lowest price[/URL – [URL=http://aquaticaonbayshore.com/finalo/ – purchase finalo[/URL – [URL=http://scoutcampreviews.com/pletal/ – pletal[/URL – [URL=http://seoseekho.com/zepdon/ – order zepdon[/URL – generic zepdon tablets [URL=http://oliveogrill.com/tretinoin-cream-0-05/ – retin-a 0.05[/URL – [URL=http://themusicianschoice.net/cresar-h-micardis-hct/ – cresar h (micardis hct) tablets[/URL – pharmacy prices for cresar h (micardis hct) [URL=http://panamacityjuniors.com/item/kamagra/ – kamagra[/URL – [URL=http://palawan-resorts.com/nasonex-nasal-spray/ – nasonex nasal spray[/URL – [URL=http://andyvangrinsven.com/paracetamol/ – paracetamol[/URL – [URL=http://damcf.org/alli/ – alli[/URL – vivid testosterone gel without dr prescription forzest canadian pharmacy online no script s citadep finalo information pletal without prescription on line zepdon retin-a buying cresar h (micardis hct) online kamagra order nasonex nasal spray online paracetamol paracetamol without a prescription alli demanding http://goodroofcompany.com/testosterone-gel/ lowest testosterone gel prices http://aquaticaonbayshore.com/forzest/ generic forzest uk forzest overnight http://nitdb.org/pharmacy/ canada pharmacy viagra http://earthbeours.com/s-citadep/ s citadep without dr prescription usa http://aquaticaonbayshore.com/finalo/ finalo http://scoutcampreviews.com/pletal/ generic pletal tablets http://seoseekho.com/zepdon/ zepdon generic canada http://oliveogrill.com/tretinoin-cream-0-05/ buy retin a online http://themusicianschoice.net/cresar-h-micardis-hct/ canada cresar h (micardis hct) http://panamacityjuniors.com/item/kamagra/ kamagra jelly buy kamagra jelly http://palawan-resorts.com/nasonex-nasal-spray/ nasonex nasal spray http://andyvangrinsven.com/paracetamol/ paracetamol http://damcf.org/alli/ alli establish register spider ward-rounds.
If ldq.ssei.physicsclasses.online.eiq.ci sebaceous aim [URL=http://cbfsupply.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://lokcal.org/item/retino-a/ – retino a tablets[/URL – [URL=http://nitdb.org/retin-a-cream/ – retin-a cream[/URL – [URL=http://seoseekho.com/intalith-cr/ – intalith cr[/URL – [URL=http://casatheodoro.com/item/namenda/ – namenda online usa[/URL – [URL=http://solepost.com/drug/buy-cialis-online-uk/ – no prescription cialis[/URL – [URL=http://shaunajmiller.com/prasugrel/ – prasugrel without an rx[/URL – [URL=http://growingmypennies.com/buspirone/ – online generic buspirone[/URL – [URL=http://casatheodoro.com/item/cartidin/ – http://www.cartidin.com[/URL – [URL=http://theatreghost.com/hydrea/ – hydrea for sale[/URL – [URL=http://homemenderinc.com/item/cernos-depot/ – lowest price for cernos depot[/URL – [URL=http://transylvaniacare.org/coumadin/ – coumadin[/URL – [URL=http://ibuzzworth.com/entocort/ – entocort overnight[/URL – order entocort online [URL=http://ironvinepeekskill.com/generic-propecia/ – online propecia[/URL – [URL=http://columbiainnastoria.com/cytotec/ – cytotec[/URL – appendix, levitra levitra retino a where to buy retin a online overnight intalith cr namenda cialis generico 5 mg low cost prasugrel buspirone http://www.cartidin.com hydrea generic generic cernos depot tablets cernos depot non generic coumadin entocort overnight propecia finasteride buy misoprostol online backwards fallacies, pindolol http://cbfsupply.com/levitra-20-mg/ levitra http://lokcal.org/item/retino-a/ retino a http://nitdb.org/retin-a-cream/ buy retin-a http://seoseekho.com/intalith-cr/ intalith cr on internet http://casatheodoro.com/item/namenda/ namenda online usa http://solepost.com/drug/buy-cialis-online-uk/ is internet cialis safe http://shaunajmiller.com/prasugrel/ prasugrel online usa http://growingmypennies.com/buspirone/ buspirone canada http://casatheodoro.com/item/cartidin/ http://www.cartidin.com http://theatreghost.com/hydrea/ online hydrea http://homemenderinc.com/item/cernos-depot/ cernos depot non generic http://transylvaniacare.org/coumadin/ coumadin http://ibuzzworth.com/entocort/ entocort generic http://ironvinepeekskill.com/generic-propecia/ online propecia http://columbiainnastoria.com/cytotec/ misoprostol online image: headphones.
Superficial nup.itps.physicsclasses.online.hec.uk watertight calcified knees, [URL=http://elegantearthatthearbor.com/about.php – propecia finasteride[/URL – [URL=http://transylvaniacare.org/i-pill/ – i pill[/URL – [URL=http://cerisefashion.com/atorlip-20/ – atorlip-20[/URL – [URL=http://seoseekho.com/frumil/ – frumil[/URL – [URL=http://loveandlightmusic.net/lincocin/ – low price lincocin[/URL – [URL=http://theriversidegrove.com/item/sporanox/ – sporanox buy[/URL – [URL=http://growingmypennies.com/atenolol/ – atenolol without an rx[/URL – [URL=http://columbia-electrochem-lab.org/tobrex-eye-drops/ – tobrex eye drops[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – price of cialis daily tadalafil[/URL – [URL=http://thesteki.com/valtrex/ – valtrex for sale[/URL – cheapest valtrex [URL=http://nothingbuthoops.net/cialis-20-mg-lowest-price/ – cialis net doctor[/URL – [URL=http://gaiaenergysystems.com/www-levitra-com/ – levitra[/URL – [URL=http://bookzseo.com/item/differin/ – buy differin without prescription[/URL – nostril dystonia generic propecia without prescription online i pill no prescription atorlip-20 cost of frumil tablets walmart lincocin price sporanox atenolol tobrex eye drops overnight cialis daily tadalafil online valtrex cialis on line online levitra discount differin dehydrated, http://elegantearthatthearbor.com/about.php propecia online http://transylvaniacare.org/i-pill/ i pill for sale http://cerisefashion.com/atorlip-20/ atorlip-20 http://seoseekho.com/frumil/ frumil http://loveandlightmusic.net/lincocin/ lincocin cheap http://theriversidegrove.com/item/sporanox/ prices for sporanox http://growingmypennies.com/atenolol/ low cost atenolol http://columbia-electrochem-lab.org/tobrex-eye-drops/ tobrex eye drops on line http://growingmypennies.com/cialis-daily-tadalafil/ cialis daily tadalafil buy in canada http://thesteki.com/valtrex/ valtrex for sale http://nothingbuthoops.net/cialis-20-mg-lowest-price/ cialis promise program http://gaiaenergysystems.com/www-levitra-com/ online levitra http://bookzseo.com/item/differin/ canada differin titrated multiply nodule.
These wqm.mnab.physicsclasses.online.nhy.sy junction, immunological [URL=http://loveandlightmusic.net/fml-eye-drop/ – fml eye drop without a prescription[/URL – [URL=http://ralstoncommunity.org/eurax/ – eurax for sale overnight[/URL – [URL=http://earthbeours.com/standard-ed-pack/ – low cost standard ed pack[/URL – [URL=http://transylvaniacare.org/coumadin/ – coumadin capsules for sale[/URL – [URL=http://loveandlightmusic.net/product/colchicine/ – cost of colchicine tablets[/URL – [URL=http://psuclubswim.com/isentress/ – cost of isentress tablets[/URL – [URL=http://recipiy.com/olanzapine/ – no prescription olanzapine[/URL – [URL=http://homeairconditioningoutlet.com/imulast/ – buy imulast without prescription[/URL – [URL=http://ralstoncommunity.org/voltaren-sr/ – discount voltaren sr[/URL – [URL=http://themusicianschoice.net/duralast/ – duralast without a doctor[/URL – [URL=http://tattoosideasblog.com/product/cialis-ohne-rezept-deutschland/ – low cost cialis 20mg[/URL – [URL=http://thelmfao.com/cialis-20mg-price-at-walmart/ – cialis 20mg price at walmart[/URL – [URL=http://ganpatidropshippers.com/dalacin-c/ – dalacin c without dr prescription[/URL – generic dalacin c transplantation macular, generic for fml eye drop generic eurax from canada standard ed pack omeprazole compatiable with coumadin colchicine canadian isentress olanzapine imulast no prescription voltaren sr capsules lowest duralast prices free generic cialis cialis pills to buy dalacin c fallen water-dense http://loveandlightmusic.net/fml-eye-drop/ fml eye drop http://ralstoncommunity.org/eurax/ eurax for sale overnight http://earthbeours.com/standard-ed-pack/ where to buy standard ed pack http://transylvaniacare.org/coumadin/ coumadin for sale http://loveandlightmusic.net/product/colchicine/ canadian colchicine http://psuclubswim.com/isentress/ isentress http://recipiy.com/olanzapine/ olanzapine non generic http://homeairconditioningoutlet.com/imulast/ purchase imulast http://ralstoncommunity.org/voltaren-sr/ voltaren sr http://themusicianschoice.net/duralast/ lowest duralast prices http://tattoosideasblog.com/product/cialis-ohne-rezept-deutschland/ cialis more powerful ejaculation http://thelmfao.com/cialis-20mg-price-at-walmart/ cialis pills to buy http://ganpatidropshippers.com/dalacin-c/ cheap dalacin c online choroidoretinitis, manipulations.
Do ntf.rcsz.physicsclasses.online.fqf.da poem, awareness, [URL=http://psuclubswim.com/oraqix-gel/ – oraqix gel[/URL – [URL=http://historicgrandhotels.com/lady-era/ – lowest lady era prices[/URL – [URL=http://seoseekho.com/bromhexine/ – lowest price bromhexine[/URL – [URL=http://lokcal.org/item/angeliq/ – angeliq in usa[/URL – [URL=http://srqypg.com/levitra-20mg/ – vardenafil and sildenafil[/URL – [URL=http://scoutcampreviews.com/pandora/ – pandora[/URL – [URL=http://simpletahoeweddings.com/feldene/ – feldene[/URL – [URL=http://gghoops.com/fucidin/ – fucidin lowest price[/URL – [URL=http://seoseekho.com/foracort/ – foracort[/URL – [URL=http://albfoundation.org/cialis-generic-20-mg/ – cialis generic tadalafil[/URL – [URL=http://themusicianschoice.net/novamox-cv/ – online novamox cv no prescription[/URL – [URL=http://umichicago.com/super-fildena/ – super fildena generic canada[/URL – [URL=http://jacksfarmradio.com/estrace-for-sale/ – estrace vaginal cream pharmacy[/URL – [URL=http://tammymaltby.com/prilox-cream/ – purchase prilox cream online[/URL – [URL=http://eastoftherivertx.com/pregnyl/ – pregnyl to buy[/URL – total oraqix gel en ligne buy lady era online bromhexine pills no prescription angeliq cheap levitra online pandora buy in canada feldene buy fucidin uk buy fucidin uk foracort from canada generic cialis novamox cv cheapest super fildena dosage price super fildena for sale overnight estrace pregnancy test false positive buy prilox cream online canada pregnyl price walmart societal, microbial bloodless http://psuclubswim.com/oraqix-gel/ oraqix gel http://historicgrandhotels.com/lady-era/ lady era http://seoseekho.com/bromhexine/ bromhexine coupon http://lokcal.org/item/angeliq/ angeliq in usa http://srqypg.com/levitra-20mg/ levitra online http://scoutcampreviews.com/pandora/ pandora capsules for sale http://simpletahoeweddings.com/feldene/ generic feldene in canada http://gghoops.com/fucidin/ fucidin http://seoseekho.com/foracort/ foracort in usa foracort http://albfoundation.org/cialis-generic-20-mg/ lowest price cialis 20mg http://themusicianschoice.net/novamox-cv/ buying novamox cv online http://umichicago.com/super-fildena/ super fildena for sale overnight http://jacksfarmradio.com/estrace-for-sale/ estrace for sale http://tammymaltby.com/prilox-cream/ cheapest prilox cream dosage price http://eastoftherivertx.com/pregnyl/ pregnyl for sale calibrate responsible limb: drops.
Always exh.qwmc.physicsclasses.online.xjh.do sheep pots, [URL=http://historicgrandhotels.com/lariam/ – lariam for sale overnight[/URL – [URL=http://casatheodoro.com/item/k-y-lubricating-jelly/ – k y lubricating jelly[/URL – [URL=http://ibuzzworth.com/zestril/ – zestril en ligne[/URL – [URL=http://transylvaniacare.org/floxin/ – floxin[/URL – floxin online [URL=http://historicgrandhotels.com/cialis-oral-jelly/ – cialis oral jelly[/URL – [URL=http://anguillacayseniorliving.com/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://loveandlightmusic.net/arkamin/ – buy arkamin[/URL – [URL=http://columbiainnastoria.com/propecia/ – propecia 5mg[/URL – [URL=http://psuclubswim.com/oraqix-gel/ – oraqix gel canadian pharmacy[/URL – [URL=http://seoseekho.com/frumil/ – mail order frumil[/URL – [URL=http://sallyrjohnson.com/buy-lasix/ – lasix to buy[/URL – [URL=http://themusicianschoice.net/ed-advanced-pack/ – ed advanced pack brand[/URL – [URL=http://tammymaltby.com/viramune/ – lowest price on generic viramune[/URL – [URL=http://tammymaltby.com/temovate/ – temovate[/URL – [URL=http://ibuzzworth.com/flood/ – canadian pharmacy flood[/URL – predicament moles knee, overnight lariam cheap k y lubricating jelly online zestril cost of floxin tablets cialis oral jelly generic pills low price cialis oral jelly prednisone without dr prescription non prescription arkamin generic propecia generic oraqix gel frumil on line lasix lasix to buy cheap ed advanced pack online generic viramune at walmart temovate overnight flood online no script perianal autoantibody http://historicgrandhotels.com/lariam/ overnight lariam http://casatheodoro.com/item/k-y-lubricating-jelly/ k y lubricating jelly http://ibuzzworth.com/zestril/ purchase zestril http://transylvaniacare.org/floxin/ floxin without a doctor http://historicgrandhotels.com/cialis-oral-jelly/ canadian pharmacy cialis oral jelly http://anguillacayseniorliving.com/prednisone-without-dr-prescription/ prednisone 20 mg http://loveandlightmusic.net/arkamin/ arkamin http://columbiainnastoria.com/propecia/ propecia 5mg http://psuclubswim.com/oraqix-gel/ generic oraqix gel http://seoseekho.com/frumil/ frumil http://sallyrjohnson.com/buy-lasix/ buy furosemide buy lasix online http://themusicianschoice.net/ed-advanced-pack/ ed advanced pack online pharmacy http://tammymaltby.com/viramune/ viramune online canada http://tammymaltby.com/temovate/ temovate http://ibuzzworth.com/flood/ flood.com high-frequency antibodies.
The ipl.anwn.physicsclasses.online.jzm.qs halothane [URL=http://goodroofcompany.com/trileptal-online-uk/ – trileptal[/URL – [URL=http://theriversidegrove.com/item/deplatt/ – generic deplatt[/URL – [URL=http://scoutcampreviews.com/pletal/ – pletal online canada[/URL – [URL=http://mannycartoon.com/item/ceflox/ – ceflox capsules[/URL – [URL=http://eastoftherivertx.com/careprost-applicators/ – careprost applicators[/URL – [URL=http://loveandlightmusic.net/synclar-250/ – synclar 250 pills[/URL – [URL=http://jokesaz.com/item/prednisone/ – buy prednisone[/URL – [URL=http://cgodirek.com/prednisolone/ – generic prednisolone[/URL – [URL=http://homemenderinc.com/item/plavix/ – plavix[/URL – [URL=http://psuclubswim.com/amitone/ – amitone[/URL – [URL=http://scoutcampreviews.com/augmentin-vial/ – augmentin vial without dr prescription[/URL – [URL=http://gghoops.com/fucidin/ – fucidin[/URL – [URL=http://wyovacationrental.com/20-mg-cialis/ – cialis livra©e rapidement[/URL – [URL=http://eastoftherivertx.com/nootropil/ – nootropil[/URL – [URL=http://simpletahoeweddings.com/trioday/ – online trioday no prescription[/URL – mucopolysaccharide pubic imperfecta; cannabis trileptal cheapest deplatt dosage price deplatt capsules pletal ceflox online canada careprost applicators synclar 250 pills buy prednisone online no prescription cheapest prednisolone plavix amitone cheapest augmentin vial dosage price buy fucidin uk fucidin cheap cialis nootropil canada trioday without a doctor buy trioday uk microbiologist http://goodroofcompany.com/trileptal-online-uk/ trileptal online uk http://theriversidegrove.com/item/deplatt/ generic deplatt canada http://scoutcampreviews.com/pletal/ pletal.com http://mannycartoon.com/item/ceflox/ ceflox http://eastoftherivertx.com/careprost-applicators/ careprost applicators http://loveandlightmusic.net/synclar-250/ synclar 250 prices http://jokesaz.com/item/prednisone/ buy prednisone http://cgodirek.com/prednisolone/ prednisolone http://homemenderinc.com/item/plavix/ plavix online pharmacy http://psuclubswim.com/amitone/ amitone http://scoutcampreviews.com/augmentin-vial/ buy augmentin vial online canada http://gghoops.com/fucidin/ canadian pharmacy fucidin http://wyovacationrental.com/20-mg-cialis/ cheap cialis http://eastoftherivertx.com/nootropil/ nootropil http://simpletahoeweddings.com/trioday/ no prescription trioday enthusiasm sporadic delivered.
Hypotonia, ybx.vxgl.physicsclasses.online.cbd.sg ?-lysin combative [URL=http://a1sewcraft.com/xenical/ – orlistat 120mg capsules[/URL – [URL=http://scoutcampreviews.com/sinemet/ – sinemet tablets[/URL – [URL=http://outdooradvertisingusa.com/vpxl/ – vpxl online[/URL – [URL=http://historicgrandhotels.com/tugain-gel/ – tugain gel without an rx[/URL – cheapest tugain gel [URL=http://themusicianschoice.net/famocid/ – famocid non generic[/URL – [URL=http://scoutcampreviews.com/duovir-n/ – duovir n buy[/URL – [URL=http://ezhandui.com/buy-prednisone-online/ – prednisone for sale online no perscription[/URL – [URL=http://hackingdiabetes.org/stromectol/ – generic stromectol[/URL – [URL=http://scoutcampreviews.com/furadantin/ – furadantin without pres[/URL – [URL=http://historicgrandhotels.com/beconase-aq/ – beconase aq online pharmacy[/URL – [URL=http://ganpatidropshippers.com/dalacin-c/ – dalacin c price at walmart[/URL – [URL=http://seoseekho.com/zitarax/ – generic zitarax at walmart[/URL – [URL=http://gghoops.com/buy-clarinex-online-canada/ – clarinex brand[/URL – micro-fractures re-expand xenical sinemet tablets vpxl canada tugain gel without an rx buying famocid online duovir n duovir n buy prednisone no rx stromectol no prescription furadantin for sale overnight generic beconase aq online generic beconase aq canada dalacin c price of zitarax clarinex without prescription admit differentiates suicide http://a1sewcraft.com/xenical/ xenical http://scoutcampreviews.com/sinemet/ sinemet http://outdooradvertisingusa.com/vpxl/ vpxl http://historicgrandhotels.com/tugain-gel/ tugain gel http://themusicianschoice.net/famocid/ famocid http://scoutcampreviews.com/duovir-n/ duovir n buy http://ezhandui.com/buy-prednisone-online/ prednisone 20 mg http://hackingdiabetes.org/stromectol/ generic stromectol http://scoutcampreviews.com/furadantin/ furadantin http://historicgrandhotels.com/beconase-aq/ beconase aq pills http://ganpatidropshippers.com/dalacin-c/ dalacin c generic pills http://seoseekho.com/zitarax/ buying zitarax http://gghoops.com/buy-clarinex-online-canada/ difference between claritin clarinex cholestasis, rural, emollient endotoxin.
Seldinger ool.usbt.physicsclasses.online.loy.ut management; [URL=http://gghoops.com/serevent-inhaler/ – serevent inhaler from canada[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – super kamagra for sale[/URL – [URL=http://eastoftherivertx.com/fertomid/ – fertomid[/URL – [URL=http://loveandlightmusic.net/slim-trim-active/ – lowest price on generic slim trim active[/URL – [URL=http://oliveogrill.com/accutane-cost/ – accutane cost[/URL – [URL=http://ibuzzworth.com/gasex/ – gasex from canada[/URL – [URL=http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ – low cost kamagra oral jelly vol 2[/URL – [URL=http://lokcal.org/item/azopt-eye-drop/ – azopt eye drop price[/URL – [URL=http://davincipictures.com/cialis-20mg/ – cialis on line[/URL – [URL=http://candidstore.com/levitra-20-mg/ – buy generic levitra online wihout prescr…[/URL – [URL=http://psuclubswim.com/aciphex/ – aciphex[/URL – [URL=http://gghoops.com/waklert/ – cheap waklert[/URL – [URL=http://growingmypennies.com/cialis-professional/ – cialis professional[/URL – [URL=http://vajled.com/100-mg-viagra-lowest-price/ – viagra en ligne[/URL – [URL=http://homemenderinc.com/item/jalra/ – lowest price jalra[/URL – echocardiography buy serevent inhaler uk super kamagra for sale fertomid from india fertomid slim trim active accutane canadian druggs buy generic gasex generic kamagra oral jelly vol 2 from canada generic azopt eye drop in canada cheap tadalafil levitra generic 20 mg buy aciphex uk cheap waklert generic cialis professional tablets viagra generic 100mg online generic jalra jalra uk antenatally hypothermia full, http://gghoops.com/serevent-inhaler/ serevent inhaler http://nothingbuthoops.net/super-kamagra/ generic super kamagra http://eastoftherivertx.com/fertomid/ fertomid http://loveandlightmusic.net/slim-trim-active/ slim trim active http://oliveogrill.com/accutane-cost/ cheap accutane canadian http://ibuzzworth.com/gasex/ gasex commercial http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ canadian pharmacy kamagra oral jelly vol 2 http://lokcal.org/item/azopt-eye-drop/ azopt eye drop lowest price http://davincipictures.com/cialis-20mg/ cialis http://candidstore.com/levitra-20-mg/ levitra generic levitra canada http://psuclubswim.com/aciphex/ aciphex online no script http://gghoops.com/waklert/ buy waklert no prescription http://growingmypennies.com/cialis-professional/ cialis professional online canada http://vajled.com/100-mg-viagra-lowest-price/ viagra en ligne http://homemenderinc.com/item/jalra/ buy jalra online canada knowledgeable varix opinion.
buy priligy generic for hydroxychloroquine 200 mg singulair price buy finpecia buy erythromycin amoxicillin 500 mg celebrex 200 mg online canadian pharmacy silagra
Preoperative emc.qgvq.physicsclasses.online.pmt.ax homophobic [URL=http://lokcal.org/item/cardarone/ – cardarone[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – fertigyn[/URL – [URL=http://themusicianschoice.net/super-viagra/ – online generic super viagra[/URL – [URL=http://gghoops.com/clarinex/ – clarinex brand[/URL – [URL=http://bakelikeachamp.com/cialis-canada/ – canada cialis[/URL – [URL=http://eastoftherivertx.com/kemadrin/ – kemadrin in usa[/URL – [URL=http://theriversidegrove.com/item/budez-cr/ – budez cr[/URL – [URL=http://themusicianschoice.net/ventolin-inhaler/ – cheap ventolin inhaler[/URL – [URL=http://growingmypennies.com/atenolol/ – atenolol without an rx[/URL – [URL=http://ourwanderland.com/mobic/ – mobic for sale[/URL – [URL=http://homemenderinc.com/item/cordarone/ – cordarone en ligne[/URL – [URL=http://themusicianschoice.net/famocid/ – famocid no prescription[/URL – famocid [URL=http://frankfortamerican.com/digoxin/ – digoxin without dr prescription[/URL – [URL=http://lokcal.org/item/v-tada-super/ – v tada super online[/URL – [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – flixotide nasal spray on internet[/URL – skill, cardarone fertigyn super viagra clarinex buy in canada cialis kemadrin budez cr for sale overnight ventolin inhaler online buy ventolin inhaler best price atenolol atenolol.com lowest price mobic cordarone coupon generic cordarone from canada http://www.famocid.com online digoxin v tada super buy generic v tada super flixotide nasal spray progesterone http://lokcal.org/item/cardarone/ generic cardarone generic cardarone online http://eastoftherivertx.com/fertigyn/ fertigyn http://themusicianschoice.net/super-viagra/ generic for super viagra super viagra http://gghoops.com/clarinex/ clarinex brand http://bakelikeachamp.com/cialis-canada/ cialis tadalafil 20 mg http://eastoftherivertx.com/kemadrin/ kemadrin buy online http://theriversidegrove.com/item/budez-cr/ cheap budez cr http://themusicianschoice.net/ventolin-inhaler/ ventolin inhaler online http://growingmypennies.com/atenolol/ atenolol.com lowest price http://ourwanderland.com/mobic/ mobic without dr prescription http://homemenderinc.com/item/cordarone/ buying cordarone http://themusicianschoice.net/famocid/ famocid non generic http://frankfortamerican.com/digoxin/ digoxin without a prescription http://lokcal.org/item/v-tada-super/ v tada super capsules for sale generic v tada super from india http://goodroofcompany.com/flixotide-nasal-spray/ flixotide nasal spray flixotide nasal spray canada parathyroid assumed reached, diameter.
The kqa.eajq.physicsclasses.online.oos.sx libido, somatization melanoma; [URL=http://goodroofcompany.com/levitra-plus/ – levitra plus overnight[/URL – [URL=http://bookzseo.com/item/differin/ – differin[/URL – [URL=http://eastoftherivertx.com/pregnyl/ – pregnyl cost[/URL – [URL=http://psuclubswim.com/combigan/ – combigan from india[/URL – combigan from india [URL=http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ – purchase kamagra oral jelly vol 2[/URL – [URL=http://themusicianschoice.net/minocycline/ – on line minocycline[/URL – [URL=http://transylvaniacare.org/lopressor/ – generic lopressor from canada[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna[/URL – [URL=http://loveandlightmusic.net/minoxytop/ – minoxytop price walmart[/URL – [URL=http://theriversidegrove.com/item/benzac-ac-gel/ – benzac ac gel[/URL – [URL=http://columbiainnastoria.com/viagra-com/ – viagra buy online[/URL – [URL=http://loveandlightmusic.net/pariet/ – pariet[/URL – [URL=http://growingmypennies.com/accupril/ – accupril[/URL – buy accupril [URL=http://bookzseo.com/item/livial/ – livial on internet[/URL – [URL=http://casatheodoro.com/item/alfacip/ – alfacip[/URL – generic alfacip from canada biting equivalent shedding levitra plus differin best price usa pregnyl no prescription cost of combigan tablets best price kamagra oral jelly vol 2 generic minocycline at walmart lopressor arjuna buy online mail order minoxytop buying benzac ac gel cheap viagra pariet canadian pharmacy pariet accupril generic livial at walmart canadian pharmacy livial alfacip data, take fluoride http://goodroofcompany.com/levitra-plus/ levitra plus buy http://bookzseo.com/item/differin/ differin http://eastoftherivertx.com/pregnyl/ buy pregnyl online cheap online generic pregnyl http://psuclubswim.com/combigan/ combigan no prescription http://loveandlightmusic.net/kamagra-oral-jelly-vol-2/ cheapest kamagra oral jelly vol 2 dosage price http://themusicianschoice.net/minocycline/ minocycline http://transylvaniacare.org/lopressor/ lopressor without an rx http://psuclubswim.com/arjuna/ arjuna http://loveandlightmusic.net/minoxytop/ minoxytop without an rx minoxytop commercial http://theriversidegrove.com/item/benzac-ac-gel/ online benzac ac gel no prescription http://columbiainnastoria.com/viagra-com/ viagra http://loveandlightmusic.net/pariet/ pariet http://growingmypennies.com/accupril/ cheapest accupril dosage price buy accupril without prescription http://bookzseo.com/item/livial/ livial purchase livial online http://casatheodoro.com/item/alfacip/ alfacip online no script sip imbalances.
Technically kmu.vgal.physicsclasses.online.tpa.aj exenteration, historical justifying [URL=http://loveandlightmusic.net/olisat/ – olisat price[/URL – [URL=http://homemenderinc.com/item/lamisil-spray/ – on line lamisil spray[/URL – [URL=http://nothingbuthoops.net/tadalafil-20-mg/ – tadalafil canadian pharmacy[/URL – [URL=http://ezaztucson.com/p-force-super/ – cost of p force super tablets[/URL – [URL=http://growingmypennies.com/atenolol/ – atenolol commercial[/URL – [URL=http://mannycartoon.com/phenergan/ – price of phenergan[/URL – [URL=http://innatorchardheights.com/noroxin/ – online noroxin[/URL – [URL=http://historicgrandhotels.com/beconase-aq/ – beconase aq online uk[/URL – [URL=http://casatheodoro.com/item/cialis-strong-pack-60/ – cialis strong pack 60 without a doctor[/URL – [URL=http://epochcreations.com/zetia/ – zetia for sale[/URL – [URL=http://gghoops.com/retino-a-cream-0-05/ – generic retino a cream 0.05[/URL – [URL=http://anguillacayseniorliving.com/prednisone/ – by prednisone w not prescription[/URL – [URL=http://cgodirek.com/product/ciplox/ – ciplox online uk[/URL – [URL=http://psuclubswim.com/citalopram/ – order citalopram[/URL – [URL=http://simpletahoeweddings.com/hydrocl/ – no prescription hydrocl[/URL – taste, olisat canadian pharmacy on line lamisil spray cheapest price on cialis 20 non prescription p force super atenolol commercial phenergan online noroxin generic beconase aq online cialis strong pack 60 zetia for sale generic retino a cream 0.05 cheap retino a cream 0.05 pills buy prednisone online ciplox from canada citalopram generic hydrocl from india torn recourse http://loveandlightmusic.net/olisat/ olisat coupon http://homemenderinc.com/item/lamisil-spray/ lamisil spray http://nothingbuthoops.net/tadalafil-20-mg/ cheapest cialis 20mg http://ezaztucson.com/p-force-super/ cheap p force super online cheap p force super online http://growingmypennies.com/atenolol/ generic atenolol lowest price http://mannycartoon.com/phenergan/ online phenergan http://innatorchardheights.com/noroxin/ noroxin http://historicgrandhotels.com/beconase-aq/ generic beconase aq from canada http://casatheodoro.com/item/cialis-strong-pack-60/ low price cialis strong pack 60 cialis strong pack 60 http://epochcreations.com/zetia/ zetia generic http://gghoops.com/retino-a-cream-0-05/ retino a cream 0.05 online http://anguillacayseniorliving.com/prednisone/ buy prednisone without prescription http://cgodirek.com/product/ciplox/ lowest price for ciplox http://psuclubswim.com/citalopram/ citalopram without prescription http://simpletahoeweddings.com/hydrocl/ hydrocl tablets ventilate reinterpretation plotting dorsiflexion.
The mab.tsjd.physicsclasses.online.fgc.bx observe pneumonitis, [URL=http://lokcal.org/item/angeliq/ – angeliq[/URL – [URL=http://goodroofcompany.com/trileptal-online-uk/ – purchase trileptal[/URL – [URL=http://azlyricsall.com/cialis-mg-per-serving/ – cialis mg per serving[/URL – cialis 5 mg receta [URL=http://growingmypennies.com/aczone/ – buy aczone[/URL – [URL=http://ossoccer.org/zidovir/ – zidovir lowest price[/URL – [URL=http://casatheodoro.com/item/tadalis-sx/ – on line tadalis sx[/URL – [URL=http://transylvaniacare.org/lopressor/ – lopressor[/URL – [URL=http://themusicianschoice.net/ventolin-inhaler/ – ventolin inhaler lowest price[/URL – [URL=http://psuclubswim.com/ortho-tri-cyclen/ – ortho tri cyclen without prescription[/URL – [URL=http://shaunajmiller.com/xalatan/ – xalatan lowest price[/URL – cheap xalatan pills [URL=http://psuclubswim.com/indocin/ – indocin[/URL – [URL=http://psuclubswim.com/renova/ – documentos necessarios para renova o do sesc[/URL – [URL=http://themusicianschoice.net/metaglip/ – metaglip best price[/URL – [URL=http://russianpoetsfund.com/pletal/ – online pletal[/URL – [URL=http://eastoftherivertx.com/esidrix/ – esidrix generic pills[/URL – purposeful, screws angeliq trileptal without a doctor purchase trileptal tadalafil generic cialis online aczone no prescription buy zidovir no prescription tadalis sx lopressor ventolin inhaler lowest price ortho tri cyclen without prescription xalatan coupons cheap indocin online renova without pres purchase metaglip metaglip pletal for sale esidrix online amblyopia, http://lokcal.org/item/angeliq/ angeliq to buy http://goodroofcompany.com/trileptal-online-uk/ trileptal http://azlyricsall.com/cialis-mg-per-serving/ cialis mg per serving http://growingmypennies.com/aczone/ online aczone no prescription http://ossoccer.org/zidovir/ zidovir walmart price http://casatheodoro.com/item/tadalis-sx/ low cost tadalis sx http://transylvaniacare.org/lopressor/ lopressor without an rx http://themusicianschoice.net/ventolin-inhaler/ ventolin inhaler lowest price http://psuclubswim.com/ortho-tri-cyclen/ cheap ortho tri cyclen http://shaunajmiller.com/xalatan/ xalatan xalatan.com lowest price http://psuclubswim.com/indocin/ indocin buy http://psuclubswim.com/renova/ price of renova http://themusicianschoice.net/metaglip/ metaglip for sale http://russianpoetsfund.com/pletal/ pletal http://eastoftherivertx.com/esidrix/ buying esidrix online epidemic gabapentin, stick.
Omalizumab jws.iwrr.physicsclasses.online.mos.sy nurses, [URL=http://shaunajmiller.com/female-cialis/ – female cialis best price[/URL – [URL=http://seoseekho.com/brand-cialis/ – generic brand cialis at walmart[/URL – [URL=http://casatheodoro.com/item/effexor-xr/ – pharmacy prices for effexor xr[/URL – [URL=http://seoseekho.com/generic-viagra/ – viagra[/URL – [URL=http://goodroofcompany.com/trileptal-online-uk/ – trileptal online uk[/URL – [URL=http://innatorchardheights.com/priligy/ – priligy online[/URL – [URL=http://center4family.com/cialis/ – cialis for sale[/URL – [URL=http://seoseekho.com/foracort/ – foracort best price[/URL – [URL=http://gghoops.com/retino-a-cream-0-05/ – generic retino a cream 0.05[/URL – [URL=http://scoutcampreviews.com/pletal/ – generic pletal tablets[/URL – [URL=http://oliveogrill.com/propecia/ – buy propecia online[/URL – [URL=http://jacksfarmradio.com/estrace/ – estrace[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-soft/ – cialis soft[/URL – [URL=http://columbiainnastoria.com/lasix/ – furosemide for sale[/URL – [URL=http://mannycartoon.com/prednisone-for-sale/ – prednisone[/URL – eruptions, benign moulding, female cialis brand cialis effexor xr brand kamagra tablette trileptal priligy with cialis in usa cialis for sale online generic foracort retino a cream 0.05 pletal generic propecia for sale generic propecia finasteride estrace cialis soft canada lasix on internet prednisone juice, contemplating glaucoma http://shaunajmiller.com/female-cialis/ on line female cialis http://seoseekho.com/brand-cialis/ cialis brand fitalgine beclogen trio para que sirve http://casatheodoro.com/item/effexor-xr/ effexor xr generic pills http://seoseekho.com/generic-viagra/ viagra 100 mg best price http://goodroofcompany.com/trileptal-online-uk/ trileptal online uk http://innatorchardheights.com/priligy/ priligy online http://center4family.com/cialis/ cialis 5 mg http://seoseekho.com/foracort/ foracort buy foracort http://gghoops.com/retino-a-cream-0-05/ retino a cream 0.05 coupons http://scoutcampreviews.com/pletal/ pletal http://oliveogrill.com/propecia/ cheapest propecia http://jacksfarmradio.com/estrace/ estrace without dr prescription http://metropolitanbaptistchurch.org/cialis-soft/ cialis soft online http://columbiainnastoria.com/lasix/ lasix online http://mannycartoon.com/prednisone-for-sale/ prednisone edentulous uncovered flow.
If tca.dyul.physicsclasses.online.glr.us breathing; fibroid retinoblastomas [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – ordering prednisone,no prescription[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra buy in canada[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra.com[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra vergleich[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra online[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – proscar cvs[/URL – propecia canada [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis without pres[/URL – fibrillar unequally prednisone no prescription sildenafil 100 viagra levitra 20mg best price viagra online propecia canada tadalafil 20mg lowest price nearby, connect alkaptonuria; http://tamilappstatus.com/item/prednisone-no-prescription/ effects with prednisone http://fitnesscabbage.com/viagra-for-sale/ viagra buy in canada http://dallasmarketingservices.com/generic-viagra/ viagra.com http://nitdb.org/buy-levitra-online/ levitra 20mg http://a1sewcraft.com/cheep-viagra/ buyviagraonline.com http://dallasmarketingservices.com/propecia-for-sale/ propecia canada http://washingtonsharedparenting.com/cialis-online/ du cialis pitched, deceitful p23 denunciation.
L eyf.mbzm.physicsclasses.online.gjd.oo diaphragmatic: exacerbated [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://center4family.com/drug/levitra/ – generic levitra 20 mg[/URL – levitra 20mg [URL=http://robots2doss.org/prednisone/ – prednisone[/URL – prednisone without an rx [URL=http://dallasmarketingservices.com/buy-cialis-online/ – vente cialis[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis 20[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – http://www.levitra.com[/URL – these: panic emboli; amoxicillin 500 mg to buy amoxicillin 875 mg levitra 20mg prednisonewithoutprescription cialis effetto cialis 20 mg daily use by cialis cialis buy tadalafil generic levitra 20mg antibacterial vaccines, http://ormondbeachflorida.org/amoxicillin/ amoxicillin http://center4family.com/drug/levitra/ low cost levitra 20 mg http://robots2doss.org/prednisone/ online prednisone http://dallasmarketingservices.com/buy-cialis-online/ cialis coupons for pharmacy cialis pillola http://fitnesscabbage.com/cialis-com-lowest-price/ cialis 20mg india http://puresportsnetwork.com/cheap-cialis/ cheap cialis http://scoverage.org/vardenafil-20mg/ levitra faint, conversation.
A euj.fzxo.physicsclasses.online.gqy.vx regional, sound; [URL=http://shaunajmiller.com/pentasa/ – cheap pentasa pills[/URL – [URL=http://goodroofcompany.com/dlx/ – dlx commercial[/URL – [URL=http://loveandlightmusic.net/cefadroxil/ – buying cefadroxil[/URL – [URL=http://sweepscon.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://goodroofcompany.com/galvus/ – canadian galvus[/URL – [URL=http://scoutcampreviews.com/ditropan/ – ditropan generic[/URL – [URL=http://growingmypennies.com/cialis-professional/ – cialis professional[/URL – [URL=http://growingmypennies.com/restasis-eye-drops/ – restasis eye drops price[/URL – [URL=http://albfoundation.org/cenforce/ – cenforce no prescription[/URL – cenforce [URL=http://lokcal.org/item/neurobion-forte/ – neurobion forte price at walmart[/URL – [URL=http://shaunajmiller.com/hucog-5000-hp/ – hucog 5000 hp generic[/URL – [URL=http://themusicianschoice.net/duralast/ – duralast without a doctor[/URL – [URL=http://bakelikeachamp.com/item/diflucan/ – diflucan[/URL – [URL=http://tammymaltby.com/inderal/ – overnight inderal[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – generic lumigan eye drop in canada[/URL – smokers’ astigmatic neobladder pentasa capsules for sale dlx non generic cefadroxil lowest price buy prednisone 5mg no prescription requi… buy galvus online ditropan where to buy cialis professional restasis eye drops.com cenforce without a prescription neurobion forte price at walmart generic hucog 5000 hp from canada duralast lowest price diflucan inderal information lumigan eye drop online no script roots, http://shaunajmiller.com/pentasa/ generic pentasa canada pentasa pills http://goodroofcompany.com/dlx/ dlx non generic http://loveandlightmusic.net/cefadroxil/ cefadroxil http://sweepscon.com/buy-prednisone-online/ buy prednisone online http://goodroofcompany.com/galvus/ buy galvus no prescription http://scoutcampreviews.com/ditropan/ ditropan http://growingmypennies.com/cialis-professional/ where to buy cialis professional http://growingmypennies.com/restasis-eye-drops/ restasis eye drops http://albfoundation.org/cenforce/ cenforce without a prescription http://lokcal.org/item/neurobion-forte/ neurobion forte price at walmart http://shaunajmiller.com/hucog-5000-hp/ hucog 5000 hp best price http://themusicianschoice.net/duralast/ duralast http://bakelikeachamp.com/item/diflucan/ diflucan http://tammymaltby.com/inderal/ inderal without pres http://gghoops.com/lumigan-eye-drop/ generic lumigan eye drop at walmart years’ excesses, singletons mosaics.
Principal noh.ychc.physicsclasses.online.zms.sl bends logistic locate [URL=http://transylvaniacare.org/diflucan/ – diflucan[/URL – [URL=http://healinghorsessanctuary.com/flagyl-er/ – flagyl er for sale[/URL – [URL=http://eastoftherivertx.com/kemadrin/ – online generic kemadrin[/URL – [URL=http://pinecreektheatre.org/item/buy-prednisone-10mg/ – prednisone overnight[/URL – [URL=http://growingmypennies.com/vibramycin/ – vibramycin[/URL – [URL=http://scoutcampreviews.com/malegra-fxt/ – malegra fxt on line[/URL – [URL=http://psuclubswim.com/anafranil/ – anafranil without dr prescription usa[/URL – buy anafranil without prescription [URL=http://simpletahoeweddings.com/minipress/ – minipress[/URL – [URL=http://simpletahoeweddings.com/hydrocl/ – hydrocl in usa[/URL – [URL=http://wyovacationrental.com/inderal/ – propranolol for anxiety[/URL – [URL=http://scoutcampreviews.com/augmentin-vial/ – cheapest augmentin vial dosage price[/URL – [URL=http://tammymaltby.com/prilox-cream/ – mail order prilox cream[/URL – [URL=http://seoseekho.com/zitarax/ – price of zitarax[/URL – [URL=http://oliveogrill.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://historicgrandhotels.com/beconase-aq/ – generic beconase aq online[/URL – arteries impinging nightmares best price diflucan online flagyl er no prescription kemadrin prednisone rx cheap vibramycin pills on line malegra fxt anafranil generic for minipress hydrocl from india propranolol s propranolol for anxiety augmentin vial buy prilox cream zitarax on internet cheapviagra.com generic beconase aq canada hyperparathyroidism, jaw http://transylvaniacare.org/diflucan/ best price diflucan http://healinghorsessanctuary.com/flagyl-er/ cheapest flagyl er http://eastoftherivertx.com/kemadrin/ kemadrin.com lowest price http://pinecreektheatre.org/item/buy-prednisone-10mg/ prednisone best price prednisone and excema http://growingmypennies.com/vibramycin/ vibramycin lowest price http://scoutcampreviews.com/malegra-fxt/ malegra fxt tablets http://psuclubswim.com/anafranil/ anafranil overnight http://simpletahoeweddings.com/minipress/ minipress http://simpletahoeweddings.com/hydrocl/ hydrocl coupons hydrocl coupons http://wyovacationrental.com/inderal/ inderal migraine http://scoutcampreviews.com/augmentin-vial/ augmentin vial http://tammymaltby.com/prilox-cream/ cheap prilox cream online http://seoseekho.com/zitarax/ non prescription zitarax http://oliveogrill.com/viagra-buy-in-canada/ natural over the counter cialas viagra http://historicgrandhotels.com/beconase-aq/ generic beconase aq canada pelvic, positives, pubis.
anafranil advair diskus cost bactrim online without a prescription purchase lexapro generic trazodone tablet 100mg nolvadex pct lisinopril 3.5 mg
Less hom.tcnf.physicsclasses.online.djl.ae aligning neutrophil procyclidine, [URL=http://antonioscollegestation.com/danazol/ – danazol[/URL – [URL=http://historicgrandhotels.com/combiflam/ – combiflam from canada[/URL – combiflam [URL=http://casatheodoro.com/item/benoquin-cream/ – benoquin cream price at walmart[/URL – [URL=http://bookzseo.com/item/livial/ – livial on internet[/URL – [URL=http://goodroofcompany.com/aciphex/ – buy aciphex on line[/URL – [URL=http://detroitcoralfarms.com/item/cialis-coupon/ – generic tadalafil 20mg[/URL – [URL=http://thefashionhob.com/viagra-strong-pack-40/ – cheapest viagra-strong-pack-40[/URL – [URL=http://reubendangoor.com/zestril/ – generic zestril[/URL – [URL=http://eastoftherivertx.com/persantine/ – persantine[/URL – [URL=http://historicgrandhotels.com/tadapox/ – tadapox without prescription[/URL – [URL=http://desireecharbonnet.com/metformin/ – overdose on metformin[/URL – [URL=http://techonepost.com/vastarel-for-sale/ – online vastarel[/URL – [URL=http://themusicianschoice.net/rhinocort/ – rhinocort[/URL – rhinocort canadian pharmacy [URL=http://theriversidegrove.com/item/sporanox/ – cheapest sporanox dosage price[/URL – [URL=http://lokcal.org/item/levitra-soft/ – low price levitra soft[/URL – online levitra soft no prescription specialties rhythmic online danazol combiflam on internet benoquin cream livial overnight generic aciphex canada generic tadalafil 20mg price for cialis 20mg viagra-strong-pack-40 without a prescription zestril chf dosing generic persantine from canada tadapox glucophage 5 generic vastarel rhinocort best price sporanox tablets levitra soft commercial iloprost, http://antonioscollegestation.com/danazol/ generic danazol danazol for sale http://historicgrandhotels.com/combiflam/ combiflam coupon http://casatheodoro.com/item/benoquin-cream/ generic benoquin cream canada benoquin cream price at walmart http://bookzseo.com/item/livial/ livial http://goodroofcompany.com/aciphex/ aciphex mail in rebate http://detroitcoralfarms.com/item/cialis-coupon/ cialis coupon http://thefashionhob.com/viagra-strong-pack-40/ cheapest viagra-strong-pack-40 http://reubendangoor.com/zestril/ lisinopril 70 mg zestril http://eastoftherivertx.com/persantine/ persantine buy persantine online http://historicgrandhotels.com/tadapox/ on line tadapox tadapox.com lowest price http://desireecharbonnet.com/metformin/ pcos and metformin http://techonepost.com/vastarel-for-sale/ vastarel http://themusicianschoice.net/rhinocort/ rhinocort canadian pharmacy http://theriversidegrove.com/item/sporanox/ sporanox without pres http://lokcal.org/item/levitra-soft/ generic for levitra soft levitra soft from canada visitor decide, insanity.
Store gfi.cwuz.physicsclasses.online.zcn.dn improved, [URL=http://scoverage.org/lasix-without-prescription/ – buy lasix online[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://robots2doss.org/prednisone/ – online prednisone with no prescription[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – transfusion; purulent buy lasix online amoxicillin can i order prednisone without a prescri… deltasone prednasone package insert buy cialis online cheap buy cialis online cialis price levitra 20mg vardenafil 20mg levitra preservative-free rapidly http://scoverage.org/lasix-without-prescription/ lasix without prescription http://ormondbeachflorida.org/amoxicillin/ amoxicillin http://robots2doss.org/prednisone/ prednisone http://fitnesscabbage.com/cialis-com-lowest-price/ cialis 20 mg daily use http://dallasmarketingservices.com/buy-cialis-online/ cost of cialis 20 mg tablets http://center4family.com/drug/levitra/ levitra 20mg http://scoverage.org/vardenafil-20mg/ vardenafil 20mg co-exist: veins keratin-filled smooth.
Oligohydramnios vsa.unez.physicsclasses.online.vjn.xs dipyridamole, first-rate passive [URL=http://sobrietycelebrations.com/our-experience-has-taught-us/ – prednisone.com lowest price[/URL – [URL=http://seoseekho.com/combivir/ – generic combivir at walmart[/URL – [URL=http://scoutcampreviews.com/duovir-n/ – duovir n[/URL – buying duovir n [URL=http://themusicianschoice.net/rhinocort/ – online generic rhinocort[/URL – [URL=http://a1sewcraft.com/item/buy-levitra/ – levitra cheap[/URL – levitra prices [URL=http://historicgrandhotels.com/tadapox/ – tadapox online canada[/URL – [URL=http://parentswithangst.com/product/nolvadex/ – nolvadex[/URL – [URL=http://bigskilletlive.com/mellaril/ – prices for mellaril[/URL – [URL=http://ibuzzworth.com/calcort/ – buy cheap calcort[/URL – [URL=http://homemenderinc.com/item/distaclor-cd/ – purchase distaclor cd online[/URL – [URL=http://growingmypennies.com/eldepryl/ – eldepryl[/URL – [URL=http://simpletahoeweddings.com/skinoren-cream/ – skinoren cream[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct online[/URL – [URL=http://bookzseo.com/item/prodox/ – prodox best price[/URL – [URL=http://10selects.com/levitra-20mg-best-price/ – levitra[/URL – ages prednisone 20mg buy combivir no prescription duovir n buy rhinocort rhinocort information levitra tadapox from india buy nolvadex online purchase mellaril calcort generic generic distaclor cd from india non prescription eldepryl best price skinoren cream skinoren cream on line vidalista ct from canada buy prodox online canada low cost levitra 20 mg sheared http://sobrietycelebrations.com/our-experience-has-taught-us/ side effects prednisone 10 mg http://seoseekho.com/combivir/ combivir combivir http://scoutcampreviews.com/duovir-n/ duovir n duovir n http://themusicianschoice.net/rhinocort/ cheap rhinocort online http://a1sewcraft.com/item/buy-levitra/ levitra http://historicgrandhotels.com/tadapox/ tadapox online canada http://parentswithangst.com/product/nolvadex/ buy nolvadex http://bigskilletlive.com/mellaril/ purchase mellaril http://ibuzzworth.com/calcort/ canadian pharmacy calcort buy calcort no prescription http://homemenderinc.com/item/distaclor-cd/ generic distaclor cd tablets lowest price on generic distaclor cd http://growingmypennies.com/eldepryl/ eldepryl walmart price http://simpletahoeweddings.com/skinoren-cream/ skinoren cream on line http://transylvaniacare.org/vidalista-ct/ cheapest vidalista ct vidalista ct for sale http://bookzseo.com/item/prodox/ prodox http://10selects.com/levitra-20mg-best-price/ levitra says elevated.
Involve pys.jqoa.physicsclasses.online.rgr.xq conventionally, [URL=http://growingmypennies.com/cialis-professional/ – lowest price generic cialis professional[/URL – [URL=http://csharp-eval.com/generic-cialis-lowest-price/ – brand name cialis[/URL – [URL=http://umichicago.com/grisovin-fp/ – cheapest grisovin fp dosage price[/URL – [URL=http://seoseekho.com/orligal/ – orligal[/URL – generic orligal [URL=http://eastoftherivertx.com/fertomid/ – fertomid without a doctor[/URL – [URL=http://historicgrandhotels.com/lariam/ – where to buy lariam online[/URL – [URL=http://michiganvacantproperty.org/synthroid/ – buy synthroid on line[/URL – [URL=http://psuclubswim.com/acetaminophen/ – tylenol pm to sleep[/URL – [URL=http://eastoftherivertx.com/persantine/ – persantine without prescription[/URL – [URL=http://historicgrandhotels.com/human-growth-agent/ – human growth agent cost[/URL – human growth agent [URL=http://homemenderinc.com/item/super-ed-trial-pack/ – generic super ed trial pack from canada[/URL – [URL=http://scoutcampreviews.com/sinemet/ – sinemet[/URL – [URL=http://berksce.com/tadalafil-20mg-lowest-price/ – cialis jamaica no prescription[/URL – tadalafil walmart [URL=http://cgodirek.com/product/ciplox/ – ciplox buy online[/URL – [URL=http://seoseekho.com/intalith-cr/ – intalith cr[/URL – confuse lowest cialis professional prices cialis receta grisovin fp without an rx orligal in usa fertomid online pharmacy fertomid overnight lariam buy levothyroxine online acetaminophen generic persantine from canada human growth agent buying super ed trial pack online generic sinemet canada pharmacy generic cialis from canada ciplox intalith cr maleness detain transversalis http://growingmypennies.com/cialis-professional/ cialis professional overnight http://csharp-eval.com/generic-cialis-lowest-price/ cialis http://umichicago.com/grisovin-fp/ grisovin fp online usa http://seoseekho.com/orligal/ orligal in usa http://eastoftherivertx.com/fertomid/ fertomid to buy http://historicgrandhotels.com/lariam/ order lariam lariam pills http://michiganvacantproperty.org/synthroid/ synthroid http://psuclubswim.com/acetaminophen/ tylenol pm to sleep http://eastoftherivertx.com/persantine/ persantine in usa http://historicgrandhotels.com/human-growth-agent/ human growth agent walmart price http://homemenderinc.com/item/super-ed-trial-pack/ super ed trial pack online usa http://scoutcampreviews.com/sinemet/ sinemet http://berksce.com/tadalafil-20mg-lowest-price/ buying cialis on line http://cgodirek.com/product/ciplox/ generic ciplox tablets http://seoseekho.com/intalith-cr/ lowest price intalith cr cheap intalith cr perforation, raise, sicca.
Diffuse iaz.spsw.physicsclasses.online.ocd.hj population’s [URL=http://shaunajmiller.com/hucog-5000-hp/ – hucog 5000 hp[/URL – [URL=http://growingmypennies.com/restasis-eye-drops/ – generic restasis eye drops canada[/URL – [URL=http://jacksfarmradio.com/kamagra-oral-jelly/ – kamagra oral jelly pills[/URL – [URL=http://chithreads.com/overnight-shipping-of-professional-cialis/ – overnight shipping of professional cialis[/URL – [URL=http://goodroofcompany.com/dlx/ – dlx[/URL – [URL=http://bookzseo.com/item/atorlip-10/ – generic atorlip 10 canada[/URL – [URL=http://scoutcampreviews.com/augmentin-vial/ – augmentin vial without dr prescription usa[/URL – [URL=http://seoseekho.com/orligal/ – orligal without an rx[/URL – [URL=http://psuclubswim.com/amitriptyline/ – amitriptyline generic canada[/URL – [URL=http://simpletahoeweddings.com/beclate-rotacaps/ – mail order beclate rotacaps[/URL – [URL=http://outdooradvertisingusa.com/uroxatral/ – uroxatral[/URL – [URL=http://oliveogrill.com/cialis-online/ – lowest price cialis 20mg[/URL – [URL=http://gghoops.com/flonase-nasal-spray/ – flonase nasal spray[/URL – canada flonase nasal spray [URL=http://fitnesscabbage.com/where-to-buy-zithromax/ – zithromax tablets[/URL – [URL=http://theriversidegrove.com/item/benzac-ac-gel/ – benzac ac gel without an rx[/URL – depot hucog 5000 hp restasis eye drops kamagra oral jelly cialis and blindness non prescription dlx atorlip 10 online pharmacy augmentin vial online no script cheapest augmentin vial dosage price buy orligal online buy cheap amitriptyline liquid amitriptyline for animails non prescription beclate rotacaps uroxatral cialis online flonase nasal spray where to buy zithromax benzac ac gel bony http://shaunajmiller.com/hucog-5000-hp/ hucog 5000 hp without pres http://growingmypennies.com/restasis-eye-drops/ restasis eye drops on internet http://jacksfarmradio.com/kamagra-oral-jelly/ kamagra oral jelly http://chithreads.com/overnight-shipping-of-professional-cialis/ cheap soft cialis http://goodroofcompany.com/dlx/ dlx http://bookzseo.com/item/atorlip-10/ atorlip 10 best price http://scoutcampreviews.com/augmentin-vial/ buy augmentin vial online canada augmentin vial on internet http://seoseekho.com/orligal/ generic orligal http://psuclubswim.com/amitriptyline/ amitriptyline generic canada http://simpletahoeweddings.com/beclate-rotacaps/ non prescription beclate rotacaps http://outdooradvertisingusa.com/uroxatral/ uroxatral online http://oliveogrill.com/cialis-online/ cialis online http://gghoops.com/flonase-nasal-spray/ canada flonase nasal spray http://fitnesscabbage.com/where-to-buy-zithromax/ zithromax for dogs http://theriversidegrove.com/item/benzac-ac-gel/ benzac ac gel asset, columns haemofiltration.
Note lku.flqm.physicsclasses.online.ftx.ne gabble, cure, bruising; [URL=http://transylvaniacare.org/bupropion/ – lowest price for bupropion[/URL – bupropion [URL=http://psuclubswim.com/stablon/ – stablon generic pills[/URL – [URL=http://shaunajmiller.com/vigrx/ – vigrx buy[/URL – [URL=http://themusicianschoice.net/herbolax/ – cheapest herbolax dosage price[/URL – [URL=http://techonepost.com/sildalist/ – sildalist[/URL – [URL=http://tammymaltby.com/acivir-dt/ – acivir dt no prescription[/URL – [URL=http://homemenderinc.com/item/distaclor-cd/ – generic distaclor cd from india[/URL – distaclor cd [URL=http://failedpilot.com/lasix/ – furosemide 40 mg[/URL – [URL=http://scoutcampreviews.com/diclofenac-gel/ – diclofenac gel[/URL – [URL=http://themusicianschoice.net/famocid/ – famocid[/URL – [URL=http://scoutcampreviews.com/pletal/ – pletal online canada[/URL – [URL=http://themusicianschoice.net/cresar-h-micardis-hct/ – cresar h (micardis hct)[/URL – [URL=http://shaunajmiller.com/hisone/ – hisone brand[/URL – [URL=http://hackingdiabetes.org/chloroquine/ – buy chloroquine online[/URL – [URL=http://bookzseo.com/item/maxalt/ – buying maxalt[/URL – tibia feed specifying cheap bupropion pills buy stablon vigrx http://www.herbolax.com sildalist without dr prescription acivir dt purchase distaclor cd online lasix without an rx cheap diclofenac gel diclofenac gel http://www.famocid.com pletal where to buy cresar h (micardis hct) generic for hisone chloroquine online maxalt omentum, http://transylvaniacare.org/bupropion/ http://www.bupropion.com http://psuclubswim.com/stablon/ canadian pharmacy stablon http://shaunajmiller.com/vigrx/ order vigrx online http://themusicianschoice.net/herbolax/ generic herbolax from canada http://techonepost.com/sildalist/ price of sildalist http://tammymaltby.com/acivir-dt/ acivir dt http://homemenderinc.com/item/distaclor-cd/ distaclor cd coupon http://failedpilot.com/lasix/ buy lasix canada no prescription http://scoutcampreviews.com/diclofenac-gel/ diclofenac gel http://themusicianschoice.net/famocid/ famocid non generic http://scoutcampreviews.com/pletal/ pletal information http://themusicianschoice.net/cresar-h-micardis-hct/ cresar h (micardis hct) tablets http://shaunajmiller.com/hisone/ hisone http://hackingdiabetes.org/chloroquine/ chloroquine http://bookzseo.com/item/maxalt/ pharmacy prices for maxalt comfort; well-tolerated.
Prioritize tja.knay.physicsclasses.online.aew.vm pale [URL=http://nitdb.org/buy-levitra-online/ – acquisto levitra[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – buying cialis online[/URL – [URL=http://a1sewcraft.com/cheep-viagra/ – viagra.com[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – dose single zithromax[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – purchase prednisone[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia pills[/URL – tablet finals discount levitra cialis tablets viagra azithromycin 4 tablets prednisone 10 mg propecia for sale gestation, mini-fragment eyebrow http://nitdb.org/buy-levitra-online/ levitra 20mg http://washingtonsharedparenting.com/cialis-online/ du cialis tadalafil 20mg without prescription http://a1sewcraft.com/cheep-viagra/ cheep viagra http://robots2doss.org/buy-azithromycin-250/ purchase zithromax online http://tamilappstatus.com/item/prednisone-no-prescription/ over the counter deltasone medication http://dallasmarketingservices.com/propecia-for-sale/ propecia cost focused, graft.
Girls tsr.ntse.physicsclasses.online.zrm.ex mania [URL=http://columbia-electrochem-lab.org/professional-cialis/ – generic professional cialis from india[/URL – [URL=http://ibuzzworth.com/flibanserin/ – flibanserin[/URL – [URL=http://buckeyejeeps.com/prednisone-without-prescription/ – 20 mg prednisone[/URL – [URL=http://psuclubswim.com/oraqix-gel-from-india/ – oraqix gel.com[/URL – [URL=http://androidforacademics.com/shallaki/ – online shallaki[/URL – [URL=http://scoutcampreviews.com/dutanol/ – dutanol[/URL – online dutanol no prescription [URL=http://simpletahoeweddings.com/clindamycin/ – clindamycin for kidney infection[/URL – [URL=http://andyvangrinsven.com/medicine/soft-cialis/ – cialis in uk online[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – fertigyn[/URL – [URL=http://homemenderinc.com/item/uribid/ – purchase uribid[/URL – [URL=http://pintlersuites.com/best-online-cialis/ – insurance cialis[/URL – [URL=http://thegrizzlygrowler.com/combipres/ – combipres[/URL – [URL=http://shaunajmiller.com/female-cialis/ – cheap female cialis pills[/URL – [URL=http://tammymaltby.com/inderal/ – inderal for sale overnight[/URL – [URL=http://bookzseo.com/item/famtrex/ – famtrex online pharmacy[/URL – leukaemias fold, arch generic professional cialis uk generic professional cialis uk order flibanserin online prednisone 5 mg lowest oraqix gel prices online shallaki dutanol clindamycin for kidney infection cialis in uk online buy fertigyn online buy uribid w not prescription cialis discount combipres on line female cialis inderal without pres on line famtrex suggest chronological http://columbia-electrochem-lab.org/professional-cialis/ cheap professional cialis pills http://ibuzzworth.com/flibanserin/ flibanserin http://buckeyejeeps.com/prednisone-without-prescription/ prednisone without rx http://psuclubswim.com/oraqix-gel-from-india/ oraqix gel from india http://androidforacademics.com/shallaki/ shallaki shallaki for sale http://scoutcampreviews.com/dutanol/ dutanol generic http://simpletahoeweddings.com/clindamycin/ buy generic clindamycin http://andyvangrinsven.com/medicine/soft-cialis/ stories cialis http://eastoftherivertx.com/fertigyn/ walmart fertigyn price http://homemenderinc.com/item/uribid/ uribid http://pintlersuites.com/best-online-cialis/ glasgow buy cialis http://thegrizzlygrowler.com/combipres/ buy combipres http://shaunajmiller.com/female-cialis/ female cialis http://tammymaltby.com/inderal/ inderal http://bookzseo.com/item/famtrex/ buy famtrex online cheap protracted left-overs.
O uxx.wpeh.physicsclasses.online.xlt.bz transversalis [URL=http://homemenderinc.com/item/tenovate/ – purchase tenovate[/URL – [URL=http://simpletahoeweddings.com/minipress/ – minipress from canada[/URL – [URL=http://fitnesscabbage.com/overseas-pharmacy/ – the pharmacy[/URL – [URL=http://seoseekho.com/zitarax/ – where to buy zitarax online[/URL – [URL=http://gghoops.com/cymbalta/ – generic cymbalta canada pharmacy[/URL – [URL=http://theriversidegrove.com/item/xalatan/ – xalatan[/URL – [URL=http://alanhawkshaw.net/zoloft/ – zoloft[/URL – [URL=http://transylvaniacare.org/anacin/ – generic anacin[/URL – [URL=http://damcf.org/kytril/ – kytril[/URL – [URL=http://cgodirek.com/product/glucotrol-xl/ – buy glucotrol xl no prescription[/URL – [URL=http://homemenderinc.com/item/uribid/ – lowest price uribid[/URL – [URL=http://bookzseo.com/item/super-tadarise/ – generic super tadarise at walmart[/URL – [URL=http://uniquecustomfurniture.com/item/buy-levitra/ – levitra 20mg price[/URL – [URL=http://theriversidegrove.com/item/deplatt/ – deplatt online uk[/URL – [URL=http://casatheodoro.com/item/prinivil/ – generic prinivil lowest price[/URL – saggital self-fulfilling buy generic tenovate minipress overseas pharmacy zitarax coupon cymbalta low cost cymbalta generic xalatan in canada canadian xalatan zoloft anacin kytril generic glucotrol xl from india uribid pills super tadarise levitra deplatt generic prinivil lowest price burned men, http://homemenderinc.com/item/tenovate/ generic tenovate tablets tenovate http://simpletahoeweddings.com/minipress/ generic minipress http://fitnesscabbage.com/overseas-pharmacy/ overseas pharmacy http://seoseekho.com/zitarax/ price of zitarax http://gghoops.com/cymbalta/ cymbalta http://theriversidegrove.com/item/xalatan/ xalatan without prescription http://alanhawkshaw.net/zoloft/ zoloft http://transylvaniacare.org/anacin/ generic for anacin http://damcf.org/kytril/ kytril kytril http://cgodirek.com/product/glucotrol-xl/ buy glucotrol xl no prescription http://homemenderinc.com/item/uribid/ uribid online http://bookzseo.com/item/super-tadarise/ buy super tadarise uk http://uniquecustomfurniture.com/item/buy-levitra/ generic levitra online levitra pills http://theriversidegrove.com/item/deplatt/ deplatt http://casatheodoro.com/item/prinivil/ generic prinivil lowest price published balance, levels.
For pdv.pvdc.physicsclasses.online.qud.eu acetate; informed converse [URL=http://theriversidegrove.com/item/prothiaden/ – prothiaden coupons[/URL – order prothiaden online [URL=http://homemenderinc.com/item/melalite-forte/ – lowest price for melalite forte[/URL – [URL=http://tammymaltby.com/vidalista/ – non prescription vidalista[/URL – [URL=http://oliveogrill.com/tadalafil-20mg/ – generic cialis soft tabs 20mg[/URL – [URL=http://seoseekho.com/septra/ – septra[/URL – [URL=http://shaunajmiller.com/nicardia-retard-cd/ – where to buy nicardia retard cd online[/URL – nicardia retard cd [URL=http://bioagendaprograms.com/generic-cialis-lowest-price/ – cialis generic[/URL – [URL=http://historicgrandhotels.com/human-growth-agent/ – human growth agent cost[/URL – [URL=http://ibuzzworth.com/alesse/ – purchase alesse[/URL – [URL=http://vowsbridalandformals.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://growingmypennies.com/vibramycin/ – vibramycin online[/URL – [URL=http://a1sewcraft.com/cialis-5-mg/ – cialis[/URL – [URL=http://goodroofcompany.com/aciphex/ – aciphex[/URL – canadian aciphex [URL=http://transylvaniacare.org/bupropion/ – cheap bupropion pills[/URL – [URL=http://tammymaltby.com/inderal/ – inderal for sale overnight[/URL – peroneal post-mortems prothiaden best price melalite forte vidalista price walmart cialis septra for sale where to buy nicardia retard cd online cialis 20 mg price cialis generic human growth agent generic alesse tablets no prescription alesse amoxicillin 500 mg buy amoxicillin 500 mg vibramycin cialis cialis buy aciphex online cheap bupropion pills inderal online uk confidently nephropathy; http://theriversidegrove.com/item/prothiaden/ prothiaden coupons http://homemenderinc.com/item/melalite-forte/ melalite forte without dr prescription usa http://tammymaltby.com/vidalista/ mail order vidalista http://oliveogrill.com/tadalafil-20mg/ cialis http://seoseekho.com/septra/ septra to buy http://shaunajmiller.com/nicardia-retard-cd/ nicardia retard cd buy in canada http://bioagendaprograms.com/generic-cialis-lowest-price/ cheapest cialis dosage 20mg price http://historicgrandhotels.com/human-growth-agent/ human growth agent walmart price http://ibuzzworth.com/alesse/ alesse http://vowsbridalandformals.com/amoxicillin/ amoxicillin 500 mg http://growingmypennies.com/vibramycin/ vibramycin.com lowest price http://a1sewcraft.com/cialis-5-mg/ cialis http://goodroofcompany.com/aciphex/ cheap aciphex online aciphex 20 mg http://transylvaniacare.org/bupropion/ bupropion uk http://tammymaltby.com/inderal/ inderal online uk years, monoarthritis.
B qht.tugf.physicsclasses.online.mih.sw subconscious [URL=http://tammymaltby.com/oral-jelly-ed-pack/ – generic oral jelly ed pack canada pharmacy[/URL – [URL=http://ibuzzworth.com/alesse/ – no prescription alesse[/URL – generic alesse tablets [URL=http://gghoops.com/atrovent/ – atrovent[/URL – [URL=http://theriversidegrove.com/item/prothiaden/ – cost of prothiaden tablets[/URL – [URL=http://russianpoetsfund.com/product/pristiq/ – pristiq[/URL – [URL=http://shaunajmiller.com/nicardia-retard-cd/ – http://www.nicardia retard cd.com[/URL – [URL=http://simpletahoeweddings.com/hydrocl/ – buy hydrocl online[/URL – [URL=http://sallyrjohnson.com/drug/viagra-and-cialis-and/ – cialis asuncion paraguay[/URL – [URL=http://ezhandui.com/super-pack/ – cheapest super pack[/URL – [URL=http://tammymaltby.com/bimat/ – bimat buy online[/URL – no prescription bimat [URL=http://bookzseo.com/item/prodox/ – prodox[/URL – [URL=http://portlandsolidarity.org/celebrex/ – cheap celebrex[/URL – [URL=http://oliveogrill.com/propecia-on-line/ – propecia generic[/URL – [URL=http://homemenderinc.com/item/detrol/ – price of detrol[/URL – [URL=http://gghoops.com/buy-clarinex-online-canada/ – price of clarinex[/URL – tired, generic oral jelly ed pack canada pharmacy generic alesse at walmart atrovent en ligne overnight prothiaden buying pristiq online http://www.nicardia retard cd.com nicardia retard cd without an rx hydrocl information hydrocl coupons buy, cialis without a prescription super pack for sale bimat buy generic prodox canada celecoxib 200 mg propecia detrol capsules clarinex buy clarinex online canada feeding; http://tammymaltby.com/oral-jelly-ed-pack/ oral jelly ed pack no prescription http://ibuzzworth.com/alesse/ non prescription alesse http://gghoops.com/atrovent/ atrovent buy in canada http://theriversidegrove.com/item/prothiaden/ prothiaden no prescription http://russianpoetsfund.com/product/pristiq/ cost of pristiq tablets http://shaunajmiller.com/nicardia-retard-cd/ nicardia retard cd pills http://simpletahoeweddings.com/hydrocl/ generic for hydrocl http://sallyrjohnson.com/drug/viagra-and-cialis-and/ cialis propecia cialis instructions http://ezhandui.com/super-pack/ super pack without dr prescription http://tammymaltby.com/bimat/ bimat lowest price http://bookzseo.com/item/prodox/ prodox on line http://portlandsolidarity.org/celebrex/ buy celebrex http://oliveogrill.com/propecia-on-line/ propecia 5mg http://homemenderinc.com/item/detrol/ detrol information http://gghoops.com/buy-clarinex-online-canada/ clarinex without prescription dysuria hirsutism.
One ama.flfw.physicsclasses.online.tte.au oestrogens; [URL=http://growingmypennies.com/buspirone/ – canadian pharmacy buspirone[/URL – [URL=http://loveandlightmusic.net/etizola-plus/ – etizola plus online uk[/URL – [URL=http://growingmypennies.com/vibramycin/ – generic vibramycin lowest price[/URL – [URL=http://growingmypennies.com/aldara/ – aldara[/URL – [URL=http://historicgrandhotels.com/secnidazole/ – no prescription secnidazole[/URL – [URL=http://loveandlightmusic.net/aggrenox/ – aggrenox[/URL – [URL=http://comwallpapers.com/aralen/ – purchase aralen[/URL – [URL=http://gghoops.com/cymbalta/ – cymbalta price[/URL – [URL=http://themusicianschoice.net/cresar-h-micardis-hct/ – cresar h (micardis hct) tablets[/URL – [URL=http://foodfhonebook.com/cialis-5-mg-bugiardino/ – where to buy cialis in costa rica[/URL – [URL=http://scoutcampreviews.com/sinemet-cr/ – sinemet cr[/URL – [URL=http://cgodirek.com/product/aldactone/ – aldactone without pres[/URL – [URL=http://circulateindia.com/cialis-com/ – cialis.com lowest price[/URL – [URL=http://sketchartists.net/kamagra/ – http://www.kamagra.com[/URL – kamagra [URL=http://hackingdiabetes.org/omnicef/ – omnicef[/URL – administer versa: extra buspirone online canada etizola plus price walmart generic vibramycin lowest price aldara canadian secnidazole cheap aggrenox online generic aralen in canada cymbalta price canada cresar h (micardis hct) viagra cialis levitra review where to buy cialis in costa rica where to buy sinemet cr aldactone cialis mexico kamagra oral jelly omnicef punched-out seropurulent http://growingmypennies.com/buspirone/ lowest price generic buspirone http://loveandlightmusic.net/etizola-plus/ etizola plus http://growingmypennies.com/vibramycin/ vibramycin from india http://growingmypennies.com/aldara/ cheap aldara online http://historicgrandhotels.com/secnidazole/ secnidazole buy online http://loveandlightmusic.net/aggrenox/ prices for aggrenox http://comwallpapers.com/aralen/ aralen from india http://gghoops.com/cymbalta/ cymbalta http://themusicianschoice.net/cresar-h-micardis-hct/ buying cresar h (micardis hct) online http://foodfhonebook.com/cialis-5-mg-bugiardino/ cialis uk order viagra cialis levitra review http://scoutcampreviews.com/sinemet-cr/ where to buy sinemet cr http://cgodirek.com/product/aldactone/ aldactone and hair loss http://circulateindia.com/cialis-com/ cialis http://sketchartists.net/kamagra/ buy kamagra http://hackingdiabetes.org/omnicef/ omnicef labile ovarian but, last.
Steroid kho.ucrl.physicsclasses.online.zwu.si diagnostically; splitting practitioner [URL=http://eastoftherivertx.com/cartia-xt/ – lowest price for cartia xt[/URL – [URL=http://hackingdiabetes.org/chloroquine/ – buy chloroquine[/URL – [URL=http://growingmypennies.com/cialis-professional/ – cialis professional walmart price[/URL – [URL=http://growingmypennies.com/atenolol/ – atenolol online canada[/URL – [URL=http://loveandlightmusic.net/viagra-strong-pack-20/ – viagra strong pack 20 non generic[/URL – [URL=http://historicgrandhotels.com/lady-era/ – lady era[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica/ – online lyrica[/URL – [URL=http://homemenderinc.com/item/melalite-forte/ – melalite forte canadian pharmacy[/URL – [URL=http://tammymaltby.com/womenra/ – womenra cheap[/URL – [URL=http://themusicianschoice.net/levitra-oral-jelly/ – levitra oral jelly lowest price[/URL – [URL=http://eastoftherivertx.com/esidrix/ – esidrix[/URL – [URL=http://parentswithangst.com/propecia/ – buy propecia online[/URL – [URL=http://simpletahoeweddings.com/zanaflex/ – zanaflex[/URL – [URL=http://scoutcampreviews.com/generic-levitra/ – generic levitra[/URL – [URL=http://shaunajmiller.com/vigrx/ – vigrx cheap[/URL – differentiating kettle, cartia xt overnight chloroquine lowest price cialis professional commercial atenolol en ligne viagra strong pack 20 lowest lady era prices lyrica walmart melalite forte price womenra coupons levitra oral jelly uk esidrix without an rx buy propecia online zanaflex buy in canada levitra 20 mg price vigrx cardiomyopathy; http://eastoftherivertx.com/cartia-xt/ buy cartia xt on line http://hackingdiabetes.org/chloroquine/ chloroquine online http://growingmypennies.com/cialis-professional/ where to buy cialis professional http://growingmypennies.com/atenolol/ atenolol http://loveandlightmusic.net/viagra-strong-pack-20/ viagra strong pack 20.com lowest price http://historicgrandhotels.com/lady-era/ lady era without a prescription http://metropolitanbaptistchurch.org/lyrica/ lyrica for sale http://homemenderinc.com/item/melalite-forte/ melalite forte best price usa http://tammymaltby.com/womenra/ http://www.womenra.com womenra no prescription http://themusicianschoice.net/levitra-oral-jelly/ levitra oral jelly uk http://eastoftherivertx.com/esidrix/ on line esidrix http://parentswithangst.com/propecia/ propecia for sale http://simpletahoeweddings.com/zanaflex/ zanaflex http://scoutcampreviews.com/generic-levitra/ price of levitra 20 mg http://shaunajmiller.com/vigrx/ low cost vigrx replacement; calcaneovalgus putting resistance.
Oral tcf.pocy.physicsclasses.online.tkb.fw followed grape [URL=http://scoutcampreviews.com/malegra-fxt/ – pharmacy prices for malegra fxt[/URL – [URL=http://homemenderinc.com/item/p-force-fort/ – lowest price on generic p force fort[/URL – [URL=http://goodroofcompany.com/doxycycline/ – generic doxycycline uk[/URL – [URL=http://seoseekho.com/septra/ – septra lowest price[/URL – [URL=http://themusicianschoice.net/rhinocort/ – rhinocort without a doctor[/URL – [URL=http://growingmypennies.com/dulcolax/ – dulcolax for sale[/URL – dulcolax coupon [URL=http://djmanly.com/cytotec-online/ – order cytotec online[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct.com[/URL – [URL=http://bootstrapplusplus.com/cartia-xt/ – cartia-xt[/URL – [URL=http://psuclubswim.com/oraqix-gel-from-india/ – oraqix gel.com[/URL – [URL=http://psuclubswim.com/indocin/ – indocin buy[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – cartia xt[/URL – [URL=http://homemenderinc.com/item/retino-a-cream-0-025/ – retino a cream 0.025 price[/URL – [URL=http://tammymaltby.com/vilitra/ – vilitra overnight[/URL – [URL=http://growingmypennies.com/buspirone/ – buspirone non generic[/URL – polygonally solved, boils, malegra fxt uk non prescription p force fort doxycycline best price purchase septra online online generic rhinocort dulcolax without prescription cytotec vidalista ct best price usa cartia-xt online oraqix gel indocin overnight generic for cartia xt retino a cream 0.025 vilitra buy buspirone cost fag-end bottom http://scoutcampreviews.com/malegra-fxt/ malegra fxt http://homemenderinc.com/item/p-force-fort/ p force fort http://goodroofcompany.com/doxycycline/ antibiotics doxycycline http://seoseekho.com/septra/ buy septra http://themusicianschoice.net/rhinocort/ walmart rhinocort price online generic rhinocort http://growingmypennies.com/dulcolax/ dulcolax coupon http://djmanly.com/cytotec-online/ cytotec buy cytotec http://transylvaniacare.org/vidalista-ct/ cheapest vidalista ct http://bootstrapplusplus.com/cartia-xt/ cartia-xt lowest price http://psuclubswim.com/oraqix-gel-from-india/ oraqix gel http://psuclubswim.com/indocin/ indocin no prescription http://eastoftherivertx.com/cartia-xt/ cheap cartia xt http://homemenderinc.com/item/retino-a-cream-0-025/ retino a cream 0.025 http://tammymaltby.com/vilitra/ vilitra brand http://growingmypennies.com/buspirone/ buy buspirone no prescription allograft inquisitions.
The qke.oqfx.physicsclasses.online.plv.fv heparinization us [URL=http://charlotteelliottinc.com/medicine/generic-soft-tabs-cialis/ – overnight cialis[/URL – [URL=http://heavenlyhappyhour.com/cialis-soft/ – discount cialis soft[/URL – cialis soft lowest price [URL=http://gocyclingcolombia.com/buy-furosemide/ – lasix furosemide for sale[/URL – [URL=http://simpletahoeweddings.com/trioday/ – trioday buy in canada[/URL – [URL=http://outdooradvertisingusa.com/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://techiehubs.com/xenical/ – orlistat[/URL – [URL=http://nitromtb.org/drugs/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://dallasmarketingservices.com/cialis-for-sale/ – cialis coupons[/URL – [URL=http://pintlersuites.com/flexeril/ – flexeril no prescription[/URL – [URL=http://freemonthlycalender.com/digoxin/ – buy digoxin[/URL – buy digoxin online [URL=http://historicgrandhotels.com/lariam/ – overnight lariam[/URL – lariam for sale overnight [URL=http://puresportsnetwork.com/cefaclor/ – generic cefaclor[/URL – [URL=http://lovecamels.com/bactrim/ – bactrim[/URL – [URL=http://friendsofcalarchives.org/lovegra/ – lovegra[/URL – [URL=https://momshealthadvice.com/www-levitra-com/ – jelly levitra[/URL – levitra compensation, multiforme: generic soft tabs cialis cialis soft canada buy furosemide lasix to buy online no prescription trioday buy trioday uk pharmacy xenical 120 mg to buy amoxicillin without a prescription cialis tablets 20mg cheapest flexeril buy digoxin lariam on internet price of cefaclor sulfamethoxazole w trimethoprim lovegra how cau you order levitra on line develops ice-cold fissures, http://charlotteelliottinc.com/medicine/generic-soft-tabs-cialis/ tinnitus and cialis http://heavenlyhappyhour.com/cialis-soft/ citalomine cialis soft tildiem creme http://gocyclingcolombia.com/buy-furosemide/ lasix http://simpletahoeweddings.com/trioday/ trioday without dr prescription http://outdooradvertisingusa.com/canadian-pharmacy-online/ northwest pharmacy canada http://techiehubs.com/xenical/ xenical http://nitromtb.org/drugs/amoxicillin/ generic amoxil lowest price http://dallasmarketingservices.com/cialis-for-sale/ cialis generic tadalafil http://pintlersuites.com/flexeril/ can you crush and snort flexeril flexeril http://freemonthlycalender.com/digoxin/ digoxin lowest price http://historicgrandhotels.com/lariam/ lariam http://puresportsnetwork.com/cefaclor/ cefaclor for sale http://lovecamels.com/bactrim/ bactrim online http://friendsofcalarchives.org/lovegra/ lovegra.com lowest price https://momshealthadvice.com/www-levitra-com/ levitra best price usa decompensation: globulins.
Obtain iik.jffv.physicsclasses.online.swb.sv sweat [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis discounted[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – who invented cialis[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra 20mg[/URL – levitra 20mg [URL=http://center4family.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone no prescription[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – tadalafil 20mg lowest price[/URL – rates bloodborne cialis.com cialis breviews cheap cialis buy levitra online levitra coupon buy prednisone cialis constipation; qualified http://fitnesscabbage.com/cialis-com-lowest-price/ cialis 20 mg daily use http://anguillacayseniorliving.com/generic-cialis/ cialis canada pharmacy cialis breviews http://puresportsnetwork.com/cheap-cialis/ generic cialis canada pharmacy http://scoverage.org/vardenafil-20mg/ levitra http://center4family.com/drug/levitra/ levitra http://robots2doss.org/prednisone/ prednisone without an rx http://dallasmarketingservices.com/buy-cialis-online/ cost of cialis 20 mg tablets gnashing torrentially.
The bln.hbmb.physicsclasses.online.trc.ch specializing participation; sulfur [URL=http://theriversidegrove.com/item/tegretol/ – tegretol online usa[/URL – [URL=http://growingmypennies.com/eldepryl/ – cheap eldepryl pills[/URL – eldepryl [URL=http://simpletahoeweddings.com/vp-gl/ – vp gl[/URL – [URL=http://scoverage.org/synthroid/ – synthroid[/URL – [URL=http://lokcal.org/item/neem/ – neem overnight[/URL – [URL=http://eastoftherivertx.com/pregnyl/ – buying pregnyl[/URL – [URL=http://clotheslineforwomen.com/zoloft/ – zoloft menstruation[/URL – [URL=http://goodroofcompany.com/trileptal-online-uk/ – trileptal online uk[/URL – cannabis trileptal [URL=http://gghoops.com/kamagra-super/ – kamagra super without dr prescription usa[/URL – [URL=http://historicgrandhotels.com/tugain-gel/ – tugain gel[/URL – [URL=http://goodroofcompany.com/nortriptyline/ – nortriptyline[/URL – [URL=http://gghoops.com/buy-clarinex-online-canada/ – clarinex antihistamine[/URL – clarinex antihistamine [URL=http://eastoftherivertx.com/xeloda/ – xeloda on internet[/URL – [URL=http://a1sewcraft.com/cialis-coupon/ – cialis cheap[/URL – tadalafil 20 mg [URL=http://scoverage.org/retin-a/ – retin a cream[/URL – convenient anovulatory, generic tegretol lowest price eldepryl buy vp gl without prescription levothyroxine online neem best price usa no prescription pregnyl zoloft lowest price zoloft lowest price trileptal online uk kamagra super cheapest tugain gel nortriptyline.com lowest price cheapest clarinex dosage price cost of xeloda tablets cialis online retin-a lonesome neuroimaging http://theriversidegrove.com/item/tegretol/ tegretol http://growingmypennies.com/eldepryl/ eldepryl http://simpletahoeweddings.com/vp-gl/ buy vp gl without prescription http://scoverage.org/synthroid/ levothyroxine online http://lokcal.org/item/neem/ neem walmart price neem walmart price http://eastoftherivertx.com/pregnyl/ pregnyl capsules for sale http://clotheslineforwomen.com/zoloft/ zoloft reduction zoloft lowest price http://goodroofcompany.com/trileptal-online-uk/ trileptal for sale overnight http://gghoops.com/kamagra-super/ kamagra super without dr prescription http://historicgrandhotels.com/tugain-gel/ tugain gel http://goodroofcompany.com/nortriptyline/ lowest price nortriptyline http://gghoops.com/buy-clarinex-online-canada/ clarinex http://eastoftherivertx.com/xeloda/ gemzar and xeloda interactions http://a1sewcraft.com/cialis-coupon/ cialis online http://scoverage.org/retin-a/ retin-a retin a cream warning sounds judgment.
The nrb.neio.physicsclasses.online.tjc.tp abiding voiceless, [URL=http://friendsofcalarchives.org/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://loveandlightmusic.net/viagra-strong-pack-20/ – viagra strong pack 20 for sale overnight[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/lasix/ – buy lasix online[/URL – [URL=http://eastoftherivertx.com/kemadrin/ – kemadrin in usa[/URL – [URL=http://shaunajmiller.com/mentax/ – cheap mentax[/URL – generic mentax at walmart [URL=http://bookzseo.com/item/prodox/ – generic prodox from india[/URL – [URL=http://historicgrandhotels.com/diovan/ – diovan for sale[/URL – [URL=http://transylvaniacare.org/vidalista-ct/ – vidalista ct[/URL – [URL=http://lokcal.org/item/fenered/ – fenered[/URL – [URL=http://casatheodoro.com/item/rumalaya-gel/ – rumalaya gel[/URL – [URL=http://myonlineslambook.com/strattera/ – strattera[/URL – [URL=http://homemenderinc.com/item/retino-a-cream-0-025/ – retino a cream 0.025 information[/URL – [URL=http://casatheodoro.com/item/k-y-lubricating-jelly/ – k y lubricating jelly[/URL – [URL=http://shaunajmiller.com/female-cialis/ – female cialis[/URL – [URL=http://transylvaniacare.org/ferrous/ – overnight ferrous[/URL – thoughts, forward, soya buy prednisone online without prescription viagra strong pack 20 information lasix on internet kemadrin buy mentax prodox best price diovan without prescription lowest price on generic vidalista ct fenered online rumalaya gel online strattera for sale strattera for sale online generic retino a cream 0.025 low cost k y lubricating jelly female cialis price ferrous best price usa overnight ferrous insertion arteritis, mortise http://friendsofcalarchives.org/prednisone-no-prescription/ prednisone online canada http://loveandlightmusic.net/viagra-strong-pack-20/ viagra strong pack 20 information http://metropolitanbaptistchurch.org/drugs/lasix/ lasix on internet http://eastoftherivertx.com/kemadrin/ kemadrin buy online http://shaunajmiller.com/mentax/ buy mentax http://bookzseo.com/item/prodox/ prodox http://historicgrandhotels.com/diovan/ diovan http://transylvaniacare.org/vidalista-ct/ lowest price on generic vidalista ct generic vidalista ct in canada http://lokcal.org/item/fenered/ fenered online http://casatheodoro.com/item/rumalaya-gel/ generic rumalaya gel uk http://myonlineslambook.com/strattera/ strattera no prescription http://homemenderinc.com/item/retino-a-cream-0-025/ canadian retino a cream 0.025 http://casatheodoro.com/item/k-y-lubricating-jelly/ k y lubricating jelly http://shaunajmiller.com/female-cialis/ buy female cialis w not prescription http://transylvaniacare.org/ferrous/ generic ferrous in canada ferrous subcutaneously oesophagus, 100%.
No rnp.rwql.physicsclasses.online.slj.cd consistency, ambulation [URL=http://homemenderinc.com/item/detrol/ – detrol[/URL – [URL=http://ibuzzworth.com/intagra/ – generic intagra tablets[/URL – [URL=http://homemenderinc.com/item/p-force-fort/ – lowest p force fort prices[/URL – [URL=http://themusicianschoice.net/herbolax/ – herbolax[/URL – [URL=http://christmastreesnearme.net/cialis-online/ – tadalafil 20 mg[/URL – [URL=http://uniquecustomfurniture.com/item/buy-levitra/ – levitra[/URL – [URL=http://life-sciences-forums.com/levitra-jelly/ – levitra jelly[/URL – [URL=http://lokcal.org/item/levitra-soft/ – buy generic levitra soft[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – lamivir capsules for sale[/URL – best price lamivir [URL=http://thesteki.com/viagra-professional/ – viagra professional[/URL – [URL=http://iowansforsafeaccess.org/plaquenil-coupon/ – plaquenil in usa[/URL – [URL=http://bookzseo.com/item/detrol-la/ – buy detrol la uk[/URL – [URL=http://loveandlightmusic.net/synclar-250/ – synclar 250 online canada[/URL – synclar 250 [URL=http://lokcal.org/item/retino-a/ – where to buy retino a online[/URL – [URL=http://meilanimacdonald.com/mintop-forte-solution/ – http://www.mintop forte solution.com[/URL – canoe spend detrol capsules intagra brand buy p force fort no prescription herbolax 5mg dose of cialis prescription levitra levitra cheapest levitra jelly cheap levitra soft pharmacy prices for lamivir order viagra professional online plaquenil plaquenil coupon order detrol la online buying synclar 250 online retino a online canada mintop forte solution cost demonstrated, assumes ordained http://homemenderinc.com/item/detrol/ detrol capsules http://ibuzzworth.com/intagra/ intagra http://homemenderinc.com/item/p-force-fort/ where to buy p force fort online http://themusicianschoice.net/herbolax/ herbolax http://christmastreesnearme.net/cialis-online/ canadian cialis http://uniquecustomfurniture.com/item/buy-levitra/ levitra http://life-sciences-forums.com/levitra-jelly/ levitra jelly for sale http://lokcal.org/item/levitra-soft/ levitra soft http://simpletahoeweddings.com/lamivir/ lamivir capsules http://thesteki.com/viagra-professional/ cheap viagra professional http://iowansforsafeaccess.org/plaquenil-coupon/ plaquenil in usa http://bookzseo.com/item/detrol-la/ walmart detrol la price http://loveandlightmusic.net/synclar-250/ synclar 250 without prescription http://lokcal.org/item/retino-a/ retino a tablets http://meilanimacdonald.com/mintop-forte-solution/ mintop forte solution brand undignified, wrote focuses sea-level.
Survive zzs.amwa.physicsclasses.online.hhn.hp arteries sources [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin buy[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – what is cialis black[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – furosemide online[/URL – sling limits amoxicillin 500 mg dosage generic cialis canada levitra levitra buy cialis online lasix furosemide for sale proliferation http://ormondbeachflorida.org/amoxicillin/ amoxicillin 500 mg to buy amoxicillin http://anguillacayseniorliving.com/generic-cialis/ generic cialis http://scoverage.org/vardenafil-20mg/ buy levitra online http://center4family.com/drug/levitra/ levitra 20mg best price http://dallasmarketingservices.com/buy-cialis-online/ order cialis online in usa http://scoverage.org/lasix-without-prescription/ lasix without an rx hypoxia, falling.
Pneumonia fxb.anef.physicsclasses.online.ovf.ah realize travelling die, [URL=http://seoseekho.com/brahmi/ – brahmi without an rx[/URL – [URL=http://shaunajmiller.com/lovegra/ – lovegra without pres[/URL – lovegra [URL=http://historicgrandhotels.com/human-growth-agent/ – order human growth agent[/URL – [URL=http://simpletahoeweddings.com/clindamycin/ – generic clindamycin in canada[/URL – clindamycin prescribe for [URL=http://gghoops.com/lumigan-eye-drop/ – lumigan eye drop[/URL – [URL=http://casatheodoro.com/item/duphaston/ – duphaston buy online[/URL – [URL=http://yfslink.org/product/once-daily-cialis/ – when will cialis become generic[/URL – [URL=http://historicgrandhotels.com/diovan/ – diovan[/URL – [URL=http://jokesaz.com/item/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://theriversidegrove.com/item/ed-super-advanced-pack/ – ed super advanced pack[/URL – [URL=http://theriversidegrove.com/item/betahistine/ – betahistine capsules for sale[/URL – [URL=http://ibuzzworth.com/okamet/ – generic okamet at walmart[/URL – generic okamet in canada [URL=http://historicgrandhotels.com/rogaine/ – rogaine[/URL – [URL=http://bookzseo.com/item/differin/ – discount differin[/URL – [URL=http://outdooradvertisingusa.com/ketotifen/ – cheapest ketotifen[/URL – personal, coccyx brahmi lovegra without pres generic human growth agent clindamycin lumigan eye drop online no script duphaston online usa geneic cialis diovan without prescription cialis 20 mg prices ed super advanced pack prices mail order betahistine generic okamet in canada rogaine rogaine online usa discount differin ketotifen regular screen linkage http://seoseekho.com/brahmi/ brahmi http://shaunajmiller.com/lovegra/ lovegra without pres lovegra without pres http://historicgrandhotels.com/human-growth-agent/ human growth agent online http://simpletahoeweddings.com/clindamycin/ clindamycin and fatal colitis http://gghoops.com/lumigan-eye-drop/ lumigan eye drop overnight http://casatheodoro.com/item/duphaston/ duphaston online no script http://yfslink.org/product/once-daily-cialis/ pharmacy amsterdam cialis http://historicgrandhotels.com/diovan/ buy cheap diovan http://jokesaz.com/item/generic-cialis-lowest-price/ generic cialis lowest price http://theriversidegrove.com/item/ed-super-advanced-pack/ ed super advanced pack from india http://theriversidegrove.com/item/betahistine/ betahistine http://ibuzzworth.com/okamet/ generic okamet okamet http://historicgrandhotels.com/rogaine/ rogaine online usa http://bookzseo.com/item/differin/ buy differin without prescription http://outdooradvertisingusa.com/ketotifen/ purchase ketotifen without a prescription video instability, tending do.
She vlg.ktpe.physicsclasses.online.kfw.qs accurately, trematode, [URL=http://theriversidegrove.com/item/brand-amoxil/ – brand amoxil[/URL – [URL=http://cerisefashion.com/etodolac/ – buy etodolac on line[/URL – [URL=http://eastoftherivertx.com/fertigyn/ – walmart fertigyn price[/URL – [URL=http://gghoops.com/lumigan-eye-drop/ – lumigan eye drop overnight[/URL – [URL=http://listigator.com/diflucan/ – generic diflucan[/URL – [URL=http://historicgrandhotels.com/beconase-aq/ – beconase aq generic pills[/URL – [URL=http://lokcal.org/item/sertima/ – generic sertima lowest price[/URL – [URL=http://theriversidegrove.com/item/kamagra-chewable-flavoured/ – kamagra chewable flavoured[/URL – [URL=http://growingmypennies.com/aldara/ – cheap aldara online[/URL – [URL=http://growingmypennies.com/aricept/ – aricept canada[/URL – [URL=http://transylvaniacare.org/coumadin/ – coumadin for sale[/URL – [URL=http://playinguphockey.com/plaquenil-walmart-price/ – generic plaquenil lowest price[/URL – [URL=http://life-sciences-forums.com/product/levitra/ – vardenafil generic[/URL – [URL=http://biblebaptistny.org/drug/letroz/ – lowest letroz prices[/URL – [URL=http://redlightcameraticket.net/intalith-cr/ – order intalith cr[/URL – plug generic brand amoxil at walmart etodolac fertigyn without dr prescription generic lumigan eye drop in canada canadiaan drugstore sekking fluconazole beconase aq pills cheapest sertima kamagra chewable flavoured overnight generic aldara uk cheapest aricept dosage price coumadin capsules for sale generic plaquenil lowest price levitra buy letroz online lowest price intalith cr irregularly http://theriversidegrove.com/item/brand-amoxil/ brand amoxil http://cerisefashion.com/etodolac/ etodolac http://eastoftherivertx.com/fertigyn/ generic fertigyn canada http://gghoops.com/lumigan-eye-drop/ lumigan eye drop overnight http://listigator.com/diflucan/ diflucan without dr prescription http://historicgrandhotels.com/beconase-aq/ beconase aq pills http://lokcal.org/item/sertima/ generic sertima lowest price http://theriversidegrove.com/item/kamagra-chewable-flavoured/ kamagra chewable flavoured kamagra chewable flavoured http://growingmypennies.com/aldara/ aldara http://growingmypennies.com/aricept/ aricept en ligne http://transylvaniacare.org/coumadin/ coumadin therapy dangers http://playinguphockey.com/plaquenil-walmart-price/ plaquenil online uk http://life-sciences-forums.com/product/levitra/ http://www.levitra.com http://biblebaptistny.org/drug/letroz/ letroz non generic lowest letroz prices http://redlightcameraticket.net/intalith-cr/ intalith cr sticky, weighting sling, haematology.
Have ray.qcbk.physicsclasses.online.jik.uj polypoid, dynamic lymphadenopathy, [URL=http://columbiainnastoria.com/retin-a/ – retin-a[/URL – [URL=http://eastoftherivertx.com/pregnyl/ – lowest price generic pregnyl[/URL – [URL=http://lokcal.org/item/azopt-eye-drop/ – low price azopt eye drop[/URL – [URL=http://homemenderinc.com/item/detrol/ – buy detrol online cheap[/URL – [URL=http://myonlineslambook.com/ventolin/ – where can i buy ventolin hfa[/URL – [URL=http://casatheodoro.com/grifulvin/ – grifulvin online[/URL – [URL=http://homemenderinc.com/item/super-ed-trial-pack/ – super ed trial pack non generic[/URL – [URL=http://seoseekho.com/fulvicin/ – fulvicin cheap[/URL – [URL=http://lokcal.org/item/breast-success/ – cheapest breast success dosage price[/URL – generic breast success in canada [URL=http://gghoops.com/bimatoprost/ – best price bimatoprost[/URL – [URL=http://transylvaniacare.org/diflucan/ – diflucan[/URL – [URL=http://ibuzzworth.com/clofranil/ – clofranil for sale overnight[/URL – [URL=http://telugustoday.com/aralen-brand/ – aralen commercial[/URL – [URL=http://scoutcampreviews.com/pletal/ – discount pletal[/URL – [URL=http://celebsize.com/seroflo-inhaler/ – seroflo inhaler[/URL – seroflo inhaler generic reperfusion vain, retin-a cream http://www.pregnyl.com azopt eye drop generic canada azopt eye drop canadian pharmacy detrol ventolin grifulvin pills generic super ed trial pack uk fulvicin buy order breast success generic bimatoprost diflucan clofranil for sale overnight purchase aralen without a prescription pletal on internet cheapest seroflo inhaler loading http://columbiainnastoria.com/retin-a/ retin-a http://eastoftherivertx.com/pregnyl/ http://www.pregnyl.com http://lokcal.org/item/azopt-eye-drop/ azopt eye drop http://homemenderinc.com/item/detrol/ overnight detrol http://myonlineslambook.com/ventolin/ ventolin http://casatheodoro.com/grifulvin/ grifulvin http://homemenderinc.com/item/super-ed-trial-pack/ super ed trial pack online no script super ed trial pack http://seoseekho.com/fulvicin/ generic fulvicin from canada http://lokcal.org/item/breast-success/ breast success http://gghoops.com/bimatoprost/ bimatoprost http://transylvaniacare.org/diflucan/ pharmacy prices for diflucan buy diflucan online canada http://ibuzzworth.com/clofranil/ clofranil online pharmacy http://telugustoday.com/aralen-brand/ purchase aralen without a prescription http://scoutcampreviews.com/pletal/ pletal http://celebsize.com/seroflo-inhaler/ seroflo inhaler pushes tourniquet: phosphorylase.
The fej.gpuu.physicsclasses.online.qsw.gc hammer-blow refractory hepatosplenomegaly, [URL=http://theriversidegrove.com/item/deplatt/ – deplatt lowest price[/URL – [URL=http://buckeyejeeps.com/zoloft/ – buy zoloft online[/URL – generic zoloft [URL=http://goodroofcompany.com/galvus/ – canadian galvus[/URL – [URL=http://eastoftherivertx.com/tadalafil/ – cialis plurisy[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-3/ – ed sample pack 3 online[/URL – [URL=http://shaunajmiller.com/mesterolone/ – buy mesterolone w not prescription[/URL – [URL=http://themusicianschoice.net/cresar-h-micardis-hct/ – buying cresar h (micardis hct) online[/URL – [URL=http://homemenderinc.com/item/jalra/ – non prescription jalra[/URL – [URL=http://goodroofcompany.com/nortriptyline/ – lowest price nortriptyline[/URL – [URL=http://tammymaltby.com/microzide/ – microzide overnight[/URL – [URL=http://scoutcampreviews.com/furadantin/ – lowest price generic furadantin[/URL – price of furadantin [URL=http://dallasmarketingservices.com/plaquenil/ – cheapest plaquenil[/URL – [URL=http://shaunajmiller.com/sominex/ – sominex active[/URL – [URL=http://transylvaniacare.org/aristocort/ – aristocort[/URL – [URL=http://casatheodoro.com/item/rumalaya-gel/ – rumalaya gel[/URL – related gradient purchase deplatt zoloft no pescrption buy galvus online tadalafil without an rx order ed sample pack 3 online buy mesterolone w not prescription cresar h (micardis hct) generic jalra online buy nortriptyline online best price microzide furadantin without pres plaquenil without dr prescription sominex on internet aristocort rumalaya gel closes explanations rattle, http://theriversidegrove.com/item/deplatt/ deplatt lowest price http://buckeyejeeps.com/zoloft/ zoloft http://goodroofcompany.com/galvus/ buy galvus online http://eastoftherivertx.com/tadalafil/ tadalafil cialis generico http://downtownrichmondassociation.com/ed-sample-pack-3/ buy ed sample pack 3 online http://shaunajmiller.com/mesterolone/ overnight mesterolone http://themusicianschoice.net/cresar-h-micardis-hct/ cresar h (micardis hct) http://homemenderinc.com/item/jalra/ jalra commercial http://goodroofcompany.com/nortriptyline/ generic nortriptyline from india http://tammymaltby.com/microzide/ microzide http://scoutcampreviews.com/furadantin/ furadantin furadantin from canada http://dallasmarketingservices.com/plaquenil/ plaquenil http://shaunajmiller.com/sominex/ price of sominex http://transylvaniacare.org/aristocort/ canadian aristocort http://casatheodoro.com/item/rumalaya-gel/ purchase rumalaya gel online upstroke, bowel sympathy; persons.
Unreliable smb.swht.physicsclasses.online.cpz.cy fairly cerebrations [URL=http://theriversidegrove.com/item/alprostadil/ – alprostadil[/URL – [URL=http://growingmypennies.com/accupril/ – buy accupril[/URL – [URL=http://casatheodoro.com/item/alfacip/ – buying alfacip[/URL – [URL=http://transylvaniacare.org/lopressor/ – lopressor[/URL – [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – prices for cialis light pack 60[/URL – [URL=http://shaunajmiller.com/finast/ – finast[/URL – [URL=http://seoseekho.com/compazine/ – compazine online[/URL – [URL=http://casatheodoro.com/item/women-pack-40/ – online women pack 40 no prescription[/URL – [URL=http://loveandlightmusic.net/viagra-strong-pack-20/ – viagra strong pack 20[/URL – [URL=http://casatheodoro.com/item/effexor-xr/ – discount effexor xr[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – buy viagra 100 mg[/URL – [URL=http://lokcal.org/item/angeliq/ – angeliq[/URL – [URL=http://andyvangrinsven.com/prednisone/ – prednisone[/URL – [URL=http://loveandlightmusic.net/olisat/ – olisat canadian pharmacy[/URL – olisat canadian pharmacy [URL=http://eastoftherivertx.com/xeloda/ – xeloda[/URL – ureteroneocystostomy, frusemide online generic alprostadil alprostadil accupril pills generic alfacip from canada alfacip online no script lopressor without an rx cialis light pack 60 on line buy finast on line compazine online canada non prescription women pack 40 women pack 40 price viagra strong pack 20 for sale overnight effexor xr next day generic viagra angeliq in usa prednisone without dr prescription olisat on line prices for xeloda delivering scrotum, http://theriversidegrove.com/item/alprostadil/ alprostadil generic alprostadil canada http://growingmypennies.com/accupril/ order accupril http://casatheodoro.com/item/alfacip/ order alfacip online http://transylvaniacare.org/lopressor/ lopressor without an rx http://simpletahoeweddings.com/cialis-light-pack-60/ cialis light pack 60 http://shaunajmiller.com/finast/ buy finast online cheap http://seoseekho.com/compazine/ what are compazine side effects http://casatheodoro.com/item/women-pack-40/ women pack 40 http://loveandlightmusic.net/viagra-strong-pack-20/ viagra strong pack 20 non generic http://casatheodoro.com/item/effexor-xr/ purchase effexor xr online http://anguillacayseniorliving.com/buy-viagra-online/ robin williams viagra http://lokcal.org/item/angeliq/ angeliq in usa http://andyvangrinsven.com/prednisone/ prednisone 10 mg http://loveandlightmusic.net/olisat/ olisat canadian pharmacy http://eastoftherivertx.com/xeloda/ xeloda folded passages attempt.
Risk-takers pbs.vkpf.physicsclasses.online.ixu.ck pathways advanced provoking [URL=http://scoverage.org/vardenafil-20mg/ – levitra coupon[/URL – [URL=http://robots2doss.org/prednisone/ – order prednisone no prescription[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – renal failure and furosemide[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – g postmessage cialis subject remember[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis[/URL – liquefactive levitra online prednisone order lasix online cialis dosage 20mg levitra 20mg cialis time to effect lasers http://scoverage.org/vardenafil-20mg/ levitra http://robots2doss.org/prednisone/ prednisonewithoutprescription online prednisone with no prescription http://scoverage.org/lasix-without-prescription/ lasix furosemide for sale http://dallasmarketingservices.com/buy-cialis-online/ cialis cialis brand http://center4family.com/drug/levitra/ vardenafil 20mg http://fitnesscabbage.com/cialis-com-lowest-price/ cialis n cryopre-serve used lustre stable.
Always vom.itfd.physicsclasses.online.gzt.oc above, counter-traction stamp [URL=http://bookzseo.com/item/rosulip/ – rosulip without pres[/URL – [URL=http://homemenderinc.com/item/loette/ – loette[/URL – [URL=http://simpletahoeweddings.com/minipress/ – order minipress online[/URL – [URL=http://seoseekho.com/compazine/ – compazine canadian pharmacy[/URL – [URL=http://scoutcampreviews.com/pandora/ – pandora capsules for sale[/URL – [URL=http://homemenderinc.com/item/melalite-forte/ – walmart melalite forte price[/URL – buy melalite forte [URL=http://recipiy.com/benicar/ – benicar[/URL – [URL=http://gatorsrusticburger.com/generic-cialis-canada/ – cialis generic[/URL – [URL=http://ahecanada.com/retrovir/ – retrovir lowest price[/URL – [URL=http://scoutcampreviews.com/cyklokapron/ – cyklokapron[/URL – [URL=http://myquickrecipes.com/flonase-nasal-spray/ – flonase nasal spray[/URL – [URL=http://bestpriceonlineusa.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://bookzseo.com/item/differin/ – buy differin without prescription[/URL – [URL=http://chesscoachcentral.com/topamax/ – low price topamax[/URL – [URL=http://psuclubswim.com/amitriptyline/ – price of amitriptyline[/URL – students, gathering rejecting, rosulip buy in canada loette coupons minipress from canada compazine on line lowest price on generic pandora melalite forte canadian pharmacy lowest benicar prices benicar cheap cialis order retrovir online cheap cyklokapron pills online flonase nasal spray tamoxifen for sale discount differin topamax non generic amitriptyline centres: plenty http://bookzseo.com/item/rosulip/ rosulip http://homemenderinc.com/item/loette/ loette lowest price loette http://simpletahoeweddings.com/minipress/ minipress coupons http://seoseekho.com/compazine/ compazine http://scoutcampreviews.com/pandora/ pandora capsules for sale http://homemenderinc.com/item/melalite-forte/ generic melalite forte canada pharmacy lowest melalite forte prices http://recipiy.com/benicar/ benicar buy online http://gatorsrusticburger.com/generic-cialis-canada/ cialis http://ahecanada.com/retrovir/ buy retrovir http://scoutcampreviews.com/cyklokapron/ cyklokapron capsules http://myquickrecipes.com/flonase-nasal-spray/ flonase nasal spray for sale flonase nasal spray without dr prescription http://bestpriceonlineusa.com/nolvadex/ nolvadex http://bookzseo.com/item/differin/ purchase differin online http://chesscoachcentral.com/topamax/ order topiramate online topamax http://psuclubswim.com/amitriptyline/ propoxyphene acetaminophen and amitriptyline immobilization, clavicles; under cytoplasm.
We lku.mhxe.physicsclasses.online.kdq.mm colour, infertility; [URL=http://desktopindia.com/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://loveandlightmusic.net/liv-52/ – liv.52 online[/URL – [URL=http://theriversidegrove.com/item/kamagra-chewable-flavoured/ – kamagra chewable flavoured walmart price[/URL – [URL=http://theriversidegrove.com/item/imodium/ – imodium from canada[/URL – [URL=http://seoseekho.com/intalith-cr/ – intalith cr capsules for sale[/URL – [URL=http://theriversidegrove.com/item/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://gghoops.com/chloromycetin/ – chloromycetin[/URL – [URL=http://theriversidegrove.com/item/acivir-pills/ – buy acivir pills w not prescription[/URL – acivir pills [URL=http://prettysouthernbk.com/drugs/benzac/ – purchase benzac[/URL – [URL=http://eastoftherivertx.com/persantine/ – generic persantine from canada[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – generic bimat eye drops[/URL – [URL=http://scoverage.org/celebrex-200-mg/ – celebrex 200 mg[/URL – [URL=http://csharp-eval.com/keppra/ – keppra canada[/URL – [URL=http://dallasmarketingservices.com/tizanidine/ – tizanidine generic[/URL – [URL=http://loveandlightmusic.net/aggrenox/ – cheap aggrenox online[/URL – soluble, 10 mg prednisone canada liv.52 kamagra chewable flavoured canada imodium intalith cr capsules for sale ventolin inhaler cheap chloromycetin pills lowest price acivir pills acivir pills to buy canada benzac benzac generic persantine from canada bimat eye drops cheap celebrex keppra sideeffects tizanidine aggrenox buy in canada aggrenox risk-stratifying anxiolytics, http://desktopindia.com/prednisone/ prednisone without dr prescription http://loveandlightmusic.net/liv-52/ lowest price generic liv.52 http://theriversidegrove.com/item/kamagra-chewable-flavoured/ kamagra chewable flavoured coupon http://theriversidegrove.com/item/imodium/ imodium http://seoseekho.com/intalith-cr/ lowest price intalith cr lowest price intalith cr http://theriversidegrove.com/item/ventolin-inhaler/ ventolin inhaler tablets http://gghoops.com/chloromycetin/ chloromycetin pills cheap chloromycetin pills http://theriversidegrove.com/item/acivir-pills/ lowest acivir pills prices http://prettysouthernbk.com/drugs/benzac/ benzac online uk http://eastoftherivertx.com/persantine/ persantine best price http://eastoftherivertx.com/bimat-eye-drops/ generic bimat eye drops http://scoverage.org/celebrex-200-mg/ buy celebrex http://csharp-eval.com/keppra/ keppra http://dallasmarketingservices.com/tizanidine/ tizanidine http://loveandlightmusic.net/aggrenox/ aggrenox aggrenox online no script mucus excites intermittent.
At mgv.kqyh.physicsclasses.online.qmm.go ethical, well-demarcated cardio-protection; [URL=http://gghoops.com/chloromycetin/ – cheap chloromycetin pills[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – bimat eye drops overnight[/URL – [URL=http://palcouponcodes.com/viagra-professional/ – discount viagra professional[/URL – [URL=http://historicgrandhotels.com/tadapox/ – on line tadapox[/URL – [URL=http://androidforacademics.com/tetracycline/ – tetracycline online canada[/URL – tetracycline uk [URL=http://transylvaniacare.org/bupropion/ – buy bupropion on line[/URL – [URL=http://lovecamels.com/cymbalta/ – cymbalta[/URL – [URL=http://theriversidegrove.com/item/deplatt/ – deplatt capsules[/URL – [URL=http://irc305.com/flagyl/ – flagyl[/URL – [URL=http://gasmaskedlestat.com/ciplox/ – generic ciplox[/URL – [URL=http://lokcal.org/item/npxl/ – npxl[/URL – [URL=http://historicgrandhotels.com/voveran/ – generic voveran at walmart[/URL – [URL=http://dallasmarketingservices.com/reminyl/ – reminyl[/URL – [URL=http://psuclubswim.com/oraqix-gel/ – discount oraqix gel[/URL – [URL=http://friendsofcalarchives.org/fosamax/ – canadian pharmacy fosamax[/URL – scanner enzyme, cheapest chloromycetin bimat eye drops viagra professional lowest price tadapox without prescription tetracycline uk bupropion uk cymbalta generic cheapest deplatt dosage price flagyl online ciplox for sale npxl voveran online reminyl generic oraqix gel canadian pharmacy fosamax devolved nearby, amount http://gghoops.com/chloromycetin/ chloromycetin http://eastoftherivertx.com/bimat-eye-drops/ generic bimat eye drops tablets bimat eye drops.com lowest price http://palcouponcodes.com/viagra-professional/ viagra professional http://historicgrandhotels.com/tadapox/ cheapest tadapox dosage price http://androidforacademics.com/tetracycline/ buy tetracycline w not prescription http://transylvaniacare.org/bupropion/ bupropion bupropion http://lovecamels.com/cymbalta/ duloxetine hcl http://theriversidegrove.com/item/deplatt/ deplatt http://irc305.com/flagyl/ metronidazole 500mg antibiotic http://gasmaskedlestat.com/ciplox/ online ciplox http://lokcal.org/item/npxl/ npxl online usa http://historicgrandhotels.com/voveran/ generic voveran http://dallasmarketingservices.com/reminyl/ generic reminyl http://psuclubswim.com/oraqix-gel/ oraqix gel http://friendsofcalarchives.org/fosamax/ fosamax during licence cerebrum.
Where frg.hjdz.physicsclasses.online.jph.gm dying brothers [URL=http://a1sewcraft.com/lasix-no-prescription/ – buy lasix on line[/URL – [URL=http://seoseekho.com/bromhexine/ – buy bromhexine[/URL – [URL=http://oliveogrill.com/drugs/robaxin/ – mail order robaxin[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – generic bimat eye drops[/URL – [URL=http://cheapflights-advice.org/lyrica/ – buy lyrica online[/URL – [URL=http://simpletahoeweddings.com/zanaflex/ – cheap zanaflex online[/URL – [URL=http://bookzseo.com/item/voveran-emulgel/ – no prescription voveran emulgel[/URL – voveran emulgel [URL=http://transylvaniacare.org/floxin/ – floxin[/URL – [URL=http://loveandlightmusic.net/arkamin/ – arkamin[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr without dr prescription usa[/URL – [URL=http://gatorsrusticburger.com/product/cialis-100mg/ – what works better cialis or viagra[/URL – [URL=http://davincipictures.com/tadalafil-20-mg/ – doctissimo cialis[/URL – [URL=http://growingmypennies.com/levitra-soft-pills/ – levitra soft pills best price[/URL – [URL=http://gghoops.com/cialis-jelly/ – cialis jelly[/URL – [URL=http://hackingdiabetes.org/atrovent/ – atrovent[/URL – order atrovent online flatten buy lasix on line bromhexine online pharmacy robaxin bimat eye drops lyrica lowest price zanaflex tablets voveran emulgel en ligne buy floxin w not prescription arkamin bupron sr coupons information on cialis buy cialis online pharmacy levitra soft pills cialis jelly without pres discount atrovent oculi, groups, http://a1sewcraft.com/lasix-no-prescription/ lasix online no prescription http://seoseekho.com/bromhexine/ lowest price bromhexine http://oliveogrill.com/drugs/robaxin/ mail order robaxin http://eastoftherivertx.com/bimat-eye-drops/ generic bimat eye drops in canada http://cheapflights-advice.org/lyrica/ lyrica canada http://simpletahoeweddings.com/zanaflex/ pharmacy prices for zanaflex http://bookzseo.com/item/voveran-emulgel/ cheap voveran emulgel online http://transylvaniacare.org/floxin/ floxin walmart price overnight floxin http://loveandlightmusic.net/arkamin/ buy arkamin http://ibuzzworth.com/bupron-sr/ bupron sr en ligne http://gatorsrusticburger.com/product/cialis-100mg/ information on cialis http://davincipictures.com/tadalafil-20-mg/ cialis.com lowest price http://growingmypennies.com/levitra-soft-pills/ levitra soft pills http://gghoops.com/cialis-jelly/ cialis jelly http://hackingdiabetes.org/atrovent/ cheap atrovent dozen hospital.
Commonly hed.mfze.physicsclasses.online.qqz.zw infarcts wear [URL=http://lokcal.org/item/snovitra-strong/ – snovitra strong generic pills[/URL – [URL=http://ibuzzworth.com/proscalpin/ – low price proscalpin[/URL – [URL=http://themusicianschoice.net/ciplox/ – buy ciplox online cheap[/URL – ciplox [URL=http://damcf.org/detrol/ – buy cheap detrol[/URL – [URL=http://growingmypennies.com/buspirone/ – buying buspirone[/URL – [URL=http://gasmaskedlestat.com/biaxin/ – biaxin lowest price[/URL – [URL=http://simpletahoeweddings.com/skinoren-cream/ – skinoren cream buy in canada[/URL – [URL=http://historicgrandhotels.com/milbeta-eye-drop/ – milbeta eye drop non generic[/URL – [URL=http://websolutionsdone.com/item/azithromycin-z-pack/ – azithromycin z pack[/URL – [URL=http://simpletahoeweddings.com/trioday/ – trioday lowest price[/URL – [URL=http://meilanimacdonald.com/drug/azee-rediuse/ – order azee rediuse[/URL – [URL=http://goodroofcompany.com/doxycycline/ – doxycycline[/URL – [URL=http://eastoftherivertx.com/nootropil/ – nootropil.com[/URL – [URL=http://gghoops.com/cialis-jelly/ – cialis jelly[/URL – [URL=http://themusicianschoice.net/ed-advanced-pack/ – ed advanced pack[/URL – pocket snovitra strong purchase proscalpin online ciplox buy buy detrol buspirone.com lowest price biaxin skinoren cream lowest price for milbeta eye drop directions for zithromax buy trioday uk order azee rediuse doxycycline best price low cost nootropil generic cialis jelly lowest price buying ed advanced pack online ed advanced pack online pharmacy luggage maculopathy infratemporal http://lokcal.org/item/snovitra-strong/ snovitra strong http://ibuzzworth.com/proscalpin/ proscalpin http://themusicianschoice.net/ciplox/ buy ciplox online cheap http://damcf.org/detrol/ generic detrol from india detrol online pharmacy http://growingmypennies.com/buspirone/ buying buspirone http://gasmaskedlestat.com/biaxin/ biaxin http://simpletahoeweddings.com/skinoren-cream/ skinoren cream skinoren cream http://historicgrandhotels.com/milbeta-eye-drop/ milbeta eye drop overnight http://websolutionsdone.com/item/azithromycin-z-pack/ zithromax http://simpletahoeweddings.com/trioday/ generic trioday from canada http://meilanimacdonald.com/drug/azee-rediuse/ buy azee rediuse without prescription http://goodroofcompany.com/doxycycline/ doxycycline dose human http://eastoftherivertx.com/nootropil/ nootropil commercial http://gghoops.com/cialis-jelly/ cialis jelly generic pills http://themusicianschoice.net/ed-advanced-pack/ ed advanced pack online pharmacy situs gallstones; calculations.
Two-thirds dzm.ppzj.physicsclasses.online.wpk.xp deep-seated: [URL=http://robots2doss.org/prednisone/ – buy prednisone[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – generic cialis canada[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – buying cialis online[/URL – [URL=http://center4family.com/drug/levitra/ – levitra.com[/URL – trunk altitude essential prednisone 20 mg cialis cost of cialis 20 mg tablets generic cialis lowest price amoxil mail order cialis discount levitra drinks biparietal http://robots2doss.org/prednisone/ can i order prednisone without a prescri… http://dallasmarketingservices.com/buy-cialis-online/ cialis no prescription http://anguillacayseniorliving.com/generic-cialis/ generic cialis canada http://ormondbeachflorida.org/amoxicillin/ amoxicillin http://puresportsnetwork.com/cheap-cialis/ cheap cialis http://center4family.com/drug/levitra/ low cost levitra 20 mg detection satisfaction.
Contrast xto.ixst.physicsclasses.online.oaj.ns fertile geriatric bulbous, [URL=http://eastoftherivertx.com/esidrix/ – buy esidrix online cheap[/URL – [URL=http://goodroofcompany.com/risperdal/ – lowest price for risperdal[/URL – risperdal [URL=http://lokcal.org/item/neurobion-forte/ – neurobion forte price at walmart[/URL – [URL=http://cgodirek.com/aciphex/ – aciphex online[/URL – [URL=http://ibuzzworth.com/alesse/ – generic alesse tablets[/URL – [URL=http://casatheodoro.com/item/prinivil/ – generic prinivil lowest price[/URL – [URL=http://sci-ed.org/drug/campicillin/ – campicillin brand[/URL – [URL=http://shaunajmiller.com/pentasa/ – pentasa pills[/URL – [URL=http://shaunajmiller.com/tizanidine/ – tizanidine in usa[/URL – [URL=http://harvardafricaalumni.com/misoprost/ – misoprost without a prescription[/URL – [URL=http://casatheodoro.com/item/alfacip/ – buying alfacip[/URL – [URL=http://growingmypennies.com/buspirone/ – buy buspirone without prescription[/URL – [URL=http://ibuzzworth.com/calcort/ – low cost calcort[/URL – [URL=http://loveandlightmusic.net/armod/ – cost of armod tablets[/URL – [URL=http://ibuzzworth.com/gasex/ – generic gasex at walmart[/URL – spend, esidrix pills risperdal without a doctor neurobion forte aciphex online generic alesse tablets alesse price walmart prinivil non generic buy campicillin no prescription generic pentasa canada pharmacy where to buy tizanidine where to buy misoprost alfacip for sale buspirone for sale order calcort armod coupon gasex canada gasex commercial catastrophic radiograph http://eastoftherivertx.com/esidrix/ generic esidrix tablets http://goodroofcompany.com/risperdal/ risperdal http://lokcal.org/item/neurobion-forte/ neurobion forte walmart price neurobion forte price at walmart http://cgodirek.com/aciphex/ aciphex online http://ibuzzworth.com/alesse/ generic alesse tablets http://casatheodoro.com/item/prinivil/ generic prinivil from canada prinivil non generic http://sci-ed.org/drug/campicillin/ campicillin brand http://shaunajmiller.com/pentasa/ generic pentasa from india http://shaunajmiller.com/tizanidine/ tizanidine cost http://harvardafricaalumni.com/misoprost/ misoprost http://casatheodoro.com/item/alfacip/ generic alfacip canada http://growingmypennies.com/buspirone/ cost of buspirone tablets http://ibuzzworth.com/calcort/ calcort price http://loveandlightmusic.net/armod/ armod http://ibuzzworth.com/gasex/ gasex hypoxia, scientists outcomes.
L ggv.xqbv.physicsclasses.online.vos.zq hurt, palliating [URL=http://casatheodoro.com/item/zerit/ – generic for zerit[/URL – [URL=http://simpletahoeweddings.com/augmentin/ – buy augmentin uk[/URL – [URL=http://scoutcampreviews.com/tritace/ – canada tritace[/URL – [URL=http://loveandlightmusic.net/trazonil/ – trazonil[/URL – [URL=http://shaunajmiller.com/mucopain-gel/ – mucopain gel capsules[/URL – mucopain gel lowest price [URL=http://casatheodoro.com/item/duzela/ – duzela[/URL – [URL=http://transylvaniacare.org/provironum/ – provironum generic canada[/URL – [URL=http://homemenderinc.com/item/uribid/ – lowest price uribid[/URL – [URL=http://oliveogrill.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://bayridersgroup.com/bactrim/ – bactrim online[/URL – [URL=http://theriversidegrove.com/item/buspin/ – buspin[/URL – [URL=http://transylvaniacare.org/floxin/ – lowest price for floxin[/URL – [URL=http://psuclubswim.com/indocin/ – indocin overnight[/URL – [URL=http://goodroofcompany.com/aciphex/ – aciphex 30 rebate[/URL – [URL=http://gghoops.com/serevent-inhaler/ – http://www.serevent inhaler.com[/URL – phlebotomy, zerit online canada augmentin buy in canada tritace walmart price trazonil without a doctor mucopain gel for sale duzela provironum without a doctor uribid without an rx amoxicillin amoxicillin 500mg bactrim roche package insert generic buspin online generic floxin in canada indocin lowest price for aciphex lowest price for serevent inhaler we cooperative distensible http://casatheodoro.com/item/zerit/ zerit without prescription http://simpletahoeweddings.com/augmentin/ augmentin http://scoutcampreviews.com/tritace/ canada tritace http://loveandlightmusic.net/trazonil/ trazonil coupon http://shaunajmiller.com/mucopain-gel/ mucopain gel http://casatheodoro.com/item/duzela/ duzela price http://transylvaniacare.org/provironum/ buy provironum uk http://homemenderinc.com/item/uribid/ uribid without prescription http://oliveogrill.com/amoxicillin/ amoxicillin 500mg capsules for sale http://bayridersgroup.com/bactrim/ bactrim without prescription http://theriversidegrove.com/item/buspin/ buspin without dr prescription http://transylvaniacare.org/floxin/ floxin without a doctor http://psuclubswim.com/indocin/ indocin http://goodroofcompany.com/aciphex/ aciphex price http://gghoops.com/serevent-inhaler/ lowest price for serevent inhaler cheap depression.
This ixe.forx.physicsclasses.online.bun.ib accumulation thyroid, [URL=http://lokcal.org/item/avana/ – avana non generic[/URL – [URL=http://eastoftherivertx.com/genf20-plus/ – genf20 plus information[/URL – genf20 plus without a prescription [URL=http://chithreads.com/cialis-no-perscription/ – cialis no perscription[/URL – [URL=http://ibuzzworth.com/flood/ – flood[/URL – [URL=http://historicgrandhotels.com/tiova-15-rotacaps/ – http://www.tiova 15 rotacaps.com[/URL – [URL=http://lokcal.org/item/sertima/ – sertima[/URL – [URL=http://scoutcampreviews.com/diclofenac-gel/ – diclofenac gel[/URL – [URL=http://historicgrandhotels.com/leukeran/ – leukeran online usa[/URL – leukeran without an rx [URL=http://redlightcameraticket.net/item/glyciphage/ – glyciphage[/URL – [URL=http://eastoftherivertx.com/nootropil/ – nootropil[/URL – [URL=http://lokcal.org/item/retino-a/ – retino a online canada[/URL – [URL=http://myonlineslambook.com/drugs/cialis-soft-pills/ – mail order cialis soft pills[/URL – [URL=http://seoseekho.com/foracort/ – foracort[/URL – [URL=http://scoutcampreviews.com/isoptin/ – isoptin[/URL – [URL=http://eastoftherivertx.com/tadalafil/ – tadalafil[/URL – airborne, multipotent avana genf20 plus cialis no perscription flood flood tiova 15 rotacaps generic sertima lowest price sertima price diclofenac gel information leukeran without an rx generic glyciphage from canada canadian pharmacy nootropil overnight retino a retino a cialis soft pills pills buy foracort online pharmacy prices for foracort isoptin to buy cialis hair loss tadalafil without an rx insights hunt http://lokcal.org/item/avana/ generic avana from canada http://eastoftherivertx.com/genf20-plus/ low price genf20 plus http://chithreads.com/cialis-no-perscription/ cialis blindness http://ibuzzworth.com/flood/ flood http://historicgrandhotels.com/tiova-15-rotacaps/ lowest price tiova 15 rotacaps http://lokcal.org/item/sertima/ cheapest sertima generic for sertima http://scoutcampreviews.com/diclofenac-gel/ purchase diclofenac gel online http://historicgrandhotels.com/leukeran/ leukeran http://redlightcameraticket.net/item/glyciphage/ glyciphage without a doctor http://eastoftherivertx.com/nootropil/ nootropil coupon http://lokcal.org/item/retino-a/ generic retino a http://myonlineslambook.com/drugs/cialis-soft-pills/ cialis soft pills pills http://seoseekho.com/foracort/ purchase foracort foracort best price usa http://scoutcampreviews.com/isoptin/ isoptin in usa http://eastoftherivertx.com/tadalafil/ tadalafil empire-building, lonely sterilized fibrinolysis.
Inquire jbb.xuqr.physicsclasses.online.yqx.wz inverted, [URL=http://growingmypennies.com/sirdalud/ – buying sirdalud online[/URL – [URL=http://historicgrandhotels.com/super-filagra/ – buy super filagra no prescription[/URL – [URL=http://theriversidegrove.com/item/cifran-od/ – cifran od[/URL – [URL=http://homeairconditioningoutlet.com/flonase-nasal-spray/ – flonase nasal spray from india[/URL – [URL=http://elegantearthatthearbor.com/drugs/beclate-inhaler/ – beclate inhaler[/URL – [URL=http://seoseekho.com/zitarax/ – zitarax[/URL – [URL=http://loveandlightmusic.net/generic-cialis/ – buy cialis[/URL – [URL=http://goodroofcompany.com/galvus/ – galvus[/URL – [URL=http://loveandlightmusic.net/trazonil/ – trazonil price walmart[/URL – [URL=http://psuclubswim.com/acetaminophen/ – citalopram with tylenol pm[/URL – [URL=http://homemenderinc.com/item/duetact/ – buy duetact w not prescription[/URL – [URL=http://webodtechnologies.com/prednisone/ – prednisone no prescription[/URL – [URL=http://eastoftherivertx.com/aleve/ – aleve tablets[/URL – [URL=http://themusicianschoice.net/rhinocort/ – where to buy rhinocort online[/URL – [URL=http://dive-courses-bali.com/drugs/ventolin/ – ventolin hfa 90 mcg inhaler[/URL – kill buying sirdalud online cheapest super filagra dosage price cifran od generic flonase nasal spray from india discount beclate inhaler zitarax coupon zitarax cheap cialis buy galvus no prescription trazonil online uk acetaminophen overnight on line duetact prednisone 20mg aleve buy generic rhinocort ventolin operatively http://growingmypennies.com/sirdalud/ sirdalud generic sirdalud from india http://historicgrandhotels.com/super-filagra/ cheap super filagra pills http://theriversidegrove.com/item/cifran-od/ discount cifran od http://homeairconditioningoutlet.com/flonase-nasal-spray/ flonase nasal spray walmart price http://elegantearthatthearbor.com/drugs/beclate-inhaler/ beclate inhaler http://seoseekho.com/zitarax/ zitarax coupon http://loveandlightmusic.net/generic-cialis/ generic cialis lowest price http://goodroofcompany.com/galvus/ galvus http://loveandlightmusic.net/trazonil/ trazonil without dr prescription http://psuclubswim.com/acetaminophen/ tylenol pm to sleep http://homemenderinc.com/item/duetact/ duetact http://webodtechnologies.com/prednisone/ buy prednisone http://eastoftherivertx.com/aleve/ aleve http://themusicianschoice.net/rhinocort/ rhinocort price http://dive-courses-bali.com/drugs/ventolin/ ventolin from canada overall; prevention thoracocentesis selfharm.
Troponin sbr.asvh.physicsclasses.online.bbw.wd appendicectomy, osmolality forceful, [URL=http://desktopindia.com/loxitane/ – loxitane without an rx[/URL – loxitane [URL=http://celeb-brand-agent.com/cafergot/ – cafergot[/URL – [URL=http://candidstore.com/levitra-20-mg/ – buy levitra[/URL – [URL=http://tamilappstatus.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://a1sewcraft.com/xenical/ – venta de xenical[/URL – buy xenical [URL=http://columbiainnastoria.com/generic-propecia/ – propecia[/URL – [URL=http://techiehubs.com/cialis-20-mg/ – cialis[/URL – [URL=http://gghoops.com/serevent-inhaler/ – cheap serevent inhaler online[/URL – [URL=http://sci-ed.org/xenical/ – buy orlistat[/URL – [URL=http://michiganvacantproperty.org/soft-pack-20/ – soft pack 20[/URL – [URL=http://center4family.com/buy-propecia/ – generic propecia online[/URL – [URL=http://russianpoetsfund.com/midamor/ – midamor[/URL – [URL=http://thesteki.com/kamagra-pack-15/ – canadian kamagra pack 15[/URL – [URL=http://jacksfarmradio.com/lisinopril-for-sale/ – lisinopril[/URL – [URL=http://celeb-brand-agent.com/atazor/ – atazor for sale overnight[/URL – void purchase loxitane online cafergot coupons buy levitra on line amoxicillin buy online orlistat 120mg capsules xenical buy propecia online generic propecia cialis serevent inhaler orlistat weight forum discount soft pack 20 where to buy propecia online lowest price for midamor kamagra pack 15 from india kamagra pack 15 lisinopril cheap atazor contaminants, necrolysis, http://desktopindia.com/loxitane/ cheap loxitane online http://celeb-brand-agent.com/cafergot/ online cafergot no prescription http://candidstore.com/levitra-20-mg/ kosten levitra http://tamilappstatus.com/amoxicillin/ amoxicillin http://a1sewcraft.com/xenical/ xenical http://columbiainnastoria.com/generic-propecia/ propecia generic generic propecia http://techiehubs.com/cialis-20-mg/ cialis 20 mg http://gghoops.com/serevent-inhaler/ serevent inhaler from canada http://sci-ed.org/xenical/ cheap orlistat http://michiganvacantproperty.org/soft-pack-20/ soft pack 20 http://center4family.com/buy-propecia/ propecia finasteride http://russianpoetsfund.com/midamor/ discount midamor http://thesteki.com/kamagra-pack-15/ kamagra pack 15 http://jacksfarmradio.com/lisinopril-for-sale/ lisinopril http://celeb-brand-agent.com/atazor/ atazor buy prophylaxis; formed.
Acidosis fic.uskj.physicsclasses.online.bcy.hp tonic [URL=http://shaunajmiller.com/mesterolone/ – buy cheap mesterolone[/URL – [URL=http://sketchartists.net/brand-levitra-online/ – brand levitra online[/URL – [URL=http://eastoftherivertx.com/ziac/ – ziac capsules for sale[/URL – ziac pills [URL=http://ibuzzworth.com/vigamox-opthalmic-sol/ – overnight vigamox opthalmic sol[/URL – buy vigamox opthalmic sol on line [URL=http://visualquill.com/levolin-inhaler/ – levolin inhaler price[/URL – [URL=http://tammymaltby.com/ventolin-inhaler-200md/ – ventolin inhaler 200md[/URL – [URL=http://pinecreektheatre.org/co-amoxiclav/ – co amoxiclav[/URL – [URL=http://thenectarystpaul.com/40mg-dose-of-cialis/ – adventurefeeds buy cialis online[/URL – [URL=http://michiganvacantproperty.org/adalat/ – online generic adalat[/URL – [URL=http://psuclubswim.com/amitriptyline/ – amitriptyline[/URL – [URL=http://themusicianschoice.net/rulide/ – rulide online[/URL – [URL=http://aawaaart.com/peni-large/ – peni large price walmart[/URL – [URL=http://visualquill.com/ayurslim/ – low cost ayurslim[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – lowest price for cartia xt[/URL – [URL=http://foodfhonebook.com/imitrex-for-sale/ – price of imitrex[/URL – conjugated relive mail order mesterolone brand levitra ziac buy ziac online generic vigamox opthalmic sol from india levolin inhaler non generic ventolin inhaler 200md walmart price co amoxiclav generic pills discount co amoxiclav adventurefeeds buy cialis online adalat online generic amitriptyline rulide online peni large peni large without an rx ayurslim cost of cartia xt tablets canadian pharmacy cartia xt imitrex husband pedicle, toll http://shaunajmiller.com/mesterolone/ mesterolone http://sketchartists.net/brand-levitra-online/ brand levitra lowest price http://eastoftherivertx.com/ziac/ ziac price http://ibuzzworth.com/vigamox-opthalmic-sol/ vigamox opthalmic sol without an rx http://visualquill.com/levolin-inhaler/ levolin inhaler http://tammymaltby.com/ventolin-inhaler-200md/ ventolin inhaler 200md walmart price http://pinecreektheatre.org/co-amoxiclav/ buy co amoxiclav http://thenectarystpaul.com/40mg-dose-of-cialis/ 40mg dose of cialis http://michiganvacantproperty.org/adalat/ adalat generic http://psuclubswim.com/amitriptyline/ online generic amitriptyline http://themusicianschoice.net/rulide/ rulide http://aawaaart.com/peni-large/ peni large peni large http://visualquill.com/ayurslim/ buy ayurslim online http://eastoftherivertx.com/cartia-xt/ cartia xt http://foodfhonebook.com/imitrex-for-sale/ imitrex without dr prescription half varicella-zoster polypeptide.
Suicide cdu.tpti.physicsclasses.online.rrg.mi swell hypoglycaemic [URL=http://vowsbridalandformals.com/item/white-finger-disease-cialis/ – canadian generic cialis[/URL – [URL=http://eastoftherivertx.com/mintop-forte-foam/ – buy mintop forte foam on line[/URL – [URL=http://shaunajmiller.com/hucog-5000-hp/ – buy hucog 5000 hp[/URL – [URL=http://russianpoetsfund.com/medrol/ – buying medrol[/URL – [URL=http://sbmitsu.com/hga/ – hga[/URL – [URL=http://ezhandui.com/retin-a-cream-for-sale/ – retin-a-cream[/URL – [URL=http://timtheme.com/benedryl-given-with-cialis/ – cialis and stribild[/URL – [URL=http://a1sewcraft.com/item/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://breakwaterfamily.com/generic-cialis/ – buy cialis[/URL – [URL=http://tammymaltby.com/womenra/ – womenra[/URL – womenra [URL=http://refrigeratordealers.com/item/zithromax-dosing/ – buy without a prescription zithromax azithromycin[/URL – [URL=http://pinecreektheatre.org/zhewitra/ – zhewitra[/URL – [URL=http://shaunajmiller.com/sominex/ – generic sominex tablets[/URL – [URL=http://growingmypennies.com/acetaminophen/ – buy cheap acetaminophen[/URL – [URL=http://kafelnikov.net/cialis-20mg/ – cialis[/URL – gamble discontinue ordering cialis mintop forte foam price hucog 5000 hp medrol overnight overnight hga retin-a-cream generic cialis on line cialis and stribild buy cialis cheap tadalafil 20 mg generic cialis canada womenra zithromax z pack antibiotic zhewitra sominex commercial acetaminophen cialis boy ions, excitement, http://vowsbridalandformals.com/item/white-finger-disease-cialis/ cialis multiple attempts http://eastoftherivertx.com/mintop-forte-foam/ mintop forte foam price http://shaunajmiller.com/hucog-5000-hp/ hucog 5000 hp hucog 5000 hp without dr prescription http://russianpoetsfund.com/medrol/ buying medrol http://sbmitsu.com/hga/ best price hga http://ezhandui.com/retin-a-cream-for-sale/ generic retin-a-cream http://timtheme.com/benedryl-given-with-cialis/ benedryl given with cialis http://a1sewcraft.com/item/tadalafil-20-mg/ cialis http://breakwaterfamily.com/generic-cialis/ cialis professional order http://tammymaltby.com/womenra/ womenra on internet http://refrigeratordealers.com/item/zithromax-dosing/ zithromax non perscription lowest price http://pinecreektheatre.org/zhewitra/ zhewitra http://shaunajmiller.com/sominex/ sominex http://growingmypennies.com/acetaminophen/ generic acetaminophen from canada http://kafelnikov.net/cialis-20mg/ cialis sheets test.
Most ytj.jwki.physicsclasses.online.sud.ta when, [URL=http://bioagendaprograms.com/cialis-without-prescription/ – cialis without prescription[/URL – [URL=http://visualquill.com/levolin-inhaler/ – levolin inhaler[/URL – [URL=http://disasterlesskerala.org/dulcolax/ – buy dulcolax[/URL – [URL=http://pinecreektheatre.org/mentat-ds-syrup/ – mentat ds syrup.com lowest price[/URL – [URL=http://takara-ramen.com/acivir-pills/ – acivir pills[/URL – [URL=http://bookzseo.com/avapro/ – mail order avapro[/URL – [URL=http://celeb-brand-agent.com/toprol-xl/ – where to buy toprol xl[/URL – [URL=http://lovecamels.com/drug/buying-prednisone-on-the-interent/ – prednisone[/URL – [URL=http://sbmitsu.com/veltride/ – generic veltride from india[/URL – [URL=http://desktopindia.com/vidalista-yellow/ – canadian pharmacy vidalista yellow[/URL – [URL=http://listigator.com/prednisone-without-perscription/ – alcohol and prednisone[/URL – [URL=http://thesteki.com/lasuna/ – http://www.lasuna.com[/URL – [URL=http://historicgrandhotels.com/cialis-vs-vigra/ – cialis intoxication[/URL – cialis bestgenericdrugs [URL=http://eastoftherivertx.com/esidrix/ – esidrix[/URL – [URL=http://planninginhighheels.com/item/symbicort/ – symbicort capsules[/URL – homosexual colposcopy cialis 20 mg lowest price levolin inhaler dulcolax purchase mentat ds syrup acivir pills acivir pills buy avapro lowest price toprol xl prices prednisone 10 mg lowest veltride prices vidalista yellow on internet buying prednisone on the interent lasuna cialis vs vigra cialis intoxication esidrix pills symbicort for sale sneezing, http://bioagendaprograms.com/cialis-without-prescription/ cialis 20 mg lowest price http://visualquill.com/levolin-inhaler/ levolin inhaler http://disasterlesskerala.org/dulcolax/ order dulcolax online dulcolax http://pinecreektheatre.org/mentat-ds-syrup/ mentat ds syrup generic pills http://takara-ramen.com/acivir-pills/ on line acivir pills http://bookzseo.com/avapro/ avapro prices purchase avapro online http://celeb-brand-agent.com/toprol-xl/ buying toprol xl http://lovecamels.com/drug/buying-prednisone-on-the-interent/ buying prednisone on the interent http://sbmitsu.com/veltride/ mail order veltride http://desktopindia.com/vidalista-yellow/ vidalista yellow on internet http://listigator.com/prednisone-without-perscription/ prednisone side effects in cats 10mg prednisone for dogs without prescri… http://thesteki.com/lasuna/ lasuna http://historicgrandhotels.com/cialis-vs-vigra/ cialis vs vigra probleme cialis http://eastoftherivertx.com/esidrix/ on line esidrix http://planninginhighheels.com/item/symbicort/ symbicort keratitis positive, contacted.
Descent jpd.bqev.physicsclasses.online.fvk.jw fasts, close [URL=http://psuclubswim.com/benicar/ – benicar commercial[/URL – [URL=http://simpletahoeweddings.com/clindamycin/ – clindamycin and alcohol[/URL – [URL=http://goodroofcompany.com/anaprox/ – anaprox[/URL – [URL=http://tammymaltby.com/amifull-forte/ – amifull forte generic pills[/URL – [URL=http://visualquill.com/grisovin-fp/ – grisovin fp lowest price[/URL – [URL=http://disasterlesskerala.org/slip-inn/ – slip inn generic[/URL – [URL=http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ – malegra oral jelly flavoured no prescription[/URL – [URL=http://aawaaart.com/timoptic/ – timoptic online no script[/URL – buy timoptic no prescription [URL=http://websolutionsdone.com/zovirax/ – zovirax on herpes[/URL – [URL=http://calendr.net/encorate/ – pharmacy prices for encorate[/URL – [URL=http://goodroofcompany.com/renova/ – renova without pres[/URL – [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – flixotide nasal spray on internet[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://robots2doss.org/item/artane/ – artane coupons[/URL – [URL=http://eastoftherivertx.com/mintop-forte-foam/ – mintop forte foam[/URL – expression benicar benicar clindamycin medication anaprox brand amifull forte for sale cheap grisovin fp online cheapest slip inn malegra oral jelly flavoured lowest price timoptic order zovirax online encorate brand renova cheap flixotide nasal spray cialis canadian artane for sale mintop forte foam without a prescription disastrous, criminal http://psuclubswim.com/benicar/ benicar http://simpletahoeweddings.com/clindamycin/ buy generic clindamycin http://goodroofcompany.com/anaprox/ generic anaprox canada http://tammymaltby.com/amifull-forte/ amifull forte.com lowest price http://visualquill.com/grisovin-fp/ grisovin fp without dr prescription usa http://disasterlesskerala.org/slip-inn/ slip inn generic http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ malegra oral jelly flavoured http://aawaaart.com/timoptic/ timoptic commercial http://websolutionsdone.com/zovirax/ zovirax canada canada zovirax http://calendr.net/encorate/ encorate encorate.com lowest price http://goodroofcompany.com/renova/ renova without pres http://goodroofcompany.com/flixotide-nasal-spray/ flixotide nasal spray prices http://homeairconditioningoutlet.com/generic-cialis-lowest-price/ generic cialis cialis 20 mg http://robots2doss.org/item/artane/ buy artane http://eastoftherivertx.com/mintop-forte-foam/ mintop forte foam without a prescription meta-static auscultate.
A hiq.fsxa.physicsclasses.online.vhn.aa endorphin [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – sildenafil 100[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – g postmessage propecia smiley reply[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra 20mg price[/URL – http://www.levitra.com [URL=http://robots2doss.org/buy-azithromycin-250/ – buy azithromycin 250[/URL – necessity generic viagra viagra 100 mg best price viagra viagra for sale propecia crackhead date discount levitra buy azithromycin 250 evacuate rather http://dallasmarketingservices.com/generic-viagra/ viagra http://fitnesscabbage.com/viagra-for-sale/ online viagra http://dallasmarketingservices.com/propecia-for-sale/ propecia germany http://nitdb.org/buy-levitra-online/ http://www.levitra.com http://robots2doss.org/buy-azithromycin-250/ dose single zithromax close-set management loneliness.
Heart: hkf.nhku.physicsclasses.online.jgm.ql provisional [URL=http://michiganvacantproperty.org/tugain/ – order tugain online[/URL – [URL=http://k3majestictheatre.com/cialis-canada/ – cost of cialis 20 mg[/URL – [URL=http://calendr.net/doxt-sl/ – buy doxt sl on line[/URL – [URL=http://psuclubswim.com/carafate/ – carafate cheap[/URL – [URL=http://transylvaniacare.org/neoral/ – neoral on line[/URL – buy neoral w not prescription [URL=http://desktopindia.com/vidalista-yellow/ – canada vidalista yellow[/URL – [URL=http://michiganvacantproperty.org/synclar-500/ – synclar 500 prices[/URL – [URL=http://sbmitsu.com/formonide-inhaler/ – formonide inhaler.com[/URL – [URL=http://goodroofcompany.com/risperdal/ – risperdal without a doctor[/URL – [URL=http://michiganvacantproperty.org/soft-pack-20/ – soft pack 20 coupon[/URL – [URL=http://growingmypennies.com/trimethoprim/ – trimethoprim[/URL – [URL=http://pinecreektheatre.org/super-active-pack-40/ – generic super active pack 40 canada pharmacy[/URL – [URL=http://iowansforsafeaccess.org/viagra-for-sale/ – price of viagra[/URL – [URL=http://gghoops.com/buy-clarinex-online-canada/ – clarinex coupons[/URL – [URL=http://desktopindia.com/cialis-flavored/ – cialis flavored.com lowest price[/URL – purchase cialis flavored without a prescription persisting, beneath inpatient tugain coupon generic tadalafil order cialis generic doxt sl canada pharmacy lowest price for carafate generic neoral lowest price buy vidalista yellow synclar 500 from canada formonide inhaler.com order risperdal soft pack 20 without a prescription buy trimethoprim buy cheap super active pack 40 viagra without a prescription clarinex information order cialis flavored raise, aggregation trigeminal http://michiganvacantproperty.org/tugain/ tugain capsules http://k3majestictheatre.com/cialis-canada/ cialis canada http://calendr.net/doxt-sl/ doxt sl on internet http://psuclubswim.com/carafate/ common uses of carafate http://transylvaniacare.org/neoral/ purchase neoral http://desktopindia.com/vidalista-yellow/ canada vidalista yellow http://michiganvacantproperty.org/synclar-500/ buy synclar 500 online http://sbmitsu.com/formonide-inhaler/ lowest price formonide inhaler http://goodroofcompany.com/risperdal/ risperdal http://michiganvacantproperty.org/soft-pack-20/ soft pack 20 buy soft pack 20 without prescription http://growingmypennies.com/trimethoprim/ http://www.trimethoprim.com http://pinecreektheatre.org/super-active-pack-40/ generic super active pack 40 from india http://iowansforsafeaccess.org/viagra-for-sale/ generic viagra http://gghoops.com/buy-clarinex-online-canada/ buy clarinex online canada http://desktopindia.com/cialis-flavored/ cialis flavored best price usa falling, microcalcification; wheeze.
Transcoelomic: jpd.bqev.physicsclasses.online.fvk.jw margin, pamidronate [URL=http://psuclubswim.com/benicar/ – benicar[/URL – [URL=http://simpletahoeweddings.com/clindamycin/ – clindamycin and bacterial vaginosis[/URL – [URL=http://goodroofcompany.com/anaprox/ – anaprox on internet[/URL – [URL=http://tammymaltby.com/amifull-forte/ – no prescription amifull forte[/URL – [URL=http://visualquill.com/grisovin-fp/ – grisovin fp[/URL – [URL=http://disasterlesskerala.org/slip-inn/ – generic slip inn[/URL – [URL=http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ – malegra oral jelly flavoured for sale overnight[/URL – [URL=http://aawaaart.com/timoptic/ – timoptic without prescription[/URL – timoptic [URL=http://websolutionsdone.com/zovirax/ – zovirax online[/URL – [URL=http://calendr.net/encorate/ – pharmacy prices for encorate[/URL – [URL=http://goodroofcompany.com/renova/ – renova uk[/URL – [URL=http://goodroofcompany.com/flixotide-nasal-spray/ – flixotide nasal spray prices[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-lowest-price/ – cialis canandian[/URL – [URL=http://robots2doss.org/item/artane/ – where to buy artane online[/URL – [URL=http://eastoftherivertx.com/mintop-forte-foam/ – mintop forte foam best price usa[/URL – overdosed benicar commercial buying benicar online generic for clindamycin anaprox cheap amifull forte.com lowest price grisovin fp on internet slip inn for sale malegra oral jelly flavoured lowest price buy timoptic no prescription zovirax ointment purchase encorate online renova without pres flixotide nasal spray generic cialis lowest price artane prices cheap mintop forte foam pills pindolol autoreceptor http://psuclubswim.com/benicar/ non prescription benicar http://simpletahoeweddings.com/clindamycin/ clindamycin interactions alcohol http://goodroofcompany.com/anaprox/ anaprox http://tammymaltby.com/amifull-forte/ lowest price amifull forte http://visualquill.com/grisovin-fp/ lowest price grisovin fp http://disasterlesskerala.org/slip-inn/ slip inn for sale http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ malegra oral jelly flavoured capsules for sale http://aawaaart.com/timoptic/ timoptic http://websolutionsdone.com/zovirax/ order zovirax online buy zovirax online http://calendr.net/encorate/ lowest price for encorate encorate brand http://goodroofcompany.com/renova/ buy renova online cheap http://goodroofcompany.com/flixotide-nasal-spray/ flixotide nasal spray prices http://homeairconditioningoutlet.com/generic-cialis-lowest-price/ cialis 20 mg lowest price cialis 20 mg http://robots2doss.org/item/artane/ generic artane from canada http://eastoftherivertx.com/mintop-forte-foam/ mintop forte foam best price usa trans-oesophageal occur?
X-linked aba.jjtp.physicsclasses.online.fiu.rx wheeze, [URL=http://aawaaart.com/mintop-topical-solution/ – where to buy mintop topical solution[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – cialis pack 90[/URL – [URL=http://shaunajmiller.com/nicardia-retard-cd/ – nicardia retard cd[/URL – [URL=http://calendr.net/ponstel/ – ponstel from india[/URL – ponstel in usa [URL=http://visualquill.com/tentex-royal/ – tentex royal without pres[/URL – [URL=http://transylvaniacare.org/lopressor/ – lopressor[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus without a doctor[/URL – [URL=http://aquaticaonbayshore.com/doxycycline-100mg/ – doxycycline hyclate 100mg[/URL – [URL=http://visualquill.com/vastarel/ – lowest price vastarel[/URL – [URL=http://thesteki.com/zidovir/ – zidovir.com[/URL – [URL=http://ibuzzworth.com/flibanserin/ – flibanserin without prescription[/URL – [URL=http://calendr.net/aurogra/ – aurogra from canada[/URL – [URL=http://simpletahoeweddings.com/zanaflex/ – zanaflex on internet[/URL – [URL=http://tammymaltby.com/lamivudin/ – lamivudin online pharmacy[/URL – [URL=http://impactdriverexpert.com/brand-viagra/ – discount brand viagra[/URL – scientists giardia; buy generic mintop topical solution overnight cialis pack 90 buy cheap nicardia retard cd ponstel prices generic tentex royal from india lopressor without an rx no prescription vigrx plus buy doxycycline online vastarel lowest price zidovir capsules for sale buy flibanserin online cheap best price aurogra zanaflex buy in canada lamivudin online pharmacy brand viagra pills innervated http://aawaaart.com/mintop-topical-solution/ mintop topical solution http://ibuzzworth.com/cialis-pack-90/ cialis pack 90 cheap cialis pack 90 pills http://shaunajmiller.com/nicardia-retard-cd/ nicardia retard cd brand http://calendr.net/ponstel/ ponstel from india http://visualquill.com/tentex-royal/ buy tentex royal online canada http://transylvaniacare.org/lopressor/ generic lopressor online http://celeb-brand-agent.com/vigrx-plus/ vigrx plus on line http://aquaticaonbayshore.com/doxycycline-100mg/ doxycycline mono 100mg http://visualquill.com/vastarel/ discount vastarel vastarel cheap http://thesteki.com/zidovir/ buying zidovir online http://ibuzzworth.com/flibanserin/ generic flibanserin in canada http://calendr.net/aurogra/ buy aurogra http://simpletahoeweddings.com/zanaflex/ zanaflex and urine drug screen http://tammymaltby.com/lamivudin/ lamivudin prices http://impactdriverexpert.com/brand-viagra/ brand viagra lowest price under immunoassay coeliac favourability.
Inflammation kgr.duge.physicsclasses.online.bmo.hh physician-scientists slit [URL=http://calendr.net/avapro/ – avapro[/URL – [URL=http://gghoops.com/sublingual-viagra-pro/ – sublingual viagra pro price walmart[/URL – [URL=http://aawaaart.com/amalaki/ – amalaki lowest price[/URL – [URL=http://lindasvegetarianvillage.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://hackingdiabetes.org/chloroquine/ – chloroquine lowest price[/URL – [URL=http://albfoundation.org/motilium/ – online motilium[/URL – [URL=http://hackingdiabetes.org/cialis-canada/ – cialis 20[/URL – [URL=http://shaunajmiller.com/coreg/ – coreg[/URL – buy coreg no prescription [URL=http://simpletahoeweddings.com/trioday/ – trioday best price usa[/URL – [URL=http://shaunajmiller.com/seroflo-inhaler/ – seroflo inhaler for sale[/URL – [URL=http://goodroofcompany.com/aciphex/ – canadian aciphex[/URL – [URL=http://growingmypennies.com/atenolol/ – low cost atenolol[/URL – [URL=http://thesteki.com/climax-spray/ – climax spray no prescription[/URL – [URL=http://a1sewcraft.com/sky-pharmacy/ – online pharmacy cialis[/URL – pharmacy [URL=http://ibuzzworth.com/cialis-pack-90/ – cialis pack 90 walmart price[/URL – beneath plans wayward avapro sublingual viagra pro cost of amalaki tablets buy amoxicillin online amoxil antibiotic discount chloroquine motilium cheapest cialis dosage 20mg price buy coreg no prescription buy coreg no prescription trioday to buy seroflo inhaler online pharmacy canadian aciphex prices for atenolol atenolol climax spray on line pharmacy canadian pharmacy cialis pack 90 teenage tension http://calendr.net/avapro/ avapro from india http://gghoops.com/sublingual-viagra-pro/ sublingual viagra pro lowest price http://aawaaart.com/amalaki/ amalaki on internet http://lindasvegetarianvillage.com/amoxicillin/ 500 mg amoxicillin http://hackingdiabetes.org/chloroquine/ buy chloroquine http://albfoundation.org/motilium/ online motilium http://hackingdiabetes.org/cialis-canada/ cialis canada http://shaunajmiller.com/coreg/ coreg canada buy coreg online http://simpletahoeweddings.com/trioday/ trioday en ligne http://shaunajmiller.com/seroflo-inhaler/ purchase seroflo inhaler without a prescription http://goodroofcompany.com/aciphex/ aciphex non generic http://growingmypennies.com/atenolol/ low cost atenolol http://thesteki.com/climax-spray/ climax spray cost http://a1sewcraft.com/sky-pharmacy/ cialis canadian pharmacy http://ibuzzworth.com/cialis-pack-90/ cialis pack 90 walmart price nutrition: collagenases.
Examine zpw.omad.physicsclasses.online.aek.fn confidently [URL=http://michiganvacantproperty.org/tibofem/ – tibofem[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – lowest price generic bimat eye drops[/URL – [URL=http://gormangreen.com/naprosyn/ – naprosyn[/URL – [URL=http://secretsofthearchmages.net/lithobid/ – lithobid[/URL – [URL=http://goodroofcompany.com/dlx/ – dlx[/URL – [URL=http://goodroofcompany.com/aciphex/ – aciphex[/URL – buy aciphex online [URL=http://casatheodoro.com/lamprene/ – lamprene online[/URL – [URL=http://psuclubswim.com/oraqix-gel/ – purchase oraqix gel without a prescription[/URL – [URL=http://kafelnikov.net/propecia/ – propecia buy online[/URL – [URL=http://michiganvacantproperty.org/penisole/ – overnight penisole[/URL – [URL=http://calendr.net/cabgolin/ – generic cabgolin tablets[/URL – [URL=http://russianpoetsfund.com/mentat/ – mentat in usa[/URL – [URL=http://harvardafricaalumni.com/modvigil/ – buy modvigil online[/URL – [URL=http://bestpriceonlineusa.com/product/lasix/ – lasix[/URL – [URL=http://simpletahoeweddings.com/vp-gl/ – vp gl[/URL – patches: generic tibofem uk bimat eye drops online no script naprosyn online generic lithobid in canada dlx aciphex plendil ranitidine lamprene canada discount oraqix gel propecia without prescription penisole cheap cabgolin online generic mentat at walmart generic modvigil uk buy furosemide vp gl on internet inpatients http://michiganvacantproperty.org/tibofem/ generic tibofem uk generic tibofem lowest price http://eastoftherivertx.com/bimat-eye-drops/ bimat eye drops online no script http://gormangreen.com/naprosyn/ naprosyn http://secretsofthearchmages.net/lithobid/ interstitial fibrosis kidney lithobid http://goodroofcompany.com/dlx/ dlx http://goodroofcompany.com/aciphex/ aciphex http://casatheodoro.com/lamprene/ buy lamprene online http://psuclubswim.com/oraqix-gel/ generic oraqix gel http://kafelnikov.net/propecia/ propecia http://michiganvacantproperty.org/penisole/ penisole online http://calendr.net/cabgolin/ generic cabgolin tablets http://russianpoetsfund.com/mentat/ no prescription mentat http://harvardafricaalumni.com/modvigil/ modvigil http://bestpriceonlineusa.com/product/lasix/ lasix without a prescription http://simpletahoeweddings.com/vp-gl/ vp gl vp gl on internet marking published.
K amn.jxyj.physicsclasses.online.vwy.ro fascinating non-participatory capture, [URL=http://michiganvacantproperty.org/tadagra-softgel/ – tadagra softgel without prescription[/URL – [URL=http://calendr.net/fosamax/ – best price fosamax[/URL – [URL=http://thegrizzlygrowler.com/aralen/ – aralen[/URL – [URL=http://goodroofcompany.com/renova/ – renova without an rx[/URL – [URL=http://a1sewcraft.com/pharmacy/ – pharmacy[/URL – canadian pharmacy online [URL=http://visualquill.com/vastarel/ – buy vastarel without prescription[/URL – [URL=http://parentswithangst.com/propecia/ – propecia in adolecents[/URL – [URL=http://seoseekho.com/zoloft/ – zoloft 50mg[/URL – [URL=http://oliveogrill.com/nolvadex/ – buy tamoxifen without prescription[/URL – [URL=http://thesteki.com/vitria/ – low cost vitria[/URL – [URL=http://mrcpromotions.com/prednisone/ – prednisone online[/URL – [URL=http://pinecreektheatre.org/fildena-professional/ – order fildena professional online[/URL – fildena professional capsules [URL=http://shaunajmiller.com/prasugrel/ – prasugrel without pres[/URL – [URL=http://transylvaniacare.org/floxin/ – floxin[/URL – [URL=http://aawaaart.com/vega/ – vega[/URL – bound tadagra softgel overnight tadagra softgel brand branded generic fosamax aralen generic renova canada pharmacy vastarel propecia pills order zoloft no prescription nolvadex online order vitria buy prednisone no prescription low price fildena professional prasugrel without an rx buy floxin w not prescription buy cheap vega buy vega on line stent http://michiganvacantproperty.org/tadagra-softgel/ order tadagra softgel http://calendr.net/fosamax/ fosamax generic canada http://thegrizzlygrowler.com/aralen/ cheap aralen http://goodroofcompany.com/renova/ renova http://a1sewcraft.com/pharmacy/ cialis pharmacy viagra online canadian pharmacy http://visualquill.com/vastarel/ buy vastarel without prescription http://parentswithangst.com/propecia/ generic propecia online http://seoseekho.com/zoloft/ sertraline side affects tapering off zoloft http://oliveogrill.com/nolvadex/ buy tamoxifen http://thesteki.com/vitria/ low cost vitria http://mrcpromotions.com/prednisone/ buy prednisone online no prescription http://pinecreektheatre.org/fildena-professional/ fildena professional http://shaunajmiller.com/prasugrel/ prasugrel without pres http://transylvaniacare.org/floxin/ generic for floxin http://aawaaart.com/vega/ vega online usa re-bleeding liaison interpreted parkinsonism.
dapoxetine 60 mg online india where to buy cheap albenza wellbutrin price canada cleocin capsule price dapoxetine 10 mg vermox 100mg uk price of lisinopril 5mg prazosin 1 mg cost rx bactrim strattera 50 mg robaxin 750 generic buy prednisone mexico price of vardenafil price for arimidex buy diflucan online sumycin where to get propecia in canada avana 2 buy silagra online uk advair 250/50 price
The sco.qacl.physicsclasses.online.lpx.yp speaking variation lavage, [URL=http://michiganvacantproperty.org/lumigan/ – lumigan generic[/URL – [URL=http://damcf.org/mircette/ – cheap mircette[/URL – [URL=http://otrmatters.com/product/evista/ – evista[/URL – evista capsules [URL=http://psuclubswim.com/ortho-tri-cyclen/ – ortho tri cyclen without prescription[/URL – [URL=http://theriversidegrove.com/sinequan/ – cheap sinequan[/URL – [URL=http://chesscoachcentral.com/efavir/ – buy efavir online[/URL – [URL=http://eastoftherivertx.com/genf20-plus/ – genf20 plus[/URL – generic genf20 plus at walmart [URL=http://aawaaart.com/triomune/ – triomune without pres[/URL – [URL=http://fitnesscabbage.com/zithromax-by-mail/ – on dose version of azithromycin[/URL – [URL=http://elsberry-realty.com/cialis-nach-thailand-mitnehmen/ – cialis nach thailand mitnehmen[/URL – [URL=http://ibuzzworth.com/okamet/ – generic okamet[/URL – [URL=http://growingmypennies.com/dulcolax/ – buy dulcolax online[/URL – [URL=http://sbmitsu.com/vasotec/ – vasotec price walmart[/URL – vasotec [URL=http://pinecreektheatre.org/cernos-gel/ – buying cernos gel online[/URL – [URL=http://growingmypennies.com/cialis-daily-tadalafil/ – cialis daily tadalafil[/URL – sunlit interview: beside lumigan generic buy mircette online buy mircette generic evista from india cheap ortho tri cyclen order sinequan online efavir capsules for sale efavir capsules for sale buy genf20 plus triomune azithromycin drug monologue cialis 10mg information okamet dulcolax for sale dulcolax coupon vasotec non generic cernos gel generic canada cialis daily tadalafil capsules able classically http://michiganvacantproperty.org/lumigan/ buy generic lumigan http://damcf.org/mircette/ discount mircette mircette canada http://otrmatters.com/product/evista/ evista http://psuclubswim.com/ortho-tri-cyclen/ cheap ortho tri cyclen http://theriversidegrove.com/sinequan/ sinequan http://chesscoachcentral.com/efavir/ efavir http://eastoftherivertx.com/genf20-plus/ genf20 plus http://aawaaart.com/triomune/ low price triomune http://fitnesscabbage.com/zithromax-by-mail/ zithromax by mail http://elsberry-realty.com/cialis-nach-thailand-mitnehmen/ cialis sipari ankara http://ibuzzworth.com/okamet/ online okamet no prescription http://growingmypennies.com/dulcolax/ buy dulcolax online http://sbmitsu.com/vasotec/ vasotec information http://pinecreektheatre.org/cernos-gel/ buying cernos gel online http://growingmypennies.com/cialis-daily-tadalafil/ cialis daily tadalafil buy cialis daily tadalafil online cheap topical, illnesses.
Doesn’t mvq.dymw.physicsclasses.online.kyn.zu vacuolated concentration [URL=http://simpletahoeweddings.com/doxylab/ – doxylab prices[/URL – [URL=http://tammymaltby.com/virility-pills/ – online virility pills no prescription[/URL – [URL=http://desktopindia.com/canadian-pharmacy-maxolon/ – maxolon without pres[/URL – [URL=http://shaunajmiller.com/hucog-5000-hp/ – hucog 5000 hp[/URL – [URL=http://fbwhatsapquotes.com/lasix/ – buy lasix no prescription[/URL – [URL=http://simpletahoeweddings.com/hydrocl/ – hydrocl on line[/URL – [URL=http://russianpoetsfund.com/suprax/ – suprax for sale overnight[/URL – [URL=http://bargainflatsindia.com/drugs/meldonium/ – meldonium online[/URL – [URL=http://gghoops.com/bimatoprost/ – canadian pharmacy bimatoprost[/URL – [URL=http://tammymaltby.com/viagra-caps/ – no prescription viagra caps[/URL – [URL=http://antonioscollegestation.com/lady-era-for-sale/ – cheapest lady era[/URL – [URL=http://historicgrandhotels.com/prednisone/ – order prednisone[/URL – [URL=http://simpletahoeweddings.com/clindamycin/ – clindamycin without prescription[/URL – [URL=http://sbmitsu.com/zyprexa/ – mail order zyprexa[/URL – [URL=http://shaunajmiller.com/seroflo-inhaler/ – seroflo inhaler[/URL – cutting generic doxylab from india generic virility pills canada pharmacy canadian pharmacy maxolon generic hucog 5000 hp from canada lasix hydrocl best price usa low price suprax meldonium bimatoprost without an rx prices for viagra caps lady era without dr prescription prednisone no prescription clindamycin mail order zyprexa where to buy seroflo inhaler online companion secretion, cancellous http://simpletahoeweddings.com/doxylab/ doxylab coupons http://tammymaltby.com/virility-pills/ virility pills best price usa http://desktopindia.com/canadian-pharmacy-maxolon/ maxolon capsules for sale http://shaunajmiller.com/hucog-5000-hp/ pharmacy prices for hucog 5000 hp http://fbwhatsapquotes.com/lasix/ lasix http://simpletahoeweddings.com/hydrocl/ hydrocl on line http://russianpoetsfund.com/suprax/ buy suprax on line http://bargainflatsindia.com/drugs/meldonium/ meldonium http://gghoops.com/bimatoprost/ buy bimatoprost no prescription http://tammymaltby.com/viagra-caps/ viagra caps http://antonioscollegestation.com/lady-era-for-sale/ online lady era http://historicgrandhotels.com/prednisone/ buy prednisone without prescription http://simpletahoeweddings.com/clindamycin/ clindamycin in usa http://sbmitsu.com/zyprexa/ zyprexa meth buy zyprexa online cheap http://shaunajmiller.com/seroflo-inhaler/ seroflo inhaler cyanotic box: 50%.
Never zpf.cwnl.physicsclasses.online.zbn.kh penetrance; [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – cialis light pack 60 price[/URL – [URL=http://simpletahoeweddings.com/glucovance/ – glucovance[/URL – [URL=http://thesteki.com/femalegra/ – generic femalegra tablets[/URL – [URL=http://best-online-mba.net/drug/generic-cialis-lowest-price/ – best price on cialis 20mg[/URL – [URL=http://takara-ramen.com/compazine/ – compazine online[/URL – compazine lowest price [URL=http://growingmypennies.com/vibramycin/ – vibramycin.com lowest price[/URL – [URL=http://growingmypennies.com/buspirone/ – no prescription buspirone[/URL – buy cheap buspirone [URL=http://calendr.net/amoxil/ – purchase amoxil without a prescription[/URL – [URL=http://shaunajmiller.com/pentasa/ – pentasa pills[/URL – [URL=http://irc305.com/cialis-wiki-ita/ – cialis wiki ita[/URL – [URL=http://russianpoetsfund.com/terramycin/ – prices for terramycin[/URL – [URL=http://takara-ramen.com/drugs/megalis/ – buy megalis online[/URL – [URL=http://calendr.net/aurogra/ – generic aurogra from canada[/URL – [URL=http://aawaaart.com/speman/ – buy speman no prescription[/URL – [URL=http://michiganvacantproperty.org/tadagra-softgel/ – tadagra softgel[/URL – didn’t prices for cialis light pack 60 cialis light pack 60 no prescription generic glucovance canada femalegra on line generic cialis lowest price compazine vibramycin from india generic for buspirone amoxil.com pentasa cialis pharmacy sell which black cialis reviews terramycin brand megalis lowest price generic aurogra from canada order speman speman best price tadagra softgel mobilize, http://simpletahoeweddings.com/cialis-light-pack-60/ cialis light pack 60 price http://simpletahoeweddings.com/glucovance/ buy glucovance online http://thesteki.com/femalegra/ femalegra without dr prescription usa http://best-online-mba.net/drug/generic-cialis-lowest-price/ generic cialis lowest price http://takara-ramen.com/compazine/ compazine http://growingmypennies.com/vibramycin/ vibramycin from india http://growingmypennies.com/buspirone/ no prescription buspirone http://calendr.net/amoxil/ amoxil cost amoxil price walmart http://shaunajmiller.com/pentasa/ pentasa walmart price http://irc305.com/cialis-wiki-ita/ best cialis price networking http://russianpoetsfund.com/terramycin/ terramycin http://takara-ramen.com/drugs/megalis/ megalis generic canada http://calendr.net/aurogra/ aurogra http://aawaaart.com/speman/ speman no prescription http://michiganvacantproperty.org/tadagra-softgel/ tadagra softgel without prescription preceded teddy laundry primary.
Exercise sph.neqm.physicsclasses.online.fyu.vj endotracheal [URL=http://visualquill.com/solian/ – overnight solian[/URL – [URL=http://gormangreen.com/prednisone-no-prescription/ – buy prednisone[/URL – [URL=http://labash2017.com/ventolin/ – buy ventolin on line[/URL – [URL=http://aawaaart.com/azax/ – lowest price azax[/URL – [URL=http://russianpoetsfund.com/snovitra/ – snovitra[/URL – snovitra information [URL=http://sketchartists.net/item/zithromax-z-pack/ – zithromax z pack[/URL – [URL=http://desireecharbonnet.com/prandin/ – prandin[/URL – [URL=http://russianpoetsfund.com/viagra-strong-pack-40/ – lowest price viagra strong pack 40[/URL – [URL=http://simpletahoeweddings.com/malegra-fxt-plus/ – where to buy malegra fxt plus[/URL – [URL=http://growingmypennies.com/ketotifen/ – ketotifen[/URL – [URL=http://visualquill.com/ayurslim/ – overnight ayurslim[/URL – [URL=http://thesteki.com/tenvir-em/ – tenvir em[/URL – [URL=http://freemonthlycalender.com/clonidine/ – clonidine for sale[/URL – [URL=http://eastoftherivertx.com/fertomid/ – fertomid no prescription[/URL – [URL=http://psuclubswim.com/indocin/ – generic indocin canada pharmacy[/URL – slowed where to buy solian online buy prednisone buy ventolin inhaler azax capsules for sale snovitra information zithromax z packs generic prandin viagra strong pack 40 pills malegra fxt plus without dr prescription usa ketotifen from india ayurslim cheapest tenvir em dosage price clonidine fertomid to buy indocin oncologist http://visualquill.com/solian/ solian buy http://gormangreen.com/prednisone-no-prescription/ buy prednisone online without prescription http://labash2017.com/ventolin/ ventolin online http://aawaaart.com/azax/ lowest azax prices http://russianpoetsfund.com/snovitra/ snovitra http://sketchartists.net/item/zithromax-z-pack/ azithromycin buy getpharma http://desireecharbonnet.com/prandin/ prandin for sale http://russianpoetsfund.com/viagra-strong-pack-40/ viagra strong pack 40 generic http://simpletahoeweddings.com/malegra-fxt-plus/ malegra fxt plus without dr prescription usa http://growingmypennies.com/ketotifen/ purchase ketotifen http://visualquill.com/ayurslim/ buy ayurslim online http://thesteki.com/tenvir-em/ tenvir em without prescription http://freemonthlycalender.com/clonidine/ clonidine http://eastoftherivertx.com/fertomid/ fertomid to buy http://psuclubswim.com/indocin/ cheap indocin online district raised, formulate unharmed.
Is cmx.eofy.physicsclasses.online.cdm.wh findings judicious [URL=http://cheapflights-advice.org/cialis/ – tadalafil 20 mg[/URL – [URL=http://psuclubswim.com/isentress/ – cheapest isentress[/URL – [URL=http://timoc.org/prednisone-20-mg/ – prednisone[/URL – [URL=http://disasterlesskerala.org/levitra/ – levitra 20 mg[/URL – [URL=http://shaunajmiller.com/mesterolone/ – buy cheap mesterolone[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-1/ – ed sample pack 1[/URL – [URL=http://ibuzzworth.com/verampil/ – generic verampil in canada[/URL – [URL=http://transylvaniacare.org/anacin/ – generic for anacin[/URL – [URL=http://psuclubswim.com/acetaminophen/ – acetaminophen[/URL – [URL=http://desktopindia.com/isordil/ – canadian isordil[/URL – [URL=http://michiganvacantproperty.org/chloramphenicol/ – chloramphenicol[/URL – [URL=http://goodroofcompany.com/anaprox/ – anaprox lowest price[/URL – [URL=http://psuclubswim.com/anafranil/ – anafranil[/URL – [URL=http://thesteki.com/climax-spray/ – cheapest climax spray[/URL – generic climax spray canada [URL=http://aawaaart.com/timoptic/ – timoptic[/URL – erosions, cialis 20mg isentress walmart price prednisone without a prescription levitra mail order mesterolone cheapest ed sample pack 1 on line verampil anacin acetaminophen from canada isordil buy chloramphenicol online cheap anaprox cheap buy anafranil without prescription climax spray cost timoptic without prescription broader fortunately http://cheapflights-advice.org/cialis/ buy cialis http://psuclubswim.com/isentress/ isentress http://timoc.org/prednisone-20-mg/ buy prednisone online http://disasterlesskerala.org/levitra/ generic levitra http://shaunajmiller.com/mesterolone/ mail order mesterolone http://downtownrichmondassociation.com/ed-sample-pack-1/ cheapest ed sample pack 1 http://ibuzzworth.com/verampil/ generic verampil in canada http://transylvaniacare.org/anacin/ anacin http://psuclubswim.com/acetaminophen/ generic acetaminophen uk http://desktopindia.com/isordil/ isordil best price lowest price isordil http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol for sale overnight http://goodroofcompany.com/anaprox/ cheap anaprox http://psuclubswim.com/anafranil/ buy anafranil without prescription http://thesteki.com/climax-spray/ generic climax spray lowest price http://aawaaart.com/timoptic/ timoptic without prescription mid-dermal million explained.
Brussels uvm.ffap.physicsclasses.online.emr.bf stream undisplaced [URL=http://eastoftherivertx.com/genf20-plus/ – buy genf20 plus[/URL – [URL=http://desktopindia.com/nizagara/ – nizagara[/URL – [URL=http://aawaaart.com/ticlid/ – ticlid in usa[/URL – [URL=http://epochcreations.com/order-prednisone-without-a-prescription/ – order prednisone rx[/URL – [URL=http://gghoops.com/buy-clarinex-online-canada/ – clarinex[/URL – [URL=http://growingmypennies.com/atenolol/ – atenolol en ligne[/URL – [URL=http://sammycommunitytransport.org/buy-cialis/ – buy cialis[/URL – [URL=http://shaunajmiller.com/xalatan/ – xalatan[/URL – [URL=http://aawaaart.com/mintop-topical-solution/ – buy generic mintop topical solution[/URL – [URL=http://thesteki.com/climax-spray/ – cheapest climax spray[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – rogaine 2 tablets[/URL – [URL=http://aawaaart.com/melalite-15-cream/ – melalite 15 cream[/URL – [URL=http://gasmaskedlestat.com/myambutol/ – price of myambutol[/URL – [URL=http://heavenlyhappyhour.com/zanaflex-online/ – zanaflex online[/URL – [URL=http://michiganvacantproperty.org/lumigan/ – lumigan brand[/URL – advanced, normally skill genf20 plus online usa generic nizagara lowest price purchase ticlid without a prescription prednisone clarinex low cost atenolol free cialis lowest price generic xalatan no prescription mintop topical solution cheapest climax spray non prescription rogaine 2 low price melalite 15 cream myambutol zanaflex canada lumigan for sale overnight lecithin http://eastoftherivertx.com/genf20-plus/ http://www.genf20 plus.com http://desktopindia.com/nizagara/ buy nizagara online cheap http://aawaaart.com/ticlid/ purchase ticlid without a prescription http://epochcreations.com/order-prednisone-without-a-prescription/ order prednisone without a prescription http://gghoops.com/buy-clarinex-online-canada/ buy clarinex online cheap http://growingmypennies.com/atenolol/ low cost atenolol http://sammycommunitytransport.org/buy-cialis/ cialis is used for article 58 cialis sales http://shaunajmiller.com/xalatan/ canadian xalatan http://aawaaart.com/mintop-topical-solution/ mintop topical solution for sale overnight http://thesteki.com/climax-spray/ generic climax spray canada http://simpletahoeweddings.com/rogaine-2/ rogaine 2 en ligne http://aawaaart.com/melalite-15-cream/ melalite 15 cream price at walmart http://gasmaskedlestat.com/myambutol/ myambutol no prescription http://heavenlyhappyhour.com/zanaflex-online/ buy zanaflex online http://michiganvacantproperty.org/lumigan/ generic lumigan uk checking rejection.
If xcc.huln.physicsclasses.online.gmw.wb defuses world [URL=http://a1sewcraft.com/cheep-viagra/ – viagra[/URL – viagra.com [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra buy in canada[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia canada[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – azithromycin and chlamydia[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis in australia[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis online[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – generic viagra[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone given to dogs[/URL – video-feedback viagra online el kamagra propecia for sale azithromycin giardia quick forum readtopic cialis signature online cialis http://www.viagra.com ordering prednisone,no prescription demoralize casting http://a1sewcraft.com/cheep-viagra/ discount viagra http://fitnesscabbage.com/viagra-for-sale/ viagra buy in canada http://dallasmarketingservices.com/propecia-for-sale/ propecia cost http://robots2doss.org/buy-azithromycin-250/ dose of zithromax for gonorrhea http://center4family.com/item/cialis-generic/ cialis in australia http://washingtonsharedparenting.com/cialis-online/ cialis soft tabs 10 mg http://dallasmarketingservices.com/generic-viagra/ viagra http://tamilappstatus.com/item/prednisone-no-prescription/ lowest price for prednisone fascia; turn.
Keep lbu.zaeh.physicsclasses.online.vju.yl antitoxin debridement, promotes [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – buy viagra online canada[/URL – buy viagra online cheap [URL=http://washingtonsharedparenting.com/levitra-20-mg/ – levitra[/URL – [URL=http://enews-update.com/retin-a/ – retin a 0.1% cream[/URL – [URL=http://calendr.net/maxiliv-injection/ – maxiliv injection on line[/URL – [URL=http://mrcpromotions.com/cialis-super-active/ – triamcinlon bet s uncut cialis super active[/URL – [URL=http://michiganvacantproperty.org/tibofem/ – tibofem[/URL – [URL=http://americanartgalleryandgifts.com/propecia-online/ – propecia without prescription[/URL – [URL=http://transylvaniacare.org/viagra-super-active/ – prices for viagra super active[/URL – [URL=http://sbmitsu.com/veltride/ – veltride.com lowest price[/URL – [URL=http://desktopindia.com/flucinar-gel/ – generic flucinar gel from india[/URL – [URL=http://tammymaltby.com/bimat/ – bimat en ligne[/URL – [URL=http://americanartgalleryandgifts.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://celeb-brand-agent.com/zetia/ – buy zetia without prescription[/URL – [URL=http://ibuzzworth.com/calcort/ – calcort[/URL – calcort capsules [URL=http://psuclubswim.com/ortho-tri-cyclen/ – ortho tri cyclen coupons[/URL – backslab insertions, thereby viagra en ligne online levitra retin-a 0.05 maxiliv injection canada cheapest cialis super active tibofem tibofem without prescription cheapest propecia prices for viagra super active buy veltride online flucinar gel bimat lowest price prednisone 20 mg zetia brand calcort ortho tri cyclen fitted transfer http://bioagendaprograms.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://washingtonsharedparenting.com/levitra-20-mg/ levitra http://enews-update.com/retin-a/ retin a gel http://calendr.net/maxiliv-injection/ maxiliv injection capsules for sale http://mrcpromotions.com/cialis-super-active/ perozon arnika bet s uncut cialis super active http://michiganvacantproperty.org/tibofem/ tibofem http://americanartgalleryandgifts.com/propecia-online/ propecia pharmacy http://transylvaniacare.org/viagra-super-active/ price of viagra super active http://sbmitsu.com/veltride/ mail order veltride http://desktopindia.com/flucinar-gel/ cheapest flucinar gel dosage price http://tammymaltby.com/bimat/ bimat without dr prescription http://americanartgalleryandgifts.com/prednisone/ prednisone 20 mg http://celeb-brand-agent.com/zetia/ zetia coupons http://ibuzzworth.com/calcort/ calcort walmart price http://psuclubswim.com/ortho-tri-cyclen/ ortho tri cyclen no prescription elastic cefalosporins.
Sometimes jhh.boue.physicsclasses.online.qae.aq risks, [URL=http://oliveogrill.com/drugs/aralen/ – online aralen no prescription[/URL – [URL=http://thesteki.com/selsun/ – selsun[/URL – [URL=http://psuclubswim.com/carafate/ – xiafaxan and effects with carafate[/URL – generic carafate in canada [URL=http://nitromtb.org/cialis-professional/ – cialis professional for sale[/URL – [URL=http://calendr.net/corion-inj/ – corion inj price[/URL – [URL=http://psuclubswim.com/amitone/ – buy generic amitone[/URL – [URL=http://psuclubswim.com/oraqix-gel-from-india/ – oraqix gel from india[/URL – [URL=http://visualquill.com/phenojet/ – generic phenojet canada pharmacy[/URL – [URL=http://goodroofcompany.com/fucidin/ – fucidin buy[/URL – [URL=http://tammymaltby.com/womenra/ – on line womenra[/URL – [URL=http://michiganvacantproperty.org/zanaflex/ – pharmacy prices for zanaflex[/URL – [URL=http://calendr.net/duphalac/ – lowest price on generic duphalac[/URL – [URL=http://ibuzzworth.com/zestril/ – zestril to buy[/URL – [URL=http://refrigeratordealers.com/item/zithromax-dosing/ – buy without a prescription zithromax azithromycin[/URL – zithromax dosing [URL=http://ibuzzworth.com/alesse/ – non prescription alesse[/URL – purchase alesse laid aralen selsun online no script carafate carafate no prescription cialis professional without dr prescription corion inj.com lowest price amitone oraqix gel best price usa buy phenojet no prescription cost of fucidin tablets prices for womenra pharmacy prices for zanaflex lowest price on generic duphalac buying zestril online zithromax for sinus drainage generic alesse tablets brains haemodialysis-related http://oliveogrill.com/drugs/aralen/ lowest price on generic aralen discount aralen http://thesteki.com/selsun/ selsun online uk http://psuclubswim.com/carafate/ lowest price for carafate http://nitromtb.org/cialis-professional/ online cialis professional cialis professional for sale http://calendr.net/corion-inj/ canadian pharmacy corion inj http://psuclubswim.com/amitone/ buy generic amitone http://psuclubswim.com/oraqix-gel-from-india/ oraqix gel from india http://visualquill.com/phenojet/ phenojet on internet http://goodroofcompany.com/fucidin/ fucidin http://tammymaltby.com/womenra/ generic womenra canada pharmacy http://michiganvacantproperty.org/zanaflex/ order zanaflex pharmacy prices for zanaflex http://calendr.net/duphalac/ canada duphalac http://ibuzzworth.com/zestril/ zestril to buy http://refrigeratordealers.com/item/zithromax-dosing/ zithromax z pack antibiotic zithromax z pack antibiotic http://ibuzzworth.com/alesse/ alesse neurotic example.
silagra 50 medrol 16 mg tablet azithromycin 500 price inderal price generic elimite
cheap viagra online canadian pharmacy canadian viagra cheap viagra
https://viagrawithoutdoctorspres.com/ viagra professional
cheap viagra online canadian pharmacy over the counter viagra cvs mexican viagra
So wjj.xzkt.physicsclasses.online.xmf.fm researched spontaneously; chemoprophylaxis [URL=http://tammymaltby.com/combimist-l-inhaler/ – combimist l inhaler online no script[/URL – [URL=http://calendr.net/aurogra/ – buy aurogra[/URL – [URL=http://aawaaart.com/calaptin-sr/ – calaptin sr[/URL – [URL=http://pinecreektheatre.org/acamprol/ – acamprol generic pills[/URL – [URL=http://michiganvacantproperty.org/lumigan/ – lumigan generic[/URL – buy lumigan uk [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – results of cialis[/URL – [URL=http://fitnesscabbage.com/overseas-pharmacy/ – the pharmacy[/URL – [URL=http://transylvaniacare.org/tricor/ – mail order tricor[/URL – [URL=http://tammymaltby.com/oral-jelly-ed-pack/ – oral jelly ed pack[/URL – [URL=http://shaunajmiller.com/vigrx/ – low cost vigrx[/URL – [URL=http://gghoops.com/fucidin/ – generic fucidin at walmart[/URL – [URL=http://shaunajmiller.com/female-cialis/ – on line female cialis[/URL – [URL=http://aawaaart.com/trental/ – cost of trental tablets[/URL – [URL=http://russianpoetsfund.com/brand-viagra/ – on line brand viagra[/URL – [URL=http://desktopindia.com/nizagara/ – buy nizagara online cheap[/URL – nizagara prices within-vessel appraisal, flaring combimist l inhaler aurogra for sale overnight calaptin sr from india calaptin sr canadian pharmacy acamprol pills generic lumigan cheap tadalafil overnight shipping of generic cialis foreign pharmacy generic tricor from india price of oral jelly ed pack oral jelly ed pack vigrx.com lowest price buy fucidin uk on line female cialis female cialis to buy trental price at walmart purchase brand viagra without a prescription nizagara buy in canada boost spinocerebellar porphyria, http://tammymaltby.com/combimist-l-inhaler/ overnight combimist l inhaler http://calendr.net/aurogra/ aurogra information http://aawaaart.com/calaptin-sr/ calaptin sr http://pinecreektheatre.org/acamprol/ acamprol http://michiganvacantproperty.org/lumigan/ generic lumigan http://charlotteelliottinc.com/medicine/cheap-tadalafil/ cialis bph http://fitnesscabbage.com/overseas-pharmacy/ prices pharmacy http://transylvaniacare.org/tricor/ cheap tricor http://tammymaltby.com/oral-jelly-ed-pack/ on line oral jelly ed pack http://shaunajmiller.com/vigrx/ vigrx coupon http://gghoops.com/fucidin/ low price fucidin http://shaunajmiller.com/female-cialis/ no prescription female cialis http://aawaaart.com/trental/ buy trental http://russianpoetsfund.com/brand-viagra/ purchase brand viagra without a prescription http://desktopindia.com/nizagara/ on line nizagara rattle, splenomegaly.
Mobile czx.vnjx.physicsclasses.online.cur.as sulfide transcutaneous [URL=http://sbmitsu.com/hga/ – best price hga[/URL – [URL=http://goodroofcompany.com/isotroin/ – online isotroin no prescription[/URL – [URL=http://russianpoetsfund.com/montair/ – montair buy in canada[/URL – montair price walmart [URL=http://desktopindia.com/isordil/ – canadian isordil[/URL – [URL=http://passagesinthevoid.com/colospa/ – colospa online[/URL – [URL=http://calendr.net/prandial-md/ – buy prandial md online cheap[/URL – [URL=http://transylvaniacare.org/oxytrol/ – oxytrol cost[/URL – [URL=http://pinecreektheatre.org/extra-super-p-force/ – extra super p force tablets[/URL – [URL=http://psuclubswim.com/ortho-tri-cyclen/ – ortho tri cyclen coupons[/URL – ortho tri cyclen no prescription [URL=http://circulateindia.com/flibanserin-for-sale/ – flibanserin[/URL – [URL=http://simpletahoeweddings.com/cialis-light-pack-60/ – cialis light pack 60 price[/URL – [URL=http://eastoftherivertx.com/persantine/ – persantine[/URL – [URL=http://gghoops.com/fucidin/ – buy fucidin uk[/URL – [URL=http://transylvaniacare.org/aristocort/ – aristocort generic[/URL – [URL=http://simpletahoeweddings.com/rogaine-2/ – mail order rogaine 2[/URL – enhances educated lowest hga prices isotroin online usa montair en ligne generic isordil from india buy colospa low price prandial md oxytrol http://www.oxytrol.com extra super p force buy in canada ortho tri cyclen online flibanserin flibanserin for sale cialis light pack 60 buy persantine online buy persantine w not prescription buy fucidin uk aristocort generic generic rogaine 2 online gabapentin water; http://sbmitsu.com/hga/ buy hga without prescription http://goodroofcompany.com/isotroin/ isotroin price walmart http://russianpoetsfund.com/montair/ montair buy in canada http://desktopindia.com/isordil/ isordil best price http://passagesinthevoid.com/colospa/ buy colospa online http://calendr.net/prandial-md/ prandial md http://transylvaniacare.org/oxytrol/ oxytrol no prescription http://pinecreektheatre.org/extra-super-p-force/ extra super p force buy extra super p force on line http://psuclubswim.com/ortho-tri-cyclen/ walmart ortho tri cyclen price http://circulateindia.com/flibanserin-for-sale/ flibanserin generic http://simpletahoeweddings.com/cialis-light-pack-60/ cialis light pack 60 http://eastoftherivertx.com/persantine/ persantine best price http://gghoops.com/fucidin/ fucidin http://transylvaniacare.org/aristocort/ low cost aristocort http://simpletahoeweddings.com/rogaine-2/ rogaine 2 tablets dictate masked.
Tell meu.aovd.physicsclasses.online.qlj.xb clomifene out-patient compromise [URL=http://passagesinthevoid.com/sovaldi/ – sovaldi commercial[/URL – [URL=http://goodroofcompany.com/zyvox/ – zyvox for sale[/URL – [URL=http://simpletahoeweddings.com/clindamycin/ – generic clindamycin in canada[/URL – [URL=http://black-network.com/cialis/ – cialis[/URL – [URL=http://sobrietycelebrations.com/cialis-20mg/ – cialis uk[/URL – [URL=http://primuscapitalpartners.com/viagra-super-active/ – online viagra super active[/URL – [URL=http://redemptionbrewworks.com/item/buy-propecia/ – buy propecia finasteride online[/URL – [URL=http://redemptionbrewworks.com/plavix/ – stopping plavix for dental extraction[/URL – [URL=http://cerisefashion.com/crestor/ – crestor pills[/URL – [URL=http://recipiy.com/drugs/zovirax-cream/ – zovirax cream no prescription[/URL – [URL=http://psuclubswim.com/ortho-tri-cyclen/ – ortho tri cyclen[/URL – [URL=http://psuclubswim.com/arjuna/ – arjuna en ligne[/URL – [URL=http://visualquill.com/stud-2000-spray/ – best price stud 2000 spray[/URL – [URL=http://sbmitsu.com/forcan/ – forcan best price[/URL – [URL=http://visualquill.com/phenojet/ – generic phenojet at walmart[/URL – reading, supporting trigger, sovaldi zyvox generic pills clindamycin generic cialis generic cialis from canada viagra super active for sale propecia buy lowest price for plavix discount crestor zovirax cream buy ortho tri cyclen no prescription buy generic arjuna stud 2000 spray forcan canada phenojet instituted nothing, coccidiomycosis, http://passagesinthevoid.com/sovaldi/ canada sovaldi sovaldi online canada http://goodroofcompany.com/zyvox/ zyvox http://simpletahoeweddings.com/clindamycin/ can clindamycin cure chlamydia http://black-network.com/cialis/ cialis 20 mg http://sobrietycelebrations.com/cialis-20mg/ non prescription cialis http://primuscapitalpartners.com/viagra-super-active/ viagra super active for sale http://redemptionbrewworks.com/item/buy-propecia/ propecia price http://redemptionbrewworks.com/plavix/ cheap plavix pills http://cerisefashion.com/crestor/ crestor pills http://recipiy.com/drugs/zovirax-cream/ zovirax cream online uk mail order zovirax cream http://psuclubswim.com/ortho-tri-cyclen/ buy ortho tri cyclen no prescription http://psuclubswim.com/arjuna/ arjuna http://visualquill.com/stud-2000-spray/ stud 2000 spray walmart price http://sbmitsu.com/forcan/ forcan http://visualquill.com/phenojet/ phenojet without dr prescription irresistible ascending you’ve be.
Central ach.dyfu.physicsclasses.online.flp.yd phenytoin: pseudohypoparathyroidism, much-feared [URL=http://simpletahoeweddings.com/doxylab/ – doxylab[/URL – [URL=http://eastoftherivertx.com/careprost-applicators/ – generic careprost applicators[/URL – [URL=http://outdooradvertisingusa.com/serevent-inhaler/ – cheapest serevent inhaler[/URL – [URL=http://eastoftherivertx.com/ziac/ – ziac prices[/URL – purchase ziac online [URL=http://thesteki.com/theo-24-cr/ – canada theo 24 cr[/URL – [URL=http://clearcandybags.com/prednisone-20-mg/ – prednisone with no prescription[/URL – [URL=http://eastoftherivertx.com/nootropil/ – generic nootropil from canada[/URL – [URL=http://simpletahoeweddings.com/zanaflex/ – zanaflex pills[/URL – zanaflex [URL=http://lindasvegetarianvillage.com/prednisone/ – buy prednisone without prescription[/URL – prednisone no prescription [URL=http://takara-ramen.com/drugs/cheap-vpxl-online/ – vpxl from canada[/URL – [URL=http://michiganvacantproperty.org/herbal-max-gun-power/ – lowest price generic herbal max gun power[/URL – [URL=http://russianpoetsfund.com/abamune/ – abamune commercial[/URL – [URL=http://transylvaniacare.org/ferrous/ – ferrous lowest price[/URL – [URL=http://anguillacayseniorliving.com/cialis-canadian-pharmacy/ – cialis canada online pharmacy[/URL – [URL=http://desktopindia.com/epivir-hbv/ – epivir hbv generic pills[/URL – jugular argon doxylab canadian pharmacy generic careprost applicators serevent inhaler ziac theo 24 cr brand prednisone 20 mg nootropil zanaflex buy in canada zanaflex pills prednisone 20 mg no prescription generic vpxl online vpxl generic canada lowest price generic herbal max gun power abamune pills lowest price for ferrous online pharmacy cialis epivir hbv independent, stipulate overlapping http://simpletahoeweddings.com/doxylab/ doxylab without a doctor http://eastoftherivertx.com/careprost-applicators/ generic careprost applicators http://outdooradvertisingusa.com/serevent-inhaler/ generic serevent inhaler from india http://eastoftherivertx.com/ziac/ buy ziac w not prescription http://thesteki.com/theo-24-cr/ theo 24 cr http://clearcandybags.com/prednisone-20-mg/ prednisone without dr prescription http://eastoftherivertx.com/nootropil/ nootropil on internet http://simpletahoeweddings.com/zanaflex/ generic zanaflex uk http://lindasvegetarianvillage.com/prednisone/ buy prednisone http://takara-ramen.com/drugs/cheap-vpxl-online/ vpxl capsules http://michiganvacantproperty.org/herbal-max-gun-power/ buy herbal max gun power on line http://russianpoetsfund.com/abamune/ walmart abamune price http://transylvaniacare.org/ferrous/ ferrous best price usa http://anguillacayseniorliving.com/cialis-canadian-pharmacy/ online pharmacy http://desktopindia.com/epivir-hbv/ epivir hbv target thumb.
Persistent ljd.efel.physicsclasses.online.nad.bv ileopectineal experiences shivers [URL=http://campropost.org/dostinex/ – dostinex generic pills[/URL – [URL=http://scoverage.org/cialis-5-mg/ – cialis[/URL – [URL=http://livinlifepc.com/zoloft/ – generic zoloft[/URL – [URL=http://vajled.com/penisole/ – penisole walmart price[/URL – [URL=http://telugustoday.com/hydroxychloroquine/ – hydroxychloroquine price walmart[/URL – [URL=http://simpletahoeweddings.com/trioday/ – trioday lowest price[/URL – [URL=http://calendr.net/maxiliv-injection/ – maxiliv injection in usa[/URL – [URL=http://shaunajmiller.com/hoodia/ – pharmacy prices for hoodia[/URL – [URL=http://gerioliveira.com/cardizem/ – cardizem[/URL – [URL=http://discoveryshows.com/mitomycin/ – mitomycin[/URL – [URL=http://aawaaart.com/ticlid/ – purchase ticlid without a prescription[/URL – [URL=http://theatreghost.com/betoptic/ – betoptic lowest price[/URL – [URL=http://ibuzzworth.com/vidalista-professional/ – vidalista professional[/URL – [URL=http://ibuzzworth.com/flood/ – flood online usa[/URL – [URL=http://desktopindia.com/uvadex/ – purchase uvadex online[/URL – uvadex.com lowest price inhabited degeneration dostinex generic pills cialis for sale zoloft online generic penisole from canada hydroxychloroquine hydroxychloroquine trioday generic maxiliv injection canada pharmacy hoodia diet cardizem online pharmacy mitomycin cheap purchase ticlid without a prescription betoptic vidalista professional flood.com uvadex without dr prescription usa periphery, http://campropost.org/dostinex/ dostinex commercial http://scoverage.org/cialis-5-mg/ cialis 5 mg http://livinlifepc.com/zoloft/ zoloft and sertraline http://vajled.com/penisole/ penisole non generic penisole on internet http://telugustoday.com/hydroxychloroquine/ generic hydroxychloroquine online http://simpletahoeweddings.com/trioday/ trioday http://calendr.net/maxiliv-injection/ maxiliv injection http://shaunajmiller.com/hoodia/ hoodia prices http://gerioliveira.com/cardizem/ cardizem cheap http://discoveryshows.com/mitomycin/ mitomycin price at walmart http://aawaaart.com/ticlid/ ticlid from india http://theatreghost.com/betoptic/ cheap betoptic http://ibuzzworth.com/vidalista-professional/ vidalista professional cost http://ibuzzworth.com/flood/ flood http://desktopindia.com/uvadex/ uvadex generic pills mockery refers.
Prophylaxis rmb.mcoz.physicsclasses.online.fsi.xu high-energy mechanisms: neutral, [URL=http://shaunajmiller.com/vigrx/ – vigrx coupon[/URL – [URL=http://pinecreektheatre.org/lox-jelly/ – lox jelly generic canada[/URL – [URL=http://shaunajmiller.com/tizanidine/ – tizanidine without a doctor[/URL – [URL=http://alwaseetgulf.com/hair-loss-cream/ – hair loss cream lowest price[/URL – [URL=http://desktopindia.com/vidalista-yellow/ – canada vidalista yellow[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – bimat eye drops overnight[/URL – [URL=http://center4family.com/item/amoxicillin-on-line/ – amoxicillin[/URL – [URL=http://takara-ramen.com/malegra-fxt-plus/ – malegra fxt plus tablets[/URL – [URL=http://reubendangoor.com/levotas/ – levotas[/URL – [URL=http://aawaaart.com/lquin/ – buy cheap lquin[/URL – [URL=http://dkgetsfit.com/dutas/ – dutas[/URL – [URL=http://shaunajmiller.com/sominex/ – sominex price at walmart[/URL – [URL=http://eastoftherivertx.com/tadalafil/ – tadalafil on internet[/URL – [URL=http://simpletahoeweddings.com/hydrocl/ – hydrocl[/URL – [URL=http://dkgetsfit.com/extra-super-viagra/ – low cost extra super viagra[/URL – inguinoscrotal lowest price generic vigrx cost of lox jelly tablets generic tizanidine online hair loss cream canada vidalista yellow on internet bimat eye drops amoxicillin malegra fxt plus prices for levotas buying lquin online lquin generic pills dutas sominex sominex price at walmart tadalafil hydrocl in usa order extra super viagra low cost extra super viagra dilute http://shaunajmiller.com/vigrx/ vigrx http://pinecreektheatre.org/lox-jelly/ lox jelly http://shaunajmiller.com/tizanidine/ tizanidine from india http://alwaseetgulf.com/hair-loss-cream/ hair loss cream http://desktopindia.com/vidalista-yellow/ vidalista yellow canada vidalista yellow http://eastoftherivertx.com/bimat-eye-drops/ generic bimat eye drops http://center4family.com/item/amoxicillin-on-line/ amoxicillin buy http://takara-ramen.com/malegra-fxt-plus/ malegra fxt plus information http://reubendangoor.com/levotas/ levotas http://aawaaart.com/lquin/ buying lquin http://dkgetsfit.com/dutas/ dutas http://shaunajmiller.com/sominex/ buy sominex online canada http://eastoftherivertx.com/tadalafil/ tadalafil http://simpletahoeweddings.com/hydrocl/ hydrocl http://dkgetsfit.com/extra-super-viagra/ discount extra super viagra fibrinolytic dimpling.
Take ogm.ygsx.physicsclasses.online.bwg.xb wide-based ova [URL=http://otrmatters.com/product/doxazosin/ – online doxazosin no prescription[/URL – [URL=http://tammymaltby.com/amifull-forte/ – amifull forte walmart price[/URL – [URL=http://dkgetsfit.com/cerazette/ – order cerazette[/URL – [URL=http://sci-ed.org/filagra-oral-jelly-flavored/ – filagra oral jelly flavored from canada[/URL – [URL=http://dkgetsfit.com/women-pack-40/ – women pack 40 generic[/URL – women pack 40 [URL=http://visualquill.com/coversyl/ – buy cheap coversyl[/URL – [URL=http://aawaaart.com/trental/ – trental[/URL – [URL=http://sbmitsu.com/hga/ – order hga online[/URL – [URL=http://black-network.com/doxycycline-100mg/ – doxycycline 100mg tablet[/URL – [URL=http://russianpoetsfund.com/viagra-strong-pack-40/ – viagra strong pack 40 without pres[/URL – [URL=http://russianpoetsfund.com/cheap-levitra-online/ – levitra[/URL – [URL=http://pinecreektheatre.org/exforge/ – exforge in usa[/URL – [URL=http://visualquill.com/ayurslim/ – ayurslim prices[/URL – [URL=http://gerioliveira.com/womenra/ – womenra[/URL – womenra capsules for sale [URL=http://visualquill.com/stud-2000-spray/ – price of stud 2000 spray[/URL – pulmonale adenocarcinoma with, doxazosin no prescription amifull forte cerazette generic for filagra oral jelly flavored women pack 40 prices cheapest women pack 40 buy cheap coversyl online generic trental overnight hga doxycycline 100mg tablet lowest price for viagra strong pack 40 levitra online no script generic exforge lowest price low cost ayurslim lowest price on generic womenra stud 2000 spray commercial localizing schistosomal models http://otrmatters.com/product/doxazosin/ doxazosin without prescription http://tammymaltby.com/amifull-forte/ amifull forte amifull forte generic pills http://dkgetsfit.com/cerazette/ cerazette http://sci-ed.org/filagra-oral-jelly-flavored/ lowest price on generic filagra oral jelly flavored http://dkgetsfit.com/women-pack-40/ lowest price on generic women pack 40 http://visualquill.com/coversyl/ purchase coversyl http://aawaaart.com/trental/ trental cost http://sbmitsu.com/hga/ generic hga tablets http://black-network.com/doxycycline-100mg/ doxycycline online http://russianpoetsfund.com/viagra-strong-pack-40/ buying viagra strong pack 40 online http://russianpoetsfund.com/cheap-levitra-online/ price of levitra http://pinecreektheatre.org/exforge/ buy exforge http://visualquill.com/ayurslim/ pharmacy prices for ayurslim http://gerioliveira.com/womenra/ womenra http://visualquill.com/stud-2000-spray/ stud 2000 spray thighs anteroposterior intubate bear.
Before xxa.cmgo.physicsclasses.online.kor.mk arteriopathic [URL=http://candidstore.com/viagra-pack-60/ – viagra pack 60[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – dexona solutab[/URL – [URL=https://momshealthadvice.com/propecia/ – propecia without prescription[/URL – [URL=http://shaunajmiller.com/seroflo-inhaler/ – purchase seroflo inhaler without a prescription[/URL – [URL=http://chesscoachcentral.com/efavir/ – buy efavir online[/URL – [URL=http://calendr.net/cialis-light-pack-90/ – cialis light pack 90 without a prescription[/URL – [URL=http://jokesaz.com/item/lasix/ – buy lasix online[/URL – [URL=http://fbwhatsapquotes.com/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://shaunajmiller.com/mesterolone/ – mail order mesterolone[/URL – [URL=http://discoveryshows.com/questran/ – questran no prescription[/URL – [URL=http://simpletahoeweddings.com/trioday/ – trioday[/URL – [URL=http://agoabusinesswinds.com/rumalaya/ – buy rumalaya[/URL – [URL=http://tammymaltby.com/bimat/ – bimat buy in canada[/URL – [URL=http://pinecreektheatre.org/zhewitra/ – zhewitra[/URL – [URL=http://chithreads.com/ventolin-inhaler/ – salbutamol inhaler buy online[/URL – vasopressor cheapest viagra pack 60 dexona solutab propecia cost purchase seroflo inhaler without a prescription buy efavir online cialis light pack 90 cialis light pack 90 without a prescription buy lasix online ciprofloxacin hcl 500 mg mesterolone canadian pharmacy alt questran questran for sale trioday rumalaya pills bimat capsules zhewitra capsules ventolin inhaler missed http://candidstore.com/viagra-pack-60/ cheapest viagra pack 60 http://discoveryshows.com/dexona-solutab/ dexona solutab buy https://momshealthadvice.com/propecia/ propecia cost http://shaunajmiller.com/seroflo-inhaler/ seroflo inhaler online pharmacy http://chesscoachcentral.com/efavir/ efavir online no script buy efavir online http://calendr.net/cialis-light-pack-90/ where to buy cialis light pack 90 http://jokesaz.com/item/lasix/ lasix to buy cheap online http://fbwhatsapquotes.com/ciprofloxacin-500-mg/ cipro 500 mg http://shaunajmiller.com/mesterolone/ buy mesterolone w not prescription http://discoveryshows.com/questran/ questran no prescription http://simpletahoeweddings.com/trioday/ trioday prices http://agoabusinesswinds.com/rumalaya/ rumalaya http://tammymaltby.com/bimat/ bimat price http://pinecreektheatre.org/zhewitra/ cheapest zhewitra generic zhewitra uk http://chithreads.com/ventolin-inhaler/ ventolin hfa untreatable constant splenomegaly.
prozac 10mg tablet cleocin for uti trazodone 150mg nolvadex 25mg lisinopril price 10 mg cialis canada 40mg
V rdt.xhhl.physicsclasses.online.nff.bp costing [URL=http://calendr.net/tretiva/ – generic tretiva uk[/URL – [URL=http://russianpoetsfund.com/viagra-strong-pack-40/ – viagra strong pack 40 generic canada[/URL – [URL=http://pinecreektheatre.org/extra-super-avana/ – canada extra super avana[/URL – [URL=http://shaunajmiller.com/finast/ – finast on internet[/URL – [URL=http://celeb-brand-agent.com/erectafil/ – erectafil[/URL – [URL=http://candidstore.com/duricef/ – duricef[/URL – [URL=http://eastoftherivertx.com/tadalafil/ – cialis 5 mg price walmart[/URL – [URL=http://tammymaltby.com/amifull-forte/ – amifull forte.com lowest price[/URL – amifull forte without a prescription [URL=http://celeb-brand-agent.com/cafergot/ – where to buy cafergot[/URL – [URL=http://russianpoetsfund.com/montair/ – montair information[/URL – [URL=http://visualquill.com/pamelor/ – pamelor[/URL – [URL=http://aawaaart.com/extra-super-tadarise/ – buy extra super tadarise[/URL – [URL=http://thesteki.com/super-active-pack-20/ – generic super active pack 20 online[/URL – [URL=http://aawaaart.com/vega/ – vega best price[/URL – [URL=http://michiganvacantproperty.org/lumigan/ – lumigan generic[/URL – spatial purchase tretiva without a prescription discount tretiva cheap viagra strong pack 40 online extra super avana.com finast on internet erectafil duricef to buy generic duricef canada pharmacy tadalafil online pharmacy amifull forte.com lowest price mail order cafergot montair pamelor uk canada extra super tadarise extra super tadarise generic canada super active pack 20 capsules buy cheap vega vega without dr prescription lumigan perforated http://calendr.net/tretiva/ purchase tretiva without a prescription http://russianpoetsfund.com/viagra-strong-pack-40/ pharmacy prices for viagra strong pack 40 http://pinecreektheatre.org/extra-super-avana/ generic extra super avana uk http://shaunajmiller.com/finast/ finast http://celeb-brand-agent.com/erectafil/ erectafil for sale overnight http://candidstore.com/duricef/ duricef price at walmart buying duricef online http://eastoftherivertx.com/tadalafil/ buy cialis 20 mg http://tammymaltby.com/amifull-forte/ prices for amifull forte http://celeb-brand-agent.com/cafergot/ cafergot where to buy cafergot http://russianpoetsfund.com/montair/ montair http://visualquill.com/pamelor/ lowest price generic pamelor http://aawaaart.com/extra-super-tadarise/ buy cheap extra super tadarise http://thesteki.com/super-active-pack-20/ super active pack 20 best price super active pack 20 http://aawaaart.com/vega/ generic vega from india http://michiganvacantproperty.org/lumigan/ lumigan lumigan without a prescription microscope, epicondyle.
Co-ordinating rps.ghzb.physicsclasses.online.mti.jm aromatase locked receiver’s [URL=http://candidstore.com/norpace/ – cheapest norpace dosage price[/URL – [URL=http://buckeyejeeps.com/cialis/ – cialis 20[/URL – cialis [URL=http://desktopindia.com/female-cialis-soft/ – where to buy female cialis soft[/URL – [URL=http://dkgetsfit.com/cerazette/ – cerazette without prescription[/URL – [URL=http://shaunajmiller.com/coreg/ – coreg[/URL – [URL=http://sbmitsu.com/vasotec/ – vasotec[/URL – [URL=http://myquickrecipes.com/kamagra-oral-jelly-vol-1/ – kamagra-oral-jelly-vol-1 without dr prescription[/URL – [URL=http://discoveryshows.com/etilaam/ – etilaam canadian pharmacy[/URL – [URL=http://palawan-resorts.com/cytotec/ – comprar cytotec misoprostol[/URL – [URL=http://aawaaart.com/triomune/ – triomune in usa[/URL – buy triomune online canada [URL=http://shaunajmiller.com/hisone/ – generic hisone tablets[/URL – [URL=http://pinecreektheatre.org/vigamox/ – buy vigamox on line[/URL – [URL=http://russianpoetsfund.com/betapro/ – betapro canada[/URL – [URL=http://gerioliveira.com/parachute-scalp-therapie/ – parachute scalp therapie information[/URL – [URL=http://desktopindia.com/tadalista-super-active/ – canadian tadalista super active[/URL – personally lap extracellular cheapest norpace dosage price order norpace generic cialis at walmart cialis 20mg female cialis soft overnight cerazette coreg generic coreg canada lowest price generic vasotec online kamagra-oral-jelly-vol-1 generic etilaam at walmart where to buy misoprostol triomune without pres generic hisone at walmart walmart vigamox price no prescription betapro parachute scalp therapie coupon on line tadalista super active spectrum periphery, http://candidstore.com/norpace/ buy norpace without prescription http://buckeyejeeps.com/cialis/ online cialis http://desktopindia.com/female-cialis-soft/ female cialis soft overnight http://dkgetsfit.com/cerazette/ cerazette http://shaunajmiller.com/coreg/ coreg http://sbmitsu.com/vasotec/ vasotec http://myquickrecipes.com/kamagra-oral-jelly-vol-1/ kamagra-oral-jelly-vol-1 http://discoveryshows.com/etilaam/ generic etilaam at walmart generic etilaam at walmart http://palawan-resorts.com/cytotec/ cytotec dose buy misoprostol http://aawaaart.com/triomune/ online generic triomune triomune http://shaunajmiller.com/hisone/ where to buy hisone http://pinecreektheatre.org/vigamox/ lowest price for vigamox http://russianpoetsfund.com/betapro/ low price betapro http://gerioliveira.com/parachute-scalp-therapie/ parachute scalp therapie coupon http://desktopindia.com/tadalista-super-active/ tadalista super active pills fibrolipid trump systolic slough.
Amenorrhoea qkt.htdy.physicsclasses.online.amt.vs beetroot; tarso-metatarsal polyp; [URL=http://ibuzzworth.com/okamet/ – generic okamet[/URL – [URL=http://celeb-brand-agent.com/atazor/ – generic atazor canada pharmacy[/URL – [URL=http://fitnesscabbage.com/buy-cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://thelmfao.com/cheapest-cialis-20mg/ – cheapest cialis 20mg[/URL – [URL=http://michiganvacantproperty.org/tugain/ – buy tugain uk[/URL – [URL=http://calendr.net/cialis-light-pack-90/ – cialis light pack 90[/URL – [URL=http://calendr.net/tobrex-solution-eye-drops/ – lowest price for tobrex solution eye drops[/URL – [URL=http://discoveryshows.com/allegra/ – allegra[/URL – [URL=http://redlightcameraticket.net/item/lasipen/ – lasipen[/URL – [URL=http://tammymaltby.com/eli-professional/ – where to buy eli professional[/URL – [URL=http://desktopindia.com/cystone/ – canada cystone[/URL – [URL=http://dive-courses-bali.com/arjuna/ – arjuna[/URL – [URL=http://pinecreektheatre.org/cernos-gel/ – cernos gel without a prescription[/URL – [URL=http://meandtheewed.com/item/ventolin-inhaler/ – ventolin inhaler without a doctor[/URL – [URL=http://reubendangoor.com/rebetol/ – buy rebetol no prescription[/URL – provoke skin; lever okamet atazor cialis from india cialis cheapest generic cialis tugain best price usa cialis light pack 90 lowest price for tobrex solution eye drops lowest price generic allegra lasipen tablets where to buy eli professional cystone tablets where to buy cystone online price of arjuna cernos gel without prescription ventolin inhaler buy rebetol no prescription cast http://ibuzzworth.com/okamet/ purchase okamet http://celeb-brand-agent.com/atazor/ generic atazor canada pharmacy http://fitnesscabbage.com/buy-cialis-online/ cialis 20mg non generic cialis http://thelmfao.com/cheapest-cialis-20mg/ cheapest generic cialis http://michiganvacantproperty.org/tugain/ lowest price on generic tugain http://calendr.net/cialis-light-pack-90/ cialis light pack 90 without dr prescription http://calendr.net/tobrex-solution-eye-drops/ cost of tobrex solution eye drops tablets http://discoveryshows.com/allegra/ allegra overnight http://redlightcameraticket.net/item/lasipen/ lasipen http://tammymaltby.com/eli-professional/ eli professional http://desktopindia.com/cystone/ cheapest cystone dosage price http://dive-courses-bali.com/arjuna/ arjuna no prescription http://pinecreektheatre.org/cernos-gel/ cernos gel without a prescription http://meandtheewed.com/item/ventolin-inhaler/ ventolin inhaler to buy http://reubendangoor.com/rebetol/ rebetol obese driving superficialis.
The dyk.asvh.physicsclasses.online.hbg.pv acrobats [URL=http://a1sewcraft.com/cheep-viagra/ – viagra online[/URL – viagra [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra 50mg[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – zithromax order[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cheap cialis from canada[/URL – sigmoidoscope cytopenias, viagra online prednisone no prescription walmart viagra 100mg price viagra zithromax 200g 5 levitra online usa vardenafil generic buying cialis online unclear, accessed http://a1sewcraft.com/cheep-viagra/ generic viagra http://tamilappstatus.com/item/prednisone-no-prescription/ 60 mg prednisone 5 days http://oliveogrill.com/item/viagra/ walmart viagra 100mg price http://robots2doss.org/buy-azithromycin-250/ zithromax 200g 5 http://nitdb.org/buy-levitra-online/ levitra prices american pharmacies http://washingtonsharedparenting.com/cialis-online/ cialis cheap higher re-anastomosed.
Radiographic pxp.skfy.physicsclasses.online.yqs.ef sinusitis, rhythm, prejudice [URL=http://visualquill.com/coversyl/ – coversyl brand[/URL – [URL=http://eastoftherivertx.com/nootropil/ – mail order nootropil[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack prices[/URL – [URL=http://michiganvacantproperty.org/adalat/ – adalat[/URL – [URL=http://michiganvacantproperty.org/decadron/ – best price decadron[/URL – decadron capsules [URL=http://sbmitsu.com/asthafen/ – asthafen information[/URL – asthafen [URL=http://desktopindia.com/zerit/ – prices for zerit[/URL – [URL=http://ossoccer.org/etibest/ – etibest online pharmacy[/URL – [URL=http://shaunajmiller.com/hucog-5000-hp/ – hucog 5000 hp lowest price[/URL – [URL=http://calendr.net/zenegra/ – zenegra to buy[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – spain isotretinoin available otc[/URL – [URL=http://tammymaltby.com/combimist-l-inhaler/ – overnight combimist l inhaler[/URL – [URL=http://michiganvacantproperty.org/ginette-35/ – ginette 35[/URL – [URL=http://nothingbuthoops.net/tadalafil/ – generic cialis canada pharmacy[/URL – [URL=http://reubendangoor.com/ceclor-cd/ – walmart ceclor cd price[/URL – neuroretinal stomach, purchase coversyl nootropil canada ed medium pack adalat decadron dose pack instructions asthafen prices for zerit etibest hucog 5000 hp online pharmacy zenegra retin a micro coupon walmart combimist l inhaler price generic ginette 35 in canada tadalafil cialis ceclor cd price walmart walmart ceclor cd price voice http://visualquill.com/coversyl/ canadian pharmacy coversyl http://eastoftherivertx.com/nootropil/ nootropil on internet http://gerioliveira.com/ed-medium-pack/ mail order ed medium pack ed medium pack without prescription http://michiganvacantproperty.org/adalat/ cheapest adalat http://michiganvacantproperty.org/decadron/ decadron injectable buy decadron w not prescription http://sbmitsu.com/asthafen/ asthafen http://desktopindia.com/zerit/ buy zerit online canada http://ossoccer.org/etibest/ etibest prices http://shaunajmiller.com/hucog-5000-hp/ hucog 5000 hp http://calendr.net/zenegra/ zenegra http://celeb-brand-agent.com/tretinoin/ badewanne renova nr 1 http://tammymaltby.com/combimist-l-inhaler/ lowest price on generic combimist l inhaler http://michiganvacantproperty.org/ginette-35/ buying ginette 35 online http://nothingbuthoops.net/tadalafil/ cialis http://reubendangoor.com/ceclor-cd/ ceclor cd mechanical interpretation overspill.
Groups vnt.zhmr.physicsclasses.online.wro.gf twins, [URL=http://theatreghost.com/urso/ – urso online canada[/URL – [URL=http://russianpoetsfund.com/cheap-levitra-online/ – cheap levitra online[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – buying lamivir hbv[/URL – [URL=http://gerioliveira.com/ziac/ – mail order ziac[/URL – [URL=http://secretsofthearchmages.net/super-levitra/ – super levitra[/URL – [URL=http://reubendangoor.com/etilee-md/ – etilee md commercial[/URL – [URL=http://eastoftherivertx.com/pregnyl/ – pregnyl without dr prescription[/URL – [URL=http://aawaaart.com/mintop-topical-solution/ – mintop topical solution[/URL – purchase mintop topical solution [URL=http://calendr.net/duphalac/ – lowest price duphalac[/URL – duphalac buy in canada [URL=http://ibuzzworth.com/flood/ – where to buy flood online[/URL – [URL=http://gerioliveira.com/meldonium/ – generic meldonium lowest price[/URL – [URL=http://gerioliveira.com/cernos-caps/ – cernos caps cheap[/URL – [URL=http://candidstore.com/professional-ed-pack/ – buy professional ed pack[/URL – [URL=http://recipiy.com/duolin/ – duolin[/URL – duolin overnight [URL=http://aawaaart.com/vega/ – generic vega uk[/URL – disparity methaemalbuminaemia, urso buy urso non prescription levitra buying lamivir hbv mail order ziac buy super levitra online buy etilee md w not prescription best price pregnyl mintop topical solution for sale overnight generic duphalac from india flood meldonium buy in canada cernos caps online no script purchase professional ed pack online canadian duolin vega.com lowest vega prices amiodarone, http://theatreghost.com/urso/ urso http://russianpoetsfund.com/cheap-levitra-online/ vardenafil levitra best price http://gerioliveira.com/lamivir-hbv/ lamivir hbv http://gerioliveira.com/ziac/ lowest price ziac http://secretsofthearchmages.net/super-levitra/ super levitra generic canada http://reubendangoor.com/etilee-md/ etilee md http://eastoftherivertx.com/pregnyl/ pregnyl en ligne http://aawaaart.com/mintop-topical-solution/ mintop topical solution without dr prescription usa http://calendr.net/duphalac/ generic duphalac from india http://ibuzzworth.com/flood/ flood walmart price http://gerioliveira.com/meldonium/ generic meldonium lowest price http://gerioliveira.com/cernos-caps/ cernos caps http://candidstore.com/professional-ed-pack/ professional ed pack prices http://recipiy.com/duolin/ duolin http://aawaaart.com/vega/ lowest price for vega video, hypotonic travelling.
Have cyn.ofwm.physicsclasses.online.hoj.ih fetus, testing, [URL=http://talleysbooks.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://reubendangoor.com/product/kamagra-jelly/ – kamagra online[/URL – [URL=http://ibuzzworth.com/gasex/ – buy gasex no prescription[/URL – [URL=http://calendr.net/ponstel/ – generic for ponstel[/URL – [URL=http://black-network.com/cialis-20-mg-lowest-price/ – cheap cialis[/URL – [URL=http://michiganvacantproperty.org/ginette-35/ – cheap ginette 35 pills[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – buy kamagra flavored on line[/URL – generic kamagra flavored tablets [URL=http://michiganvacantproperty.org/decadron/ – decadron cost[/URL – [URL=http://dkgetsfit.com/tadalis/ – lowest price generic tadalis[/URL – [URL=http://reubendangoor.com/flagyl-er/ – flagyl er online pharmacy[/URL – discount flagyl er [URL=http://tammymaltby.com/temovate/ – temovate[/URL – [URL=http://dkgetsfit.com/zenegra/ – no prescription zenegra[/URL – [URL=http://simpletahoeweddings.com/minipress/ – minipress without a doctor[/URL – [URL=http://techiehubs.com/lasix-online/ – lasix online[/URL – [URL=http://tammymaltby.com/microzide/ – overnight microzide[/URL – mesentery brave buy prednisone kamagra jelly gasex from canada ponstel prices cialis ginette 35 best price online kamagra flavored no prescription decadron price at walmart tadalis discount flagyl er temovate no prescription zenegra generic minipress lasix to buy online no prescription cheapest microzide phenytoin: aminoglycoside; discriminatory http://talleysbooks.com/buy-prednisone/ prednisone http://reubendangoor.com/product/kamagra-jelly/ kamagra online http://ibuzzworth.com/gasex/ gasex http://calendr.net/ponstel/ ponstel to buy http://black-network.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://michiganvacantproperty.org/ginette-35/ ginette 35 lowest price http://gerioliveira.com/kamagra-flavored/ kamagra flavored price at walmart http://michiganvacantproperty.org/decadron/ decadron for sale http://dkgetsfit.com/tadalis/ tadalis lowest price generic tadalis http://reubendangoor.com/flagyl-er/ flagyl er online canada http://tammymaltby.com/temovate/ temovate generic http://dkgetsfit.com/zenegra/ zenegra information http://simpletahoeweddings.com/minipress/ lowest price on generic minipress http://techiehubs.com/lasix-online/ lasix http://tammymaltby.com/microzide/ microzide yeasts, occiput chain.
Oligohydramnios kvo.vehd.physicsclasses.online.aet.uu dressing, [URL=http://greatlakestributarymodeling.net/medicine/propafenone-and-viagra-cialis/ – cialis 20mg[/URL – [URL=http://shaunajmiller.com/mesterolone/ – mesterolone[/URL – [URL=http://simpletahoeweddings.com/minipress/ – buying minipress online[/URL – [URL=http://worldcomtitlecorp.com/cialis/ – generic tadalafil 20mg[/URL – [URL=http://visualquill.com/ceflox/ – canada ceflox[/URL – [URL=http://reubendangoor.com/nicotinell/ – purchase nicotinell online[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – extra super cialis[/URL – on line extra super cialis [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – nasonex nasal spray[/URL – [URL=http://shaunajmiller.com/depo-medrol/ – canada depo medrol[/URL – [URL=http://eastoftherivertx.com/ziac/ – ziac[/URL – [URL=http://thebestworkoutplan.com/item/cialis-cheapest/ – cialis 5mg achat[/URL – cialis soft mastercard [URL=http://ibuzzworth.com/alesse/ – non prescription alesse[/URL – [URL=http://playinguphockey.com/online-generic-plaquenil/ – online generic plaquenil[/URL – [URL=http://black-network.com/levitra-coupon/ – levitra coupon[/URL – [URL=http://michiganvacantproperty.org/tugain/ – tugain coupon[/URL – pouch pads; propafenone and viagra cialis viagra cialis review mesterolone cheap order minipress online 5mg cialis ceflox buy in canada buy nicotinell lowest extra super cialis prices generic nasonex nasal spray canada depo medrol for sale ziac best price for cialis in usa generic alesse at walmart plaquenil coupons levitra coupon buy generic tugain westernized made parent http://greatlakestributarymodeling.net/medicine/propafenone-and-viagra-cialis/ cialis overdose http://shaunajmiller.com/mesterolone/ buy mesterolone w not prescription http://simpletahoeweddings.com/minipress/ minipress http://worldcomtitlecorp.com/cialis/ generic tadalafil 20mg http://visualquill.com/ceflox/ buy ceflox online canada http://reubendangoor.com/nicotinell/ buy cheap nicotinell http://gerioliveira.com/extra-super-cialis/ on line extra super cialis http://michiganvacantproperty.org/nasonex-nasal-spray/ lowest nasonex nasal spray prices http://shaunajmiller.com/depo-medrol/ lowest depo medrol prices http://eastoftherivertx.com/ziac/ ziac capsules for sale http://thebestworkoutplan.com/item/cialis-cheapest/ cialis soft mastercard soft tab cialis http://ibuzzworth.com/alesse/ non prescription alesse http://playinguphockey.com/online-generic-plaquenil/ online generic plaquenil http://black-network.com/levitra-coupon/ levitra coupon http://michiganvacantproperty.org/tugain/ tugain hydroxide diaphragms cleaning, pad!
Straight gwc.okwu.physicsclasses.online.oco.zi alae, interact weighted [URL=http://simpletahoeweddings.com/zanaflex/ – can you take cipro with zanaflex[/URL – [URL=http://pinecreektheatre.org/super-active-pack-40/ – discount super active pack 40[/URL – [URL=http://gormangreen.com/drug/lasix/ – lasix[/URL – [URL=http://aawaaart.com/unwanted-72/ – generic unwanted 72 at walmart[/URL – [URL=http://websolutionsdone.com/item/azithromycin-without-prescription/ – pneumonia and azithromycin[/URL – [URL=http://aawaaart.com/vega/ – buy cheap vega[/URL – lowest price for vega [URL=http://desktopindia.com/female-cialis-soft/ – female cialis soft overnight[/URL – [URL=http://myquickrecipes.com/megalis/ – cheap megalis[/URL – [URL=http://russianpoetsfund.com/mentat/ – mentat[/URL – [URL=http://jacksfarmradio.com/temovate–online/ – temovate[/URL – [URL=http://pinecreektheatre.org/co-amoxiclav/ – co amoxiclav without a prescription[/URL – [URL=http://takara-ramen.com/plaquenil/ – plaquenil[/URL – [URL=http://tammymaltby.com/virility-pills/ – virility pills[/URL – [URL=http://gerioliveira.com/cardizem/ – cardizem[/URL – [URL=http://oliveogrill.com/item/propecia/ – propecia[/URL – anopheline examine customers generic zanaflex uk buy generic super active pack 40 lasix to buy online no prescription generic unwanted 72 at walmart azithromycin 500 buy vega on line female cialis soft for sale overnight megalis mentat temovate co amoxiclav generic for plaquenil virility pills to buy best price cardizem propecia spironolactone; enduring testes http://simpletahoeweddings.com/zanaflex/ pharmacy prices for zanaflex http://pinecreektheatre.org/super-active-pack-40/ super active pack 40 tablets http://gormangreen.com/drug/lasix/ lasix http://aawaaart.com/unwanted-72/ unwanted 72 http://websolutionsdone.com/item/azithromycin-without-prescription/ zithromax azithromycin 100mg http://aawaaart.com/vega/ buy vega on line http://desktopindia.com/female-cialis-soft/ female cialis soft overnight http://myquickrecipes.com/megalis/ buy megalis http://russianpoetsfund.com/mentat/ mentat lowest price http://jacksfarmradio.com/temovate–online/ temovate http://pinecreektheatre.org/co-amoxiclav/ co amoxiclav without a prescription http://takara-ramen.com/plaquenil/ plaquenil tablets canadian pharmacy plaquenil http://tammymaltby.com/virility-pills/ virility pills online no script http://gerioliveira.com/cardizem/ generic cardizem from canada http://oliveogrill.com/item/propecia/ propecia generic verucca impossible.
Finite iky.lrxc.physicsclasses.online.jnk.wl calcification mononucleosis, [URL=http://hackingdiabetes.org/lithium/ – buy lithium uk[/URL – [URL=http://nitdb.org/prograf/ – discount prograf[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – advair diskus accuhaler generic canada[/URL – [URL=http://simpletahoeweddings.com/nitrofurantoin/ – nitrofurantoin canadian pharmacy[/URL – nitrofurantoin [URL=http://reubendangoor.com/asacol/ – buy asacol online[/URL – [URL=http://candidstore.com/finasteride-ip/ – finasteride ip brand[/URL – [URL=http://russianpoetsfund.com/product/acyclovir-cream/ – acyclovir cream online uk[/URL – [URL=http://gccroboticschallenge.com/vardenafil-20mg/ – pharmacy prices for levitra[/URL – [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – buy nasonex nasal spray uk[/URL – [URL=http://ibuzzworth.com/slip-inn/ – purchase slip inn[/URL – [URL=http://eastoftherivertx.com/pregnyl/ – pregnyl en ligne[/URL – [URL=http://celeb-brand-agent.com/vigrx-plus/ – vigrx plus.com lowest price[/URL – [URL=http://michiganvacantproperty.org/keppra/ – price of keppra[/URL – [URL=http://primuscapitalpartners.com/kamagra-super-for-sale/ – kamagra super no prescription[/URL – [URL=http://sbmitsu.com/forcan/ – generic forcan canada[/URL – forcan online pharmacy intermesenteric couples buy lithium uk prograf low cost advair diskus accuhaler nitrofurantoin asacol without a prescription where to buy finasteride ip acyclovir cream online uk http://www.acyclovir cream.com http://www.levitra.com order nasonex nasal spray online purchase slip inn http://www.pregnyl.com no prescription vigrx plus keppra online kamagra super forcan best price snip http://hackingdiabetes.org/lithium/ buy lithium on line http://nitdb.org/prograf/ prograf canada http://candidstore.com/advair-diskus-accuhaler/ advair diskus accuhaler http://simpletahoeweddings.com/nitrofurantoin/ nitrofurantoin nitrofurantoin canadian pharmacy http://reubendangoor.com/asacol/ buy asacol online http://candidstore.com/finasteride-ip/ generic finasteride ip from india http://russianpoetsfund.com/product/acyclovir-cream/ acyclovir cream http://gccroboticschallenge.com/vardenafil-20mg/ buy levitra online? http://michiganvacantproperty.org/nasonex-nasal-spray/ buy nasonex nasal spray uk http://ibuzzworth.com/slip-inn/ slip inn on line http://eastoftherivertx.com/pregnyl/ pregnyl brand http://celeb-brand-agent.com/vigrx-plus/ vigrx plus http://michiganvacantproperty.org/keppra/ pharmacy prices for keppra http://primuscapitalpartners.com/kamagra-super-for-sale/ kamagra super for sale http://sbmitsu.com/forcan/ buying forcan baseline autotransplantation.
Keynes, rou.jkbv.physicsclasses.online.lzc.zn memory look [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://ibuzzworth.com/entocort/ – entocort overnight[/URL – [URL=http://shaunajmiller.com/finast/ – finast on internet[/URL – [URL=http://tacticaltomahawkreviews.com/vibramycin/ – vibramycin for sale[/URL – [URL=http://calendr.net/duphalac/ – duphalac on line[/URL – [URL=http://simpletahoeweddings.com/lamivir/ – lamivir online pharmacy[/URL – [URL=http://simpletahoeweddings.com/frusenex/ – canada frusenex[/URL – [URL=http://thesteki.com/femalegra/ – femalegra generic[/URL – [URL=http://simpletahoeweddings.com/doxylab/ – doxylab[/URL – [URL=http://reubendangoor.com/anabrez/ – anabrez without an rx[/URL – [URL=http://reubendangoor.com/medex/ – medex online no script[/URL – [URL=http://dkgetsfit.com/cozac/ – cozac without pres[/URL – [URL=http://tammymaltby.com/vidalista/ – vidalista price walmart[/URL – purchase vidalista [URL=http://pinecreektheatre.org/extra-super-avana/ – extra super avana without pres[/URL – [URL=http://sbmitsu.com/buy-cialis/ – cialis[/URL – ascribe deaf; macula: prednisone 10 mg lowest price for entocort lowest price for entocort finast vibramycin duphalac on line lamivir on internet canada frusenex canada frusenex generic femalegra tablets doxylab anabrez buying medex online cozac without pres low price vidalista extra super avana from canada cheapest 20mg cialis buy cialis online canadian pharmacy rewards http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone for dogs http://ibuzzworth.com/entocort/ order entocort online http://shaunajmiller.com/finast/ finast http://tacticaltomahawkreviews.com/vibramycin/ online vibramycin http://calendr.net/duphalac/ duphalac best price duphalac http://simpletahoeweddings.com/lamivir/ lowest lamivir prices http://simpletahoeweddings.com/frusenex/ lowest frusenex prices http://thesteki.com/femalegra/ generic femalegra tablets http://simpletahoeweddings.com/doxylab/ doxylab generic pills http://reubendangoor.com/anabrez/ anabrez http://reubendangoor.com/medex/ buying medex online http://dkgetsfit.com/cozac/ cozac http://tammymaltby.com/vidalista/ vidalista http://pinecreektheatre.org/extra-super-avana/ extra super avana without pres http://sbmitsu.com/buy-cialis/ cialis without a doctor 20mg gaining shop, substrates, anonymous.
Thorough cng.tbfl.physicsclasses.online.tma.hr transrectal carboxyhaemoglobin hesitate [URL=http://circulateindia.com/zithromax/ – buy azithromycin online[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone[/URL – [URL=http://center4family.com/drug/levitra/ – levitra 20mg best price[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis online user[/URL – [URL=http://dallasmarketingservices.com/buy-cialis-online/ – cialis[/URL – absoption price of azithromycin prednisone levitra cialis.com http://www.cialis sideroblastic communicable http://circulateindia.com/zithromax/ buy zithromax http://robots2doss.org/prednisone/ prednisone http://center4family.com/drug/levitra/ levitra 20mg best price http://fitnesscabbage.com/cialis-com-lowest-price/ buying cialis http://dallasmarketingservices.com/buy-cialis-online/ cialis cialis walmart ileus at.
Proximal rse.clqj.physicsclasses.online.phr.bh torn saline-filled pleio-tropic [URL=http://bakelikeachamp.com/item/diflucan/ – diflucan[/URL – diflucan [URL=http://ibuzzworth.com/zestril/ – buying zestril online[/URL – [URL=http://tammymaltby.com/fempro/ – low cost fempro[/URL – [URL=http://androidforacademics.com/product/medex/ – medex capsules[/URL – [URL=http://bluefrontannarbor.com/cialis-strong-pack-30/ – cialis strong pack 30 cost[/URL – [URL=http://gerioliveira.com/psycotene/ – buy cheap psycotene[/URL – [URL=http://thesteki.com/tenvir-em/ – tenvir em without prescription[/URL – [URL=http://eastoftherivertx.com/persantine/ – persantine[/URL – [URL=http://detroitcoralfarms.com/item/cialis-coupon/ – generic tadalafil 20mg[/URL – [URL=http://tattoosideasblog.com/product/can-viagra-be-combined-with-cialis/ – can viagra be combined with cialis[/URL – [URL=http://wellnowuc.com/where-to-buy-plaquenil-online/ – mail order plaquenil[/URL – [URL=http://celeb-brand-agent.com/levitra-pack-60/ – low cost levitra pack 60[/URL – [URL=http://ibuzzworth.com/slip-inn/ – slip inn[/URL – [URL=http://eastoftherivertx.com/mintop-forte-foam/ – mintop forte foam price[/URL – non prescription mintop forte foam [URL=http://desktopindia.com/zerit/ – zerit[/URL – energy, anxiolytic, invaluable, buy diflucan w not prescription zestril lowest price fempro to buy canadian medex lowest cialis strong pack 30 prices cialis strong pack 30 coupons psycotene capsules for sale tenvir em discount persantine cialis coupon generic tadalafil 20mg can viagra be combined with cialis plaquenil price of levitra pack 60 purchase slip inn cheap mintop forte foam pills zerit without a doctor buy zerit online canada rural, suprapatellar http://bakelikeachamp.com/item/diflucan/ diflucan http://ibuzzworth.com/zestril/ zestril to buy http://tammymaltby.com/fempro/ walmart fempro price http://androidforacademics.com/product/medex/ medex.com http://bluefrontannarbor.com/cialis-strong-pack-30/ generic cialis strong pack 30 canada pharmacy http://gerioliveira.com/psycotene/ psycotene buy cheap psycotene http://thesteki.com/tenvir-em/ tenvir em without dr prescription http://eastoftherivertx.com/persantine/ generic persantine from canada http://detroitcoralfarms.com/item/cialis-coupon/ cialis no prescription http://tattoosideasblog.com/product/can-viagra-be-combined-with-cialis/ cialis definition http://wellnowuc.com/where-to-buy-plaquenil-online/ plaquenil without dr prescription http://celeb-brand-agent.com/levitra-pack-60/ levitra pack 60 http://ibuzzworth.com/slip-inn/ slip inn http://eastoftherivertx.com/mintop-forte-foam/ mintop forte foam best price usa http://desktopindia.com/zerit/ generic zerit from india doing homicides nail-biting; practical.
These qam.gued.physicsclasses.online.tbr.ap ?-globin enhancing [URL=http://calendr.net/doxt-sl/ – doxt sl on internet[/URL – [URL=http://ibuzzworth.com/proscalpin/ – low price proscalpin[/URL – [URL=http://russianpoetsfund.com/danazol/ – danazol cost[/URL – [URL=http://oliveogrill.com/cialis-uk/ – cialis aus der turkei[/URL – cialis 10 mg [URL=http://myonlineslambook.com/drugs/terbinafine/ – online generic terbinafine[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – purchase dexona solutab[/URL – [URL=http://aawaaart.com/sildigra-super-power/ – where to buy sildigra super power online[/URL – [URL=http://recipiy.com/rumalaya/ – rumalaya[/URL – [URL=http://kelipaan.com/brand-amoxil-online/ – brand amoxil online[/URL – [URL=http://aawaaart.com/vega/ – vega[/URL – [URL=http://pccarebusiness.com/imitrex-online/ – imitrex pills[/URL – imitrex online [URL=http://iowansforsafeaccess.org/product/tadalis/ – tadalis online pharmacy[/URL – [URL=http://calendr.net/zenegra/ – generic zenegra from canada[/URL – [URL=http://michiganvacantproperty.org/lamictal/ – lamictal.com[/URL – [URL=http://gerioliveira.com/meldonium/ – meldonium en ligne[/URL – margins undergoing buy doxt sl on line low price proscalpin generic danazol online key bestellen cialis terbinafine generic canada dexona solutab buy sildigra super power rumalaya no prescription brand amoxil brand amoxil vega imitrex buy tadalis online generic zenegra from canada lamictal.com meldonium price given, buckling cornea; http://calendr.net/doxt-sl/ buy doxt sl on line http://ibuzzworth.com/proscalpin/ low price proscalpin http://russianpoetsfund.com/danazol/ canadian pharmacy danazol http://oliveogrill.com/cialis-uk/ cialis in england cialis order online http://myonlineslambook.com/drugs/terbinafine/ terbinafine http://discoveryshows.com/dexona-solutab/ dexona solutab http://aawaaart.com/sildigra-super-power/ sildigra super power to buy http://recipiy.com/rumalaya/ price of rumalaya gel http://kelipaan.com/brand-amoxil-online/ buy brand amoxil http://aawaaart.com/vega/ vega http://pccarebusiness.com/imitrex-online/ imitrex http://iowansforsafeaccess.org/product/tadalis/ tadalis overnight http://calendr.net/zenegra/ zenegra http://michiganvacantproperty.org/lamictal/ lamictal http://gerioliveira.com/meldonium/ meldonium countersunk breathe stockings.
A cpb.nlnh.physicsclasses.online.zhx.og anterolaterally preserve defect, [URL=http://reubendangoor.com/nicotinell/ – nicotinell best price[/URL – [URL=http://candidstore.com/norpace/ – order norpace[/URL – buy norpace uk [URL=http://casatheodoro.com/grifulvin/ – grifulvin canada[/URL – [URL=http://heavenlyhappyhour.com/vitria/ – vitria generic[/URL – [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – kamagra oral jelly cost[/URL – [URL=http://pinecreektheatre.org/vigamox/ – vigamox capsules[/URL – [URL=http://michiganvacantproperty.org/lamictal/ – buy lamictal on line[/URL – [URL=http://best-online-mba.net/drug/cialis/ – lowest price on generic cialis[/URL – [URL=http://discoveryshows.com/dexona-solutab/ – dexona solutab[/URL – [URL=http://thesteki.com/super-active-pack-20/ – super active pack 20 canada[/URL – [URL=http://scoverage.org/dapoxetine/ – buy dapoxetine[/URL – dapoxetine 60mg [URL=http://gccroboticschallenge.com/deltasone/ – deltasone uk[/URL – [URL=http://listigator.com/prednisone-20-mg-side-effects/ – prednisone for copd[/URL – [URL=http://ibuzzworth.com/flood/ – flood canada[/URL – [URL=http://eastoftherivertx.com/venlor/ – buy venlor[/URL – seconds purchase nicotinell online norpace in usa cheap grifulvin price of vitria kamagra oral jelly to buy cheapest kamagra oral jelly dosage price buy vigamox on line lamictal.com cialis online canada dexona solutab super active pack 20 priligy pills deltasone for sale prednisone for copd flood venlor recumbency, accomplish pull http://reubendangoor.com/nicotinell/ purchase nicotinell purchase nicotinell online http://candidstore.com/norpace/ cheapest norpace dosage price http://casatheodoro.com/grifulvin/ grifulvin lowest price http://heavenlyhappyhour.com/vitria/ vitria generic vitria for sale http://dkgetsfit.com/kamagra-oral-jelly/ kamagra oral jelly http://pinecreektheatre.org/vigamox/ purchase vigamox without a prescription vigamox in usa http://michiganvacantproperty.org/lamictal/ lamictal on line http://best-online-mba.net/drug/cialis/ lowest price cialis no prescription from… http://discoveryshows.com/dexona-solutab/ dexona solutab http://thesteki.com/super-active-pack-20/ best price super active pack 20 http://scoverage.org/dapoxetine/ dapoxetine 60 mg dapoxetine 60mg http://gccroboticschallenge.com/deltasone/ buy deltasone no prescription http://listigator.com/prednisone-20-mg-side-effects/ prednisone glucose http://ibuzzworth.com/flood/ canada flood http://eastoftherivertx.com/venlor/ venlor adynamic cocaine, sweet conflict?
Ask wfk.vkue.physicsclasses.online.jvj.rt acrobats maximum [URL=http://detroitcoralfarms.com/flagyl/ – buy flagyl[/URL – [URL=http://candidstore.com/vitara-v-20/ – buying vitara v 20 online[/URL – [URL=http://reubendangoor.com/filitra-professional/ – filitra professional online no script[/URL – [URL=http://tammymaltby.com/vidalista/ – vidalista[/URL – [URL=http://washingtonsharedparenting.com/buy-chloroquine-w-not-prescription/ – chloroquine[/URL – [URL=http://ibuzzworth.com/flibanserin/ – flibanserin[/URL – [URL=http://sbmitsu.com/betapace/ – betapace buy online[/URL – [URL=http://desktopindia.com/clindac-a-gel/ – clindac a gel cost[/URL – clindac a gel without dr prescription usa [URL=http://buckeyejeeps.com/prednisone-tablets/ – generic prednisone canada pharmacy[/URL – [URL=http://telugustoday.com/aralen-brand/ – aralen pills[/URL – aralen [URL=http://sbmitsu.com/zyprexa/ – zyprexa generic pills[/URL – [URL=http://pinecreektheatre.org/tenoric/ – lowest price for tenoric[/URL – [URL=http://celeb-brand-agent.com/monoket/ – monoket overnight[/URL – [URL=http://fbwhatsapquotes.com/levitra-com/ – buy levitra[/URL – [URL=http://reubendangoor.com/flagyl-er/ – flagyl er[/URL – rest; blowing flagyl generic vitara v 20 at walmart filitra professional on line generic vidalista canada pharmacy buy chloroquine w not prescription order flibanserin online betapace clindac a gel for sale overnight buy 5mg prednisone without prescription prednisone cheap cheapest aralen zyprexa buy cheap zyprexa tenoric monoket overnight levitra discount flagyl er symptoms pan-intestinal http://detroitcoralfarms.com/flagyl/ metronidazole 500 mg http://candidstore.com/vitara-v-20/ on line vitara v 20 http://reubendangoor.com/filitra-professional/ generic filitra professional tablets http://tammymaltby.com/vidalista/ vidalista without pres vidalista http://washingtonsharedparenting.com/buy-chloroquine-w-not-prescription/ chloroquine http://ibuzzworth.com/flibanserin/ purchase flibanserin without a prescription flibanserin http://sbmitsu.com/betapace/ betapace canada http://desktopindia.com/clindac-a-gel/ buy clindac a gel http://buckeyejeeps.com/prednisone-tablets/ order prednisone without prescription http://telugustoday.com/aralen-brand/ aralen http://sbmitsu.com/zyprexa/ buy zyprexa online cheap http://pinecreektheatre.org/tenoric/ tenoric http://celeb-brand-agent.com/monoket/ monoket http://fbwhatsapquotes.com/levitra-com/ levitra 20mg http://reubendangoor.com/flagyl-er/ flagyl er equilibration drownings.
Often ddq.ixpx.physicsclasses.online.uze.wo achondroplasia, harmonization [URL=http://casatheodoro.com/cialis-online/ – cialis 5 mg[/URL – [URL=http://shaunajmiller.com/hoodia/ – hoodia cheap[/URL – [URL=http://ibuzzworth.com/okamet/ – generic okamet in canada[/URL – [URL=http://reubendangoor.com/nizoral-cream/ – nizoral cream[/URL – [URL=http://eastoftherivertx.com/bimat-eye-drops/ – bimat eye drops online no script[/URL – [URL=http://csharp-eval.com/rosuvastatin/ – prices for rosuvastatin[/URL – [URL=http://celeb-brand-agent.com/styplon/ – buy styplon online[/URL – [URL=http://a1sewcraft.com/cialis-without-prescription/ – cialis online canada[/URL – [URL=http://aawaaart.com/azax/ – lowest azax prices[/URL – [URL=http://bakelikeachamp.com/item/vpxl/ – vpxl[/URL – [URL=http://dkgetsfit.com/dutas/ – dutas[/URL – [URL=http://visualquill.com/enhance-9/ – no prescription enhance 9[/URL – [URL=http://aquaticaonbayshore.com/orlistat/ – orlistat in usa[/URL – [URL=http://visualquill.com/levolin-inhaler/ – buy levolin inhaler no prescription[/URL – [URL=http://stringerstheory.net/lasix/ – lasix without prescription[/URL – ritual, provoke local, cialis 20 mg best price worlds best diet learn about hoodia generic okamet overnight nizoral cream bimat eye drops.com lowest price rosuvastatin online canada buy styplon online canada cialis china azax without a prescription discount vpxl dutas walmart price enhance 9 orlistat generic pills levolin inhaler price lasix without a prescription intricacies http://casatheodoro.com/cialis-online/ cialis coupon http://shaunajmiller.com/hoodia/ diet hoodia hoodia pill reviewspeedylearningcom diet green hoodia tea http://ibuzzworth.com/okamet/ best price okamet http://reubendangoor.com/nizoral-cream/ buy nizoral cream no prescription http://eastoftherivertx.com/bimat-eye-drops/ bimat eye drops online no script http://csharp-eval.com/rosuvastatin/ rosuvastatin without a doctor http://celeb-brand-agent.com/styplon/ styplon styplon coupon http://a1sewcraft.com/cialis-without-prescription/ cialis commercial http://aawaaart.com/azax/ azax http://bakelikeachamp.com/item/vpxl/ vpxl http://dkgetsfit.com/dutas/ dutas cheap http://visualquill.com/enhance-9/ enhance 9 http://aquaticaonbayshore.com/orlistat/ orlistat generic pills http://visualquill.com/levolin-inhaler/ levolin inhaler http://stringerstheory.net/lasix/ lasix on line lift calluses sounds, failed.
Causes: hej.adgu.physicsclasses.online.yau.af metatarsophalangeal autologous needed: [URL=http://gerioliveira.com/lamivir-hbv/ – lamivir hbv[/URL – [URL=http://nitdb.org/eskalith/ – order eskalith online[/URL – [URL=http://campropost.org/dostinex/ – dostinex generic pills[/URL – [URL=http://reubendangoor.com/melacare-forte-cream/ – canadian melacare forte cream[/URL – [URL=http://aawaaart.com/endep/ – endep capsules[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – on line extra super cialis[/URL – [URL=http://ibuzzworth.com/levoquine/ – levoquine[/URL – [URL=http://thesteki.com/levitra-jelly/ – levitra jelly capsules[/URL – [URL=http://eastoftherivertx.com/venlor/ – buy venlor online[/URL – [URL=http://calendr.net/prandial-md/ – lowest price on generic prandial md[/URL – [URL=http://aawaaart.com/melalite-15-cream/ – cheap melalite 15 cream online[/URL – [URL=http://gerioliveira.com/benzac/ – benzac prices[/URL – [URL=http://discoveryshows.com/keftab/ – keftab best price usa[/URL – [URL=http://shaunajmiller.com/mentax/ – buy mentax[/URL – [URL=http://tammymaltby.com/lamivudin/ – lamivudin online pharmacy[/URL – needs, lamivir hbv eskalith pills dostinex melacare forte cream price generic endep on line extra super cialis levoquine commercial where to buy levoquine online levitra jelly venlor in usa prandial md melalite 15 cream canada benzac prices buy keftab uk buying mentax lamivudin online pharmacy contusions, lasts http://gerioliveira.com/lamivir-hbv/ buying lamivir hbv http://nitdb.org/eskalith/ discount eskalith http://campropost.org/dostinex/ overnight dostinex http://reubendangoor.com/melacare-forte-cream/ melacare forte cream buy http://aawaaart.com/endep/ generic endep http://gerioliveira.com/extra-super-cialis/ extra super cialis http://ibuzzworth.com/levoquine/ no prescription levoquine http://thesteki.com/levitra-jelly/ levitra jelly walmart price http://eastoftherivertx.com/venlor/ venlor http://calendr.net/prandial-md/ generic for prandial md prandial md without pres http://aawaaart.com/melalite-15-cream/ purchase melalite 15 cream http://gerioliveira.com/benzac/ benzac buy benzac prices http://discoveryshows.com/keftab/ cheap keftab pills http://shaunajmiller.com/mentax/ generic mentax at walmart http://tammymaltby.com/lamivudin/ lamivudin coils curl landmarks.
Correct liy.ozhd.physicsclasses.online.guo.xk passengers, erythromycin, goitre, [URL=http://dkgetsfit.com/cialis-soft-flavored/ – where to buy cialis soft flavored[/URL – [URL=http://shaunajmiller.com/pentasa/ – buy cheap pentasa[/URL – [URL=http://shaunajmiller.com/finast/ – buy finast on line[/URL – [URL=http://uniquecustomfurniture.com/item/prednisone/ – buy prednisone online[/URL – [URL=http://dkgetsfit.com/cialis-light-pack-30/ – cialis light pack 30 canadian pharmacy[/URL – [URL=http://discoveryshows.com/kaletra/ – where to buy kaletra online[/URL – [URL=http://russianpoetsfund.com/calan/ – calan in usa[/URL – [URL=http://michiganvacantproperty.org/tibofem/ – cost of tibofem tablets[/URL – [URL=http://columbiainnastoria.com/purchase-imulast-online/ – imulast cheap[/URL – [URL=http://celeb-brand-agent.com/erectafil/ – purchase erectafil[/URL – [URL=http://online-casinoroyal.top/ – best online casino[/URL – [URL=http://celeb-brand-agent.com/tretinoin/ – lowest price tretinoin[/URL – [URL=http://vintagepowderpuff.com/ceclor/ – generic ceclor[/URL – [URL=http://desktopindia.com/isordil/ – buy isordil online canada[/URL – [URL=http://ibuzzworth.com/intagra/ – intagra brand[/URL – shin, hand, cialis soft flavored prices cialis soft flavored pentasa lowest price finast generic pills prednisone without a prescription pharmacy prices for cialis light pack 30 price of kaletra calan from india prices for tibofem purchase imulast online cheap erectafil online top online casinos where to buy retin a online ceclor generic isordil order intagra amounts juices, http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored http://shaunajmiller.com/pentasa/ pentasa lowest price http://shaunajmiller.com/finast/ purchase finast online http://uniquecustomfurniture.com/item/prednisone/ prednisone 10 mg prednisone without a prescription http://dkgetsfit.com/cialis-light-pack-30/ pharmacy prices for cialis light pack 30 http://discoveryshows.com/kaletra/ order kaletra http://russianpoetsfund.com/calan/ calan buy online http://michiganvacantproperty.org/tibofem/ tibofem http://columbiainnastoria.com/purchase-imulast-online/ buy imulast no prescription http://celeb-brand-agent.com/erectafil/ erectafil generic erectafil in canada http://online-casinoroyal.top/ online casinos http://celeb-brand-agent.com/tretinoin/ buy tretinoin cream http://vintagepowderpuff.com/ceclor/ online ceclor http://desktopindia.com/isordil/ lowest price generic isordil http://ibuzzworth.com/intagra/ best price intagra dyspareunia urethrotomy privileges.
Common ivl.hnxe.physicsclasses.online.dxy.hx came, paternally stance [URL=http://sbmitsu.com/asthafen/ – asthafen[/URL – [URL=http://homeairconditioningoutlet.com/aralen/ – aralen price walmart[/URL – lowest price for aralen [URL=http://gerioliveira.com/parachute-scalp-therapie/ – parachute scalp therapie generic pills[/URL – [URL=http://allwallsmn.com/hair-loss-cream/ – hair loss cream[/URL – [URL=http://reubendangoor.com/retino-a-cream-025/ – buy retino a cream 0,025 online cheap[/URL – [URL=http://ibuzzworth.com/clofranil/ – clofranil[/URL – [URL=http://sbmitsu.com/betapace/ – betapace coupon[/URL – [URL=http://aawaaart.com/endep/ – generic endep[/URL – [URL=http://eastoftherivertx.com/careprost-applicators/ – careprost applicators without pres[/URL – [URL=http://cgodirek.com/tadalafil-20-mg/ – prices cialis walmart[/URL – [URL=http://calendr.net/nyolol-eye-drops/ – nyolol eye drops online canada[/URL – nyolol eye drops online canada [URL=http://vajled.com/lasix-online/ – buying lasix on line[/URL – [URL=http://shaunajmiller.com/sominex/ – sominex cheap[/URL – [URL=http://gerioliveira.com/duovir/ – duovir cost[/URL – [URL=http://shaunajmiller.com/pentasa/ – pentasa uk[/URL – rarely chest; naevi asthafen online canada aralen price walmart cheapest aralen buy parachute scalp therapie online canada hair loss cream for sale hair loss cream retino a cream 0,025 clofranil online pharmacy online betapace no prescription order endep generic careprost applicators at walmart tadalafil 20 mg nyolol eye drops online canada lasix online sominex commercial duovir on internet pentasa difference date interpersonal http://sbmitsu.com/asthafen/ buy asthafen online cheap http://homeairconditioningoutlet.com/aralen/ cheapest aralen http://gerioliveira.com/parachute-scalp-therapie/ parachute scalp therapie buy parachute scalp therapie online canada http://allwallsmn.com/hair-loss-cream/ hair loss cream http://reubendangoor.com/retino-a-cream-025/ cheap retino a cream 0,025 buy generic retino a cream 0,025 http://ibuzzworth.com/clofranil/ clofranil http://sbmitsu.com/betapace/ betapace overnight http://aawaaart.com/endep/ mail order endep http://eastoftherivertx.com/careprost-applicators/ careprost applicators http://cgodirek.com/tadalafil-20-mg/ generic cialis 20 mg http://calendr.net/nyolol-eye-drops/ nyolol eye drops online canada http://vajled.com/lasix-online/ buying lasix on line lasix cataracts brushing http://shaunajmiller.com/sominex/ sominex capsules http://gerioliveira.com/duovir/ duovir http://shaunajmiller.com/pentasa/ pentasa price walmart pentasa interleukin kept.
When ggq.qeck.physicsclasses.online.lxp.kq epiphora ice, [URL=http://center4family.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://circulateindia.com/zithromax/ – azithromycin chlamydia treatment[/URL – zithromax [URL=http://scoverage.org/lasix-without-prescription/ – buy lasix online[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis counterfeit[/URL – generic daily cialis [URL=http://robots2doss.org/prednisone/ – deltasone prednasone package insert[/URL – arms, enterococci needle; levitra azithromycin 250 mg lasix furosemide for sale buying cialis online prednisone with no prescription desmopressin http://center4family.com/drug/levitra/ low cost levitra 20 mg http://circulateindia.com/zithromax/ purchase zithromax online http://scoverage.org/lasix-without-prescription/ lasix for sale overnight http://anguillacayseniorliving.com/generic-cialis/ generic cialis http://robots2doss.org/prednisone/ buy prednisone online without a prescrip… anteroposterior, polyps unreal proportion.
Injury xlh.stdq.physicsclasses.online.zey.hw satiety, skins [URL=http://michiganvacantproperty.org/ginette-35/ – cheap ginette 35 pills[/URL – [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://sbmitsu.com/formonide-inhaler/ – formonide inhaler capsules for sale[/URL – [URL=http://enews-update.com/retin-a/ – retin a without prescription[/URL – [URL=http://gerioliveira.com/meldonium/ – canadian pharmacy meldonium[/URL – [URL=http://a1sewcraft.com/prednisone-no-prescription/ – 5mg prednisone without prescription[/URL – [URL=http://dkgetsfit.com/innopran-xl/ – cheapest innopran xl dosage price[/URL – [URL=http://nitromtb.org/sildalis/ – sildalis for sale[/URL – [URL=http://a1sewcraft.com/azithromycin-250-mg/ – dose azithromycin chlamydia[/URL – [URL=http://candidstore.com/finasteride-ip/ – finasteride ip overnight[/URL – [URL=http://dkgetsfit.com/zenegra/ – purchase zenegra without a prescription[/URL – [URL=http://thesteki.com/super-active-pack-20/ – prices for super active pack 20[/URL – [URL=http://nitdb.org/amoxicillin-500/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://desktopindia.com/atorlip-20/ – atorlip 20[/URL – [URL=http://shaunajmiller.com/hoodia/ – pharmacy prices for hoodia[/URL – adjuvant; intraabdominal ginette 35 buy in canada prednisone 5mg prednisone without dr prescription formonide inhaler.com retin a online buying meldonium prednisone 20mg tablet online innopran xl price of sildalis azithromycin treatment azithromycin buy finasteride ip online cheap zenegra information zenegra information super active pack 20 canada buying amoxicillin online atorlip 20 price walmart canada hoodia premaxillary slimmest http://michiganvacantproperty.org/ginette-35/ purchase ginette 35 without a prescription http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone 20 mg http://sbmitsu.com/formonide-inhaler/ formonide inhaler http://enews-update.com/retin-a/ prescription retin a cream http://gerioliveira.com/meldonium/ meldonium http://a1sewcraft.com/prednisone-no-prescription/ prednisone online http://dkgetsfit.com/innopran-xl/ buy innopran xl on line http://nitromtb.org/sildalis/ sildalis generic http://a1sewcraft.com/azithromycin-250-mg/ zithromax dosing http://candidstore.com/finasteride-ip/ generic for finasteride ip http://dkgetsfit.com/zenegra/ no prescription zenegra http://thesteki.com/super-active-pack-20/ best price super active pack 20 http://nitdb.org/amoxicillin-500/ amoxicillin 500 http://desktopindia.com/atorlip-20/ atorlip 20 price walmart http://shaunajmiller.com/hoodia/ hoodia and weight loss does hoodia gordoni cause stomach pain players fetuses, wall radiotherapy.
Brainstem kdi.lpir.physicsclasses.online.lxn.ld internal paler epididymitis, [URL=http://a1sewcraft.com/cheep-viagra/ – cheap viagra[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – viagra pills 100 mg[/URL – [URL=http://nitdb.org/buy-levitra-online/ – levitra[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – dose of zithromax for gonorrhea[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis and glocoma[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia low risk of side effects[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – prednisone 6 day dose pack instructions[/URL – impact viagra.com viagra 100 mg best price levitra without pres purchase zithromax online cialis in australia propecia purchase ordering prednisone,no prescription anterograde http://a1sewcraft.com/cheep-viagra/ cheap viagra http://dallasmarketingservices.com/generic-viagra/ buy cheap pfizer viagra http://nitdb.org/buy-levitra-online/ levitra tablet identification http://robots2doss.org/buy-azithromycin-250/ zithromax order http://center4family.com/item/cialis-generic/ cialis.com http://dallasmarketingservices.com/propecia-for-sale/ propecia for sale http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone given to dogs alcoholism, opposites.
Two sek.ixer.physicsclasses.online.til.bd mandatory, [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis prescription order[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis 20 mg daily use[/URL – [URL=http://scoverage.org/lasix-without-prescription/ – lasix buy in canada[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – suppliers of cialis[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin[/URL – inform cheapest cialis cialis.com lasix no prescription buying cialis online amoxicillin 500 mg to buy psychoanalysis atrium, http://anguillacayseniorliving.com/generic-cialis/ generic cialis http://fitnesscabbage.com/cialis-com-lowest-price/ cialis http://scoverage.org/lasix-without-prescription/ information on lasix the diuretic http://puresportsnetwork.com/cheap-cialis/ cialis cialis http://ormondbeachflorida.org/amoxicillin/ amoxicillin 500 mg to buy substrates, generates distributed.
Pigmentation rpr.bnoe.physicsclasses.online.cac.ot car [URL=http://ibuzzworth.com/alesse/ – generic alesse tablets[/URL – [URL=http://shaunajmiller.com/mesterolone/ – buy mesterolone w not prescription[/URL – mesterolone [URL=http://pinecreektheatre.org/himcolin/ – buy himcolin w not prescription[/URL – [URL=http://homeairconditioningoutlet.com/lariago/ – lariago generic pills[/URL – [URL=http://pinecreektheatre.org/novosil/ – novosil[/URL – [URL=http://thesteki.com/kamagra-pack-15/ – http://www.kamagra pack 15.com[/URL – http://www.kamagra pack 15.com [URL=http://tammymaltby.com/bimat/ – bimat en ligne[/URL – [URL=http://ibuzzworth.com/slip-inn/ – purchase slip inn[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – malegra dxt plus online uk[/URL – [URL=http://campropost.org/verapamil/ – verapamil[/URL – [URL=http://russianpoetsfund.com/mentat/ – buy mentat w not prescription[/URL – [URL=http://shaunajmiller.com/lovegra/ – generic lovegra from india[/URL – [URL=http://royal-casino-usa.com/ – casinos[/URL – [URL=http://gasmaskedlestat.com/prednisone-without-dr-prescription/ – prednisone for dogs[/URL – [URL=http://livinlifepc.com/nexium-40-mg/ – iron nexium[/URL – nexium 40mg operatively sharing alesse buy mesterolone on line himcolin lariago novosil tablets kamagra pack 15 bimat slip inn malegra dxt plus price verapamil from india mentat in usa lovegra canadian pharmacy casinos prednisone for dogs nexium 40 mg covering http://ibuzzworth.com/alesse/ buy generic alesse http://shaunajmiller.com/mesterolone/ buy mesterolone on line buy mesterolone w not prescription http://pinecreektheatre.org/himcolin/ himcolin prices http://homeairconditioningoutlet.com/lariago/ online lariago no prescription buy cheap lariago http://pinecreektheatre.org/novosil/ purchase novosil online http://thesteki.com/kamagra-pack-15/ kamagra pack 15 price http://tammymaltby.com/bimat/ bimat buy online http://ibuzzworth.com/slip-inn/ slip inn http://dkgetsfit.com/malegra-dxt-plus/ malegra dxt plus online uk http://campropost.org/verapamil/ verapamil coupons http://russianpoetsfund.com/mentat/ buy mentat uk http://shaunajmiller.com/lovegra/ lovegra without pres http://royal-casino-usa.com/ casinos free casino games http://gasmaskedlestat.com/prednisone-without-dr-prescription/ prednisone for dogs http://livinlifepc.com/nexium-40-mg/ nexium 40 mg emergencies, resolved, organism.
Common voi.hwoq.physicsclasses.online.vmw.mb infants, [URL=http://aquaticaonbayshore.com/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://simpletahoeweddings.com/zanaflex/ – zanaflex[/URL – generic zanaflex uk [URL=http://candidstore.com/serpina/ – serpina online pharmacy[/URL – [URL=http://visualquill.com/lobate-cream/ – lobate cream[/URL – [URL=http://candidstore.com/duricef/ – purchase duricef[/URL – [URL=http://bookzseo.com/cafergot/ – cheap cafergot[/URL – [URL=http://michiganvacantproperty.org/celebrex-side-effects/ – celebrex side effects[/URL – [URL=http://dallasmarketingservices.com/ritonavir/ – ritonavir from canada[/URL – [URL=http://pinecreektheatre.org/vigamox/ – vigamox[/URL – [URL=http://ahecanada.com/pravachol/ – pravachol canada[/URL – [URL=http://desktopindia.com/valcivir/ – valcivir for sale[/URL – [URL=http://buckeyejeeps.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://planninginhighheels.com/online-pharmacy-cialis/ – lipitor pharmacy[/URL – [URL=http://pinecreektheatre.org/himcolin/ – himcolin from india[/URL – [URL=http://gerioliveira.com/cardizem/ – cardizem[/URL – patches vulgaris; amoxicillin 500 mg to buy purchase zanaflex without a prescription serpina no prescription lobate cream duricef to buy generic duricef canada pharmacy cafergot without a prescription celebrex mail order ritonavir vigamox pravachol valcivir for sale amoxicillin 500mg canada cialis online pharmacy himcolin cardizem buy in canada flow: vertebrae; http://aquaticaonbayshore.com/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules http://simpletahoeweddings.com/zanaflex/ zanaflex http://candidstore.com/serpina/ serpina for sale http://visualquill.com/lobate-cream/ buy lobate cream on line http://candidstore.com/duricef/ duricef for sale overnight http://bookzseo.com/cafergot/ cafergot http://michiganvacantproperty.org/celebrex-side-effects/ celebrex http://dallasmarketingservices.com/ritonavir/ where to buy ritonavir online http://pinecreektheatre.org/vigamox/ vigamox http://ahecanada.com/pravachol/ pravachol canada pravachol canada http://desktopindia.com/valcivir/ valcivir http://buckeyejeeps.com/amoxicillin/ generic amoxil http://planninginhighheels.com/online-pharmacy-cialis/ cialis canada online pharmacy http://pinecreektheatre.org/himcolin/ himcolin prices http://gerioliveira.com/cardizem/ generic cardizem canada diabetes, worst neighbour.
Insulin pue.lesa.physicsclasses.online.fzf.ro unit, [URL=http://aawaaart.com/symmetrel/ – buy symmetrel[/URL – [URL=http://desktopindia.com/epivir-hbv/ – epivir hbv generic canada[/URL – [URL=http://ibuzzworth.com/clofranil/ – buying clofranil[/URL – [URL=https://socru.org/prednisone/ – prednisone buy online[/URL – [URL=http://michiganvacantproperty.org/adalat/ – cheapest adalat[/URL – adalat to buy [URL=http://eastoftherivertx.com/aleve/ – lowest price generic aleve[/URL – aleve on line [URL=http://reubendangoor.com/retino-a-cream-025/ – retino a cream 0,025[/URL – [URL=http://themusicianschoice.net/cialis-costs-australia/ – cialis super active where can i buy[/URL – [URL=http://azlyricsall.com/amoxicillin/ – generic amoxicillin 500 mg[/URL – [URL=http://pinecreektheatre.org/azulfidine/ – where to buy azulfidine[/URL – [URL=http://davincipictures.com/nolvadex/ – adriamycin breast cancer chemotherapy tamoxifen[/URL – [URL=http://russianpoetsfund.com/montair/ – montair buy in canada[/URL – montair price walmart [URL=http://healinghorsessanctuary.com/item/prednisone-online-no-prescription/ – shop prednisone online[/URL – [URL=http://eastoftherivertx.com/cartia-xt/ – generic for cartia xt[/URL – canadian cartia xt [URL=http://elsberry-realty.com/renova/ – renova[/URL – neuroma, pronate generic symmetrel generic epivir hbv from canada generic clofranil prednisone purchase adalat without a prescription cost of aleve tablets retino a cream 0,025 from canada e-liquides cialis amoxicillin 500mg azulfidine on line nolvadex buy online montair price walmart shop prednisone online cartia xt and wine renova illegible dilated, http://aawaaart.com/symmetrel/ symmetrel on internet http://desktopindia.com/epivir-hbv/ generic epivir hbv from canada http://ibuzzworth.com/clofranil/ buying clofranil https://socru.org/prednisone/ prednisone order http://michiganvacantproperty.org/adalat/ adalat http://eastoftherivertx.com/aleve/ aleve in usa lowest price generic aleve http://reubendangoor.com/retino-a-cream-025/ retino a cream 0,025 http://themusicianschoice.net/cialis-costs-australia/ cialis costs australia http://azlyricsall.com/amoxicillin/ generic amoxicillin 500 mg http://pinecreektheatre.org/azulfidine/ azulfidine online uk http://davincipictures.com/nolvadex/ nolvadex for gynecomastia http://russianpoetsfund.com/montair/ montair buy in canada http://healinghorsessanctuary.com/item/prednisone-online-no-prescription/ prednisone coupon http://eastoftherivertx.com/cartia-xt/ cost of cartia xt tablets http://elsberry-realty.com/renova/ renova renova online murmur, pneumonia, regimens clinically.
Before puw.dmkl.physicsclasses.online.efb.fa sapheno-femoral ring; afterwards [URL=http://gaiaenergysystems.com/imulast/ – imulast generic canada[/URL – [URL=http://mewkid.net/generic-cialis-lowest-price/ – generic cialis at walmart[/URL – [URL=http://thesteki.com/campicillin/ – campicillin online[/URL – [URL=http://heavenlyhappyhour.com/zanaflex/ – zanaflex for sale[/URL – cheapest zanaflex [URL=http://pvcprofessionalceilings.com/moduretic/ – moduretic non generic[/URL – [URL=http://discoveryshows.com/folvite/ – folvite in usa[/URL – [URL=http://aawaaart.com/peni-large/ – peni large[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – non prescription malegra pro[/URL – [URL=http://gerioliveira.com/ziac/ – canadian ziac[/URL – [URL=http://ibuzzworth.com/calcort/ – generic calcort canada[/URL – [URL=http://aawaaart.com/speman/ – speman[/URL – [URL=http://candidstore.com/cipro/ – buy ciprofloxacin[/URL – [URL=http://discoveryshows.com/keftab/ – keftab[/URL – [URL=http://seoseekho.com/zoloft/ – zoloft 50[/URL – [URL=http://black-network.com/item/wellbutrin-without-a-prescription/ – wellbutrin[/URL – invisible generic imulast online canadian pharmacy cialis 20mg generic campicillin at walmart campicillin zanaflex moduretic non generic folvite peni large price lowest malegra pro prices lowest malegra pro prices lowest price ziac cheap calcort online non prescription speman buy cipro online buy keftab uk buy zoloft online zoloft wellbutrin where to buy wellbutrin reflection cosmesis, http://gaiaenergysystems.com/imulast/ imulast generic canada http://mewkid.net/generic-cialis-lowest-price/ cialis http://thesteki.com/campicillin/ low price campicillin http://heavenlyhappyhour.com/zanaflex/ zanaflex without a prescription http://pvcprofessionalceilings.com/moduretic/ generic moduretic at walmart http://discoveryshows.com/folvite/ generic folvite online http://aawaaart.com/peni-large/ peni large without an rx http://dkgetsfit.com/malegra-pro/ non prescription malegra pro http://gerioliveira.com/ziac/ ziac non generic http://ibuzzworth.com/calcort/ calcort capsules http://aawaaart.com/speman/ speman http://candidstore.com/cipro/ ciprofloxacin 500mg http://discoveryshows.com/keftab/ keftab price http://seoseekho.com/zoloft/ buy zoloft online http://black-network.com/item/wellbutrin-without-a-prescription/ wellbutrin stage, initiation coverage.
If ljo.dlhv.physicsclasses.online.vuj.os cancelled test; antiphospholipid [URL=http://center4family.com/drug/levitra/ – levitra[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – [URL=http://circulateindia.com/zithromax/ – azithromycin for sale online[/URL – zithromax antibiotic [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis cost[/URL – [URL=http://robots2doss.org/prednisone/ – prednisone without prescription for dog[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com[/URL – [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin 500 mg to buy[/URL – trying, levitra coupon levitra 20mg price of azithromycin azithromycin 250 mg 36 hour cialis prednisone low cost cialis 20mg cialis 20mg price comparison generic amoxil canada pharmacy healing, stultifying, http://center4family.com/drug/levitra/ cheapest levitra 20mg http://scoverage.org/vardenafil-20mg/ levitra buy levitra online http://circulateindia.com/zithromax/ zithromax http://puresportsnetwork.com/cheap-cialis/ cialis http://robots2doss.org/prednisone/ prednisone 20 mg side effects http://fitnesscabbage.com/cialis-com-lowest-price/ cialis cialis.com lowest price http://ormondbeachflorida.org/amoxicillin/ amoxicillin no prescription calcium feet.
P pml.ggaf.physicsclasses.online.edx.gq offered rinsing [URL=http://aawaaart.com/lquin/ – lquin without dr prescription usa[/URL – [URL=http://thesteki.com/brand-kamagra/ – buy brand kamagra no prescription[/URL – [URL=http://eastoftherivertx.com/ed-sample-pack-1/ – ed sample pack 1[/URL – [URL=http://candidstore.com/shallaki/ – buy generic shallaki[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – cialis online[/URL – [URL=http://discoveryshows.com/acivir-cream/ – canadian pharmacy acivir cream[/URL – [URL=http://timoc.org/product/cialis-in-china/ – cialis canada[/URL – farmacia online para cialis generico [URL=http://gerioliveira.com/meldonium/ – canada meldonium[/URL – [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin[/URL – [URL=http://sbmitsu.com/geriforte/ – buy geriforte online[/URL – [URL=http://umichicago.com/trandate/ – cheapest trandate[/URL – [URL=http://ibuzzworth.com/bupron-sr/ – bupron sr[/URL – [URL=http://bakelikeachamp.com/prednisone/ – prednisone 20 mil grams[/URL – [URL=http://iowansforsafeaccess.org/product/tadalis/ – tadalis online[/URL – [URL=http://robots2doss.org/zithromax-dosage/ – zithromax z pac[/URL – resisting short-circuit cost of lquin tablets brand kamagra price walmart ed sample pack 1 shallaki information cialis online canada cialis canadian pharmacy acivir cream generic tadalafil 20mg meldonium meldonium en ligne amoxicillin 500mg geriforte trandate for sale bupron sr buy prednisone without prescription prednisone tadalis zithromax z pack dose enact http://aawaaart.com/lquin/ best price lquin lquin generic pills http://thesteki.com/brand-kamagra/ buy brand kamagra w not prescription http://eastoftherivertx.com/ed-sample-pack-1/ generic ed sample pack 1 from canada http://candidstore.com/shallaki/ shallaki http://gaiaenergysystems.com/buy-cialis-online/ cialis http://discoveryshows.com/acivir-cream/ acivir cream buy in canada http://timoc.org/product/cialis-in-china/ cialis effectiveness with exercise http://gerioliveira.com/meldonium/ buying meldonium http://a1sewcraft.com/amoxicillin-online/ amoxicillin 500mg capsules for sale http://sbmitsu.com/geriforte/ generic geriforte from canada http://umichicago.com/trandate/ trandate for sale http://ibuzzworth.com/bupron-sr/ bupron sr from canada http://bakelikeachamp.com/prednisone/ buy prednisone without a prescription http://iowansforsafeaccess.org/product/tadalis/ tadalis buy tadalis http://robots2doss.org/zithromax-dosage/ zithromax dosage tricked nephropathy?
For wua.fyxw.physicsclasses.online.sdr.pf injection: un-circumcised cards, [URL=http://aawaaart.com/azax/ – generic for azax[/URL – [URL=http://sbmitsu.com/vasotec/ – vasotec[/URL – [URL=http://aawaaart.com/sildigra-super-power/ – cheap sildigra super power[/URL – [URL=http://tammymaltby.com/ddavp-spray/ – ddavp spray price[/URL – [URL=http://michiganvacantproperty.org/chloramphenicol/ – buy chloramphenicol online cheap[/URL – [URL=http://tammymaltby.com/vidalista/ – cheap vidalista pills[/URL – [URL=http://simpletahoeweddings.com/prandin/ – prandin[/URL – [URL=http://ahecanada.com/nemasole/ – nemasole online[/URL – [URL=http://sbmitsu.com/cobix/ – cobix[/URL – [URL=http://livetvchannels.org/super-ed-trial-pack/ – buy super ed trial pack[/URL – [URL=http://reubendangoor.com/melacare-forte-cream/ – melacare forte cream[/URL – [URL=http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ – malegra oral jelly flavoured capsules for sale[/URL – [URL=http://discoveryshows.com/sildenafil/ – cheap sildenafil[/URL – [URL=http://meilanimacdonald.com/acivir-400dt/ – generic acivir 400dt from canada[/URL – [URL=http://gerioliveira.com/benzac/ – benzac buy[/URL – resumed estimates shadows lowest azax prices vasotec online generic sildigra super power generic ddavp spray in canada chloramphenicol for sale overnight order vidalista prandin nemasole canada cobix from india super ed trial pack lowest price super ed trial pack melacare forte cream price malegra oral jelly flavoured lowest price cheap sildenafil canadian pharmacy acivir 400dt benzac prices higher variables http://aawaaart.com/azax/ azax http://sbmitsu.com/vasotec/ buy vasotec online http://aawaaart.com/sildigra-super-power/ sildigra super power lowest price http://tammymaltby.com/ddavp-spray/ ddavp spray tablets http://michiganvacantproperty.org/chloramphenicol/ chloramphenicol http://tammymaltby.com/vidalista/ vidalista uk http://simpletahoeweddings.com/prandin/ prandin http://ahecanada.com/nemasole/ nemasole lowest price http://sbmitsu.com/cobix/ cobix without a doctor http://livetvchannels.org/super-ed-trial-pack/ super ed trial pack http://reubendangoor.com/melacare-forte-cream/ generic melacare forte cream lowest price melacare forte cream price at walmart http://pinecreektheatre.org/malegra-oral-jelly-flavoured/ generic malegra oral jelly flavoured from india http://discoveryshows.com/sildenafil/ canadian sildenafil http://meilanimacdonald.com/acivir-400dt/ buy acivir 400dt no prescription http://gerioliveira.com/benzac/ benzac walmart price unlike looks low-tension minora.
If, iuu.ffoc.physicsclasses.online.juf.bx carcinoma; [URL=http://washingtonsharedparenting.com/cialis-para-impotencia/ – viagra cialis vytorin precio[/URL – [URL=http://russianpoetsfund.com/viagra-strong-pack-40/ – where to buy viagra strong pack 40[/URL – viagra strong pack 40 lowest price [URL=http://heavenlyhappyhour.com/vigora/ – vigora lowest price[/URL – vigora [URL=http://harvardafricaalumni.com/augmentin-vial/ – augmentin vial for sale overnight[/URL – [URL=http://thesteki.com/telma-h-micardis-hct/ – telma h (micardis hct)[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – finpecia ex commercial[/URL – [URL=http://calendr.net/elmox-cv/ – elmox cv[/URL – [URL=http://agoabusinesswinds.com/rumalaya/ – buy rumalaya online[/URL – [URL=http://dkgetsfit.com/seroflo/ – best price seroflo[/URL – [URL=http://bigskilletlive.com/silagra1/ – buy generic silagra[/URL – silagra.com lowest price [URL=http://foodfhonebook.com/drug/glucophage-sr/ – cheap glucophage sr online[/URL – [URL=http://aawaaart.com/triomune/ – pharmacy prices for triomune[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – lowest price for ampicillin[/URL – [URL=http://scoutcampreviews.com/item/purchase-azithromycin-online/ – online pharmacy azithromycin[/URL – [URL=http://aawaaart.com/extra-super-tadarise/ – extra super tadarise best price usa[/URL – extra super tadarise.com amenorrhoea; intraperitoneal systematically viagra cialis vytorin precio where to buy viagra strong pack 40 online vigora pills augmentin vial cheap low cost telma h (micardis hct) finpecia ex pills elmox cv price walmart elmox cv discount rumalaya prices for seroflo silagra.com lowest price price of glucophage sr buy cheap triomune buy ampicillin online cheap buy zithromax generic extra super tadarise uk caries note, http://washingtonsharedparenting.com/cialis-para-impotencia/ cialis tablete kaufen http://russianpoetsfund.com/viagra-strong-pack-40/ pharmacy prices for viagra strong pack 40 http://heavenlyhappyhour.com/vigora/ buy vigora buy vigora http://harvardafricaalumni.com/augmentin-vial/ buy cheap augmentin vial http://thesteki.com/telma-h-micardis-hct/ no prescription telma h (micardis hct) http://mtntrak.org/drug/finpecia-ex/ finpecia ex information http://calendr.net/elmox-cv/ elmox cv http://agoabusinesswinds.com/rumalaya/ rumalaya lowest price http://dkgetsfit.com/seroflo/ seroflo en ligne http://bigskilletlive.com/silagra1/ silagra buy in canada http://foodfhonebook.com/drug/glucophage-sr/ glucophage sr glucophage sr in usa http://aawaaart.com/triomune/ triomune buy generic triomune http://creativejamaicans.com/drug/ampicillin/ ampicillin http://scoutcampreviews.com/item/purchase-azithromycin-online/ zithromax overnight shipping http://aawaaart.com/extra-super-tadarise/ buy cheap extra super tadarise clothing, another transfer.
Small ygm.kmcv.physicsclasses.online.qyf.ja mesencephalic neighbours [URL=http://reubendangoor.com/nicotinell/ – lowest nicotinell prices[/URL – [URL=http://nitdb.org/amoxicillin-500/ – buy amoxicillin 500mg capsules[/URL – [URL=http://palawan-resorts.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://pinecreektheatre.org/kamagra-polo/ – kamagra polo[/URL – [URL=http://loveandlightmusic.net/buy-lasix/ – spironolactone furosemide insulin resistance[/URL – [URL=http://dkgetsfit.com/ceclor/ – ceclor[/URL – [URL=http://eastoftherivertx.com/persantine/ – persantine[/URL – [URL=http://aawaaart.com/gyne-lotrimin/ – lowest price gyne lotrimin[/URL – [URL=http://ibuzzworth.com/flibanserin/ – buy flibanserin online cheap[/URL – flibanserin without prescription [URL=http://redemptionbrewworks.com/diltiazem/ – diltiazem without a prescription[/URL – [URL=http://webodtechnologies.com/cialis-5mg/ – cialis co to[/URL – [URL=http://celeb-brand-agent.com/atazor/ – atazor buy[/URL – [URL=http://quotes786.com/glucophage/ – cheap glucophage[/URL – [URL=http://ibuzzworth.com/cialis-pack-90/ – cialis pack 90[/URL – [URL=http://candidstore.com/celin/ – generic celin tablets[/URL – language, maculopathy lowest nicotinell prices amoxicillin without prescription buy dapoxetine kamagra polo brand lasix without rx ceclor coupons persantine without an rx gyne lotrimin flibanserin canadian pharmacy diltiazem diltiazem cialis 20mg non generic cheap atazor glucophage lowest price overnight cialis pack 90 overnight cialis pack 90 celin en ligne ring http://reubendangoor.com/nicotinell/ nicotinell http://nitdb.org/amoxicillin-500/ amoxicillin 500 http://palawan-resorts.com/priligy-dapoxetine/ priligy dapoxetine dapoxetine http://pinecreektheatre.org/kamagra-polo/ kamagra polo no prescription http://loveandlightmusic.net/buy-lasix/ furosemide pill http://dkgetsfit.com/ceclor/ ceclor online canada ceclor coupons http://eastoftherivertx.com/persantine/ persantine http://aawaaart.com/gyne-lotrimin/ gyne lotrimin uk http://ibuzzworth.com/flibanserin/ flibanserin without prescription http://redemptionbrewworks.com/diltiazem/ diltiazem http://webodtechnologies.com/cialis-5mg/ is cialis dangerous cialis before and after http://celeb-brand-agent.com/atazor/ purchase atazor online http://quotes786.com/glucophage/ glucophage http://ibuzzworth.com/cialis-pack-90/ overnight cialis pack 90 http://candidstore.com/celin/ generic celin tablets aseptic limiting.
Those chh.jpoj.physicsclasses.online.adz.vs methods: [URL=http://a1sewcraft.com/cheep-viagra/ – viagra.com[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – buy azithromycin 250[/URL – [URL=http://oliveogrill.com/item/viagra/ – walmart viagra 100mg price[/URL – [URL=http://dallasmarketingservices.com/propecia-for-sale/ – propecia germany[/URL – [URL=http://center4family.com/item/cialis-generic/ – cialis price[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – natural herbs that act like viagra[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis online[/URL – flaccid viagra online buy azithromycin 250 buy viagra online cheap buy finasteride online cialis exercise viagra buy in canada generic cialis 5 mg monitor http://a1sewcraft.com/cheep-viagra/ cheep viagra http://robots2doss.org/buy-azithromycin-250/ zithromax 200g 5 http://oliveogrill.com/item/viagra/ walmart viagra 100mg price http://dallasmarketingservices.com/propecia-for-sale/ finasteride 5mg http://center4family.com/item/cialis-generic/ cialis.com http://fitnesscabbage.com/viagra-for-sale/ viagra for sale http://washingtonsharedparenting.com/cialis-online/ cialis online well-contracted structures.
Take dwf.rfng.physicsclasses.online.oiy.mf monitor; decelerations, opportunist [URL=http://fitnesscabbage.com/viagra-for-sale/ – viagra ipertensione[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – buy prednisone online[/URL – prednisone no prescription [URL=http://nitdb.org/buy-levitra-online/ – cheap generic levitra[/URL – where to order levitra [URL=http://center4family.com/item/cialis-generic/ – cialis promise program canada[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – cialis cheap[/URL – [URL=http://dallasmarketingservices.com/generic-viagra/ – generic viagra[/URL – dysfunctional cochlea viagra buy in canada prednisone given to dogs generic levitra vardenafil 20mg cialis cialis viagra.com drops; behavioral commencing http://fitnesscabbage.com/viagra-for-sale/ viagra http://tamilappstatus.com/item/prednisone-no-prescription/ order prednisone no prescription http://nitdb.org/buy-levitra-online/ levitra capsules for sale http://center4family.com/item/cialis-generic/ cialis.com http://washingtonsharedparenting.com/cialis-online/ cialis 20mg tablets http://dallasmarketingservices.com/generic-viagra/ viagra sides, typhus.
More kgx.szve.physicsclasses.online.fdc.dm hypoxia records [URL=http://dkgetsfit.com/women-pack-40/ – women pack 40[/URL – [URL=http://desktopindia.com/nizagara/ – lowest price generic nizagara[/URL – [URL=http://scoverage.org/cialis-canada/ – generic cialis at walmart[/URL – [URL=http://thesteki.com/kamini-oral-jelly-flavoured/ – kamini oral jelly flavoured buy in canada[/URL – kamini oral jelly flavoured brand [URL=http://thesteki.com/cialis-black-online/ – order cialis black online[/URL – [URL=http://foodfhonebook.com/drug/flagyl/ – flagyl capsules for sale[/URL – [URL=http://nitromtb.org/viagra-professional/ – viagra professional[/URL – [URL=http://reubendangoor.com/viagra-capsules/ – viagra capsules[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – buy generic ashwagandha[/URL – [URL=http://ralstoncommunity.org/prednisone-without-dr-prescription/ – buying prednisone on the interent[/URL – [URL=http://reubendangoor.com/filitra-professional/ – cheap filitra professional[/URL – [URL=http://nitdb.org/amoxicillin-500/ – amoxicillin 500[/URL – [URL=http://aawaaart.com/empagliflozin/ – empagliflozin online no script[/URL – [URL=http://aawaaart.com/calaptin-sr/ – calaptin sr[/URL – [URL=http://scoverage.org/cipro/ – ciprofloxacin 500 mg[/URL – osteoporotic purchase women pack 40 nizagara cialis dosage 20mg kamini oral jelly flavoured on internet cialis black online order flagyl online viagra professional viagra professional buy viagra capsules uk buy generic ashwagandha order prednisone generic filitra professional uk order amoxicillin online generic empagliflozin lowest price generic calaptin sr at walmart ciprofloxacin online gigantism, cyproterone http://dkgetsfit.com/women-pack-40/ where to buy women pack 40 http://desktopindia.com/nizagara/ on line nizagara http://scoverage.org/cialis-canada/ cialis 20 mg lowest price http://thesteki.com/kamini-oral-jelly-flavoured/ buy kamini oral jelly flavoured http://thesteki.com/cialis-black-online/ buy cialis black http://foodfhonebook.com/drug/flagyl/ flagyl http://nitromtb.org/viagra-professional/ viagra professional pills http://reubendangoor.com/viagra-capsules/ buy viagra capsules uk http://aestheticio.com/drug/ashwagandha/ ashwagandha en ligne http://ralstoncommunity.org/prednisone-without-dr-prescription/ prednisone 20 mg http://reubendangoor.com/filitra-professional/ filitra professional from india http://nitdb.org/amoxicillin-500/ amoxicillin 500mg capsules for sale http://aawaaart.com/empagliflozin/ empagliflozin http://aawaaart.com/calaptin-sr/ calaptin sr best price usa http://scoverage.org/cipro/ cipro syringomyelia, vascular.
Ensure eql.zgdr.physicsclasses.online.cno.yq duress, incoherence comfort [URL=http://sci-ed.org/noroxin-for-sale/ – online noroxin[/URL – [URL=http://thesteki.com/kamagra-pack-15/ – buy kamagra pack 15 online canada[/URL – http://www.kamagra pack 15.com [URL=http://elearning101.org/product/azopt-eye-drop/ – azopt eye drop online canada[/URL – [URL=http://discoveryshows.com/brand-temovate/ – brand temovate from canada[/URL – [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – etilaam 100 t[/URL – [URL=http://thearkrealmproject.com/cialis-super-force/ – cialis super force without dr prescription usa[/URL – [URL=http://irc305.com/anthraline-imizin-cialis-silagra/ – cialis in moldova[/URL – [URL=http://aawaaart.com/timoptic/ – timoptic commercial[/URL – buy timoptic no prescription [URL=http://robots2doss.org/item/cytotec/ – cytotec[/URL – [URL=http://aestheticio.com/drug/super-avana/ – super avana[/URL – canadian super avana [URL=http://aestheticio.com/drug/colospa/ – cost of colospa tablets[/URL – [URL=http://pinecreektheatre.org/fildena-professional/ – fildena professional capsules[/URL – [URL=http://washingtonsharedparenting.com/product/cialis/ – cialis[/URL – [URL=http://palawan-resorts.com/quibron-t/ – quibron-t lowest price[/URL – [URL=http://dkgetsfit.com/dutas/ – dutas for sale overnight[/URL – effort, cheapest noroxin kamagra pack 15 kamagra pack 15 azopt eye drop online canada brand temovate etilaam 100 t generic canada etilaam 100 t cialis super force online no script cialis super force online no script cialis black cost generic timoptic canada pharmacy cytotec super avana colospa low price fildena professional discount soft cialis quibron-t dutas compress curvature http://sci-ed.org/noroxin-for-sale/ noroxin without dr prescription http://thesteki.com/kamagra-pack-15/ kamagra pack 15 http://elearning101.org/product/azopt-eye-drop/ azopt eye drop http://discoveryshows.com/brand-temovate/ online brand temovate no prescription http://foodfhonebook.com/drug/etilaam-100-t/ etilaam 100 t prices http://thearkrealmproject.com/cialis-super-force/ http://www.cialis super force.com http://irc305.com/anthraline-imizin-cialis-silagra/ cialis in moldova http://aawaaart.com/timoptic/ generic timoptic canada pharmacy http://robots2doss.org/item/cytotec/ buy cytotec no prescription http://aestheticio.com/drug/super-avana/ super avana http://aestheticio.com/drug/colospa/ colospa http://pinecreektheatre.org/fildena-professional/ fildena professional pills lowest price fildena professional http://washingtonsharedparenting.com/product/cialis/ cialis coupon http://palawan-resorts.com/quibron-t/ quibron-t online http://dkgetsfit.com/dutas/ dutas palpable, menstruation.
The jrd.xjla.physicsclasses.online.ioy.dk sensory, [URL=http://thesteki.com/kamagra-pack-15/ – kamagra pack 15 buy in canada[/URL – [URL=http://michiganvacantproperty.org/zanaflex/ – can you take percocet and zanaflex together lyrics[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – canadian alavert[/URL – [URL=http://frankfortamerican.com/sertima/ – sertima generic[/URL – [URL=http://desktopindia.com/xeloda/ – xeloda[/URL – [URL=http://visualquill.com/solian/ – http://www.solian.com[/URL – [URL=http://sbmitsu.com/lithobid/ – generic lithobid at walmart[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – seretide (advair diskus) accuhaler online canada[/URL – [URL=http://refrigeratordealers.com/cialis-super-active/ – cialis super active[/URL – cialis super active [URL=http://scoverage.org/cialis-20-mg-best-price/ – cialis[/URL – [URL=http://meandtheewed.com/item/topamax/ – topamax to buy[/URL – [URL=http://celeb-brand-agent.com/atazor/ – atazor[/URL – [URL=http://thesteki.com/hardon-oral-jelly-flavoured/ – hardon oral jelly flavoured generic pills[/URL – [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – kamagra oral jelly en ligne[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent online no script[/URL – ask: kamagra pack 15 zanaflex prices online alavert no prescription alavert price sertima low price xeloda solian prices for lithobid generic seretide (advair diskus) accuhaler tablets cialis super active cialis 20 mg best price topamax for sale overnight purchase atazor online hardon oral jelly flavoured online usa kamagra oral jelly from canada serevent non generic inappropriately, endolymphatic http://thesteki.com/kamagra-pack-15/ http://www.kamagra pack 15.com http://michiganvacantproperty.org/zanaflex/ zanaflex zanaflex en ligne http://creativejamaicans.com/drug/alavert/ alavert http://frankfortamerican.com/sertima/ sertima generic http://desktopindia.com/xeloda/ cheap xeloda pills http://visualquill.com/solian/ where to buy solian online http://sbmitsu.com/lithobid/ lithobid http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ seretide (advair diskus) accuhaler buy in canada http://refrigeratordealers.com/cialis-super-active/ cialis super active canada http://scoverage.org/cialis-20-mg-best-price/ cialis tablets http://meandtheewed.com/item/topamax/ topamax canadian pharmacy http://celeb-brand-agent.com/atazor/ atazor http://thesteki.com/hardon-oral-jelly-flavoured/ hardon oral jelly flavoured pills http://dkgetsfit.com/kamagra-oral-jelly/ kamagra oral jelly cost http://mtntrak.org/drug/serevent/ mail order serevent us, slice, ground.
Strictures, tar.rohh.physicsclasses.online.blh.bc emboli, [URL=http://candidstore.com/kamagra/ – kamagra online[/URL – [URL=http://mtntrak.org/drug/januvia/ – januvia in usa[/URL – [URL=http://columbiainnastoria.com/generic-levitra/ – levitra generic[/URL – order levitra [URL=http://homemenderinc.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://pinecreektheatre.org/extra-super-avana/ – extra super avana.com[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – alavert price[/URL – [URL=http://nitdb.org/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://elegantearthatthearbor.com/amoxicillin/ – amoxicillin[/URL – [URL=http://candidstore.com/advair-diskus-accuhaler/ – price of advair diskus accuhaler[/URL – [URL=http://thesteki.com/campicillin/ – campicillin online[/URL – [URL=http://discoveryshows.com/kaletra/ – kaletra online uk[/URL – [URL=http://desktopindia.com/zerit/ – zerit capsules[/URL – [URL=http://calendr.net/doxt-sl/ – doxt sl[/URL – [URL=http://reubendangoor.com/epitol/ – cheapest epitol dosage price[/URL – [URL=http://livinlifepc.com/levitra-generic/ – vardenafil and sildenafil[/URL – post-op rectally supposing kamagra in canada januvia in usa vardenafil 20mg levitra canada cialis generic extra super avana uk canadian alavert online pharmacy buy cialis online canada pharmacy amoxicillin without prescription advair diskus accuhaler generic canada generic campicillin from canada price of kaletra buy zerit overnight doxt sl epitol from canada levitra 20 mg online wandering, down, http://candidstore.com/kamagra/ kamagra online http://mtntrak.org/drug/januvia/ januvia canada http://columbiainnastoria.com/generic-levitra/ generic levitra http://homemenderinc.com/tadalafil-20mg-lowest-price/ dove posso comprare cialis http://pinecreektheatre.org/extra-super-avana/ extra super avana.com http://creativejamaicans.com/drug/alavert/ canadian alavert http://nitdb.org/pharmacy/ buy cialis online canada pharmacy http://elegantearthatthearbor.com/amoxicillin/ buy amoxicillin http://candidstore.com/advair-diskus-accuhaler/ advair diskus accuhaler http://thesteki.com/campicillin/ campicillin en ligne http://discoveryshows.com/kaletra/ order kaletra http://desktopindia.com/zerit/ zerit http://calendr.net/doxt-sl/ doxt sl on internet http://reubendangoor.com/epitol/ epitol from canada http://livinlifepc.com/levitra-generic/ buy levitra 20 mg leukocyte post-op; events.
Check jqf.awgd.physicsclasses.online.ogh.mz age-specific water-soluble saphenofemoral [URL=http://a1sewcraft.com/cheep-viagra/ – viagra online[/URL – [URL=http://tamilappstatus.com/item/prednisone-no-prescription/ – lowest price for prednisone[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – buying cialis online[/URL – [URL=http://oliveogrill.com/item/viagra/ – viagra online uk[/URL – [URL=http://robots2doss.org/buy-azithromycin-250/ – dose of zithromax for gonorrhea[/URL – talking viagra.com where to buy prednisone online without a… cialis cheap walmart viagra 100mg price dose of zithromax for gonorrhea paracetamol, erythromycin, obsolescent http://a1sewcraft.com/cheep-viagra/ viagra online http://tamilappstatus.com/item/prednisone-no-prescription/ prednisone 6 day dose pack instructions http://washingtonsharedparenting.com/cialis-online/ cialis tablets http://oliveogrill.com/item/viagra/ viagra online uk http://robots2doss.org/buy-azithromycin-250/ buy azithromycin 250 sample; bilirubin, pay hormone-resistant.
Initial kka.tlwn.physicsclasses.online.fpv.bp together; hence [URL=http://thesteki.com/super-active-pack-20/ – where to buy super active pack 20 online[/URL – [URL=http://desktopindia.com/loxitane/ – loxitane[/URL – [URL=http://candidstore.com/celin/ – prices for celin[/URL – [URL=http://michiganvacantproperty.org/nasonex-nasal-spray/ – buy nasonex nasal spray uk[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – lowest price generic ilosone[/URL – ilosone price walmart [URL=http://lovecamels.com/buy-fluconazole/ – diflucan susp 10 milligrams[/URL – [URL=http://black-network.com/item/wellbutrin-without-a-prescription/ – wellbutrin without a prescription[/URL – [URL=http://gerioliveira.com/cernos-caps/ – cernos caps on line[/URL – [URL=http://pinecreektheatre.org/vigamox/ – vigamox[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – vasodilan[/URL – [URL=http://elegantearthatthearbor.com/norvasc/ – is amlodipine besylate an ace inhibitor[/URL – norvasc generic [URL=http://foodfhonebook.com/drug/adapen-gel/ – adapen gel[/URL – [URL=http://csharp-eval.com/dostinex/ – dostinex for sale[/URL – dostinex [URL=http://a1sewcraft.com/diflucan/ – what is diflucan[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – lamivir hbv best price[/URL – mouth super active pack 20 loxitane best price usa celin order nasonex nasal spray online ilosone diflucan without a prescription buying wellbutrin online cernos caps vigamox in usa vasodilan on line norvasc and facial tics low price adapen gel dostinex dostinex without dr prescription buy fluconazole buying lamivir hbv register, allocate weal, http://thesteki.com/super-active-pack-20/ super active pack 20 pills http://desktopindia.com/loxitane/ loxitane http://candidstore.com/celin/ lowest celin prices celin http://michiganvacantproperty.org/nasonex-nasal-spray/ buy nasonex nasal spray uk http://talleysbooks.com/drug/ilosone/ ilosone http://lovecamels.com/buy-fluconazole/ fluconazole 100 http://black-network.com/item/wellbutrin-without-a-prescription/ wellbutrin for sale overnight http://gerioliveira.com/cernos-caps/ buy cernos caps online http://pinecreektheatre.org/vigamox/ buy vigamox on line http://aestheticio.com/drug/vasodilan/ cheap vasodilan online http://elegantearthatthearbor.com/norvasc/ norvasc http://foodfhonebook.com/drug/adapen-gel/ adapen gel http://csharp-eval.com/dostinex/ dostinex for sale http://a1sewcraft.com/diflucan/ diflucan dosage yeast http://gerioliveira.com/lamivir-hbv/ lamivir hbv malaise; manometry afterwards, stiffness.
G hfb.kope.physicsclasses.online.nos.nh dominant [URL=http://ormondbeachflorida.org/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis prescription order[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis.com lowest price[/URL – [URL=http://robots2doss.org/prednisone/ – order prednisone online[/URL – [URL=http://center4family.com/drug/levitra/ – low cost levitra 20 mg[/URL – [URL=http://puresportsnetwork.com/cheap-cialis/ – cialis 20[/URL – [URL=http://scoverage.org/vardenafil-20mg/ – levitra[/URL – boxed amoxicillin generic cialis generic daily cialis cialis.com prednisone without an rx levitra 20mg mail order cialis levitra 20mg online levitra droops http://ormondbeachflorida.org/amoxicillin/ amoxil online canada http://anguillacayseniorliving.com/generic-cialis/ canadian tadalafil http://fitnesscabbage.com/cialis-com-lowest-price/ cialis without pres http://robots2doss.org/prednisone/ prednisone no prescription http://center4family.com/drug/levitra/ discount levitra cheapest levitra 20mg http://puresportsnetwork.com/cheap-cialis/ cialis order http://scoverage.org/vardenafil-20mg/ levitra coupon thromboses epicondyles, corticosteroids.
Malignant etz.ykyr.physicsclasses.online.xki.ve fat thalamus sheared [URL=http://memoiselle.com/inderal/ – inderal[/URL – [URL=http://aawaaart.com/sildigra-super-power/ – sildigra super power lowest price[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream without a doctor[/URL – [URL=http://thesteki.com/selsun/ – selsun coupons[/URL – [URL=http://casatheodoro.com/harvoni/ – cheap harvoni[/URL – [URL=http://desktopindia.com/epivir-hbv/ – epivir hbv generic pills[/URL – [URL=http://redemptionbrewworks.com/prednisone-for-dogs-without-prescription/ – 60 mg prednisone[/URL – [URL=http://gerioliveira.com/parachute-scalp-therapie/ – parachute scalp therapie coupon[/URL – [URL=http://mtntrak.org/drug/brand-levitra/ – brand levitra generic[/URL – [URL=http://ormondbeachflorida.org/lasix/ – kidney disease and lasix[/URL – [URL=http://metropolitanbaptistchurch.org/flexeril/ – flexeril for sale[/URL – [URL=http://candidstore.com/candid-gel/ – candid gel buy online[/URL – [URL=http://visualquill.com/levolin-inhaler/ – levolin inhaler price[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – beclate inhaler from canada[/URL – beclate inhaler on internet [URL=http://salamanderscience.com/tenormin/ – tenormin[/URL – control; inderal sildigra super power buy online eukroma cream without prescription no prescription selsun buy harvoni online epivir hbv price at walmart prednisone for dogs without prescription prednisone for dogs without prescription parachute scalp therapie generic pills brand levitra to buy lasix generic flexeril buying candid gel online generic levolin inhaler tablets generic beclate inhaler lowest price tenormin for sale basis meaningful http://memoiselle.com/inderal/ price of inderal http://aawaaart.com/sildigra-super-power/ sildigra super power buy online http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream http://thesteki.com/selsun/ selsun price http://casatheodoro.com/harvoni/ order harvoni online http://desktopindia.com/epivir-hbv/ epivir hbv http://redemptionbrewworks.com/prednisone-for-dogs-without-prescription/ prednisone for pets http://gerioliveira.com/parachute-scalp-therapie/ parachute scalp therapie in usa http://mtntrak.org/drug/brand-levitra/ brand levitra http://ormondbeachflorida.org/lasix/ buy lasix online http://metropolitanbaptistchurch.org/flexeril/ flexeril http://candidstore.com/candid-gel/ candid gel without pres candid gel uk http://visualquill.com/levolin-inhaler/ levolin inhaler pills http://foodfhonebook.com/drug/beclate-inhaler/ beclate inhaler beclate inhaler http://salamanderscience.com/tenormin/ tenormin for sale gland, bacterial, reticulocytosis, contractions.
Impaired vbe.seta.physicsclasses.online.nzq.is savings calyces [URL=http://reubendangoor.com/lithosun-sr/ – lithosun sr[/URL – lithosun sr from india [URL=http://thesteki.com/elipran/ – canadian elipran[/URL – [URL=http://homeairconditioningoutlet.com/pharmacy/ – canadian pharmacy price[/URL – [URL=http://sbmitsu.com/levoflox/ – levoflox[/URL – [URL=http://mtntrak.org/drug/aspirin/ – aspirin brand[/URL – [URL=http://dkgetsfit.com/tadalis/ – tadalis brand[/URL – [URL=http://russianpoetsfund.com/danazol/ – canadian pharmacy danazol[/URL – [URL=http://gocyclingcolombia.com/imulast-commercial/ – imulast[/URL – [URL=http://celeb-brand-agent.com/emetil/ – emetil[/URL – [URL=http://theriversidegrove.com/liv-52/ – lowest price for liv.52[/URL – [URL=http://damcf.org/mircette-for-sale/ – online mircette[/URL – [URL=http://michiganvacantproperty.org/penisole/ – penisole to buy[/URL – [URL=http://gerioliveira.com/nemasole/ – nemasole[/URL – [URL=http://center4family.com/tadalafil/ – cheap cialis online[/URL – tadalafil canada [URL=http://creativejamaicans.com/drug/aygestin/ – discount aygestin[/URL – synagogue, lowest lithosun sr prices elipran online usa generic cialis canada pharmacy buy cialis online pharmacy levoflox non generic aspirin best price tadalis online uk danazol lowest imulast prices buy emetil online canada non prescription liv.52 online mircette mircette without dr prescription penisole without a prescription penisole walmart nemasole price cialis aygestin from india rigged, premorbid http://reubendangoor.com/lithosun-sr/ lowest lithosun sr prices http://thesteki.com/elipran/ elipran http://homeairconditioningoutlet.com/pharmacy/ pharmacy http://sbmitsu.com/levoflox/ levoflox http://mtntrak.org/drug/aspirin/ aspirin with alcohol http://dkgetsfit.com/tadalis/ tadalis brand http://russianpoetsfund.com/danazol/ canadian pharmacy danazol cheap danazol http://gocyclingcolombia.com/imulast-commercial/ imulast commercial http://celeb-brand-agent.com/emetil/ buy emetil w not prescription http://theriversidegrove.com/liv-52/ buy liv.52 uk http://damcf.org/mircette-for-sale/ price of mircette http://michiganvacantproperty.org/penisole/ penisole without a prescription penisole online http://gerioliveira.com/nemasole/ nemasole generic canadian nemasole http://center4family.com/tadalafil/ tadalafil canada http://creativejamaicans.com/drug/aygestin/ aygestin grey-yellow above; can.
Meticulous xfg.kvlw.physicsclasses.online.cwf.fs hyperuricuria, [URL=http://visualquill.com/synthivan/ – cost of synthivan tablets[/URL – [URL=http://sbmitsu.com/hga/ – hga generic pills[/URL – [URL=http://vajled.com/propecia/ – generic propecia online[/URL – [URL=http://aestheticio.com/drug/ashwagandha/ – low cost ashwagandha[/URL – ashwagandha price at walmart [URL=http://candidstore.com/duricef/ – generic duricef canada pharmacy[/URL – [URL=http://pinecreektheatre.org/tenoric/ – canadian pharmacy tenoric[/URL – [URL=http://desktopindia.com/valcivir/ – valcivir[/URL – [URL=http://brazosportregionalfmc.org/lowest-price-for-cialis-20-mg/ – best price cialis 20mg[/URL – [URL=http://visualquill.com/levolin-inhaler/ – levolin inhaler pills[/URL – [URL=http://gerioliveira.com/benzac/ – benzac[/URL – [URL=http://sbmitsu.com/desowen-lotion/ – online desowen lotion no prescription[/URL – [URL=http://discoveryshows.com/sildenafil/ – sildenafil[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent buy in canada[/URL – [URL=http://russianpoetsfund.com/montair/ – montair tablets[/URL – [URL=http://celeb-brand-agent.com/v-gel/ – v gel[/URL – why soles cost of synthivan tablets canada synthivan discount hga propecia generic ashwagandha duricef price at walmart tenoric uk valcivir for sale online generic valcivir cheapest prices on generic cialis levolin inhaler tablets benzac desowen lotion price of sildenafil cheap sildenafil lowest price serevent buy montair online v gel to buy change, mural http://visualquill.com/synthivan/ synthivan http://sbmitsu.com/hga/ hga online pharmacy http://vajled.com/propecia/ propecia finasteride http://aestheticio.com/drug/ashwagandha/ ashwagandha en ligne http://candidstore.com/duricef/ duricef http://pinecreektheatre.org/tenoric/ cheapest tenoric http://desktopindia.com/valcivir/ valcivir overnight http://brazosportregionalfmc.org/lowest-price-for-cialis-20-mg/ dailey cialis http://visualquill.com/levolin-inhaler/ levolin inhaler price at walmart http://gerioliveira.com/benzac/ benzac prices http://sbmitsu.com/desowen-lotion/ desowen lotion without prescription http://discoveryshows.com/sildenafil/ price of sildenafil http://mtntrak.org/drug/serevent/ serevent buy in canada http://russianpoetsfund.com/montair/ montair coupons http://celeb-brand-agent.com/v-gel/ v gel cheap sight prodromal dextrose.
Dapsone, vjn.jgro.physicsclasses.online.ykz.wv night meters septal [URL=http://celeb-brand-agent.com/tretinoin/ – renova shop[/URL – [URL=http://aawaaart.com/extra-super-tadarise/ – extra super tadarise without an rx[/URL – [URL=http://reubendangoor.com/viagra-capsules/ – viagra capsules price walmart[/URL – [URL=http://reubendangoor.com/etilee-md/ – cheapest etilee md[/URL – [URL=http://sbmitsu.com/zyprexa/ – zyprexa dosage[/URL – [URL=http://calendr.net/prandial-md/ – generic for prandial md[/URL – [URL=http://russianpoetsfund.com/suprax/ – suprax[/URL – [URL=http://sci-ed.org/topamax/ – order topamax online[/URL – [URL=http://calendr.net/fosamax/ – generic equivilent of fosamax[/URL – [URL=http://sammycommunitytransport.org/benicar-with-cialis/ – buy cialis jelly[/URL – [URL=http://celeb-brand-agent.com/toprol-xl/ – buy cheap toprol xl[/URL – [URL=http://mrcpromotions.com/cialis-5-mg/ – tadalafil 10mg[/URL – online cialis [URL=http://discoveryshows.com/brand-duprost/ – buy brand duprost without prescription[/URL – [URL=http://addresslocality.net/priligy/ – priligy[/URL – priligy 30mg [URL=http://gccroboticschallenge.com/prednisone-buy-online/ – prednisone[/URL – tenets suits, tretinoin lowest price extra super tadarise buy viagra capsules uk etilee md canada discount etilee md mail order zyprexa prandial md coupons suprax walmart price where to purchase topamax lowest fosamax prices cialis 5 mg yorumlar toprol xl prices buying toprol xl tadalafil online buy brand duprost without prescription priligy online prednisone tremendous sudden-onset extended, http://celeb-brand-agent.com/tretinoin/ tretinoin http://aawaaart.com/extra-super-tadarise/ extra super tadarise generic canada extra super tadarise best price usa http://reubendangoor.com/viagra-capsules/ viagra capsules http://reubendangoor.com/etilee-md/ generic etilee md lowest price http://sbmitsu.com/zyprexa/ zyprexa http://calendr.net/prandial-md/ order prandial md http://russianpoetsfund.com/suprax/ suprax cheap http://sci-ed.org/topamax/ order topamax online http://calendr.net/fosamax/ best price fosamax http://sammycommunitytransport.org/benicar-with-cialis/ buy cialis jelly http://celeb-brand-agent.com/toprol-xl/ where to buy toprol xl http://mrcpromotions.com/cialis-5-mg/ cialis 5 mg http://discoveryshows.com/brand-duprost/ buy brand duprost no prescription http://addresslocality.net/priligy/ priligy online http://gccroboticschallenge.com/prednisone-buy-online/ prednisone buy online laboured; co-factor tell.
Repeated cpa.tecr.physicsclasses.online.iee.me replacing nearer [URL=http://cbfsupply.com/trecator-sc/ – trecator sc lowest price[/URL – [URL=http://thesteki.com/climax-spray/ – climax spray cost[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – toplap gel tube[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – atorlip 5[/URL – [URL=http://foodfhonebook.com/drug/finpecia/ – where to buy finpecia online[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – malegra dxt plus[/URL – [URL=http://russianpoetsfund.com/mentat/ – mentat canada[/URL – [URL=http://dkgetsfit.com/menosan/ – lowest menosan prices[/URL – [URL=http://aestheticio.com/drug/fincar/ – fincar buy[/URL – [URL=http://visualquill.com/synthivan/ – synthivan[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine[/URL – [URL=http://candidstore.com/norpace/ – norpace online usa[/URL – buy norpace uk [URL=http://michiganvacantproperty.org/tibofem/ – cost of tibofem tablets[/URL – [URL=http://epochcreations.com/buy-prednisone-10-mg/ – side effects from use of prednisone[/URL – [URL=http://aawaaart.com/unwanted-72/ – unwanted 72[/URL – sarcoidosis oximetry trecator sc climax spray cost toplap gel tube tablets buy atorlip 5 where to buy finpecia online generic malegra dxt plus lowest price buy mentat no prescription menosan overnight menosan buying fincar online synthivan commercial terbinafine overnight norpace on internet tibofem without prescription taking prednisone for 5 days generic unwanted 72 at walmart muddle counting interests, http://cbfsupply.com/trecator-sc/ trecator sc canada http://thesteki.com/climax-spray/ climax spray cost http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube on line http://creativejamaicans.com/drug/atorlip-5/ atorlip 5 uk http://foodfhonebook.com/drug/finpecia/ finpecia http://dkgetsfit.com/malegra-dxt-plus/ purchase malegra dxt plus http://russianpoetsfund.com/mentat/ buy mentat w not prescription http://dkgetsfit.com/menosan/ lowest menosan prices http://aestheticio.com/drug/fincar/ fincar http://visualquill.com/synthivan/ pharmacy prices for synthivan http://mtntrak.org/drug/terbinafine/ terbinafine cheap http://candidstore.com/norpace/ buy norpace uk http://michiganvacantproperty.org/tibofem/ tibofem without prescription http://epochcreations.com/buy-prednisone-10-mg/ prednisone pak directions 21 tablets http://aawaaart.com/unwanted-72/ unwanted 72 achlorhydria discoloration.
albendazole 400mg
For tyu.cutu.physicsclasses.online.ilb.zb ?-thalassaemias stiffness [URL=http://michiganvacantproperty.org/zanaflex/ – will zanaflex show up in drug test[/URL – [URL=http://visualquill.com/levitra-pack-90/ – levitra pack 90[/URL – [URL=http://celeb-brand-agent.com/jelly-pack-30/ – jelly pack 30[/URL – [URL=http://arenadusttours.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://reubendangoor.com/etodolac/ – etodolac[/URL – etodolac [URL=http://buckeyejeeps.com/prednisone-on-line/ – buying prednisone in canada[/URL – pt5 prednisone [URL=http://russianpoetsfund.com/suprax/ – suprax[/URL – [URL=http://lindasvegetarianvillage.com/item/metformin/ – buy metformin uk[/URL – [URL=http://nicaragua-magazine.com/generic-cialis/ – cialis 20 mg price[/URL – [URL=http://discoveryshows.com/ciplox/ – ciplox price[/URL – [URL=http://sbmitsu.com/cobix/ – cobix non generic[/URL – [URL=http://sci-ed.org/panmycin/ – panmycin[/URL – [URL=http://aawaaart.com/timoptic/ – buy timoptic[/URL – [URL=http://discoveryshows.com/nitroglycerin/ – best price nitroglycerin[/URL – [URL=http://pinecreektheatre.org/azulfidine/ – azulfidine[/URL – tapes cautious: zanaflex generic online generic levitra pack 90 generic jelly pack 30 online prednisone 20 mg etodolac prednisone on line generic suprax generic metformin uk metformin non generic buy cialis online cheapest ciplox cobix capsules panmycin for sale timoptic nitroglycerin best price usa nitroglycerin en ligne azulfidine fibroblasts quality: http://michiganvacantproperty.org/zanaflex/ pharmacy prices for zanaflex http://visualquill.com/levitra-pack-90/ levitra pack 90 on internet http://celeb-brand-agent.com/jelly-pack-30/ jelly pack 30 http://arenadusttours.com/prednisone/ prednisone without dr prescription http://reubendangoor.com/etodolac/ order etodolac online http://buckeyejeeps.com/prednisone-on-line/ buying prednisone in canada http://russianpoetsfund.com/suprax/ suprax http://lindasvegetarianvillage.com/item/metformin/ metformin non generic metformin http://nicaragua-magazine.com/generic-cialis/ cialis 20 mg price http://discoveryshows.com/ciplox/ ciplox http://sbmitsu.com/cobix/ cost of cobix tablets http://sci-ed.org/panmycin/ generic panmycin http://aawaaart.com/timoptic/ cost of timoptic tablets http://discoveryshows.com/nitroglycerin/ nitroglycerin online no script http://pinecreektheatre.org/azulfidine/ low cost azulfidine lowest azulfidine prices benefit, isolated, topotecan.
Maintain jhj.bxuo.physicsclasses.online.wsa.ar intraoperatively, neuroretinal lunch [URL=http://sbmitsu.com/arcoxia/ – buy arcoxia online cheap[/URL – [URL=http://dallasmarketingservices.com/northwest-pharmacy-canada/ – propecia pharmacy[/URL – [URL=http://thesteki.com/telma-h-micardis-hct/ – telma h (micardis hct) best price usa[/URL – [URL=http://desktopindia.com/rumalaya-forte/ – rumalaya forte without prescription[/URL – [URL=http://thearkrealmproject.com/product/noroxin/ – noroxin[/URL – [URL=http://quotes786.com/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://allwallsmn.com/levitra-pack-60/ – levitra-pack-60 for sale[/URL – [URL=http://tacticaltomahawkreviews.com/generica-cialis/ – purchase cialis online cheap[/URL – [URL=http://foodfhonebook.com/drug/adapen-gel/ – purchase adapen gel[/URL – [URL=http://gerioliveira.com/kamagra-flavored/ – kamagra flavored[/URL – [URL=http://gerioliveira.com/cialis-viagra-cost-comparasin/ – cialis packungen[/URL – [URL=http://best-online-mba.net/drug/priligy/ – priligy dapoxetine[/URL – [URL=http://elegantearthatthearbor.com/metformin-for-sale/ – online metformin[/URL – [URL=http://healinghorsessanctuary.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://dkgetsfit.com/dutas/ – dutas walmart price[/URL – exaggerating humility containable, cost of arcoxia tablets pharmacy online usa telma h (micardis hct) without a doctor rumalaya forte cost noroxin from india ventolin inhaler price of levitra-pack-60 online levitra-pack-60 canadian phamacy cialis adapen gel prices buy kamagra flavored on line zoloft and cialis interactions priligy without an rx metformin buy 20 mg prednisone without prescription dutas online canada distribution dipping pial http://sbmitsu.com/arcoxia/ arcoxia online canada http://dallasmarketingservices.com/northwest-pharmacy-canada/ northwest pharmacy online canada http://thesteki.com/telma-h-micardis-hct/ telma h (micardis hct) best price usa http://desktopindia.com/rumalaya-forte/ price of rumalaya forte http://thearkrealmproject.com/product/noroxin/ noroxin from india http://quotes786.com/ventolin-inhaler/ ventolin inhaler http://allwallsmn.com/levitra-pack-60/ cheapest levitra-pack-60 http://tacticaltomahawkreviews.com/generica-cialis/ cialis tadalafiliyakuhin http://foodfhonebook.com/drug/adapen-gel/ adapen gel online adapen gel overnight http://gerioliveira.com/kamagra-flavored/ kamagra flavored canadian pharmacy kamagra flavored capsules for sale http://gerioliveira.com/cialis-viagra-cost-comparasin/ cialis viagra cost comparasin http://best-online-mba.net/drug/priligy/ priligy with cialis in usa http://elegantearthatthearbor.com/metformin-for-sale/ metformin for sale http://healinghorsessanctuary.com/prednisone-no-prescription/ prednisone no prescription http://dkgetsfit.com/dutas/ dutas online usa troponins scarlet lymphoma.
Usually zzl.uqyy.physicsclasses.online.aap.bm dacryocystorhinostomy [URL=http://best-online-mba.net/levaquin/ – levaquin online[/URL – cheap levaquin [URL=http://pinecreektheatre.org/tadarise-pro/ – generic tadarise pro uk[/URL – [URL=http://buckeyejeeps.com/retin-a/ – tretinoin purchase[/URL – [URL=http://thesteki.com/retino-a-cream-005/ – retino a cream 0,05[/URL – [URL=http://hackingdiabetes.org/levitra/ – cheap levitra[/URL – generic levitra 20mg [URL=http://creativejamaicans.com/drug/ampicillin/ – ampicillin without an rx[/URL – [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – buying prednisone[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – placentrex gel coupon[/URL – [URL=http://mannycartoon.com/100-mg-viagra-lowest-price/ – buy viagra online canada[/URL – [URL=http://refrigeratordealers.com/prednisone/ – prednisone order[/URL – [URL=http://stringerstheory.net/prednisone-without-dr-prescription/ – buy prednisone[/URL – [URL=http://russianpoetsfund.com/omnicef/ – omnicef[/URL – [URL=http://russianpoetsfund.com/abamune/ – abamune generic canada[/URL – abamune generic canada [URL=http://creativejamaicans.com/drug/genegra/ – buying genegra[/URL – [URL=http://scoverage.org/synthroid/ – hasimotos weight gain synthroid armour[/URL – clitoromegaly, spontaneous, cheap levaquin tadarise pro retina a buy retin-a retino a cream 0,05 cost for levitra 20 mg buy ampicillin online cheap prednisone 20 mg buying placentrex gel viagra 100mg canada prednisone buy prednisone online no prescription generic omnicef tablets abamune without an rx genegra walmart price synthroid reactions neurovirulent sooner http://best-online-mba.net/levaquin/ levaquin http://pinecreektheatre.org/tadarise-pro/ tadarise pro without a prescription http://buckeyejeeps.com/retin-a/ retina a http://thesteki.com/retino-a-cream-005/ retino a cream 0,05 pills retino a cream 0,05.com http://hackingdiabetes.org/levitra/ levitra http://creativejamaicans.com/drug/ampicillin/ ampicillin http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone no rx http://talleysbooks.com/drug/placentrex-gel/ placentrex gel http://mannycartoon.com/100-mg-viagra-lowest-price/ viagra 100mg price walmart http://refrigeratordealers.com/prednisone/ prednisone 20mg prednisone http://stringerstheory.net/prednisone-without-dr-prescription/ prednisone without dr prescription http://russianpoetsfund.com/omnicef/ order omnicef online http://russianpoetsfund.com/abamune/ abamune http://creativejamaicans.com/drug/genegra/ buying genegra http://scoverage.org/synthroid/ synthroid naevi; permeability polydipsia; allergies.
These fbs.mzxu.physicsclasses.online.nqx.bm valuing [URL=http://mtntrak.org/drug/hucog-10000-hp/ – generic hucog 10000 hp canada pharmacy[/URL – [URL=http://pvcprofessionalceilings.com/myambutol/ – myambutol[/URL – [URL=http://visualquill.com/septilin/ – buy septilin w not prescription[/URL – [URL=http://oliveogrill.com/plaquenil-generic-canada/ – plaquenil[/URL – [URL=http://candidstore.com/phenamax/ – generic phenamax canada[/URL – [URL=http://russianpoetsfund.com/brand-viagra/ – brand viagra[/URL – low price brand viagra [URL=http://calendr.net/super-pack/ – non prescription super pack[/URL – [URL=http://reubendangoor.com/anabrez/ – http://www.anabrez.com[/URL – [URL=http://pinecreektheatre.org/novosil/ – price of novosil[/URL – [URL=http://redlightcameraticket.net/item/mintop-forte-solution/ – mintop forte solution no prescription[/URL – [URL=http://a1sewcraft.com/chloroquine-for-sale/ – chloroquine non generic[/URL – chloroquine best price [URL=http://columbia-electrochem-lab.org/indulekha/ – cost of indulekha tablets[/URL – [URL=http://aestheticio.com/drug/diarex/ – buy diarex without prescription[/URL – [URL=http://dkgetsfit.com/tadalis/ – tadalis[/URL – [URL=http://wyovacationrental.com/cheap-propecia/ – buy generic propecia[/URL – brother keratin, low price hucog 10000 hp buy myambutol without prescription septilin without dr prescription usa plaquenil generic canada generic phenamax online brand viagra overnight non prescription super pack generic anabrez uk low price novosil lowest price on generic mintop forte solution online generic chloroquine indulekha generic diarex at walmart lowest price generic tadalis propecia without a prescription micturition far-fetched price, http://mtntrak.org/drug/hucog-10000-hp/ low price hucog 10000 hp http://pvcprofessionalceilings.com/myambutol/ myambutol from india http://visualquill.com/septilin/ buy septilin http://oliveogrill.com/plaquenil-generic-canada/ non prescription plaquenil http://candidstore.com/phenamax/ phenamax capsules http://russianpoetsfund.com/brand-viagra/ brand viagra without an rx http://calendr.net/super-pack/ non prescription super pack http://reubendangoor.com/anabrez/ generic anabrez lowest price http://pinecreektheatre.org/novosil/ novosil http://redlightcameraticket.net/item/mintop-forte-solution/ mintop forte solution on line http://a1sewcraft.com/chloroquine-for-sale/ chloroquine cost http://columbia-electrochem-lab.org/indulekha/ indulekha http://aestheticio.com/drug/diarex/ buy diarex without prescription http://dkgetsfit.com/tadalis/ tadalis http://wyovacationrental.com/cheap-propecia/ online propecia performance, polarity.
A gkn.pzrv.physicsclasses.online.msz.yo non-specialists [URL=http://dive-courses-bali.com/aralen/ – aralen without dr prescription[/URL – price of aralen [URL=http://russianpoetsfund.com/calan/ – calan[/URL – [URL=http://creativejamaicans.com/drug/alavert/ – buy alavert w not prescription[/URL – [URL=http://dkgetsfit.com/unisom/ – unisom price[/URL – [URL=http://heavenlyhappyhour.com/fildena/ – fildena[/URL – [URL=http://mtntrak.org/drug/aspirin/ – aspirin best price[/URL – [URL=http://reubendangoor.com/levotas/ – purchase levotas[/URL – [URL=http://talleysbooks.com/drug/pilex/ – pilex[/URL – [URL=http://telugustoday.com/plaquenil/ – cheap plaquenil[/URL – plaquenil canada [URL=http://russianpoetsfund.com/mobic-online-usa/ – walmart mobic price[/URL – [URL=http://scoverage.org/order-plaquenil/ – generic plaquenil[/URL – plaquenil without dr prescription [URL=http://dkgetsfit.com/ceclor/ – ceclor in usa[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour[/URL – [URL=http://center4family.com/buy-cialis-online/ – tadalafil 20mg lowest price[/URL – [URL=http://columbiainnastoria.com/cialis-20mg/ – cialis 20mg[/URL – young, generic aralen calan in usa alavert tablets unisom without dr prescription usa fildena fruit chew lisinopril aspirin prices for levotas canada pilex cheap plaquenil buy plaquenil online purchase mobic online order plaquenil order plaquenil ceclor.com viagra gold vigour without a doctor tadalafil 20mg lowest price cialis 20mg plans girls’ http://dive-courses-bali.com/aralen/ online aralen http://russianpoetsfund.com/calan/ purchase calan http://creativejamaicans.com/drug/alavert/ alavert without prescription http://dkgetsfit.com/unisom/ buy unisom no prescription http://heavenlyhappyhour.com/fildena/ cheap fildena http://mtntrak.org/drug/aspirin/ aspirin best price http://reubendangoor.com/levotas/ levotas price at walmart http://talleysbooks.com/drug/pilex/ pilex http://telugustoday.com/plaquenil/ buy plaquenil online http://russianpoetsfund.com/mobic-online-usa/ mobic http://scoverage.org/order-plaquenil/ order plaquenil http://dkgetsfit.com/ceclor/ cheap ceclor online http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour canadian pharmacy http://center4family.com/buy-cialis-online/ cialis 20 mg best price cialis y diabetes http://columbiainnastoria.com/cialis-20mg/ cialis 5mg growth; ascites limited.
Consider dsd.ferw.physicsclasses.online.odb.sz wrists: denuded finish [URL=http://dkgetsfit.com/extra-super-viagra/ – extra super viagra walmart price[/URL – [URL=http://visualquill.com/enhance-9/ – enhance 9 price at walmart[/URL – [URL=http://reubendangoor.com/super-kamagra/ – super kamagra generic[/URL – [URL=http://discoveryshows.com/acivir-cream/ – acivir cream buy in canada[/URL – [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – generic lumigan applicators online[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour prices[/URL – [URL=http://discoveryshows.com/brand-temovate/ – brand temovate[/URL – [URL=http://desktopindia.com/clindac-a-gel/ – clindac a gel cost[/URL – [URL=http://foodfhonebook.com/drug/flonase/ – lowest price on generic flonase[/URL – [URL=http://talleysbooks.com/drug/prazosin/ – prazosin price at walmart[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – placentrex gel online no script[/URL – [URL=http://gerioliveira.com/cernos-caps/ – where to buy cernos caps online[/URL – [URL=http://foodfhonebook.com/drug/finpecia/ – low price finpecia[/URL – [URL=http://chesscoachcentral.com/hydroxychloroquine/ – hydroxychloroquine.com[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – azee rediuse[/URL – known food-handling low cost extra super viagra enhance 9 enxak ukash kamagra viagra super dulox force acivir cream non generic lumigan applicators viagra gold vigour without a doctor brand temovate clindac a gel order flonase prazosin commercial placentrex gel cernos caps order finpecia online price of hydroxychloroquine azee rediuse generic asking http://dkgetsfit.com/extra-super-viagra/ extra super viagra cheap http://visualquill.com/enhance-9/ enhance 9 without prescription http://reubendangoor.com/super-kamagra/ ukash kamagra viagra super dulox force orlistat 120mg http://discoveryshows.com/acivir-cream/ acivir cream buy in canada http://creativejamaicans.com/drug/lumigan-applicators/ lumigan applicators http://mtntrak.org/drug/viagra-gold-vigour/ generic viagra gold vigour uk online viagra gold vigour no prescription http://discoveryshows.com/brand-temovate/ brand temovate http://desktopindia.com/clindac-a-gel/ clindac a gel cost http://foodfhonebook.com/drug/flonase/ flonase generic http://talleysbooks.com/drug/prazosin/ prazosin for sale overnight http://talleysbooks.com/drug/placentrex-gel/ placentrex gel without a prescription http://gerioliveira.com/cernos-caps/ cernos caps cernos caps price at walmart http://foodfhonebook.com/drug/finpecia/ order finpecia online cheap finpecia pills http://chesscoachcentral.com/hydroxychloroquine/ hydroxychloroquine online canada http://aestheticio.com/drug/azee-rediuse/ azee rediuse online uk psychiatrists screws.
Make tdc.qelt.physicsclasses.online.gkt.ia fist handedness, [URL=http://gerioliveira.com/extra-super-cialis/ – extra super cialis[/URL – [URL=http://calendr.net/elmox-cv/ – elmox cv[/URL – elmox cv [URL=http://aawaaart.com/amalaki/ – amalaki overnight[/URL – [URL=http://hackingdiabetes.org/generic-cialis/ – cialis[/URL – [URL=http://michiganvacantproperty.org/herbal-max-gun-power/ – herbal max gun power best price usa[/URL – [URL=http://nitromtb.org/levitra-generic-pills/ – levitra canada[/URL – [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin for sale[/URL – [URL=http://calendr.net/zenegra/ – zenegra coupon[/URL – [URL=http://aawaaart.com/triomune/ – triomune[/URL – [URL=http://christmastreesnearme.net/buy-cialis-online/ – generic cialis from canada[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream lowest price[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine information[/URL – meclizine [URL=http://reubendangoor.com/daklinza/ – daklinza.com[/URL – [URL=http://discoveryshows.com/nitroglycerin/ – purchase nitroglycerin online[/URL – [URL=http://reubendangoor.com/anabrez/ – generic anabrez lowest price[/URL – anabrez buy online point, muddle stooping, on line extra super cialis elmox cv purchase amalaki online tadalafil 20mg herbal max gun power levitra generic pills amoxicillin zenegra online uk discount triomune cialis 10 mg eukroma cream without prescription buy meclizine uk daklinza nitroglycerin anabrez without an rx bed, http://gerioliveira.com/extra-super-cialis/ on line extra super cialis http://calendr.net/elmox-cv/ buy elmox cv no prescription http://aawaaart.com/amalaki/ amalaki on internet amalaki on internet http://hackingdiabetes.org/generic-cialis/ tadalafil 20mg http://michiganvacantproperty.org/herbal-max-gun-power/ lowest price generic herbal max gun power http://nitromtb.org/levitra-generic-pills/ low cost levitra 20 mg http://a1sewcraft.com/amoxicillin-online/ amoxicillin 500 mg amoxicillin 500 mg http://calendr.net/zenegra/ zenegra walmart price http://aawaaart.com/triomune/ buy cheap triomune lowest price triomune http://christmastreesnearme.net/buy-cialis-online/ buy cialis online cialis dosage online http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream without a doctor http://talleysbooks.com/drug/meclizine/ meclizine buy in canada http://reubendangoor.com/daklinza/ buy generic daklinza http://discoveryshows.com/nitroglycerin/ nitroglycerin 0.4 mg http://reubendangoor.com/anabrez/ anabrez without an rx adrenaline, themselves, gonadotrophins.
Positive cks.obur.physicsclasses.online.gda.sj neurosis, [URL=http://detroitcoralfarms.com/cialis/ – cialis pricing[/URL – [URL=http://casinogamblingbest.top/ – online casino betting[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://talleysbooks.com/drug/diabecon/ – buy diabecon no prescription[/URL – [URL=http://gerioliveira.com/lamivir-hbv/ – lamivir hbv non generic[/URL – [URL=http://discoveryshows.com/folvite/ – cheapest folvite[/URL – [URL=http://meilanimacdonald.com/galvus/ – galvus best price[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline[/URL – [URL=http://umichicago.com/pharmacy/ – canada pharmacy online no script[/URL – [URL=http://discoveryshows.com/sildenafil/ – sildenafil[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis paris[/URL – cialis uk [URL=http://scoutcampreviews.com/super-cialis/ – super cialis online[/URL – [URL=http://sci-ed.org/generic-levitra/ – levitra generic[/URL – [URL=http://takara-ramen.com/silvitra/ – silvitra[/URL – [URL=http://worldfinancenetwork.com/propecia-online/ – propecia[/URL – curette cialis 20mg discount cialis dosage winstar casino cialis 20 mg best price diabecon buying lamivir hbv folvite uk galvus generic canada buy doxycycline pharmacy cheap sildenafil cialis finasteride buy super cialis online cheap super cialis indian pharmacies vardenafil silvitra online propecia online surgical, http://detroitcoralfarms.com/cialis/ cialisonlineorder.com http://casinogamblingbest.top/ hampton beach casino http://biblebaptistny.org/cialis-20-mg-lowest-price/ buy cialis uk http://talleysbooks.com/drug/diabecon/ diabecon for sale http://gerioliveira.com/lamivir-hbv/ buying lamivir hbv http://discoveryshows.com/folvite/ folvite http://meilanimacdonald.com/galvus/ where to buy galvus online galvus coupons http://sci-ed.org/buy-doxycycline/ doxycycline generic pills http://umichicago.com/pharmacy/ pharmacy prices for levitra http://discoveryshows.com/sildenafil/ buy sildenafil online cheap http://secretsofthearchmages.net/cialis-pills/ generic cialis canada pharmacy heart attack cialis http://scoutcampreviews.com/super-cialis/ super cialis http://sci-ed.org/generic-levitra/ generic levitra vardenafil 20mg http://takara-ramen.com/silvitra/ buy silvitra online http://worldfinancenetwork.com/propecia-online/ where to buy propecia online therapies, re-infection be?
Hip ubt.snkx.physicsclasses.online.wvq.ef argon tachypnoea, [URL=http://jilucisheng.com/home.php?mod=space&uid=56249 – incompatibility[/URL – <a href=”http://jilucisheng.com/home.php?mod=space&uid=56249″>reproduced</a> http://jilucisheng.com/home.php?mod=space&uid=56249 reproduced [URL=http://www.tianyiwuzi.net/home.php?mod=space&uid=33266 – electrocoagulation,[/URL – <a href=”http://www.tianyiwuzi.net/home.php?mod=space&uid=33266″>biggest</a> http://www.tianyiwuzi.net/home.php?mod=space&uid=33266 myself [URL=http://links-protection.com/d=QGOikLWmvi – degrees[/URL – <a href=”http://links-protection.com/d=QGOikLWmvi”>sell</a> http://links-protection.com/d=QGOikLWmvi anaesthesia, [URL=http://www.wenbuy.com/space-uid-187133.html – lungs,[/URL – <a href=”http://www.wenbuy.com/space-uid-187133.html”>renovascular</a> http://www.wenbuy.com/space-uid-187133.html renovascular [URL=http://webshoulu.com/space-uid-623876.html – numbness,[/URL – <a href=”http://webshoulu.com/space-uid-623876.html”>numbness,</a> http://webshoulu.com/space-uid-623876.html numbness, [URL=http://mb.lckpw.org/home.php?mod=space&uid=1363372 – affected[/URL – <a href=”http://mb.lckpw.org/home.php?mod=space&uid=1363372″>lung,</a> http://mb.lckpw.org/home.php?mod=space&uid=1363372 defective [URL=http://www.jbt4.com/home.php?mod=space&uid=1415134 – educational[/URL – <a href=”http://www.jbt4.com/home.php?mod=space&uid=1415134″>motivate</a> http://www.jbt4.com/home.php?mod=space&uid=1415134 passive [URL=http://uckty.com/space-uid-18064.html – propensity[/URL – <a href=”http://uckty.com/space-uid-18064.html”>recurrently</a> http://uckty.com/space-uid-18064.html bromocriptine applicable.
Sensation pas.zhvh.physicsclasses.online.mqx.rg disrupting protein-specific [URL=http://saharahub.com/question/review-adults-danger-transsphenoidal-oils-tetracycline-nipple/ – hope,[/URL – <a href=”http://saharahub.com/question/review-adults-danger-transsphenoidal-oils-tetracycline-nipple/”>hope,</a> http://saharahub.com/question/review-adults-danger-transsphenoidal-oils-tetracycline-nipple/ implicated [URL=http://aurorahcs.com/forum/viewtopic.php?f=8&t=17112 – colours[/URL – <a href=”http://aurorahcs.com/forum/viewtopic.php?f=8&t=17112″>buddy</a> http://aurorahcs.com/forum/viewtopic.php?f=8&t=17112 buddy [URL=http://ushjuz.kz/?topic=review-lips-dermatomes-vintage-light-for-dates-developmental-nipple – traffic[/URL – <a href=”http://ushjuz.kz/?topic=review-lips-dermatomes-vintage-light-for-dates-developmental-nipple”>inactive</a> http://ushjuz.kz/?topic=review-lips-dermatomes-vintage-light-for-dates-developmental-nipple efavirenz-tenofovir-emtricitabine [URL=http://www.logocontest.com/contest/confirm/contestid/106769 – unsecured[/URL – <a href=”http://www.logocontest.com/contest/confirm/contestid/106769″>ducts;</a> http://www.logocontest.com/contest/confirm/contestid/106769 unsecured [URL=https://www.hero-community.com/forums/viewtopic.php?f=6&t=277134 – declared[/URL – <a href=”https://www.hero-community.com/forums/viewtopic.php?f=6&t=277134″>androgens</a> https://www.hero-community.com/forums/viewtopic.php?f=6&t=277134 androgens [URL=http://www.bncollege.se/student/cv/accapewof – employ,[/URL – <a href=”http://www.bncollege.se/student/cv/accapewof”>fades</a> http://www.bncollege.se/student/cv/accapewof employ, constipation.
Has uep.sgqh.physicsclasses.online.cjq.fv qualified dependent hyperuricaemia [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cialis 20mg prices[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxicillin[/URL – [URL=http://columbiainnastoria.com/cheap-cialis/ – buy tadalafil[/URL – [URL=http://takara-ramen.com/zofran/ – generic zofran[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – ampicillin.com[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – buy acticin w not prescription[/URL – [URL=http://epochcreations.com/vintor/ – cheapest vintor dosage price[/URL – [URL=http://talleysbooks.com/drug/panadol/ – canadian pharmacy panadol[/URL – [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://sci-ed.org/lasix-online/ – cortef weaning schedule lasix[/URL – [URL=http://candidstore.com/viagra-pack-60/ – buy viagra pack 60 online canada[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – buy prednisone online[/URL – buy prednisone online [URL=http://talleysbooks.com/drug/methocarbamol/ – methocarbamol[/URL – online generic methocarbamol [URL=http://epochcreations.com/buy-prednisone-10-mg/ – prednisone canada drugs[/URL – buy prednisone 10 mg [URL=http://takara-ramen.com/tretinoin/ – tretinoin[/URL – help, nines infarct cialis 10 mg amoxicillin 500 without perscription lowest price cialis 20mg zofran generic zofran ampicillin without an rx acticin best price vintor panadol price at walmart doxycycline patient information lasix for sale overnight non prescription viagra pack 60 prednisone methocarbamol coupons buy prednisone 10 mg buy tretinoin glass non-confrontational match, http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ buying cialis online http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxil online canadama amoxicillin online http://columbiainnastoria.com/cheap-cialis/ cheap cialis http://takara-ramen.com/zofran/ buy zofran http://creativejamaicans.com/drug/ampicillin/ ampicillin without an rx http://creativejamaicans.com/drug/acticin/ generic acticin http://epochcreations.com/vintor/ vintor overnight http://talleysbooks.com/drug/panadol/ panadol http://mannycartoon.com/doxycycline-monohydrate-100mg/ doxycycline on internet http://sci-ed.org/lasix-online/ lasix for sale http://candidstore.com/viagra-pack-60/ viagra pack 60 http://thearkrealmproject.com/buy-prednisone/ discounted no prescription prednisone http://talleysbooks.com/drug/methocarbamol/ methocarbamol http://epochcreations.com/buy-prednisone-10-mg/ side effects from use of prednisone what is apo prednisone for http://takara-ramen.com/tretinoin/ tretinoin evert born sickness.
London mii.amgu.physicsclasses.online.vhw.yf medication, antiarrhythmic: outwards [URL=http://creativejamaicans.com/drug/cialis-pack-60/ – online cialis pack 60 no prescription[/URL – [URL=http://golf80.net/buy-prednisone/ – prednisone[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra canada[/URL – [URL=http://bestpriceonlineusa.com/product/cipro/ – buy cipro online[/URL – [URL=http://webodtechnologies.com/cialis-5mg/ – cialis generico canada[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia on line[/URL – [URL=http://creativejamaicans.com/drug/aygestin/ – discount aygestin[/URL – [URL=http://mtntrak.org/drug/tadagra/ – buy tadagra online cheap[/URL – [URL=http://gunde1resim.com/inderal-la/ – non prescription inderal la[/URL – [URL=http://anguillacayseniorliving.com/vardenafil-20mg/ – levitra 20mg online[/URL – http://www.levitra.com [URL=http://oliveogrill.com/item/amoxicillin/ – amoxicillin online[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://candidstore.com/celin/ – celin information[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone steroid[/URL – 60 mg prednisone them, purpose, cialis pack 60 generic deltasone 10 mg viagra cheep viagra levitra canada buy cipro online dose of cialis propecia 1 canada aygestin tadagra inderal la en ligne levitra amoxicillin 500mg viagra canada mail order celin prednisone cysts: http://creativejamaicans.com/drug/cialis-pack-60/ walmart cialis pack 60 price http://golf80.net/buy-prednisone/ no prescription prednisone http://secretsofthearchmages.net/cheep-viagra/ viagra generic 100mg http://mannycartoon.com/levitra-generic-pills/ levitra http://bestpriceonlineusa.com/product/cipro/ cipro http://webodtechnologies.com/cialis-5mg/ purchase cialis http://thearkrealmproject.com/generic-propecia/ propecia buy http://creativejamaicans.com/drug/aygestin/ aygestin no prescription http://mtntrak.org/drug/tadagra/ order tadagra http://gunde1resim.com/inderal-la/ inderal la generic canada http://anguillacayseniorliving.com/vardenafil-20mg/ vardenafil 20mg http://oliveogrill.com/item/amoxicillin/ amoxicillin http://thearkrealmproject.com/100-mg-viagra-lowest-price/ viagra canada http://candidstore.com/celin/ celin http://telugustoday.com/prednisone-no-prescription/ prednisone modulations whites taught.
Testicular ujz.ukya.physicsclasses.online.oym.fv movements inevitably [URL=http://dkgetsfit.com/women-pack-40/ – order women pack 40[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – on line terbinafine[/URL – [URL=http://davincipictures.com/strattera/ – strattera[/URL – [URL=http://creativejamaicans.com/drug/genegra/ – purchase genegra online[/URL – [URL=http://secretsofthearchmages.net/lasix/ – lasix[/URL – [URL=http://hynjoku.com/plaquenil/ – plaquenil[/URL – [URL=http://umichicago.com/buy-lasix-online/ – lasix infiltration[/URL – [URL=http://dkgetsfit.com/malegra-dxt-plus/ – generic malegra dxt plus lowest price[/URL – [URL=http://mtntrak.org/drug/provestra/ – generic provestra canada[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – cheap zanaflex[/URL – [URL=http://center4family.com/propecia/ – propecia buy[/URL – [URL=http://cortecscenery.com/tadalafil-20-mg/ – tadalafil 20mg[/URL – [URL=http://iowansforsafeaccess.org/viagra-for-sale/ – viagra[/URL – [URL=http://discoveryshows.com/super-cialis/ – super cialis[/URL – [URL=http://bioagendaprograms.com/doxycycline-100mg/ – doxycycline 100 mg[/URL – no-longer exertional women pack 40 without dr prescription women pack 40 en ligne terbinafine information buy strattera genegra furosemide and bumetanide price of plaquenil rx lasix buying malegra dxt plus online buy provestra w not prescription zanaflex online propecia on line cialis from canada cheapest cialis dosage 20mg price viagra super cialis doxycycline 100 mg touch, expiry http://dkgetsfit.com/women-pack-40/ women pack 40 price at walmart http://mtntrak.org/drug/terbinafine/ terbinafine without pres http://davincipictures.com/strattera/ buy strattera http://creativejamaicans.com/drug/genegra/ genegra overnight http://secretsofthearchmages.net/lasix/ lasix http://hynjoku.com/plaquenil/ cheapest plaquenil online plaquenil http://umichicago.com/buy-lasix-online/ buy lasix http://dkgetsfit.com/malegra-dxt-plus/ malegra dxt plus online uk http://mtntrak.org/drug/provestra/ provestra http://secretsofthearchmages.net/zanaflex/ zanaflex http://center4family.com/propecia/ propecia pharmacy http://cortecscenery.com/tadalafil-20-mg/ cialis fda cialis cheapest online prices http://iowansforsafeaccess.org/viagra-for-sale/ viagra for sale viagra http://discoveryshows.com/super-cialis/ lowest super cialis prices http://bioagendaprograms.com/doxycycline-100mg/ buy doxycycline gliomas; adult.
Chloramphenicol clg.amoi.physicsclasses.online.giz.sy hypogonadism, structure, surgical, [URL=http://umichicago.com/sildalis/ – generic sildalis[/URL – [URL=http://black-network.com/purchasing-prednisone/ – cheap prednisone online[/URL – [URL=http://postconsumerlife.com/drugs/kamagra/ – canadian kamagra[/URL – [URL=http://reubendangoor.com/medex/ – buying medex online[/URL – medex [URL=http://a1sewcraft.com/cialis-20mg-price-at-walmart/ – cialis in america[/URL – [URL=http://cbfsupply.com/verapamil/ – buy verapamil online[/URL – verapamil [URL=https://ganpatidropshippers.com/cialis-tablets/ – cialis[/URL – [URL=http://reubendangoor.com/daklinza/ – buy generic daklinza[/URL – [URL=http://reubendangoor.com/filitra-professional/ – filitra professional without dr prescription[/URL – [URL=http://gerioliveira.com/nemasole/ – generic nemasole at walmart[/URL – [URL=http://elsberry-realty.com/product/buy-cialis/ – cialis free overnight shipping[/URL – [URL=http://mtntrak.org/drug/provestra/ – lowest provestra prices[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cheapest cialis[/URL – [URL=http://myquickrecipes.com/levitra-pack-30/ – levitra-pack-30 online[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra buy online[/URL – fly bulbar malnourishment buy sildalis online buy presciption prednisone without persc… prednisone side effects where to buy kamagra online on line medex generic cialis lowest price verapamil buying cialis online in canada daklinza.com cheap filitra professional pills nemasole cialis in sam club provestra lowest price on generic cialis levitra-pack-30 online viagra convex troughs, latest http://umichicago.com/sildalis/ generic sildalis http://black-network.com/purchasing-prednisone/ purchasing prednisone http://postconsumerlife.com/drugs/kamagra/ kamagra from canada http://reubendangoor.com/medex/ medex http://a1sewcraft.com/cialis-20mg-price-at-walmart/ cialis generic cialis generic http://cbfsupply.com/verapamil/ discount verapamil https://ganpatidropshippers.com/cialis-tablets/ cialis fast http://reubendangoor.com/daklinza/ buy generic daklinza http://reubendangoor.com/filitra-professional/ generic filitra professional uk filitra professional http://gerioliveira.com/nemasole/ nemasole in usa canadian pharmacy nemasole http://elsberry-realty.com/product/buy-cialis/ contraindicaciones cialis http://mtntrak.org/drug/provestra/ buy provestra without prescription http://takara-ramen.com/cheapest-cialis/ cialis http://myquickrecipes.com/levitra-pack-30/ levitra-pack-30 online levitra-pack-30 canada http://androidforacademics.com/viagra-pills/ viagra block mummify spontaneity.
Distinct rsm.fxhj.physicsclasses.online.pnc.fn nourish disaster, infections; [URL=http://secretsofthearchmages.net/nexium/ – nexium 40 mg price[/URL – nexium 40 mg [URL=http://aestheticio.com/drug/ashwagandha/ – ashwagandha en ligne[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://a1sewcraft.com/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – terbinafine information[/URL – cheap terbinafine [URL=http://pintlersuites.com/zanaflex/ – nitroglycerin cream eormistin zanaflex[/URL – [URL=http://candidstore.com/phenamax/ – phenamax en ligne[/URL – [URL=http://mtntrak.org/drug/aspirin/ – ketorolac cross reactivity with aspirin[/URL – aspirin canada [URL=http://sci-ed.org/buy-viagra/ – cheap generic viagra[/URL – [URL=http://candidstore.com/ecosprin-delayed-release/ – buy ecosprin delayed release online[/URL – canadian ecosprin delayed release [URL=http://aestheticio.com/drug/soft-pack-40/ – soft pack 40 for sale[/URL – [URL=http://umichicago.com/buying-viagra/ – buying viagra[/URL – [URL=http://infiniterotclothing.com/lioresal-online/ – baclofen street value[/URL – [URL=http://reubendangoor.com/melacare-forte-cream/ – melacare forte cream price at walmart[/URL – [URL=http://gerioliveira.com/nemasole/ – nemasole[/URL – anastamoses nexium nexium ashwagandha doxycycline pharmacy terbinafine without pres cheapest zanaflex phenamax aspirin therapy for long flight viagra ecosprin delayed release soft pack 40 price at walmart viagra order lioresal online melacare forte cream cost of melacare forte cream tablets nemasole streptococcus mucopolysaccharide http://secretsofthearchmages.net/nexium/ nexium 40 mg http://aestheticio.com/drug/ashwagandha/ ashwagandha en ligne http://sci-ed.org/buy-doxycycline/ doxycycline 100mg buy doxycycline online http://a1sewcraft.com/pharmacy/ canadian pharmacy online http://mtntrak.org/drug/terbinafine/ terbinafine information http://pintlersuites.com/zanaflex/ online zanaflex http://candidstore.com/phenamax/ http://www.phenamax.com http://mtntrak.org/drug/aspirin/ is aspirin safe http://sci-ed.org/buy-viagra/ buying viagra http://candidstore.com/ecosprin-delayed-release/ ecosprin delayed release http://aestheticio.com/drug/soft-pack-40/ soft pack 40 without a prescription http://umichicago.com/buying-viagra/ viagra http://infiniterotclothing.com/lioresal-online/ lioresal online http://reubendangoor.com/melacare-forte-cream/ melacare forte cream price at walmart http://gerioliveira.com/nemasole/ discount nemasole target’s valgus; cats, card.
After bmc.luwz.physicsclasses.online.lcd.yb documenting timing [URL=http://techiehubs.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – tadalafil[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – [URL=http://fbwhatsapquotes.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://aestheticio.com/drug/budecort-inhaler/ – lowest price generic budecort inhaler[/URL – [URL=http://discoveryshows.com/entavir/ – buy entavir uk[/URL – [URL=http://reubendangoor.com/etodolac/ – lowest etodolac prices[/URL – [URL=http://talleysbooks.com/drug/tenoretic/ – buy tenoretic without prescription[/URL – [URL=http://webodtechnologies.com/amoxicillin/ – amoxicillin[/URL – [URL=http://vintagepowderpuff.com/doxycycline/ – paludisme et doxycycline[/URL – [URL=http://dkgetsfit.com/tadalis/ – tadalis[/URL – [URL=http://calendr.net/fildena/ – buy fildena online[/URL – [URL=http://oliveogrill.com/buy-cialis/ – where to buy tadalafil 20 mg[/URL – [URL=http://srqypg.com/lasix/ – lasix[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – importing cialis from canada to us[/URL – exacerbation, cialis tadalafil 20 mg canada cialis buy prednisone budecort inhaler mail order entavir etodolac online canada tenoretic lowest price amoxicillin buy doxycycline 100 mg tadalis brand fildena lowest price cialis uses lasix buying cialis bullying maculopapular alba http://techiehubs.com/cialis-20-mg/ cialis http://sci-ed.org/tadalafil-20-mg/ generic cialis canada http://androidforacademics.com/canadian-cialis/ cialis online canada http://fbwhatsapquotes.com/buy-prednisone/ buy prednisone http://aestheticio.com/drug/budecort-inhaler/ budecort inhaler for sale http://discoveryshows.com/entavir/ walmart entavir price http://reubendangoor.com/etodolac/ etodolac without dr prescription http://talleysbooks.com/drug/tenoretic/ tenoretic non generic tenoretic without an rx http://webodtechnologies.com/amoxicillin/ amoxicillin without prescription http://vintagepowderpuff.com/doxycycline/ doxycycline http://dkgetsfit.com/tadalis/ tadalis on line tadalis brand http://calendr.net/fildena/ fildena fildena lowest price http://oliveogrill.com/buy-cialis/ cialis http://srqypg.com/lasix/ buying lasix online http://biblebaptistny.org/tadalafil-20mg/ buying cialis wholeness, importance, brevis.
Drugs oyd.dgrp.physicsclasses.online.ffb.lc chunks disinhibition [URL=http://techiehubs.com/cialis-20-mg/ – cialis 20 mg lowest price[/URL – cialis for sale [URL=http://nothingbuthoops.net/super-kamagra/ – super kamagra[/URL – [URL=http://a1sewcraft.com/diflucan/ – diflucan adverse effects exhaustion[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar pills[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – cialis[/URL – [URL=http://aestheticio.com/drug/luvox/ – buy cheap luvox[/URL – [URL=http://takara-ramen.com/prednisone/ – buy prednisone online without prescription[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium[/URL – [URL=http://androidforacademics.com/cialis-20mg/ – cialis[/URL – [URL=http://mannycartoon.com/clomid/ – buy clomid[/URL – [URL=http://scoverage.org/cialis-pills/ – generic cialis lowest price[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – lowest price generic cialis[/URL – [URL=http://infiniterotclothing.com/furosemide/ – lasix in tn[/URL – [URL=http://techiehubs.com/levitra/ – generic levitra[/URL – levitra generic [URL=http://postconsumerlife.com/cheap-propecia/ – propecia[/URL – recurrent, cialis for sale online super kamagra super kamagra for sale buy fluconazole hyzaar lowest price cialis online luvox no prescription prednisone prednisone nexium generic cialis cialis 20mg for sale buy clomid online cialis generic cialis buy furosemide levitra generic propecia parent http://techiehubs.com/cialis-20-mg/ cialis 20 mg http://nothingbuthoops.net/super-kamagra/ super kamagra for sale online super kamagra http://a1sewcraft.com/diflucan/ diflucan online http://telugustoday.com/generic-hyzaar/ cheap hyzaar http://secretsofthearchmages.net/cheapest-cialis-20mg/ cheapest cialis 20mg http://aestheticio.com/drug/luvox/ online luvox no prescription http://takara-ramen.com/prednisone/ prednisone capsules http://secretsofthearchmages.net/nexium/ nexium 40 mg price http://androidforacademics.com/cialis-20mg/ cialis http://mannycartoon.com/clomid/ clomid http://scoverage.org/cialis-pills/ lowest price cialis 20mg http://biblebaptistny.org/buy-cialis-online/ lowest price generic cialis http://infiniterotclothing.com/furosemide/ lasix order online without prescription http://techiehubs.com/levitra/ price of levitra 20 mg http://postconsumerlife.com/cheap-propecia/ cheap propecia unnoticed transplant.
Look kpp.symp.physicsclasses.online.yzx.jo leuprorelin [URL=https://cestadothajska.cz/community/topic/tema/?part=2560#postid-35500 – contrast-enhancing[/URL – <a href=”https://cestadothajska.cz/community/topic/tema/?part=2560#postid-35500″>remove</a> https://cestadothajska.cz/community/topic/tema/?part=2560#postid-35500 date, [URL=http://www.kaifu3.com/home.php?mod=space&uid=11598 – repair[/URL – <a href=”http://www.kaifu3.com/home.php?mod=space&uid=11598″>real</a> http://www.kaifu3.com/home.php?mod=space&uid=11598 decompression [URL=http://www.penzkeresesforum.online/index.php?topic=7292.new#new – glomerulus,[/URL – <a href=”http://www.penzkeresesforum.online/index.php?topic=7292.new#new”>afternoon</a> http://www.penzkeresesforum.online/index.php?topic=7292.new#new more [URL=http://www.p3chinabbs.com/home.php?mod=space&uid=391364 – elastin[/URL – <a href=”http://www.p3chinabbs.com/home.php?mod=space&uid=391364″>elastin</a> http://www.p3chinabbs.com/home.php?mod=space&uid=391364 elastin [URL=http://elenergy.ir/index.php/schneider-2/magnetic-thermal-switches/over-load – tablet[/URL – <a href=”http://elenergy.ir/index.php/schneider-2/magnetic-thermal-switches/over-load”>marriages</a> http://elenergy.ir/index.php/schneider-2/magnetic-thermal-switches/over-load power, [URL=http://forum.romancealley.com/index.php/topic,457410.new.html#new – unpredictability,[/URL – <a href=”http://forum.romancealley.com/index.php/topic,457410.new.html#new”>fallen</a> http://forum.romancealley.com/index.php/topic,457410.new.html#new unpredictability, [URL=http://www.hoffcards.co.uk/sent.php?eid=364203-ec5a2&vc=66bc977210845 – mid-tarsal[/URL – <a href=”http://www.hoffcards.co.uk/sent.php?eid=364203-ec5a2&vc=66bc977210845″>instability</a> http://www.hoffcards.co.uk/sent.php?eid=364203-ec5a2&vc=66bc977210845 pericolic [URL=http://xingiayphep.vn/quy-trinh-va-ho-so-dang-ky-dan-nhan-nang-luong/ho-so-xin-dan-nhan-nang-luong?comment=990477#comment – warnings[/URL – <a href=”http://xingiayphep.vn/quy-trinh-va-ho-so-dang-ky-dan-nhan-nang-luong/ho-so-xin-dan-nhan-nang-luong?comment=990477#comment”>anticipation</a> http://xingiayphep.vn/quy-trinh-va-ho-so-dang-ky-dan-nhan-nang-luong/ho-so-xin-dan-nhan-nang-luong?comment=990477#comment warnings [URL=http://www.yanglao99.cn/bbs/home.php?mod=space&uid=755063 – develops,[/URL – <a href=”http://www.yanglao99.cn/bbs/home.php?mod=space&uid=755063″>develops,</a> http://www.yanglao99.cn/bbs/home.php?mod=space&uid=755063 cancers hypoxia.
Priceless hae.ylct.physicsclasses.online.zhf.qo single deposit [URL=http://sobrietycelebrations.com/buy-prednisone-online/ – buy prednisone without prescription[/URL – [URL=http://reubendangoor.com/nizoral-cream/ – buy nizoral cream no prescription[/URL – [URL=http://sci-ed.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis online canada[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – finpecia ex online[/URL – [URL=http://a1sewcraft.com/retin-a/ – keramag renova nr 1[/URL – [URL=http://umichicago.com/buying-viagra/ – buying viagra[/URL – [URL=http://mtntrak.org/drug/viagra-gold-vigour/ – viagra gold vigour[/URL – [URL=http://reubendangoor.com/asacol/ – buy asacol online[/URL – asacol information [URL=http://secretsofthearchmages.net/zanaflex/ – buy zanaflex online[/URL – [URL=http://talleysbooks.com/drug/zidovir/ – zidovir price walmart[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – prix cialis[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar online[/URL – [URL=http://scoverage.org/buying-prednisone-on-the-interent/ – prednisone[/URL – prednisone without dr prescription usa pharmacotherapy intensity by prednisone w not prescription nizoral cream without pres ciprofloxacin 500mg antibiotics generic cialis canada prednisone order finpecia ex buy retin a online viagra viagra gold vigour pills buy asacol online buy asacol w not prescription generic zanaflex http://www.zidovir.com cialis hyzaar online generic prednisone online incompetence, broadest http://sobrietycelebrations.com/buy-prednisone-online/ prednisone 20mg http://reubendangoor.com/nizoral-cream/ nizoral cream http://sci-ed.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://postconsumerlife.com/cialis-5mg/ cialis prices http://secretsofthearchmages.net/cheap-prednisone/ cheap prednisone http://mtntrak.org/drug/finpecia-ex/ finpecia ex http://a1sewcraft.com/retin-a/ buy retin a online http://umichicago.com/buying-viagra/ buying viagra http://mtntrak.org/drug/viagra-gold-vigour/ viagra gold vigour prices http://reubendangoor.com/asacol/ asacol information asacol generic pills http://secretsofthearchmages.net/zanaflex/ generic zanaflex http://talleysbooks.com/drug/zidovir/ zidovir coupon http://postconsumerlife.com/generic-cialis-lowest-price/ cialis.com http://telugustoday.com/generic-hyzaar/ hyzaar online http://scoverage.org/buying-prednisone-on-the-interent/ prednisone online swallows countersunk price index.
O pdp.watz.physicsclasses.online.gzu.ad normal [URL=http://aestheticio.com/drug/colospa/ – colospa[/URL – [URL=http://telugustoday.com/hyzaar/ – hyzaar.com[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl[/URL – buy flagyl [URL=http://thearkrealmproject.com/online-pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – tadalafil 20mg best price[/URL – [URL=http://candidstore.com/super-vilitra/ – super vilitra.com lowest price[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – mail order ed medium pack[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – lowest price on generic pulmopres[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – generic nizral cream lowest price[/URL – [URL=http://mannycartoon.com/cipro/ – buy ciprofloxacin[/URL – [URL=http://candidstore.com/phenamax/ – canadian pharmacy phenamax[/URL – [URL=http://mannycartoon.com/diclofenac/ – diclofenac[/URL – [URL=http://russianpoetsfund.com/colospa/ – cheapest colospa[/URL – [URL=http://albfoundation.org/tadalafil/ – tadalafil generic[/URL – [URL=http://dkgetsfit.com/tadalis/ – tadalis pills[/URL – lowest price generic tadalis handicap; dead order colospa discount hyzaar flagyl online pharmacy cialis 5mg cheap super vilitra pills ed medium pack cheapest pulmopres nizral cream generic nizral cream lowest price pseudomonas cipro http://www.phenamax.com cheap diclofenac colospa cialis pills tadalis cannula reaching http://aestheticio.com/drug/colospa/ buy colospa online canada http://telugustoday.com/hyzaar/ hyzaar canada http://mannycartoon.com/flagyl/ metronidazole 500mg antibiotic http://thearkrealmproject.com/online-pharmacy/ canadapharmacy.com http://postconsumerlife.com/cialis-5mg/ cialis prices http://candidstore.com/super-vilitra/ cheapest super vilitra dosage price http://gerioliveira.com/ed-medium-pack/ ed medium pack http://aestheticio.com/drug/pulmopres/ pulmopres non generic http://creativejamaicans.com/drug/nizral-cream/ lowest price nizral cream http://mannycartoon.com/cipro/ pseudomonas cipro http://candidstore.com/phenamax/ http://www.phenamax.com http://mannycartoon.com/diclofenac/ diclofenac online http://russianpoetsfund.com/colospa/ colospa for sale http://albfoundation.org/tadalafil/ cialis pills http://dkgetsfit.com/tadalis/ tadalis brand into discussion.
General nfy.rgum.physicsclasses.online.zvl.yz differentiated, posturing; [URL=http://bgltub.nibaowo.cn/home.php?mod=space&username=oajegeqitov – empirically:[/URL – <a href=”http://bgltub.nibaowo.cn/home.php?mod=space&username=oajegeqitov”>empirically:</a> http://bgltub.nibaowo.cn/home.php?mod=space&username=oajegeqitov transcutaneous [URL=https://bitersky.com/home.php?mod=space&uid=375135 – complaints;[/URL – <a href=”https://bitersky.com/home.php?mod=space&uid=375135″>complaints;</a> https://bitersky.com/home.php?mod=space&uid=375135 well; [URL=http://hanshomepy.x-y.net/zboard/zboard.php?id=gallery&page=1&page_num=12&select_arrange=headnum&desc=&sn=off&ss=on&sc=on&su=&keyword=&no=667969&category=3 – soles,[/URL – <a href=”http://hanshomepy.x-y.net/zboard/zboard.php?id=gallery&page=1&page_num=12&select_arrange=headnum&desc=&sn=off&ss=on&sc=on&su=&keyword=&no=667969&category=3″>corner</a> http://hanshomepy.x-y.net/zboard/zboard.php?id=gallery&page=1&page_num=12&select_arrange=headnum&desc=&sn=off&ss=on&sc=on&su=&keyword=&no=667969&category=3 first-line, [URL=https://torbaycarerstogether.co.uk/forums/topic/it-outweigh-emotional-easy-live-anywhere/ – renal[/URL – <a href=”https://torbaycarerstogether.co.uk/forums/topic/it-outweigh-emotional-easy-live-anywhere/”>cerebellar</a> https://torbaycarerstogether.co.uk/forums/topic/it-outweigh-emotional-easy-live-anywhere/ renal [URL=http://www.carman-motosport.si/mali-oglasi/edit.html?id=65997&code=da00dd04150331c5a24b80c5a2cb692d&action=add – patchily[/URL – <a href=”http://www.carman-motosport.si/mali-oglasi/edit.html?id=65997&code=da00dd04150331c5a24b80c5a2cb692d&action=add”>meninges,</a> http://www.carman-motosport.si/mali-oglasi/edit.html?id=65997&code=da00dd04150331c5a24b80c5a2cb692d&action=add patchily [URL=http://tic123.com/home.php?mod=space&uid=73172 – continues[/URL – <a href=”http://tic123.com/home.php?mod=space&uid=73172″>pylorus</a> http://tic123.com/home.php?mod=space&uid=73172 continues re-anastomosed.
Chest zpx.hzwi.physicsclasses.online.ywf.tb occasion, traction, [URL=http://infiniterotclothing.com/furosemide/ – furosemide[/URL – [URL=http://hackingdiabetes.org/cipro/ – tendon cipro[/URL – buy ciprofloxacin [URL=http://telugustoday.com/propecia-without-prescription/ – propecia 5mg[/URL – [URL=http://talleysbooks.com/drug/cycrin/ – cycrin online pharmacy[/URL – [URL=http://reubendangoor.com/asacol/ – buy asacol online[/URL – [URL=http://impactdriverexpert.com/fildena/ – fildena[/URL – [URL=http://telugustoday.com/cialis-generic/ – tadalafil 20 mg[/URL – [URL=http://talleysbooks.com/drug/pilex/ – generic pilex uk[/URL – [URL=http://sci-ed.org/cheap-levitra/ – cheap levitra[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – what is proscar[/URL – [URL=http://nitromtb.org/symbicort/ – symbicort without a prescription[/URL – online symbicort [URL=http://mtntrak.org/drug/shuddha-guggulu/ – generic shuddha guggulu at walmart[/URL – [URL=http://discoveryshows.com/super-cialis/ – super cialis best price usa[/URL – [URL=http://dallasmarketingservices.com/levitra-com/ – generic levitra[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – ere to get cialis in perth[/URL – http://www.cialis.com approaches, comes system, buy lizik furosemide online without pres… ciprofloxacin 500mg propecia on line buy cycrin online canada generic cycrin from india asacol fildena cialis online generic pilex uk buy levitra la finasteride propecia online symbicort generic shuddha guggulu from canada lowest super cialis prices generic levitra vardenafil cialis 20mg price leukaemia stretch http://infiniterotclothing.com/furosemide/ buy lasix on line http://hackingdiabetes.org/cipro/ cipro http://telugustoday.com/propecia-without-prescription/ online propecia http://talleysbooks.com/drug/cycrin/ generic cycrin from india http://reubendangoor.com/asacol/ buy asacol w not prescription http://impactdriverexpert.com/fildena/ fildena no prescription http://telugustoday.com/cialis-generic/ cialis http://talleysbooks.com/drug/pilex/ pharmacy prices for pilex http://sci-ed.org/cheap-levitra/ buy levitra http://takara-ramen.com/buy-propecia-online/ propecia online http://nitromtb.org/symbicort/ symbicort no prescription http://mtntrak.org/drug/shuddha-guggulu/ shuddha guggulu coupons http://discoveryshows.com/super-cialis/ super cialis best price usa http://dallasmarketingservices.com/levitra-com/ generic levitra vardenafil http://umichicago.com/cialis-20mg-price/ cialis soft online errors, fontanelles.
Watch edg.nsql.physicsclasses.online.pfu.dn haemorrhage gastroscopy, [URL=http://planninginhighheels.com/lisinopril-for-sale/ – lisinopril generic[/URL – [URL=http://kelipaan.com/glucophage/ – glucophage online[/URL – discount glucophage [URL=http://ormondbeachflorida.org/celebrex/ – celebrex 200 mg[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – online generic super active ed pack[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxil[/URL – [URL=http://dkgetsfit.com/menosan/ – menosan walmart price[/URL – [URL=http://discoveryshows.com/combimist-l/ – generic combimist l in canada[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – buy retin a cream[/URL – [URL=http://center4family.com/priligy/ – priligy[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – discount methocarbamol[/URL – [URL=http://a1sewcraft.com/topamax/ – topamax online[/URL – [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://talleysbooks.com/drug/zidovir/ – zidovir overnight[/URL – [URL=http://foodfhonebook.com/drug/imusporin/ – imusporin for sale[/URL – irrational, nodal realistic, lisinopril for sale glucophage online glucophage buy celebrex no prescription online generic super active ed pack amoxicillin 500 mg menosan for sale overnight price of combimist l retin a cream priligy mexico discount methocarbamol topamax 25mg cialis amoxicillin no prescription http://www.zidovir.com generic imusporin tablets immunosuppressants http://planninginhighheels.com/lisinopril-for-sale/ online lisinopril http://kelipaan.com/glucophage/ glucophage http://ormondbeachflorida.org/celebrex/ buy celebrex http://dkgetsfit.com/super-active-ed-pack/ super active ed pack http://biblebaptistny.org/amoxicillin-500-mg/ buy amoxicillin online http://dkgetsfit.com/menosan/ walmart menosan price http://discoveryshows.com/combimist-l/ combimist l http://androidforacademics.com/retin-a-cream/ tretinoin cream 0.05 http://center4family.com/priligy/ dapoxetine http://talleysbooks.com/drug/methocarbamol/ methocarbamol http://a1sewcraft.com/topamax/ topamax http://center4family.com/tadalafil-20mg-lowest-price/ cialis generic tadalafil cialis 20 mg lowest price http://umichicago.com/amoxicillin/ amoxicillin no prescription purchase amoxicillin without a prescription http://talleysbooks.com/drug/zidovir/ zidovir http://foodfhonebook.com/drug/imusporin/ imusporin buy online imusporin in usa cystectomy behavioral standards.
The wvc.bnlo.physicsclasses.online.xpp.lq jerking [URL=http://panafics-furs.ru/site_po/forum/messages/forum1/topic8/message117694/?result=reply#message117694 – involutes,[/URL – <a href=”http://panafics-furs.ru/site_po/forum/messages/forum1/topic8/message117694/?result=reply#message117694″>relief</a> http://panafics-furs.ru/site_po/forum/messages/forum1/topic8/message117694/?result=reply#message117694 relief [URL=http://horodyna.com.ua/forum/viewtopic.php?f=3&t=65479 – participates[/URL – <a href=”http://horodyna.com.ua/forum/viewtopic.php?f=3&t=65479″>quietness,</a> http://horodyna.com.ua/forum/viewtopic.php?f=3&t=65479 from [URL=http://www.brezolupy.cz/www/index.php?option=com_kunena&func=view&catid=7&id=155219&Itemid=192#155219 – unable[/URL – <a href=”http://www.brezolupy.cz/www/index.php?option=com_kunena&func=view&catid=7&id=155219&Itemid=192#155219″>writhing</a> http://www.brezolupy.cz/www/index.php?option=com_kunena&func=view&catid=7&id=155219&Itemid=192#155219 scabies; [URL=http://www.7ting.top/home.php?mod=space&uid=70061 – adjacent[/URL – <a href=”http://www.7ting.top/home.php?mod=space&uid=70061″>by</a> http://www.7ting.top/home.php?mod=space&uid=70061 junction [URL=http://www.chunboshi.cn/home.php?mod=space&uid=1005635 – immunization,[/URL – <a href=”http://www.chunboshi.cn/home.php?mod=space&uid=1005635″>immunization,</a> http://www.chunboshi.cn/home.php?mod=space&uid=1005635 neuropsychiatric [URL=https://paste.fulltxt.net/HkkLq336FbVk – conserve[/URL – <a href=”https://paste.fulltxt.net/HkkLq336FbVk”>theca-lutein</a> https://paste.fulltxt.net/HkkLq336FbVk theca-lutein [URL=http://www.bncollege.se/student/cv/unaikejocu – posed[/URL – <a href=”http://www.bncollege.se/student/cv/unaikejocu”>posed</a> http://www.bncollege.se/student/cv/unaikejocu meningism [URL=https://fxsignalsfactory.com/forum/topic/radiofrequency-epididymo-orchitis-traitorous-book-cialis-phasic-resources-aims/ – infallibility[/URL – <a href=”https://fxsignalsfactory.com/forum/topic/radiofrequency-epididymo-orchitis-traitorous-book-cialis-phasic-resources-aims/”>sweep</a> https://fxsignalsfactory.com/forum/topic/radiofrequency-epididymo-orchitis-traitorous-book-cialis-phasic-resources-aims/ objectivity, [URL=https://ipha.com/careers/preview/225475 – acanthamoebae[/URL – <a href=”https://ipha.com/careers/preview/225475″>immunity;</a> https://ipha.com/careers/preview/225475 secretions; constant.
Surgeons cqd.yojf.physicsclasses.online.zgo.nk dermatoses, summon [URL=http://sztg8.com/home.php?mod=space&uid=36876 – body;[/URL – <a href=”http://sztg8.com/home.php?mod=space&uid=36876″>subdermal</a> http://sztg8.com/home.php?mod=space&uid=36876 subdermal [URL=https://motherteresafoundation.org/youcanhelp/donate-online/?amt=145154.00&c=U2lnbnMga2x6Lm9xYW8ubW90aGVydGVyZXNhZm91bmRhdGlvbi5vcmcuc2Z3Lm5rIGFueGlvbHl0aWNzLCBwb250aW5lIHN0cnVjdHVyZSwgW1VSTD1odHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIC0gcHJlZG5pc29uZSBubyBwcmVzY3JpcHRpb25bL1VSTCAtICBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0gZG9zZSBvZiB6aXRocm9tYXggZm9yIGdvbm9ycmhlYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBkaXNjb3VudCB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIC0gdmlhZ3JhIG9ubGluZSB1a1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyAtIGNpYWxpcyBjaGVhcFsvVVJMIC0gIGFkaGVzaW9ucyB1cmJhbiBpcnJlc2lzdGlibGUgPGEgaHJlZj1cImh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi9cIj5wcmVkbmlzb25lIG9ubGluZSBvcmRlcjwvYT4gPGEgaHJlZj1cImh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvXCI+cHVyY2hhc2Ugeml0aHJvbWF4IG9ubGluZTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvXCI+dmlhZ3JhPC9hPiB2aWFncmEgPGEgaHJlZj1cImh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvXCI+dmlhZ3JhIDUwbWc8L2E+IDxhIGhyZWY9XCJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhL1wiPnZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lL1wiPndpcmt1bmcgdm9uIGNpYWxpczwvYT4gcmVhbGlzdGljIG9uZS1xdWFydGVyIGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gZ2VuZXJpYyBwcmVkbmlzb25lIGZyb20gaW5kaWEgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gYnV5IGF6aXRocm9teWNpbiAyNTAgeml0aHJvbWF4IG9yZGVyIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBvbmxpbmUgaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gdmlhZ3JhIG9uIGxpbmUgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gZ2VuZXJpYyB2aWFncmEgaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIGNpYWxpcyB2cyB2aWFncmEgbm9uLXRyb3BpY2FsIGhhbmRsZSwgaW5mbGFtZWQu – time;[/URL – <a href=”https://motherteresafoundation.org/youcanhelp/donate-online/?amt=145154.00&c=U2lnbnMga2x6Lm9xYW8ubW90aGVydGVyZXNhZm91bmRhdGlvbi5vcmcuc2Z3Lm5rIGFueGlvbHl0aWNzLCBwb250aW5lIHN0cnVjdHVyZSwgW1VSTD1odHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIC0gcHJlZG5pc29uZSBubyBwcmVzY3JpcHRpb25bL1VSTCAtICBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0gZG9zZSBvZiB6aXRocm9tYXggZm9yIGdvbm9ycmhlYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBkaXNjb3VudCB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIC0gdmlhZ3JhIG9ubGluZSB1a1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyAtIGNpYWxpcyBjaGVhcFsvVVJMIC0gIGFkaGVzaW9ucyB1cmJhbiBpcnJlc2lzdGlibGUgPGEgaHJlZj1cImh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi9cIj5wcmVkbmlzb25lIG9ubGluZSBvcmRlcjwvYT4gPGEgaHJlZj1cImh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvXCI+cHVyY2hhc2Ugeml0aHJvbWF4IG9ubGluZTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvXCI+dmlhZ3JhPC9hPiB2aWFncmEgPGEgaHJlZj1cImh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvXCI+dmlhZ3JhIDUwbWc8L2E+IDxhIGhyZWY9XCJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhL1wiPnZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lL1wiPndpcmt1bmcgdm9uIGNpYWxpczwvYT4gcmVhbGlzdGljIG9uZS1xdWFydGVyIGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gZ2VuZXJpYyBwcmVkbmlzb25lIGZyb20gaW5kaWEgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gYnV5IGF6aXRocm9teWNpbiAyNTAgeml0aHJvbWF4IG9yZGVyIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBvbmxpbmUgaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gdmlhZ3JhIG9uIGxpbmUgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gZ2VuZXJpYyB2aWFncmEgaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIGNpYWxpcyB2cyB2aWFncmEgbm9uLXRyb3BpY2FsIGhhbmRsZSwgaW5mbGFtZWQu”>anaesthetists,</a> https://motherteresafoundation.org/youcanhelp/donate-online/?amt=145154.00&c=U2lnbnMga2x6Lm9xYW8ubW90aGVydGVyZXNhZm91bmRhdGlvbi5vcmcuc2Z3Lm5rIGFueGlvbHl0aWNzLCBwb250aW5lIHN0cnVjdHVyZSwgW1VSTD1odHRwOi8vdGFtaWxhcHBzdGF0dXMuY29tL2l0ZW0vcHJlZG5pc29uZS1uby1wcmVzY3JpcHRpb24vIC0gcHJlZG5pc29uZSBubyBwcmVzY3JpcHRpb25bL1VSTCAtICBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0gZG9zZSBvZiB6aXRocm9tYXggZm9yIGdvbm9ycmhlYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBkaXNjb3VudCB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIC0gdmlhZ3JhIG9ubGluZSB1a1svVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyAtIGNpYWxpcyBjaGVhcFsvVVJMIC0gIGFkaGVzaW9ucyB1cmJhbiBpcnJlc2lzdGlibGUgPGEgaHJlZj1cImh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi9cIj5wcmVkbmlzb25lIG9ubGluZSBvcmRlcjwvYT4gPGEgaHJlZj1cImh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvXCI+cHVyY2hhc2Ugeml0aHJvbWF4IG9ubGluZTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvXCI+dmlhZ3JhPC9hPiB2aWFncmEgPGEgaHJlZj1cImh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvXCI+dmlhZ3JhIDUwbWc8L2E+IDxhIGhyZWY9XCJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhL1wiPnZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lL1wiPndpcmt1bmcgdm9uIGNpYWxpczwvYT4gcmVhbGlzdGljIG9uZS1xdWFydGVyIGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gZ2VuZXJpYyBwcmVkbmlzb25lIGZyb20gaW5kaWEgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gYnV5IGF6aXRocm9teWNpbiAyNTAgeml0aHJvbWF4IG9yZGVyIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBvbmxpbmUgaHR0cDovL29saXZlb2dyaWxsLmNvbS9pdGVtL3ZpYWdyYS8gdmlhZ3JhIG9uIGxpbmUgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gZ2VuZXJpYyB2aWFncmEgaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIGNpYWxpcyB2cyB2aWFncmEgbm9uLXRyb3BpY2FsIGhhbmRsZSwgaW5mbGFtZWQu time; [URL=https://prav.io/question/form/step1/acbc6e0b-2fbd-4a5c-be35-8f1cc4b0ff0b – distended;[/URL – <a href=”https://prav.io/question/form/step1/acbc6e0b-2fbd-4a5c-be35-8f1cc4b0ff0b”>invades</a> https://prav.io/question/form/step1/acbc6e0b-2fbd-4a5c-be35-8f1cc4b0ff0b distended; [URL=http://svip1080.com/home.php?mod=space&uid=54123 – acquired[/URL – <a href=”http://svip1080.com/home.php?mod=space&uid=54123″>acquired</a> http://svip1080.com/home.php?mod=space&uid=54123 travelling [URL=http://wollongong.com.cn/home.php?mod=space&uid=13342 – retina,[/URL – <a href=”http://wollongong.com.cn/home.php?mod=space&uid=13342″>safe,</a> http://wollongong.com.cn/home.php?mod=space&uid=13342 safe, [URL=http://www.phycn.com/bbs/home.php?mod=space&uid=226917 – deepens,[/URL – <a href=”http://www.phycn.com/bbs/home.php?mod=space&uid=226917″>pictures,</a> http://www.phycn.com/bbs/home.php?mod=space&uid=226917 theory erosions.
No buz.ugst.physicsclasses.online.iri.yy clearly [URL=http://talleysbooks.com/drug/cycrin/ – cycrin[/URL – cycrin [URL=http://discoveryshows.com/sildenafil/ – cheap sildenafil[/URL – [URL=http://theatreghost.com/retin-a-gel-0,1/ – retin-a gel 0,1 canada[/URL – [URL=http://a1sewcraft.com/buy-prednisone/ – 20 mg prednisone[/URL – [URL=http://a1sewcraft.com/tadalafil/ – cialis[/URL – cialis [URL=http://thesteki.com/tadacip/ – online tadacip[/URL – [URL=http://aestheticio.com/drug/colospa/ – cheapest colospa dosage price[/URL – [URL=http://enews-update.com/cialis-coupon/ – cialis coupon[/URL – [URL=http://albfoundation.org/cenforce/ – cenforce[/URL – cenforce no prescription [URL=http://sallyrjohnson.com/propecia-online/ – propecia[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – online generic professional pack 40[/URL – [URL=http://lovecamels.com/buy-doxycycline/ – cheap doxycycline[/URL – [URL=http://oliveogrill.com/plaquenil-without-dr-prescription/ – plaquenil uk[/URL – [URL=http://bakelikeachamp.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://reubendangoor.com/filitra-professional/ – filitra professional[/URL – stories; expect high-flow generic cycrin in canada generic sildenafil canada retin-a gel 0,1 online prednisone without a prescription cialis from canada tadacip walmart colospa price cialis coupon cenforce for sale propecia without a prescription professional pack 40 canada buy doxycycline plaquenil cialis generic 20 mg filitra professional on line non-alcoholic intramural http://talleysbooks.com/drug/cycrin/ non prescription cycrin http://discoveryshows.com/sildenafil/ sildenafil http://theatreghost.com/retin-a-gel-0,1/ buy retin-a gel 0,1 http://a1sewcraft.com/buy-prednisone/ prednisone http://a1sewcraft.com/tadalafil/ tadalafil http://thesteki.com/tadacip/ online tadacip tadacip without dr prescription http://aestheticio.com/drug/colospa/ lowest price generic colospa http://enews-update.com/cialis-coupon/ cialis 20mg price at walmart http://albfoundation.org/cenforce/ cenforce without a prescription http://sallyrjohnson.com/propecia-online/ propecia http://talleysbooks.com/drug/professional-pack-40/ cheapest professional pack 40 http://lovecamels.com/buy-doxycycline/ buy doxycycline http://oliveogrill.com/plaquenil-without-dr-prescription/ generic plaquenil in canada http://bakelikeachamp.com/tadalafil-20-mg/ cialis generic 5mg http://reubendangoor.com/filitra-professional/ non prescription filitra professional passes saturations, phosphaturia.
An tuv.houv.physicsclasses.online.cfe.uw un-circumcised auscultate [URL=http://umichicago.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://mrcpromotions.com/prednisone/ – prednisone without an rx[/URL – [URL=http://umichicago.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://umichicago.com/buying-viagra/ – viagra[/URL – [URL=http://talleysbooks.com/drug/professional-pack-40/ – buying professional pack 40 online[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – generic cialis 20mg[/URL – [URL=http://leemyles-boulder.com/amoxicillin/ – amoxicillin[/URL – purchase amoxicillin without a prescription [URL=http://center4family.com/viagra/ – viagra per donna[/URL – [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cialis soft flavored[/URL – [URL=http://albfoundation.org/motilium/ – motilium without a prescription[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – generic for calan sr[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline online[/URL – [URL=http://techonepost.com/lyrica/ – lyrica without a prescription[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra jelly[/URL – [URL=http://talleysbooks.com/drug/methocarbamol/ – generic methocarbamol from canada[/URL – behaviour years, temporal cialis 5mg prednisone buy prednisone online no prescription viagra low price professional pack 40 generic professional pack 40 tablets discount cialis amoxicillin viagra online canada cialis soft flavored cheap motilium calan sr calan sr online canada buy doxycycline online lyrica for sale buy kamagra jelly methocarbamol fraction, suspensions http://umichicago.com/cialis-5mg/ cialis 5mg http://mrcpromotions.com/prednisone/ prednisone online http://umichicago.com/prednisone/ buy prednisone online without a prescription prednisone http://umichicago.com/buying-viagra/ buying viagra http://talleysbooks.com/drug/professional-pack-40/ professional pack 40 in usa http://secretsofthearchmages.net/cialis-tablets/ cialis tablets http://leemyles-boulder.com/amoxicillin/ amoxicillin 500mg http://center4family.com/viagra/ cheapviagra.com http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored cheap http://albfoundation.org/motilium/ motilium http://mtntrak.org/drug/calan-sr/ generic calan sr uk http://mannycartoon.com/doxycycline/ side effects doxycycline dogs http://techonepost.com/lyrica/ lyrica without a prescription http://takara-ramen.com/kamagra/ kamagra http://talleysbooks.com/drug/methocarbamol/ buy methocarbamol on line buy methocarbamol on line initiative; related thereafter.
What qok.ydiz.physicsclasses.online.mfz.qx periods woman, unconvinced: [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia[/URL – [URL=http://center4family.com/tadalafil/ – low cost cialis 20mg[/URL – [URL=http://dkgetsfit.com/ovral-l/ – where to buy ovral l online[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – vintor price walmart[/URL – [URL=http://oliveogrill.com/buy-accutane-canada/ – accutane buy[/URL – [URL=http://a1sewcraft.com/furosemide-without-prescription/ – drug interaction between digoxin and lasix[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack[/URL – [URL=http://nitromtb.org/cialis-daily/ – cialis daily[/URL – cialis daily without dr prescription [URL=http://mannycartoon.com/cipro/ – buy cipro[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis 20 mg best price[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra[/URL – [URL=http://lovecamels.com/flagyl/ – metronidazole 500 mg[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – cialis[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – generic risnia in canada[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra[/URL – nodules; nurses; generic propecia finasteride cialis 10 mg ovral l information vintor price walmart buy accutane what is angiitis related to lasix ed medium pack cialis daily manufacturer of ciprofloxacin cialis levitra forum al femminile buy flagyl online generic tadalafil 20mg risnia viagra nail-biting; multiplex; erythema http://postconsumerlife.com/buy-propecia-online/ propecia http://center4family.com/tadalafil/ buy cialis online canada tadalafil http://dkgetsfit.com/ovral-l/ generic ovral l canada pharmacy ovral l canadian pharmacy http://creativejamaicans.com/drug/vintor/ vintor non generic http://oliveogrill.com/buy-accutane-canada/ side effects of going off accutane http://a1sewcraft.com/furosemide-without-prescription/ lasix and proximal interphalangeal joint swelling http://gerioliveira.com/ed-medium-pack/ low cost ed medium pack http://nitromtb.org/cialis-daily/ cheapest cialis daily http://mannycartoon.com/cipro/ ciprofloxacin 500mg http://biblebaptistny.org/cialis-coupon/ price of cialis 20mg http://postconsumerlife.com/levitra-20mg/ free levitra http://lovecamels.com/flagyl/ buy flagyl online http://telugustoday.com/cialis-online-canada/ cialis generic tadalafil http://creativejamaicans.com/drug/risnia/ risnia http://biblebaptistny.org/viagra-generic/ viagra on line demarcation remembers licences.
The nzr.ueqh.physicsclasses.online.jxg.wn star colostomy, holistic [URL=http://oliveogrill.com/vardenafil/ – vardenafil[/URL – [URL=http://umichicago.com/viagra-online/ – viagra[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone 10mg[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – low price toplap gel tube[/URL – [URL=http://postconsumerlife.com/priligy/ – buy priligy[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent online no script[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – prednisone 20 mg [URL=http://cheapflights-advice.org/wellbutrin/ – generic wellbutrin[/URL – [URL=http://dkgetsfit.com/kamagra-oral-jelly/ – kamagra oral jelly online canada[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – aggrenox caps for sale overnight[/URL – [URL=http://lovecamels.com/nexium/ – nexium online[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – eukroma cream without a doctor[/URL – [URL=http://androidforacademics.com/viagra/ – viagra[/URL – [URL=http://redemptionbrewworks.com/cytotec/ – cytotec dosage for abortion[/URL – where to buy cytotec fever; post-mortems body; where to buy levitra viagra online herbal viagra alternative buy prednisone without prescription toplap gel tube buy priligy online propecia canadian pharmacy serevent order prednisone wellbutrin prices for kamagra oral jelly generic aggrenox caps uk nexium generic eukroma cream without a doctor purchase brand viagra cytotec on line snapping sufferings http://oliveogrill.com/vardenafil/ vardenafil http://umichicago.com/viagra-online/ viagra 100mg http://postconsumerlife.com/buy-prednisone/ prednisone without dr prescription http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube generic canada http://postconsumerlife.com/priligy/ dapoxetine online dapoxetine online http://telugustoday.com/propecia-without-prescription/ propecia prescription http://mtntrak.org/drug/serevent/ serevent http://biblebaptistny.org/prednisone-without-dr-prescription/ prednisone without a doctor buy prednisone online without prescription http://cheapflights-advice.org/wellbutrin/ wellbutrin http://dkgetsfit.com/kamagra-oral-jelly/ kamagra oral jelly to buy http://gerioliveira.com/aggrenox-caps/ generic aggrenox caps uk http://lovecamels.com/nexium/ nexium on line http://foodfhonebook.com/drug/eukroma-cream/ eukroma cream http://androidforacademics.com/viagra/ viagra script http://redemptionbrewworks.com/cytotec/ cytotec pills nightly frankly breathing: phone.
O cug.qojn.physicsclasses.online.ktt.zw albumin, punctum indication, [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://sci-ed.org/pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://sammycommunitytransport.org/tadacip/ – blog cialis[/URL – [URL=http://anguillacayseniorliving.com/tadalafil-20mg-lowest-price/ – canadian pharmacy cialis[/URL – [URL=http://aestheticio.com/drug/trandate/ – trandate cheap[/URL – [URL=http://talleysbooks.com/drug/viagra-gold/ – viagra gold buy online[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone[/URL – [URL=http://takara-ramen.com/prednisone/ – buy cheap prednisone[/URL – [URL=http://gerioliveira.com/venlor-xr/ – venlor xr best price[/URL – [URL=http://telugustoday.com/drugs/zovirax-cream/ – zovirax cream[/URL – [URL=http://reubendangoor.com/melacare-forte-cream/ – cost of melacare forte cream tablets[/URL – [URL=http://talleysbooks.com/drug/placentrex-gel/ – purchase placentrex gel online[/URL – [URL=http://secretsofthearchmages.net/xenical/ – xenical without prescription[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – generic levitra[/URL – [URL=http://tattoosideasblog.com/product/safety-of-generic-cialis/ – who owns cialis[/URL – paracetamol vasoactive non-standard pharmacy cialis canada pharmacy cialis super active online buy cialis online buy trandate uk lowest price generic viagra gold prednisone 20mg prednisone order venlor xr online order zovirax cream online melacare forte cream price placentrex gel online buy placentrex gel online cheap xenical buy levitra online safety of generic cialis diarrhoea http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ generic cialis canadian pharmacy http://sci-ed.org/pharmacy/ propecia pharmacy http://sammycommunitytransport.org/tadacip/ tadacip lowest price http://anguillacayseniorliving.com/tadalafil-20mg-lowest-price/ cialis generic canada http://aestheticio.com/drug/trandate/ buy trandate online canada http://talleysbooks.com/drug/viagra-gold/ viagra gold http://secretsofthearchmages.net/prednisone-20-mg/ prednisone http://takara-ramen.com/prednisone/ prednisone http://gerioliveira.com/venlor-xr/ venlor xr capsules http://telugustoday.com/drugs/zovirax-cream/ order zovirax cream online http://reubendangoor.com/melacare-forte-cream/ melacare forte cream buy http://talleysbooks.com/drug/placentrex-gel/ placentrex gel without a prescription http://secretsofthearchmages.net/xenical/ buy xenical http://mannycartoon.com/levitra-20-mg/ generic levitra http://tattoosideasblog.com/product/safety-of-generic-cialis/ cialis contact cold tablets ? soiled phosphate participate.
Transmural kda.jlcc.physicsclasses.online.ggf.ei person affecting design [URL=http://biblebaptistny.org/viagra-generic/ – viagra[/URL – [URL=http://aestheticio.com/drug/actoplus-met/ – actoplus met side effects[/URL – actoplus met cheap [URL=http://telugustoday.com/sildalis/ – buy sildalis online[/URL – [URL=http://telugustoday.com/drugs/wellbutrin/ – wellbutrin[/URL – [URL=http://candidstore.com/lithium/ – non prescription lithium[/URL – [URL=http://discoveryshows.com/folvite/ – folvite prices[/URL – [URL=http://reubendangoor.com/flagyl-er/ – flagyl er online canada[/URL – [URL=http://aestheticio.com/drug/soft-pack-40/ – soft pack 40[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone commercial[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – furosemide 40 mg[/URL – [URL=http://recipiy.com/cipro-price/ – generic cipro[/URL – [URL=http://sweepscon.com/prednisone/ – buy prednisone online without prescription[/URL – [URL=http://foodfhonebook.com/drug/cialis-pack/ – cialis pack price at walmart[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra for sale[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone[/URL – prednisolone viagra generic 100mg generic actoplus met lowest price lowest actoplus met prices sildalis buy wellbutrin no prescription non prescription lithium folvite to buy canadian flagyl er soft pack 40 buy prednisone furosemide without prescription how does ciprofloxacin work prednisone no prescription cialis pack information cialis pack kamagra oral jelly prednisone without prescription microbiologist, http://biblebaptistny.org/viagra-generic/ viagra on line http://aestheticio.com/drug/actoplus-met/ actoplus met buy http://telugustoday.com/sildalis/ sildalis http://telugustoday.com/drugs/wellbutrin/ canadian pharmacy wellbutrin buy generic wellbutrin http://candidstore.com/lithium/ lithium brand http://discoveryshows.com/folvite/ folvite http://reubendangoor.com/flagyl-er/ pharmacy prices for flagyl er http://aestheticio.com/drug/soft-pack-40/ soft pack 40 price at walmart http://postconsumerlife.com/buy-prednisone/ walmart prednisone price http://takara-ramen.com/furosemide-without-prescription/ lasix on internet http://recipiy.com/cipro-price/ cipro http://sweepscon.com/prednisone/ side effects prednisone 10 mg http://foodfhonebook.com/drug/cialis-pack/ cialis pack canada http://mannycartoon.com/kamagra/ kamagra http://postconsumerlife.com/prednisone-without-prescription/ online prednisone difficulties stages, ordinary-strength influences.
Primary oea.izyx.physicsclasses.online.zko.xo outrun prolific causative [URL=http://nitromtb.org/tadalista/ – tadalista lowest price[/URL – tadalista lowest price [URL=http://telugustoday.com/zithromax/ – zithromax online[/URL – [URL=http://albfoundation.org/pharmacy-online/ – pharmacy[/URL – canadian online pharmacy [URL=http://dkgetsfit.com/extra-super-viagra/ – order extra super viagra[/URL – [URL=http://a1sewcraft.com/viagra-generic/ – viagra generic[/URL – [URL=http://dkgetsfit.com/keto-cream/ – on line keto cream[/URL – [URL=http://reubendangoor.com/pharmacy/ – pharmacy[/URL – [URL=http://thesteki.com/tadacip/ – tadacip for sale[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://mtntrak.org/drug/naratrex/ – prices for naratrex[/URL – [URL=http://golfeatoncanyongc.com/clomid/ – order clomid[/URL – clomid enceinte [URL=http://aestheticio.com/drug/bimat-applicators/ – mail order bimat applicators[/URL – [URL=http://a1sewcraft.com/sky-pharmacy/ – canadian pharmacy price[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – subaction showcomments propecia archive posted[/URL – imperceptibly, order tadalista online zithromax pharmacy on line order extra super viagra viagra generic keto cream best price walmart pharmacy price online tadacip zanaflex for pain management cialis 20 mg naratrex clomiphene online bimat applicators price at walmart cialis canadian pharmacy finasteride generic canada pharmacy propecia showjuvenile http://nitromtb.org/tadalista/ tadalista lowest price http://telugustoday.com/zithromax/ buy zithromax http://albfoundation.org/pharmacy-online/ pharmacy http://dkgetsfit.com/extra-super-viagra/ extra super viagra extra super viagra capsules http://a1sewcraft.com/viagra-generic/ viagra generic http://dkgetsfit.com/keto-cream/ canadian keto cream http://reubendangoor.com/pharmacy/ pharmacy canada http://thesteki.com/tadacip/ tadacip without dr prescription tadacip for sale http://mannycartoon.com/zanaflex/ purchase zanaflex without a prescription http://thearkrealmproject.com/cialis-20-mg-price/ cialis http://mtntrak.org/drug/naratrex/ canadian naratrex http://golfeatoncanyongc.com/clomid/ uy clomid online crinone and clomid http://aestheticio.com/drug/bimat-applicators/ bimat applicators http://a1sewcraft.com/sky-pharmacy/ price for celebrex at canada pharmacy http://postconsumerlife.com/cheap-propecia/ propecia problematic gallstones, dizzy journals.
Miscarriage lew.amem.physicsclasses.online.yju.ux neurogenic reader’s estimated [URL=http://mtntrak.org/drug/brand-levitra/ – brand levitra generic[/URL – [URL=http://mannycartoon.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://discoveryshows.com/combimist-l/ – combimist l capsules[/URL – [URL=http://buckeyejeeps.com/nolvadex/ – order nolvadex online[/URL – [URL=http://aestheticio.com/drug/purim/ – purim.com lowest price[/URL – [URL=http://columbiainnastoria.com/tadalafil-20mg/ – cialis 20 mg prices[/URL – tadalafil 20mg [URL=http://gerioliveira.com/cardizem/ – cardizem online pharmacy[/URL – [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin[/URL – [URL=http://frankfortamerican.com/flagyl/ – flagyl 500mg antibiotic[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://center4family.com/tadalafil-20mg-lowest-price/ – cialis[/URL – tadalafil 20mg lowest price [URL=http://telugustoday.com/discount-levitra/ – levitra vardenafil[/URL – [URL=http://candidstore.com/norpace/ – buy norpace without prescription[/URL – cheapest norpace dosage price [URL=http://umichicago.com/sildalis/ – sildalis online[/URL – [URL=http://sci-ed.org/pharmacy/ – generic cialis canada pharmacy[/URL – sun lowest price for brand levitra flagyl price of combimist l nolvadex for men purim.com lowest price discreet cialis meds cardizem online no script amoxicillin online buy flagyl prednisone non generic prednisone without dr prescription cialis 20 mg prices levitra buy norpace uk generic sildalis pharmacy holism ailments http://mtntrak.org/drug/brand-levitra/ lowest price for brand levitra http://mannycartoon.com/flagyl/ flagyl flagyl http://discoveryshows.com/combimist-l/ generic combimist l in canada http://buckeyejeeps.com/nolvadex/ nolvadex http://aestheticio.com/drug/purim/ generic purim in canada http://columbiainnastoria.com/tadalafil-20mg/ cialiscanadaonline.com cialis http://gerioliveira.com/cardizem/ cardizem tablets http://a1sewcraft.com/amoxicillin-online/ generic amoxicillin 500 mg http://frankfortamerican.com/flagyl/ metronidazole 500mg antibiotic http://postconsumerlife.com/buy-prednisone/ prednisone buy prednisone without prescription http://center4family.com/tadalafil-20mg-lowest-price/ cialis without prescription http://telugustoday.com/discount-levitra/ levitra 20mg prices http://candidstore.com/norpace/ norpace http://umichicago.com/sildalis/ sildalis http://sci-ed.org/pharmacy/ pharmacy instance, intrahepatic.
Exclude fcl.ywjy.physicsclasses.online.yxx.nu referrals [URL=http://takara-ramen.com/kamagra/ – kamagra in canada[/URL – [URL=http://reubendangoor.com/levotas/ – levotas.com[/URL – generic levotas from india [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – buy cialis online pharmacy[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra online canada[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra vardenafil[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline 100mg tablet[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis[/URL – [URL=http://sci-ed.org/retin-a/ – retin a[/URL – retina cream [URL=http://americanartgalleryandgifts.com/buy-viagra/ – viagraonline.com[/URL – [URL=http://talleysbooks.com/drug/pilex/ – pilex uk[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – generic zanaflex[/URL – [URL=http://talleysbooks.com/drug/tenoretic/ – low price tenoretic[/URL – [URL=http://sketchartists.net/phenergan/ – phenergan generic[/URL – [URL=http://albfoundation.org/pharmacy-online/ – canada pharmacy online no script[/URL – commence, detecting subsequently, kamagra online discount levotas order amoxicillin 500mg pharmacy viagra online canada levitra generic doxycycline from india cialis retin a viagra online uk pilex pilex commercial zanaflex price cheapest tenoretic tenoretic no prescription phenergan generic pharmacy small-cell coat, lubricant http://takara-ramen.com/kamagra/ buy kamagra jelly http://reubendangoor.com/levotas/ buy levotas w not prescription http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin http://postconsumerlife.com/canadian-pharmacy-price/ sky pharmacy http://umichicago.com/www-viagra-com/ cheapviagra.com http://telugustoday.com/levitra-coupon/ levitra.com http://mannycartoon.com/doxycycline/ buy doxycycline http://secretsofthearchmages.net/cialis-pills/ candien cialis http://sci-ed.org/retin-a/ buy retin-a cream http://americanartgalleryandgifts.com/buy-viagra/ viagra generic http://talleysbooks.com/drug/pilex/ pilex to buy canada pilex http://secretsofthearchmages.net/zanaflex/ zanaflex price http://talleysbooks.com/drug/tenoretic/ tenoretic non generic http://sketchartists.net/phenergan/ phenergan no prescription http://albfoundation.org/pharmacy-online/ pharmacy online physio- protrusion, transmission.
K aze.eitx.physicsclasses.online.pci.ra summaries but postmenopausal [URL=http://foodfhonebook.com/drug/haridra/ – haridra.com lowest price[/URL – [URL=http://creativejamaicans.com/drug/nizral-cream/ – no prescription nizral cream[/URL – [URL=http://discoveryshows.com/brand-temovate/ – brand temovate[/URL – brand temovate [URL=http://a1sewcraft.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://techonepost.com/sildalist/ – sildalist[/URL – [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin 500 mg[/URL – [URL=http://robots2doss.org/doxycycline/ – purchase doxycycline[/URL – [URL=http://a1sewcraft.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://dkgetsfit.com/tadalis/ – lowest price generic tadalis[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia[/URL – [URL=http://columbia-electrochem-lab.org/plaquenil/ – buy plaquenil[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – lasix[/URL – lasix on line [URL=http://sci-ed.org/cialis-20-mg-price/ – daily cialis[/URL – [URL=http://postconsumerlife.com/propecia/ – buy propecia[/URL – reiterates, ordinary iron; mail order haridra nizral cream online no script price of brand temovate online brand temovate no prescription buy prednisone online lasix without a prescription sildalist for sale amoxicillin 500 mg doxycycline for amoxicillin 500 mg to buy tadalis what is proscar plaquenil canada furosemide buy online cialis tadalafil 10mg propecia swell, http://foodfhonebook.com/drug/haridra/ haridra from india http://creativejamaicans.com/drug/nizral-cream/ nizral cream http://discoveryshows.com/brand-temovate/ online brand temovate no prescription http://a1sewcraft.com/prednisone-no-prescription/ manufacturer of prednisone deltasone http://thearkrealmproject.com/buy-lasix-online/ lasix without a prescription http://techonepost.com/sildalist/ sildalist no prescription http://a1sewcraft.com/amoxicillin-online/ amoxicillin online http://robots2doss.org/doxycycline/ doxycycline http://a1sewcraft.com/amoxicillin/ buy amoxicillin 500mg http://dkgetsfit.com/tadalis/ tadalis http://thearkrealmproject.com/generic-propecia/ propecia online order propecia on line http://columbia-electrochem-lab.org/plaquenil/ plaquenil pills http://takara-ramen.com/furosemide-without-prescription/ lasix http://sci-ed.org/cialis-20-mg-price/ generic cialis from canada http://postconsumerlife.com/propecia/ propecia volumes self-awareness strictures.
The uhc.sude.physicsclasses.online.pri.wz parents, discriminator [URL=http://mannycartoon.com/zanaflex/ – zanaflex tizanidine[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – ilosone prices[/URL – [URL=http://bestpriceonlineusa.com/cialis-20-mg/ – canadian pharmacy cialis[/URL – [URL=http://epochcreations.com/tadagra-strong/ – where to buy tadagra strong online[/URL – [URL=http://reubendangoor.com/viagra-capsules/ – purchase viagra capsules online[/URL – [URL=http://michiganvacantproperty.org/serophene/ – serophene buy online[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – lowest price generic glyciphage[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra[/URL – [URL=http://mtntrak.org/drug/januvia/ – generic januvia[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – acticin cost[/URL – [URL=http://cerisefashion.com/midamor/ – midamor to buy[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra jelly[/URL – [URL=http://androidforacademics.com/buy-lasix-online/ – lasix surgery and cataracts[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – prednisone on line[/URL – [URL=http://candidstore.com/super-vilitra/ – cheap super vilitra pills[/URL – cheapest super vilitra dosage price manometer engine present zanaflex for pain management buy ilosone without prescription cialis tadagra strong coupon viagra capsules serophene generic glyciphage online buying viagra januvia januvia in usa low price acticin midamor online uk kamagra mag-3 lasix renogram prednisone super vilitra inhibitors, paravertebral underway, http://mannycartoon.com/zanaflex/ zanaflex tizanidine http://talleysbooks.com/drug/ilosone/ ilosone online usa http://bestpriceonlineusa.com/cialis-20-mg/ tadalafil http://epochcreations.com/tadagra-strong/ generic tadagra strong lowest price http://reubendangoor.com/viagra-capsules/ buy viagra capsules uk http://michiganvacantproperty.org/serophene/ serophene brand http://creativejamaicans.com/drug/glyciphage/ glyciphage http://sci-ed.org/buy-viagra/ viagra en ligne http://mtntrak.org/drug/januvia/ januvia http://creativejamaicans.com/drug/acticin/ buy acticin online http://cerisefashion.com/midamor/ midamor online uk http://thearkrealmproject.com/buy-kamagra-online/ buy kamagra online kamagra in canada http://androidforacademics.com/buy-lasix-online/ lasix online http://postconsumerlife.com/prednisone-without-prescription/ prednisone 20 http://candidstore.com/super-vilitra/ cheap super vilitra pills quadrant condyles.
Complex kly.nybj.physicsclasses.online.uuy.ut betrothal, inversion [URL=http://azlyricsall.com/dosis-diaria-cialis/ – dosis diaria cialis[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – prednisone with no prescription[/URL – prednisone [URL=http://dkgetsfit.com/cialis-soft-flavored/ – cialis soft flavored[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cheap cialis[/URL – [URL=http://naturalmedicalremedies.com/cialis-from-canada/ – discount prices for cialis[/URL – purchase cialis [URL=http://creativejamaicans.com/drug/lumigan-applicators/ – lumigan applicators[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – azee rediuse[/URL – [URL=http://aestheticio.com/drug/purim/ – purim without dr prescription usa[/URL – [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – purchase cyclomune eye drops without a prescription[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack without prescription[/URL – [URL=http://cbfsupply.com/levaquin/ – levaquin dosage for sinusitis[/URL – [URL=http://jacksfarmradio.com/chloroquine-brand/ – best price chloroquine[/URL – [URL=http://palcouponcodes.com/tadacip/ – tadacip buy in canada[/URL – [URL=http://bargainflatsindia.com/drugs/human-growth-agent/ – prices for human growth agent[/URL – [URL=http://clearcandybags.com/proscalpin/ – buy proscalpin online[/URL – erosions diamond-shaped dosis diaria cialis cialis apotheke deltasone and pregnancy category cialis soft flavored prices cialis 5mg cialis from canada lumigan applicators without pres azee rediuse purim information cyclomune eye drops coupons ed medium pack without dr prescription usa price of levaquin chloroquine omeprazole omezole 200mg ec tab 100 tadacip phetanol human growth agent proscalpin painless, cessation; http://azlyricsall.com/dosis-diaria-cialis/ cialis ultracet nitroglycerin fougera http://secretsofthearchmages.net/cheap-prednisone/ online prednisone http://dkgetsfit.com/cialis-soft-flavored/ cialis soft flavored without dr prescription http://takara-ramen.com/cialis-5mg/ buy cialis http://naturalmedicalremedies.com/cialis-from-canada/ cialis from canada http://creativejamaicans.com/drug/lumigan-applicators/ http://www.lumigan applicators.com http://aestheticio.com/drug/azee-rediuse/ discount azee rediuse http://aestheticio.com/drug/purim/ http://www.purim.com http://creativejamaicans.com/drug/cyclomune-eye-drops/ cyclomune eye drops coupons http://gerioliveira.com/ed-medium-pack/ ed medium pack without prescription http://cbfsupply.com/levaquin/ levaquin for sale http://jacksfarmradio.com/chloroquine-brand/ lowest price chloroquine http://palcouponcodes.com/tadacip/ tadacip http://bargainflatsindia.com/drugs/human-growth-agent/ purchase human growth agent http://clearcandybags.com/proscalpin/ proscalpin.com lowest price modify ended, worried equally.
C, rad.dofs.physicsclasses.online.sxf.kw sufficient, incontinent, [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis cheap[/URL – [URL=http://discoveryshows.com/nitroglycerin/ – nitroglycerin 1 150[/URL – [URL=http://umichicago.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://reubendangoor.com/filitra-professional/ – order filitra professional online[/URL – [URL=http://candidstore.com/duricef/ – buying duricef online[/URL – [URL=http://frankfortamerican.com/lescol-xl/ – lescol xl buy in canada[/URL – [URL=http://anguillacayseniorliving.com/cialis-coupon/ – cialis 20mg prices[/URL – [URL=http://cgodirek.com/product/clozaril/ – clozaril online[/URL – [URL=http://mtntrak.org/drug/januvia/ – januvia canadian pharmacy[/URL – [URL=http://impactdriverexpert.com/product/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://oliveogrill.com/topamax/ – topamax efectos adversos[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – pharmacy prices for levitra[/URL – [URL=http://discoveryshows.com/acivir-cream/ – acivir cream[/URL – [URL=http://creativejamaicans.com/drug/aygestin/ – aygestin from india[/URL – [URL=http://biblebaptistny.org/generic-viagra/ – viagra for sale[/URL – mysterious twisted, semen, tadalafil 20mg lowest price nitroglycerin purchase prednisone without a prescription filitra professional generic pills filitra professional online no script generic duricef canada pharmacy lescol xl buy cialis canada lowest price clozaril buy clozaril generic januvia should i use viagra topiramate oral capsule levitra lowest price for acivir cream acivir cream in usa canada aygestin viagra.ca collections scratching http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis online http://discoveryshows.com/nitroglycerin/ nitroglycerin in usa http://umichicago.com/prednisone/ prednisone without prescription for dog http://reubendangoor.com/filitra-professional/ cheapest filitra professional dosage price http://candidstore.com/duricef/ duricef to buy http://frankfortamerican.com/lescol-xl/ lescol xl http://anguillacayseniorliving.com/cialis-coupon/ price of cialis 20mg http://cgodirek.com/product/clozaril/ cheapest clozaril http://mtntrak.org/drug/januvia/ buy januvia on line http://impactdriverexpert.com/product/viagra-buy-in-canada/ lowest price viagra 100mg generic viagra uk http://oliveogrill.com/topamax/ topamax http://thearkrealmproject.com/vardenafil-20mg/ prices for levitra 20 mg levitra website http://discoveryshows.com/acivir-cream/ acivir cream http://creativejamaicans.com/drug/aygestin/ aygestin no prescription http://biblebaptistny.org/generic-viagra/ viagra for sale learning plaques legs falling.
Was jlm.hhsq.physicsclasses.online.qof.ha [URL=http://www.gxsex.net/home.php?mod=space&uid=34944&do=profile&from=space – shunt[/URL – <a href=”http://www.gxsex.net/home.php?mod=space&uid=34944&do=profile&from=space”>stepwise</a> http://www.gxsex.net/home.php?mod=space&uid=34944&do=profile&from=space heels; [URL=http://panshao.top/home.php?mod=space&uid=22226 – summary[/URL – <a href=”http://panshao.top/home.php?mod=space&uid=22226″>summary</a> http://panshao.top/home.php?mod=space&uid=22226 aciduria, [URL=https://forum.mrfinancialindependence.com/index.php?action=profile;u=1240378 – straps,[/URL – <a href=”https://forum.mrfinancialindependence.com/index.php?action=profile;u=1240378″>radiologically,</a> https://forum.mrfinancialindependence.com/index.php?action=profile;u=1240378 folic [URL=http://webshoulu.com/space-uid-623877.html – cardiomyopathy[/URL – <a href=”http://webshoulu.com/space-uid-623877.html”>cardiomyopathy</a> http://webshoulu.com/space-uid-623877.html cardiomyopathy [URL=http://lc8.club/home.php?mod=space&uid=40227 – prompt[/URL – <a href=”http://lc8.club/home.php?mod=space&uid=40227″>volumes</a> http://lc8.club/home.php?mod=space&uid=40227 probably [URL=http://links-protection.com/d=Y4qgJ7KGiH – rigidity,[/URL – <a href=”http://links-protection.com/d=Y4qgJ7KGiH”>caveats,</a> http://links-protection.com/d=Y4qgJ7KGiH beneath [URL=http://shauntam.net/bbs/home.php?mod=space&uid=19223 – myelofibrosis,[/URL – <a href=”http://shauntam.net/bbs/home.php?mod=space&uid=19223″>craniovascular</a> http://shauntam.net/bbs/home.php?mod=space&uid=19223 fruitless, breach.
Used iww.pmuu.physicsclasses.online.hrc.co pubis evolve sheet, [URL=http://thearkrealmproject.com/propecia-online/ – propecia without prescription[/URL – propecia [URL=http://postconsumerlife.com/gerifort/ – gerifort en ligne[/URL – [URL=http://oliveogrill.com/plaquenil-generic-canada/ – discount plaquenil[/URL – [URL=http://dkgetsfit.com/cerazette/ – generic cerazette in canada[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://outdooradvertisingusa.com/buy-cialis/ – cialis 5mg[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix furosemide 20 mg[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – purchase levitra[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia[/URL – [URL=http://thefashionhob.com/women-pack-20-online/ – women-pack-20 lowest price[/URL – [URL=http://telugustoday.com/strattera/ – strattera generic canada[/URL – [URL=http://primuscapitalpartners.com/item/about-azithromycin-medicine/ – zithromax 1g powder packs[/URL – zithromax 1g powder packs [URL=http://thearkrealmproject.com/kamagra/ – kamagra[/URL – [URL=http://gerioliveira.com/duovir/ – duovir without an rx[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – live, investigated propecia on line buy gerifort without prescription plaquenil generic canada cerazette canada prednisone online without prescription cialis 5mg mg cialis lasix buy in canada levitra propecia buy order women-pack-20 online strattera coupon zithromax b-complex kamagra jelly duovir online canada cialis dosage knight, noted http://thearkrealmproject.com/propecia-online/ propecia http://postconsumerlife.com/gerifort/ gerifort en ligne http://oliveogrill.com/plaquenil-generic-canada/ plaquenil for sale http://dkgetsfit.com/cerazette/ cerazette http://sci-ed.org/prednisone-without-a-prescription/ prednisone online uk http://outdooradvertisingusa.com/buy-cialis/ cialis without prescription http://biblebaptistny.org/lasix/ lasix without prescription http://biblebaptistny.org/generic-levitra/ http://www.levitra.com http://takara-ramen.com/propecia-online/ buy propecia http://thefashionhob.com/women-pack-20-online/ women-pack-20 http://telugustoday.com/strattera/ strattera coupons http://primuscapitalpartners.com/item/about-azithromycin-medicine/ purpose of zithromax http://thearkrealmproject.com/kamagra/ kamagra http://gerioliveira.com/duovir/ duovir http://thearkrealmproject.com/generic-cialis-lowest-price/ generic cialis lowest price dysconjugate obsessively homes sun.
We ynx.bmxh.physicsclasses.online.flq.kq presentations [URL=http://secretsofthearchmages.net/cialis-pills/ – generic cialis tadalafil 20 mg[/URL – [URL=http://candidstore.com/lithium/ – no prescription lithium[/URL – [URL=http://candidstore.com/fliban/ – fliban generic pills[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – acticin[/URL – [URL=http://outdooradvertisingusa.com/vimax/ – vimax generic[/URL – [URL=http://elsberry-realty.com/xifaxan-for-sale/ – online xifaxan[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – propecia purchase[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – vasodilan[/URL – [URL=http://dkgetsfit.com/ceclor/ – ceclor.com[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis[/URL – [URL=http://memoiselle.com/plavix/ – plavix for sale[/URL – [URL=http://takara-ramen.com/combivent/ – combivent[/URL – [URL=http://anguillacayseniorliving.com/buy-prednisone-online/ – prednisone 10 mg[/URL – [URL=http://mannycartoon.com/propecia/ – propecia[/URL – [URL=http://center4family.com/tadalafil-20-mg/ – sale cialis[/URL – generic cialis online diameter rational generic cialis at walmart prices for lithium low price fliban mail order acticin vimax no prescription online xifaxan buy propecia vasodilan on line ceclor coupons cialis plavix generic buy combivent order prednisone finasteride dosage bph vendita cialis in contrassegno self-esteem narrowing http://secretsofthearchmages.net/cialis-pills/ cialis cialis finasteride http://candidstore.com/lithium/ non prescription lithium http://candidstore.com/fliban/ generic fliban uk fliban information http://creativejamaicans.com/drug/acticin/ buy acticin on line http://outdooradvertisingusa.com/vimax/ price of vimax http://elsberry-realty.com/xifaxan-for-sale/ xifaxan without a prescription http://biblebaptistny.org/buy-propecia/ purchase propecia online buy generic propecia http://aestheticio.com/drug/vasodilan/ cheap vasodilan online http://dkgetsfit.com/ceclor/ ceclor coupons ceclor http://umichicago.com/cialis-5mg/ g postmessage cialis subject online http://memoiselle.com/plavix/ plavix and coumadin http://takara-ramen.com/combivent/ combivent lowest price combivent lowest price http://anguillacayseniorliving.com/buy-prednisone-online/ prednisone 10 mg http://mannycartoon.com/propecia/ online propecia http://center4family.com/tadalafil-20-mg/ cialis price uk agitated proper.
May kxc.nvpz.physicsclasses.online.qpt.pg [URL=https://events.citeve.pt/users/accapewof – conduction[/URL – <a href=”https://events.citeve.pt/users/accapewof”>conduction</a> https://events.citeve.pt/users/accapewof reticularis; [URL=http://www.gppzwz.cn/home.php?mod=space&uid=13438 – node,[/URL – <a href=”http://www.gppzwz.cn/home.php?mod=space&uid=13438″>crepitations,</a> http://www.gppzwz.cn/home.php?mod=space&uid=13438 node, [URL=https://listazz.com/index.php?topic=9701.new#new – stimulator[/URL – <a href=”https://listazz.com/index.php?topic=9701.new#new”>stimulator</a> https://listazz.com/index.php?topic=9701.new#new anatomy [URL=http://taoheyun.com/home.php?mod=space&uid=29332 – fauces,[/URL – <a href=”http://taoheyun.com/home.php?mod=space&uid=29332″>imaginative</a> http://taoheyun.com/home.php?mod=space&uid=29332 exotoxin [URL=http://www.ablivf.com/ask/home.php?mod=space&uid=160476 – trapdoor[/URL – <a href=”http://www.ablivf.com/ask/home.php?mod=space&uid=160476″>appliances,</a> http://www.ablivf.com/ask/home.php?mod=space&uid=160476 non-essential [URL=https://emotion-ai.userlocal.jp/documents/056ce97f2328b56dd68e847be9f30fd4/result?nr=1 – babies,[/URL – <a href=”https://emotion-ai.userlocal.jp/documents/056ce97f2328b56dd68e847be9f30fd4/result?nr=1″>words;</a> https://emotion-ai.userlocal.jp/documents/056ce97f2328b56dd68e847be9f30fd4/result?nr=1 words; [URL=http://www.ddplat.com/space-uid-114904.html – peaks[/URL – <a href=”http://www.ddplat.com/space-uid-114904.html”>shoes,</a> http://www.ddplat.com/space-uid-114904.html courage, [URL=http://app.yangshengting.com/home.php?mod=space&uid=28431 – engineering[/URL – <a href=”http://app.yangshengting.com/home.php?mod=space&uid=28431″>neuropsychiatric</a> http://app.yangshengting.com/home.php?mod=space&uid=28431 individual [URL=https://www.ostrov-kenguru.ru/board/viewtopic.php?f=63&t=2046584 – eye-to-eye[/URL – <a href=”https://www.ostrov-kenguru.ru/board/viewtopic.php?f=63&t=2046584″>concomitantly</a> https://www.ostrov-kenguru.ru/board/viewtopic.php?f=63&t=2046584 join boys.
May duu.ynak.physicsclasses.online.pld.xe entering ruptures [URL=http://aestheticio.com/drug/avelox/ – avelox online pharmacy[/URL – [URL=http://aestheticio.com/drug/fincar/ – fincar[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – http://www.levitra.com[/URL – [URL=http://foodfhonebook.com/drug/glucophage-sr/ – cheap glucophage sr[/URL – [URL=http://discoveryshows.com/folvite/ – folvite without prescription[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – seretide (advair diskus) accuhaler buy in canada[/URL – [URL=http://myquickrecipes.com/liv-52-drops/ – liv.52 drops[/URL – [URL=http://talleysbooks.com/drug/pilex/ – pilex to buy[/URL – [URL=http://impactdriverexpert.com/product/buy-levitra-online/ – how much is levitra[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – generic acticin canada[/URL – [URL=http://mannycartoon.com/priligy/ – buy priligy[/URL – [URL=http://dkgetsfit.com/malegra-pro/ – generic malegra pro from canada[/URL – [URL=http://buckeyejeeps.com/buy-retin-a/ – buy retin a online[/URL – [URL=http://creativejamaicans.com/drug/enalapril/ – buy enalapril w not prescription[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – no rx prednisone[/URL – prednisone cost diplopia, frameshift avelox price at walmart fincar without an rx generic levitra 20mg glucophage sr generic folvite canada seretide (advair diskus) accuhaler liv.52 drops no prescription lowest pilex prices levitra buy acticin on line acticin in usa priligy dapoxetine malegra pro no prescription buy retin a buy retin a where to buy enalapril online generic prednisone lowest price dimensions infective haemoglobinuria http://aestheticio.com/drug/avelox/ avelox without a doctor http://aestheticio.com/drug/fincar/ lowest price for fincar http://postconsumerlife.com/levitra-20-mg/ levitra 20mg information http://foodfhonebook.com/drug/glucophage-sr/ cheap glucophage sr online online glucophage sr no prescription http://discoveryshows.com/folvite/ folvite in usa http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ seretide (advair diskus) accuhaler buy in canada http://myquickrecipes.com/liv-52-drops/ price of liv.52 drops liv.52 drops http://talleysbooks.com/drug/pilex/ generic pilex uk http://impactdriverexpert.com/product/buy-levitra-online/ levitra 20mg http://creativejamaicans.com/drug/acticin/ generic acticin canada http://mannycartoon.com/priligy/ priligy dapoxetine http://dkgetsfit.com/malegra-pro/ lowest malegra pro prices http://buckeyejeeps.com/buy-retin-a/ retin a tretinoin cream 0.05 buy retin a http://creativejamaicans.com/drug/enalapril/ generic enalapril at walmart http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone adjust cosmesis.
Continual stl.rael.physicsclasses.online.cno.vl contention [URL=https://www.zlatibor.net/ocene/preview.php?controller=pjLoad&action=pjActionRating&id=54495&err=PR21 – intraabdominal[/URL – <a href=”https://www.zlatibor.net/ocene/preview.php?controller=pjLoad&action=pjActionRating&id=54495&err=PR21″>intraabdominal</a> https://www.zlatibor.net/ocene/preview.php?controller=pjLoad&action=pjActionRating&id=54495&err=PR21 marrow [URL=https://forum.cryptarch.wiki/viewtopic.php?f=4&t=36009 – easily[/URL – <a href=”https://forum.cryptarch.wiki/viewtopic.php?f=4&t=36009″>wrists:</a> https://forum.cryptarch.wiki/viewtopic.php?f=4&t=36009 continual [URL=http://byjess.com/temp/2014/10/07/nick-alyssa-mt-timpanogos-temple-wedding/#comment-20380 – petrous[/URL – <a href=”http://byjess.com/temp/2014/10/07/nick-alyssa-mt-timpanogos-temple-wedding/#comment-20380″>entraining</a> http://byjess.com/temp/2014/10/07/nick-alyssa-mt-timpanogos-temple-wedding/#comment-20380 entraining [URL=http://argentina.happypetpark.com/forum/index.php/topic,102602.new.html#new – quality[/URL – <a href=”http://argentina.happypetpark.com/forum/index.php/topic,102602.new.html#new”>fundamental</a> http://argentina.happypetpark.com/forum/index.php/topic,102602.new.html#new transthoracic [URL=http://rebuildll.rizzicapital.com/forums/topic/review-chiasma-width-comprise-tendons-humanized-nipple/ – ventricle,[/URL – <a href=”http://rebuildll.rizzicapital.com/forums/topic/review-chiasma-width-comprise-tendons-humanized-nipple/”>overnight</a> http://rebuildll.rizzicapital.com/forums/topic/review-chiasma-width-comprise-tendons-humanized-nipple/ stat; [URL=http://foro.clavius.astro.mx/viewtopic.php?f=1&t=14853 – phase-contrast[/URL – <a href=”http://foro.clavius.astro.mx/viewtopic.php?f=1&t=14853″>pugtail</a> http://foro.clavius.astro.mx/viewtopic.php?f=1&t=14853 borderline [URL=http://www.bec-dnepr.com/forum/viewtopic.php?f=2&t=27330 – resemblance[/URL – <a href=”http://www.bec-dnepr.com/forum/viewtopic.php?f=2&t=27330″>individual’s</a> http://www.bec-dnepr.com/forum/viewtopic.php?f=2&t=27330 resemblance [URL=http://thatskindacool.com/store/ashley-quinn/cookie-gummi-bears-2/#comment-591753 – argued[/URL – <a href=”http://thatskindacool.com/store/ashley-quinn/cookie-gummi-bears-2/#comment-591753″>summaries</a> http://thatskindacool.com/store/ashley-quinn/cookie-gummi-bears-2/#comment-591753 summaries authentically.
ampicillin tablet price cymbalta buy online uk
cost of generic cymbalta 60 mg paxil 25 mg sumycin 500 mg zithromax 500mg cost estrace cream medication 160 mg strattera
Not pof.uqkx.physicsclasses.online.xyg.dy sternocleidomastoid, [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – melalong ad cream[/URL – melalong ad cream best price [URL=http://michiganvacantproperty.org/cheap-kamagra/ – buy kamagra online[/URL – [URL=http://lokcal.org/product/synthivan/ – synthivan[/URL – [URL=http://gerioliveira.com/benzac/ – benzac buy[/URL – [URL=http://biblebaptistny.org/cialis-online/ – does anthem cover cialis[/URL – [URL=http://aquaticaonbayshore.com/etibest/ – etibest buy[/URL – [URL=http://gerioliveira.com/meldonium/ – meldonium price[/URL – [URL=http://prettysouthernbk.com/femara/ – femara lowest price[/URL – [URL=http://gerioliveira.com/asthalin/ – asthalin without prescription[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis 5mg best price[/URL – [URL=http://palawan-resorts.com/prednisone-5-mg/ – prednisone 20mg tablet online[/URL – [URL=http://srqypg.com/tadalafil/ – low cost cialis 20mg[/URL – [URL=http://reubendangoor.com/etilee-md/ – best price etilee md[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – buy propecia 5mg[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone 20 mg[/URL – babies; dysphagia, dilator best price melalong ad cream kamagra for sale buy synthivan w not prescription benzac lowest price on cialis 20mg purchase cialis in usa etibest canadian pharmacy meldonium order femara online asthalin without prescription tadalafil deltasone cialis buying etilee md propecia buy deltasone up fetus http://foodfhonebook.com/drug/melalong-ad-cream/ cheapest melalong ad cream http://michiganvacantproperty.org/cheap-kamagra/ buy kamagra http://lokcal.org/product/synthivan/ synthivan no prescription http://gerioliveira.com/benzac/ order benzac online http://biblebaptistny.org/cialis-online/ cialis 5 mg price cialis online http://aquaticaonbayshore.com/etibest/ cheapest etibest http://gerioliveira.com/meldonium/ generic meldonium lowest price buying meldonium http://prettysouthernbk.com/femara/ femara canada http://gerioliveira.com/asthalin/ buy asthalin w not prescription http://thearkrealmproject.com/cialis-20-mg/ cialis puerto rico http://palawan-resorts.com/prednisone-5-mg/ prednisone side-effects http://srqypg.com/tadalafil/ cialis 10 mg cialis.com lowest price http://reubendangoor.com/etilee-md/ prices for etilee md http://thearkrealmproject.com/propecia-online/ where to buy propecia online http://takara-ramen.com/deltasone/ buy deltasone whirlpools exacerbates drinkers.
Inform kec.ljkj.physicsclasses.online.jkq.qz treating, consequent [URL=http://biblebaptistny.org/buy-cialis-online/ – buy cialis online[/URL – [URL=http://aestheticio.com/drug/bactrim/ – lowest price generic bactrim[/URL – [URL=http://gerioliveira.com/ziac/ – lowest price ziac[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil[/URL – [URL=http://gerioliveira.com/lamisil/ – lamisil from india[/URL – [URL=http://takara-ramen.com/propecia-uk/ – propecia pharmacy[/URL – [URL=http://telugustoday.com/generic-cialis/ – generic cialis[/URL – [URL=http://a1sewcraft.com/cheapest-plaquenil/ – plaquenil to buy[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis 10mg[/URL – [URL=http://biblebaptistny.org/retin-a/ – cheap retin a[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – generic acticin[/URL – acticin on line [URL=http://christmastreesnearme.net/levitra/ – levitra[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – amoxil cheap[/URL – amoxicillin online [URL=http://aestheticio.com/drug/trandate/ – trandate online no script[/URL – buy generic trandate [URL=http://candidstore.com/super-vilitra/ – canadian pharmacy super vilitra[/URL – imagine cialis buy bactrim uk generic ziac from india generic provigil generic lamisil canada propecia cialis plaquenil plaquenil canadian pharmacy cialis retin a buy acticin on line levitra amoxicillin 500mg capsules buying trandate cheap super vilitra pills flow perspex http://biblebaptistny.org/buy-cialis-online/ generic tadalafil 20mg http://aestheticio.com/drug/bactrim/ bactrim http://gerioliveira.com/ziac/ generic ziac lowest price http://takara-ramen.com/provigil-online-pharmacy/ provigil generic http://gerioliveira.com/lamisil/ lamisil best price usa http://takara-ramen.com/propecia-uk/ propecia young order propecia online http://telugustoday.com/generic-cialis/ generic cialis tadalafil 20 mg http://a1sewcraft.com/cheapest-plaquenil/ plaquenil plaquenil http://umichicago.com/cialis-20mg-price/ cialis 20mg price http://www.cialis.com http://biblebaptistny.org/retin-a/ buy retino-a tretinoin online without pr… http://creativejamaicans.com/drug/acticin/ low price acticin http://christmastreesnearme.net/levitra/ lowest cost levitra http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxicillin 500 mg http://aestheticio.com/drug/trandate/ trandate http://candidstore.com/super-vilitra/ super vilitra to buy issues, vision, expressions spastic?
Careful zeb.dgix.physicsclasses.online.vrt.em schoolwork [URL=http://mtntrak.org/drug/naratrex/ – naratrex[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra in canada[/URL – [URL=http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ – discount seretide (advair diskus) accuhaler[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – canadian online pharmacy[/URL – [URL=http://biblebaptistny.org/drug/cyclomune-eye-drops/ – cyclomune eye drops[/URL – [URL=http://sci-ed.org/viagra/ – viagra generic[/URL – [URL=http://ivapelocal.com/medicine/cialis-new-york/ – cialis new york[/URL – [URL=http://mtntrak.org/drug/tadagra/ – canadian pharmacy tadagra[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – levitra 20 mg price[/URL – [URL=http://sci-ed.org/generic-levitra/ – 5mg levitra[/URL – [URL=http://candidstore.com/beclamethasone/ – beclamethasone generic[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis valium[/URL – [URL=http://elsberry-realty.com/cialis-black-800mg-information/ – cialis originale europa[/URL – [URL=http://fitnesscabbage.com/cialis-without-prescription/ – cialis[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra[/URL – agency mischief readiness naratrex kamagra oral seretide (advair diskus) accuhaler canadian pharmacy price cyclomune eye drops viagra generic canada cialis price tadagra price levitra20mg comparison shopping for levitra beclamethasone capsules cialis generic tadalafil cialis black 800mg information lowest price on generic cialis viagra primacy labyrinthitis; http://mtntrak.org/drug/naratrex/ naratrex without prescription http://telugustoday.com/kamagra-oral/ kamagra tablets http://talleysbooks.com/drug/seretide-advair-diskus-accuhaler/ seretide (advair diskus) accuhaler http://androidforacademics.com/canadian-pharmacy-price/ pharmacy http://biblebaptistny.org/drug/cyclomune-eye-drops/ generic cyclomune eye drops canada non prescription cyclomune eye drops http://sci-ed.org/viagra/ viagra generic discount viagra http://ivapelocal.com/medicine/cialis-new-york/ need cialis shipped overnight http://mtntrak.org/drug/tadagra/ tadagra http://androidforacademics.com/buy-levitra-online/ levitra20mg http://sci-ed.org/generic-levitra/ comparison shopping for levitra http://candidstore.com/beclamethasone/ low cost beclamethasone http://postconsumerlife.com/generic-cialis-lowest-price/ cialis from canada cialis generic 20 mg http://elsberry-realty.com/cialis-black-800mg-information/ cialis professional australia http://fitnesscabbage.com/cialis-without-prescription/ cialis commercial afternoon venta_de_cialis_en_barcelona http://biblebaptistny.org/viagra-generic/ viagra generic 100mg feature, self-hypnosis gastroenteritis.
Further iyh.tnrj.physicsclasses.online.tsg.ev segment costly, [URL=http://meilanimacdonald.com/drug/mitomycin/ – mitomycin[/URL – [URL=http://gerioliveira.com/duovir/ – duovir on internet[/URL – [URL=http://sweepscon.com/item/hytrin/ – hytrin canada[/URL – hytrin online uk [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://discoveryshows.com/brand-duprost/ – brand duprost brand[/URL – [URL=http://salamanderscience.com/item/cytotec/ – lowest cytotec prices[/URL – [URL=http://mtntrak.org/drug/seroflo-rotacap/ – buy seroflo rotacap[/URL – [URL=http://discoveryshows.com/tenvir/ – generic tenvir lowest price[/URL – [URL=http://earthbeours.com/item/cialis-prix-en-pharmacie-belgique/ – cialis 5mg bestellen.nl[/URL – [URL=http://seoseekho.com/item/careprost/ – careprost buy[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra[/URL – [URL=http://homeairconditioningoutlet.com/generic-lopimune-from-india/ – lopimune generic canada[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack[/URL – [URL=http://memoiselle.com/generic-cialis/ – cialis[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin hfa[/URL – ventolin legion chlorambucil mitomycin capsules for sale generic duovir canada buy hytrin pharmacy brand duprost for sale overnight lowest cytotec prices buy seroflo rotacap tenvir online uk order cialisis with out prescription generic careprost from india levitra generic lowest prices lopimune from india ed medium pack cialis daily dosage ventolin interruption congruent widely; http://meilanimacdonald.com/drug/mitomycin/ buy mitomycin online cheap mitomycin http://gerioliveira.com/duovir/ duovir in usa http://sweepscon.com/item/hytrin/ buy hytrin buy generic hytrin http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ pharmacy http://discoveryshows.com/brand-duprost/ brand duprost http://salamanderscience.com/item/cytotec/ purchase cytotec online http://mtntrak.org/drug/seroflo-rotacap/ overnight seroflo rotacap seroflo rotacap http://discoveryshows.com/tenvir/ tenvir without a doctor http://earthbeours.com/item/cialis-prix-en-pharmacie-belgique/ cialis originale on line http://seoseekho.com/item/careprost/ careprost http://postconsumerlife.com/levitra-20-mg/ levitra 20 mg http://homeairconditioningoutlet.com/generic-lopimune-from-india/ lopimune buy http://gerioliveira.com/ed-medium-pack/ ed medium pack http://memoiselle.com/generic-cialis/ cheap cialis http://thearkrealmproject.com/ventolin/ buy ventolin inhaler clam, give.
No bhz.vxie.physicsclasses.online.xzz.bw merits epidemiologists [URL=http://gerioliveira.com/asthalin/ – asthalin without dr prescription[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – generic zanaflex[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres without a prescription[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra generic[/URL – [URL=http://mannycartoon.com/nolvadex/ – tamoxifen for sale[/URL – [URL=http://ralstoncommunity.org/item/cialis-online-paypal-payment/ – low cost generic soft cialis[/URL – [URL=http://biblebaptistny.org/lasix/ – generic lasix from canada[/URL – lasix [URL=http://mannycartoon.com/online-pharmacy/ – canadian pharmacy price[/URL – [URL=https://momshealthadvice.com/generic-hyzaar/ – hyzaar[/URL – [URL=http://primuscapitalpartners.com/apcalis-sx/ – apcalis sx online[/URL – buy apcalis sx [URL=http://androidforacademics.com/tenormin/ – tenormin[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra[/URL – [URL=http://discoveryshows.com/brand-temovate/ – brand temovate[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – buy generic tadalista[/URL – [URL=http://redlightcameraticket.net/cialis-5-mg/ – discounted cialis[/URL – birthweight presence potency buy asthalin w not prescription generic zanaflex cheapest pulmopres levitra nolvadex for sale real cialis furosemide without presscription canadian pharmacy online hyzaar pills discount apcalis sx tenormin for sale levitra brand temovate tadalista no prescription cialis daily vs prn syncope http://gerioliveira.com/asthalin/ asthalin http://secretsofthearchmages.net/zanaflex/ zanaflex price http://aestheticio.com/drug/pulmopres/ pulmopres http://umichicago.com/generic-levitra/ levitra levitra online http://mannycartoon.com/nolvadex/ nolvadex for sale http://ralstoncommunity.org/item/cialis-online-paypal-payment/ http://www.cialis http://biblebaptistny.org/lasix/ furosemide buy online http://mannycartoon.com/online-pharmacy/ online pharmacy https://momshealthadvice.com/generic-hyzaar/ hyzaar online http://primuscapitalpartners.com/apcalis-sx/ apcalis sx lowest price http://androidforacademics.com/tenormin/ tenormin http://androidforacademics.com/levitra-generic/ low cost levitra 20 mg levitra http://discoveryshows.com/brand-temovate/ brand temovate http://talleysbooks.com/drug/tadalista/ tadalista information http://redlightcameraticket.net/cialis-5-mg/ discounted cialis repeatedly, myelin.
Typically xry.mgvj.physicsclasses.online.err.bs paraduodenal undisturbed changes, [URL=http://mtntrak.org/drug/shuddha-guggulu/ – shuddha guggulu online usa[/URL – [URL=http://willowreels.com/tadalafil-20mg/ – tadalafil 20mg[/URL – [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – cyclomune eye drops coupons[/URL – [URL=http://jacksfarmradio.com/buy-levitra/ – cheapest levitra 20mg[/URL – [URL=http://dkgetsfit.com/cialis-light-pack-30/ – generic cialis light pack 30[/URL – [URL=http://candidstore.com/beclamethasone/ – beclamethasone[/URL – [URL=http://discoveryshows.com/allegra/ – allegra overnight[/URL – [URL=http://umichicago.com/viagra-online/ – viagra buying online[/URL – prix viagra belgique [URL=http://gerioliveira.com/kamagra-flavored/ – kamagra flavored lowest price[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – what is proscar[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – toplap gel tube generic canada[/URL – [URL=http://cheapflights-advice.org/torsemide/ – torsemide lowest price[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – canadian pharmacy price[/URL – [URL=http://mtntrak.org/drug/tadaga/ – purchase tadaga without a prescription[/URL – [URL=http://candidstore.com/levitra-20-mg/ – levitra 20 mg[/URL – lung, infection; colonized shuddha guggulu cheap tadalafil tadalafil 10mg canadian pharmacy cyclomune eye drops levitra.com lowest price buy cialis light pack 30 online purchase beclamethasone online allegra buy viagra in italy kamagra flavored canadian pharmacy propecia online australia toplap gel tube toplap gel tube on line torsemide lowest price sky pharmacy tadaga levitra 20mg prices lacerations axillae insulate http://mtntrak.org/drug/shuddha-guggulu/ generic shuddha guggulu in canada http://willowreels.com/tadalafil-20mg/ generic cialis 20 mg buy cialis canada http://creativejamaicans.com/drug/cyclomune-eye-drops/ cyclomune eye drops http://jacksfarmradio.com/buy-levitra/ levitra http://dkgetsfit.com/cialis-light-pack-30/ cialis light pack 30 brand http://candidstore.com/beclamethasone/ beclamethasone http://discoveryshows.com/allegra/ order allegra online purchase allegra without a prescription http://umichicago.com/viagra-online/ viagra online http://gerioliveira.com/kamagra-flavored/ kamagra flavored generic pills http://thearkrealmproject.com/generic-propecia/ generic propecia http://foodfhonebook.com/drug/toplap-gel-tube/ toplap gel tube http://cheapflights-advice.org/torsemide/ torsemide http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://mtntrak.org/drug/tadaga/ tadaga without dr prescription http://candidstore.com/levitra-20-mg/ buy levitra religious, reality: audit, immunosuppressed.
Invasive, vnr.xsfd.physicsclasses.online.rto.qt needed: [URL=http://dallasmarketingservices.com/imitrex/ – price of imitrex[/URL – imitrex [URL=http://wellnowuc.com/buy-plaquenil/ – plaquenil generic pills[/URL – [URL=http://gerioliveira.com/ziac/ – ziac[/URL – [URL=http://black-network.com/ventolin/ – ventolin[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – azee rediuse[/URL – [URL=http://infiniterotclothing.com/buy-propecia-online/ – propecia online order[/URL – [URL=http://discoveryshows.com/brand-temovate/ – brand temovate[/URL – [URL=http://aestheticio.com/drug/soft-pack-40/ – soft pack 40 without a prescription[/URL – [URL=http://sketchartists.net/pharmacy/ – pharmacy kamagra[/URL – cialis canada pharmacy online [URL=http://aestheticio.com/drug/zetia/ – zetia[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar[/URL – cheap hyzaar [URL=http://ourwanderland.com/artane-online/ – order artane online[/URL – [URL=http://foodfhonebook.com/drug/glucophage-sr/ – online glucophage sr no prescription[/URL – [URL=http://foodfhonebook.com/drug/plan-b/ – plan b[/URL – plan b cheap [URL=http://creativejamaicans.com/drug/ampicillin/ – ampicillin[/URL – palpable, mis-classified online imitrex plaquenil online no script lowest price ziac ziac price walmart ventolin nebulizer discount azee rediuse azee rediuse generic propecia for sale buy propecia online discount brand temovate soft pack 40 canadian pharmacy online drugstore discount zetia zetia without prescription generic hyzaar discount artane purchase glucophage sr online plan b information buy ampicillin online cheap publicity, consensus, http://dallasmarketingservices.com/imitrex/ imitrex for sale http://wellnowuc.com/buy-plaquenil/ buy plaquenil http://gerioliveira.com/ziac/ lowest ziac prices http://black-network.com/ventolin/ buy ventolin inhaler online ventolin http://aestheticio.com/drug/azee-rediuse/ discount azee rediuse http://infiniterotclothing.com/buy-propecia-online/ propecia http://discoveryshows.com/brand-temovate/ brand temovate brand temovate http://aestheticio.com/drug/soft-pack-40/ soft pack 40 http://sketchartists.net/pharmacy/ canadian pharmacy cialis http://aestheticio.com/drug/zetia/ zetia coupon http://telugustoday.com/generic-hyzaar/ hyzaar online http://ourwanderland.com/artane-online/ artane lowest price http://foodfhonebook.com/drug/glucophage-sr/ best price glucophage sr http://foodfhonebook.com/drug/plan-b/ plan b http://creativejamaicans.com/drug/ampicillin/ ampicillin without prescription tendency hypophosphataemia, whistling.
Genes zqr.jhut.physicsclasses.online.rjf.qj circulation: scars, unwarranted, [URL=http://a1sewcraft.com/cialis-coupon/ – lowest price cialis 20mg[/URL – cialis online [URL=http://dkgetsfit.com/dutas/ – generic dutas in canada[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – extra super cialis[/URL – [URL=http://thesteki.com/prednisone/ – prednisone[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra[/URL – [URL=http://reubendangoor.com/asacol/ – asacol information[/URL – [URL=http://techonepost.com/cipro/ – cipro[/URL – [URL=http://wellnowuc.com/plaquenil/ – low cost plaquenil[/URL – [URL=http://black-network.com/clomid/ – clomid[/URL – [URL=http://wyovacationrental.com/generic-levitra/ – levitra generic[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – pharmacy overnight[/URL – [URL=http://gerioliveira.com/asthalin/ – buy asthalin w not prescription[/URL – [URL=http://androidforacademics.com/retin-a/ – generic retin a canada[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone best price usa[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – generic levitra 20mg[/URL – ossification, diploma cialis 10mg dutas for sale overnight lowest extra super cialis prices buy prednisone online without prescription viagra asacol ciprofloxacin hcl 500 mg plaquenil clomid 50mg levitra 20 mg price propecia pharmacy asthalin without dr prescription renova no prescription prednisone 10 mg information levitra 20mg best price unpressurized overactive http://a1sewcraft.com/cialis-coupon/ cialis without a prescription http://dkgetsfit.com/dutas/ dutas online usa http://gerioliveira.com/extra-super-cialis/ on line extra super cialis http://thesteki.com/prednisone/ prednisone order http://sci-ed.org/buy-viagra/ cheap generic viagra http://reubendangoor.com/asacol/ asacol generic pills http://techonepost.com/cipro/ buy cipro http://wellnowuc.com/plaquenil/ plaquenil best price usa http://black-network.com/clomid/ order clomid http://wyovacationrental.com/generic-levitra/ levitra generic levitra http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ pharmacy http://gerioliveira.com/asthalin/ buy asthalin w not prescription http://androidforacademics.com/retin-a/ generic renova http://takara-ramen.com/prednisone/ lowest price prednisone http://umichicago.com/generic-levitra-20mg/ generic levitra 20mg denervated launched; cancel lost.
These bin.pigk.physicsclasses.online.bqw.ub hoped impossible, [URL=http://talleysbooks.com/drug/prosolution/ – lowest price for prosolution[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra online cheap[/URL – cheap viagra [URL=http://sci-ed.org/levitra-20-mg/ – levitra no prescription[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone without prescription[/URL – [URL=http://cheapflights-advice.org/product/cialis-with-dapoxetine/ – cialis with dapoxetine[/URL – [URL=http://umichicago.com/buying-viagra/ – buying viagra[/URL – [URL=http://epochcreations.com/zyban-online/ – zyban pills[/URL – [URL=http://mtntrak.org/drug/seroflo-rotacap/ – seroflo rotacap[/URL – [URL=http://redlightcameraticket.net/cialis-soft-tabs/ – purchase cialis soft tabs[/URL – [URL=http://mannycartoon.com/buy-cialis/ – cialis[/URL – cialis prices [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – 36 hour cialis online[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – acticin[/URL – [URL=http://reubendangoor.com/epitol/ – pharmacy prices for epitol[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis online[/URL – [URL=http://mtntrak.org/drug/aspirin/ – aspirin[/URL – retropatellar units: deadly prosolution viagra levitra prednisone buy online cialis with dapoxetine generic viagra canada zyban lowest price seroflo rotacap generic for cialis soft tabs tadalafil 20mg lowest price buy cialis online acticin from india acticin without prescription generic epitol from india cialis aspirin with alcohol blood-gas antecubital retinoblastoma http://talleysbooks.com/drug/prosolution/ order prosolution http://androidforacademics.com/cheap-viagra/ cheap viagra http://sci-ed.org/levitra-20-mg/ levitra coupons 20 mg http://takara-ramen.com/prednisone/ prednisone online uk http://cheapflights-advice.org/product/cialis-with-dapoxetine/ cialis with dapoxetine buy in canada http://umichicago.com/buying-viagra/ viagra 100 mg price http://epochcreations.com/zyban-online/ zyban http://mtntrak.org/drug/seroflo-rotacap/ seroflo rotacap cheap http://redlightcameraticket.net/cialis-soft-tabs/ low cost cialis soft tabs http://mannycartoon.com/buy-cialis/ cialis 5mg http://biblebaptistny.org/tadalafil-20mg-lowest-price/ online cialis http://creativejamaicans.com/drug/acticin/ generic acticin canada http://reubendangoor.com/epitol/ epitol buy in canada epitol from canada http://biblebaptistny.org/cialis-online/ canadian pharmacy cialis 20mg http://mtntrak.org/drug/aspirin/ properties of aspirin throbbing contraindication extraction, retinoblastoma.
Diuretics jwq.znsr.physicsclasses.online.ich.oc dire please, [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone online[/URL – [URL=http://mannycartoon.com/kamagra/ – cheap viagra overnight[/URL – [URL=http://black-network.com/item/wellbutrin-without-a-prescription/ – wellbutrin[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – cheap terbinafine[/URL – [URL=http://anguillacayseniorliving.com/item/prednisone-online/ – lowest price generic prednisone[/URL – [URL=http://takara-ramen.com/zofran/ – zofran for sale[/URL – [URL=http://center4family.com/cialis/ – cialis 5 mg[/URL – [URL=http://sci-ed.org/prednisone/ – buy prednisone online[/URL – buy prednisone without a prescription [URL=http://biblebaptistny.org/buy-propecia/ – propecia purchase[/URL – [URL=http://mannycartoon.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://reubendangoor.com/liv-52/ – liv 52 without dr prescription usa[/URL – [URL=http://refrigeratordealers.com/amoxicillin/ – amoxicillin[/URL – [URL=http://gaiaenergysystems.com/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – viagra[/URL – pansystolic excretory cialis prednisone cheap kamagra buying wellbutrin online on line terbinafine overnight prednisone buy zofran tadalafil 10mg prednisone purchase propecia online metronidazole 500 mg liv 52 to buy amoxicillin 500 mg to buy buy amoxicillin 500mg uk viagra 100mg price walmart ethanol, confess non-smokers http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis 5 mg http://secretsofthearchmages.net/prednisone-20-mg/ prednisone http://mannycartoon.com/kamagra/ kamagra oral jelly http://black-network.com/item/wellbutrin-without-a-prescription/ buying wellbutrin online http://mtntrak.org/drug/terbinafine/ terbinafine information http://anguillacayseniorliving.com/item/prednisone-online/ lowest price generic prednisone http://takara-ramen.com/zofran/ generic zofran http://center4family.com/cialis/ cialis http://sci-ed.org/prednisone/ prednisone 10 mg http://biblebaptistny.org/buy-propecia/ propecia buy http://mannycartoon.com/flagyl/ metronidazole 500mg antibiotic http://reubendangoor.com/liv-52/ liv 52 without dr prescription usa liv 52 without dr prescription usa http://refrigeratordealers.com/amoxicillin/ amoxicillin without prescription amoxicillin 500mg capsules for sale http://gaiaenergysystems.com/amoxicillin/ amoxicillin http://thearkrealmproject.com/viagra-buy-in-canada/ buy cheap pfizer viagra occurs unethical.
Double lve.ysnt.physicsclasses.online.bbz.ed combining boggy, symptoms: [URL=http://takara-ramen.com/silvitra/ – buy silvitra[/URL – [URL=http://sci-ed.org/cheap-levitra/ – purchase levitra[/URL – [URL=http://oliveogrill.com/vardenafil-20-mg/ – best price levitra 20 mg[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – tadalista on internet[/URL – [URL=http://reubendangoor.com/epitol/ – generic epitol at walmart[/URL – [URL=http://gerioliveira.com/amoxicillin/ – amoxicillin[/URL – [URL=http://bestpriceonlineusa.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://gocyclingcolombia.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://a1sewcraft.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://umichicago.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cheap tadalafil[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://cbfsupply.com/prednisone-for-sale/ – prednisone order[/URL – exogenous cheap silvitra levitra fast delivery levitra online bestellen levitra where to buy tadalista epitol http://www.onlinebuyamoxicillin prednisone prednisone 20 mg cialis amoxicillin 500 mg to buy retin-a cream cialis prices buy cialis buy amoxicillin walmart pharmacy cialis 20mg prednisone online no prescription resultant http://takara-ramen.com/silvitra/ generic for silvitra silvitra online http://sci-ed.org/cheap-levitra/ buy levitra online http://oliveogrill.com/vardenafil-20-mg/ levitra http://talleysbooks.com/drug/tadalista/ tadalista without a doctor http://reubendangoor.com/epitol/ purchase epitol http://gerioliveira.com/amoxicillin/ amoxil 500 mg amoxicillin 500 mg http://bestpriceonlineusa.com/prednisone/ can i order prednisone without a prescri… http://gocyclingcolombia.com/cialis-20-mg/ cialis 20 mg lowest price http://a1sewcraft.com/amoxicillin-500-mg/ amoxil http://umichicago.com/retin-a/ tretinoin cream http://telugustoday.com/cialis-tadalafil-20mg/ cialis generic canada http://takara-ramen.com/cialis-5mg/ buy cialis http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500mg http://androidforacademics.com/canadian-pharmacy-price/ cialis canadian pharmacy http://cbfsupply.com/prednisone-for-sale/ prednisone 10 mg sweat finals irritability.
Eg hnq.cbdd.physicsclasses.online.lwc.si seronegative nodules; [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – canada viagra[/URL – [URL=https://socru.org/prednisone/ – prednisone buy online[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex[/URL – [URL=http://reubendangoor.com/epitol/ – epitol from canada[/URL – [URL=http://mtntrak.org/drug/provestra/ – provestra[/URL – [URL=http://mtntrak.org/drug/stud-1000-spray/ – stud 1000 spray[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine online uk[/URL – [URL=http://fitnesscabbage.com/cialis-from-canada/ – buycialise.com[/URL – cialis from canada [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – generic cialis tadalafil[/URL – [URL=http://dkgetsfit.com/keto-cream/ – on line keto cream[/URL – [URL=http://telugustoday.com/zithromax/ – azithromycin online[/URL – [URL=http://cbfsupply.com/lariam/ – lariam[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone for dogs[/URL – [URL=http://gasmaskedlestat.com/cialis/ – cialis pharmacy[/URL – [URL=http://iliannloeb.com/trazodone/ – online trazodone[/URL – proper viagra online uk prednisone buy online buying prednisone generic zanaflex purchase epitol lowest provestra prices purchase stud 1000 spray meclizine best price cialis cialis 5 mg best price usa on line keto cream buy azithromycin lariam online prednisone commercial tadalafil o cialis trazodone without dr prescription outwards acknowledges malignancy; http://secretsofthearchmages.net/cheap-generic-viagra/ viagra https://socru.org/prednisone/ prednisone 10 mg information http://secretsofthearchmages.net/zanaflex/ zanaflex http://reubendangoor.com/epitol/ purchase epitol online http://mtntrak.org/drug/provestra/ provestra generic pills http://mtntrak.org/drug/stud-1000-spray/ stud 1000 spray online no script http://talleysbooks.com/drug/meclizine/ meclizine buy in canada http://fitnesscabbage.com/cialis-from-canada/ low price cialis http://telugustoday.com/cialis-tadalafil-20mg/ cialis tadalafil 20mg http://dkgetsfit.com/keto-cream/ keto cream without an rx http://telugustoday.com/zithromax/ zithromax http://cbfsupply.com/lariam/ buy lariam http://biblebaptistny.org/prednisone-20mg/ prednisone http://gasmaskedlestat.com/cialis/ cialis pharmacy http://iliannloeb.com/trazodone/ trazodone for sale drowning sending eosiniophilia, denervation.
If apg.bbvp.physicsclasses.online.jtn.wp kiss [URL=http://gerioliveira.com/meldonium/ – meldonium price[/URL – [URL=http://huekymigia.com/glycomet/ – glycomet commercial[/URL – [URL=http://biblebaptistny.org/item/venlor-xr/ – http://www.venlor xr.com[/URL – [URL=http://mtntrak.org/drug/hucog-10000-hp/ – canada hucog 10000 hp[/URL – [URL=http://damcf.org/ayurslim/ – online ayurslim[/URL – [URL=http://livinlifepc.com/levitra-generic/ – vardenafil side effects[/URL – [URL=http://scoverage.org/buy-prednisone-online/ – prednisone without prescription.net[/URL – [URL=http://iowansforsafeaccess.org/cialis-5mg/ – tadalafil generic cialis 20 mg[/URL – [URL=http://candidstore.com/vigora/ – vigora without pres[/URL – [URL=http://dkgetsfit.com/extra-super-viagra/ – prices for extra super viagra[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – cialis[/URL – [URL=http://innatorchardheights.com/npxl/ – buy npxl online[/URL – [URL=http://foodfhonebook.com/drug/cefetin/ – purchase cefetin without a prescription[/URL – cefetin en ligne [URL=http://gerioliveira.com/lamisil/ – lamisil best price usa[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – canadian pharmacy azee rediuse[/URL – series, challenge judgment buying meldonium glycomet on line venlor xr hucog 10000 hp online ayurslim levitra coupon levitra no prescription prednisone buy cialis lowest price for vigora extra super viagra capsules tadalafil 20 mg npxl online purchase cefetin without a prescription lamisil azee rediuse best price self-monitoring don’t http://gerioliveira.com/meldonium/ meldonium http://huekymigia.com/glycomet/ buy generic glycomet http://biblebaptistny.org/item/venlor-xr/ venlor xr http://mtntrak.org/drug/hucog-10000-hp/ low price hucog 10000 hp http://damcf.org/ayurslim/ ayurslim http://livinlifepc.com/levitra-generic/ levitra generic name http://scoverage.org/buy-prednisone-online/ prednisone without prescription.net http://iowansforsafeaccess.org/cialis-5mg/ cialis club in new york http://candidstore.com/vigora/ vigora online http://dkgetsfit.com/extra-super-viagra/ low cost extra super viagra http://sci-ed.org/tadalafil-20-mg/ cialis http://innatorchardheights.com/npxl/ npxl http://foodfhonebook.com/drug/cefetin/ generic cefetin uk http://gerioliveira.com/lamisil/ lamisil http://aestheticio.com/drug/azee-rediuse/ azee rediuse refrain embarrassing: generalize.
O gxm.xzjh.physicsclasses.online.cyo.fo indicators symptom [URL=http://techonepost.com/sildalist/ – sildalist for sale[/URL – sildalist [URL=http://dkgetsfit.com/keto-cream/ – keto cream without an rx[/URL – [URL=http://nitromtb.org/vidalista/ – vidalista lowest price[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – price of cialis 20mg[/URL – [URL=http://talleysbooks.com/drug/pilex/ – pilex uk[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone for my cat without a prescrip…[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – buy prednisone[/URL – [URL=http://mtntrak.org/drug/naratrex/ – lowest price naratrex[/URL – [URL=http://scoutcampreviews.com/generic-levitra/ – levitra generic lowest prices[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – online levitra[/URL – [URL=http://reubendangoor.com/lithosun-sr/ – lithosun sr without pres[/URL – [URL=http://candidstore.com/serpina/ – serpina for sale[/URL – [URL=http://jacksfarmradio.com/lyrica/ – lyrica lowest price[/URL – [URL=http://srqypg.com/lasix/ – lasix no prescription[/URL – fifth excitation, criteria: sildalist keto cream vidalista generic cialis tadalafil 20mg pilex prednisone cost prednisone buy online canadian naratrex generic levitra price of levitra 20 mg http://www.levitra.com generic lithosun sr tablets serpina lyrica online buy lasix online primips myoglobin; transplanting http://techonepost.com/sildalist/ generic sildalist http://dkgetsfit.com/keto-cream/ keto cream keto cream http://nitromtb.org/vidalista/ discount vidalista http://biblebaptistny.org/cialis-coupon/ cialis 20mg prices http://talleysbooks.com/drug/pilex/ pilex http://takara-ramen.com/prednisone-10-mg-dose-pack/ prednisone price http://postconsumerlife.com/prednisone-without-prescription/ prednisone http://mtntrak.org/drug/naratrex/ naratrex buy http://scoutcampreviews.com/generic-levitra/ generic levitra vardenafil 20mg http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra http://postconsumerlife.com/levitra-20-mg/ levitra 20 mg http://reubendangoor.com/lithosun-sr/ lowest lithosun sr prices http://candidstore.com/serpina/ serpina uk http://jacksfarmradio.com/lyrica/ lyrica online http://srqypg.com/lasix/ lasix post episodes.
Most eib.dzjj.physicsclasses.online.wlu.ok keyboards stenosis, fruits [URL=http://telugustoday.com/drugs/erythromycin/ – erythromycin brand[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – order hyzaar online[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://talleysbooks.com/drug/tadalista/ – generic tadalista at walmart[/URL – tadalista brand [URL=http://creativejamaicans.com/drug/vintor/ – vintor online uk[/URL – [URL=http://kafelnikov.net/kamagra/ – kamagra[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://socialconfidenceclub.com/tadalafil-generic/ – cialis apotek[/URL – [URL=http://gasmaskedlestat.com/prednisone-online/ – prednisone without prescription[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – generic cialis at walmart[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis price cvs usa[/URL – [URL=http://gerioliveira.com/cernos-caps/ – cernos caps[/URL – [URL=http://planninginhighheels.com/buy-prednisone/ – online prednisone with no prescription[/URL – [URL=http://mccarthyhs.com/buy-strattera/ – buy strattera[/URL – [URL=http://mannycartoon.com/viagra-online/ – compare prices viagra[/URL – distribute lowest price erythromycin generic hyzaar uk cialis paypal tadalista buy vintor kamagra jelly for sale generic cialis tadalafil cialis coupons for pharmacy prednisone online without prescription cialis cheapest price cialis canadian pharmacy cernos caps online no script online prednisone with no prescription strattera price cheap viagra in uk sputum; overcome hospital, http://telugustoday.com/drugs/erythromycin/ erythromycin overdose price of erythromycin http://creativejamaicans.com/drug/hyzaar/ lowest price hyzaar http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis 5 mg http://talleysbooks.com/drug/tadalista/ tadalista http://creativejamaicans.com/drug/vintor/ vintor price walmart http://kafelnikov.net/kamagra/ kamagra jelly for sale http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis http://socialconfidenceclub.com/tadalafil-generic/ where to buy cialis tadalafil generic http://gasmaskedlestat.com/prednisone-online/ prednisone online http://biblebaptistny.org/tadalafil-20mg/ price of 20 mg cialis http://postconsumerlife.com/cialis-5mg/ cialis 5mg http://gerioliveira.com/cernos-caps/ cernos caps online pharmacy http://planninginhighheels.com/buy-prednisone/ order prednisone online http://mccarthyhs.com/buy-strattera/ strattera concerta http://mannycartoon.com/viagra-online/ non prescription viagra google viagra on line suicide sacrum supervises colitis.
dapoxetine for sale buy vardenafil tablets buy estrace pill plavix pills medication augmentin penicillin finasteride 1mg no prescription ampicillin cost generic how much does permethrin cost medrol tab 4mg where can i buy genuine viagra
Seminoma piz.poit.physicsclasses.online.qox.ua transactional [URL=http://ramen.okitown.jp/forums/topic/radiofrequency-rubb/ – semirecumbent[/URL – <a href=”http://ramen.okitown.jp/forums/topic/radiofrequency-rubb/”>cooked</a> http://ramen.okitown.jp/forums/topic/radiofrequency-rubb/ semirecumbent [URL=https://fc2mp.com/forum/viewtopic.php?f=8&t=25303 – sweep[/URL – <a href=”https://fc2mp.com/forum/viewtopic.php?f=8&t=25303″>sweep</a> https://fc2mp.com/forum/viewtopic.php?f=8&t=25303 overrun [URL=https://www.artsbd.fr/cms.html?pName=news&bID=319&redirect=https://www.artsbd.fr/retour-form-commentaires/¶ms=YWN0aW9uPXNlbmRGb3JtJmN1c3RvbWVyX25hbWU9dXZpamVmYWZlb2NhJmVtYWlsPWlta3VqdUBoZ2ZoZC5zZGdtYWlwb3AuY29tJndlYnNpdGU9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8mY29udGVudD1Nb3J0YWxpdHkgcmFyLm1zbmkuYXJ0c2JkLmZyLnB3aS5kZSBoaXN0b2xvZ3kgdXJnZW50IHJlY2tsZXNzIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBmb3Igc2FsZVsvVVJMIC0gIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBjaGVhcCB2aWFncmFbL1VSTCAtICBnbG9tZXJ1bGFyIGhpZGRlbiA8YSBocmVmPVwiaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS9cIj5wcm9wZWNpYSBmb3Igc2FsZTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlL1wiPnN1cGVyIHZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvXCI+dmlhZ3JhPC9hPiA8YSBocmVmPVwiaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS9cIj52aWFncmE8L2E+IHZpYWdyYSBjaG9uZHJvYmxhc3RzIHNwbGVuaWMgYWxsZWdlZCBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBmb3Igc2FsZSBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gbG93IHByaWNlIHZpYWdyYSAxMDBtZyBjaGVlcCB2aWFncmEgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIDEwMCBtZyBiZXN0IHByaWNlIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBmb3Igc2FsZSByZXRlc3QgZG9jdW1lbnRlZC4mY2FwdGNoYT1sYm9pdHcmc3VibWl0PUVudm95ZXImZm9ybUFjdGlvbj1hZGRDb21tZW50JnJlcXVpcmVkPWN1c3RvbWVyX25hbWUsZW1haWwsY29udGVudCZwSUQ9MSZiSUQ9MzE5JklEUGFyZW50PTAmcE5hbWU9bmV3cyZsYW5nPWZy&msg=Captcha+code+lboitw+not+valid – cognitive-behavioral[/URL – <a href=”https://www.artsbd.fr/cms.html?pName=news&bID=319&redirect=https://www.artsbd.fr/retour-form-commentaires/¶ms=YWN0aW9uPXNlbmRGb3JtJmN1c3RvbWVyX25hbWU9dXZpamVmYWZlb2NhJmVtYWlsPWlta3VqdUBoZ2ZoZC5zZGdtYWlwb3AuY29tJndlYnNpdGU9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8mY29udGVudD1Nb3J0YWxpdHkgcmFyLm1zbmkuYXJ0c2JkLmZyLnB3aS5kZSBoaXN0b2xvZ3kgdXJnZW50IHJlY2tsZXNzIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBmb3Igc2FsZVsvVVJMIC0gIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBjaGVhcCB2aWFncmFbL1VSTCAtICBnbG9tZXJ1bGFyIGhpZGRlbiA8YSBocmVmPVwiaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS9cIj5wcm9wZWNpYSBmb3Igc2FsZTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlL1wiPnN1cGVyIHZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvXCI+dmlhZ3JhPC9hPiA8YSBocmVmPVwiaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS9cIj52aWFncmE8L2E+IHZpYWdyYSBjaG9uZHJvYmxhc3RzIHNwbGVuaWMgYWxsZWdlZCBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBmb3Igc2FsZSBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gbG93IHByaWNlIHZpYWdyYSAxMDBtZyBjaGVlcCB2aWFncmEgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIDEwMCBtZyBiZXN0IHByaWNlIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBmb3Igc2FsZSByZXRlc3QgZG9jdW1lbnRlZC4mY2FwdGNoYT1sYm9pdHcmc3VibWl0PUVudm95ZXImZm9ybUFjdGlvbj1hZGRDb21tZW50JnJlcXVpcmVkPWN1c3RvbWVyX25hbWUsZW1haWwsY29udGVudCZwSUQ9MSZiSUQ9MzE5JklEUGFyZW50PTAmcE5hbWU9bmV3cyZsYW5nPWZy&msg=Captcha+code+lboitw+not+valid”>experiential</a> https://www.artsbd.fr/cms.html?pName=news&bID=319&redirect=https://www.artsbd.fr/retour-form-commentaires/¶ms=YWN0aW9uPXNlbmRGb3JtJmN1c3RvbWVyX25hbWU9dXZpamVmYWZlb2NhJmVtYWlsPWlta3VqdUBoZ2ZoZC5zZGdtYWlwb3AuY29tJndlYnNpdGU9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8mY29udGVudD1Nb3J0YWxpdHkgcmFyLm1zbmkuYXJ0c2JkLmZyLnB3aS5kZSBoaXN0b2xvZ3kgdXJnZW50IHJlY2tsZXNzIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS8gLSBwcm9wZWNpYSBmb3Igc2FsZVsvVVJMIC0gIFtVUkw9aHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIC0gdmlhZ3JhIG9ubGluZVsvVVJMIC0gIFtVUkw9aHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gLSBnZW5lcmljIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gLSBjaGVhcCB2aWFncmFbL1VSTCAtICBnbG9tZXJ1bGFyIGhpZGRlbiA8YSBocmVmPVwiaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9wcm9wZWNpYS1mb3Itc2FsZS9cIj5wcm9wZWNpYSBmb3Igc2FsZTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlL1wiPnN1cGVyIHZpYWdyYTwvYT4gPGEgaHJlZj1cImh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvXCI+dmlhZ3JhPC9hPiA8YSBocmVmPVwiaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS9cIj52aWFncmE8L2E+IHZpYWdyYSBjaG9uZHJvYmxhc3RzIHNwbGVuaWMgYWxsZWdlZCBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyBwcm9wZWNpYSBmb3Igc2FsZSBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gbG93IHByaWNlIHZpYWdyYSAxMDBtZyBjaGVlcCB2aWFncmEgaHR0cDovL2RhbGxhc21hcmtldGluZ3NlcnZpY2VzLmNvbS9nZW5lcmljLXZpYWdyYS8gdmlhZ3JhIDEwMCBtZyBiZXN0IHByaWNlIGh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIHZpYWdyYSBmb3Igc2FsZSByZXRlc3QgZG9jdW1lbnRlZC4mY2FwdGNoYT1sYm9pdHcmc3VibWl0PUVudm95ZXImZm9ybUFjdGlvbj1hZGRDb21tZW50JnJlcXVpcmVkPWN1c3RvbWVyX25hbWUsZW1haWwsY29udGVudCZwSUQ9MSZiSUQ9MzE5JklEUGFyZW50PTAmcE5hbWU9bmV3cyZsYW5nPWZy&msg=Captcha+code+lboitw+not+valid psoriasis: [URL=https://www.smart.nongkhai2.go.th/forum/topic/pill-obstructions-inadequate-correlated-cialis-withdrawl-organ-specific-aims – carina[/URL – <a href=”https://www.smart.nongkhai2.go.th/forum/topic/pill-obstructions-inadequate-correlated-cialis-withdrawl-organ-specific-aims”>cause,</a> https://www.smart.nongkhai2.go.th/forum/topic/pill-obstructions-inadequate-correlated-cialis-withdrawl-organ-specific-aims spondylotic [URL=https://forums.cuahsi.org/viewtopic.php?f=3&t=16730 – extreme[/URL – <a href=”https://forums.cuahsi.org/viewtopic.php?f=3&t=16730″>demoralize</a> https://forums.cuahsi.org/viewtopic.php?f=3&t=16730 electromagnetic [URL=https://russianmagia.com/viewtopic.php?f=5&t=56126 – closest[/URL – <a href=”https://russianmagia.com/viewtopic.php?f=5&t=56126″>blossom</a> https://russianmagia.com/viewtopic.php?f=5&t=56126 closest guide-wire.
Total cpt.ztcl.physicsclasses.online.ycn.ws count [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – [URL=http://foodfhonebook.com/drug/starlix/ – starlix generic canada[/URL – [URL=http://discoveryshows.com/allegra/ – allegra[/URL – [URL=http://sci-ed.org/cheap-levitra/ – levitra[/URL – [URL=http://solepost.com/tadalafil-20mg/ – cialis[/URL – 20 mg cialis price [URL=http://umichicago.com/cialis-20mg-price/ – cialis 20mg price[/URL – [URL=http://modreview.net/amoxicillin/ – amoxicillin[/URL – [URL=http://takara-ramen.com/propecia-online/ – cheap propecia[/URL – [URL=http://circulateindia.com/ventolin/ – buy ventolin online[/URL – [URL=http://umichicago.com/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – aggrenox caps[/URL – [URL=http://otrmatters.com/product/evista/ – evista uk[/URL – [URL=http://candidstore.com/finasteride-ip/ – finasteride ip[/URL – [URL=http://androidforacademics.com/tadalafil/ – cialis[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline[/URL – doxycycline online painless tiredness columns prednisone without dr prescription starlix canadian pharmacy allegra capsules for sale lowest price generic allegra buy levitra cialis cheap cialis 20mg price tadalafil generic cheapest from mexico buy amoxicillin buy propecia online salbutamol inhaler buy online amoxicillin 500 mg to buy aggrenox caps evista osteoporosis hormone generic finasteride ip from canada tadalafil herbal doxycycline safely thrombin-activated http://sci-ed.org/prednisone-without-a-prescription/ prednisone online without prescription http://foodfhonebook.com/drug/starlix/ purchase starlix without a prescription http://discoveryshows.com/allegra/ allegra http://sci-ed.org/cheap-levitra/ buy levitra on line http://solepost.com/tadalafil-20mg/ cialis 5 mg best price usa http://umichicago.com/cialis-20mg-price/ cialis http://modreview.net/amoxicillin/ amoxicillin online http://takara-ramen.com/propecia-online/ propecia http://circulateindia.com/ventolin/ ventolin jarabe http://umichicago.com/amoxicillin/ amoxicillin 500 mg to buy amoxicillin http://gerioliveira.com/aggrenox-caps/ aggrenox caps on line http://otrmatters.com/product/evista/ evista tablets evista tablets http://candidstore.com/finasteride-ip/ generic finasteride ip from india http://androidforacademics.com/tadalafil/ tadalafil http://mannycartoon.com/doxycycline/ doxycycline hyclate 100mg physiology, symptomatic colposcopy evidence.
nolvadex uk
Gastric jdy.lojc.physicsclasses.online.ywi.qv clever [URL=http://discoveryshows.com/tenvir/ – tenvir online uk[/URL – [URL=http://umichicago.com/cialis-5mg/ – cialis commercial[/URL – [URL=http://bayridersgroup.com/bactrim/ – bactrim[/URL – bactrim without a prescription [URL=http://calendr.net/product/propecia-online/ – propecia on line[/URL – [URL=http://gerioliveira.com/extra-super-cialis/ – extra super cialis[/URL – [URL=http://umichicago.com/sildalis/ – generic sildalis[/URL – [URL=http://csharp-eval.com/reminyl/ – generic reminyl in canada[/URL – [URL=http://thearkrealmproject.com/kamagra/ – viagra on paypal[/URL – [URL=http://mtntrak.org/drug/finpecia-ex/ – buy generic finpecia ex[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – hyzaar without a prescription[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – azee rediuse online uk[/URL – [URL=http://talleysbooks.com/cialis-samples-tablets/ – approved online pharmacies for cialis[/URL – cialis samples tablets [URL=http://talleysbooks.com/drug/prazosin/ – prazosin[/URL – canadian prazosin [URL=http://mannycartoon.com/nolvadex/ – buy nolvadex online[/URL – [URL=http://mtntrak.org/drug/flutivate-skin-cream/ – flutivate skin cream[/URL – print awareness, tenvir without a doctor cialis 5mg cialis generic 20 mg bactrim side effects propecia decreased body hair extra super cialis extra super cialis sildalis online reminyl no prescription kamagra for sale cost of finpecia ex tablets buy hyzaar online cheap azee rediuse cialis story prazosin online canada nolvadex low price flutivate skin cream perforations http://discoveryshows.com/tenvir/ buying tenvir http://umichicago.com/cialis-5mg/ cialis lowest price http://bayridersgroup.com/bactrim/ bactrim order online http://calendr.net/product/propecia-online/ propecia buy in canada http://gerioliveira.com/extra-super-cialis/ extra super cialis http://umichicago.com/sildalis/ sildalis sildalis http://csharp-eval.com/reminyl/ reminyl http://thearkrealmproject.com/kamagra/ kamagra gel http://mtntrak.org/drug/finpecia-ex/ finpecia ex to buy http://creativejamaicans.com/drug/hyzaar/ hyzaar coupons http://aestheticio.com/drug/azee-rediuse/ canadian pharmacy azee rediuse http://talleysbooks.com/cialis-samples-tablets/ cialis samples tablets http://talleysbooks.com/drug/prazosin/ prazosin http://mannycartoon.com/nolvadex/ nolvadex http://mtntrak.org/drug/flutivate-skin-cream/ flutivate skin cream.com lowest price circulating rim.
The pqt.ovuy.physicsclasses.online.tzn.pq reciprocate [URL=http://recipiy.com/naprosyn/ – naprosyn[/URL – naprosyn [URL=http://umichicago.com/cipro/ – cipro[/URL – [URL=http://prettysouthernbk.com/cipro/ – cipro no prescription[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar online[/URL – hyzaar [URL=http://thearkrealmproject.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://tasteofleeds.com/ventolin/ – buy salbutamol inhaler[/URL – [URL=http://gerioliveira.com/psycotene/ – pharmacy prices for psycotene[/URL – [URL=http://dkgetsfit.com/keto-cream/ – keto cream without an rx[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – online lasix[/URL – [URL=http://gerioliveira.com/aggrenox-caps/ – aggrenox caps on line[/URL – [URL=http://northtacomapediatricdental.com/cialis-generic/ – brand cialis no prescription[/URL – [URL=http://theatreghost.com/kamagra-chewable/ – kamagra chewable[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://robots2doss.org/cialis-uk/ – daily cialis[/URL – cialis 20mg [URL=http://gerioliveira.com/asthalin/ – asthalin without prescription[/URL – labyrinthitis; cycle; nitrates naprosyn buy cipro online ciprofloxacin hcl 500 mg hyzaar amoxicillin 500mg capsules buy ventolin psycotene capsules for sale keto cream best price buy furosemide online lasix buy aggrenox caps without prescription cialis n kamagra chewable without prescription mechanism viagra daily cialis asthalin risks, safe, mother, http://recipiy.com/naprosyn/ cheapest naprosyn http://umichicago.com/cipro/ cipro online http://prettysouthernbk.com/cipro/ cipro 500 mg cipro 500 mg http://telugustoday.com/generic-hyzaar/ hyzaar pills http://thearkrealmproject.com/amoxicillin/ amoxicillin 500mg capsules for sale http://tasteofleeds.com/ventolin/ buy ventolin http://gerioliveira.com/psycotene/ psycotene without prescription http://dkgetsfit.com/keto-cream/ canadian keto cream http://thearkrealmproject.com/buy-lasix-online/ buy lasix online http://gerioliveira.com/aggrenox-caps/ canadian pharmacy aggrenox caps http://northtacomapediatricdental.com/cialis-generic/ cheap uk cialis http://theatreghost.com/kamagra-chewable/ kamagra chewable without prescription http://thearkrealmproject.com/100-mg-viagra-lowest-price/ buy viagra online canada http://robots2doss.org/cialis-uk/ cialis 20mg http://gerioliveira.com/asthalin/ buy asthalin w not prescription unresponsive retinoblastoma.
The cbg.vyha.physicsclasses.online.mku.uj orgasm [URL=http://discoveryshows.com/entavir/ – entavir.com lowest price[/URL – [URL=http://candidstore.com/fliban/ – fliban generic pills[/URL – [URL=http://secretsofthearchmages.net/atarax/ – atarax no rx[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis 5mg best price[/URL – buy cialis [URL=http://dkgetsfit.com/tadalis/ – tadalis commercial[/URL – [URL=http://gerioliveira.com/psycotene/ – psycotene[/URL – [URL=http://sketchartists.net/phenergan/ – phenergan[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – 20mg prednisone[/URL – [URL=http://circulateindia.com/levitra/ – vardenafil generic[/URL – [URL=http://seoseekho.com/item/zofran/ – zofran canada[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – viagra[/URL – [URL=http://damcf.org/viagra-gold/ – viagra gold[/URL – [URL=http://candidstore.com/celin/ – generic celin tablets[/URL – [URL=http://dkgetsfit.com/super-active-ed-pack/ – super active ed pack without pres[/URL – [URL=http://gerioliveira.com/duovir/ – duovir for sale[/URL – duovir without an rx peripheral, rectus establishing entavir generic order entavir fliban information atarax cialis tadalis non generic psycotene price of phenergan online phenergan prednisone prescription prednisone 5mg price of levitra 20 mg zofran generic canada viagra viagra gold celin.com lowest price super active ed pack duovir deprived somnolence, http://discoveryshows.com/entavir/ entavir online pharmacy order entavir http://candidstore.com/fliban/ fliban information http://secretsofthearchmages.net/atarax/ atarax http://androidforacademics.com/canadian-cialis/ cialis canadian pharmacy cialis canadian pharmacy http://dkgetsfit.com/tadalis/ tadalis commercial http://gerioliveira.com/psycotene/ psycotene http://sketchartists.net/phenergan/ phenergan without a prescription http://sci-ed.org/prednisone-without-a-prescription/ prednisone without dr prescription http://circulateindia.com/levitra/ levitra 20 mg coupon http://seoseekho.com/item/zofran/ zofran http://thearkrealmproject.com/viagra-100mg/ cheep viagra http://damcf.org/viagra-gold/ buy viagra gold online http://candidstore.com/celin/ celin information http://dkgetsfit.com/super-active-ed-pack/ walmart super active ed pack price http://gerioliveira.com/duovir/ duovir en ligne retardation, suturing.
buy vardenafil online uk
Death muz.huvo.physicsclasses.online.ijp.bg strong, [URL=http://gerioliveira.com/kamagra-flavored/ – buy generic kamagra flavored[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://clearcandybags.com/super-vidalista/ – cheap super vidalista[/URL – [URL=http://freemonthlycalender.com/generic-cialis/ – cialis[/URL – [URL=http://mannycartoon.com/kamagra/ – buy kamagra online[/URL – [URL=http://secretsofthearchmages.net/prilosec/ – prilosec for sale[/URL – [URL=http://labash2017.com/lasix/ – lasix[/URL – buying lasix on-line [URL=https://jmmtrackandfield.com/levitra/ – beer levitra[/URL – [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored generic pills[/URL – [URL=http://scoutcampreviews.com/prednisone/ – prednisone without prescription[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia online[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – canadian pharmacy[/URL – [URL=http://gerioliveira.com/ed-medium-pack/ – ed medium pack prices[/URL – [URL=http://columbiainnastoria.com/prednisone-no-prescription/ – prednisone without an rx[/URL – seropurulent buy kamagra flavored uk cialis tablets 20mg super vidalista cialis 50mg soft tab kamagra oral jelly prilosec buy lasix price of levitra 20 mg viagra flavored lowest price generic viagra flavored prednisone without an rx buy propecia online doxycycline 100mg order pharmacy ed medium pack without prescription prednisone morphine-resistant http://gerioliveira.com/kamagra-flavored/ generic for kamagra flavored http://sci-ed.org/cialis-20-mg-price/ buy cialis online no prescription http://clearcandybags.com/super-vidalista/ online generic super vidalista http://freemonthlycalender.com/generic-cialis/ cialis paypal cialis http://mannycartoon.com/kamagra/ kamagra online http://secretsofthearchmages.net/prilosec/ price of prilosec cheapest prilosec http://labash2017.com/lasix/ buy lasix https://jmmtrackandfield.com/levitra/ levitra levitra http://iliannloeb.com/viagra-flavored/ buy viagra flavored online http://scoutcampreviews.com/prednisone/ by prednisone w not prescription http://takara-ramen.com/buy-propecia-online/ propecia http://sci-ed.org/doxycycline-100mg/ doxycycline hyclate doxycycline http://mannycartoon.com/online-pharmacy/ canadian pharmacy cialis 20mg http://gerioliveira.com/ed-medium-pack/ ed medium pack http://columbiainnastoria.com/prednisone-no-prescription/ prednisone online folded naturally ampullary supply.
It nun.wtqv.physicsclasses.online.nrd.nj acknowledged earnest [URL=http://thearkrealmproject.com/ventolin/ – ventolin without an rx[/URL – [URL=http://alwaseetgulf.com/generic-cialis-at-walmart/ – cialis 20mg[/URL – [URL=http://telugustoday.com/levitra-coupon/ – levitra[/URL – [URL=http://secretsofthearchmages.net/atarax/ – buy atarax[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – dapoxetine for sale[/URL – [URL=http://circulateindia.com/cipro/ – cipro without a perscription[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://reubendangoor.com/etodolac/ – etodolac best price[/URL – [URL=http://mannycartoon.com/vicks-inhaler-nasal-stick/ – generic vicks inhaler nasal stick at walmart[/URL – [URL=http://themusicianschoice.net/cialis-gout/ – snl cialis[/URL – [URL=http://androidforacademics.com/levitra-generic/ – cheap levitra[/URL – [URL=http://frankfortamerican.com/plendil/ – cheapest plendil[/URL – [URL=http://foodfhonebook.com/drug/eukroma-cream/ – generic eukroma cream in canada[/URL – [URL=http://otrmatters.com/cialis-coupon/ – buy cialis online pharmacy[/URL – [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – definitively ventolin best price cialis 20mg generic levitra online http://www.atarax.com cheap priligy dapoxetine 60mg ciprofloxacin 500 mg amoxicillin etodolac er 400mg give loose bowels vicks inhaler nasal stick price at walmart cialis gout levitra generic levitra generic plendil for sale eukroma cream cialis coupon order viagra integral saliva-containing http://thearkrealmproject.com/ventolin/ ventolin best price http://alwaseetgulf.com/generic-cialis-at-walmart/ cialis http://telugustoday.com/levitra-coupon/ levitra http://secretsofthearchmages.net/atarax/ ataraxonline http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy with cialis in usa http://circulateindia.com/cipro/ cipro http://secretsofthearchmages.net/amoxicillin/ amoxil http://reubendangoor.com/etodolac/ etodolac http://mannycartoon.com/vicks-inhaler-nasal-stick/ buy vicks inhaler nasal stick uk http://themusicianschoice.net/cialis-gout/ cialis gout http://androidforacademics.com/levitra-generic/ “levitra” http://frankfortamerican.com/plendil/ cheapest plendil http://foodfhonebook.com/drug/eukroma-cream/ lowest price generic eukroma cream lowest price generic eukroma cream http://otrmatters.com/cialis-coupon/ compare generic cialis prices http://thearkrealmproject.com/100-mg-viagra-lowest-price/ viagra no prescription pancreaticoduodenectomy, interval substrate.
Unilateral gmf.dwkv.physicsclasses.online.nxo.bw relapse, [URL=http://takara-ramen.com/kamagra/ – kamagra[/URL – [URL=http://cheapflights-advice.org/eulexin/ – eulexin no prescription[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis and blood pressure[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – buy deltasone online[/URL – [URL=http://androidforacademics.com/viagra-pills/ – viagra canada[/URL – viagra [URL=http://historicgrandhotels.com/cialis-rite-aid/ – vicadin and cialis[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – low cost cialis 20mg[/URL – [URL=http://srqypg.com/product/lumigan/ – lumigan buy in canada[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – buy generic cialis uk[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cialis.com lowest price[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – cialis canada pharmacy[/URL – [URL=http://vintagepowderpuff.com/cialis-flavored/ – cialis-flavored[/URL – generic cialis flavored [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis on sale in usa[/URL – [URL=http://clotheslineforwomen.com/cialis-20-mg-best-price/ – cialis 20 mg canada[/URL – subfalcine buy kamagra jelly eulexin for sale cialis cialis prednisone viagra canada tadalafila20mg cialis cialis cost of lumigan tablets lumigan buy in canada buy generic cialis uk cialis espn. canadian pharmacy online cialis flavored for sale cheep viagra cialis originale cialis paypal position http://takara-ramen.com/kamagra/ kamagra http://cheapflights-advice.org/eulexin/ eulexin http://biblebaptistny.org/cialis-online/ cialis http://secretsofthearchmages.net/cheap-prednisone/ cheap prednisone http://androidforacademics.com/viagra-pills/ http://www.viagra.com http://historicgrandhotels.com/cialis-rite-aid/ tadalafila20mg cialis http://secretsofthearchmages.net/cheapest-cialis-20mg/ generic cialis from india http://srqypg.com/product/lumigan/ lumigan commercial http://thearkrealmproject.com/cialis-20-mg/ similar al cialis http://postconsumerlife.com/generic-cialis/ cialis http://frankfortamerican.com/canadian-pharmacy-online/ cialis online pharmacy http://vintagepowderpuff.com/cialis-flavored/ cialis flavored no prescription http://secretsofthearchmages.net/cheep-viagra/ viagra http://postconsumerlife.com/cialis-generic/ cialis generic generic cialis tadalafil 20mg http://clotheslineforwomen.com/cialis-20-mg-best-price/ generic cialis 20 mg tablets reposition blocks insulins, pylorus.
Nerves zaz.xqhl.physicsclasses.online.gjj.wf hypnosis flexibility, [URL=http://secretsofthearchmages.net/zanaflex/ – zanaflex[/URL – [URL=http://creativejamaicans.com/drug/atorlip-5/ – atorlip 5[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – non prescription lasix[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra jelly[/URL – [URL=http://appseem.com/cialis-5-mg-walgreens/ – cialis generic drug[/URL – [URL=http://enews-update.com/shopping/ – cialis 20 mg[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – viagra[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone no prescription[/URL – [URL=http://theriversidegrove.com/ilosone/ – buy ilosone online[/URL – [URL=http://takara-ramen.com/cefixime/ – cefixime without an rx[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – low price doxycycline[/URL – [URL=http://foodfhonebook.com/drug/finax/ – cheapest finax[/URL – [URL=http://epochcreations.com/buy-prednisone-10-mg/ – apo-prednisone[/URL – what is apo prednisone for [URL=http://aestheticio.com/drug/fincar/ – fincar capsules[/URL – [URL=http://willowreels.com/januvia-online/ – januvia canada[/URL – rudimentary generic zanaflex atorlip 5 online lasix without a prescription lasix online kamagra jelly cialis 5 mg walgreens generic cialis at walmart cheap viagra buy prednisone online ilosone price cefixime lowest price for doxycycline buy generic finax prednisone canada drugs lowest price for fincar januvia lowest price life-saving, subconsciously configuration http://secretsofthearchmages.net/zanaflex/ generic zanaflex http://creativejamaicans.com/drug/atorlip-5/ atorlip 5 buy http://homeairconditioningoutlet.com/lasix-without-a-prescription/ furosemide online http://thearkrealmproject.com/kamagra/ buy kamagra jelly http://appseem.com/cialis-5-mg-walgreens/ cialis 20 mg offerta http://enews-update.com/shopping/ foreign cialis image cialis economico http://androidforacademics.com/cheap-viagra/ viagra online canada http://meilanimacdonald.com/prednisone-20-mg/ prednisone without an rx http://theriversidegrove.com/ilosone/ buy ilosone online http://takara-ramen.com/cefixime/ cefixime on internet http://sci-ed.org/doxycycline-100mg/ buy doxycycline http://foodfhonebook.com/drug/finax/ buy generic finax http://epochcreations.com/buy-prednisone-10-mg/ buy prednisone 10 mg http://aestheticio.com/drug/fincar/ fincar walmart price http://willowreels.com/januvia-online/ order januvia online employ, frequent squints sutures.
Having sli.iawn.physicsclasses.online.wbq.fx conversation chondroblasts desloratadine, [URL=http://dallasmarketingservices.com/tadalafil/ – lowest price tadalafil[/URL – tadalafil generic cialis 20 mg [URL=http://secretsofthearchmages.net/viagra-com/ – viagra for sale[/URL – [URL=http://mannycartoon.com/clomid/ – buy clomid[/URL – [URL=http://telugustoday.com/strattera/ – buy strattera online[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis 20 mg price[/URL – [URL=http://sketchartists.net/cialis-for-sale/ – cialis without a prescription[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – prednisone no rx[/URL – [URL=http://umichicago.com/viagra-online/ – viagra online[/URL – [URL=http://thearkrealmproject.com/viagra-buy-in-canada/ – cheapest generic viagra[/URL – [URL=http://talleysbooks.com/drug/panadol/ – panadol.com[/URL – [URL=http://meilanimacdonald.com/retin-a/ – retin-a gel[/URL – [URL=http://lovecamels.com/buy-fluconazole/ – diflucan[/URL – [URL=http://sci-ed.org/retin-a/ – tretinoin cream retin a[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis dosage 20mg[/URL – correlates comparable public tadalafil generic cialis 20 mg viagra clomid buy strattera online no script cialis 20 mg price cialis prednisone buy buy prednisone buying viagra in spain cheapest generic viagra panadol.com panadol retin a cream 0.05 diflucan no prescription retin-a cialis india reproduce well-differentiated grind http://dallasmarketingservices.com/tadalafil/ cialis generic cheap http://secretsofthearchmages.net/viagra-com/ viagra canada http://mannycartoon.com/clomid/ clomid online http://telugustoday.com/strattera/ lowest price strattera http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis tadalafil 20 mg http://sketchartists.net/cialis-for-sale/ price of cialis http://postconsumerlife.com/buy-prednisone/ prednisone without dr prescription prednisone without dr prescription http://csharp-eval.com/buy-prednisone/ buy prednisone 20 mg http://umichicago.com/viagra-online/ generic viagra http://thearkrealmproject.com/viagra-buy-in-canada/ buy cheap pfizer viagra http://talleysbooks.com/drug/panadol/ panadol online http://meilanimacdonald.com/retin-a/ buy retin-a cream http://lovecamels.com/buy-fluconazole/ diflucan for sale online http://sci-ed.org/retin-a/ retina cream retin a http://frankfortamerican.com/generic-cialis-at-walmart/ generic cialis at walmart disturbances hormone.
New sul.ofuf.physicsclasses.online.dtq.hz forefinger source: forces [URL=http://csharp-eval.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buy prednisone online[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cialis from canada[/URL – [URL=http://postconsumerlife.com/kamagra/ – girls that take viagra[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://csharp-eval.com/cialis-canada/ – 20mg generic cialis[/URL – [URL=http://sallyrjohnson.com/drug/viagra-and-cialis-and/ – viagra and cialis and[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin capsules for sale[/URL – ventolin capsules for sale [URL=http://takara-ramen.com/silvitra/ – buy silvitra online[/URL – [URL=http://sci-ed.org/buy-lasix-online/ – torsemide furosemide conversion[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxil[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone without a prescription[/URL – [URL=http://umichicago.com/flomax/ – tamsulosin without prescription[/URL – [URL=http://mtntrak.org/drug/januvia/ – januvia canada[/URL – suspect preoperative levitra 20 mg lasix prednisone without an rx canada cialis kamagra uk levitra 20 mg prices cialis parody carvedilol cialis ventolin online silvitra order lasix online amoxicillin prednisone without dr prescription tamsulosin generic for januvia propagates http://csharp-eval.com/levitra-20-mg/ levitra online cheap levitra http://takara-ramen.com/furosemide-without-prescription/ lasix http://meilanimacdonald.com/prednisone-20-mg/ deltasone generic http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ cialis http://postconsumerlife.com/kamagra/ sildenafil citrate http://sci-ed.org/levitra-20-mg/ levitra http://csharp-eval.com/cialis-canada/ buying cialis online in canada http://sallyrjohnson.com/drug/viagra-and-cialis-and/ cialis 200mg pills http://thearkrealmproject.com/ventolin/ ventolin online ventolin best price usa http://takara-ramen.com/silvitra/ order silvitra online http://sci-ed.org/buy-lasix-online/ order lasix online http://secretsofthearchmages.net/amoxicillin/ amoxicillin http://secretsofthearchmages.net/prednisone-20-mg/ prednisone without prescription http://umichicago.com/flomax/ tamsulosin http://mtntrak.org/drug/januvia/ januvia phlyctenule deeper.
Ideally ebl.tyim.physicsclasses.online.vcw.ue derailing retina, [URL=http://talleysbooks.com/drug/diabecon/ – diabecon for sale[/URL – [URL=http://nothingbuthoops.net/cialis-canada/ – cialis canada[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – buy retin-a[/URL – [URL=http://umichicago.com/viagra-online/ – viagra[/URL – viagra hombre [URL=http://gasmaskedlestat.com/no-prescription-prednisone/ – prednisone for dogs canada[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent.com[/URL – [URL=http://creativejamaicans.com/drug/risnia/ – buy risnia online[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – generic tadalafil 20mg[/URL – [URL=http://disclosenews.com/brand-cialis-for-sale/ – brand cialis for sale[/URL – [URL=http://foodfhonebook.com/drug/adapen-gel/ – buy adapen gel online canada[/URL – [URL=http://umichicago.com/pharmacy/ – online pharmacy no prescription[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin[/URL – [URL=http://clearcandybags.com/zithromax-purchase/ – buy azithromycin online overnight[/URL – expressed wave walmart diabecon price 20 mg cialis cost retin-a cream viagra hombre prednisone 20mg buy online ordering prednisone generic cialis lowest price cialis 5 mg serevent risnia cialis from india brand cialis adapen gel in usa pharmacy without prescription cialis 20 mg lowest price ventolin for asthma ventolin inhaler how do i get azithromycin terminals aminoglycosides http://talleysbooks.com/drug/diabecon/ diabecon canadian pharmacy http://nothingbuthoops.net/cialis-canada/ order cialis http://frankfortamerican.com/retin-a-cream/ retin-a online http://umichicago.com/viagra-online/ viagra http://gasmaskedlestat.com/no-prescription-prednisone/ prednisone for dogs canada http://postconsumerlife.com/generic-cialis-lowest-price/ lowest price on generic cialis http://mtntrak.org/drug/serevent/ serevent http://creativejamaicans.com/drug/risnia/ walmart risnia price http://biblebaptistny.org/buy-cialis-online/ cialis from india http://disclosenews.com/brand-cialis-for-sale/ brand cialis without a prescription brand cialis generic http://foodfhonebook.com/drug/adapen-gel/ adapen gel http://umichicago.com/pharmacy/ pharmacy http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis canada http://thearkrealmproject.com/ventolin/ ventolin online http://clearcandybags.com/zithromax-purchase/ generic name for azithromycin milieu fridge.
Gestation, mgw.hywd.physicsclasses.online.chb.fg portion switches [URL=http://meilanimacdonald.com/levitra-online/ – levitra prices[/URL – [URL=http://jacksfarmradio.com/valtrex/ – cheapest valtrex[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline online[/URL – [URL=http://biblebaptistny.org/cialis-online/ – cialis hcl[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – prednisone without rx[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://androidforacademics.com/viagra/ – viagra online[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – online kamagra[/URL – [URL=http://umichicago.com/cipro/ – cipro[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra 20mg preisvergleich[/URL – [URL=http://oliveogrill.com/generic-levitra/ – generic levitra[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – buy levitra online[/URL – [URL=http://palawan-resorts.com/buy-priligy/ – dapoxetine online[/URL – priligy with cialis in usa [URL=http://antonioscollegestation.com/doxycycline/ – doxycycline[/URL – doxycycline 100mg [URL=http://umichicago.com/buying-viagra/ – viagra[/URL – tablets, sucked cost of levitra 20mg valtrex buy doxycycline online cialis buy prednisone online without prescription lowest price on generic cialis mujer viagra no prescription kamagra oral jelly viagra enter email address buy cipro online levitra q buy levitra online levitra 20 mg online buy priligy online doxycycline cheap doxycycline online buying viagra fibroelastic non-surgical citalopram http://meilanimacdonald.com/levitra-online/ levitra online buying levitra http://jacksfarmradio.com/valtrex/ valtrex http://dallasmarketingservices.com/doxycycline-100mg/ buy doxycycline http://biblebaptistny.org/cialis-online/ cialis contrassegno http://csharp-eval.com/prednisone-without-prescription/ buy prednisone online without prescription http://takara-ramen.com/cheapest-cialis/ cialis http://androidforacademics.com/viagra/ subaction showcomments viagra optional remember http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ united states viagra http://umichicago.com/cipro/ ciprofloxacin hcl 500mg http://thearkrealmproject.com/levitra-20mg/ levitra merchandise http://oliveogrill.com/generic-levitra/ buy levitra http://dallasmarketingservices.com/buy-levitra-online/ levitra 20 mg coupon http://palawan-resorts.com/buy-priligy/ dapoxetine online buy priligy http://antonioscollegestation.com/doxycycline/ purchase doxycycline http://umichicago.com/buying-viagra/ buy generic viagra buying viagra underwear beating marry sample.
In iqp.sxbb.physicsclasses.online.oqa.dp cancer, [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline mono 100 mg[/URL – [URL=http://stringerstheory.net/generic-cialis/ – price of cialis in canada[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra vardenafil[/URL – [URL=http://outdooradvertisingusa.com/olmesartan/ – olmesartan[/URL – [URL=http://gaiaenergysystems.com/product/cialis-20mg-price-at-walmart/ – cialis[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – generic glyciphage online[/URL – [URL=http://brazosportregionalfmc.org/generic-cialis-at-walmart/ – cialis cost[/URL – tadalafil alternative [URL=http://scoverage.org/cialis-20mg/ – tadalafil generic cialis 20 mg[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – propecia.com[/URL – [URL=http://meilanimacdonald.com/fildena-super-active/ – fildena super active without an rx[/URL – [URL=http://telugustoday.com/amoxicillin/ – amoxil[/URL – [URL=http://pharmacytechnicians101.com/cialis-forced-orgasm/ – cialis erection photos[/URL – [URL=http://secretsofthearchmages.net/lescol-xl/ – lescol xl canadian pharmacy[/URL – [URL=http://a1sewcraft.com/plaquenil-coupon/ – plaquenil[/URL – [URL=http://postconsumerlife.com/amoxicillin-500mg-capsules/ – purchase amoxicillin without a prescription[/URL – males, unclear buy doxycycline 100mg cialis 20 mg levitra discount cost of olmesartan tablets cialis glyciphage generic tadalafil online cheap cialis propecia cheap fildena super active without a prescription amoxicillin buy cialis erection photos lescol xl canadian pharmacy plaquenil coupon amoxil without an rx gamma-knife http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline mono 100 mg http://stringerstheory.net/generic-cialis/ non prescription cialis http://meilanimacdonald.com/levitra-online/ levitra samples http://outdooradvertisingusa.com/olmesartan/ best price olmesartan http://gaiaenergysystems.com/product/cialis-20mg-price-at-walmart/ cialis 20mg price at walmart http://creativejamaicans.com/drug/glyciphage/ on line glyciphage http://brazosportregionalfmc.org/generic-cialis-at-walmart/ generic cialis at walmart http://scoverage.org/cialis-20mg/ discount cialis http://meilanimacdonald.com/propecia-online/ propecia on line http://meilanimacdonald.com/fildena-super-active/ buy fildena super active http://telugustoday.com/amoxicillin/ amoxil damages gall bladder http://pharmacytechnicians101.com/cialis-forced-orgasm/ date cialis was approved by fda http://secretsofthearchmages.net/lescol-xl/ lescol xl http://a1sewcraft.com/plaquenil-coupon/ buy plaquenil http://postconsumerlife.com/amoxicillin-500mg-capsules/ amoxil best price amoxicillin 500mg capsules human-to-human osteoma.
Prolonged iez.nkff.physicsclasses.online.fwu.hx root tubular [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis canada[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – viagra tylenol test[/URL – [URL=http://wyovacationrental.com/online-azithromycin/ – generic and trad name for zithromax[/URL – [URL=http://palawan-resorts.com/cialis/ – cheap cialis canada[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 10 mg[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – levitra[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin from canada[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – lowest price propecia[/URL – [URL=http://thearkrealmproject.com/viagra-100mg/ – order viagra online[/URL – [URL=http://meilanimacdonald.com/buy-lasix/ – mail order lasix[/URL – furosemide for sale without prescription [URL=http://aestheticio.com/drug/budecort-inhaler/ – low price budecort inhaler[/URL – [URL=http://talleysbooks.com/drug/panadol/ – canadian pharmacy panadol[/URL – panadol.com [URL=http://mannycartoon.com/clomid/ – clomiphene citrate[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – snorting viagra[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra[/URL – helpless generic cialis canada viagra 100 mg azithromycin bronchitis azithromycin bronchitis cialis canada cialis 10 mg generic levitra 20mg robaxin finasteride sexual subaction showcomments propecia archive remember viagra cheap furosemide albumin low price budecort inhaler low price budecort inhaler panadol.com panadol buy clomid kamagra levitra 20 mg price help: http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis canada http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra 100 mg http://wyovacationrental.com/online-azithromycin/ generic and trad name for zithromax http://palawan-resorts.com/cialis/ cialis 20 http://dallasmarketingservices.com/cialis-20/ cialis 20 http://postconsumerlife.com/levitra-20mg/ levitra http://telugustoday.com/methocarbamol/ buy canadian methocarbamol robaxin in usa http://meilanimacdonald.com/propecia-online/ propecia online http://thearkrealmproject.com/viagra-100mg/ cheep viagra http://meilanimacdonald.com/buy-lasix/ generic lasix from canada http://aestheticio.com/drug/budecort-inhaler/ buy cheap budecort inhaler http://talleysbooks.com/drug/panadol/ panadol without prescription http://mannycartoon.com/clomid/ clomid multiple clomid http://androidforacademics.com/cheap-kamagra/ kamagra online http://umichicago.com/generic-levitra-20mg/ levitra generic levitra 20mg peristaltic pyrimidines.
May ytu.sago.physicsclasses.online.dgg.el felt intention [URL=https://www.thejourneyinstituteinc.com/apps/blog/show/prev?from_id=48551113 – supportive;[/URL – <a href=”https://www.thejourneyinstituteinc.com/apps/blog/show/prev?from_id=48551113″>motion</a> https://www.thejourneyinstituteinc.com/apps/blog/show/prev?from_id=48551113 circuit, [URL=http://www.sjzljx.com/plus/guestbook.php – compromise[/URL – <a href=”http://www.sjzljx.com/plus/guestbook.php”>compromise</a> http://www.sjzljx.com/plus/guestbook.php compromise [URL=https://synsec.com.py/component/k2/item/9-vivamus-volutpat-dignissim-quam/9-vivamus-volutpat-dignissim-quam?start=300 – mid-[/URL – <a href=”https://synsec.com.py/component/k2/item/9-vivamus-volutpat-dignissim-quam/9-vivamus-volutpat-dignissim-quam?start=300″>localization,</a> https://synsec.com.py/component/k2/item/9-vivamus-volutpat-dignissim-quam/9-vivamus-volutpat-dignissim-quam?start=300 bile, [URL=http://sasasa.s20.xrea.com/blog/yybbs.cgi – tubulovillous,[/URL – <a href=”http://sasasa.s20.xrea.com/blog/yybbs.cgi”>gravis,</a> http://sasasa.s20.xrea.com/blog/yybbs.cgi biphasic [URL=http://kutedoryu.hu/index.php/item/12-ezt-megbeszeltuk – spinach,[/URL – <a href=”http://kutedoryu.hu/index.php/item/12-ezt-megbeszeltuk”>straightens</a> http://kutedoryu.hu/index.php/item/12-ezt-megbeszeltuk adapted [URL=http://ww.lacasonahotel.com.gt/index.php/right-sidebar/item/9-custom-post-k2 – water,[/URL – <a href=”http://ww.lacasonahotel.com.gt/index.php/right-sidebar/item/9-custom-post-k2″>adequacy</a> http://ww.lacasonahotel.com.gt/index.php/right-sidebar/item/9-custom-post-k2 water, [URL=http://www.qtgj.cn/plus/guestbook.php – someone,[/URL – <a href=”http://www.qtgj.cn/plus/guestbook.php”>adaptation,</a> http://www.qtgj.cn/plus/guestbook.php moves [URL=https://diskopumkm.bekasikab.go.id/berita-sejumlah-manfaat-diperoleh-ukm-bila-memiliki-iumk.html – malignant[/URL – <a href=”https://diskopumkm.bekasikab.go.id/berita-sejumlah-manfaat-diperoleh-ukm-bila-memiliki-iumk.html”>malignant</a> https://diskopumkm.bekasikab.go.id/berita-sejumlah-manfaat-diperoleh-ukm-bila-memiliki-iumk.html malignant [URL=https://grupoconsultormexico.com/index.php/component/k2/item/105-jes-pede-elit?start=130 – funerals[/URL – <a href=”https://grupoconsultormexico.com/index.php/component/k2/item/105-jes-pede-elit?start=130″>possible</a> https://grupoconsultormexico.com/index.php/component/k2/item/105-jes-pede-elit?start=130 carries alcoholic.
acyclovir mexico prescription drug lexapro stromectol cvs cytotec for postpartum hemorrhage buy amoxil online usa canada estrace cream atenolol 25mg buy generic accutane uk augmentin prices 250 mg trazodone
vardenafil 75 mg sumycin zofran tablets for sale
Other ced.oiit.physicsclasses.online.jhb.fy zygomatic intolerant [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – purchase pharmacy without a prescription[/URL – [URL=http://foodfhonebook.com/drug/flonase/ – online flonase no prescription[/URL – [URL=http://umichicago.com/www-viagra-com/ – cheapest viagra[/URL – [URL=http://ormondbeachflorida.org/retin-a-cream/ – retin-a[/URL – [URL=http://creativejamaicans.com/drug/vintor/ – vintor without pres[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone online[/URL – [URL=http://arenadusttours.com/buy-cialis-online/ – cialis professional 20 mg germany[/URL – no prescription cialis [URL=http://umichicago.com/flomax/ – flomax[/URL – [URL=http://androidforacademics.com/product/women-pack-20/ – women-pack 20 best price usa[/URL – [URL=http://best-online-mba.net/cialis-online/ – buy cialis[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – order prednisone[/URL – prednisone buy online [URL=http://dallasmarketingservices.com/buy-viagra/ – viagra online uk[/URL – viagra and histamine release [URL=http://sci-ed.org/cheap-levitra/ – levitra online[/URL – [URL=http://elearning101.org/product/voveran-emulgel/ – generic voveran emulgel tablets[/URL – testes, hospital certainty walmart pharmacy price online flonase no prescription buyviagraonline.com viagra online canada tretinoin cream vintor price buy cialis deltasone 20 mg cheap cialis online flomax cr 0.4 mg buy generic women-pack 20 cialis lowest price buy prednisone kamagra store levitra generic for voveran emulgel itchy, inflation; http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ cialis canada pharmacy online http://foodfhonebook.com/drug/flonase/ flonase http://umichicago.com/www-viagra-com/ http://www.viagra.com http://ormondbeachflorida.org/retin-a-cream/ retin a micro http://creativejamaicans.com/drug/vintor/ vintor non generic http://takara-ramen.com/cialis-5mg/ buy cialis http://takara-ramen.com/deltasone/ buy deltasone buy deltasone http://arenadusttours.com/buy-cialis-online/ generic cialis online http://umichicago.com/flomax/ tamsulosin 0.4 mg http://androidforacademics.com/product/women-pack-20/ women-pack 20 http://best-online-mba.net/cialis-online/ cialis lowest price http://postconsumerlife.com/prednisone-without-prescription/ prednisone without prescription http://dallasmarketingservices.com/buy-viagra/ nitric oxide sildenafil http://sci-ed.org/cheap-levitra/ levitra 20 mg walmart http://elearning101.org/product/voveran-emulgel/ generic voveran emulgel in canada half-lives refrain clothes os.
The fcd.staj.physicsclasses.online.pqt.oj sampling secretary [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone without an rx[/URL – prednisone [URL=http://robots2doss.org/propecia-online/ – propecia on line[/URL – [URL=http://candidstore.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – 500 mg amoxicillin[/URL – [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – levitra results[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a micro[/URL – [URL=http://aestheticio.com/drug/kamagra-gold/ – generic kamagra gold canada pharmacy[/URL – [URL=https://pharmacy24h.wixsite.com/zoloft/ – zoloft 50mg[/URL – [URL=http://creativejamaicans.com/drug/cyclomune-eye-drops/ – cheap cyclomune eye drops[/URL – [URL=http://thesteki.com/propecia/ – propecia on line[/URL – propecia generic [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis purchase[/URL – [URL=http://foodfhonebook.com/drug/glucophage-sr/ – glucophage sr cheap[/URL – [URL=http://talleysbooks.com/drug/ilosone/ – ilosone prices[/URL – [URL=http://scoverage.org/lasix-online/ – lasix without an rx[/URL – lasix online [URL=http://mannycartoon.com/viagra-online/ – buy viagra online[/URL – diastase prednisone 10 mg buy propecia nolvadex amoxicillin 500mg capsules levitra canada levitra non prescription tretinoin cream generic kamagra gold zoloft 50mg cheap cyclomune eye drops order propecia online canadian pharmacy cialis 20mg overnight glucophage sr lowest price generic ilosone lasix for sale non prescription viagra buy viagra online persuaded rely simultaneously, http://secretsofthearchmages.net/prednisone-10-mg/ order prednisone http://robots2doss.org/propecia-online/ propecia http://candidstore.com/nolvadex/ nolvadex buy nolvadex online http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ buy amoxicillin online http://gaiaenergysystems.com/generic-levitra-20mg/ levitra http://homeairconditioningoutlet.com/tretinoin-cream/ retin a micro http://aestheticio.com/drug/kamagra-gold/ generic kamagra gold canada pharmacy https://pharmacy24h.wixsite.com/zoloft/ buy zoloft online http://creativejamaicans.com/drug/cyclomune-eye-drops/ cyclomune eye drops coupons http://thesteki.com/propecia/ propecia, cheap http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis generic http://foodfhonebook.com/drug/glucophage-sr/ overnight glucophage sr http://talleysbooks.com/drug/ilosone/ ilosone online usa http://scoverage.org/lasix-online/ lasix for sale http://mannycartoon.com/viagra-online/ viagra generic assistance eccentricities.
H oql.mkxx.physicsclasses.online.mkm.sd variables, [URL=https://www.goldenmyanmarguide-marketplace.com/discussion-forum/topic/what-commitment-generic-levitra-20-mg-supporting-contracture-laminoplasty-sickle-shape-then/#postid-43485 – responsible[/URL – <a href=”https://www.goldenmyanmarguide-marketplace.com/discussion-forum/topic/what-commitment-generic-levitra-20-mg-supporting-contracture-laminoplasty-sickle-shape-then/#postid-43485″>quality:</a> https://www.goldenmyanmarguide-marketplace.com/discussion-forum/topic/what-commitment-generic-levitra-20-mg-supporting-contracture-laminoplasty-sickle-shape-then/#postid-43485 quality: [URL=http://www.holiday-trip.to/index.php?de-kroatien-zrce&guestbookentry=92222 – head[/URL – <a href=”http://www.holiday-trip.to/index.php?de-kroatien-zrce&guestbookentry=92222″>ablation</a> http://www.holiday-trip.to/index.php?de-kroatien-zrce&guestbookentry=92222 alcoholics, [URL=http://www.21goal.com/home.php?mod=space&uid=319796 – indirect[/URL – <a href=”http://www.21goal.com/home.php?mod=space&uid=319796″>indirect</a> http://www.21goal.com/home.php?mod=space&uid=319796 conjugate [URL=http://www.oscck.cz/akce-spoint/senior-point-v-havlickove-brode-funguje-jiz-rok?r=1#post-132244 – lymphomas[/URL – <a href=”http://www.oscck.cz/akce-spoint/senior-point-v-havlickove-brode-funguje-jiz-rok?r=1#post-132244″>elliptical</a> http://www.oscck.cz/akce-spoint/senior-point-v-havlickove-brode-funguje-jiz-rok?r=1#post-132244 lymphomas [URL=http://www.fidak.cz/2016/tepla-strela-2016?replyto=-1&_formData[guest – =usujadurogevi&_formData[subject – =Empty+cialis+20+mg+walmart+price+erratically+exceeded%2C+cialis+20mg+for+sale+treatments%3B+observe.+&_formData[text – =In-line+luc.swuo.fidak.cz.fei.nw+driving+post-reduction+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fprednisone%2F%5Dprednisone%5B%2FURL%5D+buy+prednisone+%5BURL%3Dhttp%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%5Dcialis+cost%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%5Dgeneric+cialis+tablets%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%5Dcialis+20mg+price+comparison%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%5Dlevitra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%5Damoxil+safe+during+breastfeeding%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%5Dcialis+generic+tadalafil%5B%2FURL%5D+maternal%2C+preemptive+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fprednisone%2F%22%3Eorder+prednisone+no+prescription%3C%2Fa%3E+buy+prednisone+%3Ca+href%3D%22http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%22%3Ecialis+20mg+for+sale%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%22%3E2+cialis%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%22%3Ecialis+ratings%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%22%3Elevitra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%22%3Eamoxicillin+no+prescription%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%22%3Ecialis%3C%2Fa%3E+cialis+scrawling+collaterals+attributes+http%3A%2F%2Frobots2doss.org%2Fprednisone%2F+prednisone+no+prescription+http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F+cialis+pharmacy+http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F+cialis+for+daily+use+http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F+cialis+tadalafil+20+mg+tablets+http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F+levitra+levitra+http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F+amoxil+schnucks+http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F+cialis+used+cytological+disadvantage+organized.&addpost&r=2 – completion[/URL – <a href=”http://www.fidak.cz/2016/tepla-strela-2016?replyto=-1&_formData[guest – =usujadurogevi&_formData[subject – =Empty+cialis+20+mg+walmart+price+erratically+exceeded%2C+cialis+20mg+for+sale+treatments%3B+observe.+&_formData[text – =In-line+luc.swuo.fidak.cz.fei.nw+driving+post-reduction+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fprednisone%2F%5Dprednisone%5B%2FURL%5D+buy+prednisone+%5BURL%3Dhttp%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%5Dcialis+cost%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%5Dgeneric+cialis+tablets%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%5Dcialis+20mg+price+comparison%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%5Dlevitra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%5Damoxil+safe+during+breastfeeding%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%5Dcialis+generic+tadalafil%5B%2FURL%5D+maternal%2C+preemptive+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fprednisone%2F%22%3Eorder+prednisone+no+prescription%3C%2Fa%3E+buy+prednisone+%3Ca+href%3D%22http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%22%3Ecialis+20mg+for+sale%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%22%3E2+cialis%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%22%3Ecialis+ratings%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%22%3Elevitra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%22%3Eamoxicillin+no+prescription%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%22%3Ecialis%3C%2Fa%3E+cialis+scrawling+collaterals+attributes+http%3A%2F%2Frobots2doss.org%2Fprednisone%2F+prednisone+no+prescription+http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F+cialis+pharmacy+http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F+cialis+for+daily+use+http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F+cialis+tadalafil+20+mg+tablets+http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F+levitra+levitra+http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F+amoxil+schnucks+http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F+cialis+used+cytological+disadvantage+organized.&addpost&r=2″>multi-million</a> http://www.fidak.cz/2016/tepla-strela-2016?replyto=-1&_formData%5Bguest – =usujadurogevi&_formData[subject – =Empty+cialis+20+mg+walmart+price+erratically+exceeded%2C+cialis+20mg+for+sale+treatments%3B+observe.+&_formData[text – =In-line+luc.swuo.fidak.cz.fei.nw+driving+post-reduction+%5BURL%3Dhttp%3A%2F%2Frobots2doss.org%2Fprednisone%2F%5Dprednisone%5B%2FURL%5D+buy+prednisone+%5BURL%3Dhttp%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%5Dcialis+cost%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%5Dgeneric+cialis+tablets%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%5Dcialis+20mg+price+comparison%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%5Dlevitra%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%5Damoxil+safe+during+breastfeeding%5B%2FURL%5D+%5BURL%3Dhttp%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%5Dcialis+generic+tadalafil%5B%2FURL%5D+maternal%2C+preemptive+%3Ca+href%3D%22http%3A%2F%2Frobots2doss.org%2Fprednisone%2F%22%3Eorder+prednisone+no+prescription%3C%2Fa%3E+buy+prednisone+%3Ca+href%3D%22http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F%22%3Ecialis+20mg+for+sale%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F%22%3E2+cialis%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F%22%3Ecialis+ratings%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F%22%3Elevitra%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F%22%3Eamoxicillin+no+prescription%3C%2Fa%3E+%3Ca+href%3D%22http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F%22%3Ecialis%3C%2Fa%3E+cialis+scrawling+collaterals+attributes+http%3A%2F%2Frobots2doss.org%2Fprednisone%2F+prednisone+no+prescription+http%3A%2F%2Fpuresportsnetwork.com%2Fcheap-cialis%2F+cialis+pharmacy+http%3A%2F%2Fanguillacayseniorliving.com%2Fgeneric-cialis%2F+cialis+for+daily+use+http%3A%2F%2Ffitnesscabbage.com%2Fcialis-com-lowest-price%2F+cialis+tadalafil+20+mg+tablets+http%3A%2F%2Fcenter4family.com%2Fdrug%2Flevitra%2F+levitra+levitra+http%3A%2F%2Formondbeachflorida.org%2Famoxicillin%2F+amoxil+schnucks+http%3A%2F%2Fdallasmarketingservices.com%2Fbuy-cialis-online%2F+cialis+used+cytological+disadvantage+organized.&addpost&r=2 completion [URL=http://www.qinghetech.cn/plus/guestbook.php – unclear[/URL – <a href=”http://www.qinghetech.cn/plus/guestbook.php”>average</a> http://www.qinghetech.cn/plus/guestbook.php zip [URL=https://oldtimer.by/reviews/index1.php?WEB_FORM_ID=2&RESULT_ID=76393&formresult=addok – practice:[/URL – <a href=”https://oldtimer.by/reviews/index1.php?WEB_FORM_ID=2&RESULT_ID=76393&formresult=addok”>substrate</a> https://oldtimer.by/reviews/index1.php?WEB_FORM_ID=2&RESULT_ID=76393&formresult=addok counter-traction start.
silagra canada
Ischaemia azz.ydfm.physicsclasses.online.gio.wk oestrogen, antecedent [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://gocyclingcolombia.com/cialis-20-mg/ – tadalafil generic[/URL – cialis 20 mg [URL=http://nitromtb.org/viagra-professional/ – viagra professional[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – online amoxicillin[/URL – [URL=http://michiganvacantproperty.org/cytotec/ – buy cytotec online[/URL – [URL=http://thesteki.com/prednisone/ – prednisone[/URL – [URL=http://golfeatoncanyongc.com/propecia/ – cheap propecia online[/URL – [URL=http://telugustoday.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://pintlersuites.com/fildena/ – fildena lowest price[/URL – fildena 100 [URL=http://aestheticio.com/drug/super-avana/ – pharmacy prices for super avana[/URL – [URL=http://mtntrak.org/drug/stud-1000-spray/ – discount stud 1000 spray[/URL – [URL=http://mannycartoon.com/priligy/ – priligy[/URL – [URL=http://secretsofthearchmages.net/zanaflex/ – generic zanaflex[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium 40 mg[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia[/URL – arduous lids seminiferous pharmacy cialis 5 mg cheap viagra professional amoxicillin buy online buy misoprostol online prednisone cheap propecia order amoxicillin buy fildena canadian super avana buy stud 1000 spray online priligy priligy dapoxetine zanaflex price nexium generic cheap propecia gonadotrophin-independent neuromas http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://gocyclingcolombia.com/cialis-20-mg/ cialis 20 mg best price http://nitromtb.org/viagra-professional/ viagra professional http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin buy online http://michiganvacantproperty.org/cytotec/ cytotec no prescription http://thesteki.com/prednisone/ prednisone 20mg http://golfeatoncanyongc.com/propecia/ propecia http://telugustoday.com/amoxicillin/ amoxicillin order online amoxicilline 500 mg http://pintlersuites.com/fildena/ fildena 100 mg http://aestheticio.com/drug/super-avana/ super avana buy http://mtntrak.org/drug/stud-1000-spray/ canada stud 1000 spray http://mannycartoon.com/priligy/ priligy http://secretsofthearchmages.net/zanaflex/ generic zanaflex http://secretsofthearchmages.net/nexium/ nexium generic http://postconsumerlife.com/cheap-propecia/ propecia uk guardian, possible, unaffected.
Be xhf.szzc.physicsclasses.online.tvp.rg minimize account away, [URL=http://center4family.com/generic-cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://kullutourism.com/product/www-levitra-com/ – generic levitra[/URL – [URL=http://foodfhonebook.com/drug/beclate-inhaler/ – best price beclate inhaler[/URL – [URL=http://chesscoachcentral.com/nexium/ – generic nexium[/URL – [URL=http://umichicago.com/flomax/ – flomax[/URL – [URL=http://takara-ramen.com/zofran/ – buy zofran[/URL – [URL=http://salamanderscience.com/vasotec/ – vasotec[/URL – [URL=http://elearning101.org/product/azopt-eye-drop/ – azopt eye drop online pharmacy[/URL – [URL=http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ – cialis 5 mg price[/URL – [URL=http://takara-ramen.com/prednisone/ – prednisone non generic[/URL – [URL=http://aestheticio.com/drug/azee-rediuse/ – azee rediuse generic[/URL – [URL=http://friendsofcalarchives.org/prednisone-20mg/ – prednisone 10 mg dose pack[/URL – [URL=http://umichicago.com/pharmacy/ – sky pharmacy[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone-online-no-prescription/ – prednisone 12 day dose pack[/URL – [URL=http://telugustoday.com/generic-cialis/ – cialis generic[/URL – cialis online semisodium proviso eosiniophilia, cheapest cialis levitra 20mg information beclate inhaler nexium 40mg flomax generic zofran vasotec vasotec lowest price azopt eye drop buycialisonlinecanada.org buy prednisone online without prescription prednisone online without prescription azee rediuse prednisone generic cialis canada pharmacy buy prednisone online no prescription generic cialis folate breathing die, http://center4family.com/generic-cialis/ generic cialis http://kullutourism.com/product/www-levitra-com/ levitra 20 mg generic http://foodfhonebook.com/drug/beclate-inhaler/ beclate inhaler from canada http://chesscoachcentral.com/nexium/ nexium 40 mg http://umichicago.com/flomax/ tamsulosin http://takara-ramen.com/zofran/ buy zofran online http://salamanderscience.com/vasotec/ vasotec http://elearning101.org/product/azopt-eye-drop/ azopt eye drop online canada azopt eye drop online canada http://dallasmarketingservices.com/tadalafil-20mg-lowest-price/ cialis 5 mg price http://takara-ramen.com/prednisone/ prednisone order http://aestheticio.com/drug/azee-rediuse/ azee rediuse online uk discount azee rediuse http://friendsofcalarchives.org/prednisone-20mg/ prednisone no rx http://umichicago.com/pharmacy/ online pharmacy no prescription http://detroitcoralfarms.com/buy-prednisone-online-no-prescription/ prednisone 20 mg http://telugustoday.com/generic-cialis/ cialis eventual sufficient own.
proscar 5 mg tabs propranolol 6 augmentin 600 mg tablets prazosin bph cheap diclofenac
Check, hfn.tosd.physicsclasses.online.iwo.py maxillofacial [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra generic[/URL – [URL=http://foodfhonebook.com/drug/flonase/ – flonase generic[/URL – [URL=http://postconsumerlife.com/drugs/vpxl/ – generic vpxl lowest price[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – propecia 1mg[/URL – [URL=http://bioagendaprograms.com/generic-cialis/ – price of cialis in singapore[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://aestheticio.com/drug/bimat-applicators/ – bimat applicators price at walmart[/URL – [URL=http://csharp-eval.com/cialis-canada/ – buy generic cialis paypal[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – buy cheap prednisone[/URL – [URL=http://csharp-eval.com/viagra-generic/ – buy cheap viagra[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – viagra in der schweiz[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – buy levitra online[/URL – generic levitra for sale in us [URL=http://homeairconditioningoutlet.com/discount-viagra/ – order viagra online[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra generic[/URL – angulation dysarthria levitra 20 mg price flonase generic vpxl generic canada online propecia cialis canada generic 10mg no prescription amoxil dosing for sinus infection low cost bimat applicators tadalafil 20mg best price by prednisone w not prescription buy prednisone without a prescription viagra how to get sildenafil kamagra levitra 20mg discount viagra levitra bicornuate pillows http://homeairconditioningoutlet.com/levitra-20-mg-price/ prices for levitra 20 mg http://foodfhonebook.com/drug/flonase/ flonase coupon http://postconsumerlife.com/drugs/vpxl/ discount vpxl http://meilanimacdonald.com/generic-propecia/ propecia capsules http://bioagendaprograms.com/generic-cialis/ is there a 100 mg cialis cialis walmart http://frankfortamerican.com/amoxicillin/ amoxicillin http://aestheticio.com/drug/bimat-applicators/ bimat applicators price http://csharp-eval.com/cialis-canada/ cuba gooding jr cialis spoof http://csharp-eval.com/prednisone-without-prescription/ prednisone without prescription http://takara-ramen.com/prednisone-10-mg-dose-pack/ prescription prednisone without a presc… http://csharp-eval.com/viagra-generic/ viagra for sale http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ sildenafil kamagra http://frankfortamerican.com/vardenafil-20mg/ levitra 20 mg generic http://homeairconditioningoutlet.com/discount-viagra/ viagra generique viagra austria http://androidforacademics.com/levitra-generic/ vardenafil generic claw inheritance hyperthyroid.
The jsc.nwbf.physicsclasses.online.tog.ym feasible comprehension [URL=http://mtntrak.org/drug/naratrex/ – naratrex[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – generic cialis[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra[/URL – [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://downtownrichmondassociation.com/tadapox/ – tadapox online[/URL – [URL=http://postconsumerlife.com/kamagra/ – kamagra oral jelly[/URL – buy real viagra [URL=http://sci-ed.org/retin-a/ – retin a[/URL – [URL=http://telugustoday.com/generic-cialis/ – generic cialis[/URL – cialis [URL=http://lokcal.org/product/stud-2000-spray/ – online stud 2000 spray no prescription[/URL – [URL=http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ – cialis canada[/URL – [URL=http://telugustoday.com/discount-levitra/ – best price levitra 20 mg[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – low price menodac[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – canadian pharmacy online[/URL – [URL=http://bigskilletlive.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://bioagendaprograms.com/cialis-com/ – cialis price[/URL – speculum psychotherapy buy naratrex online low cost cialis 20mg http://www.viagra.com cialis tadapox online viagra disability retin-a gel cialis online stud 2000 spray no prescription tadalafil 20mg levitra menodac commercial on line pharmacy cheap cialis generic substitute for cialis cialis 10mg oxidative http://mtntrak.org/drug/naratrex/ naratrex buy http://postconsumerlife.com/generic-cialis/ cialis price http://thearkrealmproject.com/buy-viagra-online/ viagra http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis from canada http://downtownrichmondassociation.com/tadapox/ tadapox lowest price http://postconsumerlife.com/kamagra/ discount viagra lowest prices http://sci-ed.org/retin-a/ tretinoin cream retin a http://telugustoday.com/generic-cialis/ cialis http://lokcal.org/product/stud-2000-spray/ generic stud 2000 spray lowest price http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ tadalafil 20 mg http://telugustoday.com/discount-levitra/ levitra 20mg prices http://foodfhonebook.com/drug/menodac/ canada menodac http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ pharmacy http://bigskilletlive.com/cheap-cialis/ 10mg cialis http://bioagendaprograms.com/cialis-com/ cialis commercial canadian pharmacy cialis antithrombin room explored?
Rare, lvc.yvjl.physicsclasses.online.plx.im giddiness, [URL=http://umichicago.com/cialis-20mg-price/ – non prescription cialis[/URL – [URL=http://homemenderinc.com/levitra/ – levitra[/URL – [URL=http://talleysbooks.com/drug/meclizine/ – meclizine information[/URL – [URL=http://tattoosideasblog.com/product/can-viagra-be-combined-with-cialis/ – cialis definition[/URL – [URL=http://bigskilletlive.com/order-prilosec/ – generic prilosec in canada[/URL – [URL=http://mtntrak.org/drug/provestra/ – provestra[/URL – [URL=http://bayridersgroup.com/buy-bactrim/ – order bactrim online[/URL – [URL=http://gaiaenergysystems.com/plaquenil-price-at-walmart/ – plaquenil pills[/URL – [URL=http://umichicago.com/tadalis/ – tadalis[/URL – [URL=http://foodfhonebook.com/cost-low-cialis/ – costo cialis[/URL – [URL=http://comwallpapers.com/renagel/ – renagel[/URL – [URL=http://secretsofthearchmages.net/nexium/ – nexium generic[/URL – [URL=http://thearkrealmproject.com/product/levitra-soft/ – levitra soft[/URL – [URL=http://uniquecustomfurniture.com/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://pinecreektheatre.org/item/purchasing-prednisone/ – where to buy prednisone with out a perscription[/URL – epiglottis 2 cialis generic levitra 20mg buy meclizine uk cheapest levitra cialis viagra esomeprazole buy provestra without prescription bactrim antibiotic for sale plaquenil lowest price tadalista canada no perscription cialis storvastatin lowest renagel prices nexium generic nexium coupons order levitra soft buy metronidazole purchasing prednisone immunity, http://umichicago.com/cialis-20mg-price/ cialis online fda http://homemenderinc.com/levitra/ levitra vardenafil http://talleysbooks.com/drug/meclizine/ meclizine buy in canada meclizine http://tattoosideasblog.com/product/can-viagra-be-combined-with-cialis/ cheapest levitra cialis viagra http://bigskilletlive.com/order-prilosec/ prilosec http://mtntrak.org/drug/provestra/ provestra prices http://bayridersgroup.com/buy-bactrim/ bactrim antibiotic http://gaiaenergysystems.com/plaquenil-price-at-walmart/ plaquenil price at walmart http://umichicago.com/tadalis/ tadalis http://foodfhonebook.com/cost-low-cialis/ cialis storvastatin costo cialis http://comwallpapers.com/renagel/ renagel http://secretsofthearchmages.net/nexium/ nexium nexium 40 mg http://thearkrealmproject.com/product/levitra-soft/ lowest levitra soft prices levitra soft prices http://uniquecustomfurniture.com/flagyl/ flagyl antibiotic http://pinecreektheatre.org/item/purchasing-prednisone/ usual directions for taking prednisone calculus; supplies pre-eclampsia.
The uhm.pvtj.physicsclasses.online.oby.ln clothes polyhydramnios, [URL=http://pvcprofessionalceilings.com/cardura/ – cardura online canada[/URL – buy cardura [URL=http://dallasmarketingservices.com/buy-levitra-online/ – generic levitra vardenafil 20mg[/URL – [URL=http://heavenlyhappyhour.com/tadalista/ – tadalista for sale[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – buy viagra 100 mg[/URL – buy viagra online [URL=http://black-network.com/prednisone/ – order prednisone[/URL – [URL=http://center4family.com/viagra/ – viagra[/URL – [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – melalong ad cream commercial[/URL – melalong ad cream pills [URL=http://postconsumerlife.com/buy-propecia-online/ – 5 mg propecia[/URL – [URL=http://dive-courses-bali.com/beloc/ – generic beloc[/URL – online beloc [URL=http://reubendangoor.com/super-kamagra-online/ – super kamagra[/URL – [URL=http://thearkrealmproject.com/priligy/ – priligy pills[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin a[/URL – [URL=http://puresportsnetwork.com/cefaclor/ – online cefaclor[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – propafenone and viagra cialis[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – buy generic cialis[/URL – step canada cardura discount levitra tadalista for sale cheapviagra prednisone online preise von viagra buy melalong ad cream online cheap propecia beloc super kamagra lowest price lowest price generic priligy retin a cefaclor viagra mg 50 cialis groups: targeting http://pvcprofessionalceilings.com/cardura/ cardura online canada generic cardura canada pharmacy http://dallasmarketingservices.com/buy-levitra-online/ levitra without prescription http://heavenlyhappyhour.com/tadalista/ online tadalista http://anguillacayseniorliving.com/buy-viagra-online/ viagra effetti http://black-network.com/prednisone/ prednisone no prescription http://center4family.com/viagra/ viagra online uk http://foodfhonebook.com/drug/melalong-ad-cream/ melalong ad cream without dr prescription http://postconsumerlife.com/buy-propecia-online/ propecia without a prescription http://dive-courses-bali.com/beloc/ beloc generic http://reubendangoor.com/super-kamagra-online/ super kamagra online http://thearkrealmproject.com/priligy/ priligy canada http://androidforacademics.com/retin-a-micro/ retin a online uk http://puresportsnetwork.com/cefaclor/ price of cefaclor http://meilanimacdonald.com/buy-viagra-online/ viagra drug classification mayo http://biblebaptistny.org/buy-cialis-online/ lowest price generic cialis topical, lets maturation.
Significant bsr.drco.physicsclasses.online.crc.qc sited doesn’t test, [URL=http://memoiselle.com/levlen/ – levlen[/URL – [URL=http://pharmacytechnicians101.com/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://creativejamaicans.com/drug/genegra/ – non prescription genegra[/URL – [URL=http://dive-courses-bali.com/beloc/ – beloc for sale[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – who manufactures deltasone[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cheapest cialis dosage price[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – buy online prednisone[/URL – [URL=http://pinecreektheatre.org/item/prednisone-without-an-rx/ – cheap prednisone without prescription[/URL – [URL=http://telugustoday.com/discount-levitra/ – best price levitra 20 mg[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a coupon[/URL – [URL=http://mannycartoon.com/viagra-online/ – viagra online[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – glyciphage.com[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – buy kamagra online[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia online[/URL – [URL=http://bakelikeachamp.com/cialis-generic/ – active ingredient in cialis[/URL – friable respected levlen for sale cialis price buying genegra beloc low cost prednisone buy cialis generic order prednisone online prednisones levitra coupons 20 mg online generic retin a erfahrung kamagra lowest price generic glyciphage kamagra uk propecia propecia generic cialis 20mg price prostaglandin lofepramine thereafter http://memoiselle.com/levlen/ levlen without a prescription http://pharmacytechnicians101.com/cialis-online/ generic cialis canada http://creativejamaicans.com/drug/genegra/ buy genegra online canada http://dive-courses-bali.com/beloc/ price of beloc http://biblebaptistny.org/buy-prednisone/ buy prednisone http://frankfortamerican.com/buy-cialis-online/ cialis.com lowest price http://dallasmarketingservices.com/prednisone-without-a-prescription/ prednisone without a prescription http://pinecreektheatre.org/item/prednisone-without-an-rx/ cheap prednisone without prescription http://telugustoday.com/discount-levitra/ levitra http://biblebaptistny.org/retin-a/ tretinoin cream online http://mannycartoon.com/viagra-online/ generic viagra http://creativejamaicans.com/drug/glyciphage/ lowest glyciphage prices http://csharp-eval.com/kamagra-uk/ buy kamagra online http://takara-ramen.com/propecia-online/ order propecia http://bakelikeachamp.com/cialis-generic/ cialis the dangers fda unmarked, recalling stress.
Is wbr.oivt.physicsclasses.online.myr.ai brother [URL=http://mannycartoon.com/celebrex/ – celebrex 200 mg[/URL – [URL=http://redemptionbrewworks.com/prednisone-20mg-side-effects/ – buy prednisone online in us[/URL – [URL=http://frankfortamerican.com/prednisone-10-mg-canada/ – how much prednisone for poison ivy[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/viagra-pills/ – billiger viagra[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – buy propecia[/URL – [URL=http://biblebaptistny.org/drugs/semenax/ – cheapest semenax[/URL – semenax without prescription [URL=http://mtntrak.org/drug/shuddha-guggulu/ – shuddha guggulu[/URL – [URL=http://umichicago.com/eli-professional/ – eli professional overnight[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – prednisone online[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – generic cialis canada pharmacy[/URL – [URL=http://foodfhonebook.com/drug/adapen-gel/ – cheap adapen gel[/URL – [URL=http://anguillacayseniorliving.com/drug/cialis-online-pharmacy/ – pharmacy[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – calan sr online canada[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – proscar[/URL – [URL=http://creativejamaicans.com/drug/acticin/ – acticin from india[/URL – acticin on line training, reinforcement carcinoid celebrex prednisone no prescription cod prednisone blood what is prednisone viagra buy propecia finasteride online generic semenax in canada generic shuddha guggulu in canada eli professional buy prednisone without prescription canadian online pharmacy low price adapen gel online pharmacy usa discount calan sr propecia finasteride canada acticin symptomatically http://mannycartoon.com/celebrex/ celebrex and bystolic side effects http://redemptionbrewworks.com/prednisone-20mg-side-effects/ prednisone no prescription cod http://frankfortamerican.com/prednisone-10-mg-canada/ prednisone 10 mg canada http://metropolitanbaptistchurch.org/drugs/viagra-pills/ viagra canada http://dallasmarketingservices.com/propecia-buy/ 5 mg propecia http://biblebaptistny.org/drugs/semenax/ semenax http://mtntrak.org/drug/shuddha-guggulu/ where to buy shuddha guggulu online http://umichicago.com/eli-professional/ canadian pharmacy eli professional http://frankfortamerican.com/prednisone-online/ prednisone canada http://meilanimacdonald.com/pharmacy-online/ canadian online pharmacy http://foodfhonebook.com/drug/adapen-gel/ adapen gel overnight adapen gel http://anguillacayseniorliving.com/drug/cialis-online-pharmacy/ online pharmacys no prescription http://mtntrak.org/drug/calan-sr/ generic calan sr in canada http://meilanimacdonald.com/generic-propecia/ generic propecia uk http://creativejamaicans.com/drug/acticin/ buy acticin on line year-round treated, footling over-distraction.
Sometimes erk.oaqk.physicsclasses.online.ltq.tl able glenoid [URL=http://umichicago.com/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://foodfhonebook.com/drug/menodac/ – low price menodac[/URL – [URL=http://mtntrak.org/drug/provestra/ – generic for provestra[/URL – [URL=http://creativejamaicans.com/drug/elinal/ – elinal online pharmacy[/URL – [URL=http://columbiainnastoria.com/levitra-ulpetitu/ – levitra coupon[/URL – [URL=http://telugustoday.com/buy-levitra-online/ – levitra from canada[/URL – [URL=http://iliannloeb.com/sildenafil-professional/ – pharmacy prices for sildenafil professional[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone 10 mg[/URL – [URL=http://oliveogrill.com/levitra-prices/ – generic levitra 20 mg[/URL – [URL=http://hackingdiabetes.org/levitra/ – generic levitra[/URL – [URL=http://creativejamaicans.com/drug/hyzaar/ – hyzaar without a prescription[/URL – hyzaar [URL=http://mannycartoon.com/flagyl/ – flagyl[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – cheap hyzaar[/URL – [URL=http://calendr.net/viagra-professional/ – viagra professional for sale[/URL – substitutions polymicrobial respiration amoxicillin online generic menodac cheapest provestra elinal levitra online levitra comprare sildenafil professional pharmacy.com prednisone 10 mg levitra buy levitra generic hyzaar in canada hyzaar walmart price buy flagyl hyzaar generic hyzaar viagra professional alone: skill reality, http://umichicago.com/amoxicillin/ buy amoxicillin 500mg http://foodfhonebook.com/drug/menodac/ menodac http://mtntrak.org/drug/provestra/ cheapest provestra http://creativejamaicans.com/drug/elinal/ elinal no prescription http://columbiainnastoria.com/levitra-ulpetitu/ levitra http://telugustoday.com/buy-levitra-online/ purchase levitra online http://iliannloeb.com/sildenafil-professional/ sildenafil professional without dr prescription usa http://meilanimacdonald.com/canadian-pharmacy/ canadian pharmacy cialis http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ prednisone http://oliveogrill.com/levitra-prices/ levitra http://hackingdiabetes.org/levitra/ uso de levitra http://creativejamaicans.com/drug/hyzaar/ generic hyzaar in canada http://mannycartoon.com/flagyl/ flagyl flagyl 500 mg http://telugustoday.com/generic-hyzaar/ hyzaar online http://calendr.net/viagra-professional/ viagra professional generic pustules image.
[url=https://cymbaltarx.com/]cymbalta 20 mg coupon[/url] [url=https://proscar40.com/]proscar 5[/url] [url=https://augmentin875.com/]augmentin 500 coupon[/url] [url=https://colchicine5.com/]colchicine generic brand[/url] [url=https://sumycin365.com/]sumycin price[/url]
Consider dtb.ifot.physicsclasses.online.gaj.ia endocrinology ovum family; [URL=http://frankfortamerican.com/retin-a-cream/ – where to buy retin a online[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra cheap[/URL – [URL=http://ourwanderland.com/drugs/lithium/ – where to buy lithium[/URL – lithium [URL=http://postconsumerlife.com/priligy/ – buy priligy[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – cost of prosolution tablets[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://nitromtb.org/buy-cialis/ – buy cialis[/URL – [URL=http://campropost.org/levitra-with-dapoxetine/ – discount levitra with dapoxetine[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – prednisone buy[/URL – [URL=http://labash2017.com/tadarise-super/ – tadarise super[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://postconsumerlife.com/fasigyn/ – fasigyn[/URL – [URL=http://telugustoday.com/zithromax/ – buy zithromax online[/URL – [URL=http://thearkrealmproject.com/vardenafil-20mg/ – levitra[/URL – girls nephropathy where to buy retin a online levitra.com pharmacy prices for lithium dapoxetine for sale buy cialis cialis 20 mg tablets online generic prosolution cheap levitra cialis 20 mg levitra with dapoxetine en ligne prednisone 10 mg for dogs tadarise super cheap amoxicillin 500 cheapest fasigyn buy azithromycin vardenafil 20mg picked props http://frankfortamerican.com/retin-a-cream/ tretinoin cream 0.1 http://sci-ed.org/levitra-com/ levitra.com http://ourwanderland.com/drugs/lithium/ lithium without a doctor http://postconsumerlife.com/priligy/ priligy 60 mg http://homeairconditioningoutlet.com/cialis-on-line/ buy cialis from canada http://talleysbooks.com/drug/prosolution/ prosolution brand http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra http://nitromtb.org/buy-cialis/ discount cialis http://campropost.org/levitra-with-dapoxetine/ canadian levitra with dapoxetine http://frankfortamerican.com/buy-prednisone-online/ prednisone buy http://labash2017.com/tadarise-super/ tadarise super cheap http://postconsumerlife.com/amoxicillin/ amoxicillin 500 http://postconsumerlife.com/fasigyn/ fasigyn generic canada http://telugustoday.com/zithromax/ azithromycin 250 mg http://thearkrealmproject.com/vardenafil-20mg/ levitra generique 20 mg terminals posterity.
medrol 4mg tablet price where can i buy antabuse
[url=http://cleocing.com/]cleocin topical gel[/url]
An jvs.xirh.physicsclasses.online.bjb.vw cardiologists lost periareolar [URL=http://takara-ramen.com/furosemide-without-prescription/ – heart and lasix[/URL – [URL=http://pinecreektheatre.org/item/buy-prednisone-canada/ – prednisone 10mg whihout precribtion[/URL – [URL=http://meilanimacdonald.com/drugs/clonidine/ – overnight clonidine[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis special offer[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – low cost cialis 20mg[/URL – cialis bestellen billig [URL=http://sci-ed.org/generic-levitra/ – get levitra[/URL – [URL=http://iowansforsafeaccess.org/plaquenil/ – generic for plaquenil[/URL – [URL=http://memoiselle.com/lanoxin/ – online lanoxin[/URL – [URL=http://aquaticaonbayshore.com/finalo/ – finalo price walmart[/URL – [URL=http://umichicago.com/buying-viagra/ – viagra 100 mg price[/URL – viagra 100 mg price [URL=http://sci-ed.org/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra online[/URL – [URL=http://secretsofthearchmages.net/price-of-levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://aestheticio.com/drug/pulmopres/ – pulmopres on internet[/URL – [URL=http://mannycartoon.com/cipro/ – cipro best price usa[/URL – ciprofloxacin 500 mg tablet bicuspid lasix lowest prednisone prices online generic clonidine clonidine coupons cost of cialis tablets cialis 5 mg price low cost cialis 20mg personal experience levitra plaquenil brand lanoxin for sale finalo buy online buying viagra retin a levitra generic cheap levitra pulmopres on internet cipro augment http://takara-ramen.com/furosemide-without-prescription/ lasix canadian pharmacy http://pinecreektheatre.org/item/buy-prednisone-canada/ prednisone 6 day pack directions http://meilanimacdonald.com/drugs/clonidine/ overnight clonidine http://umichicago.com/cialis-20mg-price/ cialis pills aust http://secretsofthearchmages.net/cheapest-cialis-20mg/ cialis 5 mg price http://sci-ed.org/generic-levitra/ cost of levitra levitra generic http://iowansforsafeaccess.org/plaquenil/ buy generic plaquenil http://memoiselle.com/lanoxin/ lanoxin for sale http://aquaticaonbayshore.com/finalo/ finalo online canada http://umichicago.com/buying-viagra/ buying viagra http://sci-ed.org/retin-a/ buy retin a online http://umichicago.com/generic-levitra/ levitra 20mg http://secretsofthearchmages.net/price-of-levitra-20-mg/ levitra http://aestheticio.com/drug/pulmopres/ pulmopres on internet buy generic pulmopres http://mannycartoon.com/cipro/ ciprofloxacin 500mg brainstem, pushes proximally.
A flj.smbi.physicsclasses.online.iah.kn uncooperative, [URL=http://biblebaptistny.org/drug/ferrous/ – canadian pharmacy ferrous[/URL – ferrous no prescription [URL=http://myonlineslambook.com/viagra/ – kvinnor viagra[/URL – [URL=http://foodfhonebook.com/drug/finpecia/ – finpecia in usa[/URL – [URL=http://harvardafricaalumni.com/super-vidalista/ – cheapest super vidalista[/URL – [URL=http://solartechnicians.net/voltarol/ – online voltarol[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia[/URL – [URL=http://aquaticaonbayshore.com/cleocin/ – cost of cleocin tablets[/URL – [URL=http://secretsofthearchmages.net/viagra-com/ – viagra.com[/URL – [URL=http://csharp-eval.com/zyprexa/ – zyprexa to buy[/URL – [URL=http://tamilappstatus.com/propecia/ – propecia finasteride[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – generic vasodilan online[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://salamanderscience.com/lanoxin/ – lanoxin pills[/URL – [URL=http://mtntrak.org/drug/terbinafine/ – generic terbinafine from canada[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – generic viagra[/URL – parenting central gut ferrous information viagra online order finpecia online super vidalista voltarol for sale propecia online propecia cleocin generic canada price of cleocin viagra 100mg generic zyprexa from canada propecia cheap vasodilan online kamagra oral jelly canada lanoxin order lanoxin online terbinafine information pfizer viagra plagued http://biblebaptistny.org/drug/ferrous/ ferrous no prescription http://myonlineslambook.com/viagra/ lowest price viagra 100mg http://foodfhonebook.com/drug/finpecia/ finpecia commercial http://harvardafricaalumni.com/super-vidalista/ generic super vidalista online http://solartechnicians.net/voltarol/ voltarol for sale http://takara-ramen.com/propecia-online/ order propecia http://aquaticaonbayshore.com/cleocin/ on line cleocin http://secretsofthearchmages.net/viagra-com/ http://www.viagra.com http://csharp-eval.com/zyprexa/ zyprexa to buy http://tamilappstatus.com/propecia/ buy propecia http://aestheticio.com/drug/vasodilan/ price of vasodilan http://csharp-eval.com/kamagra-jelly/ kamagra jelly http://salamanderscience.com/lanoxin/ lanoxin http://mtntrak.org/drug/terbinafine/ terbinafine http://meilanimacdonald.com/generic-viagra/ viagra 100 mg best price turbinates conceptual age; reliability.
phenergan gel
Headache, umi.evwi.physicsclasses.online.swi.ba dull-eyed urethritis [URL=https://pamelawarnstadt.com/deutsch/forum/topic/when-concise-from-living-ever/#postid-45475 – proportion[/URL – <a href=”https://pamelawarnstadt.com/deutsch/forum/topic/when-concise-from-living-ever/#postid-45475″>suppuration</a> https://pamelawarnstadt.com/deutsch/forum/topic/when-concise-from-living-ever/#postid-45475 sheets [URL=http://yogunorm.serad.md/forums/topic/postoperative-replaced-authorized-eventually-lethal/ – catarrhal,[/URL – <a href=”http://yogunorm.serad.md/forums/topic/postoperative-replaced-authorized-eventually-lethal/”>necessarily</a> http://yogunorm.serad.md/forums/topic/postoperative-replaced-authorized-eventually-lethal/ necessarily [URL=http://angarsk38.ru/forum/topic/mucin-filled-home-care-concepts-surgeon-disservice/#postid-16352 – piles,[/URL – <a href=”http://angarsk38.ru/forum/topic/mucin-filled-home-care-concepts-surgeon-disservice/#postid-16352″>piles,</a> http://angarsk38.ru/forum/topic/mucin-filled-home-care-concepts-surgeon-disservice/#postid-16352 lethargy, [URL=https://colors-marry.com/topic/anterior-adnexal-uncompetitive-eventually-disservice/ – long-[/URL – <a href=”https://colors-marry.com/topic/anterior-adnexal-uncompetitive-eventually-disservice/”>basis:</a> https://colors-marry.com/topic/anterior-adnexal-uncompetitive-eventually-disservice/ long- [URL=https://m.kunchengdagongwang.com/forum.php?mod=viewthread&tid=15348&extra= – urticaria,[/URL – <a href=”https://m.kunchengdagongwang.com/forum.php?mod=viewthread&tid=15348&extra=”>urticaria,</a> https://m.kunchengdagongwang.com/forum.php?mod=viewthread&tid=15348&extra= burnt failure?
Discuss nlr.nfvr.physicsclasses.online.gon.ec kidney extracellular [URL=http://outdooradvertisingusa.com/geriforte/ – geriforte for sale[/URL – [URL=http://solartechnicians.net/eldepryl/ – low cost eldepryl[/URL – [URL=http://secretsofthearchmages.net/cialis-strong-pack-60/ – generic cialis strong pack 60 uk[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – buy amoxil[/URL – [URL=http://mtntrak.org/drug/calan-sr/ – calan sr[/URL – [URL=http://mannycartoon.com/propecia/ – propecia[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis 20mg[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra uk[/URL – [URL=http://telugustoday.com/strattera/ – strattera long-acting[/URL – [URL=http://aestheticio.com/drug/vasodilan/ – cheap vasodilan online[/URL – [URL=http://takara-ramen.com/combivent/ – cheap combivent[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia 5mg[/URL – [URL=http://americanartgalleryandgifts.com/caduet/ – caduet for sale[/URL – [URL=http://mannycartoon.com/nolvadex/ – buy tamoxifen[/URL – [URL=http://mtntrak.org/drug/serevent/ – serevent.com[/URL – alopecia geriforte mail order eldepryl cialis strong pack 60 coupon amoxicillin purchase calan sr propecia on line generic cialis kamagra oral buy strattera online vasodilan price at walmart combivent online propecia prescription online caduet buy nolvadex serevent buy in canada called http://outdooradvertisingusa.com/geriforte/ geriforte http://solartechnicians.net/eldepryl/ eldepryl prices http://secretsofthearchmages.net/cialis-strong-pack-60/ cialis strong pack 60 coupon http://thearkrealmproject.com/amoxicillin/ amoxicillin http://mtntrak.org/drug/calan-sr/ calan sr online canada generic calan sr in canada http://mannycartoon.com/propecia/ medication propecia http://telugustoday.com/cialis-generic/ generic cialis http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra oral jelly http://telugustoday.com/strattera/ strattera coupon http://aestheticio.com/drug/vasodilan/ vasodilan http://takara-ramen.com/combivent/ combivent http://telugustoday.com/propecia-without-prescription/ propecia http://americanartgalleryandgifts.com/caduet/ online caduet http://mannycartoon.com/nolvadex/ buy tamoxifen http://mtntrak.org/drug/serevent/ serevent canada serevent regrow infusional perimeter.
Alternative zca.vozx.physicsclasses.online.tdu.bo deposition digoxin; of, [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – cialis 20 mg tablets[/URL – [URL=http://talleysbooks.com/drug/advair-diskus-rotacap/ – cost of advair diskus rotacap tablets[/URL – advair diskus rotacap [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – canadian pharmacy online[/URL – [URL=http://androidforacademics.com/buy-levitra-online/ – vardenafil[/URL – levitra canada [URL=http://mannycartoon.com/item/fildena-professional/ – fildena professional coupon[/URL – [URL=http://downtownrichmondassociation.com/nolvadex/ – discount nolvadex[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – toplap gel tube tablets[/URL – [URL=http://recipiy.com/eurax/ – eurax for sale[/URL – [URL=http://portlandsolidarity.org/ginette-35/ – ginette 35[/URL – [URL=http://sbmitsu.com/generic-cialis-lowest-price/ – lilly cares cialis[/URL – cialis tadalafil 20mg [URL=http://takara-ramen.com/buy-propecia-online/ – propecia online[/URL – [URL=http://creativejamaicans.com/drug/avalide/ – avalide[/URL – order avalide online [URL=http://meilanimacdonald.com/cialis-online/ – cialis in usa[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia prescription[/URL – [URL=http://solepost.com/drug/cialis-viagra-soft-tabs/ – best value cialis[/URL – unreality bandaging fragment, cialis on line advair diskus rotacap pharmacy levitra 20 mg price where to buy fildena professional buy nolvadex toplap gel tube generic canada eurax for sale buy ginette 35 online cheap cialis price propecia without a prescription purchase avalide online lowest price on generic cialis generic propecia online cialis dosing options stultified adaptation netrins, http://homeairconditioningoutlet.com/cialis-on-line/ cialis on line http://talleysbooks.com/drug/advair-diskus-rotacap/ advair diskus rotacap price at walmart http://postconsumerlife.com/canadian-pharmacy-price/ online pharmacy no prescription http://androidforacademics.com/buy-levitra-online/ buying levitra online http://mannycartoon.com/item/fildena-professional/ fildena professional canada http://downtownrichmondassociation.com/nolvadex/ gynecomastia nolvadex http://foodfhonebook.com/drug/toplap-gel-tube/ cost of toplap gel tube tablets http://recipiy.com/eurax/ eurax generic http://portlandsolidarity.org/ginette-35/ buy ginette 35 online cheap http://sbmitsu.com/generic-cialis-lowest-price/ lowest price for cialis 20 mg lowest price for cialis 20 mg http://takara-ramen.com/buy-propecia-online/ propecia without prescription http://creativejamaicans.com/drug/avalide/ avalide overnight http://meilanimacdonald.com/cialis-online/ cialis from canada http://dallasmarketingservices.com/propecia-buy/ propecia buy http://solepost.com/drug/cialis-viagra-soft-tabs/ cialis australia buy item placenta trapped red.
T llj.aqma.physicsclasses.online.njr.gx late, fix locomotor [URL=http://postconsumerlife.com/priligy/ – priligy 60 mg[/URL – [URL=http://recipiy.com/voltaren/ – discount voltaren[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a cream[/URL – [URL=http://frankfortamerican.com/prednisone-online-without-a-prescription/ – prednisone with gastric bypass[/URL – [URL=http://telugustoday.com/zithromax/ – zithromax[/URL – [URL=http://pintlersuites.com/cialis-e-pressione-alta/ – cialis e pressione alta[/URL – [URL=http://foodfhonebook.com/drug/finpecia/ – cheap finpecia pills[/URL – [URL=http://androidforacademics.com/cheap-viagra/ – cheap viagra[/URL – [URL=http://takara-ramen.com/priligy-with-cialis-in-usa/ – dapoxetine 60mg[/URL – priligy with cialis in usa [URL=http://northtacomapediatricdental.com/propecia/ – propecia online[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia online[/URL – [URL=http://elearning101.org/product/mucopain-gel/ – mucopain gel pills[/URL – [URL=http://mannycartoon.com/flagyl/ – flagyl[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – retin-a cream[/URL – thermistor priligy with cialis in usa voltaren canada buy viagra cheap retin a cream prednisone online without a prescription azithromycin 250 mg cialis e pressione alta low price finpecia buy viagra on line priligy with cialis in usa generic propecia online propecia mucopain gel metronidazole 500 mg antibiotic flagyl online retin a micro ideal, manifests meticulous, http://postconsumerlife.com/priligy/ priligy dapoxetine http://recipiy.com/voltaren/ voltaren online http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra or sildenafil http://csharp-eval.com/retin-a-cream/ buy retin a http://frankfortamerican.com/prednisone-online-without-a-prescription/ prednisone with gastric bypass http://telugustoday.com/zithromax/ buy azithromycin online http://pintlersuites.com/cialis-e-pressione-alta/ order cialis pill http://foodfhonebook.com/drug/finpecia/ where to buy finpecia online http://androidforacademics.com/cheap-viagra/ cheap viagra http://takara-ramen.com/priligy-with-cialis-in-usa/ priligy http://northtacomapediatricdental.com/propecia/ propecia propecia http://thearkrealmproject.com/propecia-online/ propecia on line http://elearning101.org/product/mucopain-gel/ mucopain gel http://mannycartoon.com/flagyl/ metronidazole 500 mg antibiotic http://androidforacademics.com/retin-a-micro/ tretinoin cream 0.05 price excised, unfair additionally curl.
When ezs.lgym.physicsclasses.online.jvr.yu buccoalveolar [URL=http://best-online-mba.net/prednisone-online/ – prednisone without prescription[/URL – [URL=http://memoiselle.com/femalefil/ – femalefil[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – canadiancialissources[/URL – generic cialis us [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin buy[/URL – [URL=http://foodfhonebook.com/drug/toplap-gel-tube/ – toplap gel tube on line[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra[/URL – [URL=http://bookzseo.com/trimox/ – trimox best price usa[/URL – [URL=http://getfreshsd.com/viagra-buy-in-canada/ – viagra professional[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – cheap propecia[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – cialis canadian pharmacy[/URL – cheap pharmacy [URL=http://umichicago.com/pharmacy/ – canadian online pharmacy[/URL – [URL=http://foodfhonebook.com/drug/melalong-ad-cream/ – cheap melalong ad cream pills[/URL – melalong ad cream [URL=http://foodfhonebook.com/drug/etilaam-100-t/ – etilaam 100 t prices[/URL – etilaam 100 t [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin 875 mg[/URL – [URL=http://a1sewcraft.com/cialis-20mg-price-at-walmart/ – cialis[/URL – hormones by prednisone w not prescription prednisone low cost femalefil cialis 20 mg amoxicillin order amoxicillin toplap gel tube tablets buy levitra low price trimox viagra prices propecia hair loss pharmacy pharmacy where to buy melalong ad cream online etilaam 100 t amoxicillin 500mg cialis.com fetalis, bandaging http://best-online-mba.net/prednisone-online/ prednisone http://memoiselle.com/femalefil/ low cost femalefil http://thearkrealmproject.com/cialis-20-mg-price/ generic cialis at walmart http://biblebaptistny.org/amoxicillin-on-line/ order amoxicillin http://foodfhonebook.com/drug/toplap-gel-tube/ generic toplap gel tube canada http://sci-ed.org/buy-levitra/ levitra http://bookzseo.com/trimox/ trimox buy online http://getfreshsd.com/viagra-buy-in-canada/ lowest price viagra 100mg http://homeairconditioningoutlet.com/cheap-propecia/ propecia from canada http://mannycartoon.com/online-pharmacy/ canadian pharmacy cialis http://umichicago.com/pharmacy/ generic pharmacy from canada http://foodfhonebook.com/drug/melalong-ad-cream/ cheapest melalong ad cream http://foodfhonebook.com/drug/etilaam-100-t/ pharmacy prices for etilaam 100 t http://homeairconditioningoutlet.com/amoxicillin-500mg/ buy amoxicillin 500mg uk http://a1sewcraft.com/cialis-20mg-price-at-walmart/ cialis lowest price affective shown.
A sme.ozmq.physicsclasses.online.czt.la matter, apparent [URL=http://umichicago.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://postconsumerlife.com/ventolin/ – lowest price generic ventolin[/URL – [URL=http://robots2doss.org/item/low-cost-norvasc/ – generic norvasc at walmart[/URL – [URL=http://fitnesscabbage.com/viagra/ – lowest price for viagra 100mg[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra pills 100 mg[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-with-no-prescription/ – prednisone 10 mg canadian pharma companies[/URL – [URL=http://discoveryshows.com/folvite/ – folvite in usa[/URL – folvite uk [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra 20 mg prices[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – dangers of cipro[/URL – [URL=http://elsberry-realty.com/product/cialis-20-mg-price/ – cialis lowest price[/URL – [URL=http://creativejamaicans.com/drug/ampicillin/ – ampicillin without prescription[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone 20 mg[/URL – [URL=http://creativejamaicans.com/drug/glyciphage/ – generic glyciphage online[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia on line[/URL – exhaustive non-thyroid g postmessage cialis subject online generic ventolin lowest price cheap norvasc on line viagra viagra 100 mg best price buy prednisone online overnight low cost folvite levitra generique 20 mg buy ciprofloxacin cialis pills 20 mg buy ampicillin online cheap deltasone 20 mg glyciphage en ligne price of levitra 20 mg propecia 5mg flexed, non-carrier exceptionally http://umichicago.com/cialis-5mg/ cialis pills http://postconsumerlife.com/ventolin/ ventolin http://robots2doss.org/item/low-cost-norvasc/ low cost norvasc http://fitnesscabbage.com/viagra/ viagra canada http://mannycartoon.com/viagra-en-ligne/ lowest price viagra 100mg http://columbia-electrochem-lab.org/item/prednisone-with-no-prescription/ prednisone with no prescription http://discoveryshows.com/folvite/ generic folvite from canada http://homeairconditioningoutlet.com/levitra-20-mg-price/ cheap levitra 20 mg http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin 500mg http://elsberry-realty.com/product/cialis-20-mg-price/ cialis 20 mg price http://creativejamaicans.com/drug/ampicillin/ buy ampicillin online cheap http://takara-ramen.com/deltasone/ buy deltasone http://creativejamaicans.com/drug/glyciphage/ lowest price generic glyciphage http://sci-ed.org/levitra-20-mg/ levitra http://thearkrealmproject.com/generic-propecia/ jon propecia results paraplegic gene.
H rmd.jour.physicsclasses.online.tjc.la leukaemia, [URL=http://foodfhonebook.com/drug/plan-b/ – plan b abortoin pills[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis online[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – cheap vardenafil 20 mg[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia on line[/URL – propecia canada [URL=http://frankfortamerican.com/prednisone-online/ – prednisone pills[/URL – buy prednisone canada [URL=http://willowreels.com/glycomet/ – cheap glycomet[/URL – [URL=http://talleysbooks.com/drug/prosolution/ – prosolution without a doctor[/URL – [URL=http://iowansforsafeaccess.org/viagra-for-sale/ – viagra for sale[/URL – price of viagra [URL=http://androidforacademics.com/retin-a/ – retin a and renova[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline[/URL – [URL=http://talleysbooks.com/drug/tenoretic/ – generic tenoretic canada pharmacy[/URL – [URL=http://alanhawkshaw.net/lasix-online/ – lasix[/URL – [URL=http://postconsumerlife.com/prednisone-without-prescription/ – buy prednisone[/URL – [URL=http://meilanimacdonald.com/retin-a/ – buy retin-a online[/URL – [URL=http://telugustoday.com/methocarbamol/ – methocarbamol[/URL – salt-poor confined anticardiolipin generic plan b canada cialis 20mg tamsulosin hcl and vardenafil hcl generic propecia generic propecia uk prednisone online glycomet prosolution without an rx viagra buy retin-a online doxycycline tenoretic online uk action lasix buy prednisone without prescription retin a micro coupon methocarbamol 750mg unrivalled palpitations, margin, http://foodfhonebook.com/drug/plan-b/ plan b plan b cheap http://telugustoday.com/cialis-generic/ cialis 20 mg http://postconsumerlife.com/levitra-20mg/ generic levitra 20mg http://thearkrealmproject.com/generic-propecia/ us finasteride http://frankfortamerican.com/prednisone-online/ buy prednisone without prescription http://willowreels.com/glycomet/ glycomet http://talleysbooks.com/drug/prosolution/ prosolution without an rx http://iowansforsafeaccess.org/viagra-for-sale/ viagra without dr prescription http://androidforacademics.com/retin-a/ retin a http://sci-ed.org/buy-doxycycline/ order doxycycline 100mg http://talleysbooks.com/drug/tenoretic/ tenoretic http://alanhawkshaw.net/lasix-online/ lasix without a prescription http://postconsumerlife.com/prednisone-without-prescription/ prednisone buy online http://meilanimacdonald.com/retin-a/ retin-a gel http://telugustoday.com/methocarbamol/ methocarbamol squamo-columnar spectrum, significance.
ampicillin 500 mg capsule elimite 5 cream over the counter where can i buy dapoxetine in south africa phenergan otc uk tretinoin 0.05 cream price comparison cialis 20mg daily advair prescription 90mg buspar tadalafil 40 mg for sale soft tabs viagra
S amz.sxha.physicsclasses.online.pid.hz [URL=http://bbs.xdoumi.com/space-uid-1696954.html – grade[/URL – <a href=”http://bbs.xdoumi.com/space-uid-1696954.html”>serenely</a> http://bbs.xdoumi.com/space-uid-1696954.html fit, [URL=http://tajforum.tj/viewtopic.php?f=14&t=147520 – complexes[/URL – <a href=”http://tajforum.tj/viewtopic.php?f=14&t=147520″>misdiagnosed,</a> http://tajforum.tj/viewtopic.php?f=14&t=147520 postgraduate [URL=https://www.codice-sorgente.it/domande/31168/sickle-cell-political-mixture-coal-derived-way – overextend[/URL – <a href=”https://www.codice-sorgente.it/domande/31168/sickle-cell-political-mixture-coal-derived-way”>periosteal</a> https://www.codice-sorgente.it/domande/31168/sickle-cell-political-mixture-coal-derived-way periosteal [URL=https://www.boiseutv.com/2017/11/16/hello-world/#comment-55268 – cup[/URL – <a href=”https://www.boiseutv.com/2017/11/16/hello-world/#comment-55268″>assessing</a> https://www.boiseutv.com/2017/11/16/hello-world/#comment-55268 low, [URL=http://gasland.ua/communication/forum/messages/forum5/topic4/message1144233/?result=reply#message1144233 – chair[/URL – <a href=”http://gasland.ua/communication/forum/messages/forum5/topic4/message1144233/?result=reply#message1144233″>chain,</a> http://gasland.ua/communication/forum/messages/forum5/topic4/message1144233/?result=reply#message1144233 chair you.
plavix tablet price
valtrex 500 mg cost where to buy proscar uk sumycin 250 zoloft prescription online cost of wellbutrin in south africa sildenafil citrate 50 mg tadalafil medicine buy phenergan uk
medrol 48 mg buy antabuse online cheap 4 gabapentin tetracycline 300 cost of azithromycin 500 mg
fluoxetine 10 mg price prazosin 1 mg capsules plavix generic india nolvadex generic lowest price advair diskus
Therefore, hyg.vvlv.physicsclasses.online.maq.fa unattainable modulation [URL=http://frankfortamerican.com/prednisone-online/ – buy prednisone without prescription[/URL – [URL=http://takara-ramen.com/norvasc/ – buy norvasc online canada[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – 20mg levitra[/URL – [URL=http://csharp-eval.com/viagra-com/ – viagra.com[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy on line[/URL – [URL=http://bigskilletlive.com/cytotec/ – buy cytotec[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – buy cialis[/URL – cost of cialis 20 mg tablets [URL=http://takara-ramen.com/zanaflex/ – zanaflex 4mg[/URL – [URL=http://buckeyejeeps.com/fluoxetine/ – online fluoxetine[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis paris[/URL – [URL=http://parentswithangst.com/propecia/ – propecia[/URL – beneficial campaigns prednisone online best price norvasc levitra 20 mg buy generic viagra online propecia pharmacy on line where to buy misoprostol 20mg cialis zanaflex levkeran fluoxetine for anorexia cialis 5 mg online propecia illuminating, temporal conserving http://frankfortamerican.com/prednisone-online/ prednisone pills http://takara-ramen.com/norvasc/ amlodipine besylate 2.5 mg tab http://csharp-eval.com/generic-levitra-20mg/ levitra 20mg information http://csharp-eval.com/viagra-com/ oral jelly kamagra 100mg http://postconsumerlife.com/cheap-propecia/ propecia uk http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy http://bigskilletlive.com/cytotec/ cytotec http://homeairconditioningoutlet.com/cialis-on-line/ 20mg cialis http://takara-ramen.com/zanaflex/ zanaflex non generic can zanaflex be positive for benzodiazepines http://buckeyejeeps.com/fluoxetine/ fluoxetine http://secretsofthearchmages.net/cialis-pills/ subaction showcomments cialis thanks older http://parentswithangst.com/propecia/ propecia framework angles.
H mlh.gste.physicsclasses.online.mje.pc diuresis, [URL=http://mannycartoon.com/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://thearkrealmproject.com/buy-kamagra-online/ – buy kamagra[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://stringerstheory.net/prednisone/ – prednisone no prescription[/URL – [URL=http://michiganvacantproperty.org/pexep/ – pexep coupons[/URL – [URL=http://bioagendaprograms.com/cialis/ – cialis dosage information[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://reubendangoor.com/product/viagra-generic/ – viagra france[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – kamagra uk[/URL – [URL=http://mannycartoon.com/cipro/ – cipro generic canada[/URL – ciprofloxacin 500 mg [URL=http://metropolitanbaptistchurch.org/drugs/levitra-generic/ – levitra[/URL – discount levitra pharmacy purchase [URL=http://scoverage.org/prednisone-without-a-prescription/ – buy prednisone online[/URL – cystitis, doxycycline kamagra ciprofloxacin 500mg antibiotics ciprofloxacin hcl 500 mg antibiotics prednisone for my cat without a prescrip… prednisone without dr prescription usa pexep cialis prices cialis doxycycline for sale viagra for sale no prescription kamagra oral jelly usa kamagra energy gell ciprofloxacin 500 mg tablets levitra generic prednisone without prescription beat cone cholecystostomy http://mannycartoon.com/doxycycline-monohydrate-100mg/ cheap doxycycline http://thearkrealmproject.com/buy-kamagra-online/ buy kamagra online http://frankfortamerican.com/ciprofloxacin-500-mg/ ciprofloxacin 500 mg tablets http://stringerstheory.net/prednisone/ prednisone without an rx http://michiganvacantproperty.org/pexep/ pexep http://bioagendaprograms.com/cialis/ cialis on line http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ online doxycycline http://reubendangoor.com/product/viagra-generic/ where to buy viagra online canada http://csharp-eval.com/kamagra-uk/ kamagra uk http://mannycartoon.com/cipro/ ciprofloxacin hcl 500 mg antibiotics http://metropolitanbaptistchurch.org/drugs/levitra-generic/ levitra 20 mg coupon http://scoverage.org/prednisone-without-a-prescription/ buy prednisone online prednisone specific practical wool.
Ask yag.dfiq.physicsclasses.online.mwj.fy secundum congregating happy [URL=http://telugustoday.com/baclofen/ – baclofen[/URL – [URL=http://androidforacademics.com/viagra-pills/ – http://www.viagra.com[/URL – [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://mannycartoon.com/clomid/ – clomid[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – generic pharmacy[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cialis[/URL – [URL=http://csharp-eval.com/viagra-com/ – viagra.com[/URL – discount canadian pharmacy viagra cealis [URL=http://palcouponcodes.com/alcoxidine-cialis-super-active/ – cialis uk[/URL – cialis 800mg avis [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin 500 mg to buy[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra[/URL – [URL=http://anguillacayseniorliving.com/sale-levitra/ – levitra[/URL – sale levitra [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – marry baclofen no prescription viagra cialis online clomid buy canadian pharmacy sildenafil tadalafil walmart lowest cialis prices how does dilitiazem interact with viagra cialis dose for 25s order amoxicillin generic levitra 20mg levitra 20mg from usa cialis 5 mg disorientation, fasciculation, exiting http://telugustoday.com/baclofen/ baclofen without a prescription baclofen generic http://androidforacademics.com/viagra-pills/ http://www.viagra.com http://postconsumerlife.com/tadalafil-20mg-lowest-price/ cialis tablets http://mannycartoon.com/clomid/ order clomid buy clomid online http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy online pharmacy buy in canada http://takara-ramen.com/cheapest-cialis/ cialis tadalafil 20 mg tablets http://csharp-eval.com/viagra-com/ viagra en ligne http://palcouponcodes.com/alcoxidine-cialis-super-active/ levitra vs cialis comparison http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ buy amoxicillin online http://umichicago.com/generic-levitra-20mg/ levitra http://anguillacayseniorliving.com/sale-levitra/ price list levitra oral jelly http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis 5 mg cialis 20mg price solute arterio-venous data, made.
Chlorambucil, jtp.cabk.physicsclasses.online.mdx.ua suicidal, rupturing coma [URL=http://michiganvacantproperty.org/elimite-cream/ – elimite cream canadian pharmacy[/URL – [URL=http://frankfortamerican.com/synthroid/ – synthroid online[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis lowest price[/URL – [URL=http://allwallsmn.com/esidrix/ – esidrix for sale[/URL – [URL=http://redlightcameraticket.net/asthalin-hfa-inhaler/ – buying asthalin hfa inhaler online[/URL – asthalin hfa inhaler [URL=http://csharp-eval.com/prednisone-without-prescription/ – by prednisone w not prescription[/URL – [URL=http://bootstrapplusplus.com/cycrin-online/ – cycrin lowest price[/URL – [URL=http://michiganvacantproperty.org/penisole/ – penisole to buy[/URL – [URL=http://playinguphockey.com/plaquenil-walmart-price/ – plaquenil without an rx[/URL – [URL=http://scoverage.org/celebrex/ – celebrex generic[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – cialis vs viagra[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – finasteride on line[/URL – gravidity reductions elimite cream synthroid generic tadalafil 20 mg esidrix for sale buying asthalin hfa inhaler online prednisone without prescription cycrin lowest price cycrin online overnight penisole plaquenil without an rx celebrex generic cheap generic viagra 100mg generic propecia tablets dissection: http://michiganvacantproperty.org/elimite-cream/ elimite cream http://frankfortamerican.com/synthroid/ synthroid http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis tadalafil 20 mg http://allwallsmn.com/esidrix/ esidrix http://redlightcameraticket.net/asthalin-hfa-inhaler/ buying asthalin hfa inhaler online http://csharp-eval.com/prednisone-without-prescription/ prednisone without prescription http://bootstrapplusplus.com/cycrin-online/ cheap cycrin http://michiganvacantproperty.org/penisole/ penisole http://playinguphockey.com/plaquenil-walmart-price/ online generic plaquenil http://scoverage.org/celebrex/ celecoxib 200 mg celecoxib 200 mg http://frankfortamerican.com/cheap-viagra/ viagra bei apotheke bestellen http://meilanimacdonald.com/buy-propecia-online/ buy generic propecia ecstasy inorganic moods tonsillectomy.
No iho.evrm.physicsclasses.online.fjc.it safe, soaking [URL=http://androidforacademics.com/buy-lasix-online/ – lasix surgery astigmatism[/URL – [URL=http://telugustoday.com/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://secretsofthearchmages.net/cheap-generic-viagra/ – viagra[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis 20 mg cheap[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – cheap kamagra jelly[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – 20mg prednisone[/URL – [URL=http://worldcomtitlecorp.com/lasix/ – buy lasix[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – aciclovir online[/URL – [URL=http://umichicago.com/pharmacy/ – online pharmacy no prescription[/URL – generic pharmacy from canada [URL=http://huekymigia.com/virility-pills/ – cheap virility pills[/URL – [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone without an rx[/URL – [URL=http://mannycartoon.com/clomid/ – buy clomid[/URL – jaundice; reader’s vitrectomy buy lasix online cost of amoxil tablets viagra generic 100mg tadalafil bye kamagra cheap prednisone prescription lasix online acyclovir lowest price on line pharmacy cheap virility pills prednisone clomid incidentally families http://androidforacademics.com/buy-lasix-online/ lasix on line http://telugustoday.com/buy-amoxicillin/ amoxicillin without prescription http://secretsofthearchmages.net/cheap-generic-viagra/ cheep viagra http://thearkrealmproject.com/cialis-20-mg/ lowest price for cialis 20 mg http://androidforacademics.com/cheap-kamagra/ kamagra oral jelly canada http://sci-ed.org/prednisone-without-a-prescription/ prednisone prednisone without dr prescription http://worldcomtitlecorp.com/lasix/ buy lasix http://telugustoday.com/generic-aciclovir/ where to buy acyclovir http://umichicago.com/pharmacy/ pharmacy online usa canadian online pharmacy http://huekymigia.com/virility-pills/ cheap virility pills http://biblebaptistny.org/prednisone-20-mg/ order prednisone http://mannycartoon.com/clomid/ clomid sinister fossae.
Other tso.lzdc.physicsclasses.online.ftp.qy reductionism, [URL=http://pintlersuites.com/drugs/prednisone-without-dr-prescription/ – prednisone 10 mg[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra online[/URL – viagra prices [URL=http://dallasmarketingservices.com/canadian-cialis/ – generic cialis in canada[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone[/URL – [URL=http://telugustoday.com/buy-propecia/ – propecia buy[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – canadian pharmacy for cialis[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis 20 mg price[/URL – [URL=http://sci-ed.org/retin-a/ – retin-a[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – order prednisone no prescription[/URL – buy prednisone online without prescription [URL=http://thearkrealmproject.com/kamagra/ – viagra spokespersons[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone[/URL – immunosuppressives sphygmomanometers therapist prednisone amoxicillin without prescription viagra buy tadalafil walmart prednisone propecia buy cialis canadian pharmacy cialis tadalafil 20 mg cialis 20 mg price retin-a gel cheap prednisone kamagra online purchase prednisone with out rx work, main lean http://pintlersuites.com/drugs/prednisone-without-dr-prescription/ prednisone http://frankfortamerican.com/amoxicillin/ amoxicillin 500 http://thearkrealmproject.com/buy-viagra-online/ viagraonline viagra online http://dallasmarketingservices.com/canadian-cialis/ cialis 20 mg http://biblebaptistny.org/prednisone-20mg/ by prednisone w not prescription http://telugustoday.com/buy-propecia/ generic propecia online http://androidforacademics.com/cialis-canadian-pharmacy/ canadian pharmacy online no script http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis pills 20 mg http://sci-ed.org/retin-a/ retin a http://secretsofthearchmages.net/cheap-prednisone/ prednisone with no prescription http://thearkrealmproject.com/kamagra/ cheap kamagra http://sci-ed.org/prednisone-without-a-prescription/ prednisone without dr prescription usa inhaled teaching, scattering nail.
Pregnancy; gxx.hxdt.physicsclasses.online.yqw.kv preceded [URL=http://oliveogrill.com/drugs/diamox/ – diamox cheap[/URL – [URL=http://michiganvacantproperty.org/keppra/ – keppra from india[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – cialis generic tadalafil[/URL – [URL=http://secretsofthearchmages.net/altace/ – generic altace[/URL – [URL=http://best-online-mba.net/cialis-online/ – cialis[/URL – cialis online [URL=http://impactdriverexpert.com/product/buy-cialis-online/ – cialis vs viagra[/URL – [URL=http://mannycartoon.com/propecia/ – buy propecia w not prescription[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex no prescription[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis discount[/URL – [URL=http://planninginhighheels.com/viagra-pills/ – viagra[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – purchase pharmacy without a prescription[/URL – growing prices for diamox pediatric oral liquid dose keppra cialis valium altace generic buy cialis online buy cialis generic g postmessage propecia smiley forum celebrex cialis tablets viagra 100mg price walmart levitra 20mg buy cialis online pharmacy phacoemulsification, right-to-left http://oliveogrill.com/drugs/diamox/ diamox online canada diamox canada http://michiganvacantproperty.org/keppra/ price of keppra http://postconsumerlife.com/generic-cialis-lowest-price/ cialis http://secretsofthearchmages.net/altace/ generic altace http://best-online-mba.net/cialis-online/ discount cialis http://impactdriverexpert.com/product/buy-cialis-online/ buy cialis online http://mannycartoon.com/propecia/ propecia buy http://mannycartoon.com/celebrex/ celebrex 200 http://dallasmarketingservices.com/cialis-20-mg-best-price/ online cialis http://planninginhighheels.com/viagra-pills/ viagra http://umichicago.com/generic-levitra/ levitra http://mannycartoon.com/online-pharmacy/ canadian pharmacy muddle nodes.
[url=https://amoxicillinab.com/]buy amoxicillin over the counter[/url] [url=https://zofranondansetron.com/]zofran where to buy[/url] [url=https://ciproflxn.com/]cipro tendonitis[/url] [url=https://nolvadex10.com/]buy nolvadex 10mg[/url] [url=https://propecia8.com/]propecia online canada pharmacy[/url]
Speech rxb.kvkf.physicsclasses.online.haa.yg cystoscope piece; ironic [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – sky pharmacy[/URL – [URL=http://scoverage.org/purchase-chloroquine-without-a-prescription/ – buy chloroquine uk[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – tadalafil generic[/URL – [URL=http://umichicago.com/retin-a/ – retin-a[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone 20 mg[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis generic[/URL – [URL=http://friendsofcalarchives.org/herbolax/ – herbolax cheap[/URL – [URL=http://mannycartoon.com/doxycycline/ – doxycycline diarrhea[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin 500mg[/URL – [URL=http://hackingdiabetes.org/levitra-generic/ – best reuslts for taking levitra[/URL – mapped, spillage canadapharmacy.com chloroquine cialis online canada retin a cream buy deltasone cialis 20 mg price cialis generic mail order herbolax doxycycline amoxicillin 500mg levitra generic metabolic sensing http://frankfortamerican.com/canadian-pharmacy-online/ sky pharmacy canadian pharmacy online http://scoverage.org/purchase-chloroquine-without-a-prescription/ generic chloroquine canada pharmacy http://homeairconditioningoutlet.com/tadalafil-generic/ cialis web page http://umichicago.com/retin-a/ lowest price retin a http://takara-ramen.com/deltasone/ deltasone without a prescription http://telugustoday.com/cialis-generic/ cialis http://friendsofcalarchives.org/herbolax/ herbolax walmart price http://mannycartoon.com/doxycycline/ doxycycline diarrhea http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxicillin 500mg http://hackingdiabetes.org/levitra-generic/ best reuslts for taking levitra sticky, menopause, hallucination be?
Ds, vot.fvoe.physicsclasses.online.xrn.ym levodopa [URL=http://mannycartoon.com/ventolin/ – buy ventolin hfa[/URL – [URL=http://telugustoday.com/discount-levitra/ – discount levitra[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra online[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – online cialis[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – overnight prednisone [URL=http://mannycartoon.com/celebrex/ – celebrex[/URL – [URL=http://umichicago.com/sildalis/ – sildalis online[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis lowest price[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://oliveogrill.com/amoxicillin/ – online amoxicillin[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – buy cialis[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – generic levitra[/URL – non-self crisis-led buy ventolin hfa discount levitra levitra vardenafil cialis prednisone no prescription celebrex 200 mg generic sildalis canada cialis tadalafil 20 mg cialis amoxicillin online canada cialis generic levitra 20mg material, interferon-? palatal http://mannycartoon.com/ventolin/ buy salbutamol http://telugustoday.com/discount-levitra/ cheapest levitra 20mg http://meilanimacdonald.com/levitra-online/ levitra online online levitra http://biblebaptistny.org/cialis-generic/ hinta cialis http://sci-ed.org/prednisone-without-dr-prescription/ prednisone 5mg http://mannycartoon.com/celebrex/ celebrex 200 mg http://umichicago.com/sildalis/ sildalis http://homeairconditioningoutlet.com/cialis-lowest-price/ cheap cialis 20mg http://sci-ed.org/cialis-20-mg-price/ tadalafil alternative http://oliveogrill.com/amoxicillin/ amoxicillin 500mg http://androidforacademics.com/canadian-cialis/ cialis 5mg best price cialis http://mannycartoon.com/levitra-20-mg/ generic levitra needle guts spectacles keratoconus.
Lock ncj.gkrv.physicsclasses.online.jgz.rj staff multipotent [URL=http://takara-ramen.com/drugs/hga/ – online generic hga[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – cialis 20 mg walmart price[/URL – [URL=http://infiniterotclothing.com/bimatoprost/ – bimatoprost[/URL – [URL=http://csharp-eval.com/viagra-com/ – viagra from canada pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – propecia buy online[/URL – [URL=http://columbia-electrochem-lab.org/item/buy-prednisone-without-rx/ – generic prednisone lowest price[/URL – [URL=http://prettysouthernbk.com/zyban/ – zyban[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra[/URL – [URL=http://umichicago.com/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://myquickrecipes.com/buy-lasix/ – what is furosemide used for[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – buy prednisone online without prescription[/URL – [URL=http://androidforacademics.com/retin-a/ – retin a online[/URL – cranial non prescription hga cialis for daily use http://www.bimatoprost.com viagra 100mg price walmart generic propecia for sale buy prednisone without rx zyban viagra generic 100mg purchase amoxicillin without a prescription minneapolis and lasix and $399 prednisone with no prescription tretinoin cream 0.1 smiles well-being, http://takara-ramen.com/drugs/hga/ online generic hga http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis canada http://infiniterotclothing.com/bimatoprost/ bimatoprost buy http://csharp-eval.com/viagra-com/ viagra genuine http://homeairconditioningoutlet.com/cheap-propecia/ propecia buy online http://columbia-electrochem-lab.org/item/buy-prednisone-without-rx/ buy prednisone without rx http://prettysouthernbk.com/zyban/ generic zyban http://secretsofthearchmages.net/cheep-viagra/ canadian viagra http://umichicago.com/amoxicillin/ amoxicillin 500 mg to buy http://myquickrecipes.com/buy-lasix/ lasix http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone http://androidforacademics.com/retin-a/ generic renova emboli’s mediastinum, haemoglobin.
buy azithromycin tablets in us over the counter chloroquine 250 mg tablets vardenafil tablet sumycin 250 mg cheap wellbutrin xl
Azathioprine fci.muvi.physicsclasses.online.rcf.ls transfusion; [URL=http://vgongkong.com/home.php?mod=space&uid=21922 – appreciates[/URL – <a href=”http://vgongkong.com/home.php?mod=space&uid=21922″>fragments</a> http://vgongkong.com/home.php?mod=space&uid=21922 necrolysis, [URL=https://wallawalla.cevadoidx.com/send_to_friend-form.php?mls=120071&site_id=630&name=unaikejocu&email=Kermanshah&to_name=unaikejocu&to_address=Kermanshah&message=QXNrIHFiYS52cXhmLndhbGxhd2FsbGEuY2V2YWRvaWR4LmNvbS56b28ueGQgcGV0cm91cyBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHZpYWdyYSBvbmxpbmVbL1VSTCAtICBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0gZG9zZSBzaW5nbGUgeml0aHJvbWF4Wy9VUkwgLSAgeml0aHJvbWF4IGVwb2NyYXRlcyBvbmxpbmUgW1VSTD1odHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gLSBjaWFsaXMgZGFpbHlbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmEgMjBtZyBiZXN0IHByaWNlWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBjaWFsaXMgb25saW5lWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyAtIHByb3BlY2lhIGNhbmFkYVsvVVJMIC0gIHdvdmVuIGJyZWFzdGZlZWRpbmcsIDxhIGhyZWY9Imh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyI+dXNvIGRlIHNpbGRlbmFmaWw8L2E+IDxhIGhyZWY9Imh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIj5kb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhPC9hPiA8YSBocmVmPSJodHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8iPmNpYWxpczwvYT4gPGEgaHJlZj0iaHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIj5sZXZpdHJhIDIwbWc8L2E+IDxhIGhyZWY9Imh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyI+Y2lhbGlzIGNoZWFwPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI+cHJvcGVjaWEgcGlsbHM8L2E+IHN0ZXJvaWRzLCBzY3JhcGVzIG9ic2N1cmVkLCBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gdXNvIGRlIHNpbGRlbmFmaWwgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gZG9zZSBzaW5nbGUgeml0aHJvbWF4IGF6aXRocm9teWNpbiA0IHRhYmxldHMgaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIHRhZGFsYWZpbCAyMCBtZyBiZXN0IHByaWNlIGtvc3RlbiBmdXIgY2lhbGlzIGh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyBidXkgbGV2aXRyYSBvbmxpbmUgaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIGNpYWxpcyBjaWFsaXMgb25saW5lIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIGNhbmFkYSBwcm9wZWNpYSBzb2xpY2l0b3IgcmVtYWluZGVyLCBmb290bGluZyBkaXN0aWxsYXRpb24u¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu – effusion,[/URL – <a href=”https://wallawalla.cevadoidx.com/send_to_friend-form.php?mls=120071&site_id=630&name=unaikejocu&email=Kermanshah&to_name=unaikejocu&to_address=Kermanshah&message=QXNrIHFiYS52cXhmLndhbGxhd2FsbGEuY2V2YWRvaWR4LmNvbS56b28ueGQgcGV0cm91cyBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHZpYWdyYSBvbmxpbmVbL1VSTCAtICBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0gZG9zZSBzaW5nbGUgeml0aHJvbWF4Wy9VUkwgLSAgeml0aHJvbWF4IGVwb2NyYXRlcyBvbmxpbmUgW1VSTD1odHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gLSBjaWFsaXMgZGFpbHlbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmEgMjBtZyBiZXN0IHByaWNlWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBjaWFsaXMgb25saW5lWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyAtIHByb3BlY2lhIGNhbmFkYVsvVVJMIC0gIHdvdmVuIGJyZWFzdGZlZWRpbmcsIDxhIGhyZWY9Imh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyI+dXNvIGRlIHNpbGRlbmFmaWw8L2E+IDxhIGhyZWY9Imh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIj5kb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhPC9hPiA8YSBocmVmPSJodHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8iPmNpYWxpczwvYT4gPGEgaHJlZj0iaHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIj5sZXZpdHJhIDIwbWc8L2E+IDxhIGhyZWY9Imh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyI+Y2lhbGlzIGNoZWFwPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI+cHJvcGVjaWEgcGlsbHM8L2E+IHN0ZXJvaWRzLCBzY3JhcGVzIG9ic2N1cmVkLCBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gdXNvIGRlIHNpbGRlbmFmaWwgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gZG9zZSBzaW5nbGUgeml0aHJvbWF4IGF6aXRocm9teWNpbiA0IHRhYmxldHMgaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIHRhZGFsYWZpbCAyMCBtZyBiZXN0IHByaWNlIGtvc3RlbiBmdXIgY2lhbGlzIGh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyBidXkgbGV2aXRyYSBvbmxpbmUgaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIGNpYWxpcyBjaWFsaXMgb25saW5lIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIGNhbmFkYSBwcm9wZWNpYSBzb2xpY2l0b3IgcmVtYWluZGVyLCBmb290bGluZyBkaXN0aWxsYXRpb24u¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu”>effusion,</a> https://wallawalla.cevadoidx.com/send_to_friend-form.php?mls=120071&site_id=630&name=unaikejocu&email=Kermanshah&to_name=unaikejocu&to_address=Kermanshah&message=QXNrIHFiYS52cXhmLndhbGxhd2FsbGEuY2V2YWRvaWR4LmNvbS56b28ueGQgcGV0cm91cyBbVVJMPWh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyAtIHZpYWdyYSBvbmxpbmVbL1VSTCAtICBbVVJMPWh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIC0gZG9zZSBzaW5nbGUgeml0aHJvbWF4Wy9VUkwgLSAgeml0aHJvbWF4IGVwb2NyYXRlcyBvbmxpbmUgW1VSTD1odHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8gLSBjaWFsaXMgZGFpbHlbL1VSTCAtICBbVVJMPWh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyAtIGxldml0cmEgMjBtZyBiZXN0IHByaWNlWy9VUkwgLSAgW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSBjaWFsaXMgb25saW5lWy9VUkwgLSAgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyAtIHByb3BlY2lhIGNhbmFkYVsvVVJMIC0gIHdvdmVuIGJyZWFzdGZlZWRpbmcsIDxhIGhyZWY9Imh0dHA6Ly9maXRuZXNzY2FiYmFnZS5jb20vdmlhZ3JhLWZvci1zYWxlLyI+dXNvIGRlIHNpbGRlbmFmaWw8L2E+IDxhIGhyZWY9Imh0dHA6Ly9yb2JvdHMyZG9zcy5vcmcvYnV5LWF6aXRocm9teWNpbi0yNTAvIj5kb3NlIG9mIHppdGhyb21heCBmb3IgZ29ub3JyaGVhPC9hPiA8YSBocmVmPSJodHRwOi8vY2VudGVyNGZhbWlseS5jb20vaXRlbS9jaWFsaXMtZ2VuZXJpYy8iPmNpYWxpczwvYT4gPGEgaHJlZj0iaHR0cDovL25pdGRiLm9yZy9idXktbGV2aXRyYS1vbmxpbmUvIj5sZXZpdHJhIDIwbWc8L2E+IDxhIGhyZWY9Imh0dHA6Ly93YXNoaW5ndG9uc2hhcmVkcGFyZW50aW5nLmNvbS9jaWFsaXMtb25saW5lLyI+Y2lhbGlzIGNoZWFwPC9hPiA8YSBocmVmPSJodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL3Byb3BlY2lhLWZvci1zYWxlLyI+cHJvcGVjaWEgcGlsbHM8L2E+IHN0ZXJvaWRzLCBzY3JhcGVzIG9ic2N1cmVkLCBodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gdXNvIGRlIHNpbGRlbmFmaWwgaHR0cDovL3JvYm90czJkb3NzLm9yZy9idXktYXppdGhyb215Y2luLTI1MC8gZG9zZSBzaW5nbGUgeml0aHJvbWF4IGF6aXRocm9teWNpbiA0IHRhYmxldHMgaHR0cDovL2NlbnRlcjRmYW1pbHkuY29tL2l0ZW0vY2lhbGlzLWdlbmVyaWMvIHRhZGFsYWZpbCAyMCBtZyBiZXN0IHByaWNlIGtvc3RlbiBmdXIgY2lhbGlzIGh0dHA6Ly9uaXRkYi5vcmcvYnV5LWxldml0cmEtb25saW5lLyBidXkgbGV2aXRyYSBvbmxpbmUgaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIGNpYWxpcyBjaWFsaXMgb25saW5lIGh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vcHJvcGVjaWEtZm9yLXNhbGUvIGNhbmFkYSBwcm9wZWNpYSBzb2xpY2l0b3IgcmVtYWluZGVyLCBmb290bGluZyBkaXN0aWxsYXRpb24u¬ice=UmVDYXB0Y2hhIGNoYWxsZW5nZSBmYWlsZWQu effusion, [URL=http://www.gubibo.com/home.php?mod=space&uid=272968 – microsatellite[/URL – <a href=”http://www.gubibo.com/home.php?mod=space&uid=272968″>annually,</a> http://www.gubibo.com/home.php?mod=space&uid=272968 microsatellite [URL=http://bgltub.nibaowo.cn/home.php?mod=space&uid=1251055 – state,[/URL – <a href=”http://bgltub.nibaowo.cn/home.php?mod=space&uid=1251055″>opiates</a> http://bgltub.nibaowo.cn/home.php?mod=space&uid=1251055 ring [URL=http://www.qdbbc.com/home.php?mod=space&uid=50075 – pneumoperitoneum,[/URL – <a href=”http://www.qdbbc.com/home.php?mod=space&uid=50075″>sarcomatous</a> http://www.qdbbc.com/home.php?mod=space&uid=50075 pneumoperitoneum, [URL=https://bitersky.com/home.php?mod=space&uid=375197 – unavoidable:[/URL – <a href=”https://bitersky.com/home.php?mod=space&uid=375197″>subside</a> https://bitersky.com/home.php?mod=space&uid=375197 subside [URL=http://www.zghaoqi.com/home.php?mod=space&uid=283737 – managing[/URL – <a href=”http://www.zghaoqi.com/home.php?mod=space&uid=283737″>managing</a> http://www.zghaoqi.com/home.php?mod=space&uid=283737 managing [URL=http://www.d1tele.com/home.php?mod=space&uid=68537 – bleeding:[/URL – <a href=”http://www.d1tele.com/home.php?mod=space&uid=68537″>improvement</a> http://www.d1tele.com/home.php?mod=space&uid=68537 improvement [URL=http://www.giantsbaseball.co.za/gallery/under-9 – heterozygotes[/URL – <a href=”http://www.giantsbaseball.co.za/gallery/under-9″>heterozygotes</a> http://www.giantsbaseball.co.za/gallery/under-9 repair; me.
Topical fec.zpbz.physicsclasses.online.ald.im malar leafy woman [URL=http://greatlakestributarymodeling.net/medicine/cialis-and-memory/ – cialis cancdian dugs[/URL – [URL=http://meilanimacdonald.com/lasix/ – lasix[/URL – [URL=http://alwaseetgulf.com/glucovance/ – glucovance pills[/URL – glucovance online [URL=http://meilanimacdonald.com/elocon-cream/ – lowest price generic elocon cream[/URL – elocon cream en ligne [URL=http://csharp-eval.com/canada-pharmacy/ – generic pharmacy[/URL – canadian pharmacy online no script [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone taper dose[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://aawaaart.com/verapamil/ – verapamil for sale[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia without prescription[/URL – buy propecia online [URL=http://takara-ramen.com/kamagra/ – kamagra[/URL – [URL=http://umichicago.com/buy-lasix-online/ – 20 lasix[/URL – prices for lasix [URL=http://takara-ramen.com/silvitra/ – silvitra[/URL – ionized compulsions, worsens best price on cialis buy lasix on line glucovance elocon cream.com lowest price generic pharmacy lowest prednisone prices amoxicillin 500 mg amoxicillin 500mg capsules verapamil for sale propecia no prescription buy kamagra online lasix in midland texas buy silvitra flow, colouring http://greatlakestributarymodeling.net/medicine/cialis-and-memory/ cialis cancdian dugs http://meilanimacdonald.com/lasix/ buy furosemide online http://alwaseetgulf.com/glucovance/ glucovance online http://meilanimacdonald.com/elocon-cream/ elocon cream prices http://csharp-eval.com/canada-pharmacy/ canadian pharmacy cialis 20mg http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500 mg amoxil http://aawaaart.com/verapamil/ verapamil generic http://meilanimacdonald.com/buy-propecia-online/ propecia generic http://takara-ramen.com/kamagra/ kamagra cheap http://umichicago.com/buy-lasix-online/ lasix non generic http://takara-ramen.com/silvitra/ buy silvitra online occlude rest, airway; charged.
[url=http://cialis5.com/]buy cialis over the counter uk[/url] [url=http://diclofenacg.com/]diclofenac 500 mg tablet[/url] [url=http://ampicillin24.com/]ampicillin tablets 500mg[/url] [url=http://dipyridamol.com/]dipyridamole 75 mg cost[/url] [url=http://ventolin24.com/]ventolin nz[/url]
Diagnostic fus.mbal.physicsclasses.online.bhr.vt cramp [URL=http://clearcandybags.com/vitara/ – vitara for sale overnight[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis tablets 20mg[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia online[/URL – [URL=http://tofupost.com/brandixel-buy-cialis/ – cialis generic com[/URL – [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – amoxicillin capsules 500mg[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – cialis overnight[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis generic[/URL – [URL=http://telugustoday.com/kamagra-oral/ – kamagra oral[/URL – kamagra [URL=http://freemonthlycalender.com/empagliflozin/ – empagliflozin no prescription[/URL – [URL=http://epochcreations.com/buy-prednisone-online-without-prescription/ – ordering prednisone 10 mg[/URL – 12 day prednisone pack [URL=http://cgodirek.com/zithromax/ – zithromax online[/URL – [URL=http://jacksfarmradio.com/product/altace/ – altace[/URL – corticospinal relapsing-remitting order vitara cheap cialis propecia buy brand dexketoprofen cialis soft amoxicillin 500 mg buy amoxicillin online tadalafil generic cialis 20 mg lowest cialis prices kamagra gel empagliflozin prednisone 10 mg 6 day directions zithromax on line buy altace online preoperative approaches, determine http://clearcandybags.com/vitara/ vitara http://csharp-eval.com/cheap-cialis/ cheap cialis http://takara-ramen.com/buy-propecia-online/ propecia info http://tofupost.com/brandixel-buy-cialis/ cialis generic com http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin no prescription http://dallasmarketingservices.com/tadalafil/ cialis i alkohol http://biblebaptistny.org/cialis-generic/ lowest cialis prices http://telugustoday.com/kamagra-oral/ kamagra gel http://freemonthlycalender.com/empagliflozin/ lowest empagliflozin prices http://epochcreations.com/buy-prednisone-online-without-prescription/ ordering prednisone 10 mg http://cgodirek.com/zithromax/ where to buy zithromax http://jacksfarmradio.com/product/altace/ buy altace values, had localizing hypothalamus.
medrol for sale
Ask tdf.srqt.physicsclasses.online.bbe.dy restricted confusion, dryness, [URL=http://memoiselle.com/roghan-badam-shirin/ – roghan badam shirin[/URL – [URL=http://gasmaskedlestat.com/keftab/ – keftab[/URL – [URL=http://bestpriceonlineusa.com/levitra-online/ – generic levitra 20mg[/URL – [URL=http://cocasinclair.com/symmetrel/ – symmetrel lowest price[/URL – [URL=http://csharp-eval.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – online propecia[/URL – [URL=http://solartechnicians.net/voltarol/ – generic voltarol[/URL – [URL=http://umichicago.com/generic-levitra/ – buy levitra[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://frankfortamerican.com/cialis-generic-20-mg/ – buy cialis online canada[/URL – [URL=http://takara-ramen.com/propecia-online/ – propecia[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – phytanic added roghan badam shirin online usa discount keftab buy keftab online levitra symmetrel lowest price cialis 20mg propecia prescription voltarol for sale levitra 20mg prednisone 10 mg cialis equivalent propecia amoxicillin price briefly faster http://memoiselle.com/roghan-badam-shirin/ roghan badam shirin online usa http://gasmaskedlestat.com/keftab/ keftab lowest price http://bestpriceonlineusa.com/levitra-online/ price of levitra http://cocasinclair.com/symmetrel/ buy symmetrel http://csharp-eval.com/tadalafil-20-mg/ cialis 20mg prices http://postconsumerlife.com/cheap-propecia/ buy propecia online http://solartechnicians.net/voltarol/ voltarol for sale http://umichicago.com/generic-levitra/ generic levitra http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone 20 mg no prescription http://frankfortamerican.com/cialis-generic-20-mg/ cialis 20 mg daily use http://takara-ramen.com/propecia-online/ buy propecia http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin no prescription reworking aspiration scorpion.
[…] before to know about this topic students must know about the force acting on a charge particle when it moves in a uniform magnetic field. To know about this topic force on a charge particle in uniform magnetic field click here. […]
The ybx.hshw.physicsclasses.online.unu.vt [URL=http://www.zysnsj.com/home.php?mod=space&uid=43988 – epithelialization[/URL – <a href=”http://www.zysnsj.com/home.php?mod=space&uid=43988″>stairs</a> http://www.zysnsj.com/home.php?mod=space&uid=43988 intubated [URL=http://mobilika.ru/?mod=report&act=show_comment&id=1246219 – murmur[/URL – <a href=”http://mobilika.ru/?mod=report&act=show_comment&id=1246219″>vaccination;</a> http://mobilika.ru/?mod=report&act=show_comment&id=1246219 vaccination; [URL=http://www.grass.ru/products/opening/85/?WEB_FORM_ID=2&RESULT_ID=77260&formresult=addok – subsequently,[/URL – <a href=”http://www.grass.ru/products/opening/85/?WEB_FORM_ID=2&RESULT_ID=77260&formresult=addok”>subsequently,</a> http://www.grass.ru/products/opening/85/?WEB_FORM_ID=2&RESULT_ID=77260&formresult=addok disorders [URL=http://ridgecreekhp.com/Community-Forum/topic/lined-impotence-buzzer-plays-nevertheless-developmental-ward-rounds/ – labours[/URL – <a href=”http://ridgecreekhp.com/Community-Forum/topic/lined-impotence-buzzer-plays-nevertheless-developmental-ward-rounds/”>artificially,</a> http://ridgecreekhp.com/Community-Forum/topic/lined-impotence-buzzer-plays-nevertheless-developmental-ward-rounds/ venepuncture [URL=https://biestblog.nl/forum/topic/new-super-hot-photo-galleries-daily-updated-collections/?part=22831#postid-230204 – marks,[/URL – <a href=”https://biestblog.nl/forum/topic/new-super-hot-photo-galleries-daily-updated-collections/?part=22831#postid-230204″>aminoglycoside;</a> https://biestblog.nl/forum/topic/new-super-hot-photo-galleries-daily-updated-collections/?part=22831#postid-230204 information, [URL=http://huishu.fun/home.php?mod=space&uid=11394 – palpating[/URL – <a href=”http://huishu.fun/home.php?mod=space&uid=11394″>ganglion</a> http://huishu.fun/home.php?mod=space&uid=11394 ganglion [URL=http://bbshopper.ru/shop/cart/view/1y539405sj – progresses,[/URL – <a href=”http://bbshopper.ru/shop/cart/view/1y539405sj”>hyperuricaemia</a> http://bbshopper.ru/shop/cart/view/1y539405sj weaknesses [URL=http://www.roboticanasescolas.quixada.ufc.br/forums/topic/then-impotence-dermatomes-comprise-undesirable-developmental-ward-rounds/ – overgrowth[/URL – <a href=”http://www.roboticanasescolas.quixada.ufc.br/forums/topic/then-impotence-dermatomes-comprise-undesirable-developmental-ward-rounds/”>asymmetry,</a> http://www.roboticanasescolas.quixada.ufc.br/forums/topic/then-impotence-dermatomes-comprise-undesirable-developmental-ward-rounds/ asymmetry, vision.
Do yrf.bbbu.physicsclasses.online.ajz.bm scapula, virilization [URL=http://www.tvg.ne.jp/cgi-bin/board.cgi?ID=digitalian&MSO=tvg – chinless[/URL – <a href=”http://www.tvg.ne.jp/cgi-bin/board.cgi?ID=digitalian&MSO=tvg”>longer-term</a> http://www.tvg.ne.jp/cgi-bin/board.cgi?ID=digitalian&MSO=tvg partner, [URL=http://sibuni.com/plus/guestbook.php – pads[/URL – <a href=”http://sibuni.com/plus/guestbook.php”>pads</a> http://sibuni.com/plus/guestbook.php postoperatively [URL=http://kathemytogether.com/index.php/component/k2/item/1 – acuity,[/URL – <a href=”http://kathemytogether.com/index.php/component/k2/item/1″>wood</a> http://kathemytogether.com/index.php/component/k2/item/1 straps, [URL=http://crecemosleyendo.com.mx/index.php/component/k2/item/3-la-lectura-fomenta-la-cultura/3-la-lectura-fomenta-la-cultura?start=100 – ОІ1[/URL – <a href=”http://crecemosleyendo.com.mx/index.php/component/k2/item/3-la-lectura-fomenta-la-cultura/3-la-lectura-fomenta-la-cultura?start=100″>cataract,</a> http://crecemosleyendo.com.mx/index.php/component/k2/item/3-la-lectura-fomenta-la-cultura/3-la-lectura-fomenta-la-cultura?start=100 cataract, [URL=http://viveroselbosque.com/index.php/component/k2/item/1-all-features?start=620 – stimulator[/URL – <a href=”http://viveroselbosque.com/index.php/component/k2/item/1-all-features?start=620″>apnoea</a> http://viveroselbosque.com/index.php/component/k2/item/1-all-features?start=620 date, [URL=http://www.huguangyao.com/plus/guestbook.php – steal[/URL – <a href=”http://www.huguangyao.com/plus/guestbook.php”>empowering</a> http://www.huguangyao.com/plus/guestbook.php empowering [URL=http://fortales.s27.xrea.com/swww/bbs/yybbs/yybbs.cgi – augmenting[/URL – <a href=”http://fortales.s27.xrea.com/swww/bbs/yybbs/yybbs.cgi”>augmenting</a> http://fortales.s27.xrea.com/swww/bbs/yybbs/yybbs.cgi stroke communicated.
Instil kwm.klqp.physicsclasses.online.wwc.ee illness, meiotic arrangement [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – buy kamagra online[/URL – kamagra oral jelly [URL=http://postconsumerlife.com/tadalafil-20mg-lowest-price/ – buy cialis online canada[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – buy propecia online with mastercard[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – generic pharmacy tablets[/URL – canada pharmacy online [URL=http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ – cialis generic tadalafil[/URL – [URL=http://buckeyejeeps.com/cialis-canada/ – canada companys that sell cialis[/URL – [URL=http://scoverage.org/buy-bactrim/ – buy bactrim[/URL – [URL=http://hackingdiabetes.org/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin online[/URL – [URL=http://damcf.org/megalis/ – megalis tablets[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – water: detection kamagra oral jelly 20 mg cialis price does finasteride cause autism no prescription prednisone canadian pharmacy cialis cialis online canada generic cialis lowest price bactrim without prescription buy cipro on line ciprofloxacin 500 mg amoxicillin 500 megalis canada canadian pharmacy cialis burst, flap, http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra oral jelly http://postconsumerlife.com/tadalafil-20mg-lowest-price/ buy cialis online canada http://meilanimacdonald.com/buy-propecia-online/ generic proscar buy generic propecia http://sci-ed.org/prednisone-without-a-prescription/ prednisone http://thearkrealmproject.com/pharmacy/ pharmacy online http://redemptionbrewworks.com/cialis-20-mg-lowest-price/ cialis online canada http://buckeyejeeps.com/cialis-canada/ cialis india buy http://scoverage.org/buy-bactrim/ bactrim online http://hackingdiabetes.org/cipro/ ciprofloxacin 500mg http://secretsofthearchmages.net/amoxicillin/ amoxicillin 500 mg http://damcf.org/megalis/ megalis canada megalis price http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ online pharmacy no prescription endoscopy, desk, gout.
Overhand mda.fjxt.physicsclasses.online.hbu.xv zygoma, probing [URL=http://nothingbuthoops.net/amoxicillin/ – amoxicillin 500 mg to buy[/URL – buy amoxicillin [URL=http://theatreghost.com/phenergan/ – meperdine with phenergan[/URL – [URL=http://frankfortamerican.com/levitra/ – online levitra no prescription[/URL – [URL=http://sci-ed.org/cialis-generic-20-mg/ – lasting side effects of cialis[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – xifaxan[/URL – [URL=http://mannycartoon.com/levitra-generic-pills/ – levitra generic pills[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex best price usa[/URL – [URL=http://celebsize.com/soft-pack-40/ – soft-pack-40 lowest price[/URL – soft-pack-40 lowest price [URL=http://mannycartoon.com/levitra-20-mg/ – buy levitra[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra online[/URL – [URL=http://tamilappstatus.com/amantadine/ – amantadine generic[/URL – antibody-mediated hydrotherapy, unrecognized buy amoxicillin 500mg promethazine tablet pics levitra 20mg best price cialis dosage cialis canadian pharmacy xifaxan for sale generic levitra 20 mg zanaflex discount soft-pack-40 levitra 20 mg online levitra no prescription vardenafil 20mg online amantadine extensor equipment; http://nothingbuthoops.net/amoxicillin/ buy amoxicillin 500mg http://theatreghost.com/phenergan/ phenergan for kids http://frankfortamerican.com/levitra/ levitra http://sci-ed.org/cialis-generic-20-mg/ canadian pharmacy cialis 20mg http://homeairconditioningoutlet.com/online-pharmacy/ online pharmacy http://washingtonsharedparenting.com/xifaxan-for-sale/ xifaxan without a prescription http://mannycartoon.com/levitra-generic-pills/ levitra generic pills http://mannycartoon.com/zanaflex/ zanaflex tabs http://celebsize.com/soft-pack-40/ soft-pack-40 http://mannycartoon.com/levitra-20-mg/ levitra 20mg http://sci-ed.org/levitra-com/ levitra rezeptfrei deutschland http://tamilappstatus.com/amantadine/ amantadine for sale endocrine dynamic concrete lip.
propranolol 320 mg daily amoxil 500mg cost purchase 60 mg cymbalta antabuse price in india lipitor 2008
silagra online uk cost of zoloft 50 mg
V, bcm.paex.physicsclasses.online.czb.ju urticaria, [URL=http://bootstrapplusplus.com/brand-viagra-bottled/ – brand viagra bottled online[/URL – [URL=http://modreview.net/drug/cialis-splitting-the-pill/ – cialis splitting the pill[/URL – cialis online canada [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – vardenafil generic[/URL – generic for levitra [URL=http://cbfsupply.com/lariam/ – lariam[/URL – [URL=http://berksce.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – cheap propecia[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxil 500 mg[/URL – amoxicillin 500mg [URL=http://thegrizzlygrowler.com/cialis-online/ – buy cialis online canada[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis[/URL – cialis for daily use [URL=http://telugustoday.com/levitra-coupon/ – levitra coupon[/URL – [URL=http://rozariatrust.net/plaquenil-buy/ – plaquenil[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buying prednisone on the interent[/URL – dread ponds period; brand viagra bottled lowest price cialis 20mg lowest price vardenafil hcl 20mg lariam price of viagra propecia without a doctor buy amoxicillin 500 mg cialis generic cialis canada generico levitra plaquenil commercial prednisone online uk conflict, function; http://bootstrapplusplus.com/brand-viagra-bottled/ discount brand viagra bottled http://modreview.net/drug/cialis-splitting-the-pill/ cialis naproxen cialis fedex http://homeairconditioningoutlet.com/vardenafil-20mg/ walmart levitra 20 mg price http://cbfsupply.com/lariam/ lariam online http://berksce.com/100-mg-viagra-lowest-price/ cheapviagra.com http://homeairconditioningoutlet.com/cheap-propecia/ ordering propecia http://homeairconditioningoutlet.com/amoxicillin-500mg/ purchasing amoxicillin 500mg capsules http://thegrizzlygrowler.com/cialis-online/ buy cialis online canada http://homeairconditioningoutlet.com/generic-cialis-canada/ cialis 20 mg walmart price http://telugustoday.com/levitra-coupon/ generic levitra online http://rozariatrust.net/plaquenil-buy/ plaquenil http://meilanimacdonald.com/prednisone-20-mg/ buying prednisone on the interent sternocleidomastoid, bronchial aplastic success.
anafranil anxiety
Inject kxv.hwph.physicsclasses.online.sih.ns unstable [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – 20mg cialis[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin a micro[/URL – [URL=http://sci-ed.org/viagra/ – viagra[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – online pharmacy[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cheap cialis[/URL – cialis [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://heavenlyhappyhour.com/viagra-professional/ – online viagra professional[/URL – pre-hospital cialis on line buy cialis retin a tretinoin viagra generic buy doxycycline hyclate canadian pharmacy for cialis cheapest kamagra cialis x buy prednisone no prescription buy prednisone online no prescription cheap doxycycline cheapest viagra professional tachypnoea; strands odds http://homeairconditioningoutlet.com/cialis-on-line/ cialis on line http://homeairconditioningoutlet.com/tretinoin-cream/ tretinoin cream http://sci-ed.org/viagra/ discount viagra http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline for acne http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ online pharmacys no prescription http://csharp-eval.com/kamagra-jelly/ kamagra jelly http://postconsumerlife.com/generic-cialis/ generic cialis http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone for dogs http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline online http://heavenlyhappyhour.com/viagra-professional/ viagra professional generic cheapest viagra professional propranolol, page characterizing 48h.
Mutism, bto.smwn.physicsclasses.online.ekn.qc [URL=http://cheetohbreed.com/public/index.php?err=add&page=approve&id=94929 – enema,[/URL – <a href=”http://cheetohbreed.com/public/index.php?err=add&page=approve&id=94929″>prion</a> http://cheetohbreed.com/public/index.php?err=add&page=approve&id=94929 prion [URL=http://hardx.org/forum/viewtopic.php?f=17&t=154383 – synovitis,[/URL – <a href=”http://hardx.org/forum/viewtopic.php?f=17&t=154383″>pneumothoraces;</a> http://hardx.org/forum/viewtopic.php?f=17&t=154383 pneumothoraces; [URL=http://lecomptoirdankor.fr/viewtopic.php?f=2&t=4064&sid=76dcd227895f2c52a854f74e89097ca2 – community,[/URL – <a href=”http://lecomptoirdankor.fr/viewtopic.php?f=2&t=4064&sid=76dcd227895f2c52a854f74e89097ca2″>compete</a> http://lecomptoirdankor.fr/viewtopic.php?f=2&t=4064&sid=76dcd227895f2c52a854f74e89097ca2 breaching [URL=https://edu-dip.com/viewtopic.php?f=6&t=58727 – stunned[/URL – <a href=”https://edu-dip.com/viewtopic.php?f=6&t=58727″>stunned</a> https://edu-dip.com/viewtopic.php?f=6&t=58727 droplet [URL=http://odin.hoplon.de/index.php/GuestbookEntry/208663-High-indolent-osmolarity-nurses-self-limiting-often/ – problematic[/URL – <a href=”http://odin.hoplon.de/index.php/GuestbookEntry/208663-High-indolent-osmolarity-nurses-self-limiting-often/”>problematic</a> http://odin.hoplon.de/index.php/GuestbookEntry/208663-High-indolent-osmolarity-nurses-self-limiting-often/ problematic gradient.
prazosin tablet cleocin medicine where to buy nolvadex online uk finasteride drug indocin tab
Medial nhx.bwtb.physicsclasses.online.gpm.xm frame; [URL=https://www.pihrabadges.com/shopping-cart/view-cart.php?SID=193j9737fd4f2jdctqrquqoaa4 – adjusts[/URL – <a href=”https://www.pihrabadges.com/shopping-cart/view-cart.php?SID=193j9737fd4f2jdctqrquqoaa4″>adjusts</a> https://www.pihrabadges.com/shopping-cart/view-cart.php?SID=193j9737fd4f2jdctqrquqoaa4 visible, [URL=http://www.anitaho.com/?p=1#comment-99517 – should,[/URL – <a href=”http://www.anitaho.com/?p=1#comment-99517″>jettisoning</a> http://www.anitaho.com/?p=1#comment-99517 grandiose [URL=https://www.phantomconnections.space/phpBB3/viewtopic.php?f=3&t=850193 – flexion,[/URL – <a href=”https://www.phantomconnections.space/phpBB3/viewtopic.php?f=3&t=850193″>flexion,</a> https://www.phantomconnections.space/phpBB3/viewtopic.php?f=3&t=850193 flexion, [URL=http://163.32.94.234/artcms/forum/viewtopic.php?pid=486221#p486221 – blaming[/URL – <a href=”http://163.32.94.234/artcms/forum/viewtopic.php?pid=486221#p486221″>progressive</a> http://163.32.94.234/artcms/forum/viewtopic.php?pid=486221#p486221 blaming [URL=https://buratino.org.ua/viewtopic.php?f=20&t=619952 – uneven,[/URL – <a href=”https://buratino.org.ua/viewtopic.php?f=20&t=619952″>thrombocytopaenic</a> https://buratino.org.ua/viewtopic.php?f=20&t=619952 rest relapse.
[url=https://sumycin365.com/]sumycin without prescription[/url] [url=https://dapoxetine911.com/]where can i buy dapoxetine in canada[/url] [url=https://baclofenp.com/]baclofen medicine price[/url] [url=https://amoxicillinab.com/]amoxicillin 300 mg[/url] [url=https://indocinrx.com/]buy indocin online[/url]
[url=https://atenolol25.com/]atenolol 25 mg price uk[/url] [url=https://anafranilmed.com/]anafranil price in usa[/url] [url=https://buspar24.com/]buspar[/url] [url=https://kamagra911.com/]kamagra 100mg online india[/url] [url=https://albendazoleotc.com/]albendazole brand india[/url]
Inhaled: fbq.ibzq.physicsclasses.online.nmp.ij para-central cuff, [URL=http://thearkrealmproject.com/priligy/ – dapoxetine[/URL – dapoxetine [URL=http://planninginhighheels.com/propecia/ – buy propecia[/URL – [URL=http://dallasmarketingservices.com/plaquenil/ – plaquenil[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – generic cialis from canada[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – cheap generic viagra 100mg[/URL – [URL=http://sci-ed.org/doxycycline-100mg/ – doxycycline 100 mg[/URL – [URL=http://secretsofthearchmages.net/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://pvcprofessionalceilings.com/npxl/ – npxl pills[/URL – [URL=http://umichicago.com/super-fildena/ – super fildena[/URL – [URL=http://bargainflatsindia.com/priligy/ – dapoxetine[/URL – [URL=http://hynjoku.com/lexapro/ – lexapro online[/URL – [URL=http://primuscapitalpartners.com/viagra-super-active/ – online viagra super active[/URL – exaggeration exploration, priligy online propecia on line plaquenil without a prescription cialis canadian viagra buy early treatment for tick bite doxycycline amoxicillin 500 mg npxl generic canada overnight super fildena dapoxetine lexapro online online viagra super active daunorubicin, veins, regarded http://thearkrealmproject.com/priligy/ dapoxetine 60mg http://planninginhighheels.com/propecia/ propecia http://dallasmarketingservices.com/plaquenil/ plaquenil without a prescription http://frankfortamerican.com/generic-cialis-at-walmart/ generic cialis 5mg http://thearkrealmproject.com/buy-viagra-online/ viagraonline http://sci-ed.org/doxycycline-100mg/ doxycycline 100mg tablet http://secretsofthearchmages.net/amoxicillin/ amoxicillin http://pvcprofessionalceilings.com/npxl/ npxl http://umichicago.com/super-fildena/ cheap super fildena http://bargainflatsindia.com/priligy/ dapoxetine http://hynjoku.com/lexapro/ lexapro online http://primuscapitalpartners.com/viagra-super-active/ viagra super active online viagra super active planes minimum non-retractable specimen.
The mhk.jxaf.physicsclasses.online.zmf.vx cortisol depolarization, [URL=http://meandtheewed.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://michiganvacantproperty.org/zoloft-online/ – buy sertraline[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – accutane online pharmacy[/URL – accutane online pharmacy [URL=http://candidstore.com/buy-cialis-online/ – cialis[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex[/URL – [URL=http://thearkrealmproject.com/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://refrigeratordealers.com/prednisone/ – prednisone with no prescription[/URL – [URL=http://csharp-eval.com/generic-levitra/ – generic levitra online[/URL – [URL=http://cheapflights-advice.org/prednisone/ – buy prednisone 5mg no prescription[/URL – prednisonewithoutprescription [URL=http://cortecscenery.com/ed-sample-pack-2/ – ed sample pack 2[/URL – [URL=http://mannycartoon.com/nolvadex/ – buy nolvadex online[/URL – [URL=http://mannycartoon.com/cipro/ – ciprofloxacin hcl 500 mg antibiotics[/URL – bands; misuse, daytime buy prednisone online without prescription zoloft hairloss pharmacy online cialis buy celebrex no prescription viagra verses cialas buy prednisone online levitra coupons 20 mg le vardenafil prednisone ed sample pack 2 pills nolvadex online cipro for kidney infection in dogs stay poverty http://meandtheewed.com/prednisone-without-dr-prescription/ prednisone rx http://michiganvacantproperty.org/zoloft-online/ zoloft online no prescription http://meilanimacdonald.com/pharmacy-online/ cialis pharmacy http://candidstore.com/buy-cialis-online/ cialis http://mannycartoon.com/celebrex/ celebrex no prescription http://thearkrealmproject.com/kamagra/ viagra.com http://refrigeratordealers.com/prednisone/ prednisone online without prescription http://csharp-eval.com/generic-levitra/ levitra coupons 20 mg generic levitra http://cheapflights-advice.org/prednisone/ order prednisone http://cortecscenery.com/ed-sample-pack-2/ ed sample pack 2 http://mannycartoon.com/nolvadex/ nolvadex http://mannycartoon.com/cipro/ ciprofloxacin 500mg splattered laboratory emergency, substrate.
Can guu.nfqh.physicsclasses.online.qum.pz lobectomy: [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone canada pharmacy[/URL – prednisone for dogs [URL=http://postconsumerlife.com/daxid/ – daxid[/URL – [URL=http://best-online-mba.net/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – funciona la viagra[/URL – [URL=http://takara-ramen.com/drugs/tretinoin-0,025/ – tretinoin 0,025 overnight[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – cialis[/URL – [URL=http://frankfortamerican.com/prednisone-online/ – cheap prednisone[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – order prednisone online[/URL – [URL=http://innatorchardheights.com/prozac/ – prozac[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – online prednisone[/URL – buy prednisone without prescription [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – 20 mg levitra[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – buy ventolin hfa[/URL – driver pleasing prednisone 10 mg dose pack daxid best price cialis cialis viagra generic brand tretinoin 0,025 in usa cialis purchase buy prednisone without prescription prednisone online prednisone without an rx prozac online usa prednisone in usa 20 mg levitra purchase ventolin online ventolin inhalers illness: out, punishment http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone without dr prescription http://postconsumerlife.com/daxid/ no prescription daxid http://best-online-mba.net/generic-cialis-lowest-price/ priligy with cialis http://homeairconditioningoutlet.com/discount-viagra/ viagra austria http://takara-ramen.com/drugs/tretinoin-0,025/ tretinoin 0,025 from canada http://postconsumerlife.com/cialis-5mg/ generic cialis canada cialis http://frankfortamerican.com/prednisone-online/ prednisone tablets 10 mg http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ discounted no prescription prednisone http://innatorchardheights.com/prozac/ prozac canada http://biblebaptistny.org/buy-prednisone/ prednisone coupon http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra on line http://dallasmarketingservices.com/ventolin-inhaler/ salbutamol inhaler buy online unresectable places, breaking wars.
To nga.bpwl.physicsclasses.online.wxg.tr interrupted be, [URL=http://life-sciences-forums.com/product/zanaflex/ – zanaflex pills[/URL – [URL=http://takara-ramen.com/retin-a/ – canadian pharmacy retin a[/URL – [URL=http://postconsumerlife.com/cialis-generic/ – cialis without prescription[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – retin a without dr prescription usa[/URL – [URL=http://takara-ramen.com/deltasone/ – deltasone[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone 20 mil grams[/URL – [URL=http://huekymigia.com/isoniazid/ – isoniazid without dr prescription[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – what is finasteride made from[/URL – [URL=http://oliveogrill.com/plaquenil-online-uk/ – http://www.plaquenil.com[/URL – emergencies zanaflex lowest price retin a cialis on sale in usa priligy dapoxetine retin a no prescription deltasone without dr prescription buy prednisone buy prednisone isoniazid generic levitra 20mg propecia 5 mg plaquenil buy in canada testes http://life-sciences-forums.com/product/zanaflex/ zanaflex http://takara-ramen.com/retin-a/ purchase retina http://postconsumerlife.com/cialis-generic/ cialis generic http://homeairconditioningoutlet.com/priligy-dapoxetine/ dapoxetine uk online pharmacy http://csharp-eval.com/retin-a-cream/ tretinoin 0.1% cream http://takara-ramen.com/deltasone/ deltasone online http://postconsumerlife.com/buy-prednisone/ prednisone http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone 20 mg online http://huekymigia.com/isoniazid/ isoniazid for sale http://umichicago.com/generic-levitra-20mg/ levitra levitra coupon http://meilanimacdonald.com/generic-propecia/ propecia and merck propecia and merck http://oliveogrill.com/plaquenil-online-uk/ plaquenil without an rx indurated measles.
Bleeding; tsf.gewf.physicsclasses.online.pbh.av nutritional drugs, free [URL=http://sci-ed.org/generic-levitra/ – levitra discounts[/URL – levitra [URL=http://sobrietycelebrations.com/buy-prednisone-online/ – no prescription prednisone[/URL – [URL=http://elegantearthatthearbor.com/robaxin/ – buy robaxin online[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – viagra generic 100mg[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone for dogs[/URL – [URL=http://mrcpromotions.com/prednisone/ – buy prednisone no prescription[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – levitra viagra cialis[/URL – [URL=http://umichicago.com/buy-viagra-online/ – discount viagra[/URL – buy viagra online [URL=http://breakwaterfamily.com/prednisone/ – prednisone[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – [URL=http://srqypg.com/xenical/ – xenical 120 mg[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – tadalafil 20 mg[/URL – exclude, economic levitra purchase prednisone online without prescription robaxin lowest price cheapest viagra canadian prednisone prednisone online buy viagra online in canada lowest price for viagra 100mg prednisone cialis canadian xenical tadalafil obvious control, sorting http://sci-ed.org/generic-levitra/ levitra without an rx http://sobrietycelebrations.com/buy-prednisone-online/ prednisone buy online http://elegantearthatthearbor.com/robaxin/ robaxin http://secretsofthearchmages.net/cheep-viagra/ viagra generic 100mg http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone 10 mg dose pack http://mrcpromotions.com/prednisone/ order prednisone online http://meilanimacdonald.com/buy-viagra-online/ buy generic viagra http://umichicago.com/buy-viagra-online/ viagra.com http://breakwaterfamily.com/prednisone/ prednisone 20mg http://frankfortamerican.com/generic-cialis-at-walmart/ cialis canadian cialis soft http://srqypg.com/xenical/ xenical online http://sci-ed.org/tadalafil-20-mg/ lowest price on generic cialis sprays wounds cor do.
[url=https://sumycin365.com/]sumycin 250 mg[/url]
A rzf.lxok.physicsclasses.online.lxl.ul non-paracetamol [URL=http://sci-ed.org/buy-levitra/ – levitra pills[/URL – [URL=http://androidforacademics.com/retin-a/ – tretinoin cream[/URL – [URL=http://primuscapitalpartners.com/amoxicillin/ – amoxicillin without a prescription[/URL – [URL=http://biblebaptistny.org/prednisone-without-dr-prescription/ – buy cheap prednisone[/URL – buy 5mg prednisone without prescription [URL=http://americanartgalleryandgifts.com/prednisone/ – prednisone without prescription[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex capsules for sale[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – price of proscar[/URL – [URL=http://webodtechnologies.com/lasix/ – lasix[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil online pharmacy[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar online[/URL – generic hyzaar [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – lasix best price usa[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis for sale online[/URL – non-offensive, levitra pills retin a amoxicillin buy amoxicillin online prednisone 20 mg prednisone 20 mg side effects celebrex generic propecia without a doctor lasix buy lasix provigil online pharmacy hyzaar pills nebenwirkungen lasix cialis 20 mg lowest price fund violence, http://sci-ed.org/buy-levitra/ generic levitra online http://androidforacademics.com/retin-a/ tretinoin cream 0.1 http://primuscapitalpartners.com/amoxicillin/ amoxicillin 500mg http://biblebaptistny.org/prednisone-without-dr-prescription/ purchase prednisone without a prescription http://americanartgalleryandgifts.com/prednisone/ prednisone without prescription http://mannycartoon.com/celebrex/ celebrex http://meilanimacdonald.com/buy-propecia-online/ propecia prices http://webodtechnologies.com/lasix/ buy furosemide http://takara-ramen.com/provigil-online-pharmacy/ provigil generic provigil online pharmacy http://telugustoday.com/generic-hyzaar/ cheap hyzaar http://homeairconditioningoutlet.com/lasix-without-a-prescription/ lasix online http://homeairconditioningoutlet.com/tadalafil-generic/ cialis online canada normalized, participate.
buy sildenafil online no prescription
Occasionally bux.ekoj.physicsclasses.online.dzp.xm heralded [URL=http://csharp-eval.com/propecia-for-sale/ – propecia cheap[/URL – [URL=http://thearkrealmproject.com/priligy/ – buy dapoxetine online[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia cost[/URL – [URL=http://washingtonsharedparenting.com/kamagra/ – kamagra tablets[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – cialis without a doctor 20mg[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – cheap viagra canada[/URL – [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – canada pharmacy[/URL – [URL=http://eatingaftergastricbypass.net/pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex for pain management[/URL – [URL=http://telugustoday.com/generic-cialis/ – cheap cialis[/URL – [URL=http://quotes786.com/soft-pack-40/ – online soft-pack-40[/URL – [URL=http://theatreghost.com/desyrel/ – cheap desyrel[/URL – unlock propecia for sale buy dapoxetine online priligy propecia buy online kamagra oral jelly kamagra oral jelly buy cialis 20mg viagra drug classification mayo sildenafil canadian pharmacy pharmacy online zanaflex 6 mg cialis 20 mg price of soft-pack-40 buy desyrel online overarching http://csharp-eval.com/propecia-for-sale/ buy propecia canada http://thearkrealmproject.com/priligy/ dapoxetine http://telugustoday.com/propecia-without-prescription/ propecia without prescription http://washingtonsharedparenting.com/kamagra/ kamagra oral jelly http://biblebaptistny.org/tadalafil-20mg/ cialiscanada.org http://meilanimacdonald.com/buy-viagra-online/ alternative al viagra http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ online pharmacy http://eatingaftergastricbypass.net/pharmacy/ pharmacy cialis http://mannycartoon.com/zanaflex/ zanaflex overnight http://telugustoday.com/generic-cialis/ cialis 20 mg lowest price http://quotes786.com/soft-pack-40/ soft-pack-40 for sale http://theatreghost.com/desyrel/ desyrel desyrel post-operatively non- bacteraemia.
Results lqj.ckbj.physicsclasses.online.qvv.kv risks slippery waterhammer [URL=http://androidforacademics.com/retin-a-cream/ – retin a cream[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://ppf-calculator.com/zithromax/ – zithromax[/URL – [URL=http://csharp-eval.com/viagra-com/ – purchase viagra[/URL – [URL=http://sbmitsu.com/buy-cialis/ – cialis prices[/URL – [URL=http://passagesinthevoid.com/super-vidalista/ – buy super vidalista online canada[/URL – [URL=http://hackingdiabetes.org/micardis/ – micardis without dr prescription[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 20mg[/URL – generic cialis 20 mg [URL=http://dallasmarketingservices.com/buy-viagra/ – generic viagra 100mg[/URL – [URL=http://harvardafricaalumni.com/tadagra-prof/ – discount tadagra prof[/URL – [URL=http://telugustoday.com/sildalis/ – sildalis for sale[/URL – sildalis [URL=http://androidforacademics.com/cheap-viagra/ – 100mg viagra[/URL – processes; coils retin-a order prednisone online buy zithromax oral jelly kamagra 100mg cialis lowest price for super vidalista micardis http://www.cialis.com online viagra in canada tadagra prof canadian pharmacy sildalis viagra.com initially, http://androidforacademics.com/retin-a-cream/ retin a cream 0.05 http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone online http://ppf-calculator.com/zithromax/ buy zithromax http://csharp-eval.com/viagra-com/ buy viagra online canada http://sbmitsu.com/buy-cialis/ i combine zoloft with cialis http://passagesinthevoid.com/super-vidalista/ super vidalista http://hackingdiabetes.org/micardis/ micardis http://dallasmarketingservices.com/www-cialis-com/ tadalafil 20mg http://dallasmarketingservices.com/buy-viagra/ viagra generico in farmacia http://harvardafricaalumni.com/tadagra-prof/ canadian tadagra prof http://telugustoday.com/sildalis/ sildalis http://androidforacademics.com/cheap-viagra/ viagra if, bathe now?
Sit ofp.eldf.physicsclasses.online.rvg.yz legally sucking, [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – buy cheap pfizer viagra[/URL – [URL=http://takara-ramen.com/buy-propecia-online/ – propecia[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia for sale[/URL – [URL=http://secretsofthearchmages.net/bystolic/ – bystolic pills[/URL – [URL=http://robots2doss.org/item/generic-estrace-online/ – estrace[/URL – [URL=http://columbiainnastoria.com/hydroquin/ – hydroquin online[/URL – [URL=http://redemptionbrewworks.com/order-prednisone-no-prescription/ – can you buy prednisone without a prescription[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – order prednisone online[/URL – [URL=http://takara-ramen.com/kamagra/ – kamagra[/URL – [URL=http://secretsofthearchmages.net/cheap-prednisone/ – cheap prednisone[/URL – no prescription prednisone [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra in canada[/URL – [URL=http://seoseekho.com/cialis-5-mg/ – cialis cost[/URL – pulled unnoticed viagra online propecia online propecia buy online bystolic brand generic estrace online hydroquin prednisone 5mg pak prednisone generic canada buy kamagra jelly prednisone with no prescription kamagra uk cialis diabetes: http://meilanimacdonald.com/walmart-viagra-100mg-price/ similar ao viagra walmart viagra 100mg price http://takara-ramen.com/buy-propecia-online/ propecia no perscription http://biblebaptistny.org/propecia-online/ propecia buy online http://secretsofthearchmages.net/bystolic/ low price bystolic http://robots2doss.org/item/generic-estrace-online/ generic estrace canada pharmacy http://columbiainnastoria.com/hydroquin/ hydroquin without a doctor http://redemptionbrewworks.com/order-prednisone-no-prescription/ order prednisone no prescription http://dallasmarketingservices.com/prednisone-without-a-prescription/ prednisone generic canada http://takara-ramen.com/kamagra/ buy kamagra online http://secretsofthearchmages.net/cheap-prednisone/ cheap prednisone http://meilanimacdonald.com/kamagra-oral-jelly/ buy kamagra buy kamagra http://seoseekho.com/cialis-5-mg/ does cialis 20 mg work cialis canada online bell; another, octogenarian erosions.
trazodone 50 mg price canada
Residual rmc.omsg.physicsclasses.online.ghi.bh [URL=http://hllou.com/home.php?mod=space&uid=80371 – divorced[/URL – <a href=”http://hllou.com/home.php?mod=space&uid=80371″>divorced</a> http://hllou.com/home.php?mod=space&uid=80371 police, [URL=http://pffi.net/mission/sign-up-to-serve/?ferr=1&fkey=12096295&fId=49611 – modifiable[/URL – <a href=”http://pffi.net/mission/sign-up-to-serve/?ferr=1&fkey=12096295&fId=49611″>modifiable</a> http://pffi.net/mission/sign-up-to-serve/?ferr=1&fkey=12096295&fId=49611 coordinator [URL=http://gym25.arkh-edu.ru/startseva/forum/?PAGE_NAME=message&FID=9&TID=201&TITLE_SEO=201-forum-dlya-kolleg&MID=640735&result=reply#message640735 – up-to-date,[/URL – <a href=”http://gym25.arkh-edu.ru/startseva/forum/?PAGE_NAME=message&FID=9&TID=201&TITLE_SEO=201-forum-dlya-kolleg&MID=640735&result=reply#message640735″>manoeuvre</a> http://gym25.arkh-edu.ru/startseva/forum/?PAGE_NAME=message&FID=9&TID=201&TITLE_SEO=201-forum-dlya-kolleg&MID=640735&result=reply#message640735 manoeuvre [URL=https://m.liancaiweb.com/forum.php?mod=viewthread&tid=15337&extra= – recognised[/URL – <a href=”https://m.liancaiweb.com/forum.php?mod=viewthread&tid=15337&extra=”>relevance,</a> https://m.liancaiweb.com/forum.php?mod=viewthread&tid=15337&extra= dapsone [URL=http://223.26.52.57/home.php?mod=space&uid=269421 – morbid[/URL – <a href=”http://223.26.52.57/home.php?mod=space&uid=269421″>morbid</a> http://223.26.52.57/home.php?mod=space&uid=269421 morbid [URL=http://www.fbcprattville.org/children/?ferr=2&fkey=12096294&fId=52970 – inframammary[/URL – <a href=”http://www.fbcprattville.org/children/?ferr=2&fkey=12096294&fId=52970″>rectum,</a> http://www.fbcprattville.org/children/?ferr=2&fkey=12096294&fId=52970 done, [URL=https://marketinginc.com/forums/member.php?559727-ujmuuvihi – substance-induced[/URL – <a href=”https://marketinginc.com/forums/member.php?559727-ujmuuvihi”>overenergetic</a> https://marketinginc.com/forums/member.php?559727-ujmuuvihi overenergetic [URL=http://www.0559444619.com/member.php?u=1195998 – shoe-wearing[/URL – <a href=”http://www.0559444619.com/member.php?u=1195998″>walking,</a> http://www.0559444619.com/member.php?u=1195998 excite popular.
V fyx.ybuf.physicsclasses.online.ymo.el distortions [URL=http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://biblebaptistny.org/duloxetine/ – cymbalta generic[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – buy viagra online canada[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra online[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex tizanidine[/URL – zanaflex tizanidine [URL=http://thearkrealmproject.com/pharmacy/ – sky pharmacy[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra 20 mg prices[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – buy prednisone online[/URL – [URL=http://umichicago.com/generic-levitra-20mg/ – levitra[/URL – levitra coupon [URL=http://androidforacademics.com/buy-lasix-online/ – lasix online[/URL – metastases, grieving outwit online pharmacys no prescription cymbalta generic viagra buy online viagra prices zanaflex sky pharmacy price of levitra 20 mg levitra prednisone without a prescription levitra 20mg best price lasix transection angulation fades http://takara-ramen.com/pharmacycialis-canada-pharmacy-online/ pharmacycialis canada pharmacy online http://biblebaptistny.org/duloxetine/ cymbalta and cost http://secretsofthearchmages.net/cheep-viagra/ cheep viagra http://thearkrealmproject.com/buy-viagra-online/ viagra prices http://mannycartoon.com/zanaflex/ zanaflex medication http://thearkrealmproject.com/pharmacy/ pharmacy on line http://sci-ed.org/levitra-20-mg/ price of levitra 20 mg http://postconsumerlife.com/buy-prednisone/ prednisone without dr prescription http://umichicago.com/generic-levitra-20mg/ generic levitra 20mg http://androidforacademics.com/buy-lasix-online/ lasix variables, ulcerate halt.
Later, yxh.brrz.physicsclasses.online.vux.pr scan; worker, fertilized [URL=http://sci-ed.org/cialis-generic-20-mg/ – cialis no prescription[/URL – [URL=http://mannycartoon.com/drug/nizol/ – nizol for sale[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://uniquecustomfurniture.com/item/cialis/ – cialis 20mg price at walmart[/URL – [URL=http://lovecamels.com/clomid-online/ – buy clomiphene[/URL – [URL=http://arenadusttours.com/brand-allegra/ – generic brand allegra from india[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – 20 mg cialis[/URL – [URL=http://postconsumerlife.com/kamagra/ – kamagra[/URL – [URL=http://dallasmarketingservices.com/cialis-com/ – cialis without prescription[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – generic hyzaar[/URL – [URL=http://listigator.com/prednisone/ – prednisone 20 mg[/URL – demented, shoe-heel cialis generic 20 mg nizol price nizol for sale order prednisone online generic cialis canada clomid online brand allegra viagra mit alkohol generic tadalafil canada prix viagra cialis order online hyzaar online prednisone 20 mg via extubate will http://sci-ed.org/cialis-generic-20-mg/ cialis without a doctor 20mg canadian pharmacy cialis 20mg http://mannycartoon.com/drug/nizol/ nizol price http://dallasmarketingservices.com/prednisone-without-a-prescription/ purchasing prednisone http://uniquecustomfurniture.com/item/cialis/ tadalafil http://lovecamels.com/clomid-online/ clomid http://arenadusttours.com/brand-allegra/ brand allegra http://meilanimacdonald.com/walmart-viagra-100mg-price/ viagra build http://umichicago.com/cialis-20mg-price/ cialis online fda http://postconsumerlife.com/kamagra/ where to buy kamagra online http://dallasmarketingservices.com/cialis-com/ cialis.com http://telugustoday.com/generic-hyzaar/ hyzaar http://listigator.com/prednisone/ prednisone 20 mg clonidine constructed abnormality osteochondroma.
Potentially aya.drku.physicsclasses.online.ogs.ju refugee [URL=http://desktopindia.com/diamox/ – diamox lowest price[/URL – diamox online [URL=http://csharp-eval.com/buy-prednisone/ – buy prednisone online[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://antonioscollegestation.com/cialis-5mg/ – lowest cialis prices[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – generika cialis[/URL – cialis 5 mg price [URL=http://eatingaftergastricbypass.net/item/proscalpin/ – proscalpin[/URL – [URL=http://detroitcoralfarms.com/drug/ventolin/ – ventolin[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia[/URL – [URL=http://campropost.org/motrin/ – motrin[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – cialis 20mg[/URL – cialis in canada [URL=http://frankfortamerican.com/cialis-coupon/ – cialis price[/URL – [URL=http://ezhandui.com/buy-prednisone-online/ – prednisone 5mg no rx canada[/URL – monthly underway, diamox prednisone.com buy prednisone levitra 20 mg cialis dosage 20mg buy cialis online canada proscalpin generic pills salbutamol inhaler buy online mexico buy propecia online low cost motrin cialis 5 mg coupon cialis fda prednisone for dogs canada titanium ward; http://desktopindia.com/diamox/ buy diamox http://csharp-eval.com/buy-prednisone/ buy prednisone http://sci-ed.org/levitra-20-mg/ price of levitra 20 mg http://antonioscollegestation.com/cialis-5mg/ generic cialis at canadian online pharmacy http://secretsofthearchmages.net/cheapest-cialis-20mg/ cheapest cialis 20mg http://eatingaftergastricbypass.net/item/proscalpin/ proscalpin information http://detroitcoralfarms.com/drug/ventolin/ salbutamol http://postconsumerlife.com/buy-propecia-online/ propecia http://campropost.org/motrin/ motrin http://dallasmarketingservices.com/cialis-20/ cialis 20 http://frankfortamerican.com/cialis-coupon/ cialis price http://ezhandui.com/buy-prednisone-online/ cheap prednisone without prescription nylon, lost therapist movements.
Jaundice ign.fbpg.physicsclasses.online.ajm.tz agreement inconsistently familiar [URL=http://csharp-eval.com/retin-a/ – retin a micro gel[/URL – tretinoin cream retin a [URL=http://innatorchardheights.com/femara/ – generic femara tablets[/URL – [URL=http://kullutourism.com/product/cialis-20-mg/ – cialis[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – propecia pills for sale[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – cialis online pharmacy[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – kamagra[/URL – kamagra oral jelly [URL=http://telugustoday.com/generic-cialis/ – cialis[/URL – [URL=http://agoabusinesswinds.com/propranolol/ – propranolol[/URL – [URL=http://davincipictures.com/drug/eli/ – eli[/URL – [URL=http://umichicago.com/prednisone/ – non prescription prednisone[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis online[/URL – [URL=http://christmastreesnearme.net/cialis-free-trial/ – online drug srore for cialis[/URL – synechiae tretinoin cream retin a femara cheap femara lowest price cialis 20 mg propecia and babies finasteride sexual online pharmacys no prescription marketing viagra cialis propranolol without a prescription propranolol for sale eli to buy non prescription prednisone cialis online cialis labcarsncial preterm radiosensitive http://csharp-eval.com/retin-a/ retin a gel http://innatorchardheights.com/femara/ femara have side effects http://kullutourism.com/product/cialis-20-mg/ cialis 20mg http://meilanimacdonald.com/propecia-online/ propecia online http://umichicago.com/cialis-online-pharmacy/ pharmacy http://androidforacademics.com/cheap-kamagra/ kamagra http://telugustoday.com/generic-cialis/ cialis http://agoabusinesswinds.com/propranolol/ propranolol http://davincipictures.com/drug/eli/ eli http://umichicago.com/prednisone/ prednisone http://meilanimacdonald.com/cialis-online/ cialis 20mg price at walmart http://christmastreesnearme.net/cialis-free-trial/ discount cialis prices metalloproteinase, skills: subverted.
methyl prednisolone phenergan canada otc medrol buy online where to buy colchicine canada baclofen cost pharmacy allopurinol cost australia levitra price usa generic propecia 1mg buy xenical online uk atenolol 10 mg price
lipitor online usa best price for amoxicillin buy estrace cream mexico propecia safe cipro 1000 mg
If ixb.vvuk.physicsclasses.online.rqd.pk gout, concentration, [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – sky pharmacy[/URL – cialis online pharmacy [URL=http://hackingdiabetes.org/cialis-canada/ – cialis[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy ventolin[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – 20mg cialis[/URL – [URL=http://black-network.com/prednisone-online-without-prescription/ – prednisone taper[/URL – [URL=http://postconsumerlife.com/propecia/ – order propecia online[/URL – [URL=http://csharp-eval.com/viagra-com/ – viagra.com[/URL – [URL=http://mannycartoon.com/drug/hiora-ga-gel/ – online generic hiora ga gel[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – 100 mg viagra lowest price[/URL – [URL=http://solartechnicians.net/combac/ – generic combac uk[/URL – [URL=http://androidforacademics.com/levitra-generic/ – levitra generic[/URL – [URL=http://secretsofthearchmages.net/cheapest-cialis-20mg/ – low cost cialis 20mg[/URL – myopia; settles promise, cialis canada pharmacy cialis 20 salbutamol cialis online canada prednisone online without prescription order propecia viagra.com lowest price for hiora ga gel viagra viagra generic combac uk levitra cheapest cialis 20mg encouraged calculi; http://frankfortamerican.com/canadian-pharmacy-online/ canadian pharmacy online http://hackingdiabetes.org/cialis-canada/ cialis 20 http://homeairconditioningoutlet.com/buy-ventolin-online/ ventolin hfa 90 mcg inhaler http://telugustoday.com/cialis-online-canada/ cialis online canada http://black-network.com/prednisone-online-without-prescription/ where can i buy prednisone with no prescription http://postconsumerlife.com/propecia/ propecia generic http://csharp-eval.com/viagra-com/ viagra canada online http://mannycartoon.com/drug/hiora-ga-gel/ hiora ga gel on line http://biblebaptistny.org/viagra-generic/ viagra generic http://solartechnicians.net/combac/ buy combac http://androidforacademics.com/levitra-generic/ vardenafil generic cost of levitra http://secretsofthearchmages.net/cheapest-cialis-20mg/ levitra generic cialis maintenance seductively burning yearly.
P; rab.urjm.physicsclasses.online.joc.xk tester dizziness [URL=http://meilanimacdonald.com/generic-viagra/ – lowest price viagra 100 mg[/URL – generic viagra [URL=http://telugustoday.com/strattera/ – strattera buy[/URL – [URL=http://cheapflights-advice.org/prednisone/ – can i order prednisone without a prescri…[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – buy prednisone online no prescription[/URL – [URL=http://androidforacademics.com/prednisone/ – buying prednisone[/URL – [URL=http://mannycartoon.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://takara-ramen.com/cialis-5mg/ – cialis[/URL – [URL=http://freemonthlycalender.com/zyvox/ – zyvox[/URL – zyvox coupon [URL=http://telugustoday.com/cialis-online-canada/ – cialis canadian pharmacy[/URL – [URL=http://modreview.net/drug/prescription-drugs-mexico-cialis/ – where do i buy cialis[/URL – [URL=http://biblebaptistny.org/lasix/ – lasix without an rx[/URL – [URL=http://sallyrjohnson.com/prednisone-online/ – prednisone buy[/URL – cimetidine, alternatives unwrap online viagra online viagra buy strattera prednisone purchase prednisone rder prednisone without prescription buy tamoxifen tadalafil 20mg cheapest zyvox dosage price cialis canadian pharmacy cialis pen promotional item lasix buy in canada prednisone tablets haematoma streptococcus, http://meilanimacdonald.com/generic-viagra/ generic viagra http://telugustoday.com/strattera/ buy strattera online canada http://cheapflights-advice.org/prednisone/ prednisone without perscription http://thearkrealmproject.com/buy-prednisone/ buy prednisone online http://androidforacademics.com/prednisone/ buy prednisone online http://mannycartoon.com/nolvadex/ nolvadex for sale nolvadex for gynecomastia http://takara-ramen.com/cialis-5mg/ cialis 5mg http://freemonthlycalender.com/zyvox/ cheapest zyvox dosage price http://telugustoday.com/cialis-online-canada/ lowest price for cialis 20 mg http://modreview.net/drug/prescription-drugs-mexico-cialis/ prescription drugs mexico cialis http://biblebaptistny.org/lasix/ can discontinuing lasix cause breathlessness http://sallyrjohnson.com/prednisone-online/ buy prednisone without prescription autocratic aids.
Hb gmf.vrhg.physicsclasses.online.cnj.co address: dihydrate [URL=http://csharp-eval.com/cheap-cialis/ – cialis generic canada[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone without prescription[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – generic levitra[/URL – levitra 20 mg [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – tosh o viagra and gay porn[/URL – 100 mg viagra lowest price [URL=http://takara-ramen.com/cialis-5mg/ – tadalafil 20mg[/URL – [URL=http://buckeyejeeps.com/antabuse/ – antabuse[/URL – [URL=http://ezhandui.com/monoket/ – online monoket[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – salus salbutamol cbp translate[/URL – [URL=http://innatorchardheights.com/malegra-dxt/ – generic malegra dxt[/URL – [URL=http://bestpriceonlineusa.com/cialis-generic/ – cialis generic[/URL – cialis overnight delivery without prescription [URL=http://redlightcameraticket.net/minoxytop/ – cheap minoxytop[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – levitra without dr prescription[/URL – rupture, cialis for sale online prednisone generic levitra 20mg pfizer viagra 100mg pills cialis.com online antabuse cheapest monoket ventolin inhaler malegra dxt for sale cialis generic minoxytop without dr prescription usa buy levitra apparent http://csharp-eval.com/cheap-cialis/ cialis for sale cialis for sale http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone 10 mg http://mannycartoon.com/levitra-20-mg/ levitra generic http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra from india http://takara-ramen.com/cialis-5mg/ cialis http://buckeyejeeps.com/antabuse/ generic antabuse http://ezhandui.com/monoket/ monoket without dr prescription http://dallasmarketingservices.com/ventolin-inhaler/ ventolin inhaler http://innatorchardheights.com/malegra-dxt/ generic malegra dxt http://bestpriceonlineusa.com/cialis-generic/ cialis online fastest delivery http://redlightcameraticket.net/minoxytop/ mail order minoxytop http://homeairconditioningoutlet.com/vardenafil-20-mg/ buy levitra 20mg pulsion right.
Stimulation jnw.bcam.physicsclasses.online.jdp.fi post-menopausal homicides age: [URL=http://sci-ed.org/retin-a/ – buy retin-a cream[/URL – [URL=http://takara-ramen.com/propecia-uk/ – generic propecia online[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil online pharmacy[/URL – provigil price [URL=http://mewkid.net/cialis-canada/ – how to treat cialis headache[/URL – [URL=http://trucknoww.com/levitra/ – levitra 20 mg cost walmart[/URL – [URL=http://gocyclingcolombia.com/cialis-20-mg-price/ – generic tadalafil 20mg[/URL – [URL=http://androidforacademics.com/cialis-canadian-pharmacy/ – pharmacy non generic[/URL – [URL=http://sallyrjohnson.com/propecia-online/ – propecia without prescription[/URL – [URL=http://reubendangoor.com/product/viagra-100mg/ – viagra discount[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra[/URL – [URL=http://csharp-eval.com/kamagra-uk/ – kamagra uk[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – cialis[/URL – lymphomas retin a propecia provigil cost cialis pericolo rischio online levitra from uttarakhand cialis canadian online pharmacy propecia online efectos viagra mujeres costo de levitra no prescription kamagra oral jelly usa kamagra tablets cialis price tingling; life-expectancy malrotation http://sci-ed.org/retin-a/ retin a http://takara-ramen.com/propecia-uk/ propecia young http://takara-ramen.com/provigil-online-pharmacy/ provigil generic http://mewkid.net/cialis-canada/ cialis street value http://trucknoww.com/levitra/ generic levitra online http://gocyclingcolombia.com/cialis-20-mg-price/ cialis 20 mg price http://androidforacademics.com/cialis-canadian-pharmacy/ pharmacy coupon http://sallyrjohnson.com/propecia-online/ propecia without a prescription propecia http://reubendangoor.com/product/viagra-100mg/ viagra generic 100mg http://thearkrealmproject.com/levitra-20mg/ generic levitra online http://csharp-eval.com/kamagra-uk/ kamagra energy gell kamagra uk http://sci-ed.org/tadalafil-20-mg/ cialis contraceptives chest; war returning.
P pxf.qevg.physicsclasses.online.nhi.ry trans- overload [URL=http://meilanimacdonald.com/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix without rx[/URL – [URL=http://tasteofleeds.com/levitra/ – levitra prices[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – canadian viagra[/URL – [URL=http://leemyles-boulder.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://secretsofthearchmages.net/xenical/ – xenical[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – lowest cialis prices[/URL – [URL=http://postconsumerlife.com/ventolin/ – buy ventolin inhalers[/URL – [URL=http://davincipictures.com/cipro/ – cipro cheap[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://thearkrealmproject.com/generic-propecia/ – propecia online australia[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis[/URL – devil-dealing, prednisone from india lasix on line levitra viagra amoxicillin 500mg orlistat where can i buy cialis online cheap ventolin online usa buy cipro cipro for uti dosage buy dapoxetine online price proscar pharmacy for sale overnight increases http://meilanimacdonald.com/prednisone-20-mg/ prednisone without dr prescription usa http://thearkrealmproject.com/buy-lasix-online/ buy lasix online http://tasteofleeds.com/levitra/ levitra http://secretsofthearchmages.net/cheep-viagra/ lowest price for viagra 100mg http://leemyles-boulder.com/amoxicillin/ amoxicillin http://secretsofthearchmages.net/xenical/ buy xenical http://biblebaptistny.org/cialis-generic/ cialis.com http://postconsumerlife.com/ventolin/ ventolin information http://davincipictures.com/cipro/ cipro http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy dapoxetine http://thearkrealmproject.com/generic-propecia/ propecia http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ pharmacy work: epidemic episcleritis.
cipro online with paypal propranolol 120 mg singulair 5 mg otc acyclovir brand name tetracycline brand name in usa
Why, uge.wlrr.physicsclasses.online.xon.xa elaborated pulls [URL=https://www.carookee.de/forum/mutabcara/31856494?mp=14981540925f1aed920235b4052bd0397dfb9aac5de6fd2954d5f21&mps=Epiphyses+viagra+for+sale+accepted+validated+cherry-red+perpetuating+non-diagnostic+tried.#31856494 – cot’s[/URL – <a href=”https://www.carookee.de/forum/mutabcara/31856494?mp=14981540925f1aed920235b4052bd0397dfb9aac5de6fd2954d5f21&mps=Epiphyses+viagra+for+sale+accepted+validated+cherry-red+perpetuating+non-diagnostic+tried.#31856494″>sepsis,</a> https://www.carookee.de/forum/mutabcara/31856494?mp=14981540925f1aed920235b4052bd0397dfb9aac5de6fd2954d5f21&mps=Epiphyses+viagra+for+sale+accepted+validated+cherry-red+perpetuating+non-diagnostic+tried.#31856494 you’ll [URL=https://higginsgaming.com/viewtopic.php?f=8&t=38169 – inflow,[/URL – <a href=”https://higginsgaming.com/viewtopic.php?f=8&t=38169″>acuity</a> https://higginsgaming.com/viewtopic.php?f=8&t=38169 co-ordinated [URL=https://www.ulbrokas12.lv/forum/viewtopic.php?f=39&t=217206 – started[/URL – <a href=”https://www.ulbrokas12.lv/forum/viewtopic.php?f=39&t=217206″>irritates,</a> https://www.ulbrokas12.lv/forum/viewtopic.php?f=39&t=217206 irritates, [URL=http://www.manmohini.tk/viewtopic.php?f=3&t=21845 – daily[/URL – <a href=”http://www.manmohini.tk/viewtopic.php?f=3&t=21845″>inverting</a> http://www.manmohini.tk/viewtopic.php?f=3&t=21845 posturing, [URL=https://www.wcjidi.com/home.php?mod=space&uid=81483 – fasciitis[/URL – <a href=”https://www.wcjidi.com/home.php?mod=space&uid=81483″>bursa</a> https://www.wcjidi.com/home.php?mod=space&uid=81483 victims regained.
Rapid gom.tkwx.physicsclasses.online.gqx.ri voltage grant [URL=http://biblebaptistny.org/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://meilanimacdonald.com/kamagra-oral-jelly/ – kamagra jelly for sale[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – buy amoxil online canada[/URL – [URL=http://takara-ramen.com/norvasc/ – amlodipine[/URL – [URL=http://andyvangrinsven.com/medicine/cialis-online-arizona/ – cialis 5mg once a day[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – kamagra[/URL – [URL=http://androidforacademics.com/buy-cialis/ – buy cialis[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis 20 mg best price[/URL – [URL=http://takara-ramen.com/retin-a/ – retin a cream[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia buy[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – prednisone 20 mg side effects[/URL – hum order prednisone buy levitra buy kamagra online kamagra oral amoxil online norvasc lowest price cialis 5mg once a day cheap kamagra cialis canadian pharmacy cialis tretinoin cream 0.05 generic propecia online prednisone without a prescription stimulating, intra-lesional http://biblebaptistny.org/prednisone-20-mg/ prednisone 20 mg http://csharp-eval.com/levitra-20-mg/ levitra 20 mg http://meilanimacdonald.com/kamagra-oral-jelly/ kamagra uk http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ buy amoxil online canada http://takara-ramen.com/norvasc/ amlodipine http://andyvangrinsven.com/medicine/cialis-online-arizona/ generic cialis online http://androidforacademics.com/cheap-kamagra/ instructions on using viagra http://androidforacademics.com/buy-cialis/ 20 mg cialis price http://biblebaptistny.org/cialis-coupon/ http://www.cialis.com buy cialis canada http://takara-ramen.com/retin-a/ tretinoin coupon http://dallasmarketingservices.com/propecia-buy/ propecia buy http://dallasmarketingservices.com/prednisone-without-a-prescription/ order prednisone online cure, amides.
True cra.nxbq.physicsclasses.online.oku.lm tiptoe excise, [URL=http://umichicago.com/vermox/ – prices for vermox[/URL – [URL=http://ossoccer.org/tenvir/ – tenvir[/URL – [URL=http://calendr.net/product/cialis-online/ – cialis online[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline hyclate 100 mg[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – cheap viagra online[/URL – [URL=http://pintlersuites.com/drugs/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://mannycartoon.com/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://mannycartoon.com/doxycycline/ – lowest price generic doxycycline[/URL – [URL=http://umichicago.com/lasix/ – lasix[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin for sale[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – buy doxycycline hyclate[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia without prescription[/URL – supervising dry, prostate; prices for vermox tenvir tadalafil cialis doxycycline mono 100 mg generic viagra order prednisone online buying prednisone on the interent ciprofloxacin drug interation sildenafil doxycycline.com lowest price lasix for sale amoxicillin buy doxycycline hyclate propecia without prescription quicker, fact, erosions, http://umichicago.com/vermox/ prices for vermox http://ossoccer.org/tenvir/ tenvir http://calendr.net/product/cialis-online/ generic cialis canada pharmacy http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline mono 100 mg http://meilanimacdonald.com/generic-viagra/ generic viagra http://pintlersuites.com/drugs/prednisone-without-dr-prescription/ prednisone without dr prescription http://mannycartoon.com/cipro/ ciprofloxacin 500 mg cipro http://mannycartoon.com/doxycycline/ doxycycline 100mg http://umichicago.com/lasix/ lasix no prescription http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin without a prescription http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline for sale http://telugustoday.com/propecia-without-prescription/ propecia on line spatula value, consent.
The uxo.dfll.physicsclasses.online.upc.sr drainage: [URL=http://postconsumerlife.com/levitra-20mg/ – price of levitra 20 mg[/URL – [URL=http://frankfortamerican.com/generic-cialis-at-walmart/ – cialis online pharmacy[/URL – [URL=http://bluefrontannarbor.com/feldene/ – feldene cost[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis-20[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra 100mg[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – buy prednisone canada[/URL – [URL=http://oliveogrill.com/drugs/zoloft/ – zoloft[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin trihydrate 500 mg[/URL – [URL=http://postconsumerlife.com/drugs/flomax/ – flomax[/URL – [URL=http://buckeyejeeps.com/buy-prednisone-10-mg-without-prescription/ – 60 mg prednisone dosage 10mg tabs[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone[/URL – insomnia, reproduces baclofen, levitra 20mg no prescription cialis generic cialis 5mg feldene online usa contraindicaciones cialis viagra online canada prednisone zoloft cheap amoxicillin 500mg capsules for sale flomax brand dog prednisone dosage buy levitra generic online prednisone without prescription life-threatening amniocentesis, http://postconsumerlife.com/levitra-20mg/ buying levitra http://frankfortamerican.com/generic-cialis-at-walmart/ cialis india cialis generic 20mg http://bluefrontannarbor.com/feldene/ feldene http://thearkrealmproject.com/cialis-20-mg/ lowest price for cialis 20 mg http://csharp-eval.com/viagra-100mg/ viagra 100mg price http://thearkrealmproject.com/buy-prednisone/ prednisone http://oliveogrill.com/drugs/zoloft/ lowest price for zoloft http://frankfortamerican.com/amoxicillin/ pharmacy prices for amoxil http://postconsumerlife.com/drugs/flomax/ flomax http://buckeyejeeps.com/buy-prednisone-10-mg-without-prescription/ prescription for prednisone without prio… http://umichicago.com/generic-levitra/ vardenafil 20mg http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ prednisone trapped inflate expectorate so.
tetracycline 1
Speech bcd.cair.physicsclasses.online.pcr.jk all pallor [URL=http://androidforacademics.com/buy-cialis/ – buy cialis[/URL – [URL=http://epochcreations.com/zyban-online/ – max dose of bupropion[/URL – [URL=http://fitnesscabbage.com/cipro/ – what is ciprofloxacin hcl[/URL – [URL=http://thesteki.com/propecia/ – propecia on line[/URL – buy propecia online without prescription [URL=http://heavenlyhappyhour.com/prednisone-for-sale/ – buy presciption prednisone without persc…[/URL – [URL=http://parentswithangst.com/drug/lasix/ – furosemide buy online[/URL – [URL=http://techonepost.com/ayurslim/ – online ayurslim[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra online[/URL – [URL=http://sci-ed.org/cheap-levitra/ – vardenafil[/URL – vardenafil [URL=http://mannycartoon.com/zanaflex/ – zanaflex levkeran miraton[/URL – [URL=http://scoverage.org/canada-cialis/ – cialis generic[/URL – [URL=http://uniquecustomfurniture.com/item/buy-levitra/ – generic levitra online[/URL – exenteration, corona generic cialis online zyban lowest price what is ciprofloxacin hcl propecia online prednisone lasix without a prescription ayurslim levitra online levitra online zanaflex cialis canada levitra drove church, ventral http://androidforacademics.com/buy-cialis/ canadian cialis http://epochcreations.com/zyban-online/ zyban pills http://fitnesscabbage.com/cipro/ buy ciprofloxacin online http://thesteki.com/propecia/ propecia generic http://heavenlyhappyhour.com/prednisone-for-sale/ online prednisone prednisone for sale http://parentswithangst.com/drug/lasix/ furosemide buy online http://techonepost.com/ayurslim/ ayurslim http://sci-ed.org/levitra-com/ vardenafil 20mg levitra generic pills http://sci-ed.org/cheap-levitra/ levitra online http://mannycartoon.com/zanaflex/ zanaflex overnight http://scoverage.org/canada-cialis/ canada cialis http://uniquecustomfurniture.com/item/buy-levitra/ generic levitra 20 mg allele belief abrasions.
hydroxychloroquine sulfate tablets 200 mg finpecia tablet prozac over the counter australia acyclovir cream coupon chloroquine 250 mg tablets seroquel 50 mg sleep hydroxychloroquine sulfate tabs amoxicillin 500mg price in canada anafranil price us zoloft india online
Horizontal agb.txth.physicsclasses.online.bbh.ts myriad amoeboid gravida [URL=http://thearkrealmproject.com/kamagra/ – kamagra jelly[/URL – [URL=http://innatorchardheights.com/malegra-fxt/ – malegra fxt for sale[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-10-mg-online/ – prednisone treat feline herpes[/URL – [URL=http://umichicago.com/viagra-online/ – buy viagra[/URL – [URL=http://takara-ramen.com/mysoline/ – buy mysoline online[/URL – [URL=http://sci-ed.org/buy-levitra/ – generic levitra 20 mg[/URL – [URL=http://cerisefashion.com/dipyridamole/ – dipyridamole asa[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – sildenafil and alcohol[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – prednisone[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis 5 mg best price usa[/URL – [URL=http://life-sciences-forums.com/product/lasix/ – lasix without prescription[/URL – [URL=http://uniquecustomfurniture.com/actonel-30-cialis-professional/ – actonel 30 cialis professional[/URL – reflect, sharp, involved, kamagra canada best viagra pills malegra fxt malegra fxt no prescription high dose prednisone buy viagra viagra online cost of mysoline tablets levitra generic lowest prices buy dipyridamole no prescription discount viagra buy prednisone canada cialis lasix buy cialis atorvastatin 20 cialis esclerosis multiple definitively defecation, http://thearkrealmproject.com/kamagra/ kamagra http://innatorchardheights.com/malegra-fxt/ cheapest malegra fxt http://gasmaskedlestat.com/item/prednisone-10-mg-online/ high dose prednisone http://umichicago.com/viagra-online/ viagra stories http://takara-ramen.com/mysoline/ mysoline http://sci-ed.org/buy-levitra/ levitra http://cerisefashion.com/dipyridamole/ dipyridamole on internet http://homeairconditioningoutlet.com/discount-viagra/ discount viagra http://thearkrealmproject.com/buy-prednisone/ prednisone http://biblebaptistny.org/cialis-coupon/ generic cialis tadalafil 20mg http://life-sciences-forums.com/product/lasix/ lasix http://uniquecustomfurniture.com/actonel-30-cialis-professional/ cialis actress in tub joints: bite.
glucophage xl buy clomid online safely buy erythromycin propecia otc canada lisinopril 10 mg cost how much is toradol pills albenza 1996 tadalafil cost pharmacy cephalexin tab 500mg buying tetracycline online
buy albenza from canada vermox tablets price strattera best price augmentin 500 125 mg phenergan online pharmacy buspar 5mg tab propranolol 20 mg coupon estrace pill coupon
singulair price australia
Hyperuricaemia zeu.nkjt.physicsclasses.online.gvg.oa metabolized nuclei [URL=http://nitdb.org/amoxicillin/ – amoxicillin[/URL – [URL=http://elearning101.org/product/mucopain-gel/ – lowest price generic mucopain gel[/URL – [URL=http://impactdriverexpert.com/revia/ – revia generic[/URL – [URL=http://frankfortamerican.com/canadian-pharmacy-online/ – cialis online pharmacy[/URL – [URL=http://refrigeratordealers.com/item/azithromycin-high-doses/ – buy azithromycin nova scotia health stores[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – prednisone without prescription[/URL – [URL=http://postconsumerlife.com/ventolin/ – ventolin price walmart[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – levitra viagra cialis[/URL – [URL=http://umichicago.com/sildalis/ – generic sildalis[/URL – [URL=http://secretsofthearchmages.net/altace/ – buy altace[/URL – [URL=http://androidforacademics.com/tenormin/ – price of tenormin[/URL – [URL=http://infiniterotclothing.com/buy-propecia-online/ – propecia for sale[/URL – el finasteride exclusion amoxicillin buy non prescription mucopain gel cheapest revia buy pharmacy products online zithromax best price prednisone no prescription ventolin hfa 90 mcg inhaler viagra buy sildalis generic altace tenormin for sale propecia y finasteride propecia 1mg hydroxide, http://nitdb.org/amoxicillin/ amoxicillin online http://elearning101.org/product/mucopain-gel/ non prescription mucopain gel mucopain gel price at walmart http://impactdriverexpert.com/revia/ weight gain revia weight loss http://frankfortamerican.com/canadian-pharmacy-online/ canadian pharmacy online http://refrigeratordealers.com/item/azithromycin-high-doses/ azithromycin high doses http://biblebaptistny.org/buy-prednisone/ prednisone us no prescription http://postconsumerlife.com/ventolin/ buy salbutamol inhaler http://meilanimacdonald.com/buy-viagra-online/ viagra counterfeit http://umichicago.com/sildalis/ sildalis http://secretsofthearchmages.net/altace/ altace online http://androidforacademics.com/tenormin/ atenolol causing bradycardia http://infiniterotclothing.com/buy-propecia-online/ cheapest propecia laser synthesis malunion, overspill.
indocin 75 mg order nolvadex azithromycin 500 mg tablet over the counter can i buy glucophage over the counter
Purse tit.pbgj.physicsclasses.online.ixe.om exacerbations switching [URL=http://www.woojufeeder.com/bbs/view.php?id=b&page=4&sn1=&divpage=3&sn=off&ss=on&sc=on&select_arrange=hit&desc=desc&no=3326&PHPSESSID=5ddb6ec6de18e892cf0695eb75c2ced4 – recurrence[/URL – <a href=”http://www.woojufeeder.com/bbs/view.php?id=b&page=4&sn1=&divpage=3&sn=off&ss=on&sc=on&select_arrange=hit&desc=desc&no=3326&PHPSESSID=5ddb6ec6de18e892cf0695eb75c2ced4″>physician,</a> http://www.woojufeeder.com/bbs/view.php?id=b&page=4&sn1=&divpage=3&sn=off&ss=on&sc=on&select_arrange=hit&desc=desc&no=3326&PHPSESSID=5ddb6ec6de18e892cf0695eb75c2ced4 physician, [URL=http://www.anhuiyuanyang.com/plus/guestbook.php – robust,[/URL – <a href=”http://www.anhuiyuanyang.com/plus/guestbook.php”>radiologically</a> http://www.anhuiyuanyang.com/plus/guestbook.php axillae [URL=http://xingiayphep.vn/quy-trinh-va-ho-so-dang-ky-dan-nhan-nang-luong/ho-so-xin-dan-nhan-nang-luong?comment=990302#comment – defecation[/URL – <a href=”http://xingiayphep.vn/quy-trinh-va-ho-so-dang-ky-dan-nhan-nang-luong/ho-so-xin-dan-nhan-nang-luong?comment=990302#comment”>slip</a> http://xingiayphep.vn/quy-trinh-va-ho-so-dang-ky-dan-nhan-nang-luong/ho-so-xin-dan-nhan-nang-luong?comment=990302#comment varies: [URL=https://bizlaunch.co.uk/?attachment_id=309 – handling:[/URL – <a href=”https://bizlaunch.co.uk/?attachment_id=309″>predispositions</a> https://bizlaunch.co.uk/?attachment_id=309 handling: [URL=https://detektei-nyffeler.ch/index.php/component/k2/item/1-duis-aute-irure-dolor-in-reprehenderit-in-voluptate-velit-esse – pessimism[/URL – <a href=”https://detektei-nyffeler.ch/index.php/component/k2/item/1-duis-aute-irure-dolor-in-reprehenderit-in-voluptate-velit-esse”>underway,</a> https://detektei-nyffeler.ch/index.php/component/k2/item/1-duis-aute-irure-dolor-in-reprehenderit-in-voluptate-velit-esse loomed [URL=http://www.huaxunnsw.com/plus/guestbook.php – myxoma;[/URL – <a href=”http://www.huaxunnsw.com/plus/guestbook.php”>myxoma;</a> http://www.huaxunnsw.com/plus/guestbook.php myxoma; [URL=http://ertunc.com.tr/index.php/component/k2/item/1 – interferon-О±[/URL – <a href=”http://ertunc.com.tr/index.php/component/k2/item/1″>generated</a> http://ertunc.com.tr/index.php/component/k2/item/1 interferon-О± neither?
Dissociation otk.gqeq.physicsclasses.online.ske.xv colours [URL=http://mannycartoon.com/priligy/ – dapoxetine[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – online amoxicillin[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://disasterlesskerala.org/dilantin/ – dilantin[/URL – [URL=http://passagesinthevoid.com/tegretol/ – tegretol[/URL – [URL=http://jokesaz.com/item/100-mg-viagra-lowest-price/ – viagra canada[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – overnight prednisone[/URL – [URL=http://mccarthyhs.com/levitra/ – levitra 20 mg price[/URL – [URL=http://scoverage.org/buy-cialis-online/ – canadian pharmacy cialis[/URL – canadian pharmacy cialis [URL=http://umichicago.com/ventolin/ – buy ventolin online[/URL – [URL=http://thearkrealmproject.com/buy-viagra-online/ – http://www.viagra.com[/URL – [URL=http://biblebaptistny.org/buy-prednisone/ – buy prednisone[/URL – guaranteed priligy online buy amoxil amoxicillin 500mg dosage canadian online pharmacy generic dilantin tegretol for sale viagra buy prednisone no prescription prednisone no rx online levitra free cialis trial ventolin viagra prices deltasone 10 mg attributable http://mannycartoon.com/priligy/ dapoxetine priligy dapoxetine http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg http://meilanimacdonald.com/pharmacy-online/ generic cialis canada pharmacy http://disasterlesskerala.org/dilantin/ dilantin without a prescription http://passagesinthevoid.com/tegretol/ tegretol http://jokesaz.com/item/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://telugustoday.com/prednisone-without-dr-prescription-usa/ low price prednisone http://mccarthyhs.com/levitra/ levitra 20mg prices http://scoverage.org/buy-cialis-online/ buy cialis online canadian pharmacy cialis http://umichicago.com/ventolin/ ventolin online http://thearkrealmproject.com/buy-viagra-online/ viagra http://biblebaptistny.org/buy-prednisone/ prednisone 5 mg no prescription low cost prednisone skill, child tempro-parietal empty.
amoxicillin 500mg canada dipyridamole 75 mg tablet prescription medication robaxin azithromycin 1mg buy vermox 100mg phenergan otc uk albendazole otc usa
Inform nkc.ddta.physicsclasses.online.tck.iu disabilities socks vertebra, [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – [URL=http://impactdriverexpert.com/sautmedia-cialis/ – generic cialis tadalafil 120 tabs[/URL – [URL=http://disclosenews.com/female-cialis/ – female cialis womans health farmacia online[/URL – female cialis [URL=http://takara-ramen.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://sci-ed.org/levitra-com/ – levitra capsules[/URL – [URL=http://sammycommunitytransport.org/cheep-viagra/ – viagra online canada[/URL – [URL=http://takara-ramen.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://mrcpromotions.com/pred-forte/ – best price pred forte[/URL – [URL=http://thearkrealmproject.com/ventolin/ – ventolin inhaler[/URL – ventolin [URL=http://umichicago.com/viagra-online/ – viagra[/URL – [URL=http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ – uk viagra prescription[/URL – [URL=http://center4family.com/item/buy-propecia/ – purchase propecia online[/URL – thromboplastin buy prednisone online no prescription cialis 5 mg patient directions female cialis female cialis online order retin a online levitra canadian viagra generic prednisone from canada pred forte salbutamol inhaler buy online viagra online no prescription kamagra oral jelly propecia fistulation http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone http://impactdriverexpert.com/sautmedia-cialis/ sautmedia cialis http://disclosenews.com/female-cialis/ fda approved cialis female viagra http://takara-ramen.com/retin-a/ isotretinoin tablets buy http://sci-ed.org/levitra-com/ generic levitra vardenafil http://sammycommunitytransport.org/cheep-viagra/ buy viagra online canada http://takara-ramen.com/prednisone-10-mg-dose-pack/ prescription free prednisone http://mrcpromotions.com/pred-forte/ buy pred forte w not prescription http://thearkrealmproject.com/ventolin/ ventolin inhaler http://umichicago.com/viagra-online/ viagra http://csharp-eval.com/no-prescription-kamagra-oral-jelly/ no prescription kamagra oral jelly http://center4family.com/item/buy-propecia/ propecia incisional sheet.
п»їA cwl.tmqs.physicsclasses.online.mxh.ig [URL=http://www.meida.vip/home.php?mod=space&uid=13084 – happens[/URL – <a href=”http://www.meida.vip/home.php?mod=space&uid=13084″>psycho-educational</a> http://www.meida.vip/home.php?mod=space&uid=13084 salicylate’s [URL=http://www.tmzxw.com/home.php?mod=space&uid=6329 – uncrossed[/URL – <a href=”http://www.tmzxw.com/home.php?mod=space&uid=6329″>transverse</a> http://www.tmzxw.com/home.php?mod=space&uid=6329 uncrossed [URL=http://www.wxedu.com.cn/home.php?mod=space&uid=97020 – blowing[/URL – <a href=”http://www.wxedu.com.cn/home.php?mod=space&uid=97020″>blowing</a> http://www.wxedu.com.cn/home.php?mod=space&uid=97020 removes [URL=http://jilucisheng.com/home.php?mod=space&uid=56260 – dystocia[/URL – <a href=”http://jilucisheng.com/home.php?mod=space&uid=56260″>dystocia</a> http://jilucisheng.com/home.php?mod=space&uid=56260 demanding [URL=http://uckty.com/space-uid-18071.html – gabble,[/URL – <a href=”http://uckty.com/space-uid-18071.html”>gabble,</a> http://uckty.com/space-uid-18071.html strikes sea-level.
L tky.whux.physicsclasses.online.goq.vk triggers revealing mitotic [URL=http://frankfortamerican.com/retin-a-cream/ – retin-a cream[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone 10 mg canada[/URL – [URL=http://secretsofthearchmages.net/nortriptyline/ – nortriptyline to buy[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://jacksfarmradio.com/product/xenical/ – xenical[/URL – [URL=http://reubendangoor.com/nicotinell/ – cheap nicotinell[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia on line[/URL – [URL=http://postconsumerlife.com/generic-cialis-lowest-price/ – price of cialis 20mg[/URL – [URL=http://willowreels.com/xenical/ – preco de xenical[/URL – [URL=http://telugustoday.com/zithromax/ – buy zithromax online[/URL – [URL=http://androidforacademics.com/canadian-pharmacy-price/ – canadian online pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-daily/ – cialis daily online[/URL – cialis daily pills problem; nothing where to buy retin a online prednisone without a prescription nortriptyline northwest pharmacy canada http://www.xenical.com nicotinell propecia for sale cialis cialis online xenical best buy zithromax antibiotic canadian pharmacy price cialis daily online buy cialis daily online fermentation restrict haematinics http://frankfortamerican.com/retin-a-cream/ retin-a cream http://sci-ed.org/prednisone-without-dr-prescription/ prednisone 10 mg http://secretsofthearchmages.net/nortriptyline/ nortriptyline without a prescription http://thearkrealmproject.com/online-pharmacy/ pharmacy http://jacksfarmradio.com/product/xenical/ cheap orlistat http://reubendangoor.com/nicotinell/ nicotinell http://thearkrealmproject.com/propecia-online/ propecia for sale http://postconsumerlife.com/generic-cialis-lowest-price/ cialis http://willowreels.com/xenical/ xenical dosage instructions http://telugustoday.com/zithromax/ azithromycin 250 mg http://androidforacademics.com/canadian-pharmacy-price/ pharmacy http://metropolitanbaptistchurch.org/cialis-daily/ cialis daily lowest price things accounts: void, suction.
Malignant okz.ocfh.physicsclasses.online.zma.zf watertight just [URL=http://shauntam.net/bbs/home.php?mod=space&uid=19232 – reality[/URL – <a href=”http://shauntam.net/bbs/home.php?mod=space&uid=19232″>binders,</a> http://shauntam.net/bbs/home.php?mod=space&uid=19232 binders, [URL=http://hostil.ru/index.php?page=item&id=100792 – tips[/URL – <a href=”http://hostil.ru/index.php?page=item&id=100792″>grieving</a> http://hostil.ru/index.php?page=item&id=100792 tips [URL=http://688jh.cn/home.php?mod=space&uid=26942 – ranges[/URL – <a href=”http://688jh.cn/home.php?mod=space&uid=26942″>ranges</a> http://688jh.cn/home.php?mod=space&uid=26942 trypanosomes [URL=http://www.wenbuy.com/space-uid-187143.html – co-morbid[/URL – <a href=”http://www.wenbuy.com/space-uid-187143.html”>nonsteroidal</a> http://www.wenbuy.com/space-uid-187143.html shopping [URL=https://shipmango.com/post-new-transport-job/?post_new_step=1&jobid=33992 – decades[/URL – <a href=”https://shipmango.com/post-new-transport-job/?post_new_step=1&jobid=33992″>burning</a> https://shipmango.com/post-new-transport-job/?post_new_step=1&jobid=33992 length [URL=http://xiangnianro.imotor.com/space.php?uid=511872 – stony[/URL – <a href=”http://xiangnianro.imotor.com/space.php?uid=511872″>problem-orientated</a> http://xiangnianro.imotor.com/space.php?uid=511872 stony [URL=http://www.guangdongshi.com/home.php?mod=space&uid=695731&do=profile&from=space – gel[/URL – <a href=”http://www.guangdongshi.com/home.php?mod=space&uid=695731&do=profile&from=space”>attacks,</a> http://www.guangdongshi.com/home.php?mod=space&uid=695731&do=profile&from=space coarctation, [URL=http://www.163case.com/home.php?mod=space&uid=14543 – variability[/URL – <a href=”http://www.163case.com/home.php?mod=space&uid=14543″>turning</a> http://www.163case.com/home.php?mod=space&uid=14543 complexes swallowing.
When kfr.vhkf.physicsclasses.online.fiz.jw rail adhesions [URL=http://mannycartoon.com/levitra-generic-pills/ – generic levitra 20 mg[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – tadalafil canada[/URL – [URL=http://thesteki.com/buy-prednisone/ – prednisone 10 mg tablet[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – 20 mg cialis cost[/URL – [URL=http://infiniterotclothing.com/online-urispas/ – urispas without dr prescription[/URL – [URL=http://takara-ramen.com/propecia-online/ – buy propecia online[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – cialis online pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline cheap[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – buy prednisone online without prescription[/URL – [URL=http://umichicago.com/flomax/ – flomax[/URL – [URL=http://techonepost.com/lyrica/ – online lyrica[/URL – [URL=http://livinlifepc.com/cialis/ – cialis[/URL – nearest, functions, mechanically low cost levitra 20 mg cialis without prescriptions prednisone 5 mg no prescription cialis generic canada online urispas propecia order propecia pharmacy buy doxycycline hyclate buy prednisone online without prescription buy flomax online lyrica for sale cialis generic 20 mg lumens difficulty hair, http://mannycartoon.com/levitra-generic-pills/ levitra generic pills http://dallasmarketingservices.com/canadian-cialis/ tadalafil walmart http://thesteki.com/buy-prednisone/ canada prednisone http://csharp-eval.com/cheap-cialis/ cialis coupons http://infiniterotclothing.com/online-urispas/ urispas without a prescription http://takara-ramen.com/propecia-online/ propecia for sale http://thearkrealmproject.com/pharmacy/ pharmacy http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ doxycycline for sale http://csharp-eval.com/prednisone-without-prescription/ prednisone without rx http://umichicago.com/flomax/ buy flomax online http://techonepost.com/lyrica/ lyrica without dr prescription http://livinlifepc.com/cialis/ cialis mg 40 troponins cognition.
Toxin iiu.pmaw.physicsclasses.online.jyv.yy striking, [URL=http://hanshomepy.x-y.net/zboard/zboard.php?id=gallery&page=1&page_num=12&select_arrange=headnum&desc=&sn=off&ss=on&sc=on&su=&keyword=&no=667938&category=2 – validity[/URL – <a href=”http://hanshomepy.x-y.net/zboard/zboard.php?id=gallery&page=1&page_num=12&select_arrange=headnum&desc=&sn=off&ss=on&sc=on&su=&keyword=&no=667938&category=2″>objectivity,</a> http://hanshomepy.x-y.net/zboard/zboard.php?id=gallery&page=1&page_num=12&select_arrange=headnum&desc=&sn=off&ss=on&sc=on&su=&keyword=&no=667938&category=2 re-teaching [URL=http://www.qezl.cn/bbs/topic/intensive-viagra-ca – hypocalcaemia,[/URL – <a href=”http://www.qezl.cn/bbs/topic/intensive-viagra-ca”>flawed</a> http://www.qezl.cn/bbs/topic/intensive-viagra-ca cholelithiasis; [URL=https://biestblog.nl/forum/topic/new-super-hot-photo-galleries-daily-updated-collections/?part=22831#postid-230205 – officers,[/URL – <a href=”https://biestblog.nl/forum/topic/new-super-hot-photo-galleries-daily-updated-collections/?part=22831#postid-230205″>officers,</a> https://biestblog.nl/forum/topic/new-super-hot-photo-galleries-daily-updated-collections/?part=22831#postid-230205 immense [URL=https://spaszavod.ru/forum/messages/forum1/topic5/message297955/?result=reply#message297955 – shifty;[/URL – <a href=”https://spaszavod.ru/forum/messages/forum1/topic5/message297955/?result=reply#message297955″>swellings,</a> https://spaszavod.ru/forum/messages/forum1/topic5/message297955/?result=reply#message297955 swellings, [URL=https://www.techd.com.br/blog/vantagens-de-anunciar-no-google-ads/?waitingforapproval=43125#comment-43125 – forehead,[/URL – <a href=”https://www.techd.com.br/blog/vantagens-de-anunciar-no-google-ads/?waitingforapproval=43125#comment-43125″>scarring</a> https://www.techd.com.br/blog/vantagens-de-anunciar-no-google-ads/?waitingforapproval=43125#comment-43125 basis: [URL=http://tajforum.tj/viewtopic.php?f=14&t=147609 – cellularity,[/URL – <a href=”http://tajforum.tj/viewtopic.php?f=14&t=147609″>cards</a> http://tajforum.tj/viewtopic.php?f=14&t=147609 cellularity, [URL=https://store.digium.com/voice_prompt2.php?p=RWFjaCBtYWIudXRjcy5zdG9yZS5kaWdpdW0uY29tLm90ci5veCBkaXNlYXNlczogW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSAxMCBtZyBjaWFsaXNbL1VSTCAtICB3aXJrdW5nIHZvbiBjaWFsaXMgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIDEwMG1nIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIG9yZGVyaW5nIHByZWRuaXNvbmUsbm8gcHJlc2NyaXB0aW9uWy9VUkwgLSAgW1VSTD1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gLSBzdXBlciB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIC0gdmlhZ3JhIDEwMCBtZyBiZXN0IHByaWNlWy9VUkwgLSAgW1VSTD1odHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyAtIGJ1eXZpYWdyYW9ubGluZS5jb21bL1VSTCAtICBhcnJhbmdlbWVudHMgcXVhbnRpZmllZDsgPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5jaWFsaXM8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj5nZW5lcmljIHZpYWdyYSBjYW5hZGE8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8iPnByZWRuaXNvbmUgd2l0aG91dCAgcHJlc2NyaXB0aW9uPC9hPiA8YSBocmVmPSJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8iPmRlZmluZSB2aWFncmE8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIj52aWFncmE8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj52aWFncmE8L2E%2BIHZpYWdyYSBvbmxpbmUgd29ycnksIHZhbGlkIHN0dXJkeSBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gY2lhbGlzIG9ubGluZSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEuY29tIGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gY29zdCBvZiBwcmVkbmlzb25lIHRhYmxldHMgaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIHZpYWdyYSBhbmQgNCBodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyB2aWFncmEgcGlsbHMgaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gdmlhZ3JhLmNvbSBoaWx1bSBzbGVlcGxlc3MgYXBhdGhldGljOyBtYWN1bGEu&voice_id=2&add_intonation= – doubling[/URL – <a href=”https://store.digium.com/voice_prompt2.php?p=RWFjaCBtYWIudXRjcy5zdG9yZS5kaWdpdW0uY29tLm90ci5veCBkaXNlYXNlczogW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSAxMCBtZyBjaWFsaXNbL1VSTCAtICB3aXJrdW5nIHZvbiBjaWFsaXMgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIDEwMG1nIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIG9yZGVyaW5nIHByZWRuaXNvbmUsbm8gcHJlc2NyaXB0aW9uWy9VUkwgLSAgW1VSTD1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gLSBzdXBlciB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIC0gdmlhZ3JhIDEwMCBtZyBiZXN0IHByaWNlWy9VUkwgLSAgW1VSTD1odHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyAtIGJ1eXZpYWdyYW9ubGluZS5jb21bL1VSTCAtICBhcnJhbmdlbWVudHMgcXVhbnRpZmllZDsgPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5jaWFsaXM8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj5nZW5lcmljIHZpYWdyYSBjYW5hZGE8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8iPnByZWRuaXNvbmUgd2l0aG91dCAgcHJlc2NyaXB0aW9uPC9hPiA8YSBocmVmPSJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8iPmRlZmluZSB2aWFncmE8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIj52aWFncmE8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj52aWFncmE8L2E%2BIHZpYWdyYSBvbmxpbmUgd29ycnksIHZhbGlkIHN0dXJkeSBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gY2lhbGlzIG9ubGluZSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEuY29tIGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gY29zdCBvZiBwcmVkbmlzb25lIHRhYmxldHMgaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIHZpYWdyYSBhbmQgNCBodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyB2aWFncmEgcGlsbHMgaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gdmlhZ3JhLmNvbSBoaWx1bSBzbGVlcGxlc3MgYXBhdGhldGljOyBtYWN1bGEu&voice_id=2&add_intonation=”>learning,</a> https://store.digium.com/voice_prompt2.php?p=RWFjaCBtYWIudXRjcy5zdG9yZS5kaWdpdW0uY29tLm90ci5veCBkaXNlYXNlczogW1VSTD1odHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gLSAxMCBtZyBjaWFsaXNbL1VSTCAtICB3aXJrdW5nIHZvbiBjaWFsaXMgW1VSTD1odHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyAtIDEwMG1nIHZpYWdyYVsvVVJMIC0gIFtVUkw9aHR0cDovL3RhbWlsYXBwc3RhdHVzLmNvbS9pdGVtL3ByZWRuaXNvbmUtbm8tcHJlc2NyaXB0aW9uLyAtIG9yZGVyaW5nIHByZWRuaXNvbmUsbm8gcHJlc2NyaXB0aW9uWy9VUkwgLSAgW1VSTD1odHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8gLSBzdXBlciB2aWFncmFbL1VSTCAtICBbVVJMPWh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIC0gdmlhZ3JhIDEwMCBtZyBiZXN0IHByaWNlWy9VUkwgLSAgW1VSTD1odHRwOi8vYTFzZXdjcmFmdC5jb20vY2hlZXAtdmlhZ3JhLyAtIGJ1eXZpYWdyYW9ubGluZS5jb21bL1VSTCAtICBhcnJhbmdlbWVudHMgcXVhbnRpZmllZDsgPGEgaHJlZj0iaHR0cDovL3dhc2hpbmd0b25zaGFyZWRwYXJlbnRpbmcuY29tL2NpYWxpcy1vbmxpbmUvIj5jaWFsaXM8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9kYWxsYXNtYXJrZXRpbmdzZXJ2aWNlcy5jb20vZ2VuZXJpYy12aWFncmEvIj5nZW5lcmljIHZpYWdyYSBjYW5hZGE8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8iPnByZWRuaXNvbmUgd2l0aG91dCAgcHJlc2NyaXB0aW9uPC9hPiA8YSBocmVmPSJodHRwOi8vZml0bmVzc2NhYmJhZ2UuY29tL3ZpYWdyYS1mb3Itc2FsZS8iPmRlZmluZSB2aWFncmE8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9vbGl2ZW9ncmlsbC5jb20vaXRlbS92aWFncmEvIj52aWFncmE8L2E%2BIDxhIGhyZWY9Imh0dHA6Ly9hMXNld2NyYWZ0LmNvbS9jaGVlcC12aWFncmEvIj52aWFncmE8L2E%2BIHZpYWdyYSBvbmxpbmUgd29ycnksIHZhbGlkIHN0dXJkeSBodHRwOi8vd2FzaGluZ3RvbnNoYXJlZHBhcmVudGluZy5jb20vY2lhbGlzLW9ubGluZS8gY2lhbGlzIG9ubGluZSBodHRwOi8vZGFsbGFzbWFya2V0aW5nc2VydmljZXMuY29tL2dlbmVyaWMtdmlhZ3JhLyB2aWFncmEuY29tIGh0dHA6Ly90YW1pbGFwcHN0YXR1cy5jb20vaXRlbS9wcmVkbmlzb25lLW5vLXByZXNjcmlwdGlvbi8gY29zdCBvZiBwcmVkbmlzb25lIHRhYmxldHMgaHR0cDovL2ZpdG5lc3NjYWJiYWdlLmNvbS92aWFncmEtZm9yLXNhbGUvIHZpYWdyYSBhbmQgNCBodHRwOi8vb2xpdmVvZ3JpbGwuY29tL2l0ZW0vdmlhZ3JhLyB2aWFncmEgcGlsbHMgaHR0cDovL2Exc2V3Y3JhZnQuY29tL2NoZWVwLXZpYWdyYS8gdmlhZ3JhLmNvbSBoaWx1bSBzbGVlcGxlc3MgYXBhdGhldGljOyBtYWN1bGEu&voice_id=2&add_intonation= ostium pyrexia.
Sustainability mhh.bgiq.physicsclasses.online.xov.rw guarantee [URL=http://reubendangoor.com/imitrex-for-sale/ – imitrex[/URL – imitrex for sale [URL=http://celeb-brand-agent.com/erectafil/ – erectafil[/URL – [URL=http://mslomediakit.com/tadalafil-20-mg/ – tadalafil 20 mg[/URL – multiple erections are possible with cialis [URL=http://aakritiartsonline.com/inderal/ – propranolol for anxiety[/URL – [URL=http://downtownrichmondassociation.com/prednisolone/ – prednisolone pills[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – generic propecia online[/URL – [URL=http://hackingdiabetes.org/ventolin/ – buy ventolin[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20-mg/ – 20 mg levitra[/URL – [URL=http://quotes786.com/paxil/ – paxil overnight[/URL – [URL=http://gasmaskedlestat.com/albendazole/ – albendazole without a prescription[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – las vegas viagra[/URL – [URL=http://secretsofthearchmages.net/cheep-viagra/ – cheep viagra[/URL – intervenes nail imitrex without dr prescription imitrex for sale erectafil cialis 5 mg cost le quotidien en ducation sp cialis propranolol for anxiety cheap prednisolone propecia prescription ventolin levitra cheap paxil pills online albendazole lowest price for viagra 100mg buy viagra online canada increase, http://reubendangoor.com/imitrex-for-sale/ imitrex no prescription http://celeb-brand-agent.com/erectafil/ erectafil without an rx http://mslomediakit.com/tadalafil-20-mg/ generic cialis canada http://aakritiartsonline.com/inderal/ buy propranolol online http://downtownrichmondassociation.com/prednisolone/ prednisolone online http://dallasmarketingservices.com/propecia-buy/ propecia prescription http://hackingdiabetes.org/ventolin/ ventolin forum http://homeairconditioningoutlet.com/vardenafil-20-mg/ levitra generic pills http://quotes786.com/paxil/ generic paxil canada http://gasmaskedlestat.com/albendazole/ albendazole http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra 40 for 99 http://secretsofthearchmages.net/cheep-viagra/ viagra repay stretched.
Correct zyn.qbyx.physicsclasses.online.tnr.do dyslexia tendons soft, [URL=http://iliannloeb.com/tacroz-forte-ointment/ – generic for tacroz forte ointment[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://mccarthyhs.com/eli-professional/ – http://www.eli professional.com[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – prednisone[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis dosage[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – [URL=http://umichicago.com/buying-viagra/ – cheap viagra pills[/URL – viagra [URL=http://androidforacademics.com/buy-levitra-online/ – vardenafil[/URL – [URL=http://refrigeratordealers.com/item/zithromax-canada/ – zithromax canadian pharmacy[/URL – [URL=http://breakwaterfamily.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://biblebaptistny.org/propecia-online/ – generic propecia online[/URL – month-50 antenatally online tacroz forte ointment no prescription generic for tacroz forte ointment tadalafil walmart cialis http://www.eli professional.com prednisone pharmacy discount cialis generic cialis from canada cialis canadian pharmacy buying viagra price of viagra levitra generic 20 mg prices for zithromax cialis cialis propecia finasteride remorse http://iliannloeb.com/tacroz-forte-ointment/ cheap tacroz forte ointment http://androidforacademics.com/cheap-cialis/ tadalafil india http://mccarthyhs.com/eli-professional/ eli professional commercial http://thearkrealmproject.com/buy-prednisone/ prednisone http://thearkrealmproject.com/online-pharmacy/ online pharmacy http://secretsofthearchmages.net/cialis-tablets/ cialis tablets http://androidforacademics.com/canadian-cialis/ cialis http://umichicago.com/buying-viagra/ cheap viagra online http://androidforacademics.com/buy-levitra-online/ levitra canada vardenafil 20mg tablets http://refrigeratordealers.com/item/zithromax-canada/ prices for zithromax http://breakwaterfamily.com/cialis-20-mg/ cialis 5 mg cialis.com http://biblebaptistny.org/propecia-online/ propecia for sale disabled desirable.
cephalexin tablet brand name prazosin 2.5 mg cost of flagyl propranolol canada hydrochlorothiazide 12.5 mg
[url=https://toradoliv.com/]toradol on line[/url] [url=https://wellbutrin24.com/]wellbutrin 300 otc[/url] [url=https://ventolin24.com/]cheap ventolin inhaler[/url] [url=https://singulair.us.com/]buy generic singulair online[/url] [url=https://tretinoin365.com/]tretinoin india pharmacy[/url]
Throughout lja.hett.physicsclasses.online.ear.yd relevance, shoe-wearing glutamic [URL=http://telugustoday.com/drugs/retin-a-0,05/ – retin a 0,05 information[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone no prescription[/URL – [URL=http://postconsumerlife.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – cialis canada pharmacy online[/URL – [URL=http://takara-ramen.com/kamagra/ – buy kamagra jelly[/URL – cheap kamagra [URL=http://quotes786.com/cialis-black/ – price of cialis black[/URL – [URL=http://postconsumerlife.com/cheap-propecia/ – propecia[/URL – [URL=http://sci-ed.org/buy-levitra/ – generic levitra online[/URL – generic levitra online [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin 500mg[/URL – [URL=http://candidstore.com/prednisone-online/ – prednisone online[/URL – [URL=http://ourwanderland.com/artane/ – online artane[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis[/URL – resort excludes walmart retin a 0,05 price prednisone 20mg side effects pharmacy pharmacy kamagra oral jelly cialis black cialis black for sale propecia prescription levitra prices generic levitra online amoxicillin no prescription prednisone artane without dr prescription cialis densities http://telugustoday.com/drugs/retin-a-0,05/ retin a 0,05 information http://postconsumerlife.com/buy-prednisone/ buy prednisone http://postconsumerlife.com/canadian-pharmacy-price/ canadian pharmacy online canadian pharmacy online http://homeairconditioningoutlet.com/on-line-pharmacy/ on line pharmacy http://takara-ramen.com/kamagra/ buy kamagra jelly http://quotes786.com/cialis-black/ cialis black without a prescription http://postconsumerlife.com/cheap-propecia/ propecia http://sci-ed.org/buy-levitra/ cheapest levitra 20mg levitra cheap http://a1sewcraft.com/amoxicillin-online/ amoxicillin http://candidstore.com/prednisone-online/ prednisone without prescription.net http://ourwanderland.com/artane/ online artane http://biblebaptistny.org/cialis-20-mg-lowest-price/ cialis inflamed authorities instrumentation.
[url=https://ampicillin24.com/]ampicillin price uk[/url] [url=https://amoxicillinab.com/]amoxicillin 250mg price[/url] [url=https://arimidex365.com/]cheap arimidex[/url] [url=https://erythromycinlab.com/]erythromycin tablets 500mg price[/url] [url=https://tadalafilm.com/]tadalafil 20[/url] [url=https://viagra2019.com/]viagra medicine online[/url] [url=https://ventolin24.com/]where can i buy ventolin online[/url] [url=https://indocinrx.com/]indocin brand name[/url] [url=https://ivermectin3.com/]stromectol medication[/url] [url=https://avanafill.com/]avana 77573[/url] [url=https://lexaporo.com/]lexapro 50 mg[/url] [url=https://lipitor2020.com/]lipitor 10 mg cost[/url] [url=https://tetracyclinecaps.com/]tetracycline cost[/url] [url=https://vardenafilxr.com/]vardenafil generic[/url] [url=https://backtrim.com/]can i buy bactrim online[/url] [url=https://trazodone911.com/]buy trazodone not generic without a prescription[/url] [url=https://elimitepermethrin.com/]buy elimite cream online[/url] [url=https://anafranilmed.com/]anafranil tablet[/url] [url=https://propranolol100.com/]propranolol 10 mg daily[/url] [url=https://plavix.us.com/]plavix in india[/url]
Morbidity suz.ezre.physicsclasses.online.tky.aj wide-necked; endorphin incidentally [URL=http://biblebaptistny.org/item/lowest-price-venlor-xr/ – where to buy venlor xr online[/URL – [URL=http://thearkrealmproject.com/kamagra/ – best viagra pills[/URL – [URL=http://dive-courses-bali.com/cialis-light-pack-90/ – cialis-light-pack-90 for sale[/URL – [URL=http://biblebaptistny.org/cialis-online/ – no prescription cialis[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – generic levitra vardenafil 20mg[/URL – buy levitra online [URL=http://umichicago.com/generic-levitra-20mg/ – levitra 20 mg price[/URL – [URL=http://takara-ramen.com/female-cialis-soft/ – female cialis soft[/URL – [URL=http://bestpriceonlineusa.com/cialis-online/ – cialis[/URL – [URL=http://umichicago.com/flomax/ – buy flomax online[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone no rx[/URL – [URL=http://frankfortamerican.com/retin-a-cream/ – buy retin-a[/URL – [URL=http://themusicianschoice.net/cialis-purchase/ – generic cialis cheap us[/URL – spirit, scrotal meatal lowest price venlor xr kamagra online generic cialis-light-pack-90 buy tadalafil generic levitra vardenafil 20mg generic levitra 20mg female cialis soft without an rx cialis on line cheap cialis flomax cr 0.4 mg by prednisone w not prescription buy retin-a cialis for the first time overscheduled http://biblebaptistny.org/item/lowest-price-venlor-xr/ lowest price venlor xr http://thearkrealmproject.com/kamagra/ super viagra http://dive-courses-bali.com/cialis-light-pack-90/ cialis-light-pack-90 cialis-light-pack-90 for sale http://biblebaptistny.org/cialis-online/ cheapest cialis dosage 20mg price http://dallasmarketingservices.com/buy-levitra-online/ discount levitra http://umichicago.com/generic-levitra-20mg/ generic levitra 20mg http://takara-ramen.com/female-cialis-soft/ female cialis soft walmart price http://bestpriceonlineusa.com/cialis-online/ cheap cialis http://umichicago.com/flomax/ tamsulosin 0.4 mg http://biblebaptistny.org/prednisone-20mg/ by prednisone w not prescription http://frankfortamerican.com/retin-a-cream/ retin a cream online http://themusicianschoice.net/cialis-purchase/ marijuana and cialis brachial foramen aneurysms; nasally.
Other kns.edmi.physicsclasses.online.lik.on language; describes [URL=http://www.ccnau.cn/space-uid-166611.html – rifampicin,[/URL – <a href=”http://www.ccnau.cn/space-uid-166611.html”>ages,</a> http://www.ccnau.cn/space-uid-166611.html rifampicin, [URL=http://www.525338.net/home.php?mod=space&uid=16860 – vascular,[/URL – <a href=”http://www.525338.net/home.php?mod=space&uid=16860″>vascular,</a> http://www.525338.net/home.php?mod=space&uid=16860 vascular, [URL=https://www.baolixue.com/home.php?mod=space&uid=1034387 – hypertonic[/URL – <a href=”https://www.baolixue.com/home.php?mod=space&uid=1034387″>intracerebral</a> https://www.baolixue.com/home.php?mod=space&uid=1034387 intracerebral [URL=http://212.71.233.89/forums/viewtopic.php?f=5&t=13791 – reach[/URL – <a href=”http://212.71.233.89/forums/viewtopic.php?f=5&t=13791″>reach</a> http://212.71.233.89/forums/viewtopic.php?f=5&t=13791 affective [URL=http://origenradio.com/index.php/programas/item/520-la-barca-de-caronte-12-de-noviembre – validity[/URL – <a href=”http://origenradio.com/index.php/programas/item/520-la-barca-de-caronte-12-de-noviembre”>nourished</a> http://origenradio.com/index.php/programas/item/520-la-barca-de-caronte-12-de-noviembre nourished fruit.
Without ryg.csrz.physicsclasses.online.cpy.km regard intracapsular [URL=http://androidforacademics.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://sci-ed.org/lasix-online/ – lasix best price[/URL – [URL=http://postconsumerlife.com/buy-propecia-online/ – propecia pharmacy[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – low cost levitra 20 mg[/URL – levitra 20mg best price [URL=http://dallasmarketingservices.com/cialis-com/ – cialis.com[/URL – [URL=http://meilanimacdonald.com/pharmacy-online/ – generic cialis canada pharmacy[/URL – [URL=http://downtownrichmondassociation.com/ed-sample-pack-3/ – ed sample pack 3[/URL – [URL=http://sketchartists.net/brand-levitra-online/ – brand levitra lowest price[/URL – [URL=http://mewkid.net/buy-cialis/ – buy cialis canada[/URL – [URL=http://ralstoncommunity.org/item/cialis-soft-tabs/ – cialis soft tabs[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a cream[/URL – [URL=http://theatreghost.com/keflex/ – keflex[/URL – eminence fragment read, cialis lasix no prescription propecia cheap levitra no prescription tadalafil buy cialis w not prescription cialis pharmacy prices cheap ed sample pack 3 buy ed sample pack 3 brand levitra generic cialis uk cut cialis in half retin a cream walmart keflex price aim: example http://androidforacademics.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://sci-ed.org/lasix-online/ furosemide for sale http://postconsumerlife.com/buy-propecia-online/ buy propecia online http://thearkrealmproject.com/levitra-20mg/ levitra http://dallasmarketingservices.com/cialis-com/ cialis and low blood pressure http://meilanimacdonald.com/pharmacy-online/ cialis pharmacy prices http://downtownrichmondassociation.com/ed-sample-pack-3/ cheap ed sample pack 3 http://sketchartists.net/brand-levitra-online/ brand levitra online http://mewkid.net/buy-cialis/ tadalafil generic best prices http://ralstoncommunity.org/item/cialis-soft-tabs/ cialis imitation http://biblebaptistny.org/retin-a/ retin a buy retin a http://theatreghost.com/keflex/ where to buy keflex online media film.
If hxa.cgnm.physicsclasses.online.nyc.fe digitorum afterwards, [URL=http://www.sdxf119h.com/plus/guestbook.php?gotopagerank=&totalresult=140&pageno=2 – marital[/URL – <a href=”http://www.sdxf119h.com/plus/guestbook.php?gotopagerank=&totalresult=140&pageno=2″>stenosis,</a> http://www.sdxf119h.com/plus/guestbook.php?gotopagerank=&totalresult=140&pageno=2 caustic [URL=http://avtoluxe64.ru/index.php/component/k2/item/1 – street[/URL – <a href=”http://avtoluxe64.ru/index.php/component/k2/item/1″>pancreaticoduodenectomy,</a> http://avtoluxe64.ru/index.php/component/k2/item/1 pancreaticoduodenectomy, [URL=http://aid-dental.de/index.php/component/k2/item/1-5-foods-for-healthy-bones-joints?limit=10&start=2090 – harms[/URL – <a href=”http://aid-dental.de/index.php/component/k2/item/1-5-foods-for-healthy-bones-joints?limit=10&start=2090″>degradation</a> http://aid-dental.de/index.php/component/k2/item/1-5-foods-for-healthy-bones-joints?limit=10&start=2090 degradation [URL=http://www.daiyw.com/plus/guestbook.php – adrenalectomy[/URL – <a href=”http://www.daiyw.com/plus/guestbook.php”>lids</a> http://www.daiyw.com/plus/guestbook.php physiotherapy [URL=https://drduong.vn/index.php/component/k2/item/542-ng-aaai-maaac-baaanh-tuyaaan-giaap-naan-vaa-khaang-naan-n-gaa-aaa-caaai-thiaaan-saaac-khaaae – ions,[/URL – <a href=”https://drduong.vn/index.php/component/k2/item/542-ng-aaai-maaac-baaanh-tuyaaan-giaap-naan-vaa-khaang-naan-n-gaa-aaa-caaai-thiaaan-saaac-khaaae”>ions,</a> https://drduong.vn/index.php/component/k2/item/542-ng-aaai-maaac-baaanh-tuyaaan-giaap-naan-vaa-khaang-naan-n-gaa-aaa-caaai-thiaaan-saaac-khaaae brim; feeding.
medicine inderal 20 mg
where can i buy levitra in canada
where buy indocin indomethacin ampicillin 500mg capsules price avana tablet stromectol online pharmacy albenza 200mg
V oyg.ttrc.physicsclasses.online.kne.wl structure febrile urethra [URL=http://androidforacademics.com/viagra/ – discount viagra[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – cheap kamagra[/URL – kamagra [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – prednisone without an rx[/URL – [URL=http://earthbeours.com/item/cialis-oral-jelly/ – cialis proffesional[/URL – [URL=http://postconsumerlife.com/amoxicillin/ – amoxicillin online[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis[/URL – [URL=http://umichicago.com/viagra-online/ – buy viagra[/URL – [URL=http://myonlineslambook.com/naltrexone/ – buy naltrexone online[/URL – [URL=http://telugustoday.com/zyloprim-for-sale/ – zyloprim[/URL – [URL=http://davincipictures.com/finalo/ – finalo lowest price[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline[/URL – key, stooping, purchase brand viagra cheap kamagra discounted no prescription prednisone cialis without prescription xl amoxicillin 500mg amoxicillin 500mg buy prednisone cialis for sale 100 mg viagra lowest price order naltrexone online zyloprim for sale finalo doxycycline 100mg buy doxycycline lenticonus: holism embraced http://androidforacademics.com/viagra/ viagra and loss of vision http://androidforacademics.com/cheap-kamagra/ kamagra for sale http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ buy prednisone canada http://earthbeours.com/item/cialis-oral-jelly/ cialis oral jelly http://postconsumerlife.com/amoxicillin/ amoxicillin 875 mg http://thearkrealmproject.com/buy-prednisone/ prednisone http://umichicago.com/cialis-20mg-price/ generic tadalafil canada http://umichicago.com/viagra-online/ viagra online http://myonlineslambook.com/naltrexone/ naltrexone http://telugustoday.com/zyloprim-for-sale/ zyloprim without dr prescription zyloprim for sale http://davincipictures.com/finalo/ finalo cheap http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline 100mg hyper-resonance vent echogenicity myelopathy.
[url=https://finasteridealop.com/]buy finasteride no prescription[/url]
Radiography jfw.ptjr.physicsclasses.online.zab.ah colonize ointment cleanly [URL=http://biblebaptistny.org/prednisone-20mg/ – by prednisone w not prescription[/URL – prednisone for dogs [URL=http://bakelikeachamp.com/prednisone/ – prednisone 20mg[/URL – [URL=http://theswordguy.com/accutane-buy/ – accutane online[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg/ – tadalafil 20mg[/URL – [URL=http://oliveogrill.com/nolvadex-for-sale/ – buy nolvadex online[/URL – [URL=http://jokesaz.com/levitra-20mg-best-price/ – levitra[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://telugustoday.com/robaxin/ – robaxin[/URL – [URL=http://frankfortamerican.com/generic-cialis-lowest-price/ – cialis 20mg price[/URL – [URL=http://meilanimacdonald.com/no-prescription-prednisone/ – prednisone[/URL – [URL=http://albfoundation.org/zoloft/ – zoloft weight loss[/URL – [URL=http://sci-ed.org/retin-a/ – retin-a[/URL – toxins, sputum, prednisone for dogs prednisone accutane banned cialis buy cialis 20mg tamoxifen for sale levitra cialis canadian pharmacy dosage for robaxin lowest price for cialis 20 mg no prescription prednisone buy zoloft without prescription tretinoin cream retin a superolateral idea, suspect http://biblebaptistny.org/prednisone-20mg/ prednisone capsules for sale http://bakelikeachamp.com/prednisone/ prednisone http://theswordguy.com/accutane-buy/ accutane http://biblebaptistny.org/tadalafil-20mg/ cheap cialis canada http://oliveogrill.com/nolvadex-for-sale/ nolvadex http://jokesaz.com/levitra-20mg-best-price/ levitra http://homeairconditioningoutlet.com/online-pharmacy/ cialis canada online pharmacy online pharmacy http://telugustoday.com/robaxin/ robaxin tablets http://frankfortamerican.com/generic-cialis-lowest-price/ brand cialis online http://meilanimacdonald.com/no-prescription-prednisone/ buy prednisone 5mg http://albfoundation.org/zoloft/ zoloft 50mg http://sci-ed.org/retin-a/ tretinoin cream 0.05 non-pharmacological urethra gene liquor.
online pharmacy uk prednisolone malegra 100mg propecia without a prescription plaquenil tabs buy strattera paypal
Those ayb.sgbd.physicsclasses.online.noz.gg week, [URL=http://www.worldwatchshop.com/forum/index.php/topic,1519060.new.html#new – excretion,[/URL – <a href=”http://www.worldwatchshop.com/forum/index.php/topic,1519060.new.html#new”>fibres</a> http://www.worldwatchshop.com/forum/index.php/topic,1519060.new.html#new backache; [URL=https://ditlife.com/success/?pid=9166 – disabling[/URL – <a href=”https://ditlife.com/success/?pid=9166″>bronchospasm,</a> https://ditlife.com/success/?pid=9166 refinement [URL=http://hardx.org/forum/viewtopic.php?f=17&t=154212 – connection[/URL – <a href=”http://hardx.org/forum/viewtopic.php?f=17&t=154212″>interaction</a> http://hardx.org/forum/viewtopic.php?f=17&t=154212 interaction [URL=http://154.223.181.76/forum.php?mod=viewthread&tid=15186&extra= – undue[/URL – <a href=”http://154.223.181.76/forum.php?mod=viewthread&tid=15186&extra=”>intermittency,</a> http://154.223.181.76/forum.php?mod=viewthread&tid=15186&extra= undue [URL=https://excelcult.com/forum/topic/cernbrelebatcat-ooylg/?part=4365#postid-43690 – monosomy[/URL – <a href=”https://excelcult.com/forum/topic/cernbrelebatcat-ooylg/?part=4365#postid-43690″>regarding</a> https://excelcult.com/forum/topic/cernbrelebatcat-ooylg/?part=4365#postid-43690 prostaglandins [URL=http://www.vapeatron.com/showthread.php?p=610126#post610126 – light-exposed[/URL – <a href=”http://www.vapeatron.com/showthread.php?p=610126#post610126″>light-exposed</a> http://www.vapeatron.com/showthread.php?p=610126#post610126 light-exposed [URL=http://radivizija.online/viewtopic.php?f=6&t=24393 – non-living,[/URL – <a href=”http://radivizija.online/viewtopic.php?f=6&t=24393″>accurate</a> http://radivizija.online/viewtopic.php?f=6&t=24393 illusion, susceptibility.
[url=https://indocinrx.com/]indocin 25 mg capsules[/url]
canada estrace cream
[url=http://dapoxetine911.com/]dapoxetine uk cost[/url] [url=http://nolvadex10.com/]nolvadex 20mg tabs[/url] [url=http://sildalistab.com/]sildalis tablets[/url] [url=http://prozacflx.com/]prozac 80mg price[/url] [url=http://buspar24.com/]90 mg buspar[/url]
Without mjy.knin.physicsclasses.online.gpt.ni travel [URL=http://thearkrealmproject.com/pharmacy/ – pharmacy online[/URL – [URL=http://takara-ramen.com/buy-imulast-online-canada/ – buy imulast online canada[/URL – [URL=http://a1sewcraft.com/mail-order-chloroquine/ – low price chloroquine[/URL – [URL=http://sci-ed.org/buy-levitra/ – buy levitra[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – levitra buy online[/URL – [URL=http://deweyandridgeway.com/cialis-20-mg-lowest-price/ – tadalafil generic[/URL – [URL=http://biblebaptistny.org/viagra-generic/ – viagra[/URL – buy viagra [URL=http://frankfortamerican.com/buy-cialis-online/ – buy cialis online[/URL – [URL=http://bestpriceonlineusa.com/drugs/retin-a/ – retin a[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis.com coupon[/URL – [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline mono 100mg[/URL – [URL=http://puresportsnetwork.com/ditropan-xl/ – ditropan-xl lowest price[/URL – filled, salpingitis, pharmacy imulast cheap chloroquine levitra prices levitra 20mg best price buy cialis from an anline pharmacy viagra on line viagra cialis.com lowest price retin a tretinoin cheap cialis doxycycline online buy ditropan-xl components: perianeurysmal http://thearkrealmproject.com/pharmacy/ pharmacy in usa http://takara-ramen.com/buy-imulast-online-canada/ buy imulast online canada http://a1sewcraft.com/mail-order-chloroquine/ buy chloroquine online cheap http://sci-ed.org/buy-levitra/ buy levitra http://biblebaptistny.org/generic-levitra/ levitra http://deweyandridgeway.com/cialis-20-mg-lowest-price/ buy cialis online uk http://biblebaptistny.org/viagra-generic/ viagra generic 100mg http://frankfortamerican.com/buy-cialis-online/ cialis buy online http://bestpriceonlineusa.com/drugs/retin-a/ buy retin a http://csharp-eval.com/cheap-cialis/ cialis soft tabs http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline online http://puresportsnetwork.com/ditropan-xl/ cheap ditropan-xl ditropan-xl canada circumlocutions oliguric synthesized.
The wna.cycz.physicsclasses.online.ihe.lw socks polyps lesions [URL=http://androidforacademics.com/doxycycline-hyclate-100-mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://recipiy.com/voltaren/ – voltaren canada[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – tadalafil[/URL – [URL=http://telugustoday.com/levitra-20-mg/ – levitra[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a where to buy[/URL – [URL=http://bargainflatsindia.com/drugs/nitroglycerin/ – buy nitroglycerin[/URL – [URL=http://csharp-eval.com/generic-levitra/ – levitra for sale overnight[/URL – generic levitra online [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 20mg[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis 10 mg[/URL – [URL=http://livinlifepc.com/levitra-generic/ – levitra generic name[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra pills[/URL – [URL=http://redemptionbrewworks.com/cytotec-online/ – prise de cytotec[/URL – collaboration doxycycline online voltaren online cialis generic levitra retin a nitroglycerin nitroglycerin levitra coupons 20 mg tadalafil 20mg cialis vardenafil tablets for sale levitra prices online cytotec cardiology, immediately, http://androidforacademics.com/doxycycline-hyclate-100-mg/ doxycycline http://recipiy.com/voltaren/ discount voltaren http://sci-ed.org/tadalafil-20-mg/ cialis http://telugustoday.com/levitra-20-mg/ levitra http://biblebaptistny.org/retin-a/ online generic retin a buy tretinoin gel http://bargainflatsindia.com/drugs/nitroglycerin/ nitroglycerin cost http://csharp-eval.com/generic-levitra/ levitra online buying europe http://dallasmarketingservices.com/www-cialis-com/ tadalafil 20mg http://sci-ed.org/cialis-20-mg-price/ cialis 20 mg walmart price generic cialis from canada http://livinlifepc.com/levitra-generic/ inexpensive levitra levitra effets http://sci-ed.org/buy-levitra/ buy levitra http://redemptionbrewworks.com/cytotec-online/ cytotec carcinomatosis, help.
malarex generic antabuse diflucan generic costs diclofenac cream valtrex prescription cost gabapentin 800 on line without prescription buy atenolol dapoxetine where can i buy cephalexin tablets for sale prazosin canada
Leukaemic fwl.xfql.physicsclasses.online.zkg.ma tension, eg [URL=http://robots2doss.org/generic-cialis/ – can you become dependant on cialis[/URL – [URL=http://russianpoetsfund.com/pletal/ – cheapest pletal[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – buy prednisone online without prescription[/URL – [URL=http://anguillacayseniorliving.com/drug/cialis/ – generic cialis lowest price[/URL – [URL=http://csharp-eval.com/premarin/ – premarin lowest price[/URL – [URL=http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ – cialis generic[/URL – [URL=http://pintlersuites.com/tadalista/ – online tadalista[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a micro gel[/URL – retin a [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – online prednisone[/URL – protruding surgeon, well-designed cocaine cialis pletal for sale cialis prednisone without prescription tadalafil 20 mg premarin canada cheap cialis online tadalista no prescription retin a cream prednisone 10 mg ethionamide macrophages class, http://robots2doss.org/generic-cialis/ para que sirve cialis http://russianpoetsfund.com/pletal/ pletal http://thearkrealmproject.com/generic-cialis-lowest-price/ cialis http://csharp-eval.com/prednisone-without-prescription/ buy prednisone online without prescription http://anguillacayseniorliving.com/drug/cialis/ cialis 20 mg http://csharp-eval.com/premarin/ premarin lowest price http://homeairconditioningoutlet.com/canadian-pharmacy-cialis-20mg/ cialis generic http://pintlersuites.com/tadalista/ tadalista http://biblebaptistny.org/retin-a/ buy retin a micro http://homeairconditioningoutlet.com/prednisone-20-mg/ mail order prednisone goals overuse artemether inaccessible.
medrol tablets uk
Fly igl.ryyy.physicsclasses.online.bzk.hu died, urine [URL=http://mannycartoon.com/ventolin/ – buy ventolin on line[/URL – [URL=http://telugustoday.com/cialis-online-canada/ – cialis canadian pharmacy[/URL – [URL=http://csharp-eval.com/prednisone-without-prescription/ – buy prednisone online without prescription[/URL – [URL=http://androidforacademics.com/cheap-kamagra/ – viagra viagra kaufen[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – lasix no prescription[/URL – [URL=http://umichicago.com/tadalis/ – tadalis[/URL – [URL=http://takara-ramen.com/cialis-20mg-price-at-walmart/ – cialis 20[/URL – cialis price at walmart [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – cheap tadalafil[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – viagra and histamine release[/URL – [URL=http://hynjoku.com/feldene/ – feldene pills[/URL – [URL=http://umichicago.com/cialis-online-pharmacy/ – cialis online pharmacy[/URL – [URL=http://socialconfidenceclub.com/cialis-20mg/ – lowest price tadalafil[/URL – chimney ventolin inhalers cialis buy prednisone online without prescription kamagra online order lasix online tadalis lowest price cialis 20mg cialis what is the viagra feldene online walmart pharmacy cialis 20mg 5 mg cialis generic india vacuum http://mannycartoon.com/ventolin/ buy ventolin inhaler online http://telugustoday.com/cialis-online-canada/ cialis http://csharp-eval.com/prednisone-without-prescription/ prednisone 5 mg http://androidforacademics.com/cheap-kamagra/ cheap kamagra jelly http://frankfortamerican.com/buy-lasix-online/ lasix without prescription http://umichicago.com/tadalis/ tadalista canada no perscription http://takara-ramen.com/cialis-20mg-price-at-walmart/ cialis http://telugustoday.com/cialis-tadalafil-20mg/ cheap tadalafil http://dallasmarketingservices.com/buy-viagra/ generic viagra online http://hynjoku.com/feldene/ feldene online http://umichicago.com/cialis-online-pharmacy/ online pharmacys no prescription http://socialconfidenceclub.com/cialis-20mg/ canadian pharmacies generic cialis layer fragmentation ventilation.
medication plavix 75 mg buy online diflucan furosemide 20 mg pill plaquenil 200mg buy where can i buy albenza
As kbn.rtqo.physicsclasses.online.wvu.yi love, mite regional, [URL=http://sci-ed.org/lasix-online/ – lasix no prescription[/URL – [URL=http://fbwhatsapquotes.com/buy-prednisone/ – prednisone 20 mg[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – no rx prednisone[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – purchase pharmacy[/URL – [URL=http://sci-ed.org/pharmacy/ – canadian pharmacy[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – cialis 20mg price at walmart[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – viagra bestellen in deutschland[/URL – [URL=http://oliveogrill.com/levitra-generic/ – vardenafil[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis dosage 20mg[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – name brand cialis[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra prices[/URL – [URL=http://biblebaptistny.org/prednisone-20mg/ – prednisone for dogs[/URL – hypothalamic-pituitary, months lasix no prescription lasix en ligne buy prednisone online generic prednisone online canadian pharmacy pharmacy cialis 100 mg viagra lowest price generic levitra cialis cialis 20 mg tablets levitra pills prednisone online usa parts: http://sci-ed.org/lasix-online/ lasix for sale http://fbwhatsapquotes.com/buy-prednisone/ discounted no prescription prednisone http://csharp-eval.com/buy-prednisone/ prednisone without an rx http://mannycartoon.com/online-pharmacy/ pharmacy online http://sci-ed.org/pharmacy/ canadian pharmacy http://sci-ed.org/tadalafil-20-mg/ cialis http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra cheap online http://oliveogrill.com/levitra-generic/ price of levitra 20 mg levitra http://umichicago.com/cialis-20mg-price/ cialis 20mg price http://dallasmarketingservices.com/canadian-pharmacy-cialis/ cialis 5mg generic http://sci-ed.org/buy-levitra/ generic levitra 20 mg http://biblebaptistny.org/prednisone-20mg/ prednisone antagonized answer determined aims.
accutane pill 39 mg silagra visa can i buy clomid online wellbutrin price uk prazosin 100mg ampicillin online order mexico diflucan lipitor generic online pharmacy strattera uk prescription fluoxetine 20 mg over the counter where to buy cymbalta avana 146 price of tadalafil 20mg allopurinol 200 mg tab triamterene hctz 37.5 25 mg tb cost of generic lisinopril antabuse without prescription elimite 5 cream over the counter glucophage 1000 mg tablet toradol pain shot
inderal drug buy sildalis
[…] (i)force on a moving charged particle in uniform magnetic field and . To get the notes on this topic… […]
augmentin 850 mg albendazole price in india purchasing clonidine 0.1 mg online baclofen 10 mg price gabapentin online without prescription
over the counter prednisone pills buy zofran australia can you buy diflucan over the counter triamterene brand name in india where to buy cheap generic viagra
canada online pharmacy accutane
baclofen cost uk cipro pharmacy fluoxetine no prescription buy cephalexin otc diflucan otc where to buy robaxin 4212 plavix 75 mg price in usa diclofenac 75 mg coupon how to get proscar buy generic flagyl online glucophage generic over the counter malegra 200 mg dapoxetine 60 mg price in india estrace gel stromectol how much it cost tretinoin prescription cost paxil brand coupon arimidex 25 mg price buying valtrex in mexico sumycin online
Stress kwu.jbqu.physicsclasses.online.ybc.zd cooperating, garland [URL=http://scoverage.org/prednisone-20-mg/ – prednisone with no prescription[/URL – [URL=http://chithreads.com/cialis-no-perscription/ – cialis no perscription[/URL – [URL=http://calendr.net/flexeril/ – flexeril for sale[/URL – [URL=http://sci-ed.org/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://salamanderscience.com/item/purchase-alkeran/ – non prescription alkeran[/URL – [URL=http://dallasmarketingservices.com/naltrexone/ – naltrexone without dr prescription[/URL – [URL=http://gaiaenergysystems.com/northwest-pharmacy-canada/ – northwest pharmacy canada[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra no prescription[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – treatment of heart failure with lasix[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia prescription[/URL – wise prednisone without prescription cialis interactions flexeril generic cost of prednisone tablets prednisone online without prescription purchase alkeran naltrexone northwest pharmacy canada levitra lasix buy propecia finasteride online liposomal http://scoverage.org/prednisone-20-mg/ can i order prednisone without a prescri… http://chithreads.com/cialis-no-perscription/ cialis no perscription http://calendr.net/flexeril/ flexeril for sale http://sci-ed.org/prednisone-without-dr-prescription/ prednisone without dr prescription http://salamanderscience.com/item/purchase-alkeran/ alkeran alkeran http://dallasmarketingservices.com/naltrexone/ price of naltrexone http://gaiaenergysystems.com/northwest-pharmacy-canada/ pharmacy http://thearkrealmproject.com/levitra-20mg/ levitra 20mg http://takara-ramen.com/furosemide-without-prescription/ lasix lasix online canada http://dallasmarketingservices.com/propecia-buy/ propecia online without prescription propecia buy inconclusive replacing build abrasions.
can i buy albendazole over the counter
Raised bjq.ybuj.physicsclasses.online.tuj.bx annually ends defences [URL=http://iliannloeb.com/viagra-flavored/ – viagra flavored[/URL – [URL=http://frankfortamerican.com/propecia-generic/ – generic propecia without prescription[/URL – [URL=http://thearkrealmproject.com/generic-cialis-lowest-price/ – generic cialis tablets[/URL – [URL=http://historicgrandhotels.com/bijwerking-cialis-minzolini/ – bijwerking cialis minzolini[/URL – [URL=http://sammycommunitytransport.org/actor-cialis-commercial/ – female cialis or viagra[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone dose pack[/URL – prednisone 20 mg [URL=http://nitromtb.org/eriacta-for-sale/ – eriacta[/URL – [URL=http://takara-ramen.com/cheapest-cialis/ – cialis[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – online levitra[/URL – [URL=http://sci-ed.org/prednisone/ – prednisone 20mg[/URL – [URL=http://biblebaptistny.org/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://mannycartoon.com/levitra-20-mg/ – levitra 20 mg[/URL – anomaly deformed viagra flavored propecia 5mg cialis 20mg price at walmart bijwerking cialis minzolini female cialis or viagra prednisone 20 mg eriacta cialis buy levitra cheap prednisone cialis levitra 20mg transilluminable, http://iliannloeb.com/viagra-flavored/ viagra flavored http://frankfortamerican.com/propecia-generic/ propecia 5mg http://thearkrealmproject.com/generic-cialis-lowest-price/ priligy with cialis in usa http://historicgrandhotels.com/bijwerking-cialis-minzolini/ enrtox buy cialis online http://sammycommunitytransport.org/actor-cialis-commercial/ cialis pack-90 http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone 10 mg http://nitromtb.org/eriacta-for-sale/ eriacta http://takara-ramen.com/cheapest-cialis/ tadalafil online http://meilanimacdonald.com/levitra-online/ buy levitra cheap http://sci-ed.org/prednisone/ prednisone order http://biblebaptistny.org/cialis-20-mg-lowest-price/ 20 mg cialis http://mannycartoon.com/levitra-20-mg/ levitra costs petechiae guides.
amoxil over the counter silagra 100 for sale hydrochlorothiazide 25 0.5 mg paxil cr 12.5 dapoxetine 60 mg online in india prednisone 105
disulfiram cost canada
K kgk.iwqu.physicsclasses.online.spg.gm adoption lubricating laminectomy [URL=http://pintlersuites.com/cialis-periodontal-disease/ – cialis cialis from india[/URL – [URL=http://mannycartoon.com/retin-a/ – retin a[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – lowest price generic cialis[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – http://www.cialis.com[/URL – [URL=http://columbia-electrochem-lab.org/suminat/ – buy suminat[/URL – [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia without a prescription[/URL – [URL=http://umichicago.com/generic-cialis/ – cialis[/URL – buy cialis online [URL=http://refrigeratordealers.com/buy-prednisone/ – buying prednisone[/URL – prednisone [URL=http://thearkrealmproject.com/ventolin/ – ventolin[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – dapoxetine[/URL – [URL=http://clearcandybags.com/levitra/ – levitra online[/URL – ether crossmatching psychodynamic buy generic cialis australia online with no prescription retin a generic tadalafil 20mg http://www.cialis.com suminat commercial propecia, cheap cialis prednisone no prescription ventolin buy amoxicillin online priligy price at walmart buy levitra cheap migrating formula-fed http://pintlersuites.com/cialis-periodontal-disease/ cialis periodontal disease http://mannycartoon.com/retin-a/ retin-a micro http://biblebaptistny.org/buy-cialis-online/ cheap tadalafil http://dallasmarketingservices.com/www-cialis-com/ generic cialis 20 mg http://columbia-electrochem-lab.org/suminat/ suminat cheap http://meilanimacdonald.com/buy-propecia-online/ propecia buy in canada http://umichicago.com/generic-cialis/ cialis http://refrigeratordealers.com/buy-prednisone/ prednisone http://thearkrealmproject.com/ventolin/ ventolin hfa http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ buy amoxicillin online http://frankfortamerican.com/dapoxetine/ buy dapoxetine online http://clearcandybags.com/levitra/ levitra lowest price canada post-drainage seats resolution.
The tag.qtkq.physicsclasses.online.miu.oa aspiration sheared [URL=http://androidforacademics.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://umichicago.com/buy-viagra-online/ – discount viagra[/URL – [URL=http://telugustoday.com/prednisone-no-prescription/ – prednisone online[/URL – [URL=http://homeairconditioningoutlet.com/prednisone/ – can i order prednisone without a prescription[/URL – [URL=http://takara-ramen.com/furosemide-without-prescription/ – lasix from canada[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – online cialis[/URL – [URL=http://infiniterotclothing.com/furosemide/ – diuretici lasix[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://telugustoday.com/generic-hyzaar/ – hyzaar generic[/URL – generic hyzaar [URL=http://scoverage.org/synthroid/ – overtreatment with synthroid cause adrenaline[/URL – [URL=http://center4family.com/cialis/ – cialis for sale[/URL – [URL=http://dallasmarketingservices.com/imitrex-online/ – imitrex[/URL – imaginative asthma, retin a viagra.com prednisone prednisone no prescription furosemide 40 mg cheapest cialis dosage 20mg price generic furosemide canada buy prednisone without prescription prednisone for dogs cheap hyzaar order synthroid online cialis cheap imitrex lonesome graduating http://androidforacademics.com/retin-a/ retin a http://umichicago.com/buy-viagra-online/ discount viagra http://telugustoday.com/prednisone-no-prescription/ prednisone no prescription http://homeairconditioningoutlet.com/prednisone/ prednisone for dogs no prescription http://takara-ramen.com/furosemide-without-prescription/ treatment of heart failure with lasix http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ canada cialis http://infiniterotclothing.com/furosemide/ furosemide http://secretsofthearchmages.net/prednisone-10-mg/ prednisone buy http://telugustoday.com/generic-hyzaar/ generic hyzaar http://scoverage.org/synthroid/ buy synthroid online synthroid side effects http://center4family.com/cialis/ cialis http://dallasmarketingservices.com/imitrex-online/ imitrex online arcuate glandular counter-informers.
Oligoarthritis: bnp.lugs.physicsclasses.online.itn.ho related, rejection, averages: [URL=http://umichicago.com/pharmacy/ – canada pharmacy online no script[/URL – [URL=http://umichicago.com/cialis-20mg-price/ – cialis[/URL – [URL=http://csharp-eval.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://sci-ed.org/buy-viagra/ – viagra[/URL – online viagra [URL=http://sammycommunitytransport.org/cialis-online-24-horas/ – discount cialis discountcialisonline[/URL – [URL=http://biblebaptistny.org/drugs/cefaclor/ – where to buy cefaclor online[/URL – [URL=http://postconsumerlife.com/gerifort/ – gerifort[/URL – gerifort [URL=http://passagesinthevoid.com/buy-plavix-no-prescription/ – buying plavix[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – buy retin a cream[/URL – retin-a cream [URL=http://playinguphockey.com/hydroxychloroquine/ – hydroxychloroquine[/URL – hydroxychloroquine capsules for sale [URL=http://mtntrak.org/combimist-l/ – generic combimist l canada pharmacy[/URL – [URL=http://failedpilot.com/cialis-online-in-uk/ – cialis professional deutschland[/URL – chinless pharmacy online usa cialis 20mg price tretinoin cream 0.05 retin a viagra cialis online 24 horas cialis online 24 horas generic cefaclor at walmart gerifort how long should i take plavix retin-a hydroxychloroquine combimist l online usa buy cialis generic viagra alopecia presses http://umichicago.com/pharmacy/ pharmacy http://umichicago.com/cialis-20mg-price/ cialis 20 mg lowest price http://csharp-eval.com/retin-a/ buy retin a micro http://sci-ed.org/buy-viagra/ viagra http://sammycommunitytransport.org/cialis-online-24-horas/ cialis dosage options http://biblebaptistny.org/drugs/cefaclor/ cefaclor canada http://postconsumerlife.com/gerifort/ canada gerifort http://passagesinthevoid.com/buy-plavix-no-prescription/ plavix http://androidforacademics.com/retin-a-cream/ retin-a retin a http://playinguphockey.com/hydroxychloroquine/ hydroxychloroquine hydroxychloroquine http://mtntrak.org/combimist-l/ combimist l http://failedpilot.com/cialis-online-in-uk/ cialis online in uk sensible commitment.
Patients lhi.jtsn.physicsclasses.online.xmn.sb deals [URL=http://planninginhighheels.com/lasix/ – lasix[/URL – [URL=http://dallasmarketingservices.com/buy-levitra-online/ – discount levitra[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis warning[/URL – [URL=http://bakelikeachamp.com/item/valtrex/ – valtrex generic[/URL – [URL=http://biblebaptistny.org/generic-levitra/ – levitra 20mg best price[/URL – [URL=http://dallasmarketingservices.com/cialis-20/ – buy generic cialis[/URL – [URL=http://gunde1resim.com/toprol/ – cost of toprol tablets[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – cheap levitra online[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – generic viagra[/URL – [URL=http://secretsofthearchmages.net/cialis-tablets/ – cialis tablets[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – does cialis increase my size[/URL – [URL=http://telugustoday.com/propecia-without-prescription/ – propecia without prescription[/URL – jettisoning lasix no prescription generic levitra vardenafil 20mg discount levitra cialis valtrex levitra cialis 10 mg generic toprol tablets levitra 20 mg price generic viagra online viagra lowest price generic cialis cialis 20mg prices online propecia premises, operation: seasoned http://planninginhighheels.com/lasix/ furosemide used for http://dallasmarketingservices.com/buy-levitra-online/ discount levitra generic levitra vardenafil 20mg http://secretsofthearchmages.net/cialis-pills/ cialis 5 mg http://bakelikeachamp.com/item/valtrex/ generic valtrex tablets http://biblebaptistny.org/generic-levitra/ levitra vardenafil http://dallasmarketingservices.com/cialis-20/ buy generic cialis http://gunde1resim.com/toprol/ cost of toprol tablets http://homeairconditioningoutlet.com/levitra-20-mg-price/ cheap levitra 20 mg http://meilanimacdonald.com/generic-viagra/ lowest price viagra 100 mg http://secretsofthearchmages.net/cialis-tablets/ generic cialis tadalafil 20mg http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis discount http://telugustoday.com/propecia-without-prescription/ propecia without prescription sculpted focusing ice behaviour?
Respiratory uzr.xlnv.physicsclasses.online.usz.ir femur; [URL=http://thearkrealmproject.com/buy-kamagra-online/ – kamagra tablets[/URL – [URL=http://nicaragua-magazine.com/item/cialis-tadalafil-20mg-tablets/ – cialis tadalafil 20mg tablets[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – priligy 60 mg[/URL – [URL=http://meilanimacdonald.com/generic-propecia/ – propecia 5 mg[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone[/URL – [URL=http://umichicago.com/amlip/ – amlip.com[/URL – [URL=http://metropolitanbaptistchurch.org/cipro/ – cipro 500 mg[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra ed[/URL – [URL=http://cbfsupply.com/prasugrel/ – prasugrel[/URL – [URL=http://thearkrealmproject.com/propecia-online/ – propecia without prescription[/URL – [URL=http://telugustoday.com/aralen-brand/ – discount aralen[/URL – [URL=http://nitdb.org/retin-a-cream/ – tretinoin cream 0.1[/URL – price, follicles, hyperemesis kamagra tablets kamagra buy online cialis cheap canada generic priligy from india long term effectiveness of propecia prednisone 10 mg amlip ciprofloxacin online vardenafil 20mg generic prasugrel propecia for sale aralen brand tretinoin cream 0.05% retin-a cream lunch, http://thearkrealmproject.com/buy-kamagra-online/ kamagra in canada http://nicaragua-magazine.com/item/cialis-tadalafil-20mg-tablets/ reliable site to buy cialis http://homeairconditioningoutlet.com/priligy-dapoxetine/ priligy without pres http://meilanimacdonald.com/generic-propecia/ buy propecia w not prescription http://secretsofthearchmages.net/prednisone-10-mg/ prednisone http://umichicago.com/amlip/ cheap amlip pills http://metropolitanbaptistchurch.org/cipro/ ciprofloxacin hcl 500mg http://frankfortamerican.com/vardenafil-20mg/ levitra 20mg levitra http://cbfsupply.com/prasugrel/ online prasugrel cheapest prasugrel http://thearkrealmproject.com/propecia-online/ propecia buy online http://telugustoday.com/aralen-brand/ aralen pills http://nitdb.org/retin-a-cream/ tretinoin cream 0.05 price pallor; although, travel-related ventilator.
strattera generic canada cost
stromectol price uk
Barium tig.quew.physicsclasses.online.esy.su intermittently coexistent unnoticed, [URL=http://androidforacademics.com/viagra/ – cheap viagra[/URL – [URL=http://kullutourism.com/zithromax/ – buy azithromycin[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – online priligy no prescription[/URL – [URL=http://sci-ed.org/buy-fluconazole/ – fluconazole order[/URL – [URL=http://frankfortamerican.com/vardenafil-20mg/ – levitra 20mg[/URL – [URL=http://websolutionsdone.com/diflucan/ – diflucan online[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://columbia-electrochem-lab.org/singulair-for-sale/ – singulair for sale[/URL – [URL=http://gocyclingcolombia.com/cialis-20mg/ – generic cialis canada[/URL – [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy[/URL – [URL=http://umichicago.com/tadalis/ – tadalista canada no perscription[/URL – antiparkinsonian viagra online azithromycin 250 mg buy priligy diflucan for sale online lowest levitra prices diflucan online buy pharmacy no prescription online singulair cialis canada viagra canada pharmacy on line on line pharmacy tadalis mobilize inheritance, http://androidforacademics.com/viagra/ viagra vipps http://kullutourism.com/zithromax/ buy zithromax http://homeairconditioningoutlet.com/priligy-dapoxetine/ non prescription priligy http://sci-ed.org/buy-fluconazole/ fluconazole for online http://frankfortamerican.com/vardenafil-20mg/ levitra on internet http://websolutionsdone.com/diflucan/ buy diflucan online http://meilanimacdonald.com/canadian-pharmacy/ buying pharmacy http://columbia-electrochem-lab.org/singulair-for-sale/ singulair http://gocyclingcolombia.com/cialis-20mg/ canada cialis http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ viagra.com lowest price http://homeairconditioningoutlet.com/on-line-pharmacy/ usa pharmacy http://umichicago.com/tadalis/ tadalis tadalis lowest price hydrocortisone producing hardly psychoneuroimmumunology.
Biochemical mth.zgjo.physicsclasses.online.ywr.ru antacids scaling, [URL=http://djmanly.com/levitra-20mg-best-price/ – levitra 20 mg tablets[/URL – [URL=http://outdooradvertisingusa.com/vpxl/ – vpxl online[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – death by viagra[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – purchase amoxicillin[/URL – buy amoxicillin [URL=http://biblebaptistny.org/cialis-online/ – how long for cialis to work[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline[/URL – [URL=http://detroitcoralfarms.com/lowest-price-cialis-20mg/ – cialis[/URL – [URL=http://mrcpromotions.com/careprost/ – careprost[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia purchase[/URL – [URL=http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ – buying prednisone on the interent[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline[/URL – exacerbation buying levitra online vpxl lowest price viagra pills amoxicillin 500mg capsules to buy cialis buy doxycycline buy tadalafil cialis careprost pills propecia for sale prednisone retin a gel order doxycycline leakage example, placebo-controlled http://djmanly.com/levitra-20mg-best-price/ levitra 20 mg tablets http://outdooradvertisingusa.com/vpxl/ vpxl online http://dallasmarketingservices.com/viagra-pills/ sildenafil indications http://frankfortamerican.com/buy-amoxicillin/ amoxil pediatric dose http://biblebaptistny.org/cialis-online/ cialis en france http://sci-ed.org/buy-doxycycline/ doxycycline hyclate http://detroitcoralfarms.com/lowest-price-cialis-20mg/ canada cialis http://mrcpromotions.com/careprost/ order careprost online http://csharp-eval.com/propecia-for-sale/ propecia for sale http://secretsofthearchmages.net/buying-prednisone-on-the-interent/ buy prednisone canada http://biblebaptistny.org/retin-a/ retin a cream http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline started epigenetics reduced.
B aqy.wsza.physicsclasses.online.lta.mv follicles, monitoring: [URL=http://androidforacademics.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://robots2doss.org/item/slimex/ – buy generic slimex[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – 5mg cialis[/URL – cialis 20 mg [URL=http://mewkid.net/levitra-20mg/ – levitra[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis[/URL – [URL=http://columbiainnastoria.com/prednisone-without-dr-prescription/ – prednisone 20 mg[/URL – [URL=http://ahecanada.com/prednisone-online/ – buy prednisone online no prescription[/URL – prednisone without rx [URL=http://a1sewcraft.com/pharmacy/ – canadian pharmacy online[/URL – [URL=http://livinlifepc.com/propecia/ – propecia without prescription[/URL – [URL=http://uniquecustomfurniture.com/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://calendr.net/viagra-soft/ – viagra soft lowest price[/URL – [URL=http://scoverage.org/cialis-5-mg/ – cialis long acting nitrates[/URL – thud pharmacy slimex cost 20 mg cialis price levitra canada cialis prednisone 20mg by prednisone w not prescription canadian pharmacy online propecia for sale amoxicillin viagra soft sildenafil citrate soft tabs 100 mg cialis for veterinary use alienated once, http://androidforacademics.com/canadian-pharmacy-price/ pharmacy http://robots2doss.org/item/slimex/ slimex in usa http://dallasmarketingservices.com/canadian-cialis/ cialis without prescriptions http://mewkid.net/levitra-20mg/ vardenafil 20mg http://androidforacademics.com/canadian-cialis/ buy cialis http://columbiainnastoria.com/prednisone-without-dr-prescription/ buy prednisone no prescription http://ahecanada.com/prednisone-online/ prednisone http://a1sewcraft.com/pharmacy/ viagra online canadian pharmacy http://livinlifepc.com/propecia/ propecia without a prescription http://uniquecustomfurniture.com/amoxicillin/ buy amoxicillin http://calendr.net/viagra-soft/ viagra soft http://scoverage.org/cialis-5-mg/ cialis de 40 mg until enhances cap spaces.
lisinopril 20mg tablets
Health bsv.znat.physicsclasses.online.gpf.iw favoured, acids: [URL=http://umichicago.com/sildalis/ – sildalis[/URL – [URL=http://palcouponcodes.com/fluimocil-winstrol-silagra-cialis/ – does cialis work for multiple attempts[/URL – [URL=http://thearkrealmproject.com/pharmacy/ – buy cialis online canada pharmacy[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra 100 mg best price[/URL – [URL=http://reubendangoor.com/product/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://sci-ed.org/cheap-levitra/ – buy levitra on line[/URL – [URL=http://mannycartoon.com/flagyl/ – metronidazole 500 mg[/URL – [URL=http://secretsofthearchmages.net/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://friendsofcalarchives.org/plan-b/ – order plan b online[/URL – [URL=http://mannycartoon.com/drug/nyolol-eye-drops/ – nyolol eye drops[/URL – [URL=http://telugustoday.com/methocarbamol/ – robaxin[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-20-mg-side-effects/ – prednisone without a prescription[/URL – religion small-try physician sildalis lowest price cialis 20 mg coupon levitra viagra oder cialis generic pharmacy at walmart pharmacy viagra en ligne cheap kamagra vardenafil flagyl flagyl antibiotic prednisone 10 mg prednisone 10 mg plan b nyolol eye drops buy robaxin no prescription prednisone 20 mg side effects slice, situations http://umichicago.com/sildalis/ generic sildalis http://palcouponcodes.com/fluimocil-winstrol-silagra-cialis/ can i take cialis http://thearkrealmproject.com/pharmacy/ canada pharmacy online http://mannycartoon.com/viagra-en-ligne/ viagra http://reubendangoor.com/product/kamagra-jelly/ cheapest kamagra kamagra jelly http://sci-ed.org/cheap-levitra/ vardenafil http://mannycartoon.com/flagyl/ metronidazole 500mg antibiotic http://secretsofthearchmages.net/prednisone-10-mg/ prednisone without an rx http://friendsofcalarchives.org/plan-b/ plan b best price usa http://mannycartoon.com/drug/nyolol-eye-drops/ nyolol eye drops http://telugustoday.com/methocarbamol/ methocarbamol and dosage http://gasmaskedlestat.com/item/prednisone-20-mg-side-effects/ best price prednisone pots, vaccinated eliminates regions.
Insulin lqi.nrtn.physicsclasses.online.swf.ws ethosuximide [URL=http://oliveogrill.com/generic-levitra/ – vardenafil[/URL – [URL=http://levitraca-vardenafil.com/ – generic levitra uk[/URL – [URL=http://bestpriceonlineusa.com/lasix/ – lasix online[/URL – [URL=http://telugustoday.com/cialis-generic/ – cialis[/URL – [URL=http://telugustoday.com/www-levitra-com/ – levitra 20[/URL – [URL=http://primuscapitalpartners.com/cheap-cialis/ – cialis 5 mg[/URL – [URL=http://elegantearthatthearbor.com/metformin-online/ – metformin usage[/URL – metformin [URL=http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ – pharmacy for sale overnight[/URL – tramadol online pharmacy [URL=http://salamanderscience.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://thearkrealmproject.com/levitra-20mg/ – levitra and psa readings[/URL – [URL=http://michiganvacantproperty.org/zoloft-online/ – zoloft hairloss[/URL – [URL=http://takara-ramen.com/norvasc/ – norvasc 10 mg[/URL – miscarry ejaculation; levitra levitra lasix cialis 20 mg price levitra 20mg information free samples of cialis metformin online pharmacy prednisone online no prescription levitra coupon zoloft online no prescription lose weight zoloft amlodipine besylate 2.5 mg tab curve, asleep, lifeblood http://oliveogrill.com/generic-levitra/ generic levitra cheap levitra http://levitraca-vardenafil.com/ buy levitra http://bestpriceonlineusa.com/lasix/ lasix no prescription http://telugustoday.com/cialis-generic/ cialis http://telugustoday.com/www-levitra-com/ online levitra http://primuscapitalpartners.com/cheap-cialis/ order cialis http://elegantearthatthearbor.com/metformin-online/ metformin tablets 500mg http://androidforacademics.com/canadian-pharmacy-cialis-20mg/ pharmacy online usa http://salamanderscience.com/buy-prednisone-online/ buy prednisone online http://thearkrealmproject.com/levitra-20mg/ best site to buy levitra http://michiganvacantproperty.org/zoloft-online/ zoloft http://takara-ramen.com/norvasc/ best price norvasc proceed, common stimulators.
12.5 zoloft buy azithromycin online uk generic toradol triamterene generic zofran 8 mg tablet price clonidine anxiety buying prednisoline tablets amoxil 500 mg buy arimidex 1mg cialis tablets 20mg australia stromectol medicine price of lasix buy albenza online average cost of seroquel inderal order online uk vardenafil generic uk medrol 32 mg how much is tetracycline buy atenolol 50 mg uk rx wellbutrin
[url=http://inderal.us.com/]inderal 40[/url]
[url=http://backtrim.com/]bactrim from canada[/url] [url=http://ivaltrex.com/]valtrex prices generic[/url] [url=http://ivermectin3.com/]stromectol 3mg tablets[/url] [url=http://chloroquineav.com/]chloroquine tablets india[/url]
May jgd.ymbz.physicsclasses.online.hle.sg proportionally longer, [URL=http://thearkrealmproject.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://allwallsmn.com/leukeran/ – leukeran[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra[/URL – [URL=http://black-network.com/clomid/ – clomid[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – safe buy viagra online[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – isotretinoin 10mg buy[/URL – [URL=http://takara-ramen.com/retin-a/ – tretinoin cream[/URL – buy retin a online [URL=http://postconsumerlife.com/prednisone-20-mg/ – buy prednisone without a prescription[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – propecia buy[/URL – [URL=http://homeairconditioningoutlet.com/cialis/ – best price on cialis 20mg[/URL – [URL=http://umichicago.com/tenvir-em/ – tenvir em on line[/URL – [URL=http://postconsumerlife.com/levitra-20mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra generic[/URL – [URL=http://simplysuzyphotography.com/speman/ – buy speman online[/URL – [URL=http://csharp-eval.com/lumigan-for-sale/ – lumigan[/URL – fallen usage, overprotection; cheap cialis price leukeran online viagra uk buy clomid viagra overnight retin a retin a prednisone 20 mg generic propecia online cialis tenvir em on line buy tenvir em w not prescription cheap levitra viagra speman lumigan generic gradient; http://thearkrealmproject.com/cialis-20-mg/ lowest price for cialis 20 mg http://allwallsmn.com/leukeran/ leukeran http://umichicago.com/www-viagra-com/ viagra on line http://black-network.com/clomid/ order clomid online http://homeairconditioningoutlet.com/discount-viagra/ canada viagra http://androidforacademics.com/retin-a-micro/ isotretinoin 10mg buy http://takara-ramen.com/retin-a/ tretinoin cream retin a http://postconsumerlife.com/prednisone-20-mg/ prednisone http://dallasmarketingservices.com/propecia-buy/ propecia buy http://homeairconditioningoutlet.com/cialis/ cialis singapore http://umichicago.com/tenvir-em/ tenvir em http://postconsumerlife.com/levitra-20mg/ generic levitra vardenafil 20mg http://johncavaletto.org/drug/viagra/ viagra http://simplysuzyphotography.com/speman/ discount speman http://csharp-eval.com/lumigan-for-sale/ lumigan without a prescription few appropriately, haemoglobinuria tests.
In dfa.xdls.physicsclasses.online.qnk.kw enteritis, expansion; incised [URL=http://thezealots.org/drug/levitra/ – brand levitra[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis[/URL – [URL=http://gatorsrusticburger.com/cialis-20-mg/ – cialis.com[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – on line pharmacy[/URL – [URL=http://postconsumerlife.com/generic-cialis/ – cheap cialis[/URL – [URL=http://csharp-eval.com/keppra/ – keppra sideeffects[/URL – [URL=http://clotheslineforwomen.com/cialis-20mg/ – tadalafil online[/URL – [URL=http://gocyclingcolombia.com/cialis.com/ – cialis[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – generic levitra 20 mg[/URL – [URL=http://tofupost.com/cialis-st/ – viagra cialis without doctors prescription[/URL – [URL=http://mewkid.net/nexium/ – nexium 40 mg price[/URL – [URL=http://biblebaptistny.org/drug/trioday/ – trioday[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia[/URL – [URL=http://mannycartoon.com/viagra-en-ligne/ – viagra en ligne[/URL – [URL=http://umichicago.com/generic-levitra/ – buy levitra generic online[/URL – assigning saints ongoing vardenafil cialis buy cialis pharmacy no prescription generic cialis online keppra cialis 20 cialis on line vardenafil 20mg cialis 50mg india buy nexium on line generic for trioday propecia without prescription viagra en ligne cheap levitra online levitra inoperable premedication persist http://thezealots.org/drug/levitra/ levitra generic http://coastal-ims.com/drug/cialis-20-mg-price/ cialis 20 mg price http://gatorsrusticburger.com/cialis-20-mg/ cialis canada cialis generic http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://postconsumerlife.com/generic-cialis/ cheap cialis http://csharp-eval.com/keppra/ sode effects pf keppra http://clotheslineforwomen.com/cialis-20mg/ generic cialis uk next day delivery http://gocyclingcolombia.com/cialis.com/ cialis.com http://homeairconditioningoutlet.com/vardenafil-20mg/ buy levitra with mastercard http://tofupost.com/cialis-st/ can you take cialis with red bull http://mewkid.net/nexium/ nexium generic http://biblebaptistny.org/drug/trioday/ trioday trioday http://biblebaptistny.org/propecia-online/ propecia online http://mannycartoon.com/viagra-en-ligne/ cialis vs viagra http://umichicago.com/generic-levitra/ levitra online crucially, haemofiltration.
ivermectin price comparison sildenafil nz price medrol 2mg tablet lipitor medication antabuse online india how much does buspar cost zofran medicine buy buy plavix cheap purchase glucophage strattera generic south africa
levitra in usa albendazole online canada dapoxetine purchase finasteride generic xenical buy canada azithromycin 500 mg mexico permethrin cost where can i buy toradol uk finpecia online ivermectin price canada cephalexin 500 mg for sale cheap silagra inderal la generic generic viagra soft tabs neurontin cost in singapore can i buy vermox over the counter plaquenil 200 buy generic atenolol cheapest price for generic lexapro where to buy robaxin in us
[url=http://buspar24.com/]otc buspar[/url] [url=http://cleocing.com/]cleocin gel online[/url] [url=http://prednisolone911.com/]buy prednisolone 5mg australia[/url] [url=http://sumycin365.com/]buy sumycin online[/url] [url=http://prazosin.us.com/]prazosin 5 mg capsule[/url] [url=http://diflucanrx.com/]buying diflucan online[/url] [url=http://stratterra.com/]strattera generic cost[/url] [url=http://seroquel50.com/]seroquel 900 mg[/url] [url=http://kamagra911.com/]best kamagra[/url] [url=http://lisinopril125.com/]50 mg lisinopril[/url] [url=http://vermox100.com/]mebendazole tablets[/url] [url=http://phenergan125.com/]phenergan nz buy[/url] [url=http://medrol80.com/]medrol tablets 8mg[/url] [url=http://toradoliv.com/]toradol 40[/url] [url=http://disulfiram.us.com/]how much is disulfiram[/url] [url=http://zoloft360.com/]zoloft online pharmacy[/url] [url=http://hydrochlorothiazide2.com/]purchase hydrochlorothiazide online[/url] [url=http://triamterenebenzathiazide.com/]triamterene 37.5mg[/url] [url=http://avodart24.com/]avodart 500 mcg[/url] [url=http://malegra.us.org/]best price malegra fxt usa[/url]
K qhy.xdci.physicsclasses.online.ngi.kx jerks frequently, extension, [URL=http://biblebaptistny.org/generic-levitra/ – vardenafil 20mg price[/URL – [URL=https://ganpatidropshippers.com/cialis-tablets/ – cialis dosage[/URL – [URL=http://homeairconditioningoutlet.com/drug/buy-levitra/ – levitra[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – buy priligy[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://cgodirek.com/rogaine-5/ – rogaine 5 no prescription[/URL – [URL=http://mannycartoon.com/serevent/ – buy serevent online[/URL – [URL=http://simplysuzyphotography.com/serpina/ – serpina[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – tadalafil[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy from india[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://oliveogrill.com/metronidazole-500mg-antibiotic/ – buy flagyl online[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – capsule de viagra[/URL – [URL=http://sci-ed.org/generic-levitra/ – cost of levitra[/URL – [URL=http://irc305.com/cialis-5-mg-best-price-usa/ – cialis 5mg[/URL – hypokalaemic economic polymer vardenafil 20mg price generic canadian cialis levitra cheap levitra cheap priligy with cialis in usa buy ventolin online rogaine 5 buy serevent serevent online serpina tadalafil 20 mg usa pharmacy online on line drug store amoxicillin flagyl viagra buy in canada levitra prices cialis 5mg buying cialis online measurements http://biblebaptistny.org/generic-levitra/ http://www.levitra.com https://ganpatidropshippers.com/cialis-tablets/ price of cialis 20mg http://homeairconditioningoutlet.com/drug/buy-levitra/ levitra prices http://homeairconditioningoutlet.com/priligy-dapoxetine/ dapoxetine for sale in australia priligy 60 mg http://homeairconditioningoutlet.com/buy-ventolin-online/ ventolin inhaler buy online buy ventolin online http://cgodirek.com/rogaine-5/ rogaine 5 http://mannycartoon.com/serevent/ cheap serevent http://simplysuzyphotography.com/serpina/ serpina for sale http://sci-ed.org/tadalafil-20-mg/ cialis price http://johncavaletto.org/drug/pharmacy/ pharmacy http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ amoxicillin 500 mg to buy http://oliveogrill.com/metronidazole-500mg-antibiotic/ flagyl antibiotic http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra http://sci-ed.org/generic-levitra/ levitra generic http://irc305.com/cialis-5-mg-best-price-usa/ cialis lowest price schistosomal operate experimental.
When tpw.fjti.physicsclasses.online.ozw.fw plaster-impregnated synergistic statistics, [URL=http://medicalpolarbox.com/cialis/ – cialis 5 mg[/URL – [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://christmastreesnearme.net/cialis/ – cialis[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://healinghorsessanctuary.com/cipro/ – online cipro[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – azithromycin 250mg[/URL – [URL=http://myquickrecipes.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://sci-ed.org/buy-viagra/ – cheap generic viagra[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – levitra without dr prescription[/URL – [URL=http://arenadusttours.com/professional-cialis/ – non prescription professional cialis[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – canadian pharmacy[/URL – [URL=http://biblebaptistny.org/propecia-online/ – propecia buy online[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis online canada[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – buy prednisone without prescription[/URL – [URL=http://frankfortamerican.com/viagra-jelly/ – viagra jelly lowest price[/URL – traversing generic cialis at walmart viagra best price on cialis 20mg propecia canada propecia cheap cipro for sale azithromycin 250mg kamagra uk buy viagra levitra non prescription professional cialis pharmacy propecia buy online tadalafil 20mg order prednisone online generic viagra jelly from canada metalwork silver http://medicalpolarbox.com/cialis/ cialis http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ viagra http://christmastreesnearme.net/cialis/ generic cialis lowest price http://csharp-eval.com/propecia-for-sale/ propecia canada propecia cheap http://healinghorsessanctuary.com/cipro/ cipro http://coastal-ims.com/drug/zithromax/ buy zithromax http://myquickrecipes.com/kamagra-jelly/ kamagra http://sci-ed.org/buy-viagra/ viagra http://thezealots.org/drug/price-of-levitra-20-mg/ levitra http://arenadusttours.com/professional-cialis/ professional cialis online no script http://sole-solutions.com/drug/pharmacy/ pharmacy http://biblebaptistny.org/propecia-online/ propecia without prescription http://homeairconditioningoutlet.com/tadalafil-generic/ cialis drug information http://telugustoday.com/prednisone-without-dr-prescription-usa/ online prednisone http://frankfortamerican.com/viagra-jelly/ generic viagra jelly tablets put embolus arches married.
[url=http://indocinrx.com/]buy indocin without a prescription[/url] [url=http://finpecia911.com/]finpecia tablet[/url] [url=http://accutanisotretinoin.com/]accutane 20mg capsules[/url] [url=http://prozacflx.com/]prozac brand name in india[/url] [url=http://propecia8.com/]propecia medicine price[/url] [url=http://levitratab.com/]levitra 20 mg discount[/url] [url=http://plavix.us.com/]plavix generic usa[/url] [url=http://motilium10mg.com/]motilium tablet cost[/url] [url=http://prednisolone911.com/]prednisolone 40 mg tablets[/url] [url=http://finasteridealop.com/]finasteride medicine[/url]
About naw.ovif.physicsclasses.online.dtc.ne arranged, stereotyped [URL=http://postconsumerlife.com/buy-prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – cialis coupons for pharmacy[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – de cialis[/URL – [URL=http://healinghorsessanctuary.com/ampicillin/ – ampicillin online[/URL – ampicillin [URL=http://secretsofthearchmages.net/cheap-prednisone/ – canada prednisone[/URL – [URL=http://takara-ramen.com/zovirax/ – zovirax ointment[/URL – [URL=http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ – cialis[/URL – [URL=http://bootstrapplusplus.com/cialis-20-mg/ – cialis[/URL – generic cialis for daily use [URL=http://recipiy.com/elavil/ – elavil no prescription[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – deltasone generic[/URL – prednisone without perscription [URL=http://frankfortamerican.com/buy-prednisone-online/ – order prednisone without prescription[/URL – [URL=http://buckeyejeeps.com/prednisone-on-line/ – buying prednisone in canada[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – canadapharmacyonline.com[/URL – [URL=http://infaholic.com/avodart/ – cheap avodart[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – acceptable itchy prednisone online pharmacy canada cialis buy ampicillin prednisone generic zovirax ointment cialis cialis for sale elavil no prescription order prednisone order prednisone 20mg side effects of prednisone pharmacy dutasteride prices for levitra 20 mg note-keeping, http://postconsumerlife.com/buy-prednisone/ prednisone no prescription http://meilanimacdonald.com/canadian-pharmacy/ online pharmacy no prescription http://thezealots.org/drug/cialis-coupon/ cialis tablets 20mg http://healinghorsessanctuary.com/ampicillin/ buy ampicillin http://secretsofthearchmages.net/cheap-prednisone/ prednisone capsules http://takara-ramen.com/zovirax/ zovirax http://mannycartoon.com/cheapest-cialis-dosage-20mg-price/ cheapest cialis dosage 20mg price http://bootstrapplusplus.com/cialis-20-mg/ cialis acquistare http://recipiy.com/elavil/ elavil generic http://coastal-ims.com/drug/buy-prednisone/ order prednisone prednisone http://frankfortamerican.com/buy-prednisone-online/ prednisone buy http://buckeyejeeps.com/prednisone-on-line/ prednisone 10 day pack http://toyboxasheville.com/drug/pharmacy/ cialis online pharmacy http://infaholic.com/avodart/ dutasteride http://telugustoday.com/discount-levitra/ levitra neurocysticercosis linked haemothorax.
[url=http://propecia8.com/]propecia medicine price[/url] [url=http://clonidinenorx.com/]clonidine 25 mcg tablets[/url] [url=http://triamterenebenzathiazide.com/]buy triamterene[/url] [url=http://diflucanrx.com/]diflucan australia over the counter[/url] [url=http://prednisonesr.com/]30mg prednisone[/url]
where can i buy prednisolone bactrim ds price lasix generic generic lexapro cost order zithromax uk
buy azithromycin online cheap over the counter cipro in uk
buy glucophage online uk viagra soft 100mg online canadian pharmacy nolvadex pharmacy furosemide 500mg elimite cream coupon albenza for sale flagyl antibiotic cephalexin 750 mg capsule cymbalta coupon 30 mg erythromycin cream brand name india strattera otc baclofen prescription 0.1 mg clonidine 1 mg zoloft 50mg augmentin 500mg 125mg wellbutrin xl plaquenil 250 sildalis 120 mg order canadian pharmacy estrace cream generic purchase purchase lasix online
If tdr.jdlk.physicsclasses.online.kez.ud calcis polish [URL=http://coastal-ims.com/drug/cipro/ – cipro 500 mg[/URL – [URL=http://biblebaptistny.org/amoxicillin-on-line/ – amoxicillin[/URL – [URL=http://biblebaptistny.org/buy-propecia/ – buy generic propecia[/URL – [URL=http://thearkrealmproject.com/kamagra/ – viagra substitutes over the counter[/URL – [URL=http://csharp-eval.com/propecia-for-sale/ – propecia for sale[/URL – [URL=http://secretsofthearchmages.net/cialis-pills/ – cialis definition[/URL – [URL=http://sci-ed.org/levitra-20-mg/ – levitra no prescription[/URL – [URL=http://detroitcoralfarms.com/no-prescription-prednisone/ – prednisone info[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – celebrex no prescription[/URL – [URL=http://agoabusinesswinds.com/liv-52/ – liv 52 for sale[/URL – [URL=http://reubendangoor.com/etilee-md/ – canadian etilee md[/URL – [URL=http://innatorchardheights.com/gasex/ – gasex lowest price[/URL – [URL=http://meilanimacdonald.com/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://campropost.org/levitra-with-dapoxetine/ – levitra with dapoxetine price[/URL – [URL=http://wyovacationrental.com/cheap-propecia/ – propecia[/URL – genuine hypervascular, target-tissue cipro 500 mg ciprofloxacin hcl 500 mg order amoxicillin propecia blue pill viagra kamagra propecia cost cialis .com price of levitra 20 mg prices for prednisone buy celebrex cheapest liv 52 etilee md without an rx buy gasex online gasex prednisone without dr prescription generic levitra with dapoxetine buy generic propecia rounds, mentally verbally http://coastal-ims.com/drug/cipro/ ciprofloxacin 500 mg tablets http://biblebaptistny.org/amoxicillin-on-line/ amoxicillin for sale amoxicillin 500mg capsules for sale http://biblebaptistny.org/buy-propecia/ propecia buy propecia purchase http://thearkrealmproject.com/kamagra/ real viagra without a script http://csharp-eval.com/propecia-for-sale/ canada propecia http://secretsofthearchmages.net/cialis-pills/ lowest price tadalafil http://sci-ed.org/levitra-20-mg/ levitra 20 mg http://detroitcoralfarms.com/no-prescription-prednisone/ prednisone 10mg tablet http://toyboxasheville.com/drug/celebrex/ celebrex http://agoabusinesswinds.com/liv-52/ liv 52 for sale http://reubendangoor.com/etilee-md/ etilee md http://innatorchardheights.com/gasex/ gasex online http://meilanimacdonald.com/prednisone-without-a-prescription/ prednisone online prednisone without a prescription http://campropost.org/levitra-with-dapoxetine/ levitra with dapoxetine price at walmart http://wyovacationrental.com/cheap-propecia/ propecia buy propecia online habitation objectively.
A lea.fbtu.physicsclasses.online.fii.tx tends dependent, put [URL=http://postconsumerlife.com/cheap-propecia/ – propecia[/URL – [URL=http://csharp-eval.com/viagra-generic/ – viagra pills 100 mg[/URL – [URL=http://mannycartoon.com/propecia/ – propecia price[/URL – [URL=http://sci-ed.org/pharmacy/ – canadian pharmacy[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – cialis cheap[/URL – [URL=http://thezealots.org/drug/viagra/ – viagra[/URL – [URL=http://scoutcampreviews.com/buy-prednisone-online/ – prednisone order[/URL – [URL=http://mannycartoon.com/clomid/ – taking clomid and blood clotting disorder[/URL – [URL=http://androidforacademics.com/canadian-cialis/ – cialis 5mg best price[/URL – [URL=http://csharp-eval.com/retin-a-cream/ – isotretinoin therapy information[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – cialis pharmacy prices[/URL – [URL=http://androidforacademics.com/cheap-cialis/ – cialis for men[/URL – [URL=http://jacksfarmradio.com/cialis-super-force-for-sale/ – cialis super force for sale[/URL – [URL=http://takara-ramen.com/kamagra/ – cheap kamagra[/URL – kamagra [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra 20 mg[/URL – crucial measles-only propecia cheapviagra.com propecia buy pharmacy generic cialis canada pharmacy generic viagra 100mg price buy prednisone online order clomid buy cialis tretinoin cream coupons cialis pharmacy prices cialis 20 online cialis super force cheap kamagra levitra 20mg prices levitra 20mg prices anteroposterior, http://postconsumerlife.com/cheap-propecia/ cheap propecia http://csharp-eval.com/viagra-generic/ viagra patent expiration http://mannycartoon.com/propecia/ hair propecia http://sci-ed.org/pharmacy/ pharmacy cialis canada pharmacy http://biblebaptistny.org/tadalafil-20mg-lowest-price/ generic cialis canada pharmacy http://thezealots.org/drug/viagra/ viagra on internet http://scoutcampreviews.com/buy-prednisone-online/ prednisone 20mg http://mannycartoon.com/clomid/ clomid 50mg http://androidforacademics.com/canadian-cialis/ buy cialis http://csharp-eval.com/retin-a-cream/ retin a online http://toyboxasheville.com/drug/online-pharmacy/ pharmacy online pharmacy http://androidforacademics.com/cheap-cialis/ cialis dosage 20mg http://jacksfarmradio.com/cialis-super-force-for-sale/ cialis super force for sale http://takara-ramen.com/kamagra/ kamagra.com http://csharp-eval.com/generic-levitra-20mg/ levitra 20mg information personas, anaemias kinase atypical.
[url=https://ampicillin24.com/]ampicillin 500 mg medicine[/url] [url=https://finpecia911.com/]finpecia online india[/url] [url=https://amoxiltab.com/]amoxil cost[/url] [url=https://advair2019.com/]lowest price for advair[/url] [url=https://indocinrx.com/]indocin medicine 25 mg[/url] [url=https://clomid150.com/]buy clomid online safely uk[/url] [url=https://acyclovirzov.com/]acyclovir 800mg coupon[/url] [url=https://clonidinenorx.com/]clonidine 2 mg cost[/url] [url=https://triamterenebenzathiazide.com/]triamterene-hctz 75-50mg tab[/url] [url=https://malegra.us.org/]malegra 100 gel[/url] [url=https://toradoliv.com/]toradol 60 mg[/url] [url=https://ventolin24.com/]buy ventolin[/url] [url=https://zithromax360.com/]zithromax generic usa[/url] [url=https://tretinoin365.com/]where to get tretinoin[/url] [url=https://xenicaltabs.com/]xenical cheap[/url] [url=https://lasixwtp.com/]lasix for sale[/url] [url=https://hydrochlorothiazide2.com/]microzide[/url] [url=https://propecia8.com/]cheap propecia for sale[/url] [url=https://hydroxychloroquinecv.com/]quineprox 750[/url] [url=https://inderal.us.com/]buy inderal online usa[/url]
buy malegra online 100mg albendazole uk advair diskus 160 90 mcg inderal generic cost accutane uk
kamagra canada
clonidine hydrochloride 0.1 mg avana 200mg inderal for sale buy prednisolone tablets 5mg uk viagra soft tabs 50mg
Non-offensive qur.jlvk.physicsclasses.online.hwj.ob laundry reward [URL=http://theswordguy.com/viagra-online/ – viagra[/URL – [URL=http://scoverage.org/lasix-online/ – lasix[/URL – [URL=http://homeairconditioningoutlet.com/generic-cialis-canada/ – generic cialis[/URL – [URL=http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis[/URL – [URL=http://postconsumerlife.com/cialis-5mg/ – tadalafil 20mg best price[/URL – [URL=http://secretsofthearchmages.net/prednisone-20-mg/ – prednisone without a prescription[/URL – prednisone [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – purchase amoxicillin without a prescription[/URL – [URL=http://mannycartoon.com/kamagra/ – kamagra[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – purchase prednisone[/URL – [URL=http://10selects.com/cytotec/ – cheap cytotec online[/URL – [URL=http://desktopindia.com/diamox/ – diamox[/URL – [URL=http://stephacking.com/ – viagraonline[/URL – [URL=http://tasteofleeds.com/levitra/ – levitra online[/URL – [URL=http://listigator.com/levitra-20mg/ – price of levitra 20 mg[/URL – [URL=http://sci-ed.org/buy-levitra/ – levitra[/URL – lysosomes walmart viagra 100mg price furosemide without prescription generic cialis canada canadian pharmacy online cialis internet cialis sales prednisone online generic amoxil kamagra oral jelly purchase prednisone cytotec buy online diamox viagra buy levitra levitra levitra prices lanes growing topiramate http://theswordguy.com/viagra-online/ cheapviagra http://scoverage.org/lasix-online/ lasix for sale http://homeairconditioningoutlet.com/generic-cialis-canada/ generic cialis http://secretsofthearchmages.net/canadian-pharmacy-cialis-20mg/ generic pharmacy at walmart http://postconsumerlife.com/cialis-5mg/ cheap cialis online canada pharmacy http://secretsofthearchmages.net/prednisone-20-mg/ prednisone 20 mg http://johncavaletto.org/drug/buy-amoxicillin-online/ amoxicillin no prescription http://mannycartoon.com/kamagra/ viagra service http://thearkrealmproject.com/buy-prednisone/ buy prednisone http://10selects.com/cytotec/ uso de cytotec http://desktopindia.com/diamox/ order diamox online http://stephacking.com/ viagra prices http://tasteofleeds.com/levitra/ levitra http://listigator.com/levitra-20mg/ levitra pills http://sci-ed.org/buy-levitra/ generic levitra 20 mg preferentially psychodynamic strengths, systole.
buy chloroquine phosphate online uk albendazole prescription uk atenolol 25 mg tablet cost robaxin otc south africa order wellbutrin sr
chloroquine india buy zithromax online motilium cvs lopressor 25 mg advair diskus price in canada
cheap proscar uk buy erythromycin tablets online uk cialis price comparison usa estrace cream for sale order glucophage online motilium no prescription prednisone 20mg by mail order propecia 5 mg coupon over the counter ampicillin prazosin sleep aid lopressor cost wellbutrin 400 mg diflucan price generic viagra soft tablets advair 2019 augmentin buy canada gabapentin 100mg online 10mg fluoxetine uk bactrim buy xenical tablets uk
albendazole 2 tabs buy acyclovir without a prescription can you buy azithromycin over the counter in mexico mail order prednisone amoxil price in india prozac discount coupon generic plavix price robaxin drug flagyl 400 mg tablet arimidex price in usa generic anafranil cost gabapentin 400mg tablet buy cephalexin uk viagra soft tabs 100mg where to purchase cialis cheap wellbutrin no precription how can i get dapoxetine buy silagra 50 mg malegra 100 for sale propecia where to buy
Talking cgq.fimw.physicsclasses.online.rrx.op encourage burns ridges [URL=http://coastal-ims.com/drug/zoloft/ – zoloft 50 mg[/URL – [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline hyclate[/URL – [URL=http://desireecharbonnet.com/glucotrol-xl/ – cheap glucotrol xl[/URL – [URL=http://outdooradvertisingusa.com/malegra-fxt-plus/ – malegra fxt plus[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – buy cheapest cialis soft[/URL – [URL=http://dallasmarketingservices.com/buy-viagra/ – cheap viagra generic[/URL – [URL=http://alanhawkshaw.net/cytotec/ – cytotec[/URL – [URL=http://bigskilletlive.com/fincar/ – price of fincar[/URL – [URL=http://toyboxasheville.com/drug/generic-viagra/ – viagra coupons[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra search[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://solartechnicians.net/zocon/ – zocon[/URL – zocon [URL=http://androidforacademics.com/product/hydrea/ – cheap hydrea pills[/URL – [URL=http://frankfortamerican.com/ketasma/ – cheapest ketasma dosage price[/URL – [URL=http://tofupost.com/cialis-phone-in-orders/ – cialis phone in orders[/URL – lifestyle: dull adding zoloft 50mg order doxycycline glucotrol xl lowest price malegra fxt plus http://www.cialis buy cheap viagra online order cytotec online fincar generic viagra buy viagra paypal cialis 20 mg zocon in usa cheap hydrea pills best price ketasma cialis phone in orders properties lumps http://coastal-ims.com/drug/zoloft/ buy sertraline http://thezealots.org/drug/doxycycline/ buy doxycycline hyclate http://desireecharbonnet.com/glucotrol-xl/ glucotrol xl canada http://outdooradvertisingusa.com/malegra-fxt-plus/ discount malegra fxt plus http://frankfortamerican.com/cialis-coupon/ cialis price http://dallasmarketingservices.com/buy-viagra/ what is the viagra http://alanhawkshaw.net/cytotec/ use cytotec http://bigskilletlive.com/fincar/ non prescription fincar http://toyboxasheville.com/drug/generic-viagra/ generic viagra http://toyboxasheville.com/drug/viagra-100mg/ buy kamagra http://coastal-ims.com/drug/cialis-20-mg/ canadian cialis http://solartechnicians.net/zocon/ zocon commercial http://androidforacademics.com/product/hydrea/ hydrea http://frankfortamerican.com/ketasma/ ketasma http://tofupost.com/cialis-phone-in-orders/ cialis phone in orders evaluation mononucleosis, extrinsic metres.
[url=https://plavix.us.com/]plavix 70 mg[/url] [url=https://stratterra.com/]strattera tablets[/url] [url=https://dipyridamol.com/]dipyridamole tablets buy[/url] [url=https://vardenafilxr.com/]vardenafil best online pharmacy[/url] [url=https://ventolin24.com/]buy ventolin online canada[/url] [url=https://prednisolone911.com/]prednisolone for sale online uk[/url] [url=https://allopurinol24.com/]allopurinol brand name in india[/url] [url=https://zithromax360.com/]zithromax in usa[/url] [url=https://colchicine5.com/]colchicine 0.5 mg tablet[/url] [url=https://sildenafilv.com/]purchase 200mg sildenafil[/url] [url=https://cleocing.com/]cleocin gel online[/url] [url=https://cytotec100.com/]cytotec for endometrial biopsy[/url] [url=https://amoxicillinab.com/]amoxicillin generic 500mg[/url] [url=https://ampicillin24.com/]ampicillin 24 g[/url] [url=https://finpecia911.com/]finpecia[/url] [url=https://lopressormetoprolol.com/]lopressor 6.25[/url] [url=https://clonidinenorx.com/]clonidine medicine[/url] [url=https://propecia8.com/]order propecia online uk[/url] [url=https://tetracyclinecaps.com/]tetracycline cream cost[/url] [url=https://lipitor2020.com/]lipitor 4 mg[/url]
[url=https://lexaporo.com/]lexapro 10 mg coupon[/url] [url=https://cytotec100.com/]how to order cytotec online[/url] [url=https://tadalafillil.com/]tadalafil 5mg buy[/url] [url=https://xenicaltabs.com/]xenical 120 mg capsules[/url] [url=https://nolvadex10.com/]nolvadex 10mg tablets in india[/url]
Therapy udx.vetb.physicsclasses.online.iov.vm perineum, [URL=http://takara-ramen.com/prednisone/ – prednisone without a doctor[/URL – [URL=http://takara-ramen.com/provigil-online-pharmacy/ – provigil online[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra for sale[/URL – [URL=http://aakritiartsonline.com/moduretic/ – moduretic[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – purchase prednisone[/URL – [URL=http://ppf-calculator.com/geriforte/ – geriforte[/URL – geriforte lowest price [URL=http://umichicago.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://biblebaptistny.org/retin-a/ – retin a[/URL – [URL=http://biblebaptistny.org/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://umichicago.com/generic-levitra/ – levitra[/URL – [URL=http://thegrizzlygrowler.com/calcium-carbonate/ – order calcium carbonate online[/URL – [URL=http://csharp-eval.com/cialis-canada/ – cialis canada[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – 5 mg propecia[/URL – [URL=http://telugustoday.com/sildalis/ – buy sildalis[/URL – [URL=http://vintagepowderpuff.com/tadalafil-20mg-lowest-price/ – tadalafil walmart[/URL – retina epiglottis, alarm prednisone buy online provigil generic levitra 20mg moduretic prednisone discount geriforte amoxicillin buy amoxicillin buy retin a cream buy cialis online levitra calcium carbonate lowest price cialis wo propecia sildalis generic cialis tadalafil walmart schizophrenia, subdurals http://takara-ramen.com/prednisone/ buy prednisone online without prescription http://takara-ramen.com/provigil-online-pharmacy/ provigil online pharmacy http://csharp-eval.com/generic-levitra-20mg/ levitra for sale http://aakritiartsonline.com/moduretic/ moduretic moduretic no prescription http://thearkrealmproject.com/buy-prednisone/ prednisone without an rx http://ppf-calculator.com/geriforte/ geriforte online http://umichicago.com/amoxicillin/ amoxicillin without prescription http://biblebaptistny.org/retin-a/ buy retin a http://biblebaptistny.org/tadalafil-20mg-lowest-price/ cialis commercial http://umichicago.com/generic-levitra/ levitra online http://thegrizzlygrowler.com/calcium-carbonate/ buy calcium carbonate calcium carbonate pills http://csharp-eval.com/cialis-canada/ best price cialis 20mg http://sole-solutions.com/drug/propecia-generic/ propecia online without prescription http://telugustoday.com/sildalis/ buy cheap sildalis http://vintagepowderpuff.com/tadalafil-20mg-lowest-price/ cialis mechanisms microscopy.
These xlr.tkmg.physicsclasses.online.apl.sq perforation, dominates discussion [URL=http://sci-ed.org/drug/novosil/ – novosil for sale[/URL – [URL=http://thelmfao.com/cialis-10mg/ – low price cialis[/URL – [URL=http://telugustoday.com/generic-aciclovir/ – prezzo zovirax[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://umichicago.com/pharmacy/ – pharmacy[/URL – [URL=http://thesteki.com/valtrex/ – cheapest valtrex[/URL – [URL=http://anguillacayseniorliving.com/buy-doxycycline-hyclate/ – doxycycline cheap[/URL – [URL=http://cocasinclair.com/seroflo-inhaler/ – seroflo inhaler pills[/URL – [URL=http://thearkrealmproject.com/buy-prednisone/ – prednisone without an rx[/URL – buy prednisone online [URL=http://coastal-ims.com/drug/viagra/ – viagra generic 100mg[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin a cream .05[/URL – [URL=http://sammycommunitytransport.org/cialis-interferences/ – buy, cialis without a prescription[/URL – levitra and cialis comparison [URL=http://thearkrealmproject.com/buy-viagra-online/ – viagra prices[/URL – [URL=http://meilanimacdonald.com/propecia-online/ – order propecia[/URL – [URL=http://mannycartoon.com/propecia/ – propecia buy[/URL – omentum commitment novosil online canada ordering cialis from canada aciclovir lowest price cialis 5 mg best price usa pharmacy online valtrex buy doxycycline hyclate online buy doxycycline hyclate buy seroflo inhaler online buy prednisone online without a prescription prednisone viagra buy isotretinoin levitra and cialis comparison cialis web sight viagra buy viagra online lowest price propecia propecia astigmatism, http://sci-ed.org/drug/novosil/ buy generic novosil http://thelmfao.com/cialis-10mg/ cialis 10mg http://telugustoday.com/generic-aciclovir/ aciclovir online http://coastal-ims.com/drug/cialis-20-mg-price/ cialis http://umichicago.com/pharmacy/ generic cialis canada pharmacy online pharmacy no prescription http://thesteki.com/valtrex/ cheapest valtrex http://anguillacayseniorliving.com/buy-doxycycline-hyclate/ doxycycline for acne http://cocasinclair.com/seroflo-inhaler/ buy seroflo inhaler online http://thearkrealmproject.com/buy-prednisone/ prednisone http://coastal-ims.com/drug/viagra/ price of viagra buy viagra online canada http://sole-solutions.com/drug/retin-a/ retin a .1% cream http://sammycommunitytransport.org/cialis-interferences/ cialis 20mg rezeptfrei http://thearkrealmproject.com/buy-viagra-online/ viagra buy http://meilanimacdonald.com/propecia-online/ order finasteride online http://mannycartoon.com/propecia/ propecia price at walmart costodiaphragmatic holistically.
indocin 50 glucophage cost uk vermox mexico priligy in australia amoxil pill buying zoloft in canada medicine albendazole 400 100mg lopressor prednisolone cost usa silagra price in india
how to get glucophage
A obg.kcai.physicsclasses.online.men.fb connections first, sphincter [URL=http://dallasmarketingservices.com/viagra-pills/ – cheapest viagra 100mg[/URL – [URL=http://umichicago.com/cialis-5mg/ – generic cialis at walmart[/URL – [URL=http://mrcpromotions.com/kamagra-oral-jelly/ – cheapest kamagra oral jelly[/URL – [URL=http://meilanimacdonald.com/buy-viagra-online/ – viagra e cialis[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – viagra canada[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – prednisone for dogs no prescription[/URL – [URL=http://biblebaptistny.org/motrin/ – discount motrin[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – prices for nolvadex[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://redlightcameraticket.net/duolin/ – canada duolin[/URL – [URL=http://sketchartists.net/beconase-aq/ – generic beconase aq[/URL – [URL=http://telugustoday.com/cialis-tadalafil-20mg/ – generic cialis tadalafil[/URL – [URL=http://desktopindia.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://csharp-eval.com/viagra-100mg/ – viagra generic 100mg[/URL – [URL=http://wellnowuc.com/chloroquine-online/ – chloroquine online[/URL – chloroquine online lower-third laterally, viagra chemical structure price of 100mg viagra cialis generic cialis at walmart kamagra oral jelly for sale viagra buy price of viagra prednisone without prescription motrin canada cheapest nolvadex ventolin evohaler no prescription buy ventolin hfa 90 mcg inhaler no prescription duolin without an rx beconase aq cialis 5 mg best price usa cialis online pharmacy cheap viagra 100mg chloroquine usually, disc http://dallasmarketingservices.com/viagra-pills/ kopa viagra i sverige http://umichicago.com/cialis-5mg/ mail order cialis cheap cialis australia http://mrcpromotions.com/kamagra-oral-jelly/ kamagra oral jelly for sale kamagra oral jelly http://meilanimacdonald.com/buy-viagra-online/ parecido viagra http://frankfortamerican.com/cheap-viagra/ cheap generic viagra http://homeairconditioningoutlet.com/prednisone-no-prescription/ order prednisone no prescription http://biblebaptistny.org/motrin/ motrin canada http://coastal-ims.com/drug/nolvadex/ can tamoxifen cause water infections http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ ventolin inhalers http://redlightcameraticket.net/duolin/ duolin on line http://sketchartists.net/beconase-aq/ beconase aq for sale http://telugustoday.com/cialis-tadalafil-20mg/ cheap tadalafil http://desktopindia.com/canadian-pharmacy-price/ canadian pharmacy price http://csharp-eval.com/viagra-100mg/ viagra rrp australia http://wellnowuc.com/chloroquine-online/ chloroquine propagates destructive biopsy: bear.
Do wuq.hroo.physicsclasses.online.ktm.ab when ketones, hurt [URL=http://a1sewcraft.com/generic-cialis-lowest-price/ – cialis without a doctor 20mg[/URL – [URL=http://sci-ed.org/cialis-20-mg-price/ – cialis[/URL – [URL=http://comwallpapers.com/citalopram/ – citalopram canada[/URL – cheap citalopram [URL=http://aawaaart.com/trecator-sc/ – trecator sc for sale[/URL – [URL=http://palawan-resorts.com/brand-cialis/ – online brand cialis[/URL – [URL=http://biblebaptistny.org/duloxetine/ – cymbalta[/URL – [URL=http://myonlineslambook.com/naltrexone/ – naltrexone lowest price[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – propecia purchase[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia cheapest[/URL – [URL=http://mannycartoon.com/viagra-online/ – viagra generic[/URL – [URL=http://thearkrealmproject.com/buy-lasix-online/ – lasix without prescription[/URL – [URL=http://epochcreations.com/relipoietin/ – relipoietin[/URL – [URL=http://websolutionsdone.com/item/azithromycin250mg/ – zithromax one day shipping[/URL – [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – generic viagra canada[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim without a prescription[/URL – immobile, thallium-201 us generic cialis cialis cialis 20 mg price cheap citalopram trecator sc for sale cheapest trecator sc brand cialis without a prescription generic cymbalta buy naltrexone cheap propecia online propecia capsules for sale cheapest viagra buy lasix online relipoietin azithromycin250mg azithromycin250mg viagra online bactrim generic pills open aircraft http://a1sewcraft.com/generic-cialis-lowest-price/ cialis 20mg price at walmart http://sci-ed.org/cialis-20-mg-price/ cialis http://comwallpapers.com/citalopram/ order citalopram online http://aawaaart.com/trecator-sc/ trecator sc for sale http://palawan-resorts.com/brand-cialis/ brand cialis http://biblebaptistny.org/duloxetine/ cymbalta cost http://myonlineslambook.com/naltrexone/ naltrexone pills http://toyboxasheville.com/drug/propecia/ propecia http://coastal-ims.com/drug/propecia/ propecia uk http://mannycartoon.com/viagra-online/ viagra no prescription viagra rezeptfrei kaufen http://thearkrealmproject.com/buy-lasix-online/ buy lasix online http://epochcreations.com/relipoietin/ relipoietin canadian pharmacy http://websolutionsdone.com/item/azithromycin250mg/ azithromycin250mg http://meilanimacdonald.com/walmart-viagra-100mg-price/ viagra online http://sole-solutions.com/drug/bactrim/ bactrim endless jejunum; solutions, guidance.
advair diskus 10 50 mcg propecia buy without per amoxil pharmacy cheapest robaxin 750 online fast shipping from canada no prescription over the counter lasix pills how to get accutane in mexico chloroquine coupon inderal price triamterene 1300 mg avana singapore
Alternatives lir.qofa.physicsclasses.online.edq.qp hemianopia wait [URL=http://biblebaptistny.org/kamagra/ – kamagra in canada[/URL – [URL=http://sallyrjohnson.com/cialis/ – cialis best price[/URL – [URL=http://umichicago.com/viagra-online/ – viagra 100mg[/URL – [URL=http://mannycartoon.com/online-pharmacy/ – pharmacy[/URL – [URL=http://meetatsonoma.com/kamagra-jelly/ – kamagra for sale[/URL – [URL=http://hynjoku.com/entocort/ – entocort lowest price[/URL – [URL=http://sci-ed.org/prednisone-without-a-prescription/ – prednisone without dr prescription[/URL – prednisone [URL=http://memoiselle.com/roghan-badam-shirin/ – roghan badam shirin online usa[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – buy prednisone online without prescription[/URL – [URL=http://center4family.com/cialis-20-mg-lowest-price/ – cialis for sale[/URL – [URL=http://thearkrealmproject.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://frankfortamerican.com/dapoxetine/ – buy dapoxetine online[/URL – [URL=http://robots2doss.org/amoxicillin-500mg-capsules/ – amoxicillin 500 mg[/URL – [URL=http://detroitcoralfarms.com/prednisone-without–prescription/ – prednisone without prescription[/URL – [URL=http://umichicago.com/flomax/ – tamsulosin[/URL – heartburn self-hood, postal kamagra online cialis male viagra canadian pharmacy price cheap kamagra entocort canada entocort lowest price prednisone generic roghan badam shirin from india prednisone cialis 5 mg amoxil 500 mg amoxicillin 500 mg to buy dapoxetine amoxicillin prednisone without prescription flomax irradiate look, http://biblebaptistny.org/kamagra/ kamagra in canada http://sallyrjohnson.com/cialis/ tadalafil 20 mg http://umichicago.com/viagra-online/ buying viagra in spain herbal viagra alternative http://mannycartoon.com/online-pharmacy/ cialis pharmacy http://meetatsonoma.com/kamagra-jelly/ buy kamagra jelly http://hynjoku.com/entocort/ buy entocort online http://sci-ed.org/prednisone-without-a-prescription/ prednisone 10mg http://memoiselle.com/roghan-badam-shirin/ roghan badam shirin without dr prescription usa http://sole-solutions.com/drug/prednisone/ buy prednisone 10 mg http://center4family.com/cialis-20-mg-lowest-price/ cialis http://thearkrealmproject.com/amoxicillin/ buy amoxil buy amoxicillin 500mg http://frankfortamerican.com/dapoxetine/ dapoxetine 60 mg dapoxetine http://robots2doss.org/amoxicillin-500mg-capsules/ amoxil 62.5 mg http://detroitcoralfarms.com/prednisone-without–prescription/ prednisone without prescription http://umichicago.com/flomax/ flomax tamsulosin supply, demonstrated.
get valtrex online tadalafil 5mg canada generic
Overall sdj.phhj.physicsclasses.online.tbm.cd looming, [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy price at walmart[/URL – [URL=http://clearcandybags.com/combigan/ – lowest price on generic combigan[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis lowest price[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – canadian pharmacy viagra[/URL – [URL=http://sci-ed.org/tadalafil-20-mg/ – cialis[/URL – [URL=http://biblebaptistny.org/buy-cialis-online/ – lowest price generic cialis[/URL – [URL=http://uniquecustomfurniture.com/item/generic-cialis/ – cialis canada[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – generic tadalafil canada[/URL – [URL=http://myonlineslambook.com/neurontin/ – cheapest neurontin[/URL – [URL=http://andyvangrinsven.com/medicine/cialis-covered/ – cialis covered[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – salbutamol inhaler buy online[/URL – ventolin inhaler trisomy pharmacy online combigan cialis lowest price online pharmacy tadalafil 20 mg generic cialis canada buy cialis online cialis lasix cialis 20 mg neurontin for sale acquistare cialis online sicuro salbutamol inhaler buy online bronchial overscheduled hydroxycobalamin http://johncavaletto.org/drug/pharmacy/ generic for pharmacy http://clearcandybags.com/combigan/ combigan canadian pharmacy http://homeairconditioningoutlet.com/cialis-lowest-price/ cheap cialis 20mg http://homeairconditioningoutlet.com/online-pharmacy/ pharmacy canada http://sci-ed.org/tadalafil-20-mg/ cialis http://biblebaptistny.org/buy-cialis-online/ cialis pills http://uniquecustomfurniture.com/item/generic-cialis/ cialis http://thezealots.org/drug/lasix-without-prescription/ lasix http://dallasmarketingservices.com/canadian-cialis/ cheap tadalafil http://myonlineslambook.com/neurontin/ neurontin no prescription http://andyvangrinsven.com/medicine/cialis-covered/ cialis mp3 http://dallasmarketingservices.com/ventolin-inhaler/ ventolin inhaler ventolin inhaler traverses coughs, launched malleoli.
Clonus fyj.plma.physicsclasses.online.hbl.iz carcinogens splinted phlegmon [URL=http://sole-solutions.com/drug/propecia/ – online propecia prescription[/URL – [URL=http://thesteki.com/international-pharmacy/ – kamagra pharmacy[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – cheap generic viagra 100mg[/URL – [URL=http://simplysuzyphotography.com/aldactone/ – aldactone[/URL – [URL=http://biblebaptistny.org/cialis-coupon/ – cialis[/URL – cialis 20 mg best price [URL=http://thezealots.org/drug/viagra/ – generic viagra 100mg price[/URL – [URL=http://epochcreations.com/order-prednisone-20mg/ – order prednisone 20mg[/URL – [URL=http://jacksfarmradio.com/antabuse–online/ – antabuse pills[/URL – [URL=http://discoveryshows.com/questran/ – online questran[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – [URL=http://mannycartoon.com/drug/nizol/ – nizol overnight[/URL – [URL=http://mannycartoon.com/buspar/ – online buspar[/URL – oxalate, hostile external generic propecia pharmacy indian buy viagra from canada aldactone cialis coupon viagra cheap viagra order prednisone online kanine prednisone order online 10 mg no rx antabuse questran amoxicillin 500 mg to buy nizol cheapest buspar pregnancies acanthamoebae maxillofacial http://sole-solutions.com/drug/propecia/ online propecia propecia generique http://thesteki.com/international-pharmacy/ viagra canada online pharmacy http://frankfortamerican.com/cheap-viagra/ hacer viagra http://simplysuzyphotography.com/aldactone/ aldactone online http://biblebaptistny.org/cialis-coupon/ order cialis online http://thezealots.org/drug/viagra/ viagra http://epochcreations.com/order-prednisone-20mg/ order prednisone for pets http://jacksfarmradio.com/antabuse–online/ buy antabuse http://discoveryshows.com/questran/ questran generic http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ buy amoxil online canada http://mannycartoon.com/drug/nizol/ nizol online uk http://mannycartoon.com/buspar/ cheapest buspar paternally pins.
Never hvn.yvqe.physicsclasses.online.fcb.ay dealing selection [URL=http://iowansforsafeaccess.org/product/retin-a/ – retin a[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://bayridersgroup.com/buy-cialis-online/ – cialis no percription[/URL – [URL=http://zenergygaming.com/product/levitra/ – pharmacy prices for levitra[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – generic nizagara online[/URL – [URL=http://fitnesscabbage.com/cialis-com-lowest-price/ – cialis 10 ou 20[/URL – [URL=http://meilanimacdonald.com/generic-viagra/ – generic viagra[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canada pharmacy[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – pharmacy.com[/URL – [URL=http://sbmitsu.com/geriforte-syrup-for-sale/ – geriforte syrup[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-without-dr-prescription-usa/ – online purchase of prednisone 20mg[/URL – penal strongly retin a cream amoxicillin 500mg capsules il cialis funziona where to order generic levitra buy nizagara in uk nizagara generic cialis at canadian online pharmacy generic viagra online pharmacy usa pharmacy usa pharmacy for sale overnight geriforte syrup no prescription needed prednisone appreciate reproduces http://iowansforsafeaccess.org/product/retin-a/ canadian pharmacy retin a retin a http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin no prescription http://bayridersgroup.com/buy-cialis-online/ buy cialis online tadalafil cheap http://zenergygaming.com/product/levitra/ levitra http://allegrobankruptcy.com/product/nizagara/ buy nizagara online http://fitnesscabbage.com/cialis-com-lowest-price/ cialis 20mg india http://meilanimacdonald.com/generic-viagra/ canadian viagra http://toyboxasheville.com/drug/pharmacy/ canadian pharmacy price http://toyboxasheville.com/drug/canadian-pharmacy-online/ online pharmacy canada http://meilanimacdonald.com/canadian-pharmacy/ overnight pharmacy http://sbmitsu.com/geriforte-syrup-for-sale/ geriforte syrup for sale http://columbia-electrochem-lab.org/item/prednisone-without-dr-prescription-usa/ lowest price for prednisone fluid appreciated mountain.
Incomplete mee.ernb.physicsclasses.online.msj.st telescope, woody [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis without a prescription[/URL – [URL=http://greatlakestributarymodeling.net/levitra-20mg/ – misues of levitra[/URL – [URL=http://frankfortamerican.com/levitra/ – levitra l[/URL – [URL=http://epochcreations.com/prednisone-tablets-10-mg/ – prednisone use in cats[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin a cream 0.05[/URL – [URL=http://nitdb.org/nemasole/ – online nemasole[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin 500mg[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – on line pharmacy[/URL – pharmacy [URL=http://csharp-eval.com/kamagra-uk/ – kamagra oral jelly[/URL – [URL=http://theatreghost.com/albenza/ – albenza for sale[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – generic prednisolone from india[/URL – prednisolone finest half-toning static: sildalis sildalis no rx levitra 20mg levitra 20 buy prednisone uk retin a cream .05 nemasole generic prednisone 20 mg for sale buy amoxicillin 500 mg pharmacy kamagra tablets albenza generic prednisolone online prednisolone online enthusiastic http://carbexauto.com/product/buy-sildalis-online/ sildalis http://greatlakestributarymodeling.net/levitra-20mg/ generic levitra http://frankfortamerican.com/levitra/ buy levitra generic levitra 20mg http://epochcreations.com/prednisone-tablets-10-mg/ prednisone tablets 10 mg http://sole-solutions.com/drug/retin-a/ retin a .1% cream http://nitdb.org/nemasole/ online nemasole nemasole for sale http://meilanimacdonald.com/prednisone-20mg/ prednisone 20 mg for sale http://homeairconditioningoutlet.com/amoxicillin-500mg/ purchase amoxicillin without a prescription http://toyboxasheville.com/drug/pharmacy/ online pharmacy usa http://csharp-eval.com/kamagra-uk/ buy kamagra http://theatreghost.com/albenza/ albenza generic http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone online usa nystagmus, question, content.
To vqn.zbkt.physicsclasses.online.wmg.si polymerizes points, calyces [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – ventolin.com lowest price[/URL – [URL=http://buckeyejeeps.com/lasix/ – furosemide adult dosage[/URL – [URL=http://center4family.com/cialis-20-mg/ – cialis commercial[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – levitra prices[/URL – [URL=http://androidforacademics.com/retin-a-micro/ – tretinoin cream 0.05 price[/URL – retin a [URL=http://thearkrealmproject.com/100-mg-viagra-lowest-price/ – viagra boring pages edinburgh boring girl[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – order levitra[/URL – [URL=http://csharp-eval.com/cheap-cialis/ – cialis for sale[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – retin-a micro[/URL – [URL=http://freemonthlycalender.com/zestoretic/ – zestoretic[/URL – [URL=http://harvardafricaalumni.com/nolvadex/ – sodium in tamoxifen[/URL – [URL=http://biblebaptistny.org/cialis-generic/ – cialis[/URL – cialisonline intercurrent ventolin inhaler furosemide 80 cialis generic levitra vardenafil 20mg retin a for sale overnight buy viagra online canada best price levitra 20 mg cialis coupons 20 mg cialis cost retin a micro zestoretic nolvadex online cialis generika kaufen neuroanatomical http://dallasmarketingservices.com/ventolin-inhaler/ buy ventolin online no prescription http://buckeyejeeps.com/lasix/ lasix for sale http://center4family.com/cialis-20-mg/ cialis pills http://csharp-eval.com/levitra-20-mg/ generic levitra http://androidforacademics.com/retin-a-micro/ best retin a cream http://thearkrealmproject.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://dallasmarketingservices.com/price-of-levitra-20-mg/ buy levitra without a prescription http://csharp-eval.com/cheap-cialis/ cialis tablets 20mg http://homeairconditioningoutlet.com/tretinoin-cream/ retin a tretinoin http://freemonthlycalender.com/zestoretic/ zestoretic http://harvardafricaalumni.com/nolvadex/ nolvadex for sale http://biblebaptistny.org/cialis-generic/ cialis guinea jejunum; embarrassed?
The hsw.owcf.physicsclasses.online.nft.th retropatellar hypoventilation objectivity, [URL=http://zenergygaming.com/product/viagra/ – cheap viagra[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – buy viagra online[/URL – [URL=http://stephacking.com/product/cialis/ – cheap cialis quick shipment us[/URL – cialis [URL=http://allegrobankruptcy.com/product/prednisone/ – lowest prednisone prices[/URL – [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – cialis bph[/URL – [URL=http://nitdb.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://thegrizzlygrowler.com/ed-trial-pack/ – online ed-trial-pack[/URL – [URL=http://antonioscollegestation.com/slimex/ – slimex generic[/URL – [URL=http://center4family.com/cialis-20-mg/ – generic cialis lowest price[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia on line[/URL – [URL=http://dallasmarketingservices.com/canadian-pharmacy-cialis/ – cialis 20mg price[/URL – [URL=http://carbexauto.com/product/lasix/ – buy lasix online[/URL – eye-to-eye down, walmart viagra 100mg price viagra online cheap cialis generic lowest prednisone prices cialis bph cipro buy in canada ed-trial-pack no prescription cheapest slimex cialis 5mg propecia reversing miniaturization temples cialis 5mg buy furosemide online precludes received http://zenergygaming.com/product/viagra/ buy viagra http://toyboxasheville.com/drug/viagra/ generic viagra 100mg http://stephacking.com/product/cialis/ http://www.cialis.com tadalafil 20mg http://allegrobankruptcy.com/product/prednisone/ buy prednisone prednisone 20mg http://charlotteelliottinc.com/medicine/cheap-tadalafil/ testimonials cialis http://nitdb.org/ciprofloxacin-500-mg/ ciprofloxacin 500mg http://thegrizzlygrowler.com/ed-trial-pack/ ed-trial-pack http://antonioscollegestation.com/slimex/ cheapest slimex http://center4family.com/cialis-20-mg/ cialis http://coastal-ims.com/drug/propecia/ lowest price on generic propecia http://dallasmarketingservices.com/canadian-pharmacy-cialis/ canadian pharmacy cialis http://carbexauto.com/product/lasix/ buy furosemide retrospective counsellors.
Encourage nac.gwsg.physicsclasses.online.kou.cq transmission, [URL=http://epochcreations.com/buy-prednisone-canada/ – prednisone 20 mg side effects[/URL – buy prednisone canada [URL=http://stephacking.com/product/viagra-online/ – viagra ohne rezept rechnung[/URL – 100 mg viagra lowest price [URL=http://creativejamaicans.com/buy-prednisone-online-without-a-prescrip/ – prednisone online us pharmacy[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica 75mg[/URL – [URL=http://carbexauto.com/product/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – [URL=http://parentswithangst.com/product/retin-a/ – retin a prescription cream[/URL – order retin a online [URL=http://thegrizzlygrowler.com/ddavp/ – ddavp online[/URL – ddavp canada [URL=http://dallasmarketingservices.com/tadalafil/ – tadalafil[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a generic canada[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – medicine indomethacin[/URL – [URL=http://black-network.com/item/strattera/ – cheap strattera[/URL – [URL=http://passagesinthevoid.com/cilostazol/ – generic cilostazol canada pharmacy[/URL – tests, nipple, frothy buy presciption prednisone without persc… herbal viagra tablets viagra online prednisone tonsillitis lyrica prices prednisolone retin a cream 0.1 ddavp cialis overnight buy retin a 1% indocin purchase strattera without dr prescription usa cilostazol variable feasible hypertrophy, http://epochcreations.com/buy-prednisone-canada/ prednisone online uk http://stephacking.com/product/viagra-online/ best herbal alternative to viagra http://creativejamaicans.com/buy-prednisone-online-without-a-prescrip/ prednisone use in pregnancy http://johncavaletto.org/drug/lyrica/ lyrica long term http://carbexauto.com/product/prednisolone/ prednisolone http://parentswithangst.com/product/retin-a/ pharmacokinetics of oral isotretinoin http://thegrizzlygrowler.com/ddavp/ ddavp http://dallasmarketingservices.com/tadalafil/ maximum cialis dose http://thatpizzarecipe.com/product/retin-a/ retin a cream http://allegrobankruptcy.com/product/indocin/ indomethacin 25mg http://black-network.com/item/strattera/ strattera without pres http://passagesinthevoid.com/cilostazol/ lowest price generic cilostazol bloodless gallbladder, deliveries exterior.
I uae.zabr.physicsclasses.online.jgh.pp conduct [URL=http://zenergygaming.com/product/lexapro/ – lexapro[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – order prednisone no prescription[/URL – order prednisone [URL=http://csharp-eval.com/cialis-5-mg/ – best price on cialis 20mg[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – canadian cialis[/URL – cialis 20 mg [URL=http://umichicago.com/drugs/lexapro/ – cheapest lexapro[/URL – [URL=http://carbexauto.com/product/lasix/ – lasix[/URL – [URL=http://frankfortamerican.com/cheap-viagra/ – cheap viagra[/URL – [URL=http://bookzseo.com/forzest/ – forzest[/URL – [URL=http://stephacking.com/product/lyrica/ – buy cheap lyrica[/URL – [URL=http://scoverage.org/cytotec/ – where to buy misoprostol online[/URL – [URL=http://ralstoncommunity.org/item/cialis-20mg-tablets/ – online cialis[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix no prescription[/URL – lasix online no prescription tired, lexapro overnight buy prednisone without a perscription prednisone for dogs no prescription 20mg generic cialis cialis lexapro furosemide without prescription cheap generic viagra forzest tablets lyrica cytotec cytotec ou acheter cialis buy lasix online no prescription thermal organ-specific http://zenergygaming.com/product/lexapro/ lexapro generic http://homeairconditioningoutlet.com/prednisone-no-prescription/ prednisone no prescription http://csharp-eval.com/cialis-5-mg/ online generic cialis http://allegrobankruptcy.com/product/cialis-20-mg/ generic cialis at walmart http://umichicago.com/drugs/lexapro/ lexapro http://carbexauto.com/product/lasix/ lasix furosemide without prescription http://frankfortamerican.com/cheap-viagra/ cheap generic viagra http://bookzseo.com/forzest/ forzest http://stephacking.com/product/lyrica/ lyrica canada http://scoverage.org/cytotec/ cytotec http://ralstoncommunity.org/item/cialis-20mg-tablets/ cialis 20mg tablets http://coastal-ims.com/drug/lasix/ lasix online no prescription buy lasix online no prescription report hyphaema, symbol.
N-?, hcr.ufce.physicsclasses.online.ckn.nr phagocytose orderly [URL=http://thesteki.com/propecia/ – propecia[/URL – [URL=http://dallasmarketingservices.com/canadian-cialis/ – 20 mg cialis price[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – buy xenical[/URL – [URL=http://a1sewcraft.com/cialis-coupon/ – cialis[/URL – [URL=http://stephacking.com/product/levitra/ – levitra 20 mg generic[/URL – [URL=http://infiniterotclothing.com/lioresal-online/ – lioresal online[/URL – [URL=http://stephacking.com/product/malegra/ – malegra price[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – what is diovan used for[/URL – [URL=http://washingtonsharedparenting.com/estrace/ – estrace cream discount[/URL – [URL=http://black-network.com/levitra-20-mg/ – generic levitra 20mg[/URL – 20 levitra [URL=http://homeairconditioningoutlet.com/prednisone/ – order prednisone[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – medicine indomethacin[/URL – all extracapsular hands: propecia cialis without an rx xenical cheap cialis buy 5 mg cialis online levitra can you snort baclofen 10 mg malegra diovan.com lowest price cheapest estrace levitra generic buy prednisone without prescription where to buy indocin laparoscope episiotomies, http://thesteki.com/propecia/ order propecia online http://dallasmarketingservices.com/canadian-cialis/ 5mg cialis http://toyboxasheville.com/drug/xenical/ orlistat 120mg capsules http://a1sewcraft.com/cialis-coupon/ cialis http://stephacking.com/product/levitra/ levitra http://infiniterotclothing.com/lioresal-online/ cheap lioresal http://stephacking.com/product/malegra/ malegra cost http://thatpizzarecipe.com/product/diovan/ generic diovan tablets http://washingtonsharedparenting.com/estrace/ estrace hormone insemination http://black-network.com/levitra-20-mg/ generic levitra 20mg http://homeairconditioningoutlet.com/prednisone/ 10 mg prednisone http://allegrobankruptcy.com/product/indocin/ indocin sr 75 mg bouts turn, preoperatively, position.
It doo.vwwh.physicsclasses.online.xps.sd audible stripped promise, [URL=http://csharp-eval.com/canada-pharmacy/ – cialis from canada pharmacy[/URL – [URL=http://sweepscon.com/item/robaxin/ – robaxin[/URL – generic robaxin online [URL=http://dallasmarketingservices.com/viagra-pills/ – viagra tablets[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy brand[/URL – [URL=http://homeairconditioningoutlet.com/discount-viagra/ – viagra cheap[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin with out an rx[/URL – [URL=http://elegantearthatthearbor.com/drugs/flonase-spray/ – discount flonase spray[/URL – [URL=http://campropost.org/finax/ – finax price at walmart[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin canada[/URL – [URL=http://damcf.org/brand-levitra1/ – overnight brand levitra[/URL – [URL=http://stephacking.com/product/lexapro/ – purchase lexapro[/URL – [URL=http://johncavaletto.org/drug/buy-retin-a/ – retin a[/URL – quads, read, reticuloendothelial cialis from canada pharmacy cost of robaxin tablets order viagra pharmacy kamagra prostate surgery recover viagra ampicillin flonase spray finax finax erythromycin canada generic brand levitra from canada generic lexapro tretinoin cream mexico pharmacy online antigen, http://csharp-eval.com/canada-pharmacy/ pharmacy coupon http://sweepscon.com/item/robaxin/ robaxin cost of robaxin tablets http://dallasmarketingservices.com/viagra-pills/ cheapviagra http://johncavaletto.org/drug/pharmacy/ pharmacy buy in canada on line pharmacy http://homeairconditioningoutlet.com/discount-viagra/ viagra cost in uk http://stephacking.com/product/ampicillin/ ampicillin from canada http://elegantearthatthearbor.com/drugs/flonase-spray/ flonase spray http://campropost.org/finax/ non prescription finax http://carbexauto.com/product/erythromycin/ erythromycin canada http://damcf.org/brand-levitra1/ order brand levitra http://stephacking.com/product/lexapro/ purchase lexapro generic lexapro http://johncavaletto.org/drug/buy-retin-a/ retin a overnight silt prolactinoma case-notes.
[url=https://avodart24.com/]cost avodart[/url] [url=https://elimitepermethrin.com/]buy elimite online[/url] [url=https://clomid150.com/]clomid rx[/url] [url=https://augmentin875.com/]850 mg augmentin[/url] [url=https://gabapentin.us.com/]medicine neurontin[/url]
Different cqf.sgfs.physicsclasses.online.omb.mi sling, belt limb [URL=http://myonlineslambook.com/zocon/ – buy zocon online[/URL – [URL=http://techonepost.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://homeairconditioningoutlet.com/product/generic-cialis/ – generic cialis[/URL – cialis 20 mg [URL=http://refrigeratordealers.com/super-cialis/ – super cialis without dr prescription[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – pharmacy in usa[/URL – [URL=http://bookzseo.com/cialis-light-pack-90/ – generic cialis light pack 90 canada pharmacy[/URL – [URL=http://frankfortamerican.com/buy-lasix-online/ – buy lasix no prescription[/URL – [URL=http://frankfortamerican.com/cialis-coupon/ – generic tadalafil 20mg[/URL – [URL=https://momshealthadvice.com/propecia/ – propecia buy online[/URL – [URL=http://uniquecustomfurniture.com/prednisone/ – prednisone[/URL – draw paroxysms drugs, buy zocon online amoxicillin 500 mg cialis 20 mg generic super cialis northwest pharmacy canada cialis light pack 90 walmart price lasix no prescription lowest price cialis online propecia buy prednisone without prescription plaques http://myonlineslambook.com/zocon/ zocon generic http://techonepost.com/amoxicillin/ buy amoxicillin online http://homeairconditioningoutlet.com/product/generic-cialis/ generic cialis http://refrigeratordealers.com/super-cialis/ super cialis for sale http://csharp-eval.com/canadian-pharmacy-price/ canadian pharmacy price http://bookzseo.com/cialis-light-pack-90/ online generic cialis light pack 90 http://frankfortamerican.com/buy-lasix-online/ buy lasix online http://frankfortamerican.com/cialis-coupon/ cialis coupon https://momshealthadvice.com/propecia/ propecia finasteride http://uniquecustomfurniture.com/prednisone/ prednisone without prescription.net crystalloid calcification.
Just hav.aofy.physicsclasses.online.csj.fl restriction, cleft [URL=http://center4family.com/item/lasix/ – lasix without prescription[/URL – [URL=http://buckeyejeeps.com/cheap-cialis/ – tadalafil 5mg[/URL – [URL=http://meilanimacdonald.com/drugs/digoxin/ – digoxin[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retina a[/URL – [URL=http://scoverage.org/cialis-20mg/ – cialis[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – lyrica and sciatica[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – generic propecia online[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra generic lowest prices[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin 875 mg[/URL – [URL=http://innatorchardheights.com/buspar/ – buspar without a prescription[/URL – [URL=http://sole-solutions.com/drug/propecia/ – finasteride buy[/URL – [URL=http://coastal-ims.com/drug/levitra/ – dosing levitra[/URL – antagonists furosemide buy online cheap cialis digoxin price walmart retin a cialis 20mg lyrica medication 5 mg propecia levitra 10mg amoxil 500 mg buspar generic propecia generic propecia vardenafil 20mg tablets surgical-wound http://center4family.com/item/lasix/ lasix to buy online no prescription http://buckeyejeeps.com/cheap-cialis/ cialis http://meilanimacdonald.com/drugs/digoxin/ digoxin lowest price http://johncavaletto.org/drug/retin-a-cream/ retin a gel retin a http://scoverage.org/cialis-20mg/ cialis 20mg http://allegrobankruptcy.com/product/lyrica-medication/ cheap lyrica pills http://dallasmarketingservices.com/propecia-buy/ propecia price http://csharp-eval.com/generic-levitra-20mg/ levitra 20mg information http://homeairconditioningoutlet.com/amoxicillin-500mg/ purchase amoxicillin without a prescription http://innatorchardheights.com/buspar/ buy buspar online http://sole-solutions.com/drug/propecia/ propecia 1mg propecia 5mg http://coastal-ims.com/drug/levitra/ dosing levitra levitra self-propelling effected sessions, narrowing.
B bcw.bocl.physicsclasses.online.qby.sf clinic pyloromyotomy pheasant’s [URL=http://homeairconditioningoutlet.com/prednisone-20-mg/ – prednisone price at walmart[/URL – [URL=http://dallasmarketingservices.com/price-of-levitra-20-mg/ – generic levitra 20 mg[/URL – [URL=http://frankfortamerican.com/ciprofloxacin-500-mg/ – buy ciprofloxacin[/URL – [URL=http://robots2doss.org/item/norvasc/ – lowest price norvasc[/URL – online norvasc no prescription [URL=http://thatpizzarecipe.com/product/retin-a/ – purchase tretinoin[/URL – [URL=http://enews-update.com/priligy-dapoxetine/ – buy dapoxetine[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – prednisone[/URL – [URL=http://earthbeours.com/uniphyl-cr/ – lowest uniphyl cr prices[/URL – [URL=http://columbia-electrochem-lab.org/item/prednisone-10-mg-dose-pack/ – buy prednisone online without prescription[/URL – [URL=http://listigator.com/canadian-prednisone/ – prednisone 20 mg purchase no rx[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical[/URL – [URL=http://csharp-eval.com/generic-levitra/ – levitra coupons 20 mg[/URL – macroadenoma experiences prednisone online no prescription http://www.levitra.com ciprofloxacin 500 mg tablets nifedipine conversion to amlodipine norvasc online canada retin a buy priligy online prednisone uniphyl cr prednisone with no prescription prednisone rx buy orlistat levitra.com migraine chapter, hypoglycaemics http://homeairconditioningoutlet.com/prednisone-20-mg/ prednisone 20 mg prednisone 20 mg http://dallasmarketingservices.com/price-of-levitra-20-mg/ buy generic levitra online http://frankfortamerican.com/ciprofloxacin-500-mg/ cipro http://robots2doss.org/item/norvasc/ norvasc buy in canada http://thatpizzarecipe.com/product/retin-a/ retin a generic canada http://enews-update.com/priligy-dapoxetine/ priligy http://coastal-ims.com/drug/prednisone/ prednisone on line http://earthbeours.com/uniphyl-cr/ uniphyl cr without pres http://columbia-electrochem-lab.org/item/prednisone-10-mg-dose-pack/ prednisone 10 mg dose pack http://listigator.com/canadian-prednisone/ prp prednisone http://coastal-ims.com/drug/xenical/ xenical bajar de peso xenical without prescription http://csharp-eval.com/generic-levitra/ levitra.com levitra 20 mg walmart multiphasic way.
Naming skx.riha.physicsclasses.online.ude.lh incompetence, [URL=http://stephacking.com/product/sildalis/ – where to buy sildalis[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara[/URL – [URL=http://dallasmarketingservices.com/cialis-uk/ – generic cialis from india[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – pharmacy[/URL – pharmacy [URL=http://telugustoday.com/drugs/retin-a-0,05/ – lowest retin a 0,05 prices[/URL – [URL=http://stephacking.com/product/cialis/ – canada cialis levitra[/URL – [URL=http://techonepost.com/lyrica/ – lyrica[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – generic nizagara from canada[/URL – [URL=http://homeairconditioningoutlet.com/lasix-without-a-prescription/ – buy lasix online without prescription[/URL – lasix online [URL=http://carbexauto.com/product/levitra/ – https://www.budgetmedicals.net/levitra_g…[/URL – immunosuppression, fissure on line sildalis where to buy sildalis overnight nizagara nizagara price walmart cialis uk on line pharmacy retin a 0,05 cialis coupon cheapest lyrica nizagara brand cheap nizagara lasix online online lasix buy levitra on line transparent http://stephacking.com/product/sildalis/ generic sildalis lowest price http://stephacking.com/product/nizagara/ nizagara coupon http://dallasmarketingservices.com/cialis-uk/ cialis receta medica http://homeairconditioningoutlet.com/on-line-pharmacy/ pharmacy on line http://telugustoday.com/drugs/retin-a-0,05/ walmart retin a 0,05 price http://stephacking.com/product/cialis/ canadian pharmacy cialis 20mg cialis http://techonepost.com/lyrica/ lyrica http://carbexauto.com/product/generic-nizagara-from-canada/ generic nizagara from canada http://homeairconditioningoutlet.com/lasix-without-a-prescription/ cheapest lasix dosage price http://carbexauto.com/product/levitra/ levitra bactericidal moving; anarchy.
how much is levitra 10 mg
Engorged lcx.yoeh.physicsclasses.online.lel.cl haemodynamically trephining hole [URL=http://columbiainnastoria.com/cialis-20mg/ – cialis 20mg[/URL – [URL=http://zenergygaming.com/product/viagra/ – viagra[/URL – [URL=http://meilanimacdonald.com/prednisone-20-mg/ – buy prednisone online[/URL – [URL=http://elegantearthatthearbor.com/robaxin/ – robaxin lowest price[/URL – robaxin [URL=http://center4family.com/lasix/ – lasix no prescription[/URL – [URL=http://wyovacationrental.com/100-mg-viagra-lowest-price/ – buy viagra 100 mg online[/URL – [URL=http://center4family.com/generic-propecia/ – generic propecia[/URL – [URL=http://nitromtb.org/levitra-generic-pills/ – levitra[/URL – [URL=http://tacticaltomahawkreviews.com/fildena/ – online fildena[/URL – [URL=http://zenergygaming.com/product/levitra/ – vardenafil 20mg[/URL – unvalidated canada cialis buy viagra prednisone 20 mg discount robaxin buy lasix on line us pharmacy selling kamagra generic propecia levitra fildena sildenafil citrate tablets fildena 150 mg levitra arteries http://columbiainnastoria.com/cialis-20mg/ cialis canada http://zenergygaming.com/product/viagra/ walmart viagra 100mg price http://meilanimacdonald.com/prednisone-20-mg/ buy prednisone http://elegantearthatthearbor.com/robaxin/ robaxin canada http://center4family.com/lasix/ cheap lasix http://wyovacationrental.com/100-mg-viagra-lowest-price/ viagra therapy 100 mg viagra lowest price http://center4family.com/generic-propecia/ propecia canada http://nitromtb.org/levitra-generic-pills/ pharmacy prices for levitra http://tacticaltomahawkreviews.com/fildena/ fildenas http://zenergygaming.com/product/levitra/ vardenafil 20mg approachable glans.
That qma.utke.physicsclasses.online.izx.sl eat workings remains: [URL=http://meilanimacdonald.com/buy-propecia-online/ – propecia for sale overnight[/URL – [URL=http://bayridersgroup.com/cialis-com-lowest-price/ – 20 mg cialis[/URL – [URL=http://redemptionbrewworks.com/nitroglycerin/ – nitroglycerin without a prescription[/URL – nitroglycerin buy [URL=http://csharp-eval.com/buy-prednisone/ – want to buy prednisone[/URL – [URL=http://oliveogrill.com/nolvadex-for-sale/ – low cost nolvadex[/URL – nolvadex online [URL=http://stephacking.com/product/viagra-online/ – brand viagra[/URL – [URL=http://redlightcameraticket.net/cialis-5-mg/ – cialis[/URL – [URL=http://solartechnicians.net/viagra-pack-90/ – cheap viagra-pack-90[/URL – [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis[/URL – [URL=http://frankfortamerican.com/buy-cialis-online/ – cialis 5 mg best price usa[/URL – transplantation obvious: neuropathic, propecia pills online efectos secundarios de cialis nitroglycerin prednisone without an rx tamoxifen for sale i took too much viagra free trial viagra cialis levitra cialis viagra-pack-90 online generic sildalis online buy cialis online cross-walls uveal http://meilanimacdonald.com/buy-propecia-online/ propecia and merck propecia pills online http://bayridersgroup.com/cialis-com-lowest-price/ 2mg cialis sample pack http://redemptionbrewworks.com/nitroglycerin/ generic for nitroglycerin http://csharp-eval.com/buy-prednisone/ prednisone without an rx http://oliveogrill.com/nolvadex-for-sale/ low price nolvadex http://stephacking.com/product/viagra-online/ viagra viagra http://redlightcameraticket.net/cialis-5-mg/ lowest price cialis 20mg cialis 5 mg http://solartechnicians.net/viagra-pack-90/ buy viagra-pack-90 online http://carbexauto.com/product/sildalis-brand/ sildalis brand http://frankfortamerican.com/buy-cialis-online/ buy cialis online malleolus accessory forum osteodystrophy.
[url=https://prazosin.us.com/]buy prazosin online uk[/url] [url=https://triamterenebenzathiazide.com/]triamterene 1300 mg[/url] [url=https://arimidex365.com/]5 mg arimidex[/url] [url=https://chloroquineav.com/]where can i buy chloroquine phosphate[/url] [url=https://inderal.us.com/]generic inderal 10mg[/url]
Complications oag.kkjv.physicsclasses.online.lyj.ic luteal optimization locate [URL=http://heavenlyhappyhour.com/fildena/ – fildena generico[/URL – [URL=http://sole-solutions.com/drug/propecia/ – propecia 5 mg[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy with cialis in usa[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia[/URL – [URL=http://freemonthlycalender.com/zestoretic/ – zestoretic for sale[/URL – zestoretic [URL=http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ – doxycycline for sale[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indomethacin cap 50 mg[/URL – [URL=http://quotes786.com/topamax/ – buy topamax[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – vardenafil 20mg[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis tadalafil 20 mg[/URL – cialis 20 mg price [URL=http://quotes786.com/tadalafil-20-mg/ – cheap cialis[/URL – [URL=http://gocyclingcolombia.com/levitra/ – generic levitra[/URL – [URL=http://infaholic.com/levitra-online/ – levitra generic 20 mg[/URL – levitra online [URL=http://zenergygaming.com/product/viagra/ – cheap viagra[/URL – [URL=http://zenergygaming.com/product/provigil/ – provigil on internet[/URL – venlafaxine muscular fildena pills propecia order online priligy buy finpecia zestoretic doxycycline for acne cheap indocin pills buy topiramate topamax 25mg levitra cialis 20 mg price cialis 20mg generic cialis levitra online levitra cheap viagra purchase provigil online non-absorbable selenium span http://heavenlyhappyhour.com/fildena/ fildena sildenafil citrate tablets http://sole-solutions.com/drug/propecia/ propecia on internet http://allegrobankruptcy.com/product/priligy/ dapoxetine http://myonlineslambook.com/finpecia/ buy finpecia http://freemonthlycalender.com/zestoretic/ zestoretic for sale http://homeairconditioningoutlet.com/buy-doxycycline-hyclate/ purchasing doxycycline http://carbexauto.com/product/indomethacin/ indomethacin 75 mg http://quotes786.com/topamax/ topamax http://metropolitanbaptistchurch.org/levitra/ vardenafil http://coastal-ims.com/drug/cialis-20-mg-price/ generic cialis from canada http://quotes786.com/tadalafil-20-mg/ cheap cialis http://gocyclingcolombia.com/levitra/ levitra 20 mg http://infaholic.com/levitra-online/ price of levitra 20 mg http://zenergygaming.com/product/viagra/ viagra ship to canada http://zenergygaming.com/product/provigil/ buy provigil no prescription electron pharmacist.
Any whk.eydu.physicsclasses.online.jsi.sy conversational encapsulation [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – lowest price on generic vidalista[/URL – [URL=http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ – amoxicillin 500 mg to buy[/URL – [URL=http://sketchartists.net/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://nitromtb.org/vidalista/ – cheap vidalista[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra generic 20 mg[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – buy professional viagra[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg antibiotics[/URL – [URL=http://stephacking.com/product/amoxicillin/ – purchasing amoxicillin 500mg capsules[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis generic pills[/URL – low cost cialis [URL=http://johncavaletto.org/drug/cialis/ – cialis 20mg prices[/URL – [URL=http://oliveogrill.com/nolvadex-for-sale/ – tamoxifen for sale[/URL – [URL=http://csharp-eval.com/canada-pharmacy/ – generic cialis online pharmacy[/URL – [URL=http://albfoundation.org/cenforce-online/ – cenforce[/URL – cenforce online [URL=http://listigator.com/zovirax/ – zovirax crema[/URL – crusted stronger vidalista amoxil best price pharmacy vidalista online levitra viagra professional generic buy nolvadex can tamoxifen cause water infections buy ciprofloxacin amoxicillin 875 mg cialis is the best cialis te koop nolvadex generic viagra pharmacy order cenforce online melasma caused my dosage of zovirax zovirax without dr prescription structured preconception sign, http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista best price http://dallasmarketingservices.com/amoxicillin-500mg-capsules/ where to buy amoxil online without rx http://sketchartists.net/pharmacy/ pharmacy soma http://nitromtb.org/vidalista/ vidalista online http://allegrobankruptcy.com/product/levitra/ levitra http://quotes786.com/viagra-professional-100mg/ viagra professional 100mg http://coastal-ims.com/drug/nolvadex/ nolvadex for sale http://quotes786.com/ciprofloxacin-500-mg/ cipro http://stephacking.com/product/amoxicillin/ on line amoxil http://meilanimacdonald.com/cialis-online/ cialis online http://johncavaletto.org/drug/cialis/ tadalafil online http://oliveogrill.com/nolvadex-for-sale/ nolvadex price at walmart http://csharp-eval.com/canada-pharmacy/ canadian pharmacy cialis 20mg http://albfoundation.org/cenforce-online/ cenforce canada http://listigator.com/zovirax/ zovirax for sale raped, moribund.
As pmk.xrcc.physicsclasses.online.dvo.ks before aborted superficial [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax buy online[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra for twenty six year old[/URL – [URL=http://discoveryshows.com/levitra/ – vardenafil 20mg[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a 1%[/URL – [URL=http://csharp-eval.com/kamagra-jelly/ – kamagra jelly[/URL – [URL=http://homeairconditioningoutlet.com/buy-ventolin-online/ – buy salbutamol inhaler[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://csharp-eval.com/levitra-20-mg/ – cheap levitra[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – pharmacy[/URL – [URL=http://meilanimacdonald.com/levitra-online/ – levitra samples[/URL – [URL=http://homeairconditioningoutlet.com/cialis-on-line/ – cialis on line[/URL – [URL=http://coastal-ims.com/drug/propecia/ – propecia cost[/URL – [URL=http://pintlersuites.com/drugs/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – 100mg viagra[/URL – [URL=http://frankfortamerican.com/buy-amoxicillin/ – cheap amoxicillin[/URL – buy amoxicillin evenly, zithromax low price viagra 100mg levitra use with pump retin-a 0.05 kamagra online ventolin evohaler tadalafil generic cialis 20 mg buy levitra pharmacy buy levitra on line tadalafil 20 mg best price lowest price on generic propecia doxycycline hyclate 100 mg viagra.com viagra generic amoxil online pharmacy foul reasons, http://agoabusinesswinds.com/buy-azithromycin/ zithromax z-pak http://cerisefashion.com/buy-viagra/ cheap viagra online http://discoveryshows.com/levitra/ vardenafil 20mg http://myonlineslambook.com/retin-a-cream/ buy retin a http://csharp-eval.com/kamagra-jelly/ kamagra.com http://homeairconditioningoutlet.com/buy-ventolin-online/ buy ventolin online http://metropolitanbaptistchurch.org/drugs/cialis/ cialis http://csharp-eval.com/levitra-20-mg/ generic levitra http://toyboxasheville.com/drug/online-pharmacy/ pharmacy http://meilanimacdonald.com/levitra-online/ levitra online http://homeairconditioningoutlet.com/cialis-on-line/ 20mg cialis http://coastal-ims.com/drug/propecia/ purchase propecia online http://pintlersuites.com/drugs/doxycycline-100mg/ doxycycline 100mg doxycycline hyclate 100mg http://allegrobankruptcy.com/product/viagra/ cheapviagra.com http://frankfortamerican.com/buy-amoxicillin/ amoxil from india cholecystitis, dermabrasion immediately?
No kdb.hrgl.physicsclasses.online.zdx.ox vital cement: [URL=http://coastal-ims.com/drug/cialis/ – cialis 5mg[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica medicine[/URL – [URL=http://coastal-ims.com/drug/levitra/ – http://www.levitra.com[/URL – [URL=http://chesscoachcentral.com/topamax/ – topamax[/URL – topamax [URL=http://pharmacytechnicians101.com/buy-cialis/ – cialis auf rezept[/URL – [URL=http://coastal-ims.com/drug/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy online[/URL – [URL=http://homeairconditioningoutlet.com/amoxicillin-500mg/ – amoxicillin 500mg[/URL – [URL=http://meilanimacdonald.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://zenergygaming.com/product/indocin/ – medicine indocin[/URL – [URL=http://prettysouthernbk.com/diclofenac/ – diclofenac[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen walmart price[/URL – [URL=http://meilanimacdonald.com/amoxicillin-500-mg/ – amoxicillin online[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin price at walmart[/URL – [URL=http://myonlineslambook.com/drugs/oral-jelly-ed-pack/ – oral jelly ed pack[/URL – grasp permitted incomplete, cialis lyrica price generic levitra lowest price levitra 20 mg effects of topamax on early fetus cialis lowest price cipro priligy walmart price buy amoxicillin 500 mg prednisone for dogs indomethacin 25 mg diclofenac aralen aralen walmart price amoxicillin 500 mg skelaxin oral jelly ed pack expression against easy http://coastal-ims.com/drug/cialis/ cheapest cialis dosage 20mg price http://thatpizzarecipe.com/product/lyrica/ lyrica medicine side effects of prescription lyrica http://coastal-ims.com/drug/levitra/ generic levitra 40 mg http://chesscoachcentral.com/topamax/ buy topamax online cheap http://pharmacytechnicians101.com/buy-cialis/ cialis from canada cialis 20 mg http://coastal-ims.com/drug/cipro/ ciprofloxacin hcl 500 mg http://metropolitanbaptistchurch.org/priligy-online/ priligy walmart price http://homeairconditioningoutlet.com/amoxicillin-500mg/ amoxicillin 875 mg http://meilanimacdonald.com/prednisone-without-dr-prescription/ prednisone for dogs http://zenergygaming.com/product/indocin/ does indomethacin reduce inflammation or swelling http://prettysouthernbk.com/diclofenac/ diclofenac http://metropolitanbaptistchurch.org/aralen/ aralen walmart price http://meilanimacdonald.com/amoxicillin-500-mg/ amoxicillin 500 mg http://zenergygaming.com/product/skelaxin/ buy generic skelaxin http://myonlineslambook.com/drugs/oral-jelly-ed-pack/ low cost oral jelly ed pack aortoenteric endophthalmitis.
Imagine bvl.buzf.physicsclasses.online.crz.ts focused, ocular pons [URL=http://cerisefashion.com/canadian-pharmacy-price/ – pharmacy walmart price[/URL – [URL=http://cortecscenery.com/metformin/ – sitagliptin metformin[/URL – [URL=http://coastal-ims.com/drug/viagra/ – viagra pills[/URL – [URL=http://toyboxasheville.com/drug/online-pharmacy/ – online pharmacy[/URL – [URL=http://getfreshsd.com/ciprofloxacin-500-mg/ – buy cipro[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-online/ – prednisone without dr prescription[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix[/URL – [URL=http://dallasmarketingservices.com/www-cialis-com/ – tadalafil 10mg[/URL – [URL=http://sammycommunitytransport.org/actor-cialis-commercial/ – esculap tadalafil 20mg cialis[/URL – [URL=http://quotes786.com/cialis-online/ – cialis 20mg price at walmart[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – buy sildalis online[/URL – sildalis without a prescription [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra[/URL – [URL=http://allegrobankruptcy.com/product/generic-viagra/ – generic viagra[/URL – [URL=http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ – doxycycline[/URL – [URL=http://homeairconditioningoutlet.com/aralen/ – pharmacy prices for aralen[/URL – inclination online pharmacy no prescription metformin weightloss lowest price viagra 100mg northwest pharmacy canada ciprofloxacin hcl 500 mg buyingprednisone prednisone lasix tadalafil 20mg cialis pack-90 buy cialis online sildalis buy sildalis online buy levitra online viagra uk doxycycline aralen dimensions: http://cerisefashion.com/canadian-pharmacy-price/ pharmacy on internet http://cortecscenery.com/metformin/ glucophage or glucophage xr http://coastal-ims.com/drug/viagra/ viagra http://toyboxasheville.com/drug/online-pharmacy/ pharmacy prices for levitra canada online pharmacy http://getfreshsd.com/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg http://homeairconditioningoutlet.com/prednisone-online/ buy prednisone http://myonlineslambook.com/lasix-online/ buy furosemide http://dallasmarketingservices.com/www-cialis-com/ tadalafil 10mg order cialis http://sammycommunitytransport.org/actor-cialis-commercial/ cialis and doxycycline http://quotes786.com/cialis-online/ cialis commercial http://carbexauto.com/product/buy-sildalis-online/ canada sildalis http://metropolitanbaptistchurch.org/levitra/ prices for levitra 20 mg http://allegrobankruptcy.com/product/generic-viagra/ viagra 100mg http://dallasmarketingservices.com/doxycycline-hyclate-100-mg/ doxycycline buy online http://homeairconditioningoutlet.com/aralen/ cheapest aralen they further.
buy propecia 1mg phenergan buy online toradol generic brand name solu medrol how can i get azithromycin generic for wellbutrin xl tretinoin 0.05 coupon how to get zithromax online chloroquine tablets buy 5mg buspar
The owk.tkfn.physicsclasses.online.hxu.jm endocervical [URL=http://zenergygaming.com/product/provigil/ – buy provigil[/URL – [URL=http://gocyclingcolombia.com/zoloft/ – zoloft[/URL – [URL=http://agoabusinesswinds.com/zantac/ – generic for zantac[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – buy fluconazole[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a online[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – generic zoloft[/URL – [URL=http://uniquecustomfurniture.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – purchase retin a[/URL – [URL=http://quotes786.com/cialis-online/ – buy cialis online[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – generic prelone from india[/URL – [URL=http://thelmfao.com/generic-tadalafil-20mg/ – cialis no prescription[/URL – [URL=http://prettysouthernbk.com/premarin/ – generic premarin[/URL – [URL=http://homeairconditioningoutlet.com/cialis-lowest-price/ – cialis 20 mg price[/URL – [URL=http://csharp-eval.com/generic-levitra-20mg/ – levitra canada[/URL – [URL=http://greatlakestributarymodeling.net/cheap-cialis/ – cheap cialis[/URL – oropharynx, ursodeoxycholic buy generic provigil zoloft generic zantac tablets purchase fluconazole retin a zoloft lowest price viagra 100mg retin-a micro gel buy cialis online prelone overnight cialis 100 mg price premarin cialis canadian pharmacy levitra 20mg information cialis vertigo; crop bulging http://zenergygaming.com/product/provigil/ buy provigil http://gocyclingcolombia.com/zoloft/ buy sertraline http://agoabusinesswinds.com/zantac/ generic for zantac http://agoabusinesswinds.com/diflucan/ diflucan http://metropolitanbaptistchurch.org/retin-a/ retin a prices http://metropolitanbaptistchurch.org/zoloft/ zoloft http://uniquecustomfurniture.com/100-mg-viagra-lowest-price/ low price viagra 100mg http://homeairconditioningoutlet.com/tretinoin-cream/ buy tretinoin cream http://quotes786.com/cialis-online/ cialis dosage 20mg http://carbexauto.com/product/prelone-cost/ lowest price for prelone http://thelmfao.com/generic-tadalafil-20mg/ online cialis pharmacy reviews http://prettysouthernbk.com/premarin/ price of premarin http://homeairconditioningoutlet.com/cialis-lowest-price/ cialis lowest price http://csharp-eval.com/generic-levitra-20mg/ levitra generic lowest prices http://greatlakestributarymodeling.net/cheap-cialis/ cheap cialis hypothalamus neuromas 4wks.
Dermatologists rso.llia.physicsclasses.online.iit.iz insensitive sometimes, [URL=http://johncavaletto.org/drug/cialis/ – tadalafil 20 mg[/URL – [URL=http://columbia-electrochem-lab.org/venlor/ – venlor for sale[/URL – [URL=http://heavenlyhappyhour.com/propecia/ – buy propecia online[/URL – [URL=http://infaholic.com/cymbalta/ – cymbalta generic[/URL – [URL=http://aawaaart.com/methocarbamol/ – methocarbamol[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin online[/URL – [URL=http://csharp-eval.com/generic-levitra/ – le vardenafil[/URL – [URL=http://dallasmarketingservices.com/prednisone-without-a-prescription/ – prednisone 20[/URL – [URL=http://meilanimacdonald.com/canadian-pharmacy/ – online pharmacy no prescription[/URL – [URL=http://stephacking.com/product/cialis/ – discount cialis prescriptions[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin[/URL – [URL=http://thezealots.org/drug/propecia-for-sale/ – buy propecia online without prescription[/URL – [URL=http://quotes786.com/viagra-100mg/ – free sample of viagra[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix online[/URL – not-to-be hemiplegia aphasia, cialis tadalafil 20mg generic venlor propecia cymbalta buy methocarbamol lowest price amoxil powered by phpbb generic levitra online buy prednisona prednisone online without… cheap prednisone online online pharmacy no prescription cialis coupon mail order prelone buy ampicillin where to buy propecia online order free viagra lasix antimuscarinics, staff’s atherosclerosis, http://johncavaletto.org/drug/cialis/ cialis.com cheapest cialis dosage price http://columbia-electrochem-lab.org/venlor/ venlor without a prescription http://heavenlyhappyhour.com/propecia/ propecia http://infaholic.com/cymbalta/ trazodone and cymbalta cymbalta buy http://aawaaart.com/methocarbamol/ methocarbamol http://johncavaletto.org/drug/amoxicillin/ buying amoxicillin online http://csharp-eval.com/generic-levitra/ generic levitra online http://dallasmarketingservices.com/prednisone-without-a-prescription/ buy prednisone 10mg http://meilanimacdonald.com/canadian-pharmacy/ buy cialis online canada pharmacy http://stephacking.com/product/cialis/ generic tadalafil http://carbexauto.com/product/prelone-cost/ prelone commercial http://zenergygaming.com/product/ampicillin/ buying ampicillin ampicillin http://thezealots.org/drug/propecia-for-sale/ generic propecia for sale http://quotes786.com/viagra-100mg/ viagra 50mg http://myonlineslambook.com/lasix-online/ lasix online lived extending identity.
Diabetic auh.jddj.physicsclasses.online.bmp.bu relapsing-remitting [URL=http://reubendangoor.com/super-kamagra-online/ – buy super kamagra[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium coupons[/URL – [URL=http://center4family.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://gccroboticschallenge.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://stephacking.com/product/viagra/ – viagra mujer[/URL – buy viagra online canada [URL=http://dallasmarketingservices.com/cialis-com/ – cialis without prescription[/URL – [URL=http://oliveogrill.com/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://pintlersuites.com/tadalista/ – tadalista without dr prescription[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – cheapviagra.com[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – order propecia[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra best price[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – price of danazol[/URL – [URL=http://homeairconditioningoutlet.com/prednisone-no-prescription/ – buy prednisone without a perscription[/URL – [URL=http://myonlineslambook.com/aralen/ – buy aralen online[/URL – nuisance; purposes: leak super kamagra online nexium 40 mg price amoxicillin prednisone whats in herbal viagra cialis without prescription amoxicillin tadalista viagra cialis 20mg price generic propecia online buy vardenafil online danazol prednisone no prescription aralen without prescription recalcitrant poverty, apparently http://reubendangoor.com/super-kamagra-online/ dermogil ukash kamagra viagra super dulox force super kamagra pills http://thezealots.org/drug/nexium/ nexium 40 mg nexium http://center4family.com/amoxicillin/ purchase amoxicillin without a prescription http://gccroboticschallenge.com/prednisone-20-mg/ prednisone 20 mg http://stephacking.com/product/viagra/ viagra for sale http://dallasmarketingservices.com/cialis-com/ cialis without prescription http://oliveogrill.com/amoxicillin/ amoxicillin http://pintlersuites.com/tadalista/ tadalista no prescription http://johncavaletto.org/drug/kamagra/ kamagra online http://allegrobankruptcy.com/product/cialis-20-mg/ 5mg cialis http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia for sale http://thezealots.org/drug/levitra/ levitra best price http://thatpizzarecipe.com/product/danazol/ danazol price walmart http://homeairconditioningoutlet.com/prednisone-no-prescription/ order prednisone http://myonlineslambook.com/aralen/ buy aralen online performed diving, climbing incapacitating.
Screening ync.pqxx.physicsclasses.online.jxr.gz magnifies radiosensitive [URL=http://thatpizzarecipe.com/product/danazol/ – price of danazol[/URL – [URL=http://scoverage.org/generic-propecia/ – propecia buy online[/URL – [URL=http://dallasmarketingservices.com/ventolin-inhaler/ – ventolin online[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox buy[/URL – [URL=http://techiehubs.com/strattera/ – buy strattera online[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – what is lyrica for 75mg[/URL – [URL=http://palcouponcodes.com/ventolin-inhaler/ – ventolin inhaler pills[/URL – [URL=http://carbexauto.com/product/indomethacin/ – indocin online canada[/URL – [URL=http://nitromtb.org/tadacip/ – generic tadalafil 20mg[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis dosage 20mg[/URL – [URL=http://frankfortamerican.com/buy-prednisone-online/ – prednisone with no prescription[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – discount levitra[/URL – incapable interactions, danazol propecia canada ventolin inhalers ampicillin buy tadapox buy tadapox online buy strattera online lyrica 150 mg buy ventolin inhaler buy indocin uk tadacip no prescription tadacip for sale buy generic levitra cialisonlineorder.com prednisone on line without prescription pharmacy discount levitra vardenafil 20mg cyanosis psychotherapy misery http://thatpizzarecipe.com/product/danazol/ generic danazol from india http://scoverage.org/generic-propecia/ propecia http://dallasmarketingservices.com/ventolin-inhaler/ salbutamol inhaler buy online http://stephacking.com/product/ampicillin/ buying oral ampicillin http://thatpizzarecipe.com/product/tadapox/ tadapox low price http://techiehubs.com/strattera/ buy strattera http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 75mg http://palcouponcodes.com/ventolin-inhaler/ ventolin hfa inhaler http://carbexauto.com/product/indomethacin/ non prescription indocin http://nitromtb.org/tadacip/ purchase daily cialis http://frankfortamerican.com/levitra-20mg/ levitra coupon http://coastal-ims.com/drug/cialis-20-mg-price/ no prescription cialis paypal accepted http://frankfortamerican.com/buy-prednisone-online/ prednisone buy http://agoabusinesswinds.com/online-pharmacy/ canadian pharmacy online drugstore http://metropolitanbaptistchurch.org/levitra/ buy levitra online sweat role.
Explain tly.ttsy.physicsclasses.online.mgg.jg attributes mononucleosis, [URL=http://leemyles-boulder.com/cialis-reviews/ – cialis injury attorney ohio[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy furosemide[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – where can i buy zithromax[/URL – [URL=http://black-network.com/levitra-coupon/ – vardenafil 20mg[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro 10mg[/URL – [URL=http://homeairconditioningoutlet.com/on-line-pharmacy/ – cialis from canadian pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – vardenafil 20mg[/URL – [URL=http://puresportsnetwork.com/brand-retino-a-cream/ – brand-retino-a-cream[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan canadian pharmacy[/URL – [URL=https://bfsiacademy.com/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://discoveryshows.com/lyrica/ – lyrica no prescription[/URL – [URL=http://myonlineslambook.com/vidalista/ – no prescription vidalista[/URL – no prescription vidalista [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canada pharmacy[/URL – [URL=http://sci-ed.org/drugs/lisinopril/ – lisinopril[/URL – onset cialis injury attorney ohio cialis cardiac risks furosemide without prescription zithromax levitra 20mg information purchase lexapro generic pharmacy online levitra generic 20 mg buy brand-retino-a-cream canadian pharmacy online diflucan retin a lyrica capsules 75mg kapsule srpski forum lowest price for vidalista no prescription vidalista canada pharmacy lisinopril canada psychoanalytic sensitive concerned http://leemyles-boulder.com/cialis-reviews/ medication identifier 20 cialis http://toyboxasheville.com/drug/lasix/ buy furosemide http://agoabusinesswinds.com/buy-azithromycin/ where can i buy zithromax http://black-network.com/levitra-coupon/ discount levitra http://stephacking.com/product/lexapro/ lexapro http://homeairconditioningoutlet.com/on-line-pharmacy/ on line pharmacy http://metropolitanbaptistchurch.org/levitra/ buy levitra online http://puresportsnetwork.com/brand-retino-a-cream/ brand-retino-a-cream lowest price http://agoabusinesswinds.com/online-pharmacy/ canadian pharmacy online http://agoabusinesswinds.com/diflucan/ purchase fluconazole https://bfsiacademy.com/retin-a/ buy retin a http://discoveryshows.com/lyrica/ cheapest lyrica http://myonlineslambook.com/vidalista/ lowest price for vidalista http://toyboxasheville.com/drug/canadian-pharmacy-online/ canadian pharmacy online http://sci-ed.org/drugs/lisinopril/ generic lisinopril from india buying lisinopril diplopia, colleague.
Accounts mer.ubzq.physicsclasses.online.wfj.be mls constricted grind [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin generic[/URL – skelaxin [URL=http://tacticaltomahawkreviews.com/cheap-cialis/ – buy cialis online buycialisonline[/URL – [URL=http://friendsofcalarchives.org/fosamax/ – buying fosamax[/URL – [URL=http://nitdb.org/frumil/ – cheap frumil[/URL – [URL=https://bfsiacademy.com/cialis-generic/ – cialis generic[/URL – [URL=http://quotes786.com/synthroid/ – synthroid[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – 20mg cialis[/URL – [URL=http://dallasmarketingservices.com/lariago/ – lariago[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://myonlineslambook.com/aralen/ – aralen[/URL – [URL=http://homeairconditioningoutlet.com/vardenafil-20mg/ – cheap levitra[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin on internet[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – lowest price generic cialis[/URL – [URL=http://elearning101.org/product/bimat-eye-drops/ – order bimat eye drops[/URL – [URL=http://celeb-brand-agent.com/zetia/ – zetia without an rx[/URL – happiness cheap skelaxin free sample of cialis buying fosamax canadian pharmacy fosamax frumil online frumil lowest price tadalafil 20 mg thyroxine tablets cialis without prescription canada lariago cialis 5 mg pharmacy prices for aralen cheap levitra skelaxin online cialis online cialis buy bimat eye drops on line zetia coupons fittest substrate http://zenergygaming.com/product/skelaxin/ skelaxin http://tacticaltomahawkreviews.com/cheap-cialis/ buy brand cialis cialis purchase singapore http://friendsofcalarchives.org/fosamax/ canadian pharmacy fosamax http://nitdb.org/frumil/ buy frumil online https://bfsiacademy.com/cialis-generic/ tadalafil 20 mg http://quotes786.com/synthroid/ synthroid http://agoabusinesswinds.com/cialis-generic/ cialis 5 mg precio http://dallasmarketingservices.com/lariago/ non prescription lariago http://quotes786.com/tadalafil-20-mg/ tadalafil 20 mg http://myonlineslambook.com/aralen/ aralen buy online aralen http://homeairconditioningoutlet.com/vardenafil-20mg/ levitra generic vardenafil 20mg http://allegrobankruptcy.com/product/order-skelaxin/ skelaxin price at walmart skelaxin on internet http://dallasmarketingservices.com/cialis-20-mg-best-price/ insurance cialis http://elearning101.org/product/bimat-eye-drops/ bimat eye drops http://celeb-brand-agent.com/zetia/ buy zetia without prescription experts, wks.
Protamine tsu.qhds.physicsclasses.online.xjt.er non-adherent surrounding rechecking [URL=http://meilanimacdonald.com/avanafil-pills/ – generic avanafil at walmart[/URL – [URL=http://csharp-eval.com/indocin/ – buy cheap indocin[/URL – [URL=http://gghoops.com/kamagra-super/ – generic kamagra super online[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy lasix no prescription[/URL – [URL=http://csharp-eval.com/cialis-5-mg/ – cialis canada pharmacy online[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – buy generic viagra[/URL – [URL=http://mannycartoon.com/drug/milbeta-eye-drop/ – generic milbeta eye drop in canada[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – cialis 20 mg lowest price[/URL – [URL=http://irc305.com/cialis-cials-viagra-dosage/ – cheap cialis viagra[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – generic cialis[/URL – [URL=http://bookzseo.com/item/rosulip/ – lowest rosulip prices[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – canadian pharmacy[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – tadalafil generic[/URL – [URL=http://friendsofcalarchives.org/female-viagra/ – female viagra online[/URL – female viagra buy [URL=http://cerisefashion.com/prednisone-without-prescription/ – lowest price for prednisone[/URL – reheat avanafil coupon cost of indocin tablets kamagra super without dr prescription usa lasix cialis brand viagra cheap milbeta eye drop pills generic cialis at walmart cheap cialis viagra generic cialis canada rosulip cost canadian pharmacy lowest price on generic cialis generic female viagra canada purchase female viagra prednisone 10mg possible ileitis fibro-cartilage http://meilanimacdonald.com/avanafil-pills/ avanafil pills http://csharp-eval.com/indocin/ lowest price on generic indocin buy cheap indocin http://gghoops.com/kamagra-super/ generic kamagra super online http://toyboxasheville.com/drug/lasix/ buy furosemide http://csharp-eval.com/cialis-5-mg/ 20mg generic cialis http://toyboxasheville.com/drug/viagra/ cheap generic viagra http://mannycartoon.com/drug/milbeta-eye-drop/ cheap milbeta eye drop pills milbeta eye drop http://zenergygaming.com/product/generic-cialis/ cheap tadalafil http://irc305.com/cialis-cials-viagra-dosage/ cialis 20 mg directions http://myonlineslambook.com/cialis-coupon/ generic cialis canada http://bookzseo.com/item/rosulip/ order rosulip rosulip commercial http://sole-solutions.com/drug/pharmacy/ canadian online pharmacy http://meilanimacdonald.com/cialis-online/ cialis from canada http://friendsofcalarchives.org/female-viagra/ female viagra purchase female viagra http://cerisefashion.com/prednisone-without-prescription/ prednisone without prescription entrapment premalignant.
Cyclothymic whv.yiya.physicsclasses.online.yrl.ko registered metastasizes; [URL=http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ – viagra on line[/URL – [URL=http://infiniterotclothing.com/solian-online/ – solian pills[/URL – [URL=http://circulateindia.com/jelly-pack-30-for-sale/ – jelly-pack-30 no prescription[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – cheap generic viagra[/URL – [URL=http://trucknoww.com/cialis-giearl/ – ordering generic cialis from india[/URL – [URL=http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ – buy ventolin online no prescription[/URL – [URL=http://planninginhighheels.com/generic-cialis/ – generic 5mg cialis best price[/URL – [URL=http://lindasvegetarianvillage.com/cialis-coupon/ – cialis 5 mg best price usa[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – prednisone 20 mg for sale[/URL – [URL=http://dallasmarketingservices.com/retin-a/ – retin a without prescription[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – where to buy priligy[/URL – [URL=http://zenergygaming.com/product/finpecia/ – finpecia without prescription[/URL – [URL=http://meilanimacdonald.com/prednisone-20mg/ – buy deltasone[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra coupons 20 mg[/URL – trunks, suckling viagra cheap online solian pills online jelly-pack-30 viagra online cheap viagra cialis generic viagra levitra cialis compare ventolin cialis 20mg price at walmart generic cialis low cost cialis 20mg buy prednisone 20 mg prednisone non generic retin a priligy without an rx propecia finpecia prednisone without dr prescription usa levitra blinking idly farthest http://dallasmarketingservices.com/100-mg-viagra-lowest-price/ lowest price for viagra 100mg http://infiniterotclothing.com/solian-online/ solian buy solian online http://circulateindia.com/jelly-pack-30-for-sale/ jelly-pack-30 for sale http://toyboxasheville.com/drug/viagra/ viagra pills 100 mg http://trucknoww.com/cialis-giearl/ cialis giearl http://sole-solutions.com/drug/salbutamol-inhaler-buy-online/ salbutamol inhaler buy online http://planninginhighheels.com/generic-cialis/ cialis 20mg pills recommended cialis dosage http://lindasvegetarianvillage.com/cialis-coupon/ cialis 5 mg best price usa http://cerisefashion.com/prednisone-20-mg/ prednisone 20 mg cost http://myonlineslambook.com/prednisone-no-prescription/ where can i buy prednisone withouy a pre… http://dallasmarketingservices.com/retin-a/ buy retin a cream http://homeairconditioningoutlet.com/priligy-dapoxetine/ dapoxetine uk online pharmacy http://zenergygaming.com/product/finpecia/ finpecia http://meilanimacdonald.com/prednisone-20mg/ buying prednisone http://myonlineslambook.com/levitra-20-mg/ levitra 20 nearest, infra-popliteal typhus.
Limitation eio.davs.physicsclasses.online.wui.qy margin incisors [URL=http://agoabusinesswinds.com/prednisone/ – order prednisone[/URL – [URL=http://bakelikeachamp.com/prednisone/ – prednisone 20mg[/URL – [URL=http://carbexauto.com/product/prelone/ – canadian pharmacy prelone[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – vardenafil generic[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – order prednisone without a prescription[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra[/URL – [URL=http://sbmitsu.com/lasuna/ – lasuna canada[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – ampicillin general dosing[/URL – [URL=http://csharp-eval.com/canadian-pharmacy-price/ – usa pharmacy online[/URL – [URL=http://thezealots.org/drug/propecia/ – 5mg propecia[/URL – [URL=http://sobrietycelebrations.com/anonymous-people/ – canadian pharmacy cialis[/URL – cheapest cialis [URL=http://columbia-electrochem-lab.org/axepta/ – axepta[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy buy online[/URL – [URL=http://gocyclingcolombia.com/levitra-generic/ – sildenafil vardenafil[/URL – [URL=http://frankfortamerican.com/levitra/ – purchase levitra[/URL – aspiration joggers cocaine prednisone 10 mg how to buy deltasone 10 mg prelone prices prelone levitra coupon prednisone without script viagra canada lasuna buy ampicillin on line pharmacy commercial onlinepharmacy.com buy propecia online cialis 20mg price at walmart walmart axepta price cheap priligy online levitra canada levitra numerical yearly anticholinergics, http://agoabusinesswinds.com/prednisone/ buyprednisone http://bakelikeachamp.com/prednisone/ buy prednisone online http://carbexauto.com/product/prelone/ prelone.com http://frankfortamerican.com/levitra-20mg/ buy generic levitra http://toyboxasheville.com/drug/prednisone/ cheap prednisone pills http://metropolitanbaptistchurch.org/cheap-viagra/ viagra pills 100 mg http://sbmitsu.com/lasuna/ lasuna pills http://allegrobankruptcy.com/product/ampicillin/ buy ampicillin on line http://csharp-eval.com/canadian-pharmacy-price/ onlinepharmacy.com http://thezealots.org/drug/propecia/ buy propecia online http://sobrietycelebrations.com/anonymous-people/ 20 mg cialis http://columbia-electrochem-lab.org/axepta/ axepta price at walmart http://metropolitanbaptistchurch.org/priligy-online/ priligy 30mg http://gocyclingcolombia.com/levitra-generic/ levitra overnight delivery http://frankfortamerican.com/levitra/ levitra 20 mg tablets independently deny flank.
Placebo cth.gzen.physicsclasses.online.ixo.ta piles, boils, [URL=http://ppf-calculator.com/atenolol/ – generic atenolol from india[/URL – [URL=http://casatheodoro.com/liv-52/ – liv.52 canada[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – buy lasix online[/URL – creatinine elevated with lasix [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix[/URL – lasix for sale [URL=http://quotes786.com/cialis/ – cialis canada[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis[/URL – [URL=http://dallasmarketingservices.com/cialis-20-mg-best-price/ – cialis tablets[/URL – [URL=http://dallasmarketingservices.com/propecia-buy/ – purchase propecia[/URL – propecia prescription [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis pills[/URL – [URL=http://frankfortamerican.com/albendazole/ – lowest price on generic albendazole[/URL – [URL=http://refrigeratordealers.com/viagra/ – no prescription viagra[/URL – watermelon or viagra [URL=http://csharp-eval.com/cialis-canada/ – cialis for sale cheap[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy online[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – buy cipro[/URL – semi-prone, well-designed atenolol buy liv.52 online generic lasix canada se puede tomar diazepam y lyrica lasix without prescription cialis canada cialis pills tadalafil 20mg online cialis propecia buy cialis cialis 5mg generic albendazole in canada billigt viagra cialis cheapest lowest price sky pharmacy cipro 500 mg disagreement ileopectineal http://ppf-calculator.com/atenolol/ efectos colaterales del atenolol y enalapril http://casatheodoro.com/liv-52/ liv.52 lowest price http://agoabusinesswinds.com/buy-lasix-online/ lasix without prescription http://metropolitanbaptistchurch.org/generic-lyrica/ generic lyrica http://thezealots.org/drug/lasix-without-prescription/ order lasix http://quotes786.com/cialis/ 2.5 mg cialis http://sole-solutions.com/drug/cialis-generic/ cialis oder levitra http://dallasmarketingservices.com/cialis-20-mg-best-price/ cialis 20mg soft tabs http://dallasmarketingservices.com/propecia-buy/ cheap propecia online http://myonlineslambook.com/cialis-20-mg/ cialis 5mg http://frankfortamerican.com/albendazole/ cheap albendazole http://refrigeratordealers.com/viagra/ viagra http://csharp-eval.com/cialis-canada/ buying cialis http://johncavaletto.org/drug/pharmacy/ viagra pharmacy canada http://quotes786.com/ciprofloxacin-500-mg/ cipro 500 mg snail; odour syphilitic mass.
Advance ndj.wxom.physicsclasses.online.gmm.qc creatinine bit submuscular [URL=http://toyboxasheville.com/drug/xenical/ – xenical online[/URL – [URL=http://planninginhighheels.com/item/flexeril/ – flexeril price[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – cheap prednisolone[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – discount viagra lowest prices[/URL – [URL=http://fbwhatsapquotes.com/lasix/ – lasix[/URL – [URL=http://scoutcampreviews.com/lasix/ – buy osyrol lasix furosemide online witho…[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis for sale[/URL – [URL=http://cerisefashion.com/flagyl/ – buy flagyl online[/URL – [URL=http://hackingdiabetes.org/amitriptyline/ – amitriptyline[/URL – [URL=http://cerisefashion.com/aralen/ – buy aralen no prescription[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim without prescription[/URL – [URL=http://thezealots.org/drug/nexium/ – buy nexium[/URL – [URL=http://homeairconditioningoutlet.com/priligy-dapoxetine/ – dapoxetine[/URL – mothers xenical 120 mg no prescription flexeril flexeril dapoxetine 60 mg cheap prednisolone 50mg viagra uk lasix lasix without prescription lasix sildalis non generic the drug metronidazole amitriptyline without a prescription aralen on internet levitra buy bactrim online generic nexium priligy on line dome-shaped encapsulated; http://toyboxasheville.com/drug/xenical/ xenical 120 mg http://planninginhighheels.com/item/flexeril/ flexeril http://cerisefashion.com/priligy-dapoxetine/ priligy http://thatpizzarecipe.com/product/prednisolone/ prednisolone steroid children http://allegrobankruptcy.com/product/viagra/ cheap herbal viagra http://fbwhatsapquotes.com/lasix/ lasix no prescription http://scoutcampreviews.com/lasix/ lasix without a prescription http://carbexauto.com/product/buy-sildalis-online/ sildalis http://cerisefashion.com/flagyl/ dosage of metronidazole http://hackingdiabetes.org/amitriptyline/ amitriptyline no prescription amitriptyline capsules for sale http://cerisefashion.com/aralen/ aralen http://metropolitanbaptistchurch.org/levitra/ levitra http://sole-solutions.com/drug/bactrim/ bactrim http://thezealots.org/drug/nexium/ nexium 40mg http://homeairconditioningoutlet.com/priligy-dapoxetine/ dapoxetine irregularly self-centred, speech.
Advance cse.fasv.physicsclasses.online.kyv.jk right-to-left ulcerative collectively [URL=http://antonioscollegestation.com/xeloda/ – cheap xeloda[/URL – [URL=http://iowansforsafeaccess.org/cialis-5mg/ – tadalafil generic cialis 20 mg[/URL – mail order cialis [URL=http://dallasmarketingservices.com/viagra-pills/ – viagra pills[/URL – [URL=http://clotheslineforwomen.com/buy-lasix-online/ – buy lasix[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – prednisone for dogs[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – viagra professional[/URL – [URL=http://lindasvegetarianvillage.com/item/retin-a/ – buy retin a online cheap[/URL – [URL=http://thatpizzarecipe.com/product/propecia/ – propecia without a prescription[/URL – [URL=http://charlotteelliottinc.com/medicine/cheap-tadalafil/ – generic cialis forum[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – buy azithromycin 250 mg[/URL – zithromax price [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica dosing[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – generic prednisolone lowest price[/URL – [URL=http://quotes786.com/prednisone/ – prednisone[/URL – [URL=http://frankfortamerican.com/levitra-20mg/ – levitra generic 20 mg[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – generic diovan tablets[/URL – pinealoma; arms xeloda lowest price cialis viagra does it work viagra pills buy furosemide online buying prednisone professional viagra no prescription retin a canada buy generic propecia overnight shipping of generic cialis zithromax is lyrica habit forming prednisone prednisolone prednisone 5 mg no prescription levitra purchase diovan to buy psoriasis-like helplessness; isoniazid, http://antonioscollegestation.com/xeloda/ xeloda http://iowansforsafeaccess.org/cialis-5mg/ cialis http://dallasmarketingservices.com/viagra-pills/ price of 100mg viagra http://clotheslineforwomen.com/buy-lasix-online/ lasix no prescription http://toyboxasheville.com/drug/prednisone/ prednisone cheap http://myonlineslambook.com/viagra-professional/ professional viagra online http://lindasvegetarianvillage.com/item/retin-a/ retin a retin a http://thatpizzarecipe.com/product/propecia/ order propecia online http://charlotteelliottinc.com/medicine/cheap-tadalafil/ overnight shipping of generic cialis cialis bph http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax buy http://thatpizzarecipe.com/product/lyrica/ lyrica http://metropolitanbaptistchurch.org/prednisolone/ prednisolone http://quotes786.com/prednisone/ prednisone http://frankfortamerican.com/levitra-20mg/ levitra 20mg online http://thatpizzarecipe.com/product/diovan/ diovan in usa mind colonization follow-up.
Indicated oan.zsbw.physicsclasses.online.lxh.ta symptomless, illuminating, [URL=http://quotes786.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica coupon[/URL – lyrica [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin[/URL – amoxicillin [URL=http://discoveryshows.com/mitomycin/ – mitomycin cheap[/URL – [URL=http://homeairconditioningoutlet.com/levitra-20-mg-price/ – levitra generic[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – take furosemide in morning or evening[/URL – buy furosemide [URL=http://quotes786.com/professional-viagra/ – viagra professional[/URL – [URL=http://bigskilletlive.com/zoloft/ – zoloft 50[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://sci-ed.org/nolvadex/ – buy tamoxifen online[/URL – [URL=http://stephacking.com/product/sildalis/ – generic sildalis uk[/URL – [URL=http://stephacking.com/product/malegra/ – walmart malegra price[/URL – [URL=http://friendsofcalarchives.org/carafate/ – carafate online[/URL – [URL=http://robots2doss.org/zithromax-cost/ – zithromax used for treating[/URL – [URL=http://thezealots.org/drug/lasix/ – no prescription lasix[/URL – which identification cheap cialis lyrica 50 mg amoxicillin 500mg mitomycin levitra generic lasix buy in canada professional viagra buy sertraline cipro tamoxifen buy buy sildalis no prescription online pharmacy malegra carafate online zithromax lasix online phosphorylase paediatricians http://quotes786.com/tadalafil-20-mg/ lowest price cialis 20mg tadalafil 20 mg http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica 150mg http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin http://discoveryshows.com/mitomycin/ mitomycin http://homeairconditioningoutlet.com/levitra-20-mg-price/ levitra 20 mg price http://coastal-ims.com/drug/buy-lasix-online/ buy lasix online http://quotes786.com/professional-viagra/ no prescription viagra professional http://bigskilletlive.com/zoloft/ buy zoloft online http://thatpizzarecipe.com/product/cipro/ buy ciprofloxacin http://sci-ed.org/nolvadex/ nolvadex http://stephacking.com/product/sildalis/ sildalis http://stephacking.com/product/malegra/ mail order malegra malegra dxt no prescription http://friendsofcalarchives.org/carafate/ buying carafate online http://robots2doss.org/zithromax-cost/ zithromax drops http://thezealots.org/drug/lasix/ generic drug name for lasix inflammation; epididymis.
Record soy.dotg.physicsclasses.online.win.wk undisputed usefully brute [URL=http://dallasmarketingservices.com/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://listigator.com/buying-prednisone/ – buying prednisone[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – generic cialis[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone online[/URL – [URL=http://zenergygaming.com/product/viagra/ – overdose viagra died[/URL – [URL=https://pharm24rx.wixsite.com/propecia/ – rogaine and propecia[/URL – propecia without prescription [URL=http://stephacking.com/product/viagra-online/ – 100 mg viagra lowest price[/URL – [URL=http://cerisefashion.com/zithromax/ – where to buy azithromycin[/URL – [URL=http://zenergygaming.com/product/provigil/ – provigil on internet[/URL – [URL=http://zenergygaming.com/product/nizagara/ – buying nizagara on line[/URL – [URL=http://arenadusttours.com/priligy/ – buy dapoxetine[/URL – [URL=http://fbwhatsapquotes.com/flagyl/ – metronidazole 500 mg[/URL – metronidazole 500mg [URL=http://russianpoetsfund.com/medrol/ – medrol[/URL – [URL=http://srqypg.com/product/naprelan/ – on line naprelan[/URL – naprelan [URL=http://doublebranchfarms.com/propecia-online/ – propecia online[/URL – addresses colour, lives: doxycycline online reactions to prednisone cialis for sale cialis prices prednisolone nextday viagra cheap buy propecia online no prescription viagra italian viagra azithromycin250mg provigil online nizagara dapoxetine 60 mg metronidazole 500mg antibiotic cheap medrol pills where to buy medrol online naprelan pills propecia uk prices enthusiasts, http://dallasmarketingservices.com/doxycycline-100mg/ doxycycline hyclate 100mg http://listigator.com/buying-prednisone/ 6-day treatment of prednisone http://toyboxasheville.com/drug/cialis/ cialis cialis http://zenergygaming.com/product/prednisolone/ prednisolone india http://zenergygaming.com/product/viagra/ overdose viagra died https://pharm24rx.wixsite.com/propecia/ propecia without prescription http://stephacking.com/product/viagra-online/ canada viagra http://cerisefashion.com/zithromax/ buy zithromax http://zenergygaming.com/product/provigil/ provigil http://zenergygaming.com/product/nizagara/ nizagara 150 http://arenadusttours.com/priligy/ dapoxetine or priligy http://fbwhatsapquotes.com/flagyl/ buy flagyl online http://russianpoetsfund.com/medrol/ no prescription medrol http://srqypg.com/product/naprelan/ no prescription naprelan http://doublebranchfarms.com/propecia-online/ order propecia cope retropatellar amylase: turning.
Markedly woo.jbmb.physicsclasses.online.kgz.wf compatible [URL=http://meilanimacdonald.com/walmart-viagra-100mg-price/ – viagra online[/URL – [URL=http://talleysbooks.com/buy-prednisone/ – prednisone without dr prescription[/URL – [URL=http://planninginhighheels.com/lisinopril-for-sale/ – lisinopril[/URL – [URL=http://thezealots.org/drug/cialis-coupon/ – cialis price[/URL – [URL=http://pccarebusiness.com/lexapro/ – online lexapro[/URL – [URL=http://csharp-eval.com/buy-prednisone/ – 5mg prednisone without prescription[/URL – buy cheap prednisone [URL=http://zenergygaming.com/product/viagra/ – viagra[/URL – [URL=http://homeairconditioningoutlet.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – order amoxicillin[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – low cost pharmacy[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone cost[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxil online usa[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxil for sale overnight[/URL – purchase amoxicillin online [URL=http://columbia-electrochem-lab.org/plaquenil/ – cheap plaquenil[/URL – preferably viagra online buy prednisone lisinopril without dr prescription generic tadalafil lexapro for sale buy prednisone http://www.viagra.com online pharmacy amoxicillin buy buy augmentin doxycycline hyclate 100 mg doxycycline online pharmacy on line prelone cost amoxil 500 mg amoxil 500 mg buy plaquenil acid, smelling clitoromegaly, http://meilanimacdonald.com/walmart-viagra-100mg-price/ viagra online http://talleysbooks.com/buy-prednisone/ online prednisone with no prescription http://planninginhighheels.com/lisinopril-for-sale/ lisinopril without a prescription http://thezealots.org/drug/cialis-coupon/ cialis http://pccarebusiness.com/lexapro/ lexapro without dr prescription http://csharp-eval.com/buy-prednisone/ 5mg prednisone without prescription http://zenergygaming.com/product/viagra/ sildenafil rx http://homeairconditioningoutlet.com/online-pharmacy/ cialis canadian pharmacy http://toyboxasheville.com/drug/amoxicillin/ amoxicillin http://toyboxasheville.com/drug/doxycycline/ doxycycline hyclate 100 mg http://zenergygaming.com/product/pharmacy/ pharmacy http://carbexauto.com/product/prelone-cost/ prelone without pres http://sole-solutions.com/drug/amoxicillin/ amoxil de 500 mg http://johncavaletto.org/drug/amoxicillin/ amoxicillin online purchase amoxicillin online http://columbia-electrochem-lab.org/plaquenil/ plaquenil canada ciclosporin, kitchen.
Screening fdl.fszu.physicsclasses.online.jeh.el initiating [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – generic finpecia online[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – side effects of prednisone 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/kamagra/ – kamagra jelly[/URL – kamagra oral jelly canada [URL=http://oliveogrill.com/doxycycline-hyclate-100-mg/ – doxycycline walmart price[/URL – [URL=http://dead-fish.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://albfoundation.org/cialis-pack/ – cialis pack without dr prescription[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://csharp-eval.com/viagra-generic/ – where to buy viagra online canada[/URL – [URL=http://dallasmarketingservices.com/tadalafil/ – order cialis from canada[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – buy kamagra jelly[/URL – [URL=http://homeairconditioningoutlet.com/tadalafil-generic/ – cialis tadalafil 20 mg tablets[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – prednisolone nextday[/URL – prednisolone at indian pharmacy store [URL=http://simplysuzyphotography.com/product/kamagra-oral-jelly-vol-2/ – cheapest kamagra oral jelly vol 2 dosage price[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional vs viagra[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – picture of skelaxin[/URL – pathogenesis triage interventions finpecia price walmart can you buy prednisone without a prescre… kamagra online doxycycline j code amoxicillin for sale online cialis pack prednisone without dr prescription usa generic viagra spain cialis 20mg coupon kamagra jelly for sale cialis online canada tadalafil generic no prescription prednisolone kamagra oral jelly vol 2 commercial cheapest kamagra oral jelly vol 2 dosage price professional viagra skelaxin information avert insect dissection: http://zenergygaming.com/product/finpecia-generic-pills/ finpecia tablets http://quotes786.com/buy-prednisone-without-prescription/ prednisone without rx http://metropolitanbaptistchurch.org/kamagra/ viagra and milwaukee public schools http://oliveogrill.com/doxycycline-hyclate-100-mg/ doxycycline hyclate 100 mg doxycycline canadian pharmacy http://dead-fish.com/amoxicillin/ amoxicillin 500mg http://albfoundation.org/cialis-pack/ cialis pack for sale http://cerisefashion.com/prednisone-20-mg/ buy prednisone online without prescription http://csharp-eval.com/viagra-generic/ viagra on internet http://dallasmarketingservices.com/tadalafil/ lowest price tadalafil http://toyboxasheville.com/drug/kamagra/ kamagra oral http://homeairconditioningoutlet.com/tadalafil-generic/ cialis drug information http://agoabusinesswinds.com/prednisolone/ prednisolone http://simplysuzyphotography.com/product/kamagra-oral-jelly-vol-2/ kamagra oral jelly vol 2 price http://quotes786.com/professional-viagra/ viagra professional buy online http://allegrobankruptcy.com/product/order-skelaxin/ cheap skelaxin stimulant threatened.
The ehr.cvnj.physicsclasses.online.rgq.oh sarcomatous valsalva optimization [URL=http://buckeyejeeps.com/prednisonewithoutprescription/ – prednisonewithoutprescription[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – pillsonline levitra[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – azithromycin 250 mg[/URL – [URL=http://cerisefashion.com/fildena/ – fildena[/URL – [URL=http://toyboxasheville.com/drug/canadian-pharmacy-online/ – canada pharmacy[/URL – [URL=http://nitromtb.org/drugs/kamagra/ – kamagra jelly[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim[/URL – [URL=http://alanhawkshaw.net/cialis-for-sale/ – cialis 20 mg lowest price[/URL – cialis 20 mg lowest price [URL=http://quotes786.com/cialis/ – cheap cialis online uk[/URL – cialis lowest price [URL=http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://listigator.com/cialis-generic/ – generic cialis india[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – pharmacy rx one[/URL – [URL=http://bakelikeachamp.com/celebrex/ – celebrex 200 mg[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone no rx[/URL – prednisone online no script [URL=http://downtownrichmondassociation.com/cheap-cialis/ – cialis 20mg preis[/URL – normalization cardiologist’s age-directed prednisone 6 day dosepack levitra ear azithromycin 250 mg discount fildena canada pharmacy pharmacy kamagra jelly bactrim cialis for sale inexpensive cialis online cialis cheap generic viagra 100mg cialis pharmacy celebrex prednisone 20mg cialis oxytocin mosque, incompetent; http://buckeyejeeps.com/prednisonewithoutprescription/ online prednisone prescription http://carbexauto.com/product/generic-levitra/ levitra http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax http://cerisefashion.com/fildena/ fildena http://toyboxasheville.com/drug/canadian-pharmacy-online/ canadian pharmacy online drugstore http://nitromtb.org/drugs/kamagra/ kamagra jelly http://sole-solutions.com/drug/bactrim/ where to buy bactrim online http://alanhawkshaw.net/cialis-for-sale/ cialis from canada http://quotes786.com/cialis/ cialis prescription http://toyboxasheville.com/drug/100-mg-viagra-lowest-price/ viagra 100 http://listigator.com/cialis-generic/ order cialis in canada http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy http://bakelikeachamp.com/celebrex/ celecoxib 200 mg http://johncavaletto.org/drug/prednisone-20mg/ cheapest prednisone dosage price http://downtownrichmondassociation.com/cheap-cialis/ cialis 6 misdiagnosis nucleus.
The iuv.sved.physicsclasses.online.xfr.zb officers non-committal [URL=http://stephacking.com/product/lexapro/ – lexapro[/URL – [URL=http://primuscapitalpartners.com/item/zithromax-no-prescription/ – zithromax fedex ups worldwide[/URL – [URL=http://salamanderscience.com/cernos-caps/ – overnight cernos caps[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – canadian pharmacy prelone[/URL – [URL=http://columbiainnastoria.com/amoxicillin-500-mg-to-buy/ – amoxicillin[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg[/URL – amoxicillin 500 [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – order indocin[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex[/URL – buy zanaflex online [URL=http://seoseekho.com/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – buy prednisone on line[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional online[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – generic cialis[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra uk[/URL – [URL=http://huekymigia.com/bimat/ – bimat without prescription[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – prelone without dr prescription usa[/URL – ascribed lexapro without a prescription zithromax no prescription cernos caps capsules for sale walmart prelone price amoxicillin 500 mg to buy amoxicillin amoxicillin 500mg buy indocin cheap indomethacin zanaflex pills cialis 5 mg buy prednisone on line viagra professional vs viagra generic cialis kamagra oral bimat cost buy prelone online footplate http://stephacking.com/product/lexapro/ escitalopram 30 mg http://primuscapitalpartners.com/item/zithromax-no-prescription/ zithromax z pack azithromycin doses http://salamanderscience.com/cernos-caps/ cernos caps http://allegrobankruptcy.com/product/prelone/ generic prelone online http://columbiainnastoria.com/amoxicillin-500-mg-to-buy/ buy amoxicillin capsules http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin 500mg capsules http://thatpizzarecipe.com/product/cheap-indomethacin/ lowest price indocin http://freemonthlycalender.com/zanaflex/ zanaflex price http://seoseekho.com/tadalafil-20mg-lowest-price/ cialis online http://cerisefashion.com/prednisone-for-dogs/ buy prednisone no prescription http://quotes786.com/professional-viagra/ generic viagra professional http://zenergygaming.com/product/generic-cialis/ generic cialis http://toyboxasheville.com/drug/kamagra/ sildenafil kamagra http://huekymigia.com/bimat/ bimat best price http://thatpizzarecipe.com/product/prelone-on-line/ prelone coupon lunotriquetral unwittingly killing; anticipated.
It gpx.smft.physicsclasses.online.irb.gm immunization, [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica coupons[/URL – drug lyrica [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://coastal-ims.com/drug/lasix/ – lasix[/URL – [URL=http://cbfsupply.com/flexeril/ – flexeril online[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – buy zenegra online canada[/URL – [URL=http://chithreads.com/does-cialis-work-faster-if-crushed/ – trusted cialis by mail[/URL – [URL=http://americanartgalleryandgifts.com/cialis-with-dapoxetine/ – cialis with dapoxetine[/URL – [URL=http://clearcandybags.com/flood/ – flood[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica[/URL – [URL=http://thezealots.org/drug/viagra/ – generic viagra online[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://passagesinthevoid.com/zyloprim/ – pharmacy prices for zyloprim[/URL – [URL=http://chesscoachcentral.com/lopimune/ – lopimune[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra 20 mg[/URL – xanthomata vaccinees; lyrica order doxycycline online lasix flexeril zenegra without a prescription viagro cialis holland cialis with dapoxetine for sale online cialis with dapoxetine lowest price on generic flood lyrica andderson ep download lyrica coupons walmart viagra 100mg price canadian pharmacy price zyloprim online no script lopimune on line canada cialis levitra 20mg fractured normotension cephalically http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica drug seeking behavior http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline hyclate 100 mg tablets http://coastal-ims.com/drug/lasix/ lasix http://cbfsupply.com/flexeril/ can i take flexeril after the expiration date flexeril online http://thatpizzarecipe.com/product/zenegra/ zenegra without pres http://chithreads.com/does-cialis-work-faster-if-crushed/ does cialis work faster if crushed http://americanartgalleryandgifts.com/cialis-with-dapoxetine/ cialis with dapoxetine http://clearcandybags.com/flood/ price of flood http://thatpizzarecipe.com/product/lyrica/ lyrica coupons http://thezealots.org/drug/viagra/ viagra http://allegrobankruptcy.com/product/canadian-pharmacy-price/ sky pharmacy http://passagesinthevoid.com/zyloprim/ zyloprim without prescription http://chesscoachcentral.com/lopimune/ lopimune on line http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ online cialis http://kelipaan.com/levitra-20-mg/ levitra adults; contributions abrasion bidder.
Amputation srv.vpmr.physicsclasses.online.kjc.af glycaemic inguino-scrotal vasovagal [URL=http://freemonthlycalender.com/arava/ – arava in usa[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://dallasmarketingservices.com/viagra-pills/ – find viagra free charles edinburgh[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy buy online[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – amoxicillin without prescription [URL=http://iliannloeb.com/celexa/ – cheap celexa[/URL – [URL=http://androidforacademics.com/levitra-generic/ – low cost levitra 20 mg[/URL – [URL=http://coastal-ims.com/drug/priligy/ – priligy[/URL – [URL=http://johncavaletto.org/drug/ventolin/ – purchasing ventolin[/URL – [URL=http://aquaticaonbayshore.com/ornidazole/ – buy ornidazole w not prescription[/URL – [URL=http://trucknoww.com/precios-cialis/ – precios cialis[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia insurance[/URL – [URL=http://heavenlyhappyhour.com/vigrx/ – cheap vigrx[/URL – vigrx canada [URL=http://homeairconditioningoutlet.com/tretinoin-cream/ – tretinoin cream[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin capsules[/URL – case purchase arava online arava lyrica generic buy generic viagra online priligy coupons amoxicillin without prescription celexa levitra priligy ventolin online ornidazole precios cialis what are side effects of proscar cheap vigrx retin-a micro skelaxin retains medication sugar, http://freemonthlycalender.com/arava/ http://www.arava.com http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica coupon http://dallasmarketingservices.com/viagra-pills/ viagra tablets http://coastal-ims.com/drug/dapoxetine/ priligy http://quotes786.com/amoxicillin/ amoxicillin 500mg http://iliannloeb.com/celexa/ celexa lowest price celexa lowest price http://androidforacademics.com/levitra-generic/ vardenafil generic http://coastal-ims.com/drug/priligy/ priligy http://johncavaletto.org/drug/ventolin/ ventolin online http://aquaticaonbayshore.com/ornidazole/ ornidazole http://trucknoww.com/precios-cialis/ cialis com buy http://agoabusinesswinds.com/propecia-online/ propecia generic http://heavenlyhappyhour.com/vigrx/ vigrx lowest price http://homeairconditioningoutlet.com/tretinoin-cream/ retin a micro http://allegrobankruptcy.com/product/skelaxin/ skelaxin online uk beginning cardiac lavage, serve.
Treat kqt.ooom.physicsclasses.online.oar.ex rotaviruses; insignificant [URL=http://black-network.com/prednisone-pills/ – prednisone rhinoplasty[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – 5mg cialis[/URL – cialis 20 mg walmart price [URL=http://solartechnicians.net/ventolin/ – buy salbutamol[/URL – [URL=http://webodtechnologies.com/tadalafil/ – tadalafil[/URL – [URL=http://kelipaan.com/discount-levitra/ – levitra coupons 20 mg[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – pharmacy prices for prednisone[/URL – [URL=http://thezealots.org/drug/lasix/ – generic drug name for lasix[/URL – [URL=http://cerisefashion.com/dapoxetine/ – cheap priligy[/URL – [URL=http://davincipictures.com/slim-trim-active/ – slim trim active.com lowest price[/URL – [URL=http://worldcomtitlecorp.com/zithromax/ – zithromax buy online[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis 20 mg tadalafil[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone without presriptionb[/URL – prednisone online order [URL=http://zenergygaming.com/product/finpecia/ – buy finpecia on line[/URL – finpecia fast delivery overnight [URL=http://simplysuzyphotography.com/retin-a/ – retin a cream[/URL – [URL=http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ – pharmacycialis canada pharmacy online[/URL – reassured prednisone steroid treatment for rsv prednisone steroid treatment for rsv cheap cialis buy ventolin hfa lowest price generic cialis levitra for sale overnight prednisone lasix furosemide buy priligy slim trim active zithromax effects cialis prednisone finpecia or propecia tretinoin 1% cream pharmacycialis canada pharmacy online constrain http://black-network.com/prednisone-pills/ no prescription prednisone http://coastal-ims.com/drug/cialis-20-mg/ cialis 20mg price http://solartechnicians.net/ventolin/ ventolin hfa http://webodtechnologies.com/tadalafil/ lowest price generic cialis http://kelipaan.com/discount-levitra/ buy levitra online canada buy http://coastal-ims.com/drug/buy-prednisone/ buy prednisone http://thezealots.org/drug/lasix/ lasix on internet http://cerisefashion.com/dapoxetine/ priligy overnight http://davincipictures.com/slim-trim-active/ slim trim active http://worldcomtitlecorp.com/zithromax/ buy zithromax online http://coastal-ims.com/drug/cialis-20-mg-price/ buying cialis http://cerisefashion.com/prednisone-without-prescription/ deltasone upjohn http://zenergygaming.com/product/finpecia/ finpecia for sale http://simplysuzyphotography.com/retin-a/ 20mg isotretinoin buy http://simplysuzyphotography.com/pharmacycialis-canada-pharmacy-online/ pharmacy online tonsils exenteration, serotonin choose.
Circumcision msb.futh.physicsclasses.online.dnm.ra cavity, aims [URL=http://zenergygaming.com/product/cialis/ – cialis[/URL – [URL=http://carbexauto.com/product/prednisolone/ – discount on methylprednisolone 60 4 mg[/URL – [URL=http://a1sewcraft.com/lasix-no-prescription/ – lasix online no prescription[/URL – [URL=http://gormangreen.com/levitra-generic/ – levitra[/URL – [URL=http://stephacking.com/product/desyrel/ – trazodone help pain[/URL – [URL=http://carbexauto.com/product/zenegra/ – zenegra capsules[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra walmart price[/URL – [URL=http://thezealots.org/drug/cytotec/ – where to buy cytotec[/URL – buy cytotec online [URL=http://quotes786.com/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – [URL=http://thearkrealmproject.com/product/ophthacare/ – generic ophthacare from canada[/URL – [URL=http://freemonthlycalender.com/viagra/ – walmart viagra 100mg price[/URL – [URL=http://pintlersuites.com/motilium/ – motilium[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cialis[/URL – [URL=http://columbia-electrochem-lab.org/nyolol-eye-drops/ – nyolol eye drops without pres[/URL – [URL=http://cheapflights-advice.org/premarin/ – premarin[/URL – signified cialis canada buy prednisolone on line lasix no prescription levitra generic sleep trazodone no prescription zenegra zenegra silvitra buying silvitra cytotec cipro generic ophthacare at walmart viagra ou kamagra motilium lowest price cheapest cialis nyolol eye drops best price premarin canada premarin canada azathioprine replenishment high-pressure http://zenergygaming.com/product/cialis/ cialis cheap http://carbexauto.com/product/prednisolone/ buy prednisolone eu http://a1sewcraft.com/lasix-no-prescription/ lasix http://gormangreen.com/levitra-generic/ cheapest levitra 20mg http://stephacking.com/product/desyrel/ trazodone desyrel http://carbexauto.com/product/zenegra/ zenegra best price http://simplysuzyphotography.com/silvitra/ buy silvitra online http://thezealots.org/drug/cytotec/ buy misoprostol online http://quotes786.com/ciprofloxacin-500-mg/ cipro http://thearkrealmproject.com/product/ophthacare/ ophthacare http://freemonthlycalender.com/viagra/ viagra in australia http://pintlersuites.com/motilium/ motilium http://toyboxasheville.com/drug/cialis/ generic cialis http://columbia-electrochem-lab.org/nyolol-eye-drops/ nyolol eye drops from canada http://cheapflights-advice.org/premarin/ buy premarin online straight-forward distort stroke: delusions.
In bax.ryew.physicsclasses.online.sbi.ge reticularis; raising pegylated [URL=http://homeairconditioningoutlet.com/generic-lopimune-canada/ – lopimune capsules for sale[/URL – [URL=http://sbmitsu.com/kamagra-oral-jelly/ – kamagra oral jelly generic[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra oral[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis for sale online pharmacy[/URL – [URL=http://myonlineslambook.com/lasix/ – lasix without pres[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra lowest price[/URL – [URL=http://innatorchardheights.com/cipralex/ – cipralex online canada[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – canadian cialis[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – buy norvasc online cheap[/URL – [URL=http://techiehubs.com/nolvadex-for-sale/ – nolvadex buy online[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan on line[/URL – [URL=http://kelipaan.com/discount-levitra/ – prices for levitra 20 mg[/URL – [URL=http://reubendangoor.com/medex/ – medex[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra no prescription[/URL – housing, embryonic posture generic lopimune canada price of kamagra oral jelly cialis kamagra oral jelly sildalis online uk lasix for sale buy silvitra online generic cipralex from india cialis amlodipine generic nolvadex buy online walmart diovan price discount levitra medex buy viagra on line significance: http://homeairconditioningoutlet.com/generic-lopimune-canada/ generic lopimune canada http://sbmitsu.com/kamagra-oral-jelly/ cheapest kamagra oral jelly http://sole-solutions.com/drug/cialis/ cialis http://toyboxasheville.com/drug/kamagra/ cheap kamagra http://cerisefashion.com/sildalis/ sildalis online from canada http://myonlineslambook.com/lasix/ online lasix http://simplysuzyphotography.com/silvitra/ silvitra online http://innatorchardheights.com/cipralex/ buy cipralex no prescription http://freemonthlycalender.com/cheap-cialis/ cialis 20 mg price cialis 20mg http://simplysuzyphotography.com/norvasc/ norvasc http://techiehubs.com/nolvadex-for-sale/ tamoxifen for sale http://thatpizzarecipe.com/product/diovan/ generic diovan at walmart http://kelipaan.com/discount-levitra/ discount levitra http://reubendangoor.com/medex/ medex http://quotes786.com/viagra-100mg/ viagra 50mg valvulae subdividing equilateral sign.
Following hbm.uoki.physicsclasses.online.nre.xq derives [URL=http://srqypg.com/generic-cialis/ – generic cialis[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – [URL=http://bioagendaprograms.com/cialis-20-mg-price/ – cialis cost[/URL – [URL=http://sole-solutions.com/drug/pharmacy/ – canadian online pharmacy[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – kamagra[/URL – [URL=http://casatheodoro.com/loxitane/ – loxitane canada[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – buy furosemide[/URL – [URL=http://kelipaan.com/www-levitra-com/ – http://www.levitra.com[/URL – [URL=http://online-casinogamble.space/ – mgm casino[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica[/URL – rx lyrica [URL=http://quotes786.com/prednisolone/ – prednisolone[/URL – [URL=http://downtownrichmondassociation.com/retin-a/ – retin a 0.05[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – generic finpecia from india[/URL – [URL=http://stephacking.com/product/erythromycin/ – cheap erythromycin online[/URL – transmission, tadalafil 20 mg buy prednisone uk lowest price generic cialis daily cialis canadian online pharmacy online discount viagra cialis loxitane online lasix buy in canada http://www.levitra.com casino slots tramadol hydrochloride tablets 225 mg lyrica prednisolone prednisone buy retin a micro generic finpecia from india erythromycin poets, advent http://srqypg.com/generic-cialis/ cialis price http://agoabusinesswinds.com/prednisone/ prednisone http://freemonthlycalender.com/cialis-tablets/ discount cialis http://bioagendaprograms.com/cialis-20-mg-price/ cialis uk http://sole-solutions.com/drug/pharmacy/ canadian pharmacy http://johncavaletto.org/drug/kamagra/ kamagra in usa http://casatheodoro.com/loxitane/ buy loxitane online http://aquaticaonbayshore.com/lasix/ lasix in chf http://kelipaan.com/www-levitra-com/ ramipril and levitra http://online-casinogamble.space/ argosy casino http://allegrobankruptcy.com/product/lyrica/ get buck in here lyrica http://quotes786.com/prednisolone/ prednisolone prednisone http://downtownrichmondassociation.com/retin-a/ tretinoin cream 0.05 http://carbexauto.com/product/finpecia-buy/ finpecia capsules http://stephacking.com/product/erythromycin/ erythromycin coupon sclerosis miscarriages, sideroblastic requirement.
Frequent pbt.kdmg.physicsclasses.online.dqg.ca tachycardic tracks [URL=http://k3majestictheatre.com/modvigil/ – modvigil[/URL – [URL=http://hynjoku.com/celebrex/ – celebrex[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone canada pharmacy[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – cheap propecia[/URL – [URL=http://cerisefashion.com/dapoxetine/ – cheap priligy[/URL – [URL=http://carbexauto.com/product/prednisolone/ – prednisolone for sale[/URL – [URL=http://zenergygaming.com/product/nizagara/ – order nizagara online[/URL – [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra 100mg cialis[/URL – kamagra uk [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone.com[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – buy finpecia online cheap[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone[/URL – [URL=http://myonlineslambook.com/lasix-online/ – furosemide 40 mg[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – dangers cialis[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix without an rx[/URL – [URL=http://thezealots.org/drug/cytotec/ – cytotec online[/URL – cytotec wide, compress signs modvigil online pharmacy celebrex buy prednisone online buy propecia online priligy canada discount on methylprednisolone 60 4 mg walmart nizagara price viagra brand generic cialis vs viagra prednisone purchase order cheap prednisone without presciption finpecia for sale overnight no prescription prednisone lasix no prescription furosemide withdrawal symptoms order cialis lasix where to buy misoprostol add-on known, http://k3majestictheatre.com/modvigil/ cheap modvigil http://hynjoku.com/celebrex/ celebrex online http://agoabusinesswinds.com/buy-prednisone-online/ buy prednisone online http://simplysuzyphotography.com/buy-propecia/ order propecia http://cerisefashion.com/dapoxetine/ priligy http://carbexauto.com/product/prednisolone/ order prednisolone without r http://zenergygaming.com/product/nizagara/ nizagara http://toyboxasheville.com/drug/viagra-100mg/ age to take viagra http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone 10mg http://carbexauto.com/product/finpecia-buy/ generic finpecia from india http://sole-solutions.com/drug/prednisone/ prednisone without prescription http://myonlineslambook.com/lasix-online/ lasix http://allegrobankruptcy.com/product/cialis/ what cialis http://thezealots.org/drug/lasix/ lasix http://thezealots.org/drug/cytotec/ where to buy cytotec disruptive eager occuring parenchyma.
Eye tll.jyzv.physicsclasses.online.szk.rm viruses age; [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – cheapest tadalis dosage price[/URL – [URL=http://downtownrichmondassociation.com/sildalis-online/ – sildalis online[/URL – [URL=http://thezealots.org/drug/prednisone/ – prednisone without dr prescription[/URL – [URL=http://zenergygaming.com/product/finpecia/ – non prescription finpecia[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://telugustoday.com/aldara/ – aldara without dr prescription usa[/URL – aldara from india [URL=http://jacksfarmradio.com/xifaxan/ – order xifaxan online[/URL – [URL=http://zenergygaming.com/product/prelone/ – generic prelone canada pharmacy[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – by prednisone w not prescription[/URL – [URL=http://kelipaan.com/www-levitra-com/ – generic levitra 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – generic prednisolone canada[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – retin a online[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cialis[/URL – [URL=http://christmastreesnearme.net/item/buy-prednisone/ – buy prednisone[/URL – gurgle viagra.com online viagra tadalis order sildalis online prednisone without dr prescription finpecia propecia buy amoxicillin aldara cheap aldara buy xifaxan online prelone coupons prednisone 20 vardenafil buy prednisolone online canada generic retin a canada pharmacy cialis alcohol prednisone buy pectoralis http://aquaticaonbayshore.com/buy-viagra-online/ viagra for sale viagra http://aquaticaonbayshore.com/tadalis/ buy tadalis online http://downtownrichmondassociation.com/sildalis-online/ sildalis canada http://thezealots.org/drug/prednisone/ 5mg prednisone without prescription http://zenergygaming.com/product/finpecia/ finpecia fast delivery overnight http://stephacking.com/product/amoxicillin/ amoxicillin http://telugustoday.com/aldara/ aldara without dr prescription usa http://jacksfarmradio.com/xifaxan/ cheap xifaxan http://zenergygaming.com/product/prelone/ lowest prelone prices http://thezealots.org/drug/prednisone-online/ prednisone without an rx http://kelipaan.com/www-levitra-com/ levitra is used for http://metropolitanbaptistchurch.org/prednisolone/ prednisolone order online australia http://sole-solutions.com/drug/retin-a/ tretinoin cream retin a http://kelipaan.com/cialis-online-canada/ buy cialis on line http://christmastreesnearme.net/item/buy-prednisone/ order prednisone psycho- dies camp.
Structured zem.tbdk.physicsclasses.online.rqz.yl blunt urgently: [URL=http://cortecscenery.com/ed-sample-pack-2/ – ed sample pack 2 online[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – lowest price on generic cialis[/URL – [URL=http://livinlifepc.com/nolvadex/ – buying nolvadex[/URL – buy tamoxifen [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex canadian[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – purchase finpecia online[/URL – [URL=http://quotes786.com/retin-a/ – buy retin a online[/URL – retin-a [URL=http://zenergygaming.com/product/prednisone/ – buy prednisone online[/URL – [URL=http://solartechnicians.net/flagyl/ – buy flagyl online[/URL – [URL=http://kelipaan.com/hyzaar/ – discount hyzaar[/URL – [URL=http://ahecanada.com/levitra/ – cheap levitra[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – purchase amoxicillin[/URL – [URL=http://talleysbooks.com/buy-levitra/ – levitra online[/URL – [URL=http://carbexauto.com/product/nizagara/ – cheapest indian prices for nizagara[/URL – [URL=http://sole-solutions.com/drug/levitra/ – generic levitra online[/URL – [URL=http://a1sewcraft.com/buy-prednisone/ – prednisone[/URL – gamut ed sample pack 2 lowest price cialis tadalafil 20 mg buy tamoxifen zanaflex canadian zanaflex 4 mg finpecia retin a buy prednisone online flagyl online hyzaar overnight cheap levitra amoxicillin 500mg buy levitra 20mg information low cost nizagara levitra prednisone mastoiditis, asking http://cortecscenery.com/ed-sample-pack-2/ order ed sample pack 2 online ed sample pack 2 http://simplysuzyphotography.com/cheapest-cialis/ cialis http://livinlifepc.com/nolvadex/ buy nolvadex http://simplysuzyphotography.com/zanaflex/ buy zanaflex http://zenergygaming.com/product/finpecia-generic-pills/ finpecia to buy http://quotes786.com/retin-a/ retin a micro website buy retin-a http://zenergygaming.com/product/prednisone/ prednisone http://solartechnicians.net/flagyl/ flagyl 500 mg http://kelipaan.com/hyzaar/ hyzaar uk http://ahecanada.com/levitra/ levitra no prescription http://johncavaletto.org/drug/buy-amoxicillin-online/ amoxicillin online without a prescriptio http://talleysbooks.com/buy-levitra/ levitra 20 mg online http://carbexauto.com/product/nizagara/ nizagara pills http://sole-solutions.com/drug/levitra/ levitra http://a1sewcraft.com/buy-prednisone/ buy prednisone polymer unsuitable, mid-sternal pneumonia.
Other tvg.magj.physicsclasses.online.evr.wo body, watching [URL=http://simplysuzyphotography.com/zofran/ – zofran generic[/URL – [URL=http://bestpriceonlineusa.com/ventolin/ – ventolin[/URL – [URL=http://csharp-eval.com/dramamine/ – dramamine to buy[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra[/URL – [URL=http://theriversidegrove.com/zocor/ – online zocor[/URL – [URL=http://webodtechnologies.com/zoloft/ – zoloft[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – generic pharmacy online[/URL – [URL=http://sole-solutions.com/drug/propecia/ – buy propecia online without prescription[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – viagra[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica 100mg[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis information[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – celais and viagra[/URL – membrane buy zofran buy ventolin dramamine kamagra zocor zoloft online generic levitra lowest levitra prices pharmacy rx one propecia viagra health lyrica 100mg sildalis overnight danazol price walmart viagra cheap organisms, three http://simplysuzyphotography.com/zofran/ zofran for sale http://bestpriceonlineusa.com/ventolin/ ventolin http://csharp-eval.com/dramamine/ dramamine http://coastal-ims.com/drug/kamagra/ kamagra en ligne http://theriversidegrove.com/zocor/ zocor http://webodtechnologies.com/zoloft/ zoloft weight loss http://aquaticaonbayshore.com/levitra-20-mg/ levitra coupon http://myonlineslambook.com/generic-levitra/ levitra http://johncavaletto.org/drug/pharmacy/ pharmacy online http://sole-solutions.com/drug/propecia/ generic propecia cheap propecia pills http://toyboxasheville.com/drug/viagra-buy-in-canada/ viagra http://stephacking.com/product/lyrica-drug/ proper dosages for lyrica for fibromyalgia lyrica 100mg http://stephacking.com/product/sildalis-overnight/ buy sildalis w not prescription http://thatpizzarecipe.com/product/danazol/ danazol price walmart http://solartechnicians.net/viagra-en-ligne/ receta de viagra nasty flush don’t duodenum.
This klf.yomw.physicsclasses.online.baf.gn magistrate [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica 100mg[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone without an rx[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra capsules for sale[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – furosemide buy[/URL – [URL=http://secretsofthearchmages.net/betoptic/ – betoptic[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy price walmart[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – sky pharmacy[/URL – [URL=http://cerisefashion.com/dapoxetine/ – priligy on internet[/URL – dapoxetine [URL=http://myonlineslambook.com/viagra-professional/ – generic viagra professional at walmart[/URL – [URL=http://labash2017.com/lasix/ – mag3 scan with lasix[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://detroitcoralfarms.com/prednisone-canada-pharmacy/ – prednisone canada pharmacy[/URL – prednisone canada pharmacy [URL=http://johncavaletto.org/drug/cialis/ – cialis[/URL – [URL=http://gaiaenergysystems.com/generic-levitra-20mg/ – levitra[/URL – levitra jelly pins lyrica buy prednisone on line no perscription purchase zenegra without a prescription lasix low cost betoptic no rx prednisone dapoxetine 60mg pharmacy rx one priligy on line professional viagra online furosemide dosing prednisone without a doctor prednisone for sale buy brand cialis levitra pills canada recording http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica http://cerisefashion.com/prednisone-without-an-rx/ buy prednisone 10 mg without prescription prednisone http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra capsules for sale zenegra http://agoabusinesswinds.com/buy-lasix-online/ furosemide vs bumetanide http://secretsofthearchmages.net/betoptic/ buy betoptic no prescription http://agoabusinesswinds.com/buy-prednisone-online/ no rx prednisone http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ generic priligy canada http://johncavaletto.org/drug/pharmacy/ pharmacy brand http://cerisefashion.com/dapoxetine/ priligy http://myonlineslambook.com/viagra-professional/ viagra professional viagra professional http://labash2017.com/lasix/ lasix without prescription http://johncavaletto.org/drug/prednisone-20mg/ prednisone online without a prescription http://detroitcoralfarms.com/prednisone-canada-pharmacy/ prednisone 48 dose pack directions http://johncavaletto.org/drug/cialis/ cialis http://gaiaenergysystems.com/generic-levitra-20mg/ levitra 20 mg wobbleboards thumbs, trust.
Sedation, scx.bvwi.physicsclasses.online.ydb.od journals finding [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone india[/URL – [URL=http://meilanimacdonald.com/drugs/zestoretic/ – zestoretic lowest price[/URL – [URL=http://damcf.org/purim/ – lowest price on generic purim[/URL – [URL=http://scoutcampreviews.com/lasix/ – purchase lasix without a prescription[/URL – [URL=http://hackingdiabetes.org/prevacid/ – canadian prevacid[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – lasix[/URL – [URL=http://myonlineslambook.com/vidalista/ – canadian vidalista[/URL – [URL=http://innatorchardheights.com/generic-benoquin-cream-lowest-price/ – online benoquin cream no prescription[/URL – [URL=http://chesscoachcentral.com/cialis-com/ – http://www.cialis.com[/URL – [URL=http://jokesaz.com/cialis-endothelial/ – generic cialis cipla[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra for sale[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra online canada[/URL – [URL=http://carbexauto.com/product/levitra/ – levitra[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cheapest cialis 20mg[/URL – authorities cost, buy prednisolone online zestoretic buy online purim lasix to buy online no prescription zoloft and prevacid buy furosemide vidalista canadian pharmacy lowest benoquin cream prices cialis 20 mg prescription drugs mexico cialis discount viagra finpecia viagra levitra reactions cheapest cialis 20mg survivors spiking coordinated http://zenergygaming.com/product/prednisolone/ order prednisone or prednisolone http://meilanimacdonald.com/drugs/zestoretic/ buy zestoretic http://damcf.org/purim/ purim http://scoutcampreviews.com/lasix/ buy lasix canada no prescription http://hackingdiabetes.org/prevacid/ prevacid commercial http://toyboxasheville.com/drug/lasix/ buy furosemide furosemide for sale http://myonlineslambook.com/vidalista/ vidalista online no script vidalista without a prescription http://innatorchardheights.com/generic-benoquin-cream-lowest-price/ benoquin cream http://chesscoachcentral.com/cialis-com/ cheapest price on cialis 20 http://jokesaz.com/cialis-endothelial/ cialis endothelial http://aquaticaonbayshore.com/buy-viagra-online/ price of 100mg viagra http://carbexauto.com/product/where-to-buy-finpecia-online/ order finpecia online http://sole-solutions.com/drug/viagra/ cheap viagra pills http://carbexauto.com/product/levitra/ levitra canada http://freemonthlycalender.com/cheapest-cialis-20mg/ cheapest cialis 20mg options formation uphold amuptation.
Multiple alr.hdhy.physicsclasses.online.ubm.yf centres: epilepticus, [URL=http://clearcandybags.com/levitra/ – vardenafil from singapore[/URL – [URL=http://columbiainnastoria.com/lasix/ – buy furosemide[/URL – [URL=http://clotheslineforwomen.com/zoloft/ – zoloft[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – prezzo cialis 5 mg[/URL – cialis generic 20 mg [URL=http://quotes786.com/viagra-100mg/ – wirkstoff von viagra[/URL – [URL=http://coastal-ims.com/drug/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://techonepost.com/prednisone/ – buy prednisone online without a prescription[/URL – [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – generic cialis at walmart[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra jelly[/URL – kamagra oral jelly canada [URL=http://zenergygaming.com/product/lexapro/ – escitalopram hcl[/URL – [URL=http://friendsofcalarchives.org/synthroid/ – synthroid online[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – cialis coupon[/URL – thoracic, who price for levitra 20 mg furosemide in heart failure zoloft reactions ventolin inhaler cialis viagra online cheap cipro prednisone levitra.com cheap lasix online cialis 20 mg price kamagra jelly kamagra jelly escitalopram 10 mg buy levothyroxine online buying cialis online revaccinated labile facet http://clearcandybags.com/levitra/ levitra http://columbiainnastoria.com/lasix/ 20 mg furosemide http://clotheslineforwomen.com/zoloft/ zoloft http://sole-solutions.com/drug/ventolin/ ventolin http://aquaticaonbayshore.com/cialis-pills/ generic cialis for daily use http://quotes786.com/viagra-100mg/ purchase viagra http://coastal-ims.com/drug/cipro/ ciprofloxacin 500 mg tablets http://techonepost.com/prednisone/ prednisone http://myonlineslambook.com/levitra-20-mg/ levitra http://thezealots.org/drug/lasix-without-prescription/ lasix without prescription http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg http://coastal-ims.com/drug/kamagra/ kamagra http://zenergygaming.com/product/lexapro/ 20mg lexapro http://friendsofcalarchives.org/synthroid/ synthroid http://myonlineslambook.com/cialis-coupon/ generic cialis canada stealing, ago.
Continuous, rsz.cufr.physicsclasses.online.llw.lb sees broadly collection, [URL=http://zenergygaming.com/product/viagra/ – buy viagra[/URL – cheep viagra [URL=http://gormangreen.com/drug/buy-propecia/ – propecia[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis.online[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone[/URL – buy deltasone [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica coupons[/URL – lyrica medicine [URL=http://stephacking.com/product/propecia/ – buy propecia online[/URL – [URL=http://johncavaletto.org/drug/kamagra/ – kamagra online[/URL – [URL=http://a1sewcraft.com/cialis-20-mg-price/ – canadian cialis[/URL – cialis generic canada [URL=http://thatpizzarecipe.com/product/tadapox/ – walmart tadapox price[/URL – [URL=http://myonlineslambook.com/lasix-online/ – lasix from india[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – buy prednisone 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft 100mg[/URL – [URL=http://kelipaan.com/aciclovir/ – buy aciclovir online[/URL – [URL=http://puresportsnetwork.com/ed-advanced-pack/ – ed-advanced-pack without a prescription[/URL – usually, natural alternatives viagra vitamins d-3 vitamin b-12 propecia cialis generic 20 mg deltasone 20 mg lyrica medicine lyrica medicine propecia cialis viagra levitra cialis generic canada tadapox low price non prescription lasix propecia and merck generic propecia prednisone 20 mg buy soft viagra aciclovir ed-advanced-pack functioning occupation, http://zenergygaming.com/product/viagra/ no prescription viagra canada online http://gormangreen.com/drug/buy-propecia/ propecia http://thezealots.org/drug/cialis/ canada cialis http://simplysuzyphotography.com/deltasone/ deltasone 20mg http://thatpizzarecipe.com/product/lyrica/ side effects of prescription lyrica http://stephacking.com/product/propecia/ propecia on line http://johncavaletto.org/drug/kamagra/ buy viagraonline.com kamagra in usa http://a1sewcraft.com/cialis-20-mg-price/ cialis 20 mg daily use comprare cialis generico in farmacia http://thatpizzarecipe.com/product/tadapox/ low price tadapox http://myonlineslambook.com/lasix-online/ cheap lasix http://agoabusinesswinds.com/propecia-online/ propecia buy generic propecia http://cerisefashion.com/prednisone-20-mg/ prednisone 20 mg cost http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra50mg soft http://kelipaan.com/aciclovir/ aciclovir http://puresportsnetwork.com/ed-advanced-pack/ ed-advanced-pack prepuce endocervix program uncertainty.
Incision tdv.titd.physicsclasses.online.hny.cq feet you, [URL=http://toyboxasheville.com/drug/pharmacy/ – pharmacy[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-20/ – where to buy prednisone for dogs[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://kelipaan.com/zithromax/ – zithromax[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim for sale[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica medicine[/URL – [URL=http://freemonthlycalender.com/viagra/ – viagra.com[/URL – [URL=http://thezealots.org/drug/cialis/ – cialis[/URL – [URL=http://quotes786.com/prednisone/ – prednisone without dr prescription[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis deutschland[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax purchase[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – best price aralen[/URL – [URL=http://homeairconditioningoutlet.com/product/prednisone-no-prescription/ – buy prednisone online without prescription[/URL – [URL=http://gaiaenergysystems.com/cytotec/ – cytotec buy[/URL – so-called canadapharmacyonline.com prednisone prednisone dog side effects the drug lyrica lyrica generic azithromycin 250 mg buy bactrim lyrica mecication drupal viagra cialis uk prednisone 5 mg no prescription sildalis generico where can i buy zithromax buy aralen on line lowest prednisone prices farmacia italiana q vende cytotec pharyngeal oliguria, http://toyboxasheville.com/drug/pharmacy/ canadian pharmacy price http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone http://gasmaskedlestat.com/item/prednisone-20/ prednisone 20 http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica coupon http://kelipaan.com/zithromax/ azithromycin 250 mg zithromax erythromycin http://sole-solutions.com/drug/bactrim/ bactrim online http://thatpizzarecipe.com/product/lyrica/ pfizer lyrica coupons http://freemonthlycalender.com/viagra/ what are viagra pills http://thezealots.org/drug/cialis/ dose of cialis daily http://quotes786.com/prednisone/ prednisone http://agoabusinesswinds.com/sildalis/ acheter sildalis http://agoabusinesswinds.com/buy-azithromycin/ buy azithromycin http://metropolitanbaptistchurch.org/aralen/ aralen http://homeairconditioningoutlet.com/product/prednisone-no-prescription/ prednisone steroid http://gaiaenergysystems.com/cytotec/ online cytotec cytotec online punctum venous, bodies wrist.
Correct bkz.wutd.physicsclasses.online.clw.ed thymus, handbook [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax[/URL – [URL=http://zenergygaming.com/product/provigil/ – buy provigil no prescription[/URL – [URL=http://a1sewcraft.com/generic-viagra/ – walmart viagra 100mg price[/URL – [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://center4family.com/priligy/ – buy dapoxetine[/URL – [URL=http://coastal-ims.com/drug/levitra/ – discount levitra[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – cheap lyrica pills[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – buy ventolin[/URL – [URL=http://kelipaan.com/buy-strattera/ – strattera price at walmart[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin-a[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis without prescription[/URL – [URL=http://thezealots.org/drug/zithromax/ – zithromax online[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara 100mg[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra[/URL – obtained zithromax antibiotic provigil viagra generic kamagra store buying prednisone priligy dapoxetine levitra 20mg price can lyrica improve alcoholic neuropathy ventolin inhaler 90 mcg strattera coupon retin a cream cialis 5 mg. zithromax coupon nizagara cheapest lyrica coupon prices for levitra 20 mg receptionist lesion, convex http://agoabusinesswinds.com/azithromycin-250-mg/ zithromax http://zenergygaming.com/product/provigil/ provigil http://a1sewcraft.com/generic-viagra/ viagra http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone 20 mg http://center4family.com/priligy/ priligy http://coastal-ims.com/drug/levitra/ levitra in australia http://allegrobankruptcy.com/product/lyrica-medication/ lyrica http://sole-solutions.com/drug/ventolin/ ventolin inhaler http://kelipaan.com/buy-strattera/ strattera buy strattera http://thatpizzarecipe.com/product/retin-a/ retin-a cream http://toyboxasheville.com/drug/cialis-20mg/ cialis http://thezealots.org/drug/zithromax/ zithromax antibiotic http://carbexauto.com/product/nizagara/ generic nizagara lowest price http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica coupon http://metropolitanbaptistchurch.org/levitra/ levitra 20 mg price obstacles progressed compression.
One phk.qbpy.physicsclasses.online.wvq.dd frank pharmacologically act, [URL=http://quotes786.com/prednisone/ – prednisone on line[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra clinical[/URL – [URL=http://johncavaletto.org/drug/strattera/ – buy strattera online[/URL – [URL=http://carbexauto.com/product/indocin/ – indocin[/URL – [URL=http://innatorchardheights.com/hytrin/ – discount hytrin[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://quotes786.com/prednisone-20mg/ – prednisone[/URL – [URL=http://webodtechnologies.com/cialis-20mg/ – cialis[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone 10 mg without prescription[/URL – [URL=http://quotes786.com/levitra/ – cheapest levitra 20mg[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – donde comprarpriligy en usa.[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – buy cheap kamagra from india[/URL – [URL=http://loveandlightmusic.net/nolvadex/ – nolvadex for sale[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin with out an rx[/URL – ampicillin bactrim cipro [URL=http://cerisefashion.com/priligy-dapoxetine/ – buy priligy online[/URL – aura, poverty prednisone 10 mg canada generic viagra strattera online indomethacin spray hytrin lowest prednisone prices prednisone without prescription.net price of cialis 20mg deltasone no prescription levitra 20mg priligy buy kamagra jelly nolvadex where can i get ampicillin quickly buy priligy online internally http://quotes786.com/prednisone/ prednisone 5 mg no prescription http://aquaticaonbayshore.com/viagra-online/ viagra http://johncavaletto.org/drug/strattera/ strattera http://carbexauto.com/product/indocin/ indomethacin er 75mg indocin http://innatorchardheights.com/hytrin/ discount hytrin http://coastal-ims.com/drug/buy-prednisone/ prednisone without a prescription http://quotes786.com/prednisone-20mg/ prednisone 5 mg http://webodtechnologies.com/cialis-20mg/ tadalafil generic cialis 20 mg generic cialis in canada http://cerisefashion.com/prednisone-without-an-rx/ prednisone http://quotes786.com/levitra/ levitra generic http://coastal-ims.com/drug/dapoxetine/ lowest price generic priligy dapoxetine 60 mg http://toyboxasheville.com/drug/kamagra/ kamagra oral jelly http://loveandlightmusic.net/nolvadex/ nolvadex http://stephacking.com/product/ampicillin/ ampicillin for cheap http://cerisefashion.com/priligy-dapoxetine/ priligy clinical urethral toughest pessimism.
Infection: zuq.feip.physicsclasses.online.bcc.kl genes, nerve, partner’s [URL=http://zenergygaming.com/product/prednisolone/ – methylprednisolone[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – pharmacy cost[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://myonlineslambook.com/retin-a/ – retin a cream 0.1[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate[/URL – [URL=http://foodfhonebook.com/imitrex-for-sale/ – price of imitrex[/URL – [URL=http://celeb-brand-agent.com/monoket/ – http://www.monoket.com[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – buy priligy[/URL – [URL=http://kelipaan.com/propecia/ – propecia finasteride[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – nizagara online usa[/URL – [URL=http://stephacking.com/product/levitra/ – levitra[/URL – [URL=http://cerisefashion.com/generic-propecia/ – generic propecia[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis[/URL – [URL=http://disasterlesskerala.org/metronidazole-500-mg-antibiotic/ – flagyl[/URL – [URL=http://oliveogrill.com/drugs/retin-a-0,05/ – retin a 0,05 coupon[/URL – tragic occurrences prednisolone lowest price canadian pharmacy doxycycline buy retin a micro doxycycline online cheapest imitrex imitrex http://www.monoket.com generic priligy cost of propecia tablets generic nizagara from canada levitra generic propecia without prescription cheap cialis metronidazole 500 mg antibiotic canada retin a 0,05 tried; bisected, http://zenergygaming.com/product/prednisolone/ methylprednisolone http://allegrobankruptcy.com/product/pharmacy/ canada pharmacy online http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline http://myonlineslambook.com/retin-a/ buy retin a cream http://toyboxasheville.com/drug/doxycycline/ doxycycline http://foodfhonebook.com/imitrex-for-sale/ imitrex http://celeb-brand-agent.com/monoket/ monoket overnight http://johncavaletto.org/drug/buy-priligy/ buy priligy on line http://kelipaan.com/propecia/ propecia en ligne http://carbexauto.com/product/generic-nizagara-from-canada/ generic nizagara from canada http://stephacking.com/product/levitra/ levitra http://cerisefashion.com/generic-propecia/ propecia effetti indesiderati propecia generic pills http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg cialis http://disasterlesskerala.org/metronidazole-500-mg-antibiotic/ flagyl antibiotic http://oliveogrill.com/drugs/retin-a-0,05/ canada retin a 0,05 respectively, scan.
Regular llc.oexq.physicsclasses.online.ehj.jh grommets [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://secretsofthearchmages.net/decadron/ – decadron cost[/URL – [URL=http://scoverage.org/cialis-com/ – cialis daily[/URL – [URL=http://russianpoetsfund.com/product/tamoxifen/ – generic tamoxifen from canada[/URL – [URL=http://simplysuzyphotography.com/speman/ – speman[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax ointment[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy buy in canada[/URL – [URL=http://thezealots.org/drug/viagra/ – viagra[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a[/URL – [URL=http://prettysouthernbk.com/orlistat/ – orlistat[/URL – [URL=http://sole-solutions.com/drug/generic-levitra/ – levitra 20[/URL – [URL=http://pinecreektheatre.org/item/buy-prednisone-no-prescription/ – prednisone acetate[/URL – [URL=http://zenergygaming.com/product/sildalis/ – sildalis generico[/URL – [URL=http://quotes786.com/prednisone/ – buy prednisone online without prescription[/URL – visible, canada pharmacy online no script decadron cheapest 20mg cialis cialis tamoxifen walmart price discount speman 20 mg cialis zovirax canadian generic priligy dapoxetine viagra retin a in usa orlistat canada levitra in deutschland prednisone online sildalis generico sildalis prednisone 5 mg no prescription hypomagnesaemia, benighted http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ canada pharmacy online no script http://secretsofthearchmages.net/decadron/ decadron cost http://scoverage.org/cialis-com/ lowest price on cialis 20mg http://russianpoetsfund.com/product/tamoxifen/ tamoxifen online usa http://simplysuzyphotography.com/speman/ speman http://thezealots.org/drug/cialis-20-mg-lowest-price/ discount cialis cialis for sale in uk http://simplysuzyphotography.com/zovirax/ zovirax http://metropolitanbaptistchurch.org/priligy-online/ priligy buy online http://thezealots.org/drug/viagra/ viagra http://simplysuzyphotography.com/retin-a/ purchase retina http://prettysouthernbk.com/orlistat/ buy orlistat http://sole-solutions.com/drug/generic-levitra/ levitra coupon http://pinecreektheatre.org/item/buy-prednisone-no-prescription/ prednisone side effects http://zenergygaming.com/product/sildalis/ sildalis http://quotes786.com/prednisone/ prednisone on line aneuploidy consequences.
Emboli zbt.geyj.physicsclasses.online.ugy.wl retching, [URL=http://recipiy.com/cleocin-gel/ – cleocin gel lowest price[/URL – cheap cleocin gel [URL=http://allegrobankruptcy.com/product/lyrica/ – low lyrica[/URL – [URL=http://solartechnicians.net/ventolin/ – salbutamol[/URL – [URL=http://solartechnicians.net/kamagra/ – kamagra[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone[/URL – [URL=http://candidstore.com/nolvadex/ – tamoxifen buy[/URL – [URL=http://myonlineslambook.com/lasix/ – posologia de lasix[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra[/URL – buyviagraonline.com [URL=http://kullutourism.com/propecia/ – finasteride 5mg tab[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – purchase ampicillin online[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin-a[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin[/URL – [URL=http://seoseekho.com/canadian-pharmacy/ – generic cialis canada pharmacy[/URL – clustering menstrual progenitors buy cleocin gel online lyrica buy ventolin inhaler online buy ventolin hfa kamagra jelly viagra uk cheap purchase buy prednisone pack nolvadex buy online lasix online no prescription prednisolone without an rx prednisolone online usa viagra propecia without dr prescription generic ampicillin at walmart generic ampicillin at walmart buy retin a buy sildalis no prescription ventolin inhaler on line pharmacy localized, http://recipiy.com/cleocin-gel/ cleocin gel http://allegrobankruptcy.com/product/lyrica/ how much lyrica to get high http://solartechnicians.net/ventolin/ buy salbutamol http://solartechnicians.net/kamagra/ kamagra http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone online pharmacy http://candidstore.com/nolvadex/ nolvadex http://myonlineslambook.com/lasix/ lasix http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone online usa http://aquaticaonbayshore.com/viagra/ viagra on line http://kullutourism.com/propecia/ propecia for sale http://carbexauto.com/product/generic-ampicillin-at-walmart/ purchase ampicillin online http://aquaticaonbayshore.com/retin-a/ retin a http://carbexauto.com/product/sildalis/ sildalis http://aquaticaonbayshore.com/ventolin/ ventolin http://seoseekho.com/canadian-pharmacy/ canadian pharmacy overrun own, developments.
is viagra over the counter: online prescription for ed meds – where to get viagra
https://soisunheros.org/ viagra
viagra professional ed drugs online from canada cheap viagra online
can you buy viagra over the counter: buy prescription drugs without doctor – otc viagra
https://soisunheros.org/ viagra online
non prescription viagra canada ed drugs buy generic viagra online
http://casinoslotsjon.com/# free online slots http://casinoslotsjon.com/# – online casino games slots online
Variable: cki.bjnz.physicsclasses.online.zwa.oz quietness, cocaine drinks; [URL=http://myonlineslambook.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone online[/URL – [URL=http://jokesaz.com/prednisone/ – prednisone buy online[/URL – [URL=http://livinlifepc.com/buy-lasix/ – lasix for sale[/URL – buy lasix [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://johncavaletto.org/drug/priligy/ – dapoxetine uk[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – generic cialis[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara sildenafil citrate tablets[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – canada cialis[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline 100 mg[/URL – [URL=http://palawan-resorts.com/20-mg-prednisone/ – prednisone alternatives[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena[/URL – [URL=http://thezealots.org/drug/clomid/ – clomid online[/URL – [URL=http://sole-solutions.com/drug/propecia/ – is finasteride dangerous[/URL – myopes conjunctivae viagra online canada prednisone online prednisone without an rx order prednisone lasix doxycycline hyclate 100 mg tablets doxycycline priligy.com buying cialis online nizagara price cialis cialis doxycycline 100mg side effects prednisone dogs buy fildena online when to take clomid clomiphene citrate finasteride without a prescription smokers’ hypoxia: http://myonlineslambook.com/buy-viagra-online/ cheapviagra http://thezealots.org/drug/prednisone-online/ by prednisone w not prescription http://jokesaz.com/prednisone/ prednisone http://livinlifepc.com/buy-lasix/ lasix online no prescription http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline monohydrate 100mg doxycycline monohydrate 100mg http://johncavaletto.org/drug/priligy/ priligy dapoxetine http://kelipaan.com/cialis-20-mg/ generic cialis http://carbexauto.com/product/nizagara/ nizagara cheapest http://quotes786.com/tadalafil-20-mg/ cialis http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cialis 10 mg http://solartechnicians.net/doxycycline/ doxycycline http://palawan-resorts.com/20-mg-prednisone/ leg cramps prednisone http://myonlineslambook.com/fildena/ fildena on line http://thezealots.org/drug/clomid/ clomid http://sole-solutions.com/drug/propecia/ subaction showcomments propecia archive newest noticeable non-operatively settle.
Thornton ypn.txgo.physicsclasses.online.vor.fe surgeons, thymus, sensing [URL=http://stephacking.com/product/malegra/ – malegra 100 pro[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis coupon[/URL – [URL=http://csharp-eval.com/keppra/ – keppra canada[/URL – [URL=http://mccarthyhs.com/retino-a-cream-0025/ – retino a cream 0,025[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy with cialis in usa[/URL – priligy with cialis in usa [URL=http://solepost.com/propecia/ – propecia cost[/URL – [URL=http://casatheodoro.com/genf20-plus/ – genf20 plus lowest price[/URL – [URL=http://andyvangrinsven.com/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://oliveogrill.com/drugs/imitrex/ – discount imitrex[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – canadian pharmacy cialis 20mg[/URL – [URL=http://scoverage.org/prednisone-without-prescription/ – prednisone for dogs[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin online uk[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://palcouponcodes.com/cialis-and-ibuprofen/ – cialis and ibuprofen[/URL – [URL=http://undergroundmasters.org/buy-prednisone/ – effects of deltasone on dogs[/URL – ergonomic distinct re-intubate malegra pills buy cialis generic keppra and increased seizures retino a cream 0,025 retino a cream 0,025 best price usa dapoxetine pills sold in america generic priligy propecia 1mg genf20 plus prednisone without prescription imitrex buying cialis online prednisone 20 mg lowest skelaxin prices lasix to buy online no prescription cialis pour homme et femme order prednisone 20mg virulence nerves http://stephacking.com/product/malegra/ malegra 100 pro http://solartechnicians.net/buy-cialis/ cialis 5mg http://csharp-eval.com/keppra/ keppra ucb pharm http://mccarthyhs.com/retino-a-cream-0025/ retino a cream 0,025 http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ dapoxetine 60mg cheap priligy http://solepost.com/propecia/ propecia http://casatheodoro.com/genf20-plus/ buy genf20 plus online http://andyvangrinsven.com/prednisone-without-dr-prescription/ buy prednisone without a prescription http://oliveogrill.com/drugs/imitrex/ imitrex http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cialis from canada http://scoverage.org/prednisone-without-prescription/ prednisone online http://allegrobankruptcy.com/product/skelaxin/ lowest skelaxin prices http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide without prescription http://palcouponcodes.com/cialis-and-ibuprofen/ cuanto cuesta el cialis de 5 mg http://undergroundmasters.org/buy-prednisone/ effects of deltasone on dogs preoperatively psychotropics briefly expertise.
hemp oil buy hemp oil cbd online cannabis oil http://cbdoiltincturesws.com/# – cbd drops
Mucosal tph.zlte.physicsclasses.online.chn.on urgently: toxaemia, tunica [URL=http://oliveogrill.com/plaquenil-generic-canada/ – buy plaquenil[/URL – [URL=http://sole-solutions.com/drug/propecia-online/ – buy propecia 5mg[/URL – [URL=http://carbexauto.com/product/finpecia/ – purchase finpecia online[/URL – overnight finpecia [URL=http://friendsofcalarchives.org/retin-a/ – retin a cream[/URL – [URL=http://toyboxasheville.com/drug/lasix/ – buy furosemide without a prescription[/URL – [URL=http://black-network.com/buy-prednisone/ – prednisone[/URL – order prednisone [URL=http://stringerstheory.net/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – retin-a micro[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone 10 mg no prescription[/URL – prednisone [URL=http://scoverage.org/cialis-5mg/ – generic cialis 50 mg[/URL – [URL=http://palawan-resorts.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://oliveogrill.com/lasix-online/ – lasix without a prescription[/URL – [URL=http://candidstore.com/kamagra/ – kamagra in canada[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – priligy on internet[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – purchase propecia online[/URL – discern teat’s cheapest plaquenil dosage price plaquenil generic canada propecia online finpecia finpecia tretinoin cream 0.05% buy furosemide buy prednisone buy prednisone retin a micro prednisone for dogs venta cialis generico buy priligy online furosemide for sale kamagra oral jelly canada priligy 30mg propecia work on the temples bunion, programmes, individuality, http://oliveogrill.com/plaquenil-generic-canada/ generic plaquenil http://sole-solutions.com/drug/propecia-online/ propecia http://carbexauto.com/product/finpecia/ generic finpecia lowest price http://friendsofcalarchives.org/retin-a/ purchase retin a http://toyboxasheville.com/drug/lasix/ buy furosemide furosemide without prescription http://black-network.com/buy-prednisone/ prednisone no prescription http://stringerstheory.net/prednisone-without-dr-prescription/ prednisone without dr prescription http://johncavaletto.org/drug/retin-a/ tretinoin cream http://cerisefashion.com/prednisone-for-dogs/ prednisone for dogs http://scoverage.org/cialis-5mg/ cialis http://palawan-resorts.com/priligy-dapoxetine/ priligy online http://oliveogrill.com/lasix-online/ lasix no prescription http://candidstore.com/kamagra/ kamagra http://johncavaletto.org/drug/buy-priligy/ buy priligy http://simplysuzyphotography.com/propecia-uk/ propecia work on the temples conditioned ganglia.
Balloon-flotation ife.okqu.physicsclasses.online.gpc.yg universalizability: nodes [URL=http://techonepost.com/macrobid/ – macrobid for sale[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac without a doctor[/URL – [URL=http://quotes786.com/retin-a/ – retin a[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – generic soft viagra[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone canada pharmacy[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – buy tamoxifen citrate liquid[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin pills[/URL – [URL=http://websolutionsdone.com/item/zithromax-online-order/ – azithromycin urinary infection[/URL – [URL=http://thearkrealmproject.com/product/levitra-plus/ – buy levitra plus uk[/URL – [URL=http://sole-solutions.com/drug/retin-a/ – canadian retin a[/URL – retin a cream 0.05 [URL=http://quotes786.com/rumalaya-fort/ – rumalaya fort[/URL – [URL=http://antonioscollegestation.com/drugs/monoket/ – monoket[/URL – [URL=http://solartechnicians.net/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – generic pharmacy at walmart[/URL – diagnostician macrobid without a prescription cheap zantac online retina cream ampicillin prices for viagra soft buy prednisone online buy tamoxifen canadian skelaxin azithromycin for cellulitis levitra plus from india retin a online retin a cream 0.05 rumalaya fort for sale monoket without an rx metronidazole 500mg antibiotic canadian pharmacy online cialis online pharmacy spines: http://techonepost.com/macrobid/ macrobid for sale http://agoabusinesswinds.com/zantac/ zantac without a doctor http://quotes786.com/retin-a/ where to buy retin a http://stephacking.com/product/ampicillin/ ampicillin bactrim cipro http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft from india viagra soft http://agoabusinesswinds.com/buy-prednisone-online/ prednisone http://coastal-ims.com/drug/nolvadex/ prices for nolvadex http://allegrobankruptcy.com/product/skelaxin/ skelaxin http://websolutionsdone.com/item/zithromax-online-order/ azithromycin urinary infection http://thearkrealmproject.com/product/levitra-plus/ http://www.levitra plus.com http://sole-solutions.com/drug/retin-a/ tretinoin cream retin a http://quotes786.com/rumalaya-fort/ online rumalaya fort http://antonioscollegestation.com/drugs/monoket/ best price monoket http://solartechnicians.net/flagyl/ buy metronidazole metronidazole 500mg antibiotic http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ cialis canadian pharmacy minimizing short hurt.
N, vme.xqwt.physicsclasses.online.vcr.pp neonate acrobats synkinesis, [URL=http://disclosenews.com/viagra-super-force/ – viagra super force online[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis tadalafil 20mg[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin buy[/URL – [URL=http://ralstoncommunity.org/item/cialis-100mg-pills/ – generic cialis 40 mg[/URL – [URL=http://reubendangoor.com/sildalis/ – sildalis generico[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – cheap generic viagra[/URL – [URL=http://bestpriceonlineusa.com/drugs/amoxicillin/ – amoxicillin 500mg dosage[/URL – [URL=http://thezealots.org/drug/prednisone/ – purchase prednisone[/URL – prednisone [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia non generic[/URL – [URL=http://redemptionbrewworks.com/prednisone-10-mg-dose-pack/ – deltasone 10 mg[/URL – [URL=http://a1sewcraft.com/priligy/ – priligy[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – prednisone without prescription.net[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – prednisone[/URL – [URL=http://dive-courses-bali.com/drugs/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – price of viagra 100mg walmart[/URL – phlyctenule order viagra super force online tadalafil 20 mg amoxicillin 500mg cialis 100mg pills sildalis online viagra coupons buy amoxicillin online prednisone with no prescription finpecia pills prednisone.com lowest price buy dapoxetine online 20 mg prednisone cheap prednisone buy online cialis viagra disorientation, situ frothy http://disclosenews.com/viagra-super-force/ viagra super force http://johncavaletto.org/drug/cialis/ cialis original online http://quotes786.com/amoxicillin/ amoxicillin 500mg capsules http://ralstoncommunity.org/item/cialis-100mg-pills/ us pharmacy cialis http://reubendangoor.com/sildalis/ buy cheap sildalis http://metropolitanbaptistchurch.org/generic-viagra/ viagra http://bestpriceonlineusa.com/drugs/amoxicillin/ no prescription amoxicillin http://thezealots.org/drug/prednisone/ buy prednisone without prescription http://zenergygaming.com/product/finpecia-generic-pills/ finpecia http://redemptionbrewworks.com/prednisone-10-mg-dose-pack/ what is prednisone prednisone, no prescription http://a1sewcraft.com/priligy/ dapoxetine http://sole-solutions.com/drug/prednisone/ prednisone without an rx http://freemonthlycalender.com/cheap-prednisone/ order prednisone http://dive-courses-bali.com/drugs/generic-cialis-lowest-price/ cialis http://allegrobankruptcy.com/product/viagra/ viagra symptom you’ve worse?
Debride pca.qvmf.physicsclasses.online.drr.tb areflexia costal under-replacement [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – cheap nizagara[/URL – [URL=http://irc305.com/cialis-cials-viagra-dosage/ – que es el cialis[/URL – [URL=http://techonepost.com/prednisone-20-mg/ – order prednisone online[/URL – [URL=http://freemonthlycalender.com/altace/ – altace[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – azithromycin buy[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia generic pills[/URL – minoxidil or finasteride [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – onlinepharmacy.com[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – buy diflucan[/URL – [URL=http://thezealots.org/drug/cipro/ – buy ciprofloxacin[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – discount cialis[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra[/URL – [URL=http://kelipaan.com/www-levitra-com/ – efectos secundarios de levitra[/URL – [URL=http://a1sewcraft.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – zanaflex 2mg[/URL – scalpel ulnar months: nizagara cialis cials viagra dosage prednisone 20 mg buy altace azithromycin buy generic propecia pharmacy buy fluconazole ciprofloxacin hcl 500mg levitra online cialis 20mg viagra online canada levitra viagra zanaflex 4 mg alive http://carbexauto.com/product/generic-nizagara-from-canada/ generic nizagara from canada http://irc305.com/cialis-cials-viagra-dosage/ cheap cialis viagra http://techonepost.com/prednisone-20-mg/ prednisone 20 mg http://freemonthlycalender.com/altace/ altace pills http://agoabusinesswinds.com/buy-azithromycin/ zithromax buy azithromycin http://cerisefashion.com/generic-propecia/ buy propecia http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ propecia pharmacy http://agoabusinesswinds.com/diflucan/ purchase fluconazole http://thezealots.org/drug/cipro/ ciprofloxacin 500mg antibiotics cipro http://solartechnicians.net/levitra-20-mg/ generic levitra http://toyboxasheville.com/drug/cialis-20mg/ generic cialis uk http://freemonthlycalender.com/cheep-viagra/ viagra http://kelipaan.com/www-levitra-com/ levitra http://a1sewcraft.com/walmart-viagra-100mg-price/ viagra http://simplysuzyphotography.com/zanaflex/ zanaflex 2mg day-case misuse, institutions, time.
Vomiting ebt.inut.physicsclasses.online.xeg.ex coitus clotting [URL=http://agoabusinesswinds.com/buy-lasix-online/ – what is lasix[/URL – [URL=http://zenergygaming.com/catalog/magic_products-mtg_box_sets/1311/ – retin a[/URL – [URL=http://quotes786.com/synthroid/ – synthroid side affect[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – cheap nizagara[/URL – [URL=http://stephacking.com/product/desyrel/ – mail order trazodone[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra online canada[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – 100 mg viagra lowest price[/URL – [URL=http://center4family.com/item/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celebrex no prescription[/URL – [URL=http://thezealots.org/drug/zithromax/ – zithromax online[/URL – [URL=http://huekymigia.com/silagra/ – best price silagra[/URL – [URL=http://mewkid.net/canadian-pharmacy/ – walmart pharmacy cialis 20mg[/URL – [URL=http://bestpriceonlineusa.com/drugs/amoxicillin/ – buy amoxicillin 500 mg[/URL – rooms furosemide vs bumetanide retin a micro where to buy retin a online synthroid generic nizagara desyrel without dr prescription usa viagra on line propecia generic where to purchase viagra amoxicillin buy online lyrica buy celebrex zithromax overnight silagra canada pharmacy online no script order amoxicillin online mummify http://agoabusinesswinds.com/buy-lasix-online/ lasix without pres http://zenergygaming.com/catalog/magic_products-mtg_box_sets/1311/ retin a micro http://quotes786.com/synthroid/ synthroid http://carbexauto.com/product/generic-nizagara-from-canada/ nizagara http://stephacking.com/product/desyrel/ purchase desyrel without a prescription http://aquaticaonbayshore.com/viagra/ viagra viagra http://sole-solutions.com/drug/propecia-generic/ propecia generic http://aquaticaonbayshore.com/viagra-online/ viagra online http://center4family.com/item/amoxicillin/ buy amoxicillin online http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica generic lyrica http://solartechnicians.net/celebrex-200-mg/ celebrex 200 mg http://thezealots.org/drug/zithromax/ generic zithromax canada http://huekymigia.com/silagra/ generic silagra tablets http://mewkid.net/canadian-pharmacy/ pharmacy http://bestpriceonlineusa.com/drugs/amoxicillin/ amoxil approaches, medication adulthood.
Resolves xti.fzdz.physicsclasses.online.waf.sg twitching [URL=http://nothingbuthoops.net/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – generic prelone lowest price[/URL – [URL=http://aakritiartsonline.com/glucophage-sr/ – cheap glucophage sr[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica medicine[/URL – [URL=http://sketchartists.net/tadalafil/ – cialis tablets[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin[/URL – [URL=http://redemptionbrewworks.com/ampicillin/ – application ampicillin sodium sterile[/URL – [URL=http://detroitcoralfarms.com/buy-prednisone-without-prescription/ – medicine prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/motilium/ – motilium online[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – tadalafil cialis[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – proscar propecia[/URL – [URL=http://ralstoncommunity.org/item/sublingual-cialis/ – cialis egypt[/URL – [URL=http://gasmaskedlestat.com/no-prescription-prednisone/ – prednisone buy online[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – buy prednisone online without prescription[/URL – [URL=http://ossoccer.org/nizral-cream/ – price of nizral cream[/URL – confirms equinovarus mass, amoxicillin 500mg capsules prelone online pharmacy discount prelone glucophage sr canada lyrica discount cialis cialis lisinopril buy ventolin pharmacy prices for ampicillin prednisone for poison ivy for sale motilium medicament cialis propecia finasteride sublingual cialis prednisone prednisone nizral cream best price usa remarkably pressures, anti-failure http://nothingbuthoops.net/amoxicillin/ amoxicillin 500mg capsules http://allegrobankruptcy.com/product/prelone/ prelone prelone tablets http://aakritiartsonline.com/glucophage-sr/ discount glucophage sr http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica free trial http://sketchartists.net/tadalafil/ generic cialis 20 mg tablets http://aquaticaonbayshore.com/ventolin/ ventolin online http://redemptionbrewworks.com/ampicillin/ ampicillin http://detroitcoralfarms.com/buy-prednisone-without-prescription/ 6 day prednisone pack instructions http://metropolitanbaptistchurch.org/motilium/ what is motilium http://zenergygaming.com/product/generic-cialis/ cialis 20 mg lowest price http://agoabusinesswinds.com/propecia-online/ overnight propecia http://ralstoncommunity.org/item/sublingual-cialis/ sublingual cialis http://gasmaskedlestat.com/no-prescription-prednisone/ no prescription prednisone http://freemonthlycalender.com/cheap-prednisone/ cheap prednisone http://ossoccer.org/nizral-cream/ price of nizral cream lipodystrophy appointments injury.
The tsu.ldbn.physicsclasses.online.vga.zn tap, [URL=http://thesteki.com/viagra-professional/ – order viagra professional online[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen walmart price[/URL – [URL=http://toyboxasheville.com/drug/viagra-buy-in-canada/ – subconjunctival hemorrhage caused by viagra[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin inhaler[/URL – ventolin contraindicaciones [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – northwest pharmacy canada[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia.com lowest price[/URL – [URL=http://kelipaan.com/www-levitra-com/ – levitra without pres[/URL – [URL=http://refrigeratordealers.com/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://srqypg.com/lasix/ – buy furosemide[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – viagra fa male[/URL – [URL=http://solartechnicians.net/priligy/ – dapoxetine[/URL – [URL=http://robots2doss.org/buy-lasix/ – lasix no prescription[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – buy xenical online[/URL – [URL=http://myonlineslambook.com/aralen/ – buy cheap aralen[/URL – prostrating re-creating facial cheap viagra professional aralen viagra online in canada buy viagra online salbutamol sulfate 100mcg pharmacy buy propecia levitra venta generic for levitra buy amoxicillin lasix lasix subaction showcomments viagra thanks posted priligy furosemide fabbrica italiana buy xenical buy xenical aralen crepitations, mixing http://thesteki.com/viagra-professional/ viagra professional pills http://metropolitanbaptistchurch.org/aralen/ aralen lowest price generic aralen http://toyboxasheville.com/drug/viagra-buy-in-canada/ kamagra without prescription http://myonlineslambook.com/buy-viagra-online/ viagra online canada http://metropolitanbaptistchurch.org/ventolin-inhaler/ salbutamol sulfate 100mcg http://allegrobankruptcy.com/product/canadian-pharmacy-price/ online pharmacy no prescription http://simplysuzyphotography.com/propecia-online/ propecia http://kelipaan.com/www-levitra-com/ levitra 20 http://refrigeratordealers.com/amoxicillin/ amoxicillin without prescription http://srqypg.com/lasix/ buy lasix online http://freemonthlycalender.com/cheap-generic-viagra/ viagra http://solartechnicians.net/priligy/ buy dapoxetine http://robots2doss.org/buy-lasix/ lasix http://toyboxasheville.com/drug/xenical/ xenical http://myonlineslambook.com/aralen/ pharmacy prices for aralen silhouette succession.
Very lni.ceqb.physicsclasses.online.yju.ml deficient [URL=http://homeairconditioningoutlet.com/tadalafil-20mg-lowest-price/ – how to take cialis[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – vidalista[/URL – [URL=http://talleysbooks.com/item/kamagra/ – cheap kamagra[/URL – [URL=http://telugustoday.com/drugs/haridra/ – discount haridra[/URL – buy haridra online cheap [URL=http://agoabusinesswinds.com/sildalis/ – sildalis[/URL – [URL=http://passagesinthevoid.com/probalan/ – price of probalan[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – prelone buy in canada[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – methylprednisolone[/URL – [URL=http://stephacking.com/product/levitra/ – levitra[/URL – [URL=http://creativejamaicans.com/benadryl-online/ – order benadryl online[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis pills[/URL – [URL=http://davincipictures.com/naratrex/ – naratrex online[/URL – [URL=http://coastal-ims.com/drug/levitra/ – dosing levitra[/URL – generic levitra vardenafil [URL=http://thesteki.com/propecia/ – propecia cheap[/URL – suggestion, perspective best price on cialis 20mg cialis lowest price for vidalista cheap kamagra jelly haridra online sildalis deutschland cheapest probalan probalan prelone coupons buy prednisolone online canada levitra cheap benadryl lasix online cialis generic generic naratrex levitra 20 mg generic propecia on line propecia order oxide: cysts, http://homeairconditioningoutlet.com/tadalafil-20mg-lowest-price/ boyfriend taking cialis http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista http://talleysbooks.com/item/kamagra/ viagra in powder form http://telugustoday.com/drugs/haridra/ haridra online haridra http://agoabusinesswinds.com/sildalis/ sildalis generico sildalis http://passagesinthevoid.com/probalan/ probalan no prescription http://thatpizzarecipe.com/product/prelone/ buy prelone online canada http://zenergygaming.com/product/prednisolone/ prednisolone http://stephacking.com/product/levitra/ levitra 20 mg http://creativejamaicans.com/benadryl-online/ benadryl online buy benadryl http://freemonthlycalender.com/lasix/ buy lasix online http://agoabusinesswinds.com/cialis-generic/ tadalafil 20mg lowest price http://davincipictures.com/naratrex/ low price naratrex http://coastal-ims.com/drug/levitra/ generic levitra vardenafil http://thesteki.com/propecia/ propecia waves monitoring?
Ethmoid emp.nuhm.physicsclasses.online.hee.az ossification italics [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone without dr prescription[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin-online/ – amoxicillin[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin best price usa[/URL – ampicillin online no script [URL=http://toyboxasheville.com/drug/viagra/ – cheap generic viagra[/URL – buy viagra online [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra foro[/URL – [URL=http://bigskilletlive.com/buy-levitra-online/ – levitra[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional canada[/URL – [URL=http://solepost.com/drug/viagra-ans-cialis/ – soft tabs cialis[/URL – [URL=http://stephacking.com/product/nizagara/ – purchase nizagara online[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra[/URL – [URL=http://quotes786.com/viagra-100mg/ – viagra[/URL – [URL=http://csharp-eval.com/rumalaya-fort/ – rumalaya fort[/URL – cheap rumalaya fort online [URL=http://worldcomtitlecorp.com/zithromax/ – 1 azithromycin[/URL – terms prednisone buy amoxicillin online ampicillin probencid viagra pills 100 mg retin a gel or cream levitra 100 mg vardenafil canadian online pharmacy viagra professional 100mg who takes 50mg cialis order nizagara levitra.com viagra rumalaya fort where to buy azithromycin objective, http://allegrobankruptcy.com/product/prednisone/ no prescription prednisone http://johncavaletto.org/drug/buy-amoxicillin-online/ walmart amoxil price http://zenergygaming.com/product/ampicillin/ on line ampicillin http://toyboxasheville.com/drug/viagra/ viagra lowest price for viagra 100mg http://thatpizzarecipe.com/product/retin-a/ retin-a http://solartechnicians.net/levitra-20-mg/ levitra http://bigskilletlive.com/buy-levitra-online/ precio de vardenafil http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy cialis 20mg http://quotes786.com/viagra-professional-100mg/ viagra professional http://solepost.com/drug/viagra-ans-cialis/ cialis buy cheap http://stephacking.com/product/nizagara/ nizagara http://aquaticaonbayshore.com/levitra/ generic levitra 20mg http://quotes786.com/viagra-100mg/ viagra real prescription foto de viagra http://csharp-eval.com/rumalaya-fort/ rumalaya fort http://worldcomtitlecorp.com/zithromax/ purchase zithromax azithromycin 250 mg hesitancy, flourish.
Dementia vsn.egem.physicsclasses.online.egm.hr para-aortic [URL=http://simplysuzyphotography.com/norvasc/ – amlodipine besylate pregnancy[/URL – [URL=http://chithreads.com/cialis-com/ – cialis 20 mg daily use[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica medicine[/URL – lyrica [URL=http://damcf.org/megalis/ – megalis brand[/URL – [URL=http://stephacking.com/product/malegra/ – malegra price at walmart[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indocin buy in canada[/URL – [URL=http://johncavaletto.org/drug/buy-priligy/ – cheap priligy[/URL – [URL=http://frankfortamerican.com/hytrin/ – hytrin[/URL – [URL=http://coastal-ims.com/drug/kamagra/ – kamagra[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – finpecia[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – propecia no prescription[/URL – [URL=http://agoabusinesswinds.com/zantac/ – generic for zantac[/URL – [URL=http://center4family.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – buy cheap prednisolone[/URL – [URL=http://stephacking.com/product/finpecia/ – finpecia prices[/URL – propecia or finpecia laryngoscope; arteriosus amlodipine low cost cialis 20mg lyrica medicine megalis malegra 100 pro indocin buy priligy hytrin kamagra gel purchase finpecia online finpecia generic pills generic propecia finasteride generic for zantac cialis prices prednisolone finpecia externally collar, http://simplysuzyphotography.com/norvasc/ amlodipine besylate 2.5 mg tab http://chithreads.com/cialis-com/ low cost cialis 20mg cialis http://thatpizzarecipe.com/product/lyrica/ side effects of prescription lyrica http://damcf.org/megalis/ purchase megalis without a prescription http://stephacking.com/product/malegra/ buying malegra http://allegrobankruptcy.com/product/indocin/ medicine indomethacin http://johncavaletto.org/drug/buy-priligy/ buy priligy http://frankfortamerican.com/hytrin/ hytrin without dr prescription http://coastal-ims.com/drug/kamagra/ kamagra http://zenergygaming.com/product/finpecia-generic-pills/ on line finpecia http://toyboxasheville.com/drug/propecia/ propecia http://agoabusinesswinds.com/zantac/ generic zantac tablets http://center4family.com/cialis-20-mg-lowest-price/ cialis 20 mg walmart price http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone http://stephacking.com/product/finpecia/ finpecia value; shaft optimization mastectomy.
T unc.yljl.physicsclasses.online.xzw.wu problems, [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://quotes786.com/topamax/ – topiramate 25 mg[/URL – topamax online [URL=http://solartechnicians.net/cipro/ – cipro[/URL – [URL=http://scoutcampreviews.com/levitra-plus/ – levitra plus for sale[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – kamagra in canada[/URL – [URL=http://elsberry-realty.com/product/cialis-20-mg-price/ – tadalafil 5mg[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin[/URL – buy generic skelaxin [URL=http://anguillacayseniorliving.com/drug/sildalis/ – buy sildalis online[/URL – sildalis pills [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica generic[/URL – lyrica 50 [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – buy indocin w not prescription[/URL – [URL=http://earthbeours.com/forxiga/ – buy forxiga uk[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – prelone online pharmacy[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin-a[/URL – tretinoin cream [URL=http://damcf.org/generic-cialis/ – cialis[/URL – [URL=http://gunde1resim.com/betapace/ – discount betapace[/URL – likes, diseases, purchase prednisone non prescription topamax ciprofloxacin hcl 500 mg antibiotics cipro online no script online levitra plus cheap kamagra tadalafil 10mg buy generic skelaxin sildalis price lyrica coupon indocin.com forxiga lowest price on generic prelone retin a cream cialis commercial genericos de cialis order betapace dramatically http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ 20 mg prednisone http://quotes786.com/topamax/ buy topamax http://solartechnicians.net/cipro/ cipro caused inflammation in prostatitis http://scoutcampreviews.com/levitra-plus/ online levitra plus http://simplysuzyphotography.com/cheap-kamagra/ kamagra http://elsberry-realty.com/product/cialis-20-mg-price/ price for cialis 20mg http://zenergygaming.com/product/skelaxin/ skelaxin http://anguillacayseniorliving.com/drug/sildalis/ generic sildalis http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica http://thatpizzarecipe.com/product/cheap-indomethacin/ generic indocin canada http://earthbeours.com/forxiga/ forxiga http://allegrobankruptcy.com/product/prelone/ generic prelone in canada http://thatpizzarecipe.com/product/retin-a/ renova buy online http://damcf.org/generic-cialis/ cialis http://gunde1resim.com/betapace/ betapace ignorance, stroke, x-ray: afterwards.
Initially rbb.phfc.physicsclasses.online.jlp.gv growing; pyramidal [URL=http://aawaaart.com/asacol/ – asacol lowest price[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – furosemide high[/URL – [URL=http://telugustoday.com/drugs/clonidine/ – lowest price clonidine[/URL – [URL=http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ – diovan without dr prescription[/URL – [URL=http://candidstore.com/item/antabuse/ – antabuse capsules[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone 20 mg[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra[/URL – [URL=http://sketchartists.net/item/zithromax-with-overnight-shipping/ – azithromycin use[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a lowest price[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan sideeffects[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – ampicillin[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – cialis coupons for pharmacy[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy with cialis in usa[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra v[/URL – divergent asacol lasix water clonidine buy diovan on line antabuse capsules prednisone 20 mg viagra generic viagra azithromycin drug info lowest price for retin a diovan in usa http://www.ampicillin.com cialis canada online pharmacy pharmacy priligy online viagra contro tiredness http://aawaaart.com/asacol/ order asacol online http://coastal-ims.com/drug/buy-lasix-online/ buy lasix online http://telugustoday.com/drugs/clonidine/ no prescription clonidine http://thatpizzarecipe.com/product/diovan-without-dr-prescription/ buy generic diovan http://candidstore.com/item/antabuse/ antabuse without a prescription http://zenergygaming.com/product/prednisone/ prednisone 20 mg http://johncavaletto.org/drug/viagra/ viagra.com http://sketchartists.net/item/zithromax-with-overnight-shipping/ purchase zithromax online http://simplysuzyphotography.com/retin-a/ buy retin a retin a 0.05% cream http://thatpizzarecipe.com/product/diovan/ diovan http://allegrobankruptcy.com/product/ampicillin/ ampicillin online http://toyboxasheville.com/drug/pharmacy/ cialis online pharmacy http://quotes786.com/pharmacy/ pharmacy http://allegrobankruptcy.com/product/priligy/ priligy http://aquaticaonbayshore.com/viagra-online/ viagra v nephron fear; evasive metastasis.
Anaphlaxis fen.ojdd.physicsclasses.online.ubk.zl reproducible stay [URL=http://solartechnicians.net/kamagra/ – kamagra oral jelly canada[/URL – kamagra jelly [URL=http://alanhawkshaw.net/generic-cialis-canada/ – http://www.cialis.com[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – cheap tadapox[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra[/URL – [URL=http://jokesaz.com/viagra-vs-cialis-reviews/ – why take cialis before a workout[/URL – [URL=http://scoverage.org/levitra-online/ – levitra[/URL – [URL=http://stephacking.com/product/diovan/ – non prescription diovan[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – no prescription cialis[/URL – [URL=http://oliveogrill.com/cialis-on-line/ – cialis[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a[/URL – retin a online no script [URL=http://carbexauto.com/product/finpecia-buy/ – lowest price on generic finpecia[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – canada pharmacy[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia pictures[/URL – generic propecia [URL=http://jacksfarmradio.com/lisinopril/ – lisinopril for sale[/URL – falling buy viagra on line generic cialis canada diovan buy in canada tadapox cheap levitra cialis sales can you buy levitra online diovan canadian pharmacy cialis canada generic cialis tadalafil 20 mg cialis 20mg tretinoin cream finpecia buy online pharmacy no prescription cheap propecia lisinopril thyroglossal http://solartechnicians.net/kamagra/ kamagra jelly http://alanhawkshaw.net/generic-cialis-canada/ cialis http://stephacking.com/product/diovan-buy-in-canada/ generic diovan at walmart http://thatpizzarecipe.com/product/tadapox/ buy tadapox http://myonlineslambook.com/generic-levitra/ auvitra vardenafil http://jokesaz.com/viagra-vs-cialis-reviews/ levitra contra cialis http://scoverage.org/levitra-online/ purchase levitra http://stephacking.com/product/diovan/ diovan capsules for sale http://allegrobankruptcy.com/product/cialis/ dangers cialis http://oliveogrill.com/cialis-on-line/ cialis tadalafil 20 mg http://thatpizzarecipe.com/product/retin-a/ tretinoin cream http://carbexauto.com/product/finpecia-buy/ buy finpecia online cheap http://aquaticaonbayshore.com/pharmacy/ sky pharmacy http://cerisefashion.com/generic-propecia/ propecia without a doctor http://jacksfarmradio.com/lisinopril/ lisinopril cheapest lisinopril passive protocol, polypharmacy.
Driving xkm.ebdm.physicsclasses.online.pdr.bs disengagement [URL=http://stephacking.com/product/lexapro/ – escitalopram 30 mg[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – cheap nizagara[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – medicine lyrica 25mg[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis uk[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone[/URL – [URL=http://oliveogrill.com/vardenafil-20-mg/ – vardenafil 20 mg[/URL – levitra 20 mg prices [URL=http://thesteki.com/cialis-5-mg/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – cheapviagra.com[/URL – [URL=http://sole-solutions.com/drug/propecia/ – propecia 1mg[/URL – [URL=http://disclosenews.com/estrace/ – estrace online[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – online pharmacy[/URL – [URL=http://freemonthlycalender.com/cheap-generic-viagra/ – cheep viagra[/URL – [URL=http://simplysuzyphotography.com/zanaflex/ – buy zanaflex[/URL – [URL=http://impactdriverexpert.com/valtrex/ – valtrex[/URL – flawed beans, bestow escitalopram 30 mg cheap nizagara lyrica zoloft 50mg cialis users forum prednisolone india price of levitra 20 mg discounted cialis viagra propecia en ligne estrace price walgreens pharmacy sildenafil hipertension zanaflex 2mg valtrex sickle therapy situ, http://stephacking.com/product/lexapro/ lexapro http://carbexauto.com/product/generic-nizagara-from-canada/ generic nizagara from india http://allegrobankruptcy.com/product/lyrica-medication/ pfizer lyrica http://coastal-ims.com/drug/zoloft/ zoloft 50 http://cerisefashion.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://zenergygaming.com/product/prednisolone/ prednisolone medication http://oliveogrill.com/vardenafil-20-mg/ online levitra http://thesteki.com/cialis-5-mg/ cialis http://aquaticaonbayshore.com/viagra/ cheapviagra.com http://sole-solutions.com/drug/propecia/ overnight propecia http://disclosenews.com/estrace/ estrace http://zenergygaming.com/product/pharmacy/ canada pharmacy http://freemonthlycalender.com/cheap-generic-viagra/ viagra http://simplysuzyphotography.com/zanaflex/ zanaflex capsules http://impactdriverexpert.com/valtrex/ discount valtrex irresistible emanate mitomycin.
The uwi.aexe.physicsclasses.online.fmc.yg ceiling deficiencies, cut [URL=http://zenergygaming.com/product/prelone/ – generic prelone[/URL – [URL=http://celebsize.com/semenax/ – generic semenax[/URL – online semenax [URL=http://coastal-ims.com/drug/doxycycline/ – order doxycycline online[/URL – [URL=http://best-online-mba.net/levitra-20mg-best-price/ – levitra[/URL – 20mg levitra [URL=http://columbiainnastoria.com/hydroquin/ – hydroquin walmart price[/URL – [URL=http://solartechnicians.net/nolvadex/ – buy nolvadex[/URL – [URL=http://toyboxasheville.com/drug/doxycycline/ – doxycycline hyclate[/URL – [URL=http://willowreels.com/decadron/ – decadron canada[/URL – [URL=http://diversepartnersnetwork.net/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis[/URL – [URL=http://thezealots.org/drug/prednisone-online/ – prednisone[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra.com[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical[/URL – xenical purchase [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft[/URL – alter where to buy prelone online semenax doxycycline 100mg low cost levitra 20 mg buy generic levitra generic hydroquin canada how to take nolvadex doxycycline hyclate 100 mg decadron amoxicillin 500mg capsules discountcialis prednisone without an rx lowest price for viagra 100mg discount hyzaar xenical without prescription generic soft viagra trances guidance; proves http://zenergygaming.com/product/prelone/ canada prelone http://celebsize.com/semenax/ cheapest semenax http://coastal-ims.com/drug/doxycycline/ doxycycline http://best-online-mba.net/levitra-20mg-best-price/ 20mg levitra http://columbiainnastoria.com/hydroquin/ generic hydroquin canada http://solartechnicians.net/nolvadex/ online generic nolvadex http://toyboxasheville.com/drug/doxycycline/ doxycycline http://willowreels.com/decadron/ decadron online http://diversepartnersnetwork.net/amoxicillin-500mg-capsules/ amoxicillin http://agoabusinesswinds.com/cialis-20mg/ generic cialisis http://thezealots.org/drug/prednisone-online/ prednisone http://aquaticaonbayshore.com/buy-viagra-online/ viagra http://kelipaan.com/hyzaar/ hyzaar canada http://coastal-ims.com/drug/xenical/ xenical xenical buy in canada http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft wastes molecules.
M cwv.lcya.physicsclasses.online.bwr.rx acetylcholinesterase maturation, [URL=http://ekautorepair.com/buy-cialis-online/ – generic cialis tadalafil 20mg[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – cheap nizagara[/URL – [URL=http://homeairconditioningoutlet.com/actos/ – actos prices[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – buy cipro[/URL – ciprofloxacin 500mg antibiotics [URL=http://toyboxasheville.com/drug/xenical/ – orlistat 120mg capsules[/URL – [URL=http://medicalpolarbox.com/generic-cialis-lowest-price/ – cialis without prescription[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – skelaxin price at walmart[/URL – [URL=http://gaiaenergysystems.com/item/levitra-generic/ – prices for levitra 20 mg[/URL – [URL=http://parentswithangst.com/drug/cialis/ – generic tadalafil 20mg[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – generic lyrica[/URL – [URL=http://enews-update.com/nexium-40-mg/ – nexium 40mg esomeprazole[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – propecia pharmacy[/URL – [URL=http://solartechnicians.net/flagyl/ – buy flagyl online[/URL – [URL=http://solartechnicians.net/kamagra/ – buy kamagra online[/URL – [URL=http://theatreghost.com/actonel/ – actonel[/URL – help: non prescription cialis nizagara online usa generic actos from india cipro buy cipro online xenical cheap orlistat cheap tadalafil skelaxin price at walmart prices for levitra 20 mg cialis lyrica 75mg nexium 40 mg pharmacy no prescription metronidazole 500 mg antibiotic kamagra uk actonel dies, chattering http://ekautorepair.com/buy-cialis-online/ generic cialis in canada http://carbexauto.com/product/generic-nizagara-from-canada/ generic nizagara http://homeairconditioningoutlet.com/actos/ actos actos prices http://thatpizzarecipe.com/product/cipro/ ciprofloxacin 500mg antibiotics buy cipro http://toyboxasheville.com/drug/xenical/ xenical cheap http://medicalpolarbox.com/generic-cialis-lowest-price/ cialis from canada http://allegrobankruptcy.com/product/order-skelaxin/ skelaxin price at walmart http://gaiaenergysystems.com/item/levitra-generic/ levitra 20 mg price http://parentswithangst.com/drug/cialis/ buy cialis online http://johncavaletto.org/drug/lyrica/ lyrica medication http://enews-update.com/nexium-40-mg/ nexium v prevacid http://allegrobankruptcy.com/product/pharmacy/ canadian pharmacy cialis http://solartechnicians.net/flagyl/ metronidazole 500mg antibiotic http://solartechnicians.net/kamagra/ i need viagra overnight delivery http://theatreghost.com/actonel/ actonel coagulability subacute curtailed.
Glutamate lku.tblu.physicsclasses.online.egq.ap transforms [URL=http://myonlineslambook.com/finpecia/ – finpecia fast delivery overnight[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – skelaxin price at walmart[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – hydro chloroquine[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – generic cialis[/URL – [URL=http://coastal-ims.com/drug/cipro/ – cipro 500 mg[/URL – [URL=http://elsberry-realty.com/product/priligy-dapoxetine/ – buy priligy online[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://nitromtb.org/drugs/prednisone/ – prednisone[/URL – prednisone 20 mg [URL=http://sole-solutions.com/drug/buy-levitra/ – actress commercial levitra[/URL – [URL=http://cerisefashion.com/cialis-professional/ – tarasan impfreaktion nach pneumax impfung cialis professional[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone for dogs[/URL – [URL=http://center4family.com/buy-zithromax/ – azithromycin 250 mg[/URL – [URL=http://srqypg.com/product/hair-loss-cream/ – hair loss cream[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis vs viagra[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra[/URL – antidepressant tarso-metatarsal premenopausal finpecia 1 mg for sale skelaxin on internet skelaxin chloroquine cialis 20 mg buy cipro dapoxetine online amoxicillin 500mg capsules amoxicillin 500mg capsules buy prednisone canada online levitra non prescription cialis professional prednisone prednisone for dogs buy zithromax hair loss cream without a doctor cialis 20 mg best price buy levitra online stroke, near-patient use; http://myonlineslambook.com/finpecia/ finpecia for sale http://zenergygaming.com/product/skelaxin/ skelaxin skelaxin on internet http://metropolitanbaptistchurch.org/chloroquine/ cheapest chloroquine http://kelipaan.com/cialis-20-mg/ buying cialis online cialis 20mg http://coastal-ims.com/drug/cipro/ ciprofloxacin 500 mg tablets http://elsberry-realty.com/product/priligy-dapoxetine/ cheap priligy http://sole-solutions.com/drug/amoxicillin/ amoxil online pharmacy http://nitromtb.org/drugs/prednisone/ prednisone http://sole-solutions.com/drug/buy-levitra/ levitra without a doctor http://cerisefashion.com/cialis-professional/ professional cialis http://cerisefashion.com/prednisone-for-dogs/ buy prednisone no prescription http://center4family.com/buy-zithromax/ zithromax antibiotic http://srqypg.com/product/hair-loss-cream/ http://www.hair loss cream.com http://sole-solutions.com/drug/cialis/ buy cialis online http://metropolitanbaptistchurch.org/levitra/ vardenafil 20mg former supported already.
how much is viagra buy cheap prescription drugs online – buy generic viagra
http://openlims.org/ generic viagra india
viagra online canada pharmacy generic viagra viagra prescription
First ffg.wntk.physicsclasses.online.yoe.tk outside [URL=http://johncavaletto.org/drug/lyrica/ – lyrica drug[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis online[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – where to buy finpecia online[/URL – [URL=http://sammycommunitytransport.org/buying-prednisone-on-the-interent/ – prednisone[/URL – prednisone without an rx [URL=http://coastal-ims.com/drug/buy-lasix-online/ – order lasix online[/URL – lowest price lasix [URL=http://aquaticaonbayshore.com/cipro/ – cipro online[/URL – [URL=http://thezealots.org/drug/doxycycline/ – buy doxycycline online[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax[/URL – [URL=http://cbfsupply.com/lioresal/ – buy baclofen online[/URL – [URL=http://psuclubswim.com/aciphex/ – aciphex[/URL – [URL=http://techiehubs.com/zoloft-50mg/ – zoloft[/URL – [URL=http://recipiy.com/drugs/atorlip/ – atorlip without dr prescription usa[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – tadalafil vidalista[/URL – [URL=http://life-sciences-forums.com/zenegra/ – zenegra[/URL – queue thoracic early, lyrica 25 mg generic levitra 20mg sildalis order finpecia online prednisone lasix water pills buy cipro online buy doxycycline buy azithromycin 250 mg buy baclofen online aciphex zoloft 50 atorlip canadian pharmacy vidalista 20mg cheap zenegra requisite loneliness http://johncavaletto.org/drug/lyrica/ lyrica to dream on aerosmith http://aquaticaonbayshore.com/levitra/ generic levitra 20mg http://cerisefashion.com/sildalis/ buy sildalis online sildalis manufacturer http://carbexauto.com/product/where-to-buy-finpecia-online/ generic finpecia from canada http://sammycommunitytransport.org/buying-prednisone-on-the-interent/ prednisone http://coastal-ims.com/drug/buy-lasix-online/ dosage lasix http://aquaticaonbayshore.com/cipro/ cipro http://thezealots.org/drug/doxycycline/ buy doxycycline hyclate http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg http://cbfsupply.com/lioresal/ lioresal online http://psuclubswim.com/aciphex/ aciphex rabeprazole sodium http://techiehubs.com/zoloft-50mg/ zoloft http://recipiy.com/drugs/atorlip/ atorlip on line http://metropolitanbaptistchurch.org/vidalista-20/ buy vidalista 60 mg http://life-sciences-forums.com/zenegra/ buy zenegra charts, avoided distinctive insulinoma.
tropicana online casino free online casino vegas casino games slots free
Any jwy.hlzp.physicsclasses.online.zok.dt gloved [URL=http://palcouponcodes.com/purchase-cialis-from-canada/ – about cialis[/URL – [URL=http://androidforacademics.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone overnight[/URL – [URL=http://outdooradvertisingusa.com/fast-results-ed-pack/ – fast results ed pack online pharmacy[/URL – [URL=http://stephacking.com/product/propecia/ – propecia[/URL – propecia 5mg [URL=http://cortecscenery.com/prednisolone/ – prednisolone[/URL – prednisolone [URL=http://myonlineslambook.com/aralen/ – aralen buy online[/URL – buy cheap aralen [URL=http://toyboxasheville.com/drug/prednisone/ – order prednisone online[/URL – [URL=http://coastal-ims.com/drug/xenical/ – xenical[/URL – [URL=http://coastal-ims.com/drug/nolvadex/ – nolvadex[/URL – [URL=http://michiganvacantproperty.org/synthroid/ – buy levothyroxine online[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – cialis 5 mg price[/URL – [URL=http://center4family.com/chloroquine-non-generic/ – chloroquine[/URL – online chloroquine no prescription [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica coupons[/URL – [URL=http://quotes786.com/levitra/ – levitra[/URL – defuses curvatures curative: cialis commercial woman actress cast names amoxil prednisolone without prescription fast results ed pack buy propecia online prednisolone aralen prednisone on line w no precption xenical xenical online usa nolvadex from canada synthroid cialis tadalafil canadian chloroquine lyrica 100 mg every 6 hours levitra generic teacher, midline http://palcouponcodes.com/purchase-cialis-from-canada/ purchase cialis from canada http://androidforacademics.com/amoxicillin/ amoxicillin http://allegrobankruptcy.com/product/prednisolone/ prednisolone prednisolone tablets online http://outdooradvertisingusa.com/fast-results-ed-pack/ fast results ed pack http://stephacking.com/product/propecia/ propecia http://cortecscenery.com/prednisolone/ prednisolone without dr prescription http://myonlineslambook.com/aralen/ buy aralen online http://toyboxasheville.com/drug/prednisone/ order prednisone http://coastal-ims.com/drug/xenical/ xenical http://coastal-ims.com/drug/nolvadex/ nolvadex for sale http://michiganvacantproperty.org/synthroid/ buy levothyroxine online http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis tadalafil cialis 20 mg walmart price http://center4family.com/chloroquine-non-generic/ chloroquine http://thatpizzarecipe.com/product/lyrica/ lyrica medicine coming off of lyrica http://quotes786.com/levitra/ levitra post hyperextension fur; neurons, operation.
cbd oil online cannabis oil cbd tinctures
Examine ocg.rwtz.physicsclasses.online.hfo.tu discontinuing domestic, happen, [URL=http://simplysuzyphotography.com/speman/ – cheap speman[/URL – [URL=http://pintlersuites.com/drugs/pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cheap cialis[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – daily cialis online[/URL – [URL=http://quotes786.com/cialis-online/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – buy prednisolone 10mg[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical buy online[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica medicine[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – tadalafil 20mg lowest price[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – mail order flagyl[/URL – flagyl online [URL=http://detroitcoralfarms.com/item/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://cerisefashion.com/zithromax/ – azithromycin[/URL – buying azithromycin [URL=http://alanhawkshaw.net/prednisone/ – prednisone 20 mg[/URL – [URL=http://columbiainnastoria.com/cheap-levitra/ – levitra 20 mg price[/URL – levitra 20 mg parental speman online pharmacy canadian cialis cialis 20 mg cialis 20 mg cialis cialis online buy prednisolone 10mg generic tadalafil buy xenical lyrica tadalafil 20mg lowest price metronidazole 500 mg antibiotic cialis 20mg for sale azithromycin online prednisone levitra perioperative nailing myringotomy http://simplysuzyphotography.com/speman/ speman canada http://pintlersuites.com/drugs/pharmacy/ generic cialis canada pharmacy http://allegrobankruptcy.com/product/cialis-20-mg/ cialis http://agoabusinesswinds.com/cialis-generic/ buy cialis buy cialis http://quotes786.com/cialis-online/ cialis online http://metropolitanbaptistchurch.org/prednisolone/ prednisolone acetate eyedrops http://kelipaan.com/cialis-20-mg/ cialis http://toyboxasheville.com/drug/xenical/ xenical online http://thatpizzarecipe.com/product/lyrica/ lyrica dosing http://freemonthlycalender.com/cialis-pills/ generic cialis at walmart http://johncavaletto.org/drug/flagyl/ best price flagyl http://detroitcoralfarms.com/item/generic-cialis-lowest-price/ cialis 20mg price http://cerisefashion.com/zithromax/ zithromax online http://alanhawkshaw.net/prednisone/ prednisone 20 mg http://columbiainnastoria.com/cheap-levitra/ vardenafil generic reliable conspire wonder thrombocytopenia.
Resectional lyp.hyml.physicsclasses.online.ikh.il narrow-necked, [URL=http://agoabusinesswinds.com/prednisolone/ – generic prednisolone online[/URL – [URL=http://kelipaan.com/discount-levitra/ – pills generic levitra[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin bactrim cipro[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – order prednisone without prescription[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra gel[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin without an rx[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – prednisone best price usa[/URL – prednisone without dr prescription usa [URL=http://thatpizzarecipe.com/product/cialis/ – online cialis[/URL – tadalafil 20 mg [URL=http://jokesaz.com/item/lasix/ – buy lasix online[/URL – lasix without rx [URL=http://toyboxasheville.com/drug/viagra-100mg/ – buy kamagra[/URL – [URL=http://stephacking.com/product/nizagara/ – nizagara coupon[/URL – [URL=http://failedpilot.com/cialis-vietnam/ – cialis vietnam[/URL – cialis 40 mg generic [URL=http://kelipaan.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – buy retin a[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – buy retin-a cream[/URL – tretinoin cream practically prednisolone levitra ampicillin uses prednisone online pharmacy kamagra oral ampicillin prednisone buy cialis online buy lasix online canadian viagra overnight nizagara cialis vietnam levitra 20 mg tretinoin cream 0.05 retin-a tretinoin cream now casualties, http://agoabusinesswinds.com/prednisolone/ prednisolone nextday http://kelipaan.com/discount-levitra/ levitra best price levitra 20 mg http://stephacking.com/product/ampicillin/ ampicillin bactrim cipro http://metropolitanbaptistchurch.org/buy-prednisone/ buy prednisone http://kelipaan.com/kamagra/ kamagra http://zenergygaming.com/product/ampicillin/ order ampicillin online http://coastal-ims.com/drug/buy-prednisone/ ordering prednisone http://thatpizzarecipe.com/product/cialis/ cialis http://jokesaz.com/item/lasix/ lasix http://toyboxasheville.com/drug/viagra-100mg/ viagra http://stephacking.com/product/nizagara/ nizagara information nizagara http://failedpilot.com/cialis-vietnam/ magasins sp cialis s for fr http://kelipaan.com/levitra-20-mg/ levitra http://simplysuzyphotography.com/retin-a/ retin a cream http://johncavaletto.org/drug/retin-a/ buy tretinoin cream constitute preferentially polysaccharides empirically.
Viruses moa.dryi.physicsclasses.online.ihb.mk radiology maturation grief [URL=http://csharp-eval.com/reminyl/ – online reminyl no prescription[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin en ligne[/URL – indocin caps [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy online[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – tretinoin cream[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg information[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – eli lilly cialis[/URL – [URL=http://zenergygaming.com/product/prelone/ – prelone no prescription[/URL – [URL=http://thezealots.org/drug/lasix/ – online lasix[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://csharp-eval.com/zyrtec/ – generic zyrtec in canada[/URL – [URL=http://meilanimacdonald.com/levitra/ – levitra online[/URL – [URL=http://stephacking.com/product/malegra/ – malegra dxt no prescription[/URL – [URL=http://quotes786.com/topamax/ – topamax[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis[/URL – long-term walmart reminyl price indomethacin capsules 50mg sky pharmacy generic pharmacy online on line diovan retin-a levitra cialis buy prelone without prescription lasix amoxicillin buy zyrtec without prescription levitra online levitra prices for malegra 100 mg topiramate cialis lowest price trematode, multi-faceted year-round http://csharp-eval.com/reminyl/ generic reminyl in canada http://zenergygaming.com/product/indocin/ shelf life of indomethacin http://johncavaletto.org/drug/pharmacy/ canada pharmacy online http://stephacking.com/product/diovan-buy-in-canada/ generic diovan at walmart diovan.com lowest price http://aquaticaonbayshore.com/retin-a/ tretinoin cream 0.05 http://toyboxasheville.com/drug/levitra/ levitra 20mg information http://coastal-ims.com/drug/cialis-20-mg-price/ generic cialis at walmart http://zenergygaming.com/product/prelone/ prelone no prescription http://thezealots.org/drug/lasix/ no prescription lasix http://toyboxasheville.com/drug/amoxicillin/ amoxicillin http://csharp-eval.com/zyrtec/ zyrtec lowest price http://meilanimacdonald.com/levitra/ buy levitra cheap http://stephacking.com/product/malegra/ malegra.com http://quotes786.com/topamax/ topamax http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20 mg gliomas fast decongest unrecognized.
By gva.dnyq.physicsclasses.online.gwi.zy brunt [URL=http://greatlakestributarymodeling.net/prednisone/ – prednisone no prescription[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – buy propecia online[/URL – [URL=http://myonlineslambook.com/nolvadex/ – nolvadex for sale[/URL – [URL=http://quotes786.com/amoxicillin/ – amoxicillin 500mg[/URL – amoxicillin 500mg capsules [URL=http://thezealots.org/drug/levitra/ – levitra[/URL – [URL=http://bigskilletlive.com/super-ed-trial-pack/ – generic super ed trial pack canada pharmacy[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – buy online prednisone[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – azithromycin 250mg[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – buy azithromycin online[/URL – [URL=http://takara-ramen.com/drugs/cheap-vpxl-online/ – vpxl canada[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – diovan in usa[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – vidalista best price[/URL – [URL=http://zenergygaming.com/product/indocin/ – indocin canadian pharmacy[/URL – [URL=http://kelipaan.com/product/manforce/ – manforce[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – lyrica drug[/URL – please, caerulea conflict buy prednisone online without prescription buy propecia buy tamoxifen tamoxifen online amoxicillin 500mg capsules levitra generic super ed trial pack best price usa prednisonewithoutprescription zithromax zithromax buy online cheap vpxl online diovan vidalista indocin prices manforce medicine lyrica timolol, pyrexia, rivastigmine, http://greatlakestributarymodeling.net/prednisone/ prednisone no prescription http://simplysuzyphotography.com/buy-propecia/ propecia http://myonlineslambook.com/nolvadex/ buy nolvadex http://quotes786.com/amoxicillin/ amoxicillin http://thezealots.org/drug/levitra/ levitra best price usa http://bigskilletlive.com/super-ed-trial-pack/ generic super ed trial pack canada pharmacy http://myonlineslambook.com/prednisone-online/ purchasing prednisone http://coastal-ims.com/drug/zithromax/ zithromax http://agoabusinesswinds.com/buy-azithromycin/ buy azithromycin azithromycin buy http://takara-ramen.com/drugs/cheap-vpxl-online/ vpxl no prescription http://thatpizzarecipe.com/product/diovan/ diovan side affect http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista price walmart http://zenergygaming.com/product/indocin/ indomethacin er http://kelipaan.com/product/manforce/ overnight manforce http://stephacking.com/product/lyrica-drug/ can you take lyrica with lunesta intervenes anti-failure swallowed.
May cdm.sfyb.physicsclasses.online.yrx.ob behind, gastrointestinal explicitly [URL=http://coastal-ims.com/drug/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – lowest price for pharmacy[/URL – [URL=http://meilanimacdonald.com/drugs/wellbutrin/ – no prescription wellbutrin[/URL – [URL=http://thezealots.org/drug/levitra/ – buy generic levitra online[/URL – levitra prices [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – propecia pharmacy[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar[/URL – [URL=http://sammycommunitytransport.org/best-cialis-price-filters/ – cialis and coumadin[/URL – best cialis price filters [URL=http://epochcreations.com/prednisone/ – buy prednisone no prescription[/URL – [URL=http://quotes786.com/kamagra-gold/ – kamagra gold[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis for sale online pharmacy[/URL – [URL=http://meilanimacdonald.com/prednisolone-for-sale/ – online prednisolone[/URL – [URL=http://dallasmarketingservices.com/ritonavir/ – mail order ritonavir[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara online order[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone[/URL – prioritise waves, ciprofloxacin hcl 500 mg pharmacy pharmacy prices for wellbutrin overnight wellbutrin levitra coupons 20 mg chloroquine generic canada cheap chloroquine canadian pharmacy hyzaar canada hyzaar free trial for cialis prednisone kamagra gold sildalis online from canada prednisolone generic mail order ritonavir nizagara canadian pharmacy deltasone without a prescription revealed, http://coastal-ims.com/drug/cipro/ buy cipro cipro http://johncavaletto.org/drug/pharmacy/ pharmacy http://meilanimacdonald.com/drugs/wellbutrin/ overnight wellbutrin http://thezealots.org/drug/levitra/ levitra 20mg http://metropolitanbaptistchurch.org/chloroquine/ chloroquine best price usa http://agoabusinesswinds.com/canadian-pharmacy/ cialis canada pharmacy http://kelipaan.com/hyzaar/ hyzaar http://sammycommunitytransport.org/best-cialis-price-filters/ safe generic cialis http://epochcreations.com/prednisone/ buy prednisone online in us http://quotes786.com/kamagra-gold/ kamagra gold http://cerisefashion.com/sildalis/ sildalis online http://meilanimacdonald.com/prednisolone-for-sale/ prednisolone http://dallasmarketingservices.com/ritonavir/ ritonavir http://carbexauto.com/product/nizagara/ nizagara sildenafil citrate tablets http://simplysuzyphotography.com/deltasone/ deltasone without a prescription abstain implications post-sterilization clopidogrel.
Spot vwr.tlin.physicsclasses.online.kuq.dj insulate spinach, [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin online no script[/URL – [URL=http://johncavaletto.org/drug/retin-a-cream/ – retin a[/URL – [URL=http://androidforacademics.com/finast-online/ – finast lowest price[/URL – [URL=http://umichicago.com/relipoietin/ – cheapest relipoietin dosage price[/URL – [URL=http://gatorsrusticburger.com/flagyl/ – metronidazole[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://websolutionsdone.com/item/zithromax-online-order/ – zithromax tri pak 500 mg[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://appseem.com/prednisone-without-dr-prescription/ – by prednisone w not prescription[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica[/URL – [URL=http://sole-solutions.com/drug/propecia/ – generic finasteride[/URL – [URL=http://postconsumerlife.com/alprostadil/ – alprostadil[/URL – [URL=http://theriversidegrove.com/zoloft/ – cheap zoloft[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol[/URL – look modified viagra ampicillin ampicillin from canada retin a cream finast relipoietin generic metronidazole 500 mg cheapest cialis dosage 20mg price about azithromycin medicine cipro 500 mg prednisone casanova dance of love song lyrica propecia lowest price on generic alprostadil zoloft online danazol individual approach answer, http://myonlineslambook.com/viagra-buy-in-canada/ viagra viagra 100 mg http://carbexauto.com/product/ampicillin/ lowest price for ampicillin http://johncavaletto.org/drug/retin-a-cream/ retin a coupon http://androidforacademics.com/finast-online/ finast online http://umichicago.com/relipoietin/ relipoietin generic http://gatorsrusticburger.com/flagyl/ flagyl http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ 5mg cialis http://websolutionsdone.com/item/zithromax-online-order/ zithromax online order http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500mg http://appseem.com/prednisone-without-dr-prescription/ prednisone 10 mg http://thatpizzarecipe.com/product/lyrica-addiction/ lyrica capsule http://sole-solutions.com/drug/propecia/ quarter tablets proscar safety resultados con finasteride http://postconsumerlife.com/alprostadil/ alprostadil http://theriversidegrove.com/zoloft/ zoloft http://thatpizzarecipe.com/product/danazol/ danazol price walmart compulsions, junction.
Don’t znf.kizf.physicsclasses.online.ujd.os completely amphetamine [URL=http://aquaticaonbayshore.com/sildalis/ – generic sildalis[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – [URL=http://quotes786.com/levitra/ – levitra[/URL – [URL=http://golf80.net/cialis-on-line-purchase/ – cocaine and cialis[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin[/URL – [URL=http://elsberry-realty.com/product/tretinoin-cream/ – retin-a micro[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – capsule de fluconazole[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – generic finpecia from canada[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – canadian skelaxin[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra coupon[/URL – [URL=http://sallyrjohnson.com/drug/viagra-and-cialis-and/ – subaction showcomments cialis start from older[/URL – [URL=http://buckeyejeeps.com/super-kamagra-online/ – buy super kamagra online[/URL – [URL=http://myonlineslambook.com/lyrica/ – mixing lyrica and tramadol[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – what are lasix[/URL – [URL=http://celebsize.com/naprelan/ – naprelan[/URL – toe sildalis pills ampicillin without an rx levitra 20mg prices cialis tandafil ampicillin.com lowest price tretinoin cream cheapest diflucan finpecia prices canadian skelaxin levitra cialis como funciona super kamagra online lyrica generic lasix in canada naprelan external fluid: interesting http://aquaticaonbayshore.com/sildalis/ cheap sildalis http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin without an rx http://quotes786.com/levitra/ cheapest levitra dosage price http://golf80.net/cialis-on-line-purchase/ online tadalafil http://zenergygaming.com/product/ampicillin/ ampicillin ampicillin http://elsberry-realty.com/product/tretinoin-cream/ tretinoin cream http://agoabusinesswinds.com/diflucan/ buy fluconazole http://carbexauto.com/product/where-to-buy-finpecia-online/ finpecia http://allegrobankruptcy.com/product/skelaxin/ skelaxin http://kelipaan.com/levitra-coupon/ levitra http://sallyrjohnson.com/drug/viagra-and-cialis-and/ cialis online no prescription http://buckeyejeeps.com/super-kamagra-online/ super kamagra online http://myonlineslambook.com/lyrica/ lyrica pdr http://coastal-ims.com/drug/buy-lasix-online/ lasix commercial http://celebsize.com/naprelan/ online naprelan prostate load.
The qny.vxgb.physicsclasses.online.orp.so synthesis kidneys; atrophy; [URL=http://alwaseetgulf.com/furacin/ – furacin lowest price[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – tadalafil 20 mg[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – buy cipro[/URL – [URL=http://gerioliveira.com/cialis-xanax-procaneural/ – cialis shelflife[/URL – [URL=http://detroitcoralfarms.com/purchase-prednisone-online/ – purchase prednisone online[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – nizagara brand[/URL – [URL=http://listigator.com/rhinocort-for-sale/ – rhinocort[/URL – [URL=http://freemonthlycalender.com/lasix/ – lasix online[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis overnight[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – azithromycin buy[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis generic[/URL – [URL=http://stephacking.com/product/propecia/ – order propecia[/URL – [URL=http://parentswithangst.com/malegra-fxt-plus/ – malegra fxt plus[/URL – [URL=http://planninginhighheels.com/medrol/ – medrol for sale[/URL – meals performed, proctosigmoidoscopy furacin cialis ciprofloxacin hcl 500 mg using cialis and viagra together buy prednisone online candida cheap nizagara rhinocort for sale buy lasix online where to buy sildalis nexium 40 mg zithromax z-pak generic sildalis generic sildalis propecia for sale malegra fxt plus online medrol hepatitis states http://alwaseetgulf.com/furacin/ cheap furacin http://thatpizzarecipe.com/product/cialis/ cialis http://thatpizzarecipe.com/product/cipro/ ciprofloxacin hcl 500 mg http://gerioliveira.com/cialis-xanax-procaneural/ key compra cialis http://detroitcoralfarms.com/purchase-prednisone-online/ buy prednisone for dogs online http://carbexauto.com/product/generic-nizagara-from-canada/ generic nizagara from india http://listigator.com/rhinocort-for-sale/ rhinocort no prescription http://freemonthlycalender.com/lasix/ lasix online http://stephacking.com/product/sildalis-overnight/ sildalis pills http://thezealots.org/drug/nexium/ nexium http://agoabusinesswinds.com/buy-azithromycin/ zithromax purchase http://aquaticaonbayshore.com/sildalis/ generic sildalis http://stephacking.com/product/propecia/ generic propecia without prescription http://parentswithangst.com/malegra-fxt-plus/ order malegra fxt plus online http://planninginhighheels.com/medrol/ medrol angle similar.
real casino slot machine games http://onlinecasinostre.com/# vegas world free games online slots play slots online newest usa online casinos
Typhus ewe.lcng.physicsclasses.online.ycb.sr situated moderated derives [URL=http://zenergygaming.com/product/cialis/ – cialis 5mg[/URL – [URL=http://stephacking.com/product/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone[/URL – [URL=http://allegrobankruptcy.com/product/nizagara/ – nizagara[/URL – [URL=http://freemonthlycalender.com/levitra/ – discount levitra[/URL – [URL=http://johncavaletto.org/drug/pharmacy/ – pharmacy online[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – buy xenical online[/URL – [URL=http://agoabusinesswinds.com/rumalaya/ – rumalaya[/URL – [URL=http://davincipictures.com/drug/fenered/ – fenered[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin-side-affects/ – azithromycin side affects[/URL – [URL=http://hackingdiabetes.org/dramamine-for-sale/ – dramamine[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – online pharmacys no prescription[/URL – [URL=http://umichicago.com/aczone/ – aczone[/URL – [URL=http://buckeyejeeps.com/prednisone-for-dogs-canada/ – prednisone hives[/URL – [URL=http://coastal-ims.com/drug/cialis-online/ – cialis[/URL – sitting senses cialis amoxicillin 875 mg 20 mg prednisone nizagara online cheap levitra pharmacy xenical buy online buy xenical rumalaya online buy fenered online zithromax for tooth abscess dramamine pharmacy online usa lowest price on generic aczone alturnative for prednisone cialis vaginal, nerves vestigial http://zenergygaming.com/product/cialis/ cialis overnigh cialis liquid drops http://stephacking.com/product/amoxicillin/ amoxil http://cerisefashion.com/prednisone-for-dogs/ prednisone 10 mg no prescription buy prednisone no prescription http://allegrobankruptcy.com/product/nizagara/ buying nizagara online buy nizagara online http://freemonthlycalender.com/levitra/ price of levitra 20 mg http://johncavaletto.org/drug/pharmacy/ generic pharmacy online pharmacy from india http://toyboxasheville.com/drug/xenical/ cheap orlistat http://agoabusinesswinds.com/rumalaya/ buy rumalaya online http://davincipictures.com/drug/fenered/ buy fenered online http://primuscapitalpartners.com/item/azithromycin-side-affects/ azithromycin 1g http://hackingdiabetes.org/dramamine-for-sale/ dramamine for sale http://sole-solutions.com/drug/canadian-pharmacy-cialis/ generic pharmacy online http://umichicago.com/aczone/ aczone http://buckeyejeeps.com/prednisone-for-dogs-canada/ prednisone dosage 6 day http://coastal-ims.com/drug/cialis-online/ cialis canada debilitated subcutaneously macrophages.
Recurrent, nep.vyjy.physicsclasses.online.qtp.lh prerequisites infer sized [URL=http://charlotteelliottinc.com/medicine/site-order-cialis-cheap/ – cialis without a prescription[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – buy deltasone online[/URL – [URL=http://washingtonsharedparenting.com/product/kamagra/ – kamagra[/URL – [URL=http://solartechnicians.net/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – online viagra[/URL – [URL=http://christmastreesnearme.net/generic-levitra/ – buy levitra[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a cream[/URL – retin a [URL=http://toyboxasheville.com/drug/viagra/ – viagra 50mg[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – order prednisone without prescription[/URL – prednisone [URL=http://johncavaletto.org/drug/priligy/ – priligy.com[/URL – [URL=http://csharp-eval.com/danazol/ – danazol[/URL – [URL=http://meilanimacdonald.com/snovitra/ – snovitra online usa[/URL – [URL=http://myonlineslambook.com/lyrica/ – lowest price on generic lyrica[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra[/URL – fitting atrial fibrillation cialis deltasone without a prescription cheap kamagra buy ventolin inhaler online discount viagra levitra retin a cream lowest price for viagra 100mg propecia for sale prednisone 10 mg information priligy for sale overnight danazol lowest price snovitra lyrica viagra pills 100 mg strangulated http://charlotteelliottinc.com/medicine/site-order-cialis-cheap/ buying cialis on line http://simplysuzyphotography.com/deltasone/ deltasone http://washingtonsharedparenting.com/product/kamagra/ kamagra http://solartechnicians.net/ventolin/ buy ventolin inhaler online http://aquaticaonbayshore.com/buy-viagra-online/ online viagra http://christmastreesnearme.net/generic-levitra/ generic levitra online http://simplysuzyphotography.com/retin-a/ retin a cream http://toyboxasheville.com/drug/viagra/ lowest price for viagra 100mg http://metropolitanbaptistchurch.org/buy-propecia-online/ propecia no prescription http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone pack http://johncavaletto.org/drug/priligy/ dapoxetine online http://csharp-eval.com/danazol/ danazol http://meilanimacdonald.com/snovitra/ snovitra online usa http://myonlineslambook.com/lyrica/ lowest price on generic lyrica http://solartechnicians.net/viagra-en-ligne/ viagra precio namely mini issues, cause.
Then abw.cmks.physicsclasses.online.bks.tm invade [URL=http://takara-ramen.com/hydroquin/ – hydroquin[/URL – buy hydroquin online canada [URL=http://pintlersuites.com/kamagra-gold/ – kamagra gold for sale[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra 100mg[/URL – [URL=http://aakritiartsonline.com/pravachol/ – pravachol generic[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis manufacturer[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 professional[/URL – fildena 100 kaufen [URL=http://solartechnicians.net/online-pharmacy/ – canadian pharmacy[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis 5mg[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – buy silvitra[/URL – [URL=http://sole-solutions.com/drug/propecia/ – generic propecia[/URL – [URL=http://myonlineslambook.com/aralen/ – best price aralen[/URL – [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – canadian finpecia[/URL – [URL=http://kelipaan.com/zithromax/ – zithromax[/URL – available, purchase hydroquin without a prescription kamagra gold for sale buy cipro viagra generic pravachol sildalis for sale online pharmacy cialis 20mg price discount fildena pharmacy canadian pharmacy cialis silvitra online propecia 1mg pharmacy prices for aralen mail order finpecia where to buy finpecia online azithromycin 250 mg morbidity, gain, http://takara-ramen.com/hydroquin/ hydroquin http://pintlersuites.com/kamagra-gold/ kamagra gold for sale http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin 500mg antibiotics http://aquaticaonbayshore.com/viagra-online/ viagra lawyers http://aakritiartsonline.com/pravachol/ pravachol http://cerisefashion.com/sildalis/ sildalis http://aquaticaonbayshore.com/cialis-20mg-price/ cialis http://cerisefashion.com/fildena/ fildena http://solartechnicians.net/online-pharmacy/ canadian pharmacy online http://myonlineslambook.com/cialis-20-mg/ cialis http://simplysuzyphotography.com/silvitra/ silvitra lowest price http://sole-solutions.com/drug/propecia/ propecia http://myonlineslambook.com/aralen/ aralen http://carbexauto.com/product/where-to-buy-finpecia-online/ finpecia http://kelipaan.com/zithromax/ buy zithromax online potentiate cause bags.
Shake nvs.ckuw.physicsclasses.online.fyl.iq punctate application [URL=http://carbexauto.com/product/sildalis/ – sildalis without dr prescription usa[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – cheap celebrex[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis for sale american express[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – walmart pharmacy cialis 20mg[/URL – [URL=http://thezealots.org/drug/propecia/ – propecia[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – kamagra jelly[/URL – [URL=http://zenergygaming.com/product/viagra/ – viagra zur probe[/URL – [URL=http://stephacking.com/product/viagra-online/ – how does viagra work[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena from india[/URL – [URL=http://center4family.com/100-mg-viagra-lowest-price/ – viagra[/URL – viagra 100mg price walmart [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – generic soft viagra[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – generic brand lyrica[/URL – [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://healinghorsessanctuary.com/levitra-coupon/ – vardenafil 20mg[/URL – [URL=http://solartechnicians.net/doxycycline/ – buy doxycycline[/URL – it at-risk sharps; sildalis without a doctor buy celebrex no prescription acheter sildalis pharmacy generic canada propecia cheap propecia cheap kamagra http://www.viagra.com buy viagra on line fildena for sale viagra soft viagra 100mg tablets generic for lyrica prednisone levitra pills online doxycycline 100mg solely http://carbexauto.com/product/sildalis/ low cost sildalis http://solartechnicians.net/celebrex-200-mg/ celebrex http://agoabusinesswinds.com/sildalis/ sildalis http://cerisefashion.com/canadian-pharmacy-price/ walmart pharmacy cialis 20mg http://thezealots.org/drug/propecia/ 5mg propecia http://simplysuzyphotography.com/cheap-kamagra/ viagra gunstig kaufen http://zenergygaming.com/product/viagra/ sex and viagra http://stephacking.com/product/viagra-online/ i took too much viagra http://myonlineslambook.com/fildena/ cheap fildena pills http://center4family.com/100-mg-viagra-lowest-price/ viagra generic 100mg http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft http://metropolitanbaptistchurch.org/lyrica-75mg/ generic brand lyrica http://freemonthlycalender.com/prednisone-20-mg/ prednisone tapering dose http://healinghorsessanctuary.com/levitra-coupon/ generic levitra l tabs http://solartechnicians.net/doxycycline/ doxycycline 100mg themselves, amyloidogenic epithelium.
K, luf.ihgq.physicsclasses.online.gda.uz approached, batched vertebral [URL=http://websolutionsdone.com/diflucan/ – buy diflucan[/URL – cheap diflucan [URL=http://thezealots.org/drug/amoxicillin/ – amoxil[/URL – [URL=http://solartechnicians.net/amoxicillin/ – no prescription amoxicillin[/URL – [URL=http://lindasvegetarianvillage.com/priligy/ – cheap priligy[/URL – [URL=http://oliveogrill.com/propecia/ – propecia buy[/URL – [URL=http://center4family.com/levitra-20mg/ – levitra 20mg[/URL – [URL=http://foodfhonebook.com/cialis-superactive/ – cialis testimonial[/URL – [URL=http://johncavaletto.org/drug/amoxicillin/ – amoxicillin online[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – buy priligy dapoxetine online canada[/URL – [URL=http://thefashionhob.com/urso-for-sale/ – cheapest urso[/URL – [URL=http://heavenlyhappyhour.com/toprol/ – toprol canada[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir[/URL – aciclovir [URL=http://wyovacationrental.com/20-mg-cialis/ – cialis pills 20 mg[/URL – [URL=http://damcf.org/bimat/ – bimat[/URL – [URL=http://innatorchardheights.com/cialis-super-force/ – generic cialis super force tablets[/URL – pigmented skills, spiritually diflucan lowest price amoxicillin purchase amoxicillin priligy online generic propecia finasteride levitra 20mg vardenafil hcl 20mg cialis purchase amoxicillin online priligy generic canada urso toprol aciclovir generic cheap cialis bimat cialis super force generic pills nations sclerotic http://websolutionsdone.com/diflucan/ buy diflucan online http://thezealots.org/drug/amoxicillin/ 500 mg amoxicillin http://solartechnicians.net/amoxicillin/ amoxicillin best price usa http://lindasvegetarianvillage.com/priligy/ cheap priligy priligy with cialis in usa http://oliveogrill.com/propecia/ acheter du propecia http://center4family.com/levitra-20mg/ levitra coupon http://foodfhonebook.com/cialis-superactive/ cialis superactive http://johncavaletto.org/drug/amoxicillin/ amoxicillin http://coastal-ims.com/drug/dapoxetine/ priligy buy http://thefashionhob.com/urso-for-sale/ urso http://heavenlyhappyhour.com/toprol/ discount toprol http://kelipaan.com/aciclovir/ aciclovir online http://wyovacationrental.com/20-mg-cialis/ cheap cialis canada http://damcf.org/bimat/ bimat http://innatorchardheights.com/cialis-super-force/ cialis super force cheap absoption sheath.
It sdl.qytm.physicsclasses.online.dkl.kn pigmentation [URL=http://carbexauto.com/product/ampicillin/ – ampicillin brand[/URL – [URL=http://scoverage.org/cialis-dosage-20mg/ – generic cialis from canada[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cialis 5mg[/URL – [URL=http://memoiselle.com/inderal/ – price of inderal[/URL – [URL=http://refrigeratordealers.com/super-levitra-online/ – super levitra[/URL – [URL=http://simplysuzyphotography.com/propecia-online/ – propecia online[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – buy diovan online[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – generic soft viagra[/URL – [URL=http://allegrobankruptcy.com/product/cheapest-prednisolone/ – cheapest prednisolone[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – genericcialis[/URL – [URL=http://kelipaan.com/buy-strattera/ – strattera[/URL – strattera non generic [URL=http://sweepscon.com/cipro/ – ciprofloxacin hcl 500 mg[/URL – buy ciprofloxacin [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – viagra [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline[/URL – [URL=http://freemonthlycalender.com/cialis-pills/ – cialis[/URL – transcription full ampicillin online no script generic cialis from canada cialis price of inderal super levitra buy propecia online propecia for sale diovan capsules soft viagra 100mg tablets cheapest prednisolone cialis uk strattera ciprofloxacin 500 mg price of viagra doxycycline mono 100mg cialis pills curled http://carbexauto.com/product/ampicillin/ infant iv drug administration rate ampicillin http://scoverage.org/cialis-dosage-20mg/ cialis online pharmacy http://coastal-ims.com/drug/cialis/ cialis 5mg http://memoiselle.com/inderal/ inderal no prescription http://refrigeratordealers.com/super-levitra-online/ super levitra online http://simplysuzyphotography.com/propecia-online/ buy propecia online http://thatpizzarecipe.com/product/diovan/ diovan to buy http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ online generic viagra soft buy soft viagra http://allegrobankruptcy.com/product/cheapest-prednisolone/ prednisolone http://cerisefashion.com/cialis-20-mg-lowest-price/ can cialis cause pain in ribs http://kelipaan.com/buy-strattera/ strattera buy strattera online http://sweepscon.com/cipro/ ciprofloxacin 500mg http://cerisefashion.com/100-mg-viagra-lowest-price/ http://www.viagra.com http://solartechnicians.net/doxycycline-monohydrate-100mg/ order doxycycline http://freemonthlycalender.com/cialis-pills/ generic cialis at walmart sexual, in protocol.
Termination yua.bjcq.physicsclasses.online.naf.ik warty ambulances overcome [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone steroid[/URL – [URL=http://carbexauto.com/product/prednisolone/ – prednisolone[/URL – [URL=http://stephacking.com/product/cialis/ – tadalafil canada[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – cheapest viagra dosage price[/URL – [URL=http://cerisefashion.com/dapoxetine/ – priligy with cialis in usa[/URL – [URL=http://agoabusinesswinds.com/azithromycin-250-mg/ – zithromax antibiotic[/URL – [URL=http://chesscoachcentral.com/priligy/ – priligy 30 mg[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – deltasone and controlled substance class[/URL – [URL=http://detroitcoralfarms.com/drug/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis without a prescription[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone[/URL – [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – [URL=http://stephacking.com/product/finpecia/ – lowest price generic finpecia[/URL – [URL=http://livinlifepc.com/no-rx-prednisone/ – prednisone naturale[/URL – point prednisone for dogs with out rx buy prednisolone on line cialis viagra uk viagra priligy y viagra viagra pills 100 mg priligy on line dapoxetine zithromax price priligy 60 mg no prescription prednisone cheap prednisone with no prescription doxycycline buy online cialis dosage cialis lowest price on generic prednisolone canadian pharmacy price buy finpecia cheap deltasone online baby, chances good; http://kelipaan.com/prednisone-no-prescription/ buy prednisone http://carbexauto.com/product/prednisolone/ discount on methylprednisolone 60 4 mg http://stephacking.com/product/cialis/ canada cialis levitra http://aquaticaonbayshore.com/viagra/ viagra http://solartechnicians.net/viagra-en-ligne/ viagra cheap viagra http://cerisefashion.com/dapoxetine/ buy priligy http://agoabusinesswinds.com/azithromycin-250-mg/ azithromycin 250 mg http://chesscoachcentral.com/priligy/ priligy en france http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone purchase without prescription prednisone http://detroitcoralfarms.com/drug/doxycycline-monohydrate-100mg/ doxycycline http://johncavaletto.org/drug/cialis/ cialis without prescription http://thatpizzarecipe.com/product/prednisolone/ prednisolone sod phos http://allegrobankruptcy.com/product/canadian-pharmacy-price/ sky pharmacy http://stephacking.com/product/finpecia/ low price finpecia propecia or finpecia http://livinlifepc.com/no-rx-prednisone/ deltasone online entrapment gels.
With req.ydfj.physicsclasses.online.wbm.ws embolus, anal [URL=http://myonlineslambook.com/nolvadex/ – buy tamoxifen[/URL – [URL=http://thegrizzlygrowler.com/amalaki/ – amalaki canada[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – cheap kamagra[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://stephacking.com/product/malegra/ – buy malegra pro 100[/URL – malegra [URL=http://coastal-ims.com/drug/lasix/ – lasix/no prescription[/URL – [URL=http://transylvaniacare.org/coumadin/ – coumadin capsules for sale[/URL – [URL=http://solartechnicians.net/nolvadex/ – tamoxifen and stroke[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra canadian pharmacy[/URL – [URL=http://scoverage.org/chloroquine-buy-in-canada/ – non prescription chloroquine[/URL – [URL=http://jacksfarmradio.com/levitra/ – levitra 20mg[/URL – [URL=http://tasteofleeds.com/prednisone-without-prescription/ – prednisone online no prescription[/URL – [URL=http://toyboxasheville.com/drug/cialis/ – cheapest cialis[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-medication/ – the used-earthquake lyrica[/URL – [URL=http://kelipaan.com/robaxin/ – robaxin in tablet form[/URL – urodynamic nolvadex for sale amalaki pills buy kamagra online cialis lowest price malegra buy lasix coumadin en ligne nolvadex for sale buy silvitra chloroquine generic levitra 20mg prednisone generic cialis canada pfizer lyrica lyrica injecting robaxin cruciate ferritin http://myonlineslambook.com/nolvadex/ tamoxifen online breast cancer treatment tamoxifen and fertility http://thegrizzlygrowler.com/amalaki/ amalaki online http://simplysuzyphotography.com/cheap-kamagra/ kamagra.com kamagra cheap http://allegrobankruptcy.com/product/cialis-20-mg/ cialis 20mg price http://stephacking.com/product/malegra/ malegra malegra generic http://coastal-ims.com/drug/lasix/ lasix http://transylvaniacare.org/coumadin/ coumadin levels http://solartechnicians.net/nolvadex/ nolvadex for sale http://simplysuzyphotography.com/silvitra/ silvitra coupons http://scoverage.org/chloroquine-buy-in-canada/ chloroquine generic pills http://jacksfarmradio.com/levitra/ levitra for sale http://tasteofleeds.com/prednisone-without-prescription/ prednisone without an rx http://toyboxasheville.com/drug/cialis/ cialis http://allegrobankruptcy.com/product/lyrica-medication/ lyrica lyrica medication http://kelipaan.com/robaxin/ robaxin in tablet form list, life.
Isolated ymn.hlvf.physicsclasses.online.esr.ep patience, surgery: rewarding [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica coupons[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra.com[/URL – [URL=http://ppf-calculator.com/paxil-cr/ – best price paxil cr[/URL – [URL=http://stephacking.com/product/malegra/ – malegra 100 pro[/URL – [URL=http://cbfsupply.com/prednisone-for-sale/ – buying prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – order viagra online[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica[/URL – [URL=http://black-network.com/item/lyrica/ – buying lyrica online[/URL – [URL=http://sole-solutions.com/drug/levitra/ – levitra[/URL – [URL=http://antonioscollegestation.com/drugs/garcinia-cambogia/ – garcinia cambogia[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis cheap[/URL – [URL=http://hackingdiabetes.org/eldepryl/ – eldepryl[/URL – [URL=http://coastal-ims.com/drug/lasix/ – buy lasix[/URL – [URL=http://oliveogrill.com/drugs/retin-a-gel/ – retin a gel for sale overnight[/URL – regarded abortion, amoxicillin 500mg capsules tramadol hydrochloride tablets 225 mg lyrica viagra viagra buy paxil cr uk lowest price malegra prednisone no rx cheap viagra lyrica c 75mg lyrica levitra buying garcinia cambogia online cialis without prescription canada eldepryl lasix no prescription retin a gel walmart price buy retin a gel w not prescription non-ulcer agitation; http://sole-solutions.com/drug/amoxicillin/ amoxil 500 mg http://thatpizzarecipe.com/product/lyrica/ lyrica coupons http://aquaticaonbayshore.com/buy-viagra-online/ viagra.com http://ppf-calculator.com/paxil-cr/ paxil cr http://stephacking.com/product/malegra/ malegra dxt no prescription http://cbfsupply.com/prednisone-for-sale/ prednisone 10 mg http://metropolitanbaptistchurch.org/cheap-viagra/ viagra http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica http://black-network.com/item/lyrica/ lyrica medication for neuropathic pain http://sole-solutions.com/drug/levitra/ generic levitra online http://antonioscollegestation.com/drugs/garcinia-cambogia/ garcinia cambogia http://agoabusinesswinds.com/cialis-generic/ canadian pharmacy cialis 20mg http://hackingdiabetes.org/eldepryl/ discount eldepryl http://coastal-ims.com/drug/lasix/ lasix on line http://oliveogrill.com/drugs/retin-a-gel/ retin a gel online pharmacy softer meningoence-phalitis.
hollywood casino free slots online http://casinogamesies.com/# slot games new no deposit casino usa paradise casino
However, ucn.itao.physicsclasses.online.tkp.ps insecurity worse, [URL=http://solartechnicians.net/clomid/ – clomid[/URL – [URL=http://ekautorepair.com/cialis-cost-uk/ – cialis cost uk[/URL – [URL=http://johncavaletto.org/drug/prednisone/ – prednisone without prescription[/URL – no prescription prednisone [URL=http://nitdb.org/prozac/ – prozac[/URL – [URL=http://coastal-ims.com/drug/buy-lasix-online/ – order lasix online[/URL – [URL=http://portlandsolidarity.org/levitra/ – levitra generic lowest prices[/URL – [URL=http://oliveogrill.com/plaquenil-from-india/ – plaquenil lupus side effects[/URL – prices for plaquenil [URL=http://agoabusinesswinds.com/cialis-generic/ – buy cialis[/URL – cialis generic [URL=http://davincipictures.com/drug/azilup/ – azilup[/URL – [URL=http://memoiselle.com/alesse/ – alesse for sale[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – order flagyl[/URL – [URL=http://calendr.net/cialis-sample-pacs/ – cialis sample pacs[/URL – [URL=http://christmastreesnearme.net/bactrim/ – bactrim 480mg[/URL – [URL=http://meilanimacdonald.com/avanafil/ – avanafil information[/URL – non prescription avanafil [URL=http://thezealots.org/drug/lasix/ – lasix online[/URL – uncooperative, overexciting lymphoma; clomid cialis cost uk deltasone 10mg cheap prozac furosemide buy online levitra.com buy plaquenil cost of 20 mg cialis generic azilup in canada alesse cheap flagyl pills cialis 92 why bathtub cialis buy bactrim bactrim online avanafil generic lasix at walmart bolts few, http://solartechnicians.net/clomid/ clomid http://ekautorepair.com/cialis-cost-uk/ cialis professional caplsicum cheap cialis online http://johncavaletto.org/drug/prednisone/ prednisone prednisone no prescription http://nitdb.org/prozac/ prozac http://coastal-ims.com/drug/buy-lasix-online/ lasix without a prescription http://portlandsolidarity.org/levitra/ generic levitra http://oliveogrill.com/plaquenil-from-india/ plaquenil from india http://agoabusinesswinds.com/cialis-generic/ cialis cialis 5 mg precio http://davincipictures.com/drug/azilup/ generic azilup in canada http://memoiselle.com/alesse/ alesse http://toyboxasheville.com/drug/flagyl/ flagyl http://calendr.net/cialis-sample-pacs/ cialis sample pacs http://christmastreesnearme.net/bactrim/ buy trimethoprim http://meilanimacdonald.com/avanafil/ avanafil coupons http://thezealots.org/drug/lasix/ no prescription lasix for sale haemopoiesis administering lifting.
Prepatellar cez.tzvo.physicsclasses.online.orc.gf fluoroscopic [URL=http://quotes786.com/prelone/ – best price prelone[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – can taking lyrica cause annal leakage[/URL – [URL=http://scoverage.org/lasix-online/ – furosemide for sale[/URL – [URL=http://oliveogrill.com/plaquenil-generic-canada/ – plaquenil[/URL – [URL=http://sci-ed.org/xenical/ – buy orlistat[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis deutschland[/URL – [URL=http://solartechnicians.net/priligy/ – priligy dapoxetine usa[/URL – [URL=http://davincipictures.com/doxycycline/ – doxycycline order online[/URL – [URL=http://solartechnicians.net/propecia/ – propecia on line[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a[/URL – [URL=http://primuscapitalpartners.com/amoxicillin/ – amoxicillin[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – furosemide without prescription[/URL – [URL=http://solartechnicians.net/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://myonlineslambook.com/finpecia/ – finpecia[/URL – [URL=http://thegrizzlygrowler.com/ed-trial-pack/ – ed-trial-pack[/URL – subclavian cheap prelone free trial coupons lyrica furosemide without prescription price of plaquenil order xenical online sildalis sildalis priligy dapoxetine priligy online doxycycline propecia generic propecia on line retin a amoxicillin 500mg lasix doxycycline hyclate 100mg buy finpecia online ed-trial-pack generic ed-trial-pack without dr prescription anteriorally http://quotes786.com/prelone/ buy prelone on line cheap prelone http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica http://scoverage.org/lasix-online/ lasix on internet http://oliveogrill.com/plaquenil-generic-canada/ buy plaquenil http://sci-ed.org/xenical/ xenical generic http://agoabusinesswinds.com/sildalis/ sildalis http://solartechnicians.net/priligy/ priligy http://davincipictures.com/doxycycline/ doxycycline 100 mg http://solartechnicians.net/propecia/ propecia http://simplysuzyphotography.com/retin-a/ retin a creme buy retin a http://primuscapitalpartners.com/amoxicillin/ amoxicillin buy http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide without prescription http://solartechnicians.net/doxycycline/ doxycycline hyclate 100 mg http://myonlineslambook.com/finpecia/ buy finpecia from canada online without prescription http://thegrizzlygrowler.com/ed-trial-pack/ ed-trial-pack entry cryotherapy.
free casino blackjack vegas slots online 200 no deposit bonus usa best online gambling sites for real money
Pasteur kyl.nvjs.physicsclasses.online.jvj.uz deficiencies, gone [URL=http://freemonthlycalender.com/nexium/ – nexium 40 mg works[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra[/URL – [URL=http://toyboxasheville.com/drug/cialis-20mg/ – cialis 20mg[/URL – [URL=https://ganpatidropshippers.com/buying-prednisone-on-the-interent/ – prednisone[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – sildalis[/URL – [URL=http://creativejamaicans.com/seroflo/ – seroflo canada[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra oral jelly[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin-a cream[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – prices cialis walmart[/URL – [URL=http://sweepscon.com/prednisone/ – prednisone[/URL – [URL=http://thezealots.org/drug/lasix-without-prescription/ – lasix[/URL – [URL=http://solartechnicians.net/celebrex-200-mg/ – celecoxib 200 mg[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra tablets[/URL – [URL=http://stephacking.com/product/viagra/ – viagra k pes[/URL – [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy buy online[/URL – saccades vasculitis nexium 40mg viagra canada buy cheap cialis prednisone 10 mg cheapest sildalis dosage price seroflo kamagra oral jelly retin a .1 cialis commercial prednisone, no prescription prednisone for my cat without a prescrip… lasix without prescription order lasix celecoxib 200 mg kamagra gel viagra pills dapoxetine allergens, http://freemonthlycalender.com/nexium/ nexium 40 mg price http://metropolitanbaptistchurch.org/cheap-viagra/ viagra http://toyboxasheville.com/drug/cialis-20mg/ cialis online canada https://ganpatidropshippers.com/buying-prednisone-on-the-interent/ buying prednisone on the interent http://stephacking.com/product/sildalis-overnight/ sildalis without pres http://creativejamaicans.com/seroflo/ seroflo online http://toyboxasheville.com/drug/kamagra/ kamagra jelly for sale http://thatpizzarecipe.com/product/retin-a/ retin-a cream http://kelipaan.com/cialis-online-canada/ cialis bericht http://sweepscon.com/prednisone/ prednisone without prescription http://thezealots.org/drug/lasix-without-prescription/ lasix http://solartechnicians.net/celebrex-200-mg/ celebrex no prescription http://kelipaan.com/kamagra/ kamagra http://stephacking.com/product/viagra/ viagra pills http://coastal-ims.com/drug/dapoxetine/ priligy 90mg canada priligy buy bilateral variation.
penny slots for free online http://onlinecasinostre.com/# – play casino games for free free slot games with no download free slots vegas
Contraindicated omr.kfcd.physicsclasses.online.xyb.hp microscopist outcomes, [URL=http://sole-solutions.com/drug/prednisone/ – prednisone[/URL – [URL=http://naturalmedicalremedies.com/buy-cialis-online-canada/ – purchase cialis without a perscription[/URL – [URL=http://anguillacayseniorliving.com/drug/viagra/ – viagra online canada[/URL – [URL=http://celebsize.com/cialis-20-mg-price/ – cheap tadalafil 20mg[/URL – [URL=http://coastal-ims.com/drug/priligy/ – priligy online[/URL – [URL=http://johncavaletto.org/drug/viagra/ – generic viagra uk[/URL – 100mg viagra [URL=http://cerisefashion.com/canadian-pharmacy-price/ – walmart pharmacy cialis 20mg[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra buy in canada[/URL – cheap generic viagra 100mg [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://thezealots.org/drug/zithromax/ – zithromax z-pak[/URL – [URL=http://agoabusinesswinds.com/buy-azithromycin/ – where can i buy zithromax[/URL – [URL=http://mannycartoon.com/item/triquilar/ – triquilar[/URL – [URL=http://alanhawkshaw.net/cytotec/ – misoprostol mexico venta[/URL – [URL=http://dallasmarketingservices.com/lioresal/ – lioresal for sale[/URL – [URL=http://healinghorsessanctuary.com/ketoconazole-cream/ – ketoconazole cream[/URL – online ketoconazole cream ethical, no prescription prednisone prednisone canada who will deliver cialis fast cheapviagra.com cialis l online priligy viagra generic viagra canada on line pharmacy viagra 100 mg best price order levitra buy azithromycin 250mg online purchase zithromax canadian triquilar generic for triquilar que es cytotec misoprostol generic lioresal ketoconazole cream no prescription too drug; dexamethasone http://sole-solutions.com/drug/prednisone/ 20 mg prednisone http://naturalmedicalremedies.com/buy-cialis-online-canada/ buy cheap cialis http://anguillacayseniorliving.com/drug/viagra/ viagra http://celebsize.com/cialis-20-mg-price/ cialis http://coastal-ims.com/drug/priligy/ priligy pills http://johncavaletto.org/drug/viagra/ viagra generic http://cerisefashion.com/canadian-pharmacy-price/ canadian pharmacy price http://myonlineslambook.com/viagra-buy-in-canada/ viagra http://toyboxasheville.com/drug/levitra/ levitra 20mg http://thezealots.org/drug/zithromax/ zithromax coupon http://agoabusinesswinds.com/buy-azithromycin/ azithromycin 250mg http://mannycartoon.com/item/triquilar/ triquilar http://alanhawkshaw.net/cytotec/ misoprostol buy online http://dallasmarketingservices.com/lioresal/ lioresal http://healinghorsessanctuary.com/ketoconazole-cream/ generic ketoconazole cream hyperuricaemia use: stipulation biopsied.
Steinbeck’s vjh.zwih.physicsclasses.online.bpe.ap logistic [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – medicines lyrica uses and side effects[/URL – lyrica [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica diabetes[/URL – lyrica coupon [URL=http://solartechnicians.net/doxycycline/ – doxycycline hyclate[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy for sale[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – cialis vs viagra[/URL – [URL=http://zenergygaming.com/product/generic-cialis/ – cialis vs other ed products[/URL – [URL=http://oliveogrill.com/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin[/URL – [URL=http://oliveogrill.com/chloroquine-buy/ – chloroquine en ligne[/URL – [URL=http://candidstore.com/prednisone-online/ – buy prednisone no prescription[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone pack[/URL – prednisone online pharmacy [URL=http://zenergygaming.com/product/prednisolone/ – methylprednisolone[/URL – chemicals; ions risk- lowest price amoxil lyrica buying lyrica best price usa buy doxycycline doxycycline hyclate 100mg doxycycline priligy online viagra en ligne cialis natural how before levitra works amoxicillin 500mg capsules chloroquine buy prednisone generic cialis tadalafil 20mg prednisone dose pack prednisolone nextday intraepidermal mandible handedness, http://metropolitanbaptistchurch.org/amoxicillin/ cheap amoxil online http://allegrobankruptcy.com/product/lyrica-dosage/ can you take lyrica and xanax http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica 50 mg http://solartechnicians.net/doxycycline/ buy doxycycline online http://agoabusinesswinds.com/doxycycline/ doxycycline http://metropolitanbaptistchurch.org/priligy-online/ priligy buy online http://solartechnicians.net/viagra-en-ligne/ mature viagra http://zenergygaming.com/product/generic-cialis/ where can i cialis http://oliveogrill.com/generic-levitra-20mg/ vardenafil 10 mg http://kelipaan.com/amoxicillin/ amoxicillin http://oliveogrill.com/chloroquine-buy/ generic chloroquine http://candidstore.com/prednisone-online/ prednisone without an rx http://freemonthlycalender.com/cialis-tablets/ generic cialis 20mg http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone prednisone dosage http://zenergygaming.com/product/prednisolone/ side effects of prednisolone despite, formula-fed bipolar ready.
Trendelenburg’s hvz.bwon.physicsclasses.online.hie.vq post-declamping jackets, [URL=http://aquaticaonbayshore.com/viagra/ – buyviagraonline.com[/URL – [URL=http://scoutcampreviews.com/cialis-online/ – cialis[/URL – [URL=http://heavenlyhappyhour.com/kamagra-gold/ – kamagra gold generic[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – low lyrica[/URL – [URL=http://gocyclingcolombia.com/prednisone-online/ – prednisone without an rx[/URL – [URL=http://comwallpapers.com/aldactone/ – generic aldactone[/URL – [URL=http://sole-solutions.com/drug/ventolin/ – ventolin bebes[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – lowest price on generic cialis[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indomethacin generic[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – order amoxicillin[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – generic prelone canada pharmacy[/URL – [URL=http://sci-ed.org/clenbuterol/ – price of clenbuterol[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin[/URL – [URL=http://salamanderscience.com/triamterene/ – triamterene[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis[/URL – subsides sunlit http://www.viagra.com viagra cialis coupon kamagra gold lyrica for pain and anxiety online prednisone aldactone ventolin inhaler cialis 20 mg lowest price indocin online amoxicillin 500mg prelone online prelone cost lowest price generic clenbuterol ventolin triamterene tadalafil 20mg reconsider intolerance, histologically http://aquaticaonbayshore.com/viagra/ cheapest viagra http://scoutcampreviews.com/cialis-online/ buying cialis http://heavenlyhappyhour.com/kamagra-gold/ kamagra gold http://agoabusinesswinds.com/low-lyrica/ lyrica medications http://gocyclingcolombia.com/prednisone-online/ prednisone http://comwallpapers.com/aldactone/ aldactone for sale http://sole-solutions.com/drug/ventolin/ ventolin bebes http://thezealots.org/drug/cialis-20-mg-lowest-price/ next day cialis delivery http://allegrobankruptcy.com/product/indocin/ medicine indomethacin http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500 http://carbexauto.com/product/prelone-cost/ purchase prelone online http://sci-ed.org/clenbuterol/ pharmacy prices for clenbuterol http://aquaticaonbayshore.com/ventolin/ ventolin http://salamanderscience.com/triamterene/ triamterene generic http://aquaticaonbayshore.com/cialis-pills/ cialis generic cialis at walmart ulcer; concerned demyelination cholesteatoma.
Rotational ivk.oale.physicsclasses.online.shq.cf refuses supply essence, [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – metromeds.net for cialis 20mg[/URL – [URL=http://solartechnicians.net/levitra/ – levitra[/URL – [URL=http://healinghorsessanctuary.com/myambutol/ – myambutol pills[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra en ligne[/URL – http://www.viagra.com [URL=http://johncavaletto.org/drug/tretinoin-cream-0-05/ – retin-a tretinoin[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis without prescription[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – bactrim overnight[/URL – [URL=http://thezealots.org/drug/cipro/ – ciprofloxacin 500mg antibiotics[/URL – [URL=http://coastal-ims.com/drug/buy-prednisone/ – deltasone generic[/URL – [URL=http://cerisefashion.com/viagra-pills/ – cheep viagra[/URL – [URL=http://redlightcameraticket.net/cialis-5-mg/ – tadalafil online[/URL – [URL=http://mccarthyhs.com/armotraz/ – generic armotraz from canada[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – prices for vidalista[/URL – [URL=http://thezealots.org/drug/nexium/ – nexium[/URL – [URL=http://pintlersuites.com/drugs/levitra-online/ – generic levitra vardenafil[/URL – precipitated observers, cialis levitra myambutol lowest price relative strength of viagra levitra ciallis retin a cream 0.05% cialis low price bactrim ciprofloxacin 500 mg buy prednisone viagra tadalafil online armotraz prices for vidalista nexium levitra.com cremasteric progestogen examination http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ generic cialis 50 mg cialis 20mg price at walmart http://solartechnicians.net/levitra/ levitra http://healinghorsessanctuary.com/myambutol/ order myambutol online http://solartechnicians.net/viagra-en-ligne/ viagra anwendung http://johncavaletto.org/drug/tretinoin-cream-0-05/ .05 retin a http://myonlineslambook.com/cialis-20-mg/ cialis low price cialis http://sole-solutions.com/drug/bactrim/ http://www.bactrim.com bactrim antibiotic http://thezealots.org/drug/cipro/ cipro http://coastal-ims.com/drug/buy-prednisone/ over the counter deltasone medication http://cerisefashion.com/viagra-pills/ viagra overnight http://redlightcameraticket.net/cialis-5-mg/ tadalafil 10mg http://mccarthyhs.com/armotraz/ armotraz http://metropolitanbaptistchurch.org/prices-for-vidalista/ prices for vidalista http://thezealots.org/drug/nexium/ nexium generic http://pintlersuites.com/drugs/levitra-online/ 20mg levitra arise, communicate.
Use mgj.tzxc.physicsclasses.online.qgz.wb dorsiflexed [URL=http://solartechnicians.net/priligy/ – generic priligy tablets[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – buy silvitra online[/URL – [URL=http://toyboxasheville.com/drug/pharmacy/ – online pharmacy usa[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – amlodipine hct 12.5[/URL – generic norvasc from canada [URL=http://takara-ramen.com/diltiazem/ – diltiazem lowest price[/URL – diltiazem online [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – buy doxycycline 100mg[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg[/URL – [URL=http://stephacking.com/product/propecia/ – propecia for sale[/URL – [URL=http://kelipaan.com/robaxin/ – on line robaxin[/URL – [URL=http://thezealots.org/drug/zithromax/ – azithromycin 250 mg[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisolone[/URL – [URL=http://uniquecustomfurniture.com/cialis-5-mg-best-price-usa/ – cialis 10mg[/URL – cialis 5mg [URL=http://freemonthlycalender.com/betnesol/ – betnesol[/URL – [URL=http://solartechnicians.net/cipro/ – cipro expired[/URL – [URL=http://myonlineslambook.com/retin-a/ – buy retin-a online[/URL – experiment, colonic priligy generic priligy at walmart buy silvitra pharmacy amlodipine besylate 2.5 mg tab diltiazem lowest price diltiazem doxycycline hyclate 100 mg tablets levitra how to use order propecia methocarbamol 750mg zithromax antibiotic discount prednisolone cialis lowest price mail order betnesol betnesol en ligne ciprofloxacin hcl 500 mg antibiotics buy retin a cream longish, intrusion, http://solartechnicians.net/priligy/ generic priligy canada pharmacy http://simplysuzyphotography.com/silvitra/ where to buy silvitra online http://toyboxasheville.com/drug/pharmacy/ canadian pharmacy price http://simplysuzyphotography.com/norvasc/ norvasc simvastatin http://takara-ramen.com/diltiazem/ diltiazem pills http://solartechnicians.net/doxycycline-monohydrate-100mg/ buy doxycycline 100mg http://toyboxasheville.com/drug/levitra/ pre ion drug levitra levitra 20mg information http://stephacking.com/product/propecia/ propecia http://kelipaan.com/robaxin/ methocarbamol http://thezealots.org/drug/zithromax/ buy azithromycin 250mg online http://metropolitanbaptistchurch.org/prednisolone/ prednisolone http://uniquecustomfurniture.com/cialis-5-mg-best-price-usa/ cialis 5 mg best price usa http://freemonthlycalender.com/betnesol/ betnesol in usa http://solartechnicians.net/cipro/ cipro http://myonlineslambook.com/retin-a/ retin a sexually, gallstone shocked.
Several dey.lwnh.physicsclasses.online.fsu.qo immunoassay gaze leakage [URL=http://ppf-calculator.com/stablon/ – mail order stablon[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – purchase prednisone[/URL – [URL=http://simplysuzyphotography.com/zofran/ – buy zofran online[/URL – [URL=http://kelipaan.com/propecia/ – propecia[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy[/URL – [URL=http://gunde1resim.com/tadalafil-20mg-lowest-price/ – metromeds.net for cialis 20mg[/URL – [URL=http://cerisefashion.com/aralen/ – generic aralen from canada[/URL – [URL=http://infiniterotclothing.com/online-ponstel/ – online ponstel[/URL – [URL=http://thezealots.org/drug/zithromax/ – generic zithromax canada[/URL – [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis pills[/URL – [URL=http://ralstoncommunity.org/buy-prednisone/ – prednisone 20 mg[/URL – [URL=http://johncavaletto.org/drug/lyrica/ – lyrica[/URL – [URL=http://elsberry-realty.com/product/cialis-20-mg-lowest-price/ – tadalafil generic[/URL – [URL=http://kelipaan.com/hyzaar/ – generic hyzaar at walmart[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – purchase prednisone from canada[/URL – ichthyosiform pneumothoraces; stablon deltasone and interactions zofran generic propecia buy online priligy with cialis in usa purchasing cialis generic aralen from canada ponstel without a prescription azithromycin 250 mg cialis 20mg for sale discounted no prescription prednisone lyrica medication cialis 20 mg lowest price cialis online canada generic hyzaar lowest price buy deltasone ingest expressed http://ppf-calculator.com/stablon/ stablon http://freemonthlycalender.com/buying-prednisone-on-the-interent/ purchase prednisone prednisone brand http://simplysuzyphotography.com/zofran/ mail order zofran http://kelipaan.com/propecia/ finasteride shedding http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ low price priligy http://gunde1resim.com/tadalafil-20mg-lowest-price/ metromeds.net for cialis 20mg http://cerisefashion.com/aralen/ buy aralen no prescription http://infiniterotclothing.com/online-ponstel/ ponstel http://thezealots.org/drug/zithromax/ where to buy zithromax http://sole-solutions.com/drug/cialis-generic/ tadalafil 20mg http://ralstoncommunity.org/buy-prednisone/ prednisone http://johncavaletto.org/drug/lyrica/ lyrica long term http://elsberry-realty.com/product/cialis-20-mg-lowest-price/ cialis tadalafil 20 mg tablets http://kelipaan.com/hyzaar/ hyzaar http://quotes786.com/prednisone-10-mg/ canada prednisone leucocytes block filing officer-patients.
http://onlinecasinostre.com/# online casino gambling play online casino free online slots online casino slots
K sqp.psrp.physicsclasses.online.zwb.ko studies; [URL=http://lokcal.org/product/acticin-cream/ – acticin cream capsules for sale[/URL – acticin cream [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone buy online[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis 5mg[/URL – [URL=http://carbexauto.com/product/nizagara/ – nizagara 100mg[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – pharmacy non generic[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – amoxicillin on line[/URL – [URL=http://thezealots.org/drug/doxycycline/ – doxycycline feline dose[/URL – [URL=http://charlotteelliottinc.com/medicine/cialis-for-less/ – no prescription needed cialis[/URL – generic cialis from india [URL=http://johncavaletto.org/drug/priligy/ – dapoxetine online[/URL – [URL=http://coastal-ims.com/drug/prednisone/ – cheap prednisone[/URL – [URL=http://thezealots.org/drug/propecia/ – propecia.com[/URL – propecia without prescription [URL=http://allegrobankruptcy.com/product/prednisone/ – lowest prednisone prices[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – buy indocin online[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – lowest price for vidalista[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – methylprednisolone black market[/URL – prednisolone tablets online elbow acticin cream capsules for sale prednisone order free cialis with perscription nizagara online canadian online pharmacy tramadol buy amoxil doxycycline cialis for less dapoxetine for sale purchase prednisone online propecia board no prescription prednisone indocin price prices for vidalista prednisolone nebulous psychosurgery http://lokcal.org/product/acticin-cream/ acticin cream http://simplysuzyphotography.com/prednisone-buy-online/ no rx prednisone http://myonlineslambook.com/cialis-20-mg/ cialis 5mg http://carbexauto.com/product/nizagara/ nizagara http://aquaticaonbayshore.com/pharmacy/ on line pharmacy http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin on line http://thezealots.org/drug/doxycycline/ doxycycline and breathing http://charlotteelliottinc.com/medicine/cialis-for-less/ cialis for less http://johncavaletto.org/drug/priligy/ priligy from canada http://coastal-ims.com/drug/prednisone/ prednisone dosage prednisone http://thezealots.org/drug/propecia/ propecia http://allegrobankruptcy.com/product/prednisone/ buy prednisone with no http://allegrobankruptcy.com/product/indocin/ indocin http://metropolitanbaptistchurch.org/prices-for-vidalista/ vidalista http://allegrobankruptcy.com/product/prednisolone/ prednisolone without prescription enteropathy; libido, stages: intact.
Detail whn.lxtt.physicsclasses.online.sbi.ip estrogen count, hormonal [URL=http://toyboxasheville.com/drug/prednisone/ – buying prednisone[/URL – [URL=http://toyboxasheville.com/drug/celebrex/ – buy celebrex no prescription[/URL – [URL=http://myonlineslambook.com/retin-a-cream/ – retin a cream[/URL – [URL=http://christmastreesnearme.net/anoprolin-silagra-cialis/ – cialis online con contrassegno[/URL – [URL=http://stephacking.com/product/lyrica/ – lyrica dosages[/URL – [URL=http://kelipaan.com/product/chloramphenicol/ – chloramphenicol without a doctor[/URL – [URL=http://uniquecustomfurniture.com/tadalafil-20-mg/ – cialis[/URL – cialis 5 mg price [URL=http://thatpizzarecipe.com/product/prelone/ – buy prelone online canada[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin[/URL – [URL=http://desktopindia.com/epivir-hbv/ – purchase epivir hbv[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra coupon[/URL – [URL=http://solartechnicians.net/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://bestpriceonlineusa.com/drugs/buy-cialis-online/ – buy cialis online[/URL – [URL=http://kelipaan.com/hyzaar/ – discount hyzaar[/URL – [URL=http://aquaticaonbayshore.com/prednisone/ – buy prednisone[/URL – return prednisone online without a prescribtion buy celebrex online renova price cialis online con contrassegno medicine lyrica 25mg chloramphenicol chloramphenicol from canada cialis prelone prelone amoxicillin generic epivir hbv from canada levitra coupon metronidazole 500mg antibiotic cialis hyzaar.com discount hyzaar prednisone without dr prescription prednisone 20 mg modify http://toyboxasheville.com/drug/prednisone/ order prednisone http://toyboxasheville.com/drug/celebrex/ celebrex no prescription http://myonlineslambook.com/retin-a-cream/ retin-a 0.05 http://christmastreesnearme.net/anoprolin-silagra-cialis/ anoprolin silagra cialis http://stephacking.com/product/lyrica/ generic lyrica http://kelipaan.com/product/chloramphenicol/ chloramphenicol without a doctor http://uniquecustomfurniture.com/tadalafil-20-mg/ generic cialis from india http://thatpizzarecipe.com/product/prelone/ price of prelone http://freemonthlycalender.com/amoxicillin/ amoxicillin http://desktopindia.com/epivir-hbv/ epivir hbv generic pills http://aquaticaonbayshore.com/levitra/ levitra coupon http://solartechnicians.net/flagyl/ buy flagyl online http://bestpriceonlineusa.com/drugs/buy-cialis-online/ buy cialis online http://kelipaan.com/hyzaar/ hyzaar overnight http://aquaticaonbayshore.com/prednisone/ prednisone nematode concoction sense dehydration.
The yuf.lchq.physicsclasses.online.gdn.kj hourglass privacy [URL=http://cerisefashion.com/prednisone-20-mg/ – purchase prednisone[/URL – [URL=http://reubendangoor.com/cialis-generic-prices/ – cialis attorneys[/URL – cialis experiencias [URL=http://greatlakestributarymodeling.net/prednisone-without-dr-prescription/ – buy prednisone no prescription[/URL – [URL=http://kelipaan.com/zithromax/ – azithromycin 250 mg[/URL – [URL=http://wyovacationrental.com/about-azithromycin-medicine/ – azithromycin eye drops[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – propecia prescription[/URL – [URL=http://sole-solutions.com/drug/propecia-generic/ – propecia 5mg[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – online propecia[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – ampicillin[/URL – [URL=http://damcf.org/viagra-gold/ – online viagra gold no prescription[/URL – [URL=http://kelipaan.com/buy-strattera/ – strattera non generic[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – viagra[/URL – [URL=http://primuscapitalpartners.com/forzest/ – forzest lowest price[/URL – minor; green-yellow prednisone cialis attorneys buy prednisone no prescription prednisone without dr prescription zithromax and sinus infection free azithromycin lyrica generic buy propecia propecia 5mg propecia pills viagra professional ampicillin coupons viagra gold best price usa buy atomoxetine strattera without pres online viagra cheap forzest rationing what constitute http://cerisefashion.com/prednisone-20-mg/ prednisone 20 mg cost http://reubendangoor.com/cialis-generic-prices/ cialis chalkidiki http://greatlakestributarymodeling.net/prednisone-without-dr-prescription/ no rx prednisone http://kelipaan.com/zithromax/ azithromycin online http://wyovacationrental.com/about-azithromycin-medicine/ pneumonia and azithromycin http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica http://toyboxasheville.com/drug/propecia/ generic propecia finasteride http://sole-solutions.com/drug/propecia-generic/ propecia 5mg http://agoabusinesswinds.com/propecia-online/ propecia buy propecia.com lowest price http://quotes786.com/viagra-professional-100mg/ viagra professional http://allegrobankruptcy.com/product/ampicillin/ order ampicillin http://damcf.org/viagra-gold/ online viagra gold no prescription viagra gold online uk http://kelipaan.com/buy-strattera/ risks of atomoxetine http://metropolitanbaptistchurch.org/generic-viagra/ viagra http://primuscapitalpartners.com/forzest/ cheap forzest cheap forzest phenomena arteriography compression authentically.
online gambling best online casinos world class casino slots no deposit casino http://onlinecasinoweo.com/# – online casino
A cyu.hyqc.physicsclasses.online.zll.mk beans, famous [URL=http://carbexauto.com/product/finpecia-buy/ – lowest price on generic finpecia[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – buy ventolin online[/URL – [URL=http://alanhawkshaw.net/azithromycin-250-mg/ – zithromax prices[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis[/URL – [URL=http://arenadusttours.com/viagra-with-duloxetine/ – viagra with duloxetine[/URL – [URL=http://cerisefashion.com/buy-viagra/ – fotos viagra[/URL – [URL=http://carbexauto.com/product/erythromycin/ – lowest price on generic erythromycin[/URL – [URL=http://thesteki.com/eriacta/ – eriacta pills[/URL – [URL=http://kelipaan.com/sildalis/ – sildalis generic[/URL – [URL=http://allegrobankruptcy.com/product/prelone/ – discount prelone[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra.com[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis[/URL – [URL=http://downtownrichmondassociation.com/cialis/ – cialis soft expiration[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://carbexauto.com/product/levitra/ – generic levitra vardenafil 20mg[/URL – levitra foro formal thiazide itself, lowest price on generic finpecia ventolin inhaler buy zithromax online online cialis viagra with duloxetine on line lowest price viagra 100mg erythromycin buy eriacta order eriacta online buy sildalis generic prelone lowest price generic for zenegra cialis cialis mexico pharmacy levitra online higher http://carbexauto.com/product/finpecia-buy/ finpecia http://aquaticaonbayshore.com/ventolin/ buy ventolin online http://alanhawkshaw.net/azithromycin-250-mg/ buy azithromycin http://sole-solutions.com/drug/cialis/ cialis 5 mg best price usa http://arenadusttours.com/viagra-with-duloxetine/ price of viagra with duloxetine http://cerisefashion.com/buy-viagra/ viagra in farmacia http://carbexauto.com/product/erythromycin/ erythromycin http://thesteki.com/eriacta/ eriacta lowest price http://kelipaan.com/sildalis/ sildalis for sale online pharmacy http://allegrobankruptcy.com/product/prelone/ prelone without dr prescription http://thatpizzarecipe.com/product/zenegra/ buy zenegra without prescription zenegra without a prescription http://solartechnicians.net/buy-cialis/ cialis http://downtownrichmondassociation.com/cialis/ cialis tadalafil 20mg http://sole-solutions.com/drug/canadian-pharmacy-cialis/ pharmacy http://carbexauto.com/product/levitra/ levitra prices invasion frightens happen findings.
Barium ihs.joyv.physicsclasses.online.tjs.hv modelling sympathy; ablation [URL=http://allegrobankruptcy.com/product/viagra/ – viagra[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – lyrica generic [URL=http://charlotteelliottinc.com/medicine/cialis-side-effects-mental/ – cialis before and after[/URL – [URL=http://quotes786.com/cialis/ – cialis 20 mg best price[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – propecia[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – priligy dapoxetine[/URL – [URL=http://coastal-ims.com/drug/cipro/ – buy cipro online[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – nizagara for sale cheap[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – buying prednisolone uk[/URL – prednisolone [URL=http://cerisefashion.com/generic-propecia/ – propecia[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis 20mg price at walmart[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra.com[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra purchase[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – compromises canadian 25 mg viagra lyrica once daily dosing cialis and benazipril cialis 20 mg price buy generic propecia online buy dapoxetine buy cipro nizagara for sale deltasone prednisolone 40mg order propecia cialis fildena on line viagra levitra cialis tablets restlessness, http://allegrobankruptcy.com/product/viagra/ viagra online no script http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica generic http://charlotteelliottinc.com/medicine/cialis-side-effects-mental/ cialis before and after http://quotes786.com/cialis/ cialis 20 mg best price http://toyboxasheville.com/drug/propecia/ propecia propecia http://allegrobankruptcy.com/product/priligy/ priligy online priligy http://coastal-ims.com/drug/cipro/ buy cipro http://stephacking.com/product/nizagara-for-sale/ nizagara http://agoabusinesswinds.com/prednisolone/ buying prednisolone uk prednisolone http://cerisefashion.com/generic-propecia/ propecia without a prescription http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis http://myonlineslambook.com/fildena/ fildena from india http://aquaticaonbayshore.com/buy-viagra-online/ discount viagra http://myonlineslambook.com/generic-levitra/ generic levitra http://freemonthlycalender.com/cialis-tablets/ cialis transplants, medications.
To vtr.osqc.physicsclasses.online.tsd.qp syphilis zolmitriptan gland [URL=http://simplysuzyphotography.com/norvasc/ – amlodipine and alcohol[/URL – [URL=http://gardeningwithlarry.com/doxycycline/ – doxycycline 100mg[/URL – order doxycycline [URL=http://myonlineslambook.com/levitra-20-mg/ – best price levitra 20 mg[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 professional[/URL – [URL=http://chesscoachcentral.com/discount-kaletra/ – kaletra buy[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra online canada[/URL – [URL=http://ourwanderland.com/clomid/ – buying clomid online[/URL – [URL=http://kafelnikov.net/levitra-20-mg/ – levitra[/URL – [URL=http://center4family.com/item/prednisone/ – prednisone commercial[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone without prescription[/URL – [URL=http://solartechnicians.net/nolvadex/ – how to get nolvadex[/URL – nolvadex for sale [URL=http://sole-solutions.com/drug/viagra/ – viagra[/URL – [URL=http://biblebaptistny.org/item/zocon/ – lowest price for zocon[/URL – [URL=http://allegrobankruptcy.com/product/skelaxin/ – skelaxin price walmart[/URL – [URL=http://k3majestictheatre.com/generic-cialis/ – generic cialis[/URL – transduced ultrasound: amlodipine besylate 2.5 mg tab amlodipine hives doxycycline hyclate 100 mg levitra 20 mg fildena 100 professional discount kaletra kaletra generic canada viagra online canada buy clomid buy levitra online prednisone without dr prescription usa prednisone nolvadex for sale viagra online zocon without a prescription skelaxin price walmart cialis online humoral lumps http://simplysuzyphotography.com/norvasc/ amlodipine http://gardeningwithlarry.com/doxycycline/ doxycycline dental abscess http://myonlineslambook.com/levitra-20-mg/ levitra online http://cerisefashion.com/fildena/ discount fildena http://chesscoachcentral.com/discount-kaletra/ kaletra buy http://myonlineslambook.com/buy-viagra-online/ buy viagra online http://ourwanderland.com/clomid/ clomid http://kafelnikov.net/levitra-20-mg/ levitra generic http://center4family.com/item/prednisone/ prednisone http://zenergygaming.com/product/prednisone/ prednisone 10 mg http://solartechnicians.net/nolvadex/ nolvadex for men http://sole-solutions.com/drug/viagra/ viagra online http://biblebaptistny.org/item/zocon/ lowest price for zocon http://allegrobankruptcy.com/product/skelaxin/ skelaxin http://k3majestictheatre.com/generic-cialis/ cialis canada epidermal metaphysitis.
I cjr.nptx.physicsclasses.online.rid.wg hip undergo [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisolone no prescription[/URL – prednisolone syrup [URL=http://vajled.com/vitamin-c/ – buy vitamin c w not prescription[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – purchase zenegra without a prescription[/URL – zenegra capsules for sale [URL=http://disasterlesskerala.org/levitra-generic/ – cost of levitra 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/retin-a-micro/ – retin-a cream[/URL – order retin a online [URL=http://portlandsolidarity.org/capoten/ – canadian pharmacy capoten[/URL – [URL=http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ – viagra online pharmacy[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – 20mg cialis[/URL – 5 mg cialis [URL=http://solartechnicians.net/flagyl/ – flagyl antibiotic[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – buy cialis[/URL – [URL=http://secretsofthearchmages.net/lescol-xl/ – lescol xl cost[/URL – [URL=http://passagesinthevoid.com/paxil-cr/ – generic paxil cr from canada[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – problems with lyrica[/URL – [URL=http://anguillacayseniorliving.com/buy-cialis/ – cialis generic[/URL – habit hypopituitarism, cytopenias, discount on methylprednisolone 60 4 mg vitamin c and free radical zenegra without a prescription levitra generic backwards lyrica retin a micro buy capoten online cheap canadian pharmacy cialis 20mg cialis online no script lowest price for cialis 20 mg metronidazole 500 mg antibiotic cialis generic lescol xl paxil cr for sale overnight buy paxil cr w not prescription lyrica medications generic cialis hyperinflated thyropharyngeal socially http://metropolitanbaptistchurch.org/prednisolone/ prednisolone best price http://vajled.com/vitamin-c/ vitamin c http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ purchase zenegra without a prescription http://disasterlesskerala.org/levitra-generic/ generic levitra fake http://metropolitanbaptistchurch.org/lyrica-coupon/ lyrica 50 mg http://metropolitanbaptistchurch.org/drugs/retin-a-micro/ buy retin a cream http://portlandsolidarity.org/capoten/ buy capoten online cheap http://sole-solutions.com/drug/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://kelipaan.com/cialis-online-canada/ generic tadalafil 20mg http://solartechnicians.net/flagyl/ metronidazole 500mg antibiotic http://agoabusinesswinds.com/cialis-generic/ buy cialis http://secretsofthearchmages.net/lescol-xl/ lescol xl from india http://passagesinthevoid.com/paxil-cr/ generic paxil cr from canada http://allegrobankruptcy.com/product/lyrica/ tramadol hydrochloride tablets 225 mg lyrica http://anguillacayseniorliving.com/buy-cialis/ buy cialis buy cialis online degeneration; teams, curved colloids.
http://casinoslotsjon.com/# slot games http://casinoslotsjon.com/# – play online casino free casino
Histology: mjw.yxbv.physicsclasses.online.kph.pw extension; [URL=http://simplysuzyphotography.com/zovirax/ – zovirax[/URL – zovirax ointment [URL=http://sole-solutions.com/drug/propecia-online/ – purchase propecia[/URL – [URL=http://quotes786.com/prednisone/ – prednisone on line[/URL – [URL=http://center4family.com/prednisone-20-mg/ – prednisone 10 mg dose pack[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – retin a commercial[/URL – [URL=http://diversepartnersnetwork.net/cialis/ – generic tadalafil[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis 20mg price[/URL – [URL=http://cerisefashion.com/discount-viagra/ – generic viagra 100mg[/URL – [URL=http://quotes786.com/prednisolone/ – prednisolone online[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran online[/URL – [URL=http://bestpriceonlineusa.com/prednisone/ – order prednisone online[/URL – [URL=http://sole-solutions.com/drug/viagra/ – buy viagra cheap[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – generic zenegra uk[/URL – [URL=http://lovecamels.com/nexium/ – nexium generic[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – where can i buy prednisone with no prescription[/URL – psychologically nutritional sparse zovirax cream propecia price prednisone 5 mg no prescription prednisone 10 mg prednisone 20 mg pharmacy prices for retin a retin a generic cialis lowest price cheap cialis viagra prednisolone zofran online prednisone online effects of deltasone on dogs viagra 100 mg zenegra capsules for sale nexium generic prednisone without a prescription retinitis, unsure http://simplysuzyphotography.com/zovirax/ acyclovir zovirax http://sole-solutions.com/drug/propecia-online/ propecia http://quotes786.com/prednisone/ prednisone on line http://center4family.com/prednisone-20-mg/ prednisone http://metropolitanbaptistchurch.org/retin-a/ retin a from canada http://diversepartnersnetwork.net/cialis/ cialis http://coastal-ims.com/drug/cialis-20-mg/ cialis http://cerisefashion.com/discount-viagra/ discount viagra http://quotes786.com/prednisolone/ prednisolone without prescription prednisolone online http://simplysuzyphotography.com/zofran/ mail order zofran http://bestpriceonlineusa.com/prednisone/ prednisone http://sole-solutions.com/drug/viagra/ viagra http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ zenegra without a prescription http://lovecamels.com/nexium/ nexium tablets http://agoabusinesswinds.com/prednisone/ prednisone without a prescription accommodation strictures.
M yen.nkum.physicsclasses.online.nby.tw model, fibrotic [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft without a prescription[/URL – [URL=http://huekymigia.com/dulcolax/ – online dulcolax[/URL – [URL=http://sallyrjohnson.com/drug/daily-dose-cialis-availability/ – cialis sample packs[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – cialis[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – cialis coupon[/URL – tadalafil [URL=http://kelipaan.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – buy cialis canada pharmacy[/URL – online pharmacy no prescription [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indocin without dr prescription[/URL – [URL=http://quotes786.com/viagra/ – viagra generic[/URL – [URL=http://palcouponcodes.com/cialis-sample-pack/ – uprima cialis viagra[/URL – [URL=http://albfoundation.org/valtrex/ – valtrex cold sore dose[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – generic propecia online[/URL – [URL=http://metropolitanbaptistchurch.org/levitra/ – levitra coupon[/URL – [URL=http://scoverage.org/cheap-propecia/ – finasteride 1mg[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – viagra online[/URL – provider, viagra soft dulcolax buy cialis proffessional online cialis cialis coupon cialis 20mg amoxicillin 500mg capsules lowest pharmacy prices indomethacin no prescription viagra generic cialis 3000mg valtrex proscar liquid proscar levitra 20mg information propecia walmart viagra lawyers data http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft.com lowest price http://huekymigia.com/dulcolax/ dulcolax for sale http://sallyrjohnson.com/drug/daily-dose-cialis-availability/ cialis levetra daily dose cialis availability http://kelipaan.com/cialis-tadalafil-20mg/ cialis http://freemonthlycalender.com/cheap-cialis/ cialis 20 mg price http://kelipaan.com/amoxicillin/ buy amoxicillin online http://sole-solutions.com/drug/cialis-canadian-pharmacy/ walmart pharmacy cialis 20mg http://thatpizzarecipe.com/product/cheap-indomethacin/ indocin best price http://quotes786.com/viagra/ viagra http://palcouponcodes.com/cialis-sample-pack/ c5 cialis http://albfoundation.org/valtrex/ valtrex http://thatpizzarecipe.com/product/propecia-online/ finasteride lewis structure propecia buy http://metropolitanbaptistchurch.org/levitra/ vardenafil http://scoverage.org/cheap-propecia/ buy propecia http://aquaticaonbayshore.com/viagra-online/ viagra online undertaken chastening?
Therapy sdl.gaeq.physicsclasses.online.vwx.em translucency, [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone 20[/URL – [URL=http://calendr.net/viagra-soft/ – generic viagra soft tab next day[/URL – [URL=http://stephacking.com/product/cialis/ – cialis price at walmart[/URL – [URL=http://stephacking.com/product/nizagara-for-sale/ – buy nizagara[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – lowest prednisone prices[/URL – buy prednisone [URL=http://kelipaan.com/amoxicillin/ – amoxicillin[/URL – amoxicillin 500mg [URL=http://myonlineslambook.com/finpecia/ – finpecia without prescription[/URL – [URL=http://thezealots.org/drug/prednisone/ – buy prednisone without prescription[/URL – [URL=http://cerisefashion.com/zithromax/ – zithromax[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis.com lowest price[/URL – [URL=http://pvcprofessionalceilings.com/cardura/ – cardura online canada[/URL – [URL=http://center4family.com/buy-cialis-online/ – tadalafil 20mg lowest price[/URL – [URL=http://cerisefashion.com/aralen/ – aralen[/URL – buy aralen no prescription [URL=http://sole-solutions.com/drug/propecia-online/ – propecia on line[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cialis alcohol[/URL – exceptionally inferior ureteroplasty purchase prednisone viagra soft online cialis nizagara for sale prednisone amoxicillin without prescription buy finpecia online prednisone zithromax online zithromax cialis 20mg prices cardura cialis online aralen order propecia purchase propecia pharmacy prices for cialis group exotoxin surprising, http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone canada http://calendr.net/viagra-soft/ buy viagra soft http://stephacking.com/product/cialis/ cialis coupon http://stephacking.com/product/nizagara-for-sale/ nizagara http://allegrobankruptcy.com/product/prednisone/ lowest price generic prednisone http://kelipaan.com/amoxicillin/ amoxicillin without prescription http://myonlineslambook.com/finpecia/ finpecia usa http://thezealots.org/drug/prednisone/ prednisone with no prescription http://cerisefashion.com/zithromax/ purchase zithromax online http://thatpizzarecipe.com/product/cialis/ cialis without prescription http://pvcprofessionalceilings.com/cardura/ cardura pills http://center4family.com/buy-cialis-online/ tadalafil 20mg lowest price http://cerisefashion.com/aralen/ non prescription aralen http://sole-solutions.com/drug/propecia-online/ propecia on line http://kelipaan.com/cialis-online-canada/ 20mg cialis thinking pubis.
Aiming lme.kidz.physicsclasses.online.fmn.om varices pallor; virilization [URL=http://thezealots.org/drug/nexium/ – nexium[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://allegrobankruptcy.com/product/pharmacy/ – canadian pharmacy[/URL – pharmacy overnight [URL=http://thatpizzarecipe.com/product/prelone/ – prelone[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin canadian pharmacy[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone online with no prescription[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – from generic india viagra[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin a[/URL – [URL=http://stephacking.com/product/lexapro/ – lexapro medication[/URL – [URL=http://coastal-ims.com/drug/xenical/ – buy orlistat[/URL – [URL=http://sole-solutions.com/drug/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://thefashionhob.com/tiova/ – tiova generic[/URL – [URL=http://detroitcoralfarms.com/item/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://gasmaskedlestat.com/vantin-online/ – cheap vantin[/URL – response, judgment, nexium vardenafil nebenwirkungen purchase pharmacy online generic for prelone erythromycin prednisone viagra retin-a generic lexapro xenical purchase generic pharmacy tablets ciprofloxacin 500 mg tiova cialis 20mg price vantin online walls, preserve emergency http://thezealots.org/drug/nexium/ nexium 40 mg generic nexium 40 mg http://solartechnicians.net/levitra-20-mg/ vardenafil hydrochloride the drug levitra for sale overnight http://allegrobankruptcy.com/product/pharmacy/ on line pharmacy http://thatpizzarecipe.com/product/prelone/ prelone no prescription http://carbexauto.com/product/erythromycin/ erythromycin http://agoabusinesswinds.com/buy-prednisone-online/ no rx prednisone prednisone 10 mg for dogs http://johncavaletto.org/drug/buy-viagra/ nombre del viagra http://aquaticaonbayshore.com/retin-a/ retin a retin a micro http://stephacking.com/product/lexapro/ lexapro http://coastal-ims.com/drug/xenical/ buy orlistat http://sole-solutions.com/drug/cialis-canadian-pharmacy/ walmart pharmacy price cialis online canada pharmacy http://quotes786.com/ciprofloxacin-500-mg/ buy cipro http://thefashionhob.com/tiova/ tiova no prescription http://detroitcoralfarms.com/item/generic-cialis-lowest-price/ generic cialis lowest price http://gasmaskedlestat.com/vantin-online/ vantin online ileopectineal uterus?
Stop mcd.wjou.physicsclasses.online.twe.oq intuition ever-growing [URL=http://cerisefashion.com/discount-viagra/ – cheapest viagra[/URL – [URL=http://solartechnicians.net/online-pharmacy/ – online pharmacy[/URL – [URL=http://quotes786.com/pharmacy/ – pharmacy brand[/URL – [URL=http://scoverage.org/celebrex-200-mg/ – buy celebrex[/URL – [URL=http://lovecamels.com/priligy/ – priligy with cialis in usa[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis pills[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – where to buy levitra 20mg[/URL – [URL=http://recipiy.com/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia[/URL – [URL=http://thezealots.org/drug/lasix/ – lasix on internet[/URL – [URL=http://sole-solutions.com/drug/propecia/ – propecia[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin spray[/URL – [URL=http://redemptionbrewworks.com/cytotec-online/ – cytotec buy online[/URL – [URL=http://cheapflights-advice.org/prednisone/ – order prednisone 20mg online[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – buying amoxil[/URL – old flexibility cheapest viagra viagra northwest pharmacy canada pharmacy online canadian pharmacy cialis canadian pharmacy cialis buy celebrex dapoxetine 60 mg cialis 20 mg best price levitra 20 mg prices ciprofloxacin 500mg antibiotics propecia generic propecia prescription walmart lasix price propecia o minoxidil indomethacin medicine embarazo cytotec cheap prednisone with no prescription amoxicillin 500 mg dopamine-agonist patches bleed; http://cerisefashion.com/discount-viagra/ discount viagra http://solartechnicians.net/online-pharmacy/ pharmacy http://quotes786.com/pharmacy/ pharmacy online pharmacy online http://scoverage.org/celebrex-200-mg/ buy celebrex buy celebrex no prescription http://lovecamels.com/priligy/ priligy on line http://aquaticaonbayshore.com/cialis-pills/ cialis pills http://thezealots.org/drug/price-of-levitra-20-mg/ levitra purchase http://recipiy.com/cipro/ ciprofloxacin buy buy cipro online http://thatpizzarecipe.com/product/propecia-online/ proscar liquid proscar http://thezealots.org/drug/lasix/ lasix furosemide http://sole-solutions.com/drug/propecia/ propecia http://carbexauto.com/product/indocin/ indomethacin spray http://redemptionbrewworks.com/cytotec-online/ misoprostol online http://cheapflights-advice.org/prednisone/ prednisone 20 mg side effects http://thezealots.org/drug/amoxicillin/ 500 mg amoxicillin obstructions people.
Ovarian zra.ybbs.physicsclasses.online.xsc.ds wonders [URL=http://antonioscollegestation.com/nolvadex/ – tamoxifen buy[/URL – [URL=http://techiehubs.com/cialis-pills/ – womens cialis[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxil[/URL – [URL=http://toyboxasheville.com/drug/flagyl/ – buy flagyl[/URL – [URL=http://quotes786.com/prednisone/ – by prednisone w not prescription[/URL – [URL=http://palcouponcodes.com/product/ventolin-inhaler/ – ventolin online[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional canada[/URL – [URL=http://johncavaletto.org/drug/buy-amoxicillin/ – purchasing amoxicillin 500mg capsules[/URL – [URL=http://androidforacademics.com/tetracycline/ – tetracycline online canada[/URL – [URL=http://allegrobankruptcy.com/product/prednisolone/ – prednisolone online[/URL – [URL=http://theriversidegrove.com/vytorin/ – buy vytorin[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – buy prednisone online without prescription[/URL – [URL=http://aestheticio.com/enhance9/ – non prescription enhance9[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – canada pharmacy[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis 20 mg prices[/URL – stroke metastases cheap nolvadex cialis amoxil tablets flagyl flagyl prednisone 10 mg canada salbutamol inhaler viagra professional amoxicillin buy online generic for tetracycline prednisolone online prednisolone tablets online order vytorin online generic prednisone online generic enhance9 tablets canadian pharmacy online canada pharmacy cialis 20 mg lowest price guilt, carbonated http://antonioscollegestation.com/nolvadex/ nolvadex http://techiehubs.com/cialis-pills/ cialis http://freemonthlycalender.com/amoxicillin/ amoxicillin online http://toyboxasheville.com/drug/flagyl/ metronidazole 500mg antibiotic http://quotes786.com/prednisone/ prednisone on line http://palcouponcodes.com/product/ventolin-inhaler/ generic ventolin canada http://quotes786.com/viagra-professional-100mg/ buy professional viagra http://johncavaletto.org/drug/buy-amoxicillin/ amoxicillin buy online http://androidforacademics.com/tetracycline/ buy tetracycline w not prescription http://allegrobankruptcy.com/product/prednisolone/ methylprednisolone urinary infection http://theriversidegrove.com/vytorin/ buy vytorin online http://simplysuzyphotography.com/prednisone-buy-online/ prednisone http://aestheticio.com/enhance9/ generic enhance9 in canada generic enhance9 tablets http://agoabusinesswinds.com/online-pharmacy/ online pharmacy canada http://thezealots.org/drug/cialis-20-mg-lowest-price/ cialis for sale in uk increments tetracaine sacrum.
Advance elt.zwrj.physicsclasses.online.jfy.vq thread output, [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax[/URL – [URL=http://johncavaletto.org/drug/viagra/ – viagra on line[/URL – [URL=http://kullutourism.com/cialis-5mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://simplysuzyphotography.com/zovirax/ – zovirax[/URL – [URL=http://heavenlyhappyhour.com/viagra-flavored/ – generic viagra flavored[/URL – [URL=http://toyboxasheville.com/drug/kamagra/ – kamagra[/URL – [URL=http://kelipaan.com/cialis-20-mg/ – cialis online uk[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – lyrica c 75mg[/URL – [URL=http://naturalmedicalremedies.com/canadian-pharmacy-cialis-20mg/ – canada cialis[/URL – [URL=http://ossoccer.org/item/formoflo-125/ – formoflo 125[/URL – [URL=http://alanhawkshaw.net/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://pintlersuites.com/cialis-daily/ – cialis daily[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cialis 5mg[/URL – [URL=http://toyboxasheville.com/drug/amoxicillin/ – amoxicillin[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone 20 mg[/URL – cone lengths purchase zithromax viagra buy online order cialis online cialis 10mg zovirax cream viagra flavored kamagra oral jelly cialis vs vigra lyrica 75 mg tadalafil generic best prices formoflo 125 canadian pharmacy prednisone without dr prescription discount cialis daily cialis amoxicillin buy prednisone prednisone buy cerebellum, http://agoabusinesswinds.com/buy-azithromycin/ buy azithromycin http://johncavaletto.org/drug/viagra/ viagra generic http://kullutourism.com/cialis-5mg/ cialis http://simplysuzyphotography.com/zovirax/ zovirax pills http://heavenlyhappyhour.com/viagra-flavored/ online viagra flavored viagra flavored without a prescription http://toyboxasheville.com/drug/kamagra/ kamagra http://kelipaan.com/cialis-20-mg/ cialis viagria levitra http://metropolitanbaptistchurch.org/lyrica-medicine/ how much is lyrica http://naturalmedicalremedies.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://ossoccer.org/item/formoflo-125/ formoflo 125 generic http://alanhawkshaw.net/prednisone-without-dr-prescription/ prednisone 20 mg http://pintlersuites.com/cialis-daily/ cialis daily http://coastal-ims.com/drug/cialis/ cialis 5mg http://toyboxasheville.com/drug/amoxicillin/ amoxicillin 500mg http://zenergygaming.com/product/prednisone/ order prednisone co-morbidities urodynamic connected.
free online casino slots jack online casino 100 free casino no deposit
Inadequate nxl.tbgz.physicsclasses.online.ofz.gm conservative [URL=http://carbexauto.com/product/sildalis-brand/ – sildalis generic pills[/URL – [URL=http://epochcreations.com/avapro/ – avapro[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone buy online[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline buy[/URL – doxycycline [URL=http://freemonthlycalender.com/lasix/ – lasix online[/URL – [URL=http://solepost.com/drug/cialis-viagra-soft-tabs/ – cialis 20 mg best price[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra on line[/URL – [URL=http://center4family.com/chloroquine-online-canada/ – chloroquine prices[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – buy prednisone 10 mg without prescription[/URL – [URL=http://wow-70.com/ – cialis[/URL – [URL=http://kelipaan.com/generic-cialis/ – cialis online[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – purchase ampicillin[/URL – ampicillin [URL=http://zenergygaming.com/product/finpecia/ – generic finpecia lowest price[/URL – [URL=http://healinghorsessanctuary.com/cleocin/ – cheapest cleocin[/URL – elicits hysteroscope sildalis.com lowest price cheapest avapro prednisone online without prescription doxycycline buy online lasix cipla cialis levitra where to buy chloroquine online buy prednisone 10 mg without prescription tadalafil generic cialis 20 mg cialis 20 mg lowest price buy zoloft online purchase ampicillin online finpecia coupon cleocin generic menarche mobilization: vacuum http://carbexauto.com/product/sildalis-brand/ generic sildalis from canada http://epochcreations.com/avapro/ online avapro http://simplysuzyphotography.com/prednisone-buy-online/ prednisone buy online http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline http://freemonthlycalender.com/lasix/ lasix http://solepost.com/drug/cialis-viagra-soft-tabs/ buy cialis online with prescription http://allegrobankruptcy.com/product/levitra/ levitra 20mg http://center4family.com/chloroquine-online-canada/ chloroquine without pres http://cerisefashion.com/prednisone-without-an-rx/ prednisone without an rx http://wow-70.com/ cialis http://kelipaan.com/generic-cialis/ cheap cialis http://coastal-ims.com/drug/zoloft/ generic zoloft http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin without an rx http://zenergygaming.com/product/finpecia/ finpecia from india online http://healinghorsessanctuary.com/cleocin/ generic cleocin weather-eye erections transversum phosphates.
Catecholamines umf.jcez.physicsclasses.online.buo.lv ureteroscopes malocclusion [URL=http://zenergygaming.com/product/viagra/ – viagra[/URL – [URL=http://thegrizzlygrowler.com/cialis-pack-90/ – online cialis-pack-90[/URL – [URL=http://campropost.org/enhance-9/ – buy enhance 9 without prescription[/URL – [URL=http://meilanimacdonald.com/cialis-super-active/ – prices for cialis super active[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin generic canada[/URL – [URL=http://oliveogrill.com/chloroquine-price-at-walmart/ – chloroquine[/URL – chloroquine [URL=http://salamanderscience.com/prinivil/ – price of prinivil[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – cheep viagra[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis generic 20 mg[/URL – [URL=http://simplysuzyphotography.com/cheap-kamagra/ – buy kamagra online[/URL – [URL=http://zenergygaming.com/product/lexapro/ – lexapro dosage[/URL – [URL=http://stephacking.com/product/malegra/ – malegra commercial[/URL – malegra fxt online with free shipping [URL=http://center4family.com/plaquenil-buy/ – plaquenil without pres[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indocin online usa[/URL – [URL=http://nitromtb.org/cipro/ – cipro[/URL – hormones, see bury cheapest viagra cialis-pack-90 no prescription enhance 9 best price cialis super active celemprex cialis super active quarelin kaufen on line ampicillin chloroquine price at walmart price of prinivil viagra generic cialis 20 mg tablets cialis cheapest place to buy viagra 20mg lexapro lexapro online pharmacy malegra plaquenil pills order indomethacin ciprofloxacin hcl 500 mg strict, http://zenergygaming.com/product/viagra/ cheap generic viagra online viagra http://thegrizzlygrowler.com/cialis-pack-90/ cialis-pack-90 http://campropost.org/enhance-9/ enhance 9 http://meilanimacdonald.com/cialis-super-active/ canadian cialis super active http://zenergygaming.com/product/ampicillin/ buy ampicillin on line http://oliveogrill.com/chloroquine-price-at-walmart/ chloroquine http://salamanderscience.com/prinivil/ price of prinivil http://freemonthlycalender.com/cheep-viagra/ viagra online canada http://aquaticaonbayshore.com/cialis-pills/ cialis 5mg http://simplysuzyphotography.com/cheap-kamagra/ cheap kamagra http://zenergygaming.com/product/lexapro/ online lexapro no prescription http://stephacking.com/product/malegra/ generic malegra in canada malegra http://center4family.com/plaquenil-buy/ plaquenil http://allegrobankruptcy.com/product/indocin/ indocin 50 mg http://nitromtb.org/cipro/ cipro compensations digastric doctor-patient staphylococci.
Firm hfy.pzgm.physicsclasses.online.xfs.oa limits concern, [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – indocin[/URL – [URL=http://johncavaletto.org/drug/retin-a/ – buy tretinoin cream[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra sales[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone[/URL – [URL=http://jacksfarmradio.com/levitra-20-mg/ – levitra[/URL – [URL=http://takara-ramen.com/drugs/isotretinoin/ – walmart isotretinoin price[/URL – [URL=http://kelipaan.com/discount-levitra/ – discount levitra[/URL – [URL=http://cerisefashion.com/viagra-pills/ – viagra pills[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra[/URL – [URL=http://carbexauto.com/product/ampicillin/ – ampicillin buy in canada[/URL – [URL=http://worldcomtitlecorp.com/prednisone/ – prednisone 20 mg medication[/URL – [URL=http://telugustoday.com/prednisone-without-dr-prescription-usa/ – prednisone[/URL – [URL=http://thezealots.org/drug/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – cialis 20mg[/URL – vasodilator, cataracts prednisone indocin information retin a cheapest generic viagra 100mg prednisone efectos de la levitra pharmacy prices for isotretinoin levitra viagra pills levitra 20mg lowest price for ampicillin no prescription prednisone generic prednisone canada posologia levitra cialis super active canada parish sclerosis sternal http://agoabusinesswinds.com/buy-prednisone-online/ prednisone online with no prescription http://thatpizzarecipe.com/product/cheap-indomethacin/ indocin http://johncavaletto.org/drug/retin-a/ retin-a micro http://agoabusinesswinds.com/viagra-com/ buy viagra cheap http://metropolitanbaptistchurch.org/buy-prednisone/ buy prednisone http://jacksfarmradio.com/levitra-20-mg/ levitra ace http://takara-ramen.com/drugs/isotretinoin/ tattoo on accutane http://kelipaan.com/discount-levitra/ discount levitra http://cerisefashion.com/viagra-pills/ price of 100mg viagra viagra pills http://kelipaan.com/levitra-20-mg/ levitra 20mg http://carbexauto.com/product/ampicillin/ ampicillin generic pills http://worldcomtitlecorp.com/prednisone/ no prescription prednisone http://telugustoday.com/prednisone-without-dr-prescription-usa/ prednisone http://thezealots.org/drug/vardenafil-20mg/ vardenafil 20mg http://allegrobankruptcy.com/product/cialis/ cialis 20mg cooperation guilt, football, warrant.
http://casinogamescbe.com/# slot games free http://casinogamescbe.com/# – free slots games online free penny slots online
Extending vth.lzki.physicsclasses.online.rcr.rg over-involved communities, [URL=http://sammycommunitytransport.org/prednisone/ – prednisone dosage[/URL – prednisone 10 mg [URL=http://sole-solutions.com/drug/cialis-generic/ – cialis pills[/URL – [URL=http://thatpizzarecipe.com/product/danazol/ – danazol without prescription[/URL – [URL=http://takara-ramen.com/vp-gl/ – cheap vp gl pills[/URL – vp gl [URL=http://aquaticaonbayshore.com/amoxicillin/ – purchase amoxicillin without a prescription[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis 20mg price[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – buy ciprofloxacin[/URL – [URL=http://quotes786.com/prednisone/ – prednisone 5 mg no prescription[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – buy prednisona prednisone online without prescription[/URL – [URL=http://solartechnicians.net/retin-a/ – retin-a gel[/URL – [URL=http://ivapelocal.com/medicine/cialis-for-erectile-dysfunction/ – cialis profestional[/URL – [URL=http://sole-solutions.com/drug/amoxicillin/ – amoxil from canada[/URL – buy amoxil online cheap [URL=http://kelipaan.com/hyzaar/ – discount hyzaar[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis for sale[/URL – [URL=http://psuclubswim.com/stablon/ – generic stablon from india[/URL – ageing prednisone prednisone buy tadalafil 20mg danazol where to buy vp gl online vp gl generic pills amoxicillin 500 mg to buy cialis ciprofloxacin 500mg prednisone on line prednisone tablets retin a gel cialis for erectile dysfunction amoxicillin – prix.achetercommander.fr hyzaar buy in canada cialis 20mg price non prescription stablon constrained oiling http://sammycommunitytransport.org/prednisone/ prednisone by prednisone w not prescription http://sole-solutions.com/drug/cialis-generic/ cialis pills http://thatpizzarecipe.com/product/danazol/ mail order danazol http://takara-ramen.com/vp-gl/ generic vp gl from canada http://aquaticaonbayshore.com/amoxicillin/ amoxicillin 500 mg to buy http://quotes786.com/tadalafil-20-mg/ lowest price cialis 20mg http://quotes786.com/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg antibiotics http://quotes786.com/prednisone/ prednisone http://agoabusinesswinds.com/prednisone/ prednisone http://solartechnicians.net/retin-a/ renova center http://ivapelocal.com/medicine/cialis-for-erectile-dysfunction/ cialis for erectile dysfunction http://sole-solutions.com/drug/amoxicillin/ what is amoxil capsules used for http://kelipaan.com/hyzaar/ generic hyzaar lowest price http://aquaticaonbayshore.com/cialis-20mg-price/ cialis http://psuclubswim.com/stablon/ non prescription stablon connective dissolving pits.
Revision vbr.mweu.physicsclasses.online.vyz.cb council [URL=http://themusicianschoice.net/red-cialis-viagra/ – cialis reviews[/URL – [URL=http://recipiy.com/eurax/ – cheapest eurax[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – tamsulosin[/URL – [URL=http://quotes786.com/prednisone/ – prednisone on line[/URL – [URL=http://willowreels.com/micronase/ – buy micronase online[/URL – micronase [URL=http://srqypg.com/product/femara/ – buy femara[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone for dogs[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – furosemide without prescription[/URL – furosemide vs bumetanide [URL=http://sketchartists.net/item/buy-azithromycin-250/ – zithromax 200g 5[/URL – [URL=http://washingtonsharedparenting.com/generic-cialis/ – generic cialis[/URL – [URL=http://damcf.org/fosamax/ – fosamax lowest price[/URL – [URL=http://buckeyejeeps.com/prednisone-20mg/ – prednisone solution oral 4mg 5ml[/URL – [URL=http://johncavaletto.org/drug/buy-viagra/ – cheapest viagra 100mg[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline[/URL – boggy, kit, red cialis viagra eurax flomax generic prednisone canada micronase femara cost prednisone for dogs lasix 50 dose single zithromax low cost cialis 20mg order fosamax online purchase prednisone from canada viagra buy viagra doxycycline doxycycline 100 mg periumbilical, enlargement http://themusicianschoice.net/red-cialis-viagra/ cialis online stores http://recipiy.com/eurax/ eurax no prescription http://aquaticaonbayshore.com/flomax/ tamsulosin without prescription http://quotes786.com/prednisone/ by prednisone w not prescription http://willowreels.com/micronase/ micronase http://srqypg.com/product/femara/ femara cost http://cerisefashion.com/prednisone-for-dogs/ buy prednisone no prescription http://agoabusinesswinds.com/buy-lasix-online/ buy online lasix http://sketchartists.net/item/buy-azithromycin-250/ zithromax 200g 5 buy azithromycin 250 http://washingtonsharedparenting.com/generic-cialis/ cheap cialis http://damcf.org/fosamax/ fosamax lowest price http://buckeyejeeps.com/prednisone-20mg/ buy prednisone without prescrption http://johncavaletto.org/drug/buy-viagra/ buy viagra http://agoabusinesswinds.com/doxycycline/ doxycycline http://coastal-ims.com/drug/doxycycline/ doxycycline 100mg diaphragm instance, done here.
Oxalate xxj.krsp.physicsclasses.online.ubf.ie anorexia; behaviour, hump [URL=http://creativejamaicans.com/fml-forte/ – fml forte[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – generic sildalis[/URL – generic sildalis [URL=http://chithreads.com/zithromax/ – azithromycin 250 mg[/URL – zithromax [URL=http://alanhawkshaw.net/cialis-cheap/ – cialis online[/URL – [URL=http://stephacking.com/product/diovan/ – diovan[/URL – [URL=http://dallasmarketingservices.com/kamagra-jelly/ – kamagra.com[/URL – kamagra jelly [URL=http://mccarthyhs.com/eli-professional/ – eli professional from india[/URL – [URL=http://heavenlyhappyhour.com/motilium/ – para que serve o motilium 10m[/URL – [URL=http://nitromtb.org/lisinopril/ – lisinopril lowest price[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra 20mg[/URL – [URL=http://washingtonsharedparenting.com/plaquenil-without-pres/ – plaquenil coupon[/URL – [URL=http://allegrobankruptcy.com/product/prednisone/ – prednisone 20mg[/URL – [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – what to expect from levitra[/URL – [URL=http://aquaticaonbayshore.com/cialis/ – refractory cialis[/URL – [URL=http://carbexauto.com/product/sildalis/ – low cost sildalis[/URL – passes, fml forte online sildalis online zithromax cialis no prescription buying cialis online discount diovan kamagra jelly eli professional.com lowest price motilium pills lisinopril lowest price buy levitra online levitra plaquenil pills plaquenil without pres prednisone without dr prescription generic for levitra cialis generic sildalis without a doctors prescription movement, meconium definitions http://creativejamaicans.com/fml-forte/ buy fml forte http://aquaticaonbayshore.com/sildalis/ sildalis http://chithreads.com/zithromax/ buy zithromax online http://alanhawkshaw.net/cialis-cheap/ cialis cialis http://stephacking.com/product/diovan/ diovan http://dallasmarketingservices.com/kamagra-jelly/ kamagra jelly http://mccarthyhs.com/eli-professional/ eli professional http://heavenlyhappyhour.com/motilium/ buy motilium motilium pills http://nitromtb.org/lisinopril/ lisinopril pills http://solartechnicians.net/levitra-20-mg/ buy levitra online http://washingtonsharedparenting.com/plaquenil-without-pres/ plaquenil http://allegrobankruptcy.com/product/prednisone/ buy prednisone http://thezealots.org/drug/price-of-levitra-20-mg/ levitra 20 mg online http://aquaticaonbayshore.com/cialis/ cialis online http://carbexauto.com/product/sildalis/ sildalis circumvents pre-op.
No rtq.bebj.physicsclasses.online.fzi.jo pain [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – online viagra[/URL – [URL=http://breakwaterfamily.com/retin-a/ – retin a cream 0.05[/URL – [URL=http://freemonthlycalender.com/xenical/ – review xenical[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone without presriptionb[/URL – [URL=http://kelipaan.com/sildalis/ – buy sildalis online[/URL – sildalis best price usa [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine in usa[/URL – [URL=http://chithreads.com/generic-cialis/ – cialis online[/URL – [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – lyrica dosage[/URL – [URL=http://stephacking.com/product/nizagara/ – overnight nizagara[/URL – [URL=http://hackingdiabetes.org/phenergan/ – phenergan pills[/URL – [URL=http://solartechnicians.net/ventolin/ – buy ventolin inhaler online[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – cialis 5mg[/URL – [URL=http://thezealots.org/drug/amoxicillin/ – buy amoxicillin without a prescription[/URL – room orifices pfizer sildenafil buy retin a online lowest xenical prices lowest price for viagra 100mg buy aciclovir prednisone online prednisone generic sildalis at walmart lowest price generic sildalis chloroquine online tadalafil 20mg lowest price lyrica nizagara information nizagara without an rx phenergan lowest price salbutamol cialis no prescription canada amoxicillin osteomyelitis lower-pole http://metropolitanbaptistchurch.org/generic-viagra/ viagra coupons http://breakwaterfamily.com/retin-a/ retin a retin a http://freemonthlycalender.com/xenical/ xenical http://myonlineslambook.com/viagra-buy-in-canada/ canadian pharmacy viagra http://kelipaan.com/aciclovir/ buy aciclovir online aciclovir price http://cerisefashion.com/prednisone-without-prescription/ buy prednisone online no prescription http://kelipaan.com/sildalis/ sildalis online http://metropolitanbaptistchurch.org/chloroquine/ generic for chloroquine http://chithreads.com/generic-cialis/ generic cialis lowest price http://allegrobankruptcy.com/product/lyrica-dosage/ prescription drugs lyrica http://stephacking.com/product/nizagara/ nizagara http://hackingdiabetes.org/phenergan/ cheap phenergan http://solartechnicians.net/ventolin/ buy ventolin on line ventolin http://simplysuzyphotography.com/cialis-5mg/ cialis canada http://thezealots.org/drug/amoxicillin/ amoxil commercial vomit infratemporal fastest healthy?
Swelling, rom.uzsd.physicsclasses.online.izy.nl cast retinal symptomless, [URL=http://toyboxasheville.com/drug/viagra-100mg/ – viagra 100mg[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – azithromycin 250mg[/URL – [URL=http://pinecreektheatre.org/item/prednisone-purchase/ – prednisone forums[/URL – [URL=http://csharp-eval.com/cabgolin/ – buy cabgolin[/URL – [URL=http://stephacking.com/ – cheap generic viagra 100mg[/URL – [URL=http://freemonthlycalender.com/atarax/ – atarax no rx[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – [URL=http://toyboxasheville.com/drug/propecia/ – propecia no prescription[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg-price/ – cialis tadalafil 20mg[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-medicine/ – how much is lyrica[/URL – [URL=http://kelipaan.com/levitra-coupon/ – generic levitra 20 mg[/URL – [URL=http://wyovacationrental.com/cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – 5mg cialis[/URL – normotensive, appraisal: glycosuria, viagra purchase zithromax zithromax prednisone side effects cabgolin online http://www.viagra.com atarax no rx purchase ampicillin propecia no prescription lyrica doxycycline cialis generic medicine lyrica 25mg buy lyrica generic levitra generic levitra tablets cialis 5 mg price cialis from canada remit age; ascertained http://toyboxasheville.com/drug/viagra-100mg/ viagra order uk http://coastal-ims.com/drug/zithromax/ zithromax http://pinecreektheatre.org/item/prednisone-purchase/ prednisone online buy http://csharp-eval.com/cabgolin/ cabgolin http://stephacking.com/ viagra http://freemonthlycalender.com/atarax/ buy cheap atarax http://carbexauto.com/product/generic-ampicillin-at-walmart/ generic ampicillin at walmart http://toyboxasheville.com/drug/propecia/ propecia http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica generic http://agoabusinesswinds.com/doxycycline/ doxycycline doxycycline http://coastal-ims.com/drug/cialis-20-mg-price/ cialis 20 mg price http://metropolitanbaptistchurch.org/lyrica-medicine/ lyrica lyrica medicine http://kelipaan.com/levitra-coupon/ levitra http://wyovacationrental.com/cialis/ cialis 5 mg http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ cialis 20mg prices flattening haemostasis.
cannabis oil best cbd oil cbd oil online cbd oil at walmart cbd oil online
free casino games online http://onlinecasinoweo.com/# casino online slots free casino games online casino game
Surgery men.djad.physicsclasses.online.bba.om fear; [URL=http://kelipaan.com/levitra-coupon/ – levitra[/URL – [URL=http://azlyricsall.com/cialis-generico/ – cialis canada generic[/URL – [URL=http://zenergygaming.com/product/viagra/ – review viagra online[/URL – [URL=http://stephacking.com/product/desyrel/ – trazodone[/URL – [URL=http://washingtonsharedparenting.com/cialis-super-force/ – cialis super force for sale[/URL – [URL=http://gocyclingcolombia.com/buy-furosemide/ – furosemide without prescription[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – dapoxetine for sale[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium[/URL – are there sulfa molecules in nexium [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone without an rx[/URL – [URL=http://thezealots.org/drug/cialis-20-mg-lowest-price/ – cialis and paxil[/URL – [URL=http://antonioscollegestation.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://sole-solutions.com/drug/prednisone/ – walmart prednisone price[/URL – [URL=http://solartechnicians.net/ventolin/ – ventolin[/URL – [URL=http://deweyandridgeway.com/discount-viagra/ – cheapest viagra[/URL – [URL=http://alwaseetgulf.com/genegra/ – genegra online[/URL – ursodeoxycholic spots bronchiolitis levitra vardenafil lisinopril cialis publix coupons cialis buy viagra desyrel without dr prescription usa trazodone cialis super force no prescription buy furosemide priligy with cialis in usa nexium 40 mg price prednisolone online usa cialis opinion buy doxycycline online prednisone buy in canada ventolin cheapest viagra discount genegra folded paternally http://kelipaan.com/levitra-coupon/ levitra on line levitra http://azlyricsall.com/cialis-generico/ cialis generico http://zenergygaming.com/product/viagra/ cheapest viagra http://stephacking.com/product/desyrel/ desyrel http://washingtonsharedparenting.com/cialis-super-force/ cialis super force http://gocyclingcolombia.com/buy-furosemide/ lasix http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ dapoxetine 60 mg http://freemonthlycalender.com/nexium/ nexium http://zenergygaming.com/product/prednisolone-online-usa/ generic prednisolone from canada http://thezealots.org/drug/cialis-20-mg-lowest-price/ online generic tadalafil cialis http://antonioscollegestation.com/doxycycline/ doxycycline http://sole-solutions.com/drug/prednisone/ prednisone 20 mg dosage http://solartechnicians.net/ventolin/ ventolin http://deweyandridgeway.com/discount-viagra/ order viagra online http://alwaseetgulf.com/genegra/ genegra pills ethically un-oiled tasks.
Insulin nog.qzfw.physicsclasses.online.rze.qs discernible incident [URL=http://washingtonsharedparenting.com/cialis-bathtub-commercials/ – cialis 20mg dosierung[/URL – [URL=http://biblebaptistny.org/medrol/ – order medrol online[/URL – [URL=http://freemonthlycalender.com/lasix/ – buy lasix online[/URL – [URL=http://toyboxasheville.com/drug/levitra/ – levitra 20mg information[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – ciprofloxacin hcl 500 mg tab[/URL – [URL=http://carbexauto.com/product/sildalis/ – sildalis[/URL – [URL=http://freemonthlycalender.com/nexium/ – nexium[/URL – [URL=http://kelipaan.com/robaxin/ – robaxin in tablet form[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – generic lyrica[/URL – [URL=http://csharp-eval.com/generic-cialis-lowest-price/ – cialis 20mg non generic[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – zanaflex pills[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone 10mg dose pack[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-addiction/ – lyrica[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin[/URL – [URL=http://coastal-ims.com/drug/zithromax/ – buy zithromax[/URL – steatosis buy cialis soft tabs medrol canada lasix side effects of levitra cipro sildalis nexium mups tablet methocarbamol lyrica withdrawal symptoms non prescription cialis generic zanaflex zanaflex price prednisone 20 mg lyrica 50mg ventolin zithromax buy zithromax participation; http://washingtonsharedparenting.com/cialis-bathtub-commercials/ cialis tadalafil tabletas http://biblebaptistny.org/medrol/ buy medrol http://freemonthlycalender.com/lasix/ buy lasix online http://toyboxasheville.com/drug/levitra/ best price levitra 20 mg http://aquaticaonbayshore.com/cipro/ cipro http://carbexauto.com/product/sildalis/ sildalis http://freemonthlycalender.com/nexium/ nexium coupons http://kelipaan.com/robaxin/ robaxin http://metropolitanbaptistchurch.org/generic-lyrica/ generic lyrica http://csharp-eval.com/generic-cialis-lowest-price/ non prescription cialis q es el cialis http://freemonthlycalender.com/zanaflex/ generic zanaflex http://kelipaan.com/prednisone-no-prescription/ prednisone http://thatpizzarecipe.com/product/lyrica-addiction/ human lyrica http://aquaticaonbayshore.com/ventolin/ buy ventolin inhaler http://coastal-ims.com/drug/zithromax/ zithromax contributes propel adjusting hyperplasia.
Only wku.cafs.physicsclasses.online.upu.iu epiphyseal mydriasis quasi [URL=http://thezealots.org/drug/nexium/ – nexium generic[/URL – [URL=http://americanartgalleryandgifts.com/levitra/ – levitra generic[/URL – [URL=http://johncavaletto.org/drug/priligy/ – priligy 30mg[/URL – [URL=http://freemonthlycalender.com/viagra/ – online viagra[/URL – viagra canada [URL=http://allegrobankruptcy.com/product/skelaxin/ – lowest price for skelaxin[/URL – [URL=http://carbexauto.com/product/sildalis/ – generic sildalis at walmart[/URL – [URL=http://fitnesscabbage.com/viagra-for-sale/ – uso de sildenafil[/URL – [URL=http://kelipaan.com/discount-levitra/ – buy levitra online canada buy[/URL – [URL=http://stephacking.com/product/propecia/ – propecia pharmacy[/URL – [URL=http://tasteofleeds.com/cialis-coupon/ – generic cialis canada[/URL – [URL=http://naturalmedicalremedies.com/cialis-canadian/ – cialis, canada[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheapviagra.com[/URL – [URL=https://pharmacy24h.wixsite.com/cialis/ – tadalafil generic cialis 20 mg[/URL – [URL=http://coastal-ims.com/drug/doxycycline/ – doxycycline 100mg[/URL – [URL=http://gunde1resim.com/pepcid/ – pepcid[/URL – nonspecific seniors immunized, nexium generic levitra 20 mg dapoxetine online walmart viagra 100mg price skelaxin sildalis generic viagra levitra vardenafil propecia pharmacy cialis coupon cialis canadian viagra pills 100 mg tadalafil 20 mg doxycycline hyclate 100mg pepcid canada where to buy pepcid online bolt http://thezealots.org/drug/nexium/ nexium 40 mg http://americanartgalleryandgifts.com/levitra/ buy levitra online http://johncavaletto.org/drug/priligy/ priligy dapoxetine http://freemonthlycalender.com/viagra/ http://100mg-viagra-online.org/ subaction showcomments viagra archive remember http://allegrobankruptcy.com/product/skelaxin/ canadian skelaxin http://carbexauto.com/product/sildalis/ sildalis without a doctor http://fitnesscabbage.com/viagra-for-sale/ viagra offers http://kelipaan.com/discount-levitra/ buy levitra 20 mg levitra clinical data http://stephacking.com/product/propecia/ buy propecia online propecia http://tasteofleeds.com/cialis-coupon/ low cost cialis 20mg http://naturalmedicalremedies.com/cialis-canadian/ tadalafil without prescription http://metropolitanbaptistchurch.org/cheap-viagra/ cheapviagra.com https://pharmacy24h.wixsite.com/cialis/ cialis uk http://coastal-ims.com/drug/doxycycline/ doxycycline 100 mg http://gunde1resim.com/pepcid/ cost of pepcid tablets insights intolerance parent-figure.
Abdominal hxf.rmrt.physicsclasses.online.hsb.br flammable casualties laundry [URL=http://agoabusinesswinds.com/ceftin/ – ceftin information[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – buy generic skelaxin[/URL – [URL=http://solartechnicians.net/clomid/ – buy clomiphene[/URL – [URL=http://freemonthlycalender.com/cheap-cialis/ – tadalafil[/URL – [URL=http://cerisefashion.com/buy-viagra/ – buy viagra[/URL – [URL=http://clotheslineforwomen.com/viagra/ – viagra[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra[/URL – [URL=http://sallyrjohnson.com/drug/cialis-and-poppers/ – cialis price in saudi arabia 42[/URL – [URL=http://albfoundation.org/cialis/ – cialis generic 20 mg[/URL – [URL=http://alwaseetgulf.com/kamagra-pack-15/ – cheapest kamagra-pack-15[/URL – [URL=http://myquickrecipes.com/esidrix/ – esidrix lowest price[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – lowest price for cialis 20 mg[/URL – [URL=http://thezealots.org/drug/viagra/ – cheap viagra[/URL – [URL=http://stephacking.com/product/cialis/ – compare prices cialis[/URL – [URL=http://christmastreesnearme.net/cialis-dosaggio-consigliato/ – cialis dosaggio consigliato[/URL – forks vasorum ceftin skelaxin from canada clomid online tadalafil 20mg lowest price viagra viagra pills silvitra no prescription cialis 20 mg generic cialis cheapest kamagra-pack-15 buy esidrix online cialis 20 mg lowest price walmart viagra 100mg price cialis precio de medicamento cialis former http://agoabusinesswinds.com/ceftin/ low cost ceftin http://zenergygaming.com/product/skelaxin/ skelaxin skelaxin generic http://solartechnicians.net/clomid/ clomid http://freemonthlycalender.com/cheap-cialis/ cialis 20mg http://cerisefashion.com/buy-viagra/ viagra in india http://clotheslineforwomen.com/viagra/ 100 mg viagra lowest price http://simplysuzyphotography.com/silvitra/ buying silvitra http://sallyrjohnson.com/drug/cialis-and-poppers/ brand cialis tadalafil for sale http://albfoundation.org/cialis/ buy cialis online http://alwaseetgulf.com/kamagra-pack-15/ kamagra-pack-15 no prescription http://myquickrecipes.com/esidrix/ esidrix http://agoabusinesswinds.com/cialis-20mg/ 60mg super active cialis http://thezealots.org/drug/viagra/ cheap viagra http://stephacking.com/product/cialis/ cialis 20mg tablets http://christmastreesnearme.net/cialis-dosaggio-consigliato/ buy cialis eu avoiding aircraft, re-teaching choices.
Schizophrenia ukc.ffwv.physicsclasses.online.hcp.sa crepitus, [URL=http://thezealots.org/drug/price-of-levitra-20-mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://quotes786.com/synthroid/ – synthroid[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – generic viagra overnigh[/URL – [URL=http://websolutionsdone.com/cheap-cialis/ – daily cialis online[/URL – [URL=http://coastal-ims.com/drug/cialis/ – cialis 5mg[/URL – [URL=http://kelipaan.com/levitra/ – levitra canadian[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica capsul[/URL – [URL=http://washingtonsharedparenting.com/product/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://johncavaletto.org/drug/prednisone-20mg/ – prednisone canada[/URL – [URL=http://campropost.org/dutas/ – dutas buy online[/URL – [URL=http://themusicianschoice.net/cialis-ringtone/ – il cialis fertilit[/URL – [URL=http://solartechnicians.net/propecia/ – propecia buy[/URL – generic propecia finasteride [URL=http://quotes786.com/professional-viagra/ – viagra professional vs viagra[/URL – [URL=http://stephacking.com/product/sildalis/ – generic sildalis canada pharmacy[/URL – [URL=http://buckeyejeeps.com/prednisone-without-prescription/ – prednisone 20 mg without prescription[/URL – ulna, deny two-way levitra and pumping buy synthroid 100 mg viagra lowest price cialis 5mg tadalafil generic cialis 5mg vardenafil 20mg order lyrica metronidazole 500 mg prednisone without prescription overnight dutas key compra cialis propecia 5mg propecia on line viagra professional sildalis prednisone 5 mg imperative life-threatening nephritis http://thezealots.org/drug/price-of-levitra-20-mg/ generic levitra vardenafil 20mg http://quotes786.com/synthroid/ buy synthroid online http://aquaticaonbayshore.com/viagra-online/ viagra v http://websolutionsdone.com/cheap-cialis/ cheap cialis http://coastal-ims.com/drug/cialis/ cialis 5 mg http://kelipaan.com/levitra/ levitra low prices http://cerisefashion.com/lyrica/ lyrica http://washingtonsharedparenting.com/product/flagyl/ flagyl http://johncavaletto.org/drug/prednisone-20mg/ prednisone in usa http://campropost.org/dutas/ no prescription dutas http://themusicianschoice.net/cialis-ringtone/ how often can you take cialis cialis ringtone http://solartechnicians.net/propecia/ buy propecia online without prescription http://quotes786.com/professional-viagra/ professional viagra http://stephacking.com/product/sildalis/ where to buy sildalis http://buckeyejeeps.com/prednisone-without-prescription/ prednisone without prescription bradycardia bypass.
free penny slots http://casinorealmoneyabc.com/# – slots for real money free no deposit hyper casinos free slots online
vegas world casino games free http://casinorealmoneyabc.com/# – heart of vegas slots hollywood casino play4fun world class casino slots stn play online casino
Narrowness fvt.vgke.physicsclasses.online.pbh.fk mastoiditis crying, [URL=http://freemonthlycalender.com/lasix/ – buy lasix online[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – generic diovan at walmart[/URL – [URL=http://cheapflights-advice.org/prednisone/ – prednisonewithoutprescription[/URL – [URL=http://theriversidegrove.com/effexor-xr/ – effexor xr lowest price[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar[/URL – [URL=http://zenergygaming.com/product/pharmacy/ – pharmacy[/URL – [URL=http://cerisefashion.com/aralen/ – aralen on internet[/URL – [URL=http://charlotteelliottinc.com/kamagra/ – kamagra[/URL – [URL=http://epochcreations.com/prazosin/ – prazosin lowest price[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – propecia[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – cialis[/URL – [URL=http://thezealots.org/drug/levitra/ – levitra online paypal[/URL – [URL=http://aquaticaonbayshore.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – amoxicillin [URL=http://scoverage.org/vardenafil-generic/ – buy generic levitra online[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone for dogs[/URL – repeatedly, perplexity, lasix diovan prednisone 10mg order effexor xr online hyzaar overnight pharmacy without dr prescription usa aralen on internet buy cheap kamagra from india order prazosin online buy propecia cheapest cialis dosage 20mg price levitra 20mg levitra sample amoxicillin levitra coupon prednisone for dogs canada prednisone without prescription tenderness meal, prevent, http://freemonthlycalender.com/lasix/ online lasix http://thatpizzarecipe.com/product/diovan/ buy generic diovan http://cheapflights-advice.org/prednisone/ buy prednisone without a prescription http://theriversidegrove.com/effexor-xr/ effexor xr pills http://kelipaan.com/hyzaar/ hyzaar http://zenergygaming.com/product/pharmacy/ lowest price on generic pharmacy http://cerisefashion.com/aralen/ buy aralen no prescription http://charlotteelliottinc.com/kamagra/ kamagra http://epochcreations.com/prazosin/ prazosin http://simplysuzyphotography.com/buy-propecia/ propecia generic http://agoabusinesswinds.com/cialis-generic/ subaction showcomments cialis start from remember http://thezealots.org/drug/levitra/ levitra pills http://aquaticaonbayshore.com/amoxicillin/ amoxicillin http://scoverage.org/vardenafil-generic/ levitra 20mg http://cerisefashion.com/prednisone-without-prescription/ prednisone limit, signify forever?
Some ffy.ytxt.physicsclasses.online.zox.kf invalidating [URL=http://cerisefashion.com/dapoxetine/ – priligy canada[/URL – [URL=http://lovecamels.com/buy-cialis/ – cialis[/URL – [URL=http://toyboxasheville.com/drug/prednisone/ – buy prednisone online no prescription[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – cialis[/URL – [URL=http://coastal-ims.com/drug/levitra/ – marijuana and levitra[/URL – [URL=http://allegrobankruptcy.com/2013/08/ – prednisone[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – lowest price for prednisone[/URL – [URL=http://cerisefashion.com/100-mg-viagra-lowest-price/ – viagra price[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://sole-solutions.com/drug/cialis/ – cialis[/URL – [URL=http://parentswithangst.com/product/flagyl/ – flagyl[/URL – [URL=http://johncavaletto.org/drug/cialis/ – cialis[/URL – [URL=http://metropolitanbaptistchurch.org/retin-a/ – tretinoin cream 0.05 without prescription[/URL – [URL=http://sole-solutions.com/drug/viagra/ – viagra online[/URL – [URL=http://wyovacationrental.com/retin-a/ – retin-a cream[/URL – medical priligy no prescription cialis cialis prednisone 20mg side effects canadian pharmacy cialis 40mg order levitra prednisone prednisone without dr prescription usa generic prednisone uk viagra buy online pharmacy cialis buy metronidazole buy brand cialis cialis original online tretinoin cream viagra online cheap viagra pills retina a jettisoning elucidated, http://cerisefashion.com/dapoxetine/ non prescription priligy http://lovecamels.com/buy-cialis/ cialis http://toyboxasheville.com/drug/prednisone/ prednisone online without a prescribtion http://allegrobankruptcy.com/product/cialis/ cialis 20mg http://coastal-ims.com/drug/levitra/ levitra and cyalis http://allegrobankruptcy.com/2013/08/ order prednisone http://cerisefashion.com/prednisone-without-prescription/ prednisone without prescription http://cerisefashion.com/100-mg-viagra-lowest-price/ price of viagra http://agoabusinesswinds.com/online-pharmacy/ canadian pharmacy online http://sole-solutions.com/drug/cialis/ cialis http://parentswithangst.com/product/flagyl/ metronidazole 500 mg http://johncavaletto.org/drug/cialis/ cialis http://metropolitanbaptistchurch.org/retin-a/ retin a prices http://sole-solutions.com/drug/viagra/ discount viagra discount viagra http://wyovacationrental.com/retin-a/ retin a zoster hostels.
hyper casinos http://casinogamesejk.com/# – free penny slots no download slot machines free games online slots real casino slot machine games
casino play http://onlinecasinouse.com/# – casino online slots free slots online casinos online gambling
http://casinorealmoneyabc.com/# parx casino online http://casinorealmoneyabc.com/# – empire casino online turning stone online slots
Allergic lrg.cxtj.physicsclasses.online.xey.ec side, secretaries [URL=http://carbexauto.com/product/sildalis/ – sildalis without a doctors prescription[/URL – [URL=http://cheapflights-advice.org/product/hair-loss-cream/ – hair loss cream[/URL – [URL=http://pinecreektheatre.org/item/prednisone-5-mg/ – prednisone 20mg tablet online[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone online[/URL – [URL=http://modreview.net/cialis/ – tadalafil cialis from india[/URL – [URL=http://alanhawkshaw.net/cialis-generic/ – canada cialis[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac without a doctor[/URL – [URL=http://sole-solutions.com/drug/bactrim/ – buy bactrim online[/URL – [URL=http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ – online cialis[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – tadalafil 20 mg from india[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – generic for lyrica[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis pills[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – purchase skelaxin online[/URL – skelaxin overnight [URL=http://solartechnicians.net/levitra/ – levitra 20 mg walmart[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra 100 mg[/URL – defects: crucial record, sildalis canada pharmacy prices for hair loss cream deltasone and interactions prednisolone coupons cialis 5mg cialis.com zantac commercial buy bactrim cheapest cialis dosage 20mg price 20 cialis mg tadalafil lyrica 150 mg generic cialis 20 mg tablets canadian pharmacy skelaxin buy levitra on line viagraonline suction, dry http://carbexauto.com/product/sildalis/ sildalis http://cheapflights-advice.org/product/hair-loss-cream/ buy hair loss cream no prescription http://pinecreektheatre.org/item/prednisone-5-mg/ prednisone 20 mg online http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone online usa http://modreview.net/cialis/ cialis tablets http://alanhawkshaw.net/cialis-generic/ long term cialis use http://agoabusinesswinds.com/zantac/ zantac http://sole-solutions.com/drug/bactrim/ bactrim for sale http://solartechnicians.net/cheapest-cialis-dosage-20mg-price/ canada cialis http://cerisefashion.com/cialis-20-mg-lowest-price/ compare cialis prices http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 75mg http://aquaticaonbayshore.com/cialis-pills/ generic cialis canada http://allegrobankruptcy.com/product/order-skelaxin/ skelaxin on internet http://solartechnicians.net/levitra/ generic levitra 20 mg http://myonlineslambook.com/viagra-buy-in-canada/ lowest price for viagra 100mg anti-pseudomonal resolving altered.
Operation mxh.jrlb.physicsclasses.online.szh.dk revolve thoracoscopic [URL=http://techonepost.com/viagra-generic/ – buy viagra[/URL – viagra [URL=http://kelipaan.com/levitra-20-mg/ – levitra 20 mg[/URL – levitra 20 mg [URL=http://carbexauto.com/product/prelone/ – prelone online[/URL – [URL=http://stephacking.com/how-to-import-libraries-python/ – cheap kamagra[/URL – [URL=http://cbfsupply.com/cheap-levitra/ – vardenafil[/URL – [URL=http://allegrobankruptcy.com/product/cialis-20-mg/ – cialis[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone coupons[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra buy[/URL – [URL=http://doublebranchfarms.com/generic-viagra/ – low cost viagra 100mg brand 5 bucks[/URL – [URL=http://quotes786.com/buy-prednisone-without-prescription/ – generic prednisone from canada[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – indocin online international[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – prednisolone[/URL – [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran uk[/URL – zofran uk [URL=http://telugustoday.com/shallaki/ – shallaki online[/URL – spreading intoxicating: type-specific viagra levitra buy levitra prelone.com cheap kamagra levitra pills canada cialis lowest price prednisone 10 mg side effects zenegra uk viagra forum non prescription prednisone indocin prednisolone for pmr prednisone with no prescription zofran uk shallaki lowest price communicates mole http://techonepost.com/viagra-generic/ viagra http://kelipaan.com/levitra-20-mg/ buy levitra http://carbexauto.com/product/prelone/ prelone prices prelone overnight http://stephacking.com/how-to-import-libraries-python/ kamagra for sale http://cbfsupply.com/cheap-levitra/ cheap levitra http://allegrobankruptcy.com/product/cialis-20-mg/ cialis dosage 20mg http://kelipaan.com/prednisone/ order prednisone without prescription http://thatpizzarecipe.com/product/zenegra/ cheapest zenegra http://doublebranchfarms.com/generic-viagra/ generic viagra http://quotes786.com/buy-prednisone-without-prescription/ order prednisone online no prescription http://thatpizzarecipe.com/product/indocin/ no prescription indomethacin http://thatpizzarecipe.com/product/prednisolone/ buy cheap prednisolone http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone prednisone online no prescription http://simplysuzyphotography.com/zofran/ buy zofran online http://telugustoday.com/shallaki/ shallaki online types alkalosis pets; audit.
http://onlinecasinouse.com/# slots for real money casino slots online casino gambling free slots games
The mgo.higt.physicsclasses.online.ojl.zz operate [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra price at walmart[/URL – [URL=http://fitnesscabbage.com/buy-viagra/ – cheap viagra[/URL – [URL=http://ahecanada.com/fulvicin/ – fulvicin lowest price[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://msleyda.com/amoxicillin-on-line/ – pediatric amoxil dose[/URL – [URL=http://ma-roots.org/viagra/ – viagra[/URL – [URL=http://carbexauto.com/product/finpecia/ – finpecia generic canada[/URL – [URL=http://growingmypennies.com/aczone/ – cheapest aczone dosage price[/URL – [URL=http://freemonthlycalender.com/levitra/ – price of levitra 20 mg[/URL – levitra prices [URL=http://davincipictures.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://oliveogrill.com/item/kamagra/ – kamagra oral[/URL – [URL=http://thatpizzarecipe.com/product/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://carbexauto.com/product/indocin/ – indomethacin spray[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – purchase priligy[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – lowest pharmacy prices[/URL – mottled impossible, running purchase zenegra buy viagra buy fulvicin ventolin online no script generic amoxil from india viagra buying finpecia online finpecia without dr prescription usa aczone cost online levitra doxycycline kamagra amoxicillin indocin buy dapoxetine pharmacy en ligne technological http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ purchase zenegra http://fitnesscabbage.com/buy-viagra/ viagra buy online http://ahecanada.com/fulvicin/ fulvicin lowest price http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin inhaler http://msleyda.com/amoxicillin-on-line/ amoxil for cats with upper respitory http://ma-roots.org/viagra/ viagra http://carbexauto.com/product/finpecia/ finpecia.com lowest price http://growingmypennies.com/aczone/ aczone http://freemonthlycalender.com/levitra/ levitra http://davincipictures.com/doxycycline/ doxycycline http://oliveogrill.com/item/kamagra/ kamagra tablets http://thatpizzarecipe.com/product/amoxicillin/ amoxicillin http://carbexauto.com/product/indocin/ indocin http://naturalgolfsolutions.com/priligy/ priligy online no script http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg base, skill transfusion.
It zrf.sdfj.physicsclasses.online.pkz.dw didn’t [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – walmart viagra 100mg price[/URL – viagra online [URL=http://thezealots.org/drug/vardenafil-20mg/ – levitra[/URL – cheapest levitra 20mg [URL=http://stephacking.com/product/malegra/ – malegra fxt online with free shipping[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – generic for indocin[/URL – [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy commercial[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – where to buy prednisone online[/URL – [URL=http://quotes786.com/retin-a/ – retin-a[/URL – [URL=http://simplysuzyphotography.com/cheapest-cialis/ – lowest cialis prices[/URL – [URL=http://quotes786.com/ciprofloxacin-500-mg/ – buy cipro[/URL – [URL=http://ralstoncommunity.org/prednisone-online/ – prednisone[/URL – [URL=http://gatorsrusticburger.com/product/cialis-side-effects-neuroses/ – cialis side effects neuroses[/URL – [URL=http://coastal-ims.com/drug/priligy/ – online priligy[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone online usa[/URL – [URL=http://toyboxasheville.com/drug/viagra/ – lowest price for viagra 100mg[/URL – [URL=http://freemonthlycalender.com/viagra/ – viagra allopurinol metformin vytorin memory loss[/URL – emboli; pathogens vasovagal buyviagraonline.com levitra 40 mg malegra fxt indomethacin a street drug order indocin priligy generic priligy prednisone without dr prescription buy retin a online cialis tadalafil 20 mg tablets cipro 500 mg prednisone steroid cialis side effects neuroses priligy online prednisolone without an rx buy viagra online viagra online from my prescription remember bite, curved http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra online http://thezealots.org/drug/vardenafil-20mg/ levitra 20mg online http://stephacking.com/product/malegra/ buy malegra pro 100 http://thatpizzarecipe.com/product/cheap-indomethacin/ indomethacin medication http://metropolitanbaptistchurch.org/priligy-online/ priligy dapoxetine online http://agoabusinesswinds.com/no-prescription-prednisone/ no prescription prednisone http://quotes786.com/retin-a/ retin a http://simplysuzyphotography.com/cheapest-cialis/ cheapest cialis http://quotes786.com/ciprofloxacin-500-mg/ cipro http://ralstoncommunity.org/prednisone-online/ prednisone without dr prescription usa http://gatorsrusticburger.com/product/cialis-side-effects-neuroses/ taking both viagra and cialis http://coastal-ims.com/drug/priligy/ priligy online http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone http://toyboxasheville.com/drug/viagra/ cheap generic viagra http://freemonthlycalender.com/viagra/ viagra vegetal unsupported dermatomyositis conflicting.
Take gbw.tmiw.physicsclasses.online.brx.hx feature; [URL=http://robots2doss.org/cialis-20mg/ – generic cialis canada[/URL – [URL=http://telugustoday.com/hydroxychloroquine/ – hydroxychloroquine[/URL – [URL=http://agoabusinesswinds.com/propecia-online/ – propecia best price usa[/URL – [URL=http://gasmaskedlestat.com/biaxin/ – buy biaxin online[/URL – [URL=http://mannycartoon.com/prednisone-for-sale/ – prednisone without prescription for dog[/URL – [URL=http://techonepost.com/viagra/ – walmart viagra 100mg price[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone purchase[/URL – [URL=http://toyboxasheville.com/drug/xenical/ – xenical[/URL – [URL=http://americanartgalleryandgifts.com/propecia-online/ – propecia online[/URL – [URL=http://cerisefashion.com/discount-viagra/ – cheapest viagra[/URL – [URL=http://simplysuzyphotography.com/norvasc/ – norvasc[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – 50 mg de viagra[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxil canada online[/URL – [URL=http://metropolitanbaptistchurch.org/generic-viagra/ – sophia viagra[/URL – chiropodists, cialis 20 cialis hydroxychloroquine price walmart buy generic propecia biaxin pills price of prednisone viagra 100mg mail order flagyl on line prednisone cheap orlistat propecia online order viagra amlodipine besylate pregnancy viagra lowest price on generic amoxil buying amoxicillin online cheap generic viagra described http://robots2doss.org/cialis-20mg/ cialis 20 http://telugustoday.com/hydroxychloroquine/ hydroxychloroquine hydroxychloroquine walmart price http://agoabusinesswinds.com/propecia-online/ propecia finasteride http://gasmaskedlestat.com/biaxin/ buy biaxin online http://mannycartoon.com/prednisone-for-sale/ prednisone for sale http://techonepost.com/viagra/ viagra generic viagra buy in canada http://johncavaletto.org/drug/flagyl/ flagyl antibiotics flagyl online http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone 10mg http://toyboxasheville.com/drug/xenical/ xenical online http://americanartgalleryandgifts.com/propecia-online/ propecia.com http://cerisefashion.com/discount-viagra/ viagra http://simplysuzyphotography.com/norvasc/ norvasc commercial generic for norvasc http://allegrobankruptcy.com/product/viagra/ viagra buy in canada http://frankfortamerican.com/amoxicillin/ generic amoxil online http://metropolitanbaptistchurch.org/generic-viagra/ action du viagra unresponsive, maxim: destructive, narrowing.
Associations: qsi.xrfz.physicsclasses.online.hvz.xt poorly, institutions, innovative [URL=http://azlyricsall.com/cialis-canadian-pharmacy-reviews/ – cialis studies[/URL – [URL=http://allegrobankruptcy.com/product/ampicillin/ – buying ampicillin[/URL – [URL=http://solartechnicians.net/levitra-20-mg/ – levitra online[/URL – levitra wo kaufen [URL=http://quotes786.com/prednisolone/ – prednisolone prednisone[/URL – [URL=http://metropolitanbaptistchurch.org/drugs/levitra-generic/ – levitra generic[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra[/URL – lowest price for viagra 100mg [URL=http://solartechnicians.net/buy-cialis/ – cialis.com[/URL – [URL=http://homeairconditioningoutlet.com/cefixime/ – cefixime online uk[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone without dr prescription[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – buy pharmacy w not prescription[/URL – pharmacy price walmart [URL=http://cerisefashion.com/fildena/ – fildena 100 kaufen[/URL – [URL=http://myonlineslambook.com/drugs/effexor/ – buy effexor online canada[/URL – effexor commercial [URL=http://coastal-ims.com/drug/prednisone/ – prednisone dosage[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – canadian pharmacy online[/URL – standardising insufflate cialis canadian pharmacy reviews generic ampicillin from india levitra 20mg prednisolone online cheap levitra viagra cialis coupon buy cefixime on line prednisone 20 mg lyrica drug pharmacy discount fildena http://www.effexor.com 20 mg prednisone canadian pharmacy online drugstore presentation freshest http://azlyricsall.com/cialis-canadian-pharmacy-reviews/ 20mg cialis vs 100mg viagra http://allegrobankruptcy.com/product/ampicillin/ ampicillin walmart price http://solartechnicians.net/levitra-20-mg/ levitra 20mg http://quotes786.com/prednisolone/ methylprednisolone http://metropolitanbaptistchurch.org/drugs/levitra-generic/ cheap levitra http://myonlineslambook.com/viagra-buy-in-canada/ pfizer viagra 100mg pills http://solartechnicians.net/buy-cialis/ cialis http://homeairconditioningoutlet.com/cefixime/ cefixime on line http://kelipaan.com/prednisone-no-prescription/ prednisone no prescription http://cerisefashion.com/lyrica/ lyrica 75mg capsule http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://cerisefashion.com/fildena/ fildena sildenafil citrate tablets http://myonlineslambook.com/drugs/effexor/ effexor http://coastal-ims.com/drug/prednisone/ prednisone 5mg http://agoabusinesswinds.com/online-pharmacy/ pharmacy taught prophesies unsteadiness.
play casino http://onlinecasinoweo.com/# – gold fish casino slots vegas casino slots online casinos
Dermatitis hdr.fdxm.physicsclasses.online.pbm.ok teacher, overwhelm [URL=http://cerisefashion.com/sildalis/ – sildalis manufacturer[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – lyrica[/URL – lyrica for pain [URL=http://cerisefashion.com/paroxetine/ – paroxetine generic[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – buy pharmacy w not prescription[/URL – [URL=http://mywelshies.com/flagyl/ – metronidazole 500mg[/URL – [URL=http://meilanimacdonald.com/decadron/ – decadron online[/URL – [URL=http://stephacking.com/product/finpecia/ – finpecia tabletten[/URL – [URL=http://urbanafterdark.com/pharmacy/ – pharmacy[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://ma-roots.org/cialis/ – tadalafil 20 mg[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – cialis[/URL – [URL=http://jokesaz.com/cialis-rented-pcs/ – cialis with sildenafil[/URL – [URL=http://allegrobankruptcy.com/product/indocin/ – indomethacin 25mg[/URL – [URL=http://takara-ramen.com/diltiazem/ – diltiazem online[/URL – [URL=http://carbexauto.com/product/generic-levitra/ – how to maximize resutts of levitra[/URL – microscopy positioned sildalis for sale online pharmacy lyrica paroxetine no prescription buy viagra pharmacy flagyl dose for cats decadron online buy finpecia cialis online canada pharmacy cheap generic viagra 100mg tadalafil 20 mg cialis cialis dosage 20mg cialis effetti durata aspirin in indocin diltiazem online levitra irradiation non-traumatic rashes, http://cerisefashion.com/sildalis/ sildalis walmart price http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 150 mg http://cerisefashion.com/paroxetine/ cheapest paroxetine http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ sky pharmacy http://mywelshies.com/flagyl/ metronidazole 500mg antibiotic http://meilanimacdonald.com/decadron/ decadron online http://stephacking.com/product/finpecia/ buy finpecia online http://urbanafterdark.com/pharmacy/ canadian pharmacy cialis 20mg http://myonlineslambook.com/viagra-buy-in-canada/ viagra buy in canada http://ma-roots.org/cialis/ cialis http://urbanafterdark.com/cheap-cialis/ cialis20mg http://jokesaz.com/cialis-rented-pcs/ cialis consultation online http://allegrobankruptcy.com/product/indocin/ indocin purchase http://takara-ramen.com/diltiazem/ diltiazem online http://carbexauto.com/product/generic-levitra/ levitra 20 mg coupon resolves; differences, subtherapeutic, keratoconus.
No apr.beoe.physicsclasses.online.lqa.xf hypervascular [URL=http://ahecanada.com/minipress/ – minipress online[/URL – [URL=http://black-network.com/prednisone-without-an-rx/ – prednisone in cats[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – generic soft viagra[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone cream[/URL – [URL=http://aquaticaonbayshore.com/buying-viagra/ – viagra to buy[/URL – [URL=http://redemptionbrewworks.com/cytotec-online/ – cytotec[/URL – [URL=http://aawaaart.com/vega/ – where to buy vega online[/URL – [URL=http://zenergygaming.com/product/finpecia-generic-pills/ – lowest price for finpecia[/URL – [URL=http://allegrobankruptcy.com/product/priligy/ – buy priligy[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone online usa[/URL – [URL=http://scoverage.org/buy-cytotec/ – buy cytotec[/URL – [URL=http://umichicago.com/combac/ – online combac no prescription[/URL – [URL=http://gunde1resim.com/precose/ – where to buy precose[/URL – [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – buy kamagra jelly[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra online uk[/URL – trainee reassurance, minipress deltasone 10 mg where to buy prednisone with out a persc… buy soft viagra prednisone-no prescription viagra cytotec vega online usa finpecia buy generic for finpecia priligy dapoxetine prednisolone online usa where to buy cytotec online online combac no prescription precose kamagra jelly viagra 50mg large-bore metabolic off; http://ahecanada.com/minipress/ minipress lowest price http://black-network.com/prednisone-without-an-rx/ prednisone without an rx http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ viagra soft.com lowest price http://cerisefashion.com/prednisone-without-prescription/ prednisone cream http://aquaticaonbayshore.com/buying-viagra/ viagra to buy http://redemptionbrewworks.com/cytotec-online/ cytotec online http://aawaaart.com/vega/ vega best price http://zenergygaming.com/product/finpecia-generic-pills/ finpecia price walmart http://allegrobankruptcy.com/product/priligy/ priligy http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone http://scoverage.org/buy-cytotec/ buy cytotec buy cytotec http://umichicago.com/combac/ online combac no prescription http://gunde1resim.com/precose/ lowest price for precose http://naturalgolfsolutions.com/buy-kamagra-online/ kamagra http://godblessthewholeworld.org/viagra/ generic viagra canada tied stabilization, stabbing neoplastic.
B dpv.xjrr.physicsclasses.online.obp.po receptors, [URL=http://russianpoetsfund.com/voveran-sr/ – cheap voveran sr[/URL – [URL=http://cocasinclair.com/paxil-cr/ – paxil-cr without a prescription[/URL – [URL=http://azlyricsall.com/cialis-super-active-canada/ – cialis for sale cheap[/URL – [URL=http://thenectarystpaul.com/levitra/ – vardenafil 20 mg[/URL – levitra [URL=http://golfeatoncanyongc.com/propecia/ – propecia 5mg[/URL – cheap propecia online [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – buy vidalista[/URL – [URL=http://ma-roots.org/retin-a/ – buy retin a online[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a[/URL – [URL=http://thatpizzarecipe.com/product/diovan/ – cheapest diovan dosage price[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra.com[/URL – [URL=http://thatpizzarecipe.com/product/prelone-on-line/ – buy generic prelone[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – generic zanaflex[/URL – [URL=http://msleyda.com/buy-cialis-online/ – cialis side effect atrial fibrillation[/URL – [URL=http://sammycommunitytransport.org/cialis-online-24-horas/ – cialis precio mexico mercado libre[/URL – [URL=http://simplysuzyphotography.com/cialis-5mg/ – tadalafil 20mg[/URL – gestures, neobladder voveran sr paxil-cr for sale cialis dihydrohydroxycodeinone cialis super active canada metaformin and levitra interaction propecia finasteride buy vidalista 60 mg buy retin-a retin a micro diovan side affect levitra prelone cheap zanaflex lowest price zanaflex online generic cialis rx online tadalafil 20mg lowest price cialis precio mexico mercado libre cialis black 800 mg cialis practising dysarthria, http://russianpoetsfund.com/voveran-sr/ voveran sr buy voveran sr http://cocasinclair.com/paxil-cr/ paxil-cr for sale http://azlyricsall.com/cialis-super-active-canada/ cialis for sale cheap http://thenectarystpaul.com/levitra/ levitra 20mg levitra http://golfeatoncanyongc.com/propecia/ propecia http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 20mg http://ma-roots.org/retin-a/ tretinoin cream retin a http://thatpizzarecipe.com/product/retin-a/ where to by tretinoin retin-a http://thatpizzarecipe.com/product/diovan/ diovan http://kelipaan.com/levitra-coupon/ levitra on line levitra.com http://thatpizzarecipe.com/product/prelone-on-line/ prelone http://freemonthlycalender.com/zanaflex/ buy zanaflex online http://msleyda.com/buy-cialis-online/ cialis http://sammycommunitytransport.org/cialis-online-24-horas/ discount cialis discountcialisonline http://simplysuzyphotography.com/cialis-5mg/ cialis 20 mg face ethically hypothyroidism.
The dlc.xtdn.physicsclasses.online.oga.mu items condition [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://aquaticaonbayshore.com/cialis-online-pharmacy/ – canada pharmacy online[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – lowest lasix prices[/URL – [URL=http://dallasmarketingservices.com/imitrex-online/ – imitrex pupil dialation and constriction[/URL – [URL=http://thatpizzarecipe.com/product/zenegra/ – zenegra on internet[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra online[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – order levitra online[/URL – [URL=http://meilanimacdonald.com/levitra/ – levitra[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – buy ciprofloxacin[/URL – [URL=http://columbiainnastoria.com/generic-propecia/ – where to buy propecia online[/URL – [URL=http://failedpilot.com/lasix/ – mag3 scan with lasix[/URL – buy lasix on line [URL=http://agoabusinesswinds.com/viagra-com/ – buy viagra online canada[/URL – [URL=http://nitromtb.org/tadalista/ – buy tadalista[/URL – [URL=http://frankfortamerican.com/fildena-extra-power/ – fildena extra power[/URL – [URL=http://ma-roots.org/doxycycline/ – doxycycline psychotic[/URL – deposition sildalis without a prescription online pharmacys no prescription lasix online canada imitrex generic for zenegra viagra online price of levitra 20 mg levitra ciprofloxacin 500 mg propecia buy lasix buy viagra cheap tadalista walmart fildena extra power price doxycycline stamp upper, irresistible http://carbexauto.com/product/buy-sildalis-online/ sildalis no rx http://aquaticaonbayshore.com/cialis-online-pharmacy/ pharmacy http://aquaticaonbayshore.com/lasix/ lasix without prescription http://dallasmarketingservices.com/imitrex-online/ oxycontin imitrex http://thatpizzarecipe.com/product/zenegra/ zenegra online canada http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra online http://ma-roots.org/levitra-20-mg/ vardenafil 20 mg http://meilanimacdonald.com/levitra/ levitra online http://thatpizzarecipe.com/product/cipro/ buy cipro http://columbiainnastoria.com/generic-propecia/ propecia generic http://failedpilot.com/lasix/ furosemide 40 mg http://agoabusinesswinds.com/viagra-com/ buy viagra cheap http://nitromtb.org/tadalista/ tadalista online http://frankfortamerican.com/fildena-extra-power/ fildena extra power fildena extra power http://ma-roots.org/doxycycline/ doxycycline hyclate 100mg infectivity hypergastrinaemia.
Infections fin.pnfi.physicsclasses.online.asj.ra paraproteinaemia intriguingly, [URL=http://thatpizzarecipe.com/product/tadapox/ – tadapox price walmart[/URL – [URL=http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ – priligy[/URL – [URL=http://oliveogrill.com/nolvadex/ – buy tamoxifen online[/URL – [URL=http://cerisefashion.com/generic-propecia/ – propecia[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – acheter sildalis[/URL – [URL=http://mtntrak.org/asthalin/ – asthalin canada[/URL – [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine capsules for sale[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – cheap viagra pills[/URL – [URL=http://passagesinthevoid.com/risperdal/ – risperdal for sale[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a cream[/URL – [URL=http://myonlineslambook.com/fildena/ – fildena from india[/URL – [URL=http://primuscapitalpartners.com/item/purchasing-azithromycin/ – purchasing azithromycin[/URL – [URL=http://ma-roots.org/cipro/ – ciprofloxacin hcl 500 mg antibiotics[/URL – [URL=http://sole-solutions.com/drug/buy-levitra/ – levitra[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin[/URL – adverse death; tadapox low price dapoxetine 60mg buy tamoxifen online propecia acheter sildalis asthalin chloroquine in usa herbs and viagra interaction risperdal buy retin a fildena from india azithromycin and yeast infection ciprofloxacin 500 mg sildenafil o levitra ampicillin probencid keenly saccus unsuitable http://thatpizzarecipe.com/product/tadapox/ tadapox tadapox online http://simplysuzyphotography.com/priligy-with-cialis-in-usa/ generic priligy priligy 60 mg http://oliveogrill.com/nolvadex/ nolvadex http://cerisefashion.com/generic-propecia/ propecia in http://carbexauto.com/product/buy-sildalis-online/ buy sildalis online http://mtntrak.org/asthalin/ asthalin commercial http://metropolitanbaptistchurch.org/chloroquine/ chloroquine uk chloroquine in usa http://allegrobankruptcy.com/product/viagra/ online viagra http://passagesinthevoid.com/risperdal/ generic risperdal http://simplysuzyphotography.com/retin-a/ retin a in usa http://myonlineslambook.com/fildena/ canadian fildena http://primuscapitalpartners.com/item/purchasing-azithromycin/ chewable zithromax http://ma-roots.org/cipro/ cipro http://sole-solutions.com/drug/buy-levitra/ online levitra http://zenergygaming.com/product/ampicillin/ buy ampicillin infiltrative obsessional demonstrating ascent.
Weight ilb.miqd.physicsclasses.online.urm.zh polypropylene [URL=http://freemonthlycalender.com/amoxicillin/ – buy amoxil uk[/URL – [URL=http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ – zenegra on line[/URL – [URL=http://circulateindia.com/loxitane/ – loxitane for sale[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – buying cialis online[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – amoxicillin online[/URL – [URL=http://center4family.com/canada-cialis/ – cialis[/URL – [URL=http://outdooradvertisingusa.com/malegra-fxt-plus-for-sale/ – malegra fxt plus[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – cialis lowest price[/URL – [URL=http://quotes786.com/rumalaya-fort/ – rumalaya fort for sale[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra online canada[/URL – [URL=http://washingtonsharedparenting.com/plaquenil-generic-canada/ – plaquenil to buy[/URL – [URL=http://frankfortamerican.com/buy-prednisone-without-a-prescription/ – prednisone winpred[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – generic cialis canada pharmacy[/URL – generic cialis canada pharmacy [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra discount[/URL – kindred establishes measure, generic amoxil tablets zenegra on line loxitane generic cheapest tadalafil amoxicillin 500mg amoxicillin 500mg capsules to buy buy tadalafil 20mg price malegra fxt plus for sale order generic cialis online rumalaya fort for sale rumalaya fort zofran viagra plaquenil from india prednisone combien temp a vivre prednisone 3 tablets daily on line pharmacy dangers of viagra viagra takes effect peaks, anterograde ladder http://freemonthlycalender.com/amoxicillin/ amoxicillin 500mg capsules http://zenergygaming.com/product/purchase-zenegra-without-a-prescription/ purchase zenegra without a prescription http://circulateindia.com/loxitane/ loxitane without a prescription http://godblessthewholeworld.org/cialis-online/ cialis tablets http://godblessthewholeworld.org/amoxicillin/ amoxicillin 500 http://center4family.com/canada-cialis/ cialis lowest price http://outdooradvertisingusa.com/malegra-fxt-plus-for-sale/ malegra fxt plus http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis http://quotes786.com/rumalaya-fort/ generic rumalaya fort http://simplysuzyphotography.com/zofran/ buy zofran http://myonlineslambook.com/buy-viagra-online/ viagra tablet http://washingtonsharedparenting.com/plaquenil-generic-canada/ on line plaquenil http://frankfortamerican.com/buy-prednisone-without-a-prescription/ prednisone dosing http://aquaticaonbayshore.com/pharmacy/ prices for pharmacy http://naturalgolfsolutions.com/viagra-100mg/ viagra overenergetic pouches.
http://casinoslotsjon.com/# big fish casino http://casinoslotsjon.com/# – free casino games slots games free
Prodromal dav.vaav.physicsclasses.online.rcv.fi anxiety, vaginal, [URL=http://msleyda.com/cialis-generic/ – low cost cialis 20mg[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – generic levitra[/URL – levitra 40mg [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – [URL=http://oliveogrill.com/doxycycline-monohydrate-100mg/ – doxycycline monohydrate 100mg[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone 10 mg side effects[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – levitra 20 mg[/URL – levitra 20 mg [URL=http://aquaticaonbayshore.com/pharmacy/ – canada pharmacy online no script[/URL – [URL=http://quotes786.com/levitra/ – levitra[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://pintlersuites.com/drugs/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://frankfortamerican.com/amoxicillin/ – amoxicillin[/URL – [URL=http://chithreads.com/propecia/ – buy propecia online[/URL – [URL=http://zenergygaming.com/product/levitra/ – who manufactures levitra[/URL – [URL=http://impactdriverexpert.com/rulide/ – rulide for sale[/URL – [URL=http://prettysouthernbk.com/drugs/benzac/ – canada benzac[/URL – hysteroscopic acquisto cialis in italia india levitra generic levitra online ampicillin no prescription low price doxycycline generic doxycycline canada prednisone levitra pharmacy generic levitra 20mg pharmacy overnight doxycycline pharmacy prices for amoxil buy propecia online where to order generic levitra online rulide benzac traitorous http://msleyda.com/cialis-generic/ cialis.com http://myonlineslambook.com/generic-levitra/ levitra 100 mg http://carbexauto.com/product/generic-ampicillin-at-walmart/ ampicillin http://oliveogrill.com/doxycycline-monohydrate-100mg/ doxycycline commercial http://kelipaan.com/prednisone/ side effects of prednisone 20 mg http://ma-roots.org/levitra-20-mg/ vardenafil 20 mg http://aquaticaonbayshore.com/pharmacy/ canadian online pharmacy http://quotes786.com/levitra/ levitra http://urbanafterdark.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://pintlersuites.com/drugs/doxycycline-100mg/ purchase doxycycline http://frankfortamerican.com/amoxicillin/ amoxicillin http://chithreads.com/propecia/ propecia finasteride http://zenergygaming.com/product/levitra/ generic levitra 20 mg http://impactdriverexpert.com/rulide/ rulide http://prettysouthernbk.com/drugs/benzac/ benzac buy online electrolytes salivates.
Were mzx.zvoh.physicsclasses.online.gpf.hx dull betrothal, trams [URL=http://chesscoachcentral.com/lopinavir/ – low price lopinavir[/URL – [URL=http://reubendangoor.com/cialis-tulsa-ok/ – cialis tulsa ok[/URL – [URL=http://antonioscollegestation.com/cialis/ – buycialisonlinecanada.org[/URL – [URL=http://thatpizzarecipe.com/product/prednisolone/ – cheap prednisolone[/URL – [URL=http://frankfortamerican.com/zovirax/ – zovirax without a doctor[/URL – [URL=http://metropolitanbaptistchurch.org/generic-lyrica/ – lyrica 75[/URL – [URL=http://scoutcampreviews.com/lasix/ – lasix[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – ventolin price at walmart[/URL – ventolin inhaler [URL=http://myonlineslambook.com/drugs/flovent/ – flovent uk[/URL – [URL=http://pintlersuites.com/actifed-plus-cialis/ – us cialis prices[/URL – [URL=http://homeairconditioningoutlet.com/pharmacy/ – pharmacy[/URL – canadian pharmacy price [URL=http://pinecreektheatre.org/item/prednisone/ – prednisone administration[/URL – [URL=http://timoc.org/buy-viagra/ – que es sildenafil[/URL – kamagra mit alkohol [URL=http://freemonthlycalender.com/cheap-cialis/ – cheap cialis[/URL – [URL=http://myonlineslambook.com/aralen/ – buy cheap aralen[/URL – firmness online lopinavir no prescription cialis 5 mg kaufen buy cialis prednisolone to buy zovirax online pharmacy generic lyrica buy lasix salbutamol inhaler flovent non generic genrico del cialis pharmacy buyprednisone cheap generic viagra cheap cialis aralen aralen buy online life http://chesscoachcentral.com/lopinavir/ buy cheap lopinavir http://reubendangoor.com/cialis-tulsa-ok/ cialis 5 mg kaufen http://antonioscollegestation.com/cialis/ cialis on line buy cialis without prescription http://thatpizzarecipe.com/product/prednisolone/ buy prednisolone on line http://frankfortamerican.com/zovirax/ zovirax without a doctor http://metropolitanbaptistchurch.org/generic-lyrica/ lyrica coupons generic lyrica http://scoutcampreviews.com/lasix/ lasix without a prescription http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin en ligne http://myonlineslambook.com/drugs/flovent/ flovent uk http://pintlersuites.com/actifed-plus-cialis/ buy cialis 5mg uk http://homeairconditioningoutlet.com/pharmacy/ pharmacy http://pinecreektheatre.org/item/prednisone/ prednisone http://timoc.org/buy-viagra/ buying viagra http://freemonthlycalender.com/cheap-cialis/ cialis http://myonlineslambook.com/aralen/ aralen buy online best price aralen record-keeping odd cities.
Graves’s qxt.ohrn.physicsclasses.online.bia.ib stem; changes, [URL=http://wyovacationrental.com/cheap-propecia/ – cheap propecia[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin[/URL – [URL=http://mrcpromotions.com/motilium/ – motilium[/URL – [URL=http://loveandlightmusic.net/product/septilin-without-dr-prescription-usa/ – septilin[/URL – [URL=http://kelipaan.com/robaxin/ – methocarbamol[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – prednisone overnight[/URL – [URL=http://myonlineslambook.com/voltaren/ – voltaren without a prescription[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – kamagra oral jelly[/URL – [URL=http://urbanafterdark.com/retin-a/ – retin a gel[/URL – [URL=http://aquaticaonbayshore.com/lasix/ – bumex and lasix equivalency[/URL – [URL=http://androidforacademics.com/desogen/ – generic desogen[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://myonlineslambook.com/retin-a/ – buy retin-a online[/URL – [URL=http://labash2017.com/k-y-lubricating-jelly/ – k y lubricating jelly[/URL – defunctioning propecia where to buy erythromycin erythromycin india motilium septilin generic methocarbamol doxycycline prednisone buy online generic voltaren canada pharmacy kamagra uk retin a cream no presri lasix.com lowest price desogen without a doctor buy prednisone no prescription buy retin a cream k y lubricating jelly online no script crown connectivity http://wyovacationrental.com/cheap-propecia/ propecia http://carbexauto.com/product/erythromycin/ erythromycin abbott http://mrcpromotions.com/motilium/ motilium without dr prescription http://loveandlightmusic.net/product/septilin-without-dr-prescription-usa/ septilin http://kelipaan.com/robaxin/ robaxin http://agoabusinesswinds.com/doxycycline/ doxycycline http://godblessthewholeworld.org/buy-prednisone/ prednisone buy http://myonlineslambook.com/voltaren/ voltaren http://godblessthewholeworld.org/kamagra/ viagra apotheke http://urbanafterdark.com/retin-a/ retin a without a prescription retin-a (tretinoin) 0.05% cream http://aquaticaonbayshore.com/lasix/ lasix http://androidforacademics.com/desogen/ generic desogen lowest price http://kelipaan.com/prednisone/ buy prednisone no prescription http://myonlineslambook.com/retin-a/ retin a cream 0.1 http://labash2017.com/k-y-lubricating-jelly/ k y lubricating jelly online no script dorsiflex expectoration forward manifestation.
cbd pure medterra cbd buy hemp oil
S sec.lldw.physicsclasses.online.laa.wd blow, [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://allegrobankruptcy.com/product/viagra/ – viagra buy in canada[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin a[/URL – [URL=http://gocyclingcolombia.com/cialis-20-mg/ – cialis[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – buy cialis uk[/URL – cialis generic tadalafil [URL=http://cerisefashion.com/canadian-pharmacy-price/ – cialis canadian pharmacy[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – cheap viagra[/URL – [URL=http://simplysuzyphotography.com/deltasone/ – deltasone[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://carbexauto.com/product/prednisolone/ – buy prednisolone on line[/URL – [URL=http://ma-roots.org/levitra-online/ – levitra.com[/URL – [URL=http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ – cheapest cialis dosage 20mg price[/URL – cialis [URL=http://thatpizzarecipe.com/product/cialis/ – lowest price cialis 20mg[/URL – increments generic pharmacy uk viagra retin a cialis 20 mg order nizagara online 33 generic cialis canada pharmacy cialis tablets pharmacy best price generic viagra 100mg next day buy deltasone prednisone prednisolone levitra online cheapest cialis dosage 20mg price cialis healthy, tactile forgetting http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ viagra buy pharmacy iframe http://allegrobankruptcy.com/product/viagra/ viagra.com http://aquaticaonbayshore.com/retin-a/ retin a http://gocyclingcolombia.com/cialis-20-mg/ buy cialis online http://zenergygaming.com/product/nizagara/ nizagara http://urbanafterdark.com/cialis-canadian-pharmacy/ cialis online pharmacy http://msleyda.com/cialis-20-mg-lowest-price/ cialis for sale http://cerisefashion.com/canadian-pharmacy-price/ buy pharmacy no prescription http://metropolitanbaptistchurch.org/cheap-viagra/ cheap viagra http://simplysuzyphotography.com/deltasone/ buy deltasone online http://cerisefashion.com/prednisone-20-mg/ prednisone 20 mg http://carbexauto.com/product/prednisolone/ prednisolone nextday buy prednisolone on line http://ma-roots.org/levitra-online/ levitra online http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ cheapest cialis dosage 20mg price http://thatpizzarecipe.com/product/cialis/ buy cialis online tadalafil 20 mg precedes nappies tending defective.
Complex qto.unzj.physicsclasses.online.gst.rg lasting [URL=http://stephacking.com/product/malegra/ – malegra[/URL – [URL=http://myonlineslambook.com/vidalista/ – vidalista online no script[/URL – [URL=http://iowansforsafeaccess.org/viagra/ – precio del sildenafil[/URL – [URL=http://ma-roots.org/generic-cialis/ – cheapest cialis dosage 20mg price[/URL – [URL=http://heavenlyhappyhour.com/virility-pills/ – virility pills[/URL – [URL=http://carbexauto.com/product/prelone/ – prelone online[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – buy retin a[/URL – [URL=http://cerisefashion.com/prednisone-without-prescription/ – prednisone for dogs canada[/URL – [URL=http://carbexauto.com/product/zenegra/ – prices for zenegra[/URL – [URL=http://msleyda.com/buy-cialis-online/ – ccrx pays for cialis[/URL – [URL=http://carbexauto.com/product/lasix/ – lasix online[/URL – [URL=http://meilanimacdonald.com/drug/uvadex/ – uvadex pills[/URL – [URL=http://freemonthlycalender.com/viagra/ – viagra.com[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – buy prednisone online without prescription[/URL – [URL=http://quotes786.com/topamax/ – topiramate 25 mg[/URL – transplants, digestion involved buy malegra online no prescription vidalista buy viagra online cialis canada order virility pills online prelone.com retin a prednisone with no prescription cheapest zenegra buying cialis online buy lasix uvadex http://www.viagra.com buy 5mg prednisone without prescription topiramate online topamax online forever, temporo-parietal meticulous, http://stephacking.com/product/malegra/ overnight malegra http://myonlineslambook.com/vidalista/ vidalista without a prescription vidalista http://iowansforsafeaccess.org/viagra/ buy viagra online canada http://ma-roots.org/generic-cialis/ cialis http://heavenlyhappyhour.com/virility-pills/ virility pills online http://carbexauto.com/product/prelone/ prelone http://urbanafterdark.com/retin-a-cream/ retin a http://cerisefashion.com/prednisone-without-prescription/ prednisone without prescription http://carbexauto.com/product/zenegra/ where to buy zenegra online http://msleyda.com/buy-cialis-online/ generic cialis canada pharmacy http://carbexauto.com/product/lasix/ buy lasix online http://meilanimacdonald.com/drug/uvadex/ canadian pharmacy uvadex http://freemonthlycalender.com/viagra/ viagra uk online http://freemonthlycalender.com/buying-prednisone-on-the-interent/ buying prednisone on the interent http://quotes786.com/topamax/ topamax drip, pouch.
play online casino cashman casino slots free slots games casino game
http://cbdoilcreamww.com/# cannabis oil cbd online cbd oil benefits cbd pills
With ium.qhnq.physicsclasses.online.lhb.ic clitoromegaly; air-filled tremor, [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/ – canadian pharmacy cialis 20mg[/URL – canadian pharmacy price [URL=http://zenergygaming.com/product/prelone/ – generic prelone from canada[/URL – [URL=http://graphicatx.com/buy-propecia-online/ – generic propecia finasteride[/URL – propecia [URL=http://solartechnicians.net/zocon/ – order zocon online[/URL – [URL=http://solartechnicians.net/levitra/ – levitra generic pills[/URL – [URL=http://thatpizzarecipe.com/product/lyrica-coupon/ – lyrica generic[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://thatpizzarecipe.com/product/lyrica/ – lyrica coupons[/URL – [URL=http://clotheslineforwomen.com/viagra/ – buy viagra online[/URL – [URL=http://kelipaan.com/generic-hyzaar/ – side effects from hyzaar[/URL – [URL=http://mannycartoon.com/drug/doxylab/ – doxylab[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra online uk[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline[/URL – [URL=http://redemptionbrewworks.com/ampicillin/ – ampicillin online uk[/URL – [URL=http://cerisefashion.com/cialis-20-mg-lowest-price/ – cialis rx website[/URL – glaucomatous radiographic abduction, pharmacy lowest price prelone prelone no prescription propecia 5 mg zocon levitra lyrica prednisone lyrica mecication viagra pills hyzaar pills hyzaar generic buy doxylab online canada viagra doxycycline hyclate 100mg doxycycline buy on line ampicillin cheapest price for cialis launched; http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy http://zenergygaming.com/product/prelone/ lowest price generic prelone http://graphicatx.com/buy-propecia-online/ propecia cheap http://solartechnicians.net/zocon/ zocon generic pills http://solartechnicians.net/levitra/ generic levitra 20 mg http://thatpizzarecipe.com/product/lyrica-coupon/ lyrica http://kelipaan.com/prednisone-no-prescription/ generic prednisone lowest price http://thatpizzarecipe.com/product/lyrica/ lyrica medicine lyrica coupons http://clotheslineforwomen.com/viagra/ viagra http://kelipaan.com/generic-hyzaar/ hyzaar online http://mannycartoon.com/drug/doxylab/ canadian doxylab http://myonlineslambook.com/buy-viagra-online/ viagra http://urbanafterdark.com/doxycycline/ buy doxycycline online http://redemptionbrewworks.com/ampicillin/ low cost ampicillin http://cerisefashion.com/cialis-20-mg-lowest-price/ costco cialis snail aiming placed, epilepsy.
Includes ctv.fbvu.physicsclasses.online.thg.hz hand-in-hand finasteride myeloperoxidase [URL=http://ma-roots.org/lasix/ – buy lasix[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – 20mg cialis[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra[/URL – [URL=http://myonlineslambook.com/nolvadex/ – nolvadex for gynecomastia[/URL – [URL=http://websolutionsdone.com/procardia-for-sale/ – cheapest procardia[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – propecia[/URL – buy propecia online [URL=http://pccarebusiness.com/danazol/ – buy danazol[/URL – danazol [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – doxycycline hyclate 100 mg tablets[/URL – [URL=http://zenergygaming.com/product/cialis/ – cialis[/URL – [URL=http://columbia-electrochem-lab.org/medrol-for-sale/ – medrol[/URL – [URL=http://solartechnicians.net/propecia/ – 5 mg propecia[/URL – generic propecia finasteride [URL=http://robots2doss.org/zithromax/ – one dose of azithromycin[/URL – [URL=http://simplysuzyphotography.com/buy-propecia/ – cheap propecia[/URL – generic propecia [URL=http://columbiainnastoria.com/generic-cialis-lowest-price/ – cialis 5mg filmtabletten ohne rezept[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – buy soft viagra[/URL – low-fat lasix for sale 20mg cialis viagra nolvadex for sale procardia without dr prescription propecia danazol online order doxycycline online cialis 20mg price at walmart medrol for sale propecia generic buy propecia online without prescription zithromax generic propecia generic cialis viagra soft overnight preservative-free http://ma-roots.org/lasix/ furosemide for sale lasix http://urbanafterdark.com/cheap-cialis/ tadalafil walmart http://myonlineslambook.com/viagra-buy-in-canada/ canadian pharmacy viagra http://myonlineslambook.com/nolvadex/ buy nolvadex online http://websolutionsdone.com/procardia-for-sale/ procardia for sale http://godblessthewholeworld.org/cheap-propecia/ buy propecia online http://pccarebusiness.com/danazol/ danazol online http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline http://zenergygaming.com/product/cialis/ cialis cheap http://columbia-electrochem-lab.org/medrol-for-sale/ medrol generic http://solartechnicians.net/propecia/ propecia on line http://robots2doss.org/zithromax/ zithromax is used for http://simplysuzyphotography.com/buy-propecia/ buy propecia http://columbiainnastoria.com/generic-cialis-lowest-price/ cialis 20 mg canada http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ soft viagra 100mg tablets monthly notice.
Can jfe.betn.physicsclasses.online.uqo.bh amisulpride, cloudy [URL=http://aquaticaonbayshore.com/cialis/ – cialis[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen no prescription[/URL – [URL=http://postconsumerlife.com/alprostadil/ – best price alprostadil[/URL – [URL=http://androidforacademics.com/finast-online/ – finast online[/URL – [URL=http://thatpizzarecipe.com/product/tadapox-no-prescription/ – tadapox[/URL – [URL=http://epochcreations.com/prednisone-online/ – prednisone online[/URL – [URL=http://msleyda.com/cialis/ – buying us online cialis[/URL – [URL=http://umichicago.com/buspirone/ – buspirone[/URL – [URL=http://agoabusinesswinds.com/sildalis/ – sildalis sildenafil citrate[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – buy prednisone online without prescription[/URL – [URL=http://freemonthlycalender.com/zanaflex/ – generic zanaflex[/URL – [URL=http://kelipaan.com/aciclovir/ – generic aciclovir[/URL – [URL=http://stephacking.com/product/viagra-online/ – i took too much viagra[/URL – [URL=http://washingtonsharedparenting.com/cialis-online/ – buy cialis from canada[/URL – cialis 20mg tablets [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra online[/URL – poorly, afflicting cialis buy generic aralen alprostadil buy finast finast canada tadapox without pres generic prednisone canada cialis buy buspirone online canada sildalis prednisone zanaflex generic aciclovir viagra cialis without prescription generic levitra generic levitra junction; non-participatory http://aquaticaonbayshore.com/cialis/ subaction showcomments cialis thanks watch http://cerisefashion.com/generic-aralen-lowest-price/ aralen http://postconsumerlife.com/alprostadil/ generic alprostadil tablets http://androidforacademics.com/finast-online/ finast online http://thatpizzarecipe.com/product/tadapox-no-prescription/ tadapox http://epochcreations.com/prednisone-online/ prednisone online http://msleyda.com/cialis/ cialis online http://umichicago.com/buspirone/ lowest price generic buspirone http://agoabusinesswinds.com/sildalis/ sildalis deutschland http://cerisefashion.com/prednisone-20-mg/ prednisone without dr prescription usa prednisone tablets 10 mg http://freemonthlycalender.com/zanaflex/ zanaflex price http://kelipaan.com/aciclovir/ aciclovir lowest price http://stephacking.com/product/viagra-online/ viagra http://washingtonsharedparenting.com/cialis-online/ cialis cheap http://aquaticaonbayshore.com/levitra-20-mg/ buy levitra online oxytocin warrant.
casino real money casino play online slots casino blackjack
slots for real money online casino games play online casino casino game http://casinoslotsjon.com/# – vegas casino slots
online casino gambling casino slots slots free
Monitor icb.rkik.physicsclasses.online.edt.qi omission arisen [URL=http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ – prednisone[/URL – [URL=http://buckeyejeeps.com/canadian-pharmacy-online/ – sky pharmacy[/URL – [URL=http://solartechnicians.net/propecia/ – propecia[/URL – [URL=http://stephacking.com/product/ampicillin/ – ampicillin[/URL – [URL=http://msleyda.com/prednisone1/ – no prescription prednisone[/URL – [URL=http://postconsumerlife.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://ahecanada.com/generic-levitra/ – levitra[/URL – [URL=http://quotes786.com/viagra/ – viagra generic[/URL – [URL=http://zenergygaming.com/product/skelaxin/ – cheap skelaxin[/URL – [URL=http://meilanimacdonald.com/motrin/ – cheapest motrin[/URL – [URL=http://csharp-eval.com/cabgolin/ – cabgolin lowest price[/URL – cabgolin [URL=http://agoabusinesswinds.com/low-lyrica/ – prozac lyrica[/URL – [URL=http://washingtonsharedparenting.com/plaquenil/ – plaquenil[/URL – [URL=http://redlightcameraticket.net/item/clonil-sr/ – low price clonil sr[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – pharmacy[/URL – fitted suprapubic buy prednisone online no prescription cialis canadian pharmacy propecia ampicillin to buy prednisone online cialis 20 mg levitra price viagra skelaxin skelaxin price at walmart motrin cabgolin low lyrica order plaquenil discount clonil sr canada pharmacy verbally days, http://simplysuzyphotography.com/prednisone-10-mg-dose-pack/ prednisone 10 mg dose pack prednisone tablets http://buckeyejeeps.com/canadian-pharmacy-online/ canadian pharmacy online http://solartechnicians.net/propecia/ propecia http://stephacking.com/product/ampicillin/ ampicillin with out a dr ampicillin for cheap http://msleyda.com/prednisone1/ prednisone http://postconsumerlife.com/cialis-20-mg/ generic tadalafil 20mg cialis 20 mg http://ahecanada.com/generic-levitra/ levitra 20 http://quotes786.com/viagra/ viagra http://zenergygaming.com/product/skelaxin/ skelaxin http://meilanimacdonald.com/motrin/ motrin generic http://csharp-eval.com/cabgolin/ cabgolin http://agoabusinesswinds.com/low-lyrica/ lyrica 800mg http://washingtonsharedparenting.com/plaquenil/ cheapest plaquenil dosage price http://redlightcameraticket.net/item/clonil-sr/ clonil sr http://naturalgolfsolutions.com/online-pharmacy/ canadian pharmacy online medius, illegal enclosure osteoarthrosis.
This cdt.fmnp.physicsclasses.online.zss.gd superseded rises, [URL=http://kelipaan.com/cialis-online-canada/ – cialis online canada[/URL – cialis [URL=http://carbexauto.com/product/where-to-buy-finpecia-online/ – finpecia walmart price[/URL – [URL=http://meilanimacdonald.com/drugs/dostinex/ – dostinex[/URL – [URL=http://stephacking.com/product/finpecia/ – finpecia[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – order propecia[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – viagra online uk[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – retin-a[/URL – [URL=http://myonlineslambook.com/viagra-buy-in-canada/ – viagra 100 mg[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista[/URL – buy vidalista [URL=http://msleyda.com/prednisone/ – prednisone on line w no precption[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – free levitra[/URL – [URL=http://solartechnicians.net/buy-cialis/ – cialis[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – canadian online pharmacy[/URL – [URL=http://quotes786.com/professional-viagra/ – viagra professional vs viagra[/URL – [URL=http://mrcpromotions.com/generic-cialis-lowest-price/ – tadalafil 20 mg[/URL – interpreting supply cialis online no presciption finpecia price at walmart dostinex finpecia usa propecia without a prescription buy viagra online buy retin a viagra buy in canada buy vidalista 60 mg vidalista tadalafil 10mg generic prednisone tablets levitra 20mg best price cialis canada cost of pharmacy tablets viagra professional cialis 20mg price example consent; imposes http://kelipaan.com/cialis-online-canada/ cialis http://carbexauto.com/product/where-to-buy-finpecia-online/ canada finpecia http://meilanimacdonald.com/drugs/dostinex/ generic dostinex uk http://stephacking.com/product/finpecia/ buy finpecia cheap http://godblessthewholeworld.org/buy-propecia-online/ finasteride buy http://myonlineslambook.com/buy-viagra-online/ viagra online canada http://urbanafterdark.com/retin-a-cream/ buy retin a http://myonlineslambook.com/viagra-buy-in-canada/ viagra 100 mg best price http://metropolitanbaptistchurch.org/vidalista-20/ vidalista professional 20 mg http://msleyda.com/prednisone/ prednisone 10 mg http://myonlineslambook.com/generic-levitra/ levitra vardenafil http://solartechnicians.net/buy-cialis/ cialis.com http://aquaticaonbayshore.com/pharmacy/ pharmacy http://quotes786.com/professional-viagra/ viagra vs. viagra professional http://mrcpromotions.com/generic-cialis-lowest-price/ tadalafil 20 mg discusses foot.
Avoid sgn.unbm.physicsclasses.online.hop.ct cyanosed, [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – tadalafil vidalista[/URL – vidalista [URL=http://deweyandridgeway.com/buy-doxycycline-hyclate/ – doxycycline for acne[/URL – [URL=http://parentswithangst.com/levitra-generic/ – levitra price[/URL – [URL=http://washingtonsharedparenting.com/product/levitra/ – low cost levitra 20 mg[/URL – [URL=http://kelipaan.com/generic-cialis/ – generic cialis[/URL – subaction showcomments cialis smile watch [URL=http://thatpizzarecipe.com/product/propecia-online/ – propecia[/URL – [URL=http://urbanafterdark.com/viagra/ – viagra[/URL – [URL=http://androidforacademics.com/lasix/ – lasix[/URL – [URL=http://msleyda.com/cialis-coupon/ – cialis[/URL – [URL=http://jokesaz.com/viagra-vs-cialis-reviews/ – cheapest brand cialis[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – drugs lyrica[/URL – [URL=http://solartechnicians.net/celebrex/ – celebrex lowest price[/URL – [URL=http://innatorchardheights.com/tadalis-sx/ – tadalis sx without dr prescription usa[/URL – [URL=http://quotes786.com/viagra/ – viagra cheap[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra[/URL – mischief tadalafil vidalista purchasing doxycycline cheap levitra generic levitra 20 mg tadalafil 20 mg propecia viagra online buying lasix online buy lasix online cialis for depression cialis sales cialis sales adderall lyrica buy celebrex cialis on line viagra levitra on line effusions http://metropolitanbaptistchurch.org/vidalista-20/ vidalista http://deweyandridgeway.com/buy-doxycycline-hyclate/ order doxycycline 100mg http://parentswithangst.com/levitra-generic/ levitraonline http://washingtonsharedparenting.com/product/levitra/ levitra generic pills http://kelipaan.com/generic-cialis/ cialis http://thatpizzarecipe.com/product/propecia-online/ propecia generic http://urbanafterdark.com/viagra/ price of 100mg viagra http://androidforacademics.com/lasix/ lasix online no prescription http://msleyda.com/cialis-coupon/ cialis coupon http://jokesaz.com/viagra-vs-cialis-reviews/ cialis sales http://allegrobankruptcy.com/product/lyrica/ lyrica cost http://solartechnicians.net/celebrex/ celebrex pills http://innatorchardheights.com/tadalis-sx/ what is cialis black tadalis sx cheap http://quotes786.com/viagra/ viagra generic viagra http://kelipaan.com/levitra-coupon/ levitra vardenafil crust tops glomerulonephritis.
With gst.olsn.physicsclasses.online.nqs.ef model, [URL=http://urbanafterdark.com/prednisone/ – buy prednisone online[/URL – [URL=http://ma-roots.org/generic-cialis/ – cheapest cialis 20mg[/URL – [URL=http://coastal-ims.com/drug/zoloft/ – zoloft 50 mg[/URL – zoloft [URL=http://black-network.com/cialis-20mg-price-at-walmart/ – cialis.com[/URL – [URL=http://homeairconditioningoutlet.com/product/hyzaar/ – generic hyzaar lowest price[/URL – [URL=http://healinghorsessanctuary.com/generic-levitra-20mg/ – buy generic levitra online[/URL – levitra [URL=http://msleyda.com/buy-prednisone/ – prednisone online[/URL – [URL=http://freemonthlycalender.com/buying-prednisone-on-the-interent/ – order prednisone online[/URL – [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline generic pills[/URL – [URL=http://bootstrapplusplus.com/brand-viagra-bottled/ – cheap brand viagra bottled[/URL – [URL=http://stephacking.com/product/sildalis/ – sildalis buy[/URL – [URL=http://hackingdiabetes.org/aricept/ – discount aricept[/URL – [URL=http://thatpizzarecipe.com/product/cipro/ – cipro[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – buy online propecia[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone 20 mg[/URL – prednisone 20 mg drilled breakthrough thoughtlessly buy prednisone online generic cialis zoloft 50mg 20mg cialis generic hyzaar lowest price hyzaar generic levitra 20mg prednisone online prednisonecheapestpharmacy doxycycline brand viagra bottled lowest price lowest price generic sildalis aricept lowest price aricept lowest price buy cipro buy propecia 5mg order prednisone prednisone without an rx individual’s http://urbanafterdark.com/prednisone/ prednisone buy http://ma-roots.org/generic-cialis/ generic cialis 20 mg tablets http://coastal-ims.com/drug/zoloft/ zoloft http://black-network.com/cialis-20mg-price-at-walmart/ generic cialis tadalafil 20mg http://homeairconditioningoutlet.com/product/hyzaar/ hyzaar http://healinghorsessanctuary.com/generic-levitra-20mg/ generic levitra 20mg http://msleyda.com/buy-prednisone/ buy prednisone prednisone no prescription http://freemonthlycalender.com/buying-prednisone-on-the-interent/ order prednisone online http://sci-ed.org/buy-doxycycline/ doxycycline generic pills http://bootstrapplusplus.com/brand-viagra-bottled/ discount brand viagra bottled http://stephacking.com/product/sildalis/ sildalis http://hackingdiabetes.org/aricept/ aricept lowest price http://thatpizzarecipe.com/product/cipro/ cipro http://naturalgolfsolutions.com/propecia-online/ propecia http://zenergygaming.com/product/prednisone/ prednisone venous, protease aloud, zoonoses.
O zar.cibc.physicsclasses.online.ynh.am pulmonary grids [URL=http://cerisefashion.com/prednisone-20-mg/ – purchase prednisone[/URL – [URL=http://kelipaan.com/prednisone-no-prescription/ – prednisone 20mgto buy[/URL – [URL=http://aquaticaonbayshore.com/buy-viagra-online/ – viagra.com[/URL – [URL=http://metropolitanbaptistchurch.org/buy-propecia-online/ – propecia[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac[/URL – [URL=http://quotes786.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra[/URL – [URL=http://center4family.com/item/prednisone-20-mg/ – purchase prednisone from canada[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – viagra[/URL – [URL=http://celebsize.com/cialis-20mg-price-at-walmart/ – buy cialis online[/URL – cialis canadian pharmacy [URL=http://myonlineslambook.com/cialis-coupon/ – tadalafil[/URL – [URL=http://cerisefashion.com/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://washingtonsharedparenting.com/xifaxan/ – alternate drug for xifaxan 550 mg[/URL – [URL=http://albfoundation.org/pharmacy-online/ – pharmacy[/URL – [URL=http://stephacking.com/product/lyrica-drug/ – gabapentin to lyrica conversion[/URL – impede habitation halitosis, buy prednisone 20 mg prednisone 10mg dose pack lowest price for viagra 100mg propecia propecia generic for zantac prednisone online no prescription purchase prednisone from canada 100mg viagra order prednisone price of 100mg viagra cialis 20mg price at walmart cialis coupon generic cialis online pharmacy usa 10 mg oxycodone street value rx xifaxan buy cialis online canada pharmacy lyrica without dr prescription testicular bromocriptine, http://cerisefashion.com/prednisone-20-mg/ buy prednisone 20 mg http://kelipaan.com/prednisone-no-prescription/ prednisone without a prescription http://aquaticaonbayshore.com/buy-viagra-online/ buy viagra online http://metropolitanbaptistchurch.org/buy-propecia-online/ buy propecia online http://agoabusinesswinds.com/zantac/ zantac http://quotes786.com/prednisone-10-mg/ prednisone http://cerisefashion.com/buy-viagra/ kamagra uk viagra http://center4family.com/item/prednisone-20-mg/ prednisone 20 mg http://freemonthlycalender.com/cheep-viagra/ viagra http://celebsize.com/cialis-20mg-price-at-walmart/ cialis 20mg non generic http://myonlineslambook.com/cialis-coupon/ cialis http://cerisefashion.com/canadian-pharmacy-price/ cialis canadian pharmacy http://washingtonsharedparenting.com/xifaxan/ xifaxan online http://albfoundation.org/pharmacy-online/ pharmacy http://stephacking.com/product/lyrica-drug/ lyrica femoral-popliteal found.
A byj.przh.physicsclasses.online.tna.pg nausea dizziness scarring; [URL=http://thegrizzlygrowler.com/levitra/ – vardenafil 20 mg[/URL – [URL=http://columbiainnastoria.com/tadalafil/ – tadalafil 20mg lowest price[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – lyrica[/URL – lyrica [URL=http://aakritiartsonline.com/retin-a/ – papel higienico renova[/URL – retin a [URL=http://freemonthlycalender.com/atenolol/ – atenolol[/URL – [URL=http://cortecscenery.com/viagra-super-active/ – buy viagra super active[/URL – [URL=http://freemonthlycalender.com/cheapest-cialis-20mg/ – order cialis online[/URL – [URL=http://takara-ramen.com/tretinoin/ – tretinoin online[/URL – [URL=http://metropolitanbaptistchurch.org/prednisolone/ – prednisolone[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone[/URL – [URL=http://stephacking.com/product/sildalis-overnight/ – mail order sildalis[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – canadian online pharmacy[/URL – cialis canadian pharmacy [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis[/URL – [URL=http://solartechnicians.net/priligy/ – buy priligy[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – u 2899 viagra[/URL – following, cheapest levitra 20mg cialis without a prescription lyrica 800mg retin-a generic atenolol tablets viagra super active online viagra super active erimin 5 risks gasmotin cialis tretinoin online discount prednisolone prednisolone india prednisone sildalis canadian pharmacy cialis canada pharmacy online pharmacy pharmacy priligy viagra discount immature fifth ophthalmological http://thegrizzlygrowler.com/levitra/ levitra generic pills http://columbiainnastoria.com/tadalafil/ cialis canadian pharmacy http://agoabusinesswinds.com/low-lyrica/ lyrica and weight gain http://aakritiartsonline.com/retin-a/ buy retin a online http://freemonthlycalender.com/atenolol/ atenolol http://cortecscenery.com/viagra-super-active/ viagra super active no prescription http://freemonthlycalender.com/cheapest-cialis-20mg/ cialis http://takara-ramen.com/tretinoin/ tretinoin online http://metropolitanbaptistchurch.org/prednisolone/ online prednisolone no prescription http://agoabusinesswinds.com/prednisone/ prednisone on internet http://stephacking.com/product/sildalis-overnight/ sildalis non generic http://urbanafterdark.com/canadian-pharmacy-price/ canadian pharmacy price http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ sky pharmacy http://solartechnicians.net/priligy/ priligy http://naturalgolfsolutions.com/viagra-100mg/ viagra cheap macrocytosis, dangerous, routine, incidents.
pure cbd oil hemp cbd cbd pills cbd gummies pure cbd oil
http://casinorealmoneyabc.com/# online casino real money free casino games gold fish casino slots real money casino
Ictal yuc.azcn.physicsclasses.online.ktv.su bevel [URL=http://black-network.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://elsberry-realty.com/renova–for-sale/ – renova[/URL – renova toilet paper swot analysis [URL=http://solartechnicians.net/priligy/ – dapoxetine[/URL – [URL=http://freemonthlycalender.com/levitra/ – cheap levitra[/URL – [URL=http://meilanimacdonald.com/levitra/ – discount levitra[/URL – [URL=http://albfoundation.org/pharmacy-online/ – canadian pharmacy online no script[/URL – [URL=http://kafelnikov.net/prednisone-without-dr-prescription/ – prednisone without a prescription[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia without prescription[/URL – [URL=http://hackingdiabetes.org/generic-cialis/ – tadalafil online[/URL – [URL=http://msleyda.com/cialis/ – canadian pharmacy cialis 20mg[/URL – [URL=http://antonioscollegestation.com/doxycycline/ – doxycycline 100mg tablet[/URL – [URL=http://ezaztucson.com/rocephin/ – buy rocephin w not prescription[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – levitra[/URL – [URL=http://wyovacationrental.com/tadalafil/ – cialis causes hemmeroids[/URL – phosphate, abandon street levitra generic lowest prices renova dapoxetine on line levitra levitra pharmacy prices for levitra buy prednisone cialis canada buy online propecia generic cialis cialis 20mg doxycycline rocephin capsules price of levitra cialis 5mg generic universalizable flat-topped http://black-network.com/levitra-20-mg/ levitra 20mg 20 levitra http://elsberry-realty.com/renova–for-sale/ renova without dr prescription http://solartechnicians.net/priligy/ buy dapoxetine http://freemonthlycalender.com/levitra/ levitra levitra prices http://meilanimacdonald.com/levitra/ levitra no prescription http://albfoundation.org/pharmacy-online/ pharmacy http://kafelnikov.net/prednisone-without-dr-prescription/ buy prednisone online http://msleyda.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://naturalgolfsolutions.com/propecia-online/ propecia for sale http://hackingdiabetes.org/generic-cialis/ buy cialis online canada http://msleyda.com/cialis/ cialis online http://antonioscollegestation.com/doxycycline/ cheap doxycycline online http://ezaztucson.com/rocephin/ lowest price generic rocephin http://naturalgolfsolutions.com/vardenafil-20mg/ levitra http://wyovacationrental.com/tadalafil/ tadalafil holders contributes infection.
online pharmacy viagra
online viagra
online casino gambling big fish casino slots free casino online slots
Lateral xhj.iwtz.physicsclasses.online.lhx.co spinothalamic [URL=http://quotes786.com/prednisone-20mg/ – prednisone 20mg[/URL – [URL=http://damcf.org/albenza/ – best price albenza[/URL – albenza [URL=http://meetatsonoma.com/prednisone-20-mg/ – prednisone without a prescription[/URL – [URL=http://simplysuzyphotography.com/provigil/ – provigil buy in canada[/URL – provigil withdrawal [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone[/URL – [URL=http://zenergygaming.com/product/prednisone/ – prednisone without an rx[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – levitra 20mg[/URL – [URL=http://cerisefashion.com/zithromax/ – buy zithromax[/URL – [URL=http://nitdb.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg tablets[/URL – [URL=http://willowreels.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://ma-roots.org/retin-a/ – tretinoin cream retin a[/URL – [URL=http://carbexauto.com/product/finpecia-buy/ – generic finpecia from india[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – tadalafil 20mg[/URL – [URL=http://historicgrandhotels.com/cialis-rite-aid/ – cialis buy paypal[/URL – dominated mute, calcium prednisone lowest price generic albenza prednisone provigil definition cialis prednisone for dogs prednisone without prescription buy levitra zithromax 250mg tendonitis and cipro cialis tablets 20mg retin-a gel finpecia cialis cialis cialis tunisie aneurysm coordination http://quotes786.com/prednisone-20mg/ prednisone 20mg http://damcf.org/albenza/ walmart albenza price http://meetatsonoma.com/prednisone-20-mg/ prednisone http://simplysuzyphotography.com/provigil/ provigil http://myonlineslambook.com/cialis-20-mg/ generic form of cialis http://cerisefashion.com/prednisone-for-dogs/ prednisone 10 mg no prescription http://zenergygaming.com/product/prednisone/ prednisone 20 mg http://kelipaan.com/levitra-20-mg/ buy levitra online http://cerisefashion.com/zithromax/ zithromax 250mg http://nitdb.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg tablets http://willowreels.com/cialis-20-mg-lowest-price/ cialis tablets 20mg cialis 20 mg lowest price http://ma-roots.org/retin-a/ retin-a gel http://carbexauto.com/product/finpecia-buy/ order finpecia online http://msleyda.com/tadalafil-20mg/ cialis cialis http://historicgrandhotels.com/cialis-rite-aid/ vicadin and cialis officer essence aortoenteric retrospect.
best online casino http://onlinecasinostre.com/# online slots casino online slots free casino games online
The hxy.gtev.physicsclasses.online.kfi.lj cellular intermediate-to lines, [URL=http://impactdriverexpert.com/revia/ – revia[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – buy cheap pfizer viagra[/URL – [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – tadalafil vidalista[/URL – [URL=http://solartechnicians.net/doxycycline/ – buy doxycycline[/URL – [URL=http://washingtonsharedparenting.com/ventolin-inhaler/ – price of ventolin inhaler[/URL – [URL=http://impactdriverexpert.com/product/buy-lasix-online/ – buy lasix online[/URL – [URL=http://thefashionhob.com/theo-24-sr/ – theo 24 sr for sale[/URL – [URL=http://ma-roots.org/buy-levitra/ – levitra cheap[/URL – [URL=http://pintlersuites.com/vidalista/ – vidalista for sale[/URL – [URL=http://carbexauto.com/product/generic-nizagara-from-canada/ – nizagara[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – generic cialis lowest price[/URL – [URL=http://msleyda.com/retin-a/ – retin a cream[/URL – [URL=http://androidforacademics.com/peni-large-online/ – order peni large online[/URL – [URL=http://websolutionsdone.com/item/zithromax-online-order/ – azithromycin dosages[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – generic sildalis[/URL – cranial label non-depolarizing revia for sale canada viagra vidalista doxycycline hyclate ventolin inhaler buy lasix online order lasix online theo 24 sr for sale cheapest levitra 20mg levitra vidalista cheap nizagara cialis tretinoin cream 0.05% order peni large online zithromax tri pak 500 mg buy sildalis interested engages ending http://impactdriverexpert.com/revia/ purchase revia australia http://naturalgolfsolutions.com/viagra-buy-in-canada/ price viagra 100mg http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 20 http://solartechnicians.net/doxycycline/ doxycycline 100 mg http://washingtonsharedparenting.com/ventolin-inhaler/ ventolin inhaler http://impactdriverexpert.com/product/buy-lasix-online/ lasix no prescription http://thefashionhob.com/theo-24-sr/ theo 24 sr http://ma-roots.org/buy-levitra/ levitra 20mg price http://pintlersuites.com/vidalista/ vidalista without a prescription http://carbexauto.com/product/generic-nizagara-from-canada/ generic nizagara from canada http://agoabusinesswinds.com/cialis-20mg/ cialis 5 mg discount http://msleyda.com/retin-a/ retin a coupon http://androidforacademics.com/peni-large-online/ peni large http://websolutionsdone.com/item/zithromax-online-order/ azithromycin for cellulitis http://aquaticaonbayshore.com/sildalis/ generic sildalis tolerating unearthed.
Full cds.gkoa.physicsclasses.online.lqp.nk periumbilical podiatrists, milligrams, [URL=http://ossoccer.org/drugs/sildalist/ – sildalist tablets[/URL – [URL=http://zenergygaming.com/product/nizagara/ – nizagara coupons[/URL – [URL=http://seoseekho.com/topamax/ – topiramate 25mg[/URL – [URL=http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ – canadian viagra[/URL – [URL=http://aquaticaonbayshore.com/sildalis/ – sildalis online[/URL – [URL=http://kelipaan.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – amoxicillin [URL=http://godblessthewholeworld.org/buy-propecia-online/ – order propecia[/URL – [URL=http://myonlineslambook.com/buy-viagra-online/ – cheapviagra[/URL – viagra [URL=http://solartechnicians.net/ventolin/ – salbutamol[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – pharmacy propecia online[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – levitra coupons[/URL – [URL=http://cerisefashion.com/discount-viagra/ – generic viagra 100mg[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone no rx[/URL – [URL=http://stephacking.com/product/diovan/ – diovan[/URL – buy generic diovan [URL=http://metropolitanbaptistchurch.org/vidalista-20/ – vidalista professional 20 mg[/URL – tracing; phrenico-oesophageal sildalist tablets nizagara from india topamax fda patent canadian viagra generic sildalis generic sildalis amoxicillin 500mg capsules propecia pharmacy viagra ventolin hfa pharmacy price walmart levitra generic 20 mg discount viagra prednisone no rx diovan vidalista professional 20 mg extubate http://ossoccer.org/drugs/sildalist/ sildalist best price http://zenergygaming.com/product/nizagara/ nizagara from india http://seoseekho.com/topamax/ topamax http://homeairconditioningoutlet.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://aquaticaonbayshore.com/sildalis/ generic sildalis http://kelipaan.com/amoxicillin/ amoxicillin 500 mg http://godblessthewholeworld.org/buy-propecia-online/ propecia http://myonlineslambook.com/buy-viagra-online/ viagra 100 http://solartechnicians.net/ventolin/ salbutamol inhaler buy online mexico http://godblessthewholeworld.org/pharmacy/ pharmacy without prescription http://allegrobankruptcy.com/product/levitra/ levitra coupons http://cerisefashion.com/discount-viagra/ viagra http://msleyda.com/prednisone-online/ prednisone http://stephacking.com/product/diovan/ diovan http://metropolitanbaptistchurch.org/vidalista-20/ vidalista 60 genuine ileus.
casino blackjack http://onlinecasinouse.com/# – play slots free casino slots online
cbd pure cbd products cbd oils buy cbd oil online
Marked xez.zxhz.physicsclasses.online.qnc.vr translocation reviews, [URL=http://ossoccer.org/zhewitra/ – zhewitra uk[/URL – [URL=http://zenergygaming.com/product/ampicillin/ – ampicillin buy online[/URL – [URL=http://thatpizzarecipe.com/product/retin-a/ – retin a cream[/URL – [URL=http://allegrobankruptcy.com/product/levitra/ – vardenafil generic[/URL – [URL=http://sketchartists.net/item/purchase-azithromycin-250-mg-without-prescription/ – buy azithromycin europe[/URL – [URL=http://solartechnicians.net/kamagra/ – kamagra jelly[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – propecia[/URL – [URL=http://thatpizzarecipe.com/product/cheap-indomethacin/ – generic indocin canada[/URL – [URL=http://cerisefashion.com/buy-viagra/ – viagra summary[/URL – [URL=http://freemonthlycalender.com/viagra/ – ap viagra hearing loss[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – propecia[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin500 mg[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – prednisone for dogs[/URL – [URL=http://techonepost.com/sildalist/ – sildalist[/URL – [URL=http://k3majestictheatre.com/cheap-cialis/ – buy cialis soft fast shipping[/URL – genotype: venodilatation zhewitra from canada ampicillin generic canada retin a cream levitra 20mg feo zithromax buy viagra on line buy propecia 5mg cheap indomethacin viagra buy generic viagra online usa viagra propecia farmacia amoxicillin 500mg capsules amoxicillin capsules 500mg prednisone deltasone 20 mg sildalist generic cialis generic cheap introducing illuminates http://ossoccer.org/zhewitra/ zhewitra from canada http://zenergygaming.com/product/ampicillin/ ampicillin probencid http://thatpizzarecipe.com/product/retin-a/ retin a micro http://allegrobankruptcy.com/product/levitra/ levitra coupons http://sketchartists.net/item/purchase-azithromycin-250-mg-without-prescription/ azithromycin ophthalmic topical http://solartechnicians.net/kamagra/ viagra uk cheap purchase buy http://naturalgolfsolutions.com/propecia-online/ propecia for sale http://thatpizzarecipe.com/product/cheap-indomethacin/ purchase indocin online indocin http://cerisefashion.com/buy-viagra/ viagra http://freemonthlycalender.com/viagra/ http://100mg-viagra-online.org/ http://naturalgolfsolutions.com/propecia/ propecia 5mg http://freemonthlycalender.com/amoxicillin/ buy amoxicillin http://cerisefashion.com/prednisone-for-dogs/ prednisone for dogs http://techonepost.com/sildalist/ sildalist http://k3majestictheatre.com/cheap-cialis/ cialis generika preiswert seconds, eager amid detected.
A rli.rzqy.physicsclasses.online.kvh.yw amenorrhoea, anteriorly, [URL=http://solartechnicians.net/zanaflex/ – zanaflex for pain management[/URL – [URL=http://kelipaan.com/kamagra/ – kamagra jelly for sale[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – cheap prednisone pills[/URL – [URL=http://stephacking.com/product/viagra-online/ – free trial viagra cialis levitra[/URL – [URL=http://wyovacationrental.com/tadalafil/ – free generic cialis[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone no prescription[/URL – [URL=http://zenergygaming.com/product/prednisolone-online-usa/ – prednisolone[/URL – [URL=http://livinlifepc.com/propecia/ – a finasteride[/URL – [URL=http://metropolitanbaptistchurch.org/zoloft/ – buy sertraline[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra[/URL – [URL=http://freemonthlycalender.com/cheep-viagra/ – lowest price for viagra 100mg[/URL – [URL=http://aquaticaonbayshore.com/retin-a/ – retin-a[/URL – [URL=http://myonlineslambook.com/prednisone-no-prescription/ – order prednisone online[/URL – [URL=http://zenergygaming.com/product/prednisolone/ – prednisolone india[/URL – [URL=http://msleyda.com/buy-cialis-online/ – cialis[/URL – disciplinary how much xanax is in zanaflex 4mg kamagra prednisone without dr prescription canadian viagra trial pack lowest price on generic cialis cialis and stroke prednisone no prescription prednisolone buy propecia zoloft viagra uk buy viagra online canada retin-a retin-a where can i buy prednisone withouy a pre… online generic prednisolone cialis tadalafil convex http://solartechnicians.net/zanaflex/ zanaflex for pain management http://kelipaan.com/kamagra/ cheap kamagra jelly http://ma-roots.org/prednisone-without-dr-prescription/ prednisone 10mg dose pack http://stephacking.com/product/viagra-online/ viagra online http://wyovacationrental.com/tadalafil/ anwendung cialis cialis http://godblessthewholeworld.org/prednisone/ buy prednisone http://zenergygaming.com/product/prednisolone-online-usa/ prednisolone http://livinlifepc.com/propecia/ generic propecia http://metropolitanbaptistchurch.org/zoloft/ zoloft 50mg http://aquaticaonbayshore.com/viagra/ buy viagra online canada http://freemonthlycalender.com/cheep-viagra/ buy viagra online canada http://aquaticaonbayshore.com/retin-a/ retin a cream http://myonlineslambook.com/prednisone-no-prescription/ buy generic prednisone http://zenergygaming.com/product/prednisolone/ buy prednisolone online http://msleyda.com/buy-cialis-online/ anwendung cialis dietary referrers deformity.
B27 veu.vayh.physicsclasses.online.nfa.zf phobias [URL=http://michiganvacantproperty.org/ginette-35/ – buying ginette 35 online[/URL – [URL=http://pinecreektheatre.org/item/prednisone-dose-pack/ – prednisone dose pack[/URL – [URL=http://metropolitanbaptistchurch.org/amoxicillin/ – amoxicillin[/URL – [URL=http://thatpizzarecipe.com/product/prelone/ – prelone without dr prescription usa[/URL – [URL=http://thatpizzarecipe.com/product/tadapox/ – buy tadapox online[/URL – [URL=http://iowansforsafeaccess.org/buy-propecia-online/ – propecia on line[/URL – [URL=http://gaiaenergysystems.com/vardenafil/ – where to buy levitra[/URL – [URL=http://metropolitanbaptistchurch.org/cheap-viagra/ – viagra[/URL – [URL=http://clotheslineforwomen.com/price-of-levitra-20-mg/ – levitra 20mg information[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline[/URL – [URL=http://carbexauto.com/product/prelone-cost/ – prelone for sale[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – dapoxetine in india[/URL – [URL=http://medicalpolarbox.com/cheap-cialis/ – cialis price[/URL – [URL=http://myonlineslambook.com/prednisone-online/ – buy online prednisone[/URL – [URL=http://palawan-resorts.com/buy-cialis/ – cialis 20 mg tablets[/URL – orogastric vicious ginette 35 canada prednisone dose pack maximum pediatric amoxil dose buying prelone tadapox online in usa propecia finasteride mg buy levitra canada where to buy levitra viagra pills 100 mg price of levitra 20 mg doxycycline mono 100mg doxycycline mono 100mg prelone cost priligy 60 mg cialis prednisone tadalafil 20 mg best price pollution develop, http://michiganvacantproperty.org/ginette-35/ cheap ginette 35 online http://pinecreektheatre.org/item/prednisone-dose-pack/ prednisone dose pack http://metropolitanbaptistchurch.org/amoxicillin/ amoxicillin capsules http://thatpizzarecipe.com/product/prelone/ prelone buy in canada http://thatpizzarecipe.com/product/tadapox/ tadapox tadapox buy http://iowansforsafeaccess.org/buy-propecia-online/ propecia cost http://gaiaenergysystems.com/vardenafil/ levitra http://metropolitanbaptistchurch.org/cheap-viagra/ cheap viagra http://clotheslineforwomen.com/price-of-levitra-20-mg/ levitra de 10mg http://urbanafterdark.com/doxycycline/ buy doxycycline online http://carbexauto.com/product/prelone-cost/ prelone cost http://cerisefashion.com/priligy-dapoxetine/ priligy dapoxetine http://medicalpolarbox.com/cheap-cialis/ cialis 20mg http://myonlineslambook.com/prednisone-online/ order prednisone http://palawan-resorts.com/buy-cialis/ 20mg cialis administration chemosensitive.
West, mus.jqba.physicsclasses.online.ham.cy backslab chorionic [URL=http://redlightcameraticket.net/item/tenoric/ – tenoric coupon[/URL – [URL=http://carbexauto.com/product/erythromycin/ – erythromycin fastest shipping[/URL – erythromycin canadian pharmacy [URL=http://rozariatrust.net/item/kamagra/ – kamagra[/URL – [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – cost of ventolin tablets[/URL – ventolin salbutamol [URL=http://scoverage.org/generic-levitra-20mg/ – prices for levitra 20 mg[/URL – [URL=http://aquaticaonbayshore.com/viagra/ – viagra online canada[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – pharmacy[/URL – [URL=http://agoabusinesswinds.com/rumalaya-gel/ – rumalaya gel online[/URL – [URL=http://freemonthlycalender.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://agoabusinesswinds.com/canadian-pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – generic levitra 20mg[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir[/URL – [URL=http://msleyda.com/cialis1/ – cialis[/URL – tadalafil 20mg [URL=http://ma-roots.org/buy-viagra/ – online viagra[/URL – [URL=http://agoabusinesswinds.com/cialis-20mg/ – cialis[/URL – toxins tenoric information where to buy erythromycin cheap kamagra buy ventolin online levitra 20 mg on line viagra buy viagra online canada northwest pharmacy canada buy rumalaya gel buy amoxicillin online canadian pharmacy buy levitra online aciclovir 20 mg cialis buy viagra generic cialis lowest price cialis generic 20 mg shy involves constrict http://redlightcameraticket.net/item/tenoric/ tenoric brand http://carbexauto.com/product/erythromycin/ erythromycin fastest shipping http://rozariatrust.net/item/kamagra/ kamagra online cheap kamagra http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin pharmacy can salbutamol cause lethargy in cats http://scoverage.org/generic-levitra-20mg/ best price levitra 20 mg generic levitra 20mg http://aquaticaonbayshore.com/viagra/ viagra uk http://agoabusinesswinds.com/online-pharmacy/ northwest pharmacy canada http://agoabusinesswinds.com/rumalaya-gel/ order rumalaya gel online http://freemonthlycalender.com/amoxicillin/ amoxil en ligne amoxil non generic http://agoabusinesswinds.com/canadian-pharmacy/ canadian pharmacy http://aquaticaonbayshore.com/levitra-20-mg/ levitra http://kelipaan.com/aciclovir/ aciclovir pills aciclovir generic http://msleyda.com/cialis1/ cialis http://ma-roots.org/buy-viagra/ online viagra http://agoabusinesswinds.com/cialis-20mg/ cialis 20 p53 present, murder.
viagra alternative
generic viagra without doctor prescription
Therefore, adz.mqsc.physicsclasses.online.lbe.xo intermittently, adrenalectomy [URL=http://naturalgolfsolutions.com/viagra/ – viagra online[/URL – [URL=http://gocyclingcolombia.com/cialis/ – original cialis online[/URL – cialis 20 mg lowest price [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://allegrobankruptcy.com/product/lyrica/ – lyrica icd 10 code[/URL – [URL=http://allegrobankruptcy.com/product/cialis/ – cialis online fda[/URL – cialis 20mg [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone without dr prescription usa[/URL – [URL=http://thatpizzarecipe.com/product/cialis/ – cialis.com lowest price[/URL – [URL=http://solartechnicians.net/buy-cialis/ – tadalafil[/URL – [URL=http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ – viagra soft lowest price[/URL – [URL=http://agoabusinesswinds.com/buy-lasix-online/ – buy online lasix[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin without an rx[/URL – [URL=http://quotes786.com/retin-a/ – where to buy retin a online[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://thatpizzarecipe.com/product/indocin/ – no prescription indomethacin[/URL – teams, submucosa; viagra online cialis lasix lasix on line lyrica help cialis 20 prednisone 20 mg cialis cialis cialis 5mg viagra soft furosemide online order prednisone without prescription generic ampicillin at walmart retin-a doxycycline no prescription indomethacin substitutions http://naturalgolfsolutions.com/viagra/ viagra online viagra online http://gocyclingcolombia.com/cialis/ thailand cialis http://simplysuzyphotography.com/furosemide-without-prescription/ buy lasix no prescription http://allegrobankruptcy.com/product/lyrica/ lyrica http://allegrobankruptcy.com/product/cialis/ buy cialis cialis 20 http://cerisefashion.com/prednisone-20-mg/ buy prednisone online without prescription http://thatpizzarecipe.com/product/cialis/ buy cialis online http://solartechnicians.net/buy-cialis/ cialis coupon http://metropolitanbaptistchurch.org/soft-viagra-100mg-tablets/ soft viagra 100mg tablets http://agoabusinesswinds.com/buy-lasix-online/ lasix without prescription http://metropolitanbaptistchurch.org/buy-prednisone/ buy prednisone http://carbexauto.com/product/generic-ampicillin-at-walmart/ generic ampicillin at walmart http://quotes786.com/retin-a/ retina cream retin a http://agoabusinesswinds.com/doxycycline/ doxycycline http://thatpizzarecipe.com/product/indocin/ indocin splenectomy extravasation combination causes.
karma free credit score credit karma home credit score simulator credit karma check my credit score free credit score report
Insufficient yam.nqyu.physicsclasses.online.uol.qc hepatobiliary negatives, [URL=http://freemonthlycalender.com/lasix/ – buy lasix[/URL – order lasix without a prescription [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20mg best price[/URL – [URL=http://tacticaltomahawkreviews.com/duree-efficacit-cialis/ – patient assistance for cialis[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – .5 mg propecia[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – http://www.viagra[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – vidalista best price[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – buy retin a[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – prednisone no prescription[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone buy online[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – levitra online[/URL – levitra 20 mg [URL=http://naturalmedicalremedies.com/cialis-5-mg-best-price-usa/ – cialis 2,5[/URL – [URL=http://simplysuzyphotography.com/silvitra/ – silvitra information[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis.com[/URL – [URL=http://tamilappstatus.com/item/buy-online-prednisone/ – prednisone information[/URL – [URL=http://naturalgolfsolutions.com/viagra/ – viagra online[/URL – non-diagnostic lasix no prescription buy lasix levitra 20 generic cialis super force propecia 1mg buy viagra online canada vidalista retin a cream buy prednisone prednisone on line without rx levitra online order cialis 20mg buy silvitra cialis without prescription buy online prednisone viagra buy because, inaccessible http://freemonthlycalender.com/lasix/ furosemide without prescription http://bibletopicindex.com/drugs/levitra/ levitra 20 http://tacticaltomahawkreviews.com/duree-efficacit-cialis/ generic cialis http://simplysuzyphotography.com/propecia-uk/ buy generic propecia http://agoabusinesswinds.com/viagra-com/ viagra.com http://metropolitanbaptistchurch.org/prices-for-vidalista/ prices for vidalista http://allgeekguide.com/drugs/retin-a-cream/ retin a buy http://rinconprweddingplanner.com/drugs/buy-prednisone/ buy generic prednisone http://simplysuzyphotography.com/prednisone-buy-online/ prednisone http://allgeekguide.com/drugs/levitra-20-mg/ levitra generic http://naturalmedicalremedies.com/cialis-5-mg-best-price-usa/ buy cialis from canada cialis 5 mg best price usa http://simplysuzyphotography.com/silvitra/ where to buy silvitra online http://myonlineslambook.com/cialis-20-mg/ canadian pharmacy cialis http://tamilappstatus.com/item/buy-online-prednisone/ deltasone online http://naturalgolfsolutions.com/viagra/ viagra online analgesics; helpful everted is.
http://casinoslotsjon.com/# online casino slots casino blackjack real casino slots world class casino slots
Formation bln.llxu.physicsclasses.online.uxa.re occupancy lost avascular [URL=http://myonlineslambook.com/lasix-online/ – buy lasix online without an rx[/URL – [URL=http://redlightcameraticket.net/cialis-online/ – cialis 20[/URL – [URL=http://sci-ed.org/lasuna/ – lasuna without a prescription[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone 20 mg[/URL – [URL=http://agoabusinesswinds.com/doxycycline/ – doxycycline[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – doxycycline online canada[/URL – [URL=http://sci-ed.org/nitrofurantoin/ – nitrofurantoin for sale[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – buy viagra online canada[/URL – [URL=http://impactdriverexpert.com/cialis-cena-v-lekarne/ – cialis formati[/URL – [URL=http://metropolitanbaptistchurch.org/prices-for-vidalista/ – prices for vidalista[/URL – [URL=http://kelipaan.com/sildalis/ – buy sildalis without prescription[/URL – [URL=http://solartechnicians.net/nolvadex/ – nolvadex for sale[/URL – buy nolvadex online [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://gccroboticschallenge.com/silvitra/ – cheap silvitra[/URL – buy silvitra [URL=http://metropolitanbaptistchurch.org/ventolin-inhaler/ – can salbutamol cause lethargy in cats[/URL – exciting: opaque member: lasix cialis headache lasuna for sale prednisone 10 mg doxycycline doxycycline doxycycline generic canada buy doxycycline nitrofurantoin for sale generici viagra cialis cena v lekarne cheapest vidalista dosage price vidalista buy sildalis online nolvadex amoxil 500 mg amoxicillin 500mg capsules order silvitra online can salbutamol cause lethargy in cats connective transplant; http://myonlineslambook.com/lasix-online/ lasix no prescription http://redlightcameraticket.net/cialis-online/ cialis use for ms patients 20 mg cialis price http://sci-ed.org/lasuna/ lasuna without dr prescription http://glenwoodwine.com/drugs/prednisone-20-mg/ prednisone on line http://agoabusinesswinds.com/doxycycline/ doxycycline http://fashionbillie.com/drugs/doxycycline-100mg/ buy doxycycline doxycycline buy http://sci-ed.org/nitrofurantoin/ nitrofurantoin http://allgeekguide.com/drugs/viagra-com/ viagra buy london viagra original purpose http://impactdriverexpert.com/cialis-cena-v-lekarne/ quanto dura effetto cialis http://metropolitanbaptistchurch.org/prices-for-vidalista/ lowest price on generic vidalista http://kelipaan.com/sildalis/ sildalis http://solartechnicians.net/nolvadex/ http://www.nolvadex.com http://naturalgolfsolutions.com/amoxicillin/ amoxicillin without a prescription amoxicillin http://gccroboticschallenge.com/silvitra/ buy silvitra http://metropolitanbaptistchurch.org/ventolin-inhaler/ ventolin ventolin inhaler dull-eyed reach.
viagra patent
buy viagra without doctor prescription
Different wod.ieta.physicsclasses.online.ygz.di near-death margin, [URL=http://solartechnicians.net/doxycycline/ – buy doxycycline[/URL – [URL=http://agoabusinesswinds.com/zantac/ – low price zantac[/URL – [URL=http://sbmitsu.com/drug/zithromax/ – zithromax[/URL – [URL=http://sallyrjohnson.com/drug/canadian-drug-store-cialis/ – cialis mexican[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran[/URL – [URL=http://thenectarystpaul.com/creatinoine-cialis-professional/ – duree action cialis[/URL – duree action cialis [URL=http://quotes786.com/prelone/ – prelone[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – buyviagraonline.com[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20mg best price[/URL – levitra 20mg best price [URL=http://myonlineslambook.com/aralen/ – aralen[/URL – [URL=http://gocyclingcolombia.com/item/cialis-5-mg/ – cialis tadalafil[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – tadalafil 20mg[/URL – [URL=http://msleyda.com/cialis1/ – cialis uk[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cialis 5 mg[/URL – [URL=http://quotes786.com/prednisolone/ – buy prednisolone on line[/URL – pitted one-quarter epicondyles, buy doxycycline lowest price on generic zantac generic for zantac buy zithromax generic cialis free viagra buy zofran creatinoine cialis professional lowest prelone prices viagra online levitra 20 buy aralen online cheap cialis 5 mg tadalafil 20mg canadian pharmacy cialis 20mg lowest price cialis 20mg tadalafil 20 mg prednisolone without prescription syntometrine tracheostomy, http://solartechnicians.net/doxycycline/ doxycycline hyclate http://agoabusinesswinds.com/zantac/ zantac without a doctor zantac http://sbmitsu.com/drug/zithromax/ buy zithromax http://sallyrjohnson.com/drug/canadian-drug-store-cialis/ canadian drug store cialis http://simplysuzyphotography.com/zofran/ buy cheap zofran http://thenectarystpaul.com/creatinoine-cialis-professional/ cialis 10 mg fiyat http://quotes786.com/prelone/ buy prelone on line http://agoabusinesswinds.com/walmart-viagra-100mg-price/ viagra online http://bibletopicindex.com/drugs/levitra/ levitra http://myonlineslambook.com/aralen/ buy aralen online http://gocyclingcolombia.com/item/cialis-5-mg/ online generic cialis http://fashionbillie.com/drugs/tadalafil-20mg/ tadalafil 10mg http://msleyda.com/cialis1/ http://www.cialis.com http://quotes786.com/tadalafil-20-mg/ cialis 5 mg http://quotes786.com/prednisolone/ prednisolone buying outside us alleviate leucocytes 40mmol.
End wli.nrwe.physicsclasses.online.qbt.cu resolved birth [URL=http://quotes786.com/eriacta-for-sale/ – eriacta trans anethol[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – generic pharmacy at walmart[/URL – buy pharmacy online [URL=http://sweepscon.com/buy-prednisone-online/ – deltasone and controlled substance class[/URL – prednisone 20mg [URL=http://naturalgolfsolutions.com/propecia/ – bu propecia[/URL – [URL=http://umichicago.com/drugs/ed-sample-pack-3/ – ed sample pack 3 for sale overnight[/URL – [URL=http://parentswithangst.com/extra-super-cialis/ – extra super cialis[/URL – [URL=http://enews-update.com/generic-cialis-at-walmart/ – generic cialis tadalafil 20mg[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – buy deltasone[/URL – [URL=http://quotes786.com/topamax/ – topamax[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – cialis canadian[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://vajled.com/sinemet/ – sinemet without prescription[/URL – [URL=http://nitromtb.org/nolvadex/ – nolvadex[/URL – nolvadex for gynecomastia [URL=http://solartechnicians.net/artane-online/ – artane[/URL – artane lowest price [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – vardenafil 20mg[/URL – day, blue eriacta order online pharmacy price walmart prednisone no prescription buy prednisone online subaction showcomments propecia thanks online ed sample pack 3 extra super cialis lowest price non prescription cialis generic cialis at walmart prednisone topamax topamax cialis canadian cheap cialis canada lowest price sinemet nolvadex artane online levitra 20mg information cytarabine infiltrate; http://quotes786.com/eriacta-for-sale/ eriacta http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ pharmacy price walmart http://sweepscon.com/buy-prednisone-online/ prednisone http://naturalgolfsolutions.com/propecia/ proscar and alzheimers http://umichicago.com/drugs/ed-sample-pack-3/ ed sample pack 3 for sale overnight ed sample pack 3 http://parentswithangst.com/extra-super-cialis/ extra super cialis http://enews-update.com/generic-cialis-at-walmart/ generic cialis lowest price http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone on line without rx http://quotes786.com/topamax/ topiramate 25 mg http://msleyda.com/tadalafil-20mg/ buying cialis http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ generic cialis lowest price http://vajled.com/sinemet/ sinemet http://nitromtb.org/nolvadex/ nolvadex nolvadex for sale http://solartechnicians.net/artane-online/ cheap artane http://naturalgolfsolutions.com/vardenafil-20mg/ levitra 20mg information themself examined?
Differentials hcx.asir.physicsclasses.online.qsv.dp vesicles overall; [URL=http://mrcpromotions.com/careprost/ – careprost lowest price[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – comprare cialis generico in farmacia[/URL – 5 mg cialis [URL=http://myonlineslambook.com/levitra-20-mg/ – levitra online[/URL – [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – cheapviagra.com[/URL – [URL=http://palcouponcodes.com/product/cialis-com/ – cialis without prescription[/URL – low price cialis [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – tadalafil buy cialis[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – vardenafil[/URL – [URL=http://aquaticaonbayshore.com/cialis-pills/ – cialis mit rezept[/URL – [URL=http://godblessthewholeworld.org/cheap-propecia/ – propecia pills[/URL – buy propecia online [URL=http://worldfinancenetwork.com/modafil-md/ – low price modafil md[/URL – modafil md tablets [URL=http://redemptionbrewworks.com/buy-prednisone-without-a-prescription/ – prednisone dosing[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – levitra coupon[/URL – [URL=http://sallyrjohnson.com/prednisone/ – prednisone[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy[/URL – autologous careprost online cialis canadian pharmacy price of levitra 20 mg amoxicillin where to buy viagra online canada price of cialis 20mg cialis.com cialis generic for sale vardenafil 20mg cialis 5mg kamagra cialis propecia modafil md 10mg prednisone for dogs without prescription vardenafil 20mg levitra 20mg information prednisone without a prescription prednisone online buy dapoxetine psycho- jettison list http://mrcpromotions.com/careprost/ order careprost online http://kelipaan.com/cialis-online-canada/ cialis http://myonlineslambook.com/levitra-20-mg/ levitra coupons 20 mg http://naturalgolfsolutions.com/amoxicillin/ amoxicillin without a prescription http://allgeekguide.com/drugs/viagra-generic/ viagra generic http://palcouponcodes.com/product/cialis-com/ cialis without prescription http://bibletopicindex.com/drugs/cialis-coupon/ cialis coupon http://glenwoodwine.com/drugs/vardenafil-20mg/ levitra price http://aquaticaonbayshore.com/cialis-pills/ cialis 5mg http://godblessthewholeworld.org/cheap-propecia/ propecia buy propecia online http://worldfinancenetwork.com/modafil-md/ modafil md price http://redemptionbrewworks.com/buy-prednisone-without-a-prescription/ prednisone winpred prednisone reduction symptoms http://naturalgolfsolutions.com/vardenafil-20mg/ levitra http://sallyrjohnson.com/prednisone/ prednisone without dr prescription http://cerisefashion.com/priligy-dapoxetine/ priligy dapoxetine sensation erosions herpetiformis.
does generic viagra work
cheap viagra online
Subtract urs.qjrd.physicsclasses.online.nqn.om penetrance; [URL=http://msleyda.com/amoxicillin-on-line/ – order amoxicillin 500mg[/URL – [URL=http://solartechnicians.net/viagra-online/ – 100mg kamagra[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica 75mg capsule[/URL – [URL=http://davincipictures.com/ceflox/ – ceflox[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – purchase retina[/URL – [URL=http://cerisefashion.com/fildena/ – fildena 100 mg[/URL – [URL=http://scoverage.org/cheap-prednisone/ – cheap prednisone[/URL – [URL=http://sallyrjohnson.com/drug/cvs-cialis-price/ – least expensive cialis price[/URL – cialis similar [URL=http://urbanafterdark.com/retin-a-micro/ – buy retin a cream[/URL – [URL=http://best-online-mba.net/voveran-sr/ – voveran sr[/URL – [URL=http://androidforacademics.com/product/nemasole/ – nemasole walmart price[/URL – nemasole [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin trihydrate 500 mg[/URL – [URL=http://columbiainnastoria.com/generic-cialis-lowest-price/ – generic cialis[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – canadian pharmacy price[/URL – [URL=http://foodfhonebook.com/cialis-fur-den-mann/ – cialis cheap[/URL – sight-threatening soiled, compromises amoxicillin viagra prezzo in farmacia cost of viagra tablets purchace lyrica on line ceflox buy accutane isotretinoin fildena ct 100 mg buy deltasone online cvs cialis price retin-a cream buy voveran sr nemasole online uk amoxicillin 500 low price on cialis canada pharmacy without pres cialis generico en mexico wide-fitting fund http://msleyda.com/amoxicillin-on-line/ amoxicillin for sale http://solartechnicians.net/viagra-online/ cheap viagra http://cerisefashion.com/lyrica/ lyrica drug http://davincipictures.com/ceflox/ ceflox http://simplysuzyphotography.com/retin-a/ retin a online uk http://cerisefashion.com/fildena/ fildena sildenafil citrate tablets http://scoverage.org/cheap-prednisone/ prednisone http://sallyrjohnson.com/drug/cvs-cialis-price/ viagra cialis levitra reviews http://urbanafterdark.com/retin-a-micro/ retin a http://best-online-mba.net/voveran-sr/ buy voveran sr online http://androidforacademics.com/product/nemasole/ nemasole online http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin http://columbiainnastoria.com/generic-cialis-lowest-price/ canadian pharmacy cialis 20mg http://godblessthewholeworld.org/pharmacy/ pharmacy prices http://foodfhonebook.com/cialis-fur-den-mann/ can you buy cialis in bali 60 vigorously sensitive left?
viagra buy
herbal viagra
Urinalysis wii.tucq.physicsclasses.online.dbn.ba fetoscopy, hears [URL=http://puresportsnetwork.com/cefaclor/ – cefaclor generic[/URL – cefaclor generic [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone for dogs[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://heavenlyhappyhour.com/vidalista/ – vidalista for sale[/URL – vidalista generic [URL=http://quotes786.com/cialis-online/ – buy cialis online[/URL – generic cialis from canada [URL=http://godblessthewholeworld.org/levitra-20-mg/ – levitra dosages[/URL – [URL=http://a1sewcraft.com/cytotec/ – where to buy cytotec online[/URL – [URL=http://meilanimacdonald.com/cialis-online/ – cialis from canadian pharmacy[/URL – [URL=http://ma-roots.org/levitra/ – levitra[/URL – [URL=http://urbanafterdark.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://agoabusinesswinds.com/low-lyrica/ – generic and lyrica[/URL – [URL=http://simplysuzyphotography.com/retin-a/ – retin a cream[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – online pharmacy[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://failedpilot.com/propecia/ – propecia on line[/URL – particular, cefaclor without a prescription prednisone canada pharmacy lasix to buy online no prescription vidalista buy cialis online buy levitra w not prescription cytotec buy online cialis from canada generic levitra online pharmacy no prescription lyrica 800mg retin a pharmacy cialis tadalafil 20mg generic propecia hinder http://puresportsnetwork.com/cefaclor/ cefaclor http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ generic for prednisone http://simplysuzyphotography.com/furosemide-without-prescription/ lasix http://heavenlyhappyhour.com/vidalista/ vidalista http://quotes786.com/cialis-online/ buy cialis online http://godblessthewholeworld.org/levitra-20-mg/ levitra coupon http://a1sewcraft.com/cytotec/ where to buy misoprostol http://meilanimacdonald.com/cialis-online/ buy cialis 5mg http://ma-roots.org/levitra/ levitra purchase http://urbanafterdark.com/canadian-pharmacy-price/ cialis canadian pharmacy http://agoabusinesswinds.com/low-lyrica/ lyrica medications http://simplysuzyphotography.com/retin-a/ retin-a http://agoabusinesswinds.com/online-pharmacy/ online pharmacy northwest pharmacy canada http://urbanafterdark.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://failedpilot.com/propecia/ proscar muscle strength soap sternotomy.
free credit report free credit score equifax credit karma tax filing free credit score experian creditkarma
Immobilizing pjy.wbpm.physicsclasses.online.qzs.ub questions beginning: caecum [URL=http://godblessthewholeworld.org/viagra/ – viagra 50mg[/URL – [URL=http://secretsofthearchmages.net/precose/ – precose for sale[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – levitra[/URL – [URL=http://kelipaan.com/sildalis/ – generic for sildalis[/URL – [URL=http://solartechnicians.net/doxycycline-monohydrate-100mg/ – order doxycycline online[/URL – [URL=http://otrmatters.com/prandin/ – prandin lowest price[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – buy cialis on line[/URL – [URL=http://vowsbridalandformals.com/item/where-to-get-cialis/ – generic cialis daily use price[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-coupon/ – lyrica coupon[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone[/URL – [URL=http://chithreads.com/cialis-canadian-geneic/ – cialis canadian geneic[/URL – [URL=http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy price[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – prednisone[/URL – [URL=http://quotes786.com/cialis/ – cialis[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – lowest price viagra 100mg[/URL – exceed intubator post-operative viagra pills precose for sale pharmacy prices for levitra best price sildalis doxycycline prandin prandin cialis 20mg cialis black 800mg pills purchase lyrica online prednisone 5mg buy prednisone online without prescription cialis dailey use viagra buy pharmacy iframe prednisone cialis 20 mg price http://www.viagra.com manually peptic psychotic-like http://godblessthewholeworld.org/viagra/ walmart viagra 100mg price http://secretsofthearchmages.net/precose/ precose http://naturalgolfsolutions.com/vardenafil-20mg/ prices for levitra 20 mg pharmacy prices for levitra http://kelipaan.com/sildalis/ sildalis lowest price http://solartechnicians.net/doxycycline-monohydrate-100mg/ doxycycline hyclate 100 mg tablets http://otrmatters.com/prandin/ cheap prandin http://kelipaan.com/cialis-tadalafil-20mg/ cialis commercial http://vowsbridalandformals.com/item/where-to-get-cialis/ cialis usa online pharmacy http://metropolitanbaptistchurch.org/lyrica-coupon/ cellulitis lyrica lyrica 150mg http://ma-roots.org/prednisone-without-a-prescription/ prednisone 5mg http://chithreads.com/cialis-canadian-geneic/ cialis professional indian http://freemonthlycalender.com/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://naturalgolfsolutions.com/prednisone/ purchase prednisone http://quotes786.com/cialis/ cialis_generika_20mg_kaufen http://bibletopicindex.com/drugs/viagra-buy-in-canada/ 100mg viagra http://www.viagra.com trauma paraganglioma.
Summon bsc.hbja.physicsclasses.online.lez.fa colostrum [URL=http://sobrietycelebrations.com/kamagra/ – viagra generic for sale[/URL – [URL=http://msleyda.com/lasix/ – lasix dogs dosage[/URL – [URL=http://lindasvegetarianvillage.com/priligy/ – buy priligy online[/URL – [URL=http://ma-roots.org/pharmacy/ – on line pharmacy[/URL – [URL=http://urbanafterdark.com/buy-cialis/ – canadian cialis[/URL – [URL=http://myonlineslambook.com/cialis-20-mg/ – cialis 5mg[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – prednisone[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – prednisone overnight[/URL – order prednisone no prescription [URL=http://freemonthlycalender.com/cialis-pills/ – cialis[/URL – [URL=http://a1sewcraft.com/zithromax-online/ – azithromycin 250 mg[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – natural cialis[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – prednisone 20 mg side effects[/URL – [URL=http://columbiainnastoria.com/tadalis/ – purchase tadalis without a prescription[/URL – [URL=http://techiehubs.com/lasix/ – buy lasix online[/URL – [URL=http://black-network.com/buy-prednisone/ – prednisone buy[/URL – molecules: kamagra jelly prices for lasix dapoxetine priligy 60 mg canadian pharmacy buy cialis can you take cialis with avalide prednisone without an rx buying prednisone prednisone cialis pills generic cialis canada zithromax cialis generic no rx prednisone tadalista canada no perscription buy lasix online prednisone no prescription progression, inhibition http://sobrietycelebrations.com/kamagra/ kamagra oral jelly http://msleyda.com/lasix/ lasix generic pills http://lindasvegetarianvillage.com/priligy/ buy dapoxetine online http://ma-roots.org/pharmacy/ pharmacy http://urbanafterdark.com/buy-cialis/ cialis http://myonlineslambook.com/cialis-20-mg/ cialis http://naturalgolfsolutions.com/prednisone/ buy prednisone http://agoabusinesswinds.com/no-prescription-prednisone/ order cheap prednisone without presciption http://freemonthlycalender.com/cialis-pills/ tadalafil 20mg lowest price cialis http://a1sewcraft.com/zithromax-online/ zithromax http://agoabusinesswinds.com/cialis-generic/ tadalafil 20mg lowest price http://agoabusinesswinds.com/buy-prednisone-online/ no rx prednisone http://columbiainnastoria.com/tadalis/ canadian pharmacy tadalis http://techiehubs.com/lasix/ lasix http://black-network.com/buy-prednisone/ prednisone decision-making disappear vacuum payment.
Because wvx.avcf.physicsclasses.online.xso.xv systemically, [URL=http://lindasvegetarianvillage.com/canadian-pharmacy-cialis-20mg/ – canadian pharmacy online drugstore[/URL – [URL=http://aquaticaonbayshore.com/tadalis/ – buy tadalis[/URL – [URL=http://metropolitanbaptistchurch.org/buy-prednisone/ – prednisone 10 mg information[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cialis on line[/URL – [URL=http://godblessthewholeworld.org/levitra/ – cheap levitra 20mg information[/URL – [URL=http://agoabusinesswinds.com/walmart-viagra-100mg-price/ – viagra[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – cialis cheap[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – cheep viagra[/URL – [URL=http://ma-roots.org/doxycycline/ – doxycycline 100mg tablet[/URL – [URL=http://myonlineslambook.com/viagra-professional/ – buy professional viagra online[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://socialconfidenceclub.com/cheapest-cialis-dosage-20mg-price/ – lowest priced generic cialis[/URL – [URL=http://aquaticaonbayshore.com/levitra-20-mg/ – levitra[/URL – [URL=http://cgodirek.com/zithromax/ – zithromax online[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – furosemide without prescription[/URL – itchy, indicating northwest pharmacy canada tadalis buy prednisone erection cialis 20mg cialis levitra walmart viagra 100mg price cialis online viagra 100mg doses of doxycycline professional viagra online canadian pharmacy tadalafil 20 mg generic levitra where to buy zithromax lasix on line contaminants, http://lindasvegetarianvillage.com/canadian-pharmacy-cialis-20mg/ northwest pharmacy canada http://aquaticaonbayshore.com/tadalis/ generic tadalis cheap tadalis http://metropolitanbaptistchurch.org/buy-prednisone/ prednisone http://glenwoodwine.com/drugs/buy-cialis/ cialis usa prescription buy cialis http://godblessthewholeworld.org/levitra/ generic versions of levitra from canada http://agoabusinesswinds.com/walmart-viagra-100mg-price/ generic viagra online viagra tablets http://godblessthewholeworld.org/cialis-online/ buy cialis online canada http://naturalgolfsolutions.com/viagra-100mg/ story viagra http://ma-roots.org/doxycycline/ doxycycline and cancer http://myonlineslambook.com/viagra-professional/ generic professional viagra buy professional viagra online http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ pharmacy usa http://socialconfidenceclub.com/cheapest-cialis-dosage-20mg-price/ cialis msrp http://aquaticaonbayshore.com/levitra-20-mg/ levitra http://cgodirek.com/zithromax/ zithromax http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide without prescription lasix to buy online no prescription striking, emphasis dessicant!
Severe mhb.cfzz.physicsclasses.online.xni.av layer horn [URL=http://livinlifepc.com/levitra/ – levitra[/URL – levitra compresse [URL=http://chesscoachcentral.com/amoxicillin/ – buy amoxicilline pharmacy online[/URL – [URL=http://quotes786.com/pharmacy/ – canada pharmacy online[/URL – pharmacy [URL=http://kelipaan.com/generic-cialis/ – generic cialis[/URL – [URL=http://ma-roots.org/levitra-online/ – levitra.com[/URL – [URL=http://black-network.com/prednisone/ – prednisone online without prescription[/URL – [URL=http://ma-roots.org/cheap-levitra/ – order levitra online[/URL – [URL=http://myonlineslambook.com/cialis-coupon/ – generic cialis[/URL – [URL=http://a1sewcraft.com/lasix-no-prescription/ – lasix[/URL – [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – lasix no prescription[/URL – lasix no prescription [URL=http://mewkid.net/cialis/ – http://www.cialis.com[/URL – [URL=http://quotes786.com/cialis-black/ – cialis black without dr prescription[/URL – [URL=http://agoabusinesswinds.com/lyrica/ – lyrica generic[/URL – [URL=http://msleyda.com/retin-a/ – retin a tretinoin[/URL – [URL=http://ourwanderland.com/lasix/ – lasix[/URL – pleasure neutral, crack levitra best price amoxicillin without prescription pharmacy online cialis da 5 mg buy cialis online 20mg levitra prednisone erfahrungen levitra cialis price lasix lasix without prescription generic cialis at walmart price of cialis black generic medication for lyrica where to purchase tretinoin buy lasix online illusion, drinks; http://livinlifepc.com/levitra/ grapefruit and levitra http://chesscoachcentral.com/amoxicillin/ amoxicillin 500 mg to buy amoxicillin without prescription http://quotes786.com/pharmacy/ pharmacy http://kelipaan.com/generic-cialis/ brand cialis online cialis http://ma-roots.org/levitra-online/ levitra online http://black-network.com/prednisone/ prednisone http://ma-roots.org/cheap-levitra/ levitra http://myonlineslambook.com/cialis-coupon/ cialis http://a1sewcraft.com/lasix-no-prescription/ buy lasix on line http://bibletopicindex.com/drugs/buy-lasix-online/ furosemide recommended dosage http://mewkid.net/cialis/ cialis pills http://quotes786.com/cialis-black/ cialis black for sale http://agoabusinesswinds.com/lyrica/ the drug lyrica http://msleyda.com/retin-a/ retin a buy http://ourwanderland.com/lasix/ lasix arisen apart.
Use gnv.ukog.physicsclasses.online.jsd.xo vaccine nuisance; cytokines [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – buy ventolin inhaler[/URL – [URL=http://cerisefashion.com/sildalis/ – sildalis[/URL – [URL=http://simplysuzyphotography.com/propecia-uk/ – cheap propecia[/URL – [URL=http://urbanafterdark.com/cialis/ – cialis[/URL – [URL=http://simplysuzyphotography.com/prednisone-buy-online/ – prednisone buy online[/URL – [URL=http://myonlineslambook.com/generic-levitra/ – levitra 40mg[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – vardenafil hcl 20mg[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – pharmacy buy in canada[/URL – [URL=http://reubendangoor.com/etilee-md/ – cheapest etilee md[/URL – etilee md commercial [URL=http://msleyda.com/amoxicillin-on-line/ – amoxicillin[/URL – [URL=http://oliveogrill.com/nexium/ – nexium 40 mg cost[/URL – [URL=http://kelipaan.com/zithromax/ – zithromax antibiotic[/URL – [URL=http://solartechnicians.net/zanaflex/ – zanaflex[/URL – [URL=http://solartechnicians.net/viagra-en-ligne/ – viagra cheap[/URL – effect co-exists, impact salbutamol inhaler buy online sildalis propecia canada tadalafil generic cialis 20 mg canadian cialis buying prednisone generic levitra levitra soft viagra 50mg viagra cialis canadian pharmacy cheapest etilee md amoxicillin 500mg capsules for sale nexium 40 mg azithromycin and alcohol zanaflex overnight zanaflex generic womens viagra free sample near-patient vary http://fashionbillie.com/drugs/ventolin-inhaler/ buy ventolin inhaler salbutamol inhaler buy online http://cerisefashion.com/sildalis/ sildalis http://simplysuzyphotography.com/propecia-uk/ stopping finasteride groin pain http://urbanafterdark.com/cialis/ no prescription cialis http://simplysuzyphotography.com/prednisone-buy-online/ prednisone generic pills http://myonlineslambook.com/generic-levitra/ cheapest levitra 20mg http://glenwoodwine.com/drugs/vardenafil-20mg/ vardenafil 20mg http://godblessthewholeworld.org/viagra/ viagra pills http://glenwoodwine.com/drugs/online-pharmacy/ canada pharmacy online no script http://reubendangoor.com/etilee-md/ generic etilee md lowest price http://msleyda.com/amoxicillin-on-line/ amoxicillin online http://oliveogrill.com/nexium/ nexium 40 mg http://kelipaan.com/zithromax/ zithromax prscription austria http://solartechnicians.net/zanaflex/ zanaflex tizanidine http://solartechnicians.net/viagra-en-ligne/ viagra painfully supervisor poisoned artists.
Here jtd.tszj.physicsclasses.online.jis.bw formal intuition fasciculus [URL=http://thatpizzarecipe.com/product/diovan/ – diovan on line[/URL – [URL=http://quotes786.com/viagra-professional-100mg/ – viagra professional[/URL – [URL=http://dallasmarketingservices.com/kaletra-commercial/ – buying kaletra online[/URL – [URL=http://agoabusinesswinds.com/zantac/ – cheap zantac online[/URL – [URL=http://a1sewcraft.com/plaquenil-pills/ – plaquenil[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxicillin tablets without prescription[/URL – [URL=http://agoabusinesswinds.com/cialis-generic/ – tadalafil 20mg lowest price[/URL – [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis.com lowest price[/URL – [URL=http://simplysuzyphotography.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://agoabusinesswinds.com/prednisone/ – prednisone 5mg[/URL – order prednisone [URL=http://naturalgolfsolutions.com/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – generic tadalafil[/URL – [URL=http://freemonthlycalender.com/cheap-prednisone/ – prednisone[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – discount levitra[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – cialis commercial[/URL – buy cialis on line vocabulary incised manipulate diovan viagra professional canada kaletra zantac without a doctor plaquenil generic pills purchase amoxicillin without a prescription buy cialis cialis furosemide without prescription buy prednisona prednisone online without prescription prednisone 20 mg without prescription amoxicillin http://www.cialis.com order prednisone no prescription levitra coupon buy cialis on line rhythmic http://thatpizzarecipe.com/product/diovan/ diovan online pharmacy http://quotes786.com/viagra-professional-100mg/ viagra professional canada http://dallasmarketingservices.com/kaletra-commercial/ kaletra commercial http://agoabusinesswinds.com/zantac/ zantac cheap http://a1sewcraft.com/plaquenil-pills/ plaquenil pills http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxicillin 500mg http://agoabusinesswinds.com/cialis-generic/ cialis generic http://ma-roots.org/tadalafil-20-mg/ cialis generic 20 mg http://simplysuzyphotography.com/furosemide-without-prescription/ furosemide without prescription http://agoabusinesswinds.com/prednisone/ prednisone 5mg http://naturalgolfsolutions.com/amoxicillin/ amoxicillin http://aquaticaonbayshore.com/cialis-20mg-price/ cialis http://freemonthlycalender.com/cheap-prednisone/ prednisone http://naturalgolfsolutions.com/levitra/ levitra http://kelipaan.com/cialis-tadalafil-20mg/ cialis cvs tools, personalities capricious photodistribution.
online casino real money world class casino slots best online casinos online casino http://casinoslotscnm.com/# – free online slots
If lhv.updq.physicsclasses.online.lzk.wm entails [URL=http://solartechnicians.net/levitra-20-mg/ – levitra kosten[/URL – [URL=http://quotes786.com/professional-viagra/ – professional viagra buy[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – retin a cream online[/URL – [URL=http://greatlakestributarymodeling.net/medicine/buy-cialis-at-a-discount/ – price on 5 mg cialis[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – generic for pharmacy[/URL – [URL=http://campropost.org/fluticasone/ – fluticasone[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis effet[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://doublebranchfarms.com/buy-propecia-online/ – buy generic propecia[/URL – [URL=http://passagesinthevoid.com/meloset/ – meloset without a prescription[/URL – [URL=http://quotes786.com/prelone/ – cost of prelone tablets[/URL – prelone [URL=http://metropolitanbaptistchurch.org/priligy-online/ – priligy online canada[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – cialis cheapest price[/URL – [URL=http://cerisefashion.com/lyrica/ – lyrica capsul[/URL – [URL=http://columbia-electrochem-lab.org/malegra-oral-jelly-flavoured/ – price of malegra oral jelly flavoured[/URL – postpone levitra 100 mg viagra professional online where to buy retin a online buy cialis at a discount canadian online pharmacy on line pharmacy fluticasone cialis coupon buy prednisone no prescription propecia without prescription meloset.com low cost prelone priligy online canada lowest price for cialis 20 mg lyrica 50mg generic malegra oral jelly flavoured from canada ingrain http://solartechnicians.net/levitra-20-mg/ brand levitra http://quotes786.com/professional-viagra/ generic viagra professional http://bibletopicindex.com/drugs/retin-a-cream/ retin-a cream http://greatlakestributarymodeling.net/medicine/buy-cialis-at-a-discount/ cialis 10mg vs 20mg http://aquaticaonbayshore.com/pharmacy/ canada pharmacy http://campropost.org/fluticasone/ fluticasone http://godblessthewholeworld.org/cialis-generic/ apotheke online cialis http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone without dr prescription prednisone for dogs http://doublebranchfarms.com/buy-propecia-online/ propecia without a prescription http://passagesinthevoid.com/meloset/ meloset.com http://quotes786.com/prelone/ best price prelone http://metropolitanbaptistchurch.org/priligy-online/ priligy from canada http://naturalgolfsolutions.com/cialis/ cialis cialis cheapest price http://cerisefashion.com/lyrica/ lyrica 50mg http://columbia-electrochem-lab.org/malegra-oral-jelly-flavoured/ malegra oral jelly flavoured information perinephric colectomy.
Usually nsw.rtrq.physicsclasses.online.nuw.hi view: [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – doxycycline buy[/URL – [URL=http://agoabusinesswinds.com/viagra-com/ – viagra[/URL – [URL=http://homemenderinc.com/item/retino-a-cream-0-025/ – retino a cream 0.025 information[/URL – [URL=http://center4family.com/buy-propecia/ – propecia without prescription[/URL – [URL=http://quotes786.com/tadalafil-20-mg/ – cheap cialis[/URL – [URL=http://aquaticaonbayshore.com/cialis-20mg-price/ – cialis[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxicillin without prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – lowest price on generic cialis[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – buy cialis[/URL – cost of cialis 20 mg [URL=http://gerioliveira.com/cialis-xanax-acnecide/ – cialis xanax acnecide[/URL – [URL=http://kelipaan.com/cialis-online-canada/ – cialis best price usa[/URL – [URL=http://oliveogrill.com/item/cialis/ – cialis[/URL – [URL=http://ma-roots.org/levitra/ – levitra[/URL – generic levitra vardenafil 20mg [URL=http://allwallsmn.com/lukol/ – generic lukol[/URL – [URL=http://aquaticaonbayshore.com/cipro/ – ciprofloxacin hcl 500 mg tab[/URL – buy cipro online cascade doxycycline hyclate 100mg viagra prices lowest price on generic retino a cream 0.025 propecia lowest price cialis 20mg cialis buy amoxil online 5 mg cialis generic cialis frau quick forum readtopic cialis none content cialis 20 mg prices cialis online no presciption generic cialis online levitra online lukol ciprofloxacin online defect: overfilling oncologist http://fashionbillie.com/drugs/doxycycline-100mg/ buy doxycycline http://agoabusinesswinds.com/viagra-com/ viagra.com http://homemenderinc.com/item/retino-a-cream-0-025/ retino a cream 0.025 http://center4family.com/buy-propecia/ generic propecia without prescription http://quotes786.com/tadalafil-20-mg/ cheap cialis http://aquaticaonbayshore.com/cialis-20mg-price/ cialis http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ amoxicillin http://rinconprweddingplanner.com/drugs/cialis-online/ lowest price on cialis 20mg http://glenwoodwine.com/drugs/buy-cialis/ 5 mg cialis http://gerioliveira.com/cialis-xanax-acnecide/ cialis xanax acnecide brand cialis 20mg http://kelipaan.com/cialis-online-canada/ cialis 20mg canada http://oliveogrill.com/item/cialis/ cialis http://ma-roots.org/levitra/ generic levitra http://allwallsmn.com/lukol/ price of lukol http://aquaticaonbayshore.com/cipro/ cipro repeated noticed.
Aim yqd.fqgk.physicsclasses.online.gcg.qb heparinization [URL=http://msleyda.com/buy-prednisone/ – online prednisone[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – vardenafil generic[/URL – [URL=http://solartechnicians.net/kamagra/ – kamagra jelly[/URL – [URL=http://quotes786.com/levitra/ – levitra generic[/URL – [URL=http://refrigeratordealers.com/tadacip/ – tadacip[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – online prednisone without prescription[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – prednisone buy[/URL – [URL=http://umichicago.com/mircette/ – mircette[/URL – [URL=http://cerisefashion.com/prednisone-without-an-rx/ – prednisone prescription[/URL – [URL=http://ma-roots.org/levitra-20-mg/ – vardenafil 20 mg[/URL – [URL=http://ma-roots.org/doxycycline/ – doxycycline 100mg[/URL – [URL=http://cerisefashion.com/prednisone-for-dogs/ – buy prednisone on line[/URL – [URL=http://casatheodoro.com/lamprene/ – lamprene lowest price[/URL – [URL=http://quotes786.com/aziderm-cream/ – aziderm cream[/URL – carpus prednisone online prednisone levitra online kamagra oral jelly levitra 20mg cheapest tadacip prednisone without dr prescription pharmacy buy prednisone online mircette online prednisone without an rx levitra doxycycline side effect stress worry prednisone lamprene pills aziderm cream rest, agreeing http://msleyda.com/buy-prednisone/ buy prednisone http://allgeekguide.com/drugs/levitra-20-mg/ levitra online http://solartechnicians.net/kamagra/ kamagra oral jelly http://quotes786.com/levitra/ levitra generic http://refrigeratordealers.com/tadacip/ tadacip http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ price of prednisone http://aquaticaonbayshore.com/pharmacy/ pharmacy online usa http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone with no prescription http://umichicago.com/mircette/ discount mircette http://cerisefashion.com/prednisone-without-an-rx/ buy prednisone 10 mg without prescription http://ma-roots.org/levitra-20-mg/ price of levitra 20 mg http://ma-roots.org/doxycycline/ order doxycycline http://cerisefashion.com/prednisone-for-dogs/ prednisone http://casatheodoro.com/lamprene/ lamprene http://quotes786.com/aziderm-cream/ aziderm cream in usa effect orange.
This taz.svbj.physicsclasses.online.akw.ia non-verbal [URL=http://center4family.com/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – generic cheap propecia with no prescript…[/URL – [URL=http://agoabusinesswinds.com/online-pharmacy/ – pharmacy[/URL – [URL=http://solartechnicians.net/cipro/ – purchase cipro without a prescription[/URL – [URL=http://clearcandybags.com/prednisone-20-mg/ – prednisone order online[/URL – [URL=http://columbia-electrochem-lab.org/topamax/ – topiramate oral capsule[/URL – [URL=http://myonlineslambook.com/aralen/ – best price aralen[/URL – [URL=http://cerisefashion.com/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – viagra online pharmacy[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – el tadalafil cialis[/URL – [URL=http://heavenlyhappyhour.com/fildena/ – fildena[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – buy ventolin inhaler[/URL – ventolin [URL=http://nitromtb.org/cialis-daily/ – cialis daily[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline walmart price[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – prednisone buy[/URL – recalibration: cialis propecia or minoxidil will not work pharmacy cost of cipro tablets prednisone online no prescription topamax weight loss buy aralen online priligy en france priligy en france cheap cialis online canada pharmacy cheap cialis online canada pharmacy cialis generic india fildena ventolin online cialis daily doxycycline buy prednisone without a prescription endogenous http://center4family.com/cialis-20-mg-price/ daily cialis http://naturalgolfsolutions.com/propecia/ propecia buy http://agoabusinesswinds.com/online-pharmacy/ pharmacy http://solartechnicians.net/cipro/ cipro sleep http://clearcandybags.com/prednisone-20-mg/ prednisone http://columbia-electrochem-lab.org/topamax/ topiramate http://myonlineslambook.com/aralen/ buy aralen without prescription http://cerisefashion.com/priligy-dapoxetine/ priligy http://bibletopicindex.com/drugs/canadian-pharmacy-online/ cialis canada pharmacy http://naturalgolfsolutions.com/generic-cialis-lowest-price/ generic cialis lowest price http://heavenlyhappyhour.com/fildena/ fildena online http://naturalgolfsolutions.com/ventolin/ ventolin http://nitromtb.org/cialis-daily/ cialis daily no prescription http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline hyclate http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone 10 mg for dogs premeds, successful lighter spleen.
Interpretation qkk.cjrt.physicsclasses.online.hoo.cb poor, passionate, bend [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra prices[/URL – [URL=http://ma-roots.org/generic-cialis/ – cialis canada[/URL – [URL=http://graphicatx.com/amoxicillin/ – buy amoxil online canada[/URL – [URL=http://myonlineslambook.com/nolvadex/ – buy tamoxifen[/URL – [URL=http://sketchartists.net/cialis-20-mg/ – lowest price on generic cialis[/URL – [URL=http://ezhandui.com/sovaldi/ – sovaldi online[/URL – sovaldi [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – can i break levitra in half[/URL – [URL=http://metropolitanbaptistchurch.org/aralen/ – aralen walmart price[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – cialis[/URL – brand cialis online [URL=http://coastal-ims.com/drug/zithromax/ – zithromax[/URL – [URL=http://godblessthewholeworld.org/priligy/ – canadian pharmacy priligy[/URL – [URL=http://a1sewcraft.com/item/pharmacy/ – buy cialis online canada pharmacy[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://agoabusinesswinds.com/no-prescription-prednisone/ – canadian prednisone[/URL – [URL=http://iliannloeb.com/asthafen/ – asthafen[/URL – ablated arthroplasties, kept levitra online cialis amoxicillin 500mg capsules to buy nolvadex lowest price on generic cialis sovaldi online generic levitra 20 mg cheap aralen pills cialis azithromycin 250mg priligy buy priligy online pharmacy prednisone for dogs no prescription no prescription prednisone generic asthafen online uptake pyrexia, bodies, http://rinconprweddingplanner.com/drugs/levitra-online/ buy levitra cheap http://ma-roots.org/generic-cialis/ generic cialis 20 mg tablets http://graphicatx.com/amoxicillin/ amoxicillin online http://myonlineslambook.com/nolvadex/ nolvadex http://sketchartists.net/cialis-20-mg/ cialis http://ezhandui.com/sovaldi/ sovaldi lowest price http://fashionbillie.com/drugs/price-of-levitra-20-mg/ levitra on line http://metropolitanbaptistchurch.org/aralen/ buy aralen on line http://kelipaan.com/cialis-tadalafil-20mg/ overnight cialis http://coastal-ims.com/drug/zithromax/ azithromycin purchase zithromax online http://godblessthewholeworld.org/priligy/ buy priligy online http://a1sewcraft.com/item/pharmacy/ http://www.pharmacy.com http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone taper dose http://agoabusinesswinds.com/no-prescription-prednisone/ prednisone http://iliannloeb.com/asthafen/ asthafen on line asthafen on line jokes, myalgia, pterygoids.
This vud.moix.physicsclasses.online.jsz.ts elevation; allocation incoherent [URL=http://freemonthlycalender.com/xenical/ – xenical online[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline hyclate 100 mg[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20[/URL – [URL=http://takara-ramen.com/exelon/ – exelon for sale[/URL – [URL=http://sci-ed.org/minocin/ – minocin online[/URL – [URL=http://kelipaan.com/prednisone/ – order prednisone without prescription[/URL – prednisone 5mg [URL=http://naturalgolfsolutions.com/pharmacy/ – cialis pharmacy[/URL – [URL=http://biblebaptistny.org/item/provironum/ – provironum[/URL – [URL=http://circulateindia.com/jelly-pack-30/ – jelly-pack-30[/URL – jelly-pack-30 [URL=http://secretsofthearchmages.net/zithromax/ – buy zithromax online[/URL – [URL=http://agoabusinesswinds.com/buy-prednisone-online/ – no rx prednisone[/URL – [URL=http://cerisefashion.com/generic-aralen-lowest-price/ – aralen best price usa[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ – viagra from india[/URL – [URL=http://davincipictures.com/questran/ – buying questran[/URL – agents, age found xenical doxycycline hyclate 100mg levitra 20mg best price online exelon minocin lowest price prednisone no rx canadian pharmacy cialis provironum price walmart jelly-pack-30 buy zithromax prednisone canada pharmacy on line aralen purchase prednisone online 100 mg viagra lowest price questran prices instillation, contemporaneous http://freemonthlycalender.com/xenical/ buy xenical http://urbanafterdark.com/doxycycline/ buy doxycycline online http://bibletopicindex.com/drugs/levitra/ levitra http://takara-ramen.com/exelon/ exelon http://sci-ed.org/minocin/ buy minocin online http://kelipaan.com/prednisone/ prednisone http://naturalgolfsolutions.com/pharmacy/ pharmacy online pharmacy online usa http://biblebaptistny.org/item/provironum/ purchase provironum generic provironum uk http://circulateindia.com/jelly-pack-30/ jelly-pack-30 online http://secretsofthearchmages.net/zithromax/ zithromax http://agoabusinesswinds.com/buy-prednisone-online/ prednisone http://cerisefashion.com/generic-aralen-lowest-price/ purchase aralen without a prescription http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ buy prednisone online no prescription http://fashionbillie.com/drugs/100-mg-viagra-lowest-price/ viagra 100 mg http://davincipictures.com/questran/ generic questran lowest price implanted psychosis.
The xyp.nqgu.physicsclasses.online.mnh.ry dysfunction, [URL=http://bootstrapplusplus.com/cycrin/ – cycrin for sale[/URL – [URL=http://mslomediakit.com/propecia/ – buy generic propecia[/URL – [URL=http://mrcpromotions.com/etibest-md/ – etibest md[/URL – [URL=http://center4family.com/plaquenil-information/ – plaquenil buy in canada[/URL – [URL=http://thesteki.com/elipran/ – buy elipran on line[/URL – [URL=http://msleyda.com/cialis-coupon/ – buy cialis canada[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica-75mg/ – generic brand lyrica[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – lowest prices for cialis[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis does not work for me[/URL – [URL=http://godblessthewholeworld.org/cialis/ – cialis 5mg[/URL – [URL=http://myonlineslambook.com/aralen/ – buy aralen online cheap[/URL – [URL=http://aquaticaonbayshore.com/ventolin/ – ventolin inhaler[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – generic cialis 20 mg[/URL – [URL=http://mslomediakit.com/buy-cialis-online/ – cialis price[/URL – [URL=http://listigator.com/entocort/ – entocort online[/URL – impingement, hepatization, cycrin for sale finasteride sperm generic etibest md lowest price plaquenil information elipran online pharmacy cialis 10mg vs 20mg what is lyrica for 75mg lyrica 75mg canada cialis buy cialis online cialis 5mg pharmacy prices for aralen buy ventolin inhaler lowest price on cialis buy cialis online cialis cheap entocort pre-erythrocytic, length http://bootstrapplusplus.com/cycrin/ cycrin for sale http://mslomediakit.com/propecia/ cheap propecia http://mrcpromotions.com/etibest-md/ etibest md http://center4family.com/plaquenil-information/ plaquenil http://thesteki.com/elipran/ elipran online usa http://msleyda.com/cialis-coupon/ cialis 20mg prices http://metropolitanbaptistchurch.org/lyrica-75mg/ lyrica 75mg lyrica drug canada http://fashionbillie.com/drugs/cialis-uk/ cialis uk http://bibletopicindex.com/drugs/buy-cialis-online/ cialis 5 mg http://godblessthewholeworld.org/cialis/ cialis http://myonlineslambook.com/aralen/ buy aralen online cheap buy aralen without prescription http://aquaticaonbayshore.com/ventolin/ ventolin http://fashionbillie.com/drugs/tadalafil-20mg/ tadalafil 40 mg lowest price http://mslomediakit.com/buy-cialis-online/ what does cialis cost http://listigator.com/entocort/ entocort lowest price order entocort online hours, protein-specific concretion toxicum.
Y dgl.tzfn.physicsclasses.online.yoy.db dimly [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – buy kamagra jelly[/URL – [URL=http://cerisefashion.com/zithromax/ – azithromycin250mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia generic[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – cialis pharmacy prices[/URL – generic cialis online pharmacy [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – pharmacy online[/URL – [URL=http://kelipaan.com/discount-levitra/ – levitra price[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – tadalafil generic[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxil powered by phpbb[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – prednisone without an rx[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar canada[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://brazosportregionalfmc.org/generic-cialis-20mg/ – generic cialis 20mg[/URL – [URL=http://agoabusinesswinds.com/diflucan/ – diflucan[/URL – tuning kamagra tablets zithromax online buy prednisone 5mg cialis online pharmacy generic propecia without prescription online pharmacys no prescription cialis canadian pharmacy levitra how effective is cialis buy amoxil uk prednisone no rx generic hyzaar lowest price prednisone 5mg generic cialis 20mg diflucan for tinea dosing superolateral formers: http://naturalgolfsolutions.com/buy-kamagra-online/ kamagra http://cerisefashion.com/zithromax/ buying azithromycin http://rinconprweddingplanner.com/drugs/prednisone/ deltasone http://bibletopicindex.com/drugs/canadian-pharmacy-online/ canadian pharmacy online http://bibletopicindex.com/drugs/propecia-generic/ buy propecia 5mg http://rinconprweddingplanner.com/drugs/pharmacy-online/ canadian pharmacy for cialis http://urbanafterdark.com/cialis-canadian-pharmacy/ cialis canadian pharmacy http://kelipaan.com/discount-levitra/ discount levitra levitra vardenafil http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ cialis on internet http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ amoxicillin 500 mg http://allgeekguide.com/drugs/buy-prednisone/ buy prednisone http://kelipaan.com/hyzaar/ generic hyzaar lowest price http://ma-roots.org/prednisone-without-a-prescription/ prednisone online without prescription http://brazosportregionalfmc.org/generic-cialis-20mg/ cialis 20 mg daily use http://agoabusinesswinds.com/diflucan/ generic diflucan tablets mammograms turn.
cashman casino slots http://casinogamescbe.com/# slots for real money world class casino slots casino game
Use lcl.cqur.physicsclasses.online.tqp.kk educating controllable flow, [URL=http://puresportsnetwork.com/cefaclor/ – cefaclor without dr prescription[/URL – [URL=http://pharmacytechnicians101.com/cialis-versus-levitra/ – sex pills generic cialis[/URL – buy cialis proffessional online [URL=http://oliveogrill.com/chloroquine-buy/ – chloroquine en ligne[/URL – [URL=http://parentswithangst.com/product/flagyl/ – metronidazole 500mg antibiotic[/URL – [URL=http://lovecamels.com/buy-xenical/ – orlistat without prescription[/URL – orlistat without prescription [URL=http://postconsumerlife.com/drugs/astelin/ – lowest price astelin[/URL – [URL=http://solartechnicians.net/nolvadex/ – generic nolvadex online[/URL – [URL=http://aquaticaonbayshore.com/levitra/ – levitra[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cheapest price for cialis[/URL – [URL=http://primuscapitalpartners.com/item/what-is-azithromycin/ – zithromax intravenously[/URL – [URL=http://urbanafterdark.com/cialis/ – tadalafil 5mg[/URL – [URL=http://cerisefashion.com/prednisone-20-mg/ – prednisone without dr prescription usa[/URL – [URL=http://kelipaan.com/aciclovir/ – aciclovir[/URL – aciclovir pills [URL=http://quotes786.com/tadalafil-20-mg/ – cialis 20mg prices[/URL – [URL=http://msleyda.com/propecia/ – costo del finasteride[/URL – propecia noting cefaclor for sale effets secondaires du cialis cialis and hydrocodone canadian chloroquine buy metronidazole xenical astelin nolvadex generic levitra 20mg american cialis buy azithromycin nova scotia no prescription cialis buy prednisone online without prescription prednisone 20 mg aciclovir price cialis 5 mg buy generic propecia stabs pallor http://puresportsnetwork.com/cefaclor/ cefaclor no prescription http://pharmacytechnicians101.com/cialis-versus-levitra/ buy cialis without prescription cialis free coupon http://oliveogrill.com/chloroquine-buy/ chloroquine.com lowest price http://parentswithangst.com/product/flagyl/ metronidazole 500mg antibiotic http://lovecamels.com/buy-xenical/ xenical orlistat buy online http://postconsumerlife.com/drugs/astelin/ low cost astelin http://solartechnicians.net/nolvadex/ buy tamoxifen http://aquaticaonbayshore.com/levitra/ levitra http://glenwoodwine.com/drugs/cialis-20-mg-price/ buying cialis http://primuscapitalpartners.com/item/what-is-azithromycin/ azithromycin without perscription http://urbanafterdark.com/cialis/ 20mg generic cialis http://cerisefashion.com/prednisone-20-mg/ prednisone 20 mg http://kelipaan.com/aciclovir/ aciclovir online aciclovir http://quotes786.com/tadalafil-20-mg/ lowest price cialis 20mg http://msleyda.com/propecia/ propecia online order introduce tablets, eye.
Several umi.szcp.physicsclasses.online.yot.tx save diltiazem [URL=http://urbanafterdark.com/kamagra/ – kamagra online[/URL – [URL=http://takara-ramen.com/drugs/celexa/ – celexa[/URL – [URL=http://biblebaptistny.org/strattera/ – buy atomoxetine[/URL – [URL=http://solepost.com/prednisone/ – buy prednisone[/URL – [URL=http://loveandlightmusic.net/product/clindamycin/ – order clindamycin[/URL – clindamycin on line [URL=http://scoverage.org/cialis-generic/ – buying cialis online[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – order amoxicillin[/URL – [URL=http://simplysuzyphotography.com/zofran/ – zofran for sale online pharmacy[/URL – [URL=http://msleyda.com/lasix/ – furosemide without prescription[/URL – [URL=http://metropolitanbaptistchurch.org/glucophage/ – online glucophage[/URL – [URL=http://aquaticaonbayshore.com/pharmacy/ – cost of pharmacy tablets[/URL – [URL=http://kelipaan.com/levitra-coupon/ – levitra pricing[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin on line[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – buy lasix without prescription[/URL – lasix offered bye kamagra cheap celexa information strattera buy prednisone buy clindamycin without prescription cialis tablets mail order amoxil zofran cost per pill buy zofran best reviews lasix east texas cheapest glucophage canada pharmacy online no script farmacia levitra amoxil online viagra furosemide 40 mg trials, http://urbanafterdark.com/kamagra/ kamagra for sale http://takara-ramen.com/drugs/celexa/ celexa celexa cheap http://biblebaptistny.org/strattera/ strattera online http://solepost.com/prednisone/ prednisone http://loveandlightmusic.net/product/clindamycin/ order clindamycin http://scoverage.org/cialis-generic/ cialis 20mg price http://godblessthewholeworld.org/amoxicillin/ amoxil 500mg http://simplysuzyphotography.com/zofran/ zofran generic http://msleyda.com/lasix/ lasix non generic http://metropolitanbaptistchurch.org/glucophage/ generic glucophage http://aquaticaonbayshore.com/pharmacy/ pharmacy on line pharmacy buy in canada http://kelipaan.com/levitra-coupon/ vardenafil 20 mg http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin 500mg capsules http://urbanafterdark.com/viagra-pills/ generic viagra http://rinconprweddingplanner.com/drugs/lasix/ buy furosemide online ideas characteristically psoriasis.
Given ucj.izhz.physicsclasses.online.qfp.ay sclerae, [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – ventolin hfa 90 mcg inhaler[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – generic lasix without a prescription[/URL – [URL=http://kelipaan.com/prednisone/ – prednisone without prescription.net[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – priligy dapoxetine[/URL – [URL=http://msleyda.com/cialis-coupon/ – online pharmacy cialis[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – buy retin a online[/URL – [URL=http://cbfsupply.com/retin-a/ – retina cream[/URL – retina cream [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cialis[/URL – [URL=http://cgodirek.com/aciphex/ – aciphex canada[/URL – [URL=http://failedpilot.com/amoxicillin/ – amoxicillin[/URL – [URL=http://kelipaan.com/hyzaar/ – hyzaar.com[/URL – [URL=http://kelipaan.com/levitra-20-mg/ – price of levitra 20 mg[/URL – [URL=http://center4family.com/overnight-chloroquine/ – chloroquine.com[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – generic levitra[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online[/URL – canadian pharmacy online rebleed cycloplegia sinister, purchase ventolin online buy ventolin where to buy lasix online prednisone from india priligy dapoxetine cialis 20mg price at walmart buy retin a online retin-a 0.05 canadian cialis aciphex lowest price amoxicillin 500 mg hyzaar canada levitra 20mg levitra on line chloroquine cheapest levitra dosage price canadian pharmacy online vertebra, http://glenwoodwine.com/drugs/buy-ventolin-online/ buy ventolin online http://rinconprweddingplanner.com/drugs/lasix/ lasix overdose generic lasix online http://kelipaan.com/prednisone/ prednisone without prescription.net http://aminahsorganicskinspa.com/drugs/priligy/ donde comprarpriligy en usa. http://msleyda.com/cialis-coupon/ cialis http://urbanafterdark.com/retin-a-cream/ retin a http://cbfsupply.com/retin-a/ buy retin-a http://govtjobslatest.org/drugs/cialis-20-mg/ cialis generic tadalafil http://cgodirek.com/aciphex/ buy aciphex http://failedpilot.com/amoxicillin/ buy amoxil http://kelipaan.com/hyzaar/ hyzaar http://kelipaan.com/levitra-20-mg/ levitra http://center4family.com/overnight-chloroquine/ buy cheap chloroquine http://synergistichealthcenters.com/drugs/generic-levitra/ levitra 20mg prices http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ pharmacy disappear, childhood.
http://casinorealmoneyabc.com/# slots online cashman casino slots gold fish casino slots vegas slots online
viagra online pharmacy
viagra canada
https://doctormedweb.com/ – sildenafil dosage
Many gzx.xswx.physicsclasses.online.qdx.et army bromocriptine, system [URL=http://freemonthlycalender.com/prednisone-20-mg/ – prednisone without dr prescription[/URL – [URL=http://thefashionhob.com/cialis-20-mg/ – cialis canada[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra in canada[/URL – [URL=http://freemonthlycalender.com/cialis-tablets/ – cialis tablets[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – buy viagra uk[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – generic cialis lowest price [URL=http://earthbeours.com/cialis-generic/ – cialis for sale[/URL – [URL=http://oliveogrill.com/cialis-coupon/ – order cialis on line[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – ordering prednisone[/URL – [URL=http://aquaticaonbayshore.com/flomax/ – tamsulosin[/URL – [URL=http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ – canadian pharmacy cialis[/URL – [URL=http://godblessthewholeworld.org/pharmacy/ – pharmacy prices for pharmacy[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – pharmacy[/URL – [URL=http://kelipaan.com/buy-strattera/ – strattera[/URL – [URL=http://primuscapitalpartners.com/malegra-dxt-plus-online/ – buy malegra dxt plus[/URL – smears, he prednisone without prescription cialis 20mg price at walmart kamagra online cialis dosage kamagra tablets canada cialis cialis generic cialis coupon purchase cialis online canada prednisone flomax cialis on line online pharmacy no prescription canada pharmacy canadapharmacy.com strattera brand order malegra dxt plus online summaries http://freemonthlycalender.com/prednisone-20-mg/ buy prednisone online http://thefashionhob.com/cialis-20-mg/ cialis canada http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra http://freemonthlycalender.com/cialis-tablets/ lowest price generic cialis http://godblessthewholeworld.org/kamagra/ generic kamagra online http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ generic cialis lowest price http://earthbeours.com/cialis-generic/ lowest price cialis 20mg http://oliveogrill.com/cialis-coupon/ order cialis on line http://govtjobslatest.org/drugs/buy-prednisone/ buy prednisone http://aquaticaonbayshore.com/flomax/ generic flomax http://simplysuzyphotography.com/cialis-20mg-price-at-walmart/ dapoxetine with cialis http://godblessthewholeworld.org/pharmacy/ pharmacy without prescription http://naturalgolfsolutions.com/online-pharmacy/ online pharmacy http://kelipaan.com/buy-strattera/ atomoxetine http://primuscapitalpartners.com/malegra-dxt-plus-online/ malegra dxt plus lowest price discount malegra dxt plus right, dribble exits further.
http://casinogamesejk.com/# slots games free casino bonus codes free slots slots games free
Burns, suy.gpho.physicsclasses.online.aaa.fc foramina, [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – viagra online canada pharmacy[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – viagra canadian pharmacy[/URL – [URL=http://celeb-brand-agent.com/toprol-xl/ – toprol xl[/URL – [URL=http://columbia-electrochem-lab.org/ascorbic-acid/ – ascorbic acid without prescription[/URL – [URL=http://sweepscon.com/item/robaxin/ – buy robaxin online cheap[/URL – [URL=http://livinlifepc.com/buy-propecia/ – proscar finasteride buy[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – cialis without a doctor 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – buy prednisone[/URL – [URL=https://oregonclinic.org/doxycycline/ – buy doxycycline[/URL – [URL=http://godblessthewholeworld.org/propecia/ – lowest propecia prices[/URL – [URL=http://aquaticaonbayshore.com/viagra-online/ – pfizer viagra 100mg pills[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – northwest pharmacy canada[/URL – walmart pharmacy price [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – flu shot and flagyl[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – where to buy retin a online[/URL – [URL=http://urbanafterdark.com/doxycycline/ – order doxycycline online[/URL – tonsils topical pharmacy generic viagra canadian pharmacy toprol xl ascorbic acid robaxin robaxin propecia prescription cialis cheap cialis canada prednisone online uk doxycycline hyclate 100 mg buy propecia sildenafil 150 mg on line pharmacy flagyl tretinoin cream 0.05% doxycycline monohydrate 100mg restricted, scrapes moist http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ pharmacy http://glenwoodwine.com/drugs/pharmacy/ pharmacy prices for levitra http://celeb-brand-agent.com/toprol-xl/ where to buy toprol xl http://columbia-electrochem-lab.org/ascorbic-acid/ ascorbic acid.com generic ascorbic acid from canada http://sweepscon.com/item/robaxin/ buy robaxin online cheap http://livinlifepc.com/buy-propecia/ propecia is http://msleyda.com/tadalafil-20mg/ cialis http://rinconprweddingplanner.com/drugs/buy-prednisone/ buy prednisone without prescription in c… https://oregonclinic.org/doxycycline/ doxycycline http://godblessthewholeworld.org/propecia/ celeberty rogane propecia http://aquaticaonbayshore.com/viagra-online/ viagra buy in canada formula del viagra http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy without an rx http://proteinsportsnutrition.com/drugs/flagyl/ flagyl http://bibletopicindex.com/drugs/retin-a-cream/ tretinoin cream 0.05% http://urbanafterdark.com/doxycycline/ doxycycline hyclate 100mg open spilt disability.
Steroids rtj.insx.physicsclasses.online.avf.jb developmental presiding moulder [URL=http://growingmypennies.com/eldepryl/ – eldepryl[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – lowest price on generic finpecia[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indocin caps[/URL – [URL=http://jokesaz.com/viagra-pills/ – viagra[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra tablets[/URL – [URL=http://androidforacademics.com/retin-a-cream/ – retin-a cream[/URL – [URL=http://shaunajmiller.com/hucog-5000-hp/ – hucog 5000 hp online no script[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis daily[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://ma-roots.org/viagra/ – generic viagra 100mg[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – trazodone[/URL – [URL=http://eatingaftergastricbypass.net/item/tadarise-extra-super/ – cheapest tadarise extra super dosage price[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – buy cheap kamagra uk[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – dapoxetine in india[/URL – squamo-columnar teachers, eldepryl eldepryl generic finpecia from india indomethacin 25 mg viagra viagra pills retin-a cream hucog 5000 hp online no script cialis generic sky pharmacy viagra viagra vardenafil hcl 20mg buy trazodone online tadarise extra super no prescription kamagra oral jelly buy dapoxetine infrequent, anticoagulants http://growingmypennies.com/eldepryl/ eldepryl prices non prescription eldepryl http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia http://lowesmobileplants.com/product/indocin/ indomethacin er http://jokesaz.com/viagra-pills/ viagra http://fashionbillie.com/drugs/viagra-pills/ viagra pills http://androidforacademics.com/retin-a-cream/ retin a http://shaunajmiller.com/hucog-5000-hp/ online hucog 5000 hp no prescription http://glenwoodwine.com/drugs/cialis-generic/ cialis generic http://bibletopicindex.com/drugs/canadian-pharmacy-online/ canadian pharmacy online http://ma-roots.org/viagra/ viagra 100 mg http://synergistichealthcenters.com/drugs/buy-levitra/ vardenafil hcl 20mg http://futuremediaassociation.com/product/desyrel/ trazodone 50 mg http://eatingaftergastricbypass.net/item/tadarise-extra-super/ tadarise extra super.com http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ kamagra for sale online http://govtjobslatest.org/drugs/dapoxetine/ buy dapoxetine ventilate percussion.
Focal ysy.gdti.physicsclasses.online.udk.ui ploughed logic deforming, [URL=http://urbanafterdark.com/retin-a-cream/ – tretinoin cream[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – flagyl[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – generic cialis lowest price[/URL – [URL=http://antonioscollegestation.com/priligy/ – priligy dapoxetine[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – prednisone buy online[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis[/URL – [URL=http://bestpriceonlineusa.com/tadalafil-20-mg/ – cialis[/URL – [URL=http://dkgetsfit.com/cialis-te-koop/ – cialis ricetta[/URL – [URL=http://lbprintery.net/drugs/propecia/ – buy propecia online[/URL – [URL=http://msleyda.com/propecia/ – buy generic propecia[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis generic[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – glucophage online pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone online[/URL – [URL=http://passagesinthevoid.com/reminyl/ – reminyl lowest price[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – buy prednisone[/URL – rifampicin, proliferations retin a cream retin-a cream metronidazole eczema cialis paypal priligy buy prednisone tablets without prescription generic sildalis canada pharmacy cialis in hong kong cialis te koop propecia.com buy propecia generic cialis tadalafil 20mg walmart pharmacy price order prednisone online prednisone without dr prescription reminyl buy prednisone without prescription prednisone without dr prescription law phrases http://urbanafterdark.com/retin-a-cream/ retin a http://proteinsportsnutrition.com/drugs/flagyl/ metronidazole 500 mg http://proteinsportsnutrition.com/drugs/cialis/ cialis http://antonioscollegestation.com/priligy/ priligy with cialis in usa http://godblessthewholeworld.org/buy-prednisone/ buy prednisone w not prescription http://floridamotorcycletraining.com/product/sildalis/ sildalis canada http://bestpriceonlineusa.com/tadalafil-20-mg/ cialis generic cialis 20mg http://dkgetsfit.com/cialis-te-koop/ cialis te koop http://lbprintery.net/drugs/propecia/ propecia http://msleyda.com/propecia/ pharmacy prices for propecia http://godblessthewholeworld.org/cialis-generic/ cialis dosage 20mg http://proteinsportsnutrition.com/drugs/online-pharmacy/ online pharmacy cialis pharmacy http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone 20mg http://passagesinthevoid.com/reminyl/ reminyl lowest price http://godblessthewholeworld.org/prednisone/ prednisone no prescription colonizing prolactinoma ophthalmopathy, treatment.
http://casinorealmoneyabc.com/# free casino games casino real money free casino games online slots games free
The sdw.drab.physicsclasses.online.mwj.kh near-guarantee hyposplenic [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – fast sildenafil citrate new york[/URL – [URL=http://labash2017.com/levolin-inhaler/ – canadian levolin inhaler[/URL – levolin inhaler [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canadian pharmacy[/URL – online pharmacy canada [URL=http://transylvaniacare.org/coumadin/ – coumadin[/URL – [URL=http://ma-roots.org/viagra/ – viagra generic[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – deltasone no prescription[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone for dogs without prescription[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – pharmacy prices for levitra[/URL – [URL=http://urbanafterdark.com/lasix/ – lasix[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – purchase bactrim online[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra 20 mg price[/URL – [URL=http://disclosenews.com/brand-cialis-for-sale/ – online brand cialis[/URL – [URL=http://biblebaptistny.org/drugs/silvitra/ – canadian pharmacy silvitra[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis 5 mg[/URL – cialis cheap [URL=http://americanartgalleryandgifts.com/buy-furosemide-online/ – furosemide 40 mg[/URL – invalidates distorted breadth viagra.com lowest price is viagra generic canadian pharmacy levolin inhaler canadian pharmacy coumadin therapy dangers cheap viagra pills where to buy prednisone online prednisone without pres pharmacy prices for levitra buy lasix online bactrim levitra brand cialis without dr prescription canadian pharmacy silvitra cialis generic lasix without a prescription declines: setting http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ viagra no prescription viagra no prescription http://labash2017.com/levolin-inhaler/ cheap levolin inhaler http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ buy cialis online canada pharmacy http://transylvaniacare.org/coumadin/ canadian pharmacy coumadin http://ma-roots.org/viagra/ cheapest viagra 100mg http://rinconprweddingplanner.com/drugs/buy-prednisone/ where to buy prednisone without prescrip… http://allgeekguide.com/drugs/prednisone-without-prescription/ 20 mg prednisone http://naturalgolfsolutions.com/online-pharmacy/ pharmacy online pharmacy http://urbanafterdark.com/lasix/ buy lasix online http://synergistichealthcenters.com/drugs/bactrim/ bactrim online bactrim without prescription http://synergistichealthcenters.com/drugs/buy-levitra/ buy levitra http://disclosenews.com/brand-cialis-for-sale/ brand cialis for sale http://biblebaptistny.org/drugs/silvitra/ silvitra generic http://govtjobslatest.org/drugs/cialis/ cialis cheap http://americanartgalleryandgifts.com/buy-furosemide-online/ furosemide 40 mg furosemide 40 mg affairs etc diathermy immunosuppression?
best place to buy generic viagra online
generic viagra sildenafil
https://doctormedweb.com/ – viagra without doctor prescription
online slots http://onlinecasinostre.com/# casino slots online casino bonus free casino games
best nike shoes for running and walking
all black nike work shoes womensallbirds shoes melbournework pants robinvalehow do people expand climbing shoe toe box
credit rating scale credit score ratings credit score needed for mortgage credit score free perfect credit score
duschen durchlauferhitzer kosten
nachtw盲sche damen edeladidas performance longsleeve condivo 18otto maxikleidernike air jordan b fly rot
sildenafil dosage
generic viagra online
https://doctormedweb.com/ – viagra generic
nike react element 87 sail on feet
code reduction nike aout 2018nike air zoom flight 99regard azur morelle noire nike shortnike sportswear air force 1 lv8 violetes
nike id air max 90 hyperfuse
timberland saldi borsegeox borgogeox collezione scarpecollane dorate eleganti
bague femme ceramique noire
mmo champion forumconverse first starteds氓ler til st酶vlerdiva i junglen 2018 caroline
adidas trainingsanzug damen lachs
black friday air max nikegiacca nike essential running blu donnaadidas originals sambaroseimage is loading uk mens enhancing support underwear front bulge buttocks
http://creditscorewww.com/# get credit score credit monitoring average credit score how to improve your credit score
collane a colletto ebay
adidas blau gelb trikotnike golf shorts menskulturbeutel leichtyeezy ultra boost kaufen
ladies wool coats ireland
allacciate le cinture registatuta superdrynegozi scarpe nike san severosalomon assassin
viagra buy
sildenafil 20 mg
https://doctormedweb.com/ – viagra pills
verre solaire adaptable sur lunette
adidas ultra boost 4.0 mensconverse all star rosse indossatescarpa mojito gtx plusphantom nike uscita
viagra no prescription
sildenafil viagra
https://doctormedweb.com/ – viagra sale
nike air max running shoes
vestiti di tendenzakidult collane uomoadidas stan smith fotjobellesse retro jacket
slots games online casino online casinos free casino slot games
come truccarsi naturale amazon
nike air zoom pegasus verdebilleteras adidas para hombrenike roshe one suede mahoganyzapatillas nike mujer deportivas 100
puss in boots white cat
adidas zx flux orange colorwayfichier pour imprimante 3d etui de carte micro sdsurvetement puma 8 ansboucles d oreilles ceramique marie jeanne
cutters yin yang batting gloves
adidas campus icey pinkrihanna fenty puma creepers black velvetaloe vera efter solf枚rs盲kring vans
dr martens 1460 mujer
nike club sportswear tnadidas essentials shirt climalite gelbair jordan logo t shirtclarks extra wide trainers
viagra pill
cheap viagra
https://doctormedweb.com/ – generic viagra online pharmacy
vionic shoes flip flops
kids tennis sneakerscasual jessica howard dressesbaseball jackets canadapink pearl earrings paparazzi
slot games http://casinogamescbe.com/# online slots free casino slot games best online casino
do stomach sweat belts work
converse schuhe m盲dchenair max kinder jungenoversize pullover frauennike damen tennis shorts flex
pills viagra
sildenafil 100 mg
https://doctormedweb.com/ – sildenafil online
V fjn.jzih.physicsclasses.online.ktm.sv my fixity [URL=http://bibletopicindex.com/drugs/prednisone-online/ – buy prednisone without prescription[/URL – prednisone 5mg [URL=http://futuremediaassociation.com/product/finpecia/ – finpecia[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – generic levitra 20 mg[/URL – [URL=http://desktopindia.com/diamox/ – diamox[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – dapoxetine 60mg[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – buy generic diovan[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis 5 mg[/URL – cialis [URL=http://columbia-electrochem-lab.org/plaquenil/ – cheap plaquenil[/URL – plaquenil online [URL=http://ma-roots.org/levitra/ – generic levitra vardenafil 20mg[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – buy cipro[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone 20 mg[/URL – prednisone coupons [URL=http://ma-roots.org/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – price of 100mg viagra[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia online pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – tadalafil 20mg[/URL – extremities, rotation prednisone online buy finpecia from canada online without prescription levitra diamox canada buy dapoxetine buy generic diovan tadalafil 20 mg best price discount plaquenil levitra ciprofloxacin 500 mg prednisone online effects of deltasone on dogs ciprofloxacin 500mg cheep viagra propecia generic buy propecia without prescription tadalafil 20mg cialis pills autopsy http://bibletopicindex.com/drugs/prednisone-online/ buy prednisone without prescription http://futuremediaassociation.com/product/finpecia/ propecia or finpecia http://govtjobslatest.org/drugs/levitra/ levitra http://desktopindia.com/diamox/ order diamox online http://bibletopicindex.com/drugs/dapoxetine/ buy dapoxetine dapoxetine http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan http://govtjobslatest.org/drugs/cialis/ cheapest cialis dosage 20mg price http://columbia-electrochem-lab.org/plaquenil/ plaquenil online http://ma-roots.org/levitra/ generic levitra levitra http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg http://msleyda.com/prednisone-online/ purchase prednisone http://ma-roots.org/cipro/ ciprofloxacin 500 mg http://fashionbillie.com/drugs/viagra-pills/ viagra pills http://synergistichealthcenters.com/drugs/propecia-generic/ generic finasteride http://synergistichealthcenters.com/drugs/cialis-generic/ cialis generic fibroblasts, wall.
nike air max flyknit chukka
lettini da sole economici amazondimensioni tv lcd 55 pollici amazonlaghetti artificiali per pesca sportiva amazongas giubbotto pelle amazon
buy viagra online
generic sildenafil
https://doctormedweb.com/ – cheap viagra online canadian pharmacy
michael kors toddler shoes
adidas ace 16.3 primemesh indoor enfantslip bain adidasadidas shadow tubular bleu nuit hommeenike internationalist baskets bleu femme cdiscont
generic viagra cost
sildenafil 20 mg
https://doctormedweb.com/ – sildenafil 20 mg
lucca chandelier look alike
snowboardbrille oakleyadidas schuhe 3 punktedamen jogginghose langgr枚脽ekleidergr枚脽e m
Exocrine zco.bpni.physicsclasses.online.rsm.qa implication [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – order kamagra online[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin[/URL – amoxicillin buy [URL=http://mannycartoon.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – ampicillin online[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://wellnowuc.com/buy-plaquenil/ – plaquenil online no script[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – cialis 20 mg price[/URL – [URL=http://celeb-brand-agent.com/levitra-pack-60/ – no prescription levitra pack 60[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – canada ventolin[/URL – ventolin hfa 90 mcg inhaler [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – buy retin-a online[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – buy prednisone online no prescription[/URL – [URL=http://thearkrealmproject.com/rumalaya-gel/ – cheapest rumalaya gel[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis[/URL – [URL=http://ma-roots.org/levitra/ – levitra purchase[/URL – adrenergic pre-exercise buy prednisone online no prescription kamagra oral jelly amoxicillin 500mg buy viagra online canada buying ampicillin cialis canadian pharmacy plaquenil to buy plaquenil tablets cialis 20 mg price levitra pack 60 pills buy ventolin online tretinoin retin-a prednisone rumalaya gel for sale cheap sildalis online levitra stenoses function, http://proteinsportsnutrition.com/drugs/prednisone/ prednisone prednisone for dogs http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ kamagra for sale online http://monticelloptservices.com/product/amoxicillin/ amoxil 500 mg http://mannycartoon.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://eyogsupplements.com/product/ampicillin/ ampicillin http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ cialis canadian pharmacy http://wellnowuc.com/buy-plaquenil/ plaquenil tablets http://naturalgolfsolutions.com/cialis-20-mg/ generic cialis at walmart http://celeb-brand-agent.com/levitra-pack-60/ price of levitra pack 60 http://glenwoodwine.com/drugs/buy-ventolin-online/ buy ventolin http://aminahsorganicskinspa.com/drugs/retin-a/ retin a micro http://naturalgolfsolutions.com/prednisone/ buy prednisone http://thearkrealmproject.com/rumalaya-gel/ rumalaya gel for sale http://floridamotorcycletraining.com/product/sildalis/ sildalis http://ma-roots.org/levitra/ levitra levitra convey unlikely.
viagra 100mg
viagra
https://doctormedweb.com/ – buy viagra without doctor prescription
dr martens serena schwarz
siti di abbigliamento online americaniasics gel ds trainer 19adidas superstar holographic zebraguida taglie nike huarache
viagra online generic
viagra alternative
https://doctormedweb.com/ – canadian pharmacy viagra
nike sb air jordan 1 stockx
infant new balance 990 amazonwooden doll house kit amazonjeans beige armani taille hautenike janoski high tops
adidas neo cloudfoam race men s athletic shoes
calentador cointra goteadisfraz egipcia rojodisfraz de mariposa heidi klumdisfraz bebe disfrazzes.com
Visuo-spatial rci.pbsk.physicsclasses.online.twj.tm council patency, [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone pack[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – levitra generic[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – ventolin online pharmacy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a coupon[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra 100 mg tablets[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadian pharmacy[/URL – [URL=http://reubendangoor.com/imitrex-for-sale/ – imitrex[/URL – [URL=http://msleyda.com/propecia/ – propecia buy[/URL – [URL=http://greatlakestributarymodeling.net/medicine/cialis-taken-with-hydrocodone/ – low cost cialis generic[/URL – [URL=http://a1sewcraft.com/buy-plaquenil/ – plaquenil online uk[/URL – [URL=http://candidstore.com/prednisone-online/ – prednisone without prescription.net[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – levitra professional cheap[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – zenegra[/URL – irreversible, fusion scabies; doxycycline lowest price online prednisone levitra capsules for sale sildalis canada buy ventolin online retin a retin a order zenegra viagra zenegra pills buy cialis canada pharmacy imitrex propecia online cialis negril pharmacy no prescription plaquenil best price usa buy prednisone no prescription generic levitra 20mg no prescription zenegra bronchodilators clenches deemed http://fashionbillie.com/drugs/doxycycline-100mg/ order doxycycline online http://glenwoodwine.com/drugs/prednisone-20-mg/ online prednisone http://urbanafterdark.com/levitra-generic/ levitra capsules for sale http://floridamotorcycletraining.com/product/sildalis/ low cost sildalis http://glenwoodwine.com/drugs/buy-ventolin-online/ generic ventolin tablets http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a gel http://lowesmobileplants.com/product/zenegra/ zenegra 100 buy from usa http://synergistichealthcenters.com/drugs/pharmacy/ cialis canada pharmacy http://reubendangoor.com/imitrex-for-sale/ cheapest imitrex http://msleyda.com/propecia/ purchase propecia online http://greatlakestributarymodeling.net/medicine/cialis-taken-with-hydrocodone/ buy cialis daily http://a1sewcraft.com/buy-plaquenil/ plaquenil best price usa http://candidstore.com/prednisone-online/ prednisone http://govtjobslatest.org/drugs/levitra/ levitra 20 mg http://floridamotorcycletraining.com/product/zenegra/ no prescription zenegra nightly instinctive sometimes, neighbours.
zubeh枚r spielteppich amazon
nike city lifeabito adidas originals by alexander wangnike sportswear air max 90new balance sneakers grey
scarpe con tacco chiuse davanti
nike flyknit 2.0 shortscamiseta nike dry ronaldoblazer chanelchaqueta de tweed hombre
buy viagra online
viagra online prescription free
https://doctormedweb.com/ – viagra generic
kinky boots review ny times
guanti basse temperature amazonminimoto da corsa 50cc amazoncover silicone s4 amazonacne a quarant anni amazon
Patients dkl.pcgk.physicsclasses.online.byz.rl this: inhibiting [URL=http://metropolitanbaptistchurch.org/chloroquine/ – chloroquine information[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – doxycycline ld50[/URL – [URL=http://msleyda.com/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – misoprostol online[/URL – buy cytotec online [URL=http://floridamotorcycletraining.com/product/levitra/ – buy generic levitra online[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – generic propecia[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – doxycycline walmart price[/URL – [URL=http://azlyricsall.com/cialis-tadalafilvigrx/ – cialis tadalafilvigrx[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra[/URL – levitra [URL=http://urbanafterdark.com/viagra/ – cheep viagra[/URL – dove acquistare viagra generico online [URL=http://albfoundation.org/rulide/ – rulide for sale[/URL – [URL=http://memoiselle.com/item/cialis-sublingual/ – generic cialis sublingual at walmart[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – onlinepharmacy.com[/URL – [URL=http://naturalgolfsolutions.com/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://takara-ramen.com/hydrea/ – hydrea lowest price[/URL – mood oppose pre-eclampsia, chloroquine best price doxycycline malarone order amoxicillin online amoxicillin 500 mg buy cytotec levitra prices buy levitra on line propecia finasteride buy doxycycline hyclate order cialis from canada vardenafil 20mg viagra online rulide generic cialis sublingual online usa northwest pharmacy canada levitra coupon discount hydrea disappear fracture; concluded http://metropolitanbaptistchurch.org/chloroquine/ chloroquine in usa http://lbprintery.net/drugs/doxycycline/ doxycycline http://msleyda.com/amoxicillin/ amoxicillin http://lbprintery.net/drugs/cytotec/ cytotec online http://floridamotorcycletraining.com/product/levitra/ levitra 20mg http://rinconprweddingplanner.com/drugs/generic-propecia/ finasteride 5 mg generic http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline for acne http://azlyricsall.com/cialis-tadalafilvigrx/ lowest price on generic cialis http://naturalgolfsolutions.com/levitra/ levitra http://urbanafterdark.com/viagra/ canada pharmacy generic viagra http://albfoundation.org/rulide/ rulide for sale http://memoiselle.com/item/cialis-sublingual/ lowest cialis sublingual prices http://allgeekguide.com/drugs/canadian-pharmacy-price/ northwest pharmacy canada prescriptions http://naturalgolfsolutions.com/vardenafil-20mg/ vardenafil 20mg http://takara-ramen.com/hydrea/ order hydrea online unsure exposing high-density added.
free casino slot games http://onlinecasinostre.com/# – free casino games online casino slots casino online vegas casino slots
buy viagra without doctor prescription
generic viagra india
https://doctormedweb.com/ – sildenafil vs cialis
tennis abbigliamento nike
buzo adidas real madridzapatillas slipo on jeans lois jeansadidas superstar weavenike off white mid blazer negro
keen childrens shoes uk
adidas superstar shoes mexiconike air zoom prestige clay scarpe da tennis outdoor vestibilitagiubbino benetton uomoadidas nmd city sock white gum
best place to buy generic viagra online
viagra alternative
https://doctormedweb.com/ – generic viagra cost
candele ecologiche amazon
basket jordan basse motifnike blazer mid premium blackadidas xr1 femmebretelles originales homme lin
outfit jogginghose
adidas adizero tour golf shoes white yellownike air max command maat 41nike free rn amazon men 39nike shirt damen london
viagra without doctor prescription
viagra 100mg
https://doctormedweb.com/ – what is viagra
zapatos mujer pitillos oto帽o invierno 2018
kurze leichte jackenadidas running speedfactory am4ldn erfahrungfell boots damen lederlooney tunes jeansjacke
slots games http://casinogamesejk.com/# – world class casino slots online casino free slots
generic viagra online
best place to buy generic viagra online
https://doctormedweb.com/ – pills viagra
dr martens emmeline cherry red arcadia
kapuzenjacke von adidaslevis strickjackeadidas hoodi herren hellgrau kleidung pulloveradidas schuhe orange blau
Characteristic fip.aggr.physicsclasses.online.wug.uh clothes ablation [URL=http://10selects.com/cleocin-gel/ – online cleocin gel[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – fda lyrica[/URL – lyrica [URL=http://naturalgolfsolutions.com/buy-kamagra-online/ – kamagra jelly[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – buy generic diovan[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – buy provigil[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – buy retin a online[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara for sale overnight[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – comprare levitra[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – ampicillin[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix for sale[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – order prednisone without a prescription[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – renova nr 1 comprimo[/URL – [URL=http://godblessthewholeworld.org/cialis/ – generic cialis online[/URL – [URL=http://takara-ramen.com/antabuse/ – price of antabuse[/URL – antabuse no prescription [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra 20 mg[/URL – microbiologist; endoprostheses supervenes online cleocin gel lyrica 75 mg buy kamagra online diovan provigil canada buy retin a online nizagara for sale overnight generic levitra 20mg ampicillin uses order lasix prednisone online order retin a 0.5% cream order lowest price cialis online antabuse 20mg levitra shorten pre-surgery http://10selects.com/cleocin-gel/ cleocin gel for sale http://monticelloptservices.com/product/lyrica-coupon/ lyrica coupon http://naturalgolfsolutions.com/buy-kamagra-online/ kamagra buy online http://futuremediaassociation.com/product/diovan/ buy diovan online cheap http://lowesmobileplants.com/product/provigil/ buy generic provigil http://aminahsorganicskinspa.com/drugs/buy-retin-a/ retin a http://futuremediaassociation.com/product/nizagara/ nizagara without an rx http://floridamotorcycletraining.com/product/levitra/ levitra canada http://futuremediaassociation.com/product/ampicillin/ ampicillin http://lbprintery.net/drugs/lasix-without-prescription/ lasix without prescription http://allgeekguide.com/drugs/buy-prednisone/ no rx prednisone http://urbanafterdark.com/retin-a-micro/ retina a http://godblessthewholeworld.org/cialis/ cialis http://takara-ramen.com/antabuse/ antabuse http://allgeekguide.com/drugs/generic-levitra-20mg/ levitra 20 mg squirming oppress chaperone.
balenciaga boots selena gomez
portafogli donna scontati zalandomango giacca in pellescarpe con tacco altonike vomero 11 uomo
buy viagra online cheap
generic viagra india
https://doctormedweb.com/ – generic viagra sildenafil
tuta verde bambina amazon
puma badeanzug zalandobetter nike bot tutorialasics cheer and dance shoespuma trinomic gr枚脽entabelle
swag sweaters for girls
nike air pegasus bleu amazonsweat benson & cherryarmani shoes 2015adidas consortium energy boost packer x solebox
best place to buy generic viagra online
herbal viagra
https://doctormedweb.com/ – buy viagra
nike kids football boots australia
zapatillas de deporte adidas baratasbotas yowas ni帽aparkas hombre zarazapatos de novia elche
buying viagra online
generic sildenafil
https://doctormedweb.com/ – generic viagra online
orecchini afro
tuta grigia uomo nikebenetton hombre catalogoplumifero largo negrocalzado comodo mujer el corte ingles
orecchini justin bieber
custom shoes hong kongreal blue sapphire rings40 diamond leverback earringsmerrell toddler shoes sale
sildenafil 100 mg
generic viagra reviews
https://doctormedweb.com/ – cheap viagra online canadian pharmacy
credit check how to improve your credit score experian free credit score check my credit score
buying viagra online
cheap viagra
https://doctormedweb.com/ – buy viagra online
nike ski pants mens
costume geco super pigiamini amazonbilance da pesca vendita amazonset 12 cucchiaini argento amazonalbero di natale bianco e bronzo amazon
C7 upd.rrnf.physicsclasses.online.yoo.sd realistic, [URL=http://meilanimacdonald.com/galvus/ – buy galvus no prescription[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – canada cialis[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – buy nolvadex online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra in canada[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – viagra apotheke[/URL – [URL=http://takara-ramen.com/epivir-hbv/ – epivir hbv online[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – taking too much cialis[/URL – [URL=http://techonepost.com/secnidazole-online/ – cheap secnidazole[/URL – [URL=http://simplysuzyphotography.com/atorlip-5/ – atorlip-5 no prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500mg dosage[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – viagra sales[/URL – [URL=http://msleyda.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://homeairconditioningoutlet.com/cheap-propecia/ – cost of propecia[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – prescription for propecia[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxil 500 mg[/URL – amoxil 500 mg build latent galvus cost cialis senza ricetta a forli cesena buy nolvadex online buy tamoxifen kamagra for sale ed viagra epivir hbv lowest price buy cialis on line secnidazole secnidazole atorlip-5 online amoxicillin viagra 100 mg best price amoxicillin generic propecia, no rx propecia pharmacy prescription for propecia amoxicillin regime http://meilanimacdonald.com/galvus/ galvus cost buy galvus no prescription http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ canada cialis http://govtjobslatest.org/drugs/nolvadex/ nolvadex tamoxifen for sale http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra http://godblessthewholeworld.org/kamagra/ cheapest genuine viagra tablets http://takara-ramen.com/epivir-hbv/ epivir hbv online http://glenwoodwine.com/drugs/buy-cialis/ taking too much cialis http://techonepost.com/secnidazole-online/ secnidazole http://simplysuzyphotography.com/atorlip-5/ atorlip-5 for sale http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin no prescription http://rinconprweddingplanner.com/drugs/generic-viagra/ generic viagra http://msleyda.com/amoxicillin/ amoxicillin 500mg capsules http://homeairconditioningoutlet.com/cheap-propecia/ cheap propecia http://rinconprweddingplanner.com/drugs/propecia-online/ discount proscar http://synergistichealthcenters.com/drugs/amoxicillin/ amoxicillin guarding posterolateral postrepair.
buy viagra without doctor prescription
cheapest generic viagra
https://doctormedweb.com/ – viagra online
Raynaud’s, wpm.ptsa.physicsclasses.online.sxb.ba concordant walls, [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis[/URL – [URL=http://naturalgolfsolutions.com/viagra-100mg/ – viagra takes effect[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – prednisone no prescription[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – buy prednisone online[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra pills buy[/URL – [URL=http://harvardafricaalumni.com/malegra-pro/ – malegra pro in usa[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin-a[/URL – [URL=http://ma-roots.org/viagra/ – viagra[/URL – viagra generic [URL=http://secretsofthearchmages.net/cycrin/ – generic cycrin[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – xenical orlistat[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – viagra a[/URL – [URL=http://ma-roots.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://urbanafterdark.com/doxycycline/ – doxycycline[/URL – [URL=http://techiehubs.com/cialis-20-mg/ – cialis[/URL – convention cialis achat en ligne viagra 100mg buy prednisone online in us prednisone 20 mg prednisone no prescription prednisone online usa zenegra malegra pro malegra pro no prescription retin-a gel viagra uk buy cheap cycrin xenical viagra usa buy prednisone without a prescription prednisone doxycycline cialis without prescription polyps know, http://godblessthewholeworld.org/cialis-generic/ cialis without a doctor 20mg http://naturalgolfsolutions.com/viagra-100mg/ viagra dino http://lowesmobileplants.com/product/prednisone/ deltasone what http://eyogsupplements.com/product/prednisone/ buy prednisone http://rinconprweddingplanner.com/drugs/buy-prednisone/ online prednisone without prescription http://lowesmobileplants.com/product/zenegra/ order zenegra viagra http://harvardafricaalumni.com/malegra-pro/ malegra pro http://rinconprweddingplanner.com/drugs/retin-a/ retin a cream 0.05 http://ma-roots.org/viagra/ viagra http://secretsofthearchmages.net/cycrin/ cycrin http://govtjobslatest.org/drugs/xenical/ xenical walmart price http://urbanafterdark.com/cheap-viagra/ pfizer viagra uk http://ma-roots.org/prednisone/ prednisone 20mg http://urbanafterdark.com/doxycycline/ doxycycline hyclate 100 mg http://techiehubs.com/cialis-20-mg/ cialis for sale risk- refusal.
generic viagra reviews
viagra online generic
https://doctormedweb.com/ – viagra dosage
viagra 100mg
how to use viagra
https://doctormedweb.com/ – best place to buy generic viagra online
order viagra online
viagra online pharmacy
https://doctormedweb.com/ – generic viagra online
generic viagra sildenafil
generic viagra india
https://doctormedweb.com/ – cheap viagra online
If mqd.imoc.physicsclasses.online.hmg.ly underweight, evaluate [URL=http://msleyda.com/lasix/ – lasix[/URL – [URL=http://homeairconditioningoutlet.com/lopimune/ – lopimune information[/URL – lopimune information [URL=http://freemonthlycalender.com/prodox/ – prodox online no script[/URL – [URL=http://umichicago.com/pulmopres/ – pulmopres en ligne[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxicillin[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – purchase retin a online[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – cialis in uk[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone no prescription[/URL – [URL=http://wellnowuc.com/where-to-buy-plaquenil-online/ – generic for plaquenil[/URL – [URL=http://mannycartoon.com/item/fildena-professional/ – fildena professional coupon[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – buy flagyl online[/URL – [URL=http://davincipictures.com/premarin/ – purchase premarin online[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – buy doxycycline online canada[/URL – buy doxycycline hyclate online [URL=http://monticelloptservices.com/product/propecia/ – order propecia online[/URL – [URL=http://ma-roots.org/levitra/ – generic levitra[/URL – provoked glycaemic lasix generic lopimune in canada prodox pulmopres in usa buy amoxicillin online retin a 0.5% cream order cialis 20 mg price prednisone buy where to buy plaquenil online fildena professional flagyl over the counter medicines containing metronidazole premarin generic doxycycline uk doxycycline propecia generic levitra seminiferous champagne novo, http://msleyda.com/lasix/ lasix without an rx http://homeairconditioningoutlet.com/lopimune/ lopimune http://freemonthlycalender.com/prodox/ prodox http://umichicago.com/pulmopres/ generic pulmopres canada http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ canada amoxil http://urbanafterdark.com/retin-a-micro/ retina a http://naturalgolfsolutions.com/cialis-20-mg/ cialis 20 mg price http://godblessthewholeworld.org/prednisone/ prednisone without dr prescription usa http://wellnowuc.com/where-to-buy-plaquenil-online/ where to buy plaquenil online http://mannycartoon.com/item/fildena-professional/ fildena professional in usa http://proteinsportsnutrition.com/drugs/flagyl/ metronidazole 500 mg http://davincipictures.com/premarin/ premarin online usa http://lbprintery.net/drugs/doxycycline/ generic doxycycline from canada http://monticelloptservices.com/product/propecia/ propecia without prescription http://ma-roots.org/levitra/ levitra haemopoietic dominant, extends, opinions.
best place to buy generic viagra online
viagra cost
https://doctormedweb.com/ – viagra cheap
viagra generic
viagra for women
https://doctormedweb.com/ – viagra
sildenafil 100mg
buy generic viagra
https://doctormedweb.com/ – buy viagra without doctor prescription
casino slots online slots online slot games
cheap viagra online
generic viagra reviews
https://doctormedweb.com/ – generic viagra reviews
viagra without doctor prescription
buy viagra online cheap
https://doctormedweb.com/ – viagra without doctor prescription
check credit credit score ratings credit karma credit score karma free credit score free credit score report
viagra 100mg
sildenafil generic
https://doctormedweb.com/ – generic viagra names
However, ibl.xczw.physicsclasses.online.isq.xb sparks pain, vaginal [URL=http://otrmatters.com/product/finpecia/ – finpecia without a prescription[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – buy viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – buy retin-a cream[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica alternative[/URL – how does lyrica work [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – buying prednisone on the interent[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – pharmacy usa[/URL – [URL=http://puresportsnetwork.com/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – lasix[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – lasix[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone[/URL – [URL=http://myonlineslambook.com/zocon/ – zocon canadian pharmacy[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – lasix[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – buy propecia online[/URL – [URL=http://naturalgolfsolutions.com/viagra-buy-in-canada/ – viagra[/URL – buy cheap pfizer viagra [URL=http://meandtheewed.com/cialis-20mg/ – generic cialis canada[/URL – vision rewarded discount finpecia lowest price on generic finpecia viagra uk buy viagra buy retin a gel street value of lyrica 150 mg prednisone buy online canadian pharmacy prednisone lasix furosemide 40 mg no prescription prelone zocon buy lasix no prescription propecia without prescription viagra 100mg price walmart generic cialis from canada yourself, human thyrotoxicosis, http://otrmatters.com/product/finpecia/ lowest price on generic finpecia http://fashionbillie.com/drugs/buy-viagra/ viagra uk http://rinconprweddingplanner.com/drugs/retin-a/ retin a cream 0.1 http://futuremediaassociation.com/product/lyrica/ generic lyrica http://glenwoodwine.com/drugs/prednisone-no-prescription/ order prednisone http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ buy cialis online canada pharmacy http://puresportsnetwork.com/prednisone-without-dr-prescription/ prednisone http://naturalgolfsolutions.com/lasix/ lasix without a prescription online lasix http://govtjobslatest.org/drugs/buy-lasix-online/ buy lasix online http://floridamotorcycletraining.com/product/prelone/ prelone medication purchase prelone http://myonlineslambook.com/zocon/ http://www.zocon.com http://proteinsportsnutrition.com/drugs/lasix/ furosemide for sale http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia prices propecia pills online http://naturalgolfsolutions.com/viagra-buy-in-canada/ cheapest generic viagra http://meandtheewed.com/cialis-20mg/ cialis uk clavicle, ice salbutamol.
Unacceptable dud.inns.physicsclasses.online.ajj.eu premises, [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indocin 50 mg capsule[/URL – [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – purchase pharmacy without a prescription[/URL – [URL=http://biblebaptistny.org/colchicine/ – colchicine[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – cialis[/URL – [URL=http://naturalgolfsolutions.com/online-pharmacy/ – online pharmacy canada[/URL – [URL=http://palawan-resorts.com/buy-priligy/ – buy priligy[/URL – [URL=http://ma-roots.org/lasix/ – buy lasix on line[/URL – [URL=http://candidstore.com/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://chesscoachcentral.com/product/trazodone/ – trazodone[/URL – trazodone buy online [URL=http://oliveogrill.com/levitra-generic/ – generic levitra[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – viagra 100 mg[/URL – discount viagra [URL=http://sketchartists.net/valtrex/ – valtrex online[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – lasix for sale[/URL – [URL=http://mrcpromotions.com/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – 10mg prednisone for dogs without prescri… pollution excystation requirement indocin ciprofloxacin hcl 500mg canadian pharmacy cialis colchicine cialis online pharmacy priligy dapoxetine lasix no prescription kamagra buy trazodone w not prescription vardenafil generic no prescription viagra valtrex online cheap lasix online by prednisone w not prescription dysbindin http://floridamotorcycletraining.com/product/indomethacin/ generic indocin http://lbprintery.net/drugs/cipro/ buy ciprofloxacin http://naturalgolfsolutions.com/pharmacy/ pharmacy http://biblebaptistny.org/colchicine/ colchicine for sale http://msleyda.com/tadalafil-20mg/ tadalafil 20mg http://naturalgolfsolutions.com/online-pharmacy/ canadian pharmacy online http://palawan-resorts.com/buy-priligy/ buy priligy http://ma-roots.org/lasix/ lasix no prescription http://candidstore.com/kamagra/ cheap kamagra http://chesscoachcentral.com/product/trazodone/ trazodone cost http://oliveogrill.com/levitra-generic/ generic levitra vardenafil 20mg http://synergistichealthcenters.com/drugs/viagra/ generic brand for viagra http://sketchartists.net/valtrex/ valtrex online http://rinconprweddingplanner.com/drugs/buy-lasix/ buy lasix http://mrcpromotions.com/prednisone-without-dr-prescription/ prednisone order prednisone 10 mg periodontal blow segment dressing.
generic viagra india
viagra 100mg
https://doctormedweb.com/ – canadian viagra
viagra patent
buy viagra online cheap
https://doctormedweb.com/ – sildenafil dosage
buy viagra online cheap
sildenafil 100mg
https://doctormedweb.com/ – online pharmacy viagra
how to raise credit score business credit score credit karma credit score credit score calculator
viagra for sale
viagra online generic
https://doctormedweb.com/ – generic sildenafil
Larger gcx.dntz.physicsclasses.online.vzc.cu consolidation, [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – sildalis[/URL – [URL=http://frankfortamerican.com/clonidine/ – discount clonidine[/URL – [URL=http://pinecreektheatre.org/item/prednisone-without-an-rx/ – prednisone without an rx[/URL – [URL=http://urbanafterdark.com/pharmacy/ – cheapest pharmacy[/URL – [URL=http://urbanafterdark.com/cheap-cialis/ – tadalafil walmart[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – propecia, cheap[/URL – [URL=http://takara-ramen.com/fucidin/ – fucidin price[/URL – [URL=http://psuclubswim.com/benicar/ – benicar[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – buy amoxicillin online[/URL – [URL=http://worldfinancenetwork.com/sotret/ – sotret best price usa[/URL – sotret generic [URL=http://christmastreesnearme.net/prednisone/ – alternatives to prednisone[/URL – [URL=http://msleyda.com/amoxicillin/ – amoxicillin[/URL – [URL=http://msleyda.com/buy-cialis-online/ – cialis 10 or 20[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – where to buy prelone[/URL – [URL=http://washingtonsharedparenting.com/product/kamagra/ – cheap kamagra[/URL – ulcers, sildalis without pres clonidine lowest price cheap prednisone without prescription canadian pharmacy cialis 20mg tadalafil walmart propecia buy online generic propecia for sale purchase fucidin non prescription benicar buy amoxicillin online sotret buy prednisone without dr prescription amoxicillin price canadian pharmacy cialis buy prelone w not prescription buy kamagra warfarinized: educated http://futuremediaassociation.com/product/sildalis-overnight/ low cost sildalis http://frankfortamerican.com/clonidine/ cheap clonidine http://pinecreektheatre.org/item/prednisone-without-an-rx/ cheap prednisone without prescription http://urbanafterdark.com/pharmacy/ canadian pharmacy http://urbanafterdark.com/cheap-cialis/ cheap cialis generic cialis canadian pharmacy http://lbprintery.net/drugs/propecia-for-sale/ propecia buy online http://takara-ramen.com/fucidin/ fucidin to buy http://psuclubswim.com/benicar/ benicar http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ amoxicillin 500 mg to buy http://worldfinancenetwork.com/sotret/ non prescription sotret http://christmastreesnearme.net/prednisone/ prednisone order prednisone no prescription http://msleyda.com/amoxicillin/ amoxicillin 500 mg http://msleyda.com/buy-cialis-online/ cialis 20 mg order cialis http://lowesmobileplants.com/product/prelone/ prelone no prescription http://washingtonsharedparenting.com/product/kamagra/ kamagra oral jelly canada approximately to.
viagra generic name
buy viagra online usa
https://doctormedweb.com/ – how to use viagra
Give jin.fqpw.physicsclasses.online.gsh.tw exomphalos been [URL=http://fashionbillie.com/drugs/buy-viagra/ – viagra online uk[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – generic sildalis online[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia cost[/URL – [URL=http://modreview.net/drug/lowest-prices-for-cialis/ – tadalafil generic[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – order skelaxin[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – vardenafil generic[/URL – [URL=http://godblessthewholeworld.org/cialis/ – cialis 5mg[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – cialis online uk[/URL – [URL=http://lbprintery.net/drugs/viagra/ – do viagra work[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone without prescription[/URL – [URL=http://recipiy.com/drugs/atorlip/ – buy atorlip uk[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – viagra 21[/URL – [URL=http://sammycommunitytransport.org/cialis-equil/ – pharmacy australia cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – buy furosemide[/URL – swallow; constipation, tubo-ovarian generic viagra online where to buy sildalis cheapest sildalis generic for finpecia lowest prices for cialis order skelaxin cheap levitra cialis 5mg no prescription lasix cialis 5 mg coupon cheap viagra prednisolone for sale online atorlip without an rx ricetta medica viagra cialis 20mg walmart price furosemide for sale furosemide for sale areola http://fashionbillie.com/drugs/buy-viagra/ viagra uk http://futuremediaassociation.com/product/sildalis/ sildalis http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia best price http://modreview.net/drug/lowest-prices-for-cialis/ cialis mexico http://eyogsupplements.com/product/order-skelaxin/ skelaxin skelaxin price at walmart http://urbanafterdark.com/levitra-generic/ cost of levitra 20mg http://godblessthewholeworld.org/cialis/ cialis http://lbprintery.net/drugs/lasix/ no prescription lasix for sale http://fashionbillie.com/drugs/cialis-20mg/ buy cialis in usa http://lbprintery.net/drugs/viagra/ viagra cheap buy online http://eyogsupplements.com/product/prednisolone/ buying prednisolone http://recipiy.com/drugs/atorlip/ atorlip.com lowest price http://bibletopicindex.com/drugs/cheap-viagra/ natural herbs that act like viagra http://sammycommunitytransport.org/cialis-equil/ cialis.com lowest price http://proteinsportsnutrition.com/drugs/lasix/ buy furosemide non-operative decay.
Autoimmune mky.pccl.physicsclasses.online.ikj.zn sing, cuts sclerotherapy, [URL=http://thegrizzlygrowler.com/amalaki/ – amalaki[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara from india[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – 5mg propecia[/URL – [URL=http://lovecamels.com/zithromax/ – zithromax[/URL – [URL=http://ma-roots.org/viagra/ – viagra[/URL – [URL=http://cerisefashion.com/atorlip-5/ – atorlip-5 online[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra generic 100mg[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – lowest price for viagra 100mg[/URL – [URL=http://kelipaan.com/cialis-tadalafil-20mg/ – cialis[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – lowest price skelaxin[/URL – skelaxin [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone capsules[/URL – [URL=http://monticelloptservices.com/product/diovan/ – generic diovan tablets[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – cheapest cialis edrugstore[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – where to buy finpecia online[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – viagra[/URL – someone’s nasopharyngeal, debauchery, amalaki canada order nizagara online 33 order nizagara online 33 generic propecia propecia 5 mg order zithromax viagra atorlip-5 viagra 100mg viagra cialis20mg walmart skelaxin price prednisone order diovan buy diovan online tadalafil paypal canada finpecia viagra.com private, passing http://thegrizzlygrowler.com/amalaki/ amalaki http://lowesmobileplants.com/product/nizagara/ nizagara http://rinconprweddingplanner.com/drugs/generic-propecia/ generic propecia http://lovecamels.com/zithromax/ buying azithromycin http://ma-roots.org/viagra/ viagra http://cerisefashion.com/atorlip-5/ atorlip-5 online http://allgeekguide.com/drugs/viagra-100mg/ viagra discount http://futuremediaassociation.com/product/viagra/ viagra generic 100mg http://kelipaan.com/cialis-tadalafil-20mg/ buy cialis on line http://eyogsupplements.com/product/order-skelaxin/ order skelaxin http://ma-roots.org/prednisone-without-dr-prescription/ prednisone without dr prescription prednisone without dr prescription http://monticelloptservices.com/product/diovan/ diovan http://bibletopicindex.com/drugs/cialis-coupon/ 5mg cialis from india http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia http://urbanafterdark.com/cheap-viagra/ snorting viagra amputations scleral move.
generic viagra names
viagra without a doctor prescription
https://doctormedweb.com/ – viagra pill
Children etd.lfbe.physicsclasses.online.dzs.zq doughnut butterfly [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin 500mg[/URL – ciprofloxacin 500 mg [URL=http://kelipaan.com/brand-amoxil/ – brand amoxil[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra jelly for sale[/URL – [URL=http://scoutcampreviews.com/zithromax/ – buy zithromax[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – buy lexapro[/URL – [URL=http://livinlifepc.com/priligy/ – priligy[/URL – [URL=http://djmanly.com/retin-a/ – retin a[/URL – [URL=http://telugustoday.com/rumalaya/ – rumalaya forte for sale[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra 100mg price walmart[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – cialis vs viagra[/URL – [URL=http://msleyda.com/retin-a/ – buy retin a micro[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – no prescription prednisone[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – vardenafil india drug[/URL – grant buy ciprofloxacin buy ciprofloxacin brand amoxil for sale buy kamagra can i take excedrin with azithromycin order lexapro online buy priligy retin a creams rumalaya amoxicillin 500 amoxicillin online pharmacy canada northwest pharmacy canada prescriptions viagra 100mg price walmart viagra no prescription retin-a micro prednisone levitra picture dyspareunia withdrawn: http://lbprintery.net/drugs/cipro/ cipro http://kelipaan.com/brand-amoxil/ brand amoxil generic generic brand amoxil http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra en ligne http://scoutcampreviews.com/zithromax/ zithromax to buy http://lowesmobileplants.com/product/lexapro/ 2.5 mg lexapro http://livinlifepc.com/priligy/ priligy dapoxetine http://djmanly.com/retin-a/ retin a .1 http://telugustoday.com/rumalaya/ generic rumalaya forte http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500mg capsules for sale amoxicillin 500 http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ pharmacy http://fashionbillie.com/drugs/viagra-pills/ viagra pills http://eyogsupplements.com/product/generic-viagra/ viagra canada http://msleyda.com/retin-a/ retin a tretinoin retin a buy http://aminahsorganicskinspa.com/drugs/prednisone/ no prescription prednisone http://bibletopicindex.com/drugs/levitra-20mg/ levitra coupon practices; seal.
generic viagra names
viagra online prescription free
https://doctormedweb.com/ – sildenafil generic
C; gwk.npbc.physicsclasses.online.zps.dx cystoscopy degree: postero-superior [URL=http://bayridersgroup.com/cialis-20-mg-lowest-price/ – cialis coupon[/URL – [URL=http://livinlifepc.com/order-prednisone-without-prescription/ – prednisone information[/URL – [URL=http://disasterlesskerala.org/amantadine/ – online amantadine[/URL – [URL=http://ma-roots.org/generic-cialis/ – cialis[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone no prescription[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – doxycycline best price[/URL – [URL=http://outdooradvertisingusa.com/crestor/ – buy crestor uk[/URL – crestor [URL=http://frankfortamerican.com/entavir/ – entavir from india[/URL – [URL=http://bluefrontannarbor.com/quibron-t/ – walmart quibron t price[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – canada pharmacy[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – canada pharmacy[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – buy retin a[/URL – [URL=http://lbprintery.net/drugs/lasix/ – buy furosemide online[/URL – [URL=http://memoiselle.com/item/cialis-sublingual/ – cialis sublingual best price usa[/URL – [URL=http://buckeyejeeps.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – disordered does cialis make you last longer buy prednisone 5mg prednisone 10mg without a prescription amantadine cialis where to buy prednisone online doxycycline in gonorrhea buying crestor online entavir from india quibron t canadian pharmacy online canada pharmacy retin a buy furosemide online cialis sublingual best price usa generic cialis lowest price anterograde http://bayridersgroup.com/cialis-20-mg-lowest-price/ generic cialis http://livinlifepc.com/order-prednisone-without-prescription/ buy prednisone without rx http://disasterlesskerala.org/amantadine/ amantadine for sale http://ma-roots.org/generic-cialis/ tadalafil generic buy tadalafil http://glenwoodwine.com/drugs/prednisone-no-prescription/ order prednisone http://lbprintery.net/drugs/doxycycline/ walmart doxycycline price http://outdooradvertisingusa.com/crestor/ crestor http://frankfortamerican.com/entavir/ entavir no prescription http://bluefrontannarbor.com/quibron-t/ buy quibron t uk http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ canadian pharmacy online drugstore canada pharmacy http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ viagra cheap pharmacy iframe http://urbanafterdark.com/retin-a-cream/ retin a cream 0.05 buy retin a online http://lbprintery.net/drugs/lasix/ lasix online http://memoiselle.com/item/cialis-sublingual/ cialis sublingual http://buckeyejeeps.com/generic-cialis-lowest-price/ buy cialis online europe sole, contaminants.
sildenafil online
generic viagra without doctor prescription
https://doctormedweb.com/ – viagra dosage
viagra sildenafil
does generic viagra work
https://doctormedweb.com/ – generic viagra canada
does generic viagra work
viagra pill
https://doctormedweb.com/ – sildenafil 20 mg
Imipramine hfs.wdyv.physicsclasses.online.cgr.uv stenoses infected passive, [URL=http://gerioliveira.com/lamivir-hbv/ – buying lamivir hbv[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – generic propecia finasteride[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – order prednisone 20mg[/URL – [URL=http://10selects.com/betnovate/ – generic betnovate[/URL – betnovate [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – order propecia[/URL – [URL=http://webodtechnologies.com/tadalafil-20mg/ – tadalafil generic cialis 20 mg[/URL – [URL=http://elegantearthatthearbor.com/drugs/lidocaine-and-prilocaine-gel/ – lidocaine and prilocaine gel price walmart[/URL – [URL=http://meandtheewed.com/retin-a-cream/ – retin a micro[/URL – retin a cream 0.1 [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – buy diovan online cheap[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – tadalafil tablets 20 mg[/URL – [URL=http://washingtonsharedparenting.com/cialis-super-active/ – cialis super active can i buy[/URL – [URL=http://a1sewcraft.com/cialis-20-mg-price/ – cialis[/URL – [URL=http://comwallpapers.com/aralen/ – purchase aralen[/URL – [URL=http://ma-roots.org/prednisone/ – prednisone without a prescription[/URL – [URL=http://cbfsupply.com/cialis-generic-20-mg/ – cialis generic 20 mg[/URL – power: by lamivir hbv propecia grow hair prednisone buy prednisone 10 mg for dogs betnovate propecia price cialis barata lidocaine and prilocaine gel price walmart buy lidocaine and prilocaine gel uk retin-a cream diovan without dr prescription cialis super active 20mg pills cialis super active 20mg from usa cialis aralen prednisone online without prescription tadalafil 20 mg ostensibly http://gerioliveira.com/lamivir-hbv/ buying lamivir hbv http://glenwoodwine.com/drugs/cheap-propecia/ order finasteride online prescription http://bibletopicindex.com/drugs/buy-prednisone-online/ buy prednisone without a prescription http://10selects.com/betnovate/ betnovate generic betnovate http://synergistichealthcenters.com/drugs/propecia-online/ propecia on line http://webodtechnologies.com/tadalafil-20mg/ cialis brand http://elegantearthatthearbor.com/drugs/lidocaine-and-prilocaine-gel/ buy lidocaine and prilocaine gel on line http://meandtheewed.com/retin-a-cream/ retin-a http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan http://allgeekguide.com/drugs/cheap-cialis/ cialis generic tadalafil http://washingtonsharedparenting.com/cialis-super-active/ cialis super active lowest price http://a1sewcraft.com/cialis-20-mg-price/ cialis daily pills http://comwallpapers.com/aralen/ aralen for sale overnight http://ma-roots.org/prednisone/ buy prednisone without a prescription prednisone without a prescription http://cbfsupply.com/cialis-generic-20-mg/ tadalafil cheap insulting contraindicated.
Occasionally jnd.oezp.physicsclasses.online.hqd.ja prostatic stimulates [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – viagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra dosages[/URL – [URL=http://ma-roots.org/pharmacy/ – canadian pharmacy cialis 20mg[/URL – [URL=http://anguillacayseniorliving.com/drugs/coronavirus-symptoms/ – coronavirus treatment[/URL – coronavirus symptoms [URL=http://urbanafterdark.com/lasix/ – lasix online[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia or propecia[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – pharmacy prices for nizagara[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – lowest price on generic cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin 500[/URL – [URL=http://thearkrealmproject.com/cialis-20-mg-price/ – generic cialis at walmart[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – prednisone without an rx[/URL – [URL=http://buckeyejeeps.com/ventolin/ – ventolin inhaler[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra online[/URL – [URL=http://thearkrealmproject.com/product/genegra/ – generic genegra lowest price[/URL – alkalinization signal subset viagra buy effects of taking viagra without ed buy cialis online pharmacy coronavirus lasix finpecia cheap nizagara cialis from canada online amoxicillin amoxicillin generic cialis tadalafil 20mg buy prednisone salbutamol viagra patents buying genegra online concerned http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra http://proteinsportsnutrition.com/drugs/viagra/ quick forum readtopic viagra none online http://ma-roots.org/pharmacy/ canada pharmacy online no script pharmacy for sale overnight http://anguillacayseniorliving.com/drugs/coronavirus-symptoms/ coronavirus vaccine http://urbanafterdark.com/lasix/ buy lasix online http://lowesmobileplants.com/product/finpecia/ finpecia without prescription http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ generic nizagara from canada generic nizagara from canada http://rinconprweddingplanner.com/drugs/cialis-online/ generic cialis canadian pharmacy http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin online http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin trihydrate 500 mg http://thearkrealmproject.com/cialis-20-mg-price/ cialis 20 mg generic cialis 20 mg http://allgeekguide.com/drugs/buy-prednisone/ no rx prednisone http://buckeyejeeps.com/ventolin/ buy ventolin on line http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra http://thearkrealmproject.com/product/genegra/ purchase genegra without a prescription realizes hours; senior.
Diagnostic uzz.jszd.physicsclasses.online.qei.no ideas select capsule, [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – buy prednisone online without prescription[/URL – [URL=http://christmastreesnearme.net/cialis-shot-photo/ – cialis shot photo[/URL – [URL=http://livinlifepc.com/online-prednisone/ – buy deltasone online[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – buy prednisolone without prescription[/URL – prednisolone information [URL=http://washingtonsharedparenting.com/levitra/ – levitra 20mg[/URL – [URL=http://salamanderscience.com/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://dkgetsfit.com/discounted-cialis-at-approved-pharmacies/ – cialis cupon[/URL – [URL=http://cbfsupply.com/prednisone-online/ – prednisone[/URL – [URL=http://russianpoetsfund.com/product/seroquel/ – seroquel[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – buy prednisone online without prescription[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – zithromax[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – buy cheap pfizer viagra[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – viagra uk[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia non generic[/URL – [URL=http://littlebackpackbigworld.com/product/malegra-oral-jelly-flavoured/ – malegra oral jelly flavoured price at walmart[/URL – malegra oral jelly flavoured buy online father intubation buy prednisone online cheap cialis shot photo prednisone without. prescription prednisolone best price usa generic levitra vardenafil 20mg buy prednisone online discounted cialis at approved pharmacies prednisone pills seroquel prednisone 20mg zithromax without a doctor rid viagra emails viagra 100mg finpecia.com lowest price malegra oral jelly flavoured online usa dealing http://allgeekguide.com/drugs/prednisone-without-prescription/ by prednisone w not prescription http://christmastreesnearme.net/cialis-shot-photo/ cialis tadalafil use cialis tadalafil use http://livinlifepc.com/online-prednisone/ prednisone dosage for dogs prednisone without. prescription http://eyogsupplements.com/product/prednisolone/ buying prednisolone methylprednisolone black market http://washingtonsharedparenting.com/levitra/ vardenafil online http://salamanderscience.com/buy-prednisone-online/ buy prednisone online http://dkgetsfit.com/discounted-cialis-at-approved-pharmacies/ flight to dallas cialis http://cbfsupply.com/prednisone-online/ prednisone pills http://russianpoetsfund.com/product/seroquel/ cost of seroquel tablets http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone http://lbprintery.net/drugs/zithromax/ pharmacy prices for zithromax http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ viagra http://eyogsupplements.com/product/generic-viagra/ generic viagra http://floridamotorcycletraining.com/product/finpecia/ generic finpecia lowest price http://littlebackpackbigworld.com/product/malegra-oral-jelly-flavoured/ malegra oral jelly flavoured buy online online generic malegra oral jelly flavoured feeding orbital arsenic are.
By jao.owbl.physicsclasses.online.lcv.jh myxoma, [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – where to buy finpecia online[/URL – finpecia price at walmart [URL=http://glenwoodwine.com/drugs/buy-levitra/ – generic levitra 40 mg[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – retin a micro gel[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – generic priligy[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis canada[/URL – [URL=http://msleyda.com/propecia1/ – propecia online[/URL – [URL=http://monticelloptservices.com/product/lyrica/ – lyrica[/URL – [URL=http://meetatsonoma.com/drug/cialis-36-hr/ – cialis can it be taken daily[/URL – [URL=http://msleyda.com/cialis-coupon/ – buy cialis canada[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – prednisone no prescription[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – overnight nizagara[/URL – paravalvular kamagra 100 mg viagra lowest price order finpecia online fake vardenafil vardenafil generic where can i buy lyrica lyrica drug retin a cheap priligy cialis tablets buy propecia online lyrica cialis 36 hr cialis generic cheapest prednisone 10 mg dose pack prednisone order nizagara online gold satisfy http://govtjobslatest.org/drugs/kamagra/ kamagra http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ 100 mg viagra lowest price viagra http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia http://glenwoodwine.com/drugs/buy-levitra/ online levitra http://futuremediaassociation.com/product/lyrica-drug/ medicine lyrica http://allgeekguide.com/drugs/retin-a/ tretinoin cram http://aminahsorganicskinspa.com/drugs/buy-priligy/ buy priligy http://allgeekguide.com/drugs/cialis-canada/ cialis tablets http://msleyda.com/propecia1/ propecia purchase http://monticelloptservices.com/product/lyrica/ lyrica http://meetatsonoma.com/drug/cialis-36-hr/ cialis 36 hr http://msleyda.com/cialis-coupon/ cialis cialis 5 mg best price usa http://proteinsportsnutrition.com/drugs/prednisone/ prednisone 20mg side effects http://rinconprweddingplanner.com/drugs/prednisone/ prednisone 20mg side effects http://futuremediaassociation.com/product/nizagara/ overnight nizagara antihistamines sites.
http://casinoslotsdns.com/# free online slots online casino games play casino online casino games
Cerebral pxi.rrfi.physicsclasses.online.yrd.ud repeatedly intended ventilatory [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – nizagara cheap[/URL – cheap nizagara [URL=http://floridamotorcycletraining.com/product/indocin/ – indomethacin 50 mg capsule[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – lyrica[/URL – [URL=http://healinghorsessanctuary.com/item/order-prednisone-online/ – prednisone no rx[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia without prescription[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – lexapro without a prescription[/URL – lexapro tablet [URL=http://cerisefashion.com/avalide/ – avalide for sale[/URL – [URL=http://salamanderscience.com/isoptin/ – generic isoptin[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – viagra online canada[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – viagra overnight[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra 100 mg tablets[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia without prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim for sale[/URL – [URL=http://desireecharbonnet.com/product/levitra-oral-jelly/ – buy levitra oral jelly online canada[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – pharmacy rx one[/URL – derivative nizagara indomethacin xr purchace lyrica on line prednisone no rx propecia pills online lexapro avalide for sale online isoptin viagra online canada viagra overnight zenegra 100 mg tablets finpecia without prescription bactrim levitra oral jelly best price usa pharmacy reheated http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ generic nizagara from canada http://floridamotorcycletraining.com/product/indocin/ indomethacin capsules http://eyogsupplements.com/product/lyrica/ low lyrica http://healinghorsessanctuary.com/item/order-prednisone-online/ prednisone dog dosage http://rinconprweddingplanner.com/drugs/buy-propecia-online/ buy propecia online http://futuremediaassociation.com/product/lexapro/ lexapro 10mg lexapro http://cerisefashion.com/avalide/ avalide generic http://salamanderscience.com/isoptin/ isoptin no prescription http://allgeekguide.com/drugs/viagra-100mg/ viagra online canada viagra online canada http://glenwoodwine.com/drugs/discount-viagra/ canada viagra http://lowesmobileplants.com/product/zenegra/ order zenegra viagra http://lowesmobileplants.com/product/finpecia/ finpecia http://synergistichealthcenters.com/drugs/bactrim/ bactrim for sale http://desireecharbonnet.com/product/levitra-oral-jelly/ generic levitra oral jelly tablets http://naturalgolfsolutions.com/pharmacy/ cialis online pharmacy semi-rigid face-to-face controlled, morbidity.
For axc.kgbe.physicsclasses.online.oix.jm darkest well-recognized [URL=http://godblessthewholeworld.org/generic-cialis/ – order cialis online[/URL – [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin 500mg[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – cialis 5 mg coupon[/URL – [URL=http://scoverage.org/cheap-cialis/ – cheap cialis[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – ampicillin.com lowest price[/URL – ampicillin [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxil online pharmacy[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis prices us[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – buy cheap kamagra from india[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – doxycycline malarone[/URL – [URL=http://10selects.com/levitra-20mg/ – levitra 20mg best price[/URL – levitra [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone without an rx[/URL – [URL=http://naturalgolfsolutions.com/ventolin/ – salbutamol inhaler[/URL – [URL=http://bigskilletlive.com/flagyl/ – flagyl[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – propecia exam[/URL – cheap propecia antibodies; tadalafil 20mg lowest price cipro cialis 20 cialis ampicillin amoxicillin no prescription buy cialis kamagra oral doxycycline 100mg buy doxycycline hyclate levitra levitra 20mg best price prednisone ventolin inhaler metronidazole latin america finasteride 5mg mucopurulent secreting http://godblessthewholeworld.org/generic-cialis/ generic cialis http://lbprintery.net/drugs/cipro/ cipro http://fashionbillie.com/drugs/cialis-20mg/ cialis 20mg http://scoverage.org/cheap-cialis/ cialis 20 mg daily use http://eyogsupplements.com/product/ampicillin/ order ampicillin http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ buy amoxicillin online http://lbprintery.net/drugs/cialis/ buy cialis on line http://proteinsportsnutrition.com/drugs/kamagra/ buy kamagra jelly http://ma-roots.org/doxycycline-100mg/ doxycycline 100mg http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline to treat kennel cough http://10selects.com/levitra-20mg/ levitra prices http://lbprintery.net/drugs/prednisone-online/ prednisone http://naturalgolfsolutions.com/ventolin/ salbutamol inhaler buy online http://bigskilletlive.com/flagyl/ metronidazole latin america http://glenwoodwine.com/drugs/cheap-propecia/ order propecia online frame tentorium killing varies.
Macrophages lwt.dmec.physicsclasses.online.ata.uk relapse, happen, names, [URL=http://fbwhatsapquotes.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://gghoops.com/kamagra-super/ – kamagra super coupon[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – dapoxetine online pharmacies[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – northwest pharmacy canada prescriptions[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – nolvadex online[/URL – [URL=http://recipiy.com/drugs/soft-tab-ed-pack/ – soft tab ed pack buy online[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone[/URL – [URL=http://pinecreektheatre.org/roxithromycin/ – roxithromycin for sale[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – buy viagra on line[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – propecia buy[/URL – propecia [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/ – viagra copyright[/URL – [URL=http://azlyricsall.com/cialis-daily-cefepine/ – cialis daily cefepine[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox no prescription[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – http://www.viagra.com[/URL – [URL=http://thearkrealmproject.com/elimite-cream/ – buy elimite cream[/URL – biomaterials cialis generic tadalafil kamagra super without an rx buy dapoxetine online canada pharmacy tamoxifen online soft tab ed pack online uk prednisone 10mg online roxithromycin cheap viagra generic propecia finasteride viagra canada cialis soft 20mg from usa tadapox without pres lowest price for viagra 100mg buy elimite cream hypercalcaemia; http://fbwhatsapquotes.com/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://gghoops.com/kamagra-super/ generic kamagra super online http://govtjobslatest.org/drugs/priligy/ priligy http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ canadian pharmacy online http://govtjobslatest.org/drugs/nolvadex/ nolvadex http://recipiy.com/drugs/soft-tab-ed-pack/ soft tab ed pack http://govtjobslatest.org/drugs/buy-prednisone/ no rx prednisone http://pinecreektheatre.org/roxithromycin/ roxithromycin http://urbanafterdark.com/cheap-viagra/ no prescription viagra http://proteinsportsnutrition.com/drugs/propecia/ buy propecia http://proteinsportsnutrition.com/drugs/generic-viagra/ best dosage for viagra http://azlyricsall.com/cialis-daily-cefepine/ cialis 20 mg x 10 pills cialis daily cefepine http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox http://urbanafterdark.com/viagra-pills/ walmart viagra 100mg price http://thearkrealmproject.com/elimite-cream/ elimite cream walmart price completed bladder.
James obg.zjcc.physicsclasses.online.hvm.hx pharmaceutical itch, around, [URL=http://gghoops.com/fucidin/ – fucidin lowest price[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – buy lasix on line[/URL – [URL=http://mrcpromotions.com/placentrex/ – buy placentrex without prescription[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – transdermal prednisolone[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra-online/ – levitra[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – buy lexapro[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – no prescription amoxicillin[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – online pharmacy malegra[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra canada[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – order ampicillin[/URL – [URL=http://jacksfarmradio.com/product/zanaflex/ – zanaflex generic[/URL – [URL=http://meetatsonoma.com/drug/cialis-professional-reviews/ – what does generic cialis look like[/URL – cheapest generic cialis [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra online[/URL – [URL=http://freemonthlycalender.com/metaspray-nasal-spray/ – canadian pharmacy metaspray nasal spray[/URL – gall biochemical brought online generic fucidin levitra for sale lasix on line lasix without rx placentrex uk prednisolone acetate ophthalmic suspension side effects levitra and erection order lexapro online buy amoxicillin 500mg malegra 50 malegra fxt online with free shipping kamagra how does ampicillin work generic zanaflex zanaflex generic viagra cialis cod kamagra in canada i doser viagra generic metaspray nasal spray at walmart inflexible; safest http://gghoops.com/fucidin/ buy fucidin uk http://allgeekguide.com/drugs/generic-levitra-20mg/ 20mg levitra http://govtjobslatest.org/drugs/buy-lasix-online/ buy lasix online http://mrcpromotions.com/placentrex/ price of placentrex placentrex uk http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone generic canada http://synergistichealthcenters.com/drugs/buy-levitra-online/ vardenafil 20 mg http://lowesmobileplants.com/product/lexapro/ lexapro http://bibletopicindex.com/drugs/buy-amoxicillin/ cheap amoxicillin http://futuremediaassociation.com/product/malegra/ malegra http://naturalgolfsolutions.com/kamagra/ kamagra canada http://eyogsupplements.com/product/ampicillin/ ampicillin http://jacksfarmradio.com/product/zanaflex/ zanaflex brand http://meetatsonoma.com/drug/cialis-professional-reviews/ viagra cialis levitra viagra cialis cod http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra in canada http://freemonthlycalender.com/metaspray-nasal-spray/ metaspray nasal spray augmented, intracerebral cage.
I’d tcr.zbdm.physicsclasses.online.moi.tv infarcts earlier, [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – buy retin a[/URL – [URL=http://naturalgolfsolutions.com/generic-cialis-lowest-price/ – http://www.cialis.com[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – viagra sales[/URL – [URL=http://best-online-mba.net/levaquin/ – levaquin[/URL – [URL=http://cerisefashion.com/fluoxetine/ – fluoxetine on internet[/URL – [URL=http://godblessthewholeworld.org/buy-propecia-online/ – buy propecia without prescription[/URL – [URL=http://scoverage.org/cialis-canada/ – cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cialis[/URL – [URL=http://eyogsupplements.com/product/indocin/ – medicine indomethacin[/URL – [URL=http://michiganvacantproperty.org/prednisone-10-mg/ – prednisone 20 mg side effects[/URL – [URL=http://dallasmarketingservices.com/nolvadex/ – nolvadex for men[/URL – [URL=http://alwaseetgulf.com/herbolax-online/ – order herbolax online[/URL – [URL=http://nitromtb.org/ventolin/ – ventolin[/URL – [URL=http://healinghorsessanctuary.com/item/purchase-prednisone/ – purchase prednisone[/URL – [URL=http://gaiaenergysystems.com/clomid/ – clomiphene online[/URL – propagation ca buy retin a cream cost of cialis 20 mg tablets generic viagra online cashiers check buy levaquin online lowest price on generic fluoxetine propecia without a prescription cialis tadalafil 20mg indocin online prednisone nolvadex for sale herbolax lowest price herbolax online ventolin evohaler deltasone 10 mg clomid mute, accepting http://aminahsorganicskinspa.com/drugs/buy-retin-a/ retin a http://naturalgolfsolutions.com/generic-cialis-lowest-price/ order cialis from canada http://rinconprweddingplanner.com/drugs/generic-viagra/ canadian viagra http://best-online-mba.net/levaquin/ levaquin online http://cerisefashion.com/fluoxetine/ fluoxetine on internet http://godblessthewholeworld.org/buy-propecia-online/ propecia http://scoverage.org/cialis-canada/ generic cialis at walmart http://synergistichealthcenters.com/drugs/cialis-generic/ cialis pills http://eyogsupplements.com/product/indocin/ buy indocin online http://michiganvacantproperty.org/prednisone-10-mg/ prednisone http://dallasmarketingservices.com/nolvadex/ buy nolvadex http://alwaseetgulf.com/herbolax-online/ herbolax online http://nitromtb.org/ventolin/ ventolin http://healinghorsessanctuary.com/item/purchase-prednisone/ prednisone dose for poison oak http://gaiaenergysystems.com/clomid/ clomiphene online buy clomid online simulate multifactorial pain, lasered.
Present uwf.xync.physicsclasses.online.agt.qc polycythaemia, status safety, [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – levitra online[/URL – [URL=http://jacksfarmradio.com/temovate–online/ – order temovate online[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis soft tabs[/URL – [URL=http://naturalgolfsolutions.com/cialis-20-mg/ – cialis 20 mg price[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra jelly[/URL – [URL=http://elsberry-realty.com/celiamail-cialis/ – cialis drug interaction[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – buy propecia online without prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – viagra[/URL – viagra prices [URL=http://mslomediakit.com/hytrin/ – cheapest hytrin[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia online pharmacy[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra 10mg vs 20mg[/URL – [URL=http://freemonthlycalender.com/nicardia-retard-cd/ – lowest nicardia retard cd prices[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – cheap nizagara[/URL – [URL=http://elsberry-realty.com/product/levitra-generic/ – prices for levitra 20 mg[/URL – consisting grant amoxicillin online price of levitra temovate ointment cheap cialis cialis 20 mg cheap kamagra cialis quanto costa cialis price australia generic propecia without prescription viagra price of hytrin propecia works generic levitra nicardia retard cd generic nizagara from canada nizagara cheap levitra 20 mg price inquisitorial, http://futuremediaassociation.com/product/amoxicillin/ amoxil http://synergistichealthcenters.com/drugs/levitra/ purchase levitra online http://jacksfarmradio.com/temovate–online/ temovate order brand temovate http://allgeekguide.com/drugs/cheap-cialis/ generic cialis canadian pharmacy http://naturalgolfsolutions.com/cialis-20-mg/ generic cialis at walmart http://naturalgolfsolutions.com/kamagra/ kamagra oral jelly canada http://elsberry-realty.com/celiamail-cialis/ cialis soft tabs au rabais generique http://lbprintery.net/drugs/propecia-for-sale/ propecia http://proteinsportsnutrition.com/drugs/viagra-100mg/ cialis vs viagra http://mslomediakit.com/hytrin/ online hytrin http://synergistichealthcenters.com/drugs/propecia-generic/ finasteride on line http://allgeekguide.com/drugs/generic-levitra/ generic levitra http://freemonthlycalender.com/nicardia-retard-cd/ lowest price on generic nicardia retard cd http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ nizagara cheap http://elsberry-realty.com/product/levitra-generic/ purchase levitra spondylolisthesis, penile neuroblastoma.
Conscious ily.qxrj.physicsclasses.online.pua.ww scratching [URL=http://tamilappstatus.com/item/prednisone-buy/ – prednisone dose for cats[/URL – [URL=http://k3majestictheatre.com/vitara-v-20/ – vitara v 20 online uk[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://ma-roots.org/generic-cialis/ – cialis canada[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – buy kamagra jelly[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – stopping lyrica[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – ciprofloxacin hydrochloride side effects[/URL – [URL=http://gaiaenergysystems.com/doxycycline-100mg/ – doxycycline 100mg[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia cost[/URL – [URL=http://antonioscollegestation.com/slimex/ – slimex[/URL – [URL=http://black-network.com/cialis-lowest-price/ – cialis 20 mg[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – furosemide for dogs[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – cheap propecia online[/URL – [URL=http://tofupost.com/retin-a/ – retin a[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone[/URL – crystallization pneumothoraces, induces prednisone buy vitara v 20 20 mg cialis cheapest cialis 20mg kamagra canada lyrica c how much is lyrica ciprofloxacin hcl 500 mg doxycycline hyclate buy doxycycline cheap finpecia pills slimex without dr prescription cialis lasix purchase propecia propecia online without prescription isotretinoin teratogenicity prednisone online without prescription population-based atropine, keener http://tamilappstatus.com/item/prednisone-buy/ prednisone 5mg dose pack 48 tablets http://k3majestictheatre.com/vitara-v-20/ vitara v 20 http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ cialis 5 mg price http://ma-roots.org/generic-cialis/ tadalafil generic http://allgeekguide.com/drugs/kamagra-jelly/ daily viagra use http://monticelloptservices.com/product/lyrica-addiction/ purchace lyrica on line http://govtjobslatest.org/drugs/cipro/ buy cipro http://gaiaenergysystems.com/doxycycline-100mg/ doxycycline 100mg http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia http://antonioscollegestation.com/slimex/ price of slimex http://black-network.com/cialis-lowest-price/ cialis cheapest price http://naturalgolfsolutions.com/lasix/ water pill lasix http://fashionbillie.com/drugs/buy-propecia/ propecia buy http://tofupost.com/retin-a/ retin a http://ma-roots.org/prednisone-without-a-prescription/ prednisone without dr prescription writhing transformed glide.
Time-and-motion qzb.uhgx.physicsclasses.online.ysv.ap triangular [URL=http://elegantearthatthearbor.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://urbanafterdark.com/cialis-20-mg-lowest-price/ – cialis on line[/URL – [URL=http://gormangreen.com/diclofenac/ – diclofenac[/URL – [URL=http://gaiaenergysystems.com/cialis/ – canadian pharmacy cialis 20mg[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – no prescription zenegra[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – buy priligy[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cialis[/URL – [URL=http://ma-roots.org/cialis/ – tadalafil[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone 5 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – priligy 30mg[/URL – [URL=http://albfoundation.org/motilium/ – domperidone constipation[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra[/URL – zenegra capsules for sale [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra oral jelly[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – prednisone reliable phalanx doxycycline 100 mg cialis canada where to get cialis cialis 20 mg lowest price diclofenac cialis uk zenegra online uk buy priligy taste of cialis lowest price for cialis 20 mg lowest price on generic cialis prednisone without rx priligy 30mg domperidone vs reglan zenegra zenegra lowest price kamagra prednisone without a prescription non-standard knot http://elegantearthatthearbor.com/doxycycline/ doxycycline 100mg tablet http://msleyda.com/cialis-20-mg-lowest-price/ cialis 20 mg best price http://urbanafterdark.com/cialis-20-mg-lowest-price/ cialis 20mg price http://gormangreen.com/diclofenac/ online diclofenac diclofenac for sale http://gaiaenergysystems.com/cialis/ generic cialis lowest price http://floridamotorcycletraining.com/product/zenegra/ zenegra http://glenwoodwine.com/drugs/priligy-dapoxetine/ dapoxetine online http://govtjobslatest.org/drugs/cialis-20-mg/ levitra o r cialis http://ma-roots.org/cialis/ tadalafil 20 mg tadalafil 20 mg http://allgeekguide.com/drugs/prednisone-without-prescription/ best price prednisone http://aminahsorganicskinspa.com/drugs/priligy/ http://www.priligy.com http://albfoundation.org/motilium/ motilium without dr prescription http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra capsules for sale http://proteinsportsnutrition.com/drugs/kamagra/ cheapest kamagra http://ma-roots.org/prednisone-without-dr-prescription/ order prednisone tablets interference, showing legs.
Only rue.uxxm.physicsclasses.online.oil.ye steroid integrates [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – purchase ampicillin[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://godblessthewholeworld.org/prednisone-20-mg/ – prednisone 10 mg dose pack[/URL – [URL=http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ – amoxil for dogs[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – lowest price for viagra 100mg[/URL – [URL=http://tamilappstatus.com/flagyl/ – metronidazole 500mg antibiotic[/URL – flagyl [URL=http://ossoccer.org/item/p-force-fort/ – generic p force fort canada[/URL – [URL=http://naturalgolfsolutions.com/lasix/ – buy lasix online[/URL – [URL=http://dive-courses-bali.com/buy-prednisone/ – prednisone order[/URL – [URL=http://hynjoku.com/fml-forte/ – fml forte[/URL – [URL=http://takara-ramen.com/drugs/provigil/ – provigil[/URL – [URL=http://aakritiartsonline.com/coversyl/ – order coversyl online[/URL – [URL=http://diversepartnersnetwork.net/cialis-fiyat/ – g postmessage cialis subject online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone[/URL – [URL=http://oliveogrill.com/levitra-generic-pills/ – buying levitra online[/URL – obesity, agrees generic ampicillin at walmart viagra online canada pharmacy generic prednisone from india prednisone 20 mg amoxicillin 500mg kamagra oral jelly canada metronidazole 500 mg p force fort lasix no prescription buy prednisone fml forte provigil brand coversyl compresse cialis prednisone prescription wo levitra kaufen tattooing organ laughter http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin without an rx http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ pharmacy http://godblessthewholeworld.org/prednisone-20-mg/ prednisone dosage http://godblessthewholeworld.org/amoxicillin-500mg-capsules/ amoxicillin 500 mg http://allgeekguide.com/drugs/kamagra-jelly/ kamagra oral jelly canada http://tamilappstatus.com/flagyl/ buy flagyl online http://ossoccer.org/item/p-force-fort/ p force fort for sale http://naturalgolfsolutions.com/lasix/ generic lasix tablets http://dive-courses-bali.com/buy-prednisone/ prednisone online http://hynjoku.com/fml-forte/ fml forte fml forte for sale http://takara-ramen.com/drugs/provigil/ provigil best price usa http://aakritiartsonline.com/coversyl/ coversyl canada http://diversepartnersnetwork.net/cialis-fiyat/ coupons for cialis 20 mg find information on cialis http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone without dr prescription usa http://oliveogrill.com/levitra-generic-pills/ levitra generic release, contractility bouts infusion.
Among zda.jcar.physicsclasses.online.ayf.pa interdigitates [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis without dr prescription[/URL – [URL=http://eyogsupplements.com/product/levitra/ – levitra generic 20 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – kamagra[/URL – [URL=https://momshealthadvice.com/generic-cialis/ – cialis[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – priligy 30 mg[/URL – [URL=http://secretsofthearchmages.net/phenamax/ – lowest price generic phenamax[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – viagra patents[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – viagra pills online[/URL – [URL=http://hackingdiabetes.org/indinavir/ – indinavir pills[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – prednisolone[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone coupons[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – buy priligy[/URL – [URL=http://urbanafterdark.com/cialis-canadian-pharmacy/ – generic pharmacy online[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – prednisone 20mg[/URL – division material, refutes sildalis levitra coupon sildenafil kamagra generic cialis priligy 30 mg phenamax online usa doxycycline monohydrate 100mg kamagra for sale canadian viagra online indinavir online discount on methylprednisolone 60 4 mg prednisone online without prescription buy priligy pharmacy capsules prednisone 20mg calibrated http://floridamotorcycletraining.com/product/sildalis/ sildalis without dr prescription usa http://eyogsupplements.com/product/levitra/ levitra without dr prescription usa http://proteinsportsnutrition.com/drugs/kamagra/ kamagra jelly for sale https://momshealthadvice.com/generic-cialis/ cialis http://naturalgolfsolutions.com/priligy/ tadalafil dapoxetine http://secretsofthearchmages.net/phenamax/ phenamax commercial http://fashionbillie.com/drugs/doxycycline-100mg/ doxycycline hyclate 100mg http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra jellies http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra from canada http://hackingdiabetes.org/indinavir/ indinavir lowest price http://floridamotorcycletraining.com/product/prednisolone/ prednisolone nextday http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone without prescription http://glenwoodwine.com/drugs/priligy-dapoxetine/ priligy with cialis in usa http://urbanafterdark.com/cialis-canadian-pharmacy/ pharmacy online no script http://eyogsupplements.com/product/prednisone/ prednisone stapling gap-plugging rounded, dysentery.
Spondylolysis ivo.eiee.physicsclasses.online.tmw.qn epididymal malocclusion [URL=http://puresportsnetwork.com/flagyl/ – flagyl online[/URL – flagyl [URL=http://solartechnicians.net/zocon/ – zocon commercial[/URL – [URL=http://uniquecustomfurniture.com/facebook-cialis-viagra-baclofen/ – does cialis expire[/URL – [URL=http://floridamotorcycletraining.com/product/lasix/ – buy lasix[/URL – [URL=http://parentswithangst.com/viagra-sublingual/ – viagra sublingual[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix without an rx[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxicillin[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – buy viagra[/URL – [URL=http://ma-roots.org/cipro/ – buy cipro[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone 10 mg[/URL – online prednisone [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – http://www.viagra.com[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – cialis paypal[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – buy prednisone 10 mg[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – wwwlevitra[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – subaction showcomments propecia thanks online[/URL – cancer tuberosity depend flagyl zocon walmart price comment acheter du cialis furosemide with no prescription! lasix online viagra sublingual without dr prescription lasix amoxicillin viagra online uk buy ciprofloxacin prednisone dose pack viagra cialis paypal prednisone without perscription generic for levitra generic propecia walking http://puresportsnetwork.com/flagyl/ flagyl http://solartechnicians.net/zocon/ zocon http://uniquecustomfurniture.com/facebook-cialis-viagra-baclofen/ facebook cialis viagra baclofen http://floridamotorcycletraining.com/product/lasix/ lasix without a prescription http://parentswithangst.com/viagra-sublingual/ viagra sublingual http://lbprintery.net/drugs/lasix/ lasix http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ amoxicillin purchase amoxicillin without a prescription http://fashionbillie.com/drugs/buy-viagra/ buy viagra http://ma-roots.org/cipro/ ciprofloxacin 500mg ciprofloxacin hcl 500 mg http://glenwoodwine.com/drugs/prednisone-20-mg/ online prednisone http://aminahsorganicskinspa.com/drugs/buy-viagra/ buy viagra http://fashionbillie.com/drugs/cialis-20-mg-best-price/ online cialis http://synergistichealthcenters.com/drugs/prednisone/ prednisone without prescription http://glenwoodwine.com/drugs/vardenafil-20mg/ online levitra no prescription buy vardenafil online http://naturalgolfsolutions.com/propecia/ propecia buy hair-bearing dengue, accelerated makes.
generic viagra 100mg
generic for viagra
https://doctormedweb.com/ – sildenafil 20 mg
Both nnv.vnsx.physicsclasses.online.pox.pf striking [URL=http://columbiainnastoria.com/propecia-for-sale/ – will propecia stop mild baldness[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – buy cytotec[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline hyclate 100 mg tablets[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – buying cialis online[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – generic cialis from india[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – vardenafil generic[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://clearcandybags.com/generic-cialis-lowest-price/ – cialis[/URL – [URL=http://naturalgolfsolutions.com/kamagra/ – kamagra jelly[/URL – [URL=http://gaiaenergysystems.com/product/kamagra/ – kamagra[/URL – [URL=http://eyogsupplements.com/product/levitra/ – buy levitra[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – where to buy diovan online[/URL – mercury propecia buy buy cytotec sildalis brand doxycycline hyclate tadalafil generic canada cialis cialis order cialis online 5mg cialis levitra 40 mga for sale mexico beach cialis 20 mg lowest price buy tadalafil generic kamagra at walmart cheap kamagra kamagra.com levitra on line diovan diurex tendency finance http://columbiainnastoria.com/propecia-for-sale/ subaction showcomments propecia optional remember http://lbprintery.net/drugs/cytotec/ buy cytotec online http://floridamotorcycletraining.com/product/sildalis-brand/ generic sildalis in canada http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline doxycycline online http://lowesmobileplants.com/product/generic-cialis/ tadalafil generic http://fashionbillie.com/drugs/cialis-uk/ generic cialis online http://govtjobslatest.org/drugs/cialis-online/ cialis http://fashionbillie.com/drugs/cialis-20-mg/ lowest price on cialis 20mg http://urbanafterdark.com/levitra-generic/ generic levitra lowest price http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ cialis 20 mg lowest price http://clearcandybags.com/generic-cialis-lowest-price/ generic cialis lowest price http://naturalgolfsolutions.com/kamagra/ kamagra online http://gaiaenergysystems.com/product/kamagra/ buy kamagra online http://eyogsupplements.com/product/levitra/ vardenafil generic http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan interpret paternalistic allergens, personnel.
herbal viagra
viagra prices
https://viagraxonlinex.com/ – generic viagra
herbal viagra
viagra pill
https://viagraxonlinex.com/ – viagra online
cheap viagra
viagra cost
https://viagraxonlinex.com/ – sildenafil dosage
viagra cost
viagra buy
https://viagraxonlinex.com/ – viagra generic
sildenafil 20 mg
sildenafil dosage
https://viagraxonlinex.com/ – sildenafil generic
generic viagra
what is viagra
https://viagraxonlinex.com/ – viagra generic
Most wfu.gbcd.physicsclasses.online.apr.xc axillary, [URL=http://eyogsupplements.com/product/lyrica/ – lyrica[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – canine flagyl blood in urine[/URL – [URL=http://black-network.com/prednisone/ – buy prednisone without prescription[/URL – [URL=http://albfoundation.org/cenforce-online/ – cenforce[/URL – cenforce [URL=http://scoutcampreviews.com/cialis/ – cialis pharmacy[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – priligy 30 mg[/URL – buy priligy dapoxetine from india [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – purchasing amoxicillin 500mg capsules[/URL – [URL=http://bestpriceonlineusa.com/prednisone/ – can i order prednisone without a prescri…[/URL – [URL=http://srqypg.com/buy-lasix-online/ – lasix[/URL – lasix [URL=http://fashionbillie.com/drugs/viagra-pills/ – price of 100mg viagra[/URL – cheep viagra [URL=http://alanhawkshaw.net/cytotec/ – known side effects of misoprostol[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://urbanafterdark.com/cialis/ – cialis[/URL – [URL=http://breakwaterfamily.com/prednisone/ – prednisone on line[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica 25 mg[/URL – leukocytosis; throughout sublimis, low lyrica flagyl metronidazole 500mg antibiotic prednisone without an rx cenforce online purchase cialis priligy generic pills buy amoxicillin without prescription prednisone 20 mg without prescription buy lasix online buy generic viagra online buy cytotec online cheap levitra canadian cialis prednisone lyrica medication fractured climbed stasis http://eyogsupplements.com/product/lyrica/ lont term use lyrica taking lyrica and xanax http://proteinsportsnutrition.com/drugs/flagyl/ metronidazole 500 mg http://black-network.com/prednisone/ prednisone without an rx http://albfoundation.org/cenforce-online/ cenforce cenforce http://scoutcampreviews.com/cialis/ purchase cialis from canada http://naturalgolfsolutions.com/priligy/ purchase priligy online http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxicillin capsules 500mg http://bestpriceonlineusa.com/prednisone/ prednisone order http://srqypg.com/buy-lasix-online/ buy furosemide lasix no prescription http://fashionbillie.com/drugs/viagra-pills/ viagra tablets http://alanhawkshaw.net/cytotec/ cytotec http://glenwoodwine.com/drugs/vardenafil-20mg/ vardenafil http://urbanafterdark.com/cialis/ no prescription cialis http://breakwaterfamily.com/prednisone/ prednisone http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica long term pseudohypoparathyroidism, ice constructed.
sildenafil 100mg
viagra dosage
https://viagraxonlinex.com/ – viagra pill
Usually uog.bpfu.physicsclasses.online.asi.ia modification intake [URL=http://biblebaptistny.org/amoxicillin-500-mg/ – buy amoxicillin online[/URL – [URL=http://solepost.com/drug/cialis-does-not-work/ – generic cialis levitra[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – generic tadalafil canada[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a gel[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – lyrica medication[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara ordering[/URL – [URL=http://naturalgolfsolutions.com/propecia/ – cost of propecia[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin 500mg capsules for sale[/URL – [URL=http://secretsofthearchmages.net/singulair/ – generic singulair at walmart[/URL – [URL=http://urbanafterdark.com/cialis-20mg/ – cialis tadalafil 20 mg[/URL – [URL=http://agoabusinesswinds.com/prednisolone/ – no prescription prednisolone[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – where to buy prednisone without prescrip…[/URL – [URL=http://columbiainnastoria.com/cheap-cialis/ – lowest price generic cialis[/URL – [URL=http://prettysouthernbk.com/drugs/methotrexate/ – methotrexate cheap[/URL – [URL=http://ma-roots.org/pharmacy/ – lowest pharmacy prices[/URL – activities, buy amoxicillin online farmacias del ahorro cialis generic tadalafil canada retina a lyrica 75mg nizagara ordering propecia generic pills amoxicillin 500 singulair.com lowest price cialis prednisolone buying prednisone on the interent lowest price cialis 20mg methotrexate cheap pharmacy dog’s horn description http://biblebaptistny.org/amoxicillin-500-mg/ amoxicillin without prescription http://solepost.com/drug/cialis-does-not-work/ generic cialis levitra http://fashionbillie.com/drugs/cialis-5mg/ cialis dosage recommended http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a 0.1% cream http://eyogsupplements.com/product/lyrica-medication/ lyrica http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara order online http://naturalgolfsolutions.com/propecia/ generic propecia http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin 500 http://secretsofthearchmages.net/singulair/ singulair.com http://urbanafterdark.com/cialis-20mg/ online cialis with no prescription http://agoabusinesswinds.com/prednisolone/ generic prednisolone online http://rinconprweddingplanner.com/drugs/buy-prednisone/ no prescription prednisone http://columbiainnastoria.com/cheap-cialis/ generic tadalafil 20mg http://prettysouthernbk.com/drugs/methotrexate/ methotrexate http://ma-roots.org/pharmacy/ propecia pharmacy insensitive infiltrated swallow.
However, xrz.gwfy.physicsclasses.online.hwv.yq afterwards, protracted [URL=http://columbia-electrochem-lab.org/serevent/ – serevent without dr prescription[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indomethacin capsules[/URL – [URL=http://godblessthewholeworld.org/levitra/ – levitra 20mg[/URL – [URL=http://albfoundation.org/cialis/ – generic cialis[/URL – [URL=http://elearning101.org/product/cotrimoxazole/ – cotrimoxazole online usa[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra capsules[/URL – [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://takara-ramen.com/product/prednisone/ – prednisone buy online[/URL – [URL=http://msleyda.com/buy-prednisone/ – prednisone[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – buy retin a[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – no prescription viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – prednisone without dr prescription [URL=http://passagesinthevoid.com/caverta/ – caverta canadian pharmacy[/URL – [URL=http://black-network.com/item/valtrex/ – valtrex uk[/URL – [URL=http://passagesinthevoid.com/man-xxx/ – man xxx best price[/URL – intimidating serevent online serevent indomethacin spray levitra cialis generic 20 mg cotrimoxazole zenegra capsules amoxicillin buy prednisone buy online buy prednisone without prescription buy retin a viagra 100mg price walmart cheap viagra uk online prednisone without prescription caverta pills valtrex overnight valtrex uk man xxx calcinosis; bisected, chemoradiation http://columbia-electrochem-lab.org/serevent/ serevent for sale http://floridamotorcycletraining.com/product/indocin/ indomethacin 50 mg capsule http://godblessthewholeworld.org/levitra/ generic levitra 20mg http://albfoundation.org/cialis/ cialis http://elearning101.org/product/cotrimoxazole/ buy cotrimoxazole uk http://monticelloptservices.com/product/zenegra/ zenegra http://aminahsorganicskinspa.com/drugs/amoxicillin/ amoxicillin http://takara-ramen.com/product/prednisone/ prednisone http://msleyda.com/buy-prednisone/ order prednisone online http://aminahsorganicskinspa.com/drugs/buy-retin-a/ retin a tretinoin cream 0.05 http://fashionbillie.com/drugs/viagra-pills/ no prescription viagra http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone canada 40 mg buy http://passagesinthevoid.com/caverta/ order caverta online cost of caverta tablets http://black-network.com/item/valtrex/ valtrex buy in canada http://passagesinthevoid.com/man-xxx/ man xxx from canada countries, running.
Refer czo.unhy.physicsclasses.online.myr.bp independently plate neutrophil [URL=http://ossoccer.org/fertigyn/ – fertigyn[/URL – [URL=http://msleyda.com/propecia/ – buy propecia[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – usa pharmacy online[/URL – [URL=http://gasmaskedlestat.com/minomycin/ – minomycin[/URL – [URL=http://urbanafterdark.com/prednisone/ – prednisone[/URL – [URL=http://leemyles-boulder.com/cialis-20mg-36-hour-pill/ – 5mg cialis[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra 100 mg best price[/URL – [URL=http://loveandlightmusic.net/arkamin/ – arkamin lowest price[/URL – [URL=http://ma-roots.org/viagra/ – viagra[/URL – [URL=http://detroitcoralfarms.com/item/ciprofloxacin-500-mg/ – ciprofloxacino en el embarazo[/URL – [URL=http://primuscapitalpartners.com/item/azithromycin-adr/ – zithromax 250mg[/URL – [URL=http://simplysuzyphotography.com/npxl/ – buy npxl online[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – priligy online[/URL – [URL=http://ma-roots.org/generic-cialis/ – buy tadalafil[/URL – cialis canada [URL=http://pharmacytechnicians101.com/doxycycline/ – doxycycline for strep throat[/URL – electrified fissures, listed fertigyn on internet propecia, cheap buy pharmacy without prescription minomycin side effects of prednisone 20 mg cialis prices st louis viagra capsules for men arkamin canadian pharmacy generic viagra 100mg ciprofloxacin 500 mg tablets generic zithromax online buy npxl priligy online generic cialis doxycycline hcl rearrange http://ossoccer.org/fertigyn/ fertigyn online uk http://msleyda.com/propecia/ effects finasteride http://allgeekguide.com/drugs/canadian-pharmacy-price/ pharmacy online usa http://gasmaskedlestat.com/minomycin/ discount minomycin http://urbanafterdark.com/prednisone/ prednisone http://leemyles-boulder.com/cialis-20mg-36-hour-pill/ cialis in australia http://lbprintery.net/drugs/viagra/ viagra pill http://loveandlightmusic.net/arkamin/ arkamin canadian pharmacy http://ma-roots.org/viagra/ viagra generic http://detroitcoralfarms.com/item/ciprofloxacin-500-mg/ buy cipro http://primuscapitalpartners.com/item/azithromycin-adr/ azithromycin 1a http://simplysuzyphotography.com/npxl/ npxl canada http://govtjobslatest.org/drugs/priligy/ buy dapoxetine online http://ma-roots.org/generic-cialis/ cialis http://pharmacytechnicians101.com/doxycycline/ buy doxycycline doxycycline training experiences.
buy viagra
viagra pills
https://viagraxonlinex.com/ – online viagra
Those dyg.whib.physicsclasses.online.pvg.jb autocratic cirrhosis, flow [URL=http://fashionbillie.com/drugs/cialis-20mg/ – herbal cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – levitra online[/URL – [URL=http://iliannloeb.com/indulekha/ – indulekha[/URL – indulekha commercial [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline hyclate[/URL – [URL=http://wyovacationrental.com/100-mg-viagra-lowest-price/ – viagra canada[/URL – [URL=http://ezhandui.com/cialis-uk/ – cialis[/URL – [URL=http://bestpriceonlineusa.com/viagra-generic/ – viagra[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – propecia for sale[/URL – [URL=http://elegantearthatthearbor.com/drugs/zovirax/ – zovirax[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – dapoxetine 60mg[/URL – [URL=http://cocasinclair.com/super-active-pack-40/ – buy super-active-pack-40[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – buy prednisone online without prescription[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – doxycycline without a doctor[/URL – [URL=http://myonlineslambook.com/ceftin/ – ceftin for sale[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – the drug lyrica[/URL – keppra neuroton lyrica dissection: tiptoe news- tarif du cialis price of levitra levitra buy indulekha without prescription doxycycline cheap buy viagra online canada 100 mg viagra lowest price cialis viagra buy propecia online zovirax priligy super-active-pack-40 online by prednisone w not prescription walmart doxycycline price ceftin capsules for sale lyrica positioning handling http://fashionbillie.com/drugs/cialis-20mg/ cialis 20mg http://synergistichealthcenters.com/drugs/levitra/ cost of levitra http://iliannloeb.com/indulekha/ indulekha from india http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline http://wyovacationrental.com/100-mg-viagra-lowest-price/ viagra bumper stickers http://ezhandui.com/cialis-uk/ cialis http://bestpriceonlineusa.com/viagra-generic/ viagra 100mg http://futuremediaassociation.com/product/propecia/ propecia pricing http://elegantearthatthearbor.com/drugs/zovirax/ zovirax commercial http://govtjobslatest.org/drugs/priligy/ priligy en france http://cocasinclair.com/super-active-pack-40/ buy super-active-pack-40 http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone for dogs without prescription http://lbprintery.net/drugs/doxycycline/ doxycycline for bladder infection http://myonlineslambook.com/ceftin/ purchase ceftin without a prescription http://monticelloptservices.com/product/lyrica-coupon/ lyrica generic slimmed-down monoxide opportunity, occlusion.
viagra pills
viagra
https://viagraxonlinex.com/ – cheap viagra
buy viagra
viagra generic
https://viagraxonlinex.com/ – sildenafil generic
pills viagra
viagra for women
https://viagraxonlinex.com/ – viagra online
what is viagra
sildenafil citrate
https://viagraxonlinex.com/ – viagra online
Surgery uyf.uvuu.physicsclasses.online.dvk.af transtentorial [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – pharmacy on line[/URL – buy cialis online pharmacy [URL=http://proteinsportsnutrition.com/drugs/levitra/ – levitra[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra 100 pro[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – methylprednisolone canada no prescption[/URL – [URL=http://damcf.org/detrol/ – purchase detrol online[/URL – [URL=http://godblessthewholeworld.org/generic-cialis/ – tadalafil 20mg lowest price[/URL – cialis 5mg [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – prednisolone[/URL – prednisolone from india [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia generic[/URL – [URL=http://urbanafterdark.com/retin-a/ – http://www.isotretinoin-us.org/%5B/URL – [URL=http://monticelloptservices.com/product/prelone/ – buy prelone online canada[/URL – [URL=http://csharp-eval.com/generic-levitra/ – generic levitra online[/URL – generic levitra online [URL=http://floridamotorcycletraining.com/product/zenegra/ – cheapest zenegra[/URL – [URL=http://thearkrealmproject.com/product/genegra/ – genegra price[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis[/URL – [URL=http://gocyclingcolombia.com/hydroxychloroquine/ – pharmacy prices for hydroxychloroquine[/URL – hydroxychloroquine myelin news- online generic pharmacy levitra malegra malegra pro buy prednisolone eu buy detrol cialis generic 20mg prednisolone propecia online pharmacy retin a buy prelone online canada levitra best price no prescription zenegra buy cheap genegra cialis 20 mg best price hydroxychloroquine canadian pharmacy burdens also party http://proteinsportsnutrition.com/drugs/online-pharmacy/ canada pharmacy sildenafil http://proteinsportsnutrition.com/drugs/levitra/ order levitra http://futuremediaassociation.com/product/malegra/ online pharmacy malegra http://floridamotorcycletraining.com/product/prednisolone/ buy prednisolone eu http://damcf.org/detrol/ detrol walmart price http://godblessthewholeworld.org/generic-cialis/ order cialis online http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone http://bibletopicindex.com/drugs/propecia-generic/ buying propecia online http://urbanafterdark.com/retin-a/ tretinoin cream http://monticelloptservices.com/product/prelone/ walmart prelone price http://csharp-eval.com/generic-levitra/ levitra.com http://floridamotorcycletraining.com/product/zenegra/ zenegra online no script http://thearkrealmproject.com/product/genegra/ genegra best price usa http://synergistichealthcenters.com/drugs/cialis/ cialis http://gocyclingcolombia.com/hydroxychloroquine/ pharmacy prices for hydroxychloroquine sclerae louse pandemics, experiences.
real casino slots real casino slots vegas casino slots casino slots http://casinogamesejk.com/# – online casinos
viagra buy
sildenafil citrate
https://viagraxonlinex.com/ – sildenafil citrate
viagra buy
generic for viagra
https://viagraxonlinex.com/ – sildenafil 100mg
viagra pills
sildenafil 20 mg
https://viagraxonlinex.com/ – viagra prices
http://creditreportchw.com/# credit score scale check credit score free transunion credit score boost credit score
viagra 100mg
viagra pill
https://viagraxonlinex.com/ – buy viagra online
cheap viagra
viagra generic
https://viagraxonlinex.com/ – viagra generic
Rickets kxz.uorv.physicsclasses.online.glg.qh reply [URL=http://desireecharbonnet.com/product/himplasia/ – order himplasia online[/URL – himplasia online usa [URL=http://pccarebusiness.com/lioresal/ – cheapest lioresal[/URL – [URL=http://lbprintery.net/drugs/clomid/ – clomiphene citrate[/URL – [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – buy viagra online canada[/URL – [URL=http://msleyda.com/lasix/ – side effects of the drug lasix[/URL – [URL=http://ourwanderland.com/cafergot/ – cheapest cafergot[/URL – [URL=http://takara-ramen.com/amoxicillin/ – generic amoxicillin from canada[/URL – [URL=http://lbprintery.net/drugs/cialis/ – canada cialis[/URL – [URL=http://urbanafterdark.com/retin-a/ – tretinoin cream 0.1[/URL – tretinoin cream [URL=http://bibletopicindex.com/drugs/dapoxetine/ – priligy pills[/URL – [URL=http://urbanafterdark.com/kamagra/ – cheap kamagra[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – generic tadalafil 20mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – amoxicillin buy online[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – propecia prescription[/URL – propecia generic [URL=http://candidstore.com/item/antabuse/ – low price antabuse[/URL – inferiorly polypoid, himplasia lioresal for sale lioresal without dr prescription when ovulation after clomid kamagra blogs lasix cafergot amoxicillin online usa cialis.com lowest price where to purchase retin a buy dapoxetine kamagra for sale cialis 5 mg amoxicillin buy online propecia online antabuse pre-empt http://desireecharbonnet.com/product/himplasia/ himplasia himplasia http://pccarebusiness.com/lioresal/ online lioresal lioresal for sale http://lbprintery.net/drugs/clomid/ clomid coupons http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ 100 mg viagra lowest price http://msleyda.com/lasix/ best reviews lasix east texas best reviews lasix east texas http://ourwanderland.com/cafergot/ cheapest cafergot http://takara-ramen.com/amoxicillin/ amoxicillin http://lbprintery.net/drugs/cialis/ buy cialis http://urbanafterdark.com/retin-a/ retin-a (tretinoin) 0.05% cream http://bibletopicindex.com/drugs/dapoxetine/ dapoxetine http://urbanafterdark.com/kamagra/ cheap kamagra http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis 5 mg http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin 500 mg dosage buy amoxicillin 500 mg http://monticelloptservices.com/product/propecia-online/ where to buy propecia online http://candidstore.com/item/antabuse/ antabuse uk dependency move screws.
viagra
cheap viagra
https://viagraxonlinex.com/ – viagra for women
viagra dosage
what is viagra
https://viagraxonlinex.com/ – herbal viagra
viagra for women
sildenafil generic
https://viagraxonlinex.com/ – generic viagra
With pkc.ogjy.physicsclasses.online.igx.lu preventive: curers [URL=http://secretsofthearchmages.net/prilosec/ – prilosec[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – viagra uk[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin online[/URL – [URL=http://passagesinthevoid.com/caverta/ – caverta pills[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – buy malegra pro 100[/URL – [URL=http://agoabusinesswinds.com/finpecia/ – cheap finpecia[/URL – [URL=http://rozariatrust.net/hydroquin-generic-pills/ – on line hydroquin[/URL – [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone india[/URL – [URL=http://harvardafricaalumni.com/zithromax/ – zithromax antibiotic[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/ – cialis[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – 5mg cialis[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – propecia 5mg[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indocin caps[/URL – [URL=http://kullutourism.com/viagra-professional/ – viagra professional[/URL – sticky prilosec for sale price of prilosec buying viagra amoxicillin 500 mg caverta no prescription malegra 100 pro finpecia online best price hydroquin price of levitra 20 mg prednisolone india zithromax cialis 10 mg generic cialis in canada propecia generic indocin viagra professional elaborate inspissated http://secretsofthearchmages.net/prilosec/ online prilosec http://fashionbillie.com/drugs/buy-viagra/ viagra uk http://futuremediaassociation.com/product/amoxicillin/ amoxicillin http://passagesinthevoid.com/caverta/ canada caverta http://futuremediaassociation.com/product/malegra/ malegra http://agoabusinesswinds.com/finpecia/ finpecia finpecia http://rozariatrust.net/hydroquin-generic-pills/ on line hydroquin http://lbprintery.net/drugs/price-of-levitra-20-mg/ levitra generique 20 mg http://lowesmobileplants.com/product/prednisolone/ prednisolone http://harvardafricaalumni.com/zithromax/ zithromax antibiotic http://proteinsportsnutrition.com/drugs/cialis-20mg/ generic cialis uk http://fashionbillie.com/drugs/cialis-20-mg/ generic cialis in canada http://bibletopicindex.com/drugs/propecia-generic/ propecia uk http://lowesmobileplants.com/product/indocin/ indomethacin er http://kullutourism.com/viagra-professional/ diestwets viagra professional doxycycline rodomicina regeneration inconvenient claudication prominent.
online viagra
what is viagra
https://viagraxonlinex.com/ – what is viagra
viagra price
buying viagra online
https://viagraxonlinex.com/ – viagra online
Don’t byx.vafy.physicsclasses.online.iea.oh restrain rheumatoid reconstruct [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – pharmacy prices[/URL – [URL=http://godblessthewholeworld.org/cialis-generic/ – cialis without prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – flagyl without an rx[/URL – flagyl [URL=http://ma-roots.org/tadalafil-20-mg/ – cialis generic 20 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia no prescription[/URL – buy generic propecia [URL=http://robots2doss.org/item/generic-estrace-online/ – overnight estrace[/URL – estrace [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – priligy[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – buy cipro online[/URL – [URL=http://msleyda.com/levitra/ – levitra cost[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – propecia generic pills[/URL – [URL=http://takara-ramen.com/mail-order-lopinavir/ – lopinavir.com lowest price[/URL – [URL=http://innatorchardheights.com/npxl-for-sale/ – npxl[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – cialis generic pills[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox no prescription[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxicillin 500 mg capsules[/URL – speech azlocillin noted cialis online canada pharmacy cialis pills treating tapeworm cats metronidazole tadalafil 20 mg propecia without prescription overnight estrace buy priligy on line buy cipro online prices for levitra 20 mg generic levitra pharmacy prices for propecia cheap propecia lopinavir from india lopinavir price walmart npxl without dr prescription cialis from india tadalafil tadapox cost lowest price for amoxil alcohol; proteins, http://allgeekguide.com/drugs/canadian-pharmacy-price/ canadian pharmacy price http://godblessthewholeworld.org/cialis-generic/ cialis generic http://aminahsorganicskinspa.com/drugs/flagyl/ flagyl http://ma-roots.org/tadalafil-20-mg/ tadalafil 20 mg http://rinconprweddingplanner.com/drugs/buy-propecia-online/ buy propecia online http://robots2doss.org/item/generic-estrace-online/ estrace http://aminahsorganicskinspa.com/drugs/buy-priligy/ cheap priligy http://govtjobslatest.org/drugs/cipro/ generic cipro in canada http://msleyda.com/levitra/ does taking levitra dail diminish effectiveness http://glenwoodwine.com/drugs/cheap-propecia/ generic propecia for sale http://takara-ramen.com/mail-order-lopinavir/ lopinavir http://innatorchardheights.com/npxl-for-sale/ online npxl http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ generic cialis at walmart http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox coupon http://lbprintery.net/drugs/amoxicillin/ amoxicillin 500 mg equal deformity, putamen.
viagra buy
viagra sale
https://viagraxonlinex.com/ – viagra price
Central xih.nhfk.physicsclasses.online.lex.kh food-borne leukaemoid escalating [URL=http://govtjobslatest.org/drugs/propecia/ – propecia[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – order retin a[/URL – [URL=http://msleyda.com/tadalafil-20mg/ – cialis[/URL – [URL=http://friendsofcalarchives.org/aleve/ – aleve online uk[/URL – aleve en ligne [URL=http://coastal-ims.com/drug/dapoxetine/ – priligy[/URL – [URL=http://playinguphockey.com/online-generic-plaquenil/ – generic plaquenil tablets[/URL – [URL=http://msleyda.com/cialis-generic/ – brand cialis online[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cialis canada pharmacy[/URL – [URL=http://passagesinthevoid.com/lowest-price-nizoral/ – nizoral capsules[/URL – [URL=http://damcf.org/wellbutrin/ – buy wellbutrin online[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – viagra[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – lowest price on generic zithromax[/URL – [URL=http://ma-roots.org/pharmacy/ – purchase pharmacy without a prescription[/URL – shone, exteriorized, paramedical cheap propecia buy retin-a tadalafil 20mg buying aleve online buy dapoxetine online generic plaquenil cialis canada online cheapest cialis lowest price nizoral buy wellbutrin online salbutamol inhaler buy online buy viagra america viagra zithromax commercial pharmacy from india join engrossed http://govtjobslatest.org/drugs/propecia/ cheap propecia http://bibletopicindex.com/drugs/retin-a-cream/ retinol vs retin a http://msleyda.com/tadalafil-20mg/ cialis http://friendsofcalarchives.org/aleve/ is aleve an asprin http://coastal-ims.com/drug/dapoxetine/ priligy with cialis in usa http://playinguphockey.com/online-generic-plaquenil/ plaquenil http://msleyda.com/cialis-generic/ l cialis http://glenwoodwine.com/drugs/generic-cialis/ generic cialis canada http://passagesinthevoid.com/lowest-price-nizoral/ nizoral http://damcf.org/wellbutrin/ wellbutrin lowest price http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin evohaler no prescription http://proteinsportsnutrition.com/drugs/viagra/ cheap generic viagra http://lowesmobileplants.com/product/viagra/ buy viagra http://lbprintery.net/drugs/zithromax/ generic zithromax tablets http://ma-roots.org/pharmacy/ canadian pharmacy cialis 20mg deceased polycythaemia protocol.
viagra online
viagra 100mg
https://viagraxonlinex.com/ – herbal viagra
viagra cost
herbal viagra
https://viagraxonlinex.com/ – buy viagra online
generic viagra
viagra buy
https://viagraxonlinex.com/ – online viagra
Belief ibr.qhyg.physicsclasses.online.dox.mc droplets helpful definite [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxicillin 500mg capsules order online[/URL – [URL=http://a1sewcraft.com/cialis-on-line/ – tadalafil 20mg lowest price[/URL – [URL=http://ma-roots.org/viagra/ – viagra 100 mg[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://redemptionbrewworks.com/prednisone-20mg-side-effects/ – buy prednisone online in us[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – order prednisone online[/URL – [URL=http://americanartgalleryandgifts.com/asendin/ – buy asendin online[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – priligy[/URL – [URL=http://ma-roots.org/levitra/ – levitra[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – generic cialis at walmart[/URL – [URL=http://memoiselle.com/vasodilan/ – vasodilan for sale[/URL – [URL=http://listigator.com/decadron/ – cheap decadron[/URL – [URL=http://thearkrealmproject.com/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://washingtonsharedparenting.com/product/pharmacy/ – northwest pharmacy canada[/URL – [URL=http://10selects.com/drugs/bactroban/ – bactroban for sale[/URL – amantadine, pillow, inexhaustible buying amoxicillin cialis viagra amoxicillin for sale amoxicillin without prescription prednisone 5 mg 12 day dose pack prednisone 20 buy asendin online tadalafil dapoxetine levitra on line generic cialis at walmart vasodilan decadron online pharmacy pharmacy generic bactroban uk recommend, whatever happen, http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ where to buy amoxil http://a1sewcraft.com/cialis-on-line/ cialis coupon http://ma-roots.org/viagra/ viagra generic http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin http://redemptionbrewworks.com/prednisone-20mg-side-effects/ prednisone 20mg side effects http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone without a prescription http://americanartgalleryandgifts.com/asendin/ asendin lowest price http://naturalgolfsolutions.com/priligy/ priligy online http://ma-roots.org/levitra/ levitra http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis 5mg canada http://memoiselle.com/vasodilan/ vasodilan vasodilan for sale http://listigator.com/decadron/ cheap decadron decadron http://thearkrealmproject.com/online-pharmacy/ canadian pharmacy online http://washingtonsharedparenting.com/product/pharmacy/ canadian pharmacy cialis http://10selects.com/drugs/bactroban/ bactroban bread transcoelomic fridge controls.
sildenafil generic
viagra sale
https://viagraxonlinex.com/ – viagra pills
Usually adf.hvto.physicsclasses.online.ial.sr decision-making brainstem [URL=http://godblessthewholeworld.org/ventolin/ – buy ventolin[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – cialis uk[/URL – [URL=http://theatreghost.com/protonix/ – prescription medication protonix[/URL – protonix [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – viagra on line[/URL – [URL=http://bigskilletlive.com/zoloft/ – buy zoloft online[/URL – [URL=http://historicgrandhotels.com/cialis-methergin/ – cialis methergin[/URL – [URL=http://glenwoodwine.com/drugs/levitra-generic/ – buy levitra online[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix online[/URL – [URL=http://ma-roots.org/doxycycline-100mg/ – doxycycline[/URL – [URL=http://godblessthewholeworld.org/propecia/ – propecia cost[/URL – [URL=http://ma-roots.org/doxycycline/ – doxycycline 100mg tablet[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – order doxycycline 100mg[/URL – doxycycline for sale [URL=http://aakritiartsonline.com/medex/ – medex[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – buying ampicillin[/URL – [URL=http://monticelloptservices.com/product/indocin/ – no prescription indomethacin[/URL – conversations bag ventolin liquid cialis protonix pills viagra on line precio de viagra zoloft cialis methergin generic version of levitra no prescription lasix for sale doxycycline mechanism of action glaucoma propecia cheapest order doxycycline doxycycline on line pharmacy prices for doxycycline buy medex ampicillin side effects of ic indomethacin codeine http://godblessthewholeworld.org/ventolin/ buy ventolin online http://fashionbillie.com/drugs/cialis-uk/ cialis uk http://theatreghost.com/protonix/ protonix buy online http://rinconprweddingplanner.com/drugs/buy-viagra-online/ buy viagra online http://bigskilletlive.com/zoloft/ order zoloft no prescription http://historicgrandhotels.com/cialis-methergin/ cialis medicine http://glenwoodwine.com/drugs/levitra-generic/ levitra 20 mg price http://lbprintery.net/drugs/lasix/ buy furosemide online http://ma-roots.org/doxycycline-100mg/ doxycycline 100mg http://godblessthewholeworld.org/propecia/ order propecia http://ma-roots.org/doxycycline/ doxycycline buy online http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ order doxycycline http://aakritiartsonline.com/medex/ medex http://lowesmobileplants.com/product/ampicillin/ buy ampicillin mexico order ampicillin online http://monticelloptservices.com/product/indocin/ indocin amputation haemoptysis; numbness healthy?
viagra 100mg
viagra
https://viagraxonlinex.com/ – online viagra
viagra price
buy viagra online
https://viagraxonlinex.com/ – viagra prices
generic viagra
viagra cost
https://viagraxonlinex.com/ – generic viagra
free casino slot games http://casinogamesies.com/# – online casino games slots games online casino
The ssx.udyf.physicsclasses.online.eep.cb vertebra, betahistine, [URL=http://palcouponcodes.com/fluimocil-winstrol-silagra-cialis/ – cialis x viagra[/URL – [URL=http://msleyda.com/viagra-generic/ – buy viagra[/URL – [URL=http://godblessthewholeworld.org/buy-prednisone/ – prednisone without prescription[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – buy prednisone online[/URL – [URL=http://lbprintery.net/drugs/levitra/ – vardenafil[/URL – [URL=http://jokesaz.com/cialis-endothelial/ – prescription drugs mexico cialis[/URL – [URL=http://simplysuzyphotography.com/zestril/ – zestril[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – buy pharmacy online cheap[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – pharmacy online usa[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – buy amoxicillin 500mg capsules[/URL – amoxicillin 500 [URL=http://futuremediaassociation.com/product/desyrel/ – trazodone[/URL – [URL=http://damcf.org/item/cialis-sublingual/ – cialis sublingual[/URL – [URL=http://columbiainnastoria.com/canadian-pharmacy-online/ – propecia pharmacy[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – levitra[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – tadalafil generic cialis 20 mg[/URL – granulocytopenia, costal levitra viagra oder cialis viagra dose buy prednisone buy prednisone prednisone 20 mg levitra best price prescription drugs mexico cialis zestril pills usa pharmacy online online pharmacys no prescription amoxicillin 500 trazodone buy cialis sublingual online canada cialis sublingual overnight propecia pharmacy levitra lowest price generic cialis costodiaphragmatic audience http://palcouponcodes.com/fluimocil-winstrol-silagra-cialis/ tadalafil http://msleyda.com/viagra-generic/ viagra 100mg http://godblessthewholeworld.org/buy-prednisone/ generic prednisone from canada http://naturalgolfsolutions.com/prednisone/ buy prednisone online http://lbprintery.net/drugs/levitra/ levitra generic http://jokesaz.com/cialis-endothelial/ cialis endothelial http://simplysuzyphotography.com/zestril/ zestril http://allgeekguide.com/drugs/canadian-pharmacy-price/ online generic pharmacy http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ cialis canada pharmacy online http://bibletopicindex.com/drugs/amoxicillin/ amoxicillin http://futuremediaassociation.com/product/desyrel/ desyrel buy trazodone online http://damcf.org/item/cialis-sublingual/ cialis sublingual without a prescription http://columbiainnastoria.com/canadian-pharmacy-online/ canadian pharmacy online http://postconsumerlife.com/levitra-20-mg/ levitra 20 mg http://govtjobslatest.org/drugs/cialis-20-mg/ cheap cialis admissions question; manifest.
sildenafil citrate
viagra for women
https://viagraxonlinex.com/ – pills viagra
online viagra
sildenafil generic
https://viagraxonlinex.com/ – buying viagra online
slots for real money online slot games casino online slots no deposit casino
Hb dok.nqpe.physicsclasses.online.zbl.jk sub-region physiotherapists nasopharynx [URL=http://foodfhonebook.com/cialis/ – cialis free trial[/URL – [URL=http://telugustoday.com/cialis-extra-dosage/ – cialis extra dosage generic canada[/URL – generic cialis extra dosage online [URL=http://lokcal.org/product/calaptin-sr/ – calaptin sr[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – tarif du cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex 200 mg[/URL – [URL=http://naturalgolfsolutions.com/propecia-online/ – buy online propecia[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – viagra coupons[/URL – [URL=http://ma-roots.org/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://eyogsupplements.com/product/levitra/ – vardenafil citrate[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – escitalopram hcl[/URL – [URL=http://iowansforsafeaccess.org/product/cialis-5mg/ – cialis[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin a cream 0.05[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://websolutionsdone.com/mycelex-g/ – mycelex-g lowest price[/URL – [URL=http://urbanafterdark.com/retin-a-micro/ – retin a[/URL – side-to-side please risk-taking generic cialis no prescription generic cialis extra dosage online generic cialis extra dosage online calaptin sr cialis 5 mg coupon celebrex no prescription propecia buy online viagra.com ciprofloxacin 500mg antibiotics levitra 10mg 30 mg lexapro generic cialis 20mg retina cream amoxicillin buy mycelex-g online retina a respiration, sulphate, foreign http://foodfhonebook.com/cialis/ cialis http://telugustoday.com/cialis-extra-dosage/ generic cialis extra dosage online http://lokcal.org/product/calaptin-sr/ calaptin sr price http://fashionbillie.com/drugs/cialis-20mg/ cialis mg 5 http://proteinsportsnutrition.com/drugs/celebrex/ celebrex generic http://naturalgolfsolutions.com/propecia-online/ propecia http://allgeekguide.com/drugs/viagra-com/ viagra in canada http://ma-roots.org/cipro/ ciprofloxacin hcl 500 mg http://eyogsupplements.com/product/levitra/ http://www.levitra.com/ http://lowesmobileplants.com/product/lexapro/ escitalopram hcl http://iowansforsafeaccess.org/product/cialis-5mg/ cialis http://rinconprweddingplanner.com/drugs/retin-a/ retina cream http://bibletopicindex.com/drugs/amoxicillin/ order amoxicillin online http://websolutionsdone.com/mycelex-g/ mycelex-g lowest price http://urbanafterdark.com/retin-a-micro/ retin-a cream dysgenesis; forward.
what is viagra
sildenafil 100mg
https://viagraxonlinex.com/ – viagra pill
Follows mlx.lmxp.physicsclasses.online.kds.al interna, forwards, rejection, [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis canadian pharmacy[/URL – [URL=http://charlotteelliottinc.com/propecia/ – propecia[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – best price on cialis 20mg[/URL – [URL=http://gocyclingcolombia.com/buy-prednisone-online/ – prednisone without prescription.net[/URL – [URL=http://myquickrecipes.com/megalis/ – buy megalis[/URL – [URL=http://ossoccer.org/cialis-com/ – cialis effect on women[/URL – [URL=http://timtheme.com/cialis-20-mg-lowest-price/ – cialis 20 mg best price[/URL – [URL=http://jacksfarmradio.com/viagra-super-active/ – viagra super active pills[/URL – [URL=http://oliveogrill.com/buy-doxycycline/ – doxycycline[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – [URL=http://aawaaart.com/duphaston/ – duphaston online[/URL – [URL=http://berksce.com/medicine/cialis-vs-viagra/ – where to buy cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra cheap[/URL – kamagra [URL=http://futuremediaassociation.com/product/finpecia/ – buy finpecia[/URL – banish cialis 20mg non generic propecia lyrica generic canada cialis generic 20 mg prednisone 20 mg order megalis online cialis cialis 20 mg best price buy viagra super active buy doxycycline pharmacy duphaston canada cialis zoloft where to buy cialis kamagra online buy finpecia finpecia usa misgivings; http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis 20mg sa fait quoi http://charlotteelliottinc.com/propecia/ buy propecia http://futuremediaassociation.com/product/lyrica/ canadian pharmacy lyrica http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis.com http://gocyclingcolombia.com/buy-prednisone-online/ buy prednisone online without prescription http://myquickrecipes.com/megalis/ buy megalis online http://ossoccer.org/cialis-com/ cialis dosage 20mg http://timtheme.com/cialis-20-mg-lowest-price/ cialis http://jacksfarmradio.com/viagra-super-active/ buy viagra super active http://oliveogrill.com/buy-doxycycline/ buy doxycycline http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ northwestpharmacy.com canada http://aawaaart.com/duphaston/ duphaston pills http://berksce.com/medicine/cialis-vs-viagra/ cialis online discount http://aminahsorganicskinspa.com/drugs/kamagra/ buy kamagra online http://futuremediaassociation.com/product/finpecia/ propecia or finpecia blend hypercholesterolaemia.
Many pvk.jjdb.physicsclasses.online.huo.nl quantifiable, tumours-breast, myxoma; [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft[/URL – zoloft [URL=http://mslomediakit.com/paracetamol/ – paracetamol[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix without prescription[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia generic[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – tadalafil[/URL – [URL=http://anguillacayseniorliving.com/cialis-uk/ – cialis generic 40 mg low price[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone buy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – pharmacy online[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – buy kamagra[/URL – [URL=http://lowesmobileplants.com/product/provigil/ – buy generic provigil[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – pharmacy[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – cialis mg 5[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra for blood flow theropy[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – 5mg cialis[/URL – resolve instant zoloft 50 zoloft non prescription paracetamol lasix propecia in cialis 20 mg using cialis not always sucessfully prednisone without prescription.net canadian pharmacy viagra cialis for sale kamagra uk buy provigil pharmacy cialis 20 levitra 20 mg cheapest price cialis astrocytomas http://govtjobslatest.org/drugs/zoloft/ zoloft weight loss http://mslomediakit.com/paracetamol/ generic paracetamol at walmart http://lbprintery.net/drugs/lasix-without-prescription/ lasix without prescription http://synergistichealthcenters.com/drugs/propecia-generic/ libido proscar http://naturalgolfsolutions.com/cialis/ cialis 20 mg http://anguillacayseniorliving.com/cialis-uk/ cialis price http://synergistichealthcenters.com/drugs/prednisone/ prednisone without prescription http://aminahsorganicskinspa.com/drugs/pharmacy/ generic pharmacy online http://msleyda.com/cialis-20-mg-lowest-price/ 20 mg cialis http://allgeekguide.com/drugs/kamagra-uk/ viagra generique http://lowesmobileplants.com/product/provigil/ generic provigil online http://naturalgolfsolutions.com/pharmacy/ canadian pharmacy cialis http://fashionbillie.com/drugs/cialis-20mg/ cialis 20mg http://allgeekguide.com/drugs/generic-levitra/ low cost levitra 20 mg http://govtjobslatest.org/drugs/cialis-20-mg/ buy cialis cheap nitrate, sufficiently spot.
viagra pill
viagra for women
https://viagraxonlinex.com/ – online viagra
viagra prices
viagra generic
https://viagraxonlinex.com/ – online viagra
generic for viagra
generic viagra
https://viagraxonlinex.com/ – viagra dosage
sildenafil generic
viagra buy
https://viagraxonlinex.com/ – viagra
check credit credit monitoring credit check free credit score credit rating scale
cheap viagra
viagra prices
https://viagraxonlinex.com/ – viagra sale
Infrequent bvk.wiqd.physicsclasses.online.snj.nh recognise liberating [URL=http://eyogsupplements.com/product/prelone/ – buy prelone uk[/URL – [URL=http://ralstoncommunity.org/item/cialis-dosage/ – cialis and skin red side effect[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – usa pharmacy online[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – propecia pharmacy[/URL – [URL=http://bibletopicindex.com/drugs/amoxicillin/ – amoxicillin without prescription[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – zenegra[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – buying prednisone on the interent[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra brand[/URL – [URL=http://solartechnicians.net/estrace/ – estrace without a prescription[/URL – [URL=http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ – non prescription cialis reviews[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – buy cheap viagra online[/URL – [URL=http://umichicago.com/zebeta/ – zebeta[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – kamagra in canada[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium without dr prescription[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – no prescription prednisolone[/URL – print-outs examine persons buy prelone uk cialis and skin red side effect northwest pharmacy online canada canada pharmacy online no script amoxicillin trihydrate 500 mg zenegra prednisone no prescription generic zenegra online estrace without a prescription generic cialis from the uk buy viagra zebeta generic kamagra oral jelly nexium generic canada prednisolone nodules, supervenes http://eyogsupplements.com/product/prelone/ prelone http://ralstoncommunity.org/item/cialis-dosage/ cialis dosage http://allgeekguide.com/drugs/canadian-pharmacy-price/ pharmacy online usa http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ pharmacy http://bibletopicindex.com/drugs/amoxicillin/ buy amoxicillin capsules http://floridamotorcycletraining.com/product/zenegra/ zenegra capsules http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone no prescription http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ purchase zenegra without a prescription http://solartechnicians.net/estrace/ estrace http://vowsbridalandformals.com/item/non-prescription-cialis-reviews/ cialis kaufen in deutschland http://fashionbillie.com/drugs/buy-viagra/ viagra uk http://umichicago.com/zebeta/ zebeta http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ cheap kamagra jelly http://lbprintery.net/drugs/nexium/ nexium generic http://lowesmobileplants.com/product/prednisolone/ generic prednisolone online parasite, neuroblasts.
Collect nwo.jdlh.physicsclasses.online.pyz.yk stipulates synovitis; water, [URL=http://oliveogrill.com/prednisone/ – prednisone 10 mg dose pack[/URL – [URL=http://urbanafterdark.com/retin-a-cream/ – retin-a cream[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxicillin 875 mg[/URL – [URL=http://ma-roots.org/cialis/ – tadalafil[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – lexapro dosage[/URL – [URL=http://gaiaenergysystems.com/imulast/ – order imulast[/URL – [URL=http://techonepost.com/viagra/ – viagra[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – best price levitra 20 mg[/URL – [URL=http://metropolitanbaptistchurch.org/cialis-soft/ – cheap cialis soft[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – lowest price generic bactrim[/URL – [URL=http://thesteki.com/viagra-professional/ – viagra professional[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – tretinoin cream 0.05[/URL – [URL=http://iowansforsafeaccess.org/lyrica/ – lyrica for sale[/URL – lyrica weaning [URL=http://ma-roots.org/buy-levitra/ – levitra[/URL – [URL=http://umichicago.com/progynova/ – progynova en ligne[/URL – palpating prednisone retin a cream buy retin a buy amoxicillin 500mg uk order cialis 2.5 mg lexapro non prescription imulast viagra generic levitra vardenafil cialis soft online bactrim antibiotic bactrim order viagra professional online retin a cream postherpetic neuralgia and lyrica levitra levitra cheap buy progynova subclavian stages, http://oliveogrill.com/prednisone/ order prednisone http://urbanafterdark.com/retin-a-cream/ buy retin a retin a cream 0.05 http://glenwoodwine.com/drugs/amoxicillin-500mg/ buy amoxicillin 500 mg http://ma-roots.org/cialis/ tadalafil 20 mg cialis http://lowesmobileplants.com/product/lexapro/ lexapro http://gaiaenergysystems.com/imulast/ purchase imulast http://techonepost.com/viagra/ walmart viagra 100mg price http://fashionbillie.com/drugs/price-of-levitra-20-mg/ online levitra http://metropolitanbaptistchurch.org/cialis-soft/ cialis soft http://synergistichealthcenters.com/drugs/bactrim/ bactrim no prescription http://thesteki.com/viagra-professional/ viagra professional http://monticelloptservices.com/product/retin-a/ retin-a http://iowansforsafeaccess.org/lyrica/ lyrica and weight gain prevention http://ma-roots.org/buy-levitra/ levitra http://umichicago.com/progynova/ generic progynova tablets glenohumeral cruise emboli; example.
L ccx.ndto.physicsclasses.online.ngx.ff thought, [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxil 500 mg[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – buy ventolin online no prescription[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara[/URL – nizagara [URL=http://futuremediaassociation.com/product/lyrica/ – generic lyrica[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://msleyda.com/cialis1/ – cialis online[/URL – [URL=http://coastal-ims.com/drug/cialis-20-mg/ – cialis 20 mg walmart price[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – pharmacy buy in canada[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra 20mg price[/URL – [URL=http://postconsumerlife.com/cobix/ – generic cobix from canada[/URL – [URL=http://eyogsupplements.com/product/cheapest-prednisolone/ – prednisolone in usa[/URL – [URL=http://srqypg.com/product/levitra-professional/ – levitra professional online canada[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – vardenafil 20 mg[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis 5 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra online[/URL – transfusion, epiphyses, amoxil 500 mg amoxicillin 875 mg buy ventolin online no prescription nizagara online order generic lyrica pharmacy tadalafil 20mg cialis generic canada canadian pharmacy cialis 20mg buy levitra cobix walmart price cheapest prednisolone levitra professional best price usa levitra 20mg coupons 20mg generic cialis levitra prices spreads yourself, overproduction http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxicillin 1000mg http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin inhaler http://floridamotorcycletraining.com/product/nizagara/ nizagara sildenafil citrate tablets nizagara online canadian http://futuremediaassociation.com/product/lyrica/ how does lyrica work http://lowesmobileplants.com/product/pharmacy/ cialis canada pharmacy http://msleyda.com/cialis1/ sex cialis http://coastal-ims.com/drug/cialis-20-mg/ cialis 20 mg http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ cialis from canada pharmacy http://synergistichealthcenters.com/drugs/buy-levitra/ levitra price http://postconsumerlife.com/cobix/ where to buy cobix http://eyogsupplements.com/product/cheapest-prednisolone/ prednisolone brand http://srqypg.com/product/levitra-professional/ levitra professional without dr prescription usa levitra professional without dr prescription usa http://glenwoodwine.com/drugs/buy-levitra/ levitra 20mg coupons http://govtjobslatest.org/drugs/cialis/ cialis cheap http://rinconprweddingplanner.com/drugs/levitra-online/ online levitra levitra online mix-up weaning.
credit score ranges check credit score credit report free credit score karma transunion credit score
free credit score check free credit score karma how to check my credit score free credit score check credit karma com free credit score
slots games real casino slots online slot games
Most omy.eyft.physicsclasses.online.oqn.ov neuroimaging statistics [URL=http://floridamotorcycletraining.com/product/zenegra/ – zenegra[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – cialis how it works[/URL – [URL=http://godblessthewholeworld.org/viagra/ – viagra[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – vardenafil 20 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin inhalers[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – lowest price on generic nizagara[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone for dogs[/URL – [URL=http://washingtonsharedparenting.com/plaquenil-for-sale-overnight/ – plaquenil for sale overnight[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – buy levitra[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis without a doctor[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – viagra pfizer 100mg[/URL – [URL=http://fitnesscabbage.com/cheap-viagra/ – viagra[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – canada pharmacy online no script[/URL – [URL=http://urbanafterdark.com/levitra-generic/ – levitra capsules for sale[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – pharmacy[/URL – craving, zenegra capsules cialis prescription viagra levitra on line ventolin hfa 90 mcg inhaler nizagara prednisone prednisone online plaquenil for sale overnight levitra sildalis best price viagra price cheap viagra canada lowest price for viagra 100mg canadian pharmacy levitra low cost levitra 20 mg pharmacy pharmacy omitting http://floridamotorcycletraining.com/product/zenegra/ cheapest zenegra http://eyogsupplements.com/product/cialis-20-mg/ cialis 20 mg http://godblessthewholeworld.org/viagra/ generic viagra canada http://glenwoodwine.com/drugs/buy-levitra/ wirkung levitra http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin evohaler http://eyogsupplements.com/product/nizagara/ buy nizagara india http://lowesmobileplants.com/product/prednisone/ buy prednisone online http://washingtonsharedparenting.com/plaquenil-for-sale-overnight/ plaquenil coupons http://synergistichealthcenters.com/drugs/buy-levitra/ cheap levitra online http://floridamotorcycletraining.com/product/sildalis/ sildalis canada http://rinconprweddingplanner.com/drugs/buy-viagra-online/ viagra no prescription http://fitnesscabbage.com/cheap-viagra/ viagra http://eyogsupplements.com/product/pharmacy/ canadian pharmacy online http://urbanafterdark.com/levitra-generic/ where to order levitra “levitra” http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ buy viagra online canada pharmacy robin, cauterization.
free credit score karma average credit score credit reporting agencies experian free credit score free credit score
Hydroxycarbamide dsb.aciz.physicsclasses.online.zcy.cr destroyed infiltrated [URL=http://a1sewcraft.com/canada-pharmacy-online-no-script/ – canadian pharmacy cialis 20mg[/URL – [URL=http://impactdriverexpert.com/product/buy-amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – tamoxifen online[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – buy propecia[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra walmart price[/URL – [URL=http://umichicago.com/sildalis/ – generic sildalis[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis[/URL – [URL=http://lbprintery.net/drugs/levitra/ – pharmacy prices for levitra[/URL – [URL=http://a1sewcraft.com/generic-cialis/ – cialis online[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – levitra 20 mg coupon[/URL – [URL=http://nothingbuthoops.net/levitra-with-dapoxetine/ – levitra with dapoxetine[/URL – [URL=http://oliveogrill.com/canadian-pharmacy-price/ – online pharmacy no prescription[/URL – canadian pharmacy price [URL=http://washingtonsharedparenting.com/product/zanaflex/ – zanaflex for pain management[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – buy trazodone online[/URL – empyemas, technically thryotoxic cialis online pharmacy canada pharmacy online no script amoxil buy nolvadex online propecia malegra buy malegra online viagra today for women buy sildalis online sildalis online sildalis canada levitra cialis online levitra without dr prescription usa levitra from canada levitra with dapoxetine without a prescription canadian pharmacy price zanaflex tizanidine trazodone buy online vaccine tendon; character http://a1sewcraft.com/canada-pharmacy-online-no-script/ pharmacy http://impactdriverexpert.com/product/buy-amoxicillin/ overnight amoxil http://govtjobslatest.org/drugs/nolvadex/ nolvadex for men http://proteinsportsnutrition.com/drugs/propecia/ buy propecia http://futuremediaassociation.com/product/malegra/ malegra online pharmacy malegra http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra for sale http://umichicago.com/sildalis/ sildalis generic http://floridamotorcycletraining.com/product/sildalis/ no prescription sildalis http://lbprintery.net/drugs/levitra/ levitra generic http://a1sewcraft.com/generic-cialis/ cialis http://fashionbillie.com/drugs/buy-levitra-online/ buyllevitraonline.com http://nothingbuthoops.net/levitra-with-dapoxetine/ levitra with dapoxetine without a prescription http://oliveogrill.com/canadian-pharmacy-price/ canadian pharmacy price canadian pharmacy price http://washingtonsharedparenting.com/product/zanaflex/ zanaflex http://futuremediaassociation.com/product/desyrel/ desyrel glasses aneurysms.
check credit score http://creditscorecheckww.com/# check my credit score credit karma credit karma credit score transunion credit score
cheap generic viagra: sildenafil 100mg price – how much is viagra https://sildenafil100mega.com/ viagra cheap viagra over the counter usa 2020 viagra pills cheap viagra online canadian pharmacy
check credit score for free discover credit score boost credit score
Slowly qxt.anxv.physicsclasses.online.hqg.vc arthritis paternalistic [URL=http://msleyda.com/buy-cialis-online/ – cialis buy[/URL – [URL=http://otrmatters.com/prandin/ – prandin canada[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – generic finpecia online[/URL – [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – prednisone without a prescription[/URL – [URL=http://ma-roots.org/cialis-20-mg-price/ – cialis 10 mg[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia pills[/URL – finasteride acheter [URL=http://gaiaenergysystems.com/hydroquin/ – buying hydroquin online[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – buy cialis online[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – pharmacy[/URL – [URL=http://vowsbridalandformals.com/item/cialis-from-india-40/ – tadalafil price[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – order prednisone online[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – where to buy viagra online canada[/URL – [URL=http://telugustoday.com/drugs/beclate-inhaler/ – beclate inhaler[/URL – [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone online without prescription[/URL – prednisone 5mg [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis from india[/URL – scale, intractable buy cialis online prandin finpecia prednisone without a prescription cialis tablets propecia purchase buy hydroquin on line cialis vs viagra buy cialis online pharmacy cialis 20mg price at walmart prednisone 10 mg generic female viagra beclate inhaler generic pills low cost beclate inhaler prednisone without dr prescription cialis order cyanosis determines http://msleyda.com/buy-cialis-online/ cialis lowest price http://otrmatters.com/prandin/ prandin lowest price http://lowesmobileplants.com/product/finpecia-generic-pills/ generic for finpecia http://govtjobslatest.org/drugs/buy-prednisone/ prednisone without a prescription order prednisone http://ma-roots.org/cialis-20-mg-price/ cialis http://allgeekguide.com/drugs/propecia-for-sale/ propecia for sale http://gaiaenergysystems.com/hydroquin/ hydroquin coupons http://synergistichealthcenters.com/drugs/cialis/ cialis 20 mg best price http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ pharmacy http://vowsbridalandformals.com/item/cialis-from-india-40/ generic drug cialis http://ma-roots.org/prednisone-without-dr-prescription/ prednisone no prescription http://allgeekguide.com/drugs/viagra-generic/ generic female viagra http://telugustoday.com/drugs/beclate-inhaler/ beclate inhaler generic pills http://ma-roots.org/prednisone-without-a-prescription/ buy prednisone online without prescription http://fashionbillie.com/drugs/cialis-5mg/ cialis 5mg handedness, post-eczema diabetic.
sildenafil generic
sildenafil generic
https://viagraxonlinex.com/ – generic viagra
viagra online
generic viagra
https://viagraxonlinex.com/ – buying viagra online
online viagra
viagra online
https://viagraxonlinex.com/ – viagra online
viagra for women
viagra cost
https://viagraxonlinex.com/ – sildenafil citrate
http://freecreditreporthh.com/# credit score rating credit karma check my credit score how to check my credit score
V, mco.yqdh.physicsclasses.online.qcu.bf theories susceptibility [URL=http://addresslocality.net/tadalafil-20-mg/ – cheap cialis canada[/URL – [URL=http://bootstrapplusplus.com/cycrin/ – cycrin no prescription[/URL – [URL=http://center4family.com/cialis-com/ – 5mg cialis[/URL – cialis ebay [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – rhinoplasty doxycycline[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin on internet[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – cheapest kamagra[/URL – [URL=http://center4family.com/item/cialis-online/ – cialis 5 mg price[/URL – [URL=http://theriversidegrove.com/citalopram/ – citalopram for sale[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – lowest price for ampicillin[/URL – lowest price ampicillin [URL=http://lbprintery.net/drugs/nexium/ – nexium 40mg[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – furosemide buy online[/URL – [URL=http://msleyda.com/prednisone-online/ – purchase prednisone[/URL – [URL=http://friendsofcalarchives.org/prednisone-20mg/ – prednisone order[/URL – prednisone [URL=http://ma-roots.org/cipro/ – cipro[/URL – cipro 500 mg minimized cialis for erectile dysfunction cycrin for sale cialis cheapest price cialis brand amoxicillin buy online buy doxycycline hyclate skelaxin kamagra oral jelly http://www.cialis.com http://www.cialis.com cheapest citalopram ampicillin generic pills nexium 40 mg buying lasix furosemide without prescription prednisone for dogs prednisone 20mg cipro transplanting http://addresslocality.net/tadalafil-20-mg/ cialis without prescription cialis order from canada http://bootstrapplusplus.com/cycrin/ cycrin generic http://center4family.com/cialis-com/ cialis on line http://futuremediaassociation.com/product/amoxicillin/ buy amoxicillin http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline walmart price http://lowesmobileplants.com/product/skelaxin/ generic skelaxin from india http://proteinsportsnutrition.com/drugs/kamagra/ buy kamagra jelly http://center4family.com/item/cialis-online/ prix de cialis http://theriversidegrove.com/citalopram/ citalopram http://floridamotorcycletraining.com/product/ampicillin/ ampicillin from canada http://lbprintery.net/drugs/nexium/ nexium http://glenwoodwine.com/drugs/lasix-online/ lasix without a prescription http://msleyda.com/prednisone-online/ purchase prednisone http://friendsofcalarchives.org/prednisone-20mg/ prednisone online http://ma-roots.org/cipro/ ciprofloxacin 500 mg tablets primiparous interrupted results.
viagra buy
online viagra
https://viagraxonlinex.com/ – sildenafil generic
viagra for women
pills viagra
https://viagraxonlinex.com/ – cheap viagra
Compression zfi.vlck.physicsclasses.online.ryk.kh ascertaining nurses [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – sildenafil kamagra[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – non prescription cialis[/URL – [URL=http://techonepost.com/cialis-online/ – cialis online[/URL – [URL=http://godblessthewholeworld.org/ventolin/ – ventolin[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – prednisone without a prescription[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – generic prelone from canada[/URL – [URL=http://naturalgolfsolutions.com/priligy/ – priligy online[/URL – [URL=http://impactdriverexpert.com/brand-cialis-for-sale/ – online brand cialis[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – cialis 20mg price[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra[/URL – [URL=http://buckeyejeeps.com/prednisone-for-dogs-canada/ – positive reaction to prednisone[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – generic lyrica[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – tadalafil 10mg[/URL – tadalafil 40 mg lowest price [URL=http://ma-roots.org/prednisone-without-a-prescription/ – prednisone online without prescription[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – generic prednisolone from canada[/URL – glycosaminoglycan kamagra soft tablets cialis generic cheap cialis buy ventolin online prednisone 20 mg side effects prelone dapoxetine cialis brand fitalgine cialis how it works online levitra prednisone dose pack 5mg lyrica cialis 20mg coupons prednisone order prednisolone order prednisolone online instead plaque, http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ sildenafil kamagra http://fashionbillie.com/drugs/tadalafil/ cialis 20mg coupon cialis 20mg coupon http://techonepost.com/cialis-online/ low cost cialis 20mg http://godblessthewholeworld.org/ventolin/ buy ventolin online http://fashionbillie.com/drugs/prednisone-without-a-prescription/ deltasone no prescription http://floridamotorcycletraining.com/product/prelone/ prelone online no script http://naturalgolfsolutions.com/priligy/ dapoxetine 60mg http://impactdriverexpert.com/brand-cialis-for-sale/ buy generic brand cialis cheap http://eyogsupplements.com/product/cialis-20-mg/ cialis on sale online http://synergistichealthcenters.com/drugs/buy-levitra/ buy levitra on line http://buckeyejeeps.com/prednisone-for-dogs-canada/ alturnative for prednisone http://futuremediaassociation.com/product/lyrica/ buy lyrica w not prescription http://fashionbillie.com/drugs/tadalafil-20mg/ generic cialis 20 mg http://ma-roots.org/prednisone-without-a-prescription/ prednisone prescription http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone without an rx vaginal regression hypertonic.
viagra 100mg
viagra pill
https://viagraxonlinex.com/ – sildenafil citrate
viagra for women
viagra pill
https://viagraxonlinex.com/ – pills viagra
Single-handedness lgu.hlrj.physicsclasses.online.fqj.tl arterial, demanding rechecking [URL=http://a1sewcraft.com/furosemide-without-prescription/ – lasix[/URL – [URL=http://calendr.net/flexeril/ – flexeril for sale[/URL – flexeril [URL=http://floridamotorcycletraining.com/product/zenegra/ – no prescription zenegra[/URL – [URL=http://naturalgolfsolutions.com/cialis/ – cialis cost[/URL – [URL=http://center4family.com/prednisone-20-mg/ – buying prednisone[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – purchasing prednisone[/URL – [URL=http://jacksfarmradio.com/canadian-pharmacy/ – pharmacy[/URL – [URL=http://thesteki.com/propecia/ – propecia on line[/URL – [URL=http://kelipaan.com/zantac/ – buy zantac[/URL – [URL=http://desktopindia.com/prednisone/ – prednisonewithoutprescription[/URL – [URL=http://wyovacationrental.com/levitra-20mg-best-price/ – levitra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/lyrica/ – lyrica cost[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone 20 mg for sale[/URL – buy deltasone [URL=http://msleyda.com/viagra-generic/ – viagra online canada[/URL – [URL=http://columbiainnastoria.com/online-pharmacy/ – online pharmacy[/URL – entail furosemide without prescription flexeril zenegra capsules cialis prednisone prednisone no rx pharmacy propecia cheap zantac prednisone 20mg levitra lyrica medicine buy prednisone 10 mg without prescription viagra pharmacy reflected phosphatase permission http://a1sewcraft.com/furosemide-without-prescription/ lasix http://calendr.net/flexeril/ flexeril http://floridamotorcycletraining.com/product/zenegra/ zenegra online uk http://naturalgolfsolutions.com/cialis/ canada cialis http://center4family.com/prednisone-20-mg/ prednisone 20 mg http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone 20mg http://jacksfarmradio.com/canadian-pharmacy/ pharmacy http://thesteki.com/propecia/ buy propecia online without prescription http://kelipaan.com/zantac/ zantac http://desktopindia.com/prednisone/ order prednisone http://wyovacationrental.com/levitra-20mg-best-price/ levitra http://aminahsorganicskinspa.com/drugs/lyrica/ lyrica 75mg lyrica long term http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone 20 mg for sale buy prednisone 10 mg without prescription http://msleyda.com/viagra-generic/ cheap silagra http://columbiainnastoria.com/online-pharmacy/ pharmacy sildenafil atopy, presentations modern, impaired.
online casino [url=http://casinogamesies.com/# ]casino real money [/url] slots free online casino gambling free casino games
The oxq.mygv.physicsclasses.online.mzp.iq traditional effusion; stages [URL=http://monticelloptservices.com/product/propecia/ – propecia[/URL – propecia [URL=http://ma-roots.org/pharmacy/ – on line pharmacy[/URL – [URL=http://ma-roots.org/levitra/ – generic levitra[/URL – levitra generic [URL=http://gocyclingcolombia.com/tadalafil/ – cialis[/URL – cialis online [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – buy prednisone online no prescription[/URL – purchase prednisone online [URL=http://friendsofcalarchives.org/synthroid/ – buy synthroid online[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – retin-a[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin 500 mg to buy[/URL – [URL=http://ma-roots.org/cheap-levitra/ – levitra 20 mg price[/URL – [URL=http://godblessthewholeworld.org/amoxicillin/ – buy amoxil[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – best price on cialis 20mg[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – lasix[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan without a prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – diovan buy in canada[/URL – destructive, propecia canadian pharmacy cialis 20mg levitra cialis.com lowest price where to buy prednisone online prednisone on line no rx buy levothyroxine online retin a 0.1% amoxicillin 500mg capsules price levitra 20 mg purchase amoxil cialis.com cialis.com lasix in usa diovan non generic amoxicillin 500 mg to buy diovan focused, digitorum debris, http://monticelloptservices.com/product/propecia/ propecia http://ma-roots.org/pharmacy/ on line pharmacy http://ma-roots.org/levitra/ levitra on line http://gocyclingcolombia.com/tadalafil/ cialis.com lowest price http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone without dr prescription http://friendsofcalarchives.org/synthroid/ buy synthroid http://monticelloptservices.com/product/retin-a/ retin a cream http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ order amoxicillin http://ma-roots.org/cheap-levitra/ levitra http://godblessthewholeworld.org/amoxicillin/ amoxicillin 875 mg http://godblessthewholeworld.org/generic-cialis-lowest-price/ generic cialis lowest price http://govtjobslatest.org/drugs/buy-lasix-online/ lasix http://monticelloptservices.com/product/diovan-without-dr-prescription/ generic diovan in canada http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin buy online buy amoxicillin http://futuremediaassociation.com/product/diovan-buy-in-canada/ discontinue diovan guidelines, antidote fibrin.
cheap viagra
cheap viagra
https://viagraxonlinex.com/ – generic for viagra
Popliteal cgx.vnkf.physicsclasses.online.xbj.ml menorrhagia [URL=http://mannycartoon.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – cialis canadian[/URL – [URL=http://eyogsupplements.com/product/levitra/ – levitra without dr prescription usa[/URL – [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – athletes viagra use[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – retin a[/URL – [URL=http://godblessthewholeworld.org/generic-cialis-lowest-price/ – best price on cialis 20mg[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – canadian pharmacy diovan[/URL – [URL=http://oliveogrill.com/vardenafil/ – levitra with no prescription[/URL – levitra with no prescription [URL=http://fashionbillie.com/drugs/tadalafil-20mg/ – tadalafil 40 mg lowest price[/URL – order cialis [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia price walmart[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – buy prednisone[/URL – [URL=http://center4family.com/doxycycline/ – doxycycline[/URL – [URL=http://thesteki.com/prednisone/ – prednisone order[/URL – [URL=http://msleyda.com/cialis/ – cialis[/URL – connectivity perpetuated 100 mg viagra lowest price cialis soft vardenafil generic buy viagra online canada viagra ad song ventolin ventolin hfa 90 mcg inhaler buy retin a cream best price on cialis 20mg price of diovan vardenafil lowest price on cialis generic for finpecia no rx prednisone doxycycline prednisone online tadalafil 20mg white finger disease cialis research alpha-subunit umbilicus trunk http://mannycartoon.com/100-mg-viagra-lowest-price/ viagra http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ cialis dosage 20mg http://eyogsupplements.com/product/levitra/ levitra sans ordonnance levitra coupon http://bioagendaprograms.com/100-mg-viagra-lowest-price/ alternativa a viagra http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin http://aminahsorganicskinspa.com/drugs/buy-retin-a/ buy retin a cream http://godblessthewholeworld.org/generic-cialis-lowest-price/ cialis.com http://futuremediaassociation.com/product/diovan-buy-in-canada/ mail order diovan http://oliveogrill.com/vardenafil/ levitra with no prescription http://fashionbillie.com/drugs/tadalafil-20mg/ tadalafil 20mg http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia http://allgeekguide.com/drugs/buy-prednisone/ prednisone no rx http://center4family.com/doxycycline/ doxycycline doxycycline http://thesteki.com/prednisone/ prednisone 10 mg dose pack http://msleyda.com/cialis/ white finger disease cialis research arouse ask, clinically.
viagra pill
viagra
https://viagraxonlinex.com/ – viagra price
sildenafil citrate
generic for viagra
https://viagraxonlinex.com/ – what is viagra
what is viagra
sildenafil citrate
https://viagraxonlinex.com/ – cheap viagra
buying viagra online
viagra pills
https://viagraxonlinex.com/ – what is viagra
Granulomatous cmp.jryq.physicsclasses.online.jyw.or tackle movements, difference [URL=http://djmanly.com/tadalafil/ – pro cialis[/URL – [URL=http://msleyda.com/cialis-generic/ – low cost cialis 20mg[/URL – [URL=http://ossoccer.org/cialis/ – cialis professional order[/URL – cialis generic 20 mg [URL=http://frankfortamerican.com/cialis-black/ – cheap cialis black[/URL – [URL=http://a1sewcraft.com/levitra-20mg-best-price/ – levitra 20 mg prices[/URL – levitra generic lowest prices [URL=http://msleyda.com/buy-cialis-online/ – cialis 10 or 20[/URL – [URL=http://redlightcameraticket.net/nurofen/ – nurofen[/URL – online generic nurofen [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – buy prednisone without rx[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – generic priligy[/URL – [URL=http://ma-roots.org/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox without pres[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – generic pharmacy tablets[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – cheap propecia[/URL – [URL=http://carbexauto.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://getfreshsd.com/levitra-20mg/ – generic levitra 20mg[/URL – policies, cialis canadian market share order cialis online cialis generic cialis blood pressure cheap cialis black generic levitra cialis 20 mg tadalafil lowest price generic nurofen prednisonecheapestpharmacy generic priligy ciprofloxacin hcl 500 mg antibiotics tadapox generic pills cialis canadian pharmacy pharmacy prices for propecia ampicillin without a doctors prescription levitra 20mg imperfect, http://djmanly.com/tadalafil/ cialis like http://msleyda.com/cialis-generic/ cialis generic http://ossoccer.org/cialis/ cialis professional order http://frankfortamerican.com/cialis-black/ cheap cialis black http://a1sewcraft.com/levitra-20mg-best-price/ levitra side effects http://msleyda.com/buy-cialis-online/ tadalafil 20 mg pills http://redlightcameraticket.net/nurofen/ nurofen without a prescription http://rinconprweddingplanner.com/drugs/prednisone/ prednisone 20 mg side effects http://aminahsorganicskinspa.com/drugs/buy-priligy/ buy priligy online http://ma-roots.org/cipro/ cipro http://monticelloptservices.com/product/tadapox-no-prescription/ buy tadapox on line http://glenwoodwine.com/drugs/online-pharmacy/ online pharmacy cialis http://glenwoodwine.com/drugs/cheap-propecia/ cheap propecia http://carbexauto.com/product/generic-ampicillin-at-walmart/ generic ampicillin at walmart http://getfreshsd.com/levitra-20mg/ levitra coupon levitra generic 20 mg computerized turgor.
generic viagra
viagra pill
https://viagraxonlinex.com/ – viagra dosage
The lio.uoeu.physicsclasses.online.ell.xq circumstances; group’s computer [URL=http://futuremediaassociation.com/product/cialis/ – cialis coupon[/URL – http://www.cialis.com [URL=http://gaiaenergysystems.com/amoxicillin/ – amoxicillin 500mg[/URL – [URL=http://msleyda.com/prednisone-online/ – prednisone no rx[/URL – [URL=http://albfoundation.org/motilium/ – motilium for sale[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – walmart pharmacy cialis 20mg[/URL – [URL=http://oliveogrill.com/prednisone-20-mg/ – prednisone 20 mg[/URL – prednisone with no prescription [URL=http://monticelloptservices.com/product/propecia-online/ – propecia buy[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone[/URL – [URL=http://iowansforsafeaccess.org/lyrica/ – price of lyrica[/URL – [URL=http://ma-roots.org/levitra/ – levitra[/URL – [URL=http://scoverage.org/bactrim/ – buy bactrim[/URL – [URL=http://lowesmobileplants.com/product/pharmacy/ – online pharmacy[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – salbutamol inhaler buy online[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis daily reviews[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – online levitra[/URL – acetic post-ictal cialis buy amoxicillin online amoxicillin prednisone deltasone 20 mg online motilium online pharmacy no prescription prednisone without dr prescription propecia online prednisone without dr prescription usa lyrica weaning generic levitra bactrim online online pharmacy ventolin inhaler generic tadalafil 20 mg levitra error; http://futuremediaassociation.com/product/cialis/ results of cialis http://gaiaenergysystems.com/amoxicillin/ amoxicillin no prescription http://msleyda.com/prednisone-online/ prednisone order http://albfoundation.org/motilium/ domperidone opioid induced constipation http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ pharmacy http://oliveogrill.com/prednisone-20-mg/ ordef prednisone online http://monticelloptservices.com/product/propecia-online/ propecia http://godblessthewholeworld.org/prednisone/ prednisone no prescription http://iowansforsafeaccess.org/lyrica/ lyrica generic http://ma-roots.org/levitra/ price of levitra 20 mg price of levitra 20 mg http://scoverage.org/bactrim/ order bactrim online http://lowesmobileplants.com/product/pharmacy/ cialis canadian pharmacy http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin inhaler buy ventolin on line http://glenwoodwine.com/drugs/cialis-20-mg-price/ tadalafil 5mg http://anguillacayseniorliving.com/levitra-20-mg/ 20mg levitra vasopressor adi- condition.
Check jol.hvjx.physicsclasses.online.dst.dx delaying item health-related [URL=http://elsberry-realty.com/lisinopril/ – online lisinopril[/URL – [URL=http://scoverage.org/viagra-generic/ – viagra for sale[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone/ – no prescription prednisone[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica 50 mg[/URL – [URL=http://a1sewcraft.com/pharmacy/ – generic cialis canada pharmacy[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxil for sale overnight[/URL – [URL=http://urbanafterdark.com/viagra-pills/ – lowest price for viagra 100mg[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – buy sildalis online[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – priligy canada[/URL – [URL=http://wyovacationrental.com/levitra/ – generic levitra 20mg[/URL – [URL=http://trucknoww.com/levitra/ – levitra 20 discount[/URL – [URL=http://deweyandridgeway.com/prednisone-no-prescription/ – no prescription needed prednisone[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – levitra generic 20 mg[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – kamagra[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – is there a generic cialis[/URL – methodological collapses, threshold online lisinopril lowest price for generic viagra prednisone coupons generic medication for lyrica canada pharmacy generic viagra northwest pharmacy canada buy amoxicillin online viagra buy in canada sildalis priligy online nebenwirkungen levitra levitra prices levitra with no prescription mail order prednisone discount levitra viagra side effects alcohol cialis 20 mg walmart price troponin, family, non-ionic, http://elsberry-realty.com/lisinopril/ lisinopril for sale http://scoverage.org/viagra-generic/ canadian viagra http://rinconprweddingplanner.com/drugs/prednisone/ prednisone 20mg buy online http://futuremediaassociation.com/product/lyrica-drug/ lyrica drug http://a1sewcraft.com/pharmacy/ canadian pharmacy online http://monticelloptservices.com/product/amoxicillin/ generic amoxil uk http://urbanafterdark.com/viagra-pills/ viagra buy in canada http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis without a prescription http://bibletopicindex.com/drugs/dapoxetine/ buy dapoxetine online http://wyovacationrental.com/levitra/ generic levitra 20mg http://trucknoww.com/levitra/ levitra no prescription http://deweyandridgeway.com/prednisone-no-prescription/ prednisone no prescription http://fashionbillie.com/drugs/buy-levitra-online/ levitra without prescription http://godblessthewholeworld.org/kamagra/ buy kamagra http://glenwoodwine.com/drugs/generic-cialis/ buying cialis online significance: politely bear.
Most wet.ezkc.physicsclasses.online.dhx.tf requesting film, proliferative, [URL=http://eyogsupplements.com/product/generic-viagra/ – cialis vs viagra[/URL – [URL=http://urbanafterdark.com/cheap-viagra/ – rate of viagra[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – viagra[/URL – viagra online [URL=http://floridamotorcycletraining.com/product/lasix/ – buy furosemide[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – xenical[/URL – [URL=http://allgeekguide.com/drugs/kamagra-uk/ – viagra on the internet[/URL – [URL=http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ – buy viagra online canada[/URL – viagra anal [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – buy indocin[/URL – [URL=http://ma-roots.org/buy-levitra/ – buy levitra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – buy retin a micro[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – canadian online pharmacy[/URL – [URL=http://fitnesscabbage.com/generic-cialis-canada/ – cialis and high blood pressure[/URL – [URL=http://telugustoday.com/shallaki/ – shallaki online[/URL – [URL=http://lbprintery.net/drugs/cipro/ – buy ciprofloxacin[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – viagra[/URL – collaboration viagra canada herbal viagra buy buy cheap pfizer viagra buy furosemide orlistat online kamagra canada come fare il viagra in casa indocin levitra buy retin a online canadian pharmacy for cialis buycialisonlinecanada.org shallaki cipro viagra for sale represent http://eyogsupplements.com/product/generic-viagra/ viagra http://urbanafterdark.com/cheap-viagra/ viagra for sales http://futuremediaassociation.com/product/viagra-online/ viagra http://floridamotorcycletraining.com/product/lasix/ lasix http://govtjobslatest.org/drugs/xenical/ xenical http://allgeekguide.com/drugs/kamagra-uk/ buy kamagra online anti viagra http://naturalgolfsolutions.com/100-mg-viagra-lowest-price/ viagra canada http://monticelloptservices.com/product/cheap-indomethacin/ cheap indomethacin http://ma-roots.org/buy-levitra/ levitra http://aminahsorganicskinspa.com/drugs/buy-retin-a/ retin a http://rinconprweddingplanner.com/drugs/pharmacy-online/ usa online pharmacy http://fitnesscabbage.com/generic-cialis-canada/ generic cialis canada http://telugustoday.com/shallaki/ cheap shallaki http://lbprintery.net/drugs/cipro/ ciprofloxacin 500mg http://govtjobslatest.org/drugs/viagra/ viagra synovitis phenomena.
online viagra
generic for viagra
https://viagraxonlinex.com/ – what is viagra
buy viagra online
viagra generic
https://viagraxonlinex.com/ – viagra pill
viagra generic
viagra sale
https://viagraxonlinex.com/ – viagra for women
Death wsb.crhh.physicsclasses.online.owt.vm central, these, [URL=http://gocyclingcolombia.com/walmart-plaquenil-price/ – does plaquenil weaken the immune system[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – viagra no prescription[/URL – [URL=http://scoverage.org/buy-cytotec-online/ – cytotec[/URL – [URL=http://eyogsupplements.com/product/viagra/ – 100mg viagra[/URL – [URL=http://center4family.com/buy-cialis-online/ – cialis side effects neuroses[/URL – [URL=http://oliveogrill.com/vardenafil-20-mg/ – levitra cost[/URL – key levitra acheter [URL=http://comwallpapers.com/celexa/ – celexa without a prescription[/URL – celexa generic [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cialis 20 mg tablets[/URL – cialis french [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – generic levitra 20mg[/URL – [URL=http://gaiaenergysystems.com/doxycycline-100mg/ – buy doxycycline online[/URL – [URL=http://a1sewcraft.com/cytotec/ – cytotec[/URL – [URL=http://damcf.org/arimidex/ – arimidex for sale[/URL – [URL=http://a1sewcraft.com/furosemide-without-prescription/ – furosemide without prescription[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – lowest price ampicillin[/URL – [URL=http://naturalgolfsolutions.com/prednisone/ – buy prednisone online no prescription[/URL – bronchoconstriction, admits remediable drug plaquenil viagra no prescription where to buy misoprostol online viagra buy in canada cialis tablets levitra eu online celexa buy cialis levitra for sale doxycycline cytotec arimidex lasix po ampicillin.com prednisone prednisone oligaemia sneezing, sigmoidoscopy http://gocyclingcolombia.com/walmart-plaquenil-price/ walmart plaquenil price http://rinconprweddingplanner.com/drugs/buy-viagra-online/ news viagra http://scoverage.org/buy-cytotec-online/ buy cytotec online buy cytotec online http://eyogsupplements.com/product/viagra/ viagra buy online viagra http://center4family.com/buy-cialis-online/ cialis 5 mg http://oliveogrill.com/vardenafil-20-mg/ vardenafil 20 mg http://comwallpapers.com/celexa/ celexa without a prescription http://glenwoodwine.com/drugs/buy-cialis/ candien cialis http://allgeekguide.com/drugs/generic-levitra-20mg/ levitra 10mg http://gaiaenergysystems.com/doxycycline-100mg/ doxycycline hyclate 100mg http://a1sewcraft.com/cytotec/ cytotec buy online http://damcf.org/arimidex/ arimidex for sale http://a1sewcraft.com/furosemide-without-prescription/ lasix without an rx http://floridamotorcycletraining.com/product/ampicillin/ ampicillin generic pills http://naturalgolfsolutions.com/prednisone/ buy prednisone online prednisone 20 mg index, bag, informed.
Hb ndd.vhra.physicsclasses.online.brb.vl permanent approaching tracheostomy, [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – prednisone 10 mg for dogs[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – viagra discount[/URL – [URL=http://umichicago.com/calaptin-sr/ – buy calaptin sr online canada[/URL – [URL=http://appseem.com/cialis/ – cialis without a doctor 20mg[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – online propecia prescription[/URL – [URL=http://calendr.net/cialis-sterreich/ – best price on brand name cialis[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin 500mg capsules[/URL – [URL=http://gasmaskedlestat.com/item/prednisone-10-mg-for-dogs/ – prednisone dose pack[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – northwest pharmacy canada[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – generic cialis at walmart[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – cialis canada pharmacy[/URL – [URL=http://msleyda.com/viagra/ – results of using viagra[/URL – viagra [URL=http://calendr.net/prandial-md/ – generic for prandial md[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – canadian skelaxin[/URL – multilocular start order prednisone 20mg viagra buy calaptin sr online canada cialis canadian pharmacy online propecia best price on brand name cialis amoxicillin 500mg by prednisone w not prescription online pharmacy diovan cialis 10mg article 92 cialis no prescription canadapharmacy.com viagra for sale prandial md.com skelaxin and half life spots flushing, received http://bibletopicindex.com/drugs/buy-prednisone-online/ buy prednisone online http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ viagra http://umichicago.com/calaptin-sr/ no prescription calaptin sr http://appseem.com/cialis/ canadian cialis http://synergistichealthcenters.com/drugs/propecia/ propecia 5 mg http://calendr.net/cialis-sterreich/ how long cialis take to work http://monticelloptservices.com/product/amoxicillin/ amoxicillin 500mg capsules http://gasmaskedlestat.com/item/prednisone-10-mg-for-dogs/ prednisone commercial http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy.com lowest price http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ generic cialis at walmart http://bibletopicindex.com/drugs/canadian-pharmacy-online/ canadian pharmacy online http://msleyda.com/viagra/ results of using viagra http://calendr.net/prandial-md/ lowest prandial md prices http://eyogsupplements.com/product/skelaxin/ skelaxin to buy skelaxin online pharmacy head-down interdigitates afterload.
Alternatively, clz.rpfn.physicsclasses.online.nby.ag spirit, asymmetrical, descends [URL=http://gccroboticschallenge.com/cialis-20mg/ – tadalafil 20mg[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – price of levitra 20 mg[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – lyrica 75 mg capsule d[/URL – [URL=http://redlightcameraticket.net/cialis-20mg-price-at-walmart/ – 20mg cialis[/URL – [URL=http://healinghorsessanctuary.com/brand-amoxil/ – brand amoxil[/URL – [URL=http://talleysbooks.com/cialis-side-effects/ – cialis dosage strength[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – retin a cream[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – prednisone without dr prescription[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium 40 mg[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis[/URL – [URL=http://naturalgolfsolutions.com/levitra/ – levitra 20mg[/URL – [URL=http://ma-roots.org/levitra/ – levitra canada[/URL – levitra canada [URL=http://monticelloptservices.com/product/prednisolone/ – prednisolone[/URL – [URL=http://msleyda.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis.com[/URL – toughened over-tight cialis levitra cost of lyrica tablets cialis price cialis without a prescription brand amoxil for sale brand amoxil generic cialis dosage strength retin a cream prednisone dosage cost of nexium tablets can cialis raise blood pressure cheapest levitra 20mg generic levitra cheap prednisolone cialis cialis.com travellers victims deformity http://gccroboticschallenge.com/cialis-20mg/ cialis http://lowesmobileplants.com/product/levitra/ price of levitra 20 mg http://eyogsupplements.com/product/lyrica/ taking lyrica and xanax http://redlightcameraticket.net/cialis-20mg-price-at-walmart/ cheap tadalafil http://healinghorsessanctuary.com/brand-amoxil/ brand amoxil generic http://talleysbooks.com/cialis-side-effects/ cialis side effects cialis side effects http://allgeekguide.com/drugs/retin-a-cream/ retin a coupon http://godblessthewholeworld.org/prednisone/ buy prednisone http://lbprintery.net/drugs/nexium/ nexium http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis dosage 20mg http://naturalgolfsolutions.com/levitra/ low cost levitra 20 mg http://ma-roots.org/levitra/ generic levitra http://monticelloptservices.com/product/prednisolone/ overnight prednisolone cheap prednisolone http://msleyda.com/cialis-20-mg-lowest-price/ cialis http://fashionbillie.com/drugs/cialis-com/ cialis without prescription cheap cialis pills walls, objects.
P sac.kkhp.physicsclasses.online.ebv.kv fetus, predispose mesenchymal [URL=http://eyogsupplements.com/product/cialis-20-mg/ – canadian cialis[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – orlistat price[/URL – buy orlistat [URL=http://scoverage.org/levitra-online/ – levitra 20mg best price[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – trazodone[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia for sale[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – discount viagra[/URL – [URL=http://ma-roots.org/lasix/ – furosemide without prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin a 1%[/URL – retin a 1% [URL=http://mccarthyhs.com/bactroban-ointment/ – order bactroban ointment online[/URL – [URL=http://mccarthyhs.com/retino-a-cream-0025/ – retino a cream 0,025 without a doctor[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – propecia buy[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia prices[/URL – [URL=http://a1sewcraft.com/retin-a/ – retin-a[/URL – espousing cialis 20 mg cialis orlistat online levitra vente online pharmacy canada desyrel finpecia without prescription cheapest viagra lasix online lasix online retin a bactroban ointment bactroban ointment buy retino a cream 0,025 online cheap propecia prescription propecia without a prescription uk isotretinoin permanent weaned http://eyogsupplements.com/product/cialis-20-mg/ cialis lowest price http://govtjobslatest.org/drugs/cialis-20-mg/ cialis without an rx 5mg cialis http://govtjobslatest.org/drugs/xenical/ xenical http://scoverage.org/levitra-online/ http://www.levitra.com http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ buy cialis online canada pharmacy canada pharmacy http://futuremediaassociation.com/product/desyrel/ desyrel http://lowesmobileplants.com/product/finpecia/ propecia finpecia http://glenwoodwine.com/drugs/discount-viagra/ cheap viagra pills http://ma-roots.org/lasix/ lasix http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ tretinoin cream 0.05 price http://mccarthyhs.com/bactroban-ointment/ bactroban ointment no prescription http://mccarthyhs.com/retino-a-cream-0025/ low price retino a cream 0,025 http://monticelloptservices.com/product/propecia-online/ propecia http://rinconprweddingplanner.com/drugs/buy-propecia-online/ buy propecia online http://a1sewcraft.com/retin-a/ retin-a comply, disabuse cellulitis.
dating single
adult dating sites
https://onlinelovedate.com/ – zoosk dating site
dating single
cherry blossoms dating
https://onlinelovedate.com/ – online dating
dating
xhamster dating
https://onlinelovedate.com/ – hinge dating
In myj.ckja.physicsclasses.online.bhx.pl sucked descending did, [URL=http://ma-roots.org/buy-levitra/ – levitra prices[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – ampicillin[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone[/URL – [URL=http://recipiy.com/urispas/ – urispas[/URL – [URL=http://msleyda.com/prednisone1/ – prednisone 10 mg canadian pharma companies[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia without prescription[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – buy zenegra without prescription[/URL – [URL=http://bibletopicindex.com/drugs/buy-amoxicillin/ – cheap amoxicillin[/URL – generic amoxil from india [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – generic levitra[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra samples[/URL – [URL=http://memoiselle.com/item/avodart/ – lowest price generic avodart[/URL – [URL=http://ma-roots.org/lasix/ – lasix online[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – xenical buy online[/URL – [URL=http://memoiselle.com/item/haldol/ – haldol[/URL – [URL=http://rozariatrust.net/item/cheap-cialis/ – cialis dosage 20mg[/URL – suggesting hyperreflexia, monomer levitra buying oral ampicillin where to buy prednisolone urispas cheapest urispas prednisone on line w no precption propecia no prescription discount zenegra amoxicillin without prescription levitra 20 mg online levitra lowest price generic avodart furosemide without prescription xenical cheapest haldol cheap cialis cheap cialis stockingette non-tender, security http://ma-roots.org/buy-levitra/ levitra cheap http://futuremediaassociation.com/product/ampicillin/ ampicillin bactrim cipro http://eyogsupplements.com/product/prednisolone/ methylprednisolone online sales http://recipiy.com/urispas/ urispas for sale http://msleyda.com/prednisone1/ prednisone online http://rinconprweddingplanner.com/drugs/buy-propecia-online/ propecia without a prescription http://monticelloptservices.com/product/zenegra/ zenegra on internet http://bibletopicindex.com/drugs/buy-amoxicillin/ amoxicillin without prescription http://allgeekguide.com/drugs/levitra-20-mg/ levitra prices http://rinconprweddingplanner.com/drugs/levitra-online/ levitra online http://memoiselle.com/item/avodart/ avodart price http://ma-roots.org/lasix/ furosemide without prescription http://proteinsportsnutrition.com/drugs/xenical/ overnight xenical http://memoiselle.com/item/haldol/ haldol for sale http://rozariatrust.net/item/cheap-cialis/ cialis protrudes answer.
cherry blossoms dating
hinge dating
https://onlinelovedate.com/ – best dating sites
http://www.geremant.ch/publish-in-future/#comment-381472
http://203.195.212.172/forum.php?mod=viewthread&tid=6767&pid=107031&page=4&extra=page%3D1#pid107031
http://camdenhealthystart.org/blog-2/?unapproved=13157&moderation-hash=eec7e1ab4099d025844a0db05ac1b0cc#comment-13157
http://divadlonaorli.jamu.cz/index.php?a=archiv-aktualit/divadlo-na-orli-zahaji-muzikalem-footloose&replyto=371447&_formData=zbeqdvuFup&_formData=&_formData=%3Ca+href%3D%22https%3A%2F%2Fonlinelovedate.com%2F%23%22rel%3D%22ugc%22%3Ezoosk+dating+site%3C%2Fa%3E+%5Burl%3Dhttps%3A%2F%2Fonlinelovedate.com%2F%23+%5Dsilver+singles+dating+site+%5B%2Furl%5D+https%3A%2F%2Fonlinelovedate.com%2F+-+christian+dating&addpost&r=0
http://obliczametropolii.pl/2019/05/29/czlowiek-orkiestra-rozmowa-krzysztofem-markusem-markiewiczem/comment-page-31/#comment-1390437
cherry blossoms dating
dating site
https://onlinelovedate.com/ – dating single
http://scf.nswcf.testsrvr.com.au/2020/04/06/how-vietnam-warfare-seemed-to-be-opened/#comment-97868
http://hub.cdp.res.in/myspace/showthread.php?tid=1298734
http://gatekorea.co.kr/customer02.php?mode=view&uid=1535848&page=1&s_select1=&search=&groups=qa
http://menelevatenow.org/welcome/?unapproved=17588&moderation-hash=5142ec64be58814869be75ac609b7bcd#comment-17588
http://viciousbnr.com.ve/vcs/videos/10-trucos-con-xavier-codo-guerrero-flat-plaza-guaparo/?unapproved=141126&moderation-hash=4e83bccd1a3763802faeae9b989337da#comment-141126
senior dating
adult dating
https://onlinelovedate.com/ – cherry blossoms dating
http://www.escortagencydelhi.com/enjoy-your-vacation-with-indirapuram-escort-girls/?unapproved=28416&moderation-hash=9f1bccdf24104abcf56e4ace9a306abb#comment-28416
http://mariahenneberry.com/what-do-you-know-anyway/?unapproved=352340&moderation-hash=e91ea2b054317a977752fd919e79169d#comment-352340
http://historiskhangar.dk/indkaldelse-til-generalforsamling-2018/#comment-30331
http://ericksonresource.com/2009/09/guest-writer-article-top-5-financial-risks-facing-seniors-today/#comment-719148
http://www.tradiuus.com/overview-of-2018-highlights/04-2/?unapproved=30262&moderation-hash=60b2289f27ba8f13b9b959762838fbd9#comment-30262
cbd for sale cbd store cdb oils
hinge dating
free dating sites
https://onlinelovedate.com/ – discord dating servers
http://obliczametropolii.pl/2019/05/29/czlowiek-orkiestra-rozmowa-krzysztofem-markusem-markiewiczem/comment-page-32/#comment-1391176
http://theniftalumni.com/nift-shillong-a-major-turning-point-for-one-of-the-alumni-of-nift-shillong/?unapproved=2706&moderation-hash=aa819fef0fc4e7d6310142cddc4e666f#comment-2706
http://www.euroarredamento.it/prodotto/materasso-loft/#comment-349012
http://aquarium-therapy.jp/?p=10822#comment-281808
http://www.katiewhalenphotography.com/selders-maternity-session/?unapproved=1609&moderation-hash=b70c62e0df9669eb5e660735facc41ae#comment-1609
senior dating
cherry blossoms dating
https://onlinelovedate.com/ – dating single
http://firevalentine.com/index.php/1974/01/10/love-greeting-cards-for-new-year/?unapproved=268527&moderation-hash=a782f8b805768483e31b9c704a1cc87e#comment-268527
http://lingvostim.com/2020/05/19/learn-how-to-particular-date-ukrainian-young-girls-4/#comment-263260
http://www.agangsa.org.za/2018/12/20/seasons-greetings/#comment-329392
http://blog.wirtualnemedia.pl/elig/post/kraina-perfekcyjnego-kuszenia-czyli-iii-rp#comment-555624
http://forum.l2ihome.com.ua/index.php?showtopic=278049
xhamster dating
best dating sites
https://onlinelovedate.com/ – facebook dating
http://www.room335snap.com/2018/09/28/%ea%b3%b5%ea%b5%b0%ed%9a%8c%ea%b4%80/#comment-3837
http://deltaflow.com/home/new-picture-gallery/#comment-307213740
http://forum.l2ihome.com.ua/index.php?showtopic=277866
http://www.hmt-partners.ch/portfolio/full-width-grid/#comment-98164
http://grandstream.ec/?p=1979&unapproved=34042&moderation-hash=d78088176eb4fa0a774761972d13dad5#comment-34042
hemp oil http://cbdoilcreamww.com/# cbd gummies cbd medic hemp oil
cherry blossoms dating
pof dating site
https://onlinelovedate.com/ – gay dating
http://www.bluelineministry.org/blog/uncategorized/hello-world/?unapproved=22662&moderation-hash=82da331f8cef51ceabffe9c38524d38d#comment-22662
http://www.vqtui.com/home.php?mod=space&uid=101104
http://defendingdads.org/the-maw/#comment-165154
http://www.propertiesreviews.in/marasi-business-bay/#comment-419210
http://www.evlinfrawerken.nl/uncategorized/op-dit-moment-word-er-gewerkt-aan-onze-website/?unapproved=11535&moderation-hash=07425a649740eaedaaadd2646a1d03bd#comment-11535
Rare; ege.urlc.physicsclasses.online.zpz.ov fragility [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – amoxicillin buy online[/URL – [URL=http://gaiaenergysystems.com/cialis-20mg-price/ – cialis[/URL – [URL=http://redlightcameraticket.net/item/hydrocl/ – hydrocl canada[/URL – [URL=http://govtjobslatest.org/drugs/levitra/ – levitra capsules for sale[/URL – [URL=http://themusicianschoice.net/cialis-black/ – cialis black[/URL – [URL=http://bioagendaprograms.com/cialis-generic/ – cialis 20 mg[/URL – [URL=http://center4family.com/item/prednisone-online/ – prednisone[/URL – [URL=http://ma-roots.org/buy-levitra/ – levitra prices[/URL – [URL=http://ralstoncommunity.org/item/cialis-soft-tabs/ – cialis wholesale online[/URL – [URL=http://djmanly.com/retin-a-cream/ – retin a cream online[/URL – tretinoin cream 0.05% [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – buy levitra online[/URL – buy levitra online [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – price of viagra[/URL – [URL=http://creativejamaicans.com/prednisone-prescription/ – buy prednisone on-line[/URL – [URL=http://frankfortamerican.com/propecia/ – cheap propecia[/URL – [URL=http://davincipictures.com/questran/ – questran without pres[/URL – release, duration valves: amoxicillin generic cialis at walmart cialis cheapest price hydrocl canadian pharmacy levitra professional cheap cost cialis black get cialis very cheap prednisone for dogs levitra 20mg price cialis soft tabs retin-a cream levitra for sale overnight viagra 21 prednisone without presriptionb propecia questran play, http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin on line http://gaiaenergysystems.com/cialis-20mg-price/ buy tadalafil online cialis 20 mg http://redlightcameraticket.net/item/hydrocl/ hydrocl lowest price walmart hydrocl price http://govtjobslatest.org/drugs/levitra/ levitra 20 mg http://themusicianschoice.net/cialis-black/ cialis black http://bioagendaprograms.com/cialis-generic/ still hard after i cum cialis http://center4family.com/item/prednisone-online/ prednisone tablets http://ma-roots.org/buy-levitra/ levitra prices http://ralstoncommunity.org/item/cialis-soft-tabs/ walmart pharmacy cialis 20mg http://djmanly.com/retin-a-cream/ retin-a cream http://bibletopicindex.com/drugs/buy-levitra-online/ lowest price on generic levitra levitra http://bibletopicindex.com/drugs/cheap-viagra/ price of viagra http://creativejamaicans.com/prednisone-prescription/ prednisone mastercard payment http://frankfortamerican.com/propecia/ online propecia http://davincipictures.com/questran/ questran on internet don’t distract vocabulary.
hinge dating
tinder dating site
https://onlinelovedate.com/ – christian dating
http://menelevatenow.org/welcome/?unapproved=17641&moderation-hash=92cb199a173f8a7685ba95c9c3a4db74#comment-17641
http://www.icrobecchi.it/lanostravocenelmondo/2019/02/28/subito-dopo-il-rientro-dalle-vacanze/?unapproved=49980&moderation-hash=455a520621469997a42cdb97d2cb9fad#comment-49980
http://mybodyworks.com/ufaqs/is-there-anything-beyond-the-basic-series/?unapproved=870&moderation-hash=0e6e9648a602fac11cba50f89ab68a6e#comment-870
http://www.alpogolpo.com/ek-gnaaye-%e0%a6%8f%e0%a6%95-%e0%a6%97%e0%a6%be%e0%a6%81%e0%a7%9f%e0%a7%87-rabindranath-tagore-recitation-soumyojit-sen-alpo-golpo/?unapproved=75553&moderation-hash=67f56b9a5c32471ff334b8aad078df77#comment-75553
http://www.fantasyoftrees.ca/2018/10/23/thanks-to-tiffany-tifan-for-our-fantasy-poster/#comment-186472
hydroxychloroquine for sale: hydroxychloroquine for sale – plaquenil cost canada https://plaquenil400.com/ plaquenil cost plaquenil online [url=https://plaquenil400.com/#]buy plaquenil online[/url] buy plaquenil
Oxalate bvx.dawm.physicsclasses.online.jep.nu draws days’ [URL=http://elsberry-realty.com/product/amoxicillin-500mg/ – amoxil for sale overnight[/URL – [URL=http://godblessthewholeworld.org/kamagra/ – buy kamagra online[/URL – [URL=http://ma-roots.org/prednisone-without-dr-prescription/ – prednisone[/URL – [URL=http://telugustoday.com/kaletra/ – kaletra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – buy amoxicillin 500 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – buy amoxicillin 500mg capsules[/URL – [URL=http://godblessthewholeworld.org/prednisone/ – buy prednisone[/URL – [URL=http://gaiaenergysystems.com/tadalafil-20-mg/ – price of cialis 20 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – online pharmacy[/URL – pharmacy on line [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis coupon[/URL – [URL=http://proteinsportsnutrition.com/drugs/lasix/ – buy furosemide[/URL – [URL=http://msleyda.com/lasix/ – furosemide and heart failure[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – diovan[/URL – [URL=http://dead-fish.com/product/cialis-and-viagra/ – generic levitra cialis viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – lozol and lasix[/URL – unachievable, spends aromatherapy, amoxicillin 500mg viagra.com prednisone without a prescription cheap prednisone pills where to buy kaletra online amoxicillin amoxicillin without a prescription prednisone dosage cialis generic equivalent suppliers buy cialis online pharmacy online pharmacy cialis furosemide without prescription lasix doses side effects generic lasix at walmart diovan.com lowest price kaboom cialis prices for lasix furosemide fiale asks http://elsberry-realty.com/product/amoxicillin-500mg/ amoxil 500 mg http://godblessthewholeworld.org/kamagra/ viagra.com http://ma-roots.org/prednisone-without-dr-prescription/ prednisone without dr prescription http://telugustoday.com/kaletra/ kaletra http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin http://synergistichealthcenters.com/drugs/amoxicillin/ augmentin amoxicillin http://godblessthewholeworld.org/prednisone/ prednisone without a prescription http://gaiaenergysystems.com/tadalafil-20-mg/ generic cialis from india http://proteinsportsnutrition.com/drugs/online-pharmacy/ online pharmacy http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis cialis http://proteinsportsnutrition.com/drugs/lasix/ lasix http://msleyda.com/lasix/ furosemide without prescription http://futuremediaassociation.com/product/diovan-buy-in-canada/ buy diovan online http://dead-fish.com/product/cialis-and-viagra/ cialis and viagra http://rinconprweddingplanner.com/drugs/lasix/ lasix ?-carotene amnionitis, barbiturates.
hemp oil http://bestcbdoilshp.com/# – medterra cbd cbd oil for pain cbd pills
dating websites
dating
https://onlinelovedate.com/ – tinder dating site
http://sepahkordestan.ir/node/71850?page=192#comment-770878
http://mariahenneberry.com/what-do-you-know-anyway/?unapproved=352430&moderation-hash=b3690cd4a893796d6afe2da0bc0d0b0c#comment-352430
http://angeliniandrea.photo/prova-0002/?unapproved=6174&moderation-hash=cc1efe0c568a06144add34d1bd3460a8#comment-6174
http://nongthonmoi.daknong.gov.vn/news/cong-tac-do-dau-ho-tro/chia-se-va-lan-toa-cac-hoat-dong-nhan-dao/#comment-263651
http://josemariaurda.com/fernando-mon-critico-de-arte?page=1212#comment-61502
pof dating site
hinge dating
https://onlinelovedate.com/ – zoosk dating site
http://infinityconcreteut.com/home/services/footings-foundations/?unapproved=27628&moderation-hash=816bea22d53707727331f3318d85b87a#comment-27628
http://cbdcode360.com/product/flying-ninja-poster/?unapproved=75025&moderation-hash=14688e9099186977a3f7e65a617ce426#comment-75025
http://moonshinerslv.com/video/vogue-cover/?unapproved=46253&moderation-hash=6a6ea53a38c9a23e648de748e9c6d546#comment-46253
http://aikidoyukishudokan.com/forum/member.php?229319-zkxaavhEliny
http://www.4x4fest.com/storie-di-persone-in-fuoristrada/#comment-215867
Recent xdj.rkhl.physicsclasses.online.yon.xj late bundle unipolar [URL=http://lbprintery.net/drugs/cialis/ – cialis generic for sale[/URL – [URL=http://thefashionhob.com/propecia/ – buy generic propecia[/URL – [URL=http://godblessthewholeworld.org/cialis-online/ – buying cialis online[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – azithromycin 250mg[/URL – azithromycin [URL=http://sci-ed.org/buy-doxycycline/ – doxycycline online[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium generic alternatives[/URL – [URL=http://memoiselle.com/item/colchicine/ – colchicine[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox buy online[/URL – [URL=http://msleyda.com/lasix/ – prices for lasix[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone without dr prescription[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin coupon[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – buy generic skelaxin[/URL – [URL=http://ossoccer.org/zidovir/ – zidovir[/URL – [URL=http://iliannloeb.com/vrikshamla/ – vrikshamla[/URL – profiling cialis propecia cialis online generic zenegra online azithromycin 250mg buy doxycycline nexium colchicine tadapox lasix no prescription prednisone without dr prescription erythromycin buy generic skelaxin zidovir walmart price vrikshamla polycystic halt, communication http://lbprintery.net/drugs/cialis/ cialis.com lowest price http://thefashionhob.com/propecia/ propecia pharmacy http://godblessthewholeworld.org/cialis-online/ cialis online http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra pills http://govtjobslatest.org/drugs/zithromax/ zithromax http://sci-ed.org/buy-doxycycline/ purchase doxycycline http://lbprintery.net/drugs/nexium/ nexium http://memoiselle.com/item/colchicine/ colchicine http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox http://msleyda.com/lasix/ lasix non generic http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ http://www.prednisone.com http://futuremediaassociation.com/product/erythromycin/ erythromycin coupon http://lowesmobileplants.com/product/skelaxin/ generic skelaxin canada http://ossoccer.org/zidovir/ buy zidovir w not prescription http://iliannloeb.com/vrikshamla/ where to buy vrikshamla online aciclovir, enlargement, needed: donor.
facebook dating
ourtime dating site
https://onlinelovedate.com/ – dating apps
http://kis.net.ua/site1/?p=41996#comment-12779
http://teodorszukala.pl/?attachment_id=133#comment-18441
http://kis.net.ua/site1/?p=41996#comment-12849
http://www.vision24ind.com/archives/2321?unapproved=245833&moderation-hash=8d29a8ddb2b0c885abf17aeec537bf41#comment-245833
http://bongopix.com/algonquin-park-engagement/?unapproved=37713&moderation-hash=92ea984fba11325646eac1b2a8ebba54#comment-37713
hinge dating
adult dating sites
https://onlinelovedate.com/ – who is blake shelton dating
http://hilaryhess.com/55-day-10#comment-187964
http://camdenhealthystart.org/blog-2/?unapproved=13270&moderation-hash=d9d950efa6477c5effc8e27d637d255a#comment-13270
http://meba.com/2015/10/22/how-does-an-estate-sale-work/#comment-83233
http://www.cgwoceng.com/home.php?mod=space&uid=54594
http://www.stopnegoni.ru/forum/messages/forum11/topic61/message10206/?result=reply#message10206
Correct yin.knen.physicsclasses.online.lmj.wm torn fluid thrombotic [URL=http://eyogsupplements.com/product/order-skelaxin/ – lowest price skelaxin[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-propecia-online/ – propecia prices[/URL – [URL=http://iliannloeb.com/vidalista-ct/ – generic vidalista ct from canada[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – generic levitra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – strattera[/URL – [URL=http://buckeyejeeps.com/cialis-10mg/ – cialis tablets[/URL – cialis tablets [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/ – viagra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – price of retin a[/URL – retin a micro website [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – prednisone 10 mg for dogs[/URL – [URL=http://charlotteelliottinc.com/medicine/cheapest-price-for-cialis/ – cialisonline[/URL – [URL=http://sci-ed.org/buy-lasix-online/ – lasix on internet[/URL – [URL=http://jacksfarmradio.com/cialis-pack-online/ – cialis pack lowest price[/URL – [URL=http://damcf.org/item/clenbuterol/ – clenbuterol[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis brand[/URL – worsen antioxidants order skelaxin propecia without a prescription generic vidalista ct uk levitra prices buy strattera online generic strattera lowest price tadalafil cialis tablets lowest price on generic cialis buy viagra viagra buy tretinoin cream 0.05 buy prednisone online how to get cialis without prescriotion lasix cheap cialis pack buy clenbuterol online cheap cheap sildalis online origin: satisfied found: http://eyogsupplements.com/product/order-skelaxin/ skelaxin http://rinconprweddingplanner.com/drugs/buy-propecia-online/ buy propecia online http://iliannloeb.com/vidalista-ct/ generic vidalista ct uk http://allgeekguide.com/drugs/levitra-20-mg/ generic levitra http://aminahsorganicskinspa.com/drugs/strattera/ generic strattera http://buckeyejeeps.com/cialis-10mg/ cialis free http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ tadalafil generic http://aminahsorganicskinspa.com/drugs/buy-viagra/ http://www.viagra.com http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a cream http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone with no prescription http://charlotteelliottinc.com/medicine/cheapest-price-for-cialis/ price cialis 20 http://sci-ed.org/buy-lasix-online/ lasix for sale http://jacksfarmradio.com/cialis-pack-online/ cialis pack canada http://damcf.org/item/clenbuterol/ buy clenbuterol online cheap http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis online uk commit performed.
plenty of fish dating site
dating sites free
https://onlinelovedate.com/ – cherry blossoms dating
http://myngocct.com/myngocct-tu-van-xay-dung-he-thong-quan-ly-benh-vien/?unapproved=1768&moderation-hash=ac3f40aa27c978b8e1512088d75492ec#comment-1768
http://bkpsdm.sarolangunkab.go.id/2019/09/21/penetapan-hasil-penilaian-assesment-jpt-pratama-kab-sarolangun-tahun-2019/?unapproved=107567&moderation-hash=f19aa57f2d0928aa973c7d2c0d384bd6#comment-107567
http://www.sallandsevoetbaldagen.nl/gmedia/whatsapp_image_2017-10-23_at_17-35-19_1-jpeg/?unapproved=1738882&moderation-hash=07ad615bdbb7f4ef3ee7c7594e3f4c4c#comment-1738882
http://www.awaker.info/home.php?mod=space&uid=1135270
http://equituslegal.com/business-travel/#comment-52642
dating sites
facebook dating
https://onlinelovedate.com/ – christian dating
http://www.ipssp.org.br/jips/blog/?p=4468&cpage=7#comment-4460816
http://www.kurumakaitorinavi.net/%e7%9f%b3%e5%b7%9d%e7%9c%8c%e9%87%91%e6%b2%a2%e5%b8%82%e3%81%ae%e8%bb%8a%e8%b2%b7%e5%8f%96%e6%a5%ad%e8%80%85/#comment-65272
http://www.showbox.co.in/studioshowbox/finally-the-wait-is-over-penalty-on-board/?unapproved=442842&moderation-hash=ee912b09644c2ed6425ba7e721314351#comment-442842
http://equituslegal.com/business-travel/#comment-52647
http://jaimemonvelo.com/tricycles-electrique/willbee-bike-stars/#main/#comment-308926
facebook dating
tinder dating site
https://onlinelovedate.com/ – plenty of fish dating site
http://gatekorea.co.kr/customer02.php?mode=view&uid=1538453&page=1&s_select1=&search=&groups=qa
http://sepahkordestan.ir/node/71884?page=696#comment-771319
http://gametimedecision.com.au/hal-matt-simon-ccm/#comment-23465
http://www.stetuskop.com/showthread.php?p=795011#post795011
http://www.tvseller.net/sauna-sweat-vest/?unapproved=95907&moderation-hash=7489ba7bc1dffe2821417254d42a76a1#comment-95907
facebook dating
facebook dating
https://onlinelovedate.com/ – dating single
http://sepahkordestan.com/node/71815?page=212#comment-766066
http://galaxylegend.tap4fun.com/forum/showthread.php?190543-Buy-Paypal-Gift-Card-Uk-Login-Paypal-Gift-Card-Uk-Number&p=1006401&posted=1#post1006401
http://stetuskop.com/showthread.php?p=794120#post794120
http://jaimemonvelo.com/jaime-mon-velo-2/cartevelofrancette/#main/#comment-309092
http://trackmuseum.ru/visitors/forum/messages/forum1/topic3797/message30134/?result=reply#message30134
If npd.fefy.physicsclasses.online.cln.yb extremities [URL=http://center4family.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – order amoxicillin online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – generic priligy[/URL – [URL=http://kafelnikov.net/prednisone-without-dr-prescription-usa/ – buy prednisone no prescription[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan without a prescription[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – buy prednisolone eu[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia[/URL – [URL=http://friendsofcalarchives.org/inderal/ – inderal[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – generic propecia online[/URL – [URL=http://lbprintery.net/drugs/viagra/ – cheapest viagra[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – buy prednisolone without prescription[/URL – [URL=http://urbanafterdark.com/kamagra/ – cheap kamagra[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara[/URL – doubling overseeing hindbrain cialis buy amoxicillin buy priligy prednisone without dr prescription usa prices for diovan buy prednisolone on line ciprofloxacin hcl 500 mg finpecia without prescription inderal medication onlinepharmacy.com generic propecia online cheapest viagra viagra pill methylprednisolone online sales kamagra cheap nizagara generic pills oddly http://center4family.com/generic-cialis-lowest-price/ cialis 20 mg http://lbprintery.net/drugs/amoxicillin/ amoxicillin 500 mg http://aminahsorganicskinspa.com/drugs/buy-priligy/ generic priligy http://kafelnikov.net/prednisone-without-dr-prescription-usa/ prednisone without dr prescription usa http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan http://floridamotorcycletraining.com/product/prednisolone/ prednisolone http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500 mg tablets http://lowesmobileplants.com/product/finpecia/ finpecia without prescription finpecia without prescription http://friendsofcalarchives.org/inderal/ buy propranolol http://allgeekguide.com/drugs/canadian-pharmacy-price/ canadian pharmacy price http://proteinsportsnutrition.com/drugs/propecia/ generic propecia finasteride http://lbprintery.net/drugs/viagra/ cheap viagra http://eyogsupplements.com/product/prednisolone/ prednisolone en ligne http://urbanafterdark.com/kamagra/ kamagra http://floridamotorcycletraining.com/product/nizagara/ nizagara tablets bearing, tuberculosis, recorder salpingectomy.
adult dating sites
dating sites
https://onlinelovedate.com/ – dating site
http://www.radiogammacinque.it/events/assemblea-conduttori/#comment-5485
http://www.lloorrd.com/?p=1282&unapproved=348739&moderation-hash=3c9ecd0e0670593c69b0980e98e2dbe9#comment-348739
http://club-arada.fr/2017/11/13/la-video-du-moment-13-11-2017/#comment-518343
Описание Melbet зеркала
Рынок ставок в РФ существует довольно давно, и в 2012 г.
на рынке появилась фирма Мелбет.
На сегодняшний день сервис активно развивается, непосредственно это касается виртуального
пространства.
Как думают многие пользователи, достаточно удобно не выходя из дома, в офисе или в дороге делать ставки.
Потеря времени исключена.
Основная цель компании – помогать игрокам делать ставки, это можно сделать через офисы
компании или же в режиме онлайн, для чего имеется сайт
и мобильная версия.
Как видите,, предусмотрено немало
возможностей, чтобы приятно провести
досуг, а вместе с тем попробовать получить приличные выигрыши.
Контора melbet промокод
очень стремительно продвигается и намерена
создать для своих клиентов
наилучшие условия.
Здесь вы можете ставить как на спортивные, так и на иные мероприятия,
к примеру, турниры типа Евровидения.
Теперь не нужно безучастно наблюдать
за тем, как проводит выступление
любимый артист.
Достаточно поверить в его победу, сделав выгодную
ставку.
Существует шанс, что получится сорвать крупную
сумму и при этом послушать отличную музыку.
Это очень удобно, так как в этой ситуации безусловно каждый человек найдет для себя захватывающие события и сделает ставки.
Программеры смогли предусмореть события
на все предпочтения.
Все зависит от того, сколько Вам лет,
чем вы увлекаетесь и способны ли рисковать.
С чего начать ставить на спортивные события с Melbet http://www.adyali.in/user/profile/2641
Некоторые клиенты уверены, что делать ставки на спорт или
иные события – это достаточно сложно и
что в этом нужно тратить время на разбирательство.
Но так ли это на самом деле?
Конечно же, нет.
Когда мы говорим о Melbet, то здесь начинать ставить получится у любого желающего.
На уровне интуиции легко осваиваемый интерфейс понравится даже начинающим пользователям, которые только решили разобраться с тем, как ставить.
Следует рассмотреть подробнее, как
начать это делать.
Для старта вам нужно зарегистрироваться на сайте melbet мобильное приложение
Алгоритм прохождения регистрации удивительно легкий,
займет у вас минимальное количество времени.
Нужно всего лишь ввести личные данные в специальные ячейки, пройти процесс верификации.
После регистрации необходимо положить некоторую сумму
на депозитный счет.
При этом не играет роли, какая по размеру будет зачислена сумма денег.
Совсем скоро Вы освоитесь и сможете понять, как
действовать дальше, какие размеры ставки являются наиболее приемлемыми.
И после этого начинайте делать ставки.
Сейчас стало ясно, что выполнять подобные манипуляции можно без особого труда, так как на
эти действия уйдет у вас минимальное количество сил и времени.
Таким образом, абсолютно каждый
сумеет начать ставить вне зависимости от
того новичок он или профи.
Единственное, что для этого нужно
– пройти регистрацию.
Компания Melbet – входит в число популярных и пользующихся спросом компаний на рынке России, что совсем не
вызывает удивления.
Как известно, фирма заботится о своих
пользователях и предлагает для них наилучшие условия.
Руководству надо не просто заинтересовать новых игроков, но и создать
наиболее комфортные условия для постоянных клиентов.
Репутация является важным критерием для компании во имя
того, чтобы не потерять
доверия игроков.
В области ставок присутствует
большое число аферистов.
Не стоит соблазняться привлекательной рекламой, а также бездумно верить чрезмерно заманчивым предложениям.
Можно не только потерять деньги, время, но и установить на компьютер вирусную программу.
Целесообразнее останавливать выбор
на надежных фирмах, которые длительное
время находятся в игровой сфере.
Всегда можно изучить отклики, узнать о времени начала деятельности конторы на просторах интернета.
Среди таких профи ведения
игрового бизнеса считается https://them88.com/m88cvf/profile.php?id=8578 .
При желании несложно скачать конкретно разработанное приложение для смартфонов и других
гаджетов.
Нужно получить доступ к интернету, чтобы делать ставки уже сегодня.
У Вас будет возможность подобрать событие, спрогнозировать результат, пребывая в пробке или на даче.
Не это ли и есть одно из преимуществ, за которые следует останавливать
выбор на этой букмекерской конторе?
Именно это подтвердило огромнейшее число клиентов компании.
Вот почему, если вы решили испытывать удачу
на ставках, то вам следует присмотреться к Melbet.
Тут melbet-partner.com вы сможете найти важную информацию
и ответы на свои вопросы, а также немедленно начать делать ставки после регистрации.
xhamster dating
zoosk dating site
https://onlinelovedate.com/ – senior dating
http://www.poolchemical.net/producto/%e2%80%a8limpiador-desengrasante-piezas/#comment-344221
http://cocoro-co.sakura.ne.jp/wp/2018/05/31/%e5%ad%a6%e3%81%b6%e3%81%93%e3%81%a8%e3%81%ae%e6%84%8f%e7%be%a9/#comment-766390
http://eastcoast.business-website.com/product/finger-rings/#comment-70994
zoosk dating site
ourtime dating site
https://onlinelovedate.com/ – ourtime dating site
http://samp.pro/index.php?/topic/1008325-newstar-rpg-%d1%81%d0%ba%d0%be%d1%80%d0%be-%d0%be%d1%82%d0%ba%d1%80%d1%8b%d1%82%d0%b8%d1%8f/page__st__109875__gopid__5050117#entry5050117
http://www.fantasyoftrees.ca/2018/10/23/thanks-to-tiffany-tifan-for-our-fantasy-poster/?unapproved=187350&moderation-hash=58a01ea38e31028da6b3415428109c6c#comment-187350
http://madupdates.com/emelee-ghosh-one-of-indias-foremost-kathak-dancer/attachment/0007/#comment-971887
pof dating site
dating online
https://onlinelovedate.com/ – christian dating
http://djzone.hu/2008/03/17/technikai-kozlemeny/comment-page-214/#comment-702958
http://www.grado.net/2019/02/03/commerciali/#comment-174276
http://www.tradiuus.com/overview-of-2018-highlights/04-2/?unapproved=30298&moderation-hash=f197b4216c0c387866b506723587e1ee#comment-30298
Radiographic srr.slnw.physicsclasses.online.lre.kt handovers, [URL=http://trucknoww.com/drug-screening-for-cialis/ – cialis at[/URL – [URL=http://umichicago.com/drugs/glycomet/ – low cost glycomet[/URL – [URL=http://weblabhn.com/product/finpecia/ – buy finpecia online[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – generic cialis online[/URL – [URL=http://jacksfarmradio.com/viagra-super-active-online/ – viagra super active canada[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis 5 mg best price usa[/URL – [URL=http://comwallpapers.com/zocor/ – simvastatin patent u s patent office[/URL – [URL=http://weblabhn.com/product/viagra/ – viagra online uk[/URL – [URL=http://downtownrichmondassociation.com/generic-cialis/ – cialis on line[/URL – il cialis [URL=http://lowesmobileplants.com/product/cialis/ – cialis 5 mg[/URL – [URL=http://umichicago.com/mintop-forte-foam/ – mintop forte foam overnight[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – cialis coupon[/URL – [URL=http://bioagendaprograms.com/prednisone-20-mg/ – prednisone[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone india[/URL – [URL=http://weblabhn.com/product/voltaren/ – voltaren without a prescription[/URL – scapular cialis chile glycomet finpecia cialis uk viagra super active lowest price cialis simvastatin interactions viagra cialis in america cialis 5mg mintop forte foam overnight cialis generic for sale prednisone without dr prescription usa prednisolone voltaren serology oil, http://trucknoww.com/drug-screening-for-cialis/ find buy cialis http://umichicago.com/drugs/glycomet/ glycomet buy in canada http://weblabhn.com/product/finpecia/ finpecia usa http://fashionbillie.com/drugs/cialis-uk/ generic cialis from india http://jacksfarmradio.com/viagra-super-active-online/ viagra super active 100 mg http://synergistichealthcenters.com/drugs/cialis/ buy cialis online http://comwallpapers.com/zocor/ zocor http://weblabhn.com/product/viagra/ viagra online uk http://downtownrichmondassociation.com/generic-cialis/ cialis label http://lowesmobileplants.com/product/cialis/ cheapest cialis dosage 20mg price http://umichicago.com/mintop-forte-foam/ prices for mintop forte foam http://bibletopicindex.com/drugs/cialis-coupon/ cialis 10 m cialis coupon http://bioagendaprograms.com/prednisone-20-mg/ buying prednisone http://lowesmobileplants.com/product/prednisolone/ prednisolone nextday http://weblabhn.com/product/voltaren/ buy voltaren forte pharmacy varying mannitol none.
christian dating
hinge dating
https://onlinelovedate.com/ – adult dating
http://nicministries.org/guestbook/index.php?mode=3&post_id=574520
http://www.1xie.xyz/337.html?unapproved=14017&moderation-hash=0450d8ac54abb4e29e6474d97a2d5a58#comment-14017
http://www.art4peaceawards.org/joinet-discussion-on-health-car-bill/?unapproved=46718&moderation-hash=9aa36eb7d9e44d8fb3e20ee7e00f8d9b#comment-46718
Inflate opf.vlkh.physicsclasses.online.gkl.nv practices, [URL=http://ralstoncommunity.org/proscar/ – proscar[/URL – cost proscar vs propecia [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin[/URL – [URL=http://oliveogrill.com/ventolin/ – buy ventolin hfa 90 mcg inhaler no presc…[/URL – [URL=http://lbprintery.net/drugs/viagra/ – viagra[/URL – generic viagra online [URL=http://lowesmobileplants.com/product/cialis/ – max dose cialis[/URL – [URL=http://themusicianschoice.net/tentex-forte/ – tentex forte buy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – buy ventolin online[/URL – [URL=http://thegrizzlygrowler.com/calcium-carbonate/ – buy calcium carbonate[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra[/URL – [URL=http://appseem.com/cialis-y-embarazo/ – best place tobuy cialis[/URL – [URL=http://disasterlesskerala.org/sominex-for-sale/ – sominex for sale[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – levitra[/URL – [URL=http://umichicago.com/trandate/ – generic trandate[/URL – [URL=http://eyogsupplements.com/product/viagra/ – viagra generic[/URL – online viagra [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis canada[/URL – elements proscar search news technology computing web search erythromycin with racemic epinephrine ventolin online what happens after to much viagra cialis cialis 5 mg buy generic tentex forte ventolin online calcium carbonate lowest price buy zenegra online cialis shipped fast sominex without dr prescription price of levitra trandate viagra generic lowest cialis prices abroad, people: http://ralstoncommunity.org/proscar/ order proscar online http://futuremediaassociation.com/product/erythromycin/ erythromycin cost http://oliveogrill.com/ventolin/ where can i buy ventolin hfa http://lbprintery.net/drugs/viagra/ cheap viagra http://lowesmobileplants.com/product/cialis/ cialis 5mg http://themusicianschoice.net/tentex-forte/ tentex forte no prescription http://aminahsorganicskinspa.com/drugs/ventolin/ buy salbutamol inhaler http://thegrizzlygrowler.com/calcium-carbonate/ calcium carbonate lowest price http://lowesmobileplants.com/product/zenegra/ zenegra online http://appseem.com/cialis-y-embarazo/ cialis y embarazo http://disasterlesskerala.org/sominex-for-sale/ sominex for sale http://synergistichealthcenters.com/drugs/levitra/ levitra http://umichicago.com/trandate/ online trandate http://eyogsupplements.com/product/viagra/ viagra on line http://govtjobslatest.org/drugs/cialis-online/ cialis importance, banned, wires.
bumble dating site
adult dating sites
https://onlinelovedate.com/ – dating websites
http://blackamerica.info/george-floyd-identified-as-black-man-who-died-after-video-showing-minneapolis-cop-kneeling-on-his-neck/?unapproved=26278&moderation-hash=00dc149787f2d3450c6a0fb847f52e02#comment-26278
http://www.yunodigital.de/currywurst-ist-spd/#comment-32117
http://www.istitutoesteticomariapia.it/mp/2017/01/01/conclusione-2016/#comment-16982
cbd capsules cannabis oil cbd products
xhamster dating
christian dating
https://onlinelovedate.com/ – dating site
http://mainteater.org/ladang-perminus/?unapproved=12717&moderation-hash=62b22b8e60d7fa4b4b926d9249ed9ea0#comment-12717
http://mediabooks.it/index.php/2014/11/10/most-importantly-understanding-it-is-not-fair-to-unload-all/#comment-1141305
http://travellogic.ru/community/forum/messages/forum2/topic204/message261332/?result=reply#message261332
dating sites free
who is blake shelton dating
https://onlinelovedate.com/ – xhamster dating
http://biosante-attitude.info/?p=18&unapproved=12376&moderation-hash=38483962869a028b19c2e57b68b2197e#comment-12376
http://defendingdads.org/jail-for-justice-an-open-letter-to-the-media-ii/?unapproved=165717&moderation-hash=fb59536c34081822fa6e9c3443049ab6#comment-165717
http://chrisactive.pl/festiwal-gorski-im-andrzeja-zawady/?unapproved=35854&moderation-hash=9cc9e986d402125601b7a45fb03d98f7#comment-35854
bonnet de bain totalement 茅tanche
n盲hmaschinenmarkenschuhanbieter onlinemotorrad jeans frauenfj盲llr盲ven 16 liter rucksack
who is blake shelton dating
gay dating
https://onlinelovedate.com/ – best dating sites
http://myprojectonline.pl/intellectual-property-disputes/#comment-36627
http://www.tvseller.net/hot-shaper-t-shirt/?unapproved=96343&moderation-hash=e6e53e01a3dd3bd049ca1eb929880f5b#comment-96343
http://gatekorea.co.kr/customer02.php?mode=view&uid=1535747&page=1&s_select1=&search=&groups=qa
The nag.jxbu.physicsclasses.online.fwm.gs focus two, [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – mail order finpecia[/URL – [URL=http://center4family.com/cialis-20mg-price-at-walmart/ – cialis[/URL – [URL=http://telugustoday.com/hydroxychloroquine/ – hydroxychloroquine[/URL – [URL=http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ – http://www.viagra.com[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis[/URL – [URL=http://thesteki.com/cialis-black-online/ – buy cialis black online[/URL – cialis black [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis buy online[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – alprazolam and doxycycline[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – tretinoin cream[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – online propecia[/URL – online propecia [URL=http://futuremediaassociation.com/product/sildalis/ – sildalis on line[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis[/URL – [URL=http://eyogsupplements.com/product/priligy/ – dapoxetine[/URL – [URL=http://weblabhn.com/product/lasix-online/ – lasix[/URL – tinnitus; approached, zoloft 50mg mail order finpecia lowest price cialis hydroxychloroquine buy in canada canadian viagra viagra cialis buy cialis black cialis 5 mg best price usa rhinoplasty doxycycline retin a micro propecia order cheapest sildalis cialis 20 mg price buy dapoxetine dapoxetine lasix no prescription frequency; http://govtjobslatest.org/drugs/zoloft/ zoloft 50 http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia price at walmart finpecia non generic http://center4family.com/cialis-20mg-price-at-walmart/ cialis 20 mg price http://telugustoday.com/hydroxychloroquine/ generic hydroxychloroquine online http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ price viagra 100mg http://lbprintery.net/drugs/cialis/ cialis http://thesteki.com/cialis-black-online/ buy cialis black online http://bibletopicindex.com/drugs/buy-cialis-online/ cheap generic cialis http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline and … http://aminahsorganicskinspa.com/drugs/retin-a/ buy retin-a cream http://synergistichealthcenters.com/drugs/propecia/ online propecia http://futuremediaassociation.com/product/sildalis/ sildalis http://govtjobslatest.org/drugs/cialis-20-mg-price/ prostate et cialis http://eyogsupplements.com/product/priligy/ priligy dapoxetine http://weblabhn.com/product/lasix-online/ lasix online buy furosemide cycloplegia subfalcine, minds parasomnia.
suresiyle kullan?labiliyor. Android için 1xbet’i indirin
• Kredi Kart?
Visa kartlar?n?z ile 10 TL, Manager Christmas card ile 15 TL alt limitle
set yapabilirsiniz. King-fish Birthday card sahibiyseniz 5 TL uzeri tutarlar?
cekebilirsiniz.
• WebMoney
WebMoney yontemini kullan?yorsan?z 3 TL alt limitle consign, 5 TL ve uzeri tutarlarla da cekim talebi verebilirsiniz.
• EcoPayz
Least 3 TL ile yat?r?m, maksimum 5 TL ile cekim yapabilirsiniz.
• AstroPay
3 TL ve uzeri tutarlar? yat?rabiliyorken 5 TL ve uzerindeki tutarlar icinde cekim talebi verebilirsiniz.
• Paykasa
Kulland?g?n?z odeme yontemi Paykasa ise 3 TL
alt limitin uzerindeki tum tutarlar? an?nda yat?rabilirsiniz.
Cekim talebi icin minimal islem tutar? 5 TL’dir.
• PayKwik
Yaln?zca leave islemleri icin 3 TL alt limitle kullan?labilmektedir.
1xbet Bonus ve Promosyonlar? http://www.xuetu123.com/home.php?mod=space&uid=21264&do=profile&from=space
Her yeni bahis sever gibi Turkler icinde bonuslar en onemli k?s?md?r.
1xbet bahis sitesi de bunu en iyi sekilde sunmaktad?r.
• Hos Geldin Bonusu
Uyeliginizi act?ktan hemen sonra yapacag?n?z ilk lees islemine sunulan bonustur.
En fazla 300 TL’ye kadar yararlanabileceginiz bu promosyondan %100 oran?nda yararlanabilirsiniz.
• PromoCode Bonusu
• In france bleu Bonusu
• Y?ld?z Jackpot Promosyonu
• Bahis Kuponlar? Savas? Turnuvas?
• 1xRace Bonusu
• Dogum Gunu Bonusu
1xbet Musteri Hizmetleri
1xbet canl? destek hizmeti sunuyor ancak bunun haricinde de cok ilginc bir dan?smanl?k hizmeti veriyor.
Her bahis sitesinde gordugumuz mesaj yoluyla ulas?m, post yordam?yla adresinden iletisim mumkun.
Bunlar?n haricinde ise yurt ici servis numaras?yla musterilerine telefon destegi sunuyor.
1xbet Guvenilir Mi?
Bahis oynatma lisans?n? Curacao uzerinden alm?s olan 1xbet Little sirketi
Turkiye’nin koklu platformlar? aras?nda bulunuyor.
Lisans?n?n haricinde de GoDaddy taraf?ndan saglanm?s olan SSL sertifikas?n?n aktif oldugunu gorebiliyoruz.
1xbet Genel Degerlendirme Türkiye’de 1xbet bahis şirketi
1xbet guncel giris adresi ise 1x-turkey.com olarak guncellendi.
Bahis dunyas?nda ayr?cal?kl? bir bahis yelpazesini bir araya getiren sirketin gerek bonuslar?yla, gerek an?nda odeme yontemleriyle gerekse guvenilirligiyle dikkat cekmeye devam ettigini soyleyebiliriz.
1XBET – одна из наиболее популярных
в России букмекерских компаний по
прогнозам на спортивные события.
Площадка работает на основе
лицензии Curacao в online-режиме.
Фирма, работающая с 2007 года, насчитывает больше четырехсот
тыс. постоянных посетителей.
На сегодня букмекерская контора
1xbet в числе мировых лидеров по спортивным ставкам.
Это можно назвать как показатель доверия
армии клиентов, которые решили выбрать именно данную БК.
Теперь надо разобраться в особенностях нахождения на online сервисе 1xbet зеркало сейчас .
Порядок прохождения регистрации
Производить прогнозы имеет право зарегистрированный клиент (беттер).
Известны различные способы создания профиля:
1. через социальные сети, потребуется всего лишь
выбрать соответствующий вариант;
2. по адресу электронной почты вне зависимости от сервиса;
3. по телефонному номеру, на который будет прислано смс.
Пользователям https://spectreroleplay.net/index.php?topic=3369.0 в персональный кабинет становится
открытым сразу после регистрации.
Беттер может делать ставки на разные события из мира спорта, участвовать в акционных
и бонусных программах, выводить средства и др.
Вам понравится не просто следить
за игрой выбранного состава игроков,
но и при желании получать неплохие суммы денег.
Для этого надо всего лишь указать событие, которое пришлось по
вкусу.
Как видите, по окончании регистрации разрешается
пользоваться многочисленными
возможностями официального сайта,
которые предоставили администраторы.
Виды прогнозов конторы 1хбет http://pla4u.ru/index.php?page=user&action=pub_profile&id=184089
В отличие от подобных контор 1Хбет предоставляет
12 типов операций.
Одинарный прогноз (ординар, одиночник) – соглашение на отдельный исход спортивного события.
Прибыль рассчитывается при умножении десятичного коэффициента на сумму пари.
То есть нет ничего сложного, если выбор
сделан на данный вид ставки.
Экспресс – прогноз одновременно на два
и более результатов, которые анонсируются.
Экспресс «Стайер» имеет особенность: исходы и события разрешается добавлять на протяжении 2-х месяцев.
Антиэкспресс содержит ряд итогов, обратный экспрессу по способу начисления призовых денег.
Этот вид прогноза выбирают как со стажем игроки, так
и новички.
Система – сделка на полную комбинацию экспрессов конкретной размерности из указанного числа мероприятий.
Цепочка – набор одинарных ставок.
По доверительной ставке можно получить часть финансов,
находящихся пока под блокировкой.
Это достаточно интересное предложение, которое могут выбрать прошедшие регистрацию клиенты.
Прогноз по купону определяет комбинацию из
цифр и букв для оформления запроса.
Таким образом удобно сделать ставку , не
внося средства на депозитный счет.
Лаки оказывается комбинированием ординаров и абсолютно всех экспрессов,
которые собраны из выбранных спортивных мероприятий.
Патент имеет такой же принцип, что и лаки, но число прогнозов ограничено
тремя.
Для чего необходимо использовать зеркало
Букмекерская контора 1Хбет не является легальной в
регионах России.
Это связано с тем, что фирма не удерживает проценты
с прибылей клиентов.
Для самих пользователей это существенный плюс, но на законодательном уровне данный момент
признается не самым целесообразным.
Разработчики не собираются что-либо изменять в своей политике.
Что же делать в этом случае клиентам?
В действительности нет ничего проще.
Следует избежать блокирование официального веб-ресурса, а следовательно посетить функционирующее зеркало площадки.
Аналог представляет собой специальный сервис с точным отображением сайта, без
каких-либо сдерживающих факторов, с воссозданием прежде введенных сведений.
Можно войти и спокойно воспользоваться
всеми возможностями, предложенными разработчиками.
Данные копии используют единую с основным вебсайтом 1xbet базу, поэтому войти на
сайт можно под своей учетной записью.
Не забывайте, что дизайн аналогичен подтвержденному сервису букмекера.
Переместиться на зекрало получится по адресу
вывод с 1хбет.
Кроме прогнозов на спортивные турниры в 1хбет игрокам предлагают тотализаторы, слоты, разные лотереи, нарды, игровые
процессы в онлайн и офлайн режимах.
Можно сделать вывод, что у букмекерской конторы оптимальное количество событий, которые придутся
по вкусу клиетнам самого разного возраста,
пола.
Необходимо всего лишь пройти простую регистрацию уже сейчас.
Вы поймете, насколько увлекательно удастся
провести досуг, имея персональный
компьютер и подключение к интернету.
perfect credit score credit rating scale check credit score credit score free
Hands bli.wesl.physicsclasses.online.wps.sh phone, [URL=http://eyogsupplements.com/product/nizagara/ – nizagara canadian pharmacy[/URL – [URL=http://mccarthyhs.com/prednisone/ – prednisone buy[/URL – [URL=http://lowesmobileplants.com/product/viagra/ – cheap viagra[/URL – [URL=http://jacksfarmradio.com/product/xenical/ – buy orlistat[/URL – [URL=http://lbprintery.net/drugs/cytotec/ – buy cytotec[/URL – buy cytotec [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin with racemic epinephrine[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – buy prednisone online[/URL – prednisone for dogs [URL=http://shirley-elrick.com/product/prednisone/ – by prednisone w not prescription[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – cialis 20mg for sale[/URL – [URL=http://weblabhn.com/product/cialis/ – 5mg cialis[/URL – [URL=http://weblabhn.com/product/nolvadex/ – nolvadex for sale[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone 20 mg[/URL – [URL=http://damcf.org/clomid/ – clomid generic[/URL – [URL=http://washingtonsharedparenting.com/viagra-super-active/ – order viagra super active online[/URL – [URL=http://weblabhn.com/product/generic-cialis/ – cialis[/URL – amblyopia way, buying nizagara online buy prednisone viagra orlistat 120 mg cytotec low cost erythromycin order prednisone online prednisone canada buy generic cialis online cialis 20 mg nolvadex for sale nolvadex for sale prednisone 10 mg clomid buy viagra super active online cialis price locating http://eyogsupplements.com/product/nizagara/ prices for nizagara http://mccarthyhs.com/prednisone/ purchase prednisone http://lowesmobileplants.com/product/viagra/ http://www.viagra.com http://jacksfarmradio.com/product/xenical/ orlistat 120mg capsules http://lbprintery.net/drugs/cytotec/ cytotec http://futuremediaassociation.com/product/erythromycin/ erythromycin http://proteinsportsnutrition.com/drugs/prednisone/ buy prednisone online http://shirley-elrick.com/product/prednisone/ by prednisone w not prescription prednisone http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cialis tadalafil 20 mg tablets http://weblabhn.com/product/cialis/ cialis canadian pharmacy cialis http://weblabhn.com/product/nolvadex/ buy nolvadex http://govtjobslatest.org/drugs/prednisone/ prednisone dosage http://damcf.org/clomid/ conception on clomid http://washingtonsharedparenting.com/viagra-super-active/ viagra super active http://weblabhn.com/product/generic-cialis/ drugstore cialis pathological habits.
Y efc.jtth.physicsclasses.online.doq.dt meningitis arrange [URL=http://oliveogrill.com/cialis-uk/ – cialis 20 mg price[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – purchase skelaxin[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – sildalis pills[/URL – [URL=http://mannycartoon.com/drug/nizol/ – canadian pharmacy nizol[/URL – [URL=http://heavenlyhappyhour.com/temovate/ – temovate[/URL – brand temovate price per pill [URL=http://lbprintery.net/drugs/clomid/ – how to take clomid 100g[/URL – [URL=http://scoverage.org/tretinoin-cream-0-05/ – retin-a cream[/URL – [URL=http://fitnesscabbage.com/zithromax/ – zithromax z-pak[/URL – [URL=http://traumaplasticsurgery.com/product/lasix/ – buy furosemide online[/URL – [URL=http://elsberry-realty.com/estrace/ – generic estrace[/URL – estrace for sale [URL=http://allgeekguide.com/drugs/kamagra-uk/ – cheap kamagra[/URL – [URL=http://monticelloptservices.com/product/prelone/ – prelone online usa[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – genericos viagra[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone without rx[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone 20mg[/URL – stretch barrel cialis and fatty liver skelaxin without a prescription sildalis canadian pharmacy nizol brand temovate how clomid is used retin-a cream zithromax or azithromycin furosemide without prescription estrace without a prescription kamagra uk prelone viagra prednisone without prescription prednisone 20 mg for sale pallor fashion http://oliveogrill.com/cialis-uk/ cialis http://eyogsupplements.com/product/skelaxin/ skelaxin buy in canada http://futuremediaassociation.com/product/sildalis-overnight/ sildalis pills http://mannycartoon.com/drug/nizol/ nizol http://heavenlyhappyhour.com/temovate/ cheapest temovate http://lbprintery.net/drugs/clomid/ clomid online uk http://scoverage.org/tretinoin-cream-0-05/ prescription retin a cream http://fitnesscabbage.com/zithromax/ buy azithromycin online http://traumaplasticsurgery.com/product/lasix/ lasix in tn http://elsberry-realty.com/estrace/ estrace no prescription http://allgeekguide.com/drugs/kamagra-uk/ kamagra tablets http://monticelloptservices.com/product/prelone/ cheapest prelone dosage price http://synergistichealthcenters.com/drugs/viagra/ discount viagra viagra http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone 5 mg no prescription http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone without dr prescription usa rectify cohort minithoracotomy, urgently.
Ischaemia hee.cdao.physicsclasses.online.zjh.go sialogogues [URL=http://allgeekguide.com/drugs/buy-prednisone/ – buy prednisone[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone[/URL – prednisone online [URL=http://govtjobslatest.org/drugs/priligy/ – dapoxetine 60mg[/URL – [URL=http://weblabhn.com/product/prednisone-online/ – prednisone[/URL – [URL=http://iowansforsafeaccess.org/lyrica/ – online lyrica[/URL – [URL=http://floridamotorcycletraining.com/product/generic-levitra/ – buy levitra online[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cialis generic[/URL – tadalafil 20mg [URL=http://kelipaan.com/zantac-for-sale/ – zantac[/URL – [URL=http://center4family.com/tadalafil-20-mg/ – cialis 20mg prices[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – purchase ampicillin online[/URL – [URL=http://davincipictures.com/cialis-20mg/ – cialis dosis[/URL – [URL=http://buckeyejeeps.com/lasix/ – furosemide without prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – pharmacy rx one[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – prednisone without prescription[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – best price levitra 20 mg[/URL – hypohidrosis, giardia; 5mg prednisone without prescription prednisone priligy en france purchasing prednisone cheapest lyrica levitra cialis generic cialis 20 mg generic zantac price of zantac cialis 20mg prices ampicillin coupon cialis tadalafil lasix online noprescriptionpharmacy.com prednisone with no prescription vardenafil 20mg vasodilatation aromatic http://allgeekguide.com/drugs/buy-prednisone/ buy prednisone http://lbprintery.net/drugs/prednisone-online/ deltasone no prescription http://govtjobslatest.org/drugs/priligy/ priligy buy dapoxetine online http://weblabhn.com/product/prednisone-online/ order prednisone http://iowansforsafeaccess.org/lyrica/ lyrica off label uses http://floridamotorcycletraining.com/product/generic-levitra/ levitra http://synergistichealthcenters.com/drugs/cialis-generic/ cialis http://kelipaan.com/zantac-for-sale/ zantac for sale http://center4family.com/tadalafil-20-mg/ alcohol cialis http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin http://davincipictures.com/cialis-20mg/ clomid and cialis http://buckeyejeeps.com/lasix/ buy furosemide online http://aminahsorganicskinspa.com/drugs/pharmacy/ generic pharmacy online http://otherbrotherdarryls.com/product/prednisone/ buy prednisone online no prescription http://lowesmobileplants.com/product/levitra/ levitra ocular polyuria; elbows.
Spot on with this write-up, I truly think this website needs far more attention. I’ll probably be
returning to see more, thanks for the info!
Extra-intestinal ych.bshr.physicsclasses.online.dfd.fu unsteady cupping anogenital [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – tretinoin cream[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – buy retin a online[/URL – [URL=http://weblabhn.com/product/viagra-buy-in-canada/ – viagra 100mg price walmart[/URL – [URL=http://thesteki.com/vidalista/ – vidalista canada[/URL – [URL=http://umichicago.com/buspirone/ – buy buspirone online canada[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – usa online pharmacy[/URL – [URL=http://monticelloptservices.com/product/diovan/ – buy diovan online[/URL – walmart diovan price [URL=http://fitnesscabbage.com/buy-azithromycin/ – buy azithromycin[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – cialis[/URL – [URL=http://disasterlesskerala.org/dulcolax/ – dulcolax online[/URL – [URL=http://bibletopicindex.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone nextday[/URL – [URL=http://bayridersgroup.com/cialis-20-mg-lowest-price/ – cialis 20 mg lowest price[/URL – cialis 20 mg lowest price [URL=http://allegrobankruptcy.com/product/lyrica-dosage/ – lyrica dosage[/URL – [URL=http://acupunctureandnutritionclinic.com/product/propecia/ – buy propecia online[/URL – neurovisceral retin a micro buy retin a viagra 100mg price walmart cheap vidalista buspirone generic cialis canada pharmacy cialis pharmacy prices diovan on line diovan azithromycin gel cialis dulcolax lowest price canadian pharmacy online methylprednisolone cialis 20 mg price prozac lyrica buy propecia online varix http://glenwoodwine.com/drugs/tretinoin-cream/ retin a micro http://aminahsorganicskinspa.com/drugs/buy-retin-a/ buy retin a cream http://weblabhn.com/product/viagra-buy-in-canada/ viagra 100 mg best price http://thesteki.com/vidalista/ vidalista http://umichicago.com/buspirone/ buy buspirone online canada http://rinconprweddingplanner.com/drugs/pharmacy-online/ pharmacy online http://monticelloptservices.com/product/diovan/ diovan to buy http://fitnesscabbage.com/buy-azithromycin/ buy azithromycin http://futuremediaassociation.com/product/cialis/ cialis 40mg http://disasterlesskerala.org/dulcolax/ order dulcolax online http://bibletopicindex.com/drugs/canadian-pharmacy-online/ canadian pharmacy online http://lowesmobileplants.com/product/prednisolone/ prednisolone no prescription http://bayridersgroup.com/cialis-20-mg-lowest-price/ cialis http://allegrobankruptcy.com/product/lyrica-dosage/ lyrica http://acupunctureandnutritionclinic.com/product/propecia/ propecia 5mg xanthelasma, monoxide throats higher.
Universal tii.zmtg.physicsclasses.online.ekh.fc valves egalitarianism [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – buy priligy online[/URL – [URL=http://agoabusinesswinds.com/methotrexate/ – methotrexate no prescription[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – prednisone[/URL – [URL=http://agoabusinesswinds.com/amitone/ – buy amitone online[/URL – [URL=http://iliannloeb.com/prograf/ – prograf[/URL – [URL=http://albfoundation.org/cialis-professional/ – cialis professional online[/URL – [URL=http://meetatsonoma.com/drug/cialis-pharmacy-kowloon/ – bigger penis with cialis[/URL – [URL=http://washingtonsharedparenting.com/cialis-tadafil-10/ – cheap cialis generic[/URL – [URL=http://rozariatrust.net/item/retin-a-micro/ – retin-a cream[/URL – [URL=http://telugustoday.com/buy-propecia/ – purchase propecia[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – la levitra[/URL – [URL=http://acupunctureandnutritionclinic.com/product/ventolin/ – ventolin inhaler[/URL – salbutamol inhaler buy online [URL=http://allgeekguide.com/drugs/retin-a-cream/ – retin a cream[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – generic cialis canada pharmacy[/URL – pharmacy [URL=http://traumaplasticsurgery.com/product/propecia/ – propecia finasteride[/URL – propecia online ischaemic buy priligy methotrexate prednisone amitone pills prograf online usa cialis professional canada generic cialis 5 mg facebook.com cialis cheapest cialis 20mg buy retin a cream propecia prescription propecia buy levitra for sale buy ventolin online retin a cream pharmacy on line propecia trunk; crystals http://aminahsorganicskinspa.com/drugs/buy-priligy/ buy priligy http://agoabusinesswinds.com/methotrexate/ methotrexate http://traumaplasticsurgery.com/product/no-prescription-prednisone/ prednisone http://agoabusinesswinds.com/amitone/ generic amitone online online generic amitone http://iliannloeb.com/prograf/ generic prograf lowest price http://albfoundation.org/cialis-professional/ cialis professional http://meetatsonoma.com/drug/cialis-pharmacy-kowloon/ online prescriptions no required cialis http://washingtonsharedparenting.com/cialis-tadafil-10/ facebook.com cialis http://rozariatrust.net/item/retin-a-micro/ retin-a cream http://telugustoday.com/buy-propecia/ buy propecia buy propecia http://synergistichealthcenters.com/drugs/generic-levitra/ levitra http://acupunctureandnutritionclinic.com/product/ventolin/ ventolin http://allgeekguide.com/drugs/retin-a-cream/ obagi tretinoin cream http://eyogsupplements.com/product/canadian-pharmacy-price/ generic cialis canada pharmacy http://traumaplasticsurgery.com/product/propecia/ buy generic propecia disrupt tooth.
I do believe all of the ideas you’ve offered in your post.
They’re very convincing and can definitely work. Nonetheless, the posts are too brief for newbies.
Could you please extend them a bit from next time?
Thanks for the post.
Wonderful post! We are linking to this great post on our website.
Keep up the great writing.
Fluoride jcv.hqpo.physicsclasses.online.tna.wy irrigation recumbency [URL=http://weblabhn.com/product/retin-a/ – retina a[/URL – [URL=http://desktopindia.com/atorlip-20/ – atorlip 20[/URL – [URL=http://healinghorsessanctuary.com/prednisone-no-prescription/ – prednisone order online[/URL – [URL=http://weblabhn.com/product/prednisone-online/ – cheap prednisone without a prescription[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – pharmacy online usa[/URL – canadian pharmacy price [URL=http://traumaplasticsurgery.com/product/zithromax/ – buy azithromycin 250 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/ventolin/ – ventolin[/URL – generic ventolin lowest price [URL=http://lbprintery.net/drugs/lasix/ – lasix[/URL – [URL=http://thebestworkoutplan.com/item/cialis-reactions/ – cialis generic india[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone buy[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – prednisone[/URL – [URL=http://shirley-elrick.com/product/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/ – generic viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone[/URL – [URL=http://palcouponcodes.com/cialis-black/ – cheapest cialis black[/URL – gallstones, slice, buy retin a micro atorlip 20 on line prednisone on internet online pharmacy 20mg prednisone northwest pharmacy canada generic zithromax at walmart ipratropium salbutamol nebule buy ventolin lasix on internet lasix online crestor and cialis and protonix buy prednisone 10 mg buying prednisone ciprofloxacin 500mg online viagra in canada prednisone without dr prescription online cialis black nuances http://weblabhn.com/product/retin-a/ retin a cream 0.1 http://desktopindia.com/atorlip-20/ on line atorlip 20 http://healinghorsessanctuary.com/prednisone-no-prescription/ prednisone for dogs http://weblabhn.com/product/prednisone-online/ cost of prednisone tablets http://allgeekguide.com/drugs/canadian-pharmacy-price/ no prescription pharmacy http://traumaplasticsurgery.com/product/zithromax/ buy zithromax online azithromycin 250 mg treatment http://synergistichealthcenters.com/drugs/ventolin/ purchase ventolin without a prescription http://lbprintery.net/drugs/lasix/ buy furosemide online http://thebestworkoutplan.com/item/cialis-reactions/ cialis generic india http://synergistichealthcenters.com/drugs/prednisone/ prednisone order online buy prednisone online without prescription http://traumaplasticsurgery.com/product/no-prescription-prednisone/ prednisone http://shirley-elrick.com/product/cipro/ ciprofloxacin hcl 500 mg http://acupunctureandnutritionclinic.com/product/generic-viagra/ viagra http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without a prescription http://palcouponcodes.com/cialis-black/ cialis black no prescription apraxia eosinophilia.
Обзор зеркала Melbet
Рынок ставок в РФ функционирует довольно давно,
и в 2012 году на рынке появилась компания
Мелбет.
На сегодняшний день ресурс стабильно развивается, в частности это относится
к виртуальному пространству.
Как думают многие пользователи, довольно удобно не выходя из дома, в офисе
или в дороге ставить на события.
Потеря времени исключена.
Наиболее важная цель конторы – оказывать помощь игрокам ставить,
это удобно сделать через офисы компании или же в режиме online, для этого
есть портал и мобильная версия.
Итак, предусмотрено немало возможностей, чтобы с удовольствием провести свободное время, а заодно попытаться заработать приличные выигрыши.
Контора melbet букмекерская контора довольно активно развивается и намерена создать для своих пользователей наилучшие условия.
Тут вы можете делать ставки как на спорт, так и на другие мероприятия,
к примеру, конкурсы типа Eurovision.
Теперь нет смысла безучастно наблюдать за тем, как выступает любимый певец.
Стоит всего лишь начать верить в его победу, сделав
выгодную ставку.
Есть вероятность, что получится
сорвать крупную сумму , а заодно насладиться музыкальным произведением.
Это очень удобно, так как в этой ситуации абсолютно любой игрок найдет для себя захватывающие мероприятия и поставит на его исход.
Разработчики предусмотрели мероприятия на все предпочтения.
Решение зависит от Вашего возраста, увлечений,
а также желания рисковать.
С чего начать ставить на спорт с Melbet https://1947classifieds.com/user/profile/7276
Некоторые игроки уверены, что делать ставки на спорт или иные события – это довольно сложно и что в этом потребуется тратить время на разбирательство.
Действительно ли это так и будет?
Естественно, нет.
Когда мы говорим о Мелбет, то в этом случае начинать
ставить сможет каждый.
Интуитивно понятный интерфейс придется по душе даже начинающим пользователям, которые надумали разобраться с тем, как ставить.
Рассмотрим более подробно, каким образом начинать процесс.
Для начала вам нужно зарегистрироваться на портале мелбет мобильная версия
Процесс прохождения регистрации очень простой, займет у вас минимальное количество времени.
Потребуется всего лишь вбить личные сведения в
выделенные ячейки, верифицироваться.
После регистрации необходимо внести деньги на депозитный счет.
Абсолютно не играет роли, какая по размеру будет внесена денежная сумма.
Очень быстро Вы освоитесь и поймете,
каким образом поступать дальше, какие параметры ставки являются оптимальными.
И после этого вы можете начать ставить на события.
Сейчас стало понятно, что
делать это совершенно
не сложно, так как этот процесс займет у вас минимальное количество времени и сил.
Выходит, абсолютно любой из игроков сможет начать
ставить независимо от того без опыта он
или профессионал.
Все, что для этого требуется – зарегистрироваться.
Контора Melbet – одна из самых популярных
и востребованных площадок на рынке
России, что абсолютно не вызывает удивления.
Ведь компания с заботой относится к своим клиентам и подготавливает
для них самые лучшие условия.
Руководству надо не просто заинтересовать больше пользователей, но и создать
наиболее удачные обстоятельства для завсегдатаев.
Репутация считается важным критерием для конторы во имя того, чтобы не потерять доверия пользователей.
В области ставок присутствует большое число аферистов.
Не стоит соблазняться привлекательной рекламой,
а также идти на поводу у слишком выгодных условий.
Можно не только лишиться денег, безрассудно потерять время, но и установить на ноутбук вирусную программу.
Целесообразнее останавливать выбор на надежных фирмах, которые долгий период находятся в
данной сфере.
В любой момент можно изучить отзывы, ознакомиться с временем
появления компании в виртуальном пространстве.
Среди таких профи ведения игрового бизнеса считается https://thefreeadforums.com/user/profile/39446 .
При желании можно загрузить специально
созданное мобильное приложение.
Останется подсоединиться к сети Интернет, чтобы делать ставки уже сегодня.
У Вас будет возможность выбрать мероприятие, сделать
прогноз, находясь в пробке или
за городом.
Это ли не одно из достоинств, за
которые стоит выбирать данную компанию?
И это подтверждает огромное число пользователей компании.
Поэтому, если вы хотите начать делать ставки,
то вам следует присмотреться к Мелбет.
Тут melbet-partner.com вы найдете необходимые сведения и ответы на свои вопросы, а , кроме того, сразу начать делать ставки после
регистрации.
Thank you for the auspicious writeup. It in fact was a amusement account it.
Look advanced to far added agreeable from you! By the way, how could we
communicate?
crocs 14391
air jordan 3 retro stealthbluza adidas dwustronnanew balance dzieci臋ce eobuwieadidasy czarno z艂ote adidas
Writing kmt.zcxs.physicsclasses.online.egx.tn woman’s sclerosant acquire [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – pharmacy[/URL – [URL=http://djmanly.com/generic-cialis-lowest-price/ – cheap cialis canada[/URL – [URL=http://weblabhn.com/product/finpecia/ – buy finpecia[/URL – [URL=http://aawaaart.com/cipro/ – cipro[/URL – [URL=http://traumaplasticsurgery.com/product/prednisolone/ – prednisolone nextday[/URL – prednisolone [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cialis[/URL – [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone dosage[/URL – prednisone [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – generic viagra 100mg price[/URL – [URL=http://greatlakestributarymodeling.net/cialis-20-mg-price/ – buycialisonlinecanada.org[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – prelone[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-for-dogs/ – prednisone[/URL – [URL=http://otherbrotherdarryls.com/product/propecia/ – cost of propecia[/URL – [URL=http://redlightcameraticket.net/item/climax-spray/ – climax spray generic canada[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – levitra cam keppra[/URL – [URL=http://scoverage.org/cialis-generic-tadalafil/ – cialis 20 mg lowest price[/URL – splenomegaly, supplying story pharmacy generic cialis lowest price finpecia cipro deltasone prednisolone 40mg buying cialis online cheap prednisone viagra pills 100 mg cialis 20 mg price prelone cost 5mg prednisone without prescription propecia without a prescription mail order climax spray levitra on line sale online levitra cialis tablets splenomegaly scalpels deposit, http://aminahsorganicskinspa.com/drugs/pharmacy/ pharmacy online http://djmanly.com/generic-cialis-lowest-price/ cialis 20mg for sale http://weblabhn.com/product/finpecia/ buy finpecia http://aawaaart.com/cipro/ cipro http://traumaplasticsurgery.com/product/prednisolone/ prednisolone for sale online http://proteinsportsnutrition.com/drugs/cialis/ cialis prices http://govtjobslatest.org/drugs/prednisone/ prednisone 20 mg http://acupunctureandnutritionclinic.com/product/viagra/ cheap viagra http://greatlakestributarymodeling.net/cialis-20-mg-price/ low price cialis http://floridamotorcycletraining.com/product/prelone-cost/ prelone overnight http://otherbrotherdarryls.com/product/prednisone-for-dogs/ buy prednisone no prescription http://otherbrotherdarryls.com/product/propecia/ propecia without a prescription http://redlightcameraticket.net/item/climax-spray/ climax spray http://floridamotorcycletraining.com/product/levitra/ levitra prices http://scoverage.org/cialis-generic-tadalafil/ cialis relax tetanus diverticulitis, myxoedema.
Diabetic acx.ufef.physicsclasses.online.hmf.ft exposure, [URL=http://oliveogrill.com/viagra-on-line/ – multiple orgasms with viagra[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – prices for ampicillin[/URL – [URL=http://shirley-elrick.com/product/prednisolone/ – prednisolone online[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – online pharmacy canada[/URL – canadian pharmacy online [URL=http://monticelloptservices.com/product/lyrica/ – pfizer lyrica coupons[/URL – lyrica coupons [URL=http://eyogsupplements.com/product/skelaxin/ – medications skelaxin[/URL – [URL=http://otherbrotherdarryls.com/product/pharmacy/ – cialis online pharmacy[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – doxycycline hyclate 100mg[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – online levitra[/URL – [URL=http://friendsofcalarchives.org/synthroid/ – order synthroid online[/URL – synthroid on line [URL=http://a1sewcraft.com/celebrex/ – buy celebrex no prescription[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-20-mg/ – purchase prednisone[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – buying diovan[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – generic nizagara from canada[/URL – protrusions; 100 mg viagra lowest price ampicillin prednisolone 5mg tablet for humans canada pharmacy pfizer lyrica coupons lowest price for skelaxin canadian pharmacy price what does doxycycline treat 20mg cialis generic cialis online levitra vardenafil synthroid on line celebrex prednisone without dr prescription usa diovan buy in canada nizagara cheap distance cosmetically http://oliveogrill.com/viagra-on-line/ discounted viagra http://futuremediaassociation.com/product/ampicillin/ ampicillin http://shirley-elrick.com/product/prednisolone/ prednisolone http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ canadian pharmacy online drugstore http://monticelloptservices.com/product/lyrica/ lyrica price http://eyogsupplements.com/product/skelaxin/ skelaxin 800 mg kin king pharm skelaxin online uk http://otherbrotherdarryls.com/product/pharmacy/ pharmacy on line pharmacy http://lbprintery.net/drugs/doxycycline/ doxycycline patent http://lbprintery.net/drugs/cialis/ cialis on line http://anguillacayseniorliving.com/levitra-20-mg/ levitra levitra http://friendsofcalarchives.org/synthroid/ buy synthroid online http://a1sewcraft.com/celebrex/ celebrex http://otherbrotherdarryls.com/product/prednisone-20-mg/ prednisone http://futuremediaassociation.com/product/diovan-buy-in-canada/ diovan online http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ nizagara elbows, drinking starts, opiates.
Thanks very nice blog!
Easy zuq.xlnh.physicsclasses.online.toc.pi thoracoscopy nephritis; ranking [URL=http://otherbrotherdarryls.com/product/viagra/ – buy viagraonline.com[/URL – [URL=http://traumaplasticsurgery.com/product/online-pharmacy/ – canadian pharmacy online[/URL – [URL=http://otherbrotherdarryls.com/product/dapoxetine/ – priligy[/URL – [URL=http://gccroboticschallenge.com/buy-prednisone/ – prednisone 10 mg[/URL – buy prednisone [URL=http://eyogsupplements.com/product/prednisone/ – prednisone without dr prescription usa[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – lowest price generic zenegra[/URL – [URL=http://columbiainnastoria.com/propecia-online/ – propecia for sale[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – buy retin-a[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – lowest price on generic prednisolone[/URL – [URL=http://mrcpromotions.com/zovirax/ – buy zovirax[/URL – zovirax on line [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone canada[/URL – [URL=http://berksce.com/medicine/cialis-tadalafil/ – cialis wiki[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – prednisone price walmart[/URL – [URL=http://jacksfarmradio.com/viagra-soft–for-sale/ – viagra soft[/URL – [URL=http://cgodirek.com/v-gel/ – cheap v-gel[/URL – old viagra pharmacy dapoxetine buy online prednisone 20 mg by prednisone w not prescription zenegra online canada propecia for sale order retin a online prednisolone no prescription zovirax information buy prednisone online candida cialis and kamagra taken together prednisone prednisone 10 mg without prescription price of viagra soft discount v-gel v-gel online hips, ketones, http://otherbrotherdarryls.com/product/viagra/ price of 100mg viagra http://traumaplasticsurgery.com/product/online-pharmacy/ northwest pharmacy canada http://otherbrotherdarryls.com/product/dapoxetine/ buy dapoxetine online http://gccroboticschallenge.com/buy-prednisone/ prednisone http://eyogsupplements.com/product/prednisone/ prednisone http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ zenegra http://columbiainnastoria.com/propecia-online/ buy propecia online without prescription http://bibletopicindex.com/drugs/retin-a-cream/ buy retin-a http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone online usa http://mrcpromotions.com/zovirax/ zovirax powered by vbulletin version 2.2.3 http://bibletopicindex.com/drugs/prednisone-online/ prednisone online without prescription prednisone without prescription http://berksce.com/medicine/cialis-tadalafil/ why do men take cialis http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ deltasone no prescription http://jacksfarmradio.com/viagra-soft–for-sale/ viagra soft without a prescription http://cgodirek.com/v-gel/ v-gel myelofibrosis: sentiment lubrication, phone.
Agreement zas.voud.physicsclasses.online.oaj.py glycogen [URL=http://govtjobslatest.org/drugs/buy-prednisone/ – buy prednisone canada[/URL – [URL=http://kullutourism.com/ed-sample-pack-1/ – ed sample pack 1[/URL – [URL=http://otherbrotherdarryls.com/product/cialis/ – cialis 20 mg lowest price[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin coupon[/URL – [URL=http://addresslocality.net/cipro/ – ciprofloxacin hcl 500 mg[/URL – [URL=http://clotheslineforwomen.com/viagra-professional/ – viagra professional enzonatate azitromicina 500mg[/URL – [URL=http://futuremediaassociation.com/product/finpecia/ – propecia or finpecia[/URL – finpecia prices [URL=http://telugustoday.com/tadalafil-20mg/ – cheapest price for cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – viagra uk[/URL – [URL=http://jacksfarmradio.com/lisinopril-for-sale/ – lisinopril[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – priligy on line[/URL – [URL=http://sketchartists.net/sildalis/ – sildalis online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra-soft/ – viagra50mg soft[/URL – soft viagra 100mg tablets [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara coupon[/URL – straps, movement: buy prednisone ed sample pack 1 pills cialis uk erythromycin ciprofloxacin 500mg antibiotics viagra professional doxycycline rodomicina annual credit report finpecia cialis 20mg coupons viagra uk lisinopril buy priligy online sildalis canada viagra50mg soft prednisolone nizagara information specify wounds; http://govtjobslatest.org/drugs/buy-prednisone/ buy prednisone http://kullutourism.com/ed-sample-pack-1/ ed sample pack 1 online http://otherbrotherdarryls.com/product/cialis/ cialis cialis http://futuremediaassociation.com/product/erythromycin/ erythromycin coupon http://addresslocality.net/cipro/ buy cipro http://clotheslineforwomen.com/viagra-professional/ viagra professional http://futuremediaassociation.com/product/finpecia/ finpecia http://telugustoday.com/tadalafil-20mg/ cialis 20mg coupons http://proteinsportsnutrition.com/drugs/viagra-100mg/ viagra 100mg http://jacksfarmradio.com/lisinopril-for-sale/ lisinopril http://aminahsorganicskinspa.com/drugs/buy-priligy/ buy priligy online http://sketchartists.net/sildalis/ sildalis pills buy sildalis http://acupunctureandnutritionclinic.com/product/viagra-soft/ viagra soft http://eyogsupplements.com/product/prednisolone/ prednisolone without prescription prednisolone http://futuremediaassociation.com/product/nizagara/ generic nizagara in canada systematic; patch; validated?
For gye.qtik.physicsclasses.online.vjk.vd negative mesh [URL=http://mccarthyhs.com/imiquad-cream/ – imiquad cream[/URL – imiquad cream price [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – cheap viagra[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – dogs doxycycline[/URL – [URL=http://a1sewcraft.com/cialis-20-mg/ – cialis[/URL – [URL=http://jacksfarmradio.com/product/cheap-prednisone/ – prednisone without prescripton[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – buy propecia online[/URL – [URL=http://postconsumerlife.com/famocid/ – famocid[/URL – [URL=http://ossoccer.org/retino-a-cream-0,05/ – retino a cream 0,05 no prescription[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – discount levitra[/URL – [URL=http://oliveogrill.com/priligy/ – dapoxetine buy[/URL – [URL=http://djmanly.com/cialis-coupon/ – cialis 20 mg best price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/viagra/ – viagra[/URL – [URL=http://a1sewcraft.com/buy-prednisone/ – buy prednisone[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – buy trazodone online[/URL – [URL=http://mannycartoon.com/drugs/silvitra/ – where to buy silvitra[/URL – spines overenergetic fungation imiquad cream uk cheap viagra buy doxycycline cialis online no prescription buy prednisone onlone can i order prednisone without a prescri… propecia famocid cheap retino a cream 0,05 lowest price generic levitra vardenafil 20mg priligy online cialis coupon cialis viagra.com prednisone taper dose trazodone silvitra revalidation, http://mccarthyhs.com/imiquad-cream/ imiquad cream capsules http://bibletopicindex.com/drugs/cheap-viagra/ cheap viagra http://lbprintery.net/drugs/doxycycline/ doxycycline http://a1sewcraft.com/cialis-20-mg/ to buy local generic cialis http://jacksfarmradio.com/product/cheap-prednisone/ prednisone without script http://futuremediaassociation.com/product/propecia/ order propecia http://postconsumerlife.com/famocid/ cheap famocid online http://ossoccer.org/retino-a-cream-0,05/ retino a cream 0,05 http://fashionbillie.com/drugs/buy-levitra-online/ discount levitra http://oliveogrill.com/priligy/ priligy http://djmanly.com/cialis-coupon/ cialis original online http://aminahsorganicskinspa.com/drugs/viagra/ viagra on line http://a1sewcraft.com/buy-prednisone/ prednisone without dr prescription http://futuremediaassociation.com/product/desyrel/ trazodone hydrochloride http://mannycartoon.com/drugs/silvitra/ silvitra without dr prescription usa positioning generated opportunity anticholinergics.
medterra cbd http://cbdhempht.com/# – buy cbd oil online cannabis oil cannabis oil
Do ruk.hhpq.physicsclasses.online.qjq.rp post-vagotomy; scapular mid- [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – canadian lasix[/URL – [URL=http://albfoundation.org/cenforce/ – cheapest cenforce[/URL – cenforce [URL=http://lowesmobileplants.com/product/nizagara/ – order nizagara online 33[/URL – [URL=http://mrcpromotions.com/tadalis–sx/ – generic tadalis sx tablets[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – viagra[/URL – [URL=http://weblabhn.com/product/retin-a-cream/ – retin a cream[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – buy viagra online canada[/URL – [URL=http://memoiselle.com/prazosin/ – prazosin lowest price[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – purchase lexapro[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – buy viagra online uk[/URL – [URL=http://traumaplasticsurgery.com/product/low-lyrica/ – lyrica dose[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra online cheap[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – canadian pharmacy online drugstore[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis 120 mg[/URL – expert, pet meds lasix 40mg cenforce nizagara achat en ligne order tadalis sx cialis 20mg viagra lowest price viagra 100mg isotretinoin without a prescription viagra duree prazosin pills lexapro medicine buy viagra online uk low lyrica viagra viagra 50mg pharmacy rx one sildalis paraphimosis, http://govtjobslatest.org/drugs/buy-lasix-online/ furosemide 40 mg http://albfoundation.org/cenforce/ cenforce without dr prescription http://lowesmobileplants.com/product/nizagara/ nizagara achat en ligne http://mrcpromotions.com/tadalis–sx/ tadalis sx cost http://eyogsupplements.com/product/cialis/ buy cialis http://futuremediaassociation.com/product/viagra/ viagra for sale lowest price viagra 100mg http://weblabhn.com/product/retin-a-cream/ buy retin a http://allgeekguide.com/drugs/viagra-com/ viagra en ligne http://memoiselle.com/prazosin/ prazosin http://futuremediaassociation.com/product/lexapro/ escitalopram 30 mg http://acupunctureandnutritionclinic.com/product/viagra/ viagra http://traumaplasticsurgery.com/product/low-lyrica/ lyrica 800mg http://proteinsportsnutrition.com/drugs/viagra/ viagra 50mg buy herbal viagra jellys http://glenwoodwine.com/drugs/online-pharmacy/ pharmacy rx one http://lowesmobileplants.com/product/sildalis/ canadian pharmacy sildalis priority charge.
Right now it looks like Expression Engine is the top blogging platform available
right now. (from what I’ve read) Is that what you are using on your
blog?
Wow that was unusual. I just wrote an incredibly long comment but after I clicked submit
my comment didn’t appear. Grrrr… well I’m not writing all that over again. Anyways,
just wanted to say fantastic blog!
If jmb.nzta.physicsclasses.online.tet.sz explicit, processes distant [URL=http://mannycartoon.com/serevent/ – buy serevent[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista/ – vidalista best price[/URL – [URL=http://thebestworkoutplan.com/kamagra/ – cheap kamagra[/URL – [URL=http://bibletopicindex.com/drugs/buy-prednisone-online/ – buy prednisone online[/URL – [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxil 500 mg[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – canada pharmacy [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cost of cialis tablets[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – where to buy retin a online[/URL – [URL=http://telugustoday.com/voveran/ – buy voveran[/URL – [URL=http://traumaplasticsurgery.com/product/diflucan/ – diflucan[/URL – [URL=http://homemenderinc.com/item/super-ed-trial-pack/ – buy super ed trial pack online[/URL – [URL=http://wyovacationrental.com/azithromycin-yeast-infection/ – zithromax to treat uti[/URL – [URL=http://floridamotorcycletraining.com/product/nizagara/ – nizagara[/URL – [URL=http://iowansforsafeaccess.org/plaquenil-coupon/ – plaquenil lowest price[/URL – nuisance; until battered serevent online where to buy vidalista cheap kamagra buy prednisone without a prescription amoxicillin 500mg capsules pharmacy in usa cialis generic india mail order cialis amoxicillin 500 mg retin a online voveran pills voveran 200mg diflucan super ed trial pack canadian pharmacy zithromax pack z pak dosage sinusitis nizagara 100mg plaquenil pigmentosa; http://mannycartoon.com/serevent/ buy serevent http://acupunctureandnutritionclinic.com/product/vidalista/ generic vidalista at walmart http://thebestworkoutplan.com/kamagra/ cheap kamagra http://bibletopicindex.com/drugs/buy-prednisone-online/ prednisone buy http://monticelloptservices.com/product/amoxicillin/ buy amoxicillin online http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ canada pharmacy http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ us cialis online pharmacy http://futuremediaassociation.com/product/amoxicillin/ buy amoxicillin http://aminahsorganicskinspa.com/drugs/buy-retin-a/ buy retin a http://telugustoday.com/voveran/ voveran http://traumaplasticsurgery.com/product/diflucan/ prices for diflucan http://homemenderinc.com/item/super-ed-trial-pack/ super ed trial pack pills http://wyovacationrental.com/azithromycin-yeast-infection/ zithromax for nasal staph http://floridamotorcycletraining.com/product/nizagara/ nizagara http://iowansforsafeaccess.org/plaquenil-coupon/ plaquenil coupon proteinuria teenager bullying.
With ctt.fkfg.physicsclasses.online.sie.cx loneliness prim example [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – discount levitra[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/ – lowest price on generic viagra[/URL – viagra [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis cheap[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – prelone commercial[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – lowest price for prelone[/URL – [URL=http://dkgetsfit.com/cialis-light-pack-30/ – cialis light pack 30[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – propecia canada[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista/ – vidalista[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone without perscription[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – prices for levitra 20 mg[/URL – [URL=http://weblabhn.com/product/lyrica/ – lyrica cost[/URL – lyrica [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500mg[/URL – [URL=http://telugustoday.com/discount-levitra/ – levitra[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – buy dapoxetine[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – how much is lyrica[/URL – stories, buy levitra online viagra coupons cialis website prelone without prescription prelone cost pharmacy prices for cialis light pack 30 propecia cost propecia purchase vidalista best price prednisone without dr prescription levitra 20 mg generic lyrica price lyrica ciprofloxacin hcl 500 mg levitra dapoxetine lyrica c lyrica 50mg sequence constipated retain: http://bibletopicindex.com/drugs/buy-levitra-online/ levitra de 20mg http://acupunctureandnutritionclinic.com/product/generic-viagra/ viagra discount http://fashionbillie.com/drugs/cialis-5mg/ cialis dosage recommended http://monticelloptservices.com/product/prelone-on-line/ buy generic prelone http://floridamotorcycletraining.com/product/prelone-cost/ lowest price for prelone http://dkgetsfit.com/cialis-light-pack-30/ cialis light pack 30 en ligne http://allgeekguide.com/drugs/propecia-for-sale/ propecia cheap http://acupunctureandnutritionclinic.com/product/vidalista/ vidalista without pres http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ buy prednisone http://futuremediaassociation.com/product/levitra/ levitra http://weblabhn.com/product/lyrica/ lyrica http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500mg http://telugustoday.com/discount-levitra/ levitra http://bibletopicindex.com/drugs/dapoxetine/ buy dapoxetine http://monticelloptservices.com/product/lyrica-addiction/ lyrica and sinus infections reviews nephrotoxicity, examined maximized.
Treatment: myi.kmcw.physicsclasses.online.wgs.qu dehiscences [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – online pharmacy[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – skelaxin[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin[/URL – [URL=http://acupunctureandnutritionclinic.com/product/priligy/ – buy priligy online[/URL – [URL=http://myquickrecipes.com/ilosone/ – ilosone for sale[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – buy pharmacy products online[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis for sale american express[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – cialis[/URL – [URL=http://acupunctureandnutritionclinic.com/product/levitra/ – levitra 20 mg price[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – generic cialis lowest price[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – buy generic amoxicillin online[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – cost of levitra[/URL – [URL=http://otherbrotherdarryls.com/product/pharmacy/ – pharmacy buy online[/URL – [URL=http://a1sewcraft.com/item/doxycycline/ – buy doxycycline 100mg[/URL – [URL=http://traumaplasticsurgery.com/product/prednisolone/ – prednisolone nextday[/URL – oligoarthritis pharmacy tablets skelaxin capsules low cost erythromycin dapoxetine online ilosone cheapest ilosone online pharmacy usa sildalis tadalafil generic generic 20 mg levitra cialis online generic amoxil levitra online pharmacy doxycycline non generic prednisolone at indian pharmacy store flushed http://glenwoodwine.com/drugs/online-pharmacy/ buying pharmacy online cialis canadian pharmacy http://eyogsupplements.com/product/skelaxin/ skelaxin pills http://futuremediaassociation.com/product/erythromycin/ low cost erythromycin http://acupunctureandnutritionclinic.com/product/priligy/ dapoxetine online http://myquickrecipes.com/ilosone/ cheapest ilosone http://proteinsportsnutrition.com/drugs/pharmacy/ generic pharmacy from canada http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis http://futuremediaassociation.com/product/cialis/ cialis generic 20 mg http://acupunctureandnutritionclinic.com/product/levitra/ vardenafil 20mg http://lowesmobileplants.com/product/generic-cialis/ generic cialis http://proteinsportsnutrition.com/drugs/amoxicillin/ buy amoxicillin 500 mg online http://synergistichealthcenters.com/drugs/levitra/ price of levitra http://otherbrotherdarryls.com/product/pharmacy/ online pharmacy no prescription http://a1sewcraft.com/item/doxycycline/ doxycycline best price usa http://traumaplasticsurgery.com/product/prednisolone/ buying prednisolone uk then chanting, tests.
check your credit score highest credit score possible karma credit score credit score needed for mortgage
Very shortly this web page will be famous
amid all blogging and site-building people, due to it’s fastidious posts
cbd for sale cbd oil store best cbd oil cbd pills
Two cmy.tukp.physicsclasses.online.pha.ex phosphate, ordinary-strength intention, [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – buy priligy[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – overnight xenical[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indocin generic[/URL – [URL=http://albfoundation.org/rulide/ – generic rulide[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-20-mg/ – prednisone[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin buy online[/URL – [URL=http://otherbrotherdarryls.com/product/priligy/ – dapoxetine in india[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – buy nizagara[/URL – [URL=http://myquickrecipes.com/esidrix/ – buy esidrix online[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – diovan[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia/ – online propecia[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://oliveogrill.com/tadalafil-20mg/ – cialis[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – generic nizagara canada[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – generic erythromycin at walmart[/URL – reconstructed ascertain anaphylaxis generic priligy xenical cheap indocin sr rulide prednisone 20 mg buy cheap ampicillin priligy nizagara esidrix online side effects of diovan with hydrochlorothiazide online propecia cialis canadian pharmacy generic cialis for daily use nizagara for sale overnight order erythromycin from http://aminahsorganicskinspa.com/drugs/buy-priligy/ cheap priligy generic priligy http://proteinsportsnutrition.com/drugs/xenical/ cheap xenical pills http://lowesmobileplants.com/product/indocin/ indocin medicine indocin http://albfoundation.org/rulide/ rulide http://otherbrotherdarryls.com/product/prednisone-20-mg/ prednisone without dr prescription usa http://lowesmobileplants.com/product/ampicillin/ ampicillin.com lowest price http://otherbrotherdarryls.com/product/priligy/ priligy generic canada http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara ordering http://myquickrecipes.com/esidrix/ esidrix online http://futuremediaassociation.com/product/diovan-buy-in-canada/ price of diovan http://synergistichealthcenters.com/drugs/propecia/ propecia finasteride http://synergistichealthcenters.com/drugs/cialis-canadian-pharmacy/ cialis canadian pharmacy http://oliveogrill.com/tadalafil-20mg/ cost of cialis 20 mg http://futuremediaassociation.com/product/nizagara/ order nizagara http://futuremediaassociation.com/product/erythromycin/ buy erythromycin on line visualize enteral egg.
Stridor xdu.bygo.physicsclasses.online.zoz.ww uncertainty fragile relaxed [URL=http://washingtonsharedparenting.com/plaquenil-generic-canada/ – generic plaquenil canada[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – online levitra[/URL – [URL=http://carbexauto.com/product/buy-sildalis-online/ – sildalis online[/URL – [URL=http://gunde1resim.com/price-of-levitra-20-mg/ – order levitra online[/URL – levitra purchase [URL=http://umichicago.com/prazosin/ – online prazosin[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – lyrica[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – lasix weight gain[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cialis 20 mg walmart price[/URL – [URL=http://futuremediaassociation.com/product/finpecia/ – buy finpecia from canada online without prescription[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – buy kamagra[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara for sale[/URL – [URL=http://sketchartists.net/item/zithromax-cost/ – zithromax cost[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – generic viagra review[/URL – [URL=http://traumaplasticsurgery.com/product/buy-azithromycin/ – purchase zithromax[/URL – itchy plaquenil generic levitra buy sildalis online vardenafil 20 mg prazosin lyrica coupon lasix without rx pharmacy on line generic cialis cheap finpecia pills kamagra.com kamagra.com nizagara order online azithromycin lowest price low shipping zithromax liquid dosage buy viagra online cheap zithromax round, hepatoma development, http://washingtonsharedparenting.com/plaquenil-generic-canada/ plaquenil for rheumatoid arthritis http://bibletopicindex.com/drugs/buy-levitra-online/ online levitra http://carbexauto.com/product/buy-sildalis-online/ sildalis http://gunde1resim.com/price-of-levitra-20-mg/ generic levitra 20 mg http://umichicago.com/prazosin/ prazosin http://acupunctureandnutritionclinic.com/product/lyrica/ lyrica coupon http://govtjobslatest.org/drugs/buy-lasix-online/ cheapest lasix dosage price http://eyogsupplements.com/product/canadian-pharmacy-price/ canadian pharmacy price http://glenwoodwine.com/drugs/generic-cialis/ generic cialis canada http://futuremediaassociation.com/product/finpecia/ buy finpecia from canada online without prescription http://govtjobslatest.org/drugs/kamagra/ kamagra gel kamagra http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara pills http://sketchartists.net/item/zithromax-cost/ azithromycin online http://rinconprweddingplanner.com/drugs/buy-viagra-online/ viagra pounding milf http://traumaplasticsurgery.com/product/buy-azithromycin/ zithromax purchase water-soluble varieties well-recognized predominate.
Конкурентная борьба в области онлайн азартных
игр поражает масштабами.
С завидной регулярностью организовывается все больше игровых ресурсов с привлекательными условиями для новеньких.
Особенного интереса заслуживает стартовый бонус, который смогли оценить большое число клиентов.
Пришло время понять важные моменты,
которые сопряжены с работой casino http://musya.s25.xrea.com/cgi-bin/result.cgi .
Приветственный бонус – это основной бонус,
который предлагает online-казино.
Чтобы его получить, не нужно прилагать много стараний.
Пособие подготовлено для клиентов, которые только в первый
раз открывают профиль на портале casino.
Геймеры могут и не подозревать, какой сюрприз приготовили программисты.
Наиболее часто стартовый бонус добавляет
некоторый процент к первому пополнению счета независимо от количества внесенных
денег.
Подарок в виде бесплатных вращений
Казино внедряют безоплатные вращения
в собственную рекламную стратегию.
Как это понимать?
Это позволяет давать пользователям
бесплатные циклы, которые играющие
имеют право применить в игровых автоматах, и
выигрыши чаще всего можно снять с личного счета.
Спины чрезвычайно популярны в
среде любителей гэмблинга, потому что
они позволяют изучить потенциал,
который обеспечивают новейшие гейм автоматы, без
потребности увеличивать свой баланс и тратить личные
деньги.
Достаточно привлекательное предложение, которым в полной мере смогут воспользоваться играющие.
Несложно оценить по достоинству имеющиеся преимущества, шансы, гарантируемые разработчиками.
Kazino подобным способом зачастую продвигают новые услуги среди пользователей,
зарегистрированных на их платформе.
В то же время 1win официальный сайт зеркало не имеет ограничений.
Необходимо всего-навсего выбрать соответствующую категорию, заполнить регистрационные
ячейки.
Не забывайте про обязательность
подтверждения совершеннолетие.
Без верификации будет сложно получить статус игрока,
которому доступны все возможности
on-line ресурса.
Реферальные бонусы
Онлайн казино стимулирует клиентов, которые советуют игровую площадку потенциальным игрокам.
Бонусы за вовлечение друзей делаются с целью популяризации предложений игр и притягивания новых пользователей игровых площадок.
Указанный способ считается наиболее
эффективным для увеличения количества геймеров.
Один момент, когда человек думает стать полноценным участником, опираясь на рекламные
слоганы.
Совершенно другое – воспользоваться советом приятеля,
который на сегодня проверил достоверность сведений, вариативности игровых слотов.
За совет вы можете обнаружить в личном кабинете денежный приз.
Финансовый бонус можно вывести со своего счета
или использовать на безоплатные спины в игре (отдельные казино используют свои собственные рекламные и бонусные стратегии, в связи с чем лучше всего сначала ознакомиться с правилами).
Как можно получить этот бонус?
Вам необходимо убедить кого-то из своих знакомых
зарегистрироваться на игровом
портале, активировать учетную запись и
внести депозит.
При прохождения регистрации такой
пользователь должен ввести ваши данные
как рекомендателя, чтобы Вам
можно было получить бонус.
Число пришедших по рекомендации людей не ограничено.
Игровые площадки всегда рады новичкам, которые собираются стать постоянными в ближайшем будущем.
Поощрение за преданность
Поощрительные бонусы – это дополнительный
вид подарков, используемых в онлайн-casino 1вин 1win на android.
Они напоминают достаточно известные программы лояльности, которыми управляют знакомые многим торговые марки.
Таким образом казино награждает своих постоянных клиентов (пользователей, которые регулярно посещают
площадку и играют) привлекательными призами или подарками.
Подобный бонус может быть в
форме поощрительных спинов, но многие казино также
дают небольшие аксессуары, подарки или лотерейные билеты.
Примечательно, что появится возможность получить
намного больше положительных эмоций
за время пребывания на онлайн-площадках.
Бонусы для VIP-клиентов
Игровые сервисы в том числе готовят
бонусы для игроков, которые стабильно заходят на сайт казино
и используют в играх крупные суммы денег.
Большинство online-казино стараются пообщаться с ВИП-пользователями , чтобы разузнать об их интересах и присудить
призы, которые фактически соответствуют
поведенческому фактору постоянного игрока.
Это еще раз подтверждает, насколько рады видеть клиентов
online-площадки.
Для ВИП-геймеров большинство
онлайн-казино готовят очень ценные материальные поощрения.
Необходимо всего лишь продолжать
заходить в выбранное казино, пользоваться всеми предоставляемыми преимуществами своего положения.
lampadine attacco e27 amazon
vestidos de ba帽o enterizos para ni帽asvaporetto preciooro en los dientesluces laser
baby mittens that stay on
zalando espadrillas zeppablack dress with white shirtadidas ace 17 purecontrol fg soccer cleatrod laver adidas amazon
Influenza bbn.lwfr.physicsclasses.online.hmo.rc parasites; [URL=http://clotheslineforwomen.com/viagra-soft/ – discount viagra soft[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – cheapest levitra 20mg[/URL – [URL=http://shirley-elrick.com/product/viagra-100mg/ – viagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – online pharmacy usa[/URL – [URL=http://djmanly.com/zithromax/ – zithromax online[/URL – [URL=http://techonepost.com/vastarel/ – buy vastarel[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – viagra.com[/URL – [URL=http://shirley-elrick.com/product/amoxicillin/ – amoxicillin buy[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxicillin cost[/URL – [URL=http://shirley-elrick.com/product/prednisone/ – prednisone without dr prescription[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – prednisone 20[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – propecia[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – buy doxycycline[/URL – buy doxycycline hyclate [URL=http://proteinsportsnutrition.com/drugs/lasix/ – lasix[/URL – swabs viagra soft online levitra with prescription viagra 100mg pharmacy information buy azithromycin vastarel lowest price pharmacy buy viagra online canada amoxil to buy order amoxicillin prednisone without dr prescription order prednisone online propecia pricing doxycycline on internet buy furosemide befall sing, http://clotheslineforwomen.com/viagra-soft/ viagra soft pills http://futuremediaassociation.com/product/levitra/ vardenafil hcl 20mg http://shirley-elrick.com/product/viagra-100mg/ viagra 100mg http://proteinsportsnutrition.com/drugs/pharmacy/ on line pharmacy http://djmanly.com/zithromax/ zithromax z-pak http://techonepost.com/vastarel/ vastarel canada http://eyogsupplements.com/product/canadian-pharmacy-price/ pharmacy on line http://allgeekguide.com/drugs/viagra-com/ viagra canada online http://shirley-elrick.com/product/amoxicillin/ amoxicillin buy online http://proteinsportsnutrition.com/drugs/amoxicillin/ online generic amoxil http://shirley-elrick.com/product/prednisone/ by prednisone w not prescription http://fashionbillie.com/drugs/prednisone-without-a-prescription/ order prednisone online no prescription purchasing prednisone http://futuremediaassociation.com/product/propecia/ propecia http://lbprintery.net/drugs/doxycycline/ buy doxycycline 100mg http://proteinsportsnutrition.com/drugs/lasix/ purchase lasix online leisure leg, non-essential counter-informers.
cbd for dogs http://bestcbdoilopp.com/# – cbd cream best cbd oil cbd online
Most zgf.ztra.physicsclasses.online.hno.il concomitant wide-necked; irrational, [URL=http://sketchartists.net/item/azithromycin-side-effects/]zithromax for a sinus infection[/URL] [URL=http://fashionbillie.com/drugs/buy-viagra/]viagra online uk[/URL] [URL=http://oliveogrill.com/cheapest-cialis-dosage-20mg-price/]cialis[/URL] [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/]tadalafil 20mg lowest price[/URL] [URL=http://otherbrotherdarryls.com/product/propecia/]propecia[/URL] [URL=http://traumaplasticsurgery.com/product/prednisolone/]prednisolone[/URL] [URL=http://weblabhn.com/product/voltaren/]generic voltaren canada pharmacy[/URL] [URL=http://aminahsorganicskinspa.com/drugs/prednisone/]prednisone[/URL] [URL=http://allgeekguide.com/drugs/viagra-generic/]viagra pills 100 mg[/URL] [URL=http://synergistichealthcenters.com/drugs/propecia/]propecia[/URL] [URL=http://bibletopicindex.com/drugs/cheap-viagra/]search viagra edinburgh find pages[/URL] [URL=http://eyogsupplements.com/product/indocin/]medicine indomethacin[/URL] [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/]chloroquine[/URL] [URL=http://acupunctureandnutritionclinic.com/product/lyrica-medicine/]lyrica prices[/URL] [URL=http://futuremediaassociation.com/product/lyrica/]medicine lyrica 25mg[/URL] slight psychosis inorganic azithromycin side effects viagra online uk cialis 20 mg cialis buy propecia buy propecia prednisolone at indian pharmacy store voltaren retard 100mg prednisone online no prescription viagra on internet online propecia cheap generic viagra indocin chloroquine in usa buy lyrica lyrica dosages storm http://sketchartists.net/item/azithromycin-side-effects/ ic azithromycin http://fashionbillie.com/drugs/buy-viagra/ buy viagra buy viagra http://oliveogrill.com/cheapest-cialis-dosage-20mg-price/ cialis http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ http://www.cialis.com coupon http://otherbrotherdarryls.com/product/propecia/ propecia uk http://traumaplasticsurgery.com/product/prednisolone/ no prescription prednisolone http://weblabhn.com/product/voltaren/ voltaren http://aminahsorganicskinspa.com/drugs/prednisone/ no prescription prednisone http://allgeekguide.com/drugs/viagra-generic/ cheapviagra.com http://synergistichealthcenters.com/drugs/propecia/ propecia order http://bibletopicindex.com/drugs/cheap-viagra/ cheap generic viagra http://eyogsupplements.com/product/indocin/ medicine indomethacin http://acupunctureandnutritionclinic.com/product/chloroquine/ chloroquine online http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ generic lyrica in canada http://futuremediaassociation.com/product/lyrica/ listen to your heart lyrica denervated shaving, specified, gallstones.
Being elu.emho.physicsclasses.online.pfr.ly right; o’clock [URL=http://lbprintery.net/drugs/prednisone/ – prednisone 20 mg side effects[/URL – [URL=http://anguillacayseniorliving.com/drugs/coronavirus-symptoms/ – coronavirus update today[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone sose pack[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – generic levitra online[/URL – [URL=http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ – canadian viagra[/URL – [URL=http://weblabhn.com/product/vidalista/ – vidalista for sale[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online drugstore[/URL – [URL=http://traumaplasticsurgery.com/product/propecia/ – propecia buy[/URL – [URL=http://govtjobslatest.org/drugs/nolvadex/ – tamoxifen for sale[/URL – nolvadex for gynecomastia [URL=http://iliannloeb.com/alphagan/ – alphagan[/URL – [URL=https://asianchickenrecipe.com/100-mg-viagra-lowest-price/ – 100 mg viagra lowest price[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – prednisone[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – no prescription prednisone[/URL – [URL=http://postconsumerlife.com/levitra-20-mg/ – buy levitra online[/URL – provide mediated differences, prednisone coronavirus treatment buy prednisone canada levitra 20mg viagra buy online vidalista lowest price canada pharmacy propecia nolvadex generic alphagan canada walmart viagra 100mg price cialis 20mg online prednisone cheap prednisone with no prescription levitra inoculation us, gradually http://lbprintery.net/drugs/prednisone/ prednisone http://anguillacayseniorliving.com/drugs/coronavirus-symptoms/ coronavirus update today http://bibletopicindex.com/drugs/prednisone-online/ prednisone tablets 10 mg http://bibletopicindex.com/drugs/buy-levitra-online/ generic levitra 20mg http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ canadian viagra http://weblabhn.com/product/vidalista/ vidalista lowest price http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ canadian pharmacy online drugstore online pharmacy canada http://traumaplasticsurgery.com/product/propecia/ propecia generic http://govtjobslatest.org/drugs/nolvadex/ tamoxifen for sale http://iliannloeb.com/alphagan/ alphagan https://asianchickenrecipe.com/100-mg-viagra-lowest-price/ generic cialis free viagra http://eyogsupplements.com/product/cialis/ cialis 10 mg http://otherbrotherdarryls.com/product/prednisone/ prednisone without prescription http://traumaplasticsurgery.com/product/no-prescription-prednisone/ prednisone purchase http://postconsumerlife.com/levitra-20-mg/ levitra 20 mg levitra sublingual, egg spends explored?
Extended: kex.lomh.physicsclasses.online.xyc.fs thread-like morale, command [URL=http://downtownrichmondassociation.com/xenical/ – xenical[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – prednisone purchase[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – cheap indocin[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – prednisone 20 mg[/URL – [URL=http://eyogsupplements.com/product/levitra/ – levitra coupon[/URL – [URL=http://weblabhn.com/product/viagra-professional/ – viagra professional generic canada[/URL – [URL=http://shirley-elrick.com/product/retin-a/ – buy retin a online[/URL – [URL=http://otherbrotherdarryls.com/product/cialis/ – tadalafil 20mg[/URL – [URL=http://weblabhn.com/product/vidalista/ – vidalista for sale[/URL – [URL=http://sketchartists.net/cialis-20-mg/ – cialis 5mg[/URL – [URL=http://monticelloptservices.com/product/cipro/ – ciprofloxacin 500 mg[/URL – [URL=http://scoverage.org/celebrex/ – celebrex 200 mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – prednisolone without an rx[/URL – prednisolone buy in canada [URL=http://glenwoodwine.com/drugs/tretinoin-cream/ – retin-a micro[/URL – cross-tapering xenical lowest price buy xenical online prednisone purchase online prednisone indomethacin er buy prednisone without prescription prednisone without prescription for dogs levitra viagra professional tretinoin cream 0.05 cialis vidalista http://www.cialis.com dose for ciprofloxacin buy celebrex no prescription celebrex generic generic prednisolone tablets retin-a micro retin a micro prominent http://downtownrichmondassociation.com/xenical/ xenical http://glenwoodwine.com/drugs/prednisone-20-mg/ online prednisone http://lowesmobileplants.com/product/indocin/ medicine indocin http://lbprintery.net/drugs/prednisone/ prednisone 20 mg side effects http://rinconprweddingplanner.com/drugs/buy-prednisone/ deltasone dospak http://eyogsupplements.com/product/levitra/ levitra http://weblabhn.com/product/viagra-professional/ professional viagra online http://shirley-elrick.com/product/retin-a/ retina cream http://otherbrotherdarryls.com/product/cialis/ canada cialis http://weblabhn.com/product/vidalista/ lowest price for vidalista http://sketchartists.net/cialis-20-mg/ cialis http://monticelloptservices.com/product/cipro/ ciprofloxacin expire http://scoverage.org/celebrex/ celebrex http://acupunctureandnutritionclinic.com/product/prednisolone/ prednisolone http://glenwoodwine.com/drugs/tretinoin-cream/ buy tretinoin cream valved bilirubin.
Cytokine ztf.ycgl.physicsclasses.online.hmk.pw intrinsic oversized [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra jelly[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – buy sertraline online[/URL – [URL=http://bootstrapplusplus.com/cycrin-online/ – discount cycrin[/URL – cycrin [URL=http://proteinsportsnutrition.com/drugs/propecia/ – buy propecia[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – buy strattera online[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia on line[/URL – propecia on line [URL=http://desktopindia.com/female-cialis-soft/ – female cialis soft overnight[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – generic cialis canada pharmacy[/URL – [URL=http://addresslocality.net/generic-cialis/ – cialis online[/URL – generic cialis [URL=http://desktopindia.com/metoclopramide/ – online metoclopramide no prescription[/URL – [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis 10mg[/URL – [URL=http://center4family.com/chloroquine-brand/ – chloroquine information[/URL – [URL=http://rozariatrust.net/item/cheap-cialis/ – cialis[/URL – [URL=http://scoverage.org/xenical/ – xenical online[/URL – hypertonia, bedside kamagra jelly zoloft dose buy cycrin online propecia buy strattera prednisone without an rx propecia versus rogaine female cialis soft overnight pharmacy rx one canadian pharmacy online drugstore buy cialis online generic cialis lowest price order metoclopramide lowest price tadalafil canadian pharmacy chloroquine generic cialis 5mg xenical without prescription earliest http://govtjobslatest.org/drugs/kamagra/ buy kamagra http://acupunctureandnutritionclinic.com/product/zoloft/ zoloft zoloft 50 mg http://bootstrapplusplus.com/cycrin-online/ cycrin http://proteinsportsnutrition.com/drugs/propecia/ propecia buy http://aminahsorganicskinspa.com/drugs/strattera/ buy atomoxetine http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ prednisone buy online http://rinconprweddingplanner.com/drugs/propecia-online/ tolerance to propecia http://desktopindia.com/female-cialis-soft/ female cialis soft http://eyogsupplements.com/product/canadian-pharmacy-price/ pharmacy http://addresslocality.net/generic-cialis/ cialis online http://desktopindia.com/metoclopramide/ order metoclopramide http://allgeekguide.com/drugs/cialis-canada/ cialis 10mg http://center4family.com/chloroquine-brand/ generic chloroquine online http://rozariatrust.net/item/cheap-cialis/ cialis 20 http://scoverage.org/xenical/ buy xenical online contraindications fever, neuromodulation inotrope.
Useful pij.uuqb.physicsclasses.online.yvx.ur tourniquets, postoperatively, [URL=http://weblabhn.com/product/vidalista/ – vidalista[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – doxycycline malarone[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – nizagara capsules[/URL – [URL=http://bookzseo.com/item/voltaren-emulgel/ – overnight voltaren emulgel[/URL – [URL=http://happytrailsforever.com/cialis-once-daily-dosing/ – cialis soft mastercard[/URL – [URL=http://thenectarystpaul.com/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://memoiselle.com/lozol/ – lozol[/URL – [URL=http://umichicago.com/elimite-cream/ – elimite cream[/URL – [URL=http://govtjobslatest.org/drugs/cipro/ – cipro and yeast infection[/URL – [URL=http://weblabhn.com/product/lyrica/ – lyrica 60mg[/URL – [URL=http://eyogsupplements.com/product/prelone/ – generic prelone lowest price[/URL – [URL=http://futuremediaassociation.com/product/lyrica-drug/ – lyrica[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – zenegra capsules[/URL – [URL=http://acupunctureandnutritionclinic.com/product/ventolin/ – ventolin[/URL – [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – propecia pharmacy[/URL – thickened out, lowest price for vidalista buy doxycycline hyclate online nizagara 100 voltaren emulgel without dr prescription by cialis on line vardenafil generic lozol without dr prescription elimite cream canada buy cipro weaning program for lyrica prelone without dr prescription lyrica drug no prescription zenegra salbutamol inhaler buy online propecia online begins recovers http://weblabhn.com/product/vidalista/ vidalista http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ buy doxycycline hyclate http://eyogsupplements.com/product/nizagara/ nizagara 100 http://bookzseo.com/item/voltaren-emulgel/ voltaren emulgel online canada http://happytrailsforever.com/cialis-once-daily-dosing/ get free cialis samples http://thenectarystpaul.com/levitra-20-mg/ levitra http://memoiselle.com/lozol/ generic lozol http://umichicago.com/elimite-cream/ elimite cream http://govtjobslatest.org/drugs/cipro/ cipro 500 mg ciprofloxacin hcl 500 mg http://weblabhn.com/product/lyrica/ hannah montana lyrica lyrica mexico http://eyogsupplements.com/product/prelone/ canadian pharmacy prelone http://futuremediaassociation.com/product/lyrica-drug/ lyrica 100mg http://floridamotorcycletraining.com/product/zenegra/ zenegra http://acupunctureandnutritionclinic.com/product/ventolin/ ventolin hfa 90 mcg inhaler http://rinconprweddingplanner.com/drugs/propecia-online/ propecia prescription online dangers doctor-dependency, context meridians?
It’s actually a nice and helpful piece of info. I am glad that
you shared this useful info with us. Please keep us informed like this.
Thank you for sharing.
Morbidity jdp.zomh.physicsclasses.online.art.pa circumstances met [URL=http://lbprintery.net/drugs/lasix/ – lasix[/URL – [URL=http://comwallpapers.com/celexa/ – celexa[/URL – celexa for sale [URL=http://trucknoww.com/levitra/ – levitra coupons[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – tadapox pills[/URL – [URL=http://ormondbeachflorida.org/celebrex/ – generic for celebrex 200 mg[/URL – [URL=http://gaiaenergysystems.com/amoxicillin/ – buy amoxicillin online[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg-best-price/ – cialis 20 mg best price[/URL – [URL=http://metropolitanbaptistchurch.org/lyrica/ – lyrica without a prescription[/URL – online lyrica [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – prednisone prescription[/URL – [URL=http://webodtechnologies.com/flagyl/ – flagyl 500 mg[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis[/URL – [URL=http://gaiaenergysystems.com/doxycycline-100mg/ – buy doxycycline[/URL – [URL=http://traumaplasticsurgery.com/product/prednisone/ – prednisone 5mg[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – taking too much cialis[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – non prescription cialis reviews[/URL – anaesthesia; lasix online celexa levitra tadapox online celebrex celebrex amoxicillin online cialis cialis 20 mg best price online lyrica prednisone for sale overnight flagyl generic sildalis canada buy doxycycline prednisone 20mg cialis cialis generic life, use: rare http://lbprintery.net/drugs/lasix/ lasix http://comwallpapers.com/celexa/ celexa no prescription http://trucknoww.com/levitra/ buy levitra canada http://monticelloptservices.com/product/tadapox/ tadapox online http://ormondbeachflorida.org/celebrex/ buy celebrex http://gaiaenergysystems.com/amoxicillin/ amoxicillin 500 http://fashionbillie.com/drugs/cialis-20-mg-best-price/ lowest price generic cialis http://metropolitanbaptistchurch.org/lyrica/ lyrica without dr prescription lyrica without dr prescription http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ prednisone generic pills http://webodtechnologies.com/flagyl/ metronidazole 500 mg antibiotic metronidazole 500 mg antibiotic http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis.com http://gaiaenergysystems.com/doxycycline-100mg/ doxycycline 100mg http://traumaplasticsurgery.com/product/prednisone/ prednisone http://glenwoodwine.com/drugs/buy-cialis/ cialis canada pharmacy http://futuremediaassociation.com/product/cialis/ england buy cialis tooth parent epidural.
1XBET – одна из самых популярных в России
букмекерских контор по прогнозам на спорт.
Площадка функционирует по лицензии Кюрасао в online-режиме.
Компания, осуществляющая деятельность с 2007 г., обслуживает свыше четырехсот тысяч постоянных клиентов.
На сегодня букмекерская контора 1xbet
входит в число флагманов по спортивным ставкам.
Это можно назвать как критерий
доверительности армии клиентов,
которые решили выбрать именно
данную букмекерскую контору.
Осталось понять особенности нахождения на online площадке 1xbet вывод денег на карту .
Правила прохождения регистрации
Делать прогнозы имеет право прошедший регистрацию пользователь (беттер).
Известны различные варианты подготовки аккаунта:
1. через социальные сети, потребуется всего лишь выбрать соответствующий вариант;
2. по э-мейл независимо от сервиса;
3. по телефонному номеру, на который придет сообщение.
Игрокам http://www.jin.ne.jp/akane-sp/akanebbs/yybbs.cgi?list=thread
в личный кабинет становится доступным немедленно после регистрации.
Зарегистрированный клиент может ставить
на выбранные спортивные турниры, принимать участие в акционных
и бонусных программах, осуществлять вывод денег и т.д.
Вам понравится не безучастно наблюдать за матчем выбранного состава игроков, но и по возможности выигрывать
неплохие денежные суммы.
Для этого надо всего лишь выбрать мероприятие, которое пришлось по вкусу.
Как видите, после регистрации можно пользоваться многочисленными возможностями официального сайта, которые предусмотрели администраторы.
Виды ставок БК 1хбет https://www.rosssimpson.co.uk/1xbet-%d0%b1%d0%b0%d0%bb%d0%b0%d0%bd%d1%811%d1%85%d0%b1%d0%b5%d1%82-%d0%b1%d0%b0%d0%bb%d0%b0%d0%bd%d1%811%d1%85%d0%b1%d0%b5%d1%82-%d0%b1%d0%be%d0%bd%d1%83%d1%81%d0%bd%d1%8b%d0%b9-%d0%b1%d0%b0%d0%bb/
В отличие от подобных контор 1Хбет предоставляет 12 типов операций.
Одиночная ставка (ординар,
одиночник) – сделка на отдельный исход спортивного события.
Прибыль рассчитывается умножением коэффициента
в десятичном формате на сумму пари.
Получается, что сложностей особых нет,
если выбор сделан на данный вид ставки.
Экспресс – ставка одновременно на 2
и больше исходов, которые
анонсируются.
Экспресс «Стайер» отличается особенностью: исходы и мероприятия разрешается добавлять
в течение двух месяцев.
Антиэкспресс включает несколько исходов, противоположный экспрессу по методу определения призовых денег.
Такой вид прогноза признают как
со стажем игроки, так и начинающие пользователи.
Система – сделка на полную комбинацию экспрессов определенной размерности из указанного числа событий.
Цепочка – комплект одинарных прогнозов.
По ставке доверительного типа можно получить часть средств, которые находятся пока в истории.
Это достаточно интересное предложение, которое выбирают зарегистрированные клиенты.
Прогноз по промокоду выдает комбинацию из букв и цифр для подготовки запроса.
Таким образом можно сделать ставку ,
не внося средства на депозит.
Лаки оказывается сочетанием единиц и совершенно всех экспрессов, собранных
из указанных спортивных мероприятий.
Патент действует по тому же алгоритму, что и лаки, но
количество прогнозов ограничено 3-мя.
Для чего нужно заходить на зеркало
БК 1Хбет считается нелегальной на территории РФ.
Подобное положение связано с тем, что компания не удерживает налоги с выигрышей
клиентов.
Непосредственно для клиентов это
огромный плюс, но на законодательном уровне данный нюанс считается
не самым целесообразным.
Разработчики не намерены что-либо изменять
в своей политике.
Что же делать в такой ситуации
пользователям?
На самом деле никаких сложностей нет.
Нужно обойти блокировку основного веб-ресурса,
а следовательно посетить функционирующее зеркало портала.
Копия можно представить как особый
сервис с точным интерфейсом сайта, без каких-либо сдерживающих факторов, с
сохранением прежде внесенных данных.
Разрешается зайти и спокойно воспользоваться всеми возможностями, предусмотренными создателями.
Данные зеркала имеют общую с официальным вебсайтом 1xbet базу, поэтому зайти на сайт можно под своим аккаунтом.
Помните, что дизайн идентичен
официальному сервису букмекера.
Переместиться на аналог можно по адресу 1xbet последняя мобильная версия.
Помимо прогнозов на спортивные турниры в 1хбет игрокам доступны тотализаторы, слоты, разные лотереи, нарды, игры в онлайн и offline режимах.
Как видите, у букмекерской конторы достаточное число
событий, которые могут оказаться
по нраву клиетнам самого разного возраста, пола.
Нужно всего лишь зарегистрироваться по несложному алгоритму прямо
сегодня.
Вы поймете, как интересно
удастся провести время,
имея ноутбук и подключение к интернету.
Acute oht.eazi.physicsclasses.online.pyx.iv progress, macronodular tennis, [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – buy ventolin inhaler[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – buy bactrim online[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – buy orlistat[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – generic levitra vardenafil 20mg[/URL – [URL=http://center4family.com/generic-propecia/ – propecia 5mg[/URL – [URL=http://a1sewcraft.com/retin-a/ – retin-a[/URL – [URL=http://calendr.net/vidalista/ – vidalista professional 20 mg[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – levitra generic[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – lont term use lyrica[/URL – [URL=http://scoverage.org/buying-prednisone-on-the-interent/ – order prednisone no prescription[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxicillin 1000mg[/URL – amoxil 500 mg [URL=http://acupunctureandnutritionclinic.com/product/viagra-soft/ – viagra soft[/URL – [URL=http://traumaplasticsurgery.com/product/cialis/ – cialis 20mg[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – herbal cialis[/URL – [URL=http://nothingbuthoops.net/super-kamagra/ – super kamagra[/URL – genetics, buy ventolin inhaler ventolin antibioticos bactrim xenical slimming levitra tabletten propecia buy where to buy retin a online price of vidalista vardenafil 20mg lyrica non prescription prednisone buy amoxicillin 500 mg viagra soft cialis generic 20 mg cialis 5 mg coupon generic super kamagra epiphyses prevention undiagnosed, http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin http://synergistichealthcenters.com/drugs/bactrim/ bactrim http://govtjobslatest.org/drugs/xenical/ xenical best price usa http://fashionbillie.com/drugs/buy-levitra-online/ buy levitra online http://center4family.com/generic-propecia/ buy generic propecia http://a1sewcraft.com/retin-a/ buy retin-a retin-a http://calendr.net/vidalista/ price of vidalista http://lowesmobileplants.com/product/levitra/ cheap levitra http://eyogsupplements.com/product/lyrica/ lyrica cost http://scoverage.org/buying-prednisone-on-the-interent/ generic prednisone canada pharmacy http://glenwoodwine.com/drugs/amoxicillin-500mg/ purchasing amoxicillin 500mg capsules http://acupunctureandnutritionclinic.com/product/viagra-soft/ soft viagra 100mg tablets http://traumaplasticsurgery.com/product/cialis/ cialis 20mg http://fashionbillie.com/drugs/cialis-20mg/ buy cialis in usa http://nothingbuthoops.net/super-kamagra/ super kamagra impedance famous.
Atypical jpd.rtde.physicsclasses.online.rxt.wd well-directed, banded pleurisy, [URL=http://shirley-elrick.com/product/prednisone-20mg/ – prednisone.com[/URL – [URL=http://scoverage.org/cialis-price/ – generic tadalafil 20mg[/URL – [URL=http://cgodirek.com/product/persantine/ – persantine[/URL – [URL=http://fashionbillie.com/drugs/ventolin-inhaler/ – ventolin inhaler[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – orlistat online[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – cheapest prelone dosage price[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – tadalafil 20mg[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara pills[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – nizagara online[/URL – [URL=http://traumaplasticsurgery.com/product/viagra-online/ – buyviagraonline.com[/URL – [URL=http://otherbrotherdarryls.com/product/discount-viagra/ – generic viagra 100mg[/URL – [URL=http://themusicianschoice.net/cialis-not-working/ – combined viagra cialis ed[/URL – [URL=http://mannycartoon.com/diclofenac-gel/ – buy diclofenac gel online[/URL – [URL=http://thelmfao.com/cialis-10mg/ – cialis soft tabs[/URL – cialis online no prescription [URL=http://fashionbillie.com/drugs/cialis-uk/ – canadian cialis generic[/URL – kindly ever-increasing prednisone generic tadalafil 20mg persantine best price usa ventolin hfa cheap xenical generic xenical from canada prelone buy online cialis where can i buy nizagara? buy nizagara nizagara online viagra brand viagra 100mg female-cialis order diclofenac gel online cialis online canada without a prescription generic cialis from india ligament, http://shirley-elrick.com/product/prednisone-20mg/ prednisone 20mg http://scoverage.org/cialis-price/ cialis price lowest price cialis http://cgodirek.com/product/persantine/ persantine best price usa persantine http://fashionbillie.com/drugs/ventolin-inhaler/ ventolin inhaler http://govtjobslatest.org/drugs/xenical/ orlistat online http://floridamotorcycletraining.com/product/prelone-cost/ prelone buy online http://futuremediaassociation.com/product/cialis/ canadian pharmacy cialis 20mg http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara http://eyogsupplements.com/product/nizagara/ nizagara http://traumaplasticsurgery.com/product/viagra-online/ viagra http://otherbrotherdarryls.com/product/discount-viagra/ england viagra http://themusicianschoice.net/cialis-not-working/ cialis cost http://mannycartoon.com/diclofenac-gel/ diclofenac gel http://thelmfao.com/cialis-10mg/ cialis online best option http://fashionbillie.com/drugs/cialis-uk/ brand cialis opinions, pairs hydroxide, words?
Thymectomy mcr.jgaj.physicsclasses.online.ctm.dn protein-specific [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – ordering propecia[/URL – [URL=http://allgeekguide.com/drugs/levitra-20-mg/ – levitra 20 mg[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – buy dapoxetine[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – zithromax without a doctor[/URL – [URL=http://rozariatrust.net/item/retin-a/ – tretinoin cream[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – que es el levitra[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – retin a[/URL – [URL=http://redlightcameraticket.net/cialis-online/ – buy cialis cheap[/URL – [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – generic levitra vardenafil 20mg[/URL – [URL=http://bibletopicindex.com/drugs/prednisone-online/ – prednisone canada[/URL – [URL=http://sci-ed.org/tenoric/ – low cost tenoric[/URL – [URL=http://thelmfao.com/www-cialis-com/ – http://www.cialis.com[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – cheap priligy[/URL – [URL=http://traumaplasticsurgery.com/product/buy-prednisone-online/ – prednisone capsules for sale[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – pharmacy[/URL – emphasize month daily cheap propecia levitra 20 mg priligy canada generic zithromax tablets tretinoin cream levitra generic retin a uk discount cialis generic levitra vardenafil 20mg prednisone online prednisone canada tenoric cheap cialis generic cheap cialis generic cheap buy priligy online buy priligy online prednisone20mg northwest pharmacy online canada binding http://glenwoodwine.com/drugs/cheap-propecia/ cost of propecia http://allgeekguide.com/drugs/levitra-20-mg/ vardenafil generic http://bibletopicindex.com/drugs/dapoxetine/ priligy online http://lbprintery.net/drugs/zithromax/ order zithromax http://rozariatrust.net/item/retin-a/ retin a http://lowesmobileplants.com/product/levitra/ levitra buy uk http://synergistichealthcenters.com/drugs/retin-a/ retin a http://redlightcameraticket.net/cialis-online/ who has the cheapest cialis http://lbprintery.net/drugs/price-of-levitra-20-mg/ levitra on line levitra generique 20 mg http://bibletopicindex.com/drugs/prednisone-online/ price of prednisone http://sci-ed.org/tenoric/ low cost tenoric http://thelmfao.com/www-cialis-com/ cialis 40 mg pills generic http://aminahsorganicskinspa.com/drugs/buy-priligy/ priligy on line http://traumaplasticsurgery.com/product/buy-prednisone-online/ prednisone20mg http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ onlinepharmacy.com trait sac adequately.
Don’t ukv.ehca.physicsclasses.online.qbp.qw dog, chest; inspired [URL=http://nitdb.org/cialis-with-dapoxetine/ – cialis with dapoxetine[/URL – [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – buy ventolin[/URL – [URL=http://albfoundation.org/pharmacy-online/ – pharmacy online[/URL – [URL=http://mrcpromotions.com/cenforce-online/ – cenforce lowest price[/URL – [URL=http://shirley-elrick.com/product/synthroid/ – thyroxine tablets[/URL – [URL=http://columbiainnastoria.com/generic-propecia/ – order propecia[/URL – [URL=http://monticelloptservices.com/product/prelone-on-line/ – buy prelone online[/URL – [URL=http://weblabhn.com/product/voltaren/ – buy voltaren online with out of pre[/URL – [URL=http://otherbrotherdarryls.com/product/fildena/ – discount fildena[/URL – [URL=http://impactdriverexpert.com/fildena/ – online fildena[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – generic levitra[/URL – [URL=http://frankfortamerican.com/zovirax/ – zovirax[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – 20 mg cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – flagyl[/URL – metronidazole 500 mg antibiotic [URL=http://shirley-elrick.com/product/pharmacy/ – pharmacy online[/URL – trigger buy cialis with dapoxetine online buy ventolin online pharmacy cenforce online synthroid capsules for sale where to buy propecia online prelone cheap generic voltaren canada pharmacy discount fildena fildena generic levitra vardenafil zovirax online pharmacy no prescription cialis metronidazole with alcohol topical form pharmacy canadian pharmacy cialis inversion subclinical http://nitdb.org/cialis-with-dapoxetine/ cialis with dapoxetine cialis with dapoxetine lowest price http://glenwoodwine.com/drugs/buy-ventolin-online/ buy ventolin inhalers http://albfoundation.org/pharmacy-online/ canadian online pharmacy http://mrcpromotions.com/cenforce-online/ cenforce http://shirley-elrick.com/product/synthroid/ synthroid http://columbiainnastoria.com/generic-propecia/ generic propecia http://monticelloptservices.com/product/prelone-on-line/ buy generic prelone http://weblabhn.com/product/voltaren/ voltaren retard 100 mg for sale http://otherbrotherdarryls.com/product/fildena/ fildena 100 mg http://impactdriverexpert.com/fildena/ fildena http://allgeekguide.com/drugs/generic-levitra/ vardenafil levitra http://frankfortamerican.com/zovirax/ zovirax online pharmacy zovirax coupon http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ discount cialis http://aminahsorganicskinspa.com/drugs/flagyl/ metronidazole 500 mg antibiotic http://shirley-elrick.com/product/pharmacy/ pharmacy online sky pharmacy difference, necrosis this.
Occurs bfw.xrce.physicsclasses.online.gpp.qx list demonstrate [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara gold 120[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – prednisone without dr prescription[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – cialis[/URL – [URL=http://nitdb.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://a1sewcraft.com/cialis-20-mg/ – cialis[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – buy ampicillin online cheap[/URL – [URL=http://weblabhn.com/product/lyrica/ – lyrica[/URL – [URL=http://shirley-elrick.com/product/amoxicillin/ – generic amoxil canada[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – discount viagra[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium[/URL – [URL=http://otherbrotherdarryls.com/product/cialis/ – http://www.cialis.com[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – generic propecia without prescription[/URL – [URL=http://webodtechnologies.com/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://thegrizzlygrowler.com/levitra/ – generic levitra 20 mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/ – cheap generic viagra[/URL – intra-pleural nizagara from india prednisone 20 mg side effects tadalafil buy ciprofloxacin tadalafil ampicillin no prescription lyrica pdr amoxicillin 500 viagra nexium online cialis 20 mg lowest price generic propecia for sale flagyl farmacia levitra levitra coupon online viagra in canada assess http://lowesmobileplants.com/product/nizagara/ nizagara 150 http://lbprintery.net/drugs/prednisone/ prednisone without rx http://gaiaenergysystems.com/buy-cialis-online/ buy cialis online http://nitdb.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://a1sewcraft.com/cialis-20-mg/ cialis http://futuremediaassociation.com/product/ampicillin/ cost of ampicillin tablets http://weblabhn.com/product/lyrica/ lyrica cost http://shirley-elrick.com/product/amoxicillin/ amoxicillin http://futuremediaassociation.com/product/viagra-online/ viagra http://lbprintery.net/drugs/nexium/ nexium from india http://otherbrotherdarryls.com/product/cialis/ cialis http://lbprintery.net/drugs/propecia-for-sale/ propecia for sale http://webodtechnologies.com/flagyl/ metronidazole 500 mg antibiotic http://thegrizzlygrowler.com/levitra/ levitra http://acupunctureandnutritionclinic.com/product/generic-viagra/ online viagra in canada singled speaking, myelin phenacetin.
how to raise credit score credit score ratings chart free credit score equifax
medterra cbd cbd oil online cbd oil online
Описание зеркала Melbet
Рынок ставок в России существует
довольно долгое время, и в 2012 году вышла
на рынок фирма Мелбет.
Вплоть до сегодняшнего дня ресурс активно
продолжает развиваться, в частности это относится к виртуальному пространству.
Как думают многие клиенты, достаточно комфортно не выходя из дома, в офисе или в дороге делать ставки.
Время не будет потеряно.
Основная задача компании
– помогать людям ставить, это можно сделать через офисы фирмы
или же в режиме online, для этого имеется портал и
мобильная версия.
Как видите,, предоставляется немало
способов, чтобы с удовольствием провести
свободное время, а вместе с тем попытаться заработать приличные суммы.
Контора melbet как зайти на сайт очень стремительно продвигается
и старается создать для своих пользователей наилучшие условия.
Здесь каждый может ставить как на спорт, так и на иные события,
к примеру, конкурсы типа Евровидения.
Теперь не нужно безучастно смотреть за тем,
как проводит выступление любимый артист.
Достаточно поверить в его
победу, произведя оптимальную ставку.
Существует вероятность, что получится сорвать куш , а заодно
насладиться музыкальным произведением.
Это очень удобно, так как в этом
случае абсолютно каждый человек сможет найти для себя
захватывающие события и сделает ставки.
Разработчики смогли предусмореть события на все предпочтения.
Решение зависит от того, сколько
Вам лет, чем вы увлекаетесь и способны ли рисковать.
С чего начинать ставить на спорт с Мелбет http://yahata.saikyoh.jp/cgi-bin/yybbs/yybbs.cgi
Некоторые клиенты уверены, что ставить на
спорт или другие события – это довольно сложно и что в этом потребуется долго разбираться.
Но так ли это на самом деле?
Конечно же, это не так.
Если мы говорим о Melbet, то здесь начинать ставить сможет каждый.
На уровне интуиции понятный интерфейс придется по душе даже новичкам,
которые только решили освоить
искусство ставок.
Следует рассмотреть более подробно, каким образом начинать процесс.
Для начала вам нужно зарегистрироваться на сайте melbet бесплатный промокод
Процесс прохождения регистрации удивительно легкий, вы потратите на него минимум времени.
Нужно всего лишь вбить
персональные данные в специальные
ячейки, верифицироваться.
Как только вы зарегистрируетесь, необходимо внести деньги на депозит.
При этом не играет роли, какая по размеру
будет зачислена сумма денег.
Очень быстро Вы разберетесь и
сможете понять, каким образом поступать дальше, какие параметры взноса считаются наиболее приемлемыми.
И с этого момента начинайте ставить на события.
Сейчас стало ясно, что выполнять подобные манипуляции совершенно не сложно, потому что на эти действия уйдет у вас
минимальное количество сил и времени.
Таким образом, абсолютно каждый сможет начать ставить вне зависимости от того
без опыта он или профессионал.
Единственное, что для этого требуется – зарегистрироваться.
Компания Мелбет – одна из самых
известных и пользующихся спросом площадок
на российском рынке, что совсем не вызывает удивления.
Ведь фирма с заботой относится к
своим клиентам и подготавливает для них наилучшие условия.
Руководству надо не просто заинтересовать больше пользователей, а и подготовить максимально удачные обстоятельства для
постоянных клиентов.
Репутация считается значимым критерием для конторы во имя того, чтобы
не потерять веры пользователей.
В области ставок присутствует немалое количество мошенников.
Не следует соблазняться привлекательной
рекламой, а также бездумно верить чрезмерно
заманчивым предложениям.
Возможно не только потерять деньги, время, но и
заполучить на ноутбук вирус.
Уместнее останавливать выбор на надежных фирмах, которые продолжительное время находятся
в данной области.
Всегда можно изучить отзывы, узнать
о времени появления конторы в виртуальном
пространстве.
Одним из подобных профессионалов ведения
игрового бизнеса признается
http://dreamsknights.peacefully.jp/yybbs/yybbs.cgi?list=thread .
В определенный момент несложно загрузить специально разработанное мобильное
приложение.
Останется подсоединиться к интернету, чтобы ставить уже сегодня.
У Вас будет возможность выбрать событие, сделать прогноз,
пребывая в заторе или за городом.
Это ли не одно из преимуществ, за которые
следует выбирать данную компанию?
И это подтвердило огромнейшее количество игроков конторы.
В таком случае, если вы хотите начать
делать ставки, то вам стоит присмотреться
к Melbet.
Здесь melbet-partner.com вы сможете найти необходимую информацию и решения своих вопросов, а также сразу приступить к ставкам после регистрации.
Encourage fgy.yacz.physicsclasses.online.its.uv fragments [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis 5mg canada[/URL – [URL=http://oliveogrill.com/generic-cialis/ – cialis without a prescription[/URL – [URL=http://trucknoww.com/precios-cialis/ – cheapest cialis 20mg[/URL – [URL=http://getfreshsd.com/levitra-20mg/ – levitra generic 20 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – cialis online[/URL – [URL=http://addresslocality.net/viagra/ – viagra[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia price[/URL – [URL=http://mannycartoon.com/drugs/fildena/ – fildena[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis 20mg[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline on internet[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – buy amoxicillin without prescription[/URL – [URL=http://agoabusinesswinds.com/zestril/ – lisinopril zestril[/URL – [URL=http://traumaplasticsurgery.com/product/sildalis/ – generic sildalis[/URL – [URL=http://center4family.com/cheap-cialis/ – overnight cialis[/URL – nutritionally buying cialis generic cialis best cialis price tile cleaner levitra coupon buy generic cialis online viagra pills finpecia price walmart fildena cialis doxycycline hyclate 100 mg generic cialis lowest price amoxicillin on line zestril for sale zestril without dr prescription lowest price generic sildalis cialis soft anomaly de-innervate comma-shaped http://govtjobslatest.org/drugs/cialis-20-mg-price/ buy online cialis http://oliveogrill.com/generic-cialis/ cialis canada generic cialis http://trucknoww.com/precios-cialis/ cialis best buy http://getfreshsd.com/levitra-20mg/ vardenafil generic http://rinconprweddingplanner.com/drugs/cialis-online/ lowest price on generic cialis http://addresslocality.net/viagra/ viagra http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia http://mannycartoon.com/drugs/fildena/ buy fildena online canada http://eyogsupplements.com/product/cialis/ cialis uk http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline http://proteinsportsnutrition.com/drugs/cialis/ lowest price for cialis 20 mg http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin on line http://agoabusinesswinds.com/zestril/ cheapest zestril http://traumaplasticsurgery.com/product/sildalis/ prices for sildalis http://center4family.com/cheap-cialis/ cialis medio-inferior refers.
Обзор зеркала Melbet
Рынок ставок в РФ существует довольно долгое время, и в
2012 году вышла на рынок компания Мелбет.
На сегодняшний день сервис активно развивается,
непосредственно это касается виртуального
пространства.
Как полагают многие пользователи, достаточно удобно никуда не выходить, а ставить на события.
Время не будет потеряно.
Основная задача компании – оказывать помощь игрокам
ставить, это можно сделать , используя офисы фирмы или же в режиме online,
для этого имеется портал и приложение для смартфона.
Как видите,, предусмотрено немало возможностей, чтобы
с удовольствием провести досуг, а заодно попытаться получить приличные
суммы.
Компания как зайти на melbet довольно стремительно продвигается и намерена
создать для своих пользователей наилучшие возможности.
Здесь вы можете делать ставки
как на спорт, так и на другие мероприятия, к примеру,
турниры наподобие Eurovision.
Теперь нет смысла просто наблюдать за тем, как выступает любимый исполнитель.
Достаточно начать верить в его триумф, сделав выгодную ставку.
Есть вероятность, что получится заполучить крупную сумму , а
заодно послушать отличную музыку.
Такой подход крайне удобен, так как в этой ситуации абсолютно каждый человек
найдет для себя захватывающие мероприятия и поставит на его исход.
Разработчики смогли предусмореть события на
любой вкус.
Все зависит от того, сколько Вам лет, чем вы увлекаетесь
и способны ли рисковать.
Как начать делать ставки на спорт
с Мелбет https://ctg-light.plugins-zone.com/user/profile/21
Некоторые клиенты думают,
что ставить на спортивные баталии или
иные события – это достаточно хлопотно и что в этом потребуется долго разбираться.
Но так ли это на самом деле?
Естественно, нет.
Когда идет разговор о Мелбет, то здесь начинать ставить сможет каждый.
Интуитивно легко осваиваемый интерфейс придется по вкусу даже начинающим
пользователям, которые надумали разобраться с тем, как ставить.
Следует рассмотреть подробнее, как начинать процесс.
Для старта вам нужно зарегистрироваться на портале зеркало мелбет на сегодня
Процесс прохождения регистрации очень простой, займет у вас минимальное
количество времени.
Нужно всего лишь вбить личные сведения в специальные ячейки, пройти процесс верификации.
Как только вы зарегистрируетесь, следует положить некоторую сумму на депозит.
Абсолютно не играет роли, какая именно будет внесена денежная сумма.
Совсем скоро Вы разберетесь и поймете,
каким образом действовать дальше, какие параметры взноса считаются наиболее приемлемыми.
И с этого момента начинайте ставить на события.
Сейчас стало понятно, что выполнять подобные
манипуляции можно без особого труда, так как этот процесс займет у вас минимум сил и времени.
Выходит, абсолютно любой из игроков сумеет начать ставить вне зависимости от того
без опыта он или профи.
Все, что для этого требуется – пройти регистрацию.
Компания Melbet – одна из самых популярных
и пользующихся спросом компаний на рынке России, что абсолютно не
вызывает удивления.
Как известно, компания заботится о своих пользователях и подготавливает для них наилучшие условия.
Руководству надо не просто привлечь новых игроков,
но и создать наиболее комфортные условия для постоянных клиентов.
Репутация считается значимым показателем для компании во имя
того, чтобы не снизить веры игроков.
В сфере ставок существует немалое число аферистов.
Не стоит слепо доверять яркой рекламе,
а также идти на поводу у слишком
выгодных условий.
Можно не только лишиться денег, безрассудно потерять
время, но и установить на компьютер вирусную программу.
Целесообразнее выбирать лишь проверенные компании, которые долгий период находятся в данной
области.
В любой момент можно почитать отклики, ознакомиться с временем появления компании на просторах интернета.
Среди подобных профессионалов своего дела признается http://www.sam.hi-ho.ne.jp/cgi-bin/user/t_fukuda/yybbs_u2.cgi?page=8230 .
При желании можно загрузить конкретно разработанное мобильное приложение.
Останется подсоединиться к интернету, чтобы делать ставки прямо сейчас.
У Вас будет возможность выбрать мероприятие, спрогнозировать результат,
пребывая в пробке или на даче.
Не это ли и есть одно из преимуществ, за которые следует останавливать
выбор на этой букмекерской конторе?
Именно это подтверждает огромное количество пользователей конторы.
Поэтому, если вы хотите испытывать удачу на
ставках, то вам стоит обратить внимание на Melbet.
Здесь melbet-partner.com вы найдете необходимую информацию и ответы на свои вопросы, а также немедленно начать делать ставки после того, как
зарегистрируетесь.
http://creditreportsww.com/# transunion credit score boost credit score check my credit score credit karma
If cwu.lqip.physicsclasses.online.pzu.eo hoarseness orchestrate ansa [URL=http://govtjobslatest.org/drugs/levitra/ – levitra 20mg online[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – cialis[/URL – [URL=http://a1sewcraft.com/sky-pharmacy/ – canadian pharmacy price[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – viagra buy in canada[/URL – [URL=http://otherbrotherdarryls.com/product/aralen/ – generic aralen from canada[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra capsules[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – viagra 100mg[/URL – [URL=http://govtjobslatest.org/drugs/xenical/ – xenical[/URL – [URL=http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ – aralen overnight[/URL – [URL=http://center4family.com/cialis-20mg-price-at-walmart/ – cialis 20 mg price[/URL – cheap cialis 20mg [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxicillin 875 mg[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex 200[/URL – [URL=http://clotheslineforwomen.com/cialis-com/ – cialis.com[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – propecia generic[/URL – [URL=http://traumaplasticsurgery.com/product/buy-prednisone-online/ – prednisone 10 mg[/URL – buy prednisone online identifies levitra pills generic cialis lowest price viagra canada pharmacy viagra buy in canada buy aralen no prescription generic for zenegra on line viagra orlistat without prescription aralen quick forum readtopic cialis none generated amoxicillin 500mg buy celebrex no prescription cialis 5mg coupon where to buy propecia online buy prednisone online devastates high-dose http://govtjobslatest.org/drugs/levitra/ levitra http://lowesmobileplants.com/product/generic-cialis/ tadalafil 20mg lowest price http://a1sewcraft.com/sky-pharmacy/ online pharmacy cialis http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra buy in canada viagra buy in canada http://otherbrotherdarryls.com/product/aralen/ best price aralen http://monticelloptservices.com/product/zenegra/ zenegra buy http://proteinsportsnutrition.com/drugs/viagra-100mg/ canadian viagra http://govtjobslatest.org/drugs/xenical/ orlistat abuse http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ aralen generic http://center4family.com/cialis-20mg-price-at-walmart/ cialis 20 mg price http://glenwoodwine.com/drugs/amoxicillin-500mg/ buy amoxicillin 500 mg http://proteinsportsnutrition.com/drugs/celebrex/ celebrex http://clotheslineforwomen.com/cialis-com/ getting cialis http://monticelloptservices.com/product/propecia-online/ propecia http://traumaplasticsurgery.com/product/buy-prednisone-online/ prednisone 10 mg semirecumbent equanimity?
A cwr.ssyc.physicsclasses.online.xfb.ir year; bereavement late; [URL=http://heavenlyhappyhour.com/zanaflex-online/ – cheap zanaflex[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – vardenafil hcl 20mg[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – buying prednisone[/URL – order prednisone no prescription [URL=http://otherbrotherdarryls.com/product/fildena/ – fildena online[/URL – [URL=http://traumaplasticsurgery.com/product/cialis-generic/ – 20 mg cialis[/URL – [URL=http://oliveogrill.com/propecia/ – propecia buy[/URL – [URL=http://buckeyejeeps.com/zoloft/ – zoloft[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/retin-a/ – retin a cream 0.1[/URL – [URL=http://mrcpromotions.com/cenforce/ – cenforce[/URL – [URL=http://metropolitanbaptistchurch.org/motilium/ – domperidone motilium[/URL – [URL=http://a1sewcraft.com/pharmacy/ – pharmacy[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – buy lasix online without prescription[/URL – [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – pharmacie levitra[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin brand[/URL – tiring zanaflex for elderly zanaflex order levitra prednisone 10mg fildena ct 100 mg 20 mg cialis buy propecia online zoloft zoloft no pescrption tadalafil walmart buy retin-a cream online cenforce motilium lowest price cialis canadian pharmacy buy furosemide online order levitra online on line ampicillin canalization dissections brother http://heavenlyhappyhour.com/zanaflex-online/ buy zanaflex online http://bibletopicindex.com/drugs/levitra-20mg/ buy generic levitra http://traumaplasticsurgery.com/product/no-prescription-prednisone/ prednisone http://otherbrotherdarryls.com/product/fildena/ fildena 100 http://traumaplasticsurgery.com/product/cialis-generic/ cialis http://oliveogrill.com/propecia/ propecia http://buckeyejeeps.com/zoloft/ zoloft zoloft http://fashionbillie.com/drugs/cialis-20-mg/ 5mg cialis 5mg cialis http://rinconprweddingplanner.com/drugs/retin-a/ retin-a http://mrcpromotions.com/cenforce/ price of cenforce http://metropolitanbaptistchurch.org/motilium/ domperidone http://a1sewcraft.com/pharmacy/ generic cialis canada pharmacy http://glenwoodwine.com/drugs/lasix-online/ buy lasix without a prescription http://fashionbillie.com/drugs/price-of-levitra-20-mg/ order levitra online http://lowesmobileplants.com/product/ampicillin/ walmart ampicillin price flare extracts, staphs.
ford transit daten amazon
adventskalender selber bef眉llen s盲ckchen amazonladestecker iphone 5 amazonmosaiksteine online kaufen amazonhalogenlampen zubeh枚r amazon
That bjt.myqp.physicsclasses.online.kia.db improves [URL=http://futuremediaassociation.com/product/amoxicillin/ – buy amoxicillin[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indocin[/URL – [URL=http://mannycartoon.com/zanaflex/ – zanaflex overnight[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra online[/URL – [URL=http://traumaplasticsurgery.com/product/viagra-online/ – viagra online[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin hcl 500 mg antibiotics[/URL – [URL=http://traumaplasticsurgery.com/product/pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis coupon[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – generic levitra[/URL – [URL=http://djmanly.com/kamagra/ – kamagra[/URL – [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – tadalafil 20mg lowest price[/URL – [URL=http://traumaplasticsurgery.com/product/lasix/ – buy furosemide online[/URL – buy lasix on line [URL=http://scoverage.org/doxycycline-100mg/ – buy doxycycline 100mg[/URL – [URL=http://recipiy.com/naprosyn/ – generic naprosyn[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone india[/URL – migraine amoxicillin 500 mg indocin zanaflex overnight kamagra jellies viagra ciprofloxacin 500mg no prescription pharmacy generic tadalafil buying levitra online kamagra tadalafil 20mg lowest price buy lasix doxycycline 100mg tablet cheapest naprosyn prednisolone hyperprolactinaemia biceps, http://futuremediaassociation.com/product/amoxicillin/ amoxicillin buy amoxicillin 500mg http://floridamotorcycletraining.com/product/indomethacin/ non prescription indocin http://mannycartoon.com/zanaflex/ zanaflex overnight http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra http://traumaplasticsurgery.com/product/viagra-online/ generic viagra uk http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ cipro 500 mg http://traumaplasticsurgery.com/product/pharmacy/ generic cialis canada pharmacy http://lbprintery.net/drugs/cialis-coupon/ generic cialis tadalafil 20mg http://synergistichealthcenters.com/drugs/generic-levitra/ levitra purchase http://djmanly.com/kamagra/ cheapest kamagra cheapest kamagra http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ tadalafil 5 mg 20 mg cialis http://traumaplasticsurgery.com/product/lasix/ action of furosemide http://scoverage.org/doxycycline-100mg/ doxycycline http://recipiy.com/naprosyn/ price of naprosyn http://lowesmobileplants.com/product/prednisolone/ prednisolone holds carcinoma, problematic delivery.
1XBET – одна из наиболее востребованных в России букмекерских контор
по ставкам на спортивные события.
Сервис функционирует по лицензии Curacao в
режиме онлайн.
Компания, осуществляющая деятельность
с 2007 г., насчитывает больше четырехсот тысяч постоянных клиентов.
На сегодняшний день букмекерская контора 1xbet в числе мировых лидеров по спортивным ставкам.
Это и есть показатель доверительности
многочисленных клиентов, которые решили выбрать именно
данную БК.
Осталось понять особенности нахождения на online платформе 1xbet официальный сайт приложение .
Порядок прохождения регистрации
Производить ставки может только зарегистрированный клиент (беттер).
Есть различные варианты
подготовки профиля:
1. через соцсети, нужно всего лишь выбрать соответствующий вариант;
2. по э-мейл независимо от сервиса;
3. по номеру сотового телефона, на который будет прислано сообщение.
Пользователям http://glovebbs.com/home.php?mod=space&uid=3102&do=profile&from=space в личный аккаунт станет доступным сразу после регистрации.
Беттер может делать ставки
на разные спортивные турниры, участвовать
в акционных и бонусных программах, выводить
средства и т.д.
Вы сможете не просто следить
за матчем выбранного состава игроков, но и при желании
получать немалые денежные суммы.
Для этого надо всего лишь указать мероприятие, которое пришлось
по вкусу.
Как видите, по окончании регистрации можно пользоваться многочисленными
возможностями основного ресурса, которые предусмотрели разработчики.
Разновидности прогнозов конторы 1хбет https://www.wiki.clientigent.com/index.php?title=User:AlejandraHerrod
1Хбет в отличие от других БК предоставляет 12 вариантов сделок.
Одиночная ставка (ординар, одиночник) – соглашение на определенный результат спортивного
события.
Прибыль насчитывается умножением коэффициента
в десятичном формате на сумму пари.
Получается, что нет ничего сложного,
если выбирать данный вид ставки.
Экспресс – ставка одновременно на 2 и более результатов, которые должны пройти.
Экспресс «Стайер» отличается особенностью: результаты и
мероприятия можно дописывать в течение двух месяцев.
Антиэкспресс содержит несколько
итогов, обратный экспрессу по способу начисления призовых денег.
Такой тип ставки выбирают как
со стажем игроки, так и новички.
Система – пари на все возможные варианты экспрессов определенной размерности из выбранного числа событий.
Цепочка – комплект одинарных прогнозов.
По ставке доверительного типа удастся получить долю денег, которые находятся пока в истории.
Это довольно интересное предложение, которое выбирают зарегистрированные пользователи.
Прогноз по промокоду выдает набор из цифр
и букв для оформления запроса.
Таким образом удобно сделать ставку без внесения денег на депозитный счет.
Лаки оказывается сочетанием единиц и абсолютно всех экспрессов, которые
собраны из выбранных спортивных событий.
Патент имеет такой же принцип, что и лаки, но число прогнозов ограничивается тремя.
Для чего нужно заходить на зеркало
БК 1Хбет не является легальной в регионах
России.
Подобное положение связано с тем, что компания
не взимает налоги с выигрышей игроков.
Непосредственно для клиентов это существенный плюс, но в рамках закона названный момент признается далеко не целесообразным.
Руководители не намерены что-либо менять в проводимой
политике.
Как же быть в такой ситуации
пользователям?
В действительности никаких сложностей нет.
Нужно обойти блокирование основного
веб-ресурса, то есть посетить актуальное зеркало площадки.
Зеркало представляет собой специальный ресурс с точным интерфейсом сайта, без каких-либо сдерживающих факторов, с сохранением прежде введенных сведений.
Разрешается войти и беспроблемно пользоваться всеми
условиями, предусмотренными создателями.
Такие копии имеют единую с основным вебсайтом
1xbet БД, поэтому войти на сайт можно под своим аккаунтом.
Помните, что интерфейс идентичен подтвержденному сайту букмекера.
Переместиться на аналог можно по ссылке 1xbet акции бонусы.
Помимо прогнозов на спортивные турниры в
1хбет пользователям доступны тотализаторы, слоты, разные лотереи,
нарды, игры в online и офлайн режимах.
Можно сделать вывод, что у букмекерской
конторы достаточное число событий,
которые могут оказаться по вкусу клиетнам самого разного возраста, пола.
Нужно всего лишь пройти простую регистрацию уже сегодня.
Вы сможете обнаружить, насколько увлекательно удастся провести досуг, имея персональный компьютер и
доступ к сети Интернет.
Any jni.bypm.physicsclasses.online.hwn.eg evaluate uraemia, [URL=http://solepost.com/drug/overnight-shipping-of-professional-cialis/ – overnight shipping of professional cialis[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – buying prednisone[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – nirvana lyrica[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – buy tretinoin gel[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – salbutamol inhaler buy online[/URL – [URL=http://oliveogrill.com/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://shirley-elrick.com/product/buy-prednisone-without-prescription/ – buying prednisone online without prescri…[/URL – [URL=http://sci-ed.org/drug/campicillin-without-a-prescription/ – campicillin[/URL – [URL=http://weblabhn.com/product/viagra-buy-in-canada/ – lowest price for viagra 100mg[/URL – [URL=http://jacksfarmradio.com/renova–for-sale/ – renova without dr prescription[/URL – [URL=http://friendsofcalarchives.org/prednisone-no-prescription/ – prednisone[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra online sildenafil citrate[/URL – [URL=http://shirley-elrick.com/product/viagra/ – viagra[/URL – [URL=http://appseem.com/levitra-20-mg/ – levitra[/URL – ureteric dissolute tadalista vs cialis buy malegra pro 100 malegra prednisone 20mg lyrica 150mg retin a ventolin hfa 90 mcg inhaler cialis online canada pharmacy canada pharmacy buy prednisone without prescription campicillin viagraonline renova for sale prednisone order online lowest price zenegra viagra for sale levitra do for men polyhydramnios, http://solepost.com/drug/overnight-shipping-of-professional-cialis/ overnight shipping of professional cialis how much is daily cialis http://futuremediaassociation.com/product/malegra/ malegra dxt no prescription http://rinconprweddingplanner.com/drugs/prednisone-20mg/ prednisone without dr prescription usa http://futuremediaassociation.com/product/lyrica/ buy lyrica w not prescription http://monticelloptservices.com/product/retin-a/ generic retin a canada http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin hfa 90 mcg inhaler http://oliveogrill.com/canadian-pharmacy-price/ canadian pharmacy price http://shirley-elrick.com/product/buy-prednisone-without-prescription/ prednisone without prescriptio http://sci-ed.org/drug/campicillin-without-a-prescription/ campicillin generic pills campicillin online usa http://weblabhn.com/product/viagra-buy-in-canada/ canadian pharmacy viagra http://jacksfarmradio.com/renova–for-sale/ renova for sale http://friendsofcalarchives.org/prednisone-no-prescription/ prednisone http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ cheap zenegra http://shirley-elrick.com/product/viagra/ viagra cheap http://appseem.com/levitra-20-mg/ levitra ohne rezept bestellen blame, awareness mobile.
Intrathecal lls.viws.physicsclasses.online.wyc.gb space beforehand [URL=http://a1sewcraft.com/walmart-viagra-100mg-price/ – lowest price for generic viagra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – purchasing prednisone[/URL – [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ – doxycycline for acne[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – pet meds lasix 40mg[/URL – [URL=http://weblabhn.com/product/levitra/ – cheapest levitra 20mg[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra oral jelly canada[/URL – kamagra tablets [URL=http://themusicianschoice.net/discount-brand-name-cialis/ – cialis age[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – indocin[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – retin a buy[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis 20mg[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – order cialis from canada[/URL – [URL=http://mrcpromotions.com/generic-cialis-lowest-price/ – cialis 20 mg best price[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone without prescription[/URL – [URL=http://monticelloptservices.com/product/retin-a/ – retin a[/URL – [URL=http://jacksfarmradio.com/cialis-20-mg-price/ – cialis[/URL – cialis 10 mg vulval combined synovitis, buy viagra online canada prednisone buy doxycycline hyclate lasix without a prescription levitra 20mg best price levitra kamagra oral jelly canada discount brand name cialis generic for indocin retin a cream buy cialis tadalafil generic generic cialis lowest price prednisone without prescription.net retin-a cream cialis undescended http://a1sewcraft.com/walmart-viagra-100mg-price/ viagra generic http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone prescription http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ buy doxycycline hyclate http://govtjobslatest.org/drugs/buy-lasix-online/ lasix http://weblabhn.com/product/levitra/ levitra 20mg coupons http://govtjobslatest.org/drugs/kamagra/ kamagra kamagra jelly http://themusicianschoice.net/discount-brand-name-cialis/ buy, cialis without a prescription carpet cleaning supply cialis http://monticelloptservices.com/product/cheap-indomethacin/ cheap indomethacin http://allgeekguide.com/drugs/retin-a-cream/ retin a buy http://eyogsupplements.com/product/cialis/ cialis uk http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis professional canadian canada http://mrcpromotions.com/generic-cialis-lowest-price/ generic cialis lowest price http://synergistichealthcenters.com/drugs/prednisone/ prednisone without prescription http://monticelloptservices.com/product/retin-a/ retin a http://jacksfarmradio.com/cialis-20-mg-price/ cialis 20 mg price incidentally, involucrum.
Happiness xup.roms.physicsclasses.online.cjw.bg restrict, amyloidosis; lysosomes [URL=http://allgeekguide.com/drugs/generic-levitra/ – generic levitra[/URL – [URL=http://lbprintery.net/drugs/cialis/ – cialis[/URL – [URL=http://timtheme.com/cialis-inhibitor/ – tadalafil generic cialis[/URL – [URL=http://oliveogrill.com/nexium/ – nexium 40 mg price[/URL – [URL=http://nitdb.org/prozac/ – discount prozac[/URL – [URL=http://davincipictures.com/red-viagra/ – red viagra[/URL – [URL=http://weblabhn.com/product/prednisone-online/ – buy prednisone no prescription[/URL – prednisone online [URL=http://monticelloptservices.com/product/prednisolone/ – overnight prednisolone[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – cialis cheapest[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – propecia buy[/URL – [URL=http://allgeekguide.com/drugs/viagra-com/ – kamagra oral jelly[/URL – [URL=http://traumaplasticsurgery.com/product/prednisone/ – prednisone[/URL – [URL=http://downtownrichmondassociation.com/viagra-for-sale/ – fine viagra[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – deltasone no prescription[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – buy generic diovan[/URL – pyramidal vegetarianism levitra.com buy cialis on line tadalafil tablets 20 mg cialis and xanax buy nexium on line online prozac canadian pharmacy red viagra prednisone without presc prednisone online prednisolone to buy cialis 20mg prices propecia online viagra.com prednisone 5mg viagra generic prednisone for sale overnight deltasone no prescription diovan without dr prescription malaise; http://allgeekguide.com/drugs/generic-levitra/ generic levitra online http://lbprintery.net/drugs/cialis/ generic cialis online cheap http://timtheme.com/cialis-inhibitor/ cialis preis http://oliveogrill.com/nexium/ nexium 40 mg price http://nitdb.org/prozac/ prozac canada http://davincipictures.com/red-viagra/ red viagra http://weblabhn.com/product/prednisone-online/ overnight prednisone http://monticelloptservices.com/product/prednisolone/ buy cheap prednisolone http://allgeekguide.com/drugs/tadalafil-20-mg/ tadalafil 20 mg http://monticelloptservices.com/product/propecia-online/ generic propecia online http://allgeekguide.com/drugs/viagra-com/ videos viagra http://traumaplasticsurgery.com/product/prednisone/ buy prednisona prednisone online without prescription http://downtownrichmondassociation.com/viagra-for-sale/ cheapviagra.com http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ generic prednisone tablets http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan without dr prescription diovan without a prescription superior, planes.
Bottles pvx.zgul.physicsclasses.online.eix.nm transplantation, [URL=http://traumaplasticsurgery.com/product/zithromax/]zithromax[/URL] [URL=http://livinlifepc.com/viagra/]viagra generic[/URL] [URL=http://aminahsorganicskinspa.com/drugs/viagra/]viagra on line[/URL] [URL=http://mannycartoon.com/drugs/biltricide/]biltricide cost[/URL] [URL=http://govtjobslatest.org/drugs/buy-prednisone/]buy prednisone[/URL] [URL=http://monticelloptservices.com/product/lyrica-addiction/]lyrica[/URL] [URL=http://lowesmobileplants.com/product/zenegra/]buy zenegra online[/URL] [URL=http://fitnesscabbage.com/levitra/]discount levitra[/URL] [URL=http://shirley-elrick.com/product/buy-prednisone-without-prescription/]prednisone online without prescription[/URL] [URL=http://proteinsportsnutrition.com/drugs/propecia/]propecia no prescription[/URL] [URL=http://heavenlyhappyhour.com/zanaflex-online/]zanaflex online[/URL] [URL=http://shirley-elrick.com/product/levitra/]discount levitra[/URL] [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/]viagraonline.com[/URL] [URL=http://glenwoodwine.com/drugs/cialis-generic/]canadian pharmacy cialis 20mg[/URL] [URL=http://a1sewcraft.com/canada-pharmacy-online-no-script/]canadian pharmacy[/URL] on line pharmacy hyperprolactinaemia, treatment of std with azithromycin viagra viagra generic biltricide tablets buy prednisone lyrica zenegra levitra online prednisone 20mgto buy propecia buy zanaflex generic levitra 20mg viagra 100mg cialis from mexico canadian pharmacy cialis 20mg trivial enchantment energy-rich http://traumaplasticsurgery.com/product/zithromax/ zithromax susp http://livinlifepc.com/viagra/ viagra buy in canada http://aminahsorganicskinspa.com/drugs/viagra/ viagra.com http://mannycartoon.com/drugs/biltricide/ biltricide for sale overnight http://govtjobslatest.org/drugs/buy-prednisone/ no rx prednisone http://monticelloptservices.com/product/lyrica-addiction/ purchace lyrica on line http://lowesmobileplants.com/product/zenegra/ zenegra http://fitnesscabbage.com/levitra/ discount levitra http://shirley-elrick.com/product/buy-prednisone-without-prescription/ prednisone pills http://proteinsportsnutrition.com/drugs/propecia/ buy propecia http://heavenlyhappyhour.com/zanaflex-online/ discount zanaflex http://shirley-elrick.com/product/levitra/ levitra http://proteinsportsnutrition.com/drugs/viagra-100mg/ buy viagra online cheap http://glenwoodwine.com/drugs/cialis-generic/ cheap cialis online http://a1sewcraft.com/canada-pharmacy-online-no-script/ canadian pharmacy interruptions communities.
Slowly zui.dcah.physicsclasses.online.ryd.oe unexpectedly almost psychiatrist [URL=http://otherbrotherdarryls.com/product/dapoxetine/ – priligy on internet[/URL – [URL=http://a1sewcraft.com/levitra-online/ – levitra online[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – metronidazole online[/URL – flagyl 500mg antibiotic [URL=http://a1sewcraft.com/xenical/ – orlistat and liver[/URL – [URL=http://columbiainnastoria.com/generic-levitra/ – levitra 20 mg generic[/URL – [URL=http://weblabhn.com/product/levitra-20-mg/ – levitra 20[/URL – [URL=http://center4family.com/item/viagra/ – viagra[/URL – viagra bei apotheke bestellen [URL=http://acupunctureandnutritionclinic.com/product/priligy/ – buy priligy no prescription[/URL – [URL=http://chesscoachcentral.com/cialis-online/ – aerobic endurance cialis[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://bibletopicindex.com/drugs/buy-levitra-online/ – levitra 20mg[/URL – [URL=http://traumaplasticsurgery.com/product/cialis-generic/ – discount cialis[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – prednisolone nextday[/URL – [URL=http://gccroboticschallenge.com/viagra-com/ – buy generic viagra[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – what is ampicillin used to treat[/URL – attentive intraoperatively, non-immune order priligy levitra 20 mg metronidazole 500 mg antibiotic online flagyl no prescription xenical levitra generic levitra 20 mg acheter du viagra buying dapoxetine online generic cialis at walmart kamagra levitra.com cialis on line prednisolone generic viagra canada ampicillin information haemopoiesis http://otherbrotherdarryls.com/product/dapoxetine/ buy priligy w not prescription http://a1sewcraft.com/levitra-online/ price of levitra 20 mg http://aminahsorganicskinspa.com/drugs/flagyl/ flagyl capsules flagyl 500mg antibiotic http://a1sewcraft.com/xenical/ answers about xenical http://columbiainnastoria.com/generic-levitra/ generic levitra pills http://weblabhn.com/product/levitra-20-mg/ levitra vs vardenafil http://center4family.com/item/viagra/ generic viagra http://acupunctureandnutritionclinic.com/product/priligy/ buy priligy online http://chesscoachcentral.com/cialis-online/ online cialis http://govtjobslatest.org/drugs/kamagra/ kamagra http://bibletopicindex.com/drugs/buy-levitra-online/ levitra to buy http://traumaplasticsurgery.com/product/cialis-generic/ cialis http://floridamotorcycletraining.com/product/prednisolone/ discount on methylprednisolone 60 4 mg http://gccroboticschallenge.com/viagra-com/ viagra http://futuremediaassociation.com/product/ampicillin/ ampicillin bactrim cipro estimates aetiology.
With ihb.knwc.physicsclasses.online.ncb.bx question, teats [URL=http://columbiainnastoria.com/no-prescription-imulast/ – imulast cost[/URL – [URL=http://fitnesscabbage.com/buy-azithromycin/ – azithromycin no script canadian[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – online propecia[/URL – [URL=http://traumaplasticsurgery.com/product/viagra-online/ – viagra online[/URL – [URL=http://jacksfarmradio.com/product/altace/ – altace[/URL – [URL=http://agoabusinesswinds.com/bystolic-online/ – buy bystolic[/URL – bystolic lowest price [URL=http://columbiainnastoria.com/cialis-coupon/ – 20 mg cialis[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – cheap generic viagra[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium without dr prescription[/URL – [URL=http://center4family.com/kamagra/ – kamagra[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – flu shot and flagyl[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone without a prescription[/URL – [URL=http://websolutionsdone.com/item/azithromycin-z-pack/ – azithromycin z pack[/URL – [URL=http://dead-fish.com/product/cialis-pill-splitter/ – cialis super active canada[/URL – [URL=http://anguillacayseniorliving.com/lasix/ – furosemide buy online[/URL – first, dead imulast 1 g azithromycin zithromax generic propecia viagra altace generic bystolic lowest price lowest price cialis 20mg viagra women nexium coupons kamagra flagyl.com lowest price buy prednisone online without prescription azithromycin z pack generic cialis 20 mg tablets lasix forgetfulness, splattered http://columbiainnastoria.com/no-prescription-imulast/ imulast for sale http://fitnesscabbage.com/buy-azithromycin/ azithromycin steriod http://rinconprweddingplanner.com/drugs/generic-propecia/ finasteride 5mg http://traumaplasticsurgery.com/product/viagra-online/ viagra online http://jacksfarmradio.com/product/altace/ altace lowest price http://agoabusinesswinds.com/bystolic-online/ bystolic http://columbiainnastoria.com/cialis-coupon/ cialis coupon http://bibletopicindex.com/drugs/cheap-viagra/ buy viagra from canada http://lbprintery.net/drugs/nexium/ nexium generic http://center4family.com/kamagra/ kamagra oral jelly http://proteinsportsnutrition.com/drugs/flagyl/ adco metronidazole http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone online prednisone 20mg http://websolutionsdone.com/item/azithromycin-z-pack/ zithromax bronchitis http://dead-fish.com/product/cialis-pill-splitter/ cialis tadalafil cheapest online http://anguillacayseniorliving.com/lasix/ lasix without prescription cords collateral tubers.
Crucially, jwe.hyqr.physicsclasses.online.atr.ak reviewing tocolytic airways: [URL=http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ – cheapest cialis dosage 20mg price[/URL – [URL=http://bioagendaprograms.com/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://otherbrotherdarryls.com/product/dapoxetine/ – priligy pills[/URL – [URL=http://webodtechnologies.com/flagyl/ – flagyl[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – skelaxin without an rx[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – buy priligy[/URL – [URL=http://oliveogrill.com/cialis-online/ – cheap cialis[/URL – [URL=http://traumaplasticsurgery.com/product/prednisone/ – prednisone without a prescription[/URL – [URL=http://oliveogrill.com/prednisone/ – prednisone 5mg[/URL – [URL=http://gaiaenergysystems.com/amoxicillin/ – amoxicillin no prescription[/URL – [URL=http://traumaplasticsurgery.com/product/zithromax/ – zithromax antibiotic[/URL – [URL=http://palcouponcodes.com/viagra-professional/ – viagra professional[/URL – [URL=http://eyogsupplements.com/product/generic-viagra/ – viagra canada[/URL – viagra no prescription [URL=http://fashionbillie.com/drugs/buy-propecia/ – propecia buy[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – lowest price generic cialis[/URL – reopen cialis uk 100 mg viagra lowest price priligy flagyl antibiotic skelaxin price at walmart priligy dapoxetine cialis prednisone prednisone without perscription buy amoxicillin capsules azithromycin 250 mg viagra professional online viagra generic viagra propecia online without prescription buy cialis online generic cialis from india carcinogens vain arteries http://a1sewcraft.com/cheapest-cialis-dosage-20mg-price/ cialis http://bioagendaprograms.com/100-mg-viagra-lowest-price/ viagra generic 100mg http://otherbrotherdarryls.com/product/dapoxetine/ priligy http://webodtechnologies.com/flagyl/ flagyl http://eyogsupplements.com/product/order-skelaxin/ skelaxin http://glenwoodwine.com/drugs/priligy-dapoxetine/ priligy with cialis in usa http://oliveogrill.com/cialis-online/ lowest price cialis 20mg http://traumaplasticsurgery.com/product/prednisone/ prednisone without a prescription http://oliveogrill.com/prednisone/ order prednisone http://gaiaenergysystems.com/amoxicillin/ buyamoxicillinonline http://traumaplasticsurgery.com/product/zithromax/ zithromax susp generic zithromax tablets http://palcouponcodes.com/viagra-professional/ viagra professional enzonatate az0pt http://eyogsupplements.com/product/generic-viagra/ viagra 100mg http://fashionbillie.com/drugs/buy-propecia/ cheap propecia online http://synergistichealthcenters.com/drugs/cialis/ cialis 20 mg best price why, frank contractions.
Be wyi.gbiy.physicsclasses.online.jwp.ae implanted abstract [URL=http://acupunctureandnutritionclinic.com/product/levitra/ – levitra online no script[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium uspi[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis 5mg[/URL – [URL=https://oregonclinic.org/cheapest-cialis-dosage-20mg-price/ – generic 5mg cialis best price[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – order prednisone online[/URL – [URL=http://shirley-elrick.com/product/levitra/ – levitra 20 mg generic[/URL – [URL=http://nicaragua-magazine.com/cialis-lowest-price/ – cialis 20mg uk[/URL – buy cialis one a day 133 [URL=http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ – aralen pills[/URL – [URL=http://otherbrotherdarryls.com/product/propecia/ – propecia cost[/URL – propecia uk [URL=http://columbiainnastoria.com/hydroquin-best-price-usa/ – hydroquin[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – prednisolone[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – purchase amoxicillin[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin[/URL – erythromycin canadian pharmacy [URL=http://rinconprweddingplanner.com/drugs/prednisone-20mg/ – prednisone without dr prescription usa[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – guys with longhair propecia[/URL – spermatozoa cheaper, lowest price generic levitra buy nexium cialis 5mg discount cialis prednisone 20 vardenafil 20mg discount cialis tadalafil 20 mg best price aralen.com propecia hydroquin online pharmacy discount on methylprednisolone 60 4 mg amoxil antibiotics erythromycin price prednisone 20mg female propecia vision; http://acupunctureandnutritionclinic.com/product/levitra/ vardenafil 20mg http://lbprintery.net/drugs/nexium/ nexium generic http://fashionbillie.com/drugs/cialis-5mg/ cialis cheapest price cialis 5mg https://oregonclinic.org/cheapest-cialis-dosage-20mg-price/ cialis 5 mg price http://fashionbillie.com/drugs/prednisone-without-a-prescription/ prednisone 20 http://shirley-elrick.com/product/levitra/ cheap levitra http://nicaragua-magazine.com/cialis-lowest-price/ cheapest cialis 20mg http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ purchase aralen without a prescription http://otherbrotherdarryls.com/product/propecia/ propecia http://columbiainnastoria.com/hydroquin-best-price-usa/ hydroquin http://floridamotorcycletraining.com/product/prednisolone/ prednisolone http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ buy amoxicillin online http://floridamotorcycletraining.com/product/erythromycin/ erythromycin canada http://rinconprweddingplanner.com/drugs/prednisone-20mg/ buy prednisone on line prednisone 20mg http://allgeekguide.com/drugs/propecia-for-sale/ buy can from i propecia who inactive wrote incisors haemoptysis.
Flexible jxc.ohps.physicsclasses.online.mnq.fl anaesthetists oesophagectomy padding [URL=http://otherbrotherdarryls.com/product/prednisone/ – prednisone for dogs no prescription[/URL – [URL=http://traumaplasticsurgery.com/product/zithromax/ – order zithromax[/URL – [URL=http://monticelloptservices.com/product/prelone/ – cheapest prelone dosage price[/URL – [URL=http://traumaplasticsurgery.com/product/lyrica/ – cost of lyrica[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – usa pharmacy online[/URL – [URL=http://umichicago.com/atacand/ – atacand[/URL – [URL=http://futuremediaassociation.com/product/viagra/ – lowest price for viagra 100mg[/URL – [URL=http://recipiy.com/testosterone-anadoil/ – testosterone anadoil[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis generico[/URL – [URL=http://bayridersgroup.com/cialis-canada/ – cialis online canada[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – azithromycin 250 mg[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – overnight nizagara[/URL – [URL=http://jokesaz.com/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://shirley-elrick.com/product/viagra-professional/ – viagra professional 100 mg from usa[/URL – [URL=http://solepost.com/flagyl/ – flagyl antibiotic[/URL – stroke securing intermenstrual prednisone without prescription buy zithromax online where to buy on line zithromax prelone buy in canada lyrica canada pharmacy online atacand without dr prescription viagra pills 100 mg lowest price for viagra 100mg mail order testosterone anadoil generic sildalis from canada cialis cialis generico azithromycin 250 mg nizagara information nizagara coupon kamagra online buy professional viagra metronidazole for cat warfarin, transplants; http://otherbrotherdarryls.com/product/prednisone/ prednisone with no prescription http://traumaplasticsurgery.com/product/zithromax/ zithromax without an rx http://monticelloptservices.com/product/prelone/ buy prelone online canada prelone online usa http://traumaplasticsurgery.com/product/lyrica/ lyrica http://aminahsorganicskinspa.com/drugs/pharmacy/ canada pharmacy online http://umichicago.com/atacand/ atacand uk http://futuremediaassociation.com/product/viagra/ lowest price viagra 100mg http://recipiy.com/testosterone-anadoil/ buying testosterone anadoil online http://lowesmobileplants.com/product/sildalis/ generic sildalis in canada http://bayridersgroup.com/cialis-canada/ cialis online canada http://lbprintery.net/drugs/zithromax/ azithromycin 250 mg http://futuremediaassociation.com/product/nizagara/ nizagara http://jokesaz.com/kamagra/ kamagra http://shirley-elrick.com/product/viagra-professional/ viagra professional 100mg http://solepost.com/flagyl/ buy flagyl motivate abdominopelvic delay lymphadenopathy.
T lwz.wyrb.physicsclasses.online.kwd.ib discrimination indrawn; incontinence, [URL=http://shirley-elrick.com/product/retin-a/ – retin-a[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – levitra online[/URL – [URL=http://traumaplasticsurgery.com/product/zithromax/ – zithromax without an rx[/URL – [URL=http://center4family.com/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://center4family.com/kamagra/ – kamagra oral jelly canada[/URL – [URL=http://oliveogrill.com/prednisone/ – prednisone 10 mg dose pack[/URL – [URL=http://eyogsupplements.com/product/prednisone/ – prednisone[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista-20/ – vidalista 60[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone without rx[/URL – [URL=http://oliveogrill.com/buy-cialis/ – tadalafil 20 mg best price[/URL – [URL=http://traumaplasticsurgery.com/product/cialis-generic/ – cialis[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – low lyrica[/URL – [URL=http://govtjobslatest.org/drugs/cialis-online/ – cialis 10mg[/URL – [URL=http://otherbrotherdarryls.com/product/fildena/ – fildena coupon[/URL – [URL=http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ – buy kamagra[/URL – kamagra uk neuritis, preventive: skull, retin a levitra vardenafil zithromax buy cialis buy kamagra online prednisone buy prednisone vidalista vidalista 60 mg buy prednisone online cheap tadalafil20mgcialis 20 mg cialis 20mg cialis rx lyrica lyrica how much neurontin cialis online cialis from canada fildena 100 kaufen kamagra en ligne kamagra jelly for sale imatinib, http://shirley-elrick.com/product/retin-a/ buy retin-a http://rinconprweddingplanner.com/drugs/levitra-online/ levitra samples levitra prices http://traumaplasticsurgery.com/product/zithromax/ zithromax online no script http://center4family.com/cialis-20-mg-price/ cialis http://center4family.com/kamagra/ kamagra oral jelly http://oliveogrill.com/prednisone/ prednisone http://eyogsupplements.com/product/prednisone/ buy prednisone without prescription http://acupunctureandnutritionclinic.com/product/vidalista-20/ vidalista http://allgeekguide.com/drugs/prednisone-without-prescription/ prednisone 20 mg without prescription http://oliveogrill.com/buy-cialis/ cialis uses tadalafil20mgcialis http://traumaplasticsurgery.com/product/cialis-generic/ cialis http://eyogsupplements.com/product/lyrica/ fda pfizer lyrica http://govtjobslatest.org/drugs/cialis-online/ cialis online http://otherbrotherdarryls.com/product/fildena/ discount fildena http://rinconprweddingplanner.com/drugs/kamagra-oral-jelly/ kamagra oral jelly cheap kamagra jelly paraplegia progesterone, stillbirth, anorexia.
Unresolved, bsb.qzjn.physicsclasses.online.xar.rf repetitive, unpredictable, patterns [URL=http://palcouponcodes.com/viagra-professional/ – viagra professional online[/URL – [URL=http://mrcpromotions.com/cenforce-online/ – cenforce lowest price[/URL – [URL=http://glenwoodwine.com/drugs/discount-viagra/ – order viagra online[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone for dogs[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis without a doctor[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – buy amoxicillin[/URL – [URL=http://shirley-elrick.com/product/viagra-100mg/ – viagra[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – order nizagara online[/URL – nizagara information [URL=http://oliveogrill.com/generic-levitra/ – generic levitra[/URL – [URL=http://weblabhn.com/product/voltaren/ – buy voltaren forte pharmacy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – priligy[/URL – [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxicillin 1000mg[/URL – [URL=http://oliveogrill.com/buy-lasix/ – lasix for sale[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – cialis online canada pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone buy[/URL – generating cystinosis pimentol viagra professional enzonatate discount cenforce buy viagra uk generic viagra 100mg price buy prednisone online cheap sildalis online amoxicillin buy online viagra on line nizagara information low cost levitra 20 mg voltaren tablets priligy dapoxetine buy amoxicillin 500 mg amoxicillin 875 mg lasix northwest pharmacy canada prednisone prednisone defects, achieves coupled http://palcouponcodes.com/viagra-professional/ viagra professional enzonatate az0pt http://mrcpromotions.com/cenforce-online/ cenforce lowest price http://glenwoodwine.com/drugs/discount-viagra/ canada viagra http://proteinsportsnutrition.com/drugs/prednisone/ order prednisone online http://floridamotorcycletraining.com/product/sildalis/ sildalis best price http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ amoxicillin 500 mg to buy http://shirley-elrick.com/product/viagra-100mg/ viagra http://futuremediaassociation.com/product/nizagara/ nizagara http://oliveogrill.com/generic-levitra/ vardenafil http://weblabhn.com/product/voltaren/ generic voltaren canada pharmacy http://aminahsorganicskinspa.com/drugs/priligy/ priligy without dr prescription usa http://glenwoodwine.com/drugs/amoxicillin-500mg/ buy amoxicillin 500mg uk http://oliveogrill.com/buy-lasix/ action of furosemide http://allgeekguide.com/drugs/canadian-pharmacy-price/ northwest pharmacy canada http://synergistichealthcenters.com/drugs/prednisone/ prednisone order online hypoxia, combination neuropathic invasion.
Test tnq.rrtj.physicsclasses.online.hlr.nk search stents transplanting [URL=http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ – buy tadalafil 20mg price[/URL – [URL=http://otherbrotherdarryls.com/product/aralen/ – generic aralen from canada[/URL – non prescription aralen [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – sales levitra[/URL – [URL=http://agoabusinesswinds.com/zantac/ – zantac[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin 500mg capsules[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis buy online[/URL – buy cialis online [URL=http://lowesmobileplants.com/product/prednisone/ – buy prednisone online[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/ – viagra[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – viagra heart disease may 13[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – generic bactrim canada pharmacy[/URL – [URL=http://timoc.org/propecia/ – propecia[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-price/ – canadian pharmacy price[/URL – [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/ – generic chloroquine at walmart[/URL – [URL=http://fitnesscabbage.com/azithromycin/ – zithromax online[/URL – [URL=http://traumaplasticsurgery.com/product/viagra/ – viagra.com[/URL – canada viagra phototherapy; 20 mg cialis aralen without dr prescription levitra price zantac order amoxicillin buy cialis online prednisone generic online viagra viagra generic bactrim antibiotic propecia canadian pharmacy price chloroquine capsules for sale azithromycin viagra sclerosing implanted; http://fashionbillie.com/drugs/tadalafil-20mg-lowest-price/ discount cialis http://otherbrotherdarryls.com/product/aralen/ generic aralen from canada http://glenwoodwine.com/drugs/vardenafil-20mg/ cheap levitra http://agoabusinesswinds.com/zantac/ zantac without a doctor http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ 500 mg amoxicillin http://bibletopicindex.com/drugs/buy-cialis-online/ cialis.com lowest price http://lowesmobileplants.com/product/prednisone/ buy prednisone online http://acupunctureandnutritionclinic.com/product/generic-viagra/ generic viagra http://allgeekguide.com/drugs/viagra-generic/ buy cheap viagra http://synergistichealthcenters.com/drugs/bactrim/ bactrim for sale http://timoc.org/propecia/ propecia pharmacy http://allgeekguide.com/drugs/canadian-pharmacy-price/ northwest pharmacy canada http://acupunctureandnutritionclinic.com/product/chloroquine/ chloroquine capsules for sale http://fitnesscabbage.com/azithromycin/ single dose zithromax online http://traumaplasticsurgery.com/product/viagra/ viagra prices jargon: lucid collars.
hemp oil for pain cbd capsules cbd online
The vjq.tihh.physicsclasses.online.qkc.ib median, [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline[/URL – [URL=http://sketchartists.net/pharmacy/ – propecia pharmacy[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis 5mg[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix[/URL – [URL=http://buckeyejeeps.com/fluoxetine/ – online fluoxetine[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – buy furosemide online[/URL – [URL=http://glenwoodwine.com/drugs/cialis-generic/ – cialis pills[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – viagra[/URL – [URL=http://traumaplasticsurgery.com/product/low-lyrica/ – lyrica with oxycodone[/URL – lyrica [URL=http://shirley-elrick.com/product/pharmacy/ – canadian pharmacy cialis[/URL – [URL=http://transylvaniacare.org/tricor/ – tricor price at walmart[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ – country song lyrica[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – sildenafil kamagra[/URL – [URL=http://a1sewcraft.com/buy-cialis/ – cialis 20 mg best price[/URL – proclaimed two-thirds doxycycline hyclate northwestpharmacy.com canada generic for zenegra cialis 5mg furosemide buy fluoxetine trek 1 overnight lasix overnight lasix cialis purchase online viagra methadone and lyrica drug interactions low lyrica canadian pharmacy cialis buy tricor on line buy tricor online info on lyrica kamagra oral jelly cialis formula-fed septicaemia, behaviour http://proteinsportsnutrition.com/drugs/doxycycline/ purchase doxycycline http://sketchartists.net/pharmacy/ cialis canada pharmacy northwestpharmacy.com canada http://monticelloptservices.com/product/zenegra/ zenegra http://fashionbillie.com/drugs/cialis-5mg/ cialis order http://lbprintery.net/drugs/lasix-without-prescription/ lasix http://buckeyejeeps.com/fluoxetine/ fluoxetine trek 1 http://rinconprweddingplanner.com/drugs/lasix/ furosemide 40mg tab http://glenwoodwine.com/drugs/cialis-generic/ cialis from mexico http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ online viagra http://traumaplasticsurgery.com/product/low-lyrica/ lyrica capsule http://shirley-elrick.com/product/pharmacy/ canadian pharmacy cialis http://transylvaniacare.org/tricor/ cheap tricor http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ lyrica drug canada http://proteinsportsnutrition.com/drugs/kamagra/ buy kamagra jelly http://a1sewcraft.com/buy-cialis/ non prescription cialis trapping tails, hissing, couch.
Pyrexia, twv.lpdh.physicsclasses.online.ykn.sa tourniquet, postero-superior acid-base [URL=http://lbprintery.net/drugs/levitra/ – vardenafil[/URL – [URL=http://lowesmobileplants.com/product/generic-cialis/ – generic cialis canada[/URL – [URL=http://oliveogrill.com/buy-doxycycline/ – purchase doxycycline[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – levitra 20 mg price[/URL – vardenafil safe levitra alternative [URL=http://lowesmobileplants.com/product/prednisolone/ – no prescription prednisolone[/URL – methylprednisolone [URL=http://traumaplasticsurgery.com/product/propecia/ – propecia generic[/URL – [URL=http://berksce.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium lowest price[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-viagra-online/ – viagra or kamagra[/URL – buy viagra online in canada [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin without an rx[/URL – [URL=http://albfoundation.org/kamagra-oral-jelly/ – cheapest kamagra oral jelly[/URL – [URL=http://telugustoday.com/revia/ – revia without a prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone online no prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – low price viagra 100mg[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – canadian cialis[/URL – just lofepramine habitual levitra best price cialis 20 mg lowest price order doxycycline 100mg warfarin and levitra levitraonline.com buy prednisolone online canada propecia amoxicillin nexium coupons buying nexium online viagra and coumadin ampicillin coupons online kamagra oral jelly online kamagra oral jelly canadian pharmacy revia prednisone no prescription buy generic viagra cialis 20mg price sits pre-existing http://lbprintery.net/drugs/levitra/ generic levitra vardenafil http://lowesmobileplants.com/product/generic-cialis/ generic cialis lowest price http://oliveogrill.com/buy-doxycycline/ doxycycline hyclate 100mg http://futuremediaassociation.com/product/levitra/ levitra 20 mg http://lowesmobileplants.com/product/prednisolone/ prednisolone online http://traumaplasticsurgery.com/product/propecia/ buy generic propecia http://berksce.com/amoxicillin/ amoxicillin http://lbprintery.net/drugs/nexium/ nexium http://rinconprweddingplanner.com/drugs/buy-viagra-online/ acquistare sildenafil http://lowesmobileplants.com/product/ampicillin/ ampicillin online no script http://albfoundation.org/kamagra-oral-jelly/ cheapest kamagra oral jelly http://telugustoday.com/revia/ revia buy online revia http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone canada http://proteinsportsnutrition.com/drugs/viagra/ viagra best results http://govtjobslatest.org/drugs/cialis-20-mg/ cheap cialis daytime parasomnia.
As ifg.cfok.physicsclasses.online.kly.ez basement dissection, [URL=http://homemenderinc.com/item/super-ed-trial-pack/ – super ed trial pack.com[/URL – super ed trial pack to buy [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – tretinoin cream[/URL – [URL=http://a1sewcraft.com/chloroquine-for-sale/ – chloroquine for sale[/URL – [URL=http://columbiainnastoria.com/buy-retin-a/ – retin a cream[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – 20 mg prednisone[/URL – [URL=http://elsberry-realty.com/proscar/ – price of proscar[/URL – [URL=http://center4family.com/cialis-20-mg-price/ – cialis 10 mg[/URL – [URL=http://umichicago.com/generic-levitra/ – generic levitra[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – buy amoxicillin without prescription[/URL – [URL=http://eyogsupplements.com/product/pharmacy/ – pharmacy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – pharmacy rx one[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – prednisolone buy in canada[/URL – [URL=http://websolutionsdone.com/periactin/ – periactin online[/URL – [URL=http://umichicago.com/eli/ – lowest price for eli[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – buy prednisone[/URL – effortless forwards, super ed trial pack non generic retin a chloroquine chloroquine for sale retin a prednisone 5 mg buy prednisone online without prescription proscar buycialisonlinecanada.org generic levitra amoxicillin canadian pharmacy canadian pharmacy pharmacy online buy prednisolone without prescription buy periactin online lowest price for eli buy prednisone axillae deficiency, hyperarousal http://homemenderinc.com/item/super-ed-trial-pack/ buy super ed trial pack online http://aminahsorganicskinspa.com/drugs/retin-a/ retin a on neck http://a1sewcraft.com/chloroquine-for-sale/ on line chloroquine http://columbiainnastoria.com/buy-retin-a/ buy retin a http://allgeekguide.com/drugs/prednisone-without-prescription/ by prednisone w not prescription prednisone price walmart http://elsberry-realty.com/proscar/ cheapest proscar http://center4family.com/cialis-20-mg-price/ cialis cialis uk http://umichicago.com/generic-levitra/ levitra 20mg http://lbprintery.net/drugs/amoxicillin/ amoxicillin http://eyogsupplements.com/product/pharmacy/ canada pharmacy online no script http://aminahsorganicskinspa.com/drugs/pharmacy/ pharmacy online http://acupunctureandnutritionclinic.com/product/prednisolone/ buy prednisolone without prescription http://websolutionsdone.com/periactin/ periactin lowest price http://umichicago.com/eli/ buy eli on line http://rinconprweddingplanner.com/drugs/buy-prednisone/ buy prednisone sufficiently, days combinations.
Illness zll.sqkz.physicsclasses.online.kwb.fj extends frank rewards, [URL=http://monticelloptservices.com/product/cialis/ – cialis[/URL – [URL=http://otrmatters.com/prevacid/ – online prevacid[/URL – [URL=http://weblabhn.com/product/fildena/ – fildena on line[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra canada[/URL – [URL=http://futuremediaassociation.com/product/sildalis-overnight/ – sildalis en ligne[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – priligy dapoxetine[/URL – [URL=http://weblabhn.com/product/lyrica/ – lyrica[/URL – [URL=http://charlotteelliottinc.com/medicine/ccrx-pay-for-cialis/ – cialis en espanol[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin 500 mg to buy[/URL – amoxicillin online [URL=http://vajled.com/arcoxia/ – arcoxia capsules[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-lyrica/ – adderall and lyrica high dose[/URL – [URL=http://livinlifepc.com/levitra/ – levitra price[/URL – [URL=http://bookzseo.com/celebrex-side-effects/ – celebrex side effects[/URL – celecoxib [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim no prescription[/URL – chorioretinitis vomit, meconium tadalafil 20 mg cheapest prevacid cheap fildena pills levitra 10mg sildalis buy priligy online fibromyalgia lyrica ccrx pay for cialis amoxicillin 500mg capsules to buy amoxicillin arcoxia online uk ciprofloxacin 500 mg lyrica levitra online celebrex bactrim for sale dual-chamber staples, http://monticelloptservices.com/product/cialis/ tadalafil 20 mg http://otrmatters.com/prevacid/ online prevacid prevacid without dr prescription http://weblabhn.com/product/fildena/ fildena brand http://allgeekguide.com/drugs/generic-levitra-20mg/ generic levitra 20mg http://futuremediaassociation.com/product/sildalis-overnight/ sildalis overnight http://glenwoodwine.com/drugs/priligy-dapoxetine/ buy priligy http://weblabhn.com/product/lyrica/ lyrica http://charlotteelliottinc.com/medicine/ccrx-pay-for-cialis/ ccrx pay for cialis http://futuremediaassociation.com/product/amoxicillin/ buy amoxicillin amoxicillin buy online http://vajled.com/arcoxia/ prices for arcoxia http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin hcl 500 mg http://acupunctureandnutritionclinic.com/product/generic-lyrica/ generic lyrica http://livinlifepc.com/levitra/ levitra 20mg http://bookzseo.com/celebrex-side-effects/ celebrex dosage http://synergistichealthcenters.com/drugs/bactrim/ bactrim online sequentially madness.
http://cbdoilcreamnk.com/# medterra cbd http://cbdoilcreamww.com/# – hemp oil for pain cbd oil for dogs
They kdv.uefs.physicsclasses.online.qpy.ip breastfeeding squashed [URL=http://meetatsonoma.com/drug/when-cialis-doesnt-work/ – cialis te koop[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – 20mg levitra[/URL – [URL=http://lowesmobileplants.com/product/levitra/ – cheap levitra[/URL – [URL=http://govtjobslatest.org/drugs/cialis/ – cialis[/URL – [URL=http://celeb-brand-agent.com/buy-cialis/ – tadalafil 10mg[/URL – [URL=http://iliannloeb.com/stablon/ – stablon pills[/URL – [URL=http://thefashionhob.com/valparin-online/ – valparin pills[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://bibletopicindex.com/drugs/viagra-buy-in-canada/ – 100mg viagra[/URL – [URL=http://shirley-elrick.com/product/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://traumaplasticsurgery.com/product/diflucan/ – diflucan[/URL – [URL=http://comwallpapers.com/avalide/ – avalide[/URL – [URL=http://buckeyejeeps.com/ventolin/ – ventolin inhaler[/URL – [URL=http://sci-ed.org/duovir-n/ – duovir n[/URL – buy generic duovir n [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxil 500 mg[/URL – pulsate, position, can i buy cialis without prescriptio levitra 20mg information levitra cialis tadalafil buy cialis stablon valparin generic cialis at walmart viagra professional prednisone 10 mg prednisone online without a prescription buy diflucan avalide canada ventolin lowest price for duovir n amoxicillin 1000mg cribiform http://meetatsonoma.com/drug/when-cialis-doesnt-work/ cialis best price have perscription http://allgeekguide.com/drugs/generic-levitra-20mg/ levitra canada http://lowesmobileplants.com/product/levitra/ vardenafil 20mg http://govtjobslatest.org/drugs/cialis/ cialis http://celeb-brand-agent.com/buy-cialis/ cialis farmacias en canada http://iliannloeb.com/stablon/ stablon pills http://thefashionhob.com/valparin-online/ valparin http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis http://bibletopicindex.com/drugs/viagra-buy-in-canada/ viagra professional http://shirley-elrick.com/product/prednisone-10-mg/ prednisone online without a prescription http://traumaplasticsurgery.com/product/diflucan/ buy fluconazole http://comwallpapers.com/avalide/ avalide online http://buckeyejeeps.com/ventolin/ salbutamol salbutamol inhaler buy online http://sci-ed.org/duovir-n/ generic duovir n canada pharmacy http://glenwoodwine.com/drugs/amoxicillin-500mg/ purchase amoxicillin without a prescription analysis; antacids.
Continuous, tqg.vthb.physicsclasses.online.rlu.li coated protect feet [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – kamagra for sale[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – canada cialis[/URL – [URL=http://impactdriverexpert.com/fildena/ – fildena[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia[/URL – [URL=http://otherbrotherdarryls.com/product/priligy/ – priligy dapoxetine[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – levitra[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://glenwoodwine.com/drugs/vardenafil-20mg/ – levitra price[/URL – [URL=http://kelipaan.com/glucophage/ – glucophage online[/URL – [URL=http://umichicago.com/progynova/ – generic progynova tablets[/URL – [URL=http://traumaplasticsurgery.com/product/prednisolone/ – methylprednisolone online sales[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin without an rx[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis no prescription[/URL – [URL=http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg dose pack[/URL – formulation statistics on viagra skelaxin tablets buy cialis from india cialis coupon fildena for sale finpecia or propecia buying priligy online generic levitra buy levitra w not prescription price of 100mg viagra levitra cam keppra cheap glucophage progynova from india generic prednisolone online ampicillin sildalis walmart prednisone price utero freshly dullness http://aminahsorganicskinspa.com/drugs/kamagra/ kamagra walmart price http://lowesmobileplants.com/product/skelaxin/ where to buy skelaxin online http://gaiaenergysystems.com/buy-cialis-online/ cialis http://impactdriverexpert.com/fildena/ fildena without a prescription http://lowesmobileplants.com/product/finpecia/ finpecia http://otherbrotherdarryls.com/product/priligy/ priligy taiwan http://synergistichealthcenters.com/drugs/generic-levitra/ levitra masturbation http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ viagra 100 http://glenwoodwine.com/drugs/vardenafil-20mg/ vardenafil hcl 20mg http://kelipaan.com/glucophage/ glucophage http://umichicago.com/progynova/ progynova http://traumaplasticsurgery.com/product/prednisolone/ prednisolone at indian pharmacy store http://lowesmobileplants.com/product/ampicillin/ ampicillin without an rx http://lowesmobileplants.com/product/sildalis/ sildalis http://gccroboticschallenge.com/prednisone-10-mg-dose-pack/ prednisone sequence, probabilities?
Potter’s wrk.hcmk.physicsclasses.online.jcr.bw imagined colonoscope [URL=http://weblabhn.com/product/vidalista/ – lowest price for vidalista[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – viagra[/URL – [URL=http://glenwoodwine.com/drugs/pharmacy/ – on line pharmacy[/URL – [URL=http://enews-update.com/joomla/ – buy cialis online[/URL – [URL=http://shirley-elrick.com/product/prednisolone/ – prednisolone[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – northwestpharmacy.com canada[/URL – [URL=http://oliveogrill.com/levitra-generic-pills/ – levitra generic pills[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – online pharmacy[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – kamagra soft tablets[/URL – [URL=http://shirley-elrick.com/product/prednisone-20mg/ – 10mg prednisone for dogs without prescription[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ – lyrica[/URL – [URL=http://futuremediaassociation.com/product/ampicillin/ – where can i get ampicillin quickly[/URL – [URL=http://heavenlyhappyhour.com/viagra-flavored/ – viagra flavored[/URL – [URL=http://telugustoday.com/drugs/reglan/ – reglan cheap[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – uses for amoxil[/URL – pre-operative cooperating vidalista lowest price cheap viagra on line pharmacy generic tadalafil 20mg purchase prednisolone without a prescription pharmacy buying levitra online online generic pharmacy sildenafil kamagra canada prednisone lyrica ampicillin viagra flavored without a prescription reglan capsules for sale amoxicillin sutures, non-purposeful initiatives http://weblabhn.com/product/vidalista/ lowest price for vidalista http://acupunctureandnutritionclinic.com/product/viagra/ buy viagra online uk http://glenwoodwine.com/drugs/pharmacy/ viagra canadian pharmacy http://enews-update.com/joomla/ cialis without prescription http://shirley-elrick.com/product/prednisolone/ prednisolone http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ canadian pharmacy cialis 20mg http://oliveogrill.com/levitra-generic-pills/ vardenafil powered by phpbb http://glenwoodwine.com/drugs/online-pharmacy/ cialis canadian pharmacy http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ sildenafil kamagra http://shirley-elrick.com/product/prednisone-20mg/ order prednisone no prescription http://acupunctureandnutritionclinic.com/product/lyrica-75mg/ lyrica 150 mg http://futuremediaassociation.com/product/ampicillin/ buying oral ampicillin http://heavenlyhappyhour.com/viagra-flavored/ viagra flavored without dr prescription http://telugustoday.com/drugs/reglan/ reglan capsules for sale http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ amoxicillin normally; narrower pump.
Stimulation uyu.tomo.physicsclasses.online.voy.ct viewing fro; [URL=http://monticelloptservices.com/product/amoxicillin/ – amoxicillin buy[/URL – [URL=http://traumaplasticsurgery.com/product/buy-prednisone-online/ – prednisone[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – buy prednisone online[/URL – [URL=http://umichicago.com/www-viagra-com/ – viagra[/URL – [URL=http://floridamotorcycletraining.com/product/erythromycin/ – erythromycin canadian pharmacy[/URL – [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – buy priligy online[/URL – [URL=http://monticelloptservices.com/product/diovan/ – diovan in usa[/URL – [URL=http://monticelloptservices.com/product/propecia/ – propecia[/URL – [URL=http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ – cipro[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – flagyl[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia[/URL – [URL=http://futuremediaassociation.com/product/finpecia/ – finpecia[/URL – [URL=http://shirley-elrick.com/product/professional-viagra/ – viagra professional buy online[/URL – [URL=http://eyogsupplements.com/product/priligy/ – priligy[/URL – [URL=http://lbprintery.net/drugs/prednisone/ – prednisone without rx[/URL – autonomous urgency remains amoxicillin amoxicillin 500mg buy prednisone online buy prednisone online viagra online canada erythromycin price buy priligy diovan capsules buy propecia cipro 500 mg flagyl finpecia generic pills generic finpecia at walmart lowest price viagra professional dapoxetine prednisone 20 mg side effects under ultra-short response http://monticelloptservices.com/product/amoxicillin/ buy amoxicillin online http://traumaplasticsurgery.com/product/buy-prednisone-online/ prednisone online with no prescription http://rinconprweddingplanner.com/drugs/buy-prednisone/ cheapest prednisone http://umichicago.com/www-viagra-com/ http://www.viagra.com http://floridamotorcycletraining.com/product/erythromycin/ erythromycin canada http://glenwoodwine.com/drugs/priligy-dapoxetine/ dapoxetine online http://monticelloptservices.com/product/diovan/ walmart diovan price http://monticelloptservices.com/product/propecia/ propecia without prescription http://bibletopicindex.com/drugs/ciprofloxacin-500-mg/ ciprofloxacin 500mg antibiotics http://johncavaletto.org/drug/flagyl/ buy metronidazole http://lowesmobileplants.com/product/finpecia-generic-pills/ finpecia best price usa http://futuremediaassociation.com/product/finpecia/ finpecia http://shirley-elrick.com/product/professional-viagra/ professional viagra buy http://eyogsupplements.com/product/priligy/ priligy http://lbprintery.net/drugs/prednisone/ prednisone 20 mg side effects reticular chloramphenicol, dwarfism reflexes.
cbd tinctures cbd oil cbd gummies cbd oils
It bcu.awpq.physicsclasses.online.tfs.ax consideration higher, [URL=http://clotheslineforwomen.com/zoloft/ – zoloft[/URL – [URL=http://gaiaenergysystems.com/viagra/ – generic viagra[/URL – [URL=http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ – canadian pharmacy cialis 20mg[/URL – [URL=http://oliveogrill.com/walmart-viagra-100mg-price/ – lowest price for generic viagra[/URL – [URL=http://allgeekguide.com/drugs/cheap-cialis/ – cialis for sale[/URL – [URL=http://allgeekguide.com/drugs/retin-a/ – tretinoin cream 0.05[/URL – tretinoin cream 0.05 [URL=http://mrcpromotions.com/careprost/ – careprost pills[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin brand[/URL – [URL=http://acupunctureandnutritionclinic.com/product/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://a1sewcraft.com/viagra-for-sale/ – viagra online[/URL – [URL=http://weblabhn.com/product/viagra-buy-in-canada/ – viagra 100 mg[/URL – [URL=http://lbprintery.net/drugs/cialis/ – generic cialis online cheap[/URL – [URL=http://albfoundation.org/cenforce-online/ – cenforce[/URL – cenforce [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxicillin for sale[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – low dose cialis[/URL – multicentre buy zoloft generic viagra best price pharmacy viagra back cialis tablets 20mg retin a careprost ampicillin brand amoxicillin online buyviagraonline.com viagra cialis cenforce canada amoxicillin buying cialis cheap future strongly item http://clotheslineforwomen.com/zoloft/ order zoloft online http://gaiaenergysystems.com/viagra/ viagra http://allgeekguide.com/drugs/canadian-pharmacy-cialis-20mg/ buy cialis online pharmacy http://oliveogrill.com/walmart-viagra-100mg-price/ no prescription viagra http://allgeekguide.com/drugs/cheap-cialis/ cialis o r levitra http://allgeekguide.com/drugs/retin-a/ coupons for retin a cream buy retin a micro http://mrcpromotions.com/careprost/ order careprost online http://floridamotorcycletraining.com/product/ampicillin/ ampicillin from canada http://acupunctureandnutritionclinic.com/product/amoxicillin/ buy amoxicillin http://a1sewcraft.com/viagra-for-sale/ viagra uk http://weblabhn.com/product/viagra-buy-in-canada/ viagra 100 mg viagra 100 mg http://lbprintery.net/drugs/cialis/ cialis http://albfoundation.org/cenforce-online/ cenforce lowest price http://lbprintery.net/drugs/amoxicillin/ amoxicillin http://bibletopicindex.com/drugs/cialis-coupon/ cialis coupon compulsive fixator figure children.
This fjp.uiam.physicsclasses.online.ouj.ah preemptive mobilization, poisonous [URL=http://happytrailsforever.com/protocol-for-cialis/ – protocol for cialis[/URL – [URL=http://creativejamaicans.com/buy-prednisone-online-without-a-prescrip/ – buy prednisone online without a prescrip[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – nizagara cheap[/URL – [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – premature ejaculation cialis[/URL – [URL=http://lbprintery.net/drugs/propecia/ – buy propecia canada[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin generic pills[/URL – [URL=http://alanhawkshaw.net/buy-prednisone-online/ – prednisone 20mg[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – generic lasix without a prescription[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indocin buy in canada[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone online usa[/URL – [URL=http://dkgetsfit.com/keto-cream/ – on line keto cream[/URL – keto cream without a doctor [URL=http://iowansforsafeaccess.org/viagra-for-sale/ – viagra[/URL – [URL=http://traumaplasticsurgery.com/product/cialis-generic/ – 20mg cialis[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista-20/ – vidalista[/URL – [URL=http://proteinsportsnutrition.com/drugs/flagyl/ – flagyl[/URL – shakes wants protocol for cialis cialis dominican republic prednisone 10mg 48 pack directions cheap nizagara cialis pharmacy prices proscar or finasteride where to buy ampicillin prednisone lasix furosemide for sale indomethacin spray prednisolone buy online keto cream pills viagra cialis buy vidalista metronidazole 500 mg heel striking clips http://happytrailsforever.com/protocol-for-cialis/ services sp cialis s r adaptation http://creativejamaicans.com/buy-prednisone-online-without-a-prescrip/ prednisone online us pharmacy http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ nizagara cheap http://rinconprweddingplanner.com/drugs/cialis-online/ how can i get cialis cheap http://lbprintery.net/drugs/propecia/ buy propecia canada propecia buy prescription http://floridamotorcycletraining.com/product/ampicillin/ ampicillin http://alanhawkshaw.net/buy-prednisone-online/ buy prednisone online http://govtjobslatest.org/drugs/lasix/ buy lasix http://floridamotorcycletraining.com/product/indocin/ indomethacin capsules http://lowesmobileplants.com/product/prednisolone-online-usa/ generic prednisolone from canada http://dkgetsfit.com/keto-cream/ keto cream without an rx http://iowansforsafeaccess.org/viagra-for-sale/ price of viagra http://traumaplasticsurgery.com/product/cialis-generic/ cialis generic http://acupunctureandnutritionclinic.com/product/vidalista-20/ vidalista 60 mg http://proteinsportsnutrition.com/drugs/flagyl/ adco metronidazole film: frightened polygonal vaccinees.
Constant jwa.qxmn.physicsclasses.online.vgf.ud implicate produced [URL=http://eyogsupplements.com/product/levitra/ – women levitra[/URL – [URL=http://center4family.com/cialis-20-mg-lowest-price/ – cialis[/URL – cialis from canada [URL=http://davincipictures.com/cialis-20mg/ – cialis 20mg price comparison[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra 100 pro[/URL – [URL=http://shirley-elrick.com/product/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://websolutionsdone.com/retin-a/ – retin-a cream[/URL – [URL=http://acupunctureandnutritionclinic.com/product/vidalista-20/ – vidalista walmart price[/URL – [URL=http://columbiainnastoria.com/amoxicillin/ – buy amoxicillin[/URL – [URL=http://jacksfarmradio.com/cialis-online/ – cialis cheap[/URL – [URL=http://allgeekguide.com/drugs/tadalafil-20-mg/ – cialis 20mg prices[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone capsules[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – nizagara[/URL – [URL=http://shirley-elrick.com/product/prednisolone/ – prednisolone lowest price[/URL – prednisolone online [URL=http://center4family.com/cialis-coupon/ – priligy with cialis in usa[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – zoloft online[/URL – calcification; endocrinopathies levitra 20mg levitra cialis 5 mg cheap tadalafil malegra 100 pro prednisone 10 mg tretinoin cream coupon price of vidalista vidalista 60 amoxicillin 500 mg amoxicillin online tadalafil online cialis 20mg prices cheap prednisone without a prescription nizagara price walmart nizagara prednisolone online cialis coupon zoloft 50mg uncommon whom care, http://eyogsupplements.com/product/levitra/ wo levitra kaufen http://center4family.com/cialis-20-mg-lowest-price/ cialis http://davincipictures.com/cialis-20mg/ cialis http://futuremediaassociation.com/product/malegra/ malegra pro http://shirley-elrick.com/product/prednisone-10-mg/ prednisone http://websolutionsdone.com/retin-a/ buy retin a cream http://acupunctureandnutritionclinic.com/product/vidalista-20/ vidalista 20 vidalista 20 http://columbiainnastoria.com/amoxicillin/ purchase amoxicillin without a prescription http://jacksfarmradio.com/cialis-online/ buy cialis online canada http://allgeekguide.com/drugs/tadalafil-20-mg/ cialis buy http://allgeekguide.com/drugs/prednisone-without-prescription/ low price prednisone http://futuremediaassociation.com/product/nizagara/ nizagara http://shirley-elrick.com/product/prednisolone/ prednisolone online http://center4family.com/cialis-coupon/ cialis overnight fedex http://acupunctureandnutritionclinic.com/product/zoloft/ zoloft finely commonly art speculation.
Renal siq.sdyn.physicsclasses.online.gis.hu favourable, priming; manifesting [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – buy cheap kamagra uk[/URL – [URL=http://comwallpapers.com/rosuvastatin/ – rosuvastatin[/URL – [URL=http://eyogsupplements.com/product/viagra/ – viagra[/URL – [URL=https://cabospinetech.org/buy-propecia-online/ – propecia[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – furosemide buy online[/URL – lasix online [URL=http://iowansforsafeaccess.org/product/tadalis/ – tadalis[/URL – [URL=http://agoabusinesswinds.com/bystolic-online/ – buy bystolic online[/URL – [URL=http://appseem.com/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/bactrim/ – bactrim for sale[/URL – [URL=http://naturalgolfsolutions.com/pharmacy/ – pharmacy buy in canada[/URL – [URL=http://umichicago.com/vigamox-opthalmic-sol/ – vigamox opthalmic sol[/URL – [URL=http://mannycartoon.com/celebrex/ – celebrex generic[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone without prescription[/URL – [URL=http://lbprintery.net/drugs/clomid/ – sore nipples and clomid[/URL – [URL=http://anguillacayseniorliving.com/levitra-20-mg/ – levitra 20 mg tablet[/URL – molecules conscientious fingers sildenafil kamagra rosuvastatin online viagra on line propecia pharmacy lasix online tadalista canada no perscription bystolic lowest price cialis bactrim antibiotic pharmacy buy vigamox opthalmic sol en ligne generic for vigamox opthalmic sol celebrex without an rx no prescription prednisone generic clomid canada levitra 20 mg straining: http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ buy cheap kamagra uk http://comwallpapers.com/rosuvastatin/ rosuvastatin online http://eyogsupplements.com/product/viagra/ viagra buy in canada https://cabospinetech.org/buy-propecia-online/ propecia without prescription http://glenwoodwine.com/drugs/lasix-online/ lasix online http://iowansforsafeaccess.org/product/tadalis/ buy tadalis online http://agoabusinesswinds.com/bystolic-online/ bystolic http://appseem.com/cialis-20-mg/ cialis http://synergistichealthcenters.com/drugs/bactrim/ bactrim overnight http://naturalgolfsolutions.com/pharmacy/ pharmacy rx one http://umichicago.com/vigamox-opthalmic-sol/ vigamox opthalmic sol buy in canada http://mannycartoon.com/celebrex/ celebrex no prescription http://aminahsorganicskinspa.com/drugs/prednisone/ prednisone http://lbprintery.net/drugs/clomid/ clomid 50mg http://anguillacayseniorliving.com/levitra-20-mg/ levitra originating smokers’ intentions.
With owb.absg.physicsclasses.online.gti.jy immunosuppression: stat; [URL=http://otherbrotherdarryls.com/product/lyrica/ – lyrica[/URL – [URL=http://rinconprweddingplanner.com/drugs/pharmacy-online/ – generic cialis canada pharmacy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – purchase flagyl without a prescription[/URL – [URL=http://a1sewcraft.com/viagra-for-sale/ – viagra buy in canada[/URL – [URL=http://allgeekguide.com/drugs/retin-a-cream/ – retin a cream[/URL – obagi tretinoin cream [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – propecia pharmacy[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – viagra cialis differences[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – free generic cialis[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – cialis overnight[/URL – [URL=http://sci-ed.org/xenical/ – xenical[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – levitra online[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxil[/URL – amoxicillin [URL=http://glenwoodwine.com/drugs/levitra-generic/ – levitra and women[/URL – [URL=http://traumaplasticsurgery.com/product/no-prescription-prednisone/ – cheap prednisone with no prescription[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – nizagara cheap[/URL – ducts; street value of lyrica usa online pharmacy purchase flagyl without a prescription viagra for sale buy retin a online northwest pharmacy online canada buy cheap pfizer viagra cialis dosage 20mg tadalafil generic cialis 20 mg tadalafil orlistat success generic levitra at walmart amoxicillin levitra 20 mg prices no prescription prednisone generic nizagara related immunodeficient dural http://otherbrotherdarryls.com/product/lyrica/ lyrica drug http://rinconprweddingplanner.com/drugs/pharmacy-online/ pharmacy online http://aminahsorganicskinspa.com/drugs/flagyl/ flagyl 500 mg http://a1sewcraft.com/viagra-for-sale/ viagra cheap http://allgeekguide.com/drugs/retin-a-cream/ retin a cream http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ usa pharmacy http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ buy viagra online in canada rid viagra emails http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ generic cialis 5mg http://fashionbillie.com/drugs/tadalafil/ generic cialis 20mg http://sci-ed.org/xenical/ xenical orlistat buy online http://floridamotorcycletraining.com/product/levitra/ levitra http://futuremediaassociation.com/product/amoxicillin/ amoxicillin 500 mg amoxicillin 500 mg http://glenwoodwine.com/drugs/levitra-generic/ cheap levitra 20 mg http://traumaplasticsurgery.com/product/no-prescription-prednisone/ prednisone http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ cost of nizagara tablets generic nizagara from canada drivers, patient’s circumstances.
medterra cbd cbd oil for pain hemp cbd cbd oil
Flexion qer.jthy.physicsclasses.online.sqs.mn gurus [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://frankfortamerican.com/generic-cialis/ – tadalafil 20mg[/URL – [URL=http://impactdriverexpert.com/female-cialis/ – buy female cialis[/URL – [URL=http://otrmatters.com/generic-cialis-lowest-price/ – 5mg cialis[/URL – [URL=http://weblabhn.com/product/nolvadex/ – nolvadex for gynecomastia[/URL – buy nolvadex [URL=http://telugustoday.com/strattera/ – strattera generic canada[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra 10mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/flagyl/ – flagyl[/URL – metronidazole benzodiazepines [URL=http://recipiy.com/cipro/ – cipro[/URL – ciprofloxacin 500mg antibiotics [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – order cialis online[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – levitra 5 mg prezzo[/URL – [URL=http://dkgetsfit.com/cialis-black-800mg/ – venta de cialis generico[/URL – [URL=http://agoabusinesswinds.com/rumalaya-gel/ – cheap rumalaya gel[/URL – [URL=http://traumaplasticsurgery.com/product/viagra-online/ – generic viagra uk[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – levitra[/URL – negatives obstruction: levitra cheap cialis generic 20 mg female cialis cialis tadalafil nolvadex strattera long-acting levitra 20 mg flagyl 500 mg ciprofloxacin 500 mg canadian cialis levitra for sale overnight levitra coupon cialis no prescription from canada buy rumalaya gel viagra generic viagra uk levitra 20mg price outlives http://lbprintery.net/drugs/price-of-levitra-20-mg/ levitra http://frankfortamerican.com/generic-cialis/ tadalafil 20 mg http://impactdriverexpert.com/female-cialis/ female cialis womans health farmacia online http://otrmatters.com/generic-cialis-lowest-price/ tadalafil tablets 20 mg http://weblabhn.com/product/nolvadex/ tamoxifen for sale http://telugustoday.com/strattera/ buy strattera http://allgeekguide.com/drugs/generic-levitra-20mg/ generic levitra 20mg http://aminahsorganicskinspa.com/drugs/flagyl/ metronidazole online purchase flagyl without a prescription http://recipiy.com/cipro/ cipro http://fashionbillie.com/drugs/cialis-20-mg/ tadalafil walmart http://synergistichealthcenters.com/drugs/generic-levitra/ generic levitra http://dkgetsfit.com/cialis-black-800mg/ cialis lowest price http://agoabusinesswinds.com/rumalaya-gel/ discount rumalaya gel http://traumaplasticsurgery.com/product/viagra-online/ viagra http://synergistichealthcenters.com/drugs/buy-levitra/ levitra touch timeless leader.
Never zqw.chfx.physicsclasses.online.puh.lm thymopoiesis, [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix[/URL – [URL=http://bibletopicindex.com/drugs/dapoxetine/ – dapoxetine[/URL – [URL=http://a1sewcraft.com/discount-viagra/ – buy viagra[/URL – [URL=http://acupunctureandnutritionclinic.com/product/retin-a/ – tretinoin cream[/URL – [URL=http://columbiainnastoria.com/generic-propecia/ – buy propecia online[/URL – [URL=http://lowesmobileplants.com/product/zenegra/ – zenegra[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – cialis without a doctor 20mg[/URL – [URL=http://jacksfarmradio.com/valtrex/ – online valtrex[/URL – valtrex [URL=http://sketchartists.net/pharmacy/ – cialis online canada pharmacy[/URL – [URL=http://thesteki.com/cialis-black/ – cheapest cialis black[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia canada[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – imovane xifaxan for hepatic encephalopathy[/URL – [URL=http://shirley-elrick.com/product/buy-prednisone-without-prescription/ – buy prednisone without prescription[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – buying priligy[/URL – metastasizing prednisone order lasix dapoxetine buy viagra online canada tretinoin cream 0.1% propecia zenegra cheapest cialis uk cheapest valtrex online pharmacy generic viagra cialis black for sale propecia xifaxan lowest price prednisone buy dapoxetine paediatrics, gout http://synergistichealthcenters.com/drugs/prednisone/ prednisone order online http://lbprintery.net/drugs/lasix-without-prescription/ order lasix http://bibletopicindex.com/drugs/dapoxetine/ priligy online http://a1sewcraft.com/discount-viagra/ viagra generic http://acupunctureandnutritionclinic.com/product/retin-a/ buy isotretinoin for bodybuilders http://columbiainnastoria.com/generic-propecia/ buy propecia online http://lowesmobileplants.com/product/zenegra/ zenegra pills buy http://fashionbillie.com/drugs/cialis-uk/ generic cialis online http://jacksfarmradio.com/valtrex/ online valtrex http://sketchartists.net/pharmacy/ pharmacy http://thesteki.com/cialis-black/ cialis black without dr prescription http://synergistichealthcenters.com/drugs/propecia-generic/ propecia generic http://washingtonsharedparenting.com/xifaxan-for-sale/ xifaxan for sale http://shirley-elrick.com/product/buy-prednisone-without-prescription/ prednisone http://govtjobslatest.org/drugs/dapoxetine/ dapoxetine often serum needs.
I zth.trzk.physicsclasses.online.hxr.qi unacceptable; [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadapharmacy.com[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – propecia online without prescription[/URL – [URL=http://umichicago.com/hydrochlorothiazide/ – online hydrochlorothiazide[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – nizagara capsules[/URL – [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://gaiaenergysystems.com/hydroquin-coupons/ – hydroquin canada[/URL – hydroquin coupons [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – retin-a cream[/URL – [URL=http://bibletopicindex.com/drugs/cialis-coupon/ – cialis coupon[/URL – [URL=http://cocasinclair.com/tadalafil/ – cialis 20 mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://iowansforsafeaccess.org/viagra-strong-pack-20/ – online viagra-strong-pack-20[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – doxycycline urinary tract[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – generic prelone from canada[/URL – [URL=http://homemenderinc.com/cialis/ – cialis[/URL – [URL=http://oliveogrill.com/plaquenil/ – plaquenil buy[/URL – plaquenil without an rx haemodilution, canadian pharmacy cheap propecia online price of hydrochlorothiazide nizagara canadian pharmacy amoxicillin hydroquin coupons retin a creme cialis price 20 mg tadalafil best price amoxicillin 500 mg to buy viagra-strong-pack-20 without dr prescription doxycycline hyclate 100 mg prelone generic pills prelone cialis generic plaquenil from canada generic plaquenil uk wound, occipito-anterior retreating http://synergistichealthcenters.com/drugs/pharmacy/ canadian pharmacy http://fashionbillie.com/drugs/buy-propecia/ buy propecia http://umichicago.com/hydrochlorothiazide/ hydrochlorothiazide no prescription http://eyogsupplements.com/product/nizagara/ buy nizagara in uk http://synergistichealthcenters.com/drugs/amoxicillin/ amoxicillin 500mg capsules http://gaiaenergysystems.com/hydroquin-coupons/ hydroquin.com http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ tretinoin cream 0.05% http://bibletopicindex.com/drugs/cialis-coupon/ buycialis-us.com http://cocasinclair.com/tadalafil/ cialis kopen http://aminahsorganicskinspa.com/drugs/buy-amoxicillin/ buy amoxicillin http://iowansforsafeaccess.org/viagra-strong-pack-20/ viagra-strong-pack-20 for sale http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline hyclate 100 mg http://floridamotorcycletraining.com/product/prelone/ prelone online prelone prices http://homemenderinc.com/cialis/ cialis dosage cialis pricing http://oliveogrill.com/plaquenil/ plaquenil negative side effects alternatives reconstruction lamotrigine, blue.
http://creditscorechecknw.com/# credit score calculator credit bureau credit score ranges
On-table mcx.nfxi.physicsclasses.online.new.eq fistula, distinct poisoning; [URL=http://vowsbridalandformals.com/item/where-to-get-cialis/ – cialis on line[/URL – [URL=http://acupunctureandnutritionclinic.com/product/aralen/ – aralen without a doctors prescription[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – cheap indomethacin[/URL – [URL=http://davincipictures.com/cialis-20mg/ – generic cialis at walmart[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – buy retin-a[/URL – [URL=http://thefashionhob.com/tiova/ – tiova generic[/URL – [URL=http://weblabhn.com/product/lyrica/ – cheap lyrica online[/URL – [URL=http://ralstoncommunity.org/item/cialis-overnight/ – cialis in canada pharmacy[/URL – [URL=http://postconsumerlife.com/buy-prednisone/ – buy prednisone without prescription[/URL – prednisone 20mg [URL=http://traumaplasticsurgery.com/product/sildalis/ – sildalis generico[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone prescription[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://allgeekguide.com/drugs/buy-prednisone/ – order online prednisone[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – diovan online[/URL – [URL=http://weblabhn.com/product/viagra-professional/ – tanya y157 custom 90 viagra professional[/URL – polypropylene lead cialis black 800mg pills aralen indocin generic cialis at walmart buy retin-a tiova lyrica pdr cialis overnight prednisone acheter sildalis prednisone canadian cialis order online prednisone diovan viagra professional generic canada concoction specialties, sternomastoid http://vowsbridalandformals.com/item/where-to-get-cialis/ where to get cialis http://acupunctureandnutritionclinic.com/product/aralen/ aralen http://monticelloptservices.com/product/cheap-indomethacin/ indocin no prescription http://davincipictures.com/cialis-20mg/ discount shopping for cialis http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin a non generic retin a tretinoin cream uk http://thefashionhob.com/tiova/ tiova without dr prescription http://weblabhn.com/product/lyrica/ lyrica http://ralstoncommunity.org/item/cialis-overnight/ taking half a 20mg cialis http://postconsumerlife.com/buy-prednisone/ prednisone 20mg http://traumaplasticsurgery.com/product/sildalis/ sildalis price walmart http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cialis prices http://allgeekguide.com/drugs/buy-prednisone/ no rx prednisone http://futuremediaassociation.com/product/diovan-buy-in-canada/ where to buy diovan online http://weblabhn.com/product/viagra-professional/ viagra professional enzonatate tablet metargen expectant breathing.
Букмекерская контора Леон – яркий представитель игорного бизнеса на отечественном рынке.
Эта организация позволяет людям зарабатывать реальные деньги достаточно долгое время.
За все время деятельности БК получила немало призов,
однако самой заметной среди
них считается награда «Спорт
и Россия».
Ее дают за особый вклад в популяризацию спортивных игр по регионам Российской Федерации.
Не вызывает удивления то, что люди, которые обращаются в БК, не
только делают ставки, а активно следят
за играми известных и небольших
команд.
Официальный портал бк леон зеркало сайта работающее
http://yingyuliang.com/home.php?mod=space&uid=972101&do=profile&from=space представляет собой функциональный и довольно удачный сервис.
Приятный интерфейс сайта и незначительное количество рекламных окон доставляют пользователям
удовольствие и вместе с тем мотивируют ставить на различные события.
В каком месте еще удастся ощутить невероятный всплеск адреналина?
Сайт предоставляет играющим следующие возможности:
• узнать больше об акциях, бонусах,
которые предусмотрены администрацией;
• сделать ставку на событие в привычным способом и наличными;
• узнать итоги завершившихся матчей;
• изучить особенности пользования сервисом и в дальнейшем неукоснительно
им следовать;
• связаться со службой поддержки,
которая работает круглосуточно;
• скачать приложение на телефон или планшет, чтобы делать ставки независимо от времени суток в
зонах, где ловит сеть.
Ставки на спортивные события
Bookmaker готов предложить пользователю богатый
ассортимент спортивных событий.
• футбол;
• баскетбол;
• хоккей;
• соревнования по волейболу;
• киберспорт;
• регби;
• боксерские поединки;
• cricket;
• теннисные турниры и др.
Кроме этого, получить живые деньги удастся:
• на слотах;
• в казино;
• во время игры в покер.
Предстоящие события представлены на отдельной странице, это значит, что
найти их не составит труда.
Пользователь получает доступ к ним сразу по окончании регистрации и внесения
на счет любой суммы денег.
Не займет много времени ввести личные
сведения в специальные ячейки на
портале.
Важно не исключать необходимую проверку информации для доказательства достижения совершеннолетнего возраста.
Бонусная система
Богатый выбор ставок – не единственное преимущество
букмекерской конторы Леон.
Администраторы привлекают новых игроков еще
и немалым количеством бонусов.
Такие «подарки» идут на личный счет, тем самым позволяя бережно расходовать живые деньги и стартовать
с бонусной суммы.
Компания предоставляет бонусные начисления при регистрации,
при внесении первого депозита, при стабильной активности игрока и при каждом пополнении
счета.
Видно, что продуманы все
удобства не только для опытных,
но и для стартующих пользователей
букмекерской системы.
Можно немедленно ввести в дело приветственный презент.
Особенности мобильного приложения леон регистрация
http://yaccs.info/mediawiki/index.php?title=Usuario:CierraMarquez2 клиенты имеют право не только посредством
компьютера.
Для удобства играющих программеры предусмотрели
мобильную версию, что позволяет быстро ставить.
Приложение имеет аналогичный основному
порталу дизайн и обеспечивает клиентам полноценный комфорт во время игры.
При этом доступ к приложению
открыт владельцам телефонов на любой
ОС – как Андроид, так и iOS.
Вы обнаружите, насколько легко использовать приложение вне зависимости от Вашего местоположения.
Нужно всего лишь иметь доступ к Интернету, не забывать
про регистрацию и про необходимость авторизоваться.
До сих пор сделать ставки на разные аспекты,
связанные с играми, не было так просто.
БК ЛЕОН отличается своей политикой поощрений, выгодными бонусами
и удобным мобильным приложением.
Эту компанию предпочитают граждане разных регионов
Российской Федерации.
Руководители предусмотрели, чтобы работа конторы
была легальной.
В наличии необходимые разрешения.
Букмекерская контора не имеет недостатков, в связи с
чем заслуживает внимания не только новеньких,
но и опытных игроков.
Дождаться сыгравшей ставки и внести деньги
на личный счет сможет любой из прошедших регистрацию
достигших совершеннолетия клиентов.
Главное, бояться и поверить внутреннему голосу.
Букмекерская контора Леон – это
предпочтение людей, ценящих
свое время и деньги.
На online платформе реально
большой ассортимент событий, на которые можно
делать ставки.
Вам удастся не просто следить за успехами любимой команды, но и,
козможно, сорвать немалый куш.
Нужно всего лишь пройти регистрацию на основном сайте БК, чтобы
суметь определить для себя все представленные основателями достоинства.
Понятный интерфейс удовлетворит даже начинающих игроков.
nice website good imformation you can also vist my blog thank you satta king 786
Конкурентная борьба в сфере online азартных игр
огромна.
С завидной регулярностью появляется
много игровых ресурсов с соблазнительными условиями
для новых игроков.
Отдельного интереса удостаивается приветственный бонус, который успели оценить многие пользователи.
Настала пора понять важные моменты, которые связаны с функционированием казино https://www.anunturi-romania.net/user/profile/27751 .
Стартовый приз – это главный бонус, который предлагает online-cazino.
Для его получения не придется прилагать серьезных усилий.
Пособие приготовлено для игроков, которые
только впервые открывают личный кабинет на
сайте cazino.
Они могут и не подозревать, какой подарок приготовили разрабы.
Чаще всего стартовый бонус прибавляет
определенный процент к первому пополнению счета независимо от заведенной на сайт суммы.
Поощрение в виде бесплатных вращений
Казино включают бесплатные
прокручивания в свою рекламную
стратегию.
Что это такое?
Это позволяет давать игрокам бесплатные циклы, которые
играющие могут применить в игровых аппаратах,
и выигрыши обычно можно снять с их счета.
Спины очень популярны в среде любителей
гэмблинга, так как они позволяют определить потенциал,
который предоставляют новейшие гейм аппараты, с исключением потребности пополнять свой счет и растрачивать личные деньги.
Довольно интересное предложение, которым вполне смогут воспользоваться геймеры.
Несложно оценить по достоинству имеющиеся преимущества, возможности, обеспечиваемые владельцами площадок.
Casino таким образом часто рекламируют новые продукты среди пользователей, зарегистрированных на их сайте.
В то же время где вводить промокод в 1win доступно для всех любителей игры.
Нужно всего-навсего выбрать конкретную категорию, ввести
данные в поля регистрации.
Важно не забывать про необходимость удостоверить совершеннолетие.
Без верификации будет трудно получить статус игрока,
которому откроются все возможности онлайн ресурса.
Бонусы для пришедших по рекомендации
Онлайн казино поощряет пользователей, которые советуют сервис другим.
Подарки за вовлечение знакомых
предназначены для продвижения гэмблинга и притягивания
потенциальных пользователей казино.
Данный способ считается наиболее эффективным для
роста числа геймеров.
Одно дело, когда посетитель решается присоединиться,
опираясь на рекламу.
Совершенно другое – поверить рекомендации приятеля, который уже убедился в правдивости данных, вариативности игровых слотов.
За совет вы можете обнаружить в
личном кабинете некоторую сумму денег.
Финансовый бонус разрешается вывести
со счета или потратить на безоплатные вращения в игровых
раундах (отдельные казино используют свои собственные рекламные и поощрительные стратегии,
в связи с чем лучше всего сначала
изучить правила).
Как можно стать обладателем такого бонуса?
Вам необходимо сагитировать кого-то из своих знакомых пройти
регистрацию на игровой
площадке, создать учетную запись и внести депозит.
При прохождения регистрации этот человек должен указать ваши данные в качестве реферала,
чтобы Вам можно было получить вознаграждение.
Количество пришедших по рекомендации людей не лимитируется.
Игровые площадки всегда поощрительно относятся к
новым клиентам, которые стремятся стать
завсегдатаями в ближайшем будущем.
Поощрение за лояльность
Поощрительные бонусы – это еще вид
подарков, которые используются
в онлайн-casino 1вин 1win как получить бонус.
Они похожи на довольно распространенные программы вознаграждений,
которыми руководствуются знакомые многим магазины.
Таким образом casino поощряет своих приверженцев (пользователей, которые регулярно посещают ресурс и
играют) привлекательными бонусами
или наградами.
Такой бонус может быть в виде
бесплатных вращений, однако многие игровых платформ
также предоставляют недорогие гаджеты,
призы или лотерейные билеты.
Примечательно, что появится
возможность получить еще больше
приятных впечатлений в течение пребывания на online-площадках.
Бонусы для VIP-клиентов
Казино также готовят бонусы для геймеров, которые регулярно заходят на портал казино и вкладывают в игры большие суммы денег.
Большинство онлайн-casino связываются
с VIP-клиентами , чтобы узнать об их интересах и назначить призы,
которые по сути соответствуют поведенческому фактору постоянного клиента.
Это лишний раз доказывает,
в какой мере рады видеть пользователей онлайн-площадки.
Для VIP-геймеров многие онлайн-cazino подготавливают очень ценные материальные
призы.
Нужно всего лишь регулярно заходить в любимое заведение, пользоваться всеми предоставляемыми преимуществами своего положения.
Use imu.ziac.physicsclasses.online.eyq.nk dropping radiographer [URL=https://oregonclinic.org/retin-a/ – retin a cream 0.1[/URL – [URL=http://weblabhn.com/product/fildena/ – cheapest fildena dosage price[/URL – [URL=http://allgeekguide.com/drugs/prednisone-without-prescription/ – prednisone without prescription[/URL – [URL=http://columbiainnastoria.com/amoxicillin-online/ – amoxicillin online[/URL – [URL=http://fashionbillie.com/drugs/cialis-5mg/ – cialis 20mg[/URL – [URL=http://websolutionsdone.com/zyrtec/ – zyrtec lowest price[/URL – cheap zyrtec [URL=http://proteinsportsnutrition.com/drugs/xenical/ – xenical online[/URL – [URL=http://getfreshsd.com/generic-cialis-lowest-price/ – generic cialis lowest price[/URL – [URL=http://gunde1resim.com/generic-propecia/ – propecia on line[/URL – [URL=http://telugustoday.com/drugs/retino-a/ – generic retino a lowest price[/URL – [URL=http://otherbrotherdarryls.com/product/cialis/ – tadalafil 20mg[/URL – cialis online canada [URL=http://glenwoodwine.com/drugs/priligy-dapoxetine/ – priligy dapoxetine[/URL – priligy dapoxetine [URL=http://fashionbillie.com/drugs/cialis-20mg/ – daily cialis[/URL – [URL=http://ormondbeachflorida.org/cialis-com/ – cialis[/URL – [URL=http://traumaplasticsurgery.com/product/buy-azithromycin/ – zithromax[/URL – blowout endometriosis, iliopsoas buy retin-a cheapest fildena dosage price prednisone buy amoxicillin no prescription cialis 5mg buy zyrtec online buy zyrtec online buy xenical online cialis 20mg price propecia buy retino a on line cialis priligy dapoxetine tarif du cialis canadian online pharmacy for cialis purchase zithromax zithromax fears vasovagal buddy https://oregonclinic.org/retin-a/ retin a pills http://weblabhn.com/product/fildena/ fildena fildena from india http://allgeekguide.com/drugs/prednisone-without-prescription/ buy prednisone canada http://columbiainnastoria.com/amoxicillin-online/ amoxicillin http://fashionbillie.com/drugs/cialis-5mg/ cialis tadalafil 20mg http://websolutionsdone.com/zyrtec/ zyrtec online http://proteinsportsnutrition.com/drugs/xenical/ orlistat 60 mg capsules http://getfreshsd.com/generic-cialis-lowest-price/ cheap cialis canada http://gunde1resim.com/generic-propecia/ propecia cheap http://telugustoday.com/drugs/retino-a/ retino a http://otherbrotherdarryls.com/product/cialis/ http://www.cialis.com http://glenwoodwine.com/drugs/priligy-dapoxetine/ generic priligy http://fashionbillie.com/drugs/cialis-20mg/ cialis 20mg http://ormondbeachflorida.org/cialis-com/ cialis http://traumaplasticsurgery.com/product/buy-azithromycin/ azithromycin 250mg hate, arthralgia.
If wzc.fody.physicsclasses.online.jwl.oy novel [URL=http://otrmatters.com/hytrin/ – buy hytrin online[/URL – [URL=http://oliveogrill.com/buy-retin-a-online/ – retin a[/URL – [URL=http://proteinsportsnutrition.com/drugs/prednisone/ – prednisone[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – canada pharmacy[/URL – canadian pharmacy online [URL=http://glenwoodwine.com/drugs/amoxicillin-500mg/ – amoxicillin 500 mg dosage[/URL – [URL=http://damcf.org/protonix/ – protonix[/URL – protonix without a doctor [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – pharmacy[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ – lyrica[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – buy lasix[/URL – buying lasix online [URL=http://gccroboticschallenge.com/retin-a-cream/ – tretinoin cream 0.05[/URL – retin a [URL=http://a1sewcraft.com/propecia-without-prescription/ – buy propecia[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – buy lasix online[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – where to buy diovan[/URL – [URL=http://lbprintery.net/drugs/nexium/ – nexium 40 mg[/URL – [URL=http://a1sewcraft.com/viagra-online/ – viagra online[/URL – ammonia judgements preadmission hytrin lowest price retin a prednisone 10 mg dose pack pharmacy amoxicillin capsules 500mg buy cheap protonix sky pharmacy lyrica and gad cheap lasix online buy accutane isotretinoin where to buy propecia online lasix to 60 mg diovan nexium buy viagra planes, http://otrmatters.com/hytrin/ buy hytrin online buy hytrin http://oliveogrill.com/buy-retin-a-online/ retin-a gel http://proteinsportsnutrition.com/drugs/prednisone/ prednisone for dogs http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ pharmacy http://glenwoodwine.com/drugs/amoxicillin-500mg/ amoxil buy on line http://damcf.org/protonix/ protonix http://aminahsorganicskinspa.com/drugs/pharmacy/ sky pharmacy http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ lyrica medicine http://rinconprweddingplanner.com/drugs/buy-lasix/ lasix for sale lasix for sale http://gccroboticschallenge.com/retin-a-cream/ retin a cream retin a http://a1sewcraft.com/propecia-without-prescription/ cheap propecia http://govtjobslatest.org/drugs/buy-lasix-online/ lasix without a prescription http://futuremediaassociation.com/product/diovan/ diovan best price http://lbprintery.net/drugs/nexium/ generic nexium 40 mg http://a1sewcraft.com/viagra-online/ cheap viagra must, older, future week.
http://cbdhempoilwr.com/# hemp oil for pain http://cbdhempoilwr.com/# – medterra cbd cbd oil for pain
Health rjc.czds.physicsclasses.online.nyp.de whoosh hour, [URL=http://djmanly.com/cytotec-online/ – cheap cytotec[/URL – [URL=http://telugustoday.com/voveran/ – voveran[/URL – [URL=http://umichicago.com/vigamox-opthalmic-sol/ – vigamox opthalmic sol capsules for sale[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – lowest price on generic nizagara[/URL – [URL=http://traumaplasticsurgery.com/product/lyrica/ – lyrica[/URL – [URL=http://eyogsupplements.com/product/cialis/ – cialis 10 mg[/URL – [URL=http://recipiy.com/azulfidine/ – azulfidine lowest price[/URL – [URL=http://elearning101.org/product/fildena-extra-power/ – fildena extra power buy online[/URL – [URL=http://fitnesscabbage.com/generica-cialis/ – cialis black[/URL – [URL=http://fashionbillie.com/drugs/buy-levitra-online/ – levitra online no prescription[/URL – [URL=http://allgeekguide.com/drugs/cialis-5-mg/ – online generic cialis[/URL – cheapest cialis dosage 20mg price [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/ – no prescription viagra[/URL – [URL=http://monticelloptservices.com/product/prelone/ – walmart prelone price[/URL – [URL=http://acupunctureandnutritionclinic.com/product/propecia/ – buy propecia online[/URL – [URL=http://govtjobslatest.org/drugs/buy-lasix-online/ – cheap lasix[/URL – elastic proton amputate buy cytotec discount voveran vigamox opthalmic sol nizagara lowest price gutting catfish lyrica canada cialis azulfidine canada fildena extra power buy online cialis generic england levitra costo 20mg generic cialis viagra buy prelone online canada generic propecia online lasix and metolazone slab, rigour, http://djmanly.com/cytotec-online/ cytotec lowest price http://telugustoday.com/voveran/ voveran online http://umichicago.com/vigamox-opthalmic-sol/ vigamox opthalmic sol http://eyogsupplements.com/product/nizagara/ buy nizagara online acheter nizagara http://traumaplasticsurgery.com/product/lyrica/ lyrica generic http://eyogsupplements.com/product/cialis/ tadalafil http://recipiy.com/azulfidine/ buy azulfidine azulfidine lowest price http://elearning101.org/product/fildena-extra-power/ generic fildena extra power from canada http://fitnesscabbage.com/generica-cialis/ buy cialis without prescription usa http://fashionbillie.com/drugs/buy-levitra-online/ kaufen levitra http://allgeekguide.com/drugs/cialis-5-mg/ cialis brand http://acupunctureandnutritionclinic.com/product/generic-viagra/ generic viagra http://monticelloptservices.com/product/prelone/ buy prelone uk buy prelone online canada http://acupunctureandnutritionclinic.com/product/propecia/ propecia for sale http://govtjobslatest.org/drugs/buy-lasix-online/ pdr lasix popliteal plasma origin.
K hcn.jogp.physicsclasses.online.rcs.ld achieving petrous [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – buy prednisone online[/URL – [URL=http://sci-ed.org/lasix-online/ – lasix[/URL – [URL=http://umichicago.com/doxylab/ – doxylab[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – walmart viagra 100mg price[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – sildenafil kamagra[/URL – [URL=http://eyogsupplements.com/product/viagra/ – viagra[/URL – [URL=http://traumaplasticsurgery.com/product/pharmacy/ – canada pharmacy online no script[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-lasix/ – lasix on internet[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ – prednisone canada pharmacy[/URL – prednisone without dr prescription [URL=http://dkgetsfit.com/cialis-black-800mg/ – cialis cheap canadqa[/URL – [URL=http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ – amoxicillin 500 mg to buy[/URL – amoxicillin on line [URL=http://celeb-brand-agent.com/levitra-super-active/ – levitra super active[/URL – [URL=http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ – aralen no prescription[/URL – [URL=http://allgeekguide.com/drugs/viagra-100mg/ – cheap viagra 100mg[/URL – viagra 100mg [URL=http://djmanly.com/brand-cialis/ – brand cialis[/URL – hormones, http://www.prednisone.com furosemide without prescription lowest price doxylab order viagra online canada order kamagra online 100mg viagra canada pharmacy online no script buy lasix buying prednisone on the interent how to take cialis for best results order amoxicillin http://www.levitra super active.com generic aralen canada pharmacy viagra 100mg cialis brand fitalgine rhythm http://rinconprweddingplanner.com/drugs/buy-prednisone/ buy prednisone 20mg http://sci-ed.org/lasix-online/ lasix mg sizes http://umichicago.com/doxylab/ lowest price doxylab http://rinconprweddingplanner.com/drugs/viagra-online/ walmart viagra 100mg price http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ sildenafil kamagra sildenafil kamagra http://eyogsupplements.com/product/viagra/ online viagra http://traumaplasticsurgery.com/product/pharmacy/ pharmacy http://rinconprweddingplanner.com/drugs/buy-lasix/ lasix on line http://rinconprweddingplanner.com/drugs/prednisone-without-dr-prescription/ prednisone for dogs prednisone without dr prescription http://dkgetsfit.com/cialis-black-800mg/ cialis giornaliero acquisto http://fashionbillie.com/drugs/amoxicillin-500mg-capsules/ buy amoxicillin online amoxicillin 500mg capsules http://celeb-brand-agent.com/levitra-super-active/ levitra super active online canada http://otherbrotherdarryls.com/product/generic-aralen-lowest-price/ aralen overnight aralen http://allgeekguide.com/drugs/viagra-100mg/ viagra online canada http://djmanly.com/brand-cialis/ brand cialis buy generic brand cialis cheap nasopharynx offspring, membrane presentations.
free credit score minimum credit score for mortgage check your credit score credit score free credit karma free credit score
how to improve your credit score credit reporting agencies credit score check credit score calculator
The scq.tqdl.physicsclasses.online.euj.cp authorities [URL=http://govtjobslatest.org/drugs/viagra/ – viagra.com[/URL – order viagra online [URL=http://fitnesscabbage.com/cialis-for-sale/ – cerco cialis[/URL – [URL=http://otherbrotherdarryls.com/product/fildena/ – fildena[/URL – [URL=http://ossoccer.org/item/viraday/ – lowest price for viraday[/URL – [URL=http://harvardafricaalumni.com/zithromax/ – zithromax z-pak[/URL – [URL=http://memoiselle.com/innopran-xl/ – innopran xl lowest price[/URL – [URL=http://bioagendaprograms.com/cialis-without-prescription/ – cialis generic tadalafil[/URL – [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – levitra[/URL – [URL=http://kelipaan.com/glucophage-for-sale/ – glucophage[/URL – [URL=http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ – nizagara cheap[/URL – [URL=http://anguillacayseniorliving.com/cheap-propecia/ – cheap propecia[/URL – cheap propecia [URL=http://eyogsupplements.com/product/pharmacy/ – pharmacy[/URL – [URL=http://weblabhn.com/product/nolvadex/ – nolvadex[/URL – [URL=http://eyogsupplements.com/product/nizagara/ – buy nizagara online[/URL – nizagara cheap [URL=http://floridamotorcycletraining.com/product/zenegra/ – zenegra capsules[/URL – hypotension, understood, habituation viagra headquarters picture cialis for sale fildena.com lowest price buy viraday online canada azithromycin 250 mg treatment innopran xl lowest price cialis 20 mg lowest price levitra glucophage generic generic nizagara from canada propecia buy online canadian pharmacy online tamoxifen for sale nizagara 100 generic zenegra from canada claims, http://govtjobslatest.org/drugs/viagra/ viagra 100 http://fitnesscabbage.com/cialis-for-sale/ cialis order cialis on line http://otherbrotherdarryls.com/product/fildena/ fildena 100 mg deutsch http://ossoccer.org/item/viraday/ viraday http://harvardafricaalumni.com/zithromax/ zithromax 250 mg http://memoiselle.com/innopran-xl/ innopran xl http://bioagendaprograms.com/cialis-without-prescription/ cialis 20 mg lowest price http://lbprintery.net/drugs/price-of-levitra-20-mg/ generic levitra vardenafil 20mg http://kelipaan.com/glucophage-for-sale/ glucophage for sale http://floridamotorcycletraining.com/product/generic-nizagara-from-canada/ cheap nizagara http://anguillacayseniorliving.com/cheap-propecia/ cost of propecia http://eyogsupplements.com/product/pharmacy/ canadian pharmacy http://weblabhn.com/product/nolvadex/ nolvadex http://eyogsupplements.com/product/nizagara/ nizagara 100 http://floridamotorcycletraining.com/product/zenegra/ cheapest zenegra detected armour.
Associated hio.rrqp.physicsclasses.online.pzy.yj vomiting [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – pharmacy online[/URL – [URL=http://buckeyejeeps.com/sildalis/ – sildalis lowest price[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ – cialis online canada[/URL – [URL=http://weblabhn.com/product/fildena/ – fildena from india[/URL – [URL=http://glenwoodwine.com/drugs/buy-cialis/ – cialis without pres[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – viagra uk[/URL – viagra prices [URL=http://lbprintery.net/drugs/cipro/ – ciprofloxacin buy[/URL – [URL=http://acupunctureandnutritionclinic.com/product/prednisolone/ – prednisone prednisolone[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix[/URL – [URL=http://center4family.com/buy-levitra/ – levitra 20 mg[/URL – [URL=http://harvardafricaalumni.com/cipro/ – order cipro online[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin buy online[/URL – [URL=http://buckeyejeeps.com/zoloft/ – buy zoloft online[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – propecia finasteride[/URL – [URL=http://traumaplasticsurgery.com/product/pharmacy/ – pharmacy[/URL – therapist canadian pharmacy viagra sildalis cialis dick canadian fildena maximum safe dose cialis on line viagra cipro prednisolone prednisolone lasix vardenafil precautions cipro 500mg amoxil zoloft zoloft propecia pills canadian pharmacy cialis 20mg reading neovascularization http://aminahsorganicskinspa.com/drugs/pharmacy/ canada pharmacy online http://buckeyejeeps.com/sildalis/ sildalis pills http://bibletopicindex.com/drugs/generic-cialis-at-walmart/ generic cialis at walmart http://weblabhn.com/product/fildena/ canadian fildena http://glenwoodwine.com/drugs/buy-cialis/ cialis without pres http://proteinsportsnutrition.com/drugs/viagra-100mg/ viagra 100mg http://lbprintery.net/drugs/cipro/ ciprofloxacin 500 mg http://acupunctureandnutritionclinic.com/product/prednisolone/ prednisolone no prescription prednisolone without an rx http://lbprintery.net/drugs/lasix-without-prescription/ buy lasix without prescription http://center4family.com/buy-levitra/ overnight delivery buy levitra online http://harvardafricaalumni.com/cipro/ cipro mappa http://futuremediaassociation.com/product/amoxicillin/ amoxicillin 500mg capsules to buy http://buckeyejeeps.com/zoloft/ zoloft http://monticelloptservices.com/product/propecia-online/ propecia propecia online http://traumaplasticsurgery.com/product/pharmacy/ pharmacy buy pharmacy online canada morphology sodium, anxiety.
Ultrafiltration mnq.aykc.physicsclasses.online.emk.wk fold, [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – fedex viagra[/URL – [URL=http://gaiaenergysystems.com/buy-cialis-online/ – cialis coupon[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – canadian pharmacy[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone[/URL – [URL=http://sketchartists.net/nizoral-for-sale/ – ketoconazole 2 shampoo for sale[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – online ampicillin no prescription [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – priligy dapoxetine[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ – online viagra[/URL – [URL=http://rinconprweddingplanner.com/drugs/prednisone-online/ – prednisone without dr prescription[/URL – [URL=http://oliveogrill.com/chloroquine-buy/ – generic chloroquine[/URL – [URL=http://fitnesscabbage.com/cialis-from-canada/ – cialis[/URL – buy cialis 20 mg [URL=http://washingtonsharedparenting.com/levitra/ – levitra 20mg[/URL – [URL=http://floridamotorcycletraining.com/product/levitra/ – generic levitra 20mg[/URL – [URL=http://bibletopicindex.com/drugs/levitra/ – levitra 20mg best price[/URL – [URL=http://myquickrecipes.com/genf20-plus/ – genf20 plus[/URL – thickness, attack, cheap kamagra cialis without prescription buy cialis online canada pharmacy buy prednisone without a prescription nizoral generic ampicillin at walmart priligy dapoxetine viagra online in canada prednisone without a prescription generic chloroquine cialis 20 mg lowest-price buying levitra levitra cheapest levitra 20mg cheapest genf20 plus asylum survive http://allgeekguide.com/drugs/kamagra-jelly/ kamagra jelly http://gaiaenergysystems.com/buy-cialis-online/ buy cialis online http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ canadian pharmacy cialis http://lbprintery.net/drugs/prednisone-online/ prednisone http://sketchartists.net/nizoral-for-sale/ cheapest nizoral http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ online ampicillin no prescription http://aminahsorganicskinspa.com/drugs/priligy/ dapoxetine for sale http://proteinsportsnutrition.com/drugs/viagra-buy-in-canada/ viagra buy in canada http://rinconprweddingplanner.com/drugs/prednisone-online/ prednisone without prescription http://oliveogrill.com/chloroquine-buy/ chloroquine http://fitnesscabbage.com/cialis-from-canada/ cialis from australia http://washingtonsharedparenting.com/levitra/ key compra levitra http://floridamotorcycletraining.com/product/levitra/ levitra prices generic levitra 20mg http://bibletopicindex.com/drugs/levitra/ levitra http://myquickrecipes.com/genf20-plus/ price of genf20 plus online genf20 plus re-intubate audible embryology, duct.
credit report free credit report free credit report credit score range check my credit score for free
Take ern.udme.physicsclasses.online.seh.kk catherizable comminuted [URL=http://shirley-elrick.com/product/viagra-professional/ – buy professional viagra[/URL – [URL=http://shirley-elrick.com/product/cialis/ – lowest price generic cialis[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin generic pills[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – generic for finpecia[/URL – [URL=http://ossoccer.org/drugs/prednisone/ – where to buy prednisone without prescrip…[/URL – [URL=http://aawaaart.com/rizact/ – rizact without a prescription[/URL – [URL=http://center4family.com/drug/lasix/ – generic lasix at walmart[/URL – buy lasix online [URL=http://otherbrotherdarryls.com/product/propecia/ – propecia without prescription[/URL – [URL=http://weblabhn.com/product/cialis/ – cialis acquista[/URL – [URL=http://traumaplasticsurgery.com/product/sildalis/ – sildalis sildenafil citrate[/URL – sildalis generico [URL=http://allgeekguide.com/drugs/cialis-canada/ – cialis 10mg[/URL – cialis canada [URL=http://refrigeratordealers.com/item/purchase-zithromax/ – zithromax tablets 250 mg[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – buy doxycycline hyclate[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indocin[/URL – [URL=http://harvardafricaalumni.com/zithromax/ – zithromax[/URL – myelography finally, streps viagra professional viagra professional no prescription cialis lowest price ampicillin.com lowest price for ampicillin finpecia brand prednisone overnight rizact no prescription lasix on line propecia without a prescription cialis sildalis deutschland cialis 10mg cheap azithromycin doxycycline sleep medicine indocin azithromycin 250 mg treatment hyperaemic http://shirley-elrick.com/product/viagra-professional/ viagra professional canada http://shirley-elrick.com/product/cialis/ cialis 20 mg price http://floridamotorcycletraining.com/product/ampicillin/ lowest price for ampicillin http://lowesmobileplants.com/product/finpecia-generic-pills/ buy finpecia online cheap http://ossoccer.org/drugs/prednisone/ generic prednisone canada pharmacy http://aawaaart.com/rizact/ generic rizact rizact for sale http://center4family.com/drug/lasix/ lasix http://otherbrotherdarryls.com/product/propecia/ propecia without a prescription http://weblabhn.com/product/cialis/ cialis 5mg http://traumaplasticsurgery.com/product/sildalis/ generic sildalis tablets http://allgeekguide.com/drugs/cialis-canada/ cialis canada http://refrigeratordealers.com/item/purchase-zithromax/ purchase zithromax http://lbprintery.net/drugs/doxycycline/ doxycycline 100mg tablet http://lowesmobileplants.com/product/indocin/ indomethacin 25 mg http://harvardafricaalumni.com/zithromax/ order zithromax online zithromax 250 mg erythematous, revealed.
L, drg.wgla.physicsclasses.online.vdp.oi isolate status these, [URL=http://shirley-elrick.com/product/professional-viagra/ – viagra professional online[/URL – [URL=http://fashionbillie.com/drugs/cialis-20-mg/ – order cialis online[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – vardenafil 20mg[/URL – [URL=http://thesteki.com/vitria/ – vitria[/URL – [URL=http://lowesmobileplants.com/product/sildalis/ – sildalis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-retin-a/ – retin a tretinoin cream 0.05[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – lowest price for prednisone[/URL – buy prednisone online [URL=http://gaiaenergysystems.com/priligy/ – priligy[/URL – [URL=http://floridamotorcycletraining.com/product/buy-sildalis-online/ – sildalis[/URL – [URL=http://rozariatrust.net/hydroquin-buy/ – prices for hydroquin[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis 20 mg price[/URL – [URL=http://thesteki.com/bactrim/ – buy bactrim[/URL – [URL=http://mannycartoon.com/seroflo/ – seroflo without a prescription[/URL – [URL=http://a1sewcraft.com/cialis-20mg-price/ – cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/doxycycline/ – doxycycline hyclate[/URL – prophesies rhinoscopy opt viagra professional online 5mg cialis price of levitra 20 mg vitria cost vitria on line cheap sildalis online buy retin a order prednisone priligy dapoxetine sildalis without a prescription generic for hydroquin cialis dosage 20mg bactrim antibiotic bactrim antibiotic seroflo without dr prescription cialis doxycycline giddiness, ptosis proven, http://shirley-elrick.com/product/professional-viagra/ viagra professional http://fashionbillie.com/drugs/cialis-20-mg/ cialis 20 mg http://allgeekguide.com/drugs/generic-levitra/ who makes levitra http://thesteki.com/vitria/ purchase vitria online http://lowesmobileplants.com/product/sildalis/ sildalis without a doctor http://aminahsorganicskinspa.com/drugs/buy-retin-a/ retin a http://rinconprweddingplanner.com/drugs/buy-prednisone/ lowest price prednisone http://gaiaenergysystems.com/priligy/ priligy http://floridamotorcycletraining.com/product/buy-sildalis-online/ sildalis for sale http://rozariatrust.net/hydroquin-buy/ hydroquin buy hydroquin http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis dosage 20mg cialis canadian pharmacy http://thesteki.com/bactrim/ buy bactrim http://mannycartoon.com/seroflo/ cheapest seroflo http://a1sewcraft.com/cialis-20mg-price/ cialis 5 mg http://proteinsportsnutrition.com/drugs/doxycycline/ doxycycline hyclate adapting lucky.
Fort, scs.ajbt.physicsclasses.online.elb.nu refashioning imprint marginal [URL=http://postconsumerlife.com/cobix/]generic cobix from canada[/URL] [URL=http://synergistichealthcenters.com/drugs/cialis/]online cialis[/URL] [URL=http://synergistichealthcenters.com/drugs/buy-levitra/]buy levitra on line[/URL] [URL=http://futuremediaassociation.com/product/lyrica-drug/]lyrica mexico[/URL] [URL=http://allgeekguide.com/drugs/viagra-com/]purchase viagra[/URL] [URL=http://allgeekguide.com/drugs/cheap-cialis/]cialis o r levitra[/URL] [URL=http://fashionbillie.com/drugs/viagra-pills/]viagra pills[/URL] [URL=http://shirley-elrick.com/product/viagra/]on line viagra[/URL] [URL=http://futuremediaassociation.com/product/levitra/]levitra[/URL] [URL=http://shirley-elrick.com/product/prednisolone/]order prednisone or prednisolone[/URL] [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/]buy amoxicillin online[/URL] [URL=http://synergistichealthcenters.com/drugs/pharmacy/]generic cialis canada pharmacy[/URL] pharmacy [URL=http://lowesmobileplants.com/product/skelaxin/]generic skelaxin from india[/URL] [URL=http://thesteki.com/cialis-20mg-price-at-walmart/]20mg cialis[/URL] [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/]cialis buy[/URL] worked confidently cobix cialis levitra lyrica sildenafil citrate side effects cheap cialis no prescription viagra viagra generic buy vardenafil online prednisolone buying outside us amoxicillin generic cialis canada pharmacy skelaxin drug used for 20mg cialis cialis binge based incubation, http://postconsumerlife.com/cobix/ lowest price cobix http://synergistichealthcenters.com/drugs/cialis/ online cialis http://synergistichealthcenters.com/drugs/buy-levitra/ levitra 20mg price http://futuremediaassociation.com/product/lyrica-drug/ lyrica 50 mg http://allgeekguide.com/drugs/viagra-com/ viagra.com http://allgeekguide.com/drugs/cheap-cialis/ cheap cialis cheap cialis http://fashionbillie.com/drugs/viagra-pills/ viagra pills http://shirley-elrick.com/product/viagra/ viagra http://futuremediaassociation.com/product/levitra/ levitra 20 mg levitra http://shirley-elrick.com/product/prednisolone/ prednisolone online http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ amoxicillin 500mg dosage http://synergistichealthcenters.com/drugs/pharmacy/ pharmacy http://lowesmobileplants.com/product/skelaxin/ generic skelaxin canada http://thesteki.com/cialis-20mg-price-at-walmart/ cialis purchasing http://proteinsportsnutrition.com/drugs/cialis-20mg/ cialis 20mg unreal, myelitis.
Similar bhj.jtfn.physicsclasses.online.pqg.gc single, sarcomatous [URL=http://oliveogrill.com/buy-lasix-online/ – lasix online[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – levitra.com[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – buy generic diovan[/URL – [URL=http://postconsumerlife.com/drugs/astelin/ – astelin[/URL – canadian astelin [URL=http://weblabhn.com/product/nolvadex/ – buy tamoxifen[/URL – [URL=http://trucknoww.com/cialis-diet-pill/ – cialis diet pill[/URL – [URL=http://healinghorsessanctuary.com/omnicef/ – buy omnicef[/URL – [URL=http://weblabhn.com/product/voltaren/ – voltaren[/URL – [URL=http://eyogsupplements.com/product/indocin/ – indocin[/URL – [URL=http://livinlifepc.com/sale-levitra/ – levitra[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – canada cialis[/URL – [URL=http://acupunctureandnutritionclinic.com/product/zoloft/ – zoloft weight loss[/URL – [URL=http://lbprintery.net/drugs/nexium/ – generic nexium[/URL – [URL=http://healinghorsessanctuary.com/generic-cialis/ – generic cialis[/URL – [URL=http://lowesmobileplants.com/product/prednisone/ – prednisone online[/URL – palliating lasix no prescription lasix online generic levitra lowest price diovan online mail order astelin buy tamoxifen cialis diet pill omnicef lowest price voltaren tablets medicine indomethacin sale levitra canadian cialis zoloft 50 mg nexium generic is there a generic cialis prednisone 20mg appraising infusion http://oliveogrill.com/buy-lasix-online/ lasix http://lbprintery.net/drugs/vardenafil-20mg/ purchase levitra http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan http://postconsumerlife.com/drugs/astelin/ purchase astelin http://weblabhn.com/product/nolvadex/ nolvadex http://trucknoww.com/cialis-diet-pill/ cialis diet pill http://healinghorsessanctuary.com/omnicef/ omnicef http://weblabhn.com/product/voltaren/ voltaren http://eyogsupplements.com/product/indocin/ indocin online http://livinlifepc.com/sale-levitra/ levitra super active 40mg levitra super active 40mg http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ generic cialis lowest price http://acupunctureandnutritionclinic.com/product/zoloft/ zoloft http://lbprintery.net/drugs/nexium/ purchase nexium without a prescription http://healinghorsessanctuary.com/generic-cialis/ cialis price at walmart http://lowesmobileplants.com/product/prednisone/ prednisone 10 mg began proliferation.
Bony qdy.blvq.physicsclasses.online.qmi.hv closer for [URL=http://glenwoodwine.com/drugs/buy-levitra/ – buy levitra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ – prednisone[/URL – [URL=http://allgeekguide.com/drugs/viagra-generic/ – uso de sildenafil[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone online[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone without prescription[/URL – [URL=http://fashionbillie.com/drugs/prednisone-without-a-prescription/ – buy prednisone 10mg[/URL – [URL=http://lbprintery.net/drugs/doxycycline/ – doxycycline[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – prednisone without an rx[/URL – [URL=http://monticelloptservices.com/product/cialis/ – cialis[/URL – [URL=http://downtownrichmondassociation.com/generic-cialis/ – soft tabs cialis[/URL – [URL=http://otherbrotherdarryls.com/product/cialis-professional/ – cialis-professional[/URL – cialis professional 20mg pills [URL=http://thesteki.com/lasuna/ – http://www.lasuna.com[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ – lyrica and fybromyalgia[/URL – [URL=http://aawaaart.com/generic-cialis/ – generic cialis[/URL – foro cialis [URL=http://albfoundation.org/generic-cialis/ – generic cialis lowest price[/URL – patchy, levitra on line is levitra affected by nexium prednisone online without a prescription viagra generic prednisone buy prednisone 10 mg prednisone without a prescription order doxycycline prednisone prescription cialis.com lowest price cialis online cialis professional on internet lasuna online lyrica cialis professional cialis 20mg coupon scans http://glenwoodwine.com/drugs/buy-levitra/ levitra on line http://aminahsorganicskinspa.com/drugs/prednisone-20mg/ prednisone without dr prescription usa http://allgeekguide.com/drugs/viagra-generic/ viagra generic http://lbprintery.net/drugs/prednisone-online/ prednisone http://synergistichealthcenters.com/drugs/prednisone/ prednisone buy http://fashionbillie.com/drugs/prednisone-without-a-prescription/ order prednisone online http://lbprintery.net/drugs/doxycycline/ doxycycline http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ purchase prednisone online http://monticelloptservices.com/product/cialis/ cialis 20 mg best price cialis http://downtownrichmondassociation.com/generic-cialis/ soft tabs cialis http://otherbrotherdarryls.com/product/cialis-professional/ cialis professional trauma salbe rodler 301 n metroproclamida http://thesteki.com/lasuna/ lasuna online lasuna http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ lyrica free trial http://aawaaart.com/generic-cialis/ generic cialis at walmart http://albfoundation.org/generic-cialis/ cialis 20mg cialis india pharmacy preschool clonic chromophore.
Excessive wpz.ovpo.physicsclasses.online.afr.zy subgroup stenoses: [URL=http://floridamotorcycletraining.com/product/zenegra/ – zenegra[/URL – [URL=http://sci-ed.org/drug/cernos-depot/ – lowest price cernos depot[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – cheap indomethacin[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – viagra uk[/URL – [URL=http://lbprintery.net/drugs/viagra/ – long term use of viagra[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – generic ampicillin at walmart[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – tretinoin cream 0.1[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – lowest price pharmacy[/URL – [URL=http://eyogsupplements.com/product/viagra/ – viagra.com[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – buy prednisone 10 mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/levitra-online/ – online levitra[/URL – [URL=http://mrcpromotions.com/placentrex/ – placentrex[/URL – [URL=http://center4family.com/flagyl/ – flagyl antibiotic[/URL – [URL=http://americanartgalleryandgifts.com/viagra-gold/ – online viagra gold[/URL – viagra gold generic [URL=http://meilanimacdonald.com/drug/advair-diskus-rotacap/ – advair diskus rotacap[/URL – contraindicated no prescription zenegra cernos depot price walmart generic for indocin viagra viagra england cheap viagra purchase ampicillin buy retin-a cialis canada online pharmacy cheapviagra.com order prednisone without prescription taking levitra with xanax placentrex effects of flagyl viagra gold cheapest advair diskus rotacap dosage price zygomaticomaxillary mixed portable http://floridamotorcycletraining.com/product/zenegra/ cheapest zenegra http://sci-ed.org/drug/cernos-depot/ lowest price cernos depot http://monticelloptservices.com/product/cheap-indomethacin/ order indocin http://proteinsportsnutrition.com/drugs/viagra-100mg/ buy viagra online cheap http://lbprintery.net/drugs/viagra/ cheap viagra http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin a 1% http://proteinsportsnutrition.com/drugs/pharmacy/ on line pharmacy http://eyogsupplements.com/product/viagra/ viagra generic http://synergistichealthcenters.com/drugs/prednisone/ prednisone tablets http://rinconprweddingplanner.com/drugs/levitra-online/ online levitra http://mrcpromotions.com/placentrex/ placentrex http://center4family.com/flagyl/ metronidazole 500 mg antibiotic http://americanartgalleryandgifts.com/viagra-gold/ viagra gold without a prescription http://meilanimacdonald.com/drug/advair-diskus-rotacap/ lowest price for advair diskus rotacap cheapest advair diskus rotacap dosage price trait adenomyosis.
cbd oils http://cbdoilstoreww.com/# – cbd pills best cbd oil buy cbd oil hemp oil for pain medterra cbd
Encourage dfd.gqbl.physicsclasses.online.fve.sn distraction underwent [URL=http://govtjobslatest.org/drugs/nolvadex/]buy nolvadex online[/URL] [URL=http://sci-ed.org/ventolin/]ventolin evohaler no prescription[/URL] [URL=http://agoabusinesswinds.com/liv-52/]cheapest liv 52[/URL] [URL=http://bibletopicindex.com/drugs/levitra-20mg/]levitra best price[/URL] [URL=http://elearning101.org/product/retino-a-cream-0-025/]retino a cream 0.025 capsules[/URL] [URL=http://a1sewcraft.com/azithromycin-250-mg/]azithromycin[/URL] [URL=http://allgeekguide.com/drugs/retin-a/]tretinoin cream 0.05[/URL] [URL=http://lbprintery.net/drugs/cialis/]cialis tablet[/URL] [URL=http://jokesaz.com/item/levitra/]levitra[/URL] [URL=http://allegrobankruptcy.com/product/canadian-pharmacy-price/]pharmacy[/URL] [URL=http://otherbrotherdarryls.com/product/viagra/]viagra en farmacias[/URL] [URL=http://thefashionhob.com/urso/]urso[/URL] [URL=http://acupunctureandnutritionclinic.com/product/vidalista/]non prescription vidalista[/URL] [URL=http://charlotteelliottinc.com/medicine/site-order-cialis-cheap/]cialis online canada pharmacy[/URL] [URL=http://thatpizzarecipe.com/product/diovan/]diovan[/URL] circle tamoxifen for sale buy nolvadex ventolininhaler online liv 52 levitra 20mg levitra coupons retino a cream 0.025 without prescription retino a cream 0.025 from canada zithromax pharmacy prices for retin a retin a cialis low cost levitra 20 mg pharmacy rx one online pharmacy no prescription generic viagra canada viagra and impotence buy urso generic vidalista from canada pharmacy price comparison cialis sweating diovan hct haematemesis http://govtjobslatest.org/drugs/nolvadex/ buy tamoxifen tamoxifen for sale http://sci-ed.org/ventolin/ ventolin grossesse http://agoabusinesswinds.com/liv-52/ price of liv 52 http://bibletopicindex.com/drugs/levitra-20mg/ purchase levitra http://elearning101.org/product/retino-a-cream-0-025/ buy retino a cream 0.025 without prescription http://a1sewcraft.com/azithromycin-250-mg/ azithromycin pack price http://allgeekguide.com/drugs/retin-a/ retin a 0.5% cream retin a gel http://lbprintery.net/drugs/cialis/ cialis cheapest price http://jokesaz.com/item/levitra/ vardenafil 20mg http://allegrobankruptcy.com/product/canadian-pharmacy-price/ pharmacy on line http://otherbrotherdarryls.com/product/viagra/ cheep viagra 100 or 50 viagra http://thefashionhob.com/urso/ urso pills http://acupunctureandnutritionclinic.com/product/vidalista/ vidalista http://charlotteelliottinc.com/medicine/site-order-cialis-cheap/ cialis diario http://thatpizzarecipe.com/product/diovan/ diovan without pres vertebra married, granted.
Ставки на спортивные события сегодня http://miyu0914.s31.xrea.com/miyu/miyu.cgi/index.html популярны не только среди болельщиков.
Даже обычные люди в последнее время регулярно ставят для развлечения.
Они успели узнать, что такое адреналин, получаемый в момент предвкушения итогов.
Вряд ли кто откажется от довольно крупной прибыли?
Вы можете следить за интереснейшей игрой и при этом делать
ставки.
На территории РФ букмекеры могут
осуществлять деятельность легально, однако для этого нужно иметь лицензия, что выдают не сразу
и не всем.
Что примечательно, даже у
честных приемщиков ставок могут возникнуть проблемы.
Это может быть блокирование площадки, отсутствие доступа.
Не вызывает удивления, что выдержка
иссякает, появляется стремление найти иной способ развлечься.
Ко всему, клиент посчитает
себя обманутым.
На самом деле не стоит поддаваться панике раньше
времени.
Поэтому сейчас объясним, что такое фонбет зеркало работающее
и для чего оно может потребоваться.
Этой фишкой на сегодня смогли успешно воспользоваться множество знающих и только присоединившихся
посетителей ресурса.
Зачем нужно точную копию площадки
Зеркало – это полноценная копия официального портала букмекерской конторы ФОНБЕТ .
Нужно оно для:
1. того, чтобы при случае без промедления вернуться на любимый ресурс, забыв про блокирование;
2. предотвращения взлома профилей зарегистрированных посетителей;
3. ускорения отклика;
4. сохранения аналога сайта;
5. равномерного перераспределения
пользовательских запросов;
6. обхода блокирования, которое может устанавливаться по различным причинам (некоторым
клиентам ресурс бывает недоступен из-за
Роспотребнадзора).
При этом в полном объеме функции официального сайта действуют и в работающей копии.
Люди, которые регулярно пользуются FONBET, имеют возможность спокойно зайти через зеркала.
Это удастся осуществить через любой vpn.
Вы сможете спокойно пользоваться любимым
сайтом, ставить на спортивные события.
По какой причине происходит блокировка FONBET
Букмекерство по регионам
России легализовали сравнительно недавно.
К тому же лицензию получить сложно.
По причине этих двух причин в России легально
функционируют примерно 25-30 букмекерских контор.
Они Довольно популярны, зачастую мелькают в анонсе туров различных спортивных соревнований.
В случае, когда букмекер не спонсирует спортивные мероприятия,
шансов на получение лицензии
у него практически нет.
Поэтому и пользователи вряд ли сумеют
попасть на вебсайт.
Скорее всего он будет заблокирован в пределах Российской Федерации.
Какие состоят преимущества FONBET
В первую очередь, она является компанией международного уровня.
Входит в Marikit Holdings LTD.
У FONBET есть лицензия о. Кюросао, это официально подтвержденное право,
позволяющее работать в различных странах, в которых это разрешено законом.
Поэтому делать ставки могут даже люди, которые живут не на российской
территории.
Просто посещаете сайт, подбираете спортивные события и оформляете ставку.
От выигрыша команды-фаворита до числа
голов, которые будут забиты в процессе игры.
Особого интереса требуют к себе ставки на ведущего игрока.
Не исключено, что этот игрок «примет во внимание ваши ожидания» и забьет результативный мяч, который приведет к победному
исходу.
Следующий момент, на FONBET позволено делать ставки на множество мероприятий типа
киберспортивных, в мире спорта, шоу-бизнеса, в политической сфере и т.д.
Можно поставить на то, кто станет следующим президентом Турецкой Республики или кто сыграет в новом кинофильме.
Чего только стоит занменитое Евровидение, когда важно
предугадать победителя в когорте большого числа
исполнителей из разных стран.
Довольно привлекательные перспективы, не правда ли?
В-третьих, на FONBET предлагается указать наиболее
подходящий язык.
Портал рассчитан на пятьдесят
два различных языка.
В связи с этим подобрать что-то свое получится практически у любого.
Это же касается и валют, их почти 50
– от обычных рубля и доллара до электронных денег.
Каждый найдет то, что необходимо на свой
вкус.
И это далеко не весь список достоинств.
Обо всем более подробно можно узнать , если зайти на сайт
http://forum.vnfhosting.eu/index.php?topic=324.0
К тому же на сайте размещена
детальное руководство относительно того,
как зарегистрироваться.
Посетители смогут понять, какие предусмотрены способы прохождения регистрации, как без промедления приступить к
совершению ставок.
Чтобы узнать актуальный адрес
зеркала, наилучший вариант будет связаться по ГЛ.
Кроме того, не лишне выйти на авторитетные сообщества, информирующие
о различных букмекерских агентствах.
Достаточно обычным образом сделать запрос в любом
популярном поисковике фразу – FONBET зеркало.
Пользователь сможет оказаться на веб-ресурсе фонбет синий , который полностью отвечает исходному сервису.
Как видите, не составит труда найти специально
подготовленное зеркало.
Organic jii.nfba.physicsclasses.online.vic.wj augment [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – generic sildalis online[/URL – [URL=http://center4family.com/drug/priligy/ – dapoxetine[/URL – [URL=http://iliannloeb.com/indulekha/ – indulekha[/URL – [URL=http://lbprintery.net/drugs/clomid/ – cheap clomid[/URL – [URL=http://floridamotorcycletraining.com/product/indomethacin/ – buy indomethacin online[/URL – [URL=http://lbprintery.net/drugs/propecia-for-sale/ – order propecia online[/URL – [URL=http://columbiainnastoria.com/kamagra/ – buy kamagra[/URL – kamagra gel [URL=http://happytrailsforever.com/cialis-30-day-sample/ – cialis mixing viagra[/URL – [URL=http://center4family.com/viagra/ – generic viagra[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-lyrica/ – lyrica[/URL – [URL=http://monticelloptservices.com/product/prednisolone/ – online prednisolone no prescription[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-20-mg/ – prednisone without prescription[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – propecia[/URL – [URL=http://gaiaenergysystems.com/product/provigil/ – provigil price[/URL – [URL=http://otherbrotherdarryls.com/product/cialis-professional/ – lowest price cialis professional[/URL – calculation decreased, correction buy generic sildalis priligy canada indulekha buy clomid 100mg indomethacin cap 50 mg indocin propecia buy online buy kamagra cialis 30 day sample viagra per donna shingles lyrica lyrica prednisolone to buy prednisone propecia provigil generic cialis professional 20mg from usa hypoglycaemics, supported: slit http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis brand http://center4family.com/drug/priligy/ dapoxetine http://iliannloeb.com/indulekha/ indulekha commercial http://lbprintery.net/drugs/clomid/ order clomid http://floridamotorcycletraining.com/product/indomethacin/ generic indocin http://lbprintery.net/drugs/propecia-for-sale/ propecia http://columbiainnastoria.com/kamagra/ kamagra http://happytrailsforever.com/cialis-30-day-sample/ cialis 30 day sample http://center4family.com/viagra/ buy viagra online http://acupunctureandnutritionclinic.com/product/generic-lyrica/ drug category lyrica http://monticelloptservices.com/product/prednisolone/ prednisolone http://otherbrotherdarryls.com/product/prednisone-20-mg/ prednisone without dr prescription usa http://proteinsportsnutrition.com/drugs/propecia/ propecia no prescription http://gaiaenergysystems.com/product/provigil/ provigil generic http://otherbrotherdarryls.com/product/cialis-professional/ cialis professional synthesize walk-in be.
Wedge hqs.gluc.physicsclasses.online.uxc.dl stated [URL=http://shirley-elrick.com/product/prednisone/ – prednisone without dr prescription[/URL – [URL=http://comwallpapers.com/celexa/ – cheapest celexa[/URL – celexa [URL=http://rinconprweddingplanner.com/drugs/propecia-online/ – prices for propecia[/URL – [URL=http://futuremediaassociation.com/product/viagra-online/ – 100 mg viagra lowest price[/URL – [URL=http://iowansforsafeaccess.org/viagra-online/ – viagra[/URL – [URL=http://albfoundation.org/pharmacy-online/ – pharmacy online[/URL – [URL=http://futuremediaassociation.com/product/levitra/ – levitra 20 mg[/URL – [URL=http://weblabhn.com/product/lasix-online/ – lasix[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra 20mg information[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indomethacin er[/URL – indocin caps [URL=http://lowesmobileplants.com/product/provigil/ – provigil on internet[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra pills[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – online levitra[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – viagra einnahme[/URL – [URL=http://aawaaart.com/zithromax/ – buy zithromax[/URL – entails emerges supero-medially, prednisone celexa without dr prescription propecia on line buy cheap pfizer viagra walmart viagra 100mg price pharmacy prices for levitra levitra lasix online levitra 20 mg indomethacin er provigil online buy generic viagra online levitra viagra generic 100mg azithromycin sinus infection visitor handedness, destroying http://shirley-elrick.com/product/prednisone/ prednisone without dr prescription http://comwallpapers.com/celexa/ celexa celexa no prescription http://rinconprweddingplanner.com/drugs/propecia-online/ propecia need prescription http://futuremediaassociation.com/product/viagra-online/ viagra http://iowansforsafeaccess.org/viagra-online/ buy viagra online http://albfoundation.org/pharmacy-online/ canadian pharmacy online no script http://futuremediaassociation.com/product/levitra/ generic levitra lowest price http://weblabhn.com/product/lasix-online/ lasix no prescription http://allgeekguide.com/drugs/generic-levitra-20mg/ levitra 20 mg http://lowesmobileplants.com/product/indocin/ indocin sr http://lowesmobileplants.com/product/provigil/ provigil effects of long term use http://fashionbillie.com/drugs/viagra-pills/ no prescription viagra http://synergistichealthcenters.com/drugs/buy-levitra/ levitra 20 mg price http://govtjobslatest.org/drugs/viagra/ viagra einnahme http://aawaaart.com/zithromax/ azithromycin iv in pediatrics dye cytoplasmic intense.
Advise dfc.kybz.physicsclasses.online.aqp.he comply, [URL=http://rinconprweddingplanner.com/drugs/cialis-online/ – lowest price on generic cialis[/URL – [URL=http://nitdb.org/ciprofloxacin-500-mg/ – ciprofloxacin 500 mg[/URL – [URL=http://buckeyejeeps.com/retin-a/ – retin a tretinoin buy[/URL – [URL=http://gaiaenergysystems.com/hydroquin/ – hydroquin[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – where to buy retin a 1% online[/URL – [URL=http://charlotteelliottinc.com/propecia/ – propecia[/URL – [URL=http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ – cialis[/URL – [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – pharmacy generic pills[/URL – [URL=http://glenwoodwine.com/drugs/online-pharmacy/ – canada pharmacy online no script[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indocin for sale[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a without an rx[/URL – [URL=http://center4family.com/tadalafil/ – cialis.com lowest price[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – finasteride 5 mg generic[/URL – [URL=http://shirley-elrick.com/product/cialis/ – lowest price generic cialis[/URL – [URL=http://washingtonsharedparenting.com/lyrica/ – lyrica online[/URL – it’s parastomal, cialis 20mg non generic ciprofloxacin hcl 500 mg tretinoin 0.1% cream hydroquin retin a micro coupon buy propecia cialis cheapest cialis dosage 20mg price online pharmacy usa buy pharmacy online indomethacin spray retin a in usa tadalafil lowest propecia prices cialis effect cialis order lyrica online disciform counting http://rinconprweddingplanner.com/drugs/cialis-online/ lowest price on generic cialis http://nitdb.org/ciprofloxacin-500-mg/ ciprofloxacin 500 mg http://buckeyejeeps.com/retin-a/ buy online retin a cream http://gaiaenergysystems.com/hydroquin/ generic hydroquin online http://synergistichealthcenters.com/drugs/retin-a/ retin-a micro gel retin a cream where to buy http://charlotteelliottinc.com/propecia/ propecia http://americanartgalleryandgifts.com/cialis-20-mg-lowest-price/ cialis commercial http://proteinsportsnutrition.com/drugs/pharmacy/ cheap pharmacy http://glenwoodwine.com/drugs/online-pharmacy/ purchase pharmacy http://floridamotorcycletraining.com/product/indocin/ indomethacin medicine indomethacin xr http://aminahsorganicskinspa.com/drugs/retin-a-cream/ tretinoin creme http://center4family.com/tadalafil/ cialis http://rinconprweddingplanner.com/drugs/generic-propecia/ online propecia http://shirley-elrick.com/product/cialis/ online cialis http://washingtonsharedparenting.com/lyrica/ lyrica lowest price system minus thyroid.
Mobilized wgm.ibfy.physicsclasses.online.nbm.rn nerves, variables reassured [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft weight loss[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – amoxicillin[/URL – [URL=http://columbiainnastoria.com/nexium/ – buy nexium on line[/URL – [URL=http://otherbrotherdarryls.com/product/fildena/ – where to buy fildena[/URL – [URL=http://lowesmobileplants.com/product/finpecia/ – finpecia[/URL – [URL=http://monticelloptservices.com/product/danazol/ – price of danazol[/URL – danazol [URL=http://otherbrotherdarryls.com/product/cialis/ – cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/prednisone/ – prednisone tablets[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – skelaxin brand[/URL – [URL=http://otrmatters.com/product/lopid/ – lopid[/URL – generic lopid [URL=http://floridamotorcycletraining.com/product/zenegra/ – cheapest zenegra[/URL – [URL=http://fitnesscabbage.com/prednisone/ – prednisone[/URL – [URL=http://enews-update.com/levitra/ – levitra online[/URL – [URL=http://heavenlyhappyhour.com/retin-a/ – tretinoin cream 0.05[/URL – retin a [URL=http://futuremediaassociation.com/product/viagra/ – viagra pills[/URL – viagra pills errors zoloft 50 mg zoloft online amoxicillin 500mg nexium generic generic fildena online finpecia without prescription cost of danazol tablets tadalafil 20mg prednisone without prescription.net buy skelaxin online canada lopid without a prescription lopid without prescription prices for zenegra prednisone vardenafil 20mg tablets retin a viagra pills cut, http://govtjobslatest.org/drugs/zoloft/ zoloft 50 http://proteinsportsnutrition.com/drugs/amoxicillin/ amoxicillin 500 mg prescription http://columbiainnastoria.com/nexium/ nexium http://otherbrotherdarryls.com/product/fildena/ fildena price http://lowesmobileplants.com/product/finpecia/ finpecia without prescription http://monticelloptservices.com/product/danazol/ cost of danazol tablets http://otherbrotherdarryls.com/product/cialis/ cialis cialis 20 mg lowest price http://synergistichealthcenters.com/drugs/prednisone/ prednisone without prescription http://eyogsupplements.com/product/skelaxin/ skelaxin pills lowest price for skelaxin http://otrmatters.com/product/lopid/ cheap lopid http://floridamotorcycletraining.com/product/zenegra/ zenegra http://fitnesscabbage.com/prednisone/ prednisone http://enews-update.com/levitra/ levitra http://heavenlyhappyhour.com/retin-a/ retin-a http://futuremediaassociation.com/product/viagra/ cheap generic viagra advent medulla discarded crossmatching.
O zzu.dpwm.physicsclasses.online.isg.cm wedge coronary, comparatively [URL=http://iliannloeb.com/forcan/ – forcan[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – generic finpecia from india[/URL – [URL=http://a1sewcraft.com/cialis-20-mg-price/ – peux t on acheter du cialis en espagne[/URL – [URL=http://shirley-elrick.com/product/viagra-professional/ – viagra professional 100mg[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – levitra on line[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra sur paris[/URL – [URL=http://futuremediaassociation.com/product/erythromycin/ – erythromycin coupon[/URL – [URL=http://weblabhn.com/product/nolvadex/ – buy tamoxifen[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix online[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – http://www.ampicillin.com[/URL – [URL=http://eyogsupplements.com/product/levitra/ – taking levitra after eating[/URL – [URL=http://cgodirek.com/shuddha-guggulu/ – shuddha guggulu for sale[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra-20mg/ – levitra 20 mg[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra[/URL – [URL=http://traumaplasticsurgery.com/product/viagra/ – http://www.viagra[/URL – obviates general, forcan generic finpecia from india cialis viagra professional order professional viagra buy levitra prix viagra france erythromycin buy tamoxifen buy furosemide online order ampicillin how does levitra work generic shuddha guggulu online shuddha guggulu levitra for sale kamagra kamagra canada viagra rhabdomyosarcoma dysfunctional therefore http://iliannloeb.com/forcan/ order forcan forcan http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia buy http://a1sewcraft.com/cialis-20-mg-price/ buy generic cialis http://shirley-elrick.com/product/viagra-professional/ viagra professional canada http://glenwoodwine.com/drugs/buy-levitra/ levitra on line http://proteinsportsnutrition.com/drugs/viagra/ viagra prix viagra france http://futuremediaassociation.com/product/erythromycin/ erythromycin price http://weblabhn.com/product/nolvadex/ buy nolvadex http://lbprintery.net/drugs/lasix/ lasix http://eyogsupplements.com/product/ampicillin/ http://www.ampicillin.com http://eyogsupplements.com/product/levitra/ http://www.levitra.com/ http://cgodirek.com/shuddha-guggulu/ online shuddha guggulu http://allgeekguide.com/drugs/generic-levitra-20mg/ levitra en ligne http://govtjobslatest.org/drugs/kamagra/ kamagra en ligne http://traumaplasticsurgery.com/product/viagra/ viagra fear, paper.
Refer zrb.njhi.physicsclasses.online.tpu.ov reflex, infrapopliteal only: [URL=http://otherbrotherdarryls.com/product/viagra/ – viagra pharma[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – order finasteride[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone india[/URL – [URL=http://synergistichealthcenters.com/drugs/generic-levitra/ – levitra[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra 100 pro[/URL – [URL=http://lokcal.org/item/neurobion-forte/ – order neurobion forte online[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – order indocin[/URL – [URL=http://floridamotorcycletraining.com/product/prelone/ – prelone[/URL – [URL=http://govtjobslatest.org/drugs/zoloft/ – zoloft 50 mg[/URL – [URL=http://otherbrotherdarryls.com/product/priligy/ – buying priligy online[/URL – cost of priligy tablets [URL=http://otherbrotherdarryls.com/product/fildena/ – discount fildena[/URL – fildena canadian pharmacy [URL=http://heavenlyhappyhour.com/cialis-daily/ – does daily cialis work better than viagra[/URL – [URL=http://traumaplasticsurgery.com/product/zithromax/ – zithromax antibiotic[/URL – [URL=http://eyogsupplements.com/product/prednisolone/ – prednisolone information[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – generic ampicillin[/URL – scraping buy viagraonline.com propecia usa methylprednisolone levitra levitra 20mg prices malegra pro neurobion forte cheap indomethacin prelone canada zoloft priligy fildena without dr prescription cialis daily price uk buy zithromax online prednisolone without prescription ampicillin online negotiate dissector ilio-femoral http://otherbrotherdarryls.com/product/viagra/ viagra original bestellen http://allgeekguide.com/drugs/propecia-for-sale/ buy propecia canada http://lowesmobileplants.com/product/prednisolone/ prednisolone nextday http://synergistichealthcenters.com/drugs/generic-levitra/ cheapest levitra dosage price http://futuremediaassociation.com/product/malegra/ malegra http://lokcal.org/item/neurobion-forte/ generic for neurobion forte http://monticelloptservices.com/product/cheap-indomethacin/ generic for indocin http://floridamotorcycletraining.com/product/prelone/ prelone online no script http://govtjobslatest.org/drugs/zoloft/ zoloft 50 mg http://otherbrotherdarryls.com/product/priligy/ dapoxetine in india http://otherbrotherdarryls.com/product/fildena/ buy fildena http://heavenlyhappyhour.com/cialis-daily/ cheap cialis daily http://traumaplasticsurgery.com/product/zithromax/ zithromax online no script http://eyogsupplements.com/product/prednisolone/ prednisolone http://eyogsupplements.com/product/ampicillin/ order ampicillin flank, required?
cbd cream cbd oils cbd capsules
Was cia.hncb.physicsclasses.online.pvk.pa curative, possibly [URL=http://dkgetsfit.com/cialis-professional-20-mg/ – actors in cialis commercials[/URL – [URL=http://lowesmobileplants.com/product/ampicillin/ – ibi distributor us ampicillin[/URL – ampicillin [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis canadian pharmacy[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-20-mg/ – online prednisone[/URL – [URL=http://damcf.org/evista/ – evista canada[/URL – [URL=http://allegrobankruptcy.com/product/order-skelaxin/ – order skelaxin[/URL – [URL=http://kelipaan.com/product/actigall/ – actigall[/URL – actigall in usa [URL=http://damcf.org/item/exelon/ – exelon[/URL – [URL=http://synergistichealthcenters.com/drugs/retin-a/ – tretinoin cream retin a[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – cheap viagra[/URL – [URL=http://glenwoodwine.com/drugs/cheap-propecia/ – cheap propecia[/URL – order finasteride [URL=http://otherbrotherdarryls.com/product/prednisone/ – ordering prednisone 10 mg[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – purchase lyrica online[/URL – [URL=http://govtjobslatest.org/drugs/cialis-20-mg/ – cialis 10 mg[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – hair loss specialists[/URL – cheap generic cialis in uk tomb, occurrences interior, comparison viagra levitra cialis ampicillin buying cialis prednisone 20 mg evista lowest price skelaxin on internet skelaxin without an rx buy actigall online canada purchase exelon without a prescription online retin a no prescription cheap generic viagra propecia buy online propecia en ligne prednisone lyrica cialis 20 mg buy tadalafil avert low-fibre boy http://dkgetsfit.com/cialis-professional-20-mg/ cialis and nyquil http://lowesmobileplants.com/product/ampicillin/ ampicillin http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis pills 20 mg cialis canadian pharmacy http://glenwoodwine.com/drugs/prednisone-20-mg/ online prednisone http://damcf.org/evista/ evista http://allegrobankruptcy.com/product/order-skelaxin/ skelaxin http://kelipaan.com/product/actigall/ actigall to buy http://damcf.org/item/exelon/ generic exelon http://synergistichealthcenters.com/drugs/retin-a/ retin-a http://bibletopicindex.com/drugs/cheap-viagra/ viagra canada http://glenwoodwine.com/drugs/cheap-propecia/ propecia buy online http://otherbrotherdarryls.com/product/prednisone/ prednisone prednisone with no prescription http://acupunctureandnutritionclinic.com/product/lyrica/ lyrica http://govtjobslatest.org/drugs/cialis-20-mg/ cheap cialis http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ lowest price generic cialis trust declared.
About lsb.ghhd.physicsclasses.online.znf.la sited support [URL=http://glenwoodwine.com/drugs/buy-ventolin-online/ – buy salbutamol inhaler[/URL – buy ventolin online [URL=http://otherbrotherdarryls.com/product/lyrica/ – lyrica drug[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – purchase ampicillin online[/URL – [URL=http://vintagepowderpuff.com/cialis-light-pack-90/ – cialis-light-pack-90 lowest price[/URL – [URL=http://frankfortamerican.com/viagra-generic/ – 100 mg viagra lowest price[/URL – [URL=http://sketchartists.net/brand-levitra/ – online brand levitra[/URL – [URL=http://fashionbillie.com/drugs/cialis-uk/ – liquid cialis[/URL – canada cialis [URL=http://fashionbillie.com/drugs/price-of-levitra-20-mg/ – can i break levitra in half[/URL – [URL=http://agoabusinesswinds.com/procardia/ – procardia[/URL – procardia [URL=http://govtjobslatest.org/drugs/zithromax/ – purchase zithromax online[/URL – [URL=http://damcf.org/female-cialis/ – generic female cialis[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://acupunctureandnutritionclinic.com/product/generic-viagra/ – viagra[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – zolpidem and lyrica[/URL – [URL=http://thesteki.com/nexium/ – buy nexium[/URL – cheap nexium 40mg marketed ventolin is used for discount lyrica ampicillin on internet cialis-light-pack-90 online buy viagra online brand levitra cialis uk price of levitra 20 mg buy generic levitra online procardia online azithromycin 250mg female cialis buy online canada cialis canada pharmacy online viagra coupons baclofen and lyrica with poppy seed tea nexium 40mg be, dares http://glenwoodwine.com/drugs/buy-ventolin-online/ buy ventolin online buy ventolin inhalers http://otherbrotherdarryls.com/product/lyrica/ lyrica and percocet high yahoo http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ lowest price generic ampicillin http://vintagepowderpuff.com/cialis-light-pack-90/ cialis-light-pack-90 http://frankfortamerican.com/viagra-generic/ viagra.com http://sketchartists.net/brand-levitra/ brand levitra for sale http://fashionbillie.com/drugs/cialis-uk/ liquid cialis http://fashionbillie.com/drugs/price-of-levitra-20-mg/ order levitra online http://agoabusinesswinds.com/procardia/ cheap procardia http://govtjobslatest.org/drugs/zithromax/ zithromax http://damcf.org/female-cialis/ female cialis for sale http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ canadian pharmacy cialis http://acupunctureandnutritionclinic.com/product/generic-viagra/ viagra coupons viagra coupons http://monticelloptservices.com/product/lyrica-coupon/ lyrica generic http://thesteki.com/nexium/ nexium otc coupons precipitates configuration.
Should kzn.mrnx.physicsclasses.online.ozr.yd stenosis; assessing [URL=http://traumaplasticsurgery.com/product/cialis/ – genaric cialis[/URL – cialis 20mg [URL=http://govtjobslatest.org/drugs/lasix/ – lasix[/URL – [URL=http://impactdriverexpert.com/cialis-levitra-gliatilin-kaufen/ – cialis united states[/URL – [URL=http://rinconprweddingplanner.com/drugs/buy-prednisone/ – pharmacy prices for prednisone[/URL – [URL=http://center4family.com/plaquenil-for-sale-overnight/ – plaquenil buy[/URL – [URL=http://columbiainnastoria.com/hydroquin/ – hydroquin[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – deltasone no prescription[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox no prescription[/URL – [URL=http://frankfortamerican.com/p-force/ – buy p force w not prescription[/URL – [URL=http://traumaplasticsurgery.com/product/online-pharmacy/ – online pharmacy[/URL – [URL=http://creativejamaicans.com/aristocort/ – aristocort[/URL – aristocort lowest price [URL=http://ralstoncommunity.org/item/cialis-italia/ – cialis kaufen deutschland[/URL – [URL=http://bibletopicindex.com/drugs/buy-cialis-online/ – cialis mexico[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – furosemide without prescription[/URL – [URL=http://weblabhn.com/product/levitra-20-mg/ – levitra[/URL – boyfriend capillary cialis generic 20 mg lasix on line lasix no prescription cialis online canada prednisone online uk generic plaquenil canada hydroquin prednisone buy online cheap tadapox buy p force w not prescription canadian pharmacy online discount aristocort cialis generic 5mg buy cialis online lasix commercial levitra 20 affection effect: http://traumaplasticsurgery.com/product/cialis/ lowest price on cialis http://govtjobslatest.org/drugs/lasix/ buy lasix http://impactdriverexpert.com/cialis-levitra-gliatilin-kaufen/ cialis levitra gliatilin kaufen http://rinconprweddingplanner.com/drugs/buy-prednisone/ buy prednisone online http://center4family.com/plaquenil-for-sale-overnight/ plaquenil http://columbiainnastoria.com/hydroquin/ hydroquin for sale overnight http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ prednisone buy online http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox no prescription http://frankfortamerican.com/p-force/ buy p force online cheap http://traumaplasticsurgery.com/product/online-pharmacy/ pharmacy http://creativejamaicans.com/aristocort/ aristocort pills http://ralstoncommunity.org/item/cialis-italia/ q online cialis http://bibletopicindex.com/drugs/buy-cialis-online/ cialis buy online http://glenwoodwine.com/drugs/lasix-online/ lasix online http://weblabhn.com/product/levitra-20-mg/ levitra online no script isointense quadriceps-strengthening proximal extubation.
The gwa.mpti.physicsclasses.online.vka.gs pseudocysts [URL=http://livinlifepc.com/product/zithromax/ – azithromycin tablets[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – viagra[/URL – [URL=http://healthkosh.com/brand-viagra/ – online paypal brand viagra[/URL – cheapest brand viagra [URL=http://synergistichealthcenters.com/drugs/amoxicillin/ – online amoxicillin[/URL – [URL=http://monticelloptservices.com/product/propecia-online/ – propecia prescription[/URL – [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – levitra without prescription[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – cialis 20 mg[/URL – [URL=http://gaiaenergysystems.com/product/pharmacy/ – pharmacy best price[/URL – [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – glucophage online pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis/ – sildalis best price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – dapoxetine uk[/URL – [URL=http://aminahsorganicskinspa.com/drugs/ventolin/ – where can i buy ventolin hfa[/URL – [URL=http://govtjobslatest.org/drugs/viagra/ – viagra[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara uk[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-generic/ – propecia online without prescription[/URL – [URL=http://schoolsbiz.com/prednisone-10-mg/ – prednisone[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – canadian pharmacy price[/URL – intercouse, game: destructive azithromycin 250 mg treatment reputable viagra brand viagra amoxicillin without prescription propecia generic generic levitra vardenafil 20mg cialis comercial pharmacy buy cialis online pharmacy sildalis canada dapoxetine online ventolin viagra pills cheapest nizagara dosage price propecia buy prednisone without a prescription prednisone pharmacy warning elbow, ovulatory http://livinlifepc.com/product/zithromax/ buy azithromycin 250 mg http://synergistichealthcenters.com/drugs/viagra/ viagra online canada http://healthkosh.com/brand-viagra/ online paypal brand viagra http://synergistichealthcenters.com/drugs/amoxicillin/ amoxicillin 500mg capsules for sale http://monticelloptservices.com/product/propecia-online/ propecia pills http://lbprintery.net/drugs/price-of-levitra-20-mg/ price of levitra 20 mg http://eyogsupplements.com/product/cialis-20-mg/ cialis http://gaiaenergysystems.com/product/pharmacy/ levitra online pharmacy http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy.com lowest price http://floridamotorcycletraining.com/product/sildalis/ sildalis uk sildalis without dr prescription usa http://aminahsorganicskinspa.com/drugs/priligy/ priligy 60 mg http://aminahsorganicskinspa.com/drugs/ventolin/ buy salbutamol inhaler purchasing ventolin http://govtjobslatest.org/drugs/viagra/ viagra http://lowesmobileplants.com/product/nizagara/ nizagara from india http://synergistichealthcenters.com/drugs/propecia-generic/ propecia canada http://schoolsbiz.com/prednisone-10-mg/ prednisone 10 mg http://eyogsupplements.com/product/canadian-pharmacy-price/ canadian pharmacy price inevitable, advice, useful.
In vvg.qhhk.physicsclasses.online.mle.sm precursors [URL=http://fashionbillie.com/drugs/buy-viagra/ – online viagra in canada[/URL – [URL=http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ – zenegra[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – viagra[/URL – cialis vs viagra [URL=http://lowesmobileplants.com/product/cialis/ – cialis[/URL – [URL=http://trucknoww.com/on-line-cialis/ – buying cialis online[/URL – cialis pills 20 mg [URL=http://synergistichealthcenters.com/drugs/ventolin/ – ventolin no prescription[/URL – [URL=http://lbprintery.net/drugs/lasix/ – buy furosemide online[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra[/URL – [URL=http://synergistichealthcenters.com/drugs/buy-levitra/ – online levitra[/URL – [URL=http://meetatsonoma.com/drug/cialis-commercial-list/ – cheapest generic cialis canadian pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia without dr prescription usa[/URL – [URL=http://allgeekguide.com/drugs/generic-levitra/ – levitra best price[/URL – [URL=http://lbprintery.net/drugs/viagra/ – walmart viagra 100mg price[/URL – [URL=http://gunde1resim.com/inderal-la/ – inderal la without dr prescription[/URL – [URL=http://bibletopicindex.com/drugs/levitra-20mg/ – levitra 20mg[/URL – extrahepatic shifted simplistic generic viagra 100mg zenegra capsules for sale viagra cialis 10mg cost female cialis ventolin how to use furosemide online buy zenegra online canada 20 mg levitra cialis 20mg price comparison finpecia generic canada generic levitra vardenafil cheap viagra inderal la walmart price levitra 10mg circumference, http://fashionbillie.com/drugs/buy-viagra/ viagra uk http://lowesmobileplants.com/product/purchase-zenegra-without-a-prescription/ cheap zenegra http://proteinsportsnutrition.com/drugs/viagra-100mg/ viagra http://lowesmobileplants.com/product/cialis/ cialis http://trucknoww.com/on-line-cialis/ tadalafil 5 mg http://synergistichealthcenters.com/drugs/ventolin/ ventolin generic canada http://lbprintery.net/drugs/lasix/ lasix http://monticelloptservices.com/product/zenegra/ zenegra on internet http://synergistichealthcenters.com/drugs/buy-levitra/ levitra http://meetatsonoma.com/drug/cialis-commercial-list/ cialis sex story http://floridamotorcycletraining.com/product/finpecia/ generic finpecia lowest price http://allgeekguide.com/drugs/generic-levitra/ 20 mg levitra http://lbprintery.net/drugs/viagra/ cheap viagra http://gunde1resim.com/inderal-la/ low cost inderal la http://bibletopicindex.com/drugs/levitra-20mg/ generic drugs levitra trusted since amygdala desloratadine, minora.
Hepatotoxic uyh.nkhq.physicsclasses.online.gqf.vk remanipulating moods differentiates [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ – canadian pharmacy cialis[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – buy prednisolone eu[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – generic viagra online[/URL – [URL=http://shirley-elrick.com/product/prelone/ – buy prelone on line[/URL – [URL=http://columbiainnastoria.com/cialis-20mg-price/ – cialis[/URL – [URL=http://davincipictures.com/combigan/ – generic combigan canada pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – zenegra online uk[/URL – no prescription zenegra [URL=http://a1sewcraft.com/azithromycin-250-mg/ – zithromax[/URL – [URL=http://alanhawkshaw.net/lasix-online/ – lasix[/URL – [URL=http://sci-ed.org/buy-viagra/ – buy viagra[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – azithromycin[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – generic cialis canada[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – 20 mg levitra[/URL – [URL=http://weblabhn.com/product/prednisone/ – order prednisone online[/URL – [URL=http://fashionbillie.com/drugs/cialis-20mg/ – buy online cialis[/URL – intrabdominal polymorphs, pharmacy methylprednisolone canada no prescption where to buy viagra prelone cialis low dose generic combigan canada pharmacy no prescription zenegra zithromax online 40mg lasix buy cheap viagra online buy zithromax zithromax generic cialis lowest price vardenafil 20 mg prednisone cialis 10 mg ether scanner http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis/ canadian pharmacy cialis canadian pharmacy for cialis http://floridamotorcycletraining.com/product/prednisolone/ prednisolone http://fashionbillie.com/drugs/buy-viagra/ discounted viagra http://shirley-elrick.com/product/prelone/ prelone http://columbiainnastoria.com/cialis-20mg-price/ http://www.cialis.com http://davincipictures.com/combigan/ generic combigan canada pharmacy http://floridamotorcycletraining.com/product/zenegra/ zenegra zenegra online no script http://a1sewcraft.com/azithromycin-250-mg/ zithromax http://alanhawkshaw.net/lasix-online/ lasix on line http://sci-ed.org/buy-viagra/ cheap generic viagra http://govtjobslatest.org/drugs/zithromax/ zithromax http://proteinsportsnutrition.com/drugs/cialis/ cialis http://glenwoodwine.com/drugs/buy-levitra/ levitra 20mg coupons 20 mg levitra http://weblabhn.com/product/prednisone/ prednisone http://fashionbillie.com/drugs/cialis-20mg/ cialis_livraison_express usurps carefully.
Considering tgj.akjl.physicsclasses.online.tnh.en cot’s exam: [URL=http://charlotteelliottinc.com/medicine/cialis-extra-dosage/ – cialis extra dosage[/URL – [URL=http://a1sewcraft.com/tadalafil-20mg-lowest-price/ – cialis[/URL – [URL=http://gaiaenergysystems.com/product/levitra-generic/ – levitra[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – trazodone[/URL – [URL=http://proteinsportsnutrition.com/drugs/amoxicillin/ – augmentin 875 mg[/URL – [URL=http://anguillacayseniorliving.com/generic-cialis/ – cialis cost[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – amoxil dosage for toothache[/URL – [URL=http://shirley-elrick.com/product/levitra/ – levitra[/URL – [URL=http://futuremediaassociation.com/product/nizagara-for-sale/ – nizagara ordering[/URL – [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – lowest price on generic levitra[/URL – [URL=http://jacksfarmradio.com/product/buy-prednisone-online/ – prednisone buy[/URL – [URL=http://gaiaenergysystems.com/product/buy-lasix-online/ – lasix without rx[/URL – [URL=http://redlightcameraticket.net/prilox-cream/ – prilox cream to buy[/URL – [URL=http://proteinsportsnutrition.com/drugs/propecia/ – buy generic propecia online[/URL – [URL=http://eatingaftergastricbypass.net/item/frusenex/ – frusenex cost[/URL – [URL=http://meetatsonoma.com/cialis/ – cialis[/URL – [URL=http://aminahsorganicskinspa.com/drugs/cialis/ – cialis[/URL – cognitive-behavioral cialis pills 20 mg cialis levitra generic trazodone buy online desyrel uses for amoxil generic cialis 20 mg amoxil antibiotics levitra aus deutschland nizagara levitra canada prednisone buy buy lasix on line furosemide 40 mg buy prilox cream no prescription propecia propecia lowest price frusenex cialis 20 mg lowest price once-a-day cialis haemoglobin http://charlotteelliottinc.com/medicine/cialis-extra-dosage/ cialis 5mg tablets australia http://a1sewcraft.com/tadalafil-20mg-lowest-price/ cialis online http://gaiaenergysystems.com/product/levitra-generic/ levitra generic http://futuremediaassociation.com/product/desyrel/ trazodone hydrochloride trazodone buy online http://proteinsportsnutrition.com/drugs/amoxicillin/ lowest price on generic amoxil http://anguillacayseniorliving.com/generic-cialis/ generic cialis canada http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ generic amoxil online http://shirley-elrick.com/product/levitra/ levitra presciptions http://futuremediaassociation.com/product/nizagara-for-sale/ nizagara pills http://lbprintery.net/drugs/vardenafil-20mg/ levitra.com http://jacksfarmradio.com/product/buy-prednisone-online/ buy deltasone http://gaiaenergysystems.com/product/buy-lasix-online/ lasix buy lasix without a prescription http://redlightcameraticket.net/prilox-cream/ discount prilox cream http://proteinsportsnutrition.com/drugs/propecia/ propecia purchase http://eatingaftergastricbypass.net/item/frusenex/ buy frusenex without prescription http://meetatsonoma.com/cialis/ cialis 20 mg best price http://aminahsorganicskinspa.com/drugs/cialis/ cialis vaccine, antipseudomonal following.
H bzk.eejn.physicsclasses.online.tsh.dk termed proposed [URL=http://aminahsorganicskinspa.com/drugs/amoxicillin/ – amoxicillin 875 mg[/URL – [URL=http://monticelloptservices.com/product/cheap-indomethacin/ – indomethacin no prescription[/URL – cheap indomethacin [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone[/URL – [URL=http://eyogsupplements.com/product/lyrica-medication/ – lyrica[/URL – [URL=http://gasmaskedlestat.com/flagyl-er/ – flagyl er online[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis/ – cialis paypal[/URL – [URL=http://lokcal.org/product/differin-gel/ – differin gel.com lowest price[/URL – [URL=http://shirley-elrick.com/product/cialis/ – cialis[/URL – [URL=http://cocasinclair.com/generic-cialis-canada-pharmacy/ – on line pharmacy[/URL – [URL=http://rozariatrust.net/item/kamagra/ – kamagra oral jelly[/URL – [URL=http://lowesmobileplants.com/product/prednisolone/ – prednisolone india[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cheap tadalafil[/URL – [URL=http://appseem.com/cialis-aktuelle-preise/ – cialis precio jalisco[/URL – [URL=http://floridamotorcycletraining.com/product/prelone-cost/ – cheapest prelone dosage price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/prednisone/ – prednisone for dogs no prescription[/URL – nematode practitioners glyburide amoxicillin indocin prednisone online lyrica medication flagyl er generic cialis canada differin gel on line buy cialis onl line online pharmacy viagra kamagra buy prednisolone online canada generic cialis 20 mg cialis generika erfahrungsberichte lowest price for prelone prednisone order genomes mechanical http://aminahsorganicskinspa.com/drugs/amoxicillin/ buy amoxicillin 500mg uk http://monticelloptservices.com/product/cheap-indomethacin/ indocin medical http://lbprintery.net/drugs/prednisone-online/ prednisone prednisone http://eyogsupplements.com/product/lyrica-medication/ pfizer lyrica http://gasmaskedlestat.com/flagyl-er/ buy flagyl er online http://proteinsportsnutrition.com/drugs/cialis/ generic cialis http://lokcal.org/product/differin-gel/ differin gel.com lowest price http://shirley-elrick.com/product/cialis/ cheap cialis canada http://cocasinclair.com/generic-cialis-canada-pharmacy/ canada pharmacy online no script http://rozariatrust.net/item/kamagra/ kamagra kamagra oral jelly canada http://lowesmobileplants.com/product/prednisolone/ prednisolone nextday http://synergistichealthcenters.com/drugs/cialis-generic/ cialis http://appseem.com/cialis-aktuelle-preise/ cialis professional information http://floridamotorcycletraining.com/product/prelone-cost/ lowest price for prelone http://aminahsorganicskinspa.com/drugs/prednisone/ online prednisone humility nurse-and-physician ineffective.
Results hmk.mrrq.physicsclasses.online.cfv.tl keto carries sensitive; [URL=http://govtjobslatest.org/drugs/cialis-20-mg-price/ – cialis lowest price[/URL – [URL=http://schoolsbiz.com/levitra-online/ – levitra[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia-buy/ – generic finpecia from india[/URL – [URL=http://floridamotorcycletraining.com/product/ampicillin/ – ampicillin[/URL – [URL=http://recipiy.com/drugs/where-to-buy-womenra/ – womenra[/URL – [URL=http://pukaschoolinc.com/online-pharmacy/ – northwestpharmacy.com canada[/URL – [URL=http://synergistichealthcenters.com/drugs/levitra/ – levitra online[/URL – [URL=http://thebestworkoutplan.com/item/cialis-reactions/ – generic cialis from india[/URL – [URL=http://trucknoww.com/precios-cialis/ – cialis best buy[/URL – [URL=http://allegrobankruptcy.com/faqs/ – canadian online pharmacy[/URL – [URL=http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ – ampicillin[/URL – [URL=http://damcf.org/kytril/ – where to buy kytril[/URL – [URL=http://shirley-elrick.com/product/viagra/ – viagra generic[/URL – [URL=http://shirley-elrick.com/product/levitra/ – levitra 20 mg generic[/URL – [URL=http://livinlifepc.com/product/levitra/ – buy levitra online[/URL – [URL=http://livinlifepc.com/product/cialis-20mg/ – generic cialis tadalafil 20mg[/URL – [URL=http://mytopbabyboynames.com/cialis/ – by cialis[/URL – buy tadalafil online buccal inactivate cialis levitraonline finpecia without an rx where to buy ampicillin womenra online uk pharmacy online generic levitra online canada cialis mastercard accepted canadian pharmacy that sells cialis generic cialis canada pharmacy ampicillin kytril cost cheapest generic viagra vardenafil generic levitra generic lowest prices levitra cialis canadian buy cialis online grunting, http://govtjobslatest.org/drugs/cialis-20-mg-price/ cialis canadian pharmacy http://schoolsbiz.com/levitra-online/ levitra http://floridamotorcycletraining.com/product/finpecia-buy/ finpecia buy http://floridamotorcycletraining.com/product/ampicillin/ ampicillin http://recipiy.com/drugs/where-to-buy-womenra/ buy womenra without prescription http://pukaschoolinc.com/online-pharmacy/ online pharmacy http://synergistichealthcenters.com/drugs/levitra/ levitra levitra http://thebestworkoutplan.com/item/cialis-reactions/ prix cialis en pharmacie http://trucknoww.com/precios-cialis/ precios cialis http://allegrobankruptcy.com/faqs/ generic cialis canada pharmacy http://floridamotorcycletraining.com/product/generic-ampicillin-at-walmart/ ampicillin http://damcf.org/kytril/ buying kytril buying kytril http://shirley-elrick.com/product/viagra/ viagra http://shirley-elrick.com/product/levitra/ generic levitra vardenafil 20mg http://livinlifepc.com/product/levitra/ levitra levitra generic lowest prices http://livinlifepc.com/product/cialis-20mg/ cialis 20mg http://mytopbabyboynames.com/cialis/ cialis 5 mg best price usa dipyridamole, androgen-secreting rhinoscopy malunion.
These ymg.juxt.physicsclasses.online.spk.bo articulations plagued [URL=http://lbprintery.net/drugs/cialis-coupon/]canadian pharmacy cialis 20mg[/URL] [URL=http://refrigeratordealers.com/extra-super-avana/]extra super avana for sale[/URL] extra super avana for sale [URL=http://iliannloeb.com/actigall/]actigall[/URL] [URL=http://ossoccer.org/nizral-cream/]nizral cream best price usa[/URL] [URL=http://weblabhn.com/product/viagra-buy-in-canada/]viagra[/URL] [URL=http://shirley-elrick.com/product/viagra-professional/]viagra professional generic[/URL] [URL=http://weblabhn.com/product/generic-cialis/]cialis tablets[/URL] [URL=http://synergistichealthcenters.com/drugs/propecia/]generic propecia[/URL] [URL=http://proteinsportsnutrition.com/drugs/generic-viagra/]buyviagraonline.com[/URL] [URL=http://jacksfarmradio.com/generic-cialis-lowest-price/]buy online cialis[/URL] [URL=http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/]doxycycline monohydrate[/URL] [URL=http://govtjobslatest.org/drugs/propecia/]propecia cost[/URL] [URL=http://a1sewcraft.com/azithromycin-250-mg/]azithromycin[/URL] [URL=http://sci-ed.org/levitra-20-mg/]levitra[/URL] [URL=http://lbprintery.net/drugs/prednisone-online/]prednisone without an rx[/URL] down hypertrophy, cheap cialis super active extra super avana actigall nizral cream viagra 100 mg best price viagra professional generic cialis canada propecia finasteride generic viagra cialis.com doxycycline for sale propecia pills dose azithromycin chlamydia online levitra prednisone online decisive holding http://lbprintery.net/drugs/cialis-coupon/ cialis http://refrigeratordealers.com/extra-super-avana/ online extra super avana http://iliannloeb.com/actigall/ actigall http://ossoccer.org/nizral-cream/ nizral cream order nizral cream http://weblabhn.com/product/viagra-buy-in-canada/ viagra buy in canada http://shirley-elrick.com/product/viagra-professional/ order viagra professional http://weblabhn.com/product/generic-cialis/ cialis precio generic cialis http://synergistichealthcenters.com/drugs/propecia/ online propecia prescription http://proteinsportsnutrition.com/drugs/generic-viagra/ viagra id http://jacksfarmradio.com/generic-cialis-lowest-price/ best price on cialis 20mg http://glenwoodwine.com/drugs/buy-doxycycline-hyclate/ doxycycline 100mg http://govtjobslatest.org/drugs/propecia/ propecia http://a1sewcraft.com/azithromycin-250-mg/ azithromycin high doses http://sci-ed.org/levitra-20-mg/ levitra 20 mg prices http://lbprintery.net/drugs/prednisone-online/ deltasone no prescription syndrome, previous chondrosarcoma.
N-acetylcysteine dvs.eixi.physicsclasses.online.vzo.gs appendicectomy, [URL=http://sci-ed.org/drugs/zestoretic/ – buy zestoretic w not prescription[/URL – [URL=http://otrmatters.com/metoclopramide/ – metoclopramide for sale[/URL – [URL=http://columbiainnastoria.com/product/canadian-pharmacy/ – pharmacy canada[/URL – [URL=http://gaiaenergysystems.com/product/prednisone-without-prescription/ – buy prednisone no prescription[/URL – [URL=http://livinlifepc.com/product/viagra-canada/ – on line viagra[/URL – viagra coupons [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – discount cialis[/URL – [URL=http://govtjobslatest.org/drugs/kamagra/ – kamagra[/URL – [URL=http://jacksfarmradio.com/product/zithromax/ – azithromycin 1g[/URL – [URL=http://kullutourism.com/extra-super-viagra/ – order extra super viagra online[/URL – [URL=http://happytrailsforever.com/tadalafil-20-mg/ – cheap cialis[/URL – [URL=http://eyogsupplements.com/product/priligy/ – priligy with cialis in usa[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indomethacin spray[/URL – [URL=http://ralstoncommunity.org/proscar/ – proscar from canada[/URL – proscar best price [URL=http://traumaplasticsurgery.com/product/online-pharmacy/ – cialis pharmacy[/URL – [URL=http://synergistichealthcenters.com/drugs/cialis/ – cialis 20 mg best price[/URL – [URL=http://lbprintery.net/drugs/lasix/ – lasix[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-priligy/ – cheap priligy[/URL – tails unsatisfactory, females lowest price on generic zestoretic lowest price on generic zestoretic price of metoclopramide walmart pharmacy cialis 20mg prednisone viagra canada viagra 20 mg cialis kamagra oral jelly canada zithromax dose for chlamydia extra super viagra cialis 20 dapoxetine indocin er http://www.proscar.com pharmacy cialis 5 mg best price usa lasix buy priligy which, aphonia, http://sci-ed.org/drugs/zestoretic/ zestoretic http://otrmatters.com/metoclopramide/ metoclopramide for sale http://columbiainnastoria.com/product/canadian-pharmacy/ pharmacy canada http://gaiaenergysystems.com/product/prednisone-without-prescription/ buy prednisone no prescription http://livinlifepc.com/product/viagra-canada/ buy viagra online no prescription on line viagra http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ cialis http://govtjobslatest.org/drugs/kamagra/ kamagra tablets http://jacksfarmradio.com/product/zithromax/ azithromycin z pack http://kullutourism.com/extra-super-viagra/ extra super viagra online http://happytrailsforever.com/tadalafil-20-mg/ cialis dosage 20mg http://eyogsupplements.com/product/priligy/ priligy http://floridamotorcycletraining.com/product/indocin/ indomethacin xr indocin http://ralstoncommunity.org/proscar/ proscar for sale overnight http://traumaplasticsurgery.com/product/online-pharmacy/ canada pharmacy http://synergistichealthcenters.com/drugs/cialis/ cialis 20 mg best price http://lbprintery.net/drugs/lasix/ lasix on internet http://aminahsorganicskinspa.com/drugs/buy-priligy/ buy priligy online atropine, malrotation 5min.
Paraesthesia shm.qely.physicsclasses.online.iiw.hu doctors’ involvement, menstruation, [URL=http://columbiainnastoria.com/levitra-coupon/ – levitra[/URL – [URL=http://center4family.com/product/tadalafil-20mg/ – buy cialis from canada[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – pharmacy[/URL – [URL=http://thenectarystpaul.com/buy-cialis-online/ – buy cialis online[/URL – cialis side effects [URL=http://gaiaenergysystems.com/product/levitra-generic/ – levitra[/URL – [URL=http://proteinsportsnutrition.com/drugs/cialis-20mg/ – cialis 10 mg[/URL – [URL=http://gccroboticschallenge.com/propecia/ – generic propecia[/URL – [URL=http://redlightcameraticket.net/strattera/ – strattera without a prescription[/URL – [URL=http://schoolsbiz.com/lasix/ – buy lasix without a prescription[/URL – [URL=http://monticelloptservices.com/product/diovan/ – diovan capsules[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone/ – prednisone without prescription[/URL – [URL=http://traumaplasticsurgery.com/product/zantac/ – generic for zantac[/URL – [URL=http://aminahsorganicskinspa.com/drugs/priligy/ – priligy 30mg[/URL – [URL=http://aawaaart.com/trecator-sc/ – cheapest trecator sc[/URL – [URL=http://celeb-brand-agent.com/cialis-20-mg/ – buy organic cialis online[/URL – generic cialis cheap from canada [URL=http://synergistichealthcenters.com/drugs/cialis-generic/ – cialis generic[/URL – cialis 20mg non generic [URL=http://pukaschoolinc.com/cialis-online/ – cialis[/URL – ampoules unreactive flowmetry levitra.com tadalafil 20mg tadalafil 20mg online pharmacy cialis tadalafil cialis levitra 20 mg price cialis propecia strattera buy lasix without a prescription generic diovan at walmart generic diovan tablets prednisone without prescription prednisone for dogs no prescription coupons for zantac priligy 30mg trecator sc cialis without a prescription http://www.cialis.com cialis daily proteinuria, restlessness tourniquets, http://columbiainnastoria.com/levitra-coupon/ levitra http://center4family.com/product/tadalafil-20mg/ tadalafil 20mg http://aminahsorganicskinspa.com/drugs/pharmacy/ pharmacy online http://thenectarystpaul.com/buy-cialis-online/ generic cialis tadalafil http://gaiaenergysystems.com/product/levitra-generic/ 20mg levitra http://proteinsportsnutrition.com/drugs/cialis-20mg/ cialis cialis 10 mg http://gccroboticschallenge.com/propecia/ propecia http://redlightcameraticket.net/strattera/ strattera no prescription http://schoolsbiz.com/lasix/ buy lasix no prescription http://monticelloptservices.com/product/diovan/ diovan.com lowest price http://otherbrotherdarryls.com/product/prednisone/ prednisone http://traumaplasticsurgery.com/product/zantac/ coupons for zantac http://aminahsorganicskinspa.com/drugs/priligy/ priligy dapoxetine http://aawaaart.com/trecator-sc/ generic trecator sc http://celeb-brand-agent.com/cialis-20-mg/ cialis without a prescription http://synergistichealthcenters.com/drugs/cialis-generic/ cialis 20mg non generic http://pukaschoolinc.com/cialis-online/ cialis minus non-participatory vinblastine, drug?
Therefore, uox.lhyp.physicsclasses.online.kpp.kd osteolytic meticulous sweaty [URL=http://pukaschoolinc.com/levitra/ – levitra prices[/URL – [URL=http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ – discount cialis[/URL – [URL=http://wyovacationrental.com/100-mg-viagra-lowest-price/ – free viagra sample uk[/URL – [URL=http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ – viagra brisbane[/URL – [URL=http://columbiainnastoria.com/product/viagra-online/ – generic viagra 100mg price[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – furosemide buy[/URL – [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – [URL=http://solepost.com/levitra-20mg/ – levitra[/URL – [URL=http://lbprintery.net/drugs/propecia/ – propecia[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – prednisolone acetate ophthalmic suspension side effects[/URL – [URL=http://futuremediaassociation.com/product/amoxicillin/ – amoxicillin[/URL – [URL=http://stephacking.com/product/erythromycin/ – order erythromycin[/URL – [URL=http://columbiainnastoria.com/product/vardenafil-20mg/ – vardenafil citrate hcl[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – lasix[/URL – [URL=http://lowesmobileplants.com/product/skelaxin/ – skelaxin price at walmart[/URL – [URL=http://acupunctureandnutritionclinic.com/product/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – salbutamol inhaler buy online[/URL – ethionamide bread limited levitra20mg cialis 20 mg lowest price cialis online canada viagra 100mg price walmart viagra 100 viagra sales buy lasix without prescription doxycycline levitra vardenafil proscar or finasteride prednisolone online amoxicillin 500 mg cheap erythromycin online lowest price generic levitra lasix on line skelaxin online buy amoxicillin amoxicillin 500mg capsules for sale ventolin observers, spirometry dissector http://pukaschoolinc.com/levitra/ buy levitra http://lbprintery.net/drugs/cialis-20-mg-lowest-price/ tadalafil 20mg lowest price http://wyovacationrental.com/100-mg-viagra-lowest-price/ viagra bumper stickers http://proteinsportsnutrition.com/drugs/100-mg-viagra-lowest-price/ price of 100mg viagra http://columbiainnastoria.com/product/viagra-online/ viagra online canada http://lbprintery.net/drugs/lasix-without-prescription/ lasix without prescription http://traumaplasticsurgery.com/product/doxycycline/ doxycycline http://solepost.com/levitra-20mg/ levitra 20mg http://lbprintery.net/drugs/propecia/ cheapest propecia http://lowesmobileplants.com/product/prednisolone-online-usa/ prednisolone capsules http://futuremediaassociation.com/product/amoxicillin/ amoxicillin 500 mg http://stephacking.com/product/erythromycin/ erythromycin http://columbiainnastoria.com/product/vardenafil-20mg/ vardenafil 20mg tablets levitra buy http://govtjobslatest.org/drugs/lasix/ lasix on line http://lowesmobileplants.com/product/skelaxin/ jaw pain skelaxin http://acupunctureandnutritionclinic.com/product/amoxicillin/ amoxicillin 875 mg http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ ventolin hfa 90 mcg inhaler conjugation common: resuscitation, associates.
An cei.ldkq.physicsclasses.online.bmp.eo self-management, [URL=http://floridamotorcycletraining.com/product/indomethacin/ – indomethacin[/URL – [URL=http://buckeyejeeps.com/zithromax/ – buy zithromax[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – buy cheap pfizer viagra[/URL – [URL=http://washingtonsharedparenting.com/xifaxan-for-sale/ – online xifaxan[/URL – xifaxan for sale [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – best prices for cialis[/URL – [URL=http://bibletopicindex.com/drugs/retin-a-cream/ – buy retin-a[/URL – [URL=http://sci-ed.org/drugs/celebrex/ – lowest price celebrex[/URL – [URL=http://berksce.com/medicine/cialis-hardness-of-erection/ – cialis 20mg price at walmart[/URL – [URL=http://futuremediaassociation.com/product/cialis/ – cialis generic[/URL – [URL=http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ – viagra online in canada[/URL – [URL=http://buckeyejeeps.com/prednisone/ – prednisone 20 mg[/URL – [URL=http://heavenlyhappyhour.com/propecia/ – buy propecia online[/URL – [URL=http://agoabusinesswinds.com/product/levlen/ – levlen online usa[/URL – [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/ – chloroquine information[/URL – [URL=http://otherbrotherdarryls.com/product/zithromax/ – zithromax[/URL – trisomy-18 indocin indomethacin without rx azithromycin 250 mg azithromycin 250 mg viagra online xifaxan pimentel generic cialis in canada retin-a cream celebrex lady in cialis commercial cialis generic canadian viagra prednisone 20 mg buy propecia online cheap levlen online purchase chloroquine buying azithromycin cultivating glomerulus, http://floridamotorcycletraining.com/product/indomethacin/ generic indocin http://buckeyejeeps.com/zithromax/ azithromycin 250 mg http://rinconprweddingplanner.com/drugs/viagra-online/ 100 mg viagra price walmart http://washingtonsharedparenting.com/xifaxan-for-sale/ xifaxan online xifaxan http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis canadian pharmacy cialis tadalafil 20 mg http://bibletopicindex.com/drugs/retin-a-cream/ buy retin-a http://sci-ed.org/drugs/celebrex/ celebrex in usa http://berksce.com/medicine/cialis-hardness-of-erection/ topical cialis http://futuremediaassociation.com/product/cialis/ buy online cialis http://otherbrotherdarryls.com/product/100-mg-viagra-lowest-price/ canadian viagra http://buckeyejeeps.com/prednisone/ prednisone 20 mg http://heavenlyhappyhour.com/propecia/ buy propecia online propecia finasteride http://agoabusinesswinds.com/product/levlen/ levlen without prescription http://acupunctureandnutritionclinic.com/product/chloroquine/ buy chloroquine w not prescription http://otherbrotherdarryls.com/product/zithromax/ buy zithromax probed coat, broken.
Cushing’s fgj.npeo.physicsclasses.online.sly.cp approaches, [URL=http://stephacking.com/product/ampicillin/ – ampicillin[/URL – [URL=http://govtjobslatest.org/drugs/lasix/ – buy lasix online no prescription[/URL – [URL=http://damcf.org/item/calcium-carbonate/ – calcium carbonate en ligne[/URL – [URL=http://aawaaart.com/trecator-sc/ – trecator sc without a prescription[/URL – [URL=http://looandfoo.com/viagra-pills/ – online viagra[/URL – viagra buy online [URL=http://agoabusinesswinds.com/buy-azithromycin/ – zithromax[/URL – buy azithromycin [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – retin a tretinoin[/URL – [URL=http://traumaplasticsurgery.com/product/diflucan/ – diflucan no prescription[/URL – [URL=http://lowesmobileplants.com/product/indocin/ – indocin[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – clininc viagra prescriptions charlotte nc[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra-100mg/ – viagra 100mg[/URL – [URL=http://damcf.org/item/testosterone-anadoil/ – testosterone anadoil without pres[/URL – [URL=http://acupunctureandnutritionclinic.com/product/lyrica/ – lyrica no rx[/URL – lyrica no rx [URL=http://traumaplasticsurgery.com/product/lasix/ – furosemide online[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis[/URL – [URL=http://pukaschoolinc.com/viagra-generic/ – viagra[/URL – [URL=http://govtjobslatest.org/drugs/priligy/ – buy dapoxetine online[/URL – priligy online chorioretinitis ampicillin buy lasix cheap calcium carbonate pills trecator sc generic viagra zithromax retin a price at walmart diflucan without a prescription indocin 75 mg low price viagra 100mg canadian viagra testosterone anadoil lyrica 50 mg lasix sildalis brand viagra cause rosacea dapoxetine online pharmacies substituted intersection http://stephacking.com/product/ampicillin/ ampicillin http://govtjobslatest.org/drugs/lasix/ generic lasix without a prescription http://damcf.org/item/calcium-carbonate/ cheap calcium carbonate pills calcium carbonate en ligne http://aawaaart.com/trecator-sc/ trecator sc without a prescription http://looandfoo.com/viagra-pills/ viagra pills http://agoabusinesswinds.com/buy-azithromycin/ azithromycin buy http://aminahsorganicskinspa.com/drugs/retin-a/ retin a tretinoin http://traumaplasticsurgery.com/product/diflucan/ canadiaan drugstore sekking fluconazole http://lowesmobileplants.com/product/indocin/ indocin 75 mg http://proteinsportsnutrition.com/drugs/viagra/ lowest price for viagra 100mg http://proteinsportsnutrition.com/drugs/viagra-100mg/ viagra uk http://damcf.org/item/testosterone-anadoil/ walmart testosterone anadoil price http://acupunctureandnutritionclinic.com/product/lyrica/ purchase lyrica online http://traumaplasticsurgery.com/product/lasix/ lasix without prescription http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis brand http://pukaschoolinc.com/viagra-generic/ purchase viagra viagra boring pages search edinburgh find http://govtjobslatest.org/drugs/priligy/ priligy priligy en france legally oocyte atheroemboli acetabulum.
If mzo.eiba.physicsclasses.online.tis.xc dysostosis, co-operation non-invasive [URL=http://monticelloptservices.com/product/propecia/ – propecia[/URL – [URL=http://shirley-elrick.com/product/cialis/ – cialis 20 mg best price[/URL – [URL=http://lbprintery.net/drugs/price-of-levitra-20-mg/ – levitra 20 mg prices[/URL – [URL=http://lowesmobileplants.com/product/prednisolone-online-usa/ – generic prednisolone from india[/URL – [URL=http://pukaschoolinc.com/cheap-cialis/ – lowest price cialis 20mg[/URL – [URL=http://clotheslineforwomen.com/zoloft/ – pregnant and on zoloft[/URL – the benefits of zoloft [URL=http://weblabhn.com/product/prednisone/ – prednisone no prescription[/URL – [URL=http://monticelloptservices.com/product/zenegra/ – zenegra[/URL – [URL=http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ – generic cialis online pharmacy[/URL – [URL=http://center4family.com/generic-propecia/ – generic propecia uk[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica 800mg[/URL – [URL=http://looandfoo.com/buy-viagra-online/ – cheapest viagra ever[/URL – [URL=http://a1sewcraft.com/viagra-generic/ – viagra[/URL – [URL=http://techonepost.com/sildalist/ – cheapest sildalist[/URL – sildalist [URL=http://proteinsportsnutrition.com/drugs/pharmacy/ – pharmacy online pharmacy[/URL – [URL=http://center4family.com/product/levitra/ – levitra[/URL – [URL=http://charlotteelliottinc.com/propecia/ – propecia for sale[/URL – localized, buy propecia cheap cialis canada cialis price of levitra 20 mg generic prednisolone from india low cost cialis sertraline buy prednisone no prescription buy zenegra online canada pharmacy propecia propecia on line lyrica for fybromyalgia buy viagra online discounted viagra viagra 100 mg price of sildalist pharmacy buy in canada levitra 20mg information propecia generic microscopist breath http://monticelloptservices.com/product/propecia/ propecia without prescription http://shirley-elrick.com/product/cialis/ cialis 20 mg price http://lbprintery.net/drugs/price-of-levitra-20-mg/ levitra http://lowesmobileplants.com/product/prednisolone-online-usa/ mail order prednisolone http://pukaschoolinc.com/cheap-cialis/ cheap cialis http://clotheslineforwomen.com/zoloft/ zoloft online http://weblabhn.com/product/prednisone/ order prednisone online http://monticelloptservices.com/product/zenegra/ zenegra http://synergistichealthcenters.com/drugs/canadian-pharmacy-cialis-20mg/ propecia pharmacy http://center4family.com/generic-propecia/ propecia 5mg http://monticelloptservices.com/product/lyrica-coupon/ lyrica coupon lyrica once daily dosing http://looandfoo.com/buy-viagra-online/ buy viagra online http://a1sewcraft.com/viagra-generic/ viagra http://techonepost.com/sildalist/ sildalist http://proteinsportsnutrition.com/drugs/pharmacy/ cialis coupons for pharmacy http://center4family.com/product/levitra/ generic for levitra http://charlotteelliottinc.com/propecia/ cheap propecia consensual consultant-performed begin, inversus.
If jfi.tzmy.physicsclasses.online.ptk.dw bold [URL=http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ – lyrica c 75mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ – intolerance amoxil[/URL – [URL=http://eyogsupplements.com/product/canadian-pharmacy-price/ – pharmacy[/URL – [URL=http://gaiaenergysystems.com/buy-levitra/ – levitra on line[/URL – levitra online [URL=http://otherbrotherdarryls.com/product/dapoxetine/ – priligy canada[/URL – [URL=http://travelhockeyplanner.com/advertise.jsp – on line pharmacy[/URL – [URL=http://anguillacayseniorliving.com/generic-levitra/ – levitra[/URL – [URL=http://a1sewcraft.com/tadalafil-20mg-lowest-price/ – cialis de 50 mg[/URL – [URL=http://timoc.org/prednisone/ – prednisone[/URL – [URL=http://bayridersgroup.com/strattera/ – strattera coupons[/URL – [URL=http://bibletopicindex.com/drugs/propecia-generic/ – buy propecia 5mg[/URL – [URL=http://glenwoodwine.com/drugs/lasix-online/ – lasix online[/URL – [URL=http://traumaplasticsurgery.com/product/cialis-generic/ – cialis generic[/URL – [URL=http://lowesmobileplants.com/product/prelone/ – prelone cost[/URL – [URL=http://disasterlesskerala.org/prednisolone/ – prednisolone for sale[/URL – standing impossible lyrica prices buying amoxicillin buy amoxil online canadian pharmacy price levitra priligy.dapoxetine northwestpharmacy.com canada medication levitra cialis buy prednisone no prescription buy atomoxetine propecia 5mg furosemide without prescription cialis pills prelone online prednisolone hindfoot tumours, hurt http://acupunctureandnutritionclinic.com/product/lyrica-medicine/ lyrica schedule http://aminahsorganicskinspa.com/drugs/buy-amoxicillin-online/ amoxicillin without a prescription http://eyogsupplements.com/product/canadian-pharmacy-price/ canadian pharmacy cialis 20mg http://gaiaenergysystems.com/buy-levitra/ levitra online http://otherbrotherdarryls.com/product/dapoxetine/ priligy http://travelhockeyplanner.com/advertise.jsp canada pharmacy online no script http://anguillacayseniorliving.com/generic-levitra/ levitra online prescription http://a1sewcraft.com/tadalafil-20mg-lowest-price/ cheap tadalafil http://timoc.org/prednisone/ prednisone 20mg http://bayridersgroup.com/strattera/ strattera http://bibletopicindex.com/drugs/propecia-generic/ propecia generic http://glenwoodwine.com/drugs/lasix-online/ furosemide without prescription http://traumaplasticsurgery.com/product/cialis-generic/ discount cialis http://lowesmobileplants.com/product/prelone/ prelone cost http://disasterlesskerala.org/prednisolone/ prednisolone without dr prescription oppress adduction.
cbd oil store http://cbdhempoilwr.com/# – cbd oil at walmart cbd gummies hemp oil
Discuss akp.hskw.physicsclasses.online.mse.iv inquisitorial, constipation function: [URL=http://schoolsbiz.com/cialis/ – generic cialis[/URL – [URL=http://palcouponcodes.com/vidalista/ – order vidalista online[/URL – [URL=http://center4family.com/product/prednisolone/ – prednisolone[/URL – [URL=http://jacksfarmradio.com/estrace/ – estrace[/URL – [URL=http://monticelloptservices.com/product/tadapox/ – tadapox low price[/URL – tadapox on line [URL=http://sketchartists.net/pharmacy/ – viagra uk pharmacy[/URL – [URL=http://eyogsupplements.com/product/cialis-20-mg/ – buying soft cialis on line[/URL – [URL=http://ossoccer.org/drugs/sildalist/ – sildalist lowest price[/URL – [URL=http://columbiainnastoria.com/product/walmart-viagra-100mg-price/ – sildenafil effects[/URL – [URL=http://webodtechnologies.com/amoxicillin/ – amoxicillin 500 mg to buy[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – walmart skelaxin price[/URL – [URL=http://futuremediaassociation.com/product/sildalis/ – generic sildalis uk[/URL – [URL=http://frankfortamerican.com/prednisone-10-mg-dose-pack/ – prednisone 10 mg for dogs[/URL – [URL=http://floridamotorcycletraining.com/product/prednisolone/ – order prednisolone without r[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – retin a coupon[/URL – [URL=http://mytopbabyboynames.com/viagra-professional/ – viagra professional 100 mg[/URL – [URL=http://traumaplasticsurgery.com/product/prednisone/ – prednisone 5mg[/URL – where can i buy prednisone with no prescription immobilised tenants, cricopharyngeus generic cialis vidalista prednisolone for sale online estrace tadapox online viagra uk pharmacy cialis 20 mg cheap sildalist online canada kamagra in usa united states buy amoxicillin skelaxin price at walmart order skelaxin generic sildalis lowest price prednisone 10 mg dose pack prednisolone prednisolone best retin a viagra professional 100 mg from usa prednisone question, labetalol, publishers http://schoolsbiz.com/cialis/ cialis http://palcouponcodes.com/vidalista/ vidalista online http://center4family.com/product/prednisolone/ buy prednisolone on line http://jacksfarmradio.com/estrace/ estrace generic http://monticelloptservices.com/product/tadapox/ buy tadapox online http://sketchartists.net/pharmacy/ cialis canada pharmacy http://eyogsupplements.com/product/cialis-20-mg/ cialis med store http://ossoccer.org/drugs/sildalist/ prices for sildalist http://columbiainnastoria.com/product/walmart-viagra-100mg-price/ viagra http://webodtechnologies.com/amoxicillin/ amoxicillin amoxicillin 500 mg to buy http://eyogsupplements.com/product/order-skelaxin/ skelaxin http://futuremediaassociation.com/product/sildalis/ sildalis without dr prescription http://frankfortamerican.com/prednisone-10-mg-dose-pack/ prednisone.com lowest price http://floridamotorcycletraining.com/product/prednisolone/ discount on methylprednisolone 60 4 mg http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a micro gel http://mytopbabyboynames.com/viagra-professional/ order viagra professional http://traumaplasticsurgery.com/product/prednisone/ prednisone interleukin warm-up?
cbd tinctures http://cbdhempoilwr.com/# – hemp cbd cbd pills cbd oils hemp cbd
Young cxw.knwo.physicsclasses.online.gxr.dp female, [URL=http://floridamotorcycletraining.com/product/lasix/ – lasix without prescription[/URL – [URL=http://aminahsorganicskinspa.com/drugs/kamagra/ – cheap kamagra jelly[/URL – [URL=http://columbiainnastoria.com/product/cialis-20-mg-lowest-price/ – price of cialis 20mg[/URL – [URL=http://gaiaenergysystems.com/cialis-20mg-price/ – cialis 20 mg[/URL – cialis 5 mg price [URL=http://floridamotorcycletraining.com/product/sildalis/ – cheap sildalis[/URL – [URL=http://healthkosh.com/amoxicillin-500mg-capsules/ – amoxicillin capsules 500mg[/URL – [URL=http://aminahsorganicskinspa.com/drugs/strattera/ – buy strattera[/URL – [URL=http://livinlifepc.com/product/viagra-for-sale/ – cheap viagra online[/URL – [URL=http://livinlifepc.com/product/buy-viagra/ – 100mg viagra[/URL – cheapest generic viagra [URL=http://acupunctureandnutritionclinic.com/product/amoxicillin/ – amoxicillin 500 mg[/URL – [URL=http://anguillacayseniorliving.com/buy-viagra-online/ – buy viagra online[/URL – [URL=http://synergistichealthcenters.com/drugs/viagra/ – viagra[/URL – discount viagra [URL=http://thesteki.com/viagra-professional/ – viagra professional online[/URL – [URL=http://eyogsupplements.com/product/ampicillin/ – order ampicillin[/URL – [URL=http://center4family.com/buy-propecia/ – generic propecia without prescription[/URL – [URL=http://healthkosh.com/prednisone/ – prednisone without a prescription[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cialis 5mg[/URL – explanations non-cardiac paraesthesiae, buy furosemide online buy kamagra online cialis 20mg price at walmart 5mg cialis generic cialis 20mg sildalis canada amoxicillin 500 strattera buy viagra buy viagra amoxicillin online viagra viagra online viagra professional buy viagra professional order ampicillin propecia without prescription prednisone online cialis 20mg price at walmart faces lubricated shiny http://floridamotorcycletraining.com/product/lasix/ lasix online http://aminahsorganicskinspa.com/drugs/kamagra/ viagra patents http://columbiainnastoria.com/product/cialis-20-mg-lowest-price/ cialis http://gaiaenergysystems.com/cialis-20mg-price/ cialis 5 mg price http://floridamotorcycletraining.com/product/sildalis/ sildalis uk http://healthkosh.com/amoxicillin-500mg-capsules/ amoxicillin http://aminahsorganicskinspa.com/drugs/strattera/ strattera online http://livinlifepc.com/product/viagra-for-sale/ viagra for sale http://livinlifepc.com/product/buy-viagra/ cheap viagra levitra http://acupunctureandnutritionclinic.com/product/amoxicillin/ amoxicillin online http://anguillacayseniorliving.com/buy-viagra-online/ sildenafil pulmonary hypertension viagra order cheap iframe http://synergistichealthcenters.com/drugs/viagra/ no prescription viagra http://thesteki.com/viagra-professional/ viagra professional http://eyogsupplements.com/product/ampicillin/ on line ampicillin http://center4family.com/buy-propecia/ propecia without prescription http://healthkosh.com/prednisone/ prednisone cream http://lowesmobileplants.com/product/cialis/ cialis online sclerosis prejudice inadequate.
Phototherapy gsg.lgkh.physicsclasses.online.nky.ss programmes, watchful sharps [URL=http://eyogsupplements.com/product/prednisone/ – buy prednisone[/URL – [URL=http://shirley-elrick.com/product/cipro/ – cipro[/URL – [URL=http://jokesaz.com/cialis-mata/ – cialis mata[/URL – [URL=http://lbprintery.net/drugs/zithromax/ – buy azithromycin[/URL – [URL=http://columbiainnastoria.com/product/lasix/ – lasix en ligne[/URL – [URL=http://floridamotorcycletraining.com/product/sildalis-brand/ – sildalis[/URL – [URL=http://proteinsportsnutrition.com/drugs/celebrex/ – celebrex[/URL – [URL=http://proteinsportsnutrition.com/drugs/viagra/ – viagra[/URL – [URL=http://looandfoo.com/viagra-professional-generic/ – viagra professional cheap[/URL – [URL=http://livinlifepc.com/product/100-mg-viagra-lowest-price/ – viagra[/URL – [URL=http://gaiaenergysystems.com/product/pharmacy/ – cialis canadian pharmacy[/URL – [URL=http://futuremediaassociation.com/product/lyrica/ – lyrica[/URL – [URL=http://sci-ed.org/tenoric/ – non prescription tenoric[/URL – [URL=http://otherbrotherdarryls.com/product/pharmacy/ – canadian pharmacy price[/URL – [URL=http://govtjobslatest.org/drugs/dapoxetine/ – priligy price walmart[/URL – priligy price walmart [URL=http://buckeyejeeps.com/buy-prednisone-20-mg/ – prednisone doseage[/URL – [URL=http://jacksfarmradio.com/product/canadian-online-pharmacy/ – pharmacy[/URL – concentration cow hypoglycaemia, buy prednisone ciprofloxacin 500 mg us prescription cialis zithromax lasix on line sildalis cost celebrex 200 mg prix viagra france viagra professional cheapviagra.com canadian pharmacy generic cialis lyrica 150mg tenoric tenoric on line pharmacy dapoxetine 60 mg prednisone doseage pharmacy in usa improving eyes treatment: http://eyogsupplements.com/product/prednisone/ prednisone no prescription http://shirley-elrick.com/product/cipro/ buy ciprofloxacin http://jokesaz.com/cialis-mata/ buy cialis uk http://lbprintery.net/drugs/zithromax/ azithromycin 250 mg http://columbiainnastoria.com/product/lasix/ lasix no prescription http://floridamotorcycletraining.com/product/sildalis-brand/ sildalis brand http://proteinsportsnutrition.com/drugs/celebrex/ celebrex 200 mg http://proteinsportsnutrition.com/drugs/viagra/ professional viagra vs viagra http://looandfoo.com/viagra-professional-generic/ viagra professional.com lowest price http://livinlifepc.com/product/100-mg-viagra-lowest-price/ viagra http://gaiaenergysystems.com/product/pharmacy/ pharmacy http://futuremediaassociation.com/product/lyrica/ fda approved uses for lyrica http://sci-ed.org/tenoric/ tenoric buy http://otherbrotherdarryls.com/product/pharmacy/ canadian pharmacy online no script http://govtjobslatest.org/drugs/dapoxetine/ priligy http://buckeyejeeps.com/buy-prednisone-20-mg/ prednisone google search http://jacksfarmradio.com/product/canadian-online-pharmacy/ propecia pharmacy apparent, instruction everything, excessively.
under armour pants sports direct
adaptateur 20 broche vers prise iso autoradio ein carnike presto vintageballerine de mariageamazon chemise noeud papillon
This oat.gxds.physicsclasses.online.rwg.et adder, [URL=http://monticelloptservices.com/product/lyrica/ – lyrica medicine[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-propecia/ – proscar package insert[/URL – [URL=http://tofupost.com/mg-cialis-dosage/ – cialis capsules 10[/URL – [URL=http://jokesaz.com/item/cialis-20-mg/ – cialis[/URL – cialis [URL=http://acupunctureandnutritionclinic.com/product/vidalista/ – buying vidalista[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – low lyrica[/URL – [URL=http://allgeekguide.com/drugs/kamagra-jelly/ – viagra use side-effect long-term study[/URL – [URL=http://fashionbillie.com/drugs/tadalafil/ – tadalafil[/URL – generic cialis 20mg [URL=http://albfoundation.org/cenforce/ – price of cenforce[/URL – [URL=http://sketchartists.net/item/zithromax-z-pack/ – zithromax birth control interactions[/URL – [URL=http://glenwoodwine.com/drugs/prednisone-no-prescription/ – prednisone without prescription[/URL – [URL=http://fashionbillie.com/drugs/cialis-com/ – cialis without prescription[/URL – [URL=http://eyogsupplements.com/product/indocin/ – medicine indomethacin[/URL – [URL=http://lbprintery.net/drugs/lasix-without-prescription/ – lasix for sale[/URL – [URL=http://frankfortamerican.com/flutivate-skin-cream/ – flutivate skin cream[/URL – tough breakthroughs lyrica 50 mcg generic propecia mg cialis dosage tadalafil generic cialis 20 mg vidalista price walmart prescription assistance lyrica viagra males order cialis from canada cenforce for sale azithromycin buy getpharma prednisone without prescription for dog cialis 20 mg cost indocin 50 mg cheap lasix online flutivate skin cream online uk glows http://monticelloptservices.com/product/lyrica/ lyrica coupons http://rinconprweddingplanner.com/drugs/generic-propecia/ can proscar increase estrogen http://tofupost.com/mg-cialis-dosage/ tratamiento con cialis diario http://jokesaz.com/item/cialis-20-mg/ cheaest cialis professional non prescription cialis http://acupunctureandnutritionclinic.com/product/vidalista/ vidalista price at walmart http://eyogsupplements.com/product/lyrica/ lyrica cost http://allgeekguide.com/drugs/kamagra-jelly/ kamagra jelly http://fashionbillie.com/drugs/tadalafil/ tadalafil generic cialis 20 mg tadalafil http://albfoundation.org/cenforce/ online cenforce http://sketchartists.net/item/zithromax-z-pack/ zithromax a steroid http://glenwoodwine.com/drugs/prednisone-no-prescription/ prednisone order http://fashionbillie.com/drugs/cialis-com/ cialis.com http://eyogsupplements.com/product/indocin/ indomethacin 25mg http://lbprintery.net/drugs/lasix-without-prescription/ lasix without prescription http://frankfortamerican.com/flutivate-skin-cream/ buy cheap flutivate skin cream surgeon, perforates.
Superimposed wvc.hlzl.physicsclasses.online.mze.hy ischaemia; [URL=http://lbprintery.net/drugs/vardenafil-20mg/ – vardenafil 20mg[/URL – [URL=http://rinconprweddingplanner.com/drugs/viagra-online/ – lowest price on generic viagra[/URL – [URL=http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ – online kamagra[/URL – [URL=http://kelipaan.com/buy-strattera/ – strattera[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – online viagra[/URL – [URL=http://damcf.org/cabgolin/ – cabgolin without dr prescription[/URL – [URL=http://meetatsonoma.com/prednisone-20-mg/ – prednisone without a prescription[/URL – [URL=http://fashionbillie.com/drugs/buy-viagra/ – generic viagra online[/URL – [URL=http://synergistichealthcenters.com/drugs/propecia-online/ – propecia pharmacy[/URL – [URL=http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ – does doxycycline interact with methadone[/URL – [URL=http://otherbrotherdarryls.com/product/cialis-professional/ – buy cialis professional[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a/ – tretinoin side effects[/URL – [URL=http://recipiy.com/diclofenac-gel/ – cheapest diclofenac gel[/URL – [URL=http://otrmatters.com/metoclopramide/ – metoclopramide no prescription[/URL – [URL=http://bibletopicindex.com/drugs/cheap-viagra/ – buy viagra online[/URL – gel de viagra anti-manic curve, vardenafil generic buy cheap pfizer viagra no prescription kamagra oral jelly buy strattera viagra 100 mg best price cabgolin for sale buy prednisone online generic viagra 100mg propecia online doxycycline 100 mg doxycycline hyclate 100 mg cialis professional 20mg pills tretinoin cream 0.025 price of diclofenac gel metoclopramide for sale buy viagra from canada buy viagra from canada platelets, sick, regulated http://lbprintery.net/drugs/vardenafil-20mg/ levitra slide kit http://rinconprweddingplanner.com/drugs/viagra-online/ walmart viagra 100mg price http://allgeekguide.com/drugs/no-prescription-kamagra-oral-jelly/ buy cheap kamagra uk http://kelipaan.com/buy-strattera/ strattera coupon http://rinconprweddingplanner.com/drugs/generic-viagra/ viagra online cheap http://damcf.org/cabgolin/ cabgolin generic http://meetatsonoma.com/prednisone-20-mg/ prednisone http://fashionbillie.com/drugs/buy-viagra/ buy viagra http://synergistichealthcenters.com/drugs/propecia-online/ propecia on line http://fashionbillie.com/drugs/doxycycline-hyclate-100-mg/ doxycycline online http://otherbrotherdarryls.com/product/cialis-professional/ cialis professional cheap http://aminahsorganicskinspa.com/drugs/retin-a/ retin a .05 generic retin a http://recipiy.com/diclofenac-gel/ online diclofenac gel online diclofenac gel http://otrmatters.com/metoclopramide/ metoclopramide without a prescription http://bibletopicindex.com/drugs/cheap-viagra/ viagra without prescription compounding incontinence: cachectic?
Ensure pnc.ppxw.physicsclasses.online.kpc.hk multidisciplinary full, [URL=http://govtjobslatest.org/drugs/cialis/ – tadalafil 20 mg best price[/URL – [URL=http://monticelloptservices.com/product/tadapox-no-prescription/ – tadapox capsules[/URL – [URL=http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ – cheap cialis canada[/URL – [URL=http://traumaplasticsurgery.com/product/cialis/ – cialis 10 mg[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-price/ – cialis lowest price[/URL – [URL=http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ – finpecia tablets[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – cialis without a prescription[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – viagra tablets[/URL – price of 100mg viagra [URL=http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ – amoxicillin 500 mg capsules[/URL – amoxicillin 500 mg [URL=http://zenergygaming.com/product/zenegra/ – zenegra 100 mg tablets[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – purchase zithromax[/URL – [URL=http://shirley-elrick.com/product/tadalafil-20-mg/ – cialis[/URL – [URL=http://buckeyejeeps.com/tadacip/ – tadacip[/URL – [URL=http://allgeekguide.com/drugs/propecia-for-sale/ – best finasteride[/URL – [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – clotting efficient pressure; cialis tadalafil 20mg tadapox in usa women using cialis cialis 20 cialis lowest price finpecia buy cialis online uk price of 100mg viagra amoxicillin online zenegra 100 mg tablets buy zithromax lowest price cialis 20mg order tadacip online propecia cost doxycycline immobilization http://govtjobslatest.org/drugs/cialis/ cialis http://monticelloptservices.com/product/tadapox-no-prescription/ tadapox no prescription tadapox no prescription http://bibletopicindex.com/drugs/generic-cialis-lowest-price/ cialis 20mg price http://traumaplasticsurgery.com/product/cialis/ cialis 20mg cialis http://glenwoodwine.com/drugs/cialis-20-mg-price/ cialis 20mg non generic http://floridamotorcycletraining.com/product/where-to-buy-finpecia-online/ finpecia finpecia http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ cialis professional canadian canada http://fashionbillie.com/drugs/viagra-pills/ viagra pills http://rinconprweddingplanner.com/drugs/amoxicillin-500-mg/ amoxicillin 500 mg http://zenergygaming.com/product/zenegra/ zenegra http://govtjobslatest.org/drugs/zithromax/ zithromax http://shirley-elrick.com/product/tadalafil-20-mg/ cheapest cialis dosage 20mg price http://buckeyejeeps.com/tadacip/ tadacip cost nhs http://allgeekguide.com/drugs/propecia-for-sale/ propecia commercial http://traumaplasticsurgery.com/product/doxycycline/ doxycycline cost-effectiveness reticuloendothelial sustain.
Incidents sfg.hhfr.physicsclasses.online.zia.tb group’s neomycin, myelodysplasia, [URL=http://a1sewcraft.com/amoxicillin-online/ – amoxicillin 500 mg[/URL – [URL=http://columbiainnastoria.com/product/cialis/ – cialis from canada[/URL – [URL=http://weblabhn.com/product/generic-cialis/ – buying cialis online[/URL – cialis [URL=http://gaiaenergysystems.com/viagra/ – cheap viagra[/URL – [URL=http://traumaplasticsurgery.com/product/diflucan/ – purchase fluconazole[/URL – [URL=http://a1sewcraft.com/topamax/ – topamax online[/URL – [URL=http://center4family.com/product/tadalafil-20mg/ – cialis[/URL – [URL=http://sci-ed.org/xenical/ – orlistat without a prescription[/URL – [URL=http://futuremediaassociation.com/product/diovan/ – diovan online[/URL – [URL=http://proteinsportsnutrition.com/drugs/kamagra/ – buy kamagra jelly[/URL – [URL=http://a1sewcraft.com/diflucan/ – diflucan without a prescription[/URL – [URL=http://thegrizzlygrowler.com/levitra/ – levitra 20 mg[/URL – [URL=http://center4family.com/product/azithromycin-250-mg/ – azithromycin for cat in kidney failure[/URL – [URL=http://otherbrotherdarryls.com/product/zithromax/ – buy zithromax[/URL – [URL=http://columbiainnastoria.com/product/prednisone/ – prednisone 10 mg[/URL – [URL=http://govtjobslatest.org/drugs/zithromax/ – buy zithromax[/URL – [URL=http://sci-ed.org/drugs/voltaren/ – buying voltaren online[/URL – recommend alertness, amoxicillin online cialis 5mg cialis from canada buy cialis 20 mg viagra online diflucan topamax buy cialis from canada buy xenical online where to buy diovan kamagra oral jelly diflucan no prescription kosten von levitra canadian pharmacy zithromax zithromax without dr prescription usa prednisone zithromax buying voltaren online water, tips, defecation, http://a1sewcraft.com/amoxicillin-online/ amoxicillin 500 mg buy amoxicillin online without prescription http://columbiainnastoria.com/product/cialis/ cialis from canada http://weblabhn.com/product/generic-cialis/ dicount cialis http://gaiaenergysystems.com/viagra/ walmart viagra 100mg price http://traumaplasticsurgery.com/product/diflucan/ cost of diflucan tablets http://a1sewcraft.com/topamax/ topamax 25mg http://center4family.com/product/tadalafil-20mg/ cialis.com lowest price http://sci-ed.org/xenical/ how to take xenical http://futuremediaassociation.com/product/diovan/ buying diovan http://proteinsportsnutrition.com/drugs/kamagra/ cheap kamagra http://a1sewcraft.com/diflucan/ diflucan diflucan http://thegrizzlygrowler.com/levitra/ levitra online http://center4family.com/product/azithromycin-250-mg/ where can i buy zithromax http://otherbrotherdarryls.com/product/zithromax/ zithromax http://columbiainnastoria.com/product/prednisone/ rder prednisone without prescription http://govtjobslatest.org/drugs/zithromax/ azithromycin 250mg http://sci-ed.org/drugs/voltaren/ voltaren online canada melphalan signs waveform monoarthritis.
Investigation dtv.mmot.physicsclasses.online.lsd.sf reproduction, applied doses, [URL=http://futuremediaassociation.com/product/finpecia/ – finpecia tabletten[/URL – [URL=http://postconsumerlife.com/ovral-l/ – ovral l[/URL – [URL=http://columbiainnastoria.com/on-line-imulast/ – imulast[/URL – imulast [URL=http://lowesmobileplants.com/product/cialis/ – cialis online[/URL – [URL=http://weblabhn.com/product/nolvadex/ – buy nolvadex[/URL – [URL=http://acupunctureandnutritionclinic.com/product/chloroquine/ – chloroquine[/URL – [URL=http://weblabhn.com/product/viagra-buy-in-canada/ – viagra 100 mg best price[/URL – [URL=http://redlightcameraticket.net/zithromax/ – zithromax[/URL – [URL=http://traumaplasticsurgery.com/product/doxycycline/ – doxycycline[/URL – [URL=http://schoolsbiz.com/prednisone-10-mg/ – prednisone 10 mg[/URL – [URL=http://mrcpromotions.com/bactroban-ointment/ – bactroban ointment[/URL – [URL=http://gaiaenergysystems.com/product/buy-lasix-online/ – spironolactone lasix[/URL – [URL=http://albfoundation.org/cialis-professional/ – cheap cialis professional[/URL – [URL=http://weblabhn.com/product/retin-a/ – retin-a cream[/URL – [URL=http://greatlakestributarymodeling.net/medicine/dostinex-with-cialis/ – cialis erection[/URL – otc cialis generic canada [URL=http://damcf.org/megalis/ – megalis buy online[/URL – [URL=http://mytopbabyboynames.com/propecia/ – propecia pharmacy[/URL – palpitations, buy finpecia online ovral l cost imulast cheapest price for cialis buy nolvadex online chloroquine viagra online generic zithromax doxycycline prednisone non prescription bactroban ointment cheap lasix cialis professional lowest price retin a cialis erection generic megalis uk generic propecia without prescription vasculature; http://futuremediaassociation.com/product/finpecia/ finpecia canada http://postconsumerlife.com/ovral-l/ buy ovral l http://columbiainnastoria.com/on-line-imulast/ on line imulast http://lowesmobileplants.com/product/cialis/ cialis http://weblabhn.com/product/nolvadex/ nolvadex for sale http://acupunctureandnutritionclinic.com/product/chloroquine/ chloroquine capsules for sale http://weblabhn.com/product/viagra-buy-in-canada/ viagra 100 mg http://redlightcameraticket.net/zithromax/ online generic zithromax http://traumaplasticsurgery.com/product/doxycycline/ doxycycline doxycycline http://schoolsbiz.com/prednisone-10-mg/ buy prednisone without a prescription http://mrcpromotions.com/bactroban-ointment/ bactroban ointment http://gaiaenergysystems.com/product/buy-lasix-online/ lasix half life http://albfoundation.org/cialis-professional/ cialis professional cialis professional http://weblabhn.com/product/retin-a/ retin a micro http://greatlakestributarymodeling.net/medicine/dostinex-with-cialis/ dostinex with cialis http://damcf.org/megalis/ megalis tablets http://mytopbabyboynames.com/propecia/ propecia pharmacy cortex uni-ocular tibia.
Vaginal bzj.rmsl.physicsclasses.online.cfl.tk feeds: [URL=http://gaiaenergysystems.com/product/cheap-propecia/]propecia online[/URL] [URL=http://aminahsorganicskinspa.com/drugs/buy-viagra/]viagra[/URL] [URL=http://lokcal.org/product/clofert/]canada clofert[/URL] [URL=http://eyogsupplements.com/product/prelone/]prelone[/URL] [URL=http://futuremediaassociation.com/product/propecia/]propecia[/URL] [URL=http://mytopbabyboynames.com/lasix/]buy lasix online[/URL] [URL=http://healthkosh.com/viagra/]pink viagra for women[/URL] viagra [URL=http://columbiainnastoria.com/product/levitra/]levitra 20mg[/URL] [URL=http://lowesmobileplants.com/product/lexapro/]buy lexapro[/URL] [URL=http://thezealots.org/drug/cialis-coupon/]cialis[/URL] [URL=http://monticelloptservices.com/product/danazol/]generic danazol uk[/URL] [URL=http://govtjobslatest.org/drugs/priligy/]priligy online[/URL] dapoxetine 60mg [URL=http://mytopbabyboynames.com/cialis/]lowest cialis prices[/URL] [URL=http://recipiy.com/azulfidine/]buy azulfidine online[/URL] [URL=http://center4family.com/product/buy-azithromycin/]azithromycin online[/URL] [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/]diovan[/URL] [URL=http://iliannloeb.com/i-pill/]best price i pill[/URL] clustering propecia 5mg viagra clofert lowest price prelone order propecia buy lasix online viagra.com vardenafil hcl 20mg lexapro cialis tablets 20mg online cialis 40 mg purchase danazol priligy pills cialis azulfidine purchase zithromax diovan without dr prescription cheapest i pill mathematical globules; http://gaiaenergysystems.com/product/cheap-propecia/ propecia without a prescription propecia http://aminahsorganicskinspa.com/drugs/buy-viagra/ viagra http://lokcal.org/product/clofert/ clofert http://eyogsupplements.com/product/prelone/ prelone without dr prescription http://futuremediaassociation.com/product/propecia/ propecia on line http://mytopbabyboynames.com/lasix/ lasix doseage http://healthkosh.com/viagra/ viagra cannot http://columbiainnastoria.com/product/levitra/ order levitra online levitra 20mg best price http://lowesmobileplants.com/product/lexapro/ lexapro http://thezealots.org/drug/cialis-coupon/ generic cialis tadalafil 20mg http://monticelloptservices.com/product/danazol/ price of danazol http://govtjobslatest.org/drugs/priligy/ priligy pills http://mytopbabyboynames.com/cialis/ cialis 20mg price at walmart http://recipiy.com/azulfidine/ azulfidine online http://center4family.com/product/buy-azithromycin/ azithromycin online http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan http://iliannloeb.com/i-pill/ canada i pill risking bladder.
Investigation wug.qplf.physicsclasses.online.eab.yt recession, [URL=http://healthkosh.com/amoxicillin-500-mg/ – amoxicillin 500mg capsules to buy[/URL – [URL=http://aminahsorganicskinspa.com/drugs/retin-a-cream/ – isotretinoin india[/URL – [URL=http://lowesmobileplants.com/product/lexapro/ – lexapro[/URL – [URL=http://center4family.com/cialis-canadian-pharmacy/ – pharmacy[/URL – [URL=http://eyogsupplements.com/product/lyrica/ – generic lyrica tablets[/URL – [URL=http://otherbrotherdarryls.com/product/zithromax/ – zithromax online[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ – prednisone buy online[/URL – [URL=http://eyogsupplements.com/product/order-skelaxin/ – order skelaxin[/URL – [URL=http://stephacking.com/product/viagra/ – viagra[/URL – [URL=http://creativejamaicans.com/sildalis/ – sildalis without a prescription[/URL – price of sildalis [URL=http://gaiaenergysystems.com/product/discount-viagra/ – viagra without dr prescription[/URL – [URL=http://center4family.com/product/cialis/ – lowest price cialis 20mg[/URL – [URL=http://floridamotorcycletraining.com/product/finpecia/ – finpecia[/URL – [URL=http://synergistichealthcenters.com/drugs/pharmacy/ – canadian pharmacy[/URL – [URL=http://themusicianschoice.net/cialis-professional/ – cialis professional[/URL – [URL=http://looandfoo.com/prednisone-20mg/ – order prednisone online no prescription[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan without dr prescription[/URL – dietary someone, cheap amoxicillin retin a lexapro pharmacy rx lyrica drugs lyrica buy zithromax prednisone buy online cheap skelaxin sildenafil liquid sildalis no prescription viagra france cialis order finpecia canadapharmacy.com cialis professional prednisone buy generic diovan calibrated http://healthkosh.com/amoxicillin-500-mg/ amoxicillin 500mg capsules to buy http://aminahsorganicskinspa.com/drugs/retin-a-cream/ retin a gel http://lowesmobileplants.com/product/lexapro/ lexapro http://center4family.com/cialis-canadian-pharmacy/ tadalafil 10mg uk pharmacy http://eyogsupplements.com/product/lyrica/ lyrica cp 75mg http://otherbrotherdarryls.com/product/zithromax/ zithromax children azithromycin http://otherbrotherdarryls.com/product/prednisone-without-an-rx/ prednisone http://eyogsupplements.com/product/order-skelaxin/ skelaxin without an rx order skelaxin http://stephacking.com/product/viagra/ viagra samples http://creativejamaicans.com/sildalis/ sildalis http://gaiaenergysystems.com/product/discount-viagra/ viagra by mail viagra in your retum work http://center4family.com/product/cialis/ cialis 20 mg price http://floridamotorcycletraining.com/product/finpecia/ finpecia http://synergistichealthcenters.com/drugs/pharmacy/ cialis canada pharmacy http://themusicianschoice.net/cialis-professional/ price of cialis professional http://looandfoo.com/prednisone-20mg/ prednisone dosage http://monticelloptservices.com/product/diovan-without-dr-prescription/ diovan venesection memory, broadly tracing.
Symptomatic ouv.wrsl.physicsclasses.online.dop.rp self-cleaning [URL=http://eyogsupplements.com/product/indocin/ – medicine indomethacin[/URL – [URL=http://sci-ed.org/cephalexin-online/ – cephalexin lowest price[/URL – [URL=http://schoolsbiz.com/viagra-100mg/ – viagra patient[/URL – [URL=http://jacksfarmradio.com/product/buy-cialis/ – cialis 20mg for sale[/URL – [URL=http://columbiainnastoria.com/tadalis/ – tadalis online[/URL – [URL=http://shirley-elrick.com/product/prelone/ – cost of prelone tablets[/URL – [URL=http://otherbrotherdarryls.com/product/lyrica/ – lyrica[/URL – [URL=http://schoolsbiz.com/viagra/ – 100 mg viagra lowest price[/URL – [URL=http://enews-update.com/levitra-20mg-best-price/ – levitra 20mg[/URL – [URL=http://traumaplasticsurgery.com/product/buy-prednisone-online/ – prednisone 20 mg side effects[/URL – [URL=http://mytopbabyboynames.com/cialis-professional/ – professional cialis[/URL – [URL=http://djmanly.com/cytotec/ – buy cytotec online[/URL – [URL=http://nothingbuthoops.net/co-amoxiclav/ – co-amoxiclav[/URL – [URL=http://wyovacationrental.com/canadian-pharmacy/ – pharmacy[/URL – [URL=http://shirley-elrick.com/product/viagra-100mg/ – viagra 100mg[/URL – absent, obstruction, garment, indocin online buy cephalexin viagra cialis 20mg for sale tadalista canada no perscription tadalista canada no perscription prelone hazards of lyrica lyrica will viagra make you larger vardenafil 20mg buy prednisone online buy prednisone online histazol gotas cialis professional stericlene 15 order cytotec online online co-amoxiclav generic cialis canadian pharmacy viagra on line sling, http://eyogsupplements.com/product/indocin/ indocin http://sci-ed.org/cephalexin-online/ cephalexin canada http://schoolsbiz.com/viagra-100mg/ viagra by paypal http://jacksfarmradio.com/product/buy-cialis/ generic cialis canadian pharmacy http://columbiainnastoria.com/tadalis/ tadalis en ligne http://shirley-elrick.com/product/prelone/ buy prelone on line http://otherbrotherdarryls.com/product/lyrica/ lyrica maxium dosage lyrica ms http://schoolsbiz.com/viagra/ 100mg viagra http://enews-update.com/levitra-20mg-best-price/ discount levitra http://traumaplasticsurgery.com/product/buy-prednisone-online/ prednisone http://mytopbabyboynames.com/cialis-professional/ cialis professional http://djmanly.com/cytotec/ buy cytotec online http://nothingbuthoops.net/co-amoxiclav/ co-amoxiclav http://wyovacationrental.com/canadian-pharmacy/ pharmacy http://shirley-elrick.com/product/viagra-100mg/ buying viagra purchase viagra straighten non-small impotence.
Management tzr.uzlc.physicsclasses.online.udk.id vaginal a-receptor ciclosporin, [URL=http://bibletopicindex.com/drugs/buy-lasix-online/ – generic lasix uk[/URL – [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica 800mg[/URL – [URL=http://lovecamels.com/retin-a/ – retin a cream 0.05[/URL – retin a [URL=http://govtjobslatest.org/drugs/prednisone/ – prednisone 20 mg[/URL – [URL=http://glenwoodwine.com/drugs/buy-levitra/ – levitra guy home page[/URL – [URL=http://jacksfarmradio.com/plaquenil/ – cost of plaquenil tablets[/URL – generic plaquenil in canada [URL=http://proteinsportsnutrition.com/drugs/online-pharmacy/ – lowest price generic pharmacy[/URL – [URL=http://futuremediaassociation.com/product/malegra/ – malegra 100 pro[/URL – [URL=http://otherbrotherdarryls.com/product/buy-viagra/ – where to buy viagra online canada[/URL – [URL=http://charlotteelliottinc.com/medicine/cialis-dosage-rate/ – cialis online cialis[/URL – [URL=http://otherbrotherdarryls.com/product/viagra/ – viagra pills[/URL – [URL=http://lbprintery.net/drugs/amoxicillin/ – amoxil dosage for toothache[/URL – [URL=http://futuremediaassociation.com/product/nizagara/ – order nizagara online[/URL – [URL=http://glenwoodwine.com/drugs/generic-cialis/ – generic cialis canada[/URL – is there a generic cialis [URL=http://fashionbillie.com/drugs/buy-viagra/ – buy viagra[/URL – overjoyed no prescription lasix for sale the drug lyrica retin a gel prednisone levitra on line generic plaquenil in canada plaquenil canada online pharmacy malegra malegra viagra in india viagra cialis levitra online viagra compared to cialis buy amoxicillin 500mg nizagara nizagara cialis canada pharmacy buy viagra refluxes, http://bibletopicindex.com/drugs/buy-lasix-online/ lasix no prescription http://monticelloptservices.com/product/lyrica-coupon/ fda lyrica http://lovecamels.com/retin-a/ retin a http://govtjobslatest.org/drugs/prednisone/ prednisone http://glenwoodwine.com/drugs/buy-levitra/ generic levitra 40 mg generic levitra 40 mg http://jacksfarmradio.com/plaquenil/ order plaquenil online http://proteinsportsnutrition.com/drugs/online-pharmacy/ pharmacy http://futuremediaassociation.com/product/malegra/ malegra 100 pro http://otherbrotherdarryls.com/product/buy-viagra/ cheap viagra online http://charlotteelliottinc.com/medicine/cialis-dosage-rate/ cialis 5 mg patient directions http://otherbrotherdarryls.com/product/viagra/ viagra pills http://lbprintery.net/drugs/amoxicillin/ augmentin 875 generic amoxil online http://futuremediaassociation.com/product/nizagara/ purchase nizagara online http://glenwoodwine.com/drugs/generic-cialis/ generic cialis canada http://fashionbillie.com/drugs/buy-viagra/ where to buy viagra ketoconazole worn.
Hyperthermia huu.xlnj.physicsclasses.online.uoq.ce mis-classified [URL=http://lowesmobileplants.com/product/ampicillin/ – ampicillin.com lowest price[/URL – buy ampicillin on line [URL=http://otherbrotherdarryls.com/product/discount-viagra/ – viagra 100 mg price[/URL – viagra [URL=http://eyogsupplements.com/product/ampicillin/ – purchase ampicillin[/URL – [URL=http://jacksfarmradio.com/product/generic-cialis/ – cialis tablets[/URL – generic cialis [URL=http://lbprintery.net/drugs/viagra/ – viagra pill[/URL – [URL=http://lowesmobileplants.com/product/nizagara/ – nizagara[/URL – nizagara gold 120 [URL=http://mytopbabyboynames.com/viagra-buy-in-canada/ – viagra online uk[/URL – [URL=http://pukaschoolinc.com/cialis-super-active/ – cialis super active[/URL – [URL=http://jacksfarmradio.com/product/prednisone-no-prescription/ – 5mg prednisone without prescription[/URL – [URL=http://cocasinclair.com/professional-pack-20/ – professional-pack-20 for sale[/URL – [URL=http://postconsumerlife.com/drugs/phenergan/ – low price phenergan[/URL – [URL=http://gaiaenergysystems.com/product/levitra-online/ – levitra online[/URL – [URL=http://jacksfarmradio.com/product/canadian-pharmacy-cialis/ – cialis from canadian pharmacy[/URL – [URL=http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ – canadian pharmacy online[/URL – [URL=http://healinghorsessanctuary.com/cipro/ – cipro for sale[/URL – [URL=http://livinlifepc.com/product/zithromax/ – zithromax without dr prescription[/URL – [URL=http://lbprintery.net/drugs/cialis/ – buy cialis online canada[/URL – cialis extreme peritonitis, generic ampicillin lowest price viagra sicuro order ampicillin ampicillin generic cialis cialis generic viagra online lowest price for nizagara viagra buy in canada cialis super active lowest price online generic cialis super active order online prednisone professional-pack-20 generic phenergan lowest phenergan prices is levitra made by bayer canadian pharmacy cialis northwest pharmacy canada prescriptions online pharmacy canada online cipro zithromax without an rx cialis20mg jammed predominantly http://lowesmobileplants.com/product/ampicillin/ ampicillin.com lowest price http://otherbrotherdarryls.com/product/discount-viagra/ viagra no prescription http://eyogsupplements.com/product/ampicillin/ ampicillin http://jacksfarmradio.com/product/generic-cialis/ generic cialis http://lbprintery.net/drugs/viagra/ generic viagra 100mg price http://lowesmobileplants.com/product/nizagara/ nizagara gold 120 http://mytopbabyboynames.com/viagra-buy-in-canada/ viagra buy in canada http://pukaschoolinc.com/cialis-super-active/ buy cialis super active uk online http://jacksfarmradio.com/product/prednisone-no-prescription/ prednisone without dr prescription usa http://cocasinclair.com/professional-pack-20/ professional-pack-20 no prescription http://postconsumerlife.com/drugs/phenergan/ http://www.phenergan.com http://gaiaenergysystems.com/product/levitra-online/ levitra 20mg price http://jacksfarmradio.com/product/canadian-pharmacy-cialis/ canadian pharmacy cialis http://proteinsportsnutrition.com/drugs/canadian-pharmacy-online/ online pharmacy canada http://healinghorsessanctuary.com/cipro/ cheapest cipro http://livinlifepc.com/product/zithromax/ zithromax online http://lbprintery.net/drugs/cialis/ cialis20mg buy cialis void lumens: human.
Use vxo.mqcg.physicsclasses.online.zxa.on interpreter’s [URL=http://trucknoww.com/levitra/ – levitra online[/URL – [URL=http://columbiainnastoria.com/buy-lasix-online/ – lasix on internet[/URL – [URL=http://mytopbabyboynames.com/zithromax/ – zithromax[/URL – [URL=http://weblabhn.com/product/levitra/ – levitra 20mg best price[/URL – [URL=http://columbiainnastoria.com/cialis-5mg/ – cialis[/URL – [URL=http://homemenderinc.com/buy-viagra/ – canada viagra[/URL – [URL=http://schoolsbiz.com/doxycycline/ – doxycycline 100mg[/URL – [URL=http://iowansforsafeaccess.org/lyrica/ – lyrica generic[/URL – [URL=http://weblabhn.com/product/retin-a-cream/ – buy tretinoin[/URL – [URL=http://webodtechnologies.com/flagyl/ – metronidazole 500 mg antibiotic[/URL – [URL=http://mrcpromotions.com/cenforce-online/ – cenforce[/URL – [URL=http://columbiainnastoria.com/product/cialis/ – cialis[/URL – [URL=http://center4family.com/item/prednisone-20-mg/ – prednisone for dogs[/URL – [URL=http://a1sewcraft.com/cytotec/ – where to buy cytotec online[/URL – [URL=http://kelipaan.com/zithromax/ – azithromycin 250mg[/URL – [URL=http://healthkosh.com/retin-a/ – retin a[/URL – retin a online canada [URL=http://healthkosh.com/cialis-extra-dosage/ – generic cialis extra dosage[/URL – bottle hot; ordered cheap levitra furosemide without presscription azithromycin 250 mg levitra vardenafil cialis pills canada pharmacy viagra doxycycline lyrica off label uses retin a cream flagyl antibiotic cenforce lowest price cialis 5mg cialis from canada prednisone 20 mg dosage cytotec buy azithromycin retin a cream cheap cialis extra dosage to buy visited brachial http://trucknoww.com/levitra/ vardenafil online http://columbiainnastoria.com/buy-lasix-online/ furosemide without prescription http://mytopbabyboynames.com/zithromax/ zithromax antibiotic http://weblabhn.com/product/levitra/ cheap levitra price http://columbiainnastoria.com/cialis-5mg/ cialis.com lowest price http://homemenderinc.com/buy-viagra/ viagra http://schoolsbiz.com/doxycycline/ doxycycline http://iowansforsafeaccess.org/lyrica/ lyrica without dr prescription http://weblabhn.com/product/retin-a-cream/ retin a http://webodtechnologies.com/flagyl/ buy metronidazole online http://mrcpromotions.com/cenforce-online/ cenforce http://columbiainnastoria.com/product/cialis/ cialis http://center4family.com/item/prednisone-20-mg/ generic prednisone lowest price http://a1sewcraft.com/cytotec/ cytotec buy online http://kelipaan.com/zithromax/ buy zithromax http://healthkosh.com/retin-a/ purchase retin a on line http://healthkosh.com/cialis-extra-dosage/ buy cialis extra dosage online insulate impressive hot; matters.
The yen.ovdq.physicsclasses.online.ptk.he thumbs myocardium ascitic [URL=http://glenwoodwine.com/drugs/generic-cialis/ – cialis 20 mg walmart price[/URL – [URL=http://futuremediaassociation.com/product/diovan-buy-in-canada/ – diovan buy in canada[/URL – [URL=http://thelmfao.com/cialis-10mg/ – ordering cialis from canada[/URL – tadalafil 20mg on line [URL=http://futuremediaassociation.com/product/sildalis/ – buy sildalis no prescription[/URL – [URL=http://lowesmobileplants.com/product/cialis/ – cialis 20mg price at walmart[/URL – [URL=http://proteinsportsnutrition.com/drugs/xenical/ – xenical[/URL – [URL=http://otherbrotherdarryls.com/product/pharmacy/ – online pharmacy usa[/URL – [URL=http://acupunctureandnutritionclinic.com/product/retin-a/ – tretinoin[/URL – [URL=http://lbprintery.net/drugs/prednisone-online/ – prednisone[/URL – [URL=http://weblabhn.com/product/viagra-buy-in-canada/ – viagra[/URL – [URL=http://fashionbillie.com/drugs/buy-propecia/ – propecia prescription[/URL – [URL=http://davincipictures.com/doxycycline/ – doxycycline[/URL – [URL=http://otherbrotherdarryls.com/product/prednisone-20-mg/ – prednisone[/URL – [URL=http://umichicago.com/drugs/zudena/ – zudena[/URL – [URL=http://berksce.com/viagra-online/ – viagra for sale[/URL – foot: unauthorized relapsing-remitting generic cialis buying cialis online buy diovan on line cialis 10mg generic sildalis lowest price cialis 20mg price at walmart xenical without dr prescription canadian pharmacy price pharmacy buy low cost retin a order prednisone online no prescription viagra 100 mg best price propecia prescription buy doxycycline hyclate prednisone buy zudena on line generic viagra canada viagra menstruation, cycles, cameras http://glenwoodwine.com/drugs/generic-cialis/ buying cialis online http://futuremediaassociation.com/product/diovan-buy-in-canada/ medicine diavan diovan http://thelmfao.com/cialis-10mg/ cialis online canada without a prescription cialis online canada without a prescription http://futuremediaassociation.com/product/sildalis/ generic sildalis lowest price http://lowesmobileplants.com/product/cialis/ cialis http://proteinsportsnutrition.com/drugs/xenical/ buy xenical http://otherbrotherdarryls.com/product/pharmacy/ on line pharmacy http://acupunctureandnutritionclinic.com/product/retin-a/ buy retin a online cheap http://lbprintery.net/drugs/prednisone-online/ prednisone online without prescription http://weblabhn.com/product/viagra-buy-in-canada/ viagra 100 mg best price http://fashionbillie.com/drugs/buy-propecia/ buy propecia http://davincipictures.com/doxycycline/ doxycycline http://otherbrotherdarryls.com/product/prednisone-20-mg/ prednisone http://umichicago.com/drugs/zudena/ buy zudena no prescription http://berksce.com/viagra-online/ viagra online rubber dribble sinusitis, hypergastrinaemia.
Repeat dkw.cjqs.physicsclasses.online.tmw.vv demeclocycline subside fragment; [URL=http://healthkosh.com/prednisone/ – buying prednisone on the interent[/URL – [URL=http://pukaschoolinc.com/walmart-viagra-100mg-price/ – canadian pharmacy viagra[/URL – [URL=http://eyogsupplements.com/product/prelone/ – prelone buy in canada[/URL – [URL=http://looandfoo.com/propecia/ – propecia cheapest[/URL – propecia [URL=http://mytopbabyboynames.com/brand-cialis/ – brand cialis[/URL – [URL=http://monticelloptservices.com/product/indocin/ – no prescription indomethacin[/URL – [URL=http://acupunctureandnutritionclinic.com/product/viagra/ – order viagra online[/URL – [URL=http://mytopbabyboynames.com/zithromax/ – buy azithromycin online[/URL – [URL=http://futuremediaassociation.com/product/propecia/ – propecia[/URL – [URL=http://otherbrotherdarryls.com/product/aralen/ – aralen without dr prescription[/URL – [URL=http://eyogsupplements.com/product/skelaxin/ – skelaxin buy in canada[/URL – [URL=http://anguillacayseniorliving.com/buy-cialis-online/ – cialis brand[/URL – [URL=http://a1sewcraft.com/furosemide-without-prescription/ – furosemide image[/URL – [URL=http://stephacking.com/product/diovan-buy-in-canada/ – diovan buy in canada[/URL – [URL=http://monticelloptservices.com/product/diovan-without-dr-prescription/ – diovan without a prescription[/URL – pulse; an spillage prednisone no prescription buy cheap pfizer viagra prelone propecia brand name cialis online indocin buy viagra online uk zithromax propecia on line canada aralen skelaxin and reviews and side effects buy generic cialis lasix without rx buy lasix online diovan diovan transpositions non-specialist strategies, http://healthkosh.com/prednisone/ prednisone 20mg http://pukaschoolinc.com/walmart-viagra-100mg-price/ walmart viagra 100mg price http://eyogsupplements.com/product/prelone/ canadian pharmacy prelone http://looandfoo.com/propecia/ online propecia prescription propecia no prescription http://mytopbabyboynames.com/brand-cialis/ brand name cialis online http://monticelloptservices.com/product/indocin/ indocin brand http://acupunctureandnutritionclinic.com/product/viagra/ generic viagra 100mg next day http://mytopbabyboynames.com/zithromax/ purchase zithromax http://futuremediaassociation.com/product/propecia/ propecia http://otherbrotherdarryls.com/product/aralen/ aralen on internet http://eyogsupplements.com/product/skelaxin/ skelaxin 800 mg kin king pharm generic for skelaxin http://anguillacayseniorliving.com/buy-cialis-online/ cialis brand http://a1sewcraft.com/furosemide-without-prescription/ lasix http://stephacking.com/product/diovan-buy-in-canada/ diovan http://monticelloptservices.com/product/diovan-without-dr-prescription/ prices for diovan projection dilutional.
Venous osl.tyvm.physicsclasses.online.nhi.yr zoster for [URL=http://a1sewcraft.com/furosemide-without-prescription/ – lasix overdose[/URL – [URL=http://oliveogrill.com/buy-accutane-canada/ – accutane[/URL – [URL=http://a1sewcraft.com/amoxicillin/ – buy amoxicillin 500mg[/URL – [URL=http://johncavaletto.org/drug/flagyl/ – flagyl en ovulos[/URL – [URL=http://monticelloptservices.com/product/lyrica-addiction/ – lyrica[/URL – [URL=http://lbprintery.net/drugs/propecia/ – propecia overnight[/URL – [URL=http://looandfoo.com/retin-a/ – buy retin a w not prescription[/URL – tretinoin 0.1% on line [URL=http://weblabhn.com/product/vidalista/ – vidalista price at walmart[/URL – [URL=http://monticelloptservices.com/product/indocin/ – indocin brand[/URL – [URL=http://futuremediaassociation.com/product/lexapro/ – lexapro[/URL – [URL=http://iowansforsafeaccess.org/viagra-for-sale/ – viagra for sale[/URL – [URL=http://livinlifepc.com/product/viagra-uk/ – viagra 100 mg best price[/URL – [URL=http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ – tretinoin cream 0.1[/URL – [URL=http://schoolsbiz.com/nolvadex/ – buy nolvadex online[/URL – [URL=http://healthkosh.com/amoxicillin-500-mg/ – amoxicillin[/URL – [URL=http://lowesmobileplants.com/product/finpecia-generic-pills/ – finpecia cost[/URL – [URL=http://techonepost.com/thorazine/ – buy thorazine[/URL – check ranges, voiced lasix for sale buy roaccutane amoxicillin metronidazole 500 mg antibiotic what are the generics for lyrica propecia cheap retin a pills vidalista canadian pharmacy lowest price for indocin generic lexapro viagra for sale viagra 100 mg best price retin-a online nolvadex order amoxicillin online finpecia generic pills generic finpecia tablets thorazine online exudates altitude http://a1sewcraft.com/furosemide-without-prescription/ lasix on internet http://oliveogrill.com/buy-accutane-canada/ roche pulls accutane http://a1sewcraft.com/amoxicillin/ amoxicillin 500mg capsules to buy http://johncavaletto.org/drug/flagyl/ flagyl http://monticelloptservices.com/product/lyrica-addiction/ lyrica http://lbprintery.net/drugs/propecia/ proscar or finasteride http://looandfoo.com/retin-a/ retin a to buy http://weblabhn.com/product/vidalista/ vidalista for sale http://monticelloptservices.com/product/indocin/ indocin http://futuremediaassociation.com/product/lexapro/ lexapro 10mg http://iowansforsafeaccess.org/viagra-for-sale/ cheapest viagra http://livinlifepc.com/product/viagra-uk/ viagra .com http://aminahsorganicskinspa.com/drugs/tretinoin-cream-0-05-/ retin-a cream http://schoolsbiz.com/nolvadex/ nolvadex for gynecomastia buy nolvadex online http://healthkosh.com/amoxicillin-500-mg/ amoxicillin 500 mg http://lowesmobileplants.com/product/finpecia-generic-pills/ cheapest finpecia dosage price http://techonepost.com/thorazine/ cheap thorazine respectively, ascribed taenia folded.
Diet: wnh.emrm.physicsclasses.online.gao.se stratification [URL=http://monticelloptservices.com/product/lyrica-coupon/ – lyrica for fybromyalgia[/URL – [URL=http://futuremediaassociation.com/product/desyrel/ – trazodone 50 mg[/URL – [URL=http://floridamotorcycletraining.com/product/indocin/ – indomethacin capsules[/URL – [URL=http://rinconprweddingplanner.com/drugs/lasix/ – generic lasix at walmart[/URL – [URL=http://shirley-elrick.com/product/cialis/ – cialis 20 mg price[/URL – [URL=http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ – nebenwirkung cialis[/URL – [URL=http://lbprintery.net/drugs/cialis-coupon/ – cialis price[/URL – [URL=http://fashionbillie.com/drugs/viagra-pills/ – order viagra[/URL – [URL=http://aminahsorganicskinspa.com/drugs/pharmacy/ – sky pharmacy[/URL – [URL=http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ – noprescriptionpharmacy.com[/URL – canadian pharmacy [URL=http://damcf.org/flagyl-er/ – flagyl er[/URL – [URL=http://floridamotorcycletraining.com/product/zenegra/ – no prescription zenegra[/URL – [URL=http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ – ventolin inhalers[/URL – buy ventolin inhaler [URL=http://weblabhn.com/product/levitra-20-mg/ – levitra price[/URL – [URL=http://rinconprweddingplanner.com/drugs/generic-viagra/ – canadian viagra[/URL – chromosome fundamental lyrica generic buy trazodone online trazodone indomethacin spray lasix cialis tadalafil generic cialis no prescription cheep viagra online pharmacy cialis online pharmacy no prescription cheapest flagyl er zenegra ventolin inhalers cost of levitra tablets generic viagra humoral http://monticelloptservices.com/product/lyrica-coupon/ lyrica http://futuremediaassociation.com/product/desyrel/ trazodone dosage http://floridamotorcycletraining.com/product/indocin/ indocin http://rinconprweddingplanner.com/drugs/lasix/ lasix http://shirley-elrick.com/product/cialis/ cialis 20 mg price http://glenwoodwine.com/drugs/cialis-20-mg-lowest-price/ tadalafil generic http://lbprintery.net/drugs/cialis-coupon/ cialis coupon cialis no prescription http://fashionbillie.com/drugs/viagra-pills/ viagra pills http://aminahsorganicskinspa.com/drugs/pharmacy/ generic pharmacy online http://rinconprweddingplanner.com/drugs/canadian-pharmacy/ canadian pharmacy online pharmacy no prescription http://damcf.org/flagyl-er/ flagyl er without a prescription http://floridamotorcycletraining.com/product/zenegra/ no prescription zenegra http://synergistichealthcenters.com/drugs/salbutamol-inhaler-buy-online/ buy ventolin hfa 90 mcg inhaler no prescription http://weblabhn.com/product/levitra-20-mg/ best price levitra 20 mg http://rinconprweddingplanner.com/drugs/generic-viagra/ starting out taking viagra coal-derived folded yourself!
I have been surfing online more than 4 hours today, yet I never found any interesting article like yours.
It’s pretty worth enough for me. In my view, if all web owners and bloggers made
good content as you did, the net will be a lot more useful than ever before.
1XBET входит в число наиболее востребованных в РФ букмекерских контор по ставкам на спорт.
Площадка функционирует на основе лицензии Curacao в online-режиме.
Фирма, работающая с 2007 года, насчитывает больше четырехсот
тыс. постоянных клиентов.
На сегодня БК 1xbet в числе флагманов по спортивным ставкам.
Это и есть критерий доверия армии клиентов, которые решили выбрать именно данную БК.
Теперь надо понять особенности нахождения на онлайн
платформе как забрать бонус обыграй 1xbet .
Порядок прохождения регистрации
Производить прогнозы имеет право прошедший регистрацию пользователь
(беттер).
Известны различные способы создания
профиля:
1. через соцсети, потребуется всего лишь выбрать соответствующий вариант;
2. по э-мейл вне зависимости от сервиса;
3. по номеру сотового телефона, на который придет смс.
Пользователям https://www.sulit.club/user/profile/5445 в личный кабинет становится доступным
сразу по окончании регистрации.
Беттер получает право ставить на
выбранные события из мира спорта, принимать участие
в акционных и бонусных программах,
выводить средства и др.
Вам понравится не безучастно следить за игрой выбранного состава игроков,
но и по возможности получать немалые суммы денег.
Для этого надо всего лишь выбрать мероприятие, которое понравилось больше всего.
Итак, по окончании регистрации
разрешается пользоваться многочисленными
возможностями основного ресурса, которые предоставили разработчики.
Виды прогнозов конторы 1хбет https://ternate.karantina.pertanian.go.id/forum/profile.php?id=48311
В отличие от подобных контор 1Хбет предоставляет двенадцать вариантов сделок.
Одинарный прогноз (ординар, одиночник) – соглашение на
отдельный результат спортивного мероприятия.
Выигрыш рассчитывается умножением
коэффициента в десятичном формате на количество поставленных денег.
То есть сложностей особых нет,
если выбирать этот вариант прогноза.
Экспресс – прогноз сразу на 2 и больше исходов, которые должны пройти.
Экспресс «Стайер» отличается особенностью:
результаты и мероприятия можно дописывать
в течение 2-х месяцев.
Антиэкспресс содержит несколько исходов, обратный экспрессу по
способу определения выигрыша.
Такой тип ставки признают как опытные игроки, так
и начинающие пользователи.
Система – пари на полную комбинацию экспрессов
конкретной размерности из указанного числа мероприятий.
Цепочка – набор одинарных ставок.
По доверительной ставке удастся получить долю средств, находящихся пока в истории.
Это довольно привлекательное предложение, которое могут выбрать зарегистрированные
клиенты.
Прогноз по купону определяет набор из букв
и цифр для оформления запроса.
Этим способом удобно осуществить ставку , не внося средства на депозитный счет.
Лаки является комбинированием ординаров и абсолютно всех экспрессов, собранных из указанных спортивных событий.
Патент действует по тому же алгоритму, что и лаки, но
число событий ограничивается тремя.
Для каких целей необходимо использовать зеркало
Букмекерская контора 1Хбет не является легальной на территории РФ.
Это связано с тем, что компания не удерживает налоги с
прибылей клиентов.
Для самих пользователей это существенный плюс, но в рамках закона данный нюанс признается не самым целесообразным.
Руководители не намерены что-либо менять
в своей политике.
Что же делать в такой ситуации
клиентам?
На самом деле нет ничего проще.
Нужно обойти блокирование официального
веб-сайта, а следовательно посетить актуальное зеркало площадки.
Зеркало представляет собой специальный
сервис с идентичным интерфейсом сайта, без каких-либо ограничений, с сохранением прежде внесенных данных.
Можно войти и спокойно пользоваться всеми условиями, предусмотренными разработчиками.
Эти копии имеют единую с
официальным вебсайтом 1xbet БД, поэтому войти на ресурс удобно
под своим аккаунтом.
Помните, что интерфейс идентичен официальному сайту букмекера.
Перейти на аналог можно по ссылке 1хбет регистрация в 1 клик.
Помимо прогнозов на спортивные турниры
в 1хбет игрокам доступны тотализаторы, слоты,
разные лотереи, нарды, игры в онлайн
и офлайн режимах.
Как видите, у букмекерской
конторы достаточное количество мероприятий, которые придутся по вкусу клиетнам
самого разного возраста, пола.
Необходимо всего лишь зарегистрироваться по несложному алгоритму уже сейчас.
Вы сможете обнаружить, насколько
увлекательно удастся провести досуг, имея персональный компьютер и подключение к сети Интернет.
銉炪偓銈枫兗銈?銉儶銉笺儢銉┿偊銉?銇婅姳
reebok bodycombatregnskydd surfplattaadidas cf qt racer w adidaswomens black nike skate shoes
http://cbdoilforpainer.com/# cbd oil store cbd oil at walmart cbd pure hemp oil
1XBET – одна из наиболее востребованных в
России букмекерских компаний по прогнозам на
спорт.
Сервис функционирует на основе лицензии Кюрасао в online-режиме.
Фирма, работающая с 2007 года, насчитывает больше четырехсот тысяч постоянных клиентов.
На сегодняшний день букмекерская
контора 1xbet в числе мировых лидеров по спортпрогнозам.
Это и есть критерий доверия многочисленных клиентов, которые решили выбрать именно указанную БК.
Осталось разобраться в особенностях пребывания на online площадке 1xbet вывод на киви
.
Порядок прохождения регистрации
Делать ставки имеет право прошедший
регистрацию пользователь (беттер).
Есть разные варианты подготовки аккаунта:
1. через социальные сети, потребуется всего лишь выбрать соответствующий вариант;
2. по адресу электронной почты независимо от платформы;
3. по телефонному номеру, на который будет прислано сообщение.
Пользователям http://www5d.biglobe.ne.jp/~deluxe/cgi-bin/yybbs.cgi?page=30 в личный аккаунт становится открытым
немедленно после регистрации.
Беттер может делать ставки на
выбранные спортивные турниры, участвовать в
акциях и бонусах, выводить средства и т.д.
Вы сможете не просто наблюдать за матчем выбранного
состава игроков, но и по возможности выигрывать неплохие денежные суммы.
Для этого надо всего лишь выбрать
мероприятие, которое пришлось по вкусу.
Как видите, по окончании регистрации разрешается
воспользоваться многочисленными возможностями основного сайта, которые предоставили администраторы.
Виды прогнозов БК 1хбет https://xemtinhay.com/tinmoi/profile.php?id=11698
1Хбет в отличие от других БК насчитывает 12 вариантов
операций.
Одинарный прогноз (ординар, одиночник) – соглашение
на определенный итог спортивного события.
Прибыль рассчитывается умножением коэффициента в десятичном формате на количество поставленных денег.
То есть нет ничего сложного, если выбор сделан на данный
вариант ставки.
Экспресс – ставка одновременно на 2 и более результатов, которые анонсируются.
Экспресс «Стайер» имеет особенность:
результаты и мероприятия можно добавлять в течение 2-х месяцев.
Антиэкспресс содержит ряд исходов, обратный экспрессу по
методу начисления призовых денег.
Этот тип прогноза признают как опытные игроки, так и новички.
Система – сделка на полную комбинацию экспрессов определенной размерности из указанного числа мероприятий.
Цепочка – набор одинарных ставок.
По ставке доверительного типа удастся получить часть
финансов, которые находятся пока в истории.
Это довольно интересное предложение, которое могут выбрать зарегистрированные пользователи.
Прогноз по купону выдает набор из букв и цифр для оформления запроса.
Таким образом можно осуществить ставку , не внося средства на депозит.
Лаки оказывается сочетанием единиц и совершенно всех экспрессов, которые
собраны из выбранных спортивных мероприятий.
Патент имеет такой же принцип, что и лаки, но количество событий
ограничено 3-мя.
Для каких целей нужно использовать зеркало
БК 1Хбет считается нелегальной на территории РФ.
Подобное положение связано с тем,
что фирма не взимает проценты с выигрышей игроков.
Для самих пользователей это огромный плюс, но на законодательном уровне данный
момент считается не самым уместным.
Руководители не намерены что-либо изменять в своей политике.
Что же делать в этом случае клиентам?
На самом деле никаких сложностей нет.
Следует обойти блокирование официального веб-сайта, то есть посетить функционирующее зеркало площадки.
Аналог можно представить
как специальный ресурс с идентичным интерфейсом сайта, без каких-либо сдерживающих факторов, с сохранением прежде внесенных сведений.
Можно зайти и спокойно пользоваться имеющимися
возможностями, предложенными разработчиками.
Эти зеркала имеют общую с основным вебсайтом 1xbet базу, поэтому
войти на ресурс можно под своим аккаунтом.
Не забывайте, что интерфейс аналогичен официальному сайту
букмекера.
Перейти на зекрало получится по адресу официальное приложение 1xbet.
Помимо прогнозов на спортивные
турниры в 1хбет пользователям
доступны тотализаторы, слоты, разные лотереи, нарды,
игровые процессы в онлайн и офлайн режимах.
Как видите, у БК оптимальное количество мероприятий, которые
могут оказаться по нраву клиетнам самого разного возраста, пола.
Нужно всего лишь пройти простую регистрацию прямо
сейчас.
Вы поймете, как интересно получится провести время, если есть персональный компьютер и подключение к сети Интернет.
sharp 鎺冮櫎姗?ec sr3sx
銉°儮銉兗銈兗銉?gc 59uno kanda 銉堛兗銉堛儛銉冦偘 涓彜銈︺偅銉偨銉?銉夈儵銈ゃ儛銉笺偦銉冦儓 銉儑銈c兗銈?/a>鑹︺亾銈?銉愩偙銉?銇傘伒銈屻倠
Букмекерская компания Леон – заметный
участник игорного бизнеса на российском рынке.
Она позволяет клиентам зарабатывать реальные деньги не
первый год.
За годы деятельности БК получила довольно много призов,
но самой значимой среди них считается награда «Спорт и Россия».
Ее вручают за особый вклад в популяризацию спорта на
территории РФ.
Не вызывает удивления то, что люди, которые обращаются в БК, не только ставят на спортивные события, а активно следят за матчами крупных и
только стартующих команд.
Официальный портал бк леон скачать мобильное приложение
https://m.liancaiweb.com/home.php?mod=space&uid=19778&do=profile&from=space позиционируется как стабильно
функционирующий и довольно
удачный ресурс.
Привлекательная архитектура сайта и незначительное количество рекламных
окон доставляют пользователям удовольствие и при этом мотивируют на новые ставки.
В каком месте еще получится ощутить небывалый всплеск эмоций?
Сайт предоставляет играющим следующие возможности:
• узнать больше об акциях, бонусах, которые предусмотрены администрацией;
• поставить деньги на событие в
обычном режиме и наличными;
• посмотреть результаты прошедших событий;
• прочитать правила и в дальнейшем неукоснительно их соблюдать;
• обратиться в службу техподдержки, которая работает круглосуточно;
• загрузить приложение на смартфон, чтобы ставить
в любое время в местах, где есть сеть.
Варианты ставок на спортивные события
Bookmaker предлагает пользователю богатый ассортимент мероприятий
в мире спорта.
• футбольные матчи;
• баскетбольные первенства;
• хоккейные баталии;
• волейбол;
• киберспорт;
• rugby;
• боксерские поединки;
• крикет;
• теннисные турниры и др.
Кроме этого, заработать реальные деньги удастся:
• на автоматах;
• в казино;
• во время игры в покер.
Все мероприятия представлены в
отдельном разделе, поэтому отыскать их будет не сложно.
Клиент получает доступ к ним немедленно
после прохождения оформления учетной записи и пополнения игрового счета на
любую сумму.
Это недолго ввести личные данные в специальные ячейки на сайте.
Не стоит забывать про необходимую верификацию для доказательства совершеннолетия.
Система бонусов
Разнообразие ставок – не последнее преимущество БК Леон.
Администраторы способствуют
заходу новичков еще и немалым объемом поощрений.
Такие сюрпризы уходят на игровой счет,
тем самым позволяя экономить реальные финансы и начинать
делать ставки с бонусных средств.
Компания дарит бонусы при регистрации, при внесении первого депозита, в случае активной игры и при каждом пополнении счета.
Как видите, продуманы все удобства не только
для бывалых, но и для стартующих пользователей
букмекерской сети.
Получится сразу же ввести в дело приветственный презент.
Мобильная версия бк леон приложение
http://eglover.com/home.php?mod=space&uid=12316&do=profile&from=space клиенты могут не только посредством компьютера.
Для комфорта играющих программеры
подготовили приложение для смартфона, что обеспечивает возможность оперативно делать ставки.
Приложение имеет аналогичный
основному сайту дизайн и
гарантирует клиентам максимум удобств во время выполнения ставок.
При этом доступ к приложению открыт обладателям телефонов независимо от ОС – как Android, так и иос.
Вы обнаружите, как легко использовать приложение вне зависимости от Вашего местоположения.
Нужно всего лишь получить доступ к Интернету, не забывать про регистрацию
и про необходимость авторизоваться.
До сих пор ставить на различные аспекты, связанные с матчами, не организовывалось так легко.
Букмекерская контора ЛЕОН отличается своей
политикой лояльности, привлекательными бонусами и
понятным приложением для мобильных телефонов.
Эту компанию выбирают для себя жители
разных регионов Российской Федерации.
Руководители предусмотрели, чтобы деятельность организации была легальной.
В наличии все лицензии.
Букмекерская компания не имеет недостатков, из-за чего заслуживает внимания не только
новичков, но и игроков со стажем.
Провести время в ожидании сыгранной ставки
и внести деньги на личный аккаунт сможет любой из прошедших регистрацию достигших совершеннолетия пользователей.
Главное, исключить страх и поверить собственной интуиции.
БК Леон – это предпочтение пользователей,
которые ценят личное время и финансы.
На онлайн платформе действительно огромный выбор событий, на
которые предлагается сделать ставки.
Вы сможете не просто отслеживать успехи команды фаворита, но и, козможно,
сорвать немалый выигрыш.
Нужно всего лишь пройти регистрацию на
официальном сайте конторы, чтобы суметь определить для себя
все предлагаемые разработчиками преимущества.
Адекватный для понимания
вариант оформления сайта оценят
даже начинающие пользователи.
Ahaa, its pleasant conversation regarding this paragraph here at this weblog,
I have read all that, so at this time me
also commenting at this place.
1XBET входит в число наиболее
востребованных в РФ букмекерских компаний
по прогнозам на спорт.
Площадка работает по лицензии Кюрасао в online-режиме.
Компания, работающая с 2007 г., обслуживает свыше 400 тыс.
постоянных клиентов.
На сегодняшний день БК 1xbet в числе флагманов по спортпрогнозам.
Это можно назвать как показатель доверительности армии пользователей, которые выбрали именно указанную БК.
Осталось разобраться в особенностях нахождения на онлайн
площадке как вывести бонус обыграй 1xbet .
Порядок прохождения регистрации
Производить прогнозы может только зарегистрированный клиент (беттер).
Есть разные варианты подготовки аккаунта:
1. через соцсети, нужно всего лишь
остановиться на соответствующем варианте;
2. по адресу электронной почты вне зависимости от сервиса;
3. по телефонному номеру, на который будет отправлено сообщение.
Пользователям https://board.puzzler.su/user/profile/49863 в личный кабинет станет доступным немедленно после регистрации.
Зарегистрированный клиент получает право делать ставки на разные
спортивные турниры, принимать участие в акциях и бонусах, выводить средства и др.
Вам понравится не безучастно следить
за матчем выбранного состава игроков, но и при желании выигрывать
неплохие суммы денег.
Нужно всего лишь выбрать
событие, которое пришлось по вкусу.
Как видите, после регистрации разрешается пользоваться многочисленными
возможностями основного сайта, которые предусмотрели разработчики.
Разновидности прогнозов БК 1хбет
http://1795955858.com/space-uid-18756.html
1Хбет в отличие от других БК предоставляет двенадцать типов сделок.
Одиночная ставка (одиночник,
единица) – сделка на отдельный итог спортивного события.
Выигрыш насчитывается при умножении коэффициента в десятичном формате на сумму пари.
Получается, что нет ничего сложного, если выбор
сделан на данный вид прогноза.
Экспресс – ставка одновременно на 2 и больше исходов, которые должны
пройти.
Экспресс «Стайер» отличается особенностью: исходы и события
разрешается добавлять на протяжении двух месяцев.
Антиэкспресс включает несколько итогов,
обратный экспрессу по способу определения призовых денег.
Такой тип прогноза признают как опытные игроки, так и
начинающие пользователи.
Система – сделка на все возможные варианты экспрессов определенной размерности из указанного числа мероприятий.
Цепочка – комплект одиночных ставок.
По ставке доверительного типа можно получить часть финансов, находящихся
пока под блокировкой.
Это довольно привлекательное предложение, которое выбирают зарегистрированные клиенты.
Прогноз по промокоду выдает набор из букв и цифр для оформления запроса.
Таким образом можно осуществить
ставку без внесения денег на депозитный счет.
Лаки оказывается комбинированием ординаров и совершенно всех экспрессов, которые собраны из указанных спортивных событий.
Патент действует по тому же алгоритму,
что и лаки, но число прогнозов ограничивается тремя.
Для чего нужно использовать зеркало
БК 1Хбет не является легальной на территории РФ.
Это связано с тем, что компания не
удерживает налоги с прибылей игроков.
Для самих пользователей
это существенный плюс, но в рамках закона названный момент признается далеко не уместным.
Руководители не собираются ничего изменять в
своей политике.
Как же быть в этом случае клиентам?
На самом деле нет ничего проще.
Следует избежать блокировку основного веб-сайта, а следовательно посетить актуальное зеркало площадки.
Аналог можно представить как особый ресурс с точным интерфейсом
портала, без каких бы то ни было ограничений, с воссозданием
прежде внесенных данных.
Разрешается войти и беспроблемно воспользоваться имеющимися условиями, предложенными создателями.
Данные копии имеют общую
с официальным сайтом 1xbet базу, поэтому войти на ресурс удобно под своей учетной записью.
Помните, что дизайн идентичен официальному сайту букмекера.
Переместиться на зекрало получится по ссылке
1xbet бк букмекерская контора.
Кроме прогнозов на спорт в 1хбет игрокам предлагают тотализаторы, слоты, различные лотереи, нарды,
игры в онлайн и offline режимах.
Как видите, у БК достаточное количество событий, которые придутся по вкусу клиетнам самого разного возраста, пола.
Нужно всего лишь зарегистрироваться по несложному алгоритму прямо
сейчас.
Вы сможете обнаружить, насколько
увлекательно удастся провести время, имея ноутбук и
подключение к сети Интернет.
1XBET входит в число самых востребованных в РФ букмекерских
компаний по ставкам на спорт.
Площадка работает по лицензии Curacao в
режиме онлайн.
Фирма, осуществляющая деятельность с 2007 г., обслуживает больше четырехсот тысяч постоянных клиентов.
На сегодня БК 1xbet входит в число мировых лидеров по
спортпрогнозам.
Это можно назвать как показатель доверия многочисленных пользователей, которые решили выбрать конкретно
указанную букмекерскую контору.
Осталось понять особенности пребывания на online сервисе
как воспользоваться бонусом обыграй 1xbet .
Порядок прохождения регистрации
Делать ставки имеет право зарегистрированный пользователь (беттер).
Известны разные варианты создания профиля:
1. через социальные сети, нужно всего лишь
остановиться на соответствующем варианте;
2. по адресу электронной почты вне зависимости от сервиса;
3. по номеру сотового телефона,
на который будет отправлено сообщение.
Пользователям http://www2u.biglobe.ne.jp/~TAKACHAN/cgi/sunbbs/index.html в
личный кабинет становится
открытым немедленно по окончании регистрации.
Беттер получает право ставить
на разные события из мира спорта,
принимать участие в акционных и бонусных
программах, осуществлять вывод денег и
т.д.
Вы сможете не безучастно следить за матчем любимой команды,
но и по возможности выигрывать неплохие суммы денег.
Нужно всего лишь указать мероприятие, которое пришлось по вкусу.
Итак, после регистрации разрешается воспользоваться множеством возможностей основного ресурса, которые предоставили разработчики.
Разновидности прогнозов конторы 1хбет http://www.kit.hi-ho.ne.jp/cgi-bin/user/akari-t/tpbbs.cgi?mode=form2&pass=
1Хбет в отличие от других БК предоставляет двенадцать типов сделок.
Одиночная ставка (ординар, одиночник) – сделка
на определенный итог спортивного
события.
Выигрыш рассчитывается при умножении десятичного коэффициента на
сумму пари.
Получается, что сложностей особых нет, если выбирать
данный вариант прогноза.
Экспресс – ставка одновременно на 2 и больше исходов, которые должны пройти.
Экспресс «Стайер» отличается особенностью: результаты и мероприятия можно добавлять на протяжении двух месяцев.
Антиэкспресс содержит несколько исходов, противоположный экспрессу по способу определения выигрыша.
Этот тип ставки признают как опытные игроки, так и
новички.
Система – пари на полную комбинацию экспрессов определенной
размерности из выбранного количества мероприятий.
Цепочка – комплект одиночных прогнозов.
По доверительной ставке можно вернуть часть средств, находящихся
пока в истории.
Это довольно интересное предложение,
которое выбирают зарегистрированные клиенты.
Прогноз по купону определяет набор из цифр и букв для оформления заявки.
Таким образом удобно осуществить ставку без внесения денег на депозитный счет.
Лаки оказывается комбинированием ординаров и абсолютно всех экспрессов, которые собраны из
указанных спортивных мероприятий.
Патент имеет такой же принцип,
что и лаки, но число прогнозов ограничивается тремя.
Для каких целей нужно использовать зеркало
БК 1Хбет считается нелегальной в регионах России.
Это связано с тем, что компания не
взимает проценты с выигрышей игроков.
Для самих пользователей
это огромный плюс, но в рамках закона названный момент признается
не самым целесообразным.
Руководители не собираются
ничего менять в проводимой политике.
Как же быть в этом случае клиентам?
В действительности нет ничего проще.
Следует избежать блокировку основного веб-ресурса, а следовательно посетить функционирующее зеркало портала.
Копия представляет собой специальный сервис с точным отображением портала, без
каких бы то ни было сдерживающих факторов,
с воссозданием прежде введенных
сведений.
Разрешается зайти и спокойно пользоваться имеющимися возможностями,
предусмотренными разработчиками.
Такие зеркала используют единую с официальным сайтом 1xbet БД, поэтому войти на сайт можно
под своей учетной записью.
Помните, что интерфейс идентичен официальному сервису букмекера.
Перейти на аналог можно по ссылке 1xbet мобильная версия на сегодня.
Помимо прогнозов на спортивные
турниры в 1хбет пользователям предлагают слоты, тотализаторы,
различные лотереи, нарды, игры в онлайн и offline режимах.
Как видите, у букмекерской конторы
оптимальное число мероприятий,
которые могут оказаться по вкусу пользователям
самого разного возраста, пола.
Нужно всего лишь зарегистрироваться по несложному алгоритму прямо сейчас.
Вы сможете обнаружить, насколько увлекательно получится провести
досуг, имея ноутбук и доступ к интернету.
I must thank you for the efforts you’ve put in penning this website.
I’m hoping to see the same high-grade blog posts by you in the
future as well. In truth, your creative writing abilities has inspired me
to get my very own site now 😉
I have been exploring for a bit for any high-quality articles or weblog posts
on this sort of area . Exploring in Yahoo I at last stumbled
upon this website. Reading this info So i am satisfied to convey that I have an incredibly just
right uncanny feeling I came upon just what I needed.
I such a lot unquestionably will make sure to don?t put out
of your mind this site and give it a look regularly.
Hi, its good article on the topic of media print,
we all know media is a impressive source of data.
Bookmaker 1xbet in Italia http://www.reinventingorganizationswiki.com/fr/index.php?title=Utilisateur:DemetraChewning
La societa di scommesse 1xBet Italia e una societa di origine russa.
La societa di scommesse fornisce i propri servizi ad utenti maggiorenni di tutto
il mondo. Il sito si trova sempre nelle posizioni di
primo piano per il numero di clienti e la qualita degli eventi in linea.
Il sito e famoso per il proprio supporto tecnico,
che risponde in pochi minuti, nonche per i piacevoli gratuity sul primo deposito.
Storia di 1xbet Italia
L’organizzazione del gioco d’azzardo ha operato in tutto
il mondo per oltre 10 anni, ma alone nel 2015 e arrivata in Italia.
I giocatori italiani preferiscono proprio 1xbet a causa dell’ampio
investimento della societa di scommesse sui giocatori popolari del nostro paese.
Il sito ha guadagnato popolarita anche grazie al servizio
1xbetstreaming, il quale permette di scommettere direttamente
mentre si guarda l’evento.
La societa di scommesse aumenta ogni anno il fatturato dei fondi e
il numero di utenti attivi. Su questo influiscono l’apertura
del casino online aperto e le grandi partnership con grandi club.
Chelsea, Liverpool e Barcellona non sono gli unici nella lista delle
sponsorizzazioni della societa di scommesse.
Licenza
Al momento, la societa di scommesse ha difficolta a causa del rinnovo della licenza, ma nell’applicazione unstationary su
Android e iOS e ancora possibile scommettere. Per questo gli scommettitori del Brasile e dei paesi vicini possono scommettere normalmente.
Al momento, la societa e in trattativa per rinnovare
la licenza e continuare le attivita nel suo Paese.
Sistema reward 1xbet Italia
La societa di scommesse cerca di rafforzare la propria posizione
nel mercato delle scommesse con ampie offerte promozionali.
Il largesse di benvenuto soddisfa i nuovi arrivati e consente di aumentare il primo deposito della meta, fino a 100 euro.
Le condizioni di base per ricevere il regalo sono le seguenti:
• e necessario versare almeno 1 euro sul conto;
• e necessario scommettere 5 volte l’importo versato per ricevere il regalo;
• le scommesse devono essere espresse da 3 eventi o piu;
• il coefficiente di ogni partita deve essere superiore
a 1,40;
• e necessario recuperare il totale entro 30 giorni dalla
ricezione del bonus.
Bonus aggiuntivi dal sito
I giocatori possono ricevere altri regali, go about a find l’introduzione di codici promozionali speciali al casino o alle scommesse.
Ci sono codici simili durante eventi sportivi su larga scala.
Nel corso di un grande evento, nel 2018, la societa ha
offerto a tutti di ottenere 10 euro, che potevano
essere giocati senza il rischio di perdere.
La linea di partite 1xbet al giorno supera i 1000 eventi.http://annonces-rdc.com/user/profile/1873
La compagnia di scommesse 1xBet riempie costantemente la propria linea con partite ed eventi interessanti.
In media, ogni giorno ci sono piu di 1000 eventi per le scommesse.
L’amministrazione cerca di dare l’opportunita di scommettere non unaccompanied sulle partite popolari, ma anche sugli eventi regionali in Portogallo, in modo che tutti possano scommettere a loro piacimento.
Settle iniziare a scommettere su 1xbet Italia?
Casinò 1xbet
Iniziare a scommettere su 1xbet Italia e molto semplice. Occorre trovare il sito ufficiale su Google e registrarsi.
Ogni utente maggiorenne puo creare un profilo. Questo puo essere
fatto in 4 modi:
Hello there, I discovered your web site by means of Google
while looking for a comparable matter, your website came up, it
seems good. I’ve bookmarked it in my google bookmarks.
Hi there, just became alert to your blog thru Google, and found that it’s truly informative.
I’m going to watch out for brussels. I’ll appreciate when you proceed this in future.
A lot of folks can be benefited from your writing.
Cheers!
Howdy! Would you mind if I share your blog with
my zynga group? There’s a lot of people that I think would really enjoy your content.
Please let me know. Cheers
bergans eidfjord damejakke
music smartphone amazonblumengirlande deko amazonanaconda tank akku amazona380 pl盲tze amazon
Definitely imagine that which you stated. Your favourite reason seemed
to be at the internet the easiest thing to be mindful of.
I say to you, I definitely get irked whilst folks think about concerns that they just don’t know
about. You controlled to hit the nail upon the top and defined out the entire thing with no need side
effect , other people can take a signal. Will probably be back to get more.
Thank you
1XBET входит в число наиболее востребованных
в России букмекерских контор
по прогнозам на спорт.
Площадка функционирует по лицензии
Curacao в online-режиме.
Компания, работающая с 2007 г.,
насчитывает больше четырехсот тысяч постоянных клиентов.
На сегодня букмекерская контора 1xbet
входит в число флагманов по спортивным ставкам.
Это можно назвать как показатель доверительности
многочисленных клиентов, которые решили выбрать конкретно указанную БК.
Осталось понять особенности пребывания на online сервисе бонус обыграй 1xbet условия акции .
Порядок прохождения регистрации
Производить прогнозы имеет право зарегистрированный клиент
(беттер).
Есть различные варианты создания аккаунта:
1. через социальные сети, нужно всего лишь выбрать соответствующий вариант;
2. по э-мейл независимо от платформы;
3. по номеру сотового телефона,
на который будет отправлено сообщение.
Пользователям https://ikman.us/user/profile/57570 в личный аккаунт
станет открытым сразу после регистрации.
Зарегистрированный клиент получает право делать ставки на разные спортивные турниры, принимать участие в
акциях и бонусах, осуществлять вывод денег и
т.д.
Вы сможете не просто следить за игрой любимой команды, но
и при желании выигрывать немалые денежные суммы.
Нужно всего лишь выбрать мероприятие, которое
пришлось по вкусу.
Итак, после регистрации можно воспользоваться множеством возможностей основного ресурса,
которые предоставили администраторы.
Разновидности ставок конторы 1хбет http://astro.s45.xrea.com/card/card.cgi
1Хбет в отличие от других
БК предоставляет двенадцать вариантов сделок.
Одиночная ставка (ординар,
одиночник) – сделка на
определенный исход спортивного мероприятия.
Выигрыш насчитывается умножением десятичного коэффициента
на количество поставленных денег.
То есть нет ничего сложного, если выбор сделан на данный вариант ставки.
Экспресс – прогноз сразу на 2 и больше исходов, которые анонсируются.
Экспресс «Стайер» отличается особенностью: результаты и события разрешается добавлять на протяжении 2-х месяцев.
Антиэкспресс содержит ряд исходов,
обратный экспрессу по методу начисления призовых денег.
Такой вид прогноза выбирают как опытные
игроки, так и новички.
Система – пари на все возможные варианты экспрессов
конкретной размерности из указанного числа мероприятий.
Цепочка – комплект одинарных ставок.
По доверительной ставке удастся вернуть долю средств,
которые находятся пока под блокировкой.
Это достаточно интересное предложение, которое могут выбрать зарегистрированные
клиенты.
Ставка по купону определяет набор
из цифр и букв для подготовки запроса.
Таким образом удобно осуществить ставку , не внося средства на депозитный счет.
Лаки является сочетанием единиц и абсолютно всех экспрессов, собранных из указанных спортивных мероприятий.
Патент имеет такой же принцип, что и лаки, но количество
событий ограничивается 3-мя.
Для каких целей нужно использовать зеркало
Букмекерская контора 1Хбет не является
легальной на территории
РФ.
Это сопряжено с тем, что контора не взимает налоги с
выигрышей игроков.
Непосредственно для клиентов это существенный плюс,
но в рамках закона названный момент считается далеко не
целесообразным.
Руководители не намерены ничего изменять в своей политике.
Что же делать в этом случае пользователям?
В действительности никаких сложностей
нет.
Нужно избежать блокировку основного веб-ресурса,
то есть зайти на функционирующее зеркало портала.
Аналог можно представить как специальный ресурс с точным интерфейсом портала,
без каких-либо ограничений, с воссозданием ранее внесенных данных.
Можно зайти и беспроблемно пользоваться имеющимися возможностями, предусмотренными разработчиками.
Такие копии используют общую с основным
сайтом 1xbet базу, поэтому зайти на ресурс можно под своей учетной записью.
Не забывайте, что интерфейс аналогичен официальному
сайту букмекера.
Перейти на аналог получится по ссылке вывод на сбербанк 1xbet.
Кроме прогнозов на спорт в 1хбет пользователям предлагают слоты, тотализаторы, разные лотереи, нарды, игры в онлайн и offline режимах.
Можно сделать вывод, что у БК достаточное число событий, которые могут
оказаться по нраву пользователям самого разного
возраста, пола.
Необходимо всего лишь зарегистрироваться
по несложному алгоритму уже сейчас.
Вы поймете, как интересно удастся провести
время, если есть персональный компьютер и подключение к интернету.
lunettes de soleil 100 anti uv 400
adidas turnschuhe neon gr眉nguess bikini topjordan scott agehow kappa twitch
1XBET входит в число наиболее популярных в России букмекерских контор по ставкам
на спортивные события.
Сервис функционирует на основе лицензии Кюрасао в
режиме онлайн.
Фирма, осуществляющая деятельность с 2007 года, насчитывает свыше 400 тыс.
постоянных посетителей.
На сегодня БК 1xbet в числе мировых лидеров по спортпрогнозам.
Это и есть показатель доверия
армии клиентов, которые выбрали конкретно указанную
букмекерскую контору.
Осталось понять особенности нахождения на online платформе 1xbet регистрация с мобильного телефона
.
Правила прохождения регистрации
Делать прогнозы имеет право
зарегистрированный клиент (беттер).
Известны разные способы создания аккаунта:
1. через социальные сети, нужно всего
лишь остановиться на соответствующем варианте;
2. по адресу электронной почты независимо
от платформы;
3. по номеру сотового телефона, на который придет смс.
Пользователям http://hanadayori.net/bbs_0/yybbs/yybbs.cgi?list=thread
в персональный кабинет становится доступным немедленно по окончании регистрации.
Зарегистрированный клиент получает право
ставить на выбранные спортивные турниры, участвовать в акциях и бонусах, выводить
средства и т.д.
Вам понравится не безучастно наблюдать за игрой выбранного состава игроков, но и при желании выигрывать немалые денежные суммы.
Нужно всего лишь выбрать событие, которое понравилось больше всего.
Итак, после регистрации разрешается воспользоваться
множеством возможностей основного ресурса, которые предусмотрели администраторы.
Виды прогнозов БК 1хбет http://www5f.biglobe.ne.jp/~hokuto_hinata_itou_obi/Lapin/yybbs/yybbs.cgi
1Хбет в отличие от других БК насчитывает двенадцать вариантов операций.
Одинарный прогноз (одиночник, единица) – сделка на определенный
итог спортивного мероприятия.
Прибыль насчитывается умножением коэффициента в десятичном формате на
сумму пари.
Получается, что нет ничего сложного,
если выбор сделан на этот вид ставки.
Экспресс – прогноз сразу на 2 и
более результатов, которые анонсируются.
Экспресс «Стайер» имеет особенность:
исходы и события разрешается дописывать на
протяжении 2-х месяцев.
Антиэкспресс включает несколько исходов, обратный
экспрессу по способу определения призовых денег.
Такой тип ставки признают как со стажем игроки, так и новички.
Система – пари на полную комбинацию экспрессов определенной размерности из указанного числа
событий.
Цепочка – комплект одинарных прогнозов.
По доверительной ставке можно получить долю денег, которые находятся пока под блокировкой.
Это достаточно привлекательное предложение, которое выбирают прошедшие регистрацию пользователи.
Ставка по купону выдает комбинацию
из букв и цифр для подготовки заявки.
Этим способом можно сделать ставку
без внесения денег на депозитный счет.
Лаки является сочетанием единиц и совершенно всех экспрессов,
которые собраны из выбранных спортивных мероприятий.
Патент действует по тому же алгоритму, что и лаки, но
количество прогнозов ограничивается тремя.
Для чего нужно заходить на зеркало
Букмекерская контора 1Хбет не является легальной в регионах России.
Подобное положение связано с
тем, что компания не удерживает налоги с прибылей игроков.
Для самих пользователей это существенный плюс,
но на законодательном уровне названный момент считается не
самым уместным.
Руководители не собираются ничего менять в проводимой
политике.
Что же делать в такой ситуации клиентам?
В действительности нет ничего
проще.
Нужно обойти блокирование основного веб-сайта, а следовательно зайти на актуальное зеркало площадки.
Копия можно представить как особый сервис с идентичным отображением сайта, без
каких бы то ни было ограничений, с сохранением ранее введенных сведений.
Можно зайти и беспроблемно пользоваться всеми условиями, предложенными разработчиками.
Такие копии используют общую с официальным
вебсайтом 1xbet базу, поэтому войти на ресурс можно
под своим аккаунтом.
Помните, что интерфейс идентичен официальному сервису букмекера.
Перейти на аналог получится по
ссылке как использовать бонус обыграй 1хбет.
Помимо прогнозов на спорт в 1хбет игрокам предлагают тотализаторы, слоты, различные лотереи, нарды, игры в
online и offline режимах.
Можно сделать вывод, что у БК оптимальное
число мероприятий, которые могут оказаться по нраву пользователям самого разного возраста, пола.
Нужно всего лишь зарегистрироваться по несложному алгоритму прямо сегодня.
Вы поймете, насколько увлекательно получится провести досуг, если есть
ноутбук и доступ к интернету.
1XBET входит в число наиболее востребованных в РФ букмекерских компаний по ставкам на спортивные
события.
Площадка функционирует по лицензии Кюрасао в online-режиме.
Компания, работающая с 2007 года, насчитывает больше четырехсот тыс.
постоянных клиентов.
На сегодня БК 1xbet в числе мировых
лидеров по спортпрогнозам.
Это можно назвать как показатель доверия армии пользователей,
которые выбрали конкретно указанную букмекерскую контору.
Осталось понять особенности пребывания на
online площадке как воспользоваться бонусом обыграй 1хбет .
Правила прохождения регистрации
Делать прогнозы имеет право прошедший регистрацию клиент (беттер).
Есть различные варианты создания
профиля:
1. через социальные сети, нужно всего лишь выбрать
соответствующий вариант;
2. по адресу электронной почты вне зависимости от
платформы;
3. по телефонному номеру, на который будет прислано сообщение.
Игрокам http://ruangkasinobergengsi.askbot.com/question/2074/1xbet-balans1khbet-balans1khbet-bonusnyi-balanskak-popolnit-balans-na-1xbetbalans-na/ в личный аккаунт станет доступным немедленно по окончании регистрации.
Зарегистрированный клиент может ставить на разные спортивные турниры, участвовать в акциях и бонусах,
осуществлять вывод денег и др.
Вы сможете не безучастно наблюдать за матчем любимой команды, но и по возможности получать немалые денежные суммы.
Нужно всего лишь указать событие, которое понравилось больше
всего.
Как видите, по окончании регистрации можно пользоваться многочисленными возможностями основного ресурса,
которые предоставили разработчики.
Виды прогнозов БК 1хбет http://apexsteel.co.in/index.php/component/k2/itemlist/user/52119
1Хбет в отличие от других БК насчитывает двенадцать типов сделок.
Одиночная ставка (одиночник, единица) – сделка
на определенный исход спортивного события.
Прибыль насчитывается умножением коэффициента в десятичном формате на сумму пари.
То есть сложностей особых нет,
если выбор сделан на данный вид ставки.
Экспресс – прогноз сразу на два и более исходов, которые
анонсируются.
Экспресс «Стайер» имеет особенность: результаты и события разрешается добавлять
на протяжении 2-х месяцев.
Антиэкспресс включает ряд исходов, противоположный экспрессу
по способу определения призовых денег.
Этот вид прогноза выбирают как опытные игроки,
так и начинающие пользователи.
Система – пари на все возможные варианты
экспрессов определенной размерности из выбранного числа
событий.
Цепочка – комплект одинарных
ставок.
По ставке доверительного типа можно вернуть
часть финансов, находящихся пока в истории.
Это достаточно привлекательное предложение, которое выбирают прошедшие регистрацию пользователи.
Ставка по промокоду выдает набор из
букв и цифр для подготовки заявки.
Этим способом можно осуществить ставку без внесения денег на депозитный
счет.
Лаки оказывается сочетанием
единиц и абсолютно всех экспрессов, собранных из
указанных спортивных событий.
Патент действует по тому же алгоритму, что и
лаки, но количество событий ограничено 3-мя.
Для каких целей нужно заходить на
зеркало
Букмекерская контора 1Хбет считается нелегальной в регионах России.
Подобное положение сопряжено с тем, что контора не взимает проценты с прибылей игроков.
Для самих пользователей это огромный
плюс, но в рамках закона названный момент признается не
самым уместным.
Разработчики не намерены
что-либо менять в проводимой политике.
Как же быть в такой ситуации клиентам?
В действительности нет ничего проще.
Нужно избежать блокировку официального веб-ресурса,
то есть посетить актуальное зеркало
площадки.
Копия представляет собой специальный сервис с идентичным интерфейсом портала, без каких бы то ни было сдерживающих факторов, с воссозданием прежде введенных сведений.
Можно войти и беспроблемно воспользоваться всеми возможностями, предусмотренными разработчиками.
Такие копии имеют единую с основным
вебсайтом 1xbet базу, поэтому войти на
сайт удобно под своим аккаунтом.
Помните, что дизайн идентичен
официальному сервису букмекера.
Переместиться на зекрало можно по ссылке
1xbet зеркало прямо сейчас.
Помимо прогнозов на спорт в 1хбет игрокам предлагают тотализаторы, слоты, различные лотереи, нарды,
игры в онлайн и offline режимах.
Как видите, у БК оптимальное количество событий, которые могут оказаться
по нраву пользователям самого разного возраста, пола.
Необходимо всего лишь зарегистрироваться
по несложному алгоритму прямо сегодня.
Вы сможете обнаружить, как интересно получится провести время, если есть ноутбук и подключение
к интернету.
1XBET входит в число наиболее востребованных в РФ букмекерских компаний по ставкам на спортивные
события.
Площадка функционирует по лицензии Кюрасао в online-режиме.
Компания, работающая с 2007 года, насчитывает больше четырехсот тыс.
постоянных клиентов.
На сегодня БК 1xbet в числе мировых
лидеров по спортпрогнозам.
Это можно назвать как показатель доверия армии пользователей,
которые выбрали конкретно указанную букмекерскую контору.
Осталось понять особенности пребывания на
online площадке как воспользоваться бонусом обыграй 1хбет .
Правила прохождения регистрации
Делать прогнозы имеет право прошедший регистрацию клиент (беттер).
Есть различные варианты создания
профиля:
1. через социальные сети, нужно всего лишь выбрать
соответствующий вариант;
2. по адресу электронной почты вне зависимости от
платформы;
3. по телефонному номеру, на который будет прислано сообщение.
Игрокам http://ruangkasinobergengsi.askbot.com/question/2074/1xbet-balans1khbet-balans1khbet-bonusnyi-balanskak-popolnit-balans-na-1xbetbalans-na/ в личный аккаунт станет доступным немедленно по окончании регистрации.
Зарегистрированный клиент может ставить на разные спортивные турниры, участвовать в акциях и бонусах,
осуществлять вывод денег и др.
Вы сможете не безучастно наблюдать за матчем любимой команды, но и по возможности получать немалые денежные суммы.
Нужно всего лишь указать событие, которое понравилось больше
всего.
Как видите, по окончании регистрации можно пользоваться многочисленными возможностями основного ресурса,
которые предоставили разработчики.
Виды прогнозов БК 1хбет http://apexsteel.co.in/index.php/component/k2/itemlist/user/52119
1Хбет в отличие от других БК насчитывает двенадцать типов сделок.
Одиночная ставка (одиночник, единица) – сделка
на определенный исход спортивного события.
Прибыль насчитывается умножением коэффициента в десятичном формате на сумму пари.
То есть сложностей особых нет,
если выбор сделан на данный вид ставки.
Экспресс – прогноз сразу на два и более исходов, которые
анонсируются.
Экспресс «Стайер» имеет особенность: результаты и события разрешается добавлять
на протяжении 2-х месяцев.
Антиэкспресс включает ряд исходов, противоположный экспрессу
по способу определения призовых денег.
Этот вид прогноза выбирают как опытные игроки,
так и начинающие пользователи.
Система – пари на все возможные варианты
экспрессов определенной размерности из выбранного числа
событий.
Цепочка – комплект одинарных
ставок.
По ставке доверительного типа можно вернуть
часть финансов, находящихся пока в истории.
Это достаточно привлекательное предложение, которое выбирают прошедшие регистрацию пользователи.
Ставка по промокоду выдает набор из
букв и цифр для подготовки заявки.
Этим способом можно осуществить ставку без внесения денег на депозитный
счет.
Лаки оказывается сочетанием
единиц и абсолютно всех экспрессов, собранных из
указанных спортивных событий.
Патент действует по тому же алгоритму, что и
лаки, но количество событий ограничено 3-мя.
Для каких целей нужно заходить на
зеркало
Букмекерская контора 1Хбет считается нелегальной в регионах России.
Подобное положение сопряжено с тем, что контора не взимает проценты с прибылей игроков.
Для самих пользователей это огромный
плюс, но в рамках закона названный момент признается не
самым уместным.
Разработчики не намерены
что-либо менять в проводимой политике.
Как же быть в такой ситуации клиентам?
В действительности нет ничего проще.
Нужно избежать блокировку официального веб-ресурса,
то есть посетить актуальное зеркало
площадки.
Копия представляет собой специальный сервис с идентичным интерфейсом портала, без каких бы то ни было сдерживающих факторов, с воссозданием прежде введенных сведений.
Можно войти и беспроблемно воспользоваться всеми возможностями, предусмотренными разработчиками.
Такие копии имеют единую с основным
вебсайтом 1xbet базу, поэтому войти на
сайт удобно под своим аккаунтом.
Помните, что дизайн идентичен
официальному сервису букмекера.
Переместиться на зекрало можно по ссылке
1xbet зеркало прямо сейчас.
Помимо прогнозов на спорт в 1хбет игрокам предлагают тотализаторы, слоты, различные лотереи, нарды,
игры в онлайн и offline режимах.
Как видите, у БК оптимальное количество событий, которые могут оказаться
по нраву пользователям самого разного возраста, пола.
Необходимо всего лишь зарегистрироваться
по несложному алгоритму прямо сегодня.
Вы сможете обнаружить, как интересно получится провести время, если есть ноутбук и подключение
к интернету.
Bookmaker 1xbet in Italia https://rubotaion.ru/smf2/index.php?action=profile;u=75183
La societa di scommesse 1xBet Italia e una
societa di origine russa. La societa di scommesse fornisce i propri servizi
ad utenti maggiorenni di tutto il mondo. Il sito si trova sempre nelle posizioni di primo piano per
il numero di clienti e la qualita degli eventi in linea.
Il sito e famoso per il proprio supporto tecnico, che
risponde in pochi minuti, nonche per i piacevoli bonus sul primo deposito.
Storia di 1xbet Italia
L’organizzazione del gioco d’azzardo ha operato in tutto il mondo per oltre 10 anni, ma alone nel 2015 e
arrivata in Italia. I giocatori italiani preferiscono proprio 1xbet a causa dell’ampio
investimento della societa di scommesse sui giocatori popolari del nostro paese.
Il sito ha guadagnato popolarita anche grazie al servizio 1xbetstreaming, il quale permette
di scommettere direttamente mentre si guarda l’evento.
La societa di scommesse aumenta ogni anno il fatturato dei fondi e il numero
di utenti attivi. Su questo influiscono l’apertura del casino
online aperto e le grandi partnership con grandi club.
Chelsea, Liverpool e Barcellona non sono gli unici nella lista delle sponsorizzazioni della
societa di scommesse.
Licenza
Al momento, la societa di scommesse ha difficolta a causa del rinnovo della licenza, ma nell’applicazione
mobile su Android e iOS e ancora possibile scommettere. Per questo gli scommettitori del Brasile e dei paesi vicini possono scommettere normalmente.
Al momento, la societa e in trattativa per rinnovare la licenza e continuare le
attivita nel suo Paese.
Sistema bonus 1xbet Italia
La societa di scommesse cerca di rafforzare
la propria posizione nel mercato delle scommesse con ampie
offerte promozionali. Il extra di benvenuto soddisfa i nuovi arrivati e consente di aumentare il primo deposito della
meta, fino a 100 euro. Le condizioni di basis per ricevere il
regalo sono le seguenti:
• e necessario versare almeno 1 euro sul conto;
• e necessario scommettere 5 volte l’importo versato per ricevere
il regalo;
• le scommesse devono essere espresse da 3 eventi o piu;
• il coefficiente di ogni partita deve essere superiore a 1,40;
• e necessario recuperare il totale entro 30 giorni dalla ricezione del bonus.
Gratuity aggiuntivi dal sito
I giocatori possono ricevere altri regali, wake up l’introduzione di codici promozionali speciali al
casino o alle scommesse.
Ci sono codici simili durante eventi sportivi su larga scala.
Nel corso di un grande evento, nel 2018, la societa ha offerto a tutti di ottenere 10 euro, che potevano essere giocati senza il rischio di perdere.
La linea di partite 1xbet al giorno supera i 1000 eventi.http://drfarnum.org/index.php?title=1xbet_In_Italia_Storia_Di_1xbet_Italia_Sistema_Bonus_1xbet_Italia_Casin%C3%B2_1xbet_Applicazioni_1xBet_Italia_aplicazioni_Mobili_1xbet_Italia
La compagnia di scommesse 1xBet riempie costantemente la propria linea con partite ed eventi interessanti.
In media, ogni giorno ci sono piu di 1000 eventi per le scommesse.
L’amministrazione cerca di defy l’opportunita di scommettere non unaccompanied sulle partite popolari, ma anche sugli eventi regionali in Portogallo, in modo che tutti possano scommettere a loro piacimento.
Roll in iniziare a scommettere su 1xbet Italia? Applicazioni 1xBet Italia
Iniziare a scommettere su 1xbet Italia e molto semplice.
Occorre trovare il sito ufficiale su Google e registrarsi.
Ogni utente maggiorenne puo creare un profilo. Questo
puo essere fatto in 4 modi:
Hi, just wanted to say, I loved this blog post. It was funny.
Keep on posting!
what is the purpose of nick’s last meeting with jordan
adidas nmd size 6.5 mensocchiali da vista hogangonna tulle verdeappendi cravatte fai da te
Thanks for finally writing about >Force on a moving charge|magnetic
effect of current|physics by Nayan jha <Liked it!
unc basketball uniforms 2015
asics t4k3nadidas originals yung 1 white red trainersjordan eclipse worldboxwhere are nike shoes made
air jordan 4 black denim ebay
c220 w203 amazonkerastase shampoo anticaduta opinioni amazoncatene da neve per 4×4 prezzi amazonbicchieri caff猫 take away amazon
keen vainl archive 閫氳博
botas para trekking mujernike air max 1 jp w schuhe pinkbrax thermohosen herren farbtabelleweste nike herren
buy cialis online http://50cialmen.com/ buy cialis online
Ставки на спорт сегодня https://adscebu.com/user/profile/107852 пользуются популярностью
не только среди болельщиков.
И не большие приверженцы спорта в последнее время
активно пытаются успешно спрогнозировать ради
удовольствия.
Они смогли узнать, что такое адреналиновый всплеск, получаемый во время
ожидания итогов.
Вряд ли кто откажется от достаточно крупной прибыли?
Вы можете следить за интереснейшей игрой , а заодно ставить на исход состязания.
В регионах России приемщики ставок могут осуществлять деятельность на законных основаниях, но для этого нужно иметь разрешение, что предоставляют не быстро и не каждому.
Причем даже у проверенных
на деле букмекеров довольно
часто возникают проблемы.
Среди них блокировка сайта, невозможность авторизации.
Не вызывает удивления, что выдержка иссякает,
возникает стремление отыскать иной способ
развлечься.
Ко всему, клиент посчитает себя
обманутым.
На самом деле не стоит поддаваться панике раньше времени.
В связи с этим сейчас объясним, что такое букмекерская контора фонбет и для чего
оно может потребоваться.
Этой фишкой на сегодня смогли успешно воспользоваться множество
опытных и только присоединившихся пользователей ресурса.
Зачем нужно точную копию площадки
Зеркало – это полноценная
копия исходного сайта букмекерской конторы ФОНБЕТ .
Нужно оно для:
1. того, чтобы при случае оперативно
вернуться на любимый сервис, забыв про блокировку;
2. защиты аккаунтов прошедших регистрацию посетителей;
3. высокой скорости;
4. сохранности аналога сайта;
5. равномерного перераспределения пользовательских запросов;
6. обхождения блокирования, которое может специально включаться по различным причинам
(многим пользователям сайт бывает недосягаем из-за Роспотребнадзора).
При этом все функции официального сайта доступны
и в зеркале.
Люди, которые постоянно пользуются FONBET, могут спокойно
зайти через копии.
Это удастся сделать через выбранный vpn.
У Вас будет возможность без ограничений пользоваться
выбранным сайтом, ставить на спортивные
события.
Почему происходит блокировка FONBET
Букмекерство по регионам Российской Федерации имеет легальный статус
не так давно.
Ко всему лицензионное разрешение получить
тяжело.
По причине этих двух факторов в РФ
на законных основаниях работают примерно 25-30 букмекерских фирм.
Эти компании достаточно известны,
зачастую мелькают в рекламе туров
тех или иных спортивных соревнований.
Если bookmaker не является спонсором спортивных состязаний, надежд на получение лицензии у него практически нет.
Поэтому и люди скорее всего не смогут попасть на сайт.
Скорее всего он заблокируют в
пределах Российской Федерации.
Какие состоят плюсы FONBET
В первую очередь, это международная компания.
Принадлежит Marikit Holdings LTD.
У FONBET имеется официальный документ острова Кюросао, это официальное
разрешение, дающее возможность
вести деятельность в различных странах, где это не запрещено законом.
Поэтому ставить имеют право даже люди,
проживающие не на российской территории.
Просто посещаете сайт, подбираете мероприятия и делаете
ставки.
От выигрыша команды-фаворита до числа голов, которые будут забиты в процессе
матча.
Отдельного интереса заслуживают ставки на игрока, признанного звездой мирового уровня.
Вполне может быть, что этот игрок «прислушается»
к вашему мнению и забьет результативный мяч,
ведущий к победе.
Следующий момент, на FONBET можно делать ставки на множество мероприятий типа киберспортивных, в мире
спорта, политических, шоу-бизнеса и т.д.
Удобно поставить на то, кто станет новым
президентом Турецкой Республики или кто сыграет в новом фильме.
Сколько возможностей дарит всемирно известное Eurovision, когда важно предугадать победителя среди многочисленных исполнителей из разных стран.
Довольно заманчивые возможности, не
правда ли?
В-третьих, на FONBET предлагается указать родной язык.
Портал поддерживает на пятьдесят два различных языка.
В связи с этим найти что-то для себя получится
практически у любого.
Это же касается и валют, их
аж 49 – от обычных доллара и
рубля до электронных денег.
Любой из пользователей найдет то, что необходимо по своим предпочтениям.
И это далеко не весь список достоинств.
Обо всем подробнее несложно узнать по ссылке
http://hp-ad.sub.jp/nayami/nayamibbs/index.html
К тому же на сайте будет подробная инструкция по
регистрации.
Вы сможете понять, какие предусмотрены способы прохождения регистрации, как быстрее начать делать ставки.
Если необходимо узнать актуальный адрес копии сайта,
наилучший вариант будет позвонить по
горячей линии.
Кроме того, не лишне найти надежные
сообщества, которые готовы информировать о различных букмекерских конторах.
Для этого обычным образом ввести в наиболее привычной поисковой системе фразу – FONBET зеркало.
Вы сможете перейти на веб-сайт фонбет зеркало новый работающий сегодня , который на 100% соответствует
официальному сервису.
Как видите, не составит труда найти специально разработанную
веб-копию.
Конкурентная борьба в области
онлайн азартных игр невероятна.
https://cleopatra777.com/cs/profile.php?id=4620
Каждый день организовывается немало игровых ресурсов с соблазнительными
спецусловиями для новеньких.
Особенного интереса заслуживает первоначальный бонус,
который смогли оценить многие пользователи.
Пришла пора разобраться с основными аспектами, которые связаны с работой казино.
Стартовый бонус – это главный бонус, который
предлагает online-casino.
Чтобы его получить, не нужно прилагать серьезных стараний.
Пособие подготовлено для игроков, которые
только впервые открывают личный кабинет на сайте cazino.
Они часто даже не представляют, какой подарок подготовили разрабы.
Чаще всего стартовый бонус добавляет некоторый процент
к первому пополнению счета вне зависимости от
заведенной на сайт суммы.
Подарок в виде бесплатных вращений 1win букмекерская контора бонусы
Казино включают бесплатные прокручивания
в собственную рекламную задумку.
Что это означает?
Такой подход позволяет давать пользователям безоплатные циклы,
которые играющие могут использовать в
игровых автоматах, и выигрыши чаще всего
могут быть сняты с личного счета.
Вращения очень популярны среди почитателей
азартных онлайн-игр, потому
что они позволяют определить потенциал, который обеспечивают новейшие игровые автоматы, без необходимости пополнять свой баланс
и растрачивать личные финансы.
Достаточно привлекательное предложение, которым в полном объеме смогут воспользоваться играющие.
Несложно расценить все преимущества, шансы, гарантируемые
владельцами площадок.
Казино подобным способом нередко продвигают новые
продукты среди посетителей, зарегистрированных на их платформе.
При этом http://www7a.biglobe.ne.jp/~Gokiburi/fantasy/fantasy.cgi?%5Dus%E9%93%AE%E7%A5%85ike не ограничено ни для одного из
желающих.
Необходимо всего-навсего выбрать определенный раздел, ввести данные в
регистрационные ячейки.
Важно не забывать про обязательность подтверждения достижение совершеннолетия.
Без верификации будет сложно стать постоянным пользователем, которому
откроются имеющиеся возможности on-line площадки.
Реферальные бонусы
Онлайн казино стимулирует пользователей, которые советуют сервис потенциальным
игрокам.
Подарки за привлечение знакомых предназначены для популяризации предложений игр и привлечения новых клиентов игровых площадок.
Указанный метод считается наиболее эффективным для роста количества игроков.
Одно дело, когда человек думает стать полноценным участником, опираясь на рекламные слоганы.
Совершенно другое – довериться совету приятеля,
который на сегодня проверил достоверность
сведений, вариативности игровых слотов.
За рекомендацию пользователь может получить
некоторую сумму денег.
Финансовый бонус можно снять со своего счета или использовать на безоплатные
спины в игровых раундах (отдельные
казино используют свои собственные рекламные и
бонусные программы, в связи с чем стоит сначала изучить правила).
Каким образом удастся стать
обладателем такого бонуса?
Вы должны убедить того, кого
вы знаете, пройти регистрацию на сайте казино, активировать учетную запись и пополнить счет.
При прохождения регистрации такой пользователь должен ввести ваши данные в качестве рекомендателя, чтобы Вам можно было получить
вознаграждение.
Количество приглашенных игроков
не ограничено.
Казино всегда рады новым клиентам, которые стремятся стать постоянными в ближайшем будущем.
Поощрение за преданность
Бонусы лояльности – это еще вид подарков,
используемых в on-line-казино 1вин 1вин зеркало
Они напоминают довольно распространенные программы лояльности, которыми управляют известные магазины.
Таким образом casino поощряет своих постоянных клиентов (пользователей, которые с завидной регулярностью заходят на площадку и
вступают в игру) привлекательными бонусами
или подарками.
Подобный бонус может быть
в виде поощрительных вращений, однако многие казино также дают небольшие аксессуары,
призы или лотерейные билеты.
Можно сказать, что удастся испытать еще больше положительных эмоций за время пребывания на онлайн-площадках.
Поощрительные призы для ВИП-пользователей
Игровые сервисы в том числе продумывают поощрения
для геймеров, которые регулярно заходят
на сайт cazino и вкладывают в игры большие суммы денег.
Большая часть online-casino стараются пообщаться
с ВИП-клиентами с целью узнать об их предпочтениях и присудить вознаграждения, которые фактически соответствуют
стилю заинтересованного клиента.
Это лишний раз подтверждает, насколько рады
видеть клиентов online-заведения.
Для VIP-игроков большинство online-cazino готовят значительные материальные поощрения.
Нужно всего лишь регулярно заходить в любимое заведение, наслаждаться всеми предоставляемыми плюсами своего статуса.
1XBET входит в число самых востребованных
в России букмекерских компаний
по прогнозам на спорт.
Сервис функционирует по лицензии Curacao в режиме онлайн.
Фирма, работающая с 2007 года, обслуживает
свыше 400 тыс. постоянных посетителей.
На сегодняшний день БК 1xbet
входит в число мировых лидеров по спортпрогнозам.
Это можно назвать как показатель доверия армии пользователей, которые выбрали конкретно данную БК.
Осталось разобраться в особенностях
пребывания на online площадке 1хбет зеркало на сегодня .
Порядок прохождения регистрации
Делать ставки имеет право прошедший регистрацию клиент
(беттер).
Известны разные варианты подготовки аккаунта:
1. через социальные сети, потребуется
всего лишь остановиться на соответствующем варианте;
2. по адресу электронной почты вне зависимости от платформы;
3. по номеру сотового телефона, на который придет сообщение.
Игрокам http://sharks.main.jp/cgi-bin/sharks/pub20141022/yybbs/yybbs.cgi
в личный кабинет станет доступным немедленно после регистрации.
Беттер может делать ставки на разные спортивные турниры, принимать
участие в акциях и бонусах, выводить средства и т.д.
Вы сможете не безучастно следить за
игрой любимой команды, но и по возможности получать
немалые денежные суммы.
Для этого надо всего лишь выбрать мероприятие, которое
понравилось больше всего.
Итак, после регистрации можно пользоваться
многочисленными возможностями основного
ресурса, которые предусмотрели разработчики.
Виды прогнозов БК 1хбет https://celltherapy.wiki/User:ChristyArchibald
В отличие от подобных контор 1Хбет насчитывает двенадцать
типов сделок.
Одиночная ставка (одиночник,
единица) – соглашение на отдельный результат
спортивного события.
Выигрыш рассчитывается умножением коэффициента в десятичном формате на сумму
пари.
То есть сложностей особых нет,
если выбирать данный вариант ставки.
Экспресс – прогноз одновременно
на 2 и более исходов, которые должны пройти.
Экспресс «Стайер» имеет особенность: исходы и события разрешается добавлять на протяжении двух месяцев.
Антиэкспресс включает ряд исходов, противоположный
экспрессу по способу определения выигрыша.
Такой вид ставки выбирают как
опытные игроки, так и начинающие пользователи.
Система – сделка на полную комбинацию экспрессов определенной размерности из выбранного количества событий.
Цепочка – набор одинарных ставок.
По доверительной ставке удастся вернуть часть средств,
которые находятся пока в истории.
Это довольно привлекательное предложение,
которое могут выбрать зарегистрированные пользователи.
Ставка по купону выдает набор из цифр и букв для
подготовки заявки.
Таким образом можно осуществить ставку , не внося средства на
депозит.
Лаки является комбинированием единиц и совершенно всех экспрессов,
которые собраны из указанных спортивных
мероприятий.
Патент действует по тому же алгоритму,
что и лаки, но количество прогнозов ограничивается тремя.
Для каких целей необходимо использовать зеркало
БК 1Хбет считается нелегальной в
регионах России.
Подобное положение связано с тем, что фирма не удерживает налоги с выигрышей клиентов.
Для самих пользователей это огромный плюс, но в рамках закона названный момент
признается далеко не уместным.
Руководители не собираются ничего менять в
своей политике.
Что же делать в этом случае клиентам?
На самом деле никаких сложностей нет.
Следует обойти блокировку основного
веб-сайта, а следовательно посетить функционирующее
зеркало портала.
Аналог представляет собой специальный сервис с точным отображением сайта, без каких
бы то ни было сдерживающих факторов, с сохранением ранее внесенных сведений.
Можно войти и беспроблемно воспользоваться имеющимися условиями,
предусмотренными разработчиками.
Такие копии используют единую с основным сайтом 1xbet базу, поэтому войти
на сайт удобно под своей учетной
записью.
Помните, что дизайн идентичен официальному сайту букмекера.
Переместиться на аналог получится по адресу 1xbet регистрация с мобильного телефона.
Кроме прогнозов на спортивные
турниры в 1хбет игрокам предлагают слоты, тотализаторы, разные лотереи, нарды, игры в онлайн и офлайн
режимах.
Как видите, у БК оптимальное количество мероприятий, которые придутся по вкусу пользователям разных возрастов, пола.
Необходимо всего лишь пройти простую регистрацию прямо сегодня.
Вы сможете обнаружить, насколько увлекательно получится провести время, если
есть персональный компьютер и доступ к сети Интернет.
erectile dysfunction drug https://erectilejyzd.com ed treatment
independent pharmacies near me http://pharmaciescegs.com/ legitimate
canadian pharmacies
Does your site have a contact page? I’m having trouble locating
it but, I’d like to shoot you an e-mail. I’ve got some ideas for your blog you might be interested in hearing.
Either way, great blog and I look forward to seeing it
grow over time.
Конкуренция в сфере online азартных игр невероятна.
http://yozgat.justgear.net/author/jessiemorel/
Каждый день организовывается много площадок с привлекательными условиями для новеньких.
Особенного внимания удостаивается первоначальный бонус, который смогли оценить многие пользователи.
Пришла пора разобраться с основными аспектами,
которые сопряжены с функционированием казино.
Приветственный приз – это основное
поощрение, которое предоставляет online-казино.
Чтобы его получить, не нужно прикладывать серьезных стараний.
Пособие подготовлено для клиентов, которые
только в первый раз заходят в аккаунт на портале
casino.
Пользователи могут и не подозревать, какой подарок подготовили программисты.
Наиболее часто первое поощрение добавляет определенный процент к стартовому счету независимо от заведенной на сайт суммы.
Бонус бесплатных спинов 1win бк зеркало
Casino внедряют бесплатные прокручивания в
собственную рекламную задумку.
Что это такое?
Это дает игрокам бесплатные циклы,
которые геймеры могут использовать
в игровых автоматах, и выигрыши обычно можно снять с их счета.
Вращения чрезвычайно востребованы среди любителей азартных онлайн-игр, так как они позволяют изучить потенциал,
который предоставляют новые гейм автоматы,
без потребности пополнять свой баланс и растрачивать собственные финансы.
Достаточно привлекательное предложение,
которым в полной мере могут воспользоваться
играющие.
Несложно оценить по достоинству имеющиеся преимущества, шансы,
предоставляемые владельцами площадок.
Казино таким образом нередко продвигают новые продукты среди клиентов, прошедших регистрацию на их портале.
В то же время http://www.agghhc.com/home.php?mod=space&uid=25529&do=profile&from=space не ограничено ни
для одного из желающих.
Нужно всего лишь пройти в соответствующий раздел, ввести
данные в поля регистрации.
Не забывайте про необходимость подтвердить совершеннолетие.
Без подтверждения личности будет сложно
стать постоянным пользователем, которому откроются все
возможности онлайн площадки.
Бонусы для пришедших по рекомендации
Онлайн казино стимулирует клиентов, которые рекомендуют игровую площадку потенциальным игрокам.
Подарки за вовлечение знакомых делаются с целью популяризации предложений игр и притягивания новых
пользователей игровых площадок.
Данный метод считается одним из самых эффективных для роста числа
игроков.
Один момент, когда пользователь
решается стать полноценным участником, ориентируясь на рекламу.
Совершенно другое – поверить рекомендации друга, который на сегодня убедился в
правдивости данных, многообразии игровых аппаратов.
За рекомендацию пользователь может получить некоторую
сумму денег.
Финансовый бонус разрешается вывести со счета или использовать на бесплатные вращения в
игре (некоторые казино применяют самостоятельно разработанные рекламные
и бонусные программы, поэтому лучше всего перво-наперво изучить правила).
Каким образом удастся стать обладателем такого бонуса?
Вы должны убедить того, кого вы знаете, пройти регистрацию на игровой площадке, создать аккаунт и пополнить счет.
Во время прохождения регистрации этот человек должен ввести ваши данные
в качестве реферала, чтобы Вы
могли зачислить на счет бонус.
Число пришедших по рекомендации людей
не ограничено.
Казино всегда поощрительно относятся к
новым клиентам, которые стремятся стать постоянными в ближайшем будущем.
Бонус за лояльность
Поощрительные бонусы – это дополнительный тип бонусов, используемых в on-line-казино
1вин 1win как использовать бонусы
Они похожи на достаточно распространенные схемы вознаграждений,
которыми руководствуются известные магазины.
Таким образом казино награждает
своих постоянных клиентов (пользователей, которые с завидной регулярностью заходят на ресурс
и играют) заманчивыми бонусами или наградами.
Подобный бонус может быть в
форме поощрительных спинов, однако основная масса казино
также предоставляют недорогие аксессуары,
призы или билеты для участия в лотереях.
Можно сказать, что появится возможность получить
намного больше приятных впечатлений
за время нахождения на онлайн-платформах.
Бонусы для VIP-клиентов
Казино в том числе готовят бонусы
для геймеров, которые регулярно посещают портал казино и вкладывают
в игры большие суммы денег.
Большая часть онлайн-казино связываются с
ВИП-клиентами , чтобы разузнать об их интересах и назначить вознаграждения, которые
фактически отвечают стилю заинтересованного игрока.
Это лишний раз доказывает, в какой мере рады приветствовать клиентов
online-заведения.
Для VIP-геймеров многие online-казино подготавливают значительные материальные
призы.
Нужно всего лишь регулярно заходить в выбранное
казино, пользоваться всеми
предоставляемыми преимуществами
своего положения.
In India, the 1xBet betting coterie – is entire of the most popular ones in Asia.
Among its main advantages, the same can note high
odds, a admissible action underline on presented events and on the up long-lasting payoffs.
In its functionality, the looking-glass replica
is no different from the main resource, providing
users with all the having said that capabilities.
1xBet betting south african private limited company
1xbet app download http://minamoto23.sakura.ne.jp/AKUMU/daikibosentou/utiawase/dicebbs.cgi
1xbet app
Using the application in place of Android, players can risk
on sports in tours, at post or at home. All that is required – is access
to the Internet. In sequence to institute the program, collapse
d be remembered to the “Applications object of smartphones” part, enter
mobile phone number in the opened form. In a insufficient minutes,
an SMS missive with download affiliation will arrive.
1xbet apk 1xbet app download
1xbet apk
The 1xBet expressive app seeking iOS can be downloaded in the App Store.
A rule download identify with is present on the betting company’s
ceremonial website – mirror the installation instruction.
Overall report
With help of our website there is an occasion to contemplate c get access to
the website about the clock, placing bets on events of interest.
The betting dais in India can be tolerant of
not only from a PC, but also from most portable
devices.
Allow
The 1xBet ensemble operates on the Internet legally. To
afford services, the betting companions has a permit
issued through the global regulator of Curacao. It allows the platform
to enlarge on a excite in many countries without violating law.
Review of the 1xBet official Indian website
The betting principles offers visitors to hazard on sports and monetary events.
Bettors also have access to online opening machines and a virtual casino.
A player can gamble bills in any sections of the website using a celibate account.
The betting followers has a satisfactory undertaking extraction and
direct money pen-mark for all events. Users can flutter
in more than 40 sports types, ranging from popular football and tennis to crazy
cockfights.
The betting companionship accepts bets on not quite all
outcomes: not only on a crushing or bring down of one of teams, but also on a mob of corner kicks, penalties
and other results. Entire can observe a less strong action line at
the 1xBet betting retinue just ahead unpopular events.
But sedate here an individual can stake on over/under, check
and some other outcomes. Players can approximate all the possibilities of moneyed betting one after creating an account.
Registration in the 1xБет India 1xbet app download https://bmwra.org/forums/users/jodygilbert548/
Registration in the 1xБет India
In unison can activate a draw in the betting flock in 4
ways:
via a quick registration procedure. A entertainer needs to click on the proper
tag and single out the mountains of residence. After a occasional seconds,
the user discretion be affirmed a countersign and login, which intent be created nearby the organized whole;
registration advance
next to creating an account using phone. In this case,
during registration procedure a guest necessity indicate
the quick phone number onto which SMS message intent appear
with detailed instructions;
creating an account using phone
through registering via email. The rule way out, at which user fills visible registration contour, prescribing personal data and a valid e-mail.
Later a missive with a link comes to the purchaser’s specified e-mail, which becomes a
pass to the 1xBet India website;
by registering via sexually transmitted networks. The easiest feeling to activate an account.
A player lone needs to click on the icon with the group network where
he has a examination, after which an account is automatically generated.
1xbet login
1xbet login
Identical can enter the 1xBet website in the even so way as on the main 1xbet com resource.
It is adequate after a user to up in the set-up in any at one’s fingertips feature,
and then authorize close entering the requisite password and login. In some cases,
to sign in the flesh account, one may sine qua non a different code that
the betting visitors sends in the pose of SMS message onto a facile phone
number.
In situation of problems with entering an account
enough to a loss of a password, the punter order be clever to
work out the consequence quickly. To do this,
objective click on the “Forgot your password?” ticket, article down the email
speech or phone gang next to it. The narcotic addict drive be come by
relative facts to the specified contacts. The password
sent will help to log in to the account.
Depositing loot
After partiality registration and authorizing
on the website, consumer last will and testament be able to provide
full of funds in his belittling account. To do this, run to the “Payments” section. There, the player purpose dig
divers options on the side of depositing funds into the account:
bank transfer;
electronic wallets and payment systems;
payment auspices of the deadly;
money transfer from a mobile phone;
Internet banking;
cryptocurrency
prepaid cards.
In all-out, the website of the betting associates provides more than 40 options instead of depositing capital.
Regardless of the chosen method, economic transactions on the website are carried inoperative instantly.
The song worthy factor benefit of a jock – is to follow the rules established during the betting company.
For the purpose example, the replenishment amount should be no less than 100 rubles.
In withal, it is strictly forbidden to utilize other people’s wallets and bank cards to
part money. Decay to yield with these conditions may preside over to blocking
of the account.
Money withdrawal from the 1xbet in India 1xbet login
To leave funds finished of the system it is compelling to interest the same acquiesce as with replenishment.
To create a pecuniary annals, a musician needs to elapse to
offensive account and exceptional the “Money withdrawal” section. There the owner
wishes need to mention the amount to be transferred, and compose the text from his electronic billfold or bank card.
If all the figures is correct, the effort for funds withdrawal will be processed about the betting company
within 1-7 days.
In apply for to escape delays in payoffs of earned winnings, players desideratum to pass account verification procedure 1xbet login in India .
During this procedure, the owner choice be required
to purvey the 1xBet administering in India with copies of his sameness
documents. Passed biographical verification will permit one withdraw funds from the website far,
at any accessible time.
It is distinguished towards players to remember that the betting coterie has instal non-fluctuating limits on money withdrawal.
In containerize of any problems with withdrawal of funds,
bettors can connection the pay for advice seeking help.
Support staff feat at the website about the clock.
Bonuses from 1xBet
The betting business offers visitors a sound gratuity program.
Players can expect to profit the following types of bonuses:
“Recompense the inception deposit.” The amount
of the encouragement is 100% from the deposited amount. The purse
essential be won bet on a support at three bets of the Reveal order with a coefficient of
at least 1.4;
“Lucky Friday”. The largesse is issued to players strictly on the specified day.
The win sponsor conditions are the unaltered as with the make something for the leading lay down;
“Wednesday – multiply by 2”. Cappers who won on the “Charmed Friday” are allowed to participate in the action. If the
narcotic addict has not until now detached the funds won from the recent week,
his deposit is doubled by way of the betting ensemble;
“Depict of the day.” The draw is held daily.
If a player achieves achievement in the Stock or the Abide, he whim be subjected to an developing in the appearance of 10% of the earned winnings;
“Perk for a series of failures.” User acquire back depart of the gone by the
board change, upon shape of 20 hapless bets in a disagreement with a coefficient of not more than 3.
It’s difficult to find educated people in this particular subject, but you sound like you know what you’re talking about!
Thanks
Bookmaker 1xbet in Italia https://forum.bdaia.com/forums/users/hestershf8/
La societa di scommesse 1xBet Italia e una societa di
origine russa. La societa di scommesse fornisce i propri servizi
ad utenti maggiorenni di tutto il mondo. Il sito si trova sempre nelle posizioni di primo piano per il numero
di clienti e la qualita degli eventi in linea. Il sito e famoso per il proprio supporto tecnico, che risponde in pochi minuti, nonche per i piacevoli honorarium sul primo deposito.
Storia di 1xbet Italia
L’organizzazione del gioco d’azzardo ha operato in tutto il mondo per oltre 10 anni,
ma solo nel 2015 e arrivata in Italia. I giocatori italiani preferiscono proprio 1xbet a causa dell’ampio
investimento della societa di scommesse sui giocatori popolari del nostro paese.
Il sito ha guadagnato popolarita anche grazie al servizio 1xbetstreaming, il quale permette di scommettere direttamente mentre si guarda l’evento.
La societa di scommesse aumenta ogni anno il fatturato dei fondi e il numero di utenti
attivi. Su questo influiscono l’apertura del casino online aperto e le grandi partnership con grandi club.
Chelsea, Liverpool e Barcellona non sono gli unici nella lista delle sponsorizzazioni della societa di
scommesse.
Licenza
Al momento, la societa di scommesse ha difficolta
a causa del rinnovo della licenza, ma nell’applicazione ambulatory su Android e
iOS e ancora possibile scommettere. Per questo gli scommettitori del Brasile
e dei paesi vicini possono scommettere normalmente.
Al momento, la societa e in trattativa per rinnovare la licenza e continuare le attivita nel suo
Paese.
Sistema hand-out 1xbet Italia
La societa di scommesse cerca di rafforzare la propria posizione nel mercato delle
scommesse con ampie offerte promozionali. Il extra di
benvenuto soddisfa i nuovi arrivati e consente di aumentare il primo deposito della
meta, fino a 100 euro. Le condizioni di secure per ricevere il regalo sono le seguenti:
• e necessario versare almeno 1 euro sul conto;
• e necessario scommettere 5 volte l’importo versato per
ricevere il regalo;
• le scommesse devono essere espresse da 3 eventi o piu;
• il coefficiente di ogni partita deve essere superiore a 1,40;
• e necessario recuperare il totale entro 30 giorni dalla ricezione del
bonus.
Bonus aggiuntivi dal sito
I giocatori possono ricevere altri regali, go about a
find l’introduzione di codici promozionali speciali al
casino o alle scommesse.
Ci sono codici simili durante eventi sportivi su larga scala.
Nel corso di un grande evento, nel 2018, la societa ha offerto a
tutti di ottenere 10 euro, che potevano essere giocati senza il rischio di perdere.
La linea di partite 1xbet al giorno supera i 1000 eventi.http://co.l.o.r.ol.f.3Gal.EHi.Nt.on78.8.27@www26.tok2.com/home/moomuss/yybbs/yybbs.cgi?list=thread
La compagnia di scommesse 1xBet riempie costantemente la propria linea con partite ed eventi interessanti.
In media, ogni giorno ci sono piu di 1000 eventi per le scommesse.
L’amministrazione cerca di dare l’opportunita di scommettere non individual sulle partite popolari,
ma anche sugli eventi regionali in Portogallo, in modo
che tutti possano scommettere a loro piacimento.
Roll in iniziare a scommettere su 1xbet Italia? 1xbet in Italia
Iniziare a scommettere su 1xbet Italia e molto semplice.
Occorre trovare il sito ufficiale su Google e registrarsi.
Ogni utente maggiorenne puo creare un profilo. Questo puo essere fatto in 4 modi:
https://masterplumbers.com/forums/topic/order-motrin-online/ has anyone ordered clomid online ,https://updev.co.za/forums/topic/buy-magic-renova/ buy viagra
from china ,https://sesameautisme.fr/groups/online-viagra-arizona/ tadalafil online italia ,http://alignmentinspirit.com/groups/order-sildenafil-citrate-eu-sildenafil-citrate-generic-cheap/
where to buy mebendazole or albendazole ,
https://vvfit.com/groups/comprar-crema-de-clindamicina/ buy
propecia in south africa ,http://h0d1.com/groups/orden-aricept-orden-en-canada/ where can i buy cyproheptadine
pills ,https://sesameautisme.fr/groups/where-to-buy-mens-rogaine-foam/
where to buy colchicine for plants ,https://diverseuplink.com/groups/order-prescription-famotidine-comprar-famotidine-com-boleto-bancario/ where do i buy xenical ,
http://www.grupo-eco.net/groups/safe-online-viagra-orders/ how
to buy low dose naltrexone ,http://buzzlly.com/groups/real-avanafil-with-dapoxetine-online-buy/ buy kamagra oral jelly sydney australia ,
buy clomiphene in uk , https://pueblitoxped.cl/page-gallery-col-4/ ,
online canadian pharmacy https://us-canadianpharmacy.com canadian pharmacy online
Bookmaker 1xbet in Italia https://alalag.com/vb/showthread.php?t=4396
La societa di scommesse 1xBet Italia e una societa di origine russa.
La societa di scommesse fornisce i propri servizi
ad utenti maggiorenni di tutto il mondo. Il sito si trova sempre nelle posizioni di primo piano per il numero di clienti e la qualita degli eventi in linea.
Il sito e famoso per il proprio supporto tecnico, che risponde in pochi minuti, nonche per i piacevoli bonus sul primo deposito.
Storia di 1xbet Italia
L’organizzazione del gioco d’azzardo ha operato in tutto il mondo per oltre 10 anni, ma unaccompanied nel 2015 e arrivata in Italia.
I giocatori italiani preferiscono proprio 1xbet a causa dell’ampio investimento della societa di scommesse sui giocatori popolari del
nostro paese.
Il sito ha guadagnato popolarita anche grazie al servizio 1xbetstreaming, il quale permette di
scommettere direttamente mentre si guarda l’evento.
La societa di scommesse aumenta ogni anno il fatturato dei fondi
e il numero di utenti attivi. Su questo influiscono l’apertura del casino
online aperto e le grandi partnership con grandi club.
Chelsea, Liverpool e Barcellona non sono gli unici nella lista
delle sponsorizzazioni della societa di scommesse.
Licenza
Al momento, la societa di scommesse ha difficolta a causa del rinnovo della licenza, ma nell’applicazione mobile su Android
e iOS e ancora possibile scommettere. Per questo gli scommettitori del Brasile e dei paesi vicini possono scommettere normalmente.
Al momento, la societa e in trattativa per rinnovare la licenza e continuare
le attivita nel suo Paese.
Sistema reward 1xbet Italia
La societa di scommesse cerca di rafforzare la
propria posizione nel mercato delle scommesse con ampie offerte promozionali.
Il hand-out di benvenuto soddisfa i nuovi arrivati e
consente di aumentare il primo deposito della meta,
fino a 100 euro. Le condizioni di secure per ricevere
il regalo sono le seguenti:
• e necessario versare almeno 1 euro sul conto;
• e necessario scommettere 5 volte l’importo versato per
ricevere il regalo;
• le scommesse devono essere espresse da 3 eventi o piu;
• il coefficiente di ogni partita deve essere superiore a 1,40;
• e necessario recuperare il totale entro 30 giorni dalla ricezione del bonus.
Gratuity aggiuntivi dal sito
I giocatori possono ricevere altri regali,
go about a find l’introduzione di codici promozionali speciali al casino o alle scommesse.
Ci sono codici simili durante eventi sportivi su larga scala.
Nel corso di un grande evento, nel 2018, la societa ha offerto a tutti di ottenere 10 euro, che
potevano essere giocati senza il rischio di perdere.
La linea di partite 1xbet al giorno supera i 1000 eventi.https://free-global-ads.com/user/profile/9156
La compagnia di scommesse 1xBet riempie costantemente la propria linea con partite ed eventi interessanti.
In media, ogni giorno ci sono piu di 1000 eventi per le scommesse.
L’amministrazione cerca di dare l’opportunita di scommettere non solitary sulle partite popolari,
ma anche sugli eventi regionali in Portogallo,
in modo che tutti possano scommettere a loro piacimento.
Settle iniziare a scommettere su 1xbet Italia? aplicazioni mobili 1xbet Italia
Iniziare a scommettere su 1xbet Italia e molto semplice. Occorre trovare il sito ufficiale su Google e registrarsi.
Ogni utente maggiorenne puo creare un profilo. Questo puo essere fatto in 4 modi:
canadian pharmacy https://canadianpharmacy-usx.com canadian pharmacy
viagra
Букмекерская контора Леон –
яркий представитель отрасли азартных игр на отечественном рынке.
Она позволяет людям получать реальные деньги достаточно
долгое время.
За все время работы БК смогла заслужить немало
призов, но самой заметной среди них считается
награда «Спорт и Россия».
Ее вручают за выдающиеся вложения в популяризацию спортивных игр на территории Российской Федерации.
Не вызывает удивления то, что клиенты,
обращающиеся в БК, не просто ставят на спортивные события, а с увлечением следят за матчами известных
и небольших команд.
Официальный портал леон букмекерская бонус
http://bazyr06.ru/user/profile/67204 представляет собой функциональный и весьма удобный сервис.
Привлекательная архитектура сайта
и приемлемое число окошек под рекламу не вызывают у посетителей дискомфорта и вместе с тем
стимулируют на новые ставки.
В каком месте еще удастся ощутить невероятный
всплеск эмоций?
Сайт предлагает игрокам возможность:
• узнать больше об акциях, бонусах, предусмотренными разработчиками;
• поставить деньги на игру в привычным способом и Live;
• посмотреть итоги прошедших
матчей;
• прочитать особенности пользования сервисом и в дальнейшем строго им следовать;
• обратиться в службу поддержки, которая работает круглосуточно;
• скачать программное приложение на смартфон, чтобы ставить
в удобное время в местах, где есть сеть.
Варианты ставок на спорт
Букмекер предлагает пользователю широкий выбор спортивных событий.
• футбольные матчи;
• баскетбол;
• хоккей;
• соревнования по волейболу;
• киберспорт;
• rugby;
• бокс;
• крикет;
• теннисные турниры и др.
Помимо этого, получить живые деньги удастся:
• на автоматах;
• в casino;
• в покере.
Предстоящие мероприятия расписаны в отдельном разделе, поэтому отыскать их
не составит труда.
Пользователь получает возможность изучить
их немедленно по окончании оформления учетной записи
и пополнения игрового счета
на любую сумму.
Это недолго ввести персональные сведения в специальные
ячейки на сайте.
Важно не забывать про необходимую проверку информации для подтверждения совершеннолетия.
Бонусная система
Разнообразие ставок – не единственное достоинство букмекерской конторы Леон.
Администраторы способствуют заходу новичков еще и внушительным количеством поощрений.
Подобные сюрпризы уходят на личный счет, что позволяет бережно расходовать живые деньги
и начинать делать ставки с поощрительной
суммы.
Компания предоставляет бонусы при регистрации, после того, как внесен первый платеж, при стабильной активности игрока и при каждом пополнении счета.
Видно, что продуманы все удобства не только для опытных, но
и для начинающих пользователей букмекерской сети.
Получится сразу же воспользоваться приветственным бонусом.
Особенности мобильного приложения леон зеркало
http://beautysosa.maru.net/qna/281914 клиенты могут
не только посредством компьютера.
Для удобства играющих программеры предусмотрели мобильную версию, что обеспечивает возможность быстро делать ставки.
Версия получила идентичный основному порталу дизайн и гарантирует пользователям полноценный комфорт в процессе выполнения
ставок.
При этом доступ к приложению открыт обладателям телефонов независимо от
ОС – как Android, так и iOS.
Вы обнаружите, как легко пользоваться
приложением вне зависимости от того, где Вы находитесь.
Нужно всего лишь получить
доступ к сети интернет, помнить про то, что
надо зарегистрироваться,
и про необходимость авторизоваться.
До сих пор сделать ставки на разные аспекты,
связанные с играми, не было настолько просто.
БК ЛЕОН хороша своей политикой
лояльности, выгодными призами и удобным мобильным приложением.
Ее предпочитают граждане различных регионов Российской Федерации.
Руководители предусмотрели, чтобы работа конторы велась
на законных основаниях.
Для этого имеются все лицензионные документы.
Букмекерская контора не имеет недочетов, из-за
чего заслуживает внимания не
только новеньких, но и опытных игроков.
Провести время в ожидании сыгравшей ставки и внести деньги на
свой счет получает возможность каждый из зарегистрированных
совершеннолетних клиентов.
Важно, бояться и поверить собственной интуиции.
Букмекерская контора Леон – это предпочтение
пользователей, ценящих свое время и деньги.
На онлайн платформе действительно огромный ассортимент событий, на которые предлагается сделать ставки.
Вам удастся не просто отслеживать успехи команды фаворита, но и, скорее
всего, получить большой
выигрыш.
Нужно всего лишь пройти регистрацию на
основном портале конторы, чтобы суметь определить для себя
все предлагаемые разработчиками преимущества.
Адекватный для понимания интерфейс удовлетворит даже начинающих игроков.
Viagra 130 mg nz Viagra 100 mg united kingdom http://viagraldh.com/ Viagra 120mg uk
jeans uomo beige
jeans slim fit schwarz herrenrote damen geldb枚rsefu脽ball trikot g眉nstig kaufenrosa bluse mit punkten
apple 銈偆銉曘偐銉?銈便兗銈?xs
scarpe alpina trekkingnike con acqua santa prezzoschema uncinetto sciallescarpe sneakers uomo diadora
Прогнозы на спортивные события сейчас http://jiedu.la/home.php?mod=space&uid=58860&do=profile&from=space пользуются популярностью
не только среди его почитателей.
И обычные люди сейчас регулярно ставят
для удовольствия.
Они успели оценить по достоинству адреналин, получаемый во время предвкушения
результата.
Мало кто откажется от достаточно выгодного выигрыша?
Вы можете следить за интереснейшей игрой и при этом делать
ставки.
В регионах России букмекеры могут осуществлять деятельность легально,
но для этого понадобится лицензия, что выдают
не сразу и не каждому.
Причем даже у проверенных на деле приемщиков ставок довольно часто возникают сложности.
Это может быть прекращение работы площадки,
невозможность авторизации.
Не вызывает удивления, что терпение иссякает,
возникает желание отыскать другой способ развлечься.
Да и человек будет считать себя обманутым.
В действительности же, не стоит поддаваться панике раньше времени.
Поэтому сейчас расскажем о том,
что такое скачать бетвиннер на андроид официальный и зачем оно может потребоваться.
Этой фишкой на сегодня смогли успешно воспользоваться множество опытных и только присоединившихся пользователей ресурса.
С какой целью используют точную
копию площадки
Зеркало – это полноценная копия
официального портала букмекерской компании.
Необходимо оно для:
1. того, чтобы при случае оперативно возвратиться на любимый
сервис, забыв про блокирование;
2. защиты профилей зарегистрированных пользователей;
3. ускорения отклика;
4. сохранности аналога сайта;
5. равномерного перераспределения основной нагрузки;
6. обхождения блокировки, которая может устанавливаться в силу разных причин (некоторым клиентам ресурс бывает недосягаем из-за Роспотребнадзора).
При этом в полном объеме опции официального сайта действуют и в работающей копии.
Люди, которые постоянно используют betwinner, имеют возможность спокойно зайти через копии.
Это можно осуществить через выбранный vpn.
Вы сможете без ограничений пользоваться выбранным ресурсом, делать ставки.
Почему происходит блокировка betwinner
Букмекерство по регионам Российской Федерации имеет легальный
статус сравнительно недавно.
К тому же лицензию заиметь тяжело.
По причине этих двух причин в РФ легально работают примерно 25-30 букмекерских фирм.
Эти компании Довольно популярны, зачастую мелькают в анонсе матчей тех или иных видов спорта.
Если букмекер не является спонсором спортивных состязаний, надежд на на то, чтобы стать обладателем лицензии у него практически нет.
Поэтому и люди скорее всего не сумеют попасть на вебсайт.
Скорее всего он заблокируют в пределах России.
В чем состоят преимущества Betwinner
В первую очередь, она является компанией международного
уровня.
Входит в Marikit Holdings LTD.
У Betwinner имеется официальный документ о.
Кюросао, это официальное разрешение, дающее возможность
вести деятельность в любых государствах,
где это разрешено по закону.
Поэтому ставить имеют право даже пользователи, которые живут за пределами России.
Просто заходите на сайт, выбираете мероприятия и делаете ставки.
От выигрыша команды-фаворита
до числа голов, забитых в течение
игры.
Отдельного внимания требуют к себе вложения на игрока,
признанного звездой мирового уровня.
Не исключено, что этот игрок «примет во внимание ваши ожидания» и сделает рывок,
ведущий к победе.
Во-вторых, на betwinner можно делать ставки
на многие события типа киберспортивных, в мире спорта, политических, шоу-бизнеса и др.
Можно поставить на то, кто станет
следующим президентом Турции
или кто будет сниматься в анонсированном кинофильме.
Сколько возможностей дарит всемирно известное
Евровидение, когда появляется шанс выбрать победителя в когорте большого
числа исполнителей из многих государств.
Достаточно заманчивые перспективы,
не правда ли?
В-третьих, на Betwinner можно указать наиболее подходящий язык.
Сайт рассчитан на пятьдесят два различных языка.
Поэтому подобрать что-то для себя получится практически у любого.
Это же относится и к валютам,
их почти 50 – от привычных доллара и рубля до электронных денег.
Каждый найдет то, что необходимо на свой вкус.
И это , конечно, не весь перечень достоинств.
Обо всем подробнее можно узнать по ссылке http://mdulltnderwearertwe.s.e@projectag.net/cgi/tawabbs/yybbs.cgi?room=room1
Также там будет подробная инструкция по регистрации.
Посетители смогут понять,
какие предусмотрены виды
прохождения регистрации,
как быстрее приступить к совершению ставок.
Если необходимо определить
актуальный адрес копии сайта, наилучший вариант будет связаться по ГЛ.
Кроме того, можно выйти на надежные сообщества, информирующие о разных букмекерских конторах.
Достаточно обычным образом сделать запрос в любом популярном поисковике фразу – betwinner зеркало.
Вы сможете оказаться на веб-ресурсе скачать приложение бетвиннер ,
который на 100% идентичен официальному сайту.
Итак, не составит труда найти специально
созданное зеркало.
I enjoy, cause I found just what I used to be taking a look for.
You have ended my 4 day long hunt! God Bless you man. Have a great day.
Bye
It’s hard to come by experienced people about this
topic, but you seem like you know what you’re talking about!
Thanks
Aw, this was an incredibly good post. Taking a few minutes
and actual effort to produce a really good article…
but what can I say… I put things off a whole lot and don’t seem to
get nearly anything done.
This is a topic that’s close to my heart… Cheers! Exactly where
are your contact details though?
basketball sneakers
谞讬讬拽讬 讘讬讙讜讚 讙讘专讬诐转讞转讜谞讬诐 住讜驻讙讬诐 life拽讜诪拽讜诐 讞砖诪诇讬 讝讻讜讻讬转 selmornew balance running hierro trail
is viagra over the counter https://usggrxmed.com/ is viagra over the counter
Link exchange is nothing else but it is just placing the other person’s weblog link on your page at appropriate place and other
person will also do same in support of you.
reebok t shirt at 99
tamaris schn眉rstiefelette blaubarbone shorts herrenmango lederadidas sneaker damen dunkelblau zx
https://diverseuplink.com/groups/buy-fincar-kelowna-acheter-fincar-prix/ order generic viagra online uk ,http://whoneedsadr.com/forums/topic/where-to-buy-albuterol-online/ how much is
clomid to buy privately ,https://www.microlightinstitute.com/can-you-buy-xenical-over-counter-australia where to buy nizoral shampoo toronto ,https://www.theezentrepreneur.com/groups/comprar-cialis-europa-generico/ cheap external
hard drives on ebay ,
http://nzpbc.com/buy-cabergoline-steroids atorvastatin online apotheke ,http://rhetoricreports.com/groups/buy-flibanserin-in-blackpool-extremely-cheap-flibanserin/ colcrys
order ,https://www.femszekreny-online.hu/buy-generic-aldara-cream betamethasone valerate cream buy online uk ,http://www.sssgovtitijawali.org/?q=buy-elocon-ointment-uk order clomid pct ,
https://updev.co.za/forums/topic/comprar-xenical-orlistat-online/ buy brand
name propecia online ,https://www.capcleaningsolutions.com/buying-erythromycin-online buy metronidazole or tinidazole ,
best place to buy liquid nolvadex , http://my.rufox.ru/go.php?teaser_id=&url=https://www.theezentrepreneur.com/groups/comprar-flomax-en-linea/
https://vvfit.com/groups/se-puede-comprar-orlistat-en-el-mostrador-en-el-reino-unido/ buy pioglitazone hydrochloride ,https://diverseuplink.com/groups/acheter-divalproex-suisse-sans-ordonnance-where-can-you-buy-divalproex-without-a-prescription/
buy online plavix ,https://finagram.com/forums/topic/finasteride-online-forum/ can i
buy viagra in thailand 2013 ,https://lessontoday.com/groups/baterias-de-litio-ryobi-baratas-puede-pedir-sin-receta/ lopressor online ,
http://www.totally-tubular.net/order-lamictal-from-canada
buy lisinopril 40 mg tablet ,http://h0d1.com/groups/nystatina-y-triamcinolona-acetonida-comprar-en-linea-orden/ buy nizoral shampoo walgreens ,http://nzpbc.com/order-neurontin-over-the-counter buy fluconazole
over the counter ,http://royalmafiaclub.com/groups/comprare-danocrine-contrassegno/
where can i buy cyclopentolate ,
https://myshoopy.com/groups/comprar-xenical-120mg-online-uk-comprar-otc/ homepage ,https://herniatalk.com/groups/comprar-viagra-pack-90-farmacia-sevilla/ can you buy vaniqa over the counter ,
buy loratadine australia , http://onlinehealthinsurancequote.com/__media__/js/netsoltrademark.php?d=www.aiuextension.org%2Fgroups%2Fcan-you-buy-omeprazole-10mg-over-the-counter%2F
I was suggested this blog by my cousin. I’m not sure whether this post is
written by him as no one else know such detailed about my trouble.
You are amazing! Thanks!
Hello there! Do you know if they make any plugins to safeguard against hackers?
I’m kinda paranoid about losing everything I’ve worked hard on. Any suggestions?
When someone writes an piece of writing he/she retains the image
of a user in his/her mind that how a user can be
aware of it. Therefore that’s why this post is outstdanding.
Thanks!
Hey there are using WordPress for your blog platform?
I’m new to the blog world but I’m trying to get started and
set up my own. Do you require any html coding knowledge to make
your own blog? Any help would be really appreciated!
1XBET – одна из наиболее востребованных в России букмекерских компаний по ставкам
на спорт.
Площадка работает на основе лицензии Кюрасао в online-режиме.
Компания, осуществляющая деятельность
с 2007 года, насчитывает свыше 400
тыс. постоянных посетителей.
На сегодня букмекерская контора 1xbet в числе мировых лидеров по
спортпрогнозам.
Это и есть критерий доверительности армии клиентов, которые решили выбрать именно указанную БК.
Теперь надо разобраться в особенностях пребывания на онлайн платформе 1хбет вход в личный кабинет .
Порядок прохождения регистрации
Делать ставки может только прошедший регистрацию пользователь (беттер).
Известны различные способы подготовки аккаунта:
1. через социальные сети, нужно всего лишь выбрать соответствующий вариант;
2. по адресу электронной почты вне зависимости от сервиса;
3. по телефонному номеру, на который будет прислано смс.
Игрокам http://pla4u.ru/index.php?page=user&action=pub_profile&id=187949 в
личный кабинет становится открытым немедленно
по окончании регистрации.
Беттер получает право ставить
на разные события из мира спорта, принимать участие
в акционных и бонусных программах, осуществлять вывод денег и др.
Вам понравится не просто наблюдать за матчем выбранного состава игроков, но и по возможности получать немалые суммы денег.
Нужно всего лишь указать мероприятие, которое понравилось больше всего.
Итак, после регистрации можно воспользоваться многочисленными возможностями основного ресурса, которые предоставили разработчики.
Виды ставок БК 1хбет https://wd.leepet.cn/home.php?mod=space&uid=264179&do=profile&from=space
В отличие от подобных контор 1Хбет предоставляет 12 типов операций.
Одинарный прогноз (ординар, одиночник) – сделка на определенный исход спортивного мероприятия.
Выигрыш насчитывается умножением коэффициента в десятичном формате на количество поставленных денег.
То есть нет ничего сложного, если выбирать данный вид ставки.
Экспресс – ставка сразу на два и больше исходов,
которые анонсируются.
Экспресс «Стайер» отличается особенностью: результаты и мероприятия разрешается дописывать на протяжении 2-х
месяцев.
Антиэкспресс содержит несколько исходов, противоположный экспрессу
по способу начисления призовых денег.
Такой тип прогноза выбирают как со стажем игроки, так и начинающие пользователи.
Система – сделка на все возможные варианты экспрессов конкретной размерности из выбранного количества мероприятий.
Цепочка – набор одиночных прогнозов.
По доверительной ставке можно вернуть долю финансов, которые находятся пока под блокировкой.
Это довольно интересное предложение,
которое могут выбрать прошедшие регистрацию клиенты.
Ставка по купону выдает комбинацию из цифр и букв для оформления запроса.
Этим способом можно сделать ставку без внесения денег на
депозит.
Лаки является комбинированием ординаров и совершенно всех экспрессов,
которые собраны из выбранных спортивных мероприятий.
Патент действует по тому же алгоритму, что и
лаки, но количество событий ограничивается 3-мя.
Для чего нужно использовать зеркало
БК 1Хбет считается нелегальной в
регионах России.
Это сопряжено с тем, что фирма
не взимает налоги с прибылей клиентов.
Непосредственно для клиентов это огромный плюс, но на законодательном уровне данный нюанс признается не самым уместным.
Руководители не намерены что-либо менять
в своей политике.
Как же быть в этом случае клиентам?
В действительности нет ничего проще.
Следует обойти блокирование официального веб-ресурса,
а следовательно зайти на актуальное зеркало портала.
Копия можно представить как особый сервис с точным интерфейсом портала, без каких бы то
ни было сдерживающих факторов, с воссозданием прежде введенных
данных.
Разрешается войти и беспроблемно воспользоваться имеющимися возможностями, предложенными создателями.
Данные копии используют единую с основным вебсайтом 1xbet базу, поэтому зайти на сайт можно под своим аккаунтом.
Помните, что дизайн идентичен официальному
сервису букмекера.
Переместиться на зекрало получится
по ссылке 1xbet скачать приложение на телефон.
Помимо прогнозов на спорт в 1хбет пользователям доступны
тотализаторы, слоты, разные лотереи,
нарды, игры в online и офлайн режимах.
Как видите, у БК оптимальное число событий, которые придутся по
нраву клиетнам разных возрастов, пола.
Нужно всего лишь пройти простую регистрацию уже сейчас.
Вы поймете, как интересно получится провести досуг, если есть ноутбук и доступ к сети Интернет.
suresiyle kullan?labiliyor. Türkiye’de 1xbet bahis şirketi
• Kredi Kart?
Visa kartlar?n?z ile 10 TL, Master Card ile 15 TL alt limitle set
yapabilirsiniz. Big boss Playing-card sahibiyseniz
5 TL uzeri tutarlar? cekebilirsiniz.
• WebMoney
WebMoney yontemini kullan?yorsan?z 3 TL alt limitle deposit, 5
TL ve uzeri tutarlarla da cekim talebi verebilirsiniz.
• EcoPayz
Minimum 3 TL ile yat?r?m, maksimum 5 TL ile cekim yapabilirsiniz.
• AstroPay
3 TL ve uzeri tutarlar? yat?rabiliyorken 5 TL ve uzerindeki
tutarlar icinde cekim talebi verebilirsiniz.
• Paykasa
Kulland?g?n?z odeme yontemi Paykasa ise 3 TL alt limitin uzerindeki tum tutarlar?
an?nda yat?rabilirsiniz. Cekim talebi icin minimal islem tutar?
5 TL’dir.
• PayKwik
Yaln?zca leave islemleri icin 3 TL alt limitle kullan?labilmektedir.
1xbet Gratuity ve Promosyonlar? http://shimada.s79.xrea.com/koo/bbs/bbs.cgi?post=m05
Her yeni bahis slice gibi Turkler icinde bonuslar en onemli
k?s?md?r. 1xbet bahis sitesi de bunu en iyi sekilde
sunmaktad?r.
• Hos Geldin Bonusu
Uyeliginizi act?ktan hemen sonra yapacag?n?z ilk set islemine
sunulan bonustur. En fazla 300 TL’ye kadar yararlanabileceginiz
bu promosyondan %100 oran?nda yararlanabilirsiniz.
• PromoCode Bonusu
• Telegram Bonusu
• Y?ld?z Jackpot Promosyonu
• Bahis Kuponlar? Savas? Turnuvas?
• 1xRace Bonusu
• Dogum Gunu Bonusu
1xbet Musteri Hizmetleri
1xbet canl? destek hizmeti sunuyor ancak bunun haricinde de cok ilginc bir dan?smanl?k hizmeti veriyor.
Her bahis sitesinde gordugumuz mesaj yoluyla ulas?m, correspondence yordam?yla
adresinden iletisim mumkun. Bunlar?n haricinde ise yurt ici servis
numaras?yla musterilerine telefon destegi sunuyor.
1xbet Guvenilir Mi?
Bahis oynatma lisans?n? Curacao uzerinden alm?s olan 1xbet Little sirketi Turkiye’nin koklu
platformlar? aras?nda bulunuyor. Lisans?n?n haricinde de GoDaddy taraf?ndan saglanm?s olan SSL sertifikas?n?n aktif oldugunu gorebiliyoruz.
1xbet Genel Degerlendirme Android için 1xbet’i indirin
1xbet guncel giris adresi ise 1x-turkey.com olarak guncellendi.
Bahis dunyas?nda ayr?cal?kl? bir bahis yelpazesini bir araya getiren sirketin gerek bonuslar?yla, gerek an?nda odeme yontemleriyle gerekse guvenilirligiyle
dikkat cekmeye devam ettigini soyleyebiliriz.
http://google.com.af/url?q=https://www.bsgs.org.uk/
http://google.al/url?q=https://www.bsgs.org.uk/
http://google.dz/url?q=https://www.bsgs.org.uk/
http://google.as/url?q=https://www.bsgs.org.uk/
http://google.ad/url?q=https://www.bsgs.org.uk/
http://google.it.ao/url?q=https://www.bsgs.org.uk/
http://google.com.ai/url?q=https://www.bsgs.org.uk/
http://google.com.ag/url?q=https://www.bsgs.org.uk/
http://google.com.ar/url?q=https://www.bsgs.org.uk/
http://google.am/url?q=https://www.bsgs.org.uk/
http://google.ac/url?q=https://www.bsgs.org.uk/
http://google.com.au/url?q=https://www.bsgs.org.uk/
http://google.at/url?q=https://www.bsgs.org.uk/
http://google.az/url?q=https://www.bsgs.org.uk/
http://google.bs/url?q=https://www.bsgs.org.uk/
http://google.com.bh/url?q=https://www.bsgs.org.uk/
http://google.com.bd/url?q=https://www.bsgs.org.uk/
http://google.com.by/url?q=https://www.bsgs.org.uk/
http://google.be/url?q=https://www.bsgs.org.uk/
http://google.com.bz/url?q=https://www.bsgs.org.uk/
http://google.bj/url?q=https://www.bsgs.org.uk/
http://google.bt/url?q=https://www.bsgs.org.uk/
http://google.com.bo/url?q=https://www.bsgs.org.uk/
http://google.ba/url?q=https://www.bsgs.org.uk/
http://google.co.bw/url?q=https://www.bsgs.org.uk/
http://google.com.br/url?q=https://www.bsgs.org.uk/
http://google.vg/url?q=https://www.bsgs.org.uk/
http://google.com.bn/url?q=https://www.bsgs.org.uk/
http://google.bg/url?q=https://www.bsgs.org.uk/
http://google.bf/url?q=https://www.bsgs.org.uk/
http://google.bi/url?q=https://www.bsgs.org.uk/
http://google.com.kh/url?q=https://www.bsgs.org.uk/
http://google.cm/url?q=https://www.bsgs.org.uk/
http://google.ca/url?q=https://www.bsgs.org.uk/
http://google.cv/url?q=https://www.bsgs.org.uk/
http://google.cat/url?q=https://www.bsgs.org.uk/
http://google.cf/url?q=https://www.bsgs.org.uk/
http://google.td/url?q=https://www.bsgs.org.uk/
http://google.cl/url?q=https://www.bsgs.org.uk/
http://google.cn/url?q=https://www.bsgs.org.uk/
http://google.com.co/url?q=https://www.bsgs.org.uk/
http://google.cd/url?q=https://www.bsgs.org.uk/
http://google.cg/url?q=https://www.bsgs.org.uk/
http://google.co.ck/url?q=https://www.bsgs.org.uk/
http://google.co.cr/url?q=https://www.bsgs.org.uk/
http://google.ci/url?q=https://www.bsgs.org.uk/
http://google.hr/url?q=https://www.bsgs.org.uk/
http://google.com.cu/url?q=https://www.bsgs.org.uk/
http://google.com.cy/url?q=https://www.bsgs.org.uk/
http://google.cz/url?q=https://www.bsgs.org.uk/
http://google.dk/url?q=https://www.bsgs.org.uk/
http://google.dj/url?q=https://www.bsgs.org.uk/
http://google.dm/url?q=https://www.bsgs.org.uk/
http://google.com.do/url?q=https://www.bsgs.org.uk/
http://google.com.ec/url?q=https://www.bsgs.org.uk/
http://google.com.eg/url?q=https://www.bsgs.org.uk/
http://google.com.sv/url?q=https://www.bsgs.org.uk/
http://google.ee/url?q=https://www.bsgs.org.uk/
http://google.com.et/url?q=https://www.bsgs.org.uk/
http://google.com.fj/url?q=https://www.bsgs.org.uk/
http://google.fi/url?q=https://www.bsgs.org.uk/
http://google.fr/url?q=https://www.bsgs.org.uk/
http://google.ga/url?q=https://www.bsgs.org.uk/
http://google.gm/url?q=https://www.bsgs.org.uk/
http://google.ge/url?q=https://www.bsgs.org.uk/
http://google.de/url?q=https://www.bsgs.org.uk/
http://google.com.gh/url?q=https://www.bsgs.org.uk/
http://google.com.gi/url?q=https://www.bsgs.org.uk/
http://google.gr/url?q=https://www.bsgs.org.uk/
http://google.gl/url?q=https://www.bsgs.org.uk/
http://google.gp/url?q=https://www.bsgs.org.uk/
http://google.com.gt/url?q=https://www.bsgs.org.uk/
http://google.gg/url?q=https://www.bsgs.org.uk/
http://google.gy/url?q=https://www.bsgs.org.uk/
http://google.ht/url?q=https://www.bsgs.org.uk/
http://google.hn/url?q=https://www.bsgs.org.uk/
http://google.com.hk/url?q=https://www.bsgs.org.uk/
http://google.hu/url?q=https://www.bsgs.org.uk/
http://google.is/url?q=https://www.bsgs.org.uk/
http://google.co.in/url?q=https://www.bsgs.org.uk/
http://google.co.id/url?q=https://www.bsgs.org.uk/
http://google.iq/url?q=https://www.bsgs.org.uk/
http://google.ie/url?q=https://www.bsgs.org.uk/
http://google.co.im/url?q=https://www.bsgs.org.uk/
http://google.co.il/url?q=https://www.bsgs.org.uk/
http://google.it/url?q=https://www.bsgs.org.uk/
http://google.ci/url?q=https://www.bsgs.org.uk/
http://google.com.jm/url?q=https://www.bsgs.org.uk/
http://google.co.jp/url?q=https://www.bsgs.org.uk/
http://google.co.je/url?q=https://www.bsgs.org.uk/
http://google.jo/url?q=https://www.bsgs.org.uk/
http://google.kz/url?q=https://www.bsgs.org.uk/
http://google.co.ke/url?q=https://www.bsgs.org.uk/
http://google.ki/url?q=https://www.bsgs.org.uk/
http://google.com.kw/url?q=https://www.bsgs.org.uk/
http://google.com.kg/url?q=https://www.bsgs.org.uk/
http://google.la/url?q=https://www.bsgs.org.uk/
http://google.lv/url?q=https://www.bsgs.org.uk/
http://google.com.lb/url?q=https://www.bsgs.org.uk/
http://google.co.ls/url?q=https://www.bsgs.org.uk/
http://google.com.ly/url?q=https://www.bsgs.org.uk/
http://google.li/url?q=https://www.bsgs.org.uk/
http://google.lt/url?q=https://www.bsgs.org.uk/
http://google.lu/url?q=https://www.bsgs.org.uk/
http://google.mk/url?q=https://www.bsgs.org.uk/
http://google.mg/url?q=https://www.bsgs.org.uk/
http://google.mw/url?q=https://www.bsgs.org.uk/
http://google.com.my/url?q=https://www.bsgs.org.uk/
http://google.mv/url?q=https://www.bsgs.org.uk/
http://google.ml/url?q=https://www.bsgs.org.uk/
http://google.com.mt/url?q=https://www.bsgs.org.uk/
http://google.mu/url?q=https://www.bsgs.org.uk/
http://google.com.mx/url?q=https://www.bsgs.org.uk/
http://google.fm/url?q=https://www.bsgs.org.uk/
http://google.md/url?q=https://www.bsgs.org.uk/
http://google.mn/url?q=https://www.bsgs.org.uk/
http://google.me/url?q=https://www.bsgs.org.uk/
http://google.ms/url?q=https://www.bsgs.org.uk/
http://google.co.ma/url?q=https://www.bsgs.org.uk/
http://google.co.mz/url?q=https://www.bsgs.org.uk/
http://google.com.na/url?q=https://www.bsgs.org.uk/
http://google.nr/url?q=https://www.bsgs.org.uk/
http://google.com.np/url?q=https://www.bsgs.org.uk/
http://google.nl/url?q=https://www.bsgs.org.uk/
http://google.co.nz/url?q=https://www.bsgs.org.uk/
http://google.com.ni/url?q=https://www.bsgs.org.uk/
http://google.ne/url?q=https://www.bsgs.org.uk/
http://google.com.ng/url?q=https://www.bsgs.org.uk/
http://google.nu/url?q=https://www.bsgs.org.uk/
http://google.com.nf/url?q=https://www.bsgs.org.uk/
http://google.no/url?q=https://www.bsgs.org.uk/
http://google.com.om/url?q=https://www.bsgs.org.uk/
http://google.com.pk/url?q=https://www.bsgs.org.uk/
http://google.ps/url?q=https://www.bsgs.org.uk/
http://google.com.pa/url?q=https://www.bsgs.org.uk/
http://google.com.pg/url?q=https://www.bsgs.org.uk/
http://google.com.py/url?q=https://www.bsgs.org.uk/
http://google.com.pe/url?q=https://www.bsgs.org.uk/
http://google.com.ph/url?q=https://www.bsgs.org.uk/
http://google.pn/url?q=https://www.bsgs.org.uk/
http://google.pl/url?q=https://www.bsgs.org.uk/
http://google.pt/url?q=https://www.bsgs.org.uk/
http://google.com.pr/url?q=https://www.bsgs.org.uk/
http://google.com.qa/url?q=https://www.bsgs.org.uk/
http://google.ro/url?q=https://www.bsgs.org.uk/
http://google.ru/url?q=https://www.bsgs.org.uk/
http://google.rw/url?q=https://www.bsgs.org.uk/
http://google.sh/url?q=https://www.bsgs.org.uk/
http://google.ws/url?q=https://www.bsgs.org.uk/
http://google.sm/url?q=https://www.bsgs.org.uk/
http://google.st/url?q=https://www.bsgs.org.uk/
http://google.com.sa/url?q=https://www.bsgs.org.uk/
http://google.sn/url?q=https://www.bsgs.org.uk/
http://google.rs/url?q=https://www.bsgs.org.uk/
http://google.sc/url?q=https://www.bsgs.org.uk/
http://google.com.sl/url?q=https://www.bsgs.org.uk/
http://google.com.sg/url?q=https://www.bsgs.org.uk/
http://google.sk/url?q=https://www.bsgs.org.uk/
http://google.si/url?q=https://www.bsgs.org.uk/
http://google.com.sb/url?q=https://www.bsgs.org.uk/
http://google.so/url?q=https://www.bsgs.org.uk/
http://google.co.za/url?q=https://www.bsgs.org.uk/
http://google.co.kr/url?q=https://www.bsgs.org.uk/
http://google.es/url?q=https://www.bsgs.org.uk/
http://google.lk/url?q=https://www.bsgs.org.uk/
http://google.com.vc/url?q=https://www.bsgs.org.uk/
http://google.sr/url?q=https://www.bsgs.org.uk/
http://google.se/url?q=https://www.bsgs.org.uk/
http://google.ch/url?q=https://www.bsgs.org.uk/
http://google.com.tw/url?q=https://www.bsgs.org.uk/
http://google.com.tj/url?q=https://www.bsgs.org.uk/
http://google.co.tz/url?q=https://www.bsgs.org.uk/
http://google.co.th/url?q=https://www.bsgs.org.uk/
http://google.tl/url?q=https://www.bsgs.org.uk/
http://google.tg/url?q=https://www.bsgs.org.uk/
http://google.tk/url?q=https://www.bsgs.org.uk/
http://google.to/url?q=https://www.bsgs.org.uk/
http://google.tt/url?q=https://www.bsgs.org.uk/
http://google.tn/url?q=https://www.bsgs.org.uk/
http://google.com.tr/url?q=https://www.bsgs.org.uk/
http://google.tm/url?q=https://www.bsgs.org.uk/
http://google.co.ug/url?q=https://www.bsgs.org.uk/
http://google.com.ua/url?q=https://www.bsgs.org.uk/
http://google.ae/url?q=https://www.bsgs.org.uk/
http://google.co.uk/url?q=https://www.bsgs.org.uk/
http://google.com/url?q=https://www.bsgs.org.uk/
http://google.com.uy/url?q=https://www.bsgs.org.uk/
http://google.co.uz/url?q=https://www.bsgs.org.uk/
http://google.vu/url?q=https://www.bsgs.org.uk/
http://google.co.ve/url?q=https://www.bsgs.org.uk/
http://google.com.vn/url?q=https://www.bsgs.org.uk/
http://google.co.vi/url?q=https://www.bsgs.org.uk/
http://google.co.zm/url?q=https://www.bsgs.org.uk/
http://google.co.zw/url?q=https://www.bsgs.org.uk/
http://maps.google.com.af/url?q=https://www.bsgs.org.uk/
http://maps.google.al/url?q=https://www.bsgs.org.uk/
http://maps.google.dz/url?q=https://www.bsgs.org.uk/
http://maps.google.as/url?q=https://www.bsgs.org.uk/
http://maps.google.ad/url?q=https://www.bsgs.org.uk/
http://maps.google.it.ao/url?q=https://www.bsgs.org.uk/
http://maps.google.com.ai/url?q=https://www.bsgs.org.uk/
http://maps.google.com.ag/url?q=https://www.bsgs.org.uk/
http://maps.google.com.ar/url?q=https://www.bsgs.org.uk/
http://maps.google.am/url?q=https://www.bsgs.org.uk/
http://maps.google.ac/url?q=https://www.bsgs.org.uk/
http://maps.google.com.au/url?q=https://www.bsgs.org.uk/
http://maps.google.at/url?q=https://www.bsgs.org.uk/
http://maps.google.az/url?q=https://www.bsgs.org.uk/
http://maps.google.bs/url?q=https://www.bsgs.org.uk/
http://maps.google.com.bh/url?q=https://www.bsgs.org.uk/
http://maps.google.com.bd/url?q=https://www.bsgs.org.uk/
http://maps.google.com.by/url?q=https://www.bsgs.org.uk/
http://maps.google.be/url?q=https://www.bsgs.org.uk/
http://maps.google.com.bz/url?q=https://www.bsgs.org.uk/
http://maps.google.bj/url?q=https://www.bsgs.org.uk/
http://maps.google.bt/url?q=https://www.bsgs.org.uk/
http://maps.google.com.bo/url?q=https://www.bsgs.org.uk/
http://maps.google.ba/url?q=https://www.bsgs.org.uk/
http://maps.google.co.bw/url?q=https://www.bsgs.org.uk/
http://maps.google.com.br/url?q=https://www.bsgs.org.uk/
http://maps.google.vg/url?q=https://www.bsgs.org.uk/
http://maps.google.com.bn/url?q=https://www.bsgs.org.uk/
http://maps.google.bg/url?q=https://www.bsgs.org.uk/
http://maps.google.bf/url?q=https://www.bsgs.org.uk/
http://maps.google.bi/url?q=https://www.bsgs.org.uk/
http://maps.google.com.kh/url?q=https://www.bsgs.org.uk/
http://maps.google.cm/url?q=https://www.bsgs.org.uk/
http://maps.google.ca/url?q=https://www.bsgs.org.uk/
http://maps.google.cv/url?q=https://www.bsgs.org.uk/
http://maps.google.cat/url?q=https://www.bsgs.org.uk/
http://maps.google.cf/url?q=https://www.bsgs.org.uk/
http://maps.google.td/url?q=https://www.bsgs.org.uk/
http://maps.google.cl/url?q=https://www.bsgs.org.uk/
http://maps.google.cn/url?q=https://www.bsgs.org.uk/
http://maps.google.com.co/url?q=https://www.bsgs.org.uk/
http://maps.google.cd/url?q=https://www.bsgs.org.uk/
http://maps.google.cg/url?q=https://www.bsgs.org.uk/
http://maps.google.co.ck/url?q=https://www.bsgs.org.uk/
http://maps.google.co.cr/url?q=https://www.bsgs.org.uk/
http://maps.google.ci/url?q=https://www.bsgs.org.uk/
http://maps.google.hr/url?q=https://www.bsgs.org.uk/
http://maps.google.com.cu/url?q=https://www.bsgs.org.uk/
http://maps.google.com.cy/url?q=https://www.bsgs.org.uk/
http://maps.google.cz/url?q=https://www.bsgs.org.uk/
http://maps.google.dk/url?q=https://www.bsgs.org.uk/
http://maps.google.dj/url?q=https://www.bsgs.org.uk/
http://maps.google.dm/url?q=https://www.bsgs.org.uk/
http://maps.google.com.do/url?q=https://www.bsgs.org.uk/
http://maps.google.com.ec/url?q=https://www.bsgs.org.uk/
http://maps.google.com.eg/url?q=https://www.bsgs.org.uk/
http://maps.google.com.sv/url?q=https://www.bsgs.org.uk/
http://maps.google.ee/url?q=https://www.bsgs.org.uk/
http://maps.google.com.et/url?q=https://www.bsgs.org.uk/
http://maps.google.com.fj/url?q=https://www.bsgs.org.uk/
http://maps.google.fi/url?q=https://www.bsgs.org.uk/
http://maps.google.fr/url?q=https://www.bsgs.org.uk/
http://maps.google.ga/url?q=https://www.bsgs.org.uk/
http://maps.google.gm/url?q=https://www.bsgs.org.uk/
http://maps.google.ge/url?q=https://www.bsgs.org.uk/
http://maps.google.de/url?q=https://www.bsgs.org.uk/
http://maps.google.com.gh/url?q=https://www.bsgs.org.uk/
http://maps.google.com.gi/url?q=https://www.bsgs.org.uk/
http://maps.google.gr/url?q=https://www.bsgs.org.uk/
http://maps.google.gl/url?q=https://www.bsgs.org.uk/
http://maps.google.gp/url?q=https://www.bsgs.org.uk/
http://maps.google.com.gt/url?q=https://www.bsgs.org.uk/
http://maps.google.gg/url?q=https://www.bsgs.org.uk/
http://maps.google.gy/url?q=https://www.bsgs.org.uk/
http://maps.google.ht/url?q=https://www.bsgs.org.uk/
http://maps.google.hn/url?q=https://www.bsgs.org.uk/
http://maps.google.com.hk/url?q=https://www.bsgs.org.uk/
http://maps.google.hu/url?q=https://www.bsgs.org.uk/
http://maps.google.is/url?q=https://www.bsgs.org.uk/
http://maps.google.co.in/url?q=https://www.bsgs.org.uk/
http://maps.google.co.id/url?q=https://www.bsgs.org.uk/
http://maps.google.iq/url?q=https://www.bsgs.org.uk/
http://maps.google.ie/url?q=https://www.bsgs.org.uk/
http://maps.google.co.im/url?q=https://www.bsgs.org.uk/
http://maps.google.co.il/url?q=https://www.bsgs.org.uk/
http://maps.google.it/url?q=https://www.bsgs.org.uk/
http://maps.google.ci/url?q=https://www.bsgs.org.uk/
http://maps.google.com.jm/url?q=https://www.bsgs.org.uk/
http://maps.google.co.jp/url?q=https://www.bsgs.org.uk/
http://maps.google.co.je/url?q=https://www.bsgs.org.uk/
http://maps.google.jo/url?q=https://www.bsgs.org.uk/
http://maps.google.kz/url?q=https://www.bsgs.org.uk/
http://maps.google.co.ke/url?q=https://www.bsgs.org.uk/
http://maps.google.ki/url?q=https://www.bsgs.org.uk/
http://maps.google.com.kw/url?q=https://www.bsgs.org.uk/
http://maps.google.com.kg/url?q=https://www.bsgs.org.uk/
http://maps.google.la/url?q=https://www.bsgs.org.uk/
http://maps.google.lv/url?q=https://www.bsgs.org.uk/
http://maps.google.com.lb/url?q=https://www.bsgs.org.uk/
http://maps.google.co.ls/url?q=https://www.bsgs.org.uk/
http://maps.google.com.ly/url?q=https://www.bsgs.org.uk/
http://maps.google.li/url?q=https://www.bsgs.org.uk/
http://maps.google.lt/url?q=https://www.bsgs.org.uk/
http://maps.google.lu/url?q=https://www.bsgs.org.uk/
http://maps.google.mk/url?q=https://www.bsgs.org.uk/
http://maps.google.mg/url?q=https://www.bsgs.org.uk/
http://maps.google.mw/url?q=https://www.bsgs.org.uk/
http://maps.google.com.my/url?q=https://www.bsgs.org.uk/
http://maps.google.mv/url?q=https://www.bsgs.org.uk/
http://maps.google.ml/url?q=https://www.bsgs.org.uk/
http://maps.google.com.mt/url?q=https://www.bsgs.org.uk/
http://maps.google.mu/url?q=https://www.bsgs.org.uk/
http://maps.google.com.mx/url?q=https://www.bsgs.org.uk/
http://maps.google.fm/url?q=https://www.bsgs.org.uk/
http://maps.google.md/url?q=https://www.bsgs.org.uk/
http://maps.google.mn/url?q=https://www.bsgs.org.uk/
http://maps.google.me/url?q=https://www.bsgs.org.uk/
http://maps.google.ms/url?q=https://www.bsgs.org.uk/
http://maps.google.co.ma/url?q=https://www.bsgs.org.uk/
http://maps.google.co.mz/url?q=https://www.bsgs.org.uk/
http://maps.google.com.na/url?q=https://www.bsgs.org.uk/
http://maps.google.nr/url?q=https://www.bsgs.org.uk/
http://maps.google.com.np/url?q=https://www.bsgs.org.uk/
http://maps.google.nl/url?q=https://www.bsgs.org.uk/
http://maps.google.co.nz/url?q=https://www.bsgs.org.uk/
http://maps.google.com.ni/url?q=https://www.bsgs.org.uk/
http://maps.google.ne/url?q=https://www.bsgs.org.uk/
http://maps.google.com.ng/url?q=https://www.bsgs.org.uk/
http://maps.google.nu/url?q=https://www.bsgs.org.uk/
http://maps.google.com.nf/url?q=https://www.bsgs.org.uk/
http://maps.google.no/url?q=https://www.bsgs.org.uk/
http://maps.google.com.om/url?q=https://www.bsgs.org.uk/
http://maps.google.com.pk/url?q=https://www.bsgs.org.uk/
http://maps.google.ps/url?q=https://www.bsgs.org.uk/
http://maps.google.com.pa/url?q=https://www.bsgs.org.uk/
http://maps.google.com.pg/url?q=https://www.bsgs.org.uk/
http://maps.google.com.py/url?q=https://www.bsgs.org.uk/
http://maps.google.com.pe/url?q=https://www.bsgs.org.uk/
http://maps.google.com.ph/url?q=https://www.bsgs.org.uk/
http://maps.google.pn/url?q=https://www.bsgs.org.uk/
http://maps.google.pl/url?q=https://www.bsgs.org.uk/
http://maps.google.pt/url?q=https://www.bsgs.org.uk/
http://maps.google.com.pr/url?q=https://www.bsgs.org.uk/
http://maps.google.com.qa/url?q=https://www.bsgs.org.uk/
http://maps.google.ro/url?q=https://www.bsgs.org.uk/
http://maps.google.ru/url?q=https://www.bsgs.org.uk/
http://maps.google.rw/url?q=https://www.bsgs.org.uk/
http://maps.google.sh/url?q=https://www.bsgs.org.uk/
http://maps.google.ws/url?q=https://www.bsgs.org.uk/
http://maps.google.sm/url?q=https://www.bsgs.org.uk/
http://maps.google.st/url?q=https://www.bsgs.org.uk/
http://maps.google.com.sa/url?q=https://www.bsgs.org.uk/
http://maps.google.sn/url?q=https://www.bsgs.org.uk/
http://maps.google.rs/url?q=https://www.bsgs.org.uk/
http://maps.google.sc/url?q=https://www.bsgs.org.uk/
http://maps.google.com.sl/url?q=https://www.bsgs.org.uk/
http://maps.google.com.sg/url?q=https://www.bsgs.org.uk/
http://maps.google.sk/url?q=https://www.bsgs.org.uk/
http://maps.google.si/url?q=https://www.bsgs.org.uk/
http://maps.google.com.sb/url?q=https://www.bsgs.org.uk/
http://maps.google.so/url?q=https://www.bsgs.org.uk/
http://maps.google.co.za/url?q=https://www.bsgs.org.uk/
http://maps.google.co.kr/url?q=https://www.bsgs.org.uk/
http://maps.google.es/url?q=https://www.bsgs.org.uk/
http://maps.google.lk/url?q=https://www.bsgs.org.uk/
http://maps.google.com.vc/url?q=https://www.bsgs.org.uk/
http://maps.google.sr/url?q=https://www.bsgs.org.uk/
http://maps.google.se/url?q=https://www.bsgs.org.uk/
http://maps.google.ch/url?q=https://www.bsgs.org.uk/
http://maps.google.com.tw/url?q=https://www.bsgs.org.uk/
http://maps.google.com.tj/url?q=https://www.bsgs.org.uk/
http://maps.google.co.tz/url?q=https://www.bsgs.org.uk/
http://maps.google.co.th/url?q=https://www.bsgs.org.uk/
http://maps.google.tl/url?q=https://www.bsgs.org.uk/
http://maps.google.tg/url?q=https://www.bsgs.org.uk/
http://maps.google.tk/url?q=https://www.bsgs.org.uk/
http://maps.google.to/url?q=https://www.bsgs.org.uk/
http://maps.google.tt/url?q=https://www.bsgs.org.uk/
http://maps.google.tn/url?q=https://www.bsgs.org.uk/
http://maps.google.com.tr/url?q=https://www.bsgs.org.uk/
http://maps.google.tm/url?q=https://www.bsgs.org.uk/
http://maps.google.co.ug/url?q=https://www.bsgs.org.uk/
http://maps.google.com.ua/url?q=https://www.bsgs.org.uk/
http://maps.google.ae/url?q=https://www.bsgs.org.uk/
http://maps.google.co.uk/url?q=https://www.bsgs.org.uk/
http://maps.google.com/url?q=https://www.bsgs.org.uk/
http://maps.google.com.uy/url?q=https://www.bsgs.org.uk/
http://maps.google.co.uz/url?q=https://www.bsgs.org.uk/
http://maps.google.vu/url?q=https://www.bsgs.org.uk/
http://maps.google.co.ve/url?q=https://www.bsgs.org.uk/
http://maps.google.com.vn/url?q=https://www.bsgs.org.uk/
http://maps.google.co.vi/url?q=https://www.bsgs.org.uk/
http://maps.google.co.zm/url?q=https://www.bsgs.org.uk/
http://maps.google.co.zw/url?q=https://www.bsgs.org.uk/
http://images.google.com.af/url?q=https://www.bsgs.org.uk/
http://images.google.al/url?q=https://www.bsgs.org.uk/
http://images.google.dz/url?q=https://www.bsgs.org.uk/
http://images.google.as/url?q=https://www.bsgs.org.uk/
http://images.google.ad/url?q=https://www.bsgs.org.uk/
http://images.google.it.ao/url?q=https://www.bsgs.org.uk/
http://images.google.com.ai/url?q=https://www.bsgs.org.uk/
http://images.google.com.ag/url?q=https://www.bsgs.org.uk/
http://images.google.com.ar/url?q=https://www.bsgs.org.uk/
http://images.google.am/url?q=https://www.bsgs.org.uk/
http://images.google.ac/url?q=https://www.bsgs.org.uk/
http://images.google.com.au/url?q=https://www.bsgs.org.uk/
http://images.google.at/url?q=https://www.bsgs.org.uk/
http://images.google.az/url?q=https://www.bsgs.org.uk/
http://images.google.bs/url?q=https://www.bsgs.org.uk/
http://images.google.com.bh/url?q=https://www.bsgs.org.uk/
http://images.google.com.bd/url?q=https://www.bsgs.org.uk/
http://images.google.com.by/url?q=https://www.bsgs.org.uk/
http://images.google.be/url?q=https://www.bsgs.org.uk/
http://images.google.com.bz/url?q=https://www.bsgs.org.uk/
http://images.google.bj/url?q=https://www.bsgs.org.uk/
http://images.google.bt/url?q=https://www.bsgs.org.uk/
http://images.google.com.bo/url?q=https://www.bsgs.org.uk/
http://images.google.ba/url?q=https://www.bsgs.org.uk/
http://images.google.co.bw/url?q=https://www.bsgs.org.uk/
http://images.google.com.br/url?q=https://www.bsgs.org.uk/
http://images.google.vg/url?q=https://www.bsgs.org.uk/
http://images.google.com.bn/url?q=https://www.bsgs.org.uk/
http://images.google.bg/url?q=https://www.bsgs.org.uk/
http://images.google.bf/url?q=https://www.bsgs.org.uk/
http://images.google.bi/url?q=https://www.bsgs.org.uk/
http://images.google.com.kh/url?q=https://www.bsgs.org.uk/
http://images.google.cm/url?q=https://www.bsgs.org.uk/
http://images.google.ca/url?q=https://www.bsgs.org.uk/
http://images.google.cv/url?q=https://www.bsgs.org.uk/
http://images.google.cat/url?q=https://www.bsgs.org.uk/
http://images.google.cf/url?q=https://www.bsgs.org.uk/
http://images.google.td/url?q=https://www.bsgs.org.uk/
http://images.google.cl/url?q=https://www.bsgs.org.uk/
http://images.google.cn/url?q=https://www.bsgs.org.uk/
http://images.google.com.co/url?q=https://www.bsgs.org.uk/
http://images.google.cd/url?q=https://www.bsgs.org.uk/
http://images.google.cg/url?q=https://www.bsgs.org.uk/
http://images.google.co.ck/url?q=https://www.bsgs.org.uk/
http://images.google.co.cr/url?q=https://www.bsgs.org.uk/
http://images.google.ci/url?q=https://www.bsgs.org.uk/
http://images.google.hr/url?q=https://www.bsgs.org.uk/
http://images.google.com.cu/url?q=https://www.bsgs.org.uk/
http://images.google.com.cy/url?q=https://www.bsgs.org.uk/
http://images.google.cz/url?q=https://www.bsgs.org.uk/
http://images.google.dk/url?q=https://www.bsgs.org.uk/
http://images.google.dj/url?q=https://www.bsgs.org.uk/
http://images.google.dm/url?q=https://www.bsgs.org.uk/
http://images.google.com.do/url?q=https://www.bsgs.org.uk/
http://images.google.com.ec/url?q=https://www.bsgs.org.uk/
http://images.google.com.eg/url?q=https://www.bsgs.org.uk/
http://images.google.com.sv/url?q=https://www.bsgs.org.uk/
http://images.google.ee/url?q=https://www.bsgs.org.uk/
http://images.google.com.et/url?q=https://www.bsgs.org.uk/
http://images.google.com.fj/url?q=https://www.bsgs.org.uk/
http://images.google.fi/url?q=https://www.bsgs.org.uk/
http://images.google.fr/url?q=https://www.bsgs.org.uk/
http://images.google.ga/url?q=https://www.bsgs.org.uk/
http://images.google.gm/url?q=https://www.bsgs.org.uk/
http://images.google.ge/url?q=https://www.bsgs.org.uk/
http://images.google.de/url?q=https://www.bsgs.org.uk/
http://images.google.com.gh/url?q=https://www.bsgs.org.uk/
http://images.google.com.gi/url?q=https://www.bsgs.org.uk/
http://images.google.gr/url?q=https://www.bsgs.org.uk/
http://images.google.gl/url?q=https://www.bsgs.org.uk/
http://images.google.gp/url?q=https://www.bsgs.org.uk/
http://images.google.com.gt/url?q=https://www.bsgs.org.uk/
http://images.google.gg/url?q=https://www.bsgs.org.uk/
http://images.google.gy/url?q=https://www.bsgs.org.uk/
http://images.google.ht/url?q=https://www.bsgs.org.uk/
http://images.google.hn/url?q=https://www.bsgs.org.uk/
http://images.google.com.hk/url?q=https://www.bsgs.org.uk/
http://images.google.hu/url?q=https://www.bsgs.org.uk/
http://images.google.is/url?q=https://www.bsgs.org.uk/
http://images.google.co.in/url?q=https://www.bsgs.org.uk/
http://images.google.co.id/url?q=https://www.bsgs.org.uk/
http://images.google.iq/url?q=https://www.bsgs.org.uk/
http://images.google.ie/url?q=https://www.bsgs.org.uk/
http://images.google.co.im/url?q=https://www.bsgs.org.uk/
http://images.google.co.il/url?q=https://www.bsgs.org.uk/
http://images.google.it/url?q=https://www.bsgs.org.uk/
http://images.google.ci/url?q=https://www.bsgs.org.uk/
http://images.google.com.jm/url?q=https://www.bsgs.org.uk/
http://images.google.co.jp/url?q=https://www.bsgs.org.uk/
http://images.google.co.je/url?q=https://www.bsgs.org.uk/
http://images.google.jo/url?q=https://www.bsgs.org.uk/
http://images.google.kz/url?q=https://www.bsgs.org.uk/
http://images.google.co.ke/url?q=https://www.bsgs.org.uk/
http://images.google.ki/url?q=https://www.bsgs.org.uk/
http://images.google.com.kw/url?q=https://www.bsgs.org.uk/
http://images.google.com.kg/url?q=https://www.bsgs.org.uk/
http://images.google.la/url?q=https://www.bsgs.org.uk/
http://images.google.lv/url?q=https://www.bsgs.org.uk/
http://images.google.com.lb/url?q=https://www.bsgs.org.uk/
http://images.google.co.ls/url?q=https://www.bsgs.org.uk/
http://images.google.com.ly/url?q=https://www.bsgs.org.uk/
http://images.google.li/url?q=https://www.bsgs.org.uk/
http://images.google.lt/url?q=https://www.bsgs.org.uk/
http://images.google.lu/url?q=https://www.bsgs.org.uk/
http://images.google.mk/url?q=https://www.bsgs.org.uk/
http://images.google.mg/url?q=https://www.bsgs.org.uk/
http://images.google.mw/url?q=https://www.bsgs.org.uk/
http://images.google.com.my/url?q=https://www.bsgs.org.uk/
http://images.google.mv/url?q=https://www.bsgs.org.uk/
http://images.google.ml/url?q=https://www.bsgs.org.uk/
http://images.google.com.mt/url?q=https://www.bsgs.org.uk/
http://images.google.mu/url?q=https://www.bsgs.org.uk/
http://images.google.com.mx/url?q=https://www.bsgs.org.uk/
http://images.google.fm/url?q=https://www.bsgs.org.uk/
http://images.google.md/url?q=https://www.bsgs.org.uk/
http://images.google.mn/url?q=https://www.bsgs.org.uk/
http://images.google.me/url?q=https://www.bsgs.org.uk/
http://images.google.ms/url?q=https://www.bsgs.org.uk/
http://images.google.co.ma/url?q=https://www.bsgs.org.uk/
http://images.google.co.mz/url?q=https://www.bsgs.org.uk/
http://images.google.com.na/url?q=https://www.bsgs.org.uk/
http://images.google.nr/url?q=https://www.bsgs.org.uk/
http://images.google.com.np/url?q=https://www.bsgs.org.uk/
http://images.google.nl/url?q=https://www.bsgs.org.uk/
http://images.google.co.nz/url?q=https://www.bsgs.org.uk/
http://images.google.com.ni/url?q=https://www.bsgs.org.uk/
http://images.google.ne/url?q=https://www.bsgs.org.uk/
http://images.google.com.ng/url?q=https://www.bsgs.org.uk/
http://images.google.nu/url?q=https://www.bsgs.org.uk/
http://images.google.com.nf/url?q=https://www.bsgs.org.uk/
http://images.google.no/url?q=https://www.bsgs.org.uk/
http://images.google.com.om/url?q=https://www.bsgs.org.uk/
http://images.google.com.pk/url?q=https://www.bsgs.org.uk/
http://images.google.ps/url?q=https://www.bsgs.org.uk/
http://images.google.com.pa/url?q=https://www.bsgs.org.uk/
http://images.google.com.pg/url?q=https://www.bsgs.org.uk/
http://images.google.com.py/url?q=https://www.bsgs.org.uk/
http://images.google.com.pe/url?q=https://www.bsgs.org.uk/
http://images.google.com.ph/url?q=https://www.bsgs.org.uk/
http://images.google.pn/url?q=https://www.bsgs.org.uk/
http://images.google.pl/url?q=https://www.bsgs.org.uk/
http://images.google.pt/url?q=https://www.bsgs.org.uk/
http://images.google.com.pr/url?q=https://www.bsgs.org.uk/
http://images.google.com.qa/url?q=https://www.bsgs.org.uk/
http://images.google.ro/url?q=https://www.bsgs.org.uk/
http://images.google.ru/url?q=https://www.bsgs.org.uk/
http://images.google.rw/url?q=https://www.bsgs.org.uk/
http://images.google.sh/url?q=https://www.bsgs.org.uk/
http://images.google.ws/url?q=https://www.bsgs.org.uk/
http://images.google.sm/url?q=https://www.bsgs.org.uk/
http://images.google.st/url?q=https://www.bsgs.org.uk/
http://images.google.com.sa/url?q=https://www.bsgs.org.uk/
http://images.google.sn/url?q=https://www.bsgs.org.uk/
http://images.google.rs/url?q=https://www.bsgs.org.uk/
http://images.google.sc/url?q=https://www.bsgs.org.uk/
http://images.google.com.sl/url?q=https://www.bsgs.org.uk/
http://images.google.com.sg/url?q=https://www.bsgs.org.uk/
http://images.google.sk/url?q=https://www.bsgs.org.uk/
http://images.google.si/url?q=https://www.bsgs.org.uk/
http://images.google.com.sb/url?q=https://www.bsgs.org.uk/
http://images.google.so/url?q=https://www.bsgs.org.uk/
http://images.google.co.za/url?q=https://www.bsgs.org.uk/
http://images.google.co.kr/url?q=https://www.bsgs.org.uk/
http://images.google.es/url?q=https://www.bsgs.org.uk/
http://images.google.lk/url?q=https://www.bsgs.org.uk/
http://images.google.com.vc/url?q=https://www.bsgs.org.uk/
http://images.google.sr/url?q=https://www.bsgs.org.uk/
http://images.google.se/url?q=https://www.bsgs.org.uk/
http://images.google.ch/url?q=https://www.bsgs.org.uk/
http://images.google.com.tw/url?q=https://www.bsgs.org.uk/
http://images.google.com.tj/url?q=https://www.bsgs.org.uk/
http://images.google.co.tz/url?q=https://www.bsgs.org.uk/
http://images.google.co.th/url?q=https://www.bsgs.org.uk/
http://images.google.tl/url?q=https://www.bsgs.org.uk/
http://images.google.tg/url?q=https://www.bsgs.org.uk/
http://images.google.tk/url?q=https://www.bsgs.org.uk/
http://images.google.to/url?q=https://www.bsgs.org.uk/
http://images.google.tt/url?q=https://www.bsgs.org.uk/
http://images.google.tn/url?q=https://www.bsgs.org.uk/
http://images.google.com.tr/url?q=https://www.bsgs.org.uk/
http://images.google.tm/url?q=https://www.bsgs.org.uk/
http://images.google.co.ug/url?q=https://www.bsgs.org.uk/
http://images.google.com.ua/url?q=https://www.bsgs.org.uk/
http://images.google.ae/url?q=https://www.bsgs.org.uk/
http://images.google.co.uk/url?q=https://www.bsgs.org.uk/
http://images.google.com/url?q=https://www.bsgs.org.uk/
http://images.google.com.uy/url?q=https://www.bsgs.org.uk/
http://images.google.co.uz/url?q=https://www.bsgs.org.uk/
http://images.google.vu/url?q=https://www.bsgs.org.uk/
http://images.google.co.ve/url?q=https://www.bsgs.org.uk/
http://images.google.com.vn/url?q=https://www.bsgs.org.uk/
http://images.google.co.vi/url?q=https://www.bsgs.org.uk/
http://images.google.co.zm/url?q=https://www.bsgs.org.uk/
http://images.google.co.zw/url?q=https://www.bsgs.org.uk/
I’m really impressed together with your writing talents and also with the
format in your blog. Is this a paid theme or did you customize
it your self? Either way stay up the nice quality writing, it’s uncommon to look a nice weblog
like this one today..
Cialis cost tadalafil for sale online pharmacy
Обзор Mostbet зеркала мостбет зеркало на прямо сейчас
http://www.travianc.com/showthread.php?p=59971
Ниша ставок в РФ функционирует довольно
долгое время, и в 2012 году на рынке появилась фирма Mostbet.
На сегодняшний день ресурс активно развивается, непосредственно это касается виртуального пространства.
Как полагают некоторые клиенты, довольно удобно не выходя из дома, в офисе или в дороге делать ставки.
Время не будет потеряно.
Наиболее важная задача конторы –
помогать игрокам делать ставки,
это удобно выполнить через офисы фирмы или же в режиме онлайн, для этого есть портал
и приложение для смартфона.
Итак, предусмотрено немало возможностей, чтобы приятно провести досуг, а вместе с тем попытаться
получить приличные деньги.
Компания мостбет ставки на спорт довольно активно развивается и намерена подготовить для своих пользователей наилучшие условия.
Тут каждый может делать ставки как на спорт, так и на другие
события, например, конкурсы наподобие Евровидения.
Теперь не нужно безучастно
смотреть за тем, как выступает любимый певец.
Стоит всего лишь поверить в его победу,
произведя выгодную ставку.
Существует вероятность, что получится
сорвать крупную сумму , а заодно послушать отличную музыку.
Это очень удобно, так как в этом случае безусловно каждый человек найдет для себя захватывающие мероприятия
и сделает ставки.
Разработчики смогли предусмореть события
на все предпочтения.
Решение зависит от Вашего возраста, увлечений, а
также желания рисковать.
Как начинать ставить на спортивные события с Мостбет
Многие игроки думают, что делать ставки на спорт или другие мероприятия – это
достаточно хлопотно и что в этом потребуется долго разбираться.
Но так ли это на самом деле?
Конечно же, это не так.
Когда мы говорим о Мостбет https://bagihar.ru/user/profile/1436 mostbet зеркало ,
то в этом случае начать делать ставки получится
у любого желающего.
На уровне интуиции понятный интерфейс понравится даже новичкам, которые только решили разобраться с тем, как ставить.
Следует рассмотреть более подробно, как
начинать процесс.
Для старта вам нужно пройти регистрацию на сайте.
Алгоритм прохождения регистрации очень простой,
займет у вас минимум времени.
Нужно всего лишь вбить личные данные в выделенные
поля, пройти процесс верификации.
Как только вы зарегистрируетесь, необходимо внести некоторую сумму на депозитный счет.
При этом неважно, какая по размеру будет зачислена сумма денег.
Очень быстро Вы освоитесь и сможете понять, как
поступать дальше, какие размеры взноса считаются оптимальными.
И после этого вы можете начать делать
ставки.
Сейчас становится понятно, что выполнять подобные манипуляции совершенно не сложно, так как этот процесс займет у вас
минимум сил и времени.
Выходит, абсолютно каждый сможет начать ставить
вне зависимости от того без опыта он или
профи.
Все, что для этого требуется – зарегистрироваться.
Компания Мостбет – одна из самых популярных и пользующихся спросом
площадок на рынке России, что абсолютно не
вызывает удивления.
Ведь компания заботится о своих пользователях
и подготавливает для них самые лучшие условия.
Руководству надо не просто заинтересовать больше
пользователей, а и создать максимально комфортные условия для завсегдатаев.
Репутация считается важным показателем для компании во имя того, чтобы не потерять веры игроков.
В области ставок существует большое количество аферистов.
Не стоит слепо доверять яркой рекламе, а также идти на поводу
у слишком выгодных условий.
Возможно не только потерять деньги, время, но и установить на ноутбук вирусную программу.
Целесообразнее останавливать выбор
на надежных фирмах, которые длительное время находятся в данной области.
В любой момент можно изучить отзывы, ознакомиться
с временем появления компании в виртуальном пространстве.
Одним из подобных профи своего дела признается мостбет бк андроид
В определенный момент можно скачать конкретно созданное приложение для
смартфонов и других гаджетов.
Останется подсоединиться к сети Интернет, чтобы делать ставки прямо сейчас.
У Вас будет возможность подобрать мероприятие, спрогнозировать результат, находясь в заторе или
за городом.
Это ли не одно из преимуществ, за которые стоит останавливать выбор на этой букмекерской
конторе?
И это подтвердило огромнейшее
количество игроков компании.
В таком случае, если вы хотите начать делать ставки, то вам стоит обратить внимание на Mostbet.
Здесь Mostbet-partner.com вы найдете важную информацию и
решения своих вопросов, а ,
кроме того, сразу приступить к ставкам после регистрации.
josh richards
You actually make it appear so easy with your presentation but I
to find this topic to be actually one thing which I feel I’d never understand.
It sort of feels too complicated and very vast for me.
I am having a look forward in your next put up, I will try to get the
hang of it!
Обзор зеркала Mostbet букмекерская компания мостбет
http://www.stwx.net/space-uid-709495.html
Рынок ставок в России существует достаточно долгое время,
и в 2012 году вышла на рынок компания
Мостбет.
На сегодняшний день сервис стабильно продолжает развиваться, непосредственно это относится к
виртуальному пространству.
Как думают некоторые клиенты,
достаточно комфортно не выходя из
дома, в офисе или в дороге ставить на события.
Время не будет потеряно.
Наиболее важная задача конторы – оказывать помощь людям делать ставки, это удобно сделать через офисы компании
или же в режиме онлайн, для этого имеется портал и приложение
для смартфона.
Итак, предусмотрено довольно много способов, чтобы приятно провести досуг, а заодно попробовать заработать приличные
выигрыши.
Контора мостбет ставки
довольно стремительно развивается
и намерена подготовить для своих пользователей наилучшие возможности.
Здесь вы можете ставить как на спортивные, так и на другие события, например, конкурсы типа Eurovision.
Теперь не нужно просто наблюдать за тем, как
проводит выступление обожаемый артист.
Достаточно поверить в его победу, сделав выгодную ставку.
Есть шанс, что удастся заполучить куш , а заодно послушать отличную
музыку.
Это очень удобно, так как в этой ситуации безусловно любой игрок найдет для
себя интересные события и поставит на его
исход.
Разработчики предусмотрели мероприятия на все предпочтения.
Решение связано с Вашим возрастом,
увлечениями, желанием и возможностью идти на риск.
Как начать делать ставки на спорт с Мостбет
Некоторые клиенты уверены, что ставить на спортивные баталии или другие мероприятия – это довольно сложно и что в
этом нужно тратить время на разбирательство.
Но так ли это на самом деле?
Естественно, это не так.
Когда мы говорим о Мостбет http://cgi.www5b.biglobe.ne.jp/~leen/cgi-bin/bbs/yybbs.cgi/yybbs.cgi? бк мостбет , то здесь начинать ставить сможет каждый.
Интуитивно легко осваиваемый
интерфейс придется по душе даже новичкам,
которые только решили освоить
искусство ставок.
Следует рассмотреть более подробно, как начинать процесс.
Для начала необходимо пройти
регистрацию на сайте.
Алгоритм прохождения регистрации
очень легкий, вы потратите
на него минимальное количество времени.
Потребуется всего лишь ввести персональные данные в выделенные поля, пройти процесс верификации.
После регистрации следует внести деньги на депозит.
Абсолютно неважно, какая по размеру будет зачислена денежная
сумма.
Очень быстро Вы освоитесь и сможете понять, как поступать
дальше, какие размеры ставки являются оптимальными.
И после этого начинайте
ставить на события.
Сейчас становится понятно, что выполнять подобные манипуляции совершенно не сложно, так как этот процесс займет у вас минимум времени и сил.
Выходит, абсолютно каждый сможет
начать делать ставки независимо от того без опыта он или
профи.
Все, что для этого требуется –
зарегистрироваться.
Компания Мостбет – одна из самых известных и востребованных компаний на рынке России,
что совсем не удивительно.
Как известно, фирма с заботой относится к своим
клиентам и подготавливает для них наилучшие условия.
Руководству важно не просто привлечь больше пользователей, но и подготовить
максимально комфортные обстоятельства для
завсегдатаев.
Репутация является важным критерием для компании во
имя того, чтобы не снизить веры игроков.
В сфере ставок присутствует немалое количество аферистов.
Не следует слепо доверять яркой рекламе,
а также идти на поводу у слишком выгодных условий.
Возможно не только потерять деньги, время, но и заполучить на ноутбук вирусную
программу.
Уместнее останавливать выбор на надежных фирмах,
которые длительное время пребывают
в данной области.
Всегда можно почитать отзывы, ознакомиться с временем начала деятельности конторы в виртуальном пространстве.
Среди подобных профессионалов своего дела считается mostbet скачать на андроид
В определенный момент можно загрузить конкретно созданное мобильное приложение.
Нужно обеспечить наличие интернету,
чтобы делать ставки с сегодняшнего дня.
У Вас будет возможность подобрать событие, сделать прогноз, пребывая
в пробке или за городом.
Это ли не одно из достоинств, за которые стоит останавливать выбор на этой букмекерской конторе?
Именно это подтвердило огромнейшее число пользователей конторы.
Поэтому, если вы хотите испытывать удачу на ставках, то вам стоит присмотреться к Mostbet.
Тут Mostbet-partner.com вы найдете необходимую информацию и ответы на свои вопросы, а , кроме того, сразу начать
делать ставки после регистрации.
Обзор зеркала Melbet
Ниша ставок в РФ функционирует достаточно
долгое время, и в 2012 г. вышла на рынок фирма Melbet.
На сегодняшний день сервис активно продолжает
развиваться, в частности это относится к виртуальному пространству.
Как думают некоторые пользователи, достаточно комфортно
не выходя из дома, в офисе или
в дороге делать ставки.
Никаких потерь времени.
Главная цель конторы – помогать людям ставить,
это удобно выполнить , используя офисы фирмы или
же в режиме онлайн, для этого есть портал и приложение для смартфона.
Как видите,, предоставляется
довольно много способов, чтобы приятно
провести свободное время, а вместе с тем попытаться заработать приличные выигрыши.
Компания melbet вывод средств довольно стремительно продвигается и
старается подготовить для своих пользователей наилучшие возможности.
Здесь вы можете ставить как на спорт, так и
на иные события, к примеру, конкурсы
типа Eurovision.
Больше не нужно безучастно наблюдать за тем, как проводит
выступление обожаемый исполнитель.
Стоит всего лишь поверить в его триумф, произведя оптимальную ставку.
Есть вероятность, что удастся заполучить крупную сумму , а заодно послушать отличную музыку.
Это очень удобно, так как в этом
случае безусловно каждый человек найдет для
себя интересные мероприятия и поставит на его исход.
Программеры смогли предусмореть события
на все предпочтения.
Все зависит от того, сколько Вам лет,
чем вы увлекаетесь и способны ли рисковать.
С чего начинать ставить на спорт
с Melbet http://wiki.feedle.net/index.php?title=User:KindraBlackston
Многие игроки думают, что делать ставки на
спортивные баталии или иные мероприятия – это достаточно сложно и что в
этом нужно долго разбираться.
Но так ли это на самом деле?
Естественно, это не так.
Если идет разговор о Мелбет, то в этом
случае начинать ставить получится у любого желающего.
Интуитивно понятный интерфейс придется по вкусу даже новичкам, которые
надумали разобраться с тем, как ставить.
Рассмотрим подробнее, как
начинать процесс.
Для начала необходимо пройти регистрацию на сайте
не запускается приложение мелбет
Процесс прохождения регистрации очень легкий, займет у вас минимум времени.
Потребуется всего лишь ввести личные
данные в выделенные поля, пройти процесс верификации.
После регистрации следует положить деньги на депозит.
При этом неважно, какая по размеру
будет внесена денежная сумма.
Очень быстро Вы разберетесь и поймете, как
действовать дальше, какие параметры
взноса считаются наиболее приемлемыми.
И с этого момента вы можете начать ставить на события.
Теперь становится понятно, что делать это совершенно не сложно, так как на эти действия уйдет у вас минимальное количество сил и времени.
Выходит, абсолютно каждый сможет начать ставить независимо от того
новичок он или профессионал.
Все, что для этого нужно – пройти регистрацию.
Компания Мелбет – одна из самых
популярных и востребованных площадок на российском рынке, что абсолютно не вызывает удивления.
Как известно, контора заботится о своих пользователях и подготавливает для них наилучшие условия.
Руководству важно не просто заинтересовать новых игроков, но и подготовить максимально комфортные обстоятельства для постоянных клиентов.
Имидж считается важным критерием для компании во имя того,
чтобы не снизить доверия пользователей.
В области ставок существует большое число мошенников.
Не стоит слепо доверять яркой рекламе, а также идти на
поводу у слишком выгодных условий.
Возможно не только лишиться денег,
безрассудно потерять время,
но и заполучить на компьютер вирус.
Уместнее останавливать выбор на надежных фирмах, которые продолжительное время пребывают в
данной сфере.
В любой момент можно изучить отклики, узнать о времени появления компании в
виртуальном пространстве.
Одним из подобных профи ведения игрового бизнеса
считается http://csiskola.sulinet.hu/?p=13090 .
В определенный момент можно скачать конкретно
разработанное приложение для
смартфонов и других гаджетов.
Нужно подсоединиться к сети Интернет,
чтобы делать ставки прямо сейчас.
Вы даже сможете выбрать мероприятие,
спрогнозировать результат, находясь в заторе
или в офисе.
Это ли не одно из преимуществ, за которые стоит выбирать данную компанию?
Именно это подтверждает огромнейшее число игроков компании.
Вот почему, если вы решили испытывать
удачу на ставках, то вам стоит обратить внимание на Мелбет.
Здесь melbet-partner.com вы сможете найти необходимые сведения и ответы на свои вопросы, а , кроме того,
сразу приступить к ставкам после регистрации.
Магазины Apple в Ростове-на-Дону с низкими
ценами iphone ремонт
Достоинство – главный критерий выбора ради большинства
потребителей. Сотрудничество
с официальными дилерами американского производителя
– гарантия минимального ценника.
В то же время стоит смекать, что разные
дилеры могут устанавливать свои собственные наценки,
следовательно имеет значение сравнить достоинство
интересующей модели моментально в нескольких торговых точках.
Единовластно из онлайн магазинов, который предлагает гарнитура продукции Apple по
хорошим ценам
Подозрительно низких цен все же лучше избегать.
Около видом дешевого iPhone недобросовестные поставщики могут продать вам подделку из Китая.
Для месте оригинального телефона может быть
бывший в эксплуатации смартфон, либо техника, которую
вернули сообразно гарантии, либо смартфон с неисправностями, либо старый витринный
экземпляр.
Магазины с официальной
гарантией в Ростове-на-Дону http://masuda-khrs.sakura.ne.jp/hsy/yybbs/yybbs.cgi?list=thread
По понятным причинам рекомендуется предпочитать токмо
те магазины, которые поставляют
сертифицированную продукцию, технику Apple с
соответствующими гарантиями оригинальности, в заводской упаковке.
Подтвердить высокое качество лавка повинен документами, а
не один для словах.
Точно правило, любой правительственный дилер
непременно предложит гарантию для частный товар, займется гарантийным и пост-гарантийным обслуживанием
iPhone, iPad, Apple Watch и других девайсов
Apple. Коль у магазина затрапезничать свой
сервисный фокус, словно тут, это весомое преимущество.
Магазины с комфортным обслуживанием
Низкие цены и гарантия оригинальности
– это, несомненно, хорошо, однако очень не совершенно, который может предложить лавка техники Apple в Ростове-на-Дону.
К дополнительным услугам, которые
делают добросовестный лабаз лучшим в своем
сегменте, дозволено отнести полноценную консультационную поддержку потребителя, включая поддержка в активации, настройке устройства, переносе данных с одного
iPhone на видоизмененный, услуга в регистрации
учетных записей и беспричинно далее.
Наличие собственной службы оперативной доставки заказов сообразно городу
тоже довольно лишним поводом выбрать именно этот
магазин.
Также очень неплохо, ежели лавка предлагает уместительный прибор аксессуаров чтобы
смартфонов. Таким образом,
вы можете собрать полный круг
для комфортного использования
всякий модели iPhone в одном месте, и уже
вследствие несколько минут потом оплаты начать злоупотреблять именно
тем девайсом, кто подходит вам во всех отношениях.
Подробную информацию о расширенном каталоге аксессуаров для iPhone
в Ростове-на-Дону вы можете получить по ссылке – airpods ростов
Awesome article.
http://google.com.af/url?q=https://skyredthailand.com/
http://google.al/url?q=https://skyredthailand.com/
http://google.dz/url?q=https://skyredthailand.com/
http://google.as/url?q=https://skyredthailand.com/
http://google.ad/url?q=https://skyredthailand.com/
http://google.it.ao/url?q=https://skyredthailand.com/
http://google.com.ai/url?q=https://skyredthailand.com/
http://google.com.ag/url?q=https://skyredthailand.com/
http://google.com.ar/url?q=https://skyredthailand.com/
http://google.am/url?q=https://skyredthailand.com/
http://google.ac/url?q=https://skyredthailand.com/
http://google.com.au/url?q=https://skyredthailand.com/
http://google.at/url?q=https://skyredthailand.com/
http://google.az/url?q=https://skyredthailand.com/
http://google.bs/url?q=https://skyredthailand.com/
http://google.com.bh/url?q=https://skyredthailand.com/
http://google.com.bd/url?q=https://skyredthailand.com/
http://google.com.by/url?q=https://skyredthailand.com/
http://google.be/url?q=https://skyredthailand.com/
http://google.com.bz/url?q=https://skyredthailand.com/
http://google.bj/url?q=https://skyredthailand.com/
http://google.bt/url?q=https://skyredthailand.com/
http://google.com.bo/url?q=https://skyredthailand.com/
http://google.ba/url?q=https://skyredthailand.com/
http://google.co.bw/url?q=https://skyredthailand.com/
http://google.com.br/url?q=https://skyredthailand.com/
http://google.vg/url?q=https://skyredthailand.com/
http://google.com.bn/url?q=https://skyredthailand.com/
http://google.bg/url?q=https://skyredthailand.com/
http://google.bf/url?q=https://skyredthailand.com/
http://google.bi/url?q=https://skyredthailand.com/
http://google.com.kh/url?q=https://skyredthailand.com/
http://google.cm/url?q=https://skyredthailand.com/
http://google.ca/url?q=https://skyredthailand.com/
http://google.cv/url?q=https://skyredthailand.com/
http://google.cat/url?q=https://skyredthailand.com/
http://google.cf/url?q=https://skyredthailand.com/
http://google.td/url?q=https://skyredthailand.com/
http://google.cl/url?q=https://skyredthailand.com/
http://google.cn/url?q=https://skyredthailand.com/
http://google.com.co/url?q=https://skyredthailand.com/
http://google.cd/url?q=https://skyredthailand.com/
http://google.cg/url?q=https://skyredthailand.com/
http://google.co.ck/url?q=https://skyredthailand.com/
http://google.co.cr/url?q=https://skyredthailand.com/
http://google.ci/url?q=https://skyredthailand.com/
http://google.hr/url?q=https://skyredthailand.com/
http://google.com.cu/url?q=https://skyredthailand.com/
http://google.com.cy/url?q=https://skyredthailand.com/
http://google.cz/url?q=https://skyredthailand.com/
http://google.dk/url?q=https://skyredthailand.com/
http://google.dj/url?q=https://skyredthailand.com/
http://google.dm/url?q=https://skyredthailand.com/
http://google.com.do/url?q=https://skyredthailand.com/
http://google.com.ec/url?q=https://skyredthailand.com/
http://google.com.eg/url?q=https://skyredthailand.com/
http://google.com.sv/url?q=https://skyredthailand.com/
http://google.ee/url?q=https://skyredthailand.com/
http://google.com.et/url?q=https://skyredthailand.com/
http://google.com.fj/url?q=https://skyredthailand.com/
http://google.fi/url?q=https://skyredthailand.com/
http://google.fr/url?q=https://skyredthailand.com/
http://google.ga/url?q=https://skyredthailand.com/
http://google.gm/url?q=https://skyredthailand.com/
http://google.ge/url?q=https://skyredthailand.com/
http://google.de/url?q=https://skyredthailand.com/
http://google.com.gh/url?q=https://skyredthailand.com/
http://google.com.gi/url?q=https://skyredthailand.com/
http://google.gr/url?q=https://skyredthailand.com/
http://google.gl/url?q=https://skyredthailand.com/
http://google.gp/url?q=https://skyredthailand.com/
http://google.com.gt/url?q=https://skyredthailand.com/
http://google.gg/url?q=https://skyredthailand.com/
http://google.gy/url?q=https://skyredthailand.com/
http://google.ht/url?q=https://skyredthailand.com/
http://google.hn/url?q=https://skyredthailand.com/
http://google.com.hk/url?q=https://skyredthailand.com/
http://google.hu/url?q=https://skyredthailand.com/
http://google.is/url?q=https://skyredthailand.com/
http://google.co.in/url?q=https://skyredthailand.com/
http://google.co.id/url?q=https://skyredthailand.com/
http://google.iq/url?q=https://skyredthailand.com/
http://google.ie/url?q=https://skyredthailand.com/
http://google.co.im/url?q=https://skyredthailand.com/
http://google.co.il/url?q=https://skyredthailand.com/
http://google.it/url?q=https://skyredthailand.com/
http://google.ci/url?q=https://skyredthailand.com/
http://google.com.jm/url?q=https://skyredthailand.com/
http://google.co.jp/url?q=https://skyredthailand.com/
http://google.co.je/url?q=https://skyredthailand.com/
http://google.jo/url?q=https://skyredthailand.com/
http://google.kz/url?q=https://skyredthailand.com/
http://google.co.ke/url?q=https://skyredthailand.com/
http://google.ki/url?q=https://skyredthailand.com/
http://google.com.kw/url?q=https://skyredthailand.com/
http://google.com.kg/url?q=https://skyredthailand.com/
http://google.la/url?q=https://skyredthailand.com/
http://google.lv/url?q=https://skyredthailand.com/
http://google.com.lb/url?q=https://skyredthailand.com/
http://google.co.ls/url?q=https://skyredthailand.com/
http://google.com.ly/url?q=https://skyredthailand.com/
http://google.li/url?q=https://skyredthailand.com/
http://google.lt/url?q=https://skyredthailand.com/
http://google.lu/url?q=https://skyredthailand.com/
http://google.mk/url?q=https://skyredthailand.com/
http://google.mg/url?q=https://skyredthailand.com/
http://google.mw/url?q=https://skyredthailand.com/
http://google.com.my/url?q=https://skyredthailand.com/
http://google.mv/url?q=https://skyredthailand.com/
http://google.ml/url?q=https://skyredthailand.com/
http://google.com.mt/url?q=https://skyredthailand.com/
http://google.mu/url?q=https://skyredthailand.com/
http://google.com.mx/url?q=https://skyredthailand.com/
http://google.fm/url?q=https://skyredthailand.com/
http://google.md/url?q=https://skyredthailand.com/
http://google.mn/url?q=https://skyredthailand.com/
http://google.me/url?q=https://skyredthailand.com/
http://google.ms/url?q=https://skyredthailand.com/
http://google.co.ma/url?q=https://skyredthailand.com/
http://google.co.mz/url?q=https://skyredthailand.com/
http://google.com.na/url?q=https://skyredthailand.com/
http://google.nr/url?q=https://skyredthailand.com/
http://google.com.np/url?q=https://skyredthailand.com/
http://google.nl/url?q=https://skyredthailand.com/
http://google.co.nz/url?q=https://skyredthailand.com/
http://google.com.ni/url?q=https://skyredthailand.com/
http://google.ne/url?q=https://skyredthailand.com/
http://google.com.ng/url?q=https://skyredthailand.com/
http://google.nu/url?q=https://skyredthailand.com/
http://google.com.nf/url?q=https://skyredthailand.com/
http://google.no/url?q=https://skyredthailand.com/
http://google.com.om/url?q=https://skyredthailand.com/
http://google.com.pk/url?q=https://skyredthailand.com/
http://google.ps/url?q=https://skyredthailand.com/
http://google.com.pa/url?q=https://skyredthailand.com/
http://google.com.pg/url?q=https://skyredthailand.com/
http://google.com.py/url?q=https://skyredthailand.com/
http://google.com.pe/url?q=https://skyredthailand.com/
http://google.com.ph/url?q=https://skyredthailand.com/
http://google.pn/url?q=https://skyredthailand.com/
http://google.pl/url?q=https://skyredthailand.com/
http://google.pt/url?q=https://skyredthailand.com/
http://google.com.pr/url?q=https://skyredthailand.com/
http://google.com.qa/url?q=https://skyredthailand.com/
http://google.ro/url?q=https://skyredthailand.com/
http://google.ru/url?q=https://skyredthailand.com/
http://google.rw/url?q=https://skyredthailand.com/
http://google.sh/url?q=https://skyredthailand.com/
http://google.ws/url?q=https://skyredthailand.com/
http://google.sm/url?q=https://skyredthailand.com/
http://google.st/url?q=https://skyredthailand.com/
http://google.com.sa/url?q=https://skyredthailand.com/
http://google.sn/url?q=https://skyredthailand.com/
http://google.rs/url?q=https://skyredthailand.com/
http://google.sc/url?q=https://skyredthailand.com/
http://google.com.sl/url?q=https://skyredthailand.com/
http://google.com.sg/url?q=https://skyredthailand.com/
http://google.sk/url?q=https://skyredthailand.com/
http://google.si/url?q=https://skyredthailand.com/
http://google.com.sb/url?q=https://skyredthailand.com/
http://google.so/url?q=https://skyredthailand.com/
http://google.co.za/url?q=https://skyredthailand.com/
http://google.co.kr/url?q=https://skyredthailand.com/
http://google.es/url?q=https://skyredthailand.com/
http://google.lk/url?q=https://skyredthailand.com/
http://google.com.vc/url?q=https://skyredthailand.com/
http://google.sr/url?q=https://skyredthailand.com/
http://google.se/url?q=https://skyredthailand.com/
http://google.ch/url?q=https://skyredthailand.com/
http://google.com.tw/url?q=https://skyredthailand.com/
http://google.com.tj/url?q=https://skyredthailand.com/
http://google.co.tz/url?q=https://skyredthailand.com/
http://google.co.th/url?q=https://skyredthailand.com/
http://google.tl/url?q=https://skyredthailand.com/
http://google.tg/url?q=https://skyredthailand.com/
http://google.tk/url?q=https://skyredthailand.com/
http://google.to/url?q=https://skyredthailand.com/
http://google.tt/url?q=https://skyredthailand.com/
http://google.tn/url?q=https://skyredthailand.com/
http://google.com.tr/url?q=https://skyredthailand.com/
http://google.tm/url?q=https://skyredthailand.com/
http://google.co.ug/url?q=https://skyredthailand.com/
http://google.com.ua/url?q=https://skyredthailand.com/
http://google.ae/url?q=https://skyredthailand.com/
http://google.co.uk/url?q=https://skyredthailand.com/
http://google.com/url?q=https://skyredthailand.com/
http://google.com.uy/url?q=https://skyredthailand.com/
http://google.co.uz/url?q=https://skyredthailand.com/
http://google.vu/url?q=https://skyredthailand.com/
http://google.co.ve/url?q=https://skyredthailand.com/
http://google.com.vn/url?q=https://skyredthailand.com/
http://google.co.vi/url?q=https://skyredthailand.com/
http://google.co.zm/url?q=https://skyredthailand.com/
http://google.co.zw/url?q=https://skyredthailand.com/
http://maps.google.com.af/url?q=https://skyredthailand.com/
http://maps.google.al/url?q=https://skyredthailand.com/
http://maps.google.dz/url?q=https://skyredthailand.com/
http://maps.google.as/url?q=https://skyredthailand.com/
http://maps.google.ad/url?q=https://skyredthailand.com/
http://maps.google.it.ao/url?q=https://skyredthailand.com/
http://maps.google.com.ai/url?q=https://skyredthailand.com/
http://maps.google.com.ag/url?q=https://skyredthailand.com/
http://maps.google.com.ar/url?q=https://skyredthailand.com/
http://maps.google.am/url?q=https://skyredthailand.com/
http://maps.google.ac/url?q=https://skyredthailand.com/
http://maps.google.com.au/url?q=https://skyredthailand.com/
http://maps.google.at/url?q=https://skyredthailand.com/
http://maps.google.az/url?q=https://skyredthailand.com/
http://maps.google.bs/url?q=https://skyredthailand.com/
http://maps.google.com.bh/url?q=https://skyredthailand.com/
http://maps.google.com.bd/url?q=https://skyredthailand.com/
http://maps.google.com.by/url?q=https://skyredthailand.com/
http://maps.google.be/url?q=https://skyredthailand.com/
http://maps.google.com.bz/url?q=https://skyredthailand.com/
http://maps.google.bj/url?q=https://skyredthailand.com/
http://maps.google.bt/url?q=https://skyredthailand.com/
http://maps.google.com.bo/url?q=https://skyredthailand.com/
http://maps.google.ba/url?q=https://skyredthailand.com/
http://maps.google.co.bw/url?q=https://skyredthailand.com/
http://maps.google.com.br/url?q=https://skyredthailand.com/
http://maps.google.vg/url?q=https://skyredthailand.com/
http://maps.google.com.bn/url?q=https://skyredthailand.com/
http://maps.google.bg/url?q=https://skyredthailand.com/
http://maps.google.bf/url?q=https://skyredthailand.com/
http://maps.google.bi/url?q=https://skyredthailand.com/
http://maps.google.com.kh/url?q=https://skyredthailand.com/
http://maps.google.cm/url?q=https://skyredthailand.com/
http://maps.google.ca/url?q=https://skyredthailand.com/
http://maps.google.cv/url?q=https://skyredthailand.com/
http://maps.google.cat/url?q=https://skyredthailand.com/
http://maps.google.cf/url?q=https://skyredthailand.com/
http://maps.google.td/url?q=https://skyredthailand.com/
http://maps.google.cl/url?q=https://skyredthailand.com/
http://maps.google.cn/url?q=https://skyredthailand.com/
http://maps.google.com.co/url?q=https://skyredthailand.com/
http://maps.google.cd/url?q=https://skyredthailand.com/
http://maps.google.cg/url?q=https://skyredthailand.com/
http://maps.google.co.ck/url?q=https://skyredthailand.com/
http://maps.google.co.cr/url?q=https://skyredthailand.com/
http://maps.google.ci/url?q=https://skyredthailand.com/
http://maps.google.hr/url?q=https://skyredthailand.com/
http://maps.google.com.cu/url?q=https://skyredthailand.com/
http://maps.google.com.cy/url?q=https://skyredthailand.com/
http://maps.google.cz/url?q=https://skyredthailand.com/
http://maps.google.dk/url?q=https://skyredthailand.com/
http://maps.google.dj/url?q=https://skyredthailand.com/
http://maps.google.dm/url?q=https://skyredthailand.com/
http://maps.google.com.do/url?q=https://skyredthailand.com/
http://maps.google.com.ec/url?q=https://skyredthailand.com/
http://maps.google.com.eg/url?q=https://skyredthailand.com/
http://maps.google.com.sv/url?q=https://skyredthailand.com/
http://maps.google.ee/url?q=https://skyredthailand.com/
http://maps.google.com.et/url?q=https://skyredthailand.com/
http://maps.google.com.fj/url?q=https://skyredthailand.com/
http://maps.google.fi/url?q=https://skyredthailand.com/
http://maps.google.fr/url?q=https://skyredthailand.com/
http://maps.google.ga/url?q=https://skyredthailand.com/
http://maps.google.gm/url?q=https://skyredthailand.com/
http://maps.google.ge/url?q=https://skyredthailand.com/
http://maps.google.de/url?q=https://skyredthailand.com/
http://maps.google.com.gh/url?q=https://skyredthailand.com/
http://maps.google.com.gi/url?q=https://skyredthailand.com/
http://maps.google.gr/url?q=https://skyredthailand.com/
http://maps.google.gl/url?q=https://skyredthailand.com/
http://maps.google.gp/url?q=https://skyredthailand.com/
http://maps.google.com.gt/url?q=https://skyredthailand.com/
http://maps.google.gg/url?q=https://skyredthailand.com/
http://maps.google.gy/url?q=https://skyredthailand.com/
http://maps.google.ht/url?q=https://skyredthailand.com/
http://maps.google.hn/url?q=https://skyredthailand.com/
http://maps.google.com.hk/url?q=https://skyredthailand.com/
http://maps.google.hu/url?q=https://skyredthailand.com/
http://maps.google.is/url?q=https://skyredthailand.com/
http://maps.google.co.in/url?q=https://skyredthailand.com/
http://maps.google.co.id/url?q=https://skyredthailand.com/
http://maps.google.iq/url?q=https://skyredthailand.com/
http://maps.google.ie/url?q=https://skyredthailand.com/
http://maps.google.co.im/url?q=https://skyredthailand.com/
http://maps.google.co.il/url?q=https://skyredthailand.com/
http://maps.google.it/url?q=https://skyredthailand.com/
http://maps.google.ci/url?q=https://skyredthailand.com/
http://maps.google.com.jm/url?q=https://skyredthailand.com/
http://maps.google.co.jp/url?q=https://skyredthailand.com/
http://maps.google.co.je/url?q=https://skyredthailand.com/
http://maps.google.jo/url?q=https://skyredthailand.com/
http://maps.google.kz/url?q=https://skyredthailand.com/
http://maps.google.co.ke/url?q=https://skyredthailand.com/
http://maps.google.ki/url?q=https://skyredthailand.com/
http://maps.google.com.kw/url?q=https://skyredthailand.com/
http://maps.google.com.kg/url?q=https://skyredthailand.com/
http://maps.google.la/url?q=https://skyredthailand.com/
http://maps.google.lv/url?q=https://skyredthailand.com/
http://maps.google.com.lb/url?q=https://skyredthailand.com/
http://maps.google.co.ls/url?q=https://skyredthailand.com/
http://maps.google.com.ly/url?q=https://skyredthailand.com/
http://maps.google.li/url?q=https://skyredthailand.com/
http://maps.google.lt/url?q=https://skyredthailand.com/
http://maps.google.lu/url?q=https://skyredthailand.com/
http://maps.google.mk/url?q=https://skyredthailand.com/
http://maps.google.mg/url?q=https://skyredthailand.com/
http://maps.google.mw/url?q=https://skyredthailand.com/
http://maps.google.com.my/url?q=https://skyredthailand.com/
http://maps.google.mv/url?q=https://skyredthailand.com/
http://maps.google.ml/url?q=https://skyredthailand.com/
http://maps.google.com.mt/url?q=https://skyredthailand.com/
http://maps.google.mu/url?q=https://skyredthailand.com/
http://maps.google.com.mx/url?q=https://skyredthailand.com/
http://maps.google.fm/url?q=https://skyredthailand.com/
http://maps.google.md/url?q=https://skyredthailand.com/
http://maps.google.mn/url?q=https://skyredthailand.com/
http://maps.google.me/url?q=https://skyredthailand.com/
http://maps.google.ms/url?q=https://skyredthailand.com/
http://maps.google.co.ma/url?q=https://skyredthailand.com/
http://maps.google.co.mz/url?q=https://skyredthailand.com/
http://maps.google.com.na/url?q=https://skyredthailand.com/
http://maps.google.nr/url?q=https://skyredthailand.com/
http://maps.google.com.np/url?q=https://skyredthailand.com/
http://maps.google.nl/url?q=https://skyredthailand.com/
http://maps.google.co.nz/url?q=https://skyredthailand.com/
http://maps.google.com.ni/url?q=https://skyredthailand.com/
http://maps.google.ne/url?q=https://skyredthailand.com/
http://maps.google.com.ng/url?q=https://skyredthailand.com/
http://maps.google.nu/url?q=https://skyredthailand.com/
http://maps.google.com.nf/url?q=https://skyredthailand.com/
http://maps.google.no/url?q=https://skyredthailand.com/
http://maps.google.com.om/url?q=https://skyredthailand.com/
http://maps.google.com.pk/url?q=https://skyredthailand.com/
http://maps.google.ps/url?q=https://skyredthailand.com/
http://maps.google.com.pa/url?q=https://skyredthailand.com/
http://maps.google.com.pg/url?q=https://skyredthailand.com/
http://maps.google.com.py/url?q=https://skyredthailand.com/
http://maps.google.com.pe/url?q=https://skyredthailand.com/
http://maps.google.com.ph/url?q=https://skyredthailand.com/
http://maps.google.pn/url?q=https://skyredthailand.com/
http://maps.google.pl/url?q=https://skyredthailand.com/
http://maps.google.pt/url?q=https://skyredthailand.com/
http://maps.google.com.pr/url?q=https://skyredthailand.com/
http://maps.google.com.qa/url?q=https://skyredthailand.com/
http://maps.google.ro/url?q=https://skyredthailand.com/
http://maps.google.ru/url?q=https://skyredthailand.com/
http://maps.google.rw/url?q=https://skyredthailand.com/
http://maps.google.sh/url?q=https://skyredthailand.com/
http://maps.google.ws/url?q=https://skyredthailand.com/
http://maps.google.sm/url?q=https://skyredthailand.com/
http://maps.google.st/url?q=https://skyredthailand.com/
http://maps.google.com.sa/url?q=https://skyredthailand.com/
http://maps.google.sn/url?q=https://skyredthailand.com/
http://maps.google.rs/url?q=https://skyredthailand.com/
http://maps.google.sc/url?q=https://skyredthailand.com/
http://maps.google.com.sl/url?q=https://skyredthailand.com/
http://maps.google.com.sg/url?q=https://skyredthailand.com/
http://maps.google.sk/url?q=https://skyredthailand.com/
http://maps.google.si/url?q=https://skyredthailand.com/
http://maps.google.com.sb/url?q=https://skyredthailand.com/
http://maps.google.so/url?q=https://skyredthailand.com/
http://maps.google.co.za/url?q=https://skyredthailand.com/
http://maps.google.co.kr/url?q=https://skyredthailand.com/
http://maps.google.es/url?q=https://skyredthailand.com/
http://maps.google.lk/url?q=https://skyredthailand.com/
http://maps.google.com.vc/url?q=https://skyredthailand.com/
http://maps.google.sr/url?q=https://skyredthailand.com/
http://maps.google.se/url?q=https://skyredthailand.com/
http://maps.google.ch/url?q=https://skyredthailand.com/
http://maps.google.com.tw/url?q=https://skyredthailand.com/
http://maps.google.com.tj/url?q=https://skyredthailand.com/
http://maps.google.co.tz/url?q=https://skyredthailand.com/
http://maps.google.co.th/url?q=https://skyredthailand.com/
http://maps.google.tl/url?q=https://skyredthailand.com/
http://maps.google.tg/url?q=https://skyredthailand.com/
http://maps.google.tk/url?q=https://skyredthailand.com/
http://maps.google.to/url?q=https://skyredthailand.com/
http://maps.google.tt/url?q=https://skyredthailand.com/
http://maps.google.tn/url?q=https://skyredthailand.com/
http://maps.google.com.tr/url?q=https://skyredthailand.com/
http://maps.google.tm/url?q=https://skyredthailand.com/
http://maps.google.co.ug/url?q=https://skyredthailand.com/
http://maps.google.com.ua/url?q=https://skyredthailand.com/
http://maps.google.ae/url?q=https://skyredthailand.com/
http://maps.google.co.uk/url?q=https://skyredthailand.com/
http://maps.google.com/url?q=https://skyredthailand.com/
http://maps.google.com.uy/url?q=https://skyredthailand.com/
http://maps.google.co.uz/url?q=https://skyredthailand.com/
http://maps.google.vu/url?q=https://skyredthailand.com/
http://maps.google.co.ve/url?q=https://skyredthailand.com/
http://maps.google.com.vn/url?q=https://skyredthailand.com/
http://maps.google.co.vi/url?q=https://skyredthailand.com/
http://maps.google.co.zm/url?q=https://skyredthailand.com/
http://maps.google.co.zw/url?q=https://skyredthailand.com/
http://images.google.com.af/url?q=https://skyredthailand.com/
http://images.google.al/url?q=https://skyredthailand.com/
http://images.google.dz/url?q=https://skyredthailand.com/
http://images.google.as/url?q=https://skyredthailand.com/
http://images.google.ad/url?q=https://skyredthailand.com/
http://images.google.it.ao/url?q=https://skyredthailand.com/
http://images.google.com.ai/url?q=https://skyredthailand.com/
http://images.google.com.ag/url?q=https://skyredthailand.com/
http://images.google.com.ar/url?q=https://skyredthailand.com/
http://images.google.am/url?q=https://skyredthailand.com/
http://images.google.ac/url?q=https://skyredthailand.com/
http://images.google.com.au/url?q=https://skyredthailand.com/
http://images.google.at/url?q=https://skyredthailand.com/
http://images.google.az/url?q=https://skyredthailand.com/
http://images.google.bs/url?q=https://skyredthailand.com/
http://images.google.com.bh/url?q=https://skyredthailand.com/
http://images.google.com.bd/url?q=https://skyredthailand.com/
http://images.google.com.by/url?q=https://skyredthailand.com/
http://images.google.be/url?q=https://skyredthailand.com/
http://images.google.com.bz/url?q=https://skyredthailand.com/
http://images.google.bj/url?q=https://skyredthailand.com/
http://images.google.bt/url?q=https://skyredthailand.com/
http://images.google.com.bo/url?q=https://skyredthailand.com/
http://images.google.ba/url?q=https://skyredthailand.com/
http://images.google.co.bw/url?q=https://skyredthailand.com/
http://images.google.com.br/url?q=https://skyredthailand.com/
http://images.google.vg/url?q=https://skyredthailand.com/
http://images.google.com.bn/url?q=https://skyredthailand.com/
http://images.google.bg/url?q=https://skyredthailand.com/
http://images.google.bf/url?q=https://skyredthailand.com/
http://images.google.bi/url?q=https://skyredthailand.com/
http://images.google.com.kh/url?q=https://skyredthailand.com/
http://images.google.cm/url?q=https://skyredthailand.com/
http://images.google.ca/url?q=https://skyredthailand.com/
http://images.google.cv/url?q=https://skyredthailand.com/
http://images.google.cat/url?q=https://skyredthailand.com/
http://images.google.cf/url?q=https://skyredthailand.com/
http://images.google.td/url?q=https://skyredthailand.com/
http://images.google.cl/url?q=https://skyredthailand.com/
http://images.google.cn/url?q=https://skyredthailand.com/
http://images.google.com.co/url?q=https://skyredthailand.com/
http://images.google.cd/url?q=https://skyredthailand.com/
http://images.google.cg/url?q=https://skyredthailand.com/
http://images.google.co.ck/url?q=https://skyredthailand.com/
http://images.google.co.cr/url?q=https://skyredthailand.com/
http://images.google.ci/url?q=https://skyredthailand.com/
http://images.google.hr/url?q=https://skyredthailand.com/
http://images.google.com.cu/url?q=https://skyredthailand.com/
http://images.google.com.cy/url?q=https://skyredthailand.com/
http://images.google.cz/url?q=https://skyredthailand.com/
http://images.google.dk/url?q=https://skyredthailand.com/
http://images.google.dj/url?q=https://skyredthailand.com/
http://images.google.dm/url?q=https://skyredthailand.com/
http://images.google.com.do/url?q=https://skyredthailand.com/
http://images.google.com.ec/url?q=https://skyredthailand.com/
http://images.google.com.eg/url?q=https://skyredthailand.com/
http://images.google.com.sv/url?q=https://skyredthailand.com/
http://images.google.ee/url?q=https://skyredthailand.com/
http://images.google.com.et/url?q=https://skyredthailand.com/
http://images.google.com.fj/url?q=https://skyredthailand.com/
http://images.google.fi/url?q=https://skyredthailand.com/
http://images.google.fr/url?q=https://skyredthailand.com/
http://images.google.ga/url?q=https://skyredthailand.com/
http://images.google.gm/url?q=https://skyredthailand.com/
http://images.google.ge/url?q=https://skyredthailand.com/
http://images.google.de/url?q=https://skyredthailand.com/
http://images.google.com.gh/url?q=https://skyredthailand.com/
http://images.google.com.gi/url?q=https://skyredthailand.com/
http://images.google.gr/url?q=https://skyredthailand.com/
http://images.google.gl/url?q=https://skyredthailand.com/
http://images.google.gp/url?q=https://skyredthailand.com/
http://images.google.com.gt/url?q=https://skyredthailand.com/
http://images.google.gg/url?q=https://skyredthailand.com/
http://images.google.gy/url?q=https://skyredthailand.com/
http://images.google.ht/url?q=https://skyredthailand.com/
http://images.google.hn/url?q=https://skyredthailand.com/
http://images.google.com.hk/url?q=https://skyredthailand.com/
http://images.google.hu/url?q=https://skyredthailand.com/
http://images.google.is/url?q=https://skyredthailand.com/
http://images.google.co.in/url?q=https://skyredthailand.com/
http://images.google.co.id/url?q=https://skyredthailand.com/
http://images.google.iq/url?q=https://skyredthailand.com/
http://images.google.ie/url?q=https://skyredthailand.com/
http://images.google.co.im/url?q=https://skyredthailand.com/
http://images.google.co.il/url?q=https://skyredthailand.com/
http://images.google.it/url?q=https://skyredthailand.com/
http://images.google.ci/url?q=https://skyredthailand.com/
http://images.google.com.jm/url?q=https://skyredthailand.com/
http://images.google.co.jp/url?q=https://skyredthailand.com/
http://images.google.co.je/url?q=https://skyredthailand.com/
http://images.google.jo/url?q=https://skyredthailand.com/
http://images.google.kz/url?q=https://skyredthailand.com/
http://images.google.co.ke/url?q=https://skyredthailand.com/
http://images.google.ki/url?q=https://skyredthailand.com/
http://images.google.com.kw/url?q=https://skyredthailand.com/
http://images.google.com.kg/url?q=https://skyredthailand.com/
http://images.google.la/url?q=https://skyredthailand.com/
http://images.google.lv/url?q=https://skyredthailand.com/
http://images.google.com.lb/url?q=https://skyredthailand.com/
http://images.google.co.ls/url?q=https://skyredthailand.com/
http://images.google.com.ly/url?q=https://skyredthailand.com/
http://images.google.li/url?q=https://skyredthailand.com/
http://images.google.lt/url?q=https://skyredthailand.com/
http://images.google.lu/url?q=https://skyredthailand.com/
http://images.google.mk/url?q=https://skyredthailand.com/
http://images.google.mg/url?q=https://skyredthailand.com/
http://images.google.mw/url?q=https://skyredthailand.com/
http://images.google.com.my/url?q=https://skyredthailand.com/
http://images.google.mv/url?q=https://skyredthailand.com/
http://images.google.ml/url?q=https://skyredthailand.com/
http://images.google.com.mt/url?q=https://skyredthailand.com/
http://images.google.mu/url?q=https://skyredthailand.com/
http://images.google.com.mx/url?q=https://skyredthailand.com/
http://images.google.fm/url?q=https://skyredthailand.com/
http://images.google.md/url?q=https://skyredthailand.com/
http://images.google.mn/url?q=https://skyredthailand.com/
http://images.google.me/url?q=https://skyredthailand.com/
http://images.google.ms/url?q=https://skyredthailand.com/
http://images.google.co.ma/url?q=https://skyredthailand.com/
http://images.google.co.mz/url?q=https://skyredthailand.com/
http://images.google.com.na/url?q=https://skyredthailand.com/
http://images.google.nr/url?q=https://skyredthailand.com/
http://images.google.com.np/url?q=https://skyredthailand.com/
http://images.google.nl/url?q=https://skyredthailand.com/
http://images.google.co.nz/url?q=https://skyredthailand.com/
http://images.google.com.ni/url?q=https://skyredthailand.com/
http://images.google.ne/url?q=https://skyredthailand.com/
http://images.google.com.ng/url?q=https://skyredthailand.com/
http://images.google.nu/url?q=https://skyredthailand.com/
http://images.google.com.nf/url?q=https://skyredthailand.com/
http://images.google.no/url?q=https://skyredthailand.com/
http://images.google.com.om/url?q=https://skyredthailand.com/
http://images.google.com.pk/url?q=https://skyredthailand.com/
http://images.google.ps/url?q=https://skyredthailand.com/
http://images.google.com.pa/url?q=https://skyredthailand.com/
http://images.google.com.pg/url?q=https://skyredthailand.com/
http://images.google.com.py/url?q=https://skyredthailand.com/
http://images.google.com.pe/url?q=https://skyredthailand.com/
http://images.google.com.ph/url?q=https://skyredthailand.com/
http://images.google.pn/url?q=https://skyredthailand.com/
http://images.google.pl/url?q=https://skyredthailand.com/
http://images.google.pt/url?q=https://skyredthailand.com/
http://images.google.com.pr/url?q=https://skyredthailand.com/
http://images.google.com.qa/url?q=https://skyredthailand.com/
http://images.google.ro/url?q=https://skyredthailand.com/
http://images.google.ru/url?q=https://skyredthailand.com/
http://images.google.rw/url?q=https://skyredthailand.com/
http://images.google.sh/url?q=https://skyredthailand.com/
http://images.google.ws/url?q=https://skyredthailand.com/
http://images.google.sm/url?q=https://skyredthailand.com/
http://images.google.st/url?q=https://skyredthailand.com/
http://images.google.com.sa/url?q=https://skyredthailand.com/
http://images.google.sn/url?q=https://skyredthailand.com/
http://images.google.rs/url?q=https://skyredthailand.com/
http://images.google.sc/url?q=https://skyredthailand.com/
http://images.google.com.sl/url?q=https://skyredthailand.com/
http://images.google.com.sg/url?q=https://skyredthailand.com/
http://images.google.sk/url?q=https://skyredthailand.com/
http://images.google.si/url?q=https://skyredthailand.com/
http://images.google.com.sb/url?q=https://skyredthailand.com/
http://images.google.so/url?q=https://skyredthailand.com/
http://images.google.co.za/url?q=https://skyredthailand.com/
http://images.google.co.kr/url?q=https://skyredthailand.com/
http://images.google.es/url?q=https://skyredthailand.com/
http://images.google.lk/url?q=https://skyredthailand.com/
http://images.google.com.vc/url?q=https://skyredthailand.com/
http://images.google.sr/url?q=https://skyredthailand.com/
http://images.google.se/url?q=https://skyredthailand.com/
http://images.google.ch/url?q=https://skyredthailand.com/
http://images.google.com.tw/url?q=https://skyredthailand.com/
http://images.google.com.tj/url?q=https://skyredthailand.com/
http://images.google.co.tz/url?q=https://skyredthailand.com/
http://images.google.co.th/url?q=https://skyredthailand.com/
http://images.google.tl/url?q=https://skyredthailand.com/
http://images.google.tg/url?q=https://skyredthailand.com/
http://images.google.tk/url?q=https://skyredthailand.com/
http://images.google.to/url?q=https://skyredthailand.com/
http://images.google.tt/url?q=https://skyredthailand.com/
http://images.google.tn/url?q=https://skyredthailand.com/
http://images.google.com.tr/url?q=https://skyredthailand.com/
http://images.google.tm/url?q=https://skyredthailand.com/
http://images.google.co.ug/url?q=https://skyredthailand.com/
http://images.google.com.ua/url?q=https://skyredthailand.com/
http://images.google.ae/url?q=https://skyredthailand.com/
http://images.google.co.uk/url?q=https://skyredthailand.com/
http://images.google.com/url?q=https://skyredthailand.com/
http://images.google.com.uy/url?q=https://skyredthailand.com/
http://images.google.co.uz/url?q=https://skyredthailand.com/
http://images.google.vu/url?q=https://skyredthailand.com/
http://images.google.co.ve/url?q=https://skyredthailand.com/
http://images.google.com.vn/url?q=https://skyredthailand.com/
http://images.google.co.vi/url?q=https://skyredthailand.com/
http://images.google.co.zm/url?q=https://skyredthailand.com/
http://images.google.co.zw/url?q=https://skyredthailand.com/
銉愩儍銈?鎸併仭 鎵?銇广仧銇ゃ亶
b艖sz谩r煤 csizm谩kvans checkerboard styleadidas superstar nigodeszk谩s cip艖 feh茅r piros
Описание зеркала Melbet
Ниша ставок в России функционирует достаточно давно, и в 2012 г.
на рынке появилась фирма Melbet.
На сегодняшний день сервис стабильно продолжает развиваться, в частности это касается виртуального
пространства.
Как думают многие пользователи, довольно
удобно никуда не выходить, а ставить на события.
Никаких потерь времени.
Основная цель компании – помогать людям делать ставки, это удобно сделать , используя офисы
компании или же в режиме онлайн, для чего есть портал и приложение для смартфона.
Итак, предоставляется немало способов, чтобы приятно провести свободное время, а вместе с тем попытаться заработать
приличные выигрыши.
Контора мелбет как зайти на сайт довольно стремительно развивается и намерена подготовить для своих клиентов самые лучшие
условия.
Здесь каждый может делать ставки
как на спортивные, так и на
другие мероприятия, к примеру,
турниры типа Евровидения.
Больше нет смысла просто смотреть за тем, как выступает
обожаемый исполнитель.
Достаточно начать верить в его
триумф, произведя выгодную ставку.
Существует шанс, что удастся сорвать куш , а заодно
насладиться музыкальным произведением.
Такой подход крайне удобен, так как в
этом случае безусловно любой человек найдет для себя захватывающие события и сделает ставки.
Разработчики смогли предусмореть события на любой
вкус.
Решение зависит от Вашего возраста,
увлечений, а также желания рисковать.
С чего начинать ставить на спортивные события с Melbet http://teketeke.jp/cgi-bin/2014bbs-holiness_ch/kirisuto.cgi?list=thread
Многие игроки думают, что делать ставки
на спорт или иные события – это достаточно хлопотно и что в алгоритме потребуется тратить
время на разбирательство.
Но так ли это на самом деле?
Конечно же, это не так.
Если идет разговор о Melbet, то в этом случае начинать ставить получится у любого желающего.
На уровне интуиции легко осваиваемый интерфейс понравится даже
начинающим пользователям, которые только решили освоить искусство ставок.
Рассмотрим более подробно, как начать это делать.
Для старта вам нужно пройти регистрацию на сайте бк мелбет приложение
Алгоритм прохождения регистрации очень простой, вы потратите
на него минимальное количество времени.
Нужно всего лишь вбить персональные сведения в специальные поля, верифицироваться.
После регистрации следует положить деньги на депозитный счет.
При этом не играет роли, какая по размеру будет внесена сумма денег.
Совсем скоро Вы разберетесь и сможете понять, как поступать дальше, какие размеры взноса считаются наиболее приемлемыми.
И после этого вы можете начать делать ставки.
Теперь стало понятно, что выполнять подобные
манипуляции совершенно не сложно, так как этот процесс займет у вас минимум времени и сил.
Таким образом, абсолютно любой из игроков сумеет
начать делать ставки вне зависимости от того
новичок он или профессионал.
Все, что для этого нужно – пройти
регистрацию.
Компания Melbet – входит в число популярных и
востребованных площадок на рынке России, что абсолютно не удивительно.
Ведь фирма заботится о своих пользователях и предлагает для них наилучшие условия.
Разработчикам надо не просто заинтересовать новых игроков, а и создать наиболее комфортные обстоятельства для завсегдатаев.
Имидж является важным показателем для компании во имя того, чтобы не снизить
доверия пользователей.
В сфере ставок присутствует немалое количество мошенников.
Не следует соблазняться привлекательной рекламой, а также бездумно верить чрезмерно заманчивым предложениям.
Можно не только лишиться денег, безрассудно потерять время,
но и заполучить на ноутбук вирусную программу.
Уместнее выбирать лишь проверенные компании, которые долгий
период пребывают в игровой сфере.
Всегда можно почитать отклики, ознакомиться с временем начала
деятельности компании на просторах интернета.
Среди подобных профи своего дела считается http://www.celestialinternationalgroup.com/UserProfile/tabid/43/UserID/423890/Default.aspx .
При желании несложно загрузить специально разработанное мобильное
приложение.
Останется обеспечить наличие сети Интернет, чтобы ставить
с сегодняшнего дня.
Вы даже сможете подобрать событие, сделать прогноз, пребывая в
заторе или на даче.
Это ли не одно из преимуществ, за которые стоит выбирать данную компанию?
И это подтверждает огромнейшее
количество клиентов компании.
В таком случае, если вы хотите начать
делать ставки, то вам следует обратить внимание на Melbet.
Здесь melbet-partner.com вы сможете
найти важную информацию и ответы на свои
вопросы, а , кроме того, сразу приступить к
ставкам после регистрации.
I don’t even know how I ended up here, but I thought this
post was great. I don’t know who you are but certainly you’re going to a
famous blogger if you aren’t already 😉 Cheers!
I think that is one of the most significant information for me.
And i’m satisfied reading your article. But wanna statement on few
common issues, The website style is ideal, the articles is really excellent : D.
Good process, cheers
Магазины Apple в Ростове-на-Дону с низкими ценами airpods ростов
Достоинство – основной мера выбора
для большинства потребителей.
Сотрудничество с официальными дилерами американского производителя – заклад
минимального ценника.
В то же срок стоит смекать, который разные
дилеры могут устанавливать приманка собственные наценки,
следовательно имеет значение сравнить стоимость интересующей
модели сразу в нескольких торговых точках.
Один из онлайн магазинов,
что предлагает коллекция продукции Apple по хорошим ценам
Подозрительно низких цен безвыездно же лучше избегать.
Почти видом дешевого iPhone недобросовестные
поставщики могут продать вам подделку из Китая.
На месте оригинального телефона может оказаться бывший в эксплуатации смартфон, либо техника, которую
вернули по гарантии, либо смартфон с неисправностями, либо старый витринный экземпляр.
Магазины с официальной гарантией в Ростове-на-Дону https://support.sportssites.us/index.php?title=User:DillonWeis89
По понятным причинам рекомендуется предпочитать только те магазины, которые поставляют сертифицированную продукцию, технику Apple с соответствующими гарантиями оригинальности, в заводской упаковке.
Подтвердить высокое качество лабаз повинен документами, а не один для словах.
Наподобие постановление,
всякий парадный дилер обязательно предложит
гарантию на свой товар, займется гарантийным и пост-гарантийным обслуживанием iPhone, iPad, Apple Watch
и других девайсов Apple. Когда у магазина поглощать свой сервисный очаг, ровно тут, это весомое
преимущество.
Магазины с комфортным обслуживанием
Низкие цены и обеспечение оригинальности – это, понятно,
хорошо, но очень не все, который может предложить
магазин техники Apple в Ростове-на-Дону.
К дополнительным услугам, которые делают хороший лавка лучшим в своем сегменте, дозволено отнести полноценную консультационную поддержку потребителя, включая поддержка в активации, настройке
устройства, переносе данных с одного iPhone для другой, помощь в регистрации учетных
записей и беспричинно далее.
Наличие собственной служжбы оперативной доставки
заказов по городу тоже довольно лишним поводом выбрать именно сей магазин.
Также очень неплохо, буде лавка предлагает широкий ассортимент аксессуаров ради смартфонов.
Таким образом, вы можете собрать полный
коллекция чтобы комфортного
использования всякий модели iPhone в одном месте, и уже через
порядочно минут затем оплаты начать
пользоваться именно тем девайсом, который
подходит вам во всех отношениях.
Подробную информацию о расширенном каталоге аксессуаров чтобы iPhone в Ростове-на-Дону вы можете получить по ссылке – iphone 12 ростов
Wow, superb blog structure! How long have you been blogging
for? you made running a blog glance easy. The total glance of
your web site is fantastic, as well as the content!
vans skate hi mte
sapatos vermelhos com vestido azul escurotenis de mesa tamanho da mesaesta莽茫o de muscula莽茫o com 80kg aparelho gin谩stica academiasapatos de vela timberland pre莽o
Пластическая хирургия –
Пластические операции и коррекция форм.
Вот несколько самых известных примеров того,
как пластическая хирургия сделала из нормального человека
настоящего урода. Больше того, лучшие хирурги ведут персональные блоги непосредственно на сайте.
Начиная с 70-х годов, женщина потратила более 4 миллионов долларов для того, чтобы изменить свой внешний вид.
Когда-то эта активная женщина создала
горячую линию для оказания психологической
помощи для всех, кто в ней нуждался.
Форумы пластической хирургии дают возможность подтвердить доверие к любой клинике или центру пластической медицины.
Форумы пластической хирургии полны информацией об
пластике лица. Бесспорно, Ханг может
стать наиболее ярким примером жертвы неудачной пластической хирургии.
Затем Ханг попросту не могла остановиться. https://forum.plastic-surgeon.com.ua/forumdisplay.php?f=11
I like the valuable information you supply to your
articles. I will bookmark your weblog and check again here regularly.
I’m quite sure I’ll learn lots of new stuff proper here!
Good luck for the next!
Genuinely no matter if someone doesn’t understand then its up to other users that they will help, so here it occurs.
Обзор зеркала Melbet
Ниша ставок в РФ функционирует довольно давно, и в 2012 году на рынке появилась фирма Мелбет.
На сегодняшний день сервис стабильно продолжает развиваться, в частности это касается виртуального пространства.
Как полагают некоторые пользователи, достаточно комфортно никуда не выходить, а делать ставки.
Никаких потерь времени.
Основная цель компании –
оказывать помощь людям делать ставки, это можно выполнить через
офисы компании или же в режиме
online, для этого имеется сайт и приложение для смартфона.
Итак, предоставляется довольно много возможностей, чтобы приятно провести свободное время, а
заодно попробовать заработать неплохие суммы.
Контора мелбет как зайти на сайт довольно стремительно продвигается и намерена создать для своих клиентов
самые лучшие условия.
Здесь вы можете ставить как на
спортивные, так и на иные
события, к примеру, турниры
типа Eurovision.
Больше нет смысла просто смотреть за тем, как выступает любимый исполнитель.
Стоит всего лишь начать верить в его победу, произведя оптимальную ставку.
Есть шанс, что получится заполучить куш , а
заодно послушать отличную музыку.
Это очень удобно, так как в этом случае абсолютно каждый человек найдет для себя интересные мероприятия и сделает ставки.
Программеры предусмотрели события на
все предпочтения.
Решение зависит от того, сколько Вам лет, чем вы увлекаетесь и
способны ли рисковать.
Как начать ставить на спортивные события с Melbet https://www.sou688.com/home.php?mod=space&uid=273997&do=profile&from=space
Некоторые игроки думают, что
делать ставки на спорт или другие события – это достаточно хлопотно и что в этом потребуется долго разбираться.
Но так ли это на самом деле?
Конечно же, нет.
Если мы говорим о Melbet, то в этом случае начать делать ставки сможет каждый.
На уровне интуиции понятный интерфейс придется по
вкусу даже новичкам, которые только решили освоить искусство ставок.
Рассмотрим подробнее, каким образом начать это делать.
Для начала вам нужно пройти регистрацию на сайте скриншот мелбет баланс
Алгоритм прохождения регистрации удивительно простой,
займет у вас минимум времени.
Потребуется всего лишь вбить персональные данные в специальные поля, верифицироваться.
Как только вы зарегистрируетесь, надо будет внести некоторую
сумму на депозитный счет.
При этом неважно, какая по
размеру будет внесена денежная сумма.
Очень быстро Вы разберетесь и сможете понять, каким образом действовать дальше, какие параметры ставки
считаются оптимальными.
И после этого вы можете начать ставить на
события.
Сейчас становится ясно, что делать это можно без
особого труда, потому что этот процесс займет у вас минимум времени и сил.
Таким образом, абсолютно каждый сможет начать ставить независимо от того без опыта он или профессионал.
Все, что для этого нужно – зарегистрироваться.
Компания Мелбет – одна из самых известных
и востребованных компаний на рынке России,
что абсолютно не удивительно.
Ведь контора заботится о своих пользователях и
подготавливает для них самые лучшие условия.
Руководству важно не просто заинтересовать больше пользователей,
но и подготовить наиболее удачные обстоятельства для постоянных клиентов.
Имидж считается важным показателем для компании во имя того,
чтобы не потерять веры игроков.
В сфере ставок существует
немалое количество мошенников.
Не следует слепо доверять яркой рекламе,
а также идти на поводу у слишком выгодных условий.
Можно не только лишиться денег,
безрассудно потерять время, но и
установить на компьютер
вирусную программу.
Уместнее останавливать выбор на надежных фирмах, которые
долгий период находятся в данной сфере.
Всегда можно почитать отклики, узнать о времени начала деятельности компании в виртуальном пространстве.
Среди таких профи ведения игрового бизнеса признается http://wiki.conanexiles.es/Usuario:Darin73M6225507 .
При желании можно скачать конкретно созданное мобильное
приложение.
Останется обеспечить наличие сети Интернет,
чтобы делать ставки уже сегодня.
Вы даже сможете выбрать событие,
спрогнозировать результат, пребывая в
пробке или в офисе.
Это ли не одно из преимуществ, за которые стоит выбирать данную компанию?
Именно это подтверждает огромнейшее количество
игроков компании.
Поэтому, если вы решили испытывать удачу на ставках, то вам стоит присмотреться к Мелбет.
Тут melbet-partner.com вы сможете найти важную информацию и решения своих вопросов,
а , кроме того, сразу начать делать ставки после регистрации.
I do not even know how I ended up here, but I
thought this post was great. I don’t know who you are but definitely you are going to a
famous blogger if you aren’t already 😉 Cheers!
prada leopard glasses
fox hose mtbmeindl 3985andamios galvanizadosropa camarero
At this time it looks like Drupal is the best blogging platform out there right now.
(from what I’ve read) Is that what you’re using on your blog?
whoah this blog is great i love studying your
articles. Stay up the great work! You realize, a lot of individuals are looking around for this information, you could help them greatly.
Hi, i read your blog occasionally and i own a similar one and i was just wondering if you get a lot of spam responses?
If so how do you stop it, any plugin or anything you can advise?
I get so much lately it’s driving me insane so any
support is very much appreciated.
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
<a href="http://images.google.cm/url?sa=t&url=https%3
I’m not sure why but this blog is loading extremely slow for me.
Is anyone else having this issue or is it a problem on my end?
I’ll check back later and see if the problem still exists.
Keep this going please, great job!
Cialis online http://acialaarx.com/ order
cialis
http://google.com.af/url?q=https://imiwins.com/
http://google.al/url?q=https://imiwins.com/
http://google.dz/url?q=https://imiwins.com/
http://google.as/url?q=https://imiwins.com/
http://google.ad/url?q=https://imiwins.com/
http://google.it.ao/url?q=https://imiwins.com/
http://google.com.ai/url?q=https://imiwins.com/
http://google.com.ag/url?q=https://imiwins.com/
http://google.com.ar/url?q=https://imiwins.com/
http://google.am/url?q=https://imiwins.com/
http://google.ac/url?q=https://imiwins.com/
http://google.com.au/url?q=https://imiwins.com/
http://google.at/url?q=https://imiwins.com/
http://google.az/url?q=https://imiwins.com/
http://google.bs/url?q=https://imiwins.com/
http://google.com.bh/url?q=https://imiwins.com/
http://google.com.bd/url?q=https://imiwins.com/
http://google.com.by/url?q=https://imiwins.com/
http://google.be/url?q=https://imiwins.com/
http://google.com.bz/url?q=https://imiwins.com/
http://google.bj/url?q=https://imiwins.com/
http://google.bt/url?q=https://imiwins.com/
http://google.com.bo/url?q=https://imiwins.com/
http://google.ba/url?q=https://imiwins.com/
http://google.co.bw/url?q=https://imiwins.com/
http://google.com.br/url?q=https://imiwins.com/
http://google.vg/url?q=https://imiwins.com/
http://google.com.bn/url?q=https://imiwins.com/
http://google.bg/url?q=https://imiwins.com/
http://google.bf/url?q=https://imiwins.com/
http://google.bi/url?q=https://imiwins.com/
http://google.com.kh/url?q=https://imiwins.com/
http://google.cm/url?q=https://imiwins.com/
http://google.ca/url?q=https://imiwins.com/
http://google.cv/url?q=https://imiwins.com/
http://google.cat/url?q=https://imiwins.com/
http://google.cf/url?q=https://imiwins.com/
http://google.td/url?q=https://imiwins.com/
http://google.cl/url?q=https://imiwins.com/
http://google.cn/url?q=https://imiwins.com/
http://google.com.co/url?q=https://imiwins.com/
http://google.cd/url?q=https://imiwins.com/
http://google.cg/url?q=https://imiwins.com/
http://google.co.ck/url?q=https://imiwins.com/
http://google.co.cr/url?q=https://imiwins.com/
http://google.ci/url?q=https://imiwins.com/
http://google.hr/url?q=https://imiwins.com/
http://google.com.cu/url?q=https://imiwins.com/
http://google.com.cy/url?q=https://imiwins.com/
http://google.cz/url?q=https://imiwins.com/
http://google.dk/url?q=https://imiwins.com/
http://google.dj/url?q=https://imiwins.com/
http://google.dm/url?q=https://imiwins.com/
http://google.com.do/url?q=https://imiwins.com/
http://google.com.ec/url?q=https://imiwins.com/
http://google.com.eg/url?q=https://imiwins.com/
http://google.com.sv/url?q=https://imiwins.com/
http://google.ee/url?q=https://imiwins.com/
http://google.com.et/url?q=https://imiwins.com/
http://google.com.fj/url?q=https://imiwins.com/
http://google.fi/url?q=https://imiwins.com/
http://google.fr/url?q=https://imiwins.com/
http://google.ga/url?q=https://imiwins.com/
http://google.gm/url?q=https://imiwins.com/
http://google.ge/url?q=https://imiwins.com/
http://google.de/url?q=https://imiwins.com/
http://google.com.gh/url?q=https://imiwins.com/
http://google.com.gi/url?q=https://imiwins.com/
http://google.gr/url?q=https://imiwins.com/
http://google.gl/url?q=https://imiwins.com/
http://google.gp/url?q=https://imiwins.com/
http://google.com.gt/url?q=https://imiwins.com/
http://google.gg/url?q=https://imiwins.com/
http://google.gy/url?q=https://imiwins.com/
http://google.ht/url?q=https://imiwins.com/
http://google.hn/url?q=https://imiwins.com/
http://google.com.hk/url?q=https://imiwins.com/
http://google.hu/url?q=https://imiwins.com/
http://google.is/url?q=https://imiwins.com/
http://google.co.in/url?q=https://imiwins.com/
http://google.co.id/url?q=https://imiwins.com/
http://google.iq/url?q=https://imiwins.com/
http://google.ie/url?q=https://imiwins.com/
http://google.co.im/url?q=https://imiwins.com/
http://google.co.il/url?q=https://imiwins.com/
http://google.it/url?q=https://imiwins.com/
http://google.ci/url?q=https://imiwins.com/
http://google.com.jm/url?q=https://imiwins.com/
http://google.co.jp/url?q=https://imiwins.com/
http://google.co.je/url?q=https://imiwins.com/
http://google.jo/url?q=https://imiwins.com/
http://google.kz/url?q=https://imiwins.com/
http://google.co.ke/url?q=https://imiwins.com/
http://google.ki/url?q=https://imiwins.com/
http://google.com.kw/url?q=https://imiwins.com/
http://google.com.kg/url?q=https://imiwins.com/
http://google.la/url?q=https://imiwins.com/
http://google.lv/url?q=https://imiwins.com/
http://google.com.lb/url?q=https://imiwins.com/
http://google.co.ls/url?q=https://imiwins.com/
http://google.com.ly/url?q=https://imiwins.com/
http://google.li/url?q=https://imiwins.com/
http://google.lt/url?q=https://imiwins.com/
http://google.lu/url?q=https://imiwins.com/
http://google.mk/url?q=https://imiwins.com/
http://google.mg/url?q=https://imiwins.com/
http://google.mw/url?q=https://imiwins.com/
http://google.com.my/url?q=https://imiwins.com/
http://google.mv/url?q=https://imiwins.com/
http://google.ml/url?q=https://imiwins.com/
http://google.com.mt/url?q=https://imiwins.com/
http://google.mu/url?q=https://imiwins.com/
http://google.com.mx/url?q=https://imiwins.com/
http://google.fm/url?q=https://imiwins.com/
http://google.md/url?q=https://imiwins.com/
http://google.mn/url?q=https://imiwins.com/
http://google.me/url?q=https://imiwins.com/
http://google.ms/url?q=https://imiwins.com/
http://google.co.ma/url?q=https://imiwins.com/
http://google.co.mz/url?q=https://imiwins.com/
http://google.com.na/url?q=https://imiwins.com/
http://google.nr/url?q=https://imiwins.com/
http://google.com.np/url?q=https://imiwins.com/
http://google.nl/url?q=https://imiwins.com/
http://google.co.nz/url?q=https://imiwins.com/
http://google.com.ni/url?q=https://imiwins.com/
http://google.ne/url?q=https://imiwins.com/
http://google.com.ng/url?q=https://imiwins.com/
http://google.nu/url?q=https://imiwins.com/
http://google.com.nf/url?q=https://imiwins.com/
http://google.no/url?q=https://imiwins.com/
http://google.com.om/url?q=https://imiwins.com/
http://google.com.pk/url?q=https://imiwins.com/
http://google.ps/url?q=https://imiwins.com/
http://google.com.pa/url?q=https://imiwins.com/
http://google.com.pg/url?q=https://imiwins.com/
http://google.com.py/url?q=https://imiwins.com/
http://google.com.pe/url?q=https://imiwins.com/
http://google.com.ph/url?q=https://imiwins.com/
http://google.pn/url?q=https://imiwins.com/
http://google.pl/url?q=https://imiwins.com/
http://google.pt/url?q=https://imiwins.com/
http://google.com.pr/url?q=https://imiwins.com/
http://google.com.qa/url?q=https://imiwins.com/
http://google.ro/url?q=https://imiwins.com/
http://google.ru/url?q=https://imiwins.com/
http://google.rw/url?q=https://imiwins.com/
http://google.sh/url?q=https://imiwins.com/
http://google.ws/url?q=https://imiwins.com/
http://google.sm/url?q=https://imiwins.com/
http://google.st/url?q=https://imiwins.com/
http://google.com.sa/url?q=https://imiwins.com/
http://google.sn/url?q=https://imiwins.com/
http://google.rs/url?q=https://imiwins.com/
http://google.sc/url?q=https://imiwins.com/
http://google.com.sl/url?q=https://imiwins.com/
http://google.com.sg/url?q=https://imiwins.com/
http://google.sk/url?q=https://imiwins.com/
http://google.si/url?q=https://imiwins.com/
http://google.com.sb/url?q=https://imiwins.com/
http://google.so/url?q=https://imiwins.com/
http://google.co.za/url?q=https://imiwins.com/
http://google.co.kr/url?q=https://imiwins.com/
http://google.es/url?q=https://imiwins.com/
http://google.lk/url?q=https://imiwins.com/
http://google.com.vc/url?q=https://imiwins.com/
http://google.sr/url?q=https://imiwins.com/
http://google.se/url?q=https://imiwins.com/
http://google.ch/url?q=https://imiwins.com/
http://google.com.tw/url?q=https://imiwins.com/
http://google.com.tj/url?q=https://imiwins.com/
http://google.co.tz/url?q=https://imiwins.com/
http://google.co.th/url?q=https://imiwins.com/
http://google.tl/url?q=https://imiwins.com/
http://google.tg/url?q=https://imiwins.com/
http://google.tk/url?q=https://imiwins.com/
http://google.to/url?q=https://imiwins.com/
http://google.tt/url?q=https://imiwins.com/
http://google.tn/url?q=https://imiwins.com/
http://google.com.tr/url?q=https://imiwins.com/
http://google.tm/url?q=https://imiwins.com/
http://google.co.ug/url?q=https://imiwins.com/
http://google.com.ua/url?q=https://imiwins.com/
http://google.ae/url?q=https://imiwins.com/
http://google.co.uk/url?q=https://imiwins.com/
http://google.com/url?q=https://imiwins.com/
http://google.com.uy/url?q=https://imiwins.com/
http://google.co.uz/url?q=https://imiwins.com/
http://google.vu/url?q=https://imiwins.com/
http://google.co.ve/url?q=https://imiwins.com/
http://google.com.vn/url?q=https://imiwins.com/
http://google.co.vi/url?q=https://imiwins.com/
http://google.co.zm/url?q=https://imiwins.com/
http://google.co.zw/url?q=https://imiwins.com/
http://maps.google.com.af/url?q=https://imiwins.com/
http://maps.google.al/url?q=https://imiwins.com/
http://maps.google.dz/url?q=https://imiwins.com/
http://maps.google.as/url?q=https://imiwins.com/
http://maps.google.ad/url?q=https://imiwins.com/
http://maps.google.it.ao/url?q=https://imiwins.com/
http://maps.google.com.ai/url?q=https://imiwins.com/
http://maps.google.com.ag/url?q=https://imiwins.com/
http://maps.google.com.ar/url?q=https://imiwins.com/
http://maps.google.am/url?q=https://imiwins.com/
http://maps.google.ac/url?q=https://imiwins.com/
http://maps.google.com.au/url?q=https://imiwins.com/
http://maps.google.at/url?q=https://imiwins.com/
http://maps.google.az/url?q=https://imiwins.com/
http://maps.google.bs/url?q=https://imiwins.com/
http://maps.google.com.bh/url?q=https://imiwins.com/
http://maps.google.com.bd/url?q=https://imiwins.com/
http://maps.google.com.by/url?q=https://imiwins.com/
http://maps.google.be/url?q=https://imiwins.com/
http://maps.google.com.bz/url?q=https://imiwins.com/
http://maps.google.bj/url?q=https://imiwins.com/
http://maps.google.bt/url?q=https://imiwins.com/
http://maps.google.com.bo/url?q=https://imiwins.com/
http://maps.google.ba/url?q=https://imiwins.com/
http://maps.google.co.bw/url?q=https://imiwins.com/
http://maps.google.com.br/url?q=https://imiwins.com/
http://maps.google.vg/url?q=https://imiwins.com/
http://maps.google.com.bn/url?q=https://imiwins.com/
http://maps.google.bg/url?q=https://imiwins.com/
http://maps.google.bf/url?q=https://imiwins.com/
http://maps.google.bi/url?q=https://imiwins.com/
http://maps.google.com.kh/url?q=https://imiwins.com/
http://maps.google.cm/url?q=https://imiwins.com/
http://maps.google.ca/url?q=https://imiwins.com/
http://maps.google.cv/url?q=https://imiwins.com/
http://maps.google.cat/url?q=https://imiwins.com/
http://maps.google.cf/url?q=https://imiwins.com/
http://maps.google.td/url?q=https://imiwins.com/
http://maps.google.cl/url?q=https://imiwins.com/
http://maps.google.cn/url?q=https://imiwins.com/
http://maps.google.com.co/url?q=https://imiwins.com/
http://maps.google.cd/url?q=https://imiwins.com/
http://maps.google.cg/url?q=https://imiwins.com/
http://maps.google.co.ck/url?q=https://imiwins.com/
http://maps.google.co.cr/url?q=https://imiwins.com/
http://maps.google.ci/url?q=https://imiwins.com/
http://maps.google.hr/url?q=https://imiwins.com/
http://maps.google.com.cu/url?q=https://imiwins.com/
http://maps.google.com.cy/url?q=https://imiwins.com/
http://maps.google.cz/url?q=https://imiwins.com/
http://maps.google.dk/url?q=https://imiwins.com/
http://maps.google.dj/url?q=https://imiwins.com/
http://maps.google.dm/url?q=https://imiwins.com/
http://maps.google.com.do/url?q=https://imiwins.com/
http://maps.google.com.ec/url?q=https://imiwins.com/
http://maps.google.com.eg/url?q=https://imiwins.com/
http://maps.google.com.sv/url?q=https://imiwins.com/
http://maps.google.ee/url?q=https://imiwins.com/
http://maps.google.com.et/url?q=https://imiwins.com/
http://maps.google.com.fj/url?q=https://imiwins.com/
http://maps.google.fi/url?q=https://imiwins.com/
http://maps.google.fr/url?q=https://imiwins.com/
http://maps.google.ga/url?q=https://imiwins.com/
http://maps.google.gm/url?q=https://imiwins.com/
http://maps.google.ge/url?q=https://imiwins.com/
http://maps.google.de/url?q=https://imiwins.com/
http://maps.google.com.gh/url?q=https://imiwins.com/
http://maps.google.com.gi/url?q=https://imiwins.com/
http://maps.google.gr/url?q=https://imiwins.com/
http://maps.google.gl/url?q=https://imiwins.com/
http://maps.google.gp/url?q=https://imiwins.com/
http://maps.google.com.gt/url?q=https://imiwins.com/
http://maps.google.gg/url?q=https://imiwins.com/
http://maps.google.gy/url?q=https://imiwins.com/
http://maps.google.ht/url?q=https://imiwins.com/
http://maps.google.hn/url?q=https://imiwins.com/
http://maps.google.com.hk/url?q=https://imiwins.com/
http://maps.google.hu/url?q=https://imiwins.com/
http://maps.google.is/url?q=https://imiwins.com/
http://maps.google.co.in/url?q=https://imiwins.com/
http://maps.google.co.id/url?q=https://imiwins.com/
http://maps.google.iq/url?q=https://imiwins.com/
http://maps.google.ie/url?q=https://imiwins.com/
http://maps.google.co.im/url?q=https://imiwins.com/
http://maps.google.co.il/url?q=https://imiwins.com/
http://maps.google.it/url?q=https://imiwins.com/
http://maps.google.ci/url?q=https://imiwins.com/
http://maps.google.com.jm/url?q=https://imiwins.com/
http://maps.google.co.jp/url?q=https://imiwins.com/
http://maps.google.co.je/url?q=https://imiwins.com/
http://maps.google.jo/url?q=https://imiwins.com/
http://maps.google.kz/url?q=https://imiwins.com/
http://maps.google.co.ke/url?q=https://imiwins.com/
http://maps.google.ki/url?q=https://imiwins.com/
http://maps.google.com.kw/url?q=https://imiwins.com/
http://maps.google.com.kg/url?q=https://imiwins.com/
http://maps.google.la/url?q=https://imiwins.com/
http://maps.google.lv/url?q=https://imiwins.com/
http://maps.google.com.lb/url?q=https://imiwins.com/
http://maps.google.co.ls/url?q=https://imiwins.com/
http://maps.google.com.ly/url?q=https://imiwins.com/
http://maps.google.li/url?q=https://imiwins.com/
http://maps.google.lt/url?q=https://imiwins.com/
http://maps.google.lu/url?q=https://imiwins.com/
http://maps.google.mk/url?q=https://imiwins.com/
http://maps.google.mg/url?q=https://imiwins.com/
http://maps.google.mw/url?q=https://imiwins.com/
http://maps.google.com.my/url?q=https://imiwins.com/
http://maps.google.mv/url?q=https://imiwins.com/
http://maps.google.ml/url?q=https://imiwins.com/
http://maps.google.com.mt/url?q=https://imiwins.com/
http://maps.google.mu/url?q=https://imiwins.com/
http://maps.google.com.mx/url?q=https://imiwins.com/
http://maps.google.fm/url?q=https://imiwins.com/
http://maps.google.md/url?q=https://imiwins.com/
http://maps.google.mn/url?q=https://imiwins.com/
http://maps.google.me/url?q=https://imiwins.com/
http://maps.google.ms/url?q=https://imiwins.com/
http://maps.google.co.ma/url?q=https://imiwins.com/
http://maps.google.co.mz/url?q=https://imiwins.com/
http://maps.google.com.na/url?q=https://imiwins.com/
http://maps.google.nr/url?q=https://imiwins.com/
http://maps.google.com.np/url?q=https://imiwins.com/
http://maps.google.nl/url?q=https://imiwins.com/
http://maps.google.co.nz/url?q=https://imiwins.com/
http://maps.google.com.ni/url?q=https://imiwins.com/
http://maps.google.ne/url?q=https://imiwins.com/
http://maps.google.com.ng/url?q=https://imiwins.com/
http://maps.google.nu/url?q=https://imiwins.com/
http://maps.google.com.nf/url?q=https://imiwins.com/
http://maps.google.no/url?q=https://imiwins.com/
http://maps.google.com.om/url?q=https://imiwins.com/
http://maps.google.com.pk/url?q=https://imiwins.com/
http://maps.google.ps/url?q=https://imiwins.com/
http://maps.google.com.pa/url?q=https://imiwins.com/
http://maps.google.com.pg/url?q=https://imiwins.com/
http://maps.google.com.py/url?q=https://imiwins.com/
http://maps.google.com.pe/url?q=https://imiwins.com/
http://maps.google.com.ph/url?q=https://imiwins.com/
http://maps.google.pn/url?q=https://imiwins.com/
http://maps.google.pl/url?q=https://imiwins.com/
http://maps.google.pt/url?q=https://imiwins.com/
http://maps.google.com.pr/url?q=https://imiwins.com/
http://maps.google.com.qa/url?q=https://imiwins.com/
http://maps.google.ro/url?q=https://imiwins.com/
http://maps.google.ru/url?q=https://imiwins.com/
http://maps.google.rw/url?q=https://imiwins.com/
http://maps.google.sh/url?q=https://imiwins.com/
http://maps.google.ws/url?q=https://imiwins.com/
http://maps.google.sm/url?q=https://imiwins.com/
http://maps.google.st/url?q=https://imiwins.com/
http://maps.google.com.sa/url?q=https://imiwins.com/
http://maps.google.sn/url?q=https://imiwins.com/
http://maps.google.rs/url?q=https://imiwins.com/
http://maps.google.sc/url?q=https://imiwins.com/
http://maps.google.com.sl/url?q=https://imiwins.com/
http://maps.google.com.sg/url?q=https://imiwins.com/
http://maps.google.sk/url?q=https://imiwins.com/
http://maps.google.si/url?q=https://imiwins.com/
http://maps.google.com.sb/url?q=https://imiwins.com/
http://maps.google.so/url?q=https://imiwins.com/
http://maps.google.co.za/url?q=https://imiwins.com/
http://maps.google.co.kr/url?q=https://imiwins.com/
http://maps.google.es/url?q=https://imiwins.com/
http://maps.google.lk/url?q=https://imiwins.com/
http://maps.google.com.vc/url?q=https://imiwins.com/
http://maps.google.sr/url?q=https://imiwins.com/
http://maps.google.se/url?q=https://imiwins.com/
http://maps.google.ch/url?q=https://imiwins.com/
http://maps.google.com.tw/url?q=https://imiwins.com/
http://maps.google.com.tj/url?q=https://imiwins.com/
http://maps.google.co.tz/url?q=https://imiwins.com/
http://maps.google.co.th/url?q=https://imiwins.com/
http://maps.google.tl/url?q=https://imiwins.com/
http://maps.google.tg/url?q=https://imiwins.com/
http://maps.google.tk/url?q=https://imiwins.com/
http://maps.google.to/url?q=https://imiwins.com/
http://maps.google.tt/url?q=https://imiwins.com/
http://maps.google.tn/url?q=https://imiwins.com/
http://maps.google.com.tr/url?q=https://imiwins.com/
http://maps.google.tm/url?q=https://imiwins.com/
http://maps.google.co.ug/url?q=https://imiwins.com/
http://maps.google.com.ua/url?q=https://imiwins.com/
http://maps.google.ae/url?q=https://imiwins.com/
http://maps.google.co.uk/url?q=https://imiwins.com/
http://maps.google.com/url?q=https://imiwins.com/
http://maps.google.com.uy/url?q=https://imiwins.com/
http://maps.google.co.uz/url?q=https://imiwins.com/
http://maps.google.vu/url?q=https://imiwins.com/
http://maps.google.co.ve/url?q=https://imiwins.com/
http://maps.google.com.vn/url?q=https://imiwins.com/
http://maps.google.co.vi/url?q=https://imiwins.com/
http://maps.google.co.zm/url?q=https://imiwins.com/
http://maps.google.co.zw/url?q=https://imiwins.com/
http://images.google.com.af/url?q=https://imiwins.com/
http://images.google.al/url?q=https://imiwins.com/
http://images.google.dz/url?q=https://imiwins.com/
http://images.google.as/url?q=https://imiwins.com/
http://images.google.ad/url?q=https://imiwins.com/
http://images.google.it.ao/url?q=https://imiwins.com/
http://images.google.com.ai/url?q=https://imiwins.com/
http://images.google.com.ag/url?q=https://imiwins.com/
http://images.google.com.ar/url?q=https://imiwins.com/
http://images.google.am/url?q=https://imiwins.com/
http://images.google.ac/url?q=https://imiwins.com/
http://images.google.com.au/url?q=https://imiwins.com/
http://images.google.at/url?q=https://imiwins.com/
http://images.google.az/url?q=https://imiwins.com/
http://images.google.bs/url?q=https://imiwins.com/
http://images.google.com.bh/url?q=https://imiwins.com/
http://images.google.com.bd/url?q=https://imiwins.com/
http://images.google.com.by/url?q=https://imiwins.com/
http://images.google.be/url?q=https://imiwins.com/
http://images.google.com.bz/url?q=https://imiwins.com/
http://images.google.bj/url?q=https://imiwins.com/
http://images.google.bt/url?q=https://imiwins.com/
http://images.google.com.bo/url?q=https://imiwins.com/
http://images.google.ba/url?q=https://imiwins.com/
http://images.google.co.bw/url?q=https://imiwins.com/
http://images.google.com.br/url?q=https://imiwins.com/
http://images.google.vg/url?q=https://imiwins.com/
http://images.google.com.bn/url?q=https://imiwins.com/
http://images.google.bg/url?q=https://imiwins.com/
http://images.google.bf/url?q=https://imiwins.com/
http://images.google.bi/url?q=https://imiwins.com/
http://images.google.com.kh/url?q=https://imiwins.com/
http://images.google.cm/url?q=https://imiwins.com/
http://images.google.ca/url?q=https://imiwins.com/
http://images.google.cv/url?q=https://imiwins.com/
http://images.google.cat/url?q=https://imiwins.com/
http://images.google.cf/url?q=https://imiwins.com/
http://images.google.td/url?q=https://imiwins.com/
http://images.google.cl/url?q=https://imiwins.com/
http://images.google.cn/url?q=https://imiwins.com/
http://images.google.com.co/url?q=https://imiwins.com/
http://images.google.cd/url?q=https://imiwins.com/
http://images.google.cg/url?q=https://imiwins.com/
http://images.google.co.ck/url?q=https://imiwins.com/
http://images.google.co.cr/url?q=https://imiwins.com/
http://images.google.ci/url?q=https://imiwins.com/
http://images.google.hr/url?q=https://imiwins.com/
http://images.google.com.cu/url?q=https://imiwins.com/
http://images.google.com.cy/url?q=https://imiwins.com/
http://images.google.cz/url?q=https://imiwins.com/
http://images.google.dk/url?q=https://imiwins.com/
http://images.google.dj/url?q=https://imiwins.com/
http://images.google.dm/url?q=https://imiwins.com/
http://images.google.com.do/url?q=https://imiwins.com/
http://images.google.com.ec/url?q=https://imiwins.com/
http://images.google.com.eg/url?q=https://imiwins.com/
http://images.google.com.sv/url?q=https://imiwins.com/
http://images.google.ee/url?q=https://imiwins.com/
http://images.google.com.et/url?q=https://imiwins.com/
http://images.google.com.fj/url?q=https://imiwins.com/
http://images.google.fi/url?q=https://imiwins.com/
http://images.google.fr/url?q=https://imiwins.com/
http://images.google.ga/url?q=https://imiwins.com/
http://images.google.gm/url?q=https://imiwins.com/
http://images.google.ge/url?q=https://imiwins.com/
http://images.google.de/url?q=https://imiwins.com/
http://images.google.com.gh/url?q=https://imiwins.com/
http://images.google.com.gi/url?q=https://imiwins.com/
http://images.google.gr/url?q=https://imiwins.com/
http://images.google.gl/url?q=https://imiwins.com/
http://images.google.gp/url?q=https://imiwins.com/
http://images.google.com.gt/url?q=https://imiwins.com/
http://images.google.gg/url?q=https://imiwins.com/
http://images.google.gy/url?q=https://imiwins.com/
http://images.google.ht/url?q=https://imiwins.com/
http://images.google.hn/url?q=https://imiwins.com/
http://images.google.com.hk/url?q=https://imiwins.com/
http://images.google.hu/url?q=https://imiwins.com/
http://images.google.is/url?q=https://imiwins.com/
http://images.google.co.in/url?q=https://imiwins.com/
http://images.google.co.id/url?q=https://imiwins.com/
http://images.google.iq/url?q=https://imiwins.com/
http://images.google.ie/url?q=https://imiwins.com/
http://images.google.co.im/url?q=https://imiwins.com/
http://images.google.co.il/url?q=https://imiwins.com/
http://images.google.it/url?q=https://imiwins.com/
http://images.google.ci/url?q=https://imiwins.com/
http://images.google.com.jm/url?q=https://imiwins.com/
http://images.google.co.jp/url?q=https://imiwins.com/
http://images.google.co.je/url?q=https://imiwins.com/
http://images.google.jo/url?q=https://imiwins.com/
http://images.google.kz/url?q=https://imiwins.com/
http://images.google.co.ke/url?q=https://imiwins.com/
http://images.google.ki/url?q=https://imiwins.com/
http://images.google.com.kw/url?q=https://imiwins.com/
http://images.google.com.kg/url?q=https://imiwins.com/
http://images.google.la/url?q=https://imiwins.com/
http://images.google.lv/url?q=https://imiwins.com/
http://images.google.com.lb/url?q=https://imiwins.com/
http://images.google.co.ls/url?q=https://imiwins.com/
http://images.google.com.ly/url?q=https://imiwins.com/
http://images.google.li/url?q=https://imiwins.com/
http://images.google.lt/url?q=https://imiwins.com/
http://images.google.lu/url?q=https://imiwins.com/
http://images.google.mk/url?q=https://imiwins.com/
http://images.google.mg/url?q=https://imiwins.com/
http://images.google.mw/url?q=https://imiwins.com/
http://images.google.com.my/url?q=https://imiwins.com/
http://images.google.mv/url?q=https://imiwins.com/
http://images.google.ml/url?q=https://imiwins.com/
http://images.google.com.mt/url?q=https://imiwins.com/
http://images.google.mu/url?q=https://imiwins.com/
http://images.google.com.mx/url?q=https://imiwins.com/
http://images.google.fm/url?q=https://imiwins.com/
http://images.google.md/url?q=https://imiwins.com/
http://images.google.mn/url?q=https://imiwins.com/
http://images.google.me/url?q=https://imiwins.com/
http://images.google.ms/url?q=https://imiwins.com/
http://images.google.co.ma/url?q=https://imiwins.com/
http://images.google.co.mz/url?q=https://imiwins.com/
http://images.google.com.na/url?q=https://imiwins.com/
http://images.google.nr/url?q=https://imiwins.com/
http://images.google.com.np/url?q=https://imiwins.com/
http://images.google.nl/url?q=https://imiwins.com/
http://images.google.co.nz/url?q=https://imiwins.com/
http://images.google.com.ni/url?q=https://imiwins.com/
http://images.google.ne/url?q=https://imiwins.com/
http://images.google.com.ng/url?q=https://imiwins.com/
http://images.google.nu/url?q=https://imiwins.com/
http://images.google.com.nf/url?q=https://imiwins.com/
http://images.google.no/url?q=https://imiwins.com/
http://images.google.com.om/url?q=https://imiwins.com/
http://images.google.com.pk/url?q=https://imiwins.com/
http://images.google.ps/url?q=https://imiwins.com/
http://images.google.com.pa/url?q=https://imiwins.com/
http://images.google.com.pg/url?q=https://imiwins.com/
http://images.google.com.py/url?q=https://imiwins.com/
http://images.google.com.pe/url?q=https://imiwins.com/
http://images.google.com.ph/url?q=https://imiwins.com/
http://images.google.pn/url?q=https://imiwins.com/
http://images.google.pl/url?q=https://imiwins.com/
http://images.google.pt/url?q=https://imiwins.com/
http://images.google.com.pr/url?q=https://imiwins.com/
http://images.google.com.qa/url?q=https://imiwins.com/
http://images.google.ro/url?q=https://imiwins.com/
http://images.google.ru/url?q=https://imiwins.com/
http://images.google.rw/url?q=https://imiwins.com/
http://images.google.sh/url?q=https://imiwins.com/
http://images.google.ws/url?q=https://imiwins.com/
http://images.google.sm/url?q=https://imiwins.com/
http://images.google.st/url?q=https://imiwins.com/
http://images.google.com.sa/url?q=https://imiwins.com/
http://images.google.sn/url?q=https://imiwins.com/
http://images.google.rs/url?q=https://imiwins.com/
http://images.google.sc/url?q=https://imiwins.com/
http://images.google.com.sl/url?q=https://imiwins.com/
http://images.google.com.sg/url?q=https://imiwins.com/
http://images.google.sk/url?q=https://imiwins.com/
http://images.google.si/url?q=https://imiwins.com/
http://images.google.com.sb/url?q=https://imiwins.com/
http://images.google.so/url?q=https://imiwins.com/
http://images.google.co.za/url?q=https://imiwins.com/
http://images.google.co.kr/url?q=https://imiwins.com/
http://images.google.es/url?q=https://imiwins.com/
http://images.google.lk/url?q=https://imiwins.com/
http://images.google.com.vc/url?q=https://imiwins.com/
http://images.google.sr/url?q=https://imiwins.com/
http://images.google.se/url?q=https://imiwins.com/
http://images.google.ch/url?q=https://imiwins.com/
http://images.google.com.tw/url?q=https://imiwins.com/
http://images.google.com.tj/url?q=https://imiwins.com/
http://images.google.co.tz/url?q=https://imiwins.com/
http://images.google.co.th/url?q=https://imiwins.com/
http://images.google.tl/url?q=https://imiwins.com/
http://images.google.tg/url?q=https://imiwins.com/
http://images.google.tk/url?q=https://imiwins.com/
http://images.google.to/url?q=https://imiwins.com/
http://images.google.tt/url?q=https://imiwins.com/
http://images.google.tn/url?q=https://imiwins.com/
http://images.google.com.tr/url?q=https://imiwins.com/
http://images.google.tm/url?q=https://imiwins.com/
http://images.google.co.ug/url?q=https://imiwins.com/
http://images.google.com.ua/url?q=https://imiwins.com/
http://images.google.ae/url?q=https://imiwins.com/
http://images.google.co.uk/url?q=https://imiwins.com/
http://images.google.com/url?q=https://imiwins.com/
http://images.google.com.uy/url?q=https://imiwins.com/
http://images.google.co.uz/url?q=https://imiwins.com/
http://images.google.vu/url?q=https://imiwins.com/
http://images.google.co.ve/url?q=https://imiwins.com/
http://images.google.com.vn/url?q=https://imiwins.com/
http://images.google.co.vi/url?q=https://imiwins.com/
http://images.google.co.zm/url?q=https://imiwins.com/
http://images.google.co.zw/url?q=https://imiwins.com/
adidas revenergy boost mujer
antipasti pesce per natale amazonteli fasciatoio amazondou dou abbigliamento bambino amazonmeister levigatrice orbitale amazon
cicret narukvica cijena
nike air max 1 barely rose319986607adidas s12676air jordan 1 retro high og lanike sneaker huarache run
asics running shoes gt 1000 6
colliers de serrage fap ligneaudrey hepburn lunettes de soleilboot campmaillot triangle femme
bluetooth klinke empf盲nger amazon
geci macronochelari de soare polarizati visiniipantofi vera pelleghiozdane scoala baieti
Obese individuals with binge eating have a higher life-time prevalence of mood,
anxiety, alcohol use, and person-ality disorders than obese individuals without binge eating 2—5.
viagra or cialis Obese individuals
with binge eating have a higher life-time prevalence of mood,
anxiety, alcohol use, and person-ality disorders than obese
individuals without binge eating 2—5.
Описание зеркала Mostbet mostbet официальный сайт вход регистрация моя страница
http://yoshino-net.s8.xrea.com/cgi/aska.cgi
Ниша ставок в РФ существует достаточно долгое время, и в
2012 году вышла на рынок фирма Мостбет.
На сегодняшний день ресурс стабильно развивается, в частности это относится к виртуальному пространству.
Как полагают некоторые клиенты, достаточно комфортно
не выходя из дома, в офисе или в дороге ставить на события.
Время не будет потеряно.
Главная цель компании – помогать
людям ставить, это удобно выполнить через офисы компании или же в режиме онлайн, для этого имеется сайт и приложение для смартфона.
Как видите,, предусмотрено немало способов, чтобы с удовольствием провести свободное время,
а вместе с тем попытаться заработать приличные выигрыши.
Компания мостбет войти
довольно стремительно развивается и намерена
создать для своих клиентов самые лучшие возможности.
Тут вы можете делать ставки как на спортивные, так и на иные события, к примеру, турниры типа Евровидения.
Больше не нужно просто смотреть
за тем, как выступает любимый исполнитель.
Стоит всего лишь поверить в его триумф, сделав выгодную ставку.
Существует шанс, что удастся сорвать куш
, а заодно послушать отличную музыку.
Такой подход крайне удобен, так как в этом случае безусловно каждый человек сможет найти для себя интересные мероприятия и поставит на
его исход.
Разработчики смогли предусмореть мероприятия на любой вкус.
Решение связано с Вашим
возрастом, увлечениями, желанием и возможностью идти на риск.
Как начинать делать ставки
на спорт с Мостбет
Некоторые игроки думают, что ставить на спортивные баталии или иные события
– это довольно хлопотно и что в этом нужно тратить время на разбирательство.
Но так ли это на самом деле?
Конечно же, это не так.
Если идет разговор о Мостбет http://vip.023yl.xyz/home.php?mod=space&uid=59344&do=profile&from=space мостбет войти в личный кабинет
, то в этом случае начать делать ставки получится у любого желающего.
На уровне интуиции понятный интерфейс понравится даже
новичкам, которые только решили
разобраться с тем, как ставить.
Рассмотрим более подробно, каким образом начать это делать.
Для старта необходимо зарегистрироваться на
портале.
Процесс прохождения регистрации очень простой, займет у вас минимальное количество времени.
Потребуется всего лишь
ввести персональные данные
в специальные поля, пройти процесс верификации.
После регистрации надо будет
положить некоторую сумму на депозит.
Абсолютно не играет роли, какая именно будет зачислена денежная сумма.
Совсем скоро Вы разберетесь и
поймете, как действовать дальше, какие размеры ставки считаются наиболее приемлемыми.
И после этого вы можете начать ставить на
события.
Теперь становится понятно, что выполнять подобные манипуляции
совершенно не сложно, потому что на эти действия уйдет у вас минимальное количество времени и
сил.
Выходит, абсолютно любой из игроков сумеет начать ставить независимо от того новичок он или профессионал.
Все, что для этого нужно – пройти
регистрацию.
Компания Mostbet – входит в число известных и востребованных компаний на рынке
России, что совсем не удивительно.
Ведь компания с заботой относится к своим клиентам и предлагает для них наилучшие условия.
Руководству важно не просто привлечь новых игроков, а и создать наиболее удачные обстоятельства для постоянных клиентов.
Имидж считается важным показателем для конторы во
имя того, чтобы не потерять веры пользователей.
В области ставок существует большое число мошенников.
Не следует слепо доверять яркой рекламе, а также идти на поводу у слишком выгодных
условий.
Можно не только лишиться денег, безрассудно потерять время,
но и установить на ноутбук вирус.
Уместнее выбирать лишь проверенные компании, которые длительное время
пребывают в игровой отрасли.
Всегда можно изучить отклики, узнать о времени появления
конторы на просторах интернета.
Среди таких профессионалов своего дела
считается мостбет зеркало рабочее на сегодня прямо
В определенный момент можно загрузить специально
созданное мобильное приложение.
Останется обеспечить наличие сети Интернет, чтобы
делать ставки уже сегодня.
У Вас будет возможность выбрать мероприятие,
сделать прогноз, находясь в пробке
или за городом.
Не это ли и есть одно из преимуществ, за которые стоит выбирать данную компанию?
Именно это подтвердило огромное количество пользователей конторы.
В таком случае, если вы хотите испытывать удачу на ставках, то вам стоит обратить
внимание на Mostbet.
Тут Mostbet-partner.com вы найдете необходимую информацию и
ответы на свои вопросы, а также немедленно начать делать ставки после того, как зарегистрируетесь.
In India, the 1xBet betting company – is one of the most popular ones in Asia.
To each its dominant advantages, one can note high odds, a sympathetic vigour line on presented events and on the up established payoffs.
In its functionality, the reflection copy is no unconventional from the main resource, providing users with all the yet capabilities.
1xBet betting company
1xbet app download http://www.ner.org/forums/users/kathied348195695/
1xbet app
Using the bearing for Android, players can stake
on sports in expeditions, at work or at home. All that is required – is access to the
Internet. In dictate to initiate the program, go to the “Applications object of smartphones” portion,
countersign non-stationary phone thousand in the opened form.
In a insufficient minutes, an SMS missive with download affiliation will
arrive.
1xbet apk 1xbet apk India
1xbet apk
The 1xBet mobile app since iOS can be downloaded in the App Store.
A rule download element is handy on the betting attendance’s official website – replace the installation instruction.
Unspecific word
With help of our website there is an opportunity
to collar access to the website about the clock, placing bets on events of interest.
The betting dais in India can be tolerant of not contrariwise from a PC, but also from
most non-stationary devices.
Entitle
The 1xBet troop operates on the Internet legally.
To present services, the betting companions has a empower issued through the cosmopolitan regulator of Curacao.
It allows the platform to enlarge on a excite
in multifarious countries without violating law.
Look over of the 1xBet official Indian website
The betting party line offers visitors to venture on sports and financial events.
Bettors also prepare access to online slit machines and a essential casino.
A athlete can wager mazuma in any sections of the website using a single
account. The betting company has a godlike vitality extraction and
direct small change face on all events. Users can play in more than 40 sports types, ranging from popular football and tennis
to exotic cockfights.
The betting coterie accepts bets on almost all outcomes: not sole on a superiority or get the better of of ditty of teams, but also on a tot up of corner kicks,
penalties and other results. One can check out a less unshakeable action strip at the 1xBet betting circle only before avoided events.
But equal here entire can bet on over/under, obstacle and some
other outcomes. Players can evaluate all the possibilities of moneyed betting
one after creating an account.
Registration in the 1xБет India 1xbet india
http://bbs.laotingbest.com/home.php?mod=space&uid=31263&do=profile&from=space
Registration in the 1xБет India
Unified can turn on a graph in the betting assemblage in 4 ways:
via a rapid registration procedure. A thespian needs to click on the
happy lappet and single out the country of residence.
After a occasional seconds, the drug drive be premised a countersign and login,
which wish be created next to the arrangement;
registration procedure
by creating an account using phone. In this case, during registration methodology a visitor
necessity direct attention to the mobile phone multitude onto which SMS message intent come with blow-by-blow instructions;
creating an account using phone
via registering via email. The rule choice,
at which purchaser fills out registration shape, prescribing dear observations and a valid e-mail.
Later a communiqu‚ with a association comes to the purchaser’s specified e-mail,
which becomes a pass to the 1xBet India website;
by registering via sexually transmitted networks.
The easiest crumble to motivate an account. A sportswoman however needs
to click on the icon with the group network where he has a profile, after which an account
is automatically generated.
1xbet login
1xbet login
Inseparable can enlist the 1xBet website in the even so way as on the greatest 1xbet
com resource. It is adequately after a user to up in the way in any suitable way, and then authorize away entering the life-and-death
password and login. In some cases, to enter insulting account,
anybody may demand a dear jus canonicum ‘canon law’ that the betting visitors sends in the pose of SMS message onto
a mobile phone number.
In situation of problems with entering an account enough to a loss of a open sesame, the contender drive be clever
to resolve the copy quickly. To do this, only click on the “Forgot your password?” flag, editorial down the email speak or phone handful next to it.
The owner will be obtain allied facts to the specified contacts.
The password sent pleasure arrogate to log in to the account.
Depositing coins
After fleeting registration and authorizing on the website, user will be accomplished to replace
funds in his intimate account. To do this, go to the “Payments” section.
There, the performer purpose be wise to persevere divers options for depositing funds into the account:
bank delivery;
electronic wallets and payment systems;
payment auspices of the mortal;
greenbacks over from a motorized phone;
Internet banking;
cryptocurrency
prepaid cards.
In total, the website of the betting coterie provides more than 40 options instead of depositing
capital. Regardless of the chosen method, economic transactions on the
website are carried out instantly. The one worthy trend benefit of a
sportsman – is to serve the rules established by the betting
company. In the course of example, the replenishment amount should be no less than 100 rubles.
In withal, it is strictly forbidden to use other people’s wallets and bank
cards to part money. Loser to yield with these conditions may be to blocking of
the account.
Spinach withdrawal from the 1xbet in India 1xbet login
To leave funds to of the set-up it is necessary to use the same sense
as with replenishment. To frame a fiscal acta, a musician needs to go to personal account and supreme the “Banknotes withdrawal” section.
There the alcohol wishes constraint to indicate the amount to be
transferred, and inscribe the text from his electronic notecase or bank card.
If all the data is traditional, the devotion with a view funds withdrawal
wish be processed via the betting company within 1-7 days.
In system to refrain from delays in payoffs of earned winnings, players requisite to pass account verification procedure 1xbet app download .
During this gate, the consumer pass on be
required to purvey the 1xBet administering in India with copies of his identity
documents. Passed also nett verification transfer admit undivided remove
funds from the website far, at any convenient time.
It is notable on players to commemorate that the betting presence has
introduce certain limits on in clover withdrawal. In case of any problems with withdrawal of funds, bettors can connection the
support service in regard to help. Stand by caduceus mould
at the website around the clock.
Bonuses from 1xBet
The betting business offers visitors a valid bonus program.
Players can foresee to receive the following types of bonuses:
“In behalf of the inception deposit.” The amount of the promotion is 100% from the
deposited amount. The gain requisite be won go at three bets of the Express fount with a
coefficient of at least 1.4;
“Advantageous Friday”. The tip is issued to players strictly on the specified day.
The win back conditions are the unaltered as with the recompense after the first bank;
“Wednesday – multiply by way of 2”. Cappers who won on the
“Convenient Friday” are allowed to participate in the action.
If the user has not hitherto distant the funds won from the past week,
his deposit is doubled by the betting ensemble;
“Demonstrate of the day.” The design is held daily. If a actress achieves big name in the Dance or the
Complete, he command receive an developing in the envisage of 10% of the earned winnings;
“Bonus inasmuch as a series of failures.”
Purchaser receive subsidize take a hand in of the squandered
money, upon form of 20 hapless bets in a row with a coefficient of not more than 3.
Hi there this is kind of of off topic but I was wondering if blogs use WYSIWYG editors or if you have to
manually code with HTML. I’m starting a blog soon but have no coding expertise
so I wanted to get guidance from someone with experience.
Any help would be greatly appreciated!
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
<a href="http:
It’s very easy to find out any matter on net as compared to books, as
I found this paragraph at this web page.
Excellent goods from you, man. I have bear in mind your stuff
previous to and you’re just too excellent. I really like what
you have bought here, certainly like what you’re stating
and the way in which you are saying it. You make it enjoyable and
you still care for to keep it sensible. I can not wait to read far more from you.
This is actually a terrific website.
Hmm is anyone else encountering problems with the pictures on this blog loading?
I’m trying to figure out if its a problem on my end or if
it’s the blog. Any responses would be greatly appreciated.
Fantastic web site. Lots of helpful info here. I am sending it to several buddies ans additionally
sharing in delicious. And obviously, thank you for your effort!
I was able to find good information from your blog posts.
I like the valuable info you supply for your articles.
I will bookmark your blog and check once more here regularly.
I’m rather certain I will be told plenty of new stuff proper right here!
Best of luck for the next!
http://google.com.af/url?q=https://segurodeobamacare.com/
http://google.al/url?q=https://segurodeobamacare.com/
http://google.dz/url?q=https://segurodeobamacare.com/
http://google.as/url?q=https://segurodeobamacare.com/
http://google.ad/url?q=https://segurodeobamacare.com/
http://google.it.ao/url?q=https://segurodeobamacare.com/
http://google.com.ai/url?q=https://segurodeobamacare.com/
http://google.com.ag/url?q=https://segurodeobamacare.com/
http://google.com.ar/url?q=https://segurodeobamacare.com/
http://google.am/url?q=https://segurodeobamacare.com/
http://google.ac/url?q=https://segurodeobamacare.com/
http://google.com.au/url?q=https://segurodeobamacare.com/
http://google.at/url?q=https://segurodeobamacare.com/
http://google.az/url?q=https://segurodeobamacare.com/
http://google.bs/url?q=https://segurodeobamacare.com/
http://google.com.bh/url?q=https://segurodeobamacare.com/
http://google.com.bd/url?q=https://segurodeobamacare.com/
http://google.com.by/url?q=https://segurodeobamacare.com/
http://google.be/url?q=https://segurodeobamacare.com/
http://google.com.bz/url?q=https://segurodeobamacare.com/
http://google.bj/url?q=https://segurodeobamacare.com/
http://google.bt/url?q=https://segurodeobamacare.com/
http://google.com.bo/url?q=https://segurodeobamacare.com/
http://google.ba/url?q=https://segurodeobamacare.com/
http://google.co.bw/url?q=https://segurodeobamacare.com/
http://google.com.br/url?q=https://segurodeobamacare.com/
http://google.vg/url?q=https://segurodeobamacare.com/
http://google.com.bn/url?q=https://segurodeobamacare.com/
http://google.bg/url?q=https://segurodeobamacare.com/
http://google.bf/url?q=https://segurodeobamacare.com/
http://google.bi/url?q=https://segurodeobamacare.com/
http://google.com.kh/url?q=https://segurodeobamacare.com/
http://google.cm/url?q=https://segurodeobamacare.com/
http://google.ca/url?q=https://segurodeobamacare.com/
http://google.cv/url?q=https://segurodeobamacare.com/
http://google.cat/url?q=https://segurodeobamacare.com/
http://google.cf/url?q=https://segurodeobamacare.com/
http://google.td/url?q=https://segurodeobamacare.com/
http://google.cl/url?q=https://segurodeobamacare.com/
http://google.cn/url?q=https://segurodeobamacare.com/
http://google.com.co/url?q=https://segurodeobamacare.com/
http://google.cd/url?q=https://segurodeobamacare.com/
http://google.cg/url?q=https://segurodeobamacare.com/
http://google.co.ck/url?q=https://segurodeobamacare.com/
http://google.co.cr/url?q=https://segurodeobamacare.com/
http://google.ci/url?q=https://segurodeobamacare.com/
http://google.hr/url?q=https://segurodeobamacare.com/
http://google.com.cu/url?q=https://segurodeobamacare.com/
http://google.com.cy/url?q=https://segurodeobamacare.com/
http://google.cz/url?q=https://segurodeobamacare.com/
http://google.dk/url?q=https://segurodeobamacare.com/
http://google.dj/url?q=https://segurodeobamacare.com/
http://google.dm/url?q=https://segurodeobamacare.com/
http://google.com.do/url?q=https://segurodeobamacare.com/
http://google.com.ec/url?q=https://segurodeobamacare.com/
http://google.com.eg/url?q=https://segurodeobamacare.com/
http://google.com.sv/url?q=https://segurodeobamacare.com/
http://google.ee/url?q=https://segurodeobamacare.com/
http://google.com.et/url?q=https://segurodeobamacare.com/
http://google.com.fj/url?q=https://segurodeobamacare.com/
http://google.fi/url?q=https://segurodeobamacare.com/
http://google.fr/url?q=https://segurodeobamacare.com/
http://google.ga/url?q=https://segurodeobamacare.com/
http://google.gm/url?q=https://segurodeobamacare.com/
http://google.ge/url?q=https://segurodeobamacare.com/
http://google.de/url?q=https://segurodeobamacare.com/
http://google.com.gh/url?q=https://segurodeobamacare.com/
http://google.com.gi/url?q=https://segurodeobamacare.com/
http://google.gr/url?q=https://segurodeobamacare.com/
http://google.gl/url?q=https://segurodeobamacare.com/
http://google.gp/url?q=https://segurodeobamacare.com/
http://google.com.gt/url?q=https://segurodeobamacare.com/
http://google.gg/url?q=https://segurodeobamacare.com/
http://google.gy/url?q=https://segurodeobamacare.com/
http://google.ht/url?q=https://segurodeobamacare.com/
http://google.hn/url?q=https://segurodeobamacare.com/
http://google.com.hk/url?q=https://segurodeobamacare.com/
http://google.hu/url?q=https://segurodeobamacare.com/
http://google.is/url?q=https://segurodeobamacare.com/
http://google.co.in/url?q=https://segurodeobamacare.com/
http://google.co.id/url?q=https://segurodeobamacare.com/
http://google.iq/url?q=https://segurodeobamacare.com/
http://google.ie/url?q=https://segurodeobamacare.com/
http://google.co.im/url?q=https://segurodeobamacare.com/
http://google.co.il/url?q=https://segurodeobamacare.com/
http://google.it/url?q=https://segurodeobamacare.com/
http://google.ci/url?q=https://segurodeobamacare.com/
http://google.com.jm/url?q=https://segurodeobamacare.com/
http://google.co.jp/url?q=https://segurodeobamacare.com/
http://google.co.je/url?q=https://segurodeobamacare.com/
http://google.jo/url?q=https://segurodeobamacare.com/
http://google.kz/url?q=https://segurodeobamacare.com/
http://google.co.ke/url?q=https://segurodeobamacare.com/
http://google.ki/url?q=https://segurodeobamacare.com/
http://google.com.kw/url?q=https://segurodeobamacare.com/
http://google.com.kg/url?q=https://segurodeobamacare.com/
http://google.la/url?q=https://segurodeobamacare.com/
http://google.lv/url?q=https://segurodeobamacare.com/
http://google.com.lb/url?q=https://segurodeobamacare.com/
http://google.co.ls/url?q=https://segurodeobamacare.com/
http://google.com.ly/url?q=https://segurodeobamacare.com/
http://google.li/url?q=https://segurodeobamacare.com/
http://google.lt/url?q=https://segurodeobamacare.com/
http://google.lu/url?q=https://segurodeobamacare.com/
http://google.mk/url?q=https://segurodeobamacare.com/
http://google.mg/url?q=https://segurodeobamacare.com/
http://google.mw/url?q=https://segurodeobamacare.com/
http://google.com.my/url?q=https://segurodeobamacare.com/
http://google.mv/url?q=https://segurodeobamacare.com/
http://google.ml/url?q=https://segurodeobamacare.com/
http://google.com.mt/url?q=https://segurodeobamacare.com/
http://google.mu/url?q=https://segurodeobamacare.com/
http://google.com.mx/url?q=https://segurodeobamacare.com/
http://google.fm/url?q=https://segurodeobamacare.com/
http://google.md/url?q=https://segurodeobamacare.com/
http://google.mn/url?q=https://segurodeobamacare.com/
http://google.me/url?q=https://segurodeobamacare.com/
http://google.ms/url?q=https://segurodeobamacare.com/
http://google.co.ma/url?q=https://segurodeobamacare.com/
http://google.co.mz/url?q=https://segurodeobamacare.com/
http://google.com.na/url?q=https://segurodeobamacare.com/
http://google.nr/url?q=https://segurodeobamacare.com/
http://google.com.np/url?q=https://segurodeobamacare.com/
http://google.nl/url?q=https://segurodeobamacare.com/
http://google.co.nz/url?q=https://segurodeobamacare.com/
http://google.com.ni/url?q=https://segurodeobamacare.com/
http://google.ne/url?q=https://segurodeobamacare.com/
http://google.com.ng/url?q=https://segurodeobamacare.com/
http://google.nu/url?q=https://segurodeobamacare.com/
http://google.com.nf/url?q=https://segurodeobamacare.com/
http://google.no/url?q=https://segurodeobamacare.com/
http://google.com.om/url?q=https://segurodeobamacare.com/
http://google.com.pk/url?q=https://segurodeobamacare.com/
http://google.ps/url?q=https://segurodeobamacare.com/
http://google.com.pa/url?q=https://segurodeobamacare.com/
http://google.com.pg/url?q=https://segurodeobamacare.com/
http://google.com.py/url?q=https://segurodeobamacare.com/
http://google.com.pe/url?q=https://segurodeobamacare.com/
http://google.com.ph/url?q=https://segurodeobamacare.com/
http://google.pn/url?q=https://segurodeobamacare.com/
http://google.pl/url?q=https://segurodeobamacare.com/
http://google.pt/url?q=https://segurodeobamacare.com/
http://google.com.pr/url?q=https://segurodeobamacare.com/
http://google.com.qa/url?q=https://segurodeobamacare.com/
http://google.ro/url?q=https://segurodeobamacare.com/
http://google.ru/url?q=https://segurodeobamacare.com/
http://google.rw/url?q=https://segurodeobamacare.com/
http://google.sh/url?q=https://segurodeobamacare.com/
http://google.ws/url?q=https://segurodeobamacare.com/
http://google.sm/url?q=https://segurodeobamacare.com/
http://google.st/url?q=https://segurodeobamacare.com/
http://google.com.sa/url?q=https://segurodeobamacare.com/
http://google.sn/url?q=https://segurodeobamacare.com/
http://google.rs/url?q=https://segurodeobamacare.com/
http://google.sc/url?q=https://segurodeobamacare.com/
http://google.com.sl/url?q=https://segurodeobamacare.com/
http://google.com.sg/url?q=https://segurodeobamacare.com/
http://google.sk/url?q=https://segurodeobamacare.com/
http://google.si/url?q=https://segurodeobamacare.com/
http://google.com.sb/url?q=https://segurodeobamacare.com/
http://google.so/url?q=https://segurodeobamacare.com/
http://google.co.za/url?q=https://segurodeobamacare.com/
http://google.co.kr/url?q=https://segurodeobamacare.com/
http://google.es/url?q=https://segurodeobamacare.com/
http://google.lk/url?q=https://segurodeobamacare.com/
http://google.com.vc/url?q=https://segurodeobamacare.com/
http://google.sr/url?q=https://segurodeobamacare.com/
http://google.se/url?q=https://segurodeobamacare.com/
http://google.ch/url?q=https://segurodeobamacare.com/
http://google.com.tw/url?q=https://segurodeobamacare.com/
http://google.com.tj/url?q=https://segurodeobamacare.com/
http://google.co.tz/url?q=https://segurodeobamacare.com/
http://google.co.th/url?q=https://segurodeobamacare.com/
http://google.tl/url?q=https://segurodeobamacare.com/
http://google.tg/url?q=https://segurodeobamacare.com/
http://google.tk/url?q=https://segurodeobamacare.com/
http://google.to/url?q=https://segurodeobamacare.com/
http://google.tt/url?q=https://segurodeobamacare.com/
http://google.tn/url?q=https://segurodeobamacare.com/
http://google.com.tr/url?q=https://segurodeobamacare.com/
http://google.tm/url?q=https://segurodeobamacare.com/
http://google.co.ug/url?q=https://segurodeobamacare.com/
http://google.com.ua/url?q=https://segurodeobamacare.com/
http://google.ae/url?q=https://segurodeobamacare.com/
http://google.co.uk/url?q=https://segurodeobamacare.com/
http://google.com/url?q=https://segurodeobamacare.com/
http://google.com.uy/url?q=https://segurodeobamacare.com/
http://google.co.uz/url?q=https://segurodeobamacare.com/
http://google.vu/url?q=https://segurodeobamacare.com/
http://google.co.ve/url?q=https://segurodeobamacare.com/
http://google.com.vn/url?q=https://segurodeobamacare.com/
http://google.co.vi/url?q=https://segurodeobamacare.com/
http://google.co.zm/url?q=https://segurodeobamacare.com/
http://google.co.zw/url?q=https://segurodeobamacare.com/
http://maps.google.com.af/url?q=https://segurodeobamacare.com/
http://maps.google.al/url?q=https://segurodeobamacare.com/
http://maps.google.dz/url?q=https://segurodeobamacare.com/
http://maps.google.as/url?q=https://segurodeobamacare.com/
http://maps.google.ad/url?q=https://segurodeobamacare.com/
http://maps.google.it.ao/url?q=https://segurodeobamacare.com/
http://maps.google.com.ai/url?q=https://segurodeobamacare.com/
http://maps.google.com.ag/url?q=https://segurodeobamacare.com/
http://maps.google.com.ar/url?q=https://segurodeobamacare.com/
http://maps.google.am/url?q=https://segurodeobamacare.com/
http://maps.google.ac/url?q=https://segurodeobamacare.com/
http://maps.google.com.au/url?q=https://segurodeobamacare.com/
http://maps.google.at/url?q=https://segurodeobamacare.com/
http://maps.google.az/url?q=https://segurodeobamacare.com/
http://maps.google.bs/url?q=https://segurodeobamacare.com/
http://maps.google.com.bh/url?q=https://segurodeobamacare.com/
http://maps.google.com.bd/url?q=https://segurodeobamacare.com/
http://maps.google.com.by/url?q=https://segurodeobamacare.com/
http://maps.google.be/url?q=https://segurodeobamacare.com/
http://maps.google.com.bz/url?q=https://segurodeobamacare.com/
http://maps.google.bj/url?q=https://segurodeobamacare.com/
http://maps.google.bt/url?q=https://segurodeobamacare.com/
http://maps.google.com.bo/url?q=https://segurodeobamacare.com/
http://maps.google.ba/url?q=https://segurodeobamacare.com/
http://maps.google.co.bw/url?q=https://segurodeobamacare.com/
http://maps.google.com.br/url?q=https://segurodeobamacare.com/
http://maps.google.vg/url?q=https://segurodeobamacare.com/
http://maps.google.com.bn/url?q=https://segurodeobamacare.com/
http://maps.google.bg/url?q=https://segurodeobamacare.com/
http://maps.google.bf/url?q=https://segurodeobamacare.com/
http://maps.google.bi/url?q=https://segurodeobamacare.com/
http://maps.google.com.kh/url?q=https://segurodeobamacare.com/
http://maps.google.cm/url?q=https://segurodeobamacare.com/
http://maps.google.ca/url?q=https://segurodeobamacare.com/
http://maps.google.cv/url?q=https://segurodeobamacare.com/
http://maps.google.cat/url?q=https://segurodeobamacare.com/
http://maps.google.cf/url?q=https://segurodeobamacare.com/
http://maps.google.td/url?q=https://segurodeobamacare.com/
http://maps.google.cl/url?q=https://segurodeobamacare.com/
http://maps.google.cn/url?q=https://segurodeobamacare.com/
http://maps.google.com.co/url?q=https://segurodeobamacare.com/
http://maps.google.cd/url?q=https://segurodeobamacare.com/
http://maps.google.cg/url?q=https://segurodeobamacare.com/
http://maps.google.co.ck/url?q=https://segurodeobamacare.com/
http://maps.google.co.cr/url?q=https://segurodeobamacare.com/
http://maps.google.ci/url?q=https://segurodeobamacare.com/
http://maps.google.hr/url?q=https://segurodeobamacare.com/
http://maps.google.com.cu/url?q=https://segurodeobamacare.com/
http://maps.google.com.cy/url?q=https://segurodeobamacare.com/
http://maps.google.cz/url?q=https://segurodeobamacare.com/
http://maps.google.dk/url?q=https://segurodeobamacare.com/
http://maps.google.dj/url?q=https://segurodeobamacare.com/
http://maps.google.dm/url?q=https://segurodeobamacare.com/
http://maps.google.com.do/url?q=https://segurodeobamacare.com/
http://maps.google.com.ec/url?q=https://segurodeobamacare.com/
http://maps.google.com.eg/url?q=https://segurodeobamacare.com/
http://maps.google.com.sv/url?q=https://segurodeobamacare.com/
http://maps.google.ee/url?q=https://segurodeobamacare.com/
http://maps.google.com.et/url?q=https://segurodeobamacare.com/
http://maps.google.com.fj/url?q=https://segurodeobamacare.com/
http://maps.google.fi/url?q=https://segurodeobamacare.com/
http://maps.google.fr/url?q=https://segurodeobamacare.com/
http://maps.google.ga/url?q=https://segurodeobamacare.com/
http://maps.google.gm/url?q=https://segurodeobamacare.com/
http://maps.google.ge/url?q=https://segurodeobamacare.com/
http://maps.google.de/url?q=https://segurodeobamacare.com/
http://maps.google.com.gh/url?q=https://segurodeobamacare.com/
http://maps.google.com.gi/url?q=https://segurodeobamacare.com/
http://maps.google.gr/url?q=https://segurodeobamacare.com/
http://maps.google.gl/url?q=https://segurodeobamacare.com/
http://maps.google.gp/url?q=https://segurodeobamacare.com/
http://maps.google.com.gt/url?q=https://segurodeobamacare.com/
http://maps.google.gg/url?q=https://segurodeobamacare.com/
http://maps.google.gy/url?q=https://segurodeobamacare.com/
http://maps.google.ht/url?q=https://segurodeobamacare.com/
http://maps.google.hn/url?q=https://segurodeobamacare.com/
http://maps.google.com.hk/url?q=https://segurodeobamacare.com/
http://maps.google.hu/url?q=https://segurodeobamacare.com/
http://maps.google.is/url?q=https://segurodeobamacare.com/
http://maps.google.co.in/url?q=https://segurodeobamacare.com/
http://maps.google.co.id/url?q=https://segurodeobamacare.com/
http://maps.google.iq/url?q=https://segurodeobamacare.com/
http://maps.google.ie/url?q=https://segurodeobamacare.com/
http://maps.google.co.im/url?q=https://segurodeobamacare.com/
http://maps.google.co.il/url?q=https://segurodeobamacare.com/
http://maps.google.it/url?q=https://segurodeobamacare.com/
http://maps.google.ci/url?q=https://segurodeobamacare.com/
http://maps.google.com.jm/url?q=https://segurodeobamacare.com/
http://maps.google.co.jp/url?q=https://segurodeobamacare.com/
http://maps.google.co.je/url?q=https://segurodeobamacare.com/
http://maps.google.jo/url?q=https://segurodeobamacare.com/
http://maps.google.kz/url?q=https://segurodeobamacare.com/
http://maps.google.co.ke/url?q=https://segurodeobamacare.com/
http://maps.google.ki/url?q=https://segurodeobamacare.com/
http://maps.google.com.kw/url?q=https://segurodeobamacare.com/
http://maps.google.com.kg/url?q=https://segurodeobamacare.com/
http://maps.google.la/url?q=https://segurodeobamacare.com/
http://maps.google.lv/url?q=https://segurodeobamacare.com/
http://maps.google.com.lb/url?q=https://segurodeobamacare.com/
http://maps.google.co.ls/url?q=https://segurodeobamacare.com/
http://maps.google.com.ly/url?q=https://segurodeobamacare.com/
http://maps.google.li/url?q=https://segurodeobamacare.com/
http://maps.google.lt/url?q=https://segurodeobamacare.com/
http://maps.google.lu/url?q=https://segurodeobamacare.com/
http://maps.google.mk/url?q=https://segurodeobamacare.com/
http://maps.google.mg/url?q=https://segurodeobamacare.com/
http://maps.google.mw/url?q=https://segurodeobamacare.com/
http://maps.google.com.my/url?q=https://segurodeobamacare.com/
http://maps.google.mv/url?q=https://segurodeobamacare.com/
http://maps.google.ml/url?q=https://segurodeobamacare.com/
http://maps.google.com.mt/url?q=https://segurodeobamacare.com/
http://maps.google.mu/url?q=https://segurodeobamacare.com/
http://maps.google.com.mx/url?q=https://segurodeobamacare.com/
http://maps.google.fm/url?q=https://segurodeobamacare.com/
http://maps.google.md/url?q=https://segurodeobamacare.com/
http://maps.google.mn/url?q=https://segurodeobamacare.com/
http://maps.google.me/url?q=https://segurodeobamacare.com/
http://maps.google.ms/url?q=https://segurodeobamacare.com/
http://maps.google.co.ma/url?q=https://segurodeobamacare.com/
http://maps.google.co.mz/url?q=https://segurodeobamacare.com/
http://maps.google.com.na/url?q=https://segurodeobamacare.com/
http://maps.google.nr/url?q=https://segurodeobamacare.com/
http://maps.google.com.np/url?q=https://segurodeobamacare.com/
http://maps.google.nl/url?q=https://segurodeobamacare.com/
http://maps.google.co.nz/url?q=https://segurodeobamacare.com/
http://maps.google.com.ni/url?q=https://segurodeobamacare.com/
http://maps.google.ne/url?q=https://segurodeobamacare.com/
http://maps.google.com.ng/url?q=https://segurodeobamacare.com/
http://maps.google.nu/url?q=https://segurodeobamacare.com/
http://maps.google.com.nf/url?q=https://segurodeobamacare.com/
http://maps.google.no/url?q=https://segurodeobamacare.com/
http://maps.google.com.om/url?q=https://segurodeobamacare.com/
http://maps.google.com.pk/url?q=https://segurodeobamacare.com/
http://maps.google.ps/url?q=https://segurodeobamacare.com/
http://maps.google.com.pa/url?q=https://segurodeobamacare.com/
http://maps.google.com.pg/url?q=https://segurodeobamacare.com/
http://maps.google.com.py/url?q=https://segurodeobamacare.com/
http://maps.google.com.pe/url?q=https://segurodeobamacare.com/
http://maps.google.com.ph/url?q=https://segurodeobamacare.com/
http://maps.google.pn/url?q=https://segurodeobamacare.com/
http://maps.google.pl/url?q=https://segurodeobamacare.com/
http://maps.google.pt/url?q=https://segurodeobamacare.com/
http://maps.google.com.pr/url?q=https://segurodeobamacare.com/
http://maps.google.com.qa/url?q=https://segurodeobamacare.com/
http://maps.google.ro/url?q=https://segurodeobamacare.com/
http://maps.google.ru/url?q=https://segurodeobamacare.com/
http://maps.google.rw/url?q=https://segurodeobamacare.com/
http://maps.google.sh/url?q=https://segurodeobamacare.com/
http://maps.google.ws/url?q=https://segurodeobamacare.com/
http://maps.google.sm/url?q=https://segurodeobamacare.com/
http://maps.google.st/url?q=https://segurodeobamacare.com/
http://maps.google.com.sa/url?q=https://segurodeobamacare.com/
http://maps.google.sn/url?q=https://segurodeobamacare.com/
http://maps.google.rs/url?q=https://segurodeobamacare.com/
http://maps.google.sc/url?q=https://segurodeobamacare.com/
http://maps.google.com.sl/url?q=https://segurodeobamacare.com/
http://maps.google.com.sg/url?q=https://segurodeobamacare.com/
http://maps.google.sk/url?q=https://segurodeobamacare.com/
http://maps.google.si/url?q=https://segurodeobamacare.com/
http://maps.google.com.sb/url?q=https://segurodeobamacare.com/
http://maps.google.so/url?q=https://segurodeobamacare.com/
http://maps.google.co.za/url?q=https://segurodeobamacare.com/
http://maps.google.co.kr/url?q=https://segurodeobamacare.com/
http://maps.google.es/url?q=https://segurodeobamacare.com/
http://maps.google.lk/url?q=https://segurodeobamacare.com/
http://maps.google.com.vc/url?q=https://segurodeobamacare.com/
http://maps.google.sr/url?q=https://segurodeobamacare.com/
http://maps.google.se/url?q=https://segurodeobamacare.com/
http://maps.google.ch/url?q=https://segurodeobamacare.com/
http://maps.google.com.tw/url?q=https://segurodeobamacare.com/
http://maps.google.com.tj/url?q=https://segurodeobamacare.com/
http://maps.google.co.tz/url?q=https://segurodeobamacare.com/
http://maps.google.co.th/url?q=https://segurodeobamacare.com/
http://maps.google.tl/url?q=https://segurodeobamacare.com/
http://maps.google.tg/url?q=https://segurodeobamacare.com/
http://maps.google.tk/url?q=https://segurodeobamacare.com/
http://maps.google.to/url?q=https://segurodeobamacare.com/
http://maps.google.tt/url?q=https://segurodeobamacare.com/
http://maps.google.tn/url?q=https://segurodeobamacare.com/
http://maps.google.com.tr/url?q=https://segurodeobamacare.com/
http://maps.google.tm/url?q=https://segurodeobamacare.com/
http://maps.google.co.ug/url?q=https://segurodeobamacare.com/
http://maps.google.com.ua/url?q=https://segurodeobamacare.com/
http://maps.google.ae/url?q=https://segurodeobamacare.com/
http://maps.google.co.uk/url?q=https://segurodeobamacare.com/
http://maps.google.com/url?q=https://segurodeobamacare.com/
http://maps.google.com.uy/url?q=https://segurodeobamacare.com/
http://maps.google.co.uz/url?q=https://segurodeobamacare.com/
http://maps.google.vu/url?q=https://segurodeobamacare.com/
http://maps.google.co.ve/url?q=https://segurodeobamacare.com/
http://maps.google.com.vn/url?q=https://segurodeobamacare.com/
http://maps.google.co.vi/url?q=https://segurodeobamacare.com/
http://maps.google.co.zm/url?q=https://segurodeobamacare.com/
http://maps.google.co.zw/url?q=https://segurodeobamacare.com/
http://images.google.com.af/url?q=https://segurodeobamacare.com/
http://images.google.al/url?q=https://segurodeobamacare.com/
http://images.google.dz/url?q=https://segurodeobamacare.com/
http://images.google.as/url?q=https://segurodeobamacare.com/
http://images.google.ad/url?q=https://segurodeobamacare.com/
http://images.google.it.ao/url?q=https://segurodeobamacare.com/
http://images.google.com.ai/url?q=https://segurodeobamacare.com/
http://images.google.com.ag/url?q=https://segurodeobamacare.com/
http://images.google.com.ar/url?q=https://segurodeobamacare.com/
http://images.google.am/url?q=https://segurodeobamacare.com/
http://images.google.ac/url?q=https://segurodeobamacare.com/
http://images.google.com.au/url?q=https://segurodeobamacare.com/
http://images.google.at/url?q=https://segurodeobamacare.com/
http://images.google.az/url?q=https://segurodeobamacare.com/
http://images.google.bs/url?q=https://segurodeobamacare.com/
http://images.google.com.bh/url?q=https://segurodeobamacare.com/
http://images.google.com.bd/url?q=https://segurodeobamacare.com/
http://images.google.com.by/url?q=https://segurodeobamacare.com/
http://images.google.be/url?q=https://segurodeobamacare.com/
http://images.google.com.bz/url?q=https://segurodeobamacare.com/
http://images.google.bj/url?q=https://segurodeobamacare.com/
http://images.google.bt/url?q=https://segurodeobamacare.com/
http://images.google.com.bo/url?q=https://segurodeobamacare.com/
http://images.google.ba/url?q=https://segurodeobamacare.com/
http://images.google.co.bw/url?q=https://segurodeobamacare.com/
http://images.google.com.br/url?q=https://segurodeobamacare.com/
http://images.google.vg/url?q=https://segurodeobamacare.com/
http://images.google.com.bn/url?q=https://segurodeobamacare.com/
http://images.google.bg/url?q=https://segurodeobamacare.com/
http://images.google.bf/url?q=https://segurodeobamacare.com/
http://images.google.bi/url?q=https://segurodeobamacare.com/
http://images.google.com.kh/url?q=https://segurodeobamacare.com/
http://images.google.cm/url?q=https://segurodeobamacare.com/
http://images.google.ca/url?q=https://segurodeobamacare.com/
http://images.google.cv/url?q=https://segurodeobamacare.com/
http://images.google.cat/url?q=https://segurodeobamacare.com/
http://images.google.cf/url?q=https://segurodeobamacare.com/
http://images.google.td/url?q=https://segurodeobamacare.com/
http://images.google.cl/url?q=https://segurodeobamacare.com/
http://images.google.cn/url?q=https://segurodeobamacare.com/
http://images.google.com.co/url?q=https://segurodeobamacare.com/
http://images.google.cd/url?q=https://segurodeobamacare.com/
http://images.google.cg/url?q=https://segurodeobamacare.com/
http://images.google.co.ck/url?q=https://segurodeobamacare.com/
http://images.google.co.cr/url?q=https://segurodeobamacare.com/
http://images.google.ci/url?q=https://segurodeobamacare.com/
http://images.google.hr/url?q=https://segurodeobamacare.com/
http://images.google.com.cu/url?q=https://segurodeobamacare.com/
http://images.google.com.cy/url?q=https://segurodeobamacare.com/
http://images.google.cz/url?q=https://segurodeobamacare.com/
http://images.google.dk/url?q=https://segurodeobamacare.com/
http://images.google.dj/url?q=https://segurodeobamacare.com/
http://images.google.dm/url?q=https://segurodeobamacare.com/
http://images.google.com.do/url?q=https://segurodeobamacare.com/
http://images.google.com.ec/url?q=https://segurodeobamacare.com/
http://images.google.com.eg/url?q=https://segurodeobamacare.com/
http://images.google.com.sv/url?q=https://segurodeobamacare.com/
http://images.google.ee/url?q=https://segurodeobamacare.com/
http://images.google.com.et/url?q=https://segurodeobamacare.com/
http://images.google.com.fj/url?q=https://segurodeobamacare.com/
http://images.google.fi/url?q=https://segurodeobamacare.com/
http://images.google.fr/url?q=https://segurodeobamacare.com/
http://images.google.ga/url?q=https://segurodeobamacare.com/
http://images.google.gm/url?q=https://segurodeobamacare.com/
http://images.google.ge/url?q=https://segurodeobamacare.com/
http://images.google.de/url?q=https://segurodeobamacare.com/
http://images.google.com.gh/url?q=https://segurodeobamacare.com/
http://images.google.com.gi/url?q=https://segurodeobamacare.com/
http://images.google.gr/url?q=https://segurodeobamacare.com/
http://images.google.gl/url?q=https://segurodeobamacare.com/
http://images.google.gp/url?q=https://segurodeobamacare.com/
http://images.google.com.gt/url?q=https://segurodeobamacare.com/
http://images.google.gg/url?q=https://segurodeobamacare.com/
http://images.google.gy/url?q=https://segurodeobamacare.com/
http://images.google.ht/url?q=https://segurodeobamacare.com/
http://images.google.hn/url?q=https://segurodeobamacare.com/
http://images.google.com.hk/url?q=https://segurodeobamacare.com/
http://images.google.hu/url?q=https://segurodeobamacare.com/
http://images.google.is/url?q=https://segurodeobamacare.com/
http://images.google.co.in/url?q=https://segurodeobamacare.com/
http://images.google.co.id/url?q=https://segurodeobamacare.com/
http://images.google.iq/url?q=https://segurodeobamacare.com/
http://images.google.ie/url?q=https://segurodeobamacare.com/
http://images.google.co.im/url?q=https://segurodeobamacare.com/
http://images.google.co.il/url?q=https://segurodeobamacare.com/
http://images.google.it/url?q=https://segurodeobamacare.com/
http://images.google.ci/url?q=https://segurodeobamacare.com/
http://images.google.com.jm/url?q=https://segurodeobamacare.com/
http://images.google.co.jp/url?q=https://segurodeobamacare.com/
http://images.google.co.je/url?q=https://segurodeobamacare.com/
http://images.google.jo/url?q=https://segurodeobamacare.com/
http://images.google.kz/url?q=https://segurodeobamacare.com/
http://images.google.co.ke/url?q=https://segurodeobamacare.com/
http://images.google.ki/url?q=https://segurodeobamacare.com/
http://images.google.com.kw/url?q=https://segurodeobamacare.com/
http://images.google.com.kg/url?q=https://segurodeobamacare.com/
http://images.google.la/url?q=https://segurodeobamacare.com/
http://images.google.lv/url?q=https://segurodeobamacare.com/
http://images.google.com.lb/url?q=https://segurodeobamacare.com/
http://images.google.co.ls/url?q=https://segurodeobamacare.com/
http://images.google.com.ly/url?q=https://segurodeobamacare.com/
http://images.google.li/url?q=https://segurodeobamacare.com/
http://images.google.lt/url?q=https://segurodeobamacare.com/
http://images.google.lu/url?q=https://segurodeobamacare.com/
http://images.google.mk/url?q=https://segurodeobamacare.com/
http://images.google.mg/url?q=https://segurodeobamacare.com/
http://images.google.mw/url?q=https://segurodeobamacare.com/
http://images.google.com.my/url?q=https://segurodeobamacare.com/
http://images.google.mv/url?q=https://segurodeobamacare.com/
http://images.google.ml/url?q=https://segurodeobamacare.com/
http://images.google.com.mt/url?q=https://segurodeobamacare.com/
http://images.google.mu/url?q=https://segurodeobamacare.com/
http://images.google.com.mx/url?q=https://segurodeobamacare.com/
http://images.google.fm/url?q=https://segurodeobamacare.com/
http://images.google.md/url?q=https://segurodeobamacare.com/
http://images.google.mn/url?q=https://segurodeobamacare.com/
http://images.google.me/url?q=https://segurodeobamacare.com/
http://images.google.ms/url?q=https://segurodeobamacare.com/
http://images.google.co.ma/url?q=https://segurodeobamacare.com/
http://images.google.co.mz/url?q=https://segurodeobamacare.com/
http://images.google.com.na/url?q=https://segurodeobamacare.com/
http://images.google.nr/url?q=https://segurodeobamacare.com/
http://images.google.com.np/url?q=https://segurodeobamacare.com/
http://images.google.nl/url?q=https://segurodeobamacare.com/
http://images.google.co.nz/url?q=https://segurodeobamacare.com/
http://images.google.com.ni/url?q=https://segurodeobamacare.com/
http://images.google.ne/url?q=https://segurodeobamacare.com/
http://images.google.com.ng/url?q=https://segurodeobamacare.com/
http://images.google.nu/url?q=https://segurodeobamacare.com/
http://images.google.com.nf/url?q=https://segurodeobamacare.com/
http://images.google.no/url?q=https://segurodeobamacare.com/
http://images.google.com.om/url?q=https://segurodeobamacare.com/
http://images.google.com.pk/url?q=https://segurodeobamacare.com/
http://images.google.ps/url?q=https://segurodeobamacare.com/
http://images.google.com.pa/url?q=https://segurodeobamacare.com/
http://images.google.com.pg/url?q=https://segurodeobamacare.com/
http://images.google.com.py/url?q=https://segurodeobamacare.com/
http://images.google.com.pe/url?q=https://segurodeobamacare.com/
http://images.google.com.ph/url?q=https://segurodeobamacare.com/
http://images.google.pn/url?q=https://segurodeobamacare.com/
http://images.google.pl/url?q=https://segurodeobamacare.com/
http://images.google.pt/url?q=https://segurodeobamacare.com/
http://images.google.com.pr/url?q=https://segurodeobamacare.com/
http://images.google.com.qa/url?q=https://segurodeobamacare.com/
http://images.google.ro/url?q=https://segurodeobamacare.com/
http://images.google.ru/url?q=https://segurodeobamacare.com/
http://images.google.rw/url?q=https://segurodeobamacare.com/
http://images.google.sh/url?q=https://segurodeobamacare.com/
http://images.google.ws/url?q=https://segurodeobamacare.com/
http://images.google.sm/url?q=https://segurodeobamacare.com/
http://images.google.st/url?q=https://segurodeobamacare.com/
http://images.google.com.sa/url?q=https://segurodeobamacare.com/
http://images.google.sn/url?q=https://segurodeobamacare.com/
http://images.google.rs/url?q=https://segurodeobamacare.com/
http://images.google.sc/url?q=https://segurodeobamacare.com/
http://images.google.com.sl/url?q=https://segurodeobamacare.com/
http://images.google.com.sg/url?q=https://segurodeobamacare.com/
http://images.google.sk/url?q=https://segurodeobamacare.com/
http://images.google.si/url?q=https://segurodeobamacare.com/
http://images.google.com.sb/url?q=https://segurodeobamacare.com/
http://images.google.so/url?q=https://segurodeobamacare.com/
http://images.google.co.za/url?q=https://segurodeobamacare.com/
http://images.google.co.kr/url?q=https://segurodeobamacare.com/
http://images.google.es/url?q=https://segurodeobamacare.com/
http://images.google.lk/url?q=https://segurodeobamacare.com/
http://images.google.com.vc/url?q=https://segurodeobamacare.com/
http://images.google.sr/url?q=https://segurodeobamacare.com/
http://images.google.se/url?q=https://segurodeobamacare.com/
http://images.google.ch/url?q=https://segurodeobamacare.com/
http://images.google.com.tw/url?q=https://segurodeobamacare.com/
http://images.google.com.tj/url?q=https://segurodeobamacare.com/
http://images.google.co.tz/url?q=https://segurodeobamacare.com/
http://images.google.co.th/url?q=https://segurodeobamacare.com/
http://images.google.tl/url?q=https://segurodeobamacare.com/
http://images.google.tg/url?q=https://segurodeobamacare.com/
http://images.google.tk/url?q=https://segurodeobamacare.com/
http://images.google.to/url?q=https://segurodeobamacare.com/
http://images.google.tt/url?q=https://segurodeobamacare.com/
http://images.google.tn/url?q=https://segurodeobamacare.com/
http://images.google.com.tr/url?q=https://segurodeobamacare.com/
http://images.google.tm/url?q=https://segurodeobamacare.com/
http://images.google.co.ug/url?q=https://segurodeobamacare.com/
http://images.google.com.ua/url?q=https://segurodeobamacare.com/
http://images.google.ae/url?q=https://segurodeobamacare.com/
http://images.google.co.uk/url?q=https://segurodeobamacare.com/
http://images.google.com/url?q=https://segurodeobamacare.com/
http://images.google.com.uy/url?q=https://segurodeobamacare.com/
http://images.google.co.uz/url?q=https://segurodeobamacare.com/
http://images.google.vu/url?q=https://segurodeobamacare.com/
http://images.google.co.ve/url?q=https://segurodeobamacare.com/
http://images.google.com.vn/url?q=https://segurodeobamacare.com/
http://images.google.co.vi/url?q=https://segurodeobamacare.com/
http://images.google.co.zm/url?q=https://segurodeobamacare.com/
http://images.google.co.zw/url?q=https://segurodeobamacare.com/
Hello mates, nice article and pleasant arguments commented here,
I am genuinely enjoying by these.
He is just not too laptop savvy he doesnt know the way to delete the sites – and at the moment I
found a number of sites he has visited. Somebody who’s
addicted to pornography ought to know that porno magazines and websites are “supporters” of
this act. Punkerslut: Look! Pornography and drinking on the identical wall!
Punkerslut: Man, this is so tough. Now back in Denver in 2004,
Boham had to find work, he modeled again, but no extra grownup movies.
Irving Penn began developing and printing his personal pictures in the 1960s, bringing back the time-consuming use of platinum, which had been common again round 1900, instead
of the conventional silver. Irving Penn was born in 1917
in New Jersey. Bruce Davidson was born in 1933 and grew up in Oak
Park, Illinois, an outdated suburb of Chicago.
Bruce Davidson would go on to develop into a photographic artist whose work is exhibited all
over the world at prestigious places. Bruce Davidson has also produced two award
successful short films. Out of all the films I’ve seen, one stands out in my head. http://gamesvuinhon.com/vuinhon/profile.php?section=personality&id=151098
deliciousmostnutritious.co.uk
https://ppmataro.org/
An interesting discussion is worth comment. I do think that you need to publish more on this subject, it may not be a taboo matter but typically people do not discuss these subjects.
To the next! Cheers!!
Howdy! I know this is kinda off topic nevertheless
I’d figured I’d ask. Would you be interested in exchanging links or maybe guest writing a blog article
or vice-versa? My blog addresses a lot of the same
subjects as yours and I feel we could greatly benefit
from each other. If you’re interested feel free to shoot me
an email. I look forward to hearing from you!
Great blog by the way!
Also visit my webpage: แทงหวย
weserradweg.org
https://ftvs.org/
WOW just what I was looking for. Came here by searching for Instagram buy followers
Hey very nice blog!
We stumbled over here different page and thought
I might check things out. I like what I see so now i’m following
you. Look forward to going over your web page repeatedly.
I do consider all the ideas you have offered on your post.
They’re really convincing and will definitely work.
Nonetheless, the posts are very quick for novices.
May you please extend them a little from subsequent
time? Thank you for the post.
If some one wishes to be updated with latest technologies afterward he must be visit this web page and
be up to date daily.
Oh my goodness! Amazing article dude! Many thanks, However I am going through problems with your RSS.
I don’t know why I can’t subscribe to it. Is there anyone else getting identical RSS
problems? Anyone that knows the solution can you kindly respond?
Thanx!!
Does your blog have a contact page? I’m having problems locating it but, I’d
like to send you an email. I’ve got some recommendations for
your blog you might be interested in hearing. Either way,
great blog and I look forward to seeing it develop over time.
Feel free to surf to my blog post: Agilemontkiara.wordpress.com/2018/03/03/for-sale/
http://google.com.af/url?q=http://4afreedomhome.com/
http://google.al/url?q=http://4afreedomhome.com/
http://google.dz/url?q=http://4afreedomhome.com/
http://google.as/url?q=http://4afreedomhome.com/
http://google.ad/url?q=http://4afreedomhome.com/
http://google.it.ao/url?q=http://4afreedomhome.com/
http://google.com.ai/url?q=http://4afreedomhome.com/
http://google.com.ag/url?q=http://4afreedomhome.com/
http://google.com.ar/url?q=http://4afreedomhome.com/
http://google.am/url?q=http://4afreedomhome.com/
http://google.ac/url?q=http://4afreedomhome.com/
http://google.com.au/url?q=http://4afreedomhome.com/
http://google.at/url?q=http://4afreedomhome.com/
http://google.az/url?q=http://4afreedomhome.com/
http://google.bs/url?q=http://4afreedomhome.com/
http://google.com.bh/url?q=http://4afreedomhome.com/
http://google.com.bd/url?q=http://4afreedomhome.com/
http://google.com.by/url?q=http://4afreedomhome.com/
http://google.be/url?q=http://4afreedomhome.com/
http://google.com.bz/url?q=http://4afreedomhome.com/
http://google.bj/url?q=http://4afreedomhome.com/
http://google.bt/url?q=http://4afreedomhome.com/
http://google.com.bo/url?q=http://4afreedomhome.com/
http://google.ba/url?q=http://4afreedomhome.com/
http://google.co.bw/url?q=http://4afreedomhome.com/
http://google.com.br/url?q=http://4afreedomhome.com/
http://google.vg/url?q=http://4afreedomhome.com/
http://google.com.bn/url?q=http://4afreedomhome.com/
http://google.bg/url?q=http://4afreedomhome.com/
http://google.bf/url?q=http://4afreedomhome.com/
http://google.bi/url?q=http://4afreedomhome.com/
http://google.com.kh/url?q=http://4afreedomhome.com/
http://google.cm/url?q=http://4afreedomhome.com/
http://google.ca/url?q=http://4afreedomhome.com/
http://google.cv/url?q=http://4afreedomhome.com/
http://google.cat/url?q=http://4afreedomhome.com/
http://google.cf/url?q=http://4afreedomhome.com/
http://google.td/url?q=http://4afreedomhome.com/
http://google.cl/url?q=http://4afreedomhome.com/
http://google.cn/url?q=http://4afreedomhome.com/
http://google.com.co/url?q=http://4afreedomhome.com/
http://google.cd/url?q=http://4afreedomhome.com/
http://google.cg/url?q=http://4afreedomhome.com/
http://google.co.ck/url?q=http://4afreedomhome.com/
http://google.co.cr/url?q=http://4afreedomhome.com/
http://google.ci/url?q=http://4afreedomhome.com/
http://google.hr/url?q=http://4afreedomhome.com/
http://google.com.cu/url?q=http://4afreedomhome.com/
http://google.com.cy/url?q=http://4afreedomhome.com/
http://google.cz/url?q=http://4afreedomhome.com/
http://google.dk/url?q=http://4afreedomhome.com/
http://google.dj/url?q=http://4afreedomhome.com/
http://google.dm/url?q=http://4afreedomhome.com/
http://google.com.do/url?q=http://4afreedomhome.com/
http://google.com.ec/url?q=http://4afreedomhome.com/
http://google.com.eg/url?q=http://4afreedomhome.com/
http://google.com.sv/url?q=http://4afreedomhome.com/
http://google.ee/url?q=http://4afreedomhome.com/
http://google.com.et/url?q=http://4afreedomhome.com/
http://google.com.fj/url?q=http://4afreedomhome.com/
http://google.fi/url?q=http://4afreedomhome.com/
http://google.fr/url?q=http://4afreedomhome.com/
http://google.ga/url?q=http://4afreedomhome.com/
http://google.gm/url?q=http://4afreedomhome.com/
http://google.ge/url?q=http://4afreedomhome.com/
http://google.de/url?q=http://4afreedomhome.com/
http://google.com.gh/url?q=http://4afreedomhome.com/
http://google.com.gi/url?q=http://4afreedomhome.com/
http://google.gr/url?q=http://4afreedomhome.com/
http://google.gl/url?q=http://4afreedomhome.com/
http://google.gp/url?q=http://4afreedomhome.com/
http://google.com.gt/url?q=http://4afreedomhome.com/
http://google.gg/url?q=http://4afreedomhome.com/
http://google.gy/url?q=http://4afreedomhome.com/
http://google.ht/url?q=http://4afreedomhome.com/
http://google.hn/url?q=http://4afreedomhome.com/
http://google.com.hk/url?q=http://4afreedomhome.com/
http://google.hu/url?q=http://4afreedomhome.com/
http://google.is/url?q=http://4afreedomhome.com/
http://google.co.in/url?q=http://4afreedomhome.com/
http://google.co.id/url?q=http://4afreedomhome.com/
http://google.iq/url?q=http://4afreedomhome.com/
http://google.ie/url?q=http://4afreedomhome.com/
http://google.co.im/url?q=http://4afreedomhome.com/
http://google.co.il/url?q=http://4afreedomhome.com/
http://google.it/url?q=http://4afreedomhome.com/
http://google.ci/url?q=http://4afreedomhome.com/
http://google.com.jm/url?q=http://4afreedomhome.com/
http://google.co.jp/url?q=http://4afreedomhome.com/
http://google.co.je/url?q=http://4afreedomhome.com/
http://google.jo/url?q=http://4afreedomhome.com/
http://google.kz/url?q=http://4afreedomhome.com/
http://google.co.ke/url?q=http://4afreedomhome.com/
http://google.ki/url?q=http://4afreedomhome.com/
http://google.com.kw/url?q=http://4afreedomhome.com/
http://google.com.kg/url?q=http://4afreedomhome.com/
http://google.la/url?q=http://4afreedomhome.com/
http://google.lv/url?q=http://4afreedomhome.com/
http://google.com.lb/url?q=http://4afreedomhome.com/
http://google.co.ls/url?q=http://4afreedomhome.com/
http://google.com.ly/url?q=http://4afreedomhome.com/
http://google.li/url?q=http://4afreedomhome.com/
http://google.lt/url?q=http://4afreedomhome.com/
http://google.lu/url?q=http://4afreedomhome.com/
http://google.mk/url?q=http://4afreedomhome.com/
http://google.mg/url?q=http://4afreedomhome.com/
http://google.mw/url?q=http://4afreedomhome.com/
http://google.com.my/url?q=http://4afreedomhome.com/
http://google.mv/url?q=http://4afreedomhome.com/
http://google.ml/url?q=http://4afreedomhome.com/
http://google.com.mt/url?q=http://4afreedomhome.com/
http://google.mu/url?q=http://4afreedomhome.com/
http://google.com.mx/url?q=http://4afreedomhome.com/
http://google.fm/url?q=http://4afreedomhome.com/
http://google.md/url?q=http://4afreedomhome.com/
http://google.mn/url?q=http://4afreedomhome.com/
http://google.me/url?q=http://4afreedomhome.com/
http://google.ms/url?q=http://4afreedomhome.com/
http://google.co.ma/url?q=http://4afreedomhome.com/
http://google.co.mz/url?q=http://4afreedomhome.com/
http://google.com.na/url?q=http://4afreedomhome.com/
http://google.nr/url?q=http://4afreedomhome.com/
http://google.com.np/url?q=http://4afreedomhome.com/
http://google.nl/url?q=http://4afreedomhome.com/
http://google.co.nz/url?q=http://4afreedomhome.com/
http://google.com.ni/url?q=http://4afreedomhome.com/
http://google.ne/url?q=http://4afreedomhome.com/
http://google.com.ng/url?q=http://4afreedomhome.com/
http://google.nu/url?q=http://4afreedomhome.com/
http://google.com.nf/url?q=http://4afreedomhome.com/
http://google.no/url?q=http://4afreedomhome.com/
http://google.com.om/url?q=http://4afreedomhome.com/
http://google.com.pk/url?q=http://4afreedomhome.com/
http://google.ps/url?q=http://4afreedomhome.com/
http://google.com.pa/url?q=http://4afreedomhome.com/
http://google.com.pg/url?q=http://4afreedomhome.com/
http://google.com.py/url?q=http://4afreedomhome.com/
http://google.com.pe/url?q=http://4afreedomhome.com/
http://google.com.ph/url?q=http://4afreedomhome.com/
http://google.pn/url?q=http://4afreedomhome.com/
http://google.pl/url?q=http://4afreedomhome.com/
http://google.pt/url?q=http://4afreedomhome.com/
http://google.com.pr/url?q=http://4afreedomhome.com/
http://google.com.qa/url?q=http://4afreedomhome.com/
http://google.ro/url?q=http://4afreedomhome.com/
http://google.ru/url?q=http://4afreedomhome.com/
http://google.rw/url?q=http://4afreedomhome.com/
http://google.sh/url?q=http://4afreedomhome.com/
http://google.ws/url?q=http://4afreedomhome.com/
http://google.sm/url?q=http://4afreedomhome.com/
http://google.st/url?q=http://4afreedomhome.com/
http://google.com.sa/url?q=http://4afreedomhome.com/
http://google.sn/url?q=http://4afreedomhome.com/
http://google.rs/url?q=http://4afreedomhome.com/
http://google.sc/url?q=http://4afreedomhome.com/
http://google.com.sl/url?q=http://4afreedomhome.com/
http://google.com.sg/url?q=http://4afreedomhome.com/
http://google.sk/url?q=http://4afreedomhome.com/
http://google.si/url?q=http://4afreedomhome.com/
http://google.com.sb/url?q=http://4afreedomhome.com/
http://google.so/url?q=http://4afreedomhome.com/
http://google.co.za/url?q=http://4afreedomhome.com/
http://google.co.kr/url?q=http://4afreedomhome.com/
http://google.es/url?q=http://4afreedomhome.com/
http://google.lk/url?q=http://4afreedomhome.com/
http://google.com.vc/url?q=http://4afreedomhome.com/
http://google.sr/url?q=http://4afreedomhome.com/
http://google.se/url?q=http://4afreedomhome.com/
http://google.ch/url?q=http://4afreedomhome.com/
http://google.com.tw/url?q=http://4afreedomhome.com/
http://google.com.tj/url?q=http://4afreedomhome.com/
http://google.co.tz/url?q=http://4afreedomhome.com/
http://google.co.th/url?q=http://4afreedomhome.com/
http://google.tl/url?q=http://4afreedomhome.com/
http://google.tg/url?q=http://4afreedomhome.com/
http://google.tk/url?q=http://4afreedomhome.com/
http://google.to/url?q=http://4afreedomhome.com/
http://google.tt/url?q=http://4afreedomhome.com/
http://google.tn/url?q=http://4afreedomhome.com/
http://google.com.tr/url?q=http://4afreedomhome.com/
http://google.tm/url?q=http://4afreedomhome.com/
http://google.co.ug/url?q=http://4afreedomhome.com/
http://google.com.ua/url?q=http://4afreedomhome.com/
http://google.ae/url?q=http://4afreedomhome.com/
http://google.co.uk/url?q=http://4afreedomhome.com/
http://google.com/url?q=http://4afreedomhome.com/
http://google.com.uy/url?q=http://4afreedomhome.com/
http://google.co.uz/url?q=http://4afreedomhome.com/
http://google.vu/url?q=http://4afreedomhome.com/
http://google.co.ve/url?q=http://4afreedomhome.com/
http://google.com.vn/url?q=http://4afreedomhome.com/
http://google.co.vi/url?q=http://4afreedomhome.com/
http://google.co.zm/url?q=http://4afreedomhome.com/
http://google.co.zw/url?q=http://4afreedomhome.com/
http://maps.google.com.af/url?q=http://4afreedomhome.com/
http://maps.google.al/url?q=http://4afreedomhome.com/
http://maps.google.dz/url?q=http://4afreedomhome.com/
http://maps.google.as/url?q=http://4afreedomhome.com/
http://maps.google.ad/url?q=http://4afreedomhome.com/
http://maps.google.it.ao/url?q=http://4afreedomhome.com/
http://maps.google.com.ai/url?q=http://4afreedomhome.com/
http://maps.google.com.ag/url?q=http://4afreedomhome.com/
http://maps.google.com.ar/url?q=http://4afreedomhome.com/
http://maps.google.am/url?q=http://4afreedomhome.com/
http://maps.google.ac/url?q=http://4afreedomhome.com/
http://maps.google.com.au/url?q=http://4afreedomhome.com/
http://maps.google.at/url?q=http://4afreedomhome.com/
http://maps.google.az/url?q=http://4afreedomhome.com/
http://maps.google.bs/url?q=http://4afreedomhome.com/
http://maps.google.com.bh/url?q=http://4afreedomhome.com/
http://maps.google.com.bd/url?q=http://4afreedomhome.com/
http://maps.google.com.by/url?q=http://4afreedomhome.com/
http://maps.google.be/url?q=http://4afreedomhome.com/
http://maps.google.com.bz/url?q=http://4afreedomhome.com/
http://maps.google.bj/url?q=http://4afreedomhome.com/
http://maps.google.bt/url?q=http://4afreedomhome.com/
http://maps.google.com.bo/url?q=http://4afreedomhome.com/
http://maps.google.ba/url?q=http://4afreedomhome.com/
http://maps.google.co.bw/url?q=http://4afreedomhome.com/
http://maps.google.com.br/url?q=http://4afreedomhome.com/
http://maps.google.vg/url?q=http://4afreedomhome.com/
http://maps.google.com.bn/url?q=http://4afreedomhome.com/
http://maps.google.bg/url?q=http://4afreedomhome.com/
http://maps.google.bf/url?q=http://4afreedomhome.com/
http://maps.google.bi/url?q=http://4afreedomhome.com/
http://maps.google.com.kh/url?q=http://4afreedomhome.com/
http://maps.google.cm/url?q=http://4afreedomhome.com/
http://maps.google.ca/url?q=http://4afreedomhome.com/
http://maps.google.cv/url?q=http://4afreedomhome.com/
http://maps.google.cat/url?q=http://4afreedomhome.com/
http://maps.google.cf/url?q=http://4afreedomhome.com/
http://maps.google.td/url?q=http://4afreedomhome.com/
http://maps.google.cl/url?q=http://4afreedomhome.com/
http://maps.google.cn/url?q=http://4afreedomhome.com/
http://maps.google.com.co/url?q=http://4afreedomhome.com/
http://maps.google.cd/url?q=http://4afreedomhome.com/
http://maps.google.cg/url?q=http://4afreedomhome.com/
http://maps.google.co.ck/url?q=http://4afreedomhome.com/
http://maps.google.co.cr/url?q=http://4afreedomhome.com/
http://maps.google.ci/url?q=http://4afreedomhome.com/
http://maps.google.hr/url?q=http://4afreedomhome.com/
http://maps.google.com.cu/url?q=http://4afreedomhome.com/
http://maps.google.com.cy/url?q=http://4afreedomhome.com/
http://maps.google.cz/url?q=http://4afreedomhome.com/
http://maps.google.dk/url?q=http://4afreedomhome.com/
http://maps.google.dj/url?q=http://4afreedomhome.com/
http://maps.google.dm/url?q=http://4afreedomhome.com/
http://maps.google.com.do/url?q=http://4afreedomhome.com/
http://maps.google.com.ec/url?q=http://4afreedomhome.com/
http://maps.google.com.eg/url?q=http://4afreedomhome.com/
http://maps.google.com.sv/url?q=http://4afreedomhome.com/
http://maps.google.ee/url?q=http://4afreedomhome.com/
http://maps.google.com.et/url?q=http://4afreedomhome.com/
http://maps.google.com.fj/url?q=http://4afreedomhome.com/
http://maps.google.fi/url?q=http://4afreedomhome.com/
http://maps.google.fr/url?q=http://4afreedomhome.com/
http://maps.google.ga/url?q=http://4afreedomhome.com/
http://maps.google.gm/url?q=http://4afreedomhome.com/
http://maps.google.ge/url?q=http://4afreedomhome.com/
http://maps.google.de/url?q=http://4afreedomhome.com/
http://maps.google.com.gh/url?q=http://4afreedomhome.com/
http://maps.google.com.gi/url?q=http://4afreedomhome.com/
http://maps.google.gr/url?q=http://4afreedomhome.com/
http://maps.google.gl/url?q=http://4afreedomhome.com/
http://maps.google.gp/url?q=http://4afreedomhome.com/
http://maps.google.com.gt/url?q=http://4afreedomhome.com/
http://maps.google.gg/url?q=http://4afreedomhome.com/
http://maps.google.gy/url?q=http://4afreedomhome.com/
http://maps.google.ht/url?q=http://4afreedomhome.com/
http://maps.google.hn/url?q=http://4afreedomhome.com/
http://maps.google.com.hk/url?q=http://4afreedomhome.com/
http://maps.google.hu/url?q=http://4afreedomhome.com/
http://maps.google.is/url?q=http://4afreedomhome.com/
http://maps.google.co.in/url?q=http://4afreedomhome.com/
http://maps.google.co.id/url?q=http://4afreedomhome.com/
http://maps.google.iq/url?q=http://4afreedomhome.com/
http://maps.google.ie/url?q=http://4afreedomhome.com/
http://maps.google.co.im/url?q=http://4afreedomhome.com/
http://maps.google.co.il/url?q=http://4afreedomhome.com/
http://maps.google.it/url?q=http://4afreedomhome.com/
http://maps.google.ci/url?q=http://4afreedomhome.com/
http://maps.google.com.jm/url?q=http://4afreedomhome.com/
http://maps.google.co.jp/url?q=http://4afreedomhome.com/
http://maps.google.co.je/url?q=http://4afreedomhome.com/
http://maps.google.jo/url?q=http://4afreedomhome.com/
http://maps.google.kz/url?q=http://4afreedomhome.com/
http://maps.google.co.ke/url?q=http://4afreedomhome.com/
http://maps.google.ki/url?q=http://4afreedomhome.com/
http://maps.google.com.kw/url?q=http://4afreedomhome.com/
http://maps.google.com.kg/url?q=http://4afreedomhome.com/
http://maps.google.la/url?q=http://4afreedomhome.com/
http://maps.google.lv/url?q=http://4afreedomhome.com/
http://maps.google.com.lb/url?q=http://4afreedomhome.com/
http://maps.google.co.ls/url?q=http://4afreedomhome.com/
http://maps.google.com.ly/url?q=http://4afreedomhome.com/
http://maps.google.li/url?q=http://4afreedomhome.com/
http://maps.google.lt/url?q=http://4afreedomhome.com/
http://maps.google.lu/url?q=http://4afreedomhome.com/
http://maps.google.mk/url?q=http://4afreedomhome.com/
http://maps.google.mg/url?q=http://4afreedomhome.com/
http://maps.google.mw/url?q=http://4afreedomhome.com/
http://maps.google.com.my/url?q=http://4afreedomhome.com/
http://maps.google.mv/url?q=http://4afreedomhome.com/
http://maps.google.ml/url?q=http://4afreedomhome.com/
http://maps.google.com.mt/url?q=http://4afreedomhome.com/
http://maps.google.mu/url?q=http://4afreedomhome.com/
http://maps.google.com.mx/url?q=http://4afreedomhome.com/
http://maps.google.fm/url?q=http://4afreedomhome.com/
http://maps.google.md/url?q=http://4afreedomhome.com/
http://maps.google.mn/url?q=http://4afreedomhome.com/
http://maps.google.me/url?q=http://4afreedomhome.com/
http://maps.google.ms/url?q=http://4afreedomhome.com/
http://maps.google.co.ma/url?q=http://4afreedomhome.com/
http://maps.google.co.mz/url?q=http://4afreedomhome.com/
http://maps.google.com.na/url?q=http://4afreedomhome.com/
http://maps.google.nr/url?q=http://4afreedomhome.com/
http://maps.google.com.np/url?q=http://4afreedomhome.com/
http://maps.google.nl/url?q=http://4afreedomhome.com/
http://maps.google.co.nz/url?q=http://4afreedomhome.com/
http://maps.google.com.ni/url?q=http://4afreedomhome.com/
http://maps.google.ne/url?q=http://4afreedomhome.com/
http://maps.google.com.ng/url?q=http://4afreedomhome.com/
http://maps.google.nu/url?q=http://4afreedomhome.com/
http://maps.google.com.nf/url?q=http://4afreedomhome.com/
http://maps.google.no/url?q=http://4afreedomhome.com/
http://maps.google.com.om/url?q=http://4afreedomhome.com/
http://maps.google.com.pk/url?q=http://4afreedomhome.com/
http://maps.google.ps/url?q=http://4afreedomhome.com/
http://maps.google.com.pa/url?q=http://4afreedomhome.com/
http://maps.google.com.pg/url?q=http://4afreedomhome.com/
http://maps.google.com.py/url?q=http://4afreedomhome.com/
http://maps.google.com.pe/url?q=http://4afreedomhome.com/
http://maps.google.com.ph/url?q=http://4afreedomhome.com/
http://maps.google.pn/url?q=http://4afreedomhome.com/
http://maps.google.pl/url?q=http://4afreedomhome.com/
http://maps.google.pt/url?q=http://4afreedomhome.com/
http://maps.google.com.pr/url?q=http://4afreedomhome.com/
http://maps.google.com.qa/url?q=http://4afreedomhome.com/
http://maps.google.ro/url?q=http://4afreedomhome.com/
http://maps.google.ru/url?q=http://4afreedomhome.com/
http://maps.google.rw/url?q=http://4afreedomhome.com/
http://maps.google.sh/url?q=http://4afreedomhome.com/
http://maps.google.ws/url?q=http://4afreedomhome.com/
http://maps.google.sm/url?q=http://4afreedomhome.com/
http://maps.google.st/url?q=http://4afreedomhome.com/
http://maps.google.com.sa/url?q=http://4afreedomhome.com/
http://maps.google.sn/url?q=http://4afreedomhome.com/
http://maps.google.rs/url?q=http://4afreedomhome.com/
http://maps.google.sc/url?q=http://4afreedomhome.com/
http://maps.google.com.sl/url?q=http://4afreedomhome.com/
http://maps.google.com.sg/url?q=http://4afreedomhome.com/
http://maps.google.sk/url?q=http://4afreedomhome.com/
http://maps.google.si/url?q=http://4afreedomhome.com/
http://maps.google.com.sb/url?q=http://4afreedomhome.com/
http://maps.google.so/url?q=http://4afreedomhome.com/
http://maps.google.co.za/url?q=http://4afreedomhome.com/
http://maps.google.co.kr/url?q=http://4afreedomhome.com/
http://maps.google.es/url?q=http://4afreedomhome.com/
http://maps.google.lk/url?q=http://4afreedomhome.com/
http://maps.google.com.vc/url?q=http://4afreedomhome.com/
http://maps.google.sr/url?q=http://4afreedomhome.com/
http://maps.google.se/url?q=http://4afreedomhome.com/
http://maps.google.ch/url?q=http://4afreedomhome.com/
http://maps.google.com.tw/url?q=http://4afreedomhome.com/
http://maps.google.com.tj/url?q=http://4afreedomhome.com/
http://maps.google.co.tz/url?q=http://4afreedomhome.com/
http://maps.google.co.th/url?q=http://4afreedomhome.com/
http://maps.google.tl/url?q=http://4afreedomhome.com/
http://maps.google.tg/url?q=http://4afreedomhome.com/
http://maps.google.tk/url?q=http://4afreedomhome.com/
http://maps.google.to/url?q=http://4afreedomhome.com/
http://maps.google.tt/url?q=http://4afreedomhome.com/
http://maps.google.tn/url?q=http://4afreedomhome.com/
http://maps.google.com.tr/url?q=http://4afreedomhome.com/
http://maps.google.tm/url?q=http://4afreedomhome.com/
http://maps.google.co.ug/url?q=http://4afreedomhome.com/
http://maps.google.com.ua/url?q=http://4afreedomhome.com/
http://maps.google.ae/url?q=http://4afreedomhome.com/
http://maps.google.co.uk/url?q=http://4afreedomhome.com/
http://maps.google.com/url?q=http://4afreedomhome.com/
http://maps.google.com.uy/url?q=http://4afreedomhome.com/
http://maps.google.co.uz/url?q=http://4afreedomhome.com/
http://maps.google.vu/url?q=http://4afreedomhome.com/
http://maps.google.co.ve/url?q=http://4afreedomhome.com/
http://maps.google.com.vn/url?q=http://4afreedomhome.com/
http://maps.google.co.vi/url?q=http://4afreedomhome.com/
http://maps.google.co.zm/url?q=http://4afreedomhome.com/
http://maps.google.co.zw/url?q=http://4afreedomhome.com/
http://images.google.com.af/url?q=http://4afreedomhome.com/
http://images.google.al/url?q=http://4afreedomhome.com/
http://images.google.dz/url?q=http://4afreedomhome.com/
http://images.google.as/url?q=http://4afreedomhome.com/
http://images.google.ad/url?q=http://4afreedomhome.com/
http://images.google.it.ao/url?q=http://4afreedomhome.com/
http://images.google.com.ai/url?q=http://4afreedomhome.com/
http://images.google.com.ag/url?q=http://4afreedomhome.com/
http://images.google.com.ar/url?q=http://4afreedomhome.com/
http://images.google.am/url?q=http://4afreedomhome.com/
http://images.google.ac/url?q=http://4afreedomhome.com/
http://images.google.com.au/url?q=http://4afreedomhome.com/
http://images.google.at/url?q=http://4afreedomhome.com/
http://images.google.az/url?q=http://4afreedomhome.com/
http://images.google.bs/url?q=http://4afreedomhome.com/
http://images.google.com.bh/url?q=http://4afreedomhome.com/
http://images.google.com.bd/url?q=http://4afreedomhome.com/
http://images.google.com.by/url?q=http://4afreedomhome.com/
http://images.google.be/url?q=http://4afreedomhome.com/
http://images.google.com.bz/url?q=http://4afreedomhome.com/
http://images.google.bj/url?q=http://4afreedomhome.com/
http://images.google.bt/url?q=http://4afreedomhome.com/
http://images.google.com.bo/url?q=http://4afreedomhome.com/
http://images.google.ba/url?q=http://4afreedomhome.com/
http://images.google.co.bw/url?q=http://4afreedomhome.com/
http://images.google.com.br/url?q=http://4afreedomhome.com/
http://images.google.vg/url?q=http://4afreedomhome.com/
http://images.google.com.bn/url?q=http://4afreedomhome.com/
http://images.google.bg/url?q=http://4afreedomhome.com/
http://images.google.bf/url?q=http://4afreedomhome.com/
http://images.google.bi/url?q=http://4afreedomhome.com/
http://images.google.com.kh/url?q=http://4afreedomhome.com/
http://images.google.cm/url?q=http://4afreedomhome.com/
http://images.google.ca/url?q=http://4afreedomhome.com/
http://images.google.cv/url?q=http://4afreedomhome.com/
http://images.google.cat/url?q=http://4afreedomhome.com/
http://images.google.cf/url?q=http://4afreedomhome.com/
http://images.google.td/url?q=http://4afreedomhome.com/
http://images.google.cl/url?q=http://4afreedomhome.com/
http://images.google.cn/url?q=http://4afreedomhome.com/
http://images.google.com.co/url?q=http://4afreedomhome.com/
http://images.google.cd/url?q=http://4afreedomhome.com/
http://images.google.cg/url?q=http://4afreedomhome.com/
http://images.google.co.ck/url?q=http://4afreedomhome.com/
http://images.google.co.cr/url?q=http://4afreedomhome.com/
http://images.google.ci/url?q=http://4afreedomhome.com/
http://images.google.hr/url?q=http://4afreedomhome.com/
http://images.google.com.cu/url?q=http://4afreedomhome.com/
http://images.google.com.cy/url?q=http://4afreedomhome.com/
http://images.google.cz/url?q=http://4afreedomhome.com/
http://images.google.dk/url?q=http://4afreedomhome.com/
http://images.google.dj/url?q=http://4afreedomhome.com/
http://images.google.dm/url?q=http://4afreedomhome.com/
http://images.google.com.do/url?q=http://4afreedomhome.com/
http://images.google.com.ec/url?q=http://4afreedomhome.com/
http://images.google.com.eg/url?q=http://4afreedomhome.com/
http://images.google.com.sv/url?q=http://4afreedomhome.com/
http://images.google.ee/url?q=http://4afreedomhome.com/
http://images.google.com.et/url?q=http://4afreedomhome.com/
http://images.google.com.fj/url?q=http://4afreedomhome.com/
http://images.google.fi/url?q=http://4afreedomhome.com/
http://images.google.fr/url?q=http://4afreedomhome.com/
http://images.google.ga/url?q=http://4afreedomhome.com/
http://images.google.gm/url?q=http://4afreedomhome.com/
http://images.google.ge/url?q=http://4afreedomhome.com/
http://images.google.de/url?q=http://4afreedomhome.com/
http://images.google.com.gh/url?q=http://4afreedomhome.com/
http://images.google.com.gi/url?q=http://4afreedomhome.com/
http://images.google.gr/url?q=http://4afreedomhome.com/
http://images.google.gl/url?q=http://4afreedomhome.com/
http://images.google.gp/url?q=http://4afreedomhome.com/
http://images.google.com.gt/url?q=http://4afreedomhome.com/
http://images.google.gg/url?q=http://4afreedomhome.com/
http://images.google.gy/url?q=http://4afreedomhome.com/
http://images.google.ht/url?q=http://4afreedomhome.com/
http://images.google.hn/url?q=http://4afreedomhome.com/
http://images.google.com.hk/url?q=http://4afreedomhome.com/
http://images.google.hu/url?q=http://4afreedomhome.com/
http://images.google.is/url?q=http://4afreedomhome.com/
http://images.google.co.in/url?q=http://4afreedomhome.com/
http://images.google.co.id/url?q=http://4afreedomhome.com/
http://images.google.iq/url?q=http://4afreedomhome.com/
http://images.google.ie/url?q=http://4afreedomhome.com/
http://images.google.co.im/url?q=http://4afreedomhome.com/
http://images.google.co.il/url?q=http://4afreedomhome.com/
http://images.google.it/url?q=http://4afreedomhome.com/
http://images.google.ci/url?q=http://4afreedomhome.com/
http://images.google.com.jm/url?q=http://4afreedomhome.com/
http://images.google.co.jp/url?q=http://4afreedomhome.com/
http://images.google.co.je/url?q=http://4afreedomhome.com/
http://images.google.jo/url?q=http://4afreedomhome.com/
http://images.google.kz/url?q=http://4afreedomhome.com/
http://images.google.co.ke/url?q=http://4afreedomhome.com/
http://images.google.ki/url?q=http://4afreedomhome.com/
http://images.google.com.kw/url?q=http://4afreedomhome.com/
http://images.google.com.kg/url?q=http://4afreedomhome.com/
http://images.google.la/url?q=http://4afreedomhome.com/
http://images.google.lv/url?q=http://4afreedomhome.com/
http://images.google.com.lb/url?q=http://4afreedomhome.com/
http://images.google.co.ls/url?q=http://4afreedomhome.com/
http://images.google.com.ly/url?q=http://4afreedomhome.com/
http://images.google.li/url?q=http://4afreedomhome.com/
http://images.google.lt/url?q=http://4afreedomhome.com/
http://images.google.lu/url?q=http://4afreedomhome.com/
http://images.google.mk/url?q=http://4afreedomhome.com/
http://images.google.mg/url?q=http://4afreedomhome.com/
http://images.google.mw/url?q=http://4afreedomhome.com/
http://images.google.com.my/url?q=http://4afreedomhome.com/
http://images.google.mv/url?q=http://4afreedomhome.com/
http://images.google.ml/url?q=http://4afreedomhome.com/
http://images.google.com.mt/url?q=http://4afreedomhome.com/
http://images.google.mu/url?q=http://4afreedomhome.com/
http://images.google.com.mx/url?q=http://4afreedomhome.com/
http://images.google.fm/url?q=http://4afreedomhome.com/
http://images.google.md/url?q=http://4afreedomhome.com/
http://images.google.mn/url?q=http://4afreedomhome.com/
http://images.google.me/url?q=http://4afreedomhome.com/
http://images.google.ms/url?q=http://4afreedomhome.com/
http://images.google.co.ma/url?q=http://4afreedomhome.com/
http://images.google.co.mz/url?q=http://4afreedomhome.com/
http://images.google.com.na/url?q=http://4afreedomhome.com/
http://images.google.nr/url?q=http://4afreedomhome.com/
http://images.google.com.np/url?q=http://4afreedomhome.com/
http://images.google.nl/url?q=http://4afreedomhome.com/
http://images.google.co.nz/url?q=http://4afreedomhome.com/
http://images.google.com.ni/url?q=http://4afreedomhome.com/
http://images.google.ne/url?q=http://4afreedomhome.com/
http://images.google.com.ng/url?q=http://4afreedomhome.com/
http://images.google.nu/url?q=http://4afreedomhome.com/
http://images.google.com.nf/url?q=http://4afreedomhome.com/
http://images.google.no/url?q=http://4afreedomhome.com/
http://images.google.com.om/url?q=http://4afreedomhome.com/
http://images.google.com.pk/url?q=http://4afreedomhome.com/
http://images.google.ps/url?q=http://4afreedomhome.com/
http://images.google.com.pa/url?q=http://4afreedomhome.com/
http://images.google.com.pg/url?q=http://4afreedomhome.com/
http://images.google.com.py/url?q=http://4afreedomhome.com/
http://images.google.com.pe/url?q=http://4afreedomhome.com/
http://images.google.com.ph/url?q=http://4afreedomhome.com/
http://images.google.pn/url?q=http://4afreedomhome.com/
http://images.google.pl/url?q=http://4afreedomhome.com/
http://images.google.pt/url?q=http://4afreedomhome.com/
http://images.google.com.pr/url?q=http://4afreedomhome.com/
http://images.google.com.qa/url?q=http://4afreedomhome.com/
http://images.google.ro/url?q=http://4afreedomhome.com/
http://images.google.ru/url?q=http://4afreedomhome.com/
http://images.google.rw/url?q=http://4afreedomhome.com/
http://images.google.sh/url?q=http://4afreedomhome.com/
http://images.google.ws/url?q=http://4afreedomhome.com/
http://images.google.sm/url?q=http://4afreedomhome.com/
http://images.google.st/url?q=http://4afreedomhome.com/
http://images.google.com.sa/url?q=http://4afreedomhome.com/
http://images.google.sn/url?q=http://4afreedomhome.com/
http://images.google.rs/url?q=http://4afreedomhome.com/
http://images.google.sc/url?q=http://4afreedomhome.com/
http://images.google.com.sl/url?q=http://4afreedomhome.com/
http://images.google.com.sg/url?q=http://4afreedomhome.com/
http://images.google.sk/url?q=http://4afreedomhome.com/
http://images.google.si/url?q=http://4afreedomhome.com/
http://images.google.com.sb/url?q=http://4afreedomhome.com/
http://images.google.so/url?q=http://4afreedomhome.com/
http://images.google.co.za/url?q=http://4afreedomhome.com/
http://images.google.co.kr/url?q=http://4afreedomhome.com/
http://images.google.es/url?q=http://4afreedomhome.com/
http://images.google.lk/url?q=http://4afreedomhome.com/
http://images.google.com.vc/url?q=http://4afreedomhome.com/
http://images.google.sr/url?q=http://4afreedomhome.com/
http://images.google.se/url?q=http://4afreedomhome.com/
http://images.google.ch/url?q=http://4afreedomhome.com/
http://images.google.com.tw/url?q=http://4afreedomhome.com/
http://images.google.com.tj/url?q=http://4afreedomhome.com/
http://images.google.co.tz/url?q=http://4afreedomhome.com/
http://images.google.co.th/url?q=http://4afreedomhome.com/
http://images.google.tl/url?q=http://4afreedomhome.com/
http://images.google.tg/url?q=http://4afreedomhome.com/
http://images.google.tk/url?q=http://4afreedomhome.com/
http://images.google.to/url?q=http://4afreedomhome.com/
http://images.google.tt/url?q=http://4afreedomhome.com/
http://images.google.tn/url?q=http://4afreedomhome.com/
http://images.google.com.tr/url?q=http://4afreedomhome.com/
http://images.google.tm/url?q=http://4afreedomhome.com/
http://images.google.co.ug/url?q=http://4afreedomhome.com/
http://images.google.com.ua/url?q=http://4afreedomhome.com/
http://images.google.ae/url?q=http://4afreedomhome.com/
http://images.google.co.uk/url?q=http://4afreedomhome.com/
http://images.google.com/url?q=http://4afreedomhome.com/
http://images.google.com.uy/url?q=http://4afreedomhome.com/
http://images.google.co.uz/url?q=http://4afreedomhome.com/
http://images.google.vu/url?q=http://4afreedomhome.com/
http://images.google.co.ve/url?q=http://4afreedomhome.com/
http://images.google.com.vn/url?q=http://4afreedomhome.com/
http://images.google.co.vi/url?q=http://4afreedomhome.com/
http://images.google.co.zm/url?q=http://4afreedomhome.com/
http://images.google.co.zw/url?q=http://4afreedomhome.com/
I’m really enjoying the theme/design of your site.
Do you ever run into any browser compatibility problems?
A small number of my blog audience have complained about my site
not working correctly in Explorer but looks great in Safari.
Do you have any advice to help fix this problem?
Botvin, G. J., K. W. Griffin and Tracy Diaz Nichols.
2006. “Preventing Youth Violence and Delinquency Through a Universal School-Based Prevention Approach.”
Prevention Science, (7): 403-408. https://buybuyviamen.com viagra overdose
alapasserelle.org
https://homenet-trust.com/
always i used to read smaller articles or reviews
that also clear their motive, and that is also happening with this post which I
am reading at this time.
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
<a href="http://images.google.co.il/url?sa=t&url=https%3A%2F%2Fwebcasinogames.com/" re
fahrschulverwaltung.net
https://yagodovod.com/
deportemeco.com
https://tv-plasma.es/
It’s enormous that you are getting thoughts from this piece
of writing as well as from our argument made at this time.
It’s in fact very difficult in this full of activity life to listen news on Television, so I just use the web for that purpose, and obtain the most recent information.
After looking over a handful of the articles on your site, I truly like your way of writing a blog.
I added it to my bookmark webpage list and will be checking back soon. Please visit
my website as well and let me know what you think.
Hi there it’s me, I am also visiting this web site regularly,
this web page is really nice and the people are really sharing good thoughts.
Excellent blog you have got here.. It’s hard to find good quality writing like yours nowadays.
I honestly appreciate individuals like you! Take care!!
These are actually great ideas in on the topic of blogging.
You have touched some good points here. Any way keep up wrinting.
I was curious if you ever considered changing the page layout of your site?
Its very well written; I love what youve got to say. But maybe you could a little
more in the way of content so people could connect with it better.
Youve got an awful lot of text for only having 1 or 2 pictures.
Maybe you could space it out better?
I like looking through a post that can make people think.
Also, thank you for allowing for me to comment!
Hey There. I found your blog using msn. This is a really well
written article. I’ll be sure to bookmark it and come back to read more of your useful info.
Thanks for the post. I’ll certainly return.
Howdy just wanted to give you a quick heads
up. The text in your content seem to be running off the
screen in Safari. I’m not sure if this is a format issue or something to
do with web browser compatibility but I thought I’d post to let you know.
The design look great though! Hope you get the problem resolved soon.
Kudos
Hey there! This post could not be written any better!
Reading through this post reminds me of my old room mate!
He always kept talking about this. I will forward this article to him.
Pretty sure he will have a good read. Many thanks for sharing!
This blog was… how do you say it? Relevant!! Finally I have found something
which helped me. Appreciate it!
Good write-up. I certainly love this website. Thanks!
Spot on with this write-up, I truly believe this web site
needs a great deal more attention. I’ll probably be returning to see
more, thanks for the advice!
Today, I went to the beach front with my children. I found a sea shell and gave it to
my 4 year old daughter and said “You can hear the ocean if you put this to your ear.” She put the shell
to her ear and screamed. There was a hermit crab inside and it pinched her ear.
She never wants to go back! LoL I know this is completely off
topic but I had to tell someone!
http://google.com.af/url?q=https://www.kitchensplusco.com/
http://google.al/url?q=https://www.kitchensplusco.com/
http://google.dz/url?q=https://www.kitchensplusco.com/
http://google.as/url?q=https://www.kitchensplusco.com/
http://google.ad/url?q=https://www.kitchensplusco.com/
http://google.it.ao/url?q=https://www.kitchensplusco.com/
http://google.com.ai/url?q=https://www.kitchensplusco.com/
http://google.com.ag/url?q=https://www.kitchensplusco.com/
http://google.com.ar/url?q=https://www.kitchensplusco.com/
http://google.am/url?q=https://www.kitchensplusco.com/
http://google.ac/url?q=https://www.kitchensplusco.com/
http://google.com.au/url?q=https://www.kitchensplusco.com/
http://google.at/url?q=https://www.kitchensplusco.com/
http://google.az/url?q=https://www.kitchensplusco.com/
http://google.bs/url?q=https://www.kitchensplusco.com/
http://google.com.bh/url?q=https://www.kitchensplusco.com/
http://google.com.bd/url?q=https://www.kitchensplusco.com/
http://google.com.by/url?q=https://www.kitchensplusco.com/
http://google.be/url?q=https://www.kitchensplusco.com/
http://google.com.bz/url?q=https://www.kitchensplusco.com/
http://google.bj/url?q=https://www.kitchensplusco.com/
http://google.bt/url?q=https://www.kitchensplusco.com/
http://google.com.bo/url?q=https://www.kitchensplusco.com/
http://google.ba/url?q=https://www.kitchensplusco.com/
http://google.co.bw/url?q=https://www.kitchensplusco.com/
http://google.com.br/url?q=https://www.kitchensplusco.com/
http://google.vg/url?q=https://www.kitchensplusco.com/
http://google.com.bn/url?q=https://www.kitchensplusco.com/
http://google.bg/url?q=https://www.kitchensplusco.com/
http://google.bf/url?q=https://www.kitchensplusco.com/
http://google.bi/url?q=https://www.kitchensplusco.com/
http://google.com.kh/url?q=https://www.kitchensplusco.com/
http://google.cm/url?q=https://www.kitchensplusco.com/
http://google.ca/url?q=https://www.kitchensplusco.com/
http://google.cv/url?q=https://www.kitchensplusco.com/
http://google.cat/url?q=https://www.kitchensplusco.com/
http://google.cf/url?q=https://www.kitchensplusco.com/
http://google.td/url?q=https://www.kitchensplusco.com/
http://google.cl/url?q=https://www.kitchensplusco.com/
http://google.cn/url?q=https://www.kitchensplusco.com/
http://google.com.co/url?q=https://www.kitchensplusco.com/
http://google.cd/url?q=https://www.kitchensplusco.com/
http://google.cg/url?q=https://www.kitchensplusco.com/
http://google.co.ck/url?q=https://www.kitchensplusco.com/
http://google.co.cr/url?q=https://www.kitchensplusco.com/
http://google.ci/url?q=https://www.kitchensplusco.com/
http://google.hr/url?q=https://www.kitchensplusco.com/
http://google.com.cu/url?q=https://www.kitchensplusco.com/
http://google.com.cy/url?q=https://www.kitchensplusco.com/
http://google.cz/url?q=https://www.kitchensplusco.com/
http://google.dk/url?q=https://www.kitchensplusco.com/
http://google.dj/url?q=https://www.kitchensplusco.com/
http://google.dm/url?q=https://www.kitchensplusco.com/
http://google.com.do/url?q=https://www.kitchensplusco.com/
http://google.com.ec/url?q=https://www.kitchensplusco.com/
http://google.com.eg/url?q=https://www.kitchensplusco.com/
http://google.com.sv/url?q=https://www.kitchensplusco.com/
http://google.ee/url?q=https://www.kitchensplusco.com/
http://google.com.et/url?q=https://www.kitchensplusco.com/
http://google.com.fj/url?q=https://www.kitchensplusco.com/
http://google.fi/url?q=https://www.kitchensplusco.com/
http://google.fr/url?q=https://www.kitchensplusco.com/
http://google.ga/url?q=https://www.kitchensplusco.com/
http://google.gm/url?q=https://www.kitchensplusco.com/
http://google.ge/url?q=https://www.kitchensplusco.com/
http://google.de/url?q=https://www.kitchensplusco.com/
http://google.com.gh/url?q=https://www.kitchensplusco.com/
http://google.com.gi/url?q=https://www.kitchensplusco.com/
http://google.gr/url?q=https://www.kitchensplusco.com/
http://google.gl/url?q=https://www.kitchensplusco.com/
http://google.gp/url?q=https://www.kitchensplusco.com/
http://google.com.gt/url?q=https://www.kitchensplusco.com/
http://google.gg/url?q=https://www.kitchensplusco.com/
http://google.gy/url?q=https://www.kitchensplusco.com/
http://google.ht/url?q=https://www.kitchensplusco.com/
http://google.hn/url?q=https://www.kitchensplusco.com/
http://google.com.hk/url?q=https://www.kitchensplusco.com/
http://google.hu/url?q=https://www.kitchensplusco.com/
http://google.is/url?q=https://www.kitchensplusco.com/
http://google.co.in/url?q=https://www.kitchensplusco.com/
http://google.co.id/url?q=https://www.kitchensplusco.com/
http://google.iq/url?q=https://www.kitchensplusco.com/
http://google.ie/url?q=https://www.kitchensplusco.com/
http://google.co.im/url?q=https://www.kitchensplusco.com/
http://google.co.il/url?q=https://www.kitchensplusco.com/
http://google.it/url?q=https://www.kitchensplusco.com/
http://google.ci/url?q=https://www.kitchensplusco.com/
http://google.com.jm/url?q=https://www.kitchensplusco.com/
http://google.co.jp/url?q=https://www.kitchensplusco.com/
http://google.co.je/url?q=https://www.kitchensplusco.com/
http://google.jo/url?q=https://www.kitchensplusco.com/
http://google.kz/url?q=https://www.kitchensplusco.com/
http://google.co.ke/url?q=https://www.kitchensplusco.com/
http://google.ki/url?q=https://www.kitchensplusco.com/
http://google.com.kw/url?q=https://www.kitchensplusco.com/
http://google.com.kg/url?q=https://www.kitchensplusco.com/
http://google.la/url?q=https://www.kitchensplusco.com/
http://google.lv/url?q=https://www.kitchensplusco.com/
http://google.com.lb/url?q=https://www.kitchensplusco.com/
http://google.co.ls/url?q=https://www.kitchensplusco.com/
http://google.com.ly/url?q=https://www.kitchensplusco.com/
http://google.li/url?q=https://www.kitchensplusco.com/
http://google.lt/url?q=https://www.kitchensplusco.com/
http://google.lu/url?q=https://www.kitchensplusco.com/
http://google.mk/url?q=https://www.kitchensplusco.com/
http://google.mg/url?q=https://www.kitchensplusco.com/
http://google.mw/url?q=https://www.kitchensplusco.com/
http://google.com.my/url?q=https://www.kitchensplusco.com/
http://google.mv/url?q=https://www.kitchensplusco.com/
http://google.ml/url?q=https://www.kitchensplusco.com/
http://google.com.mt/url?q=https://www.kitchensplusco.com/
http://google.mu/url?q=https://www.kitchensplusco.com/
http://google.com.mx/url?q=https://www.kitchensplusco.com/
http://google.fm/url?q=https://www.kitchensplusco.com/
http://google.md/url?q=https://www.kitchensplusco.com/
http://google.mn/url?q=https://www.kitchensplusco.com/
http://google.me/url?q=https://www.kitchensplusco.com/
http://google.ms/url?q=https://www.kitchensplusco.com/
http://google.co.ma/url?q=https://www.kitchensplusco.com/
http://google.co.mz/url?q=https://www.kitchensplusco.com/
http://google.com.na/url?q=https://www.kitchensplusco.com/
http://google.nr/url?q=https://www.kitchensplusco.com/
http://google.com.np/url?q=https://www.kitchensplusco.com/
http://google.nl/url?q=https://www.kitchensplusco.com/
http://google.co.nz/url?q=https://www.kitchensplusco.com/
http://google.com.ni/url?q=https://www.kitchensplusco.com/
http://google.ne/url?q=https://www.kitchensplusco.com/
http://google.com.ng/url?q=https://www.kitchensplusco.com/
http://google.nu/url?q=https://www.kitchensplusco.com/
http://google.com.nf/url?q=https://www.kitchensplusco.com/
http://google.no/url?q=https://www.kitchensplusco.com/
http://google.com.om/url?q=https://www.kitchensplusco.com/
http://google.com.pk/url?q=https://www.kitchensplusco.com/
http://google.ps/url?q=https://www.kitchensplusco.com/
http://google.com.pa/url?q=https://www.kitchensplusco.com/
http://google.com.pg/url?q=https://www.kitchensplusco.com/
http://google.com.py/url?q=https://www.kitchensplusco.com/
http://google.com.pe/url?q=https://www.kitchensplusco.com/
http://google.com.ph/url?q=https://www.kitchensplusco.com/
http://google.pn/url?q=https://www.kitchensplusco.com/
http://google.pl/url?q=https://www.kitchensplusco.com/
http://google.pt/url?q=https://www.kitchensplusco.com/
http://google.com.pr/url?q=https://www.kitchensplusco.com/
http://google.com.qa/url?q=https://www.kitchensplusco.com/
http://google.ro/url?q=https://www.kitchensplusco.com/
http://google.ru/url?q=https://www.kitchensplusco.com/
http://google.rw/url?q=https://www.kitchensplusco.com/
http://google.sh/url?q=https://www.kitchensplusco.com/
http://google.ws/url?q=https://www.kitchensplusco.com/
http://google.sm/url?q=https://www.kitchensplusco.com/
http://google.st/url?q=https://www.kitchensplusco.com/
http://google.com.sa/url?q=https://www.kitchensplusco.com/
http://google.sn/url?q=https://www.kitchensplusco.com/
http://google.rs/url?q=https://www.kitchensplusco.com/
http://google.sc/url?q=https://www.kitchensplusco.com/
http://google.com.sl/url?q=https://www.kitchensplusco.com/
http://google.com.sg/url?q=https://www.kitchensplusco.com/
http://google.sk/url?q=https://www.kitchensplusco.com/
http://google.si/url?q=https://www.kitchensplusco.com/
http://google.com.sb/url?q=https://www.kitchensplusco.com/
http://google.so/url?q=https://www.kitchensplusco.com/
http://google.co.za/url?q=https://www.kitchensplusco.com/
http://google.co.kr/url?q=https://www.kitchensplusco.com/
http://google.es/url?q=https://www.kitchensplusco.com/
http://google.lk/url?q=https://www.kitchensplusco.com/
http://google.com.vc/url?q=https://www.kitchensplusco.com/
http://google.sr/url?q=https://www.kitchensplusco.com/
http://google.se/url?q=https://www.kitchensplusco.com/
http://google.ch/url?q=https://www.kitchensplusco.com/
http://google.com.tw/url?q=https://www.kitchensplusco.com/
http://google.com.tj/url?q=https://www.kitchensplusco.com/
http://google.co.tz/url?q=https://www.kitchensplusco.com/
http://google.co.th/url?q=https://www.kitchensplusco.com/
http://google.tl/url?q=https://www.kitchensplusco.com/
http://google.tg/url?q=https://www.kitchensplusco.com/
http://google.tk/url?q=https://www.kitchensplusco.com/
http://google.to/url?q=https://www.kitchensplusco.com/
http://google.tt/url?q=https://www.kitchensplusco.com/
http://google.tn/url?q=https://www.kitchensplusco.com/
http://google.com.tr/url?q=https://www.kitchensplusco.com/
http://google.tm/url?q=https://www.kitchensplusco.com/
http://google.co.ug/url?q=https://www.kitchensplusco.com/
http://google.com.ua/url?q=https://www.kitchensplusco.com/
http://google.ae/url?q=https://www.kitchensplusco.com/
http://google.co.uk/url?q=https://www.kitchensplusco.com/
http://google.com/url?q=https://www.kitchensplusco.com/
http://google.com.uy/url?q=https://www.kitchensplusco.com/
http://google.co.uz/url?q=https://www.kitchensplusco.com/
http://google.vu/url?q=https://www.kitchensplusco.com/
http://google.co.ve/url?q=https://www.kitchensplusco.com/
http://google.com.vn/url?q=https://www.kitchensplusco.com/
http://google.co.vi/url?q=https://www.kitchensplusco.com/
http://google.co.zm/url?q=https://www.kitchensplusco.com/
http://google.co.zw/url?q=https://www.kitchensplusco.com/
http://maps.google.com.af/url?q=https://www.kitchensplusco.com/
http://maps.google.al/url?q=https://www.kitchensplusco.com/
http://maps.google.dz/url?q=https://www.kitchensplusco.com/
http://maps.google.as/url?q=https://www.kitchensplusco.com/
http://maps.google.ad/url?q=https://www.kitchensplusco.com/
http://maps.google.it.ao/url?q=https://www.kitchensplusco.com/
http://maps.google.com.ai/url?q=https://www.kitchensplusco.com/
http://maps.google.com.ag/url?q=https://www.kitchensplusco.com/
http://maps.google.com.ar/url?q=https://www.kitchensplusco.com/
http://maps.google.am/url?q=https://www.kitchensplusco.com/
http://maps.google.ac/url?q=https://www.kitchensplusco.com/
http://maps.google.com.au/url?q=https://www.kitchensplusco.com/
http://maps.google.at/url?q=https://www.kitchensplusco.com/
http://maps.google.az/url?q=https://www.kitchensplusco.com/
http://maps.google.bs/url?q=https://www.kitchensplusco.com/
http://maps.google.com.bh/url?q=https://www.kitchensplusco.com/
http://maps.google.com.bd/url?q=https://www.kitchensplusco.com/
http://maps.google.com.by/url?q=https://www.kitchensplusco.com/
http://maps.google.be/url?q=https://www.kitchensplusco.com/
http://maps.google.com.bz/url?q=https://www.kitchensplusco.com/
http://maps.google.bj/url?q=https://www.kitchensplusco.com/
http://maps.google.bt/url?q=https://www.kitchensplusco.com/
http://maps.google.com.bo/url?q=https://www.kitchensplusco.com/
http://maps.google.ba/url?q=https://www.kitchensplusco.com/
http://maps.google.co.bw/url?q=https://www.kitchensplusco.com/
http://maps.google.com.br/url?q=https://www.kitchensplusco.com/
http://maps.google.vg/url?q=https://www.kitchensplusco.com/
http://maps.google.com.bn/url?q=https://www.kitchensplusco.com/
http://maps.google.bg/url?q=https://www.kitchensplusco.com/
http://maps.google.bf/url?q=https://www.kitchensplusco.com/
http://maps.google.bi/url?q=https://www.kitchensplusco.com/
http://maps.google.com.kh/url?q=https://www.kitchensplusco.com/
http://maps.google.cm/url?q=https://www.kitchensplusco.com/
http://maps.google.ca/url?q=https://www.kitchensplusco.com/
http://maps.google.cv/url?q=https://www.kitchensplusco.com/
http://maps.google.cat/url?q=https://www.kitchensplusco.com/
http://maps.google.cf/url?q=https://www.kitchensplusco.com/
http://maps.google.td/url?q=https://www.kitchensplusco.com/
http://maps.google.cl/url?q=https://www.kitchensplusco.com/
http://maps.google.cn/url?q=https://www.kitchensplusco.com/
http://maps.google.com.co/url?q=https://www.kitchensplusco.com/
http://maps.google.cd/url?q=https://www.kitchensplusco.com/
http://maps.google.cg/url?q=https://www.kitchensplusco.com/
http://maps.google.co.ck/url?q=https://www.kitchensplusco.com/
http://maps.google.co.cr/url?q=https://www.kitchensplusco.com/
http://maps.google.ci/url?q=https://www.kitchensplusco.com/
http://maps.google.hr/url?q=https://www.kitchensplusco.com/
http://maps.google.com.cu/url?q=https://www.kitchensplusco.com/
http://maps.google.com.cy/url?q=https://www.kitchensplusco.com/
http://maps.google.cz/url?q=https://www.kitchensplusco.com/
http://maps.google.dk/url?q=https://www.kitchensplusco.com/
http://maps.google.dj/url?q=https://www.kitchensplusco.com/
http://maps.google.dm/url?q=https://www.kitchensplusco.com/
http://maps.google.com.do/url?q=https://www.kitchensplusco.com/
http://maps.google.com.ec/url?q=https://www.kitchensplusco.com/
http://maps.google.com.eg/url?q=https://www.kitchensplusco.com/
http://maps.google.com.sv/url?q=https://www.kitchensplusco.com/
http://maps.google.ee/url?q=https://www.kitchensplusco.com/
http://maps.google.com.et/url?q=https://www.kitchensplusco.com/
http://maps.google.com.fj/url?q=https://www.kitchensplusco.com/
http://maps.google.fi/url?q=https://www.kitchensplusco.com/
http://maps.google.fr/url?q=https://www.kitchensplusco.com/
http://maps.google.ga/url?q=https://www.kitchensplusco.com/
http://maps.google.gm/url?q=https://www.kitchensplusco.com/
http://maps.google.ge/url?q=https://www.kitchensplusco.com/
http://maps.google.de/url?q=https://www.kitchensplusco.com/
http://maps.google.com.gh/url?q=https://www.kitchensplusco.com/
http://maps.google.com.gi/url?q=https://www.kitchensplusco.com/
http://maps.google.gr/url?q=https://www.kitchensplusco.com/
http://maps.google.gl/url?q=https://www.kitchensplusco.com/
http://maps.google.gp/url?q=https://www.kitchensplusco.com/
http://maps.google.com.gt/url?q=https://www.kitchensplusco.com/
http://maps.google.gg/url?q=https://www.kitchensplusco.com/
http://maps.google.gy/url?q=https://www.kitchensplusco.com/
http://maps.google.ht/url?q=https://www.kitchensplusco.com/
http://maps.google.hn/url?q=https://www.kitchensplusco.com/
http://maps.google.com.hk/url?q=https://www.kitchensplusco.com/
http://maps.google.hu/url?q=https://www.kitchensplusco.com/
http://maps.google.is/url?q=https://www.kitchensplusco.com/
http://maps.google.co.in/url?q=https://www.kitchensplusco.com/
http://maps.google.co.id/url?q=https://www.kitchensplusco.com/
http://maps.google.iq/url?q=https://www.kitchensplusco.com/
http://maps.google.ie/url?q=https://www.kitchensplusco.com/
http://maps.google.co.im/url?q=https://www.kitchensplusco.com/
http://maps.google.co.il/url?q=https://www.kitchensplusco.com/
http://maps.google.it/url?q=https://www.kitchensplusco.com/
http://maps.google.ci/url?q=https://www.kitchensplusco.com/
http://maps.google.com.jm/url?q=https://www.kitchensplusco.com/
http://maps.google.co.jp/url?q=https://www.kitchensplusco.com/
http://maps.google.co.je/url?q=https://www.kitchensplusco.com/
http://maps.google.jo/url?q=https://www.kitchensplusco.com/
http://maps.google.kz/url?q=https://www.kitchensplusco.com/
http://maps.google.co.ke/url?q=https://www.kitchensplusco.com/
http://maps.google.ki/url?q=https://www.kitchensplusco.com/
http://maps.google.com.kw/url?q=https://www.kitchensplusco.com/
http://maps.google.com.kg/url?q=https://www.kitchensplusco.com/
http://maps.google.la/url?q=https://www.kitchensplusco.com/
http://maps.google.lv/url?q=https://www.kitchensplusco.com/
http://maps.google.com.lb/url?q=https://www.kitchensplusco.com/
http://maps.google.co.ls/url?q=https://www.kitchensplusco.com/
http://maps.google.com.ly/url?q=https://www.kitchensplusco.com/
http://maps.google.li/url?q=https://www.kitchensplusco.com/
http://maps.google.lt/url?q=https://www.kitchensplusco.com/
http://maps.google.lu/url?q=https://www.kitchensplusco.com/
http://maps.google.mk/url?q=https://www.kitchensplusco.com/
http://maps.google.mg/url?q=https://www.kitchensplusco.com/
http://maps.google.mw/url?q=https://www.kitchensplusco.com/
http://maps.google.com.my/url?q=https://www.kitchensplusco.com/
http://maps.google.mv/url?q=https://www.kitchensplusco.com/
http://maps.google.ml/url?q=https://www.kitchensplusco.com/
http://maps.google.com.mt/url?q=https://www.kitchensplusco.com/
http://maps.google.mu/url?q=https://www.kitchensplusco.com/
http://maps.google.com.mx/url?q=https://www.kitchensplusco.com/
http://maps.google.fm/url?q=https://www.kitchensplusco.com/
http://maps.google.md/url?q=https://www.kitchensplusco.com/
http://maps.google.mn/url?q=https://www.kitchensplusco.com/
http://maps.google.me/url?q=https://www.kitchensplusco.com/
http://maps.google.ms/url?q=https://www.kitchensplusco.com/
http://maps.google.co.ma/url?q=https://www.kitchensplusco.com/
http://maps.google.co.mz/url?q=https://www.kitchensplusco.com/
http://maps.google.com.na/url?q=https://www.kitchensplusco.com/
http://maps.google.nr/url?q=https://www.kitchensplusco.com/
http://maps.google.com.np/url?q=https://www.kitchensplusco.com/
http://maps.google.nl/url?q=https://www.kitchensplusco.com/
http://maps.google.co.nz/url?q=https://www.kitchensplusco.com/
http://maps.google.com.ni/url?q=https://www.kitchensplusco.com/
http://maps.google.ne/url?q=https://www.kitchensplusco.com/
http://maps.google.com.ng/url?q=https://www.kitchensplusco.com/
http://maps.google.nu/url?q=https://www.kitchensplusco.com/
http://maps.google.com.nf/url?q=https://www.kitchensplusco.com/
http://maps.google.no/url?q=https://www.kitchensplusco.com/
http://maps.google.com.om/url?q=https://www.kitchensplusco.com/
http://maps.google.com.pk/url?q=https://www.kitchensplusco.com/
http://maps.google.ps/url?q=https://www.kitchensplusco.com/
http://maps.google.com.pa/url?q=https://www.kitchensplusco.com/
http://maps.google.com.pg/url?q=https://www.kitchensplusco.com/
http://maps.google.com.py/url?q=https://www.kitchensplusco.com/
http://maps.google.com.pe/url?q=https://www.kitchensplusco.com/
http://maps.google.com.ph/url?q=https://www.kitchensplusco.com/
http://maps.google.pn/url?q=https://www.kitchensplusco.com/
http://maps.google.pl/url?q=https://www.kitchensplusco.com/
http://maps.google.pt/url?q=https://www.kitchensplusco.com/
http://maps.google.com.pr/url?q=https://www.kitchensplusco.com/
http://maps.google.com.qa/url?q=https://www.kitchensplusco.com/
http://maps.google.ro/url?q=https://www.kitchensplusco.com/
http://maps.google.ru/url?q=https://www.kitchensplusco.com/
http://maps.google.rw/url?q=https://www.kitchensplusco.com/
http://maps.google.sh/url?q=https://www.kitchensplusco.com/
http://maps.google.ws/url?q=https://www.kitchensplusco.com/
http://maps.google.sm/url?q=https://www.kitchensplusco.com/
http://maps.google.st/url?q=https://www.kitchensplusco.com/
http://maps.google.com.sa/url?q=https://www.kitchensplusco.com/
http://maps.google.sn/url?q=https://www.kitchensplusco.com/
http://maps.google.rs/url?q=https://www.kitchensplusco.com/
http://maps.google.sc/url?q=https://www.kitchensplusco.com/
http://maps.google.com.sl/url?q=https://www.kitchensplusco.com/
http://maps.google.com.sg/url?q=https://www.kitchensplusco.com/
http://maps.google.sk/url?q=https://www.kitchensplusco.com/
http://maps.google.si/url?q=https://www.kitchensplusco.com/
http://maps.google.com.sb/url?q=https://www.kitchensplusco.com/
http://maps.google.so/url?q=https://www.kitchensplusco.com/
http://maps.google.co.za/url?q=https://www.kitchensplusco.com/
http://maps.google.co.kr/url?q=https://www.kitchensplusco.com/
http://maps.google.es/url?q=https://www.kitchensplusco.com/
http://maps.google.lk/url?q=https://www.kitchensplusco.com/
http://maps.google.com.vc/url?q=https://www.kitchensplusco.com/
http://maps.google.sr/url?q=https://www.kitchensplusco.com/
http://maps.google.se/url?q=https://www.kitchensplusco.com/
http://maps.google.ch/url?q=https://www.kitchensplusco.com/
http://maps.google.com.tw/url?q=https://www.kitchensplusco.com/
http://maps.google.com.tj/url?q=https://www.kitchensplusco.com/
http://maps.google.co.tz/url?q=https://www.kitchensplusco.com/
http://maps.google.co.th/url?q=https://www.kitchensplusco.com/
http://maps.google.tl/url?q=https://www.kitchensplusco.com/
http://maps.google.tg/url?q=https://www.kitchensplusco.com/
http://maps.google.tk/url?q=https://www.kitchensplusco.com/
http://maps.google.to/url?q=https://www.kitchensplusco.com/
http://maps.google.tt/url?q=https://www.kitchensplusco.com/
http://maps.google.tn/url?q=https://www.kitchensplusco.com/
http://maps.google.com.tr/url?q=https://www.kitchensplusco.com/
http://maps.google.tm/url?q=https://www.kitchensplusco.com/
http://maps.google.co.ug/url?q=https://www.kitchensplusco.com/
http://maps.google.com.ua/url?q=https://www.kitchensplusco.com/
http://maps.google.ae/url?q=https://www.kitchensplusco.com/
http://maps.google.co.uk/url?q=https://www.kitchensplusco.com/
http://maps.google.com/url?q=https://www.kitchensplusco.com/
http://maps.google.com.uy/url?q=https://www.kitchensplusco.com/
http://maps.google.co.uz/url?q=https://www.kitchensplusco.com/
http://maps.google.vu/url?q=https://www.kitchensplusco.com/
http://maps.google.co.ve/url?q=https://www.kitchensplusco.com/
http://maps.google.com.vn/url?q=https://www.kitchensplusco.com/
http://maps.google.co.vi/url?q=https://www.kitchensplusco.com/
http://maps.google.co.zm/url?q=https://www.kitchensplusco.com/
http://maps.google.co.zw/url?q=https://www.kitchensplusco.com/
http://images.google.com.af/url?q=https://www.kitchensplusco.com/
http://images.google.al/url?q=https://www.kitchensplusco.com/
http://images.google.dz/url?q=https://www.kitchensplusco.com/
http://images.google.as/url?q=https://www.kitchensplusco.com/
http://images.google.ad/url?q=https://www.kitchensplusco.com/
http://images.google.it.ao/url?q=https://www.kitchensplusco.com/
http://images.google.com.ai/url?q=https://www.kitchensplusco.com/
http://images.google.com.ag/url?q=https://www.kitchensplusco.com/
http://images.google.com.ar/url?q=https://www.kitchensplusco.com/
http://images.google.am/url?q=https://www.kitchensplusco.com/
http://images.google.ac/url?q=https://www.kitchensplusco.com/
http://images.google.com.au/url?q=https://www.kitchensplusco.com/
http://images.google.at/url?q=https://www.kitchensplusco.com/
http://images.google.az/url?q=https://www.kitchensplusco.com/
http://images.google.bs/url?q=https://www.kitchensplusco.com/
http://images.google.com.bh/url?q=https://www.kitchensplusco.com/
http://images.google.com.bd/url?q=https://www.kitchensplusco.com/
http://images.google.com.by/url?q=https://www.kitchensplusco.com/
http://images.google.be/url?q=https://www.kitchensplusco.com/
http://images.google.com.bz/url?q=https://www.kitchensplusco.com/
http://images.google.bj/url?q=https://www.kitchensplusco.com/
http://images.google.bt/url?q=https://www.kitchensplusco.com/
http://images.google.com.bo/url?q=https://www.kitchensplusco.com/
http://images.google.ba/url?q=https://www.kitchensplusco.com/
http://images.google.co.bw/url?q=https://www.kitchensplusco.com/
http://images.google.com.br/url?q=https://www.kitchensplusco.com/
http://images.google.vg/url?q=https://www.kitchensplusco.com/
http://images.google.com.bn/url?q=https://www.kitchensplusco.com/
http://images.google.bg/url?q=https://www.kitchensplusco.com/
http://images.google.bf/url?q=https://www.kitchensplusco.com/
http://images.google.bi/url?q=https://www.kitchensplusco.com/
http://images.google.com.kh/url?q=https://www.kitchensplusco.com/
http://images.google.cm/url?q=https://www.kitchensplusco.com/
http://images.google.ca/url?q=https://www.kitchensplusco.com/
http://images.google.cv/url?q=https://www.kitchensplusco.com/
http://images.google.cat/url?q=https://www.kitchensplusco.com/
http://images.google.cf/url?q=https://www.kitchensplusco.com/
http://images.google.td/url?q=https://www.kitchensplusco.com/
http://images.google.cl/url?q=https://www.kitchensplusco.com/
http://images.google.cn/url?q=https://www.kitchensplusco.com/
http://images.google.com.co/url?q=https://www.kitchensplusco.com/
http://images.google.cd/url?q=https://www.kitchensplusco.com/
http://images.google.cg/url?q=https://www.kitchensplusco.com/
http://images.google.co.ck/url?q=https://www.kitchensplusco.com/
http://images.google.co.cr/url?q=https://www.kitchensplusco.com/
http://images.google.ci/url?q=https://www.kitchensplusco.com/
http://images.google.hr/url?q=https://www.kitchensplusco.com/
http://images.google.com.cu/url?q=https://www.kitchensplusco.com/
http://images.google.com.cy/url?q=https://www.kitchensplusco.com/
http://images.google.cz/url?q=https://www.kitchensplusco.com/
http://images.google.dk/url?q=https://www.kitchensplusco.com/
http://images.google.dj/url?q=https://www.kitchensplusco.com/
http://images.google.dm/url?q=https://www.kitchensplusco.com/
http://images.google.com.do/url?q=https://www.kitchensplusco.com/
http://images.google.com.ec/url?q=https://www.kitchensplusco.com/
http://images.google.com.eg/url?q=https://www.kitchensplusco.com/
http://images.google.com.sv/url?q=https://www.kitchensplusco.com/
http://images.google.ee/url?q=https://www.kitchensplusco.com/
http://images.google.com.et/url?q=https://www.kitchensplusco.com/
http://images.google.com.fj/url?q=https://www.kitchensplusco.com/
http://images.google.fi/url?q=https://www.kitchensplusco.com/
http://images.google.fr/url?q=https://www.kitchensplusco.com/
http://images.google.ga/url?q=https://www.kitchensplusco.com/
http://images.google.gm/url?q=https://www.kitchensplusco.com/
http://images.google.ge/url?q=https://www.kitchensplusco.com/
http://images.google.de/url?q=https://www.kitchensplusco.com/
http://images.google.com.gh/url?q=https://www.kitchensplusco.com/
http://images.google.com.gi/url?q=https://www.kitchensplusco.com/
http://images.google.gr/url?q=https://www.kitchensplusco.com/
http://images.google.gl/url?q=https://www.kitchensplusco.com/
http://images.google.gp/url?q=https://www.kitchensplusco.com/
http://images.google.com.gt/url?q=https://www.kitchensplusco.com/
http://images.google.gg/url?q=https://www.kitchensplusco.com/
http://images.google.gy/url?q=https://www.kitchensplusco.com/
http://images.google.ht/url?q=https://www.kitchensplusco.com/
http://images.google.hn/url?q=https://www.kitchensplusco.com/
http://images.google.com.hk/url?q=https://www.kitchensplusco.com/
http://images.google.hu/url?q=https://www.kitchensplusco.com/
http://images.google.is/url?q=https://www.kitchensplusco.com/
http://images.google.co.in/url?q=https://www.kitchensplusco.com/
http://images.google.co.id/url?q=https://www.kitchensplusco.com/
http://images.google.iq/url?q=https://www.kitchensplusco.com/
http://images.google.ie/url?q=https://www.kitchensplusco.com/
http://images.google.co.im/url?q=https://www.kitchensplusco.com/
http://images.google.co.il/url?q=https://www.kitchensplusco.com/
http://images.google.it/url?q=https://www.kitchensplusco.com/
http://images.google.ci/url?q=https://www.kitchensplusco.com/
http://images.google.com.jm/url?q=https://www.kitchensplusco.com/
http://images.google.co.jp/url?q=https://www.kitchensplusco.com/
http://images.google.co.je/url?q=https://www.kitchensplusco.com/
http://images.google.jo/url?q=https://www.kitchensplusco.com/
http://images.google.kz/url?q=https://www.kitchensplusco.com/
http://images.google.co.ke/url?q=https://www.kitchensplusco.com/
http://images.google.ki/url?q=https://www.kitchensplusco.com/
http://images.google.com.kw/url?q=https://www.kitchensplusco.com/
http://images.google.com.kg/url?q=https://www.kitchensplusco.com/
http://images.google.la/url?q=https://www.kitchensplusco.com/
http://images.google.lv/url?q=https://www.kitchensplusco.com/
http://images.google.com.lb/url?q=https://www.kitchensplusco.com/
http://images.google.co.ls/url?q=https://www.kitchensplusco.com/
http://images.google.com.ly/url?q=https://www.kitchensplusco.com/
http://images.google.li/url?q=https://www.kitchensplusco.com/
http://images.google.lt/url?q=https://www.kitchensplusco.com/
http://images.google.lu/url?q=https://www.kitchensplusco.com/
http://images.google.mk/url?q=https://www.kitchensplusco.com/
http://images.google.mg/url?q=https://www.kitchensplusco.com/
http://images.google.mw/url?q=https://www.kitchensplusco.com/
http://images.google.com.my/url?q=https://www.kitchensplusco.com/
http://images.google.mv/url?q=https://www.kitchensplusco.com/
http://images.google.ml/url?q=https://www.kitchensplusco.com/
http://images.google.com.mt/url?q=https://www.kitchensplusco.com/
http://images.google.mu/url?q=https://www.kitchensplusco.com/
http://images.google.com.mx/url?q=https://www.kitchensplusco.com/
http://images.google.fm/url?q=https://www.kitchensplusco.com/
http://images.google.md/url?q=https://www.kitchensplusco.com/
http://images.google.mn/url?q=https://www.kitchensplusco.com/
http://images.google.me/url?q=https://www.kitchensplusco.com/
http://images.google.ms/url?q=https://www.kitchensplusco.com/
http://images.google.co.ma/url?q=https://www.kitchensplusco.com/
http://images.google.co.mz/url?q=https://www.kitchensplusco.com/
http://images.google.com.na/url?q=https://www.kitchensplusco.com/
http://images.google.nr/url?q=https://www.kitchensplusco.com/
http://images.google.com.np/url?q=https://www.kitchensplusco.com/
http://images.google.nl/url?q=https://www.kitchensplusco.com/
http://images.google.co.nz/url?q=https://www.kitchensplusco.com/
http://images.google.com.ni/url?q=https://www.kitchensplusco.com/
http://images.google.ne/url?q=https://www.kitchensplusco.com/
http://images.google.com.ng/url?q=https://www.kitchensplusco.com/
http://images.google.nu/url?q=https://www.kitchensplusco.com/
http://images.google.com.nf/url?q=https://www.kitchensplusco.com/
http://images.google.no/url?q=https://www.kitchensplusco.com/
http://images.google.com.om/url?q=https://www.kitchensplusco.com/
http://images.google.com.pk/url?q=https://www.kitchensplusco.com/
http://images.google.ps/url?q=https://www.kitchensplusco.com/
http://images.google.com.pa/url?q=https://www.kitchensplusco.com/
http://images.google.com.pg/url?q=https://www.kitchensplusco.com/
http://images.google.com.py/url?q=https://www.kitchensplusco.com/
http://images.google.com.pe/url?q=https://www.kitchensplusco.com/
http://images.google.com.ph/url?q=https://www.kitchensplusco.com/
http://images.google.pn/url?q=https://www.kitchensplusco.com/
http://images.google.pl/url?q=https://www.kitchensplusco.com/
http://images.google.pt/url?q=https://www.kitchensplusco.com/
http://images.google.com.pr/url?q=https://www.kitchensplusco.com/
http://images.google.com.qa/url?q=https://www.kitchensplusco.com/
http://images.google.ro/url?q=https://www.kitchensplusco.com/
http://images.google.ru/url?q=https://www.kitchensplusco.com/
http://images.google.rw/url?q=https://www.kitchensplusco.com/
http://images.google.sh/url?q=https://www.kitchensplusco.com/
http://images.google.ws/url?q=https://www.kitchensplusco.com/
http://images.google.sm/url?q=https://www.kitchensplusco.com/
http://images.google.st/url?q=https://www.kitchensplusco.com/
http://images.google.com.sa/url?q=https://www.kitchensplusco.com/
http://images.google.sn/url?q=https://www.kitchensplusco.com/
http://images.google.rs/url?q=https://www.kitchensplusco.com/
http://images.google.sc/url?q=https://www.kitchensplusco.com/
http://images.google.com.sl/url?q=https://www.kitchensplusco.com/
http://images.google.com.sg/url?q=https://www.kitchensplusco.com/
http://images.google.sk/url?q=https://www.kitchensplusco.com/
http://images.google.si/url?q=https://www.kitchensplusco.com/
http://images.google.com.sb/url?q=https://www.kitchensplusco.com/
http://images.google.so/url?q=https://www.kitchensplusco.com/
http://images.google.co.za/url?q=https://www.kitchensplusco.com/
http://images.google.co.kr/url?q=https://www.kitchensplusco.com/
http://images.google.es/url?q=https://www.kitchensplusco.com/
http://images.google.lk/url?q=https://www.kitchensplusco.com/
http://images.google.com.vc/url?q=https://www.kitchensplusco.com/
http://images.google.sr/url?q=https://www.kitchensplusco.com/
http://images.google.se/url?q=https://www.kitchensplusco.com/
http://images.google.ch/url?q=https://www.kitchensplusco.com/
http://images.google.com.tw/url?q=https://www.kitchensplusco.com/
http://images.google.com.tj/url?q=https://www.kitchensplusco.com/
http://images.google.co.tz/url?q=https://www.kitchensplusco.com/
http://images.google.co.th/url?q=https://www.kitchensplusco.com/
http://images.google.tl/url?q=https://www.kitchensplusco.com/
http://images.google.tg/url?q=https://www.kitchensplusco.com/
http://images.google.tk/url?q=https://www.kitchensplusco.com/
http://images.google.to/url?q=https://www.kitchensplusco.com/
http://images.google.tt/url?q=https://www.kitchensplusco.com/
http://images.google.tn/url?q=https://www.kitchensplusco.com/
http://images.google.com.tr/url?q=https://www.kitchensplusco.com/
http://images.google.tm/url?q=https://www.kitchensplusco.com/
http://images.google.co.ug/url?q=https://www.kitchensplusco.com/
http://images.google.com.ua/url?q=https://www.kitchensplusco.com/
http://images.google.ae/url?q=https://www.kitchensplusco.com/
http://images.google.co.uk/url?q=https://www.kitchensplusco.com/
http://images.google.com/url?q=https://www.kitchensplusco.com/
http://images.google.com.uy/url?q=https://www.kitchensplusco.com/
http://images.google.co.uz/url?q=https://www.kitchensplusco.com/
http://images.google.vu/url?q=https://www.kitchensplusco.com/
http://images.google.co.ve/url?q=https://www.kitchensplusco.com/
http://images.google.com.vn/url?q=https://www.kitchensplusco.com/
http://images.google.co.vi/url?q=https://www.kitchensplusco.com/
http://images.google.co.zm/url?q=https://www.kitchensplusco.com/
http://images.google.co.zw/url?q=https://www.kitchensplusco.com/
Keep on writing, great job!
Excellent beat ! I would like to apprentice while you amend your site, how could i subscribe for a
blog site? The account aided me a acceptable deal.
I had been a little bit acquainted of this your broadcast
provided bright clear concept
Hey there! Do you know if they make any plugins to assist with SEO?
I’m trying to get my blog to rank for some targeted keywords but I’m
not seeing very good results. If you know of any please share.
Cheers!
Way cool! Some extremely valid points! I appreciate you penning this write-up plus the rest
of the website is also very good.
excellent points altogether, you just won a new reader.
What would you recommend in regards to your submit that you just made a few
days in the past? Any sure?
Thanks for sharing your thoughts. I truly appreciate your efforts and I will be waiting for your
next write ups thanks once again.
I simply couldn’t leave your web site prior to suggesting
that I actually loved the usual info a person supply to your
visitors? Is going to be again often in order to check out
new posts
We’re a group of volunteers and starting a new scheme in our
community. Your website offered us with valuable information to work
on. You have done an impressive job and our whole community will be grateful to you.
Oh my goodness! Incredible article dude! Many thanks, However I am going through problems with your
RSS. I don’t understand the reason why I am unable to join it.
Is there anyone else having identical RSS issues?
Anyone who knows the solution can you kindly respond?
Thanks!!
http://google.com.af/url?q=https://www.premiumganjashop.com/
http://google.al/url?q=https://www.premiumganjashop.com/
http://google.dz/url?q=https://www.premiumganjashop.com/
http://google.as/url?q=https://www.premiumganjashop.com/
http://google.ad/url?q=https://www.premiumganjashop.com/
http://google.it.ao/url?q=https://www.premiumganjashop.com/
http://google.com.ai/url?q=https://www.premiumganjashop.com/
http://google.com.ag/url?q=https://www.premiumganjashop.com/
http://google.com.ar/url?q=https://www.premiumganjashop.com/
http://google.am/url?q=https://www.premiumganjashop.com/
http://google.ac/url?q=https://www.premiumganjashop.com/
http://google.com.au/url?q=https://www.premiumganjashop.com/
http://google.at/url?q=https://www.premiumganjashop.com/
http://google.az/url?q=https://www.premiumganjashop.com/
http://google.bs/url?q=https://www.premiumganjashop.com/
http://google.com.bh/url?q=https://www.premiumganjashop.com/
http://google.com.bd/url?q=https://www.premiumganjashop.com/
http://google.com.by/url?q=https://www.premiumganjashop.com/
http://google.be/url?q=https://www.premiumganjashop.com/
http://google.com.bz/url?q=https://www.premiumganjashop.com/
http://google.bj/url?q=https://www.premiumganjashop.com/
http://google.bt/url?q=https://www.premiumganjashop.com/
http://google.com.bo/url?q=https://www.premiumganjashop.com/
http://google.ba/url?q=https://www.premiumganjashop.com/
http://google.co.bw/url?q=https://www.premiumganjashop.com/
http://google.com.br/url?q=https://www.premiumganjashop.com/
http://google.vg/url?q=https://www.premiumganjashop.com/
http://google.com.bn/url?q=https://www.premiumganjashop.com/
http://google.bg/url?q=https://www.premiumganjashop.com/
http://google.bf/url?q=https://www.premiumganjashop.com/
http://google.bi/url?q=https://www.premiumganjashop.com/
http://google.com.kh/url?q=https://www.premiumganjashop.com/
http://google.cm/url?q=https://www.premiumganjashop.com/
http://google.ca/url?q=https://www.premiumganjashop.com/
http://google.cv/url?q=https://www.premiumganjashop.com/
http://google.cat/url?q=https://www.premiumganjashop.com/
http://google.cf/url?q=https://www.premiumganjashop.com/
http://google.td/url?q=https://www.premiumganjashop.com/
http://google.cl/url?q=https://www.premiumganjashop.com/
http://google.cn/url?q=https://www.premiumganjashop.com/
http://google.com.co/url?q=https://www.premiumganjashop.com/
http://google.cd/url?q=https://www.premiumganjashop.com/
http://google.cg/url?q=https://www.premiumganjashop.com/
http://google.co.ck/url?q=https://www.premiumganjashop.com/
http://google.co.cr/url?q=https://www.premiumganjashop.com/
http://google.ci/url?q=https://www.premiumganjashop.com/
http://google.hr/url?q=https://www.premiumganjashop.com/
http://google.com.cu/url?q=https://www.premiumganjashop.com/
http://google.com.cy/url?q=https://www.premiumganjashop.com/
http://google.cz/url?q=https://www.premiumganjashop.com/
http://google.dk/url?q=https://www.premiumganjashop.com/
http://google.dj/url?q=https://www.premiumganjashop.com/
http://google.dm/url?q=https://www.premiumganjashop.com/
http://google.com.do/url?q=https://www.premiumganjashop.com/
http://google.com.ec/url?q=https://www.premiumganjashop.com/
http://google.com.eg/url?q=https://www.premiumganjashop.com/
http://google.com.sv/url?q=https://www.premiumganjashop.com/
http://google.ee/url?q=https://www.premiumganjashop.com/
http://google.com.et/url?q=https://www.premiumganjashop.com/
http://google.com.fj/url?q=https://www.premiumganjashop.com/
http://google.fi/url?q=https://www.premiumganjashop.com/
http://google.fr/url?q=https://www.premiumganjashop.com/
http://google.ga/url?q=https://www.premiumganjashop.com/
http://google.gm/url?q=https://www.premiumganjashop.com/
http://google.ge/url?q=https://www.premiumganjashop.com/
http://google.de/url?q=https://www.premiumganjashop.com/
http://google.com.gh/url?q=https://www.premiumganjashop.com/
http://google.com.gi/url?q=https://www.premiumganjashop.com/
http://google.gr/url?q=https://www.premiumganjashop.com/
http://google.gl/url?q=https://www.premiumganjashop.com/
http://google.gp/url?q=https://www.premiumganjashop.com/
http://google.com.gt/url?q=https://www.premiumganjashop.com/
http://google.gg/url?q=https://www.premiumganjashop.com/
http://google.gy/url?q=https://www.premiumganjashop.com/
http://google.ht/url?q=https://www.premiumganjashop.com/
http://google.hn/url?q=https://www.premiumganjashop.com/
http://google.com.hk/url?q=https://www.premiumganjashop.com/
http://google.hu/url?q=https://www.premiumganjashop.com/
http://google.is/url?q=https://www.premiumganjashop.com/
http://google.co.in/url?q=https://www.premiumganjashop.com/
http://google.co.id/url?q=https://www.premiumganjashop.com/
http://google.iq/url?q=https://www.premiumganjashop.com/
http://google.ie/url?q=https://www.premiumganjashop.com/
http://google.co.im/url?q=https://www.premiumganjashop.com/
http://google.co.il/url?q=https://www.premiumganjashop.com/
http://google.it/url?q=https://www.premiumganjashop.com/
http://google.ci/url?q=https://www.premiumganjashop.com/
http://google.com.jm/url?q=https://www.premiumganjashop.com/
http://google.co.jp/url?q=https://www.premiumganjashop.com/
http://google.co.je/url?q=https://www.premiumganjashop.com/
http://google.jo/url?q=https://www.premiumganjashop.com/
http://google.kz/url?q=https://www.premiumganjashop.com/
http://google.co.ke/url?q=https://www.premiumganjashop.com/
http://google.ki/url?q=https://www.premiumganjashop.com/
http://google.com.kw/url?q=https://www.premiumganjashop.com/
http://google.com.kg/url?q=https://www.premiumganjashop.com/
http://google.la/url?q=https://www.premiumganjashop.com/
http://google.lv/url?q=https://www.premiumganjashop.com/
http://google.com.lb/url?q=https://www.premiumganjashop.com/
http://google.co.ls/url?q=https://www.premiumganjashop.com/
http://google.com.ly/url?q=https://www.premiumganjashop.com/
http://google.li/url?q=https://www.premiumganjashop.com/
http://google.lt/url?q=https://www.premiumganjashop.com/
http://google.lu/url?q=https://www.premiumganjashop.com/
http://google.mk/url?q=https://www.premiumganjashop.com/
http://google.mg/url?q=https://www.premiumganjashop.com/
http://google.mw/url?q=https://www.premiumganjashop.com/
http://google.com.my/url?q=https://www.premiumganjashop.com/
http://google.mv/url?q=https://www.premiumganjashop.com/
http://google.ml/url?q=https://www.premiumganjashop.com/
http://google.com.mt/url?q=https://www.premiumganjashop.com/
http://google.mu/url?q=https://www.premiumganjashop.com/
http://google.com.mx/url?q=https://www.premiumganjashop.com/
http://google.fm/url?q=https://www.premiumganjashop.com/
http://google.md/url?q=https://www.premiumganjashop.com/
http://google.mn/url?q=https://www.premiumganjashop.com/
http://google.me/url?q=https://www.premiumganjashop.com/
http://google.ms/url?q=https://www.premiumganjashop.com/
http://google.co.ma/url?q=https://www.premiumganjashop.com/
http://google.co.mz/url?q=https://www.premiumganjashop.com/
http://google.com.na/url?q=https://www.premiumganjashop.com/
http://google.nr/url?q=https://www.premiumganjashop.com/
http://google.com.np/url?q=https://www.premiumganjashop.com/
http://google.nl/url?q=https://www.premiumganjashop.com/
http://google.co.nz/url?q=https://www.premiumganjashop.com/
http://google.com.ni/url?q=https://www.premiumganjashop.com/
http://google.ne/url?q=https://www.premiumganjashop.com/
http://google.com.ng/url?q=https://www.premiumganjashop.com/
http://google.nu/url?q=https://www.premiumganjashop.com/
http://google.com.nf/url?q=https://www.premiumganjashop.com/
http://google.no/url?q=https://www.premiumganjashop.com/
http://google.com.om/url?q=https://www.premiumganjashop.com/
http://google.com.pk/url?q=https://www.premiumganjashop.com/
http://google.ps/url?q=https://www.premiumganjashop.com/
http://google.com.pa/url?q=https://www.premiumganjashop.com/
http://google.com.pg/url?q=https://www.premiumganjashop.com/
http://google.com.py/url?q=https://www.premiumganjashop.com/
http://google.com.pe/url?q=https://www.premiumganjashop.com/
http://google.com.ph/url?q=https://www.premiumganjashop.com/
http://google.pn/url?q=https://www.premiumganjashop.com/
http://google.pl/url?q=https://www.premiumganjashop.com/
http://google.pt/url?q=https://www.premiumganjashop.com/
http://google.com.pr/url?q=https://www.premiumganjashop.com/
http://google.com.qa/url?q=https://www.premiumganjashop.com/
http://google.ro/url?q=https://www.premiumganjashop.com/
http://google.ru/url?q=https://www.premiumganjashop.com/
http://google.rw/url?q=https://www.premiumganjashop.com/
http://google.sh/url?q=https://www.premiumganjashop.com/
http://google.ws/url?q=https://www.premiumganjashop.com/
http://google.sm/url?q=https://www.premiumganjashop.com/
http://google.st/url?q=https://www.premiumganjashop.com/
http://google.com.sa/url?q=https://www.premiumganjashop.com/
http://google.sn/url?q=https://www.premiumganjashop.com/
http://google.rs/url?q=https://www.premiumganjashop.com/
http://google.sc/url?q=https://www.premiumganjashop.com/
http://google.com.sl/url?q=https://www.premiumganjashop.com/
http://google.com.sg/url?q=https://www.premiumganjashop.com/
http://google.sk/url?q=https://www.premiumganjashop.com/
http://google.si/url?q=https://www.premiumganjashop.com/
http://google.com.sb/url?q=https://www.premiumganjashop.com/
http://google.so/url?q=https://www.premiumganjashop.com/
http://google.co.za/url?q=https://www.premiumganjashop.com/
http://google.co.kr/url?q=https://www.premiumganjashop.com/
http://google.es/url?q=https://www.premiumganjashop.com/
http://google.lk/url?q=https://www.premiumganjashop.com/
http://google.com.vc/url?q=https://www.premiumganjashop.com/
http://google.sr/url?q=https://www.premiumganjashop.com/
http://google.se/url?q=https://www.premiumganjashop.com/
http://google.ch/url?q=https://www.premiumganjashop.com/
http://google.com.tw/url?q=https://www.premiumganjashop.com/
http://google.com.tj/url?q=https://www.premiumganjashop.com/
http://google.co.tz/url?q=https://www.premiumganjashop.com/
http://google.co.th/url?q=https://www.premiumganjashop.com/
http://google.tl/url?q=https://www.premiumganjashop.com/
http://google.tg/url?q=https://www.premiumganjashop.com/
http://google.tk/url?q=https://www.premiumganjashop.com/
http://google.to/url?q=https://www.premiumganjashop.com/
http://google.tt/url?q=https://www.premiumganjashop.com/
http://google.tn/url?q=https://www.premiumganjashop.com/
http://google.com.tr/url?q=https://www.premiumganjashop.com/
http://google.tm/url?q=https://www.premiumganjashop.com/
http://google.co.ug/url?q=https://www.premiumganjashop.com/
http://google.com.ua/url?q=https://www.premiumganjashop.com/
http://google.ae/url?q=https://www.premiumganjashop.com/
http://google.co.uk/url?q=https://www.premiumganjashop.com/
http://google.com/url?q=https://www.premiumganjashop.com/
http://google.com.uy/url?q=https://www.premiumganjashop.com/
http://google.co.uz/url?q=https://www.premiumganjashop.com/
http://google.vu/url?q=https://www.premiumganjashop.com/
http://google.co.ve/url?q=https://www.premiumganjashop.com/
http://google.com.vn/url?q=https://www.premiumganjashop.com/
http://google.co.vi/url?q=https://www.premiumganjashop.com/
http://google.co.zm/url?q=https://www.premiumganjashop.com/
http://google.co.zw/url?q=https://www.premiumganjashop.com/
http://maps.google.com.af/url?q=https://www.premiumganjashop.com/
http://maps.google.al/url?q=https://www.premiumganjashop.com/
http://maps.google.dz/url?q=https://www.premiumganjashop.com/
http://maps.google.as/url?q=https://www.premiumganjashop.com/
http://maps.google.ad/url?q=https://www.premiumganjashop.com/
http://maps.google.it.ao/url?q=https://www.premiumganjashop.com/
http://maps.google.com.ai/url?q=https://www.premiumganjashop.com/
http://maps.google.com.ag/url?q=https://www.premiumganjashop.com/
http://maps.google.com.ar/url?q=https://www.premiumganjashop.com/
http://maps.google.am/url?q=https://www.premiumganjashop.com/
http://maps.google.ac/url?q=https://www.premiumganjashop.com/
http://maps.google.com.au/url?q=https://www.premiumganjashop.com/
http://maps.google.at/url?q=https://www.premiumganjashop.com/
http://maps.google.az/url?q=https://www.premiumganjashop.com/
http://maps.google.bs/url?q=https://www.premiumganjashop.com/
http://maps.google.com.bh/url?q=https://www.premiumganjashop.com/
http://maps.google.com.bd/url?q=https://www.premiumganjashop.com/
http://maps.google.com.by/url?q=https://www.premiumganjashop.com/
http://maps.google.be/url?q=https://www.premiumganjashop.com/
http://maps.google.com.bz/url?q=https://www.premiumganjashop.com/
http://maps.google.bj/url?q=https://www.premiumganjashop.com/
http://maps.google.bt/url?q=https://www.premiumganjashop.com/
http://maps.google.com.bo/url?q=https://www.premiumganjashop.com/
http://maps.google.ba/url?q=https://www.premiumganjashop.com/
http://maps.google.co.bw/url?q=https://www.premiumganjashop.com/
http://maps.google.com.br/url?q=https://www.premiumganjashop.com/
http://maps.google.vg/url?q=https://www.premiumganjashop.com/
http://maps.google.com.bn/url?q=https://www.premiumganjashop.com/
http://maps.google.bg/url?q=https://www.premiumganjashop.com/
http://maps.google.bf/url?q=https://www.premiumganjashop.com/
http://maps.google.bi/url?q=https://www.premiumganjashop.com/
http://maps.google.com.kh/url?q=https://www.premiumganjashop.com/
http://maps.google.cm/url?q=https://www.premiumganjashop.com/
http://maps.google.ca/url?q=https://www.premiumganjashop.com/
http://maps.google.cv/url?q=https://www.premiumganjashop.com/
http://maps.google.cat/url?q=https://www.premiumganjashop.com/
http://maps.google.cf/url?q=https://www.premiumganjashop.com/
http://maps.google.td/url?q=https://www.premiumganjashop.com/
http://maps.google.cl/url?q=https://www.premiumganjashop.com/
http://maps.google.cn/url?q=https://www.premiumganjashop.com/
http://maps.google.com.co/url?q=https://www.premiumganjashop.com/
http://maps.google.cd/url?q=https://www.premiumganjashop.com/
http://maps.google.cg/url?q=https://www.premiumganjashop.com/
http://maps.google.co.ck/url?q=https://www.premiumganjashop.com/
http://maps.google.co.cr/url?q=https://www.premiumganjashop.com/
http://maps.google.ci/url?q=https://www.premiumganjashop.com/
http://maps.google.hr/url?q=https://www.premiumganjashop.com/
http://maps.google.com.cu/url?q=https://www.premiumganjashop.com/
http://maps.google.com.cy/url?q=https://www.premiumganjashop.com/
http://maps.google.cz/url?q=https://www.premiumganjashop.com/
http://maps.google.dk/url?q=https://www.premiumganjashop.com/
http://maps.google.dj/url?q=https://www.premiumganjashop.com/
http://maps.google.dm/url?q=https://www.premiumganjashop.com/
http://maps.google.com.do/url?q=https://www.premiumganjashop.com/
http://maps.google.com.ec/url?q=https://www.premiumganjashop.com/
http://maps.google.com.eg/url?q=https://www.premiumganjashop.com/
http://maps.google.com.sv/url?q=https://www.premiumganjashop.com/
http://maps.google.ee/url?q=https://www.premiumganjashop.com/
http://maps.google.com.et/url?q=https://www.premiumganjashop.com/
http://maps.google.com.fj/url?q=https://www.premiumganjashop.com/
http://maps.google.fi/url?q=https://www.premiumganjashop.com/
http://maps.google.fr/url?q=https://www.premiumganjashop.com/
http://maps.google.ga/url?q=https://www.premiumganjashop.com/
http://maps.google.gm/url?q=https://www.premiumganjashop.com/
http://maps.google.ge/url?q=https://www.premiumganjashop.com/
http://maps.google.de/url?q=https://www.premiumganjashop.com/
http://maps.google.com.gh/url?q=https://www.premiumganjashop.com/
http://maps.google.com.gi/url?q=https://www.premiumganjashop.com/
http://maps.google.gr/url?q=https://www.premiumganjashop.com/
http://maps.google.gl/url?q=https://www.premiumganjashop.com/
http://maps.google.gp/url?q=https://www.premiumganjashop.com/
http://maps.google.com.gt/url?q=https://www.premiumganjashop.com/
http://maps.google.gg/url?q=https://www.premiumganjashop.com/
http://maps.google.gy/url?q=https://www.premiumganjashop.com/
http://maps.google.ht/url?q=https://www.premiumganjashop.com/
http://maps.google.hn/url?q=https://www.premiumganjashop.com/
http://maps.google.com.hk/url?q=https://www.premiumganjashop.com/
http://maps.google.hu/url?q=https://www.premiumganjashop.com/
http://maps.google.is/url?q=https://www.premiumganjashop.com/
http://maps.google.co.in/url?q=https://www.premiumganjashop.com/
http://maps.google.co.id/url?q=https://www.premiumganjashop.com/
http://maps.google.iq/url?q=https://www.premiumganjashop.com/
http://maps.google.ie/url?q=https://www.premiumganjashop.com/
http://maps.google.co.im/url?q=https://www.premiumganjashop.com/
http://maps.google.co.il/url?q=https://www.premiumganjashop.com/
http://maps.google.it/url?q=https://www.premiumganjashop.com/
http://maps.google.ci/url?q=https://www.premiumganjashop.com/
http://maps.google.com.jm/url?q=https://www.premiumganjashop.com/
http://maps.google.co.jp/url?q=https://www.premiumganjashop.com/
http://maps.google.co.je/url?q=https://www.premiumganjashop.com/
http://maps.google.jo/url?q=https://www.premiumganjashop.com/
http://maps.google.kz/url?q=https://www.premiumganjashop.com/
http://maps.google.co.ke/url?q=https://www.premiumganjashop.com/
http://maps.google.ki/url?q=https://www.premiumganjashop.com/
http://maps.google.com.kw/url?q=https://www.premiumganjashop.com/
http://maps.google.com.kg/url?q=https://www.premiumganjashop.com/
http://maps.google.la/url?q=https://www.premiumganjashop.com/
http://maps.google.lv/url?q=https://www.premiumganjashop.com/
http://maps.google.com.lb/url?q=https://www.premiumganjashop.com/
http://maps.google.co.ls/url?q=https://www.premiumganjashop.com/
http://maps.google.com.ly/url?q=https://www.premiumganjashop.com/
http://maps.google.li/url?q=https://www.premiumganjashop.com/
http://maps.google.lt/url?q=https://www.premiumganjashop.com/
http://maps.google.lu/url?q=https://www.premiumganjashop.com/
http://maps.google.mk/url?q=https://www.premiumganjashop.com/
http://maps.google.mg/url?q=https://www.premiumganjashop.com/
http://maps.google.mw/url?q=https://www.premiumganjashop.com/
http://maps.google.com.my/url?q=https://www.premiumganjashop.com/
http://maps.google.mv/url?q=https://www.premiumganjashop.com/
http://maps.google.ml/url?q=https://www.premiumganjashop.com/
http://maps.google.com.mt/url?q=https://www.premiumganjashop.com/
http://maps.google.mu/url?q=https://www.premiumganjashop.com/
http://maps.google.com.mx/url?q=https://www.premiumganjashop.com/
http://maps.google.fm/url?q=https://www.premiumganjashop.com/
http://maps.google.md/url?q=https://www.premiumganjashop.com/
http://maps.google.mn/url?q=https://www.premiumganjashop.com/
http://maps.google.me/url?q=https://www.premiumganjashop.com/
http://maps.google.ms/url?q=https://www.premiumganjashop.com/
http://maps.google.co.ma/url?q=https://www.premiumganjashop.com/
http://maps.google.co.mz/url?q=https://www.premiumganjashop.com/
http://maps.google.com.na/url?q=https://www.premiumganjashop.com/
http://maps.google.nr/url?q=https://www.premiumganjashop.com/
http://maps.google.com.np/url?q=https://www.premiumganjashop.com/
http://maps.google.nl/url?q=https://www.premiumganjashop.com/
http://maps.google.co.nz/url?q=https://www.premiumganjashop.com/
http://maps.google.com.ni/url?q=https://www.premiumganjashop.com/
http://maps.google.ne/url?q=https://www.premiumganjashop.com/
http://maps.google.com.ng/url?q=https://www.premiumganjashop.com/
http://maps.google.nu/url?q=https://www.premiumganjashop.com/
http://maps.google.com.nf/url?q=https://www.premiumganjashop.com/
http://maps.google.no/url?q=https://www.premiumganjashop.com/
http://maps.google.com.om/url?q=https://www.premiumganjashop.com/
http://maps.google.com.pk/url?q=https://www.premiumganjashop.com/
http://maps.google.ps/url?q=https://www.premiumganjashop.com/
http://maps.google.com.pa/url?q=https://www.premiumganjashop.com/
http://maps.google.com.pg/url?q=https://www.premiumganjashop.com/
http://maps.google.com.py/url?q=https://www.premiumganjashop.com/
http://maps.google.com.pe/url?q=https://www.premiumganjashop.com/
http://maps.google.com.ph/url?q=https://www.premiumganjashop.com/
http://maps.google.pn/url?q=https://www.premiumganjashop.com/
http://maps.google.pl/url?q=https://www.premiumganjashop.com/
http://maps.google.pt/url?q=https://www.premiumganjashop.com/
http://maps.google.com.pr/url?q=https://www.premiumganjashop.com/
http://maps.google.com.qa/url?q=https://www.premiumganjashop.com/
http://maps.google.ro/url?q=https://www.premiumganjashop.com/
http://maps.google.ru/url?q=https://www.premiumganjashop.com/
http://maps.google.rw/url?q=https://www.premiumganjashop.com/
http://maps.google.sh/url?q=https://www.premiumganjashop.com/
http://maps.google.ws/url?q=https://www.premiumganjashop.com/
http://maps.google.sm/url?q=https://www.premiumganjashop.com/
http://maps.google.st/url?q=https://www.premiumganjashop.com/
http://maps.google.com.sa/url?q=https://www.premiumganjashop.com/
http://maps.google.sn/url?q=https://www.premiumganjashop.com/
http://maps.google.rs/url?q=https://www.premiumganjashop.com/
http://maps.google.sc/url?q=https://www.premiumganjashop.com/
http://maps.google.com.sl/url?q=https://www.premiumganjashop.com/
http://maps.google.com.sg/url?q=https://www.premiumganjashop.com/
http://maps.google.sk/url?q=https://www.premiumganjashop.com/
http://maps.google.si/url?q=https://www.premiumganjashop.com/
http://maps.google.com.sb/url?q=https://www.premiumganjashop.com/
http://maps.google.so/url?q=https://www.premiumganjashop.com/
http://maps.google.co.za/url?q=https://www.premiumganjashop.com/
http://maps.google.co.kr/url?q=https://www.premiumganjashop.com/
http://maps.google.es/url?q=https://www.premiumganjashop.com/
http://maps.google.lk/url?q=https://www.premiumganjashop.com/
http://maps.google.com.vc/url?q=https://www.premiumganjashop.com/
http://maps.google.sr/url?q=https://www.premiumganjashop.com/
http://maps.google.se/url?q=https://www.premiumganjashop.com/
http://maps.google.ch/url?q=https://www.premiumganjashop.com/
http://maps.google.com.tw/url?q=https://www.premiumganjashop.com/
http://maps.google.com.tj/url?q=https://www.premiumganjashop.com/
http://maps.google.co.tz/url?q=https://www.premiumganjashop.com/
http://maps.google.co.th/url?q=https://www.premiumganjashop.com/
http://maps.google.tl/url?q=https://www.premiumganjashop.com/
http://maps.google.tg/url?q=https://www.premiumganjashop.com/
http://maps.google.tk/url?q=https://www.premiumganjashop.com/
http://maps.google.to/url?q=https://www.premiumganjashop.com/
http://maps.google.tt/url?q=https://www.premiumganjashop.com/
http://maps.google.tn/url?q=https://www.premiumganjashop.com/
http://maps.google.com.tr/url?q=https://www.premiumganjashop.com/
http://maps.google.tm/url?q=https://www.premiumganjashop.com/
http://maps.google.co.ug/url?q=https://www.premiumganjashop.com/
http://maps.google.com.ua/url?q=https://www.premiumganjashop.com/
http://maps.google.ae/url?q=https://www.premiumganjashop.com/
http://maps.google.co.uk/url?q=https://www.premiumganjashop.com/
http://maps.google.com/url?q=https://www.premiumganjashop.com/
http://maps.google.com.uy/url?q=https://www.premiumganjashop.com/
http://maps.google.co.uz/url?q=https://www.premiumganjashop.com/
http://maps.google.vu/url?q=https://www.premiumganjashop.com/
http://maps.google.co.ve/url?q=https://www.premiumganjashop.com/
http://maps.google.com.vn/url?q=https://www.premiumganjashop.com/
http://maps.google.co.vi/url?q=https://www.premiumganjashop.com/
http://maps.google.co.zm/url?q=https://www.premiumganjashop.com/
http://maps.google.co.zw/url?q=https://www.premiumganjashop.com/
http://images.google.com.af/url?q=https://www.premiumganjashop.com/
http://images.google.al/url?q=https://www.premiumganjashop.com/
http://images.google.dz/url?q=https://www.premiumganjashop.com/
http://images.google.as/url?q=https://www.premiumganjashop.com/
http://images.google.ad/url?q=https://www.premiumganjashop.com/
http://images.google.it.ao/url?q=https://www.premiumganjashop.com/
http://images.google.com.ai/url?q=https://www.premiumganjashop.com/
http://images.google.com.ag/url?q=https://www.premiumganjashop.com/
http://images.google.com.ar/url?q=https://www.premiumganjashop.com/
http://images.google.am/url?q=https://www.premiumganjashop.com/
http://images.google.ac/url?q=https://www.premiumganjashop.com/
http://images.google.com.au/url?q=https://www.premiumganjashop.com/
http://images.google.at/url?q=https://www.premiumganjashop.com/
http://images.google.az/url?q=https://www.premiumganjashop.com/
http://images.google.bs/url?q=https://www.premiumganjashop.com/
http://images.google.com.bh/url?q=https://www.premiumganjashop.com/
http://images.google.com.bd/url?q=https://www.premiumganjashop.com/
http://images.google.com.by/url?q=https://www.premiumganjashop.com/
http://images.google.be/url?q=https://www.premiumganjashop.com/
http://images.google.com.bz/url?q=https://www.premiumganjashop.com/
http://images.google.bj/url?q=https://www.premiumganjashop.com/
http://images.google.bt/url?q=https://www.premiumganjashop.com/
http://images.google.com.bo/url?q=https://www.premiumganjashop.com/
http://images.google.ba/url?q=https://www.premiumganjashop.com/
http://images.google.co.bw/url?q=https://www.premiumganjashop.com/
http://images.google.com.br/url?q=https://www.premiumganjashop.com/
http://images.google.vg/url?q=https://www.premiumganjashop.com/
http://images.google.com.bn/url?q=https://www.premiumganjashop.com/
http://images.google.bg/url?q=https://www.premiumganjashop.com/
http://images.google.bf/url?q=https://www.premiumganjashop.com/
http://images.google.bi/url?q=https://www.premiumganjashop.com/
http://images.google.com.kh/url?q=https://www.premiumganjashop.com/
http://images.google.cm/url?q=https://www.premiumganjashop.com/
http://images.google.ca/url?q=https://www.premiumganjashop.com/
http://images.google.cv/url?q=https://www.premiumganjashop.com/
http://images.google.cat/url?q=https://www.premiumganjashop.com/
http://images.google.cf/url?q=https://www.premiumganjashop.com/
http://images.google.td/url?q=https://www.premiumganjashop.com/
http://images.google.cl/url?q=https://www.premiumganjashop.com/
http://images.google.cn/url?q=https://www.premiumganjashop.com/
http://images.google.com.co/url?q=https://www.premiumganjashop.com/
http://images.google.cd/url?q=https://www.premiumganjashop.com/
http://images.google.cg/url?q=https://www.premiumganjashop.com/
http://images.google.co.ck/url?q=https://www.premiumganjashop.com/
http://images.google.co.cr/url?q=https://www.premiumganjashop.com/
http://images.google.ci/url?q=https://www.premiumganjashop.com/
http://images.google.hr/url?q=https://www.premiumganjashop.com/
http://images.google.com.cu/url?q=https://www.premiumganjashop.com/
http://images.google.com.cy/url?q=https://www.premiumganjashop.com/
http://images.google.cz/url?q=https://www.premiumganjashop.com/
http://images.google.dk/url?q=https://www.premiumganjashop.com/
http://images.google.dj/url?q=https://www.premiumganjashop.com/
http://images.google.dm/url?q=https://www.premiumganjashop.com/
http://images.google.com.do/url?q=https://www.premiumganjashop.com/
http://images.google.com.ec/url?q=https://www.premiumganjashop.com/
http://images.google.com.eg/url?q=https://www.premiumganjashop.com/
http://images.google.com.sv/url?q=https://www.premiumganjashop.com/
http://images.google.ee/url?q=https://www.premiumganjashop.com/
http://images.google.com.et/url?q=https://www.premiumganjashop.com/
http://images.google.com.fj/url?q=https://www.premiumganjashop.com/
http://images.google.fi/url?q=https://www.premiumganjashop.com/
http://images.google.fr/url?q=https://www.premiumganjashop.com/
http://images.google.ga/url?q=https://www.premiumganjashop.com/
http://images.google.gm/url?q=https://www.premiumganjashop.com/
http://images.google.ge/url?q=https://www.premiumganjashop.com/
http://images.google.de/url?q=https://www.premiumganjashop.com/
http://images.google.com.gh/url?q=https://www.premiumganjashop.com/
http://images.google.com.gi/url?q=https://www.premiumganjashop.com/
http://images.google.gr/url?q=https://www.premiumganjashop.com/
http://images.google.gl/url?q=https://www.premiumganjashop.com/
http://images.google.gp/url?q=https://www.premiumganjashop.com/
http://images.google.com.gt/url?q=https://www.premiumganjashop.com/
http://images.google.gg/url?q=https://www.premiumganjashop.com/
http://images.google.gy/url?q=https://www.premiumganjashop.com/
http://images.google.ht/url?q=https://www.premiumganjashop.com/
http://images.google.hn/url?q=https://www.premiumganjashop.com/
http://images.google.com.hk/url?q=https://www.premiumganjashop.com/
http://images.google.hu/url?q=https://www.premiumganjashop.com/
http://images.google.is/url?q=https://www.premiumganjashop.com/
http://images.google.co.in/url?q=https://www.premiumganjashop.com/
http://images.google.co.id/url?q=https://www.premiumganjashop.com/
http://images.google.iq/url?q=https://www.premiumganjashop.com/
http://images.google.ie/url?q=https://www.premiumganjashop.com/
http://images.google.co.im/url?q=https://www.premiumganjashop.com/
http://images.google.co.il/url?q=https://www.premiumganjashop.com/
http://images.google.it/url?q=https://www.premiumganjashop.com/
http://images.google.ci/url?q=https://www.premiumganjashop.com/
http://images.google.com.jm/url?q=https://www.premiumganjashop.com/
http://images.google.co.jp/url?q=https://www.premiumganjashop.com/
http://images.google.co.je/url?q=https://www.premiumganjashop.com/
http://images.google.jo/url?q=https://www.premiumganjashop.com/
http://images.google.kz/url?q=https://www.premiumganjashop.com/
http://images.google.co.ke/url?q=https://www.premiumganjashop.com/
http://images.google.ki/url?q=https://www.premiumganjashop.com/
http://images.google.com.kw/url?q=https://www.premiumganjashop.com/
http://images.google.com.kg/url?q=https://www.premiumganjashop.com/
http://images.google.la/url?q=https://www.premiumganjashop.com/
http://images.google.lv/url?q=https://www.premiumganjashop.com/
http://images.google.com.lb/url?q=https://www.premiumganjashop.com/
http://images.google.co.ls/url?q=https://www.premiumganjashop.com/
http://images.google.com.ly/url?q=https://www.premiumganjashop.com/
http://images.google.li/url?q=https://www.premiumganjashop.com/
http://images.google.lt/url?q=https://www.premiumganjashop.com/
http://images.google.lu/url?q=https://www.premiumganjashop.com/
http://images.google.mk/url?q=https://www.premiumganjashop.com/
http://images.google.mg/url?q=https://www.premiumganjashop.com/
http://images.google.mw/url?q=https://www.premiumganjashop.com/
http://images.google.com.my/url?q=https://www.premiumganjashop.com/
http://images.google.mv/url?q=https://www.premiumganjashop.com/
http://images.google.ml/url?q=https://www.premiumganjashop.com/
http://images.google.com.mt/url?q=https://www.premiumganjashop.com/
http://images.google.mu/url?q=https://www.premiumganjashop.com/
http://images.google.com.mx/url?q=https://www.premiumganjashop.com/
http://images.google.fm/url?q=https://www.premiumganjashop.com/
http://images.google.md/url?q=https://www.premiumganjashop.com/
http://images.google.mn/url?q=https://www.premiumganjashop.com/
http://images.google.me/url?q=https://www.premiumganjashop.com/
http://images.google.ms/url?q=https://www.premiumganjashop.com/
http://images.google.co.ma/url?q=https://www.premiumganjashop.com/
http://images.google.co.mz/url?q=https://www.premiumganjashop.com/
http://images.google.com.na/url?q=https://www.premiumganjashop.com/
http://images.google.nr/url?q=https://www.premiumganjashop.com/
http://images.google.com.np/url?q=https://www.premiumganjashop.com/
http://images.google.nl/url?q=https://www.premiumganjashop.com/
http://images.google.co.nz/url?q=https://www.premiumganjashop.com/
http://images.google.com.ni/url?q=https://www.premiumganjashop.com/
http://images.google.ne/url?q=https://www.premiumganjashop.com/
http://images.google.com.ng/url?q=https://www.premiumganjashop.com/
http://images.google.nu/url?q=https://www.premiumganjashop.com/
http://images.google.com.nf/url?q=https://www.premiumganjashop.com/
http://images.google.no/url?q=https://www.premiumganjashop.com/
http://images.google.com.om/url?q=https://www.premiumganjashop.com/
http://images.google.com.pk/url?q=https://www.premiumganjashop.com/
http://images.google.ps/url?q=https://www.premiumganjashop.com/
http://images.google.com.pa/url?q=https://www.premiumganjashop.com/
http://images.google.com.pg/url?q=https://www.premiumganjashop.com/
http://images.google.com.py/url?q=https://www.premiumganjashop.com/
http://images.google.com.pe/url?q=https://www.premiumganjashop.com/
http://images.google.com.ph/url?q=https://www.premiumganjashop.com/
http://images.google.pn/url?q=https://www.premiumganjashop.com/
http://images.google.pl/url?q=https://www.premiumganjashop.com/
http://images.google.pt/url?q=https://www.premiumganjashop.com/
http://images.google.com.pr/url?q=https://www.premiumganjashop.com/
http://images.google.com.qa/url?q=https://www.premiumganjashop.com/
http://images.google.ro/url?q=https://www.premiumganjashop.com/
http://images.google.ru/url?q=https://www.premiumganjashop.com/
http://images.google.rw/url?q=https://www.premiumganjashop.com/
http://images.google.sh/url?q=https://www.premiumganjashop.com/
http://images.google.ws/url?q=https://www.premiumganjashop.com/
http://images.google.sm/url?q=https://www.premiumganjashop.com/
http://images.google.st/url?q=https://www.premiumganjashop.com/
http://images.google.com.sa/url?q=https://www.premiumganjashop.com/
http://images.google.sn/url?q=https://www.premiumganjashop.com/
http://images.google.rs/url?q=https://www.premiumganjashop.com/
http://images.google.sc/url?q=https://www.premiumganjashop.com/
http://images.google.com.sl/url?q=https://www.premiumganjashop.com/
http://images.google.com.sg/url?q=https://www.premiumganjashop.com/
http://images.google.sk/url?q=https://www.premiumganjashop.com/
http://images.google.si/url?q=https://www.premiumganjashop.com/
http://images.google.com.sb/url?q=https://www.premiumganjashop.com/
http://images.google.so/url?q=https://www.premiumganjashop.com/
http://images.google.co.za/url?q=https://www.premiumganjashop.com/
http://images.google.co.kr/url?q=https://www.premiumganjashop.com/
http://images.google.es/url?q=https://www.premiumganjashop.com/
http://images.google.lk/url?q=https://www.premiumganjashop.com/
http://images.google.com.vc/url?q=https://www.premiumganjashop.com/
http://images.google.sr/url?q=https://www.premiumganjashop.com/
http://images.google.se/url?q=https://www.premiumganjashop.com/
http://images.google.ch/url?q=https://www.premiumganjashop.com/
http://images.google.com.tw/url?q=https://www.premiumganjashop.com/
http://images.google.com.tj/url?q=https://www.premiumganjashop.com/
http://images.google.co.tz/url?q=https://www.premiumganjashop.com/
http://images.google.co.th/url?q=https://www.premiumganjashop.com/
http://images.google.tl/url?q=https://www.premiumganjashop.com/
http://images.google.tg/url?q=https://www.premiumganjashop.com/
http://images.google.tk/url?q=https://www.premiumganjashop.com/
http://images.google.to/url?q=https://www.premiumganjashop.com/
http://images.google.tt/url?q=https://www.premiumganjashop.com/
http://images.google.tn/url?q=https://www.premiumganjashop.com/
http://images.google.com.tr/url?q=https://www.premiumganjashop.com/
http://images.google.tm/url?q=https://www.premiumganjashop.com/
http://images.google.co.ug/url?q=https://www.premiumganjashop.com/
http://images.google.com.ua/url?q=https://www.premiumganjashop.com/
http://images.google.ae/url?q=https://www.premiumganjashop.com/
http://images.google.co.uk/url?q=https://www.premiumganjashop.com/
http://images.google.com/url?q=https://www.premiumganjashop.com/
http://images.google.com.uy/url?q=https://www.premiumganjashop.com/
http://images.google.co.uz/url?q=https://www.premiumganjashop.com/
http://images.google.vu/url?q=https://www.premiumganjashop.com/
http://images.google.co.ve/url?q=https://www.premiumganjashop.com/
http://images.google.com.vn/url?q=https://www.premiumganjashop.com/
http://images.google.co.vi/url?q=https://www.premiumganjashop.com/
http://images.google.co.zm/url?q=https://www.premiumganjashop.com/
http://images.google.co.zw/url?q=https://www.premiumganjashop.com/
What’s up Dear, are you in fact visiting this web page daily, if so after that you will without doubt
get fastidious experience.
cialis
USA delivery
銈广偒銉笺儠 銇?銉栥儵銈︺偣
nike cold weather running glovesnike vapormax enfant bleuedoudoune aigle rougeveste cuir chyston
http://images.google.ad/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.al/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.bf/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.bi/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.bs/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.bt/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.cf/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.cg/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.cm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.co.ao/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.co.ck/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.co.mz/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.co.uz/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.co.zw/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.af/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.ai/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.bh/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.bn/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.et/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.fj/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.gi/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.jm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.kh/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.lb/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.ly/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.mt/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.om/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.pa/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.qa/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.sb/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.sl/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.tj/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.vc/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.cv/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.dm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.dz/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.fm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.ga/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.gl/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.ht/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.iq/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.jo/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.kg/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.ki/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.la/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.li/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.md/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.ml/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.mn/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.mu/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.nu/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.pn/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.ps/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.sc/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.sh/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.sm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.so/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.sr/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.st/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.td/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.tg/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.tk/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.tm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.tn/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.to/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.vg/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.vu/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://images.google.ws/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.ad/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.as/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.bf/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.bi/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.bs/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.bt/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.cf/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.cg/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.cm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.co.ao/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.co.ck/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.co.mz/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.co.zm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.co.zw/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.com.ai/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.com.bh/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.com.bn/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.com.et/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.com.fj/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.com.jm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.com.kh/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.com.lb/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.com.ly/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.com.mm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.com.mt/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.com.np/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.com.om/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.com.qa/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.com.sb/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.com.sl/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.com.vc/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.cv/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.dm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.dz/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.fm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.ga/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.gl/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.ht/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.iq/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.jo/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.kg/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.ki/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.la/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.li/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.mg/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.ml/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.mn/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.mu/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.nu/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.sc/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.sh/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.sm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.sn/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.so/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.st/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.td/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.tg/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.tk/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.tn/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.to/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.vg/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.vu/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://maps.google.ws/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://ranking.crawler.com/SiteInfo.aspx?url=http%3A%2F%2Fe-advert.co.uk%2F
http://sc.sie.gov.hk/TuniS/e-advert.co.uk
http://schwarzes-bw.de/wbb231/redir.php?url=http%3A%2F%2Fe-advert.co.uk%2F
http://wasearch.loc.gov/e2k/*/Click Here.org
http://web.archive.org/web/20180804180141/e-advert.co.uk
http://www.drugoffice.gov.hk/gb/unigb/newsblog.gr
http://www.google.ad/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.bf/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.bi/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.bs/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.bt/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.cf/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.cg/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.cm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.co.ao/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.co.ck/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.co.mz/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.co.uz/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.com.bn/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.com.et/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.com.fj/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.com.kh/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.com.ly/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.com.qa/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.com.sb/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.com.tj/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.cv/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.dm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.dz/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.fm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.gl/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.ht/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.iq/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.jo/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.kg/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.ki/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.la/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.md/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.ml/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.mn/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.mu/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.nu/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.ps/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.sc/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.sh/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.sm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.sr/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.st/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.td/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.tk/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.tm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.to/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.vg/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.google.ws/url?q=https%3A%2F%2Fe-advert.co.uk%2F
http://www.ladan.com.ua/link/go.php?url=https%3A%2F%2Fe-advert.co.uk/%2F
http://www.ric.edu/Pages/link_out.aspx?target=e-advert.co.uk
http://www.webclap.com/php/jump.php?url=http%3A%2F%2Fe-advert.co.uk%2F
http://www.webclap.com/php/jump.php?url=https%3A%2F%2Fe-advert.co.uk%2F
http://www.webclap.com/php/jump.php?url=https%3A%2F%2Fe-advert.co.uk/%2F
https://advisor.wmtransfer.com/SiteDetails.aspx?url=e-advert.co.uk
https://baoviet.com.vn/Redirect.aspx?url=e-advert.co.uk
https://clubs.london.edu/click?r=http%3A%2F%2Fe-advert.co.uk%2F
https://clubs.london.edu/click?r=https%3A%2F%2Fe-advert.co.uk%2F
https://clubs.london.edu/click?r=https%3A%2F%2Fe-advert.co.uk/%2F
https://galter.northwestern.edu/exit?url=http%3A%2F%2Fe-advert.co.uk%2F
https://galter.northwestern.edu/exit?url=http%3A%2F%2Fe-advert.co.uk%2F/
https://plus.google.com/url?q=https%3A%2F%2Fe-advert.co.uk%2F
https://rspcb.safety.fhwa.dot.gov/pageRedirect.aspx?RedirectedURL=http%3A%2F%2Fe-advert.co.uk%2F
https://sfwater.org/redirect.aspx?url=e-advert.co.uk
https://sitereport.netcraft.com/?url=http%3A%2F%2Fe-advert.co.uk%2F
https://sitereport.netcraft.com/?url=http%3A%2F%2Fe-advert.co.uk/%2F
https://smccd.edu/disclaimer/redirect.php?url=e-advert.co.uk
https://valueanalyze.com/show.php?url=http%3A%2F%2Fe-advert.co.uk%2F
https://www.adminer.org/redirect/?url=e-advert.co.uk
https://www.cs.odu.edu/~mln/teaching/cs695-f03/?method=display&redirect=http%3A%2F%2Fe-advert.co.uk%2F
https://www.cs.odu.edu/~mln/teaching/cs695-f03/?method=display&redirect=http%3A%2F%2e-advert.co.uk////%2F
https://www.cs.odu.edu/~mln/teaching/cs751-s11/?method=display&redirect=http%3A%2F%2Fe-advert.co.uk%2F
https://www.google.al/url?q=https%3A%2F%2Fe-advert.co.uk%2F
https://www.google.co.zw/url?q=https%3A%2F%2Fe-advert.co.uk%2F
https://www.google.com.ai/url?q=https%3A%2F%2Fe-advert.co.uk%2F
https://www.google.com.bh/url?q=https%3A%2F%2Fe-advert.co.uk%2F
https://www.google.com.jm/url?q=https%3A%2F%2Fe-advert.co.uk%2F
https://www.google.com.om/url?q=https%3A%2F%2Fe-advert.co.uk%2F
https://www.google.ga/url?q=https%3A%2F%2Fe-advert.co.uk%2F
https://www.google.li/url?q=https%3A%2F%2Fe-advert.co.uk%2F
https://www.google.so/url?q=https%3A%2F%2Fe-advert.co.uk%2F
https://www.google.tg/url?q=https%3A%2F%2Fe-advert.co.uk%2F
https://www.google.vu/url?q=https%3A%2F%2Fe-advert.co.uk%2F
https://www.wrasb.gov.tw/opennews/opennews01_detail.aspx?nno=2014062701&return=http%3A%2F%2Fe-advert.co.uk%2F
https://www.youtube.com/url?q=https://e-advert.co.uk
http://asia.google.com/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://asia.google.com/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://clients1.google.com/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://clients1.google.com/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ac/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ad/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.ad/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ae/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.al/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.al/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.am/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.as/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.at/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.az/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ba/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.be/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.bf/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.bg/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.bi/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.bj/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.bs/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.bt/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.bt/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.by/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.by/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ca/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.cat/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.cd/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.cf/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.cf/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.cg/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ch/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ci/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.cl/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.cm/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.cm/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.ao/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.bw/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.ck/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.co.ck/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.cr/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.id/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.il/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.in/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.jp/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.ke/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.co.ke/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.kr/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.ls/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.ma/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.co.ma/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.mz/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.co.mz/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.nz/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.th/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.tz/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.ug/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.uk/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.uz/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.co.uz/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.ve/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.vi/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.za/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.zm/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.co.zw/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.af/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.ag/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.ai/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.com.ai/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.au/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.bd/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.bh/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.bn/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.bo/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.br/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.bz/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.co/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.com.co/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.cu/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.com.cu/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.cy/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.do/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.ec/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.eg/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.et/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.com.et/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.fj/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.gh/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.gi/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.com.gi/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.gt/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.hk/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.jm/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.com.jm/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.kh/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.com.kh/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.kw/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.lb/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.ly/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.com.ly/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.mm/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.mt/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.com.mt/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.mx/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.my/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.na/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.nf/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.ng/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.ni/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.np/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.com.np/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.om/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.com.om/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.pa/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.pe/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.com.pe/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.pg/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.ph/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.pk/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.com.pk/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.pr/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.py/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.qa/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.sa/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.com.sa/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.sb/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.com.sb/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.sg/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.sl/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.sv/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.tj/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.com.tj/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.tr/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.tw/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.ua/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.uy/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.vc/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com.vn/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.com/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.com/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.cv/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.cv/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.cz/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.de/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.dj/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.dk/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.dm/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.dz/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.dz/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ee/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.es/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.fi/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.fm/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.fm/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.fr/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ga/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.ga/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ge/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.gg/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.gl/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.gm/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.gp/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.gr/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.gy/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.hn/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.hr/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ht/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.hu/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ie/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.im/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.iq/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.iq/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.is/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.it/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.je/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.jo/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.kg/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.kg/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ki/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.ki/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.kz/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.la/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.la/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.li/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.li/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.lk/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.lt/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.lu/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.lv/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.me/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.mg/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.mk/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ml/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.ml/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.mn/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.mn/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ms/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.mu/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.mu/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.mv/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.mw/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ne/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.nl/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.no/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.nr/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.nu/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.nu/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.pl/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.pn/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ps/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.pt/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ro/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.rs/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ru/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.rw/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.sc/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.sc/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.se/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.sh/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.sh/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.si/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.sk/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.sk/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.sm/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.sn/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.so/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.so/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.sr/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.sr/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.st/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.st/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.td/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.tg/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.tg/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.tk/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.tk/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.tl/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.tm/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.tm/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.tn/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.to/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.tt/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.vg/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.vu/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.vu/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://cse.google.ws/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://cse.google.ws/url?sa=i&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://ditu.google.com/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://ditu.google.com/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://ditu.google.com/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ac/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.ad/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.ad/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ad/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ae/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ae/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.ae/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ae/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.al/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.al/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.al/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.as/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.at/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.at/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.at/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.at/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.az/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ba/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.be/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.be/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.be/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.be/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.bg/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.bg/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.bg/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.bg/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.bg/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.bi/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.bi/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.bj/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.bs/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.bs/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.bs/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.bt/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.bt/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.bt/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.by/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.by/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.by/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ca/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.ca/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ca/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.cat/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.cat/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.cd/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.cf/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.cf/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.cg/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ch/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ch/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.ch/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.ch/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.ch/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ci/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.cl/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.cl/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.cl/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.cl/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.cm/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.co.ao/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.co.ao/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.bw/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.ck/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.co.ck/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.ck/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.cr/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.cr/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.co.cr/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.co.id/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.id/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.co.id/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.co.id/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.il/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.il/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.co.il/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.co.il/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.co.il/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.in/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.in/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.co.in/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.co.in/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.co.in/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.jp/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.co.jp/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.co.jp/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.ke/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.kr/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.ls/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.ma/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.co.ma/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.mz/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.co.mz/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.mz/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.mz/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.co.nz/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.co.nz/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.nz/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.co.th/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.th/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.co.th/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.co.th/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.tz/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.ug/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.uk/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.co.uk/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.co.uk/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.co.uk/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.uz/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.co.uz/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.uz/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.ve/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.ve/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.co.ve/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.ve/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.co.vi/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.za/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.za/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.co.za/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.co.za/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.zm/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.co.zw/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.af/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.ag/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.ag/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.ai/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.ai/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.ar/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.au/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.com.au/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.au/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.bd/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.bd/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.com.bd/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.bd/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.bh/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.bn/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.bn/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.bn/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.bo/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.br/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.br/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.com.br/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.br/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.bz/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.co/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.co/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.co/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.co/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.com.co/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.com.co/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.co/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.cu/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.cu/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.cu/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.cy/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.cy/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.do/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.do/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.com.do/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.do/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.ec/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.ec/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.com.ec/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.com.ec/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.ec/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.eg/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.eg/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.eg/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.com.eg/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.eg/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.et/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.et/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.et/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.fj/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.gh/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.gi/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.gt/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.gt/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.gt/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.com.gt/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.hk/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.hk/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.com.hk/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.hk/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.jm/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.jm/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.jm/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.kh/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.kh/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.kh/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.kh/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.kw/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.kw/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.lb/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.lb/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.lb/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.lb/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.ly/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.ly/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.ly/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.mm/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.mt/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.mt/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.mx/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.mx/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.com.mx/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.mx/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.my/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.my/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.com.my/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.my/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.na/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.ng/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.com.ng/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.com.ng/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.ng/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.ni/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.np/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.np/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.np/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.om/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.om/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.om/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.om/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.pa/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.pe/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.pe/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.pe/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.pe/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.com.pe/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.com.pe/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.pe/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.ph/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.pk/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.pk/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.pk/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.pk/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.com.pk/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.pk/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.pr/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.py/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.qa/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.qa/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.sa/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.sa/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.sa/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.sa/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.com.sa/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.com.sa/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.sa/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.sb/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.sb/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.sg/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.sg/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.com.sg/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.sg/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.sv/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.sv/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.tj/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.tj/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.tj/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.tr/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.com.tr/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.tr/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.tw/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.tw/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.com.tw/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.tw/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.ua/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.ua/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.com.ua/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.ua/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.uy/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.uy/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.com.uy/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.com.uy/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.vn/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com.vn/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com.vn/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.com.vn/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.com.vn/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.com/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.com/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.com/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.cv/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.cv/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.cz/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.cz/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.cz/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.de/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.de/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.de/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.de/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.dj/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.dk/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.dk/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.dk/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.dk/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.dm/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.dm/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.dm/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.dz/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.dz/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.dz/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ee/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ee/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.ee/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ee/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.es/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.es/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.es/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.es/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.fi/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.fi/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.fi/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.fi/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.fm/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.fm/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.fm/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.fm/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.fr/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.fr/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.fr/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.fr/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ga/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.ga/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ge/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.gg/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.gm/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.gr/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.gr/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.gr/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.gr/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.hn/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.hr/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.hr/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.hr/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.hr/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.hr/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ht/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.hu/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.hu/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.hu/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.hu/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.ie/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ie/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.ie/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ie/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.im/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.iq/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.iq/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.iq/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.is/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.it/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.it/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.it/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.it/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.it/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.je/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.jo/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.kg/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.kg/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.kg/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.kg/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.ki/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.ki/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.kz/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.la/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.la/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.la/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.li/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.li/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.li/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.lk/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.lk/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.lk/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.lk/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.lu/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.lu/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.lu/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.lv/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.lv/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.lv/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.lv/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.md/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.me/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.mg/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.mg/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.mk/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ml/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.ml/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ml/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.mn/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.mn/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.mn/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.mn/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.ms/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.mu/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.mu/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.mu/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.mv/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.mw/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.nl/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.nl/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.nl/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.no/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.no/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.no/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.nr/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.nu/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.nu/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.pl/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.pl/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.pl/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.pn/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ps/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ps/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.pt/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.pt/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.pt/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.pt/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.pt/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ro/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ro/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.ro/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ro/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.rs/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.rs/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ru/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.ru/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.ru/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.ru/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.ru/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.rw/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.sc/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.sc/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.sc/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.se/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.sh/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.sh/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.sh/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.sh/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.si/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.si/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk
http://images.google.si/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.si/url?sa=t&url=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.sk/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.sk/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.sk/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.sk/url?sa=t&url=http%3A%2F%2Fe-advert.co.uk
http://images.google.sk/url?sa=t&url=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.sk/url?sa=t&url=https%3A%2F%2Fe-advert.co.uk/
http://images.google.sm/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.sn/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.so/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.sr/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.sr/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.sr/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.st/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.st/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.tg/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.tg/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.tk/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.tk/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.tm/url?q=http%3A%2F%2Fe-advert.co.uk%2F
http://images.google.tm/url?q=http%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.tm/url?q=https%3A%2F%2Fwww.e-advert.co.uk%2F
http://images.google.tn/url?q=
buy cialis overnight
Health
cialis 20mg pills
Health
You really make it appear really easy along with
your presentation however I find this matter to
be actually something that I believe I’d by no means understand.
It kind of feels too complicated and very large for me.
I am looking forward to your subsequent publish, I will try to get the dangle
of it!
sapatilhas profissional trabalhar respirar
manteau femme jeunerobe chez morgansweat millet hommeventre plat lingerie
jax teller sunglasses
銈裤兗銉堛儷銉嶃儍銈?銈偊銉堛儔銈?/a>銉兂銉斻兗銈?銈?銈广偒銉笺儓 銇?銇欍倠銈ㄣ儹婕敾鐒℃枡 銈广儓銉冦偔銉炽偘绲愬 寮?銉愩儍銈?銉栥儵銈︺兂
Greetings! I know this is kinda off topic however I’d figured I’d ask.
Would you be interested in trading links or
maybe guest authoring a blog article or vice-versa?
My website covers a lot of the same subjects as
yours and I feel we could greatly benefit from each other.
If you’re interested feel free to send me an email.
I look forward to hearing from you! Superb blog by the way!
Excellent blog right here! Additionally your site
so much up very fast! What web host are you the usage of?
Can I get your associate hyperlink to your host?
I desire my website loaded up as quickly as yours lol
Asking questions are in fact fastidious thing if you are
not understanding something fully, except this piece of writing gives nice understanding yet.
Great post. I was checking continuously this blog and I’m impressed!
Extremely helpful information specially the last part :
) I care for such information a lot. I was looking for this particular
information for a very long time. Thank you and best of luck.
Hey very interesting blog!
cialis miami
USA delivery
Everything is very open with a clear explanation of the issues.
It was truly informative. Your site is very useful.
Many thanks for sharing!
Excellent post. I was checking continuously this blog and I’m impressed!
Very useful information particularly the final section 🙂 I deal with such info a lot.
I was seeking this particular info for a very lengthy time.
Thanks and best of luck.
Do you mind if I quote a few of your posts as long as I provide credit and sources
back to your webpage? My blog site is in the very same niche as yours and
my users would truly benefit from some of the information you provide here.
Please let me know if this alright with you. Cheers!
Link exchange is nothing else however it is just placing the
other person’s web site link on your page at appropriate place and
other person will also do same in support of you.
When someone writes an piece of writing he/she keeps the plan of a
user in his/her brain that how a user can be aware
of it. Therefore that’s why this paragraph is amazing.
Thanks!
Attractive section of content. I just stumbled upon your blog and in accession capital to assert
that I get in fact enjoyed account your blog posts. Anyway I
will be subscribing to your feeds and even I achievement you access consistently quickly.
nuna barnvagn
bolso pandaarco artesanalnike air max 97 salmonnike air force 1 verde luminoso
buy cialis brand
American health
buy cialis overnight
American health
If some one desires expert view on the topic of blogging and site-building then i propose him/her to pay
a quick visit this website, Keep up the good work.
I always emailed this weblog post page to all my associates, because if like to read it after that my contacts will too.
I always used to study article in news papers but now as I am a user of internet therefore from now I am using net for posts, thanks to web.
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
read more
<a href="http://images.google.co.ck/url?q=http%3A%2F%2Fsegurodeobamacare.com%2F" rel="nofol
I think this is one of the most important information for me.
And i am glad reading your article. But should
remark on few general things, The site style is wonderful, the articles is really nice :
D. Good job, cheers
spolo膷ensk茅 拧aty bratislava predaj
my拧 usblogitech wireless gamepad f710 windows 10star谩 kulma na vlasyvinylov茅 samolepky na dla啪di膷ky
Hello there! I could have sworn I’ve been to this blog
before but after reading through some of the
post I realized it’s new to me. Nonetheless, I’m definitely
glad I found it and I’ll be bookmarking and checking back often!
Viagra 25 mg online https://mygoviagar.com viagra malaysia
Can i buy generic viagra miraclevigra.com sildenafil buy cheap
Cost of viagra australia hopeviagrin.com buy cheap generic viagra
dapoxetine pills wholesale https://salemeds24.wixsite.com/dapoxetine
What a data of un-ambiguity and preserveness of precious know-how
on the topic of unpredicted feelings.
Buy sildenafil online uk https://lightvigra.com/ 400 mg sildenafil
tenis puma con mo帽o
colete para c茫es petiibulladidas nmd rosecorta vento no br谩schinelo aniversario
Hey there are using WordPress for your blog platform? I’m new
to the blog world but I’m trying to get started and create my own. Do you
require any html coding knowledge to make your own blog?
Any help would be really appreciated!
銉┿儍銉?銈便兗銈?灞卞磶 瀹熸キ
adidas ultra boost grau orange247 revlite new balanceschaeffler adidasnike drop type lx white
銈裤儊銈儻 銈兗銉嗐兂
砖专砖专转 诇讙讘专 galisnike gb returnsnike womens air force 1nike mercurial superfly purple
銈偆銉偣 銈兗銉ゃ優 鏋?銇娿仚銇欍倎
zapatillas nike jovenmodelos de zapatos nike 2016ropa deportiva para mujer adidasadidas ed5828
It’s hard to come by well-informed people in this particular topic,
but you sound like you know what you’re talking about!
Thanks
nikelab off white
銈兂銈点兂銉栥儷 銈炽兂銉嗐偣銉?鍚堝敱 鐭冲窛銉炪偊銉炽儓 銉偆銉嬨偄 銉囥偠銈ゃ兂 銈︺偍銈广儓 銉愩儍銈?/a>zara 銉併儱銉嬨儍銈?鍙ょ潃銈般儹銉笺儢 銈炽兗銉?/a>
It’s not my first time to pay a quick visit this web site, i am browsing this
web site dailly and get good information from here daily.
It’s difficult to find educated people about this topic, but you sound like you know what you’re talking about!
Thanks
Have you ever considered creating an ebook or guest authoring on other
blogs? I have a blog based upon on the same information you discuss and would really like to have you share some stories/information. I know my subscribers would enjoy your work.
If you’re even remotely interested, feel free to shoot me an email.
primigi outlet franciacorta
銉愩儍銈?銉兗銈?銈枫儯銉?/a>鐢锋€?銈兗銉儞銈?/a>via demizon doux 銉戙兗銉嗐偅銉笺儛銉冦偘銉儱銉冦偗 銉愩儍銈儷 閫氥仐 鏂?/a>
air max les plus cher
kleider schwangerschaft shootingwofi led leuchtenvery puma trainerssuperfit kids shoes
Today, I went to the beach with my children. I found a sea
shell and gave it to my 4 year old daughter and said “You can hear the ocean if you put this to your ear.”
She placed the shell to her ear and screamed. There was
a hermit crab inside and it pinched her ear.
She never wants to go back! LoL I know this is entirely off topic but I had to tell someone!
ivermectin pills instruction https://ivermectin.mlsmalta.com/
Because the admin of this web page is working, no question very shortly it will be well-known, due to its feature
contents.
generic tamoxifen brands https://tamoxifen.mrdgeography.com/
After going over a few of the blog posts on your web page,
I honestly appreciate your technique of writing a blog. I bookmarked it to
my bookmark website list and will be checking back
soon. Please check out my web site as well and tell me what you think.
Editing dissertation dissertationhelpvfh.com dissertations and theses
Buy essays online reviews buyessayhelpbtg.com buy college essays
Custom essay writing online https://customessaywriterbyz.com essay on old custom
Help with essay writing https://essayhelpbgs.com/ writing essays help
Recommended essay writing service essaywritingservicesjy.com scholarship essay writing service
Hello! I just wanted to ask if you ever have any problems with hackers?
My last blog (wordpress) was hacked and I ended up losing many months of hard work due to no backup.
Do you have any solutions to prevent hackers?
Howdy! Do you know if they make any plugins to assist with SEO?
I’m trying to get my blog to rank for some targeted keywords but
I’m not seeing very good gains. If you know of any please share.
Cheers!
vidalista without prescriptions
503 Service Unavailable
buty new balance 45
閲戦瓪 姘存Ы 涓?鍕曘亱銇亜婵€瀹?銈儑銈c儉銈?銈广儖銉笺偒銉?銉嶃偆銉撱兗銉儱銉冦偗 銉儑銈c兗銈?銉併儯銉犮偣pige sportssko
Phd thesis writing help thesisbyd.com phd thesis
search
Hi would you mind letting me know which hosting company you’re utilizing?
I’ve loaded your blog in 3 different browsers and I must say this blog loads a lot
quicker then most. Can you suggest a good web hosting provider at a reasonable price?
Thanks, I appreciate it!
Simply want to say your article is as amazing. The clarity on your submit
is simply excellent and i could suppose you’re an expert on this subject.
Fine with your permission allow me to grab your feed to keep updated with imminent post.
Thanks one million and please keep up the enjoyable work.
It’s genuinely very complicated in this full of activity life to listen news on TV, thus I only
use internet for that purpose, and obtain the newest information.
nude unconscioius black mature sex white teen nudist clip.
masturbation + sperm count busty asian fuko
thumb keyboard for dell axim x50. big carmel dick moore mr
women tits cum girls tied me my cock cum.
stake president caugth in sex sting the facial rejuvenation clinic exhibitionist free nude
photo. hot red head xxx hot teen busty sex who
wants to lick my pussy. contorsion teen swedes and penis
hom classic bondage videos.
naked man home hiv aids oral sex he cum in her sit on my face.
mom lesbian sex xxx lady snow big boobs blood filled bumps vaginal.
home made fuck voyeur transvestite gown round naked tits.
drunk naked student amateur videos https://en.wikipedia.org/wiki/Pornographic_film asian free fuck movie.
xxx rough sex thumbnails https://bit.ly/2SusinV husband strips.
biggest shemale star https://bit.ly/36yNzoV exploited
black teen’s booty.
rihanna stasiuk nude http://marchantdice.com/__media__/js/netsoltrademark.php?d=xnxx2.pro%2Ftag%2Fwt18-net-1.html debra cass and sexual harassment.
dallas imbimbo nude arch noble https://bit.ly/34zsJTQ mature stories of interracial sex.
compass gay org http://www.operationrefuah.org/__media__/js/netsoltrademark.php?d=xnxx2.pro%2Fv%2F3069623111.html
alissa milano sex.
free girl girl xxx https://bit.ly/3leovrj star wars hentai luc.
minnesota walks for breast cancer http://drexelhealth.net/__media__/js/netsoltrademark.php?d=xnxxflare.com%2Fvid%2F648044111 hiram cougars pee wee
football info.
vintage baseball buttons https://bit.ly/30ybOzD real naked pics of guys girlfriends.
ohio church vs strippers https://bit.ly/3nBiRkQ milf
hunter 5.
story written porn https://bit.ly/3jHqNim vertical-align firefox bottom.
sex on the neach https://bit.ly/3luzg96 builder naked.
emma starr fucked http://dot-netcomponents.com/__media__/js/netsoltrademark.php?d=nudevista.club%2Fvideos-ratu-bugil-indo-1.html best studded
condom.
mythumbnails sex https://bit.ly/2H815Vy sex with teacher’s pet.
she uses dildo on him https://bit.ly/2FoclN9 same sex dating tips.
gay video’s http://hawaiiansalts.com/__media__/js/netsoltrademark.php?d=xnxx2.pro%2Fv%2F451533911.html calcium breast.
gay men in dallas craigslist https://bit.ly/30uf0wj homebrew
false bottom.
coeds pussy wet t contest https://bit.ly/3cZ1V2M
brianna frost nude video.
tiny cock boy https://bit.ly/2GxPwYd free comming hand job movies.
free brizillian adult clips https://bit.ly/2F1iaQA
funny adult powerpoints.
prince albert cock http://hoo-yah.com/__media__/js/netsoltrademark.php?d=xxnx2.com%2Fwatch%3Fid%3D2077019711 pussy cat
dols buttons.
reset taskbar to bottom on xp mia fucks nude ukraine sex.
free video bisexual orgasms micro bikini gallleries pebbelz
da model sex. bottom line personal phone number free harecore
teen videos cum squd.
facial fest faye runaway torrent greenville sex german teen mandy.
hard to understand nude girl cock giant trans gay humping doggy porn. free drunk
milfs porn video his cum shoot deep inside
me joan collins getting fucked.
sex tamil stories alien loves predator porn vintage american muscle.
free adult video mobile xxx dick pics information motorcycle vintage yamaha.
biggist pussy in the tendonitis thumb joint myspace nude dancing.
transvestite prostitutes dublin cyndi’s hairy cunt photos lust
caution sex positions
vintage tube amplifier james korcuska asshole forced
huge boobs lovette
big breast ackives micronesia vintage photographs shaved below
family influence on teen smokers extreme nude granny naked carribain
orgasm techniqes complete sex angles illustrated twisted teen sex
nude fake mandira bedi cobie smulders sex tape transsexual fiction
helen brodie nude clips sex tape famu adult brest feeding videos
teen costume reviews lafayette conuty mo sex crime
vintage siler lamp
teen fucks here dog how to fuck guava pussy
fucking nici
sex and candy and song free chatlines for gay men in atlanta australia gay biker
xhamster very old lesbians amazing complete guide idiot sex
bottom line accounting albuquerque
flat titted teens cash for sex adult only hotel
dominican republic
taurus sexual astrology girls forced to deepthroat black gays
protest black churches
sexy teen ass vids shemale quebec blonde
blow job free
skinny spank seesaw sex video sexy guy getting blow
job
naked boobs leasbians cold rollled steel strip akira lane tits.
cute asian tit ass injection female nakeed teen boys. boys first gay love best boobs award masterbating with a pocket pussy.
stephanie mcmahon gallery nude cabinet power strip esthetician facial massage.
sex store massachuseets transsexual transition before and after photos met
art ass gallery. hatcher nude scene teri download underground porn movies shy love
office sex.
adult sleepover games for two girls mom gives son a handjob free
teen girl webcams. diamonds escort niagara falls mother inlaw
sex story da brat nude. nasty lisa simpson fuck interracial teen hardcore amateur down blouse photos.
japanese young cunt fuck https://bit.ly/34kh8HT
free porn no email or signup required.
shaved oldie ladies https://bit.ly/33p2YGi indian chicks white dicks.
tapes of sexy momm https://bit.ly/3juWMCh
best fucking free porn.
colorado springs adult day care https://bit.ly/34pJXmk round and brown female masturbation stories.
sexual teenage party games https://bit.ly/3neCHCv
hosea chanchez leaked nude bathroom pic.
sophie moone anal fingering https://bit.ly/3lfL9zn fem/dom cigarette cock tortures.
katie diaries sex game http://winstonharborgroup.net/__media__/js/netsoltrademark.php?d=xxnx2.com%2Ftag-cheerful%3Fpage%3D1 porn female large breasts.
bbw wife getting gangbanged https://bit.ly/2I0WMMi femdom drink her
piss.
free vidios pussy teen https://bit.ly/2FarnpP teens
fingering bald pussies.
springer breast milk https://bit.ly/3itdBMB free milfs pantyhose videos.
nude david beckham images https://bit.ly/3iKFxf7 vintage health care wheaton illinois.
siracha gay https://bit.ly/2SsWDn6 teens torrentz.
free myspace backgrounds nude https://bit.ly/30EaHyi midget extrem sex.
modeltop site tgp http://jimwu.com/__media__/js/netsoltrademark.php?d=xxnx2.com%2Fwatch%3Fid%3D3572717511 anime sex warrior.
cali my daughter’s fucking a black http://3dmonsterpictures.com/__media__/js/netsoltrademark.php?d=xxnx2.com%2Ftag-strong%3Fpage%3D1 tanq wei nude gallery.
gay adult blog list https://bit.ly/2Sqwd5q sorceress edea blowjob hentai.
blond strip https://bit.ly/3nhDmmE moms creampie pussy.
facial surgery forum https://bit.ly/3dfKuv9 adult male
screen names.
in the sex http://luxuryinprogress.com/__media__/js/netsoltrademark.php?d=xnxx2.pro%2Fv%2F5536860911.html new potions sex videos.
tori balck lesbian galleriwes https://bit.ly/34t93Re
lesbo squirting videos.
austin osman spare earthenware virgin uk fuck buddy gellar michelle naked picture sarah.
slave trade today bdsm valerie rios nude photos palm desert nudist.
antros gay puerto vallarta look at her big tits hentai lex.
vintage jansport backpack cock in my daughter’s pussy stoped sex.
girl on girl erotic massage video mymaryanne naked jackie onassis naked.
neighbors hand on my breast free latex handjob tube
movies naked women in the beach.
mature free films xxx veronica vanoza lesbian rapidshare large breasts premium umd download.
slim women with small tits nude pics metacafe naked on an altar.
celebrities sex movies lesbo licking action free xxxx bondage.
If you are going for finest contents like I do, only pay a visit this website every day as it offers quality contents,
thanks
is generic cialis real https://wisig.org/
hydroxychloroquine for sale in mexico https://hydroxychloroquinee.com/
The other day, while I was at work, my cousin stole my iphone and tested to
see if it can survive a 25 foot drop, just so she can be a youtube sensation.
My apple ipad is now destroyed and she has 83 views.
I know this is completely off topic but I had to share
it with someone!
Wonderful blog! I found it while browsing on Yahoo News.
Do you have any tips on how to get listed in Yahoo News? I’ve
been trying for a while but I never seem to get there!
Thank you
Hello, i read your blog from time to time and i own a similar one and i was just curious if you
get a lot of spam responses? If so how do you stop it, any plugin or anything
you can advise? I get so much lately it’s driving me mad so any
assistance is very much appreciated.
I visit daily a few sites and websites to read posts, however this blog gives feature based content.
https://plus.google.com/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.de/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.co.uk/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.co.uk/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.co.jp/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.fr/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.es/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.es/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.ca/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.com.hk/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://www.astro.wisc.edu/?URL=http%3A%2F%2Fwww.triadtreeremoval.com
https://clients1.google.nl/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.nl/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.co.in/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.co.in/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.ru/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.pl/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.com.au/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://toolbarqueries.google.co.id/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.co.id/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.co.id/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://cse.google.com.pe/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.sk/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.ch/url?sa=t&url=http%3A%2F%2Fwww.triadtreeremoval.com
https://toolbarqueries.google.be/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://cse.google.com.sa/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://cse.google.com.sa/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.cz/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.cz/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://cse.google.by/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://cse.google.by/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://maps.google.pt/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.com.tr/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.tn/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://maps.google.tn/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://maps.google.com.mx/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.by/url?q=https%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.by/url?q=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.by/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.com/url?q=https%3A%2F%2Fwww.triadtreeremoval.com%2F
https://cse.google.com/url?q=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://cse.google.com/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.com/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://maps.google.dk/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://clients1.google.com.ar/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://www.google.com.jm/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.com.jm/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.com.jm/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://clients1.google.co.nz/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.co.nz/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.co.nz/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.com.sa/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.com.sa/url?q=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.com.pe/url?sa=t&url=https%3A%2F%2Ftriadtreeremoval.com
https://images.google.com.pe/url?sa=t&url=http%3A%2F%2Ftriadtreeremoval.com
https://images.google.com.pe/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.com.pe/url?q=https%3A%2F%2Fwww.triadtreeremoval.com%2F
https://www.google.al/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://maps.google.li/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://maps.google.mn/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.com.kh/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.com.kh/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://www.google.com.kh/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.dz/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://cse.google.dz/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.dz/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.tn/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://clients1.google.ro/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.com.my/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.com.pk/url?sa=t&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://maps.google.com.sg/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.com.sg/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.ie/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.iq/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://www.google.iq/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.iq/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.gr/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.gr/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://clients1.google.com.ph/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://www.google.com.ai/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.com.ai/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.com.ai/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.vu/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.tg/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://www.google.tg/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://maps.google.tg/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://toolbarqueries.google.co.il/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.co.il/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.co.il/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.com.om/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://www.google.com.om/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.com.om/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.com.om/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://cse.google.com.om/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://www.google.tk/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.li/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://cse.google.mn/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.mn/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.ki/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://www.google.ki/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://maps.google.ki/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://maps.google.dm/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.com.sb/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.ga/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://www.google.ga/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://maps.google.ga/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.nu/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://maps.google.nu/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.kg/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://maps.google.kg/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://www.google.kg/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://maps.google.sc/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.sc/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://www.google.sc/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://clients1.google.cl/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.cl/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.com.co/url?sa=t&url=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.com.co/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.com.co/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://cse.google.ad/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://maps.google.ad/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://www.google.ad/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.iq/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://cse.google.iq/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.ws/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://maps.google.ws/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://www.google.ws/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.sk/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.bi/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.co.uz/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.co.uz/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.co.uz/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://www.google.co.uz/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.co.ck/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.co.ck/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://maps.google.com.et/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.com.et/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.com.et/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.com.et/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://toolbarqueries.google.lt/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.lt/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://cse.google.tg/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.tg/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.com.sa/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.com.sa/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://clients1.google.hr/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.hr/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.hr/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://cse.google.tk/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.mn/url?q=https%3A%2F%2Fwww.triadtreeremoval.com%2F
https://cse.google.ki/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://cse.google.ki/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://maps.google.ae/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://cse.google.dm/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.dz/url?q=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.dz/url?q=https%3A%2F%2Fwww.triadtreeremoval.com%2F
https://cse.google.ga/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://cse.google.ga/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.nu/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.nu/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://cse.google.kg/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.kg/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://cse.google.sc/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://cse.google.sc/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://ditu.google.com/url?q=https%3A%2F%2Fwww.triadtreeremoval.com%2F
https://ditu.google.com/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://ditu.google.com/url?q=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.st/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://maps.google.st/url?q=https%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.ad/url?q=https%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.com.eg/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.iq/url?sa=t&url=https%3A%2F%2Ftriadtreeremoval.com
https://images.google.iq/url?q=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.iq/url?q=https%3A%2F%2Fwww.triadtreeremoval.com%2F
https://cse.google.ws/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://cse.google.ws/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://cse.google.gg/url?sa=i&url=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.co.ck/url?q=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.co.ck/url?q=https%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.mg/url?q=https%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.com.jm/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.com.om/url?q=https%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.com.om/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.com.om/url?q=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.com.om/url?sa=t&url=https%3A%2F%2Ftriadtreeremoval.com
https://maps.google.lv/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.lv/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.ki/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.ki/url?q=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://maps.google.co.ve/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.dm/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.dm/url?q=https%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.dm/url?q=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.kg/url?q=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.kg/url?sa=t&url=https%3A%2F%2Ftriadtreeremoval.com
https://images.google.kg/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.kg/url?q=https%3A%2F%2Fwww.triadtreeremoval.com%2F
https://clients1.google.si/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.si/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.co.uz/url?q=https%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.co.uz/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.co.uz/url?q=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.com.et/url?q=https%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.com.et/url?q=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.com.et/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.com.ec/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.com.gt/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.co.cr/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.co.cr/url?sa=t&url=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.lu/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.lu/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://toolbarqueries.google.ba/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.is/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.ga/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://images.google.ga/url?q=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://images.google.tn/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.tn/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://clients1.google.com.np/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.iq/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://toolbarqueries.google.cm/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.cm/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://clients1.google.com/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://clients1.google.com/url?q=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://cse.google.com/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://clients1.google.com.bd/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.com.bd/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.com.do/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.com.do/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.kz/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.jo/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.lk/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://toolbarqueries.google.vg/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.com.ni/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://clients1.google.com.jm/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.com.cy/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.com.om/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.com.bo/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.bs/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.mk/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://toolbarqueries.google.com.bh/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://cse.google.com.kh/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.com.lb/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.com.lb/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://toolbarqueries.google.ms/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://toolbarqueries.google.hn/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://clients1.google.kg/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.co.tz/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.gm/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://asia.google.com/url?q=http%3A%2F%2Ftriadtreeremoval.com%2F
https://asia.google.com/url?q=http%3A%2F%2Fwww.triadtreeremoval.com%2F
https://toolbarqueries.google.sn/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.sn/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.ws/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.cat/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.sh/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://toolbarqueries.google.bi/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.bi/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.co.ug/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.co.ug/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.fm/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.com.pa/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.gl/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://clients1.google.ge/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.cf/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://toolbarqueries.google.pn/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://clients1.google.tk/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://clients1.google.co.mz/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.cv/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.com.mm/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.so/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.sc/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://maps.google.com.bz/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.com.bn/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://images.google.com.ag/url?sa=t&url=https%3A%2F%2Fwww.triadtreeremoval.com
https://clients1.google.je/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
https://clients4.google.com/url?q=http%3A%2F%2Fwww.triadtreeremoval.com
Generic cialis online https://tadafcialirx.com cialis for sale
Online cialis https://vipmenciall.com/ cialis reviews
Cialis for sale https://cialmenon.com/ cialis website
dapoxetine without dr prescription https://ddapoxetine.com/
How to use viagra https://viagstorerx.com buy viagra online
Cialis pill https://gocialirx.com/ cialis website
International viagra online https://atviagrmenrx.com viagra walmart
Does viagra make you bigger xviagrnorx.com how to use viagra
First of all I would like to say awesome blog! I had a quick question which I’d like to ask if you don’t mind.
I was curious to know how you center yourself and clear
your head before writing. I have had a difficult
time clearing my thoughts in getting my thoughts out there.
I do enjoy writing but it just seems like the first 10 to 15 minutes
are lost just trying to figure out how to begin.
Any suggestions or tips? Thank you!
viagra 25 mg coupon
viagra usa prescription
valtrex 250 mg
generic cialis in usa
generic viagra over the counter how to buy viagra without prescription buy cialis 60 mg online canadian pharmacy com how to buy cialis in usa
how to get cialis discount
cialis online cheapest prices
how to get accutane australia
ivermectin for sale
tadalafil 40 mg for sale
viagra best price usa
usa tadalafil
aurogra 100
allopurinol online india
generic tadalafil us
quineprox 0.4
sildenafil citrate tablets
where to buy cialis safely india viagra generic cialis viagra online cialis soft tabs 10mg diclofenac generic gel avodart 0 5mg buy sildenafil 50mg buy stromectol uk sildenafil 20 mg mexico tadalafil pills in india
stromectol price usa
average cost of viagra 100mg
where to get sildenafil
canadian prescription pharmacy
cialis daily coupon
sildenafil 100mg price india how to buy generic viagra safely online sildenafil uk best price where to buy ivermectin cream sildenafil gel uk can you buy zovirax cream over the counter ivermectin gel cialis online can you buy viagra online ampicillin medication
viagra discount canada
generic cialis 60 mg
hydroxychloroquine name brand
buy ivermectin stromectol
cymbalta price canada
can you buy zithromax over the counter in canada
cost of 10mg cialis
viagra soft flavoured cialis 1800mg cymbalta without a prescription buy ivermectin for humans australia how to get tadalafil
otc cialis pills
cheap sildenafil 50mg
order sildenafil 100mg
cost of daily cialis best price genuine viagra female viagra drug viagra generic europe legitimate online pharmacy usa vigara cheap stromectol cialis 20 g tadalafil 20mg for sale where can i buy viagra online uk
stromectol price
cialis tadalafil 20mg
buy generic cialis buy viagra over the counter canada viagra 25mg price generic viagra without rx cialis 25 mg price
tadalafil 20 mg buy online
buy cialis online now
where can i get viagra tablets buy generic cialis online india sildenafil 50 mg price in india viagra online purchase singapore ivermectin generic cream
viagra coupon
tadalafil 20 mg best price
tadalafil medicine
can i buy viagra in india sildenafil drug coupon tadalafil daily cost tadalafil tablet online in india how much is ivermectin 12.5 mg viagra daily online pharmacy generic cialis genuine cialis online where can you buy viagra in south africa viagra online order india
cialis 120
cheap cialis canadian pharmacy
buy cialis daily
stromectol tab
cialis 20 mg lowest price
generic cialis tablets
vardenafil 40 mg tablets average cost of 10mg cialis cheap viagra online canadian pharmacy sildenafil 20 mg online can you buy tadalafil online
prednisone 5 mg buy online
tadalafil 6mg capsule
canadian online pharmacy sildenafil
cialis pharmacy uk
tadalafil buy online canada
ivermectin 6mg tablet for lice
cialis 200
hydroxychloroquine 50 mg
cialis online pharmacy india buy tretinoin 0.05 cream buying generic cialis viagra canada drugstore viagra gel price 54899 prednisone bactrim ds antibiotic sildenafil buy canada tadalafil capsules 20mg where can buy viagra
viagra 120
order real cialis
purchase cialis online cheap
cialis canada over the counter
ivermectin virus
buy tadalafil us tadalafil 30mg tablet cialis without rx how much is over the counter viagra cialis 20 mg discount coupon prices for generic seroquel online sildenafil india citalopram in canada viagra 130 mg generic lasix 40 mg
viagra online singapore
azithromycin penicillin sildenafil 200mg for sale stromectol ebay viagra pills brand levitra online 100 mg clomid pills to order how to get viagra in canada order sildenafil generic bactrim online buy generic cialis canadian pharmacy
buy cialis australia
celexa 20 mg tablet
generic viagra india 100mg
buy cialis online us retin a cream nz medication cymbalta 60 mg 1500 mg gabapentin buying antabuse online price of celexa buy viagra online without a prescription atarax liquid cialis 5mg price uk cialis with prescription
wellbutrin 30 mg
tadalafil online united states buy tadalafil 20mg price canada tadalafil 5mg price india finpecia 1mg cheap cialis prices where to buy viagra over the counter doxycycline 40 mg coupon antabuse price australia generic cymbalta no prescription buy generic cialis mastercard
where can i buy nolvadex in south africa
avana india
flagyl price
orlistat over the counter where to buy
where to buy xenical
malegra 200 tretinoin uk cialis 10mg purchase gabapentin 300mg modafinil price in india buy citalopram without script trazodone 50 mg cost sildenafil for daily use buy accutane 5mg cost of 10mg tadalafil pills
hydroxychloroquine sulfate tablets 200 mg
abilify canada pharmacy
azithromycin 500mg buy
feldene gel buy online
viagra gel australia
tadalafil 20 mg price canada
how do i buy viagra
stromectol in canada
ivermectin pills
ivermectin stromectol
cialis canadian pharmacy online
buy viagra cheap online
covid ivermectin
bupropion pharmacy prices
hydroxychloroquine 2
buy tadacip online
doxycycline 100mg lowest price
cialis generic over the counter
online generic tadalafil
cialis soft
viagra soft tabs
where to buy sildenafil citrate online
ciali
order sildenafil us
metformin over the counter usa
piroxicam 10 mg
trental 400 mg tab
indocin otc
where can you get viagra uk
how to buy sildenafil without a prescription
sildenafil rx coupon
where to buy sildenafil usa
stromectol coronavirus
zofran generic prices
canadian viagra pharmacy
buy cialis generic uk
cialis 500mg
cialis tadalafil soft chewable 20mg
viagra buy australia
price cialis uk
where to buy elimite cream over the counter
buy lexapro online
buy stromectol uk
how to purchase viagra in uk
viagra nz over the counter
buy cheap tetracycline
generic for propecia
prednisone 20mg
stromectol prices
order prednizone
propecia online uk
baclofen cheapest
metformin 1000mg without prescription
albuterol 3mg
buy vardenafil canada
accutane tablets pharmacy
phenergan rx
generic cialis free shipping
generic india viagra
where to get viagra in australia
viagra online prices
buy generic cialis uk
lasix no preiscription
indianpharmacy com
trazodone for sale
augmentin no rx
buy antabuse without prescripition
ivermectin pills human
stromectol ebay
plavix in mexico advair 230 amoxicillin 500 how much is a diflucan pill phenergan dm diclofenac prescription australia lisinopril generic 10 mg cost of synthroid 75 mcg
lisinopril 20mg tablets price
buy stromectol canada
levitra 20mg price in usa can you buy diflucan over the counter in canada canadian pharmacy diflucan purchase metformin canada stromectol 3mg tablets diflucan 150 mg online trazodone 10mg neo medrol generic albendazole online cost of neurontin clonidine rx effexor xr generic generic pharmacy online where can i buy levitra acyclovir medication prices 500 mg augmentin stromectol buy tretinoin 0.01 voltaren gel prescription bactrim 500 mg
cost of viagra pills in india cialis generic online canada viagra soft tabs online viagra south africa where can i buy generic viagra in usa buy female viagra canada viagra usa
zestril 10mg price
amoxicillin 500mg coupon
allopurinol 200 mg daily avodart 0.5 mg price brand name lexapro from canada elimite cream coupon cymbalta canada generic buy tetracycline online pharmacy accutane australia how to get lasix without a prescription
can you buy zoloft
retin-a price
accutane 30mg
phenergan generic
lisinopril tablets uk
diflucan 1 otc
lyrica 150 mg cost biaxin 500 colchicine brand name buy albendazole on line buy ventolin over the counter nz how can i get propecia avodart 0.5 mg generic bactrim uk
lisinopril 2.5 tablet brand levitra for sale
where can i buy diflucan online indocin 50 mg tablets cephalexin average cost seroquel 800 mg pill citalopram best price
cafergot pills amoxicillin cost prazosin for ptsd avodart cost canada
how to buy metformin in canada hydroxychloroquine 800 mg cost of ampicillin pills biaxin cost diclofenac gel generic drug amoxicillin online
cozaar price in india phenergan price anafranil 10 indocin 25mg cap prozac 20 mg coupon
cymbalta 50 mg
tenormin 100 tadacip 20 sale bactrim 800 160
metformin 850mg
propecia generic canada
cephalexin 500mg buy fildena 120 motilium tablets cozaar 50 mg price budesonide capsules generic online pharmacy pain medicine cipro uk suhagra 200 mg generic levitra us buy suhagra 50mg
albuterol 063 generic lopressor buy avodart online uk
hydroxychloroquine coupon tenormin drug robaxin 750 average cost of metformin where to buy tadacip ventolin 2018
valtrex over the counter australia diflucan prescription cost bactrim 168 mg levitra 40
vermox plus
strattera 60 mg cap
robaxin price uk bactrim tablet zanaflex 6 mg suhagra 100mg cheap cheap ampicillin
ampicillin drug order allopurinol online retin a 025 gel vermox cost uk can i buy erythromycin over the counter order lopressor sildalis tablets
zovirax 15g dapoxetine in us buy cafergot tablets atenolol price
cafergot medicine bactrim ds generic buy diflucan 150 mg can you buy plaquenil over the counter
bactrim forte medicine bactrim antibiotic tizanidine 4mg tab price tadacip for sale buy vermox australia allopurinol medicine india lopressor 50 mg daily generic colchicine amoxicillin 500 mg discount
where to buy ampicillin 500 without prescription amoxicillin over the counter usa buy septra ds 800/160 mg online without prescription zanaflex online plaquenil 400 mg daily tadacip 20 online budesonide price canada buy generic antabuse
cipro mexico motilium for sale albendazole medicine price
sildalis online cost for 40 mg lisinopril levitra prescription buy bactrim over the counter where to buy levitra over the counter generic levitra from canada plaquenil 200mg tablets 100
zanaflex 4mg capsule price plaquenil 250 lopressor 5 mg
levitra order
reliable canadian pharmacy cymbalta 60 mg cost can i buy ciprofloxacin over the counter lexapro canadian pharmacy cozaar 25 mg price where to buy fildena diflucan 150 mg pill cost of fluoxetine 60 mg clonidine hydrochloride get you high erectafil 20 for sale
indocin medicine 25 mg
buy cheap celebrex
how much is propecia in singapore anafranil 10
motilium australia prescription
tizanidine 2mg best metformin brand in india zofran medicine price cost of diflucan how to get albendazole albenza cvs budesonide 80 tadalafil uk cozaar generic cost where to get gabapentin
generic for prozac augmentin 625mg price in india erectafil 10 otc tadalafil singulair 10 mg buy online budecort 0.5 mg
tadacip 20 for sale
clomid for sale south africa
how much is cipro in mexico
valtrex india
levaquin prices
rx modafinil
amoxicillin nz pharmacy sildalis indocin 50 zoloft medicine price
sildalis cheap tamoxifen for men cheap propecia generic ventolin tablet medication orlistat in india price
ivermectin gel
prednisone 7.5 mg daily
retin a gel cream
cost of misoprostol tablet
zestoretic 20-25 mg
hydroxychloroquine 100mg
strattera 44 online
malegra 100 for sale
lasix canada no prescription
anafranil
viagra buy in australia
viagra online costs
how to get viagra pills
ivermectin 5 mg price
furosemide 20 mg
seroquel purchase online
fildena
retino
where can i buy biaxin propranolol 5 mg tablet generic avodart online zithromax canadian pharmacy where can i buy generic valtrex 80mg bactrim avana canada
250mg amoxicillin capsules
purchase tamoxifen citrate
buy lisinopril 5mg
accutane drug
cafergot tablets australia
finasteride 5mg tablets